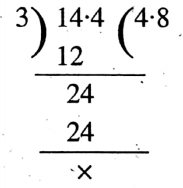WBBSE Solutions For Class 6 Maths Arithmetic Chapter 6 Multiplication And Division Of A Decimal Fraction By Whole Numbers And Decimal Fraction
Question 1. Multiply:
1. 25.04 x10
Solution :
Here we have to multiply by 10: there is only one zero in 10.
∴ The decimal point will be moved in the product one digit towards the right side.
So, 25.04 x 10 = 250.4.
2. 12.375 x 10000
Solution:
Here, we have to multiply by 10000.
It contains 4 zeroes.
The decimal point will be moved in the product 4 digits towards the right side. But the decimal number 12.375 contains 3 digits after the decimal point.
One zero will be inserted after 375 (towards the right side of 5) and then put the decimal point.
12.375 x 10000 = 123750.00
[Here we put 2 zeroes after the decimal point (on the right side of the decimal point.)]
Read and Learn More WBBSE Solutions For Class 6 Maths
3. 20.4527 x 1000000
Solution:
Here, we have to multiply by 1000000.
It contains 6 zeroes. So the decimal point will be moved in the product 6 digits towards the right side.
But the decimal number 20.4527 contains 4 digits after the decimal point.
∴ Two zeroes will be inserted after 4527 (towards the right side of 7) and then put the decimal point.
∴ 20.4527 x 1000000 = 20452700.00
4. 0.005 x 100.
Solution:
Here, we have to multiply by 100. It contains only 2 zeroes.
So the decimal point will be moved towards the right side 2 digits.
0.005 x 100 = 0.5
[If the product decimal number does not contain any integral part, we can in general keeps one zero before the decimal point.]
Question 2. Find the value of 0.001 x1010
Solution:
0.001 x 1010 = 10000000.000 (∴ The decimal point is placed before 3 zeroes from the right).
Question 3. Find the product:
1. 78.35 x 14 = 1096.90
Solution :
Here 7835 x 14 = 109690.
The multiplicand 78.35 contains 2 digits after the decimal point.
So the decimal point is put 2 digits left side from the end digit of the product.
2. 2.789 x 62 =172.918
Solution :
Here 2789 x 62 = 172918.
Since the decimal number 2.789 contains 3 digits after the decimal point, we put the decimal point 3 digits left side from the end digit of the product.
3. 101.011 x 96 = 9697.056
Solution :
Here 101.011 x 96 = 9697056.
Since the decimal number 101 Oil contains 3 digits after the decimal point, we put the decimal point 3 digits left side from the end digit of the product.
4. 0.0003 x 15 = 0.0045
Solution :
Here 3 x 15 = 45.
The multiplicand decimal number 0.0003 contains 4 digits after the decimal point.
But product 45 contains only two digits.
So 2 zeroes are inserted in the left side of product 45 and then put the decimal point so that the required product contains 4 digits after the decimal point.
One zero is put on the left side of the decimal point in the product.
5. 0.000001 x 25 = 0.000025
Solution :
Here 1 x 25 = 25.
The multiplicand decimal number contains 6 digits after the decimal point.
Product 25 contains only 2 digits.
So we insert 4 zeroes on the left side of 25 and then put the decimal point so that the required product will contain 6 digits after the decimal point and one zero is placed on the left side of the decimal point.
Question 4. Multiply:
Solution:
1. 0.67 x 0.39 = 0.2613
Solution: Here
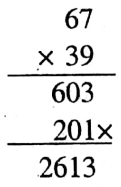
The multiplicand decimal number is 0.67 and it contains 2 digits after the decimal point and the multiplier decimal number is 0.39 and it contains 2 digits after the decimal point.
So 2 + 2 = 4 digits.
The required product will also contain 4 digits after the decimal 2613 point, which is why the required product is 0.2613.
2. 6.23 x 2.51 = 15.6373
Solution: Here
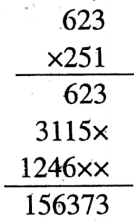
The multiplicand decimal number 6.25 contains 2 digits after the decimal point and the multiplier decimal number 2.51 contains 2 digits after the decimal point.
So 2 + 2 = 4 digits.
The required product will also contain 4 digits after the decimal point and as a result of which the required product is 15.6373
i.e., the decimal is placed 4 digits left from the end digit of the product.
3. 72.2 x 2.65 = 191.330 = 191.33
Solution :

The multiplicand decimal number 72.2 contains one digit after the decimal point and the multiplier decimal number 2.65 contains 2 digits after the decimal point. 1+2 = 3 digits.
The required product will contain 3 digits after the decimal point and so the required product is 191.330 = 191.33.
Here the end digit 0 has no value after the decimal point at the end
4. 72.156 x 12.16 = 877.41696
Solution:

5. 2.14 x 0.4 x 0.9 = 0.7704
Solution:
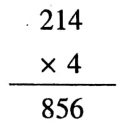
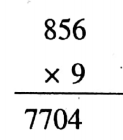
6. 0.01 x 0.0001 x 0.000001 = 0.000000000001
Solution :
1 x 1 x 1 = 1. 2 + 4 + 6= 12 digits. The required product will contain 12 digits after the decimal point.
So 11 zeroes are inserted in the left side of the product 1 (which is obtained by the multiplication of 1 x 1 x 1 by removing the decimal points) and then put the decimal point.
Question 5. Arrange in descending order
Solution :
1. 0.5 x 0.3 = 0.15
Solution:
0.5 = 0.50
0.3 = 0.30.
50 > 30 > 15,
∴ Arranging in descending order, we get, 0.5, 0.3, 0.5 x 0.3
2. 0.6 x 0.7 = 0.42
Solution :
0.6 = 0.60
0.7 = 0.70.
70 > 60 > 42
∴ Arranging in descending order, wet get, 0.7, 0.6, 0.6 x 0.7
3. 0.9 x 0.2 = 0.18
Solution :
0.9 = 0-90
0.2 = 0.20.
90 > 20 > 18
∴ Arranging in descending order, we get, 0.9, 0.2, 0.9 x 0.2
4. 0.4 x 0.8 = 0.32
Solution :
0.4 = 0.40
0.8 = 0.80.
80 >40 >32,
∴ Arranging in descending order, we get 0.8, 0.4, and 0.4 x 0.8.
5. 1.2 x 1.5 = 1.80
Solution :
1.2 = 1.20
1.5 = 1.50.
180 > 150 > 120 .
∴ Arranging in descending order, we get 1.2 x 1.5, 1.5, 1.2.
6. 2.3 x 2.4 = 5.52
Solution :
2.3 = 2.30
2.4 = 2.40.
552 > 240 > 230.
∴ Arranging in descending order, we get 2.3 x 2.4, 2.4, 2.3.
7. 6.7 x 7.2 = 48.24
Solution :
6.7 = 6.70
7.2 = 7.20
4824 > 720 > 670 ;
∴ 48.24 > 7.20 > 6.70
∴ Arranging in descending order, we get, 6.7 x 7.2, 7.2, 6.7
8. 8.2 x 1.9 = 15.58
Solution :
8.2 = 8.20
1.9 = 1.90
∴ 1558 > 820 > 190
∴ 15.58 > 8.20 > 1.90.
Arranging in descending order, we get, 8.2 x 1.9, 8.2, 1.9
Question 6. Arrange in ascending order
1. 1.4 x 1.1, 1.4, 1.1, 1.5
Solution:
14 x 1.1 = 1·54
1.4 = 1.40;
1.1 = 1.10;
1.5= 1.50
110 < 140 < 150 < 154,
1.10 < 1-40 < 1.50 < 1.54
∴ Arranging in ascending order, we get 1.1, 1.4, 1.5, 1.4 x 1.1.
2. 0-01 x 1, 0.1 x 0.01, 0.01 x 0.01, 0.1
Solution:
= 0.01 x 10.0100
= 0.1 x 0.01 0.0010
= 0.01 x 0.01
= 0.0001 x 0.1
= 0.1000
1 < 10 < 100 < 1000,
∴ 0.0001 < 0·0010 < 0·0100 < 0.1000
∴ Arranging in ascending order, we get, 0.01 x 0.01, 0.1 x 0.01, 001 × 1, 0.1
Question 7. Simplify:
1. 13.28 4.07 +2.7 × 0.02
Solution
= 13.28 4.07 +0-054.
= (13-280-054) – 4.07
= 13.3344.07 = 9.264
13.28 4.07 +2.7 × 0.02 = 9.264
2. 0.35 × 0.35 + 0.15 x 0.15 + 2 x 0-35 x 0.15
Solution
= 0.1225 +0.0225 +0.1050
=25000
= 0.25
0.35 × 0.35 + 0.15 x 0.15 + 2 x 0-35 x 0.15 = 0.25
Alternative method:
Let 0.35 = a and 0.15 = b
The given quantity = a x a + b x b+2 x a x b.
= a2 + b2+2ab
= (a + b)2
= (0-5)2
= 0.25.
Example 8. If the cost of one exercise book is 12.75, then what is the total cost of 4 exercise books?
Solution: The cost of one exercise book = 12.75
∴ The total cost of 4 exercise books (12.75 x 4)
= 51.00
= 51.
Total cost of 4 exercise books = 51
Example 9. Kartikbabu built a house on 0.35 part of his land. He cultivated fruits in 0.2 parts of the remaining land. In what part of his land did he cultivate fruits?
Solution: Let the whole of Kartikbabu’s land = 1 part.
∴ The remaining part of his land after building the house = (1 – 0.35) part
= 0.65 part.
Now 0.2 part of 0.65 part = 0·2 x 0.65
= 0.13 part.
∴ Kartikbabu cultivated fruit in 0.13 part of his land.
Question 10. Your mother asked you to purchase 2-5 kg of the pulse. If the cost of 1 kg of the pulse is 62.50, then how much money must you carry to the shop?
Solution: The cost of 1 kg of pulse = ₹ 62.50
∴ cost of 2.5 kg pulse
= ₹(62.50 x 2.5)
= ₹ 156.250
= ₹ 156.25
₹ 156.25 money must you carry to the shop.
Question 11. You had ₹ 150. With 0.3 part of your money, you bought one exercise notebook and with 0.4 part you bought your mathematics book. How much money is left with you?
Solution: 0.3 + 0.4 = 0·7 part
∴ You spent a total of 0-7 part of your money.
Now you have left (10.7) = 0.3 part of your money.
∴ You have left = 0.3 part of ₹ 150 = ₹ (3 x 150)
= ₹ 45.0
= ₹ 45.
₹ 45 money is left with you.
Alternative method :
You purchased an exercise book with
= ₹ (150 x 0.3)
= ₹ 45.
You purchased a mathematics book with
= ₹ (150 x 0.4)
= ₹ 60.
∴ You spent total
= ₹ (45+ 60)
= ₹ 105
∴ Total money is left with you
= ₹ (150 – 105)
= ₹ 45.
∴ ₹ 45 is left with you.
Question 12. What is the meaning of (31.5 ÷ 5.25)?
Solution: The meaning of (31.5 ÷ 5.25) is how many times 5.25 will be subtracted from 31.5.1
Question 13. Divide :
1.
1. 125.45 ÷ 10 = 12.545
Here in the divisor, there is only one zero after 1. So to determine the quotient, the decimal point in the dividend is moved one digit left side. Hence the quotient becomes 12.545.
2. 0.4 100 = 0.004.
Here, there are 2 zeroes after I in the divisor.
So to determine the quotient, the decimal point in the dividend is moved 2 digits towards the left side.
But then, the dividend does not contain any digit on the left side before the decimal point.
For this reason, 2 zeroes are inserted before 4 and then the decimal point is put.
So the required quotient = 0·004.
3. 23.32 ÷ 1000 = 0.02332.
There are 3 zeroes after 1 in the divisor.
So to determine the quotient the decimal point in the dividend is moved 3 digits towards the left side.
Since there are only 2 digits in the left side of the decimal point.
For this reason, one zero is inserted before 23:32 on the left side and then the decimal point is put in.
The required quotient is 0.02332.
4. 1·724 ÷ 10000 = 0.0001724.
There are 4 zeroes after 1 in the divisor.
So to determine the quotient, the decimal point in the dividend is moved 4 digits towards the left side but the dividend contains only one digit before the decimal point.
For this reason, 3 zeroes are inserted before the given dividend decimal number 1.724 and then the decimal point is put.
The required quotient is 0-0001724.
2.
1. 651-2 ÷ 4 = 162.8.
Solution:
Here removing the decimal point in the dividend we get 6512 and 6512 ÷ 4 = 1628;
Since the dividend contains a decimal point one digit before the end digit, the decimal point is also put in the quotient one digit before the end digit.
∴ The required quotient = 162.8.
2. 18 ÷ 0.2 = 18/0.2
Solution:
= 18×10 / 0.2 x 10
= 180/2
=90.
Here the decimal point in the divisor is removed by the multiplication of 10 to it.
So multiplying both the numerator and denominator by 10 we get the required result and the quotient is 90.
3. 0.225 ÷ 15 = 0.225 / 15
Solution:
= 0÷225×1000 / 15×1000
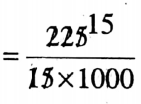
4. 875 ÷ 0.25
Solution:
= 875 x 100 / 0.25 x 100
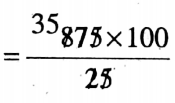
3.
1. 28.8 ÷ 1.2,
Solution:
1. 28.8 ÷ 1.2 = 28.8 / 1.2
= 28.8 / 102
= 28.8 x 10 / 1.2 x 10
= 288/12 = 24.
2. 2. 1.35 ÷ 1.5
Solution:
\(1.35 \div 1 \cdot 5=\frac{1.35}{1.5}=\frac{1.35 \times 100}{1.5 \times 100}=\frac{135}{150}=0.9\)
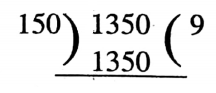
3. 3. 414.50 ÷ 0.0125
Solution:
\(414 \cdot 5 \div 0 \cdot 125=\frac{414 \cdot 5}{0 \cdot 125}=\frac{414 \cdot 5 \times 1000}{0 \cdot 125 \times 1000}=\frac{414500}{125}=3316\)

4. 0.465 ÷ 0.5
Solution:
= 0.465 x 1000 / 0.5 x 1000
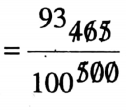
= 93/100
= 0.93.
0.465 ÷ 0.5 = 0.93.
Question 14. Simplify:
1. (45.85 – (6.29 + 15.06)} ÷ 5
Solution:
= (45.85 – (6.29 + 15.06)} ÷ 5
= (45.85 – 21.35) ÷ 5
= 24.50 ÷ 5
= 4.9.
(45.85 – (6.29 + 15.06)} ÷ 5 = 4.9.
2. {(4 – 2.07) × 2.5} ÷ 1.93
Solution:
= {(4 – 2.07) × 2.5} ÷ 1.93
= (1.93 x 2.5) ÷ 1.93
1.93 x 2.5 / 1.93
= 2.5
{(4 – 2.07) × 2.5} ÷ 1.93 = 2.5
3. (7.8 – 7.8 x 0.2) ÷ 1.2
Solution:
= (7.8 – 7.8 x 0.2) ÷ 1.2
= (7.8 – 1.56) ÷ 1.2
= 6.24 ÷ 1.2
= 6.24 x 100 / 1.2 x 100
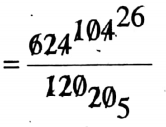
= 26/5
= 5.2
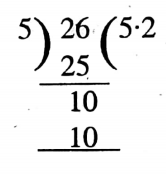
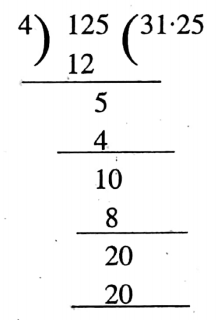
Question 15. A square is formed by bending a copper wire of length 125 centimeters. What is the length of each side of the square?
Solution: We know that each side of a square is of equal length and a square has 4 sides.
∴ The length of each side of the square = (125 ÷ 4) cm
= 31.25 cm
∴ The length of each side of the square
= 31.25 centimeters.
Question 16. The perimeter of an equilateral triangle is 14.4 cm. What is the length of each side of it?
Solution: We know that the length of each of the 3 sides of an equilateral triangle is the same.
:. The length of each side of the equilateral triangle = (14.4 ÷ 3) cm
= 4.8 cm.