Chapter 4 Work And Energy Very Short Question and Answers
Question 1. Define energy and its commercial unit. Express it in terms of Joules.
Answer:
Energy and its commercial unit.:
Energy is defined as the capacity of doing work. The commercial unit of energy is kilowatt-hour.
1 kWh = 1000 W × 3600 s = 3.6 × 106 J
Question 2. How are resources classified?
Answer:
Classification Of resources:
When energy source used is easily replenished in a short period and the reserve is limitless is called renewable source. The sources of energy which are limited in quantity and are exhaustible are called non-renewable sources of energy.
Question 3. Name the different sources of energy.
Answer:
The different sources of energy
The five sources of energy are solar energy, wind energy, geothermal energy, hydroelectric energy and biomass energy
Question 4. What are the different forms of energy?
Answer:
Different forms of energy:
The various forms include mechanical energy (potential energy + kinetic energy), chemical energy, heat energy, light energy and electrical energy.
Question 5. Define mechanical energy and its types.
Answer:
Mechanical energy and its types:
Mechanical energy is of two types i.e., the energy possessed by a body due to its motion is called kinetic energy. The energy possessed by a body due to its position or height is called potential energy.
Question 6. Define conservative and non-conservative sources of energy.
Answer:
Conservative and non-conservative sources of energy:
If the work done by a force depends only on initial and final positions but not on the path taken, then the force is said to be conservative. If the work done by a force depend on the path taken then the force is said to be non-conservative.
Question 7. Define law of conservation of energy.
Answer:
Law of conservation of energy:
Energy can neither be created nor destroyed. It can only be changed from one form to another.
Question 8. A car is moving with the uniform velocity of 50 km/h. What is the kinetic energy of the object of mass 40 kg kept in the car?
Answer:
Given:
A car is moving with the uniform velocity of 50 km/h.
We know that both objects and car are moving with the same velocity
i.e., v = 50 km/h = 50 × 103/(60 × 60)
= 13.88 m/s2
Mass of the object,
m = 40 kg
K.E. = \(\frac{1}{2} m V^2\)
K.E. = \(\frac{1}{2} \times 40 \times(13.88)^2\)
K.E. = 3853.08 J
Question 9. The acceleration due to gravity is 20 m/s2, what will be the potential energy of a body of mass 1 kg kept at the height of 10 m?
Answer:
Given:
The acceleration due to gravity is 20 m/s2,
Potential Energy = mgh
Mass, m = 1 kg
Acceleration due to gravity,
g = 20 m/s2
Height, h = 10 m
Potential Energy = 1 × 20 × 10
= 200 J
Hence, potential energy is 200 Joules.
Question 10. Calculate potential energy of water in a tank having l = 4 m, b = 3 m and h = 2, situated on top of a house whose height is 9 m.
Take rw = 1 x 103 kg/m3 and g = 10 ms-2
Answer:
Volume of water = Volume of tank
= lbh
= 4 m × 3 m × 2 m
= 24 m3
Mass of water = Volume of density
= 24 × 103 kg
Mean height of water above the ground
H = h1 + h2
= 9 m + 1 m
= 10 m
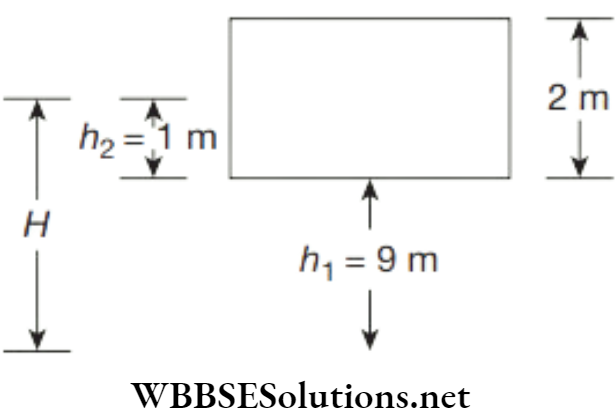
Therefore, Potential energy = MgH
= 24 × 103 × 10 × 10
= 24 × 105 J
Question 11. A body of mass 0.5 kg is in rest at a height of 20 m above the ground.
- Find its total energy.
- What is the total energy, if it starts falling freely and has fallen through a height of 5 m? (Take g = 10 ms-2)
- What conclusion can be drawn from these calculations?
Answer:
(1) P.E. of the body = mgh
= 0.5 × 10 × 20
= 100 J
K.E. of the body = \(\frac{1}{2} m V^2\)
= \(\frac{1}{2} \times 0.5 \times 0\)
= 0
Total energy = P.E. + K.E.
= 100 + 0
= 100 J
(2) 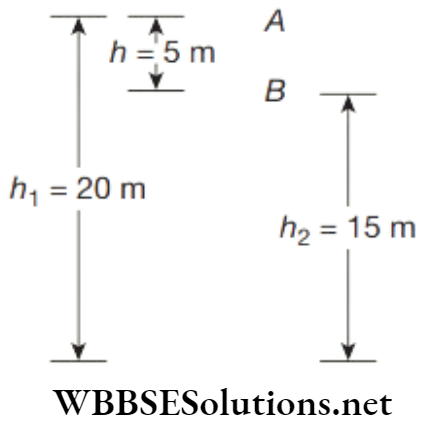
Velocity of the body at point B is given by
v2 = u2 + 2aS
= 0 + 2 × 10 × 5
= 100
∴ v = 10 ms-1
∴ Its K.E. at point B = \(\frac{1}{2} m V^2\)
= \(\frac{1}{2} \times 0.5 \times(10)^2\)
= \(\frac{1}{2} \times 0.5 \times 100\)
= 25 J
Its P.E. at point B = mgh2
= 0.5 × 10 × 15
= 75 J
Its total energy at point B = K.E. + P.E.
= 25 J + 75 J
= 100 J
Thus, we find that the total energy of a freely falling body remains constant, though its potential energy gradually change into kinetic energy.
Question 12. Calculate the kinetic energy of a body of mass 4 kg moving with the velocity of 0.2 meter per second.
Answer:
Kinetic Energy = \(\frac{1}{2} m V^2\)
Here mass = 4 kg
Velocity = 0.2 m/s
So, by putting the values in formula:
Kinetic energy = \(\frac{1}{2} \times 4 \times(0.2)^2\)
= \(\frac{1}{2} \times 4 \times 0.2 \times 0.2\)
= 0.08
Question 13. Define work and its types.
Answer:
Work and its types:
If a force is applied on a body which led to displacement in the body then work is done. Work is the product of magnitude of force and displacement.
Positive work: If a force is applied in the same direction to displacement, then work done is said to be positive.
Negative work: If a force is applied in the opposite direction of displacement, then work done is said to be negative.
Question 14. A swimmer makes a swing jump between two points, by holding one end of a rope, other end of which is tied to some higher point. What type of work is done by rope in jumping of the swimmer from one point to another?
Answer:
Zero work done.
Question 15. Calculate the work done in operating the crane, if it lifts a mass of 1600 kg through a vertical height of 40 m.
Answer:
g = 9.8 m/s2
F = mg = 1600 kg × 9.8 m/s2
= 15680 N
W = F × S = 15680 N × 40 m = 627,200 J
Question 16. How much work is done by a force of 15 N in moving an object through a distance of 2 m in the direction of force?
Answer:
W = F × S
Hence force, F = 15 N
Distance, S = 2 m
Work done, W = 15 × 2
W = 30 Joules

