Class 8 Maths

Arithmetic

• Chapter 1 Arithmetic Ratio And Proportions
• Chapter 2 Pictograph and Pie Chart
• Chapter 3 Rule Of Three
• Chapter 4 Mixture
• Chapter 5 Percentage
• Chapter 6 Time and Work

Algebra

• Chapter 1 Commutative Associative and Distributive Laws
• Chapter 2 Rational Number
• Chapter 3 Multiplication of Polynomials
• Chapter 4 Division Of Polynomials
• Chapter 5 Formulae and Their Applications
• Chapter 6 Factorisation by Formulae
• Chapter 7 Factorisation By Breaking The Middle Term
• Chapter 8 LCM
• Chapter 9 HCF
• Chapter 10 Simplification Of Fractions
• Chapter 11 Graph
• Chapter 12 Equations

Geometry

• Chapter 1 Angels
• Chapter 2 Theorems
• Chapter 3 Constructions

Geometry Chapter 3 Constructions

Constructions Introduction

You are familiar with geometrical constructions from class VI. With the help of several instruments found in the geometrical box, you have already constructed a number of geometrical figures under different conditions in classes VI and VII. In this chapter, our aim is to discuss mainly some problems and to find out their probable applications.

Read And Learn More WBBSE Solutions For Class 8 Maths

Geometry Chapter 3 Constructions  Some Questions

Question 1

Construct a triangle when its two angles and the side opposite to one of them are given.

Solution:

Given:

 

Let the two angles of a triangle be a and p. The length of the side opposite to the angle β is m.

It is required to construct the triangle.

Maths Solutions Class 8 Wbbse

Construction: Draw any straight line \(\overrightarrow{A X}\) From \(\overrightarrow{A X}\) cut off AB equal to the length m.

Draw ∠CAB and ∠DBX equal to the angle a at the endpoints A and B

of the line segment \(\overline{A B}\).

Draw ∠DBE equal to p at point B of the straight

line \(\overrightarrow{B D}\) on that side of \(\overrightarrow{B D}\) in which \(\overrightarrow{A C}\).

lies. Let BE and AC intersect each other at point F.

Then AFAB is the required triangle.

Proof: According to the construction, ∠BAF = ∠XBD

But they are corresponding angles.                   [Here \(\overline{A B}\) has intersected \(\overrightarrow{A B}\) and \(\overrightarrow{B D}\)]

Hence, \(\overrightarrow{A C}\) || \(\overrightarrow{B D}\).

Again, \(\overline{B F}\) is the transversal of the parallel

straight lines \(\overrightarrow{A C}\) and \(\overrightarrow{B D}\).

∠AFB = alternate ∠FBD.

In the ΔFAB, ∠FAB = α

∠AFB = β

and the length of the side opposite to β is

\(\overline{A B}\) = m.

Hence, ΔFAB is the required triangle (Proved).

Maths Solutions Class 8 Wbbse

Question 2

Construct a triangle when the lengths of its two sides and the angle opposite to one of them are given.

 

Solution:

Given:

 

Let b and c be the lengths of the two sides of a triangle and the angle opposite to the side b be ∠B.

It is required to construct the triangle.

Construction: Draw any straight line

\(\overrightarrow{B D}\). Now at point B of the straight

line, \(\overrightarrow{B D}\) constructs an angle ∠DBE equal to the given angle B.

Now from BE, cut off \(\overline{B A}\) equal to the length of the given side c.

With A as the center and radius equal to the length of the given side b construct an arc of a circle. Let this arc

intersects \(\overrightarrow{B D}\) at C₁ and C₂.

Join AC₁ and AC₂.

Then both ΔABC₁ and ΔABC₂ are the required triangles.

Verification: In the triangle ABC₁ if you measure the sides \(\overline{A B}\) and \(\overline{A C_1}\)

with a scale and the angle ∠ABC₁ with a protractor, you will find that AB = c,

AC₁ = b, and ∠ABC₁ is equal to ∠B.

Similarly, in the triangle ABC₂, AB = c, AC% = b, and ∠ABC₂ are equal to ∠B.

Maths Solutions Class 8 Wbbse

Question 3

Construct a triangle when the length of its one side and the angles adjacent to it are given.

Solution:

Given:

 

Let a be the length of one side of a triangle and ∠B and ∠C be the angles adjacent to side a.

It is required to construct the triangle.

Construction: Draw any straight-line BD. Now from BD cut off BC equal to the length of the side a.

Now at point B on BC draw an angle ∠CBE equal to the given angle B. Also at point C on BC

draw an angle ∠BCF equal to the given angle C. Let BE and CF intersect each other at A.

Thus, AABC is the required triangle.

Verification: Measuring the side BC with a scale and the angles ∠ABC and ∠ACB with a protractor you will find that BC = a, ∠ABC, and ∠ACB are equal to the angles B and C respectively.

Question 4

The lengths of the two sides of a triangle and the opposite angle of one side are given. To construct the triangle.

Solution:

Given:

Let, the two sides of a triangle be a and b and the angle opposite to the side b be a.

It is required to construct the triangle.

Construction: Draw any straight line \(\overline{A X}\). From \(\overline{A X}\) cut off a portion \(\overline{A B}\)  equal to a.

At a point, A draw an

angle ∠XAY equal to a. From \(\overline{A Y}\) cut off \(\overline{B C}\) = b.

Then AABC is the required triangle.

Verification: By measuring with a scale it is found that \(\overline{A B}\) = a and \(\overline{B C}\) = b, and by measuring with a protractor it is found that, ∠BCA = α.

Ganit Prabha Class 8 Solution

Question 5

To draw a straight line through a given point parallel to a given straight line.

Solution:

Let \(\stackrel{\leftrightarrow}{P Q}\) be a given straight line and R be a given point outside it.

It is required to draw a straight line through R parallel to \(\stackrel{\leftrightarrow}{P Q}\).

Construction: A point S is taken on

the straight line\(\stackrel{\leftrightarrow}{P Q}\). SR is joined.

An angle, ∠ARS is constructed at the point R on \(\overline{S R}\) which is equal to ∠RSQ and is on the opposite side of \(\overline{R S}\) in

which ∠RSQ lies. AR is produced upto the point B.

Then the straight line \(\stackrel{\leftrightarrow}{A B}\) is the required straight line which is parallel

to \(\stackrel{\leftrightarrow}{P Q}\) and passes through R.

Proof: Here is the line segment \(\overline{S R}\) intersects \(\stackrel{\leftrightarrow}{P Q}\) at S and \(\stackrel{\leftrightarrow}{A B}\) at R.

Also by construction,

∠ARS = ∠RSQ.

But they are alternate angles.

Hence, \(\stackrel{\leftrightarrow}{A B}\) || \(\stackrel{\leftrightarrow}{P Q}\).

Alternative Method:

Ganit Prabha Class 8 Solution

Let \(\stackrel{\leftrightarrow}{P Q}\) be a given straight line and R be a given point outside it.

It is required to draw a straight line

through R parallel to \(\stackrel{\leftrightarrow}{P Q}\).

Construction: A point S is taken on

the straight line \(\stackrel{\leftrightarrow}{P Q}\). \(\overline{S R}\) is joined and it is produced to T.

An angle, ∠TRB is constructed at the

point R on \(\overline{R T}\) which is equal to ∠RSQ

and is on the same side as \(\overline{R S}\) in which

∠RSQ lies. \(\overleftarrow{B R}\) is produced upto the point A.

Then the straight line \(\stackrel{\leftrightarrow}{A B}\) is the required straight line which is parallel

to \(\stackrel{\leftrightarrow}{P Q}\)  and passes through R.

Proof:  Here, \(\overline{S T}\) intersects \(\stackrel{\leftrightarrow}{P Q}\) at S and \(\stackrel{\leftrightarrow}{A B}\) at R.

Also by construction, ∠TRB – ∠RSQ. But they are corresponding angles.

Hence, \(\stackrel{\leftrightarrow}{A B}\) || \(\stackrel{\leftrightarrow}{P Q}\).

Ganit Prabha Class 8 Solution

Question 6

To divide a line segment into three equal parts.

Solution:

Given:

Let, \(\overline{A B}\) be a segment.

Construction: At point A draw any angle ∠BAC. Then ∠ABD is drawn equal to the measure of ∠BAC on the opposite side of \(\overline{A B}\) in which ∠BAC lies.

Cut off two line segments \(\overline{A E}\) and \(\overline{E F}\) of equal length from \(\overline{A C}\).

Again from \(\overline{B D}\) cut off \(\overline{B G}\) and \(\overline{G H}\) equal to the previous length.

Join \(\overline{E H}\) and \(\overline{F G}\).

They intersect the line segment \(\overline{A B}\) at points S and T.

In this way, the line segment \(\overline{A B}\) is divided at S and T into three equal parts.

It is required to divide the line segment \(\overline{A B}\) into three equal parts.

Question 7

To divide a line segment into five equal parts.

Solution:

Let \(\overline{A B}\) be a given line segment.

It is required to divide \(\overline{A B}\) into five equal parts.

Construction: A straight line \(\overline{A C}\) is drawn at point A making an angle with \(\overline{A B}\).

From \(\overline{A C}\), the line segments \(\overline{A D}\), \(\overline{D E}\), \(\overline{E F}\), \(\overline{F G}\) and \(\overline{G H}\) of equal length are cut off one after another.

\(\overline{B H}\) is joined.

Now, at points, D, E, F, and G angles are drawn making it equal to ∠AHB on the same side of \(\overline{A C}\) in which ∠AHB lies.

Let the sides of the angles intersect \(\overline{A B}\) at I, J, K, and L respectively.

Thus the line segment \(\overline{A B}\) is divided at the points I, J, K, and L into five equal parts.

Alternative method :

Let \(\overline{P Q}\) be a given line segment.

It is required to divide \(\overline{P Q}\) into five equal parts.

Construction: Any angle ∠QPR is drawn at point P.

Then, ∠PQS is drawn equal to the measure of ∠QPR on the opposite side of \(\overline{P Q}\) in which ∠QPR lies. Four line segments of equal lengths \(\overline{P A}\), \(\overline{A B}\), \(\overline{B C}\)

and \(\overline{C D}\) are cut off from \(\overline{P R}\) one after another.

Also, four line segments of former equal lengths \(\overline{Q D_1}\)_, \overline{D_1 C_1}, \overline{C_1 B_1}_, and \overline{B_1 A_1} are cut off from QS one after another.

\(\overline{A A_1}\)_, \(\overline{B B_1}\) , \(\overline{C C_1}\), and \(\overline{D D_1}\) are joined.

They intersect the line segment \(\overline{P Q}\)at E, F, G, and H respectively.

Thus the line segment \(\overline{P Q}\) is divided at points E, F, G, and H into five equal parts.

Geometry Chapter 2 Theorems

Theorems Introduction

In geometry, we obtain some properties through activities. These properties are called axioms or self-evident truths. We need not establish an axiom with the help of reasoning. On the other hand, there are also some geometrical properties that can be established with the help of reasoning. When we prove any geometrical property with logic then the property to be proved, the method of proof, and arriving at the conclusion- all stages taken as a whole is called a theorem. Thus, a geometrical property along with a proof is a theorem.

Maths Solutions Class 8 Wbbse

Propositions

By propositions, we mean the statements which propose to prove some geometrical property or to perform some geometrical construction. There are two kinds of propositions namely Theorems and Problems.

Theorem: A proposition that is proved with logic is called a Theorem.

Problem: A proposition in which some geometrical construction is performed is called a Problem.

Different parts of a proposition

A geometrical proposition has four parts :

1. General Enunciation

2. Particular Enunciation

3. Construction and

4. Proof.

1. General enunciation: The general statement of the hypothesis and the conclusion is called the general enunciation.

2. Particular enunciation: The second part of a proposition is particular enunciation. A figure is drawn according to the general enunciation. The statement of hypothesis and conclusion according to the naming of the figure is called particular enunciation.

3. Construction: It may be necessary to have some construction for the proof of the proposition. In this part, the statement of such construction is mentioned.

4. Proof: This is the final part of the proposition. In this part, the proposition is proved through a strict sequence of reasoning.

Read And Learn More WBBSE Solutions For Class 8 Maths

Converse theorem

If two theorems be such that the hypothesis of the first is the conclusion of the second and the conclusion of the first is the hypothesis of the second then those theorems are said to be converse to each other.

Corollary

If from the conclusion of a theorem, some other conclusion readily follows then it is called a corollary.

Maths Solutions Class 8 Wbbse

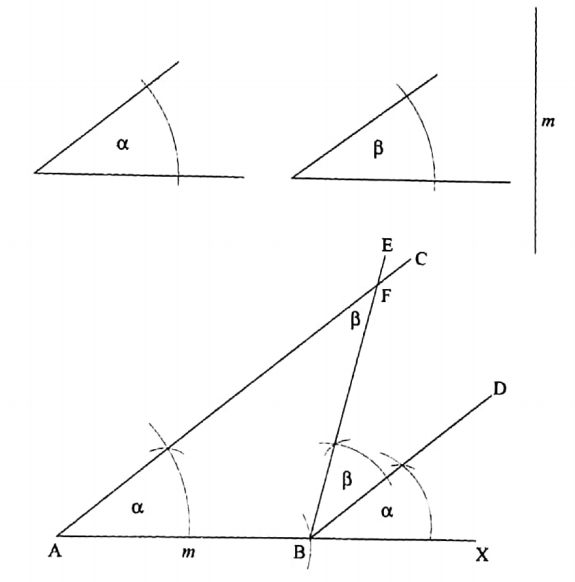
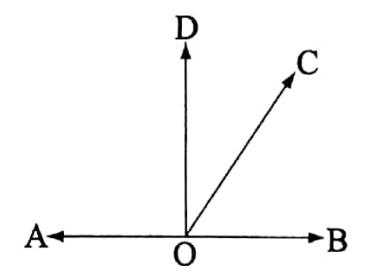
Theorem 1

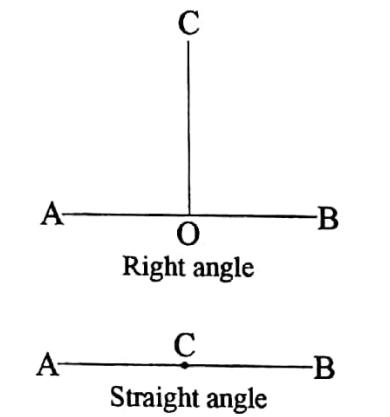
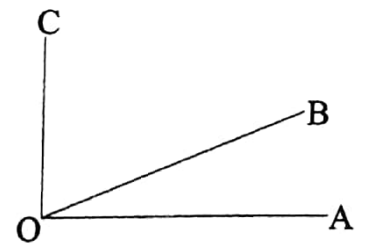
If a straight line stands on another ‘straight line, the sum of the two angles so formed is equal to two right angles.

Given:

A straight line stands on another ‘straight line, the sum of the two angles so formed is equal to two right angles.

Let \(\overleftrightarrow{A B}\) be a straight line.

\(\overrightarrow{O C}\) is another straight line that stands on AB at point O, forming the angle ∠BOC and ∠COA.

It is required to prove that, ∠BOC + ∠COA = 2 right angles.

Construction: Draw a straight line \(\overrightarrow{O D}\) perpendicular to AB at point O.

Proof : ∠BOC +∠COA =∠BOC ∠COD +∠DOA = ∠BOD +∠DOA

= 1 right angle + 1 right angle

= 2 right angles.

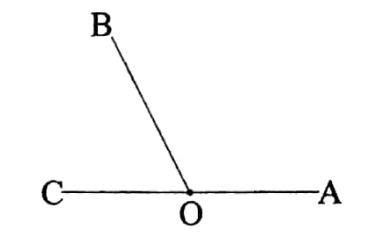
Verification of Theorem-1 :

Let \(\overleftrightarrow{A B}\) be a straight line.

\(\overrightarrow{O C}\) is another straight line that stands on

\(\overleftrightarrow{A B}\) at point O, forming the angles ∠BOC and ∠COA.

It is to be verified that ∠BOC + ∠COA = 2 right angles.

Fold the straight line \(\overleftrightarrow{A B}\) at point O in such a way that \(\overrightarrow{O A}\) coincides with  In this case the line of fold is \(\overrightarrow{O D}\).

It is clear that \(\overrightarrow{O D}\) is perpendicular to \(\overleftrightarrow{A B}\).

Measuring with a protractor it is found that,

∠BOD = 90° =∠DOA.

It means that the measure of each of the angles ∠BOD and ∠DOA is equal to 1 right angle.

Now, ∠BOC + ∠COA = ∠BOC + ∠COD ∠ DOA

= ∠BOD + ∠DOA

= 90° + 90°

= 180°

= 2 right angles.

Maths Solutions Class 8 Wbbse

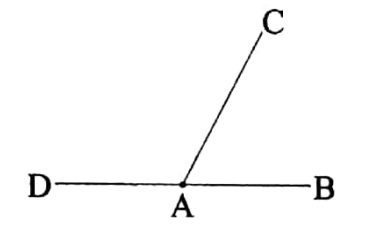
Theorem 2

If the sum of two adjacent angles is equal to two right angles, the exterior arms of the angles lie in the same straight line.

Given:

The sum of two adjacent angles is equal to two right angles, the exterior arms of the angles lie in the same straight line.

Let the sum of two adjacent angles ∠COB and ∠COA be equal to two right angles. The exterior arms of these two

adjacent angles are \(\overrightarrow{O B}\) and \(
\overrightarrow{O A}
\).

It is required to prove that  \(\overrightarrow{O B}\)  and  \(
\overrightarrow{O A}
\). lie on the same straight line.

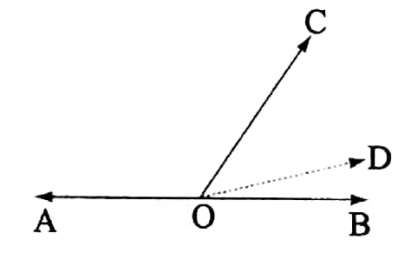
Proof: Let, \(
\overrightarrow{O B}
\)., and \(
\overrightarrow{O A}
\). are not on the same straight line.

Then \(
\overrightarrow{O A}
\). produced must pass through some other straight-line \(
\overrightarrow{O D}
\).

Now, since the straight-line \(
\overrightarrow{O C}
\). stands on the straight-line \(\overleftrightarrow{A B}\),

∠COD + ∠COA = 2 right angles.

Also by hypothesis, ∠COB + ∠COA = 2 right angles.

Hence, ∠COD + ∠COA =∠COB +∠COA

or, ∠COD = ∠COB

So,  \(
\overrightarrow{O D}
\). coincides with \(
\overrightarrow{O D}
\).

Thus, our assumption that \(
\overrightarrow{O B}
\). and  \(
\overrightarrow{O A}
\). are not on the same straight line is wrong.

Hence, \(
\overrightarrow{O B}
\). and  \(
\overrightarrow{O A}
\). lie in the same straight line.

Verification of Theorem-2 :

Draw any straight line  \(
\overrightarrow{O B}
\). With the help of a protractor draw an angle ∠BOC = 45°.

Again, with the help of the protractor draw another angle ∠COA = 135°.

Therefore,∠BOC +∠COA

= 45° + 135°

= 180°.

If a ruler is placed along the arm  \(
\overrightarrow{O B}
\). of the angle ∠BOC then it is found that

\(
\overrightarrow{O A}
\). and  \(
\overrightarrow{O B}
\). lie on the same straight line.

Some Examples

Example 1

Prove that the sum of the four angles, formed by the intersection of two straight lines, is equal to four right angles.

Solution :

Given:

The sum of the four angles, formed by the intersection of two straight lines, is equal to four right angles.

Let \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) be the two straight lines that intersect each other at point 0.

As a result of the intersection of these two straight lines, the four angles ∠BOC, ∠COA, ∠AOD, and∠DOB have been formed.

It is required to prove that :

∠BOC +∠COA + ∠AOD +∠DOB = 4 right angles.

Proof: Since \(\overrightarrow{O C}\)stands on the straight

line \(\overleftrightarrow{A B}\)at the point O therefore, ∠BOC + ∠COA = 2 right angles …….. (1)

Also since \(\overrightarrow{O D}\)stands on the straight

line AB at the point O therefore, ∠AOD + ∠DOB = 2 right angles …….. (2)

Adding (1) and (2) we get,

∠BOC + ∠COA +∠AOD + ∠DOB = 4 right angles.

Example 2

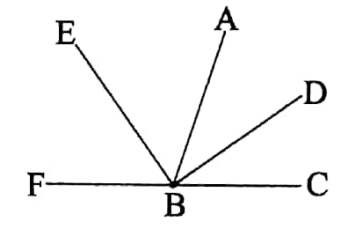
Prove that the angle between the internal and the external bisector of an angle is equal to one right angle.

Solution :

Given:

The angle between the internal and the external bisector of an angle is equal to one right angle.

Let ∠ABC be an angle whose internal bisector is \(\overrightarrow{B D}\) and whose external bisector is \(\overrightarrow{B E}\).

It is required to prove that: ∠DBE = 1 right angle

Proof: Since \(\overrightarrow{B D}\) is the bisector of ∠ABC,

:. ∠ABD = 1/2 ∠ABC …….. (1)

Also, since \(\overrightarrow{B E}\) is the bisector of ∠ABF,

∠ABE = 1/2 ∠ABF …….. (2)

Adding (1) and (2) we get,

∠ABD + ∠ABE = 1/2 (∠ABC +∠ABF)

= 1/2 x 180° = 90°

or, ∠DBE = 1 right angle.

Example 3

Prove that, if the angle formed by the bisectors of two adjacent angles is equal to 1 right angle, then the exterior sides of the adjacent angles will be on the same straight line.

Solution :

Given:

The angle formed by the bisectors of two adjacent angles is equal to 1 right angle, then the exterior sides of the adjacent angles will be on the same straight line.

Let ∠ABC and∠ABF be two adjacent angles.

\(\overrightarrow{B D}\) is the bisector of ∠ABC and \(\overrightarrow{B E}\) is the bisector of ∠ABF.

It is given that ∠DBE = 1 right angle.

It is required to prove that: BC and BF lie on the same straight line.

Proof: ∠ABC = 2∠ABD……. (1)

and ∠ABF = 2∠ABE…….. (2)

Adding (1) and (2) we get,

∠ABC + ∠ABF = 2 ∠ABD +∠ABE) = 2 x ∠DBE

= 2 x 1 right angle

= 2 right angles.

Hence, BC and BF lie in the same straight line.

Example 4

Prove that, if some straight lines stand on another straight line then the sum of the consecutive angles is equal to two right angles.

Solution :

Given:

Some straight lines stand on another straight line then the sum of the consecutive angles is equal to two right angles.

Let \(\overleftrightarrow{A B}\) be a straight line. \(\overrightarrow{O C}\), \(\overrightarrow{O D}\), and \(\overrightarrow{O E}\) be the straight lines standing on \(\overleftrightarrow{A B}\).

It is required to prove that: ∠BOC + ∠COD +∠DOE + ∠EOA = 2 right angles.

Proof: Since \(\overrightarrow{O C}\) stands on \(\overrightarrow{A B}\)

∠BOC + ∠COA = 2 right angles.

or, ∠BOC + ∠COD +∠DOE +∠EOA = 2 right angles.

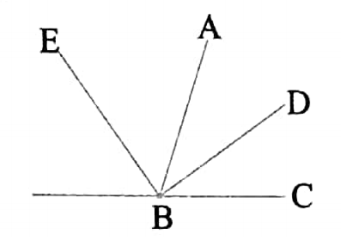
Example 5

Prove that, the sum of the consecutive angles formed by some straight lines emerging from a point is equal to four right angles.

Solution:

Given:

The sum of the consecutive angles formed by some straight lines emerging from a point is equal to four right angles.

Let O be a fixed point.

\(\overrightarrow{O A}\), \(\overrightarrow{O B}\), \(\overrightarrow{O C}\), \(\overrightarrow{O D}\), \(\overrightarrow{O E}\), \(\overrightarrow{O F}\)  be straight lines emerging from point O.

It is required to prove: ∠AOB + ∠BOC +∠COD + ∠DOE + ∠EOF +∠FOA = 4 right angles.

Construction: Produce AO to point A’.

Proof: Since A’OA is a straight line, therefore,

∠AOB +∠BOC + ∠COA = 2 right angles …. (1)

and ∠AOD + ∠DOE + ∠EOF + ∠FOA = 2 right angles …. (2)

Adding (1) and (2) we get,

∠AOB + ∠BOC + ∠COA ∠ AOD + ∠DOE + ∠EOF + ∠FOA = 4 right angles

or, ∠AOB +∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA = 4 right angles.

Example 6

Prove that, if two straight lines intersect at a point then the bisectors of the four angles are two mutually perpendicular straight lines.

Solution:

Given:

The sum of the consecutive angles formed by some straight lines emerging from a point is equal to four right angles.

Let the two straight lines \(\overleftrightarrow{P Q}\) intersect at point O.

Let, \(\overrightarrow{O A}\), \(\overrightarrow{O C}\), and \(\overrightarrow{O B}\) be the bisectors of the angles ∠POR ∠POS, ∠SOQ, and ∠ROQ respectively.

It is required to prove that \(\overline{A O B}\)and \(\overline{C O D}\) are two mutually perpendicular straight lines.

Proof: Since \(\overrightarrow{O A}\), \(\overrightarrow{O C}\), \(\overrightarrow{O B}\), and \(\overrightarrow{O D}\) are respectively the bisectors of the angles  ∠POR, ∠EOS, ∠SOQ, and ∠ROQ

∴∠AOP = 1/2  ∠POR …(1)

∠POC = 1/2 ∠POS… (2)

Adding (1) and (2) we get,

∠AOP + ∠POC = 1/2 ∠FOR +∠POS)

or, ∠AOC = 1/2 x 2 right angles = 1 right angle.

Similarly, ∠COB – ∠BOD = ∠DOA – 1 right angle

∠AOC + ∠COB = 1 right angle + 1 right angle = 2 right angles.

\(\overrightarrow{O A}\) and \(\overrightarrow{O B}\) are in the same straight line.

Similarly, \(\overrightarrow{O C}\) and \(\overrightarrow{O D}\) are in the same straight line.

Hence, \(\overline{A O B}\) and \(\overline{C O D}\) are two mutually perpendicular straight lines.

Example 7

From the figure shown below find the value of x.

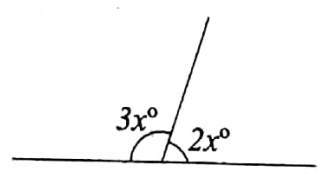
Solution:

From the given

2xº + 3xº = 180º

or, 2x + 3x = 180

or, 5x = 180

or, x = 180/5

= 36

The value of x is 36.

Example 8

Draw any straight line \(\overleftrightarrow{X Y}\). Take any two points A and B on it. At A draw any straight line \(\overrightarrow{A C}\). At B draw the straight line \(\overrightarrow{B D}\) such that ∠ABD = ∠YAC.

Show that: ∠CAB = ∠DBX.

Solution:

Any straight fine \(\overleftrightarrow{X Y}\) is drawn. A and B

are any two points on \(\overleftrightarrow{X Y}\). At point A,

any straight line \(\overrightarrow{A C}\) is drawn. Now the

straight line \(\overrightarrow{B D}\) is drawn in such a way

that ∠ABD = ∠YAC.

It is required to prove that, ∠CAB = ∠DBX.

Proof: Since \(\overrightarrow{A C}\), stands on \(\overleftrightarrow{X Y}\)

therefore, ∠YAC. + ∠CAB = 180°… (1)

Also since BD stands on \(\overleftrightarrow{X Y}\)

therefore, ∠ABD + ∠DBX = 180° …. (2)

From (1) and (2)

∠YAC + ∠CAB = ∠ABD + ∠DBX

Since ∠ABD =∠YAC

∴ ∠CAB =∠DBX.

Theorem 3

If two straight lines intersect, the vertically opposite angles are equal.

Let \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{O D}\) be any two straight lines that intersect at O.

It is required to prove that :

1. ∠AOD= vertically opposite

2. ∠AOC =vertically opposite

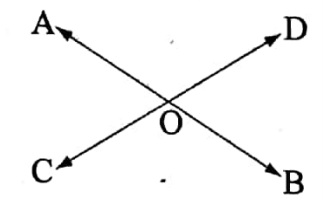
Proof: Since \(\overrightarrow{O D}\) stands on \(\overleftrightarrow{A B}\) therefore,

∠AOD ∠DOB = 2 right angles … (1)

Also since \(\overrightarrow{O B}\) stands on \(\overrightarrow{C D}\)therefore,

∠DOB +∠BOC = 2 right angles …. (2)

From (1) and (2) we get,

∠AOD + ∠DOB = ∠DOB + ∠BOC

or, ∠AOD = ∠BOC.

Also since \(\overrightarrow{O A}\) stands on \(\overrightarrow{C D}\) therefore,

∠AOC +∠AOD = 2 right angles …. (3)

and \(\overrightarrow{O D}\) stands on \(\overleftrightarrow{A B}\) therefore,

∠AOD +∠DOB = 2 right angles …. (4)

From (3) and (4) we get,

∠AOC + ∠AOD = ∠AOD + ∠DOB

:. ∠AOC =∠DOB.

Verification of Theorem-3 :

Draw any two straight lines\(\overleftrightarrow{A B}\) and

\(\overleftrightarrow{C D}\)on your paper. Let the point of intersection of \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) be 0.

Measuring with a protractor you will find that ∠AOD = ∠BOC and ∠AOC = ∠BOD.

Some Examples

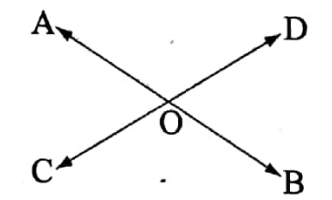
Example 1

The two straight lines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) intersect at 0. If ∠AOC = 55° then find the measures of the angles ∠AOD, ∠BOD, and∠BOC.

Solution :

Given:

The two straight lines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) intersect at 0. If ∠AOC = 55°

Since, ∠AOC = 55° therefore,∠BOD = 55°.

Again, ∠AOD = 180° – ∠AOC

= 180° – 55° = 125°

.-. ∠BOC = 125°

∠AOD = 125°,∠BOD = 55° and ∠BOC = 125°.

Example 2

Two straight lines intersect each other at a point. The sum of the three angles, out of the four angles thus formed is 315°. Find the measures of the four angles formed at that point.

Solution :

Given:

Two straight lines intersect each other at a point. The sum of the three angles, out of the four angles thus formed is 315°.

Since the sum of the three angles is 315°, therefore the measure of the fourth angle

= 360° – 315°

= 45°.

Therefore, its vertically opposite angle is also 45°.

Hence, the sum of the other two angles is 360° – 2 x 45°

= 360° – 90°

= 270°

∴ The measure of each of them

= 270º / 2

= 135°

The Measures of the angles formed at that point are 45°, 45°, 135° and 135°.

Example 3

Find the measure of the angle ∠BOC from the figure shown below.

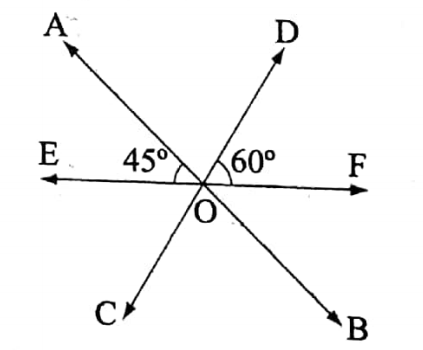
Here \(\overleftrightarrow{E F}\) is a straight line. Hence,

∠AOE + ∠AOD + ∠DOF = 180°

or, 45° ∠AOD + 60° = 180°

or, ∠AOD + 105° = 180°

or, ∠AOD = 180° – 105° = 75°

∴∠BOC = ∠AOD = 75°

Example 4

\(\overleftrightarrow{A B}\) is a straight line and O is a point on it. From 0. two straight lines \(\overrightarrow{O C}\) and \(\overrightarrow{O D}\)are drawn on the opposite sides of \(\overrightarrow{A B}\). If ∠AOC = ∠BOD then prove that \(\overrightarrow{O C}\) and \(\overrightarrow{O D}\) will lie on the same straight line

Solution:

\(\overleftrightarrow{A B}\) is a straight line and 0 is a point on it.

From O, two straight lines \(\overrightarrow{O C}\) and \(\overrightarrow{O D}\)are drawn on the opposite sides of \(\overleftrightarrow{A B}\),

such that ∠AOC = ∠BOD.

It is required to prove that :

\(\overrightarrow{O C}\) and \(\overrightarrow{O D}\) will lie on the same straight line.

Proof: It is given that∠AOC = ∠BOD …. (1)

Since, \(\overrightarrow{O C}\)stands on \(\overleftrightarrow{A B}\) therefore, ∠AOC + ∠BOC = 180°

or, ∠BOD + ∠BOC = 180°      [From (1)]

Hence, \(\overrightarrow{O C}\) and \(\overrightarrow{O D}\)will lie on the same straight line.

Example 5

Prove that, the bisectors of a pair of vertically opposite angles lie on the same straight line.

Let \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) be the two straight lines that intersect at O.

Here ∠AOC and ∠DOB are pairs of vertically opposite angles.

Let, \(\overrightarrow{O E}\) be the bisector of ∠AOC and \(\overrightarrow{O F}\) be the bisector of ∠DOB.

It is required to prove that: \(\overrightarrow{O E}\) and \(\overrightarrow{O F}\) lie on the same straight line.

Proof: Since \(\overrightarrow{O E}\)is the bisector of∠AOC,

∴ ∠AOE = ∠COE

Also, \(\overrightarrow{O F}\) is the bisector of∠DOB, ∠DOF =∠BOF

Again, ∠AOD = vertically opposite ∠BOC

Hence, ∠AOE +∠AOD +∠DOF = ∠COE +∠BOC +∠BOF

= 1/2 (∠AOE + ∠AOD + ∠DOF + ∠COE + ∠BOC +∠BOF)

= 1/2 x 4 right angles = 2 right angles

∴ ∠EOF = a straight angle

\(\overrightarrow{O E}\) and \(\overrightarrow{O F}\) lie on the same straight line

Example 6

\(\overleftrightarrow{P Q}\) and \(\overrightarrow{R S}\) are two straight lines intersecting at O. Bisector of ∠POR is \(\overrightarrow{O X}\). \(\overrightarrow{O X}\) is produced through O. Prove that it will bisect ∠SOQ,

Solution:

\(\overleftrightarrow{P Q}\) and \(\overleftrightarrow{R S}\) are two straight lines intersecting at O.

\(\overrightarrow{O X}\) is the bisector of

∠POR. \(\overleftarrow{X O}\) is produced to Y.

It is required to prove that: \(\overrightarrow{Q Y}\) bisects ∠SOQ.

Proof: ∠POX=vertically opposite ∠QOY and ∠BOX = vertically opposite ∠SOY.

Since, \(\overrightarrow{O X}\)is the bisector of∠POR therefore, ∠POX = ∠ROX Hence, ∠QOY = ∠SOY

:. \(\overrightarrow{O Y}\) bisects ∠SOQ.

Theorem 4

When a straight line cuts two other straight lines, those other two straight lines are parallel if either

1. A pair of alternate angles are equal, or,

2. A pair of interior angles on the same side of the transversal are together equal to two right angles.

Let the straight lines \(\overleftrightarrow{E F}\) intersect the straight lines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) at G and H respectively.

1. Let, ∠AGH = alternate ∠GHD.

It is required to prove that: \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are parallel to each other.

Proof: Since the straight lines \(\overleftrightarrow{A B}\) and

\(\overleftrightarrow{E F}\) intersect each other at G,

∴ ∠AGH = vertically opposite ∠EGB.

But ∠AGH =∠GHD (given)

∴∠EGB = ∠GHD

But they are corresponding angles.

∴ \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are parallel to each other.

2. Let,∠BGH + ∠GHD = 2 right angles

It is required to prove that: \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are parallel to each other.

Proof: Since the straight line \(\overleftrightarrow{G B}\) stands on the straight line \(\overleftrightarrow{E F}\)

∠EGB + ∠BGH – 2 right angles.

But, ∠BGH +∠GHD = 2 right angles (given)

∠EGB +∠BGH = ∠BGH +∠GHD

or, ∠EGB = ∠GHD.

But they are corresponding angles

\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are parallel to each other.

Verification of Theorem-4 :

1. Draw any angle ∠AGH.

Then draw another angle ∠GHD (equal in measure to∠AGH) where D is on the opposite side of \(\overline{G H}\)on which point A lies.

Extend \(\overline{A G}\) up to B and \(\overline{D H}\) in the opposite direction up to C.

Also, extend \(\overline{H G}\) up to E in one direction and up to F in another direction.

You will find that \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{C D}\).

2. Draw any angle ∠BGH. Then draw another angle ∠GHD supplementary of∠BGH, where B and D are the points on the same side of \(\overline{G H}\).

Extend \(\overline{D G}\) up to A and \(\overline{D H}\) up to C in the same direction.

Also, extend \(\overline{H G}\) up to E in one direction and up to F in another direction.

You will find that \(\overleftrightarrow{A B}\) | | \(\overleftrightarrow{C D}\).

Theorem 5

If a straight line cuts two parallel straight lines, then

1. The corresponding angles are equal.

2. The alternate angles are equal.

3. The interior angles on the same side of the transversal are together equal to two right angles.

Let the straight line \(\overleftrightarrow{E F}\) cut two parallel straight lines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) at points G and H respectively.

It is required to prove that :

1. ∠EGB= corresponding ∠GHD

2. ∠AGH= alternate ∠GHD

3. ∠BGH+ ∠GHD = 2 right angles.

Proof :

1. Let ∠EGB = not

Then let∠EGL drawn at the point G be equal to ∠GHD.

Then, the straight line \(\overleftrightarrow{E F}\)intersects two straight lines GL and \(\overleftrightarrow{C D}\) at G and H respectively and

∠EGL = corresponding ∠GHD [By assumption]

Hence, \(\overrightarrow{G L}\) || \(\overleftrightarrow{C D}\)

Thus two intersecting straight lines \(\overrightarrow{G L}\) and \(\overleftrightarrow{A B}\)are both parallel to the straight line \(\overleftrightarrow{C D}\).

But according to Playfair’s Axiom, this is impossible. Hence, ∠EGB and ∠GHD cannot be of unequal measure.

∴∠EGB = ∠GHD

1.∠EGB = ∠GHD(Proved) and ∠EGB = vertically opposite∠AGH

Hence, ∠AGH = ∠GHD

2. ∠EGB= ∠GHD (Proved)

Also since the straight line GB stands on the straight line \(\overleftrightarrow{E F}\) therefore,

∠BGH + ∠EGB = 2 right angles

Hence, ∠BGH + ∠GHD = 2 right angles.

Verification of Theorem-5 :

Draw any two parallel straight lines

\(\overleftrightarrow{A B}\)and \(\overleftrightarrow{C D}\).

Draw a transversal \(\overleftrightarrow{E F}\)which intersects \(\overleftrightarrow{A B}\) at G and \(\overleftrightarrow{C D}\) at H.

Measuring with a protractor you will find that,

1. ∠EGB= ∠GHD

2.∠AGH = ∠GHD

3. ∠BGH + ∠GHD= 180°.

Some Examples 

Example 1

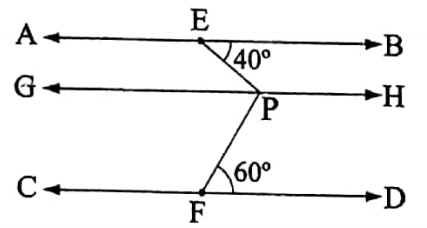
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are two parallel straight lines. E and F are two points on \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) respectively. P is a point in the region between \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) such that ∠BEP = 40° and ∠PFD = 60°. Find the measure of∠EPF.

Solution:

Draw a straight line \(\overleftrightarrow{G H}\) parallel to \(\overleftrightarrow{A B}\) or \(\overleftrightarrow{C D}\) through the point P.

Now, \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{G H}\) are parallel, and \(\overline{E P}\) is the transversal

.’. ∠GPE = alternate ∠BEP = 40°.

Again,\(\overleftrightarrow{G H}\) and \(\overleftrightarrow{C D}\) are parallel, and \(\overline{P F}\) is the transversal

∴ ∠GPF = alternate ∠PFD = 60°

∠EPF = ∠GPE + ∠GPF

= 40° + 60°

= 100°.

 

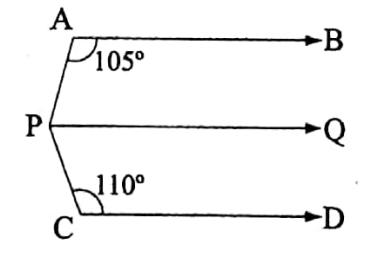
Example 2

\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are two parallel straight lines. P is a point such that ∠BAP = 105° and ∠DCP = 110°. Find the measure of ∠APC.

Solution: 

Draw a straight line \(\overrightarrow{P Q}\) parallel to \(\overleftrightarrow{A B}\)  or \(\overleftrightarrow{C D}\)

Now, since \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{P Q}\) and \(\overleftarrow{A P}\) are the transversal

∠BAP + ∠APQ = 180°

or, ∠APQ = 180° – ∠BAP

= 1∠0° – 105° = 75°

Also, since \(\overrightarrow{P Q}\) | | \(\overleftrightarrow{C D}\) and \(\overrightarrow{C P}\) is the transversal

∴ ∠QPC + ∠PCD = 180°

or, ∠QPC = 180° – ∠PCD

= 180° – 110° = 70°

∴∠APC = ∠APQ + ∠QPC

= 75° + 70°

= 145°.

Example 3

In the figure shown below \(\overleftrightarrow{B C}\) || \(\overleftrightarrow{D E}\). ∠ABC = 50°, ∠CBD = 95° and ∠EDG = 50°. Find the measures of the angles of ABFD.

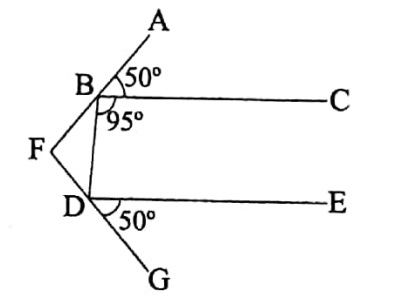
Solution:

Since ∠ABF is a straight angle, therefore, ∠ABC + ∠CBD + ∠DBF = 180°

or, 50° + 95° + ∠DBF = 180°

or, ∠DBF = 180° – 145°

= 35°

Now, \(\overleftrightarrow{B C}\)  | | \(\overleftrightarrow{D E}\) and \(\overleftrightarrow{B D}\) is the transversal

∴ ∠CBD + ∠BDE – 180°

or, ∠BDE = 180° – ∠CBD

= 180° – 95°

= 85°

Also, ∠FDG is a straight angle therefore, ∠FDB + ∠BDE + ∠EDG = 180°

or, FDB = 85° + 50° = 180°

or,∠FDB = 180° – 135°

= 45°

Hence, in the ΔBFD,

∠BFD = 180° – (∠DBF + ∠FDB)

= 180° – (35° + 45°)

= 180° – 80°

= 100°

Example 4

If the sides of one angle are respectively parallel to the sides of another angle, then the angles are either equal or supplementary.

Solution:

Let the sides \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{B C}\) of the ∠ABC

be respectively parallel to the sides \(\overleftrightarrow{D E}\) and \(\overleftrightarrow{E F}\) of the ∠DEF.

Let the point of intersection of \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{E F}\) in the first be G and that in the second figure be H.

We have to prove that:  Either ∠ABC = ∠DEF or ∠ABC and ∠DEF are supplementary.

Proof: In the first figure, since \(\overleftrightarrow{B C}\)| | \(\overleftrightarrow{F G}\)

and \(\overleftrightarrow{B A}\) is the transversal,

.’. ∠AGF = ∠ABC (corresponding angle)

Also, \(\overleftrightarrow{B A}\) || \(\overleftrightarrow{E D}\) and EF are the transversal,

∠AGF = ∠GED (corresponding angle)

∴ ∠ABC =∠GED

i.e., ∠ABC = ∠DEF.

In the second figure, since \(\overleftrightarrow{B C}\) || \(\overleftrightarrow{F H}\) and \(\overleftrightarrow{B A}\) is the transversal,

∴ ∠CBH + ∠BHF = 180°

Also, \(\overleftrightarrow{B A}\) || \(\overleftrightarrow{D E}\) and \(\overleftrightarrow{E F}\) is the transversal

.’. ∠BHF = ∠DEH (corresponding angle)

∴ ∠CBH + ∠DEH = 180°

i.e., ∠ABC +∠DEF = 180°

Hence, ∠ABC and ∠DEF are supplementary.

Example 5

The straight lines which are parallel to the same straight line are parallel to one another

solution :

Let the straight lines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) be parallel to \(\overleftrightarrow{E F}\).

It is required to prove that: \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{C D}\)

 

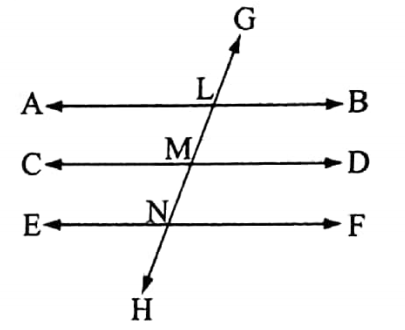
Construction: A straight line \(\overleftrightarrow{G H}\) drawn which intersects \(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\), and at the points L, M, and N respectively.

Proof: Since \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{E F}\) and \(\overleftrightarrow{G H}\) is the transversal

∴ ∠GLB= corresponding ∠LNF

Again, since \(\overleftrightarrow{C D}\) || \(\overleftrightarrow{E F}\) and \(\overleftrightarrow{G H}\) is the transversal

∴ ∠LMD = corresponding ∠LNF

Hence, ∠GLB = ∠LMD

But they are corresponding angles

∴ \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{C D}\)

Example 6

The straight lines which are perpendicular to the same straight line are parallel to one another.

Solution :

Let the straight fines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) be both perpendicular to the straight fine \(\overleftrightarrow{E F}\).

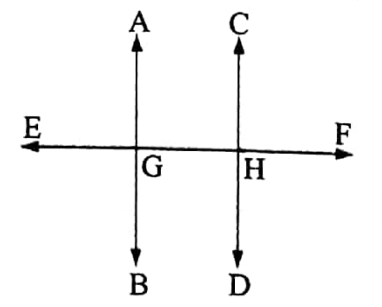
Solution:

Let the point of intersection of \(\overleftrightarrow{A B}\) and

\(\overleftrightarrow{E B}\) be G and that of \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) be H.

It is required to prove that: \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{C D}\).

Proof: Since \(\overleftrightarrow{C D}\) ⊥ \(\overleftrightarrow{E F}\)

∠CHF = 90° and since \(\overleftrightarrow{A B}\) ⊥ \(\overleftrightarrow{E F}\) ∠AGF = 90°

∠CHF = ∠AGF

But they are corresponding angles. Hence, \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{C D}\).

Theorem 6

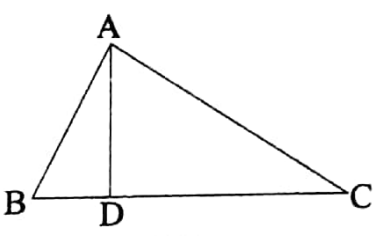
If one side of a triangle is produced, the exterior angle so formed is equal to the sum of two interior opposite angles.

Let ABC be a triangle. The side BC of the triangle is produced to point D. So, ∠ACD is an exterior angle and with respect to it ∠ABC and ∠BAC are two interior opposite angles.

It is required to prove that :

∠ACD = ∠ABC + ∠BAC.

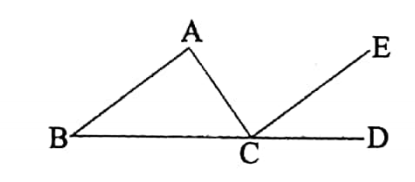
Construction: Through C draw a straight line\(\overline{C E}\) parallel to \(\overline{B A}\)

Proof: Since \(\overline{A B}\) || \(\overline{E C}\) and \(\overline{B D}\) is the transversal

.’. ∠ECD = corresponding∠ABC

Again, \(\overline{A B}\) || \(\overline{E C}\) and \(\overline{A C}\) is the transversal

∠ACE = alternate ∠BAC

Hence, ∠ECD + ∠ACE = ∠ABC + ∠BAC

or, ∠ACD = ∠ABC + ∠BAC.

Verification of Theorem-6 :

Draw any triangle ABC. Extend the side \(\overline{B C}\) up to D.

Measure with a protractor the angles ∠ACD, ∠ABC, and ∠BAC.

You will find that ∠ACD = ∠ABC +∠BAC

Theorem 7

The sum of the three angles of a triangle is equal to two right angles.

Let ABC be a triangle.

It is required to prove that: ∠ABC + ∠BCA + ∠CAB = 2 right angles.

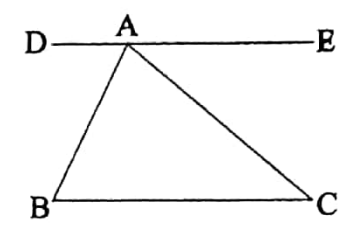
Construction: Through point A, \(\overline{D E}\) is drawn parallel to \(\overline{B C}\).

Proof: Since \(\overline{D E}\) || \(\overline{B C}\) and \(\overline{A C}\) is the transversal

∠EAC = alternate ∠BCA.

Also, since \(\overline{D E}\) || \(\overline{B C}\) and \(\overline{A B}\) is the transversal

∠DAB = alternate ∠ABC

Hence, ∠EAC + ∠DAB = ∠BCA + ∠ABC Adding ∠BAC on both sides we get,

∠EAC + ∠DAB +∠BAC =∠BCA + ∠ABC + ∠BAC

or, ∠ABC + ∠BCA + ∠CAB = ∠EAC +∠BAC + ∠DAB = 2 right angles.

Verification of Theorem-7 :

Draw any triangle ABC.

Measure its three angles with a protractor.

You will find that ∠ABC + ∠BCA + ∠CAB = 2 right angles.

Some Examples

Example 1

If the measures of the two angles of a triangle be 65° and 48° then find the measure of the third angle.

Solution :

We know that the sum of the three angles of a triangle is equal to 180°.

Hence, if any two angles be 65° and 48° then the third angle

= 180° – (65° + 48°)

= 180° – 113°

= 67°

Example 2

Between the two trianglesΔABC and A DEF if ∠ABC = ∠DEF and ∠ACB = ∠DFE then prove that ∠BAC = ∠EDF.

Solution :

Given:

ΔABC and ADEF are two triangles such that ∠ABC = ∠DEF and ∠ACB = ∠DFE.

It is required to prove that ∠BAC = ∠BDF.

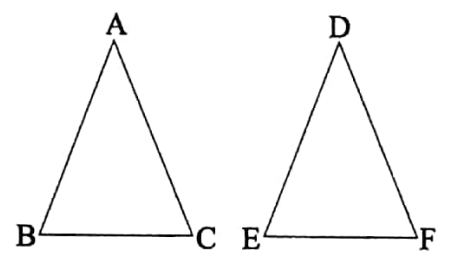
Proof: In the ΔABC,

∠ABC + ∠ACB + ∠BAC = 180° …. (1)

In the ΔDEF

∠DEF + ∠DFE + ∠EDF = 180° …. (2)

From (1) and (2) we get,

∠ABC + ∠ACB + ∠BAC = ∠DEF + ∠DFE + ∠EDF …… (3)

Also,  it is given that,

∠ABC = ∠DEF and ∠ACB = ∠DFE 

.-. ∠ABC + ∠ACB =∠DEF + ∠DFE …. (4)

By (3) – (4) we get,

∠BAC = ∠EDF.

Example 3

Prove that the two acute angles of a right-angled triangle are complementary to one another.

Solution :

Let ABC be a right-angled triangle, in which ∠ABC is a right angle.

Hence, ∠BAC and ∠BCA are the two acute angles.

It is required to prove that∠BAC and ∠BCA are complementary to one another.

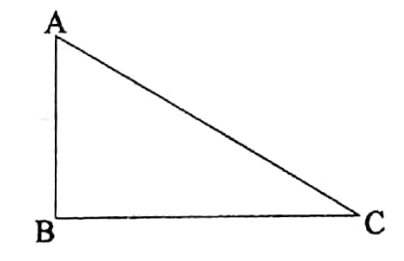
Proof: Since ABC is a triangle, therefore, ∠ABC + ∠BCA + ∠BAC = 180°

or, ∠BCA + ∠BAC = 180° – 90°            [ ∠ABC = 90°]

or, ∠BAC +∠BCA = 90°

Hence, ∠BAC and ∠BCA are complementary to one another.

Example 4

If the sides of a triangle are produced in the same order then prove that the sum of the exterior angles is equal to 360°.

Solution :

Let ABC be a triangle.

Let the sides BC, CA, and AB be produced to the points D, E, and F respectively.

Thus, three exterior angles ∠ACD, ∠BAE, and ∠CBF are produced.

It is required to prove that: ∠ACD + ∠BAE + ∠CBF = 360°.

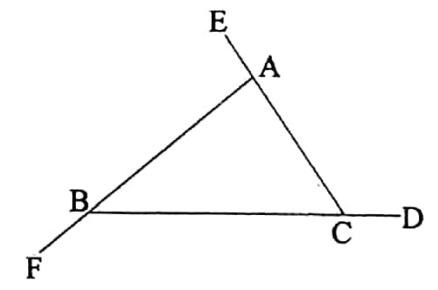
Proof: We know that, if one side of a triangle is produced, the exterior angle so formed is equal to the sum of two interior opposite angles.

∠ACD = ∠ABC + ∠BAC …….. (1)

∠BAE = ∠ABC + ∠ACB ……… (2)

∠CBF =∠ACB + ∠BAC ……… (3)

Adding (1), (2) and (3) we get, ∠ACD + ∠BAE + ∠CBF

= 2 (∠ABC + ∠ACB + ∠BAC)

= 2 x 180° [ sum of three angles of a triangle = 180]

= 360°.

Example 5

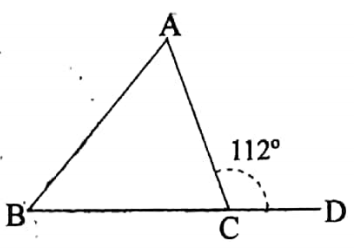
The side \(\overline{B C}\)– of the triangle, ABC is produced to D. If ∠ACD = 112° and ∠B =3/4 ∠A then what is the value of ∠B?

Solution:

Given:

The side \(\overline{B C}\)– of the triangle, ABC is produced to D.

Let ∠A = x° then ∠B = 3xº / 4

Now, ∠A + ∠B = 112º

or, xº + 3xº / 4 = 11

or, 7xº / 4 = 112º

or, xº = 112º x 4/7

∴ ∠B = 3/4 x  64º

= 48º

∠B = 48º

 

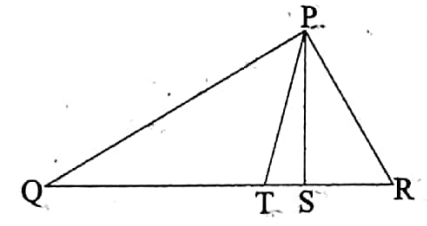
Example 6

PQR is a triangle. \(\overline{P S}\) is drawn perpendicular .from P on \(\overline{Q R}\). \(\overline{P T}\) is the bisector, of the angle ∠QPR. Prove that ∠TPS = 1/2(∠PRQ – ∠PQR).

Solution :

Given:

PQR is a triangle. \(\overline{P S}\)T \(\overline{Q R}\) and \(\overline{P T}\) is the bisector of ∠QPR.

Proof: Since ∠PST is the exterior angle of APSR

∠PRS + ∠SPR = ∠PST = 90° …. (1)

Also since ∠PSR is the exterior angle of APQS

:. ∠PQS + ∠QPS = ∠PSR = 90° …. (2)

From (1) a∠d (2)

∠PRS + ∠SPR = ∠PQS + ∠QPS

or, ∠PRS – ∠PQS

= ∠QPS – ∠SPR

= ∠QPT + ∠TPS – ∠SPR .

= ∠TPR + ∠TPS – ∠SPR

[ ∠QPT= ∠TPR]

(∠TPR – ∠SPR)+ ∠TPS

∠TPS + ∠TPS= 2. ∠TPS

Hence, ∠TPS = 1/2(∠PRS – ∠PQS)

i.e., ∠TPS = 1/2(∠PRQ – ∠PQR).

Proof: Since ∠PST is the exterior of APSR

∠PRS + ∠SPR = ∠PST = 90° …. (1)

Also since ∠PSR is the exterior angle of APQS

:. ∠PQS + ∠QPS = ∠PSR = 90° …. (2)

From (1) and (2)

∠PRS + ∠SPR = ∠PQS + ∠QPS

or, ∠PRS – ∠PQS = ∠QPS – ∠SPR = ∠QPT + ∠TPS – ∠SPR .

= ∠TPR +∠TPS – ∠SPR

[ ∠QPT= ∠TPR]

1. (∠TPR – ∠SPR)+ ∠TPS

2. ∠TPS + ∠TPS= 2. ∠TPS

Hence, ∠TPS = 1/2(∠PRS – ∠PQS)

i.e., ∠TPS = 1/2(∠PRQ – ∠PQR).

Example 7

ABC is a triangle. BO and CO are the bisectors of the angles∠ABC and ∠ACB. Prove that ∠BOC – 90° +  ∠BAC.

Solution:

Given:

ABC is a triangle.

BO and CO are the bisectors of the angles ∠ABC and∠ACB.

It is required to prove that : ∠BOC = 90° + 1/2 ∠BAC.

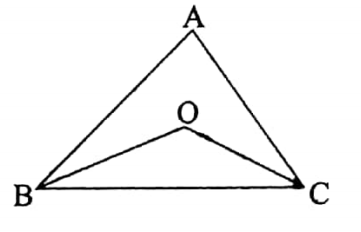
Proof: Since BO is the bisector of ∠ABC

∠OBC = 1/2 ∠ABC…….. (1)

Also since CO is the – bisector of ∠ACB

∴ ∠OCB  =∠ACB ……..(2)

Adding (1) and (2) we get,

∠OBC + ∠OCB = (∠ABC + ∠ACB) ……… (3) Now,

∠BOC = 180° – (∠OBC + ∠OCB)

= 180° – 1/2 ∠ABC + ∠ACB) [From (3)]

= 180° – 1/2 (180° – ∠BAC]

= 180° – 90° + 1/2 ∠BAC

= 90° + 1/2 ∠BAC

Example 8

ABC is a triangle. \(\overline{B O}\) and \(\overline{C O}\) are the external bisectors of the angles ∠ABC and ∠ACB. Prove that ∠BOC = 90° + 1/2 ∠BAC.

Solution :

Given:

ABC is a triangle. \(\overline{B O}\). and \(\overline{C O}\) is the external bisectors of the angles ∠ABC and ∠ACB, which means that if the sides \(\overline{A B}\) and \(\overline{A C}\) of the triangle ABC are produced to D and E respectively then \(\overline{B O}\) and \(\overline{C O}\) are the bisectors of ∠CBD and ∠BCE.

It is required to prove that: ∠BOC = 90° – 1/2 ∠BAC.

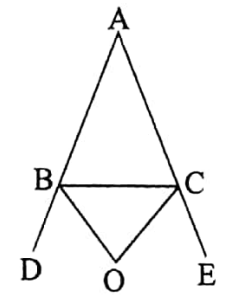
Proof: In the ΔABC, ∠CBD is an exterior angle.

∴ ∠CBD = ∠ACB + ΔBAC ……… (1)

Also, ∠BCE is an exterior angle

∴ ∠BCE = ∠ABC +ΔBAC ……… (2)

Adding (1) and (2) we get,

∠CBD + ∠BCE = ∠ACB +ΔBAC + ∠ABC + ΔBAC = 180° + ΔBAC

1/2 (∠CBD + ∠BCE) = 90° + 1/2 ABAC

or, ∠OBC + ∠OCB = 90° + 1/2 ∠BAC …….. (3)

∴ ∠BOC = 180° – (∠OBC + ∠OCB)

= 180° – (90° + 1/2 ∠BAC) [From (3)]

= 90°’- 1/2 ∠BAC.

Example 9

AB is the hypotenuse of the isosceles right-angled triangle ABC. AD is the bisector of ABAC and AD intersects BC at D. Prove that, AC + CD = AB.

Solution:

Given:

AB is the hypotenuse of the isosceles right-angled triangle ABC.

AD is the bisector of ABAC and AD intersects BC at D.

It is required to prove that, AC + CD = AB.

Construction: DE is drawn perpendicular to AB from D.

Proof: Since ΔABC is a right-angled isosceles triangle, therefore, ΔBAC = ∠ABC = 45°. i.e., ΔEBD = 45°.

Again, DE ⊥ AB ΔDEB = 90°

∴ ΔBDE = 45°.

In ΔACD and ΔADE,

∠CAD = ∠EAD (according to construction),

∠ACD = ∠AED = 90°, and AD is the common side.

∴ ΔACD ≅ ΔADE

CD = DE and AC = AE

Again since,ΔEBD – ΔBDE

DE = BE

Now, AC + CD = AE + DE = AE + BE = AB (Proved).

Example 10

In ΔABC, the external bisector of ∠ACB meets the line through point A and parallel to the side BC at point D. Prove that, ΔADC = 90° – 1/2 ∠ACB

Solution:

Given:

In.ΔABC, the external bisector of ∠ACB meets the line through point A and parallel to the side BC at point D.

It is required to prove: ΔADC = 90° – 1/2 ∠ACB.

Construction: BC is extended upto the point E.

Proof: ΔADC = 180° – ΔDAC – ΔACD

= 180° – ∠ACB – 1/2∠ACE          [  AD || BC, AC is the traversal ∠DAC = ∠ACB ]

= 180 ° – 1/2 ∠ACB – 1/2 ∠ACB – 1/2 ∠ABC – 1/2 ∠BAC

=180° – 1/2 (∠ABC + ∠ACB +∠BAC) – 1/∠ ACB

= 180° – 90° – 1/2 ∠ACB

= 90° – 1/2 ∠ACB (proved)

Polygon

A plane figure enclosed by a number of line segments is called a polygon.

A polygon is named according to the variation in the number of sides. Triangle is a polygon of three sides and a quadrilateral is a polygon of four sides.

Some examples of a polygon are:

Pentagon —A polygon having five sides.

Hexagon— A polygon having six sides.

Heptagon—A polygon having seven sides.

Octagon—A polygon having eight sides.

Nonagon—A polygon having nine sides.

Decagon—A polygon having ten sides.

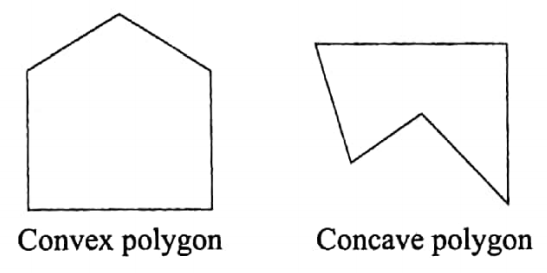
Convex polygon

A polygon without any reflex angle is called a convex polygon. In other words, it can be said that each interior angle of a convex polygon is less than two right angles. In general, by the term polygon, we mean convex polygon.

Regular polygon

If all the sides of a polygon are equal in length and the measures of all the angles are equal then the polygon is called a regular polygon. In most of cases, it is found that if the lengths of the sides of a polygon are equal then its angles are also of equal measure. For example, in an equilateral triangle, each of the three angles is 60°.

In a square, each angle is equal to 90°. In a regular pentagon, each angle is equal to 108°. In a regular hexagon, each angle is equal to 120°. But there is an exception also. All four sides of a rhombus are equal in length but its four angles are not equal to each other. So rhombus cannot be said a regular polygon.

Diagonals of a polygon

The line segments obtained by joining with a vertex of any polygon all vertices other than those which he just on both sides of it, are called the diagonals of that polygon.

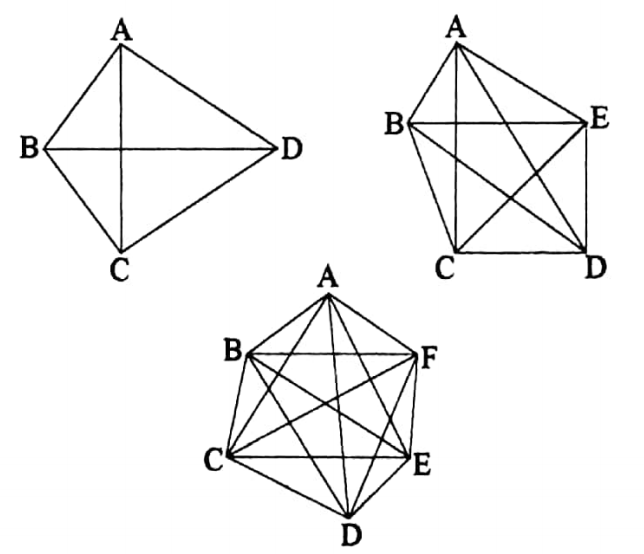
The number of diagonals of a polygon of n sides is equal to \(\frac{n(n-1)}{2}-n\)

Number of sides of a quadrilateral = 4

∴ The number of its diagonals

= \(\frac{4(4-1)}{2}-4\)

= 6-2

= 2

Number of sides of a pentagon = 5

∴ The number of its diagonals

= \(\frac{5(5-1)}{2}-5\)

= 10 – 5

= 5

Number of sides of a hexagon = 6

∴ The number of its diagonals

= \(\frac{6(6-1)}{2}-6\)

= 15-6

= 9

The Two diagonals of the quadrilateral ABCD are AC and BD.

The five diagonals of the pentagon ABCDE are AC, AD, BE, BD, and CE.

Nine diagonals of the hexagon ABCDEF are AC, AD, AE, BF, BE, BD, CF, CE, and DF.

Some information about the interior and the exterior angles of polygons

In any polygon, the number of angles is equal to the number of sides. For example, a polygon with 10 sides will have 10 angles.

By the angle of a polygon, we mean its interior angle. For example, the interior angles of the polygon ABCDEF are ∠ABC, ∠BCD, ∠CDE, ∠DEF, ∠EFA, and  ∠FAB. The adjacent supplementary angle of any interior angle is called the exterior angle of the polygon. The angles indicated in the figure are the exterior angles of the polygon ABCDEF.

The interior angles and the exterior angles obey the following relations :

1. The sum of the interior angles of a polygon of n sides is (2n-4) right angles or (2n-4) x 90°.

2. The measure of each angle of a regular polygon is the \(\frac{(2n – 4)}{n}\) right angle or, \(\frac{(2n – 4)}{n} . 90º\)

3. In any polygon the sum of one interior and one exterior angle is 180° or 2 right angles.

4. If the sides of a polygon are extended in the same order the sum of the exterior angles produced is equal to four right angles.

5. The measure of each exterior angle of a regular polygon of n sides is 4/n right angles.

Theorem 8

The sum of the interior angles of a polygon of n sides is equal to 2(n -2) right angles.

Let ABCDEF…. be a polygon of n sides. It is required to prove that, the sum of the interior angles of this polygon = 2 (n – 2) right angles.

Construction: Take any point O inside the polygon. Join the angular points A, B, C, D, E, F…. of the polygon with O.

Thus, n triangles are formed.

Proof: Since the sum of the angles of each triangle = 2 right angles therefore the sum of the angles of n triangles =

2n right angles.

Now, the sum of the angles of these n triangles = sum of the interior angles of the polygon + the sum of the angles at point O.

But the sum of the angles at the point O = 4 right angles.

∴  The sum of the interior angles of the polygon + 4 right angles = 2n right angles.

.’. sum of the interior angles of the polygon = (2n – 4) right angles = 2 (n – 2) right angles.

Verification of Theorem-8 :

Since the sum of the interior angles of a polygon depends upon its number of sides, Theorem-8 cannot be verified directly.

However, it may be verified part by part.

Some of the interior angles of a quadrilateral

= 2 (4 – 2) right angles

= 4 right angles

Some of the interior angles of a pentagon

= 2 (5 – 2) right angles

= 6 right angles

Some of the interior angles of a hexagon

= 2 (6 – 2) right angles

= 8 right angles

Thus, if you draw any quadrilateral and measure its interior angles with a protractor then you will find that the sum of the interior angles

= 4 right angles

= 360°.

Similarly, drawing any pentagon you will find that the sum of the interior angles

= 6 right angles

= 540°.

Also, drawing any hexagon you will find that the sum of the interior angles

= 8 right angles

= 720°.

Some Examples

Example 1

If the sides of a polygon are extended in the same order the sum of the exterior angles produced is equal to four right angles.

Solution :

Let, ABCDEF…. be a polygon of side n, whose sides are extended in the same order.

It is required to prove that, the sum of the exterior angles = 4 right angles.

Proof: Since, at each angular point, the sum of an interior angle and exterior angle

= 2 right angles, therefore, the sum of n interior angles + sum of n exterior angles

= 2n right angles.

or, (2n – 4) right angles + sum of n exterior angles

= 2n right angles

or, the sum of n exterior angles

= (2n – 2n + 4) right angles

= 4 right angles.

Example 2

Find the number of sides of the polygon whose sum of the interior angles is 1440°.

Solution :

Let, the number of sides of the polygon is n.

Therefore, (2n – 4) x 90 = 1440

or, 2n – 4 = 1440/90

= 16

or, 2n = 16 + 4

or, 2n = 20

or, n = 20/2

= 10

∴ The number of sides of the polygon is 10.

Example 3

Can 110° be an angle of a regular polygon?

Solution :

Let, if possible each angle of a regular polygon of n sides be 110°.

Therefore, \(\frac{(2n – 4)}{n}\) x 90 = 110

or, 9 (2n – 4) = 11 n

or, 18n – 36 = 11 n

or, 18n – 11 n = 36

or, 7n = 36

or, n = 36/7

= 5 1/7

But, since the number of sides of a polygon cannot be a fraction so 110° cannot be an angle of a regular polygon.

Example 4

Each interior angle of a regular polygon is 144°. Find the number of sides of the polygon.

Solution :

Given:

Each interior angle of the regular polygon = 144°

∴ Each exterior angle

= 180° – 144°

= 36° Number of exterior angles = 360/36

= 10

∴ Number of sides = 10

Example 5

The four angles of a pentagon are 40°, 80°, 120° and 160°. What is the measure of the fifth angle?

Solution :

Given:

The four angles of a pentagon are 40°, 80°, 120° and 160°.

The sum of the angles of a pentagon

= (2 x 5-4) right angles

= 6 right angles

= 6 x 90°

= 540°

Now, the sum of the four angles

= (40° + 80° + 120° + 160°)

= 400°

∴ The measure of the fifth angle

= (540° – 400°)

= 140°

Example 6

Each interior angle of a regular polygon is three times its exterior angle. Find the number of sides of the regular polygon.

Solution:

Given:

Each interior angle of a regular polygon is three times its exterior angle.

Let, each exterior angle = x°

∴ Each interior angle = 3x°

∴ x° + 3x° = 180°

or, 4x° = 180°

or, x° = 180° / 4

= 45°

∴ Each exterior angle = 45°

∴ Number of exterior angles = 360 / 45

= 8

∴ Number of sides = 8

Example 7

Each of the five angles of a polygon is equal to 172° and the other angles are 160° each. Find the number of sides of the polygon.

Solution:

Given:

Each of the five angles of a polygon is equal to 172° and the other angles are 160° each.

Since each of the five angles is equal to 172°,

therefore, the corresponding exterior angles are each equal to (180° – 172°) = 8°

∴ sum of those five exterior angles = 5 x 8° = 40°

∴ The sum of the other exterior angles

= 360° – 40°

= 320°

Now, some of the angles of the polygon are each equal to 160°.

Hence, the corresponding exterior angles are each equal to 180° – 160° = 20°

∴ Number of such exterior angles = 320/20

= 16

∴ Total number of sides of the polygon

= (5 + 16)

= 21

Example 8

Find the number of diagonals of a polygon of 12 sides.

Solution:

The number of diagonals of a polygon of 12 sides

= \(\frac{12(12-1)}{2}-12\)

= \(\frac{(12 . 11)}{2}-12\)

= 66 – 12

= 54.

Theorem 9

If two sides of a triangle are equal, the angles opposite to them are also equal.

Let ABC be a triangle in which AC = AB.

It is required to prove that, ∠ABC = ∠ACB

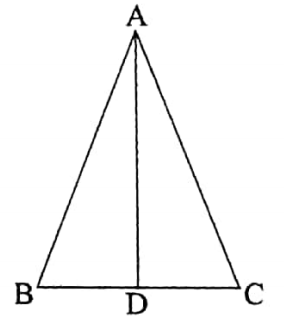
Construction: The bisector \(\overline{A D}\) of ∠BAC is drawn which intersects \(\overline{B C}\) at point D.

Proof: In the triangles ΔARD and ΔACD,

\(\overline{A B}\) = \(\overline{A C}\), \(\overline{A D}\) is common and included ∠BAD = included ∠CAD

ΔABD ≅ ΔACD

Hence,∠ABD =∠ACD

i.e., ∠ABC = ∠ACB

Verification of Theorem – 9 :

Construct a triangle ΔABC in which \(\overline{A C}\) and \(\overline{A B}\) are of equal length.

Measure the angles ∠ABC and ∠ACB, with a protractor.

You will find that they are of equal measure.

Theorem 10

If two angles of a triangle are equal, the sides opposite to these angles are also equal.

Let ABC be a triangle in which ∠ACB = ∠ABC.

It is required to prove that AB = AC. A

Construction: The bisector \(\overline{A D}\) of ∠BAC is drawn which intersects \(\overline{B C}\) at point D.

Proof: In the triangles ΔABD and ΔACD, ∠ABD = ∠ACD, ∠BAD = ∠CAD, and \(\overline{A D}\) are common.

∴ ΔABD = ΔACD

∴ \(\overline{A B}\) = \(\overline{A C}\).

Verification of Theorem-10 :

Construct a triangleΔABC in which ∠ACB = ∠ABC.

Measure the lengths of the sides \(\overline{A B}\) and \(\overline{A C}\) with a ruler.

You will find that, their lengths are the same.

Example 1

The side \(\overline{A C}\) of the triangle ABC has produced upto the point D so that \(\overline{C D}\) =\(\overline{C B}\). If the value of ∠ACB is 70° then what is the value of ∠ADB?

Solution:

Given

The side \(\overline{A C}\) of the triangle ABC has produced upto the point D so that \(\overline{C D}\) =\(\overline{C B}\).

Since ∠ACB is the exterior angle of the A BCD

∴ ∠ACB = ∠CDB + ∠CBD

Again since, CD = CB

∴ ∠CDB = ∠CBD

∴ ∠ACB = ∠CDB + ∠CBD

=2∠CDB

or, ∠CDB = 1/2 ∠ACB

= 1/2 x 70º

= 35º

∴ ∠ADB = 35º

Example 2

Side \(\overline{A B}\) of the rhombus ΔBCD is 4 cm in length and ∠BCD = 60°; what is the length of \(\overline{B D}\)?

Solution :

Given: 

Side \(\overline{A B}\) of the rhombus ΔBCD is 4 cm in length and ∠BCD = 60°

∠BCD = 60°

Also since ABCD is a rhombus

BC = CD

∠CBD = ∠CDB

But ∠CBD + ∠CDB = 180° – 60°

= 120° [ ∠BCD = 60°]

Hence, ∠CBD = ∠CDB = 60°

∴ ABCD is an equilateral triangle

∴ BD = CD = AB

= 4 cm.      [since the sides of a rhombus are equal.]

Example 3

PQR is an isosceles triangle in which \(\overline{P Q}\) = \(\overline{P R}\). The sides PQ and pp are produced to the points S and T respectively. Prove that, ∠RQS = ∠QRT and they are obtuse angles.

Solution :

Given:

PQR is an isosceles triangle in which \(\overline{P Q}\) = \(\overline{P R}\). The sides PQ and pp are produced to the points S and T respectively.

It is given that ΔPQR is an isosceles triangle in which

PQ = PR. PQ and

PR is produced to the points S and T respectively.

It is required to prove that:

1. ∠RQS – ∠QRT and

2. ∠RQS and ∠QRT are obtuse angles.

Proof :

1. In the ΔPQR,

since PQ = PR ∠PQR = ∠PRQ

Now,∠RQS = 180° – ∠PQR

= 180° – ∠PRQ = ∠QRT Hence, ∠RQS = ∠QRT.

2. PQR being a triangle, the sum of its three angles = 2 right angles.

So, ∠PQR + ∠PRQ is less than 2 right

angles. Also, as \(\overline{P Q}\) = \(\overline{P R}\).

∠PQR = ∠PRQ.

Hence, each of ∠PQR and ∠PRQ is less than 1 right angle.

Hence, their supplementary angles are greater than 1 right angle.

∴ ∠RQS and ∠QRT are obtuse angles.

Example 4

Each side of an equilateral triangle PQR is 8 cm. The midpoints of \(\overline{P Q}\) and \(\overline{P R}\) are S and T respectively. What is the length of \(\overline{S T}\)?

Solution :

Given:

Each side of an equilateral triangle PQR is 8 cm. The midpoints of \(\overline{P Q}\) and \(\overline{P R}\) are S and T respectively.

ΔPQR is an equilateral triangle in which the midpoints of \(\overline{P Q}\) and \(\overline{P R}\) are S and T respectively.

∴ \(\overline{P S}\) = 1/2 \(\overline{P Q}\)

= 1/2 \(\overline{P R}\) = \(\overline{P T}\)

∠PST = ∠PTS.

also since ΔPQR is equilateral

∴ ∠SPT = 60°

∴ ∠PST + ∠PTS = 180º – 60º

= 120º

∴ ∠PST = ∠PTS = 60º

∴ APST is equilateral.

\(\overline{S T}\) = \(\overline{P S}\)

= 1/2 \(\overline{P Q}\)

= 1/2 x 8 cm

= 4cm.

Example 5

ΔPQR is an isosceles triangle in which \(\overline{P Q}\) =\(\overline{P R}\). \(\overline{Q S}\) and rt are drawn perpendiculars from Q and R on \(\overline{P R}\) and \(\overline{P Q}\) respectively. If \(\overline{Q S}\) and RT intersect at O then prove that ΔOQR is isosceles.

Solution :

Given:

ΔPQR is an isosceles triangle in which \(\overline{P Q}\) = \(\overline{P R}\). \(\overline{Q S}\) is drawn perpendicular to \(\overline{P R}\) and

\(\overline{R T}\) is drawn perpendicular to \(\overline{P Q}\)

\(\overline{Q S}\) and \(\overline{R T}\) intersect at O.

It is required to prove that, ΔOQR is isosceles.

Proof: Since, ∠QSR = 90°

∴ ∠SRQ + ∠SQR = 90° ……. (1)

Also since, ∠RTQ = 90°

∴ ∠TQR + ∠TRQ =90° …….. (2)

From (1) and (2) we get,

∠SRQ + SQR = ∠TQR + ∠TRQ (3)

Also since, \(\overline{P Q}\) = \(\overline{P R}\)

:.∠PRQ =∠PQR

i.e., ∠SRQ =∠TQR.

Hence, from (3) ∠SQR = ∠TRQ,

i.e., ∠OQR = ∠ORQ

Hence, \(\overline{O R}\) = \(\overline{O Q}\)

ΔOQR is isosceles.

Example 6

O is a point inside the triangle ABC, such that OA=OB=OC. Prove that ∠BOC = 2 ∠B AC.

Solution :

Given:

O is a point inside the triangle ABC, such that OA=OB=OC.

ABC is a triangle.

O is a point inside the triangle ABC such that \(\overline{O A}\) = \(\overline{O B}\) = \(\overline{O C}\).

It is required to prove that, ∠BOC = 2 ∠BAC.

Proof: InΔAOB, OA = OB

:. ∠OAB = ∠OBA

∠AOB = 180° – (∠OAB + ∠OBA)

= 180° – 2∠OAB ….(1)

Also inΔAOC, OA = OC

∠OAC = ∠OCA

∠AOC = 180° – (∠OAC + ∠OCA)

= 180° – 2∠OAC ….(2)

Adding (1) and (2) we get,

∠AOB + ∠AOC = 360° – 2(∠OAB + ∠OAC)

or, 360° – ∠BOC = 360° – 2∠BAC

or, ∠BOC = 2∠BAC.

Example 7

Prove that the medians of an equilateral triangle are all equal.

Solution :

Let ABC be an equilateral triangle.

Let \(\overline{A D}\), \(\overline{B E}\), and \(\overline{C F}\) be its three medians.

It is required to prove that: \(\overline{A D}\) = \(\overline{B E}\) = \(\overline{C F}\).

Proof: Since ΔABC is equilateral, therefore,

\(\overline{A B}\) = \(\overline{A C}\)

∴ 1/2 \(\overline{A B}\) = 1/2 \(\overline{A C}\)

∴ \(\overline{B F}\) = \(\overline{C E}\)

Now in the triangles, ΔFBC and ΔEBC

\(\overline{B F}\) = \(\overline{C E}\), \(\overline{B C}\) is common to both included ∠FBC = included ∠ECB

ΔFBC ≅ ΔEBC

\(\overline{B E}\) = \(\overline{C F}\)     .……..  (1)

also, \(\overline{B C}\) = \(\overline{A B}\)

1/2 \(\overline{B C}\) = 1/2 \(\overline{A B}\)

\(\overline{C D}\) = \(\overline{A F}\)

Now in the triangles ΔADC and ΔAFC CD = AF, AC is common to both included ∠ACD = included ∠FAC

ΔADC ≅ ΔAFC

∴ \(\overline{A D}\) = \(\overline{A B}\)    …….. (2)

From (1) and (2),

\(\overline{A D}\) = \(\overline{B E}\)= \(\overline{C F}\).

Example 8

A straight line is drawn through the vertex and parallel to the base of an isosceles triangle. Prove that, it will be the external bisector of the vertical angle.

Solution :

Given:

A straight line is drawn through the vertex and parallel to the base of an isosceles triangle.

Let ΔPQR be an isosceles triangle in which

\(\overline{P Q}\) = \(\overline{P Q}\).

\(\overrightarrow{P T}\) is drawn parallel to the base QR of ΔPQR. \(\overline{P Q}\) is produced to S.

It is required to prove that, \(\overrightarrow{P T}\) is the external bisector of ∠QPR

i.e., ∠SPT = ∠TPR.

Proof: Since, \(\overrightarrow{P T}\) || \(\overrightarrow{Q R}\) and \(\overline{P R}\) is the transversal

∴ ∠TPR = alternate ∠PRQ

also, \(\overrightarrow{P T}\) || \(\overline{Q R}\) and \(\overline{S Q}\) are the transversal

∴ ∠SPT = corresponding∠PQR

Again, since \(\overline{P Q}\) = \(\overline{P R}\)

∠PQR = ∠PRQ

Hence, ∠SPT = ∠TPR.

Example 9

The Bisector of ∠BAC of ΔABC and the straight line through the midpoint D of the side AC and parallel to the side AB meet at a point E, outside BC. Prove that, ∠AEC = 1 right angle.

Solution :

Given:

The Bisector of ∠BAC of ΔABC and the straight line through the midpoint D of the side AC and parallel to the side AB meet at point E, outside BC.

EC is joined.

It is required to prove that, ∠AEC = 1 right angle.

Proof: ∠BAE = ∠EAC.

Again, ∠DEA = ∠BAE = ∠EAD

[  AB || DE, AE is the transversal

∠DEA = alternate ∠BAE ]

AD = DE. But AD – DC DE = DC

:. ∠DEC = ∠DCE,

Now, ∠AED + ∠DEC = ∠DAE + ∠DC

or, ∠AEC = ∠CAE + ∠ACE

or, ∠AEC + ∠AEC = ∠AEC + ∠CAE + ∠ACE

or, 2 ∠AEC = 180°

or, ∠AEC = 90° = 1 right angle. (Proved)

Theorem 11

If one side and the two angles at the extremities of a triangle be equal to one side and the two angles at the extremities of another triangle then the two triangles are congruent.

Let ΔABC and ADEF be the two. triangles in which \(\overline{B C}\) = \(\overline{E F}\),

∠ABC – ∠DEF and ∠ACB = ∠DFE.

It is required to prove that,ΔABC = ΔDEF.

Proof: Keeping the sides BC and EF of the triangles ABC and DEF on the same horizontal line with the vertices A and D upwards and giving ΔABC a translation of measure AD we find that the points A, B,  and C respectively coincide with the points D, E, and F and the sides AB, BC, and CA respectively coincide with the sides DE, EF, and FD.

Hence, ΔABC = ΔDEF.

Theorem 12

If the hypotenuse and the side of one right-angled triangle be equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles will be congruent.

Let ∠ACB and ∠DFE of the right-angled triangles ΔABC andΔDEF be right angles.

Let hypotenuse \(\overline{A B}\) = hypotenuse \(\overline{D E}\) and side \(\overline{A C}\) = side \(\overline{D F}\).

It is required to prove that, ΔABC ≅ ΔDEF.

Proof: Place ΔABC on ΔDEF in such a way that, point A coincides with point D, side \(\overline{A C}\)coincides with side \(\overline{D F}\) and point B falls on G which is on that side of \(\overline{D F}\) opposite to E.

Here point C will coincide with F because \(\overline{A C}\) = \(\overline{D F}\)

Thus, ΔDGF is the new position of ΔABC.

Since both ∠DFE and ∠DFG are right angles therefore EFG is a straight line and DEG is a triangle.

Now, \(\overline{D E}\) = \(\overline{A B}\) = \(\overline{D G}\)

∠DEF= ∠DGF = ∠ABC.

Now, in the triangles, ΔABC and ΔDEF,

∠ACB = ∠DFE, ∠ABC = ∠DEF and AC = DF

Hence, ΔABC ≅ ΔDEF.

Alternative proof: 

Keeping the sides BC and EF of the triangles ABC and DEF on the same horizontal line with the vertices A and D upwards and giving ΔABC a translation of measure AD we find that the points A, B, and C respectively coincide with the points D, E, and F and the sides AB, BC, and CA respectively coincide with the sides DE, EF and FD.

Hence, ΔABC ≅ΔDEF.

Some Examples

Example 1

ABCD is a quadrilateral in which \(\overline{A B}\) = \(\overline{A D}\) and \(\overline{B C}\)= \(\overline{D C}\). Prove that, the diagonal \(\overline{A C}\) of the quadrilateral ΔBCD bisects the other diagonal \(\overline{B D}\) at right angles.

Solution :

Given:

ABCD is quadrilateral in which \(\overline{A B}\) = \(\overline{A D}\)

and \(\overline{B C}\) = \(\overline{D C}\). Let the diagonals AC and

\(\overline{B D}\) of the quadrilateral ABCD intersects each other at point O.

It is required to prove that AC bisects

\(\overline{B D}\) at right angles.

\(\overline{A B}\) = \(\overline{A D}\) , \(\overline{B C}\) = \(\overline{D C}\) and \(\overline{A C}\) is common to both

ΔABC = ΔADC

Hence, ∠BAC  ≅  ∠DAC

i.e., ∠BAO = ∠DAO.

Also in the triangles ABO and ADO,

\(\overline{A B}\) = \(\overline{A D}\), \(\overline{A O}\) is common and included ∠BAO = included ∠DAO.

Hence, AΔBOA = ΔDOA.

So, \(\overline{B O}\) = \(\overline{O D}\) and ∠AOB = ∠AOD.

But ∠AOB and ∠AOD are the adjacent angles on the same straight line BD and therefore each of them is equal to 1 right angle.

\(\overline{B D}\) ⊥ \(\overline{A C}\)

Hence, \(\overline{A C}\), bisects \(\overline{B D}\) at right angles.

Example 2

Prove that the line segment joining the vertical angle of an isosceles triangle with the midpoint of the base bisects the vertical angle and is perpendicular to the base.

Solution :

Let ABC be an isosceles triangle in which \(\overline{A B}\) = \(\overline{A C}\).

Let D be the mid point of the side \(\overline{B C}\) of ΔABC.

Let us join \(\overline{A D}\).

It is required to prove that, \(\overline{A D}\) bisects ∠BAC and \(\overline{A D}\) ⊥ \(\overline{B C}\)

Proof: In the triangles ABD and ACD

\(\overline{A B}\) = \(\overline{A C}\), AD is common, and \(\overline{B D}\)= \(\overline{D C}\)

Hence, ΔABD = ΔACD

∴ ∠BAD = ∠CAD

which means that AD bisects ∠BAC and also, ∠ADB = ∠ADC,

but ∠ADB and ∠ADC are adjacent angles on the same

straight line \(\overline{B C}\) and therefore each of them is equal to 1 right angle.

It proves that AD ⊥ BC.

Example 3

Points A, B, and C are taken on a circle in such a way that \(\overline{A B}\) = \(\overline{B C}\). If 0 is the center of the circle then prove that OB is the bisector of ∠AOC.

Solution :

A, B, and C are three points on a circle having its center at O such that \(\overline{A B}\) = \(\overline{B C}\).

OB is joined.

It is required to prove that, OB is the bisector of ∠AOC.

Proof: In the triangles AOB and BOC,

AB = BC, AO = OC (both being equal to the radius of the circle), and \(\overline{O B}\) is common.

Hence, ΔAOB = ΔBOC

:. ∠AOB = ∠COB.

Hence, \(\overline{O B}\) is the bisector of ∠AOC.

Example 4

Prove that, the diagonals of a rhombus bisect each other at right angles.

Solution :

Let ABCD be a rhombus in which the two diagonals \(\overline{A C}\) and \(\overline{B D}\) intersect each other at O.

It is required to prove that, \(\overline{A C}\) and \(\overline{B D}\) bisect each other at right angles.

Proof: In the triangles ADC and ABC,

AD = AB, DC = BC, and AC is a common ΔADC ≅ ΔABC

∠DAC = ∠BAC.

Also in the triangles ADO and ABO AD = AB, AO is common and included ∠DAO = included ∠BAO

:. ΔAOD = ΔAOB

:. OD = OB and ∠AOD = ∠AOB.

But ∠AOD and ∠AOB are two adjacent angles on the same straight line DB and hence each of them is equal to 1 right angle.

∴ AO ⊥ BD.

Hence, it is proved that \(\overline{B D}\) is bisected at right angles by \(\overline{A C}\) Similarly, it can be shown that \(\overline{A C}\) is bisected at right angles by \(\overline{B D}\)

Example 5

Prove that, the perpendicular drawn from the vertex of an isosceles triangle to the base bisects the base and the vertical angle.

Solution:

Let ABC be an isosceles triangle in which AB = \(\overline{A C}\).

Let \(\overline{A D}\) be drawn perpendicular to \(\overline{B C}\)

It is required to prove that,

∠BAD = ∠CAD and \(\overline{B D}\) = \(\overline{C D}\).

Proof: In the right-angled triangles,

ABD and ACD, hypotenuse \(\overline{A B}\) =  hypotenuse \(\overline{A C}\)

AD is common in both ΔABD = ΔACD

∠BAD = ∠CAD and \(\overline{B D}\) = \(\overline{C D}\).

Example 6

PQR is a triangle. \(\overline{Q S}\) and \(\overline{R T}\) are drawn perpendiculars from Q and R on PR and PQ respectively. If \(\overline{Q S}\) = \(\overline{R T}\) then prove that, \(\overline{P Q}\) = \(\overline{P R}\).

Solution:

Given:

PQR is a triangle \(\overline{Q S}\) and \(\overline{R T}\) are drawn

perpendiculars from Q and R on PR and

\(\overline{P Q}\)respectively.

Also \(\overline{Q S}\) = \(\overline{R T}\)

It is required to prove that,

\(\overline{P Q}\) = \(\overline{P R}\).

Proof: In the right-angled triangles QSR and QTR,

\(\overline{Q S}\) = \(\overline{R T}\), \(\overline{Q R}\) is the common hypotenuse

∴ Δ QSR = Δ QTR

:. ∠SRQ = ∠TQR

i.e., ∠PRQ = ∠PQR

Hence, PQ = PR.

Example 7

O is a point within ∠PQR. Two perpendiculars \(\overline{Q S}\) and \(\overline{O T}\) are drawn on \(\overline{P Q}\) and \(\overline{Q R}\)– respectively. If \(\overline{O S}\) = \(\overline{O T}\) then proves that, ∠OQS = ∠OQT.

Solution :

Given:

O is a point in the angular region of ∠PQR.

From O, two perpendiculars \(\overline{O S}\) and \(\overline{O T}\) are drawn on \(\overline{P Q}\) and \(\overline{Q R}\) Respectively.

It is given that \(\overline{O S}\) = \(\overline{O T}\). \(\overline{Q O}\) is joined.

It is required to prove that, ∠OQS – ∠OQT.

Proof: According to the given conditions both ΔQOS and ΔQOT are right-angled triangles.

Now in the right-angled triangles, ΔQOS and ΔQOT

\(\overline{O S}\) = \(\overline{O T}\). \(\overline{Q O}\) is the common hypotenuse ΔQOS = ΔQOT

∠OQS = ∠OQT.

Example 8

Prove that, in a right-angled triangle the line segment joining the right angular point to the midpoint of the hypotenuse is half of the hypotenuse.

Solution :

Let ΔABC be a right-angled triangle of which ∠ABC = 1 right angle.

Let O be the midpoint of the hypotenuse \(\overline{A C}\).

It is required to prove that, \(\overline{B O}\) = 1/2\(\overline{A C}\)

Construction: \(\overline{B O}\) is joined and extended upto the point D in such a way that

\(\overline{B O}\) = \(\overline{O D}\). \(\overline{C D}\) is joined.

Proof: In the triangles AOB and COD,

\(\overline{A O}\) = \(\overline{O C}\), \(\overline{B O}\)= \(\overline{O D}\), and ∠AOB = vertically opposite ∠COD.

ΔAOB ≅ ΔCOD

AB = CD and ∠ABO = ∠CDO but they are alternate angles AB || DC.

Also since AB X BC CD T BC

∠DCB = 1 right angle and hence ABCD is a right-angled triangle.

Now, in the right-angled triangles, ΔABC and ΔDBC

\(\overline{A B}\) = \(\overline{C D}\), \(\overline{B C}\) is common to both included ∠ABC = included ∠DCB (both equal to 90°)

∴ ΔABC ≅ ΔDCB

\(\overline{A C}\) = \(\overline{B D}\) = 2\(\overline{B O}\)

:. \(\overline{B O}\) = 1/2 \(\overline{A C}\).

Theorem 13

If two sides of a triangle are unequal, the angle opposite to the greater side is greater than the angle opposite to the less.

Let ΔABC be a triangle in which \(\overline{A B}\) > \(\overline{A C}\).

It is required to prove that: ∠ACB > ∠ABC.

Construction: From \(\overline{A B}\), the segment \(\overline{A D}\) equal to\(\overline{A C}\) is cut off.

Let us join \(\overline{C D}\).

Proof: In the ΔACD,

since AC = AD, therefore, ∠ADC = ∠ACD.

Now, in ΔBCD,

∠ADC is the exterior angle and ∠DBC is the interior opposite angle.

:. ∠ADC > ∠DBC

i.e., ∠ADC > ∠ABC

Or, ∠ACD > ∠ABC [ ∠ADC = ∠ACD] H

ence, ∠ACB > ∠ABC        [∴ ∠ACB > ∠ACD].

Verification of Theorem-13 :

On your paper draw any triangle ABC in such a way that the side \(\overline{A B}\) > side \(\overline{A C}\)

Then measure the angles ∠ACB and ∠ABC with a protractor.

You will find that ∠ACB > ∠ABC.

Theorem 14

If two angles of a triangle are unequal, the side opposite to the greater angle is greater than the side opposite to the less.

Let ΔABC be a triangle in which ∠ACB > ∠ABC.

It is required to prove that, \(\overline{A B}\) > \(\overline{A C}\)

 

Proof: If \(\overline{A B}\) = \(\overline{A C}\) then ∠ACB = ∠ABC. But it is not true according to the hypothesis.

If \(\overline{A B}\) < \(\overline{A C}\) then ∠ACB < ∠ABC. But it is also not true according to the hypothesis.

So, AB is neither equal to nor less than \(\overline{A C}\).

Hence, the only possibility is that \(\overline{A B}\) > \(\overline{A C}\)

Verification of Theorem-14 :

On your paper draw any triangle ABC in such a way that ∠ACB >∠ABC.

Then measure the sides \(\overline{A B}\) and \(\overline{A C}\) with a ruler.

You will find that \(\overline{A B}\) > \(\overline{A C}\).

Theorem 16

Any two sides of a triangle are together greater than the third side.

Let ABC be a triangle

It is required to prove that, any two sides of ΔABC are together greater than the third side.

Let \(\overline{B C}\) be the greatest side of the ΔABC.

So it will be sufficient to prove that, \(\overline{A B}\) + \(\overline{A C}\) > \(\overline{B C}\).

Construction: The side \(\overline{B A}\) of the ΔABC is produced to D in such a way that \(\overline{A D}\) = \(\overline{A C}\) Let us join \(\overline{C D}\).

Proof: In ΔACD, since \(\overline{A D}\) = \(\overline{A C}\) according to construction, therefore, ∠ACD = ∠ADC.

Now, ∠BCD = ∠BCA + ∠ACD > ∠ADC,

i.e., ∠BCD > ∠BDC

Hence, in the ABCD since ∠BCD > ∠BDC therefore,

\(\overline{B D}\) > \(\overline{B C}\)-.

or,\(\overline{A B}\) + \(\overline{A D}\) >\(\overline{B C}\)

or, \(\overline{A B}\) + \(\overline{A C}\)– > \(\overline{B C}\)– [ AD = AC]

Verification of Theorem – 15:

in such a way that \(\overline{B C}\) is the greatest side.

Then measure the lengths of sides \(\overline{A B}\), \(\overline{A C}\), and \(\overline{B C}\)

You will find that \(\overline{A B}\) + \(\overline{A C}\) > \(\overline{B C}\)

Theorem 16

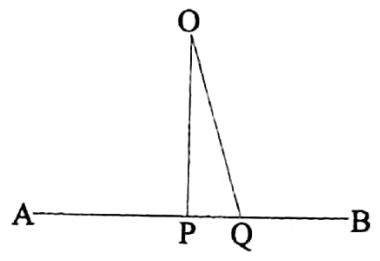
Of all line segments that can be drawn to a given straight line from a given point outside it, the perpendicular is the shortest.

Let \(\overline{A B}\) be any straight line, and O be a point outside it. From O, a line

segment \(\overline{P Q}\) is drawn which is O

perpendicular to \(\overline{A B}\) It is required to prove that, of all other line segments that can be drawn

from point O to the straight line \(\overline{A B}\), \(\overline{O P}\) is the shortest.

Construction: Let us take any point Q on the straight line \(\overline{A B}\) Let us join \(\overline{O Q}\).

Proof: In the ΔOPQ, ∠OPQ is a right angle and ∠OQP is an acute angle.

.’. ∠OQP < ∠OPQ and hence \(\overline{O P}\) < \(\overline{O Q}\).

Since this conclusion is true for any position of Q on  \(\overline{A B}\), therefore the length of \(\overline{O P}\) is the shortest.

Verification of Theorem-16 :

Take any straight line \(\overline{A B}\). From a

point O outside \(\overline{A B}\) draw a

perpendicular \(\overline{O P}\) and any other line

segment \(\overline{O Q}\). You will find that \(\overline{O P}\) < \(\overline{O Q}\)

Since it is true for any position of Q on \(\overline{A B}\), therefore the theorem is verified.

Some Examples

Example 1

Prove that, the sum of any three sides of a quadrilateral is greater than the fourth side.

Solution :

Let ABCD be a quadrilateral.

It is required to prove that, the sum of any three sides of ABCD is greater than the fourth side.

If \(\overline{D C}\) is the greatest side then it is sufficient to prove that, \(\overline{A D}\) + \(\overline{A B}\)+ \(\overline{B C}\) > 

\(\overline{D C}\)

Construction: Let us join BD.

Proof: In the ADAB

\(\overline{A D}\) + \(\overline{A B}\) >\(\overline{D B}\)  ……(1)

Also in the ADBC

\(\overline{D B}\) +\(\overline{B C}\) > \(\overline{D C}\) …..(2)

From (1) and (2)

\(\overline{A D}\) + A\(\overline{A B}\)+\(\overline{D B}\) + \(\overline{B C}\)>\(\overline{D B}\) + \(\overline{D C}\) Subtracting equal quantity \(\overline{D B}\)

From both sides, we get, \(\overline{A D}\) + \(\overline{A B}\) +\(\overline{B C}\) > \(\overline{D C}\).

Example 2

Prove that, the hypotenuse is the greatest side of a right-angled triangle.

Solution :

Let ABC be a right-angled triangle in

which ∠ABC = 90°.

Hence, AC is the hypotenuse ofΔABC.

It is required to prove that, AC is the greatest side of ΔABC.

Proof: Since, ∠ABC – 90°

∴ ∠BAC + ∠BCA = 90°.

Hence, each of ∠BAC and ∠BCA is less than 90°.

Now, since, ∠ABC > ∠BAC

:. AC > BC   (1)

also since ∠ABC > ∠ACB

\(\overline{A C}\) > \(\overline{A B}\)   (2)

From (1) and (2) it follows that,

\(\overline{A C}\) is the greatest side of the ΔABC.

Example 3

The sides \(\overline{A B}\) and \(\overline{A D}\) of the isosceles triangle ABD are equal. The side \(\overline{ADB}\) is extended upto the point C and points B and C are joined. Prove that, ∠ABC > ∠ACB.

Solution :

Given:

The sides \(\overline{A B}\) and \(\overline{A D}\)– of the isosceles triangle ABD is equal. The side \(\overline{A D}\) is

extended up to the point C. \(\overline{B C}\) is joined.

It is required to prove that, ∠ABC > ∠ACB.

Proof: In the ABCD, since ∠ADB is the exterior angle, therefore, ∠ADB > ∠DCB.

But since AB = AD ∠ADB = ∠ABD

Hence, ∠ABD > ∠DCB

also since ∠ABC > ∠ABD = ∠ABC > ∠DCB

i.e., ∠ABC > ∠ACB.

Example 4

In the triangle PQR. the side PQ is greater than the side \(\overline{P S}\).\(\overline{P S}\) is the bisector of ∠QPR which intersects \(\overline{Q B}\) at S. Prove that \(\overline{Q S}\)>\(\overline{S R}\)

Solution:

Given:

In the ΔPQR,\(\overline{P Q}\) > \(\overline{P R}\). PS is the bisector of ∠QPR, which intersects \(\overline{Q R}\) at S.

It is required to prove that, \(\overline{Q S}\) > \(\overline{S R}\).

Construction: From\(\overline{P Q}\) let us cut off a portion \(\overline{P T}\) equal to \(\overline{P R}\).

Let us join \(\overline{S T}\).

Proof: In the triangles PTS and PRS

\(\overline{P T}\) = \(\overline{P R}\), PS is common and ∠SPT = ∠SPR

APTS ≅ APRS.

\(\overline{S T}\) = \(\overline{S R}\) and∠PST = ∠PSP

In the APQS, since ∠PSP is an exterior angle.

∠PSR > ∠PQS

i.e., ∠PST > ∠PQS

Also in the ΔPST since ∠QTS is an exterior angle

∴ ∠QTS > ∠PST

∴ ∠QTS > ∠TQS

\(\overline{Q S}\) > \(\overline{S T}\)

But \(\overline{S T}\) > \(\overline{S R}\)

∴ \(\overline{Q S}\) >\(\overline{S R}\)

Example 5

ΔABC is an equilateral triangle. D is a point on \(\overline{A C}\). Prove that, \(\overline{B C}\)>\(\overline{B D}\).

Solution:

Given:

ΔABC is an equilateral triangle. D is a point on \(\overline{A C}\).

\(\overline{B D}\) is joined.

It is required to prove that, \(\overline{B C}\) > \(\overline{B D}\).

Proof: In the ΔABD, ∠BDC is the exterior angle,

∠BDC > ∠BAC

But since \(\overline{B C}\) = \(\overline{A B}\)

∠BAC = ∠BCA ∠BDC > ∠BCA

i.e., ∠BDC > ∠BCD

Hence, \(\overline{B C}\) > \(\overline{B D}\)

Example 6

D is a point within the triangle ABC. \(\overline{B D}\) and \(\overline{C D}\) are joined. Prove that, \(\overline{A B}\) + \(\overline{A C}\) >\(\overline{B D}\) + \(\overline{C D}\)

Solution :

Given:

D is a point within the triangle ABC.  \(\overline{B D}\) and \(\overline{C D}\) are joined.

ABC is a triangle. D is a point within it.

BD and CD are joined.

It is required to prove that,

\(\overline{A B}\)+ \(\overline{A C}\) > \(\overline{B D}\) + \(\overline{C D}\)

Construction: Produce BD to intersect AC at E.

Proof: In the ΔABE.

\(\overline{A B}\) +\(\overline{A B}\) > \(\overline{B E}\)

i.e., \(\overline{A B}\)+\(\overline{A E}\) > \(\overline{B D}\)+\(\overline{D E}\)-—(1)

Also in the ΔDEC,

\(\overline{D E}\) + \(\overline{E C}\) > \(\overline{C D}\)…….. (2)

Adding (1) and (2) we get,

\(\overline{A B}\) + \(\overline{A E}\) + \(\overline{D E}\) + \(\overline{E C}\) > \(\overline{B D}\) + \(\overline{D E}\) + \(\overline{C D}\)

or, \(\overline{A B}\) + \(\overline{A E}\) + \(\overline{E C}\) > \(\overline{B D}\) + \(\overline{C D}\)

or, \(\overline{A B}\) + \(\overline{A C}\) > \(\overline{B C}\) + \(\overline{C D}\).

Example 7

D is the midpoint of the side \(\overline{B C}\) of ΔABC. Prove that,\(\overline{A B}\) + \(\overline{A C}\)> 2 \(\overline{A D}\).

Solution:

Given:

D is the midpoint of the side \(\overline{B C}\) of ΔABC.

ABC is a triangle. D is the midpoint of \(\overline{B C}\)

\(\overline{A D}\) is joined.

It is required to prove that,

\(\overline{A B}\) + \(\overline{A C}\) > 2 \(\overline{A D}\).

Construction: \(\overline{A D}\) is produced upto the point H, such that \(\overline{A D}\) = \(\overline{D H}\).

Proof: In the ABD and CDH,

\(\overline{B D}\) = \(\overline{C D}\), \(\overline{A D}\) = \(\overline{D H}\)

and include ∠ADB = include ∠HDC           (Since they are vertically opposite angles)

:. ΔABD ≅ ΔCDH

\(\overline{A B}\) = \(\overline{C H}\)

Now, in the ΔACH,

\(\overline{A C}\) + \(\overline{C H}\) > \(\overline{A H}\)

or, \(\overline{A C}\) + \(\overline{A B}\) > 2\(\overline{A D}\)

\(\overline{C H}\) = \(\overline{A B}\) and \(\overline{A H}\) = 2 \(\overline{A D}\)

AB + AC >2 \(\overline{A D}\).

Example 8

Prove that, in any triangle, the sum of the medians is less than the perimeter.

Solution:

Given:

In any triangle, the sum of the medians is less than the perimeter.

Let ABC be a triangle in which \(\overline{A D}\), \(\overline{B E}\), and \(\overline{C F}\) are three medians.

It is required to prove that,

\(\overline{A D}\) + \(\overline{B E}\) + \(\overline{C F}\) < \(\overline{A B}\) + \(\overline{B C}\) + \(\overline{C A}\)

Proof:

Since, \(\overline{A D}\), \(\overline{B E}\) and \(\overline{C F}\) are the three medians of ΔABC

therefore,

\(\overline{A B}\) + \(\overline{A C}\) > 2 \(\overline{A D}\) …..(1)

\(\overline{A B}\) + \(\overline{B C}\) > 2 \(\overline{B F}\) …..(2)

\(\overline{B F}\) + \(\overline{C A}\) > 2 \(\overline{C F}\) …..(3)

Adding (1), (2) and (3) we get,

2 (\(\overline{A B}\) + \(\overline{B C}\) + \(\overline{C A}\)) > 2(\(\overline{A D}\) + \(\overline{B E}\) + \(\overline{C F}\))

or, \(\overline{A B}\) + \(\overline{B C}\) + \(\overline{C F}\) < \(\overline{A B}\) + \(\overline{B C}\) + \(\overline{C A}\).

Example 9

D is any on the extended side BC of the equilateral triangle ABC. Prove that, ∠BAD > ∠ADB.

Solution:

Given:

D is any point on the extended side BC of the equilateral triangle ABC. AD is joined.

It is required to prove that, ∠BAD > ∠ADB.

Proof: ABC is an equilateral triangle

∴ BC = AB

BD = BC + CD

∴ BD > AB ( BC = AB)

∴ in ΔABD, BD > AB

∴ ∠BAD > ∠ADB (proved).

Geometry Chapter 1 Angles

Angle

When two line segments intersect at a point, an angle is formed. Those two line segments are called the arms of that angle and the point is called the vertex of the angle.

The line segments AB and AC have intersected at point A and the angle, ∠BAC has been formed. AB and AC are the two arms of the angle and A is the vertex.

If we assume a point D on AB and another point E on AC then ∠DAE and ∠BAC will be of the same measure.

Adjacent Angles

If two angles have the same vertex and one common arm and if the two angles are on opposite sides of the common arm then the two angles are called adjacent angles.

∠POQ and ∠QOR are adjacent angles because the vertex of both angles is

O and their common arm are OQ and the two angles are on opposite sides of this common arm.

Read And Learn More WBBSE Solutions For Class 8 Maths

Perpendicular And Right Angle

If a straight line stands on another straight line in such a way that, two adjacent angles are equal then one of the straight lines is called a perpendicular to the other. Each of the two adjacent angles is called a right angle.

The straight line OC is perpendicular to AB. Both∠AOC and∠BOC are right angles.

1 right angle = 90°.

Maths Solutions Class 8 Wbbse

Straight angle

A straight line AB is drawn on a piece of paper. If point C is taken on the straight line AB then ∠ACB will be a straight angle.

1 straight angle = 180° = 2 right angles.

Acute angle, Obtuse angle, and Reflex angle

Acute angle: An angle that is less than a right angle is an acute angle.

For example, 30°, 44°, 70°, etc., are acute angles.

Obtuse angle :

An angle that is greater than one right angle but less than two right angles is called an obtuse angle.

For example, 95°, 110°, 145°, etc., are obtuse angles.

Maths Solutions Class 8 Wbbse

Reflex angle: An angle that is greater than two right angles but less than four right angles is called a reflex angle.

For example, 190°, 210°, 300°, etc., are reflex angles.

Complementary angle and supplementary angle

Complementary angle: If the sum of the two angles is equal to 90° or one right angle then each angle is called the complementary angle of the other angle.

For example, 20° and 70° are complementary angles. In ∠AOB + ∠BOC = 90°.

So, angles ∠AOB and ∠BOC are complementary angles.

We say that each of the angles ∠AOB and ∠BOC complement the other.

Supplementary angle: If the sum of the two angles is equal to 180° or two right angles then each angle is called the supplementary angle of the other angle.

For example, 100° and 80° are supplementary angles. In the figure ∠AOB +∠BOC = 180°. So, angles ∠AOB and ∠BOC are supplementary angles. We say that each of the angles ∠AOB and ∠BOC is a supplement of the other.

External angle: If any arm of an angle is extended in the direction opposite to the arm, then the angle formed by it with the other arm is called the external angle of that angle.

Let ∠BAC be an angle.

The arm BA is produced in such a way that ∠CAD is formed. Therefore, ∠CAD is the external angle of ∠BAC.

Maths Solutions Class 8 Wbbse

Note that, ∠CAD is adjacent to ∠CAB and is supplementary to ∠CAB.

 

Internal bisector of an angle

If a straight line bisects an angle, then it is called the internal bisector of that angle.

External bisector of an angle

If a straight line bisects the external angle of a given angle, then it is called the external bisector of that angle.

In the figure, BD is the internal bisector and BE is the external bisector of ∠ABC.

It can be proved that ∠EBD = 90°.

Vertically opposite angles

If two straight lines intersect each other, two pairs of angles are formed on the opposite sides of the intersecting point. Then any angle of a pair of angles is called a vertically opposite angle of the other.

The straight lines AB and CD intersect at point 0.

∠BOD is the vertically opposite angle of AOC and ∠AOD is the vertically opposite angle of ∠BOC.

The vertically opposite angles are always of the same measure.

Maths Solutions Class 8 Wbbse

:. ∠AOC = ∠BOD and ∠BOC = ∠AOD.

Transversal, Exterior angles, Interior angles, Interior opposite angles, Alternate angles, Corresponding angles

If a straight line cuts two other straight lines, the former straight line is called the transversal of those two straight lines. In the straight line, EF cuts the two straight lines AB and CD. Therefore, the straight line EF is the transversal of the straight lines AB and CD.

When a straight line cuts two other straight lines then eight angles are

formed. Among them, four angles are in the inside region of the two straight lines. These four angles are called interior angles and the other four angles are called exterior angles.

The interior angles are ∠AGH, ∠GHC, ∠GHD, and ∠HGB. The exterior angles are ∠EGA, ∠EGB, ∠CHF, and ∠FHD.

The further-off interior angle, in respect of an exterior angle, is called the interior opposite angle. For example, ∠GHD is the interior opposite angle, in respect of ∠EGB. ,

The interior angle adjacent to one exterior angle and the interior angle adjacent to a further off interior angle in respect of the same exterior angle is called alternate angles to each other.

In the figure, ∠GHD is the alternate angle of ∠AGH, and ∠GHC is the alternate angle of ∠BGH.

An exterior angle and an interior opposite angle on the same side of the transversal are called corresponding angles.

In the figure, the pair of angles (∠EGB, ∠GHD), (∠EGA, ∠GHC), (∠AGH, ∠CHF), and (∠BGH, ∠DHF) are corresponding angles.

Interior angles on the same side of the transversal

Obviously, ∠BGH and ∠GHD and also ∠AGH and ∠GHC are the interior angles on the same side of the transversal.

Classification of triangle

Triangle: A plane figure bounded by three line segments is called a triangle.

A triangle has three sides and three angles.

Three angular points are called the vertices of the triangle.

ABC is a triangle. Its three sides are AB, BC, and AC.

Its three angles are ∠ABC, ∠BCA, and ∠CAB. Its three vertices are A, B, and C.

The sum of the three angles of a triangle is equal to 2 right angles or 180°.

In any triangle, the sum of the two sides is always greater than the third side. Again, the difference between any two sides is always less than the third side.

If any angular point of a triangle is taken as a vertex then its opposite side is called it’s base.

The angle opposite to the base of a triangle is called its vertical angle.

If BC is taken as the base then ∠BAC will be its vertical angle.

The triangles are classified on the basis of

1. sides and

2. angles.

1. On the basis of sides, there are three types of triangles: equilateral triangle, isosceles triangle, and scalene triangle.

Equilateral triangle: If the lengths of the three sides of a triangle are the same then the triangle is called an equilateral triangle.

In the figure, ΔABC is an equilateral triangle.

Maths Solutions Class 8 Wbbse

Isosceles triangle: If the lengths of the two sides of a triangle are the same then the triangle is called an isosceles triangle. In the ADEF is an isosceles triangle.

Scalene triangle: If the lengths of the three sides of a triangle are unequal then the triangle is called a scalene triangle. The APQR is a scalene triangle.

2. On the basis of angles there are three types of triangles: Acute-angled triangle, obtuse-angled triangle, and right-angled triangle.

Acute-angled triangle: If each of the three angles of a triangle is acute then the triangle is called an acuteangled triangle. In the figure below ΔABC is an acuteangled triangle.

Maths Solutions Class 8 Wbbse

Obtuse-angled triangle: If any one angle of a triangle is obtuse then the triangle is called an obtuse-angle triangle.

The ADEF is an obtuse-angle triangle.

Right-angled triangle: If any one angle of a triangle is a right angle then the triangle is called a right-angled triangle.

The APQR is a right-angle triangle

The median of a triangle

The line segment obtained by joining the middle point of any side of a triangle to the opposite vertex is called the median of the triangle.

The line segment AD has been obtained by joining the midpoint D of the side BC of the triangle ABC to the opposite vertex A.

AD is the median of the triangle ABC. There are always three medians of a triangle.

Height of a triangle

The line segment obtained by drawing the perpendicular from any vertex of a triangle to the opposite side is called the height of the triangle.

AD has been drawn perpendicular from the vertex a

A to the opposite side BC of the triangle ABC.

So AD is the height of the triangle ABC.

In this case, BC is the base of the triangle.

If AC is taken as the base of the triangle then perpendicular from B on AC will be the height of the triangle.

If AB is taken as the base of the triangle then perpendicular from C on AB will be the

Maths Solutions Class 8 Wbbse

Classification of quadrilateral

Quadrilateral: A plane figure enclosed by four line segments is called a quadrilateral.

A quadrilateral has four sides and four angles. Four angular points are called the four vertices of a quadrilateral.

The line segment joining any two opposite vertices of a quadrilateral is called the diagonal of the quadrilateral.

There are two diagonals of a quadrilateral.

ABCD is a quadrilateral. Its four sides are AB, BC, CD, and DA.

Its four angles are ∠ABC, ∠BCD, ∠CDA, and ∠DAB.

Its four angular points are A, B, C, and D.

Its two diagonals are AC and BD.

the sum of the four angles of a quadrilateral = 360º.

Parallelogram: If the opposite sides of a quadrilateral are parallel then it is called a parallelogram.

Rectangle: If one angle of a parallelogram is a right angle then it is called a rectangle.

Square: If the lengths of the two adjacent sides of a rectangle are equal then it is called a square.

Trapezium: If only one pair of opposite sides of a quadrilateral are parallel then it is called a trapezium.

Isosceles trapezium: If the lengths of the non-parallel sides (i.e., oblique sides) of a trapezium are equal then it is called an isosceles trapezium.

Rhombus: If the lengths of the four sides of a quadrilateral are equal but none of the angles is a right angle then it is called a rhombus.

Axioms

Some geometrical properties are obtained through activities. They are called axioms. These geometrical properties do not require any logical proof. Great mathematician Euclid named the axioms, ‘Common notions or conceptions of thought.’ Axioms are of two types— General and Geometric. Let us state below some axioms.

Ganit Prabha Class 8 Solution

1. General axioms :

1. The quantities which are equal to the same quantity are equal to one another.

2. If equal quantities are added with equal quantities, the sums are equal.

3. If equal quantities are subtracted from equal quantities, the remainders are equal.

4. If equal quantities are added with unequal quantities, the sums are unequal.

5. If equal quantities are subtracted from unequal quantities, the remainders are unequal.

6. The same multiples of equal quantities are equal.

7. The same fractions of equal quantities are equal.

8. Every object is greater than its part.

Ganit Prabha Class 8 Solution

2. Geometric axioms:

1. If any geometrical figure (for example, a line or angle, or triangle) coincides with another geometrical figure then they are called congruent.

2. Two straight lines cannot enclose any plane surface.

3. All right angles are of equal measure.

4. Both the two intersecting straight lines cannot be parallel to a third straight line. (It is Playfair’s axiom).

5. When a straight line cuts two other straight lines, those other two straight lines are parallel if a pair of corresponding angles are equal.

6. Only one straight line can be drawn through a given point that is parallel to a given straight line.

7. Of the two triangles, if two sides and their included angle of one, are respectively equal to the two sides and their included angle of the other, then the triangles are congruent. (It is called side-angle-side congruence or SAS congruence).

8. Of the two triangles, if the two angles and one side of one, are respectively equal to the two angles and one side of the other, then the triangles are congruent. (It is called angle-angle-side congruence or ΔAS congruence.)

Some Examples

Example 1

Find the measure of the angles of an equilateral triangle.

Solution: Each angle is equal to 60°.

Ganit Prabha Class 8 Solution

Example 2

Find the measure of the angles of a right-angled isosceles triangle.

Solution: 45°, 45° and 90°.

Example 3

If one angle of a right-angled triangle is 65° then find other angles of the triangle.

Solution :

Given:

one angle of a right-angled triangle is 65°

Since the triangle is right-angled therefore one angle is 90°, and one other angle

= 180° – (90° + 65°)

= 180° – 155°

= 25°.

∴ 90° and 25°.

Other angles of the triangle 90° and 25°.

Example 4

By what name do we call the greatest side of a right-angled triangle?

Solution: Hypotenuse.

Example 5

Find the minimum and maximum number of acute angles of a triangle.

Solution: A triangle may have at least two and almost three acute angles.

Ganit Prabha Class 8 Solution

Example 6

If one angle of a triangle is twice the sum of the other two angles then find the measure of that angle.

Solution :

Given:

one angle of a triangle is twice the sum of the other two angles.

Let, the measure of that angle – x°.

Then, the sum of the other two angles

= (180 – x)

According to the question, x°

= 2(180 – x)°

or, x = 2(180 – x)

or, x = 360 – 2x

or, x + 2x= 360

or, 3x – 360

The measure of that angle is 120°.

Ganit Prabha Class 8 Solution

Example 7

The ratio of the four angles of a quadrilateral is 5: 6: 13: 12. Find the measure of the greatest angle.

Solution :

Given:

The ratio of the four angles of a quadrilateral is 5: 6: 13: 12.

Let, the measures of the angles of that quadrilateral be 5x°, 6x°, 13x°, and 12x°.

Hence, 5x° + 6x° + 13xº + 12x° = 360°

or, 36x° = 360°

or, 36x = 360

or, x = 360 / 36

= 10

Hence, the greatest angle of the quadrilateral

= 13 x 10°

= 130°.

The greatest angle of the quadrilateral is 130°.

Ganit Prabha Class 8 Solution

Example 8

Is it possible that the three sides of a triangle are, a – b, 2a, and a + b?

Solution :

Given:

a – b, 2a, And a + b.

We know that the sum of any two sides of a triangle is greater than the third side. But, in this case, (a – b) + (a + b) = a – b + a + b = 2a.

Hence, the sum of the two sides is equal to the third.

Hence, in this case, the given three lengths cannot be the sides of a triangle.

It is not possible.

Example 9

In ΔABC, if ∠A + ∠B = 135º and ∠B + ∠C = 90° then find the nature of ΔABC

Solution:

Given:

In ΔABC, if ∠A + ∠B = 135º and ∠B + ∠C = 90°

AC = (∠A+ ∠B + ∠C) – (∠A + ∠B)

= 180°- 135°

= 45°

∠A = (∠A + ∠B + ∠C)-(∠B + ∠C)

= 180° – 90°

= 90°

∠B = (∠A +∠B + ∠C) – (∠C + ∠A)

= 180° – (45° + 90°)

= 180°- 135°

= 45°

In ΔABC,

∠A = 90°,

∠B = 45°,

∠C = 45°.

.’. ΔABC is a right-angled isosceles triangle.

ΔABC is a right-angled isosceles triangle.

Example 10

In ΔABC, ∠BAC – ∠ABC = 10° and∠ACB = 50°. Find the measure of ∠ABC.

Solution :

Given:

In ΔABC, ∠BAC – ∠ABC = 10° and∠ACB = 50°

Since, ∠ACB = 50°,

therefore, ∠BAC + ∠ABC – 180º – 50° = 130°.

Now,∠BAC + ∠ABC = 130° ———-(1)

∠BAC -∠ABC = 10° ———–(2)

By (1) – (2) we get, 2∠ABC = 120°

or, ∠ABC = 120º / 2

= 60º

The measure of ∠ABC is 60°.

Ganit Prabha Class 8 Solution

Example 11

Each of the two base angles of an isosceles triangle is twice its vertical angle. Find the measure of the vertical angle.

Solution :

Given:

Each of the two base angles of an isosceles triangle is twice its vertical angle.

Let, the vertical angle be x°.

Then, each of the two base angles is 2x°.

So, x° + 2x° + 2x° = 180°

or, 5x° = 180°

or, x = 180º / 5

= 36°.

The vertical angle is 36°.

Example 12

The vertical angle A of the isosceles triangle is three times another angle B of it. What is the measure of angle A?

Solution :

Given:

The vertical angle A of the isosceles triangle is three times another angle B of it.

Let, ∠B = x°

then∠C =x° and ∠A = 3x°

∴ 3x° + x° + x° = 180°

or, 5x° = 180°

or, x° = 180° / 5

= 36°

∴ ∠A = 3x°

= 3 x 36°

= 108°

The measure of ∠A = 108°.

Example 13

In the triangle ABC, ∠A + ∠C = 140 and ∠A + 3∠B = 180°. Find the measure of the angles of the triangle.

Solution :

Given:

In the triangle ABC, ∠A + ∠C = 140 and ∠A + 3∠B = 180°.

∠B = 180° – (∠A + ∠C)

= 180° – 140° = 40°

∴ ∠A + 3 x 40° = 180°

or,∠A + 120° = 180°

or, ∠A = 180° – 120° = 60°

∴ ∠C = 180° – (∠A + ∠B)

= 180° – (60° + 40°)

= 180° – 100° = 80°

∴ ∠A = 60°, ∠B = 40°, ∠C = 80°

Example 14

The angles of a triangle are such that, 1/2 of one angle = 1/3rd of another angle = 1/4th of another angle. Find the angles of the triangle.

Solution :

Given:

The angles of a triangle are such that, 1/2 of one angle = 1/3rd of another angle = 1/4th of another angle.

Let, the equal portions be x°.

the angles are 2x°, 3x° and 4x°.

∴ 2x° + 3x° + 4x° = 180°

or, 9x° = 180°

∴ angles of the triangle are 2 x 20°, 3 x 20°, 4 x 20°

i.e., 40°, 60° and 80°.

Example 15

In the triangle, ABC, AB² + BC² = AC² and AC = 72 BC. Find the nature of the triangle.

Solution :

Given:

In the triangle, ABC, AB² + BC² = AC² and AC = 72 BC

AB² + BC² = AC²

or, AB² + BC² = (72 BC)²

or, AB² + BC² = 2 BC²

or, AB² = 2BC² – BC²

or, AB² = BC²

or, AB = BC

Hence, the triangle is a right-angled isosceles triangle whose ∠ABC = 90° and AB = BC.

∴ The triangle is isosceles right-angled.

Algebra Chapter 12 Equations

Equations Introduction

In class VII you have learned about the formation of linear equations of one variable and their solutions. Formation of equations, some useful information about equations, and rules of solving an equation have been discussed in detail in the chapter of ‘equation¹ in the book for class VII. In this chapter, our aim is to deal with a little harder problems and also to discuss some special techniques for solving algebraic equations involving one variable.

Class 8 Maths Solutions Wbbse

Method of Transportation

In an equation, usually, there are some terms on the left-hand side of the ‘=’ sign and also there are some terms on the right-hand side of the sign. If any term is taken from the left-hand side to the right-hand side or from the right-hand side to the left-hand side then a change of sign of the respective term takes place. This is called the method of transportation.

For example, if x + a = b then x = b – a, and if x + c = d then x + c – d = 0

Cross multiplication

If x/a = b/c then cx =ab. This process of multiplication of the numerator of one side of an equation by the denominator of the other side is called cross multiplication.

Method Of Alternends

If a/b = c/d then a/c = b/d.

This is called the method of alternates.

Method Of Break Term

In order to solve the equation of the form \(\frac{p}{x+a}+\frac{q}{x+b}=\frac{p+q}{x+c}\) it is convenient to proceed by writing the equation as

\(\frac{p}{x+a}+\frac{q}{x+b}=\frac{p}{x+c}+\frac{q}{x+c}\) Then is known as the method of break term.

For example, to solve the equation, \(\frac{2}{x+1}+\frac{3}{x+2}=\frac{5}{x+3}\)

write the equation as: 2 / x+ 1 + 3 / x + 2 = 2/ x + 3 + 3 / x + 3.

Read And Learn More WBBSE Solutions For Class 8 Maths

Method of division

In some cases, each fraction of an equation is written in such a way that, a part of the numerator becomes divisible by the denominator.

For example, to solve the equation,

\(\frac{4 x+5}{2 x-3}+\frac{3 x+8}{x-5}=\frac{15 x}{3 x-1}\)

Class 8 Maths Solutions Wbbse

we may proceed as follows:

\(\frac{2(2 x-3)+11}{2 x-3}+\frac{3(x-5)+23}{x-5}=\frac{5(3 x-1)+5}{3 x-1}\)

or, \(2+\frac{11}{2 x-3}+3+\frac{23}{x-5}=5+\frac{5}{3 x-1}\)

or, \(\frac{11}{2 x-3}+\frac{23}{x-5}=\frac{5}{3 x-1}\)

Algebra Chapter 12 Equations Some examples of equations

Example 1

Solve the equation : 5(x – 2) +7(x – 3) = 2(x + 3) + 3.

Solution :

Given 5(x – 2) +7(x – 3) = 2(x + 3) + 3.

5(x – 2) + 7(x – 3) = 2(x + 3) + 3

or, 5x – 10 + 7x – 21 = 2x + 6 + 3

or, 12x – 31 = 2x + 9

or, 12x – 2x = 31 + 9

or, 10x = 40

or, x = 40/10

= 4

The required solution is x = 4.

Example 2

Solve: (x – 2)(x – 3) = x² – 44.

Solution:

Given (x – 2)(x – 3) = x² – 44

or, x² – 3x -2x + 6 = x² – 44

or, x² – x² – 5x = -44 – 6

or, -5x = -50

or, x = -50 / -5

= 10

The required solution is x = 10.

Example 3

Solve: (x -+ 1) + x(x – 3) = 2x² – 8.

Solution:

Given

(x -+ 1) + x(x – 3) = 2x² – 8.

x(x + 1) + x(x – 3) = 2x² – 8

or, x² + x + x² – 3x = 2x² – 8

or, 2x² – 2x² – 2x = -8

or, -2x = -8

or, x = -8 / -2

= 4

The required solution is x = 4.

Example 4

Solve: \(\frac{x+1}{5}+x=\frac{2 x+7}{5}+2\)

Solution:

Given

\(\frac{x+1}{5}+x=\frac{2 x+7}{5}+2\).

\(\frac{x+1}{5}+x=\frac{2 x+7}{5}+2\) \(\text { or, } \frac{x+1+5 x}{5}=\frac{2 x+7+10}{5}\) \(\text { or, } 6 x+1=2 x+17 \text { or, } 6 x-2 x=17-1\) \(\text { or, } 4 x=16\) \(\text { or, } x=\frac{16}{4}=4\)

Example 5

Solve: \(\frac{2x+1}{7}+4=\frac{5-x}{3}\)

Solution:

Given \(\frac{2x+1}{7}+4=\frac{5-x}{3}\)

\(\frac{2 x+1}{7}+4=\frac{5-x}{3}\)

or, \(\frac{2 x+1+28}{7}=\frac{5-x}{3} \text { or, } \frac{2 x+29}{7}=\frac{5-x}{3} \text { or, } 6 x+87=35-7 x \text { or, } 6 x+7 x=35-87\)

or, 13x = -52

or, \(x=\frac{-52}{13}=-4\)

The required solution is x = -4.

 

Example 6

Solve: \(\frac{x+12}{6}-x=6 \frac{1}{2}-\frac{x}{12} \ldots\)

Solution:

Given \(\frac{x+12}{6}-x=6 \frac{1}{2}-\frac{x}{12} \ldots\).

\(\frac{x+12}{6}-x=6 \frac{1}{2}-\frac{x}{12}\)

or, \(\frac{x+12}{6}-x=\frac{13}{2}-\frac{x}{12}\)

or, \(\frac{x+12-6 x}{6}=\frac{78-x}{12}\)

or, \(\frac{12-5 x}{6}=\frac{78-x}{12} \text { or, } 12-5 x=\frac{78-x}{2}\)

or,  78 – x = 24 – 10x or, 10x – x = 24 – 78

or, 9x = -54

or, \(x=\frac{-54}{9}=-6\)

The required solution is x = -6

Example 7

Solve: \(\frac{x-3 a}{b}+\frac{x-3 b}{a}+\frac{x-9 a-9 b}{a+b}=0 .\)

Solution:

Given \(\frac{x-3 a}{b}+\frac{x-3 b}{a}+\frac{x-9 a-9 b}{a+b}=0 .\)

\(\frac{x-3 a}{b}+\frac{x-3 b}{a}+\frac{x-9 a-9 b}{a+b}=0\)

or, \(\frac{x-3 a}{b}-3+\frac{x-3 b}{a}-3+\frac{x-9 a-9 b}{a+b}+6=0\)

or, \(\frac{x-3 a-3 b}{b}+\frac{x-3 b-3 a}{a}\)

\(+\frac{x-9 a-9 b+6 a+6 b}{a+b}=0\)

or, \(\frac{x-3 a-3 b}{b}+\frac{x-3 a-3 b}{a}+\frac{x-3 a-3 b}{a+b}=0\)

or, \((x-3 a-3 b)\left(\frac{1}{b}+\frac{1}{a}+\frac{1}{a+b}\right)=0 \text {. }\)

Now, the left-hand side is the product of two expressions. Its value will be equal to zero if at least one of them is zero. Clearly, the second factor cannot be equal to zero because nothing is known about the values of a, b, and c.

∴ x – 3a – 3b = 0

or, x = 3a +3b

The required solution is x = 3a +3b.

Example 8

Solve: \(\frac{3}{5}(x-4)-\frac{1}{3}(2 x-9)=\frac{1}{4}(x-1)-2\)

Solution:

Given

\(\frac{3}{5}(x-4)-\frac{1}{3}(2 x-9)=\frac{1}{4}(x-1)-2\)

Multiplying both sides by 60, which is the  L.C.M of 5, 3, and 4.

36(x – 4) – 20(2x – 9) = 15(x – 1) – 120

or, 36x – 144 – 40x + 180 = 15x -15 -120

or, – 4x + 36 = 15x -135

or, 15x + 4x = 135 + 36

or, 19x = 171

or, x = 171 /19

= 9

The required solution is x = 9.

Example 9

Solve: \(\frac{x+1}{2}-\frac{5 x+9}{28}=\frac{x+6}{21}+5-\frac{x-12}{3}\)

Solution:

Given \(\frac{x+1}{2}-\frac{5 x+9}{28}=\frac{x+6}{21}+5-\frac{x-12}{3}\)

\(\frac{x+1}{2}-\frac{5 x+9}{28}=\frac{x+6}{21}+5-\frac{x-12}{3}\)

or, \(\frac{14(x+1)-(5 x+9)}{28}=\frac{x+6+105-7(x-12)}{21}\)

or, \(\frac{14 x+14-5 x-9}{28}=\frac{x+111-7 x+84}{21}\)

or, \(\frac{9 x+5}{28}=\frac{-6 x+195}{21}\)

or, \(\frac{9 x+5}{4}=\frac{-6 x+195}{3}\)

or, 27x + 15 = -24x + 780

or, 27x + 24x = 780 – 15

or, 51x = 765

or, \(x=\frac{765}{51}=15\)

The required solution is x = 15.

 

Example 10

Find the value of x from equation, \(\frac{7 x+5}{15}+\frac{2 x-5}{5}=\frac{2 x+4}{6}+\frac{5 x-2}{12}\)

Solution:

Given:-

\(\frac{7 x+5}{15}+\frac{2 x-5}{5}=\frac{2 x+4}{6}+\frac{5 x-2}{12}\) \(\frac{7 x+5}{15}+\frac{2 x-5}{5}=\frac{2 x+4}{6}+\frac{5 x-2}{12}\)

or, \(\frac{7 x+5+6 x-15}{15}=\frac{4 x+8+5 x-2}{12}\)

or,\(\frac{7 x+5+6 x-15}{15}=\frac{4 x+8+5 x-2}{12}\)

or, 45x + 30 = 52x – 40

or, 45x – 52x = -40 -30

or, -7x = -70

or, \(x=\frac{-70}{-7}=10\)

Value of x is 10.

Example 11

Solve: \(\frac{x^2+2 x+3}{x^2+3 x+5}=\frac{x+2}{x+3}\)

Solution:

Given:-

\(\frac{x^2+2 x+3}{x^2+3 x+5}=\frac{x+2}{x+3}\) \(\frac{x^2+2 x+3}{x^2+3 x+5}=\frac{x+2}{x+3}\)

or, \(\frac{x^2+2 x+3}{x+2}=\frac{x^2+3 x+5}{x+3}\)

[By the method of alternends]

or, \(\frac{x(x+2)+3}{x+2}=\frac{x(x+3)+5}{x+3}\)

or, \(x+\frac{3}{x+2}=x+\frac{5}{x+3}\)

or, \(\frac{3}{x+2}=\frac{5}{x+3}\)

or, 5x + 10 = 3x + 9 or, 5x – 3x = 9 – 10

or, 2x = -1 or, x = \(-\frac{1}{2}\)

The required solution x = \( -\frac{1}{2}\)

Example 12

Solve: \(\frac{2 x+1}{5}+\frac{7 x+2}{3}=\frac{x+3}{10}+\frac{2 x+1}{21}\)

Solution:

Given:-

\(\frac{2 x+1}{5}+\frac{7 x+2}{3}=\frac{x+3}{10}+\frac{2 x+1}{21}\) \(\frac{2 x+1}{5}+\frac{7 x+2}{3}=\frac{x+3}{10}+\frac{2 x-1}{21}\)

or, \(\frac{2 x+1}{5}-\frac{x+3}{10}=\frac{2 x-1}{21}-\frac{7 x+2}{3}\)

[By transportation]

or, \(\frac{4 x+2-x-3}{10}=\frac{2 x-1-49 x-14}{21}\)

or, \(\frac{3 x-1}{10}=\frac{-47 x-15}{21}\)

or, 63x – 21 = -470x – 150

or, 470x + 63x = 21 – 150

or, 533x = -129

or, x = \(-\frac{129}{533}\)

The required solution is x = \(-\frac{129}{533}\)

Example 13

Solve: \(\frac{1}{(x-1)(x-2)}+\frac{1}{(x-2)(x-3)}=\frac{1}{x-1} .\)

Solution:

Given:-

\(\frac{1}{(x-1)(x-2)}+\frac{1}{(x-2)(x-3)}=\frac{1}{x-1} .\) \(\frac{1}{(x-1)(x-2)}+\frac{1}{(x-2)(x-3)}=\frac{1}{x-1}\)

or, \(\frac{1}{x-2}-\frac{1}{x-1}+\frac{1}{x-3}-\frac{1}{x-2}=\frac{1}{x-1}\)

or, \(-\frac{1}{x-1}+\frac{1}{x-3}=\frac{1}{x-1}\)

or, \(\frac{1}{x-3}=\frac{2}{x-1} \text { or, } 2 x-6=x-1\)

or, 2x – x = 6 – 1 or, x = 5

The required solution is x = 5.

Example 14

Solve: \(\frac{3}{x-1}+\frac{2}{x-2}=\frac{5}{x-3}\)

Solution:

Given:-

\(\frac{3}{x-1}+\frac{2}{x-2}=\frac{5}{x-3}\) \(\frac{3}{x-1}+\frac{2}{x-2}=\frac{5}{x-3}\)

or, \(\frac{3}{x-1}+\frac{2}{x-2}=\frac{3+2}{x-3}\)

or, \(\frac{3}{x-1}+\frac{2}{x-2}=\frac{3}{x-3}+\frac{2}{x-3}\)

or, \(\frac{3}{x-1}-\frac{3}{x-3}=\frac{2}{x-3}-\frac{2}{x-2}\)

or, \(3\left(\frac{1}{x-1}-\frac{1}{x-3}\right)=2\left(\frac{1}{x-3}-\frac{1}{x-2}\right)\)

or, \(\text { 3. } \frac{-2}{(x-1)(x-3)}=2 \cdot \frac{1}{(x-3)(x-2)}\)

or, \(\frac{-3}{(x-1)(x-3)}=\frac{1}{(x-3)(x-2)}\)

Now, multiplying both sides by (x – 3) we get,

\(\frac{-3}{x-1}=\frac{1}{x-2}\)

or, x – 1 = -3x + 6 or, x + 3x = 6 + 1

or, 4x = 7

or, \(x=\frac{7}{4}=1 \frac{3}{4}\)

The required equation is \(1 \frac{3}{4}\)

Example 15

Solve: \(\frac{1}{x-2}+\frac{1}{x-6}=\frac{1}{x-3}+\frac{1}{x-5}\)

Solution:

Given :-

\(\frac{1}{x-2}+\frac{1}{x-6}=\frac{1}{x-3}+\frac{1}{x-5}\) \(\frac{1}{x-2}+\frac{1}{x-6}=\frac{1}{x-3}+\frac{1}{x-5}\)

or, \(\frac{1}{x-2}-\frac{1}{x-3}=\frac{1}{x-5}-\frac{1}{x-6}\)

or, \(\frac{x-3-x+2}{(x-2)(x-3)}=\frac{x-6-x+5}{(x-5)(x-6)}\)

or, \(\frac{-1}{(x-2)(x-3)}=\frac{-1}{(x-5)(x-6)}\)

or, (x – 5)(x – 6) = (x – 2)(x – 3)

or, x^2-11 x+30=x^2-5 x+6

or, -11x + 5x = 6 – 30

or, -6x = -24

or, x = \(\frac{-24}{-6}=4\)

The required solution is x = 4.

 

Example 16

Find the value of x from the relation \(\frac{a}{a-x}+\frac{b}{b-x}=\frac{a+b}{a+b-x} .\)

Solution:

Given:-

\(\frac{a}{a-x}+\frac{b}{b-x}=\frac{a+b}{a+b-x} .\)

From the given relation,

\(\frac{a}{a-x}+\frac{b}{b-x}=\frac{a}{a+b-x}+\frac{b}{a+b-x}\)

or, \(\frac{a}{a-x}-\frac{a}{a+b-x}=\frac{b}{a+b-x}-\frac{b}{b-x}\)

or, \(\frac{a^2+a b-a x-a^2+a x}{(a-x)(a+b-x)}=\frac{b^2-b x-a b-b^2+b x}{(a+b-x)(b-x)}\)

or, \(\frac{a b}{(a-x)(a+b-x)}=\frac{-a b}{(a+b-x)(b-x)}\)

or, \(\frac{1}{(a-x)(a+b-x)}=\frac{-1}{(a+b-x)(b-x)}\)

or, \(\frac{1}{a-x}=\frac{-1}{b-x}\)

[Multiplying both sides by a + b – x].

or, -a + x = b – x

or, x + x = a +b

or, 2x = a+ b

or, x = \(\frac{a+b}{2}\)

The required value of x is \(\frac{a+b}{2}\).

 

Example 17

Solve: [latex]\begin{aligned}
\frac{1}{(x+1)(x+2)}+\frac{1}{(x+2)(x+3)} & +\frac{1}{(x+3)(x+4)} \\
& =\frac{1}{(x+1)(x+6)}
\end{aligned}[/latex]

Solution:

From the given equation,

\(\frac{1}{(x+1)(x+2)}+\frac{1}{(x+2)(x+3)}+\frac{1}{(x+3)(x+4)}=\frac{1}{(x+1)(x+6)}\)

or, \(\frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}+\frac{1}{x+3}-\frac{1}{x+4}=\frac{1}{(x+1)(x+6)}\)

or, \(\frac{1}{x+1}-\frac{1}{x+4}=\frac{1}{(x+1)(x+6)}\)

or, \(\frac{x+4-x-1}{(x+1)(x+4)}=\frac{1}{(x+1)(x+6)}\)

or, \(\frac{3}{(x+1)(x+4)}=\frac{1}{(x+1)(x+6)}\)

or, \(\frac{3}{x+4}=\frac{1}{x+6}\)

[Multiplying both sides by (x + 1)]

or, 3x + 18 = x + 4

or, 3x – x = 4 – 18

or, 2x = -14

or, x = \(-\frac{14}{2}\) = -7

The required solution is x = -7.

 

Example 18

Solve: \(\frac{2 x+1}{2 x-1}+\frac{3 x+1}{3 x-2}=\frac{3 x+2}{3 x-1}+\frac{6 x+1}{6 x-5}\)

Solution:

From the given equation,

\(\frac{2 x+1}{2 x-1}-1+\frac{3 x+1}{3 x-2}-1=\frac{3 x+2}{3 x-1}-1+\frac{6 x+1}{6 x-5}-1\)

or, \(\frac{2 x+1-2 x+1}{2 x-1}+\frac{3 x+1-3 x+2}{3 x-2}\)

= \(\frac{3 x+2-3 x+1}{3 x-1}+\frac{6 x+1-6 x+5}{6 x-5}\)

or, \(\frac{2}{2 x-1}+\frac{3}{3 x-2}=\frac{3}{3 x-1}+\frac{6}{6 x-5}\)

or, \(\frac{6 x-4+6 x-3}{(2 x-1)(3 x-2)}=\frac{18 x-15+18 x-6}{(3 x-1)(6 x-5)}\)

or, \(\frac{12 x-7}{6 x^2-7 x+2}=\frac{3(12 x-7)}{18 x^2-21 x+5}\)

or, \((12 x-7)\left(18 x^2-21 x+5\right)=(12 x-7)\left(18 x^2-21 x+6\right)\)

or, \((12 x-7)\left(18 x^2-21 x+5-18 x^2+21 x-6\right)=0\)

or, (12x-7)(-1) = 0 or, 12x – 7 = 0

or, 12x = 7 or, x = \(\frac{7}{12}\)

The required solution is x = \(\frac{7}{12}\).

 

 

Example 19

Solve: \(\frac{x-b c}{b+c}+\frac{x-c a}{c+a}+\frac{x-a b}{a+b}=a+b+c\)

Solution:

From the given equation,

\(\frac{x-b c}{b+c}-a+\frac{x-c a}{c+a}-b+\frac{x-a b}{a+b}-c=0\)

or, \(\frac{x-b c-a b-a c}{b+c}+\frac{x-c a-b c-a b}{c+a}+\frac{x-a b-a c-b c}{a+b}=0\)

or, \((x-a b-b c-c a)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)=0\)

 

Now, the left-hand side is the product of two quantities. Its value will be equal to zero if at least one of them is zero. Clearly, the second factor cannot be equal to zero because nothing is known about the values of a, b, and c.

Hence, x – ab – be – ca = 0

or, x = ab + bc + ca

The required solution is x = ab + bc + ca.

Example 20

Solve: \(\frac{x+a^2+2 c^2}{b+c}+\frac{x+b^2+2 a^2}{c+a}+\frac{x+c^2+2 b^2}{a+b}=0 .\)

Solution:

From the given equation,

\(\begin{array}{r}
\frac{x+a^2+2 c^2}{b+c}+(b-c)+\frac{x+b^2+2 a^2}{c+a}+(c-a) \\
+\frac{x+c^2+2 b^2}{a+b}+(a-b)=0
\end{array}\)

or, \(\frac{x+a^2+2 c^2+b^2-c^2}{b+c}+\frac{x+b^2+2 a^2+c^2-a^2}{c+a}\)

\(+\frac{x+c^2+2 b^2+a^2-b^2}{a+b}=0\)

or, \(\frac{x+a^2+b^2+c^2}{b+c}+\frac{x+a^2+b^2+c^2}{c+a}\)

\(+\frac{x+a^2+b^2+c^2}{a+b}=0\)

or, \(\left(x+a^2+b^2+c^2\right)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)=0 .\)

 

Now, the left-hand side is the product of two quantities. Its value will be equal to zero if at least one of them is zero’. Clearly, the second factor cannot be equal to zero because nothing is known about the values of a, b, and c.

Hence, x + a² + b² + c² = 0

or, x = – (a² + b² + c²)

The required solution is x = – (a²+ b² + c²)

Example 21

The sum of the digits of a number of two digits is 10. if the digit in the units’ place is 4 times the digit in the tens’ place, find the number.

Solution:

Let, the digit in the tens place be x.

Then the digit in the units place = 4x

∴ The number = 10 x x + 4x

= 10x + 4x

= 14x.

Again, according to the question,

x + 4x = 10

or, 5x = 10

or, x  = 10/5

= 2

Hence, the number = 14 x 2

= 28

The number is 28.

Example 22

A number consisting of two digits is such that its digit in the tens’ place is twice that in the units’ place. If the digits are reversed, the number thus formed is 27 less than the original one. Find the number.

Solution :

Let, the digit in the units’ place be x.

Then the digit in the tens’ place = 2x.

∴ The number = 10 x 2x + x = 20x + x= 21x

If the digits are reversed, the number obtained

= 10 x x + 2x

= 12x

According to the question,

21x – 12x = 27

or, 9x = 27

or, x = 27/9

= 3

Hence, the number

= 21 x 3

= 63

The number is 63.

Example 23

The denominator of a fraction is greater than its numerator by 2. The fraction becomes 1/2 when 3 is subtracted from both the numerator and the denominator. Find the fraction.

Solution:

Let, the numerator of the fraction be x.

Then its denominator = x + 2.

Hence, the fraction = \(\frac{x}{x+2}\)

According to the question,

\(\frac{x-3}{x+2-3}=\frac{1}{2}\)

or, \(\frac{x-3}{x-1}=\frac{1}{2} \text { or, } 2 x-6=x-1\)

or, 2x – x = 6 – 1 or, x = 5

Hence, the required fraction is \(\frac{5}{7}\)

The required fraction is \(\frac{5}{7}\).

 

Example 24

The denominator of a fraction is 2 more than twice the numerator keeping the denominator unaltered then the fraction becomes 7/12. Find the fraction.

Solution:

Let, the numerator be x.

Then the denominator = 2x + 2

∴ The fraction = \(\frac{x}{2 x+2}\)

According to the question,

\(\frac{x+4}{2 x+2}=\frac{7}{12} \text { or, } 14 x+14=12 x+48\)

or, 14x – 12x = 48 – 14

or, 2x = 34

or, x = \(\frac{34}{2}=17\)

∴Numerator = 17

and denominator = 2 x 17 + 2 = 36

∴ The required fraction = \(\frac{17}{36}\)

The fraction is \(\frac{17}{36}\)

 

Example 25

₹ 624 was distributed among A, B, C, and D, If A would receive ₹ 2 more, B would receive ₹ 6 less, C would receive 5 times his money and D would receive 1/4th of his money, then they would receive equal money. How much money did each of them receive?

Solution:

Given

₹ 624 was distributed among A, B, C, and D, If A would receive ₹ 2 more, B would receive ₹ 6 less, C would receive 5 times his money and D would receive 1/4th of his money, then they would receive equal money.

Let, the equal money be ₹ x,

Then A received ₹( x – 2),

B received ₹ ( x + 6),

C received ₹ x/5 ,

D received ₹ 4x.

According to the question,

x – 2 + x + 6 + x/5 + 4x = 624

or, 6x + x/5 = 624 – 4

or, 31x / 5 = 620

or, x = 620 x 5/31 = 100

∴ A received ₹(100-2)

= ₹98

B received ₹ (100+6)

= ₹ 106

C received ₹ 100/5

= ₹ 20

D received ₹ 4 x 100

= ₹ 400.

∴ A received v 98,

B received ₹ 106,

C received ₹ 20,

D received ₹ 400.

Algebra Chapter 11 Graph

What is a graph

To construct a graph, some sort of paper is used. In the paper, there are some horizontal and vertical equidistant parallel straight lines. As a result of this, the paper is divided into some equal squares. This is called graph paper. The side of the smallest square is either 1/10th of an inch or 1 mm. The distance is measured by taking as a unit of length the side of one or more than one square. Usually, there is a bold line after each 10 smallest squares (i.e., after each 1 inch or 1 cm), x-axis and y-axis are drawn along a bold horizontal line and a bold vertical line respectively with the help of a pencil and a scale. After this, different points are plotted. The straight line or curve obtained by joining these points is a graph. Of course, in our present discussion, we shall consider only a straight line but no curve.

Plotting of points in the graph paper

Let, we have to plot the four points A (7, 8), B (- 6, 9), C (-5, – 6), and D(10, -9) on the graph paper. We draw the horizontal line XOX’ as-the x-axis. We draw the vertical line YOY’ as the y-axis. The point of intersection of these two lines, that is, point 0, is called the origin. Each axis has a scale. Let us take 1 unit length (1 small square box) = 1 along both axes. Numbers to the right of the origin along the x-axis are positive, while numbers to the left of the origin are negative. Similarly, numbers above the origin along the y-axis are positive, while numbers below the origin are negative.

1. At first moving the 7 smallest divisions towards the right along OX from the origin 0(0,0) and then moving the 8 smallest divisions upwards parallel to OY point A (7, 8) will be obtained. 7 is called the abscissa (denoted by x) or the x-coordinate of point A. 8 is called the ordinate (denoted by y) or the y-coordinate of the point A. (7,8) are the coordinates of point A, represented as A(7,8).

2. At first moving the 6 smallest divisions towards left along OX’ from the origin 0(0,0) and then moving the 9 smallest divisions upwards parallel to OY point B(- 6,9) will be obtained.

3. At first moving the 5 smallest divisions towards left along OX’ from the origin 0(0,0) and then moving the 6 smallest divisions downwards parallel to OY’ point C(-5, – 6) will be obtained.

4. At first moving the 10 smallest divisions towards the right along OX from the origin 0(0,0) and then moving the 9 smallest divisions downwards parallel to OY’ the point D (10,-9) will be obtained.

Read And Learn More WBBSE Solutions For Class 8 Maths

Some important information

1. Co-ordinates of the origin are (0,0).

2. The y coordinates of all points on the x-axis are zeroes.

3. The x coordinates of all points on the y-axis are zeroes.

4. The equation of the x-axis is y = 0.

5. The equation of the y-axis is x = 0.

6. The coordinate of each point on any straight line parallel to the x-axis is equal. Hence, the equation of any straight line parallel to the x-axis is y = c, where c is a constant.

7. The x-coordinate of each point on any straight line parallel to the y-axis is equal. Hence, the equation of any straight line parallel to the y-axis is x = c, where c is a constant.

8. The x-axis and the y-axis divide the coordinate plane into four regions, called quadrants.

1. In the first quadrant (or XOY), both the x-coordinate and the y-coordinate of a point are positive.

1st quadrant: x > 0, y > 0

2. In the second quadrant (or YOX’), the x-coordinate of a point is negative and the y-coordinate of the point is positive.

2nd quadrant: x < 0, y > 0

3. In the third quadrant (or XOY), both the x-coordinate and the y- coordinate of a point are negative.

3rd quadrant: x < 0, y < 0

4. In the fourth quadrant (or YOX), the x-coordinate of a point is positive, while the y-coordinate of the point is negative.

4th quadrant: x > 0, y < 0.

Class 8 Maths Solutions Wbbse

Algebra Chapter 11 Graph Drawing of graphs of some simple linear equations

Example 1

Draw the graphs of x = 5 and y = -7 in a figure. Find the point of intersection of those straight lines.

Solution :

Given x = 5 And y = -7

From the first equation, we get x = 5. That means, for any value of y the value of x will be 5. Therefore, by satisfying this equation we get the following values

X	5	5	5
y	1	-6	8

 

From the second equation we get, y = -7.

That means, for any value of x the value will be -7. Therefore, by satisfying this equation we get the following values :

X	8	-1	-8
y	-7	-7	-7

 

Two mutually perpendicular straight lines XOX’ and YOY’ are taken as the x-axis and y-axis respectively. Taking one side of the smallest square as the unit of length the points (5,1), (5, – 6), and (5,8) are plotted on the graph paper. Joining these points with a scale and producing both ways the graph AB of equation

x = 5 is obtained.

Again, with the same pair of axes the points (8, -7), (-1, -7), and (-8, -7) are plotted on the graph paper. Joining these points with a scale and producing both ways the graph CD of the equation

y = -7 is obtained.

AB and CD intersect each other at the point (5, -7). Hence, the required point of intersection is (5, -7).

Example 2

Draw the graph of the straight line y = 3x + 2.

Solution :

The given equation is, y = 3x + 2. From this equation we get,

X	0	2	-2
y	2	8	-4

 

Two mutually perpendicular straight lines XOX’ and YOY’ are taken as the x-axis and y-axis respectively.

 

Taking one side of the smallest square as the unit of length the points (0, 2), (2, 8), (-2, — 4) are plotted on the graph paper. Joining these points with a scale and producing both ways the graph of the given straight line is obtained.

Example 3

Draw the graph of the equation x/a + y/2 = 1. Find the portion of this graph intercepted between the axes.

Solution:

The given equation is, x/4 + y/5 = 1

or, 5x + 4y / 20 = 1

or, 5x + 4y = 20

or, 5x = 20 – 4y

or, x = 20 – 4y / 5

From the equation we get,

X	4	0	8
y	0	5	-5

 

Two mutually perpendicular straight lines XOX’ and YOY’ are taken as the x-axis and y-axis respectively.

Taking one side of the smallest square as the unit of length the points (4, 0), (0, 5), (8, – 5) are plotted on the graph paper. Joining these points with a scale and producing both ways the^ graph, of the given straight line, is obtained. * _{> ?iV} Let, the straight line intersects the x-axis at A and the y-axis at B.

Here’, OA = 4 units and OB = b units

∴ AB = √4² + 5² units

= √16 + 25 units

= √41 units

The required length is √41 units.

Example 4

Draw the graph of the equation x/5 – y/6 = 1. Find the area of the triangle formed by the graph and the axes.

Solution:

The given equation is,

x/5 – y/6 = 1

or, 6x – 5y / 30 = 1

or, 6x – 5y = 30

or, 6x = 5y + 30

or, x = 5y + 30 / 6

From this equation we get,

X	5	10	0
y	0	6	-6

 

 

Two mutually perpendicular straight lines XOX’ and YOY’ are taken as the x-axis and y-axis respectively.

Taking one side of the smallest square as the unit of length the points (5,0), (10, 6) and (0, – 6) are plotted on the graph paper. Joining these points with a scale and producing both ways the graph of the given straight line is obtained.

Let, the straight line intersects the x-axis at A and the negative y-axis at B.

Here, OA = 5 units and OB = 6 units.

.’. The required area of the triangle

= 1/2 x OA x OB sq. units.

=1/2 x 5 x 6 sq. units. = 15 sq. units.

The required area of the triangle is 15 sq. units.

Example 5

Find the graph of the function x+5 / 3. From the graph find the value of the function when x = 4. For what value of x, the value of the function will be zero.

Solution:

Drawing of the graph of the function x + 5 / 3 means drawing of y = x + 5 / 3.

Now, from this equation we, get

X	1	7	-5
y	2	4	0

 

Two mutually perpendicular straight lines XOX’ and YOY’ are taken as the x-axis and y-axis respectively.

Taking one side of the smallest square as the unit of length the points (1, 2), (7, 4), and (-5, 0) are plotted on the graph paper. Joining these points with a scale and producing both ways the graph of the given function is obtained.

From the graph, it is seen that, if x = 4, the value of the function is 3 and the value of the function is zero when x = -5.

Example 6

Solve with the help of the graph: 4x + 3y = 24 , 3x – 4y = – 7

Solution :

Given

4x + 3y = 24 , 3x – 4y = – 7.

The first equation is

4x + 3y = 24

or, 4x = 24 – 3y

or, x = 24 – 3y / 4

From this equation we get,

X	6	3	9
y	0	4	-4

 

Second equation is, 3x – 4y = -7

or, 3x = 4y – 7

or, x = 4y -7 / 3

From this equation we get,

X	-1	3	-5
y	1	4	-2

 

Two mutually perpendicular straight lines XOX and YOY’ are taken as the x-axis and y-axis respectively. Taking one side of the smallest square as the unit of length the points (6,0), (3, 4), and (9, – 4) obtained from the first equation are plotted on the graph paper. Joining these points with a scale and producing both ways the graph AB of the first equation is obtained.

Again, with the same pair of axes and the same unit the points (—1, 1), (3, 4), (-5, -2) obtained from the second equation are plotted on the graph paper. Joining these points with a scale and producing both ways the graph CD of the second equation is obtained.

The straight lines AB and CD intersect each other at point P. The coordinates of point P are (3, 4).

The required solution is x = 3, y = 4.

Example 7

Draw the graphs of the equations 4s + 3y = 11 and 5x – y  = 9. From this find their point of intersection.

Solution:

Given 4s + 3y = 11 And 5x – y  = 9.

The first equation is, 4x + 3y = 11

or, 4x = 11 – 3y

or, x = 11 – 3y / 4

From this equation we get,

X	2	-1	5
y	1	5	-3

 

The second equation is,

5x – y = 9 or, 5x = y + 9

or, x = y + 9 / 5

From this equation we get,

X	2	3	4
y	1	6	11

 

 

Two mutually perpendicular straight lines XOX’ and YOY’ are taken as the x-axis and y-axis respectively. Taking one side of the smallest square as the unit of length the points (2, 1), (—1, 5), and (5, —3) obtained from the first equation are plotted on the graph paper. Joining these points with a scale and producing both ways the graph AB of the first equation is obtained. Again, with the same pair of axes and the same unit the points (2, 1), (3, 6), (4, 11) obtained from the second equation are plotted on the graph paper. Joining these points with a scale and producing both ways the graph CD of the second equation is obtained. The straight lines AB and CD intersect each other at point P. The coordinates of point P are (2, 1).

Example 8

Find graphically the area of the triangle obtained by joining the three points (- 4, 5), (10, 8), and (-10, 11).

Solution:

Two mutually perpendicular straight lines XOX’ and YOY’ are taken as the y-axis and y- axis respectively.

Taking one side of the smallest square as the unit of length the given points are plotted on graph paper. The given points are named P, Q, and R. After this, joining the points P(- 4, 5), Q(10, 8), and R(-10, 11) the triangle PQR is obtained. The area of the triangle PQR is to be determined.

The straight lines LM and RN are drawn parallel to the x-axis through the points P and R respectively. The straight lines NM and RL are drawn parallel to the y-axis through the points Q and R. Then RLMN is a rectangle.

Now, the area of the triangle PQR = area of the rectangle RLMN – an area of the triangle RLP – an area of the triangle QPM – an area of the triangle QNR.

= (20 x 6 – 1/2 x 6 x 6 – 1/2 x 14 x 3 – 1/2 x 20 x 3) sq. units

= (120 -18 – 21 – 30) sq. units.

= 51 sq. units.

Application of graph in practical problem

We have seen that it is possible to solve two simultaneous equations with the help of a graph. It is possible to solve some special types of practical problems by the application of graphs. Of course, the range of such types of problems is limited. Usually, the application of a graph in practical problems is possible when both x and y are positive. From the graph, we may find the value of y for any value of x and also the value of x for any value of y.

Example 1

If the price of 1 kg of rice is ₹ 15, calculate with the help of the graph

1. What is the price of 2 kg of rice?

2. What quantity of rice can be obtained for ₹ 180?

Solution:

Given The Price Of 1 Kg Of Rice Is ₹ 15.

Let, the price of x kg of rice = ₹ y.

It is given that, the price of 1 kg of rice = ₹ 15

∴ price of x kg of rice = ₹ 15x

∴ y= 15x.

It is the equation of the required graph.

From this equation we get,

X	1	3	7
y	15	45	105

 

Let, on the graph paper 3 sides of the smallest square on the x-axis represent 1 kg and 1 side of the smallest square on the y-axis represent ₹ 5. The graph OP of the straight line y = 15x is drawn. From the graph, it is found that the abscissa of point Q is 5 units, and its ordinate = ₹ 75 units. Hence, the price of 5 kg of rice is  ₹ 75. Again, the ordinate of the point R is 180 units, and its abscissa = 12 units.

Hence, 12 kg of rice can be obtained for ₹180.

Example 2

If the speed of a man is 5 km per hour, calculate from the graph:

1. How far will he travel in 5 hours?

2. At what time will he travel 40 km?

Solution :

Given The Speed Of A Man Is 5 Km Per Hour.

Let, the man travels y km in x hours. It is given that,

In 1 hour the man travels 5 km

∴ In x hours the man travels 5x km.

y = 5x.

It is the equation of the required graph.

From this equation we get,

X	1	3	7
y	5	15	35

 

Let, on the graph paper 5 sides of the smallest square on the x-axis represent 1 hour and 1 side of the smallest square on the y-axis represent a distance of 1 km. The graph OP of the straight line y = 5x is drawn. From the graph, it is found that the abscissa of point Q is 5 units, and its ordinate = 25 units.

In 5 hours the man travels 25 km. Again, the ordinate of the point R is 40 units, and its abscissa = 8 units.

∴ To travel 40 km the man will take 8 hours.

Example 3

The distance of house of Anwar’s maternal uncle is 38 km from the house of Anwar. Anwar starts on a bicycle at 7 a.m. After 2 1/2  hours ride, the bicycle develops trouble. He stops for half an hour to repair it but is not successful. So he is to travel the remaining distance on foot. If the speed of cycling and walking are 12 km and 4 km per hour respectively, when does he reach the house of his maternal uncle? (Solve graphically)

Solution:

Given:-

The distance of house of Anwar’s maternal uncle is 38 km from the house of Anwar.

Anwar starts on a bicycle at 7 a.m. After 2 1/2  hours ride, the bicycle develops trouble.

He stops for half an hour to repair it but is not successful.

So he is to travel the remaining distance on foot.

If the speed of cycling and walking are 12 km and 4 km per hour respectively.

Let, on the graph paper 5 sides of the smallest square on the x-axis represent a distance of 1 km.

Anwar starts from the origin at 7 a.m. and travels by bicycle at a speed of 12 km per hour. Then after 1 hour he travels a distance of 12 km and reaches point A. After this in one more hour of traveling

12 km more he reaches point B. After

this, in 1/2 hour more traveling 6 km more he reaches point C.

After this, he stops for half an hour to repair the bicycle but in vain. The rest period of half an hour has been shown by CD.

After this Anwar starts walking at a speed of 4 km per hour and reaches E after 1 hour and then in one hour more walking 4 km he reaches his maternal uncle’s house at F. Point F is at a distance of 38 km from the starting point. The time at which he reaches point F is found in the graph. It is 5 hours after the start i.e., 12 noon.

∴ Anwar reached the house of their maternal uncle at 12 noon.

Example 4

Abani starts at 10 a.m. at the rate of 5 km per hour. two hours later Biswajit follows him by bicycle at the rate of 7 km per hour. Find graphically when and where they meet each other.

Solution:

Abani Starts At 10 A.M. At The Rate Of 5 Km Per Hour.

Two Hours Later Biswajit Follows Him By Bicycle At The Rate Of 7 Km Per Hour.

Given:-

Let, on the graph paper 5 sides of the smallest square on the x-axis represent 1 hour and 1 side of the smallest square on the y-axis represent a distance f 1 km. Let, Abani starts from the origin O and travels at a speed of 5 km per hour.

 

Let, the coordinates of point A be (1, 5). Therefore, the abscissa of point A is 1 hour and its ordinate represents 5 km. Hence point A is a point on the motion graph of Abani.

Again Biswajit starts 2 hours after Abani starts. Hence in those two hours, Biswajit has not traveled. That means the distance traveled by Biswajit in two hours is zero. After this, Biswajit starts walking at the rate of 7 km per hour. Now consider point (2, 0) as origin the of point B is plotted whose coordinates are (1, 7). Now joining point B with the point (2, 0) obtained by considering 0 as the origin and producing it we obtain the motion graph of Biswajit for the time after 2 hours.

The two motion graphs intersect each other at point C. Taking O as the origin the coordinates of point C is (7 35)

So 7 hours after Abani starts, they will meet at 5 p.m. at a distance of 35 km from the starting point.

Example 5

The total expenditure of a hostel is partly constant and partly proportional to the number of boarders. If the number of boards is 50, the total expenditure is 6000, and if the number of boards is 70, the total expenditure is 8000. Calculate graphically the total expenditure if the number of boards is 90. Also, find out the constant part of the expenditure.

Solution:

Given:-

The total expenditure of a hostel is partly constant and partly proportional to the number of boarders.

If the number of boards is 50, the total expenditure is 6000, and if the number of boards is 70, the total expenditure is 8000.

A graph is plotted using the given data. The scale chosen is as follows :

1 small div. of x-axis = 2 borders

5 small div. of y-axis = ₹ 1000

Point A corresponds to a total expenditure of ₹ 6000 for 50 borders and point B corresponds to a total expenditure of ₹ 8000 for 70 borders. The straight line joining the two points is drawn.

Point P on the straight line represents the expenditure of the hostel when the number of boarders is 90. From the graph, it is found to be ^ 10,000.

The line AB intersects the y-axis at (0,1000).

∴ The fixed component of the expenditure = ₹ 1000.

The total expenditure is ₹ 10,000

when the number of borders is 90 and the constant or fixed part of the expenditure is ₹ 1000.

∴ The total expenditure is ₹ 10,000 when the number of borders is 90 and the constant or fixed part of the expenditure is ₹ 1000.

Algebra Chapter 10 Simplification Of Fractions

Introduction

In arithmetic, you have learned a lot about fractions. By 5/7 part of an article we mean any 5 parts of the article when it is divided into 7 equal parts. Also, you know that for the fraction 5/7, 5 is the numerator and 7 is the denominator. The conception of fractions in algebra is similar to that in arithmetic.

The general form of a fraction in algebra

In algebra, we denote a fraction by a/b. Actually, it represents a fraction for any value of a and b (except b = 0). a/b may also be written saves and it indicates any a parts of a quantity when it is divided into b equal parts. In any fraction, the alphabetic symbol above the fraction line is the numerator and the alphabetic symbol below the line is the denominator. So in the fraction a/b, a is the numerator and b is the denominator.

If both the numerator and the denominator of a fraction are multiplied or divided by the same number, then the value of the fraction remains unchanged.

Thus, a/b = a x x / b x x and a/b = a ÷ x / b ÷ x

The sign of a fraction is positive when both the numerator and denominator are of the same sign (i.e., either both + or both -).

The sign of a fraction is negative when the numerator and denominator are of the opposite sign (i.e., one is + and the other is -).

The Lowest form of a fraction

Like arithmetic, an algebraic fraction can also be reduced to its lowest form.

An algebraic fraction is said to be in its lowest form when there does not exist any factor common to both the numerator and denominator.

Like arithmetic, we can reduce a fraction to its lowest form by dividing both the numerator and denominator by their H.C.F.

For Example : \(\frac{x^2 y}{x y^2}=\frac{x^2 y \div x y}{x y^2 \div x y}=\frac{x}{y}\)

In practice, to reduce a fraction into its lowest form we resolve both the numerator and denominator of the fraction into factors and then their common factors are canceled. Then the given fraction reduces to its lowest form.

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 10 Simplification Of Fractions Some examples

Example 1

Reduce \(\frac{18 x^5 y^6 z^9}{24 x^2 y^3 z^8}\) into its lowest term.

Solution:

Given \(\frac{18 x^5 y^6 z^9}{24 x^2 y^3 z^8}\).

= \(\frac{18 x^5 y^6 z^9}{24 x^2 y^3 z^8}=\frac{6 \times 3 \times x^5 \times y^6 \times z^9}{6 \times 4 \times x^2 \times y^3 \times z^8}\)

= \(\frac{3 \times x^3 \times y^3 \times z}{4}=\frac{3 x^3 y^3 z}{4}\)

Example 2 

Reduce \(\frac{56 a^5 b c^2}{42 a^2 b^3 c^4}\) into its lowest term.

Solution:

Given \(\frac{56 a^5 b c^2}{42 a^2 b^3 c^4}\).

\(\frac{56 a^5 b c^2}{42 a^2 b^3 c^4}=\frac{14 \times 4 \times a^5 \times b \times c^2}{14 \times 3 \times a^2 \times b^3 \times c^4}\)

= \(\frac{4 \times a^4}{3 \times b^2 \times c^2}=\frac{4 a^3}{3 b^2 c^2}\)

= \(\frac{4 a^3}{3 b^2 c^2}\)

Example 3

Reduce \(\frac{x^2+3 x+2}{x^2+4 x+3}\) into its lowest term.

Solution:

Given \(\frac{x^2+3 x+2}{x^2+4 x+3}\).

\(\frac{x^2+3 x+2}{x^2+4 x+3}=\frac{x^2+2 x+x+2}{x^2+3 x+x+3}\)

= \(\frac{x(x+2)+1(x+2)}{x(x+3)+1(x+3)}=\frac{(x+2)(x+1)}{(x+3)(x+1)}=\frac{x+2}{x+3}\)

= \(\frac{x+2}{x+3}\)

Example 4

Reduce \(\frac{25 x^2-36 y^2}{5 x-6 y}\) into its lowest term.

Solution:

Given \(\frac{25 x^2-36 y^2}{5 x-6 y}\).

\(\frac{25 x^2-36 y^2}{5 x-6 y}=\frac{(5 x)^2-(6 y)^2}{5 x-6 y}\)

= \(\frac{(5 x+6 y)(5 x-6 y)}{5 x-6 y}=5 x+6 y\)

= 5x + 6y

Example 5

Reduce \(\frac{15\left(a^3-b^3\right)}{25\left(a^2+a b+b^2\right)}\) into its lowest term.

Solution:

Given \(\frac{15\left(a^3-b^3\right)}{25\left(a^2+a b+b^2\right)}\)

\(\frac{15\left(a^3-b^3\right)}{25\left(a^2+a b+b^2\right)}\)

= \(\frac{5 \times 3 \times(a-b)\left(a^2+a b+b^2\right)}{5 \times 5 \times\left(a^2+a b+b^2\right)}=\frac{3(a-b)}{5}\)

= \(\frac{3(a-b)}{5}\)

Example 6

Reduce \(\frac{\left(x^3+y^3\right)\left(x^3-y^3\right)}{x^4+x^2 y^2+y^4}\) into its lowest term.

Solution:

Given

\(\frac{\left(x^3+y^3\right)\left(x^3-y^3\right)}{x^4+x^2 y^2+y^4}\)

= \(\frac{\left(x^3+y^3\right)\left(x^3-y^3\right)}{x^4+x^2 y^2+y^4}\)

= \(\frac{(x+y)\left(x^2-x y+y^2\right)(x-y)\left(x^2+x y+y^2\right)}{\left(x^2\right)^2+2 \times x^2 \times y^2+\left(y^2\right)^2-x^2 y^2}\)

= \(\frac{(x+y)(x-y)\left(x^2-x y+y^2\right)\left(x^2+x y+y^2\right)}{\left(x^2+y^2\right)^2-(x y)^2}\)

= \(\frac{(x+y)(x-y)\left(x^2-x y+y^2\right)\left(x^2+x y+y^2\right)}{\left(x^2+y^2+x y\right)\left(x^2+y^2-x y\right)}\)

= \((x+y)(x-y)=x^2-y^2\)

= \(x^2-y^2\)

 

Application of four basic operations on fractions

Addition, subtraction, multiplication, and division of fractions are similar to those in arithmetic.

For Example:

1. \(\frac{\mathrm{a}}{\mathrm{b}}+\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{ad}+\mathrm{bc}}{\mathrm{bd}}\)

2. \(\frac{\mathrm{p}}{\mathrm{q}}-\frac{\mathrm{r}}{\mathrm{s}}=\frac{\mathrm{ps}-\mathrm{qr}}{\mathrm{qs}}\)

3. \(\frac{x}{y} \times \frac{p}{q}=\frac{p x}{q y}\)

4. \(\frac{a}{b} \div \frac{c}{d}=\frac{a}{b} \times \frac{d}{c}\)

= \(\frac{\mathrm{ad}}{\mathrm{bc}}\)

 

Some Examples

Example 1

Simplify: \(\frac{9 x^2-16 y^2}{x^2-16} \times \frac{x^2-4 x}{3 x-4 y}\)

Solution:

Given \(\frac{9 x^2-16 y^2}{x^2-16} \times \frac{x^2-4 x}{3 x-4 y}\)

= \frac{9 x^2-16 y^2}{x^2-16} \times \frac{x^2-4 x}{3 x-4 y}

= \frac{(3 x)^2-(4 y)^2}{(x)^2-(4)^2} \times \frac{x(x-4)}{3 x-4 y}

= \frac{(3 x+4 y)(3 x-4 y)}{(x+4)(x-4)} \times \frac{x(x-4)}{3 x-4 y}

= \frac{x(3 x+4 y)}{x+4}

 

Example 2

Simplify: \(\frac{x^3-y^3}{x+y} \times \frac{x^2-y^2}{x^2+x y+y^2}\)

Solution:

Given \(\frac{x^3-y^3}{x+y} \times \frac{x^2-y^2}{x^2+x y+y^2}\).

= \(\frac{x^3-y^3}{x+y} \times \frac{x^2-y^2}{x^2+x y+y^2}\)

= \(\frac{(x-y)\left(x^2+x y+y^2\right)}{x+y} \times \frac{(x+y)(x-y)}{x^2+x y+y^2}\)

= \((x-y)^2\)

Example 3

Simplify: \(\frac{a}{a-b}+\frac{b}{a+b}+\frac{2 a b}{b^2-a^2} .\)

Solution:

Given \(\frac{a}{a-b}+\frac{b}{a+b}+\frac{2 a b}{b^2-a^2} .\).

= \(\frac{\mathrm{a}}{\mathrm{a}-\mathrm{b}}+\frac{\mathrm{b}}{\mathrm{a}+\mathrm{b}}+\frac{2 \mathrm{ab}}{\mathrm{b}^2-\mathrm{a}^2}\)

= \(\frac{a}{a-b}+\frac{b}{a+b}-\frac{2 a b}{a^2-b^2}\)

= \(\frac{a}{a-b}+\frac{b}{a+b}-\frac{2 a b}{(a+b)(a-b)}\)

= \(\frac{a(a+b)+b(a-b)-2 a b}{(a-b)(a+b)}\)

= \(\frac{a^2+a b+a b-b^2-2 a b}{(a-b)(a+b)}=\frac{a^2-b^2}{a^2-b^2}=1\)

 

Example 4

Simplify: \(\frac{1}{a^2-8 a+15}+\frac{1}{a^2-4 a+3}-\frac{2}{a^2-6 a+5}\)

Solution:

Given \(\frac{1}{a^2-8 a+15}+\frac{1}{a^2-4 a+3}-\frac{2}{a^2-6 a+5}\)

= a² – 8a + 15

= a² – 5a – 3a + 15

= a(a – 5) – 3 (a – 5)

= (a – 5) (a – 3) a² – 4a + 3

= a² – 3a – a + 3

= a(a – 3) – 1(a – 3)

= (a – 3) (a – 1) a² – 6a + 5

= a² – 5a – a + 5

= a(a – 5) – 1(a – 5)

= (a – 5) (a – 1)

Hence, the given expression

\(\frac{1}{a^2-8 a+15}+\frac{1}{a^2-4 a+3}-\frac{2}{a^2-6 a+5}\) = (a – 5) (a – 1)

Example 5

Simplify: \(\frac{8 a^3}{a^2+a b+b^2} \times \frac{a+b}{2 a\left(a^3+b^3\right)} \times \frac{a^4+a^2 b^2+b^4}{4 a^2} .\)

Solution:

Given \(\frac{8 a^3}{a^2+a b+b^2} \times \frac{a+b}{2 a\left(a^3+b^3\right)} \times \frac{a^4+a^2 b^2+b^4}{4 a^2} .\)

= \(\frac{8 a^3}{a^2+a b+b^2} \times \frac{a+b}{2 a\left(a^3+b^3\right)} \times \frac{a^4+a^2 b^2+b^4}{4 a^2}\)

= \(\frac{8 a^3}{a^2+a b+b^2} \times \frac{a+b}{2 a(a+b)\left(a^2-a b+b^2\right)}\times \frac{a^4+a^2 b^2+b^4}{4 a^2}\)

= \(\frac{8 a^3(a+b)\left(a^4+a^2 b^2+b^4\right)}{8 a^3(a+b)\left(a^4+a^2 b^2+b^4\right)}=1\)

 

Example: 6

Simplify: \(\frac{x-y}{x y}+\frac{y-z}{y z}+\frac{z-x}{z x} .\)

Solution: 

Given \(\frac{x-y}{x y}+\frac{y-z}{y z}+\frac{z-x}{z x} .\).

= \(\frac{x-y}{x y}+\frac{y-z}{y z}+\frac{z-x}{z x}\)

= \(\frac{x}{x y}-\frac{y}{x y}+\frac{y}{y z}-\frac{z}{y z}+\frac{z}{z x}-\frac{x}{z x}\)

= \(\frac{1}{y}-\frac{1}{x}+\frac{1}{z}-\frac{1}{y}+\frac{1}{x}-\frac{1}{z}=0\)

 

Example 7

Simplify: \(\frac{x-y}{x(x+y)} \div \frac{x^2+y^2}{2 x^2} \times \frac{2\left(x^4-y^4\right)}{x^2-2 x y+y^2}\)

Solution:

Given \(\frac{x-y}{x(x+y)} \div \frac{x^2+y^2}{2 x^2} \times \frac{2\left(x^4-y^4\right)}{x^2-2 x y+y^2}\)

= \(\frac{x-y}{x(x+y)} \div \frac{x^2+y^2}{2 x^2} \times \frac{2\left(x^4-y^4\right)}{x^2-2 x y+y^2}\)

= \(\frac{x-y}{x(x+y)} \times \frac{2 x^2}{x^2+y^2} \times \frac{2\left(x^4-y^4\right)}{x^2-2 x y+y^2}\)

= \(\frac{x-y}{x(x+y)} \times \frac{2 x^2}{x^2+y^2} \times \frac{2\left(x^2+y^2\right)(x+y)(x-y)}{(x-y)^2}\)

= 4x

 

Example 8

Simplify: \(\frac{x^2+3 x+2}{x^2+5 x+6} \times \frac{x^2+2 x-3}{x^2-4}\)

Solution:

Given \(\frac{x^2+3 x+2}{x^2+5 x+6} \times \frac{x^2+2 x-3}{x^2-4}\).

= \(\frac{x^2+3 x+2}{x^2+5 x+6} \times \frac{x^2+2 x-3}{x^2-4}\)

= \(\frac{x^2+2 x+x+2}{x^2+3 x+2 x+6} \times \frac{x^2+3 x-x-3}{x^2-4}\)

= \(\frac{x(x+2)+1(x+2)}{x(x+3)+2(x+3)} \times \frac{x(x+3)-1(x+3)}{(x+2)(x-2)}\)

= \(\frac{(x+1)(x+2)}{(x+2)(x+3)} \times \frac{(x+3)(x-1)}{(x+2)(x-2)}\)

= \(\frac{(x+1)(x-1)}{(x+2)(x-2)}=\frac{x^2-1}{x^2-4}\)

 

Example: 9

Simplify: \(\frac{x-2 y}{x y}+\frac{3 y-a}{a y}+\frac{3 x-2 a}{a x} \text {. }\)

Solution:

Given \(\frac{x-2 y}{x y}+\frac{3 y-a}{a y}+\frac{3 x-2 a}{a x} \text {. }\).

= \(\frac{x-2 y}{x y}+\frac{3 y-a}{a y}+\frac{3 x-2 a}{a x}\)

= \(\frac{a(x-2 y)+x(3 y-a)-y(3 x-2 a)}{a x y}\)

= \(\frac{a x-2 a y+3 x y-a x-3 x y+2 a y}{a x y}\)

= \(\frac{0}{a x y}=0\)

 

Example 10

Simplify: \(\frac{1}{x^2-3 x+2}+\frac{1}{x^2-5 x+6}+\frac{1}{x^2-4 x+3}\)

Solution:

Given

\(\frac{1}{x^2-3 x+2}+\frac{1}{x^2-5 x+6}+\frac{1}{x^2-4 x+3}\).

x2 – 3x + 2

= x2 – 2x – x +2

= x (x – 2) – 1 (x – 2)

= (x – 2)(x – 1)

x2 – 5x + 6 = x2 – 3x – 2x + 6

= x ( x – 3) – 2 (x – 3)

= (x – 3)(x – 2)

x2 – 4x + 3 = x2 -3x – x + 3

= x (x – 3) – 1 (x – 3)

= (x – 3)(x – 1)

∴ the given expression

= \(\frac{1}{(x-1)(x-2)}+\frac{1}{(x-2)(x-3)}+\frac{1}{(x-3)(x-1)}\)

= \(\frac{x-3+x-1+x-2}{(x-1)(x-2)(x-3)}\)

= \(\frac{3 x-6}{(x-1)(x-2)(x-3)}=\frac{3(x-2)}{(x-1)(x-2)(x-3)}\)

= \(\frac{3}{(x-1)(x-3)}=\frac{3}{x^2-4 x+3}\)

 

Example 11

Simplify: \(\frac{\frac{x^2}{5-x}+\frac{y^2}{5-y}+\frac{z^2}{5-z}+x+y+z}{\frac{x}{5-x}+\frac{y}{5-y}+\frac{z}{5-z}}\)

Solution:

Given

\(\frac{\frac{x^2}{5-x}+\frac{y^2}{5-y}+\frac{z^2}{5-z}+x+y+z}{\frac{x}{5-x}+\frac{y}{5-y}+\frac{z}{5-z}}\).

= \(\frac{\frac{x^2}{5-x}+x+\frac{y^2}{5-y}+y+\frac{z^2}{5-z}+z}{\frac{x}{5-x}+\frac{y}{5-y}+\frac{z}{5-z}}\)

= \(\frac{\frac{x^2+5 x-x^2}{5-x}+\frac{y^2+5 y-y^2}{5-y}+\frac{z^2+5 z-z^2}{5-z}}{\frac{x}{5-x}+\frac{y}{5-y}+\frac{z}{5-z}}\)

= \(\frac{\frac{5 x}{5-x}+\frac{5 y}{5-y}+\frac{5 z}{5-z}}{5-x}+\frac{y}{5-y}+\frac{z}{5-z}\)

= \(\text { 5. } \frac{\frac{x}{5-x}+\frac{y}{5-y}+\frac{z}{5-z}}{\frac{x}{5-x}+\frac{y}{5-y}+\frac{z}{5-z}}\)

= 5

 

Example 12

Simplify: \(\left(a+\frac{a x}{a-x}\right) \times\left(a-\frac{a x}{a+x}\right) \times \frac{a^2-x^2}{a^2+x^2}\)

Solution:

The given Expression \(\left(a+\frac{a x}{a-x}\right) \times\left(a-\frac{a x}{a+x}\right) \times \frac{a^2-x^2}{a^2+x^2}\)

= \(\left(a+\frac{a x}{a-x}\right) \times\left(a-\frac{a x}{a+x}\right) \times \frac{a^2-x^2}{a^2+x^2}\)

= \(\frac{a^2-a x+a x}{a-x} \times \frac{a^2+a x-a x}{a+x} \times \frac{a^2-x^2}{a^2+x^2}\)

= \(\frac{a^2}{a-x} \times \frac{a^2}{a+x} \times \frac{a^2-x^2}{a^2+x^2}\)

= \(\frac{a^4 \times\left(a^2-x^2\right)}{\left(a^2-x^2\right)\left(a^2+x^2\right)}=\frac{a^4}{a^2+x^2}\)

 

Example 13

Simplify: \(\frac{1+8 x^3}{(2-x)^2} \times \frac{4 x-x^3}{1-4 x^2} \div \frac{(1-2 x)^2+2 x}{2-5 x+2 x^2}\)

Solution:

The given expression \(\frac{1+8 x^3}{(2-x)^2} \times \frac{4 x-x^3}{1-4 x^2} \div \frac{(1-2 x)^2+2 x}{2-5 x+2 x^2}\)

= \frac{1+8 x^3}{(2-x)^2} \times \frac{4 x-x^3}{1-4 x^2} \times \frac{2-5 x+2 x^2}{(1-2 x)^2+2 x}

= \frac{1+(2 x)^3}{(2-x)^2} \times \frac{x\left(4-x^2\right)}{1-(2 x)^2} \times \frac{2-4 x-x+2 x^2}{1-4 x+4 x^2+2 x}

= \frac{(1+2 x)\left(1-2 x+4 x^2\right)}{(2-x)^2} \times \frac{x(2+x)(2-x)}{(1+2 x)(1-2 x)}\times \frac{2(1-2 x)-x(1-2 x)}{1-2 x+4 x^2}

= \frac{(1+2 x)\left(1-2 x+4 x^2\right)}{(2-x)^2} \times \frac{x(2+x)(2-x)}{(1+2 x)(1-2 x)}

= x(2 + x)

 

Example 14

Simplify: \(\frac{(b-c)^2}{(c-a)(a-b)}+\frac{(c-a)^2}{(a-b)(b-c)}+\frac{(a-b)^2}{(b-c)(c-a)} .\)

Solution:

The given expression

\(\frac{(b-c)^2}{(c-a)(a-b)}+\frac{(c-a)^2}{(a-b)(b-c)}+\frac{(a-b)^2}{(b-c)(c-a)} .\)

= \(\frac{(b-c)^3+(c-a)^3+(a-b)^3}{(a-b)(b-c)(c-a)}\)

= \(\frac{b^3-c^3-3 b c(b-c)+c^3-a^3-3 c a(c-a)+a^3-b^3-3 a b(a-b)}{(a-b)(b-c)(c-a)}\)

= \(-\frac{3}{(\mathrm{a}-\mathrm{b})(\mathrm{b}-\mathrm{c})(\mathrm{c}-\mathrm{a})}\{\mathrm{ab}(\mathrm{a}-\mathrm{b})+\mathrm{bc}(\mathrm{b}-\mathrm{c})+\mathrm{ca}(\mathrm{c}-\mathrm{a})\}\)

= \(-\frac{3}{(a-b)(b-c)(c-a)}\left\{a b(a-b)+b^2 c-b c^2+c^2 a-a^2 c\right\}\)

= \(-\frac{3}{(\mathrm{a}-\mathrm{b})(\mathrm{b}-\mathrm{c})(\mathrm{c}-\mathrm{a})}\left\{\mathrm{ab}(\mathrm{a}-\mathrm{b})-\mathrm{c}\left(\mathrm{a}^2-\mathrm{b}^2\right)+\mathrm{c}^2(\mathrm{a}-\mathrm{b})\right\}\)

= \(-\frac{3}{(\mathrm{a}-\mathrm{b})(\mathrm{b}-\mathrm{c})(\mathrm{c}-\mathrm{a})}\left\{\mathrm{ab}(\mathrm{a}-\mathrm{b})-\mathrm{c}(\mathrm{a}+\mathrm{b})(\mathrm{a}-\mathrm{b})+\mathrm{c}^2(\mathrm{a}-\mathrm{b})\right\}\)

= \(-\frac{3(\mathrm{a}-\mathrm{b})}{(\mathrm{a}-\mathrm{b})(\mathrm{b}-\mathrm{c})(\mathrm{c}-\mathrm{a})}\left\{\mathrm{ab}-\mathrm{ac}-\mathrm{bc}+\mathrm{c}^2\right\}\)

= \(-\frac{3(\mathrm{a}-\mathrm{b})}{(\mathrm{a}-\mathrm{b})(\mathrm{b}-\mathrm{c})(\mathrm{c}-\mathrm{a})}\{\mathrm{a}(\mathrm{b}-\mathrm{c})-\mathrm{c}(\mathrm{b}-\mathrm{c})\}\)

= \(-\frac{3(a-b)(b-c)(a-c)}{(a-b)(b-c)(c-a)}=\frac{3(a-b)(b-c)(c-a)}{(a-b)(b-c)(c-a)}=3\)

 

Example 15

Simplify: \(\frac{1}{x-1}+\frac{1}{x+1}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}\)

Solution:

Given

\(\frac{1}{x-1}+\frac{1}{x+1}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}\).

\(\frac{1}{x-1}+\frac{1}{x+1}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}=\frac{x+1+x-1}{(x-1)(x+1)}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}\)

= \(\frac{2 x}{x^2-1}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}=\frac{2 x^3+2 x+2 x^3-2 x}{\left(x^2-1\right)\left(x^2+1\right)}+\frac{4 x^3}{x^4+1}\)

= \(\frac{4 x^3}{x^4-1}+\frac{4 x^3}{x^4+1}=\frac{4 x^7+4 x^3+4 x^7-4 x^3}{\left(x^4-1\right)\left(x^4+1\right)}\)

= \(\frac{8 x^7}{\left(x^4\right)^2-(1)^2}=\frac{8 x^7}{x^8-1}\)

 

Example 16

Simplify: \(\frac{(b+c)\left(b^2+c^2-a^2\right)}{2 b c}+\frac{(c+a)\left(c^2+a^2-b^2\right)}{2 c a}+\frac{(a+b)\left(a^2+b^2-c^2\right)}{2 a b}\)

Solution:

Given

\(\frac{(b+c)\left(b^2+c^2-a^2\right)}{2 b c}+\frac{(c+a)\left(c^2+a^2-b^2\right)}{2 c a}+\frac{(a+b)\left(a^2+b^2-c^2\right)}{2 a b}\)

= \(\frac{1}{2}\left(\frac{\mathrm{b}+\mathrm{c}}{\mathrm{bc}}\right)\left(\mathrm{b}^2+\mathrm{c}^2-\mathrm{a}^2\right)+\frac{1}{2}\left(\frac{\mathrm{c}+\mathrm{a}}{\mathrm{ca}}\right)\left(\mathrm{c}^2+\mathrm{a}^2-\mathrm{b}^2\right)+\frac{1}{2}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{ab}}\right)\left(\mathrm{a}^2+\mathrm{b}^2-\mathrm{c}^2\right)\)

= \(\frac{1}{2}\left(\frac{1}{\mathrm{c}}+\frac{1}{\mathrm{~b}}\right)\left(\mathrm{b}^2+\mathrm{c}^2-\mathrm{a}^2\right)+\frac{1}{2}\left(\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{c}}\right)\left(\mathrm{c}^2+\mathrm{a}^2-\mathrm{b}^2\right)+\frac{1}{2}\left(\frac{1}{\mathrm{~b}}+\frac{1}{\mathrm{a}}\right)\left(\mathrm{a}^2+\mathrm{b}^2-\mathrm{c}^2\right)\)

= \(\frac{1}{2}\left[\begin{array}{c}
\frac{1}{c}\left(b^2+c^2-a^2+c^2+a^2-b^2\right)+\frac{1}{b}\left(b^2+c^2-a^2+a^2+b^2-c^2\right) \\
+\frac{1}{a}\left(c^2+a^2-b^2+a^2+b^2-c^2\right)
\end{array}\right]\)

= \(\frac{1}{2}\left[\frac{1}{c} 2 \mathrm{c}^2+\frac{1}{\mathrm{~b}} 2 \mathrm{~b}^2+\frac{1}{\mathrm{a}} 2 \mathrm{a}^2\right]=\frac{1}{2}[2 \mathrm{c}+2 \mathrm{~b}+2 \mathrm{a}]=\frac{2}{2}[\mathrm{c}+\mathrm{b}+\mathrm{a}]=\mathrm{a}+\mathrm{b}+\mathrm{c}\)

 

Algebra Chapter 9 Highest Common Factor

Elementary factor

If we cannot resolve a factor into any other factors, then such a factor is called an elementary factor. By factorization, we understand factorization as an elementary factor. The elementary factors of a³b³ are a and b because a and b cannot be resolved into any other factors.

Common factor

If two or more expressions are divisible by a factor then such a factor is called a common factor of those expressions. For example, if we consider two expressions a²b and ab²c then we see that a, b, and ab are their common factors.

The highest common factor

Two or more expressions may have more than one factor. Among the common factors of some quantities, the highest one (which is of the highest power) is called the Highest Common Factor or H.C.F. of those quantities. For example, the common factors of 2a²b³c², 3a⁴b²c³ and 4a⁵6³c² are a, b, c, a², b², c², ab, be, ca, a²b, a²c, b²c, be², abc, a²bc, ab²c, abc², a²b²c². Among them a²6²c² is of the highest power. Therefore, a²b²c² will be the H.C.F.

Process for the determination of H.C.F.

1. At first, all the given expressions are resolved into factors.

2. The required H.C.F. is the product of the common elementary factors of the highest dimension that exactly divide each of the given expressions.

3. If numerical coefficients appear before the alphabetic expressions then after finding the H.C.F. of alphabetic expressions the arithmetical H.C.F. of the numerical coefficients is written before it.

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 9 Highest Common Factor Some Examples

Example 1

To find the H.C.F. of 3xy²z², 2yz²x^2, and x²y²z.

Solution :

Given 3xy²z², 2yz²x^2, And x²y²z

x, y, and z are the elementary factors of these three expressions.

The highest powers of them which exactly divide the given expressions are x, y, z.

∴ H.C.F. = xyz

Example 2

To find, the H.C.F. of 16a²b³x⁴y⁵, 40a³b²x³y⁴, 24a⁵b⁵x³y⁴.

Solution :

Given: 16a²b³x⁴y⁵, 40a³b²x³y⁴, 24a⁵b⁵x³y⁴

H.C.F. of 16, 40, and 24 = 8.

a, b, x, y are common elementary factors.

The highest powers of them which exactly divide the expressions are a², b², x³, and y⁴.

∴ The required H.C.F. = 8a²b²x³y⁴

Example 3

Find the H.C.F. of x⁴ – 1, x⁴ – x³ + x -1.

Solution :

Given x⁴ – 1, x⁴ – x³ + x -1

First expression

= (x⁴ – 1)

= (x²+1)(x² – 1)

= (x²+1)(x+1)(x-1)

Second expression

= x⁴ – x³ + x – 1

= x³ (x – 1) + (x -1)

= (x – 1)(x³+1)

= (x-1)(x + 1)(x²-x + 1)

∴ The required H.C.F.

= (x +1)(x – 1)

= x² – 1

x⁴ – 1, x⁴ – x³ + x -1 = x² – 1

Example 4

Find the H.C.F. of x³ – 5x² + 6x, x³ + 4x² – 12x, x³ – 9x² + 14x.

Solution :

Given: x³ – 5x² + 6x, x³ + 4x² – 12x, x³ – 9x² + 14x

First expression

= x(x² – 5x + 6)

= x(x² – 2x – 3x + 6)

= x {x(x – 2) – 3(x – 2)}

= x (x – 2)(x – 3)

Second expression

= x (x² + 4x – 12)

= x (x² – 2x + 6x – 12)

= x {x (x – 2) + 6(x – 2)}

= x (x – 2) (x + 6)

Third expression

= x (x² – 9x +14)

= x (x² – 2x – 7x + 14)

= x {x (x – 2) – 7(x – 2)}

= x (x – 2) (x – 7)

.’. The required H.C.F. = x (x – 2)

x³ – 5x² + 6x, x³ + 4x² – 12x, x³ – 9x² + 14x = x (x – 2)

Example 5

Find the H.C.F. of a² – 1, a³ – 1 and a² + a – 2.

Solution :

Given a² – 1, a³ – 1 And a² + a – 2

First expression

= a² – 1

= (a + 1)(a – 1)

Second expression

= a³ – 1

= (a – 1)(a² + a + 1)

Third expression

= a² + a- 2

= a²-a + 2a-2

= a (a -1) + 2 (a – 1)

= (a – 1)(a + 2)

The required H.C.F. = a – 1

a² – 1, a³ – 1 And a² + a – 2 = a – 1

Example 6

Find the H.C.F. of x³ – 8, x² + 3x – 10, x³ + 2x² – 8x . 

Solution :

Given x³ – 8, x² + 3x – 10, x³ + 2x² – 8x

First expression

= x³ – 8

= (x)³ – (2)³

= (x – 2){(x)² + x.2 + (2)²}

= (x – 2)(x² + 2x + 4)

Second expression

= x² + 3x – 10

= x² + 5x – 2x – 10

= x ( x + 5) – 2(x + 5)

= (x+ 5)(x – 2)

Third expression

= x³ + 2x² – 8x

= x (x² + 2x – 8)

= x {x² + 4x – 2x – 8}

= x{x(x + 4) – 2(x + 4)}

= x (x + 4)(x – 2)

∴ The required H.C.F. = x – 2

x³ – 8, x² + 3x – 10, x³ + 2x² – 8x = x – 2

Example 7

Find the H.C.F. of 5(x³ – x), 4(x⁵ – x²), 7(x⁴ – 1).     

Solution :

Given 5(x³ – x), 4(x⁵ – x²), 7(x⁴ – 1)

First expression

= 5(x² – x)

= 5x (x² – 1)

= 5x (x + 1)(x – 1)

Second expression

= 4(x⁵ – x²)

= 4x² (x³ – 1)

= 4x² (x – 1)(x² + x + 1)

Third expression

= 7(x⁴ – 1)

= 7(x² + 1)(x² – 1)

= 7(x² + 1)(x + 1) (x – 1)

∴ The required H.C.F. = x – 1

5(x³ – x), 4(x⁵ – x²), 7(x⁴ – 1). = x – 1

Example 8

If the H.C.F. of x² + px + q and x² + px + q’ be x + a then show that (p – p’) a = q – q.

Solution :

Given x² + px + q And x² + px + q’ be x + a

x + a is the H.C.F. of the two given expressions therefore, it is the factor of both expressions.

Therefore, the value of the expressions will be equal to 0 if its value is 0.

Now, see x + a= 0 if x = -a,  therefore, both the expressions will be 0 if we put x = – a.

\(\text { Therefore, } \quad a^2-a p+q=0\) \(\text { and } \quad a^2-a p^{\prime}+q^{\prime}=0 \ldots \ldots \ldots \text { (2) }\)

————————————————————————-

\( \text { (subtracting) }-a p+a p^{\prime}+q-q^{\prime}=0,\)

or, – a(p – p’) = – (q – q’)

or, a(p – p’) = q – q’

or, ( p – p’) a = q – q’.

Example 9

The H.C.F, and L.C.M. of the two expressions are a² – a – 2 and a⁴ – 5a + 4. If one of the expressions be a³ + a² + a – 4, find the other.

Solution :

Given 

The H.C.F, and L.C.M. of the two expressions are a² – a – 2 and a⁴ – 5a + 4

one of the expressions a³ + a² + a – 4

The H.C.F, and L.C.M. of the two expressions are a² – a – 2 and a⁴ – 5a + 4

The product of the two expressions

= Their H.C.F. x L.C.M.

Here, the product of the two expressions

= (a² – a – 2)(a⁴ – 5a + 4)

and one expression = a³ + a² + a – 4.

.’. The required other expression

= (a² – a – 2)(a⁴ – 5a + 4) / (a³ + a² + a – 4)

= (a² – a – 2) (a -1)

= a³ – 2a² – a + 2.

Example 10

The H.C.F. and L.C.M. of two quadratic expressions are a + 1 and + 2a – a – 2, find the expressions.

Solution :

Given

The H.C.F. and L.C.M. of two quadratic expressions are a + 1 and + 2a – a – 2

Here, H.C.F. = a + 1

and L.C.M. = a³ + 2a² – a – 2

= a²(a + 2) – 1 (a + 2)

= (a² – 1)(a + 2) = (a + 1)(a – 1)(a + 2).

It is found that other than H.C.F. (a + 1), the two factors of L.C.M.  are a – 1 and a + 2.

Therefore, the required quantities are (a + 1)(a – 1) and (a + 1) (a +2),

that means a² – 1 and a² + 3a + 2.

Algebra Chapter 8 Lowest Common Multiple

Lowest Common Multiple Introduction

In arithmetic, you have learned how to find the H.C.F. i.e., the Highest Common Factor, and the L.C.M. i.e., the Lowest Common Multiple of numbers. In a similar way, we can find the H.C.F. and L.C.M. of two or more algebraic expressions. In this chapter, our aim is to find the L.C.M. of algebraic expressions by the method of factorization.

Multiple

When an expression is divisible by another expression, then the first expression is called a multiple of the second expression. For example, x²y² is a multiple of the expressions, x, y, xy, x²y, xy², etc.

Common Multiple

When an expression is divisible by each of two or more expressions, then the first expression is called the common multiple of those expressions. For example, xy, x²y², xy², etc. are divisible by each of x and y and hence they are common multiples of x and y.

The Lowest Common Multiple

Among the common multiples of some quantities, the lowest one (which is of the lowest power) is called the Lowest Common Multiple or L.C.M. of those quantities.

For Example :

L.C.M. of ab, a²b, and ab² is a²b². Here a²b² is divisible by each of the quantities ab, a²b, and ab². Moreover, a²b² is of minimum power among other quantities which are divisible by ab, a²b, and ab² (for example, a³b², a²b³, a⁴6⁴, etc.).

Determination of L.C.M. by factorization

1. First of all, the given expressions are resolved into factors.

2. The L.C.M. is the product of all kinds of factors in their highest powers.

3. If numerical coefficients appear before the alphabetic expressions then after finding the L.C.M. of the alphabetic expressions the arithmetical L.C.M. of the numerical coefficients is written before it.

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 8 Lowest Common Multiple Some Examples of L.C.M.

Example 1

Find the L.C.M. of x²yz, xy²z, and xyz².

Solution :

Given: x²yz, xy²z, And xyz²

Here, the factor with the highest power of x is the x²

The factor with the highest power of y is y²

The factor with the highest power of z is z²

Hence, the required

L.C.M. =x²y²z²

Example 2

Find the L.C.M. of 4a²6c², 8ab²c³ and 16a⁴b³c.

Solution :

Given: 4a²6c², 8ab²c³ And 16a⁴b³c.

The L.C.M. of 4, 8, and 16 is 16.

The factor with the highest power of a is a⁴

The factor with the highest power of b is b³

The factor with the highest power of c is c³

Hence, the required L.C.M. = 16a⁴b³c³

Example 3

Find the L.C.M. of a³b – ab³ and a³b² + a²b³.

Solution:

Given  a³b – ab³ And a³b² + a²b³

First expression = a³b – ab³

= ab(a² – b²) = ab(a +b) (a – b)

Second expression

= a³6² + a²b³

= a²b²(a + b)

Hence, the required L.C.M.

= a²b²(a + b) (a – b)

= a²b²(a² – b²)

The required L.C.M = a²b²(a² – b²)

Example 4

Find the L.C.M. of x² – 4x + 3 and x² – 5x + 6.

Solution :

Given x² – 4x + 3 And x² – 5x + 6

First expression = x² – 4x + 3

= x²-3x-x + 3

= x(x – 3) – l(x – 3)

= (x – 3) (x – 1)

Second expression

= x² – 5x + 6

= x² – 3x – 2x + 6

= x(x – 3) – 2(x – 3)

= (x-3)(x-2)

Hence, the required L.C.M. = (x – 1) (x – 2) (x – 3)

Example 5

Find the L.C.M. of 8(a²– 4), 12(a³ + 8) and 36(a² – 3a – 10).

Solution :

Given 8(a²– 4), 12(a³ + 8) And 36(a² – 3a – 10).

First expression

= 8(a² – 4)

= 2³ x {(a)² – (2)²}

= 2³x (a+2) (a- 2)

Second expression

= 12(a³ + 8)

= 2² x 3 x {(a)³ + (2)³}

= 2² x 3 x (a + 2) (a² – 2a + 4)

Third expression

= 36 (a² – 3a – 10)

= 2² x 3² x {a² – 5a + 2a – 10}

= 2² x 3² x {a(a – 5) + 2(a – 5)}

= 2² x 3² x (a – 5) (a + 2)

Hence, the required L.C.M.

= 2³ x 3² x (a + 2) (a – 2) (a²-2a + 4) (a – 5)

= 72 (a + 2) (a – 2) (a – 5) (a² – 2a + 4)

The required L.C.M = 72 (a + 2) (a – 2) (a – 5) (a² – 2a + 4)

Example 6

Find the L.C.M. of x³– 1, x⁴– 1,x⁴ + x²+ 1.

Solution:

Given x³– 1, x⁴– 1,x⁴ + x²+ 1

First expression

= x³ – 1

= (x)³ – (1)³

= (x – 1) (x² + x + 1)

Second expression

= x⁴ – 1

= (x²)² – (l)²

= (x² + 1) (x² – 1)

= (x²+1)(x+1)(x-1)

Third expression

= x⁴ + x² + 1

= (x²)² + 2.x².1+ (1)² -x?

= (x² + 1)² – (x)²

= (x²+1+x)(x²+ 1-x)

= (x² + x + 1) (x² – x + 1)

Hence, the required L.C.M.

= (x – 1) (x² + x +1) (x +1) (x² + 1) (x² – X + 1)

= (x – 1) (x + 1) (x² + 1) (x² + x + 1) (x² – x + 1)

The required L.C.M = (x – 1) (x + 1) (x² + 1) (x² + x + 1) (x² – x + 1)

Example 7

Find the L.C.M. of x² – y², x³ – y³, 3X² – 5x.y+ 2y².

Solution :

Given x² – y², x³ – y³, 3X² – 5x.y+ 2y²

First expression

= x² – y²

= (x + y) (x – y)

Second expression

= x³ – y³

= (x – y) (x² + xy +y²)

Third expression

= 3X² – 5x² + 2y²

= 3X² – 3xy – 2x² + 2y²

= 3x(x -y)~ 2y(x – y)

= (x-y) (3x – 2y)

Hence, the required L.C.M.

= (x+y) (x-y) (x² + xy +y²) (3x- 2y)

= (x+y) (x-y)(3x- 2y)(x² + xy +y²)

The required L.C.M = (x+y) (x-y)(3x- 2y)(x² + xy +y²)

Example 8

Find the L.C.M. of x² – y² – z² + 2yz, (x + y – z)² and x² + z² – y² + 2xz.

Solution :

Given x² – y² – z² + 2yz, (x + y – z)² And x² + z² – y² + 2xz.

First expression = x² – y² – z² + 2yz = x² – (y² – 2yz + z²)

= (x)² -xy-z)² = (x + y-z) (x-y +z)

Second expression

= (x + y – z)² 

Third expression

= x² + z² – y² + 2xz

= x² + 2xz + z² -y²

= (x + z)² – (y)²

= (x + z + y) (x + z – y)

= (x + y + z) (x – y + z)

Hence, the required L.C.M.

= (x + y- z)² (x-y+z) (x+y+z)

= (x-y+z) (x+y+z) (x + y- z)²

The required L.C.M = (x-y+z) (x+y+z) (x + y- z)²

Example 9

Find the L.C.M. of x³ – 16x, 2x³ + 9x² + 4x and x + 4.

Solution :

Given x³ – 16x, 2x³ + 9x² + 4x And x + 4.

First expression

= x³ – 16x

= xfx² – 16)

= x{(x)² – (4)²}

= x(x + 4)(x – 4)

Second expression

= 2x³ + 9x² + 4x

= x(2x² + 9x + 4)

= x(2x² + 8x + x + 4)

= x{2x(x + 4) + l(x + 4)}

= x(x + 4)(2x + 1)

Third expression

= x + 4

Hence, the required L.C.M.

= x(x + 4)(x – 4)(2x + 1)

The required L.C.M = x(x + 4)(x – 4)(2x + 1)

Example 10

Find the L.C.M. of a² – 6² + c² + 2ac, a² – 6² – c² + 26c and ab + ac + b² – c².

Solution :

Given a² – 6² + c² + 2ac, a² – 6² – c² + 26c And ab + ac + b² – c².

First expression

= a² – b² + c² + 2ac

= a² + 2ac + c² – b²

= (a + c)² – (b)²

= (a + c + b)(a + c – b)

= (a + b + c)(a – b + c)

Second expression

= a² – b² – c² + 2bc

= a² – (b² – 2bc + c²)

= (a)² – (b – c)²

= (a + b – c)(a – b + c)

Third expression

= ab + ac + b² – c²

= a(b + c) + (b + c)(b – c)

= (b + c)(a + b – c)

Hence, the required L.C.M.

= (a + b + c)(a – b + c)(a + b – c)(b + c)

= (a + b + c)(a – b + c)(a + b – c)(b + c)

The required L.C.M = (a + b + c)(a – b + c)(a + b – c)(b + c)

Example 11

Find the L.C.M. of x² – xy – 2y², 2x² – 5xy + 2y² and 2x² + xy – y².

Solution :

Given x² – xy – 2y², 2x² – 5xy + 2y² And 2x² + xy – y².

First expression

= x² – xy – 2y²

= x² – 2xy + xy – 2y²

= x(x – 2y) + y(x – 2y)

= (x- 2y)(x +y)

Second expression

= 2X² – 5xy + 2y²

= 2x² – 4xy – xy + 2y²

= 2x(x – 2y) – y(x – 2y)

= (x-2y)(2x-y)

Third expression

= 2x² + xy – y²

= 2x² + 2xy – xy -y²

= 2x(x + y) – y(x + y)

= (x + y)(2x – y)

Hence, the required L.C.M.

= (x – 2y)(x + y)(2x – y)

The required L.C.M = (x – 2y)(x + y)(2x – y)

Example 12

Find the L.C.M. of 3(x² – 9), 9(x³ + 27) and 27(x2 – 3x + 9).

Solution :

Given 3(x² – 9), 9(x³ + 27) and 27(x2 – 3x + 9)

First expression

= 3(x² – 9)

= 3{(x)² – (3)²}

= 3(x + 3)(x – 3)

Second expression

= 9(x³ + 27)

= 9{(x)³ + (3)³}

= 3² (x + 3)(x² – 3x + 9)

Third expression

= 27(x² – 3x + 9)

= 3³ (x² – 3x + 9)

Hence, the required L.C.M.

= 3³ (x + 3)(x – 3)(x² – 3x + 9)

= 27(x + 3)(x – 3)(x² – 3x + 9)

The required L.C.M = 27(x + 3)(x – 3)(x² – 3x + 9)

Algebra Chapter 7 Factorisation By Breaking The Middle Term

Factorisation By Breaking The Middle Term Introduction

In the previous chapter, we resolved the algebraic expressions into factors by using the formulae. Here also our aim is to resolve the algebraic expressions into factors but by using a different method— the method of breaking the middle term. Although this method is easier than the method discussed in the previous chapter, we cannot apply this method to all algebraic expressions due to some restrictions. This method is applicable only to those algebraic expressions which have exactly three terms and the power of the variable of the first term is twice that of the second when arranged in descending order of the power.

Factorization of the expressions of the form x² + px + q

Any algebraic expression of form \(x^2+p x+q\)  is called a quadratic expression since the highest power of x is 2. This type of expression can be factorized by splitting the middle coefficients. Here we should find two quantities such that their algebraic sum is p and product is q Let us consider the expression,

x + (a + b)x + ab.

It is of the form \(x^2+p x+q\), where a + b -p and ab = q.

Now, \(x^2+(a+b) x+a b\)

= \(x^2+a x+b x+a b\)

= x (x + a) + b(x + a)

= (x + a) (x + b).

So we may conclude that x² + px + q can be resolved into two linear factors (x + a) and (x + 6), when a + b = p and ab = q.

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 7 Factorization By Breaking The Middle Term Some Examples

Example 1

Factorize : \(x^2+7 x+12\)

Solution :

Given: \(x^2+7 x+12\)

\(x^2+7 x+12\)

= \(x^2\) + (4 + 3)x + 12

= \(x^2\) + 4x + 3x + 12

= x (x + 4) + 3(x + 4)

= (x + 4) (x + 3)

\(x^2\) + 7x + 12 = \(x^2\) + (4 + 3)x + 12

Example 2

Factorize : \(x^2-3 x-10\).

Solution :

Given: \(x^2-3 x-10\)

\(x^2-3 x-10\)

= \(x^2 – (5 – 2)x – 10\)

= \(x^2 – 5x + 2x – 10\)

= x(x – 5) + 2(x – 5)

= (x – 5) (x + 2)

\(x^2-3 x-10\) = (x – 5) (x + 2)

Example 3

Factorize : \(x^2-9 x+20\)

Solution :

Given: \(x^2-9 x+20\)

\(x^2-9 x+20\)

= \(x^2 – (5 + 4)x + 20\)

= \(x^2 – 5x – 4x + 20\)

= x(x – 5) – 4(x – 5)

= (x – 5) (x – 4)

\(x^2 – 9x + 20\) = (x – 5) (x – 4)

Example 4

Factorize : \(x^2+2 x-35\)

Solution :

Given \(x^2+2 x-35\)

\(x^2+2 x-35\)

= \(x^2+(7-5) x-35 s=x^2+7 x-5 x-35\) = x(x + 7) – 5(x + 7)

= (x + 7) (x – 5)

\(x^2+2 x-35\) = (x + 7) (x – 5)

Example 5

Factorize : 

Solution:

Given: \(x^2+20 x y+75 y^2\)

\(x^2+20 x y+75 y^2\)

= \(x^2+(15+5) x y+75 y^2\)

= \(x^2+15 x y+5 r y+75 y^2\)

= x(x + 15y) + 5y(x + 15y)

= (x + 15y) (x + by)

\(x^2+20 x y+75 y^2\). = (x + 15y) (x + by)

Example 6

Factorize : \((x+y)^2-11(x+y)+30\)

Solution :

Given: \((x+y)^2-11(x+y)+30\)

\((x+y)^2-11(x+y)+30\)

= \((x+y)^2\) – 6(x + y) – 5(x + y) + 30

= (x + y) (x + y – 6) – 5(x + y – 6)

= (x + y- 6) (x +y- 5)

\((x+y)^2-11(x+y)+30\) = (x + y- 6) (x +y- 5)

Example 7

Factorize : \((a+b)^2+(a+b)-56\)

Solution:

Given: \((a+b)^2+(a+b)-56\)

\((a+b)^2+(a+b)-56\)

= (a + b)² + 8(a + b) – 7(a + b) – 56

= (a + b) (a + b + 8) – 7(a + 6 + 8)

= (a + b + 8) (a + b – 7)

\((a+b)^2+(a+b)-56\) = (a + b + 8) (a + b – 7)

Example 8

Factorize : \(x^2+x-(a+1)(a+2)\)

Solution :

Given: \(x^2+x-(a+1)(a+2)\)

\(x^2+x-(a+1)(a+2)\)

= \(x^2\) + {(a + 2) – (a + 1)}x – (a + 1)(a + 2)

= \(x^2\) + (a + 2)x – (a + 1)x – (a + 1) (a + 2)

= x(x + a + 2) – (a + 1) (x + a + 2)

= (x + a + 2) (x – a – 1)

\(x^2\)+x-(a+1)(a+2) = (x + a + 2) (x – a – 1)

Example 9

Factorize : \(x^4-13 x^2+42\)

Solution :

Given: \(x^4-13 x^2+42\)

\(x^4-13 x^2+42\)

= \(x^4-(6+7) x^2+42\)

= \(x^4-6 x^2-7 x^2+42\)

= \(x^2\left(x^2-6\right)-7\left(x^2-6\right)\)

= \(\left(x^2-6\right)\left(x^2-7\right)\)

\(x^4-13 x^2+42=\left(x^2-6\right)\left(x^2-7\right)\)

Example 10

Factorize : \(x^6-10 x^3+16\)

Solution :

Given:

\(x^6-10 x^3+16\)

= \(x^6-(8+2) x^3+16\)

= \(x^6-8 x^3-2 x^3+16\)

= \(x^3\left(x^3-8\right)-2\left(x^3-8\right)\)

= \(\left(x^3-8\right)\left(x^3-2\right)\)

= \(\left\{(x)^3-(2)^3\right\}\left(x^3-2\right)\)

= \((x-2)\left(x^2+2 x+4\right)\left(x^3-2\right)\)

\(x^6-10 x^3+16=(x-2)\left(x^2+2 x+4\right)\left(x^3-2\right)\)

Example 11

Factorize : (p – 1) (p – 2) (p + 3) (p + 4) + 6.

Solution:

Given

(p – 1) (p – 2) (p + 3) (p + 4) + 6

(p – 1) (p – 2) (p + 3) (p + 4) + 6

= {(p – 1) (p + 3} {(p – 2) (p + 4)} + 6

= (p² + 3p – p – 3) (p² + 4p – 2p – 8) + 6

= (p² + 2p – 3) (p² + 2p – 8) + 6

Let, p² + 2p = a.

Then the given expression

= (a-3) (a-8)+ 6 = a² – 8a – 3a + 24 + 6

= a² – 11a + 30 = a² – (6 + 5)a + 30

= a² – 6a – 5a + 30

= a(a – 6) – 5(a – 6)

= (a – 6) (a – 5)

= (p² + 2p – 6) (p² + 2p – 5)             [∵ putting the value of a]

(p – 1) (p – 2) (p + 3) (p + 4) + 6 = (p² + 2p – 6) (p² + 2p – 5)

Example 12

Factorize : p2 + ( a+1/a)p + 1.

Solution:

Given  p2 + ( a+1/a)p + 1.

p2 – (a+1/a)p + 1

=p2 – a . p – 1/a . p + 1/a . a

= p(p-a) – 1/a (p-a)

= (p-a)(p – 1/a)

p2 + ( a+1/a)p + 1. = (p-a)(p – 1/a)

Example 13

Factorize : \(x^2\) – bx – (a + 36)(a + 26).

Solution :

Given \(x^2\) – bx – (a + 36)(a + 26).

\(x^2\) – bx – (a + 3b)(a + 2b)

= \(x^2\) – {(a + 3b) – (a + 2b)}x – (a + 3b)(a + 2b)

= \(x^2\) – (a + 3b)x +(a + 2b)x-(a+3b)(a+2b)

= x{x – a – 3b} + (a + 2b){x – a – 3b}

= (x – a – 3b)(x + a + 2b)

\(x^2\) – bx – (a + 36)(a + 26). = (x – a – 3b)(x + a + 2b)

Example 14

Factorize : \((x+y)^2-5 x-5 y+6\)

Solution :

Given \((x+y)^2-5 x-5 y+6\)

\((x+y)^2-5 x-5 y+6\)

= \((x+y)^2-5 x-5 y+6\)

Let, x + y = a.

Then the given expression

= \(a^2-5 a+6=a^2-2 a-3 a+6\)

= a(a – 2) – 3 (a – 2) = (a – 2) (a – 3)

= (x + y-2)(x + y-3)         [∵ putting the value of a ]

\((x+y)^2-5 x-5 y+6\) = (x + y-2)(x + y-3)

Example 15

Factorize : (x + 1)(x + 3)(x – 4)(x – 6) + 24.

Solution :

Given  (x + 1)(x + 3)(x – 4)(x – 6) + 24

= (x + l)(x – 4)(x + 3)(x – 6) + 24

= (x² – 4x + x – 4XX² – 6x + 3x – 18) + 24

= (x² – 3x – 4)(x² – 3x – 18) + 24

Let, x² – 3x = a.

Then the given expression

= a² – 18a – 4a + 72 + 24

= a² – 22a + 96

= a² – 6a – 16a + 96

= a(a – 6) — 16(a — 6)

= (a – 6) (a – 16)

= (x²-3x-6)(x²-3x- 16)           [∵ putting the value of a]

(x + 1)(x + 3)(x – 4)(x – 6) + 24 = (x²-3x-6)(x²-3x- 16)

Factorization of the expressions of the form ax ²+ bx +c

This type of quadratic expression can also be factorized by splitting the middle coefficients. Here we should find two quantities such that their algebraic sum is b and the product is ac.

Algebra Chapter 7 Factorization By Breaking The Middle Term Some Examples

Example 1

Factorize : 3x² + 8x + 5.

Solution :

Given: 3X² + 8x + 5

3X² + 8x + 5

= 3X² + (3 + 5)x + 5

= 3x² + 3x + 5x + 5

= 3x(x + 1) + 5(x + 1)

= (x + 1) (3x + 5)

3X² + 8x + 5 = (x + 1) (3x + 5)

Example 2

Factorize : 6x² + x – 40.

Solution:

Given 6x² + x – 40.

6x² + x – 40

= 6x² + (16 – 15)x – 40

= 6x² + 16x – 15* – 40

= 2x(3x + 8) – 5(3x + 8)

= (3x + 8) (2x – 5)

6x² + x – 40. = (3x + 8) (2x – 5)

Example 3

Factorize : 10x² – x – 24.

Solution :

Given 10x² – x – 24.

10x² – x – 24

= 10x² + (- 16 + 15)x – 24

= 10x² – I6x + 15x – 24

= 2x(5x – 8) + 3(5x – 8)

= (5x – 8) (2x + 3)

10x² – x – 24. = (5x – 8) (2x + 3)

Example 4

Factorize : 63x – 59x + 10.

Solution :

Given 63x – 59x + 10.

63x² – 59x + 10

= 63x² + (- 45 – 14)x + 10

= 63x² – 45x – 14x + 10

= 9x (7x – 5) – 2(7x – 5)

= (7x – 5) (9x – 2)

63x² – 59x + 10 = (7x – 5) (9x – 2)

Example 5

Factorize : 10x² + 31xy + 24y².

Solution :

Given 10x² + 31xy + 24y².

10x² + 31xy + 24y²

= 10x² + (15 + 16)xy + 24y²

= 10x² + 15xy + 16xy + 24y²

= 5x(2x + 3y) + 8y (2x + 3y)

= (2x + 3y) (5x + 8y)

10x² + 31xy + 24y². = (2x + 3y) (5x + 8y)

Example 6

Factorize : 21 (a + b)² + 8(a + b) – 45.

Solution :

Given 21 (a + b)² + 8(a + b) – 45.

21(a + b)² + 8(a + 6) – 45

= 21(a + b)² + 35(a + b) – 27(a + b) – 45

= 7(a + b) {3(a + b) + 5} – 9 {3(a + b) + 5}

= {3(a + b) + 5} (7(a + b) – 9}

= (3a + 35 + 5) (7a + 75-9)

21 (a + b)² + 8(a + b) – 45. = (3a + 35 + 5) (7a + 75-9)

Example 7

Factorize : 15(x + y)² – 26(x + y) + 8.

Solution :

Given 15(x + y)² – 26(x + y) + 8.

15(x + y)² – 26(x + y) + 8

= 15(x + y)² – 20(x + y) – 6(x + y) + 8

= 5(x + y) {3(x + y) – 4} -2{3(x + y) – 4}

= {3(x + y) – 4} {5(x + y) – 2}

= (3x + 3y-4)(5x + 5y-2)

15(x + y)² – 26(x + y) + 8. = (3x + 3y-4)(5x + 5y-2)

Example 8

Factorize : (a – 1)x² + a²xy + (a + 1)y².

Solution :

Given (a – 1)x² + a²xy + (a + 1)y².

(a – 1)x² + a²xy + (a + 1)y²

= (a – 1)x² + {(a² — 1) + l}xy + (a + 1)y²

= (a – 1)x² + (a² – 1):xy + xy + (a + 1)y²

= (a – 1)x {x + (a + l)y} + y{x + (a + 1)y}

= {x + (a + 1)y} {(a – 1)x + y}

= (x + ay + y) (ax-x +y)

(a – 1)x² + a²xy + (a + 1)y². = (x + ay + y) (ax-x +y)

Example 9

Factorize : 6x⁴ + 17x² – 45.

Solution:

Given 6x⁴ + 17x² – 45.

6x⁴ + 17x² – 45

= 6x⁴ + (27 – 10)x² – 45

= 6x⁴ + 27x² – 10x² – 45

= 3x²(2x² + 9) – 5(2x² + 9)

= (2x² + 9) (3x² – 5)

6x⁴ + 17x² – 45. = (2x² + 9) (3x² – 5)

Example 10

Factorize : 21x⁶ — 29x³ +10.

Solution :

Given 21x⁶ — 29x³ +10.

2 1x⁶ – 29x³ + 10

= 21x⁶ – (14 + 15)x³ + 10

= 2 1x⁶ – 14x³ – 15x³ + 10

= 7x³(3x³ – 2) – 5(3x³ – 2)

= (3x³ – 2) (7x³ — 5)

21x⁶ — 29x³ +10. = (3x³ – 2) (7x³ — 5)

Example 11

Factorize : 5{a²-b²)²— 8ab (a² – b²) – 13a²b².

Solution :

Given 5{a²-b²)²— 8ab (a² – b²) – 13a²b².

Let a – b = x and ab = -y

To the given expression

= 5x² – 8xy – 13y²

= 5x² – (13 – 5)xy – 13y2

= 5x² – 13xy + 5xy – 13y²

= x(5x – 13y) + y(5x – 13;y)

= (5x – 13y) (x + y)

= {5(a² – b²) – 13ab} {a² – b² + ab}

= (5a² – 5b² – 13a6) (a² – b² + ab)

5{a²-b²)²– 8ab (a² – b²) – 13a²b². = (5a² – 5b² – 13ab) (a² – b² + ab)

Example 12

Factorize : (x + 1) (x + 2) (3x— 1)(3x – 4) + 12.

Solution :

Given (x + 1) (x + 2) (3x— 1)(3x – 4) + 12.

(x + 1) (x + 2) (3x-l) (3x – 4) + 12

= {(x + 1) (3x – 1)} {(x + 2) (3x – 4)} + 12

= (3x² – x + 3x – 1) (3x² – 4x + 6x – 8) + 12

= (3x² + 2x- 1) (3x² + 2x – 8) + 12 Let, 3x² + 2x = a

The given expression

= (a – 1) (a – 8) + 12

= a² – 8a – a + 8 + 12

= a² – 9a + 20

= a – 5a – 4a + 20

= a(a -5)- 4 (a – 5)

= (a – 5) (a – 4)

= (3x² + 2x – 5) (3x² + 2x – 4)

= (3x² + 5x – 3x – 5) (3x² + 2x – 4)

= {x(3x + 5) -1(3x + 5)} (3x² + 2x – 4)

= (3x + 5) (x- 1) (3x² + 2x- 4)

(x + 1) (x + 2) (3x – 1)(3x – 4) + 12. = (3x + 5) (x – 1) (3x² + 2x – 4)