Ameerun

Algebra Chapter 8 Lowest Common Multiple

Lowest Common Multiple Introduction

In arithmetic, you have learned how to find the H.C.F. i.e., the Highest Common Factor, and the L.C.M. i.e., the Lowest Common Multiple of numbers. In a similar way, we can find the H.C.F. and L.C.M. of two or more algebraic expressions. In this chapter, our aim is to find the L.C.M. of algebraic expressions by the method of factorization.

Multiple

When an expression is divisible by another expression, then the first expression is called a multiple of the second expression. For example, x²y² is a multiple of the expressions, x, y, xy, x²y, xy², etc.

Common Multiple

When an expression is divisible by each of two or more expressions, then the first expression is called the common multiple of those expressions. For example, xy, x²y², xy², etc. are divisible by each of x and y and hence they are common multiples of x and y.

The Lowest Common Multiple

Among the common multiples of some quantities, the lowest one (which is of the lowest power) is called the Lowest Common Multiple or L.C.M. of those quantities.

For Example :

L.C.M. of ab, a²b, and ab² is a²b². Here a²b² is divisible by each of the quantities ab, a²b, and ab². Moreover, a²b² is of minimum power among other quantities which are divisible by ab, a²b, and ab² (for example, a³b², a²b³, a⁴6⁴, etc.).

Determination of L.C.M. by factorization

1. First of all, the given expressions are resolved into factors.

2. The L.C.M. is the product of all kinds of factors in their highest powers.

3. If numerical coefficients appear before the alphabetic expressions then after finding the L.C.M. of the alphabetic expressions the arithmetical L.C.M. of the numerical coefficients is written before it.

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 8 Lowest Common Multiple Some Examples of L.C.M.

Example 1

Find the L.C.M. of x²yz, xy²z, and xyz².

Solution :

Given: x²yz, xy²z, And xyz²

Here, the factor with the highest power of x is the x²

The factor with the highest power of y is y²

The factor with the highest power of z is z²

Hence, the required

L.C.M. =x²y²z²

Example 2

Find the L.C.M. of 4a²6c², 8ab²c³ and 16a⁴b³c.

Solution :

Given: 4a²6c², 8ab²c³ And 16a⁴b³c.

The L.C.M. of 4, 8, and 16 is 16.

The factor with the highest power of a is a⁴

The factor with the highest power of b is b³

The factor with the highest power of c is c³

Hence, the required L.C.M. = 16a⁴b³c³

Example 3

Find the L.C.M. of a³b – ab³ and a³b² + a²b³.

Solution:

Given  a³b – ab³ And a³b² + a²b³

First expression = a³b – ab³

= ab(a² – b²) = ab(a +b) (a – b)

Second expression

= a³6² + a²b³

= a²b²(a + b)

Hence, the required L.C.M.

= a²b²(a + b) (a – b)

= a²b²(a² – b²)

The required L.C.M = a²b²(a² – b²)

Example 4

Find the L.C.M. of x² – 4x + 3 and x² – 5x + 6.

Solution :

Given x² – 4x + 3 And x² – 5x + 6

First expression = x² – 4x + 3

= x²-3x-x + 3

= x(x – 3) – l(x – 3)

= (x – 3) (x – 1)

Second expression

= x² – 5x + 6

= x² – 3x – 2x + 6

= x(x – 3) – 2(x – 3)

= (x-3)(x-2)

Hence, the required L.C.M. = (x – 1) (x – 2) (x – 3)

Example 5

Find the L.C.M. of 8(a²– 4), 12(a³ + 8) and 36(a² – 3a – 10).

Solution :

Given 8(a²– 4), 12(a³ + 8) And 36(a² – 3a – 10).

First expression

= 8(a² – 4)

= 2³ x {(a)² – (2)²}

= 2³x (a+2) (a- 2)

Second expression

= 12(a³ + 8)

= 2² x 3 x {(a)³ + (2)³}

= 2² x 3 x (a + 2) (a² – 2a + 4)

Third expression

= 36 (a² – 3a – 10)

= 2² x 3² x {a² – 5a + 2a – 10}

= 2² x 3² x {a(a – 5) + 2(a – 5)}

= 2² x 3² x (a – 5) (a + 2)

Hence, the required L.C.M.

= 2³ x 3² x (a + 2) (a – 2) (a²-2a + 4) (a – 5)

= 72 (a + 2) (a – 2) (a – 5) (a² – 2a + 4)

The required L.C.M = 72 (a + 2) (a – 2) (a – 5) (a² – 2a + 4)

Example 6

Find the L.C.M. of x³– 1, x⁴– 1,x⁴ + x²+ 1.

Solution:

Given x³– 1, x⁴– 1,x⁴ + x²+ 1

First expression

= x³ – 1

= (x)³ – (1)³

= (x – 1) (x² + x + 1)

Second expression

= x⁴ – 1

= (x²)² – (l)²

= (x² + 1) (x² – 1)

= (x²+1)(x+1)(x-1)

Third expression

= x⁴ + x² + 1

= (x²)² + 2.x².1+ (1)² -x?

= (x² + 1)² – (x)²

= (x²+1+x)(x²+ 1-x)

= (x² + x + 1) (x² – x + 1)

Hence, the required L.C.M.

= (x – 1) (x² + x +1) (x +1) (x² + 1) (x² – X + 1)

= (x – 1) (x + 1) (x² + 1) (x² + x + 1) (x² – x + 1)

The required L.C.M = (x – 1) (x + 1) (x² + 1) (x² + x + 1) (x² – x + 1)

Example 7

Find the L.C.M. of x² – y², x³ – y³, 3X² – 5x.y+ 2y².

Solution :

Given x² – y², x³ – y³, 3X² – 5x.y+ 2y²

First expression

= x² – y²

= (x + y) (x – y)

Second expression

= x³ – y³

= (x – y) (x² + xy +y²)

Third expression

= 3X² – 5x² + 2y²

= 3X² – 3xy – 2x² + 2y²

= 3x(x -y)~ 2y(x – y)

= (x-y) (3x – 2y)

Hence, the required L.C.M.

= (x+y) (x-y) (x² + xy +y²) (3x- 2y)

= (x+y) (x-y)(3x- 2y)(x² + xy +y²)

The required L.C.M = (x+y) (x-y)(3x- 2y)(x² + xy +y²)

Example 8

Find the L.C.M. of x² – y² – z² + 2yz, (x + y – z)² and x² + z² – y² + 2xz.

Solution :

Given x² – y² – z² + 2yz, (x + y – z)² And x² + z² – y² + 2xz.

First expression = x² – y² – z² + 2yz = x² – (y² – 2yz + z²)

= (x)² -xy-z)² = (x + y-z) (x-y +z)

Second expression

= (x + y – z)² 

Third expression

= x² + z² – y² + 2xz

= x² + 2xz + z² -y²

= (x + z)² – (y)²

= (x + z + y) (x + z – y)

= (x + y + z) (x – y + z)

Hence, the required L.C.M.

= (x + y- z)² (x-y+z) (x+y+z)

= (x-y+z) (x+y+z) (x + y- z)²

The required L.C.M = (x-y+z) (x+y+z) (x + y- z)²

Example 9

Find the L.C.M. of x³ – 16x, 2x³ + 9x² + 4x and x + 4.

Solution :

Given x³ – 16x, 2x³ + 9x² + 4x And x + 4.

First expression

= x³ – 16x

= xfx² – 16)

= x{(x)² – (4)²}

= x(x + 4)(x – 4)

Second expression

= 2x³ + 9x² + 4x

= x(2x² + 9x + 4)

= x(2x² + 8x + x + 4)

= x{2x(x + 4) + l(x + 4)}

= x(x + 4)(2x + 1)

Third expression

= x + 4

Hence, the required L.C.M.

= x(x + 4)(x – 4)(2x + 1)

The required L.C.M = x(x + 4)(x – 4)(2x + 1)

Example 10

Find the L.C.M. of a² – 6² + c² + 2ac, a² – 6² – c² + 26c and ab + ac + b² – c².

Solution :

Given a² – 6² + c² + 2ac, a² – 6² – c² + 26c And ab + ac + b² – c².

First expression

= a² – b² + c² + 2ac

= a² + 2ac + c² – b²

= (a + c)² – (b)²

= (a + c + b)(a + c – b)

= (a + b + c)(a – b + c)

Second expression

= a² – b² – c² + 2bc

= a² – (b² – 2bc + c²)

= (a)² – (b – c)²

= (a + b – c)(a – b + c)

Third expression

= ab + ac + b² – c²

= a(b + c) + (b + c)(b – c)

= (b + c)(a + b – c)

Hence, the required L.C.M.

= (a + b + c)(a – b + c)(a + b – c)(b + c)

= (a + b + c)(a – b + c)(a + b – c)(b + c)

The required L.C.M = (a + b + c)(a – b + c)(a + b – c)(b + c)

Example 11

Find the L.C.M. of x² – xy – 2y², 2x² – 5xy + 2y² and 2x² + xy – y².

Solution :

Given x² – xy – 2y², 2x² – 5xy + 2y² And 2x² + xy – y².

First expression

= x² – xy – 2y²

= x² – 2xy + xy – 2y²

= x(x – 2y) + y(x – 2y)

= (x- 2y)(x +y)

Second expression

= 2X² – 5xy + 2y²

= 2x² – 4xy – xy + 2y²

= 2x(x – 2y) – y(x – 2y)

= (x-2y)(2x-y)

Third expression

= 2x² + xy – y²

= 2x² + 2xy – xy -y²

= 2x(x + y) – y(x + y)

= (x + y)(2x – y)

Hence, the required L.C.M.

= (x – 2y)(x + y)(2x – y)

The required L.C.M = (x – 2y)(x + y)(2x – y)

Example 12

Find the L.C.M. of 3(x² – 9), 9(x³ + 27) and 27(x2 – 3x + 9).

Solution :

Given 3(x² – 9), 9(x³ + 27) and 27(x2 – 3x + 9)

First expression

= 3(x² – 9)

= 3{(x)² – (3)²}

= 3(x + 3)(x – 3)

Second expression

= 9(x³ + 27)

= 9{(x)³ + (3)³}

= 3² (x + 3)(x² – 3x + 9)

Third expression

= 27(x² – 3x + 9)

= 3³ (x² – 3x + 9)

Hence, the required L.C.M.

= 3³ (x + 3)(x – 3)(x² – 3x + 9)

= 27(x + 3)(x – 3)(x² – 3x + 9)

The required L.C.M = 27(x + 3)(x – 3)(x² – 3x + 9)

Algebra Chapter 7 Factorisation By Breaking The Middle Term

Factorisation By Breaking The Middle Term Introduction

In the previous chapter, we resolved the algebraic expressions into factors by using the formulae. Here also our aim is to resolve the algebraic expressions into factors but by using a different method— the method of breaking the middle term. Although this method is easier than the method discussed in the previous chapter, we cannot apply this method to all algebraic expressions due to some restrictions. This method is applicable only to those algebraic expressions which have exactly three terms and the power of the variable of the first term is twice that of the second when arranged in descending order of the power.

Factorization of the expressions of the form x² + px + q

Any algebraic expression of form \(x^2+p x+q\)  is called a quadratic expression since the highest power of x is 2. This type of expression can be factorized by splitting the middle coefficients. Here we should find two quantities such that their algebraic sum is p and product is q Let us consider the expression,

x + (a + b)x + ab.

It is of the form \(x^2+p x+q\), where a + b -p and ab = q.

Now, \(x^2+(a+b) x+a b\)

= \(x^2+a x+b x+a b\)

= x (x + a) + b(x + a)

= (x + a) (x + b).

So we may conclude that x² + px + q can be resolved into two linear factors (x + a) and (x + 6), when a + b = p and ab = q.

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 7 Factorization By Breaking The Middle Term Some Examples

Example 1

Factorize : \(x^2+7 x+12\)

Solution :

Given: \(x^2+7 x+12\)

\(x^2+7 x+12\)

= \(x^2\) + (4 + 3)x + 12

= \(x^2\) + 4x + 3x + 12

= x (x + 4) + 3(x + 4)

= (x + 4) (x + 3)

\(x^2\) + 7x + 12 = \(x^2\) + (4 + 3)x + 12

Example 2

Factorize : \(x^2-3 x-10\).

Solution :

Given: \(x^2-3 x-10\)

\(x^2-3 x-10\)

= \(x^2 – (5 – 2)x – 10\)

= \(x^2 – 5x + 2x – 10\)

= x(x – 5) + 2(x – 5)

= (x – 5) (x + 2)

\(x^2-3 x-10\) = (x – 5) (x + 2)

Example 3

Factorize : \(x^2-9 x+20\)

Solution :

Given: \(x^2-9 x+20\)

\(x^2-9 x+20\)

= \(x^2 – (5 + 4)x + 20\)

= \(x^2 – 5x – 4x + 20\)

= x(x – 5) – 4(x – 5)

= (x – 5) (x – 4)

\(x^2 – 9x + 20\) = (x – 5) (x – 4)

Example 4

Factorize : \(x^2+2 x-35\)

Solution :

Given \(x^2+2 x-35\)

\(x^2+2 x-35\)

= \(x^2+(7-5) x-35 s=x^2+7 x-5 x-35\) = x(x + 7) – 5(x + 7)

= (x + 7) (x – 5)

\(x^2+2 x-35\) = (x + 7) (x – 5)

Example 5

Factorize : 

Solution:

Given: \(x^2+20 x y+75 y^2\)

\(x^2+20 x y+75 y^2\)

= \(x^2+(15+5) x y+75 y^2\)

= \(x^2+15 x y+5 r y+75 y^2\)

= x(x + 15y) + 5y(x + 15y)

= (x + 15y) (x + by)

\(x^2+20 x y+75 y^2\). = (x + 15y) (x + by)

Example 6

Factorize : \((x+y)^2-11(x+y)+30\)

Solution :

Given: \((x+y)^2-11(x+y)+30\)

\((x+y)^2-11(x+y)+30\)

= \((x+y)^2\) – 6(x + y) – 5(x + y) + 30

= (x + y) (x + y – 6) – 5(x + y – 6)

= (x + y- 6) (x +y- 5)

\((x+y)^2-11(x+y)+30\) = (x + y- 6) (x +y- 5)

Example 7

Factorize : \((a+b)^2+(a+b)-56\)

Solution:

Given: \((a+b)^2+(a+b)-56\)

\((a+b)^2+(a+b)-56\)

= (a + b)² + 8(a + b) – 7(a + b) – 56

= (a + b) (a + b + 8) – 7(a + 6 + 8)

= (a + b + 8) (a + b – 7)

\((a+b)^2+(a+b)-56\) = (a + b + 8) (a + b – 7)

Example 8

Factorize : \(x^2+x-(a+1)(a+2)\)

Solution :

Given: \(x^2+x-(a+1)(a+2)\)

\(x^2+x-(a+1)(a+2)\)

= \(x^2\) + {(a + 2) – (a + 1)}x – (a + 1)(a + 2)

= \(x^2\) + (a + 2)x – (a + 1)x – (a + 1) (a + 2)

= x(x + a + 2) – (a + 1) (x + a + 2)

= (x + a + 2) (x – a – 1)

\(x^2\)+x-(a+1)(a+2) = (x + a + 2) (x – a – 1)

Example 9

Factorize : \(x^4-13 x^2+42\)

Solution :

Given: \(x^4-13 x^2+42\)

\(x^4-13 x^2+42\)

= \(x^4-(6+7) x^2+42\)

= \(x^4-6 x^2-7 x^2+42\)

= \(x^2\left(x^2-6\right)-7\left(x^2-6\right)\)

= \(\left(x^2-6\right)\left(x^2-7\right)\)

\(x^4-13 x^2+42=\left(x^2-6\right)\left(x^2-7\right)\)

Example 10

Factorize : \(x^6-10 x^3+16\)

Solution :

Given:

\(x^6-10 x^3+16\)

= \(x^6-(8+2) x^3+16\)

= \(x^6-8 x^3-2 x^3+16\)

= \(x^3\left(x^3-8\right)-2\left(x^3-8\right)\)

= \(\left(x^3-8\right)\left(x^3-2\right)\)

= \(\left\{(x)^3-(2)^3\right\}\left(x^3-2\right)\)

= \((x-2)\left(x^2+2 x+4\right)\left(x^3-2\right)\)

\(x^6-10 x^3+16=(x-2)\left(x^2+2 x+4\right)\left(x^3-2\right)\)

Example 11

Factorize : (p – 1) (p – 2) (p + 3) (p + 4) + 6.

Solution:

Given

(p – 1) (p – 2) (p + 3) (p + 4) + 6

(p – 1) (p – 2) (p + 3) (p + 4) + 6

= {(p – 1) (p + 3} {(p – 2) (p + 4)} + 6

= (p² + 3p – p – 3) (p² + 4p – 2p – 8) + 6

= (p² + 2p – 3) (p² + 2p – 8) + 6

Let, p² + 2p = a.

Then the given expression

= (a-3) (a-8)+ 6 = a² – 8a – 3a + 24 + 6

= a² – 11a + 30 = a² – (6 + 5)a + 30

= a² – 6a – 5a + 30

= a(a – 6) – 5(a – 6)

= (a – 6) (a – 5)

= (p² + 2p – 6) (p² + 2p – 5)             [∵ putting the value of a]

(p – 1) (p – 2) (p + 3) (p + 4) + 6 = (p² + 2p – 6) (p² + 2p – 5)

Example 12

Factorize : p2 + ( a+1/a)p + 1.

Solution:

Given  p2 + ( a+1/a)p + 1.

p2 – (a+1/a)p + 1

=p2 – a . p – 1/a . p + 1/a . a

= p(p-a) – 1/a (p-a)

= (p-a)(p – 1/a)

p2 + ( a+1/a)p + 1. = (p-a)(p – 1/a)

Example 13

Factorize : \(x^2\) – bx – (a + 36)(a + 26).

Solution :

Given \(x^2\) – bx – (a + 36)(a + 26).

\(x^2\) – bx – (a + 3b)(a + 2b)

= \(x^2\) – {(a + 3b) – (a + 2b)}x – (a + 3b)(a + 2b)

= \(x^2\) – (a + 3b)x +(a + 2b)x-(a+3b)(a+2b)

= x{x – a – 3b} + (a + 2b){x – a – 3b}

= (x – a – 3b)(x + a + 2b)

\(x^2\) – bx – (a + 36)(a + 26). = (x – a – 3b)(x + a + 2b)

Example 14

Factorize : \((x+y)^2-5 x-5 y+6\)

Solution :

Given \((x+y)^2-5 x-5 y+6\)

\((x+y)^2-5 x-5 y+6\)

= \((x+y)^2-5 x-5 y+6\)

Let, x + y = a.

Then the given expression

= \(a^2-5 a+6=a^2-2 a-3 a+6\)

= a(a – 2) – 3 (a – 2) = (a – 2) (a – 3)

= (x + y-2)(x + y-3)         [∵ putting the value of a ]

\((x+y)^2-5 x-5 y+6\) = (x + y-2)(x + y-3)

Example 15

Factorize : (x + 1)(x + 3)(x – 4)(x – 6) + 24.

Solution :

Given  (x + 1)(x + 3)(x – 4)(x – 6) + 24

= (x + l)(x – 4)(x + 3)(x – 6) + 24

= (x² – 4x + x – 4XX² – 6x + 3x – 18) + 24

= (x² – 3x – 4)(x² – 3x – 18) + 24

Let, x² – 3x = a.

Then the given expression

= a² – 18a – 4a + 72 + 24

= a² – 22a + 96

= a² – 6a – 16a + 96

= a(a – 6) — 16(a — 6)

= (a – 6) (a – 16)

= (x²-3x-6)(x²-3x- 16)           [∵ putting the value of a]

(x + 1)(x + 3)(x – 4)(x – 6) + 24 = (x²-3x-6)(x²-3x- 16)

Factorization of the expressions of the form ax ²+ bx +c

This type of quadratic expression can also be factorized by splitting the middle coefficients. Here we should find two quantities such that their algebraic sum is b and the product is ac.

Algebra Chapter 7 Factorization By Breaking The Middle Term Some Examples

Example 1

Factorize : 3x² + 8x + 5.

Solution :

Given: 3X² + 8x + 5

3X² + 8x + 5

= 3X² + (3 + 5)x + 5

= 3x² + 3x + 5x + 5

= 3x(x + 1) + 5(x + 1)

= (x + 1) (3x + 5)

3X² + 8x + 5 = (x + 1) (3x + 5)

Example 2

Factorize : 6x² + x – 40.

Solution:

Given 6x² + x – 40.

6x² + x – 40

= 6x² + (16 – 15)x – 40

= 6x² + 16x – 15* – 40

= 2x(3x + 8) – 5(3x + 8)

= (3x + 8) (2x – 5)

6x² + x – 40. = (3x + 8) (2x – 5)

Example 3

Factorize : 10x² – x – 24.

Solution :

Given 10x² – x – 24.

10x² – x – 24

= 10x² + (- 16 + 15)x – 24

= 10x² – I6x + 15x – 24

= 2x(5x – 8) + 3(5x – 8)

= (5x – 8) (2x + 3)

10x² – x – 24. = (5x – 8) (2x + 3)

Example 4

Factorize : 63x – 59x + 10.

Solution :

Given 63x – 59x + 10.

63x² – 59x + 10

= 63x² + (- 45 – 14)x + 10

= 63x² – 45x – 14x + 10

= 9x (7x – 5) – 2(7x – 5)

= (7x – 5) (9x – 2)

63x² – 59x + 10 = (7x – 5) (9x – 2)

Example 5

Factorize : 10x² + 31xy + 24y².

Solution :

Given 10x² + 31xy + 24y².

10x² + 31xy + 24y²

= 10x² + (15 + 16)xy + 24y²

= 10x² + 15xy + 16xy + 24y²

= 5x(2x + 3y) + 8y (2x + 3y)

= (2x + 3y) (5x + 8y)

10x² + 31xy + 24y². = (2x + 3y) (5x + 8y)

Example 6

Factorize : 21 (a + b)² + 8(a + b) – 45.

Solution :

Given 21 (a + b)² + 8(a + b) – 45.

21(a + b)² + 8(a + 6) – 45

= 21(a + b)² + 35(a + b) – 27(a + b) – 45

= 7(a + b) {3(a + b) + 5} – 9 {3(a + b) + 5}

= {3(a + b) + 5} (7(a + b) – 9}

= (3a + 35 + 5) (7a + 75-9)

21 (a + b)² + 8(a + b) – 45. = (3a + 35 + 5) (7a + 75-9)

Example 7

Factorize : 15(x + y)² – 26(x + y) + 8.

Solution :

Given 15(x + y)² – 26(x + y) + 8.

15(x + y)² – 26(x + y) + 8

= 15(x + y)² – 20(x + y) – 6(x + y) + 8

= 5(x + y) {3(x + y) – 4} -2{3(x + y) – 4}

= {3(x + y) – 4} {5(x + y) – 2}

= (3x + 3y-4)(5x + 5y-2)

15(x + y)² – 26(x + y) + 8. = (3x + 3y-4)(5x + 5y-2)

Example 8

Factorize : (a – 1)x² + a²xy + (a + 1)y².

Solution :

Given (a – 1)x² + a²xy + (a + 1)y².

(a – 1)x² + a²xy + (a + 1)y²

= (a – 1)x² + {(a² — 1) + l}xy + (a + 1)y²

= (a – 1)x² + (a² – 1):xy + xy + (a + 1)y²

= (a – 1)x {x + (a + l)y} + y{x + (a + 1)y}

= {x + (a + 1)y} {(a – 1)x + y}

= (x + ay + y) (ax-x +y)

(a – 1)x² + a²xy + (a + 1)y². = (x + ay + y) (ax-x +y)

Example 9

Factorize : 6x⁴ + 17x² – 45.

Solution:

Given 6x⁴ + 17x² – 45.

6x⁴ + 17x² – 45

= 6x⁴ + (27 – 10)x² – 45

= 6x⁴ + 27x² – 10x² – 45

= 3x²(2x² + 9) – 5(2x² + 9)

= (2x² + 9) (3x² – 5)

6x⁴ + 17x² – 45. = (2x² + 9) (3x² – 5)

Example 10

Factorize : 21x⁶ — 29x³ +10.

Solution :

Given 21x⁶ — 29x³ +10.

2 1x⁶ – 29x³ + 10

= 21x⁶ – (14 + 15)x³ + 10

= 2 1x⁶ – 14x³ – 15x³ + 10

= 7x³(3x³ – 2) – 5(3x³ – 2)

= (3x³ – 2) (7x³ — 5)

21x⁶ — 29x³ +10. = (3x³ – 2) (7x³ — 5)

Example 11

Factorize : 5{a²-b²)²— 8ab (a² – b²) – 13a²b².

Solution :

Given 5{a²-b²)²— 8ab (a² – b²) – 13a²b².

Let a – b = x and ab = -y

To the given expression

= 5x² – 8xy – 13y²

= 5x² – (13 – 5)xy – 13y2

= 5x² – 13xy + 5xy – 13y²

= x(5x – 13y) + y(5x – 13;y)

= (5x – 13y) (x + y)

= {5(a² – b²) – 13ab} {a² – b² + ab}

= (5a² – 5b² – 13a6) (a² – b² + ab)

5{a²-b²)²– 8ab (a² – b²) – 13a²b². = (5a² – 5b² – 13ab) (a² – b² + ab)

Example 12

Factorize : (x + 1) (x + 2) (3x— 1)(3x – 4) + 12.

Solution :

Given (x + 1) (x + 2) (3x— 1)(3x – 4) + 12.

(x + 1) (x + 2) (3x-l) (3x – 4) + 12

= {(x + 1) (3x – 1)} {(x + 2) (3x – 4)} + 12

= (3x² – x + 3x – 1) (3x² – 4x + 6x – 8) + 12

= (3x² + 2x- 1) (3x² + 2x – 8) + 12 Let, 3x² + 2x = a

The given expression

= (a – 1) (a – 8) + 12

= a² – 8a – a + 8 + 12

= a² – 9a + 20

= a – 5a – 4a + 20

= a(a -5)- 4 (a – 5)

= (a – 5) (a – 4)

= (3x² + 2x – 5) (3x² + 2x – 4)

= (3x² + 5x – 3x – 5) (3x² + 2x – 4)

= {x(3x + 5) -1(3x + 5)} (3x² + 2x – 4)

= (3x + 5) (x- 1) (3x² + 2x- 4)

(x + 1) (x + 2) (3x – 1)(3x – 4) + 12. = (3x + 5) (x – 1) (3x² + 2x – 4)

Algebra Chapter 6 Fraction By Formulae

Fraction By Formulae Introduction

A very important topic in algebra is to resolve an expression into factors. In the previous chapter, we studied some of the very important formulae. In this chapter, our aim is to apply those formulae to resolve algebraic expressions into factors.

The sum and difference of two cubes

In the previous chapter we have seen that, (a + b) (a² – ab + b²) = a³ + b ³ and

(a – b) (a² + ab + b²) = a³ – b³.

Thus, we may conclude that the two factors of a³ + b³ are (a + b) and (a² – ab + b²),

and also the two factors of a³ – b³ are (a – b) and (a² + ab + b²).

We may also verify the above two formulae from the reverse direction as shown below

a³ + b³ = a³ + a²b – a²b – ab² + ab² + b³

= a²(a + b) – ab(a + b) + b²(a + b)

= (a + b) (a² – ab + b²).

a³ – b³ = a³ – a²b + a²b – ab² + ab² – b³

= a²(a – b) + ab(a – b) + b²(a – b)

= (a – b) (a² + ab + b²)

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 6 Fraction By Formulae Some Examples of Factors

Example 1

Factorize: x³ + 64.

Solution :

Given:

x³ + 64

x³ + 64 = (x)³ + (4)³

= (x + 4) {(x)² – x.4 + (4)²}

= (x + 4) (x² – 4x + 16)

x³ + 64 = (x + 4) (x² – 4x + 16)

Example 2

Factorize: 8a³ – 27b³.

Solution :

Given:

8a³ – 27b³.

8a³ – 27b³ = (2a)³ – (3b)³

= (2a – 3b) {(2a)² + 2a.3b + (36)²}

= (2a – 3b) (4a² + 6ab + 9b²)

8a³ – 27b³ = (2a – 3b) (4a² + 6ab + 9b²)

Example 3

Factorize: a⁶ – b⁶.

Solution :

Given:

a⁶ – b⁶

a⁶ – b⁶ = (a³)² – (b³)²

= (a³ + b³) (a³ – b³)

= (a + b) (a²-ab+b²) (a-b) (a²+ab + b²)

a⁶ – b⁶ = (a + b) (a²-ab+b²) (a-b) (a²+ab + b²)

Example 4

Factorize: 3x³ + 375.

Solution :

Given:-

3x³ + 375

3x³ + 375 = 3(x³ + 125) = 3{(x)³ + (5)³}

= 3(x + 5) {(x)² – x.5 + (5)²}

= 3(x + 5) (x² – 5x + 25)

3x³ + 375 = 3(x + 5) (x² – 5x + 25)

Example 5

Factorize: a⁴b- ab⁴.

Solution :

Given: a⁴b- ab⁴

a⁴ b- ab⁴

= ab(a³ – b³)

= ab(a – b) (a² + ab + b²)

a⁴b- ab⁴ = ab(a – b) (a² + ab + b²)

Example 6

Factorize : a³ + 3a² b+ 3ab² + 2b³.

Solution :

Given:

a³ + 3a² b + 3ab² + 2b³

a³ + 3a² b + 3ab² + 2b³

= a³ + 3a² b+ 3ab² + b³ + b³

= (a + b)³ + (b)³

= (a + b + b) {(a + b)² – (a + b).b + (b)²}

= (a + 2b) (a² + 2ab + b² – ab – b² + b²)

= (a + 2b) (a² + ab + b²)

a³ + 3a² b + 3ab² + 2b³ = (a + 2b) (a² + ab + b²)

Example 7

Factorize : 8a³ + 36a^2b + 54ab² + 27b³.

Solution :

Given:

8a³ + 36a² b + 54ab² + 27b³

8a³ + 36a² b + 54ab² + 27b³

= (2a)³ + 3 (2a)² x 3b + 3 x 2a (3b)² + (3b)³

= (2a + 3b)³

= (2a + 3b) (2a + 3b) (2a + 3b)

8a³ + 36a² b + 54ab² + 27b³ = (2a + 3b) (2a + 3b) (2a + 3b)

Example 8

Factorize: 35 – a³ + 6a² – 12a.

Solution :

Given:

35 – a³ + 6a² – 12a

35 – a³ + 6a² – 12a

= 27 + 8 – a³ + 6a² – 12a

= 27 – (a³ – 6a² + 12a – 8)

= 27 – {(a)³ – 3.(a)².2 + 3.a.(2)² – (2)³}

= (3)³ – (a – 2)³

= {3 – (a – 2)} {(3)² + 3.(a – 2) + (a – 2)²}

= (3 – a + 2) (9 + 3a – 6 + a² – 4a + 4)

= (5 – a) (a² – a + 7)

35 – a³ + 6a² – 12a = (5 – a) (a² – a + 7)

Example 9

Factorize : 8(a + b)³ + 27(6 + c)³.

Solution :

Given:

8(a + b)³ + 27(6 + c)³.

8(a + b)³ + 27(b + c)³ = {2(a + b)}³ + {3(b + c)}³

= (2a + 2b)³ + (3b + 3c)³

= (2a + 2b + 3b + 3c) {(2a + 2b)² – (2a + 2b) (3b + 3c) + (3b + 3c)²}

= (2a + 5b + 3c) {(2a)² + 2 x 2a x 2b + (2b)² – (6ab + 6ac + 6b² + 6bc) + (3b)² + 2 x 3b x 3c + (3c)²}

= (2a + 5b + 3c) {4a² + 8ab + 46² – 6ab – 6ac – 6b² – 6bc + 9b² + 18bc + 9c²}

= (2a + 56 + 3c) (4a² + 7b² + 9c² + 2ab + 12bc – 6ac)

8(a + b)³ + 27(6 + c)³.= (2a + 56 + 3c) (4a² + 7b² + 9c² + 2ab + 12bc – 6ac)

Example 10

Factorize : x³ + y³ – x(x² – y²) + y(x + y)².

Solution :

Given

x³ + y³ – x(x² – y²) + y(x + y)².

x³ + y³ – x(x² – y²) + y(x + y)²

= (x +y)(x²-xy +y²) -x(x +y)(x-y) +y(x+y)

= (x+y) {(x²-xy+y³)-x(x-y)+y(x+y)}

= (x + y) {x²– xy + y² – x² + xy + xy + y²}

= (x +y) (xy + 2y²)

= (x+y) y(x + 2y)

= y(x + y) (x + 2y)

x³ + y³ – x(x² – y²) + y(x + y)². = y(x + y) (x + 2y)

Example 11

Factorize : x³ + 9x² + 21x + 26.

Solution :

Given:

x³ + 9x² + 21x + 26.

x³ + 9x² + 21 x + 26

= (x)³ + 3(x)² + 3x (3)² + (3)³ – 1

= (x + 3)³ – (1)³

= (x + 3 – 1) {(x + 3)² + (x + 3)1 + (1)²}

= (x + 2) {x² + 3x + 9 + x + 3 + 1} .

= (x + 2) (x² + 7x + 13)

x³ + 9x² + 21x + 26. = (x + 2) (x² + 7x + 13)

Example 12

Factorize : x³ – 6xy + 12x² y- 8y³ – z + 3z²  – 3z + 1.

Solution:

Given:

x³ – 6x2y + 12xy² – 8y³ – z³ + 3z² – 3z + 1

x³ – 6x2y + 12xy² – 8y³ – z³ + 3z² – 3z + 1

= (x)³ – 3(x)² 2y + 3x(2y)² – (2y)³ – {(z)³ – 3(z)² x 1 + 3z(1)² – (1)³}

= (x – 2y)³ – (z-1)³

= {(x-2y) – (z-1)}{(x-2y)² + (x-2y) . (z-1) + (z-1)²}

= (x – 2y – z +1)(x² + 4y² + z² – 4xy + zx – 2yz – x + 2y – 2z +1)

x³ – 6x2y + 12xy² – 8y³ – z³ + 3z² – 3z + 1 = (x – 2y – z +1)(x² + 4y² + z² – 4xy + zx – 2yz – x + 2y – 2z +1)

Example 13

Factorize : 16a³ – 54(a – b)³.

Solution :

Given

16a³ – 54(a – b)³

16a³ – 54(a – b)³

= 2[8a³ – 27(a – b)³]

= 2[(2a)³ – {3(a – b)}³]

= 2{(2a)³ – (3a – 3b)³}

= 2(2a – 3a + 3b){(2a)² + 2a(3a – 3b) + (3a – 3b)²}

= 2(36 – a)(4a² + 6a² — 6ab + 9a² – 18ab + 9b²)

= 2(36 – a)(19a² — 24ab + 9b²)

16a³ – 54(a – b)³  = 2(36 – a)(19a² — 24ab + 9b²)

Example 14

Factorize: 8 – a³ + 3a^2b – 3ab² + b³.

Solution :

Given:

8 – a³ + 3a^2b – 3ab² + b³

8 – a³ + 3a²b- 3ab² + b³ = 8 – (a³ – 3a² b+ 3ab² – b³)

= (2)³ – (a – b)³

= (2 – a + b){(2)² + 2(a – b) + (a – b)²}

= (2 – a + b)(4 + 2a — 2b + a² – 2ab + b²)

= (2 – a + b)(a² — 2ab + b² + 2a – 2b + 4)

8 – a³ + 3a^2b – 3ab² + b³ = (2 – a + b)(a² — 2ab + b² + 2a – 2b + 4)

Example 15

Factorize : m³ – n³ – m(m² – n²) + n(m – n.)².

Solution :

Given

m³ – n³ – m(m² – n²) + n(m – n.)²

m³ – n³ – m(m² – n²) + n(m – rc)²

= (m – n)(m² + mn + n²) – m(m + n)(m – n) + n(m – n)²

= (m – n)(m²+ mn + n²– m²– mn+mn – n²)

= (m – n)(mn)

= mn(m – n)

m³ – n³ – m(m² – n²) + n(m – n.)² = mn(m – n)

Example 16

Factorize : 8x³+12x²+6x – y³+9y²-27y + 28.

Solution :

Given

8x³+12x²+6x – y³+9y²-27y + 28.

8x³+ 12X² + 6x – y³ + 9y² – 27y + 28

= 8x³ + I2x² + 6x + 1 -y³ + 9y² – 27y + 27

= (2x)³ + 3 (2x)² x 1 + 3 x 2x (1)² + 1- {(y)³-3y²x3 + 3y(3)²-(3)³}

= (2x + 1)³ – (y – 3)³

= {(2x + 1) – (y – 3)}{(2x + 1)² + (2x + 1)(y – 3) + (y – 3)²}

= (2x + 1 – y + 3)(4x² + 4x + 1 + 2xy – 6x + y – 3 + y² – 6y + 9)

= (2x – y + 4 x 4x² + 2xy + y² -2x- 5y + 7)

8x³+12x²+6x – y³+9y²-27y + 28. = (2x – y + 4 x 4x² + 2xy + y² -2x- 5y + 7)

Example 17

Factorize : x³-9y³– 3xy(x-y)

Solution :

Given 

x³-9y³– 3xy(x-y)

x³ – 9y³ – 3xy (x – y)

= [x³-y³– 3xy (x – y)] – 8y³

= (x- y)³ – 8y³

= (x- y)³ – (2y)³

= {(x – y)-2y} . {(x – y)² + (x – y) . 2y + (2y)²}

= (x- 3y).(x² – 2xy + y² + 2xy – 2y² + 4y²)

= (x-3y). (x² + 3y²)

x³-9y³– 3xy(x-y) = (x-3y). (x² + 3y²)

Example 18

Factorize : a³ – 9b³ + (a + b)³

Solution :

Given

a³ – 9b³ + (a + b)³

a³ – 9b³+ (a + b)³

= a³ – b³ + (a + b)³ – 8b³

= a³ – b³ +(a + b)³ – (2b)³

= (a – b) (a² + ab + b²) + {(a + b) – 2b}. {(a + b)² + (a + 6).2b + (2b)²}

= (a – b) (a² + ab + b²) + (a – b) (a² + 4ab + 7b²) = (a – b)(a² + ab + b² +a² + 4ab + 7b²)

= (a – b).(2a² + 5ab + 3b²)

a³ – 9b³ + (a + b)³ = (a – b).(2a² + 5ab + 3b²)

Example 19

Resolve into factors : 2x³ – 3x² + 3x – 1

Solution :

Given:

2x³ – 3x² + 3x – 1

2x³ – 3x² + 3x – 1 = x³ + x³ – 3x² + 3x – 1

= x³ + (x – l)³

= {x + (x – 1)} {x² – x.(x – 1)+ (x – l)²}

= (2x – 1) (x² – x² + x + x² – 2x + 1)

= (2x – 1) (x² – x + 1)

2x³ – 3x² + 3x – 1 = (2x – 1) (x² – x + 1)

Example 20

Resolve into factors : a³ – 12a – 16

Solution :

Given:

a³ – 12a – 16

a³ – 12a – 16

= a³ + 8 – 12a – 24

= a³ + 2³ – 12(a + 2)

= (a + 2) (a² – 2a +2²) – 12(a + 2)

= (a + 2) (a² – 2a + 4 – 12)

= (a + 2) (a² – 2a – 8)

= (a + 2). (a² – 4a + 2a – 8)

= (a + 2) {a(a – 4) + 2 (a – 4)}

= (a + 2) (a – 4) ( a + 2)

a³ – 12a – 16 = (a + 2) (a – 4) ( a + 2).

Chapter 5 Formulae And Their Applications

Formulae and Their Applications Introduction

In class 7 you have studied the deduction of formulae for (a + b)², (a – b)^2, and a² – b². In this chapter, we shall deduce the formulae for

(a + b)³, (a – b)³, a³ + b³ and a³ – b^3, and by the application of these formulae we shall try to solve some algebraic problems.

Formulae of (a + b)³ and (a – b)³

1. (a + b)³=a³ + 3a² b+ 3ab² + b³

= a³ + b³ + 3ab (a + b).

Proof : (a + b)³ = (a + b)² (a + b)

= (a² + 2ab + b²) (a + b)

= a³ + a² b+ 2a² b+ 2ab² + ab² + b³

= a³ + 3 a²b + 3 ab² + b³.

Also, (a + b)³ = a³ + 3a²b+ 3ab² + b³

= a³ + b³ + 3 a²b + 3ab²

= a³ + b³ + 3ab (a + b).

2. (a – b)³ = a³– 3a²b+ 3ab² – b³

= a³ – b³ – 3ab (a – b).

Proof : (a – b)³ = (a – b)² (a – b)

= (a² – 2a6 + 6²) (a – b)

= a³ – a²b- 2a²b+ 2ab² + ab² – b³

= a³ – 3a²b+ 3ab² – b³.

Also, (a – b)³ = a³ – 3a²b+ 3ab² – b³

= a³ – b³ – 3a² b+ 3ab²

= a³ – b³ — 3ab (a – b).

WBBSE Board Class 8 Math Solution

Geometric representation of the formula

 (a + b)³ = a³ + 3a²b+ 3ab² + b³

Read And Learn More WBBSE Solutions For Class 8 Maths

Prepare two cubes of sides 6 cm and 4 cm. Next prepare three parallelopipeds whose length and breadth are 6 cm each and height is 4 cm. Prepare three more parallelopipeds whose length and breadth are 4 cm each and height is 6 cm. Thus we get altogether eight solids.

The total volume of these eight solids = (6³ + 3 x 6² x 4 + 3 x 6 x 4² + 4³) cc.

Now, if we arrange these eight solids in a proper manner we get a single cube, the length of each side of which is (6 + 4) cm, and therefore its volume is

(6 + 4)³ cc.

(6 + 4)³ = 6³ + 3 x 6² x 4 + 3 x 6 x 4² + 4³

Now, taking 6 cm = a, 4 cm = 6,

we get, (a + b)³ = a³ + 3 a²b + Sab² + b³.

WBBSE Board Class 8 Math Solution

Some examples on: (a+b)³= a³+3a²b +3ab²+b³

Example 1

Find the cube of (2x + 3y).

Solution :

Given (2x + 3y).

Cube of (2x + 3y)

= (2x + 3y)³

= (2x)³+ 3 x (2x)²x 3,y + 3 x 2x (3y)²+(3y)³

= 8x² + 36x²y + 54xy² + 27y³

Cube of (2x + 3y) = 8x² + 36x²y + 54xy² + 27y³

Example 2

Find the cube of (ab + cd).

Solution :

Given:

(ab + cd)

Cube of (ab + cd)

= (ab + cd)³

= (ab)³ + 3 (ab)² x cd + 3ab x (cd)² + (cd)³

= a³b³ + 3a²b²cd + 3abc²d² + c³d³

Cube of (ab + cd) = a³b³ + 3a²b²cd + 3abc²d² + c³d³

Example 3

Find the cube of 101 with the help of the formula.

Solution :

Given Number 101.

Cube of 101

= (101)³ = (100 + 1)³

= (100)³ + 3 (100)² x 1 + 3 x 100 (1)² + (1)³

= 1000000 + 30000 + 300 + 1

= 1030301

Cube of 101 = 1030301

Example 4

Using the formula find the value of (64)³+ 3x(64)²x36 + 3x(64)x (36)²+(36)³.

Solution :

Given Formula:

(64)³+ 3x(64)²x36 + 3x(64)x (36)²+(36)³.

If we assume that 64 = a and 36 = b,

then the given expression becomes,

a³ + 3a²6 + 3a6² + 6³ = (a + 6)³

= (64 + 36)³ [Since a = 64, b= 36]

= (100)³

= 1000000

(64)³+ 3x(64)²x36 + 3x(64)x (36)²+(36)³ = 1000000

Example 5

With the help of the formula find the value of: 3.75 x 3.75 x 3.75 + 3 x 3.75 x 3.75 x 2.25 + 3 x 3.75 x 2.25 x 2.25 + 2.25 x 2.25 x 2.25.

Solution :

Given Formula:

3.75 x 3.75 x 3.75 + 3 x 3.75 x 3.75 x 2.25 + 3 x 3.75 x 2.25 x 2.25 + 2.25 x 2.25 x 2.25.

Assuming 3.75 = a

and 2.25 = 6 the given expression becomes,

a x a x a+3 x a x a x 6+3 x a x b x b+ b x b x b

= a³ + 3a²b+ 3ab² + b³ = (a + b)³

= (3.75 + 2.25)³    [Since a = 3.75 and b = 2.25]

= (6.00)³

= 216

3.75 x 3.75 x 3.75 + 3 x 3.75 x 3.75 x 2.25 + 3 x 3.75 x 2.25 x 2.25 + 2.25 x 2.25 x 2.2 = 216

Example 6

If x = 2, then find the value of 27x³ + 54x² + 36x + 8.

Solution :

Given :

x = 2

27x³ + 54x² + 36x + 8

Substitute x = 2 In Above Equation

= (3x)³ + 3 (3x)² x 2 + 3 (3x) x (2)² + (2)³

= (3x + 2)³

= (3 x 2 + 2)³ [Since x = 2]

= (6 + 2)³

= (8)³

= 512

27x³ + 54x² + 36x + 8 = 512

Example 7

If a + b – 2, then what is the value of a³ + b³ + 6ab?

Solution :

a + b = 2

Cubing both sides we get, (a + b)³ = (2)³

or, a³ + b³ + 3ab (a + b) = 8

or, a³ + 6³ + 3ab x 2 = 8 [Since a + b = 2]

or, a³ + b³ + 6ab

= 8

a³ + b³ + 6ab = 8

Example 8

If xy(x + y) = 1, then what is the value x³ + y³ – 1 / x³y³?

Solution:

xy(x + y) = 1

or, x + y = 1/xy

Cubing both sides we get,

xy(x+y) = (1/xy)³

or, x³ +y³ + 3xy (x + y) = 1/x³y³

or, x³ +y +3×1=1/x³y³       [Since xy(x +y) = 1]

or, x³ + y³ +3 = 1/x³y³

or, x³ + y³ – 1/x³y³

= -3

x³ + y³ – 1 / x³y³ = -3

Example 9

If 2x + 1/3x =4, then prove that, 27x³ + 1/8x³ = 189.

Solution:

2x + 1/3x = 4

Multiplying both sides by 3/2 we get,

3x + 1/2x = 6

Cubing both sides,

(3x)³ + (1/2x)³ + 3.3x. 1/2x. (3x + 1/2x) = (6)³

or, 27×3 + 1/8×3 + 9/2 . 6 = 216

or, 27×3 + 1/8×3  27 = 216

or, 27×3 + 1/8×3 = 189 (Proved)

Example 10

If (a² + b²)³ = (a³ + b³)², then a/b + b/a = what?

Solution :

(a² + b²)³  = (a³ + b³)²

or, (a²)³ + 3. (a²)² . b² + 3.a². (b²)² + (b²)³

= (a³)² + 2a³ b³ + (b³)²

or, a³ + 3a⁴ b² + 3a² b⁴ + b⁶ = a⁶ + 2a³ b³ + b⁶

or, 3a⁴b² + 3a²b⁴ = 2a³b³

or, 3/2 (a/b + b/a) = 1

or, a/b + b/a = 2/3

Example 11

If a + 1/ (a-5) = 7, then what is the value of (a – 5)³ + 1/ (a – 5)³

Solution:

a + 1/ (a-5) = 7

or, a – 5 + 1/ a- 5 = 2

cubing both sides we get,

\((a-5)^3+\left(\frac{1}{a-5}\right)^3+3 \cdot(a-5) \cdot \frac{1}{(\dot{a}-5)}(a-5\) \(\left.+\frac{1}{a-5}\right)=(2)^3\)

\(\text { or, }(a-5)^3+\frac{1}{(a-5)^3}+3.1 .2=8\) \(\text { or, }(a-5)^3+\frac{1}{(a-5)^3}+6=8\) \(\text { or, }(a-5)^3+\frac{1}{(a-5)^3}=2\)

Example 12

If 3x + 3/x = 2, then x3 + 1/x3 + 2 = what?

Solution:

\(3 x+\frac{3}{x}=2\) \(\text { or, } x+\frac{1}{x}=\frac{2}{3}\)

cubing both sides we get

\(x^3+\frac{1}{x^3}+3 \cdot x \cdot \frac{1}{x} \cdot\left(x+\frac{1}{x}\right)=\left(\frac{2}{3}\right)^3\) \(\text { or, } x^3+\frac{1}{x^3}+3 \cdot \frac{2}{3}=\frac{8}{27}\) \(\text { or, } x^3+\frac{1}{x^3}+2=\frac{8}{27}\)

Example 13

Simplify : (2x + 3y)³ + 3(2x + 3y)² (2x – 3y) + 3 (2x + 3y) (2x – 3y)² + (2x – 3y)³.

Solution :

Let, 2x + 3y = a and 2x – 3y = b

Then the given expression = a³ + 3a²b + 3ab² + b³

= (a + b)³ = {2x + 3y + 2x – 3y}³       [Putting a = 2x + 3y, b = 2x – 3y]

= (4x)³

= 64X³

(2x + 3y)³ + 3(2x + 3y)² (2x – 3y) + 3 (2x + 3y) (2x – 3y)² + (2x – 3y)³ = 64X³

Example 14

Simplify: (2a – b)³ + (2a+b)³ +12a(4a²– b²).

Solution :

The given expression = (2a – b)³ + (2a + b)³ + 12a(4a² – b²)

= (2a – b)³ + (2a + b)³ + 3 (4a² – b²) x 4a

= (2a- b)³ + (2a + b)³ + 3 (2a – b) (2a + b)

{(2a – b) + (2a + b)} Let, 2a – b = x

and 2a + b = y

Then the given expression = x³ + y³ + 3xy (x + y)

= (x + y)³

= (2a – b + 2a + b)³        [Putting = 2a – b, y = 2a + b]

= (4a)³

= 64a³

(2a – b)³ + (2a + b)³ + 12a(4a² – b²) = 64a³

Example 15

Find the cube of x + y + z.

Solution :

Cube of (x + y + z)

= (x + y + z)³

= {(x + y) + z}³

= (x + y)³ + 3(x + y)² z + 3(x + y) (z)² + (z)³

= x³ + 3x²y + 3xy² + y³ + 3z (x² + 2xy + y²) + 3 z²(x + y) + z³

= x³ + 3x²y + 3xy² + y³ + 3x²z + 6xyz + 3yxz + 3 xz² + 3yz² + z³

= x³ + y³ + z³ + 3x²y + 3xy² + 3 x²z + 3 xz² + 3y²z + 3yz² + 6 xyz

Cube of (x + y + z) = x³ + y³ + z³ + 3x²y + 3xy² + 3 x²z + 3 xz² + 3y²z + 3yz² + 6 xyz

Example 16

Find the cube of 2x + 3y + 4z.

Solution :

Cube of (2x + 3y + 4z)

= (2x + 3y + 4z)³

= {(2x + 3y) + 4z}³

= (2x + 3y)³+3(2x + 3y)²x4z + 3 (2x +3y)(4 z)² + (4 z)³

= (2x)³ + 3(2x)² x 3y + 3 x 2x (3y)² + (3y)³ + 12z {(2x)² + 2 x 2x x 3y + (3y)²} + 3 x I62² (2x + 3y) + 64z³

= 8x³ + 36x²y + 54xy² + 27y³ + 48x²z + 144xyz + 108y²z+ 96xz² + 144yz² + 64z³

Cube of (2x + 3y + 4z) = 8x³ + 36x²y + 54xy² + 27y³ + 48x²z + 144xyz + 108y²z+ 96xz² + 144yz² + 64z³

Geometric representation of the formula (a- b)³= a³ – 3a²b + 3ab²-b³

First of all, prepare two cubes of sides 6 cm and 4 cm and also a set of three parallelopipeds of length 10 cm, breadth 6 cm, and height 4 cm.

Now, if we arrange these five solids in a proper manner we get a single cube, the length of each side of which is 10 cm. It is found that, if we remove, the three parallelopipeds of length 10 cm, breadth 6 cm, and height 4 cm and also the cube of side 4 cm from the new cube of side 10 cm then we shall be left with the cube of side 6 cm.

∴ 6³ = 10³ – 3 x 10 x 6 x 4 – 4³.

Now since 6 = 10 – 4, the above relation gives

(10 – 4)³ = 10³ – 3 x 10 (10 – 4) x 4 – 4³

or, (10 – 4)³= 10³ – 3x 10² x 4 + 3x 10 x 4² – 4³

Now taking 10 cm = a and 4 cm = b,

we get, (a – b)³ = a³ – 3a²b + 3ab² – b³.

Some examples on :

(a – b)³ = a³ – 3a² b+3ab² – b³

Example 1

Find the cube of (3a – 4b).

Solution :

Cube of (3a – 4b)

= (3a – 4b)³

= (3a)³ – 3 (3a)² x 4b + 3 x 3a (4b)² – (4b)³

= 27a³ – 108a²b + 144ab² – 64b³

Cube of (3a – 4b) = 27a³ – 108a²b + 144ab² – 64b³

Example 2

Find the cube of (pq – rs).

Solution :

Cube of (pq – rs)

= (pq – rs)³

= (PQ)³ – 3 (pq)²rs + 3pq (rs)² – (rs)³

= p³q³ – 3p²q²rs + 3pqr²s² – r³s³

Cube of (pq – rs) = p³q³ – 3p²q²rs + 3pqr²s² – r³s³

Example 3

Expand : (5x – 1/5x)³

Solution :

(5x – 1/5x)³

= (5x)³ – 3. (5x)² . 1/5x + 3. 5x . (1/5x)² – (1/5x)³

= 125x³ -15x + 3/5x – 1/ 125 x³

(5x – 1/5x)³ = 125x³ -15x + 3/5x – 1/ 125 x³

Example 4

Find the cube of 99 with the help of the formula.

Solution :

Cube of 99

= (99)³

= (100 – 1)³

= (100)³-3 (100)² x 1 + 3 x 100 x (1)² – (1)³

= 1000000 – 30000 + 300 -1

= (1000000 + 300) – (30000 + 1)

= 1000300 – 30001

= 970299

Cube of 99 = 970299

Example 5

Using the formula find the value of (75)³-3 x (75)²x 25 + 3 x 75 x (25)² – (25)³.

Solution:

If we assume that 75 = a and 25 = b

then the given expression becomes, a³ – 3a²b + 3ab² – b³ = (a – b)³

= (75 – 25)³        [Since a = 75, b = 25]

= (50)³

= 125000

(75)³-3 x (75)²x 25 + 3 x 75 x (25)² – (25)³ = 125000

Example 6

With the help of the formula find the value of: 5.25 x 5.25 x 5.25 – 3 x 5.25 x 5.25 x 1.25 + 3 x 5.25 x 1.25 x 1.25 – 1.25 x 1.25 x 1.25.

Solution:

Given 5.25 x 5.25 x 5.25 – 3 x 5.25 x 5.25 x 1.25 + 3 x 5.25 x 1.25 x 1.25 – 1.25 x 1.25 x 1.25.

Assuming 5.25 = a and 1.25 = b

the given expression becomes,

= a x a x a-3 x a x a x b + 3 x a x b x  b – b x b x b

= a³ – 3a²b + 3a6² – b³

= (a – b)³

= (5.25 – 1.25)³ [Since a = 5.25 and b = 1.25]

= (4.00)³

=64

5.25 x 5.25 x 5.25 – 3 x 5.25 x 5.25 x 1.25 + 3 x 5.25 x 1.25 x 1.25 – 1.25 x 1.25 x 1.25 =64

Example 7

If x – 1 and y = 2, then find the value of 125x³ – 300x²y + 240xy² – 64y³.

Solution :

Given x = 1 And y = 2

125x³ – 300x²y + 240ry² – 64y³

= (5x)³ – 3 (5x)² x 4y + 3 x 5x (4y)² – (4y)³

= (5x – 4y)³

= (5 x 1 – 4 x 2)³ [Since x = 1 and y = 2]

= (5 – 8)³

= (- 3)³

= – 27

125x³ – 300x²y + 240xy² – 64y³  = – 27

Example 8

If x – y = 5, then what is the value of x³ – y³ – 15xy?

Solution :

Given:

x-y = 5

Cubing both sides we get, (x – y)³ = (5)³

or, x³ – y³ – 3xy (x – y) = 125

or, x³– y³ – 3xy.5 = 125

or, x³– y³ – 15xy = 125

= 125.

x³ – y³ – 15xy = 125.

Alternative method :

x³ – y³ – 15xy

= x³ – y³ – 3xy x 5

= x³ – y³ – 3xy x (x – y) [x – y = 5]

= (x- y)³

= (5)³

= 125

Example 9

If 2x – 2/x = 3, then what is the value of 8×3 – 8/x3?

Solution:

Given 2x – 2/x = 3

\(\left(2 x-\frac{2}{x}\right)^3=(3)^3\) \(\text { or, }(2 x)^3-\left(\frac{2}{x}\right)^3-3 \times 2 x \times \frac{2}{x}\left(2 x-\frac{2}{x}\right)=27\) \(\text { or, } 8 x^3-\frac{8}{x^3}-12 \times 3=27\left[\text { Since } 2 x-\frac{2}{x}=3\right]\) \(\text { or, } 8 x^3-\frac{8}{x^3}=27+36=63\)

Example 10

Simplify : (2a + 3d)³ – 3(2a + 3b)² (2a – 3b) + 3(2a + 3b) (2a – 3b)²– (2a – 3b)³.

Solution:

Given :-

(2a + 3d)³ – 3(2a + 3b)² (2a – 3b) + 3(2a + 3b) (2a – 3b)²– (2a – 3b)³.

Let, 2a + 3b = x and 2a – 3b = y

Then the given expression = x³ – 3x?y + 3xy² – y³

= (x – y)³

= {(2a + 3b) – (2a – 3b)}³        [Putting x = 2a + 3b and y – 2a – 3b]

= (2a + 3b – 2a + 3b)³

= (6b)³

= 216b³

(2a + 3d)³ – 3(2a + 3b)² (2a – 3b) + 3(2a + 3b) (2a – 3b)²– (2a – 3b)³ = 216b³

Example 11

Simplify : (3a – 2b)³ – (2a – b)³ – 3(3a – 2b)(2a-b)(a – b).

Solution :

Given :

(3a – 2b)³ – (2a – b)³ – 3(3a – 2b)(2a-b)(a – b).

Let, 3a -2b = x and 2a – b = y

∴ x – y = (3a – 2b) – (2a – b)

= 3a – 2b – 2a + b = a – b

Then the given expression

= x³– y³ – 3xy (x – y)

= (x – y)³

= (a – b)³ [Since x – y = a – b]

= a³– 3a² b+ 3ab² – b³

(3a – 2b)³ – (2a – b)³ – 3(3a – 2b)(2a-b)(a – b) = a³– 3a² b+ 3ab² – b³

Example 12

Find the cube of a + b – c.

Solution :

Given :- a + b – c

Cube of a + b – c = (a + b – c)³ = {(a + b) – c}³

= (a + b)³ – 3 (a+b)² c+3 (a + b) (c)²-(c)³

= a³ + 3a^2b + 3ab² + b³ – 3c (a² + 2ab + b²) + 3c² (a+b) – c³

= a³ + 3a²6 + 3ab² + b³ – 3a²c – 6abc – 3b²c + 3c²a + 3bc² – c³

= a³ + 6³ – c³ + 3a² b+ 3ab² – 3a²c + 3ac² – 3b²c + 3bc² – 6abc

Cube of a + b – c = a³ + 6³ – c³ + 3a² b+ 3ab² – 3a²c + 3ac² – 3b²c + 3bc² – 6abc

Example 13

Find the cube of a + 2b – 3c.

Solution:

Given: a + 2b – 3c

Cube of a + 2b – 3c

= (a + 2b – 3c)³

= {(a + 2b) – 3c}³

= (a + 2b)³ – 3.(a + 2b)². 3c + 3(a + 2b). (3c)² – (3c)³

= a³ + 3 (a)² x 2b + 3a (2b)² + (2b)³ – 9c (a² + 4ab + 4b²) + 27c² (a + 26) – 27c³

= a³ + 6a^2b + 12ab² + 8b³ – 9a²c – 36abc – 36b²c + 27c²a+ 54bc² – 27c³.

Cube of a + 2b – 3c = a³ + 6a^2b + 12ab² + 8b³ – 9a²c – 36abc – 36b²c + 27c²a+ 54bc² – 27c³.

Formulae of a³+ b³ and a³ – b³

1.  We have seen that,

(a + b)³ = a³ + b³ + 3ab (a + b)

Therefore, a³+b³ = (a +b)³-3ab (a+b).

2. We have seen that,

(a – b)³ = a³ – b³ — 3ab (a – b)

Therefore, a³ – b³ = (a- b)³ + 3ab (a – b)

Some Examples

Example 1

What should be multiplied with a² – ab + b² so that the product will be the sum of two cubes?

Solution :

(a + b) (a² – ab + b²) = a³ + b³,

which is the sum of two cubes.

a + b

Example 2

What should be multiplied with a² + ab + b², so that the product will be the difference between two cubes?

Solution :

(a – b)(a² + ab + b²) = a³ – b³,

which is the difference of two cubes.

= a – b

Example 3

If the sum of the cubes of the two quantities is equal to the cube of their sum, then either at least one of them will be equal to zero or their sum will be zero.

Solution :

Let the two quantities be x and y x³ + y³ = (x + y)³

or, x³ + y³ = x³ + y³ + 3xy(x + y)

or, 3xy(x + y) = 0

or, xy(x + y) = 0

∴ Either r = 0 or, y = 0

or x+y = 0 Hence proved.

Example 4

If a + b = 5 and ab = 4, then what is the value of a³ + b³?

Solution :

Given a + b = 5 And ab = 4

a³ + b³ = (a + b)³ – 3ab (a + b)

= (5)³ – 3 x 4 x 5 [Since a + b = 5 and ab = 4]

= 125 – 60

= 65

a³ + b³ = 65

Example 5

If P³ + q³ – 152 and p + q = 8, then what is the value of pq?

Solution :

Given P³ + q³ – 152 And p + q = 8.

We know that,

(p + q)³ = p³ + q³ + 3pq (p + q)

or, (8)³ = 152 + 3pq x 8

or, 512 = 152 + 24pq

or, pq = 360/24

= 15

Example 6

If x + 1/x = √3, then what is value of x³ + 1/x³

Solution:

Given x + 1/x = √3.

x³ + 1/x³ = (x + 1/x)³ – 3x 1/x  . ( x + 1/x)

= (√3)³ – 3√3

= 3√3 – 3√3

= 0

x³ + 1/x³ = 0

Example 7

If 3x + 1/2x = 5, then what is the value of 27x³ + 1/8x³?

Solution:

Given 3x + 1/2x = 5.

27x³ + 1/8x³ = (3x)³ + (1/2x)³

= (3x + 1/2x)³ – 3 x 3x 1/2x .(3x +1/2x)

= (5)³ – 9/2 x 5

= 125 – 45/2

= 250 – 45 / 2

= 205/2

= 102 ½

27x³ + 1/8x³ = 102 ½

Example 8

Find the product of (3x + 4y) and (9x² – I2xy + 16y²) with the help of the formula.

Solution :

Given (3x + 4y) And (9x² – I2xy + 16y²)

(3x + 4y) (9X² – 12xy + 16y²)

= (3x + 4y) {(3x)² – 3x x 4y + (4y)²}

= (3x)³ + (4y)³ = 27x³ + 64y³

The required product = 27x³ + 64y³.

Example 9

Find the product of (2x – y) and (4x² + 2xy + y²) with the help of the formula.

Solution :

Given

(2x – y) And (4x² + 2xy + y²)

(2x – y) (4X² + 2xy + y²)

= (2x – y) {(2x)² + 2xy + (y)²}

= (2x)³ – (y)³

= 8x³ – y³

The required product = 8x³ – y³.

Example 10

If a – b = 5 and ab = 3, then what is the value of a³ – b³?

Solution :

Given

a – b = 5

ab = 3

a³ – b³ = (a – b)³ + 3ab (a – b)

= (5)³ + 3 x 3 x 5

= 125 + 45

= 170

a³ – b³  = 170

Example 11

If a – b = 1 and a³ – b³ = 61, then what is the value of ab?

Solution :

Given a – b = 1 And a³ – b³ = 61.

(a – b)³ = a³ – b³ – 3ab(a – b)

or, (1)³ = 61 – 3ab x 1

or, 3ab = 61 – 1 = 60

or, ab = 60/3

= 20

ab = 20

Example 12

If 2x – 1/3x, then what is the value of 8x³ – 1/27x³?

Solution:

Given 2x – 1/3x

8x³ – 1/27x³ = (2x)³ – (1/3x)³

= (2x – 1/3x) + 3 x 2x x 1/3x (2x – 1/3x)

= (3)³ + 2 x 3        [Since 2x -1/3x = 3]

= 27 + 6

= 33

8x³ – 1/27x³ = 33

Example 13

If 3a – 3/a + 1 = 0, what is the value of a³ – 1/a³ + 2?

Solution:

Given, 3a – 3/a + 1 = 0 And Given Equation a³ – 1/a³ + 2

or, 3(a – 1/a) = – 1

or, (a- 1/a) = – 1/3

Now, a³ – 1/a³ + 2

= (a – 1/a) + 3.a.1/a(a – 1/a) + 2

= (-1/3)³ + 3.(-1/3) + 2        [a – 1/a = – 1/3]

= – 1/27 – 1 + 2

= 1 – 1/27

= 26/27

a³ – 1/a³ + 2 = 26/27

Example 15

If p + 1/ p+2 = 1, then what is the value of (p+2)³ + 1/(p+2)³

Solution:

Given \(p+\frac{1}{p+2}=1\)

or, \(p+\frac{1}{p+2}=1\)

Now , \((p+2)^3+\frac{1}{(p+2)^3}\)

\(=\left[(p+2)+\frac{1}{(p+2)}\right]^3-3 \cdot(p+2) \cdot \frac{1}{(p+2)}\) \(\left[(p+2)+\frac{1}{(p+2)}\right]\) \(=[p+2+1-p]^3-3 \cdot[p+2+1-p]\) \(\left[\frac{1}{p+2}=1-p\right]\) \(=3^3-3.3=27-9=18\)

(p+2)³ + 1/(p+2)³ = 18

Algebra Chapter 4 Division Of Polynomials

Division of Polynomials Introduction

In class 7 you have studied the method of division of a polynomial by a single term divisor. In this chapter, we shall extend our idea on this topic. Here we shall discuss the method of division of a polynomial by a divisor having more than one term.

Rules for division

In order to divide one polynomial by another, first of all, we arrange both dividend and divisor in the ascending or descending power of the alphabetic symbol. Here we should remember only the index law, x^m ÷ xⁿ = x^m-n

At first, the first term of the dividend is divided by the first term of the divisor. This is taken as the first term of the quotient. All the terms of the divisor are now multiplied by this term and each term of the product is placed under the corresponding term of the dividend. Subtracting this product from the dividend we get the second step of the dividend. Now dividing the first term of this new dividend by the first term of the divisor, we get the second term of the quotient. By this term, we again multiply the whole divisor and we subtract this product from the second step of the dividend. Repeating this process as far as possible we get the final quotient.

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 4 Division Of Polynomials Some examples of division

Example 1

Divide 6x⁴ – 11 x³ – 2X² + 4x + 1 by 2x² -3x -1.

Solution : 

Given:-

6x⁴ – 11 x³ – 2X² + 4x + 1 And 2x² -3x -1.

The required quotient = 3x² – x – 1

Example 2

Divide – 6x⁵ + 7x⁴ – 4x³ – 2x² + 9x + 2 by – 2x² + x + 2.

Solution:

Given:-

– 6x⁵ + 7x⁴ – 4x³ – 2x² + 9x + 2 And – 2x² + x + 2.

Example 3

Divide x⁸ + x⁴y⁴ + y⁸ by x⁴ + x²y² + y⁴.

Solution :

Given:-

x⁸ + x⁴y⁴ + y⁸ And x⁴ + x²y² + y⁴.

Example 4

Divide x³ + y³ + z³ – 3xyz by x + y + z.

Solution :

Given:-

x³ + y³ + z³ – 3xyz And x + y + z.

Example 5 

Divide a⁴+ a2b2 + b⁴ by a² -ab + b²

Solution:

Given:-

a⁴+ a2b2 + b⁴ And a² -ab + b²

Example 6

Divide a⁴x⁴+ 4 by a²x² – 2ax + 2.

Solution:

Given

a⁴x⁴+ 4 And a²x² – 2ax + 2.

Example 7

Divide a³ + 8a² + 11a -6 by a² + 2a -1.

Solution:

Given

a³ + 8a² + 11a -6 And a² + 2a -1.

 

Example 8

Divide x⁶+ x⁵+ x by x² + x +1.

Solution:

Given

x⁶+ x⁵+ x And x² + x +1.

Inexact division

In arithmetic when we divide a number by another number there may or may not be any remainder. For example when we divide 40 by 5 then there is no remainder i.e., 40 is exactly divisible by 5. But when we divide 38 by 5 then the quotient is 7 and the remainder is 3. Likewise, in algebra, when we divide one expression by another there may or may not be any remainder. Thus, when we divide an algebraic expression by another and there is a remainder then such division is called an inexact division. If q is the quotient and r is the remainder when b is divided by a,

then the complete quotient = q + r/a.

WBBSE Board Class 8 Math Solution

Example 1

Divide 2x⁶– 3x⁶+ 7x³ -16x +15 by x⁴– 2x² +4.

Solution:

Given:-

2x⁶– 3x⁶+ 7x³ -16x +15 And x⁴– 2x² +4.

Example 2

Divide 12a⁴+ 5a³ -33a² -3a + 16 by 4a² – a – 5.

Solution:

Given:

12a⁴+ 5a³ -33a² -3a + 16 And 4a² – a – 5.

Division by the method of ‘detached coefficients

There is another method of division of two polynomials. In this method, we only write successive coefficients of the dividend and divisor and then divide as before. After obtaining the quotient and remainder in terms of coefficients the alphabetic symbol is Written with successive power. If any term containing a particular power is absent either in the dividend or in the divisor, then the corresponding coefficient is taken as zero.

Example 1

Divide 6x⁴ – 7x³ + 10x² + 8x – 5 by 3x² + x – 1.

Solution :

Given 6x⁴ – 7x³ + 10x² + 8x – 5 And 3x² + x – 1.

Let us first detach the coefficients of the dividend and divisor.

Obviously, the highest power of x in the quotient is x². Hence, the required quotient is 2x² – 3x + 5.

6x⁴ – 7x³ + 10x² + 8x – 5 / 3x² + x – 1 = 2x² – 3x + 5.

Example 2

Divide 12a⁴ + 5a³ – 33a² – 3a + 16 by 4a² – a – 5.

Solution:

Given:

12a⁴ + 5a³ – 33a² – 3a + 16 And 4a² – a – 5.

Let us first detach the coefficients of the dividend and divisor.

Quotient = 3a² + 2a – 4, Remainder = 3a – 4.

Algebra Chapter 3 Multiplication Of Polynomials

Multiplication of Polynomials Introduction

You know that when two or more expressions are related to each other by the sign of addition or subtraction then a polynomial is formed and each expression of that polynomial is called a term. In this chapter, our aim is to multiply two polynomials each with more than two terms. So, in fact, this chapter is nothing but an extension of the same topic which we studied in class VII.

Rules for multiplication

Here we shall discuss the rules for multiplication in brief. The following four rules are common in any type of algebraic multiplication.

1.Commutative law : a x b = b x a.

2.Associative law : a x (b x c) = (a x b) x c.

3. Distributive law : 

1. a x (b + c) = a x b + a x c.

2. (a + b) x c = a x c + b x c.

4. Index law :

1. x^m x xⁿ = x^m+n

2. (X^m)ⁿ = x^mn

3. xº = 1.

When we multiply two polynomials we generally arrange the terms of the multiplicand and those of the multiplier in the ascending or descending powers of a variable (which is expressed by a letter of the English alphabet.)

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 3 Multiplication Of Polynomials Some examples of multiplication

Example 1

Multiply : a² – ab + b² by b²+ ab + a².

Solution:

Given:-

a² – ab + b² And b²+ ab + a².

When arranged in the descending powers of a multiplicand

= a² – ab + b² and multiplier = a² + ab + b².

Now, a² – ab + b²

The required product = a⁴+a²b²+b⁴

a² – ab + b² X b²+ ab + a² = a⁴+a²b²+b⁴

Example 2

Multiply ax + by – cz by ax – by + cz.

Solution :

Given:-

ax + by – cz And ax – by + cz.

The required product = a²x² – b²y² – c²z² + 2bcyz

ax + by – cz X ax – by + cz. = a²x² – b²y² – c²z² + 2bcyz

Example 3

Multiply : 4a – 2a² + 1 + 3a³ by 2 – 2a² + a.

Solution:

Given

4a – 2a² + 1 + 3a³ And 2 – 2a² + a.

Arranging in the descending powers of a,

we get,

multiplicand = 3a³ – 2a² + 4a + 1,

multiplier = – 2a² + a + 2.

Now, 3a³ – 2a² + 4a + 1

Example 4

Multiply: p² + g² – pq + p + q + 1 by p + q -1.

Solution :

Given

p² + q² – pq + p + q + 1 And p + q -1.

The required product = p³ + q³ -1 + 3pq

p² + g² – pq + p + q + 1 And p + q -1.= p³ + q³ -1 + 3pq

Example 5

Multiply x² + y² + z² – xy – yz – zx by  +y+ z.

Solution :

Given

x² + y² + z² – xy – yz – zx And  +y+ z.

The required product = x³ +y³ +z³ – 3xyz

x² + y² + z² – xy – yz – zx by  +y+ z. = x³ +y³ +z³ – 3xyz

Example 6

Multiply : x² + 4x + 8 by x² – 4x + 8.

Solution:

Given:-

x² + 4x + 8 And x² – 4x + 8.

The required product = x⁴ + 64

x² + 4x + 8 X x² – 4x + 8. = x⁴ + 64

Example 7

Multiply: 2x² – 3x – 1 by 3x² – x – 1.

Solution :

Given

2x² – 3x – 1 And 3x² – x – 1.

Example 8

Multiply: \(x^3-3 x^2 y^{-\frac{1}{3}}+3 x y^{\frac{2}{3}}-y^{-1} \text { by } x-y^{-\frac{1}{3}}\)

Solution:

Given

\(x^3-3 x^2 y^{-\frac{1}{3}}+3 x y^{\frac{2}{3}}-y^{-1} \text { And } x-y^{-\frac{1}{3}}\)

The required product = \(x^4-4 x^3 y^{-\frac{1}{3}}+6 x^2 y^{-\frac{2}{3}}-4 x y^{-1}+y^{-\frac{4}{3}}\)

Example 9

Multiply : a²x² – 2ax + 2 by a²x² + 2ax + 2.

Solution:

Given

a²x² – 2ax + 2 by a²x² + 2ax + 2.

The required product = a⁴x⁴ + 4

a²x² – 2ax + 2 X a²x² + 2ax + 2. = a⁴x⁴ + 4

Example 10

Multiply : 3x³ – 2x² + 2 by 2x² – x + 1.

Solution:

Given

3x³ – 2x² + 2 And 2x² – x + 1.

The required product = 6x⁵– 7x⁴ + 5x³ + 2x² – 2x + 2

3x³ – 2x² + 2 X 2x² – x + 1 = 6x⁵– 7x⁴ + 5x³ + 2x² – 2x + 2

Multiplication of more than two polynomials

In order to multiply more than two polynomials first of all we multiply any two polynomials by the method already discussed. After that, we take this product as the multiplicand and the third polynomial as the multiplier. We then find the new product. In the next stage, we multiply this product by the fourth polynomial (if any). Proceeding in this way we complete the process of multiplication.

Example 1

Find the continued product of : (a² + ab + b²), (a – b), and (a³ + b³).

Solution :

Given

(a² + ab + b²), (a – b), And (a³ + b³).

Example 2

Multiply : 2x³ – 4X² – 5 by 3X² + 4x – 2.

Solution:

Given:-

2x³ – 4X² – 5 And 3X² + 4x – 2.

Let us first detach the coefficients of the multiplicand and multiplier.

Since the term containing x is absent in the multiplicand we take the co-efficient of x as 0.

Algebra Chapter 2 Rational Number

Natural Numbers

The numbers, which were known to us in the beginning, were used to count something. These numbers are natural numbers. Thus, 1, 2, 3, 4… to infinity are called natural numbers.

Whole Numbers

When 0 is included with natural numbers, then they form whole numbers or integers. Thus, 0, 1, 2, 3, 4… to infinity are called

Positive and Negative Integers

whole numbers or integers.
The numbers 0, 1, 2, 3, 4… etc. are called positive integers, and -1, -2, -3, -4, … are negative integers.

Rational Number

Any number of the form p/q where p and q are both integers and q * 0 is called a rational number. While writing a rational number usually take the denominator as a positive integer p and express p/q in the lowest form.

Example : 3/8, 8/11, -7/12 etc.

are the rational numbers. All natural numbers, integers, and fractions are included in rational numbers. We can imagine the natural number 5 as a rational number. Because 5 =5/1 therefore, it can be expressed in the form p/q where p =5 and q = 1, p and q are both integers and q ≠ 0.

But √2 is not a rational number because it cannot be expressed in the form p/q where p and q are integers. In fact,  √2 = 1.414213…

Any decimal fraction and recurring decimal fraction may be expressed in the form p/q where p and q are integers.

Therefore, they are also rational numbers.

Read And Learn More WBBSE Solutions For Class 8 Maths

Example: 0.5 = 5/10 = 1/2;

0.9 = 9/9 = 1/1

The numbers which are not rational are called irrational numbers. Examples of some irrational numbers are

Some Decisions

1. Sum of two integers is an integer: 7 + 8=15.

2.  Product of two integers is an integer: 7 x 8 = 56.

3. The difference between two integers in a positive or negative integer: 8-4 = 4,

4-8

= -4.

4. The quotient of two integers is not always an integer: 7÷8 = 7/8,

8 ÷ 7 = 8/7.

(Only when two numbers are the same their quotient is an integer. For example, 5÷5 = 1.)

Some more decisions

If a and b are two rational numbers :

1.  a + b is a rational number.

For example 1/2 + 2/3

Given That, a + b is a rational number.

Adding The Terms 1/2 And 2/3

= 3+4 / 6

= 7/6.

Here, 7/6 is a rational number.

2. a – b is a rational number.

For example 1/2 – 2/3

Given That, a – b is a rational number

So Subtracting The Terms 1/2 And 2/3

= 3-4 / 6

= -1/6. 

Here, is a rational number.

3. a x b is a rational number.

For example 1/2 x 2/3 

Given a x b is a rational number.

So Multiply The Terms 1/2 And 2/3

1/2 x 2/3

= 1/3.

Here, 1/3 is a rational number.

4. a÷b is a rational number.

For example 1/2 ÷ 2/3

Given a ÷ b is a rational number.

= 1/2 ÷ 2/3

= 3/4

Here, 3/4 is a rational number.

Some Properties of rational numbers

1. If a and b are two rational numbers, then a + b = b + a.

That means rational numbers obey the commutative law of addition.

For example 1/2 + 2/3

= 3+4 / 6

= 7/6

2/3 + 1/2

= 4+3/6

= 7/6

∴ 1/2 + 2/3 = 2/3 + 1/2.

2. If a and b are two rational numbers, then a – b ≠ b – a.

That means the rational numbers do not obey the commutative law of subtraction.

That means the rational numbers do not obey the commutative law of subtraction.

1/2 – 2/3

= 3-4 / 6

= -1/6

2/3 – 1/2

= 4-3/6

= 1/6

∴ 1/2 – 2/3 ≠ 2/3 – 1/2.

3. If a and b are two rational numbers, then a x b = b x a.

That means rational numbers obey the commutative law of multiplication.

1/2 x 2/3 = 1/3

2/3 x 1/2 = 1/3

∴ 1/2 x 2/3 = 2/3 x 1/2.

4. If a and b are two rational numbers, then a + b x b + a.

That means the rational numbers do not obey the commutative law of division.

1/2 ÷ 2/3 = 1/2 x 3/2 = 3/4

2/3 ÷ 1/2 = 2/3 x 2/1 = 4/3

∴ 1/2 ÷ 2/3 ≠ 2/3 ÷ 1/2.

Some more Properties of rational

1.  If a, 6, and c are three rational numbers then, a + (b + c) = (a + b) + c.

That means the rational numbers obey the associative law of addition

1/2 + (2/3 + 3/4 ) = 1/2 + 8+9 / 12

= 1/2 + 17/12+= 6+17 / 12+= 23/12

(1/2 + 2/3 ) + 3/4 = 3+4 / 6 + 3/4

= 7/6 + 3/4

= 14+9 / 12

= 23/12

∴ 1/2 + (2/3 + 3/4) = (1/2 + 2/3) + 3/4.

2. If a, b, and c are three rational numbers then, a – (b – c) * (a – b) – c.

That means rational numbers do not obey the associative law of subtraction.

1/2 – (2/3 – 3/4) = 1/2 – (8-9 / 12)

= 1/2 + 1/12

= 6+1 / 12

= 7/ 12

(1/2 – 2/3 – 3/4 = 3-4 / 6 – 3/4

= -1/6 – 3/4

= -2-9 / 12

= -11/12

∴ 1/2 – (2/3 – 3/4) ≠ (1/2 – 2/3) – 3/4.

3. If a, b, and c are three rational numbers then, z x ( b x c) = (a x b) x c.

That means rational numbers obey the associative law of multiplication.

1/2 x (2/3 x 3/4) = 1/2 x 1/2

= 1/4

(1/2 x 2/3 ) x 3/4 = 1/3 x 3/4

= 1/4

∴ 1/2 x (2/3 x 3/4) = (1/2 x 2/3) x 3/4.

4. If a, b, and c are three rational numbers then, a ÷ (6 ÷ c) ≠ (a ÷ b) ÷ c.

That means rational numbers do not obey the associative law of divisions.

\(\frac{1}{2} \div\left(\frac{2}{3} \div \frac{3}{4}\right)=\frac{1}{2} \div\left(\frac{2}{3} \times \frac{4}{3}\right)\) \(=\frac{1}{2} \div \frac{8}{9}=\frac{1}{2} \times \frac{9}{8}=\frac{9}{16}\) \(\left(\frac{1}{2} \div \frac{2}{3}\right) \div \frac{3}{4}=\left(\frac{1}{2} \times \frac{3}{2}\right) \div \frac{3}{4}=\frac{3}{4} \times \frac{4}{3}=1\) \(\frac{1}{2} \div\left(\frac{2}{3} \div \frac{3}{4}\right) \neq\left(\frac{1}{2} \div \frac{2}{3}\right) \div \frac{3}{4} \text {. }\)

Distributive law

If a, b, and c are three rational numbers then,

a(b + c) = ab + ac

a(b – c) = ab – ac

\(\frac{1}{2}\left(\frac{2}{3}+\frac{3}{4}\right)=\frac{1}{2}\left(\frac{8+9}{12}\right)=\frac{1}{2} \times \frac{17}{12}=\frac{17}{24}\) \(\frac{1}{2} \times \frac{2}{3}=\frac{1}{3}, \frac{1}{2} \times \frac{3}{4}=\frac{3}{8}\) \(\frac{1}{2} \times \frac{2}{3}+\frac{1}{2} \times \frac{3}{4}=\frac{1}{3}+\frac{3}{8}=\frac{8+9}{24}=\frac{17}{24}\) \(\frac{1}{2}\left(\frac{2}{3}+\frac{3}{4}\right)=\frac{1}{2} \times \frac{2}{3}+\frac{1}{2} \times \frac{3}{4}\) \(\text { Similarly, } \frac{1}{2}\left(\frac{2}{3}-\frac{3}{4}\right)=\frac{1}{2} \times \frac{2}{3}-\frac{1}{2} \times \frac{3}{4} \text {. }\)

Algebra Chapter 12 Equations Some Examples

Example 1

Find the opposite number of addition.

1. – 3/7

2. 15/17.

Solution:

1. The opposite number of addition of – 3/7 is 3/7 because,

= – 3/7 + 3/7

= -3+3 / 7

= 0/7

= 0.

– 3/7 the opposite number of addition = 0.

2. The opposite number of addition of 15/17 is – 15/17 because,

= 15/17 – 15/17

= 15-15 / 17

= 0/17

= 0.

15/17 the opposite number of addition = 0.

Example 2

What do you mean by the reciprocal of a rational number?

Solution :

The number by which, if a rational number is multiplied to get 1 as a product is called the reciprocal or opposite number with respect to the multiplication of that rational number. It is also known as multiplicative inverse.

For Example,  the reciprocal of 5/7  is 7/5  because

5/7 x 7/5 = 1

Example 3

= { 3/7 + (-8 / 21)} + (-6/11 + 5/22}

= 9-8 / 21 + (-12 + 5) / 22

= 1/21 – 7/22

= 22-147 / 462

= -125 / 462.

{ 3/7 + (-8 / 21)} + (-6/11 + 5/22} { 3/7 + (-8 / 21)} + (-6/11 + 5/22}

Example 6

Write 4 rational numbers between 1 and 2.

Solution :

1. If x and y be two rational numbers such that x < y, then 1/2 ( x + y)is a rational number between x and y.

Observe how this rule is applied here

1 rational number between 1 and 2

= 1/2 (1+2)

= 3/2

4 rational numbers between 1 and 2 = 3/2

2. Again, 1 rational number between 1 and 3/2

= 1/2(1+2)

= 1/2(1 + 3/2)

= 5/4

1 rational number between 1 and 3/2 = 5/4

3. 1 rational number between 1 and 5/4

= 1/2 (1 + 5/4)

= 9/8

1 rational number between 1 and 5/4 = 9/8

4. 1 rational number between 1 and 9/8

= 1/2 (1 + 9/8)

= 17/16

1 rational number between 1 and 9/8 = 17/16

∴ 4 rational numbers between 1 and 2 are,

17/16, 9/8, 5/4, 3/2.

Example 7

Write 4 rational numbers equivalent to 2/3.

Solution :

\(\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6}, \quad \frac{2}{3}=\frac{2 \times 3}{3 \times 3}=\frac{6}{99},\) \(\frac{2}{3}=\frac{2 \times 4}{3 \times 4}=\frac{8}{12}, \quad \frac{2}{3}=\frac{2 \times 5}{3 \times 5}=\frac{10}{15}\)

∴ 4 rational numbers equivalent to 2/3 are,

4/6, 6/9, 8/12, 10/15.

Example 8

Write the rational number 4 as the

1. sum and

2. difference between two irrational numbers.

Solution :

1. 4 = (2 + √3) + (2 – √3).

2. 4 = (√3 + 2) – (√3 – 2).

Example 9

What should be added to 7/12 to get – 4/12?

Solution :

Let the required number be x.

Then, 7/12 + x = – 4/15

or, x = – 4/15 – 7/12

= -(4/15 + 7/12)

= – (16+35 / 60)

= – 51/60

= – 17/20.

Example 10

The sum of two rational numbers is -3. If one of them is 1/3, then find the other one.

Solution :

Given That,

The sum of two rational numbers is -3.

one of them is 1/3.

Let the other number be x.

Then, x + 1/3 = -3

or, x = – 3 – 1/3

or, x = -(3+1/3)

= -(9+1 / 3)

= -10/3

Example 11

Find the reciprocal of -5/2 x 32/15.

Solution: 

Given -5/2 x 32/15.

We have, \(-\frac{5}{8} \times \frac{32}{15}=-\frac{5 \times 32^4}{3 \times 15_3}=-\frac{4}{3}\)

∴ Reciprocal of \(-\frac{5}{8} \times \frac{32}{15}\)

= Reciprocal of \(-\frac{4}{3}\)

= \(\frac{3}{4}\)

Example 12

If x = 3 and y = 2, then find the value of (3x-4y)^y-x ÷ (4x-3y)^2y-x

Solution:

Given

x = 3 And y = 2.

We have, (3x -4y) = (3 x 3 – 4 x 2)

= (9 – 8)

= 1

(3x-4y)^y-x ÷ (4x-3y)^2y-x  = 1

(4x – 3y) = (4 x 3 – 3 x 2) = (12 – 6) = 6

∴ \((3 x-4 y)^{y-x} \div(4 x-3 y)^{2 y-x}\)

= \(\frac{(3 x-4 y)^{y-x}}{(4 x-3 y)^{2 y-x}}=\frac{(1)^{2-3}}{(6)^{2 \times 2-3}}=\frac{(1)^{-1}}{(6)^{4-3}}\)

= \(\frac{(1)^{-1}}{6}=\frac{1}{1 \times 6}=\frac{1}{6}\)

 

Algebra Chapter 1 Commutative Associative and Distributive Laws

Commutative Associate and Distributive Introduction

In class 7 you have studied commutative, associative, and distributive laws, the application of four basic operations on polynomials, the deduction of some formulae, simple factorization of quadratic expressions, and the formation of linear equations of one variable and their solution. Here we shall discuss those topics in brief for recapitulation.

Commutative, Associative, and Distributive laws

We know that if a and b are any two integers then

1. The commutative law of addition is, a+ b = b + a

2. The commutative law of multiplication is, a x b = b x a

3. Associative law of addition is, (a+ b) + c = a + (b + c)

4. The associative law of multiplication is, (a x b) x c = a x (b x c)

5. The distributive law of multiplication is

1. (a + b) x c = a x c + b x c

2. ax (b + c) = ax b + ax c

3. (a – b) x c = a x c – b x c

4. a x (b – c) – ax b~ ax c

6. The distributive law of division is

1. (a + b)÷ c = a + c + b ÷ c

2. (a-b) ÷ c = a + c-b ÷ c

But c ÷ (a + b) ≠ c + a + c ÷ b

and c ÷ (a-b) ≠ c + a- c ÷ b

Read And Learn More WBBSE Solutions For Class 8 Maths

Algebra Chapter 1 Commutative Associative and Distributive Laws Some problems with Commutative, Associative, and Distributive laws

Example 1

Rewrite 4 + 7 + 9 in two different ways such that a single bracket is used in each case.

Solution:

Given 4 + 7 + 9

Given Sum In Two Different Ways Such That A Single Bracket Is Used In Each Case:-

4 + 7 + 9 = (4+ 7)+ 9 and 4 + 7 + 9 = 4 + (7 + 9)

Example 2

Add the sum of 6 and 8 with 5 and find the result.

Solution :

Given Sum Of 6 And 8 With 5.

5 + (6 + 8)

= 5+ 14

= 19

The Result Is 19.

Example 3

Prove that: (a + b + c) x = ax + bx + cx.

Solution :

Given (a + b + c) x

(a + b + c)x

= (a + d)x [assuming b + c = d]

= ax + dx [by distributive law]

= ax + (b + c)x [putting d = b + c]

= ax + bx + cx (Proved).

(a + b + c) x = ax + bx + cx.

Example 4

Simplify a/ a-b + b / b-4.

Solution :

The given expression = a / a-b + b/b-a

= a / a-b + b / – (a-b)

= a/ a-b – b/ a-b

= a-b / a-b

= 1

a / a-b + b/b-a = 1

Example 5

Simplify : -2-[-2-{-2-(2-3-2)}].

Solution :

The given expression = – 2-[- 2-{- 2-(2-3-~2)}]

= – 2 -[-2 – {- 2 – (2 – 1)}]

= – 2 – [- 2 – {- 2 – 1}]

= – 2 – [- 2 – {- 3}]

= – 2 – [- 2 + 3]

= -2 – [1]

= – 2 – 1

= – 3

– 2-[- 2-{- 2-(2-3-~2)}] = – 3

Example 6

Simplify : x-[y + {x-(y-x-y)}]

Solution :

The given expression = x–[y + {x-{y-x-y)}]

= x-\y + {x -(y – x + y)}]

= x-\y+{x-{2y- *)}]

= x-[y + {x-2y + x}]

-x-{y + {2x- 2y}]

= x-\y + 2x-2y]

= x-[2 x-y]

= x-2x + y

= y-x

x–[y + {x-{y-x-y)}] = y-x

Polynomial

If there are many terms in an algebraic expression then, it is called a polynomial. For example, a + 5b – 8c + 9d + 7e + 8f – 11x is a polynomial.

If there is only one term in an expression, then it is called a monomial.

For example, 5x is a monomial.

If there are two or three terms, then they are called binomial and trinomial respectively.

For example, 5a + 6b is a binomial and 7a – 12b + 8c is a trinomial.

Example 1

Find the sum of 4x², – 3x², 7x².

Solution :

The required sum = 4x², – 3x², 7x²

= (4x² + 7x²) – 3x²

= 11x²  – 3x²

= 8x²

4x², – 3x², 7x² = 8x²

Example 2

Find the sum of : – 2xy, 5xy, 9.xy and -7xy.

Solution :

Here, the required sum

= – 2xy + 5xy + 9xy – 7xy

= (5xy + 9xy) – (2xy + 7xy)

= 14xy – 9xy

= 5 xy

– 2xy + 5xy + 9xy – 7xy = 5 xy

Example 3

Find the sum of the following expressions:

5x – 8y + z,

– 2x + 7y – 5z, 

3s + 5y + 3z.

Solution :

\(\begin{array}{r}
5 x-8 y+z \\
-2 x+7 y-5 z \\
3 x+5 y+3 z \\
\hline 6 x+4 y-z \\
\hline
\end{array}\)

The required sum = 6x+4y-z

Example 4

Simplify : 5a² + 2d² + 2ab + 3a² – 6b² – 5ab + 3a.

Solution :

The given expression

5a² + 2d² + 2ab + 3a² – 6b² – 5ab + 3a

= 5a² + 2b² + 2ab + 3a² – 6b² – 5ab + 3a

= (5a² + 3a²) + (2 b² – 6 b²) + (2ab – 5ab) + 3a

= 8a² – 4b² – 3ab + 3a

5a² + 2d² + 2ab + 3a² – 6b² – 5ab + 3a. = 8a² – 4b² – 3ab + 3a

Subtraction

The quantity from which the subtraction is to be made is called minuend. The quantity which is to be subtracted is called subtrahend. The result obtained after subtraction is called the difference or remainder. By subtraction of b from a, we mean the addition of the negative of b with a. It means that a – b = a + (- b).

Example 1

Subtract 5xy from 12xy.

Solution :

Given 5xy And 12xy

12xy – 5xy = 7xy

Example 2

Subtract – 9xy from 25xy

Solution:

25xy – (- 9xy) = 25xy + 9xy = 34xy.

Example 3

Subtract 5a² + 4b² + 2c² from 7a² – 3b² + 8c².

Solution :

Given 5a² + 4b² + 2c² And 7a² – 3b² + 8c².

\(\begin{array}{r}
7 a^2-3 b^2+8 c^2 \\
5 a^2+4 b^2+2 c^2 \\
-\quad- \\
\hline 2 a^2-7 b^2+6 c^2 \\
\hline
\end{array}\)

Example 4

What is to be added with a² – ab + 2b² to get a² + b²?

Solution :

The required expression = (a² + b²) – (a² – ab + 2b²)

= a² + b² – a² + ab – 2 b²

= (a² – a²) + (b² – 2b²) + ab

= – b² + ab

(a² + b²) – (a² – ab + 2b²) = – b² + ab

Multiplication

In the case of algebraic multiplication of two quantities, the sign of the product is V when the two quantities are of the same sign and the sign of the product is ‘—’ when the two quantities are of opposite signs.

This may be explained in brief as follows :

(+ x) x (+ y) = + xy

(+ x) x (- y) = – xy

(- x) x (+ y) = -xy

(- x) x (- y) = + xy

In case of finding the product of the same variable having different powers, we follow the rule x^m x xⁿ = x^m+n

Example 1

Multiply : 7x³ by 2x⁴

Solution :

Given 7x³ by 2x⁴

7x³ x 2x⁴ = 7 x 2 x x³ x x⁴

= 14 x _x³⁺⁴ 

= 14 x x⁷

= 14x⁷

7x³ x 2x⁴ = 14x⁷

Example 2

Find the product ;

(- 5p²q) x (3pq²) x (- 2p²q²).

Solution :

Given

(- 5p²q) x (3pq²) x (- 2p²q²)

The required product = (- 5p²q) x (3pq²) x (- 2p²q²)

= (- 5) x 3 x (-2) x p²⁺¹⁺² x q¹⁺²⁺²

= 30p⁵q⁵

(- 5p²q) x (3pq²) x (- 2p²q²) = 30p⁵q⁵

Example 3

Multiply : – 3p²q⁵r by – 7p³g²r⁵.

Solution :

Given – 3p²q⁵r And – 7p³g²r⁵

The required product = (- 3p²g⁵r) x (- 7p³q²r⁵)

= (- 3) x (- 7) x p²⁺³ x g⁵⁺² x r¹⁺⁵

= 21p⁵q⁷r⁶

(- 3p²g⁵r) x (- 7p³q²r⁵) = 21p⁵q⁷r⁶

Example 4

Find the product: (1/2 xy²) x (- 2/3 xy⁴) x (3x³y).

Solution :

Given

(1/2 xy²) x (- 2/3 xy⁴) x (3x³y)

= (1/2 xy²) x (- 2/3 xy⁴) x (3x³y).

= 1/2 x (- 2/3) x 3 x x¹⁺¹⁺³ x  y²⁺⁴⁺¹

= (-1) x x² x y⁷

= -x⁵y⁷

(1/2 xy²) x (- 2/3 xy⁴) x (3x³y). = -x⁵y⁷

Example 5

Multiply :7a +3b by 2a – b.

Solution :

Given 7a +3b by 2a – b

\(\begin{aligned}
& 7 a+3 b \\
& 2 a-b \\
& \hline 14 a^2+6 a b \\
& \quad-7 a b-3 b^2 \\
& \hline 14 a^2-a b-3 b^2 \\
& \hline
\end{aligned}\)

The required product = 14a²-ab-3b²

Division

In the case of algebraic division of the form

a/b = c, we call a dividend, b the divisor, and c the quotient.

If the dividend and the divisor are of the same sign, then the sign of the quotient will be + and if the dividend and the divisor are of opposite signs the sign of the quotient will be -.

This may be explained in brief as follows :

\(\frac{(+x)}{(+y)}=+\frac{x}{y}\) \(\frac{(+x)}{(-y)}=-\frac{x}{y}\) \(\frac{(-x)}{(+y)}=-\frac{x}{y}\) \(\frac{(-x)}{(-y)}=+\frac{x}{y}\)

In the case of finding the quotient of the same variable having different powers, we follow the rule x^m ÷ xⁿ = x^m+n.

We shall also take x° = 1.

Example 1

Divide 35a⁴b⁸ by 5a²b².

Solution : 

Given 35a⁴b⁸ And 5a²b²

=35a⁴b⁸ / 5a²b²

= 7a^4-2b^8-2

= 7a²b⁶

35a⁴b⁸ / 5a²b² = 7a²b⁶

Example 2

Divide (- 81m⁵n⁶) by (- 27m²n²).

Solution :

Given (- 81m⁵n⁶) And (- 27m²n²)

The required quotient

=(- 81m⁵n⁶) / (- 27m²n²).

= 3m^5-2n^6-2

= 3m³n⁴

(- 81m⁵n⁶) / (- 27m²n²) = 3m³n⁴

Example 3

Divide 4x⁵ + 3x⁴ + 8x³ + 7x by x².

Solution :

The required quotient 4x⁵ + 3x⁴ + 8x³ + 7x² / x²

\(=\frac{4 x^5+3 x^4+8 x^3+7 x^2}{x^2}=\frac{4 x^5}{x^2}+\frac{3 x^4}{x^2}+\frac{8 x^3}{x^2}+\frac{7 x^2}{x^2}\) \(=4 x^{5-2}+3 x^{4-2}+8 x^{3-2}+7 x^{2-2}\) \(=4 x^3+3 x^2+8 x^1+7 x^0\) \(=4 x^3+3 x^2+8 x+7\)

Example 4

Divide 13m²n⁴ + 16m³n³-20m⁴n² by 4m²n².

Solution:

Given 13m²n⁴ + 16m³n³-20m⁴n² And 4m²n²

= \(\frac{12 m^2 n^4+16 m^3 n^3-20 m^4 n^2}{4 m^2 n^2}\)

= \(\frac{12 m^2 n^4}{4 m^2 n^2}+\frac{16 m^3 n^3}{4 m^2 n^2}-\frac{20 m^4 n^2}{4 m^2 n^2}\)

= \(3 n^2+4 m n-5 m^2\)

 

Some important formulae

In the previous class, you learned the following three formulae :

1. (a + b)²= a² + 2ab + b².

2. (a – b)²– a² – 2ab + b².

3. a²– b² – (a + b) (a – b).

Also using the first two formulae the following five formulae can be established:

1. a²+ b² = (a + b)² – 2ab

2. a²+ b² = (a – b)² + 2ab

3. (a + b)²= (a – b)² + 4ab

4. (a – b)²= (a + b)² – 4ab.

5. ab = (a+b / 2)² – (a-b / 2)²

Algebra Chapter 1 Commutative Associative and Distributive Laws Some Examples

Example 1

Find the square of (a + 2b).

Solution :

Given (a + 2b):-

Square of (a + 2b).

= (a + 2b)²

= (a)² + 2.a.2b + (2b)²

= a²+ 4 ab+ 4 b²

Square of (a + 2b). = a²+ 4 ab+ 4 b²

Example 2

Find the square of 101.

Solution :

Given 101

Square of 101 = (101)²

= (100 + 1)²

= (100)² + 2 x 100 x 1 + (1)²

= 10000 + 200 + 1

= 10201

Square of 101 = 10201

Example 3

Simplify: (7x + 4y)2 – 2(7x+4y)(7x-4y)+(7x-4y)2.

Solution:

Given (7x + 4y)2 – 2(7x+4y)(7x-4y)+(7x-4y)2.

Let, 7x+4y = a and 7x – 4y = b.

Hence, the given expression

\(=a^2-2 a b+b^2\) \(=(a-b)^2\) \(=\{(7 x+4 y)-(7 x-4 y)\}^2\) \(=(7 x+4 y-7 x+4 y)^2\) \(=(8 y)^2=64 y^2\)

Example 4

Simplify : 0.82 x 0.82 + 2 x 0.82 x 0.18 + 0.18 x 0.18.

Solution :

Given 0.82 x 0.82 + 2 x 0.82 x 0.18 + 0.18 x 0.18.

Let, a = 0.82 and b = 0.18

Then the given expression

=a x a + 2 x a x b + b x b

= a² + 2 ab + b²

= (a + b)²

= (0.82 + 0.18)²

= (1.00)²

= (1)²

= 1

0.82 x 0.82 + 2 x 0.82 x 0.18 + 0.18 x 0.18 = 1

Example 5

Find the square of x + 2y – 3z.

Solution :

Given x + 2y – 3z.

Square of x + 2y – 3z

= (x + 2y – 3s)²

= (x + 2y)² – 2x(;c + 2y)x3z + (32)²

= (x)² + 2x x 2y + (2y)² – 6z(x + 2y) + 9z²

= x² + 4xy + 4y² – 6zx – 12yz + 9Z²

= x2 + 4y² + 9Z² + 4xy – 12yz – 6zx

x + 2y – 3z = x2 + 4y² + 9Z² + 4xy – 12yz – 6zx

Example 6

If x + y = 2 and x-y= 1, then find the value of 8xy (x² + y²).

Solution :

Given x + y = 2 and x-y= 1.

8xy(x² + y²) = 4xy x 2(x² + y²)

= {(x² + y)² -(x- y)²} {(x + y)² + (x- y)²}

= {(2)² — (1)²}{(2)² + (1)²}

= (4 – 1) (4 + 1)

= 3 x 5

= 15

8xy(x² + y²) = 15

Example 7

If 2x + 3y = 9 and xy = 3, find the value of 4x² + 9y².

Solution :

Given 2x + 3y = 9 And xy = 3.

4x² + 9y²

= (2x)² + (3y)²

= (2x + 3y)² – 2.2x3y

= (2x + 3y)² – 12xy

= (9)² – 12.3

= 81-36

=45

4x² + 9y² =45

Example 8

Express 35 as the difference between two squares.

Solution :

Given Number 35:-

35 = 7×5

= (7+5 / 2)² – (7-5 / 2)2

= (12/2)2 – (2/2)2

= (6)² – (1)²

35 = (6)² – (1)²

Expression For The Difference Between Two Squares 35 = (6)² – (1)^2.

Example 9

Find the continued product of (a + b), (a-b), (a² + b²), (a⁴ + b⁴).

Solution :

The required product = (a + b) (a – b) (a² + b²) (a⁴ + b⁴)

= (a² – b²) (a² + b²) (a⁴ + b⁴)

= {(a²)² – (b²)²} (a⁴ + b⁴)

= (a⁴ – b⁴) (a⁴ + b⁴)

= (a⁴)² – (b⁴)²

= a⁸ – b⁸

(a + b) (a – b) (a² + b²) (a⁴ + b⁴) = a⁸ – b⁸

Example 10

Express as the product of two expressions: a² – 4ab + 4b² – 4.

Solution :

Given a² – 4ab + 4b² – 4.

a² – 4ab + 4b² – 4

= (a)² – 2 x a x 2b + (2b)² – 4

= (a – 2b)² – (2)²

= (a – 2b + 2) (a – 2b – 2)

a² – 4ab + 4b² – 4 = (a – 2b + 2) (a – 2b – 2)

Factor

If the product of two or more expressions is equal to another expression, then those expressions are called the factors of the product.

For example: If p x q x _r = x, then the expressions p, q, and r are called the factors of x. Therefore, by factorization of the expression x, three factors p, q, and r are obtained.

Different methods of factorization

1. If a polynomial contains one or more common factors in each of its terms then the common factor (or factors) are taken outside the bracket according to the distributive law and the remaining portion is kept inside the bracket.

For Example: a²b + ab + ab²

= ab(a + 1 + b)

= a x b x (a + b + 1).

x3y2 + x2y3 = x2y2(x+y)

= x x x x y x y x (x+y).

a²b + ab + ab² = x x x x y x y x (x+y).

2. Some quadratic expressions may be factorized by using the formulae ; (a + b)² = a²+ 2ab + b², (a – b)² = a² – 2ab + b².

For Example: x² + 4xyz + 4y²z²

Given (a + b)² = a²+ 2ab + b², (a – b)² 

= (x)² + 2x x 2yz + (2yz)²

= (x + 2yz)²

= (x + 2yz) (x+ 2yz).

Again, 4a² – 12ab + 9b²

= (2a)² – 2 x 2a x 3b + (3b)²

= (2a – 3b)²

= (2a – 3b) (2a – 3b).

(a + b)² = a²+ 2ab + b², (a – b)² = a² – 2ab + b² = (2a – 3b) (2a – 3b).

3. Applying the formula a² – b² = (a + b) (a – b), some quadratic expressions may be factorized.

For Example 25X² – 81y²

= (5x)² – (9y)²

= (5x + 9y) (5x – 9y).

25X² – 81y² = (5x + 9y) (5x – 9y).

4. Some expressions may be factorized by simultaneous application of the formulae of (a +b)² [or (a – b)²] and a² – b².

For Example a⁴+ 4

= (a²)² + (2)²

= (a²)² + 2 x a² x 2 + (2)² – 4a²

= (a² + 2)² – (2a)²

= (a² + 2 + 2a) (a² + 2 – 2a)

= (a² + 2a +2) (a² – 2a + 2).

a⁴+ 4 = (a² + 2a +2) (a² – 2a + 2).

Algebra Chapter 1 Commutative Associative and Distributive Laws Some examples of factorization

Example 1

Factorize : 4a⁴b- 6a³b² + 12a²b³

Solution:

Given

4a⁴b- 6a³b² + 12a²b³

4a⁴b – 6a³ b²+ 12a² + b³

= 2a²b(2a² – 3ab + 6b²)

4a⁴b- 6a³b² + 12a²b³  = 2a²b(2a² – 3ab + 6b²)

Example 2

Factorize : x² – (a + b)x + ab.

Solution:

Given

x² – (a + b)x + ab.

x² -(a +b)x+ ab

= x² – ax – bx + ab

= x(x – a) – b(x – a)

= (x – a) (x – b)

x² -(a +b)x+ ab = (x – a) (x – b)

Example 3

Factorize : 9(x – y)² – 25(y – z)².

Solution :

Given

9(x – y)² – 25(y – z)².

9(x – y)² – 25(y – z)²

= {3(x – y)}² – {5(y – z)}²

= (3x – 3y)² – (5y – 5z)²

= {(3x – 3y) + (5y – 5z)} {(3x – 3y) – (5y – 5z)}

= (3x – 3y + 5y – 5z) (3x – 3y – 5y + 5z)

= (3x + 2y – 5z) (3x – 8y + 5z)

9(x – y)² – 25(y – z)² = (3x + 2y – 5z) (3x – 8y + 5z)

Example 4

Factorize : x⁴ + x²y² + y⁴.

Solution :

Given

x⁴ + x²y² + y⁴.

x⁴ + x²y² + y⁴

= (x²)² + 2.x².y² + (y²)² – x²y²

= (x² + y²)² – (xy)²

= (x² + y² + xy) (x² + y² – xy)

x⁴ + x²y² + y⁴ = (x² + y² + xy) (x² + y² – xy)

Example 5

Resolve into factors : x² – y² – 6xa+ 2ya + 8a².

Solution :

Given

x² – y² – 6xa+ 2ya + 8a².

x² – y² – 6xa + 2ya + 8a²

= x² — 6xa + 9a² – y² + 2ya – a²

= x² – 2.x. 3a + (3a)² – (y² – 2ya + a²)

= (x – 3a)² – (y – a)²

= {(x – 3a) + (y – a)} {(x – 3a) – (y – a)}

= (x – 3a + y – a) (x – 3a – y + a)

= (x + y – 4a) (x – y – 2a)

x² – y² – 6xa + 2ya + 8a² = (x + y – 4a) (x – y – 2a)

Example 6

Three factors of an expression are a ,a+1/a, and a-1/a; find the expression.

Solution:

Given

Three factors of an expression are a ,a+1/a, and a-1/a

The required expression= a(a+1/a)(a-1/a)

= a(a²-1/a²)

= a³-1/a

Linear equations of a single variable

A linear equation is one in which the power of the variable is one. In the previous class, you learned the method of finding solutions of linear equations of one variable. The procedure followed in solving such an equation can be expressed in brief:

1. If x + a = b, then x = b 

2. If x– a = b, then x = a + b.

3. If ax = b, then x = b/a

4. If x/a = b,then x = ab.

Algebra Chapter 1 Commutative Associative and Distributive Laws Some examples of equation

Example 1

Solve: 1/2(x+1) + 1/3(x+2) = 13(x-2) + 4(13-x).

Solution :

Given 1/2(x+1) + 1/3(x+2) = 13(x-2) + 4(13-x).

16 – 5(7x – 2) = 13(x – 2) + 4(13 – x)

or, 16 – 35x + 10 = 13x – 26 + 52 – 4x

or, 26 – 35x = 26 + 9x

or,-35x – 9x = 26-26

or, x = 0 / -44

∴ x = 0

1/2(x+1) + 1/3(x+2) = 13(x-2) + 4(13-x) = 0

Example 2

Solve : 3(x – 1) – (x + 2) = x + 2(x – 1).

Solution :

Given 3(x – 1) – (x + 2) = x + 2(x – 1).

3(x – 1) – (x + 2) = x + 2(x – 1)

or, 3x – 3 – x – 2 = x + 2x – 2

or, 2x – 5 = 3x – 2

or, 2x – 3x = 5 – 2

or, – x = 3

or, x = – 3

Example 3

Solve: 1/2(x + l) + 1/3(x + 2) + 1/4(x + 3) = 16.

Solution :

Given 1/2(x + l) + 1/3(x + 2) + 1/4(x + 3) = 16.

Multiplying both sides of the given equation by 12 we get,

6(x + 1) + 4(x + 2) + 3(x + 3) = 192

or, 6x + 6 + 4x + 8 + 3x + 9 = 192

or, 13x + 23 = 192 or, 13* = 192 – 23

or, 13x = 169

or, x = 169/13

∴ x = 13

Example 4

Solve: ax/b – bx/a = a²-b².

Solution :

Given ax/b – bx/a = a²-b².

\(\frac{a x}{b}-\frac{b x}{a}=a^2-b^2\) \(\text { or, } x\left(\frac{a}{b}-\frac{b}{a}\right)=a^2-b^2\) \(\text { or, } x\left(\frac{a^2-b^2}{a b}\right)=a^2-b^2\) \(\text { or, } x=a^2-b^2 \times \frac{a b}{a^2-b^2}\) \(\text { or, } x=a b\)

Example 5

Solve: x+4 / 5 + x+3 / 4 = x + 11/6.

Solution :

Given x+4 / 5 + x+3 / 4 = x + 11/6.

Multiplying both sides of the given equation by 60 we get,

12(x+4) + 15(x+3) = 10(x+11)

or, 12x + 48 + 15x + 45 = 10x + 110

or, 27x + 93 = 10x + 110

or, 27x -10 x = 110 – 93

or, 17x = 17

or, x = 17/17

= 1

x = 1

Example 6

Of the total number of fruits with a fruit vendor, 1/5 was mango, 1/4 was an apple, 2/5 was lichi and the rest 60 were oranges. Find the total number of fruits with the vendor.

Solution :

Given

Total Number Of Fruits With A Fruit Vendor Are

1/5 Was Mango,

1/4 Was An Apple,

2/5 Was Lichi, And

Rest 60 Were Oranges.

Let the total number of fruits be x.

∴ x/5 + x/4 + 2x/5 + 60 = x

or, 4x + 5x + 8x / 20= x – 60

or, 17x = 20x – 1200

or, 17x – 20x = -1200

or, -3x = -1200

or, 3x = 1200

or, x = 1200/3

= 400

The total number of fruits is 400.

Example 7

Half of a number is greater than 1/5th of it by 6. Find the number.

Solution:

Given

Half of a number is greater than 1/5th of it by 6.

Let, the number be x.

.’. Half of the number =x/2 and 1/5th of the number = x/5.

According to the question,

x/2 = x/5 + 6

or, x/2 – x/5 = 6

or, 5x – 2x /10 = 6

or, 3x/10 = 6

or, x = 6 x 10/3

= 20

The number is 20.

Example 8

The present age of the father is 7 times that of the son. After 10 years, the age of the father will be 3 times that of the son. Find the present age of the son.

Solution :

Given

The present age of the father is 7 times that of the son.

After 10 years, the age of the father will be 3 times that of the son.

Let, the present age of the son be x years then the present age of the father is 7x years. After 10 years –

age of son will be (x + 10) years and age of father will be (7x + 10) years

According to the question,

7x + 10 = 3(x+10)

or, 7x + 10 = 3x + 30

or, 7x -3x = 30 – 10

or, 4x = 20

or, x = 20/4

= 5

The present age of the son is 5 years.

Example 9

If the sum of three consecutive numbers is 90, then find the numbers.

Solution:

Given The Sum Of Three Consecutive Numbers is 90

Let, the three consecutive numbers be x, x +1, x + 2.

According to the question,

x + x + 1 + x + 2 = 90

or, 3x + 3 = 90

or, 3x = 90 – 3

= 87

or, x = 87/3

= 29

∴ The numbers are:

29, 29+1,29+2, or 29, 30, 31.

The numbers are 29, 30, and 31.

Example 10

1/3rd of the bamboo is with mud, 1/4th of it is in water, and 5 meters above the water. What is the length of the bamboo?

Solution :

Given

1/3rd Of The Bamboo Is With Mud.

1/4th Of It Is In Water And 5 Meters Above The Water.

Let, the length of the bamboo be x meters.

_∴ Length of the bamboo within mud = x/3

meters and length of the bamboo within water = x/4 meters.

According to the question,

x – (x/3 + x/4) = 5

or, x – (4x+3x / 12) = 5

or, x – 7x/12 = 5

or, 5x/12 = 5

or, x = 5 x 12/2

= 12

The length of the bamboo is 12 meters.

Example 11

The sum of the digits of a two-digit number is 10. If 18 is subtracted the digits are reversed. What is the number?

Solution:

Given

The sum of the digits of a two-digit number is 10.

If 18 is subtracted the digits are reversed.

Let, the digit in the units place be x then the digit in the tens place is 10 – x.

Therefore, the number is 10 x (10 -x) + x

If the digits are reversed the number = 10x + 10 -x = 9x + 10

According to the question.

100 – 9x – 18

or, x = 4

∴ The required number = 100 – 9 x 4

= 100 – 36

= 64

The number is 64.

Example 12

The denominator of a fraction is 2 more than its numerator and if 3 is added to the numerator and 3 is subtracted from the denominator, then the fraction becomes equal to 7/3. What is the fraction?

Solution :

Given

The denominator of a fraction is 2 more than its numerator and if 3 is added to the numerator and 3 is subtracted from the denominator, then the fraction becomes equal to 7/3.

Let, the numerator of the fraction = x,

then denominator = x + 2

Therefore, the fraction = x / x+2

According to the question,

x+3 / x+2-3 = 7/3

or, x+3 / x-1 = 7/3

or, 7x -7 = 3x+9

or, 7x -3x = 7+9

or, 4x = 16

or, x = 16/4

= 4

∴ The fraction = 4/4+2

= 4/6

The fraction is 4/6

Example 13

The present age of the father is 3 times that of the son. After 15 years the age of the father will be twice the age of the son. What are the present ages of the father and the son?

Solution :

The present age of the father is 3 times that of the son.

After 15 years the age of the father will be twice the age of the son.

Given

Let, the present age of the son be x years. Then the present age of the father is 3* years.

After 15 years age of the son will be (x + 15) years

After 15 years age of the father will be

(3x + 15) years

According to the question,

3x + 15 = 2(x+15)

or, 3x + 15 = 2xx+30

or, x = 15

∴ The present age of the son = is 15 years and the present age of the father = 15 x 3 years = 45 years.

The present age of the son is 15 years and the present age of the father is 45 years.

Example 14

Divide 830 into two parts such that 30% of one part is 4 more than 40% of the other.

Solution :

Given

Given Number 830

We Need To Divide 30% of one part is 4 more than 40% of the other:-

Let, two parts be x and (830 – x).

According to the question,

x x 30/100 = (830 – x ) x 40/100 + 4

or, 3x/10 = 2(830 – x ) / 5 + 4

or, 3x/10 – 1660 – 2x / 5 = 4

or, 3x-3320+4x / 10 = 4

or, 7x – 3320 = 40

or, 7x = 3360

or, x = 3360 / 7

= 480.

∴ One part is 480 and the other part = (830 – 480)

= 350

∴ 480 and 350.

Example 15

The numerator of a fraction is 2 less than its denominator. If 1 is added with the numerator and denominator then the fraction becomes 4/5. Find the fraction.

Solution :

Given

The numerator of a fraction is 2 less than its denominator. If 1 is added with the numerator and denominator then the fraction becomes 4/5.

Let, the denominator of the fraction = x

and numerator = x – 2

Therefore, the fraction = x – 2 / x

According to the question,

x-2+1 / x+1 = 4/5

or, x-1 / x+1 = 4/5

or, 5x – 5 = 4x + 4

or, x=9

∴ The fraction = 9-2 / 9

= 7/9.

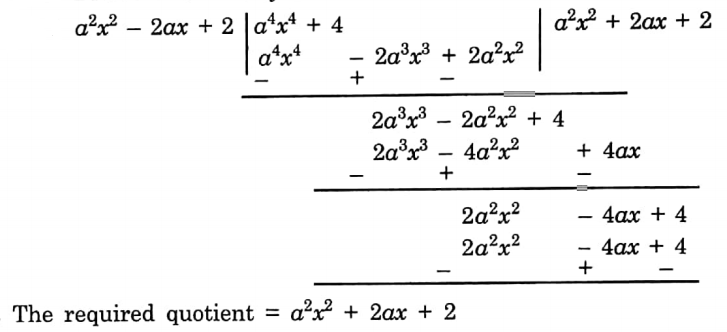
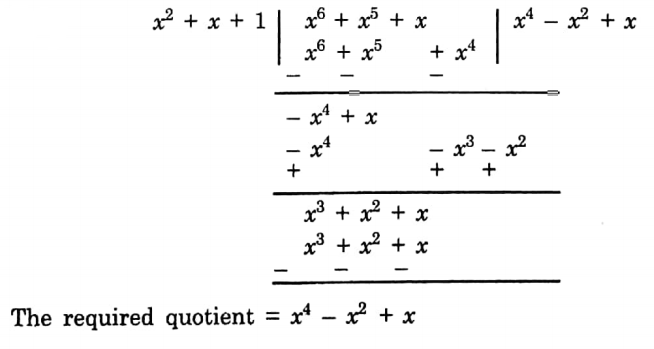
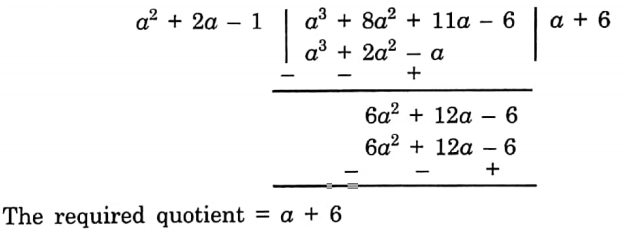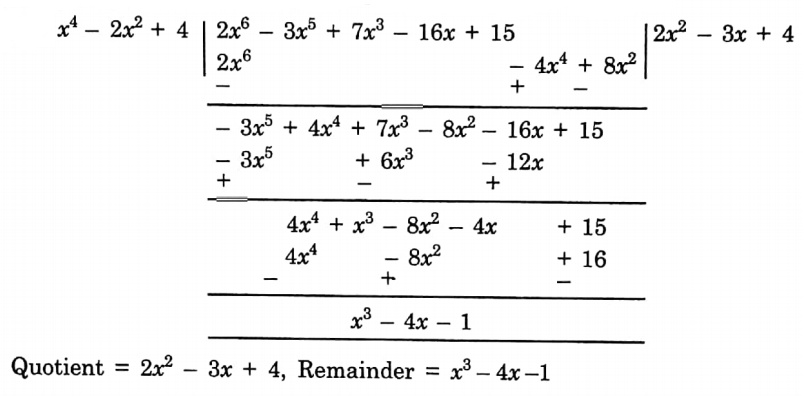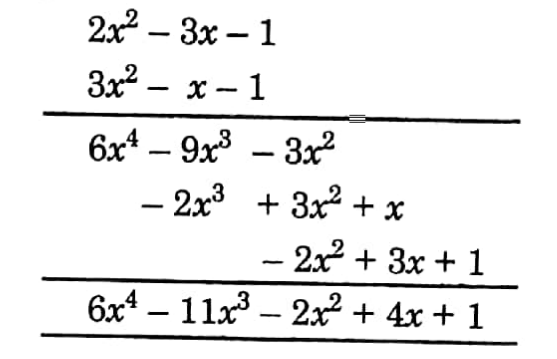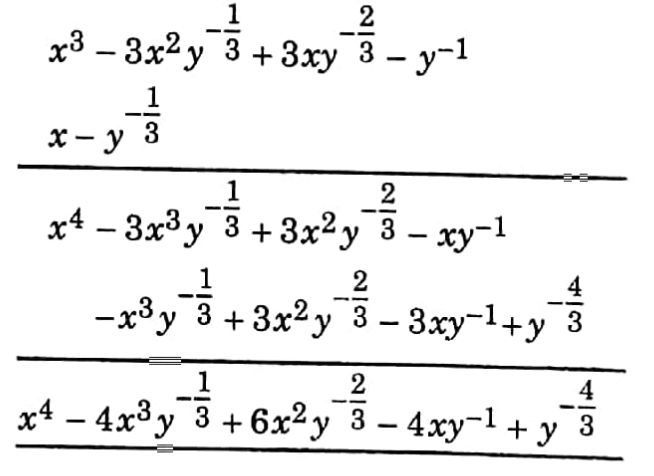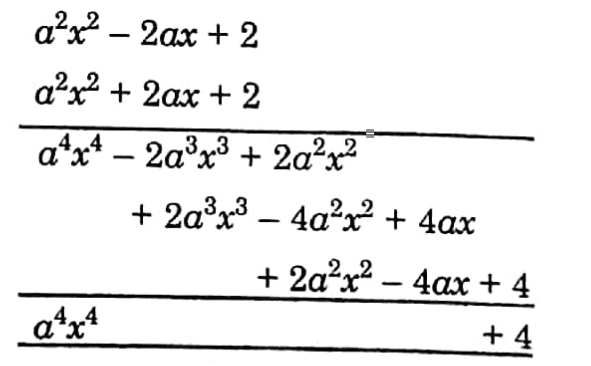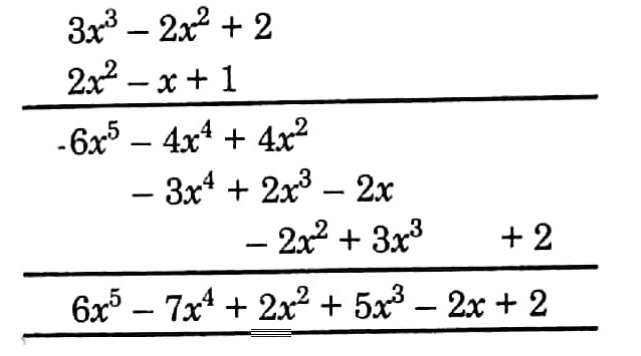Chapter 6 Time and Work

Time and Work Introduction

Some people perform a certain amount of work in a specific time. So there are three elements connected with the problems with time and work which are

1. The number of men,

2. The amount of work and

3. The span of time.

Relation between the amount of work and the span of time

If the number of men is not altered then more time will be required if the number of work increases. Let 20 persons take 15 days to plough 10 bighas of land. We have to determine the time required to plough 20 bighas of land by those 20 persons.

Here, the number of persons is unaltered. Therefore, more time will be required if the number of work increases, and less time will be required if the amount of work decreases.

Hence, in this case

20 persons plough 10 bighas of land in 15 days

’20 persons plough 1 bigha of land in 15/10 days

20 persons plough 20 bighas of land in 15/10 x 20 days

= 30 days.

Relation between the number of persons and the amount of work

If the span of time remains unaltered then more work will be done if the number of persons is increased. Let in 20 days, 10 persons can plough 15 bighas of land. We have to determine the number of bighas of land that 20 persons can plough in 20 days.

Read And Learn More WBBSE Solutions For Class 8 Maths

Here the number of days is unaltered. Therefore, if the number of persons is increased the amount of work will also increase, and if the number of persons is decreased the amount of work will also decrease.

Hence, in this case, in 20 days

10 persons can plough 15 bighas of land

1 person can plough 15/10 bighas of land

20 persons can plough 15/10 x 20 bighas of land

= 30 bighas of land

Relation between the number of persons and span of time

If the amount of work is unaltered then less time will be required if the number of persons is increased. Let, 20 persons take 30 days to plough 20 bighas of land. We have to determine the time required by 40 persons to plough 20 bighas of land.

Here, the amount of work is unaltered. Therefore, less time will be required if the number of persons is increased and more time will be required if the number of persons is decreased.

Therefore, in this case, to plough 20 bighas of land—

20 persons take 30 days

1 persons take 30 x 20 days

40 persons take 30 x 20 / 40 days

= 15 days

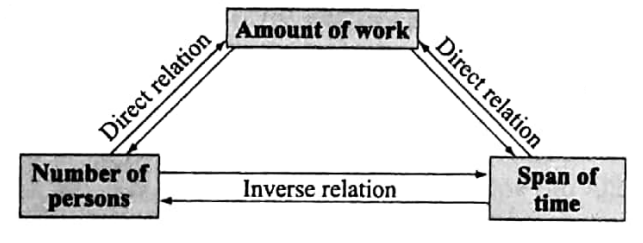
Relation among a number of persons, amount of work, and span of time

From the above discussion, we see that,

1. When a number of persons are unaltered, the amount of work is proportional to the span of time.

2. When the span of time is unaltered, the amount of work is proportional to the number of persons.

3. When the amount of work is unaltered, the number of persons is inversely proportional to the span of time. We may express the above relationships with the help of the following diagram.

Important information related to time and work

1. If a person can finish a piece of work in n days, then the work done by the person in 1 day = 1/n th part of the work.

2. If a person completes 1/n th part of a work in one day, then the time taken by the person to finish complete work = n days.

3. If A is n times as good a worker as B, then the Ratio of work done by A and B at the same time = n: 1.

4. If the number of workers to do a certain work is changed in the ratio m: n, then the ratio of time taken to finish the work changes in the ratio n: m.

5. One day’s work = 1/ Number of days required to complete the work

6. Number of days required to complete a work = 1/one day’s work

7. Number of days required to do a total work to do certain work = total work today / one day’s work

Some problems with time and work

Example 1

A cultivator can plough 6 bighas of land in 12 days. How many bighas of land will he plough in 36 days?

Solution :

Given:

A cultivator can plough 6 bighas of land in 12 days.

Number of days                   Measure of land

12                                             6 bighas

36                                             x bighas (say)

Since, the measure of land ploughed is directly proportional to the number of days,

∴ 12/36 = 6/x

or, 12 x x = 36 x 6

or, x = 36 x 6 / 12

= 18

18 bighas of land.

Alternative method :

In 12 days the cultivator can plough 6 bighas of land

In 1 day the cultivator can plough 6/12 bighas of land

In 36 days the cultivator can plough

6/12 x  36 bighas of land = 18 bighas of land.

Example 2

A carpenter can prepare 3 almirahs in 4 days. How many days will it take to prepare 12 almirahs?

Solution :

Given:

A carpenter can prepare 3 almirahs in 4 days.

Number of almirahs                       Number of days

3                                                            4

12                                                        x (say)

Since the number of almirahs prepared is directly proportional to the number of days.

∴ 3/12 = 4/x

or, 3x = 12 x 4

or,

x = 12 x 4 / 3

= 16

He will take 16 days.

Alternative method :

That carpenter can make,

3 almirahs in 4 days

1 almirah in 4/3 days

12 almirahs in  4/3 x 12 days

= 16 days.

16 days will it take to prepare 12 almirahs

Example 3

6 men can do work in 30 days. In how many days will 20 men do the work?

Solution :

Given:

6 men can do work in 30 days.

Number of men             Number of days

6                                         30

20                                     x (say)

Since the number of days is inversely proportional to the number of men

∴ 20/6 = 30/x

or, 20 x x = 30 x 6

or, x = = 9

They will do the work in 9 days.

Alternative method :

6 men can do the work in 30 days

1 man can do the work in 30 x 6 days

20 men can do the work in 30 x 6 / 20

= 9 days.

In 9 days will 20 men do the work

Example 4

A man can make 500 machine parts in 4 days working 7 hours per day. If he works for 7 days at the rate of 6 hours per day, then how many machine parts will be produced?

Solution :

Given:

A man can make 500 machine parts in 4 days working 7 hours per day. If he works for 7 days at the rate of 6 hours per day.

Total time in 4 days at the rate of 7 hours per day = (7×4) hours = 28 hours.

Total time in 7 days at the rate of 6 hours per day = (7×6) hours = 42 hours.

Total time                            Number of machine parts

28 hours                                     500

42 hours                                   x (say)

Since, the number of machine parts produced is directly proportional to the total time,

∴ 28/42 = 500/x

or, 28 x x = 500 x 42

or, x = 500 x 42 / 25

= 750

750 machine parts will be produced.

Alternative method :

That man can make

In 28 hours, 500 machine parts

In 1 hour, 500/28 machine parts

In 42 hours, 500 x42 / 28 machine parts

= 750 machine parts.

Example 5

15 people can finish work in 10 days working 8 hours per day. In how many days will 25 persons finish the work if they work 6 hours per day?

Solution :

Given:

15 people can finish work in 10 days working 8 hours per day.

Number of persons          Number of Hours       per day days

15                                             8                                    10

25                                            6                                     x (say)

Since the number of days is inversely proportional to the number of persons and is also inversely proportional to the number of hours per day, therefore,

\(\left.\begin{array}{rl}
25: 15 \\
6 & : 8
\end{array}\right\}:: 10: x\)

 

or, x 15 x 8 x 10 / 25 x 6

= 8

They will finish the work in 8 days.

Alternative method :

15 persons, working 8 hours a day can finish the work in 10 days

1 person, working 8 hours a day can finish the work in 10 x 15 days

1 person, working 1 hour a day can finish the work in 10 x 15 x 8 days

25 persons, working 1 hour a day can finish the work in 10 x 15 x 8 / 25 days

25 persons, working 6 hours a day can finish the work in 10 x 15 x 8 / 6 x 25days

= 8 days

Example 6

Ram and Shyam individually can do work in 6 hours and 8 hours respectively. How long will it take to finish the work if they work together?

Solution :

Given:

Ram and Shyam individually can do work in 6 hours and 8 hours respectively.

Ram can finish the work in 6 hours.

In 1 hour Ram can do 1/6 part

Shyam can finish the work in 8 hours

In 1 hour Shyam can do 1/8 part.

Thus, in 1 hour Ram and Shyam can do (1/6 + 1/8) part

= 4+3 / 24 part

= 7/24 part

Now, Ram and Shyam can do 7/24 part of the work in 1 hour

1 part of the work in 24/7 hours = 3 3/7 hours

They will finish the work in 3 3/7 hours.

Example 7

A and B individually complete a work in 10 hours and 12 hours respectively. If they do work together then in how many hours they will complete the work ?

Solution :

Given :

A and B individually complete a work in 10 hours and 12 hours respectively.

A can finish the work in 10 hours

In 1 hour A can do 1/10 part

B can finish the work in 12 hours

In 1 hour B can do 1/12 of part

Thus, in 1 hour A and B together can do (1/10 + 1/12) part

= 6+5 / 60 part

= 11/60 part

Now, A and B can do

11/60 part of the work in 1 hour

∴  1 part of the work in 60/11 hour

= 5 5/11 hours

They will complete the work in 5 5/11 hours.

Example 8

Rahim and Karim can finish the work in 3 days. They worked together for 2 days and after 2 more days. In how many days can Karim alone finish the work?

Solution :

Given:

Rahim and Karim can finish the work in 3 days. They worked together for 2 days and after 2 more days.

In 3 days Rahim and Karim can do 1 part

In 1 day Rahim and Karim can do 1/3 part

In 2 days Rahim and Karim can do 2/3 part

After 2 days the part of the work left = (1 – 2/3)

= 1/3 and Rahim alone can do this work in 2 days.

Now, in 2 days Rahim can do 1/3 part

in 1 day Rahim can do 1/6 part

In 1 day Karim alone can do (1/3 – 1/6) part

= 2-1 / 6

= 1/6 part of the work.

∴ Karim alone can do 1/6 part of the work in 1 day

Karim alone can do 1 part of the work in 6 days

Karim alone can finish the work in 6 days.

Example 9

Ram, Shyam, and Jadu will paint the windows of a house. Ram, Shyam, and Jadu separately can complete the work in 12, 4 and 6 days. If they do the work together, then how many days they will take to complete the work?

Solution :

Given:

Ram, Shyam, and Jadu will paint the windows of a house. Ram, Shyam, and Jadu separately can complete the work in 12, 4 and 6 days

In 12 days Ram can do 1 part

In 1 day Ram can do 1/12 part

In 4 days Shyam can do 1 part

In 1 day Shyam can do 1/4 part

In 6 days Jadu can do 1 part

In 1 day Jadu can do 1/6 part

∴ Ram, Shyam, and Jadu together can do in one day = ( 1/12 + 1/4 + 1/6) part

= 1+3+2 /12 part

= 6/12 part

= 1/2 part.

∴ The three together can do 1/2 part in 1 day

∴ They together can do 1 part in 2 days

They will complete the work in 2 days

Example 10

The work of 2 men is equal to that of 4 women. 4 men and 7 women can do work in 40 days. How long will 12 men and 6 women take to finish the work?

Solution :

Given:

The work of 2 men is equal to that of 4 women. 4 men and 7 women can do work in 40 days.

Work of 2 men = work of 4 women

Work of 1 men = work of 4/2 women

= work of 2 women

∴ Work of 4 men and 7 women

= work of (8+7) women

= work of 15 women.

Again, the work of 12 men and 16 women

= work of (24+6) women

= work of 30 women

Now, 15 women can do the work in 40 days

1 woman can do the work in 40 x 15 days

3. women can do the work in 40×15 / 30 days

= 20 days

They will finish the work in 20 days.

Example 11

A and B can complete a work separately in 20 and 25 days respectively. After 10 days of their working together, they both left. C came and completed the remaining work in 3 days. If C alone would do the work, how many days he would take to complete the work?

Solution:

Given:

A and B can complete a work separately in 20 and 25 days respectively.

After 10 days of their working together, they both left. C came and completed the remaining work in 3 days.

A and B together in 1 day can do (1/20 + 1/25) part

= 5+4 / 100 part

= 9/100 part

∴ A and B together in 10 days can do = 9/100 x 10 part

= 9/10 part

∴ C does (1 – 9/10) part

= 1/10 part of the work

C can do 1/10 part in 3 days

∴ C can do 1 part in 3 x 10 days

= 30 days

C can complete the work in 30 days.

Example 12

A, B, and C individually can do a piece of work in 10 days, 12 days, and 15 days respectively. They did the work alone for 1 day individually. How much work will be left after that?

Solution :

Given:

A, B, and C individually can do a piece of work in 10 days, 12 days, and 15 days respectively. They did the work alone for 1 day individually.

In 10 days A can do 1 part

In 1 day A can do 1/10 of part

In 12 days B can do 1 part

In 1 day B can do 1/12 part

In 15 days C can do 1 part

In 1 day C can do 1/15 of part

If A, B, and C work alone for 1 day individually, then the total work performed

= (1/10 + 1/12 + 1/15) part

= (6 + 5 + 4 / 60) part

= 15/60 part

= 1/4 part

∴ Remaining work = (1-1/4) part

= 3/4 part

3/4 part of the work will be left

Example 13

A and B can do a piece of work in 10 days and 15 days respectively. An alone did the work for 4 days and then B alone did it for 5 days. Thereafter C did the remaining work in 8 days. How long will they take to complete the work together?

Solution :

Given:

A and B can do a piece of work in 10 days and 15 days respectively.

An alone did the work for 4 days and then B alone did it for 5 days.

Thereafter C did the remaining work in 8 days.

In 10 days A can do 1 part

In 1 day A can do 1/10 part

In 4 days A can do 4/10 of part

= 2/5 part

In 15 days B can do 1 part

In 1 day B can do 1/15 part

In 5 days B can do 5/15 part

= 1/3 part

Therefore, A and B do (2/5 + 1/3) part

= (6+5 / 15) part

= 11/15 part of the work.

∴ Remaining work = ( 1 – 11/15) part

= 4/15 part

In 8 days C can do 4/15 of part

In 1 day C can do 4/ 15 x 8 part

= 1/30 part

Hence, in 1 day A, B, and C can do ( 1/10 + 1/15 + 1/30 ) part

= (3 + 2 + 1 / 30 ) part

= 6/30 part

= 1/5 part

.’. A, B, and C together can do 1/5 part in 1 day

A, B, and C together can do 1 part in 5 days.

They will complete the work in 5 days.

Example 14

A, B, and C can do a piece of work in 10 days, 12 days, and 15 days respectively. They started the work jointly. After 3 days B became ill and went away. How long will A and C take to finish the work?

Solution :

Given:

A, B, and C can do a piece of work in 10 days, 12 days, and 15 days respectively.

They started the work jointly. After 3 days B became ill and went away.

In 1 day A, B, and C can do

(1/10 + 1/12 + 1/150part

= (6+5+4 / 40)part

= 15/60 part

= 1/4 part

∴ In 3 days A, B, and C can do 3/4 part.

∴ Remaining work = (1-3/4) part

= 1/4 part

Also, in 1 day A and C can do (1/10 + 1/15) part

= (3+2 / 30) part

= 5/30 part

= 1/6 part

Hence, A and C can do 1/6 part in 1 day

A and C can do 1 part in 6 days

A and C can do 1/4 part in 6/4 days

= 3/2

= 1 1/2 days.

A and C will do the remaining work in 1 1/2 days.

Example 15

Ram and Shyam can complete a work in 20 days, Shyam and Jadu can complete that work in 15 days, and Ram and Jadu can complete that work in 20 days. How long will they take to do the work together? If Ram, Shyam, and Jadu work individually then calculate the time that will be taken by each of them separately.

Solution :

Given:

Ram and Shyam can complete a work in 20 days, Shyam and Jadu can complete that work in 15 days, and Ram and Jadu can complete that work in 20 days.

Ram and Shyam together can do it in 1 day 1/20 part

Shyam and Jadu together can do in 1 day 1/15 part

Ram and Jadu together can do in 1 day 1/20 part

2 x (Ram + Shyam + Jadu) together can do in 1 day

= (1/20 + 1/15+ 1/20) part

= 3+4+3 / 60 part

= 10/60 part

= 1/6 part

∴ Ram, Shyam, and Jadu together can do in 1 day 1/12 part

They do 1/12 part in 1 day

They do 1 part in 12 days

Now, in 1 day, Ram can do (1/12 – 1/15) part

= 5 – 4 /60 part

= 1/60 part

Ram can do 1/60 part in 1 day

Ram can do 1 part in 60 days

In 1 day, Shyam can do (1/12 -1/12) part

= 5-3 / 60 part

= 2/60 part

= 1/30 part

Shyam can do 1/30 part in 1 day

Shyam can do 1 part in 30 days

In 1 day Jadu can do (1/12 – 1/20 )part

= 1/30 part

Jadu can do 1/30 part in 1 day

Jadu can do 1 part in 30 days

The three together will do the work in 12 days.

Ram alone in 60 days,

Shyam alone in 30 days

and Jadu alone in 30 days.

Example 16

Ram, Shyam, and Jadu individually can complete a work in 5, 6, and 10 days respectively. They started doing the work together. After 2 days Ram went away. Find in how many days Shyam and Jadu will complete the remaining work.

Solution :

Given:

Ram, Shyam, and Jadu individually can complete a work in 5, 6, and 10 days respectively. They started doing the work together.

After 2 days Ram went away.

In 1 day Ram, Shyam, and Jadu can do (1/5 + 1/6 + 1/10) part

= 6+5+3 / 30 part

= 14/30 part

= 7/15 part

∴ In 2 days Ram, Shyam, and Jadu can do the 14/15 part.

∴ Remaining work = (1 – 14/15) part

= 1 1/5 part

Shyam and Jadu can do in 1 day (1/6 + 1/10) part

= (5+3 / 30)part

= 8/30 part

= 4/15 part

Shyam and Jadu can do 4/15 part in 1 day

Shyam and Jadu can do 1 part in 15/4 days

1/15 part in 15/4 x 1/15 days

= 1/4 days

Shyam and Jadu will complete the remaining work in 1/4 day.

Example 17

Ram and Shyam can do the work individually in 10 days and 15 days respectively. At first, Ram alone worked for 4 days, then Shyam alone worked for 5 days and left. Jadu came and completed the remaining work in 4 days. If Ram, Shyam, and Jadu would work together find in how many days they would complete the work.

Solution :

Given:

Ram and Shyam can do the work individually in 10 days and 15 days respectively.

At first, Ram alone worked for 4 days, then Shyam alone worked for 5 days and left.

Jadu came and completed the remaining work in 4 days.

In 10 days Ram can do 1 part

In 1 day Ram can do 1/10 part

In 4 days Ram can do 4/10 part = 2/5 part

In 15 days Shyam can do 1 part

In 1 day Shyam can do 1/15 part

In 5 days Shyam can do 5/15 part = 1/3 part

Ram and Shyam together do (2/5 + 1/3) part

= 6+5 / 15 part

= 11/15 part

∴ Jadu does(1 – 11/15)part

= 4/15 part

In 4 days Jadu can do 4/15 part

∴ In 1 day Jadu can do 1/15 part

In 1 day Ram, Shyam, and Jadu can do (1/10 + 1/15 + 1/15) part

= (3+2+2 / 30) part

The three together can do 7/30 part in 1 day

The three together can do 1 part in 30/7 days

= 4 2/7 days

They will complete the work in 4 3/7 days.

Example 18

A and B can do a piece of work in 6 days, B and C can do it in 9 days and A and C can do it in 12 days. How long will it take to do the work separately?

Solution :

Given:

A and B can do a piece of work in 6 days, B and C can do it in 9 days and A and C can do it in 12 days.

A and B together can do in 1 day 1/6 part

B and C together can do in 1 day 1/9 part

A and C together can do in 1 day 1/12 part

2 x (A, B, and C)together in 1 day do (1/6 + 1/9 +1/12) part

= 6+4+3 / 36 part

= 13/36 part

A, B, and C together in 1 day do 13/72 part = 13-8 / 72 part

= 5/72 part

∴ Adoes the work in 72/5 days = 14 2/5 days

In 1 day B does (13/72 – 1/12) part

= 13-6/72 part

= 7/72 part

∴ B does the work in 72/7 days = 10 2/7 days

In 1 day C does (13/72 – 1/6)part

= 13-12 /72part

= 1/72 part

C does the work in 72 days.

A will do the work in 14 2/5 days, B in 10 2/7 days, and C in 72 days.

Example 19

A and B together can do a piece of work in 20 days. They worked together for 15 days and then B went away. A finished the remaining work in 12 days. How many days would A and B take if they worked individually?

Solution:

Given:

A and B together can do a piece of work in 20 days.

They worked together for 15 days and then B went away.

A finished the remaining work in 12 days.

A and B together can do the work in 20 days

In 20 days they can do 1 part

In 1 day they can do 1/20 part

In 15 days they can do 15/20 part = 3/4 part

∴ Remaining work = (1 – 3/4) part

= 1/4 part

A can-do 1/4 part in 12 days

∴ A can do 1 part in 12 x 4 days = 48 days

B can do in 1 day(1/20 – 1/48) part

= 12-5 / 240 part

= 7/240 part

∴ B can do the work in 240/7 days = 34 2/7 days

A can do the work in 48 days and B can do the work in 34 2/7 days.

Example 20

A and B together can do a piece of work in 8 days. They worked together for 5 days and then B went away. The work was finished after 6 more days. In how many days will B alone finish the work?

Solution:

Given:

A and B together can do a piece of work in 8 days.

They worked together for 5 days and then B went away. The work was finished after 6 more days.

A and B together can do the work 8 days

In 8 days they do 1 part

In 1 day they do 1/8 part

In 5 days they do 5/8 part

∴ Remaining work = ( 1- 5/8)part

= 3/8 part

A can-do 3/8 part work in 6 days

∴ A can do 1 part work in 6 x 8/3 days

= 16 days

A and B together can do in 1 day 1/8 part

A alone can do in 1 day 1/16 part

∴ B alone can do in 1 day (1/8 – 1/16) part

= (2-1 / 16) part

= 1/16 part

∴ B alone can do the work in 16 days

B alone can do the work in 16 days

Pipes and Cisterns

A cistern or water tank has two types of pipes connected to it one which fills it up called the inlet and the other which empties it out called the outlet.

Since the nature of the work of the two pipes is exactly opposite, hence the work done by the inlet is considered positive whereas the work done by the outlet is considered negative. If an inlet fills up a cistern in n hours, then in 1 hour it will fill up 1/n th part of the cistern.

If an outlet empties a full cistern in m hours, then in 1 hour 1/m th part of the cistern will be emptied out by it.

Some problems with pipes and cisterns

Example  1

There are two pipes for taking water from the municipality water tank. The tank becomes empty in 4 hours by the two pipes separately. If both the pipes remain open calculate when the full tank will be empty.

Solution:

Given:

There are two pipes for taking water from the municipality water tank. The tank becomes empty in 4 hours by the two pipes separately.

By the two pipes in 1 hour can be emptied (1/4 + 1/4) part

= 1/2 part

∴ 1/2 part can be emptied in 1 hour

1 part

can be emptied in 2 hours

The full tank will be empty in 2 hours.

Example 2

There are three pipes in a tank. With these 3 pipes separately the tank can be filled up in 18, 21 and 24 hours respectively,

(a) If the 3 pipes remain open together find when the tank will be filled with water,

(b) If the first two pipes would remain open find the time to fill up the tank with water,

(c) If the last two pipes would remain open find the time to fill up the tank.

Solution :

Given:

There are three pipes in a tank. With these 3 pipes separately the tank can be filled up in 18, 21 and 24 hours respectively,

1. If the 3 pipes remain open together then in 1 hour (1/18 + 1/21 + 1/24) part

= 20+24+21 / 504 part

= 73/504 part is filled.

∴ 73/504 part is filled in 1 hour

1 part is filled in 504/73 hours

= 6 66/73 hours

2. If the first two pipes remain open together then in 1 hour (1/18 + 1/21)part

= 7+6 / 126 part

= 13/126 part is filled

∴ 13/126 part is filled in 1 hour

1 part is filled in 126/13 hours

= 9 9/13 hours

3. If the last two pipes remain open together then in 1 hour(1/24 +1/24) part

= 8+7 / 168 part

= 15/168 part is filled.

15/168 part is filled in 1 hour

1 part is filled in 168/15 hours

= 11 3/15 hours

= 11 1/5 hours

Example 3

The tank of a house can be filled up in 30 minutes by the municipality water supply pipe. All household work can be done by opening the all pipes in 4 hours. If one day the water supply pipe remains open for 25 minutes, calculate how long work can be done with that water?

Solution :

Given:

The tank of a house can be filled up in 30 minutes by the municipality water supply pipe. All household work can be done by opening the all pipes in 4 hours. If one day the water supply pipe remains open for 25 minutes.

By the water of 30 minutes, work can be done for 4 hours

By the water of 1-minute work can be done for 4/30 hours

By the water of 25 minutes, work can be done for 4/30 x 25 hours

= 10/3 hours

= 3 1/3 hours

=3 hours 20 minutes

3 hours 20 minutes work can be done.

Example 4

The first and second pipes of a tank can fill it in 8 hours and 10 hours respectively. Both the pipes remained open together for 4 hours. What part of the empty tank will be filled?

Solution :

Given:

The first and second pipes of a tank can fill it in 8 hours and 10 hours respectively. Both the pipes remained open together for 4 hours.

By the first and the second pipe, in 1 hour (1/8 + 1/10)part

= (5+4 / 40) part

= 9/40 part of the tank is filled.

∴ In 4 hours, 9/40 x 4 part

= 9/10 part of the tank is filled.

9/10 part of the tank is filled.

Example 5

A cistern can be filled by two taps A and B in 6 minutes and 3 minutes respectively. How long will it take to fill the empty cistern if the two taps are opened simultaneously?

Solution :

Given:

A cistern can be filled by two taps A and B in 6 minutes and 3 minutes respectively.

In 6 min tap A can fill 1 part of the cistern

In 1 min tap A can fill 1/6 part of the cistern

In 3 min tap B can fill 1 part of the cistern

In 1 min tap B can fill 1/3 part of the cistern

∴ In 1 minute, taps A and B can fill (1/6 + 1/3)part

= 1+2 / 6 part

= 1/2 part.

∴ Taps A and B together can fill 1/2 part of the cistern in 1 minute

1 part of the cistern in 2 minutes

The empty cistern will be filled in 2 minutes.

Example 6

A water tank may be filled in 10 minutes by a pipe. Through a hole at the bottom of the tank, the tank may be emptied in 20 minutes. Without closing the hole if the inlet pipe is opened then how long will it take to fill the empty tank?

Solution :

Given:

A water tank may be filled in 10 minutes by a pipe.

Through a hole at the bottom of the tank, the tank may be emptied in 20 minutes.

By the inlet pipe

In 10 minutes, 1 part is filled

In 1 minute, 1/10 part is filled

By the hole at the bottom of the tank

In 20 minutes, 1 part is emptied

In 2 minutes, 1/20 part is employed

Without closing the hole if the inlet pipe is opened

in 1 minute (1/10 – 1/20)part

= 1/20 part is filled.

1/20 part is filled in 1 minute

1 part is filled in 20 minutes

The empty tank will be filled in 20 minutes.

Example 7

Two taps A and B can fill a cistern in 6 minutes and 12 minutes respectively. Tap C can empty it in 8 minutes. If the three taps are opened simultaneously, then how long will it take to fill the empty cistern?

Solution :

Given:

Two taps A and B can fill a cistern in 6 minutes and 12 minutes respectively. Tap C can empty it in 8 minutes. If the three taps are opened simultaneously.

By tap A, in 1 minute, 1/6 part of the cistern is filled.

By tap B, in 1 minute, 1/12 part of the cistern is filled.

By the two taps A and B, in 1 minute, (1/6 +1/12)part

= 3/12 part

= 1/4 part of the cistern is filled.

By tap C, in 1 minute, 1/8 part of the cistern is emptied.

Therefore, if the three taps are in operation simultaneously, then in 1 minute(1/4 – 1/8)part

= 1/8 part is filled.

Therefore, 1/8 part is filled in 1 minute

1 part is filled in 8 minutes

The empty cistern will be filled in 8 minutes.

Example 8

1/4 part of a cistern is empty, and the remaining portion is filled with water. Then two taps A and B are fitted with it. The tap A can fill the cistern in 8 minutes and tap B can empty it in 4 minutes. If the two taps A and B are opened simultaneously, then how long will it take to empty the cistern ?

Solution :

Given:

1/4 part of a cistern is empty, and the remaining portion is filled with water.

Then two taps A and B are fitted with it.

The tap A can fill the cistern in 8 minutes and tap B can empty it in 4 minutes.

1/4 part of the cistern is empty.

∴ (1-1/4)part or 3/4 part is filled with water.

Now, in 1 minute tap B can empty 1/4 part and in 1 minute tap A can fill 1/8 part

∴ If taps A and B are opened simultaneously, then(1/4 – 1/8)part

= 1/8 part is emptied in 1 minute.

1/8 part is emptied in 1 minute

1 part is emptied in 8 minutes

384 part is emptied in 8 x 3/4 minutes

= 6 minutes

The cistern will be empty in 6 munites.

Example 9

A cistern has 3 pipes A, B, and C; A and B can fill it in 3 and 4 hours respectively, and C can empty it in 1 hour. If the pipes be opened in order at 3, 4, and 5 P.M., when will the cistern be empty?

Solution :

Given:

A cistern has 3 pipes A, B, and C; A and B can fill it in 3 and 4 hours respectively, and C can empty it in 1 hour. If the pipes be opened in order at 3, 4, and 5 P.M.

In 1 hour, pipe A can fill 1/3 part, pipe B can fill 1/4 part and pipe C can empty 1 part.

Now, at 5 P.M.

when the pipe C is opened(2 x 1/3 + 1/4)part

= (2/3 + 1/4)part

= (8+3 / 12)part

= 11/112 part of the cistern is filled.

When all the three pipes are in operation, in 1 hour, (1 – 1/3 +1/4) part

= (1 – 7/12)part

= 5/12 part is emptied.

∴ 5/12 part is emptied in an hour

1 part is emptied in 12/5 hours

11/12 part in emptied in 12/5 x 11/12 hours

= 11/5 hours

= 2 hours 12 minutes

Hence, the cistern will be empty for 2 hours 12 minutes after 5 P.M.

i.e., at 7-12 P.M.

The cistern will be empty at 7-12 P.M.

Example 10

A tank has two pipes A and B. A can fill the tank with water in 8 hours and B can empty it in 12 hours. If the pipe A be opened first and the pipes be opened alternatively one at a time for 1 hour each, in how many hours will the tank be filled up ?

Solution :

Given:

A tank has two pipes A and B. A can fill the tank with water in 8 hours and B can empty it in 12 hours.

If the pipe A be opened first and the pipes be opened alternatively one at a time for 1 hour each

In the first hour, pipe A fills 1/8 part of the tank.

In the second hour, pipe A is stopped and pipe B empties 1/12 part of the tank.

Thus in every two successive hours(1/8 – 1/12)part

= (3-2 / 24) part

= 1/24 part of the tank is filled.

This process will continue until there remains a portion of the tank that can be filled by pipe A alone within 1 hour.

Thus, we have to find the time when (1- 1/8) part

= 7/8 part of the tank is filled up.

Now,

1/24 part of the tank is filled in 2 hours

1 part of the tank is filled in 2 x 24 hours

7/8 part of the tank is filled in 2 x 24 x 7/8 hours

= 42 hours

Pipe A fills the remaining | part of

the tank in 1 hour and there is no necessity of opening the second pipe after that. .’. The tank will be filled in (42 + 1) hours = 43 hours.

The tank will be filled in 43 hours.

Example 11

There are 3 pipes connected to a cistern. By these three pipes individually the cistern can be filled in 20, 12, and 15 hours respectively. When the cistern was empty the first pipe only was open for some time. After this, the first pipe was closed and the other two pipes were opened simultaneously and the remaining part was filled in 3 hours. How long was the first pipe open?

Solution :

Given:

There are 3 pipes connected to a cistern. By these three pipes individually the cistern can be filled in 20, 12, and 15 hours respectively.

When the cistern was empty the first pipe only was open for some time.

After this, the first pipe was closed and the other two pipes were opened simultaneously and the remaining part was filled in 3 hours.

By the second and the third pipe in 1 hour (1/12 + 1/15)part

= (5+4 / 60)part

= 9/60 part

= 3/20 part is filled.

By the second and the third pipe in 3 hours

3 x 3/20 part

= 9/20 part is filled.

∴ The first pipe fills(1 – 9/20) part = 11/20 part

By the first pipe, 1 part is filled in 20 hours

By the first pipe, the 11/20 part is filled in 20 x 11/20 hours = 11 hours.

The first pipe was open for 11 hours.

Chapter 5 Percentage

Introduction

You are familiar with the word ‘per cent’ from your childhood. Perhaps you have heard your parents say that ‘my son has scored 95 per cent marks’, ‘at present bank interest is only 6 per cent per annum, ‘a bookseller allows 15 per cent commission’ etc. In fact, the per cent is an abbreviation of the Latin word per centum meaning per hundred. A fraction with a denominator of 100 is called

per cent. For example, 7/100 = 7 per cent. 

Per cent is denoted by the symbol “%”.

Necessity of percentage

Sometimes it becomes necessary to compare two fractions. For this purpose, we convert the fractions so that both of them have a common denominator. Then we can say that the fraction having a greater numerator, is greater than the two fractions. Let us consider an example. Suppose, there are two schools in your locality. In school A, 225 students have passed out of 300 students and in school B, 288 students have passed out of 360 students. In order to compare the performance of the two schools, we have to compare the ratios 225/300

and 288/360

Now, 225/300= 3/4

= 3 x 25 / 4 x 25

= 75/100

and, 288/360 = 4/5

4 x 20 / 5 x 20

= 80/100

Now, it is obvious that 80/100>75/100

Therefore, the performance of school B is better than that of A. Thus it becomes easy for us to compare two results when two fractions are converted to fractions having a common denominator of 100.

Read And Learn More WBBSE Solutions For Class 8 Maths

Important Formulae

1. To convert a percentage into a corresponding fraction: The number is to be written as the numerator and 100 as the denominator. Subsequently, the fraction is to be reduced to its simplest form.

Example: 10% = 10/100 

= 1/10

2. To convert a fraction into a corresponding percentage: The fraction is to be multiplied by 100 with an addition of the % symbol at the end.

Example: 2/5 = (2/5 x100)%

= 40%

3. To convert a percentage into a corresponding decimal: The percentage sign is to be removed and the decimal point is to be shifted in the number by two places to the left. 

Example: 5% = 0.05

4. To convert a decimal into a corresponding percentage: The decimal point in the number is to be shifted by two places to the right and the % symbol is to be added at the end.

Example: 0.453 = 45.3%

5. To find a given percentage of a quantity: The percentage is to be written as a fraction followed by multiplication by the quantity given.

Example: 1. x% of y = x/100 x y

2. 10% of 500 = 10/100 x 500

= 50

6. To express a given quantity as a percentage of another quantity of the same kind: The given quantity is to be divided by the other quantity followed by multiplication of the result by 100 and subsequent addition of the % symbol.

Example:

1. x as percentage of y = (x/y x 100)%

2. 20 as a percentage of ₹500 

= (20/500 x 100)%

7. To find a quantity from a given percentage of the quantity: The given quantity is to be divided by the percentage after expressing it as a fraction. 

Example :

If 20% of full marks is 40 then, full marks = 40++20

=40×100/20

= 200.

8. To find the percentage change in a quantity: The change (either increase or decrease) in the quantity is to be written as the numerator and the original quantity as the denominator followed by multiplication of the fraction by 100

1. If a quantity increases by x, percentage increase = (x/original quantity x 100 )%.

Example: An increase of 5 over the original price of a commodity of 20 means, the percentage increase

= (5/20 x 100) %

= 25%

2. If a quantity increases by x %, the new quantity

= (1+ x / 100) x original quantity

or, original quantity = new quantity / 1+ x/100

Example: An increase of 5% over the original price of a commodity of ₹200 means,

new price=₹ [(1+5/100)×200]= ₹210.

3. If a quantity decreases by x, the percentage decrease

= (x/original quantity x 100) %

Example: A decrease of 5 over the original price of a commodity of * 50 means, a percentage decrease

=(5×100)% = 10%.

4. If a quantity decreases by x%, the new quantity

= (1-x/100)x original quantity

or, original quantity = new quantity / 1- x/100

Example: A decrease of 10% over the original price of a commodity of 70 means,

new price =₹[(1-10/100)×70]= ₹63.

9. To compare between two quantities X and Y when X>Y (given) :

1. The percentage by which greater quantity (X) is greater than smaller quantity (Y),

% increase = (X-Y/Y x 100)%.

Example: The percentage by which the unit cost of 50 per kg of a certain variety of sugar is greater than that of 40 per kg of another variety is,

% increase = (50 – 40×100)% 

= 25%

2. The percentage by which the smaller quantity (Y) is less than the bigger quantity (X),

% decrease = (X-Y/ Y x 100) %.

Example: For the above-quoted example of the unit cost of two varieties of sugars,

% decreases = (50-40 / 50 x 100)% = 20%

3. When X exceeds Yby p%, then Y is Less than X by (p / 100+p x 100)%.

4. when Y is less than X by p%, then X is more than Y by (p / 100-p x 100)%

Chapter 5 Percentage Some examples of percentage

Example 1

Convert each of the following fractions into a per cent:

1. 1/4,

2. 1/2,

3. 3/4,

4. 3/8.

Solution:

1. 1/4 = 1/4 x 100%

= 25%

2. 1/2 = 1/2 x 100%

= 50%

3. 3/4 = 3/4 x 100%

= 75%

4. 3/8 = 3/8 x 100%

= 75/2%

= 37 1/2%

Example 2

Convert each of the following per cent into a vulgar fraction :

1. 25%,

2.6 2/3%,

3. 12 1/2 %,

4. 16 2/3 %.

Solution:

1. 25% = 25/100

= 1/4

2. 6 2/3% = 20/3 x 100

= 1/15

3. 12 1/2 % = 25/ 2 x 100

= 1/8

4. 16 2/3% = 50 / 3 x 100

= 1/6

Example 3

Convert each of the following percents into a decimal:

1. 25%,

2. 22.5%,

3. 41 2/3%,

4. 75%

Solution:

1. 25% = 25/100

= 0.25

2. 22.5% = 22.5/100

0.225

25% = 0.225

3. 41 2/3 % = 125 / 3 x 100

= 5/3 x 4

= 5/12

= 0.416

41 2/3 % = 0.416

4. 75% = 75/100

= 0.75

75% = 0.75

Example 4

Convert each of the following decimals into a per cent:

1. 0.28,

2. 0.125,

3. 1.25,

4. 2.75.

Solution:

1. 0.28 = 28/100

= 28%

0.28 = 28%

2. 0.125 = 125/100

= 125 / 10 x 100

= 2.5%

0.125 = 2.5%

3. 1.25 = 125/100

= 125%

1.25 = 125%

4. 2.75 = 275/100

= 275%

2.75 = 275%

Example 5

Find 25% of ₹300.

Solution:

Given:

25% And ₹300

25% of ₹300 = ₹300 x 25/100

= ₹75

25% of ₹300 = ₹75

Example 6

The ratio of hydrogen and oxygen in the water is 2:1. Find the percentage of hydrogen and oxygen in the water.

Solution:

Given:

The ratio of hydrogen and oxygen in the water is 2:1.

Since the ratio of hydrogen and oxygen in water is 2:1 therefore,

amount of hydrogen

= 2/3 part

= 2/3 x 100%

= 200/3 %

= 66 2/3 %

amount of oxygen

= 1/3 part

= 1/3 x 100%

= 100/3 %

= 33 1/3%

Hydrogen 66 2/3%, oxygen 33 1/3%.

Example 7

What per cent is 2 kg 250 gms of 0.72 quintals? 

Solution:

Given:

2 kg 250 gms And 0.72 Quintals.

2 kg 250 gms = 2.25 kg

0.72 quintals = 72 kg

∴ The required percent = 2.25/72 x 100 %

= 3.125%

3.125% per cent is 2 kg 250 gms of 0.72 quintals

Example 8

A factory used to produce 1500 bottles per month. Now 1695 bottles are produced there per month. Find the percentage of increase of production in that factory. 

Solution :

Given:

A factory used to produce 1500 bottles per month. Now 1695 bottles are produced there per month.

Previously, 1500 bottles were produced. Now 1695 bottles are produced. Production of bottles has increased by (1695 – 1500) 195 per month.

In 1500 the increase is 195

In 1 the increase is 195/1500

In 100 the increase is 195/1500 x 100 

= 13

The percentage of increase in production is 13%

Example 9

What per cent is ₹ 20 of ₹ 50?

Solution:

Given:

₹ 20 And ₹ 50.

The required percent = ₹20/₹50 x 100%

= 40%

The required percent = 40%

Example 10

The quantity of Nitrogen, Oxygen and Carbon dioxide in the air is 75.6%, 23.04% and 1.36%. Find the quantity of each in 25 litres of air.

Solution:

Given:

The quantity of Nitrogen, Oxygen and Carbon dioxide in the air is 75.6%, 23.04% and 1.36%.

In 25 litres of air, 

quantity of Nitrogen = 25 litres × 75.6% 

= 18.9 litres

quantity of Oxygen = 25 litres x 23.04%

= 5.76 litres

quantity of Carbon dioxide = 25 litres × 1.36% 

= 0.34 litre 

Nitrogen 18.9 litres, 

Oxygen 5.76 litres, 

Carbon dioxide 0.34 litre.

Example 11

40% of the number is 48. What is the number?

Solution:

Given:

40% of the number is 48.

40% of the number = 48

or, 1% of the number = 48/40

or, 100% of the number = 48/40 x 100

= 120

The number is 120.

Example 12

A man purchased a book from a book stall. He got discounts of 10% and 5% respectively. How much did the man pay if the price of the book was printed as 200? 

Solution:

Given:

A man purchased a book from a book stall. He got discounts of 10% and 5% respectively.

The printed price of the book is 200. 

Discount on the first time

 =200  x  10/100 

=20 

Price of the book after the first discount 

=(200-20)

=180 

Discount at the second time

= 180 × 5/100

=9

Price of the book after the second discount

= (180 – 9)

= 171

The price of the book is 171.

Example 13

Out of 40 students in a school, 16 failed. Find the percentage of successful candidates.

Solution :

Given:

Out of 40 students in a school, 16 failed.

The number of students who failed = 16

∴  The number of students passed = (40 – 16) = 24

.’. Out of 40 students the number of successful candidates = 24

Out of 1 student number of successful candidates = 24/40

Out of 100 students a successful 24

candidates = 24/40 x 100

= 60

The percentage of successful candidates is 60%.

Example 14

The length of each side of a square is increased by 10%. Find the percentage of increase in its area.

Solution:

Given:

The length of each side of a square is increased by 10%.

Let, the length of the side of the square = a units

Area of the square = a² sq units.

After increasing 10% the length of the beach

side = (a+a x 10/100) units

= (a + a/10)units

= 11a / 10 units

∴ Area = (11a / 10)² sq units

= 121a²/100 sq units

∴ Increase in area = (121a² / 100 – a²)sq units = 21a² / 100 sq units

In a² sq units the area increases by

21 a²  / 100 sq units

In 1 sq unit, the area increases by

21 a² / a² x 100 sq units

In 100 sq units, the area increases by

21/100 x 100 sq units = 21 aq units

It will increase by 21%

Example 15

Out of 350 mangoes in a basket, 210 mangoes were distributed among some students. Find the percentage of mangoes left in the basket.

Solution :

Given:

Out of 350 mangoes in a basket, 210 mangoes were distributed among some students.

The original number of mangoes = 350

Number of mangoes distributed = 210

Number of mangoes left in the basket = (350-210)

= 140

Therefore, percentage of the mangoes left

= 140/350  x 100 = 40 350

40% of the mangoes were left in the basket.

Example 16

15% discount L obtained if the bill of electricity is paid on time. A man got a discount of ₹ 54 by paying the bill on time. What was the amount of the bill

Solution :

Given:

15% discount L obtained if the bill of electricity is paid on time. A man got a discount of ₹ 54 by paying the bill on time.

If a discount of ₹ 15 is obtained then the amount of the bill is ₹ 10

If a discount of ₹ 1 is obtained then the amount of the bill is ₹ 100 / 15

If a discount of ₹ 54 is obtained then the

amount of the bill is ₹ 100 x 54 / 15

= ₹ 360

The amount of the bill was ₹ 360.

Example 17

Ram scored 642 marks out of 800 and Shyam scored 515 marks out of 700 in an examination. Whose performance was better ?

Solution :

Given:

Ram scored 642 marks out of 800 and Shyam scored 515 marks out of 700 in an examination.

Out of 800 marks, Ram scored 642 marks

.’. Out of 100 marks, Ram scored

642 x100 / 800 = 80.25 marks

Out of 700 marks, Shyam scored 5115 marks

∴ Out of 100 marks, Shyam scored

515 x 100 / 700

= 73.57 marks

Ram’s performance was better.

Example 18

The price of sugar has increased by 20%. Find the percentage decrease in the monthly use of sugar to keep the expenses of sugar unaltered.

Solution :

Given

The price of sugar has increased by 20%.

What price of sugar of ₹ 100 has become ₹ 120.

Therefore, on ₹ 120 the expenses should be decreased by ₹ (120 – 100)

= ₹ 20.

On ₹ 120 expenses should be decreased by ₹ 20

On ₹ 1 expenses should be decreased by

₹20 / 120

On ₹ 100 expenses should be decreased by

₹ 20/120 x 100

= ₹ 100/6

= ₹ 50/3

= ₹ 16 2/3

Monthly use of sugar decreased by 16 2/3%

Example 19

Ram’s income is greater than Shyam’s income by 20%. Find the per cent by which Shyam’s income is less than Ram’s income.

Solution :

Given:

Ram’s income is greater than Shyam’s income by 20%.

If Shyam’s income is ₹ 100, then Ram’s income is ₹ 120.

.’. Shyam’s income is less than Ram’s income by ₹ (120 – 100)

= ₹ 20.

.’. In ₹ 120, Shyam’s income is less than Ram’s income by ₹ 20

In ₹ 1, Shyam’s income is less than Ram’s income by ₹ 20/120

In ₹ 100, Shyam’s income is less than Ram’s income ₹ 20/100 x 100

= ₹ 50/3

= ₹ 16 2/3

Shyam’s income is 16 2/3% less than Ram’s income.

Example 20

When water freezes into ice, its volume is increased by 10%. By what per cent the volume will be decreased if ice melts into water.

Solution :

Given:

When water freezes into ice, its volume is increased by 10%.

100 c.c. water freezes into 110 c.c. ice.

When ice melts into the water the volume decreases in 110 cc volume = (110 – 100) c.c.

= 10 c.c.

In 110 c.c., volume decreases by 10 c.c.

In 1 c.c., volume decreases by 10/110 c.c.

In 100 c.c., volume decreases by 10/110 x 100 c.c.

= 100/11 c.c.

= 9 1/11 c.c.

The volume will be decreased by 9 1/11%

Example 21

Due to the increase in the price of sugar by 25%, a family decreases the consumption of sugar by 15%. As a result of this, what will be the percentage increase or decrease in the expenditure of sugar of that family?

Solution :

Given

Due to the increase in the price of sugar by 25%, a family decreases the consumption of sugar by 15%.

Let, the price of sugar be ₹ x per kg and the consumption of sugar be y kg.

At present

price of 1 kg of sugar is ₹ x

∴ The price of y kg of sugar is ₹ xy

Due to a 25% increase, the price of sugar per kg

= ₹ (x + x x 25/100)

= ₹ (x + x/4)

= ₹ 5x / 4

Due to a 15% decrease, in the consumption of sugar

= (y – y x 15/100)kg

= (y – 3y/20) kg

= 17y/20 kg

After rising the price

Price of 1 kg of sugar = ₹ 5x/4

Price of 17y/20 kg of sugar = ₹ 5x/4 x 17y/20

= ₹ 17xy/16

.’. Expenditure increases by

₹ (17xy / 16 – xy)

= ₹ xy/16

On ₹ xy, expenditure increases by ₹ xy/16

On ₹ 1, expenditure increases by ₹ xy / 16 x 1/xy

On ₹ 100, expenditure increases by ₹ 100/16

= ₹25/4

= ₹ 6 1/4

Expenditure will increase by 6 1/4%

Example 22

Due to the use of the high-yielding seed, a man has got a 55% production hike in paddy cultivation. But for this production, the cost of cultivation has increased by 40%. Previously a yield of ₹ 3000 was produced by investing ₹1200. Find whether his income will be increased or decreased and by how much after using a high-yielding seed.

Solution :

Given:

Due to the use of the high-yielding seed, a man has got a 55% production hike in paddy cultivation.

But for this production, the cost of cultivation has increased by 40%. Previously a yield of ₹ 3000 was produced by investing ₹1200.

Previously, the yield of ₹ 3000 was produced by investing ₹ 1200 (cost).

.’. Income was = ₹ (3000 – 1200)

= ₹ 1800

After increasing 40% the present cost of cultivation = ₹ 1200 x 140/100 = ₹ 1680

After increasing by 55% the present yield

= ₹ 3000 x 155/100

= ₹ 4650

Therefore, at present income

= ₹ (4650 – 1680)

= ₹ 2970

Therefore, income has increased by = ₹ (2970 – 1800)

= ₹ 1170

Income has increased by ₹ 1170.

Example 23

The length, breadth and height of a room are 15 m, 10 m and 5 m respectively, If the length, breadth and height be increased by 10%, find the percentage increase in the area of four walls.

Solution :

Given:

The length, breadth and height of a room are 15 m, 10 m and 5 m respectively, If the length, breadth and height be increased by 10%.

Area of the four walls of the room

= 2 x (15 + 10) x 5 sq m

= 2x25x5sqm

= 250 sq m

After a 10% increment

length becomes (15 + 15 x 10 / 100)m

= 16.5m

breadth becomes (10 + 10 x 10 / 100) m

= 11 m

height becomes (5 + 5 x 10 / 100) m

= 5.5 m

∴ Area of the four walls becomes 2 x (16.5 + 11) x 5.5 sq m

= 2 x 27.5 x 5.5 sq m

= 302.5 sq m

.’. The area of four walls increases by (302.5 – 250) sq m

= 52.5 sq m.

In 250 sq m area increases by 52.5 sq m

In 1 sq m area increases by 52.5/250 sq m

In 100 sq m area increases by 52.5 x 100 / 250 sq m

= 21 sq m.

The area of the four walls increases by 21%.

Example 24

In a legislative election, 80% of voters cast their votes and the winning candidate got 65% of the cast votes. Find the percentage of total votes he got.

Solution:

Given:

In a legislative election, 80% of voters cast their votes and the winning candidate got 65% of the cast votes.

Let, the total number of voters = x

∴ Cast votes =  x x 80/100

= 4x/5

The Winning candidate has got votes

= 4x/5 x 65/100

= 13x/25

∴ Out of x votes, he has got 13x/25 votes

Out of 1 vote, he has got 13x / 25 x x votes

Out of 100 votes, he has got 13 x 100 / 25 votes

= 52 votes

the winning candidate got 52% of the total votes.

Example 25

In an examination 52% of the examinees failed in English, 42% failed in Mathematics and 17% failed in both the subjects. If 115 examinees passed in both subjects, find the total number of examinees.

Solution:

Given:

In an examination 52% of the examinees failed in English, 42% failed in Mathematics and 17% failed in both the subjects.

If 115 examinees passed in both subjects.

(52 – 17)% or, 35% of examinees failed only in English.

(42 – 17)% or 25% of examinees failed only in Mathematics.

17% of examinees failed in both subjects.

Therefore, altogether (35 + 25 + 17)% or, 77% of examinees failed.

Hence, (100 – 77)% or, 23% of examinees passed in all.

If 23 examinees pass then the total number of examinees is 100

If 1 examinee pass then the total number of examinees is  100/23

If 115 examinees pass then the total number of examinees is 100 x 115 / 23

= 500

The total number of examinees is 500.

Example 26

The students of the school have passed 85% in Bengali, 70% in Mathematics and 65% in both subjects scoring A+. If the number of students is 120 then how many students

1. got A+ in both subjects,

2. got A+ only in Mathematics,

3. got A+ only in Bengali,

4. did not get an A+ in any subject.

Solution :

Given:

The students of the school have passed 85% in Bengali, 70% in Mathematics and 65% in both subjects scoring A+.

If the number of students is 120.

1. Number of students who got A+ in both the 65

subjects = 120 x 65/100

= 78

2. Got A+ only in Mathematics (70 – 65)% = 5%

.’. Number of students who got A+ only in Mathematics = 12 x 5/100

= 6

3. Got A+ only in Bengali = (85 – 65)% = 20%

∴ number of students who got A+ in, 20

Bengali only = 120 x 20/100

= 24.

4. Got A+ in neither subject = {120 – (78 + 6 + 24)}

= 12 students.

Got A+ in neither subject = 12 students.

Example 27

The income of a man was increased by 20% and later decreased by 20%. Find the percentage of change in his income.

Solution:

Given:

The income of a man was increased by 20% and later decreased by 20%.

If the initial income is ₹ 100 then it increases to ₹ 120.

Later, on ₹ 100 income decreases by ₹  20

Later, on ₹ 1 income decreases by ₹  20/100

Later, on ₹ 120 income decreases by ₹  20/100 x 120

= ₹ 24

Therefore, income increases by ₹ 100 by ₹ 20 and then decreases by ₹ 24.

∴ Income decreases by 4%.

Example 28

The length of a rectangle is increased by 15% and the breadth is decreased by 15%. Find the percentage increase or decrease in area.

Solution :

Given:

The length of a rectangle is increased by 15% and the breadth is decreased by 15%

Let, the length be x units and breadth be y units, then area = xy sq units.

After increasing by 15%, the length becomes

= (x + x x 115/100) units = (x + 3x/20) units

= 23x/20 units.

After decreasing by 15%, the breadth becomes

= (y – y x 15/100)units

= (y – 3y/20)units

= 17y/20 units

∴ New area = 23x/20 x 17y/20 sq units

= 391 xy/400 sq units

∴ Area decreases by  (xy – 391 xy/400) sq units = 9xy/400 sq units

on xy sq units area decreases by = 9xy/400 sq units

on 1 sq units area decreases by = 9xy/400xy sq units

on 100 sq units, the area decreases by = 9/400 x 100 sq units

= 9/4 sq units

The area will decrease by 2 1/4 %.

Example 29

In annual sports, 20% of the students took part in the 100 m race. 15% of the students in the 200 m sprint and 10% of the students in the long jump event. 5% of the students took part in all these three events. Find the number of students who did not take part in any of the events if the total number of students in the school was 780. (No students took part in two events).

Solution :

Given:

In annual sports, 20% of the students took part in the 100 m race. 15% of the students in the 200 m sprint and 10% of the students in the long jump event.

5% of the students took part in all these three events.

Took part only in 100 m race (20 – 5)% or, 15% students

Took part only in 200 m race (15 – 5)% or, 10% students

Took part only in long jump (10 – 5)% or, 5% students

∴ Took part in one or three events = (15 + 10 + 5 + 5)% or, 35% of students

∴ Took part in neither event (100 – 35)%

or, 65% of students.

∴ Took part in neither event 780 x 65/100

= 507 students.

507 students did not take part in any event.

Example 30.

A panchayat family spends 40% of the government grant on health, 35% on education and 30% of the grant for education for literacy projects. If the expenditure for the literacy project is ₹ 210000 then find

1. Total amount of grant,

2. Expenditure on education and

3. Expenditure for health.

Solution :

Given:

A panchayat family spends 40% of the government grant on health, 35% on education and 30% of the grant for education for literacy projects.

If the expenditure for the literacy project is ₹ 210000.

Let, ‘s total government grant = ₹ x

Expenditure for health = ₹ x x 40/100

= ₹ 2x / 5

Expenditure for education = ₹ x x 35/100

= ₹ 7x/20

Expenditure for a literacy project = ₹ 7x/20 x 30/100

= ₹21 x / 200

According to the question, 21x/200 = 210000

or, x = 21000 x 200/21

= 2000000

Expenditure for education = ₹ 7 x 2000000 / 20

= 700000

Expenditure for education = ₹ 2 x 2000000 / 5

= ₹ 800000

1. Total grant = ₹ 2000000,

2. expenditure for education  ₹ 700000 and

3. expenditure for health = ₹ 800000.

Example 31

Due to the use of the high-yielding seed, a man has got a 30% production hike in paddy cultivation. But for this production, the cost of cultivation has increased by 35%. Previously a yield of ₹ 1220 was produced by investing ₹ 450. Find by how much his income will be increased after using high-yielding seeds.

Solution :

Given:

Due to the use of the high-yielding seed, a man has got a 30% production hike in paddy cultivation.

But for this production, the cost of cultivation has increased by 35%. Previously a yield of ₹ 1220 was produced by investing ₹ 450.

Previously yield of ₹ 1220 was produced by investing ₹ 450.

Income was = ₹ (1220 – 450) = ₹ 770

After increasing by 35% the present cost of cultivation = ₹ 450 x 135/100

= ₹ 607.50

After increasing by 30% the present yield = ₹ 1220 x 130/100

= ₹ 1586

∴ After present income = ₹ (1586 – 607.50)

= ₹ 978.50

∴ Income has increased by = ₹ (378.50 – 770)

= ₹ 208.50

Income has increased by ₹ 208.50.

Example 32

20000 examinees were to appear in an examination. But 5% of them were absent. 60% of the examinees who had appeared in the examination passed. If the ratio of the examinees passed in the first, second and third divisions is 1:2:3, find the number of examinees passed in each division.

Solution :

Given:

20000 examinees were to appear in an examination.

But 5% of them were absent. 60% of the examinees who had appeared in the examination passed.

If the ratio of the examinees passed in the first, second and third divisions is 1:2:3.

The total number of examinees = 20000

∴  Number of absentees

= 20000 x 5%

= 1000

∴ Number of examinees present

= 20000 – 1000

= 19000

∴ The number of examinees passed

= 19000 x 60/100

= 11400

Now, the ratio of examinees passed in the first, second and third divisions is 1:2:3.

∴ Passed in the first division = 11400/6 x 1

= 1900

Passed in second division = 11400/6 x 2

= 3800

Passed in third division = 11400/6 x 3

= 5700

First division = 1900,

second division = 3800

and third division = 5700.