Classification Of Elements And Periodicity In Properties Introduction

Element Classification Principles: At present, 118 elements are known to us. It is Almost an impossible task to remember the individual properties of these elements And A larger number of compounds derived from them.

Several attempts were made by former scientists to arrange the elements in a coherent and orderly manner.

After Dalton’s Atomic theory, attempts were made to establish a correlation between the atomic masses of various elements and their properties.

But until a method for the estimation of correct atomic masses of elements was innovated, the work on the proper classification of elements could not make any significant progress.

However, after the atomic masses of elements were correctly determined, the attempts for the classification of elements received particular attention.

The way of arranging similar elements together and separating them from dissimilar elements is called the classification of elements.

Historical Background Of The Classification Of Elements Based On Atomic Weight

Dobereiner’s Law Of Triads

In 11117, German scientist Doberelnor stated that in a group of three chemically similar elements, called a triad, the atomic weight of (the middle element of each triad Is very close to the arithmetic mean of those of the other two elements.

Element Classification Principles

This was called Oohereiner’s law of triads. Some familiar triads, based on lids law, are shown below:

From the table, it is observed that the atomic weight of sodium (Na) is the average of the atomic weights of lithium (Li) and potassium (K) \(\left[\frac{7+39}{2}=23\right]\)

This relationship is only applicable to a limited number of elements and hence fails to classify all the known elements.

However, it cannot be denied that it indicated the existence of an inter-relationship between the properties and atomic weights of elements.

Law of Telluric Screw

In 1862, Chancourtois attempted to classify the elements based on atomic mass. He took a vertical cylinder with 16 equidistant lines drawn on its surface (lines are parallel to the axis of the cylinder).

He drew a spiral line or helix on the surface making an angle of 45° to the axis of the cylinder.

The atomic weights were plotted vertically along the spiral line. He arranged the elements on the helix in order of their increasing atomic weights.

It was observed that in the telluric screw, the elements that differed from each other in atomic weight by 16 or multiples of 16 fell on the same vertical line.

The elements lying on the same vertical line showed nearly the same chemical properties. However, this concept did not attract much attention.

Element Classification Principles

Newlands’ Law Of Octaves

Arranging the known elements in the ascending order of their atomic weights, Newlands, observed (1865) that properties of the eighth element, starting from a given one, is a kind of repetition of the first, like the eighth note in an octave of music. He called this regularity the law of octaves.

Starting from Li, the eighth element is Na and the eighth element following Na is K.

There exists a striking resemblance in properties among these elements. Similarly, F shows similarity with the eighth element Cl following it in properties.

The law of octaves was found to be satisfactory in the case of lighter elements from hydrogen (H) to calcium (Ca). However in the case of heavier elements beyond calcium, it lost its validity and hence, the law was discarded.

Lothar Meyer Arragngement

In 1869, Lothar Meyer, a German scientist, studied the different physical properties of the known elements and plotted a graph of atomic volume (atomic weight divided by density) against the atomic weight of various elements.

He noticed that the elements with similar properties occupied similar positions on the curve.

Based on this observation, Lothar Meyer concluded that the physical properties of the elements are a periodic function of their atomic weights.

Periodic Law

In 1869, Russian chemist, Dmitri Mendeleev, examined the relationship between the atomic weights of the elements and their physical and chemical properties.

From his studies, Mendeleev pointed out that the physical and chemical properties of elements are periodic functions of their atomic weights. This generalisation is called Mendeleev-Lothar Meyer Periodic Law or simply Mendeleev’s Periodic Law.

Element Classification Principles

Mendeleev’s Periodic law: Physical and chemical properties of elements are a periodic function of their atomic weights. This law implied that if the elements are arranged in the order of increasing atomic weights, the physical & chemical properties of the elements change regularly from one member to another and get repeated after a definite interval. This recurrence of properties ofthe elements at definite intervals is called the periodicity of elements.

Periodic classification and periodic properties: Based on the periodic law, the classification of elements according to the increasing atomic weight is called periodic classification. The properties of the elements which are directly or indirectly related to their electronic configurations and show a regular gradation when we descend in a group or move across a period in the periodic table are called periodic properties.

For example—The size of atoms or atomic radii, ionic radii, atomic volume, metallic character, ionisation enthalpy, electron affinity, electronegativity, melting point, boiling point, valency etc.

Radioactivity is not a periodic property of elements: Radioactivity is neither directly nor indirectly related to the electronic configuration of atoms. It depends on the ratio between the number of neutrons and protons present in the atom.

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

Mendeleev’s Periodic Table

Based on his periodic law, Mendeleev arranged the then-known elements in the form of a table (consisting of several rows and columns) which is known as Mendeleev’s periodic table.

Mendeleev’s original periodic table (1871) contained only 63 elements known at that time. There were no places for inert gases because these were not discovered at the time of publication of the table.

Mendeleev, however, left several blank places in the table and predicted that there must be some unknown elements which would be discovered in due course of time.

He even predicted their properties based on the properties of the adjacent elements.

Element Classification Principles

Mendeleev’s predictions were proved to be astonishingly correct when these elements were discovered later. Mendeleev’s table, now in use, is a modified version ofthe table originally designed by him. Important features of the modified form of Mendeleev’s periodic table are discussed below.

Periods and Groups: In Mendeleev’s periodic table, the elements were arranged in the increasing order of their atomic weights (but in the modified form these were arranged in increasing order of their atomic numbers) into several horizontal rows.

These horizontal rows were placed one below the other in such a way that chemically similar elements fell in the same vertical column. The horizontal rows are called periods and the vertical columns are called groups or families.

There is a gradual change in the properties of the elements with an increase in atomic mass across a period. However, elements belonging to the same group exhibit close chemical similarities.

In the modern version of Mendeleev’s table, there are seven periods (1 to 7) and nine groups (I to VIII and 0). Gr-0 consists of the inert gases (Mendeleev’s original table did not contain this group)

Main features of Mencleleov’s Periodic Table

The first period contains only 2 elements (II and He). This is called the shortest period.

The second period contains only 8 dements (Li-Bc-B-C-NO-F-Nc), beginning with alkali metal Li and ending with Inert gas No. This Is called the first short period.

The period also contains elements (Na-Mg-Al-Si-P-SCl-Ar), beginning with the alkali metal Na and ending with the Inert gas Ar. This is called the second period.

The elements of these two short periods occur in nature in very large amounts and they typify the properties of all the other members of the group to which they belong. So they are called typical elements.

Element Classification Principles

The fourth period contains 18 elements. It begins with the alkali metal K and ends with the inert gas Kr. This period is called the first long period.

The fourth period contains 10 additional elements than the second and third periods. These 10 elements (Sc to Zn) are called the transition elements. This period consists of two series (the even and the odd series).

The fifth period also contains 18 elements. It begins with the alkali metal Rb and ends with the inert gas Xe. This period is called the second long period. 10 elements from Y to Cd are called transition elements. The fifth period also consists of two series (the even and the odd series).

The sixth period contains 32 elements, and so it is called the longest period. It begins with the alkali metal Cs and ends with the inert gas Rn.

This period contains 10 transition elements (La and Hf to Hg) and 14 lanthanide elements (Ce to Lu ).

These 14 elements are also called rare earth elements because these elements were believed to be present in nature in negligible amounts.

The sixth period also consists of two series (the even and the odd series).

Element Classification Principles

The seventh period may contain a maximum of 32 elements (beginning with Fr), but all the elements have not yet been discovered. Till now 28 elements have been discovered. So it is an incomplete period.

All elements of this period are radioactive. The elements from Francium (Fr) to Uranium (U) are naturally occurring, while the elements beyond uranium are man-made.

In this period, the 14 elements beyond actinium, Ac [i.e., the elements from thorium (Th) to lawrencium (Lr) ] are called actinides, while the elements beyond uranium (U) are called transuranic elements.

WBCHSE Class 11 Chemistry Element Classification Principles

Even and odd series: Elements belonging to each of the 4th, 5th and 6th periods are divided into two series: the even and the odd series. The three even series begin with the alkali metals K, Rb and Cs, while the three odd series begin with the coinage metals Cu, Ag and Au respectively.

Subgroups: Except for the Gr-VHI and Gr-0, each of the other groups (Gr-I to VII) is divided into two subgroups designated as ‘A’ and ‘B! In long periods (4th, 5th and 6th), the elements of the even series areplacedinsubgroup-Aand those ofthe odd series are placed in subgroup-B.

In short periods (2nd and 3rd), elements of Gr-I and Gr-II are placed in subgroup-A, while those of the other groups are placed in subgroup-B. Within the same group, the properties of the elements of subgroups and B are altogether different, except for their valencies.

Element Classification Principles

However, elements of the same subgroup exhibit more or less similar properties.

For example, alkali metals of Gr-IA are closely alike. However, Gr-IA metals differ remarkably from the coinage metals of Gr-IB (Cu, Ag and Au), although they have a common valency of ‘1’.

Additional pieces of information about groups and sub-groups:

Elements of subgroup A are more electropositive than those of subgroup B. For example, Gr-VIIA elements (Mn, Tc, Re) are electropositive, while Gr-VIIB elements (F, Cl, Br and I) are electronegative characters.

Gr-VIII has no subgroups. It contains a total of 9 elements, belonging to periods 4, 5 and 6. These nine elements—Fe, Co, Ni (period-4); Ru, Rh, Pd (period-5) and Os, Ir, Pt (period-6) are arranged in this manner due to similarity in their properties and their, atomic weights are also close to v each other.

Each grip, of three elements, is called Mendeleev’s triad elements. Mendeleev coined the term ‘transitional element’ for these elements.

Element Classification Principles

Gr-0 has no subgroups. It contains inert gases: He, Ne, Ar, Kr, Xe and Rn. These elements are chemically inert and do not exhibit any tendency to combine with other elements. So they are zero-valent elements and placed in Gr-‘0′. This group acts as a bridge between highly electronegative halogens (VIIB) and highly electropositive alkali metals (IA).

Due to their similarity in chemical properties, La and 14 elements from Ce -Lu are placed together in Gr-IIIA of the 6th period. The 14 elements from Ce to Lu are called lanthanoids. For similar reasons, Ac and 14 elements from Th-Lr are placed together inGr-IIIA ofthe 7th period. The 14 elements from Th to Lr are ( called actinoids.

Importance & usefulness of Mendeleev’s periodic table Systematic Study of the elements: Mendeleev, for the first time, arranged a vast number of elements in such a way that the elements with similar chemical properties are placed in the same group.

This made the study of elements quite systematic because if the properties of one element (and its compounds) in a particular group are known, then the properties of the rest of the elements (and their compounds) can be predicted

WBCHSE Class 11 Chemistry Element Classification Principles

Prediction of new elements: Mendeleev left some gaps in the periodic table to accommodate new elements to be discovered in future. he even predicted the properties of those unknown elements based on their positions in the table.

when these elements were discovered, their properties were found to be similar as predicted By Mendeleev. For example, Mendeleev left two vacant places below b and al in gr-3 and one vacant place below.

Element Classification Principles

He named those elements eka-boron, ca-aluminium and ca-silicon respectively as he predicted that the properties of these elements would be similar to that of boron, aluminium & silicon.

In 1075, de Baisbaudron discovered eka-aluminium and named it gallium. in 1079, n. l. Nilson discovered eka-boron and named it scandium. In 1006, Winkler discovered eka-silicon and named it as germanium.

It was observed that these newly discovered elements had properties similar to those already predicted by Mendeleev before their discovery.

Correction of doubtful atomic weights: with the help of Mendeleev’s periodic table, doubtful atomic weights of some elements are rectified.

For example, Be was assigned an atomic weight of 13.5 based on its equivalent weight (4.5) and valency (wrongly taken as ‘3’ because Be had certain similarities with trivalent metal Al).

With an atomic weight of 13.5, Be should be placed between carbon (At. weight 12) and nitrogen (At. weight 14).

Element Classification Principles

But no vacant place was available In between C and N. Mendeleev asserted that Be must be bivalent because of its similarity with Mg, Ca etc. Thus he corrected its atomic weight as 4.5 X 2 = 9.0.

Defects Of Mendeleev’s Periodic Table

Discrepancy or anomaly in periodicity: Mendeleev arranged the elements in increasing order of their atomic weights. But he violated this principle in certain cases to give appropriate positions to some elements based on their properties i.e., he laid more emphasis on the properties of those elements rather than their atomic weights.

In the following four pairs of elements, elements with higher atomic weight have been placed before elements with lower atomic weight.

Position of hydrogen: Controversial position of hydrogen in the periodic table also hints at discrepancies within the table. Like the alkali metals ofGr-IA, it exhibits univalency, high reactivity, electropositive character, strong affinity for non-metals and reducing character.

On the other hand, like the halogens of Gr- VIIB, it has atomicity, high ionisation energy, non-metallic character, existence in the gaseous state at normal temperature and pressure ability to combine with milk-forming hydrides (e.g., Nall).

Element Classification Principles

Since hydrogen exhibits similarities as well as dissimilarities with both the alkali metals and the halogens, the placement of hydrogen in any one of these two groups will naturally create difficulties. So it is desirable to fix a separate position for hydrogen in Mendeleev’s periodic table.

Placement of similar elements in different groups and dissimilar elements in the same group: in some cases, elements with almost similar properties have been placed in different groups.

Example: Cu and Hg resemble in properties but Cu is Gr-IB while Hg has been placed in Gr-IIB. Likewise, elements like Ba (Gr-IIA) and Pb (Gr-IVB) have been placed in different groups.

Again, some elements with dissimilar properties have been placed in the same group.

WBCHSE Class 11 Chemistry Element Classification Principles

Example: Highly reactive alkali metals such as Li, Na, K etc., have been placed together with almost inactive coinage metals such as Cu, Ag and Au in Gr-I. Likewise, Mn, Te
and Re having no similarity with F, Cl, Br etc. have been placed together

Lack of separate positions for Gr-VIII elements: No proper place has been allotted to nine elements belonging to Gr-VIII although they have many similarities in properties.

These are arranged in three triads, one in each of the 4th (Fe, Co, Ni ), 5th(Ru, Rh, Pb) and (Os, Ir, Pt)periods

Lack of suitable positions for Lanthanoids and Actinoids: The 14 elements following La from Ce to Lu (lanthanoids) and the 14 elements following Ac from Th to Lr (actinoids) have not been allotted separate positions in the main skeleton of the periodic table.

They have been placed in two separate rows at the bottom of the table. Besides, the number of elements in the lanthanoid and actinoid series cannot be determined from Mandeleev’s periodic table.

Position of isotopes: Isotopes of an element have different atomic weights. So they should be placed at different positions in the periodic table. However, all the isotopes of any specific element are placed in a single position (i.e., same period and same group)in Mendeleev’s periodic table.

Moseley’s experiment: Atomic number determines the fundamental property of an element.

In 1913, Moseley measured the frequencies of X-rays emitted by different metals when bombarded with high-speed electrons.

He observed that the frequencies ofthe prominent X-rays emitted by different metals were different but for each metal, there was a fixed value.

Element Classification Principles

He observed further that the square root of the frequency (v) of the X-rays emitted by a metal was proportional to the atomic number but not to the atomic mass of the metal, Le., Jv = a(Z- b) where ‘a’ is the proportionality constant and is a constant for all the lines in a given series of X-rays.

Thus a plot of Tv vs Z gave a straight line but a plot of Jv vs atomic mass does not bear such alinear relationship. This led Moseley to conclude that atomic number was a better fundamental property of an element than atomic mass.

Modification Of Mendeleev’s Periodic Law

Mendeleev regarded atomic weight as the fundamental property of an element and so he considered atomic weight as the basis of periodic classification of elements.

But Moseley, from his experimental results, showed clearly that atomic number is a better fundamental property of an element than its atomic weight.

This led Moseley to suggest that atomic number (Z) should be the basis of the classification of elements. This gave birth to a new periodic law known as the modem periodic law.

Element Classification Principles

Modern Periodic Law: The physical and chemical properties ofthe elements are aperiodic functions of their atomic numbers.

This implies that, if elements are arranged in order of increasing atomic numbers, the elements with similar chemical properties are repeated after certain regular intervals.

Rectification of the discrepancy in periodicity with the help of modern periodic law:

The original periodic law, based on atomic weight, was violated in the case of four pairs of elements [(Ar, K), (Co, Ni), (Te, I), (Th, Pa)].

In each pair, an element with a higher atomic weight is placed before the element having a lower atomic weight.

Element Classification Principles

In the modern periodic table (based on the atomic number), this discrepancy disappears because the atomic numbers of K, Ni, I and Pa are greater than those of Ar, Co, Te and Th respectively.

Placement of all the isotopes of any specific element in the same position of the periodic table is quite justified as the isotopes of elements have the same atomicnumber although they have differentatomic weights.

Theoretical justification of modern periodic law: Only nuclear electrons (or more specifically valence shell electrons) take part in chemical reactions, while the atomic nucleus remains unaffected.

So it is understandable that the properties of the elements will depend upon their atomic numbers (equal to the number of electrons) rather than their atomic weight or mass numbers (equal to the total number of protons and neutrons).

Periodicity of elements

The periodic repetition of elements having similar properties after certain regular intervals when the elements are arranged in the increasing order of their atomic numbers is called periodicity.

Cause of periodicity: According to modern periodicals, there is a repetition of properties of the elements after certain regular intervals when they are arranged in order of their increasing atomic numbers.

Element Classification Principles

Again from a close study of electronic configurations of various elements, it is observed that with successive increases in atomic number, there occurs a repetition of similar outermost shell electronic configuration (valence shell electronic configuration) after certain regular intervals.

By correlating these two observations, it can be concluded that periodicity in properties is due to the recurrence of similar valence shell electronic configuration after certain regular intervals when the elements are arranged in order of increasing atomic numbers.

This can be illustrated by the following examples—

Elements of Gr-IA have outermost electronic configuration ns1 (where n = outermost principal quantum number).

These elements exhibit similar chemical properties due to their similarity in the valence shell electronic configuration.

Elements of Gr-VIIB have outermost electronic configuration ns2np5.

All the halogens exhibit similar chemical properties due to their similarity in valence shell electronic configuration.

WBCHSE Class 11 Chemistry Element Classification Principles

Inert gases belonging to group possess similar chemical properties because they have similar valence shell electronic configurations (ns2np6).

It should be noted that properties of elements get repeated only after intervals of 2, 8,18 or 32 in the atomic numbers of the elements because similar electronic configurations recur only after such intervals.

Element Classification Principles

The numbers 2, 8, 18 and 32 are called magic numbers. These numbers are very useful in locating elements with similar properties

Moderntableor Long Form Of Periodic Table Bohr’s Table:

This is an improved form of the periodic table based on modern periodic law. It is also called Bohr’s table since it follows Bohr’s scheme for the classification of the element based on the outermost electronic configuration governed by the Aufbau principle. It consists of periods and 18 groups.

Structural Features Of Long Form Of Periodic Table

Description of periods: Like Mendeleev’s modified table, it also consists ofsevenperiodswhich are numbered from as1 to 7 from top to bottom.

The period number is equal to the value of i.e., the principal quantum number corresponding to the outermost shell of the atoms of the elements belonging to that period.

Each period begins with the filling of electrons in a new energy level. Several elements in each period are twice the total number of atomic orbitals available in the energy level that are being filled.

First period: This period begins with the filling of the first energy level (n = 1). Since the first shell has only one orbital [i.e., Is), which can accommodate a maximum of two electrons, there can be only two elements in the first period. These are hydrogen (Is1) and helium (Is2).

Second period: It starts with the filling of the second energy level (n = 2). Since the second shell contains four orbitals (one 2s and three 2p), it can accommodate a maximum of (2×4) = 8 electrons. So, there are eight elements in the second period.

Element Classification Principles

It begins with lithium (Li) in which 1 electron enters the 2s -orbital (3Li: 2s1) and ends up with neon (Ne) in which the second shell gets filled (10Ne: 2sz2p6).

Third period: The third period begins with the filling of the third energy level (n = 3). This energy level contains nine orbitals (one 3s, three 3p and five 3d).

According to the Aufbau principle, 3d -orbitals will be filled up only after filling the 4s -orbital.

Consequently, the third period involves filling only four orbitals (one 3s and 3p ) which can accommodate a maximum of (2 x 4) = 8 electrons. So, there are 8 elements in the third period from (Nas1) to 18Ar(3s23p6).

Fourth period: This period corresponds to the filling of the fourth energy level (n = 4). Out of 4s,4p,4d and 4f-orbitals belonging to this shell, filling of 4d -and 4f-orbitals does not occur in this period since their energies are higher than that of even 5s -orbital.

It must however be remembered that, after filling 4s -orbital, filling of five 3d -orbitals begins since energy yf -orbital is greater than that of 4s orbital but less than it of 4p -orbital.

So the fourth period involves filling of or 9 Orbitals (one 4s, five 3d and three 4p), which can accommodate (2×9) = 18 electrons.

Therefore, the fourth period contains 18 elements from potassium (19K: 4s1) to krypton (36Kr: 4sz3d104p6).

Element Classification Principles

This period contains 10 elements more than the third period corresponding to filling off 3d -orbitals. These 10 elements [2iSc(3d14s2) to 30Zn(3d104s2)] are called the first series of transition elements.

Fifth period: The fifth period corresponds to the filling of electrons in the fifth energy level (n = 5). Like the fourth period, it also accommodates 18 elements since only nine orbitals (one 5s, five 4d and three 5p) are available for filling with electrons.

It starts with rubidium in which one electron enters 5s -orbital (37Rb: 5s1) and ends up with xenon in which the filling of 5p -orbital is complete (54Xe: 5s24d105p6). 10 elements from 39Y(5s24d1) to 48Cd(5s24d10) corresponding to filling of five 4dorbitals are called second series oftransition elements.

Sixth period: The sixth period corresponds to the filling of electrons in the sixth energy level (n = 6).

This period involves the filling of sixteen orbitals (one 6s, seven4f, five 5d and three 6p) which can accommodate a maximum of (2 X 16) = 32 electrons. So there are 32 elements in the sixth period.

It begins with caesium (Cs) in which one electron enters 6s -orbital (55Cs: 6s1) and ends up with radon in which filling of 6p -orbital is complete (86Rn: 4f145d106s26p6).

Filling up of 4f-orbitals begins with cerium(58Ce) and ends with lutetium (71Lu). These 14 elements constitute the first inner-transition series, also called lanthanoids or rare earth elements.

Element Classification Principles

These are separated from the main frame periodic table and are placed in a horizontal row at the bottom of the table Again, 10 elements lanthanum (57La), hafnium (72Hf) to mercury (80Hg), corresponding to successive filling of10 5d -orbitals, constitute the third transition series.

Seventh period: This period corresponds to the filling of electrons in the seventh energy level (n = 7). Like the sixth period, it is expected to accommodate 32 elements corresponding to the filling of 16 orbitals (one 7s, seven5f, five 6d and three 7p ).

However, at present this period is incomplete consisting of 28 elements. The last element of this period will have an atomic number of of118 and will position theinert gas family

In this period, after filling of 7s -orbital [87Fr: 7s1 and 8S1Ra: 7s2 ], the next two electrons enter the 6rf-orbital (this is against the Aufbau principle) corresponding to the elements 8gAc and goTh.

Thereafter, the filling up of 57- orbital begins with giPa and ends from Th to Lr are commonly called actinoids, which constitute the second Inner-transition series, Although Th does not contain any electron.

‘if orbital, it is considered to be a member of the actinoid series. Like lanthanoids, 14 members of the actinoid series are placed separately in a horizontal row at the hotter of the periodic table.

Description of groups: Each of the 18 groups in the long form of the periodic table consists of many elements whose atoms have similar electronic configurations ofthe outermost shell (valence shell).

The members of each group exhibit similar properties. Successive members in a group are separated by magic numbers of either 8 18 or 32.

Element Classification Principles

According to the recommendation of IUPAC (1988), the groups are numbered from 1 to 18. Designations of these groups in different systems are presented in the following table-

WBCHSE Class 11 Chemistry Element Classification Principles

Element Classification Principles

The superiority of the long form of the periodic table over Mendeleev’s periodic table

1. In the long form of the periodic table, it is easy to remember and reproduce all the elements more easily in a sequence of atomic numbers.
2. it relates the positions of the elements in the table to their electronic configurations more dearly.
3. Gradual change In properties along the periods or similarity in properties along the groups can be interpreted by considering electronic configurations of the elements.
4. For example, elements of the same group exhibit marked similarities due to similar outer electronic configurations.
5. Splitting the periodic table into s-,p-, cl- and f-blocks has made the study of the elements easier.
6. The maximum capacity of each period to accommodate a specific number of elements is related to the capacity of different electronic shells to accommodate the maximum number of electrons.
7. Due to the elimination of sub-groups, dissimilar elements do not fall In the same group. Each vertical column (group) accommodates only those elements which have similar outer electronic configurations, thereby, showing similar properties.
8. Group-VIIl elements (involving triads) of Mendeleev’s table, have been provided separate positions in groups-8, 9 and 10.
9. Elements belonging to 1, 2, and 13-17 groups are classified as representative elements, while those belonging to 3-12 groups are classified as transition elements.
10. Elements are further classified as active metals (belonging to groups 1 and 2), heavy metals (belonging to groups 3-12) and non-metals (belonging to groups 13-18).
11. Transition elements of the 4th, 5th, 6th and 7th periods are assigned appropriate positions in this periodic table.
12. The completion of each period with an inert gas element is more logical. In a period as the atomic number increases, the quantum shells are gradually filled up until an inert gas configuration is achieved at group 18.
13. It thus eliminates the even and odd series belonging to the periods 4, 5 and 6 of Defects of the long form of the periodic table

If the Position of hydrogen: The position ofhydrogen is not settled. It can be placed along with alkali metals in group 1 or with halogens in group 17, as it resembles the alkali metals as well as the halogens.

Position of helium: Based on electronic configuration, He (Is2) should be placed in group 2. But, it is placed in group 18 along with the p -block elements. No other p -block element has the electronic configuration ofthe type ns2.

Element Classification Principles

Position of lanthanoids and actinoids: Lanthanoids and actinoids have not been accommodated in the main frame of the periodic table.

Position of isotopes: Isotopeshavenotgot separate places.

Properties of isotopes of heavier elements are more or less the same, but isotopes of lighter elements differ drastically in their physical, kinetic and thermodynamic properties.

So it is not desirable to place the isotopes in the same position. Despite these limitations, the long form of the periodic table, based on electronic configurations, is much more scientific and thus finds extensive use.

Classification Of Elements Into Different Blocks

Amount In tin long form of the periodic table it has been divided Into four blocks viz, s -block, p -block, d -block and f- block.

It Is done based on the nature of atomic orbitals into which the Inst electron (the differentiating electron) gets accommodated.

Elements of s and p -blocks except Inert gases, are called representative elements, and d -block elements, on the other hand, are called transition elements.

S -block elements

Elements In which the last electron enters the -subshell of their outermost energy level (n) are called s -block elements.

Since s -subshell can accommodate a maximum of 2 electrons, only two groups are included in this block.

Elements of group-1 (alkali metals) and group-2 (alkaline earth metals) which have outermost electronic configurations rui1 and ns2 respectively constitute the s -block. This block is situated at the extreme left portion of the periodic table.

Outermost electronic configuration of t-block elements: ns1.2 Inert gas element, helium (He, Is2) Is also considered as an s -block element.

Characteristics of s-block elements:

In the case of these elements, all shells except the outermost one, are filled with electrons.

Except for H and, all other elements of this block are metals. Because of their low ionisation potential, these metals are very reactive and do not occur freely in nature.

Element Classification Principles

All the metals of this block are good reducing agents because of the value of ionisation potential.

They are good conductors of heat and electricity.

WBCHSE Class 11 Chemistry Element Classification Principles

They are soft metals. They have low melting points, boiling points and low densities as compared to the adjacent transition elements.

Cations of group-IA and group-DA elements are diamagnetic and colourless since their orbitals do not contain odd electrons.

Except for Be and Mg, -block elements impart specific colour to the flame (flame test).

Salts of these elements except dichromate, permanganate arid chromate, are colourless.

Compounds of these elements are mainly ionic (only Li and Be can form covalent compounds in many cases).

They form stable oxides with oxygen (Na1, CaO), produce chlorides with chlorine (NaCl, CaCl2) and also form salt-like hydrides (NaH, KH, CaH2) with hydrogen.

Hydroxides of these elements [except Ca(OH)2, Mg(OH)2 and Be(OH)2] are soluble in water at ordinary temperature.

Element Classification Principles

The non-luminous flame of the Bunsen burner is rich in electrons. During the flame test, metal ions are converted into short-lived neutral atoms by accepting electrons from the flame.

Valence electrons ofthese neutral atoms absorb energy from the flame and get promoted to higher energy levels.

When the electrons return to lower energy levels, the absorbed energy is emitted in the form of radiation of different wavelengths in the visible range and as a consequence, different colours, depending.

The wavelengths of emitted light radiations are Imparted to the flame. For instance, the generation of golden-yellow flame during the flame test with sodium salt is due to the transition of one electron of Na -atom from 3s -orbital to 3p -orbital and its return to 3sorbltal after a very short interval.

The ionisation potentials of Be and Mg are sufficiently high because of their smaller size. So, their electrons cannot be excited to higher energy levels by absorbing energy from the flame. As a result, they fail to respond to the flame test.

P -block elements

Elements in which the last electron enters p -subshell of their outermost energy level (n) are called p-block elements.

Since p -subshell can accommodate a maximum of six electrons, 6 groups are included in this block.

Element Classification Principles

Elements of group-13, 14, 15, 16, 17 and 18 (excluding helium) having the outermost electronic configurations: ns2np1, ns2np2, ns2np3, ns2np4, ns2np5 and ns2np6 respectively, constitute the p -block. This block is situated at the extreme right portion ofthe periodic table

The elements of group 18 are balled noble gases or inert gases. They have the shell electronic configuration ns2np6 in the outermost shell. Group-17 elements are called halogens (salt producers)’ and group-16 elements are called chalcogens (ore-forming).

These two groups of elements have high electron-gain enthalpies (high negative values of A’H) and hence readily accept one or two electrons respectively to attain the stable noble gas configuration thereby forming negative and negative anions respectively.

 

WBCHSE Class 11 Chemistry Element Classification Principles

The elements of s- and p -blocks taken together are called representative normal or main group elements. Outermost electronic config. of-flock elements: ns2np1’6

Based on electronic configuration, helium (Is2) should not be considered as a p -block element, but from the standpoint of its chemical inertness (owing to the presence of a filled valence shell) it is justified to place group-18 along with other noble gas elements.

Characteristics of block elements:

Ionisation enthalpies of p -block elements are higher as compared to those of -block elements.

Most of the p -block elements are non-metals, some are metals and a few others are metalloids and inert gases.

Element Classification Principles

The metallic character increases from top to bottom within a group non-metallic character increases from left to right along a period. Hence, metals exist at the bottom ofthe left side ofthe p -block whereas non-metals lie at the top of the right ofthe p -block. Metalloids (B, Si, Ge, As, Sb ) stand midway between them.

The oxidising character of p -block elements increases from left to right in a period and reducing character increases from top to bottom in a group.

Most of them form covalent compounds, although ionic character increases continually down the group.

Elements of this block are non-conductors of heat and electricity, except metals and graphite.

Elements of this block are mostly electronegative.

Some of them exhibit variable oxidation states or valence states. Oxidation states may be both positive and negative.

Non-metallic elements of this block form acidic oxides.

They can form both coloured and colourless compounds.

Element Classification Principles

4th, 5th and 6th-period elements can form complex compounds by coordinate covalency due to the presence of vacant d-orbitals. oa aii.

Some of the p -block elements Fe.g.-Q Si, P, S, B, Ge, Sn, As etc.) show the phenomenon of allotropy.

Carnation property is shown by some- block elements (e.g., C, Si, Ge, N, S etc.)

d-block elements (Transition elements) Elements in which the last electron enters d -the subshell of their penultimate shell (i.e., the second from the outermost) are called d -block elements, d -subshell can accommodate a maximum of 10 electrons.

Therefore, ten groups are included in d -the block. Elements of group-3 [(n-1)d1ns2], 4, 5, 6, 7, 8, 9, 10, 11 and 12 [(n- l)d10ns2] constitute the d -block.

Atoms of the elements belonging to these groups usually contain or 2 (sometimes zero) electrons in the s -s-orbital of their outermost shell (i.e., n -th shell), while the differentiating electrons are being progressively filled in, one at a time, in the d -subshell of their penultimate shell [i.e., (n- 1) -th shell].

Electronic configuration of outer shell: (n-1) d1-10ns1-2

Element Classification Principles

This block is situated in between s -and p -blocks. In fact, d -block elements form a bridge between the chemically active metals of groups 2 on one side and the less reactive elements of groups 13 and 14 on the other side.

Hence, d -block elements are called transition elements These elements have been divided into four series called the first, second, third and fourth transition series.

First transition series or 3d-series: First transition series consists of 10 elements, belonging to the 4th period, from scandium (21Sc) to zinc (3QZn) in which 3d -orbitals are being progressively filled in. Zn is not a transition element.

Second transition series or 4d-series: Second transition series also consists of 10 elements, belonging to the 5th period, from yttrium (3gY) to cadmium (48Cd) in which 4d -orbitals are being progressively filled in. Cd is not a transition element.

Third transition series or 5d-series: Third transition series also consists of 10 elements, belonging to the 6th period. These are lanthanum (57La) and elements from hafnium (72Hf) to mercury (80Hg). In all these elements, 5d orbitals are being successively filled in. Hg is not a transition element.

Element Classification Principles

Fourth transition series (6d-series: The fourth transition series is formed from a part of the seventh period and it contains 10 elements. These, are actinium (89Ac) and elements from rutherfordium (104Rf) to ununbium (112Uub), in which 6d -orbitals are being progressively filled in.

All d -block elements are not transition elements. Only those d -block elements in which atoms in their ground state or any stable oxidation state contain incompletely filled subshells are considered transition elements.

WBCHSE Class 11 Chemistry Element Classification Principles

Characteristics of d-block elements:

1. All d -block elements are metal. Their ionisation potential lies mid-way between those of s and p -block elements.
2. Elements of the 5d series (especially Pt. Au and Hg) are inert under ordinary conditions. Thus, they are known as noble metals.
3. Elements of this block exhibit variable oxidation states and valencies because ofthe presence of partially filled d orbitals in their atoms, ns -electrons and different numbers of(n-l)d electrons participate in bonding at the time of reaction with atoms of other elements.
4. They are solids (except Hg), hard and have high melting and boiling points.
5. They can form both ionic and covalent compounds.
6. They exhibit paramagnetic character due to the presence of one or more unpaired electrons in their atoms or ions (exception-Sc3+, Ti4+, Zn2+, and Cu+ which do not contain odd electrons and are diamagnetic). Fe and Co can be converted into magnets and hence, they are ferromagnetic.
7. They frequently form coloured ions in solids or solutions. With the change in their oxidation numbers, there also occurs a change in the colour ofthe formed ions.
8. d -block elements exhibit a very distinctive property of forming coloured coordination complexes.
9. This tendency may be ascribed to the small size of the atom or ion, a high nuclear charge of the ion and the presence of an incomplete d -d-orbital, capable of accepting electrons from the ligands.
10. They are less electropositive than s -block elements but more electropositive than p -block elements.
11. Several transition metals such as Cr, Mn, Fe, Co, Ni, Cu etc., and their compounds are used as catalysts.
12. Many transition metals form alloys.

F-block elements (Inner-transition elements)

Elements in which the differentiating electron (i.e., the last electron) enters the f-subshell of their antepenultimate shell (i.e., the 3rd from the outermost) are called f-block elements.

All the F-block elements belong to group 3 (3B) of the periodic table. In these elements, s -orbital last shell (n) is filled, d -subshell of the penultimate shell [i.e., (n- 1) th shell] contains 0 or 1 electron, while f-subshell of the antepenultimate shell [i.e., (n-2)th shell] gets progressively filled in.

General electronic config.: (n-2)f1-14(n-l)d0-1ns2

Lanthanide series or 4f-Series: The first series follows lanthanum (La) in the 6th period and consists of 14 elements from cerium (58Ce) to lutetium (71Lu).

These 14 elements are collectively called lanthanoids because they closely resemble lanthanum in their properties.

Element Classification Principles

These are also called rare-earth elements since most of these elements occur in very small amounts in the earth’s crust.

Actinoid series or 5f-series: The second series follows actinium (sgAc) in the 7th period and consists of 14 elements from thorium (goTh) to lawrencium (103Lr).

These 14 elements are collectively called actinoids because they closely resemble actinium in their properties.

All the actinoids are radioactive elements. 4fand 5f-series of elements are also called inner-transition elements because they form transition series within the transition elements of d -block.

Characteristics of f-block elements:

1. They are all heavy metals.
2. They exhibit variable valency. +3 oxidation state is most common. Few elements are found to occur in +2 and +4 oxidation states.
3. Some members exhibit paramagnetism due to the presence of odd electrons.
4. They form complex compounds, most of which are coloured.
5. They have high densities.
6. They generally have high melting and boiling points.
7. Within each series, the properties of the elements are quite similar. It is very difficult to separate them from a mixture.
8. Actinoids are radioactive. The first three members (Th, Pa, U ) occur in nature, while the others are man-made. The elements after uranium are called transuranic elements.

Stair-step diagonal

The right side of the long form of the periodic table is composed of p -block elements belonging to groups 13 (3A), 14(4A), 15(5A), 16(6A), 17(7A) and 18 (WlA or 0).

This segment includes four types of elements viz., metals, nonmetals, metalloids and inert gases.

Element Classification Principles

There is no sharp line of demarcation to classify the metals and non-metals, but the zig¬ zag diagonal line (looking like stair-steps) running across the periodic table from boron (B) to astatine (At) is considered as a separation between the metals and non-metals.

WBCHSE Class 11 Chemistry Element Classification Principles

This line is called the stair-step diagonal. The elements B, Si, Ge, As, Sb and Te bordering this line’ -aii d- running diagonally across the periodic table are 8 known as metalloids (which exhibit properties that are characteristics of both metals and non-metals).

The elements (except A1 ) lying between the stair-step diagonal line and the d -block elements are referred to as post-transition elements.

Classification Of Elements based on Outer Electronic Configurations

Based on electronic configurations of the ultimate and penultimate shell of the atoms, Bohr divided the elements into four classes viz., gas elements,

1. Representative elements,
2. Transition elements and
3. Inner-transition elements.

Inert gas elements

S and p -subshells of the outermost shell of the elements of this class are filled.

Except He (electronic configuration: Is2), all other inert gas elements have the valence shell electronic configuration: ns2np6.

All these elements are stable and chemically inert as their outermost shells contain octets of electrons.

Element Classification Principles

They do not normally participate in chemical reactions because the gain or loss of electrons by their atoms would disturb their stability. So, they are called inert gas elements.

Their valency being zero, they find a place in group ‘0’ or ’18 These elements act as a bridge between highly electropositive alkali metals and strongly electronegative halogens.

Representative Elements

Elements present in s – and p -blocks (except group-1) of the periodic table are known as representative elements. The electronic configuration of the outermost shell of these elements varies from ns1 to ns2np5. These consist of some metals, all non-metals and metalloids.

The name ‘representative’ has been assigned to the elements because of their frequent occurrence nature and because they typify the properties of all other members of the group to which they belong.

All the elements of groups, IIA and from 3A to VILA are included in this class.

These elements are very reactive Chemical reactivity of these elements can be ascribed to the ability of their atoms to attain inert gas electronic configuration (ns2np6 or Is2) either by gaining or losing electron(s) or by sharing one or more electron pairs with other atoms. These elements are also known as typical elements.

Transition Elements

Elements of this class are characterised by the presence of atoms in which the inner d -subshell is not filled. According to the modified definition, the elements in which atoms in their ground state or any stable oxidation state contain incompletely filled d -subshell are known as transition elements. Atoms of the elements in this class have the general electronic configuration: (n-I)dl-10 ns1-2.

Element Classification Principles

Cu, Ag and Au, despite having filled d orbitals, are regarded as transition elements. This is because at least in one stable oxidation state of these elements, d subshell remains incompletely filled.

There are four transition series corresponding to the filling of 3d,4d,5d and 6d orbitals These four series belong to the 4th. 5th. 6th and the period of the periodic table.

Each series begins with a member ofthe group-3 and ends with a member of the group-12.

Characteristics:

1. All transition elements are metallic.
2. They have more than one oxidation state or valency.
3. Their ions are coloured.
4. They form complex compounds.
5. Elements of group-12 (11B) (Zn, Cd, Hg) are not considered astransition elementsbecausetheyhaveno partially filled d -orbitals in any of their oxidation states.
6. Moreover, they do not form stable complexes and do not show characteristic colour and paramagnetism.
7. However, their tendency to form complex is much greater than that of the representative elements.
8. They exhibit properties of both transition representative elements.

Differences between typical and transition elements:

1. During the building up of an atom of a typical element by the filling of electrons in its various orbitals, the last electron goes to s -or p -orbital of the outermost shell (n).
2. However, in the case of transition elements, the last electron enters the inner d -d-orbital of(n- 1) th shell.
3. For the representative elements, atomic volume or radius decreases but ionisation enthalpy and electro negativity go on increasing with the increase in atomic number across a period.
4. In the case of the transition elements, as the last electron enters the inner (n- l)d -orbital, the extent of change is relatively small.
5. Most of the representative elements exhibit only one valency. Some elements, of course, show more than one valency.
6. But transition elements show 2 or more valencies through the participation of inner d -d-orbital electrons
7. In the case of representative elements, the tendency to form complex compounds is almost negligible while transition elements are found to show a strong tendency to produce complex compounds due to the presence of incompletely filled d -d-orbital.
8. Compounds formed by representative elements are, in general, colourless but the compounds of transition elements are mostly coloured.
9. Due to the absence of odd electron(s), compounds formed by representative elements are diamagnetic while transition metal compounds, because of the presence of odd electrons, are paramagnetic.
10. Many of the transition metals and their compounds act as catalysts in chemical reactions. Such a tendency is seldom observed in the case of representative elements.

Inner-transition elements

Elements of this class are also transition elements, although they may be distinguished from the regular transition series by their electronic configurations.

Atoms of these elements not only contain incompletely filled d -subshell [(n-l)d] but also contain incompletely filled /-subshell [(n- 2)/].

These elements comprise a transition series within a transition series and hence, they are called Inner-transition elements.

Element Classification Principles

The two series of inner-transition elements are O lanthanoids (rare earth elements) and actinoids.

In the case of 14 elements i.e., cerium (Cel to lutetium (71Lu) following lanthanum (57La), 4/- and 5d subshells remain incompletely filled. These are called lanthanoids. Their general electronic configuration is:

4f1- 14 5(io- 1 6sz Wlth increase in atomic number (58-71). the differentiating electrons of these elements enter the 4f- subshell, despite the presence of a partially filled 5d -subshell. The total electron-accommodating capacity of /-subshell Is 14.

So the number of lanthanoids is also 14. Likewise, 14 elements after actinium (89Ac), from thorium (90Th) to lawrenclum (103Lr) are called actinoids. Their general electronic configuration is 5f1’14 6d01 7s2. With the increase in atomic number (90-103), the differentiating electrons enter the 5f-subshell, despite the presence of an incompletely filled 6d -subshell. Hence, like the lanthanoids, the number of actinoids Is also 14.

Lanthanoid contraction

In the case of lanthanoids (58Ce – 71Lu), it is observed that with an increase in atomic numbers, atomic and ionic size (M3+) go on decreasing, although the decrease in Ionic radii is much more regular than that of atomic radii.

This decrease in atomic and ionic radii with an increase in atomic number in the case of lanthanoids, is known as lanthanoid contraction.

Cause Of lanthanoid contraction: The general electronic configuration of lanthanoids is: 4/’“ 5rf01 (is2. The differentiating electrons of these elements enter the 4f-subshell.

Now due to their diffused shape, f-orbitals have a very poor shielding effect. Thus with the gradual addition of the f- electrons, the atomic number increases by one unit while the shielding effect does not increase appreciably; i.c., there is a gradual increase in the effective nuclear charge acting on the outermost electrons.

Consequently, the attraction of the nucleus for the electrons in the outermost shell increases, causing the electron cloud to shrink although it’s magnitude is small. Thus, there is a gradual shrinkage in the atomic and ionic radii with an increase in atomic number.

Element Classification Principles

Precisely speaking, f-orbitals are too diffused to screen the outermost electrons effectively against the attractive force of the nucleus. Thus, there is a slow contraction in atomic and ionic radii (lanthanoid contraction).

In the same way, the d -contraction due to the accommodation of die electrons in (n- 1) d -subshell in the transition series can be interpreted. But d -orbitals are more effective in screening compared to tire f-orbitals. So this effect is less pronounced in the case of transition elements.

Element Classification Principles

Classification of elements as metals, non-metals and metalloids

All the known elements can be divided into three classes— metals, non-metals and metalloids based on their properties.

Metals: About 78% of the known elements are metals. They appear mainly on the left side and central portion of the long form ofthe periodic table.

Examples are—

1. Alkali metals,
2. Alkaline earth metals,
3. D -block elements,
4. F-block elements,
5. Higher members of p -block elements.

Metals have the following characteristics—

1. They are solids at room temperature. Mercury is an exception, which is a liquid at ordinary temperature.
2. Gallium (melting point 30°C) and caesium (melting point 29°C) are also liquids above 30°C.
3. They usually have high melting and boiling points.
4. They are good conductors of heat and electricity.
5. They are malleable (can be flattened into thin sheets) and ductile (can be drawn out into wires).

Non-metals: There are only about 20 non-metals discovered so far. They are located towards the top right-hand side of the periodic table. Hydrogen and some p-block elements are non-metals.

• Six of the non-metals (C, B, P, S, Se and I) are solid.
• Bromine is the only liquid non-metal.
• The remaining non-metals (N, O, F, Cl, H and inert gases) are gases.
• Non-metalshavelowmelting and boiling points (boron and carbon are exceptions).
• They are poor conductors of heat and electricity (graphite is a good conductor of electricity).
• Nonmetallic solids are usually brittle and are neither malleable nor ductile.

Element Classification Principles

Metalloids: There are some elements which have certain characteristics common to both metals and non-metals.

These are called semimetals or metalloids. Examples are—silicon (Si), germanium (Ge), arsenic (As), antimony (Sb) and tellurium (Te).

In most of their properties (both physical and chemical), metalloids behave as non-metals. However, they somewhat resemble the metals in their electrical conductivity. They tend to behave as semiconductors.

This property is found particularly in the case of silicon and germanium. These two metals are mainly responsible for the remarkable progress in the past five decades in the field of solid-state electronics.

Determination Of The Position Of An Element In Long Form Of Periodic Table

Since there is a close relationship between the long form of the periodic table and the electronic configuration of elements, the serial numbers of periods and groups and the type of block to which an element belongs can be predicted by following the guidelines given below:

Period: Serial number of the period = principal quantum number (n) ofthe valence shell.

Example: Mg (ls22s22pfi3s2) belongs to the third period because the principal quantum number of its valence shell is 3.

Block: The publicly into which the differentiating electron [i.e., the last electron) enters, represents the block to which the given element belongs (except He ).

Example: Sc (ls22s22p63s23pa4s23dl) belongs to d -block because the last electron [i.e., the 21st electron) enters the 3d -subshell.

Group: The group to which an element belongs can be predicted based on the number of electrons present in the outermost [i.e., fth) and the penultimate [i.e., [n —1) th] shell.

Element Classification Principles

For .s -block elements: Group-number = Number of valence electrons i.e., no. of electrons in the ns -orbital.

For p -block elements: Group-number = 10 + no. of valence electrons = 10 + no. of ns -electrons + no. of np electrons.

For d -block elements: Group-number = no. of ns- electrons + no. of (n- l)d -electrons.

For f- block elements: Group number= 3 (fixed).

Examples: Determination of the position of the elements with the following electronic configurations in the long form of the periodic table—

1. ls22s22p63s1
2. ls22s22p4
3. ls22s22p63s23p63d24s2
4. ls22s22p63s23p64s2
5. ls22s22p63s23p63d104s1

The given element belongs to s -the block because the differentiating electron (i.e., the the 11th electron) entering 3s orbital,

For this -block element, group-number = no. of electrons in the 3s -orbital =1.

Serial no. of the period = principal quantum number ofthe valence shell =

The differentiating electron [i.e., the 8th election) enters the p-subshell. So, tile given element belongs to p block, [b] Serial no. of the period = principal quantum number of the valence shell =

For this p -block element, group number= 10+ no. ofvalence electrons = 10 + number of ns electrons + no. of np -electrons =10 + 2 + 4 =16.

The differentiating electron [i.e., the 22nd electron) enters the 3d -subshell. So, the given element belongs to d -the block,

Element Classification Principles

Serial no. of the period = principal quantum number of the valence shell = 4.

For die d block element, group-number = no. of ns -electrons + no. of (n- 1)d -electrons = 2 + 2 = 4.

The differentiating electron {l.e., the 20th electron) enters the 4s -subshell. So, the given element belongs to s -block,

Serial no. of the period = principal quantum number of the valence shell =4.

For this -block element, group-number = no. of electrons in outermost shell = 2.

The differentiating electron [i.e., the 29th electron) enters the 3d -subshell. So, the given element belongs to d -block, [b] Serial no. of the period = principal quantum number of the valence shell = 4.

For this d -block element, group no. = no. of ns electrons + no. of[n- 1)d -electrons = 1 + 10 = 11.

IUPAC Nomenclature Of Transuranic Elements (Atomic Number More Than 100)

The elements beyond fermium (100) are called transfermium elements. They have atomic numbers above 101.

Fermium (100), mendelevium (101), nobelium (102), and lawrencium (103) are named after eminent scientists. Some of the elements with atomic numbers higher than 103 were synthesized and reported simultaneously by scientists from the USA and the Soviet Union.

Each group proposed different names for die same element, e.g., an element with atomic number 104 was named Rutherfordium by USA scientists while Soviet scientists named it Kurchatovium. To overcome such controversies, the

IUPAC (1977) has recommended a new method of naming these elements. This is discussed here.

Element Classification Principles

The digits expressing the atomic number of an element are represented serially (from left to right) by using the numerical roots given below.

The successive roots are written together and the name is ended by ‘ium! To avoid repetition of some letters, the following procedure is adopted.

If ‘enn’ occurs before ‘nil; the second ‘n’ of ‘enn’ is dropped.

Similarly the letter ‘i’ of ‘bi’ and ‘tri’ are dropped when they occur before ium bi+ium= bium, tri+ium= trium, enn+nil= ennil etc.

The symbol of an element is derived by writing successively the initial letters (z.e., abbreviations) of the numerical roots which constitute the name.

Element Classification Principles

 

Valency

The valency of an element is defined as the combining capacity of that element. The valency of an element is usually expressed in terms of the number of H-atoms that combine with an atom of the element.

The chemical properties of an element depend upon the number of electrons present in the outermost shell ofthe atom.

Electrons present in the outermost shell are called valence electrons and these electrons determine the valency ofthe atom.

In the case of the representative elements the valency of an atom is generally equal to either the number of valence electrons or equal to eight minus the number of valence electrons,.

However, transition and inner-transition elements exhibit variable valency involving electrons of the outermost shell as well as d- or f-electrons present in penultimate or antepenultimate shells.

Variation of valency in a period: In the case of the representative elements, the number of valence electrons increases from 1 to 7 from left to right in a period.

Oxygen-based valency increases from 1 to 7 and it becomes a zero noble gas series (because of its inertness). The maximum valency of ‘8’ is shown only by Os and Ru in 0s04 and Ru04 respectively. These two elements (transition elements) belong to group- 8 (VmB)in the periodic table.

Element Classification Principles

However, hydrogen-based and chlorine-based valency of representative elements along a period first increases from group-1 to 4 (valency= group no.) and then decreases from group-4 to 0 (valency= 8- group no).

Variation of valency in a group: On moving down a group, the number of valence electrons remains the same. Therefore, all the element groups exhibit the same valency.

Example: All the elements of group-IA (Li, Na, K, Rb etc.) have alencyT’ and that of group-2A (Mg, Ca, Sr etc.) exhibit avalencyof’21Noble gases present in group-VIIIA are zerovalent since these elements are chemically inert.

Ionisation Enthalpy or inonisation potential.

If energy is supplied to an atom, electrons may be promoted to higher energy states. If sufficient energy is supplied, one or more electrons may be removed completely from the atom leading to the formation of a cation. This energy is referred to as ionisation energy orionisation enthalpy (A/T).

Element Classification Principles

Ionisation Enthalpy or ionization potential Dentition: Ionisation enthalpy or more accurately first ionisation enthalpy of an element is defined as the amount of energy required to remove the most loosely bound electron from the valence shell of an isolated gaseous atom existing in its ground state to form a cation in the gaseous state.

Explanation: If AH1 (or I1) is the minimum amount of energy required to convert any gaseous atom in its ground state into gaseous ion M+, then the ionisation enthalpy or more accuratelyfirstionisation enthalpyofM is AH1 (orI1).

\(\begin{aligned}
& \mathrm{M}(\mathrm{g})+\Delta H\left(I_1\right) \longrightarrow \mathrm{M}^{+}(\mathrm{g})+e \\
& \text { (Isolated gaseous (Energy) (Gaseous (Electron at } \\
& \text { atom) cation) infinite distance) } \\
&
\end{aligned}\)

Element Classification Principles

Importance: The ionisation enthalpy of an element gives an idea about the tendency of its atoms to form gaseous cations.

Energy is always required to remove electrons from an atom and hence, ionisation enthalpies are always positive.

Units: It is expressed in kj per mole of atoms (kj. mol-1).

Formerly, it was expressed in electron-volt per atom (eV- atom-1) or kcal per mole of atoms (kcal. mol-1)

1ev per atom =23.06 kcalmol-1 =96.5 kl-mol¯¹.

‘Ionisation enthalpy is also called ‘ionisation potential’ because it is the minimum potential difference required in a discharge tube to remove the most loosely bound electron from an isolated gaseous atom to form a gaseous cation.

Successive ionisation enthalpies: Like the removal of the first electron from an isolated gaseous atom, it is possible to second, third etc., electrons successively from cations one after another.

The minimum amount of energy required to remove the second, third etc., electrons from unipositive, dipositive etc., ions to form M2+, M3+ etc., ions of the element are called second AH2 (or /2), tlirid AH3 (or I3 ) etc., ionisation enthalpies respectively.

Element Classification Principles

\(\begin{aligned}
& \mathrm{M}^{+}(g)+\Delta H_2\left(\text { or } I_2\right) \rightarrow \mathrm{M}^{2+}(g)+e \\
& \mathrm{M}^{2+}(g)+\Delta H_3\left(\text { or } I_3\right) \rightarrow \mathrm{M}^{3+}(g)+e
\end{aligned}\)

The second ionisation enthalpy is higher than the first ionisation enthalpy as it is more difficult to remove an electron from a cation than from a neutral atom. ] Similarly, the third ionisation enthalpy is higher than the second and so on i.e.,

AHj(or l1) < AH2(or l2) < AH3(or l3) <

If not mentioned, the term ‘ionisation enthalpy is always used to mean the first ionisation enthalpy of an element.

Formerly, first, second, third etc, ionisation enthalpies were denoted by the symbolsI, IZ, I3 etc. Such symbols will be used in many places in this book.

Factors governing ionisation enthalpy:

Atomicsize: Ionisation enthalpy decreases as the atomic size increases and vice-versa.

The attractive force between the electron (to be removed) and the nucleus is inversely proportional to the distance between them.

Thus, as the size of the atom increases, the hold of the nucleus over valence electrons decreases and consequently ionisation enthalpy decreases. For example, l1(Li)>l1(Na)>L1(K).

Element Classification Principles

The magnitude of nuclear charge: Ionisation enthalpy increases with an increase in nuclear charge and vice-versa.

This is due to the fact the force of attraction between the valence electron (to be removed) and the nucleus increases with an increase in the nuclear charge provided that the outermost electronic shell remains the same.

Screening effect of inner-shell electrons: As the screening effect or shielding effect of the inner electrons increases, the ionisation enthalpy decreases

In multi-electron atoms, the inner electronic shells act like a screen between the nucleus and the outermost electronic shell.

As a result, the nuclear attractive force acting on the electrons in the outermost shell is somewhat reduced i.e., the effective nuclear charge gets reduced to some extent.

Thus, the inner-electronic shells shield the electron (to be removed) from the nuclear attractive force, resulting in a reduction of ionisation enthalpy.

If other factors do not change, the ionisation enthalpy decreases with an increase in the number of inner electrons.

In multi-electron atoms, the ability of the electrons present in the inner shells to shield or screen the outer electrons from the attractive force of the nucleus is called the shielding effect or screening effect.

Naturally, the magnitude of the screening effect depends on the number of electrons present in the inner shells. In a particular energy level, the screening effect of the electrons presenting different subshells follows the sequencers >p> d> f.

Due to the screening effect, the valence shell electrons do not feel the full charge ofthe nucleus. The actual nuclear charge experienced by the valence shell electrons is called the effective nuclear charge.

This is given by the relation, Effective nuclear charge (Z)= total nuclear charge (Z) – screening constant (cr) where the screening constant (cr) takes into account the screening effect ofthe electrons present in the inner shells.

Element Classification Principles

Penetration effect of electronic subshells: Ionisation enthalpy increases as the penetration effect ofthe electron (to be removed) increases. It is known that in the case of multielectron atoms, the electrons in the s -s-orbital have the maximum probability of being found near the nucleus. In a given quantum shell this probability goes on decreasing in the sequence s->p-> d-> f.

This means that in a given shell, the penetration power of different subshells decreases in the order: of s->p-> d-> f-.

Now, if the penetration power of an electronic is greater, it is closer to the nucleus and held more firmly by it.

So it is more difficult to remove such an electron from the atom and consequently, ionisation enthalpy will be high.

Thus for the same shell, the energy needed to knockout an s -s-electron is greater than that required for a p-electron, which in turn will be more than that required to remove a d-electron and so on. In other words, ionisation enthalpy follows the sequence, s>p> d> f.

Effect of half-filled and filled subshells: It is known that half-filled and filled subshells have extra stability associated with them. Therefore, the removal of electrons from such subshells (having extra stability) requires more energy than expected.

Consequently, atoms having half-filled or filled subshells in their valence-shell have higher values of ionisation enthalpies.

Example: Be(ls22s2) has higher ionisation enthalpy than B(ls22s22p1) because ionisation of Be requires the removal of one electron from its filled 2s -orbital in the valence shell.

For similar reasons Mg(ls22s22p63s2) has higher ionisation enthalpy than Al(ls22s22p63s23p1)

N(ls22s22p3) has higher ionisation enthalpy than 0(ls22s22p4) because ionisation of nitrogen requires the removal of one electron from its half-filled 2p -the valence shell. Similarly, the ionisation enthalpy of P(3s23p3) is greater than that of S(3s23p4).

Effect of electronic configuration of the outermost shell:

Atoms, having the outermost electronic configuration ns2npG, are exceptionally stable because of their filled octet.

Removal of an electron from an atom having such a stable electronic configuration requires a large amount of energy.

Consequently, the noble gases He, Ne, Ar, Kr, Xe etc. (with outermost electronic configuration ns2np6) have very high ionisation enthalpy.

Variation of ionisation enthalpy in the periodic table: The periodic trends of the first ionisation energy of the elements are quite striking as seen from the graph.

The graph consists of several maxima and minima. In each period maxima occur at the noble gases which have filled the octet with the electronic configurations (ns2np6).

Element Classification Principles

Due to very high ionisation enthalpies, these elements are almost inert and show extremely low chemical reactivity.

In each period minima occur at the alkali metals which have only one electron in the outermost s -orbital. Due to very low ionisation enthalpies, these elements are highly reactive.

Variation of ionisation enthalpy across a period: For representative elements (s and p -block elements), ionisation enthalpy usually increases with increasing atomic number across a period. This is because as we move from left to right across a period—

The nuclear charge increases regularly, several shells remain the same and the addition of different electrons occurs in the same shell, and atomic size decreases.

As a result of a gradual increase in nuclear charge and a simultaneous decrease in atomic size, the valence electrons are more and more tightly held by the nucleus.

Therefore, more and more energy is needed to remove one valence electron and hence, ionisation enthalpy increases with an increase in atomic number across a period.

In any period, alkali metal has the lowest ionisation enthalpy and inert gas has the highest ionisation enthalpy.

Element Classification Principles

On careful examination of ionisation enthalpy values, some irregularities in the general trend are noticed. Can each period be explained based on different factors governing ionisation enthalpy?

Examples:

1. l1 of Be>I 1of B: Forionisation of boron (ls22s22p1), one electron is to be removed from the singly filled 2p orbital and this requires lesser energy, while for the ionisation of beryllium (ls22s2) one electron is to be removed from the more penetrating filled 2s orbital.

Furthermore, the Removal of an electron from Batom gives B+ a stable electronic configuration with a filled 2s -subshell (ls22s2) and so it requires a smaller amount of energy.

On the other hand removal of an electron from the filled 2s -orbital of Be -atom to give Be+ (1S22S1) requires a greater amount of energy.

Consequently, the first ionisation enthalpy of B is less than that of Be. of N > l1 of O: Electronic configuration of nitrogen (ls22s22p3) in which the outermost 2p -subshell is exactly half-filled is more stable than the electronic configuration of oxygen (ls22s22p4)in which the 2psubshell is neither half-filled nor filled.

Removal of 1 electron from the O -atom gives 0+ with a stable electronic configuration having a half-filled 2p -subshell (ls22s22p3), but this is not so in the case of the N -atom because N+ has the electronic configuration ls22s22p2.

In other words, the removal of an electron from the O -atom gives a cation with a more stable electronic configuration than that obtained by the removal of one electron from the N -atom. Thus, the first ionisation enthalpy of oxygen is less than that of nitrogen.

\(\mathrm{N}\left(1 s^2 2 s^2 2 p^3\right) \stackrel{-e}{\longrightarrow} \mathrm{N}^{+}\left(1 s^2 2 s^2 2 p^2\right)\) \(\mathrm{O}\left(1 s^2 2 s^2 2 p^4\right) \stackrel{-e}{\longrightarrow} \mathrm{O}^{+}\left(1 s^2 2 s^2 2 p^3\right)\)

The very high l1x value of the Exceptionally high value of the first ionisation enthalpy of neon (noble gas) amongst the elements of the 2nd period is due to its stable electronic configuration(ns2np6) ofthe outermost shell.

Variation of ionisation enthalpy down a group: For representative elements, ionisation enthalpy decreases regularly with an increase in atomic number on moving down a group from one element to the other.

Element Classification Principles

Explanation: The regular decrease in ionisation enthalpy (1.£.) may be attributed to the following factors:

On moving down a group, the atomic size increases successively due to the addition of one new electronic shell at each succeeding element.

Thus, the distance of valence shell electrons from the nucleus increases. Consequently, the nuclear attractive force on the valence electrons decreases and this, in turn, decreases the ionisation potential.

There is an increase in the shielding effect on the outermost electrons due to an increase in the number of inner electronic shells. This increased shielding effect tends to decrease the ionisation potential on moving down a group.

On moving down a group, the nuclear charge increases regularly and this increases the force of attraction of the nucleus on the valence electrons; this tends to increase the ionisation potential.

The combined effect ofthe increase in size and the shielding effect outweighs the effect of the increased nuclear charge.

Consequently, the ionisation enthalpies of the elements decrease regularly on going down a group. This is evident from the values of the first ionisation enthalpies of the elements of group-1 (alkali metals) as given in the adjacent table.

Element Classification Principles

Periodic variation of first ionisation enthalpies (eV) of the elements is evident from the following table.

Element Classification Principles

Some important facts about ionisation enthalpy:

1. The ionisation enthalpy of representative elements (s and block elements) increases from left to right across the period.
2. Exceptions are observed for some pairs of elements,
3. \(\text { e.g. } I_1(\mathrm{Be})>I_1(\mathrm{~B}) ; I_1(\mathrm{Mg})>I_1(\mathrm{Al}) ; I_1(\mathrm{~N})>I_1(\mathrm{O})\)
4. In any period, alkali metal has the least ionisation enthalpy.
   Cesium (Cs) has the lowest value of I. All the elements.
5. In each period, inert gas elements show the highest value of first ionisation enthalpy. Helium (He) has the maximum value ofI.E. of all the elements.
6. Among the representative elements, metals have low I.E., while non-metals have high values of I.E.
7. Generally, first ionisation enthalpies of transition elements (d -block elements) increase slowly from left to right in a period. This is partly due to the poor screening effect of d orbitals and partly due to electron-electron repulsive forces.
8. f-block elements also show a small change in their ionisation enthalpies on increasing atomic number.
9. From Pd to Ag, from Cd to In and also from Hg to Tl, there is a sudden decrease in ionisation enthalpy even though the atomic number increases.

Electron-gain enthalpy or electron affinity: energy is released when an electron is added to an isolated gaseous atom to convert it into a negative ion.

This energy is called electron-gain enthalpy. Electron-gain enthalpy of an atom is thus a measure of its tendency to form an anion. It is denoted by AHgg or EA.

Electron-gain enthalpy or electron affinity Definition: Electron-gain enthalpy is defined as the enthalpy change involved when an electron is added to an isolated gaseous atom in its lowest energy state (ground state) to form a gaseous ion carrying a unit negative charge.

\(\begin{aligned}
& \mathrm{X}(\mathrm{g})+e \longrightarrow \mathrm{X}^{-}(g)+\operatorname{Energy}(q) \\
& \text { Gaseous atom Electron Gaseous anion } \\
& \text { or, } \mathrm{X}(g)+e \longrightarrow \mathrm{X}^{-}(g), \quad \Delta H=-q \\
& \text { Gaseous atom Electron Gaseous anion } \\
&
\end{aligned}\)

Explanation: If q is the amount of energy released when an electron is added to the isolated gaseous atom ‘X’ in its ground state to convert to the gaseous ion X-, then the electron-gain enthalpy (electron affinity) of X is given by,AHeg = -q

Element Classification Principles

\(\begin{aligned}
\mathrm{F}(g)+e & \longrightarrow \mathrm{F}^{-}(g)+328 \mathrm{~kJ} \cdot \mathrm{mol}^{-1} \\
\text { or, } \mathrm{F}(g)+e & \longrightarrow \mathrm{F}^{-}(g), \Delta H=-328 \mathrm{~kJ} \cdot \mathrm{mol}^{-1} \\
\mathrm{Be}(g)+e & \longrightarrow \mathrm{Be}^{-}(g)-66 \mathrm{~kJ} \cdot \mathrm{mol}^{-1} \\
\text { or, } \mathrm{Be}(g)+e & \longrightarrow \mathrm{Be}^{-}(\mathrm{g}), \Delta H=66 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}
\end{aligned}\)

When an F -atom combines with an electron to form an F- ion, energy is released. So enthalpy change has a negative value. Thus electron-gain enthalpy of fluorine is given by AHeg = be supplied to convert a Be -atom to a Be ion.

So enthalpy change has a positive value. Thus electron-gain enthalpy of beryllium is givenby, by AHeg = +66 kj. mol-1.

Points to remember: QElectron-gain enthalpy of an atom is a measure of its tendency to form an anion.

Electron-gain enthalpy has usually a negative value, but it may also have a positive value, especially for noble gases.

The numerical value of the ionisation enthalpy of an I negative ion (X-) is equal to the electron-gain enthalpy of the neutral atom (X).

However, energy is usually evolved during the process of electron acceptance but energy is usually absorbed during the expulsion of electrons from an atom. So electrongain enthalpy of X and ionisation enthalpy of X- have opposite signs.

Electron-gain enthalpy with a -ve sign indicates that energy is released when the neutral atom accepts an electron (only numerical values are taken for comparison when periodicity or otherproperties are considered).

The high value of electron-gain enthalpy indicates that an added electron is strongly bound, while a low value indicates that a new electron is weakly bound to the atom.

Units: Electron-gain enthalpies are expressed in kilojoule per mole (kj. mol-1) or in electronvolt (eV) per atom.

Successive electron-gain enthalpies: Like the second and higher ionisation enthalpies, second and higher electrongain enthalpies are also possible. However, the addition of a second electron to a negative ion (X-) is opposed by the electrostatic force of repulsion.

Element Classification Principles

So energy is to be supplied for the addition ofthe second electron. Thus, the second electron-gain enthalpy of an element is positive, and so is the third, and so on.

For example, when an electron is added to an oxygen atom to form an O-ion, energy is released. However, when another electron is added to the O- ion to form the O2- ion, energy is absorbed.

First electron-gain enthalpy:

\(\begin{array}{r}
\mathrm{O}(g)+e \longrightarrow \mathrm{O}^{-}(g), \quad \Delta H_{e g}=-141 \mathrm{~kJ} \cdot \mathrm{mol}^{-1} \\
\text { Energy released }
\end{array}\)

Second electron-gain enthalpy:

\(\begin{array}{r}
\mathrm{O}^{-}(\mathrm{g})+e \longrightarrow \mathrm{O}^{2-}(\mathrm{g}), \quad \Delta H_{e g}=\underset{ }{780 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}} \\
\text { Energy absorbed }
\end{array}\)

Similarly, the first and second electron-gain enthalpies of sulphur are -200 kj mol-1 and +590 kj mol-1 respectively.

Factors governing electron-gain enthalpy: in general, the factors favouring the ionisation process disfavour the electron-gain process.

Effective nuclear charge: As effective nuclear charge (Z+) increases, the force of attraction between the nucleus and the incoming electron increases and hence, the numerical value of electron gain enthalpy increases.

Thus, the numerical magnitude ofelectrongain enthalpyof carbon (Z = 6, IE = -122 kj.mol-1 ) is greater than that ofboron(Z = 5, IE = -27 kj-mol-1).

Atomic size: As the size of the atom increases, the distance between the nucleus and the outermost shell (which receives the incoming electron) increases.

If the effective nuclear charge (Z+) per electron at the periphery is more or less the same for different species (e.g., in a group of representative elements), the force of attraction towards the nucleus of the electrons at the periphery is less for the larger species.

Consequently, the numerical magnitude of electron-gain enthalpy decreases as the atomic size increases. Thus for representative elements, the numerical value of electron-gain enthalpy decreases as the atomic number increases on moving down a group.

Nature of the orbital into which new electron gets accommodation: Orbitals which can penetrate more towards the nucleus are more suitable to accommodate the incoming electron.

Thus the ease of accommodation of Incoming eLectron follows the order ns> np> nd > nf, as the penetration effect of different orbitals follows this sequence. So the numerical magnitude of electron-gain enthalpy decreases in the sequence ns > np> nd> nf.

Nature of the outer electronic configuration: If the atoms of an element bear extra stability due to either the half-filled or full-filled subshell in their outermost level, then such atoms are very much reluctant to accept the incoming electron.

Element Classification Principles

On the other hand, if the newly added electron creates a half-filled or full-filled subshell, then the process is favoured.

Thus some ofthe elements of GrIIA(ns2), Gr-IIB[(n- l)d10ns2], Group-VA (ns2np3) and all the noble gas elements (ns2np6) have positive electron-gain enthalpies (AHeg).

On the other hand, elements of Gr-VIIA have very high electron-gain enthalpies with negative signs, because they can attain inert gas configuration accepting one electron.

Variation of electron-gain enthalpy across a period: On moving from left to right in a period, effective nuclear charge, Z nuclear charge (Z)- shielding effect of the inner shells) increases and size decreases with the increase in atomic number.

Both these factors tend to increase the nuclear attraction experienced by the incoming electron and hence, the numerical value of electron-gain enthalpy, in general, increasesin a period from left to right. It reaches a maximum value at Gr-VIIA (halogens).

Due to some characteristic electronic configuration, the general trend is violated in some cases {e.g., Be and N in the 2nd period; Mg and P in the third period).

Variation of electron-gain enthalpy down a group: For the representative elements, on moving down a group, the effective nuclear charge Z per electron at the periphery (outermost shell) remains more or less constant because the effect of increased nuclear charge is counterbalanced by the shielding effect of the inner electronic shells.

However, the atomic size gradually increases due to the addition of new quantum levels. Thus the nuclear attractive force experienced by any added electron (incoming electron) decreases as the atomic number increases, and consequently, the numerical value of electron-gain enthalpy decreases down a group.

Element Classification Principles

Some typical trends in electron-gain enthalpy & their explatition:

Experiences significant electron-electron repulsion from the other electrons present in the small-sized 2p -subshell.

On the other hand, in a chlorine atom, the added electron goes to the large-sized 3p -subshell. Hence, it experiences less electron-electron repulsion.

Another factor that favours the uptake of electrons by the Cl -atom, is that there is the possibility of the delocalisation of the increased electron density in the vacant 3d -orbital of Cl-atom.

This mechanism is not operative in F-atom because of the absence of d -orbital in the second shell. Consequently, the numerical value of electron-gain enthalpy of Cl is greater than that of F.

Electron-gain enthalpy is greater than that of O: The reason for this anomaly is similar to that of Cl versus F.

The added electron experiences considerable electron-electron repulsion from the other electrons present in the small-sized 2p -subshell of O.

This repulsion outweighs the increased attractive force of the nucleus acting on the added electron. In the S-atom, the added electron goes to the large-sized 3p -subshell.

Hence, it experiences less electron-electron repulsion. Another factor that favours the uptake of electrons by S -S-atoms is that there is a possibility ofthe delocalisation of the increased electron density in the vacant-3d -orbital of S-atom.

This mechanism is not operative in the O -atom because of the absence of any d orbital in the 2nd shell.

Element Classification Principles

Consequently, the numerical value of electron-gain enthalpy S is greater than that of O.

Gr-llA metals (e.g., Be, Mg etc.) have lower electron-gain enthalpies than Gr-IA metals (e.g., Li, Na, K efc: Gr- A metals have outer electronic configuration ns2. Hence, the addition of an extra electron brings the configuration ns2np1.

This process is disfavoured in two ways: The addition of a new electron destroys the full-filled subshell structure and 0 accommodation of the new electron occurs in the p -orbital which is less penetrating.

For alkali metals (ns1), however, accommodation of the new electron occurs in the ns -subshell giving rise to a filled ns2 configuration.

Thus, the electron-gaining process is more favourable for Gr-IA elements compared to Gr-IIA elements. Be and Mg ofGr-IIA have positive electron-gain enthalpy.

Halogens have the highest electron-gain enthalpies: This is because of the valence-shell electronic configuration of the halogensis ns2np5 and so theyrequire only one more electron to acquire the stable inert gas-like electronic configuration (ns2np&).

As a result, halogen atoms have a strong tendency to accept an additional electron. Consequently, the numerical values of their electron-gain enthalpies are very high.

Phosphorous (3s23pi3) has relatively low electron-gain enthalpy: This is because the P -atom has a relatively stable outer electronic configuration with exactly half-filled p -orbital.

Hence, it is reluctant to accept an extra electron. Consequently, it has low electron-gain enthalpy.

The electron-gain enthalpy of noble gas is high and positive:

The atoms of noble gases have a very stable outermost electronic configuration with filled subshells (ns2np6).

Any additional electron would have to be placed in an orbital ofthe next higher energy level.

The shielding effect of the inner electrons and the large distance from the nucleus makes the addition of an electron highly unfavourable. So, noble. high and adjaisitive values ofelectron-gain enthalpy.

Electronegativity

This topic will be discussed elaborately in the chapter ‘Chemical Bonding’ Here we will briefly discuss only the definition of electronegativity and its periodicity.

Electronegativity Definition: Electronegativity is defined as the tendency of an atom to attract the shared pair of electrons towards its nucleus when the atom is covalently bonded in a molecule.

Consequently, the more electronegative atom withdraws the bonding electron cloud more towards its nucleus giving rise to an accumulation of negative charge on it.

The electronegativity of an element is not its inherent property. It depends on its surrounding environment in the molecule in which the electronegativity of the element is being considered.

Element Classification Principles

Thus the electronegativity of S is different in different compounds such as H2S, S02, SFg etc.

Further, it is to be noted that unlike ionisation enthalpy and electron-gain enthalpy, electronegativity is not a measurable quantity.

Factors controlling electronegativity: Electronegativity of the elements depend on—

The atomic number of an element, i.e., the total quantity of positive charge in the nucleus of an atom,

Size of atom Or Atomicradius, number of electronicshes in an atom, oxidation state ofthe atom, state of hybridisation of the atom in the molecule under consideration. Note the electronegativity of elements.

Variation of electronegativity across a period: As Cs 0.7 At 2.2 Ford -block element, on moving down from 3d- to from left to right along a period, nuclear charge Increases while the atomic radius or size decreases.

Hence the attraction between the outer (or valence) electrons and the nucleus increases with increasing atomic number.

Consequently, the electronegativity of the atom increases from left to right across a period. Thus alkali metals of group-1 on the extreme left have the lowest electronegativity whereas, the halogensin group-17 on the right have the highest values of electronegativity in their respective periods.

This is evident from the electronegativity values ofthe elements of the second and third periods.

Variation of electronegativity down a group: As we move down a group, atomic size (radius) as well as the magnitude of nuclear charge increases but the effect of increased nuclear charge on the outer electrons is mostly counterbalanced by the screening effect of a larger number of inner electronic shells.

Hence the nuclear pull on the outer (valence) electrons decreases due to the increase of atomic size on moving down a group.

Consequently, the electronegativity of an atom decreases from top to bottom in a group. This is evident from the electronegativity values of the alkali metals of group-1 (IA) and halogen elements of group-17(VIIA)

Element Classification Principles

Ford -block element, on moving down from 3d- to 4d -series, electronegativity falls slightly but on reaching 5d series, electronegativity increases due to lanthanide contraction.

Relationship between electronegativity and non-metallic (or metallic) character of elements: Non-metallic elements have a strong tendency to gain electrons. So, electronegativity is directly related to the metallic character elements.

It can be further extended to say that electronegativity is inversely related to the metallic character of elements.

Thus the increase in electronegativity along a period is accompanied by an increase in non-metallic character (or decrease in metallic character) of elements.

Likewise, the decrease in electronegativity down a group is accompanied by a decrease in the non-metallic character (or increase in metallic character) of elements.

All these periodic trends are summarised in the given figure: (Direction arrows indicate increasing trend of the respective properties)

Element Classification Principles

Periodicity in density, melting point and boiling point

Different elements exhibit periodicity in various physical properties such as density, melting point, boiling point etc.

Periodic variation of density: On moving along a period from left to right, the density of representative elements first increases, reaches the maximum value at group-IIIA orIVA and then decreases with an increase in atomic number.

This trend is observed particularly in the case of representative elements. In a group, density generally increases from top to bottom with a rise in atomic number.

Periodic variation of melting and boiling points: On moving along a period from left to right, the melting and boiling points of representative elements first increase, reach maximum values at group IVA and thereafter go on decreasing. Minimum melting and boiling points are shown by the noble gas in the respective period.

Periodicity In Properties Of Oxides And Hydrides

Nature of oxides of the elements: On moving from left to right across a period, the basic properties and electrovalent character of oxides of elements decrease while their acidic property and covalent character gradually increase.

On the other hand, in a group, the basic property of oxides increases from top to bottom.

The nature of the oxides of transition metals depends on the oxidation state of the metals. With the increase in the oxidation state of transition metals, the acidic properties of their oxides increase.

Element Classification Principles

Example: CrO is a basic oxide, Cr203 is amphoteric and Cr03 I -a is an acidic oxide. In the case of oxides of the elements of the second period, it is observed that lithium oxide (Li20) is strongly basic. It reacts with water to produce a strong base namely lithium hydroxide (LiOH)

\(\mathrm{Li}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons 2 \mathrm{Li}^{+}+2 \mathrm{OH}^{-} \rightleftharpoons 2 \mathrm{LiOH}\)

BeO is an amphoteric oxide. It reacts with both acids and bases to form salt and water.

\(\text { Basic property: } \mathrm{BeO}+2 \mathrm{HCl} \rightarrow \mathrm{BeCl}_2+\mathrm{H}_2 \mathrm{O}\) \(\text { Acidic property: } \mathrm{BeO}+2 \mathrm{NaOH} \rightarrow \mathrm{Na}_2 \mathrm{BeO}_2+\mathrm{H}_2 \mathrm{O}\)

B203 is an acidic oxide though it possesses a slight basic property. It reacts with water to form orthoboric acid and with alkali to yield borate salt.

CO2 is an acidic oxide and it reacts with alkali to produce carbonate salt. N2O is an acidic oxide. It reacts with alkali to produce salt and water.

⇒ \(\begin{gathered}
\mathrm{B}_2 \mathrm{O}_3+3 \mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{H}_3 \mathrm{BO}_3 ; \mathrm{CO}_2+2 \mathrm{NaOH} \rightarrow \mathrm{Na}_2 \mathrm{CO}_3+\mathrm{H}_2 \mathrm{O} \\
\mathrm{N}_2 \mathrm{O}_5+2 \mathrm{NaOH} \rightarrow 2 \mathrm{NaNO}_3+\mathrm{H}_2 \mathrm{O}
\end{gathered}\)

Nature of hydrides of elements: As we move from left to right across a particular period, the tendency of the elements to form hydrides and the thermal stability, covalent character, acidic property, and volatility of the hydrides increases while the reducing property progressively decreases.

The hydrides of the strongly electropositive metals towards the left of a period are ionic having high melting points. On ionisation, they produce hydride ions (H-). Again, hydrides of non-metals towards the right of the period are covalent and have low melting and boiling points.

On moving down a group, the tendency of the elements to form hydrides decreases. The stability of the hydrides also decreases in the same sequence. Variation of other properties along any group depends on the group to which the hydride-forming element belongs.

Hydrides of alkali metals in group IA and alkaline earth metals in group 2 are salt-like polar or ionic.

These compounds are composed of positive metallic ions and negative hydride ions (H¯). On electrolysis of these ions and negative hydride ions (H-).

On electrolysis of these discharged at the cathode and anions (H- ions) at the anode; e.g., electrolysis of molten sodium hydride leads to the formation of metallic sodium at the cathode and H2 gas at the anode.

Element Classification Principles

Hydrides of the elements of groups IVA to VIIA are covalent and nonpolar; e.g., CH4, SiH4, PH3 etc., are gaseous and insoluble in water. NH3 and H2S are gaseous but soluble in water. An aqueous solution of NH3 is feebly basic and the aqueous solution of H2S is weakly acidic.

On the other hand, HC1, HBr and HI, despite being covalent compounds more soluble in water and dilute aqueous solutions, dissociate almost completely.

\(\mathrm{HX}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{X}^{-} \quad[\text { where } \mathrm{X}=\mathrm{Cl}, \mathrm{Br}, \mathrm{I}]\)

Aqueous solution of HX is strongly acidic. In electrolysis of their aqueous solutions hydrogen ions (H+) are liberated at the cathode and halide ions (X-) at the anode e.g., when an aqueous solution of hydrochloric acid is electrolysed, H2 gas is evolved at the cathode and Cl2 gas at the anode.

The trend of variation in properties of different elements in the periodic table from left to right across a period and from top to bottom in a group is shown in the given table-

Element Classification Principles

Diagonal Relationship Definition: Some elements of certain groups in the second period show similarity in properties with the diagonally opposite elements of the third period, and such similarity in properties is referred to as a diagonal relationship.

Reason for diagonal relationship: The Reason for diagonal relationship is due to opposing trends in periodic properties along a period from left to right and down the group.

For example, the atomic and ionic radius of elements decrease a periodic but increase down a group Ionisation enthalpy, electron gain enthalpy and electron negativity increase along a period but decrease down a group.

On moving diagonally, two opposite trends mutually cancel, so the elements of the period- 2 and 3 listed above are related to each other diagonally and they show similar chemical properties. Thus Li resembles Mg; Be resembles A1; and B resembles Si.

The diagonal relationship is also explained based on polarising power ofcation. On moving along the period from left to right, the charge on the cation increases, while ionic size decreases and hence polarising power increases.

Again on moving down a group, the charge on the cation remains the same, while ionic size increases. Hence polarising power decreases. So on moving diagonally, polarising power remains more or less the same and the elements exhibit similar properties.

Absence of diagonal relationship in case of long periods: Because of the intervening d – and /-series, the diagonal relationship does not hold well for long-period elements (4th, 5th… period elements).

Because the group trend of many properties in the transition series is opposite compared to that in the representative elements. However, the trend along the periods remains the same for both the representative and d -d-block elements.

Position Of Hydrogen And Inert Gases In The Periodic Table

The position of hydrogen in the periodic table is controversial. Given its chemical analogy with both the elements of group and that of group- VIIA, it can either be placed in group 2A or group VIIA. Resemblances ofhydrogen with the element.

Arguments in favour of placing hydrogen in group IA

Valency: The electronic configuration ofhydrogen is Is1 and the general electronic configuration of the elements of group-IA is ns1, i.e., like the elements of group-IA, hydrogen has only one valence electron and its valency is 1.

Element Classification Principles

Electropositive character: Like all group-IA elements, hydrogen tends to form cations by losing one electron.

\(\mathrm{Na}-e \longrightarrow \mathrm{Na}^{+} ; \mathrm{K}-e \longrightarrow \mathrm{K}^{+} ; \mathrm{H}-e \longrightarrow \mathrm{H}^{+}\)

Like elements of group-IA, hydrogen reacts with electronegative elements such as chlorine, oxygen and sulphur to produce similar type of compounds, e.g

HC1 , H20 , H2S ; NaCI , Na20 , Na2

Electrolysis of chloride compounds: Electrolysis of molten NaCl results in the deposition of metallic sodium at the cathode. Likewise, when an aqueous solution of HCl is electrolysed, H2 gas is liberated at the cathode.

\(\mathrm{NaCl} \rightleftharpoons \mathrm{Na}^{+}+\mathrm{Cl}^{-}\)

1. Cathode : Na+ + e→Na
2. Anode : Cl-e →Cl ; CI + C1→C12T
3. HCl H+ + Cl Cathode : H+ + e →H ; H + H→H2?
4. Anode : Cl–e →C1 ; C1 + C1→C12T

Reducing property: Like the elements of Gr-IA, hydrogen loses electrons easily and exhibits a reducing property.

Formation of alloy: Hydrogen dissolves in metals like Pd, Pt etc., by adsorption. This occlusion of hydrogen is comparable to the formation of alloys by elements of group IA.

Mutual displacement: Hydrogen atom(s) of hydrochloric, sulphuric or nitric acids can be displaced by the same number of atoms of group-IA elements. Again, atoms of the group-IA elements can be replaced by hydrogen atoms from the salts produced.

Formation of stable oxide: Oxides of group-IA elements are highly stable (e.g., Na20, K20 etc.). Similarly, oxide of hydrogen (H20) is also highly stable.

Formation of peroxide: Like the elements of group-IA, hydrogen also forms peroxide (H202). The analogous peroxides of group-IA elements are Na202, K202 etc.

Electron affinity: Hydrogen and the group-IA elements have comparable values of electron affinity.

In light of the above similarities between the elements of group IA and hydrogen, hydrogen can be placed along with the elements of group IA. However, the placement of hydrogen in group IA leaves six vacant places in between H and He in the first period.

Arguments in favour of placing hydrogen in group-VIIA

Electronic configuration: The electronic configuration of hydrogen is Is1 and the electronic configuration of the outermost orbit of the elements of group-VIIA is ns2np5, i.e., the outermost orbit of both hydrogen and elements of group-VILA has 1 electron less than the electronic configurations of the nearest inert gas. So, their valency 1.

Non-metallic character and atomicity: hike the dements of group-VIIA, hydrogen is also it non-metal and forms a diatomic molecule.

Formation of anion: Like the elements of group VIIA, the hydrogen atom also tends to attain the electronic configuration of Its nearest Inert gas (Me) by accepting I electron and forming anion (H” ); e.g.,

\(\mathrm{H}\left(1 s^1\right) \stackrel{+e}{\longrightarrow} \mathrm{H}^{-}\left(1 s^2\right) ; \mathrm{X}\left(n s^2 n p^5\right) \stackrel{+e}{\longrightarrow} \mathrm{X}-\left(n s^2 n p^6\right)\)

Both VIIA elements and hydrogen form electrovalent halide and hydride respectively. During the electrolysis of metallic hydrides, like halogens, hydrogen is also liberated at the anode.

Formation of covalent compounds: Just like elements of group VIIA, hydrogen reacts with different non-metals to produce covalent compounds with analogous formulas.

Compoundsinvolving11: CH4, NH3, H20, HF, SiH4. CompoundsinvolvingCl: CC14, NC13, C120, CIF, SiCl4

Substitution by halogens: H-atoms of the hydrocarbons can be substituted by Gr-VIIA elements, partially or completely.

Ionisation potential: Just like the elements of group VIIA, the ionisation, potential of hydrogen is very high but the ionisation potential of alkali metals is quite low. The following table of ionisation potentials shows the comparative picture of ionisation potential quite explicitly.

Maintenance of continuity in the periodic table: If H is placed in group YIIA, no vacant space remains between H and H. So, continuity in the periodic table is not disturbed.

From the above discussion, it is apparent that hydrogen is a unique element characterised by peculiar and distinctive unique element characterised by peculiar and distinctive position to it in the periodic table. It is reasonable to set aside a separate position for hydrogen in the periodic table. In the modern periodic table, hydrogen has been J given a completely separate place, at the top ofthe table.

Position of Inert Gases In The Periodic Table

Inert gas elements have very stable electronic configurations of their outermost or valence shell (ns2 for He and ns2np6 for others).

For this reason, these elements show little or no tendency to lose or gain electrons to form ions to give electrovalent bonds or do not share electrons with other elements to form covalent bonds. So the combining capacity or valency of these elements is zero.

Thus they are placed in group ‘zero’ ofthe periodic table. This group forms a bridge between the most electropositive alkali metal elements of group-IA and the most electronegative halogen elements of group-52A.

WBCHSE Class 11 Atomic Structure Fundamentals Discovery Of Particles

Foundations of Atomic Science Cathode rays: Discovery of electron 

William Crookes, in 1878, studied the conduction of electricity through gases. A discharge tube was filled with a gas at very low pressure (0.01 mm Hg) and the electrodes were connected to a source of high voltage \(\approx 10^4 \mathrm{~V}\). Foundations of Atomic Science

It was observed that the glass wall behind the anode began to glow with a faint greenish light called fluorescence.

Further investigations revealed that this fluorescence was due to the bombardment of the glass wall by certain invisible rays which were emitted from the cathode surface and moved towards the anode with tremendous speed.

As the rays originated from the cathode, those were called the cathode ray.

Nature of cathode rays: J.J Thomson (in 1897) and others characterized these rays based on different experimental findings.

1. Cathode rays are emitted perpendicularly from the cathode surface and travel towards the anode.
2. They cast a sharp shadow on any opaque object placed in their path. So, like ordinary light, cathode rays also travel in straight lines.
3. When a light paddle wheel (made of mica) is placed in their path, the wheel begins to rotate. This indicates that cathode rays are composed of material particles and possess momentum.
4. As cathode rays possess momentum, they can penetrate thin foil metals like aluminum.

1. Cathode rays are deflected by an electric field (towards the positive plate) as well as by a magnetic field, suggesting that cathode rays consist of negatively charged particles.
2. When these rays strike a metal foil, the foil gets heated indicating that cathode rays produce a heating effect.
3. Cathode rays ionize the gas through which they pass.
4. Like ordinary light, cathode rays affect photographic plates. This is called fogging.
5. Cathode rays produce fluorescence on the glass walls of a tube or a screen coated with zinc sulfide 1 ‘(ZnS) or barium platinocyanide Ba[Pt(CN)6].
6. Cathode rays produce X-rays when they strike against the surface of hard metals like tungsten, molybdenum, etc.
7. The characteristics of cathode rays are independent of the material of the cathode nature of the gas used in the discharge tube.
8. Considering the various properties of cathode rays, J. J. Thomson concluded that cathode rays are made of material particles, cathode rays carry a negative charge.
9. He named these negatively charged particles as negatron. Later, these particles were named electrons by G. J. Stoney (in 1874).

J. J. Thomson (1897) used discharge tubes fitted with electrodes made of different metals and filled different gases in the tube. Every time he found that the ratio of charge to mass of electrons (e/m) was the same.

⇒ \(\begin{aligned}
e / m \text { of electron } & =\frac{\text { charge of cathode ray particle }}{\text { mass of cathode ray particle }} \\
& =1.76 \times 10^8 \mathrm{C} \cdot \mathrm{g}^{-1}=1.76 \times 10^{11} \mathrm{C} \cdot \mathrm{kg}^{-1}
\end{aligned}\)

R. A. Millikan (1917) with the help of his oil drop experiment, determined the charge of an electron. Charge ofan electron (e) = -1.602 x 10^–19 C (or, -4.8 x 10^–1°esu)

No other fundamental particle is known to contain a charge lower than this. This is the minimum measurable quantity of negative charge.

The quantity of electrical charge carried by all negatively charged panicles is an integral multiple of this charge.

Hence, electronic charge is considered to be die fundamental unit of electricity and is called one unit. The mass of an electron can be calculated from the values of e and e/m.

⇒ \(\begin{array}{r}
\text { Mass of an electron }(m)=\frac{e}{e / m}=\frac{1.602 \times 10^{-19} \mathrm{C}}{1.76 \times 10^8 \mathrm{C} \cdot \mathrm{g}^{-1}} \\
=9.11 \times 10^{-28} \mathrm{~g}=9.11 \times 10^{-31} \mathrm{~kg}=0.000548 \mathrm{amu} \\
{\left[1 \mathrm{u}=1.66 \times 10^{-24} \mathrm{~g}\right]}
\end{array}\)

Mass of an electron = \(\frac{1}{1837}\) x mass of a hydrogen atom Thus, a hydrogen atom is 1837 times heavier than an electron. The mass of an electron being very small may be considered as negligible for all practical involving chemical calculations.

Therefore, an electron may be defined as a subatomic particle having a unit negative charge (1.602 x 10^-9C) & negligible mass (9.11 x 10^-28g).

The radius of an electron =2.8xl0-13cm

Electrons are universal constituents of matter: The elm ratio of negatively charged particles constituting the cathode rays was found to be the same irrespective of the nature of the cathode and the nature of the gas used in the discharge tube, thereby showing that the electrons are basic constituents of all atoms.

Atomic Structure Fundamentals

Other experiments showing the existence of electrons:

The following experiments show that the same charge-to-mass ratio exists for the electrons emitted—

1. Spontaneously from radioactive substances in the form of p-rays.
2. when ultraviolet rays are incident on the surface of active metals (e.g., Na, K, etc.).
3. When certain metal filaments are heated to a very high temperature.
4. When any form of matter is exposed to X-rays.

Origin of cathode rays in discharge tube:

1. On applying high voltage, electrons are first emitted from the surface of the cathode which travel in straight lines with high speed.
2. During their passage through the gas inside the tube, more electrons are ejected due to the bombardment of the gas molecules by the high-speed electrons.
3. On increasing the voltage in the discharge tube, the speed of the electrons increases, and the electron density in the cathode ray increases.

WBCHSE Class 11 Atomic Structure Fundamentals

Applications of cathode ray tube:

In picture tube of televisions: The picture tube of a television is a cathode ray tube. Due to fluorescence, a picture is formed on the television screen when an electron beam strikes the screen coated with a fluorescent or phosphorescent material.

In fluorescent tubes: These types of tubes are filled with gases like argon, nitrogen, etc. along with a small amount of mercury vapor under very low pressure. They are cathode ray tubes with their inner walls coated with a suitable fluorescent material.

On passing electric current, electric discharge occurs inside the tube. As a result, electrons from the cathode are transferred to the higher energy state due to collision with the atoms and molecules of the gases or the mercury vapor.

On their return to the ground state photons are emitted in the form of UV rays. These rays hit the inner walls of the tube and produce visible light.

Anode rays: Discovery of proton

1. Since negatively charged electrons are the essential constituents of all atoms and the atom as a whole is electrically neutral, it was thought that some positively charged particles must also be present in the atom.
2. Goldstein, in 1886, performed the discharge tube experiment using a perforated cathode. On passing electric discharge at low pressure, he observed that some luminous rays were emitted from the side of the anode which passed through the holes in the cathode and produced fluorescence on the glass wall coated with zinc sulfide.
3. These rays were originally called canal rays as they passed through the holes in the cathode.
4. As they travel from the side of the anode towards the cathode, these rays are also called anode rays.
5. These were named positive rays (since they were found to carry a positive charge) by J. J. Thomson (1907).

Atomic Structure Fundamentals

Characteristics of anode rays:

1. Anode rays travel in straight lines but their speed is much less than that ofthe cathode rays.
2. They consist of material particles.
3. They are positively charged as indicated by the direction of their deflection in the electric and magnetic fields.
4. From the extent of deflection in the electric field, it was proved that the particles constituting the anode rays arc are much heavier than electrons.
5. The E/M value of the particles in the anode rays is much smaller than that of the cathode ray particles.
6. Furthermore, the e/m value of the particles depends on the nature ofthe gas taken in the discharge tube.
7. The E/M value of anode ray particles is maximum when hydrogen gas (the lightest element) is used in the discharge tube.
8. The mass of the particle with this maximum e/m value is almost the same as that of an H-atom and its charge is equal to that of an electron but opposite in sign.
9. It may therefore be concluded that such anode ray particles with maximum e/m value are none other than H-atoms devoid of electrons. These were called protons by Rutherford (1911).

Anode rays produced using H₂ gas in the discharge tube consist of positively charged particles: H+ [highest e/m ], D+, H+, HD+, and D+ [lowest e/m].

WBCHSE Class 11 Atomic Structure Fundamentals

Origin of anode rays:

1. On applying high voltage between the electrodes in the discharge tube, cathode ray particles (i.e., electrons) move at a high speed toward the anode.
2. In the course of their motion, they collide with the gas molecules or atoms and knock out one or more electrons to produce positively charged ions, thereby constituting anode rays.

⇒ \(\text { A (neutral gaseous atom) } \stackrel{\text { ionised }}{\longrightarrow} \mathrm{A}^{+}+e\)

1. Thus, the anode rays are not emitted from the anode but produced from the gaseous substance present in the discharge tube.
2. So it is clear that the e/m ratio of the ray particles depends on the gaseous substance in the discharge tube. For example, the use of hydrogen to the formation of H+ ions which constitute the orhunode rays.

⇒ \(\mathbf{H} \text { (atom) }-\boldsymbol{e} \stackrel{+}{\longrightarrow} \mathbf{H}^{+} \text {(proton) }\)

E/m of proton = +9.58 x 10⁴C.g^–1

Charge of proton = + 1.602 X 10^-19 C (Or, +4.8 X 10^–10esu)

Mass of proton (m)

⇒ \(=\frac{\text { charge of a proton }}{c / m \text { of a proton }}=\frac{1.602 \times 10^{-19}}{9.58 \times 10^4}=1.6725 \times 10^{-24} \mathrm{~g}\)

This mass is nearly the same as that of an H-atom. A proton Is 1836 times heavier than an electron. So, a proton carries 1 unit of +ve charge and it is 1 836 times heavier than an electron.

Radius of a proton \(\approx 1.2 \times 10^{-13} \mathrm{~cm}\)

Atomic Structure Fundamentals

Proton is a fundamental constituent of all atoms: Taking different gases in the discharge tube experiment, it was shown that the mass of anode ray particles is minimal when hydrogen is used as the gaseous substance.

Masses of other anode ray particles produced in different experiments using different gases are always integral multiples of the mass of a proton. Thus a proton, like an electron, is also a fundamental constituent of all atoms.

Apart from the electrical discharge in gases under low pressure, protons are also emitted in certain nuclear reactions e.g., the bombardment of aluminum metal with a particle \(\left({ }_2^4 \mathrm{He}\right)\) or bombardment of nitrogen gas with neutron \(\left({ }_0^1 n\right)\)

⇒ \({ }_{13}^{27} \mathrm{Al}+{ }_2^4 \mathrm{He} \rightarrow{ }_{14}^{30} \mathrm{Si}+{ }_1^1 \mathrm{H} ; \quad{ }_7^{14} \mathrm{~N}+{ }_0^1 n \rightarrow{ }_6^{14} \mathrm{C}+{ }_1^1 \mathrm{H}\)

Differences Between Cathode And Anode Rays

Radioactivity: After the discovery of electrons and protons it is well established that the atoms are divisible into sub-atomic particles.

This was further supported by the phenomenon of radioactivity, discovered by Becquerel in 1896.

The phenomenon of spontaneous emission of active radiations by certain elements like uranium, radium, etc.

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

WBCHSE Class 11 Atomic Structure Fundamentals

Is called radioactivity, and the elements emitting such radiation are called radioactive elements.

On placing a sample of uranium mineral in a cavity made in a block of lead and allowing the emitted rays to pass through strong electric or magnetic fields, the radiation is resolved in three directions.

1. The rays which are deflected slightly towards the negative plate and hence carry + ve charge are called rays.
2. The particles present in a -rays are called particles, each particle carries 2 units +ve charge and has a mass of 4u.
3. So these are helium atoms with two units +ve charge and are represented as 2He. The rays that are deflected towards the positive plate to a larger extent must carry a -ve charge.
4. These are called p-rays. The particles present in p -rays are called P -particles. These particles have the same charge and mass as that of the electrons and are represented as Je.
5. The rays which remain undeflected are called y-rays. These are purely electromagnetic radiations.

Discovery Of Neutron

1. According to the atomic mass scale, a proton has a mass of one unit while an electron has a negligible mass.
2. If an atom comprises only electrons and protons then the mass of an atom will be almost equal to the sum of the masses of the protons present in it.
3. In practice, it is found that except for ordinary hydrogen, all other atoms have masses much greater than the sum of the masses of the protons contained by diem.
4. This led the scientists to search for a neutral particle having considerable mass. Rutherford, in 1920, predicted the presence of a fundamental particle within an atom, having no charge but one unit mass. This particle was termed a neutron.
5. James Chadwick (a student of Rutherford), in 1932, performed some scattering experiments in which he bombarded beryllium metal with fast-moving a -particles emitted from radioactive polonium.
6. He observed that new types of particle were emitted which was not deflected by the electric or magnetic field. i.e., those were neutral.
7. The mass ofsuch a particle was found to be nearly equal to that of a proton or a hydrogen atom.
8. These neutral particles having a unit mass must be the same particle i.e., neutron as predicted by Rutherford. Being neutral, neutrons are more penetrating than electrons or protons.

⇒ \({ }_4^9 \mathrm{Be}+{ }_2^4 \mathrm{He} \longrightarrow{ }_6^{12} \mathrm{C}+{ }_0^1 n\)
⇒ \(\text { Beryllium atom } \quad \alpha \text {-particle } \quad \text { Carbon atom Neutron }\)

WBCHSE Class 11 Atomic Structure Fundamentals

Mass of neutron = 1.675 x 10^-24 g

⇒ \(\approx\)mass of a proton

= 1837 x mass ofan electron

e/m of neutron = [because neutron has no charge]

Atoms of all elements except hydrogen constitute three fundamental particles—electron, proton, and neutron.

In each atom, the number of protons is equal to the number of electrons because an atom as a whole is electrically neutral. Ordinary hydrogen contains no neutron, it only contains one proton and one electron.

Subatomic particles other than an electron, proton, and neutron, are also known e.g., positron \(\left({ }_{+1}^0 e\right),\); 71 -meson, neutrino (v), photon, etc.

 

 

Structure Of Atom Numerical Examples

Question 1. An atom of an element contains 2 electrons In the first shell (n — 1 ), 8 electrons in the second shell (n = 2) and 5 electrons in the third shell (n = 3).

There are 16 neutrons in the nucleus of the atom. From these data, find—

1. The atomic no. of the element,
2. the no. of s and -electrons in the atom, mass no. of the element.

Answer: Atomic number = number of protons = number of electrons =2+8 + 5 = 15

\(\begin{array}{|c|c|c|c|}
\hline \text { Shell No. } & \begin{array}{c}
\text { Total no. of } \\
\text { electrons }
\end{array} & \begin{array}{c}
\text { No. of } \\
s \text {-electrons }
\end{array} & \begin{array}{c}
\text { No. of } \\
p \text {-electrons }
\end{array} \\
\hline 1 & 2 & 2 & 0 \\
\hline 2 & 8 & 2 & (8-2)=6 \\
\hline 3 & 5 & 2 & (5-2)=3 \\
\hline
\end{array}\) Total number of s- electron – 2 + 2+2 =6

Total number of p -electron 6 + 3 =9

The mass number of protons + number of neutrons = 15+16=31.

Question 2. Determine the number of protons present In 5.6 I16. of n sample of oxygen gas at STP, containing \({ }^{16} 0\) isotope only.
Answer: Number of oxygen molecules present in 22.4 L of the gas = 6.022×10²³.

∴ 5.6 L of oxygen at STP contains = \(=\frac{5.6 \times 6.022 \times 10^{23}}{22.4}\)

= 1.50055 x 10 23 Molecules

Number of O-atoms in the given volume of the gas

⇒ \(=2 \times 1.50055 \times 10^{23}=3.011 \times 10^{23}\)

{since oxygen is diatomic]

Now, each 16O atom contains 8 protons.

Number of protons in 3.01 1 x 10²³ atoms of oxygen

= 8 x 3.01 1 x 10²³ = 2.4088 X 10²⁴

WBCHSE Class 11 Atomic Structure Fundamentals

Question 3. Find the number of protons required to fill u sphere of 10cm3 volume. What Is the muss of those number of protons?
Answer: The radius of a proton = 1.2 x 10 13 cm (approx.)

∴ The approximate volume of a proton \(=\frac{4}{3} \pi r^3\)

⇒ \(=\frac{4}{3} \times 3.14 \times\left(1.2 \times 10^{-13}\right)^3 \mathrm{~cm}^3=7.235 \times 10^{-39} \mathrm{~cm}^3\)

∴ The number of protons which can be accommodated in the sphere of capacity 10 cm3

⇒ \(=\frac{10}{7.235 \times 10^{-39}}=1.382 \times 10^{39}\)

∴ The mass of that number of protons

1.382 x 1039 x 1.672 x H-24 g

= 2.311 x 1015g = 2.311 x 1012 kg

Atomic Structure Fundamentals

Question 4. Determine the number of neutrons and their mass, present in 7 mg of \({ }^{14}{ }_6^{14} \mathrm{C}\) Assume that the mass of I neutron = muss of 1 H-atom.
Answer: No. of neutrons present In a \({ }_6^{14} \mathrm{C} \text {-atom }\) atom = (14-6)= 8

Number of atoms in 1 gram morn or 14 g of carbon-containing only \({ }_6^{14} \mathrm{C}\) isotope 6.022 x 10²³

∴ In 7 mg or 0.007 g of carbon, the number of atoms \(=\frac{6.022 \times 10^{23} \times 0.007}{14}\)

∴ In 7 mg of carbon, the number of neutrons

∴ \(=\frac{6.022 \times 10^{23} \times 0.007 \times 8}{14}=24.088 \times 10^{20}\)

Again, mass of 6.022 x 10²³ atoms of hydrogen = 1.008 g

∴ Mass of 1 atom of hydrogen \(=\frac{1.008}{6.022 \times 10^{23}} \mathrm{~g}\)

= mass of 1 neutron [according to the given condition]

∴ Mass of 24.088 x 10²⁰ neutrons

⇒ \(=\frac{1.008 \times 24.088 \times 10^{20}}{6.022 \times 10^{23}}=4.032 \times 10^{-3} \mathrm{~g}\)

Question 5. How many different types of HC1 molecule can be produced from two natural isotopes of hydrogen C 1 H = 99% and 2I1 = 1%) and two natural isotopes of chlorine (35CI = 76% and 37CI = 24%). Arrange the molecules obtained in the decreasing order of their availability.
Answer: Four different types of HC1 molecules can be produced.

Theyare- \({ }^1 \mathrm{H}^{35} \mathrm{Cl},{ }^1 \mathrm{H}^{37} \mathrm{Cl},{ }^2 \mathrm{H}^{35} \mathrm{Cl},{ }^2 \mathrm{H}^{37} \mathrm{Cl} \text {. }\)

Since the availability of XH and 35C1 are comparatively 2H and 37C1, the decreasing order of their availability \({ }^1 \mathrm{H}^{35} \mathrm{Cl}>{ }^1 \mathrm{H}^{37} \mathrm{Cl}>{ }^2 \mathrm{H}^{35} \mathrm{Cl}>{ }^2 \mathrm{H}^{37} \mathrm{Cl}\)

Question 6. A sample of oxygen contains the isotope, 180. How many neutrons are present in 11.2L of the gas at STP?
Answer: Atomic Number of oxygen

= 8 Number of neutrons in a 180 isotope

= 18-8 = 10

∴ Number of atoms in 22.4 L of 18O isotope at STP

= 2 x 6.022 x 1023

∴ Number of neutrons in 22.4L of 180 isotopes at STP

= 10 x 2 x 6.022 x 1023 [since oxygen molecule is diatomic]

∴ Number of neutrons in 11.2Lof 180 isotopes at STP

⇒ \(\begin{aligned}
& =\frac{10 \times 2 \times 6.022 \times 10^{23} \times 11.2}{22.4} \\
& =6.022 \times 10^{24}
\end{aligned}\)

WBCHSE Class 11 Atomic Structure Fundamentals

Question 7. A sample contains two isotopes, 160 and 180. How many protons are present in 11.2L of the sample at STP? What would be the difference in the no. of protons, if the sample contains only one isotope?
Answer: Each of the atoms of 160 and 180 contains 8 protons (atomic number of oxygen = 8 ) Total number of atoms is 22.41. oxygen ( 160 and 180 ) at SIT = 6.022 X 1023×2

[since oxygen molecule is diatomic]

Number of protons in 22.4L oxygen sample at STP

= 8 X 6.022 X 10²³X 2

∴ Number of protons in 11.2 L oxygen sample at STP

⇒ \(\begin{aligned}
& =\frac{8 \times 2 \times 6.022 \times 10^{23} \times 11.2}{22.4} \\
& =4.8176 \times 10^{24}
\end{aligned}\)

If the sample contains only one isotope, then there will be no difference in the number of protons because both 16O and 180 isotopes contain 8 protons in their atoms.

Electromagnetic Radiation: Origin Of Atomic Spectra

We have already seen that Rutherford’s atomic model failed to explain the atomic spectra and stability of an atom.

In order to investigate the reasons behind the failure of the Rutherford model, scientists felt the need to explain the nature and origin of atomic spectra.

Atomic spectra result from the electromagnetic radiations emitted by the excited atoms.

These electromagnetic radiations can pass through a vacuum also. According to Newton and other physicists, light is nothing but a stream of very small particles. The phenomena of reflection, refraction, etc.

Can be successfully explained using Newton’s theory but those like dispersion, interference, etc. cannot. Thus, the particle nature of light was replaced by the wave nature of light.

Atomic Structure Fundamentals

Wave nature of electromagnetic radiation: Maxwell’s theory

James Maxwell (1865) studied the nature of light and concluded that light is transmitted in the form of electromagnetic waves, which are associated with oscillating electric and magnetic fields.

The oscillating electric and magnetic fields are perpendicular to each other and are both perpendicular to the direction of propagation ofthe wave.

The absorption or emission of radiation by a body occurs continuously.

The radiations possessing wave character, travel with the velocity of light (3 x 108m-s_1 in vacuum).

The color of the radiation depends on its wavelength.

Electromagnetic waves, unlike sound waves or water waves, do not need a material medium for propagation, Electromagnetic waves can travel through a vacuum.

Some quantities related to electromagnetic radiation

Electromagnetic spectrum: Different types of electromagnetic radiation differ only in their frequencies and hence in their wavelengths.

The order of increasing wavelengths is: cosmic rays <7 -rays < X-rays < UV rays (150-3800A) < visible light (3800-7600A) < IR-rays (7600-6 x 106A) < Microwaves < Radio waves. The complete spectrum obtained by arranging these electromagnetic radiations in order of their increasing wavelengths or decreasing frequencies is called electromagnetic spectrum.

Various types of electromagnetic radiation have different energies and are being used for different applications. Some applications of electromagnetic waves are listed below.

Limitations of electromagnetic wave theory: This theory successfully explains the properties of light such as interference and diffraction.

However, it failed to explain the phenomena such as

1. Black body radiation
2. Photoelectric effect line spectra of atoms
3. Variation of heat capacity of solids as a function of temperature.

Black body radiation: An ideal body, which emits and absorbs radiations of all frequencies is called a black body and the radiation emitted by such a body is called black body radiation.

When a substance having a high melting point is heated, viz an iron bar, it first turns red, then yellow and then glows with a white light and finally with a blue light.

According to electromagnetic wave theory, since the emission and absorption of energy occur continuously, the energy of an electromagnetic wave is supposed to be proportional to its intensity and independent of its frequency or wavelength.

So according to wave theory, a body should emit radiation ofthe same colour although its intensity may vary as the heating is continued.

We have already seen that, on applying heat, the colour of a solid changes with the rise in temperature.

The colour change indicates that the frequency of radiation emitted increases with the rise in temperature (since red light indicates low frequency and blue light indicates high). Hence, electromagnetic wave theory can’t explain black body radiation.

Atomic Structure Fundamentals

The variation of intensity with wavelength of radiation emitted by a black body at two different temperatures ( Tx and T2 ).

WBCHSE Class 11 Atomic Structure Fundamentals

It is clear that the intensity of the radiation emitted depends only on temperature.

At a given temperature, the intensity of radiation emitted increases with a decrease in wavelength reaches a maximum value at a certain wavelength and then starts decreasing with a further decrease in wavelength. (Observe the variation in the plot from right to left).

Photoelectric effect: The phenomenon of ejection of electrons from the surface of a metal when the light of a suitable wavelength falls on it, is called the photoelectric effect and the ejected electrons are called photoelectrons.

The apparatus used for studying the photoelectric effect. In the figure, Tis an evacuated glass tube fitted with two quartz windows.

Two metal plates, A and B, are fitted at two ends of the tube. The plate A is photosensitive and acts as the cathode. The plate B is the electron detector and acts as the anode. The plate electrodes are connected to a battery via a milliammeter.

When the light of a suitable wavelength strikes plate A, photoelectrons are ejected from it The electrons are attracted by detector B and so they move towards it These electrons are responsible for the flow of current through the external circuit which can be measured using the milliamm.

By measuring the strength of the current flowing through the circuit, it is possible to determine the kinetic energy ofthe electrons.

The following are a few important observations about the Velocity 3 x 108 photoelectric effect: 

1. For any given metal, there exists a minimum frequency called threshold frequency (VG).
2. At frequencies below the threshold frequency, no electrons are emitted, no matter how large the intensity of the incident light or how long the irradiation occurs.
3. The number of photoelectrons emitted per second is proportional to the intensity ofthe incident light.
4. The kinetic energy of the photoelectrons is direct radiation of a frequency of 97.8 MHz. proportional to the frequency of the incident radiation.
5. With an increase in the frequency of light, the kinetic energy of the electrons increases.
6. The kinetic energy ofthe photoelectrons are independent of the intensity ofthe incident radiation.

The observations cannot be explained based on electromagnetic wave theory. For instance:

1. According to this theory, the absorption or emission of radiation occurs continuously. Hence, the energy of light is expected to depend on the intensity of the incident light.
2. Thus, light of any frequency can be made to have sufficient energy to cause the emission of electrons, merely by increasing its intensity. However, this is not true in practice.
3. According to this theory, the energy of the ejected electrons should be proportional to the intensity of the incident light, which is not the case in reality.

Numerical examples

Question 1. Yellow light emitted from a sodium lamp has a wavelength of 580 nm. Calculate the frequency and wave number of yellow light.

Answer: \(\lambda=580 \mathrm{~nm}=580 \times 10^{-7} \mathrm{~cm}\)

[since 1nm = 10^-7 cm]

⇒ \(v=\frac{c}{\lambda}=\frac{3 \times 10^{10}}{580 \times 10^{-7}}=5.17 \times 10^{14} \mathrm{~s}^{-1}\)

⇒ \(\vec{v}=\frac{1}{\lambda}=\frac{1}{580 \times 10^{-7}}=17241.37 \mathrm{~cm}^{-1}\)

Question 2. A radio station broadcasts at a frequency of 100 MH_z. How long would it take to reach a receiving system at a distance of 300 km? Calculate the wavelength and wave number of these radiations.
Answer: Required time \(=\frac{\text { Distance }}{\text { Velocity }}=\frac{300 \times 100}{3 \times 10^8}=3 \times 10^{-3} \mathrm{~s}\)

[since Velocity of any electromagnetic radiation = 3x108m.s-1]

Wavelength of that radiation \(\lambda=\frac{c}{v}=\frac{3 \times 10^{\circ}}{100 \times 10^6}=3 \mathrm{~m}\)

[since 100MHz =1006 Hz]

Wave number (v) = 1/λ = 1/3 = 0.33m-1

Question 3. Calculate the wavelength of an electromagnetic radiation of frequency of 97.8 MHz.
Answer: Wavelength of radiation \(\lambda=\frac{c}{v}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{97.8 \times 10^6 \mathrm{~s}^{-1}}=3.06 \mathrm{~m}\)

Question 4. How long would it take a radio wave of frequency, 6.2xl08s-1 to travel from Mars to Earth, the observation distance being 8.1 x 107km?
Answer: Velocity of any electromagnetic radiation (c) 3x108m

Required time \(\begin{aligned}
=\frac{\text { Distance }}{\text { Velocity }} & =\frac{8.1 \times 10^7 \times 10^3}{3 \times 10^8} \\
& =270 \mathrm{~s}=4 \mathrm{~min} 30 \mathrm{~s}
\end{aligned}\)

Atomic Structure Fundamentals

Particle nature of electromagnetic radiation: Planck’s quantum theory

The electromagnetic wave theory could successfully explain the various phenomena of light such as interference, diffraction, polarisation, etc.

However, it failed to explain the various phenomena involving energy transfer, namely black body radiation, photoelectric effect, etc.

The failure of the classical electromagnetic theory of radiation led Max Planck (1900) to propose a new theory known as ‘Planck’s quantum theory’.

Later this theory was extended by Einstein (1905). The main points of this theory are— M Radiant energy is emitted or absorbed in the form of small, discrete packets of energy called ‘quanta’ (singular quantum). In the case of light, the quantum of energy is often called ‘photon’.

The energy of each quantum of radiation does not have a fixed value. It depends on the frequency of the emitted or absorbed radiation.

The energy possessed by each quantum of radiation is directly proportional to its frequency, i.e., Eocv or E = hv [where E = energy of each quantum or photon, v = frequency of the radiation, h = Planck’s constant (6.626 X 10_27erg-s or 6.626 x 10″34J-s )].

The total amount of energy emitted or absorbed by a body must be an integral multiple of a quantum, i.e., E = nhv [where n = number of photons, absorbed or emitted by a body]. This means the amount of energy emitted or absorbed by a body can be—hv, 2hv, 3hv, etc. but never 0.5 hv or 1.4 hv.

The energy possessed by one photon is called one quantum.

The energy possessed by one-mole photons is called one Einstein.

1 einstein = NO (or 6.022 x 10²³ ) quanta.

∴ 1 einstein energy (J5) = N0hv

Explanation of black body radiation on the basis of quantum theory: When a solid is heated, the atoms are set into oscillations emitting radiations of frequency v.

As heating is continued the atoms absorb more energy and emit radiations of higher frequency. Since the frequency of red light is minimal, an iron rod on heating first turns red and then yellow (higher frequency than red) and further turns into white and finally blue.

Explanation of the photoelectric effect on the basis of quantum theory: Einstein (1905) explained different aspects of the photoelectric effect using Planck’s quantum theory, as follows

When a light of certain frequency strikes a metal surface, photons ofthe light collide with the electrons ofthe metal. Each photon thus transfers its entire energy (hv) to each of the colliding electrons.

Photoelectrons are emitted only if the energy of the photon is sufficient to overcome the force of attraction between the electron and the nucleus. In other words, electrons are emitted from the surface of metals, when irradiated with photons of a certain minimum frequency known as threshold frequency (hv0).

The minimum energy of a photon that causes photoelectric emission is known as the photoelectric work function (hv0).

If the frequency of the incident radiation (v) is greater than the threshold frequency (v0), the excess energy of the protons Is transferred to the ejected electrons ns kinetic energy; \(\frac{1}{2} mv-W_0\). Fence, the kinetic energy of the ejected electrons Increases with an Increase In the frequency of the Incident light.

Keeping the frequency constant, If the Intensity of the incident light Is Increased, the number of photons striking the metal surface increases, This In turn Increases the number of electrons of the metal colliding with the photons, which In turn increases the strength of the photoelectric current.

The above observations are In accordance with experimental results, A plot of the kinetic energy of emitted photoelectrons against the frequency of the absorbed photons gives a straight line with slope, h.

Keeping the frequency constant, a plot of the kinetic energy of the entitled photoelectrons against the intensity of incident radiation gives n straight line parallel to the x-axis.

Dual nature of electromagnetic radiation: Prom the above discussion It Is clear that the properties of radiation like Interference or diffraction can be explained if the light is considered to have a wave nature whereas, other properties of light such as black body radiation, photoelectric effect, etc.

Can be explained, if the light is considered to have a particle nature. Thus, it is concluded that light behaves both as a wave and also as a stream of particles. Therefore light is said to have a dual nature.

Numerical Examples

Question 1. A Ray of habit or frequency SOA is incident on a metal surface and thus, absorbs 10^-7J of Calculate the number of photons Incident on the mental surface
Answer: let the number of photons incident on the metal surface = n

∴ \(n h v=10^{-7} \text { or, } \frac{n h c}{\lambda}=10^{-7}\)

Or, \(\frac{n \times 6.626 \times 10^{-34} \times 3 \times 10^8}{5000 \times 10^{-10}}=10^{-7}\)

Or, \(n=\frac{10^{-7} \times 5000 \times 10^{-10}}{6.626 \times 10^{-34} \times 3 \times 10^8}=2.51 \times 10^{11}\)

Question 2. The threshold frequency, v0 for a metal is 7.0 X 104s-1. Calculate the kinetic energy of an electron emitted, when radiation of frequency, v – 1.2 X 1015s-1, strikes this metal.
Answer: Kinetic energy of the photoelectrorts \(\left(\frac{1}{2} m v^2\right)=h\left(v-v_0\right)\)

\(\begin{aligned}
& =\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right)\left(1.2 \times 10^{15} \mathrm{~s}^{-1}-7.0 \times 10^{14} \mathrm{~s}^{-1}\right) \\
& =3.31 \times 10^{-19} \mathrm{~J}
\end{aligned}\)

Question 3. If a light with frequency 2.0 X 1016Hz emitted photo o electrons with double the kinetic energy as emitted by the light of frequency 1.25 x 1016Hz from the same metal surface, calculate the threshold frequency of the metal
Answer: Kinetic energy of photoelectrons \(\left(\frac{1}{2} m v^2\right)=h\left(v-v_0\right)\)

Given, h(2.0x 1016-vo) = h(1.25x 1016-vQ)x2

or, v0 = (2.5- 2.0) X 1016 =0.5 Xl016 =5xl015Hz

Atomic Structure Fundamentals

Question 4. When a radiation of frequency 7.5 X 1014Hz strikes a metal surface, the maximum kinetic attained by the emitted electrons is 1.6xlO-19J. Calculate the threshold frequency of the metal.
Answer: Kinetic energy ofemitted electrons \(\left(\frac{1}{2} m v^2\right)=h\left(v-v_0\right)\)

Given, 1.6 xlO-19 = h(v-v0)

Or, \(\frac{1.6 \times 10^{-19}}{6.626 \times 10^{-34}}=7.5 \times 10^{14}-v_0\)

or, v() = 7.5 x 1014-2.41 x 1014 =5.09×1014 Hz

Question 5. Calculate the energy of each quantum of electromagnetic radiation having a wavelength of 6000A. [h = 6.624 x 10^-27erg.s]
Answer: Energy of each quantum, \(E=h v=\frac{h c}{\lambda}\)

∴ \(E=6.624 \times 10^{-27} \times \frac{3 \times 10^{10}}{6000 \times 10^{-8}}=3.312 \times 10^{-12} \mathrm{erg}\)

[c = 3 x lO10cm.s-1 ; λ. = 6000A =6000 x 10^-8cm ]

Question 6. Calculate the energy of Imnl of photons of sin electromagnetic riuUntlou of frequency 2.6 X 10²³. [h = 6.026 X IO-34j.s
Answer: Energy of l mol photons = N0hv

= 0.022 X 10²³ X 6.626 X 10^–34 X 2.5 X 10H

= 99.75 kj.mol-1

Question 7. How many photons of light with wavelength 400 CBM provide 1j energy? = 6.626 X 10^-34J.s
Answer: Energy of 1 photon \(=h v=\frac{h c}{\lambda}\)

⇒ \(=\frac{6.626 \times 10^{-34} \times 3 \times 10^8}{400 \times 10^{-9}} \mathrm{~J}\)

[since 1nm= 10^-9m]

∴ No. of photons required to produce 1.0J energy

⇒ \(\begin{aligned}
& =\frac{1.0}{\left(6.626 \times 10^{-34} \times 3 \times 10^8\right) /\left(400 \times 10^{-9}\right)} \\
& =\frac{400 \times 10^{-9}}{6.626 \times 10^{-34} \times 3 \times 10^8}=2.012 \times 10^{18}
\end{aligned}\)

Question 8. Find the wave number and energy of each photon present in yellow light having wavelength 580nm. (c = 3 X 108 m.s-1 and h = 6.627 X 10^-34J.s]
Answer: Wave number \((\bar{v})=\frac{1}{\lambda}=\frac{1}{580 \times 10^{-9}} \mathrm{~m}^{-1}\)

= 1.724 X 106 m-1 [lnm = 10^-9m

Energy of each photon {E) = \(h v=h \times \frac{c}{\lambda}\)

⇒ \(=\left(6.627 \times 10^{-34}\right) \times \frac{3 \times 10^8}{580 \times 10^{-9}}=3.428 \times 10^{-19} \mathrm{~J}\)

Question 9. Calculate the frequency of light emitted when an electron drops from a higher to lower energy level of an atom and the difference between the two energy levels is 35.64 x 10^-13erg.[h = 6.624 x 10^-27erg-s]
Answer: U E1 and E2 be the two energy levels, then the difference between their energies is given by, E2-Ex = hv or, AE = hv l/i= Planck’s constant and v = frequency of light emitted].

∴ \(v=\frac{\Delta E}{h}=\frac{35.64 \times 10^{-13} \mathrm{erg}}{6.624 \times 10^{-13} \mathrm{erg} \cdot \mathrm{s}}=5.3804 \times 10^{14} \mathrm{~s}^{-1}\)

Question 10. A BOW bulb emits a monochromatic light of wavelength 480nm. Calculate the number of photons emitted per second by the bulb.
Answer: Power of the bulb =80 W = 80].s-1

Energy of a photon \(=h v=\frac{h c}{\lambda}\)

⇒ \(=\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right)\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{480 \times 10^{-9} \mathrm{~m}}=4.14 \times 10^{-19} \mathrm{~J}\)

Question 11. Calculate the wavelength of a photon (in nm) having energy of 1 eV.
Answer: Energy of1 photon, E =leV =1.609 x 10^-19j

⇒ \(\begin{aligned}
E=h v & =h \frac{c}{\lambda} \\
\text { or, } \lambda=\frac{h c}{E} & =\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{1.609 \times 10^{-19}} \\
& =12.35 \times 10^{-7} \mathrm{~m}=\frac{12.35 \times 10^{-7}}{10^{-9}} \mathrm{~nm}=1235 \mathrm{~nm}
\end{aligned}\)

Question 12. The iodine molecule absorbs radiation of wavelength 450nm to dissociate into iodine atoms. If each molecule of iodine absorbs 1 quantum of radiation, determine the kinetic energy of the iodine atom. (Bond energy of I2 = 240kJ.mol-1 )
Answer: Energy required for the dissociation of 1 mol of iodine molecules = Bond energy of I2 molecule = 240kJ

∴ The energy required for the dissociation of a single iodine molecule \(=\frac{240 \times 10^3}{6.022 \times 10^{23}} \mathrm{~J}=3.985 \times 10^{-19} \mathrm{~J}\)

Energy absorbed by each iodine molecule \(=h v=\frac{h c}{\lambda}\)

⇒ \(=\frac{6.626 \times 10^{-34} \times 3 \times 10^8}{450 \times 10^{-9}} \mathrm{~J}=4.417 \times 10^{-19} \mathrm{~J}\)

∴ The surplus energy after the dissociation of each molecule of iodine =(4.417-3.985) x 10^-19J =4.32 x 10^-20J

This surplus energy imparts kinetic energy to each iodine molecule.

The surplus energy that imparts kinetic energy to each iodine atom \(=\frac{4.32 \times 10^{-20}}{2} \mathrm{~J}=2.16 \times 10^{-20} \mathrm{~J}\)

∴ The kinetic energy of each iodine atom = 2.16 x 10^-20J.

Question 13. Calculate the energy associated with 1 mol of photon corresponding to electromagnetic radiation having a frequency of 5 X 1014Hz.
Answer: Energy associated with 1 mol of a photon is given by, E=Nhv [AT = Avogadro number, h = Planck’s constant, v = frequency of radiation]

⇒ \(\begin{aligned}
& =6.022 \times 10^{23} \times\left(6.626 \times 10^{-34}\right) \times\left(5 \times 10^{14}\right) \mathrm{J} \\
& =199.51 \times 10^3 \mathrm{~J}=199.51 \mathrm{~kJ}
\end{aligned}\)

Atomic Structure Fundamentals

Emission and absorption spectra

When light or any other electromagnetic radiation is made to pass through a spectroscope, the light separates into various components of different wavelengths, producing various coloured bands.

The set of colored bands formed is called a spectrum. Spectra can be of two types —

1. Emission spectrum and
2. Absorption spectrum

Emission spectrum: When the radiation emitted from any source such as any incandescent solid, liquid, or gaseous substance (i.e., by passing an electric discharge through a gas at low pressure or by heating some substance to high temperature) is directly analyzed through a spectroscope, the spectrum obtained is called an emission spectrum.

Depending on the source of radiation, the emission spectrum can be divided into two types—

Continuous spectrum: The spectrum produced when white light emitted from any source such as the sun, a bulb, a molten metal or any incandescent source is passed through a spectroscope is a continuous spectrum.

In this spectrum, the colours from red to violet are arranged sequentially continuously, without any break.

In this spectrum, red lies at one end and violet at the other, and the rest of the colours lie between these two colours.

The colours are so continuous that each of them appears to merge into the other. Hence, it is known as a continuous spectrum. It contains all the wavelengths of the visible range. For example— Solar spectrum.

The spectrum emitted from an incandescent source that contains all the wavelengths of light of the visible range is known as continuous spectrum. There are no. black lines in this spectrum.

Line spectrum or atomic spectrum: If a gaseous element is heated or an electric discharge is passed through the gas at low pressure and the light emitted is resolved in a spectroscope, the spectrum obtained is not a continuous spectrum.

In this case, the different coloured lines obtained are separated from each other by dark bands. The spectrum obtained is called the line spectrum.

The excited gaseous atoms are responsible for the piotirllou of such spectrum, lunco, line spectrum Is also known as the atomic spectrum.

In a lino spectrum, each line corresponds to a particular wavelength. The line spectrum of each element consists of a group of lines with certain fixed wavelengths, Every element has Its own characteristic spectrum, which is different from those of other elements.

For example, (the spectrum of sodium vapour gives two yellow lines. Hence, the line spectrum of each element characterises the atom of that element.

Therefore, the atomic spectrum of an element can be used to identify the element and Is sometimes called the fingerprint of its atoms.

Absorption spectrum: When white light emitted from a heated incandescent substance is passed through a liquid or a gaseous substance, radiations of certain wavelengths are absorbed. If the emergent radiations are resolved in a spectroscope, a few dark lines are observed, in the atoms. Otherwise continuous spectrum.

These dark lines constitute the absorption spectrum of that absorbing substance (liquid or gas).

The dark lines in the absorption spectrum are at the same place where coloured lines are obtained in the emission spectrum for the same substance. This indicates that the wavelengths of radiation absorbed in the absorption spectrum are the same as those emitted in the case of the emission spectrum.

Differences between emission and absorption spectra

Emission spectrum: Line spectrum of a hydrogen atom

1. To study the emission spectrum of hydrogen, the gas is taken in a discharge tube at low pressure, and an electric discharge is passed through it. ill H₂ molecules dissociate into energetically excited Hatoms and emit electromagnetic radiation.
2. The emitted radiation is allowed to pass through the prism in a spectroscope.
3. The resulting spectrum consists of a large number of isolated sharp lines grouped into different series, named after their discoverers. These lines constitute the line spectrum (discontinuous spectrum).
4. The visible region ofthe hydrogen spectrum can be viewed even with the naked eye. It was discovered by Balmer in 1885 and hence the series of isolated spectral lines involving the visible region is called the Balmer series.
5. Balmer observed four prominent lines (red, bluish-green, blue and violet) in the visible region and these were designated as Ha, Hy and respectively.

Balmer (1885) showed that the wave numbers (inverse of wavelengths) of the spectral lines in the visible region (Balmer series) can be expressed by the empirical formula,

⇒ \(\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right]\) ……[1]

where R is the universal constant, known as Rydberg’s constant Its value is 1.09678 x 105 cm-1. n is an integer equal to or greater than 3 (i’.e., n = 3, 4, 5, 6 v (wave number) =i, where X – wavelength.

Replacing n by 3, 4, 5 and 6 respectively the wave numbers of the spectral lines, Hy and can be calculated.

Further investigation on the line spectrum of hydrogen (using an improved spectroscope) led to the discovery of five other series lines in the ultraviolet and infrared regions. These are indicated in the adjacent table.

Rydberg (1890), showed that all series of lines in the hydrogen spectrum could be described by the following expression (similar to Balmer’s empirical formula)—

⇒ \(\bar{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\) …..[2]

where nx =1, 2, 3, 4,……, n2 = n1 + 1 , n1 + 2,…….

Atomic Structure Fundamentals

Series Of Lines In The Line Spectrum Of Hydrogen Atom 

Putting n1 = 1,2, 3, 4, 5, 6 and n2 = + 1, n1 + 2, n+3, … etc., die wave numbers of the spectral lines corresponding to Lyman, Balmer, Paschen, Brackett Pfund and Humphreys series can be calculated.

The cause of the formation of the line spectrum of hydrogen was not exactly known at that time.

However, it was believed that the line spectrum was obtained as a result of absorption and subsequent emission of energy discontinuously by the electron present in the H-atom. Hence, the line spectrum is also called an atomic spectrum.

Numerical Examples

Question 1. Calculate the wavelengths of Hff and in the emission spectrum of hydrogen. [R = 109678 cm-1 ].
Answer: Balmers equation is given by \(\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right]\)

n=3 for H and n = 6 for H

∴ \(\bar{v}_{\mathrm{H}_a}=109678\left(\frac{1}{2^2}-\frac{1}{3^2}\right)=109678 \times \frac{5}{36} \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\mathrm{H}_\alpha}=\frac{1}{\bar{v}_{\mathrm{H}_\alpha}}=\frac{36}{109678 \times 5}=6.565 \times 10^{-5} \mathrm{~cm}\)

Similarly \(\bar{v}_{\mathrm{H}_\delta}=109678\left(\frac{1}{2^2}-\frac{1}{6^2}\right)=109687 \times \frac{8}{36} \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\mathrm{H}_8}=\frac{1}{\bar{v}_{\mathrm{H}_8}}=\frac{36}{109678 \times 8}=4.10 \times 10^{-5} \mathrm{~cm}\)

Question 2. Identify the spectral line having wavelength of 4.863 x 10_5cm in the emission spectra of hydrogen.
Answer: Wave no \(\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right]\)

[Given, lamba = 4.863 x 10-5Cm]

∴ \(\bar{v}=\frac{1}{\lambda}=\frac{1}{4.863 \times 10^{-5}}=109678\left[\frac{1}{4}-\frac{1}{n^2}\right]\)

∴ \(\frac{1}{n^2}=\frac{1}{4}-\frac{1}{4.863 \times 10^{-5} \times 109678}=0.0625 \quad \text { or, } n=4\)

The spectral line with wavelength 4.863 x 10-5cm is Hbeta.

Atomic Structure Fundamentals

Question 3. Determine the wavelength and frequency of the radiation having the longest wavelength in the Lyman series of hydrogen atoms.
Answer: Rydberg’s equation \(\frac{1}{\lambda}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\): in case of lyman series. For the wavelength to be the longest, the difference in energies between the two energy levels should be minimal.

Hence, n2= 2

∴ \(\frac{1}{\lambda}=109678\left(\frac{1}{1^2}-\frac{1}{2^2}\right) \quad \text { or, } \frac{1}{\lambda}=109678\left(1-\frac{1}{4}\right)\)

∴ \(\lambda=\frac{4}{3 \times 109678}=1215.67 \times 10^{-8} \mathrm{~cm}=1215.67\)

So, the X radiation109678 has the longest wavelength in the Lyman series = 1215.67×10-8 cm.

∴ Frequency of the radiation

⇒ \(v=\frac{c}{\lambda}=\frac{3 \times 10^{10}}{1215.67 \times 10^{-8}} \mathrm{~s}^{-1}=2.467 \times 10^{15} \mathrm{~s}^{-1}\)

Question 4. The wave number of a spectral line in the Lyman series of H-atom is 82260 cm-1. Show that this line has appeared in this series due to the return of the electron from the second to the first orbit.
Answer: Wave number \(\bar{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

∴ \(\nabla=R\left[1-\frac{1}{n_2^2}\right] \text { or, } \frac{\bar{v}}{R}=1-\frac{1}{n_2^2}\)

Or, \(\frac{1}{n_2^2}=1-\frac{\bar{v}}{R}=1-\frac{82260}{109680}=\frac{27420}{109680}=\frac{1}{4}=\frac{1}{2^2}\)

∴ n2=2

This means that the electron has returned from the second to the first orbit.

Atomic Structure Fundamentals

Question 5. Calculate the shortest and longest wavelengths in the Lyman series of the hydrogen spectrum.
Answer: For the Lyman series, n1 = 1 and n2 = 2,3,4, …..

Rydberg equation \(\vec{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right],\)

The difference between nx and n2 is maximum for the shortest wavelength in the Lyman series. Hence n2 = .

∴ \(\frac{1}{\lambda_{\min }}=\bar{v}_{\max }=R\left[\frac{1}{1^2}-\frac{1}{\infty^2}\right]=R=109678 \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\min }=\frac{1}{109678}=9.117 \times 10^{-6} \mathrm{~cm}=911.7\)

Similarly, the difference between n1 and n2 is minimal for the longest wavelength in the Lyman series. Hence, n2 = 2

∴ \(\frac{1}{\lambda_{\max }}=\bar{v}_{\min }=R\left[\frac{1}{1^2}-\frac{1}{2^2}\right]=\frac{3}{4} R\)

∴ \(\begin{aligned}
\lambda_{\max } & =\frac{4}{3 R}=\frac{4}{3 \times 109678} \\
& =1215.7 \times 10^{-8} \mathrm{~cm}=1215.7 Similarly, the difference between n1 and n2 is minimal for the longest wavelength in the Lyman series. Hence, n2 = 2
\end{aligned}\)

Question 6. Show that the Balmer series appears between 3647A and 6563A in the hydrogen spectrum
Answer: For Balmer series \(\frac{1}{\lambda}=\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right], n=3,4,5, \cdots \infty\)

The Limits Of the Balmer Series Can Be obtained when n = 3 and n = 00 respectively

\(\frac{1}{\lambda_{\min }}=\bar{v}_{\max }=R\left[\frac{1}{2^2}-\frac{1}{\infty^2}\right]=\frac{R}{4}=\frac{109678}{4} \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\min }=\frac{4}{109678} \mathrm{~cm}=3647 \times 10^{-8} \mathrm{~cm}=3647 \)

Also, \(\frac{1}{\lambda_{\max }}=\bar{v}_{\min }=R\left[\frac{1}{2^2}-\frac{1}{3^2}\right]=\frac{5 R}{36}=\frac{5 \times 109678}{36} \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\max }=\frac{36}{5 \times 109678}=6564 \times 10^{-8} \mathrm{~cm}=6564 \)

Atomic Structure Fundamentals

Question 7. Calculate the wavelength of the spectral line with n2 = 3 in the Lyman series of hydrogen atoms.
Answer: In Lyman series, = 1

∴ \(\bar{v}=R\left[\frac{1}{1^2}-\frac{1}{3^2}\right]=109678 \times \frac{8}{9} \mathrm{~cm}^{-1}\)

Since n2=3

⇒ \(\lambda=\frac{1}{\bar{v}}=\frac{9}{109678 \times 8}=1.026 \times 10^{-5} \mathrm{~cm}\)

Bohr’s Atomic Model

In 1913, Neils Bohr, an eminent scientist successfully explained the stability of an atom and the cause of the appearance of line spectra with the help of Planck’s quantum theory.

He rectified the defects of Rutherford’s nuclear model and put forward a new atomic model for the hydrogen atom which is known as Bohr’s atomic model or Rutherford-Bohr’s atomic model.

Postulates Of Bohr’s Model Of Atom

The theory, put forward by Bohr regarding the structure of the H-atom, is based on three revolutionary postulates—

Postulate 1: The electron in the hydrogen atom revolves around the nucleus only in certain selected circular paths (called orbits) which are associated with definite energies. The electrons revolve only in those orbits in which the angular momentum ofthe electron is a whole number multiple of \(\frac{h}{2 \pi},\) i.e., the angular momentum of the electron, \(m v r=n \times \frac{h}{2 \pi}\), Where n= 1,2,3,4 ……….etc, m = mass of the electron, v = velocity of the electron, r = radius of the orbit, h = Planck’s constant. Thus, the angular.

Postulate 2: When an electron revolves in any selected orbit, it neither emits nor absorbs energy. The energy of an electron in a particular orbit remains constant. These orbits are, therefore, called stationary orbits although the electrons are not stationary. Electrons revolving in a stationary orbit are said to be in the stationary state.

Explanation: Each stationary orbit is considered as the energy level. The energy of an electron revolving in a stationary orbit is supposed to be the energy of that particular orbit although the orbit has no energy of its own. The energy of the orbit increases with an increase in its distance from the nucleus.

Depending on their distance from the nucleus, these orbits are divided into seven energy levels such as K, L, M, N… etc. and these are designated respectively by the numbers 1, 2, 3, 4 . . . etc.

The numbers signifying the energy levels are known as principal quantum numbers (re). These orbits can be arranged in the increasing order of their energy as follows:

K(n = 1) < L(n = 2) < M(n = 3) < N(n = 4)… etc.

Postulate 3: When an electron jumps from a higher stationary energy, level to a lower stationary energy level, it emits a fixed amount of energy in the form of radiation. On the other hand, when an electron absorbs a certain amount of energy, it moves to a higher energy level.

Electrons can never occupy a position in between two successive stationary energy levels.

Atomic Structure Fundamentals

Mathematical expression: If the frequency of radiation emitted or absorbed is assumed to be v and the energies of the higher and lower stationary orbits as E2 and E1 respectively, then the difference in energy, AE = E2-E1 =hv, [where h = Planck’s constant

[Since E2 and Ey have fixed values, the magnitude of v is also fixed. This accounts for the existence of some definite lines in the emission spectra of hydrogen. Energy is involved in the transition of electrons.

Concept of quantization of energy:

The concept of quantization of energy can be best understood by taking the following example: When a person moves down a staircase, his energy changes discontinuously.

He can have only certain definite values of energies corresponding to those of the various steps.

Alternatively, the energy of the person is quantized. However, if he goes down a ramp, his energy changes continuously, having any value corresponding to any point on the ramp. In short, energy is not quantized.

Atomic Structure Fundamentals

Calculation Of Various Quantities For Hydrogen-Like Atoms Using Bohr’s Theory

The radius of ‘faith orbit: Suppose the total quantity of positive charge in the nucleus of a hydrogen-like atom is Ze (where Z = atomic number and e = charge of a proton or an electron).

The only electron present in that atom is revolving around the nucleus in a circular orbit of radius, r with velocity, v.

According to Coulomb’s law, the attractive force of the nucleus on the electron i.e… the centripetal force = [where Ze is the total positive charge on the nucleus and e =charge of an electron].

In case of an electron revolving with velocity v, centrifugal force \(=\frac{m v^2}{r}\) [where m = mass of electron and r = radius ofthe orbit], For the stability of an atom, the centripetal force must be equal to the centrifugal force, i.e \(\frac{Z e^2}{r^2}=\frac{m v^2}{r} \quad \text { or, } v^2=\frac{Z e^2}{m r}\)

According to Bohr’s theory, the angular momentum of the revolving electron in a stationary orbit is an integral multiple \(\frac{h}{2 \pi} \text { i.e., } m v r=\frac{n h}{2 \pi}\)

[where, n = 1,2,3… etc., are whole numbers]

or, \(v=\frac{n h}{2 \pi m r} \quad \cdots[2] \quad \text { or, } v^2=\frac{n^2 h^2}{4 \pi^2 m^2 r^2} \quad \cdots[3]\)

Atomic Structure Fundamentals

hence, from equations [1] and [3] we have,

\(\begin{aligned}
& \frac{Z e^2}{m r}=\frac{n^2 h^2}{4 \pi^2 m^2 r^2} \quad \text { or, } \frac{Z e^2}{m}=\frac{n^2 h^2}{4 \pi^2 m^2 r} \\
& \text { or, } r=\frac{n^2 h^2}{4 \pi^2 m^2} \times \frac{m}{Z e^2} \text { or, } r=\frac{n^2 h^2}{4 \pi^2 m Z e^2}
\end{aligned}\)

i.e., radius of ‘n’ th orbit \(r_n=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

Equation [4] indicates the radius of with orbit of the revolving electron.

The velocity of a revolving electron in ‘n’th orbit: According to Bohr’s theory, the angular momentum of a revolving electron is given by, mvr \(=\frac{n h}{2 \pi} \quad \text { or, } r=\frac{n h}{2 \pi m v}\)

Again, the radius of ‘n’ th orbit, r \(=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

Comparing the above two relations we may write,

\(\frac{n h}{2 \pi m v}=\frac{n^2 h^2}{4 \pi^2 m Z e^2} \quad \text { or, } \frac{1}{v}=\frac{n h}{2 \pi Z e^2} \quad \text { or, } v=\frac{2 \pi Z e^2}{n h}\)

∴ The velocity of an electron revolving in the ‘n’th Bohr orbit is given by

Substituting the values of n = 1, 2, 3, etc., in this equation, the velocity of revolving electrons in different Bohr orbits can be determined.

The velocity of resolving electron in the ‘ n ‘th orbit of the H atom.

\(=\frac{2 \times \frac{22}{7} \times 1 \times\left(4.8 \times 10^{-10}\right)^2}{n \times\left(6.626 \times 10^{-27}\right)}=\frac{2.186 \times 10^8}{n} \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

Relation between the velocities of an electron in ‘n’th and first orbit: Velocity of an electron revolving in the’ n ‘th orbit.

\(\left(v_n\right)=\frac{2 \pi \mathrm{Z} e^2}{n h}\) and that in the first orbit, (v1) \(=\frac{2 \pi Z e^2}{1 \times h}\)

∴ \(\frac{v_n}{v_1}=\frac{2 \pi Z e^2}{n h} \times \frac{1 \times h}{2 \pi Z e^2}=\frac{1}{n}\)

∴ \(\frac{v_n}{v_1}=\frac{2 \pi Z e^2}{n h} \times \frac{1 \times h}{2 \pi Z e^2}=\frac{1}{n}\)

or, \(v_n=v_1 \times \frac{1}{n}\)

Relation between the radius of ‘n’th orbit and the first orbit.

Radius of ‘n th orbit \(\left(r_n\right)=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\) and the radius of the first orbit \(\left(r_1\right)=\frac{1^2 \cdot h^2}{4 \pi^2 m Z e^2}=\frac{h^2}{4 \pi^2 m Z e^2}\)

∴ \(\frac{r_n}{r_1}=\frac{n^2 h^2}{4 \pi^2 m Z e^2} \times \frac{4 \pi^2 m Z e^2}{h^2}=n^2\)

or, rn = r1 x n2

Atomic Structure Fundamentals

Total energy of an electron revolving in ‘n’th orbit: Total energy of electron revolving in ‘ n ‘th orbit, En = Kinetic energy + Potential energy

En = Kinetic energy + Potential energy

\(\begin{aligned}
& =\frac{1}{2} m v^2+\left(-\frac{Z e^2}{r}\right)=\frac{1}{2} m \times \frac{Z e^2}{m r}-\frac{Z e^2}{r} \\
& =\frac{1}{2} \frac{Z e^2}{r}-\frac{Z e^2}{r}=-\frac{Z e^2}{2 r}=-\frac{Z e^2}{2} \times \frac{1}{r}
\end{aligned}\)

Since \(v^2=\frac{Z e^2}{m r}\)

\(=-\frac{Z e^2}{2} \times \frac{4 \pi^2 m Z e^2}{n^2 h^2}\) \(r=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

Equation [6] Indicates the energy of the electron revolving in n the orbit of a Hydrogen- like Hydrogen- like Atom.

∴ For hydrogen atom, \(E_n=-\frac{2 \pi^2 m e^4}{n^2 h^2}\)

Substituting the values of m, e, n, and R in equation number[7] we have

\(E_n=-\frac{2 \times(22 / 7)^2 \times\left(9.108 \times 10^{-28} \mathrm{~g}\right) \times\left(4.8 \times 10^{-10} \mathrm{esu}\right)^4}{n^2 \times\left(6.626 \times 10^{-27} \mathrm{erg} \cdot \mathrm{s}\right)^2}\) \(=-\frac{2.176 \times 10^{-11}}{n^2} \mathrm{erg} \cdot \text { atom }^{-1}\) \(=-\frac{2.176 \times 10^{-18}}{n^2} \mathrm{~J} \cdot \mathrm{atom}^{-1}=-\frac{1312}{n^2} \mathrm{~kJ} \cdot \mathrm{mol}^{-1} \quad \cdots[7 \mathrm{a}]\)

Energies Ev E2, E3, etc., are calculated by putting n – 1, 2, 3, etc. in equation [7a] and are represented schematically in.

It is observed from these values that successive energy levels are not equidistant. The energy gap between two successive levels decreases with an increase in distance from the nucleus.

When an electron is at an infinite distance from the nucleus, its potential energy is zero.

Work done to bring the electron from an infinite distance to a distance V concerning the nucleus gives the measure of its potential energy.

The force of attraction between the nucleus and the electron is I given by, F = (applying Coulomb’s law).

∴ The potential energy of the electron at a distance ‘r’ from the nucleus \(=\int_{r=\infty}^{r=\infty} \frac{Z e^2}{r^2} d r=-\frac{Z e^2}{r}\)

Atomic Structure Fundamentals

Electronic energy as negative energy: when an electron is at an infinite distance (n = oo) from the nucleus, it experiences no force of attraction from the nucleus. Hence, the energy of the electron at an infinite distance from / the nucleus is taken as zero (E∞ = 0).

When the electron moves towards the nucleus, it experiences a force of attraction from the nucleus.

As a result, some energy is released and the energy of the electron becomes negative. Due to the release of energy, the stability of the electron occupying a fixed orbit in the atom is increased.

As the electron comes closer to the nucleus, it experiences a greater force of attraction and hence more energy is released, thereby making the electronic energy more negative. All these facts are per the expression of electronic energy,

\(E_n=-\frac{2 \pi^2 m Z^2 e^4}{n^2 h^2}\) As n decreases, the energy of the electron decreases (because it is associated with a -ve sign) and hence the stability of the electron in the atom increases.

Thus, the negative value ofthe electronic energy in an atom signifies that the stability of the electron increases as it occupies orbits closer to the nucleus.

The energy is minimal when it revolves around the nucleus occupying the first orbit (i.e., n = 1).

The ratio of the energies of an electron revolving in the V th orbit and the first orbit of the hydrogen-like atom.

⇒ \(\frac{E_n}{E_1}=\left(-\frac{2 \pi^2 m Z^2 e^4}{n^2 h^2}\right) \times \frac{1}{\left(-\frac{2 \pi^2 m Z^2 e^4}{1^2 \times h^2}\right)}=\frac{1}{n^2}\)

∴ \(E_n=E_1 \times \frac{1}{n^2}\)

The radius of the first orbit of hydrogen atom: From equation number [4], it is seen that the radius of the ‘ n ’ th orbit of a hydrogen-like atom, \(r_n=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

[where, h = Planck’s constant = 6.626 x 10 -27erg-s , m = mass of electron = 9.1 x 10-28g, e =charge of electron = 4.8 x 10-10esu]

Derivation of Rydberg’s equation

When an electron of a hydrogen atom jumps from ‘ n2 ‘th orbit to‘ ‘th orbit, let the frequency of emitted radiation be v. According to Bohr’s theory,

⇒ \(\begin{aligned}
h v=E_{n_2}-E_{n_1} & =\left(-\frac{2 \pi^2 m e^4}{n_2^2 h^2}\right)-\left(-\frac{2 \pi^2 m e^4}{n_1^2 h^2}\right)[\text { for } \mathrm{H}, Z=1] \\
& =\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)
\end{aligned}\)

⇒ \(=\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

∴ \(v=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

or, \(\frac{c}{\lambda}=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

since \(h v=E_{n_2}-E_{n_1}=\left(-\frac{2 \pi^2 m e^4}{n_2^2 h^2}\right)-\left(-\frac{2 \pi^2 m e^4}{n_1^2 h^2}\right)\)

⇒ \(=\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

∴ \(v=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Or, \(\frac{c}{\lambda}=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Since \(v=\frac{c}{\lambda}\)

Or, \(\frac{1}{\lambda}=\frac{2 \pi^2 m e^4}{c h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Since \(\frac{1}{\lambda}=\bar{v}\) = wave Number ]

or, \(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

R is a constant known as Rydberg’s constant.

Atomic Structure Fundamentals

∴ Rydberg’s constant,R \(=\frac{2 \pi^2 m e^4}{c h^3}\)

Note that earlier equation in article[11]no is2.4.4.comparable with equation [2]

Expression for wave number of spectral lines involving one-electron ions is given by

\(\bar{v}=Z^2 \times R\left(\frac{1}{n^2}-\frac{1}{n_2^2}\right) \text {, where } Z=\text { atomic number. }\) \(\bar{v}=Z^2 \times R\left(\frac{1}{n^2}-\frac{1}{n_2^2}\right) \text {, where } Z=\text { atomic number. } \)

Calculation of the value of Rydberg’s constant: Substituting the values of n, m, e, c and h in equation [12] we get,

Rydberg’s constant, \(R=\frac{2 \pi^2 m e^4}{c h^3}\)

\(\begin{aligned}
& =\frac{2 \times(3.14)^2 \times\left(9.108 \times 10^{-28} \mathrm{~g}\right) \times\left(4.8 \times 10^{-10} \mathrm{esu}\right)^4}{\left(2.9979 \times 10^{10} \mathrm{~cm} \cdot \mathrm{s}^{-1}\right) \times\left(6.626 \times 10^{-27} \mathrm{erg} \cdot \mathrm{s}\right)_4^3} \\
& =109737 \mathrm{~cm}^{-1}
\end{aligned}\)

The experimentally measured value of Rydberg’s constant is 109677 cm-1. This value of R agrees fairly well with that ofthe calculated value.

Wavelength of radiation emitted due to electronic transition from third to second Bohr orbit: Rydberg’s equation related to the frequency ofthe spectral lines of H -atom-

\(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

R= 109677 Cm-1

The wavelength of radiation (A) emitted due to the transition of an electron of a hydrogen atom from the third orbit (n = 3) to the second orbit (n = 2) can be calculated with the help of this equation.

\(\frac{1}{\lambda}=R\left(\frac{1}{2^2}-\frac{1}{3^2}\right)\)

Since \(\bar{v}=\frac{1}{\lambda} \text { and } n_1=2, n_2=3\)

Or, \(\frac{1}{\lambda}=109677 \times\left(\frac{9-4}{36}\right)=\frac{109677 \times 5}{36} .\)

∴ \(\lambda=\frac{36}{109677 \times 5}=6564.7 \times 10^{-8} \mathrm{~cm}=6564.7 \)

As the wavelength of visible light lies between 4000-8000 A, the line spectrum appears in the visible region. It represents the Balmer series.

The ionization potential of the H-atom from Rydberg’s equation: The ionisation potential of hydrogen is defined as the energy required to transfer the electron from the first orbit (n = 1) of a hydrogen atom to an infinite distance so as to form an H+ ion.

Or, \(\frac{1}{\lambda}=\frac{2 \pi^2 m e^4}{c h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\left[ \bar{v}=\frac{1}{\lambda} \text { and } R=\frac{2 \pi^2 m e^4}{c h^3}\right]\)

Or, \(\frac{c}{\lambda}=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Or, \(v=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Since \(v=\frac{c}{\lambda}\)

Atomic Structure Fundamentals

or, \(h v=\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Or, \(\Delta E=\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

[since E =Hv]

Substituting n1 = 1 and n2 = infinite in the equation, the value of the ionization potential of a hydrogen atom can be obtained.

∴ The ionization potential of H-atom (in CGS unit)

Atomic Structure Fundamentals

\(=\frac{2 \times(3.14)^2 \times\left(9.108 \times 10^{-28}\right) \times\left(4.8 \times 10^{-10}\right)^4}{\left(6.626 \times 10^{-27}\right)^2} \times\left(\frac{1}{1^2}-\frac{1}{\infty^2}\right)\)

= 2170 x 10-14 x (1 -0) =2170 x 10-14erg-atom-1

= 2170 x 10~14 X 6.24 X 1011 eV-atom-1

= 13.6 eV-atomr1 =13.6 x 1.6022 x lO-19-atom-1

= 13.6 x 1.6022 x 10-19 x 6.022 x lO-19-mol-1

= 1312kJ-mol-1

[since 1 erg = 6.24 x 1011eV]

The ionization energy of other one-electron species is given by, \(I E=(I E)_{\mathrm{H}} \times \frac{Z^2}{n^2}, \text { where }(I E)_{\mathrm{H}}\) = Inonisation Energy Of H-atom, Z = Atmotic number,n = principal Quantum number from which the electron is removed.

Number of revolutions of an electron ptt second: Velocity of an electron revolving in the ‘n’ th orbit \(v_n=\frac{2 \pi Z e^2}{n h}\)

Perimeter of the orbit = 2nrn \(=\frac{2 \pi n^2 h^2}{4 \pi^2 m Z e^2}=\frac{n^2 h^2}{2 \pi m Z e^2}\)

∴ Number of revolutions of electron in the ‘ n ’th orbit per second= \(\begin{aligned}
& =\frac{\text { Velocity }}{\text { Perimeter }}=\frac{2 \pi Z e^2}{n h}+\frac{n^2 h^2}{2 \pi m Z e^2} \\
& =\frac{2 \pi Z e^2}{n h} \times \frac{2 \pi m Z e^2}{n^2 h^2}=\frac{4 \pi^2 m Z^2 e^4}{n^3 h^3}
\end{aligned}\)

Explanation of hydrogen spectrum by Bohr’s theory

Bohr’s theory furnishes a logical explanation of the origin ground state) of six series of spectral lines in the atomic spectrum of hydrogen.

Under ordinary conditions, the revolving electron ESS Merits Of Bohr’s atomic model in the hydrogen atom exists in the lowest energy state (n = 1 ), known as the ground state.

If energy (e.g., heat, light) is available for absorption, then the electron present in the kT-shell (n=l) absorbs the energy and moves to a higher energy level [L(n = 2), Af(n = 3), N(n = 4)…..etc.]. This state is known as the excited state.

Since in a sample of hydrogen, there are a large number of atoms, the electrons in different H-atoms absorb different amounts of energies (quanta) and are promoted to different higher energy levels viz., n = 2, 3, 4,

When the source of energy is removed, electrons jump back to any lower energy level by emitting energy (quanta) as radiations of different frequencies which give rise to different lines in the spectrum. When electrons from orbits n = 2,3,4, ••• jump back to orbit n = 1, a series of lines, known as the Lyman series is obtained.

Similarly, if electrons from higher energy levels n = 3, 4, 5, 6, . . . jump back to energy level n = 2, the Balmer series will appear in the spectrum.

In the same way, when the electrons return to the third energy level (n = 3), Paschen series, to the fourth energy level (n = 4), Brackett series, to the fifth energy level (n = 5), Pfimd series and to the sixth energy level (n = 6), Humphreys series is obtained in the spectrum. The formation of six spectral series is illustrated below.

Atomic Structure Fundamentals

Thus, it is clear that a hydrogen atom containing only one electron is capable of forming several series of lines in its atomic spectrum.

Merits Of Bohr’s atomic model

Stability of an atom: One of the main postulates of Bohr’s theory regarding the structure of an atom is that an electron while revolving in its stationary orbit does not emit any energy.

So, the electron moving continuously around the nucleus in a fixed orbit will never fall on the nucleus i.e., this postulate offers a reasonable explanation regarding the stability of an atom by eliminating the main defect of Rutherford’s nuclear model.

Line spectrum of H-atom: Bohr’s atomic model is capable of explaining the discontinuous spectra formed in different one-electron systems such as H – atoms, He+ ion, Li2+ ion, etc.

Atomic Structure Fundamentals

The radius of the first orbit of H-atom: From Bohr’s theory, it has been possible to estimate the value of the radius of the first orbit (n = 1) of a hydrogen atom.

Its value is 0.529 x 10-8 cm or 0.529 A. This value has been calculated later by other methods and found to be very close to that obtained on the basis of Bohr’s theory.

Principal quantum number: The idea of principal quantum number was first established through Bohr’s model.

Energy of an electron: Based on Bohr’s theory, the energy of an electron revolving in any quantum level can be calculated and from this, it has also been possible to estimate the energy emitted or absorbed due to the transition of an electron from one energy level to another.

Thus, the relative positions of different lines in atomic spectra can be explained.

Rydberg’s constant and its value: With the help of Bohr’s theory, mathematical expression as well as the value of Rydberg’s constant can be determined.

Limitations of Bohr’s atomic model

Spectra of atoms or ions having two or more electrons (i.e., multi-electron system) cannot be explained with the help of Bohr’s theory.

1. When spectroscopes with high resolving powers were used, it was found that each line in the spectrum was split into a number of closely spaced lines (called fine structure) which could not be explained by Bohr’s theory.
2. Bohr’s theory could not explain the splitting of spectral lines under the influence of magnetic field (Zeeman effect) or electric field (Stark effect) i.e., the formation of fine structure of atomic spectra.
3. Bohr’s atomic model is two-dimensional and hence, fails to give an idea about the actual three-dimensional electronic model of the atom.
4. According to de Broglie (1923), a tiny particle like an electron has dual character i.e., an electron has a particle as well as wave nature. Bohr treated the electron only as a particle, i.e., Bohr’s model ignored the dual character of the electron.
5. According to Bohr’s atomic model, an electron moves around the nucleus along a fixed circular path with a definite velocity.
6. However, according to Heisenberg’s uncertainty principle, it is impossible to simultaneously measure both the position and velocity (or momen- turn) of a subatomic particle-like electron with absolute accuracy at a particular instant.
7. Thus, Bohr’s theory directly contradicts Heisenberg’s uncertainty principle.

Sommerfeld’s modification Of Bohr’s Theory Idea Of Elliptical Orbits

To explain the fine structure of spectral lines in the hydrogen spectrum.

Atomic Structure Fundamentals

Sommerfeld (in 1915) extended Bohr’s theory and proposed that—

1. An electron moves around a positively charged nucleus in different elliptical orbits in addition to circular orbits.
2. When the electron moves in an elliptical orbit, the nucleus remains at one of the foci.
3. When the electron moves in a circular path, the angle of revolution changes while the distance from the nucleus remains the same.
4. However, in an elliptical motion, both the angle of revolution (or radial angle) and the distance (‘ r’ or radial distance) ofthe electron from the nucleus change.
5. In order to describe an elliptical path, Sommerfeld introduced the concept of a second quantum number, called the azimuthal quantum number, denoted by the letter ‘k’ in addition to the principal quantum number n. These two quantum numbers are related to each other by the equation,

\(\frac{n}{k}=\frac{\text { length of major axis }(a)}{\text { length of minor axis }(b)}\) \(\frac{k}{n}=\frac{b}{a}=\sqrt{1-\epsilon^2}[\epsilon=\text { eccentricity }]\)

When n = k, i.e., length ofmajor axis = length of major axis, the ellipse reduces to a circle. Thus, a circular orbit is a special case of the elliptical orbit.

For each value of n, k may have n different values. These are 1, 2, 3…, n. Thus for the Bohr orbit with n – 4, there are four Sommerfeld orbits (three elliptical orbits + one circular orbit) with k = 1, 2, 3, and 4. When k = 4, the elliptical orbit reduces to a circular orbit.

Atomic Structure Fundamentals

Sommerfeld thus introduced the concept of subshells in a principal quantum shell. The difference in energy between any two subshells is quite small.

The fine structure of the hydrogen spectrum can be explained by assuming several transitions between several subshells, each characterized by different values of k but the same value of n.

To explain the splitting of spectral lines under the influence of the electric or magnetic fields, Sommerfeld suggested that the electronic orbits may lie in different planes.

Discussion:

• Bohr’s idea of ‘electrons moving in circular ‘ orbits’ was extended by Sommerfeld by introducing the concept of elliptical orbits.
• According to Einstein’s theory of relativity, the equation expressing the relation between rest mass and mass of a moving particle is given by \(=m_0 /\left(1-\frac{v^2}{c^2}\right)^{1 / 2}\) between rest mass and mass of a moving particle is given by m- mass of the moving particle, v=velocity of the moving particle, c = velocity of light).
• According to Kepler’s law, the velocity of a body moving in an elliptical orbit is maximum at the perihelion (closest to the focus) and minimum at the aphelion (farthest from the focus).

Atomic Structure Fundamentals

• Therefore, the mass of an electron moving in an elliptical orbit is maximum at the perihelion and minimum at the aphelion.
• Consequently, the electron is compelled to deviate from its original orbit to a new and identical elliptical path that lies in the same plane. Thus, the elliptical path continues its precession slowly surrounding the nucleus.
• Due to this continuous precessional motion of the elliptical orbit, the energy of the electron undergoes a slight change depending on the position of the elliptical orbit.
• The fine structure of spectral lines observed in the atomic spectra actually originates from the slight difference in energy ofthe electron.

Merits of Sommerfeld’s modification

1. Due to the introduction of azimuthal quantum numbers, the concept of multiple elliptical orbits corresponding to the same principal quantum number came into being.
2. Due to multiple values of azimuthal quantum number for the same value of the principal quantum number, the transition of an electron can occur from one quantum level to anothor which may result in multiple lines in the spectrum. Thus the fine structure of the spectrum can be explained by Sommerfeld’s theory.
3. The subshells belonging to the same principal energy levels have different eccentricities. The more is the eccentricity of a subshell, the more is the opportunity for the electrons residing in that subshell to be closer to the nucleus. Thus, the subshell wifi possesses more penetration power and the corresponding electrons belonging to the subshell will have more power to shield the nuclear charge.

Demerits of Sommerfeld’s Modification.

1. Like Bohr’s atomic model, the atomic structure proposed by Sommerfeld is also two-dimensional in nature. this model also fails to explain the three-dimensional model of atomic structure.
2. Sommerfeld’s modification also fails to explain the spectra of multi-electron atoms.
3. The relative intensities of the fines in the spectra cannot be explained by using this theory.
4. Sommerfeld’s atomic model contradicts Heisenberg’s uncertainty principle because according to the latter, it is impossible to simultaneously determine the exact position and exact momentum of an electron.

Numerical Examples

Question 1. Calculate the energy associated with the fifth orbit of H-atom, if the energy associated with the first orbit is 2.17 x 1018J.atom-1
Answer: \(E \propto \frac{1}{n^2} \text { or } E=\frac{K}{n^2}\)

∴ \(E_1=\frac{K}{1^2}(\text { for } n=1) \text { and } E_5=\frac{K}{5^2}(\text { for } n=5)\)

∴ \(\frac{E_5}{E_1}=\frac{1}{25} \quad \text { or, } E_5=\frac{E_1}{25}=\frac{-2.17 \times 10^{-18}}{25}\)

=-8.68 x 10-2° Jatom-1

Question 2. The radius of the first orbit of the H-atom is 0.53A. Find the radius of the fifth orbit.
Answer: \(r_n=r_1 \times n^2\)

∴ \(r_5=r_1 \times 5^2=0.53 \times 25=13.25\)

Atomic Structure Fundamentals

Question 3. Will there be regular variations in the energy associated with successive principal quantum numbers of hydrogen-like atoms?
Answer: No the variation will not be regular because, energy Associated with an element with an electron in n-th Orbit, En = \(=\frac{-2 \pi^2 m Z^2 e^4}{n^2 h^2}\)

For a hydrogen-like atom, \(\frac{-2 \pi^2 m Z^2 e^4}{n^2 h^2}\) = constant

∴ \(E_n=\frac{K}{n^2}\)

∴ \(E_1=\frac{K}{1^2}, E_2=\frac{K}{2^2}, E_3=\frac{K}{3^2}, E_4=\frac{K}{4^2}, \cdots \text { etc. }\)

From the values of the energy associated with the electrons, it is clear that the variation of energy in successive principal quantum numbers of hydrogen-like atoms is not regular. in fact, the spacing between the energy levels decreases, as we move outwards from the nucleus.

Question 4. Energy associated with the n-th orldt of 11 -atom Is I ‘l (i given by the expression, \(E_n=-\frac{13.6}{n^2}\). Show that \(E_{(n+1)}-E_n=\frac{13.6 \times 2}{n^3} \mathrm{eV} \text {, when ‘ } n \text { ‘ is very large. }\)
Answer: \(E_{(n+1)}-E_n=\left[-\frac{13.6}{(n+1)^2}-\left(-\frac{13.6}{n^2}\right)\right]\)

\(=\left[\frac{13.6}{n^2}-\frac{13.6}{(n+1)^2}\right] \mathrm{eV}=\frac{13.6(2 n+1)}{n^2(n+1)^2} \mathrm{eV}\)

If the value of n is very large, then (2n + l)=2n and(n+l)=n

∴ \(E_{(n+1)}-E_n=\frac{13.6 \times 2 n}{n^2 \times n^2}=\frac{13.6 \times 2}{n^3} \mathrm{eV}\)

Question 5. If an electron Is promoted from the first orbit to the third orbit of a hydrogen atom, then by how many times will the radius of the orbit be increased?
Answer: The radius ofthe n -th orbit of H -atom \(r_n=\frac{n^2 h^2}{4 \pi^2 m e^2}\)

Radius ofthe first orbit \(\left(r_1\right)=\frac{1^2 \times h^2}{4 \pi^2 m e^2}\)

Radius of the third orbit (r3) \(=\frac{3^2 \times h^2}{4 \pi^2 m e^2}\)

∴ \(\frac{r_3}{r_1}=\frac{3^2 \times h^2}{4 \pi^2 m e^2} \times \frac{4 \pi^2 m e^2}{h^2}=9 \text { i.e., } r_3=9 \times r_1 \text {. }\)

∴ The radius ofthe orbit will be increased by 9 times

Question 6. If an electron drops from the third orbit (n = 3) to the first orbit (n = 1) of the H-atom, what will be the frequency and wavelength of the radiation emitted? What would have happened if the electron jumped from the first orbit to the third orbit?
Answer: Let the frequency of the emitted radiation be v.

Then \(v=R \times c \times\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right] \mathrm{cps}\)

\(\begin{aligned}
& =109677 \times 3 \times 10^{10} \times\left(\frac{1}{1^2}-\frac{1}{3^2}\right) \\
& =329031 \times 10^{10} \times\left(1-\frac{1}{9}\right)
\end{aligned}\)

Atomic Structure Fundamentals

Since R = 109677 cm-1 and c = 3 x 1010 em s-1]

= 3.29 X 1015 X 0.889 = 2.925 X 1015 cps.

The wavelength of the emitted radiation,

\(\lambda=\frac{c}{v}=\frac{3 \times 10^{10}}{2.925 \times 10^{15}}=1.025 \times 10^{-5} \mathrm{~cm}=1025 \mathrm{~A}\)

When an electron jumps from the 1st orbit to the 3rd orbit then energy is absorbed.

The frequency and wavelength of absorbed radiation are the same i.e., the frequency and wavelength of absorbed radiation will be 2.925 x 1015 cps and 1025A respectively.

Quantities 7. Find the wavelength (in angstrom) of the photon| emitted when an electron jumps from the second Bohr orbit to the first Bohr orbit of the hydrogen atom. The ionization potential of the hydrogen atom in its ground energy state =2.17 x 10-11 erg-atom-1
Answer: Energy of the electron in the electron in first orbit (n = 1 ) of hydrogen atom \(E_1=-\frac{2 \pi^2 m e^4}{h^2}\)

The ionization potential of hydrogen atom le., the energy required to move the electron from n = 1 energy level to an infinite distance =2.17 X 10-u erg.

∴ Energy of electron in1st (n = 1) orbit =- 2.17 x 10-11 erg

\(\text { i.e., }-\frac{2 \pi^2 m e^4}{h^2}=-2.17 \times 10^{-11}\)

=1221X10-8 cm =122lA

Since 1A = 10-8 cm]

Question 8. Determine Balmer the series wavelengths of H and H Lines in the Balmer Series [ R= 109670 Cm -1]
Answer:

For Balmer series: \(\bar{v}=\frac{1}{\lambda}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

For Balmer Series N1 =2 And For The Line Hα, n2 = 3

∴ \(\frac{1}{\lambda}=109670\left[\frac{1}{2^2}-\frac{1}{3^2}\right]=109670\left(\frac{1}{4}-\frac{1}{9}\right)\)

∴ \(\lambda=\frac{36}{109670 \times 5}=6.565 \times 10^{-5} \mathrm{~cm}\)

For the line Hβ, n2 = 4

\(\frac{1}{\lambda}=109670\left[\frac{1}{2^2}-\frac{1}{4^2}\right]=109670\left(\frac{1}{4}-\frac{1}{16}\right)\)

∴ \(\lambda=\frac{16}{109670 \times 3}=4.863 \times 10^{-5} \mathrm{~cm}\)

Atomic Structure Fundamentals

Question 9. Find the velocity of the electron revolving in the third orbit of the hydrogen atom. Also, determine the number of revolutions of the electron per second around the nucleus.
Answer: The velocity of the electron revolving in the 3rd orbit around the nucleus of the hydrogen atom,

\(v_3=\frac{2 \pi e^2}{3 \times h}=\frac{2 \times 3.14 \times\left(4.8 \times 10^{-10}\right)^2}{3 \times\left(6.627 \times 10^{-27}\right)}=7.278 \times 10^7 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

The radius of the n ’ th orbit of H-atom, rn \(=\frac{n^2 h^2}{4 \pi^2 m e^2}\)

∴ Radius ofthe third orbit (r3) \(=\frac{3^2 h^2}{4 \pi^2 m e^2}\)

\(=\frac{9 \times\left(6.627 \times 10^{-27}\right)^2}{4 \times(3.14)^2 \times\left(9.108 \times 10^{-28}\right) \times\left(4.8 \times 10^{-10}\right)^2}\)

= 4.77 x 10-8 cm [m = 9.108 X 10-28 g]

Circumference ofthe third orbit

= 27πr3 = 2 x 3.14 X 4.77 X 10-8 =2.99 X 10-7cm

Atomic Structure Fundamentals

∴ Number of revolutions of electron per second around the nucleus \(=\frac{\text { Velocity }}{\text { Circumference of the orbit }}\)

\(=\frac{7.278 \times 10^7}{2.99 \times 10^{-7}}=2.43 \times 10^{14}\)

Question 10. Prove that the velocity of an electron revolving in the 1st orbit of H-atom is nearly 10-2 times that of light.
Answer: According to Bohr’s theory, mvr \(=\frac{n h}{2 \pi}\)

The radius of‘ n ‘th orbit, r \(=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

From equations [1] and [2], we have \(\frac{n h}{2 \pi m \nu}=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

\(\text { or, } \frac{1}{v}=\frac{n h}{2 \pi \mathrm{Z} e^2} \text { or, } v=\frac{2 \pi \mathrm{Z} e^2}{n h}\)

For hydrogen atom, Z = 1 ; Hence, \(\nu=\frac{2 \pi e^2}{n h}\)

For the first orbit, n = 1 , e = 4.8 x 10-1° esu,

h = 6.627 x 10-27 erg-s

∴ The velocity of moving electron in the first orbit

\(v=\frac{2 \times 3.14 \times\left(4.8 \times 10^{-10}\right)^2}{1 \times 6.627 \times 10^{-27}}\)

= 2.183 X 108 =(2.183 X 1010) X 10-2 cm-s-1

Again, the velocity of light =3 x 1010 cm-s-1

Hence, the velocity of an electron revolving in the first orbit of the H-atom is almost 10-2 times ofthe velocity of light.

Question 11. If the energy of the first Bohr orbit is – 13.58 eV, then what will be the energy of the third Bohr orbit?
Answer: Energy of n -th Bohr-orbit of H-atom, En \(=-\frac{2 \pi^2 m e^4}{n^2 h^2}\)

∴ Energy first Bohr orbit, E1 \(=-\frac{2 \pi^2 m e^4}{1^2 \times h^2}\)

∴ Energy of third Bohr orbit, E3 \(=-\frac{2 \pi^2 m e^4}{3^2 \times h^2}\)

Hence \(\frac{E_3}{E_1}=\frac{2 \pi^2 m e^4}{9 \times h^2} \times \frac{h^2}{2 \pi^2 m e^4}=\frac{1}{9}\)

∴ \(E_3=\frac{1}{9} \times E_1=\frac{1}{9} \times(-13.58) \mathrm{eV}=-1.509 \mathrm{eV}\)

Atomic Structure Fundamentals

Question 12. The velocity of an electron revolving in a certain orbit of the H-atom is \(\frac{1}{275}\) times the velocity of light. Find the orbit in which the electron is revolving.
Answer: Let the electron is revolving in the n-th orbit.

The velocity ofthe electron in the n -th orbit, \(V_n=\frac{2 \pi Z e^2}{n h}\)

[since Z=1

e= 4.8 x 10-10 esu

h = 6.626 x 10-27 erg.s]

\(=\frac{2 \times 3.14 \times\left(4.8 \times 10^{-10}\right)^2}{n \times 6.626 \times 10^{-27}}\)

Since Z=1

e = 4.8 x 10-10 esu

Atomic Structure Fundamentals

h= 6.626 x 10-27 erg.s]

\(=\frac{2.18 \times 10^8}{n} \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

Given, the velocity of revolution of the electron

\(=\frac{1}{275} \times\left(3 \times 10^{10}\right) \mathrm{cm} \cdot \mathrm{s}^{-1}=1.09 \times 10^8 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

∴ \(\frac{2.18 \times 10^8}{n}=1.09 \times 10^8\)

or, \(n=\frac{2.18 \times 10^8}{1.09 \times 10^8}=2\)

∴ The electron is revolving in the 2nd orbit of H-atom.

Question 13. According to Bohr’s theory, the energy of an electron in n-th, \(E_n=-\frac{21.76 \times 10^{-19}}{n^2} \mathrm{~J}\) J. Find the longest Wavelength of radiation required to remove one electron from the 3rd orbit of He+ ion.
Answer: Energy of the electron in n -th orbit of H-atom,

\(E_n=-\frac{2 \pi^2 m e^4}{n^2 h^2}\)

[Since Z=1]

∴ \(-\frac{2 \pi^2 m e^4}{n^2 h^2}=-\frac{21.76 \times 10^{-19}}{n^2}=21.76 \times 10^{-19}\)

Now the energy ofthe electron in’ n ‘th orbit of He+ ion.

\(E_n^{\prime}=-\frac{2 \pi^2 Z^2 m e^4}{n^2 h^2}=-\frac{2 \pi^2 \times 2^2 \times m e^4}{n^2 h^2}\)

since Z=2.

WBCHSE Class 11 Atomic Structure Fundamentals

Therefore, E’n \(=-\frac{2 \pi^2 m e^4}{n^2 h^2} \times 4\)

∴ \(E_3=-\frac{2 \pi^2 m e^4}{3^2 \times h^2} \times 4\)

Atomic Structure Fundamentals

Removal of an electron from the 3rd orbit means a transfer of electron from the 3rd orbit to n = infinite.

∴ Energy ofthe electron at an infinite distance

\(E_{\infty}=-\frac{2 \pi^2 m e^4}{\infty^2 \times h^2} \times 4=0\)

Therefore the energy required to remove the electron,

\(\Delta E=E_{\infty}-E_3=0-\left(-\frac{2 \pi^2 m e^4}{3^2 \times h^2} \times 4\right)=\frac{2 \pi^2 m e^4}{h^2} \times \frac{4}{9}\)

∴ \(\Delta E=21.76 \times 10^{-19} \times \frac{4}{9} \mathrm{~J}\)

Since \(\frac{2 \pi^2 m e^4}{h^2}=21.76 \times 10^{-19}\)

We know, AE = \(h \times \frac{c}{\lambda}\)

\(\text { or, } \quad \frac{\left(6.627 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{\lambda}=21.76 \times 10^{-19} \times \frac{4}{9}\)

[Since h = 6.627 X 10-34 j-s and c = 3 x 108m-s-1 ]

Hence \(\lambda=\frac{9 \times\left(6.627 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{21.76 \times 10^{-19} \times 4}\)

= 2056 X IO-19 m = 2056 A

1A = 10-10 m = 20556 A

[Since 1 A = 10-10m]

Atomic Structure Fundamentals

Question 14. Calculate the energy emitted when electrons of l.Og atom of hydrogen undergo transition emitting the spectra) line of lowest energy in the visible region of Its atomic spectrum [ Itf/ = l.l x 107m-1].
Answer: The given spectral line in the visible region, corresponds to the Balmer series. For Balmer series,

\(\vec{v}=R_M\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

For Lowest Energy, n1 =2 and n2=3.

∴ \(\frac{1}{\lambda}=R_H\left[\frac{1}{2^2}-\frac{1}{3^2}\right]=1.1 \times 10^7 \times \frac{5}{36}\)

The amount of energy emitted during the transition of an electron, E = hv \(=h \times \frac{c}{\lambda}=h \times c \times \frac{1}{\lambda}\)

\(=6.626 \times 10^{-34} \times 3 \times 10^8 \times\left(1.1 \times 10^7 \times \frac{5}{36}\right)=3.037 \times 10^{-19} \mathrm{~J}\)

∴ The energy emitted when electrons of gram-atom of hydrogen undergo transition =N0 x hv

= 6.022 X 1023 X (3.037 x 10-19) J = 18.28 x 104 J = 182.8 kj

Question 15. The atomic spectrum of hydrogen contains a series of four lines having wavelengths 656.5, 486.3, 434.2, and 410.3 nm. Determine the wavelength of the next line in the same series [Rg = 109678 cm-1].
Answer: As the given wavelengths lie in the visible region, they should belong to the Balmer series. For Balmer series, nx = 2. The value of n1=2 the shortest wavelength (410.3nm) can be determined using the equation,

\(\bar{v}=\frac{1}{\lambda}=R_H\left(\frac{1}{2^2}-\frac{1}{n_2^2}\right)\)

Or, \(\frac{1}{410.3 \times 10^{-7} \mathrm{~cm}}=109678 \mathrm{~cm}^{-1}\left(\frac{1}{4}-\frac{1}{n_2^2}\right)\)

Or, \(\frac{1}{n_2^2}=\frac{1}{4}-\frac{1}{410.3 \times 10^{-7} \times 109678} \quad \text { or, } \frac{1}{n_2^2}=0.25-0.22\)

Or, \(n_2^2=\frac{1}{0.03}=33.33\)

∴ N2 =6

Atomic Structure Fundamentals

Thus, the next line is obtained as a result of the transition of an electron from n2 = 7 to = 2.

∴ \(\frac{1}{\lambda}=109678\left(\frac{1}{2^2}-\frac{1}{7^2}\right) \mathrm{cm}^{-1}=25181 \mathrm{~cm}^{-1}\)

Or, \(\lambda=\frac{1}{25181}=3.971 \times 10^{-5} \mathrm{~cm}=397.1 \mathrm{~nm}\)

Question 16. The angular momentum of an electron in a Bohr’s orbit of a hydrogen atom is 3.1655 X 10-34kgm2s-1. Calculate the wavelength of the spectral line emitted when an electron falls from this level to the next lower level.
Answer: Angular momentum of an electron in ‘n-th’ Bohr orbit of H-atom, mvr \(=\frac{n h}{2 \pi}\)

Or, \(3.1655 \times 10^{-34}=\frac{n \times 6.626 \times 10^{-34}}{2 \times 3.14}\)

\(\bar{v}=\frac{1}{\lambda}=109678\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{cm}^{-1}\) \(\begin{aligned}
& =109678\left(\frac{1}{2^2}-\frac{1}{3^2}\right) \\
& \lambda=6.564 \times 10^{-5} \mathrm{~cm}
\end{aligned}\)

Since n1 = 2, n=2=3

Atomic Structure Fundamentals

Question 17. Calculate the distance of separation between the second and third orbits of the hydrogen atom.
Answer: The radius of the n-th orbit of the H-atom is given by \(r_n=0.529 \times n^2\)

∴ r3- r2 =0.529(32-22)A =0.529 X5 =2.645 A

Question 18. After absorbing an energy of 2.044 X 10-19J, the electron of the H-atom will jump to which orbit?
Answer: The energy ofthe electron in tire n-th orbit ofH-atom is,

\(E_n=\frac{-2.18 \times 10^{-19}}{n^2} \mathrm{~J}\)

The energy of an electron in the ground state (n = 1) is Ex = -21.8 X 10-19J

If tire electron absorbs an energy of 2.044 x 10—19 J, the total energy = (-21.8 x 10~19 + 20.44 x 10~19)J =-1.36 x 10-19J

∴ \(\frac{-21.8 \times 10^{-19}}{n^2}=-1.36 \times 10^{-19} \mathrm{~J}\)

∴ \(n=\sqrt{\frac{-21.8 \times 10^{-19}}{-1.36 \times 10^{-19}}}=4\)

Thus, the electron will jump to the fourth orbit.

Atomic Structure Fundamentals

Towards The Development Of Quantum Mechanical Model Of Atom

The limitations of Bohr’s model of the atom led to the development of a new improved model for atoms. Two significant concepts that led to the formulation of such a model were:

Dual nature of matter particles, Heisenberg’s uncertainty principle.

WBCHSE Class 11 Atomic Structure Fundamentals

Dual Nature Of Matter Particles: De Broglie Theory

Both the scientists, Niels Bohr and Sommerfeld regarded electrons as negatively charged particles. However, the particle nature of the electron failed to explain some of its characteristics.

In 1905, Einstein suggested that light has a dual nature i.e., both wave nature as well as particle nature.

In 1924, French physicist, Louis de Broglie concluded that just like radiations, moving electrons or other such microscopic particles are associated with wave nature i.e., they exhibit wave nature as well as particle nature.

The wave associated with a particle is called a matter wave or de Broglie wave.

The wavelength associated with a moving particle is given by the de Broglie equation \(\lambda=\frac{h}{m v}=\frac{h}{p}\) [A = wavelength of the moving particle, m = mass of the particle, v = velocity of the particle, p = momentum of tire particle, h = Planck’s constant.] All the properties of electrons and other matter particles can be explained by its wave-particle duality.

From de Broglie equation, \(\lambda \propto \frac{1}{m v}\)

Since h=Constant i.e., wavelength \(\propto \frac{1}{\text { momentum }}\)

Thus, the wavelength of the wave associated with a fast-moving particle is inversely proportional to its momentum.

Derivation of de Broglie Equation: The de Broglie equation was derived by using Planck’s quantum theory and Einstein’s equation of grass-energy equivalency. According to Planck’s quantum theory,

\(E=h v=h \times \frac{c}{\lambda}\)

where, c = velocity of light, E = energy of a photon, v = frequency and A = wavelength.

According to Einstein’s equation, E = mC2

Atomic Structure Fundamentals

where, m = mass ofa photon, c = velocity of a photon.

From [1] and [2] we have \(\frac{h c}{\lambda}=m c^2 \text { or, } \lambda=\frac{h}{m c} \cdots[3]\) de Broglie pointed out that equation (3) can be applied to fast-moving matter particles such as electrons.

∴ \(\lambda=\frac{h}{m v}\) [m = mass & v = velocity ofthe particle]

This is de Broglie equation.

The wave associated with fast-moving matter particles is called matter wave or de Broglie wave.

This type of wave is distinctively different from electromagnetic waves.

de Broglie equation has no significance for moving particles having large mass because in such cases the wavelength of the associated wave is too small for ordinary observation.

WBCHSE Class 11 Atomic Structure Fundamentals

For example, the wavelength associated with a cricket ball of mass 200 g (0.2 kg) moving with a velocity of 1 m-s-1 is—

\(\lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34}}{0.2 \times 1} \mathrm{~m}=3.31 \times 10^{-23} \mathrm{pm}\)

Such a small value of A cannot be measured.

Application of wave nature of electrons: The concept of wave nature of electrons is used in electron microscopes to get images of particles as tiny as 10A and for studying the surface structure of solid substances.

Atomic Structure Fundamentals

Angular momentum of Bohr electron from do Broglie equation: According to de Broglie, a tiny particle like electron, revolving in a circular orbit must have wave character associated with it. Thus, for the wave (associated with the moving electron) to be completely in phase, the circumference of the orbit should be an integral multiple of the wavelength, λ.

∴ 2πλ = nλ or, λ \(=\frac{2 \pi r}{n}\)

[where, r = radius of the orbit and n = an integer] From de Broglie equation \(\lambda=\frac{h}{m v}\)

[where, m = mass of electron, v = velocity of electron.]

∴ \(\frac{2 \pi r}{n}=\frac{h}{m v} \text { or, } m v r \text { (angular momentum) }=\frac{n h}{2 \pi}\)

[where, r = radius of the orbit and n = an integer] From de Broglie Equation

\(\lambda=\frac{h}{m v}\)

This is the same relation as predicted by Bohr.

Atomic Structure Fundamentals

Circumference of the electronic orbit and the wavelength associated with the electronic motion: From Bohr’s theory, angular momentum of an electron revolving in a circular orbit is an integral multiple of \(\frac{h}{2 \pi} \text { i.e., } m v r=\frac{n h}{2 \pi}\) orbit is an integral multiple of \(\frac{h}{2 \pi} \text { i.e., } m v r=\frac{n h}{2 \pi}\)

or, \(m v=\frac{n h}{2 \pi r}\)

r = radius ofthe orbit, v = velocity ofelectron. From de Broglie equation, \(\lambda=\frac{h}{m v} \quad \text { or, } m v=\frac{h}{\lambda}\)

[where λ = wavelength associated with moving electron.]
From [1] and [2] we have, \(\frac{n h}{2 \pi r}=\frac{h}{\lambda} \quad \text { or, } 2 \pi r=n \lambda\) or, 2πr = nλ

So, the circumference of the electronic orbit is an integral multiple of the wavelengths associated with the motion of electrons.

WBCHSE Class 11 Atomic Structure Fundamentals

The kinetic energy of a moving particle and the de Broglie wavelength associated with it: Kinetic energy(E) of a particle (mass = m) moving with velocity v is given by, \(E=\frac{1}{2} m v^2 \quad \text { or, } m E=\frac{1}{2} m^2 v^2 \quad \text { or, } m v=\sqrt{2 m E} \quad \cdots[1]\)

From de Broglie equation \(\lambda=\frac{h}{m \nu} \quad \text { or, } m v=\frac{h}{\lambda} \quad \cdots[2]\)

[A = wavelength associated with the moving particle] From 1 and 2 we have

\(\frac{h}{\lambda}=\sqrt{2 m E} \text { or, } \lambda=\frac{h}{\sqrt{2 m E}} \cdots[3]\)

Calculation of de Broglie wavelength of the electron from the potential applied: Ifan accelerating potential V is applied to an electron beam, the energy acquired by each electron

= e (charge in coulomb) x V(potential in volt)

Atomic Structure Fundamentals

= eV electron-volt

This energy becomes the kinetic energy of the electron.

∴ \(\frac{1}{2} m v^2=e V \quad \text { or, } \quad v=\sqrt{\frac{2 e V}{m}}\)

Substituting the values of h, m, and e in equation [1], we get \(\lambda=\frac{1.226 \times 10^{-9}}{\sqrt{V}} \mathrm{~m}\)

In place of the electron, if any other charged particle carrying Q coulomb is accelerated under a potential difference of V volt, then kinetic energy = QV. Hence \(\lambda=\frac{h}{\sqrt{2 m Q V}}\)

Numerical Examples

Question 1. Calculate the wavelength of the de Broglie wave associated with an electron moving with a velocity of 2.05 x 107m-s-1
Answer: From de Broglie equation: \(\lambda=\frac{h}{m v}\) [where A = wavelength , m = mass ofthe electron, v = velocity of the electron, \(\lambda=\frac{6.626 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right) \times\left(2.05 \times 10^7\right)}=3.548 \times 10^{-11} \mathrm{~m}\)

Question 2. Calculate the velocity of an electron having de Broglie wavelength of 200A \(\left[m=9.11 \times 10^{-31} \mathrm{~kg}, h=6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right]\)
Answer: According to de Broglie equation, \(\lambda=\frac{h}{m v}\)

∴ \(v=\frac{h}{m \lambda}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{\left(9.11 \times 10^{-31} \mathrm{~kg}\right) \times\left(200 \times 10^{-10} \mathrm{~m}\right)}\)

= 3.64 x 104m.s-1

[Since 1A =10-10m]

Question 3. Calculate the ratio of velocities of a moving electron to that of a proton associated with the same de Broglie wavelength. [mg = 9.11 x 10-31 kg, mp = 1.67 X 10-27kg, h = 6.626 X 10-34J.S]
Answer: As given in the question, Ae = Ap

∴ \(\frac{h}{m_e \nu_e}=\frac{h}{m_p \nu_p}\)

∴ \(\frac{v_e}{v_p}=\frac{m_p}{m_e}=\frac{1.67 \times 10^{-27}}{9.11 \times 10^{-31}}=1833\)

Question 4. Calculate the momentum of the particle which has a de Broglie wavelength of O.lA
Answer: \(\lambda=\frac{h}{m v}\)

∴ \(m v=\frac{h}{\lambda}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{0.1 \times 10^{-10} \mathrm{~m}}\)

= 6.626 x 10-23 kg-m-s-1.

Since 1A= 10-10m]

Question 5. Calculate the de Broglie wavelength of a proton that is moving with a kinetic energy of 5 x 10-23J.
Answer: Mass of a proton = 1.67 x 10-27kg

Kinetic energy of a proton =5 x 10 23J

∴ \(\frac{1}{2} m v^2=5 \times 10^{-23}\)

Or, \(\frac{1}{2} \times 1.67 \times 10^{-27} \times v^2=5 \times 10^{-23}\)

∴ \(v=\left(\frac{10 \times 10^{-23}}{1.67 \times 10^{-27}}\right)^{1 / 2}=244.7 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Atomic Structure Fundamentals

∴ \(\lambda=\frac{h}{m \nu}=\frac{6.626 \times 10^{-34}}{1.67 \times 10^{-27} \times 244.7}=1.62 \times 10^{-9} \mathrm{~m}\)

∴ \(\lambda=\frac{h}{m \nu}=\frac{6.626 \times 10^{-34}}{1.67 \times 10^{-27} \times 244.7}=1.62 \times 10^{-9} \mathrm{~m}\)

WBCHSE Class 11 Atomic Structure Fundamentals

Question 6. Calculate the de Broglie wavelength of an electron moving With A speed that is 1% of the speed of light.
Answer: \(\lambda=\frac{h}{m v}=\frac{6.626 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right) \times\left(3 \times 10^8 \times \frac{1}{100}\right)}\)

Question 7. Calculate the kinetic energy of an a- -particle that has a de Broglie wavelength of 8 pm.
Answer: Mass of an a -particle \(=\frac{4 \times 10^{-3}}{6.022 \times 10^{23}} \mathrm{~kg}=6.64 \times 10^{-27} \mathrm{~kg}\)

\(\lambda=\frac{h}{m v} \text { or, } v=\frac{h}{m \lambda}=\frac{6.626 \times 10^{-34}}{\left(6.64 \times 10^{-27}\right) \times\left(8 \times 10^{-12}\right)}\)

= 1.247x104m.s-1

[since 1 pm = 10-12m]

The kinetic energy of the a -particle = 1/2 mv2

\(=\frac{1}{2} \times\left(6.64 \times 10^{-27}\right) \times\left(1.247 \times 10^4\right)^2 \mathrm{~J}=5.16 \times 10^{-19} \mathrm{~J}\)

Question 8. Calculate the de Broglie wavelength of an electron accelerating in a particle accelerator through a potential difference of 110 million volt
Answer: The kinetic energy of an electron under the potential difference of of110 million volts = llOMeV =110x 106eV

∴ \(\frac{1}{2} m v^2=110 \times 10^6 \mathrm{eV}=110 \times 10^6 \times 1.602 \times 10^{-19} \mathrm{~J}\)

or, \(\frac{1}{2} \times 9.11 \times 10^{-31} \times v^2=110 \times 10^6 \times 1.602 \times 10^{-19}\)

∴ \(v=\left(\frac{2 \times 110 \times 10^6 \times 1.602 \times 10^{-19}}{9.11 \times 10^{-31}}\right)^{1 / 2}\)

= 6.22 x 109m.s-1

∴ \(\begin{aligned}
\lambda & =\frac{h}{m v}=\frac{6.626 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right) \times\left(6.22 \times 10^9\right)} \\
& =1.17 \times 10^{-13} \mathrm{~m}
\end{aligned}\)

Question 9. Find de Broglie wavelength associated with a tennis ball of mass 60 g moving with a velocity of 10 m-s-1
Answer: de Broglie wavelength, \(\lambda=\frac{h}{m v}\)

Here, h = 6.626 x 10-34 J-s

m = 60g = 60 x 10-3 kg = 6 X 10-2 kg, v = 10 m-s.1

∴ \(\lambda=\frac{6.626 \times 10^{-34}}{6 \times 10^{-2} \times 10}=1.105 \times 10^{-33} \mathrm{~m}\)

Atomic Structure Fundamentals

Question 10. Calculate the wavelength (in nm) associated with a beam of protons moving with a velocity of 103m-s-1. [Mass of proton 1.67 x 10-27kg, h = 6.63 X 10~34 J-s]
Answer: de Broglie wavelength \(\lambda=\frac{h}{m v}\)

\(=\frac{6.63 \times 10^{-34}}{1.67 \times 10^{-27} \times 10^3} \mathrm{~m}=0.40 \times 10^{-9} \mathrm{~m}=0.40 \mathrm{~nm}\)

Question 11. Calculate the wavelength of an a -particle having an energy of 6.8×10-18J.
Answer: \(\lambda=\frac{h}{\sqrt{2 m E}}=\frac{6.626 \times 10^{-34}}{\sqrt{2 \times 6.8 \times 10^{-18} \times\left(4 \times 1.67 \times 10^{-27}\right)}}\)

= 2.198 x 10-12m

Question 12. Calculate the wavelength of the wave associated with an electron beam, if the beam is accelerated by a potential difference of 5000 volts.
Answer: Kinetic energy ofthe electron = 5000 eV

= 5000x 1.602 x 10-19J

The velocity of an electron due to the applied potential difference is vms-1. Hence, kinetic energy \(=\frac{1}{2} m v^2\)

∴ \(\frac{1}{2} m v^2=5000 \times 1.602 \times 10^{-19} \mathrm{~J}\)

= 5000 x 1.602 x 10-19Kg.m2.S-1

∴ \(v=\sqrt{\frac{2 \times 5000 \times 1.602 \times 10^{-19}}{9.11 \times 10^{-31}}}=4.193 \times 10^7 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

[since mass of electron = 9.11×10-31kg]

From de Brogile Equation , we get, \(\lambda=\frac{h}{m v}\)

⇒ \(\begin{aligned}
& =\frac{6.626 \times 10^{-34}}{9.11 \times 10^{-31} \times 4.193 \times 10^7} \\
& =0.1736 \times 10^{-10} \mathrm{~m}=0.1736
\end{aligned}\)

Atomic Structure Fundamentals

Question 13. The electron of 2 -atom in the ground state absorbs energy equal to 1.5 times the minimum energy, required to remove the electron from the hydrogen atom. Calculate the wavelength of the electron emitted, [mass of electron =9.11 X 10-31kg]
Answer: Energy required to remove an electron from the ground state of H-atom = 13.6eV. Therefore, energy absorbed by the electron of H-atom = 1.5 X 13.6eV = 20.4eV

∴ Residual energy after removal ofthe electron

= (20.4- 13.6)eV = 6.8eV = 6.8 X 1.602 x 10-19

This residual energy is converted into kinetic energy.

∴ \(\frac{1}{2} m v^2=6.8 \times 1.602 \times 10^{-19}\)

∴ \(v=\sqrt{\frac{6.8 \times 1.602 \times 10^{-19}}{9.11 \times 10^{-31}}}=1.546 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

\(\begin{aligned}
\lambda=\frac{h}{m \nu} & =\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{\left(9.11 \times 10^{-31} \mathrm{~kg}\right) \times\left(1.546 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)} \\
& =4.70 \times 10^{-10} \mathrm{~m}
\end{aligned}\)

WBCHSE Class 11 Atomic Structure Fundamentals

Question 14. Find the velocity of an electron so that its momentum is equal to that of a photon Of Wavelength 650nm.
Answer: \(\lambda=\frac{h}{p}\) [from de Broglie Equation]

∴ If the momentum of electron = momentum of a photon, then A of electron =A of photon = 650nm

Applying de Broglie equation to electron, \(\lambda=\frac{h}{p}=\frac{h}{m v}\)

Atomic Structure Fundamentals

∴ \(\begin{aligned}
v=\frac{h}{m \lambda} & =\frac{6.63 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right)\left(650 \times 10^{-9}\right)} \\
& =1118.97 \mathrm{~m} \cdot \mathrm{s}^{-1}
\end{aligned}\)

Question 15. The kinetic energy of a subatomic particle is 3.60 x 10_24J. Calculate the frequency of the corresponding particle wave.
Answer: Kinetic energy \(=\frac{1}{2} m v^2=3.60 \times 10^{-24} \mathrm{~J}\)

∴ mv2 = 2 x 3.60 x 10_24J =7.2 x 10-24J For any given wav

∴ \(=\frac{v}{v}\)

∴ \(\frac{h}{m v}=\frac{v}{v} \text { or, } v=\frac{m v^2}{h}\) \(=\frac{7.2 \times 10^{-24}}{6.626 \times 10^{-34}}=1.086 \times 10^{10} \mathrm{~s}^{-1}\)

Question 16. Calculate the mass of a photon with wavelength 3.6A.
Answer: A = 3.2A =3.2 x 10-10m Velocity ofphotons (v) = velocity of light = 3 x 108m-s

From de Broglie equation, \(\lambda=\frac{h}{m v}\)

Or, \(m=\frac{h}{\lambda v}=\frac{6.626 \times 10^{-34}}{\left(3.2 \times 10^{-10}\right) \times\left(3 \times 10^8\right)}=6.9 \times 10^{-33} \mathrm{~kg}\)

Heisenberg’s Uncertainty Principle Numerical Examples

Question 1. Calculate the uncertainty in velocity (m.s-1 ) of a moving object of mass 25 g, if the uncertainty in its position is 10-5m. [h = 6.6 x 10-34 J-s]
Answer: we, know \(\Delta x \cdot \Delta p=\frac{h}{4 \pi} \text { or, } \Delta x \cdot m \Delta v=\frac{h}{4 \pi}\)

∴ \(\Delta v=\frac{6.6 \times 10^{-34}}{4 \times 3.14 \times 10^{-5} \times 0.025}=2.099 \times 10^{-28} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Question 2. An electron has a velocity of 600m-s_1 [accuracy: 0.005%]. With what accuracy can we locate the position of this electron?[mass of an electron = 9.1 x 10-31 kg, h = 6.6 x 10-34 J-s ]
Answer: According to uncertainty principle, \(\Delta x \cdot m \Delta v=\frac{h}{4 \pi}\)

Or, \(\begin{array}{r}
\Delta x=\frac{h}{4 \pi m \Delta \nu}=\frac{6.6 \times 10^{-34}}{4 \times 3.14 \times\left(9.1 \times 10^{-31}\right) \times\left(600 \times \frac{0.005}{100}\right)} \\
\quad=\frac{6.6 \times 10^{-34}}{4 \times 3.14 \times 9.1 \times 10^{-31} \times 0.03}=1.92 \times 10^{-3} \mathrm{~m}
\end{array}\)

Atomic Structure Fundamentals

Question 3. The uncertainties in position and velocity of a particle arc 10-1° in and 5.27 x 10-24 m-s-1 respectively. Calculate the mass of the particle.
Answer: According to uncertainty principle \(\Delta x \cdot \Delta p=\frac{h}{4 \pi}\)

or, \((\Delta p)^2=\frac{h}{4 \pi}\)

[since \(\Delta x=\Delta p\)

Therefore \(\Delta p=\sqrt{\frac{h}{4 \pi}} \quad \text { or, } m \Delta v=\sqrt{\frac{h}{4 \pi}} \text { or, } \Delta v=\frac{1}{2 m} \sqrt{\frac{h}{\pi}}\)

Question 4. Calculate the uncertainty in the velocity of an electron if the uncertainty in its position is of the order ±12pm.
Answer: According to uncertainly principle, Ax -mAv -h/4n.

∴ \(\Delta v=\frac{6.626 \times 10^{-34}}{4 \times 3.14 \times\left(9.11 \times 10^{-31}\right) \times\left(12 \times 10^{-12}\right)}\)

Since \(\Delta v=\frac{6.626 \times 10^{-34}}{4 \times 3.14 \times\left(9.11 \times 10^{-31}\right) \times\left(12 \times 10^{-12}\right)}\)

= 4.82 x 106m.s-1

WBCHSE Class 11 Atomic Structure Fundamentals

Question 5. Calculate the minimum uncertainty in the position of a bullet of mass 2.5g having a probable velocity between 60,000,000 and 60,000,001 m.s-1
Answer: The maximum uncertainty in velocity,

Av =60,000,001-60,000,000 =lm-s-1

According to the uncertainty principle, Ax – mAv = h/mv

∴ \(\begin{aligned}
\Delta x=\frac{h}{4 \pi m \times \Delta v} & =\frac{6.626 \times 10^{-34}}{4 \times 3.14 \times\left(2.5 \times 10^{-3}\right) \times 1} \\
& =2.12 \times 10^{-32} \mathrm{~m}
\end{aligned}\)

Atomic Structure Fundamentals

Question 6. The uncertainty in the determination of the velocity of a dust particle (of mass O.lmg) is 4.5 X 10-20 m-s Calculate the least uncertainty in its position.
Answer: \(\Delta x \times \Delta p \frac{h}{4 \pi} \text { or, } \Delta x \times m \Delta v \frac{h}{4 \pi} \text { or, } \Delta x \frac{h}{4 \pi m \times \Delta v}\)

Least uncertainty in determining its position,

\(\begin{aligned}
\Delta x & =\frac{h}{4 \pi m \times \Delta v}=\frac{6.626 \times 10^{-5}}{4 \times 3.14 \times\left(0.1 \times 10^{-6}\right) \times\left(4.5 \times 10^{-20}\right)} \\
& =1.172 \times 10^{-8} \mathrm{~m}
\end{aligned}\)

Question 7. If uncertainties in the measurement of the position and momentum of an electron are found to be equal in magnitude, then what is the uncertainty in the measurement of velocity? Comment on the result.
Answer: According to uncertainty principle, \(\Delta x \times \Delta p=\frac{h}{2 \pi}\)

Given, Ax = Ap

∴ \((\Delta p)^2=\frac{h}{4 \pi} \text { or, } \Delta p=\sqrt{\frac{h}{4 \pi}}\)

or, \(m \Delta v=\sqrt{\frac{h}{4 \pi}}, \text { or } \Delta v=\frac{1}{m} \sqrt{\frac{h}{4 \pi}}\)

\(=\frac{1}{9.11 \times 10^{-31}} \sqrt{\frac{6.626 \times 10^{-34}}{4 \times 3.14}}=7.97 \times 10^{12} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Question 8. Calculate the product of uncertainties in the position and velocity of an electron of mass 9.1 X 10-31kg, according to Heisenberg’s uncertainty principle.
Answer: According to uncertainty principle, \(\Delta x \cdot \Delta p=\frac{h}{4 \pi}\)

Or, \(\Delta x \cdot m \Delta v=\frac{h}{4 \pi} \quad \text { or, } \Delta x \cdot \Delta v=\frac{h}{4 \pi m}\)

⇒ \(=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{4 \times 3.14 \times 9.11 \times 10^{-31} \mathrm{~kg}}=5.79 \times 10^{-5} \mathrm{~m}^2 \cdot \mathrm{s}^{-1}\)

 

Shapes Of Orbitals From Wave Function

It has been stated earlier that the three-dimensional space around the nucleus in which the probability of finding an electron is maximum is called an orbital.

In order to obtain a clear idea about the shapes of orbitals, we will first discuss the variation of—

1. The radial part of the wave function,
2. Square of the radial wave function, and
3. Radial distribution function with an increase in distance from the nucleus.

Variation Of Radial Part Of Wave Function With Distance From The Nucleus

Schrodinger wave equation for the electron in a one-electron atom (H-atom) can be solved to get different expressions for wave function \((\psi)\) for different orbitals.

The orbital wave function for an electron in an atom has no physical meaning. It is simply a mathematical function of the coordinates of the electron.

However, for different orbitals the plots of the radial part of the corresponding wave functions as a function of r (distance from the nucleus) are different. depicts such plots for Is, 2s, 2p and 3s orbitals.

Atomic Structure Fundamentals

For is -orbital, the radial part of the wave function [ψ(r) or R] decreases sharply with increasing distance, r, from the dying nucleus.

For 2s -orbital ψ (r) or R, decreases sharply in the beginning, becomes zero at a particular distance, and then becomes negative as r increases.

FM 3s-orbilal \(\psi\). decreases sharply in the Beginning with an Increase In r, becomes zero At A Particcular Distance, And Then Becomes negative. On Further Increases In \(r, \psi(r)\) again becomes zero and finally becomes positive.

For 2p -orbital if \(\psi(r)\) rises from zero to a maximum, then decreases with increasing distance (r) from the nucleus. On further increase in distance, ifr(r) approaches almost zero.

For 3p -orbital,\(\psi(r)\) rises from zero and attains a maximum value. On further increase in ψ(r) begins to decrease and becomes zero at a particular distance. Then it becomes negative with a further increase in r.

Characteristic features observed in the plots of r vs Ψ(r):

1. The radial part of the wave functions for 2s, 3s, 3p, etc. orbitals can be positive or negative depending upon the distance (r) from the nucleus. These are not related to the positive and negative charges.
2. For each orbital, the radial part of the wave function Ψ(r) approaches zero as r→∞.
3. For 2s, 3s, and 3p -orbitals, one common feature for the variation of wave function Ψ(r)) with distance is that Ψ(r) becomes zero at a finite distance from the nucleus. However, for different orbitals if Ψ(r) becomes zero at different distances Ψ(r).
4. The distance Ψ(r) at which becomes zero is called a nodal point radial node or simply node. At the nodal point, the radial wave function if Ψ(r) changes its sign from positive to negative or vice versa.
5. For different orbitals, the number of radial nodes =(n-1-1).
6. This indicates that the number of radial nodes is determined by the values of the principal quantum number ( n) and azimuthal quantum number (Z) of the orbital under consideration.

Atomic Structure Fundamentals

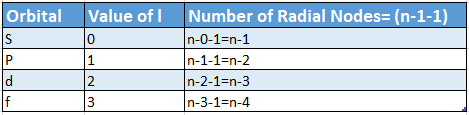
There is no relation between the positive and negative values of the wave function with the positive and negative charges.

Radial probability density [Ψ²(r) Or R²] graphs variation Of the square Of Radical Wave Function With Distance From The nucleus (r)

The square of the radial wave function, Ψ²(r) or R2 for an orbital gives the radial density.

According to the German physicist, Max Bom, the radial density, Ψ²(r) at a point gives the probability density of the electron at that point along a particular radial line.

The variation of Ψ²(r) as a function of r for different orbitals is given in the figure. The nature of these curves is different for different orbitals.

For Is -orbital, probability density is maximum near the nucleus (r≈0) and decreases sharply as we move from it.

For 2s -orbital the probability density is maximum near the nucleus (r≈0).

With increasing distance, Ψ2(r) first decreases sharply to zero and starts increasing again. After reaching a small maxima it decreases again and approaches zero as the value of r increases further.

The intermediate region (a spherical shell) where this probability density reduces to zero is called the nodal surface or simply node.

In general ns -orbital has (n- 1) nodes. Thus, the number of nodes for 2s -orbital is one, two for 3s and so on, i.e., the number of nodes increases with an increase of principal quantum number n.

Atomic Structure Fundamentals

The probability density variation for Is and 2s orbitals can be visualized in terms of charge cloud diagrams. In these diagrams, the density of the dots in a region represents the electron probability density in that region.

For 2p- Orbital Probability Density Is zero at r = 0. However, with increasing distance, it begins to increase and reaches a maximum and then decreases gradually as the distance (r) from the nucleus increases and ultimately approaches zero.

From similar plots of various orbitals, it has been found that all orbitals except s, have zero electron density at r = 0.

Radial probability distribution curve: Variation of radial distribution function (RDF) with distance from the nucleus (r)

The plot of Ψ²(r) versus r gives the probability density for the electron around the nucleus. However, in order to determine the total probability in an infinitesimally small region, we have to multiply probability density if Ψ2(r) by the volume of the region i.e., probability = Ψ²(r) x dv [where dv = volume of the region].

Since the atoms have spherical symmetry, it is more useful to discuss the probability of finding the electron in a spherical shell between the spheres of radii r and (r + dr).

The volume of such a shell of extremely small thickness, dr, is 4nr2dr. So we have, Probability = R2 x 4rrr2dr = 47tr2Ψ²(r)(r)dr [since R = Ψ²(r))].

This gives the probability of finding the electron at a particular distance (r) from the nucleus. This is called radial distribution function (RDF).

Radial distribution function (RDF) = 4πr2ψ2(r)dr

WBCHSE Class 11 Atomic Structure Fundamentals

Important information obtained from the plots of RDF vs r:

1. For all orbitals, the probability is zero at the nucleus.
2. If the point r = 0 is neglected, then it can be seen that,
3. The number of radial nodes for any orbital -n-l- 1,
4. The number of maxima (peak) for any orbital =(n-l- 1) +1 = (n-/). The peak in any curve gives the distance from the nucleus to that point where the probability of finding the electron is maximum. This is called the radius of maximum probability.
5. All the s -orbitals, except the first one (Is), have a shell-like structure, rather like an onion, or a hailstone, consisting of concentric layers of electron density. Similarly, all but the first p -p-orbital (2p) and the first dorbital (3d) have shell-like structures.
6. The first s -s-orbital (Is), first p -p-p-orbital (2p) and first orbital (3d) have two important characteristics—
7. they do not contain radial nodes and contain only one maxima.
8. Examination of the plots for Is, 2s, and 3s -orbitals shows that the most probable distance of maximum probability density increases markedly as the principal quantum number increases.
9. Furthermore, by comparing the plots for 2s and 2p, or 3s, 3p, and 3d -orbitals it is seen that the most probable radius decreases slightly as the azimuthal quantum number increases.

Shapes Of Orbitals

The angular part of the wave function, A; m(6, 0), depends on the azimuthal (/) and magnetic (m) quantum numbers but is independent ofthe principal quantum number (n).

On the other hand, the radial part of the wave function, Rn t(r), depends on the principal quantum number (n).

Thus the principal quantum number ( n) determines the size, while the azimuthal (/)and magnetic (m) quantum numbers determine the shape of an orbital.

Shape of s-orbital: From the solutions of the Schrodinger equation for s -s-orbital of H-atom, it has been known that the value of wave function ψ, or the probability of finding the electron ψ2 in space around the nucleus depends only on the distance from the nucleus but not on the direction.

Atomic Structure Fundamentals

In other words, there is an equal probability of finding the electron at a given distance in all directions Around the nucleus, i.e. ψ=f(r)

Thus all s -orbitals are spherical. For Is -orbital, RDF (the probability of finding the electron) increases as the distance from the nucleus increases and reaches a maximum value at a particular distance.

(This distance is 0.529A for the electron in the ground state of H-atom). Then this probability begins to decrease and becomes negligible at large distances.

Thus for Is -orbital, the probability of finding the electron is zero at r = 0 and also at r = oo.

Like Is -orbital, 2s -orbital is also spherical in shape.

However, 2s -orbital differs from Is -orbital in the fact that the probability of finding the electron is zero not only at r = 0 and r = ∞ but also at a particular distance between r = 0 and r – ∞.

In fact, for 2s -orbital, RDF (the probability of finding the electron) increases as the distance from the nucleus increases and reaches a maximum value. Then it begins to decrease and becomes zero at a particular distance.

The spherical shell of zero electron density is called a nodal surface or simply a node.

After crossing the nodal surface the probability of finding the electron begins to increase again and reaches a second maxima.

This second maximum represents the region of the highest electron density in a 2s orbital. This is known as an antinode.

After crossing this region of highest electron density, die probability of finding the electron again begins to decrease and approaches zero as the value of r increases further.

Thus 2s -orbital has a shell-like structure consisting of concentric layers of electron density.

3s -orbital is also spherical in shape. Its structure is similar to that of the 2s -orbital, but it differs from the 2s orbital as it has two nodal surfaces and three regions of maximum electron density.

The probability of finding the electron at the 3rd maxima is the highest and is called the antinode in a 3s -orbital.

Thus there are two nodes before the arrival of the highest probability region. These are pictorially represented in

Atomic Structure Fundamentals

Angular wave function \(\left[\mathrm{A}_{L, m}(\theta, \phi)\right]\) for s -orbital does not depend on θ and Φ.

It has non-zero values (with equal magnitude) in all possible directions. So s -orbital has no nodal plane.

Points to remember: Is, 2s, and 3s -orbitals are all spherical, but they differ from each other in the following respects—

Size and energy of ns -orbital increases as the magnitude of n increases. Thus, we have Is < 2s < 3s—.

Depending on the value of n, there are different numbers of nodes in ns -orbital. Thus, there are 0, 1, and 2 nodes for Is, 2s, and 3s -orbitals respectively.

WBCHSE Class 11 Atomic Structure Fundamentals

Shapes of ρ-orbitals: On solving the Schrodinger equation for 2p orbital of H-atom, it has been known that wave function depends on—

The distance (r) from the nucleus and also the orientation of the orbital in three-dimensional space (x, y, z).

Probability density calculation shows that each p -p-orbital consists of two sections, which are the regions of maximum electron density.

These two sections are called lobes, which are on either side ofthe plane passing through the nucleus.

The probability density of the electron is zero on this plane. It is called the nodal plane.

Atomic Structure Fundamentals

Again, the probability density of the electron is equal in both lobes, but the wave function has opposite signs in the two lobes.

Now, for p-orbitals, / = 1 and hence m = -1,0, +1. Thus there are three p-orbitals in any quantum level (except n = 1 ). The size, shape, and energy of the three p -orbitals are identical.

They differ, however, in the way the lobes are oriented. Since the lobes may be considered to lie along the three axes x, y, and z, they are assigned the designations px, py, and pz respectively.

It should be noted, however, that there is no simple relation between the values of m(-l; 0, +1) and the x, y, and z directions. The wave functions for the three p -p-orbitals are—

\(\psi_x=f(r) \cdot f(x) ; \psi_y=f(r) \cdot f(y) ; \psi_z=f(r) \cdot f(z)\)

The three p-orbitals corresponding to a particular quantum level are said to be degenerate because they have the same energy.

Thus there are three degenerate p-orbitals in each of the second n = 2, third n = 3, fourth n = 4, etc. quantum levels.

Like s -s-orbitals, p -p-orbitals increase in size and energy with an increase in the principal quantum number (n). Hence the order of increasing size and energy of various p -p-orbitals is 2p< 3p < 4p < …..

Now the number of radial nodes for 2p -orbital -n-l-l = 2-1-1 = 0. Thus 2p -orbitals [i.e., 2px, 2py, 2pz) have no radial nodes.

The number of radial nodes for p -p-orbitals of some of the higher quantum levels is given in the following table.

Atomic Structure Fundamentals

For px -orbital probability density is zero in the yz -plane. So yz -plane is the nodal plane of px -orbital. Similarly zx and xy -planes are the nodal planes for py and pz orbitals respectively.

It should be remembered that the number of nodal planes for any orbital is equal to the value of azimuthal quantum number l corresponding to that orbital.

The number of nodal planes is, however independent of the principal quantum number ‘ n ‘. The no. of nodal planes for s, p, d, and /-orbitals (belonging to any principal quantum level) are 0, 1, 2, and 3 respectively.

Shapes of d-orbitals: From solutions of the Schrodinger wave equation for 3d -orbitals of H-atom it has been known that the wave function depends on the distance from the nucleus (r) and also on two different directions in space, for example— \f/ = /(r)-/(x)-/(y) Now, for 3d -orbital, 1 = 2. Hence m = -2, -1, 0, +1, +2.

Thus there are five d -d-orbitals in the 3rd quantum level.

Atomic Structure Fundamentals

These d -d-orbitals have the same energy and hence they are degenerate. These orbitals are designated as dxydyzdzx>dx2-y2 and dz2- Probability density calculation shows that the orientations of these orbitals in space are different.

The shapes of the first four d -d-orbitals are similar to each other (which has four lobes) whereas that ofthe fifth dz2 is different (which has only two lobes).

The d -orbitals for which n is greater than three {viz., 4d, 5d, etc.) also have shapes similar to 3d -orbitals, but they differ in energy and size.

dxy -orbital has four lobes, lying in the xy -plane. The hatch lobe makes an angle of 45° with x and y-axes.

WBCHSE Class 11 Atomic Structure Fundamentals

The wave function for d -orbital has the same sign (either + or – ) in each pair of opposite lobes, but opposite signs (+ and – ) I in adjacent lobes, relating to the symmetry of the angular wave function.

The wave function if =0 along the x, y, and z axes indicates that the xz – and yz – planes represent the nodal planes of the d -orbital.

These planes are at right angles with each other. Similarly, dyz -the orbital has four lobes lying in the yz -plane, each lobe makes an angle of 45° with the y and z axes.

Atomic Structure Fundamentals

The wave function dxy =0 along the three axes (x, y, and z) indicates that the xy and xz planes constitute the nodal planes of dyz -orbital. The planes are at right angles with each other.

Similarly, dxz -the orbital has four lobes lying in the xz-plane, each lobe makes an angle of 45° with x and z-axes. The wave function ifrd =0 along the three axes (x, y and z), indicates that xy and yz -planes constitute the nodal planes of dxz -orbital. These planes are at right angles with each other.

dx2-y2 -orbital has four lobes which lie along the x and y axes in the xy -plane. The wave function xy = ψ ax2-y2 along the z-axis indicates that this orbital has two nodal planes that pass through the origin and make angles of 45° with xz and yz -planes. These two planes are at right angles with each other.

dz² -orbital has two lobes (having the same sign which lie along the z-axis and contain an annular portion surrounding the nucleus in the xy-plane. This annular portion of the orbital is called the doughnut or belly band.

A conical surface passing through the origin constitutes the nodal plane of the dz2 -orbital.

Atomic Structure Fundamentals

F-Orbitals Schrodinger wave equation gives a set of solutions when the azimuthal quantum number f has the value 3. These are called f-orbitals. For l = 3, m has the values -3, -2, -1, 0, +1, +2, +3. Thus there are seven /-orbitals.

For the existence of f-orbitals, the minimum value of the principal quantum number, n, has to be 4, as the value of l cannot be greater than (n-l).

These seven orbitals have the same energy (degenerate) but they differ in their orientations in space. The seven f-orbitals are designated.

\(\text { as }-f_{x\left(x^2-y^2\right)}, f_{y\left(x^2-y^2\right)}, f_{z\left(x^2-y^2\right)}, f_{x y z}, f_{z^3}, f_{y z^2}, f_{x z^2} \text {. }\)

1. No. spherical/radial nodes in any orbital = n-l- 1
2. No. of planar or angular nodes in any orbital = Z
3. Total no. of nodes in any orbital = n-1

Rules For Filling Up Of Electrons In Different Orbitals

The correct ground state electronic configuration of an atom is obtained on the basis of the following principles—Pauli’s exclusion principle, Hund’s rule, and the Aufbau principle.

Pauli’s exclusion principle

Principle: The knowledge of four quantum numbers is important in assigning the exact location of the electron within an atom.

After meticulous study of the line spectra of atoms, Wolfgang Pauli in 1925 proposed his exclusion principle which is widely known as Pauli’s exclusion principle.

According to this principle, no two electrons in an atom will have the same values for all four quantum numbers (n, l, m, and s).

If three of the quantum numbers of any two electrons are the same then they must differ in their fourth quantum number.

Atomic Structure Fundamentals

If the quantum numbers n, l, and m of two electrons have identical values, then the value of s should be different (+i for one and for the other).

Therefore, the corollary of this principle may be stated as—each orbital can accommodate a maximum of two electrons having an opposite spin.

With the help of Pauli’s exclusion principle, the maximum number of electrons a subshell can accommodate can be calculated. For example—

s -subshell: In the case of s -subshell, 1 = 0. Therefore m = 0. Number of orbitals in s -subshell = 1.

According to Pauli’s exclusion principle, each orbital can hold a maximum number of two electrons. So, s -subshell can accommodate a maximum of 2 electrons.

p -subshell: For p -subshell, 1=1 and m = —1,0, +1. The number of orbitals in the -subshell is three (px, py, and pz ).

According to Pauli’s exclusion principle, since each orbital can hold a maximum of 2 electrons, the maximum accommodating capacity of p -subshell {i.e., three p orbitals) =3×2 = 6 electrons.

d -subshell: In the case of d -subshell, 1 = 2, m = -2, -1, 0 +1, +2. Thus, m has 5 values indicating the presence of 5 orbitals. As the maximum number of electrons that each orbital can hold is 2, the maximum number of electrons that a d -d-subshell can accommodate is 5 X 2 = 10.

f-subshell: For /-subshell, l = 3, m = -3, -2, -1, 0, +1, +2, +3. Seven values of m indicate the presence of seven orbitals. Hence the maximum number of electrons that may be present in /-subshell is 7 x 2 = 14 .

WBCHSE Class 11 Atomic Structure Fundamentals

Pauli’s exclusion principle also permits the determination of the maximum number of electrons that can be present in a certain orbit or shell.

Example: For L -shell (n = 2), l has two values, i.e., 1 = 0 [ssubshell] and l = 1 [p -subshell].

The s -subshell can hold 2 electrons and p -subshell can accommodate 6 electrons. Therefore, the maximum accommodating capacity for L shell =(2 + 6) = 8 electrons.

Similarly, it can be shown that, the maximum number of electrons that can be accommodated in M-shell (n = 3) = 18 and the maximum number of electrons that may be present in IVshell (n = 4) =32.

Atomic Structure Fundamentals

Electron accommodating capacity of K, L, M, and JV-shell

Thus, it is seen that the maximum number of electrons accommodated in any electronic orbit with the principal quantum number’ n’ is 2n2.

Number of orbitals and electron accommodating capacity of different shells.

Hund’s multiplicity rule

This rule is helpful for deciding the mode of filling of the orbitals ofthe same energy level with electrons.

Rule: The pairing of electrons in the orbitals within the same subshell does not take place until the orbitals are singly filled up with electrons having parallel spin.

Discussion: The rule implies that orbitals with the same energy are filled up first with one electron and then the additional electron occupies the singly filled orbital orbital to form paired electrons (with opposite spin).

The energy order of the orbitals, the Aufbau principle, and the electronic configuration of atoms

Atomic Structure Fundamentals

The German word ‘Aufbau’ means ‘to build one by one! The Aufbau principle gives the sequence of gradual filling up of the different subshells of multi-electron atoms.

Aufbau principle:

Aufbau principle states that electrons are added progressively to the various orbitals in the order of increasing energy, starting with the orbital with the lowest energy.

Electrons never occupy the die orbital of higher energy leaving the orbital of lower energy vacant.

A study of the results of spectral analysis has led to the arrangement of the shells and subshell in the increasing order of their energies in the following sequence:

Is < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f< Sd < 6p < 7s < 5f< 6d ..

Electronic configuration always conforms to Pauli’s Exclusion Principle.

According to Hund’s rule, pairing of electrons in the orbitals within the same subshell (degenerate orbitals hating the same n ) cannot occur until the orbitals are singly filled up.

The energy of the subshell increases with an increase in the value of {n + l). In a multi-electron atom, the energy of a subshell, cannot be determined only by principal quantum number (n ), in exclusion of azimuthal quantum number (Z).

The correct order of energies of various subshells is determined by the (n + 1) rule or Bohr-Bury rule.

Atomic Structure Fundamentals

The implication of the rule can be better understood with the help ofthe following example.

In case of 3d -subshell, (n + Z) = (3 + 2) = 5, but for 4s -subshell, (n + Z) = (4 + 0) = 4 .

From this, it is clear that the energy of the 4s -subshell is less than that of the 3d -subshell. Hence, the electron goes to the 4s subshell first, in preference to the 3d -subshell.

If Two subshells have the same value for{n + l), then the electron enters that subshell which has a lower value of n.

For example, for 3d -subshell, {n + l) = (3 + 2) = 5 and for 4p -subshell, {n + l) = (4 + 1) = 5 In this case, the electron first enters the 3d -subshell which has a.lower value of n.

The sequence in which the subshells are filled with electrons.

Atomic Structure Fundamentals

The figure depicts the sequence of filling up of the subshells with electrons. The electronic configuration of any atom can be easily predicted from this diagram.

Exceptions to (n+1) rule: Exceptions to the {n + Z) rule are found to occur in the case of filling up of electrons in Lanthanum (La) and Actinium (Ac).

The values of {n + l) in the case of both the subshells 4/ and 5d (4 + 3 = 7 = 5 + 2) are found to be the same.

Similarly the values of (n +1) in the case of both the subshells 5/ and 6d (5 + 3 = 8 = 6 + 2) are equal. So, the order of energies of these subshells is 4/< 5d and 5/< 6d.

According to the (n + Z) rule, the expected electronic configuration of La (57) and Ac (89) should be [Xe]4/15d06s2 and [Rn]5/16d°7s2 respectively.

However, the electronic configuration of La and Ac are actually [Xe]4/ and [Rn]5/°6d17s2 respectively. In other words, lanthanum and actinium are exceptions to the (n + l) rule.

Method of writing electronic configuration of an atom 1) In order to express the electronic configuration of an atom, the principal quantum number (n = 1, 2, 3… etc.) is written first.

The symbol ofthe subsheU(s, p, d, f, etc.) is written to the right ofthe principal quantum number. For example, s -subshell of the first shell is expressed as Is; sand subshells of the second shell are expressed as 2s and 2p respectively.

Atomic Structure Fundamentals

The total number of electrons present in any subshell is then written as the right superscript of the subshell symbol.

For example, the electronic configuration, ls22s22p5 suggests that the s -subshell of the first shell contains 2 electrons, and the s, and p -subshells of the second shell contain 2 electrons and 5 electrons respectively. Thus, the total number of electrons present is equal to 9.

Examples: Electronic configuration of 17 CL atom: The atomic number of chlorine is 17. Number of electrons present in chlorine atom is 17.

Out of these 17 electrons, 2 electrons are present in the s -subshell of first shell (K-shell), 2 electrons and 6 electrons in the s – and p -subshell of the second shell (L -shell) respectively, and 2 and 5 electrons are present in the s – and p -subshell of the third shell (Mshell) respectively.

Thus, the electronic configuration of the chlorine atom is ls²2s²2p63s²3p5.

Electronic configuration of 26Fe atom: The atomic number of iron is 26. Number of electrons present in an atom of iron is 26. These 26 electrons are distributed in K, L, M, and N-shells in such a way that their electronic configuration becomes ls22s22p63s23pe3de4s2.

Here the symbol signifies an orbital and the arrow sign (↑) means an odd electron and the paired arrow sign (↓↑) stands for a pair of electrons with opposite spins.

Stability of half-filled or completely filled subshells The electronic configurations of some atoms have certain characteristic features.

It is seen that half-filled and completely filled subshells are more stable compared to nearly half-filled or nearly completely filled subshells.

Atomic Structure Fundamentals

Hence, if the (n-1)d -subshell of any atom contains 4 or 9 electrons and the ns -subshell contains 2 electrons, then one electron from the ns -subshell gets shifted to the (n-1) d subshell, thereby making a total number of either 5 or 10 electrons in it. As a result, ns -subshell is left with 1 electron instead of 2.

The extra stability of half-filled and completely filled subshells can be explained in terms of the symmetrical distribution of electrons and exchange energy.

Symmetrical distribution of electrons: The subshells with half-filled or completely filled electrons are found to have a more symmetrical distribution of electrons.

Consequently, they have lower energy which ultimately results in greater stability of the electronic configuration.

Atomic Structure Fundamentals

Electrons present in the same subshell have equal energy but their spatial distribution is different. As a result, the magnitude of the shielding effect of another is quite small and so, the electrons are more strongly attracted by the nucleus.

Interelectronic repulsion: Two types of interactions are possible between electrons of the same subshell due to interelectronic repulsive force.

Interaction due to electronic charge: The magnitude of the repulsive force acting between two electrons situated at n distance r from each other is inversely proportional to the square of the distance between them.

Atomic Structure Fundamentals

Consequently, the stability of two-electron or multi-electron ions or atoms increases with an increase in distance r. Thus, die two electrons present in the d -d-subshell prefer to be in two separate d -orbitals instead of one leading to the increased stability ofthe atom or ion.

Interaction due to rotation of electrons: Two electrons tend to remain close to each other if they have opposite spins. On the other hand, if both the electrons have parallel spin, then they prefer to remain far from each other.

The electrons occupying degenerate orbitals (orbitals of the same energy) can exchange their positions with other electrons with the same spin. In this process, exchange energy is released.

The greater the probability of exchange, the more stable the configuration. The probability of exchange is greater in the case of a half-filled or completely filled subshell.

Thus, the magnitude of exchange energy is greatest for half-filled or completely filled subshells leading to their exceptionally high stability.

This exchange energy forms the basis of Hund’s multiplicity rule. The relative magnitude of exchange energy can be calculated by the formula,

No. of exchanges \(=\frac{n !}{2 \times(n-2) !}\)

(n = number of degenerate electrons with parallel spin.)

Number of interactions in case of d4 electronic configuration

Atomic Structure Fundamentals

Total number of exchanges for d4 electronic configuration

=3+2+1=6

Number of interactions in case of d5 electronic configuration

Atomic Structure Fundamentals

Electronic configuration of ions

When an additional electron is added to an orbital of an atom, a negatively charged ion called an anion is formed while the removal of an electron from the orbital of an atom produces a positively charged ion called cation.

Electronic configuration of anions: The total number of electrons present in an anionic species is = (Z + n) where Z = atomic number and n = number of electrons gained. The electronic configuration ofthe anion is written on the basis of the total number of electrons present in it.

Examples: Fluoride ion (F-): Total number of electrons present in F- ion = (9 + 1) = 10

∴ Electronic configuration of F- ion: ls²2s²2p6

Nitride ion (N³¯ ): Total number of electrons present
in N3- ion = (7 + 3) = 10

Electronic configuration of N3- ion: ls22s22p6

Oxide ion (O²¯): Total number of electrons present in  O²¯ ion =(8 + 2) = 10.

Atomic Structure Fundamentals

∴ Electronic configuration of O2- ion: ls22s22p6

Sulphide Ion (S²¯) : Total number ofelectrons present in S2- ion =(1.6 + 2) = 18

Electronic Configuration of cations:

A total number of electrons present in a cationic species = (Z-n) where Z = atomic number and n = number of electrons lost.

For writing the electronic configuration of the cation, the electronic configuration of the neutral atom is written first.

Then requisite no. of electrons is removed from the outermost shell. Electrons from the ns -subshell should be removed before removing any electron from the (n- l)d -subshell.

The total number of electrons present in a cationic species = (Z-n) where Z = atomic number and n = number of electrons lost.

For writing the electronic configuration of the cation, the electronic configuration of the neutral atom is written first.

Then requisite no. of electrons is removed from the outermost shell. Electrons from the ns -subshell should be removed before removing any electron from the (n- l)d -subshell.

Atomic Structure Fundamentals

Examples:

Sodium ion (Na+) : Electronic configuration of \({ }_{11} \mathrm{Na}: 1 s^2 2 s^2 2 p^6 3 s^1 \text {. So, } \mathrm{Na}^{+} \text {lon: } 1 s^2 2 s^2 2 p^6\)

2. Chromium Ion (Cr3+): Electronic Configuration of

\({ }_{24} \mathrm{Cr}: 1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^5 4 s^1\)

⇒ \(\mathbf{C r}^{3+} \text { ion: } 1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^3\)

Manganese ion (Mn2+): Electronic configuration of:

Mn2+ ion: 1s22s22p63s2363d5

Ferrous (Fez+) and Ferric (Fe3+) ion: Electronic

Configuration of 26Pe: ls22s2263sz3763d64s2

Ferrous ion (Fe2+): ls22s22p63s23p63d6

Similarly, ferric ion (Fe3+): ls22s22/763s23/?63d5

Cuprous (Cu+) and Cupric (Cu2+) ion: Electronic configuration of 2gCu: ls²2s²2p63s23p63dl04s1

Cu+ ion: ls22s22/763s23/763d10

Atomic Structure Fundamentals

similarly, cupric ion (Cu2+): 1s²2s22p63s23p63d9

Orbital angular momentum of electron = Jl(l + 1) x ( l = azimuthal quantum number).

Molecules, atoms, or ions containing one or more unpaired electrons exhibit paramagnetic properties. Paramagnetic substances are attracted by the magnetic field.

The magnetic moment of paramagnetic substances depends on the number of unpaired electrons.

Magnetic moment = Jx(x + 2) BM BM = Bohr Magneton (unit of magnetic moment) x = Number of impaired electrons.

Molecules, atoms, or ions containing an even number of electrons exhibit diamagnetic properties. Diamagnetic substances are repelled by the magnetic field.

Question 1. How will you prove that electrons are negatively charged particles with a definite mass?
Answer: Under the influence of an electric field the cathode rays as well as the electron beam, are deflected towards the positive plate of the electric field. Cathode rays also neutralise the gold leaf ‘ electroscope, charged with positive electricity.

Thus it can be proved that electrons are negatively charged. A light paddle wheel placed in the path of cathode rays, begins to rotate, showing that cathode rays are made of matter particles.

Question 2. Calculate the number of particles present in 0.1 g electron.
Answer: Number of elctrons

\(\begin{aligned}
& =\frac{\text { Total mass of electrons }}{\text { Mass of Celestron }} \\
& =\frac{0.1 \mathrm{~g}}{9.11 \times 10^{-28} \mathrm{~g}} \text {-2w1.0977 } \times 10^{26}
\end{aligned}\)

Atomic Structure Fundamentals

Question 3. Calculate the mass of 1 mol electron.
Answer: Mass = Avogrado number x Mass of one electron

= (6.022 X 1023) x (9.11 X lO-28) = 0.5486 mg

Question 4. Explain why cathode rays are produced only at very low pressure of gas inside the discharge tube-
Answer: Gases being had conductor do not allow electricity to pass through them In discharge tube at high pressure.

Question 5. Mention two uses of cathode ray tubes in our daily life.
Answer: Television picture tube and fluorescent tube.

Question 5. Calculate the charge of 1 mol electron.
Answer: Charge Avogrado no, x Charge of 1 electron

a (6.022 X 1023) X (1,602 X 10-19) =9.047 X 104C

Question 6. What happens when high-velocity cathode rays strike a tungsten foil?
Answer: X-rays are emitted.

Question 7. The charge-to-mass ratio of an electron is 1836 times greater than that ofa proton. Establish a mathematical relation to compare their masses.
Answer: Given \(\frac{e}{m_e}=1836 \times \frac{e}{m_p}\) However the charge on 1 electron Is the same as that of 1 proton

\(\frac{1}{m_e}=\frac{1836}{m_p}\)

or, m2 = 1036 x me.

Question 8. Two discharge tubes containing H2 and 02 gas respectively are subjected to electrical discharge at low pressure. Will there be any difference in the nature of cathode rays and anode formed inside the tube?
Answer: In both cases, cathode rays with identical properties
are produced, because these rays are independent of the nature of the material of the cathode and the gas used in the discharge tube.

However, in these two cases, anode rays with different properties are produced since these rays depend on the nature of the gas used in the discharge tube.

Question 9. A discharge tube containing H2 gas at low pressure is subjected to high voltage. Will there be er Ission of protons from the anode?
Answer: In a discharge tube, anode rays are not emitted from the anode. Therefore protons are not emitted from the anode. However, they are produced from H2gas, by the knockout of the electrons by high-speed cathode rays.

Question 10. Explain the generation ofthe positively charged particles in
the discharge tube when hydrogen gas is used.
Answer: Due to the high voltage in the discharge tube, H2 and D2 are dissociated into H and D atoms.

Atomic Structure Fundamentals

Due to the knockout of electrons from atoms or molecules present in the discharge tube by cathode rays, H£, DJ, H+ and D+ ions are produced.

Similarly, HD+ ions are also produced by the knockout of electrons from a few HD molecules (produced by a combination of H and D atoms)

Question 11. How many protons will be needed to fill a spherical vessel of volume 10cm3? Also, calculate the mass ofthese protons.
Answer: Volume of proton \(=\frac{4}{3} \pi r^3=\frac{4}{3} \times 3.14 \times\left(1.2 \times 10^{-13}\right)^3 \mathrm{~cm}^3\)

\(\begin{aligned}
& \text { Number of protons }=\frac{\text { Volume of a sphere }}{\text { Volume of a proton }} \\
& =\frac{10}{\frac{4}{3} \times 3.14 \times\left(1.2 \times 10^{-13}\right)^3}=1.382 \times 10^{39}
\end{aligned}\)

Mass of protons = No. of protons x Mass of a proton

= (1.382 x to39) X (1.6725 X 10-24)g =2.311 x lO15g.

Atomic Structure Fundamentals

Question 12. Why was it necessary to consider the existence of neutrons in the nucleus of an atom?
Answer: The actual mass of an atom of an element, except hydrogen, Is greater than the sum of the masses of protons and electrons present in that atom. Hence, Rutherford in 1920, proposed the existence of an uncharged particle in an atom having unit mass. This particle was called the neutron.

Question 13. Who discovered the neutron?
Answer: J. Chadwick (1932).

Question 14. Between proton or neutron which one is heavier?
Answer: Neutron (1.675 x 10_24g) is slightly heavier than proton (1.6725 X 10-24g).

Question 15. Write the nuclear reaction for the emission of neutrons. Indicate the e/m value of the neutron.
Answer: When beryllium foil is bombarded with or -particles, it undergoes a nuclear reaction which primarily leads to the emission of chargeless particles called the neutron.

\({ }_4^9 \mathrm{Be}+{ }_2^4 \mathrm{He} \longrightarrow{ }_6^{12} \mathrm{C}+{ }_0^1 n\)

Question 16. Mention the symbol, charge and names of the discoverers
of positron, -meson and neutrino.
Answer: When beryllium foil is bombarded with or -particles, it undergoes a nuclear reaction which primarily leads to the emission of chargeless particles called neutrons.

Question 17. Name the experiment that helps us to determine the number of protons in the nucleus of an atom.
Answer: Moseley’s experiment on X-rays

Question 18. What is the nuclear model of the atom?
Answer: The atomic model which describes the rotation of electrons in different orbitals around the positively charged nucleus is called the nuclear model of the atom.

Question 19. Indicate the conclusions drawn by Rutherford from his particle scattering experiment.
Answer:

Question 20. Explain why Rutherford did not mention the presence of neutrons in the proposed nuclear model of the atom.
Answer: In the year 1911, when Rutherford proposed the nuclear model of the atom, the existence of neutrons was still not known (In fact, neutrons were discovered in 1932). Hence, Rutherford did not mention the presence of neutrons.

Question 21. From this experiment, it was concluded that the entire mass and positive ‘charge is present at the centre of an atom.
Answer: From Rutherford’s -particle scattering experiment, it was concluded that the entire mass and positive charge are present at the centre of an atom.

Question 22. What is the relation between Cl and S2?
Answer: Both have 18 electrons and hence, are isoelectronic

Atomic Structure Fundamentals

Question 23. Identify the isotopes and isobars from the following list of atoms with a given number of protons and neutrons.
Answer: A and B have the same number of protons but different numbers of neutrons. Hence, A and B are isotopes. C and D have different numbers of protons, but the sum of the protons and neutrons, in both cases, are the same. Hence, C and D are isobars.

Question 24. An element has an isotope with a mass number of 14. It contains 8 neutrons. Identify the element.
Answer: Mass number = No. of protons+ No. of neutrons.

Number of protons =14-8 =6

The atomic number ofthe element = 6, which means,

the element is ‘Carbon’.

Question 25. Identify the relation between the nuclides, 38Si & 3gP.
Answer: The number of neutrons in the nuclides is the same. Thus, they are isotones.

Question 26. A cation M3+ has 23 electrons. Find the atomic no. ofM.
Answer: Number of electrons present in the neutral M-atom.

Question 27. Find the total number of electrons present in l mol methane.
Answer: 1 methane (CH4) molecules 1 C-atom + 4 H- atoms Number of electrons in 1 CH4 molecule =1 X 6 + 4 X 1 = 10. Therefore, the total number of electrons in lmol of CH4 = 6.022 X 1023 X 10 = 6.022 X 1024.

Question 28. The mass number of an ion with a unit negative charge is 37. The number of neutrons present in the ion is 10.6% more than that of electrons. Identify the ion.
Answer: Let the number of protons in the ion = x. Therefore, the number of electrons =x + 1 (y the ion contains a unit negative charge). Thus, the number of neutrons =37-x.

Number of neutrons Number of electrons

=37-x-(x + 1) =36-2x

Percent of excess neutrons as compared to electrons
_ (36- 2x) x 100 x+1

Given, l3i–2.*)x 10Q = io.6
x + 1
or
36 -2x _ 106
‘ x+1 1000
or, x = 17.04=17 [v the number of protons present in
an atom or an ion cannot be a fraction]
Hence it is a chloride ion (Cl-)

Atomic Structure Fundamentals

Question 29. What are electromagnetic radiations? What is their velocity in a vacuum?
Answer: Electromagnetic waves with wavelength ranging between 0.003-0.3m are known as microwaves. As these waves collectively travel in the same direction over a long distance, they are used in radars.

Question 30. State the principle of the formation of electromagnetic radiation.
Answer: Electromagnetic waves with wavelength ranging between 0.003-0.3m are known as microwaves. As these waves collectively travel in the same direction over a long distance, they are used in radars.

Question 31. What are microwaves? Why are they used in radars?
Answer: Electromagnetic waves with wavelength ranging between 0.003-0.3m is known as microwaves.

As these waves collectively travel in the same direction over a long distance, they are used in radars.

Question 32. Arrange the various types of radiations constituting the electromagnetic spectrum, in the decreasing order of their frequencies.
Answer: The various radiations in the electromagnetic spectrum in decreasing order of their frequencies are as follows:

Cosmic rays > y-rays> X-rays> UV-rays > visible rays > microwaves > radio waves.

Question 33. Arrange the following radiations in the order of their increasing frequencies—
Answer:

The amber light of traffic signals, -2

FM radio waves,-1

X-rays-3

Cosmic rays-4

Question 34. How would you increase the strength of photoelectric current?
Answer: The strength of the photoelectric current can be increased by increasing the intensity ofthe incident radiations.

Question 35. How are the following affected by the increase in intensity ofthe incident light?

1. Threshold frequency,
2. The kinetic energy of the emitted electrons,
3. Strength photoelectric current.

Atomic Structure Fundamentals

Answer: No effect

1. Remains the same
2. Increases.

Question 36. Mention any three phenomena that can be explained with the help of the wave theory of light.
Answer: Interference, diffraction, polarisation.

Question 37. What is black body radiation Out of red and blue light, which one is associated with photons possessing higher energy?
Answer: Blue light has a higher frequency (v) than red light. The energy of each photon = hv. Consequently, the photons associated with blue light have higher energy.

Question 38. Differentiate between a quantum and a photon.
Answer: The smallest packet of energy of any electromagnetic radiation is quantum and that of light is called a photon.

Question 39. Energy associated with X-rays is higher than that of visible light— explain.
Answer: The energy of electromagnetic radiation refers to the
energy of its photons (hv).

Since, vx-ray > vvisible light -hence, hvx-ray > hv visible light Thus, the energy of X-rays is higher than that of visible light.

Question 40. Which property of electromagnetic radiation is useful in explaining the phenomena involving energy transfer?
Answer: Particle nature of electromagnetic radiation

Question 41. Give examples of the production of— Photons from electrons Electronsfrom photons.
Answer: When high-velocity electrons (cathode rays) strike the surface of hard metals like tungsten, platinum, etc., Xrays are produced.

When a light of suitable frequency or any other electromagnetic radiation strikes a metal surface, electrons are ejected from it.

Question 42. Mention die factors affecting the kinetic energy of the photoelectrons. Does the maximum kinetic energy depend on the intensity of light?
Answer: Frequency of the incident radiation and

Work function ofthe metal.

Maximum kinetic energy does not depend on the intensity ofthe incident light.

Question 43. Why does the photoelectric work function differently for different metals?
Answer: Electrons in a metal are delocalised and move freely throughout the crystal lattice of the metal.

Hence each electron has to do some work to overcome the force of attraction of the metal ions.

The amount of energy required to eject the electrons (known as work function) depends on the metal. Hence, different metals have different work functions.

Question 44. Explain— ‘The role of threshold frequency in photoelectric effect is in agreement with the particle nature of light and in disagreement with the wave nature of light’
Answer: According to the wave theory of light, the photoelectric effect can occur by increasing the intensity of the incident light. However, according to particle theory, there is a minimum frequency (threshold frequency), for each metal below which, the photoelectric effect is not possible (no matter how high the intensity of light).

Atomic Structure Fundamentals

It has been experimentally proved that the photoelectric effect depends on the frequency of the incident light but not on its intensity. The threshold frequency of each metal is unique.

Hence photoelectric effect can be successfully explained with the help of the particle nature of light.

Question 45. An electron beam hitting a ZnS screen produces scintillations on it What do you conclude?
Answer: From this phenomenon, we can conclude that electrons have a particle nature.

Question 46. An electron beam after hitting a nickel crystal produces a diffraction pattern. What do you conclude?
Answer: From this phenomenon, we can conclude that electrons have a particle nature.

Question 47. Mention the property of electromagnetic radiation (wave nature or particle nature or both) that can best explain the following phenomena—

1. Photoelectric effect
2. Interference
3. Black body radiation
4. Diffraction
5. Einstein’sequation (e = hv)
6. Planck’s equation{e – me2).

Answer:

1. Particle nature
2. Wave nature
3. Particle nature
4. Wave nature
5. Both wave and particle nature
6. Particle nature

Question 48. Give two examples of the particle nature of electromagnetic radiation.
Answer: When light of a suitable frequency strikes a metal, photoelectrons are ejected from its surface. This phenomenon (of photoelectric effect) supports the particle nature of electromagnetic radiation.

The phenomenon of black body radiation also supports the particle nature of electromagnetic radiation.

Question 49. What type of spectrum will be obtained if the electron o/Hatom approaches its nucleus inspiral pathway?
Answer: A continuous spectrum will be obtained due to the constant
emission of energy.

Question 50. Name the series of spectral lines observed in the visible region ofhydrogen spectrum.
Answer: Balmer series

Question 51. Indicate spectral regions corresponding to Lyman, Balmer, Paschen & Brackettseries in the line spectrum of hydrogen.
Answer: Lyman series →ultraviolet
Balmer series → visible
Paschen series → infrared
Brackett series → far infrared

Question 52. Which electronic transition corresponds to the third line in
the Balmer series ofthe hydrogen spectrum?
Answer: Electronic transition from the 5th orbit to the 2nd orbit.

Atomic Structure Fundamentals

Question 53. Name the five series in the atomic spectrum ofhydrogen.
Answer: Lyman, Balmer, Paschen, Brackett and Pfund.

Question 54. Why is the line spectrum of an element known as the fingerprint of its atoms?
Answer: The line spectrum of any element consists of several lines having different wavelengths. It is observed that each element has its own characteristic spectrum, different
from those of all other elements.

The spectra of any two elements can never be identical. Hence, the line spectrum of an element is known as the fingerprint of its atoms

Question 55. How would you obtain the line spectrum of hydrogen?
Answer: When hydrogen gas at low pressure is taken in the discharge tube and the light emitted on passing electric discharge is resolved in a spectroscope, the spectrum obtained is the line spectrum of hydrogen.

Question 56. Give the Rydberg formula for the calculation of the wave number of various spectral lines ofthe spectrum. What is the value Rydberg constant?
Answer: Rydberg’s formula: \(\bar{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

Where = 1, 2, 3, 4,…. etc;

n2 =ni +l. = n1 + 2, =n1 + 3, …. etc.

R = Rydberg’s constant = 109678cm-1 ; v =wave number

Question 57. Name the series of spectral lines obtained, when electrons from various energy levels jump to the first orbit in hydrogen
Answer: Lyman series

Question 58. Indicate all the possible pathways (involving one or more steps)for the transition of an excited electron from the 4th orbit to the ground state.
Answer:

• n4→ n1
• n4→ n1→ n1
• n4→ n3→ n1 and
• n4→ n3 → n2→ n1

Question 59. What are the ground state and excited state of an electron?
Answer: When the electrons in an atom are in their lowest (normal) energy state, they revolve in their respective orbits without losing energy. This state of the atom is called its ground state.

When energy is supplied to an atom by subjecting it to electric dischdt&eior high temperature, an electron in the atom may jump from its normal energy level (ground state) to some higher energy level, by absorbing a definite amount of energy. This state of the atom is called the excited state

Question 60. What is meant by the quantisation energy of an electron?
Answer: This means that the electrons in an atom have only definite values of energy

Question 61. What do you understand by stationary states?
Answer: According to Bohr’s theory of the hydrogen atom, electrons revolve around the nucleus in some fixed orbits and during its motion, the electron does not lose energy. For this reason, these orbits are known as electronic orbits at stationary states.

When an electron stays in such an orbit, it does not remain stationary at all. Had it been so, the electron, being attracted by the nucleus would have fallen onto the nucleus. The electron always remains in motion so as to overcome the influence of nuclear attractive force

Question 62. Mint is the value of Planck’s constant in the SI unit.
Answer: h = 6.626 X 10-34J-s

Question 63. Differentiate Itetween Rydbergformula & Balmerformula.
Answer: The Rydberg formula is used to calculate the wave number of
different series of lines of the spectrum of hydrogen or Hlike atoms. It is given by

\(\bar{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right] Z^2(Z=1 \text { for hydrogen })\)

Where R = Rynx = 1, 2, 3, etc, n2 = n, + 1 , n1 + 2, n1 + 3 , etc.
When nl = 2 in the Rydberg formula, it is called the Balmer
formula. Balmer formula is given by \(\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right], \text { where } n=3,4,5 \cdots \text { etc. }\)

Question 64. Why do we consider each stationary state as an energy level with a definite value?
Answer: Electrons in a particular orbit do not lose or gain energy. In other words, the energy of an electron in a particular orbit remains constant. Hence, these orbits or stationary states are known as energy levels having definite values.

Atomic Structure Fundamentals

Question 65. How many photons are emitted in the transition of the electron from the first to the first energy level of the H-atom?
Answer: There is only one electron in the H-atom. Hence, during the transition of electrons from the fourth to the first energy level, only one photon is emitted.

Question 66. How is the radius of an electronic orbit related to the principal
quantum number?
Answer: The relation between the radius (r) ofthe electronic orbit and the principal quantum number (n) is given by, Therefore, the radius of the orbit is directly proportional to the square ofthe principal quantum number.

Question 67. Prove that, the velocity of an electron revolving in the first orbit
is twice that revolving in the second orbit of the H-atom.
Answer: The velocity of the electron in the nth orbit

\(v=\frac{2 \pi e^2}{n h}\)

therefore \(m v r=\frac{n h}{2 \pi} \text { and } r=\frac{n^2 h^2}{4 \pi^2 m e^2}\)

The velocity of electron in second orbit \(v_2=\frac{2 \pi e^2}{2 \times h}\)

Therefore \(\frac{v_1}{v_2}=\frac{2 \pi e^2}{h} \times \frac{2 h}{2 \pi e^2}=2\)

therefore \(\frac{v_1}{v_2}=\frac{2 \pi e^2}{h} \times \frac{2 h}{2 \pi e^2}=2 \quad \text { or, } v_1=2 v_2\)

Question 68. Which theory forms the basis of Bohr’s atomic model?
Answer: Planck’s quantum theory.

Question 68. Bohr’s theory Is not applicable to which of the following species? (i) H, (It) He2+, (Hi) Be3+, (lv) B4+
Answer: Bohr’s theory is not applicable to He2+ because it does
not contain any electrons.

Question 69. Who proposed the concept ofdual nature of electrons?
Answer: The concept was proposed by de Broglie.

Atomic Structure Fundamentals

Question 70. Whatare de Broglie waves?
Answer: The waves associated with matter particles in motion are called matter waves or de Broglie waves.

Question 71. Write de Broglie equation for microscopic particles.
Answer: \(\lambda=\frac{h}{p}\) wavelength p = momentum of particle (mv).

Question 72. What is the relation between wave nature and particle
nature of moving particles?
Answer: Wave nature \(\propto \frac{1}{\text { particle nature }}\)

Question 73. Derive a relation between kinetic energy and de Broglie wavelength associated with a moving electron.
Answer: We know, the kinetic energy (E) of the particle moving with
velocity v, is given by, \(E=\frac{1}{2} m v^2\) or, 2E = mv2

or, 2mE = m2v2

\(m v=\sqrt{2 m E}\)

Question 74. What happens to the de Broglie wavelength associated with a moving particle if its velocity is doubled?
Answer: The de Broglie wavelength reduces to half its initial value

\(\text { [as } \left.\lambda=\frac{h}{m v} \text {, or } \lambda \propto \frac{1}{v}\right]\)

Question 75. A hard-struck cricket ball does not produce waves. Why?
Answer: Due to the large size of the cricket ball, its mass is large and hence its wavelength is negligible.

Therefore \(\lambda \propto \frac{1}{m}\)

Question 76. Two particles P and Q are moving with the same velocity, but the de Broglie wavelength of P is thrice that of Q. What do you conclude?
Answer: \(\text { Since } \lambda^{\circ} \frac{1}{m}, \lambda_P \propto \frac{1}{m_P} \text { and } \lambda_Q \propto \frac{1}{m_Q}\)

\(\frac{\lambda_P}{\lambda_Q}=\frac{m_Q}{m_P}, \text { or } \frac{m_Q}{m_P}=\frac{\lambda_P}{\lambda_Q}=\frac{3}{1} \text { or, } m_Q=3 \times m_P\)

Therefore Mass of Q is Thrice that of P.

Question 77. Compare the wavelengths of a molecule of each 02 and C02, travelling with the same velocity.
Answer: \(\text { Since } \lambda \propto \frac{1}{m} ; \quad \lambda_{\mathrm{O}_2} \propto \frac{1}{32 \mathrm{u}} \text { and } \lambda_{\mathrm{CO}_2} \propto \frac{1}{44 \mathrm{u}}\)

[ V Molar mass of 02 & CO2 are 32u & 44u respectively]

Thus, the wavelengths of a molecule of each O2 and CO2 traveling with the same velocity is in the ratio 11:8

Question 78. Why is the de Broglie wave termed a matter wave?
Answer: Since de Broglie wave is associated with fast-moving tiny material particles, it is also known as matter wave. The wavelength of such waves depends on the mass and velocity of the particles.

Atomic Structure Fundamentals

Question 79. Write the mathematical expression for Heisenberg’s uncertainty principle-
Answer: \(\Delta x \cdot \Delta p \frac{h}{4 \pi},\) where Ax and Ap are uncertainties in the determination of exact position and momentum respectively.

Question 80. For which particles is the uncertainty principle applicable?
Answer: Heisenberg’s uncertainty principle applies to tiny subatomic particles like electrons, protons, neutrons, etc.

Question 81. Is there any significance of Heisenberg’s uncertainty principle in our daily life?
Answer: In our daily life, we deal with objects of ordinary size. So the uncertainties in their position and momentum are very small as compared to the size and momentum of the n- n-object respectively. So, such uncertainties may be neglected. Thus, the uncertainty principle has no significance in our daily life.

Question 82. Why does Bohr’s model contradict Heisenberg’s uncertainty principle?
Answer: According to Bohr’s theory, negatively charged particles (electrons) inside an atom revolve around the nucleus in well-defined orbits having a fixed radius.

In order to balance the nuclear attractive force, electrons must move with a definite velocity. However, according to the uncertainty principle, it is impossible to determine simultaneously the exact position and the momentum (or velocity) of a microscopic particle like an electron. Thus, Bohr’s model contradicts Heisenberg’s uncertainty principle.

Question 83. Explain why the uncertainty principle is significant only for
subatomic particles, but not for macroscopic objects.
Answer: The position of a subatomic particle can be located accurately by illuminating it with some electromagnetic radiation.

The energy of the photon associated with such radiation is sufficient to disturb a subatomic particle so that there is uncertainty in the measurement of the position and momentum of the subatomic particles. However, this energy is insufficient to disturb a macroscopic object.

Question 84. Why is it not possible to overcome the uncertainty of Heisenberg’s principle using devices having high precision?
Answer: Heisenberg’s uncertainty principle has no relation with the precisions of measuring devices.

AVe know that the subatomic particles are very tiny and thus cannot be seen measured even under a powerful microscope; To velocity or to locate the position of the subatomic particles, they are illuminated (struck, hyprotons) with suitable electromagnetic radiation.

Hence, the precision of measuring devices is not possible in overcoming Heisenberg’s uncertainty principle.

Question 85. Is Heisenberg’s uncertainty principle applicable to a stationary electron? Explain
Answer: It is not applicable. Since the velocity of a stationary electron
is ‘zero’, (v = 0), its position can be located accurately.

Question 86. Write Schrodinger’s wave equation, indicating the significance ofthe notations used.
Answer: Schrodinger’s wave equation is based on the dual nature (wave and particle) of electrons.

Question 87. What is the basis of Schrodinger’s wave equation?
Answer: Schrodinger’s wave equation is based on the dual nature (wave and particle) of electrons.

Atomic Structure Fundamentals

Question 88. Schrodinger’s wave equation does not give us any idea about which quantum number.
Answer: Spin quantum number (s).

Question 89. What is the physical significance of & and ifr2?
Answer: The wave function has no physical significance, while 4r2 gives the probability density i.e., the probability of finding the electron at any point around the nucleus.

Question 90. Write Schrodinger’s wave equation in the briefest possible form.
Answer: The briefest form of Schrodinger’s wave equation is, Hi// = Eip, where H is known as the Hamiltonian operator.

Question 91. How many radial nodes are present in (i) 3s -orbital and (11) 2p -orbital?
Answer: Radial nodes of 3s -orbital =n-l-1 = 3-0-1 = 2

Radial nodes of 2p -orbital = n- Z-1 = 2-1-1 = 0

Question 92. How many radial nodes and planar nodes are present in 3p -orbital?
Answer: No. of radial nodes =n-Z-1 = 3-1-1 = 1
No. of planar nodes =1=1
Total no. of nodes = n- l = 3- l = 2

Question 93. How many nodal planes are present in 5d –orbital.
Answer: Number of nodal planes in 5d -orbital = 2

Question 94. Write the expression for radial distribution Junction.
Answer: RDF = 4nr2i/f2(r)dr

Question 95. Calculate the number of radial nodes and planar nodes in 2 orbital. x2-y
Answer: No. ofradial nodes =n-l-1 = 4-2-1 = 1

No. of planar nodes = 1 = 2

Question 96. What do you mean by the Acceptable values of e and Corresponding wave functions that are obtained by solving the Schrodinger wave equation for h-atom?
Answer: No, atomic orbitals do not possess a sharp boundary. This is because the electron clouds are scattered to a large distance from the nucleus. The density of electron clouds decreases with increasing distance from the nucleus but theoretically, it never becomes zero.

Question 97. Does atomic orbitals possess a sharp boundary? Explain.
Answer: No, atomic orbitals do not possess a sharp boundary. This is because the electron clouds are scattered to a large distance from the nucleus.

The density of electron clouds decreases with increasing distance from the nucleus but theoretically, it never becomes zero.

Atomic Structure Fundamentals

Question 98. What will be the sign of 2p along an axis on the two opposite sides ofthe nucleus?
Answer: The sign of 2p along an axis will be opposite on the two
opposite sides ofthe nucleus

Question 99. What will be the values of ip2 , ip2 value of – 0 ? ,>x py
Answer: When r = 0 , the value of i//2 , i/r„ and i/r, is zero (0).

Question 100. In which direction the value of(l), (ii) (III) ifr2 is the highest? Px
Answer:

• At the negative and positive direction of the x -x-axis.
• At the negative and positive direction of y -y-axis.
• At the negative and positive direction of the z-axis.

Question 101. Why do p -p-orbitals possess directional properties?
Answer: The angular part of the wave function of p -p-orbital depends on the value of 6 and <p. Thus, p -p-orbitals possess directional properties.

Question 102. Why s -orbital does not possess directional properties?
Answer: The angular part of the wave function of s -orbital does not depend on 6 and <p.

As a result, a symmetrical distribution of electron density occurs with increasing distance from the nucleus. Thus, s -the orbital is spherically symmetrical and does not possess directional properties.

Question 103. In which direction the value of/zÿ is zero?
Answer: Along the x,y and z-axis

Question 104. In which direction the value of y2 is the highest?
Answer: Along the x and y-axis.

Question 105. What do you mean by ‘doughnut’?
Answer: The two lobes of d -the orbital are distributed along the z-axis and a sphere is situated with the nucleus at its centre. This sphere is called a ‘doughnut’

Atomic Structure Fundamentals

Question 106. How many angular nodes are present in dÿ -orbital?
Identify them.
Answer: Two angular nodes are present (xz -plane and yz -plane).

Question 107. In which direction is the value ofdÿ, is zero?
Answer: Along z -the z-axis.

Question 108. How many angular nodes are present in dÿ Identify them.
Answer: Two angular nodes are present (they pass through the
origin and lie at an angle of 45° with the xz and zipline and themselves lie perpendicular to each other)

Question 109. How many angular nodes are possible for an orbital?
Answer: ‘V number of angular nodes are possible (where Z =
azimuthal quantum number).

Question 110. Does the number of angular nodes of an orbital depend on the principal quantum number?
Answer: No, it depends only on the azimuthal quantum number.

Question 111. How many angular nodes are present in s -s-orbital? Indicate the subshells present in the M -M-shell. How many orbitals are present in this shell?
Answer: s -orbital does not possess any angular nodes because the value of the angular wave function cannot be zero in any direction.

Question 112. Indicate the subshells present in the M -M-shell. How many
orbitals are present in this shell?
Answer: In the case of M-shell, the principal quantum number, n = 3. The values of azimuthal quantum no. Z are’ 0 ‘, ‘ I’ and ‘2’.

This means that the M-shell contains three subshells, namely, ‘p’ and ‘ d’. For each value of‘ Z ’, the magnetic quantum number ‘ m ’ can have 2Z + 1 values. Therefore M-shell contains 2Z+ 1 orbital.

Question 113. Write the values of the azimuthal quantum number ‘l’ in the third energy level and(it) 3d -subshell of an atom.
Answer: In the third energy level, the principal quantum number n = 3

Values of azimuthal quantum no., ‘ Z ’ are 0, 1 and 2.

For any d -subshell, 1 = 2.

Question 114. What is the maximum number of electrons that can be accommodated in the subshell with 1 = 3?
Answer: For every value of’ Z ‘, ‘ m ’ can have 2Z + 1 values.

Since For Z = 3, m can have 2Z+ 1 values, i.e., 2×3 + 1 = 7 values. Therefore, the number of orbitals in the given shell = 7.

The maximum number of electrons that can be accommodated in these orbitals =2×7 = 14 [v each orbital can accommodate a maximum of 2 electrons].

Atomic Structure Fundamentals

Question 115. What is the maximum number of electrons that can be accommodated in an orbital with m = +3?
Answer: Each value of the magnetic quantum number ‘m’ indicates only one orbital and each orbital can accommodate a maximum of 2 electrons.

This means that the orbital Indicated by m = +3 can accommodate a maximum of 2 electrons.

Question 116. Which of the following subshells have no real existence?

1. 2d)
2. 3f,
3. 4g and
4. 5d

Answer: In the case of d -subshell, 1 = 2. In the second shell ( n = 2), the values of l are 0 and 1. So there cannot be any d -d-subshell In the third shell. Therefore, we can say that there Is no real existence of a 2d subshell.

In case of/-subshell, l = 3 . In the third shell (n = 3), the values of l are 0, 1 and 2. Since there cannot be any /-subshell In this shell, there is no real existence of 3/- subshell.

ln case of g -subshell, / = 4. In the fourth shell (n = 4), the values of l are 0, 1, 2 and 3. Since there cannot be any g subshell in this shell, there is no real existence of a 4g subshell.

In the case of d -subshell, 1 = 2. In the fifth shell (n = 5), the values of l are 0, 1, 2, 3 and 4. Therefore 5d sub-shell has real existence.

Question 117. How many quantum numbers are needed to designate an orbital? Name them.
Answer: Three quantum numbers are needed to designate an orbital, namely, ‘ n ‘ l’ and ‘ m

Question 118. Identify the subshells denoted by the following:
(l)n = 4,l = 2 (ii) n = 5, l = 3
(tit) n = 6, l = 4
Answer:

1. 4d
2. 5f
3. 6g
4. 4s

Question 119. An electron is described by magnetic quantum no.m = +3. Indicate the lowest possible value of ‘n ’for this electron. (tv) n = 4,1=0
Answer: For an electron having magnetic quantum number m = +3, the lowest possible value of azimuthal quantum number ‘ l’ would be 3 and for an electron having 1 = 3, the lowest possible value for ‘ n’ would be 4.

Atomic Structure Fundamentals

In other words, the lowest possible energy level (‘n’) that the electron would occupy is the 4th shell (n = 4).

For an electron having magnetic quantum number m = +3, the lowest possible value of azimuthal quantum number ‘ l’ would be 3 and for an electron having 1 = 3, the lowest possible value for ‘ n’ would be 4.

In other words, the lowest possible energy level (‘n’) that the electron would occupy is the 4th shell (n = 4).

Question 120. Which quantum number is to be mentioned to distinguish
between theefitfrpns__present in the K -shell? £
Answer: For k-shell (n = 1), l = 0 and m = 0. This indicates that K-shell has only one orbital and this orbital can accommodate a maximum of 2 electrons having spin quantum no., ‘s’ with values +1/2 and -1/2.

So, to distinguish between the two electrons in the K-shell, it is important to indicate their spin quantum numbers.

Question 121. Write the vdltt&Wfthe magnetic quantum number for the ‘3d ’-orbitals.
Answer: For 3d orbitals, 1 = 2. Hence the values of the magnetic quantum no., ‘ m’ are +2, +1, 0, -1, -2.

Question 122. Write the values of n, l and m for 3p -subshell.
Answer: For 3p -orbitals, n = 3 , l = 1 and m = +1 , 0, -1 . Hence, 3p -subshell has 3 orbitals.

The values of and ‘ m ‘ for these orbitals are as follows:

1. n = 3, l= 1 , m = +1
2. n = 3,l=l,m = 0
3. n = 3, l = 1 , m =-1

Question 123. Which of the following two orbitals is associated with a higher energy?

1. n = 3, l = 2, m = +1
2. n = 4, l = 0, m = 0

Answer: The algebraic sum of n and / determines the energy of a given subshell. The higher the value of (n + l), of an orbital, the higher its energy. Thus, the orbital with n = 3, l= 2 is associated with a higher energy.

Question 124. Is there any difference between the angular momentum of 3p and 4p -electrons?
Answer: For any p -subshell, 1=1. The angular momentum of an electron depends on the values of all and is independent of the values of Angular momentum, \(L=\sqrt{l(l+1)} \frac{h}{2 \pi}.\).

Atomic Structure Fundamentals

Since 1=1 for both the p -subshells (3p and 4p), there is no difference in the angular momentum ofthe electrons occupying those subshells

Question 126. 4f-subshell of an atom contains 10 electrons. How many of Write the expression for the orbital angular momentum of a revolving electron.
Answer: The orbital angular momentum of the electron, ‘U is given by: L \(\sqrt{l(l+1)} \times \frac{h}{2 \pi}\)

Question 127. Write the expression for the orbital angular momentum of a
revolving electron
Answer: The orbital angular momentum of an electron, ‘U is given by: I = \(=\sqrt{l(l+1)} \times \frac{h}{2 \pi}.\)

Question 128. Mention the sequence in which the following orbitals are filled up by electrons: 3d and 4p.
Answer: The energy of a given subshell is determined by the algebraic sum of’ and ‘Vue., n + 1.

11 the ‘n +l’ values of any two subshells are equal, then the electron enters the one with lower’ n ’. In the 3d -subshell, n = 3 , l = 2 n + l = 3 + 2 = 5 In the 4p -subshell, n = 4, 1=1:.

B +1 =4 +1 = 5 Since for the 3d -subshell, n = 3 which is lower than that of 4p where n = 4, the electron first enters the 3d -subshell.

Question 129. What is the maximum number of Ad -electrons with spin quantum number s =?
Answer: For a 4d -subshell, n = 4, 1 = 2 and m = +2, +1,0, -1,-2. This implies that there are 5 orbitals in this sub-shell that can accommodate a maximum of 10 electrons.

5 of these electrons have s = +| and the remaining 5 have -i . Hence maximum number of 4d -electrons with 2 i spin quantum no., s = -1/2 is 5.

Question 130. Is it possible for atoms with even atomic numbers to contain unpaired electrons?
Answer: Atoms with even atomic numbers can have unpaired electrons. This is in accordance with Hund’s rule which states that the orbitals within the same subshell are at first filled up singly with electrons having parallel spin before pairing takes place.

For instance, in the case of a carbon atom (atomic number 6 and electronic configuration: ls22s22p1x2p1y2p0z ), there are two unpaired electrons

Question 131. Write the electronic configurations of Cu and Cr -atoms.
Answer: Electronic configuration of 2gCu

ls22s22p63s23p63d104s1

Electronic configuration of 24Cr :

ls22s22pG3s23p63d54s1

Atomic Structure Fundamentals

Question 132. Write the electronic configurations of Fe2+ and Cu+ ions.
Answer: Electronic configuration of Fe2+ (atomic number =26):

ls22s22p63s23p63d6

Electronic configuration of Cu+ (atomic number = 29 ):

1s22s22p63s23p63rf10

Question 133. Which of the following has a maximum number of unpaired electrons? (1) Mn2+Fe2+Cu2+ Cr
Answer: The following are the electronic configurations of the given ions and atoms:

1. Mn2+: ls22s22p63s23p63d5
2. Fe2+: ls22s22p63s23p63d9
3. Cu2-: ls22s22p63s23p63d9
4. Cr: ls22s22p63s23p63d54s1

Question 134. Calculate the number of unpaired electrons in the N -atom.
Answer: Electronic configuration of (atomic no. =7): ls22s22p3

According to Hund’s rule, the 3 electrons in the 2psubshell occupy the three p -p-orbitals (px, py, pz) singly.

Hence, the no. of unpaired electrons present in N = 3.

Question 135. How many electrons of the Ne -atom have clockwise spin?
Answer: Electronic configuration of Ne (atomic number = 10)

Each of the pair of electrons present in each ofthe Is, 2s, 2px, 2py, and 2pz orbitals have a clockwise spin and the other, an anti-clockwise spin. Therefore no. of electrons of Ne-atom having clockwise spin = 5.

Atomic Structure Fundamentals

Question 136. Why does an electron pair in an orbital have an opposite spin?
Answer: If a pair of electrons with parallel spin are present in the same orbital then they will repel each other.

Question 137. Write the names and symbols of an atom, a cation and an anion with the electronic configuration Is2.
Answer: Atom: Helium (He);

Cation: Lithium-ion (Li+),

Anion: Hydride ion (H- ).

Question 138. Which quantum numbers specify the size and the shape of electronic orbital?
Answer: The size of an electronic orbital is determined by the principal quantum number (n) and the azimuthal quantum number (/) determines the shape of an electronic orbital.

Question 139. Write down the values of the quantum numbers of the electron in the outermost shell of sodium.
Answer: The electron present in the outermost shell of sodium is identified as 3s1. Its principal quantum number n = 3, azimuthal quantum number 1 = 0, magnetic quantum number, m = 0 and spin quantum number, s = +1/2.

Question 140. How many nodes are there in 3s -orbital?
Answer: The spherical shell (or region) inside the s -s-orbital where electron density is zero is called the node. In the case of 3s orbital, there are two such spherical shells where the electron density is zero.

So 3s -orbital has two radial nodes but no angular node (1 = 0). So the total no. of nodes is 2. [No. of nodal surfaces =n- 1, where n is the principal quantum number]

Question 141. How many nodal points are there in 3p -orbital?
Answer: In a p -orbital the electron density, at the point where the two lobes meet is zero.

This point is called the nodal point of the p-orbital. So each of the three 3p -orbitals (viz., px, py and pz ) has only one nodal point.

Atomic Structure Fundamentals

Question 142. Indicate principal and azimuthal quantum numbers for the subshells:

1. 4s
2. 5d
3. 2p
4. 6

Answer:

1. n=4, l=0
2. n=5,l=2
3. n=2,=1
4. n=6, l=3

Question 143. Which is the lowest principal energy level that permits the existence of off-subshell?
Answer: For f-subshell the value of azimuthal quantum number Z is 3. So the lowest principal energy level that permits the existence of an f -subshell is the fourth shell (i.e, N -N-shell)

Question 144. An element (symbol M) has 26 protons in the nucleus. Write the electronic configuration of M2+ and M3+.
Answer:

26M: ls22s22p63s23p63d64s2

26m2+: ls22s22p63s23p63dG

and 26m3+ : ls22s22p6 3s2 3p63d

Atomic Structure Fundamentals

Question 145. There are 8 electrons in the 3d -subshell of an atom. Among these, what will be the maximum number of electrons with similar spin? What is the number of odd electrons?
Answer: Electronic configuration of 3d -subshell

Maximum number of electrons with the same spin = 5.

Number of odd electrons in that atom = 2.

Very Short Answer Type Question

Question 1. What are the fundamental constituents____of atom?
Answer: Electrons, protons, and neutrons are the fundamental constituents of an atom.

Question 2. Name the clement containing no neutron.
Answer: Ordinary hydrogen atom or protium:

Question 3. Name the anode ray particle with the highest value.
Answer: e/m value of proton (H+ ion) has the highest value.

Question 4. What is the consequence when cathode rays strike a hard metal surface like tungsten?
Answer: X-rays are produced.

Question 5. Why is an electron called a universal particle?
Answer: Its mass and charge are independent of its source

Question 6. What is the value of a fundamental unit of electricity?
Answer: The charge carried by one electron is said to be the fundamental unit of electricity. Its magnitude is 4.8 x 10-10 esu or 1.602 x 10~19 C.

Question 7. Besides electron, proton and neutron, name two other subatomic particles.
Answer: Positron (+°e) and Neutrino (00v).

Question 8. A cation M3+ has 23 electrons. What is the atomic number of M?
Answer: Number of electrons present in the neutral M atom = 23 + 3 = 26. So, die number of protons in the nucleus = 26. Hence, atomic number ofM is 26.

Atomic Structure Fundamentals

Question 9. Bohr’s theory is not applicable to which of the following species?

1. H ,
2. H+ ,
3. He+ ,
4. Li2+

Answer: Bohr’s theory is not applicable to proton (H+) because it does not contain any electron.

Question 10. Balmer series of hydrogen spectrum lies in which region?
Answer: It lies in the visible region ofthe spectrum.

Question 11. Mention the most important application of the de Broglie concept.
Answer: The de-Broglie concept is utilized in the construction of an electron microscope used for the measurement of the size of very small objects.

Question 12. How are the frequency and wave number of electromagnetic radiation related to each other?
Answer: \(v=\frac{c}{\lambda}=c \times \frac{1}{\lambda}=c \times \bar{v}\)

wave number \(\bar{v}=\frac{1}{\lambda}\)

Question 13. An electron beam after passing through a thin foil of gold produces a diffraction pattern (consisting of several concentric rings). What do you conclude?
Answer: Electron in motion has wage character.

Question 14. What is a quantum?
Answer: The smallest packet of energy of any radiation is called a quantum.

Question 15. What happens when an electron hits a zinc sulfide screen and what does it prove?
Answer: A scintillation is produced, which in turn proves that the electron has a particle nature.

Question 16. A scintillation is produced, which in turn proves that the electron has a particle nature.
Answer: [‘ m ‘ and ‘ e ‘ represent the mass and charge of the electron]

Question 17. Out of X-rays, y-rays, and microwaves which one has die highest and which one has die lowest frequency?
Answer: Highest frequency: y-rays; Lowest frequency: Microwave

Question 18. What is the unit of Planck’s constant in S.I.? What other physical quantity has the same unit?
Answer: The SI unit of Planck’s constant ‘h’ =kg-m2-s-1.

The SI unit of angular momentum (mv) is also kg-m2-s_1.

Atomic Structure Fundamentals

Question 19. Arrange the given subshells in the increasing order of their energies: 3d, 4p, 4s, 5p, 4d, 6s, 4f.
Answer: The sequence of energy of the given subshells is: 4s < 3d < 4p < 4d < 5p < 6s < 4/.

Question 20. What is the main difference between a wave emitted by an electric bulb and that associated with a tiny particle moving at a very high speed?
Answer: The bulb emits electromagnetic waves, while that associated with the moving particle is matter.

Question 21. Do atomic orbitals have sharp boundaries?
Answer: No, atomic orbitals do not have sharp boundaries because the probability of finding an electron even at a large distance is never zero, although it may be very small.

Question 22. At what distance from the nucleus is the radial probability maximum for the Is -orbital of the hydrogen atom? What is this distance called?
Answer: At a distance of 0.529A, the radial probability is maximum. This distance is called the Bohr radius.

Question 23. In which shell(s), there is no existence of d -subshell?
Answer: There is no existence of ‘d’ subshell in K and L -shells

Question 24. Write the values of the four quantum numbers of the electron(s) in the outermost shell of the Cr-atom.
Answer: According to the electronic configuration of b 24Cr(ls22s22p63s23p63d54s1), the outermost shell configuration of Cr-atom is: 4s1. therefore Quantum numbers for 4s1: n = 4, l = 0, m = 0 , s= \(+\frac{1}{2}\)

Question 25. Out of the four quantum numbers which one does not result from the solution of the Schrodinger wave equation?
Answer: Spin quantum number.

Question 26. Which is most paramagnetic among Cu2+, and Fe2+, and why?
Answer: From the electronic configurations it is observed that the number of unpaired electrons in Cu2+, Fe2+, and Cr3+ ions are 1, 4, and 3 respectively. So Fe2+ ion, containing the highest number of unpaired electrons, will be most paramagnetic.

Question 27. Why splitting of spectral lines is observed when the source producing the atomic spectrum is placed in a magnetic field?
Answer: In the presence of a magnetic field, the orbitals present in a sub-shell (which were originally degenerate) take up different orientations and hence their degeneracy is lost.

Quantum 28. The 4f-subshell of an atom contains 12 electrons. What is the maximum number of electrons having spins in the same direction?
Answer: Seven electrons have spin in the same direction.

Atomic Structure Fundamentals

 

Solved Questions

Question 1. What is the orbital angular momentum of a p -electron in \(\frac{h}{2 \pi}\) unit? The atomic numbers of two elements X and Y are 15 and 27 respectively. Write down the electronic configuration of X3- and Y3+ ions. State two limitations of Bohr’s theory of H-atom.
Answer: The orbital angular momentum in \(\frac{h}{2 \pi}\) unit is given by \(\sqrt{l(l+1)}\) where / = azimuthal quantum number.

For p -orbital,l= 1.

The orbital angular momentum of p -orbital in \(\frac{h}{2 \pi}\)unit

= \(=\sqrt{l(l+1)}=\sqrt{1(1+1)}=\sqrt{2} .\)

Question 2. Write two differences between orbit and orbital. Two sets of four quantum numbers of an electron are (n = 4, 1 = 3, m = 3, s = -) and n = 3, 1 = 2, 2 m = -2, s = 0). Which one of these sets is not correct and why?
Answer: The second set is incorrect because the value of s can be either \(\frac{1}{2} \text { or }-\frac{1}{2}\) but can never be zero.

Question 3. Write the electronic configuration of Cu+ and Cr2+ ions (Atomic numbers of Cu and Cr are 29 and 24 respectively).
Answer: Cu+: ls22s22/;e3A-23p63rf10

Cr2+: 1s22s22pG3s23pG3d4

Atomic Structure Fundamentals

Question 4. Write the possible values of’ m ‘ for a 4/-electron. Mention one demerit of Rutherford’s atomic model
Answer: For a 4/-elcctron, n = 4, / = 3. Thus, the possible value of m will he : +3, +2, +1, 0, -1, -2, -3

Question 5. Write the symbols of two anions isoelectronic with K+ .1
Answer: K+ion: ls22s22pG3s23pG. Two anions that are isoelectronic with K+ -ion are S2- and Cl-.

Question 6. The electronic configuration of an atom is [Z](n-2)/14(rc- l)d1ns2. What is the minimum position of the atom in the periodic table and correspondingly what is the atomic number of Z? 1+1
Find the number of impaired electrons in the atom of the element having atomic number 16. Which of the following ions does not obey Bohr’s atomic theory? He2+,Li2+,B3+,Be3
Answer: Electronic configuration of the given atom: (n-2)f1-14(n-1)d0-1ns2. So, it can be stated that the given atom belongs f-block.

lienee, the element is of group-IIIB and its electronic configuration is identical with 71Lu of the lanthanoids and 103I.r of the actinoids.

1 The lowest position available to the atom ofthe element is the 6th period and group-II2(3). Thus, it belongs to the lanthanoids and has atomic number 71.

The electronic configuration of an atom ofthe element with atomic number 16 is 1s22s22pl63s23p23p2x3plz. Thus, number of unpaired electrons is two.

Question 7. There are nine electrons in the 5f-orbital of an atom of an element Mention the maximum number of electrons that have the same spin and number of impaired electrons.
Answer: Element Mention the maximum number of electrons that have the same spin and number of impaired electrons-

imgae-

Thus, the maximum number of electrons with the same spin will be 7, and a number of unpaired electrons will be 5.

Question 8. Which rule is followed in determining the arrangement of unpaired electrons in P-atom? State the rule. Explain whether3f-orbital is present in P-atom.

Answer: First Part: Hund’s rule is followed.

Electronic configuration: I s22s22pG3s23p1x3p1x3p1x Pliosphorous atom does not contain 3/-subshell.

For 3/-subshell, n = 3 . Hence, the maximum value of / = (n- l) = 2 i.e., d -subshell.

Atomic Structure Fundamentals

Question 9. What is the stationary energy level of an electron? State one difference between Rutherford’s and Bohr’s model of atomic structure. Write the electronic configurations of Co2+ and As3+ ions. (Atomic number of Co is 27 and As is 33).
Answer: According to Bohr’s theory, the energy level in which no energy Is emitted by an electron is known as the stationary energy level of that electron. 27Co2+ : ls22s22pG3s23p63d7
33AS3+ : ls22s22p63s23p63dl04s

Question 9. In Bohr’s models of atoms the lowest angular momentum,
that an electron may have is

1. h
2. 0
3. \(\frac{h}{2 \pi}\)
4. \(\frac{h}{\pi}\)

Answer: 3. \(\frac{h}{2 \pi}\)

Question 10. State the Heisenberg’s uncertainty principle. Calculate the de Broglie wavelength associated with an electron moving with a velocity of 1.0 x 107 m/s. (Mass of an electron: 9.1 x 10-31kg
Answer: wavelength \(\lambda=\frac{h}{m v}\) [h = Planck’s constant, m = mass of an electron, v = velocity of an electron]

\(\lambda=\frac{6.626 \times 10^{-34}}{9.1 \times 10^{-31} \times 1.0 \times 10^7}=7.281 \times 10^{-11} \mathrm{~m}\)

Atomic Structure Fundamentals

Question 11. Write down the electronic configuration of 14Si and 25Mn stating the underlying principle. Which of the following orbitals is not possible? 1 p, 2d, 3s, 3f
Answer: First Part: The underlying principle is ‘The Aufbau principle! For electronic configuration see article no. 2.10.3.

Second Part: Ip, 2d, and 3f orbitals are not possible.

Question 12. Which one of the following is correct among the following sets of quantum number

1. \(n=1, l=2, m=1, s=\frac{1}{2}\)
2. \(n=3, l=1, m=0, s=\frac{1}{2}\)
3. \(n=5, l=1, m=2, s=\frac{1}{2}\)
4. \(n=4, l=1, m=-2, s=\frac{1}{2}\)

Answer: 2. \(n=3, l=1, m=0, s=\frac{1}{2}\)

Question 13. State the Pauli exclusion principle. Write the electronic configurations of 24Cr3+ and 27Co3+
Answer: Second Part: 24Cr3+: ls22s22pG3s23p63d3

27CO3+ : ls22s22p63s23p63d6

Question 14. The number of total electrons in the n-th orbit of an atom is—

1. n
2. n2
3. 2n2
4. n-1

Answer: 3. 2n2

Question 15. Mention Heisenberg’s uncertainty principle. Calculate the uncertainty of velocity of an electron which has an uncertainty in the position of lA
Answer: Second Part: According to the Heisenberg uncertainty principle,

\(\Delta x \times \Delta p\frac{h}{4 \pi} \quad \text { or } \Delta x \times m \Delta v \frac{h}{4 \pi}\)

The uncertainty in position, Ax = lA = 10 10m

\(\text { Thus, } \begin{aligned}
\Delta y=\frac{h}{\Delta x \times m \times 4 \pi} & =\frac{6.626 \times 10^{-34}}{10^{-10} \times 9.1 \times 10^{-31} \times 4 \pi} \\
& =5.794 \times 10^5 \mathrm{~m} \cdot \mathrm{s}^{-1}
\end{aligned}\)

Atomic Structure Fundamentals

Question 16. If the energy of the first Bohr’s orbit is -13.58 eV of a hydrogen atom, calculate the energy of the third Bohr’s orbit of that atom.

Answer: According to Bohr’s theory

\(E_n=-13.58 \times \frac{Z^2}{n^2} \mathrm{eV}=-13.58 \times \frac{1^2}{3^2} \mathrm{eV}=-1.5089 \mathrm{eV}\)

Question 17. The maximum how many number of electrons of the Cl atom follows the relation n + l = 3 —

1. 10
2. 8
3. 10
4. 16

Answer: 2. n + Z = 3 represents 3s and 2p orbital. Electronic configuration of Cl: ls22s22p63s23p5

Question 18. When an electron jumps down from the 5th Bohr orbit to the 3rd Bohr orbit in the H atom, how many numbers of spectral lines will be formed?
Answer: When an electron jumps down from the 5th Bohr orbit to the 3rd Bohr orbit in an H atom it can jump directly or it can jump to the 4th Bohr orbit first and from it, jump to the 3rd Bohr orbit. Thus, we get 3 spectral lines for these 3 transitions.

Question 19. How many numbers of electrons are present in one HC104 molecule?
Answer: In one molecule of HC104 molecule, total number of electrons present in it = (1 + 17 + 4 x 8) = 50

Atomic Structure Fundamentals

Question 20. Which of the following is the ground state electronic configuration of Cr (The atomic number of Cr is 24)—

1. lsz2sz2p63s23p63d44s2
2. ls22s22p63sz3p63d54i1
3. ls22s22p63s23p63d6
4. ls22s22p63s23p63d34s241

Answer: ls22s22p63s23p63rf54s1. Due to the half-filled electronic configuration of rf-subshell, Cr gets stabilized to a greater extent.

Question 21. what are the quantum numbers by which an electron In an atom can be designated? What Is the maximum number of quantum numbers that may be the same lor two electrons of an atom?
Answer: Principal quantum number (n), azimuthal quantum number (Z), magnetic quantum number (m), and spin quantum number (s) are required to designate an electron in an atom. (ii) The maximum number of quantum numbers that may be the same for two electrons of an atom is 3.

Solved Questions

Question 1. Calculate the number of electrons which will together weigh one gram. Calculate the mass and charge of one mole of electrons.
Answer: Mass of one electron = 9.11 x 10-31kg.

∴ lg or 10 3 kg = \(=\frac{1}{9.11 \times 10^{-31}} \times 10^{-3}\) electrons 9.11 x 10-31 = 1.098 x 1027 elctrons.

Mass of one electron =9.11 x 10^-31kg

So, mass of one mole of elctrons = (9.11 x 10^-31kg) x (6.022 x 1023) =5.485 x 10^-7 kg Charge on one electron = 1.602 x 10-19C.

Thus, charge on one mole of elctrons = (1.602 x 10~19C) X (6.022 x 1023) = 9.65 x 104C.

Atomic Structure Fundamentals

Question 2. Calculate the total number of electrons present in one mole of methane. Find 1 the total number and 2 the total mass of neutrons in 7 mg of 14C. (Assume that the mass of a neutron = 1.675 x 10-27kg). Find 1 the total number and 3 the total mass of protons in 34 mg of NH3 at STP. Will the answer change if the temperature and pressure are changed?
Answer: 1 molecule of CH4 contains =6 + 4 = 10 electrons. Thus, one mole or 6.022 x 1023 molecules will contain =6.022 x 1023 x 10 = 6.022 x 1024 electrons.

1. 1 mol 14C -atom = 6.022 x 1023 14C atoms = 14g

14C .One 14C -atom contains =14-6 = 8 neutrons.

14g or 14000 mg 14C = 8 x 6.022 x 1023 neutrons

Mass of one neutron = 1.675 x 10-27kg.

So, mass of 2.4088 x 1021 neutrons

= (2.4088 X 1021) X (1.675 X 10~27) =4.0347 X 10-6kg

1 mol NH3sl7g NH3=6.022 x 1023 molecules of NH3. Therefore, the number of protons present in 17g

NH3 = (6.022 X 1023) X (7 + 3) = 6.022 x 1024

Number of protons in 34mg or 0.034 g

mass 6.022 x 1024

NH’ – ITg X 0.034g = 1.2044 X 1022

Mass ofa proton = 1.6725 x 10-27kg

Mass of 1.2044 x 1022 protons

=(1.6725 x 10-27) x (1.2044 x 1022) =2.014 X 10-5kg There is no effect of temperature and pressure.

Atomic Structure Fundamentals

Question 4. Write the complete symbol for the atom with the h = 6.626 x 10-34J-s, c = 3.0 X 108m-s-1 ] given atomic number (Z) and atomic mass (A)

1. Z = 17, A = 35
2. Z= 92, A=233
3. Z = 4, A = 9

Answer: \({ }_{17}^{35} \mathrm{Cl}\)

\({ }_{92}^{233} \mathrm{U}\) \({ }_4^9 \mathrm{Be}\)

Question 5. Yellow light emitted from a sodium lamp has a wavelength (A) of 580 nm. Calculate the frequency (v) and wave number (v) of the yellow light.
Answer: Wavelength, A =580nm =580 X 10-9m =5.80 X 10-7m.

Frequency of yellow light.

\(v=\frac{c}{\lambda}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{5.80 \times 10^{-7} \mathrm{~m}}=5.17 \times 10^{14} \mathrm{~s}^{-1}\)

Speed of light, c = 3 X 108m-s-1

and wave number, \(\bar{v}=\frac{1}{\lambda}=\frac{1}{5.80 \times 10^{-7} \mathrm{~m}}\)

= 1.72 x 106m-1.

Question 6. Find the energy of each of the photons which corresponds to light of frequency 3 X 1015Hz. Have a wavelength of 0.50A
Answer: \(\begin{aligned}
E & =h v=\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^{15} \mathrm{~s}^{-1}\right) \\
& =1.988 \times 10^{-18} \mathrm{~J}
\end{aligned}\)

\(\begin{aligned}
E & =h v=\frac{h c}{\lambda}=\frac{6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s} \times 3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{0.50 \times 10^{-10} \mathrm{~m}} \\
& =3.976 \times 10^{-15} \mathrm{~J}
\end{aligned}\)

Atomic Structure Fundamentals

Question 7. Calculate the wavelength, frequency, and wavenumber of a light wave whose period is 2.0 x 10-10s.
Answer: \(\text { Frequency }(v)=\frac{1}{\text { period }}=\frac{1}{2.0 \times 10^{-10} \mathrm{~s}}=5 \times 10^9 \mathrm{~s}^{-1}\)

\(\text { Wavelength }(\lambda)=\frac{c}{\lambda}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{5 \times 10^9 \mathrm{~s}^{-1}}=6 \times 10^{-2} \mathrm{~m}\)

and wave lenght \((\bar{v})=\frac{1}{\lambda}=\frac{1}{6 \times 10^{-2} \mathrm{~m}}=16.66 \mathrm{~m}^{-1}\)

Question 8. What is the number of photons of light with a wavelength of 4000 pm that provide 1J of energy?
Answer: Wavelength of light (A) = 4000pm

= 4000 X 10-12m = 4 x 10-9m

According to Planck’s quantum theory, the energy of a photon \(E=N h v=N h \frac{c}{\lambda}\)

[N= no. of photons h= 6.626 x 10-34J-s , c = 3.0 X 108m-s-1]

\(\begin{aligned}
N=\frac{E \times \lambda}{h \times c} & =\frac{1 \mathrm{~J} \times\left(4 \times 10^{-9} \mathrm{~m}\right)}{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right)\left(3.0 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)} \\
& =2.012 \times 10^{16}
\end{aligned}\)

Atomic Structure Fundamentals

Question 9. A photon of wavelength 4 x 10-7m strikes on the metal surface, the work function of the metal is 2.13 eV. Calculate the energy of the photon (eV) the kinetic energy of the emission, and the velocity of the photoelectron (leV = 1.6020 x 10-19J)
Answer: Energy of a photon (E) = ,\(h v=\frac{h c}{\lambda}\)

\(\begin{aligned}
& =\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{4 \times 10^{-7} \mathrm{~m}} \\
& =4.97 \times 10^{-19} \mathrm{~J}
\end{aligned}\)

Or, energy of a photon \(=\frac{4.97 \times 10^{-19}}{1.602 \times 10^{-19}} \mathrm{eV}=3.10 \mathrm{eV}\)

The kinetic energy of emitted electron = energy of a photon- work function of a metal.

= (4.97 X 10-19- 2.13 X 1.602 X 10-19)J

= 1.56 X 10-19J =0.97eV

Kinetic energy of photoelctron, \(\frac{1}{2} m v^2=1.56 \times 10^{-19} \mathrm{~J}\)

\(\text { or, } v^2=\frac{2 \times 1.56 \times 10^{-19}}{m}=\frac{2 \times 1.56 \times 10^{-19}}{9.108 \times 10^{-31}}=0.34 \times 10^{12}\)

Velocity of photoelectron, v = 5.83 x 105m.s-1

Question 10. Electromagnetic radiation of wavelength 242 is just sufficient to ionize the sodium atom. Calculate the ionization energy of sodium in kJ.mol-1.
Answer: Ionisation energy ofsodium (E) = Nhv \(=N h \frac{c}{\lambda}\)

\(E=\frac{\left(6.022 \times 10^{23}\right) \times\left(6.626 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{242 \times 10^{-9}}\)

= 4346 x 105I-mol-1 = 494.6 kj-mol-1.

Atomic Structure Fundamentals

Question 11. A 25-watt bulb emits monochromatic yellow light of wavelength of 0.57 pm. Calculate the rate of emission of quanta per second.
Answer: Energy emitted bythe bulb = 25 watts = 25J-s-1.

Energy ofa photon (E) = hv \(h \frac{c}{\lambda}\)

\(\begin{aligned}
\lambda=0.57 \mu \mathrm{m}=0.57 \times 10^{-6} \mathrm{~m}, c= & 3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}, \\
& h=6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}
\end{aligned}\)

Substituting the values we get,

\(E=\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right)\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{0.57 \times 10^{-6} \mathrm{~m}}=3.49 \times 10^{-19} \mathrm{~J}\)

No. of quanta emitted \(=\frac{25 \mathrm{~J} \cdot \mathrm{s}^{-1}}{3.49 \times 10^{-19} \mathrm{~J}}=7.16 \times 10^{19} \mathrm{~s}^{-1}\)

Question 12. Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 6800 A. Calculate threshold frequency (vQ) and work function (W0) of the meta
Answer: Threshold frequency \(v_0=\frac{c}{\lambda_0}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{6800 \times 10^{-10} \mathrm{~m}}\)

= 4.41 X 1014s-1

and work function ofthe metal ( wQ) = hv0

= (6.626 X 10~34J.s) X (4.41 X lO14.s-1) =2.92 X 10-19J

Question 13. What is the wavelength of light emitted when the electron in a hydrogen atom undergoes a transition from an energy level with n = 4 to an energy level with n = 2?
Answer: According to the Rydberg equation, wave number,

\(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\) \(\bar{v}=109677\left[\frac{1}{(2)^2}-\frac{1}{(4)^2}\right] \mathrm{cm}^{-1}\)

[R = 109677 cm-1 and n2 = 4, n1 = 2]

Or, v = 109677 x\(\frac{3}{16}\) = 20564.43cm1

\(\lambda=\frac{1}{\bar{\nu}}=\frac{1}{20564.43} \mathrm{~cm}\) = 4.86 x 10-5cm =486 x 10-7crn = 486 x 10-9m = 486nm.

Atomic Structure Fundamentals

Question 14. How much energy is needed to ionize an H-atom if the electron occupies n = 5 orbit? Compare your answer with the ionization enthalpy of the H-atom (energy required to remove the electron from n = 1 orbit).
Answer: \(\begin{aligned}
& E_n=-\frac{21.76 \times 10^{-19}}{n^2} \mathrm{~J} ; E_1=-21.76 \times 10^{-19} \mathrm{~J} \\
& E_5=-\frac{21.76 \times 10^{-19}}{(5)^2}=-8.704 \times 10^{-20} \mathrm{~J} \text { and } E_{\infty}=0
\end{aligned}\)

\(\frac{\Delta E}{\Delta E^{\prime}}=\frac{8.704 \times 10^{-20} \mathrm{~J}}{21.76 \times 10^{-19} \mathrm{~J}}=4 \times 10^{-2}\)

Question 15. What is the maximum number of emission lines when the excited electron of H atom in n = 6 drops to the ground state?
Answer: The number of lines produced in a spectrum when an electron returns from the nth energy state to the ground state = Z(n2-n1) =E(6- 1) = 1(5) = 5 + 4 + 3 + 2+l = 15.

Question 16. The energy associated with the first orbit in the hydrogen atom is -2.18 x 10-18J.atom-1. What is the energy associated with the fifth orbit? Calculate the radius of Bohr’s fifth orbit for the hydrogen atom.
Answer: Energy of the first orbit (E1) = -2.18 x 10-18J-atom-1

We know that the energy of n-th orbit (En) \(=E_1 \times \frac{Z^2}{n^2}\)

\(=-2.18 \times 10^{-18} \times \frac{1^2}{n^2}\)

For H-atom, Z= 1

Thus energy of 5th Orbit (e5) \(=-2.18 \times 10^{-18} \times \frac{1^2}{5^2}\)

= -8.72×10-20 J atom-1

Bohr radius for n-th-orbit of H-atom (rn) = 0.529 x n2A

[For H-atom, Z = 1]

Bohr radius of 5th orbit, rg = 0.529 X 52A = 13.225A

Question 17. Find the wave number for the longest wavelength transition In the Balmer series of atomic hydrogen.
Answer: The equation used for explaining the line spectrum of hydrogen for \(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\) Balmer series, n1 = 2

As \(\bar{v}=\frac{1}{\lambda}, \lambda\) will be longest if n2 is minimum.

Thus, here n2 = n1 + 1 =2+1 =3 (Jt = 109677 cm-1 )

So. \(\vec{v}=R\left(\frac{1}{2^2}-\frac{1}{3^2}\right)\)

\(\text { or, } \bar{v}=109677\left(\frac{1}{2^2}-\frac{1}{3^2}\right) \mathrm{cm}^{-1}\) \(=109677 \times \frac{5}{36} \mathrm{~cm}^{-1}=1.5233 \times 10^4 \mathrm{~cm}^{-1}\)

Atomic Structure Fundamentals

Question 18. What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state? The ground state electron energy is -2.18 X 10-11 erg.
Answer: Given: energy of ground state (Ex) = -2.18 x 10-11 erg

Energy of n-th orbit, \(E_n=\frac{E_1}{n^2} \operatorname{erg}=\frac{-2.18 \times 10^{-11}}{n^2} \mathrm{erg}\)

The amount of energy required when an electron jumps from the last-orbit to 5th orbit.

\(\begin{aligned}
\Delta E=E_5-E_1 & =\frac{-2.18 \times 10^{-11}}{5^2}-\left(-2.18 \times 10^{-11}\right) \\
& =2.18 \times 10^{-11}\left(1-\frac{1}{25}\right)
\end{aligned}\)

= 2.093 X 10-u erg =2.093 X 10-18J

[v 1 erg= = 10-7 J ]

The amount of energy released when the electron returns from 5th orbit to lst-orbit =2.093 X 10-11 erg

We know that, AE = hv \(=h \frac{c}{\lambda}\)

\(\frac{h c}{\Delta E}=\frac{\left(6.626 \times 10^{-27} \mathrm{erg} \cdot \mathrm{s}\right) \times\left(3 \times 10^{10} \mathrm{~cm} \cdot \mathrm{s}^{-1}\right)}{2.093 \times 10^{-11} \mathrm{erg}}\)

= 9.497 x 10-6cm =950 x 10-8cm = 950A

Question 19. The electron energy in the hydrogen atom is given by En = (-2.18 x 10-18)/n2 J. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
Answer: \(B_2=-\frac{2.18 \times 10^{-18}}{(2)^2} \mathrm{~J}=-5.45 \times 10^{-19} \mathrm{~J}\)

Energy required to remove an electron completely from the orbit with n \(n=2, \Delta E=E_{\infty 0}-E_2=0-\left(-5.45 \times 10^{-19} \mathrm{~J}\right)\)

= 5.45x 10-19J

\(\text { Again, } \begin{aligned}
\lambda=\frac{h c}{\Delta E} & =\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{5.45 \times 10^{-19} \mathrm{~J}} \\
& =3.647 \times 10^{-7} \mathrm{~m}=3.647 \times 10^{-5} \mathrm{~cm}
\end{aligned}\)

Question 20. Calculate the wavelength of an electron moving with a velocity of 2.05 X 107m.s-1
Answer: Velocity ofan electron ( v) = 2.05 x ]07m‘S_1 According to de Broglie equation, wavelength \((\lambda)=\frac{h}{m v}\)

\(=\frac{6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}{\left(9.108 \times 10^{-31} \mathrm{~kg}\right) \times\left(2.05 \times 10^7 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}\)

Thus, the wavelength of the electron will be 3.549 x 10-11 m

Atomic Structure Fundamentals

Question 21. The mass of an electron is 9.1 x 10-31kg. If its K.E is 3.0 X 10-25J, calculate its wavelength.
Answer: Mass ofan electron (m) = 9.1 x 10-1kg

\(\mathrm{KE}=\frac{1}{2} m v^2=3.0 \times 10^{-25} \mathrm{~J}\)

Velocity of an electron \((v)=\sqrt{\frac{2 \times \mathrm{KE}}{m}}=\sqrt{\frac{2 \times 3.0 \times 10^{-25}}{9.1 \times 10^{-31} \mathrm{~kg}}}\)

= 812m.s-1

Wavelength of the moving electron \((\lambda)=\frac{h}{m v}\)

\(=\frac{6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}{\left(9.1 \times 10^{-31} \mathrm{~kg}\right) \times\left(812 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}=8.967 \times 10^{-7} \mathrm{In}\)

Question 22. Which of the following are isoelectronic species i.e., those having the same number of electrons? Na+ K+ Mg2+, Ca2+, S2-,Ar
Answer: Number of electrons present in Na+=(ll-l)=10; K+=(19-1)=18; Mg2+ =(12 —2)=10; Ca2+ =(20-2)=18; S2″ =(16+2) =18; Ar = 18.

Elance, Na+, and Mg2+ are isoelectronic because they contain 10 electrons each. K+, Ca2+, S2-, and Ar are isoelectronic because they contain 18 electrons each.

Question 23. Write the electronic configurations of the following ions: (a) H- (b) Xa- (c) O2- (d) F- What are the atomic numbers of elements whose outermost electrons are represented by (a) 3s1 (b) 2p3 and (c) 3p5? Which atoms are indicated by the following configurations?
Answer: 

1. [He]2s1
2. [Ne]3s23p3
3. [Ar]4s23d1
4. H-: Is2
5. Xa-: ls22s22p5
6. O2-: ls2s2p6
7. F-: ls22s22p6

The configuration ofthe elementwill be ls22s22ps3s1; its atomic numberwill be 11.

The configuration of the element will be 1s22s22p3; its atomic number will be 7.

The configuration of the element will be ls22s22p63s23p5; its atomic number will be 17.

lithium (Li), (Z = 3)

Phosphorous (P), (Z =15)

Scandium (Sc), (Z= 21).

Atomic Structure Fundamentals

Question 24. What is the lowest value of n that allows g-orbitals to exist?
Answer: For the existence of g-subshell, 1 should be 4. For a given orbital, the maximum value of 1 = (n-1). Thus, for 1 = 4, the minimum value of n should be 5.

Question 25. An electron is in one of the 3d orbitals. Give the possible values on n, l, and mI for this electron.
Answer: For 3d-subshell, n = 3,1 = 2 8iml = -2, -1, 0, +1, +2.

Question 26. An atom of an element contains 29 electors and 35 n = 2, 1 = 1, neutrons. Deduce the number of protons and the electronic configuration of the element.
Answer: For an electrically neutral atom, the number of protons = the number of electrons = 29.

Electronic configuration: ls22s22p63s23p63d104s1.

Question 27. Give the number of electrons in the species H+2, H2, and.
Answer: The number of electrons present in H2, H2, and 0£ is 1, 2, and 15 respectively.

Question 28. An atomic orbital has n = 3. What are the possible values of 1 and m1? List the quantum numbers (m{ and 1) of electrons for 3d orbital. Which of the following orbitals are possible? 1 p, 2s. 2p and 3f
Answer: If n = 3 , then 1 = 0, 1, 2

When I = 0, ml = 0; when l = 1 , ml = -1, 0, +1 ;

When 1 = 2, ml = -2, -1, 0, +1, +2

For 3d-subshell, n = 3 and 1 = 2; for l = 2, m1= -2,-1,+1,+2

lp is not possible because for p-subshe D,1=1. When n = 1, l cannot be 1. 2s is possible because for subshell, 1 = 0, when n = 2, 1 can be 0. 2p is possible because for p-subshell,1=1, when n = 2,1 can be 1. 3/ is not possible because for f-subshell, 1 = 3. When n = 3, cannot be 3.

Question 29. Using s, p, and d notations, describe the orbital with the following quantum numbers.

• n- 1,
• 1=0;
• n = 3;
• 1 = 1
• n = 4;
• 1 = 2;
• n = 4;
• l = 3

Answer:

• 1s
• 2s
• 4d
• 4f

Atomic Structure Fundamentals

Question 30. Explain, giving reasons, which of the following sets of quantum numbers are not possible

• n = 0, l=0, m1 = 0, ms = \(+\frac{1}{2}\)
• n = 1, l=0, m1 = 0, ms = \(-\frac{1}{2}\)
• n = 1, l=1, m1 = 0, ms = \(+\frac{1}{2}\)
• n = 2, l=1, m1 = 0, ms = \(-\frac{1}{2}\)
• n = 3, l=3, m1 = -3, ms = \(+\frac{1}{2}\)
• n = 3, l=1, m1 = 0, ms = \(+\frac{1}{2}\)

Answer: This is not possible because n cannot be zero. and are not possible because the value of n cannot be equal to 1.

Question 31. How many electrons in an atom may have the following quantum numbers?

1. n = 4,
2. ms = \(+\frac{1}{2}\)
3. n = 3, l = 0

Answer: For n = 4, the total number of electron

= 2 H2 = 2 x 42 = 32 . Among these 32 electrons, half Le., 16 electrons will have s or ms = \(+\frac{1}{2}\) and the other 16 electrons will have ms = \(-\frac{1}{2}\)

n = 3 , l = 0 means 3s -subshell. The maximum number of electrons in this subshell is two.

Question 32. Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Answer: According to Bohr’s postulate, angular momentum \(m v r=\frac{n h}{2 \pi}\) [n = principle quantum number = 1, 2, 3, 4 …]

Again, according to the de Broglie equation, for a revolving electron, wavelength \((\lambda)=\frac{h}{m v}\)

Substituting the value of A from (2) in (1) we have, 2pi r = n lambda (n = 1,2, 3, 4….)

Thus, the circumference of the Bohr orbit is an integral multiple ofthe de Broglie wavelength ofthe revolving electron.

Question 33. What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition n = 4 to n = 2 of the He+ spectrum?
Answer: For Balmer transition, n = 4 to n = 2, for He+ spectrum, the Rydberg equation is,

\(\bar{v}=\frac{1}{\lambda}=R Z^2\left(\frac{1}{2^2}-\frac{1}{4^2}\right)=R \times 2^2 \times \frac{3}{16}=\frac{3 R}{4}\)

[therefore for he, Z=2]

For Hydrogen spectrum

\(\bar{v}=\frac{1}{\lambda}=R Z^2\left(\frac{1}{n^2}-\frac{1}{n_2^2}\right)=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

According To The Question,

\(R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)=\frac{3 R}{4}\)

or, \(\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)=\frac{3}{4}\)

The equation (1) will be true if n = 1 and n -2.

For hydrogen, the spectrum transition is from n = 2 to n = 1.

Atomic Structure Fundamentals

Question 34. Calculate the energy required for the process \(\mathrm{He}^{+}(g) \rightarrow \mathrm{He}^{2+}(g)+e\) The ionization energy of the H-atom in the ground state is 2.18 X 10-18J.atom-1
Answer: The energy of an electron residing in the nth-orbit of a hydrogen-like atom/ion is En \(=-\frac{2 \pi^2 m Z^2 e^4}{n^2 h^2}\)

Ionization enthalpy for h- atom = Einfinite – E1

\(=0-\left[-\frac{2 \pi^2 m e^4 \times 1^2}{1^2 \times h^2}\right]\)

Or, \(\frac{2 \pi^2 m e^4}{h^2}=2.18 \times 10^{-18} \mathrm{~J}\)

IE = 2. 18 x 10-18(given)]

Again, ionisation enthalpy of He+ ion =E∞-El

\(=0-\left[-\frac{2 \pi^2 m e^4 \times 2^2}{1^2 \times h^2}\right]\)

Since Z=2

\(=4 \times \frac{2 \pi^2 m e^4}{h^2}=4 \times 2.18 \times 10^{-18} \mathrm{~J}=8.72 \times 10^{-18} \mathrm{~J}\)

∴ Energy required for the process = 8.72 x 10-18 J

Question 35. If the diameter of a carbon atom is 0.15 nm, calculate the number of carbon atoms that can be placed side by side in a straight line across a length of scale of length 20 cm.
Answer: Diameter (d) ofcarbon atom = 0.15nm = 0.15 x 10-9m
Length ofthe scale (Z) = 20cm = 20 x 10-2m
The number of carbon atoms that can be placed along the length ofthe scale \(=\frac{l}{d}=\frac{20 \times 10^{-2} \mathrm{~m}}{0.15 \times 10^{-9} \mathrm{~m}}=1.33 \times 10^9\)

Atomic Structure Fundamentals

Question 36. 2 X 108 atoms of carbon are arranged side by side. Calculate the radius of the carbon atom if the length of this arrangement is 2.4 cm.
Answer: Number of C-atoms (n) = 2 x 108 and length of the arrangement (Z) = 2.4cm = 2.4 x 107nm

∴ Diameter of carbon atom =l/n. Therefore, radius of
carbon atom \(=\frac{l}{2 n}=\frac{2.4 \times 10^7 \mathrm{~nm}}{2 \times 2 \times 10^8}=0.06 \mathrm{~nm}\)

Question 37. The diameter of the zinc atom is 2.6A. Calculate the radius of the zinc atom in pm and the number of atoms present in a length of 1.6 cm if the zinc atoms are arranged side by side lengthwise
Answer: Radius \(=\frac{2.6 }{2}=1.3=1.3 \times 10^{-10} \mathrm{~m}\)

= 1.3 x 10-10 x 1012pm = 130pm

Given, length = 1.6cm = 1.6 x 10-2m and diameter of an atom = 2.6A = 2×10-10m.

Atomic Structure Fundamentals

∴ Number of zinc atoms present along the length of1.6 cm

\(=\frac{1.6 \times 10^{-2} \mathrm{~m}}{2.6 \times 10^{-10} \mathrm{~m}}=6.154 \times 10^7\)

Question 38. A certain particle carries 2.5 X 10 16C of static electric charge. Find the no. electrons present in It.
Answer: Charge of electron = 1.602 x 10-19C (excluding -ye sign

∴ No. electrons contained in \(=\frac{2.5 \times 10^{-16} \mathrm{C}}{1.602 \times 10^{-19} \mathrm{C}}=1560\)

Question 39. In Millkan’s experiment, a static electric charge on the oil drops was obtained by shining X-rays. If the static electric charge on the oil drop is -1.282 x 10-18C, calculate the number of electrons present on it.
Answer: Charge of an electron =-1.602 x 10-19C

Thus, number of electrons contained in -1.282 x 10-18C Charge

\(=\frac{-1.282 \times 10^{-18} \mathrm{C}}{-1.602 \times 10^{-19} \mathrm{C}}=8\)

Question 40. In Rutherford’s experiment, generally, the thin foil of heavy atoms, like gold, platinum, etc. have been used to be bombarded by the a -particles. If the thin foil of light atoms like aluminium etc. is used, what difference would be observed from the above results?
Answer: The nucleus of heavy atoms contains a large amount of chlorine. positive charge. Thus, the a -particles that move towards the nucleus are deflected back due to strong repulsion by the nucleus. Those particles which pass through the region closer to the nucleus are deflected in different directions. On the other hand, the nucleus of light atoms contains a small amount of positive charge. Hence, a negligible number of particles are deflected back or are deflected by small angles.

Question 41. Symbol \({ }_{35}^{79} \mathrm{Br}\) and \({ }^{79} \mathrm{Br}\) symbol \({ }_{35}^{79} \mathrm{Br}\) and \({ }^{35} \mathrm{Br}\) are not acceptable. Answer briefly.
Answer: \({ }_{35}^{79} \mathrm{Br}\) is not acceptable because mass number should be written as superscript and atomic number as subscript. 35Br is not acceptable because the atomic number of an element is fixed but the mass number is not fixed. It depends on the isotopes. Thus, an indication of mass number is essential.

Atomic Structure Fundamentals

Question 42. An element with mass number 81 contains 31.7% more neutrons as compared to protons. Assign the atomic symbol.
Answer: No. of protons + no. of neutrons = mass number = 81

Let, the number of protons present in an atom = x

Number of neutrons present \(=x+\frac{31.7}{100} \times x=1.317 x\)

As given in the question, x + 1.317x = 81

or, 2.317x = 81 or, x = 34.96 = 35

Thus, number of protons = 35 l.e., atomic number = 35

The element with atomic number 35 is Br

∴ The Symbol is \({ }_{35}^{81} \mathrm{Br} \text {. }\)

Question 43. An ion with mass number 37 possesses one unit of negative charge. If the ion contains 11.1% more neutrons than electrons, find the symbol of the ion
Answer: As the ion contains one unit of negative charge, the ion has one electron more than that of the number of protons. Total number of electrons and neutrons =37 + 1 = 38. Let the number of electrons in the ion = x.

Hence, number of neutron \(=x+\frac{11.1}{100} \times x=1.111 x\)

Again, x+ l.lllx = 38 or, x = 18
Thus, the number of electrons present in the ion = 18.

Thus, the number of protons present in the ion =18-1 = 17

So, the atomic number of the element is 17 i.e., the atom is chlorine. its symbol ,\({ }_{17}^{37} \mathrm{Cl}^{-}\)

Question 44. An ion with mass number 56 contains 3 units of positive charge and 30.4% more neutrons than electrons. Assign the symbol to this ion.
Answer: The ion contains three units of positive charge. Thus, the number of electrons in the ion is three less than that of the
number of protons. Number of protons + number of neutrons mass number =56. let, the number of electrons in the ion be x.

Number of neutrons present in the ion \(=x+\frac{30.4}{100} \times x=1.304 x\)

Again, the total number of electrons and neutrons = 53. X + 1.304x = 53 or, 2.304X = 53 Thus, number of electrons present in the ion = 23 and the number of protons =23 + 3 = 26 . The element with atomic number 26 is Fe and thei£ymbol will be \({ }_{26}^{56} \mathrm{Fe}^{3+}\).

Atomic Structure Fundamentals

Question 45. Arrange falling radiations in increasing order of frequency; radiation from microwave own amber light from traffic signal radiation from FM radio cosmic ray from outer space X-rays.
Answer: Radiation from FM radio < microwave < amber light < Xrays < cosmic rays.

Question 46. Nitrogen laser produces radiation at a ‘wavelength of 337.1 nm. If the die number of photons emitted is 5.6 x 1024, calculate the power of this laser.
Answer: \(E=N h v=N h \frac{c}{\lambda}\)

\(=\frac{\left(5.6 \times 10^{24}\right) \times\left(6.626 \times 10^{-34}\right) \times\left(3.0 \times 10^8\right)}{\left(337.1 \times 10^{-9}\right)}\)

=33X106J

Question 47. Neon gas is generally used in the sign boards. If it emits strongly at 616 nm, calculate the dying frequency of emission, distance traveled by this radiation in the 30s energy of quantum, and the number of quanta present if it produces 21 of energy.
Answer: A = 616nm = 616 x 10_9m, c = 3 x 108m-s-1

Radition Frequency \(v=\frac{c}{\lambda}=\frac{3 \times 10^8}{616 \times 10^{-9}}=4.87 \times 10^{14} \mathrm{~s}^{-1}\)

Distance (s) traveled by the radiation in 30 s = ext =3 x 108m-s-1 x 30 s = 9 x 109m.

Energy of quantum

E=hv = 6.626 x IQ-34 x 4.87 x 1014 = 3.23 x 10-19J.

Number of quanta= \(\begin{aligned}
& =\frac{\text { total energy }}{\text { energy of each quantum }} \\
& =\frac{2 \mathrm{~J}}{3.23 \times 10^{-19} \mathrm{~J}}=6.19 \times 10^{18}
\end{aligned}\)

Atomic Structure Fundamentals

Question 48. In astronomical observations, signals observed from the distant stars are generally weak. If the photon detector receives a total of 3.15 x 10_18J from the radiations of 600 nm, calculate the number of photons received by the detector.
Answer: wavelength λ= 600nm = 600 x 10-9m.

Energy of phyton \(=\frac{h c}{\lambda}=\frac{\left(6.626 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{600 \times 10^{-9}}\)

= 3.313 x 10-19 J.

Number of photons detected by the detector

\(=\frac{\text { total energy recieved by the detector }}{\text { energy of each photon }}\) \(=\frac{3.15 \times 10^{-18} \mathrm{~J}}{3.313 \times 10^{-19} \mathrm{~J}}=9.15 \approx 10 \text { photons. }\)

Question 49. Lifetimes of the molecules in the excited states are often measured by using a pulsed radiantly source of duration nearly in the nano-second range. If the radiation source has a duration of 2 ns and the number of photons emitted during the pulse source is 2.5 X 1015, calculate the energy of the source.
Answer: Frequency emission (v) \(\begin{aligned}
& =\frac{1}{\text { time period }}=\frac{1}{2 \times 10^{-9} \mathrm{~s}} \\
& =0.5 \times 10^9 \mathrm{~s}^{-1}
\end{aligned}\)

The energy of emission =Nhv

= 2.5 X 1015 X 6.626 X 10-34 X 0.5 X 109

= 8.2825 X10-10J.

Question 50. The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each radiation and energy difference between two excited states.
Answer: A1 = 589nm = 589 x 10-9m

∴ Frequency, v1 \(=\frac{c}{\lambda_1}=\frac{3.0 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{589 \times 10^{-9} \mathrm{~m}}\)

λ2 = 589.6nm = 589.6 X 10-9m

∴ Frequency (v2) \(=\frac{c}{\lambda_2}=\frac{3.0 \times 10^8}{589.6 \times 10^{-9}}=5.088 \times 10^{14} \mathrm{~s}^{-1}\)

The difference in energy (AE) = E1-E2 = h(v1-v2)

= 6.626 X 10-34X (5.093- 5.088) x 1014 = 3.313 X 10-22J

Atomic Structure Fundamentals

Question 51. The work function for the cesium atom is 1.9 eV. Calculate the threshold wavelength and 0 the threshold frequency of the radiation. If the cesium element is irradiated with a wavelength of 500 nm, calculate the kinetic energy and the velocity of the ejected photoelectron.
Answer: Work function of cesium ( w0) = have = 1.9eV

∴ Threshold frequency, v0 \(=\frac{1.9 \mathrm{eV}}{h}=\frac{1.9 \times 1.602 \times 10^{-19}}{6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}\)

or, v0= 4.59 x 1014s-1

[since leV = 1.602 x 10-19J]

Again, threshold wavelength (A0) = c/v0

\(=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{4.59 \times 10^{14} \mathrm{~s}^{-1}}=6.536 \times 10^{-7} \mathrm{~m}\)

Thus threshold wavelength ofcesium = 6.536 x 10-7m

= 654 x 10-9m = 654nm

Atomic Structure Fundamentals

Threshold frequency = 4.59 x 1014s-1 Kinetic energy (KE) of the emitted electron

\(\frac{1}{2} m v^2=h v-w_0=\left(h v-h v_0\right)=h c\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)\)

or, Kinetic energy (KE)

\(=\left(6.626 \times 10^{-34}\right)\left(3 \times 10^8\right)\left(\frac{1}{500 \times 10^{-9} \mathrm{~m}}-\frac{1}{654 \times 10^{-9} \mathrm{~m}}\right)\)

or, KE = 9.36 x 10-20J; So, Kinetic energy of emitted electron 9.36 X 10-20J.

Or, \(\frac{1}{2} m v^2=9.36 \times 10^{-20}\)

Or, \(v^2=\frac{9.36 \times 10^{-20} \times 2}{9.108 \times 10^{-31}} \text { or, } v=4.53 \times 10^5\)

Hence, the velocity of the emitted electron is 4.53 x 105m.s-I

Question 52. The following results are observed when sodium metal is irradiated with different wavelengths. Calculate threshold wavelength and Planck’s constant.
Answer: let threshold wavelength = λ0nm = λ0 X 10-9m Again, Kinetic energy of emitted electron.

\(\left(\frac{1}{2} m v^2\right)=h\left(v-v_0\right)=h c\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)\)

Putting the given values in (1) we get

\(\frac{1}{2} m\left(2.55 \times 10^5\right)^2=\frac{h c}{10^{-9}}\left(\frac{1}{500}-\frac{1}{\lambda_0}\right)\) \(\frac{1}{2} m\left(4.35 \times 10^5\right)^2=\frac{h c}{10^{-9}}\left(\frac{1}{450}-\frac{1}{\lambda_0}\right)\) \(\frac{1}{2} m\left(5.35 \times 10^5\right)^2=\frac{h c}{10^{-9}}\left(\frac{1}{400}-\frac{1}{\lambda_0}\right)\)

Dividing (3) by (2) we get \(\frac{\lambda_0-450}{450 \lambda_0} \times \frac{500 \lambda_0}{\lambda_0-500}=\left(\frac{4.35}{2.55}\right)^2\)

or, λ0 = 530.88=531 nm

Substituting the value of λ0 in (4) we have \(\frac{1}{2} \times\left(9.108 \times 10^{-31}\right) \times\left(5.35 \times 10^5\right)^2\)

\(=\frac{h \times 3 \times 10^8}{10^{-9}}\left(\frac{1}{400}-\frac{1}{531}\right) \quad \text { or, } h=7.045 \times 10^{-34}\)

Value of Planck’s constant obtained = 7.045 x 10-34J.s

Question 53. The ejection of the photoelectron from the silver metal In the photoelectric effect experiment can be stopped by applying the voltage of 0.35 V when the radiation 256.7 nm is used. Calculate the work function for silver metal.
Answer: Energy of incident radiation, E = hv = work function of a metal + Kinetic energy of photoelectrons.

or, \(B=h v=h \frac{c}{\lambda}=\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{\left(256.7 \times 10^{-9} \mathrm{~m}\right)}\)

Or, E = 7.74 X 10-19J = 4.03eV

Since leV = 1.602 x10-19J)

The potential applied provides the Kinetic energy to the electron. Thus, the kinetic energy of the electron =0.35eV. So, the work function of silver metal = (4.83- 0.35)eV = 4.48eV.

Atomic Structure Fundamentals

Question 54. If the photon of the wavelength 150 pm strikes an atom and one of its inner bound electrons is ejected out with a velocity of 1.5 X 107 m>s-1, calculate the energy with which it is bound to the nucleus.
Answer: Energy of incident photon

\(=\frac{h c}{\lambda}=\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{\left(150 \times 10^{-12} \mathrm{~m}\right)}\)

= 1.3252 X 10-15J = 13.252 X 10-16J

Kinetic energy of emitted  electron \(\left(\frac{1}{2} m v^2\right)\)

\(=\frac{1}{2} \times\left(9.108 \times 10^{-31} \mathrm{~kg}\right) \times\left(1.5 \times 10^7 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)^2\)

= 1.025 X 10-16J

So, the energy with which the electron was bound to the

nucleus =(13.252 X 10-16- 1.025 X 10-16)J

= 12.227 X 10~16J = 7.632 x 103eV

Atomic Structure Fundamentals

Question 55. Emission transitions in the Paschcn series end at orbit n = 3 and start from orbit n and can be represented as v = 3.29 x 10I5(IIz) [1/32-1/n2]. Calculate the value of n if the transition is observed at 1285 nm. Find the region of the spectrum.
Answer: \(v=\frac{c}{\lambda}=\frac{3.0 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{1285 \times 10^{-9} \mathrm{~m}}=3.29 \times 10^{15}\left(\frac{1}{3^2}-\frac{1}{n^2}\right)\)

\(2.33 \times 10^{14}=3.29 \times 10^{15}\left(\frac{1}{9}-\frac{1}{n^2}\right)\) \(\text { or, } \quad \frac{2.33 \times 10^{14}}{3.29 \times 10^{15}}=\frac{1}{9}-\frac{1}{n^2} \text { or, } 0.071=\frac{1}{9}-\frac{1}{n^2}\) \(\text { or, } \frac{1}{n^2}=\frac{1}{9}-0.071 \text { or, } \frac{1}{n^2}=0.040 \text { or, } n^2=25\)

or, n – 5. Therefore, radiation corresponding to 1285 nm belongs to the infrared region.

Question 56. Calculate the wavelength for the emission transition if it starts from the orbit having a radius of 1.3225 nm and ends at 211.6 pm. Name the series to which this transition belongs and the region of the spectrum.
Answer: For a 1 electron system, the radius of the n-th orbit \(=\frac{52.9 n^2}{Z}\) pm

The radius of the orbit from which the transition of the electron occurs = 1.3225nm = 1322.5pm \(=\frac{52.9 n_1^2}{Z}\)

The radius ofthe orbit to which the electron is added.

\(r_2=211.6 \mathrm{pm}=\frac{52.9 n_2^2}{Z}\) \(\text { So, } \frac{r_1}{r_2}=\frac{1322.5}{211.6}=\frac{n_1^2}{n_2^2} \text { or, } \frac{n_1}{n_2}=2.5\)

When n1 = 5 and n2 = 2, the equation obtained for n1 and n2 is satisfied. Thus, the transition occurs from n = 5 to n = 2 and belongs to the Balmer series.

∴ Wave number (v) = 109677 \(\times\left(\frac{1}{2^2}-\frac{1}{5^2}\right)\) =2.3 x 104cm-1.

and wavelength \((\lambda)=\frac{1}{\bar{v}}=\frac{1}{2.3 \times 10^4} \mathrm{~cm}\)

= 4.35 x 10-5cm = 435nm

Thus, it lies in the visible region.

Question 57. The dual behavior of matter proposed by de Broglie led to = 1.52 x 10-38m the discovery of an electron microscope often used for the highly magnified images of biological molecules and another type of material. If the velocity of the electron in this microscope is 1.6 X106 m-s-1, calculate the de Broglie wavelength associated with this electron.
Answer: Velocity ofan electron (y) = 1.6 x 106ms_1 and mass of an electron (m) = 9.108 x 10-31kg

∴ de broglie wavelength \((\lambda)=\frac{h}{m v}\)

\(\begin{aligned}
& =\frac{6.626 \times 10^{-34}}{9.108 \times 10^{-31} \times 1.6 \times 10^6} \\
& =4.55 \times 10^{-10} \mathrm{~m}=455 \mathrm{pm}
\end{aligned}\)

Question 58. Similar to electron diffraction, a neutron diffraction microscope is also used for the determination of the structure of molecules. If the wavelength used here is 800 pm, calculate the characteristic velocity associated with the neutron.
Answer: Mass of neutron (m) = 1.675 x 10 27kg
According to de Broglie equation, wavelength \((\lambda)=\frac{h}{m v}\)

∴ Velocity ofa neutron \(v=\frac{h}{m \lambda}\)

Or, \(v=\frac{6.626 \times 10^{-34}}{1.675 \times 10^{-27} \times 800 \times 10^{-12}}\)

or, v = 494m.s-1.

Atomic Structure Fundamentals

Question 59. If the velocity of the electron in Bohr’s first orbit is j 2.19 x 106m.s-1, calculate the de Broglie wavelength associated with it.
Answer:

\(\begin{aligned}
v & =2.19 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1} ; m=9.108 \times 10^{-31} \mathrm{~kg} \\
\lambda & =\frac{h}{m v}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{\left(9.108 \times 10^{-31} \mathrm{~kg}\right) \times\left(2.19 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)} \\
& =3.32 \times 10^{-10} \mathrm{~m}=332 \times 10^{-12} \mathrm{~m}=332 \mathrm{pm}
\end{aligned}\)

Atomic Structure Fundamentals

Question 60. The velocity associated with a proton moving in a j potential difference of 1000 V is 4.37 x 103m.s-1. If the hockey ball of mass 0.1 kg is moving with this velocity, calculate the wavelength associated with this velocity.
Answer: Velocity of hockey ball =4.37x 105m-s-1 , mass = 0.1kg

∴ wave length \(\begin{aligned}
(\lambda) & =\frac{h}{m v}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{0.1 \mathrm{~kg} \times 4.37 \times 10^5 \mathrm{~m} \cdot \mathrm{s}^{-1}} \\
& =1.52 \times 10^{-38} \mathrm{~m}
\end{aligned}\)

Question 61. If the position of the electron is measured within an accuracy of ± 0.002nm, calculate the uncertainty In the momentum of the electron. Suppose the momentum of the electron Is h/(4xm x 0.05)nm, is there any problem in defining this value?
Answer: Given, Ax = 0.002nm = 2 x 10-3nm = 2 x 10-12m According to Heisenberg’s uncertainty principle.

\(\Delta x \times \Delta p=\frac{h}{4 \pi} \quad \text { or, } \Delta p=\frac{h}{4 \pi \Delta x}\) \(=\frac{6.626 \times 10^{-34}}{4 \times 3.14 \times 2 \times 10^{-12}}=2.638 \times 10^{-23} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}\)

Again Momentum of the electron

\(\begin{aligned}
& =\frac{h}{4 \pi \times 0.06 \mathrm{~nm}}=\frac{h}{4 \pi \times 5 \times 10^{-11} \mathrm{~m}} \\
& =\frac{6.606 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{4 \times 3.14 \times 5 \times 10^{-11} \mathrm{~m}}=1.055 \times 10^{-24} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}
\end{aligned}\)

The quantum numbers of six electrons are given below. Arrange them in order of increasing energy. list if any of this combinationÿ) has/ have the same energy.

• n=4, l=2, m1=-2 ms=-1/2
• n=4, l=2, m1=1 ms=+1/2
• n=4, l=2, m1=0 ms=+1/2
• n=4, l=2, m1=-2 ms=-1/2
• n=4, l=2, m1=-2 ms=+1/2
• n=4, l=2, m1=-2 ms=+1/2

Answer: The orbital occupied by the electrons that are designated by the given sets of quantum numbers are,

1. 4d
2. 3d
3. 4p
4. 3d
5. 3p
6. 4p

So, increasing the order of their energies will be—

5<2<4<6=3<1

Atomic Structure Fundamentals

Question 63. The bromine atom possesses 35 electrons. It contains 6 electrons in a 2p orbital. 6 electrons in 3p orbital and 5 electron in 4p orbital. Which of these electrons experiences the lowest effective nuclear charge?
Answer: The value of n for the 4p electrons is highest and hence they are the furthest from the nucleus and thus experience the lowest effective nuclear charge.

In a given orbit, for the same type of subshells, the higher the value of n, the lower the value of effective nuclear charge.

Question 64. Among the following pairs of orbitals which orbital will experience the larger effective nuclear charge?

1. 2s and
2. 3s,
3. 4d and
4. 4f,
5. 3d and
6. 3p

Answer:

1. 2s
2. 4d
3. 3p

Question 65. The unpaired electrons in A1 and Si are present in the 3p orbital. Which electrons will experience a more effective nuclear charge from the nucleus?
Answer: The nuclear charge of silicon (+14) is greater than that of aluminum (+13). Hence the impaired 3p -electron of silicon will experience a more effective nuclear charge.

Question 66. Indicate the number of impaired electrons in:

1. P
2. Si
3. Cr
4. Fe and
5. kr

Answer:

1. 15P = ls22s22p63s23pÿ3pÿ3pÿ ; number of unpaired electrons = 3.
2. 14Si = ls22s22p63s23pÿ3pÿ; number of unpaired electrons = 2.
3. 24Cr = ls22s22p63s23p63d54s1; number of paired electrons = 6 (5 in d-subshell &1 in s-subshell).
4. 2gFe = ls22s22p63s23p63d64s2; number of unpaired electrons in d-subshell = 4.
5. 36Kr = ls22s22p63s23p63d104s24p6; number of unpaired electrons = 0.

Question 67. How many subshells are associated with n =4? How many electrons will be present in the subshells having ms value of \(-\frac{1}{2}\) for n = 4?
Answer: For n = 4, l = 0, 1, 2, 3. Thus, the energy level with n = 4 contains four subshell (4s, 4p, 4d and 4f).

For n = 4, the number of orbitals (n)2 = (4)2 = 16.

Each orbital will have only one electron with ms = Hence, for n = 4, 16 electrons will be present in the subshells with the value of ms \(=-\frac{1}{2}.\)