Arithmetic Chapter 3 Approximate Value Exercise 3 Solved Example Problems
Approximate Value
In our daily life, in many cases, it is not possible to calculate the actual value of a quantity or the actual price or weight of a body accurately.
Therefore, in such cases for practical purpose, a value is taken nearest to the actual value, actual price, or actual weight.
It is called the approximate value of that quantity or the approximate price or weight of that body.
Suppose, ₹262.50 is to be divided among 50 boys. Then each boy will get ₹262.50 +50 =₹5.25.
Now observe that, if each boy is given ₹5 then each boy gets 25 paise less than what he would have obtained.
Again, if each boy is given ₹6 then each boy gets 75 paise more than his due.
Therefore, neither ₹5 nor ₹6 is due for that boy. Hence, this less or more is to be termed an error.
Since there is an error in both cases, therefore, the less is the amount of error more is the degree of purity.
In the above case, if ₹5 is given then an error is 25 paise and if ₹6 is given the error is 75 paise. Hence, if each is given 5 then he will be given the nearest money due for him.
Again, let ₹287.50 is to be divided among 50 boys equally. Then each boy will get ₹287.50÷ 50= ₹5.75.
Therefore, in this case, if each boy is given 6 then he will be given the nearest money due for him.
Rule: In order to calculate the approximate value instead of the actual value of any quantity, if the digit after the decimal be less than 5 (₹ 5 and paise 25 = ₹ 5.25) then it is to be ignored and if it be 5 or greater than 5 (₹ 5 and paise 75 =₹ 5.75) then 1 is to be added with the digit in the units’ place.
Approximate value of the integer
If the value of the number 5832 is written as 5000 then 832 less than the actual value is written. Again if 6000 is written instead of 5832 then, (60005832) or 168 more than the actual value is written.
Now observe that between 6000 and 5000 the former is nearer to the actual value of 5832.
Therefore, the value of 5832 in the approximate thousands of places is 6000. Similarly, the value of 5832 in the approximate hundreds’ place is 5800, and in the approximate tens’ place is 5830.
Approximate value of decimal fraction
In order to find the approximate value of any decimal fraction up to a definite decimal place, write the digits up to that decimal place and reject the next remaining digits.
But if the first digit from the left-hand side of the rejected digits be 5 or more than 5 then 1 is to be added with the last digit of that particular place.
For example, the approximate value of 3.65038 up to integer = 4. (Since, the number 6 at the left end of the rejected portion after 3 is greater than 5 therefore, 4 is the result after adding 1 with 3).
Its approximate value up to 1 decimal place =3.7 (Here, since the first digit of the rejected portion is 5 therefore, 1 is added with the previous digit.
Its approximate value up to 2 decimal places = 3.65.
(Here, since the first digit of the rejected portion is 0 therefore, nothing has been added to the previous digit.)
Its approximate value up to 3 decimal places = 3.650.
Its approximate value up to 4 decimal places = 3.6504.
Examples:
1. Find the correct value of 0.655172 up to 4 decimal places.
Solution: 0.6552 (first digit of the rejected portion is 7)
2. Express 3628753 in approximate hundred.
Solution: 3628800
3. Find the correct values of 1.218713 upto 3 and 4 decimal places and express the approximate value of their difference corrected to 2 decimal places.
Solution:

The subtracted value, when corrected upto 2 decimal places, is 0.00
Significant digit
The numbers are formed by the digits 1 to 9. They are called significant digits. If between two significant digits, there is/are one or more than one zeroes (0) then those zeroes are also taken as significant digits.
If in any decimal fraction, there is a decimal point in the beginning and there are some zeroes after the decimal point then digits other than zeroes are called significant digits. The last zero or zeroes of an integer or decimal fraction are sometimes significant digits and sometimes they are not so.
Example:
1. The approximate value of 30.23046 up to 4 significant digits 30.23. But its approximate value corrects up to 4 decimal places = 30.2305.
2. In the case of the number 0.12065 the value is correct up to 4 decimal places and also the approximate value up to 4 significant digits are both equal to 0.1207.
3. In the case of the number 0.00147, the value corrects up to one significant digit = 0.001 and the value corrects up to two significant digits= 0.0015.
4. The approximate value of 0.000240079 up to five decimal places= is 0.00024. But its approximate value up to 5 significant digits= 0.00024008.
5. In the case of the number 0.44598 the correct value up to 4 decimal places and the approximate value up to 4 significant digits are both equal to 0.4460 (Here 0 is the significant digit; here since the rejected digit is 8, therefore, adding 1 with the last digit 9 of 0.4459 we obtained 0.4460.)
6. The approximate value of 163289 up to 4 significant digits is 163300. (Here, the two zeroes are not significant digits).
7. In case of 705769, the approximate value up to a thousand and the approximate value up to a hundred are 706000 and 705800 respectively. (In both cases the last zeroes are not significant digits).
Error
If a value other than the actual value is taken then there occurs an error. In practical case this error should be as small as possible. Let us roughly take the weight of 100 kg of coal.
If the weight is taken more accurately then it may be found that the weight of coal is 99 \(\frac{1}{2}\) kg. In this \(\frac{1}{2}\) kg of coal, the loss is not significant.
But if it is gold in and that would not be negligible. Therefore, in lieu of coal then there would be a great loss if a goldsmith is compelled to measure gold more accurately.
Arithmetic Chapter 3 Approximate Value Exercise 3 Absolute Error, Relative Error, And Percentage Error
The difference between the actual value and the approximate value is called the absolute error of the approximate value.
That means, absolute error = Actual value ∼ approximate value.
The ratio of absolute error and the actual value is called the relative error.
That means, relative error = \(\frac{Absolute error}{Actual value}\).
The percentage error of the approximate value is that percentage of the actual value which the absolute error is.
That means, percentage error = \(\frac{Absolute error}{Actual value} \)
Example 1. Express 4325 kg in approximate hundred kg and find an absolute error, relative error, and percentage error.
Solution:
Given:
4325 kg
4325 kg = 4300 kg (in approximately 100 kg)
∴ absolute error = 4325 kg-4300 kg = 25 kg 25 kg
relative error = \(\frac{25 \mathrm{~kg}}{4325 \mathrm{~kg}}=\frac{1}{173}\)
and percentage error = relative error x 100 = \(\frac{1}{173}\) x100= 0.58 (correct up to 2 decimal places).
Example 2. Find the approximate value up to first two significant digits and the absolute error of 3.068.
Solution:
Given:
3.068
The approximate value of 3.068. The required sum = 13.67489.
up to first two significant digits = 3.1. absolute error = 3.068-3.1 = 0.032.
Example 3. A man measured a path of length 12 \(\frac{7}{200}\) km and told its length as 12.01 km. At this find his absolute error, relative error, and percentage error.
Solution:
Given:
A man measured a path of length 12 \(\frac{7}{200}\) km and told its length as 12.01 km.
12 \(\frac{7}{200}\) = 12.035
Absolute error = 12.035 km -12.01 km = 0.025 km
Relative error = \(\frac{0.025 \mathrm{~km}}{12035 \mathrm{~km}}=\frac{5}{2407}\)
and percentage error = \(\frac{5}{2407}\) x 100 = 0.21%
(correct up to 2 decimal places).
Arithmetic Chapter 3 Approximate Value Exercise 3 To Find The Addition And Subtraction In Approximate Value Of Decimal
Rule: When the result of addition and subtraction are to be known approximately up to a definite decimal place, it is necessary to know the next digit.
Therefore, we have to find the result of addition and subtraction up to two more digits than the digits up to which approximation is required to be done. Then the answer is to be given in approximate value as per requirement.
Example 1. What is the sum of 4.3074, 0.0028391, and 9.364 approximate up to five decimal places?
Solution:
Given:
4.3074, 0.0028391,And 9.364

Here, to get the approximate 5 decimal place the 6th decimal place must be known correctly.
So, writing up to one more decimal place i.e., 7th decimal place the sum is to be determined.
∴ The required sum = 13.67489
Example 2. Find the difference of 30.406 and 23.139 approximately up to 4 decimal places.
Solution:
Given:
30.406 And 23.139

∴ The required difference of 7.2670
Example 3. Find the sum of 7.302, 0.0865, 32.87, and 3.02 approximately up to 3 significant digits.
Solution:
Given:
7.302, 0.0865, 32.87, And 3.02
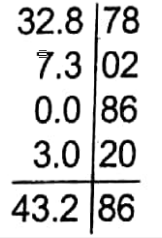
∴The required sum = 43.3.

