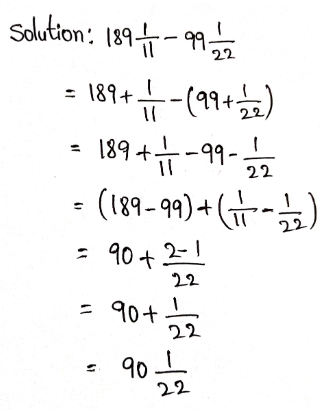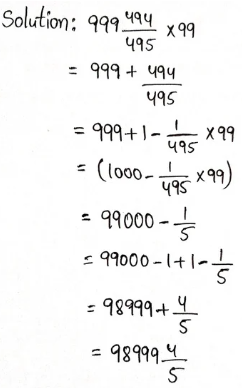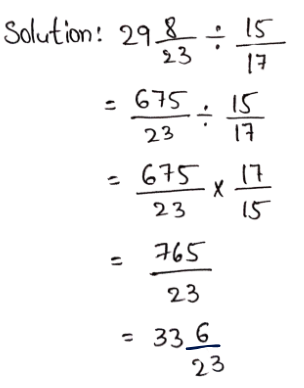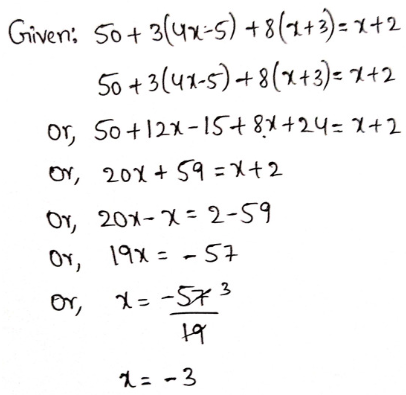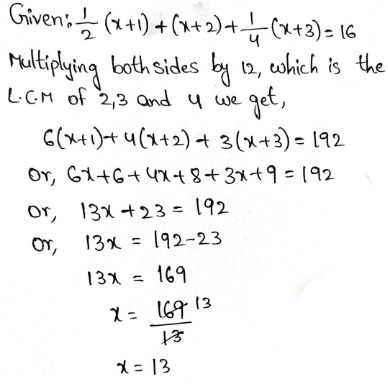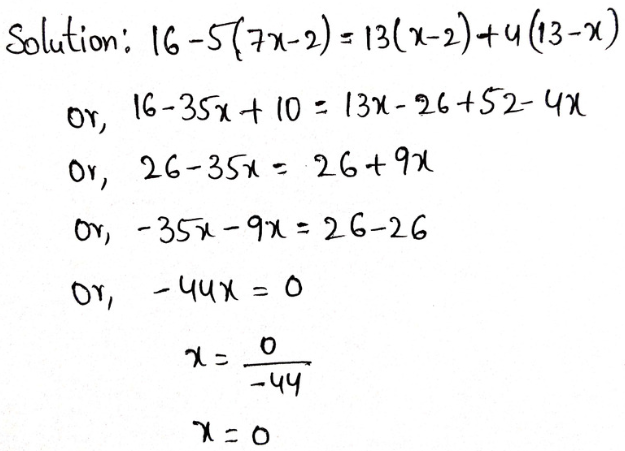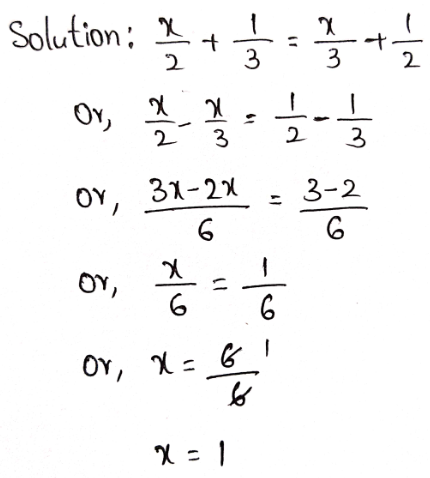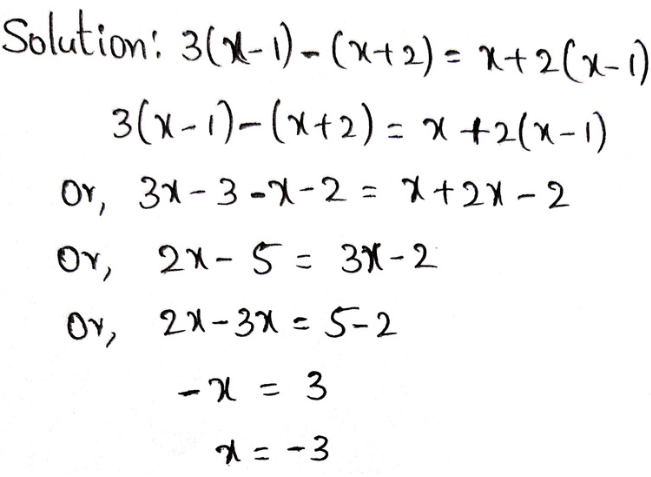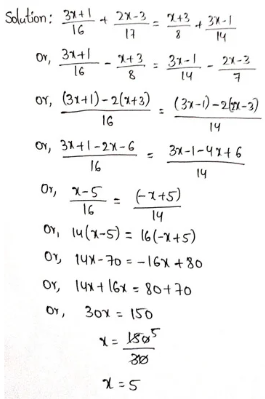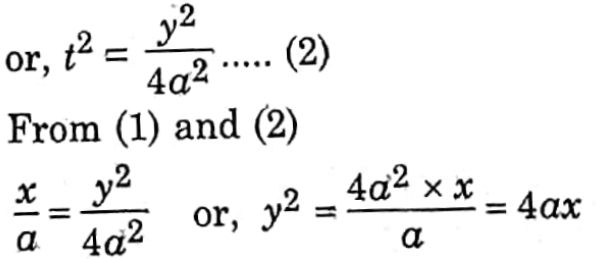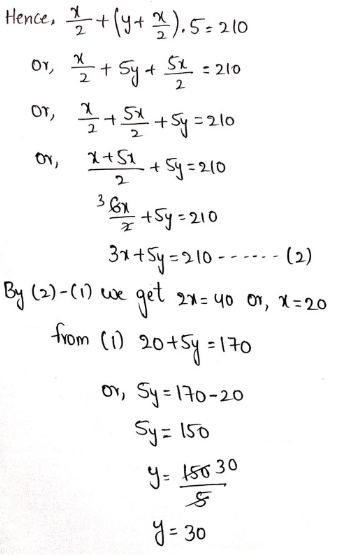Class 7 Maths

Geometry Chapter 2 Miscellaneous Constructions Exercise 2 Solved Example Problems

Introduction

In class 6 you have studied the uses of different instruments found in the geometrical box. A very important topic in geometry is to construct different geometric figures accurately with the help of those instruments.

In this chapter, our aim is to construct various geometric figures mainly with the help of a scale, protractor, pair of dividers and pair of pencil compasses. While constructing those geometrical figures you should keep in mind two important aspects.

Firstly the end of your pencil must be very sharp and the use of an eraser should be minimised. If you can draw accurate geometrical figures at this early stage then it will help you a lot in the higher classes where more complicated figures will be required to construct.

To draw a 60° angle without the help of a protractor

Without the help of a protractor, an angle is to be drawn whose measure is 60°.

Read and Learn More WBBSE Solutions For Class 7 Maths

Construction: Take any straight line AB.

With A as centre and any radius draw an arc which intersects AB at C.

Again with C as centre and same radius draw another arc which intersects the former arc at D. AD is joined.

Then ∠DAB is the required angle whose measure is 60°.

To draw a 90° and a 120° angle without the help of protractor.

Wbbse Class 7 Maths Solutions

Without the help of protractor two angles are to be drawn whose measures are 90° and 120°.

Construction: Take any straight line AB. With A as centre and any radius draw an arc which intersects AB at X.

With X as centre and any radius draw an arc which intersects AB at X. With X as center and same radius draw another arc which intersects the former arc at C.

Again with C as centre and same radius draw another arc which intersects the former arc at D.

Now, with C and D as centres and same radius draw two arcs which intersect each other at the point E. Join AD and AE.

Then  ∠EAB = 90° and ∠DAB = 120° are the two required angles.

To construct an angle equal to a given angle

Let ∠ABC be a given angle.

It is required to construct an angle equal to ∠ABC.

Construction: Take any straight-line EF in the plane of the ∠ABC. With the vertex B of ∠ABC as centre and any radius draw an arc which intersects AB and BC at M and N respectively.

Wbbse Class 7 Maths Solutions

Now with E as centre and with the same radius as before draw an arc which intersects EF at Q. Now with Q as centre and radius equal to NM draw an arc which intersects the former arc at P. Join EP and produce it upto D.

Thus, ∠DEF is equal to ∠ABC.

Verification: If you measure the angles ABC and DEF with protractor you will find that they are of equal measure.

Construction of triangles

You have learnt earlier that a triangle has six parts, namely three sides and three angles.

A definite triangle can be constructed if three mutually independent parts are known. In fact, we can construct a triangle in the following cases:

1. When the three sides of a triangle are known.
2. When the two sides and the included angle of the triangle are known.
3. When the two sides and the angle opposite to one of them are known.
4. When one side and the angles adjacent to it are known.
5. When the hypotenuse and one side of a right-angled triangle are known.

To construct a triangle when the lengths of its three sides are given

Let a, b, and c be the lengths of the three sides of a triangle.

It is required to construct the triangle.

Construction: Draw any straight-line BD. Now from BD cut off BC equal to the length of the given side a.

Wbbse Class 7 Maths Solutions

Now with B as the centre and radius equal to the length of the side c draws arc of a circle.

Again with C as the centre and radius equal to the length of the side b draw another arc of a circle on the same side of BD to cut the previous arc at A. Join BA and CA.

Thus, ΔABC is the required triangle.

Verification: You may measure the lengths of the sides BC, CA and AB of the triangle ABC by a scale.

You will find that BC = a, CA = b and AB = c.

Thus, AABC is the required triangle whose three sides are equal to a, b and c respectively.

To construct a triangle when the lengths of its two sides and their included angle are given

Let a and c be the lengths of the two sides of a triangle and their included angle be ∠B. It is required to construct the triangle.

Construction: Draw any straight line BD.

Now from BD cut off BC equal to the length of the given side a.

Now at the point B on BC draw an angle ∠CBE equal to the given angle B.

From BE cut off BA equal to the length of the given side c.

Join AC. Thus, ΔABC is the required triangle.

Verification: Measuring the sides BC and BA with a scale and the angle ∠ABC with a protractor you will find that BC = a, BA = c and ∠ABC is equal to ∠B.

Thus, ΔABC is the required triangle whose two sides are a and c and their included angle is ∠B.

Class Vii Math Solution Wbbse

To construct a triangle when the lengths of its two sides and the angle opposite to one of them are given

Let b and c be the lengths of the two sides of a triangle and the angle opposite to the side b be ∠B.

It is required to construct the triangle.

Construction: Draw any straight-line BD. Now at the point B of the straight line BD construct an angle ∠DBE equal to the given angle B.

Now from BE, cut off BA equal to the length of the given side c.

With A as centre and radius equal to the length of the given side b construct an arc of a circle.

Let this arc intersect BD at C₁ and C₂. Join AC₁ and AC₂

Then both ΔABC₁ and ΔABC₂ are the required triangles.

Verification: In the triangle ABC₁ if you measure the sides AB and AC₁ with a scale and the angle ∠ABC₁ with a protractor you will find that AB = c, AC₁ = b and ∠ABC₁ is equal to ∠B.

Similarly, in the triangle ABC₂, AB = c, AC₂ = b and ∠ABC₂ is equal to ∠B.

To construct a triangle when the length of its one side and the angles adjacent to it are given

Let a be the length of one side of a triangle and ∠B and ∠C be the angles adjacent to side a.

It is required to construct the triangle.

Class Vii Math Solution Wbbse

Construction: Draw any straight line BD. Now from BD cut off BC equal to the length of the side a.

Now at the point B on BC draw an angle ∠CBE equal to the given angle B.

Also at the point C on BC draw an angle ∠BCF equal to the given angle C.

Let BE and CF intersect each other at A. Thus, ΔABC is the required triangle.

Verification: Measuring the side BC with a scale and the angles ∠ABC and ∠ACB with protractor you will find that BC = a, ∠ABC and ∠ACB are equal to the angles B and C respectively.

To construct a right-angled triangle when the lengths of its hypotenuse and one side are given

Let the length of the hypotenuse of a right-angled triangle be b and a be the length of its another side.

It is required to construct the triangle.

Construction: Draw any straight-line BD. Now from BD cut off BC equal to the length of the side a.

Draw a perpendicular BE on BC at B. With C as the centre and radius equal to the length of the hypotenuse b draw an arc of a circle to intersect BE at A. Join AC.

Thus, ΔABC is the required triangle.

Verification: Measuring the sides BC and AC with a scale and the angle ∠ABC with a protractor you will find that, BC = a, AC = b and ∠ABC = 90°.

To construct a right-angled triangle when the length of its hypotenuse and an acute angle is given

Let the length of the hypotenuse of a right-angled triangle be b and an acute angle be a.

It is required to construct the triangle.

Class Vii Math Solution Wbbse

Construction: Draw any straight line BD. Now from BD cut off BC equal to the length of the side b. At the point B draw ∠CBY equal to the angle a. Now from the point C draw the perpendicular CN on BY.

Thus, ΔBCN is the required triangle.

Verification: Measuring the length of the side BC it is found that BC = b and measuring ∠NBC and ∠BNC with protractor it is found that ∠NBC = α and ∠BNC = 90°

Construction of quadrilaterals

You have learnt earlier that a quadrilateral has four sides. A definite quadrilateral can be constructed if five mutually independent parts are known.

In fact, we can construct a quadrilateral in the following cases:

1. When the four sides and one angle of the quadrilateral are known.
2. When the three sides and two included angle between them are known.
3. When the four sides and one diagonal of a quadrilateral are known.

Besides the above possibilities we can also construct some quadrilaterals under given conditions, such as:

1. When the two adjacent sides and their included angle of a parallelogram are given.
2. When the length of the side of a square is known.
3. When the length of the side of a rhombus and the measure of its one angle are given.

To construct a quadrilateral when the lengths of its four sides and the measure of an angle are given

Let a, b, c, d be the lengths of the four sides of a quadrilateral, and ∠X be the included angle between the sides of lengths a and b.

It is required to construct the quadrilateral.

Construction: Draw any straight line AP. From AP cut off AB equal to the length of the diagonal l.

With centers A and C and radii equal to the lengths of the sideas a and b respectively draw two arcs of circles on the same side of AC.

Let these arcs intersects at B.

Again with centred A and C and radii  equal to the given angle X.

From AQ cut off AD equal to the length of the side b. Now with centres D and B construct two arcs of the circles of radii c and d respectively.

Let these two arcs intersect each other at C. Join DC and BC.

Class Vii Math Solution Wbbse

Thus, ABCD is the required quadrilateral.

Verification: You may easily verify with scale and protractor that in the quadrilateral ABCD, AB = a, AD = b, DC = c, BC = d and ∠DAB = ∠X.

To construct a quadrilateral when the lengths of its three sides and the measures of two included angles between them are given

Let a, b, c be the lengths of the three sides of a quadrilateral and ∠X be the included angle between a and b, and ∠Y be the included angle between a and c.

It is required to construct the quadrilateral.

Construction: Draw any straight line AP. From AP, cut off AB equal to the length of the side a.

Now at the points A and B of the straight line AB draw angles ∠BAQ and ∠ABR equal to the angles X and Y respectively.

Now from AQ cut off AD equal to the length of the side b and from BR cut off BC equal to the length of the side c. Join DC.

Thus, ABCD is the required quadrilateral.

Verification: You may easily verify with scale and protractor that in the quadrilateral ABCD, AB = a, AD = b, BC = c, ∠DAB = ∠X and ∠CBA = ∠Y.

To construct a quadrilateral when the lengths of its four sides and one diagonal are given

Let, a, b, c, d be the lengths of the four sides of a quadrilateral and l be the length of its diagonal.

It is required to construct the quadrilateral.

Class Vii Math Solution Wbbse

Construction: Draw any straight line AP.

From AP cut off AC equal to the length of the diagonal l. With centres A and C and radii equal to the lengths of the sides a and b respectively draw two arcs of circles on the same side of AC.

Let these arcs intersect at B. Again with centres A and C and radii equal to the lengths of the sides c and d respectively draw two arcs of circles on the other side of AC.

Let these arcs intersect at D. Join AB, BC, AD and CD. Thus, ABCD is the required quadrilateral.

Verification: You may easily verify with a scale that in the quadrilateral ABCD, AB = a, BC = b, AD = c, CD = d and AC = l.

To construct a parallelogram when the lengths of its two adjacent sides and their included angle are given

Let a and b be the two adjacent sides and ZX be their included angle in a parallelogram. It is required to construct the parallelogram.

Construction: Draw any straight line AP. From AP cut off AB equal to the length of the side a. At the point A on AB draw an angle ∠BAQ equal to the given angle X.

From AQ, cut off AD equal to the length of the given side b.

Now with D and B as centres and radius equal to a and b respectively draw two arcs of circles intersecting each other at C. Joint BC and CD.

Thus, ABCD is the required parallelogram.

Verification: You can easily verify with scale and protractor that in the parallelogram ABCD, AB = a, AD = b, ∠BAD = X.

To construct a rectangle whose two adjacent sides are given

Let the length of the two adjacent sides of a rectangle be a and b.

It is required to construct the rectangle.

Construction: Draw any straight line AP. From AP cut off AB equal to the given side a. Now at the point A of the straight line AB construct a perpendicular AQ.

From AQ cut off AD equal to the side b.

Now draw two arcs with centres D and B and radius equal to a and b respectively which intersect each other at point C. Join BC and DC.

Thus, ABCD is the required rectangle

Verification: It can be verified easily by a scale that, for the rectangle, ABCD, AB = DC = a and AD = BC = b.

To construct a square the length of whose side is given

Let the length of the side of a square be a. It is required to construct the square.

Construction: Draw any straight line AP. From AP cut off AB equal to the given side a.

Now at the point A of the straight line AB constructs a perpendicular AQ. It is required to construct the rectangle.

Class Vii Math Solution Wbbse

Construction: Draw any straight line AP. From AP cut off AB equal to the given side a.

Now at the point A of the straight line AB construct a perpendicular AQ.

From AQ cut off AD equal to the side b.

Now draw two arcs with centres D and B and radius equal to a and b respectively which intersect each other at the point C. Join BC and DC.

Thus, ABCD is the required rectangle.

AQ cut off AD equal to the given side a.

Now with D and B as centres and radius equal to a construct two arcs of circles intersecting at C. Join BC and DC.

Thus, ABCD is the required square.

Verification: It can be verified easily by a scale that the length of each side of the square ABCD is a.

To construct a rhombus when the length of its side and the measure of one angle are given

Let the length of each side of a rhombus be a and the measure of its one angle be X.

It is required to construct the rhombus.

Construction: Draw any straight line AP. From AP cut off AB equal to the given side a.

Now at the point Aof the straight line AB construct an angle ∠BAQ equal to the given angle X.

From AQ cut off AD equal to the given side a. Now with D and B as centres and radius equal to a construct two arcs of circles intersecting at C. Join BC and DC.

Thus, ABCD is the required rhombus.

Class Vii Math Solution Wbbse

Verification: It can be verified easily with a scale and a protractor that the length of each side of the rhombus ABCD is a and the measure of the angle ∠BAD is equal to X.

 

Geometry Chapter 1 Angle Triangle And Quadrilateral Exercise 1 Solved Example Problems

Angle Triangle and Quadrilateral Introduction

In order to verify different axioms in geometry and to construct various geometrical figures, the knowledge of angles, triangles, and quadrilaterals is essential.

So, in this chapter, our aim is to discuss different types of angles, triangles, and quadrilaterals. The discussions of this chapter will help the students a lot in the future.

Wbbse Class 7 Maths Solutions

Angle

When two line segments meet at a point, an angle is formed. Those two line segments are called the arms of that angle and the point is called the vertex of the angle.

Read and Learn More WBBSE Solutions For Class 7 Maths

The line segments AB and AC have met at a point A and the angle ∠BAC is formed.

AB and AC are the two arms of the angle and A is the vertex.

If we assume a point D on AS and another point E on AC then ∠DAE and ∠BAC will be of the same measure.

Adjacent angles

If two angles have the same vertex and one common arm and if the two angles are on opposite sides of the common arm then the two angles are called adjacent angles.

∠POQ and ∠QOR are adjacent angles because the vertex of both the angles is O and their common arm is OQ and the two angles are on opposite sides of this common arm.

Perpendicular and Right angle

If a straight line stands on another straight line in such a way.that, two adjacent angles are equal then one of the straight lines is called a perpendicular to the other. Each of the two adjacent angles is called a right angle.

The straight line OC is perpendicular on AB.

Both ∠AOC and ∠BOC are right angles.

1 right angle = 90°.

Here point 0 is the foot of the perpendicular drawn from C on AB.

Straight angle

A straight line AB is drawn on a paper. If point C is taken on the straight line AB  then ∠ACB will be a straight angle. 1 straight angle = 180° = 2 right angles.

Wbbse Class 7 Maths Solutions

Acute angle, Obtuse angle, and Reflex angle

Acute angle: An angle that is less than a right angle is called an acute angle.

For example, 30°, 44°, 70°, etc., are acute angles. Since in the figure, 0°<x<90^o, hence ∠ABC = ∠x is an acute angle.

Obtuse angle: An angle that is greater than one right angle but less than two right angles is called an obtuse angle.

For example, 95°, 110°, 145°, etc., are obtuse angles. Since in the figure 90°<y<180°, hence ∠DEF = ∠y is an obtuse angle.

Reflex angle: An angle which is greater than two right angles but less than four right angles is called a reflex angle.

For example 190°, 210°, 300°, etc., are reflex angles. Since in the figures, 180°<z<360°, hence ∠AOB =∠Z is reflex angle in both the images.

Complementary angle and Supplementary angle

Complementary angle: If the sum of two angles is equal to 90° or one right angle then each angle is called the complementary angle to the other angle.

In the image, ∠BOC is the complementary angle to ∠AOC. In this case, x + y = 90°

Example: 20° is complementary to 70° as (90°-20°) = 70°.

Supplementary angle: If the sum of two angles is equal to 180° or two right angles then each angle is called the supplementary angle to the other angle. In the image, ∠BOC is the supplementary angle to ∠AOC. In the case, x + y = 180°.

Example: 100° is supplementary to 80° as (180°-100°) = 80°.

Wbbse Class 7 Maths Solutions

Vertically opposite angles

If two straight lines intersect each other, two pairs of angles are formed on the opposite sides of the intersecting point.

Then any angle of a pair of angles is called vertically opposite angle of the other.

The straight lines AB and CD intersect at the point O. ∠BOD is the vertically opposite angle of ∠AOC and ∠AOD is the vertically opposite angle of ∠BOC.

The vertically opposite angles are always of the same measure.

∴ ∠AOC = ∠BOD and ∠BOC = ∠AOD.

Transversal, Exterior angles, Interior angles, Interior opposite angles, Alternate angles, Corresponding angles

If a straight line cuts two other straight lines, the former straight line is called the transversal of those two straight lines.

In the image, the straight line EF cuts the two straight lines AB and CD.

Therefore, the straight line EF is the transversal of the straight lines AB and CD.

When a straight line cuts two other straight lines then eight angles are formed. Among them four angles are in the inside region of the two straight lines. These four angles are called interior angles and the other four angles are called exterior angles.

Wbbse Class 7 Maths Solutions

In the image, the interior angles are ∠AGH, ∠GHC, ∠GHD, and ∠HGB (or ∠3, ∠6, ∠5, and ∠4). The exterior angles are ∠EGA, ∠EGB, ∠CHF, and ∠FHD (or ∠2, ∠1, ∠7, and ∠8).

The further off interior angle, in respect of an exterior angle is called interior opposite angle.

For example, ∠GHD (or ∠5) is the interior opposite angle in respect of ∠EGB (or ∠1).

The interior angle adjacent to one exterior angle and the interior angle adjacent to further off interior angle in respect of the same exterior angle are called alternate angles to each other.

In the image, ∠GHD{or ∠5) is the alternate angle of ∠AGH (or∠3), ∠GHC (or∠6) is the alternate angle of ∠BGH (or ∠4).

An exterior angle and an interior opposite angle on the same side of the transversal are called corresponding angles.

In the images, the pair of angles [∠EGB (or ∠1), ∠GHD(or ∠5)], [∠EGA(or ∠2), ∠GHC(or ∠6), [∠AGH(or ∠3), ∠CHF(or ∠7)] and [∠BGH (or∠4), ∠DHF(or ∠8)] are corresponding angles.

Interior angles on the same side of the transversal

Obviously, ∠BGH and ∠GHD (i.e., ∠4 and ∠5) and also ∠AGH and ∠GHC (i.e., ∠3 and ∠6) are the interior angles on the same side of the transversal.

Parallel Lines and Transversal

Two lines in the same plane are said to be parallel lines if the perpendicular distance between them is the same at every intermediate pair of points when produced indefinitely in either direction.

The adjacent imges shows that AB and CD are two parallel lines.

The perpendicular distance between them at every intermediate pair of points (two perpendicular distances PQ and XY are shown in the image) is same.

If the two parallel lines are extended indefinitely in both directions, then also it would be found that the perpendicular distance between them remains same.

A pair of railway tracks is the most common example of parallel lines.

A pair of parallel straight lines (AB and CD) and their transversal EF are shown in the adjacent image.

Since the two straight lines AB and CD are parallel to each other, it can be proved that:

1. Pair of corresponding angles are equal to each other. Therefore, in this case, ∠1 = ∠5, ∠2 =∠6, ∠3 = ∠7 and ∠4 = ∠8.
2. Alternate angles are equal to each other. Therefore, in this case, ∠3 = ∠5 and ∠4 = ∠6.

Taking into account both (1) and (2) we can say that, ∠1 = ∠3 = ∠5 = ∠7 and ∠2 =∠4 = ∠6 = ∠8.

3. The sum of the interior angles on the same side of the transversal is 180° or two right angles.

∴ In this case, ∠3 +∠6 = 180° and ∠4 + ∠5 = 180°.

If a transversal crosses the parallel straight lines at right angles, it is called a perpendicular transversal.

In the adjacent image shown, XY is the perpendicular transversal to the pair of parallel lines AJB and CD.

It is clear from the imagethat, ∠3 + ∠6 = 180° (or 2 right angles) and ∠4 + ∠5 = 180° (or 2 right angles).

Class Vii Math Solution Wbbse

Some examples

Example 1. What is the sum of the angles at a point?

Solution:

Sum of the angles at a point:

An angle is measured with reference to a circle with its centre at the common endpoint of the rays. Hence, the sum of angles at a point is always 360°. It is called a full angle (see image).

Example 2. What are the values of smallest and largest geometric angles?

Solution: Smallest value = 0°, largest value = 360° (full angle or four right angles).

Example 3. Identify the acute, obtuse and reflex angles among the following: 45°, 72°, 187°, 210°, 175°, 300°, 15°, 120°, 140°

Solution:

Acute angles: 15°, 45°, 72°

Obtuse angles: 120°, 140°, 175°.

Reflex angles: 187°, 210°, 300°.

Example4. 

1. What are the values of complementary and supplementary angles to an angle θ?
2. What are the values of complementary and supplementary angles to 0°?
3. Which angle is equal to its complementary angle?
4. Which angle is equal to its supplementary angle?

Class Vii Math Solution Wbbse

Solution:

1. The complementary and supplementary angles to θ are (90°-θ) and (180°-θ) respectively.
2. Complementary angle to 0°= 90° – 0° = 90°. Supplementary angle to 0° = 180° – 0° = 180°
3. If the required angle be x°,then according to the question the complementary angle shall be also x°.∴ x + x = 2x = 90° or, x = 90°/2 = 45
4. If the required angle be x°,then according to the question the supplementary angle shall be also x°.∴ x + x = 2x = 180° or, x =180°/2 = 90°

Example 5. An angle is equal to twice its supplement. Determine its measure.

Solution: Let the required angle be x°.

According to the question, the supplementary angle = x°/2

∴ x + \(\frac{x}{2}\) = 180°

or, 2x + x = 360° or, 3x = 360° or x = 120°.

Example 6. Look at the adjacent image. For what value of x, the points A, O, and B shall lie on the same straight line?

Solution:

For A, O and B to lie on same straight line, the sum of ∠AOC and ∠BOC has to be 180°, i.e., ∠AOC + ∠BOC =180°.

∴ (6x + 5) + (4x-25) = 180

or, 10x – 20 – 180 or, 10x = 200 or, x = 20

Example 7. In the image, ∠AOC = 50°. Find out the values of other angles.

 Solution:

Vertically opposite angles are equal to each other.

∴ ∠AOC = ∠BOD = 50°.

The sum of the angles at point 0 is 360° ∠COB + ∠AOD – 360° – (50° + 50°) = 260°

Since these are vertically opposite angles, ∠COB = ∠AOD = 130°.

Example 8. Indicate two pairs of alternate angles in the image shown.

Solution: Considering PQ as transversal, ∠AEG and ∠EGH are alternate angles.

Considering RS as transversal, ∠BFH and ∠FHG are alternate angles.

Example 9. Parallel lines are shown in the images. Find the measure of angles indicated by x.

Solution: See the image.

Therefore, x+ 60° = 180° or, x = 120°

The sum of the two interior angles on the same side of the transversal is 180°.

∴ x + 140° = 180° or, x = 40°.

Class Vii Math Solution Wbbse

Example 10. In the given image if AB//CD, find x, y and z.

Solution:

∠x = 45° (Vertically opposite angle).

∠x =∠y = 45° (Alternate angle)

Since AB//CD,

∠z + ∠y = 180°.

or ∠z – 180° – ∠y – 180° – 45° = 135°.

Classification of triangle

Triangle: A plane figure bounded by three line segments is called a triangle. A triangle has three sides and three angles. Three angular points are called the vertices of the triangle.

ABC is a triangle. Its three sides are AB, BC, and AC. Its three angles are ∠ABC, ∠BCA, and ∠CAB. Its three vertices are A, B, and C.

The sum of the three angles of a triangle is equal to 2 right angles or 180°.

In any triangle, the sum of any two sides is always greater than the third side. Again, the difference of any two sides is always less than the third side.

If any angular point of a triangle is taken as a vertex then its opposite side is called its base. The angle opposite to the base of a triangle is called its vertical angle.

If BC is taken as a base then ∠BAC will be its vertical angle.

On the basis of sides there are three types of triangles: equilateral triangle, isosceles triangle, and scalene triangle.

Class Vii Math Solution Wbbse

Equilateral triangle: If the lengths of the three sides of a triangle are same then the triangle is called an equilateral triangle.

Isosceles triangle: If the lengths of the two sides of a triangle are same then the triangle is called an isosceles triangle.

Scalene triangle: If the lengths of the three sides of a triangle are unequal then the triangle is called a scalene triangle.

On the basis of angles there are three types of triangles: acute-angled triangle, obtuse-angled triangle, and right-angled triangle.

Acute-angled triangle: If each of the three angles of a triangle is acute then the triangle is called an acute angled triangle.

Obtuse-angled triangle: If any one angle of a triangle is obtuse then the triangle is called an obtuse-angled triangle.

Right-angled triangle: If any one angle of a triangle is a right angle then the triangle is called a right-angled triangle.

Median of a triangle

The line segment obtained by joining the middle point of any side of a triangle to the A opposite vertex is called the median of the triangle.

In the image, the line  segment AD has been obtained by joining the mid point D of the side BC of the triangle ABC to the opposite vertex A.

Hence, AD is a median of the triangle ABC. There are always three medians of a triangle.

The three medians of a triangle always intersect at the same point, i.e., they are concurrent.

Therefore, in each case of a triangle like scalene or equilateral or isosceles, or acutely angled or obtuse-angled or right-angled triangle, the three medians are concurrent.

Class Vii Math Solution Wbbse

The point of concurrence of the medians is known as the centroid of the triangle.

In the image, AD, BE and CF are the three medians of ΔABC.

They intersect at point G. G is the centroid of ΔABC.

Height of a triangle

The line segment obtained by drawing the perpendicular from any vertex of a triangle to the opposite side is called the height of the triangle.

In the image, AD has been drawn perpendicular from the vertex A to the opposite side BC of the triangle ABC.

Hence, AD is the height of the triangle ABC. In this case BC is the base of the triangle.

If AC is taken as the base of the triangle then the perpendicular from B on AC will be the height of the triangle.

If AB is taken as the base of the triangle then the perpendicular from C on AB will be the height of the triangle.

Some examples

Example 1. Find the measures of the angles of an equilateral triangle.

Solution:

Each angle is equal to 60° (see the adjacent image)

Example 2. What are the measures of the three angles of a right-angled isosceles triangle?

Solution:

The measures of the three angles of a right-angled isosceles triangle are 45°, 45°, and 90°. See the adjacent image.

In this case, AB = AC and ∠BAC = 90°.

Example 3. Find the maximum and maximum number of acute in a triangle.

Solution: The minimum number of acute angles is two and the maximum number is three.

Example 4. What is the nature of three points through which it is not possible to construct a triangle?

Solution: It is not possible to construct a triangle through three points when they are collinear.

Example 5. How many parts of a triangle should be known to construct it?

Solution: Three.

[Of course, it is not possible to construct a definite triangle when three angles of it are known. Because when the three angles are given then it should be assumed that actually two angles are given. If two angles of a triangle are known then automatically the third one is known. In other cases, e.g., when three sides or two sides and one angle are known, it is possible to construct a definite triangle.]

Example 6. How many straight lines may be drawn through a point?

Solution: An infinite number of straight lines may be drawn through a point.

Example 7. How many straight lines may be drawn through two points?

Solution: One straight line.

Example 8. What is the minimum number of curved lines required to enclose a region?

Solution: One.

Example 9. What is the minimum number of straight lines required to enclose a region?

Solution: Three.

Example 10. If the sum of the two angles of a triangle be 90° then what is its name?

Solution: As the sum of the two angles is 90°, the third angle must be equal to 90°. Hence the triangle is a right-angled triangle.

Example 11. A triangle is equilateral on the basis of sides. What is its name on the basis of angles?

Solution: Acute angled.

Example 12. Is it possible to construct a triangle having sides of lengths 3 cm, 4 cm, and 8 cm?

Solution: We know that the sum of the two sides of a triangle is always greater than the third.

But in this case, 3 cm + 4 cm = 7cm. It is less than 8 cm. So, it is not possible to construct a triangle in this case.

Example 13. Is it possible to construct a triangle having angles of measures 55°, 64°, and 60°?

Solution: We know that the sum of the three angles of a triangle is 180°.

But in this case the sum of the three angles is (55^o+64^o+60°) = 179°. So it is not possible to construct a triangle in this case.

Example 14. If the sum of the two acute angles of an obtuse-angled triangle be 50° then find the measure of the other angle.

Solution: The measure of the other angle of the obtuse-angled triangle = 180° – 50° = 130°.

Example 15. How many right angles may be there in a triangle?

Solution: One

Example 16. If one acute angle of a right-angled triangle be 40°, then find its other acute angle.

Solution: 50°.

Class Vii Math Solution Wbbse

Example 17. When do the two straight lines lying on a plane intersect at a point?

Solution: When they are non-parallel.

Example 18. What is the number of acute angles of a right-angled triangle?

Solution: Two.

Example 19. What is the number of medians of a triangle?

Solution: Three.

Example 20. If the angles of a triangle bear a ratio of 3:4:5, then determine the measure of the angles.

Solution:

Given:

The angles of a triangle bear a ratio of 3:4:5

Let us assume that the angles be 3x, 4y, and 5z.

∴ 3x + 4x + 5x = 180°

[ ∴ Sum of three angles of a triangle is 180°]

or 12x = 180° or, x = \(\frac{180}{2}\) = 15.

∴ The angles of the triangle will be (3x 15)°, (4×15)° and (5×15)° or 45°, 60° and 75°.

Example 21. Prove that if the measure of one angle of a triangle is equal to the sum of the rest two angles then the triangle is a right-angled one.

Solution:

Let us assume that the three angles of the triangle be ∠A, ∠B, and ∠C.

According to the question, let us assume that ∠A = ∠B + ∠C.

Now ∠A + ∠B + ∠C = 180°

or ∠A + ∠A = 180° (Since ∠A = ∠B + ∠C assumed) or, 2 ∠A = 180°

or ∠A = 180°/2 = 90° .

Therefore the triangle is a right triangle. (Proved)

Example 22. In the given image, DEIIBC. If ∠A = 65° and ∠B = 50°, then determine the values of ∠ADE, ∠AED, and∠C.

Solution:

Given:

In the given image, DEIIBC. If ∠A = 65° and ∠B = 50°

DE//BC and ADB is the transversal

∴ ∠ADE = ∠DBC = ∠B = ∠50° (corresponding angles)

The sum of three angles in ΔADE is 180°.

Classification of quadrilateral

Quadrilateral:

A plane figure enclosed by four line segments is called a quadrilateral. A quadrilateral has four sides and four angles.

Four angular points are called the four vertices of a quadrilateral.

The line segment joining any two opposite vertices of a quadrilateral is called the diagonal of the quadrilateral.

There are two diagonals of a quadrilateral. ABCD is a quadrilateral. Its four sides are

AB, BC, CD, and DA. Its four angles are ∠ABC, ∠BCD, ∠CDA, and ∠DAB.

Its four angular points are A, B, C, and D. Its two diagonals are AC and BD.

Parallelogram: If the opposite sides of a quadrilateral are parallel then it is called a parallelogram.

In the image shown is a parallelogram ABCD since the opposite sides of the quadrilateral are parallel to each other, i.e., ADIIBC and ABIIDC

∴ AB = DC and AD = BC.

The diagonals of a parallelogram bisect each other.

Class Vii Math Solution Wbbse

∴ AO = OC and BO = OD. The opposite angles of a parallelogram are equal to each other.

∴ ∠BAD = ∠BCD and ∠ADC = ∠ABC.

Since the opposite sides of a parallelogram are parallel, hence the two angles adjacent to any side are supplementary to each other.

Rectangle: If one angle of a parallelogram is a right angle then it is called a rectangle.  The diagonals of the rectangle are equal in length and they bisect each other.

Square: If the lengths of the two adjacent sides of a rectangle are equal then it is called a square.

Therefore all the sides of a square are of equal length and each angle is a right angle.

The diagonals of a square are equal in length and they bisect each other perpendicularly.

Trapezium: If only one pair of opposite sides of a quadrilateral are parallel then it is called a trapezium.

In trapezium ABCD, ABIIDC. The nonparallel sides of the trapezium are known as the oblique sides.

Isosceles trapezium: If the lengths of the non-parallel sides (i.e., oblique sides) of a trapezium are equal then it is called an isosceles trapezium. In the adjacent image, ABCD is an isosceles trapezium since AD = BC.

Rhombus: If the lengths of the four sides of a quadrilateral are equal but none of the angles is a right angle then it is called arhombus. The image ABCD is a rhombus in which AB = BC – CD – DA; but none of its angles is a right angle.

The opposite sides of a rhombus are parallel to each other. The diagonals of a rhombus are unequal in length, but they bisect each other perpendicularly. Therefore, AC ≠ BD, but AO = OC and BO = OD.

Kite: A quadrilateral in which two pairs of adjacent sides are equal is called a kite.

In the image, AB = AD and CD = CB. Thus adjacent sides of each pair are equal. The diagonals of a kite are perpendicular to each other.

Some examples Example 

Example 1. How many parts of a quadrilateral should be known to construct it?

Solution: Five.

Example 2. In this quadrilateral, there is only one pair of parallel sides.

Solution: Trapezium.

Class Vii Math Solution Wbbse

 Example 3. Which quadrilaterals have sides of equal lengths?

Solution: Square and Rhombus.

Example 4. By what name do we call a parallelogram whose one angle is a right angle?

Solution: Rectangle.

Example 5. How many diagonals and how many vertices are there in a quadrilateral?

Solution: Two diagonals and four vertices.

Example 6. What is the sum of the angles of a quadrilateral?

Solution: 360°.

Example 7. What is the difference between the two diagonals of a rectangle and the two diagonals of a rhombus?

Solution: The two diagonals of a rectangle are equal and the two diagonals of a rhombus are unequal.

Example 8. What kind of quadrilateral is it whose all the angles are equal but adjacent sides are unequal?

Solution: Rectangle.

Example 9. What kind of quadrilateral is it whose diagonals are unequal in length but are perpendicular to each other?

Solution: Rhombus.

Example 10. Name the quadrilaterals whose diagonals are equal to each other in length.

Solution: Rectangle, square and isosceles trapezium.

Example 11. What are the measures of ∠B and ∠C in the parallelogram ABCD in which ∠A = 75°?

Solution:

Given:

∠A = 75°

The opposite angles of a parallelogram are equal to each other.

∴ ∠A = ∠C = 75°.

In a parallelogram, the two angles adjacent to each side are supplementary to each other.

∴ ∠B+ ∠C= 180° (Both are adjacent to BC)

or, ∠B = 180° – ∠C = 180° – 75° = 105°

The measures of ∠B and ∠C in the parallelogram ABCD ∠B = 180° – ∠C = 180° – 75° = 105°

Example 12. If a pair of opposite angles of a parallelogram be 2x – 50° and x + 20°, then what type of parallelogram is it?

Solution:

Given:

If a pair of opposite angles of a parallelogram be 2x – 50° and x + 20°

The opposite angles are equal to each other in a parallelogram.

∴ 2x – 50 = x + 20 or, x = 70

Putting the value of x we get, (2 x 70) – 50 = 90° and 70 + 20 = 90°, i.e., each of the angles of this parallelogram is a right angle.

∴ The parallelogram in question is a rectangle.

 

 

Arithmetic Chapter 2 Ratio And Proportion Exercise 2 Solved Example Problems

Comparison of two quantities

In our practical life it is very often required to compare two quantities in terms or their magnitudes or measurements.

In fact, there are two ways of comparing quantities. We can compare two quantities either by finding the difference between them or by dividing one quantity by the other.

When we compare two numbers by division then we are determining the ratio.

Read and Learn More WBBSE Solutions For Class 7 Maths

Thus, while comparing two quantities of the same kind, the fraction expressed by how many times the first quantity is greater or smaller than the second quantity is called the ratio between the two quantities.

Suppose, a bowl of fruit contains ten apples and six oranges, then the ratio of apples to oranges is ten to six i.e., 10:6, equivalent to 5:3.

In this example the ratio of oranges to apples is 6:10 i.e., 3:5. Also, the ratio of apples to the total amount of fruits is 10: 16 or 5:8.

Mathematically speaking, if x and y are two quantities and the numerical value of y ≠ 0 then the fraction \(\frac{x}{y}\) is called the ratio of x to y and is written as x:y.

Nature of a ratio

The ratio is the quotient of two quantities of the same kind and same unit, which compares the quantities. Hence, the ratio being a fraction is an abstract number and has no unit.

The quantities forming the ratio are called the terms of the ratio in which the first number is called the antecedent while the second one is called the consequent.

∴ Ratio = antecedent consequent: antecedent consequent

= \(\frac{antecedent}{consequent}\)

Illustration with Images

 

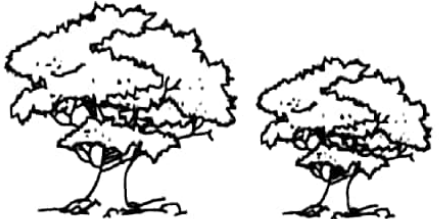
In Image 1, the height of the first tree is 40 meters and that of the second tree is 30 meters. Hence, the height of the first tree: height of the second tree = 4:3.

 

 

In image 2, in the first basket, there are 5 mangoes and in the second there are 3 mangoes.

Hence, the number of mangoes in the first basket: and the number of mangoes in the second basket = 5:3.

Also, we know that water occupies 3 parts of the Earth’s surface and land occupies 1 part of the same.

Hence, we can say that, area occupied by water: area occupied by land = 3: 1.

The symbol ‘:’ is used to denote the ratio. Thus the ratio 5 to 9 is written as 5:9 and it is read as ‘five is to nine.’

Determination of the ratio of two quantities

We can determine the ratio of two quantities of same kind. In determining the ratio, the quantities are to be expressed in the same unit.

Example: Ratio of 1 meter and 25 cm.

= \(\frac{1 meter}{25 cm}\) = \(\frac{100 cm}{25 cm}\)

= \(\frac{4}{1}\) = 4:1.

Ration of ₹ 6 and ₹ 1.52 p

= \(\frac{₹ 6}{1.50 P}\)= \(\frac{600 P}{150 p}\) = \(\frac{4}{1}\)

Concrete is a mixture of stone chips, sand and cement, normally in the ratio of 4:2:1 by volume. So there are 4+2+1 = 7 items altogether. So, the quantity of each component of concrete is

stone chips = \(\frac{4}{7}\), sand = \(\frac{2}{7}\) and cement = \(\frac{1}{7}\) part.

A ratio has no unit because it is an abstract number.

The ratio of two quantities of different kinds is not possible.

Thus 5 hours: 75 cm is inadmissible, as the comparison is not possible in this case.

Inverse ratio

If two ratios be such that, the antecedent and the consequent of the one are respectively equal to the consequent and antecedent of the other, then they are said to be inverse ratio.

Example: The inverse ratio of 2:5 is 5:2 and also the inverse ratio of 5:2 is 2:5.

Types of ratio

There are mainly two types of ratios, namely simple and compound.

Simple ratio: The ratio between two quantities of the same kind is called a simple ratio. For example, 20 cm: 25 cm 4:5 is a simple ratio.

Compound ratio: The ratio whose antecedent is the product of the antecedents of two or more simple ratios and whose consequent is the product of the consequents of those ratios is called a compound ratio of those simple ratios.

For example, the compound ratio of 2:3, 3:4 and 4:5 is (2 × 3 × 4): (3 x 4 x 5) or, 2:5.

Different types of simple ratio Simple ratios are of three different types namely

1. Ratio of greater inequality
2. Ratio of equality
3. Ratio of less inequality.

Ratio of greater inequality: The ratio in which the antecedent is greater than the consequent is called a ratio of greater inequality. For example, 25: 17.

Ratio of equality: The ratio in which the antecedent is equal to the consequent is called a ratio of equality. For example, 5:5.

Ratio of less inequality: The ratio in which the antecedent is smaller than the consequent is called a ratio of less inequality. For example, 9: 19.

Some important points about ratio

1. Since the ratio can also be considered as a fraction its value remains unchanged when both its antecedent and consequent are multiplied or divided by the same number.

Except for the ratio of equality, the value of a ratio is changed when a number is added to or subtracted from its antecedent and consequent.

2. If we add a number both to the antecedent and consequent of a ratio of greater inequality, its value will decrease.

For example: 
9: 5 = \(\frac{9}{5}\); \(\frac{9 + 3}{5 + 3}\) = \(\frac{12}{8}\) = \(\frac{3}{2}\); \(\frac{3}{2}\) < \(\frac{5}{5}\)

3. If we subtract a number both from the antecedent and consequent of a ratio of greater inequality its value will increase.

For example:
9: 5 = \(\frac{9}{5}\); \(\frac{9 – 3}{5 – 3}\) = \(\frac{6}{2}\) = \(\frac{3}{1}\); \(\frac{3}{1}\)> \(\frac{9}{5}\)

4. If we add a number both to the antecedent and consequent of a ratio of less inequality, its value will increase.

For example:
5:9 = \(\frac{5}{9}\); \(\frac{5 + 3}{9 + 3}\) = \(\frac{8}{12}\) = \(\frac{2}{3}\); \(\frac{2}{3}\)> \(\frac{5}{9}\)

5. If we subtract a number both from the antecedent and consequent of a ratio of less inequality its value will decrease.

For example:
5:9 = \(\frac{5}{9}\); \(\frac{5 – 3}{9 – 3}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\); \(\frac{1}{3}\)< \(\frac{5}{9}\)

A ratio can be expressed as a fraction. Hence, the processes applicable to the fractions are also applicable to the ratios.

For example:
1. A ratio can be expressed in the lowest form.
2. Some ratios can be converted into ratios having the same consequences.

Proportion

The equality of two ratios is called proportion. Suppose, in 3 days you can work out 45 sums and in 6 days you can work out 90 sums.

Hence, ratio of the number of days = 3:6, which in the simplest form is 1: 2.

Also the ratio of the sums worked out by you is 45: 90, which in the simplest form is 1: 2. Thus here we observe that 3:6=45:90.

Let us consider another example. If milk costs 15 per liter, the cost of 15 liters of milk is ₹ 225 and the cost of 20 liters of milk is ₹ 300.

The ratio of two quantities of milk = 15 liters: 20 liters = 15:20, which in the simplest form is 3 4.

Also the ratio of the costs of milk = ₹ 225: ₹ 300 = 225: 300, which in the simplest form is 3: 4.

Thus here we observe that 15:20 = 225: 300.

Definition: A proportion is the equality of two ratios.

We say that one ratio is proportional to the other and the four numbers forming the two ratios are in proportion.

Illustration In image 1, the ratio of bottles filled with milk: empty bottle= 2:1, and in image 2, the ratio of bottles filled with milk: empty bottle =4:2=2:1.

Since these two ratios are equal they are in proportion. When two ratios are

 

 

 

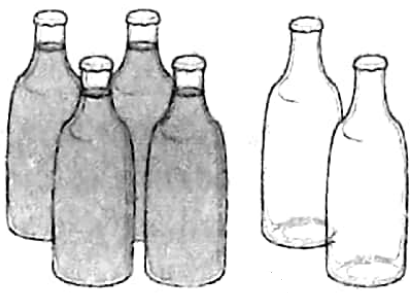
equal then instead of the sign of equality ‘ =’ we use the sign of proportion ‘: :’.

To express that, the ratio of 3 and 4 is equal to that of 9 and 12 we often write, 3:4: :9: 12. We read it ‘3 is to 4 as 9 is to 12’.

Inverse proportion or reciprocal proportion

If two ratios be such that, one of them is equal to the reciprocal of the other then we say that either of them is in reciprocal proportion of the other.

Suppose, you have to travel 400 km. If your speed is 20 km per hour then you will take 20 hours. If your speed is 25 km per hour then you will take 16 hours.

Thus, ratio of speed = \(\frac{20 km per hour}{25 km per hour}\) = \(\frac{4}{5}\)

The ratio of time required = \(\frac{20 hours}{16 hours}\) = \(\frac{5}{4}\)

Thus we see that, either of the above two ratios, is equal to the inverse of the other. These ratios are said to be in inverse proportion.

Continuous ratio

We may write the mutual ratio of many quantities of the same kind continuously with the sign of ratio.

For example: the ratio of ₹2, ₹8, ₹10, ₹16, ₹32

= ₹2: ₹8 : ₹10: ₹16: ₹32

= 2: 8: 10: 16: 32 = 1: 4: 5: 8: 16.

Continued proportion

If there be three quantities of the same kind such that the ratio of the first to the second is equal to the ratio of the second to the third then we say that the three quantities are in continued proportion.

Among the three quantities, the second quantity is called a mean proportional between the first and the third. The third quantity is called a third proportional to the first and the second.

Thus, 3, 6, and 12 are in continued proportion; because 3: 6 : : 6: 12.

Here 6 is a mean proportional between 3 and 12 and 12 is a third proportional to 3 and 6.

There may be a continued proportion of more than three quantities.

In that case, the first: the second = the second: the third = the third: the fourth = the fourth: the fifth = ….

For example, 1, 3, 9, 27, 81…. are in continued proportion.

Some properties of proportion

1. To test whether four quantities are in proportion or not we shall have to find the product of the first and the fourth and the product of the second and the third.

If these two products are equal then we say that the four quantities are in proportion; otherwise, they are not in proportion.

Example: 56: 25: 30. [Here 5 and 30 are called extremes. while 6 and 25 are called mean terms or quantities].

Here the product of the extremes i.e., the product of the first and the fourth = 5 x 30 = 150.

And the product of the means i.e., the product of the second and the third = 6 x 25 = 150.

Since these two products are equal, therefore the four quantities are in proportion.

2. If out of the 4 terms of a proportion, 3 are known, the third can easily be found out, by the following formulae.

1. An extreme = product of the means ÷ the other extreme.
2. A mean = product of the extremes ÷ the other mean.

3. If three quantities are in continued proportion, then the first: the second = the second: the third.
Hence, the first the third = (the second)². Thus, 3, 12, and 48 are in continued proportion. Here, 3 x 48 = 144 = (12)².

4. Let there be four quantities that are in proportion.

Then, by definition,
The first quantity: The second quantity = The third quantity: The fourth quantity.

Since the inverse ratio of two equal ratios are equal, therefore, the second quantity: the first quantity = the fourth quantity: the third quantity.

Thus, 4: 5 : : 28: 35.

∴ 5: 4 : : 35: 28.

5. If the four abstract numbers be in proportion then, the first: the third the second the fourth.

Thus 2: 5 = 6: 15

∴ 2: 6 = 5:15.

6. If the antecedent and the consequent of a ratio be multiplied or divided by the same number, the value of the ratio does not change.

Thus, 4:7 (4 x 5): (7 x 5) = 20: 35

Also, 10: 15 (105): (15+5)=2:3

Again, since 2:5=4:10

∴ (2x 3): (5 x 3) = (4 x 5): (10 × 5) Or, 6:15 = 20:50.

7. Let us mention some conclusions derived from proportion:

1. If \(\frac{a}{b}\) = \(\frac{c}{d}\) then

1. \(\frac{b}{a}\) = \(\frac{d}{c}\) [invertendo]
2. \(\frac{a}{c}\) = \(\frac{b}{d}\) [alternendo]
3. \(\frac{a + b}{b}\) = \(\frac{c + d}{d}\) [componendo]
4. \(\frac{a – b}{b}\) = \(\frac{c – d}{d}\) [dividendo]
5. \(\frac{a + b}{a – b}\) = \(\frac{c + d}{c – d}\) [componendo and dividendo].

2. If \(\frac{a}{b}\) = \(\frac{c}{d}\) then each ratio = \(\frac{a + c}{b + d}\)

3. If \(\frac{a}{b}\) = \(\frac{c}{d}\) then each ratio = \(\frac{a – c}{b – d}\)

4. If \(\frac{a}{b}\) = \(\frac{c}{d}\) then each ratio = \(\frac{ma + nc}{mb + nd}\)

5. \(\frac{a}{b}\) = \(\frac{c}{d}\) = \(\frac{e}{f}\) = \(\frac{g}{h}\) = ….

= \(\frac{a + c + e + g + ……}{b + d + f + h + ……}\)(addendo).

Arithmetic Chapter 2 Ratio And Proportion Exercise 2 Some Problems On Ratio

Example 1. 1 kg of rice costs ₹ 40 and 1 kg of pulse costs ₹ 100. What is the ratio of the prices of rice and pulse?

Solution:

Ratio of the prices of rice and pulse

= \(\frac{₹40}{₹100}\) = \(\frac{2}{5}\) = 2.5

The ratio of the prices of rice and pulse 2.5

Example 2. Find the ratio of ₹ 1.50 to ₹ 3.50.

Solution:

Required ratio

= \(\frac{₹1.50}{₹3.50}\) = \(\frac{150 P}{350 P}\)

= \(\frac{3}{7}\) = 3:7.

Required ratio 3:7.

Example 3. In the triangle ABC, ∠BAC = 60°, ∠ABC = 50° and ∠ACB 70° : ∠BAC : ∠ABC: ∠ACB = what?

Solution:

∠BAC: ∠ABC: ∠ACB
= 60°: 50°: 70° = 60: 50: 70=6: 5: 7

Example 4. Find the ratio of 15 minutes to 1 hour 15 minutes.

Solution:

Required ratio

= \(\frac{15 minutes}{1 hour 15 minutes}\) = \(\frac{15 minutes}{75 minutes}\)

= \(\frac{15}{75}\) = \(\frac{1}{5}\) = 1: 5

Class Vii Math Solution Wbbse

Example 5. The price of a pencil is 3 and the price of toffee is 50 paise. What is the ratio of the prices of a pencil and a toffee?

Solution:

Price of 1 pencil: the price of 1 toffee 300 paise 6

= \(\frac{₹3}{50paise}\) = \(\frac{300 paise}{50 paise}\) = \(\frac{6}{1}\)=6:1

Example 6. What is the inverse ratio of 5: 9?

Solution: 9:5.

Example 7. What is the ratio of values of a 50 p coin, a rupee coin and a two rupee coin?

Solution:

The value of a 50 p coin: the value of a rupee coin: the value of a two rupee coin.

= 50 paise: 100 paise: 200 paise = 1:2:4

Example 8. Find the compound ratio of the following: 2:3, 5:4, 6:15.

Solution:

The compound ratio of 2:3, 5:4, 6:15

= \(\frac{2x5x6}{3x4x15}\) = \(\frac{1}{3}\) = 1: 3

Example 9. Ram’s age is 12 years 6 months, Shyam’s age is 12 years 4 months and Jadu’s age is 12 years. What is the ratio of their ages?

Solution:

Ram’s age: Shyam’s age: Jadu’s age = 12 years 6 months: 12 years 4 months: 12 years

= (12 x 12+6) months: (12 x 12 + 4) months : 12 x 12 months

= 150 months: 148 months: 144 months = 75:74:72

Example 10. Find the value of x from the relation 4: 7=12:x.

Solution:

From the given relation,

we get, \(\frac{4}{7}\) = \(\frac{12}{x}\)

or, 4x = 84 or, x = \(\frac{84}{4}\) = 21

Example 11. If the ratio of two numbers be 5: 7 and their H.C.F be 13, then find the numbers.

Solution:

One number = 5 x 13 = 65
Another number = 7 x 13 = 91

∴ The numbers are 65 and 91.

Example 12.  Distinguish between x + y and x: y.

Solution:

x ÷ y is defined even when x and y are not of the same kind.

But x : y is defined only when x and y are of same kind.

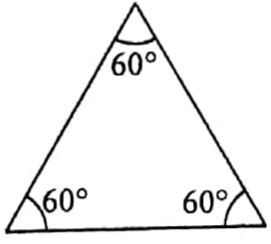
Example 13. What is the ratio of angles of an equilateral triangle?

Solution:

The angles of an equilateral triangle are 60°, 60°, and 60°.
∴ ratio of the angles = 60°: 60°: 60°=1:1:1

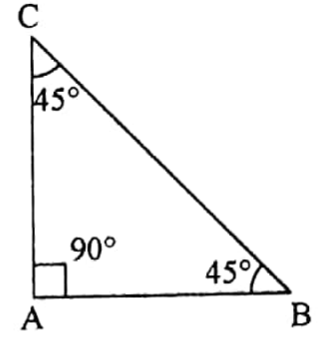
Example 14. If the ratio of the three angles of a triangle be 1:1:2 then what are the measures of the angles ?

Solution:

Let, the measures of the three angles be x°, x°, and 2x°.

According to the question, x°+x°+2x°=180°
or, 4x°= 180°

or, x° = \(\frac{180°}{4}\) = 45°

∴ Measures of the three angles are 45°, 45° and 90°

Example 15. Ratio of the runs scored by Dhoni and Koholi is 4:3 and Koholi scored 42 runs. If the runs of Dhoni would be 7 more, what would be the ratio of their runs?

Solution:

Let, the run of Dhoni = x

According to the question, \(\frac{x}{42}\) = \(\frac{4}{3}\)

or, 3x=42 × 4

or, x = \(\frac{42×4}{3}\) = 56

∴ Run of Dhoni = 56

Example 16. If out of 40 examinees, 40% failed then what is the ratio of the pass and fail? If 4 more examinees would pass then what would be the ratio of pass and fail?

Solution:

40% of 40 examinees= 40 x \(\frac{40}{100}\) = 16

If 16 examinees failed then (40 – 16) or 24 examinees passed

then ratio of pass and fail = \(\frac{24}{16}\) = \(\frac{3}{2}\) = 3 :2

If 4 more examinees would pass then the ratio of pass and fail would be = \(\frac{24+4}{16-4}\) = \(\frac{28}{12}\) = 7: 3

= 3:2, 7: 3

Example 17. In two beverages the ratio of syrup and water are 2 : 5 and 6 : 10 which beverage is sweeter ?

Solution:

In the first beverage syrup: water =2:5 = 6:15

In the second beverage syrup: water = 6 : 10

∴ Second beverage is sweeter.

∴ Second beverage.

Example 18. Between 3:5 and 4: 7, which one is greater?

Solution:

Given:

3:5 And 4: 7

L.C.M. of 5 and 7 is 35.

Now, 3:5 = \(\frac{3}{5}\) = \(\frac{3×7}{5×7}\) = \(\frac{21}{35}\)

And 4:7= \(\frac{4}{7}\) = \(\frac{4×5}{7×5}\) = \(\frac{20}{35}\)

Hence, 3: 5 is greater.

∴ 3: 5 is greater than 4 : 7.

Example 19. The ratio of the ages of Manasbabu and Dipakbabu is 7:9. If the age of Dipakbabu be If the run of Dhoni would be 7 more then run 72 years then what is the age of Manasbabu?

Solution:

Given:

The ratio of the ages of Manasbabu and Dipakbabu is 7:9. If the age of Dipakbabu be If the run of Dhoni would be 7 more then run 72 years

Let, age of Manasbabu = x years

∴ \(\frac{x}{72}\) = \(\frac{7}{9}\) or, 9x = 72 x 7

or, x = \(\frac{72×7}{9}\) = 56

∴ The age of Manasbabu is 56 years.

Example 20. If A: B=3:4 and B: C = 65, then find the value of A: B: C.

Solution:

Given:

A: B=3:4 and B: C = 65

A: B = 3:4 = (3×3): (4 x 3)=9:12

B:C = 6:5 = (6×2): (5 x 2)=12:10

∴ A: B: C = 9:12:10

∴ The value of A: B: C is 9: 12:10.

Example 21. The ratio of prices of two books is 2: 5. If the price of the first book is 32.20 what is the price of the second book?

Solution:

Given: 

The ratio of prices of two books is 2: 5. If the price of the first book is 32.20

Let, the price of the second book = x.

∴ \(\frac{32.20}{x}\) = \(\frac{2}{5}\)

or, 2x = 32.20 x 5

or, x = \(\frac{32.20 x 5}{2}\) = 80.50

∴ The price of the second book is  ₹80.50.

Example 22. The ratio of the circumference and diameter of a circle is 22:7. If the length of the diameter of a circle is 2m 1 dcm then find its circumference.

Solution:

Given:

The ratio of the circumference and diameter of a circle is 22:7. If the length of the diameter of a circle is 2m 1 dcm then find its circumference.

Let, the circumference of the circle = x dcm.

∴ \(\frac{x}{21}\) = \(\frac{22}{7}\)

or, 7x = 21 x 22

or, x = \(\frac{21 x 22}{7}\) = 66

circumference of the circle = 66 dcm = 6 m 6 dcm.

Example 23. Express \(\frac{4}{7}\): \(\frac{5}{9}\) as the ratio of integers.

Solution: \(\frac{4}{7}\) x \(\frac{9}{5}\) = \(\frac{36}{35}\) = 36: 35

Example 24. In a school from class seven out of 150 students, 90 students and from class six out of 140 students, 80 students participated in a sit and draw competition. Which of the two classes has the greater participation?

Solution:

Given:

In a school from class seven out of 150 students, 90 students and from class six out of 140 students, 80 students participated in a sit and draw competition.

In class seven, \(\frac{number of competetors}{total number of students}\)

= \(\frac{90}{150}\) = \(\frac{3}{5}\)

In class six, \(\frac{number of competetors}{total number of students}\)

= \(\frac{80}{140}\) = \(\frac{4}{7}\)

Now, \(\frac{3}{5}\) = \(\frac{3×7}{5×7}\) = \(\frac{21}{35}\)

\(\frac{4}{7}\) = \(\frac{4×5}{7×5}\) = \(\frac{20}{35}\)

Example 25. The ratio of two quantities is 5 7. If the antecedent is 40 kg, find the consequent.

Solution:

Given:

The ratio of two quantities is 5 7. If the antecedent is 40 kg,

Let the consequent be x kg.

∴ \(\frac{40 kg}{x kg}\) = \(\frac{5}{7}\)

or, \(\frac{40}{x}\) = \(\frac{5}{7}\)

or, 5x = 40 × 7 or, x = \(\frac{40 x 7}{5}\) = 56

∴ 56 kg.

The consequent 56 kg.

Example 26. Out of 100 sums, Ram got 60 sums correct. Out of 80 those sums Rahim got 50 sums correct. Who got more sums correct?

Solution:

Given:

Out of 100 sums, Ram got 60 sums correct. Out of 80 those sums Rahim got 50 sums correct.

In case of Ram,  \(\frac{correct sums}{total sums}\)

= \(\frac{60}{100}\) = \(\frac{3}{5}\)

In case of Rahim, \(\frac{correct sums}{total sums}\) =\(\frac{50}{80}\) = \(\frac{5}{8}\)

Now, \(\frac{3}{5}\) = \(\frac{3×8}{5×8}\) = \(\frac{24}{40}\)

or, \(\frac{5}{8}\) = \(\frac{5×5}{8×5}\) = \(\frac{25}{4}\)

∴ Rahim got more sums correct.

Example 27. In this year’s Madhyamik examination out of 150 examinees of the first school 100 examinees passed with grade-A. In the second school out of 100 examinees, 80 examinees passed with grade-A. Find which school has got a better result getting grade-A, in this year’s Madhyamik examination.

Solution:

Given:

In this year’s Madhyamik examination out of 150 examinees of the first school 100 examinees passed with grade-A. In the second school out of 100 examinees, 80 examinees passed with grade-A.

In the first school,

\(\frac{number of examinees getting grade-A}{total number of examinees}\)

Class Vii Math Solution Wbbse

= \(\frac{100}{150}\) = \(\frac{2}{3}\)

In the second school,

\(\frac{number of examinees getting grade-A}{total number of examinees}\)

 

= \(\frac{80}{100}\) = \(\frac{4}{5}\)

Now, \(\frac{2}{3}\) = \(\frac{2×5}{3×5}\) = \(\frac{10}{5}\)

or, \(\frac{4}{5}\) = \(\frac{4×3}{5×3}\) = \(\frac{12}{15}\)

∴ The second school has got a better result getting grade-A.

Example 28. The ratio of ages of Ram and Shyam is 8:7. If the age of Shyam be 21 years, find the age of Ram.

Solution:

Given:

The ratio of ages of Ram and Shyam is 8:7. If the age of Shyam be 21 years

Let the age of Ram be x years.

Then, \(\frac{x}{21}\) = \(\frac{8}{7}\)

or, x = \(\frac{8×21}{7}\) =24

∴ 24 years.

The age of Ram 24 years.

Wbbse Class 7 Maths Solutions

Example 29.  From a bamboo, a piece of bamboo is cut off. It is found that the ratio of the two pieces is 3:1. From the table below, find the possible length of the two pieces and the length of the bamboo.

Solution:

Given:

From a bamboo, a piece of bamboo is cut off. It is found that the ratio of the two pieces is 3:1.

In the first case, let the length of Expenses to buy new books the second piece = x dcm

∴ \(\frac{30}{x}\) = \(\frac{3}{1}\)

or, 3x = 30 or, x = 10

∴ Length of the second piece= 10 dcm and total length of the bamboo (30+10) dcm = 40 dcm.

∴ In the first case, the length of the second piece 10 dcm, and the total length of the bamboo 40 dcm.

In the second case, let the length of the first piece = y dcm

∴ \(\frac{y}{15}\) = \(\frac{3}{1}\)

or, y = 45.

∴ Length of the first piece = 45 dcm and (45+ 15) dcm = 60

∴ In the second case, the length of the first piece 45 dcm, and the total length of the bamboo = 60 dcm.

Example 30. Ratio First piece Second piece 3:1 the price of the first book is ₹ 75. If the price of the first book was ₹ 25 more what would be the required ratio prices?

Solution:

Given:

Ratio First piece Second piece 3:1 the price of the first book is ₹ 75. If the price of the first book was ₹ 25

Let the price of the second book be ₹ x

∴ \(\frac{75}{x}\) = \(\frac{3}{1}\)

or, 3x= 75 or, x = \(\frac{75}{3}\) = 25

If the price of the first book was ₹ 25 more, the required ration

= \(\frac{75+25}{25}\) = \(\frac{100}{25}\) = \(\frac{4}{1}\) = 4: 1

Example 31. In a certain year, a library received a Govt. grant of ₹ 74,350 and collected a subscription of ₹4350. They also got ₹ 1,300 by selling old papers etc. If the entire money is spent on buying new books, for binding of old books, and paying salaries to the employees in the ratio 15:3:2 then calculate for how much money new books were bought.

Solution:

Given:

In a certain year, a library received a Govt. grant of ₹ 74,350 and collected a subscription of ₹4350. They also got ₹ 1,300 by selling old papers etc. If the entire money is spent on buying new books, for binding of old books, and paying salaries to the employees in the ratio 15:3:2

That library got total money from Govt. the grant, collection of subscriptions, and selling old papers = ₹ (74,350 +4350+ 1300) = ₹ 80,000.

Expenses to by new books

Wbbse Class 7 Maths Solutions

= ₹ \(\frac{80000}{15+3+2}\) x 15 = ₹ \(\frac{80000}{20}\) x 15 = ₹ 60000

∴ New books were bought for ₹60,000

 Example 32. The ratio of daily work of A and B is 4: 3. If A can do the work in 12 days, then find the number of days required by B to do the work.

Solution:

Given:

The ratio of daily work of A and B is 4: 3. If A can do the work in 12 days

Since, the ratio of the daily work of A and B is 4:3,

∴ The work done by A in 3 days is equal to the work done by B in 4 days.

∴ Work done by A in 1 day = work done by B in \(\frac{4}{3}\) days

∴ Work done by A in 12 days

= work done by in \(\frac{4}{3}\)×12 days = 16 days.

∴ 16 days.

The number of days required by B to do the work 16 days.

Wbbse Class 7 Maths Solutions

Example 33. 1050 people have come for training at a training center. They were asked to sit in three big halls in the ratio of 11:3:3\(\frac{1}{2}\). How many people will sit in each room?

Solution:

Given:

1050 people have come for training at a training center. They were asked to sit in three big halls in the ratio of 11:3:3\(\frac{1}{2}\).

Those people were asked to sit in three big halls in the ratio

11:3:3\(\frac{1}{2}\) = 11:3:\(\frac{7}{2}\) = 22:6:7.

∴ In the first room, there will sit \(\frac{1050}{22+6+7}\) x 22 people

= \(\frac{1050}{35}\) x 22 people = 660 people

∴ In the second room, there will sit \(\frac{1050}{22+6+7}\) x 6 people

= \(\frac{1050}{35}\) x 6 people = 180 people

In the third room, there will sit \(\frac{1050}{22+6+7}\) x 7 people

= \(\frac{1050}{35}\) x 7 people = 210 people.

∴ In the first, second, and third rooms, 660 people, 180 people, and 210 people will sit respectively.

Example 34. Ram earns ₹125 in 8 days and Shyam earns ₹140 in 10 days. Find the ratio of their earnings.

Solution:

Given:

Ram earns ₹125 in 8 days and Shyam earns ₹140 in 10 days.

The earnings of Ram for 8 days = ₹125

The earnings of Ram for 1 day = ₹ \(\frac{125}{8}\)

The earnings of Shyam for 10 day = ₹140

The earnings of Shyam for 1 day = ₹ \(\frac{140}{10}\)

∴ The ration of their earnings = \(\frac{125}{8}\) : \(\frac{140}{10}\)

= \(\frac{125}{8}\) x \(\frac{10}{140}\) = 125: 112

Example 35. ₹12,100 is divided among Ram, Shyam, Jadu, and Madhu in the ratio 2:3:4:2. How much each will get?

Solution:

Given:

₹12,100 is divided among Ram, Shyam, Jadu, and Madhu in the ratio 2:3:4:2.

Ram will get

₹ \(\frac{12,100}{2+3+4+2}\) x 2

= ₹ \(\frac{12,100}{11}\) x 2 = ₹ 2200

Shyam will get

₹ \(\frac{12,100}{2+3+4+2}\) x 3 = ₹ \(\frac{12,100}{11}\) x 3 = ₹ 3300

Jadu will get

₹ \(\frac{12,100}{2+3+4+2}\) x 4 = ₹ \(\frac{12,100}{11}\) x 4 = ₹ 4400

Madhu will get

₹ \(\frac{12,100}{2+3+4+2}\) x 2 = ₹ \(\frac{12,100}{11}\) x 2 = ₹ 2200

Ram will get  ₹ 2200, Shyam will get ₹ 3300, Jadu will get ₹ 4400 and MAdhy will get ₹ 2200

Class Vii Math Solution Wbbse

Example 36. A policeman starts to chase a thief. When the thief goes 5 steps, the policeman moves 6 steps. Again, 3 steps of the police is equal to 6 steps of the thief. Find the ratio of their speeds.

Solution:

Given:

A policeman starts to chase a thief. When the thief goes 5 steps, the policeman moves 6 steps. Again, 3 steps of the police is equal to 6 steps of the thief

3 steps of the police = 6 steps of the thief

1 step of the police = \(\frac{6}{3}\) steps of the thief

6 steps of the police = \(\frac{6×6}{3}\) steps of the thief

= 12 steps of the thief

Now, in the same time, the policeman moves 6 steps and the thief moves 5 steps.

∴ The ratio of their speeds

= \(\frac{6 steps of the police}{5 steps of the thief}\)

= \(\frac{12 steps of the thief}{5 steps of the thief}\)

= \(\frac{12}{5}\) = 12: 5

Example 37. The sum of the three angles of the triangle ABC is 180°. The ratio of ∠BAC, ∠ABC, and ∠ACB is 3:5:10. If the value of ∠BAC is decreased by 10° and the value of ∠ABC is increased by 10°, calculate the new ratio of the three angles.

Solution:

Given:

The sum of the three angles of the triangle ABC is 180°. The ratio of ∠BAC, ∠ABC, and ∠ACB is 3:5:10. If the value of ∠BAC is decreased by 10° and the value of ∠ABC is increased by 10°

∠BAC= \(\frac{180^{\circ}}{3+5+10}\) x 3 =\(\frac{180^{\circ}}{18}\) x 3 = 30°

∠ABC = \(\frac{180^{\circ}}{3+5+10}\) x 5 = \(\frac{180^{\circ}}{18}\)x 5 = 50°

∠ACB = \(\frac{180^{\circ}}{3+5+10}\) x 10 = \(\frac{180^{\circ}}{18}\) x 10 = 100°

If decreased by 10°, ∠BAC = 30° -10° = 20°

If increased by 10°, ∠ABC = 50° + 10° = 60°

∴ The new ratio of the three angles

= ∠BAC: ∠ABC: ∠ACB = 20°: 60°: 100° =1:3:5

∴ The new ratio of the three angles = 1:3:5.

Example 38. Ratio of the prices of two houses is 4:3 and the price of the second house is 4,20,000. What would be the ratio of their prices if the price of the first house would have been 70,000 more?

Solution:

Given:

Ratio of the prices of two houses is 4:3 and the price of the second house is 4,20,000.

Let, the price of the first house = ₹ x

Then, \(\frac{x}{420000}\) = \(\frac{4}{3}\)

or, x = \(\frac{4 X 420000}{3}\) = 560000

Hence, the price of the first house = ₹ 560000.

If the price of the first house would have been ₹70000 more then the price of the first house would be ₹(560000+ 70000)= ₹ 630000.

Then, \(\frac{price of the first house}{price of the second house}\) = \(\frac{630000}{420000}\)

= \(\frac{63}{42}\) = \(\frac{3}{2}\) = 3:2

∴ The ratio of their prices would be 3:2.

Example 39. ₹ 9000 is divided among three friends in such a way that, the second friend gets twice the amount the first friend gets and the third friend gets half the sum of money two friends get. How much amount of money each friend will get?

Solution:

Given:

₹ 9000 is divided among three friends in such a way that, the second friend gets twice the amount the first friend gets and the third friend gets half the sum of money two friends get.

Let, the first friend gets ₹ x, the second friend gets ₹ 2x and the third friend gets ₹ \(\frac{x+2x}{2}\)= ₹ \(\frac{3x}{2}\)

∴ Ratio of the money of the three friends

=x: 2x: \(\frac{3x}{2}\)

= 1: 2: \(\frac{3}{2}\) = 2: 4: 3.

∴ First friend will get

₹ \(\frac{9000}{2+4+3}\) x 2 = ₹ \(\frac{9000}{9}\) x 2 = ₹ 2000

∴ second friend will get

₹ \(\frac{9000}{2+4+3}\) x 4 = ₹ \(\frac{9000}{9}\) x 4 = ₹ 4000

third friend will get

₹ \(\frac{9000}{2+4+3}\) x 3 = ₹ \(\frac{9000}{9}\) x 3 = ₹ 3000

∴ First friend will get ₹2000, second friend will get ₹4000 and third friend will get ₹3000

Example 40. A customer co-operative society distributes ₹ 42150 as dividends among the members from the money it can spend in a year. The remaining money is distributed as the salary of staff and loans among the people in the ratio 7: 18. If the society can spend ₹ 77575 in a year, how much money it can invest as a loan?

Solution:

Given:

A customer co-operative society distributes ₹ 42150 as dividends among the members from the money it can spend in a year. The remaining money is distributed as the salary of staff and loans among the people in the ratio 7: 18. If the society can spend ₹ 77575 in a year

In a year the cooperative society can spend ₹ 77575.

It distributes as dividends among members ₹ 42150.

Remaining money =₹ (77575-42150) = ₹ 35425.

Let, money required to distribute salary to the staff=₹ 7x.

The money invested as loan to the people = ₹ 18 x.

According to the question, 7x+18x= 35425 or, 25x = 35425

or, x= \(\frac{35425}{25}\) = 1417

∴ Money invested as loan
=₹ 1417 x 18=25506

∴ ₹  25506 is invested as loan.

Class Vii Math Solution Wbbse

Example 41. For constructing a road in the village the ratio of the money spent for last four years is 2:4:3:2. If the total money spent in those four years is 132 lac, then find how much money was spend on the second year and total money spent on first and third year.

Solution:

Given:

For constructing a road in the village the ratio of the money spent for last four years is 2:4:3:2. If the total money spent in those four years is 132 lac

Expenditure of the first year

= ₹ \(\frac{132}{2+4+3+2}\) x 2 lac = ₹ \(\frac{132}{11}\) x 2 lac

Expenditure of the second year

= ₹ \(\frac{132}{2+4+3+2}\) x 4 lac = ₹ \(\frac{132}{11}\) x 4 lac

= ₹ 48 lac

Expenditure of the third year

= ₹ \(\frac{132}{2+4+3+2}\) x 3 lac = ₹ \(\frac{132}{11}\) x 3 lac

= ₹ 36 lac

Total expenditure of the first and the third year = ₹(24+36) lac = 60 lac

∴ ₹48 lac was spent on the second year and ₹60 lac was spent on the first and the third year.

Example 42. A cooperative agricultural farm grows paddy and jute in its 35 bighas of land in a ratio of 4: 3. It earns as profit ₹ 2500 per bigha from paddy and ₹ 2800 per bigha from jute. What is the ratio of profit from paddy and jute?

Solution:

Given:

A cooperative agricultural farm grows paddy and jute in its 35 bighas of land in a ratio of 4: 3. It earns as profit ₹ 2500 per bigha from paddy and ₹ 2800 per bigha from jute.

Let, paddy be cultivated in 4x bighas of land and jute be cultivated in 3x bighas of land.

According to the question,
4x+3x= 35 or, 7x= 35 or, x = \(\frac{35}{7}\) = 5

∴ Paddy has been cultivated in 4 x 5 or 20 bighas of land and jute has been cultivated in 3 x 5 or 15 bighas of land.

Now, profit from paddy of 20 bighas of land at the rate of ₹  2500 per bigha = ₹  2500 × 20.

Also, profit from jute of 15 bighas of land at the rate of ₹  2800 per bigha = ₹ 2800 × 15.

∴ The required ratio of profit = \(\frac{ 2500 x 20}{2800×15}\) = 25:21

∴ The required ratio of profit = 25:21.

Example 43. At the time of retirement, a man got 1,96,150. He donated 20,000 to the school library and the remaining amount was divided among his wife, son, and daughter in the ratio of 5:4:4. How much money did he give to each of them?

Solution:

Given:

At the time of retirement, a man got 1,96,150. He donated 20,000 to the school library and the remaining amount was divided among his wife, son, and daughter in the ratio of 5:4:4.

From ₹ 1,96,150 if ₹  20,000 is donated to the school library then remaining money=₹ (1,96,150 – 20,000) = ₹ 1,76,150

wife gets = ₹ \(\frac{1,76,150}{5+4+4}\) x 5

= ₹ \(\frac{1,76,150}{13}\) x 5 = ₹ 67,750

son gets = ₹ \(\frac{1,76,150}{5+4+4}\) x 4

= ₹ \(\frac{1,76,150}{13}\) x 4 = ₹ 54,200

daughter gets = ₹ \(\frac{1,76,150}{5+4+4}\) x 4

= ₹ \(\frac{1,76,150}{13}\) x 4 = ₹ 54,200

∴ He gave ₹ 67,750 to his wife, ₹54,200 to his son, and ₹ 54,200 to his daughter.

Example 44. The ratio of story books and other books in a club library is 4: 3 and the number of story books is 1248. Some storybooks are purchased and thus the ratio becomes 11: 6. How many storybooks are purchased?

Solution:

Given:

The ratio of story books and other books in a club library is 4: 3 and the number of story books is 1248. Some storybooks are purchased and thus the ratio becomes 11: 6.

Let, the number of story books = 4x and the number of other books = 3x.

According to the question,
4x=1248 or, x= \(\frac{1248}{4}\) = 312

∴ Number of other books = 3 x 312 = 936.

Let, y number of story books are purchased.

∴ \(\frac{1248+y}{936}\) = \(\frac{11}{6}\)

or, 6y+7488 = 10296
or, 6y 10296-7488 or, 6y= 2808

or, y = \(\frac{2808}{6}\) = 468

∴ 468 storybooks are purchased

Class Vii Math Solution Wbbse

Example 45.  A man cultivated brinjal and potato in a ratio of 4:3 in his 35 katha lands. He made a profit of ₹150 per katha for brinjal and ₹125 per katha for potato. Calculate the ratio of profit of that man from his cultivation of brinjal and potato from his total land.

Solution:

Given:

A man cultivated brinjal and potato in a ratio of 4:3 in his 35 katha lands. He made a profit of ₹150 per katha for brinjal and ₹125 per katha for potato.

Amount of land where brinjal is cultivated

= \(\frac{35}{4+3}\) x 4 katha = \(\frac{35}{7}\) x 4 katha = 20 katha

Amount of land where potato is cultivated

= \(\frac{35}{4+3}\) x 3 kaths = \(\frac{35}{7}\) x 3 katha = 15 katha

\(\frac{Total profit from brinjal}{Total profit from potato}\)

 

= \(\frac{ ₹ 20X150}{ ₹ 15 X 125}\) = 8:5

∴ The required ratio is 8:5.

Example 46. In a school there were 660 students and the ratio of the number of boys and girls was 13:9. After a few days 30 girls joined the school but a few boys left. As a result, the ratio of the boys and the girls became 6: 5. Determine the number of boys who left the school.

Solution:

Given:

In a school there were 660 students and the ratio of the number of boys and girls was 13:9. After a few days 30 girls joined the school but a few boys left. As a result, the ratio of the boys and the girls became 6: 5.

Let, in that school the number of boys = 13x and the number of girls = 9.x.

According to the question, 13x+9x=660
or, 22x = 660

or, x = \(\frac{660}{22}\) = 30

∴ number of boys = 13 x 30 = 390 and a number of girls = 9x 30 270

Let, y number of boys left the school.

∴ 390-y-6 270+30 5

= \(\frac{390 – y}{270 + 30}\) = \(\frac{6}{5}\)

or, 5(390-y) =1800.

or, 1950-5y = 1800

or, 5y 1950-1800

or, 5y = 150

or, y = \(\frac{150}{5}\) = 30

∴ 30 boys left the school.

 

Arithmetic Chapter 2 Ratio And Proportion Exercise 2 Some Problems On Proportion

Example 1. Find whether the following proportions are true or not

1. 8:12 10:15.
2. 72:8=40:5.

Solution:

1. Here the product of the extremes =8×15 120 and the product of the means = 12 x 10 = 120. Since these two products are equal, therefore the proportion is true.
2. Here the product of the extremes = 72 × 5 = 360 and the product of the means = 8 x 40 = 320. Since these two products are not equal, therefore the proportion is not true.

Example 2.  Form the possible proportions with the numbers 8, 10, 16, and 20.

Solution:

Here we see that, 8:10 4:5, and also 16:20 = 4:5

Hence, 8:10 16:20 and 10: 8=20:16 are two proportions.

Again, 8:16 1:2 and 10: 20=1:2

∴ 8:16 10:20 and 16:8=20: 10 are two proportions

∴ The required proportions are:

1. 8:10 = 16:20
2. 10:8 = 20:16
3. 8:16 = 10:20
4. 16:8 = 20:10.

Example 3. Find the missing term in place of * in the following proportion: 16:20:8: *.

Solution:

Let, the missing term be x.

∴ \(\frac{16}{20}\) = \(\frac{8}{x}\)

or, 16x=8×20

or, x= \(\frac{8 X 20}{16}\) = 10

∴ 10.

The missing term 10.

Example 4. Find the fourth proportional of the following numbers: 12, 16, 18.

Solution:

Let, the fourth proportional be x.

∴ \(\frac{12}{16}\) = \(\frac{18}{x}\)

or, 12 X x= 16 x 18

or, x = \(\frac{16 X 18}{12}\) = 24

Example 5. Find the third proportional of the following 9:12

Solution:

Let, the third proportional be x.

∴ \(\frac{9}{12}\) = \(\frac{12}{x}\)

or, 9x= 12 x 12

or, x = \(\frac{12 X 12}{9}\) = 16

∴ 16

The third proportional is 16

Example 6. Find the mean proportional of the following numbers: 25, 81.

Solution:

Let, the mean proportion be x.

∴ \(\frac{25}{x}\) = \(\frac{x}{81}\)

or, x² = 25 x 81

or, x = 5 x 9 = 45

∴ 45.

The mean proportional 45.

Example 7. A’s money is \(\frac{2}{3}\) of B’s money and B’s money is \(\frac{4}{5}\) of C’s money. Find the ratio of A’s money to C’s money.

Solution:

Sincew, A’s money = \(\frac{2}{3}\) of B’s money

∴ \(\frac{A’s money}{B’s money}\) = \(\frac{2}{3}\)

∴ \(\frac{B’s money}{C’s money}\) = \(\frac{4}{5}\)

∴ \(\frac{A’s money}{B’s money}\) x \(\frac{B’s money}{C’s money}\) = \(\frac{2}{3}\) x \(\frac{4}{5}\)

∴ \(\frac{A’s money}{C’s money}\) = \(\frac{8}{15}\) = 8: 5

Example 8. A man used 16 ploughs to cultivate his whole land in 10 days. If he wants to cultivate the same land in 8 days, how many ploughs are required?

Solution:

Given:

A man used 16 ploughs to cultivate his whole land in 10 days. If he wants to cultivate the same land in 8 days,

No. of days
10
8

No. of ploughs
16
x (say)

If number of days decreases then the number of ploughs will increase. The number of ploughs is in inverse ratio with the number of days.

∴ 8 : 10 = 16: x

or, \(\frac{8}{10}\) = \(\frac{16}{x}\)

or, 8x = 16 x 10

or, x = \(\frac{16 X 10}{8}\) = 20

∴20 ploughs are required.

Example 9. 12 men had provision of food for 20 days. If there are 40 men, how long will the provision last?

Solution:

Given:

12 men had provision of food for 20 days. If there are 40 men

No. of men
12
40

No. of days
20
x (say)

If number of men increases then number of days will decrease. A number of days is in inverse ratio with the number of men.

∴ 40 12 = 20: x

or, \(\frac{40}{12}\) = \(\frac{20}{x}\)

or, 40x = 20 × 12

or, x = \(\frac{20 X 12}{40}\) = 6

∴ The provision will last for 6 days.

Example 10. 8 men can do a piece of work in 15 days. In how many days will 10 men finish the same work?

Solution:

Given:

8 men can do a piece of work in 15 days.

No. of men
8
10

No. of days
15
x (say)

If number of men increases then the number of days will decrease. Number of days is in inverse ratio with the number of men.

∴ 10: 8 = 15: x

or, = \(\frac{10}{8}\) or, 10x = 15 x 8

or, x = \(\frac{15 X 8}{10}\) = 12

∴ They will finish in 12 days.

Example 11. When water freezes to ice, its volume increases by 10%. Find the ratio of a certain volume of water and its corresponding volume of ice.

Solution:

Given:

When water freezes to ice, its volume increases by 10%.

Let, the volume of water be x c.c.

Then volume of ice = (x + x x \(\frac{10}{100}\)) c.c

= (x + \(\frac{x}{10}\)) c.c = \(\frac{11x}{10}\) c.c

∴ Volume of water: volume of ice = x: \(\frac{11 x}{10}\)

=1: \(\frac{11}{10}\) = 10 11.

∴ The Ration of the volume of water and ice is 10: 11

Example 12. In two types of ‘sharbat,’ the ratios of syrup and water are 2:5 and 6:10. Which one is sweeter?

Solution:

Given:

In two types of ‘sharbat,’ the ratios of syrup and water are 2:5 and 6:10.

In the first ‘sharbat’, syrup: water = 2:54:10

In the second ‘sharbat’, syrup: water 6: 10

Since in the second ‘sharbat’ the amount of syrup is more therefore the second ‘sharbat’ is sweeter.

∴ The second ‘sharbat’ is sweeter.

Example 13. The cost of 3 umbrellas or 1 chair is 600. Calculate the price of 2 umbrellas and 2 chairs.

Solution:

Given:

The cost of 3 umbrellas or 1 chair is 600.

Cost of 1 chair = cost of 3 umbrellas
Cost of 2 chairs = cost of 6 umbrellas

∴Cost of 2 umbrellas and 2 chairs = cost of (2+6) or 8 umbrellas.

No. of umbrellas
3
8

cost
₹ 600
₹ x ( say)

The cost of umbrella increases with the number of umbrellas.

Therefore, cost of an umbrella is in simple ratio with the number 0of umbrella

∴ 3: 8 = 600: x

or, \(\frac{3}{8}\) = \(\frac{600}{x}\)

or, 3x = 600 x 8

or, x = \(\frac{600 X 8}{3}\) = 1600

∴ The cost of 2 umbrellas and 2 chairs is ₹ 100

Example 14. In a flood relief camp, there is a provision of food for 4000 people for 190 days. After 30 days, 800 people went away elsewhere. Find for how many days will the remaining food last for the remaining people in the camp.

Solution:

Given:

In a flood relief camp, there is a provision of food for 4000 people for 190 days. After 30 days, 800 people went away elsewhere.

After 30 days, the number of days remaining = (190-30) days 160 days.

Number of people remaining =(4000-800) 3200.

We are to determine how long the food for 3200 people will last, which lasts 160 days for 4000 people.

No. of people
4000
3200

No. of days
160
x (say)

Number of days increases with the decrease of the number of people.

Therefore, the number of days is in inverse ratio with the number of people.

∴ 3200: 4000= 160: x

or, \(\frac{3200}{4000}\) = \(\frac{160}{x}\)

or, 3200 x = 160 x 4000

or, x = \(\frac{160 X 4000}{3200}\) = 200

∴ The remaining food will last for 200 days.

Example 15. For making a flower garland of china roses (Jaba) and Indian marigolds (gada), 105 of these flowers were collected. If the ratio of china roses and marigolds is 3:4 find how many china roses and marigolds are there. Also, find how many more china roses must be collected so that the ratio of these two types of flowers becomes equal.

Solution:

Given:

For making a flower garland of china roses (Jaba) and Indian marigolds (gada), 105 of these flowers were collected. If the ratio of china roses and marigolds is 3:4

Number of china roses

= \(\frac{105}{3 + 4}\) x 3 = \(\frac{105}{7}\) x 3 = 45

Number of marigold = \(\frac{105}{3 + 4}\) x 4 = \(\frac{105}{7}\) x 4 = 60

In order that the ratio of these two types of flowers to become equal (60-45) = 15 more china roses are to be collected.

∴ Number of china roses is 45 and the number of marigolds is 60. 15 more china roses are to be collected.

Example 16. In a factory producing machine parts, the ratio of the number of parts produced per day to the number of workers employed is 5:2. Then calculate:

1. The number of workers to be employed for the production of 125 machine parts per day.
2. The number of machine parts produced per day if 22 workers are employed.

Solution:

Given:

In a factory producing machine parts, the ratio of the number of parts produced per day to the number of workers employed is 5:2.

1. Let, the number of workers to be employed = x.

Hence, \(\frac{125}{x}\) = \(\frac{5}{2}\)

or, 5x = 125 × 2

or, x= \(\frac{125 x 2}{5}\) = 50

∴ 50 workers to be employed.

2. Let, the number of machine parts produced per day =y.

Hence, y = \(\frac{22 x 5}{2}\) = 55

∴ 55 machine parts will be produced per day.

Example 17. The ratio of the monthly income of Ram and Shyam is 25: 28. Shyam gets ₹ 600 more than Ram. What are their monthly incomes?

Solution:

Given:

The ratio of the monthly income of Ram and Shyam is 25: 28. Shyam gets ₹ 600 more than Ram.

Let the monthly income of Ram be ₹ 25x and that of Shyam be ₹ 28x.

According to the question,
28x-25x=600

or, 3x= 600 or, x = \(\frac{600}{3}\) = 200

Hence, the monthly income of Ram = ₹ 200 X 25 = ₹ 5000

and monthly income of Shyam

= ₹ 200 x 28 = ₹ 5000

∴ The monthly income of Ram is ₹ 5000, and the monthly income of Shyam is ₹ 5600

Example 18. The ratio of the ages of father and son was 4:1, 20 years ago. The ratio of their ages will be 2: 1 after 4 years. Find their present ages.

Solution:

Given:

The ratio of the ages of father and son was 4:1, 20 years ago. The ratio of their ages will be 2: 1 after 4 years.

Before 20 years, let the father’s age be 4x years and the son’s age be x years.

Therefore, at present, the father’s age is (4x+20) years and

The son’s age is (x+20) years.

Hence, after 4 years, the father’s age will be (4x+20+ 4) years = (4x+ 24) years,  and

The son’s age will be (x+20+ 4) years = (x + 24) years.

∴ According to the question, \(\frac{4x + 24}{x + 24}\) = \(\frac{2}{2}\)

or, 4x + 24 = 2x + 48

or, 4x-2x=48-24

or, 2x = 24

or, x = \(\frac{24}{2}\) = 12

∴ Father’s present age is (4 x 12 + 20) years 68 years and the son’s present age is (12+20) years = 32 years.

∴ Father’s present age is 68 years and the son’s present age is 32 years.

Example 19.  A train started from Calcutta for Madhupur and another train started from Madhupur for Calcutta at the same time. The two trains

Solution:

Given:

A train started from Calcutta for Madhupur and another train started from Madhupur for Calcutta at the same time.

 

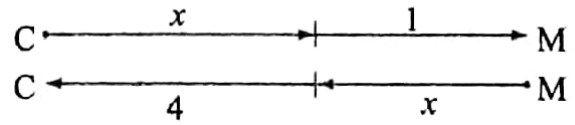
Let, after x hours of departure the two trains meet each other.

Now, the distance traveled by the first train in x hours the distance traveled by the second train in 4 hours.

Hence, the distance traveled by the first train in 1 hour the distance traveled by the second train in hours.

But according to the question,

The distance traveled by the first train in 1 hour = the distance traveled by the second train in \(\frac{4}{x}\) hours.

Hence, \(\frac{4}{x}\) or, x² = 4 or, x = 2

Hence, the first train takes (2 + 1) or 3 hours for the whole journey, and the second train takes (2+4) or 6 hours for the whole journey.

∴ Ratio of their speeds is the inverse ratio of 3 and 6 = 6:3 = 2:1.

Example 20. In a box, there are 378 coins in one rupee, 50 paise, and 25 paise coins. If the ratio of their values be 13: 11: 7, find the number of each kind of coin in the box.

Solution:

Given:

In a box, there are 378 coins in one rupee, 50 paise, and 25 paise coins. If the ratio of their values be 13: 11: 7,

Since the ratio of values of one rupee, 50 paise, and 25 paise coins is 13:11:

∴ The ratio of the number of one rupee, 50 required to complete the repair work. paise and 25 paise coins is
(13 x 1): (11 x 2): (7 x 4) = 13: 22:28

Now, 13 +22 + 28 = 63

Hence, out of 378 coins-

The number of one rupee coins

= \(\frac{13}{63}\) x 378 = 78

The number of 50 paise coins

=\(\frac{22}{63}\) x 378 =132

The number of 25 paise coins

= \(\frac{28}{63}\) x 378 = 168

∴ There are 78, one rupee coins.
132, 50 paise coins.
168, 25 paise coins.

Example 21. 20 persons decided that they would finish up the repairing work of a building within 30 days. 8 persons fell ill after 6 days of work. How many extra days would be required to complete the repair work?

Solution:

Given:

20 persons decided that they would finish up the repairing work of a building within 30 days. 8 persons fell ill after 6 days of work.

Considering a time frame of 30 days, there remains 24 days in hand after 6 days of work have passed.

When 8 persons fell ill, number of left over persons = 20 – 8 = 12

∴ The situation after 6 days is as below:

No. of persons
20
12

No. of days
24
x (say)

When number of persons reduces, number of required days increases, i.e., these two are  inverse in nature.

∴ \(\frac{20}{12}\) = \(\frac{x}{24}\)

or, x = \(\frac{20 X 24}{12}\) = 40

∴ Number of extra days required = 40-24=16

∴ 16 numbers of extra days would be required = 40 -024 = 16

Example 22. At a certain time of a day the length of the shadow of a 6m high tree becomes 8m. At the same time the shadow of an erect post measures 20m in length. Find out the height of the post.

Solution:

Given:

At a certain time of a day the length of the shadow of a 6m high tree becomes 8m. At the same time the shadow of an erect post measures 20m in length.

The length of the shadow at any point of time is directly proportional to the height of the object.

Hence,
height of object
6m
xm (say)

length of shadow
8m
20m

or, \(\frac{6}{x}\)= \(\frac{8}{20}\)

or, x = \(\frac{6 X 20}{8}\) = 15

∴ The height of the post is 15m.

 

Arithmetic Chapter 1 Revision Of Previous Lessons

Introduction
In class VI you have studied problems on

1. First four rules,
2. Vulgar fractions,
3. Decimal
4. Recurring fractions,
5. H.C.F. and L.C.M. of integers,
6. H.C.F. and L.C.M. of fractions and decimals and
7. Extraction of square roots of integers by factorisation and division.

First four rules

You know that addition, subtraction, multiplication and division are the first four rules. The entire structure of mathematics is based on these four rules. In every branch of mathematics namely arithmetic, algebra, geometry etc., we have to depend on these four rules. Let us discuss some problems on the first four rules.

Read and Learn More WBBSE Solutions For Class 7 Maths

Arithmetic Chapter 1 Revision Of Previous Lessons Exercise 1 Some Problems With The First Four Rules

Example 1. The sum of two numbers is 1040 and their difference is 304. Find the numbers.

Math Solution Of Class 7 Wbbse

Solution:

Given:

The sum of two numbers is 1040 and their difference is 304.

∴ The greater number = 1344 ÷ 2=672

Hence, the smaller number = 1040-672 = 368

∴ 672 and 368

The numbers are 672 and 368.

Class Vii Math Solution Wbbse

Example 2. The sum of the two numbers is 1000. If the greater number is thrice the smaller number, find the numbers.

Solution:

Given:

The sum of the two numbers is 1000. If the greater number is thrice the smaller number,

The greater number+ the smaller number = 1000

∴ 3 x the smaller number + the smaller number = 1000

or, 4 x the smaller number = 1000 = 250

or, the smaller number = \(\frac{1000}{4}\) = 250

Hence, the greater number = 3 x 250 = 750.

∴ 750 and 250.

The numbers are 750 and 250.

Math Solution Of Class 7 Wbbse

Example 3. The sum of two numbers is 645. If one of them is half of the other, then find the numbers.

Solution:

Given:

The sum of two numbers is 645. If one of them is half of the other,

Here, the smaller number is half of the greater number.

Hence, the greater number is twice the smaller number

Now, the greater number + the smaller number = 645

or, 2x the smaller number + the smaller number = 645

or, 3 x the smaller number = 645

or, the smaller number = \(\frac{645}{3}\) = 215

∴ The greater number = 215 x 2 = 430

∴ 430 and 215.

The numbers are 430 and 215.

Example 4. The sum of two numbers is 94792 and the greater number is 75368. Find the smaller number.

Solution:

Given:

The sum of two numbers is 94792 and the greater number is 75368.

The greater number + the smaller number = 94792

or, 75368+ the smaller number = 94792

or, the smaller number = 94792-75368 = 19424

∴  19424.

The smaller number is 19424.

Example 5. The sum of two numbers is 48925. If the smaller number is 12318, then find the greater number.

Solution:

Given:

The sum of two numbers is 48925. If the smaller number is 12318

The greater number + the smaller number = 48925

or, The greater number + 12318 = 48925

or, The greater number = 48925-12318 = 36607

∴  36607.

The greater number is 36607.

Example 6. The product of 36, 75 and another number is 218700. Find the number.

Solution:

Given:

The product of 36, 75 and another number is 218700.

Here, 36 x 75 x the required number=218700

or, the required number = \(\frac{218700}{36×75}\) = 81

∴ 81.

The number is 81.

Math Solution Of Class 7 Wbbse

Example 7. In a multiplication the multiplier is 965, and 476005 being added to the product, the sum becomes 1 million. Find the multiplicand.

Solution:

Given:

In a multiplication the multiplier is 965, and 476005 being added to the product, the sum becomes 1 million.

1 million = 1000000

When 476005 is added to the product it becomes 1000000.

Hence, the product = 1000000-476005 = 523995

Now, Multiplicand x Multiplier = 523995

or, multiplicand x 965 = 523995

or, multiplicand=523995 +965 = 543

∴  543.

The multiplicand is 543.

Example 8. What number divided by 372 gives the quotient 273 and the remainder 237?

Solution:

Given:

The number divided by 372 gives the quotient 273 and the remainder 237.

Here dividend = divisor x quotient + remainder

= 372 x 273 x 237 x = 101556 ÷ 237 = 101793

∴ 101793.

The number is 101793.

Example 9. Find the greatest number of 5 digits which is exactly divisible by 292.

Solution:

Given:

The greatest number of 5 digits which is exactly divisible by 292

The natural greatest number of 5 digits=99999

Thus, if the remainder 7 be subtracted from 99999, the result will be exactly divisible by 232.

∴ The required number= 99999-7= 99992

∴ 99992.

The greatest number is 99992.

Class Vii Math Solution Wbbse

Example 10. Find the least number of 6 digits which is exactly divisible by 215.

Solution:

Given:

The least number of 6 digits which is exactly divisible by 215

The natural least number of 6 digits = 100000

Now, 215-25 = 190

If 190 be added to 100000, the result will be divisible by 215.

∴ The required number = 100000+ 190 = 100190

∴ 100190.

The least number 100190.

Example 11. Five years ago, the father’s age was 8 times that of his son. Five years hence, the sum of their ages will be 65 years. Find their present ages.

Solution:

Given:

Five years ago, the father’s age was 8 times that of his son. Five years hence, the sum of their ages will be 65 years.

Since, after 5 years the sum of their ages will be 65 years

therefore, the sum of their present ages (65-25) years = (65-10) years 55 years.

Also, five years ago, the sum of their ages was (55-2x 5) years = 45 years.

At that time, the father’s age was 8 times that of son.

Hence, the sum of their ages was 9 times the then age of the son.

∴ At that time, the age of son was (459) or, 5 years and that of father was (5 x 8) years or 40 years.

∴ present age of father= (40+5) years = 45 years

and present age of son = (5+ 5) years = 10 years.

∴ Present age of son is 10 years and the present age of the father is 45 years.

Example 12. Find the quotient and the remainder, dividing by the factors of the divisor in the following case 7027 ÷ 105.

Solution:

Hence, the quotient = 66.

The actual remainder = the first remainder + the first divisor x the second remainder + the first divisor x the second divisor x the third remainder.

=1+3×2+3x5x6=1+6+90=97

∴ Quotient = 66, Remainder = 97.

Arithmetic Chapter 1 Revision Of Previous Lessons Exercise 1 Some Problems On Fractions

Example 1. Add together 339\(\frac{1}{10}\)+ 660\(\frac{9}{10}\) 

Solution: 339 \(\frac{1}{10}\)+ 660 \(\frac{9}{10}\)

∴ 1000.

Example 2. Subtract 189 \(\frac{1}{11}\) – 99 \(\frac{1}{22}\)

Solution: 189 \(\frac{1}{11}\) – 99 \(\frac{1}{22}\)

∴  90\(\frac{1}{22}\)

Class Vii Math Solution Wbbse

Example 3. Find the product 99990 \(\frac{494}{495}\) x 99

Solution: 999 \(\frac{494}{495}\)  × 99

∴ 98999\(\frac{4}{5}\)

Example 4.  Divide 29 \(\frac{8}{23}\) ÷ \(\frac{15}{17}\) 

Solution: 29 \(\frac{8}{23}\) ÷ \(\frac{15}{17}\)

∴ 33 \(\frac{6}{23}\)

Example 5. Simplify: 

Solution:

 

∴ \(\frac{2}{3}\)

Example 6. Add together 7.23 + 15.735 + 235.7

Solution:

Given

7.23 + 15.735 + 235.7

 

Example 7. Subtract 52.917 from 218.2

Solution:

Given:

52.917 And 218.2

 

Example 8. Multiply 33.123 by 1.25

Solution:

Given:

33.123 And 1.25

 

Example 9. Divide 67.072 by 16.

Solution:

Given:

67.072 And16

 

Example 10. Find the value of 15.8794:

1. To two places of decimal.
2. Correct to two places of decimal.

Solution:

1. The value of 15.8794 to two places of decimal = 15.87.
2. The value of 15.8794 correct to two places of decimal = 15.88.

Example 11. Convert into recurring decimal: 3 \(\frac{7}{22}\)

Class Vii Math Solution Wbbse

Solution: 3 \(\frac{7}{22}\) = \(\frac{73}{22}\)

 

Example 12. Convert into vulgar fraction 7.028

Solution: 7.028

∴ 7 \(\frac{14}{495}\)

Example 13. A man gave \(\frac{1}{3}\) of his property to his son and \(\frac{1}{5}\) of his property to his daughter. If 1267 was still left with him, what was his property?

Solution: The man gave (\(\frac{1}{3}\)+\(\frac{1}{5}\))

or, \(\frac{8}{15}\) part of his property to his son and daughter.

Therefore, (1 – \(\frac{8}{15}\))

or, \(\frac{7}{15}\) part of his property was left with him.

∴ \(\frac{7}{15}\) part of his property = ₹ 1267

∴ The whole property
= ₹1267 x \(\frac{15}{7}\) = ₹ 181 × 15 = ₹ 2715

∴ ₹ 2715.

Example 14. A post has \(\frac{1}{4}\)  of its length in mud and \(\frac{1}{5}\) of it in water and 11 metres above water. Find the whole length of the post.

Solution: (\(\frac{1}{4}\) + \(\frac{1}{5}\)) or (\(\frac{5+4}{20}\))

or, \(\frac{9}{20}\) of the post is in mud and water.

∴ (1- \(\frac{9}{20}\) or, \(\frac{11}{20}\)) of the post is above water.

∴ \(\frac{11}{20}\) of the whole post = 11 metres

∴ Lenght of the whole post = 11 x \(\frac{20}{11}\) meters.

∴ 20 meters.

Wbbse Class 7 Maths Solutions

Example 15. A man does 0.24 of a piece of work on the first day, 0.18 of it on the second day and 0.08 of it on the third day. How much of the work remains undone?

Solution:

Given:

A man does 0.24 of a piece of work on the first day, 0.18 of it on the second day and 0.08 of it on the third day.

In the first three days the man does (0.24 +0.18 +0.08) or 0.5 of the work.

Hence, (10.5) or 0.5 of the work remains undone.

∴ 0.5 of the work.

Example 16. 0.25 of the soldiers of an army died in combat, 0.15 was injured, 0.3 was captivated and the remaining 1200 soldiers escaped. How many soldiers were there in the army?

Solution:

Given:

0.25 of the soldiers of an army died in combat, 0.15 was injured, 0.3 was captivated and the remaining 1200 soldiers escaped.

(0.25 +0.15 + 0.3) or, 0.7 of the soldiers died, was injured and captivated.

Hence, (1-0.7) or, 0.3 of the soldiers escaped.

∴ 0.3 of the soldiers = 1200

∴ Total soldiers in the army = 1200 x \(\frac{10}{3}\) = 4000
∴4000.

Arithmetic Chapter 1 Revision Of Previous Lessons Exercise 1 Some Problems On H.C.F. and L.C.M.

Example 1. Find the L.C.M. of \(\frac{3}{4}\), \(\frac{5}{8}\), \(\frac{15}{16}\)

Solution:

∴ 3 \(\frac{3}{4}\)

Example 2. Find the H.C.F. of \(\frac{3}{5}\), 2 \(\frac{1}{10}\), \(\frac{6}{25}\)

Solution:

 

∴ \(\frac{3}{50}\)

Example 3. Find the L.C.M of 0.015, 0.42, and 1.5

Solution: 0.015 = 0.015
0.45 = 0.045
1.5 = 1.500

Now, let us find the L.C.M of 15, 450 and 1500

Now, 2 x 3 5 x 3 x 10 = 4500

Thus, the L.C.M of 15, 450 and 1500 is 4500

Hence the required L.C.M = 45

Example 4. Find the H.C.f of 0.4, 0.08, 0.016

Solution: 0.4 = 0.400
0.08 = 0.080
0.016 = 0.016

Let us now find the H.C.F of 400,80, 16

Thus, the H.C.F. of 400, 80, and 16 is 16

Hence, the required H.C.F. = 0.016

∴ 0.016.

Wbbse Class 7 Maths Solutions

Example 5. Three bells toll together and then at intervals of 3 \(\frac{1}{3}\), 2 \(\frac{3}{50}\) and 1 \(\frac{2}{3}\) seconds respectively. When will they toll together again?

Solution: The required time will be the L.C.M. of \(\frac{1}{3}\), 2 \(\frac{3}{50}\) and 1 \(\frac{2}{3}\) seconds i.e., the L.C.M. of \(\frac{10}{3}\), \(\frac{5}{2}\) and \(\frac{5}{3}\) seconds.

Now, the L.C.M. of \(\frac{10}{3}\), \(\frac{5}{2}\) and \(\frac{5}{3}\) seconds.

= \(\frac{L.C.M of 10,5,5}{H.C.F of 3,2,3}\) = \(\frac{10}{1}\) = 10

∴ They will toll together again after 10 seconds.

Example 6. What is the smallest number which is exactly divisible by 1 \(\frac{2}{7}\), 1 \(\frac{1}{35}\), \(\frac{45}{49}\)?

Solution: Here the numbers are

\(\frac{2}{7}\), 1 \(\frac{1}{35}\), \(\frac{45}{49}\)

i.e.., \(\frac{9}{7}\), \(\frac{36}{35}\), \(\frac{45}{49}\)

Now, the L.C.M of \(\frac{9}{7}\), \(\frac{36}{35}\), \(\frac{45}{49}\)

= \(\frac{L.C.M of 9,36,45}{H.C.F of 7,35,49}\)

= \(\frac{180}{7}\) = 25 \(\frac{5}{7}\)

∴ 25 \(\frac{5}{7}\)

Example 7. By what greatest fraction are \(\frac{14}{17}\), 3 \(\frac{1}{17}\), \(\frac{28}{34}\) exactly divisible giving integers as quotients?

Solution: Here the numbers are \(\frac{14}{17}\), 3 \(\frac{1}{17}\), \(\frac{28}{34}\)

i.e.., \(\frac{14}{17}\), \(\frac{52}{17}\), \(\frac{14}{17}\)

Now, the H.C.F. of \(\frac{14}{17}\), \(\frac{52}{17}\), \(\frac{14}{17}\)

 

= \(\frac{H.C.F of 14,52,14}{L.C.M of 17,17,17}\)

= \(\frac{2}{17}\)

∴ \(\frac{2}{17}\)

Wbbse Class 7 Maths Solutions

Example 8. By what greatest quantity must \(\frac{7}{8}\) kg, \(\frac{14}{15}\) kg and 1 \(\frac{1}{20}\) kg be divided so that the quotients are integers?

Solution: Let us first find the H.C.F. of \(\frac{7}{8}\) kg, \(\frac{14}{15}\) kg and 1 \(\frac{1}{20}\)

i.e.., of \(\frac{7}{8}\) kg, \(\frac{14}{15}\) kg and 1 \(\frac{1}{20}\)

Now, H.C.f of \(\frac{7}{8}\) kg, \(\frac{14}{15}\) kg and 1 \(\frac{1}{20}\)

= \(\frac{H.C.F of 7,14,21}{L.C.M of 8,15,20}\)

= \(\frac{7}{120}\)

∴ 2 x 2 x 5 x 2 x 3 = 120

Hence, the required quantity = \(\frac{7}{120}\) kg

∴ \(\frac{7}{120}\) kg

Example 9. By what greatest number must 2.1, 2.8, and 3.5 be divided to get integral quotients?

Solution: Here, the required number will be the H.C.F. of 2.1, 2.8, and 3.5.
Let us first find the H.C.F. of 21, 28, and 35.

Thus, H.C.F of 21, 28, and 35 is 7

Hence, H.C.F of 2.1, 2.8, and 3.5 is 0.74

∴ the required number is 0.7

Wbbse Class 7 Maths Solutions

Example 10. What least number when divided by 1.9, 0.95, and 0.076, gives integers as quotients?

Solution: The required number is the L.C.M. of 1.9, 0.95, and 0.076.
Now, 1.9 = 1.900
0.95 = 0.950
0.076 = 0.076

Now, let us find the L.C.M. of 1900, 950 and 76

∴ L.C.M. of 1900, 950 and 76
=2×2×5×5×19 = 1900

∴ L.C.M. of 1.9, 0.950, 0.076 is 1.9

∴ The required number is 1.9.

Example 11. The L.C.M. and H.C.F. of two fractions are \(\frac{4}{5}\) and \(\frac{2}{15}\) respectively. If one of them be \(\frac{2}{5}\) find the other.

Solution: We know that,

Product of two numbers = Their L.C.M.XH.C.F.

Hence, \(\frac{2}{5}\) x the other number = \(\frac{4}{5}\) x \(\frac{2}{15}\)

or, the other number= \(\frac{4}{5}\) x \(\frac{2}{15}\) x \(\frac{5}{2}\) = \(\frac{4}{15}\)

∴ \(\frac{4}{15}\)

Example 12. The product of two numbers is 0.84. If their L.C.M. be 4.2, find their H.C.F.

Solution:

L.C.M. H.C.F. = Product of the numbers

or, 4.2 x H.C.F. = 0.84

or, H.C.F. = \(\frac{0.84}{4.2}\) = 0.2

Example 13. From what least number must 5 be subtracted so that the remainder may be exactly divisible by 48, 64, 90, 120?

Solution:

∴ L.C.M. of 48, 64, 90 and 120
=2×2×2×2×3 x 5 x 4 x 3 = 2880

Hence, the required number = 2880 +5=2885

∴ The number is 2885.

Example 14. What number nearest to 100000 is exactly divisible by 2, 3, 4, 5, 6, and 7?

Solution:

Now, 100000-40=99960 and 100000+ (420-40)= 100000+ 380 = 100380 are the two numbers divisible by 420.

Between these two numbers 99960 is nearer to 100000. Hence, 99960 is the required number.

∴ 99960

Example 15. Find the greatest number that will divide 8718, 16299, and 25396 leaving the remainder 1, 2, and 3 respectively.

Solution: Since, 8718, 16299, and 25396 when divided by the required number leaves the remainder 1 , 2 and 3 respectively therefore (8718- 1), i.e., 8717, (16299- 2)

i.e., 16297 and (25396- 3)

i.e., 25393 are exactly divisible by the required number.

Hence, H.C.F. of 8717, 16297 and 25393 is the required number.

∴ The required number is 379.

Example 16. 175 mangoes and 105 oranges can be equally divided among certain number of boys and girls. Find the number.

Solution:

Hence, the number of boys and girls may be 35 or any factor of 35 i.e., 5, 7.
∴ 5, 7, 35.

 

Arithmetic Chapter 1 Revision Of Previous Lessons Exercise 1 Some Problems On Square Root

Example 1. Find the square root of 1225 by factorisation.

Solution:

Given:

1225

Now, 1225 = 5 x 5 x 7 x 7=5² x 7²

Hence, √1225 = 5 x 7=35

∴ 35.

The square root of 1225 = 35.

Example 2. Find the square root of 15625 by the division method.

Solution:

Given:

15625

∴ 125

The square root of 15625 = 125

Example 3. By what least number must 450 be multiplied to give a perfect square?

Solution:

Given:

450

Now, 450 = 2 x 3 x3x5x5=2x 3² x 5²

So, if we multiply 450 by 2 then it will be a perfect square.

Example 4. By what least number must 1323 be divided so that the quotient will be a perfect square?

Solution:

Given:

1323

Now, 1323 = 3 x 3² x 7²

So, if we divide 1323 by 3 then it will be a perfect square.

Math Solution Of Class 7 Wbbse

Example 5. The product of two numbers is 1575 and their quotinet is \(\frac{9}{7}\); find the numbers.

Solution:

Given:

The product of two numbers is 1575 and their quotinet is \(\frac{9}{7}\)

Let the smaller number be A then the greater number is \(\frac{9}{7}\) A.

Now, A x \(\frac{9}{7}\) A = 1575

or, A² = \(\frac{1575 X 7}{9}\) =175×7=1225

or, A = √1225=35

∴ The smaller number = 35 and the greater number = \(\frac{9}{7}\) × 35 = 9 x 5 = 45
∴ 35 and 45.

Example 6.  77847 soldiers were arranged in a square. After being arranged 6 soldiers were in excess. What was the number of soldiers in the front row?

Solution:

Given:

77847 soldiers were arranged in a square. After being arranged 6 soldiers were in excess.

Since there was an excess of 6 soldiers after they were arranged in the form of a square therefore,(77847 – 6) or, 77841 soldiers made the perfect square. Then the number of soldiers in the front row = √77841=279

∴ The number of soldiers in the front row = 279.

Math Solution Of Class 7 Wbbse

Example 7. Each member of a club contributed as many 25 paise as the total number of members and the total contribution was 400. Find the number of members of the club.

Solution:

Given:

Each member of a club contributed as many 25 paise as the total number of members and the total contribution was 400.

₹400 = 40000 paise
Now, number of 25 paise in 40000 paise = \(\frac{40000}{25}\) = 1600

∴ Number of members of the club = √1600 = 40 perfect square.

∴ 40.

Number of members of the club = 40.

Example 8. The length of the sides of two squares are 15 cm and 20 cm respectively. A new square is formed whose area is equal to the sum of the areas of these two squares. Find the length of the side of the new square.

Solution:

Given:

The length of the sides of two squares are 15 cm and 20 cm respectively. A new square is formed whose area is equal to the sum of the areas of these two squares.

Area of the first square= (15)² sq cm = 225 sq cm.

Area of the second square = (20)² sq cm = 400 sq cm.

Area of the new square (225+ 400) sq cm 625 sq cm.

∴The length of the side of the new square = √625 cm = 25 cm

∴ 25 cm.

The length of the side of the new square is 25 cm.

 

Arithmetic

• Chapter 1 Fractions
• Chapter 2 Ratio and Proportion
• Chapter 3 Approximate Value
• Chapter 4 Square Root of Fraction
• Chapter 5 Time and Distance
• Chapter 6 Square Measure
• Chapter 7 Bar Graph

 

Algebra

• Chapter 1 Algebra Symbols
• Chapter 2 Addition, Subtraction, Multiplication and Division Of Integers
• Chapter 3 Laws
• Chapter 4 Polynamials
• Chapter 5 Formulae and Their Applications
• Chapter 6 Factorisation
• Chapter 7 Equations

Geometry

 

• Chapter 1 Angle, Triangle and Quadrilateral
• Chapter 2 Miscellaneous Constructions
• Chapter 3 Symmetry
• Chapter 4 Congruence

 

 

Algebra Chapter 7 Equations Exercise 7 Solved Example Problems

Equations Introduction

An equation is a statement of equality that involves one or more literal numbers. The literal numbers are called unknowns or variables.

Any value of the variables that satisfy the given equation is called a solution or root of the equation. Many problems of arithmetic may be solved easily by forming equations properly and finding their solutions.

At this early stage, our aim is to form linear equations of one variable and to obtain their solutions.

Math Solution Of Class 7 Wbbse

Read and Learn More WBBSE Solutions For Class 7 Maths

Formation of equation

Suppose, we do not know the marks obtained by Ram in the examination.

But it is known that, if we add 15 marks with the marks obtained by Ram then the sum will be 90 marks.

Since, in algebra, the unknown number may be expressed by an alphabetic symbol, the marks obtained by Ram may be taken as x. Then we may express the previous statement as x + 15 = 90.

This process of equating different things is known as ‘an equation’.

The specific value of the unknown thing which satisfies the equation is known as the root of the equation.

Some useful information about equation

1. If same number is added to both sides of an equation, its sides remain equal.
2. If same number is subtracted from both sides of an equation, its sides remain equal.
3. If both sides of an equation is multiplied by the same number, its sides remain equal.
4. If both sides of an equation is divided by the same number, its sides remain equal.

Equation and identity

In an equation, two sets of expressions are equalised by a sign.

In each of these sets the known and unknown expressions are connected by the signs of addition, subtraction, multiplication or division.

Both sides become equal for a specific value of the unknown quantity.

Math Solution Of Class 7 Wbbse

Example:

x + 2 = 5 is an equation. The two sides become equal for only one value of x, namely 3. Both sides do not become equal for any value of x other than 3.

An identity is expressed in a similar manner, but its difference with the equation is that, its both sides are equal for all the values of the unknown quantity.

Example:

x+5=x+ 4+ 1 is an identity because whatever may be the value of x, its sides are always equal.

Rules for solving an equation

The specific value of the unknown quantity which satisfies an equation is called the root of the equation. The determination of the root is called the solution of the equation. In order to solve an equation some rules should be kept in mind.

1. If a positive number changes side, it becomes negative.

For Example: If x+ 5 = 2x + 10 then x= 2x + 10 – 5.

In this case, + 5 of the left-hand side has become – 5 after going to the right-hand side.

Again, if 3.v + 2 = x + 15 then 3x + 2 – 15 = x.

In this case, + 15 of the right-hand side has become – 15 after coming to the left-hand side.

2. If a negative number changes side, it becomes positive.

For Example: If 5x + 25 = 2x – 10 then 5x + 25 + 10 = 2x

Again, if 7x – 2 = 3x + 5 then 7x = 3x + 5 + 2.

3. If a number is a multiplier of the left-hand side of an equation then the right-hand side has to be divided by it while transferring it to the right-hand side.

For Example: If 3x = 27, then x = \(\frac{27}{3}\) = 9.

In this case, 3 is a multiplier of the left-hand side, so 27 on the right-hand side has to be divided by 3.

4. If a number is a divisor of the left-hand side of an equation then the right-hand side is to be multiplied by it while transferring it to the right-hand side.

For Example: If \(\frac{x}{5}\) = 7, then x= 7 x 5 = 35.

In this case, 5 is a divisor of the left-hand side, so 7 on the right-hand side has to be multiplied by 5.

Method of solution of an equation when both sides of the sign of equality contain expressions involving known and unknown quantities

1. At first, each side has to be simplified.
2. Then the terms involving the unknown quantity are to be kept in the left-hand side and the other terms should be kept on the right-hand side.
3. Now each side has to be simplified again.
4. At last, by dividing the right-hand side by the co-efficient of the left-hand side the required root of the equation may be obtained.

 

Algebra Chapter 7 Equations Exercise 7 Some Examples Of The Formation Of Equations

Example 1. Adding 16 with 8 times a number, it becomes 40. Form an equation to find the number.

Solution:

Given:

Adding 16 with 8 times a number, it becomes 40.

Let, the number be x. Its 8 times is 8x. Adding 16 with it we get 8x + 16.

Hence, from the given condition 8x + 16 = 40; it is the required equation.

Example 2. Rupees 140 was distributed among Ram, Shyam and Jadu in such a way that Shyam got, half the money of Ram and Jadu got half the money of Shyam. Form an equation to find their shares.

Solution:

Given:

Rupees 140 was distributed among Ram, Shyam and Jadu in such a way that Shyam got, half the money of Ram and Jadu got half the money of Shyam.

Let, Ram got ₹ x.

Then Shyam got ₹ \(\frac{x}{2}\)

and Jadu got ₹ \(\frac{x}{2}\) X \(\frac{1}{2}\) = ₹ \(\frac{x}{4}\)

Hence, from the given condition,

x + \(\frac{x}{2}\) +\(\frac{x}{4}\) = 140 ; it is the required equation.

Class Vii Math Solution Wbbse

Example 3. The present age of the father is 7 times that of the son. After 10 years, age of the father will be 3 times that of the son. Form an equation to find their present ages.

Solution:

Given:

The present age of the father is 7 times that of the son. After 10 years, age of the father will be 3 times that of the son.

Let, the present age of the son be x years.

Then the present age of the father is 7x years.

After 10 years—age of the son will be (x + 10) years and age of the father will be (7x +10) years

Hence, from the given condition,

7x +10 = 3 (x +10); it is the required equation.

Example 4. The half of a number is greater than \(\frac{1}{5}\) th of it by 6. Form an equation to find the number.

Solution:

Given:

The half of a number is greater than \(\frac{1}{5}\) th of it by 6.

Let, the number be x.

Half of the number is \(\frac{x}{2}\) and\(\frac{1}{5}\) th of the number is \(\frac{x}{5}\)

Hence, from the given condition, \(\frac{x}{2}\)= \(\frac{x}{5}\) + 6; it is the required equation.

Example 5. Of the total number of fruits with a fruit vendor, \(\frac{1}{5}\) was mango, \(\frac{1}{4}\) was apple, \(\frac{2}{5}\) was lichi and the rest 60 were oranges. Form an equation to find the total number of fruits with the vendor.

Solution:

Given:

Of the total number of fruits with a fruit vendor, \(\frac{1}{5}\) was mango, \(\frac{1}{4}\) was apple, \(\frac{2}{5}\) was lichi and the rest 60 were oranges.

Let, the total number of fruits be x.

Hence, from the given condition,

\(\frac{x}{5}\) +\(\frac{x}{4}\)+\(\frac{2x}{5}\)+60 = x; it is the required equation.

Example 6. Solve : \(\frac{x}{a}\) + b = \(\frac{x}{b}\)+ a .

Solution: \(\frac{x}{a}\) + b = \(\frac{x}{b}\)+ a .

Example 7. Solve: 50 + 3(4x – 5) + 8(x + 3) = x + 2.

Solution:

Given:

∴ -3.

Example 8. Solve: \(\frac{1}{2}\) (x +1) + (x + 2) + \(\frac{1}{4}\) (x + 3) = 16.

Solution:

Given:

\(\frac{1}{2}\) (x +1) + (x + 2) + \(\frac{1}{4}\) (x + 3) = 16.

∴ x= 13.

Wbbse Class 7 Maths Solutions

Example 9. \(\frac{1}{(x +1)(x +2)}\) + \(\frac{1}{x +2)(x +3)}\) + \(\frac{1}{(x +3)(x +4)}\) = \(\frac{1}{(x +1)(x +6)}\)

Solution:

Given:

\(\frac{1}{(x +1)(x +2)}\) + \(\frac{1}{x +2)(x +3)}\) + \(\frac{1}{(x +3)(x +4)}\) = \(\frac{1}{(x +1)(x +6)}\)

∴ x = -7

Example 10. Solve \(\frac{1}{(x+1)(2)}\) + \(\frac{1}{(x+3)(3)}\) = 4

Solution: \(\frac{1}{(x+1)(2)}\) + \(\frac{1}{(x+3)(3)}\) = 4

∴x= 3.

Wbbse Class 7 Maths Solutions

Example 11. Solve: 16-5 (7x-2) = 13 (x-2) + 4 (13 – x)

Solution:

Given:

16-5 (7x-2) = 13 (x-2) + 4 (13 – x)

∴ x = 0.

16-5 (7x-2) = 13 (x-2) + 4 (13 – x) = 0

Example 12. Solve \(\frac{x}{2}\) + \(\frac{1}{3}\) = \(\frac{x}{3}\) + \(\frac{1}{2}\)

Solution:

\(\frac{x}{2}\) + \(\frac{1}{3}\) = \(\frac{x}{3}\) + \(\frac{1}{2}\)

∴ x = 1

Example 13. Solve: 3 (x – 1) – (x + 2) = x + 2 (x – 1)

Solution:

3 (x – 1) – (x + 2) = x + 2 (x – 1).

∴x = – 3.

3 (x – 1) – (x + 2) = x + 2 (x – 1) = – 3.

Wbbse Class 7 Maths Solutions

Example 14. Solve: \(\frac{3x+1}{16}\) + \(\frac{2x-3}{17}\) =\(\frac{x+3}{8}\) + \(\frac{3x-1}{14}\)

Solution:

 

or, 30x = 150 or, x = \(\frac{150}{30}\) = 5

Example 15. If x = 2t and y = \(\frac{3t}{5}\) – 1, then find the value of t for which x = 5y.

Solution:

Given:

x = 2t and y = \(\frac{3t}{5}\) – 1

The relation, x = 5y will be satisfied when

2t = 5(\(\frac{3t}{5}\) – 1) or, 2t = 5(\(\frac{3t-5}{5}\))

or, 2t = 3t – 5 or, 3t – 2t = 5 or, t = 5

∴ t = 5

Example 16. If x = at² and y = 2at, find the relation between x and y.

Solution:

Given:

x = at² and y = 2at

x = at² or, at² = x or, t² =\(\frac{x}{a}\)…… (1)

Again, y = 2at or, 2at = y or, t = \(\frac{y}{2a}\)

Wbbse Class 7 Maths Solutions

Algebra Chapter 7 Equations Exercise 7 Some Problems On Equation

Example 1. If the sum of three consecutive numbers be 60. then find the numbers.

Solution:

Given:

The sum of three consecutive numbers be 60.

Let, the three consecutive numbers be x, x + 1 and x + 2

∴ According to the question, x + x+1+ x + 2 = 60

or, 3x + 3 = 60

or, 3x = 60 – 3

or, 3x = 57

or, x = \(\frac{57}{3}\) = 19

∴ The numbers are : 19, 19 + 1, 19 + 2, or, 19, 20, 21

∴19, 20, 21.

Example 2. If the sum of two numbers be 60 and their difference be 40 then find the numbers.

Solution:

Given:

The sum of two numbers be 60 and their difference be 40

Let, the greater number be x. Then the smaller number is 60 – x

According to the question, x – (60 – x) = 40

or, x – 60 + x = 40 or, 2x = 40 + 60 or, 2x = 100

or, x = \(\frac{100}{2}\) = 50

∴ The greater number = 50 and the smaller number = 60 – 50 = 10

∴ 50, 10

.’. The greater number = 50 and the smaller number = 60-50 = 10 Ans. 50,10.

Example 3. In a number of two digits, the digit in the tens’ place is greater than that of the units’ place by 3 and the sum of the digits is 11. Find the number.

Solution:

Given:

a number of two digits, the digit in the tens’ place is greater than that of the units’ place by 3 and the sum of the digits is 11.

Let, the digit in the units’ place be x.

Then the digit in the tens’ place is x + 3.

According to the question,

x + x + 3 = 11 or, 2x + 3 = 11 or, 2x = 11 – 3 or, 2x = 8

or, x = \(\frac{8}{2}\) = 4

∴ The digit in the units’ place = 4 and the digit in the tens’ place = 4 + 3 = 7

∴ The required number = 74

∴ 74.

Wbbse Class 7 Maths Solutions

Example 4. The present age of the father is 6 times that of the son. After 20 years, age of the father will be twice that of the son. Find the present age of the father.

Solution:

Given:

The present age of the father is 6 times that of the son. After 20 years, age of the father will be twice that of the son.

Let, the present age of the son be x years. Then the present age of the father is 6x years.

After 20 years— age of the son will be (x + 20) years

and age of the father will be (6x + 20) years

∴ According to the question,

6x + 20 = 2(x + 20)

or, 6x + 20 = 2x + 40

or, 6x – 2x = 40 – 20

or, 4x =20 or, x = \(\frac{20}{4}\) = 5

∴ The present age of the father is 6 x 5 years = 30 years.

∴ 30 years.

The present age of the father is 30 years.

Example 5. 1/3rd of a bamboo is within the mud, 1/4th of it  is in water and 5 metres above water. What is the length of the bamboo?

Solution:

Given:

1/3rd of a bamboo is within the mud, 1/4th of it  is in water and 5 metres above water.

Let, the length of the bamboo be x metres.

Length of the bamboo within mud = 7

metres and length of the bamboo within water = \(\frac{x}{4}\) metres

∴ According to the question, x – (\(\frac{x}{3}\) + \(\frac{x}{4}\)) = 5

or, x – \(\frac{4x+3x}{12}\) = 5

or, x – \(\frac{7x}{12}\) = 5

or, \(\frac{5x}{12}\) = 5 or, x = 5 x \(\frac{12}{5}\) = 12

∴ The length of the bamboo is 12 metres.

Example 6. The ratio of monthly incomes of two persons is 4: 5 and the ratio of their expenditures is 7: 9. If each of them saves ₹50 per month, then find the monthly income of each of them.

Solution:

Given:

The ratio of monthly incomes of two persons is 4: 5 and the ratio of their expenditures is 7: 9. If each of them saves ₹50 per month,

Let, the monthly income of  first person be ₹ 4x

and the monthly income of the second person be₹ 5x

Since each of them saves ₹50 per month

∴ Monthly expenditure of the first person = ₹(4x- 50)

and monthly expenditure of the second person = ₹ (5x – 50)

∴ According to the question,

\(\frac{4x-50}{5x-50}\) = \(\frac{7}{9}\)

or, 9(4x-50) = 7(5x-50) or, 36x – 450 = 35x- 350

or, 36x – 35x = 450 – 350

or, x = 100

∴ Monthly income of the first person = ₹ 4 x 100 =₹ 400

Monthly income of the second person = ₹ 5 x 100 =₹ 500

∴ ₹ 400 and ₹ 500.

Math Solution Of Class 7 Wbbse

Example 7. A man encashed a cheque of ₹2000 from bank. He received some five rupee notes and some ten rupee notes. If he received altogether 300 notes then what was the number of five rupee notes?

Solution:

Given:

A man encashed a cheque of ₹2000 from bank. He received some five rupee notes and some ten rupee notes. If he received altogether 300 notes

Let, the man received x number of five rupee notes and (300 – x) number of ten rupee notes.

∴ According to the question,

∴He received 200 five rupee notes.

Class Vii Math Solution Wbbse

Example 8. Total marks scored by Ram, Shyam and Jadu in an examination was 156. Shyam scored 9 marks more than Ram and Jadu scored 9 marks less than Ram. What were the marks scored by each?

Solution:

Given:

Total marks scored by Ram, Shyam and Jadu in an examination was 156. Shyam scored 9 marks more than Ram and Jadu scored 9 marks less than Ram.

Let, Ram scored x marks.

Then Shyam scored (x + 9) marks and Jadu scored (x – 9) marks

∴ According to the question, x+x + 9 + x- 9 = 156

or, 3x = 156

or, x = \(\frac{156}{3}\) = 52

Hence, Ram scored 52 marks, Shyam scored (52 + 9) marks

or 61 marks and Jadu scored (52-9) marks or 43 marks

∴ Ram scored 52 marks, Shyam scored 61 marks and Jadu scored 43 marks.

Example 9. The sum of the present ages of the father and his son is 65 years. 10 years ago, the ratio of their ages was 7: 2. Find the present ages of the father and his son.

Solution:

Given:

The sum of the present ages of the father and his son is 65 years. 10 years ago, the ratio of their ages was 7: 2.

Let, the present age of the father = x years and the present age of the son = (65 – x) years.

Then from the given condition,

\(\frac{x-10}{65-x-10}\) = \(\frac{7}{2}\)

or, 2(x – 10) = 7(55 – x) or, 2x – 20 = 385 – 7x

or, 2x + 7x = 385 + 20 or, 9x = 405

or, x = \(\frac{405}{9}\) = 45

Present age of the father = 45 years and the present age of the son = (65 – 45) years = 20 years.

∴ At present age of the father is 45 years and age of the son is 20 years.

Math Solution Of Class 7 Wbbse

Example 10. There were one rupee and five rupee coins in a money bag and the total amount was ₹170. If half of one rupee coin is replaced by five rupee coins, the amount becomes ₹210. How many one-rupee and five-rupee coins were there in the money bag at first?

Solution:

Given:

There were one rupee and five rupee coins in a money bag and the total amount was ₹170. If half of one rupee coin is replaced by five rupee coins, the amount becomes ₹210.

Let, at first there were x numbers of 1 rupee coins and y number of 5 rupee coins in the money bag.

According to the question,

x+ 5y = 170 …… (1)

If half of 1 rupee coins is replaced by 5 rupee coins, then number of

1 rupee coins  becomes x-\(\frac{x}{2}\) =\(\frac{x}{2}\) and the number of

5 rupee coins becomes Hence (y + \(\frac{x}{2}\))

Hence, \(\frac{x}{2}\) + (y + \(\frac{x}{2}\)).5 = 210

∴ Number of 1 rupee coins is 20 and that of 5 rupee coins is 30.

 Math Solution Of Class 7 Wbbse

Example 11. A train crosses a bridge 264 m long in 20 sec, but it takes 8 sec to cross a signal post by the side of the rail line. Find the length of the train and its speed.

Solution:

Given:

A train crosses a bridge 264 m long in 20 sec, but it takes 8 sec to cross a signal post by the side of the rail line.

Let, the length of the train be x m.

Then, the train takes 8 sec to cross x m and it takes 20 sec to cross (x + 264) m.

Hence, \(\frac{8}{20}\) = \(\frac{x}{x + 264}\)

or, 5x = 2x + 528 or, 5x – 2x = 528 or, 3x = 528

or, x = \(\frac{528}{3}\) = 176

∴ Length of the train is 176 m.

Also, in 8 sec the train crosses \(\frac{176}{8}\) m = 22 m

In 1 sec the train crosses 176 m

In 60×60 sec the train crosses = \(\frac{22 X 60 X 60}{1000}\) km = 79.2 km

∴ The length of the train is 176 m and its speed is 79.2 km/hour.

Example 12. A fruit seller sold some bananas at ₹10 per dozen and some guavas at ₹4 per pair and thereby got ₹368. If the number of bananas exceeds that of guava by 20, how many dozens of banana did he have?

Solution:

Given:

A fruit seller sold some bananas at ₹10 per dozen and some guavas at ₹4 per pair and thereby got ₹368. If the number of bananas exceeds that of guava by 20,

Let, that fruit seller had x guavas and (20 + x) bananas.

price of 12 bananas is ₹ 10

price of 1 banana is ₹ \(\frac{10}{12}\)

price of (20=x) banans is ₹ \(\frac{5}{6}\) (20 + x)

price of 2 guavas is ₹ 4

price of 1 guava is ₹ \(\frac{4}{2}\)

price of x guava is ₹ 2x

According to the question,

\(\frac{5}{6}\) (20 + x) + 2x = 368

 

 

Algebra Chapter 6 Factorisation Exercise 6 Solved Example Problems

Factorisation Introduction

A very important topic in algebra is to resolve an expression into factors. The idea of factors in algebra is similar to that of in arithmetic.

You have already learned about the multiple and factor of a given number in arithmetic.

For example, 35 = 5×7. Hence, factors of 35 are 1, 5, 7, and 35.

In a similar way, the factors of ab are 1, a, b, and ab. Let us now define a factor.

Math Solution Of Class 7 Wbbse

Factor

Read and Learn More WBBSE Solutions For Class 7 Maths

If the product of two or more expressions is equal to another expression then those expressions are called the factors of the product.

Example: If p x q x r = x then the expressions p, q, and r are called the factors of x.

Therefore, by factorisation of the expression x, three factors p, q, and r are obtained.

Math Solution Of Class 7 Wbbse Factorisation by a selection of common factors

If a polynomial contains one or more common factors in each of its terms then the common factor (or factors) are taken outside the bracket according to the distributive law and the remaining portion is kept inside the bracket.

Example:

\(a^2 b+a b+a b^2=a b(a+1+b)=a \times b \times(a+1+b)\) \(x^3 y^2+x^2 y^3=x^2 y^2(x+y)=x \times x \times y x y x(x+y)\)

Factorisation with the help of the formula of the square of a binomial

We know that, (a + b)² = (a + b)(a + b) and (a -b)² = (a-b) (a- b).

Some expressions can be factorised with the help of these two formulae.

Example: \(x^2+4 x y z+4 y^2 z^2\)

= \((x)^2+2 \cdot x \cdot 2 y z+(2 y z)^2=(x+2 y z)^2\)

Again, \(4 a^2-12 a b+9 b^2=(2 a)^2-2 \cdot 2 a \cdot 3 b+(3 b)^2\) 4a² – 12ab + 9b² = (2a)² – 2.2a.3b + (3b)²

= \((2 a-3 b)^2=(2 a-3 b)(2 a-3 b)\)

Wbbse Class 7 Maths Solutions

Factorisation with the help of the formula of the difference of two squares

Applying the formula a²-b² = (a + b) (a-b), some expressions can be factorised.

Example : \(25 x^2-81 y^2=(5 x)^2-(9 y)^2=(5 x+9 y)(5 x-9 y) .\)

Factorisation by the simultaneous application of the formulae of the square of a binomial and the difference of two squares

We know that, a² + 2ab + b² = (a + b)² and a² -b² = (a + b) (a-b).

Some expressions may be factorised by applying these two formulae simultaneously.

Example: \(a^4+4\)

= \(\left(a^2\right)^2+(2)^2\)

= \(\left(a^2\right)^2+2 \cdot a^2 \cdot 2+(2)^2-4 a^2\)

= \(\left(a^2+2\right)^2-(2 a)^2=\left(a^2+2+2 a\right)\left(a^2+2-2 a\right)\)

= \(\left(a^2+2 a+2\right)\left(a^2-2 a+2\right)\)

 Algebra Chapter 6 Factorisation Exercise 6 Some Examples On Factorisation

Example 1. Factorise : 3x + 12.

Solution:

Given:

3x + 12

= 3.x + 3.4 = 3 (x + 4)

∴ 3 (x +4).

3x + 12 = 3 (x +4).

Example 2. Factorise : 25m – 35n.

Solution:

Given: 25m – 35n

25m – 35n = 5 x 5m – 5 x 7n

∴ 5 (5m- 7n)

25m – 35n = 5 (5m- 7n)

Math Solution Of Class 7 Wbbse

Example 3. Factorise : \(p^2 q r+p q^2 r+p q r^2\)

Solution:

Given: \(p^2 q r+p q^2 r+p q r^2\)

 \(p^2 q r+p q^2 r+p q r^2\) = pqr (p + q + r)

∴pqr (p + q + r).

\(p^2 q r+p q^2 r+p q r^2\) = pqr (p + q + r).

Wbbse Class 7 Maths Solutions

Example 4. Factorise : \(4 a^4 b-6 a^3 b^2+12 a^2 b^3\)

Solution:

Given: \(4 a^4 b-6 a^3 b^2+12 a^2 b^3\)

\(4 a^4 b-6 a^3 b^2+12 a^2 b^3\)

∴ \(2 a^2 b\left(2 a^2-3 a b+6 b^2\right)\)

\(4 a^4 b-6 a^3 b^2+12 a^2 b^3\) = \(2 a^2 b\left(2 a^2-3 a b+6 b^2\right)\)

Example 5. Resolve into factors (ax + by) (p – q) – (ax + by) (q – r).

Solution:

Given:

(ax + by) (p-q)-(ax + by) (q – r)

= (ax +by) {(p-q)-(q- r)}

= (ax + by) (p-q-q + r)

= (ax + by) (p-2q + r)

∴ (ax +by) (p – 2q + r).

(ax + by) (p – q) – (ax + by) (q – r) = (ax +by) (p – 2q + r).

Example 6. Resolve into factors: \(x^2-(a+b) x+a b\)

Solution:

Given:

\(x^2-(a+b) x+a b\) \(x^2-(a+b) x+a b=x^2-a x-b x+a b=x(x-a)-b(x-a)\)

∴ (x-a) (x- b)

\(x^2-(a+b) x+a b\) = (x-a) (x- b)

Example 7. Resolve into factors : (P + q) (a + b) + r(a + b) + c(p + q + r).

Solution:

Given:

(P + q) (a + b) + r(a + b) + c(p + q + r)

(P + q) (a + b) + r(a + b) + c{p + q + r)

= (a + b) (p + q + r) + c(p + q + r)

∴ (p + q + r) (a + b + c)

(P + q) (a + b) + r(a + b) + c(p + q + r) = (p + q + r) (a + b + c)

Example 8. Factorise : \(\text { 2ay }-x^2-y^2+z^2 \text {. }\)

Solution:

Given:

\(\text { 2ay }-x^2-y^2+z^2 \text {. }\)

= \((z)^2-(x-y)^2\)

= {z + (x – y)} {z – (x – y)}

= (z + x – y) (z – x + y)

∴ (z + x-y)(z-x + y).

 \(\text { 2ay }-x^2-y^2+z^2 \text {. }\) = (z + x-y)(z-x + y).

Wbbse Class 7 Maths Solutions

Example 9. Resolve into factors \(9(x-y)^2-25(y-z)^2\)

Solution:

Given:

\(\left.9(x-y)^2-25(y-z)^2=\{3(x-y)\}^2-\{50-z)\right\}^2\)

= \((3 x-3 y)^2-(5 y-5 z)^2\)

= {(3x – 3y) + (5y – 5z)} {(3x – zy) – (5y – 5z)}

= (3x – 3y + 5y – 5z) (3x – 3y – 5y + 5z)

= (3x + 2y – 5z) (3x – 8y + 5z)

∴ (3x + 2y – 5z) (3x -8y+ 5z).

\(9(x-y)^2-25(y-z)^2\) = (3x + 2y – 5z) (3x -8y+ 5z).

Example 10. Resolve into factors: \(x^4+x^2 y^2+y^4\)

Solution:

Given:

\(x^4+x^2 y^2+y^4\)

= \(\left(x^2\right)^2+2 \cdot x^2 \cdot y^2+\left(y^2\right)^2-x^2 y^2\)

= \(\left(x^2+y^2\right)^2-(x y)^2\)

= \(\left(x^2+y^2+x y\right)\left(x^2+y^2-x y\right)\)

= \(\left(x^2+x y+y^2\right)\left(x^2-x y+y^2\right)\)

∴ \(\left(x^2+x y+y^2\right)\left(x^2-x y+y^2\right)\)

\(x^4+x^2 y^2+y^4\) = \(\left(x^2+x y+y^2\right)\left(x^2-x y+y^2\right)\)

Example 11. Resolve into factors : \(x^2-y^2-6 x a+2 y a+8 a^2\)

Solution:

Given:

\(x^2-y^2-6 x a+2 y a+8 a^2\)

= \(x^2-6 x a+9 a^2-y^2+2 y a-a^2\)

= \((x)^2-2 \cdot x \cdot 3 a+(3 a)^2-\left(y^2-2 y a+a^2\right)\)

= \((x-3 a)^2-(y-a)^2\)

= {(x – 3a) + (y – a)} {(x – 3a) – (y – a)}

= (x – 3a + y – a) (x – 3a – y + a)

= (x + y-4a) (x-y – 2a)

∴ (x + y- 4a) (x-y – 2a).

\(x^2-y^2-6 x a+2 y a+8 a^2\) = (x + y- 4a) (x-y – 2a).

Wbbse Class 7 Maths Solutions

Example 12. Factorise: \(4 a^2-1+9 b^2-25 c^2+12 a b-10 c\)

Solution:

Given:

\(4 a^2-1+9 b^2-25 c^2+12 a b-10 c\) \(4 a^2-1+9 b^2-25 c^2+12 a b-10 c\)

= \(4 a^2+12 a b+9 b^2-25 c^2-10 c-1\)

= \(\left(4 a^2+12 a b+9 b^2\right)-\left(25 c^2+10 c+1\right)\)

= \(\left\{(2 a)^2+2.2 a \cdot 3 b+(3 b)^2\right\}-\left\{(5 c)^2+2.5 c \cdot 1+(1)^2\right\}\)

= \((2 a+3 b)^2-(5 c+1)^2=\{(2 a+3 b)+(5 c+1)\}\{(2 a+3 b)-(5 c+1)\}\)

= (2a + 3b +5c + 1) (2a + 3b – 5c – 1)

∴ (2a + 3b + 5c + 1) (2a + 3b – 5c – 1).

\(4 a^2-1+9 b^2-25 c^2+12 a b-10 c\) = (2a + 3b + 5c + 1) (2a + 3b – 5c – 1).

Example 13. Factorise: \(9(5 c+6 d)^2-16(3 c-2 d)^2\)

Solution:

Given:

\(9(5 c+6 d)^2-16(3 c-2 d)^2\)

= \(\{3(5 c+6 d)\}^2-\{4(3 c-2 d)\}^2\)

= \((15 c+18 d)^2-(12 c-8 d)^2\)

= {(15c + 18d) + (12c – 8d)}{(15c + 18d) – (12c – 8d)}

= (15c+18d+12c-8d)(15c+18d-12c+ 8d)

∴ (27c + 10d)(3c + 26d)

\(9(5 c+6 d)^2-16(3 c-2 d)^2\) = (27c + 10d)(3c + 26d)

Wbbse Class 7 Maths Solutions

Example 14. Factorise : \(x^4+6 x^2 y^2+8 y^4\)

Solution:

Given:

\(x^4+6 x^2 y^2+8 y^4\)

= \(\left(x^2\right)^2+2 \cdot x^2 \cdot 3 y^2+\left(3 y^2\right)^2-y^4\)

= \(\left.\left(x^2+3 y^2\right)^2-y^2\right)^2\)

= \(\left(x^2+3 y^2+y^2\right)\left(x^2+3 y^2-y^2\right)\)

= \(\left(x^2+4 y^2\right)\left(x^2+2 y^2\right)\)

∴ \(\left(x^2+4 y^2\right)\left(x^2+2 y^2\right)\)

\(x^4+6 x^2 y^2+8 y^4\) = \(\left(x^2+4 y^2\right)\left(x^2+2 y^2\right)\)

Example 15. Factorise: \(3 x^2-y^2+z^2-2 x y-4 x z\)

Solution:

Given:

\(3 x^2-y^2+z^2-2 x y-4 x z\)

= \(4 x^2-4 x z+z^2-x^2-2 x y-y^2\)

= \((2 x)^2-2 \cdot 2 x \cdot z+(z)^2-\left(x^2+2 x y+y^2\right)\)

= \((2 x-z)^2-(x+y)^2\)

= {(2x – z) + (x + y)}{(2x – z) – (x + y)}

= (2x – z + x + y){2x – z – x- y)

= (3x + y – z)(x -y-z)

= (x-y- z)(3x + y-z)

∴ (x – y – z){3x + y – z).

\(3 x^2-y^2+z^2-2 x y-4 x z\) = (x – y – z){3x + y – z).

Example 16. Factorise : \(4 b^2 c^2-\left(b^2+c^2-a^2\right)^2\)

Solution:

Given:

\(4 b^2 c^2-\left(b^2+c^2-a^2\right)^2\) \(4 b^2 c^2-\left(b^2+c^2-a^2\right)^2=(2 b c)^2-\left(b^2+c^2-a^2\right)^2\)

= \(\left\{(2 b c)+\left(b^2+c^2-a^2\right)\right\}\left\{(2 b c)-\left(b^2+c^2-a^2\right)\right\}\)

= \(\left(2 b c+b^2+c^2-a^2\right)\left(2 b c-b^2-c^2+a^2\right)\)

= \(\left\{(b+c)^2-(a)^2\right\}\left\{(a)^2-(b-c)^2\right\}\)

= (b+ c + a)(b + c – a)(a + b – c)(a – b + c)

∴ (a + b + c)(a + b – c)(b + c – a)(c + a – b)

\(4 b^2 c^2-\left(b^2+c^2-a^2\right)^2\) = (a + b + c)(a + b – c)(b + c – a)(c + a – b)

Class Vii Math Solution Wbbse

Example 17. Resolve \(4 a^2-12 a b+9 b^2\) into two linear factors and find their sum.

Solution:

Given:

\(4 a^2-12 a b+9 b^2\)

= \((2 a)^2-2 \cdot 2 a \cdot 3 b+(3 b)^2\)

= \((2 a-3 b)^2=(2 a-3 b)(2 a-3 b)\)

Now, sum of the linear factors = 2a – 3b + 2a – 3b

∴ 4a – 6b

\(4 a^2-12 a b+9 b^2\) = 4a – 6b

Example 18. Resolve \(\frac{p}{q}\) – \(\frac{q}{p}\) into factors.

Solution: \(\frac{p}{q}\) – \(\frac{q}{p}\)

= \(\frac{p^2-q^2}{p q}=\frac{(p+q)(p-q)}{p q}\)

= \(\left(\frac{p+q}{p}\right)\left(\frac{p-q}{q}\right)=\left(1+\frac{q}{p}\right)\left(\frac{p}{q}-1\right)\)

\(\frac{p}{q}\) – \(\frac{q}{p}\) = \(\left(\frac{p+q}{p}\right)\left(\frac{p-q}{q}\right)=\left(1+\frac{q}{p}\right)\left(\frac{p}{q}-1\right)\)

 

Example 19. Express a – 6 as the difference of two squares and factories.

Math Solution Of Class 7 Wbbse

Solution:

a – b

= \(\left(a^{\frac{1}{2}}\right)^2-\left(b^{\frac{1}{2}}\right)^2=\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)\)

 

Example 20. Three factors of an expression are a, a + \(\frac{1}{a}\) and a – \(\frac{1}{a}\) find the expression.

Solution:

The required express

= \(a\left(a+\frac{1}{a}\right)\left(a-\frac{1}{a}\right)=a\left(a^2-\frac{1}{a^2}\right)=a^3-\frac{1}{a}\)

 

Example  21. Factorise : \(x^4-3 x^2 y^2+9 y^4\)

Solution:

Given:

\(x^4-3 x^2 y^2+9 y^4\)

= \(\left(x^2\right)^2+2 \cdot x^2 \cdot 3 y^2+\left(3 y^2\right)^2-9 x^2 y^2\)

= \(\left(x^2+3 y^2\right)^2-(3 x y)^2=\left(x^2+3 y^2+3 x y\right)\left(x^2+3 y^2-3 x y\right)\)

∴ \(\left(x^2+3 y^2+3 x y\right)\left(x^2+3 y^2-3 x y\right)\)

\(x^4-3 x^2 y^2+9 y^4\) =  \(\left(x^2+3 y^2+3 x y\right)\left(x^2+3 y^2-3 x y\right)\)

Class Vii Math Solution Wbbse

Example 22.  Factorise: \(\left(a^2-b^2\right)\left(c^2-d^2\right)-4 a b c d\)

Solution:

Given:

\(\left(a^2-b^2\right)\left(c^2-d^2\right)-4 a b c d\)

= \(a^2 c^2-a^2 d^2-b^2 c^2+b^2 d^2-4 a b c d\)

= \(a^2 c^2+b^2 d^2-2 a b c d-a^2 d^2-b^2 c^2-2 a b c d\)

= \(\left(a^2 c^2+b^2 d^2-2 a b c d\right)-\left(a^2 d^2+b^2 c^2+2 a b c d\right)\)

= \((a c-b d)^2-(a d+b c)^2\)

= (ac -bd + ad + bc) (ac – bd – ad – bc)

∴ (ac-bd + ad + bc) (ac-bd-ad-bc)

\(\left(a^2-b^2\right)\left(c^2-d^2\right)-4 a b c d\) = (ac-bd + ad + bc) (ac-bd-ad-bc)

Math Solution Of Class 7 Wbbse

Example 23. Resolve into factors \(3 x^2-y^2-z^2-2 x y-4 x z\)

Solution:

Given:

\(3 x^2-y^2-z^2-2 x y-4 x z\)

= \(4 x^2-x^2-y^2+z^2-2 x y-4 x z=4 x^2+z^2-4 x z-x^2-y^2-2 x y\)

= \((2 x-z)^2-(x+y)^2=(2 x-z+x+y)(2 x-z-x-y)\)

= (3x+y-z) (x-y-z)

∴ (3x + y-z) (x-y – z).

\(3 x^2-y^2-z^2-2 x y-4 x z\)  = (3x + y-z) (x-y – z).

Example 24. Factorise : 6xy – 9y + 4x – 6

Solution:

Given:

6xy – 9y + 4x – 6

6xy – 9y + 4x – 6 = 3y (2x – 3) + 2 (2x – 3)

∴ (2x – 3) ( 3y + 2)

6xy – 9y + 4x – 6 = (2x – 3) ( 3y + 2)

Example 25. Factorise: \(3 x^4+2 x^2 y^2-y^4\)

Solution:

Given:

\(3 x^4+2 x^2 y^2-y^4\)

= \(3 x^4+3 x^2 y^2-x^2 y^2-y^4\)

= \(3 x^2\left(x^2+y^2\right)-y^2\left(x^2+y^2\right)\)

∴ \(\left(x^2+y^2\right)\left(3 x^2-y^2\right)\)

\(3 x^4+2 x^2 y^2-y^4\) = \(\left(x^2+y^2\right)\left(3 x^2-y^2\right)\)

 

Algebra Chapter 5 formulae And Their Applications Exercise 5 Solved Example Problems

Formulae and Their Applications Introduction

The entire structure of algebra is based on some formulae. We can form some easy secting AD at G and BC at H where GD = 6. formulae by simple algebraic multiplication and we may also verify them geometrically.

Actually, every formula is an identity that is true for all values of the literals present in that identity.

The fundamental formulae are of great importance because all the harder formulae are derived from the fundamental formulae. We may define a formula as follows:

A general relation, expressed in terms of algebraic symbols is called an algebraic formula or in brief a formula.

Math Solution Of Class 7 Wbbse

Read and Learn More WBBSE Solutions For Class 7 Maths

Formula for the square of the sum of two terms

(a + b)² = (a + b) (a + b)

= a (a + b) + b (a + b)

= a² + ab + ab + b² = a² + 2 ab + b².

Thus we see that,

The square of the sum of two numbers is equal to the square of the first number plus twice the product of the two numbers plus the square of the second number.

Geometrical representation of the formula (a + b)²  = a² + 2ab + b².

In the diagram, ABCD is a square. The length of each side of ABCD = a + b.

Hence, the area of the square ABCD = (a + b)².

Now, draw a vertical line EF perpendicular to AB and intersecting AB at E and CD at F where BE = b.

Again draw a horizontal line GH perpendicular to AD and intersecting AD at G and BC and H where GD = b.

Let EF and GH intersect at P.

Math Solution Of Class 7 Wbbse

 

 

Now, area of AEPG = \(a^2\), Area of EBHP = ab, area of GPFD = ab, and area of PHCF = \(b^2\).

Thus, the sum of these four areas = \(a^2+a b+a b+b^2=a^2+2 a b+b^2\)

Since, the area of ABCD = area of (AEPG + EBHP + GPFD + PHCF)

Therefore, \((a+b)^2=a^2+2 a b+b^2\) (Proved).

Math Solution Of Class 7 Wbbse

Formula for the square of the sum of three terms \((a+b+c)^2=\{(a+b)+c\}^2\)

= \((a+b)^2+2(a+b) c+(c)^2\)

= \(a^2+2 a b+b^2+2 a c+2 b c+c^2\)

= \(a^2+b^2+c^2+2 a b+2 b c+2 c a\)

Formula for the square of the difference of two terms

\((a-b)^2=(a-b)(a-b)\)

= a (a – b) -b (a – b)

= \(a^2-a b-a b+b^2=a^2-2 a b+b^2\)

Thus we see that,

The square of the difference of two numbers is equal to the square of the first number minus twice the product of the two numbers plus the square of the second number.

Geometrical representation of the formula \((a-b)^2=a^2-2 a b+b^2\)

Let ABCD be a square of side a.

 

 

Draw a horizontal line EF perpendicular to AD and intersecting AD at E and BC at F, where AE = b.

Next draw GH perpendicular to EF, where GF = b, and draw HP perpendicular to BC produced, where CP = b.

Let GH and DC intersect at Q.

Now, area of ABCD = \(a^2\), area of EGQD = \(\left(a-b^2\right)\),

area of ABFE = ab, area of GFPH = ab, area of QCPH = \(b^2\),

Now, area of EGQD = area of (ABCD + QCPH – ABFE – GFPH)

or, \((a-b)^2=a^2+b^2-a b-a b\)

i.e., \((a-b)^2=a^2-2 a b+b^2\) (Proved).

Some relations based on the square of the sum of two terms and the square of the difference of two terms.

1. Since \((a+b)^2=a^2+2 a b+b^2\) therefore, \(a^2+b^2=(a+b)^2-2\)
2. Since \((a-b)^2=a^2-2 a b+b^2\) therefore, \(a^2+b^2=(a-b)^2+2 a b\)
3. \((a+b)^2=a^2+2 a b+b^2=a^2-l a b+b^2+4 a b-(a-b)^2+4 a b\) Hence, \((a+b)^2=(a-b)^2+4\)
4. \((a-b)^2=a^2-2 a b+b^2=a^2+2 a b+b^2-4 a b=(a+b)^2-4 a b\) Hence, \((a-b)^2=(a+b)^2-4 a b\)
5. \((a+b)^2+(a-b)^2=a^2+2 a b+b^2+a^2-2 a b+b^2=a^2+a^2+b^2+b^2\)
   \(=2 a^2+2 b^2=2\left(a^2+b^2\right)\)
   Hence, \((a+b)^2+(a-b)^2=2\left(a^2+b^2\right) .\)
6. \((a+b)^2-(a-b)^2=\left(a^2+2 a b+b^2\right)-\left(a^2-2 a b+6^2\right)\)
   \(=a^2+2 a b+b^2-a^2+2 a b-b^2=4 a b\)
   Hence, \((a+b)^2-(a-b)^2=4 a b .\)

The formula for the product of the sum and the difference of two terms.

(a +b) (a – b) = (a – b) + 6 (a – b) = a² – ab + ab – b² = a² – b².

Thus we see that, The product of the sum and the difference of two numbers is equal to the difference of the squares of those two numbers.

Geometrical representation of the formula (a + b) (a – b) = a² – b².

Let ABCD be square of side a. Draw a vertical line EF perpendicular to AB intersecting AB at E where AE = b.

Next draw a horizontal line GH perpendicular to AD and intersecting AD at G where AG = b.

Now GH intersects EF at F, BC at Q.

Here QH = b, HP is drawn perpendicular from H on DC produced.

According to the construction, the area of EBQF = area of QHPC

Now, Area of GHPD = Area of (GQCD + QHPC)

= Area of (GQCD + EBQF)

= Area of (ABCD – AEFG)

or, (a +b) (a – b) = a² – b² (Proved).

Class Vii Math Solution Wbbse

To express the product of two terms as the difference of two perfect squares,

\(a^2+2 a b+b^2=(a+b)^2\) \(a^2-2 a b+b^2=(a-b)^2\)

By subtraction, \(4 a b=(a+b)^2-(a-b)^2\)

\(a b=\frac{(a+b)^2}{4}-\frac{(a-b)^2}{4}\) \(a b=\left(\frac{a+b}{2}\right)^2-\left(\frac{a-b}{2}\right)^2\)

Algebra Chapter 5 formulae And Their Applications Exercise 5 Some Examples On (a ± b)² = a² ± 2 ab + b².

Example 1. Find the square of (x + 2y).

Solution:

Given:

(x + 2y)

Square of (x + 2y)

= \((x+2 y)^2\)

= \((x)^2+2 \cdot x \cdot 2 y+(2 y)^2=x^2+4 x y+4 y^2\)

∴ \(x^2+4 x y+4 y^2\).

The square of (x + 2y) =  \(x^2+4 x y+4 y^2\).

Example 2. Find the square of 3ab + 2bc.

Solution:

Given:

3ab + 2bc

Square of (3ab + 2bc) = \((3 a b+2 b c)^2\)

\((3 a b)^2+2 \cdot 3 a b \cdot 2 b c+(2 b c)^2=9 a^2 b^2+12 a b^2 c+4 b^2 c^2 9 a^2 b^2+12 a \cdot b^2 e+4 b^2 c^2\).

The square of 3ab + 2bc = \((3 a b)^2+2 \cdot 3 a b \cdot 2 b c+(2 b c)^2=9 a^2 b^2+12 a b^2 c+4 b^2 c^2 9 a^2 b^2+12 a \cdot b^2 e+4 b^2 c^2\).

Example 3. Find the square of 101.

Solution:

Given:

101

Square of 101

= \((101)^2=(100+1)^2\)

= \((100)^2+2 \times 100 \times 1+(1)^2=10000+200+1=10201\)

∴ 10201.

The square of 101 is 10201.

Example 4. Find the square of \(2 x^2-3 y^2\).

Solution:

Given:

\(2 x^2-3 y^2\)

Square of \(\left(2 x^2-3 y^2\right)\)

= \(\left(2 x^2-3 y^2\right)^2\)

= \(\left(2 x^2\right)^2-2 x 2 x^2 x 3 y^2+\left(3 y^2\right)^2=4 x^4-12 x^2 y^2+9 y^4\)

∴ \(4 x^4-12 x^2 y^2+9 y^4\)

The square of \(2 x^2-3 y^2\) = \(4 x^4-12 x^2 y^2+9 y^4\)

Example 5. Find the square of 498.

Solution:

Given: 498

Square of 498

= \((498)^2=(500-2)^2=(500)^2-2 \times 500 \times 2+(2)^2\)

= 250000 – 2000 + 4 = 250004 – 2000 =248004

∴ 248004.

The square of 498 is 248004.

Class Vii Math Solution Wbbse

Example 6. Simplify : \((5 a+3 b)^2+2 \cdot(5 a+3 b)(5 a-3 b)+(5 a-3 b)^2\). 

Solution :

Given:

\((5 a+3 b)^2+2 \cdot(5 a+3 b)(5 a-3 b)+(5 a-3 b)^2\)

Let 5a + 3b = x and 5a – 3b = y

Hence, the given expression = \(x^2+2 x y+y^2=(x+y)^2\)

= \((5 a+3 b+5 a-3 b)^2=(10 a)^2=100 a^2\)

∴ \(100 a^2\).

\((5 a+3 b)^2+2 \cdot(5 a+3 b)(5 a-3 b)+(5 a-3 b)^2\) = \(100 a^2\).

Example 7. Simplify : \((5 x-7 y)^2+2(5 x-7 y)(9 y-4 x)+(9 y-4 x)^2\)(5x – 7y)² + 2(5x – 7y)(9y – 4x) + (9y – 4x)².

Solution:

Given:

\((5 x-7 y)^2+2(5 x-7 y)(9 y-4 x)+(9 y-4 x)^2\)

Let, 5x -7y- a and 9y – 4x = 6

Then the given expression = \(a^2+2 a b+b^2=(a+b)^2\)

= \((5 x-7 y+9 y-4 x)^2=(x+2 y)^2=(x)^2+2 \cdot x \cdot 2 y+(2 y)^2\)

= \(x^2+4 x y+4 y^2\)

∴ \(x^2+4 x y+4 y^2\).

\((5 x-7 y)^2+2(5 x-7 y)(9 y-4 x)+(9 y-4 x)^2\)(5x – 7y)² + 2(5x – 7y)(9y – 4x) + (9y – 4x)² = \(x^2+4 x y+4 y^2\).

Example 8. Simplify \((3 a+4 b)^2-2(3 a+46)(a+4 b)+(a+4 b)^2\).

Solution:

Given:

\((3 a+4 b)^2-2(3 a+46)(a+4 b)+(a+4 b)^2\)

Let, 3a + 4b = x and a + 4b = y

Then the given expression = \(x^2-2 x y+y^2\)

= \((x-y)^2\)

= \(\{(3 a+4 b)-(a+4 b)\}^2\)

= \((3 a+4 b-a-4 b)^2=(2 a)^2=4 a^2\)

∴ \(4 a^2\)4a²

\((3 a+4 b)^2-2(3 a+46)(a+4 b)+(a+4 b)^2\) = \(4 a^2\)4a²

Example 9. Simplify \((7 x+4 y)^2-2 \cdot(7 x+4 y) x(7 x-4 y)+(7 x-A y)^2\).

Solution:

Given:

\((7 x+4 y)^2-2 \cdot(7 x+4 y) x(7 x-4 y)+(7 x-A y)^2\)

Let 7x + 4y = a and 7x – 4y = b

Hence, the given expression = \(a^2-2 a b+b^2=(a-b)^2\)

= \(\{(7 x+4 y)-(7 x-4 y))^2\)

= \(\{7 x+4 y-7 x+4 y)^2\)

= \((8 y)^2=64 y^2\)

∴ \(64 y^2\)

\((7 x+4 y)^2-2 \cdot(7 x+4 y) x(7 x-4 y)+(7 x-A y)^2\) = \(64 y^2\)

Class Vii Math Solution Wbbse

Example 10.  If x =-l then find the value of \(81 x^2-18 x+1\).

Solution:

Given:

x =-1 And \(81 x^2-18 x+1\)

\(81 x^2-18 x+1=(9 x)^2-2 \times 9 x \times 1+(1)^2\)81x² – 18x + 1 = (9x)² – 2 X 9x X 1 + (1)²

= \((9 x-1)^2=\{9(-1)-1\}^2=(-9-1)^2=(-10)^2=100\)

∴ 100.

Example 11. If p = 2, q = -1 and r = 3 then find the value of \(p^2 q^2+10 p q r+25 r^2\).

Solution:

Given:

p = 2, q = -1 and r = 3 And \(p^2 q^2+10 p q r+25 r^2\)

\(p^2 q^2+10 p q r+25 r^2\)

= \((\mathrm{pq})^2+2 \times \mathrm{pq} \times 5 r+(5 \mathrm{r})^2=(\mathrm{pq}+5 \mathrm{r})^2=\{2(-1)+5 \times 3\}^2=(-2+15)^2=(13)^2=169\)

∴ 169.

Example 12. If a = 1, b = 2 and c = -1 then find the value of \(4 a^2 b^2-20 a b c+25 c^2\).

Solution:

Given: 

a = 1, b = 2 and c = -1 And \(4 a^2 b^2-20 a b c+25 c^2\)

\(4 a^2 b^2-20 a b c+25 c^2\)

= \((2 a b)^2-2 \times 2 a b \times 5 c+(5 c)^2\)

= \((2 a b-5 c)^2=\{2 \times 1 \times 2-5(-1)\}^2\)

= \(\{4+5\}^2=(9)^2=81\)

∴ 81.

\(4 a^2 b^2-20 a b c+25 c^2\) = 81

Example 13. Find the product 201 x 201 with the help of the formula.

Solution:

\(201 \times 201=(201)^2=(200+1)^2\)

= \((200)^2+2 \times 200 \times 1+(1)^2\) = 40000 + 400 + 1 =40401

∴ 40401.

201 x 201 = 40401.

Example 14. Simplify 0.82 x 0.82 + 2 x 0.82 x 0.18 + 0.18 x 0.18.

Solution:

Let a = 0.82 and b =0.18

Then the given expression =a x a+2 x a x b+b x 6

= \(a^2+2 a b+b^2=(a+b)^2=(0.82+0.18)^2\)

= \((1.00)^2=(1)^2=1\)

∴ 1.

0.82 x 0.82 + 2 x 0.82 x 0.18 + 0.18 x 0.18 = 1.

Example 15. What is to be added with x² + 4x +\(\frac{3}{2}\) so that the sum is a perfect square?

Solution:

x² + 4x +\(\frac{3}{2}\)

= (x)² + 2.x.2 + (2)²  – (2)² +\(\frac{3}{2}\)

= (x + 2)² – 4 + \(\frac{3}{2}\)

= (x + 2)²– \(\frac{5}{2}\)

Hence, to make it a perfect square \(\frac{3}{2}\) is to be added.

Example 16. If x² – 2x + 1 = 0, then find the values of 

\(x+\frac{1}{x} \quad x^{10}+\frac{1}{x^{10}} \quad x^n+\frac{1}{x^n}\)

Solution: \(x^2-2 x+1=0\)

or, \((x-1)^2=0\)

or, x – 1 = 0

∴ x = 1

\(x+\frac{1}{x}=1+\frac{1}{1}=1+1=2\) \(x^{10}+\frac{1}{x^{10}}=(1)^{10}+\frac{1}{(1)^{10}}=1+1=2\) \(x^n+\frac{1}{x^n}=(1)^n+\frac{1}{(1)^n}=1+1=2\)

∴ 1. 2, 2. 2, 3. 2.

\(x+\frac{1}{x} \quad x^{10}+\frac{1}{x^{10}} \quad x^n+\frac{1}{x^n}\) = 1. 2, 2. 2, 3. 2.

 

Chapter 5 formulae And Their Applications Exercise 5 Some Problems On Various Formulae Derived From (a ± b)² = a² ± 2ab + b².

Example 1. Find the square of x + 2y – 3z.

Solution:

Given:

x + 2y – 3z

Square of x + 2y – 3z.

= \((x+2 y-3 z)^2\)

= \((x+2 y)^2-2 \cdot(x+2 y) \cdot 3 z+(3 z)^2\)

= \((x)^2+2 \cdot x \cdot 2 y+(2 y)^2-6 z(x+2 y)+9 z^2\)

= \(x^2+4 x y+4 y^2-6 z x-12 y z+9 z^2\)

= \(x^2+4 y^2+9 z^2+4 x y-12 y z-6 z x\)

∴ \(x^2+4 y^2+9 z^2+4 x y-12 y z-6 z x\)

The square of x + 2y – 3z = \(x^2+4 y^2+9 z^2+4 x y-12 y z-6 z x\)

Wbbse Class 7 Maths Solutions

Example 2. If a + 6 = 5 and ab = 5, find the value of a² + b².

Solution :

Given:

a + 6 = 5 and ab = 5

\(a^2+b^2=(a+b)^2-2 a b\)

= (5)²– 2.5 = 25- 10= 15

∴ 15.

a² + b²= 15.

Example 3. If a – 6 = 5 and ab = 14, find the value of a² + b².

Solution:

Given:

a – 6 = 5 and ab = 14

\(a^2+b^2=(a-b)^2+2 a b=(5)^2+2.14=25+28=53\)

∴ 53.

a² + b² = 53.

Example 4. If x + y =2 and x-y = 1, then find the value of \(8 x y\left(x^2+y^2\right)\).

Solution:

Given:

x + y =2 and x-y = 1

\(8 x y\left(x^2+y^2\right)\)

= \(4 x y \cdot 2\left(x^2+y^2\right)\)

= \(\left\{(x+y)^2-(x-y)^2\right\}\left\{(x+y)^2+(x-y)^2\right\}\)

= \(\left\{(2)^2-(1)^2\right\}\left\{(2)^2+(1)^2\right\}\)

= (4-1) (4+1) = 3 x 5 = 15

∴15.

\(8 x y\left(x^2+y^2\right)\) = 15.

Wbbse Class 7 Maths Solutions

Example 5. If 2x + 3y = 9 and xy = 3, find the value of \(4 x^2+9 y^2\).

Solution:

Given:

2x + 3y = 9 and xy = 3

\(4 x^2+9 y^2\).

= \((2 \cdot x)^2+(3 y)^2=(2 x+3 y)^2-2 \cdot 2 x \cdot 3 y=(2 x+3 y)^2-12 x y=(9)^2-12 \cdot 3=81-36=45\)

∴ 45.

\(4 x^2+9 y^2\)= 45.

Example 6. Express 35 as the difference of two squares.

Solution:

35 = 7 x 5

\(\left(\frac{7+5}{2}\right)^2-\left(\frac{7-5}{2}\right)^2\) \(\left(\frac{12}{2}\right)^2-\left(\frac{2}{2}\right)^2\)

= \((6)^2-(1)^2\)

∴ \(35=(6)^2-(1)^2\).

Example 7. Express 4xy as the difference of two perfect squares.

Solution:

4xy = 2.x.2.y

\(\left(\frac{2 x+2 y}{2}\right)^2-\left(\frac{2 x-2 y}{2}\right)^2\) \(\left\{\frac{2(x+y)}{2}\right\}^2-\left\{\frac{2(x-y)}{2}\right\}^2\)

= \((x+y)^2-(x-y)^2\)

∴ \(4 x y=(x+y)^2-(x-y)^2\).

Example 8. Express \(2\left(a^2+b^2\right)\) as the sum of two perfect squares.

Solution:

\(2\left(a^2+b^2\right)\)

= \(2 a^2+2 b^2\)

= \(a^2+a^2+b^2+b^2\)

= \(a^2+2 a b+b^2+a^2-2 a b+b^2\)

= \((a+b)^2+(a-b)^2\)

∴ \(2\left(a^2+b^2\right)=(a+b)^2+(a-b)^2\).

Wbbse Class 7 Maths Solutions

Example 9. Express 4a² + 1/4a² +1 as the difference of two perfect squares.

Solution:

\(4 a^2+\frac{1}{4 a^2}+1\)

= \((2 a)^2+2 \cdot 2 a \cdot \frac{1}{2 a}+\left(\frac{1}{2 a}\right)^2+1-2\)

= \(\left(2 a+\frac{1}{2 a}\right)^2-(1)^2\)

 

Example 10. If x = a + \(\frac{1}{a}\) and y = a – \(\frac{1}{a}\) find the value  of \(x^4+y^4-2 x^2 y^2\).

Solution:

\(x^4+y^4-2 x^2 y^2\)

= \(\left(x^2\right)^2+\left(y^2\right)^2-2 \cdot x^2 \cdot y^2=\left(x^2-y^2\right)^2\)

= \(\{(x+y)(x-y)\}^2=(x+y)^2(x-y)^2\)

\(\left\{\left(a+\frac{1}{a}\right)+\left(a-\frac{1}{a}\right)\right\}^2\left\{\left(a+\frac{1}{a}\right)-\left(a-\frac{1}{a}\right)\right\}^2\) \(\left\{a+\frac{1}{a}+a-\frac{1}{a}\right\}^2\left\{a+\frac{1}{a}-a+\frac{1}{a}\right\}^2\) \((2 a)^2 \cdot\left(\frac{2}{a}\right)^2=4 a^2 \cdot \frac{4}{a^2}=16\)

∴ 16

Example 11. If x + \(\frac{1}{4}\) = 4, then show that, x² + 1/x² = 14

Solution:

L.H.S. = \(x^2+\frac{1}{x^2}\)

= \(\left(x+\frac{1}{x}\right)^2-2 \cdot x \cdot \frac{1}{x}\)

= (4)² – 2 = 16 – 2 = 14 = R.H.S. (Proved).

Wbbse Class 7 Maths Solutions

Example 12. If 6x² – 1 = 4x, then show that, 36x² +1/x² = 28.

Solution:

6x² -1 = 4x

\((6 x)^2-2.6 x \cdot \frac{1}{x}+\left(\frac{1}{x}\right)^2=(4)^2\) \(36 x^2-12+\frac{1}{x^2}=16\) \(36 x^2+\frac{1}{x^2}=16+12\)

\(36 x^2+\frac{1}{x^2}=28\)  (Proved).

Example 13. If \(\frac{p}{6}\) + \(\frac{1}{p}\) = \(\frac{7}{6}\) then prove that \(p^2+36 / p^2=37\)

Solution: \(\frac{p}{6}\) or, p + \(\frac{6}{p}\) = 7

[Multiplying both sides by 6]

Squaring both sides,

\((p)^2+2 \cdot p \cdot \frac{6}{p}+\left(\frac{6}{p}\right)^2=(7)^2\)

or, \(p^2+12+\frac{36}{p^2}=49\)

\(p^2+\frac{36}{p^2}=49-12\)

\(p^2+\frac{36}{p^2}=37\) (Proved).

Example 14. If a + b = 9 and a – b = 5 then what is the value of a+b²/2ab?

Solution: \(\frac{a^2+b^2}{2 a b}=\frac{2\left(a^2+b^2\right)}{4 a b}\)

= \(\frac{(a+b)^2+(a-b)^2}{(a+b)^2-(a-b)^2}\)

= \(\frac{(9)^2+(5)^2}{(9)^2-(5)^2}=\frac{81+25}{81-25}=\frac{106}{56}=\frac{53}{28}=1 \frac{25}{28}\)

Example 15. If x² + y² = 4xy then prove that at⁴ + y⁴ = 14x²y².

Solution:

\(x^2+y^2=4 x y\)

or, \(\frac{x^2}{x y}+\frac{y^2}{x y}=4 \text { or, } \frac{x}{y}+\frac{y}{x}=4\)

Squaring both sides we get,

\(\frac{x^2}{y^2}+2 \cdot \frac{x}{y} \cdot \frac{y}{x}+\frac{y^2}{x^2}=16\)

or, \(\frac{x^2}{y^2}+2+\frac{y^2}{x^2}=16\)

or, \(\frac{x^2}{y^2}+\frac{y^2}{x^2}=14\)

or, \(\frac{x^4+y^4}{x^2 y^2}=14\)

or, \(x^4+y^4=14 x^2 y^2\)

Example 16. If 2a + \(\frac{1}{3a}\) = \(\frac{2}{3}\)

Solution:

2a+ \(\frac{1}{3a}\) = \(\frac{2}{3}\)

or, 3a + = \(\frac{1}{2a}\) = 1 [Multiplying both sides by \(\frac{3}{2}\)]

Squaring both sides,

\((3 a)^2+2 \cdot 3 a \cdot \frac{1}{2 a}+\left(\frac{1}{2 a}\right)^2=1\) \(9 a^2+3+\frac{1}{4 a^2}=1 \text { or, } 9 a^2+\frac{1}{4 a^2}=1-3\)

\(9 a^2+\frac{1}{4 a^2}=-2\)   (Proved).

Example 17. If a² + b² = 5ab then show that, a²/b² + b²/a²= 23.

Solution:

Given:

\(a^2+b^2=5 a b\)

or, \(\frac{a^2+b^2}{a b} \text { or, } \frac{a}{b}+\frac{b}{a}=5\)

Squaring both sides,

\(\left(\frac{a}{b}\right)^2+2 \cdot \frac{a}{b} \cdot \frac{b}{a}+\left(\frac{b}{a}\right)^2=(5)^2\)

or, \(\frac{a^2}{b^2}+2+\frac{b^2}{a^2}=25\)

or, \(\frac{a^2}{b^2}+\frac{b^2}{a^2}=25-2\)

or, \(\frac{a^2}{b^2}+\frac{b^2}{a^2}=23\) (Proved).

Example 18. Find the continued product: \((a+b)(a-b)\left(a^2+b^2\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\).

Solution:

The given expression = \((a+b)(a-b)\left(a^2+b^2\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\)

= \(\left(a^2-b^2\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\)

= \(\left(a^4-b^4\right)\left(a^4+b^4\right)\left(a^8+b^8\right)\)

= \(\left(a^8-b^8\right)\left(a^8+b^8\right)\)

∴ \(a^{16}-b^{16}\)

Example 19. Multiply with the help of the formula : \(\left(a^2+a+1\right)\left(a^2-a+1\right)\left(a^4-a^2+1\right)\).

Solution:

Given:

\(\left(a^2+a+1\right)\left(a^2-a+1\right)\left(a^4-a^2+1\right)\) \(\left(a^2+a+1\right)\left(a^2-a+1\right)\left(a^4-a^2+1\right)\)

= \(\left\{\left(a^2+1\right)+a\right\}\left\{\left(a^2+1\right)-a\right\}\left\{\left(a^4-a^2+1\right)\right\}\)

= \(\left\{\left(a^2+1\right)^2-(a)^2\right\}\left(a^4-a^2+1\right)\)

= \(\left(a^4+2 a^2+1-a^2\right)\left(a^4-a^2+1\right)=\left(a^4+a^2+1\right)\left(a^4-a^2+1\right)\)

= \(\left\{\left(a^4+1\right)+a^2\right\}\left\{\left(a^4+1\right)-a^2\right\}\)

= \(\left(a^4+1\right)^2\left(a^2\right)^2\)

= \(a^8+2 a^4+1-a^4=a^8+a^4+1\)

∴ \(a^8+a^4+1\).

Example 20. If x + y = 5 and x – y = 1, then find the value of \(8 x y\left(x^2+y^2\right)\)

Solution:

Given:

x + y = 5 and x – y = 1

\(8 x y\left(x^2+y^2\right)\)

= \(4 x y \cdot 2\left(x^2+y^2\right)\)4xy.2(x²+y²)

= \(\left\{(x+y)^2-(x-y)^2\right\}\left\{(x+y)^2+(x-y)^2\right\}\)

= \(\left\{(5)^2-(1)^2\right\}\left\{(5)^2+(1)^2\right\}\)

= (25 – 1) (25 + 1) = 24 x 26 = 624

∴ 624.

\(8 x y\left(x^2+y^2\right)\) = 624

Example 21. If x= \(\frac{a}{b}\) – \(\frac{b}{a}\) and y= \(\frac{a}{b}\) – \(\frac{b}{a}\) then show that, \(x^4+y^4-2 x^2 y^2=16\).

Solution:

= \(\left(x^2-y^2\right)^2=\{(x+y)(x-y)\}^2\)

= \(\left\{\left(\frac{a}{b}+\frac{b}{a}+\frac{a}{b}-\frac{b}{a}\right)\left(\frac{a}{b}+\frac{b}{a}-\frac{a}{b}+\frac{b}{a}\right)\right\}^2\)

= \(\left\{\left(2 \cdot \frac{a}{b}\right)\left(2 \cdot \frac{b}{a}\right)\right\}^2=\left(2 \cdot \frac{a}{b} \cdot 2 \cdot \frac{b}{a} \cdot\right)^2\)

= \((4)^2\) = 16 = R.H.S.

Example 22. If m – \(\frac{1}{m-3}\) = 5, then what is the value of (m – 3)² + 1/(m-3)²?

Solution:

m – \(\frac{1}{m-3}\) = 5

\((m-3)^2+\left(\frac{1}{m-3}\right)^2-2 \cdot(m-3) \frac{1}{(m-3)}=4\)

or, \((m-3)^2+\frac{1}{(m-3)^2}-2=4\)

or, \((m-3)^2+\frac{1}{(m-3)^2}=6\)

(m – 3)² + 1/(m-3)² = \((m-3)^2+\frac{1}{(m-3)^2}=6\)

Algebra Chapter 5 formulae And Their Applications Exercise 5 Some Examples On a² – b² = (a + b)(a – b).

Example 1. Find the product of (2a – 5b) and (2a + 5b).

Solution:

The required product = (2a – 5b) (2a + 5b)

= (2a)² – (5b)²

= 4a² – 25b² 

(2a – 5b) and (2a + 5b) = 4a² – 25b² 

Example 2.  Find the product of (1 + 5pq) and (1 – 5pq).

Solution:

The required product = (1 + 5pq) (1 – 5pq)

= (1)²-(5pq)² =1

∴ 1 – 25p²q².

(1 + 5pq) X (1 – 5pq) = 1 – 25p²q².

Example 3. Find the value of 255² – 254².

Solution:

255² – 254² = (255 + 254)(255 – 254)

= 509 x 1 = 509

∴ 509.

255² – 254² = 509.

Example 4. Find the continued product of \((a+b),(a-b),\left(a^2+b^2\right),\left(a^4+b^4\right)\).

Solution:

The required product = \((a+b)(a-b)\left(a^2+b^2\right)\left(a^4+b^4\right)\)

= \(\left(a-b^2\right)\left(a^2+b^2\right)\left(a^4+b^4\right)\)= \(\left\{\left(a^2\right)^2-\left(b^2\right)^2\right\}\left(a^4+b^4\right)\)

= \(\left(a^4-b^4\right)\left(a^4+b^4\right)\)

= \(\left(a^4-b^4\right)\left(a^4+b^4\right)\)

∴ \(a^8-b^8\).

\((a+b),(a-b),\left(a^2+b^2\right),\left(a^4+b^4\right)\) = \(a^8-b^8\).

Math Solution Of Class 7 Wbbse

Example 5. Find the product of (x -y + a) and (x +y-z).

Solution:

The required product = (x-y + z) (x+y-z)

= {x- (y – z)} {x + (y – z)}

= \((x)^2-(y-z)^2=x^2-\left(y^2-2 y z+z^2\right)\)

= \(x^2-y^2-z^2+2 y z\)

∴ \(x^2-y^2-z^2+2 y z\).

(x -y + a) a X (x +y-z) = \(x^2-y^2-z^2+2 y z\).

Example 6. Find the product of (x + 2y + 3z) and (x + 2y – 3z).

Solution:

The required product = (x + 2y + 3 z) (x + 2y – 3 z)

= {(x + 2y) + 3z} {(x + 2y) – 3z}

= \((x+2 y)^2-(3 z)^2=(x)^2+2 \cdot x \cdot 2 y+(2 y)^2-(3 z)^2\)

= \(x^2+4 x y+4 y^2-9 z^2\)

= \(x^2+4 y^2-9 z^2+4 x y\)

∴ \(x^2+4 y^2-9 z^2+4 x y\).

(x + 2y + 3z) X (x + 2y – 3z) = \(x^2+4 y^2-9 z^2+4 x y\).

Example 7. Multiply with the help of the formula 1001 x 999.

Solution:

1001 x 999 = (1000 + 1) X (1000 – 1)

= (1000)² – (1)² = 1000000 – 1 = 999999

∴ 999999.

1001 x 999 = 999999.

Math Solution Of Class 7 Wbbse

Example 8. Simplify with the help of the formula : \((2 x+3 y+4 z)^2-(3 x-2 y+4 z)^2\).

Solution:

\((2 x+3 y+4 z)^2-(3 x-2 y+4 z)^2=\{(2 x+3 y+4 z)+(3 x-2 y+4 z)\} x\{(2 x+3 y+4 z)-(3 x-2 y+4 z)\}\)

= (2x + 3y + 4z + 3x – 2y + 4z) x (2x + 3y + 4z – 3x + 2y – 4z)

= (5x + y + 8z) (- x + 5y)

= \(-5 x^2-x y-8 z x+25 x y+5 y^2+40 y z\)

= \(-5 x^2+5 y^2+24 x y+40 y z-8 z x\)

∴ \(-5 x^2+5 y^2+24 x y+40 y z-8 z x\).

\((2 x+3 y+4 z)^2-(3 x-2 y+4 z)^2\) = \(-5 x^2+5 y^2+24 x y+40 y z-8 z x\).

Example 9. Express as the product of two expressions  \(a^2-4 a b+4 b^2-4\)

Solution:

\(a^2-4 a b+4 b^2-4\)a² – 4ab + 4b² – 4

= \((a)^2-2 \cdot a \cdot 2 b+(2 b)^2-4\)

= \((a-2 b)^2-(2)^2=(a-2 b+2)(a-2 b-2)\).

\(a^2-4 a b+4 b^2-4\) = \((a-2 b)^2-(2)^2=(a-2 b+2)(a-2 b-2)\).

Algebra Chapter 4 Polynomials Exercise 4 Solved Example Problems

Polynomials Introduction

In this chapter, our aim is to study an algebraic expression, to learn what is meant by the coefficient and variable in an algebraic expression, to discuss the term and finally to apply four basic operations namely addition, subtraction, multiplication and division on a polynomial.

Here one thing should be noted with care addition and subtraction in algebra is permissible only between like terms.

On the other hand, the permissibility of multiplication and division is not restricted between like terms but can also be performed between, unlike terms.

Math Solution Of Class 7 Wbbse

Read and Learn More WBBSE Solutions For Class 7 Maths

Expression

By 20 metres, 500 gms and 4 hours the magnitudes of length, mass and time are expressed respectively.

Here it should be noted that the first part in each case is a number while the second part is unit.

Such things, which express some quantity is called an expression. In the expression 20 metres, the numerical value of length is 20 and its unit is metre.

Co-efficient and variable

If x denotes a fixed length then 8x also denotes another fixed length (which is 8 times the length denoted by x); so 8x is an expression.

Similarly, if y denotes a fixed mass then 10y also denotes another mass; so 10y is an expression.

Of the algebraic expressions 8x, 10y the first parts are numbers while the second parts are unknown. Thus, if “any number” is denoted by the alphabetic symbols x, y, z or a, b, c then their values are not fixed.

Therefore, as the values of the alphabetic symbols may vary, they are called variables. Again, if a number appears as a multiple of a variable then the number is called co-efficient. For example, in 5a the co-efficient of the variable a is 5.

It is not necessary that a co-efficient will always be a pure number. For example, in. the expression 9 abx if the variable be x then its co-efficient will be 9 ab. In this case a and b will denote fixed numbers, not variables. So, 9 ab will represent a number.

Again, if in the expression 9abx, ab is a variable then the co-efficient of ab will be 9x. In that case, the expression should be written as 9xab.

Math Solution Of Class 7 Wbbse

If an expression is indicated by a single alphabetic symbol then its co-efficient is 1. For example, in the expression x, the coefficient of x is 1. In the expression, a the co-efficient of a is 1. So, it is clear that, any expression will have a coefficient.

Term

When two or more expressions are related with each other by sign of addition or subtraction then a polynomial is formed and each expression of that polynomial is called a term.

If there is one term in an expression, then it is called a monomial. For example, 5x is a monomial.

If there are two or three terms then they are called binomial and trinomial respectively. For example, 5a + 6b is a binomial and la – 126 + 8c is a trinomial.

If there are many terms in an expression then it is called a polynomial.

For example, a + 5b – 8c + 9d + 7e + 8f – 11x is a polynomial.

Like and unlike terms

The terms in which the numerical coefficients are different but the algebraic symbols are the same are called like terms. The terms which are not like are called unlike terms.

For example, 2a and 5a are like terms, 2xy and 12xy are like terms but xy and 9x are unlike terms, 55 and 8c are unlike terms.

The operations of addition and subtraction may be performed between the like terms only, but not between the unlike terms.

We know that, the sum of 5 mangoes and 6 mangoes is (5 + 6) mangoes or 11 mangoes.

Likewise, the sum of 5x and 6x is (5x + 6x) or, 11x.

Again, the sum of 10 mangoes and 18 apples is, 10 mangoes +18 apples.

Likewise, the sum of 10x and 18y = 10x + 18y; the summation between 10x and I8y is not permissible as they are unlike terms.

Math Solution Of Class 7 Wbbse

Algebraic sum

We have mentioned earlier that summation is permissible between like terms only. The summation of like terms having same signs is similar to the process of addition in arithmetic.

For example, the sum of -5x, 7x and 8x = 5x + 7x + 8x = 20x.

Again, the sum of – 3x, -4x and -8x = – 3x – 4x – 8x = – 15x.

When the terms to be added are like but of opposite signs, their summation is not similar to the process of arithmetic.

For example, the sum of – 5x, 7x and – 4x = – 5x + 7x – 4x – 2x – 4x = – 2x.

Here, subtracting 5x from 7x we get 2x.

After subtracting 4x from 2x we get – 2x. But in arithmetic it is not possible to subtract 4x from 2x as in arithmetic we say that, the greater number cannot be subtracted from a smaller number.

Algebra Chapter 4 Polynomials Exercise 4 Some Examples Of Summation

 Example 1. Find the sum of : \(4 x^2,-3 x^2, 7 x^2\)

Solution :

Given

\(4 x^2,-3 x^2, 7 x^2\)

The required sum = \(4 x^2-3 x^2+7 x^2=\left(4 x^2+7 x^2\right)-3 x^2=11 x^2-3 x^2-8 x^2\)

∴ \(8 x^2\)

\(4 x^2,-3 x^2, 7 x^2=8 x^2\)

Example 2. Find the sum of  2xy, 5xy, 9xy and – 7xy.

Solution :

Given:

2xy, 5xy, 9xy And – 7xy

Here the required sum = – 2xy + 5xy + 9xy – 7xy

= (5xy + 9xy) – (2xy+ 7xy)

= 14 xy -9xy = 5xy

2xy, 5xy, 9xy and – 7xy = 5xy

Math Solution Of Class 7 Wbbse

Example 3. Find the sum of \(\frac{2}{5}\) ab, – \(\frac{3}{5}\) ab, \(\frac{4}{5}\) ab, and – \(\frac{1}{5}\),

Solution:

Here the required sum

= \(\frac{2}{5}\) ab, – \(\frac{3}{5}\) ab, \(\frac{4}{5}\) ab, and – \(\frac{1}{5}\),

= (\(\frac{2}{5}\) ab + \(\frac{4}{5}\) ab) – (\(\frac{3}{5}\) ab + \(\frac{1}{5}\)) ab

= \(\frac{6}{5}\) ab- \(\frac{4}{5}\) ab = \(\frac{2}{5}\) ab

= \(\frac{2}{5}\) ab

Example 4. Find the sum of the following expressions: 5x – 8y + z, – 2x + 7y — 5z, 3x + 5y + 3z.

Solution:

Given:

5x – 8y + z, – 2x + 7y — 5z, 3x + 5y + 3z

\(\begin{array}{r}
5 x-8 y+z \\
-2 x+7 y-5 z \\
3 x+5 y+3 z \\
\hline 6 x+4 y-z \\
\hline
\end{array}\)

∴ The required sum = 6x + 4y – z.

5x – 8y + z, – 2x + 7y – 5z, 3x + 5y + 3z. = 6x + 4y – z.

Example 5. Find the sum of the following expressions: \(p^2-p q+q^2, 2 p^2-3 q^2, 3 p q+8 q^2\)

Solution:

Given:

\(p^2-p q+q^2, 2 p^2-3 q^2, 3 p q+8 q^2\) \(\begin{aligned}
& p^2-p q+q^2 \\
& 2 p^2-3 q^2 \\
& 3 p q+8 q^2 \\
& \hline 3 p^2+2 p q+6 q^2 \\
& \hline
\end{aligned}\)

∴The required sum = \(3 p^2+2 p q+6 q^2\)

\(p^2-p q+q^2, 2 p^2-3 q^2, 3 p q+8 q^2=3 p^2+2 p q+6 q^2\)

Example 6. Simplify \(-5 a^2+2 b^2+2 a b+3 a^2-6 b^2-5 a b+3 a\).

Solution:

The given expression

= \(-5 a^2+2 b^2+2 a b+3 a^2-6 b^2-5 a b+3 a\)

= \(\left(5 a^2+3 a^2\right)+\left(2 b^2-6 b^2\right)+(2 a b-5 a b)+3 a\)

∴ \(8 a^2-4 b^2-3 a b+3 a\)

\(5 a^2+2 b^2+2 a b+3 a^2-6 b^2-5 a b+3 a=8 a^2-4 b^2-3 a b+3 a\)

Example 7. Find the sum of the following expressions: \(6 x^2+3 x y, x y-y^2, 2 x^2+5 y^2-3 x y\).

Solution:

Given:

\(6 x^2+3 x y, x y-y^2, 2 x^2+5 y^2-3 x y\) \(\begin{gathered}
6 x^2+3 x y \\
\quad+x y-y^2 \\
2 x^2-3 x y+5 y^2 \\
\hline 8 x^2+x y+4 y^2 \\
\hline
\end{gathered}\)

 

∴ The required sum = \(8 x^2+x y+4 y^2\).

\(\)6X²+ 3xy, xy – y², 2x² + 5y² – 3xy = 8x² + xy + 4y².

Example 8. Find the sum of the following expressions m² – \(\frac{1}{2}\) mn, \(\frac{1}{3}\) mn + n²,-m² – \(\frac{1}{4}\)n² .

Solution:

\(\begin{aligned}
& m^2+\frac{1}{2} m n \\
& +\frac{1}{3} m n+n^2 \\
& -m^2 \quad-\frac{1}{4} n^2 \\
& \left\lvert\, \begin{array}{l}
\frac{1}{2}+\frac{1}{3}=\frac{3+2}{6}=\frac{5}{6} \\
1-\frac{1}{4}=\frac{3}{4}
\end{array}\right. \\
&
\end{aligned}\)

 

∴ The required sum = –\(\frac{5}{6}\) mn + \(\frac{3}{4}\)n²

Subtraction

The quantity from which the subtraction is to be made is called minuend.

The quantity which is to be subtracted is called subtrahend. The result obtained after subtraction is called the difference or remainder.

By subtraction of b from a we mean, addition of the negative of b with a.

It means that, a – b = a + (- b). Thus to subtract one expression from another (having any number of terms in either expression), we have to change the sign of each term of the subtrahend and they will be added to the like terms of the minuend.

 

Algebra Chapter 4 Polynomials Exercise 4 Some Examples Of Subtraction

Example 1. Subtract 5xy from 12xy.

Solution: 12xy – 5xy = 7xy.

Example 2. Subtract 12x from 3x.

Solution: 3x – 12x = – 9x.

Example 3. Subtract – 9xy from 25xy.

Solution: 25xy – (- 9xy) = 25xy + 9xy = 34xy.

Example 4. Subtract \(5 a^2+\mathbf{4} b^2+2 c^2\)from \(7 a^2-3 b^2+8 c^2\).

Solution:

\(\begin{gathered}
7 a^2-3 b^2+8 c^2 \\
5 a^2+4 b^2+2 c^2 \\
-\quad-\quad- \\
\hline 2 a^2-7 b^2+6 c^2 \\
\hline
\end{gathered}\)

 

∴ \(2 a^2-7 b^2+6 c^2\).

\(5 a^2+4 b^2+2 c^2-7 a^2-3 b^2+8 c^2=2 a^2-7 b^2+6 c^2\).

Example 5. Subtract \(5 x^2-5\) from \(2 x^2+5 x y\).

Solution:

\(\begin{array}{r}
2 x^2+5 x y \\
-\quad 5 x^2+5 \\
-\quad+ \\
\hline-3 x^2+5 x y+5 \\
\hline
\end{array}\)

 

∴ \(-3 x^2+5 x y+5\).

\(5 x^2-5-2 x^2+5 x y=-3 x^2+5 x y+5\).

Example 6. What is to be added with \(a^2-\mathbf{a b}+2 \mathbf{b}^2\)a² – ab + 2b² to get \(a^2 + b^2\)?

Solution :

The required expression = \(\left(a^2+b^2\right)-\left(a^2+a b-2 b^2\right)\)

= \(\left(a^2+b^2\right)-\left(a^2+a b-2 b^2\right)\)

= \(\left(a^2-a^2\right)+\left(b^2-2 b^2\right)+a b\)

= \(-b^2 + a b\)

∴ \(-b^2 + a b\) is to be added.

Example 7. Subtract \(x^2+y^2+2 x\) from \(x^2+y^2+2 x y\).

Solution:

Given:

\(x^2+y^2-2 x y\) and \(x^2+y^2+2 x\)

\(\begin{array}{r}
x^2+y^2+2 x y \\
x^2+y^2-2 x y \\
-\quad-\quad+ \\
\hline 4 x y \\
\hline
\end{array}\)

 

∴ 4xy.

\(x^2+y^2-2 x y-x^2+y^2+2 x y=4 x y\).

Example 8. What is to be added to \(a^2+b^2+c^2\) to get \(b^2+c^2\)?

Solution:

Given

\(a^2+b^2+c^2\)

The required expression = \(\left(b^2+c^2\right)-\left(a^2+b^2+c^2\right)\)

= \(b^2+c^2-a^2-b^2-c^2=-a^2\).

∴ \(– a^2\)is to be added.

Example 9. The difference of two expressions is 3a + 6. If the greater one is \(8 a^2+5 a+9\), what will be the smaller one? (a > 0)

Solution:

\(\begin{array}{r}
8 a^2+5 a+9 \\
3 a+6 \\
-\quad- \\
\hline 8 a^2+2 a+3 \\
\hline
\end{array}\)

 

∴The smaller one is \(\)8a² + 2a + 3.

Example 10. If x = 2a – b, y = b – 3a then prove that, x – y = – (y – x).

Solution:

L.H.S. = x-y = (2a-b)-(b-3a)

= 2a – b – b + 3a = 5a – 2b.

R.H.S. = – (y-x)

= -y+x = -(b- 3a) + 2a-b

= – b +3a + 2a- b = 5a-2b.

∴ L.H.S. = R.H.S. (Proved).

Concept of index

When the same number is multiplied several times then it may be expressed in brief.

Example: 8 x 8 = 8²

8 x 8 x 8 = 8³

8 x 8 x 8 x 8 = 8⁴

8 x 8 x 8 x 8 x 8 = 8⁵.

Here 8 is called the base and the number written over 8 on the right side is the power or index.

Any number can be expanded in the index of 10.

Class Vii Math Solution Wbbse

Example: 742 = 7 x 100 + 4 x 10 + 2 = 7 x 10² + 4 x 10 + 2

4584 = 4 x 1000 + 5 x 100 + 8 x 10 + 4

= 4 x 10³ + 5 x 10² + 8 x 10 + 4

Again, 81 = 3x3x3x3 = 3⁴

Therefore, the index form of 81 is 3⁴.

Here 3 is the base and 4 is the index.

243 = 3 x 3 x 3 x 3 x 3 x 3⁵.

Therefore, index form of 243 is 3⁵. Here 3 is the base and 5 is the power.

Similarly:

1. 32= 2 x 2 x 2 x 2 x 2 = 2⁵
2. 27 = 3 x 3 x 3 = 3³
3. 625 = 5 x 5 x 5 x 5 = 5⁴
4. 729 = 3 x 3 x 3 x 3 x 3 x 3= 3⁶
5. 343= 7 x 7 x 7 = 7³

Therefore, if x is any integer,

1. x X x = x²
2. x X x ² x = x³
3. x X x X x X x = x⁴
4. x X x X x X x X x = x⁵

Again, 2 x2 x 3 x 3 = 2² x 3²

2 x 2 x 2 x 5 x 5 = 2³ x 5² 7 x 7 x 7 x 5 x 5 x 5 x 5 = 7³ x 5⁴.

Any number may be written in index form after breaking it in prime factors,

Example: 36 = 2 x 2 x 3 x 3 = 2² x 3²

75 = 3 x 5 x 5 = 3x 5²

50 = 2 x 5 x 5 = 2 x 5²

24 = 2 x 2 x 2 x 3 = 2³ x 3

Determination of greater and smaller numbers:

Between 4³ and 3⁴ which is greater and which is smaller?

4³ = 4 x 4 x 4 = 64

3⁴ = 3x3x3x3 = 81

∴ 3⁴ is greater than 4³ i.e., 3⁴ > 4³.

Some formulae :

1. x^m  X xⁿ = x^m+n
2. .x^m ÷ xⁿ = x^m–n
3. (x^m)ⁿ = x^mn
4. xⁿ X yⁿ = (xy)ⁿ  
5. x⁰ = 1

Example:

1. \(2^3 \times 2^4=2^{3+4}\)

2. \(5^8 \div 5^3=5^{8-3}=5^5\)

3. \(\left(2^3\right)^2=2^{3 \times 2}=2^6\)

4. \(5^2 \div 5^2=1\)

5. \(8^{\circ}=1\)

6. \((-3)^5 \times(-3)^3=(-3)^{5+3}=(-3)^8\)

7. \(7^2 \times 3^2=(7 \times 3)^2=21^2\)

8. \(5^3 \times 9^3=(5 \times 9)^3=45^3\)

Example 1.

\(\frac{2^5 \times 2^7}{\left(2^5\right)^2}=\frac{2^{5+7}}{2^{10}}=2^{12-10}=2^2=4\)

 

Example 2.

\(\frac{2^3 \times 3^5 \times 16}{3 \times 32}=\frac{2^3 \times 3^5 \times 2^4}{3 \times 2^5}=2^{3+4-5} \times 3^{5-1}\)

 

= \(2^2 \times 3^4=4 \times 81=324\).

To write a number from the expansion:

4 x 10³+ 2 x 10² + 3 x 10 + 5

= 4000 + 200 + 30 + 5 = 4235

5 x 10⁴+ 2 x 10³ + 1 x 10² + 2 x 10 + 3

= 50000 + 2000 + 100 + 20 + 3 = 52123.

 

Algebra Chapter 4 Polynomials Exercise 4 Simple Multiplication

In case of algebraic multiplication of two quantities, the sign of the product is + when the two quantities are of the same sign and the sign of the product is — when the quantities are of opposite signs.

This may be explained in brief as follows:

(+ x) x (+ y) = + xy

(+ x) x (- y) = – xy

(- x) x (+ y) = – xy

(- x) x (- y) = + xy

In case of finding the product of the same variable having different powers, we follow the rule x^m x xⁿ – x^m+n.

When we multiply some algebraic expressions having numerical coefficients then the numerical co-efficient of the product is equal to the product of all the coefficients.

Example 1. Multiply 7x³ by 2x⁴.

Solution: \(7 x^3 \text { by } 2 x^4=7 \times 2 \times x^3 \times x^4\)

= \(14 X x^{3+4}=14 X x^7=14 x^7\)

∴ \(14 x^7\).

\(7 x^3 \times 2 x^4=14 x^7\).

Example 2. Multiply -7p² by 8pq².

Solution: \(\left(-7 p^2\right) \times\left(8 p q^2\right)=-56 p^{2+1} q^2\)

∴ \(-56 p^3 q^2\)

\(-7 p^2 \times 8 p q^2=-56 p^3 q^2\)

Example 3. Find the product \(\left(-5 p^2 q\right) \times\left(3 p q^2\right) \times\left(-2 p^2 q^2\right)\).

Solution: The required product = \(\left(-5 p^2 q\right) \times\left(3 p q^2\right) \times\left(-2 p^2 q^2\right)\).

= \((-5) \times 3 \times(-2) \times p^{2+1+2} \times q^{1+2+2}\)

∴ \(30 p^5 q^5\)

\(\left(-5 p^2 q\right) \times\left(3 p q^2\right) \times\left(-2 p^2 q^2\right)=30 p^5 q^5\)

Example 4. Multiply  \(3 p^2 q^5 r\) by \(-7 p^3 q^2 r^5\)

Solution: The required product = \(\left(-3 p^2 q^5 r\right) \times\left(-7 p^3 q^2 r^5\right)\)

= \((-3) \times(-7) x^{p 2+3} \times q^{5+2} \times r^{1+5}=21 p^5 q^7 r^6\)

∴ \(21 p^5 q^7 r^6\)

\(3 p^2 q^5 r x-7 p^3 q^2 r^5=21 p^5 q^7 r^6\)

Example 5.  Find the product : (2xyz) x (8pqr) x (- 4abc).

Solution: The required product = (2xyz) x (8pqr) x (- 4abc)

= 2 x 8 x (- 4) x xyz pqr abc = – 64 abc pqr xyz

∴ – 64 abc pqr xyz.

(2xyz) x (8pqr) x (- 4abc) = – 64 abc pqr xyz.

Example 6. Find the product \(\left(\frac{1}{2} x y^2\right) \times\left(-\frac{2}{3} x y^4\right) \times\left(3 x^3 y\right)\)

Solution: The required product

\(\left(\frac{1}{2} x y^2\right) \times\left(-\frac{2}{3} x y^4\right) \times\left(3 x^3 y\right)\)

 

= \(\frac{1}{2}\) X – (\(\frac{2}{3}\)) X 3 X xy² X xy⁴ X x³y

= \((-1) x x^5 x y^7=-x^5 y^7\)

Multiplication of two or more terms with a single term

When we are to find the product of the form (a+b)x, then since a and b are unlike terms, it is not possible to find their sum in one term.

So we should proceed as follows: (a + b) x = a X x + b X x = ax + bx

Similarly, (a + b + c +…… ) = ax + bx + cx +

In fact, this is the distributive law of multiplication.

Wbbse Class 7 Maths Solutions

Example 1. Multiply 3a + 26 by – 2ab.

Solution: The required product

= (3a + 2b) x (- 2ab)

= 3a x (-2ab) + 2b x (- 2ab)

= \(-6 a^2 6-4 a b^2\).

∴ \(-6 a^2 6-4 a b^2\).

3a + 26 X – 2ab = \(-6 a^2 6-4 a b^2\).

Example 2. Multiply \(x^2 y z-2 x y^2 z+3 x y z^2 \text { by } 3 x y^2\).

Solution: The required product = \(\left(x^2 y z-2 x y^2 z+3 x y z^2\right) x 3 x y z\)

= \(x^2 y z \times 3 x y z-2 x y^2 z \times 3 x y z+3 x y z^2 \times 3 x y z\)

∴ \(3 x^3 y^2 z^2-6 x^2 y z^2+9 x^2 y^2 z^3\)

\(x^2 y z-2 x y^2 z+3 x y z^2 \text { by } 3 x y^2=3 x^3 y^2 z^2-6 x^2 y z^2+9 x^2 y^2 z^3\)

Example 3. Simplify: \(a^3(2 a-b)+2 b^2(a+2 b)+5\left(a^3-3 b^3\right)\).

Solution : The given expression = \(a^3(2 a-b)+2 b^2(a+2 b)+5\left(a^3-3 b^3\right)\).

= \(2 a^3-a^2 b+2 a b^2+4 b^3+5 a^3-15 b^3\)

= \(\left(2 a^3+5 a^3\right)+\left(4 b^3-15 b^3\right)-a^2 b+2 a b^2\)

∴ \(7 a^3-11 b^3-a^3 b+2 a b^2\)

\(a^3(2 a-b)+2 b^2(a+2 b)+5\left(a^3-3 b^3\right)=7 a^3-11 b^3-a^3 b+2 a b^2\)

Example 4. Simplify  2x (x – 3y) + 5y (2x + 3y) – 2x (y + 5x).

Solution: The given expression = 2x (x – 3y) + 5y (2x + 3y) -2x (y + 5x)

= \(2 x^2-6 x y+10 x y+15 y^2-2 x y-10 x^2\)

= \(\left(2 x^2-10 x^2\right)+(-6 x y+10 x y-2 x y)+15 y^2\)

∴ \(-8 x^2+2 x y+15 y^2\)

2x (x – 3y) + 5y (2x + 3y) – 2x (y + 5x) = \(-8 x^2+2 x y+15 y^2\)

Wbbse Class 7 Maths Solutions

Multiplication of a binomial expression by another binomial expression

When we are to find the product of two binomial expressions we proceed as follows (a + b) (c + d) = ac + ad + bc + bd

Thus, we see that when two binomial expressions are multiplied then each term of the multiplicand is multiplied by each term of the multiplier and all the products are finally added.

Example 1. Multiply : 7a + 36 by 2a – 6.

Solution: The required product = (7a + 36) (2a – 6)

= 7a.2a + 7a.(-b) + 3b.2a + 3b.(- b)

= \(14 a^2-7 a b+6 a b-3 b^2=14 a^2-a b-3 b^2\).

Alternative Method:

\(\begin{array}{r}
7 a+3 b \\
2 a-b \\
\hline 14 a^2+6 a b \\
-7 a b-3 b^2 \\
\hline 14 a^2-a b-3 b^2 \\
\hline
\end{array}\)

 

∴ The required product = \(14 a^2-a b-3 b^2\).

7a + 36 X 2a – 6 = \(14 a^2-a b-3 b^2\).

Example 2. Multiply \(a^2+a 6+6^2 \times a-6=a^3-6^3\) by a – 6 and find the product.

Solution:

\(\begin{aligned}
& a^2+a b+b^2 \\
& a-b \\
& \hline a^3+a^2 b+a b^2 \\
& \quad-a^2 b-a b^2-b^3 \\
& \hline a^3-b^3 \\
& \hline
\end{aligned}\)

 

∴ The required product = a³ – 6³.

\(a^2+a 6+6^2 \times a-6=a^3-6^3\).

Example 3. Multiply a + x by a – x.

Solution:

\(\begin{aligned}
& a+x \\
& a-x \\
& \hline a^2+a x \\
& -a x-x^2 \\
& \hline a^2-x^2 \\
& \hline
\end{aligned}\)

 

a + x X a – x = \(a^2-x^2\)

Class Vii Math Solution Wbbse

Example 4. Multiply \(x^4+x^2 y^2+y^4 \text { by } x^2-y^2\).

Solution:

\(\begin{aligned}
& x^4+x^2 y^2+y^4 \\
& x^2-y^2 \\
& \hline x^6+x^4 y^2+x^2 y^4 \\
& -x^4 y^2-x^2 y^4-y^6 \\
& \hline x^6-y^6 \\
& \hline
\end{aligned}\)

 

Example 5. Simplify 3(x + y) – y(3 + x) + x(y – 3).

Solution: The given expression = 3(x +y)- y(3 + x) + x(y – 3)

= 3x + 3y – 3y – xy + xy – 3x = 0

∴ 0.

3(x + y) – y(3 + x) + x(y – 3)= 0

Example 6. Simplify : (2x + 9)(x – 7) – (x – 9)(2x + 7).

Solution: The given expression = (2x + 9)(x – 7) – (x – 9)(2x + 7)

= \(\left(2 x^2-14 x+9 x-63\right)-\left(2 x^2+7 x-18 x-63\right)\)

= \(\left(2 x^2-5 x-63\right)-\left(2 x^2-11 x-63\right)\)

= \(2 x^2-5 x-63-2 x^2+11 x+63=6 x\)

∴ 6x.

(2x + 9)(x – 7) – (x – 9)(2x + 7) = 6x.

Wbbse Class 7 Maths Solutions

Example 7. Simplify : a(b – c) + b(c – a) + c(a – b).

Solution : a(b – c) + b(c – a) + c(a – b)

= ab – ac + bc – ab + ca – bc = 0

∴ 0.

a(b – c) + b(c – a) + c(a – b) = 0

Class Vii Math Solution Wbbse

Example 8. Simplify : (x + 9)(x – 7) + (x + 9)(x + 10) – (2x +1)(x + 10).

Solution : (x + 9)(x -7) + (x + 9)(x + 10) -(2x + 1)(x + 10)

= \(\left(x^2-7 x+9 x-63\right)+\left(x^2+10 x+9 x+90\right)-\left(2 x^2+20 x+x+10\right)\)

= \(\left(x^2+2 x-63\right)+\left(x^2+19 x+90\right)-\left(2 x^2+21 x+10\right)\)

= \(x^2+2 x-63+x^2+19 x+90-2 x^2-21 x-10\)

∴ 17

(x + 9)(x – 7) + (x + 9)(x + 10) – (2x +1)(x + 10) = 17

Example 9. Simplify \(-5 a-[-3 b-\{-6 c-(-3 a-\overline{5 b-4 c})\}]\)

Solution:

\(-5 a-[-3 b-\{-6 c-(-3 a-\overline{5 b-4 c})\}]\)

 

= – 5a – [ – 36 – {- 6c – (- 3a – 56 + 4c)}] = – 5a – [ – 36 – { -6c + 3a + 56 – 4c}]

= – 5a – [ – 36 – { – 10c + 3a + 56}]

= – 5a – [ – 36 + 10c – 3a – 56]

= – 5a – [ – 86 + 10c – 3a]

= – 5a + 86 – 10c + 3a = – 2a + 86 – 10c

∴ – 2a + 86 — 10c.

Example 10. Simplify \(x-[y+\{x-(y-\overline{x-y})\}]\)

Solution:

\(x-[y+\{x-(y-\overline{x-y})\}]\)

 

= x- [y + {x- (y-x+y)}]

= x – [ y + {x – (2y – x)}]

= x – {y +{x – 2y + x}]

= x – [ y + 2x – 2y]

= x – [ – y + 2x] = x + y – 2x = y – x

∴ y -x.

Simple Division

Wbbse Class 7 Maths Solutions

In case of algebraic division of the form \(/frac{a}{b}\) = c, we call a the dividend, b the divisor and c the quotient.

If the dividend and the divisor are of the same sign then the sign of the quotient will be + and if the dividend and the divisor are of opposite signs then the sign of the quotient will be This may be explained in brief as follows :

\(\frac{(+x)}{(+y)}=+\frac{x}{y}\) \(\frac{(+x)}{(-y)}=-\frac{x}{y}\) \(\frac{(-x)}{(+y)}=-\frac{x}{y}\) \(\frac{(-x)}{(-y)}=+\frac{x}{y}\)

 

In case of finding the quotient of the same variable having different powers, we follow the rule x^m ÷xⁿ = x^m–n. We shall also take x° = 1.

Example 1. Divide \(35 a^4 b^8 \text { by } 5 a^2 b^2\).

Solution: The required quotient

\(\frac{35 a^4 b^8}{5 a^2 b^2}\)

= \(7 a^{4-2} b^{8-2}=7 a^2 b^6\)

Example 2. Divide \(36 x^{12} y^8 \text { by }\left(-9 x^5 y^4\right)\).

Solution: The required quotient

\(\frac{36 x^{12} y^8}{-9 x^5 y^4}\)

 

= \(-4 x^{12-5} y^{8-4}\)

= \(-4 x^7 y^4\).

Example 3. Divide \(\left(-20 p^8 q^6\right) \text { by } 5 p^4 q^2\).

Solution: The required quotient

\(\frac{-20 p^8 q^6}{5 p^4 q^2}\)

 

= \(-4 p^{8-4} q^{8-2}\) = \(-4 p^4 q^4\)

Example 4. Divide \(\left(-81 m^5 n^6\right) \text { by }\left(-27 m^2 n^2\right)\).

Wbbse Class 7 Maths Solutions

Solution: The required quotient

\(\frac{-81 m^5 n^6}{-27 m^2 n^2}\)

 

= \(3 m^{5-2} n^{6-2}=3 m^3 n^4\)

Class Vii Math Solution Wbbse

Division of a polynomial by a monomial

We know, from the distributive law of division that, (a+ b + c) ÷ x = a÷x + b ÷ x + c ÷ x

i.e.,  \(\frac{a+b+c}{x}\) = \(\frac{a}{x}\) + \(\frac{b}{x}\) + \(\frac{c}{x}\)

Thus, we see that when a polynomial is divided by a monomial then the quotient is obtained by dividing each term of the dividend by the divisor.

Example 1. Divide 15a – 25b + 35c by 5.

Solution: The required quotient

= \(\frac{15a-25b+35c}{5}\)

= \(\frac{15a}{5}\) – \(\frac{25ba}{5}\) + \(\frac{35a}{5}\)

∴ 3a – 5b + 7c

15a – 25b + 35c X 5 = 3a – 5b + 7c

Example 2. Divide \(4 x^5+3 x^4+8 x^3+7 x^2 \text { by } x^2\).

Solution: The required quotient

\(\frac{4 x^5+3 x^4+8 x^3+7 x^2}{x^2}\) \(\frac{4 x^5}{x^2}+\frac{3 x^4}{x^2}+\frac{8 x^3}{x^2}+\frac{7 x^2}{x^2}\)

 

= \(4 x^{5-2}+3 x^{4-2}+8 x^{3-2}+7 x^{2-2}=4 x^3+3 x^2+8 x^4+7 x^0\)

= \(4 x^3+3 x^2+8 x+7\)

= \(4 x^5+3 x^4+8 x^3+7 x^2 x x^2=4 x^3+3 x^2+8 x+7\)

= \(4 x^3+3 x^2+8 x+7\)4x³ + 3X² + 8x + 7.

Wbbse Class 7 Maths Solutions

Example 3.  Divide \(12 m^2 n^4+16 m^3 n^3-20 m^4 n^2 \text { by } 4 m^2 n^2\).

Solution: The required quotient

\(\frac{12 m^2 n^4+16 m^3 n^3-20 m^4 n^2}{4 m^2 n^2}\) \(\frac{12 m^2 n^4}{4 m^2 n^2}+\frac{16 m^3 n^3}{4 m^2 n^2}-\frac{20 m^4 n^2}{4 m^2 n^2}\)

 

= \(3 m^{2-2} n^{4-2}+4 m^{3-2} n^{3-2}-5 m^{4-2} n^{2-2}=3 m^{\circ} n^2+4 m^1 n^1-5 m^2 n^{\circ}\)

∴ \(3 n^2+4 m n-5 m^2\)

\(12 m^2 n^4+16 m^3 n^3-20 m^4 n^2 \text { by } 4 m^2 n^2=3 n^2+4 m n-5 m^2\)

Example 4. Divide \(3 a b c-6 a^2 b c+5 a^2 b^2 c^2 \text { by } 3 a b c\).

Solution: The required quotient

\(\frac{3 a b c-6 a^2 b c+5 a^2 b^2 c^2}{3 a b c}\)

\(\frac{3 a b c}{3 a b c}-\frac{6 a^2 b c}{3 a b c}+\frac{5 a^2 b^2 c^2}{3 a b c}\)

∴ 1 – 2a + \(\frac{5}{3}\) abc