Tanuja Puram

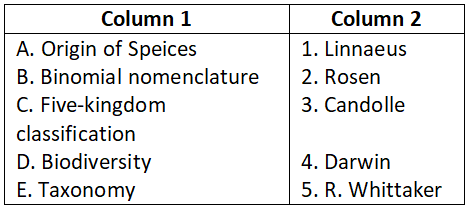
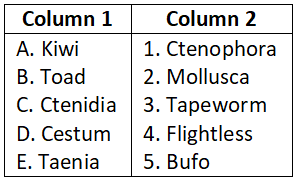
WBCHSE Class 12 Maths Solutions For The Plane

Plane A plane is a surface such that a line segment joining any two points on it lies wholly on it.

Normal To A Plane A straight line which is perpendicular to every line lying on a plane is called a normal to the plane.

All the normals to a plane are parallel to each other.

General Equation of a Plane in the Cartesian Form

Theorem 1 Every equation ax + by + cz + d = 0 of the first degree in x, y, z always represents a plane. Also, a, b, c are the direction ratios of the normal to this plane.

Proof

Let us consider a surface represented by the equation

ax + by + cz + d = 0 …(1)

Let A(x₁, y₁, z₁) and B(x₂, y₂, z₂) be any two points on the surface represented by (1). Then,

ax₁ + by₁ + cz₁ + d = 0 …(2)

and, ax₂ + by₂ + cz₂ + d = 0 …(3)

Multiplying (3) by λ and adding to (2), we get

Equations of Planes Explained

a(λx₂ + x₁) + b(λy₂ + y₁) + c(λz₂ + z₁) + d(λ+1) = 0

⇒ \(a\left(\frac{\lambda x_2+x_1}{\lambda+1}\right)+b\left(\frac{\lambda y_2+y_1}{\lambda+1}\right)+c\left(\frac{\lambda z_2+z_1}{\lambda+1}\right)+d=0\)

⇒ \(\left(\frac{\lambda x_2+x_1}{\lambda+1}, \frac{\lambda y_2+y_1}{\lambda+1}, \frac{\lambda z_2+z_1}{\lambda+1}\right)\) lies on surface (1), when λ ≠ -1.

But, these are the general coordinates of a point which divides AB in the ratio λ : 1.

Since λ may take any real value other than -1, it follows that every point of AB lies on (1).

Hence, ax + by + cz + d = 0 represents a plane.

Read and Learn More  Class 12 Math Solutions

To Show that a, b, c are the Direction Ratios of the Normal to a plane

Subtracting (2) from (3), we get

a(x₂ – x₁) + b(y₂ – y₁) + c(z₂ – z₁) = 0

⇒ a line with direction ratios a, b, c is perpendicular to an arbitrary line AB taken on plane (1) [∵ (x₂-x₁), (y₂-y₁), (z₂-z₁) are d.r.’s of AB]

⇒ a line with d.r.’s a, b, c is perpendicular to the plane (1)

⇒ a, b, c are the direction ratios of the normal to the plane (1).

Hence, ax + by + cz + d = 0 represents a plane, and a, b, c are the direction ratios of the normal to this plane.

Equation of a Plane Passing through a Given Point

Theorem 2 The equation of a plane passing through a point P(x₁,y₁,z₁) is a(x-x₁) + b(y-y₁) + c(z-z₁) = 0, where a, b, c are constants.

Proof

The general equation of a plane is

ax + by + cz + d = 0 …(1)

If this plane passes through the point P(x₁,y₁,z₁) then

ax₁ + by₁ + cz₁ + d = 0 …(2)

Subtracting (2) from (1), we get

a(x-x₁) + b(y-y₁) + c(z-z₁) = 0.

This is the general equation of a plane passing through the point P(x₁,y₁,z₁).

WBBSE Class 12 Plane Solutions

WBCHSE Class 12 Maths Solutions For The Plane Solved Examples

Example 1 Find the equation of the plane passing through the points A(2,3,4), B(-3,5,1) and C(4,-1,2).

Solution

Given 

A(2,3,4), B(-3,5,1) and C(4,-1,2)

The general equation of a plane passing through the point A(2,3,4) is given by

a(x-2) + b(y-3) + c(z-4) = 0 …(1)

Since it passes through the points B(-3,5,1) and C(4,-1,2), we have

a(-3-2) + b(5-3) + c(1-4) = 0 ⇒ -5a + 2b – 3c = 0 …(2)

a(4-2) + b(-1-3) + c(2-4) = 0 ⇒ 2a – 4b – 2c = 0 ⇒ a – 2b – c = 0 …(3)

Cross multiplying (2) and (3), we have \(\frac{a}{(-2-6)}=\frac{b}{(-3-5)}=\frac{c}{(10-2)}\)

⇒ \(\frac{a}{-8}=\frac{b}{-8}=\frac{c}{8}\)

⇒ \(\frac{a}{1}=\frac{b}{1}=\frac{c}{-1}=k \text { (say) }\)

⇒ a = k, b = k and c = -k.

Substituting a = k, b = k and c = -k in (1), we get

k(x-2) + k(y-3) – k(z-4) = 0

⇒ (x-2) + (y-3) – (z-4) = 0

⇒ x + y – z – 1 = 0.

Hence, x + y – z = 1 is the required equation of the plane.

To Show that Four Given Points are Coplanar

Suppose, we have to show that four points A, B, C, D are coplanar. We proceed in the following steps:

1. Find the equation of the plane passing through any three (say A, B, C) of the given four points.

2. Show that the fourth point D satisfies the equation obtained in step 1.

Example 2 Show that the four points A(3,2,-5), B(-1,4,-3), C(-3,8,5) and D(-3,2,1) are coplanar. Find the equation of the plane containing them.

Solution

Given

A(3,2,-5), B(-1,4,-3), C(-3,8,5) and D(-3,2,1)

The equation of the plane passing through the point A(3,2,-5) is

a(x-3) + b(y-2) + c(z+5) = 0 …(1)

If it passes through B(-1,4,-3) and C(-3,8,-5), we have

a(-1-3) + b(4-2) + c(-3+5) = 0 ⇒ – 4a + 2b + 2c = 0 ⇒ 2a – b – c = 0 …(2)

a(-3-3) + b(8-2) + c(-5+5) = 0 ⇒ -6a + 6b + 0c = 0 ⇒ a – b – 0c = 0 …(3)

Cross multiplying (2) and (3), we get

\(\frac{a}{(0-1)}=\frac{b}{(-1-0)}=\frac{c}{(-2+1)}\)

⇒ \(\frac{a}{-1}=\frac{b}{-1}=\frac{c}{-1}\)

⇒ \(\frac{a}{1}=\frac{b}{1}=\frac{c}{1}=k \text { (say) }\)

⇒ a = k, b = k and c = k in (1), we get

k(x-3) + k(y-2) + k(z+5) = 0

⇒ (x-3) + (y-2) + (z+5) = 0 ⇒ x + y + z = 0.

Thus, the equation of the plane passing through the points A(3,2,-5), B(-1,4,-3) and C(-3,8,-5) is x + y + z = 0.

Clearly, the fourth point D(-3,2,1) also satisfies x + y + z = 0.

Hence, the given four points are coplanar, and the equation of the plane containing them is x + y + z = 0.

Equation of a Plane in the Intercept Form

Theorem 3 If a plane makes intercepts of lengths a, b, c with the x-axis, y-axis and z-axis respectively, the equation of the plane is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1.\)

Proof

Let O be the origin, and let the plane meet the coordinate axes at A, B, C respectively such that OA = a, OB = b and OC = c.

So, the coordinates of these points are A(a,0,0), B(0,b,0) and C(0,0,c).

Let the equation of the given plane be

Ax + By + CZ + D = 0 …(1)

Since the given plane does not pass through O(0,0,0), D ≠ 0.

Also, since (1) passes through A(a,0,0), B(0,b,0) and C(0,0,c), we have

Aa + D = 0 ⇒ A = \(-\frac{D}{a}\),

Bb + D = 0 ⇒ B = \(-\frac{D}{b}\),

Cc + D = 0 ⇒ C = \(-\frac{D}{c}\).

Putting these values in (1), we get

\(\frac{-D x}{a}-\frac{D y}{b}-\frac{D z}{c}+D=0\)

⇒ \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) [on dividing throughout by -D].

This is the required equation of the plane in the intercept form.

Step-by-Step Solutions to Plane Geometry Problems

Example 3 Find the equation of the plane which cuts off intercepts 6,3,-4 from the axes of coordinates.

Solution

We know that the equation of a plane which cuts off intercepts a, b, c from the x-axis, y-axis and z-axis respectively, is

\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1.\)

Here, a = 6, b = 3 and c = -4.

Hence, the required equation of the plane is

\(\frac{x}{6}+\frac{y}{3}+\frac{z}{-4}=1 \Rightarrow 2 x+4 y-3 z=12.\)

Example 4 A variable plane moves in such a way that the sum of the reciprocals of its intercepts on the coordinate axes is constant. Show that the plane passes through a fixed point.

Solution

Let the equation of the variable plane be

\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) …(1)

Then, it makes intercepts a, b, c with the coordinate axes.

∴ \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=k\), where k is a constant (given)

⇒ \(\frac{1}{k a}+\frac{1}{k b}+\frac{1}{k c}=1\)

⇒ \(\frac{1}{a}\left(\frac{1}{k}\right)+\frac{1}{b}\left(\frac{1}{k}\right)+\frac{1}{c}\left(\frac{1}{k}\right)=1\)

⇒ \(\left(\frac{1}{k}, \frac{1}{k}, \frac{1}{k}\right)\) satisifes (1).

Hence, the given plane passes through a fixed point \(\left(\frac{1}{k}, \frac{1}{k}, \frac{1}{k}\right)\).

Equation of a Plane in the Normal Form

Vector Form

Theorem 1 If \(\hat{n}\) is a unit vector normal to a given plane, directed from the origin to the plane, and p is the length of the perpendicular drawn from the origin to the plane then the vector equation of the plane is \(\vec{r} \cdot \hat{n}=p .\)

Proof

Let O be the origin, and let ON be the perpendicular drawn from O to the given plane. Let ON = p.

Let \(\hat{n}\) be a unit vector along \(\overrightarrow{O N}\).

Then, \(\overrightarrow{O N}=p \hat{n}\).

Let P be an arbitrary point on the plane, and let the position vector of P be \(\vec{r}\).

Then, \(\overrightarrow{O P}=\vec{r} \text {. }\)

Since \(\overrightarrow{N P}\) lies on the plane, \(\overrightarrow{N P}\) is perpendicular to \(\hat{n}\).

∴ \(\overrightarrow{N P} \cdot \hat{n}=0\)

⇒ \((\overrightarrow{O P}-\overrightarrow{O N}) \cdot \hat{n}=0\)

⇒ \((\vec{r}-p \hat{n}) \cdot \hat{n}=0\)

⇒ \(\vec{r} \cdot \hat{n}-p \hat{n} \cdot \hat{n}=0\)

⇒ \(\vec{r} \cdot \hat{n}=p .\)

Hence, the required equation of the plane is \(\vec{r} \cdot \hat{n}=p .\)

Remark The equation of a plane which is at a distance p from the origin and which is perpendicular to \(\hat{n}\) is \(\vec{r} \cdot \hat{n}=p .\)

Corollary If \(\vec{n}\) is a vector normal to a given plane then \(\vec{r} \cdot \vec{n}=q\) represents a plane.

Proof \(\vec{r} \cdot \vec{n}=q ⇒ \vec{r} \cdot \frac{\vec{n}}{|\vec{n}|}=\frac{q}{|\vec{n}|}\)

⇒ \(\vec{r} \cdot \hat{n}=p\), where \(\frac{q}{|\vec{n}|}=p .\)

But, \(\vec{r} \cdot \hat{n}=p\) represents a plane.

∴ \(\vec{r} \cdot \vec{n}=q\) also represents a plane.

Cartesian Form

Theorem 2 If a, b, c be the direction ratios of the normal to a given plane, and p be the length of the perpendicular drawn from the origin to the given plane then the equation of the plane is ax + by + cz = p.

Proof

We know that the vector equation of a plane in the normal form is

\(\vec{r} \cdot \hat{n}=p\) …(1)

Taking \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k} \text { and } \hat{n}=a \hat{i}+b \hat{j}+c \hat{k}\), equation (1) becomes

\((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(a \hat{i}+b \hat{j}+c \hat{k})=p\)

⇒ ax + by + cz = p, which is the required equation of the plane.

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

Reduction of the General Form of the Equation of a Plane to the Normal Form

Let the general equation of the plane be ax + y + cz + d = 0. Then,

ax + by + cz + d = 0

⇒ -ax – by – cz = d …(1)

⇒ \(\frac{-a x}{\sqrt{a^2+b^2+c^2}}+\frac{-b y}{\sqrt{a^2+b^2+c^2}}+\frac{-c z}{\sqrt{a^2+b^2+c^2}}=\frac{d}{\sqrt{a^2+b^2+c^2}}\)

[on dividing (1) through out by \(\sqrt{(-a)^2+(-b)^2+(-c)^2}\)]

⇒ lx + my + nz = p, where

l = \(\frac{-a}{\sqrt{a^2+b^2+c^2}}, m=\frac{-b}{\sqrt{a^2+b^2+c^2}}\)

n = \(\frac{-c}{\sqrt{a^2+b^2+c^2}} \text { and } p=\frac{d}{\sqrt{a^2+b^2+c^2}}\).

Here l, m, n are the d.c.’s of the normal to the plane and p is the length of the perpendicular from the origin to the plane.

Solved Examples

Example 1 Find the vector equation of a plane which is at a distance of 6 units from the origin and which has \(\hat{j}\) as the unit vector normal to it.

Solution

Clearly, the required equation of the plane is \(\vec{r} \cdot \hat{j}=6 .\)

Example 2 Find the vector equation of a plane which is at a distance of 7 units from the origin and which is normal to the vector \((\hat{i}+2 \hat{j}-2 \hat{k})\)

Solution

Here, \(\vec{n}=(\hat{i}+2 \hat{j}-2 \hat{k})\) and p = 7.

∴ \(\hat{n}=\frac{\vec{n}}{|\vec{n}|}=\frac{(\hat{i}+2 \hat{j}-2 \hat{k})}{\sqrt{1^2+2^2+(-2)^2}}=\left(\frac{1}{3} \hat{i}+\frac{2}{3} \hat{j}-\frac{2}{3} \hat{k}\right)\)

Hence, the required equation of the plane is

\(\vec{r} \cdot\left(\frac{1}{3} \hat{i}+\frac{2}{3} \hat{j}-\frac{2}{3} \hat{k}\right)=7 \text {, i.e., } \vec{r} \cdot(\hat{i}+2 \hat{j}-2 \hat{k})=21 \text {. }\)

Example 3 The vector equation of a plane is \(\vec{r} \cdot(2 \hat{i}-\hat{j}+2 \hat{k})=9\). Reduce it to the normal form, and hence find the length of the perpendicular from the origin to the plane.

Solution

The equation of the given plane is

\(\vec{r} \cdot \vec{n}=9 \text {, where } \vec{n}=(2 \hat{i}-\hat{j}+2 \hat{k}) \text {. }\)

∴ \(|\vec{n}|=\sqrt{2^2+(-1)^2+2^2}=3 .\)

Now, \(\vec{r} \cdot \vec{n}=9 \Rightarrow \vec{r} \cdot \frac{\vec{n}}{|\vec{n}|}=\frac{9}{|\vec{n}|}\)

⇒ \(\vec{r} \cdot \frac{(2 \hat{i}-\hat{j}+2 \hat{k})}{3}=3\)

⇒ \(\vec{r} \cdot\left(\frac{2}{3} \hat{i}-\frac{1}{3} \hat{j}+\frac{2}{3} \hat{k}\right)=3 .\)

Thus, \(\vec{r} \cdot\left(\frac{2}{3} \hat{i}-\frac{1}{3} \hat{j}+\frac{2}{3} \hat{k}\right)=3\) is the required equation of the plane in the normal form.

The length of the perpendicular from the origin to the plane is 3 units.

Example 4 Find a unit vector normal to the plane \(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+6 \hat{k})+14=0 .\)

Solution

The equation of the given plane is

\(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+6 \hat{k})+14=0\)

⇔ \(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+6 \hat{k})=-14\)

⇒ \(\vec{r} \cdot(-2 \hat{i}+3 \hat{j}-6 \hat{k})=14\)

⇒ \(\vec{r} \cdot \vec{n}=14 \text {, where } \vec{n}=(-2 \hat{i}+3 \hat{j}-6 \hat{k})\)

⇔ \(\vec{r} \cdot \frac{\vec{n}}{|\vec{n}|}=\frac{14}{|\vec{n}|} \text {; where }|\vec{n}|=\sqrt{(-2)^2+3^2+(-6)^2}=7\)

⇒ \(\vec{r} \cdot \frac{(-2 \hat{i}+3 \hat{j}-6 \hat{k})}{7}=\frac{14}{7}\)

⇔ \(\vec{r} \cdot\left(-\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}-\frac{6}{7} \hat{k}\right)=2 \text {. }\)

Hence, the unit vector normal to the given plane is \(\hat{n}=\left(-\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}-\frac{6}{7} \hat{k}\right) .\)

Example 5 Find the direction cosines of the perpendicular from the origin to the plane \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})+3=0\).

Solution

The given equation may be written as \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})=-3\)

⇒ \(\vec{r} \cdot(-6 \hat{i}+3 \hat{j}+2 \hat{k})=3\)

⇒ \(\vec{r} \cdot \vec{n}=3 \text {, where } \vec{n}=(-6 \hat{i}+3 \hat{j}+2 \hat{k})\)

⇒ \(\vec{r} \cdot \frac{\vec{n}}{|\vec{n}|}=\frac{3}{|\vec{n}|} \text {, where }|\vec{n}|=\sqrt{(-6)^2+3^2+2^2}=7\)

⇒ \(\vec{r} \cdot \frac{(-6 \hat{i}+3 \hat{j}+2 \hat{k})}{7}=\frac{3}{7}\)

⇒ \(\vec{r} \cdot\left(-\frac{6}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{2}{7} \hat{k}\right)=\frac{3}{7} .\)

Hence, the direction cosines of the normal to the plane are \(\left(-\frac{6}{7}, \frac{3}{7}, \frac{2}{7}\right)\).

Example 6 Find the vector equation of a plane which is at a distance of 5 units from the origin and which has -1, 2, 2 as the direction ratios of a normal to it.

Solution

The direction ratios of the normal to the plane are -1, 2, 2. So, the normal vector is given by \(\hat{n}=-\hat{i}+2 \hat{j}+2 \hat{k}\).

∴ \(|\vec{n}|=\sqrt{(-1)^2+2^2+2^2}=3\)

⇒ \(\hat{n}=\frac{\vec{n}}{|\vec{n}|}=\frac{(-\hat{i}+2 \hat{j}+2 \hat{k})}{3}=\left(-\frac{1}{3} \hat{i}+\frac{2}{3} \hat{j}+\frac{2}{3} \hat{k}\right) \text {. }\)

Hence, the required equation of the plane is

\(\vec{r} \cdot \hat{n}=5 \text {, i.e., } \vec{r} \cdot\left(-\frac{1}{3} \hat{i}+\frac{2}{3} \hat{j}+\frac{2}{3} \hat{k}\right)=5 \text {. }\)

Example 7 Find the Cartesian equation of a plane whose vector equation is \(\vec{r} \cdot(2 \hat{i}+5 \hat{j}-4 \hat{k})=3\).

Solution

We have

\(\vec{r} \cdot(2 \hat{i}+5 \hat{j}-4 \hat{k})=3\)

⇔ \((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(2 \hat{i}+5 \hat{j}-4 \hat{k})=3\)

⇔ 2x + 5y – 4z = 3.

Hence, the required equation is 2x + 5y – 4z = 3.

Example 8 Find the vector equation of a plane whose Cartesian equation is 5x – 7y + 2z = 4.

Solution

We have

5x – 7y + 2z = 4.

⇔ \((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(5 \hat{i}-7 \hat{j}+2 \hat{k})=4\)

⇔ \(\vec{r} \cdot(5 \hat{i}-7 \hat{j}+2 \hat{k})=4 .\)

Hence, the required equation is \(\vec{r} \cdot(5 \hat{i}-7 \hat{j}+2 \hat{k})=4 .\)

Example 9 Find a vector normal to the plane x + 2y + 3z – 6 = 0.

Solution

We have

x + 2y + 3z = 6

⇔ \((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(\hat{i}+2 \hat{j}+3 \hat{k})=6\)

⇔ \(\hat{r} \cdot(\hat{i}+2 \hat{j}+3 \hat{k})=6 .\)

Hence, the vector normal to the given plane is \((\hat{i}+2 \hat{j}+3 \hat{k})\).

Example 10 Reduce the equation of the plane x – 2y + 2z – 9 = 0 to the normal form, and hence find the length of the perpendicular from the origin to the plane. Also, find the direction cosines of the normal to the plane.

Solution

The equation of the given plane is x – 2y + 2z = 9 …(1)

Dividing throughout by \(\sqrt{1^2+(-2)^2+2^2}\), i.e., by 3, we get

\(\frac{1}{3} x-\frac{2}{3} y+\frac{2}{3} z=3\), which is the required normal form.

The length of the perpendicular from the origin to the plane = 3 units.

The direction cosines of the normal to the plane are \(\frac{1}{3}\), –\(\frac{2}{3}\), \(\frac{2}{3}\).

Common Questions on Planes and Their Solutions

Example 11 Reduce the equation of the plane 12x – 3y + 4z + 5 = 0 to the normal form, and hence find the length of the perpendicular from the origin to the plane. Write down the direction cosines of the normal to the plane.

Solution

The given equation is

12x – 3y + 4z + 52 = 0

⇒ 12x – 3y + 4z = -52

⇒ -12x + 3y – 4z = 52 …(1)

Dividing (1) throughout by \(\sqrt{(-12)^2+3^2+(-4)^2}\), i.e., by 13, we get \(\left(\frac{-12}{13} x+\frac{3}{13} y-\frac{4}{13} z\right)=4\)

This is in the normal form, lx + my + nz = p.

The length of the perpendicular from the origin to this plane is 4 units.

The direction cosines of the normal to the plane are \(\left(\frac{-12}{13}, \frac{3}{13},-\frac{4}{13}\right)\) .

Example 12 The coordinates of the foot of the perpendicular drawn from the origin to a plane are (4, -2, -5). Find the equation of the plane.

Solution

Let O be the origin, and let N(4,-2,-5) be the foot of the perpendicular drawn from O to the given plane.

Let P(x,y,z) be an arbitrary point on the plane. Then, the d.r.’s of \(\overrightarrow{N P}\) are (x-4), (y+2), (z+5).

The d.r.’s of \(\overrightarrow{O N}\) are 4, -, -5.

Also, \(\overrightarrow{O N} \perp \overrightarrow{N P}\)

⇒ \(\overrightarrow{O N} \cdot \overrightarrow{N P}=0\)

⇒ 4(x-4) – 2(y+2) – 5(z+5) = 0

⇒ 4x – 2y – 5z – 45 = 0.

Hence, 4x – 2y – 5z = 45 is the required equation of the plane.

Example 13 Find the Cartesian form of the equation of the plane \(\vec{r}=(s-2 t) \hat{i}+(3-t) \hat{j}+(2 s+t) \hat{k} .\)

Solution

We have

\(\vec{r}=(s-2 t) \hat{i}+(3-t) \hat{j}+(2 s+t) \hat{k}\)

⇔ \((x \hat{i}+y \hat{j}+z \hat{k})=(s-2 t) \hat{i}+(3-t) \hat{j}+(2 s+t) \hat{k}\)

⇔ x = s – 2t, y = 3 – t and z = 2s + t

⇔ x – 2y = (s-6) and y + z = (3+2s) [eliminating t]

⇔ x – 2y + 6 = \(\frac{1}{2}\) (y + z – 3) [equating the values of s]

⇔ 2x – 4y + 12 = y + z – 3

⇔ 2x – 5y – z + 15 = 0.

This is the required Cartesian form of the equation of the given plane.

Equation of a Plane Parallel to a Given Plane

Vector Form

Any plane parallel to the plane \(\vec{r} \cdot \vec{n}=d_1\) is given by \(\vec{r} \cdot \vec{n}=d_2\), where the constant d2 is determined by a given condition.

Example Find the vector equation of the plane through (3,4,-1), which is parallel to the plane \(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+5 \hat{k})+2=0 .\)

Solution

Let the required equation of the plane be

\(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+5 \hat{k})=d\) …(1)

Since it passes through the point A(3,4,-1), which has the position vector \((3 \hat{i}+4 \hat{j}-\hat{k})\), we have

\((3 \hat{i}+4 \hat{j}-\hat{k}) \cdot(2 \hat{i}-3 \hat{j}+5 \hat{k})=d\)

⇔ d = [3 x 2 + 4 x (-3) + (-1) x 5] = -11.

Hence, the required equation of the plane is

\(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+5 \hat{k})+11=0 .\)

Cartesian Form

Let ax + by + cz + d = 0 be a given plane.

Then, any plane parallel to this plane is of the form ax + by + cz + k = 0, where k is determined by a given condition.

Example Find the equation of the plane which is parallel to the plane 2x – 3y + z + 8 = 0 and which passes through the point (-1,1,2).

Solution

Any plane parallel to the given plane is 2x – 3y + z + k = 0 …(1)

If it passes through (-1,1,2) then

2 x (-1) – 3 x 1 + 2 + k = 0 ⇔ k = 3.

Hence, the required equation of the plane is 2x – 3y + z + 3 = 0.

Equation of a Plane through the Intersection of Two Planes

Vector Form

Theorem 1 The equation of a plane through the intersection of two planes \(\vec{r} \cdot \overrightarrow{n_1}=q_1 and \vec{r} \cdot \overrightarrow{n_2}=q_2\) is given by \(\vec{r} \cdot\left(\overrightarrow{n_1}+\lambda \overrightarrow{n_2}\right)=q_1+\lambda q_2.\)

Proof Let π₁ and π₂ be two intersecting planes, and let their equations be \(\vec{r} \cdot \overrightarrow{n_1}=q_1 and \vec{r} \cdot \overrightarrow{n_2}=q_2.\)

Let \(\overrightarrow{r_1}\) be the position vector of a point common to them.

Then, \(\vec{r} \cdot \overrightarrow{n_1}=q_1 and \vec{r} \cdot \overrightarrow{n_2}=q_2\)

⇒ \(\overrightarrow{r_1} \cdot \overrightarrow{n_1}+\lambda\left(\overrightarrow{r_1} \cdot \overrightarrow{n_2}\right)=q_1+\lambda q_2\)

⇒ \(\overrightarrow{r_1} \cdot\left(\overrightarrow{n_1}+\lambda \overrightarrow{n_2}\right)=q_1+\lambda q_2 .\)

Thus, \(\vec{r}=\overrightarrow{r_1}\) satisfies the equation \(\vec{r} \cdot\left(\overrightarrow{n_1}+\lambda \overrightarrow{n_2}\right)=q_1+\lambda q_2\).

Hence, the equation of any plane through the intersection of two planes \(\vec{r} \cdot \overrightarrow{n_1}=q_1 and \vec{r} \cdot \overrightarrow{n_2}=q_2\) is given by

\(\vec{r} \cdot\left(\overrightarrow{n_1}+\lambda \overrightarrow{n_2}\right)=q_1+\lambda q_2\).

Theorem 2 Two Planes always intersect in a line

Proof

Let π₁ and π₂ be two intersecting planes, and let \(\vec{a}\) be the position vector of a point common to them.

Then, their equations are of the form

\((\vec{r}-\vec{a}) \cdot \overrightarrow{n_1}=0 \text { and }(\vec{r}-\vec{a}) \cdot \overrightarrow{n_2}=0\)

⇒ \((\vec{r}-\vec{a})\) is perpendicular to each one of \(\overrightarrow{n_1} \text { and } \overrightarrow{n_2}\)

⇒ \((\vec{r}-\vec{a}) is parallel to \left(\overrightarrow{n_1} \times \overrightarrow{n_2}\right)\)

⇒ \((\vec{r}-\vec{a})=\lambda\left(\vec{n}_1 \times \vec{n}_2\right)\) for some scalar λ

⇒ \(\vec{r}=\vec{a}+\lambda \vec{b}, \text { where } \vec{b}=\left(\overrightarrow{n_1} \times \overrightarrow{n_2}\right) \text {. }\)

But, we know that \(\vec{r}=\vec{a}+\lambda \vec{b}\) is the vector equation of a line.

Hence, two planes alwalys intersect in a line.

Cartesian Form

Theorem 3 The equation of a plane through the intersection of two planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is given by (a₁x + b₁y + c₁z + d₁) + λ(a₂x + b₂y + c₂z + d₂) = 0.

Proof

The given equations are

a₁x + b₁y + c₁z + d₁ = 0 …(1)

a₂x + b₂y + c₂z + d₂ = 0 …(2)

Consider the equation

(a₁x + b₁y + c₁z + d₁) + λ(a₂x + b₂y + c₂z + d₂) = 0

⇒ (a₁ + λa₂)x + (b₁ + λb₂)y + (c₁ + λc₂)z + (d₁ + λd₂) = 0 …(3)

This being a first – degree equation in x,y,z, represents a plane. In order to prove that (3) represents a plane passing through the intersection of the planes (1) and (2), it is sufficient to show that every point on the line of intersection of (1) and (2) is point on (3).

Let (α, β, γ) be a point common to (1) and (2).

Then, a₁α + b₁β + c₁γ + d₁ = 0 and a₂α + b₂β + c₂γ + d₂ = 0

⇒ (a₁α + b₁β + c₁γ + d₁) + λ(a₂α + b₂β + c₂γ + d₂) = 0

⇒ (α, β, γ)

⇒ (a₁α + b₁β + c₁γ + d₁) + λ(a₂α + b₂β + c₂γ + d₂) = 0 represents a plane through the intersection of the planes

a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0

Solved Examples

Example 1 Find the equation of the plane passing through the line of intersection of the planes 2x – 7y + 4z = 3 and 3x – 5y + 4z + 11 = 0 and the point (-2,1,3).

Solution

Any plane through the intersection of the two given plane is

(2x – 7y + 4z – 3) + λ(3x – 5y + 4z + 11) = 0 …(1)

If it passes through the point (-2,1,3), we have

[2 x (-2) – 7 x 1 + 4 x 3 – 3] + λ[3 x (-2) – 5 x 1 + 4 x 3 + 11] = 0 …(1)

⇔ -2 + 12λ = 0 ⇔ 12λ = 2 ⇔ λ = \(\frac{2}{12}\) = \(\frac{1}{6}\).

Putting λ = \(\frac{1}{6}\) in (1), we get the required equation of the plane as

(2x – 7y + 4z – 3) + \(\frac{1}{6}\) (3x – 5y + 4z + 11) = 0

⇔ (12x – 42y + 24z – 18) + (3x – 5y + 4z + 11) = 0

⇔ 15x – 47y + 28z – 7 = 0.

The equation of the plane passing through the line of intersection of the planes 15x – 47y + 28z – 7 = 0.

Example 2 Find the equation of the plane which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0 and which is perpendicular to the plane 5x + 3y – 6z + 8 = 0.

Solution

Any plane through the intersection of the two given planes is given by

(x + 2y + 3z – 4) + λ(2x + y – z + 5) = 0

⇔ (1+2λ)x + (2+λ)y + (3-λ)z + (5λ-4) = 0 …(1)

If the plane (1) is perpendicular to the plane 5x + 3y – 6z + 8 = 0, we have

5(1+2λ) + 3(2+λ) – 6(3-λ) = 0 ⇔ λ = \(\frac{7}{19}\).

Hence, the required equation of the plane is

\(\left(1+\frac{14}{19}\right) x+\left(2+\frac{7}{19}\right) y+\left(3-\frac{7}{19}\right) z+\left(\frac{35}{19}-4\right)=0\)

⇔ \(\frac{33 x}{19}+\frac{45 y}{19}+\frac{50 z}{19}-\frac{41}{19}=0\) ⇔ 33x + 45y + 50z – 41 = 0.

The equation of the plane which contains the line of intersection of the planes 33x + 45y + 50z – 41 = 0.

Example 3 Find the distance between the parallel planes 2x – y + 3z + 4 = 0 and 6x – 3y + 9z – 3 = 0.

Solution

Let P(x₁,y₁,z₁) be any point on the plane 2x – y + 3z + 4 = 0.

Then, 2x₁ – y₁ + 3z₁ + 4 = 0 ⇒ 2x₁ – y₁ + 3z₁ = -4 …(1)

∴ the distance p of the point P(x₁,y₁,z₁) from the plane 6x – 3y + 9z = 0 is given by

P = \(\frac{\left|6 x_1-3 y_1+9 z_1-3\right|}{\sqrt{6^2+(-3)^2+9^2}}=\frac{\left|3\left(2 x_1-y_1+3 z_1\right)-3\right|}{\sqrt{126}}\)

= \(\frac{|3 \times(-4)-3|}{\sqrt{126}}=\frac{15}{3 \sqrt{14}}=\frac{5}{\sqrt{14}} \text { units. }\)

The distance between the parallel planes = \(\frac{|3 \times(-4)-3|}{\sqrt{126}}=\frac{15}{3 \sqrt{14}}=\frac{5}{\sqrt{14}} \text { units. }\)

Example 4 Find the equation of a plane through the intersection of the planes \(\vec{r} \cdot(\hat{i}+3 \hat{j}-\hat{k})=5 \text { and } \vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=3\), and passing through the point (2,1,-2).

Solution

Any plane through the intersection of the two given planes is

\([\vec{r} \cdot(\hat{i}+3 \hat{j}-\hat{k})-5]+\lambda[\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})-3]=0\)

⇒ \(\hat{r} \cdot[(1+2 \lambda) \hat{i}+(3-\lambda) \hat{j}+(\lambda-1) \hat{k}]-(5+3 \lambda)=0\) …(1)

If (1) passes through (2,1,-2) then \(\hat{r}=(2 \hat{i}+\hat{j}-2 \hat{k})\) should satisfy it.

∴ \((2 \hat{i}+\hat{j}-2 \hat{k}) \cdot[(1+2 \lambda) \hat{i}+(3-\lambda) \hat{j}+(\lambda-1) \hat{k}]-(5+3 \lambda)=0\)

⇔ 2(1+2λ) + (3-λ) – 2(λ-1) – (5+3λ) = 0

⇔ 2λ = 2 ⇔ λ = 1.

Putting λ = 1 in (1), we get the required equation of the plane as \(\vec{r} \cdot(3 \hat{i}+2 \hat{j})=8 .\)

Example 5 Find the vector equation of the plane through the line of intersection of the planes \(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+4 \hat{k})=1 \text { and } \vec{r} \cdot(\hat{i}-\hat{j})+4=0\), and perpendicular to the plane \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})+8=0 .\)

Solution

Any plane through the line of intersection of the two given plane is

\([\vec{r} \cdot(2 \hat{i}-3 \hat{j}+4 \hat{k})-1]+\lambda[\vec{r} \cdot(\hat{i}-\hat{j})+4]=0\)

⇒ \(\vec{r} \cdot[(2+\lambda) \hat{i}-(3+\lambda) \hat{j}+4 \hat{k}]=1-4 \lambda\) …(1)

If this plane is perpendicular to the plane \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})+8=0\), we have

2(2+λ) + (3+λ) + 4 = 0 ⇔ 3λ + 11 = 0 ⇔ λ = \(-\frac{11}{3}\).

Putting λ = \(-\frac{11}{3}\) in (1), we get the required equation of the plane as

\(\vec{r} \cdot(-5 \hat{i}+2 \hat{j}+12 \hat{k})=47.\)

Example 6 Find the Cartesian as well as the vector equation of the plane through the intersection of the planes \(\vec{r} \cdot(2 \hat{i}+6 \hat{j})+12=0 \text { and } \vec{r} \cdot(3 \hat{i}-\hat{j}+4 \hat{k})=0\), which is at a unit distance from the origin.

Solution

Any plane through the intersection of the two given planes is given by

\([\vec{r} \cdot(2 \hat{i}+6 \hat{j})+12]+\lambda[\vec{r} \cdot(3 \hat{i}-\hat{j}+4 \hat{k})]=0\)

⇔ \(\vec{r} \cdot[(2+3 \lambda) \hat{i}+(6-\lambda) \hat{j}+(4 \lambda) \hat{k}]+12=0\) …(1)

This plane is at a unit distance from the origin.

∴ the length of the perpendicular from the origin to (1) is 1.

∴ \(\frac{12}{\sqrt{(2+3 \lambda)^2+(6-\lambda)^2+(4 \lambda)^2}}=1\)

⇔ (2+3λ)² + (6-λ)² + (4λ)² = 144

⇔ 26λ² + 40 = 144 ⇔ 26λ² = 104

⇔ λ² = 4 ⇔ λ = ±2.

Putting λ = 2 and λ = -2 in (1), we get the required equations as

\(\vec{r} \cdot(8 \hat{i}+4 \hat{j}+8 \hat{k})+12=0 \text {, and } \vec{r} \cdot(-4 \hat{i}+8 \hat{j}-8 \hat{k})+12=0\)

⇔ \(\vec{r} \cdot(2 \hat{i}+\hat{j}+2 \hat{k})+3=0 \text {, and } \vec{r} \cdot(-\hat{i}+2 \hat{j}-2 \hat{k})+3=0 \text {. }\)

In the Cartesian form, these equations are

\((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(2 \hat{i}+\hat{j}+2 \hat{k})+3=0\), and

\((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(-\hat{i}+2 \hat{j}-2 \hat{k})+3=0\)

⇔ 2x + y + 2z + 3 = 0 and -x + 2y – 2z + 3 = 0

⇔ 2x + y + 2z + 3 = 0 and x – 2y + 2z – 3 = 0.

Equation of a Plane Passing through a Given Point and Perpendicular to a Given Vector

Vector Form

Theorem 1 The vector equation of a plane passing through a point A with position vector \(\vec{a}\) and perpendicular to a given vector \(\vec{n}\) is \((\vec{r}-\vec{a}) \cdot \vec{n}=0 .\)

Proof

Let O be the origin, and let π be the given plane.

Let A be a given point on the plane with position vector \(\vec{a}\).

Let P be an arbitrary point on the plane with position vector \(\vec{r}\).

Then, \(\overrightarrow{O A}=\vec{a} \text {, and } \overrightarrow{O P}=\vec{r} \text {. }\)

∴ \(\overrightarrow{A P}=(\overrightarrow{O P}-\overrightarrow{O A})=(\vec{r}-\vec{a})\)

Let \(\overrightarrow{O N}=\vec{n}\) be normal to the plane.

Now, \(\overrightarrow{A P}\) lies in the plane and \vec{n} is normal to the plane.

∴ \(\overrightarrow{A P} \perp \vec{n}\)

⇒ \(\overrightarrow{A P} \cdot \vec{n}=0\)

⇒ \((\vec{r}-\vec{a}) \cdot \vec{n}=0 .\)

Hence, the equation of the plane passing through the point with position vector \vec{a} and perpendicular to \(\vec{n}\) is \((\vec{r}-\vec{a}) \cdot \vec{n}=0 .\)

Corollary The vector equation of the plane passing through the origin and perpendicular to \(\vec{n}\) is \(\vec{r} \cdot \vec{n}=0\).

Cartesian Form

Theorem 2 The Cartesian equation of the plane passing through a point A(x₁,y₁,z₁) and perpendicular to a line having direction ratios n1, n2, n3 is (x-x₁)n₁ + (y-y₁)n₂ + (z-z₁)n₃ = 0.

Proof

Let \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}, \vec{a}=x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k} \text { and } \vec{n}=n_1 \hat{i}+n_2 \hat{j}+n_3 \hat{k}\)

Then, \((\vec{r}-\vec{a}) \cdot \vec{n}=0\)

⇒ (x-x₁)n₁ + (y-y₁)n₂ + (z-z₁)n₃ = 0.

Equation of a Plane Passing through a Given Point and Parallel to Two Given Lines

Vector Form

Theorem 1 The vector equation of a plane passing through a given point with position vector \(\vec{a}\) and parallel to two given vector \(\vec{b}\) and \(\vec{c}\) is \((\vec{r}-\vec{a}) \cdot(\vec{b} \times \vec{c})=0 .\)

Proof

The required plane is parallel to vectors \(\vec{b}\) and \(\vec{c}\).

So, the vector \(\vec{n}=(\vec{b} \times \vec{c})\) is perpendicular to this plane.

Thus, we have to find the equation of a plane passing through the point with position vector \(\vec{a}\) and perpendicular to the vector \(\vec{n}\).

So, its equation is

\((\vec{r}-\vec{a}) \cdot \vec{n}=0 \text {, i.e., }(\vec{r}-\vec{a}) \cdot(\vec{b} \times \vec{c})=0 \text {. }\)

Hence, the required equation of the plane is \((\vec{r}-\vec{a}) \cdot(\vec{b} \times \vec{c})=0 .\)

Parametric Form

Theorem 2 The vector equation of a plane passing through a given point with position vector \(\vec{a}\) and parallel to two given vectors \(\vec{b}\) and \(\vec{c}\) is \(\vec{r}=\vec{a}+\lambda \vec{b}+\mu \vec{c}\), where λ and μ are scalars.

Proof

Let A be a given point with position vector \(\vec{a}\). Let \(\vec{r}\) be the position vector of a arbitrary point P on the plane passing through the point A, and parallel to \(\vec{b}\) and \(\vec{c}\).

∴ \(\overrightarrow{A P}=(\text { p.v. of } P)-(\text { p.v. of } A)=(\vec{r}-\vec{a})\)

Clearly, the vectors \((\vec{r}-\vec{a})\), \(\vec{b} \text { and } \vec{c}\) are coplanar.

∴ \((\vec{r}-\vec{a})\) lies in the plane of \(\vec{b}\) and \(\vec{c}\).

So, \((\vec{r}-\vec{a})\) can be expressed as a linear combination of \(\vec{b}\) and \(\vec{c}\).

∴ there exist scalars λ and μ such that

\((\vec{r}-\vec{a})=\lambda \vec{b}+\mu \vec{c} \Rightarrow \vec{r}=\vec{a}+\lambda \vec{b}+\mu \vec{c}\),

which is the required equation of the plane.

Cartesian Form

Theorem 3 The equation of the plane passing through a given point A(x₁,y₁,z₁) and parallel to two given lines having direction ratios b₁, b₂, b₃ and c₁, c₂, c₃ is

\(\left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{array}\right|=0 .\)

Proof

Let us consider a plane passing through a given point A(x₁,y₁,z₁) and parallel to two given lines having direction ratios b₁, b₂, b₃ and c₁, c₂, c₃.

Let P(x,y,z) be an arbitrary point on the plane. Then,

\(\overrightarrow{A P}\) = (p.v. of P) – (p.v. of A)

= \((x \hat{i}+y \hat{j}+z \hat{k})-\left(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}\right)\)

= \(\left(x-x_1\right) \hat{i}+\left(y-y_1\right) \hat{j}+\left(z-z_1\right) \hat{k} .\)

It is given that the plane is parallel to two lines having direction ratios b₁, b₂, b₃ and c₁, c₂, c₃.

So, the given plane is parallel to each of the vectors

\(\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k} \text { and } \vec{c}=c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}\)

∴ \(\overrightarrow{A P}\), \(\vec{b}\) and \(\vec{c}\) are coplanar, and therefore their scalar triple product must be zero.

\(\left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{array}\right|=0 .\)

This is the required equation of the plane passing through the point (x₁,y₁,z₁) and parallel to two given lines having direction ratios b₁, b₂, b₃ and c₁, c₂, c₃.

Equation of a Plane Passing through Three Given Points

Vector Form

Theorem 1 The vector equation of a plane passing through three noncollinear points with position vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) is \((\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]=0.\)

Proof

Let A, B, C be three given noncollinear points having position vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) respectively.

Let P be an arbitrary point on the plane passing through the points

A, B, C and let \(\vec{r}\) be the position vector of P. Then,

\(\overrightarrow{A P}=\text { (p.v. of } P \text { ) – (p.v. of } A)=(\vec{r}-\vec{a})\),

\(\overrightarrow{A B}=\text { (p.v. of } B \text { ) – (p.v. of } A)=(\vec{b}-\vec{a})\),

\(\overrightarrow{A C}=\text { (p.v. of } C \text { ) – (p.v. of } A)=(\vec{c}-\vec{a})\).

Since the points A, B, C, P lie on the plane, the vectors \(\overrightarrow{A P}\), \(\overrightarrow{A B}\), \(\overrightarrow{A C}\) are coplanar.

So, the scalar triple product of these vectors is 0.

∴ \([\overrightarrow{A P} \overrightarrow{A B} \overrightarrow{A C}]=0\)

⇒ \(\overrightarrow{A P} \cdot(\overrightarrow{A B} \times \overrightarrow{A C})=0\)

⇒ \((\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]=0\), which is the required equation of the plane.

Cartesian Form

Theorem 2 The equation of a plane passing through three given noncollinear points A(x₁,y₁,z₁), B(x₂,y₂,z₂) and C(x₃,y₃,z₃) is given by

\(\left|\begin{array}{lll}
x-x_1 & y-y_1 & z-z_1 \\
x-x_2 & y-y_2 & z-z_2 \\
x-x_3 & y-y_3 & z-z_3
\end{array}\right|=0 .\)

Proof

Let P(x,y,z) be an arbitrary point on the plane passing through three given noncollinear points A(x₁,y₁,z₁), B(x₂,y₂,z₂) and C(x₃,y₃,z₃). Then,

\(\overrightarrow{A P}=\text { (p.v. of } P \text { ) – (p.v. of } A)\)

= \((x \hat{i}+y \hat{j}+z \hat{k})-\left(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}\right)\)

= \(\left(x-x_1\right) \hat{i}+\left(y-y_1\right) \hat{j}+\left(z-z_1\right) \hat{k}\);

\(\overrightarrow{B P}=\text { (p.v. of } P \text { ) – (p.v. of } B)\)

= \((x \hat{i}+y \hat{j}+z \hat{k})-\left(x_2 \hat{i}+y_2 \hat{j}+z_2 \hat{k}\right)\)

= \(\left(x-x_2\right) \hat{i}+\left(y-y_2\right) \hat{j}+\left(z-z_2\right) \hat{k}\);

and \(\overrightarrow{C P}=\text { (p.v. of } P \text { ) – (p.v. of } C)\)

= \((x \hat{i}+y \hat{j}+z \hat{k})-\left(x_3 \hat{i}+y_3 \hat{j}+z_3 \hat{k}\right)\)

= \(\left(x-x_3\right) \hat{i}+\left(y-y_3\right) \hat{j}+\left(z-z_3\right) \hat{k}\)

Now, the vectors \(\overrightarrow{A P}\), \(\overrightarrow{B P}\), \(\overrightarrow{C P}\) being coplanar, their scalar triple product must be zero.

∴ \([\overrightarrow{A P} \overrightarrow{B P} \overrightarrow{C P}]=0\)

⇒ \(\left|\begin{array}{lll}
x-x_1 & y-y_1 & z-z_1 \\
x-x_2 & y-y_2 & z-z_2 \\
x-x_3 & y-y_3 & z-z_3
\end{array}\right|=0 .\) which is the required equation of the plane.

Applications of Plane Geometry in Mathematics

Angle between Two Planes

The angle between two given planes is the angle between their normals.

Vector Form

Theorem 1 If θ be the angle between two planes \(\vec{r} \cdot \overrightarrow{n_1}=q_1 \text { and } \vec{r} \cdot \overrightarrow{n_2}=q_2\)

then cos θ = \(\frac{\overrightarrow{n_1} \cdot \overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|\left|\overrightarrow{n_2}\right|} .\)

Proof

Let θ be the angle between two planes whose vector equations are \(\vec{r} \cdot \overrightarrow{n_1}=q_1 \text { and } \vec{r} \cdot \overrightarrow{n_2}=q_2.\)

Then, θ is the angle between \(\overrightarrow{n_1} and \overrightarrow{n_2}\).

∴ cos θ = \(\frac{\overrightarrow{n_1} \cdot \overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|\left|\overrightarrow{n_2}\right|} .\)

Remark The acute angle θ between θ is given by

cos θ = \(\frac{\overrightarrow{n_1} \cdot \overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|\left|\overrightarrow{n_2}\right|} .\)

Two Important Results

1. Condition for two planes to be perpendicular to each other

Two planes \(\vec{r} \cdot \overrightarrow{n_1}=q_1 \text { and } \vec{r} \cdot \overrightarrow{n_2}=q_2\) are perpendicular to each other

⇔ \(\overrightarrow{n_1} \perp \overrightarrow{n_2}\)

⇔ \(\overrightarrow{n_1} \cdot \overrightarrow{n_2}=0 .\)

2. Condition for two planes to be parallel to each other

Two planes \(\vec{r} \cdot \overrightarrow{n_1}=q_1 \text { and } \vec{r} \cdot \overrightarrow{n_2}=q_2\) are parallel to each other

⇔ \(\overrightarrow{n_1} \| \overrightarrow{n_2}\)

⇔ \(\overrightarrow{n_1}=\lambda \overrightarrow{n_2}\) for some scalar λ.

Remark 1 Any plane parallel to \(\vec{r} \cdot \vec{n}=q \text { is } \vec{r} \cdot \vec{n}=q_1 \text {. }\)

Remark 2 The equation of the plane parallel to the plane \(\vec{r} \cdot \vec{n}=q\) and passing through the point with position vector \(\vec{a}\) is \((\vec{r}-\vec{a}) \cdot \vec{n}=0 .\)

Cartesian Form

Theorem 2 Let θ be the angle between two planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0.

Then, cos θ = \(\frac{\left(a_1 a_2+b_1 b_2+c_1 c_2\right)}{\sqrt{\left(a_1^2+b_1^2+c_1^2\right)} \sqrt{\left(a_2^2+b_2^2+c_2^2\right)}} .\)

Proof

Let θ be the angle between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0

Then, θ is the angle between their normals.

But, the direction ratios of the normals to the given planes are a₁, b₁, c₁ and a₂, b₂, c₂.

∴ cos θ = \(\frac{\left(a_1 a_2+b_1 b_2+c_1 c_2\right)}{\sqrt{\left(a_1^2+b_1^2+c_1^2\right)} \sqrt{\left(a_2^2+b_2^2+c_2^2\right)}} .\)

Remark

The acute angle θ between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0

is given by cos θ = \(\frac{\left(a_1 a_2+b_1 b_2+c_1 c_2\right)}{\sqrt{\left(a_1^2+b_1^2+c_1^2\right)} \sqrt{\left(a_2^2+b_2^2+c_2^2\right)}} .\)

Two Important Results

1. Condition for two planes to be perpendicular to each other

Two planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are perpendicular to each other

⇔ their normals are perpendicular to each other

⇔ lines with direction ratios a₁, b₁, c₁ and a₂, b₂, c₂ are perpendicular to each other

⇔ a₁a₂ + b₁b₂ + c₁c₂ = 0.

2. Condition for two planes to be parallel to each other

Two planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are parallel to each other

⇔ their normals are parallel to each other

⇔ lines with direction ratios a₁, b₁, c₁ and a₂, b₂, c₂ are parallel to each other

⇔ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2} .\)

Remark 1 The equation of any plane parallel to the plane ax + by + cz + d = 0 is ax + by +cz + λ = 0

Remark 2 The equation of a plane passing through (x₁,y₁,z₁) and parallel to the plane ax + by + cz + d = 0 given by a(x-x₁) + b(y-y₁) + c(z-z₁) = 0.

Remark 3 The equation of any plane parallel to the xy-plane is z = λ.

This plane is perpendicular to the z-axis

Similarly, the equation of any plane parallel to the zx-plane is y = λ.

And, the equation of any plane parallel to the yz-plane is x = λ.

Solved Examples

Example 1 Find the angle between the planes \(\vec{r} \cdot(\hat{i}+\hat{j}+2 \hat{k})=5 \text { and } \vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=8 \text {. }\)

Solution

We know that the angle between the planes \(\vec{r} \cdot \overrightarrow{n_1}=q_1 \text { and } \vec{r} \cdot \overrightarrow{n_2}=q_2\) is given by

\(\cos \theta=\frac{\overrightarrow{n_1} \cdot \overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|\left|\overrightarrow{n_2}\right|} .\)

Here, \(\overrightarrow{n_1}=(\hat{i}+\hat{j}+2 \hat{k}) \text { and } \overrightarrow{n_2}=(2 \hat{i}-\hat{j}+\hat{k}) \text {. }\)

∴ \(\cos \theta=\frac{(\hat{i}+\hat{j}+2 \hat{k}) \cdot(2 \hat{i}-\hat{j}+\hat{k})}{|\hat{i}+\hat{j}+2 \hat{k}||2 \hat{i}-\hat{j}+\hat{k}|}\)

= \(\frac{\{1 \times 2+1 \times(-1)+2 \times 1\}}{\left\{\sqrt{1^2+1^2+2^2}\right\}\left\{\sqrt{2^2+(-1)^2+1^2}\right\}}=\frac{3}{6}=\frac{1}{2}\)

⇒ \(\theta=\frac{\pi}{3} .\)

Hence, the angle between the given planes is \(\left(\frac{\pi}{3}\right)\).

Example 2 Find the angle between the planes \(\vec{r} \cdot(2 \hat{i}+2 \hat{j}-3 \hat{k})=5 \text { and } \vec{r} \cdot(3 \hat{i}-3 \hat{j}+5 \hat{k})=6\)

Solution

We know that the angle between the planes \(\vec{r} \cdot \overrightarrow{n_1}=q_1 \text { and } \vec{r} \cdot \overrightarrow{n_2}=q_2\) is given by

\(\cos \theta=\frac{\overrightarrow{n_1} \cdot \overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|\left|\overrightarrow{n_2}\right|} .\)

Here, \(\overrightarrow{n_1}=(2 \hat{i}+2 \hat{j}-3 \hat{k}) \text { and } \overrightarrow{n_2}=(3 \hat{i}-3 \hat{j}+5 \hat{k}) \text {. }\)

∴ \(\cos \theta=\frac{(2 \hat{i}+2 \hat{j}-3 \hat{k}) \cdot(3 \hat{i}-3 \hat{j}+5 \hat{k})}{|2 \hat{i}+2 \hat{j}-3 \hat{k}||3 \hat{i}-3 \hat{j}+5 \hat{k}|}\)

= \(\frac{\{2 \times 3+2 \times(-3)+(-3) \times 5\}}{\left\{\sqrt{2^2+2^2+(-3)^2}\right\}\left\{\sqrt{3^2+(-3)^2+5^2}\right\}}\)

= \(\frac{-15}{(\sqrt{17})(\sqrt{43})}=\frac{-15}{\sqrt{731}}\)

⇒ \(\theta=\cos ^{-1}\left(\frac{-15}{\sqrt{731}}\right)\)

This is the obtuse angle between the given planes.

The acute angle between the given planes is \(\cos ^{-1}\left(\frac{-15}{\sqrt{731}}\right)\).

Example 3 Find the value of λ for which the planes \(\vec{r} \cdot(\hat{i}+2 \hat{j}+3 \hat{k})=13 \text { and } \vec{r} \cdot(\lambda \hat{i}+2 \hat{j}-7 \hat{k})=9\) are perpendicular to each other.

Solution

We know that the planes \(\vec{r} \cdot \overrightarrow{n_1}=q_1 \text { and } \vec{r} \cdot \overrightarrow{n_2}=q_2\) are perpendicular to each other only when \(\overrightarrow{n_1} \cdot \overrightarrow{n_2}=0 .\)

Here, \(\overrightarrow{n_1}=(\hat{i}+2 \hat{j}+3 \hat{k}) \text { and } \overrightarrow{n_2}=(\lambda \hat{i}+2 \hat{j}-7 \hat{k}) \text {. }\)

∴ the given planes are perpendicular to each other

⇔ \(\overrightarrow{n_1} \cdot \overrightarrow{n_2}=0 .\)

⇔ \((\hat{i}+2 \hat{j}+3 \hat{k}) \cdot(\lambda \hat{i}+2 \hat{j}-7 \hat{k})=0\)

⇔ 1 x λ + 2 x 2 + 3 x (-7) = 0 ⇔ λ = 17.

Hence, the required value of λ is 17.

Example 4 Find the angle between the planes x + y + 2z = 9 and 2x – y + z = 6.

Solution

We know that the angle between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is given by

\(\cos \theta=\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\left(\sqrt{a_1^2+b_1^2+c_1^2}\right)\left(\sqrt{a_2^2+b_2^2+c_2^2}\right)} .\)

Here, a₁ = 1, b₁ = 1, c₁ = 2, and a₂ = 2, b₂ = -1, c₂ = 1.

∴ \(\cos \theta=\frac{1 \times 2+1 \times(-1)+2 \times 1}{\left(\sqrt{1^2+1^2+2^2}\right)\left\{\sqrt{2^2+(-1)^2+1^2}\right\}}=\frac{3}{(\sqrt{6})(\sqrt{6})}=\frac{3}{6}=\frac{1}{2}\)

⇒ \(\theta=\frac{\pi}{3} .\)

Hence, the angel between the given planes is \(\left(\frac{\pi}{3}\right)\).

Examples of Finding Distance from a Point to a Plane

Example 5 Find the angle between the planes 2x – 3y + 4z = 1 and -x + y = 4.

Solution

We know that the angle between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is given by

\(\cos \theta=\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\left(\sqrt{a_1^2+b_1^2+c_1^2}\right)\left(\sqrt{a_2^2+b_2^2+c_2^2}\right)} .\)

Here, a₁ = 2, b₁ = -3, c₁ = 4, and a₂ = -1, b₂ = 1, c₂ = 0.

∴ \(\cos \theta=\frac{2 \times(-1)+(-3) \times 1+4 \times 0}{\left\{\sqrt{2^2+(-3)^2+4^2}\right\}\left\{\sqrt{(-1)^2+1^2+0^2}\right\}}\)

= \(\frac{-5}{(\sqrt{29})(\sqrt{2})}=\frac{-5}{\sqrt{58}}\)

⇒ \(\theta=\cos ^{-1}\left(\frac{-5}{\sqrt{58}}\right)\)

The acute angle between the given planes is \(\cos ^{-1}\left(\frac{-5}{\sqrt{58}}\right)\).

Example 6 Find the value of λ for which the planes 2x – 4y + 3z = 7 and x + 2y + λz = 18 are perpendicular to each other.

Solution

We know that the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are perpendicular to each other only when a₁a₂ + b₁b₂ + c₁c₂ = 0.

Here, a₁ = 2, b₁ = -4, c₁ = 3 and a₂ = 1, b₂ = 2, c₂ = λ.

∴ the given planes are perpendicular to each other

⇔ 2 x 1 + (-4) x 2 + 3 x λ = 0

⇔ 3λ = 6 ⇔ λ = 2.

Hence, λ = 2.

Example 7 Find the equation of the plane passing through the point (1,4,-2) and parallel to the plane -2x + y – 3z = 0.

Solution

The equation of a plane parallel to the given plane is of the form -2x + y – 3z = k for some scalar k.

Since it passes through (1,4,-2), we have

-2 x 1 + 4 – 3 x (-2) = k ⇔ k = 8.

Hence, the required equation of the plane is -2x + y – 3z = 8.

Example 8 Find the equation of the plane passing through the point (1,1,1) and perpendicular to each of the following planes x + 2y + 3z = 7 and 2x – 3y + 4z = 0.

Solution

Any plane through (1,1,1) is a(x1) + b(y-1) + c(z-1) = 0 …(1)

Now, (1) being perpendicular to each of the planes x + 2y + 3z = 7 and 2x – 3y + 4z = 0, we have

a x 1 + b x 2 + c x 3 = 0 ⇒ a + 2b + 3c = 0 …(2)

a x 2 + b x (-3) + c x 4 ⇒ 2a – 3b + 4c = 0 …(3)

Cross multiplying (2) and (3), we get

\(\frac{a}{(8+9)}=\frac{b}{(6-4)}=\frac{c}{(-3-4)}=k \text { (say) }\)

⇒ \(\frac{a}{17}=\frac{b}{2}=\frac{c}{-7}=k\)

⇒ a = 17k, b = 2k and c = -7k.

Putting these values in (1), we get

17k(x-1) + 2k(y-1) – 7k(z-1) = 0

⇔ 17(x-1) + 2(y-1) – 7(z-1) = 0

⇔ 17x + 2y – 7z – 12 = 0, which is the required equation of the plane.

Example 9 Find the equation of the plane passing through the points (2,2,1) and (9,3,6), and perpendicular to the plane 2x + 6y + 6z = 1.

Solution

Let the required plane passing through (2,2,1) be

a(x-) + b(y-2) + c(z-1) = 0 …(1)

Since it also passes through the point (9,3,6), we have

a(9-2) + b(3-2) + c(6-1) = 0 ⇒ 7a + b + 5c = 0 …(2)

Also, (1) being perpendicular to the plane 2x + 6y + 6z = 1, we have

2a + 6b + 6c = 0 …(3)

Cross multiplying (2) and (3), we get

\(\frac{a}{(6-30)}=\frac{b}{(10-42)}=\frac{c}{(42-2)}\)

⇒ \(\frac{a}{-24}=\frac{b}{-32}=\frac{c}{40}\)

⇒ \(\frac{a}{3}=\frac{b}{4}=\frac{c}{-5}=k \text { (say) }\)

⇒ a = 3k, b = 4k, and c = -5k

Putting these values of a, b, c in (1), we get the required equation of the plane as

3k(x-2) + 4k(y-2) – 5k(z-1) = 0

⇔ 3(x-2) + 4(y-2) – 5(z-1) = 0

⇒ 3x + 4y – 5z – 9 = 0.

Example 10 Find the equation of the plane passing through the points (2,3,4), (-3,5,1) and (4,-1,2).

Solution

The equation of the plane passing through the point (2,3,4) is a(x-2) + b(y-3) + c(z-4) = 0 …(1)

If this plane passes through the points (-3,5,1) and (4,-1,2) then

a(-3-2) + b(5-3) + c(1-4) = 0 ⇒ -5a + 2b – 3c = 0 …(2)

a(4-2) + b(-1-3) + c(2-4) = 0 ⇒ 2a – 4b – 2c = 0 …(3)

Cross multiplying (2) and (3), we get

\(\frac{a}{(-4-12)}=\frac{b}{(-6-10)}=\frac{c}{(20-4)} \Rightarrow \frac{a}{-16}=\frac{b}{-16}=\frac{c}{16}\)

⇒ \(\frac{a}{1}=\frac{b}{1}=\frac{c}{-1}=k \text { (say) }\)

⇒ a = k, b = k, c = -k.

Putting a = k, b = k, c = -k in (1), we get the required equation of the plane as

k(x-2) + k(y-3) – k(z-4) = 0

⇔ (x-2) + (y-3) – (z-4) = 0

⇔ x + y – z – 1 = 0.

Hence, the required equation of the plane is x + y – z – 1 = 0.

Angle between a Line and a Plane

The angle between a line and a plane is the complement of the angle between the line and the normal to the plane.

Vector Form

Theorem 1 If θ be the angle between the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) and the plane \(vec{r} \cdot \vec{n}=q\) then \(\sin \theta=\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|} .\)

Proof

Clearly, the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to \(\vec{b}\), and the plane \(\vec{r} \cdot \vec{n}=q\) is normal to \(\vec{n}\).

Let θ be the angle between the given line and the given plane.

Then, the angle between \(\vec{b}\) and \(\vec{n}\) is \(\left(\frac{\pi}{2}-\theta\right)\).

∴ \(\cos \left(\frac{\pi}{2}-\theta\right)=\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|} \Rightarrow \sin \theta=\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\)

Two Important Results

1. Condition for a given line to be perpendicular to a given plane

The line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is perpendicular to the plane \(\vec{r} \cdot \vec{n}=q\)

⇔ \(\vec{b}\) is perpendicular to the plane \(\vec{r} \cdot \vec{n}=q\)

⇔ \(\vec{b}\) is parallel to the normal \(\vec{n}\) to the plane

⇔ \(\vec{b}=t \vec{n}\), for some scalar t.

2. Condition for a given line to be parallel to a given plane

The line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=q\)

⇔ \(\vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=\)

⇔ \(\vec{b}\) is perpendicular to the normal \(\vec{n}\) to the plane

⇔ \(\vec{b} \cdot \vec{n}=0 .\)

Cartesian Form

Theorem 2 If θ is the angle between the line \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) and the plane a₂x + b₂y + c₂z + d = 0 then

\(\sin \theta=\frac{\left(a_1 a_2+b_1 b_2+c_1 c_2\right)}{\left(\sqrt{a_1^2+b_1^2+c_1^2}\right)\left(\sqrt{a_2^2+b_2^2+c_2^2}\right)} .\)

Proof

The direction ratios of the given line are a₁, b₁, c₁.

So, the given line is parallel to \(\vec{b} = a_1 \hat{i}+b_1 \hat{j}+c_1 \hat{k}\)

The normal to the given plane is parallel to \(\vec{n} = a_2 \hat{i}+b_2 \hat{j}+c_2 \hat{k}\).

Let θ be the angle between the given line and the given plane. Then, \(\left(\frac{\pi}{2}-\theta\right)\) is the angle between the given line and the normal to the given plane.

∴ \(\left(\frac{\pi}{2}-\theta\right) is the angle between \vec{b} and \vec{n}\)

⇒ \(\cos \left(\frac{\pi}{2}-\theta\right)=\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\)

⇒ \(\sin \theta=\frac{\left(a_1 \hat{i}+b_1 \hat{j}+c_1 \hat{k}\right) \cdot\left(a_2 \hat{i}+b_2 \hat{j}+c_2 \hat{k}\right)}{\left|a_1 \hat{i}+b_1 \hat{j}+c_1 \hat{k}\right| \cdot\left|a_2 \hat{i}+b_2 \hat{j}+c_2 \hat{k}\right|}\)

⇒ \(\sin \theta=\frac{\left(a_1 a_2+b_1 b_2+c_1 c_2\right)}{\left(\sqrt{a_1^2+b_1^2+c_1^2}\right)\left(\sqrt{a_2^2+b_2^2+c_2^2}\right)} .\)

Important Results

1. Condition for the given line to be perpendicular to the given plane

The line \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) is perpendicular to the plane a₂x + b₂y + c₂z + d = 0

⇔ the line \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) is parallel to the normal to thr plane a₂x + b₂y + c₂z + d = 0

⇔ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2} .\)

2. Condition for the given line to be parallel to the given plane

The line \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) is parallel to the plane a₂x + b₂y + c₂z + d = 0

⇔ the line \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) is perpendicular to the normal to the plane a₂x + b₂y + c₂z + d = 0

⇔ a₁a₂ + b₁b₂ + c₁c₂ = 0.

3. Distance between a line and a plane, parallel to each other

If the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=q\) then the distance between them is \(\frac{|\vec{a} \cdot \vec{n}-q|}{|\vec{n}|}\), which is the same as the distance of a point from the plane.

Summary

1. If θ is the angle between the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) and the plane \(\vec{r} \cdot \vec{n}=q\) then

\(\sin \theta=\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\)

2. The line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is perpendicular to the plane \(\vec{r} \cdot \vec{n}=q\) only when \(\vec{b}=t \vec{n}\) for some scalar t.

3. (1) The line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=q\) only when \(\vec{b} \cdot \vec{n}=0 .\)

(2) If the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=q\) then the distance between them is

\(\frac{|\vec{a} \cdot \vec{n}-q|}{|\vec{n}|}\)

(4) If θ is the angle between the line \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) and the plane a₂x + b₂y + c₂z + d = 0 then

\(\sin \theta=\frac{\left(a_1 a_2+b_1 b_2+c_1 c_2\right)}{\left(\sqrt{a_1^2+b_1^2+c_1^2}\right)\left(\sqrt{a_2^2+b_2^2+c_2^2}\right)} .\)

5. The line \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) is perpendicular to the plane a₂x + b₂y + c₂z + d = 0 only if \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\).

6. The line \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) is parallel to the plane a₂x + b₂y + c₂z + d = 0 only if a₁a₂ + b₁b₂ + c₁c₂ = 0.

Solved Examples

Example 1 Find the angle between the line \(\vec{r}=(\hat{i}+\hat{j}-3 \hat{k})+\lambda(2 \hat{i}+2 \hat{j}+\hat{k})\) and the plane \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}+2 \hat{k})=5 \text {. }\)

Solution

We know that the angle θ between the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) and the plane \(\vec{r} \cdot \vec{n}=q\) is given by

\(\sin \theta=\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\)

Here, \(\vec{b}=2 \hat{i}+2 \hat{j}+\hat{k} \text { and } \vec{n}=6 \hat{i}-3 \hat{j}+2 \hat{k} \text {. }\)

∴ \(\sin \theta=\frac{(2 \hat{i}+2 \hat{j}+\hat{k}) \cdot(6 \hat{i}-3 \hat{j}+2 \hat{k})}{|2 \hat{i}+2 \hat{j}+\hat{k}||6 \hat{i}-3 \hat{j}+2 \hat{k}|}\)

= \(\frac{\{2 \times 6+2 \times(-3)+1 \times 2\}}{\left(\sqrt{2^2+2^2+1^2}\right)\left\{\sqrt{\left.6^2+(-3)^2+2^2\right\}}\right.}=\left(\frac{8}{3 \times 7}\right)=\frac{8}{21}\)

⇒ \(\theta=\sin ^{-1}\left(\frac{8}{21}\right) .\)

Hence, the angle between the given line and the given plane is \(\sin ^{-1}\left(\frac{8}{21}\right) .\)

Example 2 Find the value of m for which the line \(\vec{r}=(\hat{i}+2 \hat{j}-\hat{k})+\lambda(2 \hat{i}+\hat{j}+2 \hat{k})\) is parallel to the plane \(\vec{r} \cdot(3 \hat{i}-2 \hat{j}+m \hat{k})=12\).

Solution

We know that the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane

\(\vec{r} \cdot \vec{n}=q \Leftrightarrow \vec{b} \cdot \vec{n}=0 .\)

Here, \(\vec{b}=2 \hat{i}+\hat{j}+2 \hat{k} \text { and } \vec{n}=3 \hat{i}-2 \hat{j}+m \hat{k} \text {. }\)

∴ the given line is parallel to the given plane

⇔ \(\vec{b} \cdot \vec{n}=0\)

⇔ \((2 \hat{i}+\hat{j}+2 \hat{k}) \cdot(3 \hat{i}-2 \hat{j}+m \hat{k})=0\)

⇔ 2 x 3 + 1 x (-2) + 2 x m = 0

⇔ 2m = -4 ⇔ m = -2.

Hence, m = -2.

Example 3 Show that the line \(\vec{r}=(2 \hat{i}-2 \hat{j}+3 \hat{k})+\lambda(\hat{i}-\hat{j}+4 \hat{k})\) is parallel to the plane \(\vec{r} \cdot(\hat{i}+5 \hat{j}+\hat{k})=5\) . Also, find the distance between them.

Solution

We know that the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=q\) only when \(\vec{b} \cdot \vec{n}=0.\)

And, the distance between the line and the plane is given by

\(\frac{|\vec{a} \cdot \vec{n}-q|}{|\vec{n}|}\)

Here, \(\vec{a}=2 \hat{i}-2 \hat{j}+3 \hat{k}, \vec{b}=\hat{i}-\hat{j}+4 \hat{k}, \vec{n}=\hat{i}+5 \hat{j}+\hat{k} \text { and } q=5 \text {. }\)

Now, \(\vec{b} \cdot \vec{n}=(\hat{i}-\hat{j}+4 \hat{k}) \cdot(\hat{i}+5 \hat{j}+\hat{k})=\{1 \times 1+(-1) \times 5+4 \times 1\}=0\)

Hence, the given line is parallel to the given plane.

Distance between the given line and the given plane

= \(\frac{|\vec{a} \cdot \vec{n}-q|}{|\vec{n}|}=\frac{|(2 \hat{i}-2 \hat{j}+3 \hat{k}) \cdot(\hat{i}+5 \hat{j}+\hat{k})-5|}{|\hat{i}+5 \hat{j}+\hat{k}|}\)

= \(\frac{|2 \times 1+(-2) \times 5+3 \times 1-5|}{\sqrt{1^2+5^2+1^2}}\)

= \(\frac{|2-10+3-5|}{\sqrt{27}}=\frac{10}{3 \sqrt{3}} \text { units. }\)

Example 4 Find the vector equation of a line passing through the point with position vector \((2 \hat{i}-3 \hat{j}-5 \hat{k})\) and perpendicular to the plane \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}+5 \hat{k})+2=0\). Also, find the point of intersection of this line and the plane.

Solution

The required line is perpendicular to the plane

\(\vec{r} \cdot(6 \hat{i}-3 \hat{j}+5 \hat{k})+2=0\) …(1)

So, the required line is parallel to \(\vec{n}=6 \hat{i}-3 \hat{j}+5 \hat{k}\)

Thus, the required line passes through the point with position vector \(\vec{a}=2 \hat{i}-3 \hat{j}-5 \hat{k}\) and is parallel to \(\vec{n}=6 \hat{i}-3 \hat{j}+5 \hat{k}\).

Hence, the vector equation of the required line is

\(\vec{r}=\vec{a}+\lambda \vec{n}, \text { i.e., } \quad \vec{r}=(2 \hat{i}-3 \hat{j}-5 \hat{k})+\lambda(6 \hat{i}-3 \hat{j}+5 \hat{k})\) …(2)

If the line (2) meets the plane (1) then

\([(2 \hat{i}-3 \hat{j}-5 \hat{k})+\lambda(6 \hat{i}-3 \hat{j}+5 \hat{k})] \cdot(6 \hat{i}-3 \hat{j}+5 \hat{k})+2=0\)

⇔ \([(2+6 \lambda) \hat{i}-(3+3 \lambda) \hat{j}+(5 \lambda-5) \hat{k}] \cdot(6 \hat{i}-3 \hat{j}+5 \hat{k})+2=0\)

⇔ 6(2+6λ) + 3(3+3λ) + 5(5λ-5) = -2

⇔ 70λ = 2 ⇔ λ = \(\frac{2}{70}\) = \(\frac{1}{35}\)

Substituting λ = \(\frac{1}{35}\) in (2), we get

\(\vec{r}=(2 \hat{i}-3 \hat{j}-5 \hat{k})+\frac{1}{35}(6 \hat{i}-3 \hat{j}+5 \hat{k})\)

⇔ \(\vec{r}=\frac{1}{35}(76 \hat{i}-108 \hat{j}-170 \hat{k}) .\)

Hence, the required point of intersection is \(\left(\frac{76}{35}, \frac{-108}{35}, \frac{-170}{35}\right)\).

Example 5 Find the angle between the line \(\frac{x-2}{3}=\frac{y+1}{-1}=\frac{z-3}{2}\) and the plane 3x + 4y + z + 5 = 0.

Solution

The given line is parallel to \(\vec{b}=3 \hat{i}-\hat{j}+2 \hat{k}\).

And, the normal to the given plane is \(\vec{n}=3 \hat{i}+4 \hat{j}+\hat{k} \text {. }\)

Let θ be the angle between the given line and the given plane.

Then, \(\sin \theta=\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}=\frac{(3 \hat{i}-\hat{j}+2 \hat{k}) \cdot(3 \hat{i}+4 \hat{j}+\hat{k})}{|3 \hat{i}-\hat{j}+2 \hat{k}| \cdot|3 \hat{i}+4 \hat{j}+\hat{k}|}\)

= \(\frac{\{3 \times 3+(-1) \times 4+2 \times 1\}}{\left\{\sqrt{3^2+(-1)^2+2^2}\right\}\left\{\sqrt{3^2+4^2+1^2}\right\}}\)

= \(\frac{7}{(\sqrt{14})(\sqrt{26})}=\sqrt{\frac{7}{52}}\)

⇒ \(\theta=\sin ^{-1}\left(\sqrt{\frac{7}{52}}\right) .\)

Hence, the angle between the given line and the given plane is \(\sin ^{-1}\left(\sqrt{\frac{7}{52}}\right) .\)

Example 6 Find the equation of the plane passing through the points (0,0,0) and (3,-1,2) and the parallel to the line \(\frac{x-4}{1}=\frac{y+3}{-4}=\frac{z+1}{7} \text {. }\)

Solution

Any plane through (0,0,0) is

a(x-0) + b(y-0) + c(z-0) = 0 ⇒ ax + by + cz = 0 …(1)

If this plane passes through (3,-1,2), we have

3a – b + 2c = 0 …(2)

Also, if the plane (1) is parallel to the given line then the normal to this plane is perpendicular to the given line.

∴ a x 1 + b x (-4) + c x 7 = 0 ⇒ a – 4b + 7c = 0 …(3)

Cross multiplying (2) and (3), we have

\(\frac{a}{(-7+8)}=\frac{b}{(2-21)}=\frac{c}{(-12+1)}=k \text { (say) }\)

⇒ \(\frac{a}{1}=\frac{b}{-19}=\frac{c}{-11}=k\)

⇒ a = k, b = -19k and c = -11k.

Substituting a = k, b = -19k and c = -11k in (1), we get the required equation of the plane as

kx – 19ky – 11kz = 0 ⇔ x – 19y – 11z = 0.

Example 7 Find the equation of the plane passing through the points (1,2,3) and (0,-1,0) and parallel to the line \(\frac{x-1}{2}=\frac{y+2}{3}=\frac{z}{-3}\).

Solution

Any plane through (1,2,3) is

a(x-1) + b(y-2) + c(z-3) = 0 …(1)

Since it passes through (0,-1,0), we have

a(0-1) + b(-1-2) + c(0-3) = 0 ⇒ a + 3b + 3c = 0 …(2)

It is being given that the plane (1) is parallel to the line

\(\frac{x-1}{2}=\frac{y+2}{3}=\frac{z}{-3}\)

∴ 2a + 3b 3c = 0 …(3)

On solving (1) and (2), we get

\(\frac{a}{(9+9)}=\frac{b}{(-3-6)}=\frac{c}{(6-3)} \Rightarrow \frac{a}{6}=\frac{b}{-3}=\frac{c}{1}\)

Hence, the required plane is

6(x-1) – 3(y-2) + 1 . (z-3) = 0

⇒ 6x – 3y + z = 3.

Real-Life Applications of Plane Geometry Concepts

Example 8 Find the equation of the plane passing through the point (0,7,-7) and containing the line \(\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z+2}{1}\).

Solution

Any plane through (0,7,-7) is

a(x-0) + b(y-7) + c(z+7) = 0 …(1)

If (1) contains the given line then it must pass through the point (-1,3,-2) and must be parallel to the given line.

If (1) passes through (-1,3,-2) then

a(-1-0) + b(3-7) + c(-2+7) = 0 ⇒ a + 4b – 5c = 0 …(2)

If (1) is parallel to the given line then

(-3)a + 2b + 1.c = 0 ⇒ -3a + 2b + c = 0 …(3)

Cross multiplying (2) and (3), we get

\(\frac{a}{(4+10)}=\frac{b}{(15-1)}=\frac{c}{(2+12)}\)

⇒ \(\frac{a}{14}=\frac{b}{14}=\frac{c}{14}\)

⇒ \(\frac{a}{1}=\frac{b}{1}=\frac{c}{1}=k \text { (say) }\)

⇒ a = k, b = k, c = k.

Putting a = k, b = k and c = k in (1), we get the required equation of the plane as

k(x-0) + k(y-7) + k(z+7) = 0

⇒ x + (y-7) + (z+7) = 0 ⇒ x + y + z = 0.

Example 9 Find the equation of the plane passing through the line of intersection of the planes x – 2y + z = 1 and 2x + y + z = 8, and parallel to the line with direction ratios 1,2,1. Find also the perpendicular distance of (1,1,1) from this plane.

Solution

The equation of a plane passing through the intersection of the given planes is

(x – 2y + z – 1) + λ(2x + y + z – 8) = 0

⇔ (1+2λ)x + (λ-2)y + (λ+1)z – (1+8λ) = 0 …(1)

Let this plane be parallel to the line with direction ratios 1, 2, 1.

Then, the normal to this plane is perpendicular to the line having the direction ratios 1, 2, 1.

∴ 1 . (1+2λ) + 2(λ-2) + 1 . (λ+1) = 0 ⇔ 5λ = 2 ⇔ \(\lambda=\frac{2}{5} \text {. }\)

Putting \(\lambda=\frac{2}{5} \text {. }\) in (1), we get the required equation of the plane as 9x – 8y + 7z – 21 = 0.

The length of the perpendicular from (1,1,1) or 9x – 8y + 7z – 21 = 0 is equal to

\(\frac{|9 \times 1-8 \times 1+7 \times 1-21|}{\sqrt{9^2+(-8)^2+7^2}}=\frac{13}{\sqrt{194}} \text { units. }\)

Example 10 Find the equation of the plane passing through the line of intersection of the planes 2x + y – z = 3, 5x – 3y + 4z + 9 = 0, and parallel to the line

\(\frac{x-1}{2}=\frac{y-3}{4}=\frac{z-5}{5}\)

Solution

The equation of a plane passing through the line of intersection of the given planes is

(2x + y – z – 3) + λ(5x – 3y + 4z + 9) = 0

⇔ (2+5λ)x + (1-3λ)y + (4λ-)λ + (9λ-3) …(1)

If this plane is parallel to the line \(\frac{x-1}{2}=\frac{y-3}{4}=\frac{z-5}{5}\) then the normal to the plane is perpendicular to this pline.

∴ 2(2+5λ) + 4(1-3λ) + 5(4λ-1) = 0

⇔ 18λ + 3 = 0 ⇔ \(\lambda=\frac{-3}{18}=\frac{-1}{6} .\)

Putting \(\lambda=\frac{-1}{6}\) in (1), we get the required equation of the plane as

\(\left(2-\frac{5}{6}\right) x+\left(1+\frac{3}{6}\right) y+\left(-\frac{4}{6}-1\right) z+\left(-\frac{9}{6}-3\right)=0\)

⇔ 7x + 9y – 10z – 27 = 0.

Example 11 Find the equation of the plane passing through (2,3,-4) and (1,-1,3), and parallel to the x-axis.

Solution

(2,3,-4) and (1,-1,3)

Let the required plane be

a(x-2) + b(y-3) + c(z+4) = 0 …(1)

Since it passes through (1,-1,3), we have

a(1-2) + b(-1-3) + c(3+4) = 0 ⇒ -a -4b + 7c = 0 …(2)

If this plane is parallel to the x-axis then the normal to the plane has the d.r.’s 1,0,0.

∴ a x 1 + b x 0 + c x 0 = 0 ⇒ a = 0.

Putting a = 0 in (2), we get 7c – 4b = 0.

Let b = k. Then, c = \(\frac{4}{7} k .\)

∴ the required plane is

0(x-2)+k(y-3)+\(\frac{4}{7}\) k(z+4)=0

⇒ 7(y-3) + 4(z+4) = 0

⇒ 7y + 4z – 5 = 0.

Hence, the required plane is 7y + 4z – 5 = 0.

Length of Perpendicular from a Point to a Plane

Vector Form

Theorem 1 The length p of the perpendicular drawn from a point with position vector \(\vec{a}\) to the plane \(\vec{r} \cdot \vec{n}=d\) is given by p = \(\frac{|\vec{a} \cdot \vec{n}-d|}{|\vec{n}|} \text {. }\)

Proof

Let π be the given plane whose equation is \(\vec{r} \cdot \vec{n}=d\) …(1)

Then, clearly \(\vec{n}\) is perpendicular to this plane.

Let A be the given point with position vector \(\vec{a}\) and let N be the foot of the perpendicular drawn from A to the given plane. Then , AN = p.

The equation of the line AN, passing through the point \(\vec{a}\) and parallel to \vec{n}, is

\(\vec{r}=\vec{a}+\lambda \vec{n}\), where λ is a scalar …(2)

Clearly, N is the point of intersection of the plane (1) and the line (2).

Substituting \(\vec{r}=\vec{a}+\lambda \vec{n}\) from (2) in (1), we get

\((\vec{a}+\lambda \vec{n}) \cdot \vec{n}=d \Rightarrow \vec{a} \cdot \vec{n}+\lambda(\vec{n} \cdot \vec{n})=d\)

⇒ \(\lambda=\frac{d-(\vec{a} \cdot \vec{n})}{|\vec{n}|^2}\)

Putting this value of λ in (2), we get the position vector of N as

\(\vec{r}=\vec{a}+\left(\frac{d-(\vec{a} \cdot \vec{n})}{|\vec{n}|^2}\right) \vec{n}\)

∴ \(\overrightarrow{A N}\) = (p.v. of N) – (p.v. of A)

= \(\vec{a}+\left(\frac{d-(\vec{a} \cdot \vec{n})}{|\vec{n}|^2}\right) \vec{n}-\vec{a}=\left(\frac{d-(\vec{a} \cdot \vec{n})}{|\vec{n}|^2}\right) \vec{n}\)

⇒ \(A N=|\overrightarrow{A N}|=\left|\frac{\mid d-(\vec{a} \cdot \vec{n})\} \vec{n}}{|\vec{n}|^2}\right|=\frac{|d-(\vec{a} \cdot \vec{n})||\vec{n}|}{|\vec{n}|^2}\)

⇒ \(A N=\frac{|d-(\vec{a} \cdot \vec{n})|}{|\vec{n}|} \Rightarrow p=\frac{|(\vec{a} \cdot \vec{n})-d|}{|\vec{n}|} .\)

Corollary Putting \(\vec{a} = \vec{0}\) in the above formula, we get the length of the perpendicular from the origin to the plane \(\vec{r} \cdot \vec{n}=d\), which is given by

\(p=\frac{|(\overrightarrow{0} \cdot \vec{n})-d|}{|\vec{n}|}=\frac{|-d|}{|\vec{n}|} .\)

Cartesian Form

Theorem 2 The length p of the perpendicular from a point A(x₁,y₁,z₁) to the plane ax + by + cz + d = 0 is given by

\(p=\left|\frac{a x_1+b y_1+c z_1+d}{\sqrt{a^2+b^2+c^2}}\right| .\)

Proof

Let N be the foot of the perpendicular drawn from the point A(x₁,y₁,z₁) to the plane ax + by + cz + d = 0.

Then, the equation on this line AN is

\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}=r \text { (say) }\) …(1)

A general point on this line is (x₁ + ar, y₁ + br, z₁ + cr).

This point coincide with N

⇔ it lies on the plane ax + by + cz + d = 0

⇔ a(x₁+ar) + b(y₁+br) + c(z₁+cr) + d = 0

⇔ \(r=\frac{-\left(a x_1+b y_1+c z_1+d\right)}{\left(a^2+b^2+c^2\right)}\) …(2)

∴ AN = \(\left\{\left(x_1+a r-x_1\right)^2+\left(y_1+b r-y_1\right)^2+\left(z_1+c r-z_1\right)^2\right\}^{1 / 2}\)

= \(\sqrt{a^2 r^2+b^2 r^2+c^2 r^2}=\left(\sqrt{a^2+b^2+c^2}\right)|r|\)

= \(\sqrt{a^2+b^2+c^2} \cdot\left|\frac{-\left(a x_1+b y_1+c z_1+d\right)}{\left(a^2+b^2+c^2\right)}\right|\) [using (2)]

= \(\left|\frac{a x_1+b y_1+c z_1+d}{\sqrt{a^2+b^2+c^2}}\right| \text {. }\)

Hence, the length p of the perpendicular from A(x1,y1,z1) to the plane ax + by + cz + d = 0 is given by

\(p=\left|\frac{a x_1+b y_1+c z_1+d}{\sqrt{a^2+b^2+c^2}}\right| .\)

Corollary Taking x₁ = 0, y₁ = 0 and z₁ = 0, we find that the length of the perpendicular from the origin to the plane ax + by + cz + d = 0 is given by

\(p=\frac{|d|}{\left|\sqrt{a^2+b^2+c^2}\right|} .\)

To Find the Distance between Parallel Planes

Let a₁x + b₁y + c₁z + d₁ = 0 and a₁x + b₁y + c₁z + d₂ = 0 be two parallel planes. Then, we take a point P(x₁,y₁,z₁) on any one of these planes and find the length of the perpendicular drawn from P(x₁,y₁,z₁) to the other plane.

Solved Examples

Example 1 Find the distance of the point \((2 \hat{i}-\hat{j}-4 \hat{k})\) from the plane \(\vec{r} \cdot(3 \hat{i}-4 \hat{j}+12 \hat{k})=9.\)

Solution

We know that the perpendicular distance of a point with position vector \(\vec{a}\) from the plane \(\vec{r} \cdot \vec{n}=d\) is given by

\(p=\frac{|\vec{a} \cdot \vec{n}-d|}{|\vec{n}|} .\)

Here, \(\vec{a}=2 \hat{i}-\hat{j}-4 \hat{k}, \vec{n}=3 \hat{i}-4 \hat{j}+12 \hat{k} \text {, and } d=9 \text {. }\)

∴ the required distance is given by

\(p=\frac{|(2 \hat{i}-\hat{j}-4 \hat{k}) \cdot(3 \hat{i}-4 \hat{j}+12 \hat{k})-9|}{\left|\sqrt{3^2+(-4)^2+(12)^2}\right|}\)

= \(\frac{|(6+4-48)-9|}{|\sqrt{169}|}=\frac{47}{13} \text { units. }\)

Example 2 Find the distance of the point (2,3,4) from the plane \(\vec{r} \cdot(3 \hat{i}-6 \hat{j}+2 \hat{k})+11=0 .\)

Solution

We know that the perpendicular distance of a point with position vector \(\vec{a}\) from the plane \(\vec{r} \cdot \vec{n}=d\) is given by

\(p=\frac{|\vec{a} \cdot \vec{n}-d|}{|\vec{n}|} .\)

Here, \(\vec{a}=2 \hat{i}+3 \hat{j}+4 \hat{k}, \vec{n}=3 \hat{i}-6 \hat{j}+2 \hat{k} \text {, and } d=-11 \text {. }\)

∴ the required distance is given by

\(p=\frac{|(2 \hat{i}+3 \hat{j}+4 \hat{k}) \cdot(3 \hat{i}-6 \hat{j}+2 \hat{k})+11|}{\left|\sqrt{3^2+(-6)^2+2^2}\right|}\)

= \(\frac{|(6-18+8)+11|}{|\sqrt{49}|}=\frac{7}{7}=1 \text { unit. }\)

Example 3 Find the distance of the point P(2,1,-1) from the plane x – 2y + 4z = 9.

Solution

The required distance

= the length of the perpendicular from P(2,1,-1) to the plane x – 2y + 4z – 9 = 0

= \(\frac{|2-2 \times 1+4 \times(-1)-9|}{\left|\sqrt{1^2+(-2)^2+4^2}\right|}=\frac{13}{\sqrt{21}} \text { units. }\)

Example 4 Find the equation of the planes x + 2y – 2z + 8 = 0, each one of which is at a distance of 2 units from the point (2,1,1).

Solution

Any plane parallel to the plane x + 2y – 2z + 8 = 0 is given by x + 2y – 2z + λ = 0 …(1)

Distance of (1) from (2,1,1) = \(\left|\frac{2+2 \times 1-2 \times 1+\lambda}{\sqrt{1^2+2^2+(-2)^2}}\right|=\left|\frac{2+\lambda}{3}\right|\)

∴ \(\left|\frac{2+\lambda}{3}\right|=2 \Rightarrow \frac{2+\lambda}{3}=2 \quad \text { or } \quad \frac{2+\lambda}{3}=-2\)

⇒ λ = 4 or λ = -8.

Putting these values of λ in (1), we get the required planes as x + 2y – 2z + 4 = 0 and x + 2y – 2z – 8 = 0.

Example 5 Find the distance between the parallel planes 2x – y + 3z + 4 = 0 and 6x – 3y + 9z – 3 = 0.

Solution

2x – y + 3z + 4 = 0 and 6x – 3y + 9z – 3 = 0

Let P(x₁, y₁, z₁) be any point on 2x – y + 3z + 4 = 0.

Then, 2x₁ – y₁ + 3z₁ = -4 …(1)

Length of the perpendicular from P(x₁,y₁,z₁) to 6x – 3y + 9z – 3 = 0 is given by

\(p=\frac{\left|6 x_1-3 y_1+9 z_1-3\right|}{\left|\sqrt{6^2+(-3)^2+9^2}\right|}=\frac{\left|3\left(2 x_1-y_1+3 z_1\right)-3\right|}{|\sqrt{126}|}\)

= \(\frac{|3 \times(-4)-3|}{|\sqrt{126}|}\) [using (1)]

= \(\frac{15}{3 \sqrt{14}}=\frac{5}{\sqrt{14}} \text { units. }\)

Example 6 Find the distance between the parallel planes \(\vec{r} \cdot(2 \hat{i}-3 \hat{j}+6 \hat{k})=5 and \vec{r} \cdot(6 \hat{i}-9 \hat{j}+18 \hat{k})+20=0 .\)

Solution

Taking \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\), the equations of the given planes become

\((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(2 \hat{i}-3 \hat{j}+6 \hat{k})=5\)

⇔ 2x – 3y + 6z = 5 …(1)

\((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(6 \hat{i}-9 \hat{j}+18 \hat{k})+20=0\)

⇔ 6x – 9y + 18z = -20 …(2)

Let P(x₁,y₁,z₁) be any point on (1).

Then, 2x₁ – 3y₁ + 6z₁ = 5 …(3)

The distance between the given planes

= length of the perpendicular from P(x₁, y₁,z₁) to the plane ()

= \(\frac{\left|6 x_1-9 y_1+18 z_1+20\right|}{\sqrt{6^2+(-9)^2+(18)^2}}=\frac{\left|3\left(2 x_1-3 y_1+6 z_1\right)+20\right|}{\sqrt{441}}\)

= \(\frac{|3 \times 5+20|}{21}\) [using (3)]

= \(\frac{35}{21}=\frac{5}{3} \text { units. }\)

Hence, the distance between the given planes is \frac{5}{3} units.

Example 7 Find the length and the coordinates of the foot of the perpendicular from the point (7,14,5) to the plane 2x + 4y – z = 2.

Solution

Any line through P(7,14,5) and perpendicular to the plane 2x + 4y – z = 2 is given by

\(\frac{x-7}{2}=\frac{y-14}{4}=\frac{z-5}{-1}=\lambda \text { (say) }\)

Any point on this line is

N(2λ + 7, 4λ + 14, -λ + 5).

If N is the foot of the perpendicular from P to the given plane then it must lie on the plane 2x + 4y – z = 2.

∴ 2(2λ + 7) + 4(4λ+14) – (-λ+5) = 2 ⇒ λ = -3.

Thus, we get the point N(1,2,8) on the plane.

Hence, the foot of the perpendicular from P(7,14,5) to the given plane is N(1,2,8).

Length of the perpendicular from P to the given plane

= PN = \(\sqrt{(7-1)^2+(14-2)^2+(5-8)^2}=\sqrt{189}=3 \sqrt{21} \text { units. }\)

Example 8 From the point P(1,2,4), a perpendicular is drawn on the plane 2x + y – 2z + 3 = 0. Find the equation, the length and the coordinates of the foot of the perpendicular.

Solution

Let PN be the perpendicular drawn from the point P(1,2,4) to the plane 2x + y – 2z + 3 = 0.

Then, the equation of the line PN is given by

\(\frac{x-1}{2}=\frac{y-2}{1}=\frac{z-4}{-2}=\lambda \text { (say). }\)

So, the coordinates of N are

N(2λ+1, λ+2, -2λ+4).

Since N lies on the plane 2x + y – 2z + 3 = 0, we have

2(2λ+1) + (λ+2) – 2(-2λ+4) + 3 = 0

⇒ \(9 \lambda=1 \Rightarrow \lambda=\frac{1}{9} .\)

∴ Coordinates of N are \(\left(\frac{2}{9}+1, \frac{1}{9}+2, \frac{-2}{9}+4\right) \text {, i.e., }\left(\frac{11}{9}, \frac{19}{9}, \frac{34}{9}\right) \text {. }\)

PN = \(\sqrt{\left(\frac{11}{9}-1\right)^2+\left(\frac{19}{9}-2\right)^2+\left(\frac{34}{9}-4\right)^2}\)

= \(\sqrt{\left(\frac{2}{9}\right)^2+\left(\frac{1}{9}\right)^2+\left(\frac{-2}{9}\right)^2}=\sqrt{\frac{4}{81}+\frac{1}{81}+\frac{4}{81}}=\sqrt{\frac{9}{81}}=\sqrt{\frac{1}{9}}=\frac{1}{3} .\)

Thus, the required equation of PN is \(\frac{x-1}{2}=\frac{y-2}{1}=\frac{z-4}{-2}\), coordinates of the foot of the perpendicular are N \(\left(\frac{11}{9}, \frac{19}{9}, \frac{34}{9}\right)\) and length PN = \(\frac{1}{3}\) unit.

Example 9 Find the length and the foot of the perpendicular from the point (1,1,2) to the plane \(\vec{r} \cdot(2 \hat{i}-2 \hat{j}+4 \hat{k})+5=0 .\)

Solution

The given Point is P(1,1,2).

The given plane is

\(\vec{r} \cdot(2 \hat{i}-2 \hat{j}+4 \hat{k})+5=0 .\)

⇔ \((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(2 \hat{i}-2 \hat{j}+4 \hat{k})+5=0\)

⇔ 2x – 2y + 4z + 5 = 0 …(1)

Any line through P(1,1,2) and perpendicular to the plane (1) is given by

\(\frac{x-1}{2}=\frac{y-1}{-2}=\frac{z-2}{4}=\lambda \text { (say). }\)

The coordinates of any point N on this line are (2λ+1) – 2(-2λ+1) + 4(4λ+2) + 5 = 0 ⇒ λ = \(-\frac{13}{24}\).

Thus, we get the point N \(\left(\frac{-1}{12}, \frac{25}{12}, \frac{-1}{6}\right) \text {. }\)

Hence, the foot of the perpendicular from P(1,1,2) to the given plane is N \(\left(\frac{-1}{12}, \frac{25}{12}, \frac{-1}{6}\right) \text {. }\)

Length of the perpendicular from P to the given plane

= PN = \(\sqrt{\left(1+\frac{1}{12}\right)^2+\left(1-\frac{25}{12}\right)^2+\left(2+\frac{1}{6}\right)^2}=\frac{13 \sqrt{6}}{12} \text { units. }\)

Example 10 Find the image of the point P(1,3,4) in the plane 2x – y + z + 3 = 0.

Solution

P(1,3,4) in the plane 2x – y + z + 3 = 0

Let Q(x₁,y₁,z₁) be the image of the point P(1,3,4) in the given plane.

The equations of the line through P(1,3,4) and perpendicular to the given plane are \(\frac{x-1}{2}=\frac{y-3}{-1}=\frac{z-4}{1}=k \text { (say). }\)

The coordinates of a general point on this line are (2k+1, -k+3, k + 4).

If N is the foot of the perpendicular from P to the given plane then N lies on the plane.

∴ 2(2k+1) – (-k+3) + (k+4) + 3 = 0

⇒ k = -1.

Thus, we get the point N(-1,4,3).

Now,N is the midpoint of PQ.

∴ \(\frac{1+x_1}{2}=-1, \frac{3+y_1}{2}=4, \frac{4+z_1}{2}=3\)

⇒ x₁ = -3, y₁ – 5, z₁ = 2.

Hence, the required image of P(1,3,4) is Q(-3,5,2).

Example 11 A variable plane which remains at a constant distance 3p from the origin cuts the coordinates axes at A, B, C. Show that the locus of the centroid of △ABC is x^-2 + y^-2 + z^-2 = p^-2.

Solution

Let the equation of the variable plane be

\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) …(1)

This plane meets the x-axis, y-axis and z-axis at the points A(a,0,0), B(0,b,0) and C(0,0,c) respectively. Let (α, β, γ) be the coordinates of the centroid of △ABC.

Then, \(\alpha=\frac{a+0+0}{3}, \beta=\frac{0+b+0}{3} \text { and } \gamma=\frac{0+0+c}{3}\)

⇒ \(\alpha=\frac{a}{3}, \beta=\frac{b}{3} \text { and } \gamma=\frac{c}{3}\)

⇒ a = 3α, b = 3β, c = 3γ …(3)

∴ 3p = length of the perpendicular from (0,0,0) to the plane (1)

⇒ \(3 p=\frac{\left|\frac{0}{a}+\frac{0}{b}+\frac{0}{c}-1\right|}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}}=\frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}}\)

⇒ \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}=\frac{1}{3 p}\)

⇒ \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=\frac{1}{9 p^2}\)

⇒ \(\frac{1}{9 \alpha^2}+\frac{1}{9 \beta^2}+\frac{1}{9 \gamma^2}=\frac{1}{9 p^2}\) [using (2)]

⇒ α^-2 + β^-2 + γ^-2 = p^-2.

Hence, the required locus is x^-2 + y^-2 + z^-2 = p^-2.

Example 12 A variable plane is at a constant distance p from the origin and meets the coordinate axes in A, B, C. Show that the locus of the centroid of the tetrahedron OABC is x^-2 + y^-2 + z^-2 = 16p^-2.

Solution

Let the equation of the variable plane be

\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) …(1)

This plane meets the x-axis, y-axis and z-axis at the points A(a,0,0), B(0,b,0) and C(0,0,c) respectively.

Let (α, β, γ) be the coordinates of the centroid of the tetrahedron OABC.

Then, \(\alpha=\frac{0+a+0+0}{4}=\frac{a}{4}, \beta=\frac{0+0+b+0}{4}=\frac{b}{4}\)

and \(\gamma=\frac{0+0+0+c}{4}=\frac{c}{4} \Rightarrow a=4 \alpha, b=4 \beta, c=4 \gamma\) …(2)

∴ p = distance of the plane (1) from (0,0,0)

⇒ \(p=\frac{\left|\frac{0}{a}+\frac{0}{b}+\frac{0}{c}-1\right|}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}}\)

⇒ \(\frac{1}{p}=\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}=\frac{1}{p^2}=\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\)

⇒ \(\frac{1}{p^2}=\frac{1}{16 \alpha^2}+\frac{1}{16 \beta^2}+\frac{1}{16 \gamma^2}\) [using (2)]

⇒ \(\frac{1}{\alpha^2}+\frac{1}{\beta^2}+\frac{1}{\gamma^2}=\frac{16}{p^2} \Rightarrow \alpha^{-2}+\beta^{-2}+\gamma^{-2}=16 p^{-2} .\)

Hence, the required locus is x^-2 + y^-2 + z^-2 = 16p^-2.

Example 13 Find the distance of the point (2,3,4) from the plane 3x + 2y + 2z + 5 = 0, measured parallel to the line \(\frac{x+3}{3}=\frac{y-2}{6}=\frac{z}{2} .\)

Solution

The point (2,3,4) from the plane 3x + 2y + 2z + 5 = 0

Let l be the given line \(\frac{x+3}{3}=\frac{y-2}{6}=\frac{z}{2}\), and let P(2,3,4) be the given point.

Let PQ || l.

Then, PQ is the line passing through P(2,3,4) and having direction ratios 3,6,2.

So, the equations of PQ are

\(\frac{x-2}{3}=\frac{y-3}{6}=\frac{z-4}{2}=\lambda \text { (say). }\)

The coordinates of any point Q on this line are (3λ+2, 6λ+3, 2λ+4).

If this point Q lies on the given plane then

3(3λ+2) + 2(6λ+3) + 2(2λ+4) + 5 = 0

⇔ 25λ + 25 = 0 ⇔ 25λ = -25 ⇔ λ = -1.

So, the coordinates of Q are (-1,-3,2).

∴ the requried distance = PQ = \(\sqrt{(2+1)^2+(3+3)^2+(4-2)^2}\)

= √49 = 7 units.

Example 14 Find the distance of the point (-2,3,-4) from the line \(\frac{x+2}{3}=\frac{2 y+3}{4}=\frac{3 z+4}{5}\), measured parallel to the plane 4x + 12y – 3z + 1 = 0.

Solution

\(\frac{x+2}{3}=\frac{2 y+3}{4}=\frac{3 z+4}{5}\)

Let P(-2,3,-4) be the given point.

Let \(\frac{x+2}{3}=\frac{2 y+3}{4}=\frac{3 z+4}{5}=\lambda\) be the given line.

A general point on this line is \(Q\left(3 \lambda-2, \frac{4 \lambda-3}{2}, \frac{5 \lambda-4}{3}\right)\)

Direction ratios of PQ are

\((3 \lambda-2+2),\left(\frac{4 \lambda-3}{2}-3\right),\left(\frac{5 \lambda-4}{3}+4\right), \text { i.e. } 3 \lambda, \frac{4 \lambda-9}{2}, \frac{5 \lambda+8}{3} \text {. }\)

Direction ratios of normal to the plane are 4,12,-3.

PQ is parallel to the given plane

⇒ PQ is perpendicular to the normal to the plane

⇒ \((4 \times 3 \lambda)+12 \times \frac{(4 \lambda-9)}{2}-3 \times \frac{(5 \lambda+8)}{3}=0\)

⇒ 12λ + 6(4λ-9) – (5λ+8) = 0 ⇒ 31λ = 62 ⇒ λ = 2.

∴ coordinates of Q are \(\left(4, \frac{5}{2}, 2\right)\).

∴ PQ = \(\sqrt{(4+2)^2+\left(\frac{5}{2}-3\right)^2+(2+4)^2}=\sqrt{36+\frac{1}{4}+36}\)

= \(\sqrt{\frac{289}{4}}=\frac{17}{2} \text { units. }\)

Condition for the Coplanarity of Two Lines

Vector Form

Theorem 1 The condition for two lines \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\) to be coplanar is that

\(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0 \text {, i.e., }\left[\overrightarrow{a_2}-\overrightarrow{a_1} \overrightarrow{b_1} \overrightarrow{b_2}\right]=0 \text {. }\)

Also, the equation of the plane containing both these lines is

\(\left(\vec{r}-\vec{a}_1\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0 \quad \text { or } \quad\left(\vec{r}-\vec{a}_2\right) \cdot\left(\vec{b}_1 \times \vec{b}_2\right)=0 \text {. }\)

Proof

The equations of the given lines are

\(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1}\) …(1)

\(\vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\) …(2)

The line (1) passes through a point A with position vector \(\overrightarrow{a_1}\) and is parallel to \(\overrightarrow{b_1}\).

The line (2) passes through a point B with position vector \(\overrightarrow{a_2}\) and is parallel to \(\overrightarrow{b_2}\).

Now, \(\overrightarrow{A B}=(\text { p.v. of } B)-(\text { p.v. of } A)=\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right) \text {. }\)

∴ the given lines are coplanar

⇔ \(\overrightarrow{A B}, \overrightarrow{b_1}, \overrightarrow{b_2}\) are coplanar

⇔ \(\overrightarrow{A B} \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0\)

⇔ \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0 .\)

Equation of the Plane Containing Both the Lines

If the lines \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\) are coplanar then their common plane is perpendicular to the vector \(\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)\), and this plane passes through each of the points \(\overrightarrow{a_1} and \overrightarrow{a_2}\).

So, its equation is

\(\left(\vec{r}-\overrightarrow{a_1}\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0 \text {, or }\left(\vec{r}-\overrightarrow{a_2}\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0 \text {. }\)

Cartesian Form

Theorem 2 The lines \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \text {, and } \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\)

are coplanar ⇔ \(\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 .\)

And, the equation of the plane containing both these lines is

\(\left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 \text { or }\left|\begin{array}{ccc}
x-x_2 & y-y_2 & z-z_2 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 \text {. }\)

Proof

The given lines are

\(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}\) …(1)

\(\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\) …(2)

The line (1) passes through a point A(x₁,y₁,z₁) and is parallel to the vector \(\overrightarrow{u_1}=a_1 \hat{i}+b_1 \hat{j}+c_1 \hat{k}.\)

Also, the line (2) passes through a point B(x₂,y₂,z₂) and is parallel to the vector \(\vec{u}_2=a_2 \hat{i}+b_2 \hat{j}+c_2 \hat{k} .\)

Now, \(\overrightarrow{A B}=(\text { p.v. of } B)-(\text { p.v, of } A)\)

= \(\left(x_2 \hat{i}+y_2 \hat{j}+z_2 \hat{k}\right)-\left(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}\right)\)

= \(\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-z_1\right) \hat{k} .\)

∴ lines (1) and (2) are coplanar

⇔ there is a plane which passes through the points A and B, and which is parallel to each of \(\overrightarrow{u_1} \text { and } \overrightarrow{u_2}\)

⇔ \(\overrightarrow{A B}, \overrightarrow{u_1}, \overrightarrow{u_2}\) are parallel to the same plane

⇔ \(\overrightarrow{A B}, \overrightarrow{u_1}, \overrightarrow{u_2}\) are coplanar

⇔ \(\left[\begin{array}{lll}
\overrightarrow{A B} & \overrightarrow{u_1} & \overrightarrow{u_2}
\end{array}\right]=0\)

⇔ \(\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 .\)

Equation of the Plane Containing Both the Lines

If the lines (1) and (2) are coplanar then their common plane is the plane containing the line (1) and parallel to the line (2), or it is the plane containing the line (2) and parallel to the line (1).

Hence, its equation is

\(\left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 \text {, or }\left|\begin{array}{ccc}
x-x_2 & y-y_2 & z-z_2 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 \text {. }\)

Solved Examples

Example 1 Show that the lines

\(\vec{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda(3 \hat{i}-\hat{j}) \text { and } \vec{r}=(4 \hat{i}-\hat{k})+\mu(2 \hat{i}+3 \hat{k})\)

are coplanar. Also, find the equation of the plane containing both these lines.

Solution

We know that the lines \(\vec{r}=\vec{a}_1+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\) are coplanar

⇔ \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0 .\)

Here, \(\overrightarrow{a_1}=\hat{i}+\hat{j}-\hat{k}, \overrightarrow{b_1}=3 \hat{i}-\hat{j}, \overrightarrow{a_2}=4 \hat{i}-\hat{k} \text { and } \vec{b}_2=2 \hat{i}+3 \hat{k} \text {. }\)

∴ \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)=(4 \hat{i}-\hat{k})-(\hat{i}+\hat{j}-\hat{k})=(3 \hat{i}-\hat{j}) .\)

\(\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
3 & -1 & 0 \\
2 & 0 & 3
\end{array}\right|\)

= \((-3-0) \hat{i}-(9-0) \hat{j}+(0+2) \hat{k}=-3 \hat{i}-9 \hat{j}+2 \hat{k}\)

∴ \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=(3 \hat{i}-\hat{j}) \cdot(-3 \hat{i}-9 \hat{j}+2 \hat{k})\)

= [3 x (-3) + (1) x (-9) + 0 x 2] = 0.

Hence, the given lines are coplanar.

The equation of the plane containing both the given lines is given by

\(\left(\vec{r}-\overrightarrow{a_1}\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0\)

⇔ \(\{\vec{r}-(\hat{i}+\hat{j}-\hat{k})\} \cdot(-3 \hat{i}-9 \hat{j}+2 \hat{k})=0\)

⇔ \(\vec{r} \cdot(-3 \hat{i}-9 \hat{j}+2 \hat{k})=(\hat{i}+\hat{j}-\hat{k}) \cdot(-3 \hat{i}-9 \hat{j}+2 \hat{k})\)

⇔ \(\vec{r} \cdot(-3 \hat{i}-9 \hat{j}+2 \hat{k})=(-3-9-2)\)

⇔ \(\vec{r} \cdot(3 \hat{i}+9 \hat{j}-2 \hat{k})+14=0\)

The equation of the plane containing both these lines \(\vec{r} \cdot(3 \hat{i}+9 \hat{j}-2 \hat{k})+14=0\)

Example 2 Show that the lines \(\frac{x}{1}=\frac{y-2}{2}=\frac{z+3}{3} \text { and } \frac{x-2}{2}=\frac{y-6}{3}=\frac{z-3}{4}\) are coplanar. Also, find the equation of the plane containing these lines.

Solution

We know that the lines

\(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \text {, and } \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\)

are coplanar ⇔ \(\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 \text {, }\)

and the equation of the plane containing these lines is

\(\left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 .\)

Here, x₁ = 0, y₁ = 2, z₁ = -3; x₂ = 2, y₂ = 6, z₂ = 3; a₁ = 1, b₁ = 2, c₁ = 3; a₂ = 2, b₂ = 3, c₂ = 4.

∴ \(\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=\left|\begin{array}{ccc}
2 & 4 & 6 \\
1 & 2 & 3 \\
2 & 3 & 4
\end{array}\right|=0 .\)

Hence, the two given lines are coplanar.

The equation of the plane containing both these lines is

\(\left|\begin{array}{ccc}
x-0 & y-2 & z+3 \\
1 & 2 & 3 \\
2 & 3 & 4
\end{array}\right|=0 \Leftrightarrow\left|\begin{array}{ccc}
x & y-2 & z+3 \\
1 & 2 & 3 \\
2 & 3 & 4
\end{array}\right|=0\)

⇔ x(8-9) – (y-2)(4-6) + (z+3)(3-4) = 0

⇔ -x + 2(y-2) – (z+3) = 0 ⇔ x – 2y + z+ 7 = 0.

Hence, the required plane is x – 2y + z + 7 = 0.

Example 3 Show that the lines

\(\frac{x-a+d}{\alpha-\delta}=\frac{y-a}{\alpha}=\frac{z-a-d}{\alpha+\delta} \text {, and } \frac{x-b+c}{\beta-\gamma}=\frac{y-b}{\beta}=\frac{z-b-c}{\beta+\gamma}\)

are coplanar.

Solution

The given lines are

\(\frac{x-(a-d)}{\alpha-\delta}=\frac{y-a}{\alpha}=\frac{z-(a+d)}{\alpha+\delta}\) …(1)

\(\frac{x-(b-c)}{\beta-\gamma}=\frac{y-b}{\beta}=\frac{z-(b+c)}{\beta+\gamma}\) …(2)

We know that the lines

\(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \text {, and } \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\)

are coplanar ⇔ \(\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0 .\)

Here, x₁ = (a-d), y₁ = a, z₁ = (a+d); x₂ = (b-c), y₂ = b, z₂ = (b+c); a₁ = (α-δ), b₁ = α, c₁ = (α+δ); and a₂ = (β-γ), b₂ = β, c₂ = (β+γ).

∴ \(\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|\)

= \(\left|\begin{array}{ccc}
(b-c)-(a-d) & b-a & (b+c)-(a+d) \\
\alpha-\delta & \alpha & \alpha+\delta \\
\beta-\gamma & \beta & \beta+\gamma
\end{array}\right|\)

= \(\left|\begin{array}{ccc}
2(b-a) & b-a & b+c-a+d \\
2 \alpha & \alpha & \alpha+\delta \\
2 \beta & \beta & \beta+\gamma
\end{array}\right| \quad\left\{C_1 \rightarrow C_1+C_3\right\}\)

= 0 [∵ C₁ and C₂ are proportional].

Hence, the given lines are coplanar.

Example 4 Find the equation of the plane which contains the two parallel lines \(\frac{x-3}{3}=\frac{y+4}{2}=\frac{z-1}{1} \text {, and } \frac{x+1}{3}=\frac{y-2}{2}=\frac{z}{1} \text {. }\)

Solution

\(\frac{x-3}{3}=\frac{y+4}{2}=\frac{z-1}{1} \text {, and } \frac{x+1}{3}=\frac{y-2}{2}=\frac{z}{1} \text {. }\)

The plane which contains the two given parallel lines must pass through the points (3,-4,1) and (-1,2,0), and must be parallel to the line having direction ratios 3,2,1.

Any plane passing through (3,-4,1) is

a(x-3) + b(y+4) + c(z-1) = 0 …(1)

If this plane passes through the point (-1,2,0) then

a(-1-3) + b(2+4) + c(0-1) = 0 ⇒ 4a – 6b + c = 0 …(2)

If the plane (1) is parallel to the line having direction ratios 3,2,1 then

3a + 2b + c = 0 …(3)

Cross multiplying (2) and (3), we get

\(\frac{a}{(-6-2)}=\frac{b}{(3-4)}=\frac{c}{(8+18)} \Leftrightarrow \frac{a}{-8}=\frac{b}{-1}=\frac{c}{26}\)

⇔ \(\frac{a}{8}=\frac{b}{1}=\frac{c}{-26}=k \text { (say) }\)

⇔ a = 8k, b = k, c = -26k.

Putting these values of a,b,c in (1), we get the required equation of the plane as

8k(x-3) + k(y+4) – 26k(z-1) = 0

⇔ 8(x-3) + (y+4) – 26(z-1) = 0 ⇔ 8x + y – 26z + 6 = 0.

The equation of the plane which contains the two parallel lines 8x + y – 26z + 6 = 0.

Chapter 1 Linear Programming

Linear Inequations in Two Variables

The inequalities of the form

ax + by ≤ c, ax + by < c, ax + by ≥ c and ax + by > c are called linear inequations in two variables x and y.

The points (x,y) for which the inequation is true, constitute its solution set.

Graph of a Linear Inequation

Let us consider an inequation, ax + by ≤ c. For drawing its graph to obtain a solution set, we proceed as under.

Step 1 Consider the equation ax + by = c, and plot the resulting line. In case of strict inequalities < or >, draw the line as dotted, otherwise mark it thick.

Step 2 Choose a point [if possible (0,0)], not lying on this line. Substitute its coordinates in the inequation. If the inequation is statisfied then shade the portion of the plane which containes the chosen point; otherwise shade the portion which does not contain this point.

The shaded portion represents the solution set. The dotted line is not a part of the shaded region while the thick line is a part of it.

Example Graph the solution set of the inequation 2x – y ≥ 1.

Solution

Consider the equation 2x – y = 1.

We may write it as \(\frac{x}{(1 / 2)}+\frac{y}{-1}=1.\)

This shows that the line 2x – y = 1 makes intercepts of \(\frac{1}{2}\) and -1 on the axes. Thus, the line meets the x-axis at A(\(\frac{1}{2}\), 0) and the y-axis at B(0, -1). We plot these points and join them by a thick line.

Consider O(0,0). Clearly, (0,0) does not satisfy the given inequation. So, out of the portions divided by this line, the one not containing O(0,0), together with the points on the line, forms the solution set.

Simultaneous Inequations

The solution set of a system of linear inequations in two variables is the set of all points (x,y) which satisfy all the inequations in the system simultaneously.

So, we find the region of the plane common to all the portions comprising the solutions sets of the given inequations. When there is no region common to all the solutions of the given inequations, we say that the solution set of the system is empty.

The linear inequations are also known as linear constraints.

WBBSE Class 12 Linear Programming Solutions

Solved Examples

Example 1 Draw the graph of the solution set of the system of inequations 2x + 3y ≥ 6, 4y ≤ 4, x ≥ 0 and y ≥ 0.

Solution

2x + 3y ≥ 6, 4y ≤ 4, x ≥ 0 and y ≥ 0

Consider the equations

2x + 3y = 6, x + 4y = 4, x = 0 and y = 0.

Now, 2x + 3y = 6 ⇒ \(\frac{x}{3}+\frac{y}{2}=1.\)

This line meets the axes at A(3,1) and B(0,2). Join these points and draw a thick line. Clearly, the portion not containing (0,0) represents the solution set of the inequation 2x + 3y ≥ 6.

Again, x + 4y = 4 ⇒ \(\frac{x}{4}+\frac{y}{1}=1 \text {. }\)

This line meets the axes at C(4,0) and D(0,1). Join these points and draw a thick line. The portion containing (0,0) represents the solution set of the inequation x + 4y ≤ 4.

X≥ 0 is represented by the y-axis and the portion on its right-hand side.

Also, y ≥ 0 is represented by the x-axis and the portion above the x-axis.

Hence, the shaded region represents the solution set of the given inequations.

Example 2 Exhibit graphically the solution set of the system of linear inequations x + y ≥ 1, 7x + 9y ≤ 63, y ≤ 5, x ≤ 6, x ≥ 0, and y ≥ 0.

Solution

x + y ≥ 1, 7x + 9y ≤ 63, y ≤ 5, x ≤ 6, x ≥ 0 and y ≥ 0

x + y = 1 meets the axes at A(1,0) and B(0,1).

Join these points by a thick line. The portion containing (0,0) is the solution set of x + y ≥ 1.

\(7 x+9 y=63 \Rightarrow \frac{x}{9}+\frac{y}{7}=1 .\)

This line meets the axes at C(9,0) and D(0,7). Join these points by a thick line. The portion containing (0,0) is the solution set of 7x + 9y ≤ 63.

y = 5 is a line parallel to the x-axis at a distance 5 from the x-axis and the portion containing O(0,0) is the solution set of the inequation y ≤ 5.

x = 6 is a line parallel to the y-axis at a distance of 6 from the y-axis and the portion containing (0,0) is the solution set of x ≤ 6.

X≥ 0 has a solution represented by the y-axis and the portion on its right. Also, y ≥ 0 has a solution represented by the x-axis and the portion above it.

The shaded region represents the solution set of the given system of inequations.

Example 3 Find the linear constraints for which the shaded area in the figure below is the solution set.

Solution

Consider the line 3x + 4y = 18.

Clearly, O(0,0) satisfies 3x + 4y ≤ 18.

The shaded area and (0,0) lie on the same side of the line 3x + 4y = 18.

So, we must have 3x + 4y ≤ 18.

Consider the line x – 6y = 3.

Clearly, (0,0) satisfies the inequation x – 6y ≤ 3.

Also, the shaded area and (0,0) lie on the same side of the line x – 6y = 3.

So, we must have x – 6y ≤ 3.

Consider the line 2x + 3y = 3.

Clearly, (0,0) satisfies the inequation 2x + 3y ≤ 3.

But, the shaded region and the point (0,0) lie on the opposite sides of the line 2x + 3y = 3.

So, we must have 2x + 3y ≥ 3.

Consider the line -7x + 14y = 14.

Clearly, (0,0) satisfies the inequation -7x + 14y ≤ 14.

Also, the shaded region and the point (0,0) lie on the same side of the line -7x + 14y = 14.

So, we must have -7x + 14y ≤ 14.

The shaded region is above the x-axis and on the right-hand side of the y-axis, so we have y ≥ 0 and x ≥ 0.

Thus, the linear constraints for which the shaded area in the given figure is the solution set, are

3x + 4y ≤ 18, x – 6y ≤ 3, 2x + 3y ≥ 3, -7x + 14y ≤ 14, x ≥ 0 and y ≥ 0.

Understanding Linear Programming Concepts

Linear Programming

Linear programming is the method used in decision-making in business for obtaining the maximum or minimum value of a liear expression, subject to satisfying certain given linear inequations.

The linear expression is known as an objective function and the linear inequations are known as linear constraints.

Linear Constrainst In business or industry we want to make the best use of our limited resources like money,labour, time, materials, ect.

The limitatiions on the resoureces can often be expressed in the form of linear inequations, known as linear constraints.

Objective Function A linear function of the involved variables, which we want to maximize or minimize, subject to the given linear constraints, is known as objective function.

Optimal Value Of An Objective Function The maximum or minimum value of an function is known as its optimal value.

Feasible Solution A set of values of the variables satisfying all the constraints is known as a feasible solution of the system of inequations.

Optimal Solution A feasible solution which leads to the optimal value of an objective function is known as an optimal solution of the system of inequations.

Optimization Techniques The processes of obtaining the optimal values of a system of inequations are called optimization techniques.

A Linear Programming Problem (LPP)

A general linear programming problem consists of maximizing or minimizing an objective function, subject to certain given constraints.

Step-by-Step Solutions to Linear Programming Problems

Formulation of a Linear programming problem (LPP)

Working rules

Step 1 Identify the unknowns in the given LPP. Denote them by x and y.

Step 2 Formulae the objective function in terms of x and y. Be sure whether it is to be maximized or minimized.

Step 3 Translate all the constraints in the form of linear inequations.

Step 4 Solved these inequations simultaneously. Mark the common area by a shaded region. This is the feasible region.

Step 5 Find the coordinates of all the vertices of the feasible region.

Step 6 Find the value of the objective function at each vertex of the feasible region.

Step 7 Find the values of x and y for which the objective function Z = ax + by has maximum or minimum value (as the case may be).

Graphical Solution of an LPP

We shall restrict ourselves to the case of an LPP in two variables. We shall consider at least three constraints or inequations. Each inequation gives rise to a line in the plane. For a simultaneous solution of these inequations, we consider the region common to their solution of these inequations, we consider the region common to their solution sets. In each case, we obtain such a region, a convex polygon, i.e., a closed region bounded by straight lines with the property that the line joining any two points of the region lies wholly in the region.

The maximum or minimum value of a linear function over a convex polygon occurs at some vertex of the polygon.

So, we look at the values of the objective function at the vertices of the set of feasible solutions. The largest of these values is the maximum value of the objective function and the smallest of these values is the minimum.

Graphical Method

It will be clear from the following solved examples.

Solved Examples

Example 1 Solve the following problem graphically: Minimize and maximize z = 3x + 9y, subject to the constraints x + 3y ≤ 60, x + y ≥ 10, x ≤ y, x ≥ 0 and y ≥ 0.

Solution

Given

Minimize and maximize z = 3x + 9y, subject to the constraints x + 3y ≤ 60, x + y ≥ 10, x ≤ y, x ≥ 0 and y ≥ 0.

Region represented by x + 3y ≤ 60

Consider the equation x + 3y = 60.

x = 0 ⇒ 3y = 60 ⇒ y = 20

y = 0 ⇒ x = 60

Plot the points A(0,20) and B(60,0). Join AB and produce it both ways.

Putting x = 0 and y = 0, we get 0 + 3 x 0 = 0 ≤ 60.

∴ O(0,0) lies in the region x + 3y ≤ 60.

So, the region containing the origin is the solution set of x + 3y ≤ 60.

Region represented by x + y ≥ 10

Consider the equation x + y = 10.

x = 0 ⇒ y = 10

y = 0 ⇒ x = 10

Plot the points C(0,10) and D(10,0). Joint CD and produce it both ways.

Now, x = 0, y = 0 ⇒ 0 + 0 ≥ 10 is not true.

∴ O(0,0) does not lie in the region x + y ≥ 10.

Region represented by x ≤ y, i.e., x – y ≤ 0

Consider the equation x = y, i.e., x – y = 0.

Clearly, x = 0 ⇒ y = 10.

And, x = 20 ⇒ y = 20.

Plot the points E(10,10) and F(20,20). Join EF and produce it both ways.

Clearly, O(0,0) satisfies x – y ≤ 0.

∴ O(0,0) lies in the region x – y ≤ 0.

We know that:

x ≥ 0 is the y-axis and the region on its RHS.

y ≥ 0 is the x-axis and the region above the x-axis.

On solving x = y and x + y = 10, we get the point G(5,5).

On solving x = y and x + 3y = 60, we get H(15,15).

Thus, the feasible region is ACGH, as shown in the figure.

Value of z = 3x + 9y:

(1) At A(0,20) it is (3 x 0 + 9 x 20) = 180.

(2) At C(0,10) it is (3 x 0 + 9 x 10) = 90.

(3) At G(5,5) it is (3 x 5 + 9 x 5) = 60.

(4). At H(15,15) it is (3 x 15 + 9 x 15) = 180.

So, the minimum value of z is 60 and its maximum value is 180.

Graphical Method in Linear Programming Explained

Example 2 A furniture dealar deals in only two items: tables and chairs. He has Rs 5000 to invest and a space to store at most 60 pieces. A table costs him Rs 250 and a chair, Rs 50. He can sell a table at a profit of Rs 50 and a chair at a profit of Rs 15. Assuming that he can sell all the items that he buys, how should he invest his money in order that he may maximize his profit?

Solution

Given

A furniture dealar deals in only two items: tables and chairs. He has Rs 5000 to invest and a space to store at most 60 pieces. A table costs him Rs 250 and a chair, Rs 50. He can sell a table at a profit of Rs 50 and a chair at a profit of Rs 15. Assuming that he can sell all the items that he buy

This problem can be formulated as under.

Let x and y be the required numbers of tables and chairs respectively. Then, clearly we have

x ≥ 0, y ≥ 0; x + y ≤ 60;

250x + 50y ≤ 5000, i.e., 5x + y ≤ 100.

Let P be the profit function. Then, P = 50x + 15y.

Now, we have to maximize P.

Now, x + y = 60 ⇒ \(\frac{x}{60}+\frac{y}{60}=1 .\)

This line meets the axes at (60,0) and (0,60). Plot these points and join them to get the line x + y = 60.

Also, 5x + y = 100 ⇒ \(\frac{x}{20}+\frac{y}{100}=1 .\)

This line meets the axes at (20,0) and (0,100). Plot these points and join them to get the line 5x + y = 100.

Also, the line x = 0 is the y-axis and the line y = 0 is the x-axis.

These four straight lines enclose the quadrilateral OABC.

The coordinates of the points O, A, B, C are (0,0), (20,0), (10,50) and (0,60) respectively.

At these points, the corresponding values of P = 50x + 15y are 0, 1000, 1250 and 900 respectively.

Clearly, it is maximum at B(10,50).

So, for a maximum profit, the dealer should purchase 10 tables and 50 chairs.

Example 3 If a young man rides his motorcycle at 25km per hour, he has to spend Rs 2 per kilometre on petrol; it he rides it at a faster speed of 40 km per hour, the petrol cost increases to Rs 5 per kilometer. He has Rs 100 to spend on petrol and wishes to find the maximum distance he can travel within one hour. Express this as a linear programming problem and then solve it.

Solution

Given

If a young man rides his motorcycle at 25km per hour, he has to spend Rs 2 per kilometre on petrol; it he rides it at a faster speed of 40 km per hour, the petrol cost increases to Rs 5 per kilometer. He has Rs 100 to spend on petrol

Suppose that the young man rides x km at 25km per hour and y km at 40km per hour. Then, we have to maximize P = x + y.

Clearly, x ≥ 0, y ≥ 0, 2x + 5y ≤ 100.

Since the available time is at most one hour, we have

\(\frac{x}{25}+\frac{y}{40} \leq 1 or 8x + 5y ≤ 200.\)

Now, we solve the system of inequations.

2x + 5y = 100 ⇒ \(\frac{x}{50}+\frac{y}{20}=1 .\)

This line meets the axes at (50,0) and (0,20). Plot these points and join them to get the line 2x + 5y = 100.

Also, 8x + 5y = 100 ⇒ \(\frac{x}{25}+\frac{y}{40}=1 \text {. }\)

This line meets the axes at (25,0) and (0,40). Plot these points and obtain the line 8x + 5y = 200.

x = 0 is the y-axis and y = 0 is the x-axis.

We find that the solution set of the above system is the shaded region OABC.

The coordinates of O, A, B, C are (0,0), (25,0), \(\left(\frac{50}{3}, \frac{40}{3}\right)\), and (0,20) respectively.

The values of P = x + y at these points are 0, 25, 30, and 20 respectively.

So, P = x + y is maximum when x = \(\frac{50}{3}\) and y = \(\frac{40}{3}\).

Thus, the young man can cover the maximum distance of 30km, if he rides \(\frac{50}{3}\) km at 25 km/h and \(\frac{40}{3}\) km at 40 km/h.

Common Types of Linear Programming Problems

Example 4 Suppose every gram of wheat provides 0.1g of proteins and 0.25g of carbohydrates, and the corresponding values for rice are 0.005 g and 0.5g respectively. Wheat costs Rs 5 and rice Rs 20 per kilogram. The minimum daily requirements of proteins and carbohydrates for an average man are 50g and 200g respectively. In what quantities should wheat and rice be mixed in the daily diet to provide the minimum daily requirements of proteins and carbohydrates at minimum cost, assuming that both wheat and rice are to be taken in the diet?

Solution

Given

Suppose every gram of wheat provides 0.1g of proteins and 0.25g of carbohydrates, and the corresponding values for rice are 0.005 g and 0.5g respectively. Wheat costs Rs 5 and rice Rs 20 per kilogram. The minimum daily requirements of proteins and carbohydrates for an average man are 50g and 200g respectively.

Let x g of wheat and y g of rice be mixed to fulfill the requirements.

Then, we have to minimize the cost function

\(Z=\frac{5 x}{1000}+\frac{20 y}{1000}, \text { i.e., } Z=\frac{x}{200}+\frac{y}{50}\) …(1)

xg of wheat and yg of rice must give at least 50g of proteins.

So, we must have

0.1x + 0.05y ≥ 50 or 2x + y ≥ 1000.

Similarly, xg of wheat and yg of rice must give at least 200 g of carbohydrates.

So, we must have

0.25x + 0.5y ≥ 200 or x + 2y ≥ 800.

Thus, we have to minimize \(Z=\frac{x}{200}+\frac{y}{50}\), subject to the constraints

x > 0, y > 0, 2x + y ≥ 1000 and x + 2y ≥ 800.

2x + y = 1000 ⇒ \(\frac{x}{500}+\frac{y}{1000}=1\)

This line meets the axes at A(500,0) and B(0,1000).

Plot these points and join them to obtain the line 2x + y = 100.

Clearly, (0,0) does not satisfy x + 2y ≥ 1000.

Again, x + 2y = 800 ⇒ \(\frac{x}{800}+\frac{y}{400}=1\)

This line meets the axes at C(800,0) and D(0,400).

Plot these points and join them to obtain the line x + 2y = 800.

Clearly, (0,0) does not satisfy x + 2y ≥ 800.

x = 0 is the y-axis and y = 0 is the x-axis.

We obtain the solution set of the above system, as shown by the shaded region.

Solving 2x + y = 1000 and x + 2y = 800, we get the point of intersection of AB and CD, given by E(400,200).

The minimum value of Z = \(\frac{x}{200}+\frac{y}{50}\) would be at some vertex of the unbounded feasible region BEC.

Clearly, at B we have x = 0, and at C we have y = 0.

Also, the value of Z at E(400,200) = \(\frac{400}{200}+\frac{200}{50}=6\).

So, we must have 400 g of wheat and 200 g of rice.

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

Example 5 A firm manufactures two types of products, A and B, and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines, M₁ and M₂. One unit of type A requires one minute of processing time on M₁ and two minutes of processing time on M₂; whereas one unit of type B requires one minute of processing time on M₁ and one minute on M₂. Machines M₁ and M₂ are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day to maximize the profit. Solve the problem graphically.

Solution

Given:

A firm manufactures two types of products, A and B, and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines, M₁ and M₂. One unit of type A requires one minute of processing time on M₁ and two minutes of processing time on M₂; whereas one unit of type B requires one minute of processing time on M₁ and one minute on M₂. Machines M₁ and M₂ are respectively available for at most 5 hours and 6 hours in a day.

Let x units of A and y units of B be produced to have a maximum profit.

Then, x ≥ 0 and y ≥ 0.

x units of A and y units of B will take (x+y) minutes on M₁.

∴ x + y ≤ 300.

x units of A and y units of B will take (2x+y) minutes on M₂.

∴ 2x + y ≤ 60.

Let Z be the profit function. Then, Z = 5x + 3y.

We have to maximize Z = 5x + 3y, subject to the constraints

x ≥ 0, y ≥ 0, x + y ≤ 300 and 2x + y ≤ 60.

Now, x + y = 300 ⇒ \(\frac{x}{300}+\frac{y}{300}=1.\)

This line meets the axes in (300,0) and (0,300).

Joining these points, we get the line x + y = 300.

Since (0,0) satisfies the inequation x + y ≤ 300, the region below the line x + y = 300 containing O(0,0) represents x + y ≤ 300.

Again, 2x + y = 360 ⇒ \(\frac{x}{180}+\frac{y}{360}=1 .\)

This line meets the axes in (180,0) and (0,360).

Joining these points, we get the line 2x + y = 360.

Since (0,0) satisfies 2x + y ≤ 360, the region below the line 2x + y = 360 containing (0,0)represents 2x + y ≤ 360.

Also, x = 0 is the y-axis and y = 0 is the x-axis.

On drawing these lines and shading the feasible region, we obtain a figure, given below.

On solving x = 0 and x + y = 300, we get the point R(0,300).

On solving x + y = 300 and 2x + y = 360, we get the point Q(60,40).

∴ the vertices of the feasible region are

O(0,0), P(180,0), Q(60,240) and R(0,300).

Values of Z = 5x + 3y at O, P, Q, R are 0, 900, 1020, 900 respectively.

∴ Z is maximum when x = 60 and y = 240.

Examples of Linear Programming Word Problems

Example 6 An aeroplane of an airline can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first-class ticket and a profit of Rs 300 is made on each economy-class ticket. The airline reserves at least 20 seats for first class. However, at least 4 times as many passengers prefer to travel by economy class than by first class. Determine how many of each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit?

Solution

Given:

An aeroplane of an airline can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first-class ticket and a profit of Rs 300 is made on each economy-class ticket. The airline reserves at least 20 seats for first class. However, at least 4 times as many passengers prefer to travel by economy class than by first class.

Let x tickets of first class and y tickets of economy class be sold to maximize the profit. Then,

x ≥ 20, y ≥ 4x, y ≥ 80 and x + y ≤ 200.

The profit function is given by Z = 400x + 300y.

Draw the graphs of the lines x = 20, y = 4x, y = 80 and x + y = 200 as shown below.

Graph of the inequation x ≥ 20

Since (0,0) does not satisfy x ≥ 20, the line x = 20 together with the region to its right-hand side, not containing (0,0), represents the region x ≥ 0.

Graph of the inequation y ≥ 4x

Clearly, since (20,0) does not satisfy the inequation y ≥ 4x, the line y = 4x together with the region to its left, not containing (20,0), represents y ≥ 4x.

Graph of the inequation y ≥ 80

Clearly, the line y = 80 and the region above this line represents y ≥ 80.

Graph of the inequation x + y ≤ 200

Clearly, (0,0) satisfies x + y ≤ 200. So, the line x + y = 200 together with the region containing O(0,0) represents x + y ≤ 200.

Thus, the shaded region in the given figure is the feasible region, whose vertices are A, B and C. A is the point of intersection of x = 20 and y = 80.

So, its coordinates are A(20,80).

On solving y = 4x and x + y = 200, we get B(40,160).

On solving x = 20 and x + y = 200, we get C(20,180).

The values of Z = 400x + 300y at A(20,80), B(40,160) and C(20,180) are respectively Rs 32000, Rs 64000 and Rs 62000.

∴ Z is maximum at x = 40, y = 160.

Example 7 A chemical industry produces two compounds, A and B. The following tbale gives the units of ingredients C and D (per kg) of compounds A and B as well as minimum requirements of C and D, and costs per kg of A and B.

Find the quantities of A and B which would minimize the cost.

Solution

Let x kg of A and y kg of B be produced. Then,

x ≥ 0, y ≥ 0, x + 2y ≥ 80 and 3x + y ≥ 75.

Then cost function is given by Z = 4x + 6y.

Thus, we have to minimize Z = 4x + 6y, subject to the constraints: x ≥ 0, y ≥ 0, x + 2y ≥ 80 and 3x + y ≥ 75.

Draw the graphs of the lines x = 0, y = 0, x + 2y = 80 and 3x + y = 75.

Since (0,0) does not satisfy the inequation x + 2y ≥ 80, the line x + 2y = 80 together with the region not containing (0,0) represents x + 2y ≥ 80.

Since (0,0) does not satisfy the inequation 3x + y ≥ 75, the line 3x + y = 75 together with the region not containing (0,0) represents 3x + y ≥ 75.

Thus, the shaded region is the feasible region.

The vertices of this region are P, Q and R.

On solving x = 0 and 3x + y = 75, we get the point P(0,75).

On solving x + 2y = 80 and 3x + y = 75, we get the point Q(14,33).

On solving y = 0 and x + 2y = 80, we get the point R(80,0).

The values of Z = 4x + 6y at the points P(0,75), Q(14,33) and R(80,0) are 450, 254 and 320 respectively.

Thus, Z is minimum at Q(14,33).

Hence, for a minimum cost, 14 kg of A and 33 kg of B must be taken.

Important Formulas in Linear Programming

Example 8 A company makes two types of belts, A and B; profits on these belts being Rs 4 and Rs 3 each respectively. Each belt of type A requires twice as much time as a belt of type B, and if all belts were of type B, the company could make 1000 belts per day. The supply of leather is sufficient for only 800 belts per day (both A and B combined). At the most 400 buckles for belts of type A and 700 for those of type B are available per day. How many belts of each type should the company make per day so as to maximize the profit?

Solution

Given

A company makes two types of belts, A and B; profits on these belts being Rs 4 and Rs 3 each respectively. Each belt of type A requires twice as much time as a belt of type B, and if all belts were of type B, the company could make 1000 belts per day. The supply of leather is sufficient for only 800 belts per day (both A and B combined). At the most 400 buckles for belts of type A and 700 for those of type B are available per day.

Let x belts of type A and y belts of type B be made.

Then, x ≥ 0, y ≥ 0, x ≤ 400, y ≤ 700 and x + y ≤ 800.

Now, 1000 belts of type B can be made in 1 day.

∴ 500 belts of type A can be made in 1 day.

∴ time taken to make x belts of type A and y belts of type B

= \(\left(\frac{x}{500}+\frac{y}{1000}\right) \text { days. }\)

∴ \(\frac{x}{500}+\frac{y}{1000} ≤ 1 i.e., 2x + y ≤ 1000\).

We have to maximize Z = 4x + 3y, subject to the constraints x ≥ 0, y ≥ 0, x ≤ 400, y ≤ 700, x + y ≤ 800 and 2x + y ≤ 1000.

We draw the graphs of the lines x = 0, y = 0, x = 400, y = 700, x + y = 800, 2x + y = 1000 as shown below.

Since (0,0) satisfies x ≤ 400, the line x = 400 together with the region containing O(0,0) represents x ≤ 400.

Since (0,0) satisfies y ≤ 700, the line y = 700 together with the region containing O(0,0) represents y ≤ 700.

Since (0,0) satisfies x + y ≤ 800, the line x + y = 800 together with the region containing O(0,0) represents x + y ≤ 800.

Since (0,0) satisfies 2x + y ≤ 1000, the line 2x + y = 1000 together with the region containing O(0,0) represents 2x + y ≤ 1000.

The y-axis and the region to its right-hand side represents x ≥ 0.

The x-axis and the region above it represents y ≥ 0.

Thus, the shaded region represents the feasible region, whose vertices are P, Q, R, S, T and U.

Clearly, the coordinates of P and Q are (0,0) and (400,0) respectively.

On solving x = 400 and 2x + y = 1000, we get R(400,200).

On solving x + y = 800 and 2x + y = 1000, we get S(200,600).

On solving y = 700 and x + y = 800, we get T(100,700).

On solving x = 0 and y = 700, we get U(0,700).

The values of Z = 4x + 3y at the points P, Q, R, S, T and E are respectively 0, 1600, 2200, 2600, 2500 and 2100.

The maximum of these values is 2600 occuring at S(200,600).

∴ Z is maximum when x = 200 and y = 600.

Thus, the company should make 200 belts of type A and 600 belts of type B to have a maximum profit.

Example 9 A company has factories located at each of the two places P and Q. From thes locations, a certain commodity is delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 7, 6 and 4 units of the commodity while the weekly production capacities of the factories at P and Q are respectively 9 and 8 units. The cost of transportation per unit is given below.

How many units should be transported from each factory to each depot in order that the transportation cost is minimum? Formulate the above LPP mathematically and then solve it.

Solution

This problem can be explained diagramatically as follows:

Let x units and y units of the commodity be transporated from the factory at P to the depots at A and B respectively. Then, (9-x-y) units will be transporated from the factory at P to the depot at C.

∴ x ≥ 0, y ≥ 0, and 9 – x – y ≥ 0 ⇒ x + y ≤ 9.

The weekly requirement of the depot at A is 7 units. So, (7-x) units will be transporated to A from the factory at Q.

Similarly, (6-y) units will be transporated to B from the factory at Q.

And, 8 – (7 – x + 6 – y) = (x+y-5) units will be transporated to C from the factory at Q.

∴ 7 – x ≥ 0, 6 – y ≥ 0 and x + y – 5 ≥ 0 i.e., x ≤ 7, y ≤ 6 and x + y ≥ 5.

The total cost of transporation is

Z = 16x + 10(7 – x) + 10y + 12(6-y) + 15(9-x-y) + 10(x+y-5)

⇒ Z = x – 7y + 227.

Now, we have to find the values of x and y which minimize

Z = x – 7y + 227, subject to the constraints

x ≥ 0, y ≥ 0, x + y ≤ 9, x ≤ 7, y ≤ 8 and x + y ≥ 5.

We draw the graphs of the lines

x = 0, y = 0, x + y = 9, x = 7, y = 6 and x + y = 5 as shown below.

Since (0,0) satisfies x + y ≤ 9, the line x + y = 9 together with the region containing O(0,0) represents x + y ≤ 9.

Since (0,0) does not satisfy x + y ≥ 5, the line x + y = 5 together with the region not containing O(0,0) represents x + y ≥ 5.

Since (0,0) satisfies x ≤ 7, the line x = 7 together with the region containing O(0,0) represents x ≤ 7.

Since (0,0) satisfies y ≤ 6, the line y = 6 together with the region containing O(0,0) represents y ≤ 6.

The y-axis and the region to its right-hand side represents x ≥ 0.

The x-axis and the region above it represents y ≥ 0.

Thus, the shaded region represents the feasible region whose vertices are R, S, T, U, V and W.

On solving y = 0 and x + y = 5, we get R(5,0).

On solving y = 0 and x = 7, we get S(7,0).

On solving x = 7 and x + y = 9, we get T(7,2).

On solving x + y = 9 and y = 6, we get U(3,6).

On solving x = 0 and y = 6, we get V(0,6).

On solving x = 0 and x + y = 5, we get W(0,5).

The values of Z = x – 7y + 227 at R, S, T, U, V and W are 32, 234, 220, 188, 185 and 192 respectively.

And, the factory at Q must deliver, 7, 0 and 1 units to A, B, C respectively.

Properties of Linear Programming Solutions

Example 10 A factory owner purchases two types of machines A and B for his factory. The requirements and the limitations for the machines are as follows:

He has maximum area of 9000m² available and 72 skilled labourers who can operate both the machines. How many machines of each type should he buy to maximize the daily output?

Solution

Let x machines of type A and y machines of type B be bought and let z be the daily output.

Then, z = 60x + 40y …(1)

Maximum area available = 9000m².

∴ 1000x + 1200y ≤ 9000

⇒ 5x + 6y ≤ 45 …(2)

Maximum labour available = 72 men.

∴ 12x + 8y ≤ 72 ⇒ 3x + 2y ≤ 18 …(3)

Now, we have to maximize z = 60x + 40y, subject to the constraints

5x + 6y ≤ 45,

3x + 2y ≤ 18m

x ≥ 0 and y ≥ 0.

Now, 5x + 6y = 45 ⇒ \(\frac{x}{9}+\frac{y}{(15 / 2)}=1\).

This line meets the axes at A(9,0) and B \(\left(0, \frac{15}{2}\right)\).

Plot these points and join them to obtain the line 5x + 6y = 45.

Clearly, (0,0) satisfies 5x + 6y ≤ 45.

So, the region below AB represents 5x + 6y ≤ 45.

Again, 3x + 2y = 18 ⇒ \(\frac{x}{6}+\frac{y}{9}=1\).

This line meets the axes at C(6,0) and D(0,9).

Plot these points and join them to obtain the line 3x + 2y = 18.

Clearly, (0,0) satisfies 3x + 2y ≤ 18.

So, the region below CD represents 3x + 2y ≤ 18.

x ≥ 0 is the region to the right of y-axis.

And, y ≥ 0 is the region above the x-axis.

On solving 5x + 6y = 45 and 3x + 2y = 18 simultaneously, we get x = \(\frac{9}{4}\) and y = \(\frac{45}{8}\).

So, the lines AB and CD intersect at E \(\left(\frac{9}{4}, \frac{45}{8}\right)\).

Thus, the corner points of the feasible region are

O(0,0), C(6,0), E \(\left(\frac{9}{4}, \frac{45}{8}\right)\) and B \(\left(0, \frac{15}{2}\right)\).

Value of daily output z = 60x + 40y :

(1) At O(0,0) it is z = (60 x 0 + 40 x 0) = 0.

(2) At C(6,0) it is z = (60 x 6 + 40 x 0) = 360.

(3) At E \(\left(\frac{9}{4}, \frac{45}{8}\right)\) it is z = \(\left(60 \times \frac{9}{4}+40 \times \frac{45}{8}\right)=360\).

(4) At B \(\left(0, \frac{15}{2}\right)\) it is z = \(\left(60 \times 0+40 \times \frac{15}{2}\right)=300\).

Thus, either (6 machines of type A and no machine of type B) or (2 machines of type A and 6 machines of type B) be used to have maximum output.

[Note \(\frac{9}{4}\) machines = 2 machines and \(\frac{45}{8}\) machines = 6 machines.]

Real-Life Applications of Linear Programming

Example 11 A retired person has Rs 70000 to invest and two types of bonds are available in the market for investment. First type of bond yields an annual income of 8% on the amount invested and the second type of bond yields 10% per annum. As per norms, he has to invest minimum of Rs 10000 in the first type and not more than R 30000 in the second type. How should he plan his investment, so as to get maximum return, after one year of investment?

Solution

Given

A retired person has Rs 70000 to invest and two types of bonds are available in the market for investment. First type of bond yields an annual income of 8% on the amount invested and the second type of bond yields 10% per annum. As per norms, he has to invest minimum of Rs 10000 in the first type and not more than R 30000 in the second type.

Let bonds A be at 8% and bonds B be at 10%.

Suppose he plans to invest Rs x in bonds A and Rs y in bonds B.

Then, clearly x + y = 70000 …(1)

He invests minimum of Rs 10000 in bonds A.

∴ x ≥ 10000 …(2)

Also, he invests not more than Rs 30000 in bonds B.

∴ y ≤ 30000 …(3)

Let z be the annual return on these investments. Then,

\(z=\frac{8 x}{100}+\frac{10 y}{100} \Rightarrow z=0.08 x+0.1 y\) …(4)

Thus, we have to maximize z, subject to the conditions

\(\left.\begin{array}{r}
x+y=7000 \\
x \geq 10000 \\
y \leq 30000
\end{array}\right\}\)

Now, x + y = 70000 ⇒ \(\frac{x}{70000}+\frac{y}{70000}=1\).

This line meets the axes at A(70000,0) and B(0, 70000).

Plot these points and joint them to obtain the line x + y = 70000.

Clearly, (0,0) satisfies x + y ≤ 70000.

So, the region below AB represents x + y ≤ 70000.

x ≥ 10000 is the region parallel to the y-axis and to the right of it beyond the line x = 10000.

Thus, the region to the right of line CD represents x ≥ 10000.

y ≤ 30000 is the region parallel to the x-axis and above it, but below the line y = 30000.

Thus, the region below the line EF and above the x-axis represents y ≤ 30000.

Thus, the corner points of the feasible region are

D(10000,0), A(70000,0), E(30000,40000) and F(10000,40000).

Value of annual return z = 0,08x + 0.1y :

(1) At D(10000,0) it is z = (0.08 x 10000 + 0.1 x 0) = 800.

(2) At A(70000,0) it is z = (0.08 x 70000 + 0.1 x 0) = 5600.

(3) At E(30000,40000) it is z = (0.08 x 30000 + 0.1 x 40000) = 6400.

(4) At F(10000,40000) it is z = (0.08 x 10000 + 0.1 x 40000) = 4800.

So, in order to get a maximum annual return, he should invest Rs 30000 in bond A and Rs 40000 in bond B.

WBCHSE Class 12 Maths Special Integrals

Some Special Integrals – Three Special Integrals

Theorem

(1) \(\int \frac{d x}{\left(a^2-x^2\right)}=\frac{1}{2 a} \log \left|\frac{a+x}{a-x}\right|+C\)

(2) \(\int \frac{d x}{\left(x^2-a^2\right)}=\frac{1}{2 a} \log \left|\frac{x-a}{x+a}\right|+C\)

(3) \(\int \frac{d x}{\left(x^2+a^2\right)}=\frac{1}{a} \tan ^{-1} \frac{x}{a}+C\)

Proof

(1) \(\int \frac{d x}{\left(a^2-x^2\right)}=\int \frac{d x}{(a+x)(a-x)}\)

= \(\int \frac{1}{2 a} \cdot\left\{\frac{(a-x)+(a+x)}{(a+x)(a-x)}\right\} d x=\frac{1}{2 a} \cdot\left[\int \frac{d x}{(a+x)}+\int \frac{d x}{(a-x)}\right]\)

= \(\frac{1}{2 a} \cdot[\log |a+x|-\log |a-x|]+C\)

= \(\frac{1}{2 a} \cdot \log \left|\frac{a+x}{a-x}\right|+C\)

∴ \(\int \frac{d x}{\left(a^2-x^2\right)}=\frac{1}{2 a} \cdot \log \left|\frac{a+x}{a-x}\right|+C\)

(2) \(\int \frac{d x}{\left(x^2-a^2\right)}=\int \frac{d x}{(x-a)(x+a)}\)

= \(\int \frac{1}{2 a} \cdot\left\{\frac{(x+a)-(x-a)}{(x-a)(x+a)}\right\} d x=\frac{1}{2 a} \cdot\left[\int \frac{d x}{(x-a)}-\int \frac{d x}{(x+a)}\right]\)

= \(\frac{1}{2 a} \cdot[\log |x-a|-\log |x+a|]+C=\frac{1}{2 a} \cdot \log \left|\frac{x-a}{x+a}\right|+C\)

∴ \(\int \frac{d x}{\left(x^2-a^2\right)}=\frac{1}{2 a} \cdot \log \left|\frac{x-a}{x+a}\right|+C\)

(3) \(\int \frac{d x}{\left(x^2+a^2\right)}=\frac{1}{a^2} \cdot \int \frac{d x}{\left(1+\frac{x^2}{a^2}\right)}\)

= \(\frac{1}{a^2} \cdot \int \frac{a d t}{\left(1+t^2\right)}\) [putting \(\frac{x}{a}\) = t and dx = a dt]

= \(\frac{1}{a} \tan ^{-1} t+C=\frac{1}{a} \tan ^{-1} \frac{x}{a}+C .\)

∴ \(\int \frac{d x}{\left(x^2+a^2\right)}=\frac{1}{a} \tan ^{-1} \frac{x}{a}+C\)

Remark If we have an integral of the form \(\int \frac{d x}{\left(a x^2+b x+c\right)}\), then we put the denominator in the form [(x+α)² ± β²] and then integrate.

Read and Learn More  Class 12 Math Solutions

WBCHSE Class 12 Maths Special Integrals 

Solved Examples

Example 1 Evaluate:

(1) \(\int \frac{d x}{\left(1-4 x^2\right)}\)

(2) \(\int \frac{d x}{\left(32-2 x^2\right)}\)

(3) \(\int \frac{x^2}{\left(1-x^6\right)} d x\)

Solution We have

(1) \(\int \frac{d x}{\left(1-4 x^2\right)}=\frac{1}{4} \cdot \int \frac{d x}{\left(\frac{1}{4}-x^2\right)}\)

= \(\frac{1}{4} \cdot \int \frac{d x}{\left\{\left(\frac{1}{2}\right)^2-x^2\right\}}\)

= \(\frac{1}{4} \cdot \frac{1}{\left(2 \times \frac{1}{2}\right)} \cdot \log \left|\frac{\frac{1}{2}+x}{\frac{1}{2}-x}\right|+C\)

[∵ \(\int \frac{d x}{\left(a^2-x^2\right)}=\frac{1}{2 a} \log \left|\frac{a+x}{a-x}\right|+C\)]

\(\frac{1}{4} \log \left|\frac{1+2 x}{1-2 x}\right|+C\)

(2) \(\int \frac{d x}{\left(32-2 x^2\right)}=\frac{1}{2} \cdot \int \frac{d x}{\left(16-x^2\right)}\)

= \(\frac{1}{2} \cdot \int \frac{d x}{\left\{(4)^2-x^2\right\}}\)

= \(\frac{1}{2} \cdot \frac{1}{(2 \times 4)} \log \left|\frac{4+x}{4-x}\right|+C\)

[∵ \(\int \frac{d x}{\left(a^2-x^2\right)}=\frac{1}{2 a} \log \left|\frac{a+x}{a-x}\right|+C\)]

= \(\frac{1}{16} \log \left|\frac{4+x}{4-x}\right|+C\)

(3) Putting x³ = t and 3x²dx = dt, we get

\(\int \frac{x^2}{\left(1-x^6\right)} d x=\frac{1}{3} \cdot \int \frac{1}{\left(1-t^2\right)} d t\)

= \(\frac{1}{3} \cdot \frac{1}{(2 \times 1)} \cdot \log \left|\frac{1+t}{1-t}\right|+C\)

[∵ \(\int \frac{d x}{\left(a^2-x^2\right)}=\frac{1}{2 a} \log \left|\frac{a+x}{a-x}\right|+C\)]

= \(\frac{1}{6} \log \left|\frac{1+x^3}{1-x^3}\right|+C\)

WBBSE Class 12 Special Integrals Solutions

Example 2 Evaluate:

\(\int \frac{\sin x}{\left(1-4 \cos ^2 x\right)} d x\)

Solution

Putting cos x = t and -sin x dx = dt, we get

\(\int \frac{\sin x}{\left(1-4 \cos ^2 x\right)} d x=-\int \frac{d t}{\left(1-4 t^2\right)}\)

= \(-\frac{1}{4} \cdot \int \frac{d t}{\left(\frac{1}{4}-t^2\right)}=-\frac{1}{4} \cdot \int \frac{d t}{\left\{\left(\frac{1}{2}\right)^2-t^2\right\}}\)

= \(-\frac{1}{4} \log \left|\frac{1+2 t}{1-2 t}\right|+C=-\frac{1}{4} \log \left|\frac{1+2 \cos x}{1-2 \cos x}\right|+C\)

Example 3 Evaluate:

(1) \(\int \frac{d x}{\left(9 x^2-1\right)}\)

(2) \(\int \frac{x}{\left(x^4-9\right)} d x\)

(3) \(\int \frac{x^2}{\left(x^2-9\right)} d x\)

Solution We have

(1) \(\int \frac{d x}{\left(9 x^2-1\right)}=\frac{1}{9} \cdot \int \frac{d x}{\left(x^2-\frac{1}{9}\right)}\)

= \(\frac{1}{9} \cdot \int \frac{d x}{\left\{x^2-\left(\frac{1}{3}\right)^2\right\}}\)

= \(\frac{1}{9} \cdot \frac{1}{\left(2 \times \frac{1}{3}\right)} \log \left|\frac{x-\frac{1}{3}}{x+\frac{1}{3}}\right|+C\)

[∵ \(\int \frac{d x}{\left(x^2-a^2\right)}=\frac{1}{2 a} \log \left|\frac{x-a}{x+a}\right|+C\)]

(2) Putting x² = t and 2x dx = dt, we get

\(\int \frac{x}{\left(x^4-9\right)} d x=\frac{1}{2} \int \frac{d t}{\left(t^2-9\right)}=\frac{1}{2} \cdot \int \frac{d t}{\left\{t^2-(3)^2\right\}}\)

= \(\frac{1}{2} \cdot \frac{1}{(2 \times 3)} \log \left|\frac{t-3}{t+3}\right|+C\)

= \(\frac{1}{12} \log \left|\frac{x^2-3}{x^2+3}\right|+C\)

(3) \(\int \frac{x^2}{\left(x^2-9\right)} d x=\int\left\{1+\frac{9}{x^2-9}\right\} d x\)

= \(\int d x+9 \int \frac{d x}{\left[x^2-(3)^2\right]}\)

= \(x+9 \cdot\left[\frac{1}{(2 \times 3)} \log \left|\frac{x-3}{x+3}\right|\right]+C\)

= \(x+\frac{3}{2} \log \left|\frac{x-3}{x+3}\right|+C\).

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

Example 4 Evaluate \(\int \frac{d x}{\left(4+25 x^2\right)} .\)

Solution We have

\(\int \frac{d x}{\left(4+25 x^2\right)}=\frac{1}{25} \cdot \int \frac{d x}{\left(\frac{4}{25}+x^2\right)}\)

= \(\frac{1}{25} \cdot \int \frac{d x}{\left\{(2 / 5)^2+x^2\right\}}\)

[∵ \(\int \frac{d x}{\left(a^2+x^2\right)}=\frac{1}{a} \tan ^{-1} \frac{x}{a}+\mathrm{C}\)]

= \(\frac{1}{10} \tan ^{-1}\left(\frac{5 x}{2}\right)+C\).

WBCHSE Class 12 Maths Special Integrals 

Example 5 Evaluate \(\int \frac{3 x}{\left(1+2 x^4\right)} d x\)

Solution

\(\int \frac{3 x}{\left(1+2 x^4\right)} d x\)

Putting x² = t and 2x dx = dt, we get

\(\int \frac{3 x}{\left(1+2 x^4\right)} d x=\frac{3}{2} \cdot \int \frac{d t}{\left(1+2 t^2\right)}\)

= \(\frac{3}{4} \cdot \int \frac{d t}{\left(\frac{1}{2}+t^2\right)}=\frac{3}{4} \cdot \int \frac{d t}{\left\{\left(\frac{1}{\sqrt{2}}\right)^2+t^2\right\}}\)

= \(\frac{3}{4} \cdot \frac{1}{(1 / \sqrt{2})} \tan ^{-1} \frac{t}{(1 / \sqrt{2})}+C\)

= \(\frac{3}{2 \sqrt{2}} \tan ^{-1}(\sqrt{2} t)+C=\frac{3}{2 \sqrt{2}} \tan ^{-1}\left(\sqrt{2} x^2\right)+C\).

\(\int \frac{3 x}{\left(1+2 x^4\right)} d x\) = \(\frac{3}{2 \sqrt{2}} \tan ^{-1}(\sqrt{2} t)+C=\frac{3}{2 \sqrt{2}} \tan ^{-1}\left(\sqrt{2} x^2\right)+C\).

Example 6 Evaluate \(\int \frac{d x}{\left(1+5 \sin ^2 x\right)}\).

Solution

\(\int \frac{d x}{\left(1+5 \sin ^2 x\right)}\)

On dividing num. and denom. by cos²x, we get

\(\int \frac{d x}{\left(1+5 \sin ^2 x\right)}=\int \frac{\left(1 / \cos ^2 x\right)}{\left(\frac{1}{\cos ^2 x}+5 \cdot \frac{\sin ^2 x}{\cos ^2 x}\right)} d x\)

= \(\int \frac{\sec ^2 x}{\left(\sec ^2 x+5 \tan ^2 x\right)} d x=\int \frac{\sec ^2 x}{\left\{\left(1+\tan ^2 x\right)+5 \tan ^2 x\right\}} d x\)

= \(\int \frac{\sec ^2 x}{\left(1+6 \tan ^2 x\right)} d x=\int \frac{d t}{\left(1+6 t^2\right)}\), where tan x = t

= \(\frac{1}{6} \int \frac{d t}{\left(\frac{1}{6}+t^2\right)}=\frac{1}{6} \cdot \int \frac{d t}{\left\{\left(\frac{1}{\sqrt{6}}\right)^2+t^2\right\}}\)

= \(\frac{1}{6} \cdot \frac{1}{(1 / \sqrt{6})} \tan ^{-1} \frac{t}{(1 / \sqrt{6})}+C=\frac{1}{\sqrt{6}} \tan ^{-1}(\sqrt{6} t)+C\)

= \(\frac{1}{\sqrt{6}} \tan ^{-1}(\sqrt{6} \tan x)+C \text {. }\)

\(\int \frac{d x}{\left(1+5 \sin ^2 x\right)}\) = \(\frac{1}{\sqrt{6}} \tan ^{-1}(\sqrt{6} \tan x)+C \text {. }\)

Step-by-Step Solutions to Special Integral Problems

Example 7 Evaluate \(\int \frac{d x}{\left(2+\sin ^2 x\right)}\)

Solution

\(\int \frac{d x}{\left(2+\sin ^2 x\right)}\)

On dividing num. and denom. by cos²x, we get

\(\int \frac{d x}{\left(2+\sin ^2 x\right)}=\int \frac{\sec ^2 x}{\left(2 \sec ^2 x+\tan ^2 x\right)} d x=\int \frac{\sec ^2 x}{\left\{2\left(1+\tan ^2 x\right)+\tan ^2 x\right\}} d x\)

= \(\int \frac{\sec ^2 x}{2+3 \tan ^2 x} d x=\int \frac{d t}{\left(2+3 t^2\right)}\), where tan x = t

= \(\frac{1}{3} \cdot \int \frac{d t}{\left(t^2+\frac{2}{3}\right)}=\frac{1}{3} \cdot \int \frac{d t}{\left(\sqrt{\frac{2}{3}}\right)^2+t^2}\)

= \(\frac{1}{3} \cdot \frac{1}{\sqrt{\frac{2}{3}}} \cdot \tan ^{-1} \frac{t}{\left(\sqrt{\frac{2}{3}}\right)}+C=\frac{1}{\sqrt{6}} \tan ^{-1} \frac{\sqrt{3} t}{\sqrt{2}}+C\)

= \(\frac{1}{\sqrt{6}} \tan ^{-1}\left(\frac{\sqrt{3} \tan x}{\sqrt{2}}\right)+C\).

\(\int \frac{d x}{\left(2+\sin ^2 x\right)}\) = \(\frac{1}{\sqrt{6}} \tan ^{-1}\left(\frac{\sqrt{3} \tan x}{\sqrt{2}}\right)+C\).

Example 8 Evaluate \(\int \frac{d x}{\left(x^2+6 x+13\right)}\).

Solution We have

\(\int \frac{d x}{\left(x^2+6 x+13\right)}=\int \frac{d x}{\left\{\left(x^2+6 x+9\right)+4\right\}}\)

= \(\int \frac{d x}{\left\{(x+3)^2+2^2\right\}}=\int \frac{d t}{\left(t^2+2^2\right)}\), where (x+3) = t

= \(\frac{1}{2} \tan ^{-1} \frac{t}{2}+C\)

= \(\frac{1}{2} \tan ^{-1} \frac{1}{2}(x+3)+C .\)

\(\int \frac{d x}{\left(x^2+6 x+13\right)}\) = \(\frac{1}{2} \tan ^{-1} \frac{1}{2}(x+3)+C .\)

Example 9 Evaluate \(\int \frac{d x}{\left(x^2+8 x+20\right)}\)

Solution We have

\(\int \frac{d x}{\left(x^2+8 x+20\right)}=\int \frac{d x}{\left\{(x+4)^2+2^2\right\}}=\int \frac{d t}{\left(t^2+2^2\right)}\), where (x+4) = t-3

= \(\frac{1}{2} \tan ^{-1} \frac{t}{2}+C\)

= \(\frac{1}{2} \tan ^{-1} \frac{1}{2}(x+4)+C\).

\(\int \frac{d x}{\left(x^2+8 x+20\right)}\) = \(\frac{1}{2} \tan ^{-1} \frac{1}{2}(x+4)+C\).

Example 10 Evaluate \(\int \frac{d x}{\left(9 x^2-12 x+8\right)}\)

Solution We have

\(\left(9 x^2-12 x+8\right)=9\left(x^2-\frac{4}{3} x+\frac{8}{9}\right)\)

= \(9\left\{\left(x^2-\frac{4}{3} x+\frac{4}{9}\right)-\frac{4}{9}+\frac{8}{9}\right\}=9\left\{\left(x-\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^2\right\}\)

∴ \(\int \frac{d x}{\left(9 x^2-12 x+8\right)}=\frac{1}{9} \cdot \int \frac{d x}{\left\{\left(x-\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^2\right\}}\)

= \(\frac{1}{9} \cdot \frac{1}{(2 / 3)} \tan ^{-1}\left\{\frac{\left(x-\frac{2}{3}\right)}{(2 / 3)}\right\}+C=\frac{1}{6} \tan ^{-1}\left(\frac{3 x-2}{2}\right)+C\).

\(\int \frac{d x}{\left(9 x^2-12 x+8\right)}\) = \(\frac{1}{9} \cdot \frac{1}{(2 / 3)} \tan ^{-1}\left\{\frac{\left(x-\frac{2}{3}\right)}{(2 / 3)}\right\}+C=\frac{1}{6} \tan ^{-1}\left(\frac{3 x-2}{2}\right)+C\).

WBCHSE Class 12 Maths Special Integrals 

Example 11 Evaluate \(\int \frac{x}{\left(x^4-x^2+1\right)} d x\).

Solution

\(\int \frac{x}{\left(x^4-x^2+1\right)} d x\)

Putting x² = t and 2x dx = dt, we get

\(\int \frac{x}{\left(x^4-x^2+1\right)} d x=\frac{1}{2} \cdot \int \frac{d t}{\left(t^2-t+1\right)}=\frac{1}{2} \cdot \int \frac{d t}{\left\{\left(t-\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2\right\}}\)

= \(\frac{1}{2} \cdot \frac{1}{\left(\frac{\sqrt{3}}{2}\right)} \tan ^{-1} \frac{\left(t-\frac{1}{2}\right)}{\left(\frac{\sqrt{3}}{2}\right)}+C\)

= \(\frac{1}{\sqrt{3}} \cdot \tan ^{-1}\left(\frac{2 t-1}{\sqrt{3}}\right)+C=\frac{1}{\sqrt{3}} \tan ^{-1}\left(\frac{2 x^2-1}{\sqrt{3}}\right)+C\)

\(\int \frac{x}{\left(x^4-x^2+1\right)} d x\). = \(\frac{1}{\sqrt{3}} \cdot \tan ^{-1}\left(\frac{2 t-1}{\sqrt{3}}\right)+C=\frac{1}{\sqrt{3}} \tan ^{-1}\left(\frac{2 x^2-1}{\sqrt{3}}\right)+C\)

Example 12 Evaluate \(\int \frac{d x}{\left(2 x^2+x-1\right)}\).

Solution We have

\(\int \frac{d x}{\left(2 x^2+x-1\right)}=\frac{1}{2} \cdot \int \frac{d x}{\left(x^2+\frac{1}{2} x-\frac{1}{2}\right)}\)

= \(\frac{1}{2} \int \frac{d x}{\left[\left\{x^2+\frac{1}{2} x+\left(\frac{1}{4}\right)^2\right\}-\frac{1}{16}-\frac{1}{2}\right]}=\frac{1}{2} \int \frac{d x}{\left[\left(x+\frac{1}{4}\right)^2-\left(\frac{3}{4}\right)^2\right]}\)

= \(\frac{1}{2} \cdot \frac{1}{2 \cdot \frac{3}{4}} \log \left|\frac{\left(x+\frac{1}{4}\right)-\frac{3}{4}}{\left(x+\frac{1}{4}\right)+\frac{3}{4}}\right|+C=\frac{1}{3} \log \left|\frac{2 x-1}{2(x+1)}\right|+C\)

Common Formulas for Special Integrals

Example 13 Evaluate \(\int \frac{d x}{\left(3 x^2+13 x-10\right)}\).

Solution We have

\(\left(3 x^2+13 x-10\right)=3\left(x^2+\frac{13}{3} x-\frac{10}{3}\right)\)

= \(3\left\{\left(x+\frac{13}{6}\right)^2-\frac{169}{36}-\frac{10}{3}\right\}=3\left\{\left(x+\frac{13}{6}\right)^2-\frac{289}{36}\right\}\)

= \(3\left\{\left(x+\frac{13}{6}\right)^2-\left(\frac{17}{6}\right)^2\right\}.\)

∴ \(\int \frac{d x}{\left(3 x^2+13 x-10\right)}=\int \frac{d x}{3\left\{\left(x+\frac{13}{6}\right)^2-\left(\frac{17}{6}\right)^2\right\}}\)

= \(\frac{1}{3} \int \frac{d t}{\left\{t^2-\left(\frac{17}{6}\right)^2\right\}}\), where [x+\(\frac{13}{6}\)] = t [/latex]

= \(\frac{1}{3} \cdot \frac{1}{\left(2 \times \frac{17}{6}\right)} \log \left|\frac{t-\frac{17}{6}}{t+\frac{17}{6}}\right|+C\)

[∵ \(\int \frac{d x}{\left(x^2-a^2\right)}=\frac{1}{2 a} \log \left|\frac{x-a}{x+a}\right|\)]

= \(\frac{1}{17} \log \left|\frac{6 t-17}{6 t+17}\right|+C\)

= \(\frac{1}{17} \log \left|\frac{6\left(x+\frac{13}{6}\right)-17}{6\left(x+\frac{13}{6}\right)+17}\right|=\frac{1}{17} \log \left|\frac{6 x-4}{6 x+30}\right|+C\)

= \(\frac{1}{17} \log \left|\frac{3 x-2}{3 x+15}\right|+C=\frac{1}{17} \log \left|\frac{(3 x-2)}{3(x+5)}\right|+C\)

= \(\frac{1}{17}\left\{\log \frac{1}{3}+\log \left|\frac{3 x-2}{x+5}\right|\right\}+C\)

= \(\frac{1}{17} \log \left|\frac{3 x-2}{x+5}\right|+k\),

where \(\frac{1}{17} \log \frac{1}{3}+C\) = k = constant.

WBCHSE Class 12 Maths Special Integrals 

Example 14 Evaluate \(\int \frac{d x}{\left(1+x-x^2\right)} .\)

Solution We have

\(\int \frac{d x}{\left(1+x-x^2\right)}=-\int \frac{d x}{\left(x^2-x-1\right)}\)

= \(-\int \frac{d x}{\left\{\left(x^2-x+\frac{1}{4}\right)-\frac{5}{4}\right\}}=-\int \frac{d x}{\left\{\left(x-\frac{1}{2}\right)^2-\left(\frac{\sqrt{5}}{2}\right)^2\right\}}\)

= \(\int \frac{d x}{\left\{\left(\frac{\sqrt{5}}{2}\right)^2-\left(x-\frac{1}{2}\right)^2\right\}}=\int \frac{d x}{\left\{\left(\frac{\sqrt{5}}{2}\right)^2-u^2\right\}}\), where [x – \(\frac{1}{2}\)] = u

= \(\frac{1}{\left(2 \times \frac{\sqrt{5}}{2}\right)} \cdot \log \left|\frac{\frac{\sqrt{5}}{2}+u}{\frac{\sqrt{5}}{2}-u}\right|+C\)

= \(\frac{1}{\sqrt{5}} \log \left|\frac{\sqrt{5}+2 u}{\sqrt{5}-2 u}\right|+C=\frac{1}{\sqrt{5}} \log \left|\frac{\sqrt{5}+2\left(x-\frac{1}{2}\right)}{\sqrt{5}-2\left(x-\frac{1}{2}\right)}\right|+C\)

= \(\frac{1}{\sqrt{5}} \log \left|\frac{\sqrt{5}+2 x-1}{\sqrt{5}-2 x+1}\right|+C=\frac{1}{\sqrt{5}} \log \left|\frac{(\sqrt{5}-1)+2 x}{(\sqrt{5}+1)-2 x}\right|+C .\)

Example 15 Evaluate \(\int \frac{d x}{\left(5-8 x-x^2\right)}\)

Solution We have

\(\int \frac{d x}{\left(5-8 x-x^2\right)}=-\int \frac{d x}{\left(x^2+8 x-5\right)}\)

= \(-\int \frac{d x}{\left\{\left(x^2+8 x+16\right)-21\right\}}=-\int \frac{d x}{\left\{(x+4)^2-(\sqrt{21})^2\right\}}\)

= \(\int \frac{d x}{\left\{(\sqrt{21})^2-(x+4)^2\right\}}=\int \frac{d t}{\left\{(\sqrt{21})^2-t^2\right\}}\), Where (x+4) = t

= \(\frac{1}{2 \sqrt{21}} \cdot \log \left|\frac{\sqrt{21}+t}{\sqrt{21}-t}\right|+C\)

= \(\frac{1}{2 \sqrt{21}} \cdot \log \left|\frac{\sqrt{21}+4+x}{\sqrt{21}-4-x}\right|+C\).

Example 16 Evaluate \(\int \frac{d x}{\left(1-6 x-9 x^2\right)} .\)

Solution We have

\(\int \frac{d x}{\left(1-6 x-9 x^2\right)}=-\int \frac{d x}{\left(9 x^2+6 x-1\right)}=-\frac{1}{9} \int \frac{d x}{\left(x^2+\frac{2}{3} x-\frac{1}{9}\right)}\)

= \(-\frac{1}{9} \cdot \int \frac{d x}{\left\{\left(x^2+\frac{2}{3} x+\frac{1}{9}\right)-\frac{2}{9}\right\}}\)

= \(-\frac{1}{9} \cdot \int \frac{d x}{\left\{\left(x+\frac{1}{3}\right)^2-\left(\frac{\sqrt{2}}{3}\right)^2\right\}}=\frac{1}{9} \cdot \int \frac{d x}{\left\{\left(\frac{\sqrt{2}}{3}\right)^2-\left(x+\frac{1}{3}\right)^2\right\}}\)

= \(\frac{1}{9} \cdot \int \frac{d x}{\left\{\left(\frac{\sqrt{2}}{3}\right)^2-t^2\right\}}\), where (x + \(\frac{1}{3}\)) = t

= \(\frac{1}{9} \cdot \frac{1}{2 \cdot \frac{\sqrt{2}}{3}} \log \left|\frac{\frac{\sqrt{2}}{3}+t}{\frac{\sqrt{2}}{3}-t}\right|+C=\frac{1}{6 \sqrt{2}} \log \left|\frac{\sqrt{2}+3 t}{\sqrt{2}-3 t}\right|+C\)

= \(\frac{1}{6 \sqrt{2}} \log \left|\frac{\sqrt{2}+3\left(x+\frac{1}{3}\right)}{\sqrt{2}-3\left(x+\frac{1}{3}\right)}\right|+C\)

= \(\frac{1}{6 \sqrt{2}} \log \left|\frac{\sqrt{2}+1+3 x}{\sqrt{2}-1-3 x}\right|+C.\)

Class 12 Integration Special Integrals 

Example 17 Evaluate \(\int \frac{\cos x}{\left(\sin ^2 x+4 \sin x+5\right)} d x\)

Solution

\(\int \frac{\cos x}{\left(\sin ^2 x+4 \sin x+5\right)} d x\)

Putting sin x = t and cos x dx = dt, we get

\(\int \frac{\cos x}{\left(\sin ^2 x+4 \sin x+5\right)} d x=\int \frac{d t}{\left(t^2+4 t+5\right)}=\int \frac{d t}{\left\{\left(t^2+4 t+4\right)+1\right\}}\)

= \(\int \frac{d t}{\left\{(t+2)^2+1^2\right\}}=\int \frac{d u}{\left(u^2+1\right)}\), where u = (t+2)

= tan^-1u + C = tan^-1(t+2) + C

= tan^-1(sin x + 2) + C.

Example 18 \(\int \frac{e^x}{\left(e^{2 x}+6 e^x+5\right)} d x\).

Solution

\(\int \frac{e^x}{\left(e^{2 x}+6 e^x+5\right)} d x\)

Putting e^x = t and e^xdx = dt, we get

\(\int \frac{e^x}{e^{2 x}+6 e^x+5} d x=\int \frac{d t}{\left(t^2+6 t+5\right)}=\int \frac{d t}{\left\{\left(t^2+6 t+9\right)-4\right\}}\)

= \(\int \frac{d t}{\left\{(t+3)^2-2^2\right\}}=\int \frac{d u}{\left(u^2-2^2\right)}\), where (t+3) = u

= \(\frac{1}{(2 \times 2)} \log \left|\frac{u-2}{u+2}\right|+C=\frac{1}{4} \log \left|\frac{t+3-2}{t+3+2}\right|+C\)

= \(\frac{1}{4} \log \left|\frac{t+1}{t+5}\right|+C=\frac{1}{4} \log \left|\frac{e^x+1}{e^x+5}\right|+C .\)

Examples of Special Integrals with Solutions

Integrals of the form \(\int \frac{(p x+q)}{\left(a x^2+b x+c\right)} d x\)

Method Let (px + q) = A. \(\frac{d}{d x}\left(a x^2+b x+c\right)\) + B

Find A and B.

Now, the integrand so obtained can be integrated easily.

Class 12 Integration Special Integrals 

Example 19 Evaluate \(\int \frac{x}{\left(x^2+x+1\right)} d x\)

Solution

Let x = A . \(\frac{d}{d x}\left(x^2+x+1\right)\) + B. Then,

x = A(2x+1) + B.

Comparing coefficients of like powers of x, we get

(2A = 1 and A + B = 0) ⇒ [A=\(\frac{1}{2}\) and B=\(\frac{-1}{2}\)].

∴ \(\int \frac{x}{\left(x^2+x+1\right)} d x=\int \frac{\frac{1}{2} \cdot(2 x+1)-\frac{1}{2}}{\left(x^2+x+1\right)} d x\)

= \(\frac{1}{2} \int \frac{(2 x+1)}{\left(x^2+x+1\right)} d x-\frac{1}{2} \int \frac{d x}{\left(x^2+x+1\right)}\)

= \(\frac{1}{2} \log \left|x^2+x+1\right|-\frac{1}{2} \int \frac{d x}{\left\{\left(x+\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2\right\}}\)

= \(\frac{1}{2} \log \left|x^2+x+1\right|-\frac{1}{2} \cdot \frac{1}{\left(\frac{\sqrt{3}}{2}\right)} \tan ^{-1}\left\{\frac{\left(x+\frac{1}{2}\right)}{\left(\frac{\sqrt{3}}{2}\right)}\right\}+C\)

= \(\frac{1}{2} \log \left|x^2+x+1\right|-\frac{1}{\sqrt{3}} \tan ^{-1}\left(\frac{2 x+1}{\sqrt{3}}\right)+C .\)

Example 20 Evaluate \(\int \frac{(3 x+1)}{\left(2 x^2-2 x+3\right)} d x\)

Solution

\(\int \frac{(3 x+1)}{\left(2 x^2-2 x+3\right)} d x\)

Let (3x+1) = A . \(\frac{d}{d x}\left(2 x^2-2 x+3\right)\) + B. Then,

(3x+1) = A(4x-2) + B

Comparing coefficients of like powers of x, we get

(4A = 3 and B – 2A = 1) ⇒ [A=\(\frac{3}{4}\) and B=\(\frac{5}{2}\)].

∴ \(\int \frac{(3 x+1)}{\left(2 x^2-2 x+3\right)} d x=\int \frac{A \cdot(4 x-2)+B}{\left(2 x^2-2 x+3\right)}\)

= \(\int \frac{\frac{3}{4} \cdot(4 x-2)+\frac{5}{2}}{\left(2 x^2-2 x+3\right)} d x=\frac{3}{4} \cdot \int \frac{(4 x-2)}{\left(2 x^2-2 x+3\right)} d x+\frac{5}{2} \int \frac{d x}{2\left(x^2-x+\frac{3}{2}\right)}\)

= \(\frac{3}{4} \log \left|2 x^2-2 x+3\right|+\frac{5}{4} \cdot \int \frac{d x}{\left\{\left(x^2-x+\frac{1}{4}\right)+\frac{5}{4}\right\}}\)

= \(\frac{3}{4} \log \left|2 x^2-2 x+3\right|+\frac{5}{4} \cdot \int \frac{d x}{\left\{\left(x-\frac{1}{2}\right)^2+\left(\frac{\sqrt{5}}{2}\right)^2\right\}}\)

= \(\frac{3}{4} \log \left|2 x^2-2 x+3\right|+\frac{5}{4} \cdot \frac{1}{\left(\frac{\sqrt{5}}{2}\right)} \tan ^{-1}\left\{\frac{\left(x-\frac{1}{2}\right)}{\left(\frac{\sqrt{5}}{2}\right)}\right\}+C\)

= \(\frac{3}{4} \log \left|2 x^2-2 x+3\right|+\frac{\sqrt{5}}{2} \tan ^{-1}\left(\frac{2 x-1}{\sqrt{5}}\right)+C \text {. }\)

Class 12 Integration Special Integrals 

Example 21 Evaluate \(\int \frac{(2 x+1)}{\left(4-3 x-x^2\right)} d x\)

Solution

\(\int \frac{(2 x+1)}{\left(4-3 x-x^2\right)} d x\)

Let (2x+1) = A . \(\frac{d}{d x}\left(4-3 x-x^2\right)\) + B.

Then, (2x+1) = A(-3-2x) + B …(1)

Comparing coefficients of like terms, we get

(-2A = 2 and -3A + B = 1) ⇒ (A = -1, B = -2).

∴ \(\int \frac{(2 x+1)}{\left(4-3 x-x^2\right)} d x=\int\left\{\frac{(-1) \cdot(-3-2 x)-2}{\left(4-3 x-x^2\right)}\right\} d x\)

= \(-\int \frac{(-3-2 x)}{\left(4-3 x-x^2\right)} d x-2 \int \frac{d x}{\left(4-3 x-x^2\right)}\)

= \(-\log \left|4-3 x-x^2\right|+2 \int \frac{d x}{\left(x^2+3 x-4\right)}\)

= \(-\log \left|4-3 x-x^2\right|+2 \int \frac{d x}{\left(x+\frac{3}{2}\right)^2-\left(4+\frac{9}{4}\right)}\)

= \(-\log \left|4-3 x-x^2\right|+2 \int \frac{d x}{\left\{\left(x+\frac{3}{2}\right)^2-\left(\frac{5}{2}\right)^2\right\}}\)

= \(-\log \left|4-3 x-x^2\right|+\frac{2}{\left(2 \times \frac{5}{2}\right)} \log \left|\frac{\left(x+\frac{3}{2}\right)-\frac{5}{2}}{\left(x+\frac{3}{2}\right)+\frac{5}{2}}\right|+C\)

= \(-\log \left|4-3 x-x^2\right|+\frac{2}{5} \log \left|\frac{x-1}{x+4}\right|+C\).

Example 22 Evaluate \(\int\left(\frac{x^2+5 x+3}{x^2+3 x+2}\right) d x\).

Solution We have

\(\frac{\left(x^2+5 x+3\right)}{\left(x^2+3 x+2\right)}=\left\{1+\frac{(2 x+1)}{x^2+3 x+2}\right\}\)

⇒ \(\int \frac{\left(x^2+5 x+3\right)}{\left(x^2+3 x+2\right)} d x=\int d x+\int \frac{(2 x+1)}{\left(x^2+3 x+2\right)} d x\) …(1)

Let (2x+1) = A . \(\frac{d}{d x}\left(x^2+3 x+2\right)+B.\) Then,

(2x+1) = A(2x+3) + B …(2)

Comparing coefficients of like powers of x, we get

(2A = 2 and 3A + B = 1) ⇒ (A=1 and B=-2).

∴ (2x+1) = (2x+3) – 2.

∴ \(I=x+\int \frac{(2 x+1)}{\left(x^2+3 x+2\right)} d x\)

= \(x+\int \frac{\{(2 x+3)-2\}}{\left(x^2+3 x+2\right)} d x=x+\int \frac{(2 x+3)}{\left(x^2+3 x+2\right)} d x-2 \int \frac{d x}{\left(x^2+3 x+2\right)}\)

= \(x+\log \left|x^2+3 x+2\right|-2 \int \frac{d x}{\left\{\left(x^2+3 x+\frac{9}{4}\right)+\left(2-\frac{9}{4}\right)\right\}}\)

= \(x+\log \left|x^2+3 x+2\right|-2 \int \frac{d x}{\left\{\left(x+\frac{3}{2}\right)^2-\left(\frac{1}{2}\right)^2\right\}}\)

= \(x+\log \left|x^2+3 x+2\right|-2 \cdot \frac{1}{\left(2 \times \frac{1}{2}\right)} \log \left|\frac{x+\frac{3}{2}-\frac{1}{2}}{x+\frac{3}{2}+\frac{1}{2}}\right|+C\)

= \(x+\log \left|x^2+3 x+2\right|-2 \log \left|\frac{x+1}{x+2}\right|+C.\)

Applications of Special Integrals in Mathematics

Integrals of the form \(\int \frac{d x}{a+b \cos ^2 x}, \int \frac{d x}{a+b \sin ^2 x}\)

and \(\int \frac{d x}{a \cos ^2 x+b \sin x \cos x+c \sin ^2 x} .\)

Method In each such an integral, we divide the numerator and denominator by cos²x and put tan x = t, sec²x dx = dt and then integrate.

Example 23 Evaluate \(\int \frac{d x}{a^2 \sin ^2 x+b^2 \cos ^2 x}\)

Solution

\(\int \frac{d x}{a^2 \sin ^2 x+b^2 \cos ^2 x}\)

Dividing the numerator and the denominator of the given integrand by cos²x, we get

\(\int \frac{d x}{\left(a^2 \sin ^2 x+b^2 \cos ^2 x\right)}=\int \frac{\sec ^2 x}{a^2 \tan ^2 x+b^2} d x\)

= \(\int \frac{d t}{\left(a^2 t^2+b^2\right)}\) [putting tan x = t]

= \(\frac{1}{a^2} \int \frac{d t}{\left[t^2+\left(\frac{b}{a}\right)^2\right]}=\frac{1}{a^2} \cdot \frac{1}{\left(\frac{b}{a}\right)} \tan ^{-1} \frac{t}{\left(\frac{b}{a}\right)}+C\)

= \(\frac{1}{a b} \tan ^{-1}\left(\frac{a t}{b}\right)+C=\frac{1}{a b} \tan ^{-1}\left(\frac{a \tan x}{b}\right)+C\).

Example 24 Evaluate:

(1) \(\int \frac{d x}{\left(1+3 \sin ^2 x\right)}\)

(2) \(\int \frac{d x}{\left(3+2 \cos ^2 x\right)}\)

Solution

(1) Dividing the numerator and denominator by cos²x, we get

\(\int \frac{d x}{\left(1+3 \sin ^2 x\right)}=\int \frac{\sec ^2 x}{\sec ^2 x+3 \tan ^2 x} d x=\int \frac{\sec ^2 x}{\left(1+4 \tan ^2 x\right)} d x\)

= \(\int \frac{d t}{\left(1+4 t^2\right)}\) [putting tan x = t]

= \(\frac{1}{4} \int \frac{d t}{\left[t^2+\left(\frac{1}{2}\right)^2\right]}\)=\(\frac{1}{4} \cdot \frac{1}{(1 / 2)} \tan ^{-1} \frac{t}{(1 / 2)}+C\)

= \(\frac{1}{2} \tan ^{-1}(2 t)+C\)=\(\frac{1}{2} \tan ^{-1}(2 \tan x)+C .\)

(2) Dividing the numerator and denominator by cos²x, we get

\(\int \frac{d x}{\left(3+2 \cos ^2 x\right)}=\int \frac{\sec ^2 x}{\left(3 \sec ^2 x+2\right)} d x=\int \frac{\sec ^2 x}{5+3 \tan ^2 x} d x\)

= \(\int \frac{d t}{\left(5+3 t^2\right)}\) [putting tan x = t]

= \(\frac{1}{3} \int \frac{d t}{\left[t^2+\left(\frac{5}{3}\right)\right]}=\frac{1}{3} \cdot \int \frac{d t}{\left[t^2+\left(\frac{\sqrt{5}}{\sqrt{3}}\right)^2\right]}\)

= \(\frac{1}{3} \cdot \frac{1}{\left(\frac{\sqrt{5}}{\sqrt{3}}\right)} \tan ^{-1} \frac{t}{\left(\frac{\sqrt{5}}{\sqrt{3}}\right)}+C=\frac{1}{\sqrt{15}} \tan ^{-1}\left(\frac{\sqrt{3} t}{\sqrt{5}}\right)+C\)

= \(\frac{1}{\sqrt{15}} \tan ^{-1}\left(\frac{\sqrt{3} \tan x}{\sqrt{5}}\right)+C.\)

Class 12 Integration Special Integrals 

Example 25 Evaluate \(\int \frac{d x}{\left(4 \sin ^2 x+5 \cos ^2 x\right)}\).

Solution

\(\int \frac{d x}{\left(4 \sin ^2 x+5 \cos ^2 x\right)}\)

On dividing the numerator and denominator by cos²x, we get

\(\int \frac{d x}{\left(4 \sin ^2 x+5 \cos ^2 x\right)}=\int \frac{\sec ^2 x}{\left(4 \tan ^2 x+5\right)} d x\)

= \(\int \frac{d t}{4 t^2+5}\) [putting tan x = t]

= \(\frac{1}{4} \int \frac{d t}{\left(t^2+\frac{5}{4}\right)}=\frac{1}{4} \cdot \int \frac{d t}{\left[t^2+\left(\frac{\sqrt{5}}{2}\right)^2\right]}=\frac{1}{4} \cdot \frac{1}{\left(\frac{\sqrt{5}}{2}\right)} \tan ^{-1} \frac{t}{\left(\frac{\sqrt{5}}{2}\right)}+C\)

= \(\frac{1}{2 \sqrt{5}} \tan ^{-1}\left(\frac{2 t}{\sqrt{5}}\right)+C=\frac{1}{2 \sqrt{5}} \tan ^{-1}\left(\frac{2 \tan x}{\sqrt{5}}\right)+C\).

Example 26 Example \(\int \frac{d x}{\left(1+3 \sin ^2 x+8 \cos ^2 x\right)}\).

Solution

\(\int \frac{d x}{\left(1+3 \sin ^2 x+8 \cos ^2 x\right)}\)

On dividing the numerator and denominator by cos²x, we get

\(\int \frac{d x}{\left(1+3 \sin ^2 x+8 \cos ^2 x\right)}=\int \frac{\sec ^2 x d x}{\sec ^2 x+3 \tan ^2 x+8}\)

= \(\int \frac{\sec ^2 x}{9+4 \tan ^2 x} d x=\int \frac{d t}{9+4 t^2}\) [putting tan x = t]

= \(\frac{1}{4} \int \frac{d t}{\left(t^2+\frac{9}{4}\right)}=\frac{1}{4} \cdot \int \frac{d t}{\left[t^2+\left(\frac{3}{2}\right)^2\right]}\)

= \(\frac{1}{4} \cdot \frac{1}{(3 / 2)} \cdot \tan ^{-1}\left\{\frac{t}{(3 / 2)}\right\}+C\)

= \(\frac{1}{6} \tan ^{-1}\left(\frac{2 t}{3}\right)+C=\frac{1}{6} \tan ^{-1}\left(\frac{2 \tan x}{3}\right)+C\)

Techniques for Evaluating Special Integrals

Class 12 Integration Special Integrals 

Example 27 Evaluate \(\int \frac{\sin x}{\sin 3 x} d x\).

Solution We have

\(\int \frac{\sin x}{\sin 3 x} d x=\int \frac{\sin x}{\left(3 \sin x-4 \sin ^3 x\right)} d x\)

= \(\int \frac{1}{\left(3-4 \sin ^2 x\right)} d x\) [dividing num. and denom. by sin x]

= \(\int \frac{\sec ^2 x}{3 \sec ^2 x-4 \tan ^2 x} d x\) [dividing num. and denom. by cos2x]

= \(\int \frac{\sec ^2 x}{3\left(1+\tan ^2 x\right)-4 \tan ^2 x} d x=\int \frac{\sec ^2 x}{\left(3-\tan ^2 x\right)} d x\)

= \(\int \frac{d t}{\left(3-t^2\right)}\), where tan x = t and sec2x dx = dt

= \(\int \frac{d t}{\left[(\sqrt{3})^2-t^2\right]}=\frac{1}{2 \sqrt{3}} \log \left|\frac{\sqrt{3}+t}{\sqrt{3}-t}\right|+C\)

= \(\frac{1}{2 \sqrt{3}} \log \left|\frac{\sqrt{3}+\tan x}{\sqrt{3}-\tan x}\right|+C\)

Example 28 Evaluate \(\int \frac{\cos x}{\cos 3 x} d x\).

Solution We have

\(\int \frac{\cos x}{\cos 3 x} d x=\int \frac{\cos x}{\left(4 \cos ^3 x-3 \cos x\right)} d x\)

= \(\int \frac{d x}{4 \cos ^2 x-3}=\int \frac{d x}{4 \cos ^2 x-3\left(\sin ^2 x+\cos ^2 x\right)}\)

= \(\int \frac{d x}{\cos ^2 x-3 \sin ^2 x}=\int \frac{\sec ^2 x}{1-3 \tan ^2 x} d x\)

[on dividing the num. and denom. by cos2x]

= \(\int \frac{d t}{1-3 t^2}, where tan x = t and sex2x dx = dt\)

= \(\frac{1}{3} \cdot \int \frac{d t}{\left(\frac{1}{3}-t^2\right)}=\frac{1}{3} \cdot \int \frac{d t}{\left[\left(\frac{1}{\sqrt{3}}\right)^2-t^2\right]}=\frac{1}{3} \cdot \frac{1}{2 \cdot \frac{1}{\sqrt{3}}} \log \left|\frac{\frac{1}{\sqrt{3}}+t}{\frac{1}{\sqrt{3}}-t}\right|+C\)

= \(\frac{1}{2 \sqrt{3}} \log \left|\frac{1+\sqrt{3} t}{1-\sqrt{3} t}\right|+C=\frac{1}{2 \sqrt{3}} \log \left|\frac{1+\sqrt{3} \tan x}{1-\sqrt{3} \tan x}\right|+C .\)

Example 29 Evaluate \(\int \frac{d x}{(2+\cos x)}\)

Solution We have

\(\int \frac{d x}{(2+\cos x)}=\int \frac{d x}{1+(1+\cos x)}=\int \frac{d x}{1+2 \cos ^2(x / 2)}=\int \frac{\sec ^2(x / 2) d x}{\sec ^2(x / 2)+2}\)

[dividing the num. and denom. by cos²(x/2)]

= \(\int \frac{\sec ^2(x / 2)}{3+\tan ^2(x / 2)} d x=2 \int \frac{d t}{3+t^2}, \text { where } \tan (x / 2)=t\)

= \(2 \cdot \int \frac{d t}{(\sqrt{3})^2+t^2}=2 \cdot \frac{1}{\sqrt{3}} \tan ^{-1} \frac{t}{\sqrt{3}}+C\)

= \(\frac{2}{\sqrt{3}} \tan ^{-1}\left[\frac{\tan (x / 2)}{\sqrt{3}}\right]+C .\)

Special Integrals Class 12 Maths 

Some More Special Integrals

Example 30 Evaluate \(\int \frac{\left(x^2+1\right)}{\left(x^4+1\right)} d x\)

Solution We have

\(\int\left(\frac{x^2+1}{x^4+1}\right) d x=\int \frac{\left(1+\frac{1}{x^2}\right)}{\left(x^2+\frac{1}{x^2}\right)} d x\) [dividing num. and denom. by x²]

= \(\int \frac{\left(1+\frac{1}{x^2}\right)}{\left(x-\frac{1}{x}\right)^2+2} d x\)

= \(\int \frac{d t}{\left[t^2+(\sqrt{2})^2\right]}\), wnere (x – \(\frac{1}{x}\)) = t and (1 + \(\frac{1}{x^2}\))dx = dt

= \(\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{t}{\sqrt{2}}\right)+C=\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{x-\frac{1}{x}}{\sqrt{2}}\right)+C\)

= \(\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{x^2-1}{\sqrt{2} x}\right)+C\)

Example 31 Evaluate \(\int \frac{\left(x^2+4\right)}{\left(x^4+16\right)} d x\)

Solution We have

\(\int\left(\frac{x^2+4}{x^4+16}\right) d x=\int \frac{\left(1+\frac{4}{x^2}\right)}{\left(x^2+\frac{16}{x^2}\right)} d x\) [dividing num. and denom. by x²]

= \(\int \frac{\left(1+\frac{4}{x^2}\right)}{\left(x-\frac{4}{x}\right)^2+8} d x\)

= \(\int \frac{d t}{\left(t^2+8\right)}\) [putting (x – \(\frac{4}{x}\)) = t and (1 + \(\frac{4}{x^2}\))dx = dt]

= \(\int \frac{d t}{t^2+(\sqrt{8})^2}\)=\(\frac{1}{\sqrt{8}} \tan ^{-1}\left(\frac{t}{\sqrt{8}}\right)+C\)

= \(\frac{1}{\sqrt{8}} \tan ^{-1} \frac{\left(x-\frac{4}{x}\right)}{\sqrt{8}}+C\)=\(\frac{1}{2 \sqrt{2}} \tan ^{-1}\left(\frac{x^2-4}{2 \sqrt{2} x}\right)+C\)

Special Integrals Class 12 Maths 

Example 32 Evaluate \(\int \frac{\left(x^2-1\right)}{\left(x^4+x^2+1\right)} d x\)

Solution We have

\(\int \frac{\left(x^2-1\right)}{\left(x^4+x^2+1\right)} d x=\int \frac{\left(1-\frac{1}{x^2}\right)}{\left(x^2+\frac{1}{x^2}+1\right)} d x\)

[dividing num. and denom. by x²]

= \(\int \frac{\left(1-\frac{1}{x^2}\right)}{\left[\left(x+\frac{1}{x}\right)^2-1\right]} d x\)

= \(\int \frac{d t}{\left(t^2-1\right)}\) [putting (x + \(\frac{1}{x}\)) = t and (1 – \(\frac{1}{x^2}\))dx = dt]

= \(\frac{1}{2} \log \left|\frac{t-1}{t+1}\right|+C=\frac{1}{2} \log \left|\frac{x+\frac{1}{x}-1}{x+\frac{1}{x}+1}\right|+C\)

= \(\frac{1}{2} \log \left|\frac{x^2-x+1}{x^2+x+1}\right|+C\)

Example 33 Evaluate \(\int \frac{d x}{\left(x^4+1\right)}\)

Solution We have

\(\int \frac{d x}{\left(x^4+1\right)}=\int \frac{\left(x^2+1\right)-\left(x^2-1\right)}{2\left(x^4+1\right)} d x\)

= \(\frac{1}{2} \int \frac{\left(x^2+1\right)}{\left(x^4+1\right)} d x-\frac{1}{2} \int \frac{\left(x^2-1\right)}{\left(x^4+1\right)} d x\)

= \(\frac{1}{2}\left[\int \frac{\left(1+\frac{1}{x^2}\right)}{\left(x^2+\frac{1}{x^2}\right)} d x-\int \frac{\left(1-\frac{1}{x^2}\right)}{\left(x^2+\frac{1}{x^2}\right)} d x\right]\)

[dividing num. and denom. of each integral by x²]

= \(\frac{1}{2}\left[\int \frac{\left(1+\frac{1}{x^2}\right)}{\left[\left(x-\frac{1}{x}\right)^2+2\right]} d x-\int \frac{\left(1-\frac{1}{x^2}\right)}{\left[\left(x+\frac{1}{x}\right)^2-2\right]} d x\right]\)

= \(\frac{1}{2}\left[\int \frac{d t}{\left[t^2+(\sqrt{2})^2\right]}-\int \frac{d u}{\left[u^2-(\sqrt{2})^2\right]}\right]\)

[putting (x – \(\frac{1}{x}\)) = t in the 1st integral, and (x + \(\frac{1}{x}\)) = u in the 2nd]

= \(\frac{1}{2}\left\{\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{t}{\sqrt{2}}\right)-\frac{1}{2 \sqrt{2}} \log \left|\frac{u-\sqrt{2}}{u+\sqrt{2}}\right|\right\}+C\)

= \(\frac{1}{2 \sqrt{2}} \tan ^{-1}\left(\frac{x-\frac{1}{x}}{\sqrt{2}}\right)-\frac{1}{4 \sqrt{2}} \log \left|\frac{x+\frac{1}{x}-\sqrt{2}}{x+\frac{1}{x}+\sqrt{2}}\right|+C\)

= \(\frac{1}{2 \sqrt{2}} \tan ^{-1}\left(\frac{x^2-1}{\sqrt{2} x}\right)-\frac{1}{4 \sqrt{2}} \log \left|\frac{x^2+1-\sqrt{2} x}{x^2+1+\sqrt{2 x}}\right|+C \text {. }\)

Real-Life Applications of Special Integrals

Example 34 Evaluate \(\int \frac{x^2}{\left(x^4+x^2+1\right)} d x\)

Solution We have

I = \(\frac{1}{2} \int \frac{2 x^2}{\left(x^4+x^2+1\right)} d x\)

= \(\frac{1}{2} \cdot \int \frac{\left(x^2-1\right)+\left(x^2+1\right)}{\left(x^4+x^2+1\right)} d x\)

= \(\frac{1}{2} \int \frac{\left(x^2-1\right)}{\left(x^4+x^2+1\right)} d x+\frac{1}{2} \int \frac{\left(x^2+1\right)}{\left(x^4+x^2+1\right)} d x\)

= \(\frac{1}{2} \int \frac{\left(1-\frac{1}{x^2}\right)}{\left(x^2+1+\frac{1}{x^2}\right)} d x+\frac{1}{2} \int \frac{\left(1+\frac{1}{x^2}\right)}{\left(x^2+1+\frac{1}{x^2}\right)} d x\)

[on dividing num. and denom. of each by x2]

= \(\frac{1}{2} \int \frac{\left(1-\frac{1}{x^2}\right)}{\left\{\left(x+\frac{1}{x}\right)^2-1\right\}} d x+\frac{1}{2} \int \frac{\left(1+\frac{1}{x^2}\right)}{\left\{\left(x-\frac{1}{x}\right)^2+(\sqrt{3})^2\right\}} d x\)

{putting (x + \(\frac{1}{x}\)) = u and (1 – \(\frac{1}{x^2}\))dx = du in I1, and (x – \(\frac{1}{x}\)) = v and (1 + \(\frac{1}{x^2}\))dx = dv in I2}

= \(\frac{1}{2} \log \left|\frac{u-1}{u+1}\right|+\frac{1}{2} \cdot \frac{1}{\sqrt{3}} \tan ^{-1} \frac{v}{\sqrt{3}}+C\)

= \(\frac{1}{2} \log \left|\frac{x+\frac{1}{x}-1}{x+\frac{1}{x}+1}\right|+\frac{1}{2 \sqrt{3}} \tan ^{-1}\left(\frac{x^2-1}{\sqrt{3} x}\right)+C\)

= \(\frac{1}{2} \log \left|\frac{x^2-x+1}{x^2+x+1}\right|+\frac{1}{2 \sqrt{3}} \tan ^{-1}\left(\frac{x^2+1}{\sqrt{3} x}\right)+C\)

Special Integrals Class 12 Maths 

Example 35 Evaluate \(\int \sqrt{\cot x} d x\)

Solution

\(\int \sqrt{\cot x} d x\)

Put cot x = t² so that -cosec²x dx = 2t dt or dx = \(\frac{-2 t}{\left(1+t^4\right)} d t\).

∴ \(\int \sqrt{\cot x} d x=-\int \frac{2 t^2}{\left(t^4+1\right)} d t\)

= \(-\int \frac{\left[\left(t^2+1\right)+\left(t^2-1\right)\right]}{\left(t^4+1\right)} d t=-\int \frac{\left(t^2+1\right)}{\left(t^4+1\right)} d t-\int \frac{\left(t^2-1\right)}{\left(t^4+1\right)} d t\)

= \(-\int \frac{\left(1+\frac{1}{t^2}\right)}{\left(t^2+\frac{1}{t^2}\right)} d t-\int \frac{\left(1-\frac{1}{t^2}\right)}{\left(t^2+\frac{1}{t^2}\right)} d t\)

= \(-\int \frac{\left(1+\frac{1}{t^2}\right)}{\left[\left(t-\frac{1}{t}\right)^2+2\right]} d t-\int \frac{\left(1-\frac{1}{t^2}\right)}{\left[\left(t+\frac{1}{t}\right)^2-2\right]} d t\)

= \(-\int \frac{d u}{\left[u^2+(\sqrt{2})^2\right]}-\int \frac{d v}{\left[v^2-(\sqrt{2})^2\right]}\)

[putting (t – \(\frac{1}{t}\)) = u in the 1st integral, and (t + \(\frac{1}{x}\)) = v in the 2nd]

= \(-\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{u}{\sqrt{2}}\right)-\frac{1}{2 \sqrt{2}} \log \left|\frac{v-\sqrt{2}}{v+\sqrt{2}}\right|+C\)

= \(-\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{t-\frac{1}{t}}{\sqrt{2}}\right)-\frac{1}{2 \sqrt{2}} \log \left|\frac{t+\frac{1}{t}-\sqrt{2}}{t+\frac{1}{t}+\sqrt{2}}\right|+C\)

= \(-\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{t^2-1}{\sqrt{2} t}\right)-\frac{1}{2 \sqrt{2}} \log \left|\frac{t^2-\sqrt{2} t+1}{t^2+\sqrt{2} t+1}\right|+C\)

= \(-\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{\cot x-1}{\sqrt{2 \cot x}}\right)-\frac{1}{2 \sqrt{2}} \log \left|\frac{\cot x-\sqrt{2 \cot x}+1}{\cot x+\sqrt{2 \cot x}+1}\right|+C\)

Example 36 Evaluate \(\int(\sqrt{\tan x}+\sqrt{\cot x}) d x\)

Solution We have

\(\int(\sqrt{\tan x}+\sqrt{\cot x}) d x\)

= \(\int\left(\sqrt{\tan x}+\frac{1}{\sqrt{\tan x}}\right) d x=\int \frac{(\tan x+1)}{\sqrt{\tan x}} d x\)

= \(\int \frac{\left(t^2+1\right)}{t} \cdot \frac{2 t}{\left(1+t^4\right)} d t\), where tan x = t2 ⇒ x = tan-1t2

⇒ \(d x=\frac{2 t}{\left(1+t^4\right)} d t\)

= \(2 \int \frac{\left(t^2+1\right)}{\left(t^4+1\right)} d t=2 \int \frac{\left(1+\frac{1}{t^2}\right)}{\left(t^2+\frac{1}{t^2}\right)} d t\) [on dividing num. and denom. by t2]

= \(2 \int \frac{\left(1+\frac{1}{t^2}\right)}{\left(t-\frac{1}{t}\right)^2+2} d t\)

= \(2 \int \frac{d u}{\left(u^2+2\right)}, where (t – [latex]\frac{1}{t}\)) = u and (1 + \(\frac{1}{t^2}\))dt = du

= \(2 \cdot \frac{1}{\sqrt{2}} \tan ^{-1} \frac{u}{\sqrt{2}}+C=\sqrt{2} \tan ^{-1} \frac{\left(t-\frac{1}{t}\right)}{\sqrt{2}}+C\) [∵ u = (t – \(\frac{1}{t}\))]

= \(\sqrt{2} \tan ^{-1} \frac{\left(t^2-1\right)}{(\sqrt{2} t)}+C=\sqrt{2} \tan ^{-1}\left(\frac{\tan x-1}{\sqrt{2 \tan x}}\right)+C\) [∵ t2 = tan x].

Example 37 Evaluate \(\int \sqrt{\tan \theta} d \theta\).

Solution

\(\int \sqrt{\tan \theta} d \theta\)

Putting tan θ = t², we get θ = tan^-1t² ⇒ \(d \theta=\frac{2 t}{\left(1+t^4\right)} d t .\)

∴ I = \(\int t \cdot \frac{2 t}{\left(1+t^4\right)} d t=\int \frac{2 t^2}{\left(t^4+1\right)} d t\)

= \(\int \frac{\left(t^2+1\right)+\left(t^2-1\right)}{\left(t^4+1\right)} d t=\int \frac{\left(t^2+1\right)}{\left(t^4+1\right)} d t+\int \frac{\left(t^2-1\right)}{\left(t^4+1\right)} d t\)

= \(\int \frac{\left(1+\frac{1}{t^2}\right)}{\left(t^2+\frac{1}{t^2}\right)} d t+\int \frac{\left(1-\frac{1}{t^2}\right)}{\left(t^2+\frac{1}{t^2}\right)} d t\)

= \(\int \frac{\left(1+\frac{1}{t^2}\right)}{\left(t-\frac{1}{t}\right)^2+2} d t+\int \frac{\left(1-\frac{1}{t^2}\right)}{\left\{\left(t+\frac{1}{t}\right)^2-2\right\}} d t\)

= \(\int \frac{d u}{\left(u^2+2\right)}+\int \frac{d v}{\left(v^2-2\right)}\),

where (t – \(\frac{1}{t}\)) = u and (t + \(\frac{1}{t}\)) = v in I1 and I2

= \(\frac{1}{\sqrt{2}} \tan ^{-1} \frac{u}{\sqrt{2}}+\frac{1}{2 \sqrt{2}} \cdot \log \left|\frac{v-\sqrt{2}}{v+\sqrt{2}}\right|+C\)

= \(\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{t-\frac{1}{t}}{\sqrt{2}}\right)+\frac{1}{2 \sqrt{2}} \cdot\left|\frac{t+\frac{1}{t}-\sqrt{2}}{t+\frac{1}{t}+\sqrt{2}}\right|+C\)

= \(\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{t^2-1}{\sqrt{2} t}\right)+\frac{1}{2 \sqrt{2}} \cdot\left|\frac{t^2-\sqrt{2} t+1}{t^2+\sqrt{2} t+1}\right|+C\), where t = \(\sqrt{\tan \theta}\).

Special Integrals Class 12 Maths 

Three More Special Integrals

Theorem

(1) \(\int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1} \frac{x}{a}+C .\)

(2) \(\int \frac{d x}{\sqrt{x^2-a^2}}=\log \left|x+\sqrt{x^2-a^2}\right|+C\).

(3) \(\int \frac{d x}{\sqrt{x^2+a^2}}=\log \left|x+\sqrt{x^2+a^2}\right|+C\).

Proof

(1) Put x = a sin θ so that dx = a cos θ dθ.

∴ \(\int \frac{d x}{\sqrt{a^2-x^2}}=\int \frac{a \cos \theta}{a \cos \theta} d \theta=\int d \theta=\theta+C=\sin ^{-1} \frac{x}{a}+C\).

Hence, \(\int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1} \frac{x}{a}+C\)

(2) Put x = a sec θ so that dx = a sec θ tan θ dθ.

∴ \(\int \frac{d x}{\sqrt{x^2-a^2}}=\int \frac{a \sec \theta \tan \theta}{a \tan \theta} d \theta\)

= \(\int \sec \theta d \theta=\log |\sec \theta+\tan \theta|+c\)

= \(\log \left|\sec \theta+\sqrt{\sec ^2 \theta-1}\right|+c\)

= \(\log \left|\frac{x}{a}+\sqrt{\left(\frac{x^2}{a^2}-1\right)}\right|+c=\log \left|\frac{x+\sqrt{x^2-a^2}}{a}\right|+c\)

= \(\log \left|x+\sqrt{x^2-a^2}\right|-\log a+c\)

= \(\log \left|x+\sqrt{x^2-a^2}\right|+C\) [taking -log a + c = C].

Hence, \(\int \frac{d x}{\sqrt{x^2-a^2}}=\log \left|x+\sqrt{x^2-a^2}\right|+C\).

(3) Put x = a tan θ so that dx = a sec²θ dθ.

∴ \(\int \frac{d x}{\sqrt{x^2+a^2}}=\int \frac{a \sec ^2 \theta}{a \sec \theta} d \theta\)

= \(\int \sec \theta d \theta=\log |\sec \theta+\tan \theta|+c\)

= \(\log \left|\sqrt{1+\tan ^2 \theta}+\tan \theta\right|+c\)

= \(\log \left|\sqrt{1+\frac{x^2}{a^2}}+\frac{x}{a}\right|+c\)

= \(\log \left|x+\sqrt{x^2+a^2}\right|-\log a+c\)

= \(\log \left|x+\sqrt{x^2+a^2}\right|+C\) [taking -log a + c = C].

Hence, \(\int \frac{d x}{\sqrt{x^2+a^2}}=\log \left|x+\sqrt{x^2+a^2}\right|+C .\)

Class 12 Maths Special Integrals Solutions 

Solved Examples

Example 1 Evaluate:

(1) \(\int \frac{d x}{\sqrt{9-25 x^2}}\)

(2) \(\int \frac{d x}{\sqrt{4 x^2-9}}\)

(3) \(\int \frac{d x}{\sqrt{16 x^2+25}}\)

Solution We have

(1) \(\int \frac{d x}{\sqrt{9-25 x^2}}=\frac{1}{5} \cdot \int \frac{d x}{\sqrt{\frac{9}{25}-x^2}}=\frac{1}{5} \cdot \int \frac{d x}{\sqrt{\left(\frac{3}{5}\right)^2-x^2}}\)

= \(\frac{1}{5} \sin ^{-1}\left(\frac{x}{3 / 5}\right)+C=\frac{1}{5} \sin ^{-1}\left(\frac{5 x}{3}\right)+C .\)

(2) \(\int \frac{d x}{\sqrt{4 x^2-9}}=\frac{1}{2} \int \frac{d x}{\sqrt{x^2-\frac{9}{4}}}=\frac{1}{2} \int \frac{d x}{\sqrt{x^2-\left(\frac{3}{2}\right)^2}}\)

= \(\frac{1}{2} \log \left|x+\sqrt{x^2-\frac{9}{4}}\right|+C\)

= \(\frac{1}{2} \log \left|2 x+\sqrt{4 x^2-9}\right|+C\).

(3) \(\int \frac{d x}{\sqrt{16 x^2+25}}=\frac{1}{4} \cdot \int \frac{d x}{\sqrt{x^2+\frac{25}{16}}}=\frac{1}{4} \cdot \int \frac{d x}{\sqrt{x^2+\left(\frac{5}{4}\right)^2}}\)

= \(\frac{1}{4} \cdot \log \left|x+\sqrt{x^2+\frac{25}{16}}\right|+C\)

= \(\frac{1}{4} \log \left|4 x+\sqrt{16 x^2+25}\right|+C .\)

Example 2 Evaluate \(\int \frac{d x}{\sqrt{15-8 x^2}}\).

Solution We have

\(\int \frac{d x}{\sqrt{15-8 x^2}}=\frac{1}{\sqrt{8}} \cdot \int \frac{d x}{\sqrt{\frac{15}{8}-x^2}}\)

= \(\frac{1}{2 \sqrt{2}} \sin ^{-1}\left\{\frac{x}{\sqrt{\frac{15}{8}}}\right\}+C=\frac{1}{2 \sqrt{2}} \sin ^{-1}\left(\sqrt{\frac{8}{15}} x\right)+C\).

Example 3 Evaluate \(\int \frac{\cos x}{\sqrt{4-\sin ^2 x}} d x\)

Solution

\(\int \frac{\cos x}{\sqrt{4-\sin ^2 x}} d x\)

Putting sin x = t and cos x dx = dt, we get

\(\int \frac{\cos x}{\sqrt{4-\sin ^2 x}} d x=\int \frac{d t}{\sqrt{4-t^2}}=\int \frac{d t}{\sqrt{2^2-t^2}}\)

= \(\frac{1}{2 \sqrt{2}} \sin ^{-1}\left\{\frac{x}{\sqrt{\frac{15}{8}}}\right\}+C=\frac{1}{2 \sqrt{2}} \sin ^{-1}\left(\sqrt{\frac{8}{15} x}\right)+C.\)

Class 12 Maths Special Integrals Solutions 

Example 4 Evaluate \(\int \frac{d x}{\sqrt{1-e^{2 x}}} .\)

Solution

\(\int \frac{d x}{\sqrt{1-e^{2 x}}} .\)

Multiplying the numerator and denominator by e^-x, we get

\(\int \frac{d x}{\sqrt{1-e^{2 x}}}=\int \frac{e^{-x} d x}{\sqrt{e^{-2 x}\left(1-e^{2 x}\right)}}=\int \frac{e^{-x}}{\sqrt{e^{-2 x}-1}} d x\)

= \(-\int \frac{d t}{\sqrt{t^2-1}}\) [putting e-x = t]

= \(-\log \left|t+\sqrt{t^2-1}\right|+C\)

= \(-\log \left|e^{-x}+\sqrt{e^{-2 x}-1}\right|+C .\)

Example 5 Evaluate \(\int \frac{2^x}{\sqrt{1-4^x}} d x\).

Solution

\(\int \frac{2^x}{\sqrt{1-4^x}} d x\)

Putting 2^x = t and (2^x log 2)dx = dt, we get

\(\int \frac{2^x}{\sqrt{1-4^x}} d x=\frac{1}{(\log 2)} \cdot \int \frac{d t}{\sqrt{1-t^2}}\)

= \(\frac{1}{(\log 2)} \cdot \sin ^{-1} t+C=\frac{1}{(\log 2)} \cdot \sin ^{-1}\left(2^x\right)+C .\)

Example 6  Evaluate \(\int \frac{x^2}{\sqrt{x^6-1}} d x\)

Solution

\(\int \frac{x^2}{\sqrt{x^6-1}} d x\)

Putting x³ = t and x²dx = \(\frac{1}{3}\) dt, we get

\(\int \frac{x^2}{\sqrt{x^6-1}} d x=\frac{1}{3} \int \frac{d t}{\sqrt{t^2-1}}=\frac{1}{3} \log \left|t+\sqrt{t^2-1}\right|+C\)

= \(\frac{1}{3} \log \left|x^3+\sqrt{x^6-1}\right|+C\).

Example 7 Evaluate:

(1) \(\int \frac{\sin x}{\sqrt{4 \cos ^2 x-1}} d x\)

(2) \(\int \frac{\sec ^2 x}{\sqrt{\tan ^2 x-4}} d x\)

Solution

(1) Putting cos x = t and -sin x dx = dt, we get

\(\int \frac{\sin x}{\sqrt{4 \cos ^2 x-1}} d x=\int \frac{-d t}{\sqrt{4 t^2-1}}=-\frac{1}{2} \int \frac{d t}{\sqrt{t^2-(1 / 2)^2}}\)

= \(-\frac{1}{2} \cdot \log \left|t+\sqrt{t^2-\frac{1}{4}}\right|+C\)

= \(-\frac{1}{2} \log \left|2 t+\sqrt{4 t^2-1}\right|+C\)

= \(-\frac{1}{2} \log \left|2 \cos x+\sqrt{4 \cos ^2 x-1}\right|+C \text {. }\)

(2) Putting tan x = t and sec²xdx = dt, we get

\(\int \frac{\sec ^2 x}{\sqrt{\tan ^2 x-4}} d x=\int \frac{d t}{\sqrt{t^2-4}}=\log \left|t+\sqrt{t^2-4}\right|+C\)

= \(\log \left|\tan x+\sqrt{\tan ^2 x-4}\right|+C\).

Class 12 Maths Special Integrals Solutions 

Example 8 Evaluate \(\int \frac{x^2}{\sqrt{x^6+a^6}} d x\)

Solution

\(\int \frac{x^2}{\sqrt{x^6+a^6}} d x\)

Putting x³ = t and x²dx = \(\frac{1}{3}\)dt, we get

\(\int \frac{x^2}{\sqrt{x^6+a^6}} d x=\frac{1}{3} \int \frac{d t}{\sqrt{t^2+\left(a^3\right)^2}}=\frac{1}{3} \log \left|t+\sqrt{t^2+a^6}\right|+C\)

= \(\frac{1}{3} \log \left|x^3+\sqrt{x^6+a^6}\right|+C .\)

Example 9 Evaluate \(\int \frac{\sec ^2 x}{\sqrt{16+\tan ^2 x}} d x.\)

Solution

\(\int \frac{\sec ^2 x}{\sqrt{16+\tan ^2 x}} d x.\)

Putting tan x = t and sec²xdx = dt, we get

\(\int \frac{\sec ^2 x}{\sqrt{16+\tan ^2 x}} d x\)=\(\int \frac{d t}{\sqrt{16+t^2}}=\log \left|t+\sqrt{t^2+16}\right|+C\)

= \(\log \left|\tan x+\sqrt{\tan ^2 x+16}\right|+C .\)

Example 10 Evaluate \(\int \sqrt{\frac{1-x}{1+x}} d x\).

Solution We have

\(\int \sqrt{\frac{1-x}{1+x}} d x=\int\left\{\frac{\sqrt{1-x}}{\sqrt{1+x}} \times \frac{\sqrt{1-x}}{\sqrt{1-x}}\right\} d x\)

= \(\int \frac{(1-x)}{\sqrt{1-x^2}} d x=\int \frac{d x}{\sqrt{1-x^2}}-\int \frac{x}{\sqrt{1-x^2}} d x\)

= \(\sin ^{-1} x+\frac{1}{2} \cdot \int \frac{(-2 x)}{\sqrt{1-x^2}} d x\)

= \(\sin ^{-1} x+\frac{1}{2} \int \frac{d t}{\sqrt{t}}\), where (1 – x2) = t and (-2x)dx = dt

= \(\sin ^{-1} x+\frac{1}{2} \int t^{-1 / 2} d t=\sin ^{-1} x+\frac{1}{2} \cdot \frac{t^{1 / 2}}{(1 / 2)}+C\)

= \(\sin ^{-1} x+\sqrt{1-x^2}+C .\)

Integrals of the form \(\int \frac{d x}{\sqrt{\left(a x^2+b x+c\right)}} .\)

Method Put (ax² + bx + c) in the form a{(x + α)² ± β²} and then integrate.

Example 11 Evaluate \(\int \frac{d x}{\sqrt{x^2-3 x+2}}\).

Solution We have

\(\int \frac{d x}{\sqrt{x^2-3 x+2}}=\int \frac{d x}{\sqrt{\left(x^2-3 x+\frac{9}{4}\right)-\frac{1}{4}}}=\int \frac{d x}{\sqrt{\left(x-\frac{3}{2}\right)^2-\left(\frac{1}{2}\right)^2}}\)

= \(\int \frac{d z}{\sqrt{z^2-\left(\frac{1}{2}\right)^2}}\), where (x – \(\frac{3}{2}\)) = z

= \(\log \left|z+\sqrt{z^2-\frac{1}{4}}\right|+C\)

[∵ \(\int \frac{d z}{\sqrt{z^2-a^2}}=\log \left|z+\sqrt{z^2-a^2}\right|+C\)]

= \(\log \left|\left(x-\frac{3}{2}\right)+\sqrt{x^2-3 x+2}\right|+C\).

Class 12 Maths Special Integrals Solutions 

Example 12 Evaluate \(\int \frac{d x}{\sqrt{5 x^2-2 x}}\).

Solution We have

\(\int \frac{d x}{\sqrt{5 x^2-2 x}}=\frac{1}{\sqrt{5}} \cdot \int \frac{d x}{\sqrt{x^2-\frac{2}{5} x}}=\frac{1}{\sqrt{5}} \cdot \int \frac{d x}{\sqrt{x^2-\frac{2}{5} x+\left(\frac{1}{5}\right)^2-\left(\frac{1}{5}\right)^2}}\)

= \(\frac{1}{\sqrt{5}} \cdot \int \frac{d x}{\sqrt{\left(x-\frac{1}{5}\right)^2-\left(\frac{1}{5}\right)^2}}=\frac{1}{\sqrt{5}} \cdot \int \frac{d t}{\sqrt{t^2-\left(\frac{1}{5}\right)^2}}\)

where (x – \(\frac{1}{5}\)) = t

= \(\frac{1}{\sqrt{5}} \cdot \log \left|t+\sqrt{t^2-\left(\frac{1}{5}\right)^2}\right|+C\)

= \(\frac{1}{\sqrt{5}} \log \left|\left(x-\frac{1}{5}\right)+\sqrt{x^2-\frac{2 x}{5}}\right|+C\)

Example 13 Evaluate \(\int \frac{\cos x}{\sqrt{\sin ^2 x-2 \sin x-3}} d x .\)

Solution

\(\int \frac{\cos x}{\sqrt{\sin ^2 x-2 \sin x-3}} d x .\)

Putting sin x = t and cos x dx = dt, we get

\(\int \frac{\cos x}{\sqrt{\sin ^2 x-2 \sin x-3}} d x=\int \frac{d t}{\sqrt{t^2-2 t-3}}=\int \frac{d t}{\sqrt{(t-1)^2-2^2}}\)

= \(\log \left|(t-1)+\sqrt{(t-1)^2-2^2}\right|+C\)

= \(\log \left|(\sin x-1)+\sqrt{\sin ^2 x-2 \sin x-3}\right|+C \text {. }\)

Example 14 Evaluate \(\int \frac{e^x}{\sqrt{5-4 e^x-e^{2 x}}} d x\).

Solution

\(\int \frac{e^x}{\sqrt{5-4 e^x-e^{2 x}}} d x\)

Putting e^x = t and e^xdx = dt, we get

\(\int \frac{e^x}{\sqrt{5-4 e^x-e^{2 x}}} d x=\int \frac{d t}{\sqrt{5-4 t-t^2}}=\int \frac{d t}{\sqrt{5-\left(t^2+4 t+4\right)+4}}\)

= \(\int \frac{d t}{\sqrt{9-(t+2)^2}}=\int \frac{d t}{\sqrt{3^2-(t+2)^2}}\)

= \(\int \frac{d z}{\sqrt{3^2-z^2}}\), where (t+2) = z

= \(\sin ^{-1} \frac{z}{3}+C=\sin ^{-1} \frac{(t+2)}{3}+C\)

= \(\sin ^{-1} \frac{\left(e^x+2\right)}{3}+C\)

Example 15 Evaluate \(\int \frac{d x}{\sqrt{2-4 x+x^2}}\)

Solution We have

\(\int \frac{d x}{\sqrt{2-4 x+x^2}}=\int \frac{d x}{\sqrt{x^2-4 x+4-2}}=\int \frac{d x}{\sqrt{(x-2)^2-(\sqrt{2})^2}}\)

= \(\log \left|(x-2)+\sqrt{(x-2)^2-2}\right|+C\)

= \(\log \left|x-2+\sqrt{x^2-4 x+2}\right|+C\).

Example 16 Evaluate \(\int \frac{d x}{\sqrt{3 x^2+6 x+12}}\)

Solution We have

\(\int \frac{d x}{\sqrt{3 x^2+6 x+12}}=\frac{1}{\sqrt{3}} \cdot \int \frac{d x}{\sqrt{x^2+2 x+4}}\)

= \(\frac{1}{\sqrt{3}} \cdot \int \frac{d x}{\sqrt{(x+1)^2+(\sqrt{3})^2}}\)

= \(\frac{1}{\sqrt{3}} \cdot \int \frac{d t}{\sqrt{t^2+(\sqrt{3})^2}}\), where (x+1) = t

= \(\frac{1}{\sqrt{3}} \log \left|t+\sqrt{t^2+3}\right|+C\)

= \(\frac{1}{\sqrt{3}} \log \left|(x+1)+\sqrt{x^2+2 x+4}\right|+C\).

WBCHSE Maths Chapter Special Integrals 

Example 17 Evaluate \(\int \frac{d x}{\sqrt{8+3 x-x^2}}\)

Solution We have

\(\int \frac{d x}{\sqrt{8+3 x-x^2}}=\int \frac{d x}{\sqrt{8-\left(x^2-3 x\right)}}=\int \frac{d x}{\sqrt{8-\left(x^2-3 x+\frac{9}{4}\right)+\frac{9}{4}}}\)

= \(\int \frac{d x}{\sqrt{\left(\frac{\sqrt{41}}{2}\right)^2-\left(x-\frac{3}{2}\right)^2}}=\sin ^{-1}\left\{\frac{\left(x-\frac{3}{2}\right)}{\left(\frac{\sqrt{41}}{2}\right)}\right\}+C\)

= \(\sin ^{-1}\left(\frac{2 x-3}{\sqrt{41}}\right)+C\).

Example 18 Evaluate \(\int \frac{d x}{\sqrt{2 x-x^2}} .\)

Solution We have

\(\int \frac{d x}{\sqrt{2 x-x^2}}=\int \frac{d x}{\sqrt{1-\left(x^2-2 x+1\right)}}\)

= \(\int \frac{d x}{\sqrt{1-(x-1)^2}}=\sin ^{-1}(x-1)+C \text {. }\)

Example 19 Evaluate \(\int \frac{d x}{\sqrt{x(1-2 x)}}\)

Solution We have

\(\int \frac{d x}{\sqrt{x(1-2 x)}}=\int \frac{d x}{\sqrt{x-2 x^2}}\)

= \(\frac{1}{\sqrt{2}} \cdot \int \frac{d x}{\sqrt{\frac{x}{2}-x^2}}=\frac{1}{\sqrt{2}} \int \frac{d x}{\sqrt{-\left(x^2-\frac{x}{2}+\frac{1}{16}\right)+\frac{1}{16}}}\)

= \(\frac{1}{\sqrt{2}} \int \frac{d x}{\sqrt{\frac{1}{16}-\left\{x^2-\frac{x}{2}+\frac{1}{16}\right\}}}=\frac{1}{\sqrt{2}} \cdot \int \frac{d x}{\sqrt{\left(\frac{1}{4}\right)^2-\left(x-\frac{1}{4}\right)^2}}\)

= \(\frac{1}{\sqrt{2}} \int \frac{d t}{\sqrt{\left(\frac{1}{4}\right)^2-t^2}}\), where (x – \(\frac{1}{4}\)) = t

= \(\frac{1}{\sqrt{2}} \sin ^{-1} \frac{t}{(1 / 4)}+C=\frac{1}{\sqrt{2}} \sin ^{-1}(4 t)+C=\frac{1}{\sqrt{2}} \sin ^{-1} 4\left(x-\frac{1}{4}\right)+C\)

= \(\frac{1}{\sqrt{2}} \sin ^{-1}(4 x-1)+C .\)

Integrals of the from \(\int \frac{(p x+q)}{\sqrt{\left(a x^2+b x+c\right)}} d x\)

Method Let (px + q) = \(A \cdot \frac{d}{d x}\left(a x^2+b x+c\right)+B\).

Now, the value of the integral can be obtained easily.

Example 20 Evaluate \(\int \frac{2 x+1}{\sqrt{x^2+2 x-1}} d x .\)

Solution

\(\int \frac{2 x+1}{\sqrt{x^2+2 x-1}} d x .\)

Let 2x + 1 = \(A \cdot \frac{d}{d x}\left(x^2+2 x-1\right)+B\)

or 2x + 1 = A(2x+2) + B.

Comparing the coefficients of like powers of x, we get

(2A = 1 and 2A + B = 1) ⇒ (A = 1 and B = -1).

∴ \(\int \frac{2 x+1}{\sqrt{x^2+2 x-1}} d x=\int \frac{1 \cdot(2 x+2)-1}{\sqrt{x^2+2 x-1}} d x\)

= \(\int \frac{2 x+2}{\sqrt{x^2+2 x-1}} d x-\int \frac{d x}{\sqrt{x^2+2 x-1}}\)

= \(\int \frac{1}{\sqrt{t}} d t-\int \frac{d x}{\sqrt{x^2+2 x+1-2}}\), where t = x2 + 2x – 1

= \(2 \sqrt{t}-\int \frac{d x}{\sqrt{(x+1)^2-(\sqrt{2})^2}}\)

= \(2 \sqrt{x^2+2 x-1}-\log \left|(x+1)+\sqrt{x^2+2 x-1}\right|+C\)

WBCHSE Maths Chapter Special Integrals 

Example 21 Evaluate \(\int \frac{(x+1)}{\sqrt{4+5 x-x^2}} d x .\)

Solution

\(\int \frac{(x+1)}{\sqrt{4+5 x-x^2}} d x .\)

Let (x+1) = \(A \cdot \frac{d}{d x}\left(4+5 x-x^2\right)+B\). Then,

(x+1) = A(5-2x) + B.

Comparing the coefficients of like powers of x, we get

(-2A = 1 and 5A + B = 1) ⇒ (A = \(-\frac{1}{2}\) and B = \(\frac{7}{2}\)).

∴ (x+1) = \(-\frac{1}{2}\)(5-2x) + \(\frac{7}{2}\).

∴ \(\int \frac{(x+1)}{\sqrt{4+5 x-x^2}} d x=\int \frac{-\frac{1}{2}(5-2 x)+\frac{7}{2}}{\sqrt{4+5 x-x^2}} d x\)

= \(-\frac{1}{2} \int \frac{(5-2 x)}{\sqrt{4+5 x-x^2}} d x+\frac{7}{2} \int \frac{1}{\sqrt{4+5 x-x^2}} d x\)

= \(-\frac{1}{2} \int \frac{1}{\sqrt{t}} d t+\frac{7}{2} \cdot \int \frac{1}{\sqrt{4-\left(x^2-5 x\right)}} d x\), where t = 4 + 5x – x2

= \(-\frac{1}{2} \cdot 2 \sqrt{t}+\frac{7}{2} \cdot \int \frac{d x}{\sqrt{4-\left(x^2-5 x+\frac{25}{4}\right)+\frac{25}{4}}}\)

= \(-\sqrt{t}+\frac{7}{2} \cdot \int \frac{d x}{\sqrt{\left(\frac{\sqrt{41}}{2}\right)^2-\left(x-\frac{5}{2}\right)^2}}\)

= \(-\sqrt{4+5 x-x^2}+\frac{7}{2} \cdot \sin ^{-1} \frac{\left(x-\frac{5}{2}\right)}{\left(\frac{\sqrt{41}}{2}\right)}+C\)

= \(-\sqrt{4+5 x-x^2}+\frac{7}{2} \sin ^{-1}\left(\frac{2 x-5}{\sqrt{41}}\right)+C .\)

Practice Problems on Special Integrals for Class 12

Example 22 Evaluate \(\int \frac{(x+3)}{\sqrt{5-4 x-x^2}} d x\).

Solution

\(\int \frac{(x+3)}{\sqrt{5-4 x-x^2}} d x\)

Let (x+3) = \(A \cdot \frac{d}{d x}\left(5-4 x-x^2\right)+B\). Then,

(x+3) = A(-4-2x) + B.

Comparing the coefficients of like powers of x, we get

(-2A = 1 and -4A + B = 3) ⇒ (A = \(-\frac{1}{2}\), B = 1).

∴ \(\int \frac{(x+3)}{\sqrt{5-4 x-x^2}} d x=-\frac{1}{2} \cdot \int \frac{(-4-2 x)}{\sqrt{5-4 x-x^2}} d x+\int \frac{d x}{\sqrt{5-4 x-x^2}}\)

= \(-\frac{1}{2} \int \frac{d t}{\sqrt{t}}+\int \frac{d x}{\sqrt{5-\left(x^2+4 x+4\right)+4}}\), where (5-4x-x2) = t

= \(-\frac{1}{2} \cdot \frac{t^{1 / 2}}{(1 / 2)}+\int \frac{d x}{\sqrt{3^2-(x+2)^2}}\)

= \(-\sqrt{t}+\sin ^{-1} \frac{(x+2)}{3}+C\)

= \(-\sqrt{5-4 x-x^2}+\sin ^{-1} \frac{(x+2)}{3}+C\)

WBCHSE Maths Chapter Special Integrals 

Three More Special Integrals

Theorem

(1) \(\int \sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+C\)

(2) \(\int \sqrt{x^2-a^2} d x=\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C\)

(3) \(\int \sqrt{x^2+a^2} d x=\frac{x}{2} \sqrt{x^2+a^2}+\frac{a^2}{2} \log \left|x+\sqrt{x^2+a^2}\right|+C .\)

Proof (1) Integrating by parts, taking 1 as the second function, we get

I = \(\int \sqrt{a^2-x^2} d x=\int\left(\sqrt{a^2-x^2} \cdot 1\right) d x\)

= \(\left(\sqrt{a^2-x^2}\right) \cdot x-\int \frac{1}{2}\left(a^2-x^2\right)^{-1 / 2}(-2 x) \cdot x d x\)

= \(x\left(\sqrt{a^2-x^2}\right)+\int \frac{x^2}{\sqrt{a^2-x^2}} d x=x\left(\sqrt{a^2-x^2}\right)+\int \frac{a^2-\left(a^2-x^2\right)}{\sqrt{a^2-x^2}} d x\)

= \(x\left(\sqrt{a^2-x^2}\right)+a^2 \int \frac{d x}{\sqrt{a^2-x^2}}-\int \sqrt{a^2-x^2} d x\)

= \(x\left(\sqrt{a^2-x^2}\right)+a^2 \sin ^{-1} \frac{x}{a}-I+c .\)

∴ \(2 I=x\left(\sqrt{a^2-x^2}\right)+a^2 \sin ^{-1} \frac{x}{a}+c\)

⇒ \(I=\frac{x}{2}\left(\sqrt{a^2-x^2}\right)+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+C\) [taking \frac{c}{2} = C].

Hence, \(\int \sqrt{a^2-x^2} d x=\frac{x}{2}\left(\sqrt{a^2-x^2}\right)+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+\mathrm{C} .\)

(2) Integrating by parts, taking 1 as the second function, we get

I = \(\int \sqrt{x^2-a^2} d x=\int\left(\sqrt{x^2-a^2} \cdot 1\right) d x\)

= \(\left(\sqrt{x^2-a^2}\right) \cdot x-\int \frac{1}{2}\left(x^2-a^2\right)^{-1 / 2}(2 x) \cdot x d x\)

= \(x\left(\sqrt{x^2-a^2}\right)-\int \frac{x^2}{\sqrt{x^2-a^2}} d x=x\left(\sqrt{x^2-a^2}\right)-\int \frac{\left(x^2-a^2\right)+a^2}{\sqrt{x^2-a^2}} d x\)

= \(x\left(\sqrt{x^2-a^2}\right)-\int \sqrt{x^2-a^2} d x-\int \frac{a^2}{\sqrt{x^2-a^2}} d x\)

= \(x\left(\sqrt{x^2-a^2}\right)-I-a^2 \log \left|x+\sqrt{x^2-a^2}\right|+c .\)

∴ \(2 I=x\left(\sqrt{x^2-a^2}\right)-a^2 \log \left|x+\sqrt{x^2-a^2}\right|+c\)

⇒ \(I=\frac{x}{2}\left(\sqrt{x^2-a^2}\right)-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C\) [taking \frac{c}{2} = C].

Hence, \(\int \sqrt{x^2-a^2} d x=\frac{x}{2}\left(\sqrt{x^2-a^2}\right)-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C .\)

(3) Integrating by parts, taking 1 as the second function, we get

I = \(\int \sqrt{x^2+a^2} d x=\int\left(\sqrt{x^2+a^2} \cdot 1\right) d x\)

= \(\left(\sqrt{x^2+a^2}\right) x-\int \frac{1}{2}\left(x^2+a^2\right)^{-1 / 2}(2 x) \cdot x d x\)

= \(x\left(\sqrt{x^2+a^2}\right)-\int \frac{x^2}{\sqrt{x^2+a^2}} d x=x\left(\sqrt{x^2+a^2}\right)-\int \frac{\left(x^2+a^2\right)-a^2}{\sqrt{x^2+a^2}} d x\)

= \(x\left(\sqrt{x^2+a^2}\right)-\int \sqrt{x^2+a^2} d x+a^2 \int \frac{d x}{\sqrt{x^2+a^2}}\)

= \(x \cdot\left(\sqrt{x^2+a^2}\right)-I+a^2 \log \left|x+\sqrt{x^2+a^2}\right|+c .\)

∴ \(2 I=x\left(\sqrt{x^2+a^2}\right)+a^2 \log \left|x+\sqrt{x^2+a^2}\right|+c\)

or I = \(\frac{x}{2}\left(\sqrt{x^2+a^2}\right)+\frac{a^2}{2} \log \left|x+\sqrt{x^2+a^2}\right|+C\) [taking \frac{c}{2} = C].

Hence, \(\int \sqrt{x^2+a^2} d x=\frac{x}{2}\left(\sqrt{x^2+a^2}\right)+\frac{a^2}{2} \log \left|x+\sqrt{x^2+a^2}\right|+C .\)

WBCHSE Maths Chapter Special Integrals 

Solved Examples

Example 1 Evaluate:

(1) \(\int \sqrt{9-x^2} d x\)

(2) \(\int \sqrt{1-4 x^2} d x\)

(3) \(\int \sqrt{16-9 x^2} d x\)

Solution

We know that \(\int \sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+C\)

∴ (1) \(\int \sqrt{9-x^2} d x=\int \sqrt{3^2-x^2} d x\)

= \(\frac{x}{2} \sqrt{9-x^2}+\frac{9}{2} \sin ^{-1} \frac{x}{3}+C .\)

(2) \(\sqrt{1-4 x^2} d x=2 \int \sqrt{\left(\frac{1}{4}-x^2\right)} d x=2 \int\left\{\sqrt{\left(\frac{1}{2}\right)^2-x^2}\right\} d x\)

= \(2\left[\frac{x}{2} \sqrt{\frac{1}{4}-x^2}+\frac{1}{8} \sin ^{-1}\left(\frac{x}{(1 / 2)}\right)\right]+C\)

= \(\frac{x}{2} \sqrt{1-4 x^2}+\frac{1}{4} \sin ^{-1}(2 x)+C .\)

(3) \(\int \sqrt{16-9 x^2} d x=3 \int\left\{\sqrt{\left(\frac{16}{9}-x^2\right)}\right\} d x=3 \int\left\{\sqrt{\left(\frac{4}{3}\right)^2-x^2}\right\} d x\)

= \(3\left[\frac{x}{2} \sqrt{\frac{16}{9}-x^2}+\frac{8}{9} \sin ^{-1} \frac{x}{(4 / 3)}\right]+C\)

= \(\frac{x}{2} \sqrt{16-9 x^2}+\frac{8}{3} \sin ^{-1}\left(\frac{3 x}{4}\right)+C .\)

Example 2 Evaluate:

(1) \(\int \sqrt{x^2-16} d x\)

(2) \(\int \sqrt{4 x^2-5} d x\)

(3) \(\int \sqrt{17 x^2-11} d x\)

Solution

We know that \(\int \sqrt{x^2-a^2} d x=\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C .\)

∴ (1) \(\int \sqrt{x^2-16} d x=\int \sqrt{x^2-4^2} d x\)

= \(\frac{x}{2} \cdot \sqrt{x^2-4^2}-\frac{16}{2} \log \left|x+\sqrt{x^2-16}\right|+C\)

= \(\frac{x}{2} \cdot \sqrt{x^2-16}-8 \log \left|x+\sqrt{x^2-16}\right|+C\)

(2) \(\int \sqrt{4 x^2-5} d x=2 \int \sqrt{x^2-\frac{5}{4}} d x=2 \cdot \int \sqrt{x^2-\left(\frac{\sqrt{5}}{2}\right)^2} d x\)

= \(\left[\frac{x}{2} \sqrt{x^2-\frac{5}{4}}-\frac{5}{8} \log \left|x+\sqrt{x^2-\frac{5}{4}}\right|\right]+C\)

= \(x \sqrt{x^2-\frac{5}{4}}-\frac{5}{4} \log \left|x+\sqrt{x^2-\frac{5}{4}}\right|+C\)

(3) \(\int \sqrt{17 x^2-11} d x=\sqrt{17} \cdot \int \sqrt{x^2-\frac{11}{17}} d x\)

= \(\sqrt{17} \cdot\left\{\frac{x}{2} \sqrt{x^2-\frac{11}{17}}-\frac{11}{34} \log \left|x+\sqrt{x^2-\frac{11}{17}}\right|\right\}+C\)

= \(\frac{x}{2} \sqrt{17 x^2-11}-\frac{11 \sqrt{17}}{34} \log \left|x+\sqrt{x^2-\frac{11}{17}}\right|+C .\)

Example 3 Evaluate \(\int \sqrt{16 x^2+25} d x\)

Solution

\(\int \sqrt{16 x^2+25} d x\)

We know that \(\int \sqrt{x^2+a^2} d x=\frac{x}{2} \sqrt{x^2+a^2}+\frac{a^2}{2} \log \left|x+\sqrt{x^2+a^2}\right|+C\)

∴ \(\int \sqrt{16 x^2+25} d x=4 \int\left\{\sqrt{x^2+\frac{25}{16}}\right\} d x=4 \int\left\{\sqrt{x^2+\left(\frac{5}{4}\right)^2}\right\} d x\)

= \(4 \cdot\left\{\frac{x}{2} \sqrt{x^2+\frac{25}{16}}+\frac{25}{32} \log \left|x+\sqrt{x^2+\frac{25}{16}}\right|\right\}+C\)

= \(\frac{x}{2} \cdot \sqrt{16 x^2+25}+\frac{25}{8} \log \left|x+\sqrt{x^2+\frac{25}{16}}\right|+C\)

WBCHSE Maths Chapter Special Integrals 

Example 4 Evaluate \(\int \sqrt{\frac{16+(\log x)^2}{x}} d x .\)

Solution

\(\int \sqrt{\frac{16+(\log x)^2}{x}} d x .\)

Putting log x = t and \(\frac{1}{x}\)dx = dt, we get

I = \(\int \sqrt{16+t^2} d t=\int \sqrt{4^2+t^2} d t\)

= \(\frac{t}{2} \sqrt{16+t^2}+\frac{16}{2} \log \left|t+\sqrt{16+t^2}\right|+C\)

= \(\frac{1}{2} \log x \cdot \sqrt{16+(\log x)^2}+8 \log \left|\log x+\sqrt{16+(\log x)^2}\right|+C\)

Example 5 Evaluate \(\int x \sqrt{x^4+1} d x\)

Solution

\(\int x \sqrt{x^4+1} d x\)

Putting x² = t and x dx = \(\frac{1}{x}\)dt, we get

I = \(\frac{1}{2} \int \sqrt{t^2+1} d t\)

= \(\frac{1}{2} \cdot\left[\frac{t}{2} \sqrt{t^2+1}+\frac{1}{2} \log \left|t+\sqrt{t^2+1}\right|\right]+C\)

= \(\frac{x^2}{4} \sqrt{x^4+1}+\frac{1}{4} \log \left|x^2+\sqrt{x^4+1}\right|+C\)

Example 6 Evaluate \(\int e^x \sqrt{e^{2 x}+4} d x\)

Solution

\(\int e^x \sqrt{e^{2 x}+4} d x\)

Putting e^x = t and e^xdx = dt, we get

I = \(\int \sqrt{t^2+4} d x\)

= \(\frac{t}{2} \cdot \sqrt{t^2+4}+\frac{4}{2} \log \left|t+\sqrt{t^2+4}\right|+C\)

= \(\frac{1}{2} e^x \sqrt{e^{2 x}+4}+2 \log \left|e^x+\sqrt{e^{2 x}+4}\right|+C\)

\(\int e^x \sqrt{e^{2 x}+4} d x\) = \(\frac{1}{2} e^x \sqrt{e^{2 x}+4}+2 \log \left|e^x+\sqrt{e^{2 x}+4}\right|+C\)

Example 7 Evaluate \(\int \cos x \sqrt{4-\sin ^2 x} d x .\)

Solution

\(\int \cos x \sqrt{4-\sin ^2 x} d x .\)

Putting sin x = t and cos x dx = dt, we get

I = \(\int \sqrt{4-t^2} d t\)

= \(\frac{t}{2} \sqrt{4-t^2}+\frac{4}{2} \sin ^{-1} \frac{t}{2}+C\)

= \(\frac{1}{2} \sin x \sqrt{4-\sin ^2 x}+2 \sin ^{-1}\left(\frac{1}{2} \sin x\right)+C .\)

Integrals of the form \(\int \sqrt{\left(a x^2+b x+c\right)} d x\)

Method Express (ax² + bx + c) as a[(x+α)² ± β²] and obtain an integral which can be evaluated easily.

Example 8 Evaluate \(\int \sqrt{x^2+3 x} d x .\)

Solution We have

\(\left(x^2+3 x\right)=\left\{x^2+3 x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2\right\}=\left(x+\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2\)

∴ \(I=\int \sqrt{x^2+3 x} d x\)

= \(\int \sqrt{\left(x+\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2} d x=\int \sqrt{t^2-\left(\frac{3}{2}\right)^2} d t\), where (x + \(\frac{3}{2}\)) = t

= \(\frac{1}{2} t \sqrt{t^2-\frac{9}{4}}-\frac{9}{8} \log \left|t+\sqrt{t^2-\frac{9}{4}}\right|+C\)

{using \(\int \sqrt{x^2-a^2} d x=\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C\)}

= \(\frac{1}{2}\left(x+\frac{3}{2}\right) \sqrt{x^2+3 x}-\frac{9}{8} \log \left|\left(x+\frac{3}{2}\right)+\sqrt{x^2+3 x}\right|+C\)

WBCHSE Maths Chapter Special Integrals 

Example 9 Evaluate \(\int \sqrt{2 x^2+3 x+4} d x\)

Solution We have

\(\left(2 x^2+3 x+4\right)=2\left(x^2+\frac{3}{2} x+2\right)\)

= \(2 \cdot\left\{\left(x^2+\frac{3}{2} x+\frac{9}{16}\right)+\left(2-\frac{9}{16}\right)\right\}=2 \cdot\left\{\left(x+\frac{3}{4}\right)^2+\left(\frac{\sqrt{23}}{4}\right)^2\right\} .\)

∴ \(\sqrt{2 x^2+3 x+4}=\sqrt{2} \cdot \sqrt{\left(x+\frac{3}{4}\right)^2+\left(\frac{\sqrt{23}}{4}\right)^2}\)

⇒ \(\int \sqrt{2 x^2+3 x+4} d x=\sqrt{2} \cdot \int \sqrt{\left(x+\frac{3}{4}\right)^2+\left(\frac{\sqrt{23}}{4}\right)^2} d x\)

= \(\sqrt{2} \int \sqrt{t^2+\left(\frac{\sqrt{23}}{4}\right)^2} d t\), where (x + \(\frac{3}{2}\)) = t

= \(\sqrt{2} \cdot\left\{\frac{t}{2} \cdot \sqrt{t^2+\frac{23}{16}}+\frac{23}{32} \log \left|t+\sqrt{t^2+\frac{23}{16}}\right|\right\}+C\)

[∵ \(\int \sqrt{t^2+a^2} d t=\frac{t}{2} \sqrt{t^2+a^2}+\frac{a^2}{2} \log \left|t+\sqrt{t^2+a^2}\right|+C\)]

= \(\frac{\sqrt{2}}{2}\left(x+\frac{3}{4}\right) \sqrt{\left(x+\frac{3}{4}\right)^2+\frac{23}{16}}+\frac{23 \sqrt{2}}{32} \log \left|\left(x+\frac{3}{4}\right)+\sqrt{x^2+\frac{3}{2} x+2}\right|+C\)

= \(\frac{(4 x+3)}{4 \sqrt{2}} \cdot \sqrt{x^2+\frac{3}{2} x+2}+\frac{23 \sqrt{2}}{32} \log \left|\frac{(4 x+3)}{4}+\frac{\sqrt{2 x^2+3 x+4}}{\sqrt{2}}\right|+C\)

= \(\frac{(4 x+3) \sqrt{2 x^2+3 x+4}}{8}+\frac{23 \sqrt{2}}{32} \log \left|\frac{(4 x+3)}{4}+\frac{\sqrt{2 x^2+3 x+4}}{\sqrt{2}}\right|+C \text {. }\)

Example 10 Evaluate \(\int \sqrt{3-2 x-2 x^2} d x\)

Solution We have

\(\left(3-2 x-2 x^2\right)=2 \cdot\left\{\frac{3}{2}-x-x^2\right\}\)

= \(2 \cdot\left[\frac{3}{2}-\left(x^2+x+\frac{1}{4}\right)+\frac{1}{4}\right]\)

= \(\left[\frac{7}{4}-\left(x+\frac{1}{2}\right)^2\right]=2 \cdot\left\{\left(\frac{\sqrt{7}}{2}\right)^2-\left(x+\frac{1}{2}\right)^2\right\}\)

∴ \(\sqrt{3-2 x-2 x^2}=\sqrt{2} \cdot \sqrt{\left(\frac{\sqrt{7}}{2}\right)^2-\left(x+\frac{1}{2}\right)^2}\)

⇒ \(\int \sqrt{3-2 x-2 x^2} d x=\sqrt{2} \cdot \int \sqrt{\left(\frac{\sqrt{7}}{2}\right)^2-\left(x+\frac{1}{2}\right)^2} d x\)

= \(\sqrt{2} \cdot \int \sqrt{\left(\frac{\sqrt{7}}{2}\right)^2-t^2} d t\), where (x + \(\frac{1}{2}\)) = t and dx = dt

= \(\sqrt{2} \cdot\left\{\frac{t}{2} \cdot \sqrt{\frac{7}{4}-t^2}+\frac{7}{8} \sin ^{-1} \frac{t}{(\sqrt{7 / 2})}\right\}+C\)

[∵ \(\int \sqrt{a^2-t^2} d t=\frac{t}{2} \sqrt{a^2-t^2}+\frac{a^2}{2} \cdot \sin ^{-1} \frac{t}{a}+C\)]

= \(\sqrt{2} \cdot\left\{\frac{1}{2}\left(x+\frac{1}{2}\right) \sqrt{\frac{7}{4}-\left(x+\frac{1}{2}\right)^2}+\frac{7}{8} \sin ^{-1} \frac{\left(x+\frac{1}{2}\right)}{(\sqrt{7} / 2)}\right\}+C\)

= \(\sqrt{2}\left\{\frac{1}{4}(2 x+1) \cdot \sqrt{\frac{3}{2}-x-x^2}+\frac{7}{8} \sin ^{-1}\left(\frac{2 x+1}{\sqrt{7}}\right)\right\}+C\)

= \(\frac{1}{4}(2 x+1) \sqrt{3-2 x-2 x^2}+\frac{7}{4 \sqrt{2}} \sin ^{-1}\left(\frac{2 x+1}{\sqrt{7}}\right)+C \text {. }\)

Integrals of the form \(\int(p x+q) \sqrt{\left(a x^2+b x+c\right)} d x\)

Method Let (px+q) = \(A \cdot \frac{d}{d x}\left(a x^2+b x+c\right)+B\).

Find A and B.

Then, we get the integrand which is easily integrable.

Example 11 Evaluate \(\int(x+3) \sqrt{3-4 x-x^2} d x .\)

Solution

\(\int(x+3) \sqrt{3-4 x-x^2} d x .\)

Let (x+3) = \(A \cdot \frac{d}{d x}\left(3-4 x-x^2\right)+B ⇔ (x+3) = A(-4-2x) + B\).

Comparing coefficients of like powers of x, we get

-2A = 1 and -4A + B = 3 ⇔ A = \(\frac{1}{2}\) and B = 1.

∴ \((x+3)=-\frac{1}{2}(-4-2 x)+1\)

⇒ \(I=\int\left\{-\frac{1}{2}(-4-2 x)+1\right\} \sqrt{3-4 x-x^2} d x\)

= \(-\frac{1}{2} \int(-4-2 x) \sqrt{3-4 x-x^2} d x+\int \sqrt{3-4 x-x^2} d x\)

= \(-\frac{1}{2} \int \sqrt{t} d t+\int \sqrt{7-\left(4 x+x^2+4\right)} d x\), where 3-4x-x2 = t

= \(\left(-\frac{1}{2} \times t^{3 / 2} \times \frac{2}{3}\right)+\int \sqrt{(\sqrt{7})^2-(x+2)^2} d x\)

= \(-\frac{1}{3}\left(3-4 x-x^2\right)^{3 / 2}+\frac{1}{2}(x+2) \sqrt{3-4 x-x^2}+\frac{7}{2} \sin ^{-1}\left(\frac{x+2}{\sqrt{7}}\right)+C\)

[∵ \(\int \sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \cdot \sin ^{-1} \frac{x}{a}+C\)]

Example 12 Evaluate \(\int(3 x-2) \sqrt{x^2+x+1} d x .\)

Solution

\(\int(3 x-2) \sqrt{x^2+x+1} d x .\)

Let (3x-2) = \(A \cdot \frac{d}{d x}\left(x^2+x+1\right)+B\)

Then, (3x-2) = A(2x+1) + b.

Comparing coefficients of like powers of x, we get

2A = 3 and A + B = -2. So, A = \(\frac{3}{2}\) and B = \(-\frac{7}{2}\)

∴ \((3 x-2)=\frac{3}{2}(2 x+1)-\frac{7}{2} .\)

So, \(\int(3 x-2) \sqrt{x^2+x+1} d x\)

= \(\int\left\{\frac{3}{2}(2 x+1)-\frac{7}{2}\right\} \sqrt{x^2+x+1} d x\)

= \(\frac{3}{2} \int(2 x+1) \sqrt{x^2+x+1} d x-\frac{7}{2} \int \sqrt{x^2+x+1} d x\)

= \(\frac{3}{2} \int \sqrt{t} d t-\frac{7}{2} \int \sqrt{\left(x^2+x+\frac{1}{4}\right)+\frac{3}{4}} d x\), where x² + x + 1 = t in the 1st integral

= \(t^{3 / 2}-\frac{7}{2} \int \sqrt{\left\{\left(x+\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2\right\}} d x\)

= \(\left(x^2+x+1\right)^{3 / 2}-\frac{7}{2} \cdot \int \sqrt{u^2+\left(\frac{\sqrt{3}}{2}\right)^2} d u\), Where u = (x + \frac{1}{2})

= \(\left(x^2+x+1\right)^{3 / 2}-\frac{7}{2}\left\{\frac{u}{2} \cdot \sqrt{u^2+\frac{3}{4}}+\frac{3}{8} \log \left|u+\sqrt{u^2+\frac{3}{4}}\right|\right\}+C\)

{∵ \(\int \sqrt{u^2+a^2} d u=\frac{u}{2} \sqrt{u^2+a^2}+\frac{a^2}{2} \log \left|u+\sqrt{u^2+a^2}\right|+C\)}

= \(\left(x^2+x+1\right)^{3 / 2}-\frac{7 u}{8} \sqrt{4 u^2+3}-\frac{21}{16} \log \left|u+\sqrt{u^2+\frac{3}{4}}\right|+C\)

= \(\left(x^2+x+1\right)^{3 / 2}-\frac{7}{8}\left(x+\frac{1}{2}\right) \sqrt{4\left(x+\frac{1}{2}\right)^2+3}-\frac{21}{16} \log \mid\left(x+\frac{1}{2}\right)+\sqrt{\left(x+\frac{1}{2}\right)^2+\frac{3}{4} \mid}+C\)

= \(\left(x^2+x+1\right)^{3 / 2}-\frac{7(2 x+1)}{8} \sqrt{x^2+x+1}-\frac{21}{16} \log \left|\frac{(2 x+1)}{2}+\sqrt{x^2+x+1}\right|+C \text {. }\)

WBCHSE Maths Chapter Special Integrals 

Example 13 Evaluate \(\int x \sqrt{x+x^2} d x\)

Solution

\(\int x \sqrt{x+x^2} d x\)

Let x = \(A \cdot \frac{d}{d x}\left(x+x^2\right)+B\). Then,

x = A(1+2x) + B …(1)

Comparing coefficients of various powers of x, we get

(2A = 1 and A + B = 0) ⇒ [A = \(\frac{1}{2}\) and B = \(-\frac{1}{2}\)].

∴ \(x=\frac{1}{2}(1+2 x)-\frac{1}{2}\)

⇒ \(\int x \sqrt{x+x^2} d x\)

= \(\int\left\{\frac{1}{2}(1+2 x)-\frac{1}{2}\right\} \sqrt{x+x^2} d x\)

= \(\frac{1}{2} \int(1+2 x) \sqrt{x+x^2} d x-\frac{1}{2} \int \sqrt{x+x^2} d x\)

= \(\frac{1}{2} \int \sqrt{t} d t-\frac{1}{2} \int \sqrt{\left\{\left(x^2+x+\frac{1}{4}\right)-\frac{1}{4}\right\}} d x\), where (x+x²) = t in the first integral

= \(\frac{1}{2} \cdot \frac{t^{3 / 2}}{(3 / 2)}-\frac{1}{2} \int \sqrt{\left\{\left(x+\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2\right\}} d x\)

= \(\frac{1}{3}\left(x+x^2\right)^{3 / 2}-\frac{1}{2} \cdot \int \sqrt{u^2-\left(\frac{1}{2}\right)^2} d u\), where (x + \(\frac{1}{2}\)) = u

= \(\frac{1}{3}\left(x+x^2\right)^{3 / 2}-\frac{1}{2}\left\{\frac{u}{2} \cdot \sqrt{u^2-\frac{1}{4}}-\frac{1}{8} \log \left|u+\sqrt{u^2-\frac{1}{4}}\right|\right\}+C\)

{∵ \(\int \sqrt{x^2-a^2} d x=\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C\)}

= \(\frac{1}{3}\left(x+x^2\right)^{3 / 2}-\frac{1}{4}\left(x+\frac{1}{2}\right) \sqrt{\left(x+\frac{1}{2}\right)^2-\frac{1}{4}}+\frac{1}{16} \log \mid\left(x+\frac{1}{2}\right) \sqrt{\left(x+\frac{1}{2}\right)^2-\frac{1}{4} \mid}+C\)

= \(\frac{1}{3}\left(x+x^2\right)^{3 / 2}-\frac{1}{8}(2 x+1) \sqrt{x+x^2}+\frac{1}{16} \log \left|\frac{(2 x+1)}{2} \cdot \sqrt{x+x^2}\right|+C\)

WBCHSE Class 12 Maths Solutions For Straight Line In Space Fundamental Concepts

This chapter consists of some important concepts of three-dimensional geometry. Though we have studied these in Class 9, yet we shall review here these fundamental concepts for ready reference.

WBBSE Class 12 Straight Line in Space Solutions

Coordinates of a Point in Space

Let O be the origin, and let OX, OY, and OZ be three mutually perpendicular lines, taken as the x-axis, y-axis, and z-axis respectively in such a way that they form a right-handed system.

The planes YOZ, ZOX, and XOY are respectively known as the yz-plane, the zx-plane, and the xy-plane.

These planes, known as the coordinate planes, divide the space into eight parts called octants.

Let P be a point in space. Through P, draw three planes PLAN, PNBM, and PLCM parallel to the yz-plane, the zx-plane, and the xy-plane respectively, and meet the x-axis, y-axis, and z-axis at points A, B, and C respectively. Complete the parallelepiped whose coterminous edges are OA, OB, and OC.

Let OA = x, OB = y and OC = z. We say that the coordinates of P are (x,y,z).

It is clear from the figure alongside that

(1) x = distance of P from the yz-plane

(2) y = distance of P from the zx-plane

(3) z = distance of P from the xy-plane

Read and Learn More  Class 12 Math Solutions

Also, we can say that

(1) the equation of the xy-plane is z = 0

(2) the equation of the zx-plane is y = 0

(3) the equation of the yz-plane is x = 0

Position Vector Of A Point In Space Let \(\hat{i}, \hat{j}, \hat{k}\) be unit vectors along OX, OY and OZ respectively.

If P(x, y, z) is a point in space, we say that the position vector (or, p.v.) of P is \((x \hat{i}+y \hat{j}+z \hat{k})\).

Some Results on Points in Space

1. Distance Between Two Points The distance between two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) is given by PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2} .\)

2. Sector Formulae

(1) If P(x,y,z) divides the join of A(x₁, y₁,z₁) and B(x₂,y₂,z₂) in the ration m:n then

\(x=\frac{\left(m x_2+n x_1\right)}{(m+n)}, y=\frac{\left(m y_2+n y_1\right)}{(m+n)}, z=\frac{\left(m z_2+n z_1\right)}{(m+n)} .\)

(2) The midpoint of the line joining A(x₁,y₁,z₁) and B(x₂,y₂,z₂) is given by

\(M\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right) .\)

(3) The centroid of △ABC with vertices A(x₁,y₁,z₁), B(x₂,y₂,z₂) and C(x₃,y₃,z₃) is given by

\(G\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right) .\)

Some Results on Lines in Space

1. Direction Cosines Of A Line If a line makes angles α, β, γ with the x-axis, y-axis and z-axis respectively then

l = cos α, m = cos β, n = cos γ are called the direction cosines (or, d.c.’s)of the line.

We always have l² + m² + n² = 1.

Remarks

(1) d.c.’s of the x-axis are 1,0,0.

(2) d.c.’s of the y-axis are 0,1,0.

(3) d.c.’s of the z-axis are 0,0,1.

2. Direction Ratios Of A Line Any three numbers a, b, c proportional to the direction cosines l, m, n respectively of a line, are called the direction ratios of the line.

Clearly, we have \(\frac{l}{a}=\frac{m}{b}=\frac{n}{c} .\)

Some Important Facts

(1) If a,b,c are the direction ratios of a line then its direction cosines are

\(l=\frac{a}{\sqrt{a^2+b^2+c^2}}, m=\frac{b}{\sqrt{a^2+b^2+c^2}}, n=\frac{c}{\sqrt{a^2+b^2+c^2}} .\)

(2) If \(\vec{r}=a \hat{i}+b \hat{j}+c \hat{k}\) then the direction ratios of \(\vec{r}\) are a,b,c.

(3) Let PQ be a line joining P(x₁,y₁,z₁) and Q(x₂,y₂,z₂). Then the direction ratios of the line PQ are (x₂ – x₁), (y₂ – y₁), (z₂ – z₁).

3. Angle Between Two Lines If θ is the angle between two lines L₁ and L₂ whose d.c.’s are l₁, m₁, n₁ and l₂, m₂, n₂ then the following hold true.

(1) cos θ = l₁l₂ + m₁m₂ + n₁n₂

(2) sin θ = \(\sqrt{\Sigma\left(m_1 n_2-m_2 n_1\right)^2}\)

(3) lines L₁ and L₂ are prependicular ⇔ l₁l₂ + m₁m₂ + n₁n₂ = 0

(4) lines L₁ and L₂ are parallel ⇔ \(\frac{l_1}{l_2}=\frac{m_1}{m_2}=\frac{n_1}{n_2}\)

WBCHSE Class 12 Maths Solutions For Straight Line In Space Solved Examples

Example 1 Find the direction cosines of a line whose direction ratios are 2, -6, 3.

Solution

Here, a = 2, b = -6, c = 3.

∴ d.c.’s are \(\frac{a}{\sqrt{a^2+b^2+c^2}}, \frac{b}{\sqrt{a^2+b^2+c^2}}, \frac{c}{\sqrt{a^2+b^2+c^2}}\),

i.e., \(\frac{2}{\sqrt{2^2+(-6)^2+3^2}}, \frac{-6}{\sqrt{2^2+(-6)^2+3^2}}, \frac{3}{\sqrt{2^2+(-6)^2+3^2}}\),

i.e., \(\frac{2}{7}, \frac{-6}{7}, \frac{3}{7} \text {. }\)

The direction cosines of a line \(\frac{2}{7}, \frac{-6}{7}, \frac{3}{7} \text {. }\)

Example 2 Find the direction cosines of each of the following vectors:

(1) \(2 \hat{i}+\hat{j}-2 \hat{k}\)

(2) \(-\hat{i}-\hat{k}\)

(3) \(-\hat{j}\)

Solution

(1) Direction ratios of the vector (\(2 \hat{i}+\hat{j}-2 \hat{k}\)) are 2, 1, -2.

∴ its d.c.’s are

\(\frac{2}{\sqrt{2^2+1^2+(-2)^2}}, \frac{1}{\sqrt{2^2+1^2+(-2)^2}}, \frac{-2}{\sqrt{2^2+1^2+(-2)^2}},\)

i.e., \(\frac{2}{3}, \frac{1}{3}, \frac{-2}{3} \text {. }\)

(2) Direction ratios of the vector (-\hat{i}-\hat{k}) are -1, 0, -1.

∴ its d.c.’s are

\(\frac{-1}{\sqrt{(-1)^2+0^2+(-1)^2}}, 0, \frac{-1}{\sqrt{(-1)^2+0^2+(-1)^2}}\)

i.e., \(\frac{-1}{\sqrt{2}}, 0, \frac{-1}{\sqrt{2}} \text {. }\)

(3) Direction ratios of the vector (-\hat{j}) are 0, -1, 0.

∴ its d.c.’s are

\(0, \frac{-1}{\sqrt{0^2+(-1)^2+0^2}},\) 0 i.e., 0, -1, 0.

Step-by-Step Solutions to Straight Line Problems

Example 3 Find the direction cosines of the line segment joining the points A(7, -5, 9) and B(5, -3, 8).

Solution

Given

The points A(7, -5, 9) and B(5, -3, 8).

Direction ratios of the line segment AB are (5 – 7), -3 -(-5), (8 – 9), i.e., -2, 2, -1.

∴ its d.c.’s are

\(\frac{-2}{\sqrt{(-2)^2+2^2+(-1)^2}}, \frac{2}{\sqrt{(-2)^2+2^2+(-1)^2}}, \frac{-1}{\sqrt{(-2)^2+2^2+(-1)^2}}\)

i.e., \(\frac{-2}{3}, \frac{2}{3}, \frac{-1}{3} \text {. }\)

The direction cosines of the line segment joining the points \(\frac{-2}{3}, \frac{2}{3}, \frac{-1}{3} \text {. }\)

Example 4 Find the angle between the lines whose direction ratios are 2,3,6 and 1,2,2.

Solution

Given 2,3,6 and 1,2,2

Direction ratios of the first line are 2,3,6.

∴ its d.c.’s are

\(\frac{2}{\sqrt{2^2+3^2+6^2}}, \frac{3}{\sqrt{2^2+3^2+6^2}}, \frac{6}{\sqrt{2^2+3^2+6^2}}\)

i.e., \(\frac{2}{7}, \frac{3}{7}, \frac{6}{7} \text {. }\)

Direction ratios of the second line are 1, 2, 2.

∴ its d.c.’ are

\(\frac{1}{\sqrt{1^2+2^2+2^2}}, \frac{2}{\sqrt{1^2+2^2+2^2}}, \frac{2}{\sqrt{1^2+2^2+2^2}}\)

i.e., \(\frac{1}{3}, \frac{2}{3}, \frac{2}{3} \text {. }\)

∴ \(\cos \theta=\left(\frac{2}{7} \times \frac{1}{3}\right)+\left(\frac{3}{7} \times \frac{2}{3}\right)+\left(\frac{6}{7} \times \frac{2}{3}\right)=\frac{20}{21}\)

⇒ \(\theta=\cos ^{-1}\left(\frac{20}{21}\right)\)

Hence, the angle between the given lines is \(\cos ^{-1}\left(\frac{20}{21}\right)\).

Example 5 Find the angle between the vectors \(\overrightarrow{r_1}=3 \hat{i}-2 \hat{j}+\hat{k}\) and \(\overrightarrow{r_2}=4 \hat{i}+5 \hat{j}+7 \hat{k}\).

Solution

The direction ratios of the first vector are 3, -2, 1.

∴ its d.c.’s are

\(\frac{3}{\sqrt{3^2+(-2)^2+1^2}}, \frac{-2}{\sqrt{3^2+(-2)^2+1^2}}, \frac{1}{\sqrt{3^2+(-2)^2+1^2}}\)

i.e., \(\frac{3}{\sqrt{14}}, \frac{-2}{\sqrt{14}}, \frac{1}{14}\)

The direction ratios of the second vector are 4,5,7.

∴ its d.c.’s are

\(\frac{4}{\sqrt{4^2+5^2+7^2}}, \frac{5}{\sqrt{4^2+5^2+7^2}}, \frac{7}{\sqrt{4^2+5^2+7^2}}\)

i.e., \(\frac{4}{3 \sqrt{10}}, \frac{5}{3 \sqrt{10}}, \frac{7}{3 \sqrt{10}}\)

∴ cos θ = \(\left(\frac{3}{\sqrt{14}} \times \frac{4}{3 \sqrt{10}}\right)+\left(\frac{-2}{\sqrt{14}} \times \frac{5}{3 \sqrt{10}}\right)+\left(\frac{1}{\sqrt{14}} \times \frac{7}{3 \sqrt{10}}\right)\)

= \(\frac{9}{3 \sqrt{140}}=\frac{3}{\sqrt{140}}=\frac{3}{2 \sqrt{35}}\)

⇒ θ = \(\cos ^{-1}\left(\frac{3}{2 \sqrt{35}}\right)\)

Hence, the angle between the given vectors is \(\cos ^{-1}\left(\frac{3}{2 \sqrt{35}}\right)\).

Example 6 Find the angles made by the vector \(\vec{r}=(\hat{i}+\hat{j}-\hat{k})\) with the coordinate axes.

Solution

Direction ratios of the given vector are 1, 1, -1.

∴ its d.c.’s are

\(\frac{1}{\sqrt{1^2+1^2+(-1)^2}}, \frac{1}{\sqrt{1^2+1^2+(-1)^2}}, \frac{-1}{\sqrt{1^2+1^2+(-1)^2}}\)

i.e., \(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{-1}{\sqrt{3}}\).

Let the given vector make angles θ₁, θ₂, and θ₃ with the x-axis, y-axis and z-axis respectively.

The d.c.’s of the x-axis are 1, 0, 0.

∴ \(\cos \theta_1=\left(\frac{1}{\sqrt{3}} \times 1\right)+\left(\frac{1}{\sqrt{3}} \times 0\right)+\left(-\frac{1}{\sqrt{3}} \times 0\right)=\frac{1}{\sqrt{3}}\)

⇒ \(\theta_1=\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right) \text {. }\)

∴ the angle between the given vector and the x-axis is \(\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right)\).

The d.c.’s of the y-axis are 0, 1, 0.

∴ \(\cos \theta_2=\left(\frac{1}{\sqrt{3}} \times 0\right)+\left(\frac{1}{\sqrt{3}} \times 1\right)+\left(-\frac{1}{\sqrt{3}} \times 0\right)=\frac{1}{\sqrt{3}}\)

⇒ \(\theta_2=\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right).\)

∴ the angle between the given vector and the y-axis is \(\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right)\)

The d.c.’s of the z-axis are 0,0,1.

∴ \(\cos \theta_3=\left(\frac{1}{\sqrt{3}} \times 0\right)+\left(\frac{1}{\sqrt{3}} \times 0\right)+\left(-\frac{1}{\sqrt{3}} \times 1\right)=\frac{-1}{\sqrt{3}}\)

⇒ \(\theta_3=\cos ^{-1}\left(\frac{-1}{\sqrt{3}}\right)\)

∴ the angle between the given vector and the z-axis is \(\cos ^{-1}\left(\frac{-1}{\sqrt{3}}\right)\)

WBCHSE Class 12 Maths Solutions For Straight Line In Space – Straight Line In Space

Equation of a Line Passing through a Given Point and Parallel to a Given Vector

Vector Form

Theorem 1 The vector equation of a straight line passing through a given point with position vector \(\overrightarrow{r_1}\) and parallel to a given vector \(\vec{m}\) is \(\vec{r}=\overrightarrow{r_1}+\lambda \vec{m}\), where λ is a scalar.

Proof

Let L be the line, passing through a given point A with position vector \(\overrightarrow{r_1}\) and parallel to a given vector \(\vec{m}\).

Let O be the origin. Then, \(\overrightarrow{O A}=\overrightarrow{r_1}\).

Let P be an arbitrary point on L, and let the position vector of P be \(\vec{r}\).

Then, \(\overrightarrow{O P}=\vec{r}\).

Clearly, \(\overrightarrow{A P} \ \vec{m}\)

⇒ \(\overrightarrow{A P}=\lambda \vec{m}\), for some scalar λ

⇒ (p.v. of P) – (p.v. of A) = \(\lambda \vec{m}\)

⇒ \(\overrightarrow{O P}-\overrightarrow{O A}=\lambda \vec{m}\)

⇒ \(\vec{r}-\overrightarrow{r_1}=\lambda \vec{m}\)

⇒ \(\vec{r}=\overrightarrow{r_1}+\lambda \vec{m}\) …(1)

Clearly, every point on the line L satisfies (1), and for any value of λ, (1) gives the position vector of a point P on the line.

Hence, \(\vec{r}=\vec{r}_1+\lambda \vec{m}\) is the desired equation.

Corollary The vector equation of a straight line passing through the origin and parallel to a given vector \(\vec{m}\) is \(\vec{r}=\lambda \vec{m}\).

Proof

Taking \(\overrightarrow{r_1}=\overrightarrow{0}\) in (1), we get the desired equation, \(\vec{r}=\lambda \vec{m}\).

Cartesian Form

Theorem 2 The equations of a straight line with direction ratios a, b, c, and passing through a point A(x₁, y_1, z₁) are

\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c} .\)

Proof

We know that the vector equation of a straight line passing through a fixed point A(x₁, y₁, z₁) with position vector \(\overrightarrow{r_1}\) and parallel to a given vector \(\vec{m}\) is given by

\(\vec{r}=\overrightarrow{r_1}+\lambda \vec{m}\) …(1), where λ is a scalar.

Let P(x, y, z) be the given point on the line with position vector \(\vec{r}\).

Then, \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k} \text { and } \overrightarrow{r_1}=x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k} \text {. }\)

Since the direction ratios of the given line are a, b, c and this line is parallel to \vec{m} are a, b, c.

∴ \(\vec{m}=a \hat{i}+b \hat{j}+c \hat{k} .\)

Putting \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}, \vec{r}_1=x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k} \text { and } \vec{m}=a \hat{i}+b \hat{j}+c \hat{k}\) in (1), we get the equation of the line as

\((x \hat{i}+y \hat{j}+z \hat{k})=\left(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}\right)+\lambda(a \hat{i}+b \hat{j}+c \hat{k})\)

⇒ \((x \hat{i}+y \hat{j}+z \hat{k})=\left(x_1+\lambda a\right) \hat{i}+\left(y_1+\lambda b\right) \hat{j}+\left(z_1+\lambda c\right) \hat{k}\)

⇒ x = x₁ + λa, y = y₁ + λb and z = z₁ + λc

⇒ \(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}=\lambda \text {. }\)

Hence, the equations of a line having direction ratios a, b, c and passing through A(x1, y1, z1) are

\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}.\)

Corollary The equations of a line having direction cosines l, m, n and passing through (x1, y1, z1) are \(\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n} .\)

Proof Since the direction cosines of a line are porportional to the direction ratios of the line, the result follows.

Equation of a Line Passing through Two Given Points

Vector Form

Theorem 3 The vector equation of a straight line passing through two points with position vectors \(\overrightarrow{r_1} \text { and } \overrightarrow{r_2}\) is given by \(\vec{r}=\overrightarrow{r_1}+\lambda\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right) .\)

Proof

Let L be the given line, passing through two given points A and B with position vectors \(\overrightarrow{r_1} \text { and } \overrightarrow{r_2}\) respectively.

Let O be the origin.

Then, \(\overrightarrow{O A}=\overrightarrow{r_1} \text { and } \overrightarrow{O B}=\overrightarrow{r_2} \text {. }\)

∴ \(\overrightarrow{A B}=(\text { p.v. of } B)-(\text { p.v, of } A)=\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right) \text {. }\)

Let P be an arbitrary point on L, having the position vector \(\vec{r} .\)

Then, \(\overrightarrow{O P}=\vec{r}\).

∴ \(\overrightarrow{A P}=(\mathrm{p} \cdot \mathrm{v} \cdot \text { of } P)-(\mathrm{p} \cdot \mathrm{v} \cdot \text { of } A)\)

= \((\overrightarrow{O P}-\overrightarrow{O A})=\left(\vec{r}-\overrightarrow{r_1}\right)\)

Since \(\overrightarrow{A P} \text { and } \overrightarrow{A B}\) are collinear vectors, we have

\(\overrightarrow{A P}=\lambda(\overrightarrow{A B})\), for some scalar λ

⇒ \(\left(\vec{r}-\overrightarrow{r_1}\right)=\lambda\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)\)

⇒ \(\vec{r}=\overrightarrow{r_1}+\lambda\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)\)

Hence, the vector equation of a line L, passing through two given points A and B with position vectors \(\overrightarrow{r_1} \text { and } \vec{r}_2\), is given by

\(\vec{r}=\overrightarrow{r_1}+\lambda\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right) .\)

Equations of Straight Lines in Space

Cartesian Form

Theorem 4 The equation of a line passing through two given points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) are given by

\(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\)

Proof

We know that the vector equation of a line passing through two points A and B with position vectors \(\overrightarrow{r_1} \text { and } \overrightarrow{r_2}\) is given by

\(\vec{r}=\overrightarrow{r_1}+\lambda\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)\) …(1)

Let A(x₁, y₁, z₁) and B(x₂, y₂, z₂) be the points on the given line with position vectors \(\overrightarrow{r_1} \text { and } \overrightarrow{r_2}\) respectively.

Let P(x, y, z) be an arbitrary point on this line with position vector \(\vec{r}\).

Then, \(\overrightarrow{r_1}=x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}\),

\(\overrightarrow{r_2}=x_2 \hat{i}+y_2 \hat{j}+z_2 \hat{k} \text { and } \vec{r}=x \hat{i}+y \hat{j}+z \hat{k} \text {. }\)

Substituting these values in (1), we get

\(x \hat{i}+y \hat{j}+z \hat{k}=\left(x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}\right)+\lambda\left[\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-z_1\right) \hat{k}\right]\)

⇒ \(\left(x-x_1\right) \hat{i}+\left(y-y_1\right) \hat{j}+\left(z-z_1\right) \hat{k}=\lambda\left[\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1 \hat{j}+\left(z_2-z_1\right) \hat{k}\right]\right.\)

⇒ \(\left(x-x_1\right)=\lambda\left(x_2-x_1\right),\left(y-y_1\right)=\lambda\left(y_2-y_1\right) \text { and }\left(z-z_1\right)=\lambda\left(z_2-z_1\right)\)

⇒ \(\frac{\left(x-x_1\right)}{\left(x_2-x_1\right)}=\frac{\left(y-y_1\right)}{\left(y_2-y_1\right)}=\frac{\left(z-z_1\right)}{\left(z_2-z_1\right)}(=\lambda)\), which are the required equatons.

Summary

1. (1) The vector equation of a line through a point with p.v. \(\overrightarrow{r_1}\) and parallel to \(\vec{m}\) is

\(\vec{r}=\overrightarrow{r_1}+\lambda \vec{m} .\)

(2) The vector equation of a line through two points with p.v.’s \(\overrightarrow{r_1} \text { and } \overrightarrow{r_2}\) is

\(\vec{r}=\overrightarrow{r_1}+\lambda\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right) .\)

2. (1) The Cartesian equations of a line with d.r.’s a, b, c and passing through A(x₁, y₁, z₁) are

\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c} .\)

(2) The Cartesian equations of a line through A(x₁, y₁, z₁) and B(x₂, y₂, z₂) are

\(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\)

WBCHSE Class 12 Maths Solutions For Straight Line In Space Solved Examples

Example 1 A line passes through the point (3, 4, 5) and is parallel to the vector \((2 \hat{i}+2 \hat{j}-3 \hat{k})\). Find the equations of the line in the vector as well as Cartesian form.

Solution

Vector equation of the given line

The given line passes through the point A(3, 4, 5) and is parallel to the vector \(\vec{m}=(2 \hat{i}+2 \hat{j}-3 \hat{k})\).

Also, the p.v. of A is \(\overrightarrow{r_1}=3 \hat{i}+4 \hat{j}+5 \hat{k} .\)

∴ the vector equation of the given line is

\(\vec{r}=\overrightarrow{r_1}+\lambda \vec{m} \Leftrightarrow \vec{r}=(3 \hat{i}+4 \hat{j}+5 \hat{k})+\lambda(2 \hat{i}+2 \hat{j}-3 \hat{k})\) …(1)

Cartesian equations of the given line

Taking \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\), equation (1) becomes

\((x \hat{i}+y \hat{j}+z \hat{k})=(3 \hat{i}+4 \hat{j}+5 \hat{k})+\lambda(2 \hat{i}+2 \hat{j}-3 \hat{k})\)

⇔ \((x \hat{i}+y \hat{j}+z \hat{k})=(3+2 \lambda) \hat{i}+(4+2 \lambda) \hat{j}+(5-3 \lambda) \hat{k}\)

⇔ x = 3 + 2λ, y = 4 + 2λ and z = 5 – 3λ

⇔ \(\frac{x-3}{2}=\frac{y-4}{2}=\frac{z-5}{-3}=\lambda .\)

Hence, \(\frac{x-3}{2}=\frac{y-4}{2}=\frac{z-5}{-3}\) are the required equations of the given line in the Cartesian form.

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

Example 2 A line is drawn in the direction of \((\hat{i}+\hat{j}-2 \hat{k})\) and it passes through a point with position vector \((2 \hat{i}-\hat{j}+4 \hat{k})\). Find the equations of the line in the vector as well as Cartesian form.

Solution

Vector equation of the given line

The given line passes through the point A having position vector \(\overrightarrow{r_1}=2 \hat{i}-\hat{j}+4 \hat{k}\), and is parallel to the vector \(\vec{m}=(\hat{i}+\hat{j}-2 \hat{k})\).

∴ the vector equation of the given line is

\(\vec{r}=\vec{r}_1+\lambda \vec{m}\)

⇔ \(\vec{r}=(2 \vec{i}-\vec{j}+4 \vec{k})+\lambda(\hat{i}+\hat{j}-2 \hat{k})\) …(1)

Cartesian equations of the given line

Taking \(\vec{r}=x \hat{i}+y \vec{j}+z \vec{k}\), equation (1) becomes

\((x \hat{i}+y \hat{j}+z \hat{k})=(2 \hat{i}-\hat{j}+4 \hat{k})+\lambda(\hat{i}+\hat{j}-2 \hat{k})\)

⇔ \((x \hat{i}+y \hat{j}+z \hat{k})=(2+\lambda) \hat{i}+(\lambda-1) \hat{j}+(4-2 \lambda) \hat{k}\)

⇔ x = 2 + λ, y = λ – 1 and z = 4 – 2λ

⇔ \(\frac{x-2}{1}=\frac{y+1}{1}=\frac{z-4}{-2}=\lambda\).

Hence, \(\frac{x-2}{1}=\frac{y+1}{1}=\frac{z-4}{-2}\) are the required equations of the given line in the Cartesian form.

Common Questions on Straight Lines in Space and Their Solutions

Example 3 Find the vector equation of a line passing through a point with the position vector \((2 \hat{i}-\hat{j}+\hat{k})\) and parallel to the line joining the points \((-\hat{i}+4 \hat{j}+\hat{k})\) and \((\hat{i}+2 \hat{j}+2 \hat{k})\). Also, find the Cartesian equivalents of the equation.

Solution

Vector equation of the given line

Let A, B, C be the given points with position vectors

\((2 \hat{i}-\hat{j}+\hat{k}),(-\hat{i}+4 \hat{j}+\hat{k}) \text { and }(\hat{i}+2 \hat{j}+2 \hat{k})\) respectively.

∴ \(\overrightarrow{B C}=(\text { p.v. of } C)-(\text { p.v. of } B)\)

= \((\hat{i}+2 \hat{j}+2 \hat{k})-(-\hat{i}+4 \hat{j}+\hat{k})=(2 \hat{i}-2 \hat{j}+\hat{k})\)

∴ the vector equation of the line passing through the point A with p.v. \((2 \hat{i}-\hat{j}+\hat{k})\), and parallel to \(\overrightarrow{B C}=(2 \hat{i}-2 \hat{j}+\hat{k})\), is

\(\vec{r}=(2 \hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-2 \hat{j}+\hat{k})\) …(1)

Cartesian equations of the given line

Taking \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\), equation (1) becomes

\((x \hat{i}+y \hat{j}+z \hat{k})=(2 \hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-2 \hat{j}+\hat{k})\)

⇔ \((x \hat{i}+y \hat{j}+z \hat{k})=(2+2 \lambda) \hat{i}+(-1-2 \lambda) \hat{j}+(1+\lambda) \hat{k}\)

⇔ x = 2 + 2λ, y = -1 -2λ and z = 1 + λ

⇔ \(\frac{x-2}{2}=\frac{y+1}{-2}=\frac{z-1}{1}=\lambda\)

Hence, \(\frac{x-2}{2}=\frac{y+1}{-2}=\frac{z-1}{1}\) are the required equations of the given line in the Cartesian form.

Example 4 Find the vector equation of the line passing through the point A(2, -1, 1), and parallel to the line joining the points B(-1, 4, 1) and C(1, 2, 2). Also, find the Cartesian equations of the line.

Solution

Vector equation of the given line

The p.v. of B = \((-\hat{i}+4 \hat{j}+\hat{k})\) and p.v. of C = \((\hat{i}+2 \hat{j}+2 \hat{k})\).

∴ \(\overrightarrow{B C}\) (p.v. of C) – (p.v. of B)

= \((\hat{i}+2 \hat{j}+2 \hat{k})-(-\hat{i}+4 \hat{j}+\hat{k})=(2 \hat{i}-2 \hat{j}+\hat{k})\)

The p.v. of A is \(\overrightarrow{r_1}=2 \hat{i}-\hat{j}+\hat{k} \text {. }\)

∴ the vector equation of the given line is

\(\vec{r}=\overrightarrow{r_1}+\lambda(\overrightarrow{B C})\)

⇔ \(\vec{r}=(2 \hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-2 \hat{j}+\hat{k})\) …(1)

Cartesian equations of the given line is

Taking \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\), equation (1) becomes

\((x \hat{i}+y \hat{j}+z \hat{k})=(2 \hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-2 \hat{j}+\hat{k})\)

⇔ \((x \hat{i}+y \hat{j}+z \hat{k})=(2+2 \lambda) \hat{i}+(-1-2 \lambda) \hat{j}+(1+\lambda) \hat{k}\)

⇔ x = 2 + 2λ, y = -1 -2λ, z = 1 + λ

⇔ \(\frac{x-2}{2}=\frac{y+1}{-2}=\frac{z-1}{1}=\lambda\)

Hence, \(\frac{x-2}{2}=\frac{y+1}{-2}=\frac{z-1}{1}\) are the required equations of the given line in the Cartesian form.

Example 5 The Cartesian equations of a line are \(\frac{x-3}{2}=\frac{y+2}{-5}=\frac{z-6}{3}\). Find the vector equation of the line.

Solution

The equations of the given line are

\(\frac{x-3}{2}=\frac{y+2}{-5}=\frac{z-6}{3}\).

This shows that the given line passes through the point A(3, -2, 6) and it is parallel to the vector \(\vec{m}=2 \hat{i}-5 \hat{j}+3 \hat{k}\).

Also, p.v. of A is \(\vec{r}_1=3 \hat{i}-2 \hat{j}+6 \hat{k} .\)

∴ the vector equation of the given line is

\(\vec{r}=\overrightarrow{r_1}+\lambda \vec{m}\)

⇔ \(\vec{r}=(3 \hat{i}-2 \hat{j}+6 \hat{k})+\lambda(2 \hat{i}-5 \hat{j}+3 \hat{k}) .\)

The vector equation of the line ⇔ \(\vec{r}=(3 \hat{i}-2 \hat{j}+6 \hat{k})+\lambda(2 \hat{i}-5 \hat{j}+3 \hat{k}) .\)

Example 6 The Cartesian equations of a line are 6x – 2 = 3y + 1 = 2z – 2.

Find (a) the direction ratios of the line, and (b) the Cartesian and vector equations of the line parallel to this line and passing through the point (2, -1, -1).

Solution

The equations of the given line are

6x – 2 = 3y + 1 = 2z – 2

⇔ \(\frac{\left(x-\frac{1}{3}\right)}{\left(\frac{1}{6}\right)}=\frac{\left(y+\frac{1}{3}\right)}{\left(\frac{1}{3}\right)}=\frac{z-1}{\left(\frac{1}{2}\right)}\)

⇔ \(\frac{\left(x-\frac{1}{3}\right)}{1}=\frac{\left(y+\frac{1}{3}\right)}{2}=\frac{z-1}{3}\).

(a) Clearly, the direction ratios of the given line are 1, 2, 3.

(b) The d.r.’s of a line parallel to the given line are 1, 2, 3.

∴ the Cartesian equations of the line passing through (2, -1, -1) and parallel to the given line are

\(\frac{x-2}{1}=\frac{y+1}{2}=\frac{z+1}{3}\)

Vector equations of the required line

The required line passes throguh the point A(2, -1, -1) and is parallel to the vector \(\vec{m}=\hat{i}+2 \hat{j}+3 \hat{k} .\)

Also, p.v. of A is \(\vec{r}_1=2 \hat{i}-\hat{j}-\hat{k}\)

∴ the vector equation of the required line is

\(\vec{r}=\vec{r}_1+\lambda \vec{m}\),

i.e., \(\vec{r}=(2 \hat{i}-\hat{j}-\hat{k})+\lambda(\hat{i}+2 \hat{j}+3 \hat{k})\).

The vector equation of the required line is \(\vec{r}=(2 \hat{i}-\hat{j}-\hat{k})+\lambda(\hat{i}+2 \hat{j}+3 \hat{k})\).

Applications of Straight Lines in Space

Example 7 Find the vector and Cartesian equations of the line passing through the points A(2, -1, 4) and B(1, 1, -2).

Solution

Vector equation of the given line

Let the position vectors of A and B be \overrightarrow{r_1} \text { and } \overrightarrow{r_2} respectively. Then,

\(\overrightarrow{r_1}=2 \hat{i}-\hat{j}+4 \hat{k} \text { and } \vec{r}_2=\hat{i}+\hat{j}-2 \hat{k}\)

∴ \(\left(\vec{r}_2-\vec{r}_1\right)=(\hat{i}+\hat{j}-2 \hat{k})-(2 \hat{i}-\hat{j}+4 \hat{k})=(-\hat{i}+2 \hat{j}-6 \hat{k}) .\)

∴ the vector equation of the line AB is

\(\vec{r}=\vec{r}_1+\lambda\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)\) for some scalar, λ,

i.e., \(\vec{r}=(2 \vec{i}-\vec{j}+4 \vec{k})+\lambda(-\vec{i}+2 \vec{j}-6 \vec{k})\) …(1)

Cartesian equations of the given line

Taking \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\), equation (1) becomes

\((x \hat{i}+y \hat{j}+z \hat{k})=(2 \hat{i}-\hat{j}+4 \hat{k})+\lambda(-\hat{i}+2 \hat{j}-6 \hat{k})\)

⇔ \((x \hat{i}+y \hat{j}+z \hat{k})=(2-\lambda) \hat{i}+(2 \lambda-1) \hat{j}+(4-6 \lambda) \hat{k}\)

⇔ x = 2 – λ, y 2λ – 1 and z = 4 – 6λ

⇔ \(\frac{x-2}{-1}=\frac{y+1}{2}=\frac{z-4}{-6}=\lambda\)

Hence \(\frac{x-2}{-1}=\frac{y+1}{2}=\frac{z-4}{-6}\) are the Cartesian equations of the given line.

NOTE A first-degree equation in the x, y, z of the form ax + by + cz + d = 0 represents a plane.

Example 8 Find the coordinates of the point where the line through A(3, 4, 1) and B(5, 1, 6) crosses the xy-plane.

Solution

A(3, 4, 1) and B(5, 1, 6)

The equations of the line AB are

\(\frac{x-3}{(5-3)}=\frac{y-4}{(1-4)}=\frac{z-1}{(6-1)} \text {, }\)

i.e., \(\frac{x-3}{2}=\frac{y-4}{-3}=\frac{z-1}{5}\) …(1)

The line (1) crosses the xy-plane at the point where z = 0. So, putting z = 0 in (1), we get

\(x=\left(3-\frac{2}{5}\right)=\frac{13}{5}, y=\left(4+\frac{3}{5}\right)=\frac{23}{5} \text { and } z=0 \text {. }\)

Hence, the line AB crosses the xy-plane at \(\left(\frac{13}{5}, \frac{23}{5}, 0\right) \text {. }\)

Example 9 Find the coordinates of the point where the line \(\frac{x-1}{2}=\frac{y-2}{-3}=\frac{z+5}{4}\) meets the plane 2x + 4y – z = 3.

Solution

The plane 2x + 4y – z = 3

Let \(\frac{x-1}{2}=\frac{y-2}{-3}=\frac{z+5}{4}=\lambda\)

Then, x = (2λ + 1), y = (2 – 3λ), and z = (4λ – 5).

∴ P(2λ + 1, 2 – 3λ, 4λ – 5) is any point on (1).

If this point lies on the plane 2x + 4y – z = 3, we have

2(2λ+1) + 4(2-3λ) – (4λ-5) = 3 ⇒ λ = 1.

Putting λ = 1, we get the required point P(3, -1, -1).

Example 10 Find the equations of the line passing through the point (-1, 3, -2) and perpendicular to each of the lines \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3} \text { and } \frac{x+2}{-3}=\frac{y-1}{2}=\frac{z+1}{5} \text {. }\)

Solution

(-1, 3, -2) and perpendicular to each of the lines \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3} \text { and } \frac{x+2}{-3}=\frac{y-1}

Let the direction ratios of the required line be a, b, c. Then, this line being perpendicular to each of the given lines, we have

a + 2b + 3c = 0 …(1)

-3a + 2b + 5c = 0 …(2)

Cross multiplying (1) and (2), we get

[latex]\frac{a}{(10-6)}=\frac{b}{(-9-5)}=\frac{c}{(2+6)}\)

⇔ \(\frac{a}{4}=\frac{b}{-14}=\frac{c}{8}=k\) (say)

⇔ a = 4k, b = -14k and c = 8k.

Thus the required line has direction ratios 4k, -14k, 8k, and it passes through the point (-1, 3, -2).

Hence, the required equations are

\(\frac{x+1}{4 k}=\frac{y-3}{-14 k}=\frac{z+2}{8 k}\)

⇔ \(\frac{x+1}{2}=\frac{y-3}{-7}=\frac{z+2}{4} \text {. }\)

Example 11 Show that the lines \(\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5} \text { and } \frac{x-8}{7}=\frac{y-4}{1}=\frac{z-5}{3}\) intersect each other. Also, find the point of their intersection.

Solution

The given lines are

\(\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5}=\lambda\) (say) …(1)

and \(\frac{x-8}{7}=\frac{y-4}{1}=\frac{z-5}{3}=\mu\) (say) …(2)

P(4λ + 5, 4λ + 7, -5λ-3) is any point on (1).

Q(7μ + 8, μ + 3, 3μ + 5) is any point on (2).

The given lines will intersect if they have a common point. This happens when P and Q coincide for some particular values of λ and μ.

Thus, the given lines will intersect if

4λ + 5 = 7μ + 8, 4λ + 7 = μ + 3 and -5λ-3 = 3μ + 5

⇔ 4λ – 7 = 3 …(1), 4λ – μ = -3 …(2), 5λ + 3μ = -8 …(3)

Solving (1) and (2), we get λ = -1 and μ = -1.

Also, these values of λ and μ satisfy (3).

Hence, the given lines intersect.

Putting λ = -1 in P, or μ = -1 in Q, we get the point of intersection of the given lines as (, 3, ).

Example 12 Show that the lines \(\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5} \text { and } \frac{x+2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}\) do not intersect.

Solution

The given lines are

\(\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5}=\lambda\) (say) …(1)

\(\frac{x+2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}=\mu\) (say) …(2)

P(3λ + 1, 2λ – 1, 5λ + 1)is any point on (1).

Q(4μ – , 3μ + 1, -2μ – 1) is any point on (2).

If possible, let the given lines intersect.

Then, P and Q coincide for some particular values of λ and μ.

In that case, we have

3λ + 1 = 4μ – 2, 2λ – 1 = 3μ + 1 and 5λ + 1 = -2μ – 1

⇔ 3λ – 4μ = -3 …(1), 2λ – 3μ = 2 …(2), 5λ + 2μ = -2 …(3).

Solving (1) and (2), we get λ = -17 and μ = -12.

However, these values of λ and μ do not satisfy (3).

Hence, the given lines do not intersect.

Example 13 Show that the lines \(\vec{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda(3 \hat{i}-\hat{j}) \text { and } \vec{r}=(4 \hat{i}-\hat{k})+\mu(2 \hat{i}+3 \hat{k})\) intersect each other. Find their point of intersection.

Solution

The given lines are

\(\vec{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda(3 \hat{i}-\hat{j})\) …(1)

\(\vec{r}=(4 \hat{i}-\hat{k})+\mu(2 \hat{i}+3 \hat{k})\) …(2)

These lines will intersect if for some particular values of λ and μ, the values of \(\vec{r}\) given by (1) and (2) are the same,

i.e., \((\hat{i}+\hat{j}-\hat{k})+\lambda(3 \hat{i}-\hat{j})=(4 \hat{i}-\hat{k})+\mu(2 \hat{i}+3 \hat{k})\) …(3)

Equating the coefficients of \(\hat{i}, \hat{j}, \hat{k}\) on both sides of (3), we get

1 + 3λ = 4μ + 2. 1 – λ = 0, and -1 = -1 + 3μ

⇔ 3λ – 2μ = 3 …(1), λ = 1 …(2), μ = 0 …(3).

Clearly, λ = 1 and μ = 0 also satisfy (1).

Putting λ = 1 in (1), we get \(\vec{r}=(4 \hat{i}+0 \hat{j}-\hat{k})\).

Hence, the point of intersection of the given lines is (4, 0, -1).

Example 14 Show that the lines \(\vec{r}=(\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k}) \text { and } \vec{r}=(\hat{i}+\hat{j}+\hat{k})+\mu(\hat{i}-\hat{j}+2 \hat{k})\) do not intersect.

Solution

The given lines are

\(\vec{r}=(\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})\) …(1)

\(\vec{r}=(\hat{i}+\hat{j}+\hat{k})+\mu(\hat{i}-\hat{j}+2 \hat{k})\) …(2)

These lines will intersect if for some particular values of λ and μ, the values of \(\vec{r}\) given by (1) and (2) are the same, i.e.,

\((\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})=(\hat{i}+\hat{j}+\hat{k})+\mu(\hat{i}-\hat{j}+2 \hat{k})\) …(3)

Equating the coefficients of \(\hat{i}, \hat{j}, \hat{k}\) on both sides of (3), we get

1 + λ = 1 + μ, 2 – λ = 1 – μ and 1 + λ = 1 + 2μ

⇒ λ – μ = 0 …(1), λ – μ = 1 …(2), λ – 2μ = 0 …(3).

From (2) and (3), we get λ = 2 and μ = 1.

And, these values of λ and μ do not satisfy (1).

Hence, the given lines do not intersect.

Example 15 Find the point on the line \(\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}\) at a distance 3√2 from the point (1, 2, 3).

Solution

The given line is

\(\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}=r\) (say) …(1)

The general point on this line is

P(3r – 2, 2r – 1, 2r + 3).

Let this point P be at a distance 3√2 from the point Q(1, 2, 3).

Then, PQ = 3√2

⇒ PQ² = (3√2)² = 18

⇒ (3r – 2 – 1)² + (2r – 1 – 2)² + (2r + 3 – 3)² = 18

⇒ (3r – 3)² + (2r – 3)² + (2r)² = 18

⇒ 17r² + 18 – 30 r = 18

⇒ 17r² – 30r = 0 ⇒ r(17r – 30) = 0

⇒ r = 0 or r = \(\frac{30}{17}\).

r = 0 ⇒ required point is P(-2, -1, 3).

r = \(\frac{30}{17}\) ⇒ required point is P(\(\frac{90}{17}\)-2, \(\frac{60}{17}\)-1, \(\frac{60}{17}\)+3), i.e.,

P(\(\frac{56}{17}, \frac{43}{17}, \frac{111}{17}\)).

Example 16 Find the foot of the perpendicular drawn from the point P(1, 6, 3) on the line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\). Also, find its distance from P.

Solution

The given line is

\(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}=r\) (say) …(1)

The general point on this line is (r, 2r + 1, 3r + 2).

Let N be the foot of the perpendicular drawn from the point P(1, 6, 3) to the given line.

Then, this point is N(r, 2r + 1, 3r + 2) for some value of r.

DRs of PN are (r-1), (2r-5), (3r-1).

DRs of given line (1) are 1, 2, 3.

Since PN ⊥ given line (1), we have

1 . (r-1) + 2 . (2r-5) + 3 . (3r-1) = 0

⇔ (r + 4r + 9r) = 14 ⇔ 14r = 14 ⇔ r = 1.

So, the required point is N(1, 3, 5).

PN = \(\sqrt{(1-1)^2+(3-6)^2+(5-3)^2}\)

= \(\sqrt{0^2+(-3)^2+2^2}=\sqrt{13} \text { units. }\)

Hence, the required foot of the perpendicular is N(1, 3, 5) and its distance from P is √13 units.

Example 17 Find the image of the point (1, 6, 3) in the line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3} .\)

Solution

(1, 6, 3) in the line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3} .\)

The given line is

\(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}=\lambda\) …(1)

Let N be the foot of the perpendicular drawn from the point P(1, 6, 3) to the given line.

∴ N has the coordinates (λ, 2λ + 1, 3λ + 2).

The direction ratios of PN are

(λ-1), (2λ + 1 – 6), (3λ + 2 – 3),

i.e., (λ-1), (2λ-5), (3λ-1).

Also, the direction ratios of the given line (1) are 1, 2, 3.

Since PN is perpendicular to the given line (1), we have

1 . (λ-1) + 2(2λ-5) + 3(3λ-1) = 0 ⇒ λ = 1.

Putting λ = 1, we get the point N(1, 3, 5).

Let M(α, β, γ) be the image of P(1, 6, 3) in the given line.

Then, N(1, 3, 5) is the midpoint of PM.

∴ \(\frac{\alpha+1}{2}=1, \frac{\beta+6}{2}=3 \text { and } \frac{\gamma+3}{2}=5\)

⇔ α = 1, β = 0 and γ = 7.

Hence, the image of P(1, 6, 3) is M(1, 0, 7).

Collinearity of Three Given Points

Theorem 1 The condition for three given points A(x₁, y₁, z₁), B(x₂, y₂, z₂) and C(x₃, y₃, z₃) to be collinear is that \(\frac{x_3-x_1}{x_2-x_1}=\frac{y_3-y_1}{y_2-y_1}=\frac{z_3-z_1}{z_2-z_1} .\)

Proof

A(x₁, y₁, z₁), B(x₂, y₂, z₂) and C(x₃, y₃, z₃)

The equations of the line AB are

\(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\) …(1)

Clearly, A< B, C will be collinear only when C lies on the line Ab. This happens when C(x₃, y₃, z₃) lies on (1).

∴ \(\frac{x_3-x_1}{x_2-x_1}=\frac{y_3-y_1}{y_2-y_1}=\frac{z_3-z_1}{z_2-z_1} .\)

Collinearity of Three Points Whose p.v.’s are Given

Theorem 2 Three points A, B, C with position vectors \(\vec{a}, \vec{b}, \vec{c}\) respectively are collinear if and only if there exist scalars μ₁, μ₂, μ₃, not all zero, such that \(\mu_1 \vec{a}+\mu_2 \vec{b}+\mu_3 \vec{c}=\overrightarrow{0} \text { and } \mu_1+\mu_2+\mu_3=0 \text {. }\)

Proof

Let A, B, C be three collinear points with position vectors \(\vec{a}, \vec{b}, \vec{c}\) respectively.

Then, the vector equation of the line AB is

\(\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})\)

⇒ \(\vec{c}=\vec{a}+\lambda(\vec{b}-\vec{a})\) [∵ A, B, C being collinear, C lies on AB]

⇒ \((1-\lambda) \vec{a}+\lambda \vec{b}-\vec{c}=\overrightarrow{0}\)

⇒ \(\mu_1 \vec{a}+\mu_2 \vec{b}+\mu_3 \vec{c}=\overrightarrow{0}\), where μ₁ + μ₂ + μ₃ = (1 – λ) + λ – 1 = 0 and μ₃ = -1 ≠ 0.

Conversely, let A, B, C be given points with position vectors \(\vec{a}, \vec{b}, \vec{c}\) respectively and μ₁, μ₂, μ₃ be scalars, not all zero, say μ₃ ≠ 0, such that

\(\mu_1 \vec{a}+\mu_2 \vec{b}+\mu_3 \vec{c}=\overrightarrow{0} \text { and } \mu_1+\mu_2+\mu_3=0\)

⇒ \(\left(\frac{\mu_1}{\mu_3}\right) \vec{a}+\left(\frac{\mu_2}{\mu_3}\right) \vec{b}+\vec{c}=\overrightarrow{0} \text { and }\left(\frac{\mu_1}{\mu_3}\right)+\left(\frac{\mu_2}{\mu_3}\right)+1=0\)

⇒ \(\left(\frac{\mu_1}{\mu_3}\right) \vec{a}-\lambda \vec{b}+\vec{c}=\overrightarrow{0} \text { and }\left(\frac{\mu_1}{\mu_3}\right)-\lambda+1=0 \text {, where }\left(\frac{\mu_2}{\mu_3}\right)=-\lambda\)

⇒ \((\lambda-1) \vec{a}-\lambda \vec{b}+\vec{c}=\overrightarrow{0} [∵ \frac{\mu_1}{\mu_3}=(\lambda-1)]\)

⇒ \(\vec{c}=(1-\lambda) \vec{a}+\lambda \vec{b}\)

⇒ the point C lies on the line AB

⇒ the points A, B, C are collinear.

Solved Examples

Example 1 Prove that the points A(2, 1, 3), B(5, 0, 5) and C(-4, 3, -1) are collinear.

Solution

A(2, 1, 3), B(5, 0, 5) and C(-4, 3, -1)

The equations of the line AB are

\(\frac{x-2}{5-2}=\frac{y-1}{0-1}=\frac{z-3}{5-3}\)

⇔ \(\frac{x-2}{3}=\frac{y-1}{-1}=\frac{z-3}{2}\) …(1)

The given points A, B, C are collinear

⇔ C lies on the line AB

⇔ C(-4, 3, -1) satisfies (1)

⇔ \(\frac{-4-2}{3}=\frac{3-1}{-1}=\frac{-1-3}{2}\)

⇔ -2 = -2 = -2, which is true.

Hence, the given points A, B, C are collinear.

Example 2 Find the value of λ for which the points A(-1, 3, 2), B(-4, 2, -2) and C(5, 5, λ) are collinear.

Solution

A(-1, 3, 2), B(-4, 2, -2) and C(5, 5, λ)

The equations of the line AB are

\(\frac{x+1}{-4+1}=\frac{y-3}{2-3}=\frac{z-2}{-2-2}\)

⇔ \(\frac{x+1}{-3}=\frac{y-3}{-1}=\frac{z-2}{-4}\)

⇔ \(\frac{x+1}{3}=\frac{y-3}{1}=\frac{z-2}{4}\) …(1)

Since A, B, C are collinear, the points C(5, 5, λ) lies on (1).

∴ \(\frac{5+1}{3}=\frac{5-3}{1}=\frac{\lambda-2}{4} \Leftrightarrow \frac{\lambda-2}{4}=2 \Leftrightarrow \lambda=10 .\)

Hence, the value of λ is 10.

Example 3 Show that the points whose position vectors are \((-2 \hat{i}+3 \hat{j}+5 \hat{k}), (\hat{i}+2 \hat{j}+3 \hat{k}) \text { and }(7 \hat{i}-\hat{k})\) are collinear.

Solution

\((-2 \hat{i}+3 \hat{j}+5 \hat{k}), (\hat{i}+2 \hat{j}+3 \hat{k}) \text { and }(7 \hat{i}-\hat{k})\)

Let A, B, C be the given points, and let their position vectors be denoted by \(\vec{a}, \vec{b}, \vec{c}\) respectively. Then,

\(\vec{a}=(-2 \hat{i}+3 \hat{j}+5 \hat{k}), \vec{b}=(\hat{i}+2 \hat{j}+3 \hat{k}) \text { and } \vec{c}=(7 \hat{i}-\hat{k})\)

∴ the vector equation of the line AB is

\(\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})\), where λ is a scalar

⇔ \(\vec{r}=(-2 \hat{i}+3 \hat{j}+5 \hat{k})+\lambda[(\hat{i}+2 \hat{j}+3 \hat{k})-(-2 \hat{i}+3 \hat{j}+5 \hat{k})]\)

⇔ \(\vec{r}=(-2 \hat{i}+3 \hat{j}+5 \hat{k})+\lambda(3 \hat{i}-\hat{j}-2 \hat{k})\) …(1)

If this line passes through the point C, we have

\(\vec{c}=(-2 \hat{i}+3 \hat{j}+5 \hat{k})+\lambda(3 \hat{i}-\hat{j}-2 \hat{k}) .\)

⇔ \((7 \hat{i}-\hat{k})=(-2 \hat{i}+3 \hat{j}+5 \hat{k})+\lambda(3 \hat{i}-\hat{j}-2 \hat{k})\)

⇔ \((9 \hat{i}-3 \hat{j}-6 \hat{k})=\lambda(3 \hat{i}-\hat{j}-2 \hat{k})\)

⇔ \(3(3 \hat{i}-\hat{j}-2 \hat{k})=\lambda(3 \hat{i}-\hat{j}-2 \hat{k})\)

⇔ λ = 3, which is a scalar.

Thus, the point C lies on the line AB.

Hence, the given points A, B, C are collinear.

Example 4 Using the vector method, find the values of λ and μ for which the points A(3, λ, μ), B(2, 0, -3) and C(1, -2, -5) are collinear.

Solution

A(3, λ, μ), B(2, 0, -3) and C(1, -2, -5)

Let \(\vec{a}, \vec{b}, \vec{c}\) be the position vectors of the given points A, B, C respectively. Then,

\(\vec{a}=3 \hat{i}+\lambda \hat{j}+\mu \hat{k}, \vec{b}=2 \hat{i}-3 \hat{k} \text { and } \vec{c}=\hat{i}-2 \hat{j}-5 \hat{k}\)

∴ the vector equation of the line Bc is

\(\vec{r}=\vec{b}+t(\vec{c}-\vec{b})\), for some scalar t

⇔ \(\vec{r}=(2 \hat{i}-3 \hat{k})+t[(\hat{i}-2 \hat{j}-5 \hat{k})-(2 \hat{i}-3 \hat{k})]\)

⇔ \(\vec{r}=(2 \hat{i}-3 \hat{k})+t(-\hat{i}-2 \hat{j}-2 \hat{k})\)

⇔ \(\vec{r}=(2-t) \hat{i}-(2 t) \hat{j}-(3+2 t) \hat{k}\) …(1)

If this line BC passes through the point A, we have

\(\vec{a}=(2-t) \hat{i}-(2 t) \hat{j}-(3+2 t) \hat{k}\), for some scalar t

⇔ \((3 \hat{i}+\lambda \hat{j}+\mu \hat{k})=(2-t) \hat{i}-(2 t) \hat{j}-(3+2 t) \hat{k}\)

⇔ 2 – t = 3, -2t = λ and -(3 + 2t) = μ

⇔ t = -1, λ = (-2) x (-1) = 2, and μ = -[3 + 2 x(-1)] = -1.

Hence, λ = 2 and μ = -1.

Angle between Two Lines

Vector Form

Let the vector equations of two given lines be \(\vec{r}=\overrightarrow{r_1}+\lambda \overrightarrow{m_1} \text { and } \vec{r}=\overrightarrow{r_2}+\mu \overrightarrow{m_2}\), where λ and μ are scalars.

Let θ be the angle between these lines.

Since the given lines are parallel to \(vec{m}_1 \text { and } \vec{m}_2\) and respectively, the angle between the given lines must be equal to the angle between \(\vec{m}_1 \text { and } \vec{m}_2\).

∴ \(\cos \theta=\frac{\vec{m}_1 \cdot \vec{m}_2}{\left|\vec{m}_1\right| \cdot\left|\vec{m}_2\right|}\)

Cartesian Form

Let the Cartesian equations of two given lines be

\(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \text { and } \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2} \text {. }\)

Then, the direction ratios of these lines are a₁, b₁, c₁ and a₂, b₂, c₂ respectively.

Let θ be the angle between these lines. Then,

\(\cos \theta=\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\left(\sqrt{a_1^2+b_1^2+c_1^2}\right)\left(\sqrt{a_2^2+b_2^2+c_2^2}\right)} .\)

Solved Examples

Example 1 Find the angle between the lines \(\vec{r}=(3 \hat{i}+2 \hat{j}-4 \hat{k})+\lambda(\hat{i}+2 \hat{j}+2 \hat{k}), and \vec{r}=(5 \hat{j}-2 \hat{k})+\mu(3 \hat{i}+2 \hat{j}+6 \hat{k}) .\)

Solution

Let θ be the angle between the given lines. The given lines are parallel to the vectors \((\hat{i}+2 \hat{j}+2 \hat{k}) \text { and }(3 \hat{i}+2 \hat{j}+6 \hat{k})\) respectively.

So, θ is the angle between these vectors.

∴ \(\cos \theta=\frac{(\hat{i}+2 \hat{j}+2 \hat{k}) \cdot(3 \hat{i}+2 \hat{j}+6 \hat{k})}{|\hat{i}+2 \hat{j}+2 \hat{k}||3 \hat{i}+2 \hat{j}+6 \hat{k}|}\)

= \(\frac{(3+4+12)}{\left(\sqrt{1^2+2^2+2^2}\right)\left(\sqrt{3^2+2^2+6^2}\right)}=\frac{19}{21}\)

⇒ \(\theta=\cos ^{-1}\left(\frac{19}{21}\right)\)

Hence, the angle between the given lines is \(\cos ^{-1}\left(\frac{19}{21}\right)\).

Example 2 Find the angle between the lines \(\frac{x+4}{3}=\frac{y-1}{5}=\frac{z+3}{4} \text { and } \frac{x+1}{1}=\frac{y-4}{1}=\frac{z-5}{2} \text {. }\)

Solution

The direction ratios of the given lines are 3, 5, 4 and 1, 1, 2.

Let θ be the angle betweeen the given lines. Then,

\(\cos \theta=\frac{(3 \times 1+5 \times 1+4 \times 2)}{\left(\sqrt{3^2+5^2+4^2}\right)\left(\sqrt{1^2+1^2+2^2}\right)}=\frac{8}{5 \sqrt{3}}=\frac{8 \sqrt{3}}{15}\)

⇒ \(\theta=\cos ^{-1}\left(\frac{8 \sqrt{3}}{15}\right)\)

Hence, the angle between the given lines is \(\cos ^{-1}\left(\frac{8 \sqrt{3}}{15}\right)\)

Example 3 Find the angle between the lines \(\frac{x+1}{1}=\frac{2 y-3}{3}=\frac{z-6}{2} \text { and } \frac{x-4}{3}=\frac{y+3}{-2}, z=5 \text {. }\)

Solution

The given equations may be written as

\(\frac{x-4}{3}=\frac{y+3}{-2}=\frac{z-5}{0}\) …(1)

\(frac{x+1}{1}=\frac{y-(3 / 2)}{(3 / 2)}=\frac{z-6}{2}\) …(2)

Let \(\vec{m}_1 \text { and } \vec{m}_2\) be the vectors parallel to (1) and (2) respectively.

Then, \(\vec{m}_1=3 \hat{i}-2 \hat{j}+0 \hat{k} \text { and } \vec{m}_2=\hat{i}+\frac{3}{2} \hat{j}+2 \hat{k} \text {. }\)

Let θ be the angle between \(\vec{m}_1 \text { and } \vec{m}_2\), and so the angle between the given lines is also θ. Then,

\(\cos \theta=\frac{\vec{m}_1 \cdot \vec{m}_2}{\left|\overrightarrow{m_1}\right|\left|\vec{m}_2\right|}=\frac{(3 \times 1-2 \times 3 / 2+0 \times 2)}{\left(\sqrt{3^2+(-2)^2+0^2}\right)\left(\sqrt{1^2+(3 / 2)^2+2^2}\right)}=0\)

⇒ \(\theta=\frac{\pi}{2}\)

Hence, the angle between the given lines is \(\left(\frac{\pi}{2}\right)\).

Examples of Finding Distance Between Two Lines in Space

Example 4 Find the angle between the lines \(\frac{5-x}{3}=\frac{y+3}{-4}, z=7 \text { and } \frac{x}{1}=\frac{1-y}{2}=\frac{z-6}{2} \text {. }\)

Solution

The given lines are

\(\frac{x-5}{-3}=\frac{y+3}{-4}=\frac{z-7}{0}\) …(1)

\(\frac{x}{1}=\frac{y-1}{-2}=\frac{z-6}{2}\) …(2)

Let \(\vec{m}_1 \text { and } \vec{m}_2\) be the vectors parallel to (1) and (2) respectively.

Then, \(\vec{m}_1=-3 \hat{i}-4 \hat{j}+0 \hat{k} \text { and } \vec{m}_2=\hat{i}-2 \hat{j}+2 \hat{k}\)

Let θ be the angle between \(\vec{m}_1 \text { and } \vec{m}_2\). Then,

\(\cos \theta=\frac{\vec{m}_1 \cdot \vec{m}_2}{\left|\vec{m}_1\right|\left|\vec{m}_2\right|}\)

= \(\frac{\{(-3) \times 1+(-4) \times(-2)+0 \times 2\}}{\left\{\sqrt{(-3)^2+(-4)^2+0^2}\right\}\left\{\sqrt{1^2+(-2)^2+2^2}\right\}}=\frac{1}{3}\)

⇒ \(\theta=\cos ^{-1}\left(\frac{1}{3}\right)\)

Hence, the angle between the given lines is \(\cos ^{-1}\left(\frac{1}{3}\right)\).

Example 5 Find the angle between two lines, one of which has direction ratios 2, 2, 1, and the other is obtained by joining the points (3, 1, 4) and (7, 2, 12).

Solution

Let L₁ and L₂ be the given lines. Then, the direction ratios of L₁ are 2, 2, 1.

And, the direction ratios of L₂ are (7 – 3), (2 – 1), (12 – 4), i.e., 4, 1, 8.

Let θ be the angle between the given lines. Then,

\(\cos \theta=\frac{(2 \times 4+2 \times 1+1 \times 8)}{\left(\sqrt{2^2+2^2+1^2}\right)\left(\sqrt{4^2+1^2+8^2}\right)}=\frac{18}{27}=\frac{2}{3}\)

⇒ \(\theta=\cos ^{-1}\left(\frac{2}{3}\right)\)

Hence, the angle between the given lines is \(\cos ^{-1}\left(\frac{2}{3}\right)\).

Example 6 Prove that the lines x = ay + b, z = cy + d, and x = a’y + b’, z = c’y + d’ are perpendicular if aa’ + cc’ + 1 = 0.

Solution

The equations of the first line are

x = ay + b, z = cy + d

⇔ \(\frac{x-b}{a}=y, \frac{z-d}{c}=y\)

⇔ \(\frac{x-b}{a}=\frac{y}{1}=\frac{z-d}{c}\) …(1)

Similarly, the equations of the second line are

\(\frac{x-b^{\prime}}{a^{\prime}}=\frac{y}{1}=\frac{z-d^{\prime}}{c^{\prime}}\) …(2)

The given lines are perpendicular to each other

⇔ aa’ + 1 x + cc’ = 0

⇔ aa’ + cc’ + 1 = 0.

Example 7 Find the value of k so that the lines \(\frac{1-x}{3}=\frac{7 y-14}{2 k}=\frac{z-3}{2} \text { and } \frac{7-7 x}{3 k}=\frac{5-y}{1}=\frac{6-z}{5}\) are at right angles.

Solution

The given equations in the standard form are

\(\frac{x-1}{-3}=\frac{y-2}{(2 k / 7)}=\frac{z-3}{2}\) …(1)

\(\frac{x-1}{(-3 k / 7)}=\frac{y-5}{-1}=\frac{z-6}{-5}\) …(2)

The direction ratios of the given lines are

\(\left(a_1=-3, b_1=\frac{2 k}{7}, c_1=2\right) \text { and }\left(a_2=\frac{-3 k}{7}, b_2=-1, c_2=-5\right)\)

The given lines are at right angles

⇔ a₁a₂ + b₁b₂ + c₁c₂ = 0

⇔ \(-3 \times\left(\frac{-3 k}{7}\right)+\left(\frac{2 k}{7}\right) \times(-1)+2 \times(-5)=0\)

⇔ \(\frac{9 k}{7}-\frac{2 k}{7}=10 \Leftrightarrow 7 k=70 \Leftrightarrow k=10 .\)

Hence, k = 10.

Miscellaneous Solved Examples

Example 1 The direction ratios of a vector are 2, -3, 4. Find its direction cosines.

Solution

2, -3, 4

Clearly, the direction cosines of the given vector are

\(\frac{2}{\sqrt{2^2+(-3)^2+4^2}}, \frac{-3}{\sqrt{2^2+(-3)^2+4^2}}, \frac{4}{\sqrt{2^2+(-3)^2+4^2}}\),

i.e., \(\frac{2}{\sqrt{29}}, \frac{-3}{\sqrt{29}}, \frac{4}{\sqrt{29}} .\)

Example 2 Find the direction cosines of the vector \(\vec{r}=6 \hat{i}+2 \hat{j}-3 \hat{k}\).

Solution

The direction ratios of \vec{r} are 6, 2, -3.

∴ the direction cosines of \(\vec{r}\) are

\(\frac{6}{\sqrt{6^2+2^2+(-3)^2}}, \frac{2}{\sqrt{6^2+2^2+(-3)^2}}, \frac{-3}{\sqrt{6^2+2^2+(-3)^2}}\)

i.e., \(\frac{6}{7}, \frac{2}{7}, \frac{-3}{7} \text {. }\)

Example 3 If a line makes angles α, β, γ with the x-axis, y-axis and z-axis respectively, prove that sin²α + sin²β + sin²γ = 2.

Solution

The direction cosines of the line are cos α, cos β, cos γ.

∴ cos²α + cos²β + cos²γ = 1

⇒ (1 – sin²α) + (1 – sin²β) + (1 – sin²γ) = 1

⇒ sin²α + sin²β + sin²γ = 2.

Example 4 Find the angle between the vectors having direction cosines \(\frac{1}{2},-\frac{1}{3}, \frac{1}{4}, \text { and } \frac{1}{3}, 1, \frac{2}{3} \text {. }\)

Solution

Let θ be the angle between the given vectors. Then,

\(\cos \theta=\frac{\left\{\frac{1}{2} \times \frac{1}{3}+\left(-\frac{1}{3}\right) \times 1+\frac{1}{4} \times \frac{2}{3}\right\}}{\sqrt{\left(\frac{1}{2}\right)^2+\left(\frac{-1}{3}\right)^2+\left(\frac{1}{4}\right)^2} \cdot \sqrt{\left(\frac{1}{3}\right)^2+(1)^2+\left(\frac{2}{3}\right)^2}}=0\)

⇒ θ = 90°.

Example 5 Find the angle between the vectors having direction ratios 3, 4, 5, and 4, -3, 5.

Solution

3, 4, 5, and 4, -3, 5

Let θ be the angle between the given vectors.

Let a₁ = 3, b₁ = 4, c₁ = 5, and a₂ = 4, b₂ = -3, c₂ = 5.

\(\cos \theta=\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\left(\sqrt{a_1^2+b_1^2+c_1^2}\right)\left(\sqrt{a_2^2+b_2^2+c_2^2}\right)}\)

= \(\frac{3 \times 4+4 \times(-3)+5 \times 5}{\left(\sqrt{3^2+4^2+5^2}\right)\left(\sqrt{4^2+(-3)^2+5^2}\right)}=\frac{25}{50}=\frac{1}{2}\)

∴ θ = 60°.

Thus, the angle between the given vectors is 60°.

Example 6 Find the angles of △ABC whose vertices are A(-1, 3, 2), B(2, 3, 5) and C(3, 5, -2).

Solution

A(-1, 3, 2), B(2, 3, 5) and C(3, 5, -2)

The d.r.’s of AB are (2+1), (3-3), (5-2), i.e., 3, 0, 3.

And, the d.r.’s of AC are (3+1), (5-3), (-2-2), i.e., 4, 2, -4.

∴ \(\cos A=\frac{[3 \times 4+0 \times 2+3 \times(-4)]}{\left(\sqrt{3^2+0^2+3^2}\right)\left(\sqrt{4^2+2^2+(-4)^2}\right)}=0 \Rightarrow \angle A=90^{\circ} \text {. }\)

The d.r.’s of BA are (-1-2), (3-3), (2-5), i.e., -3, 0, -3.

And, the d.r.’s of BC are (3-2), (5-3), (-2-5), i.e., 1, 2, -7.

∴ \(\cos B=\frac{(-3) \times 1+0 \times 2+(-3) \times(-7)}{\left(\sqrt{(-3)^2+0^2+(-3)^2}\right)\left(\sqrt{1^2+2^2+(-7)^2}\right)}=\frac{1}{\sqrt{3}}\)

⇒ \(\angle B=\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right).\)

The d.r.’s of CB are (2-3),(3-5), (5+2) i.e., -1, -2, 7.

And, the d.r.’s of CA are (-1-3), (3-5), (2+2), i.e., -4, -2, 4.

∴ \(\cos C=\frac{(-1) \times(-4)+(-2) \times(-2)+7 \times 4}{\left\{\sqrt{(-1)^2+(-2)^2+7^2}\right\}\left\{\sqrt{(-4)^2+(-2)^2+4^2}\right\}}=\sqrt{\frac{2}{3}} .\)

⇒ \(C=\cos ^{-1}\left(\sqrt{\frac{2}{3}}\right) .\)

Thus, ∠A = 90°, ∠B = \(\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right) \text { and } \angle C=\cos ^{-1}\left(\sqrt{\frac{2}{3}}\right) \text {. }\)

Example 7 Find the direction cosines of the line which is perpendicular to thr lines whose direction ratios are 1, -1, 2 and 2, 1, -1.

Solution

1, -1, 2 and 2, 1, -1

Let l, m, n be the direction cosines of the required line.

Then, l x 1 + m x (-1) + n x 2 = 0,

l x 2 + m x 1 + n x (-1) = 0

⇒ \(\left\{\begin{array}{c}
l-m+2 n=0 \\
2 l+m-n=0
\end{array}\right.\)

Cross multiplying those lines, we get

\(\frac{l}{-1}=\frac{m}{5}=\frac{n}{3}=\frac{\sqrt{l^2+m^2+n^2}}{\sqrt{(-1)^2+5^2+3^2}}=\frac{1}{\sqrt{35}}\)

∴ \(l=\frac{-1}{\sqrt{35}}, m=\frac{5}{\sqrt{35}}, n=\frac{3}{\sqrt{35}} .\)

Example 8 Find the direction cosines of the lines which are connected by the relations l – 5m + 3n = 0 and 7l² + 5m2 – 3n² = 0.

Solution

The given equations are

l – 5m + 3n = 0 …(1)

7l² + 5m² – 3n² = 0 …(2)

Putting l = (5m – 3n) from (1) in (2), we get

7(5m – 3n)² + 5m² – 3n² = 0

⇒ 6m² – 7mn + 2n² = 0

⇒ \(6\left(\frac{m}{n}\right)^2-7\left(\frac{m}{n}\right)+2=0 \Rightarrow 6 p^2-7 p+2=0, \text { where } \frac{m}{n}=p\)

⇒ (3p – 2)(2p – 1) = 0

⇒ \(p=\frac{2}{3} \text { or } p=\frac{1}{2} \Rightarrow \frac{m}{n}=\frac{2}{3} \text { or } \frac{m}{n}=\frac{1}{2} \text {. }\)

Now, \(\frac{m}{n}=\frac{2}{3} \Rightarrow \frac{m}{2}=\frac{n}{3}=\frac{5 m-3 n}{5 \times 2-3 \times 3}=\frac{l}{1}\)

⇒ \(\frac{l}{1}=\frac{m}{2}=\frac{n}{3}=\frac{\sqrt{l^2+m^2+n^2}}{\sqrt{1^2+2^2+3^2}}=\frac{1}{\sqrt{14}}\)

⇒ \(l=\frac{1}{\sqrt{14}}, m=\frac{2}{\sqrt{14}}, n=\frac{3}{\sqrt{14}} .\)

Again, \(\frac{m}{n}=\frac{1}{2} \Rightarrow \frac{m}{1}=\frac{n}{2}=\frac{5 m-3 n}{5 \times 1-3 \times 2}=\frac{l}{-1}\)

⇒ \(\frac{l}{-1}=\frac{m}{1}=\frac{n}{2}=\frac{\sqrt{l^2+m^2+n^2}}{\sqrt{(-1)^2+1^2+2^2}}=\frac{1}{\sqrt{6}}\)

⇒ \(l=\frac{-1}{\sqrt{6}}, m=\frac{1}{\sqrt{6}}, n=\frac{2}{\sqrt{6}} .\)

Hence, the direction cosines of the lines are

\(\left(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}\right) \text { and }\left(\frac{-1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, \frac{2}{\sqrt{6}}\right) \text {. }\)

Example 9 Prove that the straight lines whose direction cosines are given by the relations al + bm + cn = 0 and fmn + gnl + hlm = 0 are perpendicular to each other if \(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}=0\), and parallel if a²f² + b²g² + c²h² – 2bcgh – 2cahf – 2abfg = 0.

Solution

The given equations are

al + bm + cn = 0 …(1)

fmn + gnl + hlm = 0 …(2)

Putting \(n=\frac{-(a l+b m)}{c}\) from (1) in (2), we get

\(f m \cdot\left\{\frac{-(a l+b m)}{c}\right\}+g l \cdot\left\{\frac{-(a l+b m)}{c}\right\}+h l m=0\)

⇒ agl² + (af + bg – ch)lm + bfm² = 0

⇒ \(a g\left(\frac{l}{m}\right)^2+(a f+b g-c h) \cdot\left(\frac{l}{m}\right)+b f=0\) …(3)

Now, equation (3), being a quadratic equation in \(\left(\frac{l}{m}\right)\), will have two roots, say \(\left(\frac{l_1}{m_1}\right) \text { and }\left(\frac{l_2}{m_2}\right)\).

∴ \(\frac{l_1}{m_1} \times \frac{l_2}{m_2}=\frac{b f}{a g} \Rightarrow \frac{l_1 l_2}{b f}=\frac{m_1 m_2}{a g}\)

⇒ \(\frac{l_1 l_2}{\left(\frac{f}{a}\right)}=\frac{m_1 m_2}{\left(\frac{g}{b}\right)}=\frac{n_1 n_2}{\left(\frac{h}{c}\right)}=k\) [by symmetry].

∴ \(l_1 l_2+m_1 m_2+n_1 n_2=k\left(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}\right)\)

Thus, the given lines will be perpendicular to each other

⇔ l₁l₂ + m₁m₂ + n₁n₂ = 0

⇔ \(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}=0 .\)

The lines will be parallel only when the roots of (3) are equal.

∴ (af + bg – ch)² – 4abgf = 0

⇔ a²f² + b²g² + c²h² – 2bcgh – 2cahf – 2abfg = 0.

Example 10 Show that the straight lines whose direction cosines are given by the equations al + bm + cn = 0 and ul² + vm² + wn² = 0 are mutually perpendicular if a²(v + w) + b²(u+w) + c²(u+v) = 0, and parallel if \(\frac{a^2}{u}+\frac{b^2}{v}+\frac{c^2}{w}=0 .\)

Solution

The given equations are

al + bm + cn = 0 …(1)

ul² + vm² + wn² = 0 …(2)

Putting \(l=\frac{-(b m+c n)}{a}\) from (1) in (2), we get

\(\frac{u(b m+c n)^2}{a^2}+v m^2+w n^2=0\)

⇒ (b²u + a²v)m² + 2ubcmn + (c²u + a²w)n² = 0

⇒ \(\left(b^2 u+a^2 v\right)\left(\frac{m}{n}\right)^2+2 u b c\left(\frac{m}{n}\right)+\left(c^2 u+a^2 w\right)=0\) …(3)

Let \(\frac{m_1}{n_1} \text { and } \frac{m_2}{n_2}\) be the roots of (3).

Then, \(\frac{m_1}{n_1}, \frac{m_2}{n_2}=\frac{c^2 u+a^2 w}{b^2 u+a^2 v}\)

⇒ \(\frac{m_1 m_2}{c^2 u+a^2 w}=\frac{n_1 n_2}{b^2 u+a^2 v}=\frac{l_1 l_2}{b^2 w+c^2 v}=k\) [by symmetry]

∴ l₁l₂ + m₁m₂ + n₁n₂ = k(b²w + c²v + c²u + a²w + b²u + a²v)

The given lines are mutually perpendicular

⇔ l₁l₂ + m₁m₂ + n₁n₂ = 0

⇔ a²(v+w) + b²(w+u) + c²(u+v)= 0.

For the given lines to be parallel, the direction cosines must be equal.

∴ the roots of (3) must be equal.

∴ \(4 u^2 b^2 c^2-4\left(b^2 u+a^2 v\right)\left(c^2 u+a^2 w\right)=0 \Leftrightarrow \frac{a^2}{u}+\frac{b^2}{v}+\frac{c^2}{w}=0 .\)

Example 11 If the edges of a rectangular parallelepiped are a, b, c, prove that the angles between the four diagonals are given by \(\cos ^{-1}\left(\frac{ \pm a^2 \pm b^2 \pm c^2}{a^2+b^2+c^2}\right)\).

Solution

Let OA, OB, OC be the coterminous edges of the parallelepiped, taken along the axes in such a way that OA = a, OB = b and OC = c.

Then, the coordinates of the vertices are O(0,0,0), A(a,0,0), B(0,b,0), C(0,0,c), P(a,b,c), L(0,b,c), M(a,0,c) and N(a,b,0).

The direction ratios of the diagonals OP, AL, BM and CN are (a,b,c), (-a,b,c), (a,-b,c) and (a,b,-c) respectively.

∴ the direction cosines of OP, AL, BM and CN are

\(\left(\frac{a}{\sqrt{a^2+b^2+c^2}}, \frac{b}{\sqrt{a^2+b^2+c^2}}, \frac{c}{\sqrt{a^2+b^2+c^2}}\right)\),

\(\left(\frac{-a}{\sqrt{a^2+b^2+c^2}}, \frac{b}{\sqrt{a^2+b^2+c^2}}, \frac{c}{\sqrt{a^2+b^2+c^2}}\right)\),

\(\left(\frac{a}{\sqrt{a^2+b^2+c^2}}, \frac{-b}{\sqrt{a^2+b^2+c^2}}, \frac{c}{\sqrt{a^2+b^2+c^2}}\right)\),

\(\left(\frac{a}{\sqrt{a^2+b^2+c^2}}, \frac{b}{\sqrt{a^2+b^2+c^2}}, \frac{-c}{\sqrt{a^2+b^2+c^2}}\right)\).

Let θ₁ be the angle between OP and AL. Then,

\(\cos \theta_1=\frac{\left(-a^2+b^2+c^2\right)}{\left(a^2+b^2+c^2\right)} \quad \text { or } \theta_1=\cos ^{-1}\left(\frac{-a^2+b^2+c^2}{a^2+b^2+c^2}\right)\)

Again, let θ₂ be the angle between OP and BM. Then,

\(\cos \theta_2=\frac{\left(a^2-b^2+c^2\right)}{\left(a^2+b^2+c^2\right)} \quad \text { or } \theta_2=\cos ^{-1}\left(\frac{a^2-b^2+c^2}{a^2+b^2+c^2}\right) \text {. }\)

Similarly, the angles between the other pairs of diagonals can be obtained.

Clearly, the angles between the four diagonals can be given by

\(\cos ^{-1}\left(\frac{ \pm a^2 \pm b^2 \pm c^2}{a^2+b^2+c^2}\right) \text {. }\)

Example 12 Show that the angle between any two diagonals of a cube is \(\cos ^{-1}\left(\frac{1}{3}\right)\).

Solution

Let OA, OB, OC be the coterminous edges of a cube, taken along the axes in such a way that OA = OB = OC = a.

Then, the coordinates of the vertices of the cube are

O(0,0,0), A(a,0,0), B(0,a,0), C(0,0,a), P(a,a,a), L(0,a,a), M(a,0,a) and N(a,a,0).

The direction ratios of the diagonals OP, AL, BM and CN are (a,a,a), (-a,a,a), (a,-a,a) and (a,a,-a) respectively.

Thus, direction cosines of OP, AL, BM and CN are

\(\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right),\left(\frac{-1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right),\left(\frac{1}{\sqrt{3}}, \frac{-1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right), and \left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{-1}{\sqrt{3}}\right)\) respectively.

If θ₁ be the angle between OP and AL then

\(\cos \theta_1=\left\{\frac{1}{\sqrt{3}} \cdot\left(\frac{-1}{\sqrt{3}}\right)+\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}}+\frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}}\right\}=\frac{1}{3}\)

⇒ \(\theta_1=\cos ^{-1}\left(\frac{1}{3}\right)\)

Similarly, the angle between each one of the other pairs is \(\cos ^{-1}\left(\frac{1}{3}\right)\).

Hence, the angle between any two diagonals of the cube is \(\cos ^{-1}\left(\frac{1}{3}\right)\).

Example 13 A line makes angles α, β, γ, δ with the four diagonals of a cube. Prove that \(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma+\cos ^2 \delta=\frac{4}{3} \text {. }\).

Solution

Let OA, OB, OC be the coterminous edges of a cube, taken along the axes in such a way that OA = OB = OC = a.

Then, the coordinates of the vertices of the cube are O(0,0,0), A(a,0,0), B(0,a,0), C(0,0,a), P(a,a,a), L(0,a,a), M(a,0,a) and N(a,a,0).

The direction ratios of the diagonals OP, AL, BM and CN are (a,a,a), (-a,a,a), (a,-a,a) and (a,a,-a) respectively.

∴ the direction cosines of OP, AL, BM and CN are

\(\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right),\left(\frac{-1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right),\left(\frac{1}{\sqrt{3}}, \frac{-1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)\), and \(\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{-1}{\sqrt{3}}\right)\) respectively.

Let (l,m,n) be the direction cosines of a line which makes angles α, β, γ, δ with the four diagonals of the cube. Then,

\(\cos \alpha=\left(l \cdot \frac{1}{\sqrt{3}}+m \cdot \frac{1}{\sqrt{3}}+n \cdot \frac{1}{\sqrt{3}}\right)=\frac{(l+m+n)}{\sqrt{3}}\),

\(\cos \beta=\left\{l \cdot\left(\frac{-1}{\sqrt{3}}\right)+m \cdot \frac{1}{\sqrt{3}}+n \cdot \frac{1}{\sqrt{3}}\right\}=\frac{(-l+m+n)}{\sqrt{3}}\),

\(\cos \gamma=\left\{l \cdot \frac{1}{\sqrt{3}}+m \cdot\left(\frac{-1}{\sqrt{3}}\right)+n \cdot \frac{1}{\sqrt{3}}\right\}=\frac{(l-m+n)}{\sqrt{3}}\),

\(\cos \delta=\left\{l \cdot \frac{1}{\sqrt{3}}+m \cdot \frac{1}{\sqrt{3}}+n \cdot\left(\frac{-1}{\sqrt{3}}\right)\right\}=\frac{(l+m-n)}{\sqrt{3}}\).

On squaring and adding, we get

\(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma+\cos ^2 \delta\)

= \(\frac{1}{3} \cdot\left\{(l+m+n)^2+(-l+m+n)^2+(l-m+n)^2+(l+m-n)^2\right\}\)

= \(\frac{4}{3}\).

Example 14 If a variable line in two adjacent positions has direction cosines (l, m, n) and (l + δl, ,m + δm, n + δn), show that the small angle δθ between the two positions is given by (δθ)² = (δl)² + (δm)² + (δn)².

Solution

Clearly, we have

l² + m² + n² = 1 …(1)

and (l + δl)² + (m + δm)² + (n + δn)² = 1 …(2)

Subtracting (1) from (2), we get

(l + δl)² + (m + δm)² + (n + δn)² – (l² + m² + n²) = 0

⇒ (δl)² + (δm)² + (δn)² = -2(l . δl + m .δm + n . δn) …(3)

∴ cos δθ = l . (l + δl) + m . (m + δm) + n . (n + δn)

= (l² + m² + n²) + (l . δl + m . δm + n . δn)

= \(1-\frac{1}{2}\left\{(\delta l)^2+(\delta m)^2+(\delta n)^2\right\}\) [using (3)].

∴ (δl)² + (δm)² + (δn)² = 2(1 – cos δθ)

= \(4 \sin ^2 \frac{\delta \theta}{2}=4 \cdot\left(\frac{\delta \theta}{2}\right)^2 \quad\left[\frac{\delta \theta}{2} \text { being small, } \sin \frac{\delta \theta}{2}=\frac{\delta \theta}{2}\right]\)

= (δθ)².

Hence, (δθ)² = (δl)² + (δm)² + (δn)².

Example 15 If l₁, m₁, n₁, and l₂, m₂, n₂ be the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of them are (m₁n₂ – m₂n₁), (n₁l₂ – n₂l₁), (l₁m₂ – l₂m₁).

Solution

Let l, m, n be the direction cosines of the line perpendicular to each of the given lines. Then,

ll₁ + mm₁ + nn₁ = 0 …(1)

ll₂ + mm₂ + nn₂ = 0 …(2)

Cross multiplying (1) and (2), we get

\(\frac{l}{\left(m_1 n_2-m_2 n_1\right)}=\frac{m}{\left(n_1 l_2-n_2 l_1\right)}=\frac{n}{\left(l_1 m_2-l_2 m_1\right)}=\frac{\sqrt{l^2+m^2+n^2}}{\sqrt{\Sigma\left(m_1 n_2-m_2 n_1\right)^2}}\)

or \(\frac{l}{\left(m_1 n_2-m_2 n_1\right)}=\frac{m}{\left(n_1 l_2-n_2 l_1\right)}=\frac{n}{\left(l_1 m_2-l_2 m_1\right)}=\frac{1}{\sin \theta}\),

But, \(\theta=\frac{\pi}{2}\), and therefore, sin θ = 1.

∴ l = (m₁n₂ – m₂n₁), m = (n₁l₂ – n₂l₁) and n = (l₁m₂ – l₂m₁).

Hence, the direction cosines of the required line are (m₁n₂ – m₂n₁), (n₁l₂ – n₂l₁), (l₁m₂ – l₂m₁).

Shortest Distance between Two Lines

Coplanar Lines Two lines lying in the same plane are called coplanar lines. Coplanar lines are either parallel or intersecting.

Skew Lines Two lines in space which are not coplanar are called skew lines. Skew lines are neither parallel nor intersecting.

Line Of Shortest Distance Between Two Skew Lines If L₁ and L₂ are two skew lines then there is a unique line which is perpendicular to both the lines L₁ and L₂. This line is called the line of shortest distance between L₁ and L₂.

Shortest Distance Between Two Skew Lines The length of the line segment \(\overrightarrow{P Q}\), intercepted by two skew lines L₁ and L₂ on the common perpendicular to both the lines, is called the shortest distance (SD) between L₁ and L₂.

Remark If two lines in space intersect at a point then the shortest distance between them is zero.

To Find the Shortest Distance between Two Skew Lines

Vector Form

Theorem The shortest distance between two skew lines \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\) is given by \(d=\left|\frac{\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right) \cdot\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)}{\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|}\right| .\)

Proof Let L₁ and L₂ be two skew lines whose vector equations are respectively.

\(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1}\) …(1)

and \(\vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\) …(2)

Then, L₁ is parallel to \(\overrightarrow{b_1}\) and passes through a point A, whose position vector is \(\overrightarrow{a_1}\).

And, L₂ is parallel to \(\overrightarrow{b_2}\) and passes through a point B, whose position vector is \(\overrightarrow{a_2}\).

Let \(\overrightarrow{P Q}\) be the shortest-distance vector between L1 and L2.

Then, \(\overrightarrow{P Q} \perp \overrightarrow{b_1} \text { and } \overrightarrow{P Q} \perp \overrightarrow{b_2}\)

∴ \(\overrightarrow{P Q} \|\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)\)

∴ \(P Q=\mid \text { projection of } \overrightarrow{A B} \text { along }\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right) \mid\)

= \(\left|\frac{\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right) \cdot\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)}{\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|}\right| .\)

Condition For Two Given Lines To Intersect Suppose that the lines \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\) intersect. Then, the shortest distance between them is zero.

∴ \(\left[\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right) \overrightarrow{b_1} \overrightarrow{b_2}\right]=0\)

Remark Two lines intersect only when the shortest distance between them is zero.

Solved Examples

Example 1 Find the shortest distance between two lines whose vector equations are \(\vec{r}=(\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k}) \text { and } \vec{r}=(2 \hat{i}-\hat{j}-\hat{k})+\mu(2 \hat{i}+\hat{j}+2 \hat{k}) \text {. }\)

Solution

Comparing the given equations with the standard equations \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\), we have

\(\overrightarrow{a_1}=(\hat{i}+2 \hat{j}+\hat{k}), \overrightarrow{b_1}=(\hat{i}-\hat{j}+\hat{k})\) \(\overrightarrow{a_2}=(2 \hat{i}-\hat{j}-\hat{k}) \text { and } \overrightarrow{b_2}=(2 \hat{i}+\hat{j}+2 \hat{k}) \text {. }\)

∴ \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)=(2 \hat{i}-\hat{j}-\hat{k})-(\hat{i}+2 \hat{j}+\hat{k})=(\hat{i}-3 \hat{j}-2 \hat{k})\)

and, \(\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
1 & -1 & 1 \\
2 & 1 & 2
\end{array}\right|\)

= \((-2-1) \hat{i}-(2-2) \hat{j}+(1+2) \hat{k}\)

= \((-3 \hat{i}+3 \hat{k})\)

∴ \(\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|=\sqrt{(-3)^2+3^2}=\sqrt{18}=3 \sqrt{2} .\)

∴ SD = \(\left|\frac{\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right) \cdot\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)}{\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|}\right|\)

= \(\frac{|(-3 \hat{i}+3 \hat{k}) \cdot(\hat{i}-3 \hat{j}-2 \hat{k})|}{3 \sqrt{2}}=\frac{|(-3-0-6)|}{3 \sqrt{2}}\)

= \(\frac{|-9|}{3 \sqrt{2}}=\frac{9}{3 \sqrt{2}}=\frac{3 \sqrt{2}}{2} \text { units. }\)

The shortest distance between two lines = \(\frac{|-9|}{3 \sqrt{2}}=\frac{9}{3 \sqrt{2}}=\frac{3 \sqrt{2}}{2} \text { units. }\)

Real-Life Applications of Straight Lines in Geometry

Example 2 Find the shortest distance between the lines L₁ and L₂ whose vector equations are given below:

L₁: \(\vec{r}=\hat{i}+\hat{j}+\lambda(2 \hat{i}-\hat{j}+\hat{k})\)

L₂: \(\vec{r}=2 \hat{i}+\hat{j}-\hat{k}+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k})\)

Solution

Comparing the given equations with the standard equations \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\), we have

\(\overrightarrow{a_1}=(\hat{i}+\hat{j}), \overrightarrow{b_1}=(2 \hat{i}-\hat{j}+\hat{k})\) \(\overrightarrow{a_2}=(2 \hat{i}+\hat{j}-\hat{k}) \text { and } \overrightarrow{b_2}=(3 \hat{i}-5 \hat{j}+2 \hat{k})\)

∴ \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)=(2 \hat{i}+\hat{j}-\hat{k})-(\hat{i}+\hat{j})=(\hat{i}-\hat{k})\)

and, \(\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & -1 & 1 \\
3 & -5 & 2
\end{array}\right|\)

= \((-2+5) \hat{i}-(4-3) \hat{j}+(-10+3) \hat{k}\)

= \((3 \hat{i}-\hat{j}-7 \hat{k})\)

∴ \(\left|\vec{b}_1 \times \vec{b}_2\right|=\sqrt{3^2+(-1)^2+(-7)^2}=\sqrt{59}\)

∴ SD = \(\left|\frac{\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right) \cdot\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)}{\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|}\right|\)

= \(\frac{|(3 \hat{i}-\hat{j}-7 \hat{k}) \cdot(\hat{i}-\hat{k})|}{\sqrt{59}}=\frac{|3 \times 1-1 \times 0-7 \times(-1)|}{\sqrt{59}}\)

= \(\frac{|3-0+7|}{\sqrt{59}}=\frac{10 \sqrt{59}}{59} \text { units. }\)

The shortest distance between the lines L₁ and L₂  = \(\frac{|3-0+7|}{\sqrt{59}}=\frac{10 \sqrt{59}}{59} \text { units. }\)

Example 3 Find the shortest distance between the lines whose vector equations are

\(\vec{r}=(1-t) \hat{i}+(t-2) \hat{j}+(3-2 t) \hat{k} \text {, and }\) \(\vec{r}=(s+1) \hat{i}+(2 s-1) \hat{j}-(2 s+1) \hat{k} \text {. }\)

Solution

The given equations can be written as

\(\vec{r}=(\hat{i}-2 \hat{j}+3 \hat{k})+t(-\hat{i}+\hat{j}-2 \hat{k}) \text {, and }\) \(\vec{r}=(\hat{i}-\hat{j}-\hat{k})+s(\hat{i}+2 \hat{j}-2 \hat{k})\)

Comparing the given equations with the standard equations \(\vec{r}=\overrightarrow{a_1}+t \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+s \overrightarrow{b_2}\), we get

\(\overrightarrow{a_1}=(\hat{i}-2 \hat{j}+3 \hat{k}), \overrightarrow{b_1}=(-\hat{i}+\hat{j}-2 \hat{k})\) \(\vec{a}_2=(\hat{i}-\hat{j}-\hat{k}) \text { and } \vec{b}_2=(\hat{i}+2 \hat{j}-2 \hat{k}) \text {. }\)

∴ \(\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|=\sqrt{2^2+(-4)^2+(-3)^2}=\sqrt{29}\)

∴ SD = \(\left|\frac{\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right) \cdot\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)}{\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|}\right|\)

= \(\frac{|(2 \hat{i}-4 \hat{j}-3 \hat{k}) \cdot(\hat{j}-4 \hat{k})|}{\sqrt{29}}=\frac{|2 \times 0-4 \times 1-3 \times(-4)|}{\sqrt{29}}\)

= \(\frac{|0-4+12|}{\sqrt{29}}=\frac{8 \sqrt{29}}{29} \text { units. }\)

The shortest distance between the lines = \(\frac{|0-4+12|}{\sqrt{29}}=\frac{8 \sqrt{29}}{29} \text { units. }\)

Example 4 Show that the lines \(\vec{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda(3 \hat{i}-\hat{j}) \text { and } \vec{r}=(4 \hat{i}-\hat{k})+\mu(2 \hat{i}+3 \hat{k})\) intersect. Find their point of intersection.

Solution

Comparing the given equations with the standard equations \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\), we get

\(\overrightarrow{a_1}=(\hat{i}+\hat{j}-\hat{k}), \overrightarrow{b_1}=(3 \hat{i}-\hat{j})\) \(\overrightarrow{a_2}=(4 \hat{i}-\hat{k}) \text { and } \overrightarrow{b_2}=(2 \hat{i}+3 \hat{k}) \text {. }\)

∴ \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)=(4 \hat{i}-\hat{k})-(\hat{i}+\hat{j}-\hat{k})=(3 \hat{i}-\hat{j}) .\)

And, \(\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
3 & -1 & 0 \\
2 & 0 & 3
\end{array}\right|\)

= \((-3-0) \hat{i}-(9-0) \hat{j}+(0+2) \hat{k}\)

= \((-3 \hat{i}-9 \hat{j}+2 \hat{k})\)

∴ \(\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|=\sqrt{(-3)^2+(-9)^2+2^2}=\sqrt{94}\)

∴ SD = \(\left|\frac{\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right) \cdot\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)}{\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|}\right|\)

= \(\left|\frac{(-3 \hat{i}-9 \hat{j}+2 \hat{k}) \cdot(3 \hat{i}-\hat{j})}{\sqrt{94}}\right|\)

= \(\frac{|-9+9+0|}{\sqrt{94}}=0\)

Thus, for some particular values of λ and μ, we have

\((\hat{i}+\hat{j}-\hat{k})+\lambda(3 \hat{i}-\hat{j})=(4 \hat{i}-\hat{k})+\mu(2 \hat{i}+3 \hat{k})\)

⇒ \((1+3 \lambda) \hat{i}+(1-\lambda) \hat{j}-\hat{k}=(4+2 \mu) \hat{i}+(3 \mu-1) \hat{k}\)

⇒ 1 + 3λ = 4 + 2μ, 1 – λ = 0 and 3μ – 1 = -1

⇒ λ = 1 and μ = 0.

Thus, the position vector of the point of intersection of the given lines is given by

\(\vec{r}=(\hat{i}+\hat{j}-\hat{k})+(3 \hat{i}-\hat{j}) [putting λ = 1], i.e., \vec{r}=(4 \hat{i}-\hat{k}) .\)

Hence, the point of intersection of the given lines if P(4, 0, -1).

Example 5 Show that the lines \(\vec{r}=(\hat{i}-\hat{j})+\lambda(2 \hat{i}+\hat{k}) \text { and } \vec{r}=(2 \hat{i}-\hat{j})+\mu(\hat{i}+\hat{j}-\hat{k})\) do not intersect.

Solution

Comparing the given equations with the standard equations \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1} \text { and } \vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\), we get

\(\overrightarrow{a_1}=(\hat{i}-\hat{j}), \overrightarrow{b_1}=(2 \hat{i}+\hat{k})\) \(\vec{a}_2=(2 \hat{i}-\hat{j}) \text { and } \vec{b}_2=(\hat{i}+\hat{j}-\hat{k})\)

∴ \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)=(2 \hat{i}-\hat{j})-(\hat{i}-\hat{j})=\hat{i} .\)

And, \(\left(\vec{b}_1 \times \vec{b}_2\right)=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
2 & 0 & 1 \\
1 & 1 & -1
\end{array}\right|\)

= \((0-1) \hat{i}-(-2-1) \hat{j}+(2-0) \hat{k}\)

= \((-\hat{i}+3 \hat{j}+2 \hat{k})\)

∴ \(\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|=\sqrt{(-1)^2+3^2+2^2}=\sqrt{14}\)

∴ SD = \(\left|\frac{\left(\vec{b}_1 \times \vec{b}_2\right) \cdot\left(\vec{a}_2-\vec{a}_1\right)}{\left|\vec{b}_1 \times \vec{b}_2\right|}\right|\)

= \(\left|\frac{(-\hat{i}+3 \hat{j}+2 \hat{k}) \cdot \hat{i}}{\sqrt{14}}\right|=\frac{|-1|}{\sqrt{14}}\)

= \(\frac{1 \times \sqrt{14}}{14}=\frac{\sqrt{14}}{14} \neq 0\)

Since the shortest distance between the given lines is not zero, the given lines do not intersect.

Distance Between Parallel Lines Let L₁ and L₂ be two parallel lines. Then, these lines are clearly coplanar.

Let the equations of these lines be

\(\vec{r}=\overrightarrow{a_1}+\lambda \vec{b}\) …(1)

\(\vec{r}=\overrightarrow{a_2}+\mu \vec{b}\) …(2)

Let A be a point on L₁ with position vector \(\overrightarrow{a_1}\) and let B be a point on L₂ with position vector \(\overrightarrow{a_2}\).

Draw BM ⊥ L₁. Then, distance between L₁ and L₂ = \(|\overrightarrow{B M}|\).

Let θ be the angle between \(\overrightarrow{A B} \text { and } \vec{b}. Then, (\vec{b} \times \overrightarrow{A B})=\{|\vec{b}||\overrightarrow{A B}| \cdot \sin \theta\} \hat{n}\), where \(\hat{n}\) is a unit vector, perpendicular to the plane of L₁ and L₂.

∴ \(\vec{b} \times\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)=|| \vec{b}|| \overrightarrow{A B}|\cdot \sin \theta| \hat{n}\)

⇒ \(\vec{b} \times\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)=|\vec{b}|(B M) \vec{n}\) [∵ (AB) sin θ = BM]

⇒ \(\left|\vec{b} \times\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)\right|=|\vec{b}||\overrightarrow{B M}| . 1\) [∵ \(|\hat{n}|=1\)]

⇒ \(|\overrightarrow{B M}|=\left|\frac{\vec{b} \times\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)}{|\vec{b}|}\right| .\)

Example 6 Find the shortest distance between the lines L1 and L2, given by \(\vec{r}=\hat{i}+\hat{j}+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \text { and } \vec{r}=2 \hat{i}+\hat{j}-\hat{k}+\mu(4 \hat{i}-2 \hat{j}+2 \hat{k})\).

Solution

The given lines are

L_1: \(\vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k})\) …(1)

L_2: \(\vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+2 \mu(2 \hat{i}-\hat{j}+\hat{k})\) …(2)

These equations are of the form:

\(\vec{r}=\overrightarrow{a_1}+\lambda \vec{b} \text { and } \vec{r}=\overrightarrow{a_2}+2 \mu \vec{b}=\overrightarrow{a_2}+\mu^{\prime} \vec{b} \text {, where }\)

\(\overrightarrow{a_1}=(\hat{i}+\hat{j})\), \(\overrightarrow{a_2}=(2 \hat{i}+\hat{j}-\hat{k}), \vec{b}=(2 \hat{i}-\hat{j}+\hat{k}) \text { and } \mu^{\prime}=2 \mu \text {. }\)

Clearly, the given lines are parallel.

Now, \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)=(2 \hat{i}+\hat{j}-\hat{k})-(\hat{i}+\hat{j})=(\hat{i}-\hat{k})\)

∴ \(\left\{\vec{b} \times\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)\right\}=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
2 & -1 & 1 \\
1 & 0 & -1
\end{array}\right|\)

= \((1-0) \hat{i}-(-2-1) \hat{j}+(0+1) \hat{k}\)

= \((\hat{i}+3 \hat{j}+\hat{k})\)

⇒ \(\left|\vec{b} \times\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)\right|=\sqrt{1^2+3^2+1^2}=\sqrt{11} and |\vec{b}|=\sqrt{2^2+(-1)^2+1^2}=\sqrt{6}\)

⇒ shortest distance between L₁ and L₂

= distance between L₁ and L₂

= \(\frac{\left|\vec{b} \times\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right)\right|}{|\vec{b}|}=\frac{\sqrt{11}}{\sqrt{6}}=\left(\frac{\sqrt{11}}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}}\right)=\frac{\sqrt{66}}{6} \text { units. }\)

Shortest Distance between Two Skew Lines in the Cartesian Form

The shortest distance between the skew lines \(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \text { and } \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\) is given by

\(\mathrm{SD}=\frac{\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|}{\sqrt{D}}\)

where D = {(a₁b₂ – a₂b₁)² + (b₁c₂ – b₂c₁)² + (c₁a₂ – c₂a₁)²}.

Condition For Two Given Lines To Intersect Let L₁ and L₂ be the given lines whose equations are

\(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \text { and } \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\)

1. L₁ and L₂ intersect ⇔ SD between them is 0

⇔ \(\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0\)

2. L₁ and L₂ do not intersect ⇔ they are skew lines

⇔ \(\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right| \neq 0 .\)

Solved Examples

Example 1 Find the shortest distance between the lines

\(\frac{x+3}{-4}=\frac{y-6}{3}=\frac{z}{2} \text { and } \frac{x+2}{-4}=\frac{y}{1}=\frac{z-7}{1} \text {. }\)

Solution

Comparing the given equations with

\(\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \text { and } \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\), we get

(x₁ = -3, y₁ = 6, z₁ = 0), (x₂ = -2, y₂ = 0, z₂ = 7), (a₁ = -4, b₁ = 3, c₁ = 2) and (a₂ = -4, b₂ = 1, c₂ = 1).

Now, D = (a₁b₂ – a₂b₁)² + (b₁c₂ – b₂c₁)² + (c₁a₂ – c₂a₁)²

= (-4+12)² + (3-2)² + (-8+4)²

= (64 + 1 + 16) = 81.

∴ SD = \(\frac{1}{\sqrt{D}} \cdot\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|\)

= \(\frac{1}{\sqrt{81}} \cdot\left|\begin{array}{ccc}
-2+3 & 0-6 & 7-0 \\
-4 & 3 & 2 \\
-4 & 1 & 1
\end{array}\right|=\frac{1}{9} \cdot\left|\begin{array}{rrr}
1 & -6 & 7 \\
-4 & 3 & 2 \\
-4 & 1 & 1
\end{array}\right|\)

= \(\frac{1}{9} \cdot\{1 \cdot(3-2)+6 \cdot(-4+8)+7 \cdot(-4+12)\}=\frac{81}{9}=9 \text { units. }\)

Hence, the shortest distance between the given lines is 9 units.

Alternative Method

Example 2 Find the length and the equations of the line of shortest distance between the lines

\(\frac{x-3}{3}=\frac{y-8}{-1}=z-3 \text { and } \frac{x+3}{-3}=\frac{y+7}{2}=\frac{z-6}{4} \text {. }\)

Solution

The given equations are

\(\frac{x-3}{3}=\frac{y-8}{-1}=\frac{z-3}{1}=\lambda \text { (say) }\) …(1)

\(\frac{x+3}{-3}=\frac{y+7}{2}=\frac{z-6}{4}=\mu \text { (say) }\) …(2)

P(3λ+3, -λ+8, λ+3) is any point on (1).

Q(-3μ-3, 2μ-7, 4μ+6) is any point on (2).

The direction ratios of PQ are (-3μ – 3 – 6, 2μ + λ- 15, 4μ -λ + 3).

If PQ is the line of shortest distance then PQ is perpendicular to each of (1) and (2).

∴ \(\left\{\begin{array}{c}
3(-3 \mu-3 \lambda-6)-1 \cdot(2 \mu+\lambda-15)+1 \cdot(4 \mu-\lambda+3)=0 \\
\quad \text { and } \\
-3(-3 \mu-3 \lambda-6)+2 \cdot(2 \mu+\lambda-15)+4 \cdot(4 \mu-\lambda+3)=0
\end{array}\right.\)

⇒ \(\left\{\begin{array}{l}
-11 \lambda-7 \mu=0 \\
7 \lambda+29 \mu=0
\end{array}\right.\)

⇒ λ = 0 and μ = 0.

Thus, PQ will be the line of shortest distance with λ = 0 and μ = 0.

Substituting λ = 0 and μ = 0 in P and Q respectively, we get the points P(3, 8, 3) and Q(-3, -7, 6).

∴ SD = PQ = \(\sqrt{(-3-3)^2+(-7-8)^2+(6-3)^2}\)

= \(\sqrt{36+225+9}=\sqrt{270}=3 \sqrt{30} \text { units. }\)

Equations of the line of shortest distance means equations of PQ, given by

\(\frac{x-3}{-3-3}=\frac{y-8}{-7-8}=\frac{z-3}{6-3}\)

⇔ \(\frac{x-3}{-6}=\frac{y-8}{-15}=\frac{z-3}{3}\)

⇔ \(\frac{x-3}{2}=\frac{y-8}{5}=\frac{z-3}{-1}\)

Example 3 Find the length and the equations of the line of shortest distance between the lines

\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4} \text { and } \frac{x-2}{3}=\frac{y-4}{4}=\frac{z-5}{5} \text {. }\)

Solution

The given lines are

\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda \text { (say) }\) …(1)

\(\frac{x-2}{3}=\frac{y-4}{4}=\frac{z-5}{5}=\mu \text { (say) }\) …(2)

P(2λ+1, 3λ+2, 4λ+3) is any point on (1).

Q(3μ+2, 4μ+4, 5μ+5) is any point on (2).

The direction ratios of \overrightarrow{P Q} are (3μ – 2λ + 1, 4μ – 3λ + 2, 5μ – 4λ + 2).

If \(\overrightarrow{P Q}\) is the line of shortest distance then \(\overrightarrow{P Q}\) is perpendicular to each of (1) and (2).

∴ \(\left\{\begin{array}{l}
2(3 \mu-2 \lambda+1)+3(4 \mu-3 \lambda+2)+4(5 \mu-4 \lambda+2)=0, \\
\quad \text { and } \\
3(3 \mu-2 \lambda+1)+4(4 \mu-3 \lambda+2)+5(5 \mu-4 \lambda+2)=0
\end{array}\right.\)

⇒ \(\left\{\begin{array}{l}
38 \mu-29 \lambda+16=0 \\
50 \mu-38 \lambda+21=0
\end{array}\right.\)

⇒ \(\frac{\mu}{(-609+608)}=\frac{\lambda}{(800-798)}=\frac{1}{(-1444+1450)}\) [by cross multiplication]

⇒ \(\frac{\mu}{-1}=\frac{\lambda}{2}=\frac{1}{6}\)

⇒ \(\lambda=\frac{2}{6}=\frac{1}{3} \text { and } \mu=\frac{-1}{6} \text {. }\)

Thus PQ will be the line of shortest distance when λ = \(\frac{1}{3}\) and μ = \(-\frac{1}{6}\). Putting λ = \(\frac{1}{3}\) and μ = \(-\frac{1}{6}\) in P and Q respectively, we get the points \(P\left(\frac{5}{3}, 3, \frac{13}{3}\right) \text { and } Q\left(\frac{3}{2}, \frac{10}{3}, \frac{25}{6}\right) \text {. }\)

∴ SD = PQ = \(\sqrt{\left(\frac{3}{2}-\frac{5}{3}\right)^2+\left(\frac{10}{3}-3\right)^2+\left(\frac{25}{6}-\frac{13}{3}\right)^2}\)

= \(\sqrt{\frac{1}{36}+\frac{1}{9}+\frac{1}{36}}=\frac{1}{\sqrt{6}} \text { units }=\frac{\sqrt{6}}{6} \text { units. }\)

Hence, \(\mathrm{SD}=\frac{\sqrt{6}}{6} \text { units. }\)

Direction ratios of PQ are \(\left(\frac{3}{2}-\frac{5}{3}\right),\left(\frac{10}{3}-3\right),\left(\frac{25}{6}-\frac{13}{3}\right) \text {, } i.e., -\frac{1}{6}, \frac{1}{3}, \frac{-1}{6}, \text { i.e. }-1,2,-1 \text {. }\)

∴ the equations of the line of shortest distance are \(\frac{\left(x-\frac{5}{3}\right)}{-1}=\frac{y-3}{2}=\frac{\left(z-\frac{13}{3}\right)}{-1} .\)

Example 4 Show that the lines \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4} \text { and } \frac{x-4}{5}=\frac{y-1}{2}=z\) intersect each other. Find their point of intersection.

Solution

The given lines are

\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda \text { (say) }\) …(1)

\(\frac{x-4}{5}=\frac{y-1}{2}=\frac{z}{1}=\mu \text { (say) }\) …(2)

P(2λ+1, 3λ+2, 4λ+3) is any point on (1).

Q(5μ+4, 2μ+1, μ) is any point on (2).

If the lines (1) and (2) intersect then P and Q must coincide for some particular values of λ and μ.

This gives

2λ + 1 = 5μ + 4, 3λ + 2μ = 2 + 1 and 4λ + 3 = μ

⇔ 2λ – 5μ = 3 …(1), 3λ – 2μ = -1 …(2), and 4λ – μ = -3 …(3)

Solving (1) and (2), we get λ = -1 and μ = -1.

And, these values of λ and μ also satisfu (3).

Hence, the given lines intersect.

The point of intersection of the given lines is (-1, -1, -1), which is obtained by putting λ = -1 in P or μ = -1 in Q.

Example 5 Show that the lines \(\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5} \text { and } \frac{x-2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}\) do not intersect each other.

Solution

The given lines are

\(\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5}=\lambda \text { (say) }\) …(1)

\(\frac{x-2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}=\mu \text { (say) }\) …(2)

P(3λ+1, 2λ-1, 5λ+1) is any point on (1).

Q(4μ+2, 3μ+1, -2μ-1) is any point on (2).

If the lines (1) and (2) intersect then P and Q must coincide for some particular values of λ and μ.

This gives

3λ + 1 = 4μ + 2, 2λ – 1 = 3μ + 1, 5λ + 1 = -2μ – 1

⇔ 3λ – 4μ = 1 …(1), 2λ – 3μ = 2 …(2), and 5λ + 2μ = -2 …(3).

Solving (1) and (2), we get λ = -5 and μ = -4.

But, the values λ = -5 and μ = -4 do not satisfy (3).

Hence, the given lines do not intersect each other.

Chapter 2 Differentiation

1. Derivatives of Some Functions

In class 9, we have studied about the derivatives of algebraic and trignometric functions. We derived the following results.

(1) \(\frac{d}{d x}\left(x^n\right)=n x^{n-1}\)

(2) \(\frac{d}{d x}(\sin x)=\cos x\)

(3) \(\frac{d}{d x}(\cos x)=-\sin x\)

(4) \(\frac{d}{d x}(\tan x)=\sec ^2 x\)

(5) \(\frac{d}{d x}(\cot x)=-{cosec}^2 x\)

(6) \(\frac{d}{d x}(\sec x)=\sec x \tan x\)

(7) \(\frac{d}{d x}({cosec} x)=-{cosec} x \cot x\)

In algebra of derivatives, we have established the following rules.

Some Rules of Differentiation

(1) \(\frac{d}{d x}(u+v)=\left(\frac{d u}{d x}+\frac{d v}{d x}\right)\)

(2) \(\frac{d}{d x}(u-v)=\left(\frac{d u}{d x}-\frac{d v}{d x}\right)\)

(3) \(\frac{d}{d x}(u v)=\left(u \cdot \frac{d v}{d x}+v \cdot \frac{d u}{d x}\right)\)

(4) \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{\left(v \cdot \frac{d u}{d x}-u \cdot \frac{d v}{d x}\right)}{v^2}\)

Read and Learn More  Class 12 Math Solutions

Derivatives of Composite Functions (Chain Rule)

(1) Let y = f(t) and t = g(x). Then, \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right).\)

(2) Let y = f(t), t = g(u) and u = h(x). Then, \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d u} \times \frac{d u}{d x}\right) .\)

This rule may be extended further on more variables.

Solved Examples

Example 1 Differentiate each of the following w.r.t. x:

(1) sinx³

(2) cos³x

(3) tan √x

Solution

(1) Let y = sinx³.

Putting x³ = t, we get

y = sin t and t = x³

⇒ \(\frac{d y}{d t}=\cos t \text { and } \frac{d t}{d x}=3 x^2\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)\)

= (cos t .3x²) = 3x² cos t = 3x² cos x³.

Hence, \(\frac{d}{d x}\left(\sin x^3\right)=3 x^2 \cos x^3\).

(2) Let y = cos³x = (cos x)³.

Putting cos x = t, we get

y = t³ and t = cos x

⇒ \(\frac{d y}{d t}=3 t^2 \text { and } \frac{d t}{d x}=-\sin x\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)\)

= (-3t²sin x) = (-3 sin x)t² = (-3sin x cos²x).

Hence, \(\frac{d}{d x}\left(\cos ^3 x\right)=-3 \sin x \cos ^2 x .\)

(3) Let y = tan√x

Putting √x = t, we get

y = tan t and t = √x

⇒ \(\frac{d y}{d t}=\sec ^2 t \text { and } \frac{d t}{d x}=\frac{1}{2} x^{-1 / 2}=\frac{1}{2 \sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)\)

= \(\left(\sec ^2 t \cdot \frac{1}{2 \sqrt{x}}\right)=\frac{\sec ^2 \sqrt{x}}{2 \sqrt{x}}\) [∵ t = √x]

Hence, \(\frac{d}{d x}(\tan \sqrt{x})=\frac{\sec ^2 \sqrt{x}}{2 \sqrt{x}} .\)

WBBSE Class 12 Differentiation Solutions

Example 2 Differentiate each of the following w.r.t. x:

(1) (ax + b)^m

(2) (2x+3)⁵

(3) \(\sqrt{a x^2+2 b x+c}\)

Solution

(1) Let y = (ax + b)^m.

Putting (ax+b) = t, we get

y = t^m and t = (ax+b)

⇒ \(\frac{d y}{d t}=m t^{m-1} \text { and } \frac{d t}{d x}=a\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\left(m t^{m-1} \times a\right)=m a t^{m-1}=m a(a x+b)^{m-1} .\)

∴ \(\frac{d}{d x}(a x+b)^m=m a(a x+b)^{m-1}\)

(2) Let y = (2x+3)⁵.

Putting (2x+3) = t, we get

y = t⁵ and t = 2x+3

⇒ \(\frac{d y}{d t}=5 t^4 \text { and } \frac{d t}{d x}=2\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=10 t^4=10(2 x+3)^4 .\)

(3) Let y = \(\sqrt{a x^2+2 b x+c}\)

Putting (ax² + 2bx + c) = t, we get

y = √t and t = (ax²+2bx+c)

⇒ \(\frac{d y}{d t}=\frac{1}{2} t^{-1 / 2}=\frac{1}{2 \sqrt{t}} \text { and } \frac{d t}{d x}=(2 a x+2 b)=2(a x+b)\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\frac{1}{2 \sqrt{t}} \times 2(a x+b)=\frac{(a x+b)}{\sqrt{t}}=\frac{(a x+b)}{\sqrt{a x^2+2 b x+c}} .\)

Example 3 Differentiate sin 3x cos tx w.r.t x.

Solution

Given

sin 3x cos tx w.r.t x.

Let y = sin 3x cos 5x = \(\frac{1}{2}\)[2 cos 5x sin 3x]

= \(\frac{1}{2}\){sin (5x+3x) – sin(5x-3x)}

= \(\frac{1}{2} \cdot(\sin 8 x-\sin 2 x)=\frac{1}{2} \sin 8 x-\frac{1}{2} \sin 2 x .\)

∴ \(\frac{d y}{d x}=\frac{1}{2} \cdot \frac{d}{d x}(\sin 8 x)-\frac{1}{2} \cdot \frac{d}{d x}(\sin 2 x)\)

= \(\left(\frac{1}{2} \cdot 8 \cos 8 x-\frac{1}{2} \times 2 \cos 2 x\right)=(4 \cos 8 x-\cos 2 x) .\)

sin 3x cos tx = \(\left(\frac{1}{2} \cdot 8 \cos 8 x-\frac{1}{2} \times 2 \cos 2 x\right)=(4 \cos 8 x-\cos 2 x) .\)

Example 4 Differentiate sin 2x sin 4x w.r.t. x.

Solution

Given

sin 2x sin 4x w.r.t. x

Let y = sin 2x sin 4x = \(\frac{1}{2}\)(2 sin 4x sin 2x)

= \(\frac{1}{2}\) {cos (4x-2x) – cos (4x+2x)}

= \(\frac{1}{2}\) [cos 2x – cos 6x].

∴ \(\frac{d y}{d x}=\frac{1}{2} \cdot \frac{d}{d x}(\cos 2 x)-\frac{1}{2} \cdot \frac{d}{d x}(\cos 6 x)\)

= \(\frac{1}{2} \cdot(-2 \sin 2 x)-\frac{1}{2} \cdot(-6 \sin 6 x)\)

= (3sin 6x – sin 2x).

sin 2x sin 4x = (3sin 6x – sin 2x).

Example 5 Differentiate \(\sqrt{\frac{1-\tan x}{1+\tan x}}\) w.r.t. x.

Solution

Given

\(\sqrt{\frac{1-\tan x}{1+\tan x}}\) w.r.t. x

Let y = \(\sqrt{\frac{1-\tan x}{1+\tan x}}.\)

Putting \(\frac{(1-\tan x)}{1+\tan x)}=t\), we get

y = √t and t = \(\frac{(1-\tan x)}{1+\tan x)}\).

∴ \(\frac{d y}{d t}=\frac{1}{2} t^{-1 / 2}=\frac{1}{2 \sqrt{t}} .\)

And, \(\frac{d t}{d x}=\frac{(1+\tan x) \cdot \frac{d}{d x}(1-\tan x)-(1-\tan x) \cdot \frac{d}{d x}(1+\tan x)}{(1+\tan x)^2}\)

= \(\frac{(1+\tan x)\left(-\sec ^2 x\right)-(1-\tan x)\left(\sec ^2 x\right)}{(1+\tan x)^2}=\frac{-2 \sec ^2 x}{(1+\tan x)^2}\)

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\frac{1}{2 \sqrt{t}} \times \frac{-2 \sec ^2 x}{(1+\tan x)^2}\)

= \(\frac{-\sec ^2 x}{(1+\tan x)^2} \times \frac{\sqrt{1+\tan x}}{\sqrt{1-\tan x}}\)

= \(\frac{-\sec ^2 x}{(1+\tan x)^{3 / 2}(1-\tan x)^{1 / 2}} .\)

\(\sqrt{\frac{1-\tan x}{1+\tan x}}\) = \(\frac{-\sec ^2 x}{(1+\tan x)^{3 / 2}(1-\tan x)^{1 / 2}} .\)

Understanding Differentiation Concepts for Class 12

Example 6 If y = \(\frac{1}{\sqrt{a^2-x^2}} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Given

y = \(\frac{1}{\sqrt{a^2-x^2}} \text {, find } \frac{d y}{d x} \text {. }\)

Putting (a² – x²) = t, we get

y = \(\frac{1}{\sqrt{t}}=t^{-1 / 2}\) and t = (a² – x²)

⇒ \(\frac{d y}{d t}=-\frac{1}{2} t^{-3 / 2}=\frac{-1}{2 t^{3 / 2}} \text { and } \frac{d t}{d x}=-2 x\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\frac{-1}{2 t^{3 / 2}} \times(-2 x)=\frac{x}{t^{3 / 2}}=\frac{x}{\left(a^2-x^2\right)^{3 / 2}} .\)

Example 7 If y = cos²x², find \(\frac{d y}{d x}\).

Solution

Given: y = (cosx²)².

Putting x² = t and cos t = u, we get

y = u², u = cos t and t = x²

⇒ \(\frac{d y}{d u}=2 u, \frac{d u}{d t}=-\sin t \text { and } \frac{d t}{d x}=2 x\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= (2u) x (-sint) x 2x

= -4 x u sin t = -4x cos t sin t = -4xcosx²sinx².

∴ \(\frac{d y}{d x}=-4 x \cos x^2 \sin x^2\)

Example 8 If y = sin(cos x²), find \(\frac{d y}{d x}\)

Solution

Given

y = sin(cos x²),

Putting x² = t and cos x² = cos t = u, we get

y = sin u, u = cos t and t = x²

⇒ \(\frac{d y}{d u}=\cos u, \frac{d u}{d t}=-\sin t \text { and } \frac{d t}{d x}=2 x\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= [cos u x (-sin t) x 2x] = -2x sin t cos u

= -2x sin t cos(cos t) = -2x sin x² cos(cos x²).

∴ \(\frac{d y}{d x}=-2 x \sin x^2 \cos \left(\cos x^2\right) .\)

Example 9 If y = \(\sin (\sqrt{\sin x+\cos x}), \text { find } \frac{d y}{d x}\)

Solution

Given

y = \(\sin (\sqrt{\sin x+\cos x}), \text { find } \frac{d y}{d x}\)

Putting (sin x + cos x) = t and √t = u, we get

y = sin u, u = √t and t = (sin x + cos x)

⇒ \(\frac{d y}{d u}=\cos u_r \frac{d u}{d t}=\frac{1}{2} t^{-1 / 2}=\frac{1}{2 \sqrt{t}} \text { and } \frac{d t}{d x}=(\cos x-\sin x)\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= \(\left\{\cos u \times \frac{1}{2 \sqrt{t}} \times(\cos x-\sin x)\right\}=\frac{\cos \sqrt{t}}{2 \sqrt{t}} \cdot(\cos x-\sin x)\)

= \(\frac{\cos (\sqrt{\sin x+\cos x})}{2 \sqrt{\sin x+\cos x}} \cdot(\cos x-\sin x) \text {. }\)

Example 10 If y = \(\sin [\sqrt{\sin \sqrt{x}}] \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Given

y = \(\sin [\sqrt{\sin \sqrt{x}}] \text {, find } \frac{d y}{d x} \text {. }\)

Putting √x = t, sin√x = sin t = u and \(\sqrt{\sin \sqrt{x}}\) = √u = v, we get

y = sin v, v = √u, u =sin t and t = √x.

∴ \(\frac{d y}{d v}=\cos v ; \frac{d v}{d u}=\frac{1}{2} u^{-1 / 2}=\frac{1}{2 \sqrt{u}} ; \frac{d u}{d t}=\cos t \text { and } \frac{d t}{d x}=\frac{1}{2 \sqrt{x}} \text {. }\)

So, \(\frac{d y}{d x}=\left(\frac{d y}{d v} \times \frac{d v}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)=\left[\cos v \cdot \frac{1}{2 \sqrt{u}} \cdot \cos t \cdot \frac{1}{2 \sqrt{x}}\right]\)

= \(\left[\cos \sqrt{u} \cdot \frac{1}{2 \sqrt{u}} \cos t \cdot \frac{1}{2 \sqrt{x}}\right]\) [∵ v = √u]

= \(\frac{1}{4} \cos (\sqrt{\sin t}) \cdot \frac{1}{\sqrt{\sin t}} \cdot \cos \sqrt{x} \cdot \frac{1}{\sqrt{x}}\) [∵ u = sin t]

= \(\frac{1}{4} \cos (\sqrt{\sin \sqrt{x}}) \cdot \frac{1}{\sqrt{\sin \sqrt{x}}} \cdot \cos \sqrt{x} \cdot \frac{1}{\sqrt{x}}\) [∵ t = √x]

= \(\frac{\cos (\sqrt{\sin \sqrt{x}})}{4 \sqrt{x} \sqrt{\sin \sqrt{x}}} \cdot \cos \sqrt{x}\)

Example 11 If y = \(\frac{5 x}{\sqrt[3]{1-x^2}}+\sin ^2(2 x+3) \text {, find } \frac{d y}{d x}\).

Solution

We have

y = \(5 x\left(1-x^2\right)^{-1 / 3}+\sin ^2(2 x+3)\)

⇒ \(\frac{d y}{d x}=\frac{d}{d x}\left\{5 x\left(1-x^2\right)^{-1 / 3}\right\}+\frac{d}{d x}\left\{\sin ^2(2 x+3)\right\}\)

= \(\left\{5 x \cdot\left(\frac{-1}{3}\right)\left(1-x^2\right)^{-13} \cdot(-2 x)+\left(1-x^2\right)^{-13} \cdot 5\right\}+\{2 \sin (2 x+3) \cos (2 x+3) \cdot 2\}\)

= \(\frac{10 x^2}{3\left(1-x^2\right)^{43}}+\frac{5}{\left(1-x^2\right)^{3 / 5}}+2 \sin (4 x+6)\)

= \(\frac{10 x^2+15\left(1-x^2\right)}{3\left(1-x^2\right)^{43}}+2 \sin (4 x+6)\)

= \(\frac{\left(15-5 x^2\right)}{3\left(1-x^2\right)^{4 / 3}}+2 \sin (4 x+6) \text {. }\)

Some Results on Limits

Suppose we have to find \(\lim _{x \rightarrow a} f(x)\), where f(x) contains a series which is capable of being expanded, then after making proper expansion and simplifying, we put x =a.

Some important expansions are given below:

(1) For | x | < 1, we have the bionomial expansion

\((1+x)^n=\left\{1+n x+\frac{n(n-1)}{2 !} x^2+\frac{n(n-1)(n-2)}{3 !} x^3+\ldots\right\}\)

(2) \(\left(\frac{x^n-a^n}{x-a}\right)=\left(x^{n-1}+a x^{n-2}+a^2 x^{n-3}+\ldots+a^{n-1}\right)\)

(3) \(e^x=\left\{1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\ldots+\frac{x^n}{n !}+\ldots\right\}\)

(4) \(a^x=\left\{1+x(\log a)+\frac{x^2}{2 !}(\log a)^2+\ldots\right\}\)

(5) \(\log (1+x)=\left\{x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\ldots\right\}\)

(6) \(\sin x=\left\{x-\frac{x^3}{3 !}+\frac{x^5}{5}-\frac{x^7}{7 !}+\ldots\right\}\)

(7) \(\cos x=\left\{1-\frac{x^2}{2 !}+\frac{x^4}{4 !}-\frac{x^6}{6 !}+\ldots\right\}\)

(8) \(\tan x=\left\{x+\frac{x^3}{3 !}+\frac{2}{15} x^5+\ldots\right\}\)

We shall also make use of the following theorems on limits. The proof of these theorems is beyond the scope of this book.

Fundamental Theorems on Limits (without proof)

(1) \(\lim _{x \rightarrow a}\{f(x)+g(x)\}=\left\{\lim _{x \rightarrow a} f(x)\right\}+\left\{\lim _{x \rightarrow a} g(x)\right\}\)

(2) \(\lim _{x \rightarrow a}\{f(x)-g(x)\}=\left\{\lim _{x \rightarrow a} f(x)\right\}-\left\{\lim _{x \rightarrow a} g(x)\right\}\)

(3) \(\lim _{x \rightarrow a}\{c \cdot f(x)\}=c \cdot\left\{\lim _{x \rightarrow a} f(x)\right\}\), where c is a constant.

(4) \(\lim _{x \rightarrow a}\{f(x) \cdot g(x)\}=\left\{\lim _{x \rightarrow a} f(x)\right\} \cdot\left\{\lim _{x \rightarrow a} g(x)\right\}\)

(5) \(\lim _{x \rightarrow a}\left\{\frac{f(x)}{g(x)}\right\}=\frac{\left\{\lim _{x \rightarrow a} f(x)\right\}}{\left\{\lim _{x \rightarrow a} g(x)\right\}} \text {, provided } \lim _{x \rightarrow a} g(x) \neq 0 \text {. }\)

(6) If f(x) ≤ g(x) for all x then \(\lim _{x \rightarrow a} f(x) \leq \lim _{x \rightarrow a} g(x) .\)

Some Important Theorems on Limits

Theorem 1 Prove that \(\lim _{x \rightarrow a}\left(\frac{x^n-a^n}{x-a}\right)=n a^{n-1}\), where a > 0.

Proof

We know that \(\left(\frac{x^n-a^n}{x-a}\right)=\left(x^{n-1}+a x^{n-2}+a^2 x^{n-3}+\ldots+a^{n-1}\right) .\)

∴ \(\lim _{x \rightarrow a}\left(\frac{x^n-a^n}{x-a}\right)=\lim _{x \rightarrow a}\left(x^{n-1}+a x^{n-2}+a^2 x^{n-3}+\ldots+a^{n-1}\right)\)

= na^n-1 [putting x = a].

Hence, \(\lim _{x \rightarrow a}\left(\frac{x^n-a^n}{x-a}\right)=n a^{n-1} .\)

Theorem 2 Prove that \(\lim _{x \rightarrow 0} \frac{\log (1+x)}{x}=1\)

Proof

Expanding log(1+x), we get

\(\lim _{x \rightarrow 0} \frac{\log (1+x)}{x}=\lim _{x \rightarrow 0} \frac{\left(x-\frac{x^2}{2}+\frac{x^3}{3}-\ldots\right)}{x}\)

= \(\lim _{x \rightarrow 0}\left(1-\frac{x}{2}+\frac{x^2}{3}-\ldots\right)=1\) [putting x = 0].

Hence, \(\lim _{x \rightarrow 0} \frac{\log (1+x)}{x}=1\)

Theorem 3 Prove that \(\lim _{x \rightarrow 0}\left(\frac{e^x-1}{x}\right)=1\)

Proof

Expanding e^x, we get

\(\lim _{x \rightarrow 0}\left(\frac{e^x-1}{x}\right)=\lim _{x \rightarrow 0}\left\{\frac{\left(1+x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\ldots\right)-1}{x}\right\}\)

= \(\lim _{x \rightarrow 0} \frac{\left(x+\frac{x^2}{2 !}+\frac{x^3}{3 !}+\ldots\right)}{x}\)

= \(\lim _{x \rightarrow 0}\left(1+\frac{x}{2}+\frac{x^2}{6}+\ldots\right)=1\) [putting x = 0].

Hence, \(\lim _{x \rightarrow 0}\left(\frac{e^x-1}{x}\right)=1\)

Step-by-Step Solutions to Differentiation Problems

Theorem 4 Prove that \(\lim _{x \rightarrow 0}(1+x)^{1 / x}=e\)

Proof

Expanding (1+x)^1/x we get

\(\lim _{x \rightarrow 0}(1+x)^{1 / x}=\lim _{x \rightarrow 0}\left\{1+\frac{1}{x} \cdot x+\frac{\frac{1}{x}\left(\frac{1}{x}-1\right)}{2 !} \cdot x^2+\frac{\frac{1}{x}\left(\frac{1}{x}-1\right)\left(\frac{1}{x}-2\right)}{3 !} \cdot x^3+\ldots\right\}\)

= \(\lim _{x \rightarrow 0}\left\{1+1+\frac{(1-x)}{2 !}+\frac{(1-x)(1-2 x)}{3 !}+\ldots\right\}\)

= \(\left(1+1+\frac{1}{2 !}+\frac{1}{3 !}+\ldots\right)=e\)

∴ \(\lim _{x \rightarrow 0}(1+x)^{1 / x}=e\)

Theorem 5 Prove that \(\lim _{x \rightarrow-}\left(1+\frac{1}{x}\right)^x=e .\)

Proof

Putting \(\frac{1}{x}\) = y, we get

\(\lim _{x \rightarrow 0}\left(1+\frac{1}{x}\right)^x=\lim _{x \rightarrow 0}(1+y)^{1 / y}=e\) [∵ x → ∞, \(\frac{1}{x}\) → 0 ⇒ y → 0].

Hence, \(\lim _{x \rightarrow-}\left(1+\frac{1}{x}\right)^x=e .\)

Theorem 6 Prove that

(1) \(\lim _{x \rightarrow \infty} \frac{1}{x}=0\) and

(2) \(\lim _{x \rightarrow-\infty} \frac{1}{x}=\infty .\)

Proof

(1) Putting \(\frac{1}{x}\) = y, we get

\(\lim _{x \rightarrow \infty} \frac{1}{x}=\lim _{x \rightarrow \infty} y=0\) [as, x → ∞, \(\frac{1}{x}\) → 0 ⇒ y → 0].

Hence, \(\lim _{x \rightarrow \infty} \frac{1}{x}=0\)

(2) Clearly, when x → 0, then \(\frac{1}{x}\) → ∞.

∴ \(\lim _{x \rightarrow-\infty} \frac{1}{x}=\infty .\)

2. Derivatives of Exponential and Logarithmic Functions

Exponential Function

Let a be a real number such that a > 1.

Then, f(x) = a^x is called an exponential function.

Its domain = R and range = R⁺.

When a = e, we have the exponential function, f(x) = e^x.

This is called natural exponential function.

Logarithmic Function

Let a be a real number such that a > 1.

If ax = b, we define, log_ax = b.

We say that log of x to the base a is equal to b.

log₁₀ x is called common logarithm of x.

log_ex is called natural logarithm of x and we denote it simply by log x.

It is easy to verify the following results:

(1) log(xy) = (log x) + (log y)

(2) log \frac{x}{y} = (log x) – (log y)

(3) log (xⁿ) = n log x

(4) \(\log _a x=\frac{1}{\log _x a}\)

(5) log_xx = 1 and log 1 = 0

Derivatives of Exponential and Logarithmic Functions

We have

(1) \(\frac{d}{d x}\left(e^x\right)=e^x\)

(2) \(\frac{d}{d x}(\log x)=\frac{1}{x}\)

Derivative of a^x

Let y = a^x. Then, log y = x log a …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\log a\) ⇒ \(\frac{d y}{d x}=y(\log a)\)

⇒ \(\frac{d y}{d x}=a^x(\log a) .\)

Hence, \(\frac{d}{d x}\left(a^x\right)=a^x(\log a) .\)

Summary

(1) \(\frac{d}{d x}\left(e^x\right)=e^x\)

(2) \(\frac{d}{d x}\left(a^x\right)=a^x(\log a)\)

(3) \(\frac{d}{d x}(\log x)=\frac{1}{x}\)

(4) \(\frac{d}{d x}\left(\log _a x\right)=\frac{1}{x \log a}\)

Solved Examples

Example 1 Differentiate each of the following w.r.t. x:

(1) \(e^{x^2}\)

(2) e^-3x

(3) e^{cos x}

Solution

(1) Let y = \(e^{x^2}\).

y = e^t and t = x²

⇒ \(\frac{d y}{d t}=e^t \text { and } \frac{d t}{d x}=2 x\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\left(e^t \times 2 x\right)=\left(e^{x^2} \times 2 x\right)=2 x e^{x^2}\)

Hence, \(\frac{d}{d x}\left(e^{x^2}\right)=2 x e^{x^2} .\)

(2) Let y = e^-3x.

Puting -3x = t, we get

y = e^t and t = -3x

⇒ \(\frac{d y}{d t}=e^t \text { and } \frac{d t}{d x}=-3\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=-3 e^t=-3 e^{-3 x} .\)

Hence, \(\frac{d}{d x}\left(e^{-3 x}\right)=-3 e^{-3 x} .\)

(3) Let y = e^{cos x}

Putting cos x = t, we get

y = e^t and t = cos x

⇒ \(\frac{d y}{d t}=e^t \text { and } \frac{d t}{d x}=-\sin x\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\left(-e^t \sin x\right)=\left(-e^{\cos x} \sin x\right)\)

Hence, \(\frac{d}{d x}\left(e^{\cos x}\right)=-e^{\cos x} \sin x .\)

Key Rules of Differentiation Explained

Example 2 Differentiate each of the following w.r.t. x:

(1) sin (log x), x > 0

(2) log(log x), x > 1

Solution

(1) Let y = sin(log x).

Putting log x = t, we get

y = sin t and t = log x

⇒ \(\frac{d y}{d t}=\cos t \text { and } \frac{d t}{d x}=\frac{1}{x}\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\left(\cos t \times \frac{1}{x}\right)=\cos (\log x) \times \frac{1}{x}=\frac{\cos (\log x)}{x} .\)

Hence, \(\frac{d}{d x}\{\sin (\log x)\}=\frac{\cos (\log x)}{x} .\)

(2) Let y = log(log x).

Putting log x = t, we get

y = log t and t = log x

⇒ \(\frac{d y}{d t}=\frac{1}{t} \text { and } \frac{d t}{d x}=\frac{1}{x}\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\left(\frac{1}{t} \times \frac{1}{x}\right)=\left(\frac{1}{\log x} \times \frac{1}{x}\right)=\frac{1}{(x \log x)} .\)

∴ \(\frac{d}{d x}\{\log (\log x)\}=\frac{1}{(x \log x)}\)

Example 3 If y = \(e^{\sqrt{\cot x}} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Given: y = \(e^{\sqrt{\cot x}}\)

Putting cot x = t and \(\sqrt{\cot x}=\sqrt{t}\) = u, we get

y = e^u, u = √t and t = cot x

⇒ \(\frac{d y}{d u}=e^u, \frac{d u}{d t}=\frac{1}{2} t^{-1 / 2}=\frac{1}{2 \sqrt{t}} \text { and } \frac{d t}{d x}=-{cosec}^2 x\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= \(\left\{e^\mu \cdot \frac{1}{2 \sqrt{t}} \cdot\left(-{cosec}^2 x\right)\right\}=e^{\sqrt{\cot x}} \cdot \frac{1}{2 \sqrt{\cot x}} \cdot\left(-{cosec}^2 x\right)\)

= \(\frac{\left(-{cosec}^2 x\right) e^{\sqrt{\cot x}}}{2 \sqrt{\cot x}}\)

Example 4 If y = \(\log \tan \frac{x}{2}, \text { find } \frac{d y}{d x}\)

Solution

Given: y = \(\log \tan \frac{x}{2}\).

Putting \(\frac{x}{2}\) = t and tan\(\frac{x}{2}\) = tan t = u, we get

y = log u, u = tan t and t = \(\frac{x}{2}\)

⇒ \(\frac{d y}{d u}=\frac{1}{2} u^{-t / 2}=\frac{1}{2 \sqrt{u}}, \frac{d u}{d t}=e^t \text { and } \frac{d t}{d x}=\frac{1}{2} x^{-1 / 2}=\frac{1}{2 \sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= \(\left(\frac{1}{2 \sqrt{u}} \times e^t \times \frac{1}{2 \sqrt{x}}\right)=\left\{\frac{1}{2 \sqrt{u}} \times u \times \frac{1}{2 \sqrt{x}}\right\}=\frac{\sqrt{u}}{4 \sqrt{x}}=\frac{e^{\frac{1}{2} t}}{4 \sqrt{x}}\)

= \(\frac{e^{\frac{1}{2} \sqrt{x}}}{4 \sqrt{x}}\).

Example 5 If y = \(\frac{1}{\log \cos x} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Given: y = (log cos x)^-1.

Putting cos x = t and log cos x = log t = u, we get

y = u^-1 = \(\frac{1}{u}\), u = log t and t = cos x

⇒ \(\frac{d y}{d u}=\frac{-1}{u^2}, \frac{d u}{d t}=\frac{1}{t} \text { and } \frac{d t}{d x}=-\sin x\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= \(\left\{\frac{-1}{u^2} \times \frac{1}{t} \times(-\sin x)\right\}=\left\{\frac{1}{(\log \cos x)^2} \cdot \frac{1}{\cos x} \cdot \sin x\right\}\)

= \(\frac{\tan x}{(\log \cos x)^2}\).

Example 6 If y = \(\sqrt{e^{\sqrt{x}}} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

y = \(\sqrt{e^{\sqrt{x}}} \text {, find } \frac{d y}{d x} \text {. }\)

Putting √x = t, e^√x = e^t = u, we get

y = √u, u = e^t and t = √x

⇒ \(\frac{d y}{d u}=\frac{1}{2} u^{-1 / 2}=\frac{1}{2 \sqrt{u}}, \frac{d u}{d t}=e^t \text { and } \frac{d t}{d x}=\frac{1}{2} x^{-1 / 2}=\frac{1}{2 \sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= \(\left(\frac{1}{2 \sqrt{u}} \times e^t \times \frac{1}{2 \sqrt{x}}\right)=\left\{\frac{1}{2 \sqrt{u}} \times u \times \frac{1}{2 \sqrt{x}}\right\}=\frac{\sqrt{u}}{4 \sqrt{x}}=\frac{e^{\frac{1}{2} t}}{4 \sqrt{x}}\)

= \(\frac{e^{\frac{1}{2} \sqrt{x}}}{4 \sqrt{x}}\)

Example 7 If y = log log log x³, find \(\frac{d y}{d x}\)

Solution

Given

y = log log log x³

Let x³ = t, log x³ = log t = u and log log x³ = log u = v.

Then, y = log v, v = log u, u = log t and t = x³

⇒ \(\frac{d y}{d x}=\left(\frac{d y}{d v} \times \frac{d v}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= \(\left(\frac{1}{v} \times \frac{1}{u} \times \frac{1}{t} \times 3 x^2\right)=\frac{3 x^2}{t u v}\)

= \(\frac{3 x^2}{x^3(\log t)(\log t)}=\frac{3}{x(\log t)(\log \log t)}\)

= \(\frac{3}{x\left(\log x^3\right)\left(\log \log x^3\right)}=\frac{1}{x(\log x)\left(\log \log x^3\right)}\).

Example 8 If y = \(\sqrt{\log \left\{\sin \left(\frac{x^2}{3}-1\right)\right\}} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

y = \(\sqrt{\log \left\{\sin \left(\frac{x^2}{3}-1\right)\right\}} \text {, find } \frac{d y}{d x} \text {. }\)

Put \(\left(\frac{x^2}{3}-1\right)=t, sin \left(\frac{x^2}{3}-1\right)\) = sin t = u

and \(\log \left\{\sin \left(\frac{x^2}{3}-1\right)\right\}=\log u=v\)

Then, y = √v, where v = log u, u = sin t and t = \(\left(\frac{x^2}{3}-1\right)\).

∴ \(\frac{d y}{d v}=\frac{1}{2} v^{-1 / 2}=\frac{1}{2 \sqrt{v}} ; \frac{d v}{d u}=\frac{1}{u} ; \frac{d u}{d t}=\cos t \text { and } \frac{d t}{d x}=\frac{2 x}{3} \text {. }\)

So, \(\frac{d y}{d x}=\left(\frac{d y}{d v} \times \frac{d v}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)\)

= \(\left(\frac{1}{2 \sqrt{v}} \cdot \frac{1}{u} \cdot \cos t \cdot \frac{2 x}{3}\right)\)

= \(\frac{x}{3} \cdot \frac{\cos t}{u \cdot \sqrt{\log u}}=\frac{x}{3} \cdot \frac{\cos t}{\sin t \sqrt{\log \sin t}}\)

[∵ v = log u and u = sin t]

= \(\frac{x \cot t}{3 \sqrt{\log \sin t}}=\frac{x \cot \left(\frac{x^2}{3}-1\right)}{3 \cdot \sqrt{\log \sin \left(\frac{x^2}{3}-1\right)}}\) [∵ t = \(\left(\frac{x^2}{3}-1\right)\)].

Example 9 If y = e^x log (sin 2x), find \(\frac{d y}{d x}\).

Solution

y = e^x log (sin 2x)

We have

\(\frac{d y}{d x}=\frac{d}{d x}\left\{e^x \log (\sin 2 x)\right\}\)

= \(e^x \cdot \frac{d}{d x}\{\log (\sin 2 x)\}+\log (\sin 2 x) \cdot \frac{d}{d x}\left(e^x\right)\)

= \(e^x \cdot\left\{\frac{1}{\sin 2 x} \cdot \cos 2 x \cdot 2\right\}+\log (\sin 2 x) \cdot e^x\)

= 2 e^x cot 2x + ex log(sin 2x)

= e^x {2 cot 2x + log(sin 2x)}.

Common Questions on Differentiation and Their Solutions

Example 10 If y = e^ax cos(bx+c), find \(\frac{d y}{d x}\).

Solution

y = e^ax cos(bx+c)

We have

\(\frac{d y}{d x}=e^{a x} \cdot \frac{d}{d x}\{\cos (b x+c)\}+\cos (b x+c) \cdot \frac{d}{d x}\left(e^{a x}\right)\)

= e^ax . {-b sin(bx+c)} + cos(bx+c) . aeax

= e^ax. {a cos (bx+c) – b sin(bx+c)}.

Example 11 Differentiate \(\log \sqrt{\frac{1+\cos ^2 x}{\left(1-e^{2 x}\right)}}\)

Solution

\(\log \sqrt{\frac{1+\cos ^2 x}{\left(1-e^{2 x}\right)}}\)

Let y = \(\log \sqrt{\frac{1+\cos ^2 x}{\left(1-e^{2 x}\right)}}=\log \left(\frac{1+\cos ^2 x}{1-e^{2 x}}\right)^{1 / 2}=\frac{1}{2} \log \left(\frac{1+\cos ^2 x}{1-e^{2 x}}\right)\)

∴ \(y=\frac{1}{2} \log \left(1+\cos ^2 x\right)-\frac{1}{2} \log \left(1-e^{2 x}\right)\)

⇒ \(\frac{d y}{d x}=\frac{1}{2} \cdot \frac{1}{\left(1+\cos ^2 x\right)}(2 \cos x)(-\sin x)-\frac{1}{2} \cdot \frac{1}{\left(1-e^{2 x}\right)} \cdot\left(-2 e^{2 x}\right)\)

= \(\left\{\frac{-\sin x \cos x}{\left(1+\cos ^2 x\right)}+\frac{e^{2 x}}{\left(1-e^{2 x}\right)}\right\} .\)

Hence, \(\frac{d}{d x}\left\{\log \sqrt{\frac{1+\cos ^2 x}{\left(1-e^{2 x}\right)}}\right\}=\left\{\frac{-\sin x \cos x}{\left(1+\cos ^2 x\right)}+\frac{e^{2 x}}{\left(1-e^{2 x}\right)}\right\} \text {. }\)

Example 12 If y = \(\log \sqrt{\frac{1+\sin ^2 x}{1-\sin x}}, \text { find } \frac{d y}{d x}\).

Solution

We have

y = \(\frac{1}{2} [log (1+sin2x) – log(1-sin x)]\) …(1)

On differentiating (1) w.r.t. x, we get

\(\frac{d y}{d x}=\frac{1}{2} \cdot\left[\frac{d}{d x}\left\{\log \left(1+\sin ^2 x\right)\right\}-\frac{d}{d x}\{\log (1-\sin x)\}\right]\)

= \(\frac{1}{2} \cdot\left\{\frac{2 \sin x \cos x}{\left(1+\sin ^2 x\right)}-\frac{(-\cos x)}{(1-\sin x)}\right\}\)

= \(\frac{1}{2} \cdot\left\{\frac{\sin 2 x}{\left(1+\sin ^2 x\right)}+\frac{\cos x}{(1-\sin x)}\right\} .\)

Example 13 If y = log sin(e^x + 5x + 8), find \(\frac{d y}{d x}\).

Solution

Given: y = log sin(e^x + 5x + 8) …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(\frac{d y}{d x}=\frac{1}{\sin \left(e^x+5 x+8\right)} \cdot \cos \left(e^x+5 x+8\right) \cdot \frac{d}{d x}\left(e^x+5 x+8\right)\)

= {cot (e^x + x + 8)} (e^x + 5) = (e^x + 5). cot (e^x + 5x + 8).

Example 14 If y = \(\sqrt{x^2+1}-\log \left\{\frac{1}{x}+\sqrt{1+\frac{1}{x^2}}\right\} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

We have

y = \(\sqrt{x^2+1}-\log \left\{\frac{1}{x}+\sqrt{1+\frac{1}{x^2}}\right\}\)

⇒ \(y=\sqrt{x^2+1}-\log \left\{1+\sqrt{x^2+1}\right\}+\log x\)

⇒ \(\frac{d y}{d x}=\frac{1}{2}\left(x^2+1\right)^{-1 / 2} \cdot 2 x-\frac{1}{\left\{1+\sqrt{x^2+1}\right\}} \cdot\left\{\frac{1}{2}\left(x^2+1\right)^{-1 / 2} \cdot 2 x\right\}+\frac{1}{x}\)

= \(\frac{x}{\sqrt{x^2+1}}-\frac{1}{\left\{1+\sqrt{x^2+1}\right\}} \cdot \frac{x}{\sqrt{x^2+1}}+\frac{1}{x}\)

= \(\frac{x\left\{1+\sqrt{x^2+1}\right\}-x}{\left(\sqrt{x^2+1}\right)\left\{1+\sqrt{x^2+1}\right\}}+\frac{1}{x}=\frac{x \sqrt{x^2+1}}{\left(\sqrt{x^2+1}\right)\left\{1+\sqrt{x^2+1}\right\}}+\frac{1}{x}\)

= \(\frac{x}{\left\{1+\sqrt{x^2+1}\right\}}+\frac{1}{x}=\frac{\left(x^2+1\right)+\sqrt{x^2+1}}{x\left\{1+\sqrt{x^2+1}\right\}}\)

= \(\frac{\left(\sqrt{x^2+1}\right)\left\{\left(\sqrt{x^2+1}\right)+1\right\}}{x\left\{1+\sqrt{x^2+1}\right\}}=\frac{\sqrt{x^2+1}}{x} .\)

3. Derivaties of Inverse Trigonometric Functions

In the table given below, we mention the domain and range of various inverse trigonometric functions.

Derivatives of Inverse Trigonometric Functions

Example 1 Prove that \(\frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^2}}\), where x ∈ ]-1, 1[.

Solution

\(\frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^2}}\), where x ∈ ]-1, 1[

Let y = sin^-1x, where x ∈ ]-1,1[ and y ∈ \(]-\frac{\pi}{2}, \frac{\pi}{2}[\). Then,

y = sin^-1x ⇒ x = sin y

⇒ \(\frac{d x}{d y}=\cos y \geq 0\) since y = \(]-\frac{\pi}{2}, \frac{\pi}{2}[\)

⇒ \(\frac{d x}{d y}=\sqrt{1-\sin ^2 y}=\sqrt{1-x^2}\)

⇒ \(\frac{d y}{d x}=\frac{1}{\sqrt{1-x^2}} .\)

Example 2 Prove that \(\frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-1}{\sqrt{1-x^2}}\), where x ∈ ]-1, 1[.

Solution

\(\frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-1}{\sqrt{1-x^2}}\), where x ∈ ]-1, 1[.

Let y = cos^-1x, where x ∈ ]-1, 1[ and y ∈ \(]0, \frac{\pi}{2}[\). Then,

y = cos^-1x ⇒ x = cos y

⇒ \(\frac{d x}{d y}=-\sin y\), where sin y > 0, since y ∈ \(]0, \frac{\pi}{2}[\)

⇒ \(\frac{d x}{d y}=-\sqrt{1-\cos ^2 y}=-\sqrt{1-x^2}\)

⇒ \(\frac{d y}{d x}=\frac{-1}{\sqrt{1-x^2}}\)

Hence, \(\frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-1}{\sqrt{1-x^2}} .\)

Example 3 Prove that \(\frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{\left(1+x^2\right)}\), where x ∈ R.

Solution

\(\frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{\left(1+x^2\right)}\), where x ∈ R

Let y = tan^-1x, where x ∈ R and y ∈ \(]-\frac{\pi}{2}, \frac{\pi}{2}[\). Then,

x = tan y

⇒ \(\frac{d x}{d y}=\sec ^2 y=\left(1+\tan ^2 y\right)=\left(1+x^2\right)\)

⇒ \(\frac{d y}{d x}=\frac{1}{\left(1+x^2\right)} .\)

Hence, \(\frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{\left(1+x^2\right)} .\)

Example 4 Prove that \(\frac{d}{d x}\left(\cot ^{-1} x\right)=\frac{-1}{\left(1+x^2\right)}\), where x ∈ R.

Solution

\(\frac{d}{d x}\left(\cot ^{-1} x\right)=\frac{-1}{\left(1+x^2\right)}\), where x ∈ R

Let y = cot^-1x, where x ∈ R and y = ]0,π[. Then,

x = cot y

⇒ \(\frac{d x}{d y}=-{cosec}^2 y=-\left(1+\cot ^2 y\right)=-\left(1+x^2\right)\)

⇒ \(\frac{d y}{d x}=\frac{-1}{\left(1+x^2\right)} .\)

Hence, \(\frac{d}{d x}\left(\cot ^{-1} x\right)=\frac{-1}{\left(1+x^2\right)}\).

Applications of Differentiation in Real Life

Example 5 Prove that \(\frac{d}{d x}\left(\sec ^{-1} x\right)=\frac{1}{|x| \sqrt{x^2-1}}\), where x ∈ R – [-1,1].

Solution

\(\frac{d}{d x}\left(\sec ^{-1} x\right)=\frac{1}{|x| \sqrt{x^2-1}}\), where x ∈ R – [-1,1]

Let y = sec^-1x, where x ∈ R – [-1,1] and y ∈ ]0,π[ – {\(\frac{\pi}{2}\)}. Then,

x = sec y

⇒ \(\frac{d x}{d y}=\sec y \tan y>0\)

⇒ \(\frac{d y}{d x}=\frac{1}{\sec y \tan y}=\frac{1}{\sec y \cdot \sqrt{\sec ^2 y-1}}\)

⇒ \(\frac{d y}{d x}=\frac{1}{|x| \sqrt{x^2-1}}\)

Hence, \(\frac{d}{d x}\left(\sec ^{-1} x\right)=\frac{1}{|x| \sqrt{x^2-1}} .\)

Example 6 Prove that \(\frac{d}{d x}\left({cosec}^{-1} x\right)=\frac{-1}{|x| \sqrt{x^2-1}}\), where x ∈ R – [-1,1].

Solution

\(\frac{d}{d x}\left({cosec}^{-1} x\right)=\frac{-1}{|x| \sqrt{x^2-1}}\), where x ∈ R – [-1,1]

Let y = cosex^-1x, where x ∈ R – [-1,1] and y ∈ \(]-\frac{\pi}{2}, \frac{\pi}{2}[\) – {0}. Then,

x = cosec y

⇒ \(\frac{d x}{d y}= -{cosec} y \cot y, \text { where } {cosec} y \cot y>0\)

⇒ \(\frac{d y}{d x}=\frac{-1}{{cosec} y \cot y}=\frac{-1}{({cosec} y) \sqrt{{cosec}^2 y-1}}=\frac{-1}{|x| \sqrt{x^2-1}} .\)

Summary

(1) \(\frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^2}}\)

(2) \(\frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-1}{\sqrt{1-x^2}}\)

(3) \(\frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{\left(1+x^2\right)}\)

(4) \(\frac{d}{d x}\left(\cot ^{-1} x\right)=\frac{-1}{\left(1+x^2\right)}\)

(5) \(\frac{d}{d x}\left(\sec ^{-1} x\right)=\frac{1}{|x| \sqrt{x^2-1}}\)

(6) \(\frac{d}{d x}\left({cosec}^{-1} x\right)=\frac{-1}{|x| \cdot \sqrt{x^2-1}}\)

Solved Examples

Example 1 Differentiate the following w.r.t. x:

(1) sin^-12x

(2) tan^-1√x

(3) cos^-1(cot x)

Solution

(1) Let y = sin^-12x.

Putting 2x = t, we get y = sin^-1t and t = 2x.

Now, y = sin^-1t ⇒ \(\frac{d y}{d t}=\frac{1}{\sqrt{1-t^2}}\)

And, t = 2x ⇒ \(\frac{d t}{d x}=2\).

∴ \(\frac{d u}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\frac{2}{\sqrt{1-t^2}}=\frac{2}{\sqrt{1-4 x^2}}\) [∵ t = 2x].

Hence, \(\frac{d}{d x}\left(\sin ^{-1} 2 x\right)=\frac{2}{\sqrt{1-4 x^2}} .\)

(2) Let y = tan^-1√x.

Putting √x = t, we get y = tan^-1t and t = √x.

Now, y = tan^-1t ⇒ \(\frac{d y}{d t}=\frac{1}{\left(1+t^2\right)}\)

And, t = √x ⇒ \(\frac{d t}{d x}=\frac{1}{2} x^{-1 / 2}=\frac{1}{2 \sqrt{x}}\)

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\frac{1}{\left(1+t^2\right)} \cdot \frac{1}{2 \sqrt{x}}=\frac{1}{2 \sqrt{x}(1+x)}\) [∵ t = √x]

Hence, \(\frac{d}{d x}\left(\tan ^{-1} \sqrt{x}\right)=\frac{1}{2 \sqrt{x}(1+x)} .\)

(3) Let y = cos^-1(cot x).

Putting cot x = t, we get y = cos^-1t and t = cot x.

Now, y = cos^-1t ⇒ \(\frac{d y}{d t}=\frac{-1}{\sqrt{1-t^2}}\).

And, t = cot x ⇒ \(\frac{d t}{d x}=-{cosec}^2 x .\)

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\frac{{cosec}^2 x}{\sqrt{1-t^2}}=\frac{{cosec}^2 x}{\sqrt{1-\cot ^2 x}}\) [∵ t = cot x].

Hence, \(\frac{d}{d x}\left\{\cos ^{-1}(\cot x)\right\}=\frac{{cosec}^2 x}{\sqrt{1-\cot ^2 x}}\)

Example 2 Differentiate the following w.r.t. x:

(1) sec(tan^-1x)

(2) sin(tan^-1x)

(3) cot(cos^-1x)

Solution

(1) Let y = sec(tan^-1x).

Putting tan^-1x = t, we get y = sec t and t = tan^-1x.

Now, y = sec t ⇒ \(\frac{d y}{d t}=\sec t \tan t\).

And, t = tan^-1x ⇒ \(\frac{d t}{d x}=\frac{1}{\left(1+x^2\right)}\)

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\frac{\sec t \tan t}{\left(1+x^2\right)}=\frac{\left(\sqrt{1+\tan ^2 t}\right)(\tan t)}{\left(1+x^2\right)}\)

= \(\frac{\left(\sqrt{1+x^2}\right) x}{\left(1+x^2\right)}=\frac{x}{\sqrt{1+x^2}}\) [∵ t = tan-1x ⇒ tan t = x].

Hence, \(\frac{d}{d x}\left\{\sec \left(\tan ^{-1} x\right)\right\}=\frac{x}{\sqrt{1+x^2}}\)

(2) Let y = sin(tan^-1x).

Putting tan^-1x = t, we get y = sin t and t = tan^-1x.

Now, y = sin t ⇒ \(\frac{d y}{d t}=\cos t .\)

And, t = tan^-1x ⇒ \(\frac{d t}{d x}=\frac{1}{\left(1+x^2\right)}\)

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\cos t \cdot \frac{1}{\left(1+x^2\right)}=\frac{1}{\left(1+x^2\right)^{3 / 2}}\)

[∵ tan t = x ⇒ \(\cos t=\frac{1}{\sqrt{1+x^2}}\)].

Hence, \(\frac{d}{d x}\left\{\sin \left(\tan ^{-1} x\right)\right\}=\frac{1}{\left(1+x^2\right)^{3 / 2}}\)

(3) Let y = cot(cos^-1x).

Putting cos^-1x = t, we get y = cot t and t = cos^-1x.

Now, y = cot t ⇒ \(\frac{d y}{d t}=-{cosec}^2 t\).

And, t = cos^-1x ⇒ \(\frac{d t}{d x}=\frac{-1}{\sqrt{1-x^2}} .\)

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\frac{{cosec}^2 t}{\sqrt{1-x^2}}=\frac{1}{\left(1-x^2\right)^{3 / 2}}\)

[∵ cos t = x ⇒ \({cosec}^2 t=\frac{1}{\left(1-x^2\right)}\)].

Hence, \(\frac{d}{d x}\left\{\cot \left(\cos ^{-1} x\right)\right\}=\frac{1}{\left(1-x^2\right)^{3 / 2}}\)

Example 3 If y = sin(tan^-12x), prove that \(\frac{d y}{d x}=\frac{2}{\left(1+4 x^2\right)^{3 / 2}} \text {. }\).

Solution

y = sin(tan^-12x)

Putting tan^-12x = t, we get y = sin t and t = tan^-12x.

Now, y = sin t ⇒ \(\frac{d y}{d t}=\cos t .\)

And, t = tan^-12x ⇒ \(\frac{d t}{d x}=\left\{\frac{1}{\left(1+4 x^2\right)} \times 2\right\}=\frac{2}{\left(1+4 x^2\right)} \text {. }\)

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d t} \times \frac{d t}{d x}\right)=\left\{\cos t \times \frac{2}{\left(1+4 x^2\right)}\right\}\) …(1)

Now, t = tan^-12x ⇒ tan t = 2x

⇒ \(\sec t=\sqrt{1+\tan ^2 t}=\sqrt{1+4 x^2}\)

⇒ \(\cos t=\frac{1}{\sec t}=\frac{1}{\sqrt{1+4 x^2}}\) …(2)

Putting the value of cos t from (2) in (1), we get

\(\frac{d y}{d x}=\left\{\frac{1}{\sqrt{1+4 x^2}} \times \frac{2}{\left(1+4 x^2\right)}\right\}=\frac{2}{\left(1+4 x^2\right)^{3 / 2}} .\)

Example 4 Differentiate \(\sqrt{\cot ^{-1} \sqrt{x}}\) w.r.t. x.

Solution

\(\sqrt{\cot ^{-1} \sqrt{x}}\) w.r.t. x

Let y = \(\sqrt{\cot ^{-1} \sqrt{x}}\).

Putting √x = t and cot^-1√x = cot^-1t = u, we get

y = √u, where u = cot^-1t and t = √x.

Now, y = √u ⇒ \(\frac{d y}{d u}=\frac{1}{2} u^{-1 / 2}=\frac{1}{2 \sqrt{u}}\)

u = cot^-1t ⇒ \(\frac{d u}{d t}=\frac{-1}{\left(1+t^2\right)}\).

And, t = √x ⇒ \(\frac{d t}{d x}=\frac{1}{2} x^{-1 / 2}=\frac{1}{2 \sqrt{x}} .\)

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)=\frac{-1}{4 \sqrt{u}\left(1+t^2\right) \sqrt{x}}\)

= \(\frac{-1}{4\left(\sqrt{\cot ^{-1} t}\right)\left(1+t^2\right) \sqrt{x}}\) [∵ u = cot^-1t]

= \(\frac{-1}{4\left(\sqrt{\cot ^{-1} \sqrt{x}}\right)(1+x) \sqrt{x}}\) [∵ t = √x].

Example 5 Differentiate e^tan-1√x w.r.t. x.

Solution

e^tan-1√x w.r.t. x

Let y = e^tan-1√x.

Putting √x = t and tan^-1√x = tan^-1t = u, we get

y = e^u, where u = tan^-1t and t = √x.

Now, y = e^u ⇒ \(\frac{d y}{d u}=e^u\);

u = tan^-1t ⇒ \(\frac{d u}{d t}=\frac{1}{\left(1+t^2\right)}\)

And, t = √x ⇒ \(\frac{d t}{d x}=\frac{1}{2} x^{-1 / 2}=\frac{1}{2 \sqrt{x}}\).

∴ \(\frac{d y}{d x}=\left(\frac{d y}{d u} \times \frac{d u}{d t} \times \frac{d t}{d x}\right)=e^x \cdot \frac{1}{\left(1+t^2\right)} \cdot \frac{1}{2 \sqrt{x}}\)

= \(e^{\tan ^{-1} t} \cdot \frac{1}{\left(1+t^2\right)} \cdot \frac{1}{2 \sqrt{x}}\) [∵ u = tan^-1t]

= \(\frac{e^{\tan ^{-1} \sqrt{x}}}{2 \sqrt{x}(1+x)}\) [∵ t = √x].

Hence, \(\frac{d y}{d x}=\frac{e^{\tan ^{-1} \sqrt{x}}}{2 \sqrt{x}(1+x)}\)

Example 6 If y = \(\frac{x \sin ^{-1} x}{\sqrt{1-x^2}} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

y = \(\frac{x \sin ^{-1} x}{\sqrt{1-x^2}} \text {, find } \frac{d y}{d x} \text {. }\)

y = \(\frac{x \sin ^{-1} x}{\sqrt{1-x^2}}\) …(1)

⇒ \(y \sqrt{1-x^2}=x \sin ^{-1} x \) …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(y \cdot \frac{d}{d x}\left(\sqrt{1-x^2}\right)+\left(\sqrt{1-x^2}\right) \frac{d y}{d x}=x \cdot \frac{d}{d x}\left(\sin ^{-1} x\right)+\sin ^{-1} x \cdot \frac{d}{d x}(x)\)

⇒ \(y \cdot \frac{1}{2}\left(1-x^2\right)^{-\frac{1}{2}} \cdot(-2 x)+\left(\sqrt{1-x^2}\right) \frac{d y}{d x}=x \cdot \frac{1}{\sqrt{1-x^2}}+\sin ^{-1} x \cdot 1\)

⇒ \(\frac{-x y}{\sqrt{1-x^2}}+\left(\sqrt{1-x^2}\right) \frac{d y}{d x}=\frac{x}{\sqrt{1-x^2}}+\sin ^{-1} x\)

⇒ \(\frac{-x y}{\sqrt{1-x^2}}+\left(\sqrt{1-x^2}\right) \frac{d y}{d x}=\frac{x}{\sqrt{1-x^2}}+\sin ^{-1} x\) [using(1)]

⇒ \(-x^2 \sin ^{-1} x+\left(1-x^2\right)^{3 / 2} \frac{d y}{d x}=x\left(\sqrt{1-x^2}\right)+\left(1-x^2\right) \sin ^{-1} x\)

⇒ \(\left(1-x^2\right)^{3 / 2} \frac{d y}{d x}=x\left(\sqrt{1-x^2}\right)+\sin ^{-1} x\)

⇒ \(\frac{d y}{d x}=\frac{x\left(\sqrt{1-x^2}\right)+\sin ^{-1} x}{\left(1-x^2\right)^{3 / 2}} .\)

Example 7 Find \(\frac{d}{d x}\left[\left(\sqrt{1-x^2}\right) \sin ^{-1} x-x\right]\)

Solution

We have

\(\frac{d}{d x}\left[\left(\sqrt{1-x^2}\right) \sin ^{-1} x-x\right]\)

= \(\frac{d}{d x}\left[\left(\sqrt{1-x^2}\right) \sin ^{-1} x\right]-\frac{d}{d x}(x)\)

= \(\left(\sqrt{1-x^2}\right) \cdot \frac{d}{d x}\left(\sin ^{-1} x\right)+\left(\sin ^{-1} x\right) \cdot \frac{d}{d x}\left(\sqrt{1-x^2}\right)-1\)

= \(\left(\sqrt{1-x^2}\right) \cdot \frac{1}{\left(\sqrt{1-x^2}\right)}+\left(\sin ^{-1} x\right) \cdot \frac{1}{2}\left(1-x^2\right)^{-1 / 2} \cdot(-2 x)-1\)

= \(\left\{1-\frac{x \sin ^{-1} x}{\sqrt{1-x^2}}-1\right\}=\frac{-x \sin ^{-1} x}{\sqrt{1-x^2}} \text {. }\)

Example 8 Show that \(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}\right]=\sqrt{a^2-x^2} .\)

Solution

We have

\(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}\right]\)

= \(\frac{d}{d x}\left[\frac{x}{2} \cdot \sqrt{a^2-x^2}\right]+\frac{a^2}{2} \cdot \frac{d}{d x}\left[\sin ^{-1} \frac{x}{a}\right]\)

= \(\frac{x}{2} \cdot \frac{d}{d x}\left(\sqrt{a^2-x^2}\right)+\left(\sqrt{a^2-x^2}\right) \cdot \frac{d}{d x}\left(\frac{x}{2}\right)+\frac{a^2}{2} \cdot \frac{1}{\sqrt{1-\frac{x^2}{a^2}}} \cdot \frac{1}{a}\)

= \(\frac{x}{2} \cdot \frac{1}{2}\left(a^2-x^2\right)^{\frac{-1}{2}} \cdot(-2 x)+\left(\sqrt{a^2-x^2}\right) \cdot \frac{1}{2}+\frac{a^2}{2 \sqrt{a^2-x^2}}\)

= \(\frac{-x^2}{2 \sqrt{a^2-x^2}}+\frac{\sqrt{a^2-x^2}}{2}+\frac{a^2}{2 \sqrt{a^2-x^2}}\)

= \(\frac{-x^2+\left(a^2-x^2\right)+a^2}{2 \sqrt{a^2-x^2}}=\frac{\left(a^2-x^2\right)}{\sqrt{\left(a^2-x^2\right)}}=\sqrt{\left(a^2-x^2\right)}\)

Hence, \(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}\right]=\sqrt{a^2-x^2} .\)

4. Differentiation by Trigonometrical Transformations

Some Useful Results

(1) \((1-\cos x)=2 \sin ^2\left(\frac{x}{2}\right)\)

(2) \((1+\cos x)=2 \cos ^2\left(\frac{x}{2}\right)\)

(3) Sin 3x = (3 sin x – 4 sin³x)

(4) cos 3x = (4 cos³x – 3 cos x)

(5) \(\sin x=\frac{2 \tan (x / 2)}{1+\tan ^2(x / 2)}\)

(6) \(\cos x=\frac{1-\tan ^2(x / 2)}{1+\tan ^2(x / 2)}\)

(7) \(\tan ^{-1} x-\tan ^{-1} y=\tan ^{-1}\left\{\frac{x-y}{1+x y}\right\}\)

(8) \(\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left\{\frac{x+y}{1-x y}\right\}\)

Some Useful Substitutions

Suppose we are given sin^-1f(x), cos^-1f(x), tan^-1f(x), etc.

Rule 1. If f(x) = \(\sqrt{a^2-x^2}\), put x = a sin θ or x = a cos θ.

Rule 2. If f(x) = \(\sqrt{a^2+x^2}\), put x = a tan θ or x = a cot θ.

Rule 3. If f(x) = \(\sqrt{x^2-a^2}\), put x = a sec θ or x = a cosec θ.

Rule 4. If f(x) = \(\sqrt{a-x}\), put x = a cos 2θ.

Solved Examples

Example 1 Differentiate each of the following w.r.t. x:

(1) \(\tan ^{-1}\left(\frac{1-\cos x}{\sin x}\right)\)

(2) \(\tan ^{-1}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\)

Solution

(1) Let y = \(\tan ^{-1}\left(\frac{1-\cos x}{\sin x}\right)=\tan ^{-1}\left\{\frac{2 \sin ^2(x / 2)}{2 \sin (x / 2) \cos (x / 2)}\right\}\)

= \(\tan ^{-1}\left\{\tan \frac{x}{2}\right\}=\frac{x}{2}\)

∴ y = \(\frac{x}{2}\).

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{x}{2}\right)=\frac{1}{2} .\)

(2) Let y = \(\tan ^{-1}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)=\tan ^{-1}\left(\frac{1-\tan x}{1+\tan x}\right)\)

[on dividing num. and denom. by cos x]

= \(\tan ^{-1}\left\{\tan \left(\frac{\pi}{4}-x\right)\right\}=\left(\frac{\pi}{4}-x\right)\)

∴ \(y=\left(\frac{\pi}{4}-x\right)\)

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{\pi}{4}-x\right)=\frac{d}{d x}\left(\frac{\pi}{4}\right)-\frac{d}{d x}(x)=(0-1)=-1\).

Example 2 Differentiate w.r.t. x:

(1) \(\tan ^{-1}\left(\frac{\cos x}{1+\sin x}\right)=\tan ^{-1}\left\{\frac{\sin \left(\frac{\pi}{2}-x\right)}{1+\cos \left(\frac{\pi}{2}-x\right)}\right\}\)

(2) tan^-1(sec x + tan x)

Solution

(1) Let y = \(\tan ^{-1}\left(\frac{\cos x}{1+\sin x}\right)=\tan ^{-1}\left\{\frac{\sin \left(\frac{\pi}{2}-x\right)}{1+\cos \left(\frac{\pi}{2}-x\right)}\right\}\)

= \(\tan ^{-1}\left\{\frac{2 \sin \left(\frac{\pi}{4}-\frac{x}{2}\right) \cos \left(\frac{\pi}{4}-\frac{x}{2}\right)}{2 \cos ^2\left(\frac{\pi}{4}-\frac{x}{2}\right)}\right\}\)

= \(\tan ^{-1}\left\{\tan \left(\frac{\pi}{4}-\frac{x}{2}\right)\right\}=\left(\frac{\pi}{4}-\frac{x}{2}\right)\)

∴ \(y=\left(\frac{\pi}{4}-\frac{x}{2}\right)\)

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{\pi}{4}-\frac{x}{2}\right)=\frac{d}{d x}\left(\frac{\pi}{4}\right)-\frac{d}{d x}\left(\frac{x}{2}\right)=\left(0-\frac{1}{2}\right)=\frac{-1}{2} .\)

(2) Let y = tan^-1(sec x + tan x)

= \(\tan ^{-1}\left(\frac{1}{\cos x}+\frac{\sin x}{\cos x}\right)=\tan ^{-1}\left(\frac{1+\sin x}{\cos x}\right)\)

= \(\tan ^{-1}\left\{\frac{1-\cos \left(\frac{\pi}{2}+x\right)}{\sin \left(\frac{\pi}{2}+x\right)}\right\}\)

{∵ \(\cos \left(\frac{\pi}{2}+x\right)=-\sin x ; \sin \left(\frac{\pi}{2}+x\right)=\cos x\)}

= \(\tan ^{-1}\left\{\frac{2 \sin ^2\left(\frac{\pi}{4}+\frac{x}{2}\right)}{2 \sin \left(\frac{\pi}{4}+\frac{x}{2}\right) \cos \left(\frac{\pi}{4}+\frac{x}{2}\right)}\right\}\)

= \(\tan ^{-1}\left\{\tan \left(\frac{\pi}{4}+\frac{x}{2}\right)\right\}=\left(\frac{\pi}{4}+\frac{x}{2}\right) \text {. }\)

∴ \(y=\left(\frac{\pi}{4}+\frac{x}{2}\right)\)

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{\pi}{4}+\frac{x}{2}\right)=\frac{d}{d x}\left(\frac{\pi}{4}\right)+\frac{d}{d x}\left(\frac{x}{2}\right)=\left(0+\frac{1}{2}\right)=\frac{1}{2} .\)

Example 3 Differentiate w.r.t x:

(1) \(\tan ^{-1}\left\{\sqrt{\frac{1+\cos x}{1-\cos x}}\right\}\)

(2) \(\tan ^{-1}\left\{\sqrt{\frac{1+\sin x}{1-\sin x}}\right\}\)

Solution

(1) Let y = \(\tan ^{-1}\left\{\sqrt{\frac{1+\cos x}{1-\cos x}}\right\}=\tan ^{-1}\left\{\sqrt{\frac{2 \cos ^2(x / 2)}{2 \sin ^2(x / 2)}}\right\}\)

= \(\tan ^{-1}\left(\cot \frac{x}{2}\right)=\tan ^{-1}\left\{\tan \left(\frac{\pi}{2}-\frac{x}{2}\right)\right\}=\left(\frac{\pi}{2}-\frac{x}{2}\right)\)

∴ \(y=\left(\frac{\pi}{2}-\frac{x}{2}\right)\).

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{\pi}{2}-\frac{x}{2}\right)=\frac{d}{d x}\left(\frac{\pi}{2}\right)-\frac{d}{d x}\left(\frac{x}{2}\right)=\left(0-\frac{1}{2}\right)=\frac{-1}{2} .\)

(2) Let y = \(\tan ^{-1}\left\{\sqrt{\frac{1+\sin x}{1-\sin x}}\right\}=\tan ^{-1}\left\{\frac{1-\cos \left(\frac{\pi}{2}+x\right)}{1+\cos \left(\frac{\pi}{2}+x\right)}\right\}^{\frac{1}{2}}\)

= \(\tan ^{-1}\left\{\frac{2 \sin ^2\left(\frac{\pi}{4}+\frac{x}{2}\right)}{2 \cos ^2\left(\frac{\pi}{4}+\frac{x}{2}\right)}\right\}^{\frac{1}{2}}=\tan ^{-1}\left\{\tan \left(\frac{\pi}{4}+\frac{x}{2}\right)\right\}=\left(\frac{\pi}{4}+\frac{x}{2}\right) .\)

∴ \(y=\left(\frac{\pi}{4}+\frac{x}{2}\right)\)

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{\pi}{4}+\frac{x}{2}\right)=\frac{d}{d x}\left(\frac{\pi}{4}\right)+\frac{d}{d x}\left(\frac{x}{2}\right)=\left(0+\frac{1}{2}\right)=\frac{1}{2} .\)

Example 4 Differentiate \(\cos ^{-1}\left\{\sqrt{\frac{1+\cos x}{2}}\right\}\) w.r.t. x.

Solution

Let y = \(\cos ^{-1}\left\{\sqrt{\frac{1+\cos x}{2}}\right\}=\cos ^{-1}\left\{\sqrt{\frac{2 \cos ^2(x / 2)}{2}}\right\}\)

= \(\cos ^{-1}\{\cos (x / 2)\}=\frac{x}{2}\)

∴ y = \(\frac{x}{2}\)

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{x}{2}\right)=\frac{1}{2} .\)

Example 5 If y = \(\cot ^{-1} \sqrt{\frac{1-\sin x}{1+\sin x}}, \text { find } \frac{d y}{d x}\).

Solution

We have

\(y=\cot ^{-1} \sqrt{\frac{1-\sin x}{1+\sin x}}=\cot ^{-1} \sqrt{\frac{1+\cos \left(\frac{\pi}{2}+x\right)}{1-\cos \left(\frac{\pi}{2}+x\right)}}\)

= \(\cot ^{-1} \sqrt{\frac{2 \cos ^2\left(\frac{\pi}{4}+\frac{x}{2}\right)}{2 \sin ^2\left(\frac{\pi}{4}+\frac{x}{2}\right)}}=\cot ^{-1}\left\{\cot \left(\frac{\pi}{4}+\frac{x}{2}\right)\right\}=\left(\frac{\pi}{4}+\frac{x}{2}\right) \text {. }\)

∴ \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{\pi}{4}+\frac{x}{2}\right)=\frac{d}{d x}\left(\frac{\pi}{4}\right)+\frac{d}{d x}\left(\frac{x}{2}\right)=\left(0+\frac{1}{2}\right)=\frac{1}{2} .\)

Example 6 If y = \(\cot ^{-1} \frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}} \text { and } 0<x<\frac{\pi}{2} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

We have

\((1+\sin x)=\left\{\cos ^2(x / 2)+\sin ^2(x / 2)+2 \sin (x / 2) \cos (x / 2)\right\}\)

= \(\{\cos (x / 2)+\sin (x / 2)\}^2 .\)

\((1-\sin x)=\left\{\cos ^2(\pi / 2)+\sin ^2(\pi / 2)-2 \sin (\pi / 2) \cos (\pi / 2)\right\}\)

= \(\{\cos (x / 2)-\sin (x / 2)\}^2 .\)

∴ \(\sqrt{1+\sin x}=\sqrt{\{\cos (x / 2)+\sin (x / 2)\}^2}=\cos \left(\frac{x}{2}\right)+\sin \left(\frac{x}{2}\right)\)

and \(\sqrt{1-\sin x}=\sqrt{\{\cos (x / 2)-\sin (x / 2)\}^2}=\cos \left(\frac{x}{2}\right)-\sin \left(\frac{x}{2}\right)\)

∴ y = \(\cot ^{-1}\left\{\frac{[\cos (x / 2)+\sin (x / 2)]+[\cos (x / 2)-\sin (x / 2)]}{[\cos (x / 2)+\sin (x / 2)]-[\cos (x / 2)-\sin (x / 2)]}\right\}\)

= \(\cot ^1\left\{\frac{2 \cos (x / 2)}{2 \sin (x / 2)}\right\}=\cot ^{-1}\{\cot (x / 2)\}=\frac{x}{2}\)

⇒ \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{x}{2}\right)=\frac{1}{2}\)

Example 7 If y = \(\tan ^{-1} \frac{(\sqrt{1+\sin x}+\sqrt{1-\sin x})}{(\sqrt{1+\sin x}-\sqrt{1-\sin x})} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

We have

y = \(\tan ^{-1}\left\{\frac{(\sqrt{1+\sin x}+\sqrt{1-\sin x})}{(\sqrt{1+\sin x}-\sqrt{1-\sin x})} \times \frac{(\sqrt{1+\sin x}+\sqrt{1-\sin x})}{(\sqrt{1+\sin x}+\sqrt{1-\sin x})}\right\}\)

= \(\tan ^{-1}\left\{\frac{(1+\sin x)+(1-\sin x)+2 \sqrt{1-\sin ^2 x}}{(1+\sin x)-(1-\sin x)}\right\}=\tan ^{-1}\left(\frac{1+\cos x}{\sin x}\right)\)

= \(\tan ^{-1}\left\{\frac{2 \cos ^2(x / 2)}{2 \sin (x / 2) \cos (x / 2)}\right\}=\tan ^{-1}\left\{\cot \frac{x}{2}\right\}=\tan ^{-1}\left\{\tan \left(\frac{\pi}{2}-\frac{x}{2}\right)\right\}\)

= \(\left(\frac{\pi}{2}-\frac{x}{2}\right)\)

∴ \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{\pi}{2}-\frac{x}{2}\right)=\frac{d}{d x}\left(\frac{\pi}{2}\right)-\frac{d}{d x}\left(\frac{x}{2}\right)=\left(0-\frac{1}{2}\right)=-\frac{1}{2} .\)

Example 8 Differentiate w.r.t. x:

(1) \(\cot ^{-1}\left(\frac{1}{x}\right)\)

(2) \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\)

(3) \(\cot ^{-1}\left(\frac{1-x}{1+x}\right)\)

Solution

(1) Let y = \(\cot ^{-1}\left(\frac{1}{x}\right)\)

Putting x = tan θ, we get

\(y=\cot ^{-1}\left(\frac{1}{\tan \theta}\right)=\cot ^{-1}(\cot \theta)=\theta=\tan ^{-1} x \text {. }\)

∴ \(\frac{d y}{d x}=\frac{1}{\left(1+x^2\right)}\).

(2) Let y = \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\)

Putting x = tan θ, we get

\(y=\tan ^{-1}\left(\frac{2 \tan \theta}{1-\tan ^2 \theta}\right)=\tan ^{-1}(\tan 2 \theta)=2 \theta=2 \tan ^{-1} x\).

∴ \(\frac{d y}{d x}=\frac{2}{\left(1+x^2\right)}\)

Hence, \(\frac{d}{d x}\left\{\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\right\}=\frac{2}{\left(1+x^2\right)} .\)

(3) Let y = \(\cot ^{-1}\left(\frac{1-x}{1+x}\right)\)

Putting x = tan θ, we get

\(y=\cot ^{-1}\left(\frac{1-\tan \theta}{1+\tan \theta}\right)=\cot ^{-1}\left\{\tan \left(\frac{\pi}{4}-\theta\right)\right\}\)

= \(\cot ^{-1}\left[\cot \left\{\frac{\pi}{2}-\left(\frac{\pi}{4}-\theta\right)\right\}\right]=\left(\frac{\pi}{4}+\theta\right)=\frac{\pi}{4}+\tan ^{-1} x.\)

∴ \(\frac{d y}{d x}=\frac{1}{\left(1+x^2\right)}\).

Hence, \(\frac{d}{d x}\left\{\cot ^{-1}\left(\frac{1-x}{1+x}\right)\right\}=\frac{1}{\left(1+x^2\right)} .\)

Example 9 Differentiate w.r.t. x:

(1) \(\cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\)

(2) \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\)

(3) \(\sec ^{-1}\left(\frac{1}{2 x^2-1}\right)\)

Solution

(1) Let y = \(\cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\)

Putting x = tan θ, we get

\(y=\cos ^{-1}\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)=\cos ^{-1}(\cos 2 \theta)=2 \theta=2 \tan ^{-1} x \text {. }\)

∴ \(\frac{d y}{d x}=\frac{2}{\left(1+x^2\right)}.\)

Hence, \(\frac{d}{d x}\left\{\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\right\}=\frac{2}{\left(1+x^2\right)}.\)

(2) Let y = \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\)

Putting x = tan θ, we get

\(y=\sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^2 \theta}\right)=\sin ^{-1}(\sin 2 \theta)=2 \theta=2 \tan ^{-1} x \text {. }\)

∴ \(\frac{d y}{d x}=\frac{2}{\left(1+x^2\right)} .\)

Hence, \(\frac{d}{d x}\left\{\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\right\}=\frac{2}{\left(1+x^2\right)} .\)

(3) Let y = \(\sec ^{-1}\left(\frac{1}{2 x^2-1}\right)\)

Putting x = cos θ, we get

\(y=\sec ^{-1}\left(\frac{1}{2 \cos ^2 \theta-1}\right)=\sec ^{-1}\left(\frac{1}{\cos 2 \theta}\right)\)

= sec^-1(sec 2θ) = 2θ = 2 cos-1x.

∴ y = 2 cos^-1x.

Hence, \(\frac{d y}{d x}=2 \frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-2}{\sqrt{1-x^2}} .\)

Example 10 Differentiate w.r.t. x:

(1) cos^-1(4x³ – 3x)

(2) \(\sin ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\)

(3) \(\sec ^{-1}\left(\frac{x^2+1}{x^2-1}\right)\)

Solution

(1) Let y = cos^-1(4x³ – 3x).

Putting x = cos θ, we get

y = cos^-1(4 cos³θ – 3 cos θ) = cos^-1(cos 3 θ) = 3θ.

∴ y = 3θ ⇒ y = 3 cos^-1x

⇒ \(\frac{d y}{d x}=\frac{-3}{\sqrt{1-x^2}}\)

(2) Let y = \(\sin ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\)

Putting x = tan θ, we get

\(y=\sin ^{-1}\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)=\sin ^{-1}(\cos 2 \theta)=\sin ^{-1}\left[\sin \left(\frac{\pi}{2}-2 \theta\right)\right]\)

= \(\left(\frac{\pi}{2}-2 \theta\right)=\left(\frac{\pi}{2}-2 \tan ^{-1} x\right)\)

∴ y = \(\left(\frac{\pi}{2}-2 \tan ^{-1} x\right)\).

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left(\frac{\pi}{2}-2 \tan ^{-1} x\right)=\frac{d}{d x}\left(\frac{\pi}{2}\right)-2 \cdot \frac{d}{d x}\left(\tan ^{-1} x\right)\)

= \(\left\{0-\frac{2}{\left(1+x^2\right)}\right\}=\frac{-2}{\left(1+x^2\right)}\).

(3) Let y = \(\sec ^{-1}\left(\frac{x^2+1}{x^2-1}\right)\)

Putting x = cot θ, we get

y = \(\sec ^{-1}\left(\frac{\cot ^2 \theta+1}{\cot ^2 \theta-1}\right)=\sec ^{-1}\left(\frac{1+\tan ^2 \theta}{1-\tan ^2 \theta}\right)\)

= sec^-1 (sec 2θ) = 2θ = 2 cot^-1x.

∴ \(\frac{d y}{d x}=\frac{-2}{\left(1+x^2\right)}\).

Hence, \(\frac{d}{d x}\left\{\sec ^{-1}\left(\frac{x^2+1}{x^2-1}\right)\right\}=\frac{-2}{\left(1+x^2\right)}\).

Examples of Higher-Order Derivatives

Example 11 Differentiate \(\cot ^{-1}\left(\frac{1-x}{1+x}\right)\) w.r.t. x.

Solution

Let y = \(\cot ^{-1}\left(\frac{1-x}{1+x}\right)\)

Putting x = tan θ, we get

y = \(\cot ^{-1}\left(\frac{1-\tan \theta}{1+\tan \theta}\right)=\cot ^{-1}\left\{\tan \left(\frac{\pi}{4}-\theta\right)\right\}\)

= \(\cot ^{-1}\left[\cot \left\{\frac{\pi}{2}-\left(\frac{\pi}{4}-\theta\right)\right]\right]=\cot ^{-1}\left[\cot \left(\frac{\pi}{4}+\theta\right)\right]\)

= \(\left(\frac{\pi}{4}+\theta\right)\)

= \(\frac{\pi}{4}+\tan ^{-1} x\) [∵ x = tan θ ⇒ θ = tan^-1x].

∴ \(y=\frac{\pi}{4}+\tan ^{-1} x\)

⇒ \(\frac{d y}{d x}=\frac{d}{d x}\left\{\frac{\pi}{4}+\tan ^{-1} x\right\}=\frac{d}{d x}\left(\frac{\pi}{4}\right)+\frac{d}{d x}\left(\tan ^{-1} x\right)\)

= \(\left\{0+\frac{1}{\left(1+x^2\right)}\right\}=\frac{1}{\left(1+x^2\right)}\).

Hence, \(\frac{d y}{d x}=\frac{1}{\left(1+x^2\right)}\).

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

Example 12 Differentiate \(\tan ^{-1}\left\{\frac{\sqrt{1+x^2}-1}{x}\right\}\) w.r.t x.

Solution

Let y = \(\tan ^{-1}\left\{\frac{\sqrt{1+x^2}-1}{x}\right\}\).

Putting x = tan θ, we get

y = \(\tan ^{-1}\left\{\frac{\sqrt{1+\tan ^2 \theta}-1}{\tan \theta}\right\}=\tan ^{-1}\left\{\frac{\sec \theta-1}{\tan \theta}\right\}\)

= \(\tan ^{-1}\left\{\frac{\left(\frac{1}{\cos \theta}-1\right)}{\sin \theta} \cdot \cos \theta\right\}=\tan ^{-1}\left(\frac{1-\cos \theta}{\sin \theta}\right)\)

= \(\tan ^{-1}\left\{\frac{2 \sin ^2(\theta / 2)}{2 \sin (\theta / 2) \cos (\theta / 2)}\right\}=\tan ^{-1}\left\{\tan \frac{\theta}{2}\right\}\)

= \(\frac{\theta}{2}=\frac{1}{2} \tan ^{-1} x\)

∴ y = \(\frac{1}{2}\) tan^-1x

⇒ \(\frac{d y}{d x}=\frac{1}{2} \cdot \frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{2\left(1+x^2\right)}\)

Example 13 If \(y=\tan ^{-1}\left\{\frac{\sqrt{1+x^2}-\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right\} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Putting x² = cos θ, we get

y = \(\tan ^{-1}\left\{\frac{\sqrt{1+\cos \theta}-\sqrt{1-\cos \theta}}{\sqrt{1+\cos \theta}-\sqrt{1-\cos \theta}}\right\}\)

= \(\tan ^{-1}\left\{\frac{\sqrt{2 \cos ^2(\theta / 2)}-\sqrt{2 \sin ^2(\theta / 2)}}{\sqrt{2 \cos ^2(\theta / 2)}+\sqrt{2 \sin ^2(\theta / 2)}}\right\}\)

= \(\tan ^{-1}\left\{\frac{\sqrt{2} \cos (\theta / 2)-\sqrt{2} \sin (\theta / 2)}{\sqrt{2} \cos (\theta / 2)+\sqrt{2} \sin (\theta / 2)}\right\}=\tan ^{-1}\left\{\frac{\cos (\theta / 2)-\sin (\theta / 2)}{\cos (\theta / 2)-\sin (\theta / 2)}\right\}\)

= \(\tan ^{-1}\left\{\frac{1-\tan (\theta / 2)}{1+\tan (\theta / 2)}\right\}=\tan ^{-1}\left\{\tan \left(\frac{\pi}{4}-\frac{\theta}{2}\right)\right\}\)

= \(\left(\frac{\pi}{4}-\frac{\theta}{2}\right)=\frac{\pi}{4}-\frac{1}{2} \cos ^{-1} x^2\)

∴ \(\frac{d y}{d x}=\frac{d}{d x}\left\{\frac{\pi}{4}-\frac{1}{2} \cos ^{-1} x^2\right\}=\frac{d}{d x}\left(\frac{\pi}{4}\right)-\frac{1}{2} \cdot \frac{d}{d x}\left(\cos ^{-1} x^2\right)\)

= \(\left\{0-\frac{1}{2} \cdot \frac{-1}{\sqrt{1-x^4}} \cdot 2 x\right\}=\frac{x}{\sqrt{1-x^4}}\)

Example 14 If y = \(\sin ^{-1}\left[x \sqrt{1-x}-\sqrt{x} \sqrt{1-x^2}\right] \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Putting x = sin θ and √x = sin Φ, we get

y = sin^-1[sin θ cos Φ – sin Φ cos θ] = sin^-1[sin (θ-Φ)]

= (θ – Φ) = sin^-1x – sin^-1√x.

∴ y = sin^-1x – sin^-1√x

⇒ \(\frac{d y}{d x}=\frac{d}{d x}\left\{\sin ^{-1} x-\sin ^{-1} \sqrt{x}\right\}\)

= \(\frac{d}{d x}\left(\sin ^{-1} x\right)-\frac{d}{d x}\left\{\sin ^{-1} \sqrt{x}\right\}\)

= \(\left[\frac{1}{\sqrt{1-x^2}}-\frac{1}{2 \sqrt{x} \cdot \sqrt{1-x}}\right]\)

Example 15 Differentiate \(\tan ^{-1}\left(\frac{x^{1 / 3}+a^{1 / 3}}{1-x^{1 / 3} a^{1 / 3}}\right)\) w.r.t. x.

Solution

Let y = \(\tan ^{-1}\left(\frac{x^{1 / 3}+a^{1 / 3}}{1-x^{1 / 3} a^{1 / 3}}\right)\).

Putting x^1/3 = tan θ and a^1/3 = tan Φ, we get

y = \(\tan ^{-1}\left(\frac{\tan \theta+\tan \phi}{1-\tan \theta \tan \phi}\right)=\tan ^{-1}[\tan (\theta+\phi)]\)

= (θ + Φ) = tan^-1(x^1/3) + tan^-1(a^1/3).

∴ \(\frac{d y}{d x}=\frac{d}{d x}\left\{\tan ^{-1}\left(x^{1 / 3}\right)+\tan ^{-1}\left(a^{1 / 3}\right)\right\}\)

= \(\frac{d}{d x}\left\{\tan ^{-1}\left(x^{1 / 3}\right)\right\}+\frac{d}{d x}\left\{\tan ^{-1}\left(a^{1 / 3}\right)\right\}=\frac{1}{\left(1+x^{2 / 3}\right)} \cdot \frac{1}{3} x^{-2 / 3}\)

= \(\frac{1}{3 x^{2 / 3}\left(1+x^{2 / 3}\right)}\) [∵ tan^-1(a^1/3) = constant].

Example 16 Differentiate \(\tan ^{-1}\left(\frac{a \cos x-b \sin x}{b \cos x+a \sin x}\right)\) w.r.t. x.

Solution

Let y = \(\tan ^{-1}\left(\frac{a \cos x-b \sin x}{b \cos x+a \sin x}\right)\).

Putting a = r sin θ and b = r cos θ, we get

y = \(\tan ^{-1}\left\{\frac{r(\sin \theta \cos x-\cos \theta \sin x)}{r(\cos \theta \cos x+\sin \theta \sin x)}\right\}\)

= \(\tan ^{-1}\left\{\frac{\sin (\theta-x)}{\cos (\theta-x)}\right\}=\tan ^{-1}\{\tan (\theta-x)\}\)

= \(\theta-x=\left(\tan ^{-1} \frac{a}{b}-x\right)\) [∵ \(\frac{a}{b}\) = tan θ ⇒ θ = tan^-1 \(\frac{a}{b}\)].

∴ \(\frac{d y}{d x}=\frac{d}{d x}\left(\tan ^{-1} \frac{a}{b}-x\right)\)

= \(\frac{d}{d x}\left(\tan ^{-1} \frac{a}{b}\right)-\frac{d}{d x}(x)=-1\) [∵ tan^-1 \(\frac{a}{b}\) = constant].

Example 17 If y = \(\sin ^{-1}\left\{\frac{\sqrt{1+x}-\sqrt{1-x}}{2}\right\} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Putting x = cos 2θ, we get

y = \(\sin ^{-1}\left\{\frac{\sqrt{1+\cos 2 \theta}-\sqrt{1-\cos 2 \theta}}{2}\right\}\)

= \(\sin ^{-1}\left\{\frac{\sqrt{2 \cos ^2 \theta}-\sqrt{2 \sin ^2 \theta}}{2}\right\}=\sin ^{-1}\left\{\frac{\sqrt{2} \cos \theta-\sqrt{2} \sin \theta}{2}\right\}\)

= \(\sin ^{-1}\left\{\frac{1}{\sqrt{2}} \cos \theta-\frac{1}{\sqrt{2}} \sin \theta\right\}=\sin ^{-1}\left\{\sin \frac{\pi}{4} \cos \theta-\cos \frac{\pi}{4} \sin \theta\right\}\)

= \(\sin ^{-1}\left\{\sin \left(\frac{\pi}{4}-\theta\right)\right\}\)

= \(\left(\frac{\pi}{4}-\theta\right)=\left(\frac{\pi}{4}-\frac{1}{2} \cos ^{-1} x\right)\)

[∵ x = cos 2θ ⇒ 2θ = cos^-1x ⇒ θ = \(\frac{1}{2}\)cos-1x]

∴ y = \(\frac{\pi}{4}-\frac{1}{2} \cos ^{-1} x\)

Hence, \(\frac{d y}{d x}=\frac{d}{d x}\left\{\frac{\pi}{4}-\frac{1}{2} \cos ^{-1} x\right\}=\frac{d}{d x}\left(\frac{\pi}{4}\right)-\frac{1}{2} \frac{d}{d x}\left(\cos ^{-1} x\right)\)

= \(\left\{0-\frac{1}{2} \cdot \frac{(-1)}{\sqrt{1-x^2}}\right\}=\frac{1}{2 \sqrt{1-x^2}}\).

Example 18 Differentiate each of the following w.r.t. x:

(1) \(\tan ^{-1}\left(\sqrt{1+x^2}+x\right)\)

(2) \(\tan ^{-1}\left(\sqrt{1+x^2}-x\right)\)

Solution

(1) Let y = \(\tan ^{-1}\left(\sqrt{1+x^2}+x\right)\)

Putting x = cot θ, we get

y = \(\tan ^{-1}({cosec} \theta+\cot \theta)=\tan ^{-1}\left(\frac{1}{\sin \theta}+\frac{\cos \theta}{\sin \theta}\right)\)

= \(\tan ^{-1}\left(\frac{1+\cos \theta}{\sin \theta}\right)=\tan ^{-1}\left(\frac{2 \cos ^2(\theta / 2)}{2 \sin (\theta / 2) \cos (\theta / 2)}\right)\)

= \(\tan ^{-1}\left(\cot \frac{\theta}{2}\right)=\tan ^{-1}\left\{\tan \left(\frac{\pi}{2}-\frac{\theta}{2}\right)\right\}\)

= \(\frac{\pi}{2}-\frac{1}{2} \theta=\frac{\pi}{2}-\frac{1}{2} \cot ^{-1} x .\)

∴ \(\frac{d y}{d x}=-\frac{1}{2} \cdot \frac{-1}{\left(1+x^2\right)}=\frac{1}{2\left(1+x^2\right)}\)

Hence, \(\frac{d}{d x}\left\{\tan ^{-1}\left(\sqrt{1+x^2}+x\right)\right\}=\frac{1}{2\left(1+x^2\right)} .\)

(2) Let y = \(\tan ^{-1}\left(\sqrt{1+x^2}-x\right)\)

Putting x = cot θ, we get

y = \(\tan ^{-1}({cosec} \theta-\cot \theta)=\tan ^{-1}\left(\frac{1}{\sin \theta}-\frac{\cos \theta}{\sin \theta}\right)\)

= \(\tan ^{-1}\left(\frac{1-\cos \theta}{\sin \theta}\right)=\tan ^{-1}\left\{\frac{2 \sin ^2(\theta / 2)}{2 \sin (\theta / 2) \cos (\theta / 2)}\right\}\)

= \(\tan ^{-1}\left(\tan \frac{\theta}{2}\right)=\frac{1}{2} \theta=\frac{1}{2} \cot ^{-1} x\)

∴ \(\frac{d y}{d x}=\frac{-1}{2\left(1+x^2\right)}\).

Hence, \(\frac{d}{d x}\left\{\tan ^{-1}\left(\sqrt{1+x^2}-x\right)\right\}=\frac{-1}{2\left(1+x^2\right)}\).

Example 19 Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1+x^2}+1}{x}\right)\) w.r.t. x.

Solution

Let y = \(\tan ^{-1}\left(\frac{\sqrt{1+x^2}+1}{x}\right)\).

Putting x = tan θ, we get

y = \(\tan ^{-1}\left(\frac{\sec \theta+1}{\tan \theta}\right)=\tan ^{-1}\left(\frac{1+\cos \theta}{\sin \theta}\right)\)

= \(\tan ^{-1}\left\{\frac{2 \cos ^2(\theta / 2)}{2 \sin (\theta / 2) \cos (\theta / 2)}\right\}=\tan ^{-1}\left\{\cot \frac{\theta}{2}\right\}\)

= \(\tan ^{-1}\left\{\tan \left(\frac{\pi}{2}-\frac{\theta}{2}\right)\right\}=\left(\frac{\pi}{2}-\frac{\theta}{2}\right)=\frac{\pi}{2}-\frac{1}{2} \tan ^{-1} x\)

∴ \(\frac{d y}{d x}=-\frac{1}{2\left(1+x^2\right)} .\)

Hence, \(\frac{d}{d x}\left\{\tan ^{-1}\left(\frac{\sqrt{1+x^2}+1}{x}\right)\right\}=\frac{-1}{2\left(1+x^2\right)}\).

Example 20 Differentiate \(\cot ^{-1}\left(\sqrt{1+x^2}+x\right)\) w.r.t. x.

Solution

Let y = \(\cot ^{-1}\left(\sqrt{1+x^2}+x\right)\).

Putting x = cot θ, we get

y = \(\cot ^{-1}({cosec} \theta+\cot \theta)=\cot ^{-1}\left(\frac{1}{\sin \theta}+\frac{\cos \theta}{\sin \theta}\right)\)

= \(\cot ^{-1}\left(\frac{1+\cos \theta}{\sin \theta}\right)=\cot ^{-1}\left\{\frac{2 \cos ^2(\theta / 2)}{2 \sin (\theta / 2) \cos (\theta / 2)}\right\}\)

= \(\cot ^{-1}\left(\cot \frac{\theta}{2}\right)=\frac{\theta}{2}=\frac{1}{2} \cot ^{-1} x \text {. }\)

∴ \(\frac{d y}{d x}=\frac{-1}{2\left(1+x^2\right)}\).

Hence, \(\frac{d}{d x}\left\{\cot ^{-1}\left(\sqrt{1+x^2}+x\right)\right\}=\frac{-1}{2\left(1+x^2\right)}\).

Example 21 Differentiate \(\cos ^{-1}\left(\frac{x-x^{-1}}{x+x^{-1}}\right)\) w.r.t. x.

Solution

Let y = \(\cos ^{-1}\left(\frac{x-x^{-1}}{x+x^{-1}}\right)=\cos ^{-1}\left\{\frac{\left(x-\frac{1}{x}\right)}{\left(x+\frac{1}{x}\right)}\right\}=\cos ^{-1}\left(\frac{x^2-1}{x^2+1}\right) \text {. }\)

Putting x = tan θ, we get

y = \(\cos ^{-1}\left(\frac{\tan ^2 \theta-1}{\tan ^2 \theta+1}\right)=\cos ^{-1}(-\cos 2 \theta)=\cos ^{-1}\{\cos (\pi-2 \theta)\}\)

= (π – 2θ) = π – 2 tan^-1x.

∴ \(\frac{d y}{d x}=\frac{d}{d x}\left(\pi-2 \tan ^{-1} x\right)=\frac{d}{d x}(\pi)-2 \cdot \frac{d}{d x}\left(\tan ^{-1} x\right)=\left(0-\frac{2}{1+x^2}\right)\)

= \(\frac{-2}{\left(1+x^2\right)}\).

Example 22 If y = \(\tan ^{-1}\left(\frac{\sqrt{a}-\sqrt{x}}{1+\sqrt{a x}}\right) \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Putting √a = tan α and √x = tan θ, we get

y = \(\tan ^{-1}\left(\frac{\tan \alpha-\tan \theta}{1+\tan \alpha \tan \theta}\right)=\tan ^{-1}\{\tan (\alpha-\theta)\}=(\alpha-\theta)\)

∴ y = (α – θ) ⇒ y = tan^-1√a – tan^-1√x

⇒ \(\frac{d y}{d x}=\frac{d}{d x}\left(\tan ^{-1} \sqrt{a}\right)-\frac{d}{d x}\left(\tan ^{-1} \sqrt{x}\right)\)

= \(\left\{0-\frac{1}{(1+x)} \cdot \frac{1}{2} x^{-1 / 2}\right\}=\frac{-1}{2 \sqrt{x}(1+x)}\).

Hence, \(\frac{d y}{d x}=\frac{-1}{2 \sqrt{x}(1+x)}\).

Example 23 If y = \(\sin ^{-1}\left\{\frac{5 x+12 \sqrt{1-x^2}}{13}\right\}, \text { find } \frac{d y}{d x} \text {. }\)

Solution

We have

y = \(\sin ^{-1}\left\{\frac{5 x+12 \sqrt{1-x^2}}{13}\right\}\)

Let \(\frac{5}{13}\) = sin α and x = cos θ. Then,

cos α = \(\sqrt{1-\frac{25}{169}}=\sqrt{\frac{144}{169}}=\frac{12}{13}\)

and \(\sqrt{1-x^2}=\sqrt{1-\cos ^2 \theta}=\sqrt{\sin ^2 \theta}=\sin \theta\)

∴ y = sin^-1{sin α cos θ + cos α sin θ}

= sin^-1{sin(α+θ)}

= \(\alpha+\theta=\sin ^{-1} \frac{5}{13}+\cos ^{-1} x .\)

∴ \(\frac{d y}{d x}=\frac{d}{d x}\left\{\sin ^{-1} \frac{5}{13}+\cos ^{-1} x\right\}=\frac{d}{d x}\left\{\sin ^{-1} \frac{5}{13}\right\}+\frac{d}{d x}\left(\cos ^{-1} x\right)\)

= \(\left\{0-\frac{1}{\sqrt{1-x^2}}\right\}=\frac{-1}{\sqrt{1-x^2}}\)

Hence, \(\frac{d y}{d x}=\frac{-1}{\sqrt{1-x^2}}\)

5. Differentiation of Implicit Function

Let f(x,y) = a be a function of x and y defined in such a manner that y is not expressible directly in terms of x. Then, f(x,y) = a is called an implicit function of x and y. In differentiating such a function, we differentiate both sides of the equation termwise, keeping in mind that

\(\frac{d}{d x}\left(y^2\right)=2 y \cdot \frac{d y}{d x} ; \frac{d}{d x}\left(y^3\right)=3 y^2 \cdot \frac{d y}{d x},\) and so on.

Solved Examples

Example 1 If x³ + y³ = 3axy, find \(\frac{d x}{d y}\).

Solution

Given: x³ + y³ = 3axy …(1)

Differentiating both sides of (1) w.r.t. x, we get

\(3 x^2+3 y^2 \cdot \frac{d y}{d x}=3 a \cdot\left\{x \cdot \frac{d y}{d x}+y \cdot 1\right\}\)

⇒ \(3\left(y^2-a x\right) \cdot \frac{d y}{d x}=3\left(a y-x^2\right)\)

⇒ \(\frac{d y}{d x}=\left(\frac{a y-x^2}{y^2-a x}\right) .\)

Example 2 If ax² + 2hxy + by² + 2gx + 2fy + c = 0, find \(\frac{d x}{d y}\).

Solution

Given: ax² + 2hxy + by² + 2gx + 2fy + c = 0 …(1)

Differentiating both sides of (1) w.r.t. x, we get

\(2 a x+2 h\left(x \cdot \frac{d y}{d x}+y \cdot 1\right)+2 b y \cdot \frac{d y}{d x}+2 g+2 f \cdot \frac{d y}{d x}=0\)

⇒ \((2 a x+2 h y+2 g)+(2 h x+2 b y+2 f) \cdot \frac{d y}{d x}=0\)

⇒ \(\frac{d y}{d x}=-\left(\frac{a x+h y+g}{h x+b y+f}\right) .\)

Example 3 If \(\sqrt{1-x^2}+\sqrt{1-y^2}=a(x-y) \text {, prove that } \frac{d y}{d x}=\sqrt{\frac{1-y^2}{1-x^2}} \text {. }\)

Solution

Given: \(\sqrt{1-x^2}+\sqrt{1-y^2}=a(x-y)\) …(1)

Putting x = sin θ and y = sin Φ, it becomes

cos θ + cos Φ = a(sin θ – sin Φ)

⇒ \(\frac{\cos \theta+\cos \phi}{\sin \theta-\sin \phi}=a\)

⇒ \(\frac{2 \cos \left(\frac{\theta+\phi}{2}\right) \cos \left(\frac{\theta-\phi}{2}\right)}{2 \cos \left(\frac{\theta+\phi}{2}\right) \sin \left(\frac{\theta-\phi}{2}\right)}=a\)

⇒ \(\cot \left(\frac{\theta-\phi}{2}\right)=a \Rightarrow \theta-\phi=2 \cot ^{-1} a\)

⇒ sin^-1x – sin^-1y = 2 cot^-1a …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{\sqrt{1-x^2}}-\frac{1}{\sqrt{1-y^2}} \cdot \frac{d y}{d x}=0 .\)

Hence, \(\frac{d y}{d x}=\sqrt{\frac{1-y^2}{1-x^2}} .\)

Example 4 If \(x \sqrt{1-y^2}+y \sqrt{1-x^2}=1, \text { prove that } \frac{d y}{d x}=-\sqrt{\frac{1-y^2}{1-x^2}} .\)

Solution

We have \(x \sqrt{1-y^2}+y \sqrt{1-x^2}=1\) …(1)

Putting x = sin θ and y = cos Φ in (1), we get

sin θ cos Φ + cos θ sin Φ = 1

⇒ sin(θ + Φ)

⇒ (θ + Φ) = sin^-1(1)

⇒ sin^-1x + sin^-1y = \(\frac{\pi}{2}\) …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{\sqrt{1-x^2}}+\frac{1}{\sqrt{1-y^2}} \cdot \frac{d y}{d x}=0\)

∴ \(\frac{d y}{d x}=-\sqrt{\frac{1-y^2}{1-x^2}}\)

Example 5 If \(x \sqrt{1+y}+y \sqrt{1+x}=0 \text {, prove that } \frac{d y}{d x}=\frac{-1}{(1+x)^2} \text {. }\)

Solution

\(x \sqrt{1+y}+y \sqrt{1+x}=0\)

⇒ \(x \sqrt{1+y}=-y \sqrt{1+x}\)

⇒ x²(1+y) = y²(1+x) [on squaring both sides]

⇒ (x-y)(x + y + xy) = 0

⇒ x + y +xy = 0 [∵ x = y does not satisfy the given equation]

⇒ \(y=\frac{-x}{1+x} \text {. }\)

∴ \(\frac{d y}{d x}=-\left\{\frac{(1+x) \cdot 1-x \cdot 1}{(1+x)^2}\right\}=\frac{-1}{(1+x)^2}\)

Example 6 If sin y = x sin (a+y), prove that \(\frac{d y}{d x}=\frac{\sin ^2(a+y)}{\sin a} .\)

Solution

sin y = x sin (a+y)

⇒ \(x=\frac{\sin y}{\sin (a+y)}\) …(1)

On differentiating both sides of (1) w.r.t. y, we get

\(\frac{d x}{d y}=\frac{\sin (a+y) \cos y-\sin y \cos (a+y)}{\sin ^2(a+y)}\) [using the quotient rule]

= \(\frac{\sin (a+y-y)}{\sin ^2(a+y)}=\frac{\sin a}{\sin ^2(a+y)}\)

Hence, \(\frac{d y}{d x}=\frac{\sin ^2(a+y)}{\sin a} .\)

Example 7 If \(y \cdot \sqrt{x^2+1}=\log \left(\sqrt{x^2+1}-x\right)\), show that \(\left(x^2+1\right) \frac{d y}{d x}+x y+1=0 .\)

Solution

Given: \(y \cdot \sqrt{x^2+1}=\log \left(\sqrt{x^2+1}-x\right)\) …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(y \cdot \frac{1}{2}\left(x^2+1\right)^{-1 / 2} \cdot 2 x+\left(\sqrt{x^2+1}\right) \cdot \frac{d y}{d x}\)

= \(\frac{1}{\left\{\sqrt{x^2+1}-x\right\}} \cdot\left\{\frac{1}{2}\left(x^2+1\right)^{-1 / 2} \cdot 2 x-1\right\}\)

⇒ \(\frac{x y}{\sqrt{x^2+1}}+\left(\sqrt{x^2+1}\right) \frac{d y}{d x}=\frac{1}{\left\{\sqrt{x^2+1}-x\right\}} \cdot\left\{\frac{x}{\sqrt{x^2+1}}-1\right\}\)

⇒ \(\frac{x y}{\sqrt{x^2+1}}+\left(\sqrt{x^2+1}\right) \frac{d y}{d x}=\frac{1}{\left\{\sqrt{x^2+1}-x\right\}} \cdot \frac{\left\{x-\sqrt{x^2+1}\right\}}{\sqrt{x^2+1}}\)

⇒ \(x y+\left(x^2+1\right) \frac{d y}{d x}=-1\)

⇒ \(\left(x^2+1\right) \frac{d y}{d x}+x y+1=0 .\)

Example 8 If \(y=\sqrt{x}+\frac{1}{\sqrt{x}}\), show that [/latex]2 x \frac{d y}{d x}+y=2 \sqrt{x} .[/latex]

Solution

\(y=\sqrt{x}+\frac{1}{\sqrt{x}}\) ⇒ √x y = x + 1 …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(\sqrt{x} \cdot \frac{d y}{d x}+y \cdot \frac{1}{2} x^{-1 / 2}=1\)

⇒ \(\sqrt{x} \frac{d y}{d x}+\frac{y}{2 \sqrt{x}}=1\)

⇒ \(2 x \frac{d y}{d x}+y=2 \sqrt{x}\)

Example 9 If cos(x+y) = y sin x, find \(\frac{d x}{d y}\).

Solution

Given : cos(x+y) = y sin x …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(-\sin (x+y) \cdot \frac{d}{d x}(x+y)=y \cos x+\sin x \cdot \frac{d y}{d x}\)

⇒ \(-\sin (x+y) \cdot\left(1+\frac{d y}{d x}\right)=y \cos x+\sin x \cdot \frac{d y}{d x}\)

⇒ \(\{\sin (x+y)+\sin x\} \cdot \frac{d y}{d x}=-\{\sin (x+y)+y \cos x\}\)

⇒ \(\frac{d y}{d x}=\frac{-\{\sin (x+y)+y \cos x\}}{\{\sin (x+y)+\sin x\}} .\)

Example 10 Find \(\frac{d x}{d y}\) when \(\sin (x y)+\frac{x}{y}=x^2-y\)

Solution

Given: \(\sin (x y)+\frac{x}{y}=x^2-y\)

Differentiating both sides w.r.t. x, we get

\(\cos (x y) \cdot \frac{d}{d x}(x y)+x \cdot\left(-\frac{1}{y^2}\right) \frac{d y}{d x}+\frac{1}{y} \cdot 1=2 x-\frac{d y}{d x}\)

⇒ \(\cos (x y) \cdot\left[x \cdot \frac{d y}{d x}+y \cdot 1\right]-\frac{x}{y^2} \cdot \frac{d y}{d x}+\frac{1}{y}=2 x-\frac{d y}{d x}\)

⇒ \(\left[x \cos (x y)-\frac{x}{y^2}+1\right] \cdot \frac{d y}{d x}=2 x-\frac{1}{y}-y \cos (x y)\)

⇒ \(\left\{x y^2 \cos (x y)-x+y^2\right\} \cdot \frac{d y}{d x}=2 x y^2-y-y^3 \cos (x y) .\)

Hence, \(\frac{d y}{d x}=\left\{\frac{2 x y^2-y-y^3 \cos (x y)}{x y^2 \cos (x y)-x+y^2}\right\} .\)

Comparative Analysis of Differentiation Techniques

Example 11 If e^x + e^y = e^x+y, prove that \(\frac{d x}{d y}\) = -e^y-x.

Solution

Given: e^x + e^y = e^x+y     …(1)

On dividing through out by e^x+y, we get

e^-y + e^-x = 1 …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(e^{-y} \cdot\left(\frac{-d y}{d x}\right)+e^{-x}(-1)=0\)

⇒ \(\frac{d y}{d x}=\frac{-e^{-x}}{e^{-y}}=-e^{(y-x)} .\)

Example 12 If \(\tan ^{-1}\left(\frac{x^2-y^2}{x^2+y^2}\right)=a, \text { show that } \frac{d y}{d x}=\frac{x(1-\tan a)}{y(1+\tan a)}\)

Solution

\(\tan ^{-1}\left(\frac{x^2-y^2}{x^2+y^2}\right)=a ⇒ \frac{\left(x^2-y^2\right)}{\left(x^2+y^2\right)}=\tan a\)

∴ (x² – y²) = (x² + y²) tan a …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(2 x-2 y \cdot \frac{d y}{d x}=2 x \tan a+2 y \cdot \frac{d y}{d x} \cdot \tan a\)

⇒ \(y(1+\tan a) \frac{d y}{d x}=x(1-\tan a)\)

⇒ \(\frac{d y}{d x}=\frac{x(1-\tan a)}{y(1+\tan a)}\)

6. Differentiation Using Logarithms

When the given function is a power of some expression or a product of expressions, then we take the logarithm on both sides and differentiate termwise, as shown below.

Solved Examples

Example 1 If y = \(\sqrt{\frac{(x-3)\left(x^2+4\right)}{\left(3 x^2+4 x+5\right)}} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Given: y = \(\sqrt{\frac{(x-3)\left(x^2+4\right)}{\left(3 x^2+4 x+5\right)}}\) …(1)

Taking logarithm on both sides of (1), we get

log y = \(\frac{1}{2}\) {log(x-3) + log(x² + 4) – log(3x² + 4x + 5)}.

Differentiating both sides w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\frac{1}{2} \cdot\left\{\frac{1}{(x-3)}+\frac{2 x}{\left(x^2+4\right)}-\frac{(6 x+4)}{\left(3 x^2+4 x+5\right)}\right\}\)

⇒ \(\frac{d y}{d x}=\left(\frac{1}{2} y\right) \cdot\left\{\frac{1}{(x-3)}+\frac{2 x}{\left(x^2+4\right)}-\frac{(6 x+4)}{\left(3 x^2+4 x+5\right)}\right\}\)

= \(\frac{1}{2} \cdot \sqrt{\frac{(x-3)\left(x^2+4\right)}{\left(3 x^2+4 x+5\right)}} \cdot\left\{\frac{1}{(x-3)}+\frac{2 x}{\left(x^2+4\right)}-\frac{(6 x+4)}{\left(3 x^2+4 x+5\right)}\right\} \text {. }\)

Example 2 If y = \(\frac{\sqrt{x}(x+4)^{3 / 2}}{(4 x-3)^{43}} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

Given: \(y \frac{\sqrt{x}(x+4)^{3 / 2}}{(4 x-3)^{43}}\) …(1)

Taking logarithm on both sides of (1), we get

log y = \(\frac{1}{2}\) log x + \(\frac{3}{2}\) log (x+4) – \(\frac{4}{3}\) log (4x – 3).

On differentiating both sides w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\frac{1}{2} \cdot \frac{1}{x}+\frac{3}{2} \cdot \frac{1}{(x+4)}-\frac{4}{3} \cdot \frac{4}{(4 x-3)}\)

⇒ \(\frac{d y}{d x}=y\left[\frac{1}{2 x}+\frac{3}{2(x+4)}-\frac{16}{3(4 x-3)}\right]\)

= \(\frac{\sqrt{x}(x+4)^{3 / 2}}{(4 x-3)^{4 / 3}} \cdot\left[\frac{1}{2 x}+\frac{3}{2(x+4)}-\frac{16}{3(4 x-3)}\right]\)

Example 3 Differentiate (x+1)²(x+2)³(x+3)⁴ w.r.t. x.

Solution

(x+1)²(x+2)³(x+3)⁴ w.r.t. x

Let y = (x+1)²(X+2)³(x+3)⁴ …(1)

Taking logarithm on both sides of (1), we get

log y = 2 log(x+1) + 3 log(x+2) + 4log(x+3) …(2)

Differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\frac{2}{(x+1)}+\frac{3}{(x+2)}+\frac{4}{(x+3)}\)

⇒ \(\frac{d y}{d x}=y \cdot\left[\frac{2}{(x+1)}+\frac{3}{(x+2)}+\frac{4}{(x+3)}\right]\)

= \((x+1)^2(x+2)^3(x+3)^4 \cdot\left[\frac{2}{(x+1)}+\frac{3}{(x+2)}+\frac{4}{(x+3)}\right]\)

Example 4 Differentiate \(\sqrt{(x-1)(x-2)(x-3)(x-4)}\) w.r.t. x.

Solution

\(\sqrt{(x-1)(x-2)(x-3)(x-4)}\) w.r.t. x

Let y = \(\sqrt{(x-1)(x-2)(x-3)(x-4)}\) …(1)

Taking logarithm on both sides of (1), we get

log y = \(\frac{1}{2}\) {log (x-1) + log (x+2) + log (x-3) + log (x-4)} …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\frac{1}{2} \cdot\left\{\frac{1}{(x-1)}+\frac{1}{(x-2)}+\frac{1}{(x-3)}+\frac{1}{(x-4)}\right\}\)

⇒ \(\frac{d y}{d x}=\left(\frac{y}{2}\right) \cdot\left\{\frac{1}{(x-1)}+\frac{1}{(x-2)}+\frac{1}{(x-3)}+\frac{1}{(x-4)}\right\}\)

= \(\frac{1}{2} \cdot \sqrt{(x-1)(x-2)(x-3)(x-4)}\left\{\frac{1}{(x-1)}+\frac{1}{(x-2)}+\frac{1}{(x-3)}+\frac{1}{(x-4)}\right\} .\)

Example 5 Differentiate (e^xcos³xsin²x) w.r.t x.

Solution

(e^xcos³xsin²x) w.r.t x

Let y = e^xcos³xsin²x …(1)

Taking logarithm on both sides of (1), we get

log y = x + 3 log cos x + 2 log sin x …(2)

\(\frac{1}{y} \cdot \frac{d y}{d x}=1+\frac{3}{\cos x} \cdot(-\sin x)+\frac{2}{\sin x} \cdot \cos x\)

⇒ \(\frac{d y}{d x}=y \cdot\{1-3 \tan x+2 \cot x\}\)

= (e^xcos³xsin²x)(1-3 tan x + 2 cot x).

Example 6 Differentiate (tan x tan 2x tan 3x tan 4x) w.r.t. x.

Solution

(tan x tan 2x tan 3x tan 4x) w.r.t. x

Let y = tan x tan 2x tan 3x tan 4x …(1)

Taking logarithm on both sides of (1), we get

log y = log tan x + log tan 2x + log tan 3x + log tan 4x …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\left\{\frac{\sec ^2 x}{\tan x}+\frac{2 \sec ^2 2 x}{\tan 2 x}+\frac{3 \sec ^2 3 x}{\tan 3 x}+\frac{4 \sec ^2 4 x}{\tan 4 x}\right\}\)

⇒ \(\frac{d y}{d x}=y \cdot\left[\frac{1}{\sin x \cos x}+\frac{2}{\sin 2 x \cos 2 x}\right.\left.+\frac{3}{\sin 3 x \cos 3 x}+\frac{4}{\sin 4 x \cos 4 x}\right]\)

= \(y \cdot\left[\frac{2}{\sin 2 x}+\frac{4}{\sin 4 x}+\frac{6}{\sin 6 x}+\frac{8}{\sin 8 x}\right]\)

= [2 tan x tan 2x tan 3x tan 4x] x [coses 2x + 2 cosec 4x + 3 cosec 6x + 4 cosec 8x].

Example 7 If y = (2x + 3)^{(3x – 5)}, find \(\frac{d x}{d y}\).

Solution

y = (2x + 3)^{(3x – 5)}

Given: y = (2x + 3)^{(3x – 5)} …(1)

Taking logarithm on both sides of (1), we get

log y = (3x – 5) log (2x + 3) …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=(3 x-5) \cdot \frac{d}{d x}\{\log (2 x+3)\}+\log (2 x+3) \cdot \frac{d}{d x}(3 x-5)\)

= \((3 x-5) \cdot \frac{1}{(2 x+3)} \cdot 2+\log (2 x+3) \cdot 3\)

⇒ \(\frac{d y}{d x}=y \cdot\left\{\frac{(6 x-10)}{(2 x+3)}+3 \log (2 x+3)\right\}\)

⇒ \(\frac{d y}{d x}=(2 x+3)^{(3 x-5)} \cdot\left\{\frac{(6 x-10)}{(2 x+3)}+3 \log (2 x+3)\right\} .\)

Example 8 If y = \(\frac{5^x}{x^5} \text {, find } \frac{d y}{d x} \text {. }\)

Solution

y = \(\frac{5^x}{x^5} \text {, find } \frac{d y}{d x} \text {. }\)

Given: y = \(\frac{5^x}{x^5}\) …(1)

Taking logarithm on both sides of (1), we get

log y = log(5^x) – log(x⁵)

⇒ log y = x log 5 – 5 log x

⇒ \(\frac{1}{y} \cdot \frac{d y}{d x}=(\log 5) \cdot 1-\frac{5}{x}\) [differentiating both sides w.r.t. x]

⇒ \(\frac{d y}{d x}=y\left(\log 5-\frac{5}{x}\right)\)

⇒ \(\frac{d y}{d x}=\frac{5^x}{x^5}\left(\log 5-\frac{5}{x}\right) .\)

Example 9 Differentiate x^x w.r.t. x.

Solution

x^x w.r.t. x

Let y = x^x …(1)

Taking logarithm on both sides of (1), we get

log y = x log x …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=x \cdot \frac{d}{d x}(\log x)+\log x \cdot \frac{d}{d x}(x)\)

= \(\left(x \cdot \frac{1}{x}+\log x \cdot 1\right)=(1+\log x)\)

⇒ \(\frac{d y}{d x}=y(1+\log x)\)

⇒ \(\frac{d y}{d x}=x^x(1+\log x) .\)

Example 10 Differentiate (sin x)^x w.r.t. x.

Solution

(sin x)^x w.r.t. x

Let y = (sin x)^x      …(1)

Taking logarithm on both sides of (1), we get

log y = x log(sin x) …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=x \cdot \frac{d}{d x}\{\log (\sin x)\}+\log (\sin x) \cdot \frac{d}{d x}(x)\)

= \(x \cdot \frac{1}{\sin x} \cdot \cos x+\log (\sin x) \cdot 1\)

= x cot x + log (sin x)

⇒ \(\frac{d y}{d x}=y \cdot[x \cot x+\log (\sin x)]\)

⇒ \(\frac{d y}{d x}=(\sin x)^x[x \cot x+\log (\sin x)] .\)

Example 11 Differentiate x^sin-1x w.r.t. x.

Solution

x^sin-1x w.r.t. x

Let y = x^sin-1x …(1)

Taking logarithm on both sides of (1), we get

log y = (sin-x)(log x) …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\left(\sin ^{-1} x\right) \cdot \frac{d}{d x}(\log x)+(\log x) \cdot \frac{d}{d x}\left(\sin ^{-1} x\right)\)

= \(\left(\sin ^{-1} x\right) \frac{1}{x}+(\log x) \cdot \frac{1}{\sqrt{1-x^2}}\)

⇒ \(\frac{d y}{d x}=y \cdot\left[\frac{\sin ^{-1} x}{x}+\frac{\log x}{\sqrt{1-x^2}}\right]\)

⇒ \(\frac{d y}{d x}=x^{\sin ^{-1} x} \cdot\left\{\frac{\sin ^{-1} x}{x}+\frac{\log x}{\sqrt{1-x^2}}\right\} .\)

Example 12 Differentiate (sin x)^{log x} w.r.t. x.

Solution

(sin x)^{log x} w.r.t. x

Let y = (sin x)^{log x} …(1)

Taking logarithm on both sides of (1), we get

log y = (log x)(log sin x) …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=(\log x) \cdot \frac{d}{d x}(\log \sin x)+(\log \sin x) \cdot \frac{d}{d x}(\log x)\)

= \((\log x) \cdot \frac{1}{\sin x} \cdot \cos x+(\log \sin x) \cdot \frac{1}{x}\)

= \((\log x) \cot x+\frac{(\log \sin x)}{x}\)

⇒ \(\frac{d y}{d x}=y \cdot\left[(\log x) \cot x+\frac{(\log \sin x)}{x}\right]\)

⇒ \(\frac{d y}{d x}=(\sin x)^{\log x} \cdot\left[(\log x) \cot x+\frac{(\log \sin x)}{x}\right] .\)

Example 13 Differentiate x^x sin-1√x w.r.t. x.

Solution

x^x sin-1√x w.r.t. x

Let y = x^x sin-1√x …(1)

Taking logarithm on both sides of (1), we get

log y = x log x + log(sin-1√x) …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\frac{d}{d x}(x \log x)+\frac{d}{d x}\left\{\log \left(\sin ^{-1} \sqrt{x}\right)\right\}\)

= \(\left(x \cdot \frac{1}{x}+\log x \cdot 1\right)+\frac{1}{\sin ^{-1} \sqrt{x}} \cdot \frac{1}{\sqrt{1-x}} \cdot \frac{1}{2} x^{-1 / 2}\)

= \(\left\{(1+\log x)+\frac{1}{2\left(\sqrt{x-x^2}\right) \sin ^{-1} \sqrt{x}}\right\}\)

⇒ \(\frac{d y}{d x}=y \cdot\left\{(1+\log x)+\frac{1}{2\left(\sqrt{x-x^2}\right) \sin ^{-1} \sqrt{x}}\right\}\)

= \(\left(x^x \sin ^{-1} \sqrt{x}\right)\left\{(1+\log x)+\frac{1}{2\left(\sqrt{x-x^2}\right) \sin ^{-1} \sqrt{x}}\right\}\)

= \(\left\{\left(x^x \sin ^{-1} \sqrt{x}\right)(1+\log x)+\frac{x^x}{2\left(\sqrt{x-x^2}\right)}\right\} \text {. }\)

Example 14 Differentiate \(\frac{e^{x^2} \tan ^{-1} x}{\sqrt{1+x^2}}\) w.r.t. x.

Solution

\(\frac{e^{x^2} \tan ^{-1} x}{\sqrt{1+x^2}}\) w.r.t.

Let y = \(\frac{e^{x^2} \tan ^{-1} x}{\sqrt{1+x^2}}\) …(1)

Taking logarithm on both sides of (1), we get

log y = x² + log(tan-1x) – \(\frac{1}{2}\) log(1+x2) …(2)

On differentiating both sides of (2) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=2 x+\frac{1}{\tan ^{-1} x} \cdot \frac{1}{\left(1+x^2\right)}-\frac{1}{2} \cdot \frac{2 x}{\left(1+x^2\right)}\)

⇒ \(\frac{d y}{d x}=y\left[2 x+\frac{1}{\left(1+x^2\right) \tan ^{-1} x}-\frac{x}{\left(1+x^2\right)}\right]\)

= \(\frac{e^{x^2} \tan ^{-1} x}{\sqrt{1+x^2}},\left[2 x+\frac{1}{\left(1+x^2\right) \tan ^{-1} x}-\frac{x}{\left(1+x^2\right)}\right]\)

Example 15 Differentiate \(\left\{x^{\tan x}+\sqrt{\frac{x^2+1}{x}}\right\}\) w.r.t. x.

Solution

\(\left\{x^{\tan x}+\sqrt{\frac{x^2+1}{x}}\right\}\) w.r.t. x

Let y = v + u, where u = x^{tan x} and v = \(\sqrt{\frac{x^2+1}{x}} .\)

Now, u = x^{tan x}

⇒ log u = (tan x)(log x)

⇒ \(\frac{1}{u} \cdot \frac{d u}{d x}=(\tan x) \cdot \frac{d}{d x}(\log x)+(\log x) \cdot \frac{d}{d x}(\tan x)\) [differentiating w.r.t. x]

= (tan x).\(\frac{1}{x}\) + (log x)sec²x

⇒ \(\frac{d u}{d x}=u \cdot\left[\frac{\tan x}{x}+(\log x) \sec ^2 x\right]\)

⇒ \(\frac{d u}{d x}=x^{\tan x} \cdot\left\{\frac{\tan x}{x}+(\log x) \sec ^2 x\right\}\) …(1)

And, v = \(\sqrt{\frac{x^2+1}{x}}\)

⇒ \(\frac{1}{v} \cdot \frac{d v}{d x}=\frac{1}{2} \cdot\left\{\frac{2 x}{\left(x^2+1\right)}-\frac{1}{x}\right\}\) [differentiating w.r.t. x]

⇒ \(\frac{d v}{d x}=\frac{v}{2} \cdot\left\{\frac{2 x^2-\left(x^2+1\right)}{x\left(x^2+1\right)}\right\}\)

⇒ \(\frac{d v}{d x}=\frac{1}{2} \sqrt{\frac{x^2+1}{x}} \cdot\left\{\frac{\left(x^2-1\right)}{x\left(x^2+1\right)}\right\}\) …(2)

∴ y = u + v

⇒ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)

⇒ \(\frac{d y}{d x}=x^{\tan x} \cdot\left\{\frac{\tan x}{x}+(\log x) \sec ^2 x\right\}+\frac{1}{2} \cdot \sqrt{\frac{x^2+1}{x}} \cdot\left\{\frac{\left(x^2-1\right)}{x\left(x^2+1\right)}\right\}\)

Example 16 If Y = (x)^{cos x} + (cos x)^{sin x}, find \(\frac{d x}{d y}\).

Solution

Y = (x)^{cos x} + (cos x)^{sin x}

Let y = u + v, where u = (x)^{cos x} and v = (cos x)^{sin x}.

Now, u = (x)^{cos x}

⇒ log u = (cos x)(log x)

⇒ \(\frac{1}{u} \cdot \frac{d u}{d x}=(\cos x) \cdot \frac{d}{d x}(\log x)+(\log x) \cdot \frac{d}{d x}(\cos x)\) [on differentiating w.r.t. x]

= (cos x).\(\frac{1}{x}\) + (log x)(-sin x)

⇒ \(\frac{d u}{d x}=u \cdot\left\{\frac{\cos x}{x}-(\log x)(\sin x)\right\}\)

⇒ \(\frac{d u}{d x}=(x)^{\cos x}\left\{\frac{\cos x}{x}-(\log x)(\sin x)\right\}\) …(1)

And, v = (cos x)^{sin x}

⇒ log v = (sin x)log(cos x)

⇒ \(\frac{1}{v} \cdot \frac{d v}{d x}=(\sin x) \cdot \frac{d}{d x}\{\log (\cos x)\}+\log (\cos x) \cdot \frac{d}{d x}(\sin x)\) [on differentiating w.r.t. x]

⇒ \(\frac{d v}{d x}=v \cdot\left\{(\sin x) \cdot \frac{(-\sin x)}{\cos x}+\log (\cos x) \cdot \cos x\right\}\)

⇒ \(\frac{d v}{d x}=(\cos x)^{\sin x} \cdot\{-\sin x \tan x+\cos x \cdot \log (\cos x)\}\) …(2)

∴ y = (u+v)

⇒ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)

⇒ \(\frac{d y}{d x}=(x)^{\cos x} \cdot\left\{\frac{\cos x}{x}-(\log x) \sin x\right\}+(\cos x)^{\sin x} \cdot\{-\sin x \tan x+\cos x \cdot \log (\cos x)\}\)

Example 17 If y = (sin x)^{tan x} + (cos x)^{sec x}, find \(\frac{d x}{d y}\).

Solution

y = (sin x)^{tan x} + (cos x)^{sec x}

Let y = u + v, where u = (sin x)^{tan x} and v = (cos x)^{sec x}.

Now, u = (sin x)^{tan x}

⇒ log u = (tan x)(log sin x)

⇒ \(\frac{1}{u} \cdot \frac{d u}{d x}=(\tan x) \cdot \frac{d}{d x}(\log \sin x)+(\log \sin x) \cdot \frac{d}{d x}(\tan x)\) [on differentiating w.r.t. x]

= \((\tan x) \cdot \frac{1}{\sin x} \cdot \cos x+(\log \sin x) \cdot \sec ^2 x\)

⇒ \(\frac{d u}{d x}=u\left[1+(\log \sin x) \sec ^2 x\right]\)

⇒ \(\frac{d u}{d x}=(\sin x)^{\tan x} \cdot\left\{1+(\log \sin x) \sec ^2 x\right\}\) …(1)

And v = (cos x)^{sec x}

⇒ log v = (sec x).log(cos x)

⇒ \(\frac{1}{v} \cdot \frac{d v}{d x}=(\sec x) \cdot \frac{d}{d x}\{\log (\cos x)\}+\log (\cos x) \cdot \frac{d}{d x}(\sec x)\) [on differentiating w.r.t. x]

= \((\sec x) \cdot \frac{1}{\cos x} \cdot(-\sin x)+\log (\cos x) \cdot \sec x \tan x\)

= (sec x tan x)[log (cos x) – 1]

⇒ \(\frac{d v}{d x}=v \cdot(\sec x \tan x)[\log (\cos x)-1]\)

⇒ \(\frac{d v}{d x}=(\cos x)^{\sec x} \cdot(\sec x \tan x)[\log (\cos x)-1]\) …(2)

∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)

⇒ \(\frac{d y}{d x}=(\sin x)^{\tan x} \cdot\left\{1+(\log \sin x) \sec ^2 x\right\}+(\cos x)^{\sec x} \cdot(\sec x \tan x)[\log (\cos x)-1]\) [from (1) and (2)].

Example 18 If x^y = y^x, find \(\frac{d x}{d y}\).

Solution

x^y = y^x

Given: x^y = y^x

⇒ y log x = x log y …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(y \cdot \frac{d}{d x}(\log x)+(\log x) \cdot \frac{d}{d x}(y)=x \cdot \frac{d}{d x}(\log y)+(\log y) \cdot \frac{d}{d x}(x)\)

⇒ \(y \cdot \frac{1}{x}+(\log x) \cdot \frac{d y}{d x}=x \cdot \frac{1}{y} \cdot \frac{d y}{d x}+(\log y) \cdot 1\)

⇒ \(\left(\log x-\frac{x}{y}\right) \frac{d y}{d x}=\left(\log y-\frac{y}{x}\right)\)

⇒ \(\frac{(y \log x-x)}{y} \cdot \frac{d y}{d x}=\frac{(x \log y-y)}{x}\)

⇒ \(\frac{d y}{d x}=\frac{y(x \log y-y)}{x(y \log x-x)}\)

Example 19 If x^y . y^x = 1, find \(\frac{d x}{d y}\).

Solution

x^y . y^x = 1

Given: x^y . y^x = 1

⇒ (y log x) + (x log y) = 0 …(1) [∵ log 1 = 0]

On differentiating both sides of (1) w.r.t. x, we get

\(y \cdot \frac{d}{d x}(\log x)+(\log x) \cdot \frac{d}{d x}(y)+x \cdot \frac{d}{d x}(\log y)+(\log y) \cdot \frac{d}{d x}(x)=0\)

⇒ \(y \cdot \frac{1}{x}+(\log x) \cdot \frac{d y}{d x}+x \cdot \frac{1}{y} \cdot \frac{d y}{d x}+(\log y) \cdot 1=0\)

⇒ \(\left(\log x+\frac{x}{y}\right) \cdot \frac{d y}{d x}=-\left(\log y+\frac{y}{x}\right)\)

⇒ \(\frac{(y \log x+x)}{y} \cdot \frac{d y}{d x}=\frac{-(x \log y+y)}{x}\)

⇒ \(\frac{d y}{d x}=\frac{-y(x \log y+y)}{x(y \log x+x)} .\)

Example 20 If x^y = e^x-y, prove that \(\frac{d y}{d x}=\frac{\log x}{(1+\log x)^2}\).

Solution

x^y = e^x-y

We have

x^y = e^x-y ⇒ y log x = (x-y)

⇒ (1 + log x)y = x

⇒ \(y=\frac{x}{(1+\log x)}\) …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(\frac{d y}{d x}=\frac{(1+\log x) \cdot \frac{d}{d x}(x)-x \cdot \frac{d}{d x}(1+\log x)}{(1+\log x)^2}\)

= \(\frac{(1+\log x) \cdot 1-x \cdot \frac{1}{x}}{(1+\log x)^2}=\frac{(1+\log x-1)}{(1+\log x)^2}=\frac{\log x}{(1+\log x)^2}\)

Example 21 If x^y + y^x = a^b, find \(\frac{d x}{d y}\).

Solution

x^y + y^x = a^b

Let u = x^y and v = y^x.

Then, u + v = ab ⇒ \(\frac{d u}{d x}+\frac{d v}{d x}=0\) …(1) [∵ a^b = constant]

Now, u = x^y ⇒ log u = y log x [taking log on both sides]

⇒ \(\frac{1}{u} \cdot \frac{d u}{d x}=y \cdot \frac{1}{x}+\log x \cdot \frac{d y}{d x}\) [on differentiation]

⇒ \(\frac{d u}{d x}=u\left[\frac{y}{x}+\log x \cdot \frac{d y}{d x}\right]\)

⇒ \(\frac{d u}{d x}=x^y\left[\frac{y+x \log x \cdot \frac{d y}{d x}}{x}\right]\)

⇒ \(\frac{d u}{d x}=x^{y-1}\left[y+x \log x \cdot \frac{d y}{d x}\right]\)

And, v = y^x ⇒ log v = x log y [taking log on both sides]

⇒ \(\frac{1}{v} \cdot \frac{d v}{d x}=x \cdot \frac{1}{y} \cdot \frac{d y}{d x}+\log y\) [on differentiation]

⇒ \(\frac{d v}{d x}=v \cdot\left[\frac{x}{y} \cdot \frac{d y}{d x}+\log y\right] \Rightarrow \frac{d v}{d x}=y^x\left\{\frac{x \cdot \frac{d y}{d x}+y \log y}{y}\right\}\)

⇒ \(\frac{d v}{d x}=y^{(x-1)},\left\{x \cdot \frac{d y}{d x}+y \log y\right\} .\)

Using (1), we get \(\frac{d u}{d x}+\frac{d v}{d x}=0\)

⇒ \(x^{(y-1)}\left\{y+x \log x \cdot \frac{d y}{d x}\right\}+y^{(x-1)} \cdot\left\{x \frac{d y}{d x}+y \log y\right\}=0\)

⇒ \(\left\{x^y(\log x)+x \cdot y^{(x-1)}\right\} \cdot \frac{d y}{d x}=-\left\{y \cdot x^{(y-1)}+y^x(\log y)\right\}\)

∴ \(\frac{d y}{d x}=\frac{-\left\{y \cdot x^{(y-1)}+y^x(\log y)\right\}}{\left\{x^y(\log x)+x y^{(x-1)}\right\}} .\)

Real-Life Applications of Derivatives in Physics and Economics

Example 22 If x^x + x^y + y^x = a^b, find \(\frac{d x}{d y}\).

Solution

x^x + x^y + y^x = a^b

Let u = x^x, v = x^y and w = y^x. Then,

u + v + w = ab

⇒ \(\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}=0\) …(1) [∵ a^b = constant]

Now, u = x^x

⇒ log u = x log x

⇒ \(\frac{1}{u} \cdot \frac{d u}{d x}=x \cdot \frac{d}{d x}(\log x)+\log x \cdot \frac{d}{d x}(x)\) [on differentiating both sides w.r.t. x]

⇒ \(\frac{d u}{d x}=u\left[\frac{y}{x}+\log x \cdot \frac{d y}{d x}\right]\)

⇒ \(\frac{d u}{d x}=x^y\left[\frac{y+x \log x \cdot \frac{d y}{d x}}{x}\right]\) …(2)

And, v = x^y

⇒ log v = y log x

⇒ \(\frac{1}{v}, \frac{d v}{d x}=y \cdot \frac{d}{d x}(\log x)+(\log x) \cdot \frac{d}{d x}(y)\) [on differentiating both sides w.r.t. x]

⇒ \(\frac{d v}{d x}=v \cdot\left\{y \cdot \frac{1}{x}+(\log x) \cdot \frac{d y}{d x}\right\}\)

⇒ \(\frac{d v}{d x}=x^y\left\{\frac{y}{x}+(\log x) \frac{d y}{d x}\right\}\) …(3)

And, w = y^x

⇒ log w = x log y

⇒ \(\frac{1}{w} \cdot \frac{d w}{d x}=x \cdot \frac{d}{d x}(\log y)+(\log y) \cdot \frac{d}{d x}(x)\) [on differentiating both sides w.r.t. x]

⇒ \(\frac{d w}{d x}=w \cdot\left\{x \cdot \frac{1}{y} \cdot \frac{d y}{d x}+(\log y) \cdot 1\right\}\)

⇒ \(\frac{d w}{d x}=y^x \cdot\left\{\frac{x}{y} \cdot \frac{d y}{d x}+(\log y)\right\}\) …(4)

Using (2), (3) and (4) in (1), we get

\(x^x(1+\log x)+x^y\left\{\frac{y}{x}+(\log x) \frac{d y}{d x}\right\}+y^x \cdot\left\{\frac{x}{y} \cdot \frac{d y}{d x}+(\log y)\right\}=0\)

⇒ \(\left\{x^x(1+\log x)+y \cdot x^{(y-1)}+y^x(\log y)\right\}+\left\{x^y(\log x)+x y^{(x-1)}\right\} \frac{d y}{d x}=0\)

⇒ \(\frac{d y}{d x}=\frac{-\left\{x^x(1+\log x)+y \cdot x^{(y-1)}+y^z(\log y)\right\}}{\left\{x^y(\log x)+x y^{(x-1)}\right\}} .\)

Example 23 If y = \(x^{\left(x^x\right)}\), find [/latex]\frac{d x}{d y}[/latex].

Solution

y = \(x^{\left(x^x\right)}\)

Let x^x = u . Then, y = x^u.

∴ x log x = log u and log y = u log x.

Now, log u = x log x

⇒ \(\frac{1}{u} \cdot \frac{d u}{d x}=x \cdot \frac{d}{d x}(\log x)+\log x \cdot \frac{d}{d x}(x)\) [on differentiating w.r.t. x]

⇒ \(\frac{d u}{d x}=u \cdot\left[x \cdot \frac{1}{x}+\log x \cdot 1\right]\)

⇒ \(\frac{d u}{d x}=x^x(1+\log x)\) …(1)

And, log y = u log x

⇒ \(\frac{1}{y} \cdot \frac{d y}{d x}=u \cdot \frac{d}{d x}(\log x)+(\log x) \cdot \frac{d}{d x}(u)\)

= \(u \cdot \frac{1}{x}+(\log x) \cdot \frac{d u}{d x}\)

⇒ \(\frac{d y}{d x}=y \cdot\left[\frac{u}{x}+(\log x) \cdot \frac{d u}{d x}\right]\)

= \(x^{\left(x^x\right)} \cdot\left[\frac{x^x}{x}+(\log x)\left\{x^x(1+\log x)\right\}\right]\)

= \(x^{\left(x^x\right)} \cdot\left[x^{(x-1)}+x^x(\log x)+x^x(\log x)^2\right]\).

Example 24 If y = \((\log x)^{\cos x}+\frac{x^2+1}{x^2-1} \text {, find } \frac{d y}{d x}\)

Solution

y = \((\log x)^{\cos x}+\frac{x^2+1}{x^2-1} \text {, find } \frac{d y}{d x}\)

Let (log x)^{cos x} = u and and \(\frac{x^2+1}{x^2-1}\) = v. Then,

u = (log x)^{cos x} ⇒ log u = cos x . log(log x) …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(\frac{1}{u} \cdot \frac{d u}{d x}=\cos x \cdot \frac{d}{d x}\{\log (\log x)\}+\log (\log x) \cdot \frac{d}{d x}(\cos x)\)

= \(\cos x \frac{1}{\log x} \cdot \frac{1}{x}-(\sin x) \cdot \log (\log x)\)

∴ \(\frac{d u}{d x}=u \cdot\left\{\frac{\cos x}{x \log x}-(\sin x) \cdot \log (\log x)\right\}\)

⇒ \(\frac{d u}{d x}=(\log x)^{\cos x} \cdot\left\{\frac{\cos x}{x \log x}-(\sin x) \cdot \log (\log x)\right\} \text {. }\)

Also, v = \(\frac{\left(x^2+1\right)}{\left(x^2-1\right)} ⇒ \frac{d v}{d x}=\frac{\left(x^2-1\right) \cdot \frac{d}{d x}\left(x^2+1\right)-\left(x^2+1\right) \cdot \frac{d}{d x}\left(x^2-1\right)}{\left(x^2-1\right)^2}\)

⇒ \(\frac{d v}{d x}=\frac{\left(x^2-1\right) \cdot 2 x-\left(x^2+1\right) \cdot 2 x}{\left(x^2-1\right)^2}=\frac{-4 x}{\left(x^2-1\right)^2}\)

∴ y = u + v

⇒ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)

= \((\log x)^{\cos x} \cdot\left\{\frac{\cos x}{x \log x}-(\sin x) \cdot \log (\log x)\right\}-\frac{4 x}{\left(x^2-1\right)^2}\)

7. Derivatives of an Infinite Series

If we take out a single term from an infinite series, it remains unaffected. We utilize this result in finding the derivative of an infinite series.

Solved Examples

Example 1 If \(y=x^{x^{x \cdots \cdots}}, \text { prove that } \frac{d y}{d x}=\frac{y^2}{x(1-y \log x)}\).

Solution

\(y=x^{x^{x \cdots \cdots}}, \text { prove that } \frac{d y}{d x}=\frac{y^2}{x(1-y \log x)}\).

We know that an infinite series is not affected by the exclusion of a single term.

So, we may write the given function as y = x^y.

Now, y = x^y ⇒ log y = y log x …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=y \cdot \frac{1}{x}+\log x \cdot \frac{d y}{d x}\)

⇒ \(\left(\frac{1}{y}-\log x\right) \frac{d y}{d x}=\frac{y}{x}\)

⇒ \(\frac{(1-y \log x)}{y} \cdot \frac{d y}{d x}=\frac{y}{x}\)

⇒ \(\frac{d y}{d x}=\left\{\frac{y}{x} \times \frac{y}{(1-y \log x)}\right\} \Rightarrow \frac{d y}{d x}=\frac{y^2}{x(1-y \log x)}\)

Example 2 If \(y=\sqrt{\sin x+\sqrt{\sin x+\sqrt{\sin x+\ldots \text { to } \infty}}} \text {, prove that } \frac{d y}{d x}=\frac{\cos x}{(2 y-1)} \text {. }\)

Solution

\(y=\sqrt{\sin x+\sqrt{\sin x+\sqrt{\sin x+\ldots \text { to } \infty}}} \text {, prove that } \frac{d y}{d x}=\frac{\cos x}{(2 y-1)} \text {. }\)

We may write the given series as

\(y=\sqrt{\sin x+y} \Rightarrow y^2=(\sin x+y)\) …(1)

On differentiating both sides of (1), w.r.t. x, we get

\(2 y \cdot \frac{d y}{d x}=\cos x+\frac{d y}{d x}\)

⇒ \((2 y-1) \cdot \frac{d y}{d x}=\cos x\)

⇒ \(\frac{d y}{d x}=\frac{\cos x}{(2 y-1)} .\)

Example 3 If \(y=e^{x+e^{x+e^{x+\ldots infinity}}}, \text { prove that } \frac{d y}{d x}=\frac{y}{(1-y)} .\)

Solution

\(y=e^{x+e^{x+e^{x+\ldots infinity}}}, \text { prove that } \frac{d y}{d x}=\frac{y}{(1-y)} .\)

We may write the given series as

y = e^x+y  ⇒ log y = (x + y) …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=1+\frac{d y}{d x}\)

⇒ \(\left(\frac{1}{y}-1\right) \frac{d y}{d x}=1\)

⇒ \(\frac{(1-y)}{y}, \frac{d y}{d x}=1\)

⇒ \(\frac{d y}{d x}=\frac{y}{(1-y)} .\)

Example 4 If \(y=(\sqrt{x})^{(\sqrt{x})^{(\sqrt{x}) \ldots infinity}}\), prove that \(x\left(\frac{d y}{d x}\right)=\frac{y^2}{(2-y \log x)}\).

Solution

\(y=(\sqrt{x})^{(\sqrt{x})^{(\sqrt{x}) \ldots infinity}}\), prove that \(x\left(\frac{d y}{d x}\right)=\frac{y^2}{(2-y \log x)}\).

We may write the given series as

\(y=(\sqrt{x})^y \Rightarrow y=x^{y / 2}\)

⇒ \(\log y=\frac{y}{2} \cdot \log x\) …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(\frac{1}{y} \cdot \frac{d y}{d x}=\frac{y}{2} \cdot \frac{1}{x}+\frac{1}{2} \log x \cdot \frac{d y}{d x}\)

⇒ \(\left(\frac{1}{y}-\frac{1}{2} \log x\right) \cdot \frac{d y}{d x}=\frac{y}{2 x}\)

⇒ \(\frac{(2-y \log x)}{2 y} \cdot \frac{d y}{d x}=\frac{y}{2 x}\)

⇒ \(x \cdot \frac{d y}{d x}=\frac{y^2}{(2-y \log x)}\)

8. Derivatives of One Function With Respect To Another Function

Let f(x) and g(x) be two functions of x. In order to find the derivative of f(x) with respect to g(x), we put u = f(x) and v = g(x). Now, find \frac{d u}{d v}=\frac{(d u / d x)}{(d v / d x)}, which is the required derivative.

Example 1 Differentiate e^x w.r.t. √x.

Solution

e^x w.r.t. √x

Let u = e^x and v = √x.

Then, \(\frac{d u}{d x}=e^x \text { and } \frac{d v}{d x}=\frac{1}{2} x^{-1 / 2}=\frac{1}{2 \sqrt{x}} .\)

∴ \(\frac{d u}{d v}=\frac{(d u / d x)}{(d v / d x)}=\frac{e^x}{(1 / 2 \sqrt{x})}=2 e^x \sqrt{x}\)

Example 2 Differentiate sin²x w.r.t. e^{cos x}.

Solution

sin²x w.r.t. e^{cos x}

Let u = sin²x and v = e^{cos x}. Then,

\(\frac{d u}{d x}=2 \sin x \cos x\)

and \(\frac{d v}{d x}=e^{\cos x} \cdot(-\sin x)=(-\sin x) \cdot e^{\cos x}\)

∴ \(\frac{d u}{d v}=\frac{(d u / d x)}{(d v / d x)}=\frac{2 \sin x \cos x}{(-\sin x) e^{\cos x}}=\frac{-2 \cos x}{e^{\cos x}} .\)

Example 3 Differentiate sin^-1x w.r.t. tan^-1x.

Solution

sin^-1x w.r.t. tan^-1x

Let u = sin^-1x and v = tan^-1x.

Then, \(\frac{d u}{d x}=\frac{1}{\sqrt{1-x^2}} \text { and } \frac{d v}{d x}=\frac{1}{\left(1+x^2\right)}\)

∴ \(\frac{d u}{d v}=\frac{(d u / d x)}{(d v / d x)}=\frac{1}{\sqrt{1-x^2}} \times\left(1+x^2\right)=\frac{\left(1+x^2\right)}{\sqrt{1-x^2}}\)

Example 4 Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)\) w.r.t. tan^-1x.

Solution

\(\tan ^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)\) w.r.t. tan^-1x

Let u = \(\tan ^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)\) and v = tan^-1x.

Now, v = tan^-1x ⇒ x = tan v.

Putting x = tan v, we get

u = \(\tan ^{-1}\left\{\frac{\sqrt{1+\tan ^2 v}-1}{\tan v}\right\}=\tan ^{-1}\left(\frac{\sec v-1}{\tan v}\right)\)

= \(\tan ^{-1}\left(\frac{1-\cos v}{\sin v}\right)=\tan ^{-1}\left\{\frac{2 \sin ^2(\nu / 2)}{2 \sin (v / 2) \cos (v / 2)}\right\}\)

= \(\tan ^{-1}\left\{\tan \frac{v}{2}\right\}=\frac{v}{2}\)

∴ \(u=\frac{v}{2} \Rightarrow \frac{d u}{d v}=\frac{1}{2}\)

Example 5 Differentiate \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right) \text { w.r.t. } \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\)

Solution

\(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right) \text { w.r.t. } \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\)

Let u = \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right) and v = \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\)

Putting x = tan θ, we get

u = \(\sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^2 \theta}\right)=\sin ^{-1}(\sin 2 \theta)=2 \theta \text {, }\)

v = \(\cos ^{-1}\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)=\cos ^{-1}(\cos 2 \theta)=2 \theta \text {. }\)

∴ u = v ⇒ \(\frac{d u}{d v}=1\).

Example 6 Differentiate \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right) \cdot \text { w.r.t. } \sin ^{-1}\left(\frac{2 x}{1+x^2}\right) \text {. }\)

Solution

\(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right) \cdot \text { w.r.t. } \sin ^{-1}\left(\frac{2 x}{1+x^2}\right) \text {. }\)

Let u = \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\) and v = \(\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\)

Putting x = tan θ, we get

u = \(\tan ^{-1}\left(\frac{2 \tan \theta}{1-\tan ^2 \theta}\right)=\tan ^{-1}(\tan 2 \theta)=2 \theta\),

v = \(\sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^2 \theta}\right)=\sin ^{-1}(\sin 2 \theta)=2 \theta \text {. }\)

∴ u = v ⇒ \(\frac{d u}{d v}=1\).

Example 7 Differentiate \(\tan ^{-1}\left\{\frac{\sqrt{1+x^2}-\sqrt{1-x^2}}{\sqrt{1+x^2}+\sqrt{1-x^2}}\right\} \text { w.r.t. } \cos ^{-1} x^2\)

Solution

\(\tan ^{-1}\left\{\frac{\sqrt{1+x^2}-\sqrt{1-x^2}}{\sqrt{1+x^2}+\sqrt{1-x^2}}\right\} \text { w.r.t. } \cos ^{-1} x^2\)

Let u = \(\tan ^{-1}\left\{\frac{\sqrt{1+x^2}-\sqrt{1-x^2}}{\sqrt{1+x^2}+\sqrt{1-x^2}}\right\}\) and v = cos^-1x².

Then, cos^-1x² = v ⇒ x² = cos v.

Putting x² = cos v, we get

u = \(\tan ^{-1}\left\{\frac{\sqrt{1+\cos v}-\sqrt{1-\cos v}}{\sqrt{1+\cos v}+\sqrt{1-\cos v}}\right\}\)

= \(\tan ^{-1}\left\{\frac{\sqrt{2 \cos ^2(v / 2)}-\sqrt{2 \sin ^2(v / 2)}}{\sqrt{2 \cos ^2(v / 2)}+\sqrt{2 \sin ^2(v / 2)}}\right\}\)

= \(\tan ^{-1}\left\{\frac{\cos (v / 2)-\sin (v / 2)}{\cos (v / 2)+\sin (v / 2)}\right\}=\tan ^{-1}\left\{\frac{1-\tan (v / 2)}{1+\tan (v / 2)}\right\}\)

[dividing num. and denom. by cos(v/2)]

= \(\tan ^{-1}\left\{\tan \left(\frac{\pi}{4}-\frac{v}{2}\right)\right\}=\left(\frac{\pi}{4}-\frac{v}{2}\right) .\)

∴ \(u=\left(\frac{\pi}{4}-\frac{v}{2}\right) \Rightarrow \frac{d u}{d \nu}=\frac{-1}{2}\)

10. Second-Order Derivatives

Let f(x) be a differentiable function of x whose second-order derivative exists. We denote the second-order derivative of y w.r.t. x by \frac{d^2 y}{d x^2} or y2.

Solved Examples

Example 1 Find the second-order derivative of:

(1) x¹⁰

(2) log x

(3) tan^-1x

Solution

(1) Let y = x¹⁰. Then,

\(\frac{d y}{d x}=10 x^9 .\)

∴ \(\frac{d^2 y}{d x^2}=(10 \times 9) x^8=90 x^8 .\)

Hence, \(\frac{d^2}{d x^2}\left(x^{10}\right)=90 x^8\)

(2) Let y = log x. Then,

\(\frac{d y}{d x}=\frac{1}{x}=x^{-1} \text {. }\)

∴ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left(x^{-1}\right)=(-1) x^{(-1-1)}=-x^{-2}=\frac{-1}{x^2} .\)

Hence, \(\frac{d^2}{d x^2}(\log x)=\frac{-1}{x^2}\)

(3) Let y = tan^-1x. Then,

\(\frac{d y}{d x}=\frac{1}{\left(1+x^2\right)}=\left(1+x^2\right)^{-1} .\)

∴ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left(1+x^2\right)^{-1}\)

= \((-1)\left(1+x^2\right)^{-2} \cdot(2 x)=\frac{-2 x}{\left(1+x^2\right)^2}\)

Hence, \(\frac{d^2}{d x^2}\left\{\tan ^{-1} x\right\}=\frac{-2 x}{\left(1+x^2\right)^2}\).

Example 2 If y = (tan x + sec x), prove that \(\frac{d^2 y}{d x^2}=\frac{\cos x}{(1-\sin x)^2}\)

Solution

Given that y = (tan x + sec x).

∴ \(\frac{d y}{d x}=\sec ^2 x+\sec x \tan x=\left(\frac{1}{\cos ^2 x}+\frac{1}{\cos x} \cdot \frac{\sin x}{\cos x}\right)\)

= \(\left(\frac{1+\sin x}{\cos ^2 x}\right)=\left(\frac{1+\sin x}{1-\sin ^2 x}\right)=\frac{1}{(1-\sin x)}\)

∴ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left\{\frac{1}{(1-\sin x)}\right\}=\frac{d}{d x}(1-\sin x)^{-1}\)

= \((-1)(1-\sin x)^{-2}(-\cos x)=\frac{\cos x}{(1-\sin x)^2} \text {. }\)

Hence, \(\frac{d^2 y}{d x^2}=\frac{\cos x}{(1-\sin x)^2}\)

Example 3 If y = e^4xsin 3x, find \(\frac{d^2 y}{d x^2} .\)

Solution

Let y = e^4x sin 3x. Then,

\(\frac{d y}{d x}=3 e^{4 x} \cos 3 x+4 e^{4 x} \sin 3 x=e^{4 x}(3 \cos 3 x+4 \sin 3 x) .\)

∴ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left(\frac{d y}{d x}\right)=\frac{d}{d x}\left\{e^{4 x}(3 \cos 3 x+4 \sin 3 x)\right\}\)

= e^4x (-9sin 3x + 12 cos 3x) + 4 e^4x (3 cos 3x + 4 sin 3x)

= e^4x (7 sin 3x + 24 cos 3x).

\(\frac{d^2 y}{d x^2} .\) = e^4x (7 sin 3x + 24 cos 3x).

Example 4 If y = (x⁴ + cot x), find \(\frac{d^2 y}{d x^2}\).

Solution

We have

y = (x4 + cot x)

⇒ \(\frac{d y}{d x}=4 x^3-{cosec}^2 x\)

⇒ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left(4 x^3-{cosec}^2 x\right)\)

= \(4 \cdot \frac{d}{d x}\left(x^3\right)-\frac{d}{d x}\left({cosec}^2 x\right)\)

= (4 x 3x²) – 2 cosec x(-cosec x cot x)

= (12 x² + 2 cosec²x cot x).

\(\frac{d^2 y}{d x^2}\) = (12 x² + 2 cosec²x cot x).

Example 5 Find the second derivative of log(log x) w.r.t. x.

Solution

Let y = log(log x). Then,

\(\frac{d y}{d x}=\frac{1}{(\log x)} \cdot \frac{1}{x}=\frac{1}{(x \log x)}=(x \log x)^{-1}\)

⇒ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}(x \log x)^{-1}\)

= \((-1)(x \log x)^{-2} \cdot \frac{d}{d x}(x \log x)\)

= \(\frac{-1}{(x \log x)^2} \cdot\left(x \cdot \frac{1}{x}+\log x \cdot 1\right)=\frac{-(1+\log x)}{(x \log x)^2} .\)

log(log x) = \(\frac{-1}{(x \log x)^2} \cdot\left(x \cdot \frac{1}{x}+\log x \cdot 1\right)=\frac{-(1+\log x)}{(x \log x)^2} .\)

Example 6 If y = sin(log x), find \(\frac{d^2 y}{d x^2}\).

Solution

We have

y = sin(log x)

⇒ \(\frac{d y}{d x}=\frac{d}{d x}\{\sin (\log x)\}=\cos (\log x) \cdot \frac{1}{x}=\frac{\cos (\log x)}{x}\)

⇒ \(\frac{d^2 y}{d x^2}=\frac{d}{d x} \cdot\left\{\frac{\cos (\log x)}{x}\right\}\)

= \(\frac{x \cdot \frac{d}{d x}\{\cos (\log x)\}-\cos (\log x) \cdot \frac{d}{d x}(x)}{x^2}\)

= \(\frac{x\left\{-\sin (\log x) \cdot \frac{1}{x}\right\}-\cos (\log x) \cdot 1}{x^2}\)

= \(\frac{-\{\sin (\log x)+\cos (\log x)\}}{x^2} .\)

\(\frac{d^2 y}{d x^2}\) = \(\frac{-\{\sin (\log x)+\cos (\log x)\}}{x^2} .\)

Example 7 If e^y(x+1) = 1, prove that \(\frac{d^2 y}{d x^2}=\left(\frac{d y}{d x}\right)^2\)

Solution

We have

e^y(x+1) = 1 ⇒ \(e^y=\frac{1}{(x+1)}\) …(1)

⇒ \(y=\log \left\{\frac{1}{(x+1)}\right\}=\log 1-\log (x+1)\)

⇒ y = -log(x+1) …(2)

∴ \(\frac{d y}{d x}=\frac{-1}{(x+1)}\)

⇒ \(\frac{d^2 y}{d x^2}=\frac{1}{(x+1)^2}=\left(\frac{d y}{d x}\right)^2 \text {. }\)

Hence, \(\frac{d^2 y}{d x^2}=\left(\frac{d y}{d x}\right)^2\)

Example 8 If y = A cos nx + B sin nx, prove that \(\frac{d^2 y}{d x^2}+n^2 y=0\)

Solution

We have

y = A cos nx + B sin nx

⇒ \(\frac{d y}{d x}=\frac{d}{d x}(A \cos n x)+\frac{d}{d x}(B \sin n x)\)

= -An sin nx + B n cos nx

= n(B cos nx – A sin nx)

⇒ \(\frac{d^2 y}{d x^2}=n \cdot \frac{d}{d x}(B \cos n x-A \sin n x)\)

= \(n \cdot\left\{B \cdot \frac{d}{d x}(\cos n x)-A \cdot \frac{d}{d x}(\sin n x)\right\}\)

= n . {-B n sin nx – A n cos nx}

= -n²(A cos nx + B sin nx) = -n²y

⇒ \(\frac{d^2 y}{d x^2}+n^2 y=0\)

Example 9 If y = e^x(sin x + cos x), prove that \(\frac{d^2 y}{d x^2}-2 \frac{d y}{d x}+2 y=0\)

Solution

We have

y = e^x(sin x + cos x)

⇒ \(\frac{d y}{d x}=e^x \cdot \frac{d}{d x}(\sin x+\cos x)+(\sin x+\cos x) \cdot \frac{d}{d x}\left(e^x\right)\)

= e^x(cos x – sin x) + (sin x + cos x) . e^x = 2 e^x cos x

⇒ \(\frac{d^2 y}{d x^2}=2 \cdot \frac{d}{d x}\left(e^x \cos x\right)\)

= \(2 \cdot\left\{e^x \cdot \frac{d}{d x}(\cos x)+\cos x \cdot \frac{d}{d x}\left(e^x\right)\right\}\)

= 2 . {e^x(-sin x) + (cos x)e^x} = 2e^x(cos x – sin x).

∴ \(\left(\frac{d^2 y}{d x^2}-2 \frac{d y}{d x}+2 y\right)\)

= 2 e^x (cos x – sin x) – 4 e^x cos x + 2 e^x(sin x + cos x) = 0.

Hence, \(\frac{d^2 y}{d x^2}-2 \frac{d y}{d x}+2 y=0\)

Example 10 If y = 3 e^2x + 2 e^3x, prove that \(\frac{d^2 y}{d x^2}-5 \frac{d y}{d x}+6 y=0 .\)

Solution

We have

y = 3 e^2x + 2 e^3x …(1)

⇒ \(\frac{d y}{d x}=3 \cdot \frac{d}{d x}\left(e^{2 x}\right)+2 \cdot \frac{d}{d x}\left(e^{3 x}\right)\) [on differentiating (1) w.r.t. x]

= (3 x 2e^2x) + (2 x 3 e^3x) = (6 e^2x + 6 e^3x)

⇒ \(\frac{d y}{d x}=6\left(e^{2 x}+e^{3 x}\right)\) …(2)

On differentiating (2) w.r.t. x, we get

\(\frac{d^2 y}{d x^2}=6 \cdot\left\{\frac{d}{d x}\left(e^{2 x}\right)+\frac{d}{d x}\left(e^{3 x}\right)\right\}\)

= 6 . (2 e^2x + e^3x)

∴ \(\left(\frac{d^2 y}{d x^2}-5 \frac{d y}{d x}+6 y\right)\)

= 6(2 e^2x + 3 e^3x) – 30(e^2x + e^3x) + (18 e^2x + 12 e^3x)

= (12 – 30 + 18)e^2x + (18 – 30 + 12)e^3x = 0.

Hence, \(\left(\frac{d^2 y}{d x^2}-5 \frac{d y}{d x}+6 y\right)=0 .\)

Example 11 If y = sin^-1x, prove that \(\left(1-x^2\right) \frac{d^2 y}{d x^2}-x \frac{d y}{d x}=0 .\)

Solution

Given: y = sin^-1x …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(y_1=\frac{1}{\sqrt{1-x^2}}\)

⇒ \(y_1^2=\frac{1}{\left(1-x^2\right)}\)

⇒ (1 – x²)y₁² = 1 …(2)

On differentiating both sides of (2) w.r.t. x, we get

(1-x²) . 2y₁y₂ + y₁²₁(-2x) = 0

⇒ (1-x²)y₂ – xy₁ = 0.

Hence, \(\left(1-x^2\right) \frac{d^2 y}{d x^2}-x \frac{d y}{d x}=0 .\)

Example 12 If y = (tan^-1x)², prove that (1+x²)²y₂ + 2x(1+x²)y₁ = 2.

Solution

Given: y = (tan^-1x)² …(1)

On differentiating both sides of (1) w.r.t. x, we get

\(y_1=2 \tan ^{-1} x \cdot \frac{1}{\left(1+x^2\right)}\)

⇒ (1 + x²)y₁ = 2 tan^-1x

⇒ (1 + x²)²y₁² = 4(tan^-1x)² [on squaring both sides]

⇒ (1 + x²)²y₁² – 4y = 0 …(2)

On differentiating both sides of (2) w.r.t. x, we get

(1+x²)². 2y₁y₂ + y₁² . 2(1+x²).2x – 4y₁ = 0

⇒ (1+x²)²y₂ + 2x(1+x²)y₁ – 2 = 0.

Hence, (1+x²)²y₂ + 2x(1+x²)y₁ = 2.

Example 13 If x = a(θ + sin θ) and y = a(1 – cos θ), find \(\frac{d^2 y}{d x^2} \text { at } \theta=\frac{\pi}{2}\).

Solution

We have

x = a(θ + sin θ) and y = a(1 – cos θ)

⇒ \(\frac{d x}{d \theta}=a(1+\cos \theta) \text { and } \frac{d y}{d \theta}=a \sin \theta\)

⇒ \(\frac{d y}{d x}=\frac{(d y / d \theta)}{(d x / d \theta)}\)

= \(\frac{a \sin \theta}{a(1+\cos \theta)}=\frac{\sin \theta}{(1+\cos \theta)}=\frac{2 \sin (\theta / 2) \cos (\theta / 2)}{2 \cos ^2(\theta / 2)}=\tan \frac{\theta}{2}\)

⇒ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left(\tan \frac{\theta}{2}\right)=\frac{1}{2} \sec ^2 \frac{\theta}{2} \cdot \frac{d \theta}{d x}=\left(\frac{1}{2} \sec ^2 \frac{\theta}{2}\right) \times \frac{1}{a(1+\cos \theta)}\)

⇒ \(\left(\frac{d^2 y}{d x^2}\right)_{\theta=\frac{\pi}{2}}=\frac{1}{2} \sec ^2 \frac{\pi}{4} \cdot \frac{1}{a\left(1+\cos \frac{\pi}{2}\right)}=\frac{1}{a} .\)

Example 14 If x = (2 cos θ – cos 2θ) and y = (2 sin θ – sin 2θ), find \(\frac{d^2 y}{d x^2} \text { at } \theta=\frac{\pi}{2}\).

Solution

We have

x = (2 cos θ – cos 2θ) and y = (2 sin θ – sin 2θ)

⇒ \(\frac{d x}{d \theta}=(-2 \sin \theta+2 \sin 2 \theta) \text { and } \frac{d y}{d \theta}=(2 \cos \theta-2 \cos 2 \theta)\)

⇒ \(\frac{d y}{d x}=\frac{(d y / d \theta)}{(d x / d \theta)}=\frac{(2 \cos \theta-2 \cos 2 \theta)}{(-2 \sin \theta+2 \sin 2 \theta)}=\frac{(\cos \theta-\cos 2 \theta)}{(\sin 2 \theta-\sin \theta)}\)

= \(\frac{2 \sin \left(\frac{3 \theta}{2}\right) \sin \frac{\theta}{2}}{2 \cos \left(\frac{3 \theta}{2}\right) \sin \frac{\theta}{2}}=\tan \frac{3 \theta}{2}\)

⇒ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left(\tan \frac{3 \theta}{2}\right)=\frac{3}{2} \sec ^2 \frac{3 \theta}{2} \cdot \frac{d \theta}{d x}=\frac{3}{2} \sec ^2 \frac{3 \theta}{2} \cdot \frac{1}{2(\sin 2 \theta-\sin \theta)}\)

⇒ \(\left(\frac{d^2 y}{d x^2}\right)_{\theta=\frac{\pi}{2}}=\frac{3}{2} \cdot \sec ^2\left(\frac{3 \pi}{4}\right) \cdot \frac{1}{2\left(\sin \pi-\sin \frac{\pi}{2}\right)}\)

= \(\frac{-3}{4} \sec ^2 \frac{\pi}{4}=\frac{-3}{4} \times(\sqrt{2})^2=\frac{-3}{2}\)

[∵ \(\sec \frac{3 \pi}{4}=\sec \left(\pi-\frac{\pi}{4}\right)=-\sec \frac{\pi}{4}\)].

Chapter 1 Continuity And Differentiability Functions

Real Functions

Let R be the set of all real numbers, and let X and Y be any two nonempty subsets of R. Then, a rule f which associates to each x ∈ X, a unique real number f(x) ∈ Y is called a real function from X to Y and we write, f : X → Y.

f(x) is called the image of x or the value of the function at x. The sets X and Y are respectively known as the domain and the codomain of f.

Also, the set {f(x) : x ∈ X} is called the range of f.

Clearly, range (f) ⊆ Y.

However, if range (f) = Y, we say that f is an onto function: otherwise f is said to be an into function.

If two or more than two elements in X have the same image in Y then f is said to be a many-one function.

On the other hand, if different elements in X have different images in Y, we say that f is one-one.

Clearly, f is one-one ⇔ [f(x1) = f(x2) ⇒ x1 = x2].

A one-one onto function is called a one-to-one correspondence.

Remark 1 Sometimes a function is described only by a formula and the domain of the function is not explicitly stated. In such cases, the domain of the function is the set of all those real numbers for which the formula is meaningful.

Read and Learn More  Class 12 Math Solutions

Remark 2 Usually the domain of a real function is an interval. For any two real numbers a and b, where a<b, we define

1. closed interval [a, b] = {x ∈ R : a ≤ x ≤ b}
2. open interval ]a, b[ = {x ∈ R : a < x < b}
3. right-half open interval [a, b[ = {x ∈ R : a ≤ x < b}
4. left-half open interval ]a, b] = {x ∈ R : a < x ≤ b}
5. [a, ∞] = {x ∈ R : x > a}
6. [a, ∞] = {x ∈ R : x ≥ a}
7. [-∞, a] = {x ∈ R : x < a}
8. [-∞, a] = {x ∈ R : x ≤ a}
   Sometimes, we write, R = ]-∞, ∞[.

Some Important Functions

1. Constant Function Let c be a fixed real number. Then, the function defined by f(x) = c for all x ∈ R is called a constant function c.

Clearly, dom(f) = R and range (f) = {c}.

2. Identity Function The function defined by f(x) = x for all x ∈ R is called the identity function.

Clearly, its domain is R and its range is R.

3. Modulus Function The function defined by

\(f(x)=|x|=\left\{\begin{array}{r}
x, \text { when } x \geq 0 \\
-x, \text { when } x<0
\end{array}\right.\)

is called the modulus function.

Since the modulus of every real number is a unique non-negative real number, so domf(x) = R.

Since | x | is either o or a positive real number, we have range (f) = {| x | : x ∈ R} = set of non-negative real numbers.

4. Reciprocal Function The function defined by f(x) = \(\frac{1}{x}\) is called the reciprocal function.

Clearly, \(\frac{1}{x}\) is not defined when x = 0.

∴ dom(f) = R – {0}.

Also, y = \(\frac{1}{x}\) ⇔ x = \(\frac{1}{y}\).

Clearly, x is defined for all real numbers y except when y = 0.

∴ range (f) = R – {0}.

5. Signum Function This function is defined by f(x) = \(\left\{\begin{array}{c}
\frac{|x|}{x}, \text { when } x \neq 0 \\
0, \text { when } x=0
\end{array}\right.\)

Thus, we have f(x) = \(\left\{\begin{array}{r}
1, \text { when } x>0 \\
0, \text { when } x=0 \\
-1, \text { when } x<0 .
\end{array}\right.\)

Clearly, its domain is R and range = {-1, 0, 1}.

6. Square-Root Function Let f(x) = +√x.

We know that the negative real numbers do not have real square roots. So, f(x) is not defined when x is a negative real number.

f(x) is not defined when x is a negative real number.

∴ dom(f) = set of all non-negative real numbers real numbers = [0, ∞[.

Clearly, range (f) = {+√x : x ∈ [0, ∞[} = [0, ∞[.

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

7. Step Function Or The Greatest Integer Function

If x ∈ R then [x] is defined as the greatest integer not exceeding x.

For example, we have

[2.01] = 2; [2.9] = 2; [-1.3] = -2; [3] = 3 and [-1] = -1, etc.

Now, if we consider f(x) = [x] then clearly for each x ∈ R, [x] is defined.

So dom(f) = R.

By definition, [x] is an integer.

So, range(f) = {[x] : x ∈ R} = set of all integers.

Example Find a set of all real numbers x such that [x] = 2.

Solution Clearly, for all x such that 2 ≤ x < 3, we have f(x) = [x] = 2.

∴ required set = {x ∈ R : 2 ≤ x < 3} = [2, 3[.

8. Smallest Integer Function (or Ceiling Function) For any real number x, we define ⌈x⌉ as the smallest integer greater than or equal to x.

For example,

⌈6.3⌉ = 7, ⌈7.01⌉ = 8, ⌈-6.1⌉ = -6, ⌈-2.9⌉ = -2, ⌈-3⌉ = -3, ⌈5⌉ = 5.

The function f : R → R : f(x) = ⌈x⌉, x ∈ R is called the smallest integer function or ceiling function.

Clearly, domain (f) = R and range (f) = I.

9. Polynomial Function A function of the formula

p(x) = a₀xⁿ+ a₁x^n-1 + a₂x^n-2 + … + a_n-1x+a_n,

where a₀, a₁, a₂,…..,a_n-1,an are real numbers, a₀ ≠ 0

and n is a non-negative integer, is called a polynomial function of degree n.

Polynomials of degree 1, 2, 3 and 4 are respectively called linear, quadratic, cubic and biquadratic polynomials.

Thus, (1) f(x) = ax + b, a ≠ 0, is a linear polynomial.

(2) f(x) = ax² + bx + c, a ≠ 0, is a quadratic polynomial.

(3) f(x) = ax³ + bx² + cx + d, a ≠ 0, is a cubic polynomial.

10. Rational Function A function of the form f(x) = \(\frac{p(x)}{q(x)}\), where p(x) and q(x) are polynomials and a(x) ≠ 0, is called a rational function.

Thus, f(x) = \(\left(\frac{x^2+1}{x^3-2 x+5}\right)\) is a rational function, where x³ – 2x + 5 ≠ 0.

Graphs

Graph of a Function

For a given function f(x), the aggregate of the points (x, f(x)) is called the graph or the curve representing the function.

In practice, we plot some of the points and join them freehand to obtain the graph.

Example 1 Draw the graphs of the constant functions

1. f(x) = 2

2. f(x) = 0

3. f(x) = -2

Solution (1) When f(x) = 2 for all x ∈ R, some of the points on the graph may be taken as (0, 2), (-1, 2), (1,2) (-2, 2), (2,2), etc.

Joining these points, we obtain a line y = 2, drawn parallel to the x-axis at a distance of 2 units from it, as the required graph.

Similarly,

(2) the graph of the function f(x) = 0 is the line y = 0, i.e., the x-axis.

(3) The graph of the function f(x) = -2 is the line y = -2, drawn parallel to the x-axis at a distance of 2 units below the x-axis.

WBBSE Class 12 Continuity and Differentiability Solutions

Example 2 Draw the graphs of the linear functions

(1) f(x) = 1-x

(2) f(x) = 2x + 1

Solution (1) When f(x) = 1-x, some of the points on the graph are (0, 1), (1,0), (2,-1), (-1, 2) etc.

Joining these points, we get a line as the graph of the function.

(2) Let f(x) = 2x+1.

Some of the points on the graph are (0,1), (1,3), (-1,-1), (2,5) etc.

Joining these points, we obtain a line as the graph.

Remark The graph of a linear function is a straight line.

Example 3 Draw the graph of the identify function f(x) = x.

Solution f(x) = x is clearly a linear function whose graph must be a line. Plotting the points (0,0), (1,1), (-1,-1), etc., and joining them, we get the required graph.

Example 4 Draw the graphs of the polynomial functions

(1) f(x) = x²

(2) f(x) = 1-x²

(3) f(X) = x³-x

Solution

(1) The function f(x) = x² is a quadratic function. Some of the points on the graph are (0,0), (1,1), (-1, 1), (-2, 4), (2,4), (-3, 9), (3,9) etc.

Joining these points, we get a parabola as the graph.

(2) f(x) = 1-x² is also a quadratic function. Some of the points on the graph are (0,1), (1,0), (-1,0), (2,-3), (-2,-3), (-3,-8), (3,-8), etc.

Joining these points, we obtain a parabola as its graph.

(3) Let f(x) = x³ – x.

This is a cubic function.

Some of the points on the graph are (0,0), (-1,0), (1,0), (-0.5, 0.375), (0.5, -0.375), (2,6), (-2,-6), etc.

Joining these points, we obtain the required graph.

Remark It may be observed here that whenever (x,y) is a point on the graph then (-x,-y) is also a point on the graph. So, the graph is symmetrical about the origin.

This is an important property possessed by the graph of an odd function.

Step-by-Step Solutions to Continuity Problems

Example 5 Draw the graph of the modulus function f(x) = | x |.

Solution

f(x) = | x | = \(\left\{\begin{array}{r}
x \text { when } x \geq 0 \\
-x \text { when } x<0
\end{array}\right.\)

Some of the points on the graph are (0,0), (-1,1), (-2,2), (1,1), (2,2), etc.

Joining these points, we get the required graph.

Remark It may be observed here that whenever (x,y) is a point on the graph, then (-x,y) is also a point of it. Thus, the graph is symmetrical about the y-axis. This is an important property possessed by the graphs of even functions.

Example 6 Draw the graph of the reciprocal function f(x) = \(\frac{1}{x}\).

Solution

Clearly, f(x) = \(\frac{1}{x}\) is not defined at x = 0. Some points on the graph are (1,1), (-1,-1), (1\2,2), (2,1/2), (-1/2,-2), (-2,-1/2), (1/3,3), (-1/3,-3), (3,1/3), etc.

Joining these points, we get the required graph. Since f(x) = \(\frac{1}{x}\) is an odd function, it is symmetrical about the origin.

Example 7 Draw the graph of the square-root function f(x) = √x.

Solution

Let f be a real-valued function which associates to each non-negative real number x, its non-negative square root.

The, f: R₀⁺→ R₀⁺ : f(x) = √x, is called the square-root function.

Domain f(x) = R₀+, and range (f) = R₀⁺.

Some of the points on the graph are (0,0), (1,1), (2, 1.4), (3, 1.7), (4, 2), (5, 2.2), etc. Joining these points, we get the required graph.

Example 8 Draw the graph of the rational function f(x) = \(\frac{x^2-1}{x-1}\).

Solution

Let f(x) = \(\frac{x^2-1}{x-1}\).

Now, f(1) = \(\frac{0}{0}\), which is meaningless.

So, the function is not defined at x = 1.

Also, when x ≠ 1, we have

f(x) = \(\left(\frac{x^2-1}{x-1}\right)\) = (x+1).

This being a linear function, its graph is a straight line.

Some of the points on the graph are (0,1), (-1,0), (2,3), (3,4), (-2,-1), (-3,-2), etc.

Joining these points, we obtain the required graph. Clearly, the point (1,2) does not lie on the graph. So, it is a broken graph, and we shall say that the given function is discontinous at x = 1.

Example 9 Draw the graph of the step function f(x) = [x].

Solution

As the definition of the function indicates, for all x such that -2 ≤ x < -1,

we have f(x) = -2; for all x such that -1 ≤ x < 0,

We have f(x) = -1; for all x such that 0 ≤ x < 1,

we have f(x) = 0′ for all x such that 1 ≤ x < 2, we have f(x) = 1, and so on,

i.e., f(x) = \(\left[\begin{array}{c}
-2 \text { when } x \in[-2,-1[ \\
-1 \text { when } x \in[-1,0[ \\
0 \text { when } x \in[0,1[ \\
1 \text { when } x \in[1,2[ \\
\text { and so on. }
\end{array}\right.\)

Clearly, the function jumps at the points (-1,-2), (0, -1), (1,0), (2,1), etc.

In other words, the given function is discontinuous at each integral value of x.

Example 10 Draw the graph of the smallest integer function f(x) = ⌈x⌉.

Solution

As the definition of the function suggest,

for all x such that -3 ≤ x ≤ -2, we have f(x) = -2;

for all x such that -2 < x ≤ -1, we have f(x) = -1;

for all x such that -1 < x ≤ 0, we have f(x) = 0;

for all x such that 0 < x ≤ 1, we have f(x) = 1; and so on.

i.e., f(x) = \(\left[\begin{array}{c}
-2 \text { when } x \in]-3,-2] \\
-1 \text { when } x \in]-2,-1] \\
0 \text { when } x \in]-1,0] \\
1 \text { when } x \in] 0,1] \\
2 \text { when } x \in] 1,2] \\
3 \text { when } x \in] 2,3] \\
\text { and so on. }
\end{array}\right.\)

Plotting these points, we can get the required graph. The function jumps at the points (-2, -1), (-1, 0), (0,1), (1,2) etc., or is discontinuous at each integral value of x.

Differentiability Explained for Class 12

Example 11 Draw the graph of the signum function f(x) = \(\left\{\begin{array}{c}
\frac{|x|}{x} \text { when } x \neq 0 \\
0 \quad \text { when } x=0 .
\end{array}\right.\)

Solution

Clearly, (0,0) is a point on the graph. Now, when x > 0, we have | x | = x, and so in this case, we have, f(x) = 1, i.e., f(x) = 1 for all values of x > 0.

And, when x < 0, we have | x | = -x and therefore,

f(x) = -1 for all values of x < 0.

Hence the graph may be drawn, as shown in the adjoining figure.

Clearly, the function is broken (i.e., it is discontinuous) at each of the points x = -1,0 and 1.

Example 12 Draw the graph of the function f(x) = \(\left\{\begin{array}{l}
x^2, \text { when } x<0 \\
x, \text { when } 0 \leq x \leq 1 \\
1 / x, \text { when } 1 \leq x<\infty .
\end{array}\right.\)

Solution

Here, the graph consists of three parts. Some of the points of the graph are (-3,9), (-2,4), (-1,1), (0,0), (\(\frac{1}{2}\), \(\frac{1}{2}\)) , (\(\frac{3}{4}\), \(\frac{3}{4}\)),  (1,1), (2,\(\frac{1}{2}\)), (3,\(\frac{1}{3}\)), etc.

And, the graph may now be drawn, as shown in the adjoining figure.

Example 13 Draw the graph of the function f(x) = | x | + | x-1 |.

Solution

Let us consider the following cases.

Case 1 When x < 0

In this case, (x-1) < 0.

∴ |x| = -x and | x-1 | = -(x-1) = 1 – x.

Consequently, | x | + | x-1 | = – x + 1 – x = 1 – 2x.

Case 2 When 0 ≤ x ≤ 1

In this case, | x | = x and | x-1 | = -(x-1) = 1-x.

∴ | x | + | x-1 | = x + 1 – x = 1.

Case 3 When x > 1

In this case, | x | = x and | x-1 | = x + (x-1) = (2x-1).

Thus, we may define the above function as

\(f(x)=\left\{\begin{array}{cl}
1-2 x, & \text { when } x<0 \\
1, & \text { when } 0 \leq x \leq 1 \\
2 x-1, & \text { when } x>1
\end{array}\right.\)

So, we have

(1) a linear function 1-2x when x < 0;

(2) a constant function 1 when 0 ≤ x ≤ 1;

(3) a linear function 2x-1 when x > 1.

The corresponding points on these parts of the graph are (-1,3), (-2,5), (0,1), (1,1), (2,3), (3,5), etc.

Joining these points, we obtain the graph as shown.

Example 14 Draw the graph of the exponential function:

(1) f(x) = 2^x

(2) f(x) = \(\left(\frac{1}{3}\right)^x\)

Solution

(1) Let f(x) = 2^x.

Some of the points on the graph are

(0,1), (1,2), (2,4), (3,8), \(\left(-1, \frac{1}{2}\right)\), \(\left(-2, \frac{1}{4}\right)\), \(\left(-3, \frac{1}{8}\right)\), etc.

And so the graph takes the form, shown in the adjoining figure.

It may be observed here that the given function is strictly increasing. Also, as the value of x decreases, the corresponding value of the function decreases, and therefore, on the left-hand side of the y-axis, the curve comes closer and closer to the x-axis.

This is the case of the exponential function ax, where a > 1.

(2) Let f(x) = \(\left(\frac{1}{3}\right)^x\)

Some of the points on the graph are (-2,9), (-1,3), (0,1), \(\left(1, \frac{1}{3}\right)\), \(\left(2, \frac{1}{9}\right)\), etc.

Joining these points, we obtain the graph as shown. It follows from the graph that the given function is strictly decreasing.

On the RHS of the y-axis, the curve comes closer and closer to the x-axis.

Remark This is the case of the exponential function ax, where 0 < a < 1.

Example 15 Draw the graphs of the logarithmic functions

(1) log_ax, when a > 1

(2) log_ax, when 0 < a < 1

Solution

(1) We know that when a > 1, the function ax is strictly increasing, i.e., different values of x give different values of ax. Also, the range of this function is R. So, the function f(x) = ax is one-one onto and therefore invertible.

Its graph is of the form shown in the adjoining figure. The graph of the function g(x) = log_ax x is the reflection of the graph of f(x) = ax in the line y = x.

It may be noted that the graph passes through (1,0).

(2) We know that when 0 < a < 1, the function ax is strictly decreasing, i.e., different values of x give different values of ax. So, the function is one-one. Also, its range is R. So, it is onto. Thus, the function ax is invertible.

Its inverse is the log function reflected by the line y = x, as shown. The graph clearly passes through (1,0).

Example 16 On the same scale draw the graphs of e^x and log_ex.

Solution

Since e lies between 2 and 3, it follows that e > 1. So, it is a particular case of ax, where a > 1. The fucntion ex is strictly increasing. Also, its range is R. So, the function is one-one onto and therefore invertible.

The graph passes through the point (0,1) and comes closer and closer to the x-axis and the values of x decrease. Thus, the graph of ex may be drawn as shown in the figure. Its reflection in the line y = x gives the graph of logex.

Graphs of Trignometric Functions

1. Graph Of A Sine Function We know that a sine function is periodic with period 2π. So, we have to sketch the graph in the interval [0,2π] and then we may complete the graph by repeating it over intervals, each of length 2π. We first draw it in the interval \(\left[0, \frac{\pi}{2}\right]\). We know that it is strictly increasing in this interval. Also, we may use the table, given below.

Thus, we may draw the graph in the interval \(\left[0, \frac{\pi}{2}\right]\).

Now, we know that sin(π-x) = sin x. So we may get some other values of the function in the interval \(\left[\frac{\pi}{2}, \pi\right]\). Moreover, the function is strictly decreasing in this interval. Thus, we may draw it in the interval \(\left[\frac{\pi}{2}, \pi\right]\). Finally, we draw it in (π, 2π), using the fact that sin (π+x) = -sin x.

The graph may be completed now by making repetitions over each interval of length 2π.

Common Questions on Continuity and Differentiability

2. Graph Of A Cosine Function We know that a cosine function is periodic with period 2π. By making use of the table given below, we may first draw it in the interval \(\left[0, \frac{\pi}{2}\right]\), keeping in view that it is strictly decreasing in this interval.

Now, cos (π-x) = -cos x, so, we may draw the graph in the interval [π/2, π]. It is strictly decreasing in this interval also. Further, making use of cos(π+x) = cos x, we may draw the graph form π to 2π, as shown in the figure.

The graph may now be completed by making repetitions over each interval of length 2π.

3. Graph Of A Tangent Function We know that a tangent function is a periodic function with period π. Therefore, it is enough to draw the graph over an interval of length π. The complete graph then consists of infinitely many repetitions of the same to the let as well as to the right.

Since tan(-x) = – tanx, therefore, if (x, tan x) is any point on the graph then (-x, -tan x) is also a point on the graph. Thus, we can say that the graph of y = tan x is symmetrical in opposite quadrants.

Some of the values of the function are given below:

The graph may thus be drawn as shown below.

Similarly, the graphs of cosec x, sec x and cot x may be drawn.

Continuity

Continuity At A Point A real function f(x) is said to be continuous at a point a of its domain if \(\lim _{x \rightarrow a} f(x)\) exists and equals f(a).

Thus, f(x) is continuous at x = a if \(\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow a^{-}} f(x)=f(a) .\)

If f(x) is not continuous at a point, it is said to be discontinous at that point.

Remark f(x) is discontinuous at x = a in each of the following cases:

(1) f(a) is not defined

(2) \(\lim _{x \rightarrow a} f(x)\) does not exist

(3) \(\lim _{x \rightarrow a} f(x) \neq f(a)\) {removable discontinuity}

Geometric Idea of Continuity

Example 1 Consider the function: f(x) = \(\left\{\begin{array}{l}
1, \text { if } x \neq 0 \\
2, \text { if } x=0 .
\end{array}\right.\)

The above function is clearly defined for every real value of x.

We have, f(0) = 2.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)=\lim _{h \rightarrow 0} f(h)=1\).

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} f(-h)=1\).

∴ \(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0-} f(x)=1 \text {. So, } \lim _{x \rightarrow 0} f(x)=1\).

Thus, \(\lim _{x \rightarrow a} f(x) \neq f(0)\).

If we draw the graph of the given function, we note that we cannot draw the graph without lifting the pen. We have to lift the pen at x=0.

So, the given function is discontinuous at x = 0.

Example 2 Consider the function: f(x) = \(\begin{cases}x+2, & \text { if } x \leq 1 \\ x-2, & \text { if } x>1\end{cases}\).

The given function is defined at all points of the real line.

We have f(1) = (1 + 2) = 3.

\(\lim _{x \rightarrow 1+} f(x)=\lim _{h \rightarrow 0} f(1+h)=\lim _{h \rightarrow 0} f(1+h-2)=\lim _{h \rightarrow 0} f(h-1)=-1\).

\(\lim _{x \rightarrow 1-} f(x)=\lim _{h \rightarrow 0} f(1-h)=\lim _{h \rightarrow 0} f(1-h+2)=\lim _{h \rightarrow 0} f(3-h)=3\).

∴ \(\lim _{x \rightarrow 1+} f(x) \neq \lim _{x \rightarrow 1-} f(x) \text { and so } \lim _{x \rightarrow 1} f(x)\) does not exist.

If we draw the graph of the above function, we note that we cannot draw the graph without lifting the pen. We have to lift the pen at x = 1.

So, the given function is discontinuous at x = 1.

Solved Examples

Example 1 Show that f(x) = x³ is continuous at x = 2.

Solution

f(x) = x³

We have f(2) = 2³ = 8;

\(\lim _{x \rightarrow 2+} f(x)=\lim _{h \rightarrow 0}(2+h)^3=\lim _{h \rightarrow 0}\left(8+h^3+12 h+6 h^2\right)=8\);

\(\lim _{x \rightarrow 2-} f(x)=\lim _{h \rightarrow 0}(2-h)^3=\lim _{h \rightarrow 0}\left(8-h^3-12 h+6 h^2\right)=8\).

∴ \(\lim _{x \rightarrow 2+} f(x)=\lim _{x \rightarrow 2-} f(x)=f(2)\).

Hence, f(x) is continuous at x = 2.

Example 2 Show that f(x) = [x] is not continuous at x = n, where n is an integer.

Solution

We have f(n) = [n] = n;

\(\lim _{x \rightarrow n+} f(x)=\lim _{h \rightarrow 0} f(n+h)=\lim _{h \rightarrow 0}[n+h]=n\) {∵ [n+h] = n};

\(\lim _{x \rightarrow n-} f(x)=\lim _{h \rightarrow 0} f(n-h)=\lim _{h \rightarrow 0}[n-h]=(n-1)\) {∵ [n-h] = (n-1)}.

Thus, \(\lim _{x \rightarrow n+} f(x) \neq \lim _{x \rightarrow n-} f(x)\) and therefore, \(\lim _{x \rightarrow n} f(x)\) does not exist.

Hence, f(x) is discontinuous at x = n.

Example 3 Show that the function f(x) = \(\left\{\begin{array}{l}
x, \text { if } x \text { is an integer; } \\
0, \text { if } x \text { is not an integer }
\end{array}\right.\)

Solution

Let x = n, where n is an integer. Then f(n) = n;

\(\lim _{x \rightarrow n+} f(x)=\lim _{h \rightarrow 0} f(n+h)=0\)

[∴ (n + h) is not an integer ⇒ f(n+h) = 0];

and \(\lim _{x \rightarrow n^{-}} f(x)=\lim _{h \rightarrow 0^{-}} f(n-h)=0\)

[∴ (n-h) is not an integer ⇒ f(n-h) = 0].

∴ \(\lim _{x \rightarrow n+} f(x)=\lim _{x \rightarrow n-} f(x)=0\)

So, \(\lim _{x \rightarrow n} f(x)=0 \neq f(n)\).

Hence, f(x) is discontinuous at x = n.

Example 4 Discuss the continuity of the function f(x) at x = 0, if

f(x) = \(\begin{cases}2 x-1, & x<0 \\ 2 x+1, & x \geq 0\end{cases}\).

Solution

Clearly, f(0) = (2 x 0 + 1) = 1.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)\) = \(\lim _{h \rightarrow 0}[2(0+h)+1]=\lim _{h \rightarrow 0}(2 h+1)=1\).

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)\) = \(\lim _{h \rightarrow 0}[2(0+h)+1]=\lim _{h \rightarrow 0}(2 h+1)=1\).

Thus, \(\lim _{x \rightarrow 0+} f(x) \neq \lim _{x \rightarrow 0-} f(x)\) and therefore, \(\lim _{x \rightarrow 0} f(x)\) does not exist.

Hence, f(x) is discontinuous at x = 0.

Example 5 Show that the function f(x) = \(\left\{\begin{array}{r}
3 x-2, \text { when } x \leq 0 \\
x+1, \text { when } x>0
\end{array}\right.\) is discontinuous at x = 0.

Solution

We have, f(0) = (3 x 0 – 2) = -2.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)\) = \(\lim _{h \rightarrow 0}(h+1)=1\).

\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{h \rightarrow 0} f(0-h)\) = \(\lim _{h \rightarrow 0}[3(-h)-2]=\lim _{h \rightarrow 0}(-3 h-2)=-2\).

∴ \(\lim _{x \rightarrow 0+} f(x) \neq \lim _{x \rightarrow 0-} f(x)\) and therefore, \(\lim _{x \rightarrow 0} f(x)\) does not exist.

Hence, f(x) is discontinuous at x = 0.

Example 6 Show that the function f(x) = \(\left\{\begin{array}{c}
\frac{x}{|x|}, \text { when } x \neq 0 \\
1, \text { when } x=0
\end{array}\right.\) is discontinuous at x = 0.

Solution

It is being given that f(0) = 1.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)=\lim _{h \rightarrow 0} \frac{h}{|h|}=\lim _{h \rightarrow 0} \frac{h}{h}=1\).

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} \frac{-h}{|h|}=\lim _{h \rightarrow 0} \frac{-h}{h}=-1\).

∴ \(\lim _{x \rightarrow 0+} f(x) \neq \lim _{x \rightarrow 0-} f(x)\).

So, \(\lim _{x \rightarrow 0} f(x)\) does not exist.

Hence, f(x) is discontinuous at x = 0.

Example 7 Examine the continuity of the function f(x) = \(\left\{\begin{array}{cl}
\frac{|\sin x|}{x}, & x \neq 0 \\
1, & x=0 \text { at } x=0 .
\end{array}\right.\)

Solution

We have f(0) = 1.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)\) = \(\lim _{h \rightarrow 0} \frac{|\sin (0+h)|}{(0+h)}=\lim _{h \rightarrow 0} \frac{|\sin h|}{h}=\lim _{h \rightarrow 0} \frac{\sin h}{h}=1\).

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)\)

= \(\lim _{h \rightarrow 0} \frac{|\sin (-h)|}{-h}=\lim _{h \rightarrow 0} \frac{|-\sin h|}{-h}=\lim _{h \rightarrow 0} \frac{\sin h}{-h}=-1\).

∴ \(\lim _{x \rightarrow 0+} f(x) \neq \lim _{x \rightarrow 0-} f(x)\). So, \(\lim _{x \rightarrow 0} f(x)\) does not exist.

Hence, f(x) is discontinuous at x = 0.

Example 8 Show that the function f(x) = 2x – | x | is continuous at x = 0.

Solution

We have, f(0) = (2 x 0) – | 0 | = 0.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)\)

= \(\lim _{h \rightarrow 0}(2 h-|h|)=\lim _{h \rightarrow 0}(2 h-h)=\lim _{h \rightarrow 0} h=0\).

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)\)

= \(\lim _{h \rightarrow 0}\{2(-h)-|-h|\}=\lim _{h \rightarrow 0}(-2 h-h)=\lim _{h
\rightarrow 0}(-3 h)=0\).

Thus, \(\lim _{x \rightarrow 0+} f(x)=\lim _{x \rightarrow 0-} f(x)=0 and therefore, \lim _{x \rightarrow 0} f(x)=0\).

∴ \(\lim _{x \rightarrow 0} f(x)=f(0)=0\).

Hence, f(x) is continuous at x = 0.

Examine 9 Let f(x) = \(\left\{\begin{aligned}
|x|+3, & \text { if } x \leq-3 \\
-2 x, & \text { if }-3<x<3 \\
6 x+2, & \text { if } x \geq 3 .
\end{aligned}\right.\) Show that f(x) is continuous at x = -3 but discontinuous at x = 3.

Solution

We have f(-3) = | 3 | + 3 = (3+3) = 6.

\(\lim _{x \rightarrow(-3)+} f(x)=\lim _{h \rightarrow 0} f(-3+h)\) = \(\lim _{h \rightarrow 0}\{-2(-3+h)\}=\lim _{h \rightarrow 0}(6-2 h)=6\).

\(\lim _{x \rightarrow(-3)-} f(x)=\lim _{h \rightarrow 0} f(-3-h)\) = \(\lim _{h \rightarrow 0}(|-3-h|+3)=\lim _{h \rightarrow 0}\{|-(3+h)|+3\}\)

= \(\lim _{h \rightarrow 0}\{(3+h)+3\}=6\).

∴ \(\lim _{x \rightarrow(-3)+} f(x)=\lim _{x \rightarrow(-3)-} f(x)=6\). So, \(\lim _{x \rightarrow(-3)} f(x)=6\).

Thus, \(\lim _{x \rightarrow(-3)} f(x)=f(-3)=6\).

Hence, f(x) is continuous at x = -3.

Now, f(3) = (6 x 3 + 2) = 20.

\(\lim _{x \rightarrow 3-} f(x)=\lim _{h \rightarrow 0} f(3-h)\)

= \(\lim _{h \rightarrow 0}\{-2(3-h)\}=\lim _{h \rightarrow 0}(-6+2 h)=-6\).

Thus, \(f(3) \neq \lim _{x \rightarrow 3-} f(x)\).

Hence, f(x) is discontinuous at x = 3.

Example 10 Find the value of k for which

f(x) = \(\left\{\begin{array}{r}
k x+5, \text { when } x \leq 2 \\
x-1, \text { when } x>2
\end{array}\right.\) is continuous at x = 2.

Solution

We have, f(2) = (k x 2 + 5) = (2k + 5).

\(\lim _{x \rightarrow 2+} f(x)=\lim _{h \rightarrow 0} f(2+h)\)

= \(\lim _{h \rightarrow 0}\{(2+h)-1\}=\lim _{h \rightarrow 0}(1+h)=1\).

\(\lim _{x \rightarrow 2-} f(x)=\lim _{h \rightarrow 0} f(2-h)\)

= \(\lim _{h \rightarrow 0}\{k(2-h)+5\}=\lim _{h \rightarrow 0}\{(2 k+5)-k h\}=(2 k+5)\).

Now, \(\lim _{x \rightarrow 2} f(x)\) exists only when 2k + 5 = 1, i.e., when k = -2.

When k = -2, we have \(\lim _{x \rightarrow 2} f(x)=f(2)=1\).

Hence, f(x) is continuous at x = 2 when k = -2.

Example 11 If the following function f(x) is continuous at x = 0, find the value of k:

f(x) = \(\left\{\begin{aligned}
\frac{1-\cos 2 x}{2 x^2}, & x \neq 0 \\
k, & x=0
\end{aligned}\right.\)

Solution

We have, f(0) = k.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)\)

= \(\lim _{h \rightarrow 0} \frac{(1-\cos 2 h)}{2 h^2}=\lim _{h \rightarrow 0} \frac{2 \sin ^2 h}{2 h^2}=\lim _{h \rightarrow 0}\left(\frac{\sin h}{h}\right)^2\)

= \(\left\{\lim _{h \rightarrow 0}\left(\frac{\sin h}{h}\right)\right\}^2=(1)^2=1\).

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)\)

= \(\lim _{h \rightarrow 0}\left\{\frac{1-\cos 2(-h)}{2(-h)^2}\right\}=\lim _{h \rightarrow 0} \frac{\{1-\cos (-2 h)\}}{2 h^2}\)

= \(\lim _{h \rightarrow 0} \frac{(1-\cos 2 h)}{2 h^2}=\lim _{h \rightarrow 0} \frac{2 \sin ^2 h}{2 h^2}=\lim _{h \rightarrow 0}\left(\frac{\sin h}{h}\right)^2\)

= \(\left\{\varliminf_{h \rightarrow 0} \frac{\sin h}{h}\right\}^2=1^2=1\).

Since f(x) is continuous at x = 0, we must have

f(0) = \(\lim _{x \rightarrow 0+} f(x)=\lim _{x \rightarrow 0-} f(x)\) ⇒ k = 1.

Example 12 For what value of k is the following function continuous at x = 0?

f(x) = \(\left\{\begin{aligned}
\frac{1-\cos 4 x}{8 x^2}, & x \neq 0 \\
k, & x=0
\end{aligned}\right.\)

Solution

We have, f(0) = k.

\(\lim _{x \rightarrow 0^{+}} f(x)=\lim _{h \rightarrow 0} f(0+h)\)

= \(\lim _{h \rightarrow 0} \frac{(1-\cos 4 h)}{8 h^2}=\lim _{h \rightarrow 0} \frac{2 \sin ^2 2 h t}{8 h^2}=\lim _{h \rightarrow 0}\left(\frac{\sin 2 h}{2 h}\right)^2\)

= 1² = 1.

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)\)

= \(\lim _{h \rightarrow 0} \frac{\{1-\cos 4(-h) \mid}{8(-h)^2}=\lim _{h \rightarrow 0} \frac{\{1-\cos (-4 h)\}}{8 h^2}=\lim _{h \rightarrow 0} \frac{(1-\cos 4 h)}{8 h^2}\)

[ ∵ cos(-θ) = cosθ]

= \(\lim _{h \rightarrow 0} \frac{2 \sin ^2 2 h}{8 h^2}=\lim _{h \rightarrow 0}\left(\frac{\sin 2 h}{2 h}\right)^2\)

= 1² = 1.

∴ \(\lim _{x \rightarrow 0} f(x)=1\).

For continuity at x = 0, we must have

\(f(0)=\lim _{x \rightarrow 0} f(x) \Rightarrow k=1\) [ ∵ \(f(0)=k \text { and } \lim _{x \rightarrow 0} f(x)=1\)].

Example 13 Given that

f(x) = \(\left\{\begin{array}{rr}
\frac{(1-\cos 4 x)}{x^2}, & \text { if } x<0 \\
a, & \text { if } x=0 \\
\frac{\sqrt{x}}{\sqrt{16+\sqrt{x}}-4}, & \text { if } x>0
\end{array}\right.\).

If f(x) is continuous at x = 0, find the value of a.

Solution

We have, f(0) = a.

\(\lim _{x \rightarrow 0^{+}} f(x)=\lim _{h \rightarrow 0} f(0+h)\)

= \(\lim _{h \rightarrow 0}\left\{\frac{\sqrt{h}}{\sqrt{16+\sqrt{h}}-4}\right\}\)

= \(\lim _{h \rightarrow 0}\left\{\frac{\sqrt{h}}{\sqrt{16+\sqrt{h}}-4} \times \frac{\sqrt{16+\sqrt{h}}+4}{\sqrt{16+\sqrt{h}}+4}\right\}\)

= \(\lim _{h \rightarrow 0} \frac{\sqrt{h} \cdot\{\sqrt{16+\sqrt{h}}+4\}}{\{(16+\sqrt{h})-16\}}=\lim _{h \rightarrow 0} \frac{\sqrt{h} \cdot\{\sqrt{16+\sqrt{h}}+4\}}{\sqrt{h}}\)

= \(\lim _{h \rightarrow 0}\{\sqrt{16+\sqrt{h}}+4\}=(4+4)=8\)

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} f(-h)\)

= \(\lim _{h \rightarrow 0} \frac{\{1-\cos 4(-h)\}}{(-h)^2}=\lim _{h \rightarrow 0} \frac{\{1-\cos (-4 h)\}}{h^2}\)

= \(\lim _{h \rightarrow 0} \frac{(1-\cos 4 h)}{h^2}=\lim _{h \rightarrow 0} \frac{2 \sin ^2 2 h}{h^2}\)

= \((2 \times 4) \cdot \lim _{h \rightarrow 0} \frac{\left(\sin ^2 2 h\right)}{(2 h)^2}=8 \cdot \lim _{h \rightarrow 0}\left(\frac{\sin 2 h}{2 h}\right)^2\)

= (8 x 12) = 8.

∴ \(\lim _{x \rightarrow 0+} f(x)=\lim _{x \rightarrow 0-} f(x)=8 \Rightarrow \lim _{x \rightarrow 0} f(x)=8\).

But, by continuity of f at x = 0, we have

\(\lim _{x \rightarrow 0} f(x)=f(0) \Rightarrow a=8\) [ ∵ \(f(0)=a \text { and } \lim _{x \rightarrow 0} f(x)=8\)].

Hence, a = 8.

Example 14 If the following function f(x) is continuous at x = 0, find the values of a,b and c.

f(x) = \(\left\{\begin{array}{cc}
\frac{\sin (a+1) x+\sin x}{x} & , \text { if } x<0 \\
c & , \text { if } x=0 \\
\frac{\sqrt{x+b x^2}-\sqrt{x}}{b x^{3 / 2}} & , \text { if } x>0
\end{array}\right.\)

Solution

We have, f(0) = c.

\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{h \rightarrow 0} f(0-h)\)

= \(\lim _{h \rightarrow 0} \frac{\sin (a+1)(-h)+\sin (-h)}{(-h)}=\lim _{h \rightarrow 0} \frac{-\{\sin (a+1) h+\sin h\}}{-h}\)

= \(\lim _{h \rightarrow 0} \frac{\sin (a+1) h+\sin h}{h}=\lim _{h \rightarrow 0} \frac{2 \sin \left(\frac{a}{2}+1\right) h \cdot \cos \frac{a h}{2}}{h}\)

= \(2 \cdot \lim _{h \rightarrow 0}\left\{\frac{\sin \left(\frac{a}{2}+1\right) h}{\left(\frac{a}{2}+1\right) h} \cdot\left(\frac{a}{2}+1\right) \cdot \cos \frac{a h}{2}\right\}\)

= \(2\left(\frac{a}{2}+1\right) \cdot \lim _{h \rightarrow 0} \frac{\sin \left(\frac{a}{2}+1\right) h}{\left(\frac{a}{2}+1\right) h} \cdot \lim _{h \rightarrow 0} \cos \frac{a h}{2}\)

= (a + 2) x 1 x 1 = (a + 2).

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)\)

= \(\lim _{h \rightarrow 0}\left\{\frac{\left[\sqrt{h+b h^2}-\sqrt{h}\right]}{b h^{3 / 2}} \times \frac{\left[\sqrt{h+b h^2}+\sqrt{h}\right]}{\left[\sqrt{h+b h^2}+\sqrt{h}\right]}\right\}\)

= \(\lim _{h \rightarrow 0} \frac{\left(h+b h^2-h\right)}{b h^{3 / 2}\left(\sqrt{h+b h^2}+\sqrt{h}\right)}=\lim _{h \rightarrow 0} \frac{b h^2}{b h^2(\sqrt{1+b h}+1)}\)

= \(\lim _{h \rightarrow 0} \frac{1}{(\sqrt{1+b h}+1)}=\frac{1}{2}\).

Since f(x) is continuous at x = 0, we have

\(f(0)=\lim _{x \rightarrow 0-} f(x)=\lim _{x \rightarrow 0+} f(x) \Rightarrow c=\frac{1}{2} \text { and } a+2=\frac{1}{2}\)

∴ c = \(\frac{1}{2}\) and a = \(\frac{-3}{2}\)

Applications of Continuity and Differentiability in Real Life

Example 15 If the function f(x) = \(\left\{\begin{array}{r}
3 a x+b, \text { for } x>1 \\
11, \text { for } x=1 \\
5 a x-2 b, \text { for } x<1
\end{array}\right.\) is continuous at x = 1, find the values of a and b.

Solution

We have, f(1) = 11.

\(\lim _{x \rightarrow 1^{+}} f(x)=\lim _{h \rightarrow 0} f(1+h)\)

= \(\lim _{h \rightarrow 0}\{3 a(1+h)+b\}=\varliminf_{h \rightarrow 0}\{(3 a+b)+3 a h\}\)

= (3a + b)

\(\lim _{x \rightarrow 1-} f(x)=\lim _{h \rightarrow 0} f(1-h)\)

= \(\lim _{h \rightarrow 0}\{5 a(1-h)-2 b\}=\lim _{h \rightarrow 0}\{(5 a-2 b)-5 a h\}\)

= (5a – 2b).

Since f(x) is continuous at x = 1, we have

\(\lim _{x \rightarrow 1+} f(x)=\lim _{x \rightarrow 1^{-}} f(x)=f(1)\).

∴ 3a + b = 5a – 2b = 11.

On solving (3a + b = 11) and (5a – 2b = 11), we get a = 3, b = 2.

Hence, a = 3, b = 2.

Example 16 For what value of k is the function

f(x) = \(\left\{\begin{aligned}
k\left(x^2-2 x\right), & \text { if } x \leq 0 \\
4 x+1, & \text { if } x>0
\end{aligned}\right.\)

(1) continuous at x = 0?

(2) continuous at x = 1?

(3) continous at x = -1?

Solution

(1) we have f(0) = k(0 – 2 x 0) = 0.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)\)

= \(\lim _{h \rightarrow 0}\{4(0+h)+1\}=\lim _{h \rightarrow 0}(4 h+1)=1\)

\(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)\)

= \(\lim _{h \rightarrow 0} k\left\{(-h)^2-2(-h)\right\}=\lim _{h \rightarrow 0} k\left(h^2+2 h\right)=0\)

Thus, \(\lim _{x \rightarrow 0+} f(x) \neq \lim _{x \rightarrow 0^{-}} f(x)\), and thus \(\lim _{x \rightarrow 0} f(x)\) does not exist.

So, f(x) is not continuous at x = 0 for any value of k.

(2) f(1) = (4 x 1 + 1) = 5.

\(\lim _{x \rightarrow 1^{+}} f(x)\)=\(\lim _{h \rightarrow 0} f(1+h)\)

= \(\lim _{h \rightarrow 0}\{4(1+h)+1\}=\lim _{h \rightarrow 0}(5+4 h)=5\).

Thus, \(\lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1-} f(x)=\lim _{x \rightarrow 1} f(x)=5\).

Hence, f(x) is continuous at x = 1 for every real value of k.

(3) f(-1) = k[(-1)2 – 2 x (-1)] = 3k.

\(\lim _{x \rightarrow(-1)+} f(x)=\lim _{h \rightarrow 0} f(-1+h)\)

= \(\lim _{h \rightarrow 0} k\left\{(-1+h)^2-2(-1+h)\right\}=\lim _{h \rightarrow 0} k\left\{1+h^2-2 h+2-2 h\right\}\)

= \(\lim _{h \rightarrow 0} k\left(3+h^2-4 h\right)=3 k\).

\(\lim _{x \rightarrow(-1)-} f(x)=\lim _{h \rightarrow 0} f(-1-h)\)

 

= \(\lim _{h \rightarrow 0} k\left\{(-1-h)^2-2(-1-h)\right\}=\lim _{h \rightarrow 0}
k\left\{1+h^2+2 h+2+2 h\right\}\)

= \(\lim _{h \rightarrow 0} k\left(3+4 h+h^2\right)=3 k\).

Thus, \(\lim _{x \rightarrow(-1)+} f(x)=\lim _{x \rightarrow(-1)-} f(x)=f(-1)=3 k\).

Hence, f(x) is continuous at x = -1 for each real value of k.

Example 17 Show that the function f(x) = \(\left\{\begin{array}{r}
\frac{\sin ^2 a x}{x^2}, \text { when } x \neq 0 \\
1, \text { when } x=0
\end{array}\right.\) is discontinuous at x = 0. Redefine the function in such a way that it becomes continuous at x = a.

Solution

Clearly, f(0) = 1.

Also, \(\lim _{x \rightarrow 0} f(x)=\lim _{x \rightarrow 0} \frac{\sin ^2 a x}{x^2}=a^2 \cdot \lim _{a x \rightarrow 0}\left(\frac{\sin a x}{a x}\right)^2=a^2\).

Since \(\lim _{x \rightarrow 0} f(x) \neq f(0), f(x)\) is discontinuous at x = 0.

However, it becomes continuous if f(0) = a².

So, the desired function is f(x) = \(\left\{\begin{array}{r}
\frac{\sin ^2 a x}{x^2}, \text { when } x \neq 0 \\
a^2, \text { when } x=0
\end{array}\right.\).

Example 18 Is the function f(x) = \(\frac{(3 x+4 \tan x)}{x}\) continuous at x = 0? If not, how many the function be defined to make it continuous at this point?

Solution

Since f(x) is not defined at x = 0, it cannot be continuous at x = 0.

However, \(\lim _{x \rightarrow 0} f(x)=\lim _{x \rightarrow 0}\left(\frac{3 x+4 \tan x}{x}\right)=\lim _{x \rightarrow 0}\left[3+4 \cdot \frac{\sin x}{x} \cdot \frac{1}{\cos x}\right]\)

= \(3+4 \cdot \lim _{x \rightarrow 0}\left\{\frac{\sin x}{x}\right\} \cdot\left\{\lim _{x \rightarrow 0} \frac{1}{\cos x}\right\}=7\).

So, in order to make f(x) continuous at x = 0, we define it as

f(x) = \(\left\{\begin{aligned}
\frac{(3 x+4 \tan x)}{x}, & \text { when } x \neq 0 \\
7, \text { when } x & =0
\end{aligned}\right.\).

Example 19 Show that the function f(x) = \(\left\{\begin{array}{r}
\left(\frac{e^{1 / x}-1}{e^{1 / x}+1}\right), \text { when } x \neq 0 \\
0, \text { when } x=0
\end{array}\right.\) is discontinuous at x = 0.

Solution

Clearly, f(0) = 0.

Now, \(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)=\lim _{h \rightarrow 0} f(h)=\lim _{h \rightarrow 0}\left(\frac{e^{1 / h}-1}{e^{1 / h}+1}\right)\)

= \(\lim _{h \rightarrow 0} \frac{e^{1 / h}\left(1-\frac{1}{e^{1 / h}}\right)}{e^{1 / f t}\left(1+\frac{1}{e^{1 / h}}\right)}=\lim _{h \rightarrow 0} \frac{\left(1-\frac{1}{e^{1 / h}}\right)}{\left(1+\frac{1}{e^{1 / h}}\right)}=1\).

And, \(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} f(-h)=\lim _{h \rightarrow 0}\left(\frac{e^{-1 / h}-1}{e^{-1 / h}+1}\right)\)

= \(\lim _{h \rightarrow 0} \frac{\left(\frac{1}{e^{1 / h}}-1\right)}{\left(\frac{1}{e^{1 / h}}+1\right)}=-1\).

Thus, \(\lim _{x \rightarrow 0+} f(x) \neq \lim _{x \rightarrow 0-} f(x)\), and therefore , \(\lim _{x \rightarrow 0} f(x)\) does not exist.

Hence, f(x) is discontinuous at x = 0.

Continuous Functions

Continuity In An Interval A function f(x) is said to be continous in an open interval ]a,b[ if it is continous at each point of ]a,[.

If f(x) is defined on a closed interval [a,b], we say that

(1) f is continuous at a if \(\lim _{x \rightarrow a+} f(x)=f(a)\);

(2) f is continuous at b if \(\lim _{x \rightarrow b-} f(x)=f(b)\);

(3) f is continuous in [a,b] if it is continuous at a, at b and at each point of ]a,b[.

Continuous Functions A function f(x) is said to be continuous if it is continuous at each point of its domain.

Algebra of Continuous Functions

Theorem 1 Every constant function is continuous.

Proof

Let f(x) = c, where c is constant.

Clearly, the domain of a constant function is R.

Let a be an arbitrary real number.

Then, f(a) = c and \(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} c=c\) [∵ f(x) = c].

∴ \(\lim _{x \rightarrow a} f(x)=f(a)\).

Thus, f(x) is continuous at x = a for all a ∈ R.

Hence, f(x) is continuous.

Theorem 2 Show that the identity function is continuous.

Proof

Let f(x) = x for all x ∈ R.

Let a be an arbitrary real number. Then, f(a) = a.

And, \(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} x=a\) [∵ f(x) = x].

∴ \(\lim _{x \rightarrow a} f(x)=f(a)=a\).

This shows that f(x) is continuous at x = a for all a ∈ R.

Hence, the identity function is continuous.

Theorem 3 If f and g be continuous function then

(1) f + g is continuous

(2) f – g is continuous

(3) cf is continuous

(4) fg is continuous

(5) \(\left(\frac{f}{g}\right)\) is continuos at those points where g(x) ≠ 0.

Proof

(1) Let dom(f) = D₁ and dom(g) = D₂. Then, dom(f+g) = D₁ ∩ D₂.

Let a ∈ D₁ ∩ D₂. Then, a ∈ D₁ and a ∈ D₂.

By continuity of f and g, we have \(\lim _{x \rightarrow a} f(x)=f(a)\) and \(\lim _{x \rightarrow a} g(x)=g(a)\).

∴ \(\lim _{x \rightarrow a}(f+g)(x)=\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)\)

= f(a) + g(a) = (f+g)(a).

This shows that (f+g) is continuous at a for all a ∈ D₁ ∩ D₂.

Hence, (f+g) is continuous.

Similarly, (2) may be proved.

(3) Let dom(f) = D₁. Then, dom(cf) = D1. Let a ∈ D₁.

Then, by the continuity of f, we have \(\lim _{x \rightarrow a} f(x)=f(a)\).

∴ \(\lim _{x \rightarrow a}(c f)(x)=\lim _{x \rightarrow a} c \cdot f(x)=c \cdot \lim _{x \rightarrow a} f(x)=c \cdot f(a)=(c f)(a)\)

This shows that (cf) is continuous at a for all a ∈ D₁.

Hence, cf is continuous.

(4) Let dom(f) = D₁ and dom(g) = D₂. Then, dom(fg) = D₁ ∩ D₂.

Let a ∈ D₁ ∩ D₂. Then, a ∈ D₁ and a ∈ D₂.

By continuity of f and g, we have \(\lim _{x \rightarrow a} f(x)=f(a) \text { and } \lim _{x \rightarrow a} g(x)=g(a)\).

∴ \(\lim _{x \rightarrow a}(f g)(x)=\lim _{x \rightarrow a}[f(x) \cdot g(x)]\)

= \(\lim _{x \rightarrow a} f(x) \cdot \lim _{x \rightarrow a} g(x)=f(a) \cdot g(a)=(f g)(a)\).

This shows that fg is continuous.

(5) Let dom(f) = D₁ and dom(g) = D₂.

Then, dom\(\left(\frac{f}{g}\right)\) = [(D₁ ∩ D₂) – {x:g(x)=0}] = D (say).

Let a ∈ D. Then a ∈ D₁, a ∈ D₂ and g(a) ≠ 0.

By continuity of f and g, we have \(\lim _{x \rightarrow a} f(x)=f(a) \text { and } \lim _{x \rightarrow a} g(x)=g(a)\).

∴ \(\lim _{x \rightarrow a}\left(\frac{f}{g}\right)(x)=\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}=\frac{f(a)}{g(a)}=\left(\frac{f}{g}\right)(a)\), since g(a) ≠ 0.

Thus, \(\left(\frac{f}{g}\right)\) is continuous at a for all a ∈ D. Hence, \(\left(\frac{f}{g}\right)\) is continuous.

Theorem 4 Every polynomial function is continuous.

Proof

Let f(x) = a₀ + a₁x + a₂x² + …. + a_nxⁿ be a polynomial. We shall prove the theorem by induction on n.

When n = 0 then f(x) = a₀, which being a constant function is continuous.

When n = 1 then f(x) = a₀ + a₁x.

Clearly, f(x) is the sum of a constant function and a multiple of the identity function. It, being the sum of two continuous functions, is continuous.

Let everty polynomial of degree at most n be continuous.

Consider a general polynomial of degree (n+1), namely,

a₀ + a₁x + a₂x² + … + a_nx²ⁿ + a_n+1xⁿ⁺¹.

This can be written as a₀ + x(a₁ + a₂x + … + a_nx^n-1 + a_n+1xⁿ).

This is the sum of a constant function a0 (which is continuous) and the product of the identity function x (which is continuous) and the polynomial function a₁ + a₂x + … + a_n+1xⁿ of degree at most n (which we assumed to be continuous).

Therefore, it is continuous.

Thus, the continuity of a polynomial of degree n implies the continuity of a polynomial of degree (n+1).

Hence, by the principle of induction, everty polynomial function is continuous.

Theorem 5 Every rational function is continuous.

Proof

Let f(x) = \(\frac{p(x)}{q(x)}\), where p(x) and q(x) are polynomials.

Then, dom[p(x)] = R and dom[q(x)] = R.

∴ dom[p(x)] = dom \(\left\{\frac{p(x)}{q(x)}\right\}\) = R ∩ R – {x:q(x) = 0} = R – {x:q(x) = 0}.

Let a be an arbitrary element of domf(x).

Then, a ∈ R and q(a) ≠ 0.

But, every polynomial function being continuous, we have

\(\lim _{x \rightarrow a} p(x)=p(a) \text { and } \lim _{x \rightarrow a} q(x)=q(a) \text {. }\)

∴ \(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a}\left\{\frac{p(x)}{q(x)}\right\}=\frac{\lim _{x \rightarrow a} p(x)}{\lim _{x \rightarrow a} q(x)}=\frac{p(a)}{q(a)} \text {, where } q(a) \neq 0\).

This shows that f(x) is continuous at x = a for all a ∈ domf(x).

Hence, every rational function is continuous.

Theorem 6 Let f and g be real functions such that f o g is defined. If g is continuous at a and f is continuous at g(a), show that f o g is continuous at a.

Proof

Since f o g is defined, we have range(g) ⊆ dom(f).

Since g is continuous as a, we have \(\lim _{x \rightarrow a} g(x)=g(a)\) …(1)

Also, f being continuous at g(a), we have \(\lim _{y \rightarrow g(a)} f(y)=f\{g(a)\}\) …(2)

∴ \(\lim _{x \rightarrow a}(f \circ g)(x)=\lim _{x \rightarrow a} f\{g(x)\}=\lim _{g(x) \rightarrow g(a)} f\{g(x)\}\)

[∵ x → a ⇒ g(x) → g(a) from(1)]

= \(\lim _{y \rightarrow g(a)} f(y)=f\{g(a)\}\) [using (2)]

= (f o g)(a).

Thus, (f o g) is continuous at a.

Theorem 7 The composite of two continuous functions is continuous.

Proof

Let f and g be continuous functions such taht g o f is defined.

Then, range(f) ⊆ dom(g). Let a ∈ dom(f).

Then, a ∈ dom(f) ⇒ f(a) ∈ range(f)

⇒ f(a) ∈ dom(g) [∵ range(f) ⊆ dom(g)].

Thus, f is continuous at a, and g is continuous at f(a).

Consequently, \(\lim _{x \rightarrow a} f(x)=f(a)\) …(1)

And, \(\lim _{y \rightarrow f(a)} g(y)=g[f(a)]\) …(2)

∴ \(\lim _{x \rightarrow a}(g \circ f)(x)=\lim _{x \rightarrow a} g[f(x)]\)

= \(\lim _{f(x) \rightarrow f(a)} g[f(x)]\) [∵ x → a ⇒ f(x) → f(a) from(1)]

= \(\lim _{y \rightarrow f(a)} g(y)=g[f(a)]\) [using (2)]

= (g o f)(a).

This shows that g o f is continuous at a for all a ∈ dom(f).

Hence g o f is continuous.

An improtant result

For continuity of f at a, it is sufficient to show that \(\lim _{h \rightarrow 0} f(a+h)=f(a)\), since

f is continuous ⇔ \(\lim _{x \rightarrow a} f(x)=f(a)\)

⇔ \(\lim _{(a+h) \rightarrow a} f(a+h)=f(a)\) [putting x = (a+h)]

⇔ \(\lim _{h \rightarrow 0} f(a+h)=f(a) .\)

Theorem 8 The exponential function is continuous.

Proof

Let f(x) = e^x. Then, clearly, dom(f) = R.

Let a be an arbitraty real number. Then,

\(\lim _{x \rightarrow a} e^x=\lim _{h \rightarrow 0} e^{a+h}=\lim _{h \rightarrow 0} e^a \cdot e^h=e^a \cdot \lim _{h \rightarrow 0} e^h=e^a \times 1=e^a .\)

Thus, f(x) = e^x is continuous at x = a for all a ∈ R.

Hence, the exponential function is continuous.

Theorem 9 (1) The sine function is continuous.

(2) The cosine function is continuous.

(3) The tangent function is continuous.

Proof

(1) Let f(x) = sin x. Then, clearly dom(f) = R.

Let a be an arbitrary real number. Then,

\(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} \sin x=\lim _{h \rightarrow 0} \sin (a+h)=\lim _{h \rightarrow 0}[\sin a \cos h+\cos a \sin h]\)

= \(\sin a \cdot \lim _{h \rightarrow 0} \cos h+\cos a \cdot \lim _{h \rightarrow 0} \sin h\)

= (sin a x 1 + cos a x 0) = sin a = f(a).

Thus, \(\lim _{x \rightarrow a} f(x)=f(a)\) for all a ∈ R.

∴ f(x) = sin x is continuous at a for all a ∈ R.

Hence, sin x is continuous.

(2) Let f(x)= cos x. Clearly, dom(f) = R.

Let a be an arbitrary real number. Then,

\(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} \cos x=\lim _{h \rightarrow 0} \cos (a+h)=\lim _{h \rightarrow 0}[\cos a \cos h-\sin a \sin h]\)

 

= \(\cos a \cdot \lim _{h \rightarrow 0} \cos h-\sin a \cdot \lim _{h \rightarrow 0} \sin h=(\cos a \times 1-\sin a \times 0)\)

= cos a = f(a).

Thus, \(\lim _{x \rightarrow a} f(x)=f(a)\) for all a ∈ R.

∴ f(x) = cos x is continuous at a for all a ∈ R.

Hence, cos x is continuous.

(3) We have tan x = \(\frac{\sin x}{\cos x}\) and dom(tan x) = R – {(2n+1)\(\frac{\pi}{2}\):n ∈ I].

Let a ∈ R – {(2n+1)\(\frac{\pi}{2}\):n ∈ I]. Then,

\(\lim _{x \rightarrow a} \tan x=\lim _{x \rightarrow a} \frac{\sin x}{\cos x}=\frac{\lim _{h \rightarrow 0} \sin (a+h)}{\lim _{h \rightarrow 0} \cos (a+h)}\)

= \(\frac{\lim _{h \rightarrow 0}(\sin a \cos h+\cos a \sin h)}{\lim _{h \rightarrow 0}(\cos a \cos h-\sin a \sin h)}\)

= \(\left(\frac{\sin a \times \cos 0+\cos a \times \sin 0}{\cos a \times \cos 0-\sin a \times \sin 0}\right)=\left(\frac{\sin a \times 1+\cos a \times 0}{\cos a \times 1-\sin a \times 0}\right)\)

= tan a.

Thus, tan x is continuous at a for all a ∈ R – {(2n+1)\(\frac{\pi}{2}\):n ∈ I].

Hence, tan x is continuous

Theorem 10 The logarithmic function is continuous.

Proof

Let f(x) = log x. Then, dom(f) = set of positive real numbers.

Let a be any positive real number. Then,

\(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} \log x\)

= \(\lim \left[\log \left(a \cdot \frac{x}{a}\right)\right]=\lim _{x \rightarrow a}\left[\log a+\log \frac{x}{a}\right]\)

= \(\log a+\lim _{x \rightarrow a} \log \frac{x}{a}=\log a=f(a)\) [∵ \(\lim _{x \rightarrow a} \log \frac{x}{a}=\log 1=0\)].

Thus, f(x) = log x is continuous at a ∈ R⁺.

Hence, f(x) = log x is continuous.

Theorem 11 Sin | x | is continuous.

Proof

Let f(x) = | x | and g(x) = sin x. Then,

(g o f)(x) = g{f(x)} = g(| x |) = sin | x |.

Now, f and g being continuous, it follows that their composite (g o f) is continuous.

Hence, sin | x | is continuous.

Solved Examples

Example 1 Let f(x) = \(\begin{cases}x & \text { if } x \geq 1 \\ x^2 & \text { if } x<1\end{cases}\). Is f a continuos function ? why?

Solution

Let a be any real number. Then, three possibilities arise.

Case 1 When a > 1

In this case, f(a) = a.

Also, \(\lim _{x \rightarrow a+} f(x)=\lim _{h \rightarrow 0} f(a+h)=\lim _{h \rightarrow 0}(a+h)=a .\)

And, \(\lim _{x \rightarrow a-} f(x)=\lim _{h \rightarrow 0} f(a-h)=\lim _{h \rightarrow 0}(a-h)=a\)

[∵ a > 1 and h is very small ⇒ (a-h) > 1].

∴ \(\lim _{x \rightarrow a+} f(x)=\lim _{a \rightarrow a-} f(x)=a=f(a) .\)

So, f(x) is continuous at each a > 1.

Case 2 When a < 1

In this case, f(a) = a².

\(\lim _{x \rightarrow a+} f(x)=\lim _{h \rightarrow 0} f(a+h)=\lim _{h \rightarrow 0}(a+h)^2=a^2\)

[∵ a < 1 and h is very small ⇒ (a-h) < 1].

And, \(\lim _{x \rightarrow a^{-}} f(x)=\lim _{h \rightarrow 0} f(a-h)=\lim _{h \rightarrow 0}(a-h)^2=a^2\)

[∵ a < 1 and h is very small ⇒ (a-h) < 1].

∴ \(\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow a-} f(x)=a^2=f(a) .\)

Case 3 When a = 1

In this case, f(1) = 1.

\(\lim _{x \rightarrow 1+} f(x)=\lim _{h \rightarrow 0} f(1+h)=\lim _{h \rightarrow 0}(1+h)=1\) [∵ (1+h) > 1].

\(\lim _{x \rightarrow 1-} f(x)=\lim _{h \rightarrow 0} f(1-h)=\lim _{h \rightarrow 0}(1-h)^2=1\) [∵ (1-h) < 1].

∴ \(\lim _{x \rightarrow 1+} f(x)=\lim _{x \rightarrow 1-} f(x)=1\)

So, \(\lim _{x \rightarrow 1} f(x)=1=f(1)\).

So, f is continuous at a = 1.

Thus, from all the above three cases, it follows that f(x) is continuous at x = a for all a ∈ R.

Hence, f(x) is continuous.

Examples of Applying Rolle’s Theorem

Example 2 Prove that f(x) = | x | is a continuous function.

Solution

Let f(x) = | x | = \(\left\{\begin{array}{r}
x, \text { if } x \geq 0 \\
-x, \text { if } x<0 .
\end{array}\right.\)

Clearly, dom(f) = R.

Let a be any real number. Then, the following cases arise.

Case 1 When a < 0

In this case, f(a) = -a.

\(\lim _{x \rightarrow a+} f(x)=\lim _{h \rightarrow 0} f(a+h)=\lim _{h \rightarrow 0}\{-(a+h)\}=-a\)

[∵ a < 0 and h is very small and positive ⇒ a + h < 0].

And, \(\lim _{x \rightarrow a-} f(x)=\lim _{h \rightarrow 0} f(a-h)=\lim _{h \rightarrow 0}\{-(a-h)\}=-a .\)

[∵ a < 0 and h is very small and positive ⇒ a – h < 0].

So, \(\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow a^{-}} f(x)=-a=f(a) .\)

Thus, f(x) is continuous at each a < 0.

Case 2 When a > 0

In this case, f(a) = a.

\(\lim _{x \rightarrow a+} f(x)=\lim _{h \rightarrow 0} f(a+h)=\lim _{h \rightarrow 0}(a+h)=a\) [∵ (a+h) > 0].

\(\lim _{x \rightarrow a_{-}^{-}} f(x)=\lim _{h \rightarrow 0} f(a-h)=\lim _{h \rightarrow 0}(a-h)=a\) [∵ (a-h) > 0].

∴ \(\lim _{x \rightarrow a+} f(x)=\lim _{x \rightarrow a_{-}} f(x)=f(a) .\)

So, f(x) is continuous at each a > 0.

Case 3 When a = 0

Clearly, f(0) = 0.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)=\lim _{h \rightarrow 0} f(h)=\lim _{h \rightarrow 0} h=0 .\) \(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} f(-h)=\lim _{h \rightarrow 0}\{-(-h)\}=\lim _{h \rightarrow 0} h=0 .\)

∴ \(\lim _{x \rightarrow 0+} f(x)=\lim _{x \rightarrow 0-} f(x)=0=f(0) .\)

So, f(x) is continuous at x = 0.

Thus, from all the above cases, it follows that f(x) = | x | is continuous at a for all a ∈ R.

Hence, f(x) = | x | is continuous.

Example 3 Discuss the continuity of the function f(x) = \(\begin{cases}2 x-1, & \text { if } x<0 \\ 2 x+1, & \text { if } x \geq 0 .\end{cases}\)

Solution

When x < 0, we have f(x) = 2x – 1, which being a polynomial function, is continuous at each point where x < 0.

Also, when x > 0, we have f(x) = 2x + 1, which being a polynomial function, is continuous at each point where x > 0.

Let us consider the point x = 0.

f(0) = (2 x 0 + 1) = 1.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)=\lim _{h \rightarrow 0} f(h)=\lim _{h \rightarrow 0}(2 h+1)=1 .\)

And, \(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} f(-h)=\lim _{h \rightarrow 0}[(2(-h)-1)]=-1 .\)

∴ \(\lim _{x \rightarrow 0+} f(x) \neq \lim _{x \rightarrow 0-} f(x) .\)

So, \(\lim _{x \rightarrow 0} f(x)\) does not exist, and therefore f(x) is not continuous at x = 0.

Thus, the given function is continuous at each point except at x = 0, where it is discontinuous.

Example 4 Discuss the continuity of the function f(x) = \(\begin{cases}\frac{\sin x}{x}, & \text { if } x<0 \\ (x+1), & \text { if } x \geq 0 .\end{cases}\)

Solution

We know that sin x as well as the identity function x is continuous.

So, the quotient function, \(\frac{\sin x}{x}\) is continuous at each x < 0.

Also, when x > 0, we have f(x) = (x+1), which being a polynomial function, is continuous.

Let us consider the point x = 0.

Clearly, f(0) = (0+1) = 1.

We have f(0) = (0+1) = 1;

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)=\lim _{h \rightarrow 0}(h+1)=1\)

and, \(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} f(-h)\)

= \(\lim _{h \rightarrow 0} \frac{\sin (-h)}{-h}=\lim _{h \rightarrow 0}\left(\frac{-\sin h}{-h}\right)=\lim _{h \rightarrow 0} \frac{\sin h}{h}=1\)

∴ \(\lim _{x \rightarrow 0+} f(x)=\lim _{x \rightarrow 0-} f(x)=1\)

So, \(\lim _{x \rightarrow 0} f(x)=1=f(0) .\)

Thus, f(x) is continuous at x = 0 also.

Hence, f(x) is continuous at all points.

Example 5 Discuss the continuity of the function f(x) = \(\left\{\begin{array}{r}
\frac{x}{|x|}, \text { if } x \neq 0 \\
0, \text { if } x=0 .
\end{array}\right.\)

Solution

We know that the identity function x is continous and the modulus function | x | is continuous.

So, the quotient function \(\frac{x}{|x|}\) is continuous at each x ≠ 0.

It has already been proved that f(x) is discontinuous at x = 0.

Hence, the given function is continuous at each point, except at x = 0.

Example 6 Locate the point of discontinuity of the function f(x) = \(\left\{\begin{array}{r}
\frac{x^4-16}{x-2}, \text { if } x \neq 2 \\
16, \text { if } x=2 .
\end{array}\right.\)

Solution

The function f(x) = \(\frac{x^4-16}{x-2}\) being a rational function, is continuous at all points of its domain, i.e., for all real numbers except 2.

Now, consider the given function at x = 2.

We have f(2) = 16.

\(\lim _{x \rightarrow 2+} f(x)=\lim _{h \rightarrow 0} f(2+h)=\lim _{h \rightarrow 0}\left\{\frac{(2+h)^4-16}{2+h-2}\right\}=\lim _{2+h \rightarrow 2}\left\{\frac{(2+h)^4-2^4}{(2+h)-2}\right\}\)

= 4 x 2^4-1 = 32 [∵ \(\lim _{x \rightarrow a}\left(\frac{x^n-a^n}{x-a}\right)=n a^{n-1}\)].

Thus, \(\lim _{x \rightarrow 2+} f(x) \neq f(2)\), and therefore \(\lim _{x \rightarrow 2} f(x) \neq f(2)\).

Hence, f(x) is discontinuous at x = 2.

Graphical Interpretation of Continuity and Differentiability

Example 7 Determine the value of k so that the function f(x) = \(\left\{\begin{aligned}
k x^2, & \text { if } x \leq 2 \\
3, & \text { if } x>2
\end{aligned}\right.\) is continuous.

Solution

Since a polynomial function is continuous and a constant function is continuous, the given function is continuous for all x < 2 and for all x > 2.

So, consider the point x = 2. We have f(2) = 4k.

\(\lim _{x \rightarrow 2+} f(x)=\lim _{h \rightarrow 0} f(2+h)=\lim _{h \rightarrow 0} 3=3 .\)

And, \(\lim _{x \rightarrow 2-} f(x)=\lim _{h \rightarrow 0} f(2-h)=\lim _{h \rightarrow 0} k(2-h)^2=4 k\)

∴ for continuity, we must have 4k = 3 or k = \(\frac{3}{4}\).

Example 8 Let f(x) = \(\left\{\begin{aligned}
1, & \text { if } x \leq 3 \\
a x+b, & \text { if } 3<x<5 \\
7, & \text { if } 5 \leq x .
\end{aligned}\right.\)

Find the values of a and b so that f(x) is continuous.

Solution

We know that a constant function is continuous, and a polynomial function is continuous.

So, the given function is continuous for all x < 3; for all x > 5 and for all x lying in ]3, 5[.

Now, consider the point x = 3. We have f(3) = 1.

\(\lim _{x \rightarrow 3+} f(x)=\lim _{h \rightarrow 0} f(3+h)=\lim _{h \rightarrow 0}[a(3+h)+b]=(3 a+b) .\)

And, \(\lim _{x \rightarrow 3-} f(x)=\lim _{h \rightarrow 0}(3-h)=\lim _{h \rightarrow 0} 1=1\)

Since f(x) is given to be continuous, it must be continuous at x = 3 also.

So, we must have f(3) = \(\lim _{x \rightarrow 3-} f(x)=\lim _{x \rightarrow 3+} f(x)\), i.e., 3a + b = 1 …(1)

Again, consider the point x = 5. We have f(5) = 7.

\(\lim _{x \rightarrow 5+} f(x)=\lim _{h \rightarrow 0} f(5+h)=\lim _{h \rightarrow 0} 7=7\).

And, \(\lim _{x \rightarrow 5-} f(x)=\lim _{h \rightarrow 0} f(5-h)=\lim _{h \rightarrow 0}[a(5-h)+b]=(5 a+b) .\)

Now, by continuity of f(x) at x = 5, we have

f(5)= \(\lim _{x \rightarrow 5+} f(x)=\lim _{x \rightarrow 5-} f(x) \text { or } 5 a+b=7\)

Solving (1) and (2), we get a = 3 and b = -8.

Example 9 Show that the function f(x) = \(\sqrt{x^4+3}\) is continuous at each point.

Solution

Let g(x) = x⁴ + 3 and h(y) = √y.

Since every polynomial function is continuous at each point where x = a, it follows that g(x) is continuous at x = a.

Clearly, g(a) is positive. Moreover, \(h[g(a)]=\sqrt{g(a)}=\lim _{y \rightarrow g(a)} \sqrt{y} .\)

∴ h(y) is continuous at g(a).

Since the composite of continuous functions is continuous, it follows that (h o g) (x) is continuous.

But, (h o g)(x) = h[g(x)] = h(x⁴ + 3) = \(\sqrt{x^4+3}\) = f(x).

Hence, f(x) is continuous.

Example 10 Show that the function f(x) = | sin x + cos x | is continuos at x = π.

Solution

f(x) = | sin x + cos x |

Let g(x) = sin x + cos x and k(y) = | y |.

We shall first show that g is continuous at x = π and k is continuous at y = g(π).

 

Now, \(\lim _{x \rightarrow \pi} g(x)=\lim _{x \rightarrow \pi}(\sin x+\cos x)=\sin \pi+\cos \pi=-1\).

Also, g(π) = (sin π + cos π) = -1. ∴ \(\lim _{x \rightarrow \pi} g(x)=g(\pi)\)

So, g is continuos at x = π. Now, g(π) = -1.

∴ k[g(π)] = k(-1) = | -1 | = 1.

Now, \(\lim _{y \rightarrow(-1)+} k(y)=\lim _{y \rightarrow(-1)+}|y|=\lim _{h \rightarrow 0}|-1+h|=1\).

And, \(\lim _{y \rightarrow(-1)^{-}} k(y)=\lim _{y \rightarrow(-1)^{-}}|y|=\lim _{h \rightarrow 0}|-1-h|=1\).

∴ k[g(π)] = \(\lim _{y \rightarrow g(x)} k(y) .\) This shows that k is continuos at g(π).

Consequently, (k o g) is continuous at x = π.

But, (k o g)(x) = k[g(π)] = k(sin x + cos x) = | sin x + cos x | = f(x).

Hence, f(x) is continuous at x = π.

Differentiability

Let f(x) be a real function and a be any real number. Then, we define

(1) Right-hand derivative \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\), if it exists, is called the right-hand derivative of f(x) at x = a, and it is denoted by Rf'(a).

(2) Left-hand derivative \(\lim _{h \rightarrow 0} \frac{f(a-h)-f(a)}{-h}\), if it exists, is called the left-hand derivative of f(x) at x = a, and it is denoted by Lf'(a).

Differentiability A function f(x) is said to be differentiable at x = a, if Rf'(a) = Lf'(a).

The common value of Rf'(a) and Lf'(a) is denoted by f'(a) and it is known as the derivative of f(x) at x = a.

If, however, Rf'(a) ≠ Lf'(a), we say that f(x) is not differentiable at x = a.

Remark In each case, h is taken as positive and very small.

Solved Examples

Example 1 Show that f(x) = x² is differentiable at x = 1 and find f'(1).

Solution

f(x) = x²

Rf'(1) = \(\lim _{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}=\lim _{h \rightarrow 0} \frac{(1+h)^2-(1)^2}{h}\)

= \(\lim _{h \rightarrow 0}\left(\frac{1+h^2+2 h-1}{h}\right)=\lim _{h \rightarrow 0}(h+2)=2 .\)

And, \(L f^{\prime}(1)=\lim _{h \rightarrow 0} \frac{f(1-h)-f(1)}{-h}=\lim _{h \rightarrow 0} \frac{(1-h)^2-(1)^2}{-h}\)

= \(\lim _{h \rightarrow 0}\left(\frac{1+h^2-2 h-1}{-h}\right)=\lim _{h \rightarrow 0}(-h+2)=2\)

∴ Rf'(1) = Lf'(1) = 2.

This shows that f(x) is differentiable at x = 1 and f'(1) = 2.

Example 2 Show that f(x) = [x] is not differentiable at x = 1.

Solution

f(x) = [x]

We have Rf'(1) = \(\lim _{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}=\lim _{h \rightarrow 0} \frac{[1+h]-[1]}{h}=0\)

{∵ [1+h] = 1 and [1] = 1},

and \(Lf'(1) = \lim _{h \rightarrow 0} \frac{f(1-h)-f(1)}{-h}=\lim _{h \rightarrow 0} \frac{[1-h]-[1]}{-h}=\infty\)

{∵ [1-h] = 0 abd [1] = 1}.

Thus Rf'(1) ≠ Lf'(1).

Hence, f(x) = [x] is not differentiable at x = 1.

Example 3 (1) Show that f(x) = x^4/3 is differentiable at x = 0, and hence find f'(0).

(2) Show that f(x) = x^3/2 is not differentiable at x = 0.

Solution

(1) We have Rf'(0) = \(\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}=\lim _{h \rightarrow 0} \frac{f(h)-f(0)}{h}\)

= \(\lim _{t \rightarrow 0} \frac{h^{4 / 3}-0}{h}=\lim _{h \rightarrow 0} \frac{h^{4 / 3}}{h}=\lim _{h \rightarrow 0} h^{1 / 3}=0\)

And, Lf'(0) = \(\lim _{h \rightarrow 0} \frac{f(0-h)-f(0)}{-h}=\lim _{h \rightarrow 0} \frac{f(-h)-0}{-h}\)

= \(\lim _{h \rightarrow 0} \frac{(-h)^{4 / 3}-0}{(-h)}=\lim _{h \rightarrow 0} \frac{(-h)^{4 / 3}}{(-h)}=\lim _{h \rightarrow 0}(-h)^{1 / 3}=0\)

Thus, Rf'(0) = Lf'(0) = 0.

Hence, f(x) = x^4/3 is differentiable at x = 0 and f'(0) = 0.    

(2) Consider g(x) = x^3/2.

Now, Rg'(0) = \(\lim _{h \rightarrow 0} \frac{g(0+h)-g(0)}{h}=\lim _{h \rightarrow 0} \frac{g(h)-g(0)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{h^{3 / 2}-0}{h}=\lim _{h \rightarrow 0} \frac{h^{3 / 2}}{h}=\lim _{h \rightarrow 0} h^{1 / 2}=0\)

And, Lg'(0) = \(\lim _{t \rightarrow 0} \frac{g(0-h)-g(0)}{-h}=\lim _{h \rightarrow 0} \frac{g(-h)-g(0)}{-h}\)

= \(\lim _{h \rightarrow 0} \frac{(-h)^{3 / 2}-0}{(-h)}=\lim _{h \rightarrow 0} \frac{(-h)^{3 / 2}}{(-h)}\)

= \(\lim _{h \rightarrow 0}(-h)^{1 / 2}\), which is imaginary.

Thus, Lg'(0) does not exist.

Hence, g(x) = x^3/2 is not differentiable at x = 0.

Example 4 Show that the function f(x) = \(\begin{cases}1+x, & \text { if } x \leq 2 \\ 5-x, & \text { if } x>2\end{cases}\) is not differentiable at x = 2.

Solution Rf'(2) = \(\lim _{h \rightarrow 0} \frac{f(2+h)-f(2)}{h}=\lim _{h \rightarrow 0}\left[\frac{5-(2+h)-3}{h}\right]\)

= \(\lim _{h \rightarrow 0} \frac{-h}{h}=\lim _{h \rightarrow 0}(-1)=-1\)

And, Lf'(2) = \(\lim _{h \rightarrow 0} \frac{f(2-h)-f(2)}{-h}\)

= \(\lim _{h \rightarrow 0}\left[\frac{1+(2-h)-3}{-h}\right]=\lim _{h \rightarrow 0} \frac{-h}{-h}=\lim _{h \rightarrow 0} 1=1\)

Thus, Rf'(2) ≠ Lf'(2).

Hence, f(x) is not differentiable at x = 2.

Example 5 Let f(x) = \(\left\{\begin{array}{c}
(1+\sin x), \text { when } 0 \leq x<\frac{\pi}{2} \\
1, \text { when } x<0
\end{array}\right.\) Show that f'(0) does not exist.

Solution

We have Rf'(0) = \(\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}=\lim _{h \rightarrow 0} \frac{f(h)-f(0)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{(1+\sin h)-1}{h}=\lim _{h \rightarrow 0} \frac{\sin h}{h}=1 .\)

And, Lf'(0) = \(\lim _{h \rightarrow 0} \frac{f(0-h)-f(0)}{-h}=\lim _{h \rightarrow 0} \frac{f(-h)-f(0)}{-h}=\lim _{h \rightarrow 0} \frac{(1-1)}{-h}=0 .\)

Thus, Rf'(0) ≠ Lf'(0). Hence, f'(0) does not exist.

Example 6 Let f(x) = mx + c and f(0) = f'(0) = 1. Find f(2).

Solution

f(x) = mx + c and f(0) = f'(0) = 1

Clearly, f(0) = (m x 0 + c) = c = 1 (given).

Also, f'(0) = \(\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}=\lim _{h \rightarrow 0} \frac{f(h)-f(0)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{(m h+c)-1}{h}=\lim _{h \rightarrow 0} \frac{m h+1-1}{h}\) [∵ c=1]

= \(\lim _{h \rightarrow 0} \frac{m h}{h}=\lim _{h \rightarrow 0} m=m\)

Thus, f'(0) = 1 ⇒ m = 1.

So, f(x) = 1 . x + 1, i.e., f(x) = (x+1). Hence, f(2) = (2+1) = 3.

Relation between Continuity and Differentiability

Theorem Every differentiable function is continuous. But, every continuous function need not be differentibale.

Proof

Let f(x) be a differentiable function and let a be any real number in its domain. Then, \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}=f^{\prime}(a)\) …(1)

Now, \(\lim _{h \rightarrow 0}[f(a+h)-f(a)]=\lim _{h \rightarrow 0}\left[\frac{f(a+h)-f(a)}{h} \times h\right]\)

= \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h} \times \lim _{h \rightarrow 0} h\)

= f'(a) x 0 = 0 [using (1)].

Thus, \(\lim _{h \rightarrow 0}[f(a+h)-f(a)]=0\) or \(\lim _{h \rightarrow 0} f(a+h)=f(a)\).

This shows that f(x) is continuous at a for all a.

Hence, every differentiable function is continuous.

In order to show that a continuous function need not be differentiable, it is sufficient to give an example of a function which is continuous but not differentiable. Condiser f(x) = | x | at x = 0.

Clearly, f(0) = 0.

\(\lim _{x \rightarrow 0+} f(x)=\lim _{h \rightarrow 0} f(0+h)=\lim _{h \rightarrow 0} f(h)=\lim _{h \rightarrow 0}|h|=\lim _{h \rightarrow 0} h=0 .\)

And, \(\lim _{x \rightarrow 0-} f(x)=\lim _{h \rightarrow 0} f(0-h)=\lim _{h \rightarrow 0} f(-h)=\lim _{h \rightarrow 0}|-h|=\lim _{h \rightarrow 0} h=0\)

Thus, \(\lim _{x \rightarrow 0+} f(x)=\lim _{x \rightarrow 0-} f(x)=f(0) .\)

So, f(x) = | x | is continuous at x = 0.

But, Rf'(0) = \(\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}=\lim _{h \rightarrow 0} \frac{f(h)-f(0)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{|h|-0}{h}=\lim _{h \rightarrow 0} \frac{h}{h}=1 .\)

And, \(L f^{\prime}(0)=\lim _{h \rightarrow 0} \frac{f(0-h)-f(0)}{-h}=\lim _{h \rightarrow 0} \frac{f(-h)-f(0)}{-h}\)

= \(\lim _{h \rightarrow 0} \frac{|-h|-0}{-h}=\lim _{h \rightarrow 0} \frac{h}{-h}=-1 \text {. }\)

Thus, Rf'(0) ≠ Lf'(0).

This shows that f(x) = | x | is not differentiable at x=0. Thus, f(x) = | x | is continuous but not differentiable at x=0. Hence, a continuous function need not be differentiable.

Example 7 Show that the function f(x) = \(\left\{\begin{array}{r}
x \sin (1 / x), \text { when } x \neq 0 \\
0, \text { when } x=0
\end{array}\right.\) is continuous but not differentiable at x = 0.

Solution

We have already discussed the above function for continuity at x = 0.

Now, Rf'(0) = \(\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}=\lim _{h \rightarrow 0} \frac{h \sin (1 / h)-0}{h}\)

= \(\lim _{h \rightarrow 0} \sin (1 / h)\), which does not exist.

Hence, f(x) is not differentiable at x = 0.

Example 8 Show that f(x) = | x-2 | is continuous but not differentiable at x = 2.

Solution

We have f(2) = | 2 – 2 | = 0.

\(\lim _{x \rightarrow 2+} f(x)=\lim _{h \rightarrow 0} f(2+h)=\lim _{h \rightarrow 0}|2+h-2|=\lim _{h \rightarrow 0}|h|=\lim _{h \rightarrow 0} h=0 .\)

∴ \(\lim _{x \rightarrow 2+} f(x)=\lim _{x \rightarrow 2-} f(x)=f(2)=0 .\)

So, f(x) is continuous at x=2.

But, Rf'(2) = \(\lim _{h \rightarrow 0} \frac{f(2+h)-f(2)}{h}=\lim _{h \rightarrow 0} \frac{|2+h-2|-0}{h}\)

 

= \(\lim _{h \rightarrow 0} \frac{|h|}{h}=\lim _{h \rightarrow 0} \frac{h}{h}=1\)

And, \(L f^{\prime}(2)=\lim _{h \rightarrow 0} \frac{f(2-h)-f(2)}{-h}=\lim _{h \rightarrow 0} \frac{|2-h-2|-0}{-h}\)

= \(\lim _{h \rightarrow 0} \frac{|-h|}{-h}=\lim _{h \rightarrow 0} \frac{h}{-h}=-1\)

 

Thus, Rf'(2) ≠ Lf'(2).

 

This shows that f(x) is not differentiable at x = 2.

\(\int \cot ^2\left(\frac{x}{2}\right) d x=\int\left(\operatorname{cosec}^2 \frac{x}{2}-1\right) d x\)

 

\(2 \int \operatorname{cosec}^2 t d t-\int d x\)