WBCHSE Class 11 Physics Notes For Vibration of Strings and Air Columns

Superposition Of Waves Transverse Vibration In A String

Stretched string: A stretched string is a thin metal wire clamped between two rigid supports (A and B) with tension.

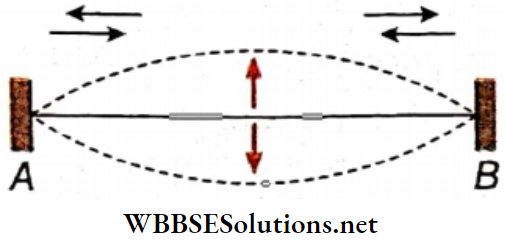
Such a string is the source of sound emitted by musical instruments like sitar, violin, piano, etc. To generate vibrations in the string, it is initially disturbed in a direction normal to its length.

This transverse disturbance is initiated usually by one of the three following methods:

1. Plucking the wire at any point—this method is used for sitar, guitar, etc.
2. Striking the wire at any point—this method is used to play a piano.
3. Bowing on the wire at any point—this method is used to play a violin.

The vibration in a stretched string has two salient features:

1. When a stretched string is displaced from its equilibrium position, two identical progressive waves are produced. These two waves travel towards the two ends of the wire. After getting reflected from the two ends, they again travel towards the opposite ends.
   • Thus, the two waves are reflected again and again from both ends. Hence, a stationary wave is generated in the string. This is known as a stationary wave in a stretched string.
   • As the string is rigidly clamped at the two ends, two nodal points are formed at the ends. One or more than one loops may be formed between them. Only one loop is shown there is no node other than A and B, and only one antinode is formed at the midpoint.
2. When the stretched string is vibrated in one or more than one loop, every point on the wire vibrates in a direction normal to the length of the wire. So, it is a transverse vibration.

Formation Of Stationary Waves In A Stretched String: Let a uniform string of length l be stretched by a tension T along the x-axis, with its ends rigidly fixed at the end x = 0 and x = l. Suppose a transverse wave is produced in the string travels along the positive x-axis and gets reflected at the fixed end, x = l.

The incident and reflected waves can be written as, y₁ = a sin (ωt- kx) and y₂ = – a sin(ωt+ kx) The equation of the resultant wave due to the superposition of the incident and the reflected progressive waves will be

y = \(y_1+y_2 =a \sin (\omega t-k x)-a \sin (\omega t+k x)\)

= \(-a[\sin (\omega t+k x)-\sin (\omega t-k x)]\)

= \(-2 a \cos \omega t \sin k x\)… (1)

(Using the relation sinA – sinB = \(2 \cos \frac{A+B}{2} \sin \frac{A-B}{2}\))

Since the supports A and B are rigid, nodes will be formed at these two points. So, y = 0 at x = 0 and y = 0 at x = l

[The coordinates of the supports A and B are x = 0 and x = l respectively, l = length of the string]

Now putting x = l and y = 0 in equation (1) we have

0 = -2a cosωt sinkl

So, for any value of t, sin kl = 0

i.e., kl = pπ, where p = 0, 1, 2, 3…..

Now if p = 0, then y = -2a cosωt sin kx

= \(-2 a \cos \omega t \sin \frac{p \pi}{l} x=0\)

i.e., for any value of t and x, y = 0.

This equation represents a vibrationless stationary string. This is not our subject of discussion.

So the significant values of p are 1, 2, 3,…..

Now, \(\frac{p \pi}{l} \quad \text { or, } \frac{2 \pi}{\lambda}=\frac{p \pi}{l} \quad \text { or, } \lambda=\frac{2 l}{p}\)…..(2)

Different Modes Of The Stationary Waves:

1. If p = 1, from equation (2), \(\lambda=2 l \text { or, } l=\frac{\lambda}{2}\). This means that two consecutive nodes must be apart by a distance equal to the length of the string, i.e., the string should vibrate in one segment.
2. If p = 2, from equation (2), \(\lambda=\frac{2 l}{2}=l \text { or, } l=\lambda\).

This means that between two nodes at the two ends of the string, there is another node. So the string must vibrate in two segments.

Generally, for the values of p = 1, 2, 3, 4,…… the stationary waves are formed in the stretched string and the string vibrates in one, two, three, four …. segments respectively. In each case, there are two nodes at the two ends of the string. Other nodes are formed according to the number of segments.

Laws Of Transverse Vibration In A Stretched String: Let a thin, uniform, and flexible wire be clamped with a tension between two rigid supports. Here, l = length of the wire, M = mass of the wire, r = radius of the wire,ρ = density of the material of the wire, and T = tension along the wire.

So, the area of cross-section = πr²;

volume of unit length of the wire = πr² · l = πr²

∴ Mass per unit length of the wire, m = \(\pi r^2 \rho=\frac{M}{l}\). This mass per unit length is often called the linear density of the wire. It is a characteristic property of the wire used because for a given wire, the linear density is fixed it is independent of the tension applied and the total length of the wire.

As proposed by the French scientist Marin Mersenne, the frequency (n) of transverse vibration in a stretched string varies with the relevant properties of the string according to the following laws:

Law Of Length: If the tension and the mass per unit length remain constant, the frequency of transverse vibration is inversely proportional to the length of the string, i.e., n ∝ \(\frac{1}{l}\), when T and m are constants.

Law Of Tension: If the length and the mass per unit length remain constant, the frequency of transverse vibration is proportional to the square root of the tension in the string, i.e., n ∝ √T, when l and m are constants.

Law Of Mass: If the length and the tension in the wire remain constant, the frequency of transverse vibration is inversely proportional to the square root of the mass per unit length of the string,

i.e., \(n \propto \frac{1}{\sqrt{m}}\), when l and T are constants.

The combination of the three laws gives, \(n \propto \frac{1}{l} \sqrt{\frac{T}{m}} \quad \text { or, } n=\text { constant } \times \frac{1}{l} \sqrt{\frac{T}{m}}\)

When the string vibrates in a single loop, the fundamental tone is emitted. In that case, the value of the above constant is \(\frac{1}{2}\). Then the frequency of the fundamental tone is \(n_1=\frac{1}{2 l} \sqrt{\frac{T}{m}}\)….(1)

It Is To Be Noted That,

1. The frequency of transverse vibration of the wire does not depend upon the total mass; it depends on mass per unit length of the wire.
2. The frequency of the wire does not depend upon the extent of stretching or the strength with which the wire is hit, causing the wire to vibrate.

Now, m = \(\pi r^2 \rho \text { or, } \sqrt{m}=\sqrt{\pi} \cdot r \cdot \sqrt{\rho} \text {. So, the law } n \propto \frac{1}{\sqrt{m}}\) means that \(n \propto \frac{1}{r \sqrt{\rho}}\).

This leads to two supplementary laws on transverse vibration in a string:

Law Of Radius: If the material of the string remains the same, the density remains constant. Thus the frequency of transverse vibration is inversely proportional to the radius of the string when the length and the tension in the string are constant;

i. e., n ∝ \(\frac{l}{r}\), when l, T, and ρ are constants.}{r}[/latex]

Law Of Density: For strings of the same radius, but made of different materials, the frequency of transverse vibration is inversely proportional to the square root of the density of the material, if the length and the tension in the string remain constant;

i. e., \(n \propto \frac{1}{\sqrt{\rho}}\), when l, T and r are constants.

Fundamental Tone And Overtones In A Stretched String: Let us consider the vibration of a stretched string in a single loop. Here, there are two nodes at the two ends, A and B, of the string and only one antinode at the mid-point.

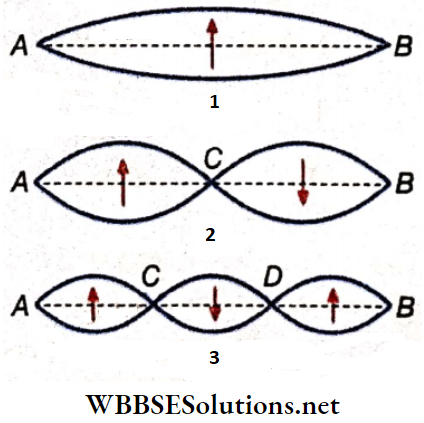
If λ is the wavelength of the stationary wave produced, the distance between two consecutive nodes.

= \(\frac{\lambda}{2}\) = length of the wire (l).

or, λ = 2l

If V is the wave velocity, the frequency is \(n_1=\frac{V}{\lambda}=\frac{V}{2 l}\)…(1)

Now, if the string vibrates in two loops, a node is formed at the mid-point (C) in addition to the nodes A and B at the two ends. So, the distance between three consecutive nodes = λ = length of the wire (l).

Therefore, the frequency is \(n_2=\frac{V}{\lambda}=\frac{V}{l}=2 \cdot \frac{V}{2 l}=2 n_1\)

Similarly, the frequency becomes \(3 n_1, 4 n_1, 5 n_1, \ldots\), vibrations in three, four, five,… loops, respectively.

The above discussions show that the lowest frequency for all the tones that can be emitted from a vibrating string is n₁. So the tone of frequency n₁ is the fundamental tone or the 1st harmonic. This means that only the fundamental tone is emitted when a stretched string vibrates in n single loop.

It is the fundamental tone that is produced by the string. But the string is making all those other possible vibrations too, all at the same time, so that the actual vibration of the string is pretty complex.

The tones with higher frequencies \(2 n_1, 3 n_1, 4 n_1, \ldots\), etc,, are the overtones. Again, the frequency of each overtone is a simple multiple of the fundamental frequency; so each overtone is a harmonic, i.e., the frequency of 2nd harmonic = 2n₁, the frequency of 3rd harmonic = 3n₁,… the frequency of p-th harmonic = pn₁ and so on.

We cannot hear the harmonics as separate notes. It may be noted that a stretched string may emit all tire even and odd harmonics. They are what give the string its rich, musical, string-like sound timbre. (The sound of a single frequency alone is mechanical, uninteresting, and unmusical sound)

If the above equation (1) is compared with equation (1), we get, V  \(=\sqrt{\frac{T}{m}}\)

where, T = tension in the string, m = mass per unit length of the string, and V = velocity of the transverse wave in the string.

The frequencies of the fundamental and the different overtones, in terms of the tension (T), the length of the wire (l), and the mass of the wire per unit length (m), are

⇒ \(n_1=\frac{1}{2 l} \sqrt{\frac{T}{m}}; n_2=2 n_1=\frac{2}{2 l} \sqrt{\frac{T}{m}} ;\)

∴ \(n_p=\frac{p}{2 l} \sqrt{\frac{T}{m}}\)….(3)

where, p = number of loops in the vibration; n_p is called the frequency of the p-th harmonic.

In principle, a vibrating string can emit all the overtones.

• But, in reality, the presence of the overtones depends on the point of initial disturbance. For example, let the mid-point of the string be plucked to initiate the vibrations. Clearly, this point will have the maximum amplitude of vibration and will become an antinode.
• So, a node at the mid-point is never obtained by plucking the mid-point. Accordingly, the harmonics having a node at the mid-point will be absent.
• These absent harmonics are the 2nd, 4th 6th harmonics. So, a vibrating string generates only the odd harmonics when it is initially plucked at the mid-point.

Initial plucking or striking at a point on the string generates an antinode at that point. At the same time, if some other point is touched loosely, then a node is formed there.

• A metal bar is used for this loose touch while playing a guitar. In this way, a good instrumentalist can control the musical sound emitted by forming nodes and antinodes at points as per his desire.
• It is possible to vibrate every wire in sitar, piano, etc. in such a way that the same wire can emit different tones simultaneously. Shows an example where the fundamental and the 2nd harmonic are being produced simultaneously. The string is vibrating in two loops to produce the 2nd harmonic.
• At the same time, the 2-loop formation is also vibrating in a single loop, so that the fundamental tone is emitted.
• We know that the quality or timbre of a musical sound depends on the number of overtones in the emitted sound and also on the relations of the overtones with the fundamental. Accordingly, it is evident that instruments like sitar, violin, piano, etc., can emit notes of very rich quality.

Superposition Of Waves – Transverse Vibration In A String Numerical Examples

Example 1. Two stretched wires made of the same material have lengths, diameters, and tensions, each in the ratio 1:2. The first wire emits a fundamental tone of frequency 200 Hz. What is the fundamental frequency of the 2nd wire?
Solution:

If d is the diameter of a wire, the mass per unit length is m = \(\frac{\pi d^2}{4} \rho\)

where ρ = density of the material of the wire. It is the same for the two wires.

Now, the fundamental frequency,

n = \(\frac{1}{2} l \sqrt{\frac{T}{m}}=\frac{1}{2 l} \sqrt{\frac{T \cdot 4}{\pi d^2 \rho}}=\frac{1}{l d} \sqrt{\frac{T}{\pi \rho}}\)

So, for the two wires, \(\frac{n_1}{n_2}=\frac{l_2}{l_1} \cdot \frac{d_2}{d_1} \cdot \sqrt{\frac{T_1}{T_2}}\)

or, \(\quad n_2=n_1 \cdot \frac{l_1}{l_2} \cdot \frac{d_1}{d_2} \cdot \sqrt{\frac{T_2}{T_1}}=200 \times \frac{1}{2} \times \frac{1}{2} \times \sqrt{\frac{2}{1}}\)

[Here, \(n_1=200\)]

∴ \(n_2=50 \sqrt{2}=70.7 \mathrm{~Hz} \text {. }\)

Example 2. The lengths of two wires made of the same material are in the ratio 2:3. Their diameters are equal and the fundamental of the shorter wire is one octave higher than that of the longer wire. Find the ratio
Solution:

The two wires are of the same material and the diameters are equal. So, the mass per unit length m is the same.

Here, the ratio 2 : 3 implies that the 1st wire is shorter

∴ \(n_1=2 n_2 \text { or, } \frac{n_1}{n_2}=\frac{2}{1} \text {. }\)

The fundamental frequency, n = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}\)

So, for the two wires, \(\frac{n_1}{n_2}=\frac{l_2}{l_1} \sqrt{\frac{T_1}{T_2}}\)

or, \(\frac{T_1}{T_2}=\left(\frac{n_1}{n_2}\right)^2 \cdot\left(\frac{l_1}{l_2}\right)^2=\left(\frac{2}{1}\right)^2 \cdot\left(\frac{2}{3}\right)^2=\frac{16}{9}\)

i.e., the ratio between the tensions is 16:9.

Example 3. A wire of density 9 g · cm^-3 Is elongated by 0.05 cm when stretched between two clamps 100 cm apart Find out the lowest frequency of transverse vibration in the wire, Given, Young’s modulus of the material of the wire = 9 x10¹¹ dyn · cm^-2.
Solution:

Length of the wire, L = 100 cm; elongation, l = 0.05 cm; density of the material, ρ = 9 g · cm^-3; Young’s modulus of the material,

Y = 9 x 10¹¹ dyn · cm^-2.

Let α = area of the cross-section of the wire

∴ Mass per unit length, m = αρ

Longitudinal stress = \(\frac{\text { tension }}{\text { area of cross-section }}=\frac{T}{\alpha}\)

longitudinal strain = \(\frac{\text { elongation }}{\text { original length }}=\frac{l}{L} .\)

∴ Y = \(\frac{\text { longitudinal stress }}{\text { longitudinal strain }}=\frac{T / \alpha}{l / L}=\frac{T L}{\alpha l}\)

or, T = \(\frac{Y \alpha l}{L}\)

The lowest frequency of transverse vibration = fundamental frequency,

n = \(\frac{1}{2 L} \sqrt{\frac{T}{m}}=\frac{1}{2 L} \sqrt{\frac{Y \alpha l}{L} \cdot \frac{1}{\alpha \rho}}=\frac{1}{2 \times 100} \sqrt{\frac{\left(9 \times 10^{11}\right) \times 0.05}{100 \times 9}}\)

= 35.36 Hz

Example 4. A stationary wave having 5 loops is generated in a 10 m long wire. What is the frequency, if the wave velocity is 20 m · s^-1?
Solution:

If λ is the wavelength, length of each loop = \(\frac{\lambda}{2}\)

∴ Length of 5 loops = 5 • \(\frac{\lambda}{2}\) = 10 m or, \(\lambda=\frac{10 \times 2}{5}\) = 4m

So, frequency, n = \(\frac{V}{\lambda}=\frac{20}{4}=5 \mathrm{~Hz}\) = 5 Hz.

Example 5. A uniform wire of length 12 m and mass 6 kg is suspended from a rigid support A mass of 2 kg is attached to the lower free end. A transverse wave of length 0.06 m is generated at the lower end of the wire. What is its wavelength when the wave reaches the upper end?
Solution:

The velocity of transverse vibration in a stretched wire, V = \(\sqrt{\frac{T}{m}}\), where T = tension in the wire and m = mass per unit length = constant, for the uniform wire.

If V₁ and V₂ are the velocities at the lower and upper ends, respectively, \(\frac{V_1}{V_2}\)=\(\sqrt{\frac{T_1}{T_2}}\)

Here, T₁ = tension at the lower end = weight of the suspended mass = 2 x 9.8 N;

T₂ = tension at the upper end = weight of the wire and the suspended mass = (2 + 6) x 9.8 = 8 x 9.8 N

The entire wire will emit a sound of a fixed frequency; so the wavelength A is proportional to the wave velocity V.

∴ \(\frac{\lambda_1}{\lambda_2}=\frac{V_1}{V_2}=\sqrt{\frac{T_1}{T_2}}\)

or, \(\lambda_2=\lambda_1 \sqrt{\frac{T_2}{T_1}}=0.06 \times \sqrt{\frac{8 \times 9.8}{2 \times 9.8}}=0.12 \mathrm{~m}\).

Example 6. A wire is stretched with negligible tension at 30°C between two rigid supports. Find the velocity Of the transverse wave in the wire at 20°C. Given, the coefficient of linear expansion, Young’s modulus, and the density of the material of the wire are α = 18 x 10^{-6 °}C^-1, Y = 12 x 10¹¹ dyn • cm^-2, and ρ = 6 g · cm^-3, respectively.
Solution:

Decrease in temperature, θ = 30-20 = 10°C; due to this decrement, the wire will tend to contract. As a result, thermal stress will be developed.

This thermal stress = Yαθ;

So the tension in the wire, T = Yαθ A, where A = area of the cross-section of the wire.

Again, mass per unit length of the wire,

m = A · 1 · ρ = Aρ

∴ The velocity of the transverse wave in the wire is

V = \(\sqrt{\frac{T}{m}}=\sqrt{\frac{Y \alpha \theta A}{A \rho}}\)

= \(\sqrt{\frac{Y \alpha \theta}{\rho}}=\sqrt{\frac{\left(12 \times 10^{11}\right) \times\left(18 \times 10^{-6}\right) \times 10}{6}}\)

= \(6000 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)