WBBSE Solutions For Class 9 Maths Arithmetic Chapter 1 Real Numbers

Arithmetic Chapter 1 Real Numbers

Arithmetic Chapter 1 Natural Numbers

1. The numbers 1, 2,.3, 4, …… (to infinity) are called Natural Numbers or Counting Numbers.
2. For the essentiality of counting different objects, these natural counting numbers have been created from the very beginning of human civilization.
3. These numbers start from 1 and end at infinity.
4. So, the series of these numbers is closed at the left and open at the right.
5. The least natural number is 1.
6. There is no greatest natural number.
7. Natural numbers are usually denoted by the English alphabet N.
8. Representing the natural numbers according to the set theory we get,
9. N= {1, 2, 3, 4, ……..} or,
10. N ={n: n ≥ 1 and n is a natural number}

Read and Learn More WBBSE Solutions For Class 9 Maths

 

 

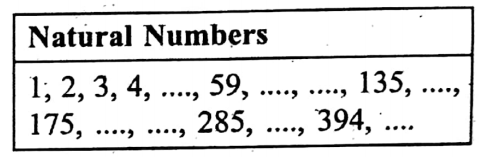
Properties and Characteristics of Natural Numbers:

1. ‘O’ is not a natural number.
2. The least natural number is 1.
3. The numerical value of two consecutive natural numbers is always 1.
4. The sum of two or more natural numbers is always a natural number.
   For example, 10 + 15 = 25, which is a natural number, and 6 + 14 + 112 = 132, which is also a natural number.
5. The subtraction of two natural numbers may or may not be a natural number.
   For example, 25 – 14 =11, which is a natural number; On the other hand, 16 – 48 = – 32, which is not a natural number.
6. The product of two natural numbers is a natural number.
   For example, 15 x 36 = 540, which is a natural number; 10 x 26 x 108 = 28080, which is a natural number.
7. The division of two natural numbers may or may not be a natural number.
   For example, 50 ÷ 2 = 25, which is a natural number; But 75 ÷ 50 = 3/2 is a fraction, not a natural number.
8. The natural numbers can be represented easily on the number line.
9. Natural numbers are not dense on the number line, i.e., there is no other natural number between two consecutive natural numbers.
10. Natural numbers are all positive numbers.

 

Arithmetic Chapter 1 Whole numbers

1. From the previous classes, it is known to all of us that 0 is not a natural number.
2. Now, the numbers, generated by adding 0 to the natural numbers are called Whole Numbers.
3. Therefore the numbers 0, 1, 2, 3, and 4, (to infinity) are called Whole Numbers.
4. Whole numbers are generally denoted by the letter W of the English alphabet.
5. W= {0, 1, 2, 3,4,…….}
6. = {x : x ≥ 0, where x is zero or a natural number}.

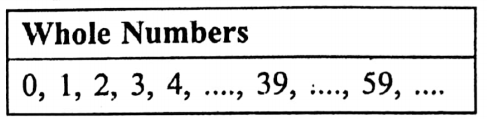
Properties and Characteristics of Whole Numbers

1. The least whole number is 0.
2. There is no greatest whole number.
3. Whole numbers are not dense on the number line.
4. The sum or product of two or more whole numbers is always a whole number.
5. The subtraction or division of two whole numbers may or may not be a whole number.

 

Arithmetic Chapter 1 Integers

1. You have already studied that all the natural numbers are positive and there exists always an additive inverse of these positive integers.
2. For example, the additive inverse of 7 is (- 7); the additive inverse of 16 is (- 16), etc.
3. These additive inverse numbers are called Negative Integers.
4. Therefore, the integers greater than 0 i.e. the numbers 1, 2, 3, 4, (to infinity) are called Positive Integers.
5. The integers less than 0 i.e. the numbers – 1, – 2, – 3, – 4, (to infinity) are called
6. Negative Integers and the number 0 is called Neither Positive nor Negative Integers.
7. Now, Negative integers, zero, and positive integers are together called integers.
8. Integers are usually denoted by I or the English alphabet Z.
9. Therefore, by set theory notation,
10. I = {…… -4, – 3, – 2, – 1, 0, 1, 2, 3, 4,………. } or,
11. Z ={….,- 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, }
12. Also, I or Z = {x: x is an integer}.
13. Moreover, Negative integers are denoted by I^– or Z^– and Positive integers are denoted by I⁺ or Z⁺.
14. ∴ I^– or Z^– = {  -4, -3,-2, – 1}.
15. and I⁺ or Z⁺ = {1, 2, 3, 4, ………}.

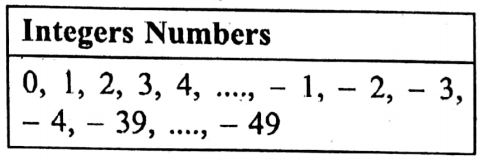
Properties and Characteristics of Integers:

1. here is no least or greatest integer.
2. Integers are expanded to infinity on both sides left and right.
3. The least positive integer is 1.
4. The greatest negative integer is – 1.
5. 0 is neither positive nor negative;
6. There exists an additive inverse of each and every integer.
7. The distance in the number line between any positive integer and its additive inverse is always equal.
8. Integers are not dense in the number line, i.e., there exists no other integer between two consecutive integers.
9. The sum, subtraction, and product of two or more integers are always an integer.
10. The division of two integers may or may not be an integer.
11. The sum of any positive integer and its additive inverse is always zero.

 

Example 1. 

 If two integers a and b be such that -2 < a < 0 and 0 < b < 2, then show that

1. (a + b)belongs to the set of whole numbers W

Solution:

Given Two Integers a And b be Such That -2 < a < 0 and 0 < b < 2

– 2 < a <0 means that a is an integer that is greater than – 2, but less than 0.

∴ a = – 1.

0 < b < 2 means that b is an integer that is greater than 0, but less than 2.

∴b = 1.

Now, (1) a + b = – 1 + 1

= 0, which is a whole number,

∴ (a + b) belongs to W. (Proved)

 

2. (a – b) belongs to the set of natural numbers N.

Solution:

Given Two Integers a And b be Such That -2 < a < 0 and 0 < b < 2

(a – b) belongs to the set of natural numbers N

a – b = – 1– 1

= – 2, which is a negative integer.

∴ (a – b) does not belong to N. (Proved)

 

3. Given Two Integers a And b be Such That -2 < a < 0 and 0 < b < 2

(b – a) belongs to the set of integers Z.

b – a = 1 – (- 1)

= 1 + 1

= 2, which is an integer.

∴ (b – a) belongs to Z. (Proved)

 

Example  2. If two negative integers n₁ and n₂ be such that n₁ ≠ – 1, n₂ ≠ – 2 and – 3 < n_1,n₂ < 3 then find the values of

1. n₁ + n₂

2. n₁ – n₂

3. n₁n₂

4. \(\frac{n_1}{n_2}\)

 

Solution:

-3 < n₁, n₂ < 3 means that both n₁ and n₂ are two such negative integers, the values of which are greater than (-3), but less than 3.

∴ The value of n₁ and n₂ are -2 and -1.

Also, given that n₁ ≠ -1

∴ n₁ = -2 and n₂ ≠ -2 ⇒ n₂ = -1.

So,

1. n₁+ n₂

= – 2 + (- 1)

= – 2 – 1

= – 3

 

2. n₁ – n₂

= – 2 + (- 1)

= – 2 + 1

= – 1

 

3. n₁. n₂

= (-2). (-1)

= 2

 

4. \(\frac{n_1}{n_2}\)

= \(\frac{n_1}{n_2}\)

= \(\frac{-2}{-1}\)

= 2

 

Example 3. If – 5 < x< 5 and x is a negative integer, then find the values of

Solution:

Given – 5 < x< 5 and x is a negative integer

The meaning of – 5 < x< 5 is that x is greater than (- 5) and less than 5.

Now, the integers which are greater than – 5 and less than 5 are – 4, – 3, – 2, – 1, 0., 1, 2, 3, and 4.

Also,x is a negative integer.

∴ The values of x are – 4, – 3, – 2, – 1.

 

Arithmetic Chapter 1 Rational Numbers

Definition:

1. The numbers that can be represented in the form \(\frac{p}{q}\)  where p and q are both integers and q ≠ 0, is called Rational Numbers.
2. For example,  is a rational number; Because 5 and 7 are both integers.
3. Therefore, all integers are Rational Numbers.
4. Moreover, any natural number can be represented in the form \(\frac{p}{q}\)  where p and q are both integers and q ≠ 0.
5. For example, 8 is a natural number, it can be represented in the form as follows
6. \(8=\frac{8}{1}(p=8, q=1)=\frac{16}{2}(p=16, q=2)=\frac{24}{3}(p=24, q=3) \text {, }\)………etc.
7. 8 is a rational number.
8. Thus, it can be easily shown that any natural number can be represented in the form \(\frac{p}{q}\) where p and q
9. q are both integers and q ≠ 0.
10. Therefore, every natural number is a rational number.
11. We can also write 0 in the form \(\frac{0}{1}\) =\(\frac{0}{2}\) = \(\frac{0}{3}\) = \(\frac{0}{4}\) = …..etc., where both the numerator and denominator
12. are integers and the denominator is never zero.
13. ∴ 0 (zero) is a rational number.
14. Thus, all natural numbers including zero, i..e., the whole numbers are all rational numbers.
15. Again, any negative integer such as -18, can be written in the form \(\frac{-18}{1}\) = \(\frac{-32}{2}\) = ……… etc.
16. both the numerator and denominator are integers and the denominator is not zero.
17. 18 is a rational number.
18. Similarly, any negative integer can be represented in the form \(\frac{p}{q}\) where p and q are both integers and q ≠ 0.
19. ∴ All the negative integers are rational numbers.
20. From the above discussion, we can say that,
21. The numbers that can be represented in the form of the division of two integers where the denominator is never zero are called rational numbers.
22. The rational numbers are usually denoted by the English alphabet Q.

Equivalent Rational Numbers:

1. You have already studied that a rational number can be represented in several manners, the value of each of which is equal.
2. Such as \(\frac{2}{3}\)  is a rational number.
3. It can be represented in different forms like  \(\frac{2}{3}\) = \(\frac{4}{6}\) = \(\frac{6}{9}\) = \(\frac{8}{12}\) = …………etc.,  where both the numerator and denominator are integers and the denominator is never zero.
4. Each of these numbers is a rational number.
5. Also, the value of each of these rational numbers is equal. These rational numbers are called equivalent rational numbers.
6. Therefore, the rational numbers which are of equal values, but of different representations are called equivalent rational numbers to each other.
7. Any rational number is usually represented in its lowest form (by simplification); i.e., the two integers forming the numerator and denominator of the lowest form (in the case of \(\frac{p}{q}\), p and q) are co-primes.

 

To insert one or more rational numbers in between two given numbers (Rational or integer):

1. Let a and b be two given numbers (rationals or integers).
2. We have to insert one or more than one rational numbers in between a and b. 
3. We can do the same by different methods as follows

Method-1.

1. When 1 rational number is to be inserted
2. The given two numbers are a and b.
3. Tthe required rational number = \(\frac{a+b}{2}\)

For example:

1. Insert one rational number between 3 and 4.

Solution:

Here, the given two numbers are 3 and 4.

So, taking a= 3 and b = 4, the required rational number

= \(\frac{a+b}{2}=\frac{3+4}{2}=\frac{7}{2}\)

 

2. Insert one rational number between 2 and \(\frac{3}{2}\).

Solution: The required rational number = \(\frac{2+\frac{3}{2}}{2}=\frac{7}{4}\)

 

3. Insert one rational number between \(\frac{5}{2}\) and 5.

Solution:

\(\frac{\frac{5}{2}+5}{2}=\frac{15}{4}\)

 

4. Insert one rational number between – 2 and \(\frac{3}{4}\).

 Solution: The required rational number = \(\frac{-2+\frac{3}{4}}{2}=\frac{\frac{-8+3}{4}}{2}=\frac{-\frac{5}{4}}{2}=-\frac{5}{8}\)

 

5. Insert one rational number between \(\frac{1}{7}\) and  \(\frac{1}{6}\).

Solution: The required rational number = \(\frac{\frac{1}{7}+\frac{1}{6}}{2}=\frac{\frac{6+7}{42}}{2}=\frac{\frac{13}{42}}{2}=\frac{13}{84}\)

 

Method-2.

When more than one rational numbers are to be inserted :

1. Let a and b be two given numbers and we have to insert n rational numbers in between them.
2. Then, the WORKING RULE is as follows:
3. Step – 1: Bind (n + 1); The result of this sum will be the denominator of all the required rational numbers.
4. Step – 2: Express an in such of its equivalent rational number, the denominator of which is the result of the sum {n + 1).
5. Step – 3: Express b as an equivalent rational number, the denominator of which is the same as that of the expression of an in STEP – 1, i.e., (n + 1).
6. Step – 4: Select n integers in between the numerator of the equivalent rational number obtained in STEP – 2 and the numerator of the equivalent rational number obtained in STEP-3. (Since n rational numbers have to be inserted).
7. Step – 5: Write down the result of the sum.
8. (n + 1) as the denominator of each of the integers obtained in STEP – 4.
9. Step – 6: Represent the rational numbers obtained in STEP – 5 as their lowest forms by simplification
10. Then, complete your answer by writing the rational numbers thus involved as the required rational numbers one after another.

For Example

1. Let 8 rational numbers are to be inserted between 6 and 7.

Then,

2. Step – 1: 8+1 = 9.

3. Step – 2: 6 = \(\frac{54}{9}\)

4. Step – 3: 7 = \(\frac{63}{9}\)

5. Step – 4: 55,56,58,59,60,61,62 [∵ these are between 54 and 53]

6. Step – 5: \(\frac{55}{9}, \frac{56}{9}, \frac{57}{9}, \frac{58}{9}, \frac{59}{9}, \frac{60}{9}, \frac{61}{9}, \frac{62}{9}\)

7. Step – 6: \(\frac{57}{9}=\frac{19}{3} ; \frac{60}{9}=\frac{20}{3}\)

∴ The Required rational numbers are \(\frac{55}{9}, \frac{56}{9}, \frac{57}{9}, \frac{58}{9}, \frac{59}{9}, \frac{60}{9}, \frac{61}{9}, \frac{62}{9}\)

 

Cautions:

1. If a and b are both rational numbers, then it may sometimes appear that the two numerators of the equivalent rational numbers obtained in STEP-2 or in STEP-3 having their denominators as the result of the sum (n + 1) are not integers.

2. For example, in the case of inserting 8 rational numbers in between \(\frac{1}{3} \text { and } \frac{1}{2}, \frac{1}{3}=\frac{3}{8+1}=\frac{3}{9}\), the numerator 3 of which is an integer, but \(\frac{1}{2}=\frac{\frac{9}{2}}{8+1}=\frac{\frac{9}{2}}{9}\) numerator \(\left(\frac{9}{2}\right)\) of which is not an integer.

3. In such a case, it is more convenient to take any multiple of (n + 1) such as 2 (n + 1), 3 (n + 1), 4 (n + 1), ………………etc. as the denominator of the rational numbers instead of (n + 1) as the same.

 

For example:

1. in the insertion of rational numbers in between \(\frac{1}{3}\) and \(\frac{1}{2}\) it is more convenient to take 6 x 9 = 54 as the denominator instead of taking
(n + 1) = 8 + 1 = 9 as the denominator.

2. Here, none of the numbers 2 x 9 = 18, 3 x 9 = 27, 4 x 9 – 36, 5 x 9 = 45 must not be taken as the denominator.

3. ∴ The selected denominator is 54.

4. So, \(\frac{1}{3}=\frac{18}{54} \text { and } \frac{1}{2}=\frac{27}{54}\)

5. Again, 8 integers in between 18 and 27 are 19, 20, 21, 22, 23, 24, 25, and 26.

6. ∴ The required rational numbers are

7. \(\frac{19}{54}, \frac{20}{54}, \frac{21}{54}, \frac{22}{54}, \frac{23}{54}, \frac{24}{54}, \frac{25}{54} \text { and } \frac{26}{54}\) i.e.,

8. \(\frac{19}{54}, \frac{10}{27}, \frac{7}{18}, \frac{11}{27}, \frac{23}{54}, \frac{4}{9}, \frac{25}{54} \text { and } \frac{13}{27}\)

9. If n is a large number, then it is not wise to follow the method described in method – 2, In this case, you should follow the general rule described in the following.

 

Method-3 : (General Rule)

Let the given numbers be a and b, where a < b and we have to insert n rational numbers in between a and b.

Then the WORKING RULE is

Step – 1: Find d, where d = \(\frac{b-a}{n+1}\)

Step – 2: Determine the rational numbers (a + d), (a + 2d), (a + 3d),…………………. , (a + nd).

Hence, the required rational numbers are (a + d), (a + Id), (a + 3d),……………………,  (a + nd)

For examples:

1. Insert 4 rational numbers between 3 and 4.

Solution:

Here, a = 3, b = 4 and n = 4.

∴ d = \(\frac{4-3}{4+1}=\frac{1}{5}\)

Now, a + d = \(3+\frac{1}{5}=\frac{16}{5}\)

a+2d= \(3+2 \times \frac{1}{5}=\frac{17}{5}\)

a+3d= \(3+3 \times \frac{1}{5}=\frac{18}{5}\)

a+4d=\(3+4 \times \frac{1}{5}=\frac{19}{5}\)

Hence, the required rational numbers are \(\frac{16}{5}, \frac{17}{5}, \frac{18}{5} \text { and } \frac{19}{5}\)

 

2. Insert 4 rational numbers in between \(\frac{1}{3}\) and \(\frac{2}{5}\).

Solution: Here, a = \(\frac{1}{3}\) , b = \(\frac{2}{5}\) n = 4.

∴ d = \(\frac{\frac{2}{5}-\frac{1}{3}}{4+1}=\frac{\frac{6-5}{15}}{5}=\frac{\frac{1}{15}}{5}=\frac{1}{75}\)

Now, \(a+d=\frac{1}{3}+\frac{1}{75}=\frac{25+1}{75}=\frac{26}{75}\);

\(a+2 d=\frac{1}{3}+2 \times \frac{1}{75}=\frac{1}{3}+\frac{2}{75}=\frac{25+2}{75}=\frac{27}{75}=\frac{9}{25}\)

\(a+3 d=\frac{1}{3}+3 \times \frac{1}{75}=\frac{1}{3}+\frac{1}{25}=\frac{25+3}{75}=\frac{28}{7.5}\);

\(a+4 d=\frac{1}{3}+4 \times \frac{1}{75}=\frac{1}{3}+\frac{4}{75}=\frac{25+4}{75}=\frac{29}{75}\);

Hence, the required rational numbers are \(\frac{26}{75}, \frac{9}{25}, \frac{28}{75} \text { and } \frac{29}{75}\)

 

Plotting of rational numbers in the number line:

We know that any integer can be represented in the form \(\frac{p}{q}\), where both p and q are integers and q ≠ 0.

Now,

1.

1. If the given rational number is to be plotted to be a positive proper fraction then we divide the distance between 0 and 1 so many equal parts as the number given in the denominator of the given rational number.
2. Then, we plot the given rational number in the number line by taking as many equal parts from 0 as are there in the numerator of the given number.
3. If the given rational number is a negative proper fraction, we perform the same procedure by taking the distance between (- 1) and 0 in the number line.
4. For example, let we have to plot the given rational number \(\frac{3}{7}\), which is a positive proper fraction in the number line.
5. Then, we first, divide the distance between 0 and 1 into 7 equal parts (since the denominator of \(\frac{3}{7}\) is 7).
6. Secondly, we take 3 (since the numerator of \(\frac{3}{7}\)  is 3) equal parts out of 7, starting from 0 to the right-hand side.
7. Thus, we plot the given rational number in the number line.
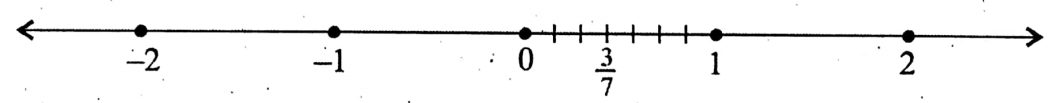
8. Similarly, we can plot the rational number which is a negative proper fraction, in the number line.
9. But in this case, we have to choose the distance in the number line between (-1) and 0.

 

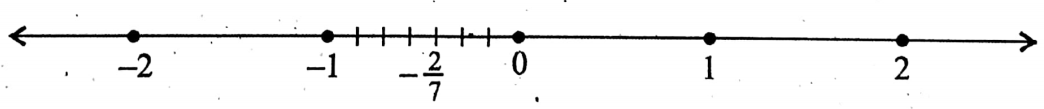
2.

1. If the given rational number, which is to be plotted is an improper fraction, then at the first, we express the number as the sum of an integral part and a proper fractional part.
2. Hence, starting from 0 on the number line, we move towards the right-hand side of 0 (if the integral part is positive) or towards the left-hand side (if the integral part is negative) so many equal parts of the number line as the integral part detects and after all, we plot the proper fractional part of the given number in the just next equal part of the number line according to the rule (1) described in the above.
3. Thus, any rational number which is an improper fraction can easily be plotted in the number line.
4. For example, let we have to plot the rational number \(\frac{17}{3}\) in the number line.
5. Then, expressing the given number as the sum of two parts an integral part and a proper fractional part, we get, \(\left(\frac{17}{3}=5+\frac{2}{3}\right)\)
6. integral part = 5 and proper fractional part = \(\frac{2}{3}\).
7.  So, moving 5 equal parts towards the right-hand side from 0 along the number line, we plot in \(\frac{2}{3}\) the 6th equal parts of the number line.
8. Therefore, the point thus plotted in the 6th equal part of the number line represents the given rational number \(\frac{17}{3}\).
9. Similarly, Plotting the rational number \(-\frac{6}{5}\) in the number line, we get the following.

Decimal expression of rational numbers :

1. By simple division method, we get,

2. \(\frac{1}{2}=0 \cdot 5\);

3. \(\frac{1}{3}=0 \cdot 333 \ldots \ldots\);

4. \(\frac{1}{4}=0.25\);

5. \(\frac{1}{5}=0 \cdot 2\);

6. \(\frac{1}{6}=0 \cdot 166 \ldots \ldots\);

7. \(\frac{1}{7}=0 \cdot 142857142857 \ldots \ldots\);

8. \(\frac{1}{8}=0 \cdot 125\);

9. \(\frac{1}{9}=0 \cdot 1111 \ldots \ldots\);

10. \(\frac{1}{10}=0 \cdot 1\);

11. \(\frac{1}{11}=0.090909\);

12. Thus, any rational number can be expressed as a decimal fraction by a simple division process.

13. Again, we see that the representing decimal fractions are either

 

Terminating decimal fractions:

1. If the decimal representation of a rational number is terminating, then we see that the denominator of the number is either 2 or 5 or any multiple of both 2 and 5, and 2 x 5 = 10.
2. Such as, \(\frac{1}{2}\) = 0 . 5 is a terminating decimal fraction and its denominator is 2.
3. Similarly, \(\frac{1}{5}\) = 0 . 2 and \(\frac{1}{10}\)= 0.1 are two terminating decimal fractions and we see that both the numbers have the denominators and 10 respectively.
4. Therefore, the rational numbers the denominator of which is 2 or 5 or any multiple of them, become terminating decimal fractions when represented in decimal fractions and vice versa.

 

Non-terminating decimal fractions:

1. The non-terminating decimal fractions, i.e., the fractions in which the division process never ends are all recurring decimal fractions.
2. One or more than one digit in this decimal fraction recures.

For Example:

1. \(\frac{1}{3}=0 \cdot 333 \ldots \ldots\) the recurring digit is 3.

2. \(\frac{1}{6}=0 \cdot 166 \ldots \ldots\) the recurring digit is 6

3. \(\frac{1}{7}=0 \cdot 142857142857 \ldots \ldots\) The recurring digits are 1, 4, 2, 8, 5, and 7.

4. \(\frac{1}{11}=0.090909\) the recurring digits are 0 and 9.

5. Therefore, the rational numbers when represented as decimal fractions are all non-terminating recurring.

6. From the above discussion, we can say that the decimal expression of a rational number is either terminating or non-terminating recurring.

7. Moreover, a number whose decimal expression is terminating or non-terminating recurring is rational.

 

Characteristics and Properties of rational numbers :

1. 0 is a rational number.
2. The rational numbers are dense in the number line, i.e., there is an infinite number of rational numbers between any two rational numbers in the number line.
3. The decimal expansion of rational numbers is either terminating or non-terminating recurring.
4. The sum of two rational numbers is a rational number, i.e., if x, y, ∈ Z, then (x + y) ∈ Z. [Closure under addition property.]
5. The product of two rational numbers is a rational number, i..e., if x, y ∈ Z, then xy ∈ Z.  [Closure under multiplication property.]
6. Associative law for addition:
   If x, y, z ∈ Z, then x + (v + z) = (x + y) + z.
7. Commutative law for addition:
   If x, y ∈ Z, then x + y = y + x.
8. If x ∈ Z, then x + 0 = x = 0 + x; 0 is called the additive identity element.
9. Ifx ∈ Z, x + (- x) = 0 = (- x) + x; (-x) is called the additive inverse of x.
10. Associative law under multiplication:
    If x, y, z ∈ Z, then x.(y.z) = (x.y).z
11. Commutative law under multiplication:
    If x, y ∈ Z, then x.y – yx.
12. If x ∈ Z, then x.1 = x = 1. x; 1 is called the multiplicative identity element.
13. Left distributive law :
    If x, y, z ∈ Z, then x.(y + z) = x.y + x.z
14. Right distributive law:
    If x, y, z e Z, then (x + y).z = x.z + yz.
15. Trichotomy law:
    If x, y ∈ Z, then either x = y or x > y or x < y.
16. Transitivity law:
    If x, y ∈ Z and if x > y and y > z, then x > z.
17. Monotone property of addition:
    If x, y, z ∈ Z, then x>y=>x+z>y + z.
18. Monotone property of multiplication:
    If x, y, z ∈ Z, then x > y => x.z > y.z (z > 0).
19. Cancellation law:
    If x, y, z ∈ Z, then x + z= y + z=>x=y

 

Arithmetic Chapter 1 Real Numbers Select The Correct Answer (MCQ)

1. 0 is a rational number. The rational number just next to it is

1. 1
2. 1/2
3. 1/10
4. Undetermined.

Solution:

0 is a rational number.

The rational number next to it is 0 0001, 0 001, 0 01, 0T, etc.

So the rational number just next to it is undetermined. ,

∴ The correct answer is 4. Undetermined.

 

2. \(\frac{p}{q}\) is a rational number, where p and q are two natural numbers and 0 < q < If the decimal expansion of \(\frac{p}{q}\) be a terminating decimal fraction, then q = 

1. 1
2. 2
3. 3
4. None of these

Solution: q is a natural number and 0 < q < 5

q={1,2, 3,4}

p is a natural number

p = 1, 2, 3, 4,……………….. etc.

If q = 1, then \(\frac{p}{q}\) is the natural number.

If q = 2, then \(\frac{p}{q}\) is the terminating decimal fraction.

If q = 3, then \(\frac{p}{q}\) is a non-terminating decimal fraction.

The correct answer is 4. None of these

 

3. The decimal expression of the rational number \(\frac{1}{2048}\) is a 

1. Terminating number.
2. Non-terminating number
3. Non-terminating recurring number
4. None of these

Solution:

= \(\frac{1}{2048}\)

= \(\frac{1}{(2)^{11}}\)

As the factors of denominators are 2.

So the number \(\frac{1}{2048}\)  is a terminating number

∴ The correct answer is 1. Terminating number.

 

 

4. The decimal expansion of  \(\frac{1}{3125}\) is

1. Non-terminating number
2. Non-terminating recurring number
3. Terminating
4. None of these

Solution:

= \(\frac{1}{3125}\)

= \(\frac{1}{(5)^5}\)

As factors denominator are 5

So the number \(\frac{1}{3125}\) is terminating.

∴ The correct answer is 3. Terminating

 

 

Arithmetic Chapter 1 Real Numbers Short Answer Type Questions

Examples 1.

Give 4 examples of rational numbers.

Solution: 4 rational numbers are \(\frac{1}{2}, \frac{2}{3}, \frac{7}{8}, \frac{5}{9}\)

 

Example 2.

Insert one rational number in between the following two given rational numbers in each case.

1. 4 and 5

Solution:

4 and 5

We get, \(\frac{4+5}{2}=\frac{9}{2}\)

∴ The required rational number = \(\frac{9}{2}\)

 

2. \(-1 \text { and } \frac{1}{2}\)

Solution:

\(-1 \text { and } \frac{1}{2}\)

We get, \(\frac{-1+\frac{1}{2}}{2}=-\frac{1}{4}\)

∴ The required rational number = \(-\frac{1}{4}\)

 

3. \(\frac{1}{4} \text { and } \frac{1}{3}\)

Solution:

\(\frac{1}{4} \text { and } \frac{1}{3}\)

We get, \(\frac{\frac{1}{4}+\frac{1}{3}}{2}=\frac{\frac{3+4}{12}}{2}=\frac{\frac{7}{12}}{2}=\frac{7}{24}\)

∴ The required rational number = \(\frac{7}{24}\)

 

4. -2 and -1

Solution:

-2 and -1

we get, \(\frac{-2+(-1)}{2}=\frac{-2-1}{2}=-\frac{3}{2}\)

∴ The required rational number = \(-\frac{3}{2}\)

 

Example  3.  is a rational number, where p and q are both integers and q * 0. The decimal expansion of \(\frac{p}{q}\) gives a terminating decimal fraction. Then, what property q must satisfy?

Solution:

We know that if the decimal expansion of a rational number is a terminating fraction, then the denominator of the rational number must be 2 or 5

or (2 or 5)

or (any multiple of 2 and 5).

q = 2 or any multiple of 2,

or, q = 5 or any multiple of 5,

or, q = any multiple of both 2 and 5.

 

Example 4. What type of number will be resulted when the sum, subtraction, product, and division (divisor is not zero) of two rational numbers are taken?

Solution:

The sum, subtraction, product, and division (Divisor is not zero) of two rational numbers is a rational number.

 

Arithmetic Chapter 1 Real Numbers Long answer-type Questions

Example 1.

Insert 3 rational numbers between each pair of rational numbers given below

1. 4 and 5

Solution:

4 and 5

We know that if a and be two rational numbers, then 3 rational numbers between a and b are given by a + d, a + 2d, and a + 3d,

where d = \(\frac{b-a}{3+1}=\frac{b-a}{4}\)

Now, Here , a = 4 and b = 5,

∴ d = \(\frac{5-4}{3+1}=\frac{1}{4}\)

∴ a + d = \(4+\frac{1}{4}=\frac{16+1}{4}=\frac{17}{4}\);

a + 2d = \(a+2 d=4+2 \times \frac{1}{4}=4+\frac{1}{2}=\frac{9}{2}\).

∴ The required rational numbers are \(\frac{17}{4}, \frac{9}{2} \text { and } \frac{19}{4}\)

 

2. \(\frac{1}{5} \text { and } \frac{1}{4}\)

Solution:

Here, a = \(\frac{1}{5}\) and b= \(\frac{1}{4}\)

∴ d = \(\frac{\frac{1}{4}-\frac{1}{5}}{3+1}=\frac{\frac{5-4}{20}}{4}=\frac{\frac{1}{20}}{4}=\frac{1}{80}\)

∴ a + d = \(\frac{1}{5}+\frac{1}{80}=\frac{16+1}{80}=\frac{17}{80}\)

a + 2d = \(\frac{1}{5}+2 \times \frac{1}{80}=\frac{1}{5}+\frac{1}{40}=\frac{8+1}{40}=\frac{9}{40}\)

a+3d = \(\frac{1}{5}+3 \times \frac{1}{80}=\frac{1}{5}+\frac{3}{80}=\frac{16+3}{80}=\frac{19}{80}\)

∴ The required rational numbers are \(\frac{17}{80}, \frac{9}{40} \text { and } \frac{19}{80}\)

 

Example 2.

Insert 5 rational numbers between \(\frac{3}{5}\) and \(\frac{4}{5}\).

Solution:

We know that 5 rational numbers between a and b are given by a + d, a + 2d, a + 3d,

a + 4d, and a + 5d, where d = \(\frac{b-a}{5+1}=\frac{b-a}{6}\)

Here a = \(\frac{3}{5}\) and b = \(\frac{4}{5}\),

∴ d = \(\frac{\frac{4}{5}-\frac{3}{5}}{6}=\frac{\frac{4-3}{5}}{6}=\frac{\frac{1}{5}}{6}=\frac{1}{30}\)

∴ a+d = \(\frac{3}{5}+\frac{1}{30}=\frac{18+1}{30}=\frac{19}{30}\)

a+2d = \(\frac{3}{5}+2 \times \frac{1}{30}=\frac{3}{5}+\frac{1}{15}=\frac{9+1}{15}=\frac{10}{15}=\frac{2}{3}[latex]

a+3d = [latex]a+3 d=\frac{3}{5}+3 \times \frac{1}{30}=\frac{3}{5}+\frac{1}{10}=\frac{6+1}{10}=\frac{7}{10}\);

a+4d = \(\frac{3}{5}+4 \times \frac{1}{30}=\frac{3}{5}+\frac{2}{15}=\frac{9+2}{15}=\frac{11}{15}\)

a+5d = \(=\frac{3}{5}+5 \times \frac{1}{30}=\frac{3}{5}+\frac{1}{6}=\frac{18+5}{30}=\frac{23}{30}\)

∴ The required rational numbers are \(\frac{19}{30}, \frac{2}{3}, \frac{7}{10}, \frac{11}{15} \text { and } \frac{23}{30}\)

 

Example 3.

Insert 6 rational numbers between each pair of rational numbers given below :

1. 3 and 4 

2. 1 and 2

Solution:

We know that 6 rational numbers between a and b are given by a + d, a + 2d, a + 3d,

a + 4d, a + 5d and a + 6d, where d = \(\frac{b-a}{6+1}=\frac{b-a}{7}\)

Now,

1. 3 and 4 

Here, a = 3 and b = 4,

∴ d = \(\frac{4-3}{7}=\frac{1}{7}\)

a+d = \(3+\frac{1}{7}=\frac{21+1}{7}=\frac{22}{7}\)

 

∴ The required rational numbers are \(\frac{22}{7}, \frac{23}{7}, \frac{24}{7}, \frac{25}{7}, \frac{26}{7} \text { and } \frac{27}{7}\)

 

2. 1 and 2

Solution:

Here, a = 1 and b = 2,

∴ d = \(\frac{2-1}{7}=\frac{1}{7}\)

∴ a+d = \(a+d=1+\frac{1}{7}=\frac{7+1}{7}=\frac{8}{7}\)

 

 

∴ The required rational numbers are \(\frac{8}{7}, \frac{9}{7}, \frac{10}{7}, \frac{11}{7}, \frac{12}{7} \text { and } \frac{13}{7}\)

 

Example 4.

Express the following rational numbers in decimal form and write what type of numbers the resulting decimal fractions are:

Solution:

1. 

 

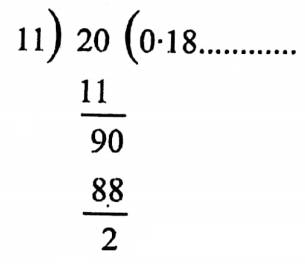
∴ 2 is the first dividend id repeated

∴ The digits 1 and 8 will repeat again and again in the long division and the division process will never end.

∴ \(\frac{2}{11}=0 \cdot 181818 \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots\)

 

2. \(4 \frac{1}{8}=\frac{33}{8}\)

Solution:

\(4 \frac{1}{8}=\frac{33}{8}\)

Now,

 

 

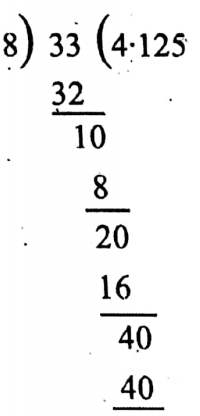
∴ \(4 \frac{1}{8}=4 \cdot 125\)

∴ The required decimal fraction is a terminating number.

 

3. 

 

 

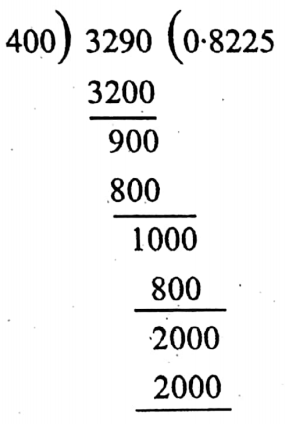
∴ \(\frac{329}{400}=0.8225\)

∴ A resulting decimal fraction is a terminating number.

 

Example 5.

Express the following decimal fractions in the form of \(\frac{p}{q}\) where p> q ∈ Z and q ≠ 0

1. \(0 \cdot \overline{6}\)

Solution:

\(0 \cdot \overline{6}\) = \(0.6666\ldots \ldots \ldots \ldots \ldots\)

Let x = \(0.6666\ldots \ldots \ldots \ldots \ldots\)

or, = 10x = \(6.6666\ldots \ldots \ldots \ldots \ldots\)

or, 10x = \(6+0.666 \ldots\ldots \ldots \ldots \)

or, 10x = 6 + x [ ∵ x = 0.6666……….. ]

or, 10x – x = 6

or, x = \(\frac{6}{9}=\frac{2}{3}\)

∴ \(0. \overline{6}=\frac{2}{3}\)

 

2. \(0.4 \overline{7}\)

Solution:

\(0.4 \overline{7}=0.4777\ldots \ldots \ldots \ldots \ldots\)

Let, x = 0.4777………

or, 10x = 4.777…………(1)

or, 100x = 47.777……………..(2)

Now (2) – (1)

100x – 10x = (47.777…………..) – (4.777……….)

90x = 43

x = \(\frac{43}{90}\)

∴ \(0.4 \overline{7}\) = \(\frac{43}{90}\)

 

3. \(0 . \overline{001}\)

Solution:

\(0 . \overline{001}\) = \(0.001001001\ldots \ldots \ldots \ldots \ldots\)

Let x = 0.00100101001………….

or, 1000x = 1.001001…………..

or, 1000x – x = 1

or 999x = 1

or, x = \(\frac{1}{999}\)

∴ \(0 . \overline{001}\) = \(\frac{1}{999}\)

 

4. 0.99999…………

Solution:

Let x = 0.999999…………….

or, 10x = 9.9999…………

or, 10x = 9 + 0.9999………

or, 10x = 9 + x [∵ 0.9999……..=x]

or, 10x – x = 9

or, 9x = 9

or, x = \(\frac{9}{9}\)

= 1

∴ 0.9999……. = 1 = \(\frac{1}{1}\ldots \ldots\).

 

Example 6.

If \(\frac{1}{7}\) = \(0 \cdot \overline{142857}\) then what will be the results of the rational fractions \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}\) and  \(\frac{6}{7}\) When without performing actual division, they are expressed as decimal fractions. Give reasons in favor of your answer.

Solution:

We have

\(\frac{2}{7}\) 

\(\frac{2}{7}\) = 2 x \(\frac{1}{7}\)

= 2 x \(0 \cdot \overline{142857}\)

= \(0 \cdot \overline{285714}\)

 

\(\frac{3}{7}\)

\(\frac{3}{7}\) = 3 x \(\frac{1}{7}\)

= 3 x \(0 \cdot \overline{142857}\)

= \(0 \cdot \overline{428571}\)

 

\(\frac{4}{7}\)

\(\frac{4}{7}\) = 4 x \(\frac{1}{7}\)

= 4 x \(0 \cdot \overline{142857}\)

= \(0 \cdot \overline{571428}\)

 

\(\frac{5}{7}\)

\(\frac{5}{7}\) = 5 x \(\frac{1}{7}\)

= 5 x \(0 \cdot \overline{142857}\)

= \(0 \cdot \overline{714285}\)

 

\(\frac{6}{7}\) 

\(\frac{6}{7}\) = 6 x \(\frac{1}{7}\)

= 6 x \(0 \cdot \overline{142857}\)

= \(0 \cdot \overline{0.857142}\)

We see from all the above non-terminating recurring numbers that the 6 digits 1, 2, 4, 5, 7, and 8 recure repeatedly in a cyclic order in the decimal expansions of the rational numbers \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}\) and  \(\frac{6}{7}\). This cyclic order is shown in the following

\(\frac{1}{7}\) starts from 1 : 142857

\(\frac{2}{7}\) starts from 2 : 285714

\(\frac{3}{7}\) starts from 4 : 428571

\(\frac{4}{7}\) starts from 5 : 571428

\(\frac{5}{7}\) starts from 7 : 714285

\(\frac{16{7}\) starts from 8 : 857142

 

 

Arithmetic Chapter 1 Real Numbers Irrational Numbers

Definition:

1. The numbers that cannot be expressed in the form \(/frac{p}{q}\).
2. where p and q are both integers and q ≠ 0, are called irrational numbers.
3. That is the number that cannot be expressed as the division of two integers (the divisor is never zero) are called irrational numbers.
4. For example √2√3. √5. √7. √10, ………….0.020020002, etc.
5. We can express √2 or √3 or….. in the following form √2 = \(=\frac{\sqrt{2}}{1}=\frac{2 \sqrt{2}}{2}=\frac{3 \sqrt{2}}{3}[latex], where p = √2 or, 2√2 or, 3√2……………… and q = 1,2,3 ……..etc.
6. In these cases, q, i.e., the denominator of the number is an integer, but p, i.e., the numerator is not an integer, for the number √2,2√2 or, 3√2……. are not integers.
7. ∴ The numbers √2 or √3 or…… cannot be expressed in the form where both p and q are integers and 90.
8. Therefore, these numbers are irrational numbers.
9. Since the number of irrational numbers is infinity, there is neither beginning nor an end to the irrational numbers.
10. Therefore, these numbers are irrational numbers.
11. Since the number of irrational numbers is infinity, there is neither beginning nor an end to the irrational numbers.

 

Decimal Expansion of Irrational Numbers:

1. Finding the square root by division process, we can express the irrational numbers in the form of a decimal fraction.
2. For example, let us express the irrational numbers

 

 

∴ √3 = 1.73205080756…………………….

Again,

 

∴ √7 = 2.645757131106……………

 

1. Thus, we can express any irrational number in the form of a decimal fraction. It is noticed that the decimal fractions thus obtained have two common criteria, namely-
   1. The decimal fraction is non-terminating, i.e., the division process never ends;
   2. the decimal fraction is non-recurring, i.e., in the resulting decimal number no digit (or digits) recure.
2. Therefore, we can say that the decimal expansion of any irrational number is non-recurring non-terminating.
3. On the other hand, if the decimal expansion of any number is non-recurring and non-terminating, then it is an irrational number.

 

1. We know that
2. √2 is a root of equation x² – 2 = 0;
3. √3 is a root of equation x² – 3 = 0;
4. √5 is a root of the equation x² – 5 = 0; etc.
5. These types of irrational numbers are called algebraic irrational numbers.
6. Therefore, the irrational numbers which are the roots of any algebraic equation are called algebraic irrational numbers.
7. And, the irrational numbers which are not the roots of any algebraic equation are called Transcendental irrational numbers.
8. For examples. π= 3.14159265358979323846264338327950……………..and e = 2.718281828………. are two transcedental irrational numbers.

 

Insertion of one or more than one irrational number in between two given rational numbers and insertion of one or more than one rational number in between two given irrational numbers:

1. Let [latex]\frac{1}{3}\) and \(\frac{1}{2}\) be two given rational numbers. We have to insert one irrational number in between them.
2. Now,
   \(\frac{1}{3}\) = 0.3333………. and \(\frac{1}{2}\) = 0.5
3. In the first number (0.3333………) the digit just next to the decimal point is 3, while in the second, it is 5
4. So, the digit just next to the decimal point of the required irrational number will be 4, which is between 3 and 5.
5. ∴ The required irrational number = 0.40400400040000.
6. Similarly, one irrational number in between \(\frac{1}{3}\) and \(\frac{1}{2}\) is 0.450450045000…………, because,
7. \(\frac{1}{3}\) = 0.333…….. and \(\frac{1}{2}\) = 0.666…………….

2.  Insertion of one or more than one rational number in between two given irrational numbers:

1.  Let √2 and √3 be two given irrational numbers.
2. We have to insert one rational number between √2 and √3.
3. Now, √21.41421356237………….. and √3=1.73205080756………..
4. We see that the integral parts of both numbers are equal (1).
5. Also, the digit just next to the decimal point is 4 in the first number and 7 in the second number. 
6. Again, the digits 5 and 6 are between 4 and 7.
7. ∴ The required rational number = 1.5.

Plotting of Irrational numbers on the number line :

1. You have learned earlier that natural numbers, whole numbers, Integers, and rational numbers can be easily plotted on the number line.
2. You have already practiced the various process and methods of plotting these numbers on the number line.
3. So, our present task is how to plot irrational numbers on the number line. In order to do so, we shall use the geometric process and shall take the help of the well-known Pythagorus’theorem.
4. But, what is Pythagoras’ theorem?

Pythagoras theorem :

Statement:

The area of the square drawn over the hypotenuse of any right-angled triangle is equal to the sum of the areas of the squares drawn over the two other sides of the triangle.

That is, let ABC be a right-angled triangle, whose B = 90°.

.. AC is the hypotenuse.

By Pythagoras’ theorem, AC2 = AB2+ BC2.

Geometrically, ACPQ = ABEF + BCRS.

Thus, according to this theorem of Pythagoras, we can write,

√2=√(1+1)=√((1)2+(1)2)

√3 = √(2+1) = √((√2)2 + (1)2)

√5 = √(4+1) = √((2)2 +(1)2)

√7=√(4+3) = √((2)2 +(√3)2)…………….etc,

 

 

Now, using these formulas we can plot any irrational number in the number line geometrically.

We also represent the irrational numbers on the number line by the process of successive magnification, expressing the numbers in decimal form.

 

Thus, we can represent the irrational numbers on the number line by two methods:

1. Geometric Method and

2. Method of successive magnification.

 

1. Geometric Method:

1. The WORKING RULE of this method is
2. STEP-1: Write the given irrational number according to Pythagoras’ theorem.
3.  STEP-2: Choose the hypotenuse and two other sides of the right-angled triangle from the formula thus obtained in STEP-1.
4. STEP-3: Cut the distance equal to the length of any of the two other sides of the right-angled triangle from the point O (which denotes O) to either the right-hand side (when the given irrational number is positive) or to the left-hand side (when the given irrational number is negative).
5. STEP-4: Draw a perpendicular straight line at the last point of this distance (obtained in STEP-3).
6.  STEP-5: Join O to the top of the perpendicular by a scale. Then, it will be the hypotenuse. 
7. STEP-6: Taking O as the center, draw an arc, the radius of which is equal to the hypotenuse obtained in STEP-5.
8. Then the point of intersection of the arc to the number line will represent the required irrational number.

 

Example 1. Locate √2 on the number line.

Solution: From the Pythagoras theorem we get, (√2)² = (1)² +(1)²

∴ hypotenuse = √2 units and the length of the two other sides of the right-angled triangle are 1 unit each.

 

 

Now,

1. Cut OA = 1 unit from the right-hand side of the origin O( √2 is positive).

2. Draw AB (= 1 unit) perpendicular to the number line at A.

3. Join O to B by a scale.

4. Taking O as the center and OB as the radius, draw an arc on the right-hand side of O.

5. Let the arc intersects the number line at C.

Then, point C will represent the required irrational number √2 on the number line, i.e. OC = √2 units.

 

Example 2. Locate √3 on the number line.

Solution:

From Pythagoras’ theorem, we get. (√3)² – (√2)² + (1)².

∴ hypotenuse√3 units and the length of one side of the right-angled triangle = √2 units and the length of the other side = 1 unit.

Also, (√2)2 = (1)2+(1)2 So, at first, we have to locate √2 on the number and then √3.

 

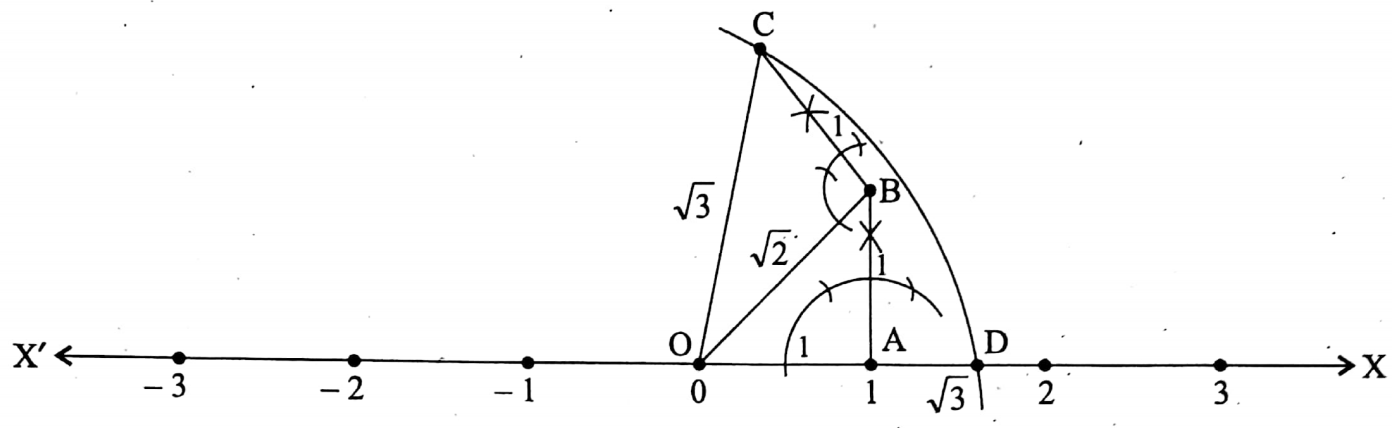
Now,

1. Cut OA = 1 unit 

2. Draw AB perpendicular to the number line such that AB = 1 unit. 

3. Join O to B by a scale. OB = √2 units.

4. Draw BC 1 OB, such that BC= 1 unit.

(√2)² +(1)² = √2+1

= √3 units.

5.  Join O to C by a scale. Then, OC = √(OB² + BC²)

= √((2)² + (1)²)

= √(2+1)

= √3 units.

6. Draw an arc on the right-hand side of O, by taking O as the center and OC as the radius.

Let the area intersects the number line in D.

Then, D will represent the required irrational number √3 on the number line, i.e., OD = √3 units.

From the above discussion you can, now easily represent the irrational numbers √5, √6, √7…etc., on the number line with the help of Pythagoras’ theorem geometrically.

 

General Rule:

We can now represent any irrational number of type √x, x>0 on the number line geometrically as follows:

 

 

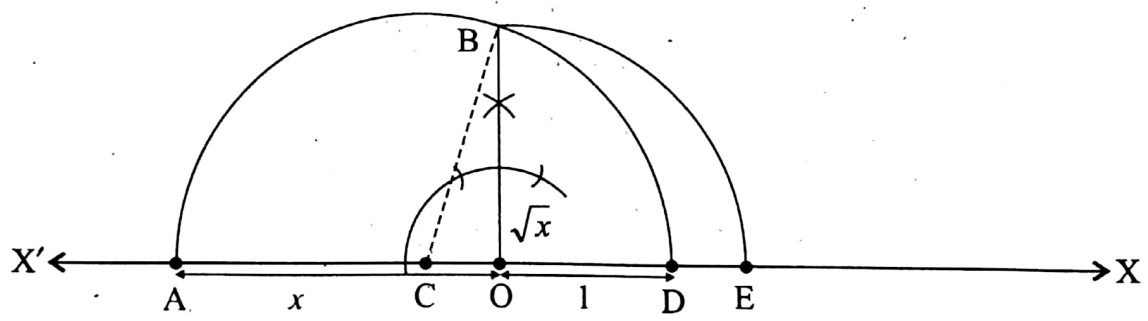
At First,

1. Draw \(\overline{\mathrm{OA}}\) = x on the number line (O denotes the number 0).

2. Take \(\overline{\mathrm{OD}}\) = 1 unit;

3. Find C, the mid-point of AD\(\overline{\mathrm{AD}}\);

4. Draw a semi-circle ABD with a center at C;

5. Draw \(\overline{\mathrm{OB}}\) perpendicular to the number line at O.

Let \(\overline{\mathrm{OB}}\) intersect the semi-circle in B.

Then, \(\overline{\mathrm{OB}}\) = √x;

6. Now, draw an arc with a center at O and a radius equal to \(\overline{\mathrm{OB}}\).

Let the arc intersects the number line in E.

Then E will represent the required irrational number √x, x>0, on the number line, i.e. OE = √x

 

Proof: AD \(\overline{\mathrm{AD}}\) = \(\overline{\mathrm{OA}}\) + \(\overline{\mathrm{OD}}\) = x + 1; C is the mid-point of \(\overline{\mathrm{AD}}\).

 

∴ \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{CD}}\) = \(\frac{x+1}{2}\)

 

Now, \(\overline{\mathrm{CO}}\) = \(\overline{\mathrm{CD}}\) – \(\overline{\mathrm{oD}}\) = \(\frac{x+1}{2}\) – 1

= \(\frac{x+1-2}{2}=\frac{x-1}{2}\)

 

Again, \(\overline{\mathrm{OB}}\) ⊥ \(\overline{\mathrm{AD}}\) [by construction]

 

∴ from the right-angled triangle BOC, by Pythagoras’ theorem, we get,

 

OB² = BC² – CO² = \(\left(\frac{x+1}{2}\right)^2\) – \(\left(\frac{x-1}{2}\right)^2\)

 

∵ \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{CD}}\)the radius of the same circle

= x.1 [∵ ab= \(\left(\frac{a+b}{2}\right)^2\) – \(\left(\frac{a-b}{2}\right)^2\) = x

∴ OB² = x

or, OB = √x.

By construction OB = OE (radius of the same circle)

OE = OB = √x

 or, OE = √x

Thus, by this general rule, we can represent any irrational number of type √x, x>0 like √3.5, √4.7, √5.3. etc geometrically.

 

Method of successive magnification:

1. The method in which any rational or irrational (Real) number can be represented on the number line by dividing the distance between two consecutive numbers into some equal parts with the help of a magnifying glass, is called the method of successive magnification.
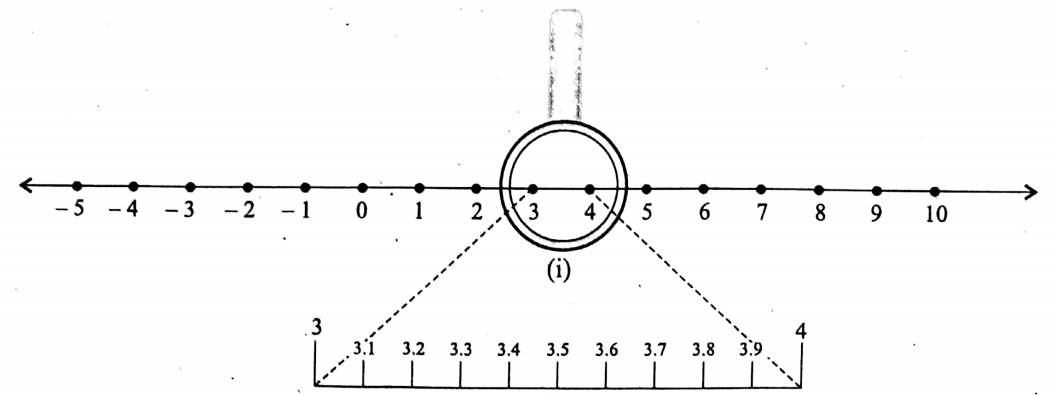
2. Let, you have to represent √11 on the number line, then you can do it by this method of successive magnification in the following manner:
3. Since√11 = 3.31662479035
4. is a non-terminating non-recurring number, the method mentioned above will be an endless one.
5. So, we usually represent an approximate value of the given number, i.e….. Of √11 by computing two or three digits after the decimal point.
6. It is regardless that he who can successively continue this process as many times so will get a more and more accurate approximation value of √11
7. Now, let you want to represent 3-316 on the number line. It is clear that the number 3.316 is a number between 3 and 4.
8. So, you should look closely at the portion of the number line between 3 and 4 and divide this portion into 10 equal parts. Locate the numbers as shown in the following.
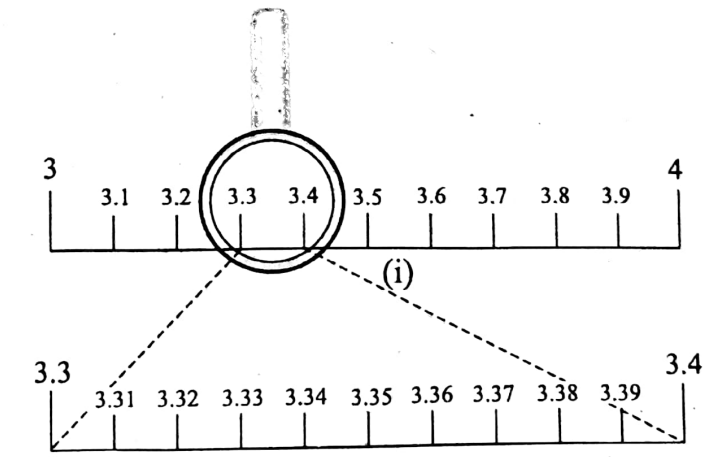
9. Now, the number 3.316 is a number between 3.3 and 3.4.
10. So, look closely at the portion between 3.3 and 3.4. of the (2) of the above.
11. Magnifying this portion with a magnifying glass, divide it into 10 equal parts.
12. Then locate the numbers as shown in the following figure.
13. Again, the number 3.316 is a number between 3.31 and 3.32.
14. Therefore, according to the same previous method, divide this portion of (1) of the above into 10 equal parts and locate the numbers as shown in the following:
15. So, the number in the 6th position of the last
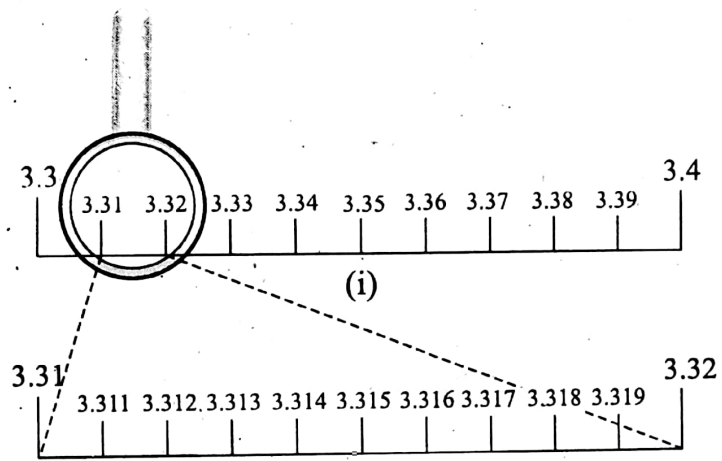
16. no (2) of the above will represent the required number 3.316 on the number line.
17. Thus, by using the magnifying glass three consecutive times, you have become successful to represent the number 3.316 on the number line.
18. If you use the magnifying glass in this manner further for 1 time, 2 times, 3 times, and so on, you will be able to represent the numbers 3.3166, 3.1662, 3.316624,……. respectively on the number line.
19. Therefore, by this long method of successive magnification, we can represent any rational or irrational numbers on the number line.
    

Characteristics and properties of Irrational numbers:

1. Irrational numbers are dense on the number line, i.e., there exist infinitely many irrational numbers in between any two irrational numbers on the number line.
2. The sum of a rational and an irrational number is an irrational number.
3. The difference between a rational and an irrational number is an irrational number.
4. The product of a non-zero rational number to an irrational number is an irrational number.
5. The division of a non-zero rational and an irrational number is an irrational number.
6. The sum, difference, product, and division of two irrational numbers may or may not be irrational numbers.
7. If x, and y be two irrational numbers, then
   1. x + y = y + x, i.e., the irrational numbers satisfy the commutative law for addition.
   2. xy= yx, i.e., the irrational numbers satisfy the commutative law for multiplication.
8. The irrational numbers obey the associative law for both addition and multiplication, i.e., if x, y, be any three irrational numbers, then
   1. x + (y + z) = (x + y) + (Associative law for addition) and
   2. x (y z) = (xy) z (Associative law for multiplication).
9. The irrational numbers obey the distributive laws, i.e., if x, y, and z be any three irrational numbers, then
   1. x (y + z) = xy+xz (Left distributive law) and
   2. (x + y) zxz+yz (Right distributive law)
10. The irrational numbers can easily be represented on the number line.

 

Arithmetic Chapter 1 Real Numbers Select The Correct Answer (MCQ)

1. If √3 = 1-732 and √27 = 5.196 then (√27-√3)² =

1. (3-464)
2. (3-464………)
3. 24
4. 12

Solution:

= (√27-√3)2

=(√3×3×3-√3)2

=(3√3-√3)2

= (2√3)2

= 12

∴ The correct answer is 4. 12

2. If n ∈ N and 10<n< 12 then, \(\frac{1}{\sqrt{n}}\)

1. √11
2. 3-317
3. \(\frac{\sqrt{11}}{11}\)
4. 3.317

Solution: n ∈ N and 10 < n < 12

So, n = 11 

∴ \(\frac{1}{\sqrt{n}}=\frac{1}{\sqrt{11}}=\frac{1 \times \sqrt{11}}{\sqrt{11} \times \sqrt{11}}=\frac{\sqrt{11}}{11}\)

∴ The correct answer is 3. \(\frac{\sqrt{11}}{11}\).

 

3. If a be the least prime number and xⁿ – aⁿ = 0 then, \(\frac{\sqrt{6}}{\sqrt{x}}\)

1. √2
2. 3
3. 1·414
4. 1·732

Solution:

xⁿ – a^{n = 0}

xⁿ = aⁿ

x = a

As a be the least prime number. So the value of a is 2.

∴ \(\frac{\sqrt{6}}{\sqrt{x}}=\frac{\sqrt{6}}{\sqrt{2}}=\frac{\sqrt{2} \times \sqrt{3}}{\sqrt{2}}=\sqrt{3}=1.732 \ldots \ldots\)

∴ The correct answer is 4. 1·732.

 

4. \(\sqrt{6+\sqrt{6+\sqrt{6+\cdots \cdots \propto}}}\)

1. A negative integer
2. A rational number
3. An irrational number
4. None of these

Solution:

Let \(\sqrt{6+\sqrt{6+\sqrt{6+\cdots \cdots \propto}}}\)

\(x^2=6+\sqrt{6+\sqrt{6+\cdots \cdots \infty}}\)

x² = 6 = x

x² – x – 6 = 0

(x – 3)(x + 2) = 0

either x – 3 = 0 or x = 2

x + 2 = 0

x = -2

∴ The correct answer is 2. A rational number

 

Arithmetic Chapter 1 Real Numbers Short Answer Type Questions

Example 1. What do you mean by irrational numbers? Give 4 examples of irrational numbers.

Solution: The numbers which cannot be represented as the division (divisor is not zero) of two integers, are called irrational numbers.

Mathematically, if a number s cannot be represented in the form \(\frac{p}{q}\) where p and q are both integers and q ≠ 0, then s is c.alled an irrational number.

If any irrational number is represented in the form of a decimal fraction, it will be an

1. non-terminating and

2. Non-recurring number.

On the other hand, the numbers, the decimal expansion of which are non-terminating and non-recurring are called irrational numbers.

 

Example 2. Give 4 examples of irrational numbers.

Solution: 4 examples of irrational numbers are √2, √3, √5, and 0.10110111011110

 

Example 3. Write 4 numbers, the decimal expansion of which are non-terminating and nonrecurring.

Solution: We know that the decimal expansion of any irrational number is non-terminating and non-recurring.

∴ the required 4 numbers are √2, √3, √5, and √6.

 

Example 4. Are the square roots of all positive integers irrational? If not, then give an example of such a positive integer, the square root of which is a rational number.

Solution: No, the square roots of all the positive integers are not irrational.

For example, 4. Because √4 = 2. which is a rational number.

 

Arithmetic Chapter 1 Real Numbers Long Answer Type Questions

Example 1. Find out which one of the following numbers is rational and which one is the irrational number :

1. √23

Solution:

∴ 4.7958315………………. is a non-terminating and non-recurring number,

∴ √23 is an irrational number.

2. √225

Solution:

 

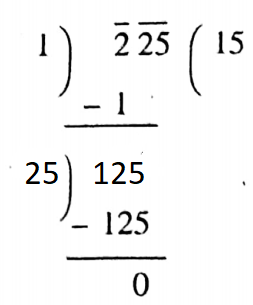
∴ √22525, which is a rational number.

∴ √225 is a rational number

 

3. 0.3796.

Solution:

0.3796 is a terminating number.

∴ 0.3796 is a rational number.

 

4. 7.478478………

Solution:

The number 7.478478… is non-terminating and recurring…

∴ 7.478478….. is a rational number.

 

5. 1.101001000100001

Solution:

The number 1.101001000100001…… is non-terminating and non-recurring.

∴ The number is irrational.

 

6. √50

Solution:

 

√50 = 7.0710678……… which is a non-terminating and non-recurring number.

.. √50 is irrational.

 

Aliter:

√50 = √(25×2) = √25 × √2 = 5√2

We know that √2 is an irrational number,

.. 5√2 is also an irrational number, [:: 5 € N]

√50 is an irrational number.

 

7. √42

Solution:

 

 

 

√42 = 6.48074069…………., which is a non-terminating and nonrecurring number.

∴ √42 is an irrational number.

 

8. √29

Solution:

 

 

√29 = 5.385164807……… which is a non-terminating and non-recurring number.

√29  is an irrational number.

 

9. -√81

Solution:

 -√81=-√(9)²

= -9

= \(-\frac{9}{1}\)

.. -√81 is a rational number.

 

10. -1000

Solution:

-√10000 = -√100x 10

= – √100 × √10

= -10x √10

Now,

 

 

 

√10 = 3.16227766….

-10√10 = -10 x 3.16227766..

=-31.6227766-

-√10000 =  – 31.6227766…..……, which is a non-terminating and non-recurring number.

-√1000 is an irrational number.

 

Example 2. Determine whether the following given numbers are rationals or irrational:

1. √47

Solution:

√47 = 6.8556546004…………..(find the square root by long division method).

Now, the number 6.8556546004…. is non-terminating and non-recurring… √47 is an irrational number.

 

2. √625

Solution:

 

.

 

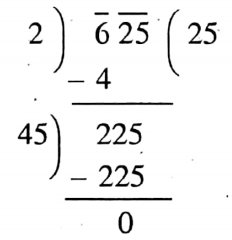√625 = 25, which is a rational number.

∴ √625 is a rational number.

 

3. 6.5757…

Solution:

6.5757…… = 6.57, Which is a non-terminating and recurring number. 

∴ 6.5757 is a rational number.

 

4. 2-√5

Solution:

2 of the number (2-√5) is rational, whereas √5 of the same number (2-√5) is irrational. 

We know that the difference between a rational and an irrational number is always irrational.

∴ (2-√5) is an irrational number.

 

5. (3+√23) -√23.

Solution:

(3+ √23) – √23=3+ √23-√23=3 which is a rational number,

∴ The given number is rational.

 

6. \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)

Solution:

\(\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2}{7}\),

where both 2 and 7 are integers and 7 ≠ 0,

∴ The given number is rational.

 

7. \(\frac{1}{\sqrt{2}}\)

Solution:

\(\frac{1}{\sqrt{2}}\);

Here, 1 is an integer, but √2 is not an integer.

So that the number \(\frac{1}{\sqrt{2}}\)  cannot be expressed in the form \(\frac{p}{q}\)

where p and q are both integers and q ≠ 0.

∴ \(\frac{1}{\sqrt{2}}\) is an irrational number.

 

8. 2π

Solution:

2 of the number 2 is rational, but л is irrational.

Now, the product of a rational number to an irrational number is always irrational.

∴ 2π is an irrational number.

 

Example 3. Insert 3 irrational numbers in between \(\frac{5}{7}\) and \(\frac{9}{11}\)

Solution:

\(\frac{5}{7}=0 \cdot \overline{714285}\) (Do the division yourself) and \(\frac{9}{11}=0 \cdot \overline{81}\) (Do the division yourself)

Now, the number formed by the next two digits of the decimal point of the first number is 71 and that of the second number is 81.

So, constructing any three irrational numbers by taking any three values between 71 and 81, we get 72072007200072000072 . . . . ., 73073007300073000073. 74074007400074000074…

Hence, the required three irrational numbers are 0.72072007200072000072…………… 0.73073007300073000073……… and 0.74074007400074000074………….., etc.

 

Example 4. Π = \(\frac{c}{d}\) is the proportion of the circumference (let c) of a circle to the diameter (let d) of it, i.e. =, where c and d are both terminating then how is an irrational number? Explain.

Solution:

When we measure the circumference and diameter of a circle with the help of a scale or by any other means, the value of these measurements is, in practical, approximate rational numbers.

Again, any smallest change in the measurement of the circumference of the circle obviously causes a change in the measurement of its diameter.

So, it is very difficult to determine that actually which one of the measurements of c and d is irrational.

We generally write Π = \(\frac{22}{7}\), But \(\frac{22}{7}\) is an approximate value of π, not accurate value. That is why though Π = \(\frac{c}{d}\), л is an irrational number.

 

Example 5.

1. Both 0.2101 and 0.2 are rational numbers.

Solution: 

Both 0.2101 and 0.2 are rational numbers.

Now, the number formed by the three digits just next to the decimal point of the first number is 210 and that of the second number is 222.

So, we can take 215 and 220 in between 210 and 222 for our consideration. (Any other two numbers can be chosen).

∴ The required two rational numbers are 0.215 and 0.220 or 0.22.

 

2. 0.232332333233332…… and 0.212112111211112….. are both irrational numbers.

Solution:

0.232332333233332…… and 0.212112111211112….. are both irrational numbers.

Now, the number formed by the three digits just next to the decimal point of the second number is 212 and that of the first number is 232.

So, we can choose any 2 numbers 220 and 230 in between 212 and 232.

∴ The required rational numbers are 0.220 or 0.22 and 0.230 or 0.23.

 

Example 6. 

1. 

1. By taking any two irrational numbers, prove that their sum is a rational number.

Solution:

Let the irrational numbers be (2+ √3) and (2-√3).

Then 2+√3+2-√3-4,

which is a rational number.

∴ The sum of two irrational numbers is a rational number. (Proved)

 

2. By taking any two irrational numbers, prove that their difference is a rational number.

Solution:

 Let the irrational numbers be (√3+1) and. (√3-1)

Now, (√3+1)-(3-1)

=√3+1-√3+1 

1+1=2, which is a rational number.

 

2. Insert in between \(\frac{1}{7}\) and \(\frac{2}{7}\)

1. A rational number.

Solution: 

\(\frac{1}{7}\) = \(0 . \overline{142857}\) and \(\frac{2}{7}\) = \(0 . \overline{285714}\) (Do the two divisions yourself).

Now, the number formed by the two digits just next to the decimal point of the first number is 14 and that of the second number is 28.

Let us choose any number 15 between 14 and 28.

∴ The required rational number is 0.15.

Alter :

The required rational number = \(\frac{\frac{1}{7}+\frac{2}{7}}{2}=\frac{3}{14}\)

 

2. An irrational number.

Solution:

An irrational number in between \(\frac{1}{7}\) and \(\frac{2}{7}\) is 0.1501500150001…………………or 0.15155155515551……………

 

Example 7. Represent the number √(9.3) on the number line.

 

 

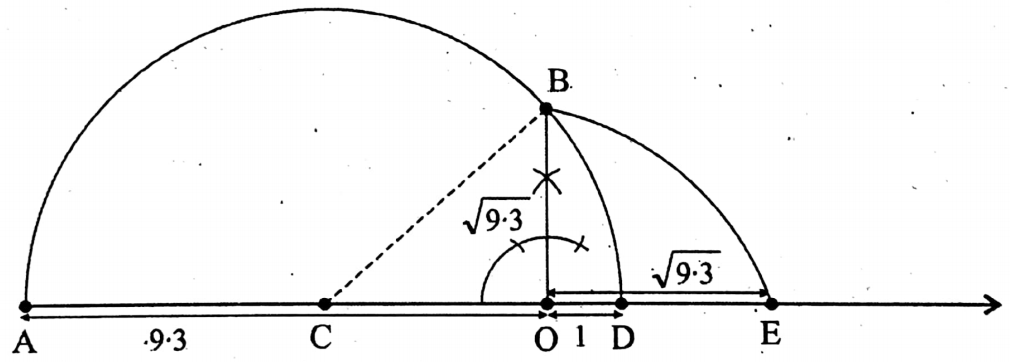
Solution:

At first,

1. Let us draw a straight line AO = 9.3 units such that O denotes the point 0 on the number line.

2. Let us then draw OD = 1 unit.

3. Let us determine the mid-point C of AD.

4. Let us draw a semi-circle with center C and radius CA or CD.

5. Let us draw OB 1 AD at O. Let OB intersects the semi-circle in B. So, OB = √(9.3).

6. Let us draw an arc with a center at O and a radius equal to OB.

Let this arc intersects the number line in E.

Therefore, point E will represent the number √(9.3) on the number line.

Proof: CO = CD-OD= \({10.3}{2}\) – 1

= 4.15     [ CD = \(\frac{A D}{2}=\frac{A O+O D}{2}=\frac{9 \cdot 3+1}{2}=\frac{10 \cdot 3}{2}\)

Now, from the right-angled triangle BOC, we get,

OB2 = BC2 – CO2 

= (5-15)2 – (4-15)2             [·.· BC=CD= \(\frac{10 \cdot 3}{2}\) = 5.15]

=26.5225-17-2225=9.3

OB2 9.3 or, OB = √(9.3),

∴ OE = OB = √(9.3).

 

Arithmetic Chapter 1 Real Numbers

In the previous sections, you have studied sufficiently- 

1. Natural numbers

2. Whole numbers

3. Integers

4. Rational numbers and

 5. Irrational numbers. 

In this section, we shall try to know about real numbers.

What is the real number?

All rational and Irrational numbers are together called real numbers.

Again, there are natural numbers, whole numbers, and integers (both positive and negative) in rational numbers.

So, we can say that natural numbers, whole numbers, integers, rational numbers, and irrational numbers are altogether called real numbers.

Any real number can be represented in any form of number by using the 10 digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 one time or more than one time, which have real values.

Since any natural, whole, integer, rational, and irrational number can be represented on the number line, and since the real numbers consist of them all the real numbers can be represented on the number line.

That is any real number can be represented on the number line by a certain point uniquely.

On the other hand, each and every point on the number line represents one and only one real number.

We can also say that any real number is either rational or irrational.

Therefore, the numbers, formed by the 10 digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 in any form, using the digits one time or more, than one time, which have real values, which can be represented on the number line and which are either rational or irrational are called real numbers.

 

For examples,

-7, 6, 5, 2, 0, 1, 2, 3,………, \(\frac{1}{2}\),\(\frac{1}{3}\),..…………,\(\frac{7}{9}\),\(\frac{10}{12}\),…………,√2, √3, √5,…..π, e………….etc, are all real numbers. 

The number of real numbers is infinity. 

The real numbers are usually denoted by R or IR.

Now, it, obviously, gives rise to the question of that is there any existence of non-real numbers.

 In reply, we must say Yes. For example, √3, √2, √1,………etc.

These numbers are called non-real or imaginary or complex numbers.

The study of these numbers is not our task in the present section.

You should study them later on in your higher mathematics classes.

 

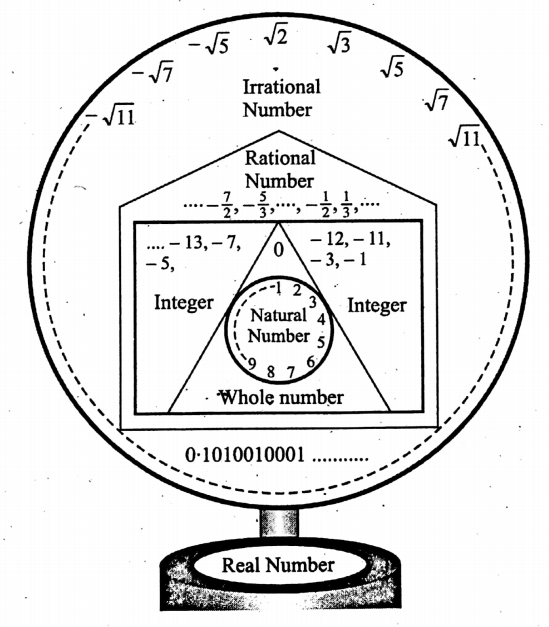
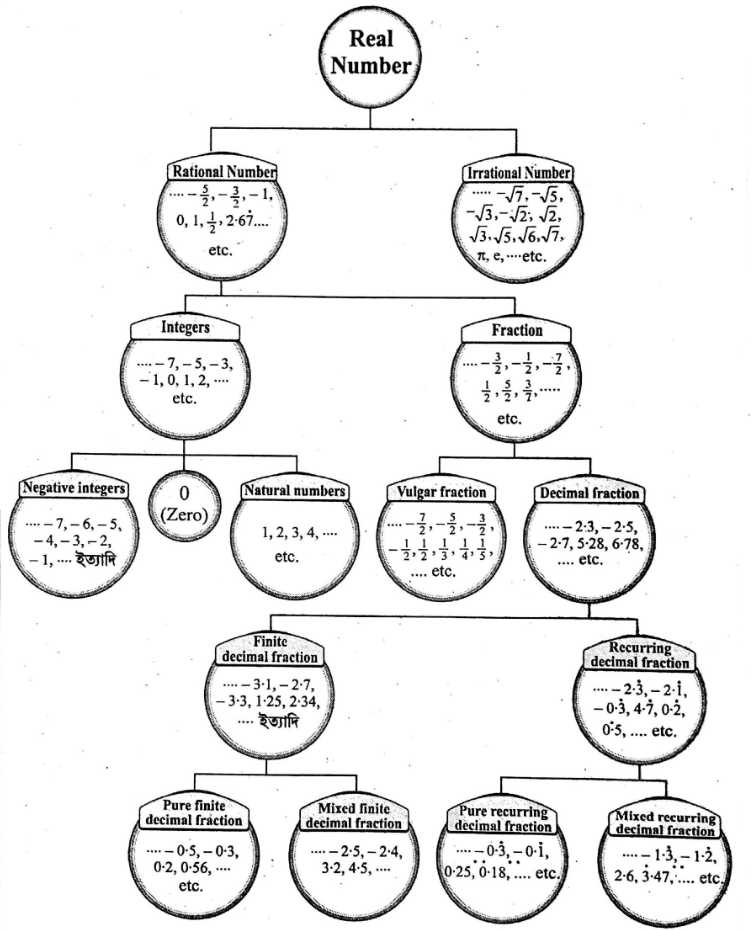
Classification of real numbers :

We can classify the real numbers into two large sections

1. Rational  Number

1. Natural numbers: 1, 2, 3, 4, ….. (to infinity)
2. Whole numbers: 0, 1, 2, 3, 4,…. (to infinity)
3. Integers:
   1. Negative integers:……..-3, -2, -1.
   2. Zero: 0
   3. Positive integers: 1, 2, 3, 4, ….…(to infinity)

Irrational numbers :

1. Negative irrationals:……– √3, −√2,\(-\frac{1}{√2}\),\(-\frac{1}{√2}\),……..
2. Positive irrationals:…….√2,……..√3,…………,√5,…………

 

Global diagram of Real numbers:

 

 

Properties of real numbers:

You have already known that real numbers include natural numbers, whole numbers, integers, rationals, and irrationals.

So, the properties that are satisfied by those numbers, are also the proporties of real numbers.

It, thus needs not to repeat the properties here.

 

 

In stead, some useful formulas of real numbers are given below.

These are called the identities of positive real numbers. If a and b be two positive real numbers, then

A most important characteristic of real numbers is that real numbers are dense on the number line, i.e., there exists infinitely many numbers in between any two real numbers at a distance of considerably shortest (what shortest the distance may be).

Another important characteristic of real numbers is that each and every real numbers can be represented by a unique point on the number line.

On the other hand a point on the number line denotes one and only one real number.

Operations on real numbers :

According to the properties of real numbers:

1. The sum, difference, product and division of two real numbers is also a real number.

2. Real numbers satisfy the associative law, commutative law, distributive law, cancellation law, etc.

3. In you earlier classes, you have studied how to operate the mathematical operations (i.e., sum, difference, product and division) on natural numbers, whole numbers, integers, i.e., on rational numbers.

4. So, in this section, we shall discuss only the operations on irrational numbers.

5. Any irrational number can be represented in the form (a+b), where a and b are both positive integers and b is not a perfect square.

6. Here, a is called the rational part and √b is called the irrational part of the number.

7. Hence, (a+√b) is the sum of a rational and an irrational number, which is definitely an irrational number.

8. The conjugate irrational number of the irrational number (a+√b) is (a-√b) and vice versa, i.e. the two irrational numbers (a+ √b) and (a-√b) are conjugate to each other.

 The properties of conjugate irrational numbers are:

1. The sum of two conjugate irrational numbers is a rational number, such as 2+ √3+2-√3=4.

2. The product of two conjugate irrational numbers is a rational number.

Such as,

(2+3)(2-3)-(2)2-(√3)-4-3-1.

3. The difference of two conjugate irrational numbers is an irrational number. Such as, (2+√3)-(2-√3)-2+√3-2+√3=2√3.

4. The division of two conjugate irrational numbers an irrational number.

Such as

 

In this division, the irrational number in the denominator have been eliminated multiplying both numerator and denominator by another irrational number, which is conjugate to the denominator. It is called the rationalisation of the denominator.

Again, for any irrational number (a+√b).

1. If a+ √b=0, then a = b = 0.

2. If a = 0, then the irrational number (a + b) becomes a purely irrational number and if b = 0, then the irrational number (a+b) becomes a rational number.

If none of a and b is zero, the irrational number (a+√b) is called a mixed irrational number. 

3. If a+√b=c+ √d, where b and d are not perfect squares, then a = c and b = d.

Rationalisation of the denominator :

To rationalise the denominator of any irrational number, we usually follow the rules given below: 

1. If the denominator of the irrational number be a purely irrational number, then we product both the numerator and denominator of the number by that very purely irrational number.

For example,

 

 

2. If the denominator be a mixed irrational number, we product both the numerator and denominator of the number by the conjugate irrational number of the denominator.

For example,

 

 

In the following examples your conception of how mathematical operations are performed on real numbers, especially on irrational numbers, will be more and more clear.

 

Arithmetic Chapter 1 Real Numbers Select The Correct Answer(MCQ)

1. Which one of the following is false? 

1. Every rational number is a real number
2. Every integer is a real number
3. Every irrational number is a real number
4. √2 is a rational number

Solution:

1. – 5,\(\frac{3}{4}\), \(\frac{5}{7}\) etc. all rational number is a real number..

2. -3, -2, 1, 5, 7, etc. All integer is a real numbers.

3. √3; √5 etc. are real numbers.

4. √2 = 1.414………….is irrational number.

∴ The correct answer is 4. √2 is a rational number

 

2. If a and b be two non-zero real numbers, then \((a b)^{-1}\)

1. (-a)(-b)
2. \(a^{-1} b^{-1} \text { or } b^{-1} a^{-1}\)
3. (-a) + (-b)
4. a.b

Solution:

\((a b)^{-1}\) = \(a^{-1} b^{-1}[/atex]

∴ The correct answer is 2. [latex]a^{-1} b^{-1} \text { or } b^{-1} a^{-1}\)

 

3. If * denotes the mathematical operation ‘addition’ and b is not a perfect square, a*√b will lie in

1. N
2. Z
3. Q
4. R

Solution:

The sum, difference, product, and division of two real numbers is also real number. 

So a + √b will be the real number (R).

∴ The correct answer is 4. R

 

4 Which one of the following is true?

1. √6+√3 =√7+ √2
2. √6+ √3>√7+ √2
3. √6+√3<√7.+√2
4. None of these

Solution:

(√6+ √3)² = (√6)² + (√3)² +2√6.√3

= 6+3+2√18

= 9+2√18 (√7+√2)²

= (√7)² + (√2)² +2.√7.√2

=7+2+2√14

=9+2√14

18 > 14

or, √18 > √14

or, 2√18 >2√14

or, 9+2√189+2√14

or, (√6+ √3)² > (√7 + √2)²

or, √6+ √3> √7+ √2

∴ The correct answer is 3. √6+√3<√7.+√2

 

Arithmetic Chapter 1 Real Numbers Short answer type Questions

Examples 1. Do the sum:

1. √12+ √108

Solution:

√12+ √108

= √4×3+√36×3

=√4× √3+√36×√3 

=2√3+6√3 

=8√3

√12+ √108 =8√3

 

2. √8+ √50

Solution:

√8+ √50

= √4×2+√25×2

= √4× √2+ √25× √2

=2√2+5√2

=7√2

√8+ √50 =7√2

 

Example 2. Subtract:

1. √175-√112

Solution :

√175-√112

=√25×7-√16×7

=√25×√7-√16×√7

=5√7-4√7

= √7

√175-√112 = √7

 

2. √147-√27.

Solution:

√147-√27

= √49×

= 3-√9×3

= √49× √3-√9× √3

=7√3-3√3

= 4√3

√147-√27 = 4√3

 

Example 3. Do the product: 

1 √7×3√7

Solution :

√7×3√7 

=3x(√7)²

= 3 x 7

= 21

√7×3√7  = 21

 

2. √18 × √72

Solution:

√18 × √72

= √(9×2) × √(36×2)

= √9 × √2 × √36 × √2

= 3√2 × 6√2

=3×6×(√2)²

=18×2

=36

√18 × √72 =36

 

3. 2√5× √32×3√2

Solution:

2√5 x √32 x 3√2

=2√5 × √16 x √2 x 3√2

=2√5 x √16 x√2 × 3√2

=2√5 × 4√2 × 3√2

=2 x 4 × 3 × √5 x √2 x √2

=24 × √5 x (√2)²

=24 × √(5×2)

=48√5

2√5 x √32 x 3√2 =48√5

 

4. (2√3+3√5) (3√2+5√3).

Solution:

(2√3+3√5) (3√2+5√3)

=2√3 × 3√2 + 2√3 x 5√3 + 3√5 × 3√2 + 3√5 x 5√3

=6 x √(3×2) + 10 x (√3)2 + 9 x √(5×2) + 15 × √(5×3)

=6√6+10×3+9√10+15√15

=6√6+30+9√10+15√15

=30+6√6+9√10+15√15

(2√3+3√5) (3√2+5√3) =30+6√6+9√10+15√15

 

Example 4. Do the division:

1. √243+ √108

Solution:

√243+ √108

 

 

2. (2+√2)+(√2-1).

Solution:

 

(2+√2)+(√2-1)

 

 

Example 5. Rationalize the denominator of

1. \(\frac{1}{\sqrt{7}}\)

Solution: 

\(\frac{1}{\sqrt{7}}\)

 

 

2. \(\frac{1}{\sqrt{5}+\sqrt{3}}\)

Solution:

\(\frac{1}{\sqrt{5}+\sqrt{3}}\)

 

 

3. \(\frac{1}{\sqrt{7}-1}\)

Solution:

\(\frac{1}{\sqrt{7}-1}\)

 

 

4. \(\frac{1}{\sqrt{7}-\sqrt{6}}\)

Solution:

 

 

 

Arithmetic Chapter 1 Real Numbers Long Answer Type Questions

Example 1. Simplify

1. 3√48 – 4√75 + 5√192

Solution:

 

 

2. (3+√3) (2+√2)

Solution:

(3+√3) (2+√2)

= 6 + 3√2 + 2√3 + √(3 x 2)

= 6 + 3√2 + 2√3 + √6

(3+√3) (2+√2) = 6 + 3√2 + 2√3 + √6

 

3. (√5 + √2)²

Solution:

(√5 + √2)²

= (√5 )² + 2 x √5 x √2 + (√2)²

= 5 + 2√10 + 2

= 7 + 2√10

(√5 + √2)² = 7 + 2√10

 

4. (√5 – √2)(√5 + √2)

Solution:

(√5 – √2)(√5 + √2)

= (√5)² – (√2)²

= 5 – 2

= 3

(√5 – √2)(√5 + √2) = 3

 

5. \(\frac{\sqrt{2}(2+\sqrt{3})}{\sqrt{3}(\sqrt{3}+1)}-\frac{\sqrt{2}(2-\sqrt{3})}{\sqrt{3}(\sqrt{3}-1)}\)

Solution:

\(\frac{\sqrt{2}(2+\sqrt{3})}{\sqrt{3}(\sqrt{3}+1)}-\frac{\sqrt{2}(2-\sqrt{3})}{\sqrt{3}(\sqrt{3}-1)}\)

 

 

Alternative Method:

1.

 

 

2.

 

6. \(\frac{3 \sqrt{2}}{\sqrt{6}+\sqrt{3}}-\frac{2 \sqrt{6}}{\sqrt{3}+1}+\frac{2 \sqrt{3}}{\sqrt{6}+2}\)

Solution:

 

 

7. \(\frac{4 \sqrt{3}}{2-\sqrt{2}}-\frac{30}{4 \sqrt{3}-\sqrt{18}}-\frac{\sqrt{18}}{3-2 \sqrt{3}}\)

Solution:

\(\frac{4 \sqrt{3}}{2-\sqrt{2}}-\frac{30}{4 \sqrt{3}-\sqrt{18}}-\frac{\sqrt{18}}{3-2 \sqrt{3}}\)

 

 

Example 2. \(a^{\frac{1}{3}} b^{-\frac{1}{3}}+a^{-\frac{1}{3}} b^{\frac{1}{3}}\), then prove that a(bx³ – 3bx – a) = b²

Solution:

\(a^{\frac{1}{3}} b^{-\frac{1}{3}}+a^{-\frac{1}{3}} b^{\frac{1}{3}}\)

 

 

Example 3. If x = \(=\frac{1}{2}\left\{\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}\right\}\) then find the value of \(\frac{2 a \sqrt{1+x^2}}{x+\sqrt{1+x^2}}\)

Solution:

 

 

Example 4. If x = \(\frac{4 \sqrt{15}}{\sqrt{5}+\sqrt{3}}\), then find the value of \(\frac{x+\sqrt{20}}{x-\sqrt{20}}+\frac{x+\sqrt{12}}{x-\sqrt{12}}\)

Solution:

x = \(\frac{4 \sqrt{15}}{\sqrt{5}+\sqrt{3}}\)

 

 

Example 5. If a (2+√3) = b(2 – √3) = 1, then find the value of \(\frac{1}{a^2+1}+\frac{1}{b^2+1}\)

Solution:

a (2+√3) = 1

or, a = \(\frac{1}{2+\sqrt{3}}\)

 

 

Again,

 

 

 

Example 6. 

1. If a = \(\frac{\sqrt{5}+1}{\sqrt{5}-1}\) and b = \(\frac{\sqrt{5}-1}{\sqrt{5}+1}\), then find the value of (5a² – 3ab + 5b²)

Solution:

a = \(\frac{\sqrt{5}+1}{\sqrt{5}-1}\) and b = \(\frac{\sqrt{5}-1}{\sqrt{5}+1}\)

 

 

Again,

 

 

2. x = \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\) and y = \(\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\)

Solution:

x = \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\) and y = \(\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\)

 

 

3. x = √3 + √2 and y = √3 – √2

Solution:

x = √3 + √2 and y = √3 – √2

 

 

Example 7. 

1. Find the value of \(\frac{a^6+a^4+a^2+1}{a^3}\) , where a = 3 + 2√2.

Solution:

a = 3 + 2√2,

 

 

2. If 2x = a + \(\frac{1}{a}\) and 2y = b + \(\frac{1}{b}\), then prove that \(x y+\sqrt{\left(x^2-1\right)\left(y^2-1\right)}=\frac{1}{2}\left(a b+\frac{1}{a b}\right)\)

Solution:

 

 

Example 8. If x = \(\frac{1}{2-\sqrt{3}}\), then find the value of (x³ – 2x² – 7x + 4).

Solution:

 

 

Example 9. 

1. If x = \(\sqrt{\frac{\sqrt{5}+1}{\sqrt{5}-1}}\), then find the value of \(\left(x-\frac{1}{x}\right)\)

Solution:

x = \(\sqrt{\frac{\sqrt{5}+1}{\sqrt{5}-1}}\)

∴ \(\frac{1}{x}\)

 

 

2. If x = 8 + √28, and then find the value of\(\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)\)

Solution:

 

 

Example 10. If x = \(\frac{\sqrt{3}}{2}\), then find the value of \(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\)

Solution:

 

 

Alternative Method:

 

 

Example 11. If x = \(\frac{n-\sqrt{m^2-4 n}}{n+\sqrt{m^2-4 n}}\), then find the value of (m² -n² -4n)(x² + 1) +2(m² + n² – 4n) x = 0.

Solution:

 

 

Example 12. If x = \(\frac{\sqrt{a+2 b}+\sqrt{a-2 b}}{\sqrt{a+2 b}-\sqrt{a-2 b}}\), then prove that bx² – ax + b = 0.

Solution:

 

 

Alternative Method:

 

Example 13. Find the value of 8xy(x² + y²), when a+y = √3, and x-y = √2.

Solution:

Given Expression

 

 

Example 14. If x = \(\frac{\sqrt{5}-1}{\sqrt{5}+1}\) and y = \(\frac{\sqrt{5}+1}{\sqrt{5}-1}then find the value of \)

Solution:

x = \(\frac{\sqrt{5}-1}{\sqrt{5}+1}\) and y = \(\frac{\sqrt{5}+1}{\sqrt{5}-1}\)

 

 

Example 15. If a²+b+2a√b = 7+4√3 and c²+d-2c√d = 1, then find the value of (a+b+c+d).

Solution:

Given a²+b+2a√b = 7+4√3 And c²+d-2c√d = 1

a²+b+2a√b = 7+4√3

 

 

Example 16. If x = 1+√2+√3 and y = 1+√2-√3 then find the value of \(\frac{x^2+4 x y+y^2}{x+y}\)

Solution:

Given If x = 1+√2+√3 And y = 1+√2-√3

x = 1+√2+√3 and y = 1+√2-√3