Algebra Chapter 5 Linear Equations In Real Problems
Chapter 5 Linear Equations In Real Problems Formation of simultaneous linear algebraic equations of real mathematical problems
We have to face different types of mathematical problems in our daily life.
To solve these problems, we generally convert them to some simultaneous linear algebraic equations.
We have discussed in the previous chapter and some of its contents in brief.
According to that discussion and applying the concepts of solving simultaneous linear equations in two variables also discussed in that chapter, we shall study the method of solving real mathematical problems in the present chapter.
For this, we need to remember the following formulae:
Read and Learn More WBBSE Solutions For Class 9 Maths
Some Special formulae:
Formula-1: Distance Velocity x Time.
Formula-2: Velocity = \(\frac{Distance}{Time}\)
Formula-3: Time = \(\frac{Distance}{Velocity}\)
Formula-4: Transformation of units from km per hour to meter per sec
\(a \mathrm{~km} / \text { hour }=\frac{a \times 1000}{60 \times 60} \mathrm{~m} / \mathrm{sec}=\frac{5 a}{18} \mathrm{~m} / \mathrm{sec}\)
Formula-5: Transformation of units from m/sec to km/hour
\(b \mathrm{~m} / \mathrm{sec}=\frac{b \times 60 \times 60}{1000} \mathrm{~km} / \text { hour }=b \times \frac{18}{5} \mathrm{~km} / \text { hour }\)Formula-6: If in steady water, the velocity of a boat = u km/hour and the velocity of the current = v km/hour (u > v), then
1. the velocity of the boat in favor of the current = (u + v) km/hour;
2. the velocity of the boat against the current = (v) km/hour.
Formula-7: From a fixed point if the velocities of two persons or of two objects be a km/hour and b km/hour (a> b), then
1. their relative velocity in the opposite directions = (a + b) km/hour;
2. their relative velocity in the same direction = (a – b) km/hour.
Formula-8:
1. If the unit’s digit and ten’s digit of a two-digit number be x and y respectively, then the number = 10y + x, and the number obtained by reversing the digits of it = 10x + y.
2. If the unit’s digit, ten’s digit, and hundred’s, digit of a three-digit number be x, y and z respectively, then the number = 100z + 10y + x
Solutions of simultaneous linear equations in two variables by different methods:
We have already discussed four methods of solving different simultaneous linear equations in two variables in the previous chapter. The methods are:
- Method of elimination
- Method of comparison
- Method of substitution
- Method of cross-multiplication.
To solve the above-mentioned equations, these methods are widely used. Observe the following examples.
Question 1. Ritadevi bought 5 pens and 3 pencils for Rs. 34 from a shop. Sumitadevi has also bought 7 pens and 6 pencils for Rs. 53 from the same shop. Find the value of each pen and of each pencil.
Solution:
Given Ritadevi bought 5 pens and 3 pencils for Rs. 34 from a shop
Sumitadevi has also bought 7 pens and 6 pencils for Rs. 53 from the same shop
Let the value of each pen = Rs
By the first condition given,5x + 3y = 34………….(1)
By the second condition given, 7x+6y= 53…………..(2).
Now, multiplying (1) by 2 we get, 10x + 6y = 68……………(3)
Subtracting (2) from (3) we get, 10x-7x = 68-53
or 3x = 15
or, x = 5
Putting x = 5 in (1) we get, 5 x 5 + 3y = 34
or, 25+ 3y = 34.
or, 3y = 34 25 or, 3y = 9 or, y= \(\frac{9}{3}\) = 3.
∴ the value of each pen is Rs. 5 and that of each pencil is Rs. 3.
Question 2. The weights of Sitadevi and Gitadevi are together 85 kilograms. If half of the weight of Sitadevi is equal to \(\frac{4}{9}\)th part of the weight of Gitadevi, then determine the weight of each separately.
Solution:
Given
The weights of Sitadevi and Gitadevi are together 85 kilograms
Let the weight of Sitadevi x kg and the weight of Gitadevi = y kg.
By the first condition given, x+y= 85………………..(1)
By the second condition given, \(x \times \frac{1}{2}=y \times \frac{4}{9} \text {, or, } x=\frac{8 y}{9}\)…………(2)
Now, substituting x = \(\frac{8y}{9}\) in (1) we get, \(\frac{8 y}{9}+y=85\)
or, 8y+9y= 85 x 9 [multiplying by 9]
or, 17y=85 x 9
or, \(y=\frac{85 \times 9}{17}\)
or, y=45
Putting y 45 in (2) we get, x = \(x=\frac{8 \times 45}{9}=40\)
∴ the weight of Sitadevi is 40 kg and the weight of Gitadevi is 45 kg.
Question 3. The present age of Sumitra is twice the present age of Sulekha. 10 years ago, the age of Sumitra was thrice the age of Sulekha. What are their present ages?
Solution:
Given
The present age of Sumitra is twice the present age of Sulekha
10 years ago, the age of Sumitra was thrice the age of Sulekha
Let the present age of Sumitra be x years and that of Sulekha be y years.
By the first condition given, x = 2y….. (1)
and by the second condition given, x − 10 = 3 (y – 10)………………(2)
Now, substituting x = 2y in (2) we get, 2y – 10 = 3 (y-10),
or, 2y – 10 = 3y – 30
or, 3y – 2y = 10 + 30
or, y = 20.
Putting y 20 in (1) we get, x = 2 x 20 = 40.
∴ the present age of Sumitra is 40 years and that of Sulekha is 20 years.
Question 4. The value of the total number of 70 notes (currency) is Rs. 590, in which there are notes of Rs. 10 and Rs. 5. Find the number of each note.
Solution:
Given:-
The value of the total number of 70 notes (currency) is Rs. 590, in which there are notes of Rs. 10 and Rs. 5.
Let the number of notes of Rs. 10 is x and that of Rs. 5 be y.
As per question, x + y = 70……. (1)
and 10x + 5y = 590…….. (2)
Multiplying (1) by 5 we get, 5x+5y= 350………. (3)
Subtracting (3) from (2) we get, 10x – 5x = 590 – 350
or, 5x = 240
or, x = 48.
Putting x = 48 in (1) we get, 48+ y = 70
or, y = 70-48 = 22
∴ The number of notes of Rs. 10 is 48 and that of Rs. 5 is 22.
Question 5. The denominator of a fraction is greater than the numerator of it by 5 and if 3 is added to both the numerator and the denominator the fraction becomes \(\frac{3}{4}\). Find the fraction.
Solution:
Given
The denominator of a fraction is greater than the numerator of it by 5
Let the numerator of the fraction be x and the denominator of it be y.
∴ the fraction = \(\frac{x}{y}\)
By the first condition given, y = x + 5….. (1)
and by the second condition given, \(\frac{x+3}{y+3}=\frac{3}{4}\)
Now substituting y = x + 5 in (2) we get, \(\frac{x+3}{x+5+3}=\frac{3}{4} \text { or, } \frac{x+3}{x+8}\) = \(\frac{3}{4}\)
or, 4x-3x=24 – 12
or, x = 12.
Putting x = 12 in (1) we get, y = 12 + 5 = 17.
∴ The required fraction = \(\frac{12}{17}\)
Alternative Method:
Let the numerator of the fraction = x,
the denominator = x + 5.
As per the question, \(\frac{x+3}{x+5+3}=\frac{3}{4} \text { or, } \frac{x+3}{x+8}=\frac{3}{4}\)
or, 4x+12= 3x + 24
or, x = 12
∴ the denominator = x+5= 12 + 5 = 17.
∴ the required fraction = \(\frac{12}{14}\)
Question 6. If 21 is added to the first number of two given numbers, it becomes twice the second number and if 12 is added to the second number, it becomes twice the first number. Find the numbers.
Solution:
Let the first number be x and the second number be y.
By the first condition given, x + 21 = 2y
or, x = 2y-21…… (1)
By the second condition given, y + 12 = 2x
or, x = \(x=\frac{y+12}{2}\)…………(2)
The L.H.S.s of both (1) and (2) are equal,
∴ the RHSs of (1) and (2) must also be equal.
∴ 2y-21 = \(\frac{y+12}{2}\)
or, 4y – 42 = y+ 12
or, 4y- y = 12 + 42
or, 3y = 54
or, y = \(\frac{54}{3}\)
= 18.
Putting y = 18 in (2) we get, x = \(x=\frac{18+12}{2}=\frac{30}{2}=15\)
∴ the required fractions are 15 and 18.
Question 7. A and B can complete \(\frac{2}{3}\)rd of a piece of work, if A works 3 days and B works 4 days together. While they can complete \(\frac{11}{12}\) part of the work, if A works 3 days and B works 6 days together. In how many days A and B will complete the work separately?
Solution:
Let A will complete the work in x days and B will complete the work in y days separately.
By the first condition given, \(\frac{3}{x}+\frac{4}{y}=\frac{2}{3}\)………….. (1)
A can complete in x days 1 part of the work
∴ A can complete in 1 day 1/x part of the work
A can complete in 3 days 3/x part of the work
Similarly, B can complete in 4 days 4/y part of the work.
By the second condition given, \(\frac{3}{x}+\frac{6}{y}=\frac{11}{12}\)…….(2)
Now, subtracting (1) from (2) we get,
\(\frac{6}{y}-\frac{4}{y}=\frac{11}{12}-\frac{2}{3} \text { or, } \frac{6-4}{y}=\frac{11-8}{12} \text { or, } \frac{2}{y}=\frac{3}{12} \text { or, } y=\frac{2 \times 12}{3}=8\)
Putting y 8 in (1) we get,
\(\frac{3}{x}+\frac{4}{8}=\frac{2}{3} \text { or, } \frac{3}{x}=\frac{2}{3}-\frac{1}{2} \text { or, } \frac{3}{x}=\frac{4-3}{6} \text { or, } \frac{3}{x}=\frac{1}{6} \text { or, } x=18\)∴ A will complete the work in 18 days and B will complete the work in 8 days separately.
Question 8. There are two kinds of syrup. In the first kind, there is 5 kg of sugar in 100 liters of syrup. While in the second kind, there is 8 kg of sugar in 100 liters of syrup. In how much quantities of these two kinds of syrup should be mixed so that there will have 93 kg of sugar in 150 liters of syrup? od valeun bebe po bad. ad hoc per amor e soltalo2
Solution:
Given:-
There are two kinds of syrup. In the first kind, there is 5 kg of sugar in 100 liters of syrup.
While in the second kind, there is 8 kg of sugar in 100 liters of syrup
Let x liters of the first kind should be mixed with y liters of the second kind of syrup. x + y = 150……. (1)
Again, In the first kind, in 100 liters of syrup, there is 5 kg of sugar.
Again, In the first kind, in 1 liter of syrup, there is 5/100 kg of sugar.
Again, In the first kind, in x liters of syrup, there is \(\frac{5x}{100}\) kg of sugar.
= x/20 kg of syrup.
In the second kind, in 100 liters of syrup, there is 8 kg of sugar.
In the second kind, in 1 liter of syrup, there is 8/100 kg of sugar.
In the second kind, in y liters of syrup, there is \(\frac{8y}{100}\) kg of sugar.
= 2/25 kg of sugar.
As per question,\(\frac{x}{20}+\frac{2 y}{25}=9 \frac{2}{3}\)
From (1) we get, y = 150 – x……………..(2)
Substituting y = (150 – x) in (2) we get, \(\frac{x}{20}+\frac{2(150-x)}{25}=9 \frac{2}{3}\)
or, \(\frac{x}{20}+\frac{300-2 x}{25}=\frac{29}{3}\)
or, \(\frac{5 x+1200-8 x}{100}=\frac{29}{3}\)
or, \(\frac{1200-3 x}{100}=\frac{29}{3}\)
or, 3600 – 9x = 2900
or, 9x = 700
or, x = \(\frac{700}{9}\) in (3) we get,
y = \(150-\frac{700}{9}=\frac{1350-700}{9}=\frac{650}{9}=72 \frac{2}{9}\)
∴ the required quantities are 77 \(\frac{7}{9}\) liters of the first kind and 72 \(\frac{2}{9}\) liters of the second kind.
Question 9. If the length and breadth of a rectangle be increased by 2 meters and 3 meters respectively, the area of the rectangle is increased by 75 sq. meters. But if the length is decreased by 2 meters and the breadth is increased by 3 meters, the area of the rectangle increases by 15 sq. meters. Find the length and breadth of the rectangle.
Solution:
Given
If the length and breadth of a rectangle be increased by 2 meters and 3 meters respectively, the area of the rectangle is increased by 75 sq. meters.
But if the length is decreased by 2 meters and the breadth is increased by 3 meters, the area of the rectangle increases by 15 sq. meters.
Let the length and breadth of the rectangle be x meters and y meters respectively.
∴ the area of the rectangle = xy sq. meters.
By the first condition given, (x+2) (y+3)= xy + 75………..(1)
By the second condition given, (x-2) (y+3)= xy + 15…………(2)
Now, subtracting (2) from (1) we get, (y+3) (x + 2 – x + 2) = 75 – 15
or, (y+3)× 4 = 60
or, y+3 = \(\frac{60}{4}\)
or, y + 3 = 15
or, y = 12.
Putting y = 12 in (1) we get, (x+2)(12+3) = x x 12 + 75
Or, (x+2) x 15 = 12x + 75
Or, 15x + 30 = x x 12+75
or, 15x-12x=75 – 30
or, 3x = 45
or, x = \(\frac{45}{3}\) = 15
∴ the length of the rectangle = is 15 meters and the breadth of the rectangle = is 12 meters.
Question 10. Babul said to Eeshan, “If you give me \(\frac{1}{3}\)rd of your money, I will have Rs. 200.” Eeshan said to Babul, “If you give me \(\frac{1}{2}\) of your money, I will have Rs. 200.” How much money did each of them possess?
Solution:
Let Eeshan have Rs. x and Babul have Rs. y
By the first condition given, y+x x \(\frac{1}{3}\) =200…….(1)
By the second condition given, x+y x \(\frac{1}{2}\) = 200……….(2)
Multiplying (2) by 2 we get, 2x + y = 400…….(3)
Now, subtracting (1) from (3) we get, 2x – \(\frac{x}{3}\) = 400 – 200
or, \(\frac{6x – x}{3}\) = 200
or, \(\frac{5x}{3}\) = 200
or, x=200 x \(\frac{3}{5}\) = 120
Putting x =120 in (3) we get, 2 x 120+ y = 400 or, 240 + y = 400
or, y = 160
∴ Eeshan possessed Rs. 120 and Babul possessed Rs. 160.
Question 11. The amount t of money was u di friends was 2 less than the original, each of them would have got Rs 18. Again, had the number number of friends been 3 more than the original, each of them would have got Rs. 12. Determine the number of friends and the amount of money. 19 ft to 190 275
Solution:
Given The amount t of money was u di friends was 2 less than the original, each of them would have got Rs 18.
Again, had the number number of friends been 3 more than the original, each of them would have got Rs. 12.
Let the number of friends is x and the amount of money be Rs.y.
By the first condition given, \(\frac{y}{x-2}\) = 18
or, y = 18(x – 2)…………..(1)
By the second condition given, \(\frac{y}{x+3}\) = 12
or, y = 12 (x+3)………(2)
The LHSs of both (1) and (2) are equal,
∴ the RHSs must also be equal.
∴ 18 (x – 2) = 12 (x + 3)
or, 18x – 36 = 12x + 36
or, 18x – 12x = 36 + 36
or, 6x = 72
or, x = \(\frac{72}{6}\) = 12
Putting x = 12 in (1) we get, y= 18 (12 – 2)
= 18 x 10
= 180.
∴ the required number of friends = 12 and the required amount of money = Rs. 180.
Question 12. There are coins of one rupee and 50 paise in a box owned by the elder brother of Mitali. The total value of the coins is Rs. 350. The sister of Mitali replaces \(\frac{1}{3}\)rd of the 50 paisa coins in the box by an equal number of one rupee coins, so that the total value of the coins now becomes Rs. 400. Determine the number of one rupee coins and 50 paisa coins each.
Solution:
Let the number of one rupee coin be x and the number of 50 paisa coins be y.
By the first condition given, x x 1 + y x \(\frac{50}{100}\) = 350
[ ∵ One 50 paisa coin = Rs. \(\frac{50}{100}\) ]
or, x + y x \(\frac{1}{2}\) = 350
or, x = 350 – \(\frac{y}{2}\)……………(1)
By the second condition given, \(\left(x+\frac{y}{3}\right) \times 1+\left(y-\frac{y}{3}\right) \times \frac{50}{100}=400\)
or, \(x+\frac{y}{3}+\frac{2 y}{3} \times \frac{1}{2}=400\)
or, \(x+\frac{y}{3}+\frac{y}{3}=400\)
or, \(x+\frac{y+y}{3}=400\)
or, \(x+\frac{2 y}{3}=400\)
or, \(x=400-\frac{2 y}{3}\)……………(2)
The LHSS of (1) and (2) are equal,
∴ the RHSS must also be equal.
∴ \(350-\frac{y}{2}=400-\frac{2 y}{3}\)
or, \(-\frac{y}{2}+\frac{2 y}{3}=400-350\)
or, \(\frac{-3 y+4 y}{6}=50\)
or, \(\frac{y}{6}=50\)
or, y = 300
Putting y 300 we get x = \(350-\frac{300}{2}\) = 350-150-200.
∴ the required number of one rupee coin is 200 and the number of 50 paisa coins is 300.
Question 13. The time required by a motor. car to travel a certain distance is 3 hours less if its velocity is increased by 9 kilometers per hour. Again, if the velocity is decreased by 6 kilometers per hour, then the time required by the car to travel the same distance is 3 hours more. Find the velocity of the car and a certain distance.
Solution:
Given
The time required by a motor. car to travel a certain distance is 3 hours less if its velocity is increased by 9 kilometers per hour.
Again, if the velocity is decreased by 6 kilometers per hour, then the time required by the car to travel the same distance is 3 hours more.
Let the velocity of the car = x km/hour and the certain distance = y km.
By the first condition given, \(\frac{y}{x+9}=\frac{y}{x}-3 \quad \text { or, } \frac{y}{x+9}=\frac{y-3 x}{x}\)
or, xy – 3x² + 9y – 27x = xy
or, -3x² – 27x = -9y
or, x2 + 9x = 3y
or, y = \(y=\frac{x^2+9 x}{3}\) …………..(1)
By the second condition given, \(\frac{y}{x-6}=\frac{y}{x}+3\)
\(\frac{y}{x-6}=\frac{y+3 x}{x}\)
or, xy – 6y + 3x² – 18x = xy
or, – 6y+ 3x²-18x = 0
or, 6y= 3x²-18x
or, 2y = x²-6x
or, y = \(y=\frac{x^2-6 x}{2}\)………(2)
Now, comparing (1) and (2) we get, \(\frac{x^2+9 x}{3}=\frac{x^2-6 x}{2}\)
or, 3×2-18x = 2x² + 18x
or, 3x² – 18x – 2x²-18x
or, x² – 36x = 0
or, x (x – 36) = 0
∴ either x = 0
or, x – 36 = 0
x = 36.
But x ≠ 0,
∴ x = 36.
Putting x 36 in (1) we get, y = \(y=\frac{(36)^2+9 \times 36}{3}\) = 540
∴ the velocity of the motor car = 36 km/hour and the certain distance = 540 kilometres.
Question 14. A number of two digits is 3 more than 4 times the sum of its digits. If the positions of the digits of the number be interchanged, then the new number thus formed is 18 more than the original number. Determine the number.
Solution:
Given
A number of two digits is 3 more than 4 times the sum of its digits.
If the positions of the digits of the number be interchanged, then the new number thus formed is 18 more than the original number.
Let the unit’s digit of the number be x and the ten’s digit of the number be y.
∴ the number = 10y+x……………(1)
By the first condition given, 10y + x = 4 (x + y) + 3
or, 10y+x=4x+4y+ 3
or, 4x+4y+ 310y-x=0
or, 3x6y+ 3 = 0
or, x-2y+ 1 = 0…………….(2) [Dividing by 3]
By the second condition given, 10x + y = 10y + x + 18
or, 10x + y – 10y – x – 18 = 0
or, 9x – 9y – 18 = 0…………….(3) [Dividing by 9]
Now, from (2) and (3) we get by the method of cross-multiplication.
\(\frac{x}{(-2) \times(-2)-1 \times(-1)}=\frac{-y}{1 \times(-2)-1 \times 1}=\frac{1}{1 \times(-1)-(-2) \times 1}\)
or, \(\frac{x}{5}=\frac{-y}{-3}=\frac{1}{1}\)
∴ \(\frac{x}{5}\) = \(\frac{1}{1}\)
or, x = 5.
Again, \(\frac{-y}{-3}=\frac{1}{1}\)
or, y = 3.
Putting x = 5 and y = 3 in (1) we get, the number = 10 x 3 + 5 = 35.
∴ the required number = 35.
Question 15. The sum of the digits of a number consisting of two digits is 14 and if 29 is subtracted from the number, then the two digits of the number become equal to each other. Find the number.
Solution:
Given
The sum of the digits of a number consisting of two digits is 14 and if 29 is subtracted from the number, then the two digits of the number become equal to each other
Let the unit’s digit and ten’s digit of the number be x and y respectively.
∴ The number = 10y + x……………..(1).
By the first condition given, x + y = 14
or, y = 14 – x…………..(2)
When 29 is subtracted from the number, the new number (y-3) + (x + 1).
10y + x – 29 = 10y + x – 30 + 1 = 10
Here, the ten’s and unit’s digits of this new number are (y-3) and (x + 1) respectively.
As per question, y3x + 1 or, 14-x-3x + 1 [Putting y=14x]
or, 11- x = x + 1
or, x + x = 11 – 1
or, 2x = 10
or, x = 5.
Putting x 5 in (2) we get, y = 14 – 59.
Now, substituting x = 5 and y = 9 in (1) we get, the number = 10 x 9 + 5 = 95.
∴ the required number = 95.
Question 16. A boatsman can travel by his boat a distance of 30 kilometers in 6 hours in favor of the current. While he comes back in 10 hours against the current. Find the velocity of the current and the velocity of the boat in still water.
Solution:
Given
A boatsman can travel by his boat a distance of 30 kilometers in 6 hours in favor of the current. While he comes back in 10 hours against the current
Let the velocity of the current be x km/h and the velocity of the boat in still water be y km/h (y > x)
∴ the velocity of the boat in favor of the current = (x + y) km / h. and the velocity of the boat against the current = (x + y) km/h [y>x]
By the first condition given, \(\frac{30}{x+y}\)……….(1)
and by the second condition given,\(\frac{30}{y-x}\)………………….(2)
Now, dividing (2) by (1) we get, \(\frac{\frac{30}{y \frac{1}{30}}}{\frac{30}{x+y}}=\frac{10}{6}\)
or, \(\frac{30}{y-x} \times \frac{x+y}{30}=\frac{5}{3}\)
or, \(\frac{x+y}{y-x}=\frac{5}{3}\)
or, 3x + 3y = 5y- 5x
or, 3x + 5x = 5y – 3y
or, 8x = 2y
or, y = 4x………. (3)
Putting y = 4x in (1) we get, \(\frac{30}{x+4x}\) = 6
or, \(\frac{30}{5x}\) = 6
Or, 30x = 30
or, x = \(\frac{30}{30}\) = 1
Putting x = 1 in (3) we get; y = 4 × 1 = 4.
∴ the velocity of the current = 1 km/h and the velocity of the boat in still water = 4 km/h.
Alternative Method:
Let the velocity of the boat in still water be x km/h and the velocity of the current be y km/h (x > y)
∴ the velocity of the boat in favor of the current = (x + y) km / h and the velocity of the boat against the current = (xy) km/h.
By the first condition given, \(\frac{30}{x+y}\) = 6
or, \(\frac{5}{x + y}\) = 1 [Dividing by 6]
or, x + y = 5
or, x+y-5=0……………(1)
By the second condition given, \(\frac{30}{x-y}\)
or, \(\frac{3}{x-y}\) = 1 [Dividing by 10]
or, x-y = 3
or, x-y-3 = 0…….(2)
From (1) and (2) we get by the method of cross-multiplication,
\(\frac{x}{1 \times(-3)-(-5) \times(-1)}=\frac{-y}{1 \times(-3)-(-5) \times 1}=\frac{1}{1 \times(-1)-1 \times 1} \text { or, } \frac{x}{-8}=\frac{-y}{2}=\frac{1}{-2}\)
∴ \(\frac{x}{-8}=\frac{1}{-2}\)
Or, \(x=\frac{-8}{-2}=4\) and \(\frac{-y}{2}=\frac{1}{-2}\)
or, \(-y=\frac{2}{-2}=-1 \text { or, } y=1\)
∴ the velocity of the current = 1 km/h and the velocity of the boat in still water 4 km/h
Question 17. A train was stopped for 1 hour for a special cause after 1 hour of its starting from the Howrah station and then traveling with a velocity of \(\frac{3}{5}\) part of past velocity, it reached the destination after 3 hours of its scheduled time. If the place of special cause were at a distance of 50 kilometers far away from the place the special cause had occurred, then the train would have reached the destination in a time which would be 1 hour and 20 minutes less than the time taken by it earlier. Calculate the total distance traveled by train and its past velocity of it.
Solution:
Let the total distance traveled by train be x km and the past velocity of it be y km/h.
∴ the scheduled time to reach the destination=- hours.
The train traveled y km in the first 1 hour.
∴ the rest distance = (x-y) km.
The train traveled this rest distance with a velocity of \(y \times \frac{3}{5} \mathrm{~km} / \mathrm{h}=\frac{3 y}{5} \mathrm{~km} / \mathrm{h}\)
∴ the time required by the train to travel this rest distance \(\frac{x-y}{\frac{3 y}{5}} \text { hours }=\frac{5 x-5 y}{3 y} \text { hours }\)
As per the question, \(1+1+\frac{5 x-5 y}{3 y}=\frac{x}{y}+3 \quad \text { or, } \frac{3 y+3 y+5 x-5 y}{3 y}=\frac{x+3 y}{y}\)
or, \(\frac{5 x+y}{3}=x+3 y\) [ ∵ y ≠ 0]
or, 5x + y = 3x + 9y
or, 5x – 3x = 9y – y
or, 2x = 8y
or, x = \(\frac{8y}{2}\) = 4y…………………(1)
If the special cause were at a distance 50 km far away from the place it had occurred then the rest distance would be (x – y – 50) km, and the required time to travel this distance would be
\(\frac{x-y-50}{\frac{3y}{5}}\) hours = \(\frac{5x-5y-250}{3y}\) hours.
As per the question, \(1+\frac{50}{y}+1+\frac{5 x-5 y-250}{3 y}=\left(\frac{x}{y}+3\right)-1 \frac{20}{60}\)
or, \(\frac{3 y+150+3 y+5 x-5 y-250}{3 y}=\frac{x+3 y}{y}-1 \frac{1}{3}\)
or, \(\frac{5 x+y-100}{3 y}=\frac{x+3 y}{y}-\frac{4}{3}\)
or, 5x + y – 100 = 3x + 9y – 4y [multiplying by 3y]
or, 5x-3x + y – 9y+ 4y = 100
or, 2x-4y= 100
or, x-2y= 50
or, 4y-2y= 50 [by (1)]
or, 2y = 50
or, y = \(\frac{50}{2}\)
or, y = 25.
Putting y 25 in (1) we get, x = 4 x 25
= 100.
∴ the train traveled a total distance of 100 km and its past velocity of it was 25 km/hour.
Question 18. Matangini got 6 as the quotient and 6 as the remainder when she had divided the number of two digits by the sum of the digits. Had she divided the number obtained by interchanging the positions of the digits by the sum of the digits, then she would get 4 as the quotient and 9 as the remainder. Determine the number.
Solution:
Given
Matangini got 6 as the quotient and 6 as the remainder when she had divided the number of two digits by the sum of the digits.
Had she divided the number obtained by interchanging the positions of the digits by the sum of the digits, then she would get 4 as the quotient and 9 as the remainder.
Let the unit’s digit and the ten’s digit of the number of x and y respectively.
∴ the number be x and y respectively.
∴ the number = 10y+x………(1)
By the first condition given, \(\frac{10 y+x-6}{x+y}=6\)
or, 10y + x – 6 = 6x + 6y
or, 6x + 6y – 10y x + 6 = 0
or, 5x – 4y + 6=0………..(2)
By the second condition given, \(\frac{10 x+y-9}{x+y}=4\)
or, 10x+y-9=4x+ 4y
or, 10x+y-9-4x-4y=0
or, 6x – 3y – 9 = 0
or, 2x – y – 3 = 0 ………..(3) [Dividing by 3]
Now, from (2) and (3) we get by the method of cross-multiplication
\(\frac{x}{(-4) \times(-3)-6 \times(-1)}=\frac{-y}{5 \times(-3)-6 \times 2}=\frac{1}{5 \times(-1)-(-4) \times 2} \quad \text { or, } \frac{x}{18}=\frac{-y}{-27}=\frac{1}{3}\)
∴ \(\frac{x}{18}=\frac{1}{3}\) or, x = 6
Again, \(\frac{-y}{-27}=\frac{1}{3}\) or, y = 9.
Now, putting x 6 and y = 9 in (1) we get,
the number = 10 x 9+ 6 = 96.
the required number = 96.
Question 19. In order to put some oranges into some boxes, Sankarbabu found that had he has been put 20 oranges more into each box, the number of boxes required would be 3 less than the original number. Again, had he put 5 oranges into each box, the number of boxes would be 1 more than the original number? Find the number of oranges and the number of boxes that Sankarbabu possessed.
Solution:
Given
putting some oranges into some boxes, Sankarbabu found that had he has been put 20 oranges more into each box, the number of boxes required would be 3 less than the original number.
Again, had he put 5 oranges into each box, the number of boxes would be 1 more than the original number
Let Sankarbabu possess x oranges and y boxes.
∴ the number of oranges that can be put into each box = \(\frac{x}{y}\)
By the first condition given, \(\frac{x}{\frac{x}{y}+20}=y-3\)
or, x = x + 20y – \(\frac{3x}{y}\) – 60
or, \(\frac{3x}{y}\) = 20y – 60
or, x = \(x=\frac{20 y^2-60 y}{3}\)…………..(1)
By the second condition given, \(\frac{x}{\frac{x}{y}-5}=y+1\)
or, x=x-5y+\(\frac{x}{y}\) -5
or, \(\frac{x}{y}\) = 5y+5
or, x = 5y²+5y………….(2)
Comparing the RHSS of (1) and (2) we get, \(\frac{20 y^2-60 y}{3}=5 y^2+5 y\) [ ∵ LHSs are equal]
or, 20y² – 60y = 15y²+ 15y
or, 5y²-75y = 0
or, y² – 15y = 0 [Dividing by 5]
or y (y – 15) = 0
or, y – 15 = 0 [ ∵ y not = 0] or, y = 15.
Putting y = 15 in (2) we get, x = 5 x (15)² + 5 x 15
or, x = 5 x 225+ 75
or, x = 1125 + 75
or, x = 1200.
∴ Sankarbabu possessed 1200 oranges and 15 boxes.
Question 20. Two trains start at the same time, one from Kolkata to Madhupur and the other from Madhupur to Kolkata. If they arrive at Madhupur and Kolkata respectively 1 hour and 4 hours after they cross each other, find the ratio of their velocities.
Solution:
Given
Two trains start at the same time, one from Kolkata to Madhupur and the other from Madhupur to Kolkata
If they arrive at Madhupur and Kolkata respectively 1 hour and 4 hours after they cross each other
Let the velocity of the first train be x km/hour and the velocity of the second train be y km/hour and let after t hours of their starting they cross each other.
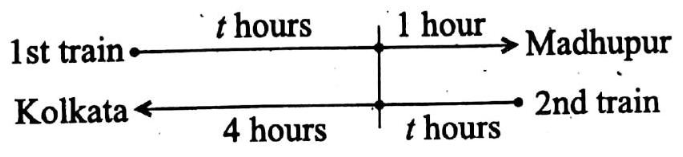
As per the question, the distance covered by the 1st train in t hours is equal to the distance covered by
the second in 1 hour.
∴ \(t x=4 y \quad \text { or, } t=\frac{4 y}{x}\)…………(1)
Again, the distance covered by the first train in 1 hour is equal to the distance covered by the second in / hours.
∴ \(x=t y \text { or, } t=\frac{x}{y}\)………….(2)
Now, comparing the RHSS of (1) and (2) we get, \(\frac{4 y}{x}=\frac{x}{y}\) [ ∵ LHSS are equal]
or, x2 = 4y2
or, x = 2y [Taking square roots of both sides]
or, \(\frac{x}{y}=\frac{2}{1} \text { or, } x: y=2: 1\)
∴ the velocity of the 1st train: the velocity of the 2nd train = 2: 1

