Motion in a Plane Multiple Choice Question And Answers

Motion in a Plane

Question 1. A particle has an initial velocity of \(3 \hat{i}+4 \hat{j}\) and an acceleration of \(0.4 \hat{i}+0.3 \hat{j}\). Its speed after 10s is

1. 10 units
2. 7 units
3. 7 √2 units
4. 8.5 units

Answer: 3. 7√2 units

In the vector form,

⇒ \(\vec{v}=\vec{u}+\vec{a} t=(3 \hat{i}+4 \hat{j})+(0.4 \hat{i}+0.3 \hat{j}) t\)

At \(t=10 \mathrm{~s}, \vec{v}=(3 \hat{i}+4 \hat{j})+(4 \hat{i}+3 \hat{j})=7 \hat{i}+7 \hat{j}\)

Hence, speed = magnitude of velocity

⇒ \(v=|7 \hat{i}+7 \hat{j}| \text { units }=\sqrt{7^2+7^2} \text { units }=7 \sqrt{2} \text { units. }\)

Question 2. A particle has an initial velocity of 9 m s^-1 due east and a constant acceleration of 2 m s^-2 due west. The distance covered by the particle in the fifth second of its motion is

1. Zero
2. 0.5 m
3. 2m
4. None of these

Answer: 2. 0.5 m

Since the acceleration is opposite to the direction of the initial velocity, the particle decelerates and comes to rest momentarily at a time t. Hence, applying the equation v = u-at, we have

0 = 9ms^-1-(2ms^-2)t

or, t = 4.5s.

In the fifth second, the particle covers equal distances in opposite directions.

Hence,

⇒ \(s_1=s_2=\frac{1}{2} a t^2=\frac{1}{2}\left(2 \mathrm{~m} \mathrm{~s}^{-2}\right)\left(\frac{1}{2} \mathrm{~s}\right)^2\)

= 0.25m.

∴ the total distance covered in the fifth second is 0.50 m.

Question 3. The x- and y-coordinates of a particle at any time t are x = 5t- 2t² and y = 10t, respectively, where x and y are in metres, and f is in seconds. The acceleration of the particle at t = 2 s is

1. 5ms^-2
2. -4ms^-2
3. -8 ms^-2
4. Zero

Answer: 2. -4ms^-2

Given that x = 5t-2t².

So, \(v_x=\frac{d x}{d t}=5-4 t\)

Similarly, y = 10t

⇒ \(v_y=\frac{d y}{d t}=10\)

Differentiating again,

⇒ \(a_x=\frac{d v_x}{d t}=-4 \text { and } a_y=\frac{d y_y}{d t}=0\)

∴ acceleration \(\vec{a}=a_x \hat{i}+a_y \hat{j}=-4 \hat{i}\) = constant.

The acceleration at t = 2 s is -4 m s^-2.

Question 4. A particle moves such that its position vector is given by \(\vec{r}=(\cos \omega t) \hat{i}+(\sin \omega t) \hat{j}\), where o is a constant. Which of the following statements is true?

1. The velocity vector is perpendicular to \(\vec{r}\), and the acceleration vector is directed towards the origin.
2. The velocity vector is perpendicular to \(\vec{r}\), and the acceleration vector is directed away from the origin.
3. The velocity and acceleration vectors are both perpendicular to \(\vec{r}\)
4. The velocity and acceleration vectors are both parallel to \(\vec{r}\).

Answer: 1. The velocity vector is perpendicular to \(\vec{r}\), and the acceleration vector is directed towards the origin.

Given that \(\vec{r}=\cos \omega t \cdot \hat{i}+\sin \omega t \cdot \hat{j}\)

∴ velocity \(\vec{v}=\frac{d \vec{r}}{d t}=-\omega \sin \omega t \cdot \hat{i}+\omega \cos \omega t \cdot \hat{j}\)

and acceleration \(\vec{a}=\frac{d \vec{v}}{d t}=-\omega^2 \cos \omega t \cdot \hat{i}-\omega^2 \sin \omega t \cdot \hat{j}=-\omega^2 \vec{r}\)

The position vector \(\vec{r}\) is directed away from the centre, but the acceleration

⇒ \(\vec{a}=-\omega^2 \vec{r}\)

is directed towards the centre.

Further, \(\vec{r} \cdot \vec{v}=(\cos \omega t \cdot \hat{i}+\sin \omega t \cdot \hat{j})(-\omega \sin \omega t \cdot \hat{i}+\omega \cos \omega t \cdot \hat{j})\)

⇒ \(-\omega \sin \omega t \cos \omega t+\omega \sin \omega t \cos \omega t=0\)

Hence, the angle between \(\vec{v}\) and \(\vec{r}\) is 90°, and thus \(\vec{v}\) is perpendicular to \(\vec{r}\).

Note The given equation represents a uniform circular motion of unit radius.

Question 5. A particle is moving in a plane such that its position coordinates (x, y) are (2 m, 3 m) at t = 0, (6 m, 7 m) at t = 2 s, and (13 m, 14 m) at t = 5 s. The average velocity vector \(\left(\vec{v}_{\text {av }}\right)\) from f = 0 to f = 5 s is

1. \(\frac{1}{5}(13 \hat{i}+14 \hat{j}) \mathrm{m} \mathrm{s}^{-1}\)
2. \(\frac{7}{3}(\hat{i}+\hat{j}) \mathrm{ms}^{-1}\)
3. \(2(\hat{i}+\hat{j}) \mathrm{m} \mathrm{s}^{-1}\)
4. \(\frac{11}{5}(\hat{i}+\hat{j}) \mathrm{m} \mathrm{s}^{-1}\)

Answer: 4. \(\frac{11}{5}(\hat{i}+\hat{j}) \mathrm{m} \mathrm{s}^{-1}\)

The position vector of the particle at \(t=0 \text { is } \vec{r}_1=2 \hat{i}+3 \hat{j}\) and that at

⇒ \(t=5 \mathrm{~s} \text { is } \vec{r}_2=13 \hat{i}+14 \hat{j} .\)

The displacement \(\Delta \vec{r}=\overrightarrow{r_2}-\overrightarrow{r_1}\) in the time interval At=5 s is \(\Delta \vec{r}=11 \hat{i}+11 \hat{j}\)

∴ The average velocity vector is

⇒ \(\vec{v}_{\mathrm{av}}=\frac{\Delta \vec{r}}{\Delta t}=\frac{11}{5}(\hat{i}+\hat{j}) \mathrm{m} \mathrm{s}^{-1}\)

Question 6. A body is moving with a velocity of 30 m s^-1 towards the east. After 10 s, its velocity becomes 40 m s^-1 towards the north. The average acceleration of the body is

1. 1 m s^-2
2. √7 m s^-2
3. 7ms^-2
4. 5 m s^-2

Answer: 2. √7 m s-2

The velocity due east is \(\vec{v}_1=\left(30 \mathrm{~m} \mathrm{~s}^{-1}\right) \hat{i}\) and the velocity due north is

⇒ \(\vec{v}_2=\left(40 \mathrm{~m} \mathrm{~s}^{-1}\right) \hat{j}\)

∴ The change in velocity vector is \(\Delta \vec{v}=\vec{v}_2-\vec{v}_1=(40 \hat{j}-30 \hat{i}) \mathrm{m} \mathrm{s}^{-1}\)

∴ The magnitude of the average acceleration is

⇒ \(\left|\vec{a}_{\mathrm{av}}\right|=\frac{|\Delta \vec{v}|}{\Delta t}=\frac{|40 \hat{j}-30 \hat{i}|}{10 \mathrm{~s}}=\frac{1}{10 \mathrm{~s}} \sqrt{40^2+30^2} \mathrm{~m} \mathrm{~s}^{-1}\)

⇒ \(\frac{50 \mathrm{~m} \mathrm{~s}^{-1}}{10 \mathrm{~s}}=5 \mathrm{~m} \mathrm{~s}^{-2}\)

Question 7. A particle moves in the ay-plane in such a way that x = a cos ωt and y = a sin ωt. The particle follows

1. An elliptical path
2. A circular path
3. A parabolic path
4. A linear path (straight line)

Answer: 2. A circular path

Given that \(x=a \sin \omega t\)

So, \(\sin \omega t=\frac{x}{a}\)

Also, \(y=a \cos \omega t \Rightarrow \cos \omega t=\frac{y}{a}\)

By squaring and adding, we obtain

⇒ \(\sin ^2 \omega t+\cos ^2 \omega t=\frac{x^2}{a^2}+\frac{y^2}{a^2} \Rightarrow x^2+y^2=a^2\)

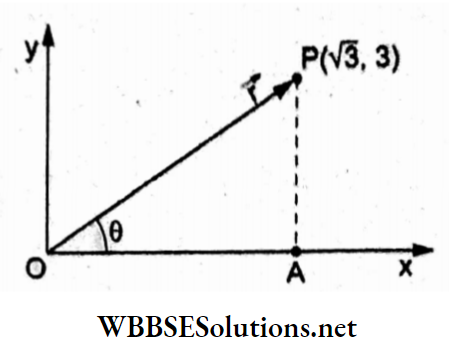
Question 8. A particle starting from the origin (0, 0) moves in a straight line in the ay-plane. Its coordinates at a later time are (√3,3). The angle made by the path of the particle with the x-axis is

1. 45°
2. 30°
3. 60°
4. 0°

Answer: 3. 60°

The instantaneous position vector of the particle is

⇒ \(\overrightarrow{O P}=\vec{r}=\sqrt{3} \hat{i}+3 \hat{j}\)

Hence,

⇒ \(\tan \theta=\frac{A P}{O A}=\frac{3}{\sqrt{3}}=\sqrt{3} \Rightarrow \theta=60^{\circ}\)

Question 9. A car is moving on a straight road towards the north with a uniform speed of 50 km h^-1 Then, it turns left through 90°. If the speed remains unchanged after turning, the increase in the velocity of the car in the turning process is

1. 70.7 km h^-1 in the southwest direction
2. Zero
3. 50 km h^-1 towards the west
4. 70.7 km h^-1 in the northwest direction

Answer: 1. 70.7 km h^-1 in the southwest direction

Initial velocity = \(\vec{v}_1=\left(50 \mathrm{~km} \mathrm{~h}^{-1}\right) \hat{j}\) and

final velocity = \(\vec{v}_2=\left(50 \mathrm{~km} \mathrm{~h}^{-1}\right)(-\hat{i})\)

∴ the change in velocity is

⇒ \(\Delta \vec{v}=\vec{v}_2-\vec{v}_1=-\left(50 \mathrm{~km} \mathrm{~h}^{-1}\right)(\hat{i}+\hat{j})\)

∴ \(|\Delta \vec{v}|=\left(50 \mathrm{~km} \mathrm{~h}^{-1}\right)|\hat{i}+\hat{j}|\)

⇒ \(50 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}b\)

= 70.7 km h ^-1.

Question 10. The maximum height attained by a projectile and its horizontal range are equal to each other if the angle of projection is given by

1. 0 = tan^-1(2)
2. 0 = tan^-1(3)
3. 0 = tan^-1(4)
4. 0 = tan^-1(5)

Answer: 3. 0 = tan^-1(3)

Horizontal range = \(R=\frac{u^2 \cdot 2 \sin \theta \cos \theta}{g}\)

and maximum height = \(H=\frac{u^2 \sin ^2 \theta}{2 g}\)

Given that R = H

Hence, \(\frac{u^2 \cdot 2 \sin \theta \cdot \cos \theta}{g}=\frac{u^2 \sin ^2 \theta}{2 g} \Rightarrow \tan \theta=4\)

⇒ \(\theta=\tan ^{-1}(4)\)

Question 11. When a projectile is at the highest point of its trajectory, the directions of its velocity and acceleration are

1. Parallel to each other
2. Antiparallel to each other
3. Perpendicular to each other
4. Inclined to each other at an angle of 60°

Answer: 3. Perpendicular to each other

The direction of the velocity is tangential to the trajectory at every point. At the highest point, the velocity is along the horizontal and the acceleration \(\vec{g}\) is vertical. So, the angle between \(\vec{g}\) and \(\vec{g}\) is 90°, and thus they are perpendicular to each other.

Question 12. A ball is projected horizontally with a velocity of 5 m s^-2 from the top of a 19.6-m-high building. How long will the ball take to hit the ground?

1. √3s
2. 2s
3. 3s
4. √2s

Answer: 2. 2s

Since the ball is projected horizontally, the velocity component uy along the vertical is zero.

So, \(h=\frac{1}{2} g t^2\)

∴ \(t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2(19.6 \mathrm{~m})}{9.8 \mathrm{~m} \mathrm{~s}^{-2}}}=2 \mathrm{~s}\)

Question 13. A bomb is dropped from an aeroplane when it is at a height h directly above a target If the aeroplane is moving at a speed v, the distance by which the bomb will miss the target is given by

1. \(2 v \sqrt{\frac{h}{g}}\)
2. \(v \sqrt{\frac{h}{2g}}\)
3. \(v \sqrt{\frac{h}{g}}\)
4. \(v \sqrt{\frac{2h}{g}}\)

Answer: 4. \(v \sqrt{\frac{2h}{g}}\)

The time when the bomb strikes the ground is \(t=\sqrt{\frac{2 h}{g}}\)

∴ the distance ahead of the target where the bomb strikes the ground is

⇒ \(x=v t=v \sqrt{\frac{2 h}{g}}\)

Question 14. The ceiling of a tunnel is 5 m high. What is the maximum horizontal distance that a ball thrown with a speed of 20 m s^-1 can go without hitting the ceiling of the tunnel?

1. 10√5m
2. 20√3m
3. 40 m
4. 30√3m

Answer: 2. 20√3m

Maximum height, \(H=\frac{u^2 \sin ^2 \theta}{2 g}=5 \mathrm{~m}\)

∴ \(\sin ^2 \theta=\frac{10 g}{u^2}=\frac{100}{20 \times 20}=\frac{1}{4} \Rightarrow \sin \theta=\frac{1}{2}\)

⇒ \(\theta=30^{\circ} \Rightarrow \sin 2 \theta=\sin 60^{\circ}=\frac{\sqrt{3}}{2}\)

∴ The maximum horizontal range is

⇒ \(\theta=30^{\circ} \Rightarrow \sin 2 \theta=\sin 60^{\circ}=\frac{\sqrt{3}}{2}\)

Question 15. A boy aims a gun at a target from a point at a horizontal distance of 100 m. If the gun can impart a horizontal velocity of 500 m s^-1 to the bullet, the height at the target where he must aim his gun in order to hit is

1. 10 cm
2. 20 cm
3. 50 cm
4. 80 cm

Answer: 2. 20 cm

The time taken to cover 100 m by the bullet is

⇒ \(t=\frac{100 \mathrm{~m}}{500 \mathrm{~m} \mathrm{~s}^{-1}}=0.2 \mathrm{~s}\)

The downward distance moved in this time is

⇒ \(y=\frac{1}{2} g t^2=\frac{1}{2} \times 10 \mathrm{~m} \mathrm{~s}^{-2} \times(0.2 \mathrm{~s})^2\)

= 20 cm.

This is the distance above the target where the gun is aimed at.

Question 16. From the top of a tower of height 40 m, a ball is projected upwards with a speed of 20 ms^-1 making an angle of 30° with horizontal. After how much time will the ball hit the ground?

1. 1s
2. 2s
3. 3s
4. 4s

Answer: 4. 4s

Consider the point of projection O as the origin and the equation of kinematics along the vertical line.

h =-40 m,

⇒ \(u_y=u \sin 30^{\circ}=\left(20 \mathrm{~m} \mathrm{~s}^{-1}\right)\left(\frac{1}{2}\right)\)

= 10ms^-1

and g = -10 m s^-2.

Applying \(h=u_y t+\frac{1}{2} g t^2\), we have

⇒ \(-40=10 t-\frac{1}{2} \times 10 t^2\)

or t²-2t-8=0 or

(t-4)(t+ 2)=0.

Hence, the permissible time is t = 4s,

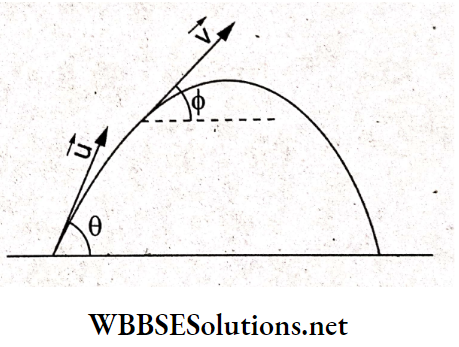
Question 17. A particle is thrown with a speed u at an angle θ to the horizontal. When the particle makes an angle Φ with the horizontal; its speed changes to v given by

1. \(v=u \cos \theta\)
2. \(v=u \cos \theta \cos \phi\)
3. \(v=u \cos \theta \sec \phi\)
4. \(v=u \sec \theta \cos \phi\)

Answer: 3. \(v=u \cos \theta \sec \phi\)

We know that during a projectile motion, the horizontal component of the velocity remains unchanged. This is due to the component of \(\vec{g}\) along the horizontal being zero.

Thus, \(v \cos \phi=u \cos \theta\)

⇒ \(v=\frac{u \cos \theta}{\cos \phi}=u \cos \theta \sec \phi\)

Question 18. An aeroplane flying at a constant velocity releases a bomb. As the bomb drops down from the aeroplane,

1. It will always be vertically below the aeroplane
2. It will be vertically below the aeroplane only if the aeroplane Is flying horizontally
3. It will be vertically below the aeroplane only if the aeroplane Is flying at an angle of 45° to the horizontal
4. It will gradually fall behind the aeroplane if the plane is flying horizontally

Answer: 1. It will always be vertically below the aeroplane

The horizontal component of the velocity of the aeroplane will always be the same as the horizontal component of the velocity Of the bomb. Hence, in all cases, the two will have the same horizontal displacement in die same time interval. So, the bomb will be vertically below the aeroplane in all cases.

Question 19. Two stones are projected simultaneously in the same vertical plane from the same point but with different speeds and at different angles to the horizontal. The path followed by one stone as seen by the other is

1. A straight vertical line
2. A straight line making a constant angle (not = 90°) with the horizontal
3. A parabola
4. A hyperbola

Answer: 2. A straight line making a constant angle (not = 90°) with the Horizontal

In a projectile motion, the velocity vector at any time is given by

⇒ \(\vec{v}=\vec{u}+\vec{g} t=(u \cos \theta) \hat{i}+(u \sin \theta-g t) \hat{j}\)

for the first stone, \(\vec{v}_1=\left(u_1 \cos \theta_1\right) \hat{i}+\left(u_1 \sin \theta_1-g t\right) \hat{j}\)

and for the second stone, \(\vec{\nabla}_2=\left(u_2 \cos \theta_2\right) \hat{i}+\left(u_2 \sin \theta_2-g t\right) \hat{j}\)

∴ the relative velocity of the first stone relative to the second stone is

⇒ \(\vec{v}_{12}=\vec{v}_1-\vec{v}_2=\left(\vec{v}_{\mathrm{r}}\right)_x-\left({\overrightarrow{v_r}}_{\mathrm{r}}\right)_y\) = constant

Hence, the die path followed by one stone as seen by the other will be a straight line making a constant with the horizontal.

Question 20. A gun kept on a horizontal road is used to hit a car travelling on the same road away from the gun at a uniform speed of 10√2 m s^-1. The car is at a distance of 150 m from the gun when it is fired at an angle of 45° to the horizontal. With what speed should the shell be projected so that it hits the car?

1. 20 ms^-1
2. 30ms^-1
3. 40ms^-1
4. 50ms^-1

Answer: 4. 50ms^-1

Let the bullet hit the car at B, where the range is

⇒ \(O B=\frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin 90^{\circ}}{10}=\frac{u^2}{10}\)

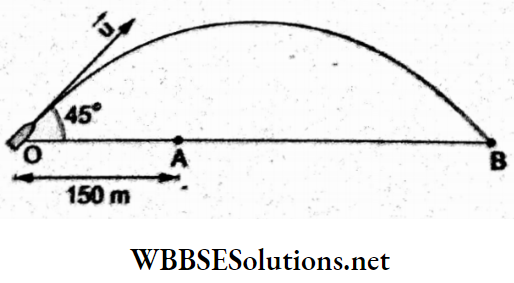
Time of flight, \(T=\frac{2 u \sin \theta}{g}=\frac{2 u}{\sqrt{2} \times 10}\)

During this time, the car travels a distance of

⇒ \(A B=\text { velocity } \times T=10 \sqrt{2} \times \frac{2 u}{10 \sqrt{2}}\)

Thus, R = OA + AB

or \(\frac{u^2}{10}\) = 150 + 2m

or u²- 20u -1500 = 0

or (u-50)(u + 30) = 0.

Hence, the permissible value of the speed of the shell is 50 m s^-1.

Question 21. A projectile has a maximum range of 200 m. What is the maximum height attained by it?

1. 28 m
2. 50 m
3. 75 m
4. 100 m

Answer: 2. 50 m

For the maximum range, the angle of projection is 0 = 45°. So

⇒ \(R_{\max }=\frac{u^2 \sin \left(2 \times 45^{\circ}\right)}{g}=\frac{u^2}{g}=200\)

Hence, the maximum height is

⇒ \(H=\frac{u^2 \sin ^2 45^{\circ}}{2 g}=\frac{1}{2}\left(\frac{u^2}{g}\right)\left(\frac{1}{\sqrt{2}}\right)^2\)

⇒ \(\frac{1}{2}(200 \mathrm{~m})\left(\frac{1}{2}\right)=50 \mathrm{~m}\)

Question 22. Which of the following remains constant during the motion of a projectile fired from a planet?

1. Kinetic energy
2. Momentum
3. The vertical component of the velocity
4. Horizontal component of the velocity

Answer: 4. Horizontal component of the velocity

For any planet, the acceleration due to gravity (\(\vec{g}\)) acts vertically downwards. So, its component along the horizontal is geos 90° = 0. Hence, the horizontal component of the velocity remains constant.

Question 23. A ball is projected at an angle of 60° with the horizontal with a kinetic energy of K. Its kinetic energy at the highest point of the trajectory will be

1. 2K
2. K
3. \(\frac{K}{2}\)
4. \(\frac{K}{4}\)

Answer: 4. \(\frac{K}{4}\)

The kinetic energy at the point of projection is \(K=\frac{1}{2} m u^2\)

Let the velocity at the maximum height be v. Since the horizontal component of the velocity remains constant, u cos 60° = v.

∴ The kinetic energy at the highest point is

⇒ \(K^{\prime}=\frac{1}{2} m v^2=\frac{1}{2} m\left(u \cos 60^{\circ}\right)^2\)

⇒ \(\frac{1}{4}\left(\frac{1}{2} m u^2\right)=\frac{K}{4}\)

Question 24. Four projectiles are projected with the same speed at the angles 20°, 35°, 60° and 75° with the horizontal. The horizontal range will be maximum for the projectile whose angle of projection is

1. 20°
2. 35°
3. 60°
4. 75°

Answer: 2. 35°

Range = \(R=\frac{u^2 \sin 2 \theta}{8}\)

For the same value of u, R oc sin 20.

Since sin 20 is maximum for θ = 35°, the range is maximum for the angle of projection θ = 35°

Question 25. The maximum height attained by a projectile is increased by 10% by increasing the speed of projection, without changing the angle of projection. The percentage increase in the horizontal range will be

1. 5%
2. 15%
3. 10%
4. 20%

Answer: 3. 10%

Maximum height = \(H=\frac{u^2 \sin ^2 \theta}{2 g}\)

Since (sin²θ)/2g is constant,

⇒ \(\frac{d H}{H}=2\left(\frac{d u}{u}\right)\)

⇒ \(2\left(\frac{d u}{u}\right)=10 \%=\frac{1}{10} \Rightarrow \frac{d u}{u}=\frac{1}{20} .\)

Horizontal range = \(R=\frac{u^2 \sin 2 \theta}{g}\)

Since (sin²θ)/g is constant,

⇒ \(\frac{d R}{R}=2\left(\frac{d u}{u}\right)=2\left(\frac{1}{20}\right)=\frac{1}{10}=10 \%\)

Question 26. A projectile has a range R and a time of flight T. If the range is doubled by increasing the speed of projection without changing the angle of projection, the time of flight will become

1. \(\frac{T}{2}\)
2. 2T
3. \(\frac{T}{\sqrt{2}}\)
4. √2T

Answer: 4. √2T

Initially, \(R=\frac{u_1^2 \sin 2 \theta}{g} \text { and } T=\frac{2 u \sin \theta}{g}\)

When the range is doubled, \(2 R=\frac{u_2^2 \sin 2 \theta}{g}\)

Hence,

⇒ \(u_1^2=\frac{u_2^2}{2} \Rightarrow u_1=\frac{u_2}{\sqrt{2}} \Rightarrow u_2=\sqrt{2} u_1\)

∴ The corresponding value of the time of light is

⇒ \(T^{\prime}=\frac{2 u_2 \sin \theta}{g}=\frac{2 \sqrt{2} u_1 \sin \theta}{g}=\sqrt{2} T .\)

Question 27. For the same range R, the maximum heights attained are h₁ and h₂. Then, R, h₁ and h₂ are related as

1. \(R=\sqrt{h_1 h_2}\)
2. \(R=2 \sqrt{h_1 h_2}\)
3. \(R=3 \sqrt{h_1 h_2}\)
4. \(R=4 \sqrt{h_1 h_2}\)

Answer: 4. \(R=4 \sqrt{h_1 h_2}\)

For the same range, the angles of projection are complementary. Hence,

⇒ \(\theta_1+\theta_2=90^{\circ}\)

For, \(\theta_1, h_1=\frac{u^2 \sin ^2 \theta}{2 g} \text { and } R=\frac{u^2 \sin 2 \theta}{g}\)

For , \(\theta_2=90^{\circ}-\theta_1, h_2=\frac{u^2 \sin ^2\left(90^{\circ}-\theta\right)}{2 g}=\frac{u^2}{2 g} \cos ^2 \theta\)

and , \(R=\frac{u^2}{g} \sin 2\left(90^{\circ}-\theta\right)=\frac{u^2}{g} \sin 2 \theta\)

∴ \(\sqrt{h_1 h_2}=\frac{u^2}{2 g} \sin \theta \cos \theta=\frac{u^2}{4 g} \sin 2 \theta=\frac{R}{4}\)

Hence, \(R=4 \sqrt{h_1 h_2}\)

Question 28. A ball is projected vertically upwards at a certain initial speed. Another ball is projected at an angle of 60° with the vertical at the same initial speed. The ratio of their maximum heights reached is

1. 4:1
2. 2:3
3. 3:2
4. 2:1

Answer: 3. 3:2

For the projection along the vertical,

⇒ \(v^2=u^2-2 g h=0 \Rightarrow h=\frac{u^2}{2 g}\)

For the projection at the angle

θ = 90°- 60°

= 30°, the maximum height is

⇒ \(H=\frac{u^2 \sin ^2 30^{\circ}}{2 g}=\frac{1}{4} h\)

∴ \(\frac{h}{H}=\frac{h}{\frac{h}{4}}=\frac{4}{1}=4: 1\)

Question 29. Two balls A and B are projected simultaneously from the same point. A is projected vertically upwards and B at 30° to the vertical. They reach the ground simultaneously. The velocities of projection of A and B are in the ratio

1. 1:√3
2. √3:1
3. 2:√3
4. √3:2

Answer: 4. √3:2

For the motion along the vertical, \(v=u_{\mathrm{A}}-g t_{\mathrm{A}}=0\). So, the time of flight (up and down) is

⇒ \(T_{\mathrm{A}}=\frac{2 u_{\mathrm{A}}}{g}\)

For the projectile motion at the angle 0 = 90°- 30° = 60°, the time of flights

⇒ \(T_{\mathrm{B}}=\frac{2 u_{\mathrm{B}} \sin 60^{\circ}}{g}=\frac{\sqrt{3} u_{\mathrm{B}}}{8} .\)

Since,

⇒ \(T_{\mathrm{A}}=T_{\mathrm{B}}, 2 u_{\mathrm{A}}=\sqrt{3} u_{\mathrm{B}}\)

⇒ \(\frac{u_{\mathrm{A}}}{u_{\mathrm{B}}}=\frac{\sqrt{3}}{2}=\sqrt{3}: 2\)

Question 30. A body is projected with a velocity \(\vec{v}=(3 \hat{i}+4 \hat{j}) \mathrm{m} \mathrm{s}^{-1}\). The maximum height attained by the body is

1. 0.8 m
2. 8 m
3. 80 m
4. 800 m

Answer: 1. 0.8 m

Given that the velocity of projection is

⇒ \(\vec{v}=(3 \hat{i}+4 \hat{j}) \mathrm{m} \mathrm{s}^{-1}=\left(v_x \hat{i}+v_y \hat{j}\right) \mathrm{m} \mathrm{s}^{-1}\)

The speed of projection is \(v=\sqrt{3^2+4^2} \cdot \mathrm{m} \mathrm{s}^{-1}=5 \mathrm{~m} \mathrm{~s}^{-1}\), and for die angle of projection 0,

⇒ \(\tan \theta=\frac{v_y}{v_x}=\frac{4}{3} \Rightarrow \sin \theta=\frac{4}{5}\)

∴ maximum height \(=H=\frac{u^2 \sin ^2 \theta}{2 g}=\frac{\left(5 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\left(\frac{4}{5}\right)^2}{20 \mathrm{~m} \mathrm{~s}^{-2}}\)

= 0.8m

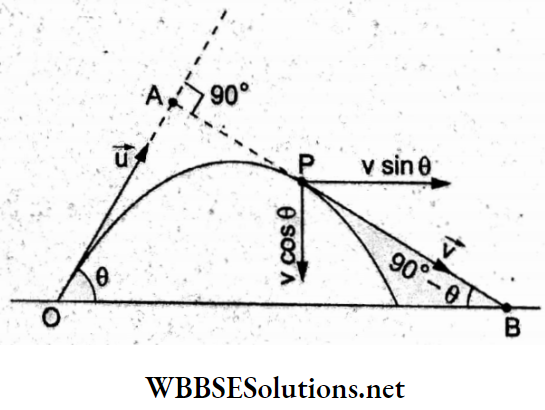
Question 31. A body is projected at an angle of 0 with the horizontal. The velocity of the body will become perpendicular to the velocity of projection after a time t equal to

1. \(\frac{2 u \sin \theta}{g}\)
2. \(\frac{u \sin \theta}{8}\)
3. \(\frac{2 u}{g \sin \theta}\)
4. \(\frac{u}{g \sin \theta}\)

Answer: 4. \(\frac{u}{g \sin \theta}\)

At O, the angle of projection is \(\theta\), and at P, the velocity vector \(\vec{v}\) is perpendicular to the direction of the velocity of projection.

In \(\triangle \mathrm{OAB}, \angle P B O=90^{\circ}-\theta\)

The components of v along the horizontal are v_x = v cos (90°- 0) = v sin 0 and v_y = v cos 0.

Since the horizontal component of the velocity remains constant,

u cos θ = v sin θ …..(1)

For motion along the vertical,

⇒ \(-v \cos \theta=u \sin \theta-g t \Rightarrow t=\frac{1}{g}(u \sin \theta+v \cos \theta)\)

Substituting \(v=\frac{u \cos \theta}{\sin \theta}\) from (i), we get

⇒ \(t=\frac{1}{g}\left(u \sin \theta+\frac{u \cos ^2 \theta}{\sin \theta}\right)=\frac{u}{g \sin \theta}\)

Question 32. The equation of the trajectory of a projectile is y- ax- bx², where a and b are constants of motion. The horizontal range of the projectile is

1. \(\frac{a}{b}\)
2. \(\frac{\sqrt{a}}{2 b}\)
3. \(\frac{a^2}{2 b}\)
4. \(\frac{a^2}{4 b}\)

Answer: 1. \(\frac{a}{b}\)

Given that y-ax- bx².

Comparing this with the equation of trajectory,

⇒ \(y=(\tan \theta) x-\left(\frac{8}{2 u^2 \cos ^2 \theta}\right) x^2\)

we get \(a=\tan \theta \text { and } b=\frac{g}{2 u^2 \cos ^2 \theta}\)

Now, horizontal range = \(R=\frac{u^2 \sin 2 \theta}{g}=\frac{2 u^2 \sin \theta \cos \theta}{g}\)

⇒ \(\frac{2 u^2 \cos ^2 \theta \tan \theta}{g}=\frac{a}{b}\)

Question 33. In the preceding question, the greatest height attained by the projectile is

1. \(\frac{a}{b}\)
2. \(\frac{a^2}{4 b}\)
3. \(\frac{\sqrt{a}}{2 b}\)
4. \(\frac{a^2}{2 b}\)

Answer: 2. \(\frac{a^2}{4 b}\)

Maximum height = \(H=\frac{u^2 \sin ^2 \theta}{2 g}=\frac{u^2 \cos ^2 \theta \tan ^2 \theta}{2 g}\)

⇒ \(\frac{2 u^2 \cos ^2 \theta \tan ^2 \theta}{4 g}=\frac{a^2}{4 b}\) [from preceding solution].

Question 34. The velocity of a projectile at the initial point A is \((2 \hat{i}+3 \hat{j}) \mathrm{m} \mathrm{s}^{-1}\). Its velocity at the point B is

1. \((2 \hat{i}+3 \hat{j}) \mathrm{m} \mathrm{s}^{-1}\)
2. \((2 \hat{i}-3 \hat{j}) \mathrm{m} \mathrm{s}^{-1}\)
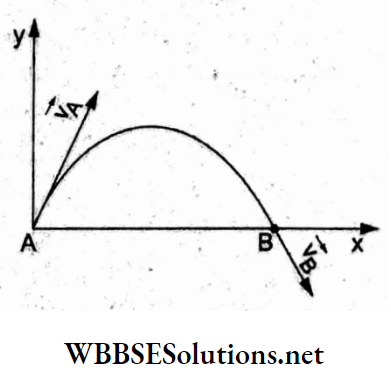
3. \((-2 \hat{i}-3 \hat{j}) \mathrm{ms}^{-1}\)
4. \((-2 \hat{i}+3 \hat{j}) \mathrm{ms}^{-1}\)

Answer: 2. \((2 \hat{i}-3 \hat{j}) \mathrm{m} \mathrm{s}^{-1}\)

Let the velocity at B be \(v_x \hat{i}+v_y \hat{j}\)

The initial velocity of projection is \(\vec{u}=2 \hat{i}+3 \hat{j}\)

So, at B in the same horizontal plane, the x-component will remain
unchanged, while the y-component will reverse its sign.

So, the velocity at B is \(\vec{v}=(2 \hat{i}-3 \hat{j}) \mathrm{ms}^{-1}\) m s^-1

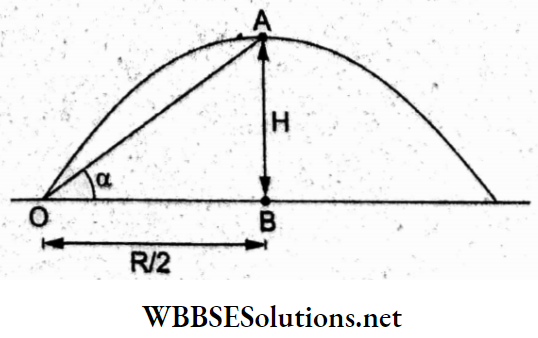
Question 35. A projectile is fired at an angle of 45° with the horizontal. The elevation angle of the projectile at its highest point as seen from the point of projection is

1. 45°
2. 60°
3. \(\tan ^{-1}\left(\frac{1}{2}\right)\)
4. \(\tan ^{-1}\left(\frac{\sqrt{3}}{2}\right)\)

Answer: 3. \(\tan ^{-1}\left(\frac{1}{2}\right)\)

The angle of elevation at the highest point A is ΔAOB = a.

⇒ \(\tan \alpha=\frac{H}{R / 2}\)

Now, \(H=\frac{u^2 \sin ^2 45^{\circ}}{2 g}=\frac{u^2}{4 g}\)

and \(\frac{R}{2}=\frac{u^2 \sin 45^{\circ} \cos 45^{\circ}}{g}=\frac{u^2}{2 g}\)

∴ \(\tan \alpha=\frac{\frac{u^2}{4 g}}{\frac{u^2}{2 g}}=\frac{1}{2} \Rightarrow \alpha=\tan ^{-1}\left(\frac{1}{2}\right)\)

Question 36. The speed of a projectile at its maximum height is half its initial speed of projection. The angle of projection is

1. 15°
2. 60°
3. 45°
4. 30°

Answer: 2. 60°

Let u = speed of projection and v = speed at maximum height.

Since the horizontal component remains the same, \(u \cos \theta=v. \text { But } v=\frac{u}{2}\)

∴ \(u \cos \theta=\frac{u}{2} \Rightarrow \cos \theta=\frac{1}{2} \Rightarrow \theta=60^{\circ}\)

Question 37. During the projection of a projectile at angles 45°- 0 and 45°+ θ, with the horizontal, the ranges described by the projectile are in the ratio

1. 2:1
2. 1:2
3. 1:1
4. 1:3

Answer: 3. 1:1

The given angles of projection are a = 45°- θ and p = 45° + θ.

a + B = 45°-  θ + 45° + θ = 90°.

So, the angles of projection are complementary.

Hence, the range will be the same in both cases and the ratio R1: R2 will be 1:1.

Question 38. A projectile is given an initial velocity of \((\hat{i}+2 \hat{j}) \mathrm{m} \mathrm{s}^{-1}, \text { where } \hat{i}\), where i is along the ground and is along the upward vertical. If g = 10 m s, the equation of the trajectory is

1. 2y = 2x- 5x²
2. 4y = 2x- 5X²
3. 4y = 2x – 25x²
4. y = 2x-5x²

Answer: 4. y = 2x-5x²

Given that the velocity of projection is \(\vec{u}=\hat{i}+2 \hat{j}\)

∴ \(u=\sqrt{u_x{ }^2+u_y{ }^2}=\sqrt{1+4}=\sqrt{5}\),

⇒ tanθ = \(\frac{2}{1} \text { and } \cos \theta=\frac{1}{\sqrt{5}}\)

The equation of the trajectory is

⇒ \(y=x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta}\)

or, \(y=2 x-\frac{10 x^2}{2(5)\left(\frac{1}{5}\right)}\)

or, y = 2x- 5X².

Question 39. A boy can throw a ball up to a maximum height of 10 m. The maximum horizontal distance to which the boy can throw the same ball will be

1. 20 √2 m
2. 10 m
3. 10 √2m m
4. 20 m

Answer: 4. 20 m

For motion along the vertical,

⇒ \(v^2=u^2-2 g h=0 \Rightarrow u^2=2 g h=2 \times 10 \times 10=200\)

For the maximum horizontal range, 0 = 45°.

So,

⇒ \(R_{\max }=\frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin 90^{\circ}}{g}=\frac{200}{10} \mathrm{~m}\)

= 20m.

Question 40. A projectile has the same range R for two angles of projection. It is launched at the same speed in both cases. If T₁ and T₂ are the times of flight in the two situations then

1. T₁T₂ is independent of R
2. \(T_1 T_2 \propto R^2\)
3. \(\frac{T_1}{T_2}=\tan \theta\)
4. \(\frac{T_1}{T_2}=\tan ^2 \theta\)

Answer: 3. \(\frac{T_1}{T_2}=\tan \theta\)

For the same range, the angles of projection must be complementary.

So, θ₁ + θ₂ = 90°

∴ \(T_1=\frac{2 u \sin \theta}{g} \text { and } T_2=\frac{2 u \sin \left(90^{\circ}-\theta\right)}{g}=\frac{2 u \cos \theta}{g}\)

∴ \(T_1 T_2=\frac{4 u^2 \sin \theta \cos \theta}{g^2}=\frac{2}{g}\left(\frac{u^2 \sin 2 \theta}{g}\right)=\frac{2 R}{g}\)

But \(\frac{T_1}{T_2}=\frac{\frac{2 u}{g} \sin \theta}{\frac{2 u}{g} \cos \theta}=\tan \theta\)

Question 41. A particle moves in a circle of radius 5 cm at a constant speed and has a time period of 0.2π s. The acceleration of the particle is

1. 25 m s^-2
2. 36 ms^-2
3. 5 ms^-2
4. 15 ms^-2

Answer: 4. 15 ms^-2

In a uniform circular motion, the acceleration is

⇒ \(a=\frac{v^2}{R}=\omega^2 R\)

Given that R = 5 cm = 5 x 10~2 m and T = 0.2n s

∴ \(a=\left(\frac{2 \pi}{0.2 \pi \mathrm{s}}\right)^2\left(5 \times 10^{-2} \mathrm{~m}\right)=5 \mathrm{~m} \mathrm{~s}^{-2}\)

Question 42. A stone tied to the end of a 1-m-long string is whirled in a horizontal circle at a constant speed. If it makes 22 revolutions in 44 seconds, what is the magnitude and direction of the acceleration of the stone?

1. \(\pi^2 \mathrm{~m} \mathrm{~s}^{-2}\), directed along the radius towards the centre
2. \(\pi^2 \mathrm{~m} \mathrm{~s}^{-2}\), directed along the radius away from the centre
3. \(\pi^2 \mathrm{~m} \mathrm{~s}^{-2}\), directed along the tangent to the circle
4. \(\frac{\pi^2}{2} \mathrm{~m} \mathrm{~s}^{-2}\), directed along the radius towards the centre

Answer: 1. \(\pi^2 \mathrm{~m} \mathrm{~s}^{-2}\), directed along the radius towards the centre

Given that the radius of the circular path = R = 1.0 m

and angular speed = \(\omega=\frac{2 \pi}{T}=2 \pi \times \text { frequency }=2 \pi \times \frac{22 \mathrm{rev}}{44 \mathrm{~s}}=\pi \mathrm{s}^{-1}\)

∴ radial acceleration = \(a=\omega^2 R=\left(\pi \mathrm{s}^{-1}\right)^2(1.0 \mathrm{~m})=\pi^2 \mathrm{~m} \mathrm{~s}^{-2}\)

In a uniform circular motion, the tangential acceleration is zero, so the net acceleration is radially directed towards the centre.

Question 43. A particle moves along a circle of radius (20/ft) m with a constant tangential acceleration. If the die velocity of the particle is 80 m s at the end of the second revolution after the motion has begun, the magnitude of the tangential acceleration is

1. 40 ms^-2
2. 64On m s^-2
3. 160ft m s^-2
4. 40tu m s^-2

Answer: 1. 40 ms^-2

Given that radius = \(=R=\frac{20}{\pi} \mathrm{m}\), velocity = v = 80 m s^-1 and angular displacement = 0 = 2 rev =4n rad. For a nonuniform circular motion,

⇒ \(\omega^2=\omega_0^2+2 \alpha \theta \Rightarrow \omega^2=2 \alpha \cdot 4 \pi\) [… \(\omega_0=0\)]

∴ angular acceleration = \(\alpha=\frac{\omega^2}{8 \pi}=\frac{v^2}{8 \pi R^2}\)

Hence, tangential acceleration = \(a=R \alpha=\frac{v^2}{8 \pi R}\)

Substituting the values, \(a=\frac{\left(80 \mathrm{~m} \mathrm{~s}^{-1}\right)^2}{8 \pi\left(\frac{20}{\pi} \mathrm{m}\right)}=40 \mathrm{~m} \mathrm{~s}^{-2}\)

Question 44. Two particles, having masses M and m, are moving in circular paths of radii R and r respectively. If their times of revolution are equal, the ratio of their angular velocities will be equal to

1. \(\frac{r}{R}\)
2. \(\frac{R}{r}\)
3. 1
4. \(\sqrt{\frac{R}{r}}\)

Answer: 3. 1

Angular velocity = \(\omega=\frac{2 \pi}{T}\)

Since the times of revolution and T2 are equal, the angular velocities

⇒ \(\omega_1 \text { and } \omega_2\) are also equal.

Thus, the ratio is \(\frac{\omega_1}{\omega_2}=1\)

Question 45. A 500-kg car takes a round turn of radius 50 m with a velocity of 36 km h^-1. The centripetal force is

1. 1000 N
2. 750 N
3. 250 N
4. 1200 N

Answer: 1. 1000 N

Centripetal force = \(F=\frac{m v^2}{\dot{R}}\)

Given that \(m=500 \mathrm{~kg}, v=36 \mathrm{~km} \mathrm{~h}^{-1}=10 \mathrm{~m} \mathrm{~s}^{-1}\)

and R = 50m.

∴ \(F=\frac{(500 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)^2}{50 \mathrm{~m}}=1000 \mathrm{~N}\)

Question 46. A ball of mass 0.25 kg attached to the end of a string of length 1.96 m is moving in a horizontal circle. The string breaks if the tension exceeds 25 N. The maximum speed with which the ball can be revolved is

1. 5 ms^-1
2. 3 m s^-1
3. 14 ms^-1
4. 3.92 ms^-1

Answer: 3. 14 ms^-1

Maximum tension = 25 N = \(\frac{m v^2}{R}\)

Hence, the maximum speed is

⇒ \(v=\sqrt{\frac{25 R}{m}} \mathrm{~m} \mathrm{~s}^{-1}=\sqrt{\frac{25 \times 1.96}{0.25}} \mathrm{~m} \mathrm{~s}^{-1}=14 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 47. An electric fan has blades each of length 30 cm (measured from the axis of rotation). If the fan is rotating at 120 rpm, the acceleration of a point on the tip of each blade is

1. 160ms^-2
2. 50.55 ms^-2
3. 47.4 ms^-2
4. 23.7 ms^-2

Answer: 3. 47.4 ms^-2

Given that radius = R = 30 cm = 30 x 10^-2 m

and angular frequency = \(=\omega=120 \mathrm{rpm}=\frac{2 \pi \times 120}{60} \mathrm{rad} \mathrm{s}^{-1}\)

∴ the centripetal acceleration is

⇒ \(a=\omega^2 R=\left(4 \pi \mathrm{rad} \mathrm{s}^{-1}\right)^2(0.3 \mathrm{~m})\)

⇒ \(4.8 \pi^2 \mathrm{~m} \mathrm{~s}^{-2}=47.4 \mathrm{~m} \mathrm{~s}^{-2}\)

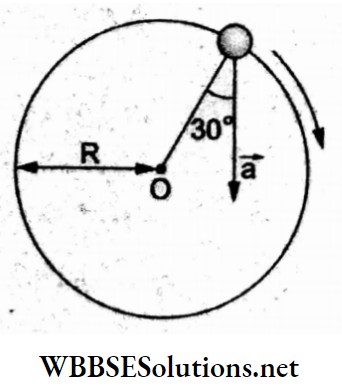
Question 48. In the given figure, a = 15 m s^-2 represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R = 2.5 m at a given time. The speed of the particle is

1. 5.7 ms^-1
2. 4.5 m s^-1
3. 5.0 ms^-1
4. 6.2 m s^-1

Answer: 1. 5.7 ms^-1

Radial acceleration aT = a cos 30°

⇒ \(\frac{v^2}{R} \Rightarrow\left(15 \mathrm{~m} \mathrm{~s}^{-2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{v^2}{2.5 \mathrm{~m}}\)

Hence, the speed of the particle is

⇒ \(v=\sqrt{15 \times \frac{\sqrt{3}}{2} \times 2.5} \mathrm{~m} \mathrm{~s}^{-1}=5.7 \mathrm{~m} \mathrm{~s}^{-1}\)

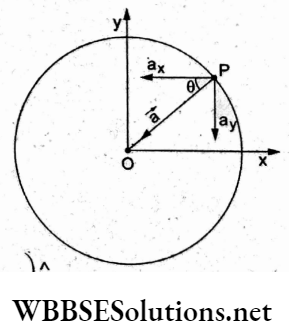
Question 49. For a particle undergoing uniform circular motion, the acceleration a at a point P(R, 0) on the circle of radius R is (where 9 is measured from die r-axis)

1. \(\left(\frac{v^2}{R}\right) \hat{i}+\left(\frac{v^2}{R}\right) \hat{j}\)
2. \(\left(-\frac{v^2}{R} \cos \theta\right) \hat{i}+\left(\frac{v^2}{R} \sin \theta\right) \hat{j}\)
3. \(\left(-\frac{v^2}{R} \sin \theta\right) \hat{i}-\left(\frac{v^2}{R} \cos \theta\right) \hat{j}\)
4. \(\left(-\frac{v^2}{R} \cos \theta\right) \hat{i}-\left(\frac{v^2}{R} \sin \theta\right) \hat{j}\)

Answer: 4. \(\left(-\frac{v^2}{R} \cos \theta\right) \hat{i}-\left(\frac{v^2}{R} \sin \theta\right) \hat{j}\)

In a uniform circular motion, the net acceleration (or centripetal acceleration) is directed radially towards the centre. Its x- and y-components relative to the origin O are both negative.

∴ \(|\vec{a}|=\frac{v^2}{R}\)

∴ \(\vec{a}=a_x \hat{i}+a_y \hat{j}=\left(-\frac{v^2}{R} \cos \theta\right) \hat{i}-\left(\frac{v^2}{R} \sin \theta\right) \hat{j}\)

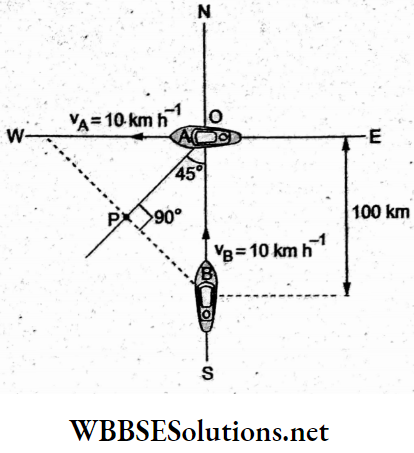
Question 50. A ship A is moving westwards with a speed of 10 km h^-1, and another ship B, 100 km south of A, is moving northwards with a speed of 10 km h^-1. The time after which the separation between them becomes minimal is

1. 5h
2. 10√2 h
3. 5 √2 h
4. 2 h

Answer: 1. 5h

The given situation is shown in the figure given on the next page. The velocity of ship A is v_A = 10 km h^-1 due west and the velocity of ship B is v_B = 10 km h^-1 due north. Initially,

OB = 100 km and the shortest distance = OP = OB cos 45°

⇒ \(\frac{100}{\sqrt{2}} \mathrm{~km}=50 \sqrt{2} \mathrm{~km}\)

The magnitude of the relative velocity is

⇒ \(v_{\mathrm{AB}}=\sqrt{v_{\mathrm{A}}^2+v_{\mathrm{B}}^2}=10 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\)

The time after which the separation between A and B is equal to

⇒ \(O P=50 \sqrt{2} \mathrm{~km} \text { is }\)

⇒ \(t=\frac{O P}{v_{\mathrm{AB}}}=\frac{50 \sqrt{2} \mathrm{~km}}{10 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}}=5h\)

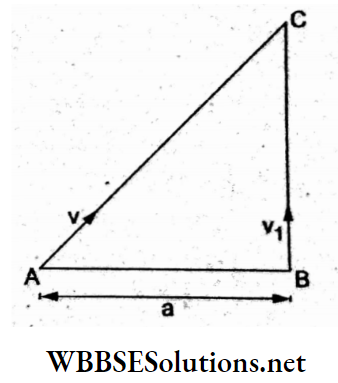
Question 51. Two boys are standing at the ends A and B of the ground, where AB = a. The boy at B starts running in a direction perpendicular to AB with a velocity v The boy at A starts running simultaneously with a velocity v and catches the other in a time t, where t equals

1. \(\frac{a}{\sqrt{v^2+v_1^2}}\)
2. \(\frac{a}{v+v_1}\)
3. \(\frac{a}{v-v_1}\)
4. \(\frac{a}{\sqrt{v^2-v_1^2}}\)

Answer: 4. \(\frac{a}{\sqrt{v^2-v_1^2}}\)

Let the meeting point of A and B be at C at the same time T.

So, AC = vT and BC = v₁T.

Now, AC² = AB² + BC²

⇒ \((v T)^2=a^2+\left(v_1 T\right)^2\)

⇒ \(T^2\left(v^2-v_1{ }^2\right)=a^2\)

⇒ \(T=\frac{a}{\sqrt{v^2-v_1^2}}\)

Question 52. The width of a river is 1 km. The velocity of a boat is 5 km h-1. The boat covers the width of the river in the shortest time of 15 min. Then, the velocity of the river stream is

1. 3 km h^-1
2. 4 km h^-1
3. √29 km h^-1
4. √41 km h^-1

Answer: 1. 3 km h^-1

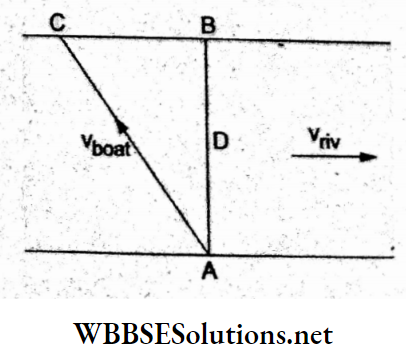
The boat moves along AC with velocity \(v_{\text {boat }}=5 \mathrm{~km} \mathrm{~h}^{-1}\).

It drifts due to the river current up to B, where BC = drift.

The actual displacement of the boat is AB = resultant velocity x time.

From the vector triangle of velocities,

⇒ \(v^2=v_{\text {boat }}^2-v_{\text {riv }}^2\)

Now, the resultant velocity is

⇒ \(v=\frac{A B}{T}=\frac{1 \mathrm{~km}}{\frac{1}{4} \mathrm{~h}}=4 \mathrm{~km} \mathrm{~h}^{-1}\)

∴ \(v_{\text {riv }}=\sqrt{v_{\text {boat }}^2-v^2}\)

⇒ \(\sqrt{\left(5 \mathrm{~km} \mathrm{~h}^{-1}\right)^2-\left(4 \mathrm{~km} \mathrm{~h}^{-1}\right)^2}=3 \mathrm{~km} \mathrm{~h}^{-1}\)

Question 53. A person aiming to reach exactly the opposite point on the bank of a river is swimming at a speed of 0.5 m s^-1 at an angle of 120° with the direction of the stream flow. The speed of the water in the stream is

1. 1.0 ms^-1
2. 0.5 m s^-1
3. 0.25 ms^-1
4. 0.433 m s^-1

Answer: 3. 0.25 ms^-1

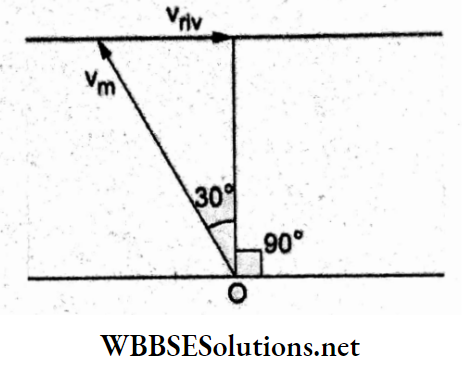
Let the speed of the river water be v_nv and that of the man be

⇒ \(v_{\mathrm{m}}=0.5 \mathrm{~m} \mathrm{~s}^{-1} \text {. }\)

As shown in the adjoining figure,

⇒ \( \sin 30^{\circ}=\frac{v_{\text {riv }}}{v_{\text {m }}}\)

or, \(v_{\text {riv }}=v_{\mathrm{m}} \sin 30^{\circ}\)

⇒ \(\left(0.5 \mathrm{~m} \mathrm{~s}^{-1}\right)\left(\frac{1}{2}\right)=0.25 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 54. A boat is sent across a river with a velocity of 8 km h^-1. If the resultant velocity of the boat is 10 km h^-1, the velocity of the river water is

1. 12.8 km h^-1
2. 10 km h^-1
3. 6kmh^-1
4. 8kmh^-1

Answer: 3. 6kmh^-1

Since the boat is directed across the river, its velocity \(\left(v_{\text {boat }}=8 \mathrm{~km} \mathrm{~h}^{-1}\right)\) makes an angle of 90° with the river current. Thus, for the resultant speed v, we have

⇒ \(v^2=v_{\text {boat }}^2+v_{\text {riv }}^2\)

⇒ \(\left(10 \mathrm{~km} \mathrm{~h}^{-1}\right)^2=\left(8 \mathrm{~km} \mathrm{~h}^{-1}\right)^2+v_{\mathrm{riv}}^2\)

⇒ \(v_{\text {riv }}=\sqrt{\left(10^2-8^2\right) \mathrm{km}^2 \mathrm{~h}^{-2}}=6 \mathrm{~km} \mathrm{~h}^{-1}\)

Question 55. An A150-m-long train is going towards the north at a speed of 10 m s^-1. A parrot is flying at 5 m s^-1 towards the south, parallel to the railway track. The time taken by the parrot to cross the train is

1. 8 s
2. 10 s
3. 12 s
4. 15 s

Answer: 2. 10 s

Given that the velocity of the train is

⇒ \(v_{\mathrm{t}}=10 \mathrm{~m} \mathrm{~s}^{-1}\)

and the velocity of the parrot (in the opposite direction) is,

⇒ \(v_{\mathrm{p}}=-5 \mathrm{~m} \mathrm{~s}^{-1}\)

∴ The relative velocity of the parrot with respect to the train is

⇒ \(\vec{v}_{\mathrm{pt}}=\vec{v}_{\mathrm{p}}-\vec{v}_{\mathrm{t}}\)

Substituting the values,\(v_{p t}=-5 \mathrm{~m} \mathrm{~s}^{-1}-10 \mathrm{~m} \mathrm{~s}^{-1}=-15 \mathrm{~m} \mathrm{~s}^{-1}\)

Thus, the parrot will appear to move at 15 m s^-1 towards the train.

∴ The time taken by the parrot to cross the train is

⇒ \(t=\frac{\text { length of train }}{\text { relative velocity of the parrot with respect to the train }}\)

⇒ \(\frac{150 \mathrm{~m}}{15 \mathrm{~m} \mathrm{~s}^{-1}}=10 \mathrm{~s}\)

Question 56. A jet aeroplane travelling from east to west at a speed of 500 km h^-1 ejects out gases of combustion at a speed of 1500 km h^-1 relative to the jet plane. What is the velocity of the gases with respect to an observer standing on the ground?

1. 1000 km h^-1 in the direction from w.est to east
2. 1000 km h^-1 in the direction from east to west
3. 2000 km h^-1 in the direction from west to east
4. 2000 km h^-1 in the direction from east to west

Answer: 1. 1000 km h^-1 in the direction from w.est to east

Let us assume the direction from the east to the west as the positive direction of the x-axis. Thus, the velocity of the jet plane is

⇒ \(\left(500 \mathrm{~km} \mathrm{~h}^{-1}\right) \hat{i}\)

Since this is relative to the ground, we can write

⇒ \(\vec{v}_{j, g r}=\left(500 \mathrm{~km} \mathrm{~h}^{-1}\right) \hat{i}\)

The velocity of the ejected gases relative to the jet plane is

⇒ \(\vec{v}_{\text {gas }, j}=\vec{v}_{\text {gas, gr }}-\vec{v}_{j, g r}\)

The velocity of the gases relative to the ground is

⇒ \(\vec{v}_{\text {gas, gr }}=\vec{v}_{\text {gas }, \mathrm{j}}+\vec{v}_{\mathrm{j}, \mathrm{gr}}\)

⇒ \(\left(-1500 \mathrm{~km} \mathrm{~h}^{-1}\right) \hat{i}+\left(500 \mathrm{~km} \mathrm{~h}^{-1}\right) \hat{i}=\left(-1000 \mathrm{~km} \mathrm{~h}^{-1}\right) \hat{i}\)

Here, the negative sign refers to the direction from the west to the east.

Question 57. A swimmer can swim in still water with a speed of 5 m s^-1. While crossing a river, his average speed is 3 m s^-1. If he crosses the river in the shortest possible time, what is the speed of the water?

1. 2 ms^-1
2. 4 m s^-1
3. 6 ms^-1
4. 8 m s^-1

Answer: 2. 4 m s^-1

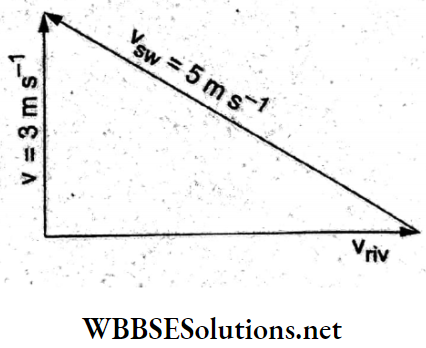
In order to cross the river in the shortest time, the resultant velocity v of the swimmer must be perpendicular to the velocity u_riv of the river current, as shown in the adjoining figure. Thus, from the figure,

⇒ \(v_{\mathrm{sw}}^2=v^2+v_{\mathrm{riv}}^2\)

⇒ \(v_{\mathrm{riv}}^2=v_{\mathrm{sw}}^2-v^2=(25-9)\left(\mathrm{m} \mathrm{s}^{-1}\right)^2=16\left(\mathrm{~m} \mathrm{~s}^{-1}\right)^2\)

velocity of the river = uriv = 4 ms^-1.

Question 58. Raindrops are falling vertically with a speed of 4 m s^-1. After some time, the wind starts blowing at a speed of 3 m s^-1 in the north-to-south direction. In order to protect himself from the rain, a man standing on the ground should hold his umbrella at an angle given by.

1. \(\theta=\tan ^{-1}\left(\frac{3}{4}\right)\) with the vertical towards the south
2. \(\theta=\tan ^{-1}\left(\frac{3}{4}\right)\) with the vertical towards the north
3. \(\theta=\cot ^{-1}\left(\frac{3}{4}\right)\) with the vertical towards ihe south
4. \(\theta=\cot ^{-1}\left(\frac{3}{4}\right)\) with the vertical towards the north

Answer: 2. \(\theta=\tan ^{-1}\left(\frac{3}{4}\right)\) with the vertical towards the north

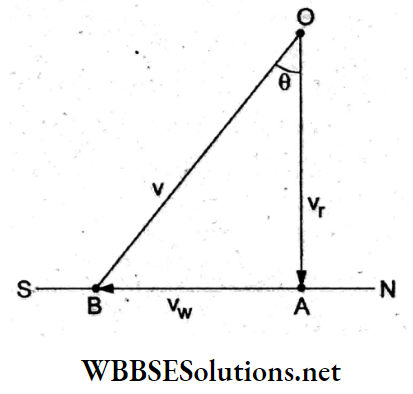
The velocity of the rain = v_r = 4 m s^-1 (directed vertically downwards) and the velocity of the wind =  v_w = 3ms⁴ (directed from the north to the south).

The motion of the raindrops will be affected simultaneously by gravity (downwards) and the wind (southwards).

Hence, the resultant velocity will be along OB (from the triangle law of vector addition).

In order to protect himself from the rain, the man must hold his umbrella tilted at an angle of 0 with the vertical (towards the north), where

⇒ \(\tan \theta=\frac{v_{\mathrm{W}}}{v_{\mathrm{r}}}=\frac{3 \mathrm{~m} \mathrm{~s}^{-1}}{4 \mathrm{~m} \mathrm{~s}^{-1}}=\frac{3}{4}\)

or, \(\theta=\tan ^{-1}\left(\frac{3}{4}\right)\)

Question 59. A swimmer can swim in still water at 4.0 km h^-1. If he swims in a river flowing at 3.0 km h^-1 and keeps his direction perpendicular to the water flow, what is his velocity relative to the ground?

1. \(5.0 \mathrm{~km} \mathrm{~h}^{-1}, \theta=\tan ^{-1}\left(\frac{3}{4}\right)\)
2. \(5.0 \mathrm{~km} \mathrm{~h}^{-1}, \theta=\tan ^{-1}\left(\frac{4}{3}\right)\)
3. \(4.0 \mathrm{~km} \mathrm{~h}^{-1}, \theta=\tan ^{-1}\left(\frac{3}{4}\right)\)
4. \(4.0 \mathrm{~km} \mathrm{~h}^{-1}, \theta=\tan ^{-1}\left(\frac{4}{3}\right)\)

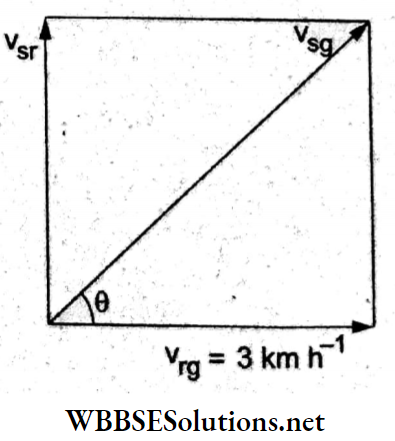
Answer: 2. \(5.0 \mathrm{~km} \mathrm{~h}^{-1}, \theta=\tan ^{-1}\left(\frac{4}{3}\right)\)

The velocity of the swimmer relative to the river current is
v_{\mathrm{sr}}=4 \mathrm{~km} \mathrm{~h}^{-1}\(\) perpendicular to the river flow. The velocity of the river
current relative to the ground is \(\)

Thus, the velocity of the swimmer relative to the ground will be

⇒ \(\vec{v}_{\mathrm{sg}}=\vec{v}_{\mathrm{sr}}+\vec{v}_{\mathrm{rg}}\)

These velocity vectors are shown in the adjoining diagram. The magnitude of the velocity of the swimmer relative to the ground is

⇒ \(v_{\mathrm{sg}}=\sqrt{4^2+3^2} \mathrm{~km} \mathrm{~h}^{-1}=5 \mathrm{~km} \mathrm{~h}^{-1}\)

The angle 0 with the direction of the flow is given by

⇒ \(\tan \theta=\frac{4}{3} \Rightarrow \theta=\tan ^{-1}\left(\frac{4}{3}\right)\)

Question 60. A man is walking on a level road at 3 km h^-1. Raindrops fall Vertically at 4.0 km h^-1. What is the velocity of the raindrops relative to the man?

1. \(5.0 \mathrm{~km} \mathrm{~h}^{-1}, \theta=\tan ^{-1}\left(\frac{3}{4}\right)\) with the vertical
2. \(5.0 \mathrm{~km} \mathrm{~h}^{-1}, \theta=\tan ^{-1}\left(\frac{4}{3}\right)\) with the vertical
3. 7.0 km h_1, 0 = 45° with the vertical
4. 5.0 km h-1, 0 = 60° with the vertical

Answer: 1. \(5.0 \mathrm{~km} \mathrm{~h}^{-1}, \theta=\tan ^{-1}\left(\frac{3}{4}\right)\) with the vertical

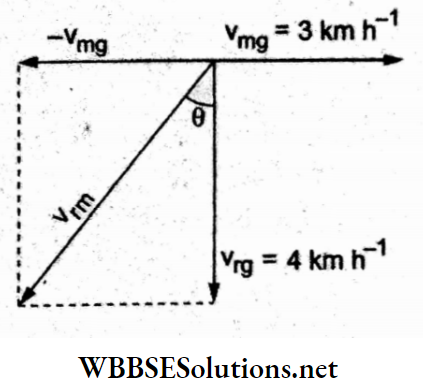
The velocities of the raindrops and the man are given relative to the ground. Thus, the velocity of the raindrops relative to the man is

⇒ \(\vec{v}_{\mathrm{rm}}=\vec{v}_{\mathrm{rg}}-\vec{v}_{\mathrm{mg}}\)

The three velocity vectors are shown in the adjoining figure. The velocity of the raindrops relative to the man is

⇒ \(v_{\mathrm{rm}}=\sqrt{4^2+3^2} \mathrm{~km} \mathrm{~h}^{-1}=5 \mathrm{~km} \mathrm{~h}^{-1}\)

The angle with the vertical is

⇒ \(\theta=\tan ^{-1}\left(\frac{3}{4}\right)\)

Question 61. Raindrops are falling vertically. When a car moves at a speed of v, the raindrops appear to fall at 60° with the horizontal, and when the speed of the car is (B + 1)v, they appear to make an angle of 45° with the vertical. The value of p is

1. 0.123
2. 0.414
3. 0.732
4. 0.24

Answer: 3. 0.732

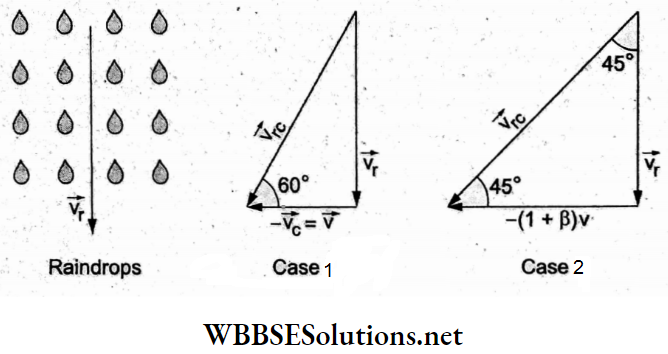
In Case 1, tan60° = \(\frac{v_{\mathrm{r}}}{v}=\sqrt{3} .\)

In Case 2, tan 45° = \(\frac{v_x}{(1+\beta) v}=1\)

∴ \(1+\beta=\sqrt{3} \Rightarrow \beta=0.732\)

Question 62. Starting from the origin at the time t = 0, with an initial velocity of \(5 \hat{j} \mathrm{~m} \mathrm{~s}^{-1}\) a particle moves in the xy-plane with a constant acceleration of \((10 \hat{j}+4 \hat{j}) \mathrm{m} \mathrm{s}^{-2}\). At a time t, its coordinates are (20 m, y₀). The values of t and y₀ are respectively

1. 5s and 25m
2. 2s and 4m
3. 2s and 18m
4. 4s and 52 m

Answer: 3. 2 s and 18m

For the motion along the x-direction,

⇒ \(u_x=0, a_x=10 \mathrm{~m} \mathrm{~s}^{-2} \text { and } x_2-x_1=x_0=20 \mathrm{~m} \text {. }\)

∴ \(20 \mathrm{~m}=\frac{1}{2}\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right) t^2 \Rightarrow t=2 \mathrm{~s}\)

For the motion along the y-direction,

⇒ \(y_0=\left(5 \mathrm{~m} \mathrm{~s}^{-1}\right)(2 \mathrm{~s})+\frac{1}{2}\left(4 \mathrm{~m} \mathrm{~s}^{-2}\right)(2 \mathrm{~s})^2=18 \mathrm{~m}\)

∴ \(t=2 \mathrm{~s} \text { and } y_0=18 \mathrm{~m}\)