WBCHSE Class 11 Physics Notes For Superposition Of Waves 

Superposition Of Waves

Principle Of Superposition Of Waves

The simultaneous progress of more than one wave through a region of space produces the phenomenon known as the superposition of waves. During superposition, each of the waves travels independently, i.e., a wave retains its individual properties though it overlaps on other waves. For example, when different musical instruments are played at a time, the notes from each instrument can be detected separately.

If more than one waves are incident simultaneously on a particle in a medium, the particle would have different displacements for each of the separate waves. But these displacements of the particle occur at the same time, i.e., a resultant displacement of the particle occurs for all the waves.

Since displacement is a vector quantity, the resultant displacement is the vector sum of all the individual displacements. This is known as the principle of superposition of waves.

Superposition Of Two Single Waves Or Two Wave Pulses:

• For example, let two wave pulses P and Q of equal displacement and of the same sign (both upward) travel with equal speed along the length of a string but in opposite directions the two wave pulses at a later instant before superposition. The result is when the two pulses superpose each other at a time t.
• It is found from that at time t, a wave pulse R of displacement equal to the sum of the displacements of wave pulses P and Q is formed. Then, after that, the wave pulses P and Q retaining their original shapes move along the string as shown.

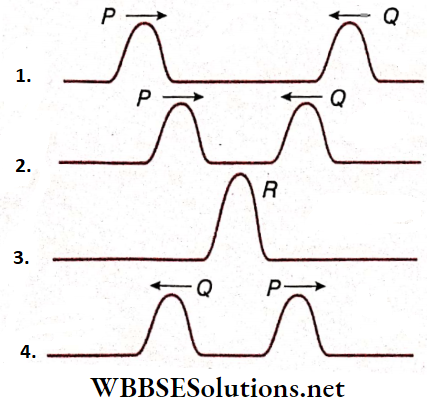
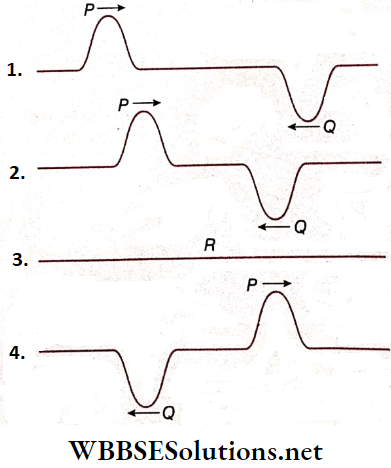
• Now, let the two wave pulses P and Q having equal displacement but of opposite signs are move along the length of a string with equal speed in opposite directions and show that after a short time, the two pulses get closer to each other.
• At the time t’, the two wave pulses superpose and produce a resultant wave pulse R of zero displacements. After that, the two wave pulses retain their original shapes and continue to move along the length of the string as shown.

Superposition Of Waves Statement: The resultant displacement of a particle In a medium due to more than one wave Is equal to the vector sum of the different displacements produced by the Individual waves separately.

Let n number of waves traveling in a medium superpose on each other. If \(\overrightarrow{y_1}, \overrightarrow{y_2}, \overrightarrow{y_3}, \cdots \cdots \vec{y}_n\) are the displacements at a point due to n waves, then the resultant displacement will be \(\vec{y}=\overrightarrow{y_1}+\overrightarrow{y_2}+\overrightarrow{y_3}+\cdots \overrightarrow{y_n}\)

If the displacements due to the two wave pulses are equal and in the same direction, i.e., \(\left|\overrightarrow{y_1}\right|=\left|\overrightarrow{y_2}\right|=A\), then from the superposition principle, the magnitude of the resultant displacement will be \(\left|\overrightarrow{y_1}\right|=A+A=2 A\), as shown.

If the displacements are equal but in opposite directions, then the magnitude of the resultant displacement will be \(|\vec{y}|=A+(-A)=A-A=0\), as shown.

• If different displacements are collinear, it is sufficient to take their algebraic sum, i.e., to determine the resultant displacement, two like vectors are added while two unlike vectors are subtracted. The principle of superposition is applicable to all types of waves, say, electromagnetic waves, sound waves, etc.
• The best example of the superposition of waves is the melody of musical instruments. Another classic example is the throwing of more than one stone in a lake. In fact, most of the sounds we produce while speaking is a superposition. In the case of light waves, this is also valid. Any light in nature we see is in general a superposition.

The Superposition Of Similar Waves Gives Rise To The Following Important Phenomena:

Stationary Waves: The superposition of two identical but oppositely directed progressive waves produces stationary waves.

Beats: Two progressive waves of the same amplitude and velocity, but of slightly different frequencies, produce beats on superposition.

Interference: Two identical progressive waves, on superposition with a constant phase difference, produce interference.

The first two of these three phenomena will be discussed in this chapter, with special emphasis on sound waves.

Superposition Waves Numerical Examples

Example 1. The displacement of a periodically vibrating particle is y = 4cos(\(\frac{1}{2}\)t) sin (1000t). Calculate the number of harmonic waves that are superposed.
Solution:

y = \(4 \cos ^2\left(\frac{1}{2} t\right) \sin (1000 t)\)

= \(2 \cdot 2 \cos ^2\left(\frac{1}{2} t\right) \cdot \sin (1000 t)\)

= 2(1 + cos t) sin (1000t)

= 2sin(1000t) + 2 sin (1000t) cost

= 2 sin(1000t) + sin(1000t+ t) + sin(1000t- t)

= 2 sin( 1000t) + 1 sin(1001t)+ 1 sin(999t)

= y₁+y₂+y₃

Here each of y₁, y₂, and y₃ is in the form of A sinωt. Thus, each of them represents a harmonic wave.

Hence, the number of superposed harmonic waves = 3.

Example 2. The displacements of a particle at the position x = 0 in a medium due to two different progressive waves are y₁ = sinπrt and y₂ = sin2πt, respectively. How many times would the particle come to rest in every second?
Solution:

According to the principle of superposition, the resultant displacement of the particle is

y = y₁ +y₂= sin4πt+sin2πt

= \(2 \sin \frac{4 \pi t+2 \pi t}{2} \cos \frac{4 \pi t-2 \pi t}{2}=2 \sin 3 \pi t \cdot \cos \pi t\)

The particle comes to rest (y = 0) when either sin3πt = 0 or cosπt = 0.

When sin3πt = 0, we have t = 0, \(\frac{1}{3}\)s, \(\frac{2}{3}\)s (t< 1s)

Again, when cosπt = 0, we have t = \(\frac{1}{2}\)s (t<1s)

∴ y = 0, when t = 0, \(\frac{1}{3}\)s, \(\frac{2}{3}\)s, \(\frac{1}{2}\)s

In every second, the particle comes to rest 4 times.

Superposition Waves Stationary Or Standing Waves

Stationary Or Standing Waves Definition: When two progressive waves of the same amplitude, frequency, and velocity traveling in opposite directions superpose in a region of space, the resultant wave is confined to that region and cannot progress through the medium. Such a type of wave is called a stationary wave or standing wave.

• A stationary wave keeps on repeating itself in a region and there is no transfer of energy along the medium in either direction. In can be explained as below.
• Let a thin metallic wire AB be stretched between two rigid supports. The wire is struck at any arbitrary point in a normal direction. Two separate waves are produced and they travel towards the two ends of the wire.
• After getting reflected from the end support, each wave starts moving towards the opposite end. As a result, they superpose in the region between A and B. The resultant wave is confined in the region AB and cannot travel like a progressive wave.

Stationary waves in a stretched string are produced in this way. These waves are the sources of notes emitted from stringed instruments like sitar, violin, etc. Stationary waves are also produced in the air columns in instruments like flute, organ, etc.

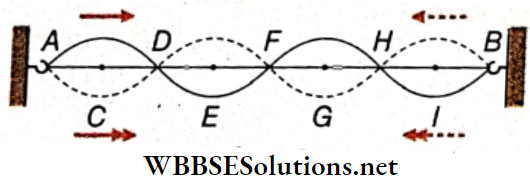
Nodes And antinodes: A stationary wave remains confined in a region and cannot progress through the medium. As a result, the waveform is such that in a few positions (like A, D, F, H, B), the particles in the medium remain stationary at all times, i.e., the wave amplitude at these positions is always zero.

These positions are called nodes. On the other hand, the particles in a few positions (like C, E, G, I) continue to vibrate with maximum amplitude—these positions are the antinodes.

Nodes And Antinodes Definition: In a stationary wave, the positions where the particles of the medium always remain at rest are called nodes, and the positions where the particles vibrate with the maximum amplitude are called antinodes.

For vibrations of a stretched string, nodes and antinodes are formed at points on the string; they are nodal points and antinodal points, respectively. Similarly, during vibrations of stretched membranes, in instruments like tabla, drum, etc., nodal lines and antinodal lines are formed, while nodal surfaces and antinodal surfaces are formed in vibrating air columns.

Loop: The region between two consecutive nodes in a stationary wave is called a loop. For example, each of AD, DF, FH, and HB is a loop. If we consider any single loop, it is evident that all the particles are either in the equilibrium position or above or below that position at any instant. As the vibrations are usually very fast, the whole loop is visible.

Now, we consider two adjacent loops. At any instant, if the particles in loop AD are below the equilibrium position along line AB, the particles in loop DF would be above line AB. So, the particles in adjacent loops of a stationary wave are in opposite phases, i.e., the phase difference is 180°.

Wavelength Of A Stationary Wave: The two antinodal points C and G are in the same phase because

1. When the displacement of the particle at C is maximum, the particle at G also goes to its maximum displaced position and
2. At every instant, the particles at C and G are on the same side relative to their equilibrium positions. Since C and G are consecutive points lying in the same phase, the distance between C and G is known as the wavelength (λ).

It is to be noted that there is another antinodal point E between C and G, but E is in the opposite phase with respect to C and G. It is observed that the distance between the nodal points A and F is also equal to CG.

Wavelength Of A Stationary Wave Definition: The distance between three consecutive nodes or three consecutive antinodes, is the wavelength (λ) of a stationary wave.

So, the length of a loop = distance between two consecutive nodes (say, AD) = \(\frac{\lambda}{2}\);

The distance between a node and the adjacent antinode (say, AC) = half of the length of a loop = \(\frac{\lambda}{4}\).

Resonant Frequency: Let us consider a string of a guitar, is stretched between its two ends. Suppose a continuous sinusoidal wave of a certain frequency is propagating along the string to the right. When the wave reaches the right end, it will reflect and begin to move towards the left.

• While moving towards the left end of the sting it must superpose with the wave that is still travelling towards the right. Similarly, after reaching the left end, the left-going wave reflects and begins to travel to the right, which results in a superposition with the left and right-going waves.
• In other words, within a very short time, we may find many overlapping traveling waves, interfering with each other.
• For certain frequencies, the interference produces a standing wave pattern accurately with nodes and antinodes. Such a standing wave is said to be produced at resonance and the string is said to be a resonator at this certain resonant frequency. If the string is oscillated at some frequency other than its resonant frequency, a standing wave is not formed.

Explanation Of The Formation Of Stationary Waves By Graphical Method: Two identical, but oppositely directed progressive waves superpose in a region of an elastic medium to produce stationary waves. The formation of these stationary waves can be explained graphically.

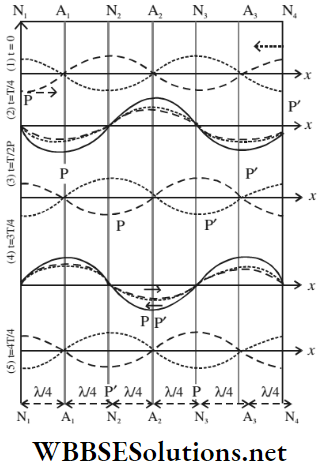
Consider a progressive wave (wave 1, denoted by a blue line) is moving towards right through a medium. Another progressive wave (wave 2, denoted by a broken blue line) of the same amplitude, frequency, and velocity is moving toward the left. The relations T = \(\frac{1}{n}\) and λ = \(\frac{V}{n}\) confirm that their time periods and wavelengths are also equal. When the two waves superpose in the region AE of the medium, the following cases can occur:

1. At the beginning of a period (time, t = 0), the two waves are in opposite phases. So, the resultant displacement is zero for every particle in the medium, i.e., every particle is in its equilibrium position. The graph of the resultant wave is the straight line AE.
2. During the time t = \(\frac{1}{4}\), the 1st wave covers a distance towards the right; the 2nd wave also travels the same distance towards the left. So, at this instant, the two waves are in the same phase.
   • The resultant displacements of the points A, C, and E become maximum, but the points B and D remain in equilibrium position. The graph of the resultant wave is shown as a red line.
3. By the time t = \(\frac{T}{2}\), both the waves have progressed further towards their direction of propagation through a distance \(\frac{\lambda}{4}\); so they are again in opposite phases. At this instant, every particle in the medium returns to its equilibrium position. So, the graph of the resultant wave becomes a straight line again.
4. At time t = \(\frac{3T}{4}\), the resultant displacement of every particle is equal but opposite to that at time t = \(\frac{T}{4}\). Here again, the points B and D remain in their equilibrium positions and the resultant displacements of the points A, C, and E become maximum. The graph of the resultant wave is again shown as a red line.
5. Finally, at time t = T, each of the progressive waves completes a period and returns to its position as that at time t = 0. As a result, each particle in this medium is in its equilibrium position again. The graph of the resultant wave again becomes a straight line.

The above discussion, on the superposition of two identical but oppositely directed progressive waves, leads to the following inferences:

1. The displacements of particles at B and D are zero at all times, i.e., they are always at rest. These points are called the nodal points. On the other hand, the particles at A, C, and E vibrate with maximum amplitudes on the two sides of the equilibrium and are known as the antinodal points.
2. The nodes and the antinodes do not travel through the medium. So the resultant wave is a stationary or standing wave.
3. The two ends B and D of the portion BD remain stationary and the intermediate points vibrate periodically across the position of equilibrium. So, a loop is formed in the portion BD of the stationary wave.

Mathematical Representation Of A Stationary Wave

Suppose each of two progressive waves has amplitude = A, frequency = n, velocity = V, time period = T = \(\frac{1}{n}\) and wavelength = \(\lambda=\frac{V}{n}\). If they approach each other from two opposite directions along the x-axis, their equations are

\(\left.\begin{array}{rl}
y_1 & =A \sin (\omega t-k x) \\
\text { and } \quad y_2 & =A \sin (\omega t+k x)
\end{array}\right\}\)…(1)

Where, ω = 2πn and \(k=\frac{2 \pi}{\lambda}\)

According to the principle of superposition of waves, the resultant displacement of a particle in the medium is

y = \(y_1+y_2\)

= \(A[\sin (\omega t-k x)+\sin (\omega t+k x)]\)

= \(2 A \sin \frac{(\omega t-k x)+(\omega t+k x)}{2} \cos \frac{(\omega t+k x)-(\omega t-k x)}{2}\)

= \(2 A \sin \omega t \cos k x=A^{\prime} \sin \omega t\)…(2)

Where, \(A^{\prime}=2 A \cos k x=2 A \cos \left(\frac{2 \pi}{\lambda} x\right)\)…(3)

Equation (2) represents a stationary wave. It cannot represent a progressive wave because a term like (ωt± kx) is not present in the argument of its trigonometric functions. The frequency of this motion is n = ω/2π, and the amplitude is \(A^{\prime}=2 A \cos \left(\frac{2 \pi}{\lambda} x\right)\), which varies harmonically and depends on the value of x.

Change Of Amplitude With Position: The amplitude will be zero at points, where

cos k x = \(\cos \left(\frac{2 \pi}{\lambda} x\right)=0=\cos \left(n+\frac{1}{2}\right) \pi\)

where n = 0, 1, 2 ……

∴ \(\frac{2 \pi x}{\lambda}=\left(n+\frac{1}{2}\right) \pi\)

or, x = \((2 n+1) \frac{\lambda}{4}\)

or, x = \(\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}, \cdots\)

These points where amplitude is zero, are called nodes. Clearly, the separation between two consecutive nodes is λ/2.

The amplitude will have a maximum value of 2A at points, where,

cos kx = \(\cos \left(\frac{2 \pi}{\lambda} x\right)= \pm 1=\cos n \pi\) [n = 0,1,2, •••]

These points of maximum amplitude are called antinodes. Clearly, the antinodes are also separated by λ/2 and are located halfway between pairs of nodes.

It is evident from equation (2) that every particle in the medium executes simple harmonic motion. The frequency of this motion is n = \(\frac{\omega}{2 \pi}\) and \(A^{\prime}=2 A \cos \left(\frac{2 \pi}{\lambda} x\right) .\)

The main features of the resultant displacement are, however, inherent in equation (3). Here, the quantity A’ represents the amplitudes of the particles at different positions (i.e., different values of x) of the medium. Evidently, the amplitude is different for different values of x.

For Example,

1. At the points x = 0, \(\frac{\lambda}{2}, \frac{2 \lambda}{2}, \frac{3 \lambda}{2}, \cdots, \frac{n \lambda}{2}\), the amplitude A’ = ±2A = maximum.These are the antinodal points. The distance between two consecutive antinodes = \(\frac{\lambda}{2}\).
2. At the points x = \(\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}, \cdots,(2 n+1) \frac{\lambda}{4}\), the amplitude A’ = 0. These are the nodal points. Here again, the distance between two consecutive nodes = \(\frac{2 \lambda}{4}=\frac{\lambda}{2}\)

The values of x also show that an antinode is present between two consecutive nodes.

Characteristics Of Stationary Waves

1. Two identical but oppositely directed progressive waves superpose to form a stationary wave.
2. Along a stationary wave, the particles at different points vibrate with different amplitudes. The points at which the amplitudes of vibration are always zero are called nodes the points with the maximum amplitudes, of vibration are called antinodes.
3. The distance between two consecutive nodes or two consecutive antinode is \(\frac{\lambda}{2}\). (λ = wavelength of the stationary wave.)
4. Nodes and mummies are fixed points; they do not change their positions with time. So. stationary waves do not travel through the medium. They remain confined to a region.
5. All die particles in a loop, between two nodes, are displaced in the same direction relative to their equilibrium positions. So, these particles are in the same phase.
6. Particles in adjacent loops are displaced in opposite directions at any instant; so they are in opposite phases.
7. All die particles come to rest simultaneously twice in each period and they cross the equilibrium position simultaneously twice in each period.
8. At the instant when all the particles are at their equilibrium positions, die potential energy of the stationary wave becomes zero, but the kinetic energy becomes maximum. On die other hand, in the maximum displaced positions, the kinetic energy becomes zero, while the potential energy becomes maximum. The total energy of the stationary wave is always conserved.
9. The changes in density and pressure are maximum at nodal points but zero at antinodal points.

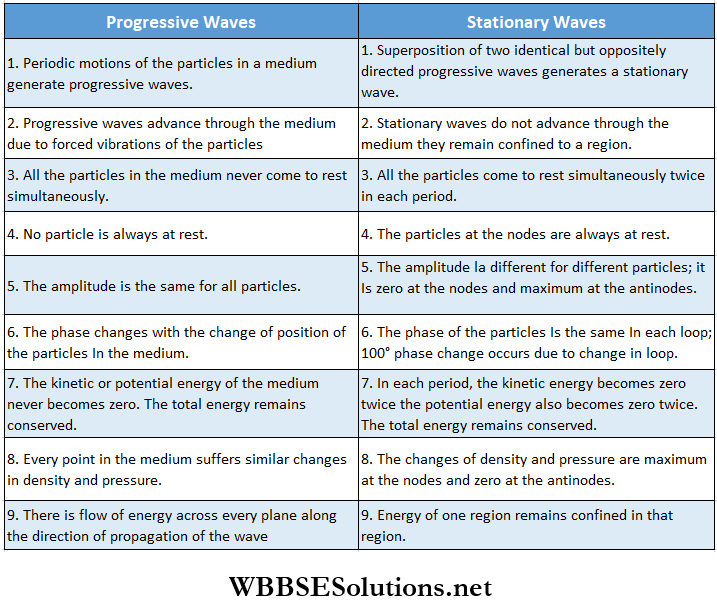
Difference Between Progressive And Stationary Waves:

Superposition Of Waves Stationary Or Standing Waves Numerical Examples

Example 1. A sound wave of frequency 80 Hz gets reflected normally from a large wall. Estimate the distance of the first node and the first antinode from the wall. Given, the velocity of sound in air = 320 m · s^-1.
Solution:

Here, the superposition of the incident and the reflected waves produces a stationary wave. The air particles adjacent to the wall cannot vibrate; so a node is developed at the wall.

Wavelength of the stationary wave, \(\lambda=\frac{V}{n}=\frac{320}{80}=4 \mathrm{~m}\)

∴ Distance of the 1st node from the wall = distance between two consecutive nodes = \(\frac{\lambda}{2}=\frac{4}{2}=2 \mathrm{~m}\)

The 1st antinode is at the midpoint between these two nodes; so its distance from the wall = 1 m.

Example 2. A wave represented by the equation y=A cos(kx-ωt) superposes on another wave to produce a stationary wave with a node at x = 0. What is the equation of this second wave?
Solution:

As a stationary wave is produced, the second wave will have the same amplitude, frequency, and velocity, but it will be oppositely directed. So its general equation will be, y’ = Acos(kx + ωt+ θ), where θ = initial phase

According to the principle of superposition, the equation of the resultant stationary wave is y_r = y+y’ = A [cos(kx-ωt) + cos(kx+ ωt+ θ)]

y_r = 0 at the point x = 0 due to the presence of a node

So, 0 = A[cos(-ωt) + cos(ωt+ θ)]

or, cosωt + cos (ωt+θ) = 0

or, cosωt = -cos(ωt+θ) = cos(ωt+θ +π)

Hence, ωt = ωt+ θ + Kπ or, θ = -π

So, the required equation is

y’ = A cos(kx + ωt-π) or, y’ = -A cos(kx + ωt).

Example 3. The equation of the vibration of a wire is y = \(5 \cos \frac{\pi x}{3} \sin 40 \pi t,\), where x and y are given in cm and t is given in s. Calculate the

1. Amplitudes and velocities of the two waves which on superposition, form the above-mentioned vibration
2. Distance between the two closest points of the wire that are always at rest;
3. The velocity of a particle at x = 1.5 cm at the instant t = \(\frac{9}{8}\)s.

Answer:

y = \(5 \cos \frac{\pi x}{3} \sin 40 \pi t=\frac{5}{2} \cdot 2 \sin 40 \pi t \cos \frac{\pi x}{3}\)

= \(\frac{5}{2}\left[\sin \left(40 \pi t+\frac{\pi x}{3}\right)+\sin \left(40 \pi t-\frac{\pi x}{3}\right)\right]\)

= \(\frac{5}{2} \sin 40 \pi\left(t+\frac{x}{120}\right)+\frac{5}{2} \sin 40 \pi\left(t-\frac{x}{120}\right)\)

= \(y_1+y_2\)

So, the resultant vibration is produced due to the superposition of two waves y₁ and y₂. Comparing these two waves with the general equation, y = \(A \sin \omega\left(t-\frac{x}{V}\right)\)

1. Amplitude, A₁ = A₂ = \(\frac{5}{2}\) = 2.5 cm; wave velocity, V₁ = 120 cm · s^-1 (towards negative x – direction) and V₂ = 120 cm · s^-1 (towards positive x-direction).

2. Wavelength, \(\lambda=\frac{V}{n}=\frac{V}{\omega / 2 \pi}=\frac{2 \pi V}{\omega}\)

The closest points that are always at rest denote two consecutive nodes. So, the distance between them = \(\frac{\lambda}{2}=\frac{\pi V}{\omega}=\frac{\pi \times 120}{40 \pi}=3 \mathrm{~cm} .\)

3. Particle velocity,

v = \(\frac{d y}{d t}=5 \cos \frac{\pi x}{3} \cdot 40 \pi \cos 40 \pi t\)

= \(200 \pi \cos \frac{\pi x}{3} \cos 40 \pi t\)

So, at x = \(1.5 \mathrm{~cm} and t=\frac{9}{8} \mathrm{~s}\),

v = \(200 \pi \cos \frac{\pi \times 1.5}{3} \cos \left(40 \pi \times \frac{9}{8}\right)\)

= \(200 \pi \cos \frac{\pi}{2} \cos 45 \pi=0 .\)

 

Superposition Of Waves Sonometer

A sonometer is an instrument designed to verify the laws of transverse vibration in a stretched string and to determine the emitted frequency.

Sonometer Description: A hollow box H is kept on a table. A uniform, thin metal wire whose one end is fixed with the rigid support R is stretched over two fixed bridges A and C, kept on the box H. This wire is passed through a small fixed pulley P and suspended beside the table.

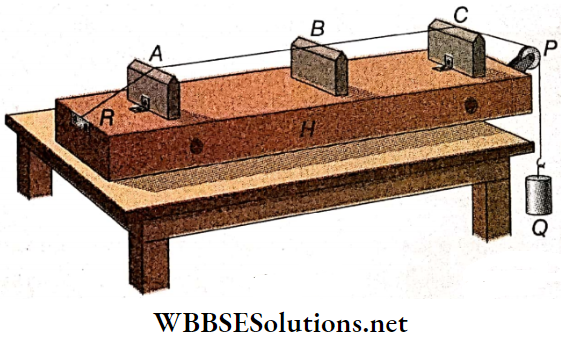
The movable bridge B can be put anywhere between A and C. Different known masses can be suspended at the free end Q of the wire to produce different tensions. More than one wire can be set similarly parallel to one another. In general, wires of different materials and of different cross sections are used.

Sonometer Working Principle: A wire of the sonometer is forced to vibrate in the region between the two bridges A and B. As a result, two nodes are generated at the ends of A and B. So, the effective length of the vibrating wire is equal to the distance between A and B.

• The handle of a vibrating tuning fork of known frequency is touched with the hollow box H. So, the wire AB vibrates at that instant due to forced vibration. Now, the length of the wire is adjusted by moving the bridge B until a resonance is achieved.
• This means that the tones emitted from the tuning fork and that from the wire are in unison and a loud sound is heard. In this situation, the frequencies become equal and the frequency of the vibrating wire is obtained from the known frequency of the tuning fork.

Verification Of The Laws Of Transverse Vibration In A String:

Law Of Length: To verify this law, only one wire of the sonometer is used and the mass suspended at the free end is kept unaltered. As a result, the mass per unit length (m) and the tension (T) of the wire remain constant. Now, a tuning fork of a known frequency (n₁) is vibrated and the bridge B of the sonometer is adjusted until the wire AB resonates. Let the length of the wire in this case be l₁. The wire is then similarly brought to resonance by using a few other tuning forks of different frequencies n₂, n₃, •••, etc. If the corresponding lengths of the wire AB at resonance are \(l_2, l_3, \cdots, \text { etc. }\) respectively, it is observed that \(n_1 l_1=n_2 l_2=n_3 l_3=\cdots\)

i.e., \(n \propto \frac{1}{l}\), when T and m are constants.

Law Of Tension: In this case, only one wire of the sonometer is used, so that the mass per unit length (m) of the wire remains constant. Moreover, if bridge B is kept at a fixed position, the length (l) of the wire does not change.

Now the wire AB is brought to resonance with different tuning forks of known frequencies n₁, n₂, n₃,….., respectively. These resonances are generated by increasing or decreasing the mass M suspended at the free end of the wire. Let the values of M at the resonances be M₁, M₂, ……, respectively. So, the corresponding values of the tension in the wire are T₁ = M₁g, T₂ = M₂g,…… Here, it is observed that,

∴ \(\frac{T_1}{T_2}=\frac{n_1^2}{n_2^2} \text { or, } \frac{n_1}{n_2}=\sqrt{\frac{T_1}{T_2}}\)

i.e., n ∝ √T, when l and m are constants.

Law Of Mass: A few wires made of different materials and having different cross sections are taken. These are known as experimental wires. The mass per unit length of the wires are different; let the values be m₁, m₂, m₃, …….., respectively Initially the 1st wire is used in the sonometer.

• Bridge B is kept at a definite position and a particular mass is suspended from its free end. The position of B and the value of the mass are not changed throughout the experiment. So the length l and the tension T remain constant.
• Now, another wire called the reference wire is set at a parallel position, and a fixed mass is hung from its free end. So the tension in the reference wire also remains fixed. Then the 1st experimental wire and the reference wire are vibrated simultaneously and resonance is obtained by adjusting the position of the movable bridge (say B’) of the reference wire.
• Let n₁ = frequency of vibration of both the wires and l₁ = length of the reference wire at resonance. The experiment is repeated by replacing the 1st experimental wire with the 2nd, 3rd,… and so on. Now, from the law of length, it is evident for the reference wire that, n₁l₁ = n₂l₂ = n₃l₃ =  …….

If the experimentally obtained values are analyzed, it is observed that \(\frac{m_1}{l_1^2}=\frac{m_2}{l_2^2}=\frac{m_3}{l_3^2}=\cdots\)

So, \(\frac{l_1^2}{l_2}=\frac{m_1}{m_2} or, \frac{l_1}{l_2}=\sqrt{\frac{m_1}{m_2}} or, \frac{n_2}{n_1}=\sqrt{\frac{m_1}{m_2}}\)

i.e., \(n_1 \sqrt{m_1}=n_2 \sqrt{m_2}=n_3 \sqrt{m_3}=\cdots\)

So, \(n \propto \frac{1}{\sqrt{m}}\), when l and T are constants.

Here, it is to be noted that the values m₁, m₂, …… correspond to the experimental wires, and l₁, l₂, ….. correspond to the reference wire. In each case, the length of the experimental wires l = constant.

However, the frequencies n₁, n₂,……. are the frequencies at resonance of the experimental wire as well as of the reference wire.

Determination of the frequency of a tuning fork by a Sonometer: The arm of a tuning fork vibrating with an unknown frequency is loosely held in contact with the hollow box of the Sonometer.

• Now the position of bridge B under the sonometer wire is adjusted until resonance is obtained. This resonance denotes that the tuning fork and the sonometer wire are vibrating with the same frequency, i.e., they are in unison.
• For the detection of the resonance, a V-shaped thin piece of paper is kept inverted at the center of the wire AB. At resonance, the amplitude of vibration at the central antinode is very large.

As a result, the wire throws away the piece of paper. If the wire vibrates in a single loop, it emits the fundamental tone. Then its frequency is,

n = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}=\frac{1}{2 l} \sqrt{\frac{M g}{m}}\)

Here, l = length of the portion of the wire AB at resonance, M = mass suspended at the free end, and m = mass per unit length of the wire.

The values of l, M, and m are measured by usual methods. By using these values of l, M, and m, the value of the frequency (n) can be determined. The calculated value of n is equal to the frequency of the tuning fork.

Superposition Of Waves Sonometer Numerical Examples

Example 1. A sonometer wire emits a tone of frequency 150 Hz. Find out the frequency of the fundamental tone emitted by the wire if the tension is increased in the ratio 9:16 and the length is doubled.
Solution:

The mass per unit length m remains the same for a single wire.

So from the relation n = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}\), we get

∴ \(\frac{n_1}{n_2}=\frac{l_2}{l_1} \sqrt{\frac{T_1}{T_2}}\)

or, \(n_2=n_1 \cdot \frac{l_1}{l_2} \sqrt{\frac{T_2}{T_1}}=150 \times \frac{1}{2} \times \sqrt{\frac{16}{9}}=100 \mathrm{~Hz}\).

Example 2. The fundamental frequency of a 100 cm long sonometer wire is 330 Hz. Find out the velocity of the transverse wave in the wire and the wavelength of the resulting sound waves in air. Given, the velocity of sound in air = 330 m · s^-1.
Solution:

For fundamental tone in a wire, two nodes are produced at the two ends, So, the length of the wire = distance between two consecutive nodes = \(\frac{\lambda}{2}\)

Here, λ = length of the transverse wave,

According to the question, \(\frac{\lambda}{2}=100 \mathrm{~cm}=1 \mathrm{~m}\)

So, λ = 2

∴ Velocity of transverse wave in the wire, V = frequency x wavelength = 330 x 2 = 660 m · s^-1

The frequency of the resulting sound waves in air will also be 330 Hz.

The velocity of sound waves in air = 330 m · s^-1.

∴ The wavelength of the resulting sound waves in air

= \(\frac{\text { velocity }}{\text { frequency }}=\frac{330}{330}=1 \mathrm{~m}\).

Example 3. A wire kept between two bridges 25 cm apart, Is stretched through a linear expansion of 0.04 cm. Find the fundamental frequency of vibration of the wire. Given, the density and Young’s modulus of the material of the wire are 10 g · cm^-3 and 9 x 10¹¹ dyn · cm^-2, respectively.
Solution:

Longitudinal strain = \(\frac{\text { linear expansion }}{\text { original length }}=\frac{x}{l}\)

Longitudinal stress = \(\frac{\text { tension in the wire }}{\text { area of cross-section }}=\frac{T}{\alpha}\)

Y = \(\frac{\text { longitudinal stress }}{\text { longitudinal strain }}=\frac{\frac{T}{a}}{\frac{x}{l}}=\frac{T l}{\alpha x}\)

or, T = \(\frac{Y \alpha x}{l}\)

Mass per unit length of the wire, m= density x area of cross-section = \(\rho \alpha\)

∴ Fundamental frequency,

n = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}=\frac{1}{2 l} \sqrt{\frac{Y \alpha x}{l} \cdot \frac{1}{\rho \alpha}}=\frac{1}{2 l} \sqrt{\frac{Y x}{l \rho}}\)

= \(\frac{1}{2 \times 25} \times \sqrt{\frac{\left(9 \times 10^{11}\right) \times 0.04}{25 \times 10}}=240 \mathrm{~Hz}\).

Example 4. The linear density of mass of a metal wire is 9.8 g · m^-1. It is kept between two rigid supports, 1 m apart, with a tension of 98 N. The midpoint of the wire is kept between the poles of an electromagnet driven by an alternating current. Find out the frequency of this alternating current that will produce resonance in the wire.
Solution:

Mass per unit length of the wire,

m = 9.8 g · m^-1 = 9.8 x 10^-3 kg · m^-1; length of the wire, l = 1m; tension in the wire, T = 98 N

∴ Fundamental frequency,

n = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}=\frac{1}{2 \times 1} \sqrt{\frac{98}{9.8 \times 10^{-3}}}=50 \mathrm{~Hz}\)

For this reason, the frequency of the alternating current is also 50Hz.

Example 5. A 1m long wire Is clamped at both ends. Find out the positions of two bridges that will divide the wire in three parts such that the fundamental frequencies are in the ratio 1:2:3.
Solution:

Here, n₁: n₂: n₃ = 1:2:3

As \(n \propto \frac{1}{l}\), we have \(l_1: l_2: l_3=1: \frac{1}{2}: \frac{1}{3}\)

So, \(l_2=\frac{l_1}{2}\) and \(l_3=\frac{l_1}{3}\)

Now, \(l_1+l_2+l_3=1\) ; so, \(l_1+\frac{l_1}{2}+\frac{l_1}{3}=1\)

or, \(\frac{11}{6} l_1=1$ or, $l_1=\frac{6}{11} \mathrm{~m}\)

Then, \(l_2=\frac{l_1}{2}=\frac{3}{11} \mathrm{~m} and l_3=\frac{l_1}{3}=\frac{2}{11} \mathrm{~m}\)

So, the first bridge is at a distance of \(\frac{6}{11}\)m from one end and the second bridge is at a distance of \(\frac{2}{11}\)m from the other end.

Example 6. The linear, density of a wire is 0.05 g · cm^-1. The wire is stretched with a tension of 4.5 x 10⁷ dyn between two rigid supports. A driving frequency of 420 Hz resonates with the wire. At the next higher frequency of 490 Hz, another resonance is observed. Find out the length of the wire.
Solution:

Let 420 Hz = frequency of the p -th harmonic.

So, 490 Hz = frequency of the (p + 1) – th harmonic.

Then, 420 = \(\frac{p}{2 l} \sqrt{\frac{T}{m}}\) and \(490=\frac{p+1}{2 l} \sqrt{\frac{T}{m}}\)

∴ \(\frac{420}{490}=\frac{p}{p+1}\) or, p=6

So, we get, 420 = \(\frac{6}{2 l} \sqrt{\frac{T}{m}}\)

or, \(l=\frac{6}{2 \times 420} \sqrt{\frac{4.5 \times 10^7}{0.05}}=214.3 \mathrm{~cm}\)

Example 7. One end of a wire of radius is sealed with the end of another wire of radius 2r. This is used as a sonometer wire with tension T, keeping the junction at the mid-point of the vibrating length. If a stationary wave having a node at the junction is generated, find out the ratio between the number of loops in the two portions.
Solution:

Let ρ₁ and ρ₂ be the densities of the materials of the two wires respectively.

Mass per unit length of the first wire, m₁ = πr²ρ₁

Mass per unit length of the second wire, \(m_2=\pi(2 r)^2 \rho_2=4 \pi r^2 \rho_2\)

∴ \(\frac{m_1}{m_2}\) =\(\frac{\rho_1}{4 \rho_2}\)

The junction is at the mid-point of the vibrating length 2l (say).

So, the vibrating length of each wire = l.

The two wires are vibrating simultaneously; so the frequency of vibration is the same. Let it be n.

Again, a node is generated at the junction; so an integral number of loops is produced in each wire. If the number of loops in the two wires are p and q, respectively, then

n = \(\frac{p}{2 l} l \sqrt{\frac{T}{m_1}} \text { and } n=\frac{q}{2 l} \sqrt{\frac{T}{m_2}}\)

∴ \(\frac{p}{2 l} \sqrt{\frac{T}{m_1}}=\frac{q}{2 l} \sqrt{\frac{T}{m_2}}\)

or, \(\frac{p}{q}=\sqrt{\frac{m_1}{m_2}}=\sqrt{\frac{\rho_1}{4 \rho_2}}=\frac{1}{2} \sqrt{\frac{\rho_1}{\rho_2}}\)

If the two wires are of the same material, then \(\rho_1=\rho_2\)

So, \(\frac{p}{q}=\frac{1}{2}\).

Superposition Of Waves Longitudinal Vibration In A String

If a string is vibrated by stretching it along its length, longitudinal waves are generated. After reflection from the end-supports, incident waves, and reflected waves superpose. So, longitudinal stationary waves are produced.

The velocity of these waves is equal to the velocity of longitudinal sound waves propagating through a string and is given by, \(V_l=\sqrt{\frac{Y}{\rho}}\)

where Y and ρ are Young’s modulus and the density of the material of the string, respectively.

Now let l = length of the string, α = area of cross-section, T = tension in the string, and x = linear expansion due to tension.

So, mass per unit length of the wire, m = pa; longitudinal strain = \(\frac{x}{l}\); longitudinal stress = \(\frac{T}{\alpha}\)

∴ Y = \(\frac{\frac{T}{\alpha}}{\frac{x}{l}}=\frac{T l}{\alpha x} \text { and } \rho=\frac{m}{\alpha}\)

∴ \(V_l=\sqrt{\frac{Y}{\rho}}=\sqrt{\frac{T l}{\alpha x} \cdot \frac{\alpha}{m}}=\sqrt{\frac{T l}{m x}}\)

We know that the velocity of transverse waves in a stretched string is \(
V_t=\sqrt{\frac{T}{m}}\)

∴ \(\frac{V_t}{V_l}=\sqrt{\frac{x}{l}}\)

For elastic metal wires, the linear expansions is much less than the original length, i.e., x<<1, so V_t <<V_l.

So, the longitudinal wave velocity in a stretched string is far greater than the transverse wave velocity.

For example, we consider a stretched string made of steel. The velocity of sound waves in steel is about 5000 m · s^-1.

This is the velocity of longitudinal waves in a steel string. If the longitudinal stationary waves in such a stretched steel string produce a fundamental tone of frequency 250 Hz, then the wavelength, \(\lambda=\frac{5000}{250}=20 \mathrm{~m}\).

So, the length of the wire, l = \(\frac{\lambda}{2}=10 \mathrm{~m}\). Clearly, it is practically impossible to construct any musical instrument with such a long string. For this reason, the longitudinal vibrations in a stretched string have no practical importance.

Superposition Of Waves Velocity Of Sound Numerical Examples

Example 1. A tuning fork of frequency 384 Hz produces the 1st and the 2nd resonances with air columns of a pipe closed at one end at lengths 22 cm and 67 cm, respectively. Find out the velocity of sound in air, and the end error for the open end of the tube.
Solution:

Velocity of sound in air, V = \(2 n\left(l_2-l_1\right)=2 \times 384 \times(67-22)=2 \times 384 \times 45\)

= 34560 \mathrm{~cm} \cdot \mathrm{s}^{-1}[/latex].

End error, c = \(\frac{1}{2}\left(l_2-3 l_1\right)=\frac{1}{2}(67-3 \times 22)\)

= \(\frac{1}{2} \times 1=0.5 \mathrm{~cm}\) .

Example 2. A 200 cm long vertical tube is filled with water, and a vibrating tuning fork of frequency 256 Hz is held over the open upper end of the tube. Then water is allowed to escape gradually through the lower end. Find out the positions of the water surface at the 1st and 2nd resonances. Neglect the end error. The velocity of sound in air = 320 m s^-1.
Solution:

The 1st resonance corresponds to the fundamental tone for the tube closed at one end. If l₁ is the length of the air column at the 1st resonance, then n = \(\frac{V}{4 l_1}\)

or, \(l_1 =\frac{V}{4 n}=\frac{320 \times 100}{4 \times 256}=31.25 \mathrm{~cm}\)

The 2nd resonance corresponds to the 1st overtone, which is the 3rd harmonic. If l₂ is the corresponding length of the air column then,

n = \(3 \cdot \frac{V}{4 I_2}\)

or, \(l_2=3 \cdot \frac{V}{4 n}=3 l_1=3 \times 31.25=93.75 \mathrm{~cm}\)

So, the height of the water surface from the bottom of the tube is respectively, (200-31.25) or 168.75 cm and (200- 93.75) or 106.25 cm.

Superposition Of Waves Conclusion

The resultant displacement of a particle in a medium due to more than one wave is equal to the vector sum of the different displacements produced by the individual waves separately. This is the principle of superposition of waves.

• When two progressive waves of the same amplitude, frequency, and velocity, traveling in opposite directions, superpose in a region of space, the resultant wave is confined to that region, and cannot progress through the medium. Such a type of wave is called a stationary wave or standing wave.
• In a stationary wave, the positions where the particles of the medium always remain at rest are called nodes and the positions where the particles vibrate with maximum amplitude, are called antinodes.
• The distance between two successive nodes or two successive antinodes is equal to half the wavelength of a stationary wave.
• The vibrating region between two successive nodes is a loop of a stationary wave. All the particles in a loop lie in the same phase and those in adjacent loops belong to opposite phases.

Laws of transverse vibrations in a stretched string: Let Z be the length of a stretched string, m be the mass per unit length of the string and T be the tension in the string. If the frequency of transverse vibrations in the string is n, then the string is n, then

1. \(n \propto \frac{1}{l}\), when T and m are constants.
2. \(n \propto \sqrt{T}\), when l  and m are constants.
3. \(n \propto \frac{1}{\sqrt{m}}\), when l  and T are constant.

The fundamental tone is emitted when a stretched string vibrates in a single loop. All the odd and even harmonics may also be emitted from the string depending on the number of loops formed during vibrations.

• A sonometer is a suitable instrument to study the vibrations in a stretched string.
• The longitudinal wave velocity in a stretched string is many times higher than the transverse wave velocity. The longitudinal waves in a string have no practical importance.
• The stationary waves in a stretched string are transverse stationary waves, whereas those in an air column are longitudinal stationary waves.
• A closed pipe (a pipe dosed at one end and open at the other) can emit its fundamental tone and only the odd harmonics. But an open pipe (a pipe with both ends open) can emit its fundamental tone and both odd and even harmonics. So an open pipe emits a musical sound of higher quality.
• The fundamental frequency of an open pipe is twice that of a closed pipe of equal length.
• The periodic rise and fall of the loudness of the resultant produced fay the superposition of two 4- If two progressive waves approach each other from two progressive sound waves of equal amplitude but of slightly different frequencies, is called beats.

The difference between the frequencies of rise two component waves of a beat is called the beat frequency. Beats are distinctly audible when the two superposing waves have a frequency difference of 10 Hz or less.

Superposition Of Waves Useful Relations For Solving Numerical Problems

If two progressive waves approach each other from two opposite directions along the x-axis, their equations are \(y_1=A \sin (\omega t-k x) \text { and } y_2=A \sin (\omega t+k x)\)

where for the two progressive waves, amplitude = A, frequency = n, velocity = V, time period = T = \(\frac{1}{n}\) and wavelength = \(\lambda=\frac{V}{n}\)

They superpose to form a stationary wave: y = y₁ + y₂ = 2A coskx sinωt = A’sinωt,

where \(A^{\prime}=2 A \cos k x=2 A \cos \left(\frac{2 \pi}{\lambda} x\right)\)

1. At x  = 0, \(\frac{\lambda}{2}, \frac{2 \lambda}{2}, \frac{3 \lambda}{2}, \cdots[latex], the amplitude is  A’ = ±2A = maximum. These antinodes of the stationary’ wave.
2. At x = [latex]\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}, \cdots\), the amplitude is A’ = 0 = minimum. These points are nodes.

For the transverse vibrations in a sealed string of length l, mass per unit length m, and tension T, the frequency is, \(n_p=\frac{p}{2 l} \sqrt{\frac{T}{m}}\) where p = a number of loops.

Let the length of a pipe be l and the velocity of sound be V. For dosed and open pipes, the wavelength and the frequency of longitudinal stationary sound waves are given in the following table:

The end error occurring at each open end of a dosed or an open pipe is c ≈ 0.6r, where r = radius of the pipe.

Then, the effective length of a dosed pipe of length l is l+ c; the effective length of an open pipe of length l is l+2c.

So, the fundamental frequencies are,

For a closed pipe, \(n_0=\frac{V}{4(l+c)}\)

For an open pipe, \(n_0=\frac{V}{2(l+2 c)}\)

In case of beat production, two sound weaves have the amplitude A and the same initial phase but have slightly different frequencies n₁ and n₂, (where n₁ > n₂). Their equations are \(y_1=A \sin 2 \pi n_1 t \text { and } y_2=A \sin 2 \pi n_2 t \text {. }\)

The equation of the resultant wave formed on superposition is, \(y=y_1+y_2=A^{\prime} \sin 2 \pi n t\)

where n = \(\frac{n_1+n_2}{2}\)

and A’ = \(2 A \cos \left\{\pi\left(n_1-n_2\right) t\right\}\)

Beat frequency = number of beats heard per second = n₁-n₂ = the difference between the frequencies of the two-component sound waves

Superposition Of Waves Very Short Answer Type Questions

Question 1. What type of wave is formed when two identical but oppositely directed progressive waves superpose?
Answer: Stationary wave

Question 2. Name the type of wave which does not transmit energy from one place to another.
Answer: Stationary wave

Question 3. If λ is the wavelength of a stationary wave, what would be the distance between two consecutive nodes?
Answer: \(\frac{\lambda}{2}\)

Question 4. If λ is the wavelength of a stationary wave, what would be the distance between a node and the adjacent antinode?
Answer: \(\frac{\lambda}{4}\)

Question 5. How many times in each period all the particles in the medium for a stationary wave, come to rest simultaneously?
Answer: Twice

Question 6. The phase is always the same for all particles between two consecutive nodes of a stationary wave. Is the statement true or false?
Answer: True

Question 7. At the instant when all the particles are at their equilibrium positions, the potential energy of a stationary wave becomes maximum. Is the statement true or false?
Answer: False

Question 8. The fundamental frequency of transverse vibration in a taut string is 200 Hz. What will be the fundamental frequency if the length of the string is doubled, with its tension unchanged?
Answer: 100 Hz

Question 9. The fundamental frequency of transverse vibration in a taut string is 200 Hz. Keeping the length of the string unaltered, if its tension is doubled, what will be the fundamental frequency?
Answer: 200√2 Hz

Question 10. How does the frequency of the fundamental tone of transverse vibration in a stretched string change when a comparatively thicker string of the same material is used?
Answer: Decreases

Question 11. At the ends of an organ pipe open at both ends, what do we always get nodes or antinodes?
Answer: Antinode

Question 12. If the fundamental frequency emitted by a pipe closed at one end is 200 Hz, what is the frequency of the first overtone?
Answer: 600 Hz

Question 13. If the fundamental frequency emitted by a pipe open at both ends is 200 Hz, what is the frequency of the first overtone?
Answer: 400 Hz

Question 14. If the fundamental frequency of a closed pipe is 200 Hz, what would be the fundamental frequency of an open pipe of equal length?
Answer: 400 Hz

Question 15. Which harmonics are present in the note produced from a pipe closed at one end?
Answer: Fundamental tone and its odd harmonics

Question 16. What will be the beat frequency when two tuning forks of frequencies 256 Hz and 260 Hz are vibrated simultaneously?
Answer: 4

Question 17. As in sound, can beats be observed by two light sources?
Answer: No

Question 18. The superposition of two progressive sound waves of equal speed and amplitude but of slightly different frequencies produces ______
Answer: Beats

Question 19. Beats are heard when two tuning forks of frequencies 256 Hz and 260 Hz are vibrated simultaneously. If some wax is dropped at one of the prongs of the first fork, how will the beat frequency change?
Answer: Increase

Superposition Of Waves Assertion Reason Type Question And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 Is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 Is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 Is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: When two vibrating tuning forks have f₁ = 300 Hz and f₂ = 350 Hz and are held close to each other, beats cannot be heard.

Statement 2: The principle of superposition is valid only when f₁ – f₂ < 10 Hz.

Answer: 3. Statement 1 is true, and statement 2 is false.

Question 2.

Statement 1: When a wave goes from one medium to another, the average power transmitted by the wave may change.

Statement 2: Due to changes in medium, amplitude, speed, wavelength, and frequency of wave may change.

Answer: 3. Statement 1 Is true, and statement 2 is false.

Question 3.

Statement 1: For a closed pipe, the 1st resonance length is 60 cm. The 2nd resonance position will be obtained at 120 cm.

Statement 2: In a closed pipe, n₂ = 3n₁, where n₁ = frequency of the fundamental tone and n₂ = frequency of the 1st overtone.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 4.

Statement 1: If two waves of some amplitude, produce a resultant wave of the same amplitude, then the phase difference between them will be 120°.

Statement 2: The velocity of sound is directly proportional to the square of its absolute temperature.

Answer: 3. Statement 1 Is true, and statement 2 is false.

Superposition Of Waves Match Column 1 With Column 2

Question 1. Three successive resonance frequencies in an organ pipe are 1310, 1834, and 2358 Hz. The velocity of sound in air is 340 m · s^-1.

Answer: 1. C, 2. A, 3. D, 4. B

Question 2. A string fixed at both ends is vibrating in resonance. In Column 1 some statements are given which can match with one or more entries in Column 2.

Answer: 1. A, B, D, 2. A, B, D 3. C, 4. A, B, C, D

Superposition Of Waves Comprehension Type Question And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A closed-air column 32 cm long is in resonance with a tuning fork. Another open-air column of length 66 cm is in resonance with another tuning fork. The two forks produce 8 beats per second when sounded together.

1. The speed of sound in air

1. 33792 cm · s^-1
2. 35790 cm · s^-1
3. 31890 cm · s^-1
4. 40980 cm · s^-1

Answer: 1. 33792 cm · s^-1

2. The frequencies of the forks

1. 230 Hz, 290 Hz
2. 250 Hz, 300 Hz
3. 264 Hz, 256 Hz
4. 150 Hz, 300 Hz

Answer: 3. 264 Hz, 256 Hz

Question 2. Find the number of possible natural oscillations of air column in a pipe whose frequencies lie below 1250 Hz. The length of the pipe is 85 cm. The velocity of sound is 340 m · s^-1. Consider the following two cases:

1. The pipe is closed from one end

1. 2
2. 4
3. 8
4. 6

Answer: 4. 6

2. The pipe is opened from both ends

1. 3
2. 7
3. 6
4. 9

Answer: 3. 6

Question 3. In the arrangement shown a mass can be hung from a string with a linear mass density of 2 x 10^-3 kg ·m^-1 that passes over a light pulley. The string is connected to a vibrator of frequency 700 Hz and the length of the string between the vibrator and the pulley is 1 m.

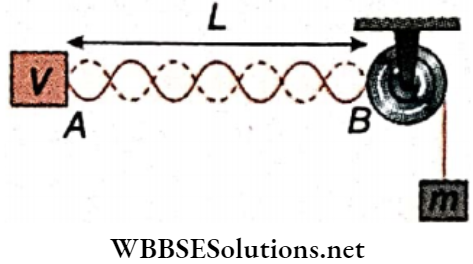
1. If the standing waves are to be observed, the largest mass that can be hung is

1. 16 kg
2. 24 kg
3. 32 kg
4. 400 kg

Answer: 4. 400 kg

2. If the mass suspended is 16 kg, then the number of loops formed in the string is

1. 1
2. 3
3. 5
4. 8

Answer: 3. 5

3. The string is set into vibrations and represented by the equation y = \(6 \sin \left(\frac{\pi x}{10}\right) \cos \left(14 \times 10^3 \pi t\right)\), where x and y are in cm and t is in s. The maximum displacement at x = 5 m from the vibrator is

1. 6 cm
2. 3 cm
3. 5 cm
4. 2 cm

Answer: 1. 6 cm

Superposition Of Waves Integer Answer Type Questions

In this type, the answer to each of the questions Is a single-digit integer ranging from 0 to 9.

Question 1. A closed organ pipe and an open organ pipe of the same length produce 2 beats when they are set into vibration simultaneously in their fundamental mode. The length of the open organ pipe is now halved and that of the closed organ pipe is doubled. What will be the number of beats produced?
Answer: 7

Question 2. The displacement y of a particle executing periodic motion is given by \(y =4 \cos ^2\left(\frac{1}{2} t\right) \sin (1000 t)\) This expression may be considered as a result of the superposition of how many simple harmonic motions?
Answer: 3

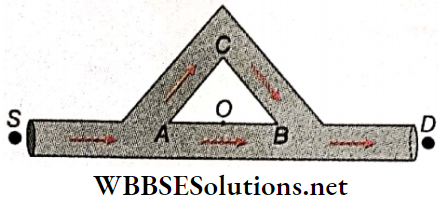
3. A sound wave starting from source S, follows two paths AOB and ACB to reach the detector D. ABC is an equilateral triangle of side l and there is silence at point D. If the maximum wavelength is nl, find the value of n.
Answer: 8

Question 4. A string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. The amplitude at the center of the string is 4 mm. Find the distance between the two points (in m) having an amplitude 2 mm.
Answer: 1