Class 9 Mathematics

Modern Algebra Chapter 2 Probability

Chapter 2 Probability Introduction

Probability:-

1. In our daily life, we have to face some events, the results of which are not certain, or it is impossible to guess about the certain results of that events. 
2. The circumstances that may evolve before the event or during the event or in the future, can not be forecasted accurately or certain results of the events can not be assumed correctly.
3. It can be forecasted the results of the events only by assumption with the help of some logical arguments, that may or may not be wrong. 
4. Such as observing the clouds in the sky, we can assume that rain may take place or there is a probability of rain.
5. Here, our assumption may be correct or incorrect, i.e., it may rain or may not rain.
6. Let us through an unbiased dice.
7. Then as a result of this event, we can say that any one of the numbers 1, 2, 3, 4, 5, and 6 may come.
8. If we assume that 4 will come, then 4 may come or may not come. 
9. So, we have to say that there is a possibility or probability of coming 4 as a result.
10. Similarly, the event of throwing an unbiased coin upwards is included in the probability theory. 
11. Here, either head or tail may occur as a result.
12. At present, probability theory is widely used in the business world, statistics, preparation of budgets, determination of principles in government and non-government organizations, and also to forecast the demands of goods.
13. Before the discussion of probability theory, we shall have some pre-knowledges about some concepts of it.
14. In the following, these conceptions have been discussed.

Read and Learn More WBBSE Solutions For Class 9 Maths

Chapter 2 Probability Random Experiment

Random Experiment:-

1. The experiments or observations in which there is a clear conception about which events may occur or what results may come, but for a certain experiment of observation, it is impossible to say about the certain results, are known as random experiments or observations.
2. Probability theory is always dealt with random experiments or observations.
3. Again, if an unbiased dice is thrown randomly in the ground, we know that the result is either 1 or 2 or 3 or 4 or 5, or 6.
4. But it is impossible to say about the certainty of the result.
5. Similarly, in a football match for a team, the result is any one of the three, win, loss, or draw.
6. So it is also an example of a random experiment.

Events:

1. Any result related to a random experiment is called an event. 
2. For example, the throwing of an unbiased coin is either head or tail.
3. Here, the occurrence of a head or tail in the coin throwing is an event of a random experiment.
4. Similarly, each of the results 1, 2, 3, 4, 5, and 6, when a dice is rolled, is also an event.

Chapter 2 Probability Mutually Exclusive Events

Probability Mutually Exclusive Events:-

1. If two or more than two events are related in such a way that they can not occur together, then the events are called mutually exclusive events.
2. If two events A and B are mutually exclusive, then \(A \cap B=\phi \text { or } P(A \cap B)=0, \text { where } \phi\) denotes the impossible event. 
3. Clearly, simple events are always mutually exclusive events.
4. The odd and even results of throwing a die are mutually exclusive events.
5. But in the same experiment, even results and the multiple of three results are not mutually exclusive events, because if the result be 6, then it is simultaneously even and a multiple of 3.

Chapter 2 Probability Impossible Event And Certain (Or Sure) Event

Impossible Event And Certain (Or Sure) Event:-

1. In any random experiment, we can think of or observe such an event that can never occur, this event is called an impossible event.
2. Impossible events are generally denoted by P (Φ) = 0, i.e., the probability of an impossible event is zero.
3. For example, let there are 4 red and 3 white balls in a box and 1 ball is withdrawn randomly. 
4. The ball will be green is an impossible event, since it can never occur.
5. Similarly, to occur 7 in a dice throwing is also an impossible event.
6. Again, in any random experiment, if we think or observe that an event must always occur in every case, then the event is called a certain or sure event.
7. For example, in the random experiment of throwing a coin, the occurrence of a head or tail is a sure event. 
8. Sure events are usually denoted by S and the probability of a sure event is 1, i.e., P (S) = 1.

Chapter 2 Probability Complementary Event

Complementary Event:-

1. In any random experiment, the negative result of a certain event is called the complementary event.
2. For example, the complementary event of the event head is not to occur head, i.e., the occurrence of a tail.
3. In the rolling of a dice, the complementary event of the event occurrence of even is not to occur even result, i.e., the occurrence of odd results.
4. The complement of an event A is usually denoted by \(\mathrm{A}^c \text { or } \mathrm{A}^{\prime} \text { or } \overline{\mathrm{A}} \text {. }\)

Chapter 2 Probability Exhaustive Events

Exhaustive Events:-

1. If two or more two events related to a random experiment be such that at least one of them must occur in the result of the experiment, then these events are known as exhaustive.
2. For example, in the random experiment of throwing an unbiased coin, if A and B are two events (where A occurrence of the head and B is = the occurrence of the tail), then the events A and B are said to be exhaustive since either A or B must occur in the result.

Chapter 2 Probability Sample Space Or Event Space

Sample Space Or Event Space:-

1. If E be a random experiment, then the simple events related to E are called simple point or event point.
2. The set of all these event points which are possible in the experiment is called the sample space or event space of experiment E.
3. Sample space is generally denoted by S.
4. Thus, the universal set of all the events in an experiment is called the sample space or event space.

Chapter 2 Probability Classical Or Mathematical Definition Of Probability

Classical Or Mathematical Definition Of Probability:-

1. Let in a random experiment E, there is n (S) number of equally probable or mutually symmetrical sample points in the sample space S of E.
2. If amongst the points in (A) number of points is included in the event A, then the ratio \(\frac{m(A)}{n(S)}\) is called the probability of the event A and it is denoted by P (A).
3. ∴ \(\mathrm{P}(\mathrm{A})=\frac{m(\mathrm{~A})}{n(\mathrm{~S})} \quad \text { or, } \mathrm{P}(\mathrm{A})=\frac{\text { Number of event points equally probable related to } \mathrm{A} \text {. }}{\text { Number of total event points in the sample space. }}\)

Chapter 2 Probability Notations

Probability Notations:-

1. Let the sample space of the random experiment E be S and A and B are two events related to E. 
2. Then, P (A) denotes the probability of the event A.
3. \(\left.\mathrm{P} \cdot\left(\mathrm{A}^c\right) \text { [or, } \mathrm{P}\left(\mathrm{A}^{\prime}\right) \text { or; } \mathrm{P}(\overline{\mathrm{A}})\right]\) denotes the probability of non-occurrence of event A.
4. \(\mathrm{P}(\mathrm{A} \cup \mathrm{B})[\text { or, } \mathrm{P}(\mathrm{A}+\mathrm{B})]\) denotes the probability of occurrence of at least one of A and B, i.e., either A or B or both A and B occurs.
5. \(P(A \cap B)[\text { or } P(A B)]\) denotes the probability of occurrence of both events A and B together.

Chapter 2 Probability Some Theorems

Theorem-1: The probability of impossible events is zero, i.e., P (Φ) = 0.

Theorem-2: If A is an event, then \(\mathrm{P}\left(\mathrm{A}^c\right)=1-\mathrm{P}(\mathrm{A}), \text { where } \mathrm{A}^c\), where A is the complement of the event A.

Theorem-3: For an event A, 0 ≤ P (A) ≤ 1.

Theorem-4: 

1. If A and B be two mutually exclusive events, then, \(P(A \cup B)=P(A)+P(B)\). 

2. If A and B are not mutually exclusive events, then \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\).

Question 1. If E is the random experiment of throwing an unbiased coin and S is its sample space and if H and T denote the events of occurrence of head and tail respectively, then

1. If one coin is thrown, then S = {H, T}, here in sample space there are only two event points H and T.

2. If two coins are thrown simultaneously or one coin is thrown two times, then S = (HH, HT, TH, TT) and there are 2² = 4 event points in the sample space. S. 

3. If three coins are thrown simultaneously or one coin is thrown three times, then find the sample space of E.

Solution: 

Given

Three coins are thrown simultaneously or one coin is thrown three times.

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT). Here, there are 2³ = 8 sample points in the sample space S.

Let A denotes the event of the occurrence of the head at first and B denotes the event of the occurrence of two heads, then A= {HHH, HHT, HTH, HTT)

and B = {HHT, HTH, THH).

Clearly, \(A \cup B\) = {HHH, HHT, HTH, HTT, THH) and \(A \cap B\) = {HHT, HTH}

Again, if X denotes the event of non-occurrence of any head, then X occurrence of at least one head= complement of X = {TTT)}

= X_c = S – X

= {HHH, HTH, HHT, HTT, THH, THT, TTH}

If m coins are thrown simultaneously or one coin is thrown m-times, then there are 2m sample points in the sample space.

Question 2. If E is a random experiment of rolling a dice and S be its sample space, then if one dice is rolled-

1.  S = {1, 2, 3, 4, 5, 6), here the number of event points is 6.

2. If two dice are rolled, find the sample space.

Solution:

Given

E is a random experiment of rolling a dice and S be its sample space.

The required sample space = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4). (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)).

Here, in the sample space, there are 6² = 36 event points.

Similarly, if 3 dice are rolled, then there will be 6³ = 216 even points in the sample space.

If the number of dice is n, then the number of event points = 6ⁿ in the sample space.

Question 3. If E is a random experiment of counting the number of telephone calls in a telephone line after a regular period of time and if S is its sample space, then

Solution:

Given

E is a random experiment of counting the number of telephone calls in a telephone line after a regular period of time.

S is its sample space.

S = {1, 2, 3, 4, 5, 6).

Here, there will have an infinite number of countable event points.

Question 4. Let the heights of a group of students be more than 4 feet and less than 6 feet. Now, if E is the random experiment of measuring the heights of the students and if S is the sample space, then 

Solution:

Given

The heights of a group of students be more than 4 feet and less than 6 feet.

E is the random experiment of measuring the heights of the students.

S is the sample space

S = {x: 4 < x <6}

Here, the height of a certain student may be a real positive number between 4 feet and 6 feet. 

Therefore, there will have infinitely many numbers of uncountable event points.

Clearly, in the given examples (1) and (2), there is a finite number of event points. 

In example (3), there is an infinite number of countable event points and in example-(4), there is an infinite number of non-countable events.

Therefore, the sample spaces of examples (1), (2), and (3) are discrete, but in example-(4), it is continuous.

Modern Algebra Chapter 1 Set Theory

Chapter 1 Set Theory Introduction 

1. Set theory is a key basis of mathematics.
2. Without the concept of set theory, any subject of mathematics like calculus, algebra, etc. can never be completely discussed.
3. George Bull, an English mathematician at first discussed set theory.
4. Later on, George L.P. Cantor, a German mathematician developed it.
5. He is called the father of modern set theory.

Read and Learn More WBBSE Solutions For Class 9 Maths

Chapter 1 Set Theory Concepts Of Sets

1. If any definition of any subject is to be made, then we have to depend on some other related subjects.
2. Because the definition is such a statement that expresses the new concepts depending on its old concepts.
3. That is why, the definition of any subject is at all impossible.
4. It is very difficult to define set theory.
5. According to their benefit of works, different persons have defined set theory differently.
6. According to Cantor-Set is a collection of certain different objects.
7. In general, a set is a collection of some well-defined different objects.
8. Here, the term ‘well-defined’ is of special significance.
9. By this term, it means whether an element x will be included in a certain set A. or not.
10. For example, it is possible to construct a set of students who have secured 60 or more than 60 in the madhyamik exam.
11. Here the student who has secured 61, is a member of that set, but who has secured 59 is not a member or element of that set.
12. But it is quite impossible to define a set by taking the intelligent students of class-9.
13. Because here the term ‘intelligent’ is not well-defined, that is, it is not possible to detect whether a certain student is intelligent or not and whether he or she will be an element of that set or not.
14. In the definition, it is noticed that the objects should be different, i.e., a certain object can not be a member of a set more than once.
15. For example, let set A consists of the roots of the equation x²- 12x +36= 0.
16. Now, the roots of x² – 12x+36= 0 are 6, 6, i.e., the roots are equal.
17. Then, A consists of only one element 6.
18. Since repeat is not allowed in the definition.

Chapter 1 Set Theory Different Symbols Relating To Set And Their Meanings

Chapter 1 Set Theory Definition Of Set

A collection of different well-defined and independent-of-order objects is called a set, i.e., a collection of objects will be said a set, if

1. The collection is well-defined.
2. Any two objects included in the collection are different from each other.
3. The objects included in the collection are independent of order.
   What is meant by a collection of well-defined objects has already been discussed earlier.
   Now, we shall explain the term independent of order.
   Order of a set means that among the objects of the set which one is at the first, which one at the second, which one at the third, …… etc.
   The objects of the set are independent of order means that the objects may take any place in the set.
   Thus the sets A = (a, e, i, o, u-) or A= (a, i, e, o, u} denote the same set.

Chapter 1 Set Use Of Symbol

Any set is usually denoted by the capital letters A, B, C, ……………X, Y, Z, etc. of English alphabets, and the elements or members of the sets are usually denoted by the small letters a, b, c, x, y, z, etc. 

Thus, if a is any element of the set A, then we write a € A and is read by a belongs to A. 

Again, if a is not an element of A, then we write A and we read it by a does not belong to A.

Chapter 1 Set Presentation Of Sets

Sets:-

There are two methods of describing sets.

1. Roster Method or Tabular Method.
2. Set-builder method or property method or statement method.

1. Roster method: The method in which all the elements of a set are expressed tabularly in a second bracket is known as the Roster method.

For examples:

1. If the vowels of English alphabets be a set V, then in the Roster method V = {a, e, i, o, u). 
2. If P denotes the set of first four prime numbers, then P= (2, 3, 5, 7).
3.  If C is the set of cube roots of 1, then C = {1, ω, ω²).
4. If N₁ denotes the set of first 6 natural numbers, then in the Roster method, N₁ = {1, 2, 3, 4, 5, 6). 

2. Set-builder method:

The method in which the characteristic or property, the elements of the set obey is expressed by a statement is known as the set-builder method.

Here no individual element is expressed in the second bracket.

Thus if each and every element of a set A obey the common property or characteristic P(x), then in the set-builder method, A is expressed as follows:

A = {x | P(x)} or, A = {x: P (x)}.

For examples:

1. If N₁ is a set of the first 6 natural numbers, then in the set builder method, N₁ is expressed as follows:

N = {x1≤x≤6 and x is an integer).

2. If V denotes the vowel of English alphabets, then V = {x: x is a vowel of English alphabets}

Chapter 1 Set Sets Of Different Types

1. Finite and Infinite Set:

The set in which the number of elements can be determined by counting them, i.e., the set in which the number of elements is finite is called a finite set.

If the number of elements of a set A is n, then n is called the degree or order of A and it is denoted by | A | or, n (A).

For examples:

1. The set A = {1, 2, 3, 4, 5, 6) is a finite set, and n (A) = 6.
2. The set V = (a, e, i, o, u) is a finite set, and n (V) = 5.

Infinite Set:

The set in which the number of elements is not countable, i.e., the number of elements is infinite, is known as an infinite set.

For examples:

1. Set of natural numbers, N = {1, 2, 3 … … ) is an infinite set.
2. A set of integers Z = {….. 3, 2, 1, 0, 1, 2, 3 ….) is an infinite set.

 

2. Singleton Set:

The set in which the number of elements is one is called a singleton set.

For examples:

1. A (2) is a singleton set,
2. B= {x: x is a positive integer and x is the root of the equation x²+2x-8=0} is a singleton set.

3. Null Set:

If the number of elements of a set is zero, then it is called a null set.

Null sets are usually denoted by o.

For examples:

1. Φ = (x: x is a whole number and 3 < x < 4) is a null set.
2. Φ = {x: x is real and roots of the equation x2+1= 0) is a null set.

4. Subset:

If two sets A and B be such that each and every element of B is an element of A, then B is called a subset of A.

It is usually denoted by B⊆ A or A ⊇ B.

For examples:

1. Let A = {1, 2, 3, 4, 5, 6, 7, 8) and B = {1, 2, 3, 4}, then B is a subset of A since each and every element of B is an element of A.
2. Let A = (a, b, c) and B = (a, b, c, d, e ), then A is a subset of B.

5. Equal Sets: 

If two sets A and B be such that every element of A is an element of B and every element of B is an element of A, i.e., if A ⊆  B and B ⊆ A, then A = B.

For examples:

1. Let A = {2, 3, 4, 5) and B = {2, 4, 3, 5), then A = B.
2. Let X = {2, 3} and Y = {x: x is the roots of x²-5x+6=0), then X = Y.

6. Proper subset and superset: 

A set A is called the proper subset of B if

1. A is a subset of B and

2. there exists at least one element in B which is not in A, i.e., at least one x ∈ B, x ∉ A.

Proper subsets are denoted by A ⊂ B.

The set B is called the superset of A and is written by B ⊃ A.

For examples :

Let N = {1, 2, 3……………} and Z = {-3, -2, -1, 0, 1, 2, 3, ……… }.

Then N ⊂ Z and N ≠ Z.

Let A = (1, 3, 5, 7) and B = {x: 1 ≤ x ≤ 8 and x = N}

A ⊂ B and A ≠ B,

∴ A ⊂ B [ ∵ 8 ∈ B, but 8 ∉ A]

7. Equivalence Sets:

Two sets A and B are said to be equivalence sets if both of them have the same number of elements.

For examples:

Let A= {1, 2, 3, 4) and B (a, b, c, d).

Here, n (A) = 4 and n (B) = 4.

∴ A and B are equivalence sets.

8. Universal Set: 

In the mathematical problems of sets, sometimes it is needed to find such a set which is the superset of all the sets consisting of the problem, i.e., all the sets of the problem are a subset of that set.

This super set is called the universal set with respect to all the sets in the specific problem.

Universal sets are usually denoted by U.

For examples:

The set of all real numbers R is a universal set with respect to all the sets of natural numbers, sets of integers, sets of rational numbers, set of irrational numbers, etc.

Also, let in a mathematical problem, A, B, and C are three sets such that A= {1, 2, 3, 4), B = (3, 4, 5}, and C = {1, 3, 5, 6, 7, 8), then with respect to A, B, C the set U = {1, 2, 3, 4, 5, 6, 7, 8} is a universal set.

1. Power Set: 

The set consisting of all the subsets of a given set A is called the power set of A and is usually denoted by P (A).

Symbolically, P (A) = (X: X ⊂ A).

For examples:

Let A = (a, b, c). P(A) = (Φ, (a), (b), (c), (a, b), (b, c), (c, a), (a, b, c}} 

Let A = {1,2}

∴ P(A)= {Φ, (1), (2), (1, 2)}

Chapter 1 Set Sets Operations On Sets

1. Union of two sets :

Let A and B be two given sets.

Then, the union of the sets A and B, denoted by \(A \cup B\), is defined by \(A \cup B\) = {x:x ∈ A or x ∈ B) i.e., \(A \cup B\) consists of all the elements of both A and B, but not repeated.

For examples:

1. Let A = (a, b, c, d) and B = (b, c, d, e)

∴ \(A \cup B\)

2. Let A = {1, 3, 5, 7……….} and B (2, 4, 6, 8……..}

∴ \(A \cup B\)

2. The intersection of two sets :

Let A and B be two given sets. 

Then the intersection of A and B, usually denoted by \(\), is defined by \(A \cap B\) = {x:x ∈ A and x ∈ B), i.e., \(A \cap B\) consists of only the common elements of both A and B.

For examples:

1. Let A = {1, 2, 3, 4, 5) and B = (2, 3, 4}

∴ \(A \cap B\) = (2, 3, 4)

2. Let A = {x:1≤x≤3, x ∈ N) and B = (x: 0≤x≤2, x ∈ N}

∴ \(A \cap B\) = (1, 2)

 

3. Disjoint sets:

If two given sets A and B be such that there is no common element in between them, then the sets are called disjoint sets.

Here, \(A \cup B\) = Φ and Φ = null set.

For examples:

Let A= {x: x is a rational number}

and B= {x: x is an irrational number}

Then clearly, \(A \cap B\) ≠ Φ

∴ A and B are disjoint sets.

4. Difference between two sets:

Let A and B be two given sets. 

Then the difference between A and B, usually denoted by A – B or B – A is defined by A-B = {x:x ∈ A and x ∉ B). 

Similarly, B A = {x: x ∈ B and x ∉ A}

i.e., (A-B) consists of those elements which are not an element of B

For examples:

Let A= (a, b, c, d, e) and B = (c, d, e, f)

∴ A – B (a, b) and B – A = {f}

 

5. Complement of a set :

With respect to a universal set U, the complement of a set A, usually denoted by A’ or A^c, is defined by

Ac = U – A = (x: x ∈ U and x ∈ A).

For examples :

Let R= (x: x is real), Q= {x: x is rational}

∴ with respect to the universal set R,

Q^c = R – Q = {x: x is irrational).

5. Symmetric Difference :

The symmetric difference of two sets A and B is usually denoted by AΔB and is defined by

\(\mathrm{A} \Delta \mathrm{B}=(\mathrm{A}-\mathrm{B}) \cup(\mathrm{B}-\mathrm{A})\)

Chapter 1 Set Sets Venn Diagram

The by which the operations on sets are presented in a befitting manner is known as Venn diagrams.

Method:

In Venn diagrams, the universal set is usually expressed by a rectangle and the subsets of the universal set are expressed by some circles which are generally shaded.

Set Operations by Venn diagrams:

1. Union of two sets:

2. Intersection of two sets:

3. disjoint Sets:

4. Difference of the two sets:

5. Complement of a set:

6. Symmetric Difference:

Statistics Chapter 2 Histogram And Frequency Polygon

Chapter 2 Histogram And Frequency Polygon Histogram:

We get some rectangles when the class intervals of any continuous grouped frequency distribution are plotted along the X-axis and the corresponding class-frequencies are plotted along the Y-axis of a graph- paper, the breadths of which are the class lengths and the lengths are the class-frequencies when they are equal or are proportionate to the frequency densities of the corresponding class-intervals when they are unequal.

We know, the area of a rectangle = Length x Breadth

= Frequency density x class-length

= \(\frac{\text { class }- \text { frequency }}{\text { class }- \text { length }} \times \text { class }- \text { length }\)

= class-frequency.

Read and Learn More WBBSE Solutions For Class 9 Maths

∴ When the class lengths are unequal, the areas of the rectangles are proportionate to the corresponding class frequencies.

Therefore, The graphical representation of the grouped frequency distribution of any continuous variable by some adjacent rectangles is known as Histogram.

If the class lengths be not all equal, then the areas of the rectangles are not proportionate to the class- frequencies. In this cases, while histograms are constructed-

The last class length is assumed as one unit.

The lengths of the other rectangles are taken as a proportion of this unit.

For example, if the frequencies of the class intervals 0 – 10, 10 – 30, 30 – 50, 50 – 80, 80 – 100, ………etc. be respectively 4, 16, 12, 18, 8,……………….. etc., then the lengths of the rectangles will be

\(\frac{4}{10} \times 10=4, \quad \frac{16}{20} \times 10=8, \frac{12}{20} \times 10=6, \frac{18}{30} \times 10=6, \frac{8}{20} \times 10=4\)……………………etc. respectively.

Then the areas of the rectangles will be proportionate to the corresponding class frequencies.

 

Chapter 2 Histogram And Frequency Polygon Method Of Construction Of Histograms

 

A working rule of construction of histograms of any given continuous grouped frequency distribution: 

STEP-1: Plot the class boundaries of the class intervals along the X-axis of a graph paper consecutively.

If the class boundaries do not start from O, the class boundaries should

be plotted from a point that is at a short distance from the origin on the right side and the part between the starting point and the origin should be marked by a curved line like     

 

 

STEP-2: The class frequencies of each class interval (or it’s proportionate) should be then plotted along the Y-axis.

In this case, follow the rule discussed above for equal or unequal class- lengths. 

STEP-3: Construct a rectangle for each of the cases thus plotted taking class lengths as breadth and class frequencies as length.

Since the values of the variable are continuous, there will be no gap between the two consecutive rectangles.

Thus, the total pictorial of the continuous rectangles as a whole will be the required histogram.

 

Chapter 2 Histogram And Frequency Polygon

Frequency Polygon:-

Like a histogram, the frequency polygon is also a graphical representation of a given data and its frequencies.

In a frequency polygon (grouped or ungrouped), the values of the variables are plotted along the X-axis, and the corresponding frequencies are plotted along the Y-axis accordingly, a polygon is constructed, which is the pictorial representation of the given frequency distribution.

Therefore, the graphical representation of a frequency distribution (grouped or ungrouped) by a polygon is called a frequency polygon.

Three methods of construction of frequency polygons are discussed below:

1. Construction of frequency polygon of ungrouped data;
2. Construction of frequency polygon of grouped data and its frequencies.

 

1. Frequency Polygon of ungrouped data:

To construct a frequency polygon of any ungrouped data and its frequencies, the values of the variables are taken as the x-coordinates and the corresponding frequencies as the y-coordinates to plot the points thus obtained.

Observe the following example:

Example: The marks obtained by 15 students in a Math exam in the Desbandhu Chittaranjan College are given below:

21, 20, 20, 19, 21, 19, 19, 22, 20, 20, 22, 21, 20, 21, 22.

Construct a frequency polygon of the above data.

Solution:

Arranging the given data we get the following frequency distribution table:

 

 

Now, the points (18, 0), (19, 3), (20, 5), (21, 4), (22, 3), and (23, 0) are plotted in white or graph paper. 

Let the points be P, A, B, C, D, Q.

Then the polygon PABCDQ is the required frequency polygon.

 

 

2. Frequency Polygon of grouped data :

We can construct a frequency polygon of a given continuous grouped frequency distribution in two methods:

1. At first, constructing a histogram and then constructing a frequency polygon from it. 
2. Constructing a frequency polygon directly, i.e., without constructing any histogram. 

 

1. Construction of frequency polygon after constructing histogram :

In this method, at first, a histogram of the given continuous grouped frequency distribution is constructed according to the above-mentioned method.

Then, the class mark of the previous class interval of the first class interval and the class mark of the interval next to the last class interval are determined.

The polygon obtained by joining the mid-points of the breadths of the rectangles in the histogram constructed firstly to the points thus determined is our required frequency polygon. 

2. Construction of frequency polygon directly, i.e., without the construction of histogram :

In this method, at first, all the class marks of the class intervals are determined.

Then plotting them along the X-axis and their corresponding frequencies along the Y-axis, some points are plotted. Later on, the polygon obtained by joining those points by straight lines is our required frequency polygon.

 

Question 1. Daily profits (in Rupees) of 50 shops in the village Bakultala are given below:

Given

Daily profits (in Rupees) of 50 shops in the village Bakultala are given below:

Daily profits (in Rupees).

 

 

Construct a histogram of the above data.

Solution:

Here, all the given class intervals are continuous.

Now, let us take X’OX as X-axis and YOY’ as Y-axis.

Selection of Scale: 

Along the X-axis the length of the sides of each smallest square = 10 units and along the Y-axis it is I unit.

Now, let us plot the class intervals along X-axis. 

Then, let us construct the rectangles for each of the class intervals taking class lengths as the breadths and the corresponding frequencies as the lengths (heights) of the rectangles.

 

 

Then the pictorial presentation of the rectangles as a whole is the required histogram.

 

Question 2. Construct a frequency polygon of the following frequency distribution after constructing a histogram of the same :

 

 

Solution:

Expressing the given data into a grouped frequency distribution we get the following table:

 

 

Now, according to the figure, let us plot the class intervals 20- 25, 25- 30, 30-35, 35-40, 40-45, 45- 50, and 50- 55 along X-axis.

The frequency of the first class interval is 20.

 

 

∴ taking the class-length 5 as the breadth (∵ 20-25 interval has the class-length 25 – 20 = 5) and the corresponding frequency 20 as the length (height), let us construct the first rectangle for the first class interval.

Similarly, all the rectangles for all the class intervals with the same breadth 5 and corresponding frequencies as the lengths (heights) are constructed.

Then the pictorial figure thus obtained by the adjacent rectangles as a whole is our required histogram.

Construction of frequency polygon :

To construct a frequency polygon let us determine the class mark of the previous class interval of the interval (20-25).

Here, class-mark = \(\frac{15+20}{2}\)

Assuming 0 as its frequency, this class mark is plotted along the X-axis. Let the mid-point be P. 

Now, taking the mid-value of the first interval (here, mid-value = \(\frac{20+25}{2}\) = 22.5) 22.5 as the x-coordinate and the corresponding frequency as the y-coordinate, let us plot a point.

 Let the point be A.

According to the same procedure, let us plot the points B (27.5, 26), C (32.5, 16), D (37.5, 10), E (42.5, 4), F (47.5, 18), G (52.5, 6).

At last, taking the mid-value of the next class-interval, i.e., (50- 60) of the last class-interval (50-55) (here, mid-value = \(\frac{55+60}{2}\) = 57.5) as the x-coordinate and 0 (as its frequency) as the y-coordinate the last point (57.5, 0) is plotted.

Let the point be Q.

Now, joining the points P, A; A, B; B, C; C, D ; D, E; E, F; F, G and G, Q by straight lines we get a polygon PABCDEFGQP, which is the required frequency polygon.

 

Question 3. Construct an independent frequency polygon of the following marks obtained by 75 students of the school of Prithas

 

 

Solution:

Let us take X’OX as the x-axis and YOY’ as the Y-axis in the graph paper.

O is the origin.

Also taking along the X-axis, side of each smallest square = 5 units and along the Y-axis, side of each smallest square 1 unit, we get the reduced coordinates

(6, 12), (8, 18), (10, 21), (12, 15), (14, 6), and (16, 3) of the coordinates (30, 12), (40, 18), (50, 21), (60, 15), (70, 6), and (80, 3).

Now, the marks obtained just before 30 will be 20, and just next to 80 will be 90.

∴ According to the scale, the reduced coordinates of (20, 0) (∵ frequency of 20 is assumed to be 0) and (90, 0) will be (4, 0) and (18, 0) respectively.

 

 

Thus plotting in the graph paper the points (4, 0), (6, 12), (8, 18), (10, 21), (12, 15), (14, 6), (16, 3) and (18, 0) let us they are respectively P, A, B, C, D, E, F and Q.

Let us join the points P. A; A, B; B, C; C, D; D, E; E, F and F, Q by straight lines.

Thus a polygon PABCDEFQP is produced.

∴ PABCDEFQP is the required frequency polygon.

 

Question 4. Construct an independent frequency polygon of the following frequency distribution : (Give scale and construction signs. Description is not necessary.)

 

 

Solution :

Selection of Scale: Along the X-axis and Y-axis, the side of each smallest square= 1 unit. 

Mid-values of the class intervals are respectively

\(\frac{0+5}{2}=2 \cdot 5, \frac{5+10}{2}=7 \cdot 5, \frac{10+15}{2}=12 \cdot 5, \frac{15+20}{2}=17 \cdot 5, \frac{20+25}{2}=22 \cdot 5 \text { and } \frac{25+30}{2}=27 \cdot 5\)

∴ the points to be plotted are P (-2.5, 0), A (2·5, 4), B (7.5, 10), C (12.5, 24), D (17.5, 12), E (22.5, 20), F (27.5, 8) and Q (32.5, 0).

 

 

∴ PABCDEFQP is the required frequency polygon.

 

Statistics Chapter 1 Frequency Distributions Of Grouped Data

Chapter 1 Frequency Distributions Of Grouped Data Variables or Variates

1. Suppose the weights of your classmates be x kg.
2. Then it is clear that x may take any value.
3. Because the weights of them are not equal.
4. Let the weight of one of them be 30 kg.
5. Then x = 30.
6. Again, let the weight of another of them be 32 kg.
7. Then, obviously, x = 32, i.e., x is here a changeable quantity, which is countable or measurable.
8. This x is called variable or variate.
9. Similarly, the heights of the learners of your class, and the daily expenditures of each of your families, are all variables or variates.

Definition:

Read and Learn More WBBSE Solutions For Class 9 Maths

1. The quantities, the values of which are changeable and measurable, i.e., the quantities which may take more than one value and are measurable, are called variables or variate.
2. Variables are generally of two types.

Such as—

1. Discontinuous or Discrete variables
2. Continuous variables.

1. Discontinuous or Discrete variables:

1. The variables which may take some but not all the values of a given certain limits of values are called discontinuous or discrete
2. For example, let the number of students present in a day be n.
3. Then n is a discontinuous or discrete variable.
4. Because, if the number of students in your class is 40, then the values of n may be 1,2, 3, 4,………….40; i.e, n may take only the integer values of the Certain given limit of values from 1 to 40.
5. But n is not capable to take the values of the limit like 1.5,2.5, 3.7,4.8, etc. for the number of students present on a certain day can never be an irrational one.
6. So that here n is a discontinuous or discrete variable.
7. For similar reasons, the number of students in your school, the number, of trees in your home, the population of your village, the number of calls in your mobile, etc. are all discontinuous or discrete variables.

2. Continuous variable:

1. The variables which are capable to take any value of a certain given limit and are measurable, are called continuous variables.

Such as—

Let the heights of the students in your class be x cm.

Then the values of x may be any number (rational or irrational) between 100 cm and 200 cm (if the heights of the students lie between this certain limit).

So, here x is a continuous variable.

For similar reasons, weights, temperatures, income, expenditure, etc. are all continuous variables.

This changeable but measurable characteristic of any quantity is called its numerical attributes.

Therefore, the numerical or quantitative attributes of any quantity are called variables or variates.

 

Chapter 1 Frequency Distributions Of Grouped Data  Attribute

There are some quantities that are changeable, but not measurable.

Such as the intelligence of man, merit, the educational standard of the students of class 9, the behavior of members of any family, etc.

These cannot be expressed by any quantity.

So, these qualitative quantities are called attributes.

Definition: 

The qualitative characteristics of any object or subject, which are changeable, but beyond of measurement, are called attributes.

Chapter 1 Frequency Distributions Of Grouped Data  Grouped Frequency Distribution

1. We have learned in the previous classes that by arranging the collected primary data in ascending or descending order, we get an arranged data or array.
2. These arrays when expressed in its simplest or shortest form are called frequency distribution.
3. Frequency distribution is of two types.

Such as-

1. Simple or ungrouped frequency distribution;
2. Class or grouped frequency distribution;

You have already studied a lot about the simplest or ungrouped frequency distribution. In the present chapter, we shall discuss about class or grouped frequency distribution. Before it, we shall clarify some terms regarding this.

1. Range: 

The difference between the highest and lowest values of any class or grouped data is called its range.

2. Class or Class-interval:

 If any finite grouped data be divided into some groups or classes; then each group is called its class or class interval.

In general, when the number of members of any grouped data is a large quantity, then they are grouped in such class intervals.

For example, let any grouped data of 1 to 100 be divided into 10 equal classes or class intervals as follows

1-10, 10-20, ………. 90-100.

Then, each of 1 – 10, 10 – 20, …………………….90 – 100 is a class or class interval.

3. Class frequency: 

The number of values in any class interval is called it’s class frequency.

For example, let there be 4 values of any variable of a grouped data between 1 to 10, namely 3, 5, 7, and 8.

Then, the class frequency of the class interval (110) will be 4.

4. Class limit: 

The two end values of any class interval are called the class limits of that class-intervals.

For example, the two class limits of the class intervals (110) are 1 and 10.

Class limits are of two types:

1. Lower class limit
2. Upper-class limit.

1. Lower class limit:

The class limit which is lower or smaller than the two class limits is called the lower class limit.

For example, between the two class limits 1 and 10 of the class interval (110), I am smaller than 10.

Therefore, here I am the lower class limit.

2. Upper-Class limit:

Between the two class limits of the class interval, the one which is greater is called the upper-class limit of that class interval.

Such as, in the class interval (1-10), 10 is greater than 1. 

So, here 10 is the upper class limit of the class interval (1-10).

5. Methods of formation of class intervals: 

We can form class intervals from grouped data in two methods.

Such as-

1. Exclusive method
2. Inclusive method.

1. Exclusive Method:

The method of formation of class intervals in which the upper limit of any class interval is taken as the lower limit of the next class interval and this upper limit is not included to that class interval, but is included in the next class interval is known as the exclusive method of formation of class-intervals.

For example, in the class intervals 1-10, 10-20, 20-30,……….., etc. the upper limits of each of the class intervals is the lower limit of the next class interval.

So, this is an exclusive method.

2. Inclusive Method:

The method of formation of class intervals in which both the lower and the upper limits are included to that class intervals is known inclusive method.

For example, in each of the class intervals 19, 10-19, 20-29, and 30-39,……………, both the lower and the upper limits are included in that class interval.

Hence, it is an inclusive method.

6. Class range:

The difference between the upper and the lower class limits of any class- interval is called the class range of that interval.

Such as the class range of the class interval (1-10) = (10-1) = 9 (by exclusive method) and 10 (by inclusive method).

7. Class boundary:

In order to fill up the gaps between two consecutive class intervals, the class limits of that intervals are extended to some limits, which are known as the class boundaries of that class interval.

For example, in order to fill up the gaps between 9 and 10 of the class intervals 19, 10 – 19 we can extend the intervals as follows: 0.5 9.5 and 9.5 19.5.

Thus, the class-interval 0.5 9.5, 0.5, and 9-5 are called the class boundaries.

It is clear that class boundaries are of two types-

1. Lower class boundaries.
2. Upper class- boundaries.

1. Lower Class-boundary:

The smaller one of the two class boundaries of any class interval is called the Lower class boundary.

For example, for the class interval (0.5 9.5), 0.5 is the lower class boundary.

2. Upper Class-boundary:

The greater one of the two class boundaries of any class interval is called the Upper-class boundary.

Such as, for the class interval (0.5 – 9.5), 9.5 is the upper class- boundary.

Method of finding class boundaries from class limits:

Let in the inclusive method, 10 class intervals are as follows

\(x_0-x_1, x_2-x_3, x_4-x_5, \ldots \ldots \ldots \ldots \cdot x_9-x_{10}\) and

let \(x_2-x_1=x_3-x_2=x_4-x_3=\cdots \cdots \cdots=x_9-x_8=d\) 

∴ Lower class-boundary of the class \(\left(x_0-x_1\right)=x_0-\frac{x_2-x_1}{2}=x_0-\frac{d}{2}\)

and upper class-boundary = \(x_1+\frac{x_2-x_1}{2}=x_1+\frac{d}{2}\)

Similarly, lower class-boundary of the class\(\left(x_4-x_5\right)=x_4-\frac{d}{2} \text { and upper class-boundary }=x_5+\frac{d}{2}\) 

For example, in the class intervals 1-9, 10-19, d = 10 – 9 = 1.

∴ the lower class boundary of the class \((1-9)=1-\frac{d}{2}=1-\frac{1}{2}=0.5\)

and upper class boundary = \(=9+\frac{d}{2}=9+\frac{1}{2}=9 \cdot 5\)

∴ the corresponding class will be (0.5 – 9.5).

 

8. Mid-value or class mark: The value of the variable of any class interval which lies just in the middle of the two class limits or class boundaries is called the class mark or the mid-value of that class interval.

∴ the mid-value of any class-interval = \(\frac{\text { Lower class-limit }+ \text { Upper class-limit }}{2}\)

= \(\frac{\text { Lower class-boundary }+ \text { Upper class-boundary }}{2}\)

Mathematically, if the lower-class limit or boundary of any class interval is x₁ and its upper-class limit or boundary is x₂, then

the mid-value of the class-interval = \(\frac{x_1+x_2}{2}\)

For example, the mid value of (10-12) = \(\frac{10+12}{2}\) = 11.

 

9. Class length:

The difference between the two class limits or class boundaries of any class- interval is called the class length of this class interval.

∴ Class-length = (upper class-limit) – (lower class-limit).

For example, the class length of the class interval (10 – 20) = 20 – 10 = 10

 

10. Relative frequency:

The ratio of the frequency of a certain class interval to the total frequency of any grouped data is called the relative frequency of that certain class interval.

∴ Relative frequency = \(\frac{\text { Class-frequency }}{\text { Total-frequency }}\)

For example, let the total frequency of any grouped data be 40 and that of the class-interval (10-20) be 6, then the relative frequency of (10-20) = \(\frac{6}{40}\) = 0.15.

Percentage of relative frequency:

Percentage of relative frequency = \(\frac{\text { Class-frequency }}{\text { Total-frequency }} \times 100 \%\)

 

11. Frequency density:

The ratio of the class frequency of any class interval of a grouped data to its class length is called the frequency density of that class interval.

∴ Frequency density = \(\frac{\text { Class-frequency }}{\text { Class-length }}\)

For example, if the class frequency of the class interval (10-20) is 6,

then its frequency density = \(\frac{6}{10}\)

= 0.6. [ ∵ class-length = 20- 10 = 10 ]

 

A working rule of preparation of grouped frequency distribution :

STEP-1: Express the given raw data as an array by arranging them in ascending or descending order.

STEP-2: Select the class intervals.

STEP-3: Determine the class frequency of each interval using tally marks.

STEP-4: Prepare the grouped frequency distribution table by putting class frequencies against each class interval.

 

Chapter 1 Frequency Distributions Of Grouped Data Cumulative Frequency Distribution

To know the number of values of any variable just before or next to a certain value of the variable, we generally use cumulative frequency distribution. In this table, the frequency written against any class- interval denotes the frequency of that class including the sum total of all the frequencies of the class- intervals before (or next) to that class interval.

Cumulative frequency distributions are of two types.

Such as-

1. Less than type cumulative frequency distribution
2. More than type cumulative frequency distribution.

 

1. Less than type cumulative frequency distribution :

In this type, the frequency written against any certain class interval is equal to the frequency of that class interval including the sum total of all the class intervals before that certain class interval, i.e., here. 

Cumulative frequency of the first class-interval frequency of the first class-interval.

Cumulative frequency of the second class-interval frequency of the first class-interval + frequency of the second class-interval.

Cumulative frequency of the third class-interval = frequency of the third class-interval + Cumulative frequency of the second class-interval,…………………….., etc.

For example, A distribution of the heights of 50 students of class 9 is as follows;

Table of Frequency Distribution

 

 

We can prepare a less-than-type cumulative frequency distribution table from this table as follows:

Less than type cumulative frequency distribution table

 

 

From the above table, we can say that the number of students having heights less than 160 cm = 22.

Similarly, the number of students having heights less than 170 cm = 44.

 

2. More than type cumulative frequency distribution :

In this type, the frequency written against any class interval is the frequency of that class interval including the total frequencies of its next all the class intervals, i.e., here.

Cumulative frequency of the first class interval = frequency of the first class interval + cumulative frequency of the second class interval.

Cumulative frequency of the second class interval = frequency of the second class interval + cumulative frequency of the third class interval.

Cumulative frequency of the third class interval = frequency of the third class interval + cumulative frequency of the fourth class interval.

………………………….., etc.

For example, by Preparing a more than type cumulative frequency distribution table from the above-mentioned example, we get,

More than type cumulative frequency distribution.

 

 

In the above table, the number of students having heights more than 160 cm is 28, and that more than 150 cm is 48.

 

Chapter 1 Frequency Distributions Of Grouped Data Select The Correct Answer (MCQ)

 

Question 1. Which one of the following is the pictorial representation of data?

1. Raw data
2. Bar diagram
3. Cumulative frequency
4. Frequency distribution

Solution:

2. Bar diagram is the correct

 

Question 2. The range of the data 12, 25, 15, 18, 17, 20, 22, 26, 6, 16, 11, 8, 19, 10, 30, 20, 32 is

1. 10
2. 15
3. 18
4. 26

Solution:

Given 

12, 25, 15, 18, 17, 20, 22, 26, 6, 16, 11, 8, 19, 10, 30, 20, 32.

The lowest value of the given data = 6 and the highest value = 32.

∴ the required range = 32 – 6

= 26

∴ 4. 26 is correct.

 

Question 3. The class length of 15, 610, ………………… is equal to

1. 4
2. 5
3. 4.5
4. 5.5

Solution:

The gap between (1-5) and (6-10) = d = 6 – 5 = 1

the lower-boundary of \((1-5)=1-\frac{d}{2}=1-\frac{1}{2}=0 \cdot 5\) and

∴ the upper boundary = \(5+\frac{d}{2}=5+\frac{1}{2}=5 \cdot 5\)

∴ the required class length is 5.5 – 0.5 = 5.5

∴ 2. 5.5 is correct.

 

Question 4. The mid-values of the class intervals of a frequency distribution are respectively 15, 20, 25,30, …… The class interval of which the mid-value is 20 is

1. 12.5 – 17.5
2. 17.5 – 22.5
3. 18-5 – 21.5 
4. 19.5 – 20.5 

Solution:

Given

The mid-values of the class intervals of a frequency distribution are respectively 15, 20, 25,30.

The lower class boundary of the class interval (17.5 – 22.5 ) = 17.5 and the upper class-boundary= 22.5.

∴ the mid-value of the class-interval = \(\frac{17 \cdot 5+22 \cdot 5}{2}=\frac{40}{2}=20\)

Also, its class length is 22.5 – 17.5 = 5 = (20 – 15). 

∴ 2. 17.5 – 22.5 is the correct answer.

 

Question 5. The mid-value of a class interval of a frequency distribution is 10 and the class length of each class is 6; The lower class limit of the class interval is

1. 6
2. 7
3. 8
4. 12

Solution:

Given 

The mid-value of a class interval of a frequency distribution is 10 and the class length of each class is 6.

Let the lower class limit be x. 

As per the question, the class-length of class = 6 

∴ upper class-limt = 6 + x

∴  the mid-value of the class-interval = \(\frac{x+6+x}{.2}\)

or, \(10=\frac{6+2 x}{2}\)      [∵ mid-value = 10]

or, 2x + 6 = 20

or, 2x = 20 – 6

or, 2x = 14

or, x = \(\frac{14}{2}\)

= 7.

∴ The required lower-limit = 7.

 

Chapter 1 Frequency Distributions Of Grouped Data Short Answer Type Questions

 

Question 1. Find the lower-class boundary of the continuous frequency distribution of which the mid-value is m and the upper-class boundary is u.

Solution: 

Given 

Mid-value is m and the upper-class boundary is u.

We know, mid-value of any class = \(\frac{\text { Lower class }- \text { boundary }+ \text { upper class – boundary }}{2}\)

⇒ m = \(m=\frac{\text { Lower class }- \text { boundary }+u}{2}\)

or, 2m = Lower class-boundary + u.

or, 2m – u = Lower class boundary.

∴ The required lower class-boundary=2m – u.

 

Question 2. The mid-value of a class interval of a continuous frequency distribution is 42 and its class length is 10. Find the lower and upper-class limits of the class interval.

Solution: 

Given 

The mid-value of a class interval of a continuous frequency distribution is 42 and its class length is 10.

Let the upper limit = x and lower limit = y

As per question, \(\frac{x+y}{2}\) = 42 …………….(1) and x-y = 10……………..(2);

From (1) we get, x + y = 84………………(3)

Adding (2) and (3) we get, x-y + x + y = 10 + 84

or, 2x = 94

or, x = 47.

Putting x = 47 in (2) we get, 47-y= 10

or, y = 47 – 10 

= 37.

∴ The required upper-limit= 47 and lower-limit= 37.

 

Question 3. Find the frequency density of the first class interval of the following frequency distribution :

 

 

Solution:

Here, the first class interval is (70-74), the upper limit = 74, and lower-limit = 70, and d 75 – 74 = 1.

∴ upper class-boundary = 74 + \(\frac{1}{2}\) = 74.5  and lower class-boundary = 70 – \(\frac{1}{2}\) = 69.5.

∴ class-length 74.5 – 69.5 = 5.

Again, the frequency of the first class interval = 3,

∴ The required frequency density = \(\frac{\text { Class-frequency }}{\text { Class-length }}=\frac{3}{5}=0.6\)

 

Question 4. Find the relative frequency of the last class interval of question no. 3 above. 

Solution:

Here, the last class interval is (8589), the class frequency of which is 8. 

Total frequency 3+ 4+ 5+ 8 = 20

∴ the required relative frequency = \(\frac{\text { Class-frequency }}{\text { Total-frequency }}=\frac{8}{20}=0.4\)

 

Question 5. Determine which of the following are attributes and which are variables :

1. Number of members of a family 

Solution: 

The number of members of the family may be any integer, 

i.e., it may take any value.     

∴ it is a variable.

 

2. Daily temperature

Solution: 

The daily temperature may take any value.    

∴ it is a variable.

 

3. Educational standard

Solution: 

Educational standard is a non-measurable quantity.

∴  it is an attribute.

 

4. Monthly income

Solution: 

The monthly income of any person may take any value, integer, or fraction.

∴ it is a variable.

 

Chapter 1 Frequency Distributions Of Grouped Data Short Answer Type Questions

 

Question 1. The number of members of each of the 40 families in your village is given below:

 

 

 

Prepare a grouped frequency distribution table of the above data taking intervals 0 – 2, 2 – 4, ………… etc.

Solution:

The given data is raw data.

Arranging them in an array, we get,

 

 

Now, using tally-mark we prepare the following grouped frequency distribution table

 

Question 2. The marks in mathematics obtained by 40 students of Hindu School, Kolkata are given below:

 

 

Prepare a grouped frequency distribution table of the above data taking the class intervals 1- 10, 11- 20,……………., 41 – 50.

Solution:

The lowest number obtained = 01 and the highest number obtained = 49.

in the inclusive method, we get the following table:

Grouped frequency distribution of the marks obtained in Mathematics.

 

 

Question 3. Hindustan Times published data on the ages of some injuries of the disastrous earthquake that occurred in Nepal on 25th April 2015 as follows:

 

 

Prepare a more than type cumulative frequency distribution table of the above data. 

Solution: More than the type cumulative frequency distribution table of 300 injuries.

 

 

Question 4. Prepare a grouped frequency distribution table of the following cumulative frequency distribution:

 

 

Solution:

Here, the total number of students = 100.

In the exclusive method, the class intervals will be 0 – 10, 10-20, 20-30, 30-40, 40 – 50, 50-60, and 60-70 and the respective frequencies will be 100-92 = 8, 92-87 = 5, 87-75 = 12, 75 – 40 =35, 40 – 16 = 24, 160 = 16 and 0.

Then we get the following table

 

 

 

 

 

Mensuration Chapter 3 Area Of Circles

Chapter 3 Area Of Circles Area of a circle

Area of circles circumscribed in Determination of in-radius and circum-radius

Area of a circle = x (radius)² = πr² [ r = radius of circle]

The area of the region closed by two concentric circles= \(\pi\left(\mathrm{R}^2-r^2\right)=\pi(\mathrm{R}+r)(\mathrm{R}-r)\)   [R and r are the radii of the circles ]

Let the sides AB, BC, CD, ………… of a regular polygon touch the circle with the center at O and the number of sides of it be n. 

Let us draw the radii OP, OQ, OR,………………contacts.

∴ these are perpendiculars to AB, BC, CD,… etc. respectively.

Read and Learn More WBBSE Solutions For Class 9 Maths

Let the radius = r, 

∴ r = OP = OQ = OR = ………..

Now, the area of the polygon ABCD ………….

= ΔOAB + ΔOBC + ΔOCD + ………..

= \(\frac{1}{2} \mathrm{AB} \cdot \mathrm{OP}+\frac{1}{2} \mathrm{BC} \cdot \mathrm{OQ}+\frac{1}{2} \mathrm{CD} \cdot \mathrm{OR}+\cdots \cdots\)

= \(\frac{1}{2} \mathrm{AB} \cdot r+\frac{1}{2} \mathrm{BC} \cdot r+\frac{1}{2} \mathrm{CD} \cdot r+\cdots \cdots\)

= \(\frac{1}{2} r(\mathrm{AB}+\mathrm{BC}+\mathrm{CD}+\cdots \cdots)\)

= \(\frac{1}{2} r \times \text { (Perimeter of the polygon) }\)

Now, if the number of sides is a large number, i.e., if n tends to infinity, then AB, BC, CD,….. etc. reduces smaller and smaller and ultimately at the limiting position they coincide with the circumference of the circle.

∴ Area of the circle = \(\frac{1}{2} r \times(\text { circumference of the circle) }\)

= \(\frac{1}{2} r \times 2 \pi r=\pi r^2\)

∴ Area of a circle = πr² (r= radius). (Proved)

 

Chapter 3 Area Of Circles  Area Of Circles Inscribed In A Square

Area Of Circles Inscribed In A Square:-

If a circle is inscribed in a square, then the diameter of the circle is equal to the equal sides of the square.

∴ Radius of the circle = \(\frac{\text { side of the square }}{2}\)

Now, if the equal sides of the square be units, then the radius of the circle = \(\frac{a}{2}\) units, 

∴ Area of the circle = \(\pi\left(\frac{a}{2}\right)^2 \text { sq-units }=\frac{\pi a^2}{4} \text { sq-units }\)

 

 

Chapter 3 Area Of Circles Area Of Circles Circumscribing A Square

Area Of Circles Circumscribing A Square:-

If a circle is circumscribed in a square, then the diameter of the circle is equal to the diagonal of the square.

Now, if the equal sides of the square be a unit, then its diagonal is √2a units.

∴ Diameter = √2a units

∴ Radius = \(\frac{\sqrt{ } 2 a}{2} \text { units }=\frac{a}{\sqrt{ } 2} \text { units. }\)

∴ Area of the circle = \(\pi \times\left(\frac{a}{\sqrt{ } 2}\right)^2 \text { sq-units }=\frac{\pi a^2}{2} \text { sq-units. }\)

 

 

Chapter 3 Area Of Circles Area Of Circles Circumscribing A Rectangle

Area Of Circles Circumscribing A Rectangle:-

If a circle is circumscribed in a rectangle, then the diameter of the circle is equal to the diagonal of the rectangle.

Now, if the length and breadth of the rectangle be a units and b units respectively,

then the diagonal of the rectangle is \(\sqrt{a^2+b^2}\) units.

∴ Diameter of the circle = \(\sqrt{a^2+b^2}\)

∴ Radius of the circle = \(\frac{\sqrt{a^2+b^2}}{2}\)

∴ Area of the circle = \(=\pi\left(\frac{\sqrt{a^2+b^2}}{2}\right)^2 \text { sq-units }=\frac{\pi}{4}\left(a^2+b^2\right) \text { sq-units }\)

 

 

Chapter 3 Area Of Circles To Find The In-Radius Of A Triangle

The In-Radius Of A Triangle:-

Let O be the in-radius of the ΔABC.

Let us draw perpendiculars OD, OE, and OF to the sides BC, CA, and AB respectively.

Let the in-radius of ΔABC be r.

∴ OD = OE = OF = r units

Now, the area of ΔABC = area ofΔOBC + area of ΔOAC + area of ΔOAB.

⇒ \(\frac{1}{2} \times \mathrm{BC} \times \mathrm{OD}+\frac{1}{2} \times \mathrm{AC} \times \mathrm{OE}+\frac{1}{2} \times \mathrm{AB} \times \mathrm{OF}\)

= \(\frac{1}{2} \times \mathrm{BC} \times r+\frac{1}{2} \times \mathrm{AC} \times r+\frac{1}{2} \times \mathrm{AB} \times r\)

= \(\frac{1}{2}(\mathrm{BC}+\mathrm{AC}+\mathrm{AB}) \times r\)

∴ Area of the triangle = \(\frac{1}{2}\) x Perimeter of the triangle x in-radius

 

 

Chapter 3 Area Of Circles To Find The In Radius And Circum Radius Of An Equilateral Triangle

 

The In Radius And Circum Radius Of An Equilateral Triangle:-

Let the equal sides of the equilateral triangle be a unit.

∴ Height of the triangle = \(\frac{\sqrt{3}}{2} a \text { units }\)

Since, the height of an equilateral triangle is also a median of it, the median 

= \(\frac{\sqrt{3}}{2} a \text { units }\)

Now, the median is divided internally at the centroid of the triangle into the ratio 2: 1,

∴  in-radius = \(\frac{1}{3} \times\left(\frac{\sqrt{3}}{2} a\right) \text { units }=\frac{a}{2 \sqrt{3}} \text { units }\)

and circum-radius = \(\frac{2}{3} \times \frac{\sqrt{3} a}{2} \text { units }=\frac{a}{\sqrt{3}} \text { units }\)

If an arc of a circle of radius r units produces an angle e at the center, then the length of that arc = \(\frac{\theta}{360} \times \text { circumference of the circle }=\frac{2 \pi r \theta}{360} \text { units. }\)

and the area of the circle = \(\frac{\theta}{360} \times \text { area of the circle }=\frac{\pi r^2 \theta}{360} \text { sq-units }\)

 

Chapter 3 Area Of Circles Select The Correct Answer (MCQ)

 

Question 1. The area of a circle is x sq-units. If the circumference is y-units and the diameter be z-units, then the value of \(\frac{x}{yz}\)is

1. \(\frac{1}{2}\)
2. \(\frac{1}{4}\)
3. 1
4. \(\frac{1}{8}\)

Solution :

The area of the circle = \(\pi\left(\frac{z}{2}\right)^2 \text { sq-units }\)

and circumference = \(y=2 \pi\left(\frac{z}{2}\right) \text { units }\)

∴ \(\frac{x}{y z}=\frac{\frac{\pi z^2}{4}}{\pi z \cdot z}=\frac{1}{4}\)

 

 

Question 2. The ratio of the areas of two squares circumscribed and inscribed in a circle is.

1. 4:1
2. 1:4
3. 2:1
4. 1:2

Solution:

Let the radius of the circle = r units.

∴ The side of the circumscribed square = diameter of the circle = 2r units and the diagonal of the inscribed square = diameter of the circle = 2r units.

The side of the square inscribed in the circle= \(\frac{\text { diagonal }}{\sqrt{2}}=\frac{2 r}{\sqrt{2}} \text { units }=\sqrt{2} r \text { units }\)

The required ratio = (2r units)²: (√2r units)² = 4r² sq-units: 2r² sq-units = 2: 1.

 

Question 3. The numerical value of the circumference and area of a circle are equal. The length of the diagonal of the circumscribed circle is

1. 4 units
2. 2 units
3. 4√2 units
4. 2√2 units

Solution: 

Let the radius of the circle is r units, 

∴ \(2 \pi r=\pi r^2 \Rightarrow r=2\)

∴ The side of the square circumscribing the circle = the diameter = 2r units 2 x 2 units = 4 units

∴ Diagonal = side x √2 = 4√2 units.

 

Question 4. The ratio of the areas of the circles circumscribing and inscribed in an equilateral triangle is

1. 4:1
2. 1:4
3. 2:1
4. 1:2

Solution: 

The circum-radius: in-radius of the equilateral triangle = \(\frac{2}{3} \times \text { height : } \frac{1}{3} \times \text { height }\)

= 2: 1

The ratio of the areas is 2²: 1² = 4: 1.

 

Chapter 3 Area Of Circles Short Answer Type Questions

 

Question 1. If the radius of a circle is increased by 10%, then what percentage of its area will be increased?

Solution:

Given

The radius of a circle is increased by 10%

Let the initial radius of the circle be 100r units.

‍ initial area = \(\pi \times(100 r \text { units })^2=10000 \pi r^2 \text { sq-units }\)

Radius when increased by 10% = \(\left[100 r \times\left(1+\frac{10}{100}\right)\right] \text { units }=110 r \text { units }\)

∴ Area after increment = \(\left(12100 \pi r^2-10000 \pi r^2\right) \text { sq-units }=2100 \pi r^2 \text { sq-units }\)

∴ Increased area = \(\left(12100 \pi r^2-10000 \pi r^2\right) \text { sq-units }=2100 \pi r^2 \text { sq-units }\)

∴ Percentage of increment = \(\left(\frac{2100 \pi r^2}{10,000 \pi r^2} \times 100\right) \%=21 \%\)

 

Question 2. If the circumference of a circle is decreased by 50%, then what percentage of its area will be decreased?

Solution: 

Given

The circumference of a circle is decreased by 50%

Let the initial radius of the circle = r units.

∴ initial circumference = 2πr units and area = πr² units.

Now, circumference after discriminant = \(\frac{2πr}{2}\) = units = πr unit [ \(50 \%=\frac{50}{100}=\frac{1}{2}\) ]

∴ Then the radius = \(\frac{\text { circumference }}{2 \pi}=\frac{\pi r}{2 \pi} \text { units }=\frac{r}{2} \text { units }\)

∴ Area after discriminant = \(\pi \times\left(\frac{r}{2}\right)^2 \text { sq-units }=\frac{\pi r^2}{4} \text { sq-units }\)

∴ Decreased area = \(\left(\pi r^2-\frac{\pi r^2}{4}\right) \text { sq-units } ₹ \frac{3 \pi r^2}{4} \text { sq-units }\)

∴ Required percentage = \(\left(\frac{\frac{3 \pi r^2}{4}}{\pi r^2} \times 100\right) \%=\left(\frac{3 \pi r^2}{4} \times \frac{1}{\pi r^2} \times 100\right) \%=75 \%\)

 

Question 3. Jaya inscribed a circle in a square. This circle is also the circumcircle of an equilateral triangle, each of whose sides are 4√3 cm. Find the diagonal of the square.

Solution:

Given

Jaya inscribed a circle in a square.

This circle is also the circumcircle of an equilateral triangle, each of whose sides are 4√3 cm.

The side of the equilateral triangle is 4√3 cm

∴ Height = \(\frac{\sqrt{3}}{2} \times 4 \sqrt{3} \mathrm{~cm}=6 \mathrm{~cm} .\)

∴ Radius of the circumcircle= \(\frac{2}{3}\) x 6 cm = 4 cm.

∴ Diameter = 2 x 4 cm = 8 cm

Since the circle is inscribed in the square, the side of the square is equal to the diameter of the circle.

∴ Side of the square = 8 cm.

The diagonal of the square = 8√2 cm.

 

 

Question 4. Sumit cut a wire into two equal parts and bent one of them into a square and the other into a circle. If the area of the square be 33 sq-cm more than that of the circle, find the length of the wire.

Solution:

Given

Sumit cut a wire into two equal parts and bent one of them into a square and the other into a circle.

The area of the square be 33 sq-cm more than that of the circle.

Let the length of the wire be 2a cm.

∴ length of each part =\(\frac{2a}{2}\) cm = a cm 

Also, let the side of the square be x cm, 

∴ Perimeter = 4x cm.

∴ 4x = a ⇒ x = \(\frac{a}{4}\)

Again, let the radius of the circle be r cm. 

∴ Circumference = 2πr cm

∴ \(2 \pi r=a \Rightarrow r=\frac{a}{2 \pi}\)

As per the question, \(\frac{14 a^2-11 a^2}{176}=33 \Rightarrow 3 a^2=33 \times 176 \Rightarrow a^2=\frac{33 \times 176}{3}\)

⇒ \(\frac{14 a^2-11 a^2}{176}=33 \Rightarrow 3 a^2=33 \times 176 \Rightarrow a^2=\frac{33 \times 176}{3}\)

⇒ \(a=\sqrt{11 \times 11 \times 16}=11 \times 4=44\)

∴ The length of the wire = 2 x 44 cm = 88 cm.

 

Chapter 3 Area Of Circles Long Answer Type Questions

 

Question 1. Palas and Piyali have drawn two circles, the radius of which is 4: 5; then find the ratio of their areas.

Solution:

Given

Palas and Piyali have drawn two circles, the radius of which is 4: 5.

Let the radii of the circles be 4r units and 5r units respectively.

The ratio of the areas of the circles = \(\pi(4 r)^2: \pi(5 r)^2=16 \pi r^2: 25 \pi r^2=16: 25\)

The required ratio = 16: 25.

 

Question 2. There is a road of the breadth of 7 m of a circular park along its outer circumference. If the circumference of the circle is 352 m, then find the area of the road. To concrete the road at a rate of Rs. 20 per sq-m, what will be the required expenditure?

Solution:

Given

There is a road of the breadth of 7 m of a circular park along its outer circumference.

The circumference of the circle is 352 m.

To concrete the road at a rate of Rs. 20 per sq-m

Let the radius of the circular park be r m.

∴ its circumference = 2πr m

As per question, 2лr = 352 ⇒ \(2 \times \frac{22}{7} \times r=352\)

⇒ \(r=\frac{352 \times 7}{2 \times 22}=56\)

The radius of the park = 56 m.

∴ Including the road the radius of the park = (56+7) m = 63 m 

∴ Including the road the area of the circle = π x 63² sq-cm

Again, the area of the circle = π x 56²

∴ The area of the road only = \(\left(\pi \times 63^2-\pi \times 56^2\right) \mathrm{sq}-\mathrm{m}=\pi\left(63^2-56^2\right) \mathrm{sq}-\mathrm{m}\)

= π x (63 + 56) x (63 – 56) sqm

= \(\frac{22}{7} \times 119 \times 7 \mathrm{sq}-\mathrm{m}=2618 \mathrm{sq}-\mathrm{m}\)

Now the expenditure to concrete the road= is Rs. 20 x 2618 

= Rs. 52360.

∴ The required area is 2618 sqm and the required expenditure = is Rs. 52360.

 

 

Question 3. There is a road of equal breadth around the circular field of Bakultala. The outer circumference of the road is 132 m more than its inner circumference. If the area of the road is 14190 sqm, then find the area of the field.

Solution:

Given

There is a road of equal breadth around the circular field of Bakultala.

The outer circumference of the road is 132 m more than its inner circumference.

the area of the road is 14190 sqm,

Let the inner radius and outer radius of the circular road be \(r_1 \mathrm{~m} \text { and } r_2\) respectively.

∴ inner circumference = \(2 \pi r_1 \mathrm{~m} \text { and outer circumference }=2 \pi r_2 \mathrm{~m} \text {. }\)

As per the question, \(2 \pi r_2-2 \pi r_1=132 \Rightarrow 2 \times \frac{22}{7}\left(r_2-r_1\right)=132\)

\(r_2-r_1=\frac{132 \times 7}{2 \times 22} \Rightarrow\left(r_2-r_1\right)=21\) ……………(1)

Given that the area of the road = 14190 sqm

∴ \(\pi\left(r_2^2-r_1^2\right)=14190 \Rightarrow\left(r_2+r_1\right)\left(r_2-r_1\right)=14190 \times \frac{7}{22} \Rightarrow\left(r_2+r_1\right) \times 21=14190 \times \frac{7}{22}\) ………………(2)

Adding (1) + (2) we get, \(r_2-r_1+r_2+r_1=21+215 \Rightarrow 2 r_2=236 \Rightarrow r_2=118\)

\(r_1=215-118=97\)    ∴ the radius of the field = 97 m

∴ The area of the circle = \(\pi r^2 \mathrm{sq}-\mathrm{m}=\frac{22}{7} \times(97)^2 \mathrm{sq}-\mathrm{m}=\frac{206998}{7} \mathrm{sq}-\mathrm{m}=29571 \frac{1}{7} \mathrm{sq}-\mathrm{m} .\)

 

Question 4. The area of a circular field is 154 sq-cm. Find the perimeter of the square circumscribing the circle and also find the area of the square. If the square would be inscribed in the circle, then what would be the perimeter and area of the square?

Solution: 

Given

The area of a circular field is 154 sq-cm.

The square would be inscribed in the circle.

Let the radius of the field = r cm,

∴ Area of the field = r² sq-cm.

As per the question, \(\pi r^2=154 \Rightarrow \frac{22}{7} \times r^2=154 \Rightarrow r^2=\frac{154 \times 7}{22} \Rightarrow r^2=49 \Rightarrow r=7\)

The radius of the field = 7 cm.

∴ Diameter of the field 2r= 2 x 7 cm = 14 cm.

The side of the square circumscribing the circular field is equal to the diameter of the field. 

∴ The perimeter of the square = 4 x side = 4 x 14 cm = 56 cm.

∴ Area of the square = (side)² = (14)² sq-cm = 196 sq-cm.

Again, when the square is inscribed in the circular field, the diagonal of the square is equal to the diameter of the field.

∴ Now, if the side of the square be x cm, then \(\sqrt{2} x=14 \Rightarrow x=\frac{14}{\sqrt{2}}=7 \sqrt{2}\)

∴ Then the perimeter of the square = 4 x side = 4 x 7√2 cm = 28 √2 cm. 

and the area of it (side)²= (7√2)² sq-cm = 98 sq-cm

The perimeter and area of the square 28 √2 cm and 98 sq-cm.

 

Question 5. Lina bought a bracelet from a fair. There is 269-5 sq-cm metal in the bracelet. If the outer diameter of the bracelet is 28 cm, find its inner radius.

Solution:

Given 

Lina bought a bracelet from a fair. There is 269-5 sq-cm metal in the bracelet.

The outer diameter of the bracelet is 28 cm.

Let the inner radius be r cm

Given that the outer-diameter = 28 cm, 

∴ outer-radius = 14 cm

There is 269.5 sq-cm metal in the bracelet.

∴ π (14² – r²) = 269.5

(196 – r²) = 269.5 x \(\frac{7}{22}\)

∴ Inner-radius = 2 x \(\frac{21}{2}\) cm = 21 cm.

 

Question 6. The radius of the circumcircle of a right-angled triangle is 5 cm and the perpendicular distance of the hypotenuse from its opposite vertex is 4 cm. Find the area of the triangle. 

Solution: 

Given 

The radius of the circumcircle of a right-angled triangle is 5 cm and the perpendicular distance of the hypotenuse from its opposite vertex is 4 cm.

We know that the circumcentre of the circumcircle of a right-angled triangle is the midpoint of the hypotenuse and its circum-radius is half of the hypotenuse.

In the ∠B is the right angle of the ΔABC.

The midpoint of the hypotenuse AC is O and BD is the perpendicular drawn from B to AC.

Now, AC = 2 x OA = 2 x 5 cm = 10 cm and BD = 4 cm.

∴ Area of ΔABC = \(\frac{1}{2}\) × AC x BD sq-cm

 = \(\frac{1}{2}\) x 10 x 4 sq-cm 20 sq-cm

∴ The required area = 20 sq-cm.

 

 

Question 7. In the given figure, OPQR is a rhombus three of whose vertices are on the circle with the center at O. If the area of the rhombus is 32√3 sq-cm, find the radius of the circle.

Solution:

Given

OPQR is a rhombus three of whose vertices are on the circle with the center at O.

The area of the rhombus is 32√3 sq-cm.

Let the radius of the circle = r cm.

OPQR is a rhombus,

∴ OP = PQ = QR = RO

∴ OP = OR radius.

OP = OQ = PQ = r cm 

∴ ΔOPQ is an equilateral triangle.

Now area of the rhombus = 2 x (area of ΔOPQ)

= \(2 \times \frac{\sqrt{3}}{4} \times r^2 \mathrm{sq}-\mathrm{cm}=\frac{\sqrt{3}}{2} r^2 \mathrm{sq}-\mathrm{cm}\)

As per the question, \(\frac{\sqrt{3}}{2} r^2=32 \sqrt{3} \Rightarrow r^2=64 \Rightarrow r=8\)

∴ The required radius = 8 cm.

 

 

Question 8. The circle inscribed in an equilateral triangle of sides 24 cm just touches the sides of the triangle. Find the area of the rest part of the triangle (let √3 = 1-732)

Solution: 

Given 

The circle inscribed in an equilateral triangle of sides 24 cm just touches the sides of the triangle.

The ΔABC is an equilateral triangle, each side of which is 24 cm. 

AD is the perpendicular drawn from A to BC. 

Since the triangle is equilateral,

∴ D bisects BC.

∴ BD = CD = \(\frac{24}{2}\) cm = 12 cm. 

The incentre and centroid of the ΔABC are the same points O.

∴ OD = \(\frac{1}{3}\) AD…………(1)

Height of the triangle ABC= AD = \(\mathrm{ABC}=\mathrm{AD}=\frac{\sqrt{3}}{2} \times 24 \mathrm{~cm}=12 \sqrt{3} \mathrm{~cm}\)

∴ from (1) we get, OD = \(\mathrm{OD}=\frac{1}{3} \times \mathrm{AD}=\frac{1}{3} \times 12 \sqrt{3} \mathrm{~cm}=4 \sqrt{3} \mathrm{~cm}\)

∴ Area of the circle = \(\pi \times(\mathrm{OD})^2=\left\{\frac{22}{7} \times(4 \sqrt{3})^2\right\} \mathrm{sq}-\mathrm{cm}\)

= \(\left(\frac{22}{7} \times 48\right) \mathrm{sq}-\mathrm{cm}=150 \cdot 86 \mathrm{sq}-\mathrm{cm}\)

Area of the ΔABC = \(\frac{\sqrt{3}}{4} \times(\text { side })^2=\frac{\sqrt{3}}{4} \times(24)^2 \mathrm{sq}-\mathrm{cm}=144 \sqrt{3} \mathrm{sq}-\mathrm{cm}\)

= 144 x 1.732 sq. cm

= 249.40 sq. cm

∴ Area of the ΔABC = (249.40 – 150.86) sq. cm

= 98.54 sq. cm

 

The area of the rest part of the triangle = 98.54 sq. cm

 

 

Question 9. ABCD is a square of side 12 cm. Four arcs, each of radius 6 cm have been drawn with centers at A, B, C, and D respectively, and in the remaining part, some sketches are also drawn. Find the perimeter and area of the sketched region.

Solution: 

Given

ABCD is a square of side 12 cm.

Four arcs, each of radius 6 cm have been drawn with centers at A, B, C, and D respectively, and in the remaining part, some sketches are also drawn.

Let the four circles drawn with centers A, B, C, and D respectively, and a radius of 6 cm intersect each other at P, Q, R, and S.

We have to find the perimeter and area of the curved region PQRS

Now, area of the square ABCD = (12)² sq-cm = 144 sq.cm

 

 

 

Each of the arcs PS, PQ, QR, and RS have produced an angle of 90° at each center. 

Since each of the radii of the circles is equal. 

∴ arc PS arc PQ = arc QR arc arc RS

= \(\frac{\text { angle produced at the centre }}{360^{\circ}} \times(\text { circumference of circle })\)

= \(\left(\frac{90^{\circ}}{360^{\circ}} \times 2 \pi \times 6\right) \mathrm{cm}=3 \pi \mathrm{cm}=3 \times \frac{22}{7} \mathrm{~cm}=\frac{66}{7} \mathrm{~cm}\)

∴ Perimeter of the curved region 

PQRS = 4 x arc Ps = (4 x \(\frac{66}{7}\)) cm

= 37 \(\frac{5}{7}\)

Again, the region APS = region BPQ = region CQR = region DRS

= \(\frac{\text { angle produced at the centre }}{360^{\circ}} \times \text { area of the circle }\)

= \(\left[\frac{90^{\circ}}{360^{\circ}} \times \pi \times(6)^2\right] \mathrm{sq}-\mathrm{cm}=\frac{198}{7} \mathrm{sq}-\mathrm{cm}\)

∴ Area of the 4 regions = \(\left(4 \times \frac{198}{7}\right) \mathrm{sq}-\mathrm{cm}=\frac{792}{7} \mathrm{sq}-\mathrm{cm}\)

Area of the curved region PQRS = (Area of the square) (Area of 4 regions)

= \(\left(144-\frac{792}{7}\right) \mathrm{sq}-\mathrm{cm}=30 \frac{6}{7} \mathrm{sq}-\mathrm{cm}\)

 

 

Alternative Method:

 The radius of each of the circles with centers at A, B, C, and D is 6 cm and the length of the arc cut by each of the four circles is part \(\frac{1}{4}\) of the circumference of the circles, and the area of each part is also \(\frac{1}{4}\) part of the area of the circle.

∴ The required perimeter = \(4 \times \frac{1}{4} \times 2 \times \frac{22}{7} \times 6 \mathrm{~cm}=37 \frac{5}{7} \mathrm{~cm}\)

and required area = \(\left\{(6+6)^2-4 \times \frac{1}{4} \times \pi \times 6^2\right\} \mathrm{sq}-\mathrm{cm}=30 \frac{6}{7} \mathrm{sq}-\mathrm{cm}\)

 

Question 10. In the given find the area of the lined region.

Solution

Area of each circle = \(\pi \times(r)^2[r=\text { radius }]=\left[\frac{22}{7} \times(3 \cdot 5)^2\right] \mathrm{sq}-\mathrm{cm}=38 \cdot 5 \mathrm{sq}-\mathrm{cm}\)

The arc PS has produced an angle of 90° at the center A.   [ABCD is a square]

∴ Area of the region APS

= \(=\frac{\text { angle produced at the centre }}{360^{\circ}} \times \text { area of circle }\)

= \(\left[\frac{90^{\circ}}{360^{\circ}} \times 38 \cdot 5\right] \mathrm{sq}-\mathrm{cm}=9.625 \mathrm{sq}-\mathrm{cm}\)

∴ The area of the lined region of the circle with the center at A

= (38.5 – 9.625) sq-cm 

= 28.875 sq-cm 

∴ The required area = (4 x 28.875) sq-cm

= 115.5 sq-cm

 

The area of the lined region = 115.5 sq-cm

 

Alternative Method:

The radius of each of the circles with centers at A, B, C, and D is 3.5 cm.

Now in the lined region, \(\frac{1}{4}\) part of the area of each of the circles must be subtracted and \(\frac{3}{4}\) part of the area of each of the circles must be added.

The area of the lined region = \(4 \times \frac{3}{4} \times \frac{22}{7} \times(3 \cdot 5)^2 \mathrm{sq}-\mathrm{cm}=115 \cdot 5 \mathrm{sq}-\mathrm{cm}\)

 

Question 11. In the given find the area and perimeter of the shaded region. 

Solution:

The perimeter of the shaded region = line segment AB + arc AB.

= \(\sqrt{\mathrm{OA}^2+\mathrm{OB}^2}\left [ \angle \mathrm{AOB}=90^{\circ}\right]+\frac{1}{4} \times 2 \times \frac{22}{7} \times 12 \mathrm{~cm}\)(radius 12 cm)

= \(\sqrt{(12)^2+(12)^2} \mathrm{~cm}+\frac{132}{7} \mathrm{~cm}\)

= \(\left(12 \sqrt{2}+\frac{132}{7}\right) \mathrm{cm}\)

= 35.83 cm

∴ Area of the shaded region

= \(\left\{\frac{1}{4} \times \frac{22}{7} \times(12)^2-\frac{1}{2} \times 12 \times 12\right\} \text { sq-cm }\)

= \(\frac{288}{7} \mathrm{sq}-\mathrm{cm}=41 \frac{1}{7} \mathrm{sq}-\mathrm{cm} .\)

 

 

Question 12. Protul has drawn an equilateral triangle ABC the side of which is 10 cm. Sumita has drawn three arcs each of length 5 cm with centers at A, B, and C, and have colored some region in the middle position. Find the area of the colored region. (Take √3 = 1.732)

Solution:

Given

Protul has drawn an equilateral triangle ABC the side of which is 10 cm.

Sumita has drawn three arcs each of length 5 cm with centers at A, B, and C, and have colored some region in the middle position.

The area of the equilateral ΔABC = \(\frac{\sqrt{3}}{4} \times(\text { side })^2=\left[\frac{\sqrt{3}}{4} \times(10)^2\right] \text { sq-cm }\)

= \(25 \sqrt{3} \mathrm{sq}-\mathrm{cm}=25 \times 1.732 \mathrm{sq}-\mathrm{cm}\)

= 43.3 sq-cm (approx.)

Since the arc PR has produced an angle of 60°. at A,

∴ Area of the region APR = \(=\frac{\text { angle produced at the centre }}{360^{\circ}}\) x (area of the circle)

= \(\left[\frac{60^{\circ}}{360^{\circ}} \times \pi \times(5)^2\right] \mathrm{sq}-\mathrm{cm}\)

= \(\left[\frac{1}{6} \times \frac{22}{7} \times 25\right] \mathrm{sq}-\mathrm{cm}=\frac{275}{21} \mathrm{sq}-\mathrm{cm}\)

Similarly, the areas of the regions BPQ and CQR are \(\frac{275}{21}\)sq-cm.

. The area of the colored region= (area of the triangle) – (area of the three equal regions)

= \(\left(43 \cdot 3-3 \times \frac{275}{21}\right) \mathrm{sq}-\mathrm{cm}=(43 \cdot 3-39 \cdot 29) \mathrm{sq}-\mathrm{cm}\)

= 4.01 sq-cm (approx.)

 

 

Question 13. Rabeya has drawn an equilateral triangle of side 21 cm on a large piece of paper. Find the area of the incircle of the triangle.

Solution:

Given

Rabeya has drawn an equilateral triangle of side 21 cm on a large piece of paper.

The side of the equilateral triangle is 21 cm.

∴ height = \(\frac{\sqrt{3}}{2} \times 21 \mathrm{~cm}=\frac{21}{2} \sqrt{3} \mathrm{~cm}\)

The median of the equilateral triangle = its height.

Now, inradius of the incircle = \(\frac{1}{3}\) x median

= \(\frac{1}{3} \times \frac{21 \sqrt{3}}{2} \mathrm{~cm}=\frac{7 \sqrt{3}}{2} \mathrm{~cm}\)

∴ Area of the incircle = \(\frac{22}{7} \times\left(\frac{7 \sqrt{3}}{2}\right)^2 \mathrm{sq}-\mathrm{cm}\)

= \(\frac{22}{7} \times \frac{7 \times \sqrt{3}}{2} \times \frac{7 \times \sqrt{3}}{2} \mathrm{sq}-\mathrm{cm}\)

= 115.5 sq. cm

The area of the incircle of the triangle = 115.5 sq. cm

 

Question 14. The perimeter of a triangle is 32 cm and the area of its incircle is 38-5 sq-cm. Find the area of the triangle.

Solution:

Given 

The perimeter of a triangle is 32 cm and the area of its incircle is 38-5 sq-cm.

Let the radius of the incircle be r cm.

∴ Area of the incle = πr² sq. cm

∴ As per the question, \(\pi r^2=\frac{385}{10} \Rightarrow \frac{22}{7} r^2=\frac{385}{10} \Rightarrow r^2=\frac{385 \times 7}{10 \times 22}=\frac{49}{4} \Rightarrow r=\frac{7}{2}=3 \cdot 5\)

∴ The radius of the incircle = 3.5 cm.

Now, area of the triangle = \(\frac{1}{2} \times \text { perimeter } \times \text { radius }=\frac{1}{2} \times 32 \times 3.5 \mathrm{sq}-\mathrm{cm}=56 \mathrm{sq}-\mathrm{cm}\)

 

Question 15. Find the radii of the incircle and circumcircle of a triangle of sides 20 cm, 15 cm and 25 cm. Also, find their areas.

Solution:

Given

A triangle of sides 20 cm, 15 cm, and 25 cm.

 20² + 15² = 400+ 225 = 625 = 25²

∴ The given triangle is a right-angled triangle, the hypotenuse of which is 25 cm.

Now, the radius of the circumcircle = \(\frac{\text { hypotenuse }}{2}=\frac{25}{2} \mathrm{~cm}=12 \frac{1}{2} \mathrm{~cm}\)

∴ Area of the circumcircle = \(\frac{22}{7} \times\left(\frac{25}{2}\right)^2 \mathrm{sq}-\mathrm{cm}=\frac{22}{7} \times \frac{625}{4} \mathrm{sq}-\mathrm{cm}\)

Again, area of the triangle = \(\frac{6875}{14} \mathrm{sq}-\mathrm{cm}=491 \frac{1}{14} \mathrm{sq}-\mathrm{cm}\)

Let the radius of the incircle be r cm,

∴ \(\frac{1}{2}\) perimeter of the triangle x r = 150

\(\frac{1}{2} \times(15+20+25) \times r=150 \Rightarrow \frac{1}{2} \times 60 \times r=150 \Rightarrow r^{\prime}=\frac{150}{30}=5\)

∴ The radius of the incircle = 5 cm

∴ Area of the incircle = \(\frac{22}{7} \times 5^2 \mathrm{sq}-\mathrm{cm}=\frac{550}{7} \mathrm{sq}-\mathrm{cm}=78 \frac{4}{7} \mathrm{sq}-\mathrm{cm}\)

Mensuration Chapter 2 Circumference Of Circles

Chapter 2 Circumference Of Circles Chord of a circle

1. Chord of a circle:

The line segment joining the two end points of an arc is called the chord of the arc.

O is the center of the circle.

C is the mid-point of the arc ACB and the straight line AB is the chord of the arc ACB.

CD ⊥ AB and CD are called the height of the arc ACB.

Read and Learn More WBBSE Solutions For Class 9 Maths

 

 

2. Ring:

The circles having the same center are called concentric. 

The region closed by two circumferences of two concentric circles is called a ring.

In, the region closed by the circumference PDQ and ACK is a ring. 

Here, PDQ is the outer circumference and ACK is the inner circumference.

 

 

Chapter 2 Circumference Of Circles Circumference Of A Circle

 

Circumference Of A Circle:-

The circumference of a circle is usually known as its perimeter. 

The measurement of the circumference of a circle is always \(\frac{22}{7}\) times its diameter.

Thus, the ratio between the circumference and the diameter of a circle is always constant. 

Proof: Let us draw two circles with co-center O and radius R and r (R > r). 

In the first circle, a regular polygon ABCD……….. is constructed, the number of sides of which is, say, n. 

Now, if OA, OB, OC, OD……etc. are joined, they intersect the second circle at a, b, c, and d.

etc., n-points.

If ab, bc, cd,……… are joined, then a regular polygon abcd………etc., is constructed in the second circle.

Now, in ΔOAB and ΔOab, \(\frac{\mathrm{OA}}{\mathrm{O} a}=\frac{\mathrm{OB}}{\mathrm{O} b}\)    [∵ OA = OB and Oa = Ob ]

Again, since ZAOB = ZaOb,

∴ the triangles ΔOAB = ΔOab are similar.

∴ \(\frac{\mathrm{AB}}{a b}=\frac{\mathrm{OA}}{\mathrm{O} a}=\frac{\mathrm{R}}{r}\)

Similarly ab bc \(\frac{\mathrm{AB}}{a b}=\frac{\mathrm{BC}}{b c}=\frac{\mathrm{CD}}{c d}=\cdots \cdots=\frac{\mathrm{R}}{r}\)

∴ \(\frac{(\mathrm{AB}+\mathrm{BC}+\mathrm{CD}+\cdots \cdots)}{(a b+b c+c d+\cdots \cdots)}=\frac{\mathrm{R}}{r}\)

i.e., \(\frac{\text { Perimeter of the polygon ABCD } \cdots \cdots}{\text { Perimeter of the polygon } a b c d \cdots \cdots}=\frac{\mathrm{R}}{r}=\frac{\text { Radius of the circle ABCD }}{\text { Radius of the circle } a b c d}\)

Now, if n→ ∞, i.e. if the number of sides n is an infinitely large number, then the perimeter of the polygon gradually coincides with the circumference of the circle.

∴ \(\frac{\text { Circumference of } \mathrm{ABCD}}{\text { Circumference of } a b c d}=\frac{\text { Radius of } \mathrm{ABCD}}{\text { Radius of } a b c d}=\frac{\mathrm{R}}{r}=\frac{2 \mathrm{R}}{2 r}=\frac{\text { Diameter of ABCD }}{\text { Diameter of } a b c d}\) = constant

∴ \(\frac{\text { Circumference of ABCD }}{\text { Diameter of } \mathrm{ABCD}}=\frac{\text { Circumference of } a b c d}{\text { Radius of } a b c d}=\text { constant }\)

This constant is usually denoted by π.

∴ Circumference of a circle = π × Diameter.

∵ Circumference of a circle = π x 2r (r = radius)

= 2πr

 

 

Chapter 2 Circumference Of Circles Select The Correct Answer (MCQ)

 

Question 1. Soma takes time \(\frac{πx}{100}\) minutes to round a circular park. Then Soma will take time to cross the park along its diameter-

1. \(\frac{x}{200}\) minutes
2. \(\frac{x}{100}\) minutes
3. \(\frac{π}{100}\)minutes
4. \(\frac{π}{200}\) minutes

Solution:

Let the radius of the park be units.

∴ diameter = 2 units and circumference = 2лr units.

Now, to round 2πr units time required by Soma is \(\frac{πx}{100}\) minutes

∴ to round 1 units time required by Soma is \(\left(\frac{\pi x}{100} \div 2 \pi r\right)\) minutes

∴ to round 2r units time required by Soma is \(\left(\frac{\pi x}{100} \times \frac{1}{2 \pi r} \times 2 r\right) \text { minutes }=\frac{x}{100} \text { minutes }\)

 

Question 2. A circle is inscribed in a square. If the side of the square is 10 cm, then the diameter of the circle is

1. 10 cm
2. 5 cm
3. 20 cm
4. 10√2 cm

Solution: 

Since the circle is inscribed in the square, the side of the square is equal to the diameter of the circle.

∴ the diameter of the circle is 10 cm.

 

Question 3. A circle is circumscribed about a square. If the side of the square is 5 cm, then the diameter of the circle is

1. 5√2 cm
2. 10√2 cm
3. 5 cm
4. 10 cm

Solution: 

Since the circle is circumscribed about the square, the diameter of the circle is equal to the diagonal of the square.

Now, the side of the square is 5 cm, 

∴ diagonal side x √2 = 5√2 cm. 

∴ the diameter of the circle = 5√2 cm.

 

Question 4. A circular ring is of breadth 5 cm. Then the difference between the ex-radius and in-radius of the ring is

1. 5 cm
2. 2.5 cm
3. 10 cm
4. None of these

Solution: 

Let the ex-radius of the ring = R cm and-in-radius of the ring = r cm.

The breadth of the ring = (R – r) cm = 5 cm (as per question)

∴ The required difference = 5 cm.

 

Chapter 2 Circumference Of Circles Short Answer Type Questions

 

Question 1. Find the ratio of the in-radius and circum-radius of a square. 

Solution: 

On-Radius And Circum-Radius Of A Square:-

Let the side of the square = a unit.

∴ Diameter of in-circle = a units and in-radius= \(\frac{a}{2}\)  units.

∴ Again, the diameter of the circum-circle = diagonal of the square = √2a units 

∴ Curcum-radius = \(\frac{\sqrt{2} a}{2} \text { units }=\frac{a}{\sqrt{2}} \text { units }\) 

∴ in-radius: circum-radius = \(\frac{a}{2}: \frac{a}{\sqrt{2}}=\frac{a}{2} \times \frac{\sqrt{2}}{a}=\frac{1}{\sqrt{2}}=1: \sqrt{2}\) 

 

Question 2. If the diameter of a circle and the side of a square are equal, then find the ratio of their perimeters.

Solution: 

Given

The diameter of a circle and the side of a square are equal

Let the diameter of the circle side of the square=2a units.

∴ The perimeter of the circle = 2πa units and the perimeter of the square = 4 x 2a units = 8a units.

The required ratio = 2πa: 8aπ: 4 = \(\frac{22}{7}\) :4 11:14

 

Question 3. The minute’s hand of a clock is of length 7 cm. To round an angle of 90°, what length of arc should it travel?

Solution:

Given 

The minute’s hand of a clock is of length 7 cm. To round an angle of 90°.

The required length = the length of the arc produced by the angle 90° at the center of a circle of radius 7 cm.

= \(\frac{Angle  at  the  centre}{360º}\) x (circumference of the circle)

= \(\frac{90º}{360º}\) x 2π x 7 cm = \(\frac{1}{4}\) x 2 x \(\frac{22}{7}\) x7 cm = 11 cm

The required length = 11 cm.

 

Question 4. If the perimeter of a semi-circle is 36 cm, then find its length of diameter.

Solution:

Given

The perimeter of a semi-circle is 36 cm.

Let the radius of the semi-circle = r cm.

∴ The perimeter of it = (πr + 2r) cm.

As per the question, πr+2r=36 

⇒ r(π+2) = 36

⇒ \(r\left(\frac{22}{7}+2\right)=36\)

⇒ \(r \times \frac{36}{7}=36 \Rightarrow r=7\)

∴ 2r= 2 x 7 cm = 14 cm. 7

The required diameter = 14 cm.

 

Chapter 2 Circumference Of Circles Long Answer Type Questions

 

Question 1. The radius of the wheel of a train is 0.35 m. If the wheel rounds 450 times in one minute, then find the velocity of the train per hour.

Solution: 

Given 

The radius of the wheel of a train is 0.35 m.

the wheel rounds 450 times in one minute.

Radius of the wheel = 0.35 m,

∴ circumference of the wheel = 2 x \(\frac{22}{7}\) x 0.35 m 

= 2.2 m 

∴ the train travels in one minute = 2.2 x 450 m 

= 990 m

∴ the train travels in one hour = 990 x 60 m

= 59400 m 

= 59.4 km

∴ the velocity of the train = 59.4 km per hour.

 

Question 2. A rectangular wire of length 18 cm and breadth 15 cm is bent into a circular wire. Then find the radius of this circular wire.

Solution:

Given

A rectangular wire of length 18 cm and breadth 15 cm is bent into a circular wire.

The length and breadth of the rectangular wire are 18 cm and 15 cm respectively.

∴ its perimeter = 2 x (18 + 15) cm = 66 cm 

Let the radius of the circular wire = r cm

∴ Circumference = 2 πг cm

As per question, = 2 πr = 66 

⇒  \(2 \times \frac{22}{7} \times r=66 \quad \Rightarrow r=\frac{21}{2}=10 \cdot 5\)

∴ the required radius = 10.5 cm.

 

Question 3. Puja and Mohammad started a competition of race at the same time and same point on a circular track of diameter 56 m. When Puja finished the race by rounding 10 times the track, Mohammad then remained one round behind Puja. How many meters was the race and by what meters Puja defeated Mohammad?

Solution: 

Given

Puja and Mohammad started a competition of race at the same time and same point on a circular track of diameter 56 m.

When Puja finished the race by rounding 10 times the track, Mohammad then remained one round behind Puja.

The diameter of the circular track = 56 m,

∴ Circumference of the track= \(\frac{22}{7}\) x 56 m 

= 176 m

∴ 1 round of the track = 176 m

∴ 10 round of the track  = 176 x 10 m = 1760 m

∴ the race was 1760 meters and Puja defeated Mohammad by 176 meters.

 

Question 4. The time taken by Rahim to travel along the diameter of a circular field is 40 sec less as he takes the time to round the field. If the speed of Rahim is 90 m per minute, then find the diameter of the field.

Solution: 

Given 

The time taken by Rahim to travel along the diameter of a circular field is 40 sec less as he takes the time to round the field.

The speed of Rahim is 90 m per minute.

Let the radius of the circular field be m.

∴ its circumference 2лrm and diameter = 2r m

The time required to travel along the circumference

= \(\frac{\text { Distance travelled }}{\text { speed }}=\frac{2 \pi r \mathrm{~m}}{90 \mathrm{~m} / \text { minute }}=\frac{2 \pi r}{90} \text { minutes }\)

And the time required to travel along the diameter = \(\frac{2 r \mathrm{~m}}{90 \mathrm{~m} / \mathrm{m}}=\frac{2 r}{90} \text { minutes }\)

As per question, \(\frac{2 \pi r}{90}-\frac{2 r}{90}=\frac{2}{3}\)    [ ∵ \(40 \mathrm{sec}=\frac{40}{60} \text { minute }=\frac{2}{3} \text { minute }\) ]

or, \(\frac{2 r}{90}(\pi-1)=\frac{2}{3} \quad \text { or, } \frac{2 r}{90}\left(\frac{22}{7}-1\right)=\frac{2}{3} \quad \text { or, } \quad \frac{2 r}{90} \times \frac{15}{7}=\frac{2}{3}\)

or, \(2 r=\frac{2 \times 90 \times 7}{3 \times 15} \quad \text { or, } 2 r=28\)

∴ the required diameter = 28 m.

 

Question 5. The ratio of the circumferences of the two circles is 2 : 3 and the difference between their radii is 2 cm. Find the diameters of the circles.

Solution:

Given

The ratio of the circumferences of the two circles is 2 : 3 and the difference between their radii is 2 cm.

Let the radius of the greater circle be \(r_1\) cm and that of the smaller one be \(r_2\) cm.

∴ \(r_1-r_2=2 \ldots(1) \text { and } 2 \pi r_2: 2 \pi r_1=2: 3 \ldots \ldots (2)\) 

From (1) we get, \(r_1=r_2+2\) ………………(3)

From (2) we get, \(\frac{2 \pi r_2}{2 \pi r_1}=\frac{2}{3} \Rightarrow 3 r_2=2 r_1 \Rightarrow r_2=\frac{2}{3} r_1\) ………………(4)

From (3) we get, \(r_1=\frac{2}{3} r_1+2 \Rightarrow 3 r_1=2 r_1+6 \Rightarrow r_1=6 \Rightarrow 2 r_1=2 \times 6=12\)

From (4) we get, \(r_2=\frac{2}{3} \times 6=4 \Rightarrow 2 r_2=2 \times 4=8\)

∴ the required diameters are 12 cm and 8 cm.

 

Question 6. Four greatest circular plates have been cut out from a circular plate of area 196 sq-cm. Find the circumference of each of the plates.

Solution: 

Given

Four greatest circular plates have been cut out from a circular plate of area 196 sq-cm.

The area of the circular plate = 196 sq-cm.

∴ length of the sides = √196 cm = 14 cm

∴ the diameter of each of the circular plates \(\frac{14}{2} \mathrm{~cm}=7 \mathrm{~cm}\)

∴ \(\text { radius }=\frac{7}{2} \mathrm{~cm}\)

∴ circumference =2 x \(\frac{22}{7}\) x \(\frac{7}{2}\) cm = 22 cm

the required circumference = 22 cm.

 

Question 7. Mahim takes the times 46 sec and 44 sec to round a circular Path of breadth 7 m 5 dem by a bicycle along the outer and inner edges respectively. Find the diameter of the circular path along the inner edge.

Solution:

Given

Mahim takes the times 46 sec and 44 sec to round a circular Path of breadth 7 m 5 dem by a bicycle along the outer and inner edges respectively.

Let the radius of the inner circle = r dem

∴ the radius of the outer circle = (r + 75) dcm [ ∵ 7 m 5 dcm = 75 dcm]

∴ Circumference of the inner circle = 2πr dem and that of the outer circle = 2π (r +75) dcm.

Since time is proportionate to distance, speed is constant.

\(\frac{\text { Circumference of the outer circle }}{\text { Circumference of the inner circle }}=\frac{\text { Time required to travel along outer edge }}{\text { Time required to travel along inner edge }}\)

⇒ \(\frac{2 \pi(r+75)}{2 \pi r}=\frac{46}{44} \Rightarrow 23 r=22 r+1650 \Rightarrow r=1650\)

∴ the required diameter = 2r dcm = 2 x 1650 dcm = 3300 dcm = 330 m.

 

Question 8. The ratio of the times required to travel along the outer edge and along the inner edge of a circular path by a bicycle is 20: 19. If the path between the edges is of breadth 5 m, then find the diameter of the inner circle.

Solution:

Given 

The ratio of the times required to travel along the outer edge and along the inner edge of a circular path by a bicycle is 20: 19.

The path between the edges is of breadth 5 m.

Let the radius of the inner circle = rm

∴ radius of the outer circle = (r+ 5) m

∴ circumference of the inner circle = 2πr m

and circumference of the outer circle = 2л (r + 5) m Since time is proportionate to distance,

\(\frac{\text { Circumference of the outer circle }}{\text { Circumference of the inner circle }}=\frac{\text { Time required to travel along the outer edge }}{\text { Time required to travel along the inner edge }}\)

∴ \(\frac{2 \pi(r+5)}{2 \pi r}=\frac{20}{19} \Rightarrow \frac{r+5}{r}=\frac{20}{19} \Rightarrow 20 r-19 r=95 \Rightarrow r=95\)

Circumference of the Outer Circle Circumference of the inner circle

∴ the required diameter is 190 m.

 

 

 

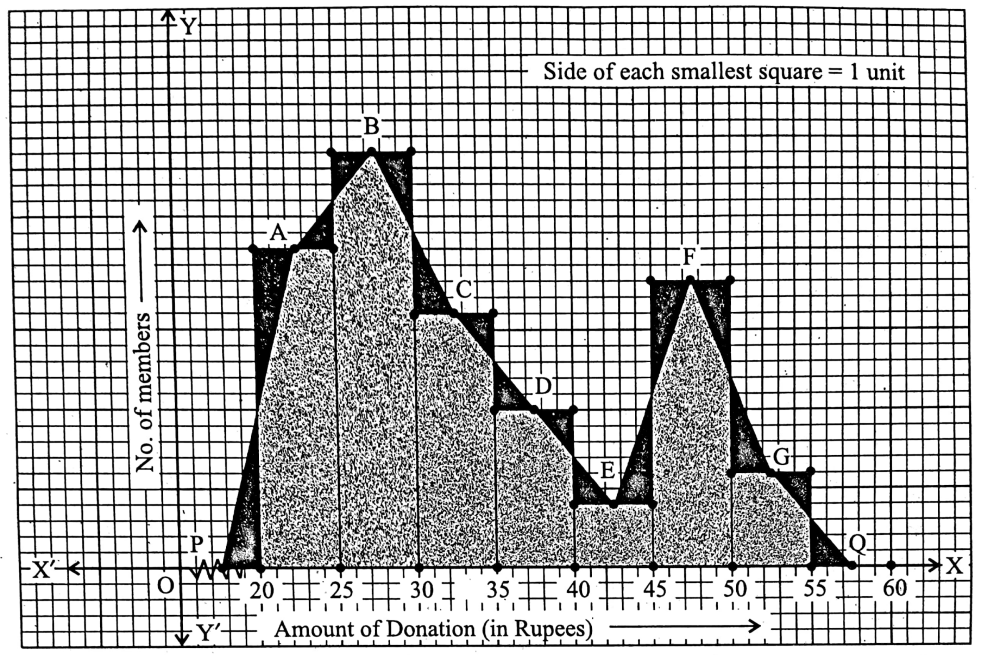
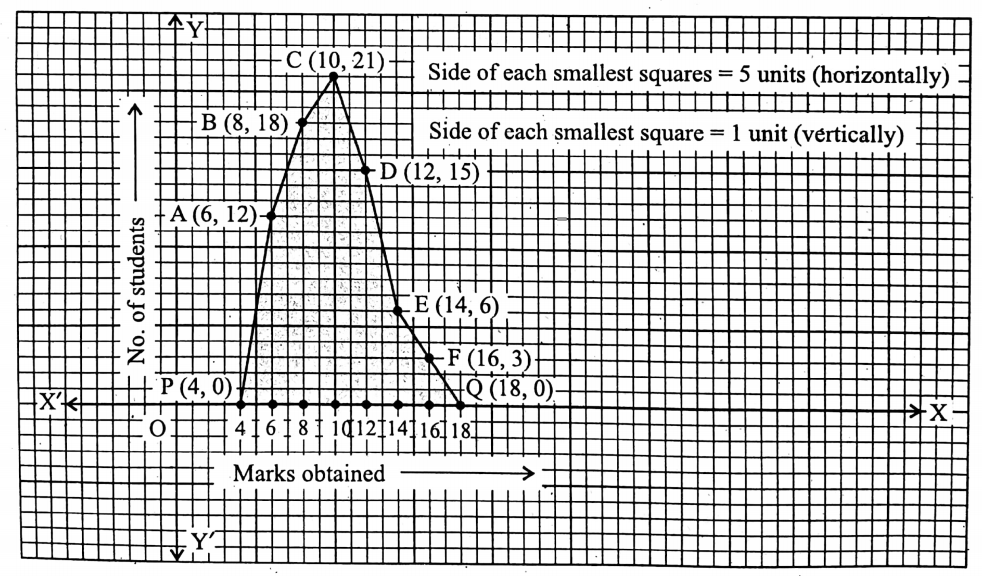
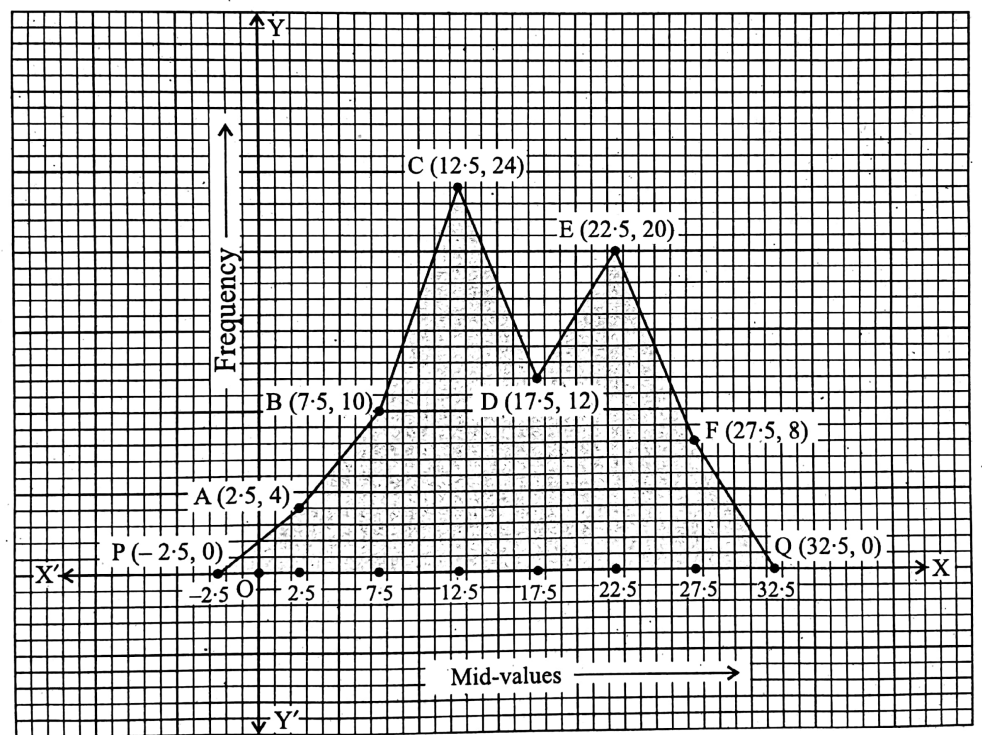
Mensuration Chapter 1 Perimeter And Area Of Triangles And Quadrilaterals

Chapter 1 Perimeter And Area Of Triangles And Quadrilaterals Triangle

1. Definition of Triangle:

The plane area closed by three straight lines is called a triangle. In the following figure.

ABC is a triangle, the vertices of which are A, B, and C, the sides are AB, BC, and CA and the angles are ∠ABC, ∠BCA, and ∠BAC 

 

2. Height of a triangle:

The perpendicular drawn from any of the vertices of a triangle to its opposite side or to its produced opposite side is called the height of the triangle.

Such as, a perpendicular AD is drawn from the vertex A to its opposite side BC.

Read and Learn More WBBSE Solutions For Class 9 Maths

Similarly, a perpendicular DG is drawn from the vertex D to its produced opposite side EF

 

 

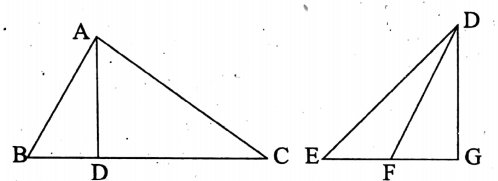
3. Base of a triangle:

The side of the triangle to which the perpendicular is drawn from the opposite vertex is called the base of the triangle with respect to that perpendicular.

Such as BC is the base of the ΔABC with respect to the perpendicular AD, and in ΔDEF, EF is the base with respect to the perpendicular DG. 

 

 

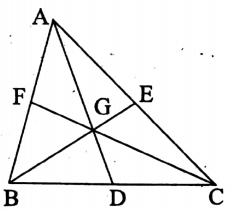
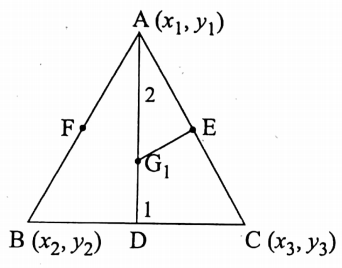
4. Median of a triangle:

The line segments obtained by joining any vertex of a triangle to the mid-point of its opposite side are called the median of the triangle.

Such as, the medians of theΔABC are AD, BE, and CF B Clearly, the medians are concurrent.

Here, the three medians coincide at G.

5. Perimeter of a triangle:

The sum of the lengths of the three sides of a triangle is called its perimeter.

In the perimeter of the ΔABC = AB + BC + CA.

6. Area of a triangle:

The triangle including its internal plane area is called the area of the triangle.

7. Types of triangles:

With respect to sides, triangles are of three types.

Namely, equilateral triangle, isosceles triangle, and scalene triangle.

Again, with respect to angles, triangles are also of three types.

Namely, acute-angled triangle, obtuse-angled triangle, and right-angled triangle.

You have already studied more of it in your previous classes.

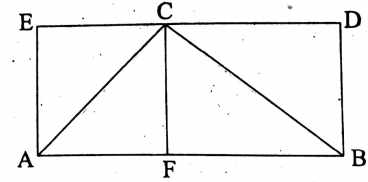
8. Formula to find the area of a triangle:

Let the base of the ΔABC be AB and its height be CF.

We have to find the area of this triangle ABC.

Let us draw a rectangle ABDE with base AB such that the ΔABC and the rectangle ABDE lie within the same parallels.

Now, the ΔABC and the ABDE have the same base AB and within the same parallels AB and DE 

∴ area of ΔABC = \(\frac{1}{2}\) x area of ABDE

∴ area of ΔABC = \(\frac{1}{2}\) x AB x DB = \(\frac{1}{2}\) × AB x CF.

∴ area of any triangle = \(\frac{1}{2}\) x base x height.

 

 

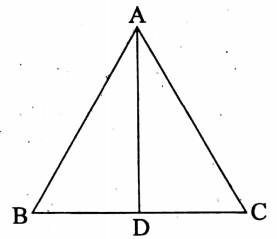
9. Area of an equilateral triangle:

Let the length of each side of an equilateral triangle be ‘a’ units, i.e., AB = BC = CA = units.

Let AD is perpendicular drawn from.

A to the base BC.

Since, the perpendicular, drawn from any vertex of an equilateral triangle to its opposite side, bisects the opposite side,

∴ BD = DC = units

Now, in a right-angled triangle ABD, AD is perpendicular, BD is the base and AB is the hypotenuse.

∴ AD² = AB² – BD² [ by Pythagoras theorem ]

= \(=a^2-\left(\frac{a}{2}\right)^2=a^2-\frac{a^2}{4}=\frac{3 a^2}{4} \Rightarrow \mathrm{AD}=\frac{\sqrt{3} a}{2}\)

Height of an equilateral triangle of side a unit \(\frac{\sqrt{3}}{2}\) x (length of each equal side)

Area of an equilateral triangle = \(\frac{1}{2}\) x BC x AD

= \(\frac{1}{2} \times a \times \frac{\sqrt{3}}{2} a \text { sq-units }=\frac{\sqrt{3}}{4} a^2 \text { sq-units. }\)

∴ Area of an equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)

 

 

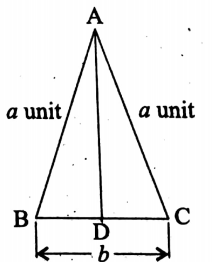
10. Area of an isosceles triangle:

Let the lengths of each of the equal sides AB and AC of the triangle ABC be a unit and the length of its base be b units.

Let us draw perpendicular AD from A to BC.

Since we know that the perpendicular drawn from the vertex of an isosceles triangle to its unequal side bisects the b unequal side,

∴ BD=DC= \(\frac{b}{2}\) units.

Now, in the right-angled triangle ABD, AD is perpendicular, BD is the base and AB is the hypotenuse.

∴ AD² = AB² – BD² [ by Pythagoras theorem]

= \(a^2-\left(\frac{b}{2}\right)^2=a^2-\frac{b^2}{4}\)

∴ \(\mathrm{AD}=\sqrt{a^2-\frac{b^2}{4}}\)

Area of the ΔABC = \(\frac{1}{2} \times \mathrm{BC} \times \mathrm{AD}=\frac{1}{2} \times b \sqrt{a^2-\frac{b^2}{4}} \text { sq-units }\)

∴ Area of an isosceles triangle = \(\frac{1}{2} \times \text { base } \times \sqrt{(\text { equal side })^2-\left(\frac{\text { unequal side }}{2}\right)^2}\)

 

 

11. Area of a Scalene triangle: 

Let the sides of a scalene triangle ABC be a, b, c.

Now, if s be the half-perimeter of ABC, then s = \(\frac{a+b+c}{2}\)

Let us draw perpendicular AD from A to BC. 

Let BD = x units and AD = h DC= ax units

∴ Area of \(\Delta \mathrm{ABC}=\frac{1}{2} \mathrm{BC} \times \mathrm{AD}=\frac{1}{2} a h\)

From the right-angled triangle ABD, we get,

\(\mathrm{AD}^2=\mathrm{AB}^2-\mathrm{BD}^2 \Rightarrow h^2=c^2-x^2\)……………(1)

and from right-angled triangle ADC, we get, 

\(\mathrm{AD}^2=\mathrm{AC}^2-\mathrm{DC}^2 \Rightarrow h^2=b^2-(a-x)^2\)…………….(2)

∴ \(b^2-(a-x)^2=c^2-x^2[\text { by (1) and (2) ] }\)

\(b^2-a^2-x^2+2 a x=c^2-x^2 \Rightarrow 2 a x=a^2-b^2+c^2 \Rightarrow x=\frac{a^2-b^2+c^2}{2 a}\)

∴ \(h^2=c^2-x^2=c^2-\left(\frac{a^2-b^2+c^2}{2 a}\right)^2=c^2-\frac{\left(a^2-b^2+c^2\right)^2}{4 a^2}=\frac{4 a^2 c^2-\left(a^2-b^2+c^2\right)^2}{4 a^2}\)

= \(\frac{\left(2 a c+a^2+c^2-b^2\right)\left(2 a c-a^2+b^2-c^2\right)}{4 a^2}\)

= \(\frac{\left\{(a+c)^2-b^2\right\}\left\{b^2-(a-c)^2\right\}}{4 a^2}\)

= \(\frac{(a+b+c)(a+c-b)(a+b-c)(b+c-a)}{4 a^2}\)

 =\(\frac{(a+b+c)(a+b+c-2 b)(a+b+c-2 c)(a+b+c-2 a)}{4 a^2}\)

= \(\frac{2 s(2 s-2 b)(2 s-2 c)(2 s-2 a)}{4 a^2}=\frac{4 s(s-a)(s-b)(s-c)}{a^2}\)

\(\Rightarrow h=\frac{2}{a} \sqrt{s(s-a)(s-b)(s-c)}\)

∴ Area of a scalene triangle of sides a,b and c

= \(\frac{1}{2} \times \mathrm{BC} \times \mathrm{AD}=\frac{1}{2} \times a \times \frac{2 \sqrt{s(s-a)(s-b)(s-c)}}{a}=\sqrt{s(s-a)(s-b)(s-c)}\)

∴ Area of a scalene triangle = \(\sqrt{s(s-a)(s-b)(s-c)}, \text { where } s=\frac{a+b+c}{2}\)  and a, b, c are sides.

 

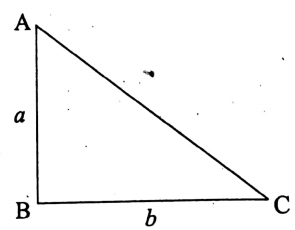
12. Area of a right-angled triangle: 

Let in the right-angled triangle ABC, ∠ABC = 90° and

the length of its adjacent sides of the right angle, i.e., of AB and AC are a units and b units respectively 

∴ area of ΔABC = \(\frac{1}{2}\) x base x height

= \(\frac{1}{2}\) x b x a sq-units 

= \(\frac{1}{2}\) ab sq-units

∴ Area of a right-angled triangle = \(\frac{1}{2}\) x (product of the lengths of the two adjacent sides of the right angle).

 

 

Chapter 1 Perimeter And Area Of Triangles And Quadrilaterals Select The Correct Answer (MCQ)

 

Question 1. The lengths of each of the equal sides of an isosceles right-angled triangle be a unit, then its perimeter is

1. (1+√2) a units
2. (2+√2) a units
3. 3a units
4. (3+2√2) a units 

Solution: 

Here, the length of each of the bases and the perpendicular of the isosceles right-angled triangle is a unit.

∴ hypotenuse = \(\sqrt{a^2+a^2} \text { units }=\sqrt{2 a^2} \text { units }=\sqrt{2} a \text { units }\)

∴ perimeter of the triangle = \(a+a+\sqrt{2} a=2 a+\sqrt{2} a=(2+\sqrt{2}) a \text { units. }\)

Question 2. If the area, perimeter, and height of an equilateral triangle be A, s, and h respectively, then the value of \(\frac{2 A}{s h}\) is

1. 1
2. 1/2
3. 1/3
4. 1/4

Solution

Let the length of the side of the equilateral triangle be x units.

area A = \(\mathrm{A}=\frac{\sqrt{3}}{4} x^2\) sq-units, perimeter s = 3x units and height h = \(h=\frac{\sqrt{3}}{2} x\)

∴ \(\frac{2 \mathrm{~A}}{s h}=\frac{2 \cdot \frac{\sqrt{3}}{4} x^2}{3 x \cdot \frac{\sqrt{3}}{2} x}=\frac{1}{3}\)

Question 3. D is a point on AC of ΔABC such that AD: DC = 3: 2; If the area of the ΔABC is 40 sq- cm, then the area of the ABDC is

1. 16 sq-cm
2. 24 sq-cm
3. 30 sq-cm
4. 36 sq-cm

Solution :

AD: DC = 3:2

\(\Rightarrow \frac{\mathrm{AD}}{\mathrm{DC}}=\frac{3}{2} \Rightarrow \frac{\mathrm{AD}}{\mathrm{DC}}+1=\frac{3}{2}+1\)

\(\Rightarrow \frac{\mathrm{AD}+\mathrm{DC}}{\mathrm{DC}}=\frac{5}{2} \Rightarrow \frac{\mathrm{AC}}{\mathrm{DC}}=\frac{5}{2}\)………….(1)

Let BE be the length of the perpendicular drawn from B to AC.

∴ area of the ΔABC = \(\frac{1}{2}\) AC x BE [ ∵ BE = height]

and area of the ΔBDC = \(\frac{1}{2}\) CD x BE

∴ \(\frac{\Delta \mathrm{BDC}}{\Delta \mathrm{ABC}}=\frac{\frac{1}{2} \times \mathrm{CD} \times \mathrm{BE}}{\frac{1}{2} \times \mathrm{AC} \times \mathrm{BE}}=\frac{\mathrm{DC}}{\mathrm{AC}}=\frac{5}{2}[\text { by (1) }]\)

∴ area of ΔBDC = \(\frac{2}{5}\) x (area of ΔABC)

= \(\frac{2}{5}\) × 40 sq-cm = 16 sq-cm

 

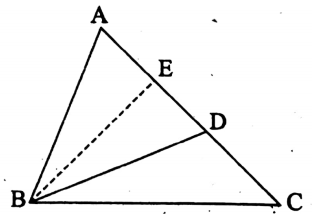
The area of the ABDC is = 16 sq-cm.

 

Question 4. If the differences between each of the sides of a triangle from its half-perimeter be 8 cm, 7 cm, and 5 cm, then the area of the triangle is

1. 20√7 sq-cm
2. 10√14 sq-cm
3. 20√14 sq-cm
4. 140 sq-cm

Solution:

Let the half-perimeter of the triangle be s cm and the sides of the triangle be a cm, b cm, and c cm.,

As per question, s-a=8; s-b= 7; s-c = 5

∴ (s-a)+(s-b)+(s-c) = 20

⇒ 3s-(a+b+c) = 20

⇒ 3s-2s=20 

⇒s=20

∴ the area of the triangle = \(\sqrt{20 \times 8 \times 7 \times 5} \mathrm{sq}-\mathrm{cm}=20 \sqrt{14} \mathrm{sq}-\mathrm{cm}\)

 

Chapter 1 Perimeter And Area Of Triangles Short Answer Type Questions

 

Question 1. The numerical value of the area and the height of an equilateral triangle are equal. Find the length of the side of the triangle.

Solution: 

Given 

The numerical value of the area and the height of an equilateral triangle are equal

Let the length of the side of the triangle be x units.

∴ area = \(\frac{\sqrt{3}}{4} x^2\) sq-units and height = \(\frac{\sqrt{3}}{2} x\)

As per the question, \(\frac{\sqrt{3}}{4} x^2=\frac{\sqrt{3}}{2} x \Rightarrow x=2 \text { units }\)

∴ the length of the sides of the triangle is 2 units.

 

Question 2. If the lengths of the sides of a triangle be doubled, then what percentage of its area will be increased?

Solution: 

Given

The lengths of the sides of a triangle be doubled

Let the sides of the triangle be units, b units, c units, half-perimeter s units, and area A sq-units.

A= \(\sqrt{s(s-a)(s-b)(s-c)} \text { sq-units, where } s=\frac{a+b+c}{2}\)

If the sides of the triangle be doubled, let its area will be A, sq-units, and perimeter be 2s, units.

∴ \(2 s_1=2 a+2 b+2 c \quad \text { or; } \quad s_1=a+b+c=2 s\)……………..(1)

∴ \(\mathrm{A}_1=\sqrt{s_1\left(s_1-2 a\right)\left(s_1-2 b\right)\left(s_1-2 c\right)}=\sqrt{2 s(2 s-2 a)(2 s-2 b)(2 s-2 c)} \text { [ by (1) ] }\)

= \(4 \sqrt{s(s-a)(s-b)(s-c)}=4 \mathrm{~A}\)

∴ percentage of increased area = \(\frac{3 \mathrm{~A}}{\mathrm{~A}} \times 100 \%=300 \%\)

∴ the required increment of the percentage of area is 300%.

 

Question 3. If the sides of a right-angled triangle be (x-2) cm, x cm, and (x + 2) cm, then what is the length of its hypotenuse?

Solution:

Given 

The sides of a right-angled triangle be (x-2) cm, x cm, and (x + 2) cm

Here, the length of the greatest side is (x + 2) cm.

length of the hypotenuse is (x+2) cm.

Now, by Pythagoras’ theorem, x² + (x-2)² = (x+2)² [x cm and (x – 2) cm are one of the perpendicular or base ]

or, x²+x²+4 – 4x = x² + 4 + 4x

⇒ x²-8x=0

⇒ x(x-8)= 0. 

∴ either x = 0 (which is impossible) or, x-8=0

⇒ x=8.

∴ the required length of the hypotenuse = (8 + 2) cm

= 10 cm.

length of its hypotenuse = 10 cm.

 

Question 4. If a square is drawn on the height of an equilateral triangle, then what will be the ratio between the areas of the triangle and the square? 

Solution:

Given 

A square is drawn on the height of an equilateral triangle

Let the side of the equilateral triangle be x units.

Height = \(\frac{\sqrt{3}}{2} x \text { units and area }=\frac{\sqrt{3}}{4} x^2 \text { sq-units }\)

∴ side of the square = \(\frac{\sqrt{3}}{2} x\) units (as per question)

∴ area of the square = \(\left(\frac{\sqrt{3}}{2} x\right)^2 \text { sq-units }=\frac{3}{4} x^2 \text { sq-units }\) 

∴ area of the triangle: area of the square = \(\frac{\sqrt{3}}{4} x^2: \frac{3}{4} x^2=\frac{\frac{\sqrt{3}}{4} x^2}{\frac{3}{4} x^2}=\frac{1}{\sqrt{3}}=1: \sqrt{3}\) 

the required ratio=1: √3.

 

Chapter 1 Perimeter And Area Of Triangles Long Answer Type Questions

 

Question 1. If the height of a triangle is decreased by 40% and its base is increased by 40%, then what change in its area will be performed?

Solution:

Given 

The height of a triangle is decreased by 40% and its base is increased by 40%

Let the base of the triangle be x units, height be y units and area be A sq-units.

∴ \(\mathrm{A}=\frac{1}{2} x y\) 

Now, the increased base = \(\left(x+x \times \frac{40}{100}\right) \text { units }=\left(x+\frac{2 x}{5}\right) \text { units }=\frac{7 x}{5} \text { units }\) 

and the decreased height = \(\left(y-y \times \frac{40}{100}\right) \text { units }=\left(y-\frac{2 y}{5}\right) \text { units }=\frac{3 y}{4} \text { units }\) 

Then, the area of the triangle = \(\frac{1}{2} \times \frac{7 \dot{x}}{5} \times \frac{3 y}{5} \text { sq-units }=\frac{21 x y}{50} \text { sq-units }\) 

∴ the area will be decreased by = \(\left(\frac{1}{2} x y-\frac{21 x y}{50}\right) \text { sq-units }=\frac{2 x y}{25} \text { sq-units }\) 

∴ the required percentage of decreased area = \(\frac{\frac{2 x y}{25}}{\frac{1}{2} x y} \times 100 \%=16 \%\) 

 

Question 2. The perimeter of an isosceles triangle is 544 cm. The length of each equal side is \(\frac{5}{6}\) part of its base. Find the area of the triangle.

Solution:

Given

The perimeter of an isosceles triangle is 544 cm. The length of each equal side is \(\frac{5}{6}\) part of its base

Let the length of the base = x cm

∴ length of each of its equal sides= \(\frac{5}{6}\)x cm

Since, the perimeter = 544 cm,

∴ \(x+\frac{5 x}{6}+\frac{5 x}{6}=544 \Rightarrow \frac{6 x+5 x+5 x}{6}=544\)

\(\Rightarrow \frac{16 x}{6}=544 \quad \Rightarrow x=544 \times \frac{6}{16}=204\)

∴ length of the base 204 cm and the length of each equal side = \(\frac{5}{6}\) x 204 cm

= 170 cm.

∴area of the triangle = \(\frac{1}{2} \times 204 \sqrt{(170)^2-\left(\frac{204}{2}\right)^2} \text { sq-cm }\)

= \(\frac{1}{2} \times 204 \sqrt{272 \times 668} \mathrm{sq}-\mathrm{cm}\)

= \(\frac{1}{2} \times 204 \times \sqrt{17 \times 16 \times 4 \times 17} \cdot \mathrm{sq}-\mathrm{cm}\)

= \(\frac{1}{2} \times 204 \times 17 \times 2 \times 4 \mathrm{sq}-\mathrm{cm}=13872 \mathrm{sq}-\mathrm{cm}\)

∴ the area of the triangle is 13872 sq-cm.

 

Question 3. If the length of the hypotenuse of a right-angled isosceles triangle is 12√2 cm, then find its area.

Solution:

Given 

The length of the hypotenuse of a right-angled isosceles triangle is 12√2 cm

Let the length of the two equal sides of the right-angled triangle adjacent to the right angle be a cm.

∴ (hypotenuse)² = a²+2 = 2a²   ∴ hypotenuse = √2a cm.

As per the question, a√2 = 12√2

⇒ a = 12

∴ area of the triangle =\(\frac{1}{2}\) base x height = \(\frac{1}{2}\) x 12 × 12 sq-cm

= 72 sq-cm

∴ the required area of the triangle = 72 sq-cm.

 

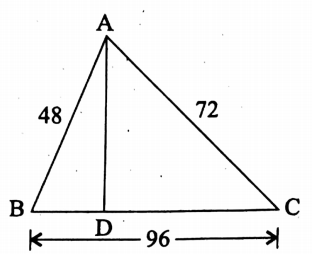
Question 4. The ratio of the sides of a triangular park is 2: 3: 4. If the perimeter of the park is 216 m, then find the distance (perpendicular) of the greatest side of the park from its opposite vertex.

Solution:

Given

The ratio of the sides of a triangular park is 2: 3: 4

The perimeter of the park is 216 m

Let the sides of the park be 2x m, 3x m, and 4x m. 

The perimeter of the park is 216 m.

∴ 2x+3x+4x = 216

or, 9x = 216

⇒ x = \(\frac{216}{24}\)

∴ The length of the sides of the park is (2 x 24) m = 48 m, (3 x 24) m = 72 m, and (4 x 24) m = 96 m.

∴ half-perimeter of the park = \(\frac{216}{2}\)m = 108m

∴ area of the park = \(\sqrt{108(108-48)(108-72)(108-96)} \text { sq-m }\)

= \(\sqrt{108 \times 60 \times 36 \times 12} \text { sq-m }\)

= \(\sqrt{12 \times 9 \times 12 \times 5 \times 6 \times 6 \times 4 \times 3} \mathrm{sq}-\mathrm{cm}\)

= 12 x 3 x 6 x 2√15 sq.cm

= 432√15 sq.cm

Let the required perpendicular distance be x m.

∴ \(\frac{1}{2} \times 96 \times x=432 \sqrt{15} \Rightarrow x=\frac{432 \sqrt{15}}{48}=9 \sqrt{15}\)

∴ The required perpendicular distance = 9√15 m.

 

 

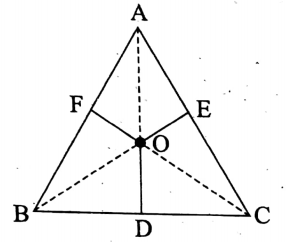
Question 5. If the perpendicular distances of the sides of an equilateral triangle from any point within the triangle be 10 cm, 12 cm, and 8 cm, then find the area of the triangle.

Solution:

Given 

The perpendicular distances of the sides of an equilateral triangle from any point within the triangle be 10 cm, 12 cm, and 8 cm

Let OD, OE, and OF be the perpendicular distances of the sides BC, CA, and AB respectively of the equilateral triangle ABC from the point O within the ΔABC. Also, let the length of the sides of the ΔABC be a cm.

Now, the area of ΔABC= area of ΔOBC + area of ΔOCA + area of ΔOAB.

\(\Rightarrow \frac{\sqrt{3}}{4} a^2=\frac{1}{2} \mathrm{BC} \times \mathrm{OD}+\frac{1}{2} \mathrm{AC} \times \mathrm{OE}+\frac{1}{2} \mathrm{AB} \times \mathrm{OF}\)

\(\Rightarrow \frac{\sqrt{3}}{4} a^2=\frac{1}{2} \times a \times 10+\frac{1}{2} \times a \times 12+\frac{1}{2} a \times 8\)

\(\Rightarrow \frac{\sqrt{3}}{4} a^2=15 a \quad \Rightarrow a=\frac{60}{\sqrt{3}}=\frac{60 \sqrt{3}}{3}=20 \sqrt{3}\)

∴ area of the triangle ABC = \(\frac{\sqrt{3}}{4}(20 \sqrt{3})^2 \cdot \mathrm{sq}-\mathrm{cm}=\frac{\sqrt{3}}{4} \times 400 \times 3 \mathrm{sq}-\mathrm{cm}=300 \sqrt{3} \mathrm{sq}-\mathrm{cm}\)

the required area = 300√3 sq-cm

 

 

Question 6. If the perimeter of a right-angled isosceles triangle is (√2+1) cm, then find the length of its hypotenuse and also its area.

Solution:

Given

The perimeter of a right-angled isosceles triangle is (√2+1) cm

Let the length of each equal side adjacent to the right angle of the right-angled isosceles triangle be a cm.

∴ Length of the hypotenuse = \(\sqrt{a^2+a^2} \mathrm{~cm}=\sqrt{2} a \mathrm{~cm}\)

The perimeter is (√2+1) cm         

:. a+a+ √2a = (√2+1)

\(\Rightarrow 2 a+\sqrt{2} a=(\sqrt{2}+1) \quad \Rightarrow \sqrt{2} a(\sqrt{2}+1)=(\sqrt{2}+1) \quad \Rightarrow a=\frac{1}{\sqrt{2}}\)

∴ Length of the hypotenuse = \(\sqrt{2} \cdot \frac{1}{\sqrt{2}} \mathrm{~cm}\) = 1 cm.

Area of f the triangle =\(\frac{1}{2} \times a \times a \mathrm{sq}-\mathrm{cm}=\frac{1}{2} a^2 \mathrm{sq}-\mathrm{cm}=\frac{1}{2} \times \frac{1}{2} \mathrm{sq}-\mathrm{cm}=\frac{1}{4} \mathrm{sq}-\mathrm{cm}\)

∴ the required length and area are 1 cm and \(\frac{1}{4}\) sq-cm respectively.

 

Question 7. If the length of the sides of an equilateral triangle is increased by 1 m each, then the area of the triangle increases by √3 sq-cm. Find the length of the side of the equilateral triangle. 

Solution:

Given

The length of the sides of an equilateral triangle is increased by 1 m each, then the area of the triangle increases by √3 sq-cm

Let the length of the equal side of the equilateral triangle be a m.

∴ Area \(\frac{\sqrt{3}}{4} a^2 \mathrm{sq}-\mathrm{m}\)

The increased length of the sides = (a + 1) m.

Then, the area becomes = \(\frac{\sqrt{3}}{4}(a+1)^2 s \mathrm{sq}-\mathrm{m}\)

As per the question, \(\frac{\sqrt{3}}{4}(a+1)^2-\frac{\sqrt{3}}{4} a^2=\sqrt{3}\)

\(\frac{\sqrt{3}}{4}\left(a^2+2 a+1-a^2\right)=\sqrt{3} \Rightarrow 2 a+1=4 \Rightarrow a=\frac{3}{2} ⇒ 1 \cdot 5\)

∴ the required length of the side = 1.5 m.

 

Question 8. The ratio of the areas of an equilateral triangle and a square is √3:2. If the length of the diagonal of the square be 60 cm, find the perimeter of the equilateral triangle. 

Solution:

Given 

The ratio of the areas of an equilateral triangle and a square is √3:2

The length of the diagonal of the square be 60 cm

Let the length of the equilateral triangle be a cm and the length of the sides of the square be x cm.

As per the question,

\(\frac{\sqrt{3}}{4} a^2: x^2=\sqrt{3}: 2 \Rightarrow \frac{\sqrt{3} a^2}{4 x^2}=\frac{\sqrt{3}}{2} \Rightarrow \frac{a^2}{x^2}=\frac{2}{1} \Rightarrow a: x=\sqrt{2}: 1\)

Also, the length of the diagonal of the square is 60 cm.

∴ \(\sqrt{2} x=60 \Rightarrow x=\frac{60}{\sqrt{2}}=30 \sqrt{2} \quad ∴ \frac{a}{x}=\sqrt{2} \Rightarrow a=\sqrt{2} x \Rightarrow a=\sqrt{2} \times 30 \sqrt{2}=60\)

∴ perimeter of the triangle = 3a cm = 3 x 60 cm, = 180 cm.

∴ the required perimeter = 180 cm.

 

Question 9. The length of the hypotenuse of the right-angled triangle and its perimeter be 13 cm and 30 cm respectively. Find the area of the triangle.

Solution:

Given 

The length of the hypotenuse of the right-angled triangle and its perimeter be 13 cm and 30 cm respectively

Let the two adjacent sides of the right angle of the right-angled triangle be a cm and b cm.

The given length of the hypotenuse is 13 cm.

∴ \(\sqrt{a^2+b^2}=13 \Rightarrow a^2+b^2=169\)

Also, perimeter = 30 cm,

∴ \(a+b+\sqrt{a^2+b^2}=30 \Rightarrow a+b+13=30 \Rightarrow a+b=17\)

\(\Rightarrow(a+b)^2=289 \quad \Rightarrow a^2+b^2+2 a b=289\)

\(\Rightarrow 169+2 a b=289 \quad \Rightarrow 2 a b=120 \quad \Rightarrow a b=60\)

Now, the area = \(\frac{1}{2}\) ab sq-cm

= \(\frac{1}{2}\) x 60 sq-cm

= 30 sq-cm

∴ the required area = 30 sq-cm.

 

Chapter 1 Perimeter And Area Of Triangles And Quadrilaterals Rectangle And Square

 

1. 

1. Area of a rectangle = Length x Breadth
   ∴ Length Area Breadth = Area ÷ Length.
   If Length = units and Breadth = b units, then the area of the rectangle = ab sq-units.
2. The perimeter of a rectangle = 2 (a + b) units.
3. The diagonal of a rectangle
   \(\sqrt{(\text { Length })^2+(\text { Breadth })^2}=\sqrt{a^2+b^2} \text { units }\)

 

2. 

1. Area of a square
   We know that the length and breadth of a square are equal.
   ∴ Area of a square = Length x Breadth = (side)², i.e., either (Length)² or, (Breadth)².
   ∴ Side of a square = √Area
2. The perimeter of a square = 4a units.
3. Diagonal of a square = \(\sqrt{a^2+a^2}\) units = a√2 units
4. Area of a square x (diagonal)² sq-units.

 

3. 

1. Area of four walls of a room
   A room is usually either rectangular or square.
   In a rectangular room, the two walls along the length are equal, and also along the breadth, the two opposite walls are equal.
2. Along the length of the wall is a rectangle, the length of which is equal to the length of the room and the breadth is the height, of the room.
3. ∴ Area of that two walls = 2 x length x height.
4. Similarly, the two walls along the breadth are also two rectangles, the length of which is the breadth of the room and the breadth is the height of the room.
5. Area of that two walls = 2 x breadth x height
6. If h is the height of the room, then the area of the four walls = 2 (length x breadth) x height
   = perimeter x height
   = 2 (a + b) h sq-units.

 

Chapter 1 Perimeter And Area Of Triangles Select The Correct Answer (MCQ)

 

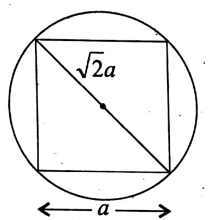
Question 1. The length of the diagonal of a square is 12√2 cm. Then the area of the square is 

1. 288 sq-cm
2. 144 sq-cm
3. 72 sq-cm
4. 18 sq-cm

Solution:

If the sides of the square be a cm, the diagonal is √2a

:. √2a = 12√2

 ⇒ a² = 144

∴ Area of the square = 144 sq-cm.

 

Question 2. If the area of a square is \(\mathbf{A}_1\), sq-units and the area of the square drawn on the diagonal of the previous square be  \(\mathbf{A}_1: \mathbf{A}_2\)

1. 1:2 
2. 2:1
3. 1:4
4. 4:1

Solution: Let the side of the first square be a unit.

∴ \(\mathrm{A}_1=a^2 \text { sq-units }\)

Again, the diagonal of the first square=√2a units.

∴ \(\mathrm{A}_2=(\sqrt{2} a)^2 \quad \Rightarrow \mathrm{A}_2=2 a^2 \text { sq-units. }\)

∴  \(\mathrm{A}_1: \mathrm{A}_2=a^2: 2 a^2=\frac{a^2}{2 a^2}=1: 2\)

 

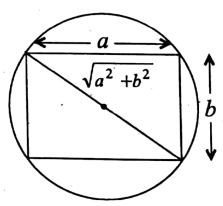
Question 3. The diagonal of a rectangle is 10 cm and the area is 62.5 sq-cm. Then the sum of its length and breadth is

1. 12 cm
2. 15 cm
3. 20 cm
4. 25 cm

Solution:

Let the length and breadth of the rectangle be a cm and b cm respectively.

∴ \(\sqrt{a^2+b^2}=10\)

a²+b² = 100 and ab = 62.5

(a+b)² = a²+b²+2ab

= 100+ 2 x 62.5

= 100+125 = 225

∴ a+b = √225 

= 15

∴ the required sum = 15 cm.

 

Question 4. The ratio of the diagonals of two squares is 5: 2. Then the ratio of their areas is

1. 5:2
2. 2:5
3. 4: 25
4. 25: 4

Solution:

Let the diagonals of the squares be 5x and 2x. 

If the sides of the squares be a and b, then

\(\sqrt{2} a=5 x \Rightarrow a=\frac{5 x}{\sqrt{2}} \quad \text { and } \quad \sqrt{2} b=2 x \Rightarrow b=\frac{2 x}{\sqrt{2}}\)

∴ The ratio of the areas \(a^2: b^2=\left(\frac{5 x}{\sqrt{2}}\right)^2:\left(\frac{2 x}{\sqrt{2}}\right)^2=\frac{25 x^2}{2}: \frac{4 x^2}{2}=\frac{25}{4}=25: 4\)

 

Chapter 1 Perimeter And Area Of Triangles Short Answer Type Questions

 

Question 1. If the sides of a square be increased by 10%, then how much percentage of its area will be increased?

Solution:

Given

The sides of a square be increased by 10%.

Let the side of the square be a unit.

∴ area = a² sq-units.

If the side is increased by 10%, then it will be

\(\left(a+a \times \frac{10}{100}\right) \text { units }=\left(a+\frac{a}{10}\right) \text { units }=\frac{11 a}{10} \text { units }\)

∴ \(\text { area }=\left(\frac{11 a}{10}\right)^2 \text { sq-units }=\frac{121 a^2}{100} \text { sq-units }\)

∴ Percentage of area increased = \(\frac{\frac{121 a^2}{100}-a^2}{a^2} \times 100 \%=\frac{\frac{21 a^2}{100}}{a^2} \times 100 \%=21 \%\)

∴ the required percentage = 21%.

 

Question 2. If the length of a rectangle is increased by 10% and its breadth is decreased by 10%, then find its percentage of increased or decreased area.

Solution: 

Given

The length of a rectangle is increased by 10% and its breadth is decreased by 10%.

Let the length of the rectangle be a unit and the breadth be b units.

∴ are ab sq-units.

Now, increased = \(\left(a+a \times \frac{10}{100}\right) \text { units }=\left(a+\frac{a}{10}\right) \text { units }=\frac{11 a}{10} \text { units }\)

Again, decreased breadth = \(\left(b-b \times \frac{10}{100}\right) \text { units }=\left(b-\frac{b}{10}\right) \text { units }=\frac{9 b}{10} \text { units }\)

∴ now area \(\frac{11 a}{10} \times \frac{9 b}{10} \text { sq-units }=\frac{99 a b}{100} \text { sq-units }\)

∴ are decreased = \(\left(a b-\frac{99 a b}{100}\right) \text { sq-units }=\frac{a b}{100} \text { sq-units }\) 

∴ percentage of decreased area = \(\frac{\frac{a b}{100}}{a b} \times 100 \%=1 \%\)

∴ the required percentage = 1% decrease.

 

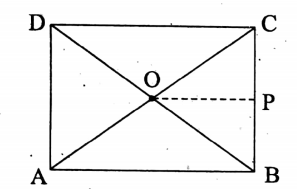
Question 3. The diagonal of a rectangle is 5 cm. The length of the perpendicular drawn to one of the breadth of the rectangle from the point of intersection of its diagonal is 2 cm. Find the breadth of the rectangle.

Solution: 

Given 

The diagonal of a rectangle is 5 cm.

The length of the perpendicular drawn to one of the breadth of the rectangle from the point of intersection of its diagonal is 2 cm.

Let O be the point of intersection of the diagonals AC and BD of the rectangle ABCD and let OP be the perpendicular drawn from O to BC.

Since O is the mid-point of AC and OP || AB

∴ AB = 2 OP

AB = 2 x 2 cm = 4 cm

∴ the length of the rectangle is 4 cm. Let the breadth of the rectangle be x cm.

∴ x² + (4)² = (5)²

 x² = 25 – 16

x² = 9

⇒ x= 3

∴ The breadth of the rectangle is 3 cm.

 

 

Question 4. The diagonal of a square is 4√2 cm. Find the length of the diagonal of the square whose area is double of the first square.

Solution:

Given 

The diagonal of a square is 4√2 cm..

Let the side of the given square be a cm.

∴ length of its diagonal As per the question, √2a = 4√2

⇒ a² = 16

area of the given square is 16 sq-units.

the area of the required square = 2 x 16 sq-units 

= 32 sq-units. 

Now, if the side of the required square is b cm, then b² = 32.

∴ b = √32 = 4√2

∴ length of the diagonal = √2 × 4√2 cm 

= 8 cm.

∴ the required diagonal = 8 cm.

 

Chapter 1 Perimeter And Area Of Triangles Long Answer Type Questions

 

Question 1. The area of rectangular land is 500 sqm. The length of the land if decreased by 3 m and its breadth if increased by 2 m, then it becomes a square. Find the length and breadth of the land.

Solution:

Given

The area of rectangular land is 500 sqm.

The length of the land if decreased by 3 m and its breadth if increased by 2 m, then it becomes a square.

Let the length of the land be x m and the breadth be y m.

As per question, xy= 500 and x – 3 = y + 2 x – y = 5……………...(1)

⇒(x-y)² = 25 (x + y)² – 4xy = 25(x+y)²

= 25+2000 [4xy = 4 x 500 = 2000] 

⇒ x + y = √2025 

⇒ x+y = 45…………..(2)

Adding (1) and (2) we get, 2x = 50

x = 25

∴ y = 45 – x

= 45 – 25

= 20

The required length is 25 m and the breadth = is 20 m.

 

Question 2. The side of a square land is 300 m. There is a wall of the same height around the square land of breadth 3 dcm. At a rate of Rs. 5000 per 100 sqm, what will be the expenditure to build a wall on the land?

Solution: 

Given

The side of a square land is 300 m.

There is a wall of the same height around the square land of breadth 3 dcm.

At a rate of Rs. 5000 per 100 sqm.

The side of the square is 300 m.

∴ area = (300)² sq-cm.

Length of the land including the wall = (300+ 0.3 +0.3) m = 300.6 m

∴ then its area = (300.6)² sqm.

∴ Area of the wall = (300.6)² – (300)² sqm = (300.6 + 300) x (300.6-300) sqm

= (600.6 x 0.6) sq-m = 360-36 sq-m

Now, for 100 sqm the expenditure = Rs. 5000

for 1 sqm the expenditure = Rs. \(\frac{5000}{100}\)

for 360.36 sqm the expenditure = \(\text { Rs. } \frac{5000 \times 360 \cdot 36}{100}\)

∴ the required expenditure = Rs. 18018.

 

Question 3. If the length of a rectangular land of area 1200 sq-cm is 40 cm, then find the area of the square drawn on the diagonal of the rectangular land.

Solution: 

Given

The length of a rectangular land of area 1200 sq-cm is 40 cm.

Length of the land = 40 cm and area = 1200 sq-cm

∴ breadth = \(\frac{1200}{40}\)

∴ diagonal = \(\sqrt{40^2+30^2} \mathrm{~cm}=\sqrt{1600+900} \mathrm{~cm}\)

= √2500 cm 

= 50 cm

∴ the required area (50)² sq-cm = 2500 sq-cm

 

 

Question 4. The area of four walls of a room is 42 sq-cm. If the area of the ground of the room is 12 sqm and its length is 4 m, then find the height of the wall.

Solution

Given

The area of four walls of a room is 42 sq-cm.

The area of the ground of the room is 12 sqm and its length is 4 m.

The area of the ground= is 12 sqm and the length

= 4 m

∴ breadth = \(\frac{12}{4}\) m

= 3 m. 

Area of four walls = 42 sqm.

∴ 2 x (length + breadth) x height = 42

⇒ 2 × (4 + 3) x height = 42 

Height = \(\frac{42}{14}\) = 3

∴ the required height = 3 m.

 

Question 5. Sujata wants to draw a picture on a rectangular paper of an area of 84 sq-cm. If the difference between the length and breadth of the paper is 5 cm, find the perimeter of the rectangular paper.

Solution: 

Given

Sujata wants to draw a picture on a rectangular paper of an area of 84 sq-cm.

The difference between the length and breadth of the paper is 5 cm.

Let the length and breadth of the paper be x cm and y cm.

Area of the paper = 84 sq-cm

Xy = 84 As per the question,  x-y = 5

∴ (x + y)² = (x − y)² + 4xy

= 52 + 4 x 84

= 25 +  336 = 361

∴ x + y = √361

∴ 2(x+y) = 2 x 19

= 38

∴ the required perimeter = 38 cm.

 

Question 6. How many meters of walls should be needed to round the square land of which the length of the diagonal is 20√2 m? At a rate of Rs. 20 per sq-m, what will be the expenditure for grass the land?

Solution:

The diagonal of the square = 20√2 m 

∴ side x √2 = 20√2 sides = 20 m.

∴ perimeter of the square = 4 x a [ a = side ] = 4 x 20 m = 80 m.

∴ The length of the required wall is 80 m. 

Area of the land = 20 x 20 sq-m = 400 sq-m 

At a rate of Rs. 20 per sq-m. the required expenditure = Rs. (400 x 20) = Rs. 8000.

 

Question 7. The ratio of the length and breadth of the hall-room of Moushumi is 9: 5 and its perimeter is 140 m. Moushumi wants to fit a tally of rectangular sizes 25 cm x 20 cm into the hall room. Then what will be the expenditure of doing this at a rate of Rs. 500 per 100 tally?

Solution: 

Given

The ratio of the length and breadth of the hall-room of Moushumi is 9: 5 and its perimeter is 140 m.

Moushumi wants to fit a tally of rectangular sizes 25 cm x 20 cm into the hall room.

The ratio of the length and the breadth of the hall room is 9:5.

Let length = 9x m and breadth = 5x m

∴ perimeter = 2 (length + breadth) = 2 (9x + 5x) m = 28x m

As per the question, 28x = 140

x = 5

∴ Length of the hall-room = 9 x 5 m = 45 m 

and breadth = 5 x 5 m = 25 m

∴ Area of the hall-room = length x breadth = (45 x 25) sq-cm 

= 1125 sq-m 

= 11250000 sq-cm

Area of a single tally = (25 x 20) sq-cm 

= 500 sq-cm

∴ required no. of tally = \(\frac{11250000}{500}\) = 22500

At a rate of Rs. 500 per 100 tallies, the required expenditure = \(\text { Rs. } \frac{500 \times 22500}{100}\)

= Rs. 112500.

At a rate of Rs. 500 per 100 tallies, the required expenditure = Rs. 112500.

 

Question 8. The ratio of the length and breadth of a rectangular field is 4: 3. To round the field it needs to walk a way of 336 m. Find the area of the field.

Solution: 

Given

The ratio of the length and breadth of a rectangular field is 4: 3.

To round the field it needs to walk a way of 336 m.

The ratio of length and breadth = 4:3.

Let length 4x m and breadth = 3x m.

∴ Perimeter = 2 (4x + 3x) m = 14x m.

As per the question, 14x= 336

⇒ x = \(\frac{336}{14}\) 

⇒ x = 24

Length of the field = 4 x 24 m = 96 m and breadth = 3 x 24 m = 72 m

∴ Area of the field = length x breadth = (96 x 72) sq-cm = 6912 sqm

the required area = 6912 sq-m.

 

Question 9. The diagonal of a rectangular field is 15 m. The difference between its length and breadth is 3 m. Find the perimeter and area of the field.

Solution:

Given

The diagonal of a rectangular field is 15 m.

The difference between its length and breadth is 3 m.

The diagonal of the given field = 15 m.

Let its breadth = x m, 

∴ length = (x + 3) m (by a question) 

∴ diagonal = \(\sqrt{x^2+(x+3)^2} \mathrm{~m}\)

As per the question, \(\sqrt{x^2+(x+3)^2}=15 \Rightarrow x^2+(x+3)^2=225 \Rightarrow x^2+x^2+6 x+9=225\)

\(2 x^2+6 x-216=0 \Rightarrow x^2+3 x-108=0 \Rightarrow x^2+(12-9) x-108=0\)

\(x^2+12 x-9 x-108=0 \Rightarrow x(x+12)-9(x+12)=0 \Rightarrow(x+12)(x-9)=0\)

∴ either x + 12 = 0

x = –12 

or, x -9=0

⇒ x=9.

But the value of x can never be negative, 

∴ x = 9.

∴ breadth of the field = 9 m and length = (9+ 3) m = 12 m. 

∴ Perimeter of the field = 2 (length + breadth) = 2 (12 + 9) m

= 42 m

Area of the field = length x breadth = 12 x 9 sqm

= 108 sqm. 

∴ the required perimeter = is 42 m and the required area

= 108 sqm.

The required perimeter = 108 sqm.

 

Question 10. The length of a rectangle is 1 \(\frac{1}{2}\) part of its breadth. To plane it, it requires Rs. 1470  at a rate of Rs. \(\frac{5}{16}\) per sqm. To fench the rectangle at a rate of Rs. 4 per meter, find the expenditure.

Solution:

Given 

The length of a rectangle is 1 \(\frac{1}{2}\) part of its breadth.

To plane it, it requires Rs. 1470  at a rate of Rs. \(\frac{5}{16}\) per sqm. To fench the rectangle at a rate of Rs. 4 per meter.

Area of the rectangle = \(\left(\text { Rs. } 1470 \div \text { Rs. } \frac{5}{16}\right) \text { sqm }\)

= \(\frac{1470 \times 16}{5} s q-m=294 \times 16 \mathrm{sq}-\mathrm{m}\)

i.e., length x breadth = 294 x 16 sq-m.

\(\frac{3}{2}\)breadth x breadth = 294 x 16 sqm     [∵ Length = \(\frac{3}{2}\) x breadth]

⇒ (breadth)² = \(\frac{294 \times 16 \times 2}{3} \text { sqm }=196 \times 16 \text { sqm }\)

⇒ breadth =  \(\sqrt{196 \times 16} \mathrm{~m}=(14 \times 4) \mathrm{m}=56 \mathrm{~m}\)

∴ Length = \(\left(56 \times \frac{3}{2}\right) \mathrm{m}=84 \mathrm{~m}\) m

= 84 m.

∴ Length of the fencing = perimeter of the rectangle

= 2 (84+ 56) m 

= 2 x 140 m

= 280 m 

∴ required expenditure= Rs. (4 x 280) = Rs. 1120.

 

Chapter 1 Perimeter And Area Of Triangles Quadrilaterals And Polygons

 

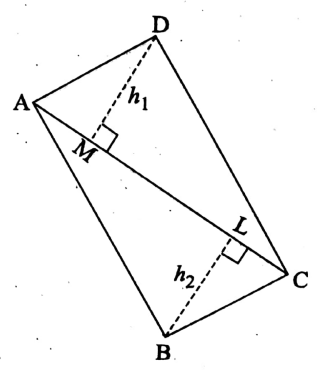
Parallelogram :

We know that the quadrilateral in which the opposite sides are parallel is known as a parallelogram.

The ABCD is a parallelogram of which AC is a diagonal and CL ⊥ AB.

∴ Area of the parallelogram

ABCD = 2 x (area of ΔABC) sq-units

= \(2 \times\left(\frac{1}{2} \times \mathrm{AB} \times \mathrm{CL}\right)\)

= (AB × CL) sq-units

 = (base x height) sq-units

If the two adjacent sides of a parallelogram be a units and b units, then

1. Perimeter of the parallelogram = 2 (a + b) = 2 (sum of any two adjacent sides).

2. Area of the parallelogram = (Base x Height) sq-units.

 

 

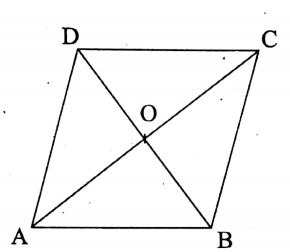
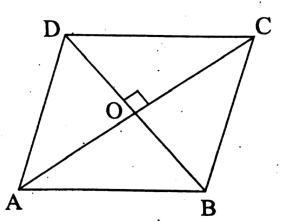
Rhombus :

We know that

1. the quadrilateral, four of whose sides are equal is known as a rhombus

2. the diagonals of a rhombus bisect each other orthogonally.

The AC and BD are the two diagonals of the rhombus ABCD, which intersect each other orthogonally at O.

Now, area of the rhombus ABCD= [(area of ΔABC) + (area of ΔADC)] sq-units

= \(\left[\left(\frac{1}{2} \times \mathrm{AC} \times \mathrm{BO}\right)+\left(\frac{1}{2} \times \mathrm{AC} \times \mathrm{OD}\right)\right] \text { sq-un }\)

= \(\frac{1}{2} \times \mathrm{AC}(\mathrm{BO}+\mathrm{OD}) \text { sq-units }=\frac{1}{2} \times \mathrm{AC} \times \mathrm{BD} \text { sq-units }\)

= \(\frac{1}{2} \times[(\text { first diagonal }) \times(\text { second diagonal })] \text { sq-units }\)

= \(\frac{1}{2} \times \text { (product of the diagonals) sq-uinits. }\)

Again, in the right-angled triangle COD,

CD² = OC² + OD²    (by Pythagoras theorem) 

= \(\left(\frac{1}{2} \mathrm{AC}\right)^2+\left(\frac{1}{2} \mathrm{BD}\right)^2=\frac{1}{4}\left(\mathrm{AC}^2+\mathrm{BD}^2\right)\)

∴ CD = \(\mathrm{CD}=\sqrt{\frac{1}{4}\left(\mathrm{AC}^2+\mathrm{BD}^2\right)}=\frac{1}{2} \sqrt{\mathrm{AC}^2+\mathrm{BD}^2}\)

= \(\frac{1}{2} \sqrt{(\text { first diagonal })^2+(\text { second diagonal })^2}\)

∴ if \(d_1 \text { and } d_2\) is the diagonals of a rhombus, then

1. Side of the rhombus = \(\frac{1}{2} \sqrt{d_1^2+d_2^2} \text { units }\).

2. Perimeter of the rhombus = \(4 \times(\text { side })=2 \sqrt{d_1^2+d_2^2}\)

3. Area of the rhombus = (Base) x (Height) square units

4. Area of the rhombus = \(\frac{1}{2} \times d_1 \times d_2 \text { sq-units }\)

 

 

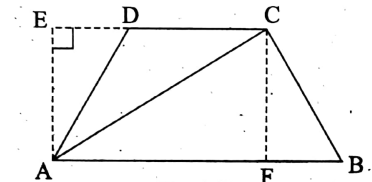
Trapezium :

We know that the quadrilateral only two of whose opposite sides are parallel is known as a trapezium.

The perpendicular distance between the two parallel sides is called the height of the trapezium.

In the, ABCD is a trapezium of which AB || DC and AC is a diagonal.

Let us draw CF ⊥ AB and AE ⊥ produced CD.

Area of the trapezium ABCD = [(area of ΔADC) + (area of ΔABC) sq-units.

= \(\left(\frac{1}{2} \times \mathrm{DC} \times \mathrm{AE}+\frac{1}{2} \times \mathrm{AB} \times \mathrm{CF}\right) \text { sq-units }=\left(\frac{1}{2} \times \mathrm{DC} \times \mathrm{CF}+\frac{1}{2} \times \mathrm{AB} \times \mathrm{CF}\right) \text { sq-units }\)

= \(\frac{1}{2} \times \mathrm{CF} \times(\mathrm{DC}+\mathrm{AB}) \text { sq-units }\)

= \(\frac{1}{2}\) (perpendicular distance of the parallel sides) x ( sum of the parallel sides) sq. units.

∴ If the two parallel sides of a trapezium be a units and b units and the height be h units, then

Area of the trapezium = \(\frac{1}{2}\) (a+b) xh sq-units.

 

 

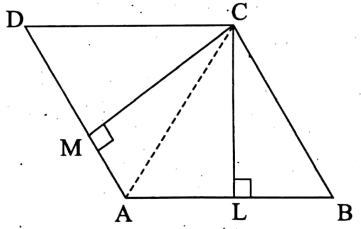
Quadrilateral :

We know that the plane region closed by four straight lines is known as a quadrilateral.

In, ABCD is a quadrilateral of which AC is a diagonal.

BL ⊥ AC and DM ⊥ AC are drawn.

∴ area of ABCD = [(area of ΔABC) + (area of ΔADC)] sq-units

= \(=\left[\left(\frac{1}{2} \times \mathrm{AC} \times \mathrm{BL}\right)+\left(\frac{1}{2} \times \mathrm{AC} \times \mathrm{DM}\right)\right] \text { sq-units }\)

= \(\frac{1}{2} \times \mathrm{AC} \times(\mathrm{BL}+\mathrm{DM}) \text { sq-units }\)

= \(\frac{1}{2}\) x (length of one diagonal) x (sum of the perpendiculars drawn from two opposite vertices to that diagonal) sq-units.

∴ If the lengths of the perpendiculars drawn from B and D of the quadrilateral ABCD to the diagonal AC be h, and h2 units respectively, then

The area of ABCD = \(\frac{1}{2}\) x AC x \(\left(h_1+h_2\right)\) sq-units.

 

 

Chapter 1 Perimeter And Area Of Triangles Select The Correct Answer (MCQ)

 

Question 1. The height of a parallelogram is one-third of its base. If the area of the parallelogram is 192 sq-cm, then its height is

1. 4 cm
2. 8 cm
3. 16 cm
4. 24 cm

Solution:

Let the height of the parallelogram be a cm (a > 0). the base is 3a cm.

∴ Area = base x height = (3a x a) sq-cm = 3a² sq-cm.

As per the question, \(3 a^2=192 \Rightarrow a^2=\frac{192}{2}=64 \Rightarrow a=8\)

∴ The required height = 8 cm.

 

Question 2. The length of each side of a rhombus is 6 cm and one of its angles is 60°. Then its area is

1. 9√3 sq-cm
2. 18√3 sq-cm
3. 36√3 sq-em
4. 6√3 sq-em

Solution:

Let in rhombus PQRS, PQ = QR = RS = SP = 6 cm and ∠PQR = 60°

Now, in ΔPQR, PQ = QR

∴ ∠QPR = ∠QRP [∵ Opposite angles of equal sides of a triangle are equal]

Again, in ΔPQR, ∠QPR + ∠PRQ + ∠RQP = 180°

∠QPR + ∠QPR + 60° = 180°

⇒ 2 ∠QPR = 120° ⇒ ∠QPR = 60°

∴ <QPR = <QRP = ∠PQR = 60°.

∴ ΔPQR is an equilateral triangle of sides 6 cm [∵ PQ QR = RP = 6 cm. ]

∴ Area of ΔPQR= \(\frac{\sqrt{3}}{4} \times(\text { side })^2=\frac{\sqrt{3}}{4} \times 6^2 \mathrm{sq}-\mathrm{cm}=\frac{\sqrt{3}}{4} \times 36 \mathrm{sq}-\mathrm{cm}=9 \sqrt{3} \mathrm{sq}-\mathrm{cm}\)

∴ The area of the rhombus PQRS = 2 x ΔPQR 

= 2 x 9√3 sq-cm 

= 18√3 sq-cm.

 

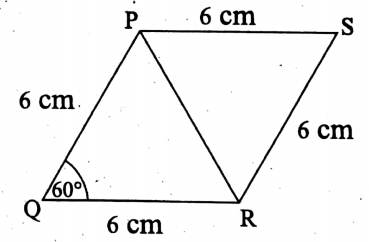
The area of the rhombus PQRS = 18√3 sq-cm.

 

Question 3. The length of a diagonal of a rhombus is thrice of its other diagonal. If the area of the rhombus is 96 sq-cm, then the length of the greater diagonal is

1. 8 cm 
2. 12 cm
3. 16 cm
4. 24 cm

Solution:

Let the diagonals of the rhombus be a cm and 3a cm (a > 0).

∴ Area of the rhombus = \(\frac{1}{2}\) x product of the diagonals product of the diagonals

= \(\left(\frac{1}{2} \times a \times 3 a\right) \text { sq-cm }\)

= \(\frac{3 a^2}{2} \mathrm{sq}-\mathrm{cm}\)

As per the question, \(\frac{3 a^2}{2}=96 \Rightarrow 3 a^2=192 \Rightarrow a^2=64 \Rightarrow a=8\)

∴ The length of the greater diagonal (3 x 8) cm = 24 cm.

 

Question 4. A rhombus and a square lie on the same base. The area of the square is x2 sq-units and the area of the rhombus is y-units, then

1. y > x²
2. y < x²
3. y = x²
4. x <y²

Solution:

The rhombus EBCF and the square ABCD lie on the same base BC.

Let the side EF of EBCF intersect the side CD of ABCD at Q.

∴ Area of the square ABCD = BC x DC = x² sq-units.

∴ Area of the rhombus EBCF = BC x CQ=y sq-units 

Now, BC x CQ < BC x DC    [∵ CQ < DC]

∴ y < x²

 

Chapter 1 Perimeter And Area Of Triangles Short Answer Type Questions

 

Question 1. The area of the parallelogram ABCD is 96 sq-cm and the length of the diagonal BD is 12 cm. Find the perpendicular distance of the diagonal BD from point A.

Solution:

Given 

The area of the parallelogram ABCD is 96 sq-cm and the length of the diagonal BD is 12 cm.

The area of the parallelogram ABCD is 96 sq-cm and the length of the diagonal BD is 12 cm.

AS is the perpendicular distance f the diagonal BD from A.

Let AS h cm (h > 0).

Now, ΔABD = \(\frac{1}{2}\) ABCD

=\(\left(\frac{1}{2} \times 96\right) \mathrm{sq}-\mathrm{cm}=48 \mathrm{sq}-\mathrm{cm}\)

Again, ΔABD = \(\frac{1}{2}\) × BD X AS

= \(\left(\frac{1}{2} \times 12 \times h\right) \mathrm{sq}-\mathrm{cm}=6 h \mathrm{sq}-\mathrm{cm}\)

As per the question, 6h = 48 

h = 8.

∴ the required length = 8 cm.

 

Question 2. The lengths of two adjacent sides of a parallelogram are 5 cm and 3 cm. If the perpendicular distance of the greatest sides of the parallelogram is 2 cm, then find the perpendicular distance between its smallest sides.

Solution:

Given 

The lengths of two adjacent sides of a parallelogram are 5 cm and 3 cm.

the perpendicular distance of the greatest sides of the parallelogram is 2 cm.

The length of the greatest sides is 5 cm and the perpendicular distance between them is 2 cm.

∴ Area of the parallelogram = 5 x 2 sq-cm = 10 sq-cm.

Let the perpendicular distance between the smallest sides be x cm.

∴ 3 x x = 10

\(\Rightarrow x=\frac{10}{3}=3 \frac{1}{3} \mathrm{~cm}\)

∴ The required distance = 3 \(\frac{1}{3}\) cm.

Question 3. The height of a rhombus is 14 cm and the length of its sides is 5 cm. Find the area of the rhombus.

Solution

Given 

The height of a rhombus is 14 cm and the length of its sides is 5 cm.

Area of the rhombus = side of rhombus x height 

= 5 x 14 sq-cm 

= 70 sq-cm. 

∴ The required area = 70 sq-cm.

 

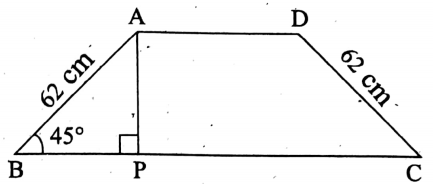
Question 4. The angle along any of the two adjacent parallel sides of an isosceles trapezium is 45°. If the length of its slant sides is 62 cm, then find the perpendicular distance between its parallel sides.

Solution:

Given

The angle along any of the two adjacent parallel sides of an isosceles trapezium is 45°.

The length of its slant sides is 62 cm.

Let in the isosceles trapezium ABCD.

AB = DC = 62 cm and ∠ABC= 45°. 

Perpendicular AP is drawn from A to BC, which is the height of the trapezium w.r.t. the side BC.

Now, in ΔAPB, ∠APB = 90°, ∠ABP = 45°

∠BAP = 180° –  ∠APB – ∠ABP

= 180° – 90° –  45°

= 45°

in ΔAPB, ∠ABP = ∠BAP. 

∴ AP = BP

Again, in ΔAPB, ∠APB = 90°.

AP² + BP² = AB² [ by Pythagoras theorem ]

∴ AP²+ AP² = AB² [∵ AP = BP]

⇒ 2AP² = AB 

⇒ \(\mathrm{AP}^2=\frac{\mathrm{AB}^2}{2} \Rightarrow \mathrm{AP}=\frac{\mathrm{AB}}{\sqrt{2}}=\frac{1}{\sqrt{2}} \times 62 \mathrm{~cm}=31 \sqrt{2} \mathrm{~cm}\)

∴ The required perpendicular distance = 31√2 cm.

 

 

Chapter 1 Perimeter And Area Of Triangles Long Answer Type Questions

 

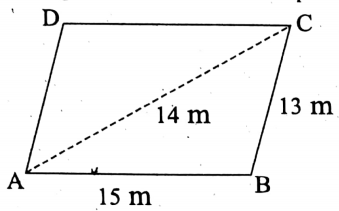
Question 1. Two adjacent sides of a field of shape parallelogram are 15 m and 13 m. If one of the diagonals of the field is 14 m, find its area.

Solution: 

Given 

Two adjacent sides of a field of shape parallelogram are 15 m and 13 m.

Let ABCD be the given parallelogram of which two adjacent sides AB and BC are of length 15 m and 13 m respectively and the length of the diagonal AC is 14 m.

∴ Half-perimeter of ΔABC = \(\frac{15+14+13}{2} \mathrm{~m}=\frac{42}{2} \mathrm{~m}=21 \mathrm{~m}\)

= \(\sqrt{21(21-15)(21-14)(21-13)} \mathrm{sq}-\mathrm{cm}\)

 = \(\sqrt{21 \times 6 \times 7 \times 8} \text { sq-cm }\)

= \(\sqrt{3 \times 7 \times 2 \times 3 \times 7 \times 2 \times 2 \times 2} \text { sq-cm }\)

= 3 x 7 x 2 x 2 sq-cm 

= 84 sq-cm

∴ area of  ABCD = 2 x area of ΔABC 

= 2 x 84 sqm 

= 168 sqm.

∴ The required area = 168 sqm.

 

 

Question 2. Two adjacent sides of a parallelogram are 25 cm and 15 cm and the length of a diagonal is 20 cm. What will be the height of the parallelogram when its base is the side of length 25 cm? 

Solution:

Given 

Two adjacent sides of a parallelogram are 25 cm and 15 cm and the length of a diagonal is 20 cm.

Let the two adjacent sides AB and BC of ABCD be 25 cm and 15 cm respectively and the length of its diagonal BD is 20 cm.

∴ Half-perimeter of ΔABD = \(\frac{25+15+20}{2} \mathrm{~cm}=\frac{60}{2} \mathrm{~cm}=30 \mathrm{~cm}\)

∴ Area of ΔABD = \(\sqrt{30(30-25)(30-15)(30-20)} \mathrm{sq}-\mathrm{cm}\)

= \(\sqrt{30 \times 5 \times 15 \times 10} \text { sq-cm }\)

= \(\sqrt{2 \times 3 \times 5 \times 5 \times 3 \times 5 \times 2 \times 5} \mathrm{sq}-\mathrm{cm}\)

= 2 x 3 x 5 x 5 sq-cm 

= 150 sq-cm

Let the required height of ABCD on the base AB be DE.

∴ \(\frac{1}{2}\) x AB x DE = 150

⇒ \(\frac{1}{2}\)  × 25 x DE

⇒ \(\mathrm{DE}=\frac{150 \times 2}{25}\)

⇒ DE = 12

∴ The required height = 12 cm.

 

 

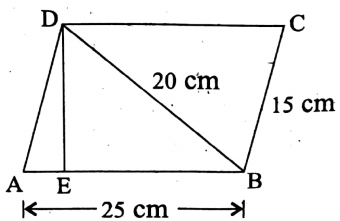
Question 3. Two adjacent sides of a parallelogram are 15 cm and 12 cm. If the perpendicular distance of the smallest sides of the parallelogram is 7.5 cm, then what is the perpendicular distance between its greatest sides?

Solution: 

Given 

Two adjacent sides of a parallelogram are 15 cm and 12 cm.

the perpendicular distance of the smallest sides of the parallelogram is 7.5 cm.

The distance between the smallest sides of the given parallelogram is 7.5 cm and the length of the smaller side is 12 cm.

∴ Area of the parallelogram = 12 x 7.5 sq-cm 

= 90 sq-cm.

Let the perpendicular distance between the greatest sides be x cm.

∴ 15 x x = 90

⇒ x=6. 

∴ The required length = 6 cm.

 

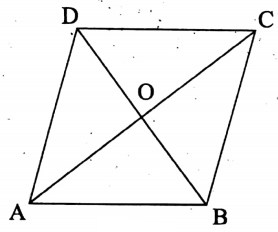
Question 4. The two diagonals of a rhombus are 15 cm and 20 cm. Find its perimeter, area, and height.

Solution:

Given 

The two diagonals of a rhombus are 15 cm and 20 cm.

Let the diagonals AC and BD of the rhombus ABCD intersect each other at O. 

Let AC 20 cm and BD = 15 cm.

∴ AO = \(\frac{\mathrm{AC}}{2}=\frac{20}{2} \mathrm{~cm}=10 \mathrm{~cm} \text { and } \mathrm{BO}=\frac{\mathrm{BD}}{2}=\frac{15}{2} \mathrm{~cm}=7 \cdot 5 \mathrm{~cm}\)

Since the diagonals of a rhombus bisect each other orthogonally,

∴ from the right-angled ΔAOB, we get,

\(\mathrm{AB}=\sqrt{\mathrm{AO}^2+\mathrm{OB}^2}=\sqrt{100+\frac{225}{4}} \mathrm{~cm}=\sqrt{\frac{625}{4}} \mathrm{~cm}=\frac{25}{2} \mathrm{~cm}=12.5 \mathrm{~cm}\)

∴ Perimeter of the rhombus = \(4 \times \frac{25}{2} \mathrm{~cm}\)

∴ Area of the rhombus = \(\frac{1}{2} \times 15 \times 20\)

Let the height of the rhombus be x cm. 

∴ \(\frac{25}{2} \times x=150\)

x = 12.

∴ Perimeter = 50 cm, Area 150 sq. cm, and Height = 12 cm

 

 

Question 5. The perimeter of a rhombus is 440 m and the perpendicular distance between its two parallel sides is 22 m. Then find the area of the rhombus.

Solution

Given 

The perimeter of a rhombus is 440 m and the perpendicular distance between its two parallel sides is 22 m

Perimeter of the given rhombus = 440 m, 

∴ 4 x side = 440 

Side = \(\frac{440}{4}\) m = 110 m.

∴ Area of the rhombus = side x perpendicular distance

= 110 x 22 sqm 

= 2420 sqm.

The area of the rhombus = 2420 sqm.

 

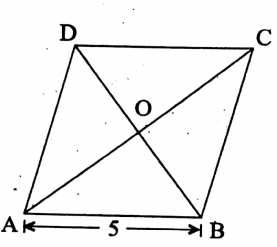
Question 6. If the perimeter of a rhombus is 20 cm and the length of one of its diagonal is 6 cm, then find the area of the rhombus.

Solution: 

Given

The perimeter of a rhombus is 20 cm and the length of one of its diagonal is 6 cm

Let the perimeter of the rhombus ABCD is 20 cm.

∴ 4 x AB = 20 cm

⇒ AB = 5 cm

Let the length of the diagonal BD is 6 cm and BD and AC intersect at O.

∴ BO = \(\frac{\mathrm{BD}}{2}=\frac{6}{2} \mathrm{~cm}=3 \mathrm{~cm}\)

∴ ∠AOB = 90°

∴ AO = \(\sqrt{\mathrm{AB}^2-\mathrm{BO}^2}=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4\)

∴ AO = 4 cm 

∴ AC = 2 x 4 cm

= 8 cm

∴ Area of the rhombus = \(\frac{1}{2}\)  x 6 x 8 sq-cm 

= 24 sq-cm

∴ The required area = 24 sq-cm.

 

 

Question 7. The area of a trapezium is 1400 sq-decametre. The perpendicular distance between its parallel sides is 20 decametres and the ratio of the lengths of the parallel sides is 3: 4. Find the lengths of the sides.

Solution: 

Given 

The area of a trapezium is 1400 sq-decametre.

The perpendicular distance between its parallel sides is 20 decametres and the ratio of the lengths of the parallel sides is 3: 4.

Let the parallel sides be 3x decametre and 4x decametre.

The area of the trapezium is 1400 sq-decametres and the perpendicular distance between the parallel sides is 20 decametres.

∴ \(\frac{1}{2}\) x (3x + 4x) x 20 = 1400 

⇒ 7x = 140

⇒ x = 20

∴ Length of the sides are 3x decametres = 3 x 20 decametres 

= 60 decametres.

and 4x decametres = 4 x 20 decametres 

= 80 decametres.

∴ The required lengths are 60 decametres and 80 decametres.

 

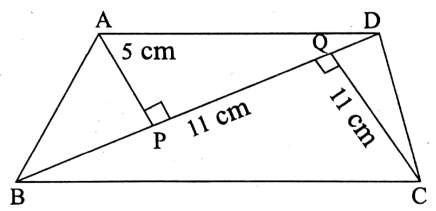
Question 8. The length of the diagonal BD of the trapezium ABCD is 11 cm and the lengths of two perpendiculars from A and C to the diagonal BD are 5 cm and 11 cm. Find the area of the trapezium ABCD.

Solution: 

Given

The length of the diagonal BD of the trapezium ABCD is 11 cm and the lengths of two perpendiculars from A and C to the diagonal BD are 5 cm and 11 cm

Let the length of the diagonal BD of the given trapezium ABCD be 11 cm and the lengths of the perpendiculars AP and CQ drawn from A and C respectively to BD. 

Given that AP = 5 cm and CQ = 11 cm.

∴ Area of ΔABD =\(\frac{1}{2} \times \text { base } \times \text { height }=\frac{1}{2} \times \mathrm{BD} \times \mathrm{AP}=\frac{1}{2} \times 11 \times 5 \mathrm{sq}-\mathrm{cm}=27.5 \mathrm{sq}-\mathrm{cm}\)

= \(\frac{1}{2}\) x 11 x 5 sq-cm 

= 27.5 sq-cm

∴ Again, area of ΔBCD = \(\frac{1}{2} \times \text { base } \times \text { height }\)

= \(\frac{1}{2} \times \mathrm{BD} \times \mathrm{CQ}=\frac{1}{2} \times 11 \times 11 \mathrm{sq}-\mathrm{cm}=60 \cdot 5 \mathrm{sq}-\mathrm{cm}\)

∴ Area of the trapezium ABCD = area of ΔABD + area of ΔBCD

= (27.5+ 60.5) sq-cm 

= 88.0 sq-cm

The required area = 88 sq-cm.

 

 

Question 9. The area of a rhombus is 2016 sq-cm and the length of each of the sides is 65 cm. Then find the lengths of its diagonals.

Solution: 

Given 

The area of a rhombus is 2016 sq-cm and the length of each of the sides is 65 cm

Let the lengths of the diagonals of the rhombus be x cm and y cm.

By the first condition given, \(\frac{1}{2} \times x \times y=2016 \Rightarrow x y=4032\) ……………….(1)

By the second condition given, \(\frac{1}{2} \sqrt{x^2+y^2}=65 \Rightarrow \sqrt{x^2+y^2}=130\)

x²+ y² = 16900 …………….(2)

We have, (x + y)² = x² + y² + 2xy = 16900 + 2 x 4032 = 16900 + 8064 = 24964

∴ x + y = 158…………..(3)

Again, (x – y)² = x² + y² -2xy

⇒ (x – y)² = 16900-8064

= 8836

∴ x – y = 94 …………………..(4)

Solving (3) and (4) we get, x= 126, y = 32

∴ the required lengths of the diagonals are 126 cm and 32 cm.

 

Question 10. The sides of a rhombus and a square are equal and the length of the diagonal of the square is 40√2 cm. If the ratio of the diagonals of the rhombus is 3: 4, then find the area of the rhombus.

Solution:

Given 

The sides of a rhombus and a square are equal and the length of the diagonal of the square is 40√2 cm

The ratio of the diagonals of the rhombus is 3: 4

Let the side of the square be a cm.

the length of the diagonal a√2 cm,

∴ a√2 = 40√2 

⇒ a = 40

∴ Let the lengths of the diagonals BD and AC be 3x cm and 4x cm.

∴ \(\mathrm{AO}=\frac{4 x}{2} \mathrm{~cm}=2 x \mathrm{~cm} \text { and } \mathrm{BO}=\frac{3 x}{2} \mathrm{~cm}\)

∴ AO² + BO² = AB²

or, \(4 x^2+\frac{9 x^2}{4}=40^2 \Rightarrow \frac{25 x^2}{4}=1600 \Rightarrow x=16\)

∴ The lengths of the diagonals 3 x 16 cm = 48 cm and

4 x 16 cm = 64 cm.

∴ Area of rhombus = \(\frac{1}{2}\) x 48 x 64 sq-cm = 1536 sq-cm.

∴The required area = 1536 sq-cm.

 

 

 

 

 

Coordinate Geometry Chapter 3 Area Of Triangles

Chapter 3 Area Of Triangles Determination of the area of the triangle formed by the given three points:

Let the coordinates of the points A, B, and C with respect to the rectangular coordinate axes \(\overleftrightarrow{X’OX}\) and \(\overleftrightarrow{Y’OY}\) are \(\left(x_1, y_1\right),\left(x_2, y_2\right) \text { and }\left(x_3, y_3\right)\) respectively.

We have to find the area of the triangle ΔABC obtained by joining these points A, B, and C.

Let us draw perpendiculars AL, BM, and CN from A, B, and C respectively to the x-axis.

Then,

Read and Learn More WBBSE Solutions For Class 9 Maths

\(\overline{\mathrm{OL}}=x_1, \overline{\mathrm{OM}}=x_2, \overline{\mathrm{ON}}=x_3\)

and \(\overline{\mathrm{AL}}=y_1, \overline{\mathrm{BM}}=y_2, \overline{\mathrm{CN}}=y_3\)

∴ \(\overline{\mathrm{LN}}=x_3-x_1, \overline{\mathrm{LM}}=x_2-x_1 ; \overline{\mathrm{NM}}=\dot{x}_2-x_3\)

Now, area of the ΔABC = [(area of the trapezium ALNC) + (area of the trapezium CNMB) – (area of the trapezium ALMB)]

= \(\frac{1}{2}(\overline{\mathrm{AL}}+\overline{\mathrm{NC}}) \cdot \overline{\mathrm{LN}}+\frac{1}{2}(\overline{\mathrm{CN}}+\overline{\mathrm{MB}}) \cdot \overline{\mathrm{NM}}-\frac{1}{2}(\overline{\mathrm{AL}}+\overline{\mathrm{BM}}) \cdot \overline{\mathrm{LM}}\)

= \(\frac{1}{2}\left(y_1+y_3\right)\left(x_3-x_1\right)+\frac{1}{2}\left(y_3+y_2\right)\left(x_2-x_3\right)-\frac{1}{2}\left(y_1+y_2\right)\left(x_2-x_1\right) \text { Sq-units }\)

= \(\frac{1}{2}\left[x_1 y_2-y_1 x_2+x_2 y_3-y_2 x_3+x_3 y_1-y_3 x_1\right] \text { Sq-units }\)

= \(=\frac{1}{2}\left[x_1 y_2-y_1 x_2+x_2 y_3-y_2 x_3+x_3 y_1-y_3 x_1\right] \text { Sq-units }\) 

∴ \(\Delta \mathrm{ABC}=\frac{1}{2}\left[y_1\left(x_2-x_3\right)+y_2\left(x_3-x_1\right)+y_3\left(x_1-x_2\right)\right] \text { Sq-units }\)

 

 

Chapter 3 Area Of Triangles To Determine The Condition Of Three Given Points To Be Collinear

 

Let \(\mathrm{A}\left(x_1, y_1\right), \mathrm{B}\left(x_2, y_2\right) \text { and } \mathrm{C}\left(x_3, y_3\right)\) be three collinear points.

∴ the area of the triangle produced by these three points must be 0. 

∴ the required condition is

\(\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]=0\) \(\Rightarrow x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)=0\)

 

Chapter 3 Area Of Triangles Select The Correct Answer (MCQ)

 

Question 1. In the right-angled triangle ABC, ∠ABC = 90°. If the coordinates of A and C be (0, 4) and (3, 0) respectively then the area of the ΔABC is

1. 12 Sq-units
2. 6 Sq-units
3. 24 Sq-units
4. 8 Sq-units

Solution:

The coordinates of A and C are (0, 4) and (3, 0) respectively, and ∠ABC = 90°.

∴ the coordinates of B are (0, 0).

area of the ΔABC = \(\frac{1}{2} \mathrm{AB} \times \mathrm{BC}\)

= \(\frac{1}{2} \times 4 \times 3 \text { Sq-units }\)

= 6 Sq-units

∴ area of the ΔABC = 6 Sq-units.

 

Question 2.  If the points (0, 0), (4, -3), and (x, y) are collinear, then 

1. x = 8, y = -6
2. x = 8, y = 6
3. x = 4, y = -6
4. x = -8, y=-6

Solution: The given points (0, 0), (4, -3), and (x, y) are collinear, then

∴ \(\frac{1}{2}[0(-3-y)+4(y-0)+x(0+3)]=0 \Rightarrow \frac{1}{2}[4 y+3 x]=0 \Rightarrow 4 y+3 x=0\)

Now, x 8, y=-6    [∵ 4y+ 3.8 = 0⇒ 4y = -24⇒ y = -6]

∴ x = 8, y = -6.

Question 3. If the area of the triangle, the vertices of which are (2, 7), (5, 1), and (x, 3), is 18 sq-units, then the value of x is

1. 10
2. 2
3. – 2
4. – 10

Solution: The area of the triangle with vertices (2, 7), (5, 1), and (x, 3) is 18 Sq-units.

∴ \(\frac{1}{2}[2(1-3)+5(3-7)+x(7-1)]=18\)

\(\frac{1}{2}[-4-20+6 x]=18\)

⇒-24+6x=36

6x=60

⇒x=10

Question 4. If the points (1, 3), (2, h), and (5, 1) are collinear, then the value of h is

1. 1
2. 0
3. 2
4. None of these

Solution: The given points are colinear, the area of the triangle formed by them is equal to zero.

Now, area of the triangle = \(\frac{1}{2}[-1(h+1)+2(-1-3)+5(3-h)] \text { Sq-units }\)

= \(\frac{1}{2}[-h-1-8+15-5 h] \text { Sq-units }\)

= \(\frac{1}{2}[-6  h+6] \text { Sq-units }\)

= (3-3h) Sq-units.

3-3h = 0 ⇒ (1-h) = 0 ⇒ h = 1.

 

Chapter 3 Area Of Triangles Short Answer Type Questions

 

Question 1. Examine whether points (2, 3), (4, 5) and (6, 5) are collinear or not.

Solution:

Given Points (2, 3), (4, 5) and (6, 5)

Let the points be A (2, 3), B (4, 5), and C (6, 5).

∴ area of ΔABC = \(\frac{1}{2}[2(5-5)+4(5-3)+6(3-5)] \text { Sq-units }\)

= \(\frac{1}{2}[0+8-12] \text { Sq-units }\)

= -2 Sq-units

Since the area of the triangle formed by the given points is not 0.

∴ the given points are not collinear.

 

Question 2. The centroid of a triangle is (6, 9) and two of its vertices are (15, 0) and (0, 10). Find the coordinates of the third vertex.

Solution:

Given

The centroid of a triangle is (6, 9) and two of its vertices are (15, 0) and (0, 10)

Let the coordinates of the third vertex be (h, k).

Two given vertices are (15, 0) and (0, 10).

∴ centroid = \(\left(\frac{15+0+h}{3}, \frac{0+10+k}{3}\right)=\left(\frac{15+h}{3}, \frac{10+k}{3}\right)\)

As per question, \(\frac{15+h}{3}=6\) ⇒ 15+h=18 ⇒h=3

Again, \(\frac{10+k}{3}=9\) ⇒ 10+k=27 ⇒ k=17

∴ the third vertex is (3, 17).

 

Question 3. If the points (a, 0), (0, b), and (1, 1) are collinear, then show that \(\frac{1}{a}+\frac{1}{b}=1\)

Solution:

Given Points (a, 0), (0, b), and (1, 1) are collinear

Since the points (a, 0), (0, b), and (1, 1) are collinear,

∴ the area of the triangle formed by them is zero.

Now, area of the triangle = \(\left.\frac{1}{2}[a(b-1)+0(1-0)+1(0-b)] \text { Sq-units }=\frac{1}{2}[a b-a-b)\right] \text { Sq-units }\)

As per question, \(\frac{1}{2}[a b-a-b]=0\) ⇒ ab – a – b = 0 ⇒  ab = a+b ⇒  a+b = ab

⇒ \(\frac{a}{a b}+\frac{b}{a b}=1\)

⇒  \(\frac{1}{b}+\frac{1}{a}=1\)

∴ \(\frac{1}{a}+\frac{1}{b}=1\)      (Proved)

 

Question 4. Find the centroid of the triangle formed by the points (xy, yz), (x, y), and (y, z).

Solution: 

Given Points (xy, yz), (x, y), and (y, z)

The required centroid = \(\left(\frac{x-y-x+y}{3}, \frac{y-z-y+z}{3}\right)=\left(\frac{0}{3}, \frac{0}{3}\right)\) =(0,0)

∴ the centroid is (0, 0).

 

Chapter 3 Area Of Triangles Long Answer Type Questions

 

Question 1. For what value of k the points (1, 1), (2, 1), and (k, 1) are collinear?

Solution:

Given Points (1, 1), (2, 1), and (k, 1)

Let the given points be A (1, 1), B (2, 1), and C (k, – 1).

The given points are collinear if ΔABC = 0

Now, ΔABC = \(\frac{1}{2}\) [1 (− 1 + 1) + 2 ( − 1 + 1) + k ( − 1 + 1)] Sq-units = \(\frac{1}{2}\) [0+0+0] Sq-units = 0

Hence, for any real value of k, the given points are collinear.

 

Question 2. Prove that the line segment obtained by joining the points (1, 2) and (-2,-4) passes through the origin.

Solution:

Given Points (1, 2) and (-2,-4)

The area of the triangle formed by the points (1, 2) and (-2,-4) and the origin (0, 0)

= \(\frac{1}{2}\) [1(−4 −0) − 2 (0 −2)+0(2+4)] Sq-units = \(\frac{1}{2}\) [-4+4+0] Sq-units 

= \(\frac{1}{2}\) x.0 Sq-units = 0

Since the area of the triangle formed by the given points is 0, the given points are collinear. Hence the line segment joining (1, 2) and (-2, -4) passes through the origin. (Proved) 

 

Question 3. Prove that the mid-point of the line segment obtained by joining the points (2, 1) and (6, 5) lie on the line segment obtained by joining the points (-4, -5) and (9, 8).

Solution:

The midpoint of the line segment was obtained by joining the points (2, 1) and (6, 5) 

= \(\left(\frac{2+6}{2}, \frac{1+5}{2}\right)\) = (4, 3).

Now, the area of the triangle formed by the points

= \(\frac{1}{2}\) [-4(8-3)+9(3+5)+4(-5-8)] Sq-units 

= \(\frac{1}{2}\) [-20+72-52] Sq-units

= \(\frac{1}{2}\) x 0 Sq-units = 0

∴ (4, 5), (9, 8), and (4, 3) are collinear.

∴ the mid-point of the line segment joining (2, 1) and (6, 5) lies on the line segment joining the points (4; 5) and (9, 8). (Proved)

 

Question 4. Find the area of the quadrilateral formed by the points (1, 4), (2, 1), (2, 3), and (3, 3).

Solution: 

Given Points (1, 4), (2, 1), (2, 3), and (3, 3)

Let the given points be A (1, 4), B(-2, 1), C (2, 3), and D (3, 3).

Let us draw the diagonal BD

Now, ΔABD = \(\frac{1}{2}\) [1(1 −3) −2(3-4)+3(4 − 1)] Sq-units

= \(\frac{1}{2}\) (-2+2+9] Sq-units

= \(\frac{9}{2}\) Sq-units.

Also, ABCD = \(\frac{1}{2}\) [-2(-3-3)+2(3-1)+3(1+3)] Sq-units

= \(\frac{1}{2}\) [12+4+12] Sq-units 

= 14 Sq-units

∴ quadrilateral ABCD = ΔABD + ΔBCD

= \(\left(\frac{9}{2}+14\right)\)

= \(18 \frac{1}{2} S q \text {-units }\)

∴ the required area = \(18 \frac{1}{2} S q \text {-units }\) Sq-units.

 

 

Question 5. The coordinates of A, B, and C are (3, 4), (4, 3), and (8,6) respectively; Find the area of the ΔABC and also find the perpendicular distance of BC from the vertex A. 

Solution:

Given

The coordinates of A, B, and C are (3, 4), (4, 3), and (8,6) respectively

The coordinates of A, B, and C are (3, 4), (- 4, 3), and (8, -6).

∴ area of ΔABC = \(\frac{1}{2}\) [3(3+6) 6)-4(-6-4)+8(4-3)] Sq-units 

= \(\frac{1}{2}\) [27+40+8] Sq-units

= \(\frac{1}{2}\) x 75 Sq-units

= 37 \(\frac{1}{2}\) Sq-units.

Now, length of BC = \(\sqrt{(-4-8)^2+(3+6)^2} \text { units }\) 

= √144+81 units 

=√225 units 

= 15 units Let the perpendicular distance of BC from A be x-units.

∴ \(\frac{1}{2} \times x \times 15=\frac{75}{2} \Rightarrow \frac{15 x}{2}=\frac{75}{2}\)

⇒ x = 5 

∴ the required length of the perpendicular is 5 units.

 

Question 6. The coordinates of A of the ΔABC are (2, 5) and the coordinates of its centroid are (-2, 1). Find the coordinates of the mid-point of BC.

Solution:

Given

The coordinates of A of the ΔABC are (2, 5) and the coordinates of its centroid are (-2, 1)

Let the mid-point of BC be D (h, k).

∴ the line segment AD is divided internally at (2, 1) into the ratio 2: 1.

∴ \(\frac{2 \times h+1 \times 2}{2+1}=-2\)

or, \(\frac{2 h+2}{3}=-2\)

or, 2h + 2 = -6

or, 2h = -8

or, h = -4

Again, \(\frac{2 \times k+1 \times 5}{2+1}=1\)

or, \(\frac{2 k+5}{3}=1\)

or, 2k + 5 = 3

or, 2k = -2

or, k = -1

∴ the mid-point of BC is (4, 1).

 

Question 7. A (1, 5), B (3, 1), and C (5, 7) are the vertices of the ΔABC. D, E, and F are the mid-points of BC, CA, and AB respectively. Find the area of ADEF and show that ΔABC = 4 ADEF.

Solution:

Given 

A (1, 5), B (3, 1), and C (5, 7) are the vertices of the ΔABC. D, E, and F are the mid-points of BC, CA, and AB respectively

The vertices of the ΔABC are given A (- 1, 5), B (3, 1), and C (5, 7).

area of ΔABC = \(\frac{1}{2}\) [-1(1-7)+3(7-5)+5(5-1)] Sq-units

= \(\frac{1}{2}\)[6+6+20] Sq-units 

= \(\frac{1}{2}\) x 32 Sq-units 

= 16 Sq-units

The mid-points of BC, CA, and AB are D, E, and F respectively.

∴ Coordinates of D = \(\left(\frac{3+5}{2}, \frac{1+7}{2}\right)\) = (4,4)

∴ Coordinates of E = \(\left(\frac{-1+5}{2}, \frac{5+7}{2}\right)\) = (2,6)

∴ Coordinates of F =  \(\left(\frac{-1+3}{2}, \frac{5+1}{2}\right)\) =(1,3)

area of ΔDEF =  \(\frac{1}{2}[4(6-3)+2(3-4)+1(4-6)] \text { Sq-units }\)

=  \(\frac{1}{2}[12-2-2] \text { Sq-units }=\frac{1}{2} \times 8 \text { Sq-units }\)

= 4 Sq-units

∴ ΔABC= 16 Sq-units = 4 x 4 Sq-units = 4 ΔDEF. (Proved)

 

Question 8. The coordinates of A, B, C, and D are (0, 1), (1, 2), (15, 2), and (4, 5) respectively. In what ratio does AC divide BD?

Solution:

Given

The coordinates of A, B, C, and D are (0, 1), (1, 2), (15, 2), and (4, 5) respectively

Let AC divides BD at P into the ratio m: n.

BD is divided at P into the ratio m: n.

∴ the coordinates of P = \(\left(\frac{4 m-n}{m+n}, \frac{-5 m+2 n}{m+n}\right)\)

Clearly, A, C, and P are collinear.

∴ the area of the triangle formed by them is zero.

∴ \(\frac{1}{2}\left[0\left(2-\frac{-5 m+2 n}{m+n}\right)+15\left(\frac{-5 m+2 n}{m+n}+1\right)+\frac{4 m-n}{m+n} \cdot(-1-2)\right]=0\)

 \(15 \times \frac{-5 m+2 n+m+n}{m+n}-\frac{3(4 m-n)}{m+n}=0 \Rightarrow \frac{15(-4 m+3 n)-3(4 m-n)}{m+n}=0\)

 \(5(-4 m+3 n)=4 m-n \quad \Rightarrow-20 m+15 n=4 m-n \quad \Rightarrow-24 m=-16 n\)

 \(\frac{m}{n}=\frac{16}{24}=\frac{2}{3} \quad \Rightarrow m: n=2: 3\)

∴ \(\overline{\mathrm{AC}} \text { divides } \overline{\mathrm{BD}}\) internally into the ratio 2: 3.

AC divides BD = 2: 3.

 

Question 9. The vertices of the triangle ABC are A (3, 0), B (0, 6), and C (6, 9). The sides AB and AC of ΔABC are intersected by DE at D and E respectively into a ratio of 1: 2. Prove by coordinate geometry that ΔABC = 9 ΔADE.

Solution:

Given 

The vertices of the triangle ABC are A (3, 0), B (0, 6), and C (6, 9).

The sides AB and AC of ΔABC are intersected by DE at D and E respectively into a ratio of 1: 2

As per the question, AB is divided at D internally into the ratio 1 2.

∴ The coordinates of D =  \(\left(\frac{1 \cdot 0+2 \cdot 3}{2+1}, \frac{1 \cdot 6+2 \cdot 0}{2+1}\right)\) = (2, 2)

Similarly, the coordinates of E =  \(\left(\frac{1 \cdot 6+2 \cdot 3}{2+1}, \frac{1 \cdot 9+2 \cdot 0}{2+1}\right)\) = (4, 3)

Now, the area of ΔABC = \(\frac{1}{2}\) [3(6-9)+0(9-0)+6(0-6)] Sq-units

= \(\frac{1}[2]\) (-9-36) Sq-units

∴ the area of ΔABC = \(\frac{45}{2}\) Sq-units     [∵ area can never be negative ]

Similarly, area of ΔADE = \(\frac{1}{2}\) [3(2−3)+2(3 +2(3-0)+4(0-2)] Sq-units

= \(\frac{1}{2}\) [−3+6–8] Sq-units 

= – \(\frac{5}{2}\) Sq-units

area of ΔADE= \(\frac{5}{2}\) Sq-units    [∵ area can never be negative ]

∴ \(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{ADE}}=\frac{\frac{45}{2}}{\frac{5}{2}}=9\)

or, ΔABC = 9 ΔADE (Proved)

ΔABC = 9 ΔADE

 

 

 

 

Coordinate Geometry Chapter 2 Section Formulas

Chapter 2 Section Formulas Determination of the coordinates of the point dividing a given line segment into a certain ratio:

Formula-1 When the line segment is divided internally

Let the coordinates of P and Q of the line segment \(\overleftrightarrow{\mathrm{PQ}}\) with respect to the axes \(\overleftrightarrow{\mathrm{OX}}\) and \(\overleftrightarrow{\mathrm{OY}}\) are \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) respectively.

Also, let the point R divides \overleftrightarrow{\mathrm{OX}} internally at a ratio m: n, i.e., PR: RQ = m: n; We have to determine the coordinates of R.

Read and Learn More WBBSE Solutions For Class 9 Maths

Let the coordinates of R be (x, y)

Now, let us draw perpendiculars PL, QM, and RN from P, Q, and R respectively to \(\overleftrightarrow{\mathrm{OX}}\) 

Also, let us draw \(\overline{\mathrm{PT}}\) perpendicular to \(\overline{\mathrm{QM}}\) from P.

Let this perpendicular intersects \(\overline{\mathrm{RN}}\) at S and \(\overline{\mathrm{QM}}\) at T.

Clearly, \(\overleftrightarrow{\mathrm{RS}}\) || \(\overleftrightarrow{\mathrm{QT}}\)

∴ \(\frac{\overline{\mathrm{PS}}}{\overline{\mathrm{PT}}}=\frac{\overline{\mathrm{RS}}}{\overline{\mathrm{QT}}}=\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{PQ}}}\)

Now,

\(\overline{\mathrm{PS}}=\overline{\mathrm{LN}}=\overline{\mathrm{ON}}-\overline{\mathrm{OL}}=x-x_1\)

\(\overline{\mathrm{PT}}=\overline{\mathrm{LM}}=\overline{\mathrm{OM}}-\overline{\mathrm{OL}}=x_2-x_1\)

\(\overline{\mathrm{RS}}=\overline{\mathrm{RN}}-\overline{\mathrm{SN}}=\overline{\mathrm{RN}}-\overline{\mathrm{PL}}=y-y_1\)

and \(\overline{\mathrm{QT}}=\overline{\mathrm{QM}}-\overline{\mathrm{TM}}=\overline{\mathrm{QM}}-\overline{\mathrm{PL}}=y_2-y_1\)

Again, \(\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{RQ}}}=\frac{m}{n}\)

or, \(\frac{\overline{\mathrm{RQ}}}{\overline{\mathrm{PR}}}\) = \(\frac{n}{m}\)

=\(\frac{n}{m} \Rightarrow \frac{\overline{\mathrm{RQ}}}{\overline{\mathrm{PR}}}+1\)

=\(\frac{n}{m}+1 \Rightarrow \frac{\overline{\mathrm{RQ}}+\overline{\mathrm{PR}}}{\overline{\mathrm{PR}}}\)

=\(\frac{n+m}{m} \Rightarrow \frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}}\)

=\(\frac{m+n}{m}\)

∴ From (1) we get, \(\frac{\overline{\mathrm{PS}}}{\overline{\mathrm{PT}}}=\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{PQ}}}\)

or, \(\frac{x-x_1}{x_2-x_1}=\frac{m}{m+n} \quad \text { or, } x(m+n)-x_1(m+n)=m x_2-m x_1\)

or, \(x(m+n)=m x_2-m x_1+m x_1+n x_1\)

or, \(x(m+n)=m x_2-m x_1+m x_1+n x_1\)

∴ \(x=\frac{m x_2+i x_1}{m+n}\)

Again, \(\frac{\overline{\mathrm{RS}}}{\overline{\mathrm{QT}}}=\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{PQ}}} \quad[\text { by }(1)]\)

or, \(\frac{y-y_1}{y_2-y_1}=\frac{m}{m+n}\)

or, \(y=\frac{m y_2+n y_1}{m+n}\) [ by simplification ]

∴ Coordinates of R is \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)

 

 

Formula-2 When the line segment is divided externally

Let the coordinates of P and Q of the line segment \(\overleftrightarrow{\mathrm{PQ}}\) with respect to the coordinate axes \(\overleftrightarrow{\mathrm{OX}}\) and \(\overleftrightarrow{\mathrm{OY}}\) be \(\left(x_1, y_1\right) \text { and }\left(x_2, y_2\right)\) respectively and let the point R divides \(\overleftrightarrow{\mathrm{PQ}}\) externally with a ratio m: n,

i.e., \(\overline{\mathrm{PR}}\): \(\overline{\mathrm{QR}}\) = m: n.

We have to determine the coordinates of R.

Let the coordinates of R be (x, y)

Let us draw perpendiculars \(\overline{\mathrm{PL}}\), \(\overline{\mathrm{QM}}\), and \(\overline{\mathrm{RN}}\) from P, Q, and R respectively to \(\overleftrightarrow{\mathrm{OX}}\).

Let us also draw perpendicular \(\overline{\mathrm{PT}}\) from P to \(\overline{\mathrm{RN}}\), which intersects \(\overline{\mathrm{QM}}\) at S and \(\overline{\mathrm{RN}}\) at T. 

Clearly, \(\overleftrightarrow{\mathrm{QS}} \| \overleftrightarrow{\mathrm{RT}}\)

∴ \(\frac{\overline{\mathrm{PS}}}{\overline{\mathrm{PT}}}=\frac{\overline{\mathrm{QS}}}{\overline{\mathrm{RT}}}=\frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}}\) …………….(1)

Now, 

\(\overline{\mathrm{PS}}=\overline{\mathrm{LM}}=\overline{\mathrm{OM}}-\overline{\mathrm{OL}}=x_2-x_1\)

\(\overline{\mathrm{PT}}=\overline{\mathrm{LN}}=\overline{\mathrm{ON}}-\overline{\mathrm{OL}}=x-x_1\)

\(\overline{\mathrm{QS}}=\overline{\mathrm{QM}}-\overline{\mathrm{SM}}=\overline{\mathrm{QM}}-\overline{\mathrm{PL}}=y_2-y_1\)

and \(\overline{\mathrm{RT}}=\overline{\mathrm{RN}}-\overline{\mathrm{TN}}=\overline{\mathrm{RN}}-\overline{\mathrm{PL}}=y-y_1\)

Again, \(\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{QR}}}=\frac{m}{n}, \quad \text { or, } \frac{\overline{\mathrm{QR}}}{\overline{\mathrm{PR}}}=\frac{n}{m} \quad \text { or, } 1-\frac{\overline{\mathrm{QR}}}{\overline{\mathrm{PR}}}=1-\frac{n}{m}\)

or, \(\frac{\overline{\mathrm{PR}}-\overline{\mathrm{QR}}}{\overline{\mathrm{PR}}}=\frac{m-n}{m} \quad \text { or, } \frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}}=\frac{m-n}{m}\)

∴ From (1) we get, \(\frac{\overline{\mathrm{PS}}}{\overline{\mathrm{PT}}}=\frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}} \text { or, } \frac{x_2-x_1}{x-x_1}=\frac{m-n}{m}\)

or, \(x(m-n)-x_1(m-n)=m x_2-m x_1\)

Or, \(x(m-n)=m x_2-m x_1+m x_1-n x_1 \text { or, } x(m-n)=m x_2-n x_1\)

∴ \(x=\frac{m x_2-n x_1}{m-n}\)

Again, \(\frac{\overline{\mathrm{QS}}}{\overline{\mathrm{RT}}}=\frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}} \quad \text { or, } \frac{y_2-y_1}{y-y_1}=\frac{m-n}{m}\)

or, \(y=\frac{m y_2-n y_1}{m-n}\)      [ by simplification ]

∴ the coordinates of R is \(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right)\)

 

 

Formula-3: Determination of coordinates of mid-point

Let the coordinates of P and Q of the line segment  \(\overline{\mathrm{PQ}}\) be \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) respectively and let R is the mid-point of \(\overline{\mathrm{PQ}}\).

Clearly, R divides PQ internally in the ratio 1: 1.

∴ the required coordinates of R are \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

 

 

Formula-4: Determination of the centroid of a triangle:

In the solid geometry section, you have studied that the medians of any triangle are concurrent and the point of intersection of the medians of the triangle is called its centroid.

We shall now prove with the help of coordinate geometry the medians of any triangle are concurrent and the centroid divides the medians internally into a radio of 2: 1.

Let D, E, and F be the mid-points of the sides BC, AC, and AB respectively of the ΔABC. 

Also, let the coordinates of its vertices A, B, and C be \(\left(x_1; y_1\right),\left(x_2, y_2\right) \text { and }\left(x_3, y_3\right)\) respectively.

Then the coordinates of D, E, and F are

\(\left(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}\right),\left(\frac{x_3+x_1}{2}, \frac{y_3+y_1}{2}\right) \text { and }\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\) respectively.

Let G be any point on AD such that \(\overline{\mathrm{AG}_1}: \overline{\mathrm{G}_1 \mathrm{D}}=2: 1\) =2: 1.

Clearly, the coordinates of G₁ will be

\(\left(\frac{2 \cdot \frac{x_2+x_3}{2}+1 \cdot x_1}{2+1}, \frac{2 \cdot \frac{y_2+y_3}{2}+1 \cdot y_1}{2+1}\right)=\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

Similarly, if G₂ and G₃ be any two points on the medians BE and CF respectively such that \(\overline{\mathrm{BG}_2}: \overline{\mathrm{G}_2 \mathrm{E}}=2: 1 \text { and } \overline{\mathrm{CG}_3}: \overline{\mathrm{G}_3 \mathrm{~F}}=2: 1\), then in a similar process discussed above we can show that the coordinates of both \(\mathrm{G}_2 \text { and } \mathrm{G}_3\) will be \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

Thus \(\mathrm{G}_1, \mathrm{G}_2, \mathrm{G}_3\) expresses the same point.

Hence, the medians \(\overline{\mathrm{AD}}\), \(\overline{\mathrm{BE}}\), and \(\overline{\mathrm{CF}}\) are concurrent and the point of intersection of them divides them internally into a ratio of 2 1.

Also, the coordinates of the centroid are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

 

Chapter 2 Section Formulas Select The Correct Answer (MCQ)

 

Question 1. The coordinates of the mid-point of the line segment joining the points (l, 2m) and (-l+2m, 2l-2m) are

1. (1, m) 
2. (1, – m)
3. (m, -1)
4. (m, 1)

Solution: 

Given line segment joining the points (l, 2m) and (-l+2m, 2l-2m)

The coordinates of the required mid-point are \(\left(\frac{l-l+2 m}{2}, \frac{2 m+2 l-2 m}{2}\right)\)

 

Question 2. If the two endpoints of the diameter of a circle be (7, 9) and (1,3); then the centre of the circle is

1. (3, 3)
2. (4, 6)
3. (3, 3)
4. (4, 6)

Solution:

Given The two endpoints of the diameter of a circle be (7, 9) and (1,3)

The mid-point of the diameter of a circle is its centre.

∴ the required centre is \(\left(\frac{7-1}{2}, \frac{9-3}{2}\right)\)

 

Question 3. If any point divides the line segment joining the points (2,5) and (- 3,-2) into the ratio 4 3 externally. Then the ordinate of the point is

1. 18
2. – 7
3. 18
4. 7

Solution:

Given 

Any point divides the line segment joining the points (2,5) and (- 3,-2) into the ratio 4 3 externally

The required ordinate = \(\frac{4 \times(-2)-3 \times(-5)}{4-3}=\frac{-8+15}{1}=7\)

 

Question 4. If P (1, 2), Q (4, 6), R (5, 7) and S (x, y) are the successive four vertices of the parallelogram PQRS, then

1. x = 2, y = 4
2. x =3, y = 4
3. x = 2, y = 3
4. x = 2, y = 5

Solution:

Given 

P (1, 2), Q (4, 6), R (5, 7) and S (x, y) are the successive four vertices of the parallelogram PQRS

The mid-point of the diagonal \(\overline{\mathrm{PR}}\) is \(\left(\frac{1+5}{2}, \frac{2+7}{2}\right)=\left(3, \frac{9}{2}\right)\)

The mid-point of the diagonal \(\overline{\mathrm{QS}}\) is \(\left(\frac{4+x}{2}, \frac{6+y}{2}\right)\)

Since the mid-points of the diagonals of a parallelogram are the same,

∴ \(\frac{4+x}{2}=3 and \frac{6+y}{2}=\frac{9}{2}\)

⇒ x+4=6

⇒x=2

⇒ y+6=9

⇒y=3

∴ x=2, y = 3

 

Chapter 2 Section Formulas Short Answer Type Questions

 

Question 1. C is the centre of a circle and AB is its diameter. The coordinates of A and C are (6, 7) and (5, 2) respectively. Find the coordinates of B.

Solution:

Given 

C is the centre of a circle and AB is its diameter. The coordinates of A and C are (6, 7) and (5, 2) respectively

Let the coordinates of point A be (6, –7) and of point B is (h, k).

∴ the coordinates of C, mid-point of AB are \(\left(\frac{6+h}{2}, \frac{-7+k}{2}\right)\)

\(\frac{6+h}{2}=5\)

⇒ h + 6 = 10

⇒ h = 4

Also, \(\frac{-7+k}{2^{\prime}}=-2\)

⇒ k-7 = -4

⇒ k=3

∴ the coordinates of B are (4, 3).

 

Question 2. The points P and Q are on the first and third quadrants respectively and their distances of them from the x-axis and y-axis are 6 units and 4 units respectively. Find the coordinates of mid-point \(\overline{\mathrm{PQ}}\).

Solution:

Given

The points P and Q are on the first and third quadrants respectively and their distances of them from the x-axis and y-axis are 6 units and 4 units respectively

Since P is on the first quadrant,

∴ both the coordinates of P will be positive.

∴ The coordinates of P are (4, 6).

Also, since Q lies on the third quadrant, both the coordinates will be negative.

∴ the coordinates of Q are (-4, -6).

∴ the coordinates of the mid-point of \(\overline{\mathrm{PQ}}\) are

\(\left(\frac{4-4}{2}, \frac{6-6}{2}\right)\) = (0,0).

∴ the required coordinates of \(\overline{\mathrm{PQ}}\) are (0, 0).

 

 

 

Question 3. The points A and B lie on the second and fourth quadrants respectively and the distances of them from the x-axis and y-axis are 8 units and 6 units respectively. Find the coordinates of the mid-point of AB.

Solution

Given

The points A and B lie on the second and fourth quadrants respectively and the distances of them from the x-axis and y-axis are 8 units and 6 units respectively

Since A lies on the second quadrant,

∴ its abscissa is negative and the ordinate is positive.

∴ coordinates of A are (- 6, 8).

Similarly, since B lies on the fourth quadrant, its abscissa is positive and the ordinate is negative.

∴ coordinates of B are (6,8).

∴ coordinates of the mid-point of \(\overline{\mathrm{AB}}\) are \(\left(\frac{-6+6}{2}, \frac{8-8}{2}\right)\) = (0,0)

∴ the required coordinates of the midpoint of \(\overline{\mathrm{AB}}\) are (0, 0).

 

 

Question 4. P is a point on the line segment \(\overline{\mathrm{AB}}\) such that AP PB. If the coordinates of A and B are (3, 4) and (5, 2) respectively find the coordinates of P.

Solution:

∵ AP = PB.

∴ P is the mid-point of \(\overline{\mathrm{AB}}\).

∴ the coordinates of P are \(\left(\frac{3-5}{2}, \frac{-4+2}{2}\right)=\left(\frac{-2}{2}, \frac{-2}{2}\right)=(-1,-1)\)

∴ the coordinates of P are (-1,-1).

 

The coordinates of P are (-1,-1)

 

Chapter 2 Section Formulas Long Answer Type Questions

 

Question 1. Determine the ratio in which the x-axis divides the line segment joining the points (5, 4) and (2, 3).

Solution:

Given 

The x-axis divides the line segment joining the points (5, 4) and (2, 3)

Let the given points be A (5; 4) and B (2, 3) and the x-axis divides \(\overline{\mathrm{AB}}\) into the ratio m: n 

∴ Coordinates of P are \(\left(\frac{2 m+5 n}{m+n}, \frac{3 m-4 n}{m+n}\right)\)

Since P lies on the x-axis, the ordinate of P is 0.

∴ \(\frac{3 m-4 n}{m+n}=0^i \Rightarrow 3 m-4 n=0 \Rightarrow 3 m=4 n \Rightarrow \frac{m}{n}=\frac{4}{3}=4: 3\)

\(\overline{\mathrm{AB}}\) is divided by the x-axis into the ratio 4: 3 internally.

 

Question 2. Determine the ratio into which the line segment joining the points (- 1, 2) and (4, 5) are intersected at the point (-11, 16).

Solution:

Given

The line segment joining the points (- 1, 2) and (4, 5) are intersected at the point (-11, 16)

Let the given points be A (1, 2) and B (4, 5) and AB is divided into the ratio m: n at (-11, 16).

∴ \(-11=\frac{m .4+n(-1)}{m+n}\)

-11m-11n = 4m-n

⇒ -15m =10n

⇒ \(\frac{m}{n}=-\frac{2}{3}\)

⇒ m: n=2: 3

Hence, \(\overline{\mathrm{AB}}\) is divided externally into the ratio 2 : 3 at (-11, 16).

 

Question 3. The coordinates of P of the APQR are (-1, -1); If the centroid of the triangle is \(\left(2, \frac{4}{3}\right)\), then find the mid-point of QR.

Solution:

Given

The coordinates of P of the APQR are (-1, -1)

Let the centroid of the APQR be G\(\left(2, \frac{4}{3}\right)\)and the mid-point of QR be S (h, k); Since

G \(\left(2, \frac{4}{3}\right)\) divides the median \(\overline{\mathrm{PS}}\) internally into the ratio 2: 1, we get,

\(\frac{2 \cdot h+1(-1)}{2+1}=2\)

⇒ 2h – 1 = 6

⇒ 2h = 7

⇒ h = \(\frac{7}{2}\)

And, \(\frac{2 \cdot k+1 \cdot(-1)}{2+1}=\frac{4}{3}\)

⇒ 2k – 1 = \(\frac{4}{3}\) x 3

⇒ 2k = 4 + 1

⇒ k = \(\frac{5}{2}\)

∴ the mid-point of \(\overline{\mathrm{QR}}\) is \(\left(\frac{7}{2}, \frac{5}{2}\right)\)

 

 

Question 4. (2, 6) is the centre of a circle and one of its chords of length 24 units is bisected at (-1, 2). Find the radius of the circle.

Solution:

Given 

(2, 6) is the centre of a circle and one of its chords of length 24 units is bisected at (-1, 2)

Let the chord AB of the circle with centre C is bisected at D.

As per the question, the coordinates of C and D are (2, 6) and (-1, 2).

∴ \(\mathrm{CD}^2=(2+1)^2+(6-2)^2=3^2+4^2=9+16=25 \text { and } \overline{\mathrm{AB}}=24\)

∴ \(\overline{\mathrm{BD}}\) = \(\frac{1}{2}\) \(\overline{\mathrm{AB}}\) = \(\frac{1}{2}\) x 24 = 12

Now, C and B are joined.

Since D is the mid-point of AB.

∴ \(\overline{\mathrm{CD}}\)  is perpendicular to \(\overline{\mathrm{AB}}\).

∴ from the right-angled triangle BCD, we get,

\(\mathrm{BC}^2=\mathrm{CD}^2+\mathrm{DB}^2=25+12^2 \Rightarrow \mathrm{BC}^2=169, \overline{\mathrm{BC}}=13\)

the required radius of the circle is 13 units.

 

 

Question 5. Determine the ratio in which the line segment joining the points (7, 3) and (-9, 6) is divided by the y-axis.

Solution: 

Given

The line segment joining the points (7, 3) and (-9, 6) is divided by the y-axis

Let the line segment joining the points (7, 3) and (-9, 6) be divided by the y-axis into the ratio mn at P.

∴ the coordinates of P are \(\left(\frac{m \cdot(-9)+n .7}{m+n}, \frac{m .6+n .3}{m+n}\right)=\left(\frac{-9 m+7 n}{m+n}, \frac{6 m+3 n}{m+n}\right)\)

Since P lies on the y-axis, 

∴ the abscissa of P is 0.

∴ \(\frac{-9 m+7 n}{m+n}=0\)

⇒ -9m + 7n = 0

⇒ +9m = +7n

⇒ \(\frac{m}{n}=\frac{7}{9}\)

∴ the required ratio is 7: 9.

 

Question 6. Prove that points A (7, 3), B (9, 6), C (10, 12) and D (8, 9) when joined consecutively produce a parallelogram.

Solution:

Given 

Points A (7, 3), B (9, 6), C (10, 12) and D (8, 9)

The mid-point of the diagonal AC of ABCD = mid-point of the line segment joining (7, 3) and (10, 12).

∴ mid-point of \(\overline{\mathrm{AC}}\) is \(\left(\frac{7+10}{2}, \frac{3+12}{2}\right)=\left(\frac{17}{2}, \frac{15}{2}\right)\)

Again, the mid-point of the diagonal BD of ABCD = mid-point of the line segment joining (9, 6) and (8, 9).

mid-point of \(\overline{\mathrm{BD}}\) is \(\left(\frac{9+8}{2}, \frac{6+9}{2}\right)=\left(\frac{17}{2}, \frac{15}{2}\right)\)

∴ Since the mid-points of both the diagonals \(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\) are \(\left(\frac{17}{2}, \frac{15}{2}\right)\)

i.e., the same,

\(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\) bisect each other.

∴ ABCD is a parallelogram. (Proved)

 

Question 7. Find (x,y) if the points (3, 2), (6, 3), (x, y) and (6, 5) produce a parallelogram when joined successively.

Solution:

Given 

The points (3, 2), (6, 3), (x, y) and (6, 5) produce a parallelogram when joined successively

Let the vertices of the parallelogram ABCD be A (3, 2), B (6, 3), C (x, y) and D (6, 5) and the diagonals AC and BD intersect each other at P.

∴ the diagonals of a parallelogram bisect each other,

P is the mid-point of both the diagonals \(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\).

∴ the coordinates of P, the mid-point of AC are \(\left(\frac{3+x}{2}, \frac{2+y}{2}\right)\)

and the coordinates of P, the mid-point of BD are \(\left(\frac{6+6}{2}, \frac{3+5}{2}\right)\) = (6,4);

∴ \(\left(\frac{3+x}{2}, \frac{2+y}{2}\right)=(6,4) \Rightarrow \frac{3+x}{2}=6 \Rightarrow x+3=12 \Rightarrow x=9\) 

and \(\frac{2+y}{2}=4 \Rightarrow y+2=8 \Rightarrow y=6\)

∴ (x, y) = (9, 6)

 

Question 8. If the points \(\left(x_1, y_1\right),\left(x_2, y_2\right),\left(x_3, y_3\right) \text { and }\left(x_4, y_4\right)\) when joined successively produce a parallelogram, prove that \(x_1+x_3=x_2+x_4 \text { and } y_1+y_3=y_2+y_4\)

Solution:

The mid-point of the diagonal joining the points \(\left(x_1, y_1\right) \text { and }\left(x_3, y_3\right)\) are

= \(\left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\right)\)

Again, the mid-point of the diagonal joining the points \(\left(x_2, y_2\right) \text { and }\left(x_4, y_4\right)=\left(\frac{x_2+x_4}{2}, \frac{y_2+y_4}{2}\right)\)

Since the diagonals of a parallelogram bisect each other, the mid-points of its diagonals will be the same.

∴ \(\left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\right)=\left(\frac{x_2+x_4}{2}, \frac{y_2+y_4}{2}\right)\)

∴ \(\frac{x_1+x_3}{2}=\frac{x_2+x_4}{2} \Rightarrow x_1+x_3=x_2+x_4\)   (proved)

Again, \(\frac{y_1+y_3}{2}=\frac{y_2+y_4}{2} \Rightarrow y_1+y_3=y_2+y_4\)     (Proved)

 

Question 9. (2, 4), (6, 2) and (- 4, 2) are the vertices of a triangle. Find the length of its medians.

Solution:

Given 

(2, 4), (6, 2) and (- 4, 2) are the vertices of a triangle

Let the given vertices be A (2, -4), B (6, -2) and C (-4, 2).

If D, E and F be the mid-points of BC, CA and AB respectively, then the coordinates of D are

\(\left(\frac{6-4}{2}, \frac{-2+2}{2}\right)\)= (1,0).

The coordinates of E are \(\left(\frac{2-4}{2}, \frac{-4+2}{2}\right)\) = (-1,-1).

The coordinates of F are \(\left(\frac{2+6}{2}, \frac{-4-2}{2}\right)\) = (4, -3)

∴ \(\overline{\mathrm{AD}}=\sqrt{(2-1)^2+(-4-0)^2}\) units = √1+16 units 

= √17 units

∴ \(\overline{\mathrm{BE}}=\sqrt{(6+1)^2+(-2+1)^2}\) units = √49+1 units 

= √50 units 

= 5√2 units

∴ \(\overline{\mathrm{CF}}=\sqrt{(-4-4)^2+(2+3)^2}\) units = √64+25 units

 = √89 units

∴ the required lengths of the medians are √17 units, 5√2 units and √89 units.

 

Question 10. Find the coordinates of the midpoint of the line segment intersected by the axes of the straight line 4x + 3y+ 12 = 0.

Solution:

Given 

straight line 4x + 3y+ 12 = 0

Putting x = 0 in 4x + 3y+ 120 we get, 3y= – 12 or, y = -4

∴ the straight line intersects the y-axis at (0, -4).

Also, putting y = 0 in 4x + 3y+ 12 = 0, we get 4x + 12 = 0 or, 4x = -12 or x = -3

∴ the straight line intersects the x-axis at (-3, 0).

So, the mid-point of (-3, 0) and (0, 4) is \(\left(\frac{-3+0}{2}, \frac{0-4}{2}\right)=\left(\frac{-3}{2},-2\right)\)

∴ the required coordinates are \(\left(\frac{-3}{2},-2\right)\)

 

Question 11. Determine the ratio in which the straight line 3x + 4y = 21 divides the line segment obtained by joining the points (-9, 5) and (7, 9).

Solution: 

Given 

The straight line 3x + 4y = 21 divides the line segment obtained by joining the points (-9, 5) and (7, 9)

Let the straight line 3x + 4y = 21 divide the line segment joining (-9, 5) and (7, 9) into the ratio m: n.

Now, the coordinates of the point of intersection are \(\left(\frac{7 m-9 n}{m+n}, \frac{9 m+5 n}{m+n}\right)\)

Clearly, this point lies on the straight line 3x + 4y = 21.

∴ \(\text { 3. } \frac{7 m-9 n}{m+n}+4 \cdot \frac{9 m+5 n}{m+n}=21\)

⇒ 21m-27n+36m+20n = 21m + 21n 

⇒ 36m = 28n

⇒ \(\frac{m}{n}=\frac{28}{36}=\frac{7}{9}\)

∴ m: n = 7:9

∴ the required ratio is 7: 9.

 

Question 12. If the points (5, 2), (x, 7), (1, 4) and (1, y) after joining successively produce a parallelogram, find the values of x and y.

Solution:

Given 

The points (5, 2), (x, 7), (1, 4) and (1, y) after joining successively produce a parallelogram

Let the given points denote the vertices A (5, 2), B (x, 7), C (- 1, 4) and D (1, y) of the parallelogram ABCD.

Then, mid-point of the diagonal AC = \(\left(\frac{5-1}{2}, \frac{2+4}{2}\right)\) = (2, 3)

Again, mid-point of the diagonal BD = \(\left(\frac{x+1}{2}, \frac{7+y}{2}\right)\)

Since mid-points of the diagonals of a parallelogram are equal.

\(\frac{x+1}{2}=2 \Rightarrow x+1=4 \Rightarrow x=3\) and

\(\frac{7+y}{2}=3 \Rightarrow y+7=6 \Rightarrow y=-1\)

∴ the values of x and y are 3 and -1 respectively.

 

 

 

Co-Ordinate Geometry Chapter 1 Distance Formulas

Chapter 1 Distance Formulas Introduction

Coordinate Geometry:-

The branch of mathematics in which different problems of geometry are solved with the help of algebra is known as coordinate geometry.

Rene Descartes, a famous French philosopher and mathematician developed this branch of mathematics and by his name, it is also known as cartesian geometry. 

Coordinate geometry is of two types:

1. Two-dimensional geometry

2. Three-dimensional geometry or solid coordinate geometry. 

Read and Learn More WBBSE Solutions For Class 9 Maths

The geometry based on any plane region is called two-dimensional geometry, while the geometry based on any solid object or space is usually called solid geometry.

Here we shall confine our discussion to two-dimensional geometry only.

Let us consider a page of this book, which is purely a plane where say O is a fixed point and \(\overleftrightarrow{\mathrm{XOX}^{\prime}}\) and \(\overleftrightarrow{\mathrm{YOY}^{\prime}}\) are two straight lines perpendicular to each other, i.e., they have divided the page plane into four sections.

Each of these sections is called a quadrant. The sections XOY, YOX’, X’OY’, and Y’OX’ are called the 1st, 2nd, 3rd, and 4th quadrants respectively 

The fixed point O is called the origin and the straight lines together are called the coordinate axes.

Separately \(\overleftrightarrow{\mathrm{XOX}^{\prime}}\) is called the x-axis or abscissa and \(\overleftrightarrow{\mathrm{YOY}^{\prime}}\) is called the y-axis or ordinate.

To express any point in this plane, firstly the digit expressing the distance along the axis (or parallel to the x-axis) and then the digit expressing the distance along the y-axis (or parallel to the y-axis) are written in a bracket.

If the coordinates of any point A be (a, b), then it is quadrant assumed that point A is at a distance of a unit from the origin O along or parallel to the x-axis and at a distance of b units along or parallel to the y-axis.

Whether the point lies on the 1st, 2nd, 3rd, or 4th quadrant or not totally depends on the signs of a and b.

Here, a is called the abscissa or x-coordinate, and b is called the ordinate or y-coordinate of point A.

Clearly, in the 1st quadrant, both the coordinates of any point are positive. In the 2nd quadrant, the abscissa is negative, but the ordinate is positive.

In the 3rd quadrant, the abscissa and the ordinate of any point are both negative, and in the 4th quadrant, the abscissa is positive, but the ordinate of any point is negative.

 

 

Chapter 1 Distance Formulas To Find The Distance Between Two Points Located At Different Positions In A Plane

 

1. Distance between two points located on the positive sides of the x-axis:

Let A (a, 0) and B (b, 0) (b> a) be two points on the positive x-axis, and O (0, 0) is the origin.

Now, AB = OB – OA 

= b-a

 

 

2. Distance between two points located on the negative side of the x-axis :

Let A (-a, 0) and B (- b, 0)(a> b) be any two points on the negative x-axis and 0 (0, 0) is the origin.

Here, AB = OA – OB

= a-b

 

 

3. Distance between two points located on the positive side of the y-axis :

Let A (0, a) and B (0, b) (b> a) be any two points located on the positive y-axis and O (0, 0) is the origin. 

Here, AB =  OB – OA

= b-a

 

 

4. Distance between two points located on the negative side of the y-axis:

Let A (0,- a) and B (0, – b)(a > b) be any two points located on the negative y-axis, and O (0, 0) is the origin.

Here, AB = OA – OB

= a-b

 

 

5. Distance between two points located on both positive and negative sides of the x-axis :

Let A (a, 0) and B (b, 0) be any two points on the both positive and negative sides of the x-axis and O (0, 0) be the origin.

Here, AB = OA + OB

= a + b

 

 

6. Distance between two points located on both the positive and negative sides of y-axis :

Let A (0, a) and B (0, b) be any two points on both positive and negative sides of the y-axis and O (0, 0) is the origin

Here, AB = OA + OB

= a + b

 

 

Chapter 1 Distance Formulas Distance Between Any Two Points In The XY-Plane

 

Let P \(\left(x_1, y_1\right) \text { and } \mathrm{Q}\left(x_2, y_2\right)\) be any two points in the XY-plane.

O (0, 0) is the origin. PR and QS are two perpendiculars drawn from P and Q respectively to the x-axis 

Again, let us draw QT ⊥ PR.

Now, SR = OR – OS

= (Abscissa of P) (Abscissa of Q)

= \(x_1-x_2\)

PT = PR – TR

= PR – QS (∵ TR = QS)

= (Ordinate of P) (Ordinate of Q)

= \(y_1-y_2\)

Now the distance between P and Q = PQ

But, from the right-angled triangle PQT, we get,

PQ² = PT² + QT²

= \(\left(y_1-y_2\right)^2+\left(x_1-x_2\right)^2\)  [∵ QT = SR = \(x_1-x_2\) ]

∴ PQ = \(\sqrt{\left(y_1-y_2\right)^2+\left(x_1-x_2\right)^2}=\sqrt{\left(y_2-y_1\right)^2+\left(x_2-x_1\right)^2}\)

∴ In the XY-plane, the distance between any two points

= √( (square of the difference of the ordinates of the points)+(square of the difference of the abscissas of the points) )

 

 

 

Chapter 1 Distance Formulas Distance Of A Point In The XY-Plane From The Origin

 

Distance Of A Point In The XY-Plane From The Origin

Let P (x, y) be any point on the XY-plane, and O (0, 0) be the origin

Again, PM ⊥ OX.

∴ OM = x and PM = y

Now, from the right-angled triangle POM, we get,

OP² = OM²+ PM² = x²+ y². 

∴ OP = \(\sqrt{x^2+y^2}\)

Also, by the distance formula, OP² = (x – 0)² + ( y – 0)² = x² + y²

∴ OP = \(\sqrt{x^2+y^2}\)

 

 

Formulas at a glance :

1. Distance of a given point P (x, y) from the origin 0 (0, 0) is \(\overline{\mathrm{OP}}=\sqrt{x^2+y^2}\) units.

2. Distance between two given points P (\(x_1-x_1\)) and Q (\(y_2-y_2\)) is \(\overline{\mathrm{PQ}}=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\) units.

 

Chapter 1 Distance Formulas Select The Correct Answer (MCQ)

 

Question 1. The distance between the points (a + b, c – d) and (a – b, c + d) is

1. \(2 \sqrt{a^2+c^2}\)
2. \(2 \sqrt{b^2+d^2}\)
3. \(\sqrt{a^2+c^2}\)
4. \(\sqrt{b^2+d^2}\)

Solution: 

Required distance = \(\sqrt{[(a+b)-(a-b)]^2+[(c-d)-(c+d)]^2}\)

= \(\sqrt{(a+b-a+b)^2+(c-d-c-d)^2}\)

= \(\sqrt{4 b^2+4 d^2}=\sqrt{4\left(b^2+d^2\right)}=2 \sqrt{b^2+d^2}\)

The distance between the points (a + b, c – d) and (a – b, c + d) is = \(\sqrt{4 b^2+4 d^2}=\sqrt{4\left(b^2+d^2\right)}=2 \sqrt{b^2+d^2}\)

Question 2. The distance between the points (x, -7) and (3, -3) is 5 units. Then the values of x are 

1. 0 or 6
2. 2 or 3
3. 5 or 1
4. – 6 or 0

Solution:

Given

The Distance Between The Points (x, -7) And (3, -3) is 5 Units

The required distance =\(\sqrt{(x-3)^2+(-7+3)^2}=\sqrt{(x-3)^2+16}\)

As per the question, \(\sqrt{(x-3)^2+16}=5 \Rightarrow(x-3)^2+16=25 \Rightarrow(x-3)^2=9\)

x – 3 = ± 3

Then,

x-3 =+3

x = 6 and x-3 = -3

x=0

x= 0 or 6.

The values of x are x= 0 or 6.

 

Question 3. If the distance of the point (x, 4) from the origin is 5 units, then the value of x is

1. ± 4
2. ± 5
3. ± 3
4. None of these

Solution:

Given

The distance of (x, 4) from the origin is 5 units.

∴ \(\sqrt{x^2+4^2}=5 \Rightarrow x^2+16=25 \Rightarrow x^2=25-16=9 \Rightarrow x= \pm 3\)

 

Question 4. The coordinates of the center of a circle are (0, 0). If the coordinates of any point on its circumference be (3, 4), then the radius of the circle is

1. 5 units
2. 4 units
3. 3 units
4. None of these

Solution:

Given 

The coordinates of the center of a circle are (0, 0).

If the coordinates of any point on its circumference be (3, 4).

Since the point (3, 4) is on the circumference of the circle, the distance between (3, 4) and (0, 0) is the radius of the circle.

∴ the required radius = \(\sqrt{3^2+4^2} \text { units }=\sqrt{9+16} \text { units }\) 

= √25 units 

= 5 units.

The radius of the circle is = 5 units.

Question 5. The distance of the point (a + b, a – b) from the origin is

1. \(2 \sqrt{a^2-b^2}\)
2. \(2 \sqrt{a^2+b^2}\)
3. \(\sqrt{2\left(a^2+b^2\right)}\)
4. None of these

Solution:

Given 

The distance of the point (a + b, a – b)

Required distance = \(\sqrt{(a+b)^2+(a-b)^2}=\sqrt{2\left(a^2+b^2\right)}\)

 

Chapter 1 Distance Formulas Short Answer Type Questions

 

Question 2. 

1. Determine the coordinates of a point on the y-axis from which the distance of the points (2, 3) and (1, 2) are equal.

Solution: 

Given:-

Coordinates of a point on the y-axis from which the distance of the points (2, 3) and (1, 2) are equal

Let the coordinates of the point on the y-axis be (0, k).

∴ the distance of (2, 3) from (0, k)=√(2-0)² + (3-k)² units.

Again, the distance of (-1, 2) from (0, k)= \(\sqrt{(2-0)^2+(3-k)^2}\) units.

As per the question, \(\sqrt{(-1-0)^2+(2-k)^2}\).

\(\sqrt{2^2+(3-k)^2}=\sqrt{1^2+(2-k)^2}\)

⇒ 4+9+k² -6k = 1+4+k²-4k

⇒-6k+4k = 1-9

⇒ 2k=8 

⇒ k=4

the required point is (0, 4).

 

2. If the square of the distance between the points (-2, a) and (a,- 3) is 85, find the value of a.

Solution: 

Given:-

square of the distance between the points (-2, a) and (a,- 3) is 85

The distance between (-2, a) and (a, – 3) = \(\sqrt{(-2-a)^2+(a+3)^2}\)

As per the question, \((-2-a)^2+(a+3)^2=85\)

\((a+2)^2+(a+3)^2=85\)

a²+4+4a+a²+9+6a = 85

2a² + 10a +13 = 85 

2a²+10+13-85 = 0

2a²+10a-72 = 0

a²+5a-36 = 0

(a+9)(a-4)=0

a = -9, 4

the values of a are 9 and 4.

 

3. Show that the distance between (1, 1) and \(\left(\frac{2 m^2}{1+m^2}, \frac{(1-m)^2}{1+m^2}\right)\) is independent of m.

Solution:

Given:-

 The distance between (1, 1) and \(\left(\frac{2 m^2}{1+m^2}, \frac{(1-m)^2}{1+m^2}\right)\)

= \(\sqrt{\left(1-\frac{2 m^2}{1+m^2}\right)^2+\left[1-\frac{(1-m)^2}{1+m^2}\right]^2}\)

= \(\sqrt{\left(\frac{1+m^2-2 m^2}{1+m^2}\right)^2+\left[\frac{1+m^2-(1-m)^2}{1+m^2}\right]^2}\)

= \(\sqrt{\frac{\left(1-m^2\right)^2}{\left(1+m^2\right)^2}+\frac{\left(1+m^2-1-m^2+2 m\right)^2}{\left(1+m^2\right)^2}}\)

= \(\frac{1}{\left(1+m^2\right)} \sqrt{\left(1-m^2\right)^2+4 m^2}\)

= \(\frac{1}{\left(1+m^2\right)} \sqrt{\left(1+m^2\right)^2}=\frac{1}{\left(1+m^2\right)} \times\left(1+m^2\right)=1\)

∴ the distance between (1, 1) and \(\left(\frac{2 m^2}{1+m^2}, \frac{(1-m)^2}{1+m^2}\right)\) is independent of m. (Proved).

 

4. The coordinates of one of the vertices of a triangle is (2, 0) and the coordinates of the mid- points of its opposite side is (5, 3). Find the length of the median.

Solution:

Given:-

The coordinates of one of the vertices of a triangle is (2, 0) and the coordinates of the mid- points of its opposite side is (5, 3)

The required length = \(\sqrt{(2-5)^2+(0-3)^2}\) units

= √9+9 units = √18 units = 3√2 units.

∴ length of the median = 3√2 units.

 

Chapter 1 Distance Formulas Long Answer Type Questions

 

Question 1. Prove that A (3, 3), B (8,-2), and C (-2,-2) are the vertices of a right-angled isosceles triangle. Also, find the length of the hypotenuse of ΔABC.

Solution:

Given That A (3, 3), B (8,-2), and C (-2,-2) are the vertices of a right-angled isosceles triangle

The three vertices of the given triangle are A (3, 3), B (8,-2), and C (-2,-2).

Now, AB =  \(\sqrt{(3-8)^2+(3+2)^2}\) units

= √25+25 units

= √50 units

BC = \(\sqrt{(8+2)^2+(-2+2)^2}\) units

=√100 units

= 10 units.

AC =  \(\sqrt{(3+2)^2+(3+2)^2}\) units

= √25+25 units

= √50 units.

AB²+ AC² = (√50)² + (√50)²

=50+50

= 100

= (10)²

= BC²       [∵ BC= 10]

Clearly, AB = AC         ∴ ΔABC is isosceles.

And AB²+ AC² = BC²         ∴ ΔABC is right-angled.

The given points are the vertices of a right-angled isosceles triangle, the length of whose hypotenuse is 10 units. (Proved)

 

Question 2. Show that the points (2, 1), (0, 0), (1, 2), and (1, 3) are the vertices of a square. 

Solution:

Given Points (2, 1), (0, 0), (1, 2), and (1, 3)

Let the given points be A (2, 1), B (0, 0), C (-1, 2), and D (1, 3).

\(\overline{\mathrm{AB}}=\sqrt{2^2+1^2}\)units

= √5 units

\(\overline{\mathrm{BC}}=\sqrt{1^2+(-2)^2}\) units

=√1+4 units

= √5 units

\(\overline{\mathrm{CD}}=\sqrt{(-1-1)^2+(2-3)^2}\) units

= √4+1 units

= √5 units;

\(\overline{\mathrm{AD}}=\sqrt{(2-1)^2+(1-3)^2}\) units

= √1+4 units

= √5 units;

∴ \(\overline{\mathrm{AB}}=\overline{\mathrm{BC}}=\overline{\mathrm{CD}}=\overline{\mathrm{AD}}\)

Again, \(\overline{\mathrm{AC}}=\sqrt{(2+1)^2+(1-2)^2}\) units

= √9+1 units

= √10 units

\(\overline{\mathrm{AC}}=\sqrt{(2+1)^2+(1-2)^2}\) units

= √9+1 units

= √10 units

\(\overline{\mathrm{BD}}=\sqrt{1^2+3^2}\)

= √1+9 units

= √10 units

∴ \(\overline{\mathrm{AC}}=\overline{\mathrm{BD}}\)

Clearly, the four sides of the quadrilateral ABCD are equal and the two diagonals are also equal.

∴ ABCD is a square. (Proved)

 

Question 3. Calculate whether the three points 0 (0, 0), A (4, 3) and B (8, 6) are collinear or not.

Solution: 

The given three points are O (0, 0), A (4, 3), and B (8, 6).

∴ \(\overline{\mathrm{OA}}=\sqrt{(+4)^2+(-3)^2}\) units = √16+9 units = √25 units = 5 units 

\(\overline{\mathrm{AB}}=\sqrt{(4-8)^2+(3-6)^2}\) units = √16+9 units = √25 units = 5 units

\(\overline{\mathrm{OB}}=\sqrt{(8)^2+(6)^2}\) units = √64+36 units = √100 units = 10 units

\(\overline{\mathrm{OA}}+\overline{\mathrm{AB}}=5+5=10=\overline{\mathrm{OB}}\)

∴ 0 (0, 0), A (4, 3), and B (8, 6) are collinear. (Proved)

 

Question 4. Show that the successive joining of the points (–7, 2), (19, 8), (15, 6), and (-11, 12) produce a parallelogram.

Solution:

Given (–7, 2), (19, 8), (15, 6), And (-11, 12)

Let the points are A (-7, 2), B (19, 8), C (15, 6), and D (11, 12)

∴ \(\overline{\mathrm{AB}}=\sqrt{(-7-19)^2+(2-8)^2}\) units = √676+36 units

= √712 units 

= √4 x 178 units 

= 2√178 units

∴ \(\overline{\mathrm{BC}}=\sqrt{(19-15)^2+(8+6)^2}\) units= √16+ 196 units -√4×53 units -2√53 units

∴ \(\overline{C D}=\sqrt{(15+11)^2+(-6+12)^2}\) units = √676+36 units = √712 units = 2√178 units

∴ \([\overline{\mathrm{AD}}=\sqrt{(-7+11)^2+(2+12)^2}/latex] units = √16+ 196 units = √212 units=2√53 units

∴ [latex]\overline{\mathrm{AB}}=\overline{\mathrm{CD}} \text { and } \overline{\mathrm{AD}}=\overline{\mathrm{BC}}\)

Clearly, the opposite sides of the quadrilateral are equal.

∴ the quadrilateral is a parallelogram. (Proved)

 

Question 5. Show that the successive joining of the points (2, 5), (5, 9), (9, 12), and (6, 8) produce a rhombus.

Solution:

Given (2, 5), (5, 9), (9, 12), And (6, 8)

Let the given points be A (2, 5), B (5, 9), C (9, 12), and D (6, 8).

∴ \(\overline{\mathrm{AB}}=\sqrt{(2-5)^2+(5-9)^2}\)units = √9+16 units = √25 units = 5 units.

∴ \(\overline{\mathrm{BC}}=\sqrt{(5-9)^2+(9-12)^2}\) units = √16+9 units = √25 units = 5 units. 

∴ \(\overline{C D}=\sqrt{(9-6)^2+(12-8)^2}\) units=√9+16 units = √25 units = 5 units.

∴ \(\overline{\mathrm{AD}}=\sqrt{(2-6)^2+(5-8)^2}\) units = √16+9 units = √25 units = 5 units.

∴ \(\overline{\mathrm{AC}}=\sqrt{(2-9)^2+(5-12)^2}\) units = √49+49 units = √98 units.

∴ \(\overline{\mathrm{BD}}=\sqrt{(5-6)^2+(9-8)^2}\) units = √1+1 units = √2 units.

∴ In the quadrilateral ABCD, \(\overline{\mathrm{AB}}=\overline{\mathrm{BC}}=\overline{\mathrm{CD}}=\overline{\mathrm{AD}} \text { and } \overline{\mathrm{AC}} \neq \overline{\mathrm{BD}}\).

i.e., the sides. of ABCD are equal, but the diagonals are not equal.

∴ ABCD is a rhombus. (Proved)

 

Question 6. The line segment joining the points (7, 1) and (9, 3) is the base of an isosceles triangle. If the abscissa of the triangle is 4, find the vertex.

Solution:

Given The line segment joining the points (7, 1) and (9, 3) is the base of an isosceles triangle

Let the vertex be (4, k).

Now, the distance between (4, k) and (7,-1) = \(\sqrt{(4-7)^2+(k+1)^2}\) units.

Again, the distance between (4, k) and (9, 3)=\(\sqrt{(4-9)^2+(k-3)^2}\) units. 

Since the given triangle is isosceles,

∴ \(\sqrt{(4-7)^2+(k+1)^2}=\sqrt{(4-9)^2+(k-3)^2}\)

⇒ \(\sqrt{9+(k+1)^2}=\sqrt{25+(k-3)^2}\)

⇒ 9+(k+1)² = 25+ (k − 3)²

⇒ 9+k²+1+2k = 25+k²+9-6k

⇒ 2k+6k = 34-10 

⇒ 8k = 24

⇒ k = 3

∴ the required vertex is (4, 3)

 

Question 7. If the point (x, y) is equidistant from the points (a + b, b- a) and (a – b, a + b), then prove that bx = ay.

Solution: 

Given

The Point (x, y) is equidistant from the points (a + b, b- a) and (a – b, a + b)

Distance between (x, y) and (a + b, b- a) = \(\sqrt{[x-(a+b)]^2+[y-(b-a)]^2}\) units 

= \(\sqrt{[x-(a+b)]^2+[y+(a-b)]^2}\) units

Distance between (x, y) and (a – b, a + b) = \(\sqrt{[x-(a-b)]^2+[y-(a+b)]^2}\) units.

As per the question, \(\sqrt{[x-(a+b)]^2+[y+(a-b)]^2}=\sqrt{[x-(a-b)]^2+[y-(a+b)]^2}\)

⇒ [x-(a+b)]² +[y+(a−b)]² = [x-(a – b)]² +[y-(a+b)]²

⇒ x² +(a+b)² -2x(a+b) + y² + (a−b)² +2y(a-b)

⇒ x² +(a-b)² -2x(a – b) + y² +(a+b)² -2y(a+b) 

⇒ 2x (a-b)-2x(a+b) = -2y(a+b)-2y(a-b)

⇒ 2x [a-b-a-b] = -2y [a+b+a-b]

⇒ 2bx=2ay

bx = ay (Proved)

 

Question 8. Prove that the circle of centre (4, 3) passes through the points (0, 0), (8, 0), (1, 7) and (1, 1). Find also the radius of the circle.

Solution:

Given The circle of centre (4, 3) passes through the points (0, 0), (8, 0), (1, 7) and (1, 1).

Let the centre of the circle be O (4, 3) and the points be A (0, 0), B (8, 0), C (1, 7) and D (1, 1).

Now, the distance of four points from the centre of the circle is

\(\sqrt{4^2+3^2}\) units=√25 units = 5 units

\(\sqrt{(4-8)^2+3^2}\) units = √25 units = 5 units

\(\sqrt{(4-1)^2+(3-7)^2}\) units = √9+16 units = √25 units = 5 units

\(\sqrt{(4-1)^2+(3+1)^2}\) units=√9+16 units = √25 units = 5 units

Clearly, the distances of all the given points from the centre of the circle are equal. 

∴ the circle passes through the given points. (Proved)

∴ The radius of the circle is 5 units.

 

Question 9. The centre of a circle is (5, 3) and its radius is 5 units. Determine the length of the chord of the circle, which is bisected at the point (3, 2).

Solution:

Given The centre of a circle is (5, 3) and its radius is 5 units

Let the centre of the circle be O (5, 3) and its chord AC is bisected at B (3,2) 

Now, \(\overline{\mathrm{OA}}\) = radius of the circle = 5 units;

\(\overline{\mathrm{OB}}=\sqrt{(5-3)^2+(3-2)^2}\) units=√4+1 units = √5 units.

From the right-angled triangle AOB, we get,

\(\mathrm{AB}^2=\mathrm{AO}^2-\mathrm{OB}^2\) units = (20 – 5)

= 20 units

AB = √20 units=2√5 units.

AC=2AB = 4√5 units

∴ the required length of the chord = 4√5 units.

 

 

Question 10. Prove that the points (2, 2), (2, 2) and (-2√3, 2√3) are the vertices of an equilateral triangle.

Solution: 

Given Points (2, 2), (2, 2) And (-2√3, 2√3)

Let the given points be A (2, 2), B (-2,-2) and C(-2√3, 2√3).

∴ \(\sqrt{(2+2)^2+(2+2)^2}\) units = √16+16 units = √32 units

\(\sqrt{(-2+2 \sqrt{3})^2+(-2-2 \sqrt{3})^2}\) units = \(\sqrt{2\left[(-2)^2+(2 \sqrt{3})^2\right]}\) units 

= \(\sqrt{2[4+12]}\) units 

= √32 units

\(\sqrt{(2+2 \sqrt{3})^2+(2-2 \sqrt{3})^2}\) units = v units

= \(\sqrt{2\left[(2)^2+(2 \sqrt{3})^2\right]}\) units 

= √2×16 units

= √32 units

Clearly, \(\overline{\mathrm{AB}}=\overline{\mathrm{BC}}=\overline{\mathrm{AC}}\)

∴ The given points are the vertices of an equilateral triangle. (Proved)