Class 11 Physics

Superposition Of Waves Long Answer Type Questions

Question 1. When you sing in the shower why is the sound heard so good?
Answer:

It is because of superposition. The sound waves you produce in the air bounce off the walls and interfere with each other in a way that produces a sweet sound.

Question 2. Which from an of a string the tone clamped will at be both absent ends, in the when note it is emitted strode at a distance of one-third of its length from one end?
Answer:

The stretched string AB is struck at the point C, where AC = \(\frac{1}{3}\)AB. As a result, an antinode will be formed at C; a node can never be formed there. So the modes of vibration, as shown in the figure, will be absent. This means that the absent ones would correspond to the 3rd, 6th 9th,… harmonics.

Question 3. What would be the change in the fundamental frequency of a stringed instrument if

1. The length of the string is doubled,
2. The tension is doubled,
3. The diameter is doubled?

Answer:

1. The frequency is inversely proportional to the length of the string. So, if the length is doubled, the fundamental frequency would be reduced to half.
2. Frequency is proportional to the square root of the tension. So, if the tension is doubled, the fundamental frequency would be √2. or 1.414 times of its initial value.
3. If the diameter is doubled, the area of the cross-section becomes 22 or 4 times the initial value. If the materials of the string is the same, the mass per unit length also becomes 4 times its original value. The frequency is inversely proportional to the square root of the mass per unit length. So, in this case, the frequency would be \(\frac{1}{\sqrt{4}} \text { or } \frac{1}{2}\) times, i.e., half the initial value.

Question 4. Compare the fundamental frequencies of the tones emitted by two pipes of equal length, one open at both ends and the other closed at one end.
Answer:

Let V be the velocity of sound in air and l, be the length of each of the pipes.

∴ The frequency of the fundamental tone emitted by the pipe open at both ends, \(n_1=\frac{V}{2 l}\)

and the frequency of the fundamental tone emitted by the pipe closed at one end, \( n_2=\frac {V}{4 l}.\)

∴ \(\frac{n_1}{n_2}=\frac{\frac{V}{2 l}}{\frac{V}{4 l}}=2 \quad \text { or, } n_1=2 n_2\)

So, the fundamental frequency for a pipe open at both ends is twice that of a pipe of the same length but closed at one end.

Example 5. A closed pipe and an open pipe emit fundamental tones of the same frequency. Find out the ratio of their lengths.
Answer:

Let the length of the closed pipe and the open pipe be l₁ and l₂, respectively. V is the velocity of sound in air.

For the closed pipe, the fundamental frequency is \(n_1=\frac{V}{4 l_1}\); for the open pipe, it is \(n_2=\frac{V}{2 l_2}\)

In the problem, \(n_1=n_2 \text { or, } \frac{V}{4 l_1}=\frac{V}{2 l_2} \text { or, } \frac{l_1}{l_2}=\frac{1}{2}\)

Therefore, the ratio of their lengths is  1: 2

Question 6. Would the frequencies of the tones emitted from a closed or an open pipe change If the temperature of the air column in the pipe increases?
Answer:

The frequencies of the tones are proportional to the velocity of sound in air, which increases with the increase of temperature. So, as the temperature increases, the frequencies of the tones emitted from the air column in the pipe would also increase.

Question 7. How would the fundamental frequency emitted from an organ pipe, open at both ends, change, If

1. An open end is suddenly closed,
2. The length of the pipe is increased,
3. The diameter of the pipe is increased?
4. What would happen if the air is blown heavily through an open end?

Answer:

1. If an open end is suddenly closed, the pipe open at both ends becomes a closed pipe of equal length. In this case, the fundamental frequency would be halved.
2. The frequency of the emitted fundamental tone is inversely proportional to the length of the pipe. So, the frequency would decrease with the increase in the length of the pipe.
3. The end error of a pipe increases with the increase in diameter. As a result, the effective length of the pipe increases. The fundamental frequency is inversely proportional to the length of the pipe; so the frequency would decrease due to this increase in effective length.
4. A heavier blow would increase the loudness of the emitted tones. Moreover, the hither (Le, 2nd, 3rd, 4th,…) harmonics would be. formed more easily.

Question 8. Why is the musical sound emitted from an open pipe more pleasant than that emitted from a closed pipe?
Answer:

A dosed pipe can emit the fundamental rone and its odd harmonics. But an open pipe can emit both the odd and the even harmonics as well as the fundamental tone. So, a note emitted from, an open pipe contains a larger number of constituent tones.

The quality of a note depends on the number of overtones present in it. Store the number of overtones present in a note, the more pleasant it sounds. This results in a higher quality of sound emitted from an open pipe.

Question 9. A stretched vibrating string is touched at a distance of 1/3 rd of its length from one end. What would happen to the musical sound emitted?
Answer:

The point of touch would be a nodal point. So only the 3rd, 6th. 9th…. harmonics, which have a node at 1/3 would be emitted. No other harmonics have a node at 1/3. So, all of them would be suppressed.

Question 10. Two tuning forks, vibrating simultaneously, produce 6 beats per second. The first of them has a frequency of 312 Hz. Some amount of wax is added to one arm of the second tuning fork; the number of beats per second reduces to 3. Find out the frequency of this second tuning fork. Is it possible to increase the beat frequency to 6 per second by adding some more wax to die second tuning fork?
Answer:

Initially, the number of beats per second is 6. So the frequency of the 2nd fork is either 312-*-6 = 318 Hz or 312 – 6 = 306 Hz. After putting the wax, the beat frequency is 3 per second.

• So the changed frequency of the 2nd fork is, either 312÷3=315Hz or 312 – 3 = 309 Hz. But the addition of wax reduces the frequency of the 2nd fork; so it cannot change from 306 Hz to 309 Hz; the actual change is from 318 Hz to 315 Hz. This means that the actual frequency of the 2nd tuning fork is 318 Hz.
• By adding a sufficient amount of wax on the 2nd fork, its frequency can be reduced from 318 Hz to 306 Hz. Then again the beat frequency would be 312 – 306 = 6 per second.

Question 11. Two Identical wires of equal lengths are stretched In such a way that their simultaneous vibrations produce 6 beats per second. The tension In one of the wires is changed slightly and it is observed that the beat frequency remains the same. How is it possible?
Answer:

The frequency of a stretched string is proportional to the square root of the tension. If the fundamental frequency in the 1st wire is more than that in the 2nd wire, the tension in the 1st ware (T₁) > the tension in the 2nd wire (T₂).

Then, n₁ = n₂ ÷ 6, where n₁ and n₂ are the fundamental frequencies of the two wires respectively. Now, the tension T₂ is increased gradually until the fundamental frequency of the 2nd wire changes to n₂‘ = n₂ ÷ 12. Under these circumstances, the frequency difference becomes, \(n_2^{\prime}-n_1=\left(n_2+12\right)-\left(n_2+6\right)=6\)

This means that 6 beats would be heard again per second.

Question 12. Three tuning forks of frequencies n-x,n, and n + x are vibrated simultaneously. If the amplitudes of vibration are equal, show that the forks would form beats.
Answer:

Let A be the amplitude of the vibration of each tuning fork.

Then, the equations of the waves are y₁ = Asin2π(n- x)t, y₂ = Asin2πnt if and y₃ = Asin2π(n + x)t.

∴ The equation of the resultant wave is

y = \(y_1+y_2+y_3\)

= \(A[\sin 2 \pi(n-x) t+\sin 2 \pi n t+\sin 2 \pi(n+x) t]\)

= \(A[\{\sin 2 \pi(n+x) t+\sin 2 \pi(n-x) t\}+\sin 2 \pi n t]\)

= \(A[2 \sin 2 \pi n t \cos 2 \pi x t+\sin 2 \pi n t]\)

= \(A(1+2 \cos 2 \pi x t) \sin 2 \pi n t\)

∴ The amplitude of the resultant wave = A(1 + 2 cos2πxt)

This amplitude clearly depends on time. As a result, the intensity of the emitted sound would also increase and decrease periodically with time [intensity ∝ (amplitude)²]. Thus beats are produced. So, beats can be produced not only due to the superposition of two waves but also due to the superposition of more than two waves.

Question 13. Three sources emitting sound waves of the same amplitude have frequencies 400 Hz, 401 Hz, and 402 Hz, respectively. Find out the number of beats heard per second.
Answer:

⇒ \(y_1=A \sin (2 \pi \cdot 400 t) ; y_2=A \sin (2 \pi \cdot 401 t)\)

⇒ \(y_3=A \sin (2 \pi \cdot 402 t)\)

∴ y = \(y_1+y_2+y_3\)

= \(A[\sin (2 \pi \cdot 400 t)+\sin (2 \pi \cdot 401 t)+\sin (2 \pi \cdot 402 t)\} \)

= \(A\left[\sin (2 \pi \cdot 401 t)+2 \sin \left\{2 \pi \frac{402+400}{2} t\right\}\right.\)

. \(\left.\cdot \cos \left\{2 \pi \frac{402-400}{2} t\right\}\right]\)

= \(A[\sin (2 \pi \cdot 401 t)+2 \sin (2 \pi \cdot 401 t) \cos 2 \pi t]\)

= \(A(1+2 \cos 2 \pi t) \sin (2 \pi \cdot 401 t)\)

Here, the amplitude of the resultant wave, \(A^{\prime}=A(1+\cos 2 \pi t).\)

This is maximum when \(\cos 2 \pi t=1=\cos 2 n \pi[n=0,1,2,3, \cdots]\)

or, t = \(n=0,1,2, \cdots\)

Then, the time interval between two consecutive maxima is Is; so the beat frequency = 1 per second.

Question 14. A 100 cm long stretched string is struck at a point 25 cm from one of its ends. Which of the overtones would be absent in the emitted note?
Answer:

At the striking point, an antinode would be formed. So, the overtones having a node at the point of 25 cm would not be formed. As 25 cm = \(\frac{100 \mathrm{~cm}}{4}=\frac{1}{4}\)(l = length of the stretched string), the absent overtones would be the 4th, 8th, 12th, …. harmonics.

Question 15. In a particular vibrating mode of a stretched string of length l clamped at both ends, n nodes are formed. What is the wavelength of the stationary wave formed in this mode?
Answer:

Both endpoints are nodes. So, the number of loops formed between the n nodes = n-1. Every loop has a length = \(\frac{\lambda}{2} \text {. So, } \frac{l}{n-1}=\frac{\lambda}{2} \text { or, } \lambda=\frac{2 l}{n-1} \text {. }\)

Question 16. The equation of two progressive waves superposing on a string is y₁ = Asin[k(x- ct)] and y₂ = Asin[k(x+ ct)]. What is the distance between two consecutive nodes?
Answer:

Here, \(y_1 \text { or } y_2=A \sin [k(x \mp c t)]\)

The general form of the two waves, y = \(A \sin \frac{2 \pi}{\lambda}(x \mp V t)\)

So, k = \(\frac{2 \pi}{\lambda} \text { or, } \lambda=\frac{2 \pi}{k}\)

∴ The distance between two consecutive nodes = \(\frac{\lambda}{2}=\frac{\pi}{k}\).

Question 17. Two waves represented as y₁ = A₁ sin ωt and y₂ = A₂ cosωt superpose at a point in space. Find out the amplitude of the resultant wave at that point.
Answer:

⇒ \(y_1=A_1 \sin \omega t ; y_2=A_2 \cos \omega t=A_2 \sin \left(\omega t+\frac{\pi}{2}\right) \text {. }\)

So, the phase difference between the two waves = \(\frac{\pi}{2}\).

Then, the amplitude of the resultant wave is A = \(\sqrt{A_1^2+A_2^2+2 A_1 A_2 \cos \frac{\pi}{2}}=\sqrt{A_1^2+A_2^2} .\)

Question 18. The length of a stretched string between two rigid supports is 40 cm. What would be the maximum length of a stationary wave that can be formed in the string?
Answer:

Let the maximum wavelength that can be formed for the given string be λ. For the stationary wave of maximum length, only two nodes are present and they are at the two ends of the string. There is only one antinode between them. So the string vibrates in a single loop. Then the length of this loop = \(\frac{\lambda}{2}\) = 40 cm; so, λ = 80 cm.

Question 19. The equation of a transverse progressive wave is y = 0.02sin(x+40t) m. Find out the tension In a wire of linear density 10^-4 kg · m^-1, if the wave travels along it.
Answer:

Comparing the given equation with the standard form y = A sin(ωt+ kx), we have k = 1 and ω = 40.

So, the wave velocity, V = \(\frac{\omega}{k}=\frac{40}{1}=40 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)

If T = tension and m = linear density of the wire,

V = \(\sqrt{\frac{T}{m}} \text { or, } T=V^2 m=(40)^2 \times 10^{-4}=0.16 \mathrm{~N}\)

Question 20. The superposition of two progressive waves produces a stationary wave represented as y = Acos(0.01x)sin(100t) m. What is the velocity I of the two-component waves?
Answer:

Two progressive waves represented as y₁ = A sin(ωt- kx) and y₂ = A sin(ωt+ kx) superpose to form a stationary wave y = y₁ + y₂ = 2A cos kx sin ωt.

Comparing the given equation with this standard form, we have k = 0.01 m^-1 and ω = 100 Hz. So the wave velocity,

V = \(\frac{\omega}{k}=\frac{100}{0.01}=10^4 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)

Example 21. A uniform wire has length I and area of cross-section α and the density of its material is ρ. If the wire is stretched with a tension T, what would be the velocity of a transverse wave traveling along It?
Answer:

Volume of unit length of the wire = unit length x area of cross-section = 1 x α = α; then linear density = mass per unit length, m = ρα.

∴ Velocity of a transverse wave, V = \(\sqrt{\frac{T}{m}}=\sqrt{\frac{T}{\rho \alpha}}\)

 Superposition Of Waves Multiple Choice Question And Answers

Question 1. A wave y= asin(ωt- kx) being superposed with another wave produces a node at x = 0. The equation of the second wave should be

1. y = asin(ωt+kx)
2. y = -asin(ωt+kx)
3. y= asin(ωt-kx)
4. y = -asin(ωt- kx)

Answer: 2. y = -asin(ωt+kx)

Question 2. At the instant when all the particles in the medium of a stationary wave are at their equilibrium positions the

1. Kinetic Energy Becomes Zero
2. Potential Energy Becomes Zero
3. Net Energy Becomes Zero
4. None Of These Becomes Zero

Answer: 2. Potential Energy Becomes Zero

Question 3. Which of the following remains constant in case of vibration of the particles in a stationary wave?

1. Velocity
2. Acceleration
3. Amplitude
4. Phase

Answer:  3. Amplitude

Question 4. When two identical sound waves superpose at a point with a phase difference of 180°,

1. The point will be a node
2. The intensity of the sound will increase at that point
3. The point will be an antinode
4. Beats will be heard

Answer: 1. The point will be a node

Question 5. The equation of a progressive wave is y = A cos (kx-ωt). This wave superposes with another wave and produces a stationary wave by creating a node at x = 0. Which of the following equations is correct for the other wave?

1. Asin(kx+ωt)
2. -Asin(kx-ωt)
3. -Acos(kx+ωt)
4. -Asin(kx-ωt)

Answer: 3. -Acos(kx+ωt)

Question 6. A fundamental tone of frequency n₁ is produced when a string stretched at both ends is vibrated. The frequency of the fundamental tone changes to n₂ when the tension in the string is doubled. What is the ratio of n₁ and n₂?

1. 1: 2
2. 2: 1
3. 1:√2
4. √2: 1

Answer: 3. 1: √2

Question 7. The waves generated due to the vibration of an air column in a pipe open at one end or a pipe open at both ends are

1. Transverse progressive waves
2. Transverse stationary waves
3. Longitudinal progressive waves
4. Longitudinal stationary waves

Answer: Longitudinal stationary waves

Question 8. When a fundamental tone is produced from a pipe of length l, open at both ends, the wavelength of the stationary wave is

1. \(\frac{l}{2}\)
2. l
3. 2l
4. 4l

Answer: 3. 2l

Question 9. If the frequency of the fundamental tone emitted from a pipe closed at one end is 200 Hz, then the frequencies of the first three overtones will be

1. 400 Hz, 600 Hz, 800 Hz
2. 600 Hz, 1000 Hz, 1400 Hz
3. 400 Hz, 800 Hz, 1200 Hz
4. 600 Hz, 800 Hz, 1000 Hz

Answer: 2. 600 Hz, 1000 Hz, 1400 Hz

Question 10. A fundamental tone is emitted from a pipe closed at one end. If the closed end is suddenly opened,

1. The pitch of the tone decreases
2. The intensity of the tone decreases
3. The pitch of the tone increases
4. The intensity of the tone increases

Answer: 3. The pitch of the tone increases

Question 11. When a fundamental tone is produced from a pipe of length l, closed at one end, the wavelength of the stationary wave is

1. \(\frac{l}{2}\)
2. l
3. 2l
4. 4l

Answer: 4. 4l

Question 12. Due to the end error in stationary waves produced in a closed or an open pipe

1. Antinodes are not formed at the closed end
2. Antinodes are formed inside the pipe very close to its open end.
3. Nodes are formed slightly outside the open end of the pipe
4. None of these

Answer: 3. Nodes are formed slightly outside the open end of the pipe

Question 13. When the temperature of the air in a closed or so open pipe increases, the frequency of stationary wave will

1. Remain the same
2. Increase
3. Decrease
4. Depending on other factors also

Answer: 2. Increase

Question 14. The frequencies of the fundamental tones in a dosed and an open, pipe are the state The talks of the lengths of the two pipes is

1. 1:1
2. 1:2
3. 2:1
4. 4:1

Answer: 2. 1:2

Question 15. While measuring the speed of sound by performing a resonance column experiment, a student gets the first resonance condition at a column length of 18 cm during winter. Repeating the same experiment during summer, he measures the column length to be x cm for the second resonance. Then,

1. 18 > x
2. x > 54
3. 54 > x > 36
4. 36 > x > 18

Answer: 2. x > 54

Question 16. A student is performing the experiment of the resonance column. The diameter of the column tube is 4cm The frequency of the turning fork is 512HZ. The air temperature is  38C in which the speed of sound is 336m/s. The zero of the meter scale coincides with the top end of the resonance column tube. When the first resonance occurs, the reading of the water level in the column is

1. 14 cm
2. 15.2 cm
3. 16.4cm
4. 17.6cm

Answer: 2. 15.2 cm

Question 17. A student is performing an experiment using a resonance column and a turning fort of frequency 244 s^-1. He is told that the air in the tube has been replaced by another (assume the fear fee column remains filled with gas). If the minimum height at which resonance occurs is (0.350 ± 0.005) m, the gas in tube is (using information: √167RT = \(640 \mathrm{~J}^{1 / 2} \cdot \mathrm{mol}^{-1 / 2}; \sqrt{140 R T}=590 \mathrm{~J}^{1 / 2} \cdot \mathrm{mol}\). The molar masses M in grams are given in fee options. Take the value of \(\sqrt{\frac{10}{M}}\) for each gas as given there)

1. Neon \(\left(M=20, \sqrt{\frac{10}{20}}=\frac{7}{10}\right)\)
2. Nitrogen \(\left(M=28, \sqrt{\frac{10}{28}}=\frac{3}{5}\right)\)
3. Oxygen \(\left(M=32, \sqrt{\frac{10}{32}}=\frac{9}{16}\right)\)
4. Argon \(\left(M=36, \sqrt{\frac{10}{36}}=\frac{17}{32}\right.\)

Answer: 4. Argon \(\left(M=36, \sqrt{\frac{10}{36}}=\frac{17}{32}\right.\)

Question 18. What should be fee beat frequency so that it is not audible to the human ear?

1. Greater than 10 Hz
2. 10 Hz
3. 5 Hz
4. Less than 5 Hz

Answer: 1. Greater than 10 Hz

Question 19. If n₁ and n₂ are fee frequencies of two sound waves, the frequency of the beat produced due to the superposition of these waves will be

1. \(n_1-n_2\)
2. \(n_1+n_2\)
3. \(\frac{n_1+n_2}{2}\)
4. \(2\left(n_1-n_2\right)\)

Answer: 1. \(n_1-n_2\)

Question 20. Beats are not observed for light waves, because

1. There is no difference in the velocities of the two light waves
2. It is impossible to stabilize the frequency difference of two light waves below 10 Hz
3. It is impossible to keep the intensities of two light waves equal or nearly equal
4. None of these

Answer: 2. It is impossible to stabilize the frequency difference of two light waves below 10 Hz

Question 21. When two waves y₁ = A sin2008πt and y₂ = A sin2008πt are superposed, the number of beats produced per second is

1. 0
2. 1
3. 4
4. 8

Answer: 3. 4

Question 22. A set of 25 tuning fork is arranged in a series of decreasing frequencies such that each fork gives 3 beats with the succeeding one. The first fork is the octave of the last. Frequency of fee 10th fork is

1. 120Hz
2. 117Hz
3. 110Hz
4. 89Hz

Answer: 2. 117Hz

Question 23. The displacement of a particle in a medium at an instant due to the effect of more than one wave is

1. Not dependent on the displacements due to the individual waves
2. Equal to the vector sum of fee displacements due to fee individual waves
3. Equal to fee displacement due to any one of the waves
4. Random due to the effect of all the waves

Answer: 2. Equal to fee vector sum of fee displacements due to fee individual waves

Question 24. A sound wave of frequency 500 Hz is advancing along the positive x-axis with a speed of 300 m · s^-1. The phase difference between the two points x₁ and x₂ is 60°. The least distance between those two points is

1. 1 mm
2. 1cm
3. 10cm
4. 1 m

Answer: 3. 10cm

Question 25. When two progressive waves y₁= 4sin(2x-6t) and \(y_2=3 \sin \left(2 x-6 t-\frac{\pi}{2}\right)\) are superposed, the amplitude of the resultant wave is

1. 5
2. 6
3. \(\frac{5}{3}\)
4. \(\frac{1}{2}\)

Answer: 1. 5

Question 26. A hollow pipe of length 0.8 m is closed at one end. At its open end, a 0.5 m long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire is 50 N and the speed of sound is 320 m • s^-1, the mass of the string is

1. 5g
2. 10 g
3. 20 g
4. 40 g

Answer: 2. 10 g

Question 27. A sound of 20dB is more intense than a sound of 10 dB by

1. 100
2. \(\frac{1}{10}\)
3. 10
4. 0.01

Answer: 3. 10

In this type of question, more than one option is correct.

Question 28. For a certain transverse standing wave on a long string, an antinode is formed at x = 0, and next to it, a node is formed at x = 0.10 m. The displacement y(t) of the string particle at x = 0 is shown.

1. The transverse displacement of the particle at x = 0.05 m and t = 0.05 s is -2√2 cm
2. Transverse displacement of the particle at x = 0.04 m and t = 0.025 s is -2 √2 cm
3. The speed of the traveling waves that interface to produce this standing wave is 2 m • s^-1
4. The transverse velocity of the string particle at x = \(\frac{1}{15}\)m and t = 0.1 s is 20π cm· s^-1

Answer:

1. The transverse displacement of the particle at x = 0.05 m and t = 0.05 s is -2√2 cm

3. The speed of the traveling waves that interface to produce this standing wave is 2 m • s^-1

4. The transverse velocity of the string particle at x = \(\frac{1}{15}\)m and t = 0.1 s is 20π cm· s^-1

Question 29. Following are equations of four waves

1. \(y_1=a \sin \omega\left(t-\frac{x}{v}\right)\)
2. \(y_2=a \cos \omega\left(t+\frac{x}{v}\right)\)
3. \(z_1=a \sin \omega\left(t-\frac{x}{v}\right)\)
4. \(z_2=a \cos \omega\left(t+\frac{x}{v}\right)\)

Which of the following statements is correct?

1. On superposition of waves (1) and (2), a traveling wave having amplitude a√2 will be formed
2. Superposition of waves (2) and (3) is not possible
3. On superposition of (1) and (2), a stationary wave having amplitude a√2 will be formed
4. On superposition of (3) and (4), a transverse stationary wave will be formed

Answer:

1. On the superposition of waves (1) and (2), a traveling wave having amplitude a√2 will be formed

4. On superposition of (3) and (4), a transverse stationary wave will be formed

Question 30. One end of a taut string of length 3m along the x-axis is fixed at x = 0. The speed of the waves in the string is 100 m · s^-1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. Obtain the possible waveforms of this stationary wave.

1. \(y(t)=A \sin \frac{\pi x}{6} \cos \frac{50 \pi t}{3}\)
2. \(y(t)=A \sin \frac{\pi x}{3} \cos \frac{100 \pi t}{3}\)
3. \(y(t)=A \sin \frac{5 \pi x}{6} \cos \frac{250 \pi t}{3}\)
4. \(y(t)=A \sin \frac{5 \pi x}{2} \cos 250 \pi t\)

Answer:

1. \(y(t)=A \sin \frac{\pi x}{6} \cos \frac{50 \pi t}{3}\)

3. \(y(t)=A \sin \frac{5 \pi x}{6} \cos \frac{250 \pi t}{3}\)

4. \(y(t)=A \sin \frac{5 \pi x}{2} \cos 250 \pi t\)

Wave Motion Introduction

When a small piece of stone is thrown into a pond, the water surface gets disturbed. The ripples formed due to this disturbance do not remain confined to the region where the stone hits the water’s surface, but it spreads in all directions along the surface.

• As the disturbance passes, the water particles start oscillating, i.e., moving up and down about their mean positions but are not displaced along the water surface. The pattern that moves along the pond due to such movement of individual particles of the medium, is called a wave.
• This wave motion transfers energy from one point to another, but no mass transport is associated with this transfer.

Wave: A wave is a disturbance that travels through a medium, whereas the particles constituting the medium do not travel.

• We are familiar with different types of waves; like sound waves, light waves, radio waves, etc. Among these, sound wave is a mechanical wave and the other two are electromagnetic waves.
• In this chapter, we are mainly concerned with mechanical waves. Mechanical waves can propagate only through a material medium, whereas electromagnetic waves do not require any material medium for propagation, i.e., they can propagate through a vacuum.

Wave Motion Mechanical Waves

The origin and propagation of mechanical waves depend on three properties of materials

1. Elasticity
2. Interia and
3. Cohesion
4. Elasticity: If any part of a material or a medium is displaced from its equilibrium position, stress is developed in it due to its elasticity. This stress tries to bring that part back to its equilibrium position.
5. Inertia: When a particle returns to its equilibrium position, it has a motion due to inertia. So the particle cannot come to rest immediately on reaching the equilibrium position. Due to the inertia of motion, it moves to the opposite side crossing the equilibrium position.
   • These two incidents— coming back to the equilibrium position due to elasticity and moving to the opposite side due to inertia of motion—happen alternately in any part of a material or a medium, causing that part to vibrate.
6. Cohesion: The adjacent molecules of a material medium attract each other. This phenomenon is called cohesion. If any part of a material medium begins to vibrate, the adjacent part is then forced to vibrate due to cohesion.
   • In this way, vibration propagates from one layer to the next. This type of propagating vibration is known as a mechanical wave.

Mechanical Waves Definition: The disturbance which travels through a material medium, due to collective vibration of the particles of the medium, is known as a mechanical wave.

Characteristics Of A Mechanical Wave:

1. For the propagation of a mechanical wave, a material medium is necessary. This wave cannot propagate through a vacuum.
2. Each particle of the medium forces the adjacent particles to vibrate, but the particle itself is not carried away from its equilibrium position; rather, the wave advances through the medium.
3. The vibrating particles of any material medium have their own mechanical energies and potential energy. This mechanical energy is forced vibration, i.e., a wave in motion transfers mechanical energy through the medium. So, this type not wave is called a mechanical wave.

Wave Motion Transverse And Longitudinal Waves

Simple Harmonic Wave: If the motion of the particles of a medium is sample harmonic, then the corresponding wave is known as a simple harmonic wave.

There Are Two Types Of Simple Harmonic Waves

1. Transverse wave and
2. Longitudinal waves

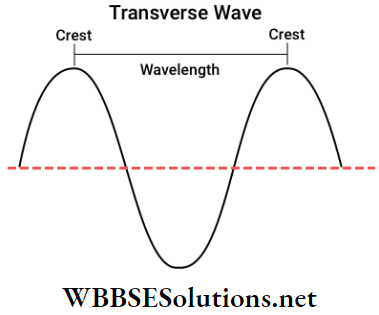
Transverse Wave Definition: A wave that propagates in a direction, perpendicular to the direction of motion of the vibrating particles of the medium, is called a transverse wave.

Examples Of Transverse Waves:

1. If a small stone is thrown into a pond, it generates waves that spread out horizontally in all directions. Now, if a small piece of cork is floated on the water surface, it oscillates vertically about its mean position. So the wave motion is directed along the horizontal direction, but the direction of motion of the cork and the vibrating water panicles are vertical. This is an example of a transverse wave.
2. A rubber rope AB is taken. The end B is fixed to a rigid support and the other end A is held in such a way that the rope is in a stretched condition. Now the end A is oscillated vertically A wave is found to be generated along the rope and it propagates towards the end B.

It is evident that the direction of vibration of each particle of the rope is perpendicular to the direction of propagation of the wave through the rope.

• The particle whose position at some instant is P occupies the position Q at another instant. Since PQ and AB are perpendicular to each other, the wave is obviously a transverse wave.
• A transverse wave can be described generally through. The straight line OBDF is the equilibrium position of the rope. Suppose at an instant, the particle at O is passing through its mean position in its course of vibration from an upward to a downward direction.
• The directions of motion of the different particles of the medium at that instant have been shown by arrows. A and E are two points having a maximum displacement in the positive direction.
• These are called crests. Again C is a point having maximum displacement in the negative direction. This is called a trough.

It is evident that at the said instant, points A and E are situated on the same side of and at the same distance from the mean position. Their velocities are also the same. In short, the conditions of motion at points A and E are the same.

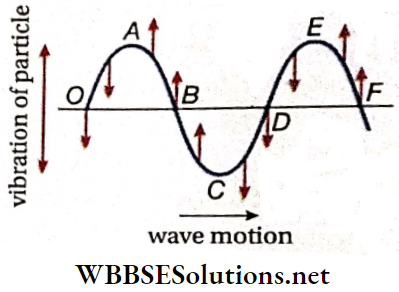
• So, these two points are in the same phase. Similarly, the points O and D, or B and F are in the same phase.
• On the other hand, the conditions of motion at points A and C are opposite. So, these two points are in opposite phases.
• Electromagnetic waves like light waves, radio waves, etc., are transverse waves. The two quantities responsible for the production of electromagnetic waves are the electric field vector and magnetic field vector, which are always perpendicular to the direction of propagation of the wave.
• Electromagnetic waves can propagate through solid, liquid, and gaseous media and even through a vacuum.

Longitudinal Wave Definition: A wave which propagates of motion of the vibrating particles of t a longitudinal wave.

Example Of Longitudinal Wave: A thin and long spring AB is taken whose spring constant is very small. The end B is fixed to a rigid support and the other end A is held in such a way that the spring is in stretched condition.

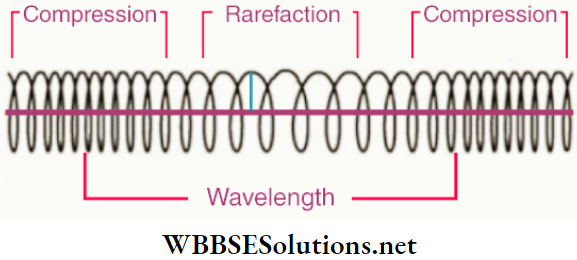
• Now the end A is made to oscillate back and forth so that a wave moves along its length to end B.
• Some coils of the spring come close to each other creating compression and some other coils move away from each other creating rarefaction.
• Compressions and rarefactions are formed alternately along the length of the spring and they propagate towards the end B.
• Since the wave motion is directed from A to B, and during compressions and rarefactions the coils of the spring oscillate parallel to the length of the spring, this wave is a longitudinal wave.

Actually, a longitudinal wave travels through a medium in the form of periodic compressions and rarefactions.

• Let the point O be the equilibrium position of a particle in a material medium. The medium may be imagined to consist of many layers of equal thickness.
• A few layers on the right side of O have been shown. Now, some energy from outside is supplied to the layer at O so that the layer oscillates along the line AB.
• When the layer moves from A to B due to oscillation, it exerts pressure on the layers in front of it. So, those layers get compressed due to the property of compressibility of solid, liquid and gaseous media.
• Thus compression takes place in the region CD of the medium due to the motion of the layer at point O from A to B.
• The opposite incident happens at the time of motion of the layer from B to A, i.e., the layers of the region CD get rarefied due to the decrease in pressure.
• By that time, the previous compression reaches the region DE by compressing the next layers leaving a rarefaction behind.

So, a complete oscillation (ABA) generates compression and a rarefaction. These compressions and rarefactions are not confined to a region, but move through the medium due to the property of compressibility, thereby producing a wave.

• Again, if we think of any array of layers, it is found that the layers alternately get compressed and rarefied parallel to the direction of wave motion.
• It is evident that density and pressure in the medium increase in the zones of compression and decrease in the zones of rarefaction.
• It is the process of propagation of sound wave in air. It is clear that a sound wave is a longitudinal mechanical wave.

Nature Of The Medium: All longitudinal waves are mechanical waves. This type of waves cannot propagate without any medium. Longitudinal waves can propagate through any solid, liquid or gaseous medium.

• These media revert to their original conditions after the external driving oscillation (like ABA) is withdrawn.
• Till that instant, compression or rarefaction passes to the next parallel layers continuously in the direction of the force applied.
• Transverse elastic waves can be formed only in solids, not in liquids and gases. This is because liquids and gases have negligible compressibility and hence cannot sustain shearing stress as they have no definite shape.
• A solid has a definite shape and it opposes any force exerted to change its shape, i.e., a solid substance can sustain shearing stress.
• So, if one of its layers oscillates, its adjacent layer is also forced to oscillate in the same direction.
• Light waves, radio waves, etc., are not mechanical waves. These are electromagnetic waves. The elasticity of the medium has no relation with the electric and magnetic fields.
• So electromagnetic waves can propagate through vacuum, as well as through solid, liquid, or gas.

Actually, the waves set up on the surface of the water are not elastic waves; they are mechanical waves produced due to Earth’s gravity.

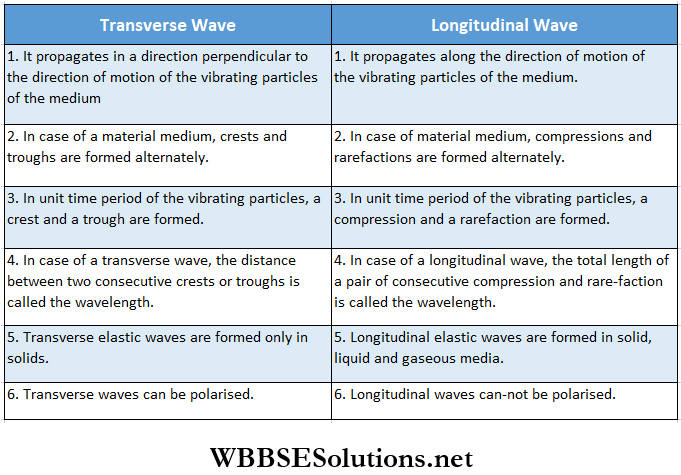
Difference Between Transverse And Longitudinal Waves:

Wave Motion Other Classifications Of Waves

Considering the nature of vibration, we classify waves as mechanical waves, electromagnetic waves, etc. Again, considering the direction of motion of the vibrating particles of the medium and that of the wave, we classify them as transverse waves and longitudinal waves.

In addition, waves can also be categorized on the basis of their different properties. A few of them are discussed below.

On the basis of the direction of energy transmission: The wave that transmits energy in a single direction is called a one-dimensional wave, For example, a transverse wave formed in a stretched string and a longitudinal wave formed In an elastic spring are one-dimensional waves.

• The wave which transmits energy along a plane is called a two-dimensional wave. The wave formed on the surface of water, when a stone is thrown on it, is two-dimensional.
• The wave which transmits energy in all directions is called a three-dimensional wave. Sound waves, light waves, radio waves, etc., are three-dimensional waves.

On the basis of characteristics of particle vibration: If the particles of a medium vibrate simply harmonically, the corresponding wave is called a simple harmonic wave. Practically most waves are produced by complex vibrations. But any complex wave may be described as a superposition of a number of simple harmonic waves.

On the basis of the limit of wave motion: If any wave advances through a medium continuously with a definite velocity, the wave is called a travelling or progressive wave. If the wave is not damped, it can propagate up to infinity. On the other hand, if the wave does not advance, but remains confined in a region, it is called a standing or stationary wave.

Wave Motion Some Physical Terms Related To Waves

Waves Phase: The quantity from which the motion of a wave can be known completely is called the phase of the wave.

Displacement, velocity, acceleration, etc., of a vibrating particle can be obtained from it. The particles at O and D are in the same phase. The particles at A and E, or the particles at C and E, are also in the same phase. Particles at A and C and particles at C and D are in opposite phases.

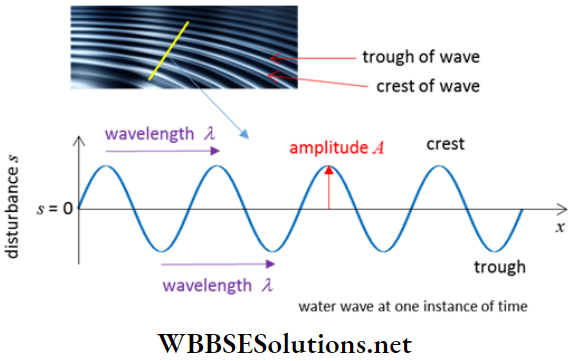
Complete Wave: The wave in between two consecutive particles, having the same phase at an instant, is known as a complete wave. Show respectively how a complete transverse wave is formed In between two consecutive crests, and how a complete longitudinal wave is formed by the combination of a compression and, a rarefaction.

Wavelength: The length of a complete wave, i.e., the distance between two consecutive particles having the same phase at an instant, is called tire wavelength (λ). OD or AE is the wavelength of the transverse wave. Again CE or DF is the wavelength of the longitudinal wave. Generally, it can be said that

The wavelength of a transverse wave = distance between any two consecutive crests or consecutive troughs.

Wavelength of a longitudinal wave = total length of a pair of successive compression and rarefaction.

In general wavelength of a wave is the distance between two consecutive points in the same phase of motion at the same instance of time.

Time period: The time required to form a complete wave, i.e., time taken by a wave to cover a distance between two consecutive particles having the same phase of vibration, is called the time period (T) of the wave.

Frequency: Frequency (n) of a wave is the number of complete waves formed in unit time.

Amplitude: The amplitude of a wave is the maximum displacement of any particle producing the wave, from its mean position. The distance of the points A, C, or E from the straight line OBDF is the amplitude of the wave.

Wave Velocity: The distance traveled by a wave in a unit of time is called its wave velocity (V). Energy is transmitted through the medium by the wave with this velocity. It may be noted that wave velocity is different from particle velocity. Particle velocity is the velocity of the particles of the medium which execute simple harmonic motions about their mean positions.

Wavefront: All the particles on a surface normal to the direction of propagation of a wave have the same phase. A surface of this type is called a wavefront. In other words, the wavefront is the locus of all points having the same phase of motion at the same instance of time.

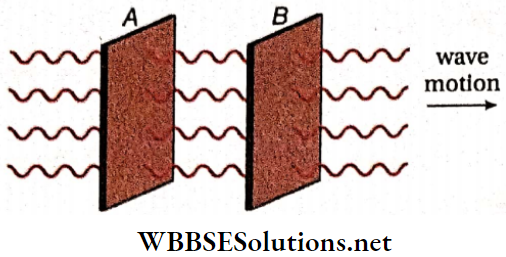
This surface is perpendicular to the direction of propagation of wave at any point. The plane A is a wavefront because the phase of all the particles lying on plane A is the same. Similarly, the plane B is another wavefront. Clearly, planes A and B are parallel.

Wavefront Definition: Any surface, that is normal to the direction of propagation of a wave, is known as a wavefront. The particles lying on a wavefront have the same phase.

Wave Ray: A normal drawn on a wavefront is called a ray. The energy of a wave is transferred from one part of the medium to another along the ray.

Relations Among The Physical Quantities

Relation Between Time Period And Frequency: If T is the time period of a wave, one complete wave is formed in time T. Therefore, the number of complete waves formed in unit time is \(\frac{1}{T}\).

So, according to the definition of frequency,

n = \(\frac{1}{T} \quad \text { or, } T=\frac{1}{n}\)…(1)

Relation Between Wavelength And Wave Number: The number of complete waves in a length λ is 1.

So, the number of complete waves in unit length is \(\frac{1}{\lambda}\). This quantity multiplied by 2π is known as the wave number k, i.e.,

k = \(2 \pi \cdot \frac{1}{\lambda}=\frac{2 \pi}{\lambda} \quad \text { or, } \lambda=\frac{2 \pi}{k}\)…(2)

Relation Among Wave Velocity, Frequency, And Wavelength: Let the frequency of a wave be n, wavelength λ, and wave velocity V. According to the definition of frequency, the number of complete waves formed in unit time is n. Again, the wave covers a distance of V in unit time. So, the length of n number of complete waves is V.

So, the length of one complete wave = \(\frac{V}{n}\);

Then, according to the definition of wavelength, \(\lambda=\frac{V}{n} \quad \text { or, } V=n \lambda\)…(3)

i.e., wave velocity = frequency x wavelength

Again if T is the time period of a wave, n = \(\frac{1}{T}\)

∴ V = \(n \lambda=\frac{\lambda}{T} \quad \text { or, } \lambda=V T\)….(4)

From equation (3), n = \(\frac{V}{\lambda}\). If more than one wave move through a medium with the same velocity, V will be a constant. In that case, \(n \propto \frac{1}{\lambda},\) i.e., frequency and wavelength will be inversely proportional to each other. So, greater the wavelength of a wave, the smaller its frequency, and vice versa.

Wave Motion Numerical Examples

Example 1. The wave generated on a water surface advances 1 m in Is. If the wavelength is 20 cm, how many waves are produced per second?
Solution:

Wavelength, λ = 20 cm;

wave velocity, V = 1 m · s^-1 = 100 cm · s^-1

If n is the frequency, V = nλ

or \(n=\frac{V}{\lambda}=\frac{100}{20}=5 \mathrm{~s}^{-1}\)

So, 5 waves are produced per second.

Example 2. A radio center broadcasts radio waves of length 300 m. What is the frequency of this wave? Given, the velocity of light = 3 x 10⁵ km · s^-1.
Solution:

Wavelength of radio wave, λ = 300 m.

Radio waves are electromagnetic waves like light and both of them have the same velocity.

So, the velocity of radio waves,

V = \(3 \times 10^5 \mathrm{~km} \cdot \mathrm{s}^{-1}=3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

∴ Frequency, n = \(\frac{V}{\lambda}=\frac{3 \times 10^8}{300}=10^6 \mathrm{~Hz}=1 \mathrm{MHz}\)

Example 3. The frequency of a tuning fork is 400 Hz and the velocity of sound in air is 320 m · s^-1. Find how far would the sound travel when the fork just completes 30 vibrations.
Solution:

Here V = 320 m · s^-1; n = 400

We know, V = nλ

∴ 320 = 400 x λ

or, \(\lambda=\frac{320}{400}=\frac{4}{5} \mathrm{~m}\)

So, when the fork completes 1 vibration, sound travels \(\frac{4}{5}\)m.

∴ When the fork completes 30 vibrations, sound travels \(\frac{4}{5}\)x30 = 24m

Example 4. A light pointer attached to one arm of a tuning fork touches a plate. The tuning fork is made to vibrate and the plate is allowed to fall freely downwards simultaneously. The tuning fork completes 8 vibrations when the pointer shows a downward displacement of 10 cm of the plate. What is the frequency of the tuning fork?
Solution:

Suppose a time t is taken by the plate to move 10 cm downwards.

So, from the relation h = \(\frac{1}{2}\)gt², we have

10 = \(\frac{1}{2}\) x 980 x t²

or, \(t^2=\frac{1}{49} \quad \text { or, } t=\frac{1}{7} \mathrm{~s}\)

The tuning fork completes 8 vibrations in that time,

So, frequency of the tuning fork = \(\frac{8}{1 / 7}=56 \mathrm{~Hz}\)

Example 5. What is the length of a compression in the sound wave, produced by a tuning fork of frequency 440 Hz? Given, the velocity of sound in air is 330 m · s^-1.
Solution:

Frequency of the sound wave (n) = frequency of the tuning fork = 440 s^-1

Velocity of sound (V) = 330 m · s^-1

∴ Wavelength, \(\lambda=\frac{V}{n}=\frac{330}{440}=\frac{3}{4} \mathrm{~m}\)

∴ Length of a compression = \(\frac{\text { wavelength }}{2}=\frac{3}{4 \times 2}\)

= 0.375 m = 37.5 cm.

Example 6. A rod hanging from a spring is dipped partly in water. The rod vibrates 180 times per minute. As a result, waves are formed on water and have 6 consecutive crests within a distance of 30 cm. Find the velocity of the wave in water.
Solution:

Here, frequency n = \(\frac{180}{60}\) = 3 Hz

There are 5 waves within 6 consecutive crests.

So, the length of these 5 waves = 30 cm

∴ Wavelength, \(\lambda=\frac{30}{5}=6 \mathrm{~cm}\)

∴ Velocity of the wave, V= nλ = 3 x 6 = 10 cm · s^-1.

Example 7. The frequency of a tuning fork is 280 advances 80 m In a medium while the tuning fork executes 70 complete oscillations. Determine the velocity of sound in that medium.
Solution:

Wavelength, \(\lambda=\frac{80}{70}\) = \(\frac{8}{7}\) cm

So, the velocity of sound in the medium,

V = \(n \lambda=280 \times \frac{8}{7}=320 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Example 8. The frequency of a tuning fork is 512 Hz. When the tuning fork makes 30 vibrations, the emitted sound travels 20 m in the air. Determine the wavelength and the velocity of sound waves in air.
Solution:

Wavelength, \(\lambda=\frac{20}{30}\) = 0.667 m

∴ Velocity of sound in air,

V = nλ = 512 x = 341.33 m · s^-1

Example 9. When two vibrating tuning forks of frequencies 50 Hz and 100 Hz touch the surface of water, they produce waves of wavelengths 0.6 cm and 0.36 cm, respectively. Compare the velocities of the two surface waves.
Solution:

If V₁ and V₂ are die velocities of die two surface waves, then

⇒ \(\frac{V_1}{V_2}=\frac{n_1 \lambda_1}{n_2 \lambda_2}=\frac{50 \times 0.6}{100 \times 0.36}=\frac{5}{6}\)

i.e., \(V_1: V_2=5: 6 .\)

 

Wave Motion Equation Of A Travelling Or Progressive Wave Numerical Examples

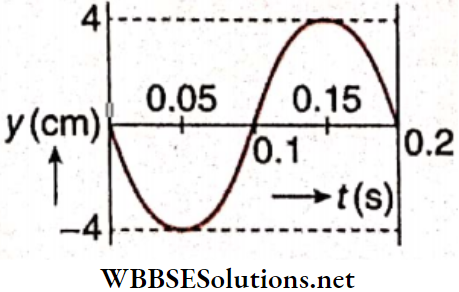
Example 1. The equation of a progressive wave is y = 15sin(660πt-0.02πx) cm. Calculate the frequency and the velocity of the wave.
Solution:

The general equation of a progressive wave is,

y = \(A \sin \omega\left(t-\frac{x}{V}\right)\)….(1)

The equation of the given wave is

y = \(15 \sin (660 \pi t-0.02 \pi x)=15 \sin 660 \pi\left(t-\frac{0.02 x}{660}\right)\)

= \(15 \sin 660 \pi\left(t-\frac{x}{660 / 0.02}\right) \mathrm{cm}\)…(2)

Comparing equations (1) and (2) we have ω = 660π

⇔ Frequency, n = \(\frac{\omega}{2 \pi}=\frac{660 \pi}{2 \pi}=330 \mathrm{~s}^{-1}=330 \mathrm{~Hz} \text {; }\)

Wave velocity, V = \(\frac{660}{0.02}=\frac{660 \times 100}{2}=33000 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

= \(330 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)

Example 2. A wave vibrating along the y-axis propagates along the negative direction of x-axis. The values of its amplitude/frequency and wavelength are 10cm, 500 Hz, and 100 cm, respectively. Write down the equation of the progressive wave.
Solution:

Amplitude, A = 10 cm; frequency n = 500 Hz and wavelength, λ = 100 cm

∴ Wave velocity, V = nλ = 500 x 100 = 5 x 10⁴ cm · s^-1

Angular frequency, ω = 2πn = 2π x 500 = 1000π Hz

Since the wave propagates along the negative x-direction, the equation of the progressive waves,

y = \(A \sin O\left(t+\frac{x}{V}\right)=10 \sin 1000 x\left(t+\frac{x}{5 \times 10^4}\right) \mathrm{cm}\)

Example 3. The equation of a progressive wave is y = 20sinπ(4t – 0.01x)cm. Determine the amplitude, frequency, wavelength, and velocity of the wave.
Solution:

The general equation of a progressive wave is y = \(A \sin \frac{2 \pi}{d}(V t-x)\)…(1)

The given equation is y = \(20 \sin \pi(4 t-0.01 x)\)

= \(20 \sin \pi\left(4 t-\frac{x}{100}\right)=20 \sin \frac{\pi}{100}(400 t-x)\)

= \(20 \sin \frac{2 \pi}{200}(400 t-x) \mathrm{cm}\)…(2)

Comparing equations (1) and (2) we have,

Amplitude, A = 20 cm; wavelength, λ = 200 cm;

Wave velocity, V = 400 cm · s^-1.

So, frequency, n = \(\frac{V}{\lambda}=\frac{400}{200}=2 \mathrm{~Hz}\)

Example 4. The equation of a progressive wave is y = \(10 \sin 2 \pi\left(\frac{t}{0.005}-\frac{x}{10}\right)\)cm; here t and x are given in CGS units. Determine the amplitude, wavelength, and velocity of the wave.
Solution:

y = \(10 \sin 2 \pi\left(\frac{t}{0.005}-\frac{x}{10}\right)\)

= \(10 \sin \frac{2 \pi}{10}\left(\frac{t}{0.0005}-x\right) \mathrm{cm}\)…(1)

Comparing equation (1) with the general equation of a progressive wave, y = \(A \sin \frac{2 \pi}{\lambda}(V t-x)\), we have,

Amplitude, A = 10 cm; wavelength, λ = 10 cm

Velocity of wave, V = \(\frac{1}{0.0005}=2000 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

Example 5. A wave traveling along the X-axis is described by the equation y(x, t) = 0.005cos(αx—βt). If the wavelength and the time period of the wave are 0.08 m and 2.0 s respectively, what are the values of α and β?
Solution:

= \(\frac{2 \pi}{\lambda}=\frac{2 \pi}{0.08}=25 \pi \mathrm{m}^{-1} ; \beta=\frac{2 \pi}{T}=\frac{2 \pi}{2}=\pi \mathrm{s}^{-1}\)

[In this question β and α are used instead of the usual symbols ω and k respectively].

Example 6. The equation of a progressive wave is given by y = 10sinπ(t-0.002x) cm. Determine

1. Maximum displacement
2. Maximum velocity and
3. Maximum acceleration of the particles of the medium,

Solution: Given the equation,

y = 10sinπ(t-0.002x) cm….(1)

General equation of a progressive wave,

y = \(A \sin \omega\left(t-\frac{x}{V}\right)\)…(2)

Comparing equations (1) and (2) we have,

A = 10 cm; \(\omega=\pi \mathrm{Hz} ; V=\frac{1}{0.002}=500 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

1. Maximum displacement of the particles of the medium = amplitude of the wave (A) =10 cm.

2. Velocity of a particle, \(v=\frac{\partial y}{\partial t}=\omega A \cos \omega\left(t-\frac{x}{V}\right) \mathrm{cm} \cdot \mathrm{s}^{-1}\)

∴ Maximum velocity of the particle = ωA = π x 10 = 31.4 cm · s^-1.

3. Acceleration of a particle,

a = \(\frac{\partial v}{\partial t}=-\omega^2 A \sin \omega\left(t-\frac{x}{V}\right) \mathrm{cm} \cdot \mathrm{s}^{-2}\)

∴ Maximum acceleration of the particle = ω²A = π² x 10 = 98.7 cm · s^-2.

Example 7. The equation y = \(y_0 \sin 2 \pi\left(n t-\frac{x}{\lambda}\right)\) expresses a transverse wave. If the maximum particle velocity is equal to four times the wave velocity, show that \(\lambda=\frac{1}{2} \pi y_0\)
Solution:

Given equation,

y = \(y_0 \sin 2 \pi\left(n t-\frac{x}{\lambda}\right)=y_0 \sin \frac{2 \pi}{\lambda}(\lambda n t-x)\)

Comparing this equation with the general equation of a progressive wave, y = \(A \sin \frac{2 \pi}{\lambda}(V t-x)\), we have,

A = y₀; V= λn

Again, particle velocity is given by v = \(\frac{\partial y}{\partial t}=\frac{2 \pi V}{\lambda} A \cos \frac{2 \pi}{\lambda}(V t-x)\)

So, maximum particle velocity, \(v_0=\frac{2 \pi V A}{\lambda}\)

According to the equation \(\frac{v_0}{V}=4 \text { or, } \frac{2 \pi A}{\lambda}=4 \text { or, } \lambda=\frac{2 \pi A}{4}=\frac{1}{2} \pi y_0\)

Example 8. A wave equation that gives a displacement along y direction Is given by y = 10^-4 sin(60t+ 2x) where x and y are in meters and f is time in seconds. Determine the wavelength, frequency, and velocity of the wave.
Solution:

Given equation is y = \(10^{-4} \sin (60 t+2 x)\)

= \(10^{-4} \sin 2(30 t+x)\)

= \(10^{-4} \sin \frac{2 \pi}{\pi}(30 t+x)\)

Comparing the given equation with the general equation of a progressive wave, y = \(A \sin \frac{2 \pi}{\lambda}(V t+x)\), we have,

Wavelength, λ =π= 3.14 m;

Wave velocity, V = 30 m · s^-1; (in the direction of negative x-axis)

Frequecy, n = \(\frac{V}{\lambda}=\frac{30}{3.14}=9.55 \mathrm{~Hz} .\)

Example 9. A wave having a frequency 200 Hz is advancing with a velocity 40 m · s^-1. What is the phase difference of two particles separated by 5 cm in the direction of wave motion?
Solution:

Here n = 200 Hz; V = 40 m · s^-1 = 4000 cm · s^-1

So, \(\lambda=\frac{V}{n}=\frac{4000}{200}=20 \mathrm{~cm}\)

∴ Phase difference = \(\frac{2 \pi}{\lambda}\) x path difference

= \(\frac{2 \pi}{20} \times 5=\frac{\pi}{2} \mathrm{rad}=90^{\circ} .\)

Example 10. \(y_1=0.1 \sin \frac{\pi}{2}(200 t-x) \mathrm{cm}\) and \(y_2=0.2 \sin \frac{\pi}{2}(200 t-x+5) \mathrm{cm}\) are two wave equations. Show that the phase difference of the two waves does not change. What is the value of that phase difference?
Solution:

Comparing the given equations of the two waves with the general equation of a progressive wave,

y = \(A \sin \frac{2 \pi}{\lambda}(V t-x)\),

The wavelength (λ) and the wave velocity (V) of the given two waves are equal. So, the two waves can propagate with any special phase (crest or trough) maintaining equal distance with respect to each other. So, the phase difference of the two waves does not change.

Phase of the first wave \(\left(\theta_1\right)=\frac{\pi}{2}(200 t-x)\)

Phase of the second wave \(\left(\theta_2\right)=\frac{\pi}{2}(200 t-x+5)\)

So, phase difference = θ₂-θ₁

= \(\frac{\pi}{2} \cdot 5=\frac{5 \pi}{2} \mathrm{rad}=\frac{5}{2} \times 180^{\circ}=450^{\circ}\)

Since 450° = 360° + 90°, the two angles 450° and 90° are equivalent, i.e., the required phase difference = 90°.

Example 11. The equation of a progressive wave is y = \(0.1 \sin \frac{\pi}{2}(200 t-x) \mathrm{cm}\)

1. What is the phase of the wave at the point x = 2 at time t =0?
2. What is the phase difference between two points separated by 8 cm?
3. How does the phase at any point change in 0.005 s?

Solution:

The phase of the given progressive wave,

θ = \(\frac{\pi}{2}(200 t-x)\) ….(1)

1. Putting x = 2, t = 0 in equation (1),

θ = \(\frac{\pi}{2}(-2)=-\pi \mathrm{rad}=-180^{\circ}\)

-180° and + 180°—these two angles are equivalent. So, θ = 180°.

2. For two points separated by 8 cm,

⇒ \(\theta_1=\frac{\pi}{2}\left(200 t-x_1\right), \theta_2=\frac{\pi}{2}\left(200 t-x_2\right)\)

∴ Phase difference = θ₂ – θ₁

= \(\frac{\pi}{2}\left(x_2-x_1\right)=\frac{\pi}{2} \times 8=4 \pi \mathrm{rad}\)

But the angle 4π rad is equivalent to 0°.

So, phase difference = 0°.

2. The required phase change

= \(\frac{\pi}{2}(200 \times 0.005)=\frac{\pi}{2} \times 1=\frac{\pi}{2} \mathrm{rad}=90^{\circ}\)

Example 12. The amplitude of a wave propagating in the positive x-direction is given by y = \(\frac{1}{1+x^2}\) at time t = 0 and by y = \(\frac{1}{1+(x-1)^2}\) at t = 2 s where x and y are in meters, The shape of the wave does not change during the propagation. What is the velocity of the wave?
Solution:

Considering the point x = 0 at t = 0, amplitude, y = \(\frac{1}{1+0^2}=1 \mathrm{~m}\)

Now, if the wave propagates up to the point x = x₁ at t = 2s, then

1 = \(\frac{1}{1+\left(x_1-1\right)^2} \quad \text { or } 1+\left(x_1-1\right)^2=1 \)

or, \(\left(x_1-1\right)^2=0 \quad \text { or, } x_1-1=0 \quad \text { or, } x_1=1 \mathrm{~m},\)

i.e., in time 2s tire phase of amplitude 1m has advanced from the point x = 0 to x = 1m.

So, the velocity of the wave = \(\frac{1}{2}\) = 0.52 m · s^-1

Example 13. A plane progressive wave of frequency 25 Has, amplitude 2,5 x 10^-5 m, and initial phase zero propagates along the negative x-direction with a velocity of 300 m · s^-1. At any Instance, what Is the phase difference between the oscillations at two points 6 m apart along the line of propagation of the wave? Also, determine the corresponding amplitude difference.
Solution:

Here, n = 25 Hz, A = 2.5 x 10^-5 m, V= 300 m · s^-1

∴ \(\lambda=\frac{V}{n}=\frac{300}{25}=12 \mathrm{~m}\)

So, two points 6 rn apart have a path difference of \(\frac{\lambda}{2}\).

∴ Phase difference = \(\frac{2 \pi}{\lambda} \cdot \frac{\lambda}{2}=\pi \mathrm{rad}=180^{\circ}\)

So, the two points are in the opposite phase. For example, if a crest is formed at a point, a trough would be formed 6m apart. However, the magnitudes of the amplitude would be the same.

∴ Amplitude difference = 0.

Example 14. The bulk modulus and the density of steel are 80 and 8 times, respectively, of those of water. Calculate the speed of sound in steel. Given, the speed of sound in water = 1493 m · s^-1.
Solution:

The velocity of sound in an elastic medium is

V = \(\sqrt{\frac{E}{\rho}}\)

Where E = modulus of elasticity of the medium ρ = density of the medium

∴ Velocity of sound in water, \(V_w=\sqrt{\frac{E_w}{\rho_w}}\)

Velocity of sound in steel, \(V_w=\sqrt{\frac{E_w}{\rho_w}}\)

∴ \(\frac{V_s}{V_w}=\sqrt{\frac{E_s}{\rho_s} \cdot \frac{\rho_w}{E_w}}=\sqrt{\frac{E_s}{E_w} \times \frac{\rho_w}{\rho_s}}=\sqrt{80 \times \frac{1}{8}}=\sqrt{10}=3.162\)

∴ \(V_s=3.162 V_w=3.162 \times 1493=4721 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)

Example 15. A wave is represented by y = \(20 \cdot \sqrt{3} \sin \left(\frac{2 \pi t}{T}-\frac{2 \pi x}{\lambda}\right) \mathrm{cm}\), Calculate the displacement of a particle at the position x = \(\frac{lambda}{6}\) on the wave at time t = \(\frac{T}{3}\)
Solution:

Given equation, \(y=20 \cdot \sqrt{3} \sin \left(\frac{2 \pi t}{T}-\frac{2 \pi x}{\lambda}\right)\)

Putting x = \(\frac{\lambda}{6}$ and $t=\frac{T}{3}\), we get

Displacement, y = \(20 \cdot \sqrt{3} \sin \left(\frac{2 \pi T}{3 T}-\frac{2 \pi \lambda}{6 \lambda}\right)=20 \cdot \sqrt{3} \sin \left(\frac{2 \pi}{3}-\frac{\pi}{3}\right)\)

= \(20 \cdot \sqrt{3} \sin \frac{\pi}{3}=20 \cdot \sqrt{3} \cdot \frac{\sqrt{3}}{2}=30 \mathrm{~cm}\)

Example 16. The equations of two waves are, \(y_1=0.30 \sin (314 t-1.57 x)\),
\(y_2=0.10 \sin (314 t-1.57 x+1.57)\) Determine the phase difference and the ratio of the intensities of the two waves.
Solution:

Phase of the first wave, θ₁ = 314t – 1.57x

Phase of the second wave, θ₂ = 314t – 1.57x +1.57

∴ The phase difference of the two waves

= \(\theta_2-\theta_1=1.57 \mathrm{rad}=1.57 \times \frac{180}{\pi}=90^{\circ}\)

We know that the intensity of a wave is proportional to the square of its amplitude.

∴ Ratio of the amplitudes of the two waves = \(\frac{A_1}{A_2}=\frac{0.30}{0.10}=\frac{3}{1}\)

∴ Ratio of the intensities of the two waves = \(\frac{I_1}{I_2}=\frac{A_1^2}{A_2^2}=\frac{9}{1}\)

Wave Motion Velocity Of Sound In Solid And Liquid Media

Sound propagates through solids and liquids as longitudinal elastic wave tike in gaseous media. But the velocities of sound in solid and liquid are different. If E is the modulus of elasticity of the medium and ρ is its density, Newton’s formula for the velocity of sound is given by,

c = \(\sqrt{\frac{E}{D}}\)…(1)

• The density of any solid or liquid is greater than that of a gas. Bin the modulus of elasticity of a solid or a liquid is much greater than the Thar of a gas.
• So, the velocity of sound in a solid or B. Liquid is greater than that in a gas. For example, the psVjcities of sound in iron and in water are about 15 times and 4.5 times that in air, respectively.
• The velocity of sound in iron is greater than that in air—it can be easily understood from a simple experiment. If one end of a long iron pipe is struck heavily, the sound of striking is heard twice at the other end of the pipe.
• Sound is heard for the first time due to its propagation through the iron and for the second time due to its propagation through the air in the pipe. An iron pipe nearly 100 m in length should be taken to hear the two sounds distinctly.

There is one important difference between solids and liquids as media of propagation of sound. The modulus of elasticity for the solid is, Young’s modulus (Y) while it is the bulk modulus (k) in the case of the liquid. So the equation (1)

For solid, c = \(\sqrt{\frac{Y}{\rho}}\)….(2)

and for liquid, c = \(\sqrt{\frac{k}{\rho}}\) …(3)

In case of steel, Y = 2 x 10¹¹ N · m^-2; ρ = 7850 kg · m^-3;

From equation (2) we get,

c = \(\sqrt{\frac{2 \times 10^{11}}{7850}} \approx 5048 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

In case of water, k = 2.1 x 10⁹ N · m^-2; ρ = 1000 kg · m^-3

From equation (3) we get, c = \(\sqrt{\frac{2.1 \times 10^9}{1000}}=1449 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Velocity Of Sound In Solid And Liquid Media Numerical Examples

Example 1. Two explosions are made simultaneously from a ship, one above the surface of the water and another just below it. Sound is heard in a hydrophone placed below water from another ship 5 km apart 11s earlier than the sound reaching the deck of the ship. What is the velocity of sound in water? Given that the velocity of sound in air = 348 m · s^-1.
Solution:

Distance between the two ships = 5 km = 5000 m

So time taken by the sound to come through air = \(\frac{5000}{348} \mathrm{~s}\)

According to the question, time is taken by the sound to come through water = \(\frac{5000}{348}-11=\frac{5000-3828}{348}=\frac{1172}{348} \mathrm{~s}\)

Therefore, the velocity of sound in water

= \(\frac{5000}{\frac{1172}{348}}=1485 \mathrm{~m} \cdot \mathrm{s}^{-1}\) (approx.)

Example 2. If one end of a long steel pipe is struck, the sound is heard twice at an interval of 3 s at the other end. What is the length of the pipe? (The velocities of sound in air = 350m · s^-1, in steel = 5000 m · s^-1)
Solution:

Let the length of the pipe be l m.

So, time is taken by the sound to come through the air in the pipe = \(\frac{l}{350}\)s

Again, time taken by die sound to come through steel =\(\frac{l}{5000}\)s

According to the question, \(\frac{l}{350}-\frac{l}{5000}=3 \quad \text { or, } l\left(\frac{1}{350}-\frac{1}{5000}\right)=3\)

or, \(l\left(\frac{100-7}{35000}\right)=3\)

or, \(l=\frac{35000 \times 3}{93}=1129 \mathrm{~m}=1.129 \mathrm{~km} .\)

Example 3. Sound moves through a liquid with a velocity 1340 m · s^-1. If the density of the liquid is 0.8 g · cm^-3, determine the compressibility of the liquid.
Solution:

We know, c = \(\sqrt{\frac{k}{\rho}}\); k = bulk modulus of the liquid

∴ k = c²ρ [c = 1340 m · s^-1 = 134 x 10³ cm · s^-1]

Again, compressibility = \(\frac{1}{k}=\frac{1}{c^2 \rho}\)

= \(\frac{1}{\left(134 \times 10^3\right)^2 \times 0.8}=\frac{1}{143648} \times 10^{-5}\)

= \(6.96 \times 10^{-11} \mathrm{~cm}^2 \cdot \mathrm{dyn}^{-1}\)

Wave Motion Musical Sound And Noise

Musical sound: The sound produced due to regular and periodic vibrations, that is pleasing to hear, is called musical sound. While singing, the vocal cords of a singer vibrate with regular periodic motion.

• Similarly when die strings of a sitar are excited to produce a certain note, diey vibrate with regular periodic motion. The sound of clapping is usually unpleasant, but rhythmic clapping of hands may produce a pleasant sound.
• This is due to the regular vibration of the source. Similarly pattern of raindrops on tin roofs or the clickers’ sound of train wheels may be sonorous.

Noise: The sound produced by an irregular or short-lived vibration is called noise. The explosion of a cracker, the firing of a gun, the horn of a car, etc., are noises.

Tone: A musical sound of a single frequency is called a tone. When the source of sound vibrates in SHM, it produces a tone. The two prongs of a tuning fork vibrate in SHM and produce the sound of a single frequency. Thus, the sound of a tuning fork is a pure tone.

Tone note: A musical sound due to a mixture of more than one frequency is called a note. The sound produced by different musical instruments consists, in general, of more than one tone. If a tone is compared with monochromatic light such as red light, a note can be compared with compound light, i.e., white light. The tones within a note are classified on the basis of their frequencies.

• Fundamental Tone: The tone with the lowest frequency present in a note is called the fundamental tone.
• Overtones: The tones in a note, other than the fundamental tone, are called overtones.
• Harmonics: Harmonics are tones having frequencies that are integral multiples of that of the fundamental tone. The fundamental tone is also a harmonic.
• Octave: A tone whose frequency is twice that of the fundamental tone is said to be the octave of the fundamental tone.

Suppose, a musical note consists of tones of frequencies 200 Hz, 300 Hz, 400 Hz, 500 Hz, and 600 Hz. So it can be said:

1. Each of these five different frequencies corresponds to a tone,
2. The combination of these five tones is a note,
3. The tone of 200 Hz is die fundamental tone,
4. The tones having frequencies 300 Hz, 400 Hz, 500 Hz, and 600 Hz are overtones,
5. Both of the tones of frequencies 400 Hz and 600 Hz are harmonics, as the frequencies are 2 and 3 umes that of the fundamental tone respectively. The tone of 400 Hz is called the second harmonic as its frequency is 2 times of the fundamental tone. Similarly, the tone of 600 Hz is called the third harmonic. The fundamental tone is called the first harmonic.
6. The tone of 400 Hz is the octave because this frequency is the mice die frequency of the fundamental tone.

Characteristics Of Musical Sound Or Note: There are three characteristics that differentiate musical notes. These are loudness, pitch, and quality.

1. Loudness: Loudness Is related to the sound energy reaching our ears per unit time. If the sound energy reaching our ears in 1 second goes up, we perceive a corresponding increase in the loudness.
2. Pitch: It is that characteristic that differentiates a sharp or shrill sound from a grave one. It increases with the Increase in frequency of the source.
3. Quality Or Timbre: It is that characteristic of a musical note that enables us to distinguish between a note emitted by one musical instrument from a note of the same loudness and pitch emitted by another instrument. It depends on the number of overtones present in a note and their relation with the fundamental tone.

Wave Motion Conclusion

A wave is a disturbance that travels through a medium, but the particles constituting the medium do not travel.

• The disturbance that travels through a material medium due to a collective vibration of the particles of the medium is known as a mechanical wave.
• It is an elastic wave if the particles vibrate due to the elasticity of the medium. If the motion of the particles of a medium is simple harmonic, the corresponding wave is known as a simple harmonic wave.
• A wave, that propagates in a direction perpendicular to the direction of motion of the vibrating particles of the medium, is called a transverse wave.
• A wave, that propagates along the direction of motion of the vibrating particles of the medium, is called a longitudinal wave.
• All longitudinal waves are mechanical waves. Longitudinal waves can be transmitted through any solid, liquid, or gaseous medium. This type of wave cannot propagate without any medium.
• Transverse elastic waves cannot be produced in liquids or gases but can be created in solids.

Some physical quantities related to waves:

1. Phase: The quantity from which the motion of a wave, except the amplitude, can be known completely is called the phase of the wave.

2. Complete Wave: The wave in between two consecutive particles having the same phase at an instant is known as a complete wave.

3. Wavelength: The length of a complete wave, i.e., the distance between two consecutive particles having the same phase at an instant is called the wavelength of the wave.

4. Time period: The time required to create a complete wave, i.e., the time taken by a wave to cover the distance between two consecutive particles having the same phase of vibration is called the time period of the wave.

5. Frequency: The frequency of a wave is the number of complete waves produced in unit time.

6. Amplitude: The amplitude of a wave is the maximum displacement from the mean position of a particle-producing tire wave.

7. Wave velocity: The distance traversed by a wave in unit time is called the wave velocity.

8. Wavefront: A surface normal to the direction of propagation of a wave is known as a wavefront. Particles lying on a wavefront have the same phase.

9. Ray: A normal drawn on a wavefront is called a ray.

The velocity with which sound wave propagates in a material medium depends on two properties of the medium density, and elasticity.

• Newton assumed that the propagation of sound through a gaseous medium is an isothermal process.
• According to Laplace, the propagation of sound through a gaseous medium is an adiabatic process.
• The pressure of a gas has no effect on the velocity of sound.
• The velocity of sound in a gas is directly proportional to the square root of its absolute temperature.
• The velocity of sound in air increases by 0.61 m · s^-1 or 61 cm · s^-1 for 1°C rise in temperature.
• The velocity of sound in moist air is greater than that in dry air.
• The velocity of sound in a gas is inversely proportional to the square root of its density.
• To obtain regular reflection of sound, the reflector must be large but the surface of the reflector need not be very smooth.
• If the reflected sound is heard separately from an original sound, it is called an echo of the original sound.
• The sensation of an inarticulate sound (sound produced by gunshot, clapping, etc.) persists in our ear for about \(\frac{1}{10}\)th of a second. This is known as the persistence of hearing.
• The velocity of sound in air at 0°C is about 330 m · s^-1.

Wave Motion Useful Relations for Solving Numerical Problems

Relation between time period (T) and frequency (n): T = \(\frac{1}{n}\)

Relation between wavelength (λ) and wave number (k): \(\lambda=\frac{2 \pi}{k}\)

Relation between frequency (n) and angular frequency ω:ω = 2πn

Wave velocity (V) = frequency (n) x wavelength (λ)

Equation of a progressive wave moving along the positive and negative direction of the x-axis:

y = \(A \sin \omega\left(t \mp \frac{x}{V}\right)=A \sin (\omega t \mp k x)\)

= \(A \sin \frac{2 \pi}{\lambda}(V t \mp x)=A \sin 2 \pi\left(\frac{t}{T} \mp \frac{x}{\lambda}\right)\)

If The equation of a progressive wave can be expressed using cosine function also.

Physical quantities related to the motion of a particle in a progressive wave:

\(\begin{array}{|l|l|}
\hline \text { Displacement } & y=A \sin (\omega t-k x \pm \phi) \\
\hline \text { Velocity } & \nu=\frac{d y}{d t}=\omega A \cos (\omega t-k x \pm \phi) \\
\hline \text { Max. velocity } & \pm \omega A \\
\hline \text { Acceleration } & a=\frac{d^2 y}{d t^2}=-\omega^2 A \sin (\omega t-k x \pm \phi) \\
\hline \text { Max, acceleration } & \pm \omega^2 A \\
\hline
\end{array}\)

 

If the particle velocity is v and the wave velocity is V, then \(\nu=-V \frac{\partial y}{\partial x}\)

Velocity of Progressive waves in different media:

\(\begin{array}{|l|l|l|}
\hline \begin{array}{l}
\text { Velocity of a long- } \\
\text { tidal wave in a } \\
\text { solid medium }
\end{array} & V=\sqrt{\frac{Y}{\rho}} & \begin{array}{l}
Y=\text { Young’s modulus of } \\
\text { the medium and } \rho= \\
\text { density of the medium }
\end{array} \\
\hline \begin{array}{l}
\text { Velocity of a long- } \\
\text { tidal wave in a } \\
\text { liquid or a gaseous } \\
\text { medium }
\end{array} & V=\sqrt{\frac{E}{\rho}} & \begin{array}{l}
E=\text { bulk modulus of the } \\
\text { medium and } \rho=\text { density } \\
\text { of the medium }
\end{array} \\
\hline
\end{array}\) \(\begin{array}{|c|c|c|}
\hline \begin{array}{l}
\text { Velocity of sound } \\
\text { wave in a gaseous } \\
\text { medium }
\end{array} & V=\sqrt{\frac{\gamma p}{\rho}} & \begin{array}{l}
p=\text { pressure of the gas, } \\
\gamma=c_p / c_\nu=\text { ratio of the } \\
\text { two specific heats of the } \\
\text { gas and } \rho=\text { density of } \\
\text { the gas }
\end{array} \\
\hline \begin{array}{l}
\text { Velocity of a trans- } \\
\text { verse wave in a } \\
\text { stretched string }
\end{array} & V=\sqrt{\frac{T}{m}} & \begin{array}{l}
T=\text { tension in the string } \\
\text { and } m=\text { mass per unit } \\
\text { length of the string }
\end{array} \\
\hline
\end{array}\)

 

If M is the mass of 1 mol of a gas, then c = \(\sqrt{\frac{\gamma R T}{M}}\)

where T = absolute temperature of the gas,

R = universal gas constant

If c₀ and c are the velocities of sound at 0°C and t °C respectively, then c = c₀(1+ 0.001830 t)

If the densities of two different gases at the same temperature and pressure are ρ₁ and ρ₂ and the velocities of sound in the two gases are c₁ and c₂ respectively, then \(\frac{c_1}{c_2}=\sqrt{\frac{\rho_2}{\rho_1}}\)

If the distance of a reflector from the source of sound is D, the time required to hear the echo is t, and the velocity of sound is V, then, 2D = Vt

Wave Motion Very Short Answer Type Questions

Question 1. What kind of energy is transmitted through an elastic wave?
Answer: Mechanical energy

Question 2. Give an example of an elastic wave.
Answer: Soundwave

Question 3. Is It possible for a transverse wave to propagate in a liquid?
Answer: No

Question 4. What kind of wave is an X-ray?
Answer: Electromagnetic

Question 5. If the direction of motion of a wave and the direction of vibration of the particles of a medium are parallel to each other, the wave is called a transverse wave.
Answer: False

Question 6. If the direction of motion of a wave and the direction of vibration of the particles of a medium are perpendicular to each other, the wave is called a ______ wave.
Answer: Transverse

Question 7. During propagation of sound, compressions and rarefactions occur so rapidly that the _______ of the gas cannot remain constant.
Answer: Temperature

Question 8. If λ is the wavelength of a transverse wave, what will be the distance between two consecutive crests?
Answer: λ

Question 9. If λ is the wavelength of a longitudinal wave, what will be the length of a compression?
Answer: \(\frac{\lambda}{2}\)

Question 10. If the velocity of sound is 330 m · s^-1, what will be the wavelength of the sound wave emitted from a tuning fork of frequency 220 Hz?
Answer: 1.5 m

Question 11. The time required to form a complete wave is called the time period of the wave. Is the statement true or false?
Answer: True

Question 12. What is the number of complete waves formed in unit time called?
Answer: Frequency

Question 13. The maximum displacement of a particle on the wave from its mean position is called the _______ of the wave.
Answer: Amplitude

Question 14. The surface of vibration of the particles of a medium having the same phase during the propagation of a wave is called the ________ of the wave.
Answer: Wavefront

Question 15. The frequency of a progressive wave x = velocity of the wave.
Answer: Wavelength

Question 16. The equation of a progressive wave is given by y = Acos\(\frac{2 \pi}{\lambda}\)(Vt-x). Find the frequency of the wave.
Answer: \(\frac{V}{\lambda}\)

Question 17. The equation of a progressive wave is given by y = \(4 \sin 20 \pi\left(t-\frac{x}{100}\right) \mathrm{cm}\). Find the amplitude of the wave.
Answer: 4cm

Question 18. The equation of a progressive wave is given by y = \(4 \sin 20 \pi\left(t-\frac{x}{100}\right) \mathrm{cm}\). Find the frequency of the wave.
Answer: 10 Hz

Question 19. The equation of a progressive wave is given by \(y=4 \sin 20 \pi\left(t-\frac{x}{100}\right) \mathrm{cm}\). Find the velocity of the wave.
Answer: 100 cm · s^-1

Question 20. Why is the sound heard in CO₂ more intense in comparison to the sound heard in the air?
Answer: Density more

Question 21. By what process does the propagation of sound through a gaseous medium take place?
Answer: Adiabatic

Question 22. What is the ratio of the velocities of sound through hydrogen and oxygen at STP?
Answer: 4: 1

Question 23. If the temperature remains constant, what will be the bulk modulus of a gas?
Answer: Equal to the pressure of the gas

Question 24. Why is the velocity of sound greater in deep water than that on its surface?
Answer: Pressure increases with the depth of water, velocity of sound increases with the increase of pressure

Question 25. Why does a violinist return his instrument on entering a warm room?
Answer: Due to an increase in temperature velocity increases

Question 26. If temperature is kept constant, the velocity of sound in a gas is independent of which of the following properties? Pressure, density, or wind flow.
Answer: Pressure

Question 27. Is the velocity of sound in dry air at constant temperature, less or greater than that in moist air?
Answer: Less

Question 28. The equation of a progressive wave is given by y = \(A \cos \omega\left(t-\frac{x}{V}\right)\). What will be the frequency and amplitude of the wave?
Answer: \(\left[\frac{\omega}{2 \pi}, A\right]\)

Question 29. What should be the minimum time interval between an original sound and its echo, so that the echo is heard separately?
Answer: \(\frac{1}{10}\)s

Question 30. The velocity of sound in air is 330 m • s^-1. What should be the minimum distance of a reflector so that a listener can hear the echo distinctly?
Answer: 16.5 m

Question 31. In a big hall, sound persists even after the original sound is stopped. What is the phenomenon called?
Answer: Reverberation

Question 32. If a sound wave enters water from the air, is the angle of refraction less or greater than the angle of incidence?
Answer: Greater

Wave Motion Assertion Reason Type Questions And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: A sound wave is regarded as a pressure wave.

Statement 2: Energy in this type of wave is transported due to the formation of compression and rarefaction in the medium in which pressure difference is created.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 2.

Statement 1: Any function of space and time that satisfies the following equation represents a wave \(\frac{d^2 y}{d x^2}=\frac{1}{V^2} \frac{d^2 y}{d t^2}\)

Statement 2: y s Asin ωt, y = Acosωt do not satisfy the above equations and hence do not represent waves.

Answer: 2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1

Wave Motion Match The Columns

Question 1. A wave is transmitted from a denser to a rarer medium.

Answer: 1. C, 2. A, 3. A, 4. A

Question 2. Three traveling sinusoidal waves on identical strings have the same tension. The mathematical form of the waves are \(y_1=A \sin (3 x-6 t), y_2=A \sin (4 x-8 t) and y_3=A \sin (6 x-12 t)\).

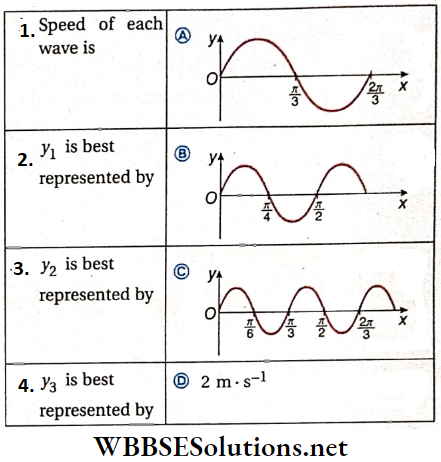
Answer: 1. D, 2. A, 3. B, 4. C

Wave Motion Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. Represents two snaps of a traveling wave on a string of mass per unit length μ = 0.25 kg · m^-1. The first snap is taken at t = 0 and the second is taken at t = 0.053 s.

1. The speed of the wave is

1. \(\frac{20}{3}\) m · s^-1
2. \(\frac{10}{3}\) m · s^-1
3. 20 m · s^-1
4. 10 m · s^-1

Answer: 2. \(\frac{10}{3}\) m · s^-1

2. The frequency of the wave is

1. \(\frac{5}{3}\) Hz
2. \(\frac{10}{3}\) Hz
3. 5 Hz
4. 10 Hz

Answer: 1. \(\frac{5}{3}\) Hz

3. The maximum speed (in m · s^-1) of the particle is

1. \(\frac{5 \pi}{13}\)
2. \(\frac{5 \pi}{13}\)
3. \(\frac{\pi}{30}\)
4. \(\frac{7 \pi}{20}\)

Answer: 3. \(\frac{\pi}{30}\)

Question 2. A sinusoidal wave is propagating in a negative x -x-direction in a string stretched along the x-axis. A particle of string at x = 2 cm is found at its mean position and it is moving in a positive y-direction at t = 1s. The amplitude of the wave, the wavelength, and the angular frequency of the wave are 0.1 m, \(\frac{\pi}{4}\) m and 4π rad • s^-1 respectively,

1. The equation of the wave is

1. y = 0.1sin[47π(t- 1) + 8(x-2)]
2. y = 0.1 sin [(t- 1) – (x-2)]
3. y = 0.1sin [4π(t- 1)-8(x-2)]
4. None of these

Answer: 1. y = 0.1sin[47π(t- 1) + 8(x-2)]

2. The speed of particle at x = 2m and t = 1 s is

1. 0.2π m · s^-1
2. 0.67π m · s^-1
3. 0.4π m · s^-1
4. 0

Answer: 3. 0.4π m · s^-1

3. The instantaneous power (in J · s^-1) transfer through x = 2 m and t = 1.125 s is

1. 10
2. \(\frac{4 \pi}{3}\)
3. \(\frac{2 \pi}{3}\)
4. Zero

Answer: 4. Zero

Question 3. Suppose a musical note consists of tones of frequencies 100 Hz, 200 Hz, 300 Hz, 400 Hz, 500 Hz, and 600 Hz.

1. What should be the frequency of the fundamental tone?

1. 200 Hz
2. 100 Hz
3. 400 Hz
4. 600 Hz

Answer: 2. 100 Hz

2. Among the frequencies the third and fourth harmonics are respectively

1. 300 Hz, 500 Hz
2. 400 Hz, 500 Hz
3. 300 Hz, 400 Hz
4. None of these

Answer: 3. 300 Hz, 400 Hz

3. Among the tones the octave is

1. 200 Hz
2. 300 Hz
3. 400 Hz
4. None

Answer: 1. 200 Hz

Wave Motion Integer Answer Type Questions

In this type, the answer to each of the questions Is a single-digit integer ranging from 0 to 9.

Question 1. A transverse wave propagating along x -axis is represented by (x, t) = 8.0sin (0.5π x – 4πt – \(\frac{\pi}{4}\)) where x is in meters and t is in seconds. Calculate the speed in m µ s^-1 of the wave.
Answer: 8

Question 2. The water waves are traveling along the surface of an ocean at a speed of 2.5 m · s^-1 and splashing up periodically against a pole. Each adjacent crest is 5 m apart. The crest splashes upon reaching the foot of the pole. How much time (in seconds) passes between each successive splashing?

Answer: 2

Wave Motion Equation Of A Travelling Or Progressive Wave

A wave, that propagates through a medium in a fixed direction, is called a progressive wave in one dimension. Suppose, due to the propagation of the wave, the panicles in the medium are subjected to forced simple harmonic motions. Obviously, the wave reaches two different panicles at two different times.

• As a result, there arises a time lag, and consequently a phase lag, between the vibrations of two different particles along the direction of wave motion.
• This time lag or phase lag depends on the velocity of the wave. If the wave travels from left to right, each particle starts vibrating later than its predecessor on the left. So, the phase of a panicle lags behind that of any other panicle on its left.

Let the positive direction of the x-axis be chosen along the direction of propagation of a one-dimensional progressive wave. O is the origin.

The particles of the medium vibrate simply harmonically. The displacement of the particle at O at any instant t from its mean position is given by, y = Asinωt

where A is the amplitude of vibration and ω is the angular frequency of the SHM executed by the particle.

If n is the frequency of the particle, ω = 2πn

y = Asin2πnt…(1)

The wave is traveling along the positive x -x-direction.

So, time taken by the wave to reach P at a distance x on the right-hand side of O is \(\frac{x}{V}\) i.e., with respect to time, the point P always lags behind the point O by \(\frac{x}{V}\). If t and t’ are the times at the points O and P, respectively, t’ = t – \(\frac{x}{V}\).

So, displacement of the particle at P is given by,

y = \(A \sin \omega t^{\prime}=A \sin \omega\left(t-\frac{x}{V}\right)=A \sin 2 \pi n\left(t-\frac{x}{V}\right)\)….(2)

This is the equation of a progressive wave traveling in the positive direction of x-axis.

If the wave propagates in the opposite direction, i.e., in the negative x-direction, we put -x in place of +x. So in that case, the equation of the progressive wave will be,

y = \(A \sin \omega\left(t+\frac{x}{V}\right)=A \sin 2 \pi n\left(t+\frac{x}{V}\right)\)…(3)

From equations (2) and (3) it is seen that the displacement of a vibrating panicle on the path of a progressive wave changes

1. With time and
2. With distance.

Each of these changes, with time or with distance, is periodic. Clearly, in each of the cases, the displacement graph of the particle (y-t graph or y-x graph) is a sine graph.

Any of the harmonic functions in sine and cosine forms may be used to express a simple harmonic motion. So we can express equations (1), (2), and (3) by cosine functions.

In equations (2) and (3), y is the displacement of a particle with respect to its mean position.

1. In the case of a transverse wave, y is perpendicular to the x-axis.
2. In the case of a longitudinal wave, y is parallel to the x-axis.

A Few Alternative Forms Of The Progressive Wave Equation: In equation (2), the angular function is, \(\theta=\omega\left(t-\frac{x}{V}\right).\)

By expressing θ in different ways, the equation of a progressive wave can be expressed in a few alternative forms

Frequency, \(n=\frac{\omega}{2 \pi} ;\) time period, \(T=\frac{1}{n}=\frac{2 \pi}{\omega}\) wavelength, \(\lambda=\frac{V}{n}\);

Wave number, \(k=\frac{2 \pi}{\lambda}=\frac{2 \pi n}{V}=\frac{\omega}{V}\)

1. \(\theta=\omega\left(t-\frac{x}{V}\right)=\omega t-\frac{\omega}{V} x=\omega t-k x\)
2. \(\theta=\omega\left(t-\frac{x}{V}\right)=\frac{\omega}{V}(V t-x)=k(V t-x)=\frac{2 \pi}{\lambda}(V t-x)\)
3. \(\theta=\omega t-k x=2 \pi\left(\frac{\omega}{2 \pi} t-\frac{k}{2 \pi} x\right)=2 \pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)

Using these values of θ, the equation of a progressive wave can be written as

\(\left.\begin{array}{rl}
y & =A \sin \omega\left(t-\frac{x}{V}\right) \\
& =A \sin (\omega t-k x) \\
& =A \sin \frac{2 \pi}{\lambda}(V t-x) \\
& =A \sin 2 \pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)
\end{array}\right\}\)…(4)

Any of these alternative forms may be used as per convenience. Remember that if we put -x in place of x, we shall get the equation of a progressive wave moving in the negative direction of the x-axis.

Phase: The concept of phase has been discussed in the chapter Simple Harmonic Motion.

The equation of a progressive wave is written as y = Asinθ

where \(\theta=\frac{2 \pi}{\lambda}(V t-x)\)…(5)

If a progressive wave is not damped, the amplitude of vibration A remains constant. Except for amplitude, all other information about the wave is obtained from the angle θ. This angle θ is called the phase angle or phase. If this phase angle is known,

1. From the values of 2 and V we get,

frequency, \(n=\frac{V}{\lambda}\); time period T = \(\frac{1}{n}=\frac{\lambda}{V}\), etc.

2. For a particle in position x, the displacement at an instant t can be determined. Obviously, the phase 6 of the wave depends on x and t. At any instant, the phase changes with distance x. Again, at any point, the phase changes with time t.

Phase Difference: The phase difference of two particles at any two positions along the progressive wave at a particular instance of time is actually the difference of the phase angles at the two positions at that instant.

If x₁ and x₂ are the positions of the two particles along the direction of propagation of the wave, the path difference on the wave between the two particles is x₂-x₁.

From equation (5), at any instant t, the phase of the two particles are, respectively,

⇒ \(\theta_1=\frac{2 \pi}{\lambda}\left(V t-x_1\right) \text { and } \theta_2=\frac{2 \pi}{\lambda}\left(V t-x_2\right)\)

∴ \(\theta_1-\theta_2=\frac{2 \pi}{\lambda}\left(x_2-x_1\right)\)

i.e., phase difference = \(\frac{2 \pi}{\lambda}\) x path difference….(6)

From equation (6) we get,

1. If the path difference of two particles is 0, λ, 2 λ,…, the phase difference becomes 0, 2π, 4π,… In this case, the particles are in the same phase.

2. If the path difference of two particles \(\frac{\lambda}{2}, \frac{3 \lambda}{2}, \frac{5 \lambda}{2}, \ldots\) the phase difference becomes π, 3π, 5π,… In this case, the particles are in opposite phases.

Cosine form of the equation of a progressive wave: The equation of a progressive wave can be written using a cosine function instead of the sine function. Then,

y = \(A \cos (\omega t-k x)=A \sin \left(\omega t-k x+\frac{\pi}{2}\right)\)….(7)

Comparing equations (4) and (7), it is evident that the phase difference between these two progressive waves is \(\frac{\pi}{2}\) or 90°.

Initial Condition: In equation (4), if x = 0 and t = 0, y = 0, i.e., at the beginning, the displacement of the particle at the origin is zero. Similarly, in equation (7), if x = 0 and t = 0, y = A, i.e., at the beginning, the displacement of the particle at the origin is maximum. Obviously, due to different initial conditions, the phase difference between the two progressive waves given by equations (4) and (7) is 90°.

Generally, the displacement of a particle at t = 0 and x = 0 may have any value between +A and -A. So, the phase of a progressive wave may be different from those in equations (4) or (7). Denoting the initial phase by ø, the general form of a progressive wave can be written as:

\(\left.\begin{array}{rl}
y & =A \sin (\omega t-k x \pm \phi) \\
& =A \sin \left[\omega\left(t-\frac{x}{V}\right) \pm \phi\right] \\
& =A \sin \left[\frac{2 \pi}{\lambda}(V t-x) \pm \phi\right] \\
& =A \sin \left[2 \pi\left(\frac{t}{T}-\frac{x}{\lambda}\right) \pm \phi\right]
\end{array}\right\}\)…..(8)

According to equation (8), at t = 0 and x = 0, the phase angle of the particle is ±ø. This is called the epoch of the progressive wave at the origin.

Partial Derivatives: The equations in this section show that y is a function of two independent variables—x and r. So y has two independent derivatives one with respect to x and the other with respect to t. They are the partial derivatives:

1. \(\frac{\partial y}{\partial x}=\frac{d y}{d x} .\), when t is considered to be a constant = rate of change of y with respect to x when t is a constant.

2. Similarly, \(\frac{\partial y}{\partial t}\) = rate of change of y with respect to t, when x is a constant.

Particle velocity and acceleration in a progressive wave: Displacement of a particle in a progressive wave, y = \(A \sin (\omega t-k x \pm \phi)\)……(9)

So, the velocity of the particle,

v = \(\frac{\partial y}{\partial t}=\omega A \cos (\omega t-k x \pm \phi)\)

or, \(\nu =v_0 \cos (\omega t-k x \pm \phi)\)…..(10)

The maximum value of the velocity of the particle = \(\pm \omega A= \pm v_0\).

This v₀ is called the velocity amplitude of the particle in a progressive wave.

From equation (9), \(\sin (\omega t-k x \pm \phi)=\frac{y}{A}\)

So, \(\cos (\omega t-k x \pm \phi)=\sqrt{1-\frac{y^2}{A^2}}=\frac{1}{A} \sqrt{A^2-y^2}\)

i.e., \(v=\omega A \cdot \frac{1}{A} \sqrt{A^2-y^2}\)

or, v = \(\omega \sqrt{A^2-y^2}\)

The phase difference between a sine function and a cosine function is 90°. So, the phase difference between displacement y and velocity v is also 90°.

From equation (11), it is also seen that if y = 0, v = ωA = v₀ and again if y = A, v = 0,

i.e., if displacement is zero, velocity is maximum and if displacement is maximum, velocity is zero.

Acceleration of the particle in a progressive wave,

a = \(\frac{\partial^2 y}{\partial t^2}=-\omega^2 A \sin (\omega t-k x \pm \phi)\)

or, a = \(-\omega^2 y\)….(12)

From this equation it is evident that the displacement of the particle y and its acceleration a are in opposite phases, i.e., the phase difference between them is 180°.

Accordingly, the phase difference between velocity and acceleration is 90°.

The maximum acceleration of the particle = \(\pm \omega^2 A= \pm a_0\)

This a₀ may be called the amplitude of acceleration of the particle in a progressive wave.

Relation between particle velocity and wave velocity in a progressive wave:

Displacement of the particle in a progressive wave, y = \(A \sin (\omega t-k x \pm \phi)\)

So, particle velocity, \(\nu=\frac{\partial y}{\partial t}=\omega A \cos (\omega t-k x \pm \phi)\)

Again, \(\frac{\partial y}{\partial x}=-k A \cos (\omega t-k x \pm \phi)\)

So, \(\frac{\partial}{\partial y}=-\frac{\omega}{k x}=-V\)

(As V is the wave velocity, \(k=\frac{\omega}{V}\) )

∴ v = -V \(\frac{\partial y}{\partial x}\)….(13)

This is the relation between particle velocity v and wave velocity V.

In case of a transverse wave, the direction of particle velocity is always perpendicular to that of wave velocity. In the case of a longitudinal wave, the direction of particle velocity is along or opposite to the direction of wave velocity.

Differential Equation Of A Progressive Wave: If y = \(A \sin (\omega t-k x \pm \phi)\)

⇒ \(\frac{\partial^2 y}{\partial t^2}=-\omega^2 A \sin (\omega t-k x \pm \phi)\)

and \(\frac{\partial^2 y}{\partial x^2}=-k^2 A \sin (\omega t-k x \pm \phi)\)

So, \(\frac{\frac{\partial^2 y}{\partial x^2}}{\frac{\partial^2 y}{\partial t^2}}=\frac{k^2}{\omega^2}=\frac{1}{V^2}\) (because wave velocity, \(V=\frac{\omega}{k}\))

or, \(\frac{\partial^2 y}{\partial x^2}=\frac{1}{V^2} \frac{\partial^2 y}{\partial t^2}\)…(14)

This equation is the differential equation of a progressive wave. Conversely, if any one-dimensional disturbance satisfies this equation, it is obviously a progressive wave.

Difference Between Particle Velocity And Wave Velocity:

1. The particles of a medium in a progressive wave do not change their positions due to their velocities. Every particle only vibrates on both sides of its mean position But the progressive wave advances through the medium with its wave velocity.
2. The velocities of the particles of the medium change continuously. It is maximum at the mean positions and zero at their extreme positions. However wave velocity remains constant for a particular medium. It depends only on the properties of the medium.
3. A progressive wave possesses energy due to the motion of the particles of the medium. This energy propagates with the wave through the medium with the velocity of the wave.
4. In a transverse wave, the direction of particle velocity is perpendicular to that of wave velocity. On the other hand, for a longitudinal wave, these two velocities are parallel.

The velocity of progressive waves in different media:

1. Velocity of a longitudinal wave in a solid medium, V = \(\sqrt{\frac{Y}{\rho}}\); Y = Young’s modulus of the medium, and ρ = density of the medium.

2. Velocity of a longitudinal wave in a liquid or gaseous medium, V = \(\sqrt{\frac{E}{\rho}}\); E = Bulk modulus of the medium, and ρ = density of the medium.

3. Velocity of sound wave in a gaseous medium, V = \(\sqrt{\frac{\gamma p}{\rho}}\); p = pressure of the gas, and γ = ratio of the two specific heats \(\left(\frac{c_p}{c_w}\right)\) of the gas.

4. Velocity of a transverse wave in a stretched string, V = \(\sqrt{\frac{T}{m}}\); T = tension in the string, and m = mass per unit length of the string.

5. Velocity of a longitudinal wave in a stretched string, \(V=\sqrt{\frac{Y}{\rho}}\); Y = Young’s modulus of the material of the string, and p ~ density of the material of the string.

6. Velocity of an electromagnetic wave, V = \(\frac{1}{\sqrt{\mu \epsilon}} ; \mu\) = permeability and ∈ = permittivity of the medium.

Characteristics Of Progressive Waves:

1. Progressive wave continuously propagates through a medium, and if not damped, it can propagate to infinity.
2. The progressive wave moves with a definite velocity. The wave velocity depends on the elastic properties and on the density of the medium. Energy is transferred with the wave through the medium with the velocity of the wave.
3. Each particle of the medium vibrates about its mean position with identical frequency and amplitude. The direction of movement of the particles may be perpendicular (transverse wave) or parallel (longitudinal wave) with respect to the direction of wave motion.
4. The velocity with which the phase of a vibrating particle of the medium is transferred to the next particle is called the wave velocity. For the same reason, it is also called the phase velocity. The phase difference between two vibrating particles is proportional to the distance of separation of the two particles along the line of wave propagation.
5. The progressive wave carries energy from one point to another without displacing the particles of the medium. Energy is transferred perpendicular to the direction of the wavefronts, i.e., along the direction of the rays.
6. Pressure and density in the medium, through which the progressive wave advances, follow the sinusoidal form of variation, like that of displacement, velocity, and acceleration.
7. A progressive wave has double periodicity. One is time periodicity determined by the time period (T) of the wave and the other is space periodicity determined by the wavelength (λ).

Different Properties Of Progressive Waves: The distinctive properties of progressive waves are explained below

Absorption: While moving through any medium, damping of the progressive wave takes place. It means that the energy of the wave gradually decreases with the increase of distance because a part of the energy of the wave is absorbed by the medium as the wave propagates.

Reflection: When a progressive wave traveling in a homogeneous medium is incident on an interface with another medium, a part of the incident wave comes back to the first medium. This phenomenon is known as the reflection of a wave. The amount of energy of the incident wave that will be reflected depends on the nature of the interface of the two media.

Refraction: When a progressive wave traveling through a homogeneous medium is incident on an interface with another medium, a part of the incident wave is transmitted into the second medium. This phenomenon is known as the refraction of a wave. In refraction, the direction of wave motion generally changes.

Interference: Let us consider two progressive waves having the same wavelength and velocity. The phase difference of the two waves is always a constant. When these two waves superpose, the amplitude of the resultant wave increases at some places and decreases at some other places of the medium. This successive increase and decrease of the amplitude of the resultant wave is called interference of waves.

Diffraction: When a progressive wave passes through the edge of an opening or of an obstacle, the direction of the wave may change. This is called the diffraction of a wave.

Scattering: In the course of propagation, when a progressive wave falls on a material particle, the particle is subject to a forced vibration. So this particle also acts as a secondary source of wave, i.e., weaves propagate in all directions from the vibrating particle. This phenomenon is called the scattering of a wave.

Polarisation: During propagation of a transverse wave through a medium, each particle of the medium vibrates on a plane perpendicular to the direction of motion of the wave.

• The plane is called the normal plane. If the vibrations of the particles on such planes arc somehow are restricted to a particular direction, then this phenomenon is called the polarisation of a wave. Obviously, polarization does not take place in case of longitudinal waves.
• It is to be noted that, polarisation does not take place in the case of sound waves. This shows that sound waves are longitudinal. On the other hand, light waves can be polarised by suitable arrangements. So light waves are transverse.

In optics, these properties of waves are discussed in detail. In this chapter, the phenomena of reflection and refraction of sound waves are mainly discussed.

Wave Motion Multiple Choice Questions And Answers

Question 1. Which one of the following phenomena differentiates transverse waves from longitudinal waves?

1. Reflection
2. Refraction
3. Polarisation
4. Interference

Answer: 3. Polarisation

Question 2. A sound wave is a

1. Transverse elastic wave
2. Transverse electromagnetic wave
3. Longitudinal elastic wave
4. Longitudinal electromagnetic wave

Answer: 3. Longitudinal elastic wave

Question 3. A light wave is a

1. Transverse elastic wave
2. Transverse electromagnetic wave
3. Longitudinal elastic wave
4. Longitudinal electromagnetic wave

Answer: 2. Transverse electromagnetic wave

Question 4. Polarisation of the sound wave does not occur, because the sound wave is

1. Transverse wave
2. Longitudinal wave
3. Progressive wave
4. Elastic wave

Answer: 2. Longitudinal wave

Question 5. If a child stands up while swinging on a swing, then the period of the swing will

1. Increase
2. Decrease
3. Remain same
4. Increase if the child is long and decrease if the child is short

Answer: 2. Decrease

Question 6. A wave is advancing along the surface of water with a velocity of 80 cm · s^-1. If the distance between two consecutive crests is 20 cm, then what will be the wavelength?

1. 80 cm
2. 20 cm
3. 4 cm
4. \(\frac{1}{4}\) cm

Answer: 2. 20 cm

Question 7. When a wave coming from a medium enters another medium, the property of the wave which remains unchanged is

1. Velocity
2. Frequency
3. Wavelength
4. Amplitude

Answer: 2. Frequency

Question 8. A wave is advancing along the surface of water with a velocity of 80 cm • s^-1. If the distance between two consecutive crests is 20 cm, then what will be the frequency of the wave?

1. 80Hz
2. 20Hz
3. 4 Hz
4. \(\frac{1}{4}\) Hz

Answer: 3. 4 Hz

Question 9. When a force F₁ acts on a particle, the frequency is 6Hz, and when a force F₂ acts, the frequency is 8 Hz. Now if both the forces act simultaneously in the same direction, then their frequency’ becomes

1. 20Hz
2. 14Hz
3. 10Hz
4. 2Hz

Answer: 3. 10Hz

Question 10. If the wavelength in a medium is reduced by 50%, keeping its velocity constant, the percentage change in its frequency is

1. 50%
2. 25%
3. 100%
4. 200%

Answer: 3. 100%

Question 11. The equation of a progressive wave is given by y = \(5 \sin \frac{\pi}{2}(100 t-x) \mathrm{cm}\). The wavelength is

1. 2 cm
2. 4 cm
3. 50 cm
4. 100 cm

Answer: 2. 4 cm

Question 12. The equation of a progressive wave is given by y = \(5 \sin \frac{\pi}{2}(100 t-x) \mathrm{cm}\). The frequency of the wave is

1. 25 Hz
2. 50 Hz
3. 100 Hz
4. 50π Hz

Answer: 1. 25 Hz

Question 13. The equation of a wave is given by y = \(10^{-4} \sin (60 t+2 x)\). Here x is expressed in metres and r in seconds. This represents a wave

1. Which is moving in the negative direction of the x-axis with a velocity of 30 m • s^-1
2. Whose wavelength is  πm
3. Whose frequency’ is \(\frac{30}{\pi}\) hz
4. All the above options are correct

Answer: 4. All the above options are correct

Question 14. The equation of a tramverse wave is given by Y = \(Y_0 \sin 2 \pi\left(f t-\frac{x}{\lambda}\right)\). If the wave velocity, then

1. \(\lambda=\frac{\pi Y_0}{4}\)
2. \(\lambda=\frac{\pi Y_0}{2}\)
3. \(\lambda=\pi Y_0\)
4. \(\lambda=2 \pi Y_0\)

Answer: 2. \(\lambda=\frac{\pi Y_0}{2}\)

Question 15. Which one of the following physical quantities moves with a wave at the same velocity?

1. Amplitude
2. Mass
3. Momentum
4. Energy

Answer: 4. Energy

Question 16. When temperature increases, the frequency of a turning fork,

1. Increases
2. Decreases
3. Remains same
4. Increases or decreases depending on the material

Answer: 2. Decreases

Question 17. The pressure, density, and ratio of two specific heats of a gas are p, ρ, and γ respectively. The velocity of sound in the gas is

1. \(\frac{\sqrt{p}}{\rho}\)
2. \(\gamma \frac{\sqrt{p}}{\rho}\)
3. \(\sqrt{\frac{\gamma p}{\rho}}\)
4. \(\sqrt{\frac{3 \gamma p}{\rho}}\)

Answer: 3. \(\sqrt{\frac{\gamma p}{\rho}}\)

Question 18. If the absolute temperature of a gas is T and the velocity’ of sound in the gas is V, then

1. V ∝ T
2. V ∝ √T
3. \(V \propto \frac{1}{T}\)
4. \(V \propto \frac{1}{\sqrt{T}}\)

Answer: 2. V ∝ √T

Question 19. The velocity of sound in moist air is greater than that in dry air, because

1. Moist air is comparatively light
2. Moist air is comparatively heavy
3. The pressure of moist air is low
4. The pressure of moist air is high

Answer: 1. Moist air is comparatively light

Question 20. Laplace concluded that the temperature of a gaseous medium cannot remain constant during the propagation of sound through it, because

1. The pressure of the gas remains constant
2. The volume of the gas remains constant
3. The particles of the medium vibrate with a large amplitude
4. The compressions and the rarefactions occur very rapidly

Answer: 4. The compressions and the rarefactions occur very rapidly

Question 21. According to Laplace’s correction, the propagation of sound through a gaseous medium is

1. An isochoric process
2. An isobaric process
3. An isothermal process
4. An adiabatic process

Answer: 4. An isochoric process

Question 22. In an adiabatic process, the bulk modulus of a gas is

1. Equal to its density
2. Greater than its density
3. Equal to its pressure
4. Greater than its pressure

Answer: 4. Greater than its pressure

Question 23. The velocity of sound in air at STP is 330 m· s^-1. If the atmospheric pressure becomes 75 cm Hg, then the velocity of sound at the same temperature will be

1. 330 m · s^-1
2. Less than 330 m · s^-1
3. Greater than 330 m · s^-1
4. Given data is insufficient

Answer: 1. 330 m · s^-1

Question 24. For 1°C rise in temperature, the velocity of sound in air increases by

1. About 2 m · s^-1
2. About 2 ft · s^-1
3. About 61 m · s^-1
4. About 61 ft · s^-1

Answer: 2. About 2 ft · s^-1

Question 25. The ratio of the velocities of sound through hydrogen and oxygen at STP is

1. 1:16
2. 1:4
3. 4:1
4. 16:1

Answer: 3. 4:1

Question 26. At what temperature the velocity of sound in a gas will increase by 10% of its value at 27 °C?

1. 29.7°C
2. 32.7°C
3. 57°C
4. 90°C

Answer: 4. 90°C

Question 27. TWo monatomic ideal gases of molecular masses m₁ and m₂ respectively are enclosed in separate containers and kept at the same temperature. The ratio of the speed of sound of 1st and 2nd gas is given by

1. \(\sqrt{\frac{m_1}{m_2}}\)
2. \(\sqrt{\frac{m_2}{m_1}}\)
3. \(\frac{m_1}{m_2}\)
4. \(\frac{m_2}{m_1}\)

Answer: 2. \(\sqrt{\frac{m_2}{m_1}}\)

Question 28. Velocity of sound is maximum in

1. Water
2. Air
3. Vacuum
4. Steel

Answer: 4. Steel

Question 29. The ratio of the speed of sound in nitrogen gas to that in helium gas, at 300K is

1. \(\sqrt{\frac{2}{7}}\)
2. \(\sqrt{\frac{1}{7}}\)
3. \(\frac{\sqrt{3}}{5}\)
4. \(\frac{\sqrt{6}}{5}\)

Answer: 3. \(\frac{\sqrt{3}}{5}\)

Question 30. During a speech, the vibration of the diaphragm of a microphone is

1. Natural vibration
2. Damped vibration
3. Forced vibration
4. Resonant vibration

Answer: 3. Forced vibration

Question 31. Phon is the unit of

1. Pitch
2. Quality
3. Timbre
4. Loudness

Answer: 4. Loudness

Question 32. A sound absorber attenuates the sound level by 20 dB. The intensity decreases by a factor of

1. 1000
2. 10000
3. 10
4. 100

Answer: 4. 100

Question 33. Which one of the following phenomena does not take place in the case of sound waves?

1. Reflection
2. Refraction
3. Polarisation
4. Interference

Answer: 3. Polarisation

Question 34. A balloon full of carbon dioxide and another full of water behaves as lenses for the refraction of sound. What will be the nature of these lenses?

1. Both are convergent
2. Both are divergent
3. The first one is divergent and the second one is convergent
4. The first one is convergent and the second one is divergent

Answer: 4. The first one is convergent and the second one is divergent

Question 35. If a man standing at any place between two hills fires a gun, how many echoes will he hear?

1. 1
2. 2
3. 4
4. More than 4

Answer: 4. More than 4

Question 36. A sound is made in sea water from the bottom of a ship and its echo is heard after a time t. If v is the velocity of sound in sea water, the depth of the sea at that place is

1. vt
2. \(\frac{v t}{2}\)
3. \(\frac{v t}{10}\)
4. \(\frac{v t}{20}\)

Answer: 2. \(\frac{v t}{2}\)

Question 37. An echo coming from a hill is heard 20 s after the original sound. If the velocity of sound in air is 330 m • s^-1, the distance of the hill will be

1. 3.3 km
2. 6.6 km
3. 1.65 km
4. 13.2 km

Answer: 1. 3.3 km

Question 38. If the velocity of sound in air and in water are 330 m · s^-1 and 1400 m · s^-1 respectively, what will be the critical angle for refraction of sound going to water from air?

1. About 29°
2. About 13.6°
3. About 76.4°
4. No critical angle in this case

Answer: 2. About 13.6°

Question 39. A source of sound of frequency 600 Hz is placed in water. The speed of sound in water and air is 1500 m/s and 300 m/s respectively. The frequency of sound recorded by an observer who is standing in air is

1. 660 Hz
2. 600 Hz
3. 540 Hz
4. None of the above

Answer: 2. 600 Hz

In this type of question, more than one option is correct.

Question 40. A wave equation that gives the displacement along the y-direction is given by y = 10^-4 sin(60t+2x) where x and y are in meters and t is time in seconds. This represents a wave

1. Traveling with a velocity of 30 m · s^-1 in the negative x -direction
2. Of wavelength πm
3. Of frequency \(\frac{30}{\pi}\) hz
4. Of amplitude 10^-4 m traveling along the negative x -direction

Answer: All options are correct

Question 41. For a transverse wave on a string, the string displacement is described by, y = f(x- at) where f represents a function and A is a negative constant. Then which of the following is/are correct statement(s)?

1. The shape of the string at time t = 0 is given by f(x)
2. The shape of the waveform doesn’t change as it moves along the string.
3. Waveform moves in the positive x -x-direction
4. The speed of the waveform is a.

Answer:

1. The shape of the string at time t = 0 is given by f(x)
2. The shape of the waveform doesn’t change as it moves along the string.

Question 42. Mark the correct statement(s) concerning waves

1. A wave can have both transverse and longitudinal components
2. A wave doesn’t result in the bulk flow of the materials of its medium
3. A wave is a traveling disturbance
4. A wave can be there even in the absence of an elastic medium

Answer: All options are correct

Question 43. Mark the correct statements.

1. Note emitted from any musical instrument is generally a combination of tones
2. A tone can be compared with compound light
3. Fundamental tone can be treated as the 1st harmonic
4. Harmonics are only the odd multiples of the fundamental tone

Answer:

1. Note emitted from any musical instrument is generally a combination of tones

3. Fundamental tone can be treated as the 1st harmonic

Question 44. Suppose a musical instrument emits sound having frequencies 250 Hz, 300 Hz, 350 Hz, 400 Hz, 450 Hz, and 500 Hz respectively.

1. Tones having frequencies 250 Hz, 300 Hz, 350 Hz, 400 Hz, 450 Hz, and 500 Hz are overtones.
2. The tone of 250 Hz is the fundamental tone
3. The combination of these six tones forms a note
4. The tone of 500 Hz is the octave

Answer:

2. The tone of 250 Hz is the fundamental tone

3. Combination of these six tones forms a note

4. The tone of 500 Hz is the octave

Wave Motion Question and Answers

Question 1. In the case of a transverse wave, do the particles of the medium vibrate in the u plane parallel to the plane of propagation of the wave?
Answer:

Let us assume that the wave is propagating along the z-axis. Then the plane of propagation of the wave, or the wavefronts, will be perpendicular to z -the axis, i.e., parallel to the xy-plane.

Again the direction of motion of tire vibrating particles of the medium in a transverse wave is perpendicular to z -the axis, i.e., parallel to the xy-plane. So, the particles of the medium vibrate in a plane parallel to the plane of propagation of the wave.

Question 2. The equation of a progressive wave In a stretched string Is given by, y = Asin(kx – ωt). What is the maximum particle velocity?
Answer:

Particle velocity, v = \(\frac{\partial y}{\partial t}=\frac{\partial}{\partial t}\{A \sin (k x-\omega t)\}\)

= \(-\omega A \cos (k x-\omega t)\)

Since the maximum value of a cosine function is ±1, the magnitude of maximum particle velocity is ωA.

Question 3. Regular reflection of sound takes place from a large rough reflector, but not regular reflection of light. On the other hand, regular reflection of light takes place from a small smooth reflector, but not regular reflection of sound. What Is the reason for this?
Answer:

To obtain effective reflection of a wave from a reflector, its size should be greater than the wavelength. The wavelength of audible sound in air varies from 1.5 cm to 16 in.

• On the other hand, the wavelength of visible light varies from 4 x 10^-7 m to 8 x 10^-7 m, i.e., the wavelength of sound is much greater than that of light. So light can be reflected from a very small reflector, but not sound.
• Again for regular reflection, the size of the notches of the surface of a reflector should be smaller than the wavelength of the wave. The wavelength of light is very small.
• So the size of the notches of the reflector should be very small, i.e., the reflector should be smooth. On the other hand, the wavelength of sound is large. So regular reflection of sound takes place even from a rough reflector.

Question 4. A sound wave travels from air to water. The angle of incidence at the surface of separation between air and water is i₁ and the angle of refraction is l₂. Snell’s law is applicable in this case. Determine which one of i₁ and i₂ is greater.
Answer:

According to Snell’s law, \(\frac{\sin i_1}{\sin i_2}\) = constant.

The value of this constant is equal to the ratio of the velocities of the wave in the two media.

i.e., \(\frac{\sin i_1}{\sin i_2}=\frac{V_1}{V_2}\)

Here, the first medium is air and the second medium is water. The velocity of sound in water is greater than that in air (i.e., V₂>V₁).

So, \(\sin i_2>\sin i_1 \quad \text { or, } \quad i_2>i_1\)

∴ i₁ is smaller than i₂.

Question 5. A balloon full of carbon dioxide and another frill of water behave as lenses for the refraction of sound. What type of lens will they resemble?
Answer:

The velocity of sound in carbon dioxide is less than that in air, i.e., when sound enters carbon dioxide from air, its velocity decreases. So in the case of refraction of sound, carbon dioxide is a denser medium relative to air.

• Hence, a balloon full of carbon dioxide, when placed in the air, behaves like a convex lens. In the case of a convex lens of glass, light rays incident on it become convergent. Similarly, sound rays passing through a balloon full of carbon dioxide become convergent.
• On the other hand, when sound enters water from the air, its velocity increases, because the velocity of sound in air is 330 m · s^-1, but that in water is about 1500 m · s^-1. So, in case of refraction of sound, water is a rarer medium than air.
• Hence, a balloon full of water behaves in an opposite manner. So in this case, since the sound wave moves to a rarer medium from a denser medium, the waves will diverge. Therefore, the balloon containing water will behave like a concave lens.

Question 6. In a progressive wave, the maximum velocity and maximum acceleration of a particle in the medium are v₀ and a₀, respectively. Find the amplitude and the frequency of the waves.
Answer:

Let the equation of a progressive wave be y = \(A \sin \omega\left(t-\frac{x}{V}\right)\)

So, particle velocity v = \(\frac{\partial y}{\partial t}=\omega A \cos \omega\left(t-\frac{x}{V}\right)\),

i.e., v₀ = ωA

Again, acceleration, a = \(\frac{\partial v}{\partial t}=-\omega^2 A \sin \omega\left(t-\frac{x}{V}\right),\)

i.e., a₀ = ω²A

So, amplitude, A = \(\frac{(\omega A)^2}{\omega^2 A}=\frac{v_0^2}{a_0}\)

And frequency, n = \(\frac{\omega}{2 \pi}=\frac{1}{2 \pi} \cdot \frac{\omega^2 A}{\omega A}=\frac{a_0}{2 \pi v_0}\).

Question 7. A plane wave of sound traveling in the air is incident upon a plane’s water surface. The angle of incidence is 60. Assuming Snell’s law to be valid for sound waves, it will be refracted into the water away from the normal. State whether the statement is true or false and explain.
Answer:

The velocity of sound in water is about 4 times that in air. So for sound waves, air is a denser medium and water is a rarer medium. In this case, the sound wave is incident on a rarer medium (water) from the denser medium (air).

• For sound waves, the critical angle in air with respect to water is about \(\sin ^{-1}\left(\frac{1}{4}\right)=14.5^{\circ}\).
• So if the angle of incidence is 60°, sound waves will not be refracted in water, rather there will be a total internal reflection from the surface of the water. So the statement is false.

Question 8. Prove that the equation \(y=4 \sin \frac{2 \pi}{15}(60 t-x) \mathrm{cm}\) represents a progressive wave.
Answer:

Here the velocity of the wave is 60 cm · s^-1.

If y₁ is the displacement of a particle at the point (x + 60) at time (t+1), then

⇒ \(y_1=4 \sin \frac{2 \pi}{15}[60(t+1)-(x+60)]\)

= \(4 \sin \frac{2 \pi}{15}(60 t-x)=y\)

So, the motion of a particle at a distance x cm at time t is identical to the motion of the particle at a distance (x + 60) cm at time (t + 1). In this case, the disturbance in the medium moves 60 cm in 1 s. So, the given equation is an equation of a progressive wave.

Question 9. If the wavelength of an X-ray is 3Å, what is the frequency of the wave? [1A = 10^-8 cm]
Answer:

Velocity of X-ray = velocity of light

= c = 3 x 10¹⁰ cm · s^-1

Wavelength, λ = 3Å = 3 x 10^-8 cm

∴ Frequency, n = \(\frac{c}{\lambda}=\frac{3 \times 10^{10}}{3 \times 10^{-8}}=10^{18} \mathrm{~Hz} .\)

Question 10. Which property of waves proves that sound wave is longitudinal?
Answer:

The polarisation property of wave proves it. It is not possible for any longitudinal wave to exhibit the phenomenon of polarisation, as in longitudinal waves, the vibrating particles always move along the direction of propagation of the wave. Since sound waves do not exhibit the phenomenon of polarisation, they are longitudinal.

Question 11. Which property of waves shows that light wave is transverse?
Answer:

The polarisation property of wave proves it. Any transverse wave exhibits the phenomenon of polarisation, as the vibrating particles always move perpendicular to the direction of propagation of the wave. Since light waves exhibit the phenomenon of polarisation, they are transverse.

Question 12. If the amplitude of a progressive wave at a distance r from a point source is A, what will be the amplitude at a distance 2r?
Answer:

Intensity of a wave ∝ (amplitude)²

Again, the intensity is inversely proportional to the square of the distance from a point source,

i.e., \(\text { intensity } \propto \frac{1}{(\text { distance })^2}\)

So, \(\text { amplitude } \propto \frac{1}{\text { distance }}\)

Hence, the amplitude will be half, i.e., \(\frac{A}{2}\) at a distance 2r,

Question 13. The equation of a wave la given by y = \(A \cos ^2\left(2 \pi n t-2 \pi \frac{x}{\lambda}\right)\), Determine the amplitude, the frequency, and the wavelength of the wave.
Answer:

y = \(A \cos ^2\left(2 \pi n t-2 \pi \frac{x}{\lambda}\right)=\frac{A}{2} \cdot 2 \cos ^2\left(2 \pi n t-2 \pi \frac{x}{\lambda}\right)\)

= \(\frac{A}{2}\left[1+\cos \left(4 \pi n t-4 \pi \frac{x}{\lambda}\right)\right] \)

= \(\frac{A}{2}+\frac{A}{2} \cos \left(4 \pi n t-4 \pi \frac{x}{\lambda}\right)\)

Here, the second term, i.e., the term containing the cosine function represents the wave. Comparing this term with the general equation y = A’ cos (ωt- kx), we have,

Amplitude, A’ = \(\frac{A}{2}\)

∴ \(\omega=4 \pi n, \text { i.e., frequency }=\frac{\omega}{2 \pi}=2 n,\)

k = \(\frac{4 \pi}{\lambda}, \text { i.e., wavelength }=\frac{2 \pi}{k}=\frac{2 \pi}{\frac{4 \pi}{\lambda}}=\frac{\lambda}{2}\).

Question 14. The equation of a progressive wave Is given by y = \(A \sin 2 \pi\left(p t-\frac{x}{5}\right)\). What Is the ratio of the maximum particle velocity of the medium to the wave velocity?
Answer:

y = \(A \sin 2 \pi\left(p t-\frac{x}{5}\right)=A \sin \left(2 \pi p t-\frac{2 \pi}{5} x\right)\)

Comparing the given equation with the general equation y = Asin(ωt- kx) we have,

∴ \(\omega=2 \pi p \text { and } k=\frac{2 \pi}{5}\)

∴ Wave velocity, V = \(\frac{\omega}{k}=\frac{2 \pi p}{\frac{2 \pi}{5}}=5 p\)

Again, particle velocity,

v = \(\frac{\partial y}{\partial t}=2 \pi p A \cos \left(2 \pi p t-\frac{2 \pi}{5} t\right)\)

Maximum particle velocity, v₀ = 2πpA

So, the ratio of the maximum panicle velocity to the wave velocity = \(\frac{v_0}{V}=\frac{2 \pi p A}{5 p}=\frac{2}{5} \pi \lambda\)

Question 15. Even if the ratio \(\frac{p}{\rho}\) for helium and oxygen are kept equal, why la the velocity of sound not equal hi the two gases?
Answer:

The velocity of sound, c = \(\sqrt{\frac{\gamma p}{\rho}}\), Though the value of the ratio \(\frac{p}{\rho}\) for the two gases are equal, the velocity of sound c differs due to the different values of γ. Oxygen Is a diatomic gas and helium Is a monatomic gas. The values of γ for these two gases are \(\frac{7}{5}\) and \(\frac{5}{3}\) respectively. So, the velocity of sound In them is not equal.

Question 16. Why Is the velocity of sound In the air higher In the rainy season than in winter?
Answer:

Both the temperature and the humidity of the air are higher in the rainy season than In winter. We know, the velocity of sound in air is given by,

c = \(\sqrt{\frac{\gamma p}{\rho}}=\sqrt{\frac{\gamma R T}{M}}\)

Since c ∝ √T, the velocity of sound increases with the increase in temperature of the air.

Again with the increase in humidity, the amount of water vapour in air also increases. The density of water vapor Is less than the density of air. So the density ρ Is less in the rainy season and the velocity of sound increases.

Hence, the velocity of sound in air is higher in the rainy season In comparison to that in winter.

Question 17. At what temperature the velocity of sound In air Is twice its value at 0°C?
Answer:

The velocity of sound (c) in the air is proportional to the square root of its absolute temp (T), i.e., c α √T.

So the velocity of sound is doubled if the absolute temperature becomes four times. Since the initial temperature is 0°C or 273 K,

The required final temperature = 4x 273 K = 1092 K

= (1092 – 273)°C = 819°C.

Question 18. The velocity of sound is generally greater in solids than in gases why?
Answer:

The velocity of sound in a solid is given by, \(V_s=\sqrt{\frac{Y}{\rho}} ;\)

Y = Young’s modulus of the solid, ρ = density of the solid

The velocity of sound in a gas is given by, \(V_g=\sqrt{\frac{k}{\rho^{\prime}}}\)

k = bulk modulus of the gas, ρ’ = density of the gas.

Although the density of a solid medium is more than that of a gaseous medium, the modulus of elasticity of a solid (Y) is many times greater than that of a gas (k).

Hence, \(\frac{Y}{\rho}>\frac{k}{\rho^{\prime}}\)

Therefore, V_s > V_g, i.e., the velocity of sound is greater in solids than in gases.

Question 19. How will the velocity of sound be affected at high altitudes?
Answer:

The temperature decreases with increasing altitude. Furthermore, the humidity of air is generally less in hill areas. So, the velocity of sound will decrease due to a decrease in both temperature and humidity.

Question 20. The speed of sound in water and in air are 1500 m • s^-1 and 300 m • s^-1 respectively. A source of sound of frequency 600 Hz is placed inside water. If the emitted sound enters air from the source, what will be its frequency?
Answer:

The frequency of the emitted sound will remain the same, i.e., 600 Hz, because the frequency of a wave does not change due to refraction.

Question 21. Determine the relationship between the rms velocity. f of the molecule of a gas and the velocity of sound in the gas.
Answer:

From the kinetic theory of gases, we have,

rms velocity of the gas molecules = \(\sqrt{\frac{3 p}{\rho}}\)

Again from the calculations of Newton and Laplace we have, the velocity of sound in a gaseous medium = \(\sqrt{\frac{\gamma p}{\rho}}\)

[γ = ratio of the two specific heats of the gas]

So, the ratio of the rms velocity and the velocity of sound in a gaseous medium = \(\sqrt{\frac{3}{\gamma}}\)

Question 22. If the velocity of sound in oxygen at STP is v, what will be the velocity of sound in helium under the same conditions?
Answer:

Velocity of sound, c = \(\sqrt{\frac{\gamma p}{\rho}}\),

i.e., if the pressure remains the same, for two different gases, \(\frac{c_1}{c_2}=\sqrt{\frac{\gamma_1}{\gamma_2}} \cdot \sqrt{\frac{\rho_2}{\rho_1}}\)

The ratio of the densities of oxygen and helium = \(\frac{16}{2}\) = 8

Again, for oxygen \(\gamma_1=\frac{7}{5}\) (oxygen is diatomic)

And for helium \(\gamma_2=\frac{5}{3}\) (helium is monatomic)

So, \(\frac{\gamma_1}{\gamma_2}=\frac{7 / 5}{5 / 3}=\frac{21}{25}\)

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{21}{25}} \times \sqrt{\frac{1}{8}}\)

As \(c_1=v, c_2=v \sqrt{\frac{25 \times 8}{21}}=3.1 v\).

Kinetic Theory Of Gases

Molecular Concept Of Matter And Its Applications

For centuries, scientists have studied the structure of matter—how it is formed and which are its smallest entities, possessing properties identical to that of the matter itself.

• In the early nineteenth century, Dalton and Avogadro for the first time proposed the theory of molecular structure of matter.
• A molecule is the smallest entity and matter is composed of molecules having all the chemical properties of the matter itself.
• The physical quantities related to molecules are number of molecules in a material body, molecular velocities, intermolecular distances, intermolecular forces, etc.
• These are the internal microscopic properties of a body. Unfortunately, these properties cannot be measured directly through experiments. As a result, we have to start with certain basic assumptions (postulates) about the behaviour of molecules.
• This gives us a picture of how molecules behave in a body. This is known as the molecular model. The next step is the application of Newton’s laws of motion on the molecules.

Now, the experimentally determined properties of a body as a whole, like pressure, temperature, and internal energy, are expected to be intimately related to the molecular model.

So Newton’s Jaws should give us expressions leading to these Bulk properties. This is essentially the object of the kinetic theory of matter.

• In short, the subject of study in which theoretical expressions of the bulk properties of a body are tamed from the application of Newton’s laws of motion on the internal molecular behaviour is called the kinetic theory of matter.
• Naturally, the values from the theoretical expressions of kinetic theory should match the experimental values. The formulas obtained from kinetic theory should be identical to the experimentally obtained thermodynamic formulas. This is actually the pre-condition for the success of kinetic theory.

This condition is beautifully obeyed in case of gases, leading to the very successful and advanced theory of the kinetic theory of gases. But this is not the case with liquids or solids. Partially successful molecular models exist for solids, but almost none so far has been developed for liquids.

Evidence of molecular motion: Molecules cannot be observed directly, but some natural phenomena clearly indicate the existence of molecular motion.

1. Diffusion: Let a gas jar filled with hydrogen gas be held upside down on another gas jar filled with carbon dioxide gas. Now the lids are removed. After an interval of time, it will be observed that the two gases will produce a homogeneous mixture in the two jars, ignoring gravitation.

• This phenomenon is called diffusion of the two gases. Clearly, molecular motion is evident in this phenomenon. Though carbon dioxide is heavier than hydrogen, CO₂ molecules move up and the hydrogen molecules move down to produce the mixture.
• The molecules of a gas randomly move at different velocities in all directions.
• So the molecules of the two gases mix and produce a homogeneous mixture. Diffusion takes place in liquids and solids also.
• If a few granules of copper sulphate are dropped at the bottom of a container filled with water, the blue colour gradually spreads throughout the whole volume of water.
• The density of copper sulphate solution is more than the density of water.
• But the solution moves up ignoring gravitation and after an interval of time, the whole mixture turns blue.
• It is an example of the motion of copper sulphate molecules diffusing into water. In a similar manner, solid phosphorus or boron can be diffused at high temperatures into solid silicon crystals to produce extrinsic semiconductors.
• In general, diffusion can be defined as the phenomenon by virtue of which movement of molecules occurs from a region of higher concentration to a region of lower concentration in a mixture till a homogeneity of concentration is established.

2. Vaporisation and vapour pressure: Liquid molecules are in motion inside the liquid. They move randomly at different velocities. Some molecules rise to the liquid surface with sufficient kinetic energy and overcome the attraction of other molecules inside the liquid.

• As a result, they may escape from the liquid. This phenomenon is called evaporation. Again, kinetic energies of molecules may be increased by applying heat. Hence, more molecules may escape from the liquid and vaporisation may occur.
• If a liquid is enclosed in a container, molecules leaving the liquid move randomly above the liquid surface. They collide with each other and hit the surface again and again. Some molecules may enter the liquid again. This leads to the vapour pressure corresponding to the vapour above the liquid surface.
• At a particular higher temperature, the kinetic energies of the molecules of the liquid become very high. In comparison, the potential energies due to intermolecular attractions become negligible. So the molecules are effectively free and all of them try to come out of the liquid at the same time. This phenomenon is called boiling of the liquid.

3. Expansion of gas: A gas spreads throughout the whole volume of its container. If the volume of the container increases, the gas spreads again to occupy the whole volume. This shows the property of random and unrestricted motion of the gas molecules.

4. Brownian motion: Very small, but still visible particles are often present as impurities in a liquid or in a gas. Observations through microscopes show that these particles move in a very random manner in all possible directions. This is known as Brownian motion.

This phenomenon can be explained by the concept of molecular motion. Molecules inside a liquid or a gas move randomly in all directions and collide time and again with small foreign particles (called Brownian particles). These collisions are directly responsible for the Brownian motion.

Kinetic Theory Of Gases Brownian Motion

British scientist, Robert Brown, first observed this continuous and irregular motion of the particles with a powerful microscope. He put some pollen grains in water.

• These grains, being very light, remained suspended in water. Brown noticed the random, continuous, and to and fro motion of these grains. However he was not able to determine the mechanisms that caused this motion.
• Albert Einstein published a paper in 1905 that explained in precise detail how the motion that Brown had observed was a result of the pollen being moved by individual water molecules.
• Brownian motion of a particle is shown. Colloids in a colloidal solution, very small feathers suspended in air, etc., are examples of randomly moving Brownian particles.

Explanation of the origin of Brownian motion: Just after the discovery of Brownian motion, scientists assumed that the reason of the origin of Brownian motion was a chemical reaction, irregular change of temperature, surface tension of liquid, etc. However from various experiments, it was proved that these explanations were not correct.

• It became possible to explain Brownian motion with the help of kinetic theory. We know that liquid or gas molecules are moving randomly and colliding with floating particles at every instant and from all directions.
• The force exerted on a floating particle of big size in any direction, due to some colliding molecules, is cancelled by the equal and opposite force due to some other molecules.
• As a result, the resultant force acting on the floating particle becomes zero and it has no Brownian motion. But if the floating particle is very tiny in size, the resultant force on it does not become zero as the colliding particles do not exert force equally from all directions.
• Hence, the floating particle moves along the direction of the resultant force and Brownian motion is observed. As molecular thrusts are random, the magnitude of the resultant force is not equal always.
• Also, the resultant force does not act always in the same direction. So the floating particle moves in a random manner in all possible directions.

Characteristics of Brownian motion:

1. The motion is perpetual, spontaneous, random and continuous. Itoo Brownian particles, even at close proximity, do not have identical motion.
2. The motion does not depend on the motion of the container.
3. The velocities of the particles increase with rise in temperature.
4. Smaller particles have higher average velocities.
5. The velocities of the particles become higher in liquids with lower viscosity.
6. The motion depends only on the mass and the size of the particle and not on the material it is made of.

Kinetic Theory Of Gases – Basic Assumptions Of Kinetic Theory Of Gases

A gas is made of atoms and molecules. The three variables—volume, pressure, and temperature, are all consequences of the motion of the molecules.

• The kinetic theory of gases relates the motion of the molecules to the volume, pressure, and temperature of the gas. Actually, the kinetic theory of gases explains the macroscopic properties of the gases, though it is a microscopic mode.
• Rudolf Clausius and James Clark Maxwell developed the kinetic theory of gases and explained gas laws in terms of motion of the gas molecules.
• In order, to formulate the kinetic theory of gases some simplifying assumptions are made about the behavior of the molecules of the ideal gas. The assumptions are

1. A gas is composed of a large number of molecules. For a particular gas, the molecules are identical. But they are different for different gases.
2. Every gas molecule behaves as a point mass. So the sum of their volumes is negligible compared to the volume of the container. The intermolecular space in the container is an empty space.
3. The molecules are in continuous and random motion in all possible directions. The value of molecular velocities varies from zero to infinity.
4. During random motion, the molecules collide with each other and with the walls of the container. These collisions are perfectly elastic. This means that the velocity changes due to collision, but the net momentum and kinetic energy remain unchanged.
5. The average distance between the molecules is sufficiently large, so that the attractive or repulsive forces between them are negligible except during collision. As a result,
   • Molecular motion is unrestricted and the gas spreads throughout the inner volume of its container
   • The potential energy of a molecule is negligible, the total energy comes from its kinetic energy only
   • Between two collisions, a molecule moves with uniform velocity (according to Newton’s first law of motion). The straight line path between two successive collisions is called a free path.
6. Every collision is instantaneous the time of a collision is negligible compared to the time taken by a molecule to describe a free path.
7. The gas is homogeneous and isotropic. This means that the properties of the gas in any small portion are identical to those in any other equivalent portion anywhere inside the container.

A gas obeying the properties outlined in these assumptions is called an ideal gas or a perfect gas. Real gases show some deviations from these properties. Real gases available to us are good approximation of an ideal gas at low pressure and high temperature.

The kinetic theoretical definitions of mass and volume of a gas are obtained directly from the above assumptions:

1. The mass of a gas is defined as the sum of the masses of the constituent molecules.
2. The volume of a gas is defined as the inner volume of the gas container.

Mean free path: The straight line path described by a molecule between two collisions is called a free path.

• The gas molecules move randomly. As a result, the lengths of the free paths vary in an irregular manner. So, to get a concrete picture, the Idea of a mean-free path becomes essential.
• It is the average distance that a molecule can travel between two successive collisions.

Mean free path Definition: The mean value of the distance travelled by a molecule between two successive collisions Is called the mean free path (λ).

• In other words, if a molecule suffers N number of collisions with other molecules when it travels through a total distance d, then the mean free path is, \(\lambda=\frac{d}{N}\).
• The basic assumptions of kinetic theory describe every molecule as a point mass. But the value of mean free path becomes theoretically infinite if the molecules are treated as geometrical points.
• So some deviations from the assumptions, are necessary. Every molecule is assumed to be a very small hard sphere of non-zero radius. Then it is possible to get an effective theoretical value of the mean free path.

An expression for the free path: Let σ = diameter of each molecule of the gas n = number of molecules per unit volume = number density of the molecules.

Let us consider a particular molecule of the gas moving with a velocity v at an instant of time. It will collide with all molecules whose centres come at a distance of cr or less along its line of motion. Now we choose a cylinder of radius cr and of length v. Clearly,

1. The axis of this cylinder is the path described by the chosen molecule in unit time, and
2. All other molecules, whose centers come within this cylinder, collide with the chosen molecule in that unit time.

The volume of this cylinder = cross-sectional area x length = πσ²v, and the number of molecules having centres in this volume = πσ²vn. So, the number of collisions per unit of time, N = πσ²vm.

The mean free path of the molecules is, therefore,

= \(\frac{\text { path described by a molecule }(d)}{\text { number of collisions }(N)}=\frac{\nu}{\pi \sigma^2 v n}\)

i.e., \(\lambda=\frac{1}{\pi \sigma^2 n}\)….(1)

This equation (1) shows that the mean free path (λ) of gas molecules is

1. Inversely proportional to the number of gas molecules (n) in a unit volume of the gas and
2. Inversely proportional to the square of molecular diameter (σ).

So, \(\lambda \propto \frac{1}{n} and \lambda \propto \frac{1}{\sigma^2}\),

i.e., \(\lambda \propto \frac{1}{\sigma^2 n} or, \lambda=\frac{k}{\sigma^2 n}\)

The constant k in equation (1) is \(\frac{1}{\pi}\). However, it has been estimated by different scientists by different other methods. The estimates give different results, but the value of k is always slightly greater or slightly less than 1. Then, the approximate expression for the mean free path is \(\lambda=\frac{1}{\sigma^2 n}\).

Kinetic Theory Of Gases – Mean Speed And Root Mean Square Speed of Gas Molecule

Molecular velocity is a vector quantity. The number of gas molecules in any container is very large. So the velocity vectors are oriented randomly in all possible directions.

• As a result, the resultant velocity vector must be zero. Consequently, the mean velocity of the molecules is also zero. Clearly, this zero value is useless as it gives no information about the order of magnitude of the molecular velocities.
• Alternatively, we may take the magnitudes only of the molecular velocities to calculate the mean. Certainly, it is non-zero and a useful quantity. We also know the molecules move in straight lines between collisions.
• So the magnitude of molecular velocity is actually the molecular speed. The calculated mean velocity is essentially the mean speed of the molecules. However, mean speed is often loosely termed as mean velocity.

Let N be the number of molecules of a gas in a closed container and, at any instant, c₁, c₂, c₃…..c_N be the magnitudes of velocities of the N molecules, respectively.

So, mean velocity or mean speed of the molecules, \(\bar{c}=\frac{c_1+c_2+c_3+\cdots+c_N}{N}\)

Mean square velocity of the molecules is defined as the mean of the squares of velocities,

⇒ \(\overline{c^2}=\frac{c_1^2+c_2^2+c_3^2+\cdots+c_N^2}{N}\)

Root mean square speed or rms speed of the molecules, defined as the square root of mean square speed,

c = \(\sqrt{\overline{c^2}}=\sqrt{\frac{c_1^2+c_2^2+c_3^2+\cdots+c_N^2}{N}}\)

The mean velocity \(\bar{c}\) and the rms speed c of the gas molecules in a container are not equal. For example, let us take three molecules with velocities 40 m · s^-1, 80 m · s^-1, and 120 m · s^-1.

Then, \(\bar{c}=\frac{40+80+120}{3}=80 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

c = \(\sqrt{\frac{(40)^2+(80)^2+(120)^2}{3}}=86.4 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

In general, the rms speed is slightly greater than the mean velocity. In kinetic theory, the role of the rms speed is comparatively more important than that of the mean velocity.

 

 

Unit 9 Behavior Of Perfect Gas And Kinetic Theory Chapter 1 Kinetic Theory Of Gases

Deduction Of Difference Gas Laws From Kinetic Theory Of Gases

We have so far developed the kinetic theory of gases to a certain stage. Now it Is possible to see that the theoretical result of kinetic theory matches exactly with the thermodynamic gas laws obtained from experiments. This proves the success of the kinetic theory of gases.

1. Boyle’s law: According to the kinetic theory of gases, \(T \propto E \text { and } E=\frac{3}{2} p V . \text { So, } p V \propto T\). If T = constant for a certain amount of gas, then pV = constant. This is Hoyle’s law.

2. Charles’ law: According to the kinetic theory of gases, \(T \propto E \text { and } E=\frac{3}{2} p V \text {. So } p V \propto T\). If p = constant for a certain amount of gas, then V ∝ T, This is Charles’ law.

3. Pressure law: According to the kinetic theory of gases, \(T \propto E \text { and } E=\frac{3}{2} p V \text {. So } p V \propto T\). If V = constant for a certain amount of gas, then p ∝ T. This is Charles’ law of pressure.

4. Joule’s law: According to the kinetic theory of gases, E = 3/2 RT. So E is a function of temperature only; it does not depend on the volume or pressure of the gas. This is Joule’s law or Mayer’s hypothesis, as discussed In the chapter First and Second Law of Thermodynamics,

5. Avogadro’s law: Let equal volumes of two gases be taken at the same pressure and temperature. The pressure, temperature, and volume are p, T, and V, respectively.

Now for the first gas,

N₁ = total number of molecules in the container,

m₁ = mass of each molecule,

c₁ = rms speed of the molecules.

Then, \(n_1=\frac{N_1}{V}\) = number of molecules per unit volume. According to kinetic theory, the pressure of the gas,

p = \(\frac{1}{3} m_1 n_1 c_1^2=\frac{1}{3} m_1 \frac{N_1}{V} c_1^2\)

Pressure being the same, so we get similarly for the second gas,

p = \(\frac{1}{3} m_2 \frac{N_2}{V} c_2^2 .\)

So, \(\frac{1}{3} m_1 \frac{N_1}{V} c_1^2=\frac{1}{3} m_2 \frac{N_2}{V} c_2^2\)

or, \(m_1 N_1 c_1^2=m_2 N_2 c_2^2\)…..(1)

Again, the temperature of the two gases is the same. So the average kinetic energy of a molecule is equal for the two gases. This means that

⇒ \(\frac{1}{2} m_1 c_1^2=\frac{1}{2} m_2 c_2^2 \text { or, } m_1 c_1^2=m_2 c_2^2\)….(2)

From relations (1) and (2), we get N₁ = N₂. So, equal So, pV = RT (1 mol of an ideal gas) volumes of different gases, at the same pressure, and Equation (4) is known as the ideal gas equation temperature, contains an equal number of molecules. This is Avognclro’s law.

6. Dalton’s law of partial pressure: The pressure of a gas mixture on the walls of its container is equal to the sum of the partial pressures exerted by constituent gases separately, at same temperature as that of the mixture, provided that the gases do not react chemically with each other—this is Dalton’s law.

Let several gases be mixed in a closed container. Their densities are, ρ₁, ρ₂, ρ₃…… and the molecular rms speeds are c₁, c₂, c₃ ….. respectively. Every gas molecule moves with its own kinetic energy, which does not depend on the motion of the other molecules. So, the net pressure on the container will be the sum of the pressures exerted by all individual molecules. Then, the pressure of the gas mixture is

p = \(\frac{1}{3} \rho_1 c_1^2+\frac{1}{3} \rho_2 c_2^2+\frac{1}{3} \rho_3 c_3^2+\cdots\)….(3)

= \(p_1+p_2+p_3+\cdots\)…..(3)

Here, p₁, p₂, p₃,……. are the partial pressures of the first second, third, … gases on the walls of the container. So equation (3) expresses Dalton’s law of partial pressure.

7. Graham’s law of diffusion: The rate of diffusion of a gas in a mixture is inversely proportional to the square root of the density of the gas—this is Graham’s law.

Let the densities of two gases be ρ₁ and ρ₂ and the rms velocities of the molecules be c₁ and c₂, respectively. The gases are allowed to diffuse with each other at the same temperature and same pressure. The diffusion is due to the motion of molecules so the rate of diffusion is clearly proportional to the rms speed of the molecules.

Now, p = \(\frac{1}{3} \rho_1 c_1^2=\frac{1}{3} \rho_2 c_2^2\)

or, \(\rho_1 c_1^2=\rho_2 c_2^2 or, \frac{c_1}{c_2}=\sqrt{\frac{\rho_2}{\rho_1}}\).

As, rate of diffusion r  ∝ c, we have \(\frac{r_1}{r_2}=\frac{c_1}{c_2}, i.e., \quad \frac{r_1}{r_2}\)= \(\sqrt{\frac{\rho_2}{\rho_1}}\)

or, \(r \propto \frac{1}{\sqrt{\rho}}\).

This is Graham’s law.

8. Ideal gas equation: According to the kinetic theory of gases, \(T \propto E \text { and } E=\frac{3}{2} p V \text {. So, } p V \propto T \text {. }\). Then, pV = kT, where k is a constant. For 1 mol of an ideal gas, this constant k is called the universal gas constant, denoted by R.

So, pV= RT (1 mol of an ideal gas)…(4)

Equation (4) is known as the ideal gas equation.

Unit 9 Behavior Of Perfect Gas And Kinetic Theory Chapter 1 Kinetic Theory Of Gases

Limitations Of Ideal Gas Laws

If a gas obeys Boyle’s law and Charles’ law accurately, then it is called an ideal gas. But in practice, real gases do not obey these ideal gas conditions in all circumstances.

Usually, a real gas behaves as an ideal gas at high temperatures and low pressures. But at low temperatures and high pressures, the behaviour deviates from that of an ideal gas.

The equation of state for 1 mol of an ideal gas is pV = RT. A real gas deviates from this equation chiefly due to the following two reasons:

1. The kinetic theory assumes that gas molecules are point masses and the volume of the molecules is negligible compared to the total volume of the gas. But every molecule, however small, has a finite volume. So their total volume is not always negligible.
   • In particular, at low temperatures and high pressures, the volume of a gas is comparatively small. In this case, the volume of the gas molecules becomes an important factor.
   • The effective volume for the motion of the molecules inside the gas container of volume V is reduced by an amount b (say). Then the equation of state for 1 mol of the gas becomes p(V-b) = RT.
2. The kinetic theory further assumes that the molecules do not attract one another. But in particular, at low temperatures and high pressures, the molecules come closer to one another.
   • As a result, the attractive forces are no longer negligible. Now, consider a molecule near the wall of the container. It experiences a resultant force towards the interior due to attractions by the other molecules. So it collides with the wall at a comparatively less velocity.

As a result, the pressure on the wall becomes less. Let p’ be the reduction of the pressure on the wall due to all these molecules, van der Waals established that \(p^{\prime}=\frac{a}{v^2}\) where a is a constant for a particular gas. Now, if p is the effective pressure on the wall, then the pressure would be \(p+p^{\prime} \text { or } p+\frac{a}{V^2}\) considering that the gas was ideal.

So the equation of state for 1 mol of a real gas becomes \(\left(p+\frac{a}{V^2}\right)(V-b)=R T\)….(1)

Equation (1) is called the van der Waals equation for a real gas. The constants a and b are known as van der Waals constants; their values depend on the nature of the gas. For n mol of a real gas, let V be its volume. Then molar volume = V/n.

Then, we get \(\left\{p+\frac{a}{(V / n)^2}\right\}\left\{\frac{V}{n}-b\right\}=R T\)

or, \(\left(p+\frac{a n^2}{V^2}\right)(V-n b)=n R T\)…(2)

This is the form of van der Waals equation for n mol of a real gas. It is to be noted that the van der Waals equation is only one of several equations of state of real gases, proposed by different scientists.

Unit 9 Behavior Of Perfect Gas And Kinetic Theory Chapter 1 Kinetic Theory Of Gases

Degree Of Freedom (DOF)

Degree Of Freedom Definition: The minimum number of independent coordinates necessary to specify the instantaneous position of a moving body is called the degree of freedom of the body.

Degree Of Freedom Example:

1. Let us consider the motion of a particle falling freely under gravity. We take the initial point as the origin and the downward line as the z-axis. Then the position of the particle at any instant is specified by the z-coordinate only.

So, the number of degrees of freedom of the particle is 1. Essentially, the degree of freedom of every one-dimensional motion is, for example, the motion of a car along a road, an ant moving on a stationary rope, etc.

2. Motions of projectiles under gravity, orbital motion of planets around the sun, circular motion, motion of an ant on the floor of a room, etc., are examples of two-dimensional motions, in each case, any one point on the plane, Is chosen as the origin and two perpendicular axes x and y are considered. Then the position of the object at any Instant Is specified by the x- and y- coordinates. So, the number of degrees of freedom in two-dimensional motion Is 2.

3. According to the kinetic theory, all gas molecules of an Ideal gas are point masses and they are In a completely random to-and-fro motion. At least three coordinates (say x, y, z) are necessary to specify the position of a molecule at any Instant.

So, the number of degrees of freedom of an Ideal gas molecule is 3. Essentially, every three-dimensional motion has 3 degrees of freedom, for example, Brownian motion, motion of a fly in a room, etc.

• In the above examples, the particle, the object, and the gas molecule all are considered to be as a point mass, which cannot undergo rotation, if the body is rigid and has a finite size, it can undergo rotation also, about any axis, So, a rigid body will have degrees of freedom both due to its translatory motion and rotatory motion.
• Like translatory motion, the rotatory can also be resolved into three mutually perpendicular components. Thus a rigid body has six degrees of freedom, 3 for translatory motion and 3 for rotatory motion.
• Now, let us consider a system of two particles or two-point masses. Each particle has three degrees of freedom, so the system has six degrees of freedom. If the two particles remain at a fixed distance from each other, then there is one definite relationship between them.
• These definite relationships are known as constraints. As a result, the number of independent coordinates required to describe the configuration of the system is reduced by one. Hence, the system has (6-1) = 5 degrees of freedom.

These 5 degrees of freedom may be interpreted in another way: degrees of freedom for the translatory motion of the centre of mass = 3 and degrees of freedom for the rotatory motion of the two particles around the center of mass = 2.

In a system consisting of N particles, if the particles possess k independent relations i.e., constraints among them, then the number of degrees of freedom of the system is given by, f = 3N – k.

Degrees of freedom of different types of gases:

1. Monatomic gas: The molecule of a monatomic gas (for example, neon, helium, argon, etc.) consists of a single atom (a point mass). At least three coordinates (say x, y, z) are necessary to specify the position of the molecule at any instant in the three-dimensional space. So, the number of degrees of freedom of a monatomic gas molecule, f = 3×1-0 = 3.

2. Diatomic gas: The molecule of a diatomic gas like hydrogen, oxygen, nitrogen etc. has two atoms in it. Two point atoms have a fixed distance between them (neglecting the vibration of the atoms in the molecules)

i. e., the number of constraints is 1. Here, N = 2 and k = 1

∴ f = 3×2-1 = 5

3. Triatomic gas: Triatomic gas molecules are of two types:

(1) In a linear molecule such as CO₂, CS₂ > HCN, etc. the three atoms are arranged in a straight line. The number of independent relations between them is only two.

∴ f = 3×3-2 – 7 i.e., such a molecule has seven degrees of freedom.

2. In a non-linear molecule like H₂O, SO₂, etc. the three atoms are located at the three vertices of a triangle. Hence, there are three fixed distances among the three atoms.

∴ f = 3×3-3 = 6

Therefore, a non-linear triatomic molecule has six degrees of freedom.

Degrees of freedom in different cases:

 

 Kinetic Theory Of Gases Conclusion

The subject of study in which theoretical expressions on the bulk properties of a body are obtained from the application of Newton’s laws of motion on the internal molecular behavior is called the kinetic theory of matter. This approach has been highly successful for gases.

• The random and perpetual motion of very small particles present as impurities in a liquid or gas is known as Brownian motion. This happens due to random collisions of the Brownian particles with the molecules in matter. This motion furnishes evidence of the molecular model.
• The kinetic theory of gases relates the motion of the molecules of the gas to the volume, pressure, and temperature of the gas. Actually, this theory explains the macroscopic properties of the gases with the help of microscopic parameters.

Three basic assumptions of the kinetic theory of gases are—

1. Molecules are point masses; the intermolecular space is much larger than the space occupied by the molecules.
2. The attraction between molecules is negligible. As a result, the molecular potential energy is zero, i.e., the energy is purely kinetic.
3. Molecular motion is continuous and random. A molecule may have any velocity between zero and infinity in any direction. A molecule may have any velocity between zero and infinity in any direction.

The straight-line path described by a molecule between two successive collisions is called a firepath. The mean value of the lengths of different free paths of different molecules of a gas is called the mean free path.

The pressure of a gas in a container depends on

1. The mass of a molecule,
2. The number of molecules in unit volume and
3. The average velocity of the molecules.

Temperature is a property of a gas, which is proportional to the total kinetic energy of the gas molecules.

Absolute zero temperature is the temperature at which the internal energy of the gas becomes zero, i.e., the molecular motion stops entirely.

The velocity which is possessed by the highest number of gas molecules in a container is called the most probable velocity.

Gases obeying Charles’ law and Boyle’s law perfectly are called ideal or perfect gases.

In general, real gases deviate from this ideal behavior, especially at

1. High pressures and
2. Low temperatures.

The minimum number of independent coordinates necessary to specify the instantaneous position of a moving particle is called the degree of freedom of the tire particle.

Principle of equipartition of energy: The average molecular kinetic energy of any substance is equally shared among the degrees of freedom; the average kinetic energy of a molecule per degree of freedom is 1/2 kT (T = absolute temperature and k = Boltzmann constant (1.38 x 10^-23 J · K^-1).

Kinetic Theory Of Gases Useful Relations For Solving Numerical Examples

Mean free path of a gas molecule (λ):

1. \(\lambda=\frac{d}{N}\) where d = total distance traveled by a molecule, N = total number of collisions suffered by that molecule through the distance d.

2. \(\lambda=\frac{1}{\pi \sigma^2 n}\) where, σ = diameter of each molecule of the gas, n = the number of molecules per volume i.e., the number density of the molecule.

Let c₁, c₂,…..c_N be the magnitudes of instantaneous velocities of N molecules in a gas. Then,

1. Mean velocity, \(\bar{c}=\frac{c_1+c_2+\cdots+c_N}{N}\)

2. Root mean square speed or rms speed, \(c=\sqrt{\frac{c_1^2+c_2^2+\cdots+c_N^2}{N}}\)

At absolute temperature T,

\(\begin{array}{|c|c|c|}
\hline \begin{array}{c}
\text { Average speed of } \\
\text { a gas molecule } \\
(c)
\end{array} & \begin{array}{c}
\text { rms speed of a } \\
\text { gas molecule } \\
(c)
\end{array} & \begin{array}{c}
\text { Most probable } \\
\text { speed of a gas } \\
\text { molecule }\left(c_m\right)
\end{array} \\
\hline \sqrt{\frac{8 k T}{\pi m}} & \sqrt{\frac{3 k T}{m}} & \sqrt{\frac{2 k T}{m}} \\
\hline
\end{array}\)

 

∴ \(\bar{c}: c: c_m=\frac{2}{\sqrt{\pi}}: \sqrt{\frac{3}{2}}: 1\)

Pressure of an ideal gas, p = \(\frac{1}{3} \rho c^2=\frac{1}{3} m n c^2\), where m- mass of a molecule, n = number of molecules in unit volume and ρ = mn = density.

The internal energy of a gas in a container, which is equal to the sum of the kinetic energies of the molecules, is

U = E = \(\frac{3}{2} p V ; \quad \text { So, } p=\frac{2}{3} \frac{E}{V}=\frac{2}{3} u \text {, }\)

where u = energy per unit volume.

• If M is the molecular weight of a gas, the rms speed of the molecules is related to temperature T of the gas by the relation, \(c=\sqrt{\frac{3 R T}{M}} \quad \text { or, } \quad c \propto \sqrt{T}\)
• The equation of state for 1 mol of an ideal gas is p V = R T.
• For real gases, volume and pressure corrections lead to the van der Waals equation of state:

⇒ \(\left(p+\frac{a}{V^2}\right)(V-b)=R T\)

• For n mol of real gas, van der Waals equation of state is \(\left(p+\frac{a n^2}{V^2}\right)(V-n b)=n R T\) [where, a, b are small positive constants ‘a’ is related to the average force of attraction between the molecules and ‘b’ Is related to the total volume of the molecules.
• The average kinetic energy of a gas molecule, e = \(\frac{3}{2} k T\)
• If some amount of gas contains N molecules, the total internal energy i.e., total kinetic energy, E = \(\frac{3}{2}Nk T\)
• For 1 mol of a gas, N = N_A = Avogadro’s number.
• Then, \(E=\frac{3}{2} N_A k T=\frac{3}{2} R T \text {, where } R=N_A k \text {. }\)
• Molar specific heat at constant volume, \(C_v=\frac{d Q}{d T}=\frac{d E}{d T}\)

If n₁ mol of a gas is mixed with n₂ mol of another gas (they do not react with each other), then,

1. Molar specific heat of the mixture at constant volume, \(C_\nu=\frac{n_1 C_{\nu_1}+n_2 C_{\nu_2}}{n_1+n_2}\) where, \(C_{\nu_1}\) = molar specific heat at constant pressure of 1st and 2nd gases respectively.

2. Molar specific heat of the gas mixture at constant pressure, \(C_p=\frac{n_1 C_{p_1}+n_2 C_{p_2}}{n_1+n_2}\) where, \(C_{p_1}\) and \(C_{p_2}\) are the molar specific heat at constant pressure of 1st and 2nd gases respectively.

3. The ratio of Cp and Cv for the mixture is,

⇒ \(\gamma=\frac{C_p}{C_v}=\frac{n_1 C_{p_1}+n_2 C_{p_2}}{n_1 C_{v_1}+n_2 C_{v_2}}\)

For 1 mol of a monatomic gas, \(C_\nu=\frac{d E}{d T}=\frac{3}{2} R ; C_p=C_\nu+R=\frac{5}{2} R ; \gamma=\frac{C_p}{C_\nu}=\frac{5}{3}\)

In general cases, if f is the number of degrees of freedom of an ideal gas molecule then \(C_\nu=\frac{f_2}{2} R ; C_p=\left(1+\frac{f}{2}\right) R ; \gamma=\frac{C_p}{C_\nu}=1+\frac{2}{f}\)

Kinetic Theory Of Gases Very Short Answer Type Questions

Question 1. What is the name of the smallest entity of matter that exhibits all the properties of that matter?
Answer: Molecule

Question 2. Which one of the following has the highest intermolecular force—solid, liquid, or gas?
Answer: Solid

Question 3. If a gas jar filled with a light gas like hydrogen is held side down on another gas jar filled with carbon dioxide, it is observed that the two gases produce a homogeneous mixture in the jars. What is the name of this process?
Answer: Diffusion

Question 4. How does the velocity of Brownian particles change due to the movement of the vessel?
Answer: No change occurs

Question 5. What is the direction of velocities of gas molecules according to the kinetic theory of gases?
Answer: All possible directions

Question 6. Gas molecules collide with each other and with the walls of the container. What is the type of these collisions? .
Answer: Perfectly elastic

Question 7. What do you call the straight line path described by a gas molecule between two successive collisions?
Answer: Free path

Question 8. Both vaporization and vapor pressure prove the ________ of molecules of a liquid.
Answer: Mobility

Question 9. Brownian motion supports the _______ of the matter.
Answer: Kinetic theory

Question 10. In Brownian motion in a medium, if the particles decrease in size, how does their velocity vary?
Answer: Increases

Question 11. Does the velocity of the particles increase or decrease, when the viscosity increases in Brownian motion in a medium?
Answer: Decreases

Question 12. Which gases obey the basic assumptions of the kinetic theory?
Answer: Ideal gases

Question 13. According to the kinetic theory of gases, every gas molecule behaves as a ________
Answer: Point mass

Question 14. According to the kinetic theory of gases, the velocity of gas molecules varies from ______ to ______
Answer: zero, infinity

Question 15. Which is greater rms speed or mean velocity?
Answer: rms speed

Question 16. Does the pressure of a gas increase or decrease when the velocity of the gas molecules increases?
Answer: Increases

Question 17. On which other factor does the pressure of a gas depend, besides the number of molecules per unit volume and the temperature of the gas?
Answer: Mass of the gas molecules

Question 18. Is the most probable velocity of gas molecules higher or lower than the mean velocity?
Answer: Lower

Question 19. Will the rms speed of oxygen and hydrogen gas molecules be the same at equal temperatures?
Answer: No, hydrogen gas will have a higher rms speed

Question 20. What is the ratio of the rms speeds of O₃ and O₂ at a certain temperature?
Answer: √2: √3

Question 21. By how many times will the pressure of a gas kept in a gas container of constant volume increase to double the rms speed of the gas molecules?
Answer: 4 times

Question 22. The velocities of the three gas molecules are 4cm · s^-1, 8 cm · s^-1, and 12 cm · s^-1, respectively. Calculate their rms speed.
Answer: 8.64 cm · s^-1

Question 23. What is the relation between rms speed and molecular mass of a gas?
Answer: rms speed is inversely proportional to the square root of the molecular mass of that gas

Question 24. Hydrogen and oxygen gases are kept in two vessels at the same temperature and pressure. What is the ratio of the rms speed of their molecules?
Answer: 4:1

Question 25. If a gas molecule of mass m and velocity u collides perpendicularly with a wall of a container, what will be the value of momentum of the molecule after the collision?
Answer: mu

Question 26. If n number of molecules, each having mass m and velocity u, perpendicularly hit the walls of a container in every second, what will be the value of the applied force?
Answer: 2mnu

Question 27. In the kinetic theory of gases, _____ is more important than mean velocity.
Answer: rms speed

Question 28. What is the name of the force that acts among the molecules of matter?
Answer: Intermolecular force

Question 29. Under which conditions do real gases behave as ideal gases?
Answer: At low pressure and high temperature

Question 30. Which property of a gas is proportional to the net internal energy of the gas molecules?
Answer: Temperature of the gas

Question 31. At which temperature does the kinetic energy of gas molecules become zero?
Answer: Absolute zero temperature

Question 32. To which gases is the van der Waals’ equation applicable?
Answer: Real gases

Question 33. If the temperature of a gas is increased at constant volume, how will the number of collisions of the molecules per unit time change?
Answer: Increase

Question 34. What is the dimension of an in van der Waals’ equation \(\left(p+\frac{a}{V^2}\right)(V-b)=R T?\)
Answer: ML^-3T^-2

Question 35. What is the dimension of b in van der Waals’ equation \(\left(p+\frac{a}{V^2}\right)(V-b)=R T?\)
Answer: L³

Question 36. What is the relation between the pressure p of a gas and its energy density?
Answer: \(\left[p=\frac{2}{3} u\right]\)

Question 37. According to the kinetic theory of gases, as there is no attractive force between the gas molecules, the entire energy of them is ______
Answer: Kinetic energy

Kinetic Theory Of Gases  Assertion Reason Type Question And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 Is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: The root mean square speeds of the molecules of different ideal gases at the same temperature are the same.

Statement 2: The average translational kinetic energy of molecules of a different ideal gas is same at the same temperature.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 2.

Statement 1: The rms speed of oxygen molecules (O₂) at an absolute temperature T is c. If the temperature is doubled and oxygen gas dissociates into atomic oxygen, the rms speed remains unchanged.

Statement 2: The rms speed of the molecules of a gas is directly proportional to √T/M.

Answer: 1. Statement 1 is true, and statement 2 Is true statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: The total translational kinetic energy of all the molecules of a given mass of an ideal gas is 1.5 times the product of its pressure and volume.

Statement 2: The molecules of a gas collide with each other and the velocities of the molecules change due to the collision.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 4.

Statement 1: The mean free path of gas molecules, varies inversely with the density of the gas.

Statement 2: The mean free path of gas molecules is defined as the average distance traveled by a molecule between two successive collisions.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 5.

Statement 1: The following show \(\frac{pV}{T}\) versus p graph for a certain mass of O₂ gas at two temperatures T₁ and T₂. It follows from the graph that T₁ > T₂.

Statement 2: At higher temperatures, real gas behaves more like an ideal gas.

Answer: 1. Statement 1 is true, and statement 2 Is true statement 2 is a correct explanation for statement 1.

Question 6.

Statement 1: For an ideal gas, at a constant temperature, the product of the pressure and the volume is constant.

Statement 2: The mean square velocity of die molecules is inversely proportional to mass.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 7.

Statement 1: The total translational kinetic energy of all the molecules of a given mass of an ideal gas is 1.5 times the product of its pressure and volume.

Statement 2: The molecules of a gas collide with each other and the velocities of the molecules change due to the collision.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Kinetic Theory Of Gases Match Column 1 with Column 2

Question 1.

Answer: 1. C, 2. B, D 3. A, 4. A

Question 2.

Answer: 1. C, 2. B, 3. A

Question 3.

R = universal gas constant, f = number of degrees of freedom, T = temperature.

Answer: 1. C, 2. B, 3. A

Question 4. Match the following columns according to the graph.

Answer: 1. C, 2. A, 3. B

Kinetic Theory Of Gases Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. The pressure exerted by an ideal gas is p = \(\frac{1}{3} \frac{M}{V} c^2\), where the symbols have their usual meanings. Using standard gas equation, pV = RT, we find that \(c^2=\frac{3 R T}{M} \quad \text { or } \quad c^2 \propto T\) Average kinetic energy of translation of 1 mol of gas = \(\frac{1}{2} M c^2=\frac{3 R T}{2}\)

1. Average thermal energy of a helium atom at room temperature (27°C) is (given, Boltzmann constant k= 1.38 x 10^-23 J · K^-1)

1. 2.16 x 10²¹ J
2. 6.21 x 10²¹ J
3. 6.21 x 10^-21 J
4. 6.21 x 10^-23 J

Answer: 3. 6.21 x 10²¹ J

2. Average thermal energy of 1 mol of helium at this temperature is (given, gas constant for 1 mol = 8.31 J · mol^-1 · K^-1)

1. 3.74 x 10³ J
2. 3.74 x 10^-3 J
3. 3.47 x 10⁶ J
4. 3.47X10^-6 J

Answer: 1. 3.74 x 10³ J

3. At what temperature, when pressure remains unchanged, will the rms speed of hydrogen double its value at STP?

1. 819 K
2. 819 °C
3. 1000K
4. 1000°C

Answer: 2. 819 °C

4. At what temperature, when pressure remains unchanged, will the rms speed of a gas be half its value at 0°C?

1. 204.75 K
2. 204.75 °C
3. -204.75 K
4. -204.75 °C

Answer: 4. -204.75 °C

Question 2. If c₁, c₂, c₃ …. are random speeds of gas molecules at a certain moment then average velocity c_av = \(\frac{c_1+c_2+c_3+\cdots+c_n}{n}\) and root mean square speed of gas molecules,

⇒ \(c_{\mathrm{rms}}=\sqrt{\frac{c_1^2+c_2^2+c_3^2+\cdots+c_n^2}{n}}=c.\)

Further, c² ∝ T or, c ∝ √T.

At 0 K, c =0, i.e., molecular motion stops,

1. If three molecules have velocities 0.5km · s^-1, 1 km · s^-1 and 2 km · s^-1, the ratio of rms speed and average velocity is

1. 0.134
2. 1.34
3. 1.134
4. 13.4

Answer: 3. 1.134

2. The temperature of a certain mass of a gas is doubled. The rms speed of its molecules becomes n times, where n is

1. \(\sqrt{2}\)
2. 2
3. \(\frac{1}{\sqrt{2}}\)
4. \(\frac{1}{2}\)

Answer: 1. \(\sqrt{2}\)

3. KE per molecule of the gas in the above question becomes x times, where x is

1. \(\frac{1}{2}\)
2. \(\frac{1}{4}\)
3. 4
4. 2

Answer: 4. 2

4. KE per mole of hydrogen at 100°C (given R = 8.31 J · mol^-1 · K^-1) is

1. 4946 J
2. 4649 J
3. 4496 J
4. 4699J

Answer: 2. 4649 J

5. At what temperature, when pressure remains constant, will the rms speed of the gas molecules be increased by 10% of? rms speed at STP?

1. 57.3 K
2. 57.3 °C
3. 557.3 K
4. -57.3 °C

Answer: 2. 57.3 °C

Question 3. A cubical box of side lm contains helium gas (atomic weight = 4) at pressure 10 N • m^-2. During an observation time of 1s, an atom traveling with rms speed parallel to one of the edges of the cube was found to make 500 hits with a particular wall without any collision with other atoms.

1. Evaluate the temperature of the gas.

1. 125K
2. 160K
3. 181K
4. 185K

Answer: 2. 160K

2. Evaluate the average kinetic energy per atom.

1. 3.31 x 10^-21 J
2. 3.75 x 10⁶ J
3. 3.81 x 10^-15 J
4. 3.22 x 10³ J

Answer: 1. 3.31 x 10^-21 J

3. Evaluate the total mass of the helium gas in the box.

1. 9×10^-4 kg
2. 5x 10^-3 kg
3. 3 x 10^-4 kg
4. 7 x 10^-3 kg

Answer: 3. 7 x 10^-3 kg

Kinetic Theory Of Gases Integer Answer Type Questions

In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.

Question 1. Two identical cylinders contain helium at 3.5 standard atmospheres and argon at 2.5 standard atmospheres respectively. If both these gases are filled in one of the cylinders, what would be the pressure of the mixture?
Answer: 6

Question 2. The rms speed of molecules of a gas at -73 °C and 1 standard atmosphere pressure is 100 m · s^-1. The temperature of the gas is increased to 527°C and pressure is doubled. The rms speed becomes k times. What is the value of k?
Answer: 2

Question 3. The density of a gas is 6 x 10^-2 kg· m^-3 and the root mean square speed of the gas molecules is 500 m · s^-1. The pressure exerted by the gas on the walls of the vessel is n x 10³ N · m^-2. Find the value of n.
Answer: 5

Question 4. A gas has molar heat capacity c = 37.55 J · mol^-1 · K^-1, in the process pT = constant. Find the number of degrees of freedom of the molecules of the gas.
Answer: 5

Question 5. A vessel has 6g of hydrogen at pressure p and temperature 500 K. A small hole is made in it so that hydrogen leaks out How much hydrogen (in g) leaks out if the final pressure is \(\frac{p}{2}\) and temperature falls to 300K?
Answer: 1

 

Kinetic Theory Of Gases – Pressure Of A Perfect Gas According To The Kinetic Theory

Gas molecules, due to their random motion, collide continuously with the inner walls of its container. As a result, an outward force or thrust acts on the walls. The pressure of a gas is defined as the force exerted normally by the gas molecules on unit area of the walls of its container.

There are a large number of molecules in the container and they have random velocities in all possible directions. Statistically, on unit surface of any wall of the container, equal number of molecules collide with equal average velocity. As a result, the gas exerts equal pressure on the walls in all directions.

It is evident that the pressure of a gas is high, if

1. The gas molecules are heavy so that a large force acts on the walls,
2. The molecules move fast, so that a big impact is exerted on the walls and
3. The molecules are densely situated so that the number of collisions with the walls is high.

This means that the pressure of a gas on the walls of its container depends on

1. The mass of each molecule,
2. Average velocity of the molecules and
3. The number of molecules in a unit volume inside the container.

Derivation of the Expression for Pressure of an Ideal Gas: Let us take a cubical container.

It is filled with a gas. The inside surfaces of the container are such that the molecules suffer elastic collisions with them.

Let l be the length of each side of the container, m be the mass of each gas molecule and N be the total number of molecules in the container.ρ

Sp, A = \(l^2=\text { area of each of the six inner surfaces, }\)

V = \(l^3=\text { volume of the gas of the container, }\)

M = \(m N=\text { mass of the gas, }\)

ρ = \(\frac{M}{V}=\frac{m N}{V}=\frac{m N}{l^3}=\text { density of the gas, }\)

n = \(\frac{N}{V}=\frac{N}{\beta}\)= number of molecules in unit volume

= number density of the gas

= molecular concentration

Then, ρ = mn

Now, one corner O of the cubical container is taken as the origin, and the x, y, and z axes are chosen along the three mutually perpendicular sides at O.

Let c be the velocity of a gas molecule and u, v, w be the velocity components along the three axes, respectively.

So, c² = u² + v² + w²

Now, let us consider only the parallel surfaces R and S, which are perpendicular to the x-axis. As the collisions are elastic, the molecule hits the surface R at velocity u and rebounds from this surface In the opposite direction, i.e., the velocity of the molecule will he -u.

But v and w do not change In this case. So, for surfaces R and s, only the velocity component u or -u should be considered.

Thus, mu = momentum of the molecule before collision,

mu = momentum of the molecule after the collision,

So, a change in the momentum of the molecule

= final momentum- initial momentum

= – mu -(mu) = -2mu

After a collision at R, the molecule moves towards S, Again the collision is S brings the molecule back to R, The effective distance traveled by the molecule between two collisions with the same surface = 2l.

The time taken between these two collisions, t = \(\frac{2 l}{u}\)

So, the rate of change in momentum of the molecule \(\frac{-2 m u}{\frac{2 m}{u}}=-\frac{m u^2}{1}\)

From Newton’s second law of motion, die force exerted by the surface R on the molecule = –\(\frac{m u^2}{l}\);

Again, horn Newton’s third law, the equal and opposite force exerted by the molecule on the die surface R = +\(\frac{m u^2}{l}\).

Then, pressure on surface R due to the molecule

= \(\frac{\text { force }}{\text { surface area }}=\frac{\frac{m u^2}{1}}{p^2}=\frac{m u^2}{p^3}=\frac{m u^2}{V}\)

Now, we consider all the N molecules and die components u₁, u₂…., u_N respectively of velocities along the x-axis.

So, the net pressure on surface R, due to all the N molecules in the container, Is \(p_x=\frac{m_1}{v}\left(u_1^2+u_2^2+\cdots+u_N^2\right)\)

Similarly, the pressure on surfaces perpendicular to die y and z axes, respectively, are \(p_y =\frac{m}{v}\left(v_1^2+v_2^2+\cdots+v_N^2\right)\)

and \(p_2 =\frac{m}{v}\left(w_1^2+w_2^2+\cdots+w_N^2\right)\)

As the gas exerts equal pressure in all directions, \(p_{\mathrm{x}}=p_y=p_z=p=\) pressure of the gas.

So, p= \(\frac{1}{3}\left(p_x+p_y+p_z\right)\)

= \(\frac{1}{3}\frac{m}{V}[\left(u_1^2+u_2^2+\cdots+u_N^2\right)+\left(v_1^2+v_2^2+\cdots+v_N^2\right)\)

…. + \(\left.\left(w_1^2+w_2^2+\cdots+w_N^2\right)\right]\)

= \(\frac{1}{3} \frac{m}{V}\left[\left(u_1^2+v_1^2+w_1^2\right)+\left(u_2^2+v_2^2+w_2^2\right)+\right.\)

…… + \(\left(u_N^2+v_N^2+w_N^2)\right]\)

= \(\frac{1}{3} \frac{m}{V}\left(c_1^2+c_2^2+\cdots+c_N^2\right)\)

= \(\frac{1}{3} \cdot \frac{m N}{V} \cdot \frac{\left.\left.c_1^2+c_2^2+\cdots+v_N^2+w_N^2\right)\right]}{N}\)

= \(\frac{1}{3} m \frac{N c^2}{V}\left[c^2=\frac{c_1^2+c_2^2+\cdots c_N^2}{N}(c=\text { ms speed })\right]\)

= \(\frac{1}{3} \frac{M_0}{V} c^2 \text { [total mass of the gas, } M_0=m N]\)

= \(\frac{1}{3} \rho c^2\left[\text { density of the gas, } \rho=\frac{M_0}{V}\right]\)…(1)

This expression shows that pressure depends on the total volume V, but not on the length l of the cubical container. This means that the expression is true for containers of all shapes.

This is the expression for the pressure of an ideal gas, according to kinetic theory.

From equation (1), \(c=\sqrt{\frac{3 p}{\rho}}\)….(2)

In this relation, pressure p and density ρ are bulk thermodynamic properties that are measured by experiments. So, from these measured values, we get an estimate of the rms speed c of the molecules.

Molecular number density: The number of molecules in unit volume N/V = n, this ‘n’ is called the molecular number density of gas.

Now, density, \(\rho=\frac{M_0}{V}=\frac{m N}{V}=m n\)

∴ From equation (1) we get, p = \(\frac{1}{3} m n c^2\)….(3)

This equation is mainly used in chemistry. It can be understood that the pressure of gas depends on three quantities

1. Mass of gas molecule (m),
2. Number of gas molecules in unit volume (n) and
3. rms Speed of the molecules.

Kinetic Theory Of Gases – Pressure Of A Perfect Gas According To The Kinetic Theory Numerical Examples

Example 1. The velocity of 10 gas molecules in a container, are 2, 3, 3, 4, 4, 4, 5, 5,7, and 10 km • s^-1, respectively. Find out the mean velocity and rms speed.
Solution:

Mean velocity, \(\bar{c}=\frac{2+3+3+4+4+4+5+5+7+10}{10}=\frac{47}{10}\)

= \(4.7 \mathrm{~km} \cdot \mathrm{s}^{-1} ;\)

rms speed \(\tilde{c}=\sqrt{\frac{2^2+3^2+3^2+4^2+4^2+4^2+5^2+5^2+7^2+10^2}{10}}\)

= \(\sqrt{\frac{269}{10}}=\sqrt{26.9}=5.1865 \mathrm{~km} \cdot \mathrm{s}^{-1} .\)

Example 2. Find out the rms speed of a gas of density 2 g · L^-1 at 76 cm Hg pressure. Given, density of mercury = 13.6 g · cm^-3 and 980 cm · s^-2
Solution:

p = \(76 \times 13.6 \times 980 \mathrm{dyn} \cdot \mathrm{cm}^{-2},\)

ρ = \(2 \mathrm{~g} \cdot \mathrm{L}^{-1}=\frac{2}{1000} \mathrm{~g} \cdot \mathrm{cm}^{-3}\)

So, rms speed,

c = \(\sqrt{\frac{3 p}{\rho}}\)

= \(\sqrt{\frac{3 \times 76 \times 13.6 \times 980 \times 1000}{2}}\)

= \(3.9 \times 10^4 \mathrm{~cm} \cdot \mathrm{s}^{-1}=0.39 \mathrm{~km} \cdot \mathrm{s}^{-1} .\)

Example 3. Determine the rms speed of air molecules at STP. Given, the density of mercury = 13.6 g · cm^-3; the density of air = 0.00129 g · cm^-3
Solution:

p = \(76 \times 13.6 \times 980 \mathrm{dyn} \cdot \mathrm{cm}^{-2},\)

ρ = \(0.00129 \mathrm{~g} \cdot \mathrm{cm}^{-3}\)

∴ c = \(\sqrt{\frac{3 p}{\rho}}=\sqrt{\frac{3 \times 76 \times 13.6 \times 980}{0.00129}}\)

= \(4.85 \times 10^4 \mathrm{~cm} \cdot \mathrm{s}^{-1}=0.485 \mathrm{~km} \cdot \mathrm{s}^{-1} .\)

Example 4. The rms speed of hydrogen molecules at STP 1.85 km s^-1. What is the density of hydrogen gas?
Solution:

Here, c = 1.85 km · s^-1 = 1.85 x 10⁵ cm · s^-1

p = 76 x 13.0 x 980 dyn · cm^-2

From the equation p = \(\frac{1}{3} \rho c^2\) we get,

ρ = \(\frac{3 p}{c^2}=\frac{3 \times(76 \times 13.6 \times 980)}{\left(1.85 \times 10^5\right)^2}\)

= \(0.000089 \mathrm{~g} \cdot \mathrm{cm}^{-3} .\)

Example 5. Find out the rms speed of nitrogen gas molecules at 0°C. The density of nitrogen gas at STP = 1.25 g · L^-1 and the density of mercury = 13.6 g · cm^-3.
Solution:

p = 76 x 13.6 x 980 dyn cm^-2,

ρ = 1.25 g · L^-1 = 1.25 x 10^-3 g · cm^-3

rms speed, = \(\sqrt{\frac{3 p}{\rho}}\)

= \(\sqrt{\frac{3 \times(76 \times 13.6 \times 980}{1.25 \times 10^{-3}}}\)

= \(4.93 \times 10^4 \mathrm{~cm} \cdot \mathrm{s}^{-1} .\)

Example 6. Find out the ratio of the rms speeds of hydrogen and nitrogen molecules at STP.
Solution:

According to Avogadro’s law, at STP the volume of 1 mol gas is 22.4L.

∴ Density of hydrogen \(\rho_{\mathrm{H}}=\frac{2}{22.4} \mathrm{~g} \cdot \mathrm{L}^{-1}\)

and density of nitrogen, \(\rho_{\mathrm{N}}=\frac{28}{22.4} \mathrm{~g} \cdot \mathrm{L}^{-1}\)

∴ The ratio of the rms speeds of hydrogen and nitrogen is,

⇒ \(\frac{c_{\mathrm{H}_2}}{c_{\mathrm{N}_2}}=\frac{\sqrt{\frac{3 p}{\rho_{\mathrm{H}}}}}{\sqrt{\frac{3 p}{\rho_{\mathrm{N}}}}}=\sqrt{\frac{\rho_{\mathrm{N}}}{\rho_{\mathrm{H}}}}=\sqrt{\frac{28}{2}}=\sqrt{\frac{14}{1}}=3.74: 1\)

Kinetic Theory Of Gases – Principle Of Equipartition Of Energy

The principle of equipartition of energy in kinetic theory came essentially from the concept of degrees of freedom. we have seen that the pressure of an ideal gas is p = \(\frac{1}{3}\left(p_x+p_y+p_z\right)\)

The number of degrees of freedom of an ideal gas molecule = 3. Clearly, it led to a factor of 1/3.

So, we get \(p=\frac{1}{3} \rho c^2 \text { or, } c^2=\frac{3 p}{\rho}\)(c = rms speed of the gas molecules).

Again, the total kinetic energy of the molecules in 1 mol of an ideal gas is \(\frac{3}{2} p V=\frac{3}{2} R T\). So, it may be said that the molecular kinetic energy of 1 mol of an ideal gas for each degree of freedom is \(\frac{1}{2}\) RT Scientist Ludwig Boltzmann analysed the motion of a single molecule in an ideal gas and theoretically established the principle of equipartition of energy

Statement of the principle of equipartition of energy: The average molecular kinetic energy of any substance is equally shared among the degrees of freedom; the average kinetic energy of a single molecule associated with each degree of freedom is \(\frac{1}{2} k T\)(T= absolute temperature, k = Boltzmann constant = 1.38 x 10^-23 J · K^-1)

The number of degrees of freedom of an ideal gas molecule = 3. So, from the equipartition principle, the average kinetic energy of a molecule = 3 x \(\frac{1}{2}kT\) = \(\frac{3}{2}\)kT. The molecule has no potential energy. So, the average total energy of a molecule is e = \(\frac{3}{2}\)kT

Again, the total energy of 1 mol of an ideal gas is E = \(\frac{3}{2}\)RT.

So, the number of molecules in 1 mol of a gas = \(\frac{E}{e}\) = \(\frac{R}{k}\).

Clearly, this is the Avogadro number N_A, i.e., \(N_A=\frac{R}{k} \text { or, } R=N_A k\)

This is the relation between the universal gas constant R, the Avogadro number N_A, and the Boltzmann constant k. Then the total energy of 1 mol of an ideal gas is \(E=\frac{3}{2} N_A k T\)

For any amount of ideal gas containing N molecules, \(E=\frac{3}{2} N_A k T\). This relation is widely used particularly in chemistry.

It is to be noted that the equipartition principle is applicable to all substances, not only to gases. For any substance, solid, liquid, or gas, the average molecular kinetic energy associated with each degree of freedom is \(\frac{1}{2}\)kT.

For ideal gases, the molecular potential energy is zero; so it is easy to calculate the total energy. But for real gases, liquids, or solids, the potential energy calculations are not easy. However, for these substances, the kinetic energy strictly follows the principle of equipartition.

Specific heat of a gas: The first law of thermodynamics is written as

dQ = dE+ dW [E is taken for internal energy]

At constant volume, dV = 0; so dW = pdV = 0.

Then, dQ = dE.

So, the heat absorbed or released at constant volume for a temperature change dT of 1 mol of gas is dQ = C_vdT.

Here, C_v = molar specific heat at constant volume.

Then, \(C_v=\frac{d Q}{d T}=\frac{d E}{d T}\)

In the case of monatomic gas: The kinetic theory assumes that the ideal gas molecules are monatomic. Actually, gases like helium, neon, and argon are monatomic. For 1 mol of such a gas, E = \(\frac{3}{2}\)RT

So, \(C_v=\frac{d E}{d T}=\frac{3}{2} R\)

The molar-specific heat at constant pressure is C_p.

∴ \(C_p-C_\nu=R \quad \text { or, } C_p=C_\nu+R=\frac{3}{2} R+R=\frac{5}{2} R\)

The ratio between the two specific heats is \(\gamma=\frac{C_p}{C_v}=\frac{5}{3}=1.67\)

This value tallies with the experimentally determined values of γ in the case of helium, neon, etc.

In Case Of diatomic gas: The molecules of gases like oxygen, nitrogen, hydrogen, etc., are diatomic. The number of degrees of freedom of a diatomic molecule = 5; so for 1 mol of such a gas, E = \(\frac{5}{2}\) RT.

Then, \(C_\nu=\frac{d E}{d T}=\frac{5}{2} R ; C_p=C_\nu+R=\frac{5}{2} R+R=\frac{7}{2} R\)

∴ \(\gamma=\frac{C_p}{C_v}=\frac{7}{5}=1.4\)

This value of γ is also supported by experiments.

In general cases: if f is the number of degrees of free-dom of an ideal gas molecule then, the energy of 1 mol of such a gas E = \(\frac{f}{2}\)RT

⇒ \(C_\nu=\frac{f_R}{2} ; \quad C_p=\frac{f_2}{2} R+R=\left(\frac{f+2}{2}\right) R\)

So, \(\gamma=\frac{C_p}{C_v}=\frac{f+2}{f}=1+\frac{2}{f}\).

Specific heats of helium and hydrogen gases: We know that, R ≈ 2 cal • mol^-1 • °C^-1 For helium gas,

⇒ \(C_v=\frac{3}{2} R=\frac{3}{2} \times 2=3 \mathrm{cal} \cdot \mathrm{mol}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

⇒ \(C_p=\frac{5}{2} R=\frac{5}{2} \times 2=5 \mathrm{cal} \cdot \mathrm{mol}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

The molecular weight of helium =4.

So the specific heats are, \(c_\nu=\frac{C_v}{4}=\frac{3}{4}=0.75 \mathrm{cal} \cdot \mathrm{g}^{-1 \cdot{ }^{\circ} \mathrm{C}^{-1}}\)

⇒ \(c_p=\frac{C_p}{4}=\frac{5}{4}=1.25 \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

For hydrogen gas,

⇒ \(C_v=\frac{5}{2} R=\frac{5}{2} \times 2=5 \mathrm{cal} \cdot \mathrm{mol}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

⇒ \(C_p=\frac{7}{2} R=\frac{7}{2} \times 2=7 \mathrm{cal} \cdot \mathrm{mol}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

The molecular weight of hydrogen = 2.

So, the specific heats of hydrogen gas are,

⇒ \(c_\nu=\frac{C_\nu}{2}=\frac{5}{2}=2.5 \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

and \(c_p=\frac{C_p}{2}=\frac{7}{2}=3.5 \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

It may be noted that the value of c_p for helium gas and the values of both c_v and c_p for hydrogen gas are greater than the specific heat of water (1 cal · g^-1 · C^-1).

c_v, c_p, and γ of a gas mixture: Let n₁ mol of a gas (molar specific heat at constant volume and constant pressure be \(C_{v_1} \text { and } C_{p_1}\) respectively) is mixed with n₂ mol of a gas (molar specific heat at constant volume and constant pressure be \(C_{\nu_2} \text { and } C_{p_2}\) respectively) such that they do not react chemically.

Therefore, the thermal capacity of (n₁ + n₂) mol gas of the mixture at constant volume is \(n_1 C_{v_1}+n_2 C_{v_2}\)

Hence, at constant volume effective molar specific heat of the mixture is, \(C_v=\frac{n_1 C_{v_1}+n_2 C_{v_2}}{n_1+n_2}\)

Similarly, at constant pressure, the effective molar specific heat of the mixture is \(C_p=\frac{n_1 C_{p_1}+n_2 C_{p_2}}{n_1+n_2}\)

∴ Ratio of the two molar specific heats of the mixure, \(\gamma=\frac{C_p}{C_v}=\frac{n_1 C_{p_1}+n_2 C_{p_2}}{n_1 C_{v_1}+n_2 C_{v_2}}\)

Now, if f₁ and f₂ be the degress of freedom of the molecules of two gases respectively then,

⇒ \(C_{v_1}=\frac{f_1}{2} R ; C_{p_1}=C_{v_1}+R=\left(\frac{f_1}{2}+1\right) R\)

and \(C_{v_2}=\frac{f_2}{2} R ; C_{p_2}=C_{v_2}+R=\left(\frac{f_2}{2}+1\right) R\)

Putting these values in equation(1), we can find γ of the gas mixure.

Kinetic Theory Of Gases – Principle Of Equipartition Of Energy Numerical Examples

Example 1. The rms speed of the molecules of an ideal gas at STP is 0.5 km · s^-1. Find the density of the gas. What will be the density at 21°C if the pressure remains the same? Given, atmospheric pressure = 10⁵ N · m^-2
Solution:

rms speed, \(c=\sqrt{\frac{3 p}{\rho}}; so \rho=\frac{3 p}{c^2}\).

Here, p = \(10^5 \mathrm{~N} \cdot \mathrm{m}^{-2}\),

c = \(0.5 \mathrm{~km} \cdot \mathrm{s}^{-1}=0.5 \times 1000 \mathrm{~m} \cdot \mathrm{s}^{-1}=500 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

∴ \(\rho=\frac{3 \times 10^5}{(500)^2}=1.2 \mathrm{~kg} \cdot \mathrm{m}^{-3}\)

At constant pressure, \(c \propto \frac{1}{\sqrt{\rho}}; also c \propto \sqrt{T}. So, \rho \propto \frac{1}{T}\)

Then, \(\frac{\rho_0}{\rho_{21}}=\frac{T_{21}}{T_0}\)

or, \(\rho_{21}= \rho_0 \frac{T_0}{T_{21}}\)

(\(T_0=0^{\circ} \mathrm{C}=273 \mathrm{~K}, T_{21}=21^{\circ} \mathrm{C}=(21+273) \mathrm{K}=294 \mathrm{~K}\))

= \(1.2 \times \frac{273}{294}=1.11 \mathrm{~kg} \cdot \mathrm{m}^{-3}\).

Example 2. Find out the energy of 1 mol of a gas and its average molecular kinetic energy at 27°C. Given, R = 8.3×10⁷ erg mol.Kl and N_A = 6.02 x 10²³ mol^-1.
Solution:

The energy of 1 mol of the gas is

E = \(\frac{3}{2} R T=\frac{3}{2} \times\left(8.3 \times 10^7\right) \times 300\left[T=27^{\circ} \mathrm{C}=300 \mathrm{~K}\right]\)

= 3.735 x 10¹⁰ erg

Average molecular kinetic energy is

e = \(\frac{3}{2} k T=\frac{3}{2} \frac{R}{N_A} T=\frac{3}{2} \times \frac{\left(8.3 \times 10^7\right) \times 300}{6.02 \times 10^{23}}\)

= \(6.2 \times 10^{-14} \mathrm{erg} .\)

Example 3. The average kinetic energy of a molecule in a gas at STP is 5.6 x 10^-14 erg. Find out the number of molecules per volume of the gas. Given, density of mercury = 13.6 g · cm^-3
Solution:

Pressure of the gas, p

= \(\frac{2}{3}\) x energy of gas molecules per unit volume

= \(\frac{2}{3}\) x n x average kinetic energy of 1 molecule

where n = number of molecules per unit volume of the gas

∴ n = \(\frac{3 p}{2 \times \text { average kinetic energy of } 1 \text { molecule }}\)

= \(\frac{3 \times(76 \times 13.6 \times 980)}{2 \times\left(5.6 \times 10^{-14}\right)}=2.71 \times 10^{19} .\)

Example 4. Find out the temperature at which the rms speed of nitrogen molecules will be equal to the escape velocity from the earth’s gravity. Given, the mass of a nitrogen atom = 23.24 x 10^-24 g; average radius of the earth = 6390 km; g = 980 cm · s^-2; Boltzmann constant = 1.37 x 10^-16 erg · °C^-1.
Solution:

rms speed of a molecule = \(\sqrt{\frac{3 R T}{M}} ;\)

escape velocity = \(\sqrt{2 g R_1}\), where Rl = radius of the earth.

According to the question, \(\sqrt{\frac{3 R T}{M}}=\sqrt{2 g R_1}\)

T = \(\frac{2}{3} \frac{g M R_1}{R}\)

Now, R = Nk and M = mN

where m = mass of a nitrogen molecule

= 2 x (23.24 X 10^-24) g ;

N = number of nitrogen molecules

So, T = \(\frac{2}{3} \cdot \frac{g m N R_1}{N k}=\frac{2}{3} \cdot \frac{g m R_1}{k}\)

= \(\frac{2}{3} \times \frac{980 \times\left(2 \times 23.24 \times 10^{-24}\right) \times\left(6390 \times 10^5\right)}{1.37 \times 10^{-16}}\)

= \(1.42 \times 10^5 \mathrm{~K} .\)

Example 5. Find out the temperature at which the average kinetic energy of a gas molecule will be equal to the energy gained by an electron on acceleration across a potential difference of 1 V. Given, Boltzmann constant = 1.38 x 10^-23 J · K^-1; charge of an electron = 1.6 x 10^-19 C.
Solution:

Energy gained by the electron

= 1 eV = (1.6 x 10~19 C) x 1 V = 1.6 x 1019 J.

Average kinetic energy of a gas molecule

= \(\frac{3}{2}\)kT = \(\frac{3}{2}\) x (1.38 x 1^-23) x T J

∴ 1.6 x 10^-19 = \(\frac{3}{2}\) x (1.38 x 10^-23) x T

or, \(T=\frac{2}{3} \times \frac{1.6 \times 10^{-19}}{1.38 \times 10^{-23}}=7729 \mathrm{~K}=7456^{\circ} \mathrm{C}\)

Example 6. Find out the molecular kinetic energy of 1 mol of oxygen gas at STP. Given, the molecular weight of oxygen = 32 density of oxygen at STP = 1.43 g · L^-1 density of mercury = 13.6 g · cm^-3.
Solution:

The volume of 1 mol or 32 g oxygen

= \(\frac{32}{1.43} \mathrm{~L}=\frac{32 \times 10^3}{1.43} \mathrm{~cm}^3 \text {; }\)

At STP, pressure p = 76 x 13.6 x 981 dyn · cm^-2; temperature, T = 0°C = 273 K.

∴ The molecular kinetic energy of 1 mol oxygen gas at STP (diatomic gas) is

E = \(\frac{5}{2} R T=\frac{5}{2} \frac{p V}{T} T=\frac{5}{2} p V\)

= \(\frac{5}{2} \times(76 \times 13.6 \times 981) \times \frac{32 \times 10^3}{1.43}\)

= \(5.67 \times 10^{10} \mathrm{erg} .\)

Example 7. At what temperature will the rms speed of a hydrogen molecule be equal to that of an oxygen molecule at 47°C?
Solution:

The molecular weights of oxygen and hydrogen, respectively, are M₁ = 32 and M₂ = 2.

rms speed, c = \(\sqrt{\frac{3 R T}{M}}\)

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2} \cdot \frac{M_2}{M_1}}\)

Here, \(c_1=c_2 and T_1=47^{\circ} \mathrm{C}=320 \mathrm{~K}\)

∴ \(\frac{T_1}{T_2} \cdot \frac{M_2}{M_1}=1\)

or, \(T_2 =T_1 \cdot \frac{M_2}{M_1}=320 \times \frac{2}{32}\)

= \(20 \mathrm{~K}=(20-273)^{\circ} \mathrm{C}=-253^{\circ} \mathrm{C} .\)

Example 8. 0.76 g of a mixture of hydrogen and oxygen gases has a volume of 2 L, temperature of 300 K, and pressure of 10⁵ N · m^-2. Find out the individual masses of hydrogen and oxygen in the mixture.
Solution:

Let the number of moles of hydrogen and oxygen be n₁ and n₂ respectively.

Then, the pressure of the mixture

p = \(\frac{n_1 R T}{V}+\frac{n_2 R T}{V}=\left(n_1+n_2\right) \frac{R T}{V}\)

or, \(n_1+n_2=\frac{p V}{R T}=\frac{10^5 \times\left(2 \times 10^{-3}\right)}{8.3 \times 300}=0.08\)…(1)

Now, the mass of hydrogen gas = 2n₁ and the mass of oxygen gas = 32n₂.

So, 2n₁ + 32n₂ = 0.76

or, n + 16n₂ = 0.38….(2)

(2)-(1)

15n₂ = 0.3 or, n₂ = 0.02

Then from (1), n₁ = 0.08 – 0.02 = 0.06

∴ Mass of hydrogen = 2 x 0.06 = 0.12 g and mass of oxygen = 32 x 0.02 = 0.64g

Example 9. Find out the number of molecules in a gas of volume 20cm³ at a pressure of 76 cm of mercury, and at 27°C. Given, the average molecule kinetic energy at 27°C = 2 x 10^-14 erg.
Solution:

The pressure of the gas,

p = \(\frac{1}{3} \rho c^2=\frac{1}{3} \frac{m N}{V} {c^2}\)

[m = mass of a molecule, N = number of molecules]

or, N = \(\frac{3 p V}{m c^2}=\frac{3 p V}{2 \times \frac{1}{2} m c^2}\)

[average molecular kinetic energy = \(\frac{1}{2}\) = 2 x 10^-14 erg]

= \(\frac{3 \times(76 \times 13.6 \times 980) \times 20}{2 \times\left(2 \times 10^{-14}\right)}\)

= 1.52 x 10²¹

Example 10. Find the temperature at which the average kinetic energy of a gas molecule will be equal to the energy of a photon in 600Å radiation. Given, the Boltzmann constant, k = 1.38 X 10^-23 J · K^-1; Planck’s constant, h = 6.625 x 10^-34 J · s.
Solution:

Let the required temperature = T.

Average molecular kinetic energy = \(\frac{3}{2}\)kT;

Energy of a photon = hv = \(\frac{h c}{\lambda}\)

[Here, λ = 6000Å = 6000 x 10^-10 m]

According to the question, \(\frac{3}{2} k T=\frac{h c}{\lambda}\)

∴ T = \(\frac{2}{3} \frac{h c}{\lambda k}=\frac{2}{3} \times \frac{\left(6.625 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{\left(6000 \times 10^{-10}\right) \times\left(1.38 \times 10^{-23}\right)}\)

= 1.6 x 10⁴ K.

Example 11. Some amount of oxygen gas contained in a vessel has a density of 1.429 kg · m^-3 at STP. The temperature is increased until the pressure is doubled. Neglecting the change in volume of the vessel, find the rms speed of the oxygen molecules.
Solution:

Mass and volume of the gas remain the same; so the density also remains the same.

So, ρ =1.429 kg · m^-3 = 1.429 x 10^-3 g · cm^-3

In the first case, rms speed of oxygen molecules,

⇒ \(c_1=\sqrt{\frac{3 p_1}{\rho}}=\sqrt{\frac{3 \times(76 \times 13.6 \times 980)}{1.429 \times 10^{-3}}}=46114 \mathrm{~cm} \cdot \mathrm{s}^{-1} .\)

In the second case, p₂ = 2p₁

∴ \(\frac{c_2}{c_1}=\sqrt{\frac{p_2}{p_1}}=\sqrt{2}\)

or, \(c_2=\sqrt{2} c_1=46114 \times \sqrt{2}=65215 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

Example 12. Two ideal gases at absolute temperatures T₁ and T₂ are mixed with each other. If the molecular mass and the number of molecules are m₁, n₁, and m₂, n₂, respectively, find out the temperature of the mixture.
Solution:

Molecular kinetic energy of the first gas = \(n_1 \cdot \frac{3}{2} k T_1\) and that of the second gas = \(n_2 \cdot \frac{3}{2} k T_2\)

So the net energy = \(\frac{3}{2} k\left(n_1 T_1+n_2 T_2\right)\)

The number of molecules in the mixture = n₁ + n₂.

Let the temperature of the mixture be T.

The total molecular kinetic energy = \(\left(n_1+n_2\right) \cdot \frac{3}{2} k T\)

From the principle of energy conservation \(\left(n_1+n_2\right) \cdot \frac{3}{2} k T=\frac{3}{2} k\left(n_1 T_1+n_2 T_2\right)\)

or, T = \(\frac{n_1 T_1+n_2 T_2}{n_1+n_2}\) .

Example 13. 2 mol of a monatomic gas is mixed with 1 mol of a diatomic gas, Find out the value of γ of the mixture.
Solution:

For the monatomic gas, \(\gamma_1=1+\frac{2}{f}=1+\frac{2}{3}=\frac{5}{3}\)

where f = number of degrees of freedom

For the diatomic gas, \(\gamma_2=1+\frac{2}{f}=1+\frac{2}{5}=\frac{7}{5}\)

[f = 3 for a monatomic gas and f = 5 for a diatomic gas]

So, for the mixture, \(\gamma=\frac{n_1 \gamma_1+n_2 \gamma_2}{n_1+n_2}=\frac{2 \times \frac{5}{3}+1 \times \frac{7}{5}}{2+1}=1.58\)

Example 14. The mean free path for the collision of nitrogen molecules at STP is 6.44 x 10^-6 cm. What is the mean time interval between collisions? Given, R = 8.31 x 10⁷ erg · mol^-1 · K^-1; molecular mass of nitrogen = 28.
Solution:

rms speed, c = \(\sqrt{\frac{3 R T}{M}}=\sqrt{\frac{3 \times\left(8.31 \times 10^7\right) \times 273}{28}} \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

∴ Mean time interval between collisions = \(\frac{\text { mean free path }}{\text { rms velocity }}\)

= \(6.44 \times 10^{-6} \times \sqrt{\frac{28}{3 \times\left(8.31 \times 10^7\right) \times 273}}\)

= \(1.306 \times 10^{-10} \mathrm{~s}\)

Example 15. The mass of a hydrogen molecule is 3.32 x 10^-27 kg. 10²³ such molecules hit every second on a rigid wall of area 2 cm² at an angle of 45° with horizontal with a velocity of 10³ m · s^-1. If the molecules are reflected with the same velocity, then what is the pressure exerted on the wall?
Solution:

Suppose the molecules are incident along PO and reflected along OQ.

Here, ∠PON = ∠NOQ = 45°.

Change of momentum normal to the wall for each hydrogen molecule = 2mvcos45°.

∴ Net change of momentum in a second

= exerted force = n· 2mvcos45°

(where, n = number of molecules)

∴ Pressure exerted on the wall = \(\frac{\text { force }}{\text { area }}=\frac{n \cdot 2 m \nu \cos 45^{\circ}}{\text { area }}\)

= \(\frac{10^{23} \times 2 \times\left(3.32 \times 10^{-27}\right) \times 10^3 \times \frac{1}{\sqrt{2}}}{2 \times 10^{-4}}\)

= \(2.35 \times 10^3 \mathrm{~N} \cdot \mathrm{m}^{-2}\)

Example 16. 22 g of CO₂ gas at 27°C is mixed with 16g of O₂ gas at 37° C. What will be the temperature of the mixture?
Solution:

22 g CO₂= \(\frac{22}{44}\) or  \(\frac{1}{2}\) mol of CO₂

16 g O₂ =  \(\frac{16}{32}\) or  \(\frac{1}{2}\) mol O₂

Temperature of the mixture, T = \(\frac{n_1 T_1+n_2 T_2}{n_1+n_2}=\frac{\frac{1}{2}(27+273)+\frac{1}{2}(37+273)}{\frac{1}{2}+\frac{1}{2}}\)

= \(305 \mathrm{~K}=32^{\circ} \mathrm{C}\)

Example 17. A mixture of 8g oxygen, 14g nitrogen, and 22g carbon dioxide is contained in a vessel of volume 4L. What will be the pressure of the gas mixture if the temperature of the mixture is 27°C? [Given R = 8.315 J · mol^-1 K^-1]
Solution:

We know, pV = nRT [n =number of moles]

or, \(p=\frac{n R T}{V}=\frac{g}{M} \cdot \frac{R T}{V}\)

[g = mass of the gas, M = atomic weight of the gas]

Pressure exerted by \(\mathrm{O}_2 \text { is } p_{\mathrm{O}_2}=\frac{8}{32} \cdot \frac{R T}{V}=\frac{1}{4} \frac{R T}{V}\)

Pressure exerted by N is \(p_{\mathrm{N}_2}=\frac{14}{28} \cdot \frac{R T}{V}=\frac{1}{2} \frac{R T}{V}\)

and pressure exerted by \(\mathrm{CO}_2 \text { is } p_{\mathrm{CO}_2}=\frac{22}{44} \cdot \frac{R T}{V}=\frac{1}{2} \frac{R T}{V}\)

According to Dalton’s law, the pressure of the gas mixture,

p = \(p_{\mathrm{O}_2}+p_{\mathrm{N}_2}+p_{\mathrm{CO}_2}=\frac{R T}{V}\left(\frac{1}{4}+\frac{1}{2}+\frac{1}{2}\right)=\frac{5}{4} \frac{R T}{V} \)

= \(\frac{5}{4} \times \frac{8.315 \times 300}{4 \times 10^{-3}}=7.795 \times 10^5 \mathrm{~N} / \mathrm{m}^2\)

Example 18.  1 mol of He at 57°C is mixed with 1 mol of Ar at 27°C. Find the temperature of the gas mixture.
Solution:

Average kinetic energy of 1 mol gas

= \(\frac{3}{2} R T=\frac{3}{2} k N_A T\)

Average kinetic energy of 1 mol of He =

= \(\frac{3}{2} k N_A(273+57)=\frac{3}{2} k N_A \times 330\)

Average kinetic energy of 1 mol of Ar

= \(\frac{3}{2} k N_A(273+27)=\frac{3}{2} k N_A \times 330\)

After mixing the two gases, the number of atoms in the mixture = 2 N_A.

Let the temperature of the mixture is T.

Average kinetic energy of the mixture = \(\frac{3}{2} \times 2 N_A k T\)

∴ From the principle of conservation of energy,

⇒ \(\frac{3}{2} \times 2 N_A k T=\frac{3}{2} k N_A \times 330+\frac{3}{2} k N_A \times 300\)

or, T = \(\frac{1}{2}\)(330 + 300) = 315K = (315 – 273) = 42°C.

Example 19. Find the minimum radius of the planet of density 5.5 x 10³ kg/m³ and temperature 427°C which can hold O₂ in its atmosphere. [Given G = 6.67 x 10^-11 N · m^-2 · kg^-2 and R = 8.3 J · mol^-1 · K^-1
Solution:

The escape velocity of any object at the surface of the planet of radius r and mass M₁ is

v = \(\sqrt{\frac{2 G M_1}{r}}=\sqrt{\frac{2 G}{r} \cdot \frac{4}{3} \pi r^3 \rho}]\)

[where ρ is the material density of the planet]

= \(\sqrt{\frac{8}{3} G \pi r^2 \rho}\)

rms speed of a gas of molecular weight M at an absorb temperature T is \(c=\sqrt{\frac{3 R T}{M}}\)

Since the planet holds O₂, hence v_min = c

∴ \(\sqrt{\frac{8}{3} G \pi r_{\min } \rho}=\sqrt{\frac{3 R T}{M}}\)

(\(r_{\min }\)= minimum radius of the planet)

or, \(\frac{8}{3} G \pi r_{\min }^2 \rho=\frac{3 R T}{M}\)

or, \(r_{\min }^2=\frac{9 R T}{8 G \pi \rho M}\)

or, \(r_{\min }=\sqrt{\frac{9 R T}{8 G \pi \rho M}}\)

= \(\sqrt{\frac{9 \times 8.3 \times(427+273) \times 7}{8 \times 6.67 \times 10^{-11} \times 22 \times 5.5 \times 10^3 \times 32 \times 10^{-3}}}\)

= \(421 \times 10^3 \mathrm{~m}=421 \mathrm{~km} .\)

Example 20. 1 mol O₂ at temperature 27°C at STP (1.01 x 10⁵ N/m²) IJS kept in a vessel. Find the number of collisions the molecules experience (in SI) per second per unit area with the wall of the vessel. [Given Boltzmann constant k = 138 x 10¹³ J/K]
Solution:

Number of molecules in 1 mol of 02 = 6.023 x 1023

∴ Mass of a molecule, m = \(\frac{32}{6.023 \times 10^{23} \times 1000}\)

= \(5.316 \times 10^{-26} \mathrm{~kg}\)

Momentum of the molecule, P = mv = \(m \sqrt{\frac{3 k T}{m}}=\sqrt{3 k T m}\)

Change in momentum due to each collision,

ΔP = \(2 P=2 \sqrt{3 k T m}\)

= \(2 \sqrt{3 \times 1.38 \times 10^{-23} \times 300 \times 5.316 \times 10^{-26}}\)

= \(5.139 \times 10^{-23} \mathrm{~kg} \cdot \mathrm{m} \cdot \mathrm{s}^{-1}\)

If the molecules experience ‘n’ number of collisions per second per square meter of the wall, then the pressure of the gas will be

p = nΔP or, 1.01 x 10⁵ = n x 5.139 x 10^-23

or, n = 1.965 x 10²⁷.

Example 21. 0.014kg N₂ gas at 27°C is kept in a dosed vessel, How much heat is required to double the rms of the N₂ molecules?
Solution:

Heat received, ΔQ = nC_vΔT

[C_v = molar specific heat at constant volume

Here, \(n=\frac{0.014 \times 1000}{28}=\frac{1}{2}\)

For diatomic molecule C_v = \(\frac{5}{2}\)R

and rms speed of N₂ molecule, c ∝ √T

∴ To double the velocity c, the temperature should be 4 T.

∴ \(\Delta Q=\frac{1}{2} \times \frac{5}{2} R \times(4 T-T)\)

= \(\frac{5}{4} \times 2 \times(273+27) \times 3\left[because R=2 \mathrm{cal} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\right]\)

= 2250 cal

Example 22. If 2 mol of a gas at constant pressure, requires 70 cal heat to increase its temperature from 30°C to 35°C, then find its degrees of freedom.
Solution:

Work done at constant pressure,

ΔW = pΔV = nRΔT =2x2x5

[ΔT = (308-303) = 5K] = 20 cal

Given that, heat received, ΔQ = nC_pΔT = 70 cal.

∴ \(C_p=\frac{70}{2 \times 5}=7 \mathrm{cal} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\)

∴ \(C_v=C_p-R=7-2=5 \mathrm{cal} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\)

∴ \(\gamma=\frac{C_p}{C_v}=\frac{7}{5}\)

Again, \(\gamma=1+\frac{2}{f}\)

∴ 1 + \(\frac{2}{f}=\frac{7}{5}\)

or, \(\frac{2}{f}=\frac{7}{5}-1=\frac{7-5}{5}=\frac{2}{5}\)

∴ f = 5

Degree of freedom of the gas molecule is 5.

 

 Kinetic Theory Of Gases

Interpretation Of Temperature From Kinetic Theory

Total energy (E) of gas molecules: According to the kinetic theory, the potential energy of gas molecules = 0; the entire energy of the gas comes from the kinetic energy of the molecules.

∴ E = \(\frac{1}{2} m c_1^2+\frac{1}{2} m c_2^2+\cdots+\frac{1}{2} m c_N^2\)

[m = mass of each molecule; c₁, c₂,….. c_N = velocity of the N molecules in the container]

= \(\frac{1}{2} m\left(c_1^2+c_2^2+\cdots+c_N^2\right)=\frac{1}{2} m N \frac{c_1^2+c_2^2+\cdots+c_N^2}{N}\)

As mN = M = mass of the gas,

and c = \(\sqrt{\frac{c_1^2+c_2^2+\cdots+c_N^2}{N}}\)

= rms speed of the molecules,

∴ E = \(\frac{1}{2} M c^2=\frac{1}{2} M \cdot \frac{3 p}{\rho}\left[\text { As } p=\frac{1}{3} \rho c^2, \text { we have } c^2=\frac{3 p}{\rho}\right]\)

Again, as \(\frac{M}{\rho}\) = V = volume of the gas, we get

E = \(\frac{3}{2} p V\)…(1)

This is the expression for the total energy of a gas.

Relation between pressure and energy density: Energy density of a gas (u) = energy per unit volume = \(\frac{E}{V}\)

From relation (1), \(\frac{E}{V}=\frac{3}{2} p\)…(1)

or, \(u=\frac{3}{2} p \quad \text { or, } \quad p=\frac{2}{3} u\)…(2)

So, the pressure of a gas is \(\frac{2}{3}\)rd of its energy density. This relation (2) is a fundamental one, valid for all ideal gases.

Effect of heat absorbed by a gas: when a gas absorbs heat from its surroundings, two effects occur simultaneously.

1. The temperature of the gas increases.
2. Heat is converted to some other form of energy inside the gas. It is nothing but the kinetic energy of the molecules. This means that the kinetic energy of the molecules increases.

These two effects suggest that the temperature of a gas and the kinetic energy of its molecules are intimately related with each other. The definition of temperature in kinetic theory comes from this concept.

Idea of temperature: Temperature (T) is a property of a gas, which is proportional to the kinetic energy of the gas molecules.

So, T ∝ E or, T = aE where a is a constant.

The constant a may have any value. Different values of a will give different temperature scales. Usually, the value of a is so chosen that the temperature scale is an exact match with the experimental Kelvin scale of temperature.

Let us take 1 mol of an ideal gas. Then E is the kinetic energy of the molecules present in 1 mol of the gas. Then we choose \(a=\frac{2}{3 R}\), where

R = universal gas constant = 8.31 J · mol · K^-1

Then, for 1 mol of an ideal gas, \(T=\frac{2}{3 R} E \quad \text { or, } \quad E=\frac{3}{2} R T\)….(3)

With this choice of a, the quantity T becomes exactly the same as the Kelvin temperature.

• We know that the potential energy of an ideal gas molecule is zero. So the total internal energy is essentially the kinetic energy of the molecules. But for real gases and also for liquids and solids, the molecular potential energy is not zero.
• Then the total internal energy becomes the sum of the molecular kinetic and potential energies. Here, it must be noted that the temperature is taken to be proportional to the kinetic energy only of the molecules.
• In this way, the concept of temperature is extended to all gases, liquids, and solids. This means that temperature is a property of all substances and is proportional to the kinetic energy of the molecules in the substance.

The proportionality constant is taken in such a way that the values of temperature exactly match with the values of the Kelvin scale. For this, the required absolute constant is the Boltzmann constant.

The idea of absolute zero of temperature: By definition, T ∝ E; so E = 0 when T = 0. This defines the absolute zero of temperature. It is the temperature at which the internal energy of the gas becomes zero, i.e., the molecular motions stop entirely.

Variation of the rms speed of gas molecules: Let M = molecular weight of a gas. Then, mass of 1 mol of the gas = M g.

The density of the gas is ρ = \(\frac{M}{V}\); so M = ρV.

Now, p = \(\frac{1}{3} \rho c^2 \text { or, } c^2=\frac{3 p}{\rho}=\frac{3 p V}{\rho V}=\frac{3 R T}{M}\)

∴ c = \(\sqrt{\frac{3 R T}{M}}\)….(3)

As R = constant and for a particular gas, M = constant, we get c ∝ √T. So, the rms speed of gas molecules is proportional to the square root of the temperature of the gas.

Most probable velocity of gas molecules: The kinetic theory assumes that a gas molecule may have a velocity between zero and infinity. But in reality, the number of molecules with very low or very high velocities is extremely small The majority of molecules have intermediate velocities.

• Maxwell analysed the phenomenon with his velocity distribution curve. This curve has a peak at P and the point P corresponds to a velocity c_m.
• Among all velocities, the velocity c_m is possessed by the highest number of gas molecules. This c_m is known as the most probable velocity.

The most probable velocity of gas molecules Definition: The velocity which is possessed by the highest number of gas molecules in a container is called the most probable velocity.

Shows that, in general, c_m is less than both the mean velocity \(\bar{c}\) and the rms speed c of gas molecules.

Actually, cm< \(\bar{c}\) <c.

Theoretically, we get an absolute temperature of T,

⇒ \(c_m=\sqrt{\frac{2 R T}{M}}, \bar{c}=\sqrt{\frac{8 R T}{\pi M}}, c=\sqrt{\frac{3 R T}{M}}\)

So, \(c_m: \bar{c}: c=\sqrt{2}: \sqrt{\frac{8}{\pi}}: \sqrt{3}=1: \frac{2}{\sqrt{\pi}}: \sqrt{\frac{3}{2}} .\)

Interpretation Of Temperature From Kinetic Theory Numerical Examples

Example 1. At what temperature will the rms speed of molecules of nitrogen gas be twice of that at 0°C?
Solution:

T₁ = 0°C = 273 K; rms speed at 0°C = c₁

At temperature T₂, rms speed = c₂ = 2 c₁.

As \(c=\sqrt{\frac{3 R T}{M}}\),

∴ \(c \propto \sqrt{T}\), we have \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

or, \(T_2 =T_1\left(\frac{c_2}{c_1}\right)^2=273 \times\left(\frac{2}{1}\right)^2=1092 \mathrm{~K}\)

= \((1092-273)^{\circ} \mathrm{C}=819^{\circ} \mathrm{C} .\)

Example 2. The temperature of a gas rises from 27°C to  327°C. Show that the rms speed of the gas molecules would be √2 times its initial value at die final higher temperature.
Solution:

T₁ = 27°C = (27 + 273) K = 300 K;

T₂ = 327°C = (327 + 273) K = 600 K.

As \(c \propto \sqrt{T}\), we have \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

or, \(c_2=c_1 \sqrt{\frac{T_2}{T_1}}=c_1 \sqrt{\frac{600}{300}}=\sqrt{2} c_1\)

Example 3. The rms speed of oxygen gas molecules at STP is 4.5 x 10⁴ cm · s^-1. Find out the same for carbon dioxide gas molecules at STP. Given, the molecular weights of oxygen and carbon dioxide are 32 and 44, respectively.
Solution:

We know, c = \(\sqrt{\frac{3 R T}{M}}\)

As the temperature is the same for both the gases, \(c \propto \frac{1}{\sqrt{M}}\)

So, \(\frac{c_{\mathrm{O}_2}}{c_{\mathrm{CO}_2}}=\sqrt{\frac{M_2}{M_1}}\)

[M₁ = molecular weight of O₂, M₂ = molecular weight of CO₂]

or, \(c_{\mathrm{CO}_2}=c_{\mathrm{O}_2} \sqrt{\frac{M_1}{M_2}}=4.5 \times 10^4 \times \sqrt{\frac{32}{44}}\)

= \(3.84 \times 10^4 \mathrm{~cm} \cdot \mathrm{s}^{-1} .\)

Example 4. Find out the kinetic energy of 2g of nitrogen gas at 27°C, Given, R = 8.3 x 10⁷ erg mol^-1 K^-1
Solution:

The Kinetic energy of the molecules of 1 mol gas = 3/2 RT

Here, T = 27°C = (27 + 273) K = 300 K ; mass of 1 mol nitrogen gas = 28 g.

So, the kinetic energy of the molecules in 2 g of nitrogen gas

= \(\frac{2}{28} \times \frac{3}{2} R T=\frac{3}{28} R T=\frac{3 \times\left(8.3 \times 10^7\right) \times 300}{28}\)

= \(2.668 \times 10^9 \mathrm{erg}=2.668 \times 10^2 \mathrm{~J}=266.8 \mathrm{~J} .\)

Example 5. At what temperature the average kinetic energy of the molecules of a perfect gas be doubled than that at 20°C?
Solution:

Here, T₁ = 20 °C = 293 K.

As the average kinetic energy of gas molecules is proportional to the absolute temperature of the gas, the required temperature,

T₂ = 2 x 293 = 586 K = (586 – 273) °C = 313 °C

Question 6. Find out the temperature at which the molecular rms speed of a gas would be 1/3rd its value at 100°C.
Solution:

Let the required temperature be T₂K, molecular rms speed at this temperature be c_2, and that at 100°C be c₁.

According to the question, \(c_2=\frac{1}{3} c_1\)

Here, \(T_1=100^{\circ} \mathrm{C}=(100+273) \mathrm{K}=373 \mathrm{~K}\)

As \(c \propto \sqrt{T}\), we have, \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

or, \(T_2=T_1\left(\frac{c_2}{c_1}\right)^2 =373 \times\left(\frac{1}{3}\right)^2=\frac{373}{9}=41.44 \mathrm{~K}\)

= \((41.44-273)^{\circ} \mathrm{C}=-231.56^{\circ} \mathrm{C}\).