Elasticity Long Answer Type Questions And Answers
Question 1. Which is more elastic steel or diamond?
Answer:
Magnitude of elastic limit is the degree of elasticity of a material. Higher the elastic limit of a material, greater is its degree of elasticity. The elastic limit of diamond is more than that of steel and hence diamond is more elastic than steel.
Question 2. Explain why the temperature of a wire under tension will change if it snaps suddenly.
Answer:
The temperature of a wire under tension will change if it snaps suddenly
During elongation of a wire the work done remains stored as elastic potential energy in the wire. When the wire snaps suddenly, that stored potential energy is transformed into heat energy resulting in increase in temperature.
Question 3. Two bodies M and N of equal mass are hung separately from two lightweight springs. Force constants of the springs are k1 and k2. The bodies are set to vibrate so that their maximum velocities are equal. Find the ratio of the amplitudes of vibration of the two bodies.
Answer:
Two bodies M and N of equal mass are hung separately from two lightweight springs. Force constants of the springs are k1 and k2. The bodies are set to vibrate so that their maximum velocities are equal.
A body suspended from a spring will acquire maximum velocity at the equilibrium position in its path of vibration. At that position potential energy of the body becomes zero and its energy becomes totally kinetic.
Let the amplitude of vibration of the body M be x1 and that of N be x2. Since they are of equal mass and their maximum velocities are also the same, their maximum kinetic energies will also be equal.
[Maximum kinetic energy = 1/2 x mass x (maximum velocity)2]. This kinetic energy transforms into the potential energy (1/2kx2) of the body at the end of its amplitude.
∴ \(\frac{1}{2} k_1 x_1^2=\frac{1}{2} k_2 x_2^2 \text { or, } \frac{x_1}{x_2}=\sqrt{\frac{k_2}{k_1}} \text {. }\)
Question 4. Springs are usually made of steel but not of copper. Why?
Answer:
Springs are usually made of steel but not of copper.
Elasticity of steel is more than that of copper. It means that the elastic limit of steel is greater. Let us consider two springs of the same size, one of steel and another of copper.
An equal tensile force is applied on both springs. On slowly increasing the magnitude of the applied force on the two springs it is seen that, at a certain stage the steel spring still behaves like an elastic body but the copper spring undergoes a permanent deformation.
For this reason, springs are usually made of steel but not of copper. Moreover, copper is costlier than steel. However, copper springs may be used where the applied force is not very high.
Question 5. On the basis of the moduli of elasticity distinguish between solid, liquid, and gaseous substances.
Answer:
We know that there are three moduli of elasticity
- Young’s modulus,
- Bulk modulus and
- Modulus of rigidity.
Since solids have definite length, volume, and shape, it has all the three moduli of elasticity. Liquid and gaseous substances have no definite length or shape, but have volume only.
Hence a liquid or a gaseous substance only has bulk modulus. This modulus of a gas is much less than that of a liquid. But the bulk moduli of a solid and a liquid are nearly equal in magnitude.
Question 6. The Poisson’s ratio of a wire is σ. Show that if e is the longitudinal strain due to an applied force, the volume strain will be e( 1 – 2σ).
Answer:
The Poisson’s ratio of a wire is σ.
Suppose, the length of the wire is l, radius is r and its volume is V.
∴ V = πr2l
or, dV = \(\pi r^2 d l+2 \pi l r d r=\pi r^2 d l-2 \pi r^2 \sigma d l\)
[\(\sigma=\frac{-d r / r}{d l / l}\), dr = \(-r \sigma \frac{d l}{l}\)]
= \(\pi r^2 d l(1-2 \sigma)\)
∴ Volume strain = \(\frac{d V}{V}=\frac{\pi r^2 d l(1-2 \sigma)}{\pi r^2 l}=\frac{d l}{l}(1-2 \sigma)\)
= \(e(1-2 \sigma)\left[\text { given that } \frac{d l}{l}=e\right]\)
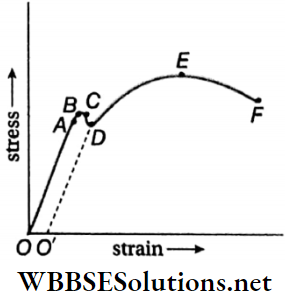
Question 7. In the case of an elastic body which one is more fundamental—stress or strain?
Answer:
When an elastic body gets strained under the influence of external forces, a reaction force develops inside the body. This is the source of stress. This stress helps the deformed body to regain its original shape. It means that only when strain is produced in a body, a stress is developed within it. So, elastic strain is more fundamental than stress.
Question 8. Within elastic limit the Poisson’s ratio depends only on the nature of the material but not on the stress applied”—explain.
Answer:
With the increase in stress, longitudinal strain as well as lateral strain will increase proportionately. As a result, Poisson’s ratio remains fixed, because
Poisson’s ratio = \(\frac{\text { lateral strain }}{\text { longitudinal strain }}\); hence with in elastic limit Poisson’s ratio is independent of the stress applied.
Question 9. For a steel wire, if the diameter is larger, it can withstand a greater load. Why?
Answer:
We know that, breaking stress = \(\frac{\text { breaking load }}{\text { area of cross-section of the wire }}\)
or, breaking load = breaking stress x area of cross-section of the wire
= breaking stress x \(\frac{\pi d^2}{4}\)
[d = diameter of the wire]
Since for a particular material, the breaking stress is fixed, a wire with a larger diameter (d) is able to withstand a greater load.
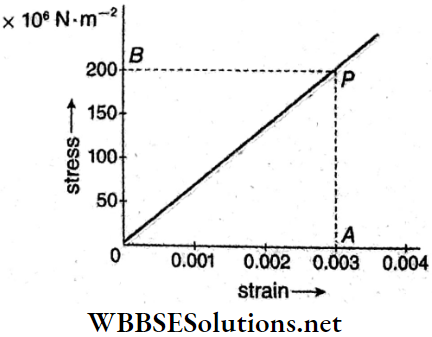
Question 10. In the Fig, load-elongation graphs of two wires made of two different materials A and B are shown. The wires have the same length and the same area of cross-section. Which material has a greater value of F?
Answer:
For the same load F, elongations in the wires made of materials A and B are l1 and l2 respectively.
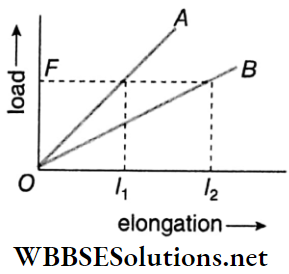
Since their initial lengths are the same, (longitudinal strain)A < (longitudinal strain)B.
Now Y = \(\frac{\text { longitudinal stress }}{\text { longitudinal strain }}\)
Hence, YA> YB.
Question 11. Load-elongation graphs of two wires A and B, made of the same material and of equal initial length are shown in the Fig. Which wire is thicker?
Answer:
Y = \(\frac{F L}{\alpha l}\)
or, Y = \(\frac{F L}{\alpha l}\)(α = area of cross-section of the wires)
F, L, and Y are the same for the two wires
∴ \(\alpha \propto \frac{1}{l}\)
So the wire of smaller elongation has a larger cross-section.
∴ (α)A>(α)B
Hence, the wire A is thicker than the wire B.
Question 12. Young’s moduli of two rods of equal length and equal cross-section are Y1 and Y2. These rods are joined end to end forming a composite rod-system. Prove that the equivalent Young’s modulus of the composite system of rods = \(\frac{2 Y_1 Y_2}{Y_1+Y_2} .\)
Answer:
Young’s moduli of two rods of equal length and equal cross-section are Y1 and Y2. These rods are joined end to end forming a composite rod-system.
Let for applied force F, elongations of the two rods be /j and /2 respectively.
∴ \(l_1=\frac{F L}{Y_1 A} ; l_2=\frac{F L}{Y_2 A}\)
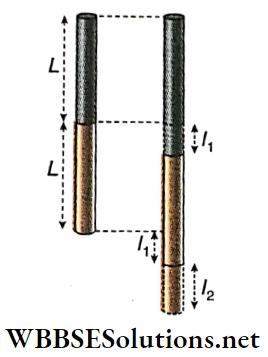
A = area of cross-section of each rod;
L = original length of each rod.
Now, equivalent Young’s modulus of the composite rod-system,
Y = \(\frac{\frac{F}{A}}{\frac{l_1+L_2}{2 L}}=\frac{2 F L}{A\left(l_1+l_2\right)}\)
= \(\frac{2 F L}{A\left[\frac{F L}{Y_1 A}+\frac{F L}{Y_2 A}\right]}\)
= \(\frac{2}{\frac{1}{Y_1}+\frac{1}{Y_2}}=\frac{2 Y_1 Y_2}{Y_1+Y_2}\)
Question 13. State whether the values of Young’s moduli for thin and thick iron wires of equal length will be different.
Answer:
Young’s moduli of two iron wires of the same length but of different thicknesses cannot be different because it depends only on the material of the wire.
Question 14. Can a steel wire be elongated to twice its initial length by hanging a load from its end?
Answer:
By hanging a load from its free end, a steel wire can¬not be elongated to twice its initial length. This is because the wire snaps before attaining that elongation, as it crosses its breaking load.
Question 15. How does the value of modulus of elasticity change due to increase in temperature?
Answer:
In most cases, the value of elastic modulus decreases slightly due to increase in temperature
Question 16. A hanging wire of length L is elongated by an amount l with a load M attached to Its free end. Prove that the elastic potential energy stored In the wire Is 1/2 Mgl.
Answer:
A hanging wire of length L is elongated by an amount l with a load M attached to Its free end.
Elastic potential energy stored in the wire
= 1/2 x force x increase in length
= 1/2 x Mgx l = 1/2 Mgl.
Question 17. A spring balance gives erroneous readings if It is used frequently over a long period of time. Explain.
Answer:
A spring balance gives erroneous readings if It is used frequently over a long period of time.
On using a spring balance frequently over a long period of time, its elastic property degrades and it deforms permanently. As a result, the elongation of the spring is more than the elongation it should suffer for a given load suspended at its free end. So, we get a wrong reading.
Question 18. An elastic wire is cut into two equal halves. Deter – mine whether there will be any change in the maxi¬mum load that each half can carry.
Answer:
An elastic wire is cut into two equal halves.
Young’s modulus, Y = \(\frac{\text { stress }}{\text { strain }}\). For maximum load, the stress is the breaking stress. For wires of the same material, both Y and the breaking stress have fixed characteristic values.
So, when a wire carries the maximum load, the strain acquires a particular value. This value is independent of the initial length of the wire. Therefore, two wires of the same material of lengths L1 and L2, can carry the same maximum load.
Question 19. The breaking force for a wire is F. What will be the breaking force for
- two parallel wires of same size and
- for a single wire of double the thickness?
Answer:
1. When two wires of the same size are suspended in parallel; a force equal to 2F has to be applied on the parallel combination, so that a force equal to the breaking force for the wire acts on each of the two wires.
2. Now, F = \(\frac{Y a l}{L}=\frac{Y\left(\pi d^2\right) l}{4 L}\)
or, F ∝ d2
If the wire is of double the thickness i.e., of double the diameter then breaking force will be 4F.
Elasticity Short Questions And Answers
Question 1. A spring is cut into two equal pieces. What is the spring the constant of each part if the spring constant of the original spring is k,
Solution:
A spring is cut into two equal pieces.
Let us consider that the spring elongates by x when a force F is applied on it. So, the force constant of the spring, k = F/x.
Now, if the spring is cut into two equal parts, then on the application of the same force F, each part of the spring will elongate by x/2.
The force constant each part, \(k^{\prime}=\frac{F}{\frac{x}{2}}=\frac{2 F}{x}=2 k\)
Question 2. A spring having spring constant k is cut into two parts in the ratio 1:2. Find the spring constants of the two parts.
Solution:
A spring having spring constant k is cut into two parts in the ratio 1:2.
Let the initial length of the spring be x.
The spring constant of a particular spring is inversely proportional to its length.
∴ kx = constant.
When the spring is cut into two parts in the ratio 1:2, the length of the two parts are x/3 and 2x/3 respectively.
⇒\(k_1 \frac{x}{3}=k x \text { or, } k_1=3 k\)
and \(k_2 \cdot \frac{2 x}{3}=k x \text { or, } k_2=\frac{3 k}{2}\)
Question 3. The length of a metal wire is L1. when the tension is T1 and L2 when the tension is T2 The unstretched length of the wire is
- \(\frac{L_1+L_2}{2}\)
- \(\sqrt{L_1 L_2}\)
- \(\frac{T_2 L_1-T_1 L_2}{T_2-T_1}\)
- \(\frac{T_2 L_1+T_1 L_2}{T_2+T_1}\)
Answer:
Young’s modulus, Y = \(\frac{\text { stress }}{\text { strain }}\)
or, strain = \(\frac{\text { stress }}{\text { strain }}\)
If the length of the wire is L0 when there is no tension in the string, then in the first case, stress = \(\frac{T_1}{\alpha}\) and strain = \(\frac{L_1-L_0}{L_0}\)
[a = area of cross-section = constant (approximately)]
So, \(\frac{L_1-L_0}{L_0}=\frac{T_1}{\alpha Y} \quad \text { or, } \frac{1}{\alpha Y}=\frac{1}{T_1}\left(\frac{L_1}{L_0}-1\right)\)
Similarly in the second case, \(\frac{1}{\alpha Y}=\frac{1}{T_2}\left(\frac{L_2}{L_0}-1\right)\)
So, \(\frac{1}{T_1}\left(\frac{L_1}{L_0}-1\right)=\frac{1}{T_2}\left(\frac{L_2}{L_0}-1\right)\)
or, \(\frac{1}{L_0}\left(\frac{L_1}{T_1}-\frac{L_2}{T_2}\right)=\frac{1}{T_1}-\frac{1}{T_2}\)
or, \(\frac{1}{L_0} \frac{T_2 L_1-T_1 L_2}{T_1 T_2}=\frac{T_2-T_1}{T_1 T_2}\)
∴ \(L_0=\frac{T_2 L_1-T_1 L_2}{T_2-T_1}\)
The option 3 is correct
Question 4. A liquid of bulk modulus k is compressed by applying an external pressure such that its density increased by 0.04% . The pressure applied on the liquid is
- k/10000
- k/10000
- 1000k
- 0.01k
Answer:
k = \(\frac{p}{\frac{\Delta V}{V}}\)
or, \(p=k \times \frac{\Delta V}{V}=k \times \frac{\Delta \rho}{\rho}=k \times 0.01 \%=\frac{k}{10000}\)
The option 1 is correct.
Question 5. The stress along the length of a rod (with rectangular cross section) is 1% of the Young’s modulus of its material. What is the approximate percentage of change of its volume? (Poisson’s ratio of the material of the rod is 0.3)
- 3%
- 1%
- 0.7%
- 0.4%
Answer:
Let, volume of the rod, V = xyz and Young’s modulus of its material of the rod = Y
Now, \(\frac{F}{A}=Y \times 1 \%\)
or, \(Y \times \frac{\Delta x}{x}=\frac{Y}{100}\)
or, \(\frac{\Delta x}{x}=0.01\)
∴ \(\frac{\Delta V}{V}=\frac{\Delta x}{x}+\frac{\Delta y}{y}+\frac{\Delta z}{z}\)
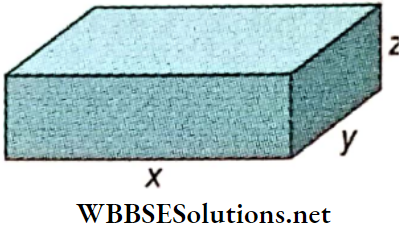
= \(\frac{\Delta x}{x}-\sigma \frac{\Delta x}{x}-\sigma \frac{\Delta x}{x}\) ……..(1)
[Poisson’s ratio, \(\sigma=\frac{\text { lateral strain }}{\text { longitudinal strain }}=\frac{\frac{\Delta y}{y}}{\frac{\Delta x}{x}}=\frac{\frac{\Delta z}{z}}{\frac{\Delta x}{x}}\)]
Negative symbol in equation (1) implies that, as length increases due to stress, value of y and z decreases simultaneously.
∴ From equation (1),
∴ \(\frac{\Delta V}{V}=0.01-2 \times 0.3 \times 0.01=0.004=0.4 \%\)
The option 4 is correct.
Question 6. When a rubber band is stretched by a distance x, it exerts a restoring force of magnitude F = ax + bx2, where a and b are constants. The work done in stretching the unstretched rubber band by L isothermal
- \(a L^2+b L^3\)
- \(\frac{1}{2}\left(a L^2+b L^3\right)\)
- \(\frac{a L^2}{2}+\frac{b L^3}{3}\)
- \(\frac{1}{2}\left(\frac{a L^2}{2}+\frac{b L^3}{3}\right)\)
Answer:
⇒ \(\int d W=\int F d l\)
W = \(\int_0^L a x d x+\int_0^L b x^2 d x=\frac{a L^2}{2}+\frac{b L^3}{3}\)
The option 3 is correct.
Question 7. A man grows into a giant such that his linear dimensions increase by a factor of 9. Assuming that his density remains same, the stress in the leg will change by a factor of
- 9
- 1/9
- 81
- 1/81
Answer:
According to the question, \(\frac{V_f}{V_i}=(9)^3\)
So, \(\frac{m_f}{m_i}=(9)^3\)
Also, \(\frac{A_f}{A_i}=(9)^2\)
Stress = \(\frac{\text { force }}{\text { area }}=\frac{m \times g}{A}\)
∴ \(\frac{S_f}{S_i}=\frac{m_f}{m_i} \times \frac{A_i}{A_f}=(9)^3 \times \frac{1}{(9)^2}=9\)
The option 1 is correct.
Question 8. An external pressure P is applied on a cube at 0°C so that it is equally compressed from all sides. K is the bulk modulus of the material of the cube and α is its coefficient of linear expansion. Suppose we want to bring the cube to its original size by heating. The temperature should be raised by
- \(\frac{P}{3 \alpha K}\)
- \(\frac{P}{\alpha K}\)
- \(\frac{3 \alpha}{P K}\)
- \(3 P K \alpha\)
Answer:
Bulk modulus, K= \(\frac{P}{\left(\frac{\Delta V}{V}\right)}\)
∴ \(\frac{\Delta V}{V}=\frac{P}{K}[\Delta V= change in volume]\)
If we bring back the cube to its original size by increasing the temperature Δt,
⇒ \(\Delta V=V \cdot \gamma \Delta t\)
or, \(\Delta t=\frac{\Delta V}{V} \cdot \frac{1}{\gamma}=\frac{\Delta V}{V} \cdot \frac{1}{3 \alpha}=\frac{P}{3 k \alpha}\)
The option (1) is correct.
Question 9. A solid sphere of radius r made of a soft material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the surface of the liquid, covering entire cross-section of cylindrical container. When a mass m is placed on the surface of the piston to compress the liquid, the fractional decrement in the radius of the sphere, (dr/r) is
- \(\frac{m g}{3 K a}\)
- \(\frac{m g}{K a}\)
- \(\frac{K a}{m g}\)
- \(\frac{K a}{3 m g}\)
Answer:
Bulk modulus, K = \(-V \frac{d p}{d V}\)
or, \(-\frac{d V}{V}=\frac{d p}{K}\)
or, \(\frac{-3 d r}{r}=\frac{\frac{m g}{a}}{K}\left[because V=\frac{4}{3} \pi r^3\right]\)
or, \(\frac{d r}{r}=-\frac{m g}{3 K a} \quad therefore\left|\frac{d r}{r}\right|=\frac{m g}{3 K a}\)
The option 1 is correct
Question 10. Copper of fixed volume V is drawn into wire of length l. When this wire is subjected to a constant force F, the extension produced in the wire is Δl. Which of the following graphs is a straight line?
- Δl versus 1/l
- Δl versus l2
- Δl versus 1/l2
- Δl versus l
Answer:
Y = \(\frac{F l}{A \Delta l} \text { or, } \Delta l=\frac{F l}{A Y}=\frac{F l^2}{V Y}\)
∴ \(\Delta l \propto l^2\)
The option 2 is correct.
Question 11. The approximate depth of an ocean is 2700 m. The compressibility of water is 45.4 x 10-11 Pal-1 and density of water is 103kg/m3. What fractional compression of water will be obtained at the bottom of the ocean?
- 0.8 x 10-2
- 1.0 x 10-2
- 1.2 x 10-2
- 1.4×10-2
Answer:
Due to AP amount of increase in pressure, there is AV
amount of compression in volume V.
So, fractional compression = \(\frac{\Delta V}{V}\)
and compressibility, K = \(\frac{1}{V} \frac{\Delta V}{\Delta P}\)
Now consider the magnitude, \(\frac{\Delta V}{V}=K \Delta P\)
Here, ΔP = hρg = 2700 x 103 x 10 Pa [taking g = 10m/s2]
Hence, fractional compression, \(\frac{\Delta V}{V} =\left(45.4 \times 10^{-11}\right) \times\left(2700 \times 10^3 \times 10\right)\)
= \(1.226 \times 10^{-2}\)
The option 3 is correct.
Question 12. The density of a metal at normal pressure is p. Its density when it is subjected to an excess pressure p is p’ . If B is bulk modulus of the metal, the ratio of \(\frac{e^{\prime}}{\rho}\)
- \(1+\frac{B}{p}\)
- \(\frac{1}{1-\frac{p}{B}}\)
- \(1+\frac{p}{B}\)
- \(\frac{1}{1+\frac{P}{B}}\)
Answer:
Volume strain = change in pressure = p
Initial volume, V = \(\frac{M}{\rho}\)
Final volume, \(V^{\prime}=\frac{M}{\rho^{\prime}}\)
Change in volume, \(V^{\prime}-V=M\left(\frac{\rho-\rho^{\prime}}{\rho^{\prime} \rho}\right)\)
∴ Volume strain = \(=\frac{V^{\prime}-V}{V}=\frac{\rho-\rho^{\prime}}{\rho^{\prime}}\)
∴ \(B=-\frac{p V}{V^{\prime}-V}=-\frac{p \times \rho^{\prime}}{\rho-\rho^{\prime}}\)
or, \(\underset{B}{p}=-\frac{\rho-\rho^{\prime}}{\rho^{\prime}}=\frac{\rho^{\prime}-\rho}{\rho^{\prime}}\)
or, \(\frac{\rho}{\rho^{\prime}}=1-\frac{p}{B}\)
∴ \(\frac{\rho^{\prime}}{\rho}=\frac{1}{1-\frac{p}{B}}\)
The option 2 is correct.
Question 12. Two wires are made of the same material and have the same volume. The first wire has cross-sectional area A and the second wire has cross-sectional area 3A. If the length of the first wire is increased by Δl. on applying a force F, how much force is needed to stretch the second wire by the same amount?
- 4F
- 6F
- 9F
- F
Answer:
In case of first wire, Y = \(\frac{F / A}{\Delta l / l_0}=\frac{F l_0}{A \Delta l}\)
or, \(F=\frac{Y A \Delta l}{l_0}\)
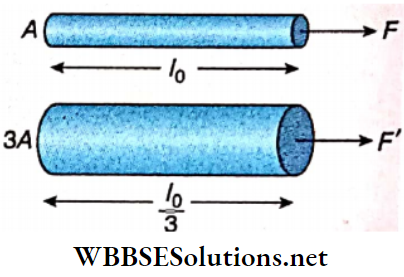
In case of second wire,
Y = \(\frac{F^{\prime} / 3 A}{\frac{\Delta l}{l_0 / 3}}=\frac{F^{\prime} l_0}{9 A \Delta l}\)
or, \(F^{\prime}=\frac{9 Y A \Delta l}{l_0}=9 F\)
The option 3 is correct.
Question 13. Which type of substances are called elastomers? Give one example.
Answer:
Elastomers:
Elastomers are those materials for which stress-strain variation is not a straight line within elastic limit. An elastomer is a polymer with viscoelasticity (colloquially elasticity), generally having low Young’s modulus and high failure strain compared with other materials.
Example: Rubber.
Question 14. Bridges are declared unsafe after long use. Why?
Answer:
Bridges are declared unsafe after long use.
A bridge undergoes alternating stress and strain for a large number of times during its use. A bridge loses its elastic strength when it is used for long time. Therefore, the amount of strain for a given stress will become large and ultimately the bridge will collapse. So, they are declared unsafe after long use.
Question 15. What are elastomers? Give two examples for the same.
Answer:
Elastomers:
Elastomers (elastic polymers) are materials of low Young’s modulus but of very high elastic limits. Such a material can withstand high strain but can still develop sufficient stress to bring it back to its initial size and shape.
Examples: natural rubber, thermoplastics.
Question 16. What is the value of rigidity modulus of elasticity for an incompressible liquid?
Answer:
Value of rigidity modulus of elasticity for an incompressible liquid
A liquid, compressible or incompressible, does not have any define shape; it cannot withstand shear. So it can never generate any shearing stress. Hence the rigidity modulus of elasticity of a liquid is zero.
Question 17. Which type of energy is stored in the spring of wrist watch?
Answer:
Potential energy is stored in the spring of wrist watch.
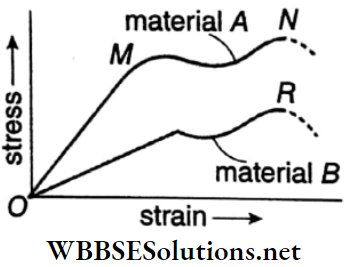
Question 18. The stress-strain graph for materials A and B are as shown in the graphs are drawn to the same scale, which graph represents property of ductile materials? Justify your answer.
Answer:
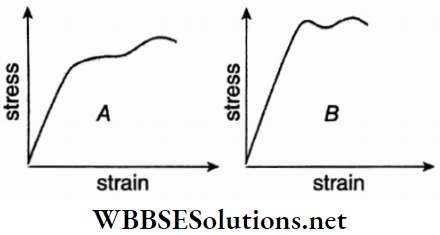
The graph for material A represents the property of ductile material because of its greater plastic range.
Question 19. A two wires A and B of length l, radius r, and length 21, radius 2 r having same Young’s modulus Y are hung with a weight mg as shown in figure. What is the net elongation in the two wires?
Answer:
A two wires A and B of length l, radius r, and length 21, radius 2 r having same Young’s modulus Y are hung with a weight mg as shown in figure.
The length and radius of wire A are l and r and that of wire B are 2l and 2 r respectively.
If l1 and l2 be the individual elonga¬tion of wire A and wire B, then the net elongation,
∴ \(\Delta l =\Delta l_1+\Delta l_2=\frac{m g l}{\pi r^2 Y}+\frac{m g(2 l)}{\pi(2 r)^2 Y}\)
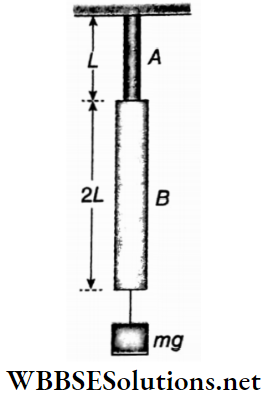
= \(\left(\frac{m g l}{\pi r^2 Y}+\frac{2 m g l}{4 \pi r^2 Y}\right)=\frac{4 m g l+2 m g l}{4 \pi r^2 Y}=\frac{3}{2} \frac{m g l}{\pi r^2 Y}\)
Question 20. Which of the two forces-deforming or restoring is responsible for the elastic behaviour of substance?
Answer:
Restoring force is responsible for the elastic behaviour of substance.
Elasticity Assertion Reason Type Question And Answers
Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.
- Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
- Statement 1 is true, statement 2 is true; statement D is not a correct explanation for statement 1.
- Statement 1 is true, statement 2 is false.
- Statement 1 is false, statement 2 is true.
Question 1.
Statement 1: Young’s modulus for a perfectly plastic body is zero.
Statement 2: For a perfectly plastic body, restoring force is zero.
Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
Question 2.
Statement 1: If length of a rod is doubled the breaking load remains unchanged.
Statement 2: Breaking load is equal to the elastic limit
Answer: 3. Statement 1 is true, statement 2 is false.
Question 3.
Statement 1: Ductile metals are used to prepare thin wires.
Statement 2: In the stress-strain curve of ductile metals, the length between the points representing elastic limit and breaking points is very small.
Answer: 3. Statement 1 is true, statement 2 is false.
Question 4.
Statement 1: The restoring force F on a stretched string at extension x is related to the potential energy U as F = \(=-\frac{d U}{d x}\)
Statement 2: F = -kx and U = 1/2kx2, where k is the spring constant.
Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
Question 5.
Statement 1: Identical springs of steel and copper are equally stretched. More work will be done on the steel spring.
Statement 2: Steel is more elastic than copper.
Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
Question 6.
Statement 1: A hollow shaft is found to be stronger than a solid shaft made of same material.
Statement 2: The torque required to produce a given twist in hollow cylinder is greater than that required to twist a solid cylinder of same size and same material.
Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
Question 7.
Statement 1: The bridges are declared unsafe after a long use.
Statement 2: Elastic strength of bridges decreases with time.
Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
Question 8.
Statement 1: Stress is the internal force per unit area of a body.
Statement 2: Rubber is less elastic than steel.
Answer: 2. Statement 1 is true, statement 2 is true; statement D is not a correct explanation for statement 1.
Elasticity Very Short Answer Type Questions
Question 1. Between rubber and steel—which one is more elastic?
Answer: Steel
Question 2. Which one is more elastic—steel or diamond?
Answer: Diamond
Question 3. State whether the elasticity of a metallic substance increases or decreases with the rise in temperature.
Answer: Decreases
Question 4. ‘Strain has no unit’—state whether the statement is true or false.
Answer: True
Question 5. Write down the dimension of stress.
Answer: ML-1T-2
Question 6. Can the length of a steel wire be doubled by hanging a load from its end?
Answer: No
Question 7. Under which kind of stress does a body undergo a change in shape without changing its volume?
Answer: Shearing stress
Question 8. Which property of a spring is represented by its force constant?
Answer: Stiffness of the spring
Question 9. Between steel and copper—which one is usually used to make springs?
Answer: steel
Question 10. Write down the dimension of force constant.
Answer: MT-2
Question 11. Can liquid and gaseous substances withstand shearing strain?
Answer: No
Question 12. Which property of a metal is manifested when compressional stress more than the yield point is developed?
Answer: Plastic property
Question 13. On what factor does the breaking stress of a wire depend?
Answer: On the material of the wire
Question 14. State whether a body undergoes a change in volume due to shearing stress only.
Answer: No
Question 15. ‘Young’s modulus depends on temperature’—state whether it is true or false?
Answer: True
Question 16. Write down the dimension of elastic limit.
Answer: MLT-2
Question 17. A wire is halved by cutting it. Would there be any change in the breaking load due to this?
Answer: No
Question 18. All bodies are _______ elastic in reality.
Answer: Partly
Question 19. Strain is a ______ quantity.
Answer: Dimensionless
Question 20. During change in length of a wire or change in volume of a body, ______ stress is developed.
Answer: Normal
Question 21. During change in shape of a body, stress is developed.
Answer: Shearing
Question 22. Compressibilities of solidsand liquids are very _____, but that of a gaseous substance is much ______
Answer: low, higher
Question 23. Modulus of rigidity is a characteristic of ________.
Answer: Solids
Question 24. Poisson’s ratio depends on the of a body.
Answer: Material
Question 25. Loss in elastic ability of a body due to rapid change in the load applied on it is called _____
Answer: Elastic fatigue
Question 26. What is the SI unit of force constant?
Answer: N · m-1
Question 27. ______ are usually made of not of copper.
Answer: Springs, steel
Question 28. The magnitude of the _______ per unit cross-sectional area on a body is the breaking stress.
Answer: Breaking load
Question 29. Write the name of a substance whose elasticity does not change with the change in temperature.
Answer: Invar
Question 30. What is defined by dividing stress by strain within elastic limit?
Answer: Elastic modulus
Question 31. For which kind of substance is Young’s modulus physically meaningful?
Answer: Solid
Question 32. Two iron wires of equal length are taken. One of them is thick and the other is thin. In which case will Young’s modulus be greater?
Answer: Wall be same in either case
Question 33. What is the Poisson’s ratio of a substance whose volume remains unchanged under elastic strains?
Answer: 1/2
Question 34. A wire is cut into two parts. What will be the change in Young’s modulus of the parts?
Answer: No change occurs
Question 35. What is the range of theoretical values of Poisson’s ratio?
Answer: -1 to 1/2
Question 36. Write down the dimension of Poisson’s ratio with respect to M, L and T.
Answer: M0L0T0
Question 37. What is the value of Young’s modulus for a perfectly rigid body?
Answer: Infinite
Question 38. Name the reciprocal of bulk modulus.
Answer: Compressibility
Question 39. What is the dimension of elastic modulus?
Answer: ML-1T-2
Question 40. What is the relation between Y, K and σ?
Answer: Y = 3K(1-2σ)
Question 41. What is the relation between Y, n and <x?
Answer: Y = 2n(1 +σ)
Question 42. What is the value of Young’s modulus for a perfectly plastic body?
Answer: Zero
Question 43. What will be the change in temperature of a stretched wire if it snaps suddenly?
Answer: Temperature increases
Question 44. Which type of energy is stored when an elastic wire is elongated by stretching?
Answer: Potential
Question 45. In a stretched wire, potential energy stored per unit volume = 1/2 x _____ x _____
Answer: stress, strain
Question 46. Force constants of two springs are k1 and k2(k1 >k2)
- The springs are elongated by the same amount and
- The springs are elongated by applying the same force. Then for which of the springs is more work performed?
Answer:
- The first spring,
- The second spring
Question 47. Force constants of two springs are k1 and k2. What will be the equivalent force constant of the spring system when the springs are joined in a parallel combination?
Answer: k1 + k2
Elasticity Match Column 1 With Column 2
Question 1.

Answer: 1. C, 2. B, 3. A, 4. D
Question 2.
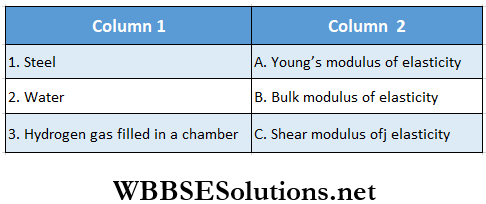
Answer: 1. A, B, C, 2. B, 3. B
Question 3.
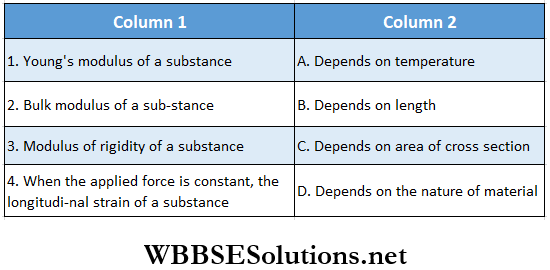
Answer: 1. A, D, 2. A, D, 3. A, D, 4. C
Question 4.
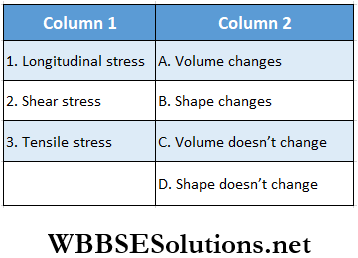
Answer: 1. A, B, C 2. B, C, 3. A, D
Elasticity Comprehension Type Question And Answers
Read the following passages carefully and answer the questions at the end of them.
Question 1. According to Hooke’s law, within the elastic limit = stress/strain constant. This constant depends on the type of strain or the type of force acting. Tensile stress might result in compressional or elongative strain however, a tangential stress can only cause a shearing strain. After crossing the elastic limit, the material undergoes elongation and beyond a stage beaks. All modulus of elastically are basically constants for the materials under stress.
1. Two wires of same material have length and radius l, r and 2l, r/2 respectively. The ratio of their Young’s modulus is
- 1:2
- 2:3
- 2:1
- 1:1
Answer: 4. 1:1
2. After crossing the yield region, the material will have
- Reduced stress
- Increased stress
- Breaking stress
- Constant stress
Answer: 1. Reduced stress
3. If stress/strain is x in elastic region and y in yield region, then
- x = y
- x > y
- x < y
- x = 2y
Answer: 2. x > y
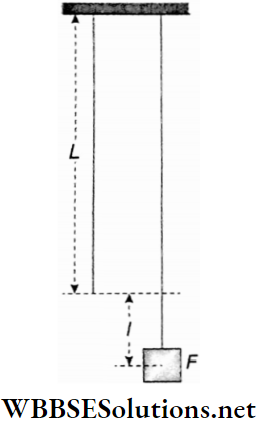
Question 2. A sphere of radius 0.1 m and mass 8π kg is attached to the lower end of a steel wire of length 5 m and diameter 10-3 m. The wire is suspended from 5.22 m high ceiling of a room. When the sphere is made to swing as a simple pendulum, it just grazes the floor at the lowest point. Given, Young’s modulus of steel is 1.994 x 1011 N • m-2.
1. What is the extension of the wire at the mean position when the sphere is oscillating?
- 0.01m
- 0.02 m
- 0.03 m
- 0.04 m
Answer: 2. 0.02 m
2. The tension in the wire at the mean position when the sphere is oscillating is
- 199.4 πN
- 19.94 πN
- 1.994 πN
- 0.1994 πN
Answer: 3. 1.994 πN
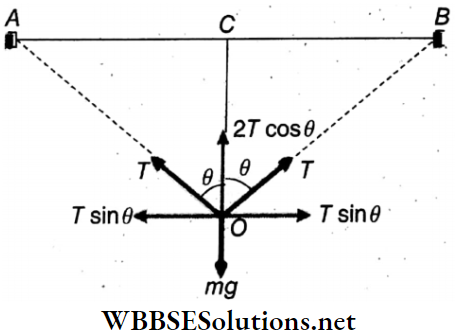
Question 3. A light rod of length 2 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross section 10-3m2 and the other is of brass of cross-section 2 x 10-3 m2. Young’s modulus for steel is 2 x 1011 N • m-2 and for brass is 1011 N • m-2.
1. Find out the position along the rod at which a weight may be hung to produce equal stress in both wires.
- 1.39m
- 1.30m
- 1.33m
- 1.24m
Answer: 3. 1.33m
2. Find out the position along the rod at which a weight may be hung to produce equal strains on both wires.
- 1m
- 1.2m
- 0.87m
- 1.05m
Answer: 1. 1m
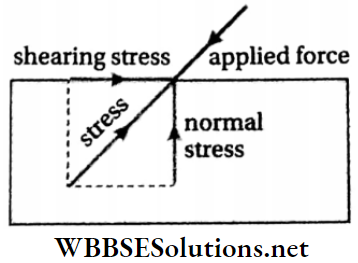
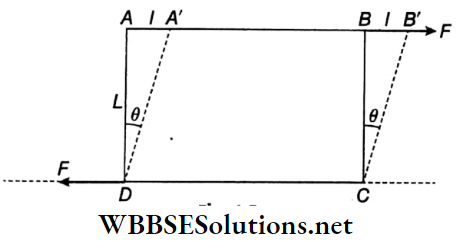
Question 4. A bar of cross-section A is subjected to equal and opposite tensile force F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in Fig.
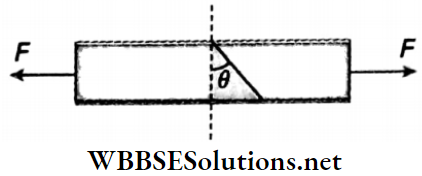
1. The tensile stress at this plane in terms of F, A and θ is
- \(\frac{F \cos ^2 \theta}{A}\)
- \(\frac{F}{A \cos ^2 \theta}\)
- \(\frac{F \sin ^2 \theta}{A}\)
- \(\frac{F}{A \sin ^2 \theta}\)
Answer: 1. \(\frac{F \cos ^2 \theta}{A}\)
2. Find the value of θ for which the tensile stress is
- 0°
- 90°
- 45°
- 60°
Answer: 1. 0°
3. What is the shearing stress at the plane in terms of F, A, and θ?
- \(\frac{F \cos 2 \theta}{2 A}\)
- \(\frac{F \sin 2 \theta}{2 A}\)
- \(\frac{F \sin \theta}{A}\)
- \(\frac{F \cos \theta}{A}\)
Answer: 2. \(\frac{F \sin 2 \theta}{2 A}\)
Question 5. To measure Poisson’s ratio for rubber, the apparatus shown in Fig is used. T is a piece of thin-walled rubber tubing nearly 1 m long and 2 cm in diameter. The lower end is closed and is joined to a hanger H on which slotted weights can be slipped. The upper end is closed by a rubber bung containing a capillary tube C. The whole of the rubber tube and part of the capillary tube are filled with water. The apparatus is supported on a rigid support. When the weights are inserted in the hanger, the length of the rubber tube increases, and meniscus of water in C is observed to fall. The extension in the rubber tube is measured using a vernier microscope.
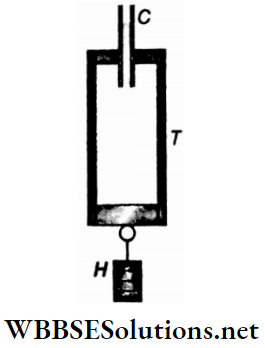
Let V, a and l be the inner volume, area iv. The stress in the string is of cross section and length respectively of the tube. Then V = al = πR2l ; R is the inner radius of the tube and r is the radius of the capillary tube. Let dx be the fall in the level of the meniscus of the capillary tube.
1. What is the Poisson’s ratio?
- \(\sigma=\left(1-\frac{r}{R} \frac{d x}{d V}\right)\)
- \(\sigma=\frac{1}{2}\left(1-\frac{r}{R} \frac{d x}{d V}\right)\)
- \(\sigma=\frac{1}{2}\left(1-\frac{r^2}{R^2} \frac{d x}{d \nu}\right)\)
- \(\sigma=\left(1-\frac{r^2}{R^2} \frac{d x}{d \nu}\right)\)
Answer: 3. \(\sigma=\frac{1}{2}\left(1-\frac{r^2}{R^2} \frac{d x}{d \nu}\right)\)
2. The nature of graph between dx and dl is
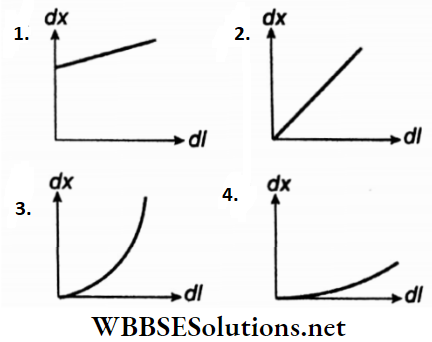
Answer: 2.
Question 6. One end of a string of length L and cross-sectional area A is fixed to a support and the other end is fixed to a bob of mass m. The bob is revolved in a horizontal circle of radius r with an angular velocity ω such that the string makes an angle θ with the vertical. Young’s modulus is Y.
1. The angular velocity w is equal to
- \(\sqrt{\frac{g \sin \theta}{r}}\)
- \(\sqrt{\frac{g \cos \theta}{r}}\)
- \(\sqrt{\frac{g \tan \theta}{r}}\)
- \(\sqrt{\frac{g \cot \theta}{r}}\)
Answer: 3. \(\sqrt{\frac{g \tan \theta}{r}}\)
2. The tension T in the string is
- \(\frac{m g}{\cos \theta}\)
- \(\frac{m g}{\sin \theta}\)
- \(\frac{m g}{\tan \theta}\)
- \(m\left(g^2+r^2 \omega^4\right)^2\)
Answer: 1. \(\frac{m g}{\cos \theta}\)
3. The increase ΔL in length of the string is
- \(\frac{T L}{A Y}\)
- \(\frac{m g L}{A Y \cos \theta}\)
- \(\frac{m g L}{A Y \sin \theta}\)
- \(\frac{m g L}{A Y}\)
Answer: 3. \(\frac{m g L}{A Y \sin \theta}\)
4. The stress in the string is
- \(\frac{m g}{A}\)
- \(\frac{m g}{A}\left(1-\frac{r}{L}\right)\)
- \(\frac{m g}{A}\left(1+\frac{r}{L}\right)\)
- \(\frac{m g}{A}\left(\frac{r}{L}\right)\)
Answer: 1. \(\frac{m g}{A}\left(\frac{r}{L}\right)\)
Elasticity Integer Answer Type Question And Answers
Question 1. In this type, the answer to each of the questions is a single-digit Integer ranging from 0 to 9. 1. A 0.1 kg mass is suspended from a wire of negligible mass. The length of the wire is 1 m and its cross-sectional area is 4.9 x 10-7 m2. If the mass is pulled a little in the vertically downward direction and released it performs simple harmonic motion of angular frequency 140 rad • s-1. If the Young’s modulus of the material of the wire is n x 109 N • m-2. Find the value of n.
Answer: 4
Question 2. Two wires A and B have the same length and area of cross section. But Young’s modulus of A is two times the Young’s modulus of B. Then what is the ratio of the force constant of A to that of B?
Answer: 2
Question 3. For a wire of length l, maximum change in length under stress conditions is 2 mm. What is the change in length (in mm) under same conditions when length of wire is halved?
Answer: 1
Question 4. The density of water at the surface is 1030 kg • m-3 and bulk modulus of water is 2 x 109 N • m-2. What is the approximate change in density (in kg • m-3) of water in a lake at a depth of 400 m below the surface?
Answer: 2
Question 5. A body of mass 3.14 kg is suspended from one end of a wire of length 10.0 m. The radius of the wire is changing uniformly from 9.8 x 10-4 m at one end to 5.0 x 10-4 m at the other end. Find the change in the length of the wire in mm. Young’s modulus of the material of the wire is 2x 1011 N • m-2.
Answer: 1