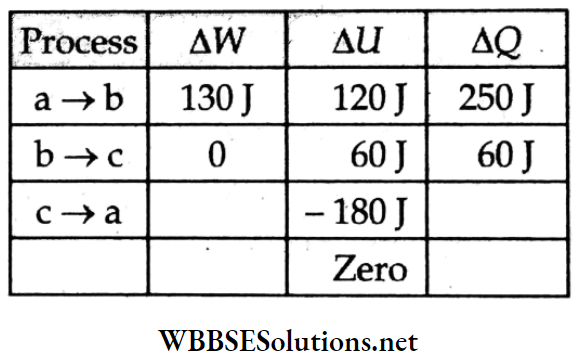
Mechanical Properties of Matter Elasticity Surface Tension and Viscosity
Question 1. Which of the following has no dimensions?
- Young modulus
- Stress
- Poisson ratio
- Compressibility
Answer: 3. Poisson ratio
Poisson ratio = \(\sigma=\frac{\text { lateral strain }}{\text { longitudinal strain }}\)
As strain is dimensionless, the Poisson ratio also has no dimensions.
Question 2. The dimensional formula for the modulus of rigidity is
- ML-2r-2
- ML-3T-2
- ML2T-2
- ML-1T-2
Answer: 4. ML-1T-2
Modulus of rigidity = \(\eta=\frac{\text { tangential stress }}{\text { shear strain }}\)
Shear strain is dimensionless, so
⇒ \([\eta]=\frac{[\text { force }]}{[\text { area }]}=\mathrm{ML}^{-1} \mathrm{~T}^{-2}\)
Question 3. Which of the following symbols does not denote a unit of the Young modulus?
- MPa
- dyn cm-2
- Nm-1
- Nm-2
Answer: 3. Nm-1
Y is \(\frac{fprce}{area}\) ,so the newton per metre (N m-1) is not a unit of Y
Question 4. A 10-m-long steel wire of a cross-sectional area 10-5 m2 subjected to an extensional force of 2500 N elongates by 1.0 cm. The Young modulus for steel is
- 2.5 x 107 N m-2
- 2.5 x 109 N m-2
- 2.5 x 1011 N m-2
- 3.0 x 1010 N m-2
Answer: 3. 2.5 x 1011 N m-2
⇒ \(Y=\frac{\frac{F}{A}}{\frac{\Delta L}{L}}=\frac{\frac{2500 \mathrm{~N}}{10^{-5} \mathrm{~m}^2}}{\frac{1 \times 10^{-2} \mathrm{~m}}{10 \mathrm{~m}}}\)
= \(2.5 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}\)
Question 5. The theoretical value of the Poisson ratio lies between
- -∞ and +∞
- -1 and +1
- 0 and +1
- -1 and +\(\frac{1}{2}\)
Answer: 4. -1 and +\(\frac{1}{2}\)
Theoretically, the value of the Poisson ratio lies between-1 and + \(\frac{1}{2}\)
Question 6. If the longitudinal strain for a wire is 0.03 and its Poisson ratio is 0.5, its lateral strain is
- 0.003
- 0.0075
- 0.015
- 0.4
Answer: 3. 0.015
Poisson ratio = \(\sigma=\frac{\text { lateral strain }}{\text { longitudinal strain }}\)
∴ 0.5 = \(\frac{\text { lateral strain }}{0.03}\)
lateral strain = 0.015
Question 7. The relation between the Young modulus (Y), bulk modulus (B), and modulus of rigidity (n) is
- \(\frac{1}{Y}=\frac{1}{B}+\frac{1}{\eta}\)
- \(\frac{3}{Y}=\frac{1}{\eta}+\frac{1}{3 B}\)
- \(\frac{1}{Y}=\frac{3}{\eta}+\frac{1}{3 B}\)
- \(\frac{1}{\eta}=\frac{3}{Y}+\frac{1}{3 B}\)
Answer: 2. \(\frac{3}{Y}=\frac{1}{\eta}+\frac{1}{3 B}\)
The relation connecting Y, n, and B is
⇒ \(\frac{3}{Y}=\frac{1}{\eta}+\frac{1}{3 B}\)
Question 8. A uniform steel wire of a cross-sectional area of 4 mm² is stretched by 0.1 mm by some stretching force. How much will another steel wire of the same length but of a cross-sectional area of 8 mm² get stretched by the same stretching force?
- 0.5 mm
- 1.0 mm
- 0.05 mm
- 0.08 mm
Answer: 3. 0.05 mm
⇒ \(Y=\frac{F}{A} \cdot \frac{L}{\Delta L}\)
Given that F and L are constant.
∴ Δ1 . ΔL1 = Δ2.ΔL2
(4mm²)(0.1mm) = (8mm²)ΔL2
ΔL2 = 0.05mm.
Question 9. The breaking force for a wire of diameter D of a material is F. The breaking force for a wire of the same material of radius D is
- \(\frac{F}{4}\)
- F
- 2F
- 4F
Answer: 4. 4F
The breaking stress for a given material is constant. Thus, the breaking force (F) is proportional to the area (A).
Here, \(F=k \pi\left(\frac{D}{2}\right)^2\)
and F’ = knD² = 4F.
Question 10. A cube is subjected to a uniform volume compression. If the length of each side of the cube is reduced by 2%, the bulk strain is
- 0.02
- 0.03
- 0.04
- 0.06
Answer: 4. 0.06
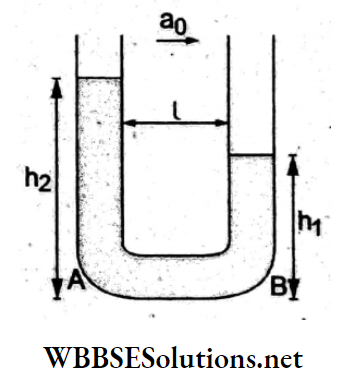
Volume strain = \(\frac{\Delta V}{V}\)
∵ V = L³,
∴ \(\frac{\Delta V}{V}=3\left(\frac{\Delta L}{L}\right)\)
= 3(2%)
= 6%
= 0.06′
Question 11. The energy density in a stretched string is equal to
- stress x strain
- \(\frac{stress}{strain}\)
- \(\frac{1}{2}\) (stress x strain)
- \(\frac{strain}{stress}\)
Answer: 3. \(\frac{1}{2}\) (stress x strain)
The elastic energy stored is
U = \(\frac{1}{}2\) (stress)(strain)(volume).
∴ energy density = \(\frac{U}{\text { volume }}=\frac{1}{2}\) (stress)(strain).
Question 12. A wire fixed at the upper end stretches by a length l by applying a stretching force F. The work done in this stretching is stress
- \(\frac{E}{2l}\)
- Fl
- 2Fl
- \(\frac{Fl}{2}\)
Answer: 4. \(\frac{Fl}{2}\)
Work done = \(\frac{1}{2}\)(stretching force)(stretch)
= \(\frac{1}{2}\)Fl.
Question 13. A uniform wire suspended vertically from one of its ends is stretched by a 20-kg load suspended from the lower end. The load stretched the wire by 1 mm. The elastic energy stored in the wire is
- 0.1 J
- 0.21 J
- 10 J
- 20 J
Answer: 1. 0.1 J
Given that F = 20 kg F
= 200 N
and stretch = 1 mm
= 1 x 10-3 m.
∴ energy stored = U = \(\frac{1}{2}\)Fl
= 0.1 J.
Question 14. If S is the stress and Y is the Young modulus of the material of a wire, the energy stored per unit volume in the wire is
- \(\frac{2Y}{S}\)
- \(\frac{S^2}{2 Y}\)
- \(\frac{S}{2Y}\)
- 2S²Y
Answer: 2. \(\frac{S^2}{2 Y}\)
Energy density = \(\frac{1}{2}\) (stress)(strain)
= \(\frac{1}{2} \text { (stress) }\left(\frac{\text { stress }}{Y}\right)\)
= \(\frac{S^2}{2 Y}\)
Question 15. A pendulum made of a uniform wire of cross-sectional area A has a time period of T. When an additional mass M is added to its bob, the time period changes to TM. If Y is the Young modulus of the wire then is equal to
- \(\left[\left(\frac{T_M}{T}\right)^2-1\right] \frac{A}{M g}\)
- \(\left[\left(\frac{T_M}{T}\right)^2-1\right] \frac{M g}{A}\)
- \(\left[1-\left(\frac{T_M}{T}\right)^2\right] \frac{A}{M g}\)
- \(\left[1-\left(\frac{T}{T_M}\right)^2\right] \frac{A}{M g}\)
Answer: 1. \(\left[\left(\frac{T_M}{T}\right)^2-1\right] \frac{A}{M g}\)
⇒ \(T=2 \pi \sqrt{\frac{L}{g}} \text { and } T_M=2 \pi \sqrt{\frac{L+\Delta L}{g}}\)
∴ \(\frac{T_M}{T}=\sqrt{\frac{L+\Delta L}{L}} \Rightarrow\left(\frac{T_M}{T}\right)^2=1+\frac{\Delta L}{L}\)
But \(Y=\frac{F L}{A \cdot \Delta L}=\frac{M g L}{A \cdot \Delta L}\)
∴ \(\frac{1}{Y}=\frac{A \cdot \Delta L}{M g L}=\left[\left(\frac{T_M}{T}\right)^2-1\right] \frac{A}{M g}\)
Question 16. The potential-energy function for the force between two atoms in a diatomic molecule is approximately given by \(U(x)=\frac{a}{x^{12}}-\frac{b}{x^6}\) where a and b are two constants, and x is the distance between the atoms. If the dissociation energy is \(D=U(x=\infty)-U_{\mathrm{eq}}\) then D is equal to
- \(\frac{b^2}{6 a}\)
- \(\frac{b^2}{2 a}\)
- \(\frac{b^2}{12 a}\)
- \(\frac{b^2}{4 a}\)
Answer: 4. \(\frac{b^2}{4 a}\)
Potential energy = U = \(\frac{a}{x^{12}}-\frac{b}{x^6}\)
Force = \(F=-\frac{d U}{d x}=\frac{12 a}{x^{13}}-\frac{6 b}{x^7}\)
For equilibrium, F = 0
x6 = \(\frac{2a}{b}\)
U at x = ∞ is zero, and U at equilibrium, when x = \(x=\left(\frac{2 a}{b}\right)^{1 / 6}\), will be equal to
⇒ \(\frac{a}{\left(\frac{2 a}{b}\right)^2}-\frac{b}{\frac{2 a}{b}}=-\frac{b^2}{4 a}\)
∴ dissociation energy = \(=\frac{b^2}{4 a}\)
Question 17. If in a wire of Young modulus Y, a longitudinal strain of x is produced, the value of the potential energy stored in its unit volume will be
- Yx²
- 2Yx²
- 0.5Yx²
- 0.5Y²x
Answer: 4. 0.5Y²x
Elastic potential energy density = \(\frac{U}{\text { volume }}=\frac{1}{2}\) (stress)(strain)
= \(\frac{1}{2}\) [Y(strain)(strain)]
= \(\frac{1}{2}\) Y(strain)²
= 0.5Yx²
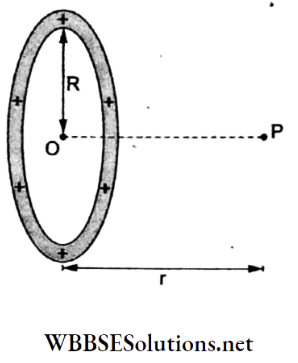
Question 18. A metal ring of initial radius r and cross-sectional area A is fitted onto a wooden disc of radius R > r. If the Young modulus of the metal is Y, the tension in the ring is
- \(\frac{A Y R}{r}\)
- \(\frac{Y r}{AR}\)
- \(\frac{A Y(R-r)}{r}\)
- \(\frac{Y(R-r)}{A r}\)
Answer: 3. \(\frac{A Y(R-r)}{r}\)
Initial length = L = 2πr and final length = 2πR.
∴ extension = AL = final length- initial length = (R- r).
∴ tension = \(F=\frac{Y A \cdot \Delta L}{L}\)
= \(\frac{Y A \cdot 2 \pi(R-r)}{2 \pi r}\)
= \(\frac{A Y(R-r)}{r}\)
Question 19. The compressibility of water is 4 x 10-5 per unit atmospheric pressure. The decrease in the volume of 100 cm3 water under a pressure of 100 atm will be
- 0.4 cm3
- 4 x 10–5 cm3
- 0.025 cm3
- 0.004 cm3
Answer: 1. 0.4 cm3
Compressibility = \(\frac{1}{B}=\frac{\Delta V}{p V}\)
∴ \(4 \times 10^{-5} \mathrm{~atm}=\frac{\Delta V}{\left(100 \times 10^{-6} \mathrm{~m}^3\right)(100 \mathrm{~atm})}\)
∴ the decrease in volume = AV = 4 x 10-7 m³
= 0.4 cm3.
Question 20. The breaking stress of a wire depends upon the
- Length of the wire
- The radius of the wire
- Material of the wire
- The shape of its cross-section
Answer: 3. Material of the wire
The breaking stress does not depend on the shape and size of the wire. It depends on the material of the wire.
Question 21. The length of a metal wire is l2under a tension of T1and l1 under a tension of T2. The natural length of the wire is
- \(\frac{l_1+l_2}{2}\)
- \(\sqrt{h_1 l_2}\)
- \(\frac{l_1 T_2-l_2 T_1}{T_2-T_1}\)
- \(\frac{h_1 T_2+l_2 T_1}{T_1+T_2}\)
Answer: 3. \(\frac{l_1 T_2-l_2 T_1}{T_2-T_1}\)
Let U be the original length of the wire,
∴ under the tension T1 stretch = l1-l
and under the tendon Tystretch = l2-l
∵ stretching force = extension
∴ \(\frac{T_1}{T_2}=\frac{l_1-l}{l_2-l}\)
Hence, \(l=\frac{l_1 T_2-l_2 T_1}{T_2-T_1}\)
Question 22. A steel cable with a cross-sectional area of 3 cm² has an elastic limit of 2.4 x 108 N m-2. The maximum upward acceleration that can be given to a 1200-kg elevator supported by this cable, if the stress is not to exceed one-third of its elastic limit, is (assuming g = 10 m s-2)
- 12 ms-2
- 10ms-2
- 8ms-2
- 7ms-2
Answer: 2. 10ms-2
Maximum tension = \(\frac{1}{3}\) (stress)(area)
= \(\frac{1}{3}\left(2.4 \times 10^8 \mathrm{Nm}^{-2}\right)\left(3 \times 10^{-4} \mathrm{~m}^2\right)\)
= 2.4 x 104N
Ifais the maximum upward acceleration of die elevator,
tension = T= m(g +a)
2.4 X104N = (1200 kg)(10 ms-2 + a)
a = 10 ms-2
Question 23. The Young modulus for a steel wire is 2 x 1011 Pa and- its elastic limit is 2.5 x 108 Pa. By how much can a steel wire of 3 m length and 2 mm diameter be stretched before its elastic limit is reached?
- 3.75 mm
- 7.50 mm
- 4.75 mm
- 4.00 mm
Answer: 1. 3.75 mm
The maximum stretching force is
F = (elastic limit)(area of cross-section)
= (2.5 x 108 N m-2)(rc)(10-3 m)²
= 2.5n x 10²N.
∴ the length by which the wire can be stretched is
⇒ \(\Delta L=\frac{F}{A} \cdot \frac{L}{Y}=\frac{250 \times \pi \times 3}{\pi \times 10^{-6} \times 2 \times 10^{11}}\)
= 3.75 x 10-3m
= 3.75 mm.
Question 24. For a constant hydraulic stress P on an object of bulk modulus B, the fractional change in the volume of the object will be
- \(\frac{P}{B}\)
- \(\frac{B}{P}\)
- \(\sqrt{\frac{P}{B}}\)
- \(\left(\frac{B}{P}\right)^2\)
Answer: 3. \(\sqrt{\frac{P}{B}}\)
∵ bulk modulus = B = \(B=\frac{P}{\frac{\Delta V}{V}}\),
∴ fractionalchange in volume = \(\frac{\Delta V}{V}=\frac{P}{B}\)
Question 25. Four wires having the following lengths and diameters are made of the same material. Which of these will have the largest extension when the same tension is applied?
- Length = 50 cm and diameter = 0.5 mm
- Length = 100 cm and diameter =1 mm
- Length = 200 cm and diameter = 2 mm
- Length = 300 cm and diameter = 3 mm
Answer: 1. Length = 50 cm and diameter = 0.5 mm
Youngmodulus = Y = \(Y=\frac{\frac{F}{A}}{\frac{\Delta L}{L}}-\frac{4 F L}{\pi D^2 \cdot \Delta L}\)
For all the four wires, Y and F are the same.
Hence, \(\Delta L \propto \frac{L}{D^2}\)
In (a), \(\frac{L}{D^2}=\frac{50 \mathrm{~cm}}{(0.05 \mathrm{~cm})^2}=20 \times 10^3 \mathrm{~cm}^{-1}\)
In (b), \(\frac{L}{D^2}=\frac{100 \mathrm{~cm}}{(0.1 \mathrm{~cm})^2}=10 \times 10^3 \mathrm{~cm}^{-1}\)
In (c), \(\frac{L}{D^2}=\frac{200 \mathrm{~cm}}{(0.2 \mathrm{~cm})^2}=5 \times 10^3 \mathrm{~cm}^{-1}\)
In (d), \(\frac{L}{D^2}=\frac{300 \mathrm{~cm}}{(0.3 \mathrm{~cm})^2}=3.3 \times 10^3 \mathrm{~cm}^{-}\)
Hence, AL is maximum in option (1)
Question 26. The approximate depth of an ocean is 2700 m. The compressibility of water is 45.4 x 1011 Pa-1 and the density of water is 10³ kg m. What fractional compression of water will be obtained at the bottom of the ocean?
- 1.0 x 10-2
- 12 x 10-2
- 1.4 x 10-2
- 0.8 x 10-2
Answer: 2. 12 x 10-2
The excess pressure at the bottom is
Ap = hpg = (2700 m)(10³ kg m)(10 m s-2) = 27 x 106 Pa.
∵ bulk modulus = B = V \(V\left(\frac{\Delta p}{\Delta V}\right)\)
∴ compressibility = \(\kappa=\frac{1}{B}=\frac{1}{V} \cdot \frac{\Delta V}{\Delta p}\)
∴ the fractional compression in volume is
⇒ \(\frac{\Delta V}{V}\) = k . Ap
= (45.4 x10-11Pa-1)(27 x106 Pa)
= 1.2 x 10-2.
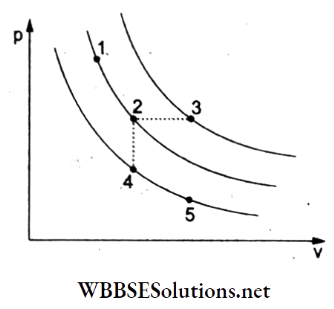
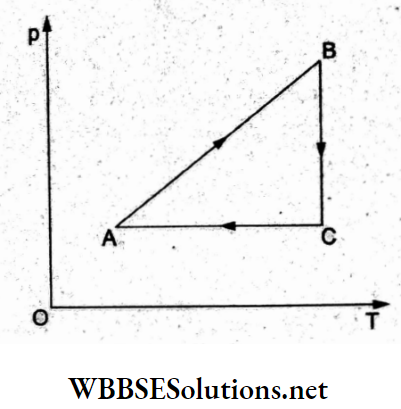
Question 27. Copper of a fixed volume (V) is drawn into a wire of length l. When the wire is subjected to a constant force F, the extension produced in the wire is Al. Which of the following graphs is a straight line?
- Al versus \(\frac{1}{l}\)
- Al versus l²
- AZ versus \(\frac{1}{l^2}\)
- Al versus l
Answer: 2. Al versus l²
Volume = V= Al.
Young modulus = Y = \(=Y=\frac{\frac{F}{A}}{\frac{\Delta l}{l}}=\frac{F l}{A \cdot \Delta l}\)
∴ extension = \(\Delta l=\frac{F l}{Y A}=\frac{F l^2}{Y V}\)
∴ Δl ∝ l², so the Δl-versus-l² graph is a straight line
Question 28. The Young modulus of steel is twice that of brass. Two wires of the same length and the same area of cross-section, one of steel and another of brass, are suspended from the same roof. If we want the lower ends of the wires to be at the same level, the weights added to the steel and brass wires must be in the ratio
- 1:1
- 1:2
- 2:1
- 4:1
Answer: 3. 2:1
Let and be the required weights to produce the same extension
⇒ \(\Delta L=\frac{w L}{Y A}\)
Thus, \(\frac{w_{\mathrm{gt}} L}{Y_{\mathrm{st}} A}=\frac{w_{\mathrm{br}} L}{Y_{\mathrm{br}} A}\)
⇒ \(\frac{w_{\mathrm{st}}}{\omega_{\mathrm{br}}}\)
= \(\frac{Y_{\mathrm{st}}}{Y_{\mathrm{br}}}\)
= \(\frac{2}{1} \Rightarrow w_{\mathrm{st}}: w_{\mathrm{br}}=2: 1\)
Question 29. Which among the following materials is the most elastic?
- Iron
- Copper
- Quartz
- Rubber
Answer: 3. Quartz
Quartz is the closest approach to a perfectly elastic material.
Question 30. A substance breaks down by a stress of 106 N m-2. If the density of the material of a wire is 3 x 10³ kg m-3, the length of the wire which will break under its own weight when suspended vertically will be
- 66.6 m
- 60.0 m
- 30.3 m
- 33.3 m
Answer: 3. 30.3 m
Breaking stress = \(\frac{m g}{A}=\frac{(A L) \rho g}{A}=L \rho g\)
∴ L = \(\frac{\text { breaking stress }}{\rho g}\)
= \(\frac{10^6 \mathrm{~N} \mathrm{~m}^{-2}}{\left(3 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}\)
= 33.3 m.
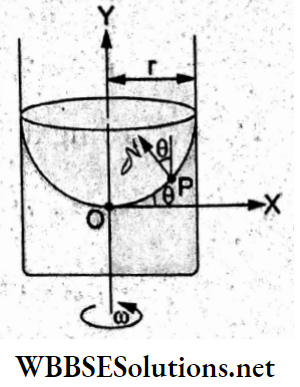
Question 31. A body of mass m = 10 kg is attached to a wire of length 0.3 m. Calculate the maximum angular velocity with which it can be rotated in a horizontal circle. (Given that the breaking stress of the wire = 4.8 x 107 N m-2 and the area of cross-section of the wire = 10-6 m².)
- 4 rad s-1
- 8 rad s-1
- 1 rad s-1
- 2 rad s-1
Answer: 1. 4 rad s-1
The breaking force is the tension produced in the wire while the body undergoes a circular motion.
Thus, tension = F = (breaking stress)(area of cross-section)
∴ mω²l = (4.8 x 107Nm-2)(10-6 m2) = 48 N
∴ angular frequency =ω = \(\sqrt{\frac{48^{\prime} \mathrm{N}}{(10 \mathrm{~kg})(0.3 \mathrm{~m})}}\)
= \(4 \mathrm{rad} \mathrm{s}^{-1}\)
Question 32. A sphere of radius 3 cm is subjected to a pressure of 100 atm. Its volume decreases by 0.3 cm³. What is the bulk modulus of its material?
- 4π x 105 atm
- 4π x 106 atm
- 4π x 3 x 10³ atm
- 4π x 108 atm
Answer: 3. 4π x 3 x 10³ atm
Bulk modulus = \(B=\frac{\text { stress }}{\text { volume strain }}\)
⇒ \(V\left(\frac{\Delta p}{\Delta V}\right)\)
= \(\frac{\frac{4}{3} \pi(3 {~cm})^3(100 {~atm})}{0.3 {~cm}^3}\)
= 4π x 3 x 10³ atm.
Question 33. A solid sphere of radius R made of a material of bulk modulus B is surrounded by a liquid contained in a cylindrical container. A massless piston of area A floats on the surface of the liquid. When a block of mass m is placed on the piston to compress the liquid, the fractional change in the radius of the sphere is
- \(\frac{m g}{3 A R}\)
- \(\frac{m g}{A}\)
- \(\frac{m g}{3 A B}\)
- \(\frac{m g}{A B}\)
Answer: 3. \(\frac{m g}{3 A B}\)
Volume of the sphere = V = \(\frac{4}{3} \pi R^3\)
∴ \(\frac{\Delta V}{V}=3\left(\frac{\Delta R}{R}\right)\)
bulk modulus = \(B=V\left(\frac{\Delta p}{\Delta V}\right)\)
∴ \(\frac{\Delta V}{V}=\frac{\Delta p}{B}=\frac{\frac{m g}{A}}{B}=\frac{m g}{A B}\)
⇒ \(3\left(\frac{\Delta R}{R}\right)=\frac{m g}{A B}\)
⇒ \(\frac{\Delta R}{R}=\frac{m g}{3 A B}\)
Question 34. A given quantity of an ideal gas is at a pressure p and an absolute temperature T. The isothermal bulk modulus of the gas is
- \(\frac{2p}{3}\)
- p
- \(\frac{3}{2}\)
- 2p
Answer: 2. p
For an isothermal process, pV = constant.
∴ P.ΔV + V.Δp = 0
⇒ \(p=-V\left(\frac{\Delta p}{\Delta V}\right)=\frac{\Delta p}{-\frac{\Delta V}{V}}\)
=\(\frac{\text { stress }}{\text { volume strain }}\)
= B
Thus, bulk modulus = B = p.
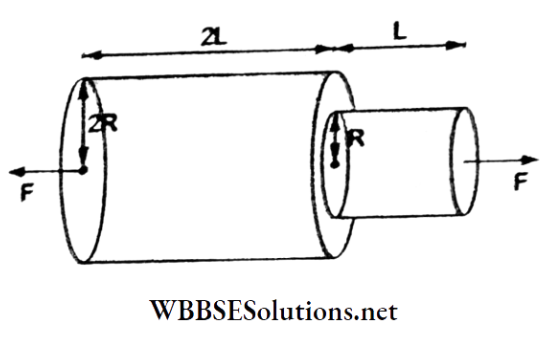
Question 35. One end of a thick horizontal copper wire of length 2L and radius 2R is welded to one end of a thin horizontal copper wire of length L and radius R. When this arrangement is stretched by applying equal forces at the two ends, the ratio of the elongation in the thin wire to that in the thick wire is equal to
- 0.25
- 0.50
- 2
- 4
Answer: 3. 2
The elongation in the thin wire is
⇒ \(h=\frac{F L}{\pi R^2 Y}\)
The elongation in the thick wire is
⇒ \(h_2=\frac{F(2 L)}{\pi(2 R)^2 Y}\)
∴ \(\frac{h_1}{h_2}=\frac{L}{2 L} \cdot \frac{4 R^2}{R^2}=2\)
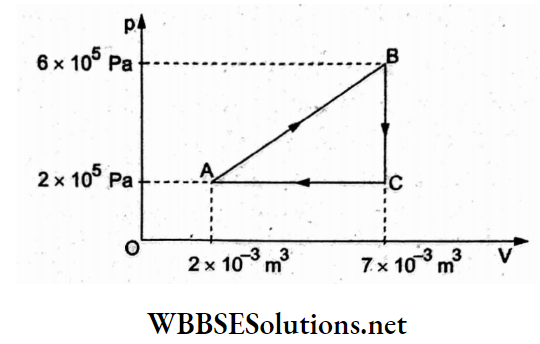
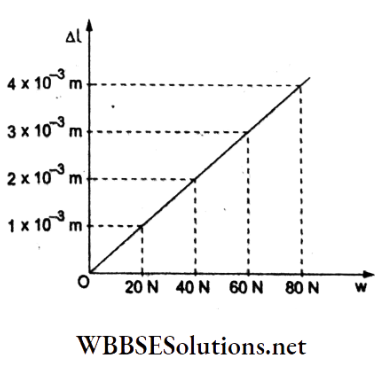
Question 36. The adjoining graph shows the extension (Al) of a wire of length 1 m suspended 4xio-3m from a rigid support at one end with a load w connected to the other end. If the cross-sectional area of the wire is 10-6 m², calculate 1 x 10 m the Young modulus of the material of the wire.
- 2 x1011 N m-2
- 2 x 10-11 N m-2
- 2 x 1012 Nm-2
- 2 x 1013 N m-2
Answer: 1. 2 x1011 N m-2
From the given load-extension graph, when the load is w = 20 N, the extension is Al = 1 x 10-4 m.
Young modulus = Y = \(\frac{w / A}{\Delta l / l}\)
= \(\frac{(20 \mathrm{~N})(1 \mathrm{~m})}{\left(10^{-6} \mathrm{~m}^2\right)\left(1 \times 10^{-4} \mathrm{~m}\right)}\)
= 2 x 1011 Nm-2.
Question 37. A longitudinal strain is possible in
- Solids
- Liquids
- Gases
- All of these
Answer: 1. Solids
The longitudinal strain is possible only in solids.
Question 38. Which of the following affects the elasticity of a substance? Choose the best option,
- Impurity of the substance
- Hammering and annealing
- A change in temperature
- All of these
Answer: 4. All of these
Impurity, hammering, and temperature variation affect the elastic property of a substance.
Question 39. For a constant hydraulic stress on an object, the fractional change \(\left(\frac{\Delta V}{V}\right)\) in the object’s volume and its bulk modulus are related as
- \(\frac{\Delta V}{V} \propto B^2\)
- \(\frac{\Delta V}{V} \propto \frac{1}{B}\)
- \(\frac{\Delta V}{V} \propto B\)
- \(\frac{\Delta V}{V} \propto \frac{1}{B^2}\)
Answer: 2. \(\frac{\Delta V}{V} \propto \frac{1}{B}\)
Bulk modulus = B = \(\frac{\text { strese }}{\frac{\Delta V}{V}}\)
∴ \(B \propto \frac{1}{\frac{\Delta V}{V}} \Rightarrow \frac{\Delta V}{V} \propto \frac{1}{B}\)
Question 40. The shear modulus is zero for
- Solids only
- Liquids only
- Gases only
- Both liquids and gases
Answer: 3. Gases only
In solids and liquids, a shearing strain may exist, so they have a shear modulus. But in gases, there is no shearing and hence no shear modulus.
Question 41. A uniform wire of length l is extended to a new length l’. The work done is
- \(\frac{Y A}{l}\left(l^{\prime}-l\right)\)
- \(\frac{Y A}{l}\left(l^{\prime}-l\right)^2\)
- \(\frac{Y A}{2 l}\left(l^{\prime}-l\right)^2\)
- \(\frac{2 Y A}{l}\left(l^{\prime}-l\right)^2\)
Answer: 3. \(\frac{Y A}{2 l}\left(l^{\prime}-l\right)^2\)
Work done = W = strain energy stored = \(\frac{1}{2}\)(stress)(strain)(volume),
stress = Y(strain) = \(Y\left(\frac{l-l}{I}\right)\) and volume = Al.
∴ \(W=\frac{1}{2} Y\left(\frac{l^{\prime}-l}{l}\right)\left(\frac{l^{\prime}-l}{l}\right)(A l)\)
= \(\frac{Y A}{2 l}\left(l^{\prime}-l\right)^2\)
Question 42. The bulk modulus of the material of a sphere is B. If it is subjected to a uniform pressure p, the fractional decrease in its radius is
- \(\frac{p}{B}\)
- \(\frac{3p}{B}\)
- \(\frac{B}{3p}\)
- \(\frac{p}{3B}\)
Answer: 4. \(\frac{p}{3B}\)
Volume = V = \(\frac{4}{3} \pi R^3\)
⇒ \(\frac{\Delta V}{V}=3\left(\frac{\Delta R}{R}\right)\)
⇒ \(\frac{\Delta R}{R}=\frac{1}{3}\left(\frac{\Delta V}{V}\right)\) ….(1)
Bulk modulus = B = \(\left(\frac{V}{\Delta V}\right) p=\frac{R p}{3 \Delta R}\) [from(1)]
⇒ \(\frac{\Delta R}{R}=\frac{p}{3 B}\)
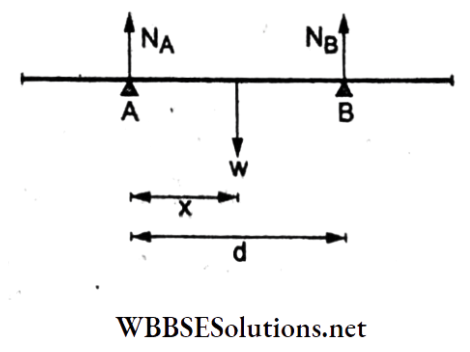
Question 43. A uniform rod of weight w is supported by two parallel knife edges A and B, and it is in equilibrium in a horizontal position. The two knives are at a distance d from each other. The center of mass of the rod is at a distance x from A. The normal reaction on A is
- \(\frac{wx}{d}\)
- \(\frac{wd}{x}\)
- \(\frac{w(d-x)}{d}\)
- \(\frac{w(d-x)}{x}\)
Answer: 3. \(\frac{w(d-x)}{d}\)
Let NA and NB be the normal reactions at the knife edges A and B respectively, and w be the weight, as shown. To find NA, we take the moments of the forces about B, which gives
NAd – w(d – x) = 0 [ ∵ the system is in equilibrium]
⇒ \(N_{\mathrm{A}}=\frac{w(d-x)}{d}\)
Question 44. If the ratios of the diameters, length,s and Young moduli of the steel and copper wires shown in the given figure are p, q and s respectively, the corresponding ratio of the increases in their lengths would be
- \(\frac{5 q}{2 s p^2}\)
- \(\frac{7 q}{5 s p^2}\)
- \(\frac{2 q}{5 s p}\)
- \(\frac{7 q}{5 s p}\)
Answer: 2. \(\frac{7 q}{5 s p^2}\)
Young6 modulus = Y = \(\frac{\frac{F}{A}}{\frac{\Delta L}{L}}=\frac{4 F L}{\pi D^2 \cdot \Delta L}\)
∴ extension = \(\Delta L=\frac{4 F L}{\pi D^2 \gamma}\)
For steel, \(\Delta L_{\mathrm{st}}=\frac{4 F_{\mathrm{st}} L_{\mathrm{st}}}{\pi D_{\mathrm{st}}^2 Y_{\mathrm{st}}}\)
Similarly, for copper, \(\Delta L_{C u}=\frac{4 F_{C u} L_{C u}}{\pi D_{C u}^2 Y_{C u}}\)
∴ \(\frac{\Delta L_{\mathrm{st}}}{\Delta L_{\mathrm{Cu}}}=\frac{F_{\mathrm{st}}}{F_{\mathrm{Cu}}} \frac{L_{\mathrm{st}}}{L_{\mathrm{Cu}}}\left(\frac{D_{\mathrm{cu}}}{D_{\mathrm{st}}}\right)^2\left(\frac{Y_{\mathrm{cu}}}{Y_{\mathrm{st}}}\right)\)
⇒ \(\left(\frac{7 m g}{5 m g}\right)(q)\left(\frac{1}{p}\right)^2\left(\frac{1}{s}\right)\)
= \(\frac{7 q}{5 s p^2}\)
Question 45. A uniform cylindrical rod of length L and radius r is made of a material whose Young modulus of elasticity is Y. When this rod is heated by a temperature AT and simultaneously subjected to a net longitudinal compressional force F, its length remains unchanged. The coefficient of volume expansion of the material of the rod is nearly equal to
- \(\frac{F}{3 \pi r^2 Y \cdot \Delta T}\)
- \(\frac{6 F}{\pi r^2 \gamma \cdot \Delta T}\)
- \(\frac{9 F}{\pi r^2 Y \cdot \Delta T}\)
- \(\frac{3 F}{\pi r^2 Y \cdot \Delta T}\)
Answer: 4. \(\frac{3 F}{\pi r^2 Y \cdot \Delta T}\)
The coefficient of linear expansion is given by
⇒ \(\alpha=\frac{1}{L} \cdot \frac{\Delta L}{\Delta T}=\frac{\text { longitudinal strain }}{\Delta T}\)
∴ Young modulus = Y = \(\frac{\text { stress }}{\text { strain }}=\frac{\frac{F}{A}}{\alpha \cdot \Delta T}\)
⇒ \(\alpha=\frac{F}{Y A \cdot \Delta T}\)
Hence, the coefficient of volume expansion is
⇒ \(\gamma=3 \alpha=\frac{3 F}{A Y \cdot \Delta T}=\frac{3 F}{\pi r^2 Y \cdot \Delta T}\)
Question 46. When a block of mass M is suspended by a long wire of length L, the extension produced is l. The elastic potential energy stored in the stretched wire is
- Mgl
- MgL
- \(\frac{1}{2}\) MgL
- \(\frac{1}{2}\) Mgl
Answer: 4. \(\frac{1}{2}\) Mgl
The elastic potential energy in a stretched wire is given by
⇒ \(U=\frac{1}{2} k x^2=\frac{1}{2}(k x) x=\frac{1}{2} F_{\max }\) (extension)
= \(\frac{1}{2}\)(stretching force)(stretch)
= \(\frac{1}{2}\) Mgl
Question 47. A boy’s catapult is made of a rubber cord, which is 42 cm long with 6 mm diameter of cross section and of a negligible mass. The boy keeps a stone weighing 0.02 kg on it and stretches the cord by 20 cm by applying a constant force. When released, the stone flies off with a velocity of 20 m s-1. Neglect the change in the area of the cross-section of the cord while stretched. The Young modulus of rubber is close to
- 5 x 104 N m-2
- 4 x 108 N m-2
- 3 x 106 N m-2
- 2 x 103 N m-2
Answer: 3. 3 x 106 N m-2
The elastic potential energy stored in the rubber cord on stretching is
⇒ \(U=\frac{1}{2} \text { (stress) (strain)(volume) }\)
⇒ \(\frac{1}{2} Y(\text { strain })^2 \text { (volume) }\)
⇒ \(\frac{1}{2} Y\left(\frac{\Delta L}{L}\right)^2 A L\)
= \(\frac{Y(\Delta L)^2 A}{2 L}\)
This energy appears as the KE of the stone.
Thus, \(\frac{1}{2} m v^2=\frac{Y(\Delta L)^2 A}{2 L}\)
∴ Young modulus = Y = \(\frac{m v^2 L}{(\Delta L)^2 A}\)
Substituting the appropriate values, we have
⇒ \(Y=\frac{\left(2 \times 10^{-2} \mathrm{~kg}\right)\left(20 \mathrm{~m} \mathrm{~s}^{-1}\right)^2(0.42 \mathrm{~m})}{\left(2 \times 10^{-1} \mathrm{~m}\right)^2(3.14)\left(3 \times 10^{-3} \mathrm{~m}\right)^2} \approx 3 \times 10^6 \mathrm{~N} \mathrm{~m}^{-2}\)
Question 48, The elastic limit of brass is 379 MPa. What should be the minimum diameter of a brass rod if it is to support a 400-N load without exceeding the elastic limit?
- 1.00 mm
- 1.16 mm
- 1.86 mm
- 0.90 mm
Answer: 2. 1.16 mm
The elastic limit is the maximum permissible stress for a given material.
Thus,
⇒ \(379 \times 10^6 \mathrm{~Pa}=\frac{400 \mathrm{~N}}{\pi\left(\frac{d}{2}\right)^2}=\frac{1600 \mathrm{~N}}{\pi d^2}\)
∴ minimum diameter = d = \(\sqrt{\frac{1600 \mathrm{~N}}{(3.14)\left(379 \times 10^6 \mathrm{~N} \mathrm{~m}^{-2}\right)}}\)
= 1.159 mm ≈ 1.16 mm.
Question 49. A wire of length L and an area of cross-section A is hanging from a fixed support. The length of the wire changes to L1 when a block of mass M is suspended from its free end. The expression for its Young modulus is
- \(\frac{M g\left(L_1-L\right)}{A L}\)
- \(\frac{M g L}{A L_1}\)
- \(\frac{M g L}{A\left(L_1-L\right)}\)
- \(\frac{M g L_1}{A L}\)
Answer: 3. \(\frac{M g L}{A\left(L_1-L\right)}\)
Young modulus = Y = \(\frac{\text { stress }}{\text { longitudinal strain }}\)
⇒ \(\frac{\frac{F}{A}}{\frac{\Delta L}{L}}\)
= \(\frac{\frac{M g}{A}}{\frac{\left(L_1-L\right)}{L}}\)
= \(\frac{M g L}{A\left(L_1-L\right)}\)
Question 50. A 2-m-long rope of uniform cross-sectional area 2 cm² is being pulled by two persons towards themselves, each exerting a force of 100 N on the rope. If the rope extends in length by 1 cm, the Young modulus of the material of the rope is
- 2 x 106 N m-2
- 1 x 108 Nm-2
- 1 x 1010 N m-2
- 1 x 107 N m-2
Answer: 2. 1 x 108 Nm-2
Given that tension = F = 100 N, L = 2 m,
ΔL = 1 cm =1 x 10² m and A = 2 x 10-4 m².
∴ \(Y=\frac{\frac{F}{A}}{\frac{\Delta L}{L}}=\frac{F}{A} \cdot \frac{L}{\Delta L}\)
= \(\frac{(100 \mathrm{~N})(2 \mathrm{~m})}{\left(2 \times 10^{-4} \mathrm{~m}^2\right)\left(1 \times 10^{-2} \mathrm{~m}\right)}\)
= 100 x 106Nm-2
= 1 x 108 N m-2.
Question 51. If the liquid in a capillary tube neither rises nor falls inside it, the angle of contact is
- 0°
- 180°
- 90°
- 45°
Answer: 3. 90°
When the angle of contact is 0 = 90°, the surface tension acts perpendicular to the wall of the capillary tube and its vertically upward component will be zero. Hence, there will be no rise of the liquid column.
In the other words, h = \(\frac{2 S \cos \theta}{r \rho g}\)
= 0 for θ
= 90°.
Question 52. The pressures inside two soap bubbles are 1.01 atm and 1.03 atm. The ratio of their volumes is
- 27:1
- 3:1
- 127:101
- None of these
Answer: 1. 27:1
The excess pressure inside a soap bubble is given by p = \(\frac{\Delta S}{R}\)
∴ \(\frac{p_1}{p_2}=\frac{R_2}{R_1}\)
Hence, the ratio of die volumes is
⇒ \(\frac{V_1}{V_2}=\left(\frac{R_1}{R_2}\right)^3\)
= \(\left(\frac{p_2}{p_1}\right)^3\)
= \(\left(\frac{0.03}{0.01}\right)^3\)
= 27:1.
Question 53. The wettability of a surface by a liquid depends primarily on the
- Viscosity of the liquid
- Surface tension of the liquid
- Density of lhe liquid
- The angle of contact between the surface and the liquid
Answer: 4. Angle of contact between the surface and the liquid
The wettability of a solid surface by a liquid depends on the angle of contact 0. Liquids with 0 < 90° wet, and liquids with 0 > 90° do not wet. For no wetting (glass-mercury pair), the adhesive force (Fgl-Hg) is less than the cohesive force (FHg-Hg)- For wetting (glass-water pair), the adhesive force (Fgl-W) is greater than the cohesive force (Fw_w).
Question 54. A certain number of spherical drops, each of radius r, of a liquid coalesce into a single drop of radius R and volume V. If T is the surface tension of the liquid then
- Energy released = \(4 V T\left(\frac{1}{r}-\frac{1}{R}\right)\)
- Energy absorbed = \(3 V T\left(\frac{1}{r}+\frac{1}{R}\right)\)
- Energy released = \(=3 V T\left(\frac{1}{r}-\frac{1}{R}\right)\)
- Energy is neither released nor absorbed
Answer: 3. Energy’released = \(=3 V T\left(\frac{1}{r}-\frac{1}{R}\right)\)
Since the volume remains constant, V = \(\frac{4}{3} \pi R^3=N\left(\frac{4}{3} \pi r^3\right)\)
Initial surface area = Ai = N(4πr²) and final surface area = Af = 4πR². Since liquids have the property to contract, the final surface area will be less than the initial surface area, and thus energy is released.
The energy released = ΔU = surface tension x ΔA
= T(N.4πr² – 4πR²)
= \(\left(N \cdot \frac{4}{3} \cdot \frac{\pi r^3}{r}-\frac{4 \pi}{3} \cdot \frac{R^3}{R}\right)\)
= \(3 V T\left(\frac{1}{r}-\frac{1}{R}\right)\)
Question 55. A square wireframe of side L is dipped in a liquid. On taking it out, a membrane is formed. If the surface tension of the liquid is T, the force acting on the wireframe will be
- 2TL
- 4TL
- 8TL
- 10TL
Answer: 3. 8TL
The membrane in the air has two surfaces.
The total force acting on the frame is
F = (surface tension)(perimeter) x 2
= (T)(4L)(2)
= 8TL
Question 56. At its critical temperature, the surface tension of a liquid
- Is zero
- Is infinity
- Is the same as that at any other temperature
- Cannot be determined
Answer: 1. Is zero
The surface tension decreases with an increase in temperature and its value is zero at the critical temperature.
Question 57. Two spherical soap bubbles of radii a and b in a vacuum coalesce under isothermal conditions. The resulting bubble has a radius equal to
- \(\frac{a+b}{2}\)
- \(\frac{a b}{a+b}\)
- \(\sqrt{a^2+b^2}\)
- a + b
Answer: 3. \(\sqrt{a^2+b^2}\)
In a vacuum under isothermal conditions, the surface energy remains unchanged. Thus,
8πa²S + 8πb²S = 8πR²S.
⇒ \(R=\sqrt{a^2+b^2}\)
Question 58. The surface tension of a soap solution is 25 x 10-3 Nml The excess pressure in a soap bubble of diameter 1 cm is
- 10 Pa
- 20 Pa
- 5 Pa
- None of these
Answer: 2. 20 Pa
The excess pressure inside each soap bubble is
⇒ \(\Delta p=\frac{4 S}{r}\)
= \(\frac{4\left(25 \times 10^{-3} \mathrm{~N} \mathrm{~m}^{-1}\right)}{0.5 \times 10^{-2} \mathrm{~m}}\)
=20 Pa
Question 59. The force required to separate two glass plates of area 10-2 m², with a 0.05-mm-thick film of water between them, is (given that surface tension of water = 70 x 10-3 N m-1)
- 25 N
- 20 N
- 14 N
- 28 N
Answer: 4. 28 N
The pressure difference across the glass plates due to a thin layer of water of thickness d is given by
⇒ \(\Delta p=\frac{S}{R}=\frac{S}{\frac{d}{2}}=\frac{2 S}{d}\)
Hence, the required force is
⇒ \(F=A \cdot \Delta p\)
= \(\frac{\left(10^{-2} \mathrm{~m}^2\right)\left(2 \times 70 \times 10^{-3} \mathrm{~N} \mathrm{~m}^{-1}\right)}{0.05 \times 10^{-3} \mathrm{~m}}\)
= 28 N.
Question 60. For different capillaries of radius r, the condition for liquid rise (h) above the free surface of the liquid is
- \(\frac{h}{r}\) = constant
- hr = constant
- h + r = constant
- h-r = constant
Answer: 2. hr = constant
The capillary rise due to the surface tension (S) is given by
⇒ \(h=\frac{2 S \cos \theta}{r \rho g}\)
For a given solid-liquid pair; S, 0, p, and are constant.
Hence, the products also constant.
Question 61. The excess pressure inside a soap bubble of radius r is proportional to
- r
- \(\frac{1}{r}\)
- r2
- \(\frac{1}{r^2}\)
Answer: 2. \(\frac{1}{r}\)
The excess pressure inside a soap bubble is Δp = 4S/r, which is proportional to 1/r.
Question 62. When the temperature is increased, the angle of contact of a liquid
- Increases
- Decreases
- Remains the same
- First increases and then decreases
Answer: 1. Increases
When the temperature rises, the surface tension decreases, and the angle of contact increases.
Question 63. The radius of a soap bubble is r and the surface tension of the soap solution is T. Keeping the temperature constant, the extra energy needed to double the radius of the bubble by blowing is
- 8πr²T
- 16πr²T
- 24πr²T
- 32πr²T
Answer: 3. 24πr²T
The extra energy required = work done
= (surface tension)(increase in surface area)
= \(T\left[2.4 \pi(2 r)^2-2.4 \pi(r)^2\right]=24 \pi r^2 T\)
Question 64. A work of 3.0 x 10-4J is required to stretch a soap film from 10 cm x 6 cm to 10 cm x 11 cm. The surface tension of the soap solution is
- 5 x 10-2 N m-1
- 3 x 10-2 N m-1
- 1.5 x 10-2 N m-1
- 1.2 x 10-2Nm-1
Answer: 2. 3 x 10-2 N m-1
Work done = (surface tension) (increase in surface area)
=> 3.0 x 10-4J =T[2(110 x 10-4cm2-60 x 104m2)]
= T(10-2m2)
⇒ \(T=\frac{3.0 \times 10^{-4} \mathrm{~J}}{10^{-2} \mathrm{~m}^2}\)
= \(3.0 \times 10^{-2} \mathrm{Nm}^{-1}\)
Question 65. One large soap bubble of diameter D breaks into 27 bubbles, each having a surface tension of T. The change in the surface energy is
- 2πTD²
- 4πTD2
- πTD2
- 8πTD2
Answer: 2. 4πTD²
Assuming the volume of air enclosed to be unchanged,
⇒ \(\frac{4}{3} \pi\left(\frac{D}{2}\right)^3=27 \times \frac{4}{3} \pi r^3\)
∴ the radius of the smaller bubble is r = D/6.
Now, the increase in surface area is
⇒ \(\Delta S=27 \times 2\left(4 \pi r^2\right)-2 \times\left[4 \pi\left(\frac{D}{2}\right)^2\right]\)
⇒ \(27 \times 8 \pi\left(\frac{D}{6}\right)^2-2 \times 4 \pi\left(\frac{D}{2}\right)^2\)
= \(4 \pi D^2\)
Hence, the increase in surface energy is
⇒ \(\Delta U=T(\Delta A)=4 \pi T D^2\)
Question 66. A mercury drop of radius 1 cm is broken into 106 droplets of equal sizes. The work done is (the surface tension of mercury being 35 x 10-2 N m-1)
- 4.35 x 10-2 J
- 4.35 x 10-3 J
- 4.35 x l0-6J
- 4.35 x 10-8 J
Answer: 1. 4.35 x 10-2 J
Since the volume remains unchanged,
⇒ \(\frac{4}{3} \pi R^3=10^6 \cdot \frac{4}{3} \pi r^3\)
⇒ \(r=\frac{R}{100}\)
∴ work done = T.ΔA
⇒ \(T \cdot 4 \pi\left(10^6 \cdot r^2-R^2\right)=T \cdot 4 \pi\left(10^6 \cdot \frac{R^2}{10^4}-R^2\right)\)
= 4πT(99R²)
== 4(3.14)(35 x 10-2 N m-1) x 99(1 x 10-2m)2
= 4.35 x 10-2 J.
Question 67. Eight identical mercury droplets coalesce into one mercury drop. The energy changes by a factor of
- 1
- 2
- 4
- 6
Answer: 2. 2
⇒ \(V=\frac{4}{3} \pi R^3\)
= \(8 \times \frac{4}{3} \pi r^3\)
⇒ \(r=\frac{R}{2}\)
Initial surface energy = Ui = 4πR2T
and final surface energy = Uf = 8(4πr²)T.
⇒ \(8 \times 4 \pi\left(\frac{R}{2}\right)^2 T\)
= \(2\left(4 \pi R^2 T\right)\)
= \(2 U_i\)
Thus, increases by a factor of 2.
Question 68. There is a small bubble at one end and a bigger bubble at the other end of the tube, as shown in the figure. Which of the following statements is true?
- The smaller bubbles will grow until they collapse.
- The bigger bubbles will grow until they collapse.
- They remain in equilibrium.
- None of these.
Answer: 2. The bigger bubbles will grow until they collapse.
If p0 be the pressure outside then
inside the smaller bubble, \(p_1=p_0+\frac{4 T}{r}\)
and inside the bigger bubble, \(p_2=p_0+\frac{4 T}{R}\)
∵ r < R;
∴ p1 > p2
Hence, air will flow from the smaller bubble to the bigger bubble, which will further grow until both the bubbles collapse.
Question 69. A 15-cm-long capillary tube is vertically dipped in water. The water rises up to 7 cm. If the entire setup is put in a freely falling elevator, the length of the water column in the capillary tube will be
- 3.5 cm
- 15 cm
- 6 cm
- 8 cm
Answer: 2. 15 cm
During free fall (under gravity), the system is in a state of artificial weightlessness.
So, effectivelyg = 0.
Hence, gravity does not work but the force of surface tension still acts and the maximum ascent of the water column occurs in the full length of the tube (up to 15 cm).
Question 70. The surface tension of a liquid decreases with a rise in the
- Viscosity of the liquid
- Temperature of the liquid
- Diameter of the container
- Thickness of the container
Answer: 2. Temperature of the liquid
The surface tension decreases with rise in temperature as
Sθ = S0 (l – αθ),
where a is the temperature coefficient of surface tension.
Question 71. The potential energy of a soap bubble having a surface tension equal to 0.04 N m-1 and of diameter 1 cm is
- 6π x 10-6 J
- 4π x 10-6 J
- 2π x 10-6 J
- 8π x 10-6 J
Answer: 4. 8n x 10-6J
Potential energy = U = T x surface area
= T x 2(4πR²)
= 8πTR²
= Sπ (0.04 N m-1) (0.5 x 10-2 m)2
= 8π X 10-6 J.
Question 72. When there are no external forces, the shape of a small liquid drop is determined by the
- Surface tension of the liquid
- Viscosity of the liquid
- Temperature of air
- Density of the liquid
Answer: 1. Surface tension of the liquid
The shape of a free liquid drop is determined by its molecular forces, which gives rise to its surface tension
Question 73. Raindrops are spherical due to their
- Viscosity
- Surface tension
- Thrust on dropping
- Residual pressure
Answer: 2. Surface tension
A liquid surface tends to contract due to its surface tension and assumes a spherical shape, which has the minimum surface area for a given volume.
Question 74. For a liquid to rise in a capillary tube, the angle of contact should be
- An acute angle
- An obtuse angle
- A right angle
- None of these
Answer: 1. An acute angle
A liquid rises in a capillary tube if the angle of contact (0) between the solid-liquid pair is acute. The vertically upward component of the surface tension (T cos θ) makes the liquid rise.
Question 75. Two small drops of mercury, each of radius R, coalesce into a single large drop. The ratio of the total surface energies before and after the change is
- 1:21/3
- 21/3:1
- 2:1
- 1:2
Answer: 2. 21/3:1
Volume, \(V=2\left(\frac{4}{3} \pi R^3\right)\)
= \(\frac{4}{3} \pi R^{\prime 3}\)
R’ = 21/3R.
Now, Ui = T(2 x 4πR2)
and Uf = T (4πR2)
= T(4π)22/3 R²
∴ \(\frac{U_i}{U_f}=\frac{2 R^2}{2^{2 / 3} R^2}=2^{1 / 3}: 1\)
Question 76. A thread is tied slightly loose to a wireframe. The frame is dipped in a soap solution and then taken out. The frame is completely covered with a soap film, as shown in the figure. When the portion A is punctured with a pin, the thread
- Becomes concave towards A
- Becomes convex towards A
- Remains in its initial position
- Becomes either concave or convex towards A depending on
the size of A relative to B.
Answer: 1. Becomes concave towards A
When portion A is punctured, the soap film will start contracting and the circular hole created will gradually increase in size. This will lead the thread to become concave towards A.
Question 77. A capillary tube of radius r is immersed in water and the water rises to a height of h. The mass of the water in the capillary tube is 5 g. Another capillary tube of radius 2r is immersed in water. The mass of water that will rise in this tube is
- 2.5 g
- 5.0 g
- 10 g
- 20 g
Answer: 3. 10 g
In a capillary rise, surface tension = T = \(\frac{{rhpg}}{2 \cos \theta}\)
So, \(r h=\frac{2 T \cos \theta}{\rho g}=\text { constant }\)
⇒ \(r h=2 r h^{\prime}\)
⇒ \(h^{\prime}=\frac{h}{2}\)
Now, \(m=\pi r^2 h\)
and \(m^{\prime}=\pi(2 r)^2\left(\frac{h}{2}\right)\)
∴ \(\frac{m^{\prime}}{m}=\frac{2 \pi r^2 h}{\pi r^2 h}=2\)
m = 2m
= 10g.
Question 78. A rectangular film of a liquid is extended from an area of 4 cm x 2 cm to 5 cm x 4 cm. If the work done is 3 x 10-4 J, the value of the surface tension of the liquid is
- 0.25 N m-1
- 8.0 Nm-1
- 0.125 Nm-1
- 0.2 Nm-1
Answer: 3. 0.125 Nm-1
Work done = (surface tension)(increase in surface area)
3 x 10-4 J = T[2(20 x 10-4 m²-8 x 10-4m²)]
∴ suface tension = T = \(\frac{3 \times 10^{-4} \mathrm{~J}}{2 \times 12 \times 10^{-4} \mathrm{~m}^2}\)
= \(0.125 \mathrm{Nm}^{-1}\)
Question 79. Three liquids of densities p1, p2, and p3 (where p1 > p2 > p3), and having the same value of surface tension rise to equal heights in three identical capillaries. The angles of contact θ1, θ2 and θ3 obey the relation
- \(\frac{\pi}{2}>\theta_1>\theta_2>\theta_3>0\)
- \(0 \leq \theta_1<\theta_2<\theta_3<\frac{\pi}{2}\)
- \(\frac{\pi}{2}<\theta_1<\theta_2<\theta_3<\pi\)
- \(\pi>\theta_1>\theta_2>\theta_3>\frac{\pi}{2}\)
Answer: 2. \(0 \leq \theta_1<\theta_2<\theta_3<\frac{\pi}{2}\)
The rise of a liquid in a capillary tube is given by
⇒ \(h=\frac{2 T \cos \theta}{r \rho g}\)
So, \(\frac{\cos \theta}{\rho}=\frac{h r g}{2 T}\)
∴ for the three given capillaries,
⇒ \(\frac{\cos \theta_1}{\rho_1}=\frac{\cos \theta_2}{\rho_2}=\frac{\cos \theta_3}{\rho_3}\)
Given that p1 > p2 > p3
∴ cos θ1 > cos θ2 > cos θ3.
Hence, \(0 \leq \theta_1<\theta_2<\theta_3<\frac{\pi}{2}\)
Question 80. Two soap bubbles of radii R1 and R2 (where R1 > R2) come into contact, as shown in the adjoining figure. The radius of curvature of the common surface is given by
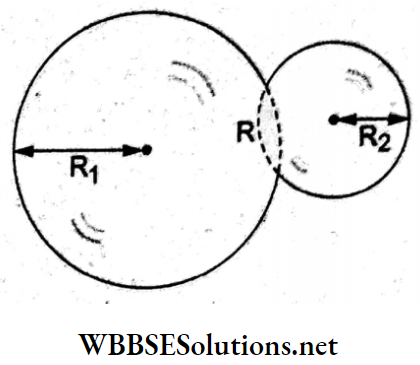
- \(R=\frac{R_1+R_2}{2}\)
- \(R=\frac{R_1-R_2}{2}\)
- \(R=\frac{R_1 R_2}{R_1-R_2}\)
- \(R=\frac{R_1 R_2}{R_1+R_2}\)
Answer: 3. \(R=\frac{R_1 R_2}{R_1-R_2}\)
If p0ise the pressure outside the bubbles, the pressure inside the larger bubble is \(p_1=p_0+\frac{4 T}{R_1}\) and that inside the smaller bubble is \(p_2=p_0+\frac{4 T}{R_2}\)
Since p2 > P1, the pressure difference across the common surface is
⇒ \(\Delta p=p_2-p_1=\frac{4 T}{R}\)
⇒ \(4 T\left(\frac{1}{R_2}-\frac{1}{R_1}\right)=\frac{4 T}{R}\)
⇒ \(R=\frac{R_1 R_2}{R_1-R_2}\)
Question 81. A liquid drop at a temperature of 0, isolated from its surroundings breaks into a number of droplets. The temperature of the droplets will be
- Equal to θ
- Greater than θ
- Less than θ
- Either of the three, depending on the surface tension of the liquid
Answer: 3. Less than θ
When the drop breaks into droplets, the total surface area increases, leading to a greater surface energy. This extra energy is drawn from the internal energy of the drop and it cools down. The temperature of the droplets will be less than θ.
Question 82. The adjoining figure shows two soap bubbles A (smaller) and B (larger) formed at the two open ends of a tube, with its valve V closed. When the valve is opened, air can flow freely between the bubbles. Which of the following options is true?
- There will be no change in the size of the bubbles.
- The bubbles will become of equal size.
- The sizes of A and B will get interchanged.
- A will become smaller and B will become larger.
Answer: 4. A will become smaller and B will become larger.
The air pressure is greater inside the smaller bubble. Hence, air flows from the smaller bubble to the larger bubble. So, A will become smaller and B will become larger.
Question 83. The arms of a manometer consist of tubes B of radii and r2 (where r1 > r2) filled with a liquid of surface tension S, as shown in the figure. Find the expression for h (the level difference of the menisci at A and B) in terms of r1,r2 and S.
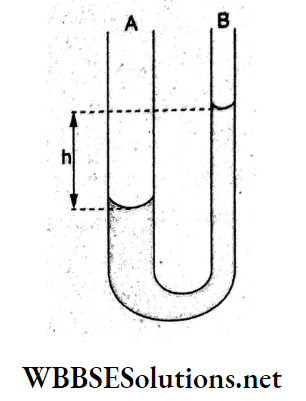
- \(\frac{S}{\rho g}\left(\frac{r_1-r_2}{r_1 r_2}\right)\)
- \(\frac{2 S}{\rho g}\left(\frac{r_1-r_2}{r_1 r_2}\right)\)
- \(\frac{S}{2 \rho g}\left(\frac{r_1+r_2}{r_1 r_2}\right)\)
- \(\frac{S}{\rho g}\left(\frac{r_1+r_2}{r_1 r_2}\right)\)
Answer: 2. \(\frac{2 S}{\rho g}\left(\frac{r_1-r_2}{r_1 r_2}\right)\)
Let p0 be the atmospheric pressure.
∴ the pressure below the meniscus at A is \(p_1=p_0-\frac{2 S}{r_1}\)
and that below the meniscus B is \(p_2=p_0-\frac{2 S}{r_2}\)
Equalizing the pressure in the same level at A, we have,
p1 = p2 + hpg
⇒ \(p_0-\frac{2 S}{r_1}=p_0-\frac{2 S}{r_2}+h \rho g\)
⇒ \(h=\frac{2 S}{\rho g}\left(\frac{r_1-r_2}{r_1 r_2}\right)\)
Question 84. A soap bubble is blown slowly at the end of a tube by a pump supplying air at a constant rate. Which of the following graphs correctly represents the variation of the excess pressure inside the bubble with time?
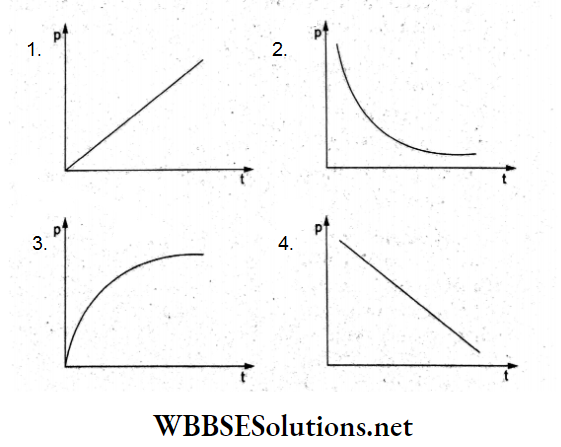
Answer: 2.
The excess pressure inside a soap bubble of radius r is
p = \(\frac{4S}{r}\)
So, \(p \propto \frac{1}{r}\)
Since air is supplied at a constant rate, the radius r will be proportional
to time.
Thus, pt = constant, which is represented by the curve given in option (2)
Question 85. The pressure inside two soap bubbles is 1.01 atm and 1.02 atm respectively. The ratio of their respective volumes is equal to
- 8
- 4
- 16
- 2
Answer: 1. 8
The excess pressure inside the first bubble is
Pi = \(\frac{4 S}{r_1}\)
= 1.01 atm – 1.0 atm
= 0.01 atm,
and that for the second bubble is
⇒ \(p_2=\frac{4 S}{r_2}=1.02 \mathrm{~atm}-1 \mathrm{~atm}=0.02 \mathrm{~atm}\)
∴ \(\frac{p_2}{p_1}=\frac{r_1}{r_2}=\frac{0.02 \mathrm{~atm}}{0.01 \mathrm{~atm}}\)
= 2.
Hence, \(\frac{V_1}{V_2}=\frac{r_1^3}{r_2^3}\)
= 8.
Question 86. An ice cube floating in a gravity-free space melts and converts into water. The shape of this water is
- A cylinder
- An ellipsoid
- A sphere
- Unpredictable
Answer: 3. A sphere
In a gravity-free space, any volume of liquid (when free) assumes a spherical shape. Hence, the ice cube will assume the shape of a large spherical drop.
Question 87. Consider an ice cube of edge L kept in a gravity-free space. Assuming the densities of ice and water to be equal, the surface area of the water formed when the ice melts will be
- (36π)½L²
- (6π)1/3L²
- (36π)1/3L²
- None of these
Answer: 3. (36π)1/3L²
The ice cube of edge L will assume the shape of a sphere of radius R when it melts. Since its volume is unchanged,
⇒ \(L^3=\frac{4}{3} \pi R^3 \Rightarrow R=\left(\frac{3}{4 \pi}\right)^{1 / 3}\)
∴ the final surface area of the spherical drop is
⇒ \(4 \pi R^2=4 \pi\left(\frac{3}{4 \pi}\right)^{2 / 3} L^2=(36 \pi)^{1 / 3} L^2\)
Question 88. A soap bubble having a radius of 1 mm is blown from a detergent solution having a surface tension of 2.5 x 10-2Nm-2. The pressure inside the bubble equals a depth z0 below the free surface of water in a container. Taking = 10 ms-2 and density of water = 10³ kgm-3, the value of z0 is
- 100 cm
- 10 cm
- 1 cm
- 0.5 cm
Answer: 3. 1 cm
The excess pressure inside a soap bubble is given by \(\Delta p=\frac{4 T}{R}\), which is equal to the pressure due to a column (of height z0) of water (p = Z0pg).
∴ \(\frac{4 T}{R}=z_0 \rho g\)
⇒ \(z_0=\frac{4 T}{\rho g R}\)
Hence, \(z_0=\frac{4\left(2.5 \times 10^{-2} \mathrm{~N} \mathrm{~m}^{-1}\right)}{\left(10^3 \mathrm{~kg} \mathrm{~m}^{-3}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)\left(1 \times 10^{-3} \mathrm{~m}\right)}=10^{-2} \mathrm{n}\)
= 1 cm.
Question 89. The ratio of the surface tensions of mercury and water is given to be 7.5, while the ratio of their densities is 13.6. Their contact angles with their glass containers are close to 135° and 0° respectively. It is observed that mercury gets depressed by an amount of h in a capillary tube of radius rv while water rises by the same amount of h in a capillary tube of radius r2. The ratio \(\frac{r_1}{r_2}\) is then close to
- \(\frac{4}{5}\)
- \(\frac{2}{5}\)
- \(\frac{2}{3}\)
- \(\frac{3}{5}\)
Answer: 2. \(\frac{2}{5}\)
The depression of mercury in the capillary tube is
⇒ \(h_{\mathrm{Hg}}=\frac{r_1 h_1 \rho_{\mathrm{Hg}} g}{2 S_{\mathrm{Hg}} \cos \theta_{\mathrm{Hg}}}\)
and the rise of the water level is
⇒ \(h_w=\frac{r_2 h_2 \rho_w g}{2 S_w \cos \theta_w}\)
Given that hHg= hw.
∴ \(\frac{r_1 h_1 \rho_{\mathrm{Hg}} g}{2 S_{\mathrm{Hg}} \cos \theta_{\mathrm{Hg}}}=\frac{r_2 h_2 \rho_{\mathrm{w}} g}{2 S_{\mathrm{w}} \cos \theta_{\mathrm{w}}}\)
∴ \(\frac{r_1}{r_2}=\frac{h_2}{h_1} \cdot \frac{\rho_{\mathrm{w}}}{\rho_{\mathrm{Hg}}} \cdot \frac{S_{\mathrm{Hg}}}{S_{\mathrm{w}}} \cdot \frac{\cos \theta_{\mathrm{Hg}}}{\cos \theta_{\mathrm{w}}}\)
Substituting the appropriate values,
⇒ \(\frac{r_1}{r_2}=\left(\frac{h}{h}\right)\left(\frac{1}{13.6}\right)\left(\frac{7.5}{1}\right)\left(\frac{1}{\sqrt{2}}\right)\)
= 0.4
= \(\frac{2}{5}\)
Question 90. The work done to blow a soap bubble of radius 5 cm is (given that surface tension of the soap solution = 0.1 N m-1)
- 6.28 x 10-3 J
- 3.14 x 10-2 J
- 2.5 x 10-2 J
- 5.8 x 10-3 J
Answer: 1. 6.28 x 10-3 J
The work done in blowing a soap bubble is
W = (surface tension)(increase in surface area)
= S.ΔA = S(8πR²).
Substituting the values,
W= (0.1 N m-1) [8 x 3.14 x(5x 10-2 m)2]
= 62.8 x 10-4 J
= 6.28 x 10-3 J.
Question 91. In an isothermal process, two water drops each of a radius 1 mm are combined to form a bigger drop. The amount of energy released during the process is (given that surface tension = 0.1 N m-1)
- 1 μJ
- 0.75 μJ
- 0.5 μJ
- 0.25 μJ
Answer: 3. 0.5 μJ
Let R be the radius of the bigger drop.
∴ \(\left(\frac{4}{3} \pi r^3\right) \times 2=\frac{4}{3} \pi R^3\)
=> R = 21/3r.
The change in the surface area of the drops is
ΔA = 4πr².2-4πR²
= 4π(2r² -22/3r2)
= 4πr2(2-22/3).
Since the surface area decreases, energy is released. This energy is
given by
All = S.ΔA = (0.1 Nm-1)[4 x 3.14 x (10-3 m)2(2-1.58)]
= 0.52 x 10-6 J ≈ 0.5 mmmJ
Question 92. A soap bubble, blown by a mechanical pump at the mouth of a tube, increases in volume with time at a constant rate. The graph that correctly depicts, the time dependence of the pressure inside the die bubble is
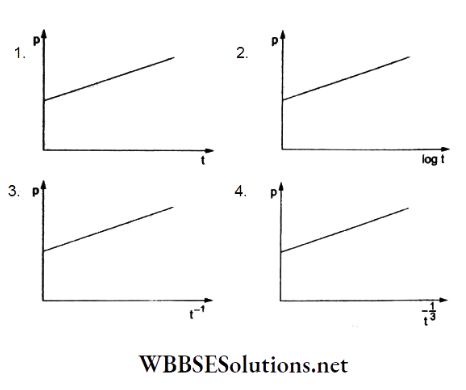
Answer: 4.
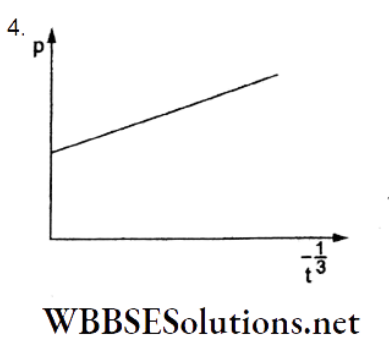
The volume of a soap bubble is \(V=\frac{4}{3} \pi R^3\).
∴ \(\frac{d V}{d t}=4 \pi R^2 \frac{d R}{d t}=\text { constant (given) }\)
∴ R2dR = (constant)dt.
Integrating,
⇒ \(\frac{R^3}{3}=(\text { constant }) t\)
⇒ \(R \propto t^{1 / 3}\)
For a soap bubble, a pressure difference is
⇒ \(p-p_0=\frac{4 S}{R}=\frac{k}{t^{1 / 3}}\)
⇒ \(p=p_0+\frac{k}{t^{1 / 3}}\)
This shows that the graph in option (4) is correct.
Question 93. A capillary tube of radius 0.15 mm is dipped in a liquid of A density 667 kg m-3. Find the height to which the liquid will rise. [Given that surface tension of the liquid = (1/20) N m-1 and angle of contact = 60°]
- 0.02 m
- 0.01 m
- 0.05 m
- 0.04 m
Answer: 4. 0.04 m
The rise of tire liquid (h) in a capillary is given by
⇒ \(T=\frac{r h \rho g}{2 \cos \theta}\)
⇒ \(h=\frac{2 T \cos \theta}{r \rho g}\)
On substituting the given values,
⇒ \(h=\frac{2\left(\frac{1}{20} \mathrm{~N} \mathrm{~m}^{-1}\right) \cos 60^{\circ}}{\left(0.15 \times 10^{-3} \mathrm{~m}\right)\left(667 \mathrm{~kg} \mathrm{~m}^{-3}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}\)
= 0.05m.
Question 94. The pressure inside two soap bubbles is 1.01 atm and 1.02 atm. The ratio of their volumes is
- 4:1
- 8:1
- 1:8
- 1:4
Answer: 2. 8:1
The excess pressure (pi -p0) in a soap bubble is \(\frac{4T}{R}\)
Hence, \(\frac{4 T}{R_1}\) = 1.01 atm-1 atm
= 0.01 atm
and \(\frac{4 T}{R_2}\) 1.02 atm-1 atm = 0.02 atm.
∴ \(\frac{R_1}{R_2}=\frac{0.02 \mathrm{~atm}}{0.01 \mathrm{~atm}}\)
= 2.
⇒ \(\frac{V_1}{V_2}=\left(\frac{R_1}{R_2}\right)^3=2^3\)
=8
V1:V2 =8:1
Question 95. A capillary tube made of glass and of radius 0.15 mm is dipped vertically in a beaker filled with a liquid of surface tension 5 x 10-2 Nm -1 and density 667 kg m-3. The capillary rise is h. It is observed that tangents drawn from the meniscus from two diametrically opposite points are inclined at 60°. The value of h is
- 0.049 m
- 0.172 m
- 0.087 m
- 0.137 m
Answer: 3. 0.087 m
Capillary rise = h = \(\frac{2 T \cos \theta}{r \rho g}\)
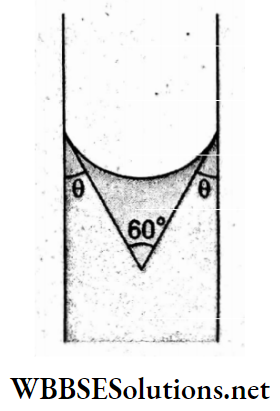
= \(\frac{2\left(5 \times 10^{-2} \mathrm{~N} \mathrm{~m}^{-1}\right)\left(\cos 30^{\circ}\right)}{\left(0.15 \times 10^{-3} \mathrm{~m}\right)\left(667 \mathrm{~kg} \mathrm{~m}^{-3}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}\)
⇒ \(\frac{1.732 \times 5 \times 10^{-2}}{0.15 \times 667 \times 10^{-2}} \mathrm{~m}\)
= 0.087 m.
Question 96. A capillary tube of radius r is immersed vertically in water, and the water rises to a height of h. The mass of the water in the capillary is 5 g. Another capillary tube of radius 2r is immersed in water. The mass of the water that will rise in this tube is
- 5.0 g
- 10.0 g
- 20.0 g
- 2.5 g
Answer: 2. 10.0 g
The weight of the liquid column in the capillary tube is balanced by the force due to surface tension.
Hence, 2πrTcos θ = mg.
For the capillary tube of radius 2r, let the mass of the liquid that rises be m’.
∴ 2π(2r)Tcos θ = m’g.
Hence, \(\frac{m^{\prime}}{m}=2\)
=> m’ = 2m
= 2(5 g)
=10g.
Question 97. Ablockofdensitydx and massMmovesdownwards with a uniform speed in glycerine of density d2. What is the viscous force acting on the die block?
- Mgd1
- Mgd2
- \(M g\left(1-\frac{d_1}{d_2}\right)\)
- \(M g\left(1-\frac{d_2}{d_1}\right)\)
Answer: 4. \(M g\left(1-\frac{d_2}{d_1}\right)\)
Weight of the block (acting downwards) = Mg,
weight of the liquid = buoyant force (acting upwards)
⇒ \(M^{\prime} g=V d_2 g=\left(\frac{M}{d_1}\right) d_2 g\)
and f = viscous force (upward).
Since the motion is uniform, net force = 0.
∴ \(M g-M\left(\frac{d_2}{d_1}\right) g-f=0\)
⇒ \(f=M g\left(1-\frac{d_2}{d_1}\right)\)
Question 98. An object is moving through a liquid. The viscous damping force acting on it is proportional to the velocity. The dimensions of the constant of proportionality are
- ML-1T-1
- MLT-1
- M0LT-1
- ML0T-1
Answer: 4. ML0T-1
Viscous damping force = f = kv.
∴ \([k]=\frac{[f]}{[v]}\)
= \(\frac{\mathrm{MLT}^{-2}}{\mathrm{LT}^{-1}}\)
= \(\mathrm{ML}^0 \mathrm{~T}^{-1}\)
Question 99. Which of the following is not a dimensional quantity?
- Acceleration due to gravity
- Surface tension
- Reynolds number
- Velocity of light
Answer: 3. Reynolds number
The critical velocity is given by \(v_c=\frac{k \eta}{\rho R}\) where the Reynolds number k is dimensionless.
Question 100. The Reynolds number for fluid flow through a pipe is independent of the
- Viscosity of the fluid
- Velocity of the fluid
- Length of the pipe
- Diameter of the pipe
Answer: 3. Length of the pipe
In a fluid flow, critical velocity = \(v_c=\frac{k \eta}{\rho D}\) where the Reynolds number
k is independent of the length of the pipe.
Question 101. When a steel ball is dropped in an oil,
- The ball attains a constant velocity after some time
- The speed of the ball will keep on increasing
- The ball stops after some time
- None of the above takes place
Answer: 1. The ball attains a constant velocity after some time
A steel ball dropped in oil will experience its’ weight (downward), buoyant force (upward), and viscous force (upward). The viscous force gradually increases with speed, and the net force becomes zero when the ball finally attains a constant terminal velocity.
Question 102. The ratio of the terminal velocities of two drops of radii R and R/2 is
- 1:1
- 2:1
- 4:1
- 1:4
Answer: 3. 4:1
Terminal velocity = \(v=\frac{2}{9} \cdot \frac{(\rho-r) r^2}{\eta}\)
∴ v ∝ r²
⇒ \(\frac{v_1}{v_2}=\frac{R^2}{(R / 2)^2}\)
= \(\frac{4}{1}\)
v1: v2 = 4: 1
Question 103. The volume of a liquid flowing per unit of time through a tube of radius r and length l whose ends are maintained at a pressure difference P is given by \(V=\frac{\pi Q P r^4}{\eta l}\) where t is the coefficient of viscosity and Q is equal to
- 8
- \(\frac{1}{8}\)
- 16
- \(\frac{1}{16}\)
Answer: 2. \(\frac{1}{8}\)
The volume flowing per unit of time is given by Poiseuille’s equation, i.e,
⇒ \(V=\frac{\pi P r^4}{8 \eta l}\)
Comparing this with the given equation, we have Q = \(\frac{1}{8}\)
Question 104. The radii of two drops of a liquid are in the ratio of 3: 2. Their terminal velocities are in the ratio
- 2:3
- 3:2
- 9:4
- 4:9
Answer: 3. 9:4
The ratio of the terminal velocities is
⇒ \(\frac{v_1}{v_2}=\frac{r_1^2}{r_2^2}\)
= \(\left(\frac{3}{2}\right)^2\)
= \(\frac{9}{4}\)
Question 105. The coefficient of viscosity of hot air
- Is Greater Than The Coefficient Of Viscosity Of Cold Air
- Is The Same As The Coefficient Of Viscosity Of Cold Air
- Is Smaller Than The Coefficient Of Viscosity Of Cold Air
- Increases or decreases depending on the external pressure
Answer: 1. Is Greater Than The Coefficient Of Viscosity Of Cold Air
An increase in gas temperature causes the gas molecules to collide more often and thus increases the gas viscosity. Hence, hot air is more viscous than cold air.
Question 106. The viscous force exerted by a liquid flowing between two plates in a streamline flow depends upon
- The velocity gradient in the direction perpendicular to the plates only
- The areas of the plates only
- The coefficient of viscosity of the plates only
- All of these
Answer: 4. All of these
The viscous force exerted by a liquid flowing between two horizontal plates is given by
⇒ \(F=-\eta A \frac{d v}{d z}\)
which depends on all the three factors given in options (1), (2), and (3).
Question 107. Under a constant-pressure head, the volume flowing per unit time through a tube is V. If the length of the tube is doubled and the diameter of the bore is halved, the rate of flow would become
- \(\frac{V}{4}\)
- 16V
- \(\frac{V}{8}\)
- \(\frac{V}{32}\)
Answer: 4. \(\frac{V}{32}\)
The rate of flow is given by
⇒ \(V=\frac{\pi P r^4}{8 \eta l}\)
Hence, the new rate of flow will be
⇒ \(V^{\prime}=\frac{\pi P}{8 \eta} \cdot \frac{\left(\frac{r}{2}\right)^4}{2 l}\)
= \(\frac{\pi P r^4}{8 \eta l} \cdot \frac{1}{32}\)
= \(\frac{V}{32}\)
Question 108. A spherical ball is dropped in a p-long column of liquid. Which of the following three plots (P, Q, and R) represents the variation of gravitational force with time, that of viscous force with time, and that of the net force acting on the ball with time respectively?
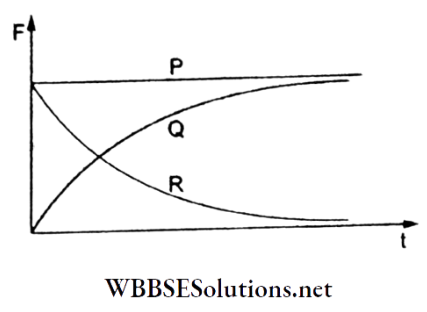
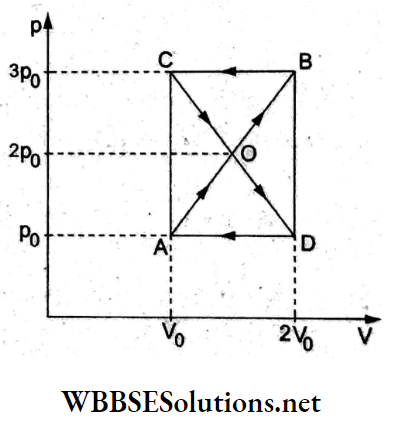
- Q, R, and P
- R, Q, and P
- P, Q, and R
- R, P, and Q
Answer: 3. P, Q, and R
The gravitational force (= weight = mg) remains constant (given by the plot P). The viscous force gradually increases with time and becomes constant when the terminal velocity is reached (represented by the plot Q). The net force gradually decreases and has a zero value when the motion becomes uniform (shown by plot R).
Question 109. A lead shot of 1 mm diameter falls through a long column of glycerine. The variation of its velocity (v) with the distance covered (s) is represented by
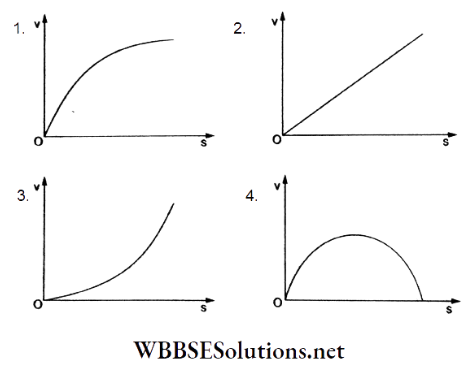
Answer: 1.
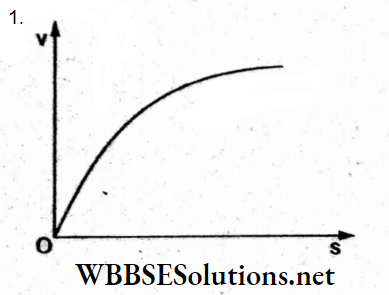
Initially, the velocity increases due to gravity. Simultaneously, a viscous force acts, so the lead shot attains a constant terminal velocity, as shown in the graph in option (1).
Question 110. A sphere of mass M and radius R is falling in a viscous fluid. The terminal velocity attained by the falling object will be proportional to
- R²
- R
- \(\frac{1}{R}\)
- \(\frac{1}{R^2}\)
Answer: 1. R²
The terminal velocity of a spherical body falling under gravity in a viscous fluid is given by
⇒ \(v=\frac{2}{9} \cdot \frac{\rho-\sigma}{\eta} \cdot R^2\)
⇒ \(v \propto R^2\)
Question 111. A raindrop reaching the ground with a terminal velocity has a momentum of p. Another drop of twice its radius, also reaching the ground with a terminal velocity, will have a momentum of
- 4p
- 16p
- 8p
- 32p
Answer: 4. 32p
The terminal velocity is given by v ∝ r², and the mass is given by
⇒ \(m=\frac{4}{3} \pi r^3 \rho \propto r^3\)
Hence, the momentum is given by p ∝ r³.
For the smaller drop, p = kr5.
For a larger drop, p’ = k(2r) = 32kr5.
∴ \(\frac{p^{\prime}}{p}=32\)
p’ = 32p
Question 112. A cylindrical drum, open at the top, contains 30 liters of water. It drains out through a small hole at the bottom. 10 liters of water comes out in a time of the next 10 liters in a further time t2 and the last 10 liters in a further time t3. Then,
- t1 = t2 = t3
- t1>t2<t3
- t1<t2<t3
- \(\frac{1}{t_1}+\frac{1}{t_2}=\frac{1}{t_3}\)
Answer: 3. t1<t2<t3
The velocity of efflux is given by \(v=\sqrt{2 g x}\), where x is the height of the liquid. As the water drains out, x reduces, so v reduces. This reduces the rate of drainage. Hence, it requires a longer time to drain out the same volume of water. Thus,
t1<t2<t3
Question 113. A solid sphere of radius R acquires a terminal velocity while falling under gravity through a viscous fluid having the coefficient of viscosity r1. The sphere is broken into 27 identical solid spheres. If each of these small spheres acquires a terminal velocity of v2 while falling through the same fluid, the ratio v1/v1 equals
- 9
- \(
- 27
- [latex]\frac{1}{9}\)
Answer: 1. 9
The terminal velocity of a sphere falling through a viscous medium under gravity is given by
⇒ \(v=\frac{2}{9} \cdot \frac{r^2(\rho-\sigma) g}{\eta}\)
Thus, v1 = kr2….(1)
When the drop is split up into 27 droplets of equal radii r0 then,
⇒ \(\frac{4}{3} \pi r^3=27 \cdot \frac{4}{3} \pi r_0^3\)
Hence, r0 = \(\frac{r}{3}\) and its terminal velocity is
⇒ \(v_2=k r_0^2=k\left(\frac{r}{3}\right)^2\)…..(2)
∴ \(\frac{v_1}{v_2}=\frac{r^2}{\left(\frac{r}{3}\right)^2}=9\)
Question 114. A small hole of area of cross-section 2 mm² is punched near the bottom of a fully filled open tank of height 2 m. Taking =10 m s-2, the rate of flow of water through the open hole would be nearly
- 12.6 x 10-6 m3 s-1
- 8.9 x 10-6 m3 s-1
- 2.23 x 10-6 m3s-1
- 6.4 x 10-6 m3 s-1
Answer: 1. 12.6 x 10-6 m3 s-1
According to Torricelli’s law, the efflux speed of a liquid at a depth of h is \(v=\sqrt{2 g h}\) and thus the volume flowing per unit time is
V = (area) (velocity)
= A\(v=\sqrt{2 g h}\)
= \(\left(2 \times 10^{-6} \mathrm{~m}^2\right) \sqrt{2\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(2 \mathrm{~m})}\)
= \(=4 \times 10^{-6} \times \sqrt{10} \mathrm{~m}^3 \mathrm{~s}^{-1}\)
= 12.6 x 10-6 m3 s-1.
Question 115. Water from a pipe is coming at a rate of 100 litres per minute. If the radius of the pipe is 5 cm, the Reynolds number for the flow is of the order of (given that density of water = 1000 kg m-3 and coefficient of viscosity of water =1 mPa s)
- 106
- 103
- 104
- 102
Answer: 3. 104
The volume flowing per unit time is given by V = (area ofcross section)(velocity) = Av.
Since critical velocity = \(v_{\mathrm{c}}=\frac{k \eta}{\rho R}\)
∴ \(\frac{V}{A}=\frac{k \eta}{\rho R}\)
Hence, Reynolds number = k\(\frac{V \rho R}{A \eta}\) ,
Substituting the proper radius, we obtain
⇒ \(k=\frac{\left(100 \mathrm{~L} \mathrm{~min}^{-1}\right)\left(10^3 \mathrm{~kg} \mathrm{~m}^{-3}\right)}{\pi\left(5 \times 10^{-2} \mathrm{~m}\right)\left(10^{-3} \mathrm{~Pa} \mathrm{~s}\right)} \approx \frac{\left(\frac{100 \times 10^{-3}}{60}\right)\left(10^3\right)}{(3.14)\left(5 \times 10^{-5}\right)}\)
⇒ \(\frac{10^7}{3.14 \times 300} \approx 10^4\)
Question 116. Water flows into a large tank with a flat bottom at the rate of 10-4 m3 s-1 Water is also leaking out of a hole of area 1 cm² at its bottom. If the height of the water in the tank remains steady then this height is close to
- 4 cm
- 3 cm
- 5 cm
- 1.7 cm
Answer: 3. 5 cm
The water level will remain steady if in flow rate = outflow rate.
Hence, V = Av = A\(\sqrt{2 g h}\)
⇒ \(h=\frac{V^2}{2 A^2 g}=\frac{\left(10^{-4} \mathrm{~m}^3 \mathrm{~s}^{-1}\right)^2}{2\left(10^{-4} \mathrm{~m}^2\right)^2\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}\)
⇒ \(\frac{10^{-8}}{2 \times 10^{-7}} \mathrm{~m}\)
= \(\frac{1}{20}\)
= 5 cm.
Question 117. A spherical ball of radius r and density p is released from a height h above the surface of a viscous liquid. If the terminal velocity gained by the ball in die liquid is the same as that before entering the liquid then h is proportional to
- r4
- r3
- r2
- r
Answer: 1. r4
The velocity of the ball just before entering the liquid is v = \(\sqrt{2 g h}\)
Its terminal velocity in the liquid will be
⇒ \(v_{\mathrm{t}}=\frac{2}{9} \cdot \frac{r^2(\rho-\sigma) g}{\eta}=k r^2\)
∴ \(\sqrt{2 g h}=k r^2\)
⇒ \(h=\frac{k^2 r^4}{2 g} \propto r^4\)