WBCHSE Class 11 Physics Work And Energy Notes

Energy

A body can do work by the transfer of some amount of energy.

Energy Definition: The total amount of work that a body can do is the same as its total amount of energy. Hence, energy and work are equivalent physical quantities, having the same units and dimensions. Both are scalar quantities.

Energy is manifested in nature in different forms:

1. Mechanical energy
2. Heat energy
3. Light energy
4. Sound energy
5. Magnetic energy
6. Electrical energy
7. Chemical energy
8. Atomic energy

In all-natural events, energy changes from one form to another. In fact, every natural phenomenon can be interpreted as a sequence of energy transformations.

Energy Examples:

1. In an electric bulb, electrical energy is converted into heat energy at first, and then into light energy.
2. In an electric fan, electrical energy changes into mechanical energy.
3. In a telephone, sound energy is converted into electrical energy (during speaking), and electrical energy into sound energy (during listening).
4. In hydroelectric plants, water stored in a high reservoir flows downwards and its potential energy changes into kinetic energy. This kinetic energy rotates the turbines which generate electrical energy.
5. Water from sea, river and other water bodies evaporate and forms clouds. This water eventually returns to the earth in the form of rain. The potential energy of the clouds converts into the kinetic energy of the raindrops.
6. On burning coal, chemical energy is converted into heat and light energy.

We observe such numerous incidents of energy transformations in daily life. But neither energy is created nor destroyed in such incidents. Energy can only get transferred from one body to another or can change its form. As soon as a body loses energy, another body gains it in equal amounts. Hence the total energy in the universe remains the same. This is the law of conservation of energy.

Law Of Conservation Of Energy: Energy cannot be created or destroyed. It can only be converted from one form to another.

• It means that the total energy in the universe remains constant.
• After the introduction of Einstein’s theory of relativity, the law of conservation of energy was corrected and the law of conservation of mass energy was established.
• This means that mass and energy in the universe are not conserved individually.
• Only mechanical energy is discussed in detail in the following sections.

Work And Energy – Conservation Force

Conservation Force Definition: A system in which the total mechanical energy i.e., the sum of its kinetic and potential energy [remains conserved, is called a conservative system. The forces acting in such a system are called conservative forces.

Conservation Force Example: Gravitational force, restoring force of spring or elastic force, electrostatic force, force between the magnetic poles, etc., are conservative forces.

Work is done to lift a body against gravity and is stored as potential energy. While returning to its initial position, the body uses this stored energy and does work that is exactly equal to the initial work done while lifting. Hence energy is conserved.

Work Done In A Dosed Path Under A Conservative Force: For a conservative system, the work done depends only on the initial and final positions. It does not depend on the path taken in reaching the final position from the initial position.

• This means that the sum of the kinetic and potential energies remains constant throughout.
• It also implies that if a body goes around a complete loop so that its final and initial positions are the same, then the total work done is zero. For any conservative force, the work done is reversible.
• Hence if work done against a force can be restored, the force is called conservative. Also if work done by a force in a closed path equals to zero, the force is called conservative.

Thus in a conservative system, it is possible to restore the initial work done.

Suppose a body gets displaced by dx along the x-axis under the action of a conservative force F (which may vary with position) also acting along the x-axis. Therefore the work done by the conservative force dW = F(x)dx.

Since change in potential energy is negative of work done, then change in potential energy for this displacement dx is given by dU = -F(x)

In a three-dimensional reference frame, this equation is dU = \(-\vec{F} \cdot d \vec{r}\)….(1)

Work And Energy – Conservation Of Mechanical Energy Of A Particle In A Conservative System

Suppose a conservative force \(\vec{F}\), acting on a particle of mass m moves, it from point A to point B.

If the velocity of the particle at any point of its motion in the force field is v, then \(\vec{F} \cdot d \vec{r}=m \frac{d \vec{v}}{d t} \cdot \vec{v} d t=m \vec{v} \cdot d \vec{v}=m d\left(\frac{1}{2} v^2\right)\)

∴ Work done, to take the particle from A to B, by force \(\vec{F}\),

W = \(\int_A^B \vec{F} \cdot d \vec{r}=\left[\frac{1}{2} m v^2\right]_A^B=\frac{1}{2} m v_B^2-\frac{1}{2} m v_A^2\)…(1)

where v_A and v_B are the velocities of the particle at A and B respectively.

Equation (1), we know \(\vec{F} \cdot d \vec{r}=-d U\)

∴ \(\int_A^B \vec{F} \cdot d \vec{r}=-\int_A^B d U=U_A-U_B\)

= difference in potential energy between the points A and B…(2)

Comparing (1) and (2), \(U_A-U_B=\frac{1}{2} m v_B^2-\frac{1}{2} m v_A^2\)…(2)

Equation (3) establishes that in a conservative field when the kinetic energy of a particle increases, its potential energy decreases.

∴ \(\frac{1}{2} m v_A^2+U_A=\frac{1}{2} m v_B^2+U_B\)…(4)

If K_A and K_B are the kinetic energies of the particle at A and B respectively, then

K_A+U_B = K_B+ U_B or, K + U = constant (E).

Hence in a conservative field i.e., in a conservative system (where no dissipation of energy occurs due to forces like friction, etc.), at each point sum of potential energy and kinetic energy remains constant.

In other words, total mechanical energy (E) of a particle in a conservative system remains constant. This is the statement of the principle of conservation of mechanical energy.

Total mechanical energy In a free fall under gravity remains constant: Let a body of mass m be at rest at point A. DE, the earth’s surface is taken as the reference plane and the height of point A from DE is h. As the body is at rest it has potential energy only and no kinetic energy.

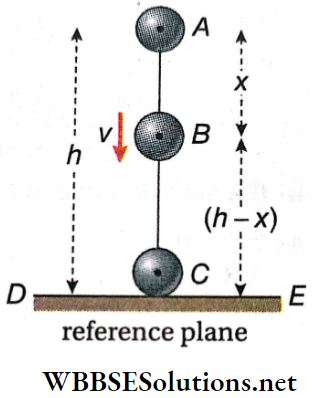
Potential energy at A = mgh

Kinetic energy at A = 0

Total mechanical energy at A = mgh + 0 = mgh

Now the body is released and it starts falling freely. When the body reaches a point B, it acquires a velocity v.

At B, the body has both potential energy (due to its height) and kinetic energy (due to its motion).

Let AB = x

∴ Potential energy at B = mg(h- x)

Kinetic energy at B = \(\frac{1}{2} m v^2=\frac{1}{2} m \cdot 2 g x\)

= mgx (because \(v^2=u^2+2\) as and u=0)

∴ Total mechanical energy at B = mg(h-x) + mgx = mgh

= total energy at A.

Also at C, when the body is about to touch the reference plane, its potential energy becomes zero. If the velocity acquired at that point is V, then kinetic energy at C

= \(\frac{1}{2} m V^2=\frac{1}{2} m \cdot 2 g h\left[because V^2=2 g h\right]\)

= mgh

Total mechanical energy at C = mgh + 0 = mgh

∴ Total energy at A = total energy at B = total energy at C.

Therefore, the total mechanical energy (= potential energy + kinetic energy) of a freely falling body, under the action of i gravity, remains conserved at all positions.

As the body touches the ground, both its potential energy and kinetic energy become zero; the entire mechanical energy transforms into heat, sound, and other forms of energy.

Total Mechanical Energy Of A Body, Falling Under Gravity Along A Frictionless Inclined Surface, Remains Constant: Let a body of mass m be at rest at a point A on a frictionless plane of inclination θ. Earth’s surface CD is taken as the reference plane.

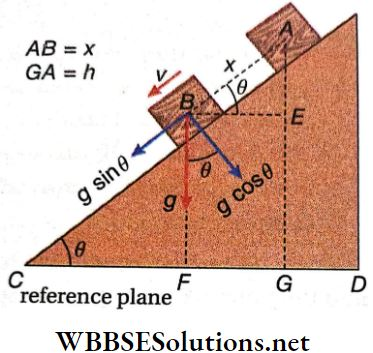
Let the height of point A from the reference plane, GA = h. Being at rest, the body has no kinetic energy at A.

The potential energy at A = mgh Kinetic energy at A = 0

∴ Total mechanical energy at A = mgh + 0 = mgh

On releasing the body, it falls along the incline and reaches a point B such that, AB = x. Let the velocity of the body at B be v.

Acceleration of the body along the incline, a = gsinθ.

∴ \(v^2=0+2 g \sin \theta \cdot x=2 g x \sin \theta \quad \text { [as } v^2=u^2+2 a s \text { ] }\)

∴ Kinetic energy at \(B=\frac{1}{2} m v^2=\frac{1}{2} \cdot m \cdot 2 g x \sin \theta\)

= mgx sinθ

The perpendicular height of B from CD plane = FB = GE = GA-EA = h-x sinθ

(because \(\sin \theta=\frac{E A}{A B} \quad \text { or, }E A=A B \sin \theta=x \sin \theta\))

∴ The potential energy at B = mg(h-x sinθ)

∴ Total mechanical energy at B

= mg(h- xsinθ) + mgx sinθ

= mgh = total energy at A

At point C, i.e., where the body just touches the plane CD, it has no potential energy. If the velocity of the body at that moment is V, then

V² = 0 + 2g sinθ · AC = 2gsinθ · AC

and hence, kinetic energy at C = \(\frac{1}{2}\) m · 2g sinθ · AC = mgh

[sinθ = \(\frac{G A }{A C}\) = \(\frac{h}{A C}\) or, AC sinθ = h]

∴ Total energy at C = 0 + mgh = mgh

Thus, total mechanical energy at A = total mechanical energy at B = total mechanical energy at C.

Hence, the total mechanical energy of a body, moving along a frictionless inclined plane under gravity, is conserved.

Total Mechanical Energy Of A Hydrogen Gas-Filled Balloon Rising Upwards Remains Constant: Let us assume that air and earth form a system. If the earth’s surface is taken as the plane of reference, when the balloon is at rest on the ground, both its potential and kinetic energy = 0, i.e., total mechanical energy = 0.

Now the balloon is released. Upthrust, T due to air on the balloon is more than the weight, mg of the balloon filled with gas and so the balloon rises up. Let the mass of the gas-filled balloon = m and the mean resultant upward force on it = F – T – mg.

∴ Acceleration of the balloon = \(\frac{F}{m}\). If the velocity of the balloon is v at a height h from the earth surface, then

v2² = 2\(\frac{F}{m}\)h [according to the formula v² = u² + 2as]

Hence, kinetic energy at h = \(\frac{1}{2}\)= \(\frac{1}{2}\)m 2 \(\frac{F}{m}\)h = Fh

We know that when a stone falls freely under gravity, the work done is negative. Similarly, when the balloon rises by itself (without the help of any external agent) under the effect of the mean upward resultant force F, the work done is also negative. Here, the upthrust is not applied by an external agent.

So, at height h the change in potential energy = -Fh. As the initial potential energy of the balloon on the ground was zero, the total potential energy at a height h = -Fh.

∴ The total mechanical energy of the balloon at height h = potential energy + kinetic energy = – Fh + Fh = 0 = total energy of the balloon on the ground before its release.

Thus, the total mechanical energy remains conserved for a hydrogen gas-filled balloon when it is rising up. It is to be noted that, with the increase in height h, the kinetic energy increases but the potential energy decreases equally.

Actually, the expression mgh for potential energy should be modified for a balloon as (mg- T)h, where T is the upward thrust exerted on the balloon by the air surrounding it. For a hydrogen-filled balloon, the upward thrust is greater than its weight, i.e., T> mg. So the potential energy (mg-T)h is negative; this negative value goes on increasing with an increase in height h.

Another similar event is observed when a piece of wood is held at the bottom of a bucket full of water. When it is released, it floats up by itself. It can be shown that the total mechanical energy remains conserved. As the piece of wood rises upwards, its kinetic energy gradually increases and the potential energy decreases equally.

Work And Energy – Conservation Of Mechanical Energy Of A Particle In A Conservative System Numerical Examples

Example 1. After falling from a height of 200 m, water flows horizontally with a certain velocity. Ignoring any energy dissipation, find the velocity of flow.
Solution:

Potential energy changes into kinetic energy during the free fall of water.

Let mass of water = m, height = h, final velocity = v

Here, at a height of 200 m

potential energy (P.E.)_i = mgh and kinetic energy (K.E.)_i = 0

when water falls and flows horizontally, potential energy, (P.E.)_f = 0 and kinetic energy (K.E.)_f = \(\frac{1}{2}\)mv²

∴ From the conservation of mechanical energy we,

∴ mgh = \(\frac{1}{2}\)mv

or, \(\nu=\sqrt{2 g h}=\sqrt{2 \times 9.8 \times 200}\)

= \(62.61 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

= 62.61 m · s^-1

Example 2. The mass of the bob of a simple pendulum is 10 g and the effective length is 13 cm. The bob is pulled 5 cm away from the vertical and then released. What will be the kinetic energy of the bob when it passes through the lowest point?
Solution:

We observe that, the energy of the bob at point B = potential energy = mgh = 10 x 980 x AC.

Here OA = OB = 13 cm and CB = 5 cm.

∴ OC = \(\sqrt{13^2-5^2}\)

= \(\sqrt{144}=12 \mathrm{~cm}\)

∴ AC = OA-OC = 13 – 12 = 1 cm.

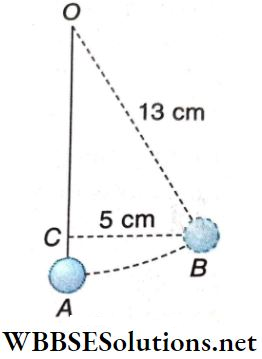
∴ Potential energy of the bob at B = 10 x 980 x 1 = 9800 erg

∴ The kinetic energy of the bob at the lowest point A = potential energy of the bob at B = 9800 erg.

Example 3. After a collision with an ideal spring, a body of mass 8 g, moving with a constant velocity of 10 cm· s^-1 comes to rest Force constant of the spring is 200 dyn · cm^-1. If the total kinetic energy of the body is spent in compressing the spring, find the compression.
Solution:

Here, the kinetic energy of the body transforms into the potential energy of the spring.

∴ \(\frac{1}{2} m v^2=\frac{1}{2} k x^2\), where x = compression of the spring

∴ x = \(\sqrt{\frac{m v^2}{k}}=\sqrt{\frac{8 \times 10^2}{200}}=2 \mathrm{~cm}\) .

Example 4. The effective length of a pendulum is 50 cm and the mass of the bob is 4 g. The bob is drawn to one side until the string is horizontal and is then released. When the string makes an angle 60° with the vertical, what is the velocity and the kinetic energy of the bob?
Solution:

OB is the horizontal position of the string.

At B, the total energy of the bob

= potential energy = mgh = (4 x 980 x 50) erg

At C, the total energy of the bob = kinetic energy + potential energy

= kinetic energy + 4 x 980 x AD

(cos 60° = \(\frac{OD}{OC}\) or, OD = \(\frac{50}{2}\) = 25 cm

∴ AD = OA – OD – 50-25 = 25 cm)

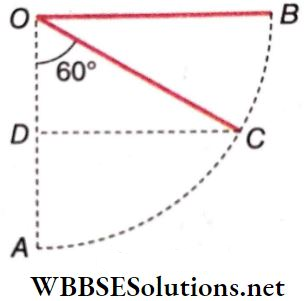
According to the law of conservation of energy, the energy of the bob at C = energy of the bob at B

or, K.E. of the bob at C + P.E. of the bob at C = K.E. of the bob at B + P.E. of the bob at B

or, \(\frac{1}{2} m v^2+4 \times 980 \times 25=0+4 \times 980 \times 50\) (v = velocity of bob at C)

or, \(\frac{1}{2} m v^2=4 \times 980 \times 25=98000\)

∴ \(v^2=\frac{98000 \times 2}{4} \quad \text { or, } v=\sqrt{49000}=222.36 \mathrm{~cm} \cdot \mathrm{s}^{-1}\).

Example 5. The mass of the bob of a pendulum is 100 g and the length of the string is 1 m. The bob is initially held in such a way that the string is horizontal. The bob is then released. Find the kinetic energy of the bob when the string makes an angle of

1. 0° and
2. 30° with the vertical.

Solution:

When the string is horizontal, the height of the bob above its lowest position = 1 m = 100 cm.

The energy of the bob at point P = potential energy of the bob

= mgh = 100 x 980 x 100 = 98 x 10⁵ erg.

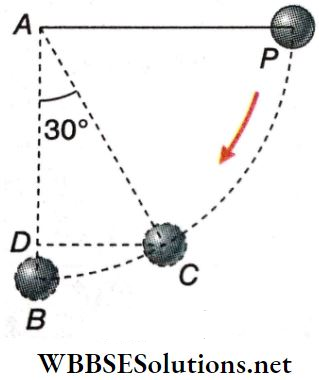
1. At 0° angle with the vertical, the string holds the bob at its lowermost position. Hence, energy at B = kinetic energy of the bob = initial potential energy = 98 x 10 erg.

2. When the string makes a 30° angle with the vertical, the height of the bob from its lowermost position

= BD = BA – DA = 100- AC cos30°

= \(100\left(1-\frac{\sqrt{3}}{2}\right)=13.4 \mathrm{~cm}\)

Potential energy of the bob at C = 100 x 980 x 13.4 erg;

kinetic energy at this position = initial potential energy- potential energy at C

= 98 x 10⁵ -(100 x 980 x 13.4) = 8486800 erg.

Example 6. A body of mass 1 kg falls to the ground from the roof of a building 20 m high. Find its

1. Initial potential energy,
2. Velocity when it reaches the ground,
3. Maximum kinetic energy and
4. Kinetic and potential energies at a position 2 m above the earth’s surface.

Solution:

1. Initial potential energy of the body = mgh = 1 x 9.8 x 20 = 196 J.

2. Suppose the body touches the ground with velocity v. Potential energy at roof level = kinetic energy just before touching the ground.

∴ 196 = \(\frac{1}{2}\) x 1 x v²

∴ v² = 392 and v = 19.8 m · s^-1

3. Maximum kinetic energy = initial potential energy = 196 J

4. Potential energy at a height of 2 m = 1×9.8×2 =19.6J

∴  Kinetic energy at that height of 2 m = decrease in initial potential energy = 196 – 19.6 = 176.4 J.

Example 7. A pump lifts 200 L of water per minute through a height of 5 m and ejects it through an orifice 2 cm in diameter. Find the velocity of efflux of water and the power of the pump.
Solution:

Volume of water lifted by the pump in is = \(\frac{200}{60}=\frac{10}{3} \mathrm{~L}=\frac{10^4}{3} \mathrm{~cm}^3 \text {. }\)

Mass of this volume of water = \(\frac{10^4}{3} g=\frac{10}{3} \mathrm{~kg}\)

∴ Increase in potential energy in 1 second

= \(\frac{10}{3}\) x 9.8×5 J · s^-1 = 163.33 J

∴ Power of the pump to raise water up to the height of 5m = 163.33 W.

If the velocity of efflux is v, then \(\pi r^2 \times v=\frac{10^4}{3}\)

or, \(\nu=\frac{10^4 \times 7}{3 \times 22 \times(1)^2}=1061 \mathrm{~cm} \cdot \mathrm{s}^{-1}=10.61 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)

The kinetic energy of the amount of water thrown out per second

= \(\frac{1}{2}\) x \(\frac{10}{3}\) x(10.61)² J =187.62 J

∴ Power of efflux = 187.62 W

∴ Total power of the pump = 163.33 + 187.62 = 350.95 W.

Example 8. A body of mass 10 kg is raised to a height of 10 m with an upward force of 196 N. Find the work done by the upward force and the work done against gravitation. Show that the total energy in this case is equal to the work done by the upward force. [g = 9.8 m · s^-2]
Solution:

Work done by the upward force, W = force x displacement

= 196 N x 10 m = 1960 N · m = 1960 J.

Upward acceleration of the body in the absence of gravity,

a’ = \(\frac{\text { upward force }}{\text { mass }}=\frac{196}{10}=19.6 \mathrm{~m} \cdot \mathrm{s}^{-2}\)

∴ Effective upward acceleration, a = a’ -g = 19.6-9.8 = 9.8 m · s^-2

If the body starts from rest, and attains a velocity v at the height of 10 m, then from v² = u² + 2 as, v² = 2 x 9.8 x 10 m² · s^-2

∴  Kinetic energy of the body at this height,

K = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) x 10 x 2 x 9.8 x 10 = 980 J

Work done against gravitational force,

W’ = force due to gravity x displacement = mass x acceleration due to gravity x displacement = 10 x 9.8 x 10 = 980 J

This work done against gravitational pull gets stored as potential energy V of the body. Hence, V = 980 J.

∴ Total mechanical energy of the body at a height of 10 m = V + K= 980 + 980 = 1960 J = W

So, a part of the work done by the upward force changes into kinetic energy of the body, and the other part transforms itself into the stored potential energy. Thus, the total energy and work done by the upward force are equal.

Example 9. A body of mass 10 kg moving with a speed of 2.0 m · s^-1 on a frictionless table strikes a mounted spring and comes to rest. If the force constant of the spring be 4 x 10⁵ N · m^-1, then what will be the compression on the spring?
Solution:

The kinetic energy of the body is E = \(\frac{1}{2}\)mv², where m and v be the mass and the speed of the body respectively.

On striking the spring, the kinetic energy of the spring due to compression is completely converted into the potential energy of the spring.

If the spring is compressed through a distance x then its potential energy is U = \(\frac{1}{2}\)kx²

∴ \(\frac{1}{2}\) mv2 = \(\frac{1}{2}\)kx2

or, x = \(v \sqrt{\frac{m}{k}}=2 \times \sqrt{\frac{10}{4 \times 10^5}}=10^{-2} \mathrm{~m}=1 \mathrm{~cm}\)

Example 10. Shows two blocks of masses m₁ = 3 kg and m₂ = 5 kg, both moving towards the right on a frictionless surface with speeds u₁ = 10 m · s^-1 and u₁ = 4 m · s^-1 respectively. To the back side of m₂ an ideal spring of force constant 1000 N · m^-1 is attached. Calculate the maximum compression of the spring when the blocks collide.

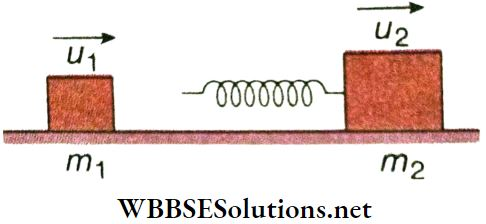
Solution:

m₁ = 3kg, m₂ = 5kg, u₁ = 10 m · s^-1, u₂ = 4 m ·  s^-1

Force constant, k = 1000 N · m^-1

Let v be the speed of the combination.

Using the law of conservation of linear momentum, m₁u₁ + m₂u₂ =(m₁ + m₂)v

∴ v = \(\frac{m_1 u_1+m_2 u_2}{m_1+m_2}=\frac{3 \times 10+5 \times 4}{3+5}=6.25 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Also, let x be the maximum compression of the spring when the blocks collide.

∴ From conservation of mechanical energy, we get \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2}\left(m_1+m_2\right) v^2+\frac{1}{2} k x^2\)

or, \(500 x^2=380-312.5=67.5\)

∴ x = \(\sqrt{\frac{67.5}{500}} \approx 0.367 \mathrm{~m}\)

Work And Energy – Non-Conservative Force

Non-Conservative Force Definition: In the presence of resistive forces in a system, mechanical energy does not remain conserved and gets dissipated. Such a system is called a non-conservative system and the resistive force is called a non-conservative force or dissipative force.

Non-Conservative Force Example: Frictional force is a non-conservative force.

• Frictional force resists the motion of an object. Thus on slid¬ing a body over a rough surface, work done against friction does not get stored in the body as potential energy.
• Frictional force always acts opposite to the direction of motion. To move a body from its initial position to a final position, some amount of work is done to overcome friction.
• If the body is brought back to its initial position along the same path, again some work is done to overcome friction. Thus, each time the body moves, some energy is lost. It can therefore be stated that, it is not possible to restore the initial work done in a non-conservative system.

Work Done In A Closed Path Under A Non-Conservative Force: The total work done to move a body under a non-conservative force along a closed path once completely, is positive or negative but never zero. For example, to slide a body over a rough surface from one point to another, work has to be done against friction.

To return the body to its initial position by sliding it over the same surface following any path, work has to be done against friction again. So, the total amount of work done is not zero in a closed path. Hence, a force is called non-conservative when work done against it cannot be restored. Alternatively, when the work done by a force in a closed path is not zero, the force is called nonconservative.

Work And Energy – Mass Energy Equivalence

The principle of mass-energy equivalence can be obtained from Einstein’s famous theory of relativity.

Mass is a form of energy. Mass can be converted into energy and vice versa. If m amount of mass of a substance is completely converted to energy, then the amount of energy liberated is, E = mc² (c = velocity of light in vacuum = a constant)

According to this equation, the equivalent energy of mass m is E, and the equivalent mass of energy E is m

Mass Energy Equivalence Example:

1. In CGS system c = 3 x 10¹⁰ cm · s^-1

∴ Equivalent energy of 1 g mass

= 1 x (3 x 10¹⁰)²= 9 x 10²⁰ erg = 9 x 10¹³ J

Again in \(\mathrm{SI}\), \(c=3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Hence equivalent energy of 1 kg mass = \(1 \times\left(3 \times 10^8\right)^2=9 \times 10^{16} \mathrm{~J} .\)

2. Mass of an electron = \(9.1 \times 10^{-28} \mathrm{~g}\)

Equivalent energy of the mass of 1 electron = \(9.1 \times 10^{-28} \times\left(3 \times 10^{10}\right)^2 \mathrm{erg}\)

= \(\frac{9.1 \times 10^{-28} \times 9 \times 10^{20}}{1.6 \times 10^{-12}} \mathrm{eV}\)

= \(0.511 \times 10^6 \mathrm{eV}=0.511 \mathrm{MeV} .\)

The increase or decrease in energy of an electron while crossing a potential difference of 1V is called 1 electronvolt (eV). 1 eV = 1.6 x 10^-12 erg.

Rest Mass: Einstein’s theory of relativity also informs us that the mass of a substance is not a constant quantity but depends on the velocity of the substance. Especially if the velocity of an object becomes comparable to that of light, then its mass increases significantly.

That is why to measure the true mass of an object as an intrinsic property, the object should be at rest with respect to the observer. The mass of the object thus measured is called its rest mass and the equivalent energy is called rest energy. For example, the rest mass of an electron =9.1 x 10^-28 g, and the rest energy is 0.511 MeV.

Unit Of Mass And Energy: As mass and energy are equivalent to each other, their units are also the same. Sometimes mass is given in units of energy, and energy is given in units of mass. For example, ‘energy of 1g’ denotes 9 x 10²⁰ erg amount of energy; or mass of ‘9 x 10¹⁶ J’ represents a mass of 1 kg. From this equivalence, it can be stated that the rest mass of an electron is 0.511 MeV.

Law Of Conservation Of Mass-Energy: During the mutual transformation of mass and energy, the law of conservation of mass or the law of conservation of energy cannot be applied separately. It becomes the law of conservation of mass energy.

The total amount of mass energy in nature Is constant, it can never be created or destroyed. It can only change from one form to another.

Mass can be transformed into energy only within an atom. The energy thus obtained from mass is the source of atomic energy. When gamma rays with an energy of a few MeV or more enter the electric field of a heavy nucleus, it can be transformed into an electron and a positron (an electron-like particle but of positive charge). This is an example of the transformation of energy to mass.

Two-Dimensional Collisions Numerical Examples

Example 1. Two particles of masses m₁ and m₂, moving with velocities u₁ and u₁, respectively, and making an angle θ between them, collide with each other. After the collision, the 1st particle travels in the initial direction of motion of the 2nd, and vice-versa. Find the velocities of the two particles after collision. Under what condition, would this collision be elastic?
Solution:

Suppose v₁, v₂ are the velocities of the two particles, respectively, after collision. The particles before and after collision move as shown. It also shows the chosen directions of the x and the y-axis.

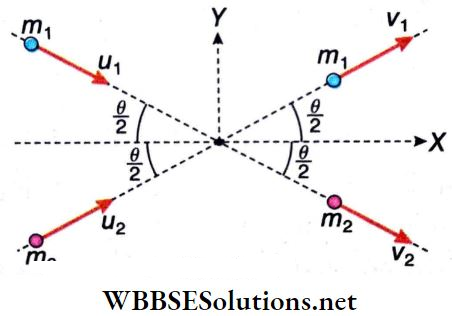
For momentum conservation along the x-axis, we get, \(m_1 u_1 \cos \frac{\theta}{2}+m_2 u_2 \cos \frac{\theta}{2}=m_1 v_1 \cos \frac{\theta}{2}+m_2 v_2 \cos \frac{\theta}{2},\)

or, \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)….(1)

Similarly, along the y-axis, we get, \(-m_1 u_1 \sin \frac{\theta}{2}+m_2 u_2 \sin \frac{\theta}{2}=m_1 v_1 \sin \frac{\theta}{2}-m_2 v_2 \sin \frac{\theta}{2}\)

or, \(-m_1 u_1+m_2 u_2=m_1 v_1-m_2 v_2\)……(2)

Adding equations (1) and (2), \(2 m_2 u_2=2 m_1 v_1\)

or, \(v_1=\frac{m_2}{m_1} u_2\)…(3)

Subtracting equation (2) from (1), \(2 m_1 u_1=2 m_2 v_2\)

or, \(v_2=\frac{m_1}{m_2} u_1\)…..(4)

The kinetic energy before collision is, \(K_1=\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\)

and that after collision is \(K_2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2=\frac{1}{2} m_1\left(\frac{m_2}{m_1} u_2\right)^2+\frac{1}{2} m_2\left(\frac{m_1}{m_2} u_1\right)^2\)

= \(\frac{1}{2} \frac{m_2}{m_1} m_2 u_2^2+\frac{1}{2} \frac{m_1}{m_2} m_1 u_1^2\)

Here, K₁ ≠K₂; so the collision is inelastic, in general. As a m special case, it would be an elastic collision if K₁ = K₂. It is possible only when m₁ = m₂, i.e., the two particles are of equal masses.

Example 2. A bomb explodes and splits up Into three fragments. Two fragments, each of mass 200 g, move away from each other making an angle of 120°, at a speed of 100 m · s^-1. Find the direction and velocity of the third fragment whose mass is 500 g. Also, find out the energy released in an explosion.
Solution:

The velocity of fragments A and B along OA and OB. A and B have equal mass and speed. From the law of conservation of linear momentum, the third piece must move along OD, in the direction opposite to the resultant of OA and OB.

If the velocity of the third piece is v, then taking the components along the line CD in the CGS system, 500 v = 200 x 10⁴ cos60° + 200 x 10⁴ cos60°

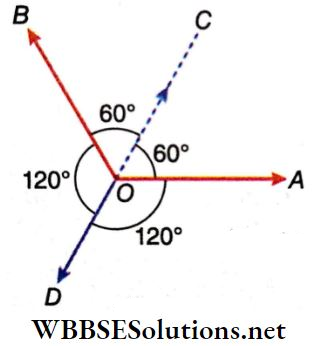
or, v = \(\frac{200 \times 10^4}{500}=4 \times 10^3 \mathrm{~cm} \cdot \mathrm{s}^{-1}=40 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Hence, the velocity of the third fragment is 40 m · s^-1. It moves so as to make an angle 120° with each of OA and OB. The energy released due to the explosion is the kinetic energy of the three fragments.

∴ Energy released = \(\frac{1}{2} \times 200 \times\left(10^4\right)^2\)

+ \(\frac{1}{2} \times 200 \times\left(10^4\right)^2+\frac{1}{2} \times 500 \times\left(4 \times 10^3\right)^2\)

= \(2400 \times 10^7 \mathrm{ergs}=2400 \mathrm{~J} .\)

Example 3. A spaceship while flying in space, splits up into three equal parts, due to an explosion. One fragment keeps moving in the same direction; the other two fly off at 60° to the original direction, on either side. If the energy released due to the explosion is twice the kinetic energy of the spaceship, find the kinetic energy of each of the fragments.
Solution:

Let the mass of the spaceship be 3m and the initial speed be u.

Hence, mass of each fragment = m.

Let their velocities be v₁, v_2, and v₃ after the explosion.

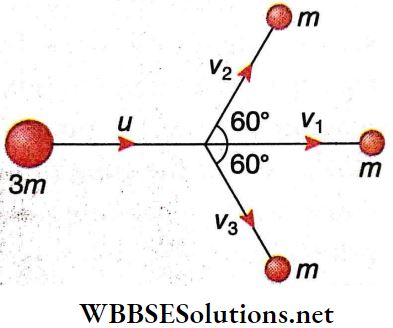
Applying the conservation of momentum law along the direction perpendicular to the original direction of motion,

0 = mv₂ sin60°- mv₃ sin60°

or, mv₂ sin60° – mv₃ sin60°

or, v₂ = v₃ = v (say)

Applying the law of conservation of linear momentum along the original direction of motion,

3 mu = mv₁ + 2mv cos60°

or, 3u = v₁ + v…(1)

The kinetic energy of the spaceship before explosion E= 1/2 x 3mu²

Energy released during the explosion, \(E_r=\frac{1}{2} m\left(v_1^2+2 v^2\right)-\frac{1}{2} \cdot 3 m u^2\)

According to the problem, \(E_r=2 E \quad \text { or, } \frac{1}{2} m\left(v_1^2+2 v^2\right)-\frac{1}{2} \cdot 3 m u^2=2 \times \frac{1}{2} \cdot 3 m u^2\)

or, \(v_1^2+2 v^2-3 u^2=6 u^2\)

or, \(v_1^2+2 v^2=9 u^2\)….(2)

Solving (1) and (2), v₁ =u and v = 2 u

Hence, the kinetic energy of the first fragment after the explosion

= \(\frac{1}{2} m v_1^2=\frac{1}{2} m u^2=\frac{1}{2} \cdot \frac{2}{3} \cdot E=\frac{1}{3} E\)

the kinetic energy of each of the other two fragments

= \(\frac{1}{2} m v^2=\frac{1}{2} m(2 u)^2=2 m u^2=2 \cdot \frac{2}{3} E=\frac{4}{3} E\)

 

Work And Energy Conclusion

If a body undergoes a displacement due to a force acting on it, work is said to be done, and the product of force and displacement is the measure of the work done.

Work Done Against A Force: Consider a particle on which some forces are acting. When an external agent causes a displacement opposite to the direction of the resultant of these forces, work is said to be done against the force.

Work Done By A Force: Consider a particle on which some forces are acting. The resultant of these forces can cause a displacement. This is said to be work done by a force.

• If a force acts at right angles to the direction of displacement of a body, no work is done by the force. This force is called a no-work force.
• The rate of doing work with respect to time is called power. That is work done in unit time is called power.
• Energy is the capacity to do work.
• The ability of a body to do work due to its speed, special position, or special configuration, or all of these, is called its mechanical energy.
• Mechanical energy is of two types— kinetic energy and potential energy.
• The ability of a body to do work due to its speed is called its kinetic energy.
• The ability of a body to do work due to its special position or configuration is called its potential energy.
• The ability of a body to do work, acquired due to its rise against gravity, is called its gravitational potential energy.
• Gravitational potential energy depends on the chosen plane of reference. This energy may also have a negative value.
• The ability of a body to do work, gained due to its special shape, is called elastic potential energy.

Law Of Conservation Of Energy: Energy can neither be created nor destroyed.

Mass-Energy Equivalence: In this universe, the total sum of mass and energy is a constant. This is the law of conservation of mass energy. Mass and energy are equivalent; one can be converted into the other.

• If the total momentum and the total kinetic energy of a system are conserved, the collision is termed as an elastic collision.
• If the total momentum is conserved, but the total kinetic energy is not, it is an inelastic collision.

Coefficient Of Restitution: The coefficient of restitution is defined as the ratio of the velocity with which the two bodies separate after a collision to their velocity of approach before the collision.

1. For elastic collision, e = 1.
2. For perfectly inelastic collision, e = 0.
3. For partially elastic collision, 0 < e < 1.

A system in which the total mechanical energy remains conserved is called a conservative system. Forces acting in such a system are called conservative forces.

In a system where resistive forces are present, the mechanical energy is not conserved. Such systems are called non-conservative systems. Forces of resistance are called dissipative forces.

Work And Energy Useful Relations For Solving Numerical Problems

When a force \(\vec{F}\) acting on a body is associated with a displacement \(\vec{s}\), work done, W = \(\vec{F}\) · \(\vec{s}\) = Fs cosθ, where θ is the angle between \(\vec{F}\) and \(\vec{s}\).

For a variable force \(\vec{F}\), if the displacement of a particle is from A to B, the total work done is

W = \(\int_A^B \vec{F} \cdot d \vec{s}\)

= \(\int_A^B F \cos \theta d s\)

Power (P) = \(\frac{\text { work }(W)}{\text { time }(t)}\) = force (F) x velocity of the body(v)

Kinetic energy = \(\frac{1}{2}\) mv²

For a moving object of mass m, and kinetic energy E, momentum p = √2mE

Gravitational potential energy = mgh

Within the elastic limit, the elastic potential energy of a spring (stretched or compressed by x) = \(\frac{1}{2}\)kx², where k is the spring constant.

Efficiency of a machine

= \(\frac{\text { work output from the machine }}{\text { energy input to the machine }} \times 100 \%\)

In a conservative field, total energy (E) = kinetic energy (K) + potential energy (V) = constant.

The energy equivalent of a mass m is, E = mc², where c is the velocity of light in a vacuum.

Law of conservation of momentum during a linear collision between two bodies: m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

In case of elastic collision

1. \(u_1-u_2=v_2-v_1\) and
2. \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)

Coefficient of restitution, e = \(\frac{v_2-v_1}{u_1-u_2}\)

In case of collision of a falling body with a fixed horizontal plane, total distance traveled before coming to rest, d = \(h \frac{1+e^2}{1-e^2}\)

Work And Energy Very Short Answer Type Questions

Question 1. A force is acting on a body in motion, but is not doing any work. Give an example of such a force.
Answer: Centripetal force on a body, in a uniform circular motion

Question 2. Is work a vector or a scalar quantity?
Answer: Scalar quantity

Question 3. What is the amount of work done by a force when the body moves in a circular path?
Answer: Zero

Question 4.In a tug-of-war game, which of the teams does effective work?
Answer: The stronger team

Question 5. A person is carrying a bucket of water and is in a lift moving up with uniform velocity. Is the person doing any work on the bucket of water? Will the energy of the bucket and water remain constant?
Answer: No

Question 6. A motor drives a belt at a constant velocity of v m · s^-1. If m kg of sand falls on the belt per second, what is the rate of work done by the force exerted by the belt on the sand?
Answer: 1/2mv³W

Question 7. A boy tried to lift a bucketful of water but failed. What is the work done by him?
Answer: Zero

Question 8. What is the work done by the tension in the string during the oscillation of a simple pendulum?
Answer: Zero

Question 9. A box was lifted vertically through a height of 6 m in 3 s. If the box had been lifted in a zig-zag way in 5 s, the work done would have been the same. Is the statement true or false?
Answer: True

Question 10. 1 kg · m = ________ J.
Answer: 9.8

Question 11. A force \(\vec{F}=(5 \hat{i}+3 \hat{j}+2 \hat{k}) \mathrm{N}\) acts on a particle, and the particle moves from the origin to a point \(\vec{r}=(2 \hat{i}-\hat{j}) \mathrm{m}\). What will be the work done on the particle?
Answer: 7

Question 12. How many joules are in 1 MeV?
Answer: 1.6 x 10^-13J

Question 13. What is the unit of energy?
Answer: Joule

Question 14. Does the kinetic energy of a ball, thrown inside a moving train, depend on the speed of the train?
Answer: No

Question 15. Which type of energy is lost in doing work against friction?
Answer: Mechanical energy

Question 16. A small car and a lorry are moving with the same kinetic energy. Brakes are applied to produce the same force against the motion. Which one will cover a greater distance before stopping?
Answer: Both cover the same distance

Question 17. When a body falls on the ground from a height, it becomes slightly warm—why?
Answer: Kinetic energy changes to heat energy

Question 18. Is the resistance due to air a conservative force?
Answer: No

Question 19. What happens to internal energy, when the temperature of the body increases?
Answer: Increases

Question 20. What type of energy is stored in the spring of a watch?
Answer: Potential energy

Question 21. The kinetic energies of a heavy and a light object are the same. Momentum of which object will be higher?
Answer: Heavy

Question 22. Momenta of a light and a heavy body are the same. Which body has greater kinetic energy.?
Answer: Lighter

Question 23. If E is the kinetic energy of a body of mass m, what will be its momentum?
Answer: \(\sqrt{2 m E}\)

Question 24. An object breaks up into two masses m₁ and m₂ due to explosion. The two fragments move in opposite directions. What will be the relation between the kinetic energy and the masses?
Answer: Inversely

Question 25. What is the loss of KE of a freely falling body of mass m, during the t th second?
Answer: [1/2 mg²(2t – 1)]

Question 26. The increase in momentum of a body is 100%. What will be the increase in its kinetic energy?
Answer: 300

Question 27. The increase in kinetic energy of a body is 69%. What will be the increase in its momentum?
Answer: 30

Question 28. Which physical quantity in conserved during both the elastic and inelastic collisions?
Answer: Momentum

Question 29. Two objects coalesce after a collision with each other. What is the coefficient of restitution?
Answer: 0

Question 30. The coefficient of restitution between a ball and a horizontal floor is e = 1/2. If the ball falls from a height of 10 m, after its impact with the floor, the ball bounces up to a height of ______.
Answer: 2.5m

Work And Energy Assertion Reason Type Questions And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: The absolute PE of a system as measured by two different persons at the same time can be different.

Statement 2: The value of the absolute PE of a system depends upon the reference value chosen.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 2.

Statement 1: Work done by normal contact force can be non-zero.

Statement 2: Normal contact force is always perpendicular to the displacement of the object. (Here displacement is measured with respect to a frame of reference attached to the two surfaces in contact.)

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: In a circular motion, work done by the centripetal force is not always zero.

Statement 2: If the speed of the particle increases or decreases in a circular motion, net force, acting on the particle is not directed toward the center.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 4.

Statement 1: When a body moves uniformly in a circle its momentum goes on changing but its kinetic energy remains constant.

Statement 2: \(\vec{p}=m \vec{v}, \mathrm{KE}=\frac{1}{2} m v^2\). In circular motion \(\vec{v}\) changes, v² does not change.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 5.

Statement 1: If a particle of mass m is connected to a light rod and whirled in a vertical circle of radius R, then to complete the circle, the minimum velocity of the particle at the lowest point is \(\sqrt{5 g R}\).

Statement 2: Mechanical energy is conserved and for the minimum velocity at the lowest point, the velocity at the highest point will be zero.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 6.

Statement 1: Work done by constant force is equal to the magnitude of force multiplied by displacement.

Statement 2: Work done is a scalar quantity. It may be positive, negative, or zero.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 7.

Statement 1: If work done by a conservative force is negative then potential energy associated with that force should increase.

Statement 2: This is from the reaction Δu = -W. Here Au is change in potential energy and W is work done by conservative force.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Work And Energy Match Column A With Column B.

Question 1. The displacement time graph of a body is shown.

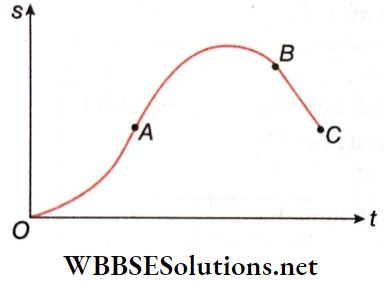
Answer: 1. A, 2. B, C, D, 3. B, C, D, 4. C

Question 2. A force F = kx (where k is a positive constant) is acting on a particle. In Column A displacements (x) are given and in Column B work done by the force is given.

Answer: 1. B, 2. A, 3. C

Question 3.

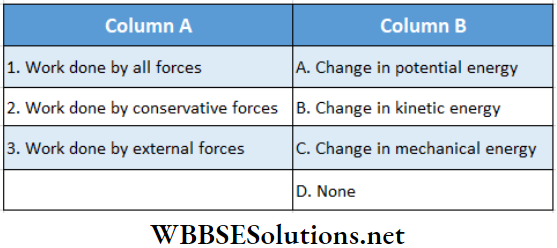
Answer: 1. B, 2. D, 3. C

Question 4. The system is released from rest. Friction is absent and string is massless. In time t = 0.3 s (take g = 10 m · s^-2)

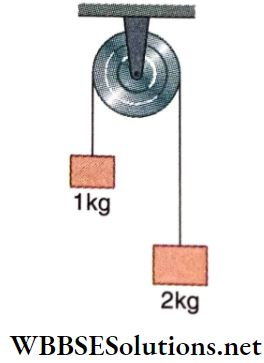
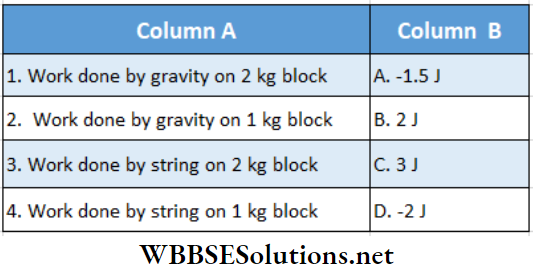
Answer: 1. C, 2. A, 3. D, 4. B

Question 5.

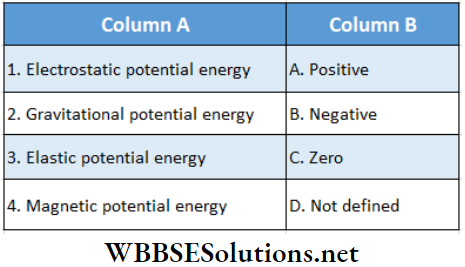
Answer: 1. A, B, C, 2. B, C, 3. A, C, 4. A, B, C

Question 6. A particle is suspended from a string of length R. It is given a velocity u = \(3 \sqrt{g R}\) at the bottom.

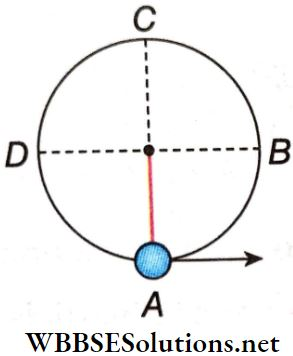
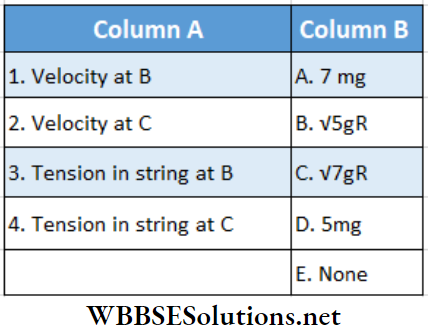
Answer: 1. C, 2. B, 3. A, 4. E

Work And Energy Question And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A body of mass 2 kg starts from rest and moves with uniform acceleration. It acquires a velocity 20 m · s^-1 in 4 s.

1. Power exerted on the body at 2 s is

1. 50 W
2. 100 W
3. 150 W
4. 200 W

Answer: 2. 100 W

2. Average power transferred to the body in the first 2 s is

1. 50 W
2. 100W
3. 150 W
4. 200 W

Answer: 1. 50 W

Question 2. A ball of mass m is dropped from a height H above a level floor as shown. After striking the ground it bounces back and reaches up to the height h.

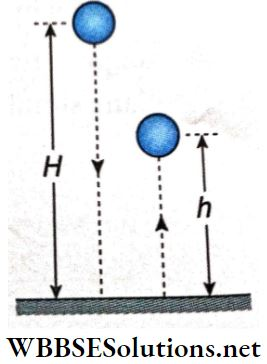
1. During the collision, the part of the KE which appears in other forms (other than KE or PE) is (this part of the energy is termed as lost energy as it cannot be utilized properly)

1. mgH
2. mgh
3. mgH – mgh
4. Zero

Answer: 3. mgH – mgh

2. The speed of the ball just after the collision is

1. \(\sqrt{2 g H}\)
2. \(\sqrt{2} g h\)
3. \(\sqrt{2 g(H-h)}\)
4. None of these

Answer: 2. \(\sqrt{2} g h\)

3. If the lost energy in the collision is half of the value computed in Question (1), and H = \(\frac{3 h}{2}\), then the height attained by the ball after the collision is

1. \(\frac{7 h}{4}\)
2. \(\frac{3 h}{4}\)
3. \(\frac{3 h}{2}\)
4. \(\frac{9 h}{5}\)

Answer: 1. \(\frac{7 h}{4}\)

Question 3. A block of 2.5 kg is pulled 2.20 m along a frictionless horizontal table by a constant force of 16 N directed at 45° above the horizontal.

1. Work done by the applied force is

1. 25 J
2. 27 J
3. 24.9 J
4. 22.5 J

Answer: 3. 24.9 J

2. Work done by the normal force exerted by the table is

1. 24.9 J
2. Zero
3. 27 J
4. 27.5 J

Answer: 2. Zero

3. Work done by the force of gravity is

1. 24.9 J
2. 27 J
3. Zero
4. 27.5 J

Answer: 3. Zero