WBCHSE Class 11 Physics Simple Harmonic Motion Long Answer Type Questions

Oscillation And Waves  Simple Harmonic Motion Long Answer Type Questions

Question 1. Simple harmonic motion is a periodic motion, but alt periodic motions are not simple harmonic — explain.
Answer:

The motion that repeats itself at regular intervals of time is called periodic motion. If the periodic motion is

1. Linear and
2. The acceleration of the particle executing the motion is proportional to its displacement front the position of equilibrium and is always directed towards the mean position, only then the motion of the particle is said to be simple harmonic.

The motion of the hands of a dock or the motion of the planets and satellites are periodic in nature. But as these motions do not satisfy the above conditions, they cannot he called simple harmonic. So it can be said that all simple harmonic motions are periodic but all periodic motions are not simple harmonic.

Read and Learn More Class 11 Physics Long Answer Questions

Question 2. What should be the displacement of a particle, executing SHM, from Its position of equilibrium so that the velocity of the particle is half of its maximum velocity?
Answer:

If the angular frequency of a particle executing SHM is ω and the amplitude of motion is A, then the maximum velocity of the particle = ωA

For a displacement x, velocity of the particle, v = \(\omega \sqrt{A^2-x^2}\)

According to the question, \(\omega \sqrt{A^2-x^2}=\frac{1}{2} \omega A\)

or, \(\frac{A}{2}=\sqrt{A^2-x^2} \text { or, } \frac{A^2}{4}=A^2-x^2\)

or, \(x^2=A^2-\frac{A^2}{4} \text { or, } x^2=\frac{3}{4} A^2\)

or, x = \(\pm \frac{\sqrt{3}}{2} A\); this is the required displacement.

Question 3. What should be the displacement of a particle, executing SHM, from its position of equilibrium so that its acceleration is half of its maximum acceleration?
Answer:

According to the definition of SHM, acceleration ∝ displacement.

So, the acceleration of the particle will be half of its maximum value, if the displacement is half of the maximum displacement, i.e… half the amplitude.

Example 4. What should be the displacement of a particle, executing SHM, from its position of equilibrium so that the kinetic energy of the particle is half of its max imum kinetic energy?
Answer:

Maximum kinetic energy of a particle executing SHM = \(\frac{1}{2}\)mω²A²

When the displacement of the particle is x from the position of equilibrium, kinetic energy of the particle = \(\frac{1}{2}\)mω²(A² – x²)

According to the question, \(\frac{1}{2} m \omega^2\left(A^2-x^2\right)=\frac{1}{2} \times \frac{1}{2} m \omega^2 A^2\)

or, \(A^2-x^2=\frac{A^2}{2}\)

or, \(x^2=A^2-\frac{A^2}{2}=\frac{A^2}{2}\)

or, \(x= \pm \frac{A}{\sqrt{2}}\); this is the required displacement.

Question 5. What should be the displacement of a particle, executing SHM, from its position of equilibrium so that the kinetic energy and the potential energy of the particle are equal?
Answer:

Kinetic energy of a particle executing SHM = \(\frac{1}{2}\) mω²(A² – x²).

Its potential energy = \(\frac{1}{2}\)mω²x²

According to the question, \(\frac{1}{2} m \omega^2\left(A^2-x^2\right)=\frac{1}{2} m \omega^2 x^2 \text { or, } A^2-x^2=x^2\)

or, \(2 x^2=A^2 or, x^2=\frac{A^2}{2}\)

or, x = \(\pm \frac{A}{\sqrt{2}}\); this is the required displacement.

Question 6. Two equal masses M and N are suspended from the ends of two separate weightless springs having spring constants k₁ and k₂. If the maximum velocities of the two masses for their vertical oscillations are the same, what is the ratio of the amplitudes of vibration of M and N?
Answer:

If angular frequency = ω and amplitude = A, then maximum velocity = ωA.

So for the two given masses, ω₁A₁ = ω₂A₂

or, \(\frac{A_1}{A_2}=\frac{\omega_2}{\omega_1}=\frac{\frac{2 \pi}{T_2}}{\frac{2 \pi}{T_1}}=\frac{T_1}{T_2}=\frac{2 \pi \sqrt{\frac{m_1}{k_1}}}{2 \pi \sqrt{\frac{m_2}{k_2}}}\)

or, \(\frac{A_1}{A_2}=\sqrt{\frac{k_2}{k_1}} \quad\left[because m_1=m_2=m\right]\).

Question 7. A weight is suspended from a spring balance and the time period for its vertical oscillatory motion is T. The spring is divided into two equal parts and from any one of them the same weight is suspended. Determine the time period of the vertical oscillatory motion of that spring.
Answer:

If the increase in length of the spring is l due to the suspension of the weight, then spring constant, k = \(\frac{mg}{l}\), i.e., if the weight remains constant, then k \(\frac{1}{T}\).

Now, if the spring is halved and the same weight is suspended, then the increase in length is also halved. So the spring constant (k) is doubled.

Now, time period, T = \(2 \pi \sqrt{\frac{m}{k}} \text { or, } T \propto \frac{1}{\sqrt{k}}\)

So, as k is doubled, the time period becomes \(\frac{1}{\sqrt{2}}\)times the original time period, i.e., the required time period = \(\frac{T}{\sqrt{2}}\).

Question 8. Show that the equation x = Asinωt represents a simple harmonic motion.
Answer:

The equation of displacement is, x = Asinωt

∴ Velocity, v = \(\frac{dx}{dt}\) = ωAcosωt

and acceleration, a = \(\frac{dv}{dt}\) = -ω²Asinωt = -ω²x.

Now, from the equation, a = -ω²x, it is evident that

1. The acceleration of the particle is proportional to the displacement and
2. The direction of acceleration is opposite to that of displacement, i.e., the acceleration is directed towards the position of equilibrium. So, by definition, it is a simple harmonic motion.

Question 9. The potential energy of a spring pendulum, with a mass m connected to it, is given by V = \(\frac{1}{2}\)kx² (where x = displacement from the position of equilibrium and k = a constant). How does the applied force on the mass vary with displacement?
Answer:

Suppose, the force applied on the mass m = F.

If V is the potential energy of the spring pendulum, then F = \(-\frac{d V}{d x}=-\frac{d}{d x}\left(\frac{1}{2} k x^2\right)=-\frac{1}{2} k \cdot 2 x=-k x\)

So, the applied force F is proportional to x and acts in a direction opposite to that of x.

Question 10. A billiard boll strikes perpendicularly on one side of a smooth billiard table and after rebounding it strikes the opposite side. As there is no friction the motion continues. Thus the ball makes a to and fro oscillation with repeated rebounds. Is the motion of the billiard ball simple harmonic?
Answer:

In this case, if the collision of the billiard ball with the edge of the table is elastic, then the motion of the billiard ball is periodic. But all periodic motions are not simple harmonic.

• If in a periodic motion, the acceleration of the particle is proportional to its displacement from the position of equilibrium and is directed towards it, then that periodic motion of the particle is called simple harmonic.
• The billiard ball oscillates to and fro with repeated rebounds, but it does not fulfill the above conditions of SHM. The table is smooth. So the ball has no acceleration on its path of motion except at the time of collision with the two edges of the table. Hence, the motion is not simply harmonic.

Question 11. A small spherical body is placed on the concave side of a curved surface of radius of curvature R The curved surface is placed on a table. The spherical body is displaced a little from its position of equilibrium and then released. If the displacement of the body is very small in comparison to the radius of curvature of the curved surface, show that the spherical body will perform an SHM and also calculate its time period.
Answer:

The spherical body of mass m is displaced a little from its position of equilibrium A’, and then released. Suppose the body is at B at any instant. O is the center of curvature of the concave surface. ∠A’OB = θ(say).

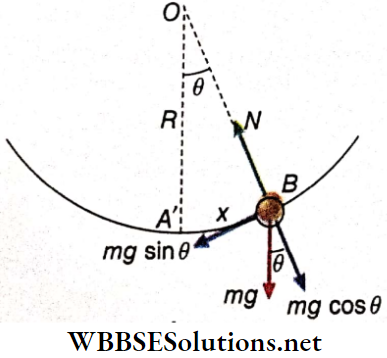
The weight mg of the spherical body at B in resolved into two mutually perpendicular components;

1. mgcosθ, acting perpendicular to the concave surface at B, and
2. mgsinθ, acting tangentially to the concave surface at B.

The normal reaction N balances the component mgcosθ.

The component mgsinθ produces an acceleration of the spherical body.

∴ Acceleration of the spherical body is, a = \(\frac{-m g \sin \theta}{m}\)

(Negative sign indicates that m acceleration and displacement are mutually opposite in direction]

= -gsinθ = -gθ [as θ is very small, sinθ = θ]

= \(\frac{-g.x}{R}\) [x = displacement of the body from A = Rθ]

i.e., a = \(-omega^2 x \text {, where } \omega=+\sqrt{g / R} \text {. }\)

Therefore, the motion of the spherical body is simple harmonic.

Time period of the SHM, T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{R}{g}}\)

Question 12. A body of mass m is Suspended from a weightless wire of length l. If Y Is Young’s modulus of the material of the wire, calculate the frequency of vibration In the vertical direction.
Answer:

If the mass m causes an elongation x of the wire, then longitudinal stress = Young’s modulus x longitudinal strain = Y · \(\frac{x}{l}\)

By definition, longitudinal stress = reaction force acting per unit area

∴ Reaction force = longitudinal stress x α [α = cross-sectional area of the wire]

= \(\frac{Y x}{l} \times \alpha=\frac{Y x \alpha}{l}\)

This reaction force acts as the restoring force.

So, acceleration of mass m, a = \(\frac{\text { restoring force }}{m}=\frac{Y x \alpha}{m l}\)

∴ Frequency, \(n=\frac{1}{2 \pi} \sqrt{\frac{\text { acceleration }}{\text { displacement }}}=\frac{1}{2 \pi} \sqrt{\frac{a}{x}}=\frac{1}{2 \pi} \sqrt{\frac{Y a}{m l}}\)

Question 13. A wooden cylinder floats in water with a length h immersed Into it. If it is pushed a little inside water and then released, show that it will perform a simple harmonic motion. Calculate the time period of this motion.
Answer:

Let the cross-sectional area of the cylinder be α.

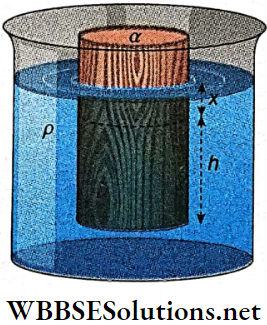
According to Archimedes’ principle,

The weight of the cylinder = weight of the displaced water at equilibrium = hαρg; [ρ = density of water]

Mass of the cylinder, m = hαρ

If the cylinder is pushed through a distance x inside the water, then an extra buoyant force acts on the cylinder in the upward direction. It tries to bring the cylinder back to its equilibrium position.

So the restoring force, F = extra buoyant force

= weight of the extra water displaced = -xαρg

∴ Acceleration of the cylinder,

a = \(\frac{F}{m}=\frac{-x \alpha \rho g}{h \alpha \rho}=\frac{-g}{h} \cdot x=-\omega^2 x\left[\text { where } \omega=\sqrt{\frac{g}{h}}\right]\)

As the motion of the cylinder obeys the equation a = -ω²x, it is simple harmonic.

Time period of the motion, T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{h}{g}} .\)

Question 14. An object attached to a spring is executing a SHM. If the spring constant of the spring is increased, what changes in its frequency will be noticed?
Answer:

Time period, T = \(2 \pi \sqrt{\frac{m}{k}}\); frequency, \(n=\frac{1}{T}=\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\).

Hence, \(n \propto \sqrt{k}\)

Therefore, the frequency will increase with the increase of the spring constant k.

Question 15. A particle of mass m executes SHM with an amplitude A. If its mass is changed to 1/4 m, then what will be its

1. New frequency and
2. Total energy?

Answer:

Frequency, \(n=\frac{\omega}{2 \pi}=\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\), where k= force constant.

Let \(n^{\prime}\) be the changed frequency.

∴ \(\frac{n}{n^{\prime}}=\sqrt{\frac{m^{\prime}}{m}} \text { or, } n^{\prime}\)=\(n \sqrt{\frac{m}{m^{\prime}}}=n \sqrt{\frac{m}{\frac{1}{4} m}}=2 n \text {, }\)

i.e., the frequency will be doubled.

Total energy, \(E=\frac{1}{2} m \omega^2 A^2=\frac{1}{2} k A^2\), i.e., the total energy remains the same.

Question 16. The equation, = \(\frac{d^2 x}{d t^2}+\alpha x=0\), represents an SHM. Find its time period.
Answer:

Comparing the given equation with the general equation of SHM, \(\frac{d^2 x}{d t^2}+\omega^2 x=0\), we get, ω²=α or, ω = √a

∴ Time period, T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\alpha}} .\)

Question 17. What is the time period of the SHM indicated by the function sin²ωt?
Answer:

sin²ωt = \(\frac{1}{2}(1-\cos 2 \omega t)=\frac{1}{2}-\frac{1}{2} \cos 2 \omega t\)

Here, \(\frac{1}{2} \cos 2 \omega t\) indicates an SHM whose angular frequency = 2ω.

∴ Time period, \(T=\frac{2 \pi}{2 \omega}=\frac{\pi}{\omega}\).

Question 18. Write the equation of motion of a particle executing SHM if at t = 0, its displacement is maximum.
Answer:

The equation of SHM of a particle is x = Asin(ωt+ α)

Now if at t = 0, the displacement is maximum, i.e., x = A, then,

A = \(A \sin (\omega \cdot 0+\alpha) \text { or, } \sin \alpha=1=\sin \frac{\pi}{2} \text { or, } \alpha=\frac{\pi}{2}\)

So, the equation of the particle executing SHM is, x = \(A \sin \left(\omega t+\frac{\pi}{2}\right) \text { or, } x=A \cos \omega t \text {. }\)

Question 19. If the time period and amplitude are T and A respectively, then find the time taken by a particle executing SHM to reach the position x = \(\frac{A}{2}\) from x = A.
Answer:

Equation of an SHM, x = Acoscot – Acos\(\frac{2 \pi}{t}\)t.

Now at t = 0, x = A; when x = \([\frac{A}{2}\), we get from the above equation,

∴ \(\frac{A}{2}=A \cos \frac{2 \pi}{T} t \text { or, } \cos \frac{2 \pi}{T} t=\frac{1}{2}=\cos \frac{\pi}{3} \text { or, } t=\frac{T}{6}\)

The particle takes a time of \(\frac{T}{6}\) to move from x = A to x = \(\frac{A}{2}\)

Question 20. A simple harmonic motion is represented as x = Asinωt+ Bcosωt. Find its amplitude and initial phase.
Answer:

x = \(A \sin \omega t+B \cos \omega t\)

= \(\sqrt{A^2+B^2}\left[\frac{A}{\sqrt{A^2+B^2}} \sin \omega t+\frac{B}{\sqrt{A^2+B^2}} \cos \omega t\right]\)

= \(\sqrt{A^2+B^2}[\cos \theta \sin \omega t+\sin \theta \cos \omega t]\)

= \(\sqrt{A^2+B^2} \sin (\omega t+\theta)\)

Comparing with the general equation x=Asin(ωt+∅) of SHM, we get,

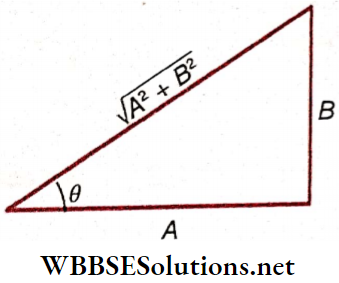
Amplitude = \(\sqrt{A^2+B^2}\)

Initial phase = \(\theta=\tan ^{-1}\left(\frac{B}{A}\right)\)