WBCHSE Class 11 Physics Notes For Viscosity And Surface Tension

 Viscosity And Surface Tension

The flow of fluids is of two types

1. Laminar or streamline flow and
2. Turbulent flow.

Laminar or Streamline Flow Definition: A smooth, uninterrupted flow in ordered layers, without any energy transfer between the layers, is called a laminar streamline or steady flow.

The velocity of a fluid along its flow, in general, depends on its position and on time. This means that the fluid velocity may be different at different points, and at any particular point, it may also change with time.

Mathematically speaking, for a one-dimensional fluid flow along the x- direction, the fluid velocity \(\vec{v}\) is a function of position x and time t, i.e., \(\vec{v}\) = f(x, t).

For a laminar or streamline motion, the fluid satisfies the condition that \(\vec{v}\) is a function of x only, and not of r. It means that, at any particular point along the fluid flow, the magnitude and the direction of the fluid velocity do not change with time, although the velocity may be different at different points. In short, \(\vec{v}\) = f(x), but \(\vec{v}\) ≠ f(t)

In Fig a laminar flow for a liquid is shown. At points A, B, C, and D, let the flow velocities at any instant be ν_A, ν_B, ν_c, and ν_D respectively. Also at any subsequent time, a liquid particle that reaches the point A will have the velocity ν_A similarly, at point B, the velocity will be ν_B at point C the velocity will be ν_C and at point D. the velocity will be ν_D. It means that each particle of the liquid follows the velocity of its preceding particle and moves along the same path.

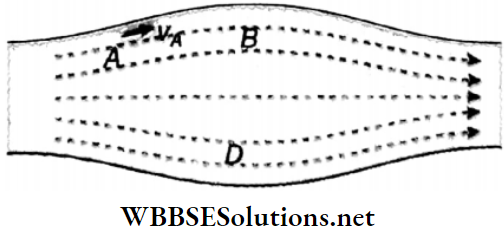
Streamline: In the case of streamline motion, the paths along which the particles of the fluid move are called streamlines. A tangent drawn at any point on this path indicates the direction of motion of the fluid at that point.

Properties of streamlining:

1. Two streamlines never intersect each other. Otherwise, at the point of intersection of two streamlines, two tangents can be drawn and hence two directions of motion of the particle are possible. Hut, in streamlined motion, any particle can move in one direction only and hence two streamlines can never intersect.

2. In the flow tube, where the streamlines are crowded together, the velocity of flow is higher. Where they are spaced, the velocity of flow is lower.

A special case of streamlined flow is a steady flow, for which the fluid velocity is a constant at all points along this flow at all times. So this velocity in neither a function of time, not of position. Example: a sufficiently slow liquid flow along a narrow uniform horizontal tube.

Turbulent Flow: In general, the motion of a fluid is streamlined, if its velocity does not exceed a definite limiting value. The limiting value of velocity is called the critical velocity.

If the velocity of a fluid exceeds the critical velocity, then the flow becomes turbulent, and in some regions, eddies and vortices are formed. This kind of flow is called a turbulent flow.

Turbulent Flow Definition: If the velocity of a fluid along its flow continuously and randomly changes in magnitude and direction, then it is called a turbulent or disorderly flow.

The path of fluid particles in turbulent flow is shown in Fig At every point along the flow, both the magnitude and the direction of fluid velocity change with time.

Turbulent Flow Experiment: Reynolds demonstrated the difference between streamline and turbulent flow by a simple experiment. a discharge pipe Q is attached horizontally to a vertical water-filled cylinder P. The flow rate may be varied with a valve at the end of the pipe.

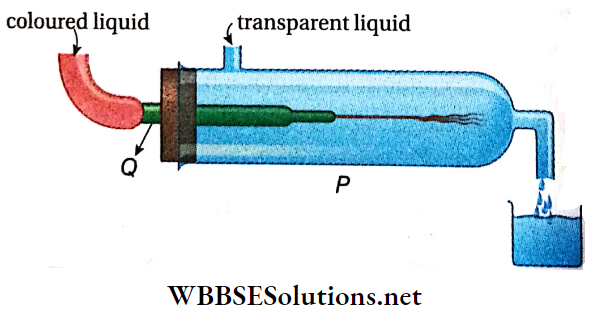
• To make the flow behaviour visible, we use KMnO₄ solution, which is injected centrally into the horizontal pipe through a very narrow tube (diameter < 1 mm), positioned to avoid additional turbulence.
• If the velocity of the transparent liquid is low, the coloured liquid is observed to travel continuously in the form of a thread, indicating a streamline flow.
• As the flow of the transparent liquid is increased gradually, the coloured thread gets disrupted and later on the coloured liquid begins to move randomly, or forms eddies and vortices and mixes with the transparent liquid.
• The velocity of the transparent liquid at which this disturbance starts is called the critical velocity. It depends on the nature of the liquid, the cross-section of the tube, etc.

Viscosity And Surface Tension Viscosity: When a liquid flows slowly over a fixed horizontal surface, i.e., when the flow is laminar, the layer of the liquid in contact with the fixed surface remains at rest due to adhesion.

• The layer just above it moves slowly over the lower one, the third layer moves faster over the second one, and so on. The velocities of the layers of liquid increase with the increase in distance from the horizontal rigid surface.
• For two consecutive horizontal layers inside the liquid, the upper layer moves with a velocity greater than that of the lower one.
• The upper layer tends to accelerate the lower layer, while the lower layer tends to retard the upper one. In this way, the two adjacent layers tend to decrease their relative velocity—as if a tangential force acts on the upper layer and tries to oppose its motion.
• This tangential force is called viscous force. Therefore, to maintain a constant relative motion between the layers, an external force must act. If no external force acts, then the relative motion between the layers will cease and the flow of the liquid will stop.

Viscosity Definition: The property by virtue of which a liquid opposes the relative motion between its adjacent layers is called viscosity of the liquid.

Comparison of viscosity with friction: Viscosity is a general property of a fluid. The frictional force acting between two solid surfaces resembles in many ways the viscosity of a liquid.

• Hence, viscosity is called internal friction of a liquid. Like friction, the viscous force is absent if a liquid is at rest.
• The difference between the frictional force in solids and viscosity in liquids is that the viscous force depends on the area of liquid surface while the frictional force does not.

Viscosity and mobility of different liquids: Viscosities of different liquids are different. If alcohol and oil are poured separately into two identical vessels and stirred, then oil will come to rest earlier. This shows that the viscosity of oil is greater.

The greater the viscosity of a liquid, the lesser is its mobility. For example, the viscosity of honey is more than that of water and hence honey flows much slower than water. Coal tar has the least mobility.

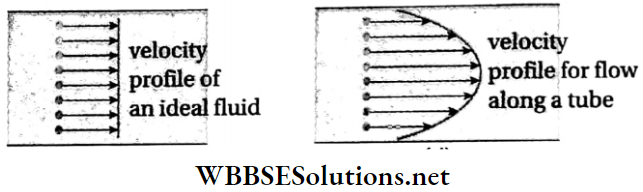
Velocity profile: The surface formed by joining the end points of the velocity vectors of different layers of any section of a flowing liquid is called its velocity profile. Velocity profile for flow above a horizontal surface is shown in Fig.

Velocity profile of a non-viscous liquid: An ideal liquid is non-viscous. For such a liquid, there is no resistance due to viscosity. The velocities of the different layers are the same.

Every particle in a given cross-section of the liquid moves forward with the same velocity. On joining the ends of these velocity vectors, we get a plane surface. Therefore, we can say that the velocity profile of a non-viscous liquid is linear (on 2D graph).

Velocity profile of a viscous liquid: When a viscous liquid flows through a horizontal tube, the layer of liquid in contact with the wall of the tube remains stationary due to adhesion. So the velocity of that layer is zero.

• The layer of the liquid which flows along the axis of the tube has the maximum velocity. As we progress from the centre towards the walls, the velocity decreases.
• Therefore, on joining the ends of the velocity vectors, we get a parabolic surface. The velocity profile of a viscous liquid is a parabola (on 2D graph).

Coefficient of Viscosity: Let PQ be a solid horizontal surface. A liquid is in streamline motion over the surface PQ. Two liquid surfaces CD and MN are at distances x and (x+dx) respectively from the fixed solid surface. The velocity of layer CD is ν and that of layer MN is ν+ dν.

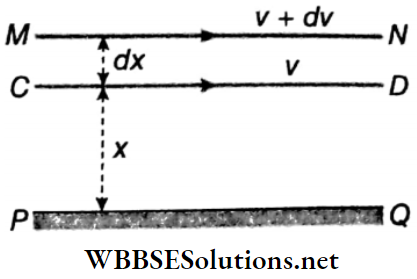
Due to the viscosity of the liquid, an opposing force acts between these two layers and tries to slow down the relative motion of the layers. If this opposing viscous force is F, then for streamline motion of the liquid, Newton proved that

1. F ∝ A; A = area of cross-section of the liquid surface, and
2. \(F \propto \frac{d v}{d x} ; \frac{d v}{d x}\) = velocity gradient = rate of change of velocity with distance perpendicular to the direction of flow.

∴ \(F \propto A \frac{d v}{d x} \text { or, } F=-\eta A \frac{d v}{d x}\) ….(1)

Here, η is a constant known as the coefficient of viscosity. Its value depends on the nature of the liquid.

Equation (1) is known as Newton’s formula for the streamline flow of a viscous liquid. Liquids that obey this law are called Newtonian liquids and liquids that do not obey this law are called non-Newtonian liquids.

From equation (1), we get, \(\eta=\frac{F}{A \frac{d v}{d x}}\)

If A = 1 and \(\frac{d v}{d x}=1\), then η = F; from this, we can define the coefficient of viscosity.

Coefficient of Viscosity Definition: The coefficient of viscosity of a liquid is defined as the required tangential force acting per unit area to maintain unit relative velocity between two liquid layers unit distance apart.

Units of coeffcient of viscocity: \(\eta=\frac{F}{A \frac{d v}{d x}}=\frac{F d x}{A d \nu}\)

So, unit of \(\eta=\frac{\mathrm{N} \cdot \mathrm{m}}{\mathrm{m}^2 \cdot\left(\mathrm{m} \cdot \mathrm{s}^{-1}\right)}=\mathrm{N} \cdot \mathrm{s} \cdot \mathrm{m}^{-2}=\mathrm{Pa} \cdot \mathrm{s}\)

Unit:

• dyn · s · cm^-2 CGS System or g · cm^-1 · s^-1
• N · s · m^-2 or Pa · s or kg · m^-1 · s^-1 SI

Relation: \(1 \mathrm{~kg} \cdot \mathrm{m}^{-1} \cdot \mathrm{s}^{-1}=\frac{1 \mathrm{~kg}}{1 \mathrm{~m} \times 1 \mathrm{~s}}=\frac{1000 \mathrm{~g}}{100 \mathrm{~cm} \times 1 \mathrm{~s}}\)

= 10 g · cm^-1 · s^-1

Poise and decompose: The coefficient of viscosity of a liquid is 1 poise, when a tangential force of 1 dyn is required to maintain a relative velocity of 1 cm · s^-1 between two parallel layers of the liquid 1 cm apart where each layer has an area of 1 cm².

So, 1 poise is the CGS unit of the coefficient of viscosity η.

1 poise = 1 dyn • s • cm^-2 = 1 g • cm^-1 • s^-1.

As, 1 kg · m^-1 · s^-1 = 10g · cm^-1 • s^-1 = 10 poise,

the SI unit of η is called 1 decapoise = 10 poise.

The coefficient of viscosity of a liquid is 1 decompose, when a tangential force of 1 newton is required to maintain a relative velocity of 1 m · s^-1 between two parallel layers separated by  distance of 1 m, where each layer has an area of 1 m².

Dimension of coefficient of viscosity: \([\eta]=\frac{[\mathrm{F}]}{[\mathrm{A}]\left[\frac{d \nu}{d x}\right]}=\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^2 \cdot \frac{\mathrm{LT}^{-1}}{\mathrm{~L}}}=\mathrm{ML}^{-1} \mathrm{~T}^{-1}\)

Effect of pressure and temperature on the coefficient of viscosity:

Effect of pressure: Usually, viscosity increases with pressure. In less viscous liquids, the viscosity increases at a low rate with pressure.

• But for highly viscous liquids, an increase in pressure results in a rapid rise in its viscosity. However, water behaves differently and, with an increase in pressure, its viscosity decreases.
• From the kinetic theory of gases, it is known that a change in pressure does not affect the viscosity of a gas. But for a large increase (or decrease) in pressure, viscosity is affected.

Effect of temperature: Usually, the coefficient of viscosity of liquids decreases with a rise in temperature. The relation between temperature and coefficient of viscosity is rather complicated. One commonly used equation relating these two is

⇒ \(\eta_t=\frac{A}{(1+B t)^C}\)

where, η_t = coefficient of viscosity of a liquid at t°C and A, B, and C are constants for a particular fluid.

For gases, the coefficient of viscosity increases with an increase in temperature.

Critical Velocity and Reynolds Number

Critical velocity: The maximum velocity of a fluid, up to which the flow of the fluid is streamlined and beyond which the flow becomes turbulent, is regarded as the critical velocity for that fluid.

On gradually increasing the velocity of a fluid, the streamline flow does not become turbulent abruptly. Rather this change occurs gradually.

With the help of experimental demonstration and also by dimensional analysis, it can be proved that the critical velocity (ν_c) of a fluid is

1. Inversely proportional to the density (ρ) of the fluid,
2. Directly proportional to the coefficient of viscosity (η) of the fluid, and
3. Inversely proportional to the characteristic length (l) of the channel. So,

⇒ \(v_c \propto \frac{\eta}{\rho l} \text { or, } v_c=N_c \cdot \frac{\eta}{\rho l}\) …..(1)

In the case of a tube, the characteristic length is the diameter of the tube while, for a canal, the characteristic length is its breadth.

If, for a liquid, ρ and η are known and its critical velocity ν_c can be determined experimentally during its flow through a tube of diameter l, then from equation (1), the value of the constant N_c for that liquid can be determined. This value is nearly 2300.

For any velocity ν of the fluid flow, equation (1) can also be written in an equivalent form as

⇒ \(v=N \cdot \frac{\eta}{\rho l} \text { or, } N=\frac{\rho l v}{\eta}\)…….(1)

N is called the Reynolds number.

Special cases:

1. If ν<ν_c, i.e., the velocity of fluid flow is less than the critical velocity, then comparing equations (1) and (2), we can say that N<N_c. It means that the value of Reynolds number is less than 2300. So, if the value of Reynolds number is less than 2300, then the flow will be streamlined.

2. On the other hand, if ν>ν_c, i.e., the velocity of the fluid is greater than the critical velocity, then N >N_c, and hence the value of Reynolds number will be greater than 2300. If Reynolds number is greater than 2300, then the flow will be turbulent.

Dimension of Reynolds number: From equation (2) we get, dimension of N

= \(\frac{\text { dimension of } \rho \times \text { dimension of } l \times \text { dimension of } \nu}{\text { dimension of } \eta}\)

= \(\frac{M L^{-3} \cdot L \cdot L T^{-1}}{M L^{-1} T^{-1}}=1\)

So, N is a dimensionless quantity; it is a pure number.

Reynolds number: A dimensionless number N= \(\frac{\rho l v}{\eta}\) can be formed by combining the characteristic length (l) of a fluid channel and the velocity (v), density (ρ) and coefficient of viscosity (η) of the fluid the magnitude of N determines whether the fluid flow is streamlined or turbulent. This number N is called the Reynolds number.

• In the above discussion, 2300 is an approximate value of Nc. Usually, for N < 2000, the fluid flow is streamlined, and for N> 3000 the fluid flow is turbulent. If N lies between 2000 and 3000, the streamline flow of a fluid gradually changes into turbulent flow.
• In the above discussion, 2300 is an approximate value of N_c. Usually, for N < 2000, the fluid flow is streamlined, and for N > 3000 the fluid flow is turbulent. If N lies between 2000 and 3000, the streamline flow of fluid gradually changes into turbulent flow.
• As N is a pure number, its value does not depend on the system of units chosen. For a particular flow, the value of N remains the same.

If the radius of a tube of flow is considered, instead of its diameter, then the effective value is, N_c ≈ 1150.

Viscosity And Surface Tension Numerical Example

Example: A plate of area 100 cm2 is floating on an oil of depth 2 mm. The coefficient of viscosity of oil is 15.5 poise. What horizontal force is required to move the plate horizontally with a velocity of 3 cm · s^-1?
Solution:

The viscous force, F = \(\eta A \frac{d v}{d x}\)

Here, A = 100 cm², η = 15.5 poise,

dν = 3 cm · s^-1 and dx = 2 mm = 0.2 cm.

∴ F = 15.5 x 100 x 3/0.2 = 23250 dyn

So the required horizontal force is 23250 dyn.

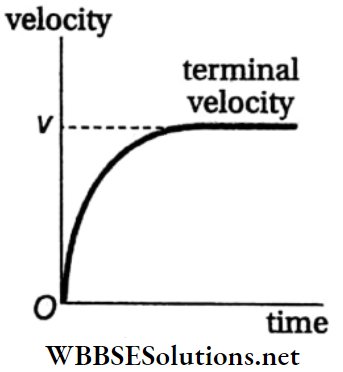
Terminal Velocity of a Body in a Viscous Medium and Stokes’ Law: When a body falls through a viscous medium (liquid or gas), it drags a layer of the fluid adjacent to it due to adhesion. But fluid layers at a large distance from the body are at rest.

• As a result, there is relative motion between different layers of the fluid at different distances from the body. But the viscosity of the fluid opposes this relative motion.
• The opposing force due to viscosity increases with increase in the velocity of the body due to the gravitational acceleration g. If the body is small in size, then after an interval of time the opposing upward force (i.e., viscous force and buoyant force) becomes equal to the downward force (weight of the body).
• Then the effective force acting on the body becomes zero and the body begins to fall through the medium with a uniform velocity, called the terminal velocity. A graph representing the change in velocity of a falling object with time is shown in Fig.

Stokes’ law: Stokes proved that, if a small sphere of radius r is falling with a terminal velocity ν through a medium of coefficient of viscosity η, then the opposing force acting on the sphere due to viscosity is

F = 6 πηrν ………..(1)

Equation (1) expresses Stokes.

1. To establish Stokes’ law, the following assumptions are
   made.
2. The fluid medium must be infinite and homogeneous. E3D The sphere must be rigid with a smooth surface.
3. The sphere must not slip when falling through the medium.
4. The fluid motion adjacent to the falling sphere must be streamlined.
5. The sphere must be small in size, but it must be greater than the intermolecular distance of the medium.

Equation for terminal velocity: if the density of the material of the sphere is ρ, then the weight of the sphere = \(\frac{4}{3} \pi r^3 \rho g .\)

If the density of the fluid medium is σ, then the upward buoyant force acting on the sphere = \(\frac{4}{3} \pi r^3 \sigma g\)

∴ The resultant downward force acting on the sphere =

= \(\frac{4}{3} \pi r^3 \rho g-\frac{4}{3} \pi r^3 \sigma g=\frac{4}{3} \pi r^3(\rho-\sigma) g\)….(2)

If the sphere attains terminal velocity, then

⇒ \(6 \pi \eta r \nu=\frac{4}{3} \pi r^3(\rho-\sigma) g \text { or, } \nu=\frac{2}{9} \frac{r^2(\rho-\sigma) g}{\eta}\) ….(3)

So, from equation (3), we see that the terminal velocity obeys the following rules.

1. Terminal velocity is directly proportional to the square of the radius of the sphere.
2. It is directly proportional to the difference of densities of the material of the sphere and that of the medium.
3. It is inversely proportional to the coefficient of viscosity of the medium.

If the density of the body is less than the density of the medium, i.e., ρ < σ, then it is clear that the terminal velocity becomes negative. Hence, the velocity of the body will be in the upward direction. For this reason, air or other gas bubbles move upwards through water.

Applications of Stokes’ law:

1. Falling of rain drops through air: Water vapour condenses on the particles suspended in air far above the ground to form tiny water droplets. The average radius of these tiny water droplets is 0.001 cm (approx.)

• Assuming the coefficient of viscosity of air as 1.8 x 10^-4  poise (approx.) the terminal velocity of these droplets is calculated as 1.2 cm · s^-1 (approx.) which is negligible. So, these water droplets float in the sky. Collectively these droplets form clouds.
• But as they coalesce to form larger drops, their terminal velocities increase. For example, the terminal velocity of a water droplet of radius 0.01cm becomes 120 cm · s^-1 (approx.). As a result, they cannot float any longer and so they come down as rain.

2. Coming down with the help of a parachute: When a soldier jumps from a flying airplane, he falls with acceleration due to gravity but due to viscous drag in air, the acceleration goes on decreasing till he acquires terminal velocity.

The soldier then descends with constant velocity and opens his parachute close to the ground at a pre-calculated moment, so that he may land safely near his destination.

Terminal Velocity Numerical Examples

Example 1. An oil drop of density 950 kg · m^-3 and radius 10^-6 m is falling through air. The density of air is 1.3 kg · m^-3 and its coefficient of viscosity is 181 x 10^-7 SI unit. Determine the terminal velocity of the oil drop, [g = 9.8 m · s^-2]
Solution:

Terminal velocity, \(\nu=\frac{2}{9} \cdot \frac{r^2(\rho-\sigma) g}{\eta}\)

[Here, ρ = 950 kg · m^-3 ; r = 10^-6 m; σ = 1.3 kg · m^-3; η = 181 x 10^-7 SI]

= \(\frac{2}{9} \cdot \frac{\left(10^{-6}\right)^2(950-1.3) \times 9.8}{181 \times 10^{-7}}\)

= \(1.14 \times 10^{-4} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Example 2. An air bubble of radius 1 cm is rising from the bottom of a long liquid column. If its terminal velocity is 0.21 cm · s^-1, calculate the coefficient of viscosity of the liquid. Given that the density of the liquid is 1.47 g · cm^-3. Ignore the density of air.
Solution:

Coefficient of viscosity of the liquid, \(\eta=\frac{2}{9} \cdot \frac{r^2(\rho-\sigma) g}{v}\)

[Here, r = 1cm; v = -0.21 cm · s^-1; ρ = 0; cσ = 1.41 g · cm^-3]

= \(\frac{2}{9} \times \frac{(1)^2(0-1.47) \times 980}{-0.21}=1524.4 \text { poise. }\)

 

Viscosity And Surface Tension Surface Tension Of Liquids

All liquids possess a special property—a tendency to minimise its surface area. This tendency of a liquid surface to contract its area is called surface tension. From our practical experience, we know that water droplets, or a small amount of mercury always takes the shape of a sphere.

• In the absence of external forces, all liquids always take a spherical shape. For a given volume, the surface area of a sphere is the least and hence a liquid drop has a natural tendency to take the shape of a sphere.
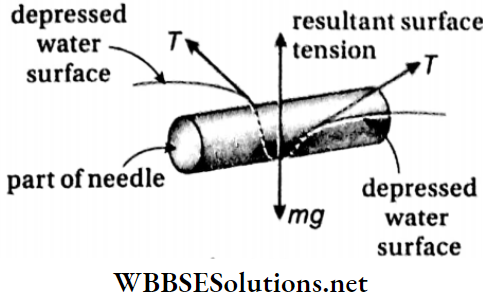
• If a clean dry needle is placed horizontally on the surface of water, then it is observed that the needle floats on water. The water surface under the needle is slightly depressed.
• Insects like spiders and mosquitoes are able to walk on the surface of water. Where their legs touch, the water surface becomes slightly depressed.
• From such observations, it seems that the surface of water behaves like a stretched rubber membrane.

Experimental demonstration: A wire loop is dipped into a soap solution. A thin soap film will be formed in the loop when it is taken out of the solution. This film acts as the free surface of the liquid.

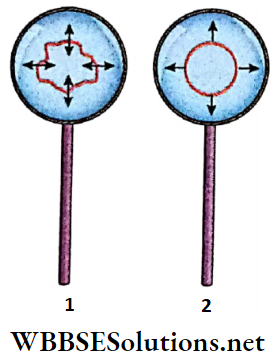
A wet cotton thread loop, after being dipped in soap solution, is put on the film. No change is seen in the shape of the loop. The soap film inside the loop is now punctured with a fine needle and it is observed that the cotton thread pulls itself into a circle. What is the reason behind this observation?

• Initially, there was soap film inside and outside the cotton loop. Every point on the loop experienced equal and opposite forces tangential to the surface of the film. These two forces balanced each other. As a result, no resultant force acted on the loop.
• After the film inside the loop was removed, the inward force vanished and only the film outside the loop exerted a force on the thread. We know that among all plane surfaces having the same boundary length, the area of a circle is the greatest.
• Hence, a circle formed by the loop occupies the maximum area. So, the area of the film in between the loop and the thread reduces to a minimum. From this, it can be inferred clearly that the film has a tendency to minimize its area.
• It can be concluded that a tension always acts on the free surface of a liquid and that the free surface behaves as a stretched-thin membrane. Due to this tension, the free surface of any liquid has a tendency to contract so as to occupy the minimum area. This tension is known as surface tension.

Surface tension: Surface tension is the property of the free surface of a liquid due to which the liquid behaves as a stretched thin membrane and has a tendency to contract so as to minimise the surface area.

• As a reason behind the origin of surface tension, it can be said that the molecules of a liquid attract each other by cohesive force [the force of attraction which acts between the molecules of same material is called cohesive force).
• Equal cohesive force acts on the molecule inside the liquid from all directions.
• Consequently, the resultant cohesive force on the molecule is zero. But, no cohesive forces act on the molecules of the free surface of the liquid to the outward direction. So, the cohesive force inside the liquid is not balanced.
• As a result, a resultant cohesive force acts on each molecule of the free surface in the downward direction. Thus, the free surface of a liquid tends to have the least surface area.
• Let us imagine a straight line on the free surface of a liquid. Due to the tendency of the liquid surface to contract, the molecules on the opposite sides of the line try to move away from each other. This can be seen in the following experiment.

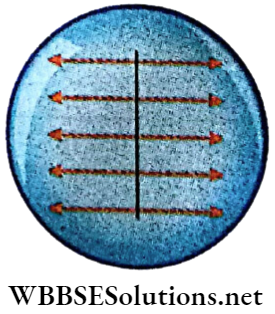
If a matchstick is placed on a water Surface, it remains at rest. But when a drop of alcohol is put on water on one side of the stick, the stick moves in the opposite direction.

1. The water surface exerts an equal pressure on both sides of the stick. This force is normal to the stick.

2. When a drop of alcohol is put on water, the force on that side is weaker and the stick is pulled away by the stronger tangential force towards the opposite side.

Hence, surface tension can also be defined as follows:

Surface tension Definition: The tangential force per unit length on a liquid surface, that acts along the normal on either side of an imaginary line on that surface, is called the surface tension of the liquid.

Units:

• dyn · cm^-1 CGS System
• N · m SI

Relation: \(1 \mathrm{~N} \cdot \mathrm{m}^{-1}=\frac{1 \mathrm{~N}}{1 \mathrm{~m}}=\frac{10^5 \mathrm{dyn}}{10^2 \mathrm{~cm}}=10^3 \mathrm{dyn} \cdot \mathrm{cm}^{-1}\)

Dimensional: \([\text { Surface tension }]=\frac{[\text { force }]}{\text { [length }]}=\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}}=\mathrm{MT}^{-2}\)

Surface Energy: We know that on the free surface of a liquid, the surface tension always tries to minimize the surface area. So, to increase the area of the surface of the liquid, an external force is needed.

• The external force does work to increase the area of the surface of the liquid, and the work done remains stored inside the surface of the liquid as potential energy.
• The surface energy of a liquid is measured by the work done to increase the area of the surface of a liquid by unity.

Units:

• erg · cm^-2 CGS System
• J · m^-2 SI

Relation: \(1 \mathrm{~J} \cdot \mathrm{m}^{-2}=\frac{1 \mathrm{~J}}{1 \mathrm{~m}^2}=\frac{10^7 \mathrm{erg}}{10^4 \mathrm{~cm}^2}=10^3 \mathrm{erg} \cdot \mathrm{cm}^{-2}\)

Dimension: \([\text { Surface energy }]=\frac{[\text { work }]}{[\text { area }]}=\frac{\mathrm{ML}^2 \mathrm{~T}^{-2}}{\mathrm{~L}^2}=\mathrm{MT}^{-2}\)

Relation between surface tension and surface energy: A rectangular wire frame PQRS is taken. A wire AB can move along PQ and SR.

When the frame is dipped into a soap solution and taken out, a thin film is formed within the frame.

As a result, the surface tension acts normally on the wire AB and tangentially to the surface of the film. This force tries to contract the film surface and pulls the wire AB towards QR. To keep the wire AB in its position, an equal but opposite force needs to be applied on it.

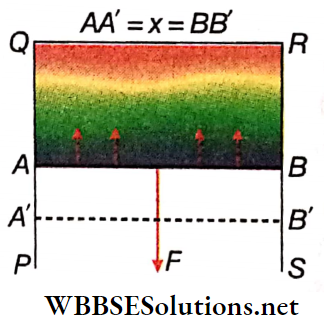
Let the length of the wire AB be l; the surface tension of the liquid be T.

∴ The net force acting on the wire AB in the direction QR = 2lT. [The film has two surfaces and surface tension acts on each surface, therefore the net force has the factor of 2]

∴ To keep the wire AB still, the force required to be applied in the opposite direction, F = 2lT

Now, the amount of work done in displacing the wire AB through a short distance δx against the surface tension (assuming the force F to be a constant throughout the displacement) so that it comes to the new position A’B’ is

Fδx = 2lTδx

Due to this, the total increase in the area of the film surface = 2 lδx.

This work remains stored as potential energy on the film surface.

∴ Work done for unit increase in area against the surface tension = \(\frac{2 l T \delta x}{2 l \delta x}=\) = T

So, the potential energy stored per unit area or the surface energy is numerically equal to the surface tension of the liquid. Note that the temperature is assumed to be constant.

Alternative definition of surface tension: Keeping the temperature constant, the amount of work done in increasing the area of a liquid surface by unity is called the surface tension of that liquid at that temperature.

Units:

• erg · cm^-2 CGS System
• J · m^-2 SI Units

Dimension: According to the alternative definition,

⇒ \([\text { surface tension }]=\frac{[\text { work }]}{[\text { area }]}=\frac{\mathrm{ML}^2 \mathrm{~T}^{-2}}{\mathrm{~L}^2}=\mathrm{MT}^{-2}\)

Total surface energy: in the discussion, it was assumed that, during increase in the area of a liquid surface under the influence of an applied force, the temperature remains constant. But, in practice, some molecules from inside the liquid rise to its surface during the expansion of the surface.

• A resultant attraction exerted by the other molecules inside the liquid acts on these moving molecules. Therefore, these molecules on reaching the surface lose their linear kinetic energy and the average linear kinetic energy of the total liquid decreases.
• Since the temperature is directly proportional to the average kinetic energy, the temperature of the surface of the liquid decreases with an increase in its area. To keep the temperature constant, the liquid surface absorbs heat from its surroundings.

To increase the area of a liquid surface keeping the temperature constant, energy may be supplied in two ways

1. Mechanical energy to increase the surface area and
2. Heat energy to keep the temperature constant. The total of these two energies should actually be the surface energy.

So, the increase in potential energy per unit surface area or stored surface energy (E) = mechanical energy or work done (T) + heat (h) required for unit area

i.e., E = T+h……(1)

From thermodynamics, it can be proved that, h = \(-\theta \frac{d T}{d \theta}\)

[θ = temperature in absolute scale and dT/dθ = rate of increase in surface tension due to increase in temperature]

∴ E = \(T-\theta \frac{d T}{d \theta}\)…..(2)

Now, with the increase in temperature, the surface tension decreases and hence \(-\theta \frac{d T}{d \theta}\) is a negative quantity.

So, h is a positive quantity.

∴ E = \(T+\theta \frac{d T}{d \theta}\)…..(3)

when only the magnitudes are considered.

Again, at the absolute zero temperature, i.e., when θ = 0, E = T.

So, at any temperature except absolute zero, the total surface energy of a liquid is always greater than the surface tension of that liquid.

Factors Affecting Surface Tension of a Liquid: Surface tension of a liquid depends on the following factors.

1. Temperature of the liquid: With an increase in the temperature, the surface tension of almost all liquids decreases. For a small change in temperature, the relation between surface tension and temperature is

T’ = \(T\left[1-\alpha\left(t^{\prime}-t\right)\right]\)

Here, T and T’ are the surface tensions at temperatures t and t’ respectively]

For a given liquid, α is a constant quantity. It is called the temperature coefficient of surface tension.

It is experimentally verified that at a specific temperature of every liquid, the surface tension of the liquid disappears. This temperature is called the critical temperature of that liquid.

2. Pollution: If impurities are present on a liquid surface, then the surface tension of that liquid usually decreases. For example, when an oil or a fat-like substance is poured over water, it forms a thin film over the surface of water. This decreases the original surface tension of water.

3. Presence of dissolved substances: if a liquid contains dissolved inorganic substances, then the surface tension of that liquid increases. Again, if the liquid contains dissolved organic matter, then its surface tension decreases. For example, the surface tension of pure water is 0.072 N · m^-1.

If common salt (inorganic substance) is dissolved in water, then its surface tension becomes 0.083 N · m^-1 (approx.), but the surface tension of soap-water (organic substance) is approximately 0.030 N · m^-1.

4. Medium above the liquid surface: The surface tension of a liquid depends on the nature of the medium above the free surface of that liquid. For example, the surface tension of water is about 72 dyn · cm^-1 in the presence of dry air above the surface of water, but is about 70 dyn · cm^-1 when there is moist air above the surface of water at the same temperature.

5. Presence of electric charge: The surface tension of a liquid decreases due to the presence of electric charge on the surface of the liquid.

Some Phenomena in Connection with Surface Tension

1. Camphor darts to and fro when put on the Surface Of water: Camphor is soluble in water. When put on water, the portion that comes into contact with the water begins to dissolve. The part which gets dissolved in water contaminates the water and the surface tension of that part decreases. Due to this difference in surface tension, a net unbalanced force acts on the piece of camphor, and consequently, the piece of camphor darts to and fro on the surface of water.

2. Hair of a paint brush cling together when the brush is brought out of water: The hair of a brush lie apart while immersed in water because, inside water, the surface tension is absent. But when the brush is brought out of the water, a thin film of water clings to the hair, and the surface tension tries to contract the area of the film hence the hair clings together.

3. Turbulent sea calms down If oil is poured on the water: The surface tension of pure water is more than that of oily water. When oil is poured over sea water, the oil spreads in the direction of motion of the waves leaving uncovered sea water at the rear. Hence, the surface tension of the water ahead of the waves is lower than that of the water behind the waves. The water at the rear pulls the water at the front and, as a result, high waves become lower.

4. When oil is poured on water, it spreads readily Over the entire surface: Since the surface tension of pure water is greater than the surface tension of oil, a tensile force acts on the surface of oil. Due to this tensile force, oil spreads readily over the entire surface of water.

5. When chalk dust is sprinkled on water and a few drops of alcohol is added, then the dust particles rapidly spread on the water surface: Alcohol decreases the surface tension. Due to unequal surface tension on different parts of the water surface, the chalk particles spread rapidly on the surface of water.

6. Water cannot seep in through the cloth of raincoats, umbrellas and tents: The minute pores in the cloth of raincoats etc. trap air molecules. However, these pores are too small to let rain droplets enter, because the droplets retain their spherical shape due to surface tension, and the diameters of the spheres are greater than that of the pores. So, the rainwater falling on the cloth simply flows off.

7. A needle Coin float on water surface: A needle floats due to the surface tension of water. The surface of water where the needle is placed experiences a slight depression due to the surface tension of water. So, the water exerts an upward force on the needle which balances its weight (acting downwards). Therefore, a needle can float if it is placed carefully on a calm water surface.

Viscosity And Surface Tension Surface Tension Of Liquids Numerical Examples

Example 1. The surface tension of water at 20 °C is 72 dyn · cm^-1 and for water dT/dθ = -0.146 dyn · cm^-1 · K^-1. What is the total surface energy of water?
Solution:

We know that the total surface energy of water,

E = T – θ dT/dθ = 72 – 293 x (-0.146) [20°C = 293 K]

= 72 + 42.778 = 114.778 erg · cm^-2.

Example 2. A drop of water of radius 1 mm is to be divided into 10⁶ point drops of equal size. How much mechanical work should be done? The surface tension of water = 72 dyn · cm^-1.
Solution:

Let the radius of each point drop be r

∴ \(\frac{4}{3} \pi r^3 \times 10^6=\frac{4}{3} \pi\left(\frac{1}{10}\right)^3 \quad \text { or, } r=0.001 \mathrm{~cm}\)

The surface area of the original drop = \(4 \pi\left(\frac{1}{10}\right)^2 \mathrm{~cm}^2\)

and the total surface area of 10⁶ point drops = 10⁶ x 4π(0.001)² = 4π cm².

∴ Increase in surface area = \(4 \pi-4 \pi\left(\frac{1}{10}\right)^2=4 \pi \times 0.99 \mathrm{~cm}^2\)

= \(4 \pi-4 \pi\left(\frac{1}{10}\right)^2=4 \pi \times 0.99 \mathrm{~cm}^2\)

∴ Mechanical work done = increase in surface area x surface tension

= 72 x 4π x 0.99 = 895.73 erg

Example 3. 1000 water droplets having a radius of 0.01 cm each coalesce to form a single big drop. What will be the decrease in energy? The surface tension of water = 72 dyn · cm^-1
Solution:

Let the radius of the single big drop be R.

∴ \(\frac{4}{3} \pi R^3=\frac{4}{3} \pi(0.01)^3 \times 1000 \quad \text { or, } R=0.1 \mathrm{~cm}\)

Surface area of the big drop = 4π (0.1)² cm²

Total surface area of 1000 droplets

= 4π (0.01)² x 1000 cm²

∴ Decrease in area

= 4π (0.01)² x 1000-4π(0.1)²

= 4π(0.1 -0.01) = 47 x 0.09 cm³

∴ Decrease in energy = 4π x 0.09 x 72 = 81.43 erg.

Example 4. A rectangular glass slab measures 0.1 m x 0.0154 m x 0.002 m and its weight in air is 80.36 x 10^-3 N. The slab is immersed half in water keeping its length and thickness horizontal. What will be the apparent weight of the slab? The surface tension of water is 72 x 10^-3 N · m^-1.
Solution:

While it is immersed, the following forces act on the glass slab

1. Weight of the slab acting downwards,
2. Upward buoyant force due to the weight of displaced water and
3. Downward force due to surface tension.

Now, weight of the slab = 80.36 x 10^-3 N

Buoyant force = weight of displaced water

= \(0.1 \times \frac{0.0154}{2} \times 0.002 \times 1000 \times 9.8\)

= 15.092 x 10^-3 N

Force due to surface tension

= 2 x (0.1 + 0.002) x 72 x 10^-3 N

= 14.688 x 10^-3 N

∴ The apparent weight of the slab

= 80.36 x 10^-3 – 15.092 x 10^-3 + 14.688 x 10^-3

= 79.956 x 10^-3 N.

Example 5. The radius of a soap bubble is increased from 1 cm to 3 cm. What amount of work is done for this? The surface tension of soap-water is 26 dyn • cm^-1•
Solution:

Work done = increase in area x surface tension =

47{(3)²-(1)²} x 26 x 2 [the soap-bubble has two surfaces]

= 5227.6 erg = 5.2276 x 10^-4 J.

Example 6. Determine the surface energy of a liquid film formed on a ring of area 0.15 m². The surface tension of the liquid = 5 N · m^-1.
Solution:

Surface energy, E = 2 x surface tension x area =2 x 5 x 0.15= 1.5 J

Example 7. Determine the surface energy of a soap-water film formed on a frame of area 10^-3 m². Surface tension of soap-water = 70 x 10^-3 N · m^-1.
Solution:

Surface energy = 2 x surface tension x area

= 2 x 70 x 10^-3 x 10^-3 = 14 x 10^-5 J.

Example 8. What will be the work done to form a soap bubble of radius 5 cm? The surface tension of soap-water = 70 dyn · cm^-1
Solution:

Work done =2 x 4πr² x T =8πr² T

[r = radius of the soap-bubble and T = surface tension of soap-water]

= 8 x 22/7 x (5)² x 70 = 44000 erg

= 0.0044 J.

Example 9.  If a large number of water droplets of diameter 2rcm each coalesce to form a large water drop of diameter 2jRcm, then prove that the rise in tem-perature of water is \(\frac{3 T}{J}\left(\frac{1}{r}-\frac{1}{R}\right)\). Here, T is the surface tension of water and J is the mechanical equivalent of heat.
Solution:

If the number of small water droplets is n, then the dissipation of surface energy, W = (4πr²n-4πR²)T.

We know that W = JH and H = heat absorbed = msθ

[where m = mass of the larger water drop, s = specific heat of water, 6θ = temperature increase]

H = \(\frac{W}{J}=\frac{T}{J} \times 4 \pi\left(n r^2-R^2\right)\)

or, \(\frac{4}{3} \pi R^3 \cdot 1 \cdot \theta=\frac{T}{J} \times 4 \pi\left(n r^2-R^2\right)\)

⇒ \({\left[because m=\frac{4}{3} \pi R^3 \cdot 1=\frac{4}{3} \pi R^3 \text { and } s=1 \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot{ }^{\circ} \mathrm{C}-1\right]}\)

or, \(\theta= \frac{3 T}{J} \frac{\left(n r^2-R^2\right)}{R^3}\)

⇒ \({\left[\text { here, } n \cdot \frac{4}{3} \pi r^3=\frac{4}{3} \pi R^3 \text { or, } R^3=n r^3 \text { or, } n=\frac{R^3}{r^3}\right]}\)

= \(\frac{3 T}{J}\left[\frac{R^3}{r^3} \cdot \frac{r^2}{R^3}-\frac{1}{R}\right]\)

= \(\frac{3 T}{J}\left(\frac{1}{r}-\frac{1}{R}\right)\)

Example 10. Water is filled upto a height h in a beaker of radius R as shown in the Fig. 3.24. The density of water is p, the surface tension of water is T and the atmospheric pressure is P₀. Consider a vertical section ABCD of the water column through a diameter of the beaker. What is the force on water on one side of this section by water on the other side of this section?

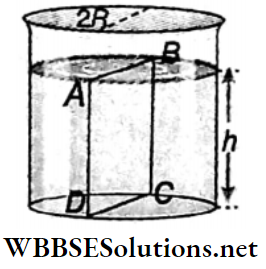
Solution:

The force acted on the liquid of left side by the liquid of right side is equal to the resultant of the following two forces.

1. Force due to surface tension =2RT (right side).

2. Impulse due to the exerted pressure by the liquid of height h

= \(\left(P_0+\frac{\rho g h}{2}\right) \times 2 R h\) [where \(\frac{\rho g h}{2}\)= average pressure on the plane A B C D]

= \(2 P_0 R h+\dot{R} \rho g h^2\) (along left side)

∴ The resultant force on the plane ABCD = \(2 P_0 R h+R \rho g h^2-2 R T\)

Example 11. When water in a beaker is gradually heated, a bubble formed at the lower surface of the beaker starts to rise up from the bottom of the beaker. The radius of the spherical bubble is R and the radius of the circular region of the bubble touched with the lower surface of the container is r(r<<R). Show that, the value of r will be \(R^2 \sqrt{\frac{2 \rho_u g}{3 T}}\) just before the detached from the lower surface of the container [where, ρ_w = density of water, T = surface tension of water]. Consider, though the density and surface tension are unchanged with the increase in temperature, but the density of air changes significantly.

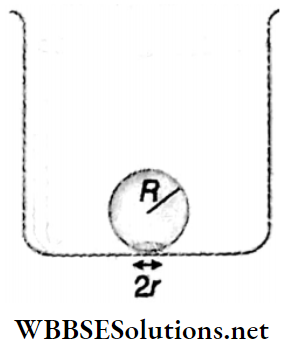
Solution:

At that instant when the bubble is just detached from the lower surface of the beaker, the buoyancy force = the force due to surface tension.

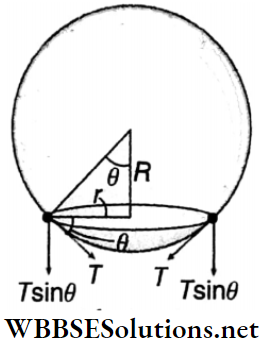
Now, the net force due to surface tension = (2πr)T sinθ (directed downward)

and the buoyancy force = \(\frac{4}{3} \pi R^3 \rho_w g\) (directed upward)

In this case, \(\frac{4}{3} \pi R^3 \rho_w g=(T)(2 \pi r) \sin \theta\)

[as θ is very small, sin/θ ≈ tanθ = r/R]

or, \(\frac{4}{3} \pi R^3 \rho_w g=(T)(2 \pi r)\left(\frac{r}{R}\right)\)

or, \(\frac{4}{3} \pi R^3 \rho_w g=T \cdot 2 \pi \frac{r^2}{R}\)

or, \(r^2=\frac{2\left(R^4 \rho_w g\right)}{3 T}\)

∴ r = \(R^2 \sqrt{\frac{2 \rho_w g}{3 T}}\)

Pressure Difference Between The Two Sides Of A Curved Liquid Surface

1. Suppose the free surface of a liquid is plane. A molecule lying on its surface is attracted by other surface molecules equally in all directions. So the resultant tangential force on the molecule is zero.

2. If the free surface of the liquid is concave, then every molecule on the surface experiences an upward resultant force due to attraction by other surface molecules.

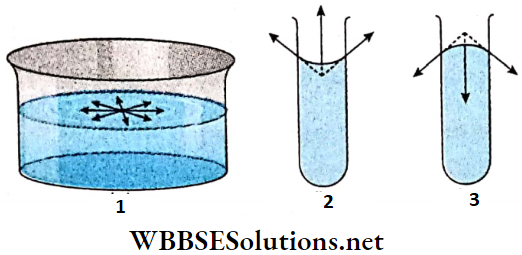
3. If the liquid surface is convex, then the resultant force on a molecule on the surface due to attraction by other surface molecules will be directed downwards.

• Obviously, there must be a difference of pressure between the two sides of a curved surface for equilibrium of it. This difference of pressure i.e., the excess pressure force will balance the resultant force due to surface tension. The pressure on the concave side must be greater than the pressure on the convex side.
• We shall now calculate the excess pressure on the concave side of spherical surfaces in case of a liquid drop, an air bubble in a liquid, and a soap bubble.

Excess pressure inside a liquid drop: Let us consider a liquid drop of radius R of a liquid of surface tension T. Every molecule on its surface experiences a resultant pull normally inwards due to surface tension.

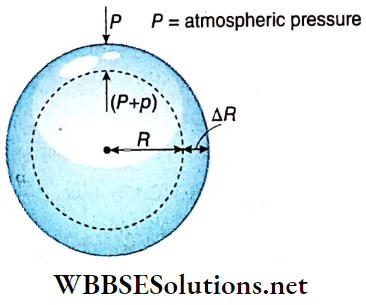
So the internal pressure of the drop becomes greater than the pressure outside it. The internal excess pressure of the drop produces a force acting outwards which balances the force due to surface tension and maintains the equilibrium of the drop.

Suppose, external pressure on the drop =P, internal pressure of the drop = (P+ p).

So, the excess pressure inside the drop = p.

Suppose this internal excess pressure acting normally outwards increases the radius of the drop from R to R + ΔR i.e., it increases the surface area of the drop. Here ΔR is taken to be so small that the pressure inside the drop may be taken as unchanged.

Work done by the excess pressure,

W = Excess pressure x area x displacement

= p · 4πR² · ΔR ………(1)

Increase of surface area of the liquid drop,

⇒ \(\Delta A =4 \pi(R+\Delta R)^2-4 \pi R^2\)

= \(4 \pi\left\{R^2+2 R \cdot \Delta R+(\Delta R)^2-R^2\right\}\)

= \(8 \pi R \cdot \Delta R\) ; [neglecting the term \((\Delta R)^2\) which is very small]

∴ Increase in surface energy,

E = increase in surface area x surface tension

= 8πR · ΔR · T …….(2)

This increase in surface energy of the liquid drop takes place at the cost of work done by the excess pressure i.e., E = W.

So, from equation (1) and (2) we have, p · 4πR² · ΔR = 8π R ⋅ ΔR · T

or, p = 2T/R …..(3)

Excess pressure inside an air bubble in a liquid: Let us consider an air bubble of radius R formed in a liquid of surface tension T. Like a liquid drop the air bubble has also one surface in contact with the liquid.

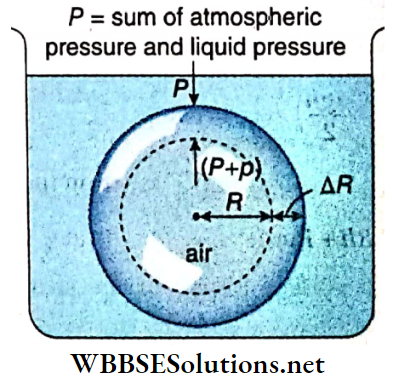
So proceeding similarly as in the case of a liquid drop we can prove that the excess pressure inside the air bubble in a liquid is given by p = 2T/R.

Excess pressure inside a soap bubble: Let us consider a thin soap bubble of radius R formed from a soap solution of surface tension T.

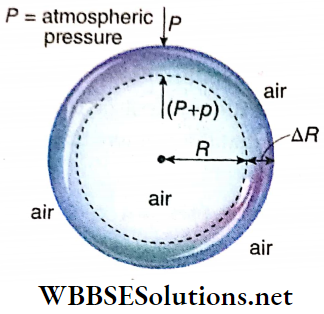
Suppose, the pressure outside the bubble = P, internal pressure =(P+p)

So, the excess pressure inside the bubble = p. Suppose, the radius of the bubble increases from R to R + ΔR due to this internal excess pressure acting normally outwards, i.e., the surface area of the bubble increases.

Here ΔR is taken to be so small that the pressure inside the bubble may be taken as unchanged.

Work done by the excess pressure,

W = excess pressure x area x displacement = p · 4πR² · ΔR …..(1)

The soap bubble has two liquid surfaces in contact with air, one inside the bubble and the other outside the bubble.

So, increase of surface area of the soap bubble,

⇒ \(\Delta A =2\left[4 \pi(R+\Delta R)^2-4 \pi R^2\right]\)

= \(8 \pi\left[R^2+2 R \cdot \Delta R+(\Delta R)^2-R^2\right]\)

= \(16 \pi R \cdot \Delta R\) ; [neglecting the term] \((\Delta R)^2\) which is very small]

∴ Increase in surface energy,

E = increase in surface area x surface tension

= 16 πR · ΔR · T……….(2)

This increase in surface energy of the soap bubble takes place at the cost of work done by the excess pressure i.e., E = W

So, from equations (1) and (2) we have,

⇒ \(p \cdot 4 \pi R^2 \cdot \Delta R=16 \pi R \cdot \Delta R \cdot T\)

p = \(\frac{4 T}{R}\)

Viscosity And Surface Tension Bubble  Numerical Examples

Example 1. Find the excess pressure inside a rainwater drop of diameter 0.02cm. The surface tension of water = 0.072 N · m^-1.
Solution:

Water drop has only one curved surface.

So, excess pressure of a water drop, p =2T/r where, T = surface tension of water

r = radius of a water drop = 0.002/2 = 0.01 cm = 0.01 x 10m

∴ p = \(=\frac{2 \times 0.072}{0.01 \times 10^{-2}}=1440 \mathrm{~N} \cdot \mathrm{m}^{-2}\)

Example 2. Surface tension of soap solution = 27 dyn • cm^-1. Calculate the excess pressure (in N • m^-2) inside a soap bubble of radius 3 cm.
Solution:

The excess pressure inside a soap bubble,

p = \(\frac{4 T}{r}=\frac{4 \times 27}{3}=36 \mathrm{dyn} \cdot \mathrm{cm}^{-2}=3.6 \mathrm{~N} \cdot \mathrm{m}^{-2} \text {. }\)

Example 3. Find the pressure inside an air bubble of radius 0.1mm just inside the surface of water. Surface tension of water = 72 dyn · cm^-1
Solution:

Excess pressure inside an air bubble

= \(\frac{2 T}{r}=\frac{2 \times 72}{0.01}\)

[T = 72 dyn · cm^-1 and r = 0.1 mm = 0.01 cm] = 14400 dyn · cm^-2.

Atmospheric pressure = 76 x 13.6 x 980 dyn · cm^-2

∴ Total pressure inside an air bubble = (76 x 13.6 x 980 + 14400)

= 1.0274 x 106 dyn · cm^-2.

Example 4. The excess pressure inside a soap bubble of radius 8mm raises the height of an oil column by 2mm. Find the surface tension of the soap solution. Density of the oil = 0.8 g · cm^-3.
Solution:

Excess pressure in a soap bubble (p) = 4πr.

Again, p = hρg, h = height of the oil column.

Now, \(\frac{4 T}{r}=h \rho g \text { or, } T=\frac{h \rho g \times r}{4}=\frac{0.2 \times 0.8 \times 980 \times 0.8}{4}\)

[h = 2mm = 0.2cm; ρ = 0.8 g • cm^-3, g = 980cm · s^-2 and r = 8mm = 0.8cm],

∴ T = 31.36 dyn · cm^-1

Example 5. In an isothermal process, two soap bubbles of radii a and b combine and form a bubble of radius c. If the external pressure is p, then prove that the surface tension of the soap solution is \(T=\frac{p\left(c^3-a^3-b^3\right)}{4\left(a^2+b^2-c^2\right)}\)
Solution:

We know, the excess pressure inside the soap bub¬ble = internal pressure – external pressure.

∴ For the bubble of radius a, excess pressure, \(\frac{4 T}{a}=p_a-p\)

∴ \(p_a=\left(p+\frac{4 T}{a}\right)\)

Similarly, for the bubble of radius b, \(p_b=\left(p+\frac{4 T}{b}\right)\)

For the bubble of radius c, \(p_c=\left(p+\frac{4 T}{c}\right)\)

Boyle’s law is applicable in isothermal process.

According to this law, \(p_a V_a+p_b V_b=p_c V_c\)

or, \(\left(p+\frac{4 T}{a}\right) \times \frac{4}{3} \pi a^3+\left(p+\frac{4 T}{b}\right) \times \frac{4}{3} \pi b^3\)

= \(\left(p+\frac{4 T}{c}\right) \times \frac{4}{3} \pi c^3\)

or, \(\left(p+\frac{4 T}{a}\right) a^3+\left(p+\frac{4 T}{b}\right) b^3=\left(p+\frac{4 T}{c}\right) c^3\)

or, \(4 T\left(a^2+b^2-c^2\right)=p\left(c^3-a^3-b^3\right)\)

∴ T = \(\frac{p\left(c^3-a^3-b^3\right)}{4\left(a^2+b^2-c^2\right)} .\)

Example 6. Two soap bubbles of radii 0.04 m and 0.03 m are combined in such a way that a common surface is formed between the two bubbles. What is the radius of curvature of the common surface?
Solution:

Let, the radii of the two soap bubbles are r₁ and r₂, and the internal pressures are p₁ and p₂ respectively.

The radius of the common surface = r, atmospheric pressure = p₀

For the first bubble, \(p_1-p_0=\frac{4 T}{r_1}\)

and for the second bubble, \(p_2-p_0=\frac{4 T}{r_2}\)

where, T = surface tension of soap solution.

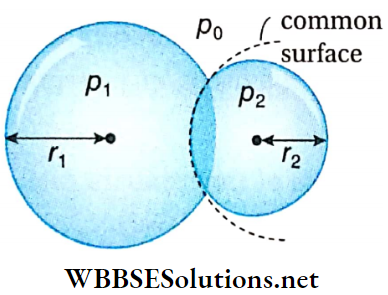
Subtracting (1) from (2) we get,

⇒ \(p_2-p_1 = 4 T\left(\frac{1}{r_2}-\frac{1}{r_1}\right)=4 T\left(\frac{1}{0.03}-\frac{1}{0.04}\right)\)

= \(\frac{4 \times 100}{12} \times T\) ……(3)

But, for the common surface, \(p_2-p_1=\frac{4 T}{r}\)……..(4)

Comparing (3) and (4) we get, \(\frac{4 T}{r}=\frac{4 \times 100}{12} \times T\)

∴ r = 0.12 m.

 

Viscosity And Surface Tension Conclusion

Streamline flow: A smooth, uninterrupted flow of fluid in ordered layers, without any energy transfer between the layers, is called a laminar or streamline flow.

Streamline: In a smooth flow, the path along which any fluid particle moves is called a streamline.

Turbulent flow: If the velocity of a fluid along its flow continuously and randomly changes in magnitude and direction then it is called a turbulent or disorderly flow.

Viscosity: The property by virtue of which a liquid resists the relative motion between its adjacent layers is called viscosity of that liquid.

Velocity profile: The surface obtained by joining the terminal points of the velocity vectors of different layers of a flowing liquid at any section of it is called its velocity profile.

• In case of flow of a non-viscous liquid along a tube, the velocity profile becomes flat
• In case of flow of a viscous liquid along a tube, the velocity profile becomes parabolic.

Velocity gradient: In a horizontal streamline flow, the rate of change of velocity with distance \(\left(\frac{d u}{d x}\right)\) in a direction perpendicular to the flow of the liquid is called the velocity gradient. Dimension of velocity gradient \(\left(\frac{d u}{d x}\right)=\frac{\mathrm{LT}^{-1}}{\mathrm{~L}}=\mathrm{T}^{-1} .\)

Coefficient of viscosity: The tangential viscous force acting per unit area between two parallel liquid layers having unit velocity gradient between them is called the coefficient of viscosity of that liquid.

Units of coefficient of viscosity:

CGS system: dyn • s • cm^-2 or g • cm^-1 • s^-1 or poise

SI: N • s • m^-2 or Pa • s or kg • m^-1 • s^-1 or decapoise

Dimension of coefficient of viscosity: ML^-1T^-1.

• Usually the viscosity of a liquid increases with the increase in pressure and decreases with the increase in temperature.
• Pressure has almost no effect on the viscosity of a gas. With the increase in temperature, the viscosity of a gas increases.

Critical velocity: When the velocity of a fluid does not exceed a certain limiting value, the flow of the fluid remains streamline, but when the velocity exceeds that particular limiting value, the flow becomes turbulent. The limiting value of that velocity is called critical velocity.

Reynolds number N is a dimensionless quantity. For N< 2000, the fluid motion is streamlined. If N> 3000, then the fluid motion becomes turbulent. As the value of N gradually changes from 2000 to 3000, the pure streamline flow gradually changes into a fully turbulent flow.

Terminal velocity: When a body falls through a viscous medium under the influence of gravity, the viscosity of the medium offers resistance against its motion.

If the body is small, then after a certain time the magnitude of this upward viscous force become equal to the net force creating the motion. Then the body attains a uniform velocity through the medium. This uniform velocity of the body is called the terminal velocity.

Equation of continuity: In the case of streamline flow of a fluid (liquid or gas), the mass of fluid flowing per second through any cross-section of the tube of flow always remains constant. This is called the equation of continuity.

Bernoulli’s theorem: For the streamline flow of an ideal liquid, the sum of the potential energy, the kinetic energy, and the energy due to pressure per unit volume of the liquid remains constant at every point on the streamline. It leads to the relation

⇒ \(\frac{v^2}{2 g}+h+\frac{p}{\rho g}=\text { constant }\)

or, velocity head + elevation head + pressure head = constant.

Torricelli’s theorem: The velocity of efflux of a liquid, confined in a container through an orifice at some depth of the container is equal to the velocity acquired by a body falling freely from rest under gravity from the free surface of the liquid to the orifice.

Surface tension: Surface tension is a property of the free surface of a liquid due to which it behaves as a stretched thin membrane and has a tendency to con¬tract so as to minimise the surface area.

Units of surface tension:

• CGS system: dyn · cm^-1
• SI: N • m^-1

Dimension of surface tension: MT^-1.

Surface energy: The potential energy per unit area of the surface film is called surface energy.

or, surface energy = \(\frac{\text { work done in increasing the surface area }}{\text { increase in surface area }} \text {. }\)

• The surface energy per unit area is numerically equal to the surface tension of a liquid (if temperature remains constant)
• At any temperature except absolute zero, the total surface energy of a liquid is always greater than the surface tension.
• The surface tension of all liquids decreases with the rise in temperature. At the critical temperature of a liquid, the surface tension vanishes.
• If a liquid surface is contaminated with impurities, then the surface tension of that liquid usually decreases.
• If an inorganic substance is dissolved in a liquid, then the surface tension increases, but if an organic substance is dissolved, then the surface tension decreases.
• The presence of electric charges on the surface of a liquid causes a decrease in the surface tension.

Due to surface tension, capillary action is observed in liquids.

• When a liquid is in contact with a solid, the angle between the solid surface and the tangent to the free surface of the liquid at the point of contact, measured from inside the liquid is called the angle of contact for that specific pair of solid and liquid.
• If the angle of contact is less than 90°, then the liquid is said to wet the solid, and it rises in a capillary tube. But if the angle of contact is more than 90°, then the liquid does not wet the solid, and falls in a capillary tube.

Jurin’s law: The rise or fall of a liquid in a capillary tube is inversely proportional to the radius of the tube.

Viscosity And Surface Tension Useful Relations For Solving Numerical Problems

For two adjacent layers of a flowing liquid, if the opposing force acting is F, the area of the liquid surface is A and the velocity gradient is \(\frac{d v}{d x}\), then the coefficient of viscosity, \(\eta=\frac{F}{A \frac{d y}{d x}}\)

If Reynolds number is N, velocity of fluid flow is v, characteristic length of the fluid is l, the coefficient of viscosity is η and density of the fluid is ρ, then N = \(\frac{e l v}{\eta}\).

If a small sphere of radius r falls through a medium having a coefficient of viscosity η with a terminal velocity v, then the opposing force acting on the sphere due to viscosity is F = 6πηrv and the terminal velocity of the sphere is,

v = \(\frac{2}{9} \frac{r^2(\rho-\sigma) g}{\eta}\)

where ρ and σ are the densities of the material of the sphere and the material of the medium respectively.

If the cross-sectional area at any place of a tube of flow is a and the velocity of the fluid at that place is v, then the equation of continuity is expressed as, vα = constant.

Bernoulli’s theorem: \(\frac{v^2}{2 g}+h+\frac{p}{\rho g}\) = constant,

where \(\frac{v^2}{2 g}\) is the velocity head, h is the elevation head, and \(\frac{p}{\rho g}\) is the pressure head.

Torricelli’s theorem: The velocity of efflux of a liquid through an orifice situated at a depth h of its container is, v = √2gh

Surface tension = \(\frac{\text { tangential force }}{\text { length }}\)

Work done to increase the area of a liquid surface by unity at constant temperature = surface energy stored per unit area = surface tension.

If the radius of a capillary tube is r, the density’ of liquid is ρ the angle of contact of the liquid with respect to the material of the tube is θ and the surface tension of the liquid is T, then the rise of the liquid in that capillary tube is

h = \(\frac{2 T \cos \theta}{r \rho g}\)

The excess pressure inside a spherical drop or bubble \(p=\frac{2 T}{r}\)

where T = surface tension and r = radius of curvature

The excess pressure inside a spherical soap bubble \(p=\frac{4 T}{r}\)

where T = surface tension and r = radius of curvature.

Viscosity And Surface Tension Assertion Reason Type Question And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true statement n is a correct explanation for statement 1.
2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, statement 2 is true.

Question 1.

Statement 1: The stream of water flowing at high speed from a garden hose pipe tends to spread like a fountain when held vertically up, but tends to narrow down when held vertically down.

Statement 2: In any steady flow of an incompressible fluid, the volume flow rate of the fluid remains constant.

Answer: 1. Statement 1 is true, statement 2 is true statement n is a correct explanation for statement 1.

Question 2.

Statement 1: The viscosity of liquid increases with rise in temperature.

Statement 2: Viscosity of a liquid is the property of the liquid by virtue of which it opposes the relative motion amongst its different layers.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 3.

Statement 1: All the rain drops hit the surface of the earth with the same constant velocity.

Statement 2: An object falling through a viscous medium eventually attains a terminal velocity.

Answer: 1. Statement 1 is true, statement 2 is true statement n is a correct explanation for statement 1

Question 4.

Statement 1: Air flows from a small bubble to a large bubble when they are connected to each other by a capillary tube.

Statement 2: The excess pressure because of surface tension inside a spherical bubble decreases as its radius increases.

Answer: 1. Statement 1 is true, statement 2 is true statement n is a correct explanation for statement 1

Question 5.

Statement 1: When height of the tube is less than the rise in liquid in a capillary tube, the liquid does not overflow.

Statement 2: Product of radius of meniscus and height of liquid In the capillary tube always remains constant.

Answer: 1. Statement 1 is true, statement 2 is true statement n is a correct explanation for statement 1

Question 6.

Statement 1: It is easier to spray water in which some soap is dissolved.

Statement 2: Soap is easier to spread.

Answer: 3. Statement 1 is true, statement 2 is false.

Question 7.

Statement 1: A needle placed carefully on the surface of water may float, whereas a ball of the same material will always sink.

Statement 2: The buoyancy of an object depends both on the material and shape of the object.

Answer: 3. Statement 1 is true, statement 2 is false.

Question 8.

Statement 1: A large force is required to draw apart normally two glass plates enclosing a thin water film.

Statement 2: Water works as glue and sticks two glass plates.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 9.

Statement 1: Tiny drops of liquid resist deforming forces better than bigger drop.

Statement 2: Excess pressure inside a drop is directly proportional to surface tension.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 10.

Statement 1: The uplift of the wing of an aircraft moving horizontally is caused by a pressure difference between the upper and lower faces of the wing.

Statement 2: The velocity of air moving along the upper surface is higher than that along the lower surface.

Answer: 1. Statement 1 is true, statement 2 is true statement n is a correct explanation for statement 1