WBCHSE Class 11 Physics Notes For Newtonian Gravitation And Planetary Motion

 Newtonian Gravitation And Planetary Motion

Newtonian Gravitation And Planetary Motion Introduction: Since ancient times, scientists have been extremely curious to learn more about the stars and planets.

• Since the time of Copernicus, it is known that planets move around the sun. But to investigate the cause and nature of this motion, it was necessary to know the exact positions of the planets in the sky at different times.
• Astrophysicist Tycho Brahe, for many years, observed the positions of planets without a telescope (Galileo discovered the telescope after the death of Brahe) and published a lot of information about this.
• Kepler analysed the observational findings of Tycho Brahe and arrived at three laws about planetary motion. These laws are known as Kepler’s laws of planetary motion.

Read and Learn More: Class 11 Physics Notes

 Newtonian Gravitation And Planetary Motion – Kepler’s Laws

Kepler’s Laws First Law: Every planet moves in an elliptical orbit with the sun at one of its foci.

Kepler’s Laws Second Law: The line joining the sun and a planet sweep out equal areas in equal intervals of time, i.e., the areal velocity of a planet is constant.

Kepler’s Laws Third Law: The square of the time period of revolution of a planet is directly proportional to the cube of the length of the semi-major axis of its elliptical orbit.

The orbits of planets are known as Keplerian orbits while their motions are known as Keplerian motions.

Proof Of Kepler’s Second Law: Let us consider a planet of mass m moving in an elliptical orbit with the sun at focus S. Also, let \(\vec{r}\) be the position vector of the planet with respect to the sun and \(\vec{F}\) be the required centripetal force for the planet.

The torque exerted on this planet by this force about the sun, \(\)

(\(\vec{r}\) and \(\vec{F}\) are oppositely directed)

But \(\) (\(\vec{L}\) = angular momentum of the planet)

∴ \(\frac{d \vec{L}}{d t}=0 \quad \text { or, } \vec{L}=\text { constant }\)

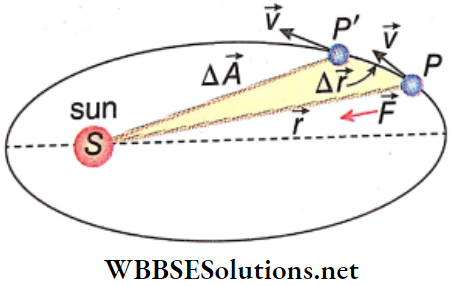
Now, if the planet moves from position P to P’ in very small time A t, then the area swept out by the radius vector \(\vec{r}\) is,

⇒ \(\Delta \vec{A}=\text { area of triangular region } S P P^{\prime}\)

= \(\frac{1}{2} \vec{r} \times \overrightarrow{P P^{\prime}}\)

Now, \(\quad \overrightarrow{P P^{\prime}} =\Delta \vec{r}=\vec{v} \Delta t=\frac{\vec{p}}{m} \Delta t\)

∴ \(\quad \Delta \vec{A}=\frac{1}{2} \vec{r} \times \frac{\vec{p}}{m} \Delta t\)

or, \(\quad \frac{\Delta \vec{A}}{\Delta t}=\frac{1}{2 m}(\vec{r} \times \vec{p})=\frac{\vec{L}}{2 m}\) (because \(\vec{L}=\vec{r} \times \vec{p}\))

Hence, \(\quad \frac{\Delta \vec{A}}{\Delta t}=\text { constant }\) (because \(\vec{L} \text { and } m\)) are constant

Thus, the areal velocity of the planet remains constant, i.e., the radius vector joining the sun and a planet sweeps out equal areas in equal intervals of time.

Gravitational Attraction Of Extended Bodies

Any extended body comprises a large number of particles. Thus, to find the mutual force of attraction between two extended bodies, the force of attraction between each particle of the first body and that of the second body is to be determined individually.

• The resultant of these forces, given by the vector addition method, gives the magnitude and direction of the force of attraction between the two extended bodies. Clearly, this method is complicated and unwieldy. This method can only be used in the case of regular-shaped bodies.
• But in the case of two extended bodies, however large they may be, if the distance separating them is much greater than their sizes, it can be assumed that the entire mass of each body is concentrated at its centre of mass. As a result, two extended bodies can be considered as two particles at their respective centres of mass.
• In this way, the complication involved in applying Newton’s law of gravitation may be removed. This approach can be applied to celestial bodies, like the earth and the moon, even if they are large in size and cannot be considered as particles.
• The distance between them is so large in comparison to their sizes that they may be considered as particles situated at their respective centres of mass for the purpose of measuring the gravitational force between them.

Now taking M = mass of the earth, m = mass of the moon and r = the distance between their centres of mass, the force of gravitation between them = \(\frac{G M m}{r^2}\).

When the distance between the two bodies is small compared to their sizes, this method of calculation fails.

When the gravitational attraction between a homogeneous spherical body and a particle situated outside the body is considered, it is assumed that the entire mass of the spherical body is concentrated at its centre of mass.

Hence, the earth, the sun, the moon and other planets are taken as spherical and the law is applied. A substance is called homogeneous when the physical properties (like density) of its different parts are identical.

Newtonian Gravitation And Planetary Motion – Sun Earth Moon Numerical Examples

Example 1. Assuming that the moon moves around the earth in a circular orbit of radius 3.8 x 10⁵ km in 27 days and the earth moves around the sun in a circular orbit of radius 1.5 x 10⁸ km in 365 days, find the ratio of the masses of the sun and the earth.
Solution:

From Kepler’s law, \(\frac{T^2}{r^3}\) = constant

where T = time period, r = radius of the orbit.

If the mass of the sun is M₀ and the radius of the earth’s orbit around the sun is r₀, the orbital speed,

⇒ \(v_0=\sqrt{\frac{G M_0}{r_0}}\)

∴ Time period T₀ of the earth = \(\frac{2 \pi r_0}{v_0}=2 \pi r_0 \sqrt{\frac{r_0}{G M_0}}=2 \pi \sqrt{\frac{r_0^3}{G M_0}}\)

Similarly, if the mass of the earth is M, the radius of the moon’s orbit is r, time period,

T = \(2 \pi \sqrt{\frac{r^3}{G M}}\)

∴ \(\frac{T}{T_0}=\sqrt{\left(\frac{r}{r_0}\right)^3 \frac{M_0}{M}} \text { or, }\left(\frac{T}{T_0}\right)^2=\left(\frac{r}{r_0}\right)^3 \cdot \frac{M_0}{M}\)

or, \(\frac{M_0}{M}=\left(\frac{T}{T_0}\right)^2 \cdot\left(\frac{r_0}{r}\right)^3=\left(\frac{27}{365}\right)^2 \cdot\left(\frac{1.5 \times 10^8}{3.8 \times 10^5}\right)^3\)

= 3.37 x 10⁵ = 337000

Hence, the sun is 337000 times more massive than the Earth.

Example 2. Find the mass of the sun considering the orbit of the earth to be circular. Given, a distance of the earth from the sun = 1.49 x 10¹³ cm and G = 6.66 x 10^-8 CGS unit.
Solution:

Let the mass of the sun be M₀, the distance of the earth from the sun r, and the time period of the earth around the sun T.

∴ Mass of the Sun, \(M_0=\frac{4 \pi^2 r^3}{G T^2}\)

= \(\frac{4 \times \pi^2 \times\left(1.49 \times 10^{13}\right)^3}{6.67 \times 10^{-8} \times(365 \times 24 \times 60 \times 60)^2}\)

= \(2 \times 10^{33} \mathrm{~g}=2 \times 10^{30} \mathrm{~kg}\)

Newtonian Gravitation And Planetary Motion – Mass And Average Density Of The Earth Numerical Examples

Example 1. The average density of the earth is 5500 kg · m^-3, the gravitational constant is 6.7 x 10^-11 N · m² · kg^-2 and the radius of the earth is 6400 km. Using the given values, find the magnitude of the acceleration due to gravity on the surface of the earth.
Solution:

It is known \(\rho=\frac{3 g}{4 \pi R G}\)

or, \(g=\frac{4 \pi \rho R G}{3}\)

g =\(\frac{4 \times 22 \times 5500 \times 6400 \times 10^3 \times 6.7 \times 10^{-11}}{7 \times 3}\)

= \(9.88 \mathrm{~m} \cdot \mathrm{s}^{-2} .\)

Example 2. If the earth is considered as a solid sphere of iron of; radius 6.37 x 10⁶ m and of density 7.86 g · cm^-3, what will be the magnitude of the acceleration due to gravity on the earth’s surface? Gravitational constant = 6.58 x 10^-8 CGS unit.
Solution:

It is known \(\rho=\frac{3 g}{4 \pi R G}\)

∴ g = \(\frac{4 \pi \rho R G}{3}=\frac{4 \times 22 \times 7.86 \times 6.37 \times 10^8 \times 6.58 \times 10^{-8}}{7 \times 3}\)

= \(1380.55 \mathrm{~cm} \cdot \mathrm{s}^{-2}\)

Newtonian Gravitation And Planetary Motion Conclusion

The force with which any two material particles in the universe attract each other is called gravitation.

Newton’s Law Of Gravitation: Any two material particles in the universe attract each other along their line of joining. This force of attraction is directly proportional to the product of the masses of the two particles and inversely proportional to the square of the distance separating them.

• The amount of force with which any two material particles of unit mass kept at a unit distance apart attract each other is called the gravitational constant.
• If a body of unit mass is kept at a point in any gravita¬tional field, the gravitational force acting on that body is called gravitational intensity at that point.
• The amount of work done to bring a body of unit mass from infinity to any point in a gravitational field is called the gravitational potential at that point.
• The force with which anybody on or near the earth’s surface is attracted by the earth is called gravity.
• The acceleration produced in a body falling under the influence of the force of gravity is called the acceleration due to gravity.

Kepler’s laws related to the motion of planets and satellites:

1. First Law: Keeping the sun at one of the foci, each planet revolves in an elliptical path around the sun.
2. Second Law: The line joining the sun and a planet covers equal areas in equal intervals of time.
3. Third Law: The square of the time period of revolution of a planet around the sun is directly proportional to the cube of the semimajor axis of its orbit.

The minimum velocity that should be given to a body so that it can escape from the earth or other planets or sat¬ellites is called its escape velocity.

Some uses of an artificial satellite:

1. Weather information,
2. Communication,
3. Military and defence surveillance,
4. Remote sensing.

If the relative angular velocity of an artificial satellite revolving in the equatorial plane is zero with respect to the diurnal motion of the earth, then, from the earth’s surface, the satellite appears to be at rest at the same place. This kind of satellite is called a geostationary satellite.

Newtonian Gravitation And Planetary Motion Useful Relations For Solving Numerical Problems

If the distance between two particles of masses m₁ and m₂ is r and if the mutual force of attraction between the two particles is F, then according to Newton’s law of gravitation,

F = \(\) where G is the gravitational constant whose value in SI is 6.67 x 10^-11 N · m² · kg^-2.

Gravitational intensity at a point situated at a distance r from the centre of a body of mass M is E = \(\frac{G M}{r^2}\)

Work done in bringing a body of unit mass from infinity to the position r, i.e., the gravitational potential at a distance r from the centre of a body of mass M is V = –\(\frac{G M}{r}\)

The relation between the gravitational field intensity and potential is E = \(\frac{d V}{d r}\)

Acceleration due to gravity at any point on the earth’s surface, g = \(\frac{G M}{R^2}\), where M is the mass and R is the radius of the earth, and G is the gravitational constant.

The relation between the gravitational constant G and the mean density (ρ) of the earth is \(\frac{3 g}{4 \pi R G}\).

1. The relation between the acceleration due to gravity at an altitude h above the surface of the earth (g’) and the acceleration due to gravity on the earth’s surface (g) is g’ = g(1-\(\frac{2h}{R}\)) (this equation is valid for h<<R)
2. The relation between the acceleration due to gravity at a depth h below the earth’s surface (g’) with the acceleration due to gravity on the earth’s surface (g) is g’ = g = (1-\(\frac{h}{R}\)
3. The value of the acceleration due to gravity at θ – latitude (g’) of the earth is \(g^{\prime}=g\left(1-\frac{\omega^2 R}{g} \cos ^2 \theta\right)\)
   1. At the poles, θ = 90° ; so, g’ = g.
   2. At the equator, θ = 0°; so, \(g^{\prime}=g\left(1-\frac{\omega^2 R}{g}\right)\)

If a planet of mass m revolves around the sun of mass M₀ along a circular path of radius r, then the orbital speed of that planet, v = \(v=\sqrt{\frac{G M_0}{r}}.\).

Orbital angular velocity, \(\omega=\sqrt{\frac{G M_0}{r^3}}\)

Time period of revolution, T = \(T=2 \pi \sqrt{\frac{r^3}{G M_0}}\)

The value of the escape velocity of a body from the surface of the earth, \(v_e=\sqrt{2 g R}.\).

If the mass of the earth = M, radius of the earth = R, mass of an artificial satellite = m, the orbital speed of the satellite = v and the height of the orbit above the surface of the earth = h, then the orbital speed of the artificial satellite, v \(=\sqrt{\frac{G M}{R+h}}\) and the time period of revolution of the satellite, T = \(2 \pi \sqrt{\frac{r^3}{8}}\), where r = R+h.

In the case of a satellite revolving very close to the surface of the earth, its orbital speed, \(v=\sqrt{g R}\)

and the time period of revolution, T = \(2 \pi \sqrt{\frac{R}{g}}\)

If the mass of the earth = M, the radius of the earth = R, the mass of a geostationary satellite = m, the distance of the satellite from the centre of the earth = r and its time period of revolution = T, then the orbital speed of the geostationary satellite,

v = \(\sqrt{\frac{g R^2}{r}}\)

and the height of the orbit of the geostationary satellite, r \(=\left(\frac{g R^2 T^2}{4 \pi^2}\right)^{1 / 3}\)

If an artificial satellite of mass m revolves along a circular path of radius r, the kinetic energy of the satellite,

K = \(\frac{G M M}{2 r}\) [where M = mass of the earth]

The potential energy is U = –\(\frac{G M m}{r}\)

Total energy of the satellite, E = –\(\frac{G M m}{2r}\)

Newtonian Gravitation And Planetary Motion Assertion Reason Type Questions And Answers

Direction: These questions have statement 1 and statement 2 of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, statement 1 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is true; statement 2 is false.

Question 1.

Statement 1: The force of gravitation between a sphere of mass M₁ and a rod of mass M₂ is = \(\frac{G M_1 M_2}{r} \text {. }\)

Statement 2: Newton’s law of gravitation holds correct for point masses.

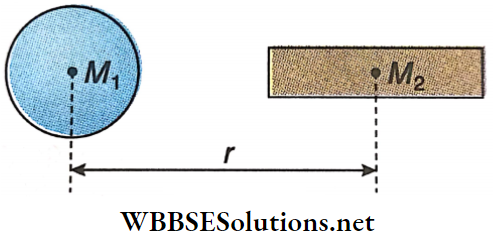
Answer: 4. Statement 1 is true; statement 2 is false.

Question 2.

Statement 1: An astronaut in an orbiting space station above the earth experiences weightlessness

Statement 2: An object moving around the earth under the influence of the earth’s gravitational force is in a state of free fall.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: If time period of a satellite revolving in a circular orbit in the equatorial plane is 24 h, then it must be a geostationary satellite.

Statement 2: Time period of a geostationary satellite is 24 hours.

Answer: 4. Statement 1 is true; statement 2 is false.

Question 4.

Statement 1: Gravitational force between two masses in the air is F. If they are immersed in the water force will remain F.

Statement 2: Gravitational force does not depend on the medium between the masses.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 5.

Statement 1: The binding energy of a satellite does not depend upon the mass of the satellite.

Statement 2: Binding energy is the negative value of the total energy of the satellite.

Answer: 4. Statement 1 is true; statement 2 is false.

Question 6.

Statement 1: Kepler’s laws for planetary motion are a consequence of Newton’s laws.

Statement 2: Kepler’s laws can be derived by using Newton’s laws.

Answer: 4. Statement 1 is true; statement 2 is false.

Newtonian Gravitation And Planetary Motion Match Column A With Column B.

Question 1.

Answer: 1. A, C, 2. A, B, C, D, 3. A, B, C, D, 4. A, C, D

Question 2. In Column A, four artificial satellites of Earth are shown. In Column B, some statements are given related to motion or other facts about the satellites.

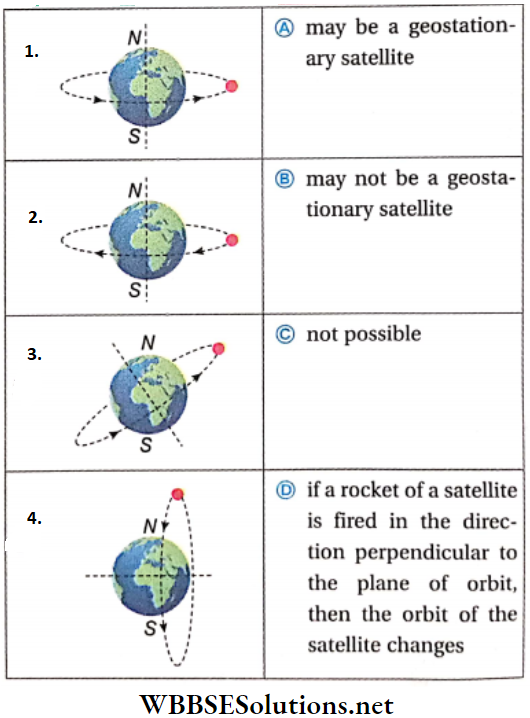
Answer: 1. A, D, 2. B, D, 3. B, D, 4. C

Question 3.

Answer: 1. C, 2. B, 3. A

Question 4. In the elliptical orbit of a planet, as the planet moves from the apogee position to the perigee position, match the following columns.

Answer: 1. C, 2. B, 3. B, 4. A

Newtonian Gravitation And Planetary Motion Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. The PE of the earth-satellite system is shown by a solid line as a function of distance r (the separation between the earth’s centre and satellite). The total energy of two objects which may or may not be bound to earth are shown in the graph by dotted lines,

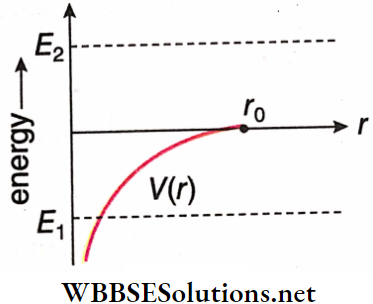
1. Mark the correct statement(s).

1. The object having total energy E₁ is the bounded one
2. The object having total energy E₂ is the bounded one
3. Both objects are bounded

Answer: 1. The object having total energy E₁ is the bounded one

2. If the object having total energy E₁ is having the same PE curve as shown, then

1. r₀ is the maximum distance of the object from the earth’s centre
2. This object and earth system is a bounded one
3. The KE of the object is zero when r = r₀
4. All of the above

Answer: 4. All of the above

3. If both the objects gave the same PE curve as shown, then

1. For the object having total energy E₂, all values of r are possible
2. For the object having total energy E₂ only values of r < r₀ are possible
3. For the object having total energy E₁ all values of r are possible
4. None of the above

Answer: 1. For the object having total energy E₂, all values of r are possible

Question 2. A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a. The centre of the shell falls on the surface of the inner sphere.

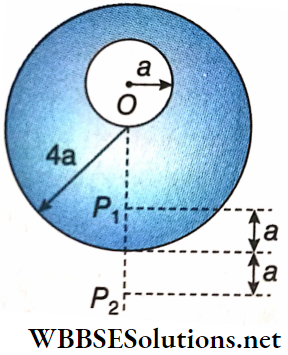
1. Find the gravitational field intensity at point P₁.

1. \(\frac{G M}{16 a^2}\)
2. \(\frac{G M}{8 a^2}\)
3. \(\frac{G M}{2 a^2}\)
4. \(\frac{G M}{4 a^2}\)

Answer: 1. \(\frac{G M}{16 a^2}\)

2. Find the gravitational field intensity at point P₂.

1. \(\frac{21 G M}{900 a^2}\)
2. \(\frac{61 G M}{450 a^2}\)
3. \(\frac{61 G M}{900 a^2}\)
4. \(\frac{61 G M}{1800 a^2}\)

Answer: 3. \(\frac{61 G M}{900 a^2}\)

Question 3. The gravitational field in a region is given by \(\vec{E}=\left(5 \mathrm{~N} \cdot \mathrm{kg}^{-1}\right) \hat{i}+\left(12 \mathrm{~N} \cdot \mathrm{kg}^{-1}\right) \hat{j}\)

1. Find the magnitude of the gravitational force acting on a particle of mass 2 kg placed at the origin.

1. 26 N
2. 30 N
3. 20 N
4. 35 N

Answer: 1. 26 N

2. Find the potential at the points (12 m, 0) and (0,5 m) if the potential at the origin is taken to be zero.

1. -30J · kg^-1_, -30 J · kg^-1
2. -40J · kg^-1_, -30 J · kg^-1
3. -60J · kg^-1_, -60 J · kg^-1
4. -40J · kg^-1_, -50 J · kg^-1

Answer: 3. -60J · kg^-1_, -60 J · kg^-1

3. Find the change in gravitational potential energy if a particle of mass 2 kg is taken from the origin to the point (12 m, 5 m).

1. -225 J
2. -240 J
3. -245 J
4. -250 J

Answer: 2. -240 J

4. Find the change in potential energy if the particle is taken from (12 m, 0) to (0,5 m).

1. -10 J
2. -50 J
3. Zero
4. -60 J

Answer: 3. Zero

Newtonian Gravitation And Planetary Motion Integer Answer Type Questions

In this type, the answer to each of the questions Is a single-digit integer ranging from 0 to 9.

Question 1. Gravitational acceleration on the surface of a planet is (√6/11)g, where g is the gravitational acceleration on the surface of the earth. The average mass density of the planet is \(\frac{2}{3}\)times that of the earth. If the escape speed on the surface of the earth is taken to be 11 km · s^-1, the escape speed on the surface of the planet in km · s^-1 will be
Answer: 3

Question 2. A binary star consists of two stars A (mass 2.2 M_s) and B (mass 11 M_s), where M_s is the mass of the sun. They are separated by distance d and are rotating about their centre of mass, which is stationary. The ratio of the total angular momentum of the binary star to the angular momentum of star B about the centre of mass is
Answer: 6

Question 3. A particle is projected vertically upwards from the surface of the earth of radius R, with a kinetic energy equal to half of the minimum value needed for it to escape. The maximum height to which it rises above the surface of the earth is nR. What should be the value of n?
Answer: 1

Question 4. The time period of a satellite A, whose orbital radius is r₀, is T₀ and the time period of a satellite B having radius 4r₀ is T_B. Find the ratio of T_B and T₀.
Answer: 8

Question 5. Two particles of masses m₁ and m₂ are kept at a separation of r. When a third particle is kept at a distance of \(\frac{d}{3}\) from m, then it does not experience any net force. Determine the ratio \(\frac{m_2}{m_1}\).
Answer: 4