WBCHSE Class 11 Physics Notes For Kinetic Theory Of Gases

Kinetic Theory Of Gases

Molecular Concept Of Matter And Its Applications

For centuries, scientists have studied the structure of matter—how it is formed and which are its smallest entities, possessing properties identical to that of the matter itself.

• In the early nineteenth century, Dalton and Avogadro for the first time proposed the theory of molecular structure of matter.
• A molecule is the smallest entity and matter is composed of molecules having all the chemical properties of the matter itself.
• The physical quantities related to molecules are number of molecules in a material body, molecular velocities, intermolecular distances, intermolecular forces, etc.
• These are the internal microscopic properties of a body. Unfortunately, these properties cannot be measured directly through experiments. As a result, we have to start with certain basic assumptions (postulates) about the behaviour of molecules.
• This gives us a picture of how molecules behave in a body. This is known as the molecular model. The next step is the application of Newton’s laws of motion on the molecules.

Now, the experimentally determined properties of a body as a whole, like pressure, temperature, and internal energy, are expected to be intimately related to the molecular model.

So Newton’s Jaws should give us expressions leading to these Bulk properties. This is essentially the object of the kinetic theory of matter.

• In short, the subject of study in which theoretical expressions of the bulk properties of a body are tamed from the application of Newton’s laws of motion on the internal molecular behaviour is called the kinetic theory of matter.
• Naturally, the values from the theoretical expressions of kinetic theory should match the experimental values. The formulas obtained from kinetic theory should be identical to the experimentally obtained thermodynamic formulas. This is actually the pre-condition for the success of kinetic theory.

This condition is beautifully obeyed in case of gases, leading to the very successful and advanced theory of the kinetic theory of gases. But this is not the case with liquids or solids. Partially successful molecular models exist for solids, but almost none so far has been developed for liquids.

Evidence of molecular motion: Molecules cannot be observed directly, but some natural phenomena clearly indicate the existence of molecular motion.

1. Diffusion: Let a gas jar filled with hydrogen gas be held upside down on another gas jar filled with carbon dioxide gas. Now the lids are removed. After an interval of time, it will be observed that the two gases will produce a homogeneous mixture in the two jars, ignoring gravitation.

• This phenomenon is called diffusion of the two gases. Clearly, molecular motion is evident in this phenomenon. Though carbon dioxide is heavier than hydrogen, CO₂ molecules move up and the hydrogen molecules move down to produce the mixture.
• The molecules of a gas randomly move at different velocities in all directions.
• So the molecules of the two gases mix and produce a homogeneous mixture. Diffusion takes place in liquids and solids also.
• If a few granules of copper sulphate are dropped at the bottom of a container filled with water, the blue colour gradually spreads throughout the whole volume of water.
• The density of copper sulphate solution is more than the density of water.
• But the solution moves up ignoring gravitation and after an interval of time, the whole mixture turns blue.
• It is an example of the motion of copper sulphate molecules diffusing into water. In a similar manner, solid phosphorus or boron can be diffused at high temperatures into solid silicon crystals to produce extrinsic semiconductors.
• In general, diffusion can be defined as the phenomenon by virtue of which movement of molecules occurs from a region of higher concentration to a region of lower concentration in a mixture till a homogeneity of concentration is established.

2. Vaporisation and vapour pressure: Liquid molecules are in motion inside the liquid. They move randomly at different velocities. Some molecules rise to the liquid surface with sufficient kinetic energy and overcome the attraction of other molecules inside the liquid.

• As a result, they may escape from the liquid. This phenomenon is called evaporation. Again, kinetic energies of molecules may be increased by applying heat. Hence, more molecules may escape from the liquid and vaporisation may occur.
• If a liquid is enclosed in a container, molecules leaving the liquid move randomly above the liquid surface. They collide with each other and hit the surface again and again. Some molecules may enter the liquid again. This leads to the vapour pressure corresponding to the vapour above the liquid surface.
• At a particular higher temperature, the kinetic energies of the molecules of the liquid become very high. In comparison, the potential energies due to intermolecular attractions become negligible. So the molecules are effectively free and all of them try to come out of the liquid at the same time. This phenomenon is called boiling of the liquid.

3. Expansion of gas: A gas spreads throughout the whole volume of its container. If the volume of the container increases, the gas spreads again to occupy the whole volume. This shows the property of random and unrestricted motion of the gas molecules.

4. Brownian motion: Very small, but still visible particles are often present as impurities in a liquid or in a gas. Observations through microscopes show that these particles move in a very random manner in all possible directions. This is known as Brownian motion.

This phenomenon can be explained by the concept of molecular motion. Molecules inside a liquid or a gas move randomly in all directions and collide time and again with small foreign particles (called Brownian particles). These collisions are directly responsible for the Brownian motion.

Kinetic Theory Of Gases Brownian Motion

British scientist, Robert Brown, first observed this continuous and irregular motion of the particles with a powerful microscope. He put some pollen grains in water.

• These grains, being very light, remained suspended in water. Brown noticed the random, continuous, and to and fro motion of these grains. However he was not able to determine the mechanisms that caused this motion.
• Albert Einstein published a paper in 1905 that explained in precise detail how the motion that Brown had observed was a result of the pollen being moved by individual water molecules.
• Brownian motion of a particle is shown. Colloids in a colloidal solution, very small feathers suspended in air, etc., are examples of randomly moving Brownian particles.

Explanation of the origin of Brownian motion: Just after the discovery of Brownian motion, scientists assumed that the reason of the origin of Brownian motion was a chemical reaction, irregular change of temperature, surface tension of liquid, etc. However from various experiments, it was proved that these explanations were not correct.

• It became possible to explain Brownian motion with the help of kinetic theory. We know that liquid or gas molecules are moving randomly and colliding with floating particles at every instant and from all directions.
• The force exerted on a floating particle of big size in any direction, due to some colliding molecules, is cancelled by the equal and opposite force due to some other molecules.
• As a result, the resultant force acting on the floating particle becomes zero and it has no Brownian motion. But if the floating particle is very tiny in size, the resultant force on it does not become zero as the colliding particles do not exert force equally from all directions.
• Hence, the floating particle moves along the direction of the resultant force and Brownian motion is observed. As molecular thrusts are random, the magnitude of the resultant force is not equal always.
• Also, the resultant force does not act always in the same direction. So the floating particle moves in a random manner in all possible directions.

Characteristics of Brownian motion:

1. The motion is perpetual, spontaneous, random and continuous. Itoo Brownian particles, even at close proximity, do not have identical motion.
2. The motion does not depend on the motion of the container.
3. The velocities of the particles increase with rise in temperature.
4. Smaller particles have higher average velocities.
5. The velocities of the particles become higher in liquids with lower viscosity.
6. The motion depends only on the mass and the size of the particle and not on the material it is made of.

Kinetic Theory Of Gases – Basic Assumptions Of Kinetic Theory Of Gases

A gas is made of atoms and molecules. The three variables—volume, pressure, and temperature, are all consequences of the motion of the molecules.

• The kinetic theory of gases relates the motion of the molecules to the volume, pressure, and temperature of the gas. Actually, the kinetic theory of gases explains the macroscopic properties of the gases, though it is a microscopic mode.
• Rudolf Clausius and James Clark Maxwell developed the kinetic theory of gases and explained gas laws in terms of motion of the gas molecules.
• In order, to formulate the kinetic theory of gases some simplifying assumptions are made about the behavior of the molecules of the ideal gas. The assumptions are

1. A gas is composed of a large number of molecules. For a particular gas, the molecules are identical. But they are different for different gases.
2. Every gas molecule behaves as a point mass. So the sum of their volumes is negligible compared to the volume of the container. The intermolecular space in the container is an empty space.
3. The molecules are in continuous and random motion in all possible directions. The value of molecular velocities varies from zero to infinity.
4. During random motion, the molecules collide with each other and with the walls of the container. These collisions are perfectly elastic. This means that the velocity changes due to collision, but the net momentum and kinetic energy remain unchanged.
5. The average distance between the molecules is sufficiently large, so that the attractive or repulsive forces between them are negligible except during collision. As a result,
   • Molecular motion is unrestricted and the gas spreads throughout the inner volume of its container
   • The potential energy of a molecule is negligible, the total energy comes from its kinetic energy only
   • Between two collisions, a molecule moves with uniform velocity (according to Newton’s first law of motion). The straight line path between two successive collisions is called a free path.
6. Every collision is instantaneous the time of a collision is negligible compared to the time taken by a molecule to describe a free path.
7. The gas is homogeneous and isotropic. This means that the properties of the gas in any small portion are identical to those in any other equivalent portion anywhere inside the container.

A gas obeying the properties outlined in these assumptions is called an ideal gas or a perfect gas. Real gases show some deviations from these properties. Real gases available to us are good approximation of an ideal gas at low pressure and high temperature.

The kinetic theoretical definitions of mass and volume of a gas are obtained directly from the above assumptions:

1. The mass of a gas is defined as the sum of the masses of the constituent molecules.
2. The volume of a gas is defined as the inner volume of the gas container.

Mean free path: The straight line path described by a molecule between two collisions is called a free path.

• The gas molecules move randomly. As a result, the lengths of the free paths vary in an irregular manner. So, to get a concrete picture, the Idea of a mean-free path becomes essential.
• It is the average distance that a molecule can travel between two successive collisions.

Mean free path Definition: The mean value of the distance travelled by a molecule between two successive collisions Is called the mean free path (λ).

• In other words, if a molecule suffers N number of collisions with other molecules when it travels through a total distance d, then the mean free path is, \(\lambda=\frac{d}{N}\).
• The basic assumptions of kinetic theory describe every molecule as a point mass. But the value of mean free path becomes theoretically infinite if the molecules are treated as geometrical points.
• So some deviations from the assumptions, are necessary. Every molecule is assumed to be a very small hard sphere of non-zero radius. Then it is possible to get an effective theoretical value of the mean free path.

An expression for the free path: Let σ = diameter of each molecule of the gas n = number of molecules per unit volume = number density of the molecules.

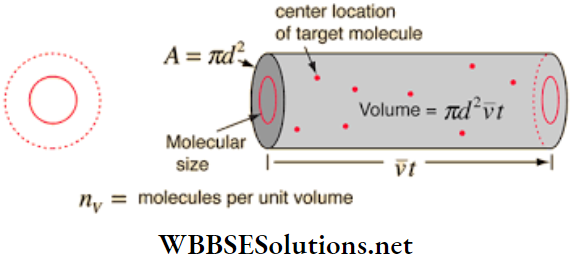
Let us consider a particular molecule of the gas moving with a velocity v at an instant of time. It will collide with all molecules whose centres come at a distance of cr or less along its line of motion. Now we choose a cylinder of radius cr and of length v. Clearly,

1. The axis of this cylinder is the path described by the chosen molecule in unit time, and
2. All other molecules, whose centers come within this cylinder, collide with the chosen molecule in that unit time.

The volume of this cylinder = cross-sectional area x length = πσ²v, and the number of molecules having centres in this volume = πσ²vn. So, the number of collisions per unit of time, N = πσ²vm.

The mean free path of the molecules is, therefore,

= \(\frac{\text { path described by a molecule }(d)}{\text { number of collisions }(N)}=\frac{\nu}{\pi \sigma^2 v n}\)

i.e., \(\lambda=\frac{1}{\pi \sigma^2 n}\)….(1)

This equation (1) shows that the mean free path (λ) of gas molecules is

1. Inversely proportional to the number of gas molecules (n) in a unit volume of the gas and
2. Inversely proportional to the square of molecular diameter (σ).

So, \(\lambda \propto \frac{1}{n} and \lambda \propto \frac{1}{\sigma^2}\),

i.e., \(\lambda \propto \frac{1}{\sigma^2 n} or, \lambda=\frac{k}{\sigma^2 n}\)

The constant k in equation (1) is \(\frac{1}{\pi}\). However, it has been estimated by different scientists by different other methods. The estimates give different results, but the value of k is always slightly greater or slightly less than 1. Then, the approximate expression for the mean free path is \(\lambda=\frac{1}{\sigma^2 n}\).

Kinetic Theory Of Gases – Mean Speed And Root Mean Square Speed of Gas Molecule

Molecular velocity is a vector quantity. The number of gas molecules in any container is very large. So the velocity vectors are oriented randomly in all possible directions.

• As a result, the resultant velocity vector must be zero. Consequently, the mean velocity of the molecules is also zero. Clearly, this zero value is useless as it gives no information about the order of magnitude of the molecular velocities.
• Alternatively, we may take the magnitudes only of the molecular velocities to calculate the mean. Certainly, it is non-zero and a useful quantity. We also know the molecules move in straight lines between collisions.
• So the magnitude of molecular velocity is actually the molecular speed. The calculated mean velocity is essentially the mean speed of the molecules. However, mean speed is often loosely termed as mean velocity.

Let N be the number of molecules of a gas in a closed container and, at any instant, c₁, c₂, c₃…..c_N be the magnitudes of velocities of the N molecules, respectively.

So, mean velocity or mean speed of the molecules, \(\bar{c}=\frac{c_1+c_2+c_3+\cdots+c_N}{N}\)

Mean square velocity of the molecules is defined as the mean of the squares of velocities,

⇒ \(\overline{c^2}=\frac{c_1^2+c_2^2+c_3^2+\cdots+c_N^2}{N}\)

Root mean square speed or rms speed of the molecules, defined as the square root of mean square speed,

c = \(\sqrt{\overline{c^2}}=\sqrt{\frac{c_1^2+c_2^2+c_3^2+\cdots+c_N^2}{N}}\)

The mean velocity \(\bar{c}\) and the rms speed c of the gas molecules in a container are not equal. For example, let us take three molecules with velocities 40 m · s^-1, 80 m · s^-1, and 120 m · s^-1.

Then, \(\bar{c}=\frac{40+80+120}{3}=80 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

c = \(\sqrt{\frac{(40)^2+(80)^2+(120)^2}{3}}=86.4 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

In general, the rms speed is slightly greater than the mean velocity. In kinetic theory, the role of the rms speed is comparatively more important than that of the mean velocity.

 

 

Unit 9 Behavior Of Perfect Gas And Kinetic Theory Chapter 1 Kinetic Theory Of Gases

Deduction Of Difference Gas Laws From Kinetic Theory Of Gases

We have so far developed the kinetic theory of gases to a certain stage. Now it Is possible to see that the theoretical result of kinetic theory matches exactly with the thermodynamic gas laws obtained from experiments. This proves the success of the kinetic theory of gases.

1. Boyle’s law: According to the kinetic theory of gases, \(T \propto E \text { and } E=\frac{3}{2} p V . \text { So, } p V \propto T\). If T = constant for a certain amount of gas, then pV = constant. This is Hoyle’s law.

2. Charles’ law: According to the kinetic theory of gases, \(T \propto E \text { and } E=\frac{3}{2} p V \text {. So } p V \propto T\). If p = constant for a certain amount of gas, then V ∝ T, This is Charles’ law.

3. Pressure law: According to the kinetic theory of gases, \(T \propto E \text { and } E=\frac{3}{2} p V \text {. So } p V \propto T\). If V = constant for a certain amount of gas, then p ∝ T. This is Charles’ law of pressure.

4. Joule’s law: According to the kinetic theory of gases, E = 3/2 RT. So E is a function of temperature only; it does not depend on the volume or pressure of the gas. This is Joule’s law or Mayer’s hypothesis, as discussed In the chapter First and Second Law of Thermodynamics,

5. Avogadro’s law: Let equal volumes of two gases be taken at the same pressure and temperature. The pressure, temperature, and volume are p, T, and V, respectively.

Now for the first gas,

N₁ = total number of molecules in the container,

m₁ = mass of each molecule,

c₁ = rms speed of the molecules.

Then, \(n_1=\frac{N_1}{V}\) = number of molecules per unit volume. According to kinetic theory, the pressure of the gas,

p = \(\frac{1}{3} m_1 n_1 c_1^2=\frac{1}{3} m_1 \frac{N_1}{V} c_1^2\)

Pressure being the same, so we get similarly for the second gas,

p = \(\frac{1}{3} m_2 \frac{N_2}{V} c_2^2 .\)

So, \(\frac{1}{3} m_1 \frac{N_1}{V} c_1^2=\frac{1}{3} m_2 \frac{N_2}{V} c_2^2\)

or, \(m_1 N_1 c_1^2=m_2 N_2 c_2^2\)…..(1)

Again, the temperature of the two gases is the same. So the average kinetic energy of a molecule is equal for the two gases. This means that

⇒ \(\frac{1}{2} m_1 c_1^2=\frac{1}{2} m_2 c_2^2 \text { or, } m_1 c_1^2=m_2 c_2^2\)….(2)

From relations (1) and (2), we get N₁ = N₂. So, equal So, pV = RT (1 mol of an ideal gas) volumes of different gases, at the same pressure, and Equation (4) is known as the ideal gas equation temperature, contains an equal number of molecules. This is Avognclro’s law.

6. Dalton’s law of partial pressure: The pressure of a gas mixture on the walls of its container is equal to the sum of the partial pressures exerted by constituent gases separately, at same temperature as that of the mixture, provided that the gases do not react chemically with each other—this is Dalton’s law.

Let several gases be mixed in a closed container. Their densities are, ρ₁, ρ₂, ρ₃…… and the molecular rms speeds are c₁, c₂, c₃ ….. respectively. Every gas molecule moves with its own kinetic energy, which does not depend on the motion of the other molecules. So, the net pressure on the container will be the sum of the pressures exerted by all individual molecules. Then, the pressure of the gas mixture is

p = \(\frac{1}{3} \rho_1 c_1^2+\frac{1}{3} \rho_2 c_2^2+\frac{1}{3} \rho_3 c_3^2+\cdots\)….(3)

= \(p_1+p_2+p_3+\cdots\)…..(3)

Here, p₁, p₂, p₃,……. are the partial pressures of the first second, third, … gases on the walls of the container. So equation (3) expresses Dalton’s law of partial pressure.

7. Graham’s law of diffusion: The rate of diffusion of a gas in a mixture is inversely proportional to the square root of the density of the gas—this is Graham’s law.

Let the densities of two gases be ρ₁ and ρ₂ and the rms velocities of the molecules be c₁ and c₂, respectively. The gases are allowed to diffuse with each other at the same temperature and same pressure. The diffusion is due to the motion of molecules so the rate of diffusion is clearly proportional to the rms speed of the molecules.

Now, p = \(\frac{1}{3} \rho_1 c_1^2=\frac{1}{3} \rho_2 c_2^2\)

or, \(\rho_1 c_1^2=\rho_2 c_2^2 or, \frac{c_1}{c_2}=\sqrt{\frac{\rho_2}{\rho_1}}\).

As, rate of diffusion r  ∝ c, we have \(\frac{r_1}{r_2}=\frac{c_1}{c_2}, i.e., \quad \frac{r_1}{r_2}\)= \(\sqrt{\frac{\rho_2}{\rho_1}}\)

or, \(r \propto \frac{1}{\sqrt{\rho}}\).

This is Graham’s law.

8. Ideal gas equation: According to the kinetic theory of gases, \(T \propto E \text { and } E=\frac{3}{2} p V \text {. So, } p V \propto T \text {. }\). Then, pV = kT, where k is a constant. For 1 mol of an ideal gas, this constant k is called the universal gas constant, denoted by R.

So, pV= RT (1 mol of an ideal gas)…(4)

Equation (4) is known as the ideal gas equation.

Unit 9 Behavior Of Perfect Gas And Kinetic Theory Chapter 1 Kinetic Theory Of Gases

Limitations Of Ideal Gas Laws

If a gas obeys Boyle’s law and Charles’ law accurately, then it is called an ideal gas. But in practice, real gases do not obey these ideal gas conditions in all circumstances.

Usually, a real gas behaves as an ideal gas at high temperatures and low pressures. But at low temperatures and high pressures, the behaviour deviates from that of an ideal gas.

The equation of state for 1 mol of an ideal gas is pV = RT. A real gas deviates from this equation chiefly due to the following two reasons:

1. The kinetic theory assumes that gas molecules are point masses and the volume of the molecules is negligible compared to the total volume of the gas. But every molecule, however small, has a finite volume. So their total volume is not always negligible.
   • In particular, at low temperatures and high pressures, the volume of a gas is comparatively small. In this case, the volume of the gas molecules becomes an important factor.
   • The effective volume for the motion of the molecules inside the gas container of volume V is reduced by an amount b (say). Then the equation of state for 1 mol of the gas becomes p(V-b) = RT.
2. The kinetic theory further assumes that the molecules do not attract one another. But in particular, at low temperatures and high pressures, the molecules come closer to one another.
   • As a result, the attractive forces are no longer negligible. Now, consider a molecule near the wall of the container. It experiences a resultant force towards the interior due to attractions by the other molecules. So it collides with the wall at a comparatively less velocity.

As a result, the pressure on the wall becomes less. Let p’ be the reduction of the pressure on the wall due to all these molecules, van der Waals established that \(p^{\prime}=\frac{a}{v^2}\) where a is a constant for a particular gas. Now, if p is the effective pressure on the wall, then the pressure would be \(p+p^{\prime} \text { or } p+\frac{a}{V^2}\) considering that the gas was ideal.

So the equation of state for 1 mol of a real gas becomes \(\left(p+\frac{a}{V^2}\right)(V-b)=R T\)….(1)

Equation (1) is called the van der Waals equation for a real gas. The constants a and b are known as van der Waals constants; their values depend on the nature of the gas. For n mol of a real gas, let V be its volume. Then molar volume = V/n.

Then, we get \(\left\{p+\frac{a}{(V / n)^2}\right\}\left\{\frac{V}{n}-b\right\}=R T\)

or, \(\left(p+\frac{a n^2}{V^2}\right)(V-n b)=n R T\)…(2)

This is the form of van der Waals equation for n mol of a real gas. It is to be noted that the van der Waals equation is only one of several equations of state of real gases, proposed by different scientists.

Unit 9 Behavior Of Perfect Gas And Kinetic Theory Chapter 1 Kinetic Theory Of Gases

Degree Of Freedom (DOF)

Degree Of Freedom Definition: The minimum number of independent coordinates necessary to specify the instantaneous position of a moving body is called the degree of freedom of the body.

Degree Of Freedom Example:

1. Let us consider the motion of a particle falling freely under gravity. We take the initial point as the origin and the downward line as the z-axis. Then the position of the particle at any instant is specified by the z-coordinate only.

So, the number of degrees of freedom of the particle is 1. Essentially, the degree of freedom of every one-dimensional motion is, for example, the motion of a car along a road, an ant moving on a stationary rope, etc.

2. Motions of projectiles under gravity, orbital motion of planets around the sun, circular motion, motion of an ant on the floor of a room, etc., are examples of two-dimensional motions, in each case, any one point on the plane, Is chosen as the origin and two perpendicular axes x and y are considered. Then the position of the object at any Instant Is specified by the x- and y- coordinates. So, the number of degrees of freedom in two-dimensional motion Is 2.

3. According to the kinetic theory, all gas molecules of an Ideal gas are point masses and they are In a completely random to-and-fro motion. At least three coordinates (say x, y, z) are necessary to specify the position of a molecule at any Instant.

So, the number of degrees of freedom of an Ideal gas molecule is 3. Essentially, every three-dimensional motion has 3 degrees of freedom, for example, Brownian motion, motion of a fly in a room, etc.

• In the above examples, the particle, the object, and the gas molecule all are considered to be as a point mass, which cannot undergo rotation, if the body is rigid and has a finite size, it can undergo rotation also, about any axis, So, a rigid body will have degrees of freedom both due to its translatory motion and rotatory motion.
• Like translatory motion, the rotatory can also be resolved into three mutually perpendicular components. Thus a rigid body has six degrees of freedom, 3 for translatory motion and 3 for rotatory motion.
• Now, let us consider a system of two particles or two-point masses. Each particle has three degrees of freedom, so the system has six degrees of freedom. If the two particles remain at a fixed distance from each other, then there is one definite relationship between them.
• These definite relationships are known as constraints. As a result, the number of independent coordinates required to describe the configuration of the system is reduced by one. Hence, the system has (6-1) = 5 degrees of freedom.

These 5 degrees of freedom may be interpreted in another way: degrees of freedom for the translatory motion of the centre of mass = 3 and degrees of freedom for the rotatory motion of the two particles around the center of mass = 2.

In a system consisting of N particles, if the particles possess k independent relations i.e., constraints among them, then the number of degrees of freedom of the system is given by, f = 3N – k.

Degrees of freedom of different types of gases:

1. Monatomic gas: The molecule of a monatomic gas (for example, neon, helium, argon, etc.) consists of a single atom (a point mass). At least three coordinates (say x, y, z) are necessary to specify the position of the molecule at any instant in the three-dimensional space. So, the number of degrees of freedom of a monatomic gas molecule, f = 3×1-0 = 3.

2. Diatomic gas: The molecule of a diatomic gas like hydrogen, oxygen, nitrogen etc. has two atoms in it. Two point atoms have a fixed distance between them (neglecting the vibration of the atoms in the molecules)

i. e., the number of constraints is 1. Here, N = 2 and k = 1

∴ f = 3×2-1 = 5

3. Triatomic gas: Triatomic gas molecules are of two types:

(1) In a linear molecule such as CO₂, CS₂ > HCN, etc. the three atoms are arranged in a straight line. The number of independent relations between them is only two.

∴ f = 3×3-2 – 7 i.e., such a molecule has seven degrees of freedom.

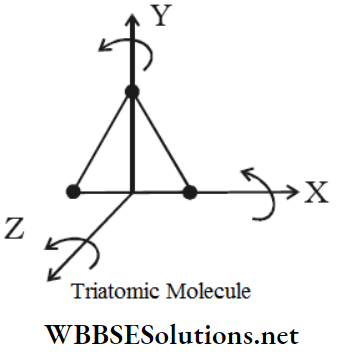
2. In a non-linear molecule like H₂O, SO₂, etc. the three atoms are located at the three vertices of a triangle. Hence, there are three fixed distances among the three atoms.

∴ f = 3×3-3 = 6

Therefore, a non-linear triatomic molecule has six degrees of freedom.

Degrees of freedom in different cases:

 

 Kinetic Theory Of Gases Conclusion

The subject of study in which theoretical expressions on the bulk properties of a body are obtained from the application of Newton’s laws of motion on the internal molecular behavior is called the kinetic theory of matter. This approach has been highly successful for gases.

• The random and perpetual motion of very small particles present as impurities in a liquid or gas is known as Brownian motion. This happens due to random collisions of the Brownian particles with the molecules in matter. This motion furnishes evidence of the molecular model.
• The kinetic theory of gases relates the motion of the molecules of the gas to the volume, pressure, and temperature of the gas. Actually, this theory explains the macroscopic properties of the gases with the help of microscopic parameters.

Three basic assumptions of the kinetic theory of gases are—

1. Molecules are point masses; the intermolecular space is much larger than the space occupied by the molecules.
2. The attraction between molecules is negligible. As a result, the molecular potential energy is zero, i.e., the energy is purely kinetic.
3. Molecular motion is continuous and random. A molecule may have any velocity between zero and infinity in any direction. A molecule may have any velocity between zero and infinity in any direction.

The straight-line path described by a molecule between two successive collisions is called a firepath. The mean value of the lengths of different free paths of different molecules of a gas is called the mean free path.

The pressure of a gas in a container depends on

1. The mass of a molecule,
2. The number of molecules in unit volume and
3. The average velocity of the molecules.

Temperature is a property of a gas, which is proportional to the total kinetic energy of the gas molecules.

Absolute zero temperature is the temperature at which the internal energy of the gas becomes zero, i.e., the molecular motion stops entirely.

The velocity which is possessed by the highest number of gas molecules in a container is called the most probable velocity.

Gases obeying Charles’ law and Boyle’s law perfectly are called ideal or perfect gases.

In general, real gases deviate from this ideal behavior, especially at

1. High pressures and
2. Low temperatures.

The minimum number of independent coordinates necessary to specify the instantaneous position of a moving particle is called the degree of freedom of the tire particle.

Principle of equipartition of energy: The average molecular kinetic energy of any substance is equally shared among the degrees of freedom; the average kinetic energy of a molecule per degree of freedom is 1/2 kT (T = absolute temperature and k = Boltzmann constant (1.38 x 10^-23 J · K^-1).

Kinetic Theory Of Gases Useful Relations For Solving Numerical Examples

Mean free path of a gas molecule (λ):

1. \(\lambda=\frac{d}{N}\) where d = total distance traveled by a molecule, N = total number of collisions suffered by that molecule through the distance d.

2. \(\lambda=\frac{1}{\pi \sigma^2 n}\) where, σ = diameter of each molecule of the gas, n = the number of molecules per volume i.e., the number density of the molecule.

Let c₁, c₂,…..c_N be the magnitudes of instantaneous velocities of N molecules in a gas. Then,

1. Mean velocity, \(\bar{c}=\frac{c_1+c_2+\cdots+c_N}{N}\)

2. Root mean square speed or rms speed, \(c=\sqrt{\frac{c_1^2+c_2^2+\cdots+c_N^2}{N}}\)

At absolute temperature T,

\(\begin{array}{|c|c|c|}
\hline \begin{array}{c}
\text { Average speed of } \\
\text { a gas molecule } \\
(c)
\end{array} & \begin{array}{c}
\text { rms speed of a } \\
\text { gas molecule } \\
(c)
\end{array} & \begin{array}{c}
\text { Most probable } \\
\text { speed of a gas } \\
\text { molecule }\left(c_m\right)
\end{array} \\
\hline \sqrt{\frac{8 k T}{\pi m}} & \sqrt{\frac{3 k T}{m}} & \sqrt{\frac{2 k T}{m}} \\
\hline
\end{array}\)

 

∴ \(\bar{c}: c: c_m=\frac{2}{\sqrt{\pi}}: \sqrt{\frac{3}{2}}: 1\)

Pressure of an ideal gas, p = \(\frac{1}{3} \rho c^2=\frac{1}{3} m n c^2\), where m- mass of a molecule, n = number of molecules in unit volume and ρ = mn = density.

The internal energy of a gas in a container, which is equal to the sum of the kinetic energies of the molecules, is

U = E = \(\frac{3}{2} p V ; \quad \text { So, } p=\frac{2}{3} \frac{E}{V}=\frac{2}{3} u \text {, }\)

where u = energy per unit volume.

• If M is the molecular weight of a gas, the rms speed of the molecules is related to temperature T of the gas by the relation, \(c=\sqrt{\frac{3 R T}{M}} \quad \text { or, } \quad c \propto \sqrt{T}\)
• The equation of state for 1 mol of an ideal gas is p V = R T.
• For real gases, volume and pressure corrections lead to the van der Waals equation of state:

⇒ \(\left(p+\frac{a}{V^2}\right)(V-b)=R T\)

• For n mol of real gas, van der Waals equation of state is \(\left(p+\frac{a n^2}{V^2}\right)(V-n b)=n R T\) [where, a, b are small positive constants ‘a’ is related to the average force of attraction between the molecules and ‘b’ Is related to the total volume of the molecules.
• The average kinetic energy of a gas molecule, e = \(\frac{3}{2} k T\)
• If some amount of gas contains N molecules, the total internal energy i.e., total kinetic energy, E = \(\frac{3}{2}Nk T\)
• For 1 mol of a gas, N = N_A = Avogadro’s number.
• Then, \(E=\frac{3}{2} N_A k T=\frac{3}{2} R T \text {, where } R=N_A k \text {. }\)
• Molar specific heat at constant volume, \(C_v=\frac{d Q}{d T}=\frac{d E}{d T}\)

If n₁ mol of a gas is mixed with n₂ mol of another gas (they do not react with each other), then,

1. Molar specific heat of the mixture at constant volume, \(C_\nu=\frac{n_1 C_{\nu_1}+n_2 C_{\nu_2}}{n_1+n_2}\) where, \(C_{\nu_1}\) = molar specific heat at constant pressure of 1st and 2nd gases respectively.

2. Molar specific heat of the gas mixture at constant pressure, \(C_p=\frac{n_1 C_{p_1}+n_2 C_{p_2}}{n_1+n_2}\) where, \(C_{p_1}\) and \(C_{p_2}\) are the molar specific heat at constant pressure of 1st and 2nd gases respectively.

3. The ratio of Cp and Cv for the mixture is,

⇒ \(\gamma=\frac{C_p}{C_v}=\frac{n_1 C_{p_1}+n_2 C_{p_2}}{n_1 C_{v_1}+n_2 C_{v_2}}\)

For 1 mol of a monatomic gas, \(C_\nu=\frac{d E}{d T}=\frac{3}{2} R ; C_p=C_\nu+R=\frac{5}{2} R ; \gamma=\frac{C_p}{C_\nu}=\frac{5}{3}\)

In general cases, if f is the number of degrees of freedom of an ideal gas molecule then \(C_\nu=\frac{f_2}{2} R ; C_p=\left(1+\frac{f}{2}\right) R ; \gamma=\frac{C_p}{C_\nu}=1+\frac{2}{f}\)

Kinetic Theory Of Gases Very Short Answer Type Questions

Question 1. What is the name of the smallest entity of matter that exhibits all the properties of that matter?
Answer: Molecule

Question 2. Which one of the following has the highest intermolecular force—solid, liquid, or gas?
Answer: Solid

Question 3. If a gas jar filled with a light gas like hydrogen is held side down on another gas jar filled with carbon dioxide, it is observed that the two gases produce a homogeneous mixture in the jars. What is the name of this process?
Answer: Diffusion

Question 4. How does the velocity of Brownian particles change due to the movement of the vessel?
Answer: No change occurs

Question 5. What is the direction of velocities of gas molecules according to the kinetic theory of gases?
Answer: All possible directions

Question 6. Gas molecules collide with each other and with the walls of the container. What is the type of these collisions? .
Answer: Perfectly elastic

Question 7. What do you call the straight line path described by a gas molecule between two successive collisions?
Answer: Free path

Question 8. Both vaporization and vapor pressure prove the ________ of molecules of a liquid.
Answer: Mobility

Question 9. Brownian motion supports the _______ of the matter.
Answer: Kinetic theory

Question 10. In Brownian motion in a medium, if the particles decrease in size, how does their velocity vary?
Answer: Increases

Question 11. Does the velocity of the particles increase or decrease, when the viscosity increases in Brownian motion in a medium?
Answer: Decreases

Question 12. Which gases obey the basic assumptions of the kinetic theory?
Answer: Ideal gases

Question 13. According to the kinetic theory of gases, every gas molecule behaves as a ________
Answer: Point mass

Question 14. According to the kinetic theory of gases, the velocity of gas molecules varies from ______ to ______
Answer: zero, infinity

Question 15. Which is greater rms speed or mean velocity?
Answer: rms speed

Question 16. Does the pressure of a gas increase or decrease when the velocity of the gas molecules increases?
Answer: Increases

Question 17. On which other factor does the pressure of a gas depend, besides the number of molecules per unit volume and the temperature of the gas?
Answer: Mass of the gas molecules

Question 18. Is the most probable velocity of gas molecules higher or lower than the mean velocity?
Answer: Lower

Question 19. Will the rms speed of oxygen and hydrogen gas molecules be the same at equal temperatures?
Answer: No, hydrogen gas will have a higher rms speed

Question 20. What is the ratio of the rms speeds of O₃ and O₂ at a certain temperature?
Answer: √2: √3

Question 21. By how many times will the pressure of a gas kept in a gas container of constant volume increase to double the rms speed of the gas molecules?
Answer: 4 times

Question 22. The velocities of the three gas molecules are 4cm · s^-1, 8 cm · s^-1, and 12 cm · s^-1, respectively. Calculate their rms speed.
Answer: 8.64 cm · s^-1

Question 23. What is the relation between rms speed and molecular mass of a gas?
Answer: rms speed is inversely proportional to the square root of the molecular mass of that gas

Question 24. Hydrogen and oxygen gases are kept in two vessels at the same temperature and pressure. What is the ratio of the rms speed of their molecules?
Answer: 4:1

Question 25. If a gas molecule of mass m and velocity u collides perpendicularly with a wall of a container, what will be the value of momentum of the molecule after the collision?
Answer: mu

Question 26. If n number of molecules, each having mass m and velocity u, perpendicularly hit the walls of a container in every second, what will be the value of the applied force?
Answer: 2mnu

Question 27. In the kinetic theory of gases, _____ is more important than mean velocity.
Answer: rms speed

Question 28. What is the name of the force that acts among the molecules of matter?
Answer: Intermolecular force

Question 29. Under which conditions do real gases behave as ideal gases?
Answer: At low pressure and high temperature

Question 30. Which property of a gas is proportional to the net internal energy of the gas molecules?
Answer: Temperature of the gas

Question 31. At which temperature does the kinetic energy of gas molecules become zero?
Answer: Absolute zero temperature

Question 32. To which gases is the van der Waals’ equation applicable?
Answer: Real gases

Question 33. If the temperature of a gas is increased at constant volume, how will the number of collisions of the molecules per unit time change?
Answer: Increase

Question 34. What is the dimension of an in van der Waals’ equation \(\left(p+\frac{a}{V^2}\right)(V-b)=R T?\)
Answer: ML^-3T^-2

Question 35. What is the dimension of b in van der Waals’ equation \(\left(p+\frac{a}{V^2}\right)(V-b)=R T?\)
Answer: L³

Question 36. What is the relation between the pressure p of a gas and its energy density?
Answer: \(\left[p=\frac{2}{3} u\right]\)

Question 37. According to the kinetic theory of gases, as there is no attractive force between the gas molecules, the entire energy of them is ______
Answer: Kinetic energy

Kinetic Theory Of Gases  Assertion Reason Type Question And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 Is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: The root mean square speeds of the molecules of different ideal gases at the same temperature are the same.

Statement 2: The average translational kinetic energy of molecules of a different ideal gas is same at the same temperature.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 2.

Statement 1: The rms speed of oxygen molecules (O₂) at an absolute temperature T is c. If the temperature is doubled and oxygen gas dissociates into atomic oxygen, the rms speed remains unchanged.

Statement 2: The rms speed of the molecules of a gas is directly proportional to √T/M.

Answer: 1. Statement 1 is true, and statement 2 Is true statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: The total translational kinetic energy of all the molecules of a given mass of an ideal gas is 1.5 times the product of its pressure and volume.

Statement 2: The molecules of a gas collide with each other and the velocities of the molecules change due to the collision.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 4.

Statement 1: The mean free path of gas molecules, varies inversely with the density of the gas.

Statement 2: The mean free path of gas molecules is defined as the average distance traveled by a molecule between two successive collisions.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 5.

Statement 1: The following show \(\frac{pV}{T}\) versus p graph for a certain mass of O₂ gas at two temperatures T₁ and T₂. It follows from the graph that T₁ > T₂.

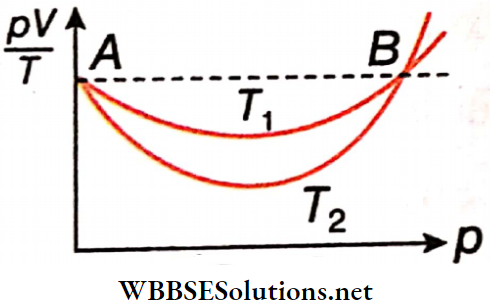
Statement 2: At higher temperatures, real gas behaves more like an ideal gas.

Answer: 1. Statement 1 is true, and statement 2 Is true statement 2 is a correct explanation for statement 1.

Question 6.

Statement 1: For an ideal gas, at a constant temperature, the product of the pressure and the volume is constant.

Statement 2: The mean square velocity of die molecules is inversely proportional to mass.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 7.

Statement 1: The total translational kinetic energy of all the molecules of a given mass of an ideal gas is 1.5 times the product of its pressure and volume.

Statement 2: The molecules of a gas collide with each other and the velocities of the molecules change due to the collision.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Kinetic Theory Of Gases Match Column 1 with Column 2

Question 1.

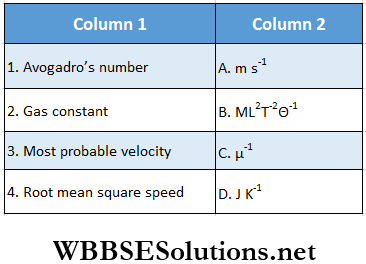
Answer: 1. C, 2. B, D 3. A, 4. A

Question 2.

Answer: 1. C, 2. B, 3. A

Question 3.

R = universal gas constant, f = number of degrees of freedom, T = temperature.

Answer: 1. C, 2. B, 3. A

Question 4. Match the following columns according to the graph.

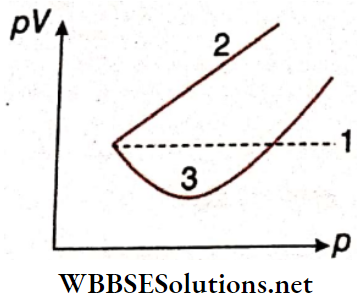
Answer: 1. C, 2. A, 3. B

Kinetic Theory Of Gases Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. The pressure exerted by an ideal gas is p = \(\frac{1}{3} \frac{M}{V} c^2\), where the symbols have their usual meanings. Using standard gas equation, pV = RT, we find that \(c^2=\frac{3 R T}{M} \quad \text { or } \quad c^2 \propto T\) Average kinetic energy of translation of 1 mol of gas = \(\frac{1}{2} M c^2=\frac{3 R T}{2}\)

1. Average thermal energy of a helium atom at room temperature (27°C) is (given, Boltzmann constant k= 1.38 x 10^-23 J · K^-1)

1. 2.16 x 10²¹ J
2. 6.21 x 10²¹ J
3. 6.21 x 10^-21 J
4. 6.21 x 10^-23 J

Answer: 3. 6.21 x 10²¹ J

2. Average thermal energy of 1 mol of helium at this temperature is (given, gas constant for 1 mol = 8.31 J · mol^-1 · K^-1)

1. 3.74 x 10³ J
2. 3.74 x 10^-3 J
3. 3.47 x 10⁶ J
4. 3.47X10^-6 J

Answer: 1. 3.74 x 10³ J

3. At what temperature, when pressure remains unchanged, will the rms speed of hydrogen double its value at STP?

1. 819 K
2. 819 °C
3. 1000K
4. 1000°C

Answer: 2. 819 °C

4. At what temperature, when pressure remains unchanged, will the rms speed of a gas be half its value at 0°C?

1. 204.75 K
2. 204.75 °C
3. -204.75 K
4. -204.75 °C

Answer: 4. -204.75 °C

Question 2. If c₁, c₂, c₃ …. are random speeds of gas molecules at a certain moment then average velocity c_av = \(\frac{c_1+c_2+c_3+\cdots+c_n}{n}\) and root mean square speed of gas molecules,

⇒ \(c_{\mathrm{rms}}=\sqrt{\frac{c_1^2+c_2^2+c_3^2+\cdots+c_n^2}{n}}=c.\)

Further, c² ∝ T or, c ∝ √T.

At 0 K, c =0, i.e., molecular motion stops,

1. If three molecules have velocities 0.5km · s^-1, 1 km · s^-1 and 2 km · s^-1, the ratio of rms speed and average velocity is

1. 0.134
2. 1.34
3. 1.134
4. 13.4

Answer: 3. 1.134

2. The temperature of a certain mass of a gas is doubled. The rms speed of its molecules becomes n times, where n is

1. \(\sqrt{2}\)
2. 2
3. \(\frac{1}{\sqrt{2}}\)
4. \(\frac{1}{2}\)

Answer: 1. \(\sqrt{2}\)

3. KE per molecule of the gas in the above question becomes x times, where x is

1. \(\frac{1}{2}\)
2. \(\frac{1}{4}\)
3. 4
4. 2

Answer: 4. 2

4. KE per mole of hydrogen at 100°C (given R = 8.31 J · mol^-1 · K^-1) is

1. 4946 J
2. 4649 J
3. 4496 J
4. 4699J

Answer: 2. 4649 J

5. At what temperature, when pressure remains constant, will the rms speed of the gas molecules be increased by 10% of? rms speed at STP?

1. 57.3 K
2. 57.3 °C
3. 557.3 K
4. -57.3 °C

Answer: 2. 57.3 °C

Question 3. A cubical box of side lm contains helium gas (atomic weight = 4) at pressure 10 N • m^-2. During an observation time of 1s, an atom traveling with rms speed parallel to one of the edges of the cube was found to make 500 hits with a particular wall without any collision with other atoms.

1. Evaluate the temperature of the gas.

1. 125K
2. 160K
3. 181K
4. 185K

Answer: 2. 160K

2. Evaluate the average kinetic energy per atom.

1. 3.31 x 10^-21 J
2. 3.75 x 10⁶ J
3. 3.81 x 10^-15 J
4. 3.22 x 10³ J

Answer: 1. 3.31 x 10^-21 J

3. Evaluate the total mass of the helium gas in the box.

1. 9×10^-4 kg
2. 5x 10^-3 kg
3. 3 x 10^-4 kg
4. 7 x 10^-3 kg

Answer: 3. 7 x 10^-3 kg

Kinetic Theory Of Gases Integer Answer Type Questions

In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.

Question 1. Two identical cylinders contain helium at 3.5 standard atmospheres and argon at 2.5 standard atmospheres respectively. If both these gases are filled in one of the cylinders, what would be the pressure of the mixture?
Answer: 6

Question 2. The rms speed of molecules of a gas at -73 °C and 1 standard atmosphere pressure is 100 m · s^-1. The temperature of the gas is increased to 527°C and pressure is doubled. The rms speed becomes k times. What is the value of k?
Answer: 2

Question 3. The density of a gas is 6 x 10^-2 kg· m^-3 and the root mean square speed of the gas molecules is 500 m · s^-1. The pressure exerted by the gas on the walls of the vessel is n x 10³ N · m^-2. Find the value of n.
Answer: 5

Question 4. A gas has molar heat capacity c = 37.55 J · mol^-1 · K^-1, in the process pT = constant. Find the number of degrees of freedom of the molecules of the gas.
Answer: 5

Question 5. A vessel has 6g of hydrogen at pressure p and temperature 500 K. A small hole is made in it so that hydrogen leaks out How much hydrogen (in g) leaks out if the final pressure is \(\frac{p}{2}\) and temperature falls to 300K?
Answer: 1