WBCHSE Class 11 Physics Notes For Expansion Of Gases

Expansion Of Gases Introduction

Gases expand on heating and contract on cooling, like solids and liquids. Like liquids, gases too do not have any fixed shape and therefore the linear or the surface expansion of a gas is irrelevant.

Only the change in volume with the change in temperature is of importance. Other characteristic features of gaseous expansions, compared to those of solids and liquids, are discussed below.

1. The coefficient of volume expansion for a gas has a much higher value than that for solids and liquids. For a certain rise in temperature, the expansion of the container is negligible compared to the expansion of the gas in it. Hence, the apparent expansion of gas is practically the same as real expansion and is usually not reckoned separately unless a very high accuracy is required.
2. Unlike solids and liquids, the volume of a fixed mass of a gas is considerably affected due to any change in pressure. So, the effects of both temperature and pressure have to be studied in connection with the expansion or contraction of a gas. While studying the effect of one, the other is usually kept constant.
3. The rate of expansion or contraction, due to the change in either pressure or temperature, does not differ for different gases. Unlike solids and liquids, the coefficient of expansion is the same for all gases.

The state of a fixed mass of gas is therefore determined by the parameters

1. Volume,
2. Pressure and
3. Temperature.

The rules, that govern the change of one parameter with the change of another keeping the third one constant, are called gas laws.

1. It should be mentioned here that the pressure of a gas means the pressure exerted by the gas. In equilibrium (i.e., when each parameter of the gas is a constant) the pressure exerted by the gas and the pressure applied on the gas are equal.
2. The gas which follows Boyle’s law and Charles’ law at any temperature and pressure is called an ideal gas. In reality, an ideal gas does not exist. However, the ideal gas concept provides a very useful tool for the analysis of real gases.

 Expansion Of Gases Charles Law

The relationship between the volume and temperature of a fixed mass of gas at constant pressure was investigated experimentally by the French scientist Charles in 1787.

• He concluded that at constant pressure a fixed volume of all gases would expand by the same amount for an equal rise in temperature. Gay Lussac arrived at almost the same result in 1802.
• He found that the coefficient of volume expansion of all gases has the same value if pressure is kept constant. In 1842 Regnault showed that the experimental value of this coefficient is 1/273 per degree Celsius.
• Charles’ law is enunciated by combining the experimental results of Gay Lussac and Regnault.

Statement: When pressure is kept constant, the volume of a fixed mass of gas increases or decreases by 1/273 th part of its volume at 0°C, for each degree Celsius rise or fall in temperature.

Mathematical expression: Let V₀ be the volume of a mass m of a gas at 0°C. As per Charles’ law, the volume at 1°C will be

⇒ \(V_1=V_0+\frac{V_0}{273}=V_0\left(1+\frac{1}{273}\right)\)

The volume of the gas at \(2^{\circ} \mathrm{C}\),

⇒ \(V_2=V_0+\frac{2 V_0}{273}=V_0\left(1+\frac{2}{273}\right)\)

∴ The volume of the gas at \(t^{\circ} \mathrm{C}\),

⇒ \(V_t=V_0+\frac{V_0 t}{273}=V_0\left(1+\frac{t}{273}\right)\)….(1)

Similarly, if temperature is decreased by t°C, i.e., at a temperature -t°C, the volume of the gas becomes \(V_{-t}=V_0\left(1-\frac{t}{273}\right)\)

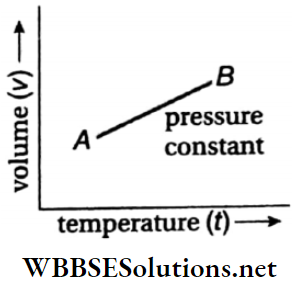
Therefore, at constant pressure volume of a fixed mass of gas changes linearly with its temperature. So, at fixed pressure, a graph plotted between the volume of a gas of a fixed mass and its temperature gives a straight line (AB).

Expansion Of Gases Pressure Law

The law that relates the change in pressure of a fixed mass of a gas at a fixed volume, with change in temperature is called pressure law or Regnault’s law.

Statement: When volume is kept constant, the pressure of a fixed mass of gas increases or decreases by1/273th part of its pressure at 0°C, for each degree centigrade rise or fall in temperature.

Mathematical expression: Let p₀ be the pressure of a fixed mass of a gas at 0°C. The pressure is p_t when the temperature is raised to t °C.

Therefore the pressure of the gas at 1°C, \(p_1=p_0+\frac{p_0}{273}=p_0,\left(1+\frac{1}{273}\right)\)

and the pressure of the gas at t°C, \(p_t=p_0+\frac{p_0 t}{273}=p_0\left(1+\frac{t}{273}\right)\)

Similarly, the pressure of the gas at -t°C, \(p_{-t}=p_0-\frac{p_0 t}{273}=p_0\left(1-\frac{t}{273}\right)\)

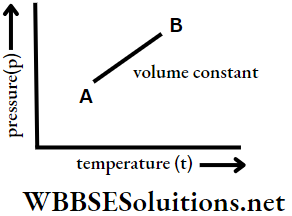
Hence the change in pressure of a fixed mass of gas is linearly related to the change in temperature at constant volume.

So, at constant volume, a graph plotted between the pressure of a gas of fixed mass and its temperature gives a straight line.

The increase in either the volume or the pressure of a gas with a rise in temperature is loosely termed as thermal expansion, although an increase in pressure is not actually an expansion.

Expansion Of Gases – Alternative Forms Of Charles Law And Pressure Law

Charles’ law: Suppose a fixed mass of a gas. at constant pressure, has volume V₀ at 0°C, at V₁ at t₁°C and V₂ at t₂°C. From Charles’ law.

⇒ \(V_1=V_0\left(1+\frac{t_1}{273}\right)=V_0\left(\frac{273+t_1}{273}\right)=\frac{V_0}{273} \cdot T_1\)

[where T₁ = t₁ + 273]

Obviously, the temperature t₁ in the Celsius scale is the same as the temperature T₁ K in the Kelvin scale.

Similarly, \(V_2=\frac{V_0}{273} \cdot T_2\)

where \(T_2=t_2+273\)

Here, \(t_2{ }^{\circ} \mathrm{C}=T_2 \mathrm{~K}\).

∴ \(\frac{V_1}{V_2}=\frac{T_1}{T_2}=\) constant

or, \(V \propto T\) at constant pressure.

Hence, Charles’ law can also be stated as the volume of a fixed mass of gas at constant pressure is directly proportional to its temperature in an absolute scale.

Pressure law: Suppose a fixed mass of a gas at constant volume has pressure p₀ at 0°C, p₁ at t₁ °C. and p₂ at t₂ °C. Hence, from pressure law.

⇒ \(p_1=p_0\left(1+\frac{t_1}{273}\right)=\frac{p_0}{273}\left(273+t_1\right)=\frac{p_0}{273} \times T_1\)

where \(T_1=t_1+273\)

It is dear that the temperature t°C is the same as the temperature T₁K.

Similarly, \(p_2=\frac{p_0}{273} \times T_2\) [where T₂ = t₂ + 273]

Here, t₂ °C = T₂ K.

∴ \(\frac{p_1}{p_2}=\frac{T_1}{T_2} \quad \text { or, } p \propto T\), at constant volume.

Hence, pressure law can be expressed as. the pressure of a fixed mass of a gas at constant volume is directly proportional to its temperature in an absolute scale.

Expansion Of Gases- Combination Of Boyles Law And Charles

Ideal or Perfect gas: The gases that obey Bodes and Charles’ law at any temperature are called ideal gases.

The equation obtained by combining Boyles’s law and Charles’ law is called the equation of the state of an ideal gas.

From Bovle’s law, \(V \propto \frac{1}{p}\) when T is constant.

From Charles’ law, V∝T when p is constant.

∴ \(V \propto \frac{T}{p}\) when both p and T vary

or, pV= kT ….(1)

where k is a constant whose value depends on the units of p, V, T, and the mass of the gas. If a gas of fixed mass occupies a volume V₁ at pressure p₁ and temperature T₁, and after a general change, a volume V₂, at pressure p₂, and temperature T₂, then

⇒ \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\)….(2)

It is known that the physical property of an ideal gas of fixed mass depends on its pressure, volume, and temperature.

Hence, the equation pV = kT is called the equation of state of an ideal gas.

Note that no real gas totally follows this equation of state.

The deviation, though small at ordinary temperature and pressure, becomes significant at high pressure and at low- temperature.

Expansion Of Gases Absolute Scale Of Temperature

From Charles’ law, If a fixed mass of gas at constant pressure occupies a volume V₀ at 0°C, then at t°C its volume will be \(V_t=V_0\left(1+\frac{t}{273}\right)\)

Now if the temperature is reduced to t = -273°C

⇒ \(V_t=V_0\left(1-\frac{273}{273}\right)=0\), i.e., the volume of the gas vanishes at -273°C temperature.

Similarly from pressure law, if a fixed mass of a gas at constant volume has a pressure p at 0°C, then at t°C its pressure will be \(p_t=p_0\left(1+\frac{t}{273}\right) \text {. }\)

Now if the temperature is reduced to t = -273 °C, \(p_t=p_0\left(1-\frac{273}{273}\right)=0\), i.e., the pressure of the gas vanishes at -273°C temperature.

So, at -273 °C, the volume and pressure of a fixed mass of gas have worked out to be zero.

If the temperature could be lowered below -273 °C, the pressure and volume would have been negative, which is meaningless. Hence, the lowest conceivable temperature in this universe is -273 °C.

Therefore -273 °C is called the absolute zero of temperature, or simply, absolute zero. More precisely, the value of absolute zero is -273.15°C.

Definition: The temperature at which the volume and the pressure of a gas reduce to zero is called the absolute zero of temperature. This temperature is the lowest temperature in reality.

Taking absolute zero i.e., -273°C as zero, a new scale of temperature was developed by Lord Kelvin, and it is called the absolute scale of temperature or Kelvin scale after the inventor.

In this scale, the temperature reading is denoted by A (absolute) or K (Kelvin). Each degree in this scale is taken equal to a degree in the Celsius scale. Hence, the scale of temperature where -273°C is taken as zero (0) and each degree is equal to a degree in Celsius scale, is called the absolute scale or Kelvin scale.

The freezing point of water (0°C) in an absolute scale is 273 K and the boiling point of water (100°C) in this scale is 373 K.

If any temperature is represented by t°C in the Celsius scale and by TK on the Kelvin scale, then, T = t + 273.

In the Kelvin scale, a temperature may be zero or positive. A negative Kelvin temperature does not exist.

0° K In Fahrenheit scale: in the relation \(\frac{C}{5}=\frac{F-32}{9}\), putting C = -273°C (0K) we have, \(\frac{-273}{5}=\frac{F-32}{9}\) or, F = – 459.4°F.

Incidentally, gas laws are valid as long as the matter remains in a gaseous state. All gases get liquified much before they attain the absolute zero temperature. No gas can be cooled to the temperature of absolute zero, and as such, zero volume or zero pressure of a gas is never realized in practice.

Absolute scale of temperature—why it is so named: The selection of 0 degrees in Celsius and Fahrenheit scale has no scientific reason behind it. The freezing point of water is taken arbitrarily as 0°C and the boiling point as 100°C in the Celsius scale.

• But the selection of 0 degrees in absolute scale is scientific as it denotes the temperature at which the volume and pressure of any ideal gas would reduce to zero. This is the lowest conceivable temperature in this universe.
• In addition, the scale does not depend on the nature of the gas. Hence, it is justified to call it the absolute scale of temperature.

Expansion Of Gases Universal gas Constant

The equation of state for an ideal gas is pV = kT. The value of the constant k depends on the mass of the gas used. Keeping pressure (p) and temperature (T) constant, if the mass of a gas is doubled, the volume is also doubled.

• So k is doubled. We can conclude that k is directly proportional to the mass of the gas.
• When one gram-molecule or one mole of an ideal gas is taken, the constant k is written as R. As per Avogadro’s law, at the same temperature and pressure, volume of 1 gram-molecule of any gas is the same.
• Therefore, the value of the constant R, for all 1-gram-molecule ideal gases, is the same. Hence, R is called the universal gas constant or molar gas constant.

Hence, for 1 gram-molecule of any ideal gas,

pV = RT ….(1) f the volume of n gram-molecule of gas is V, then the volume of 1 gram-molecule of gas, = V/n

Then from equation (1) we get, \(p \cdot \frac{V}{n}=R T \quad \text { or, } p V=n R T\)….(2)

Obviously, for mg of a gas of molecular weight M the number of moles, n = m/n

∴ pV = \(\frac{m}{M} R T\)….(3)

Comparing equation(3) with the gas equation pV = kT, k = \(\frac{m}{M} R T\)

Therefore for 1 gram of gas, k = \(\frac{R}{M}\) = r (say), r is also a constant and is called the specific gas constant.

As the molecular weights of different gases are different, the magnitude of this constant is also different for different gases.

Magnitude of universal or molar gas constant: From equation (1) above, the relation R = \(\frac{p V}{T}\) is valid for any ideal gas at any temperature and pressure.

Hence, R is also equal to \(\frac{p_0 V_0}{T_0}\) where p₀ = 76 cm Hg
(standard pressure) = 76 x 13.596 x 980.665 dyn · cm^-2, T₀ (standard temperature) = 0 + 273 = 273 K and V₀ = the volume at STP of 1 mol of a gas = 22.4 litre, as per Avogadro’s law.

∴ R = \(\left(76 \times 13.596 \times 980.665 \mathrm{dyn} \cdot \mathrm{cm}^{-2}\right) \frac{\times 22.4 \times 1000 \mathrm{~cm}^3 \cdot \mathrm{mol}^{-1}}{273 \mathrm{~K}}\)

= 8.314 x 10⁷ dyn · cm · mol^-1 · K^-1

= 8.314 x 10⁷ erg · mol”1 · K^-1

= 8.314 J · mol^-1 · K^-1

Magnitude of specific gas constant: Value of r for agasis r= R/M.

1. For hydrogen, molecular weight = 2,

r = \(frac{R}{2}=\frac{8.314 \times 10^7}{2}\)

= \(4.16 \times 10^7 \mathrm{erg} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}\)

2. For oxygen, molecular weight = 32

r = \(\frac{R}{32}=\frac{8.314 \times 10^7}{32}\)

= \(0.26 \times 10^7 \mathrm{erg} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}\)

3. For nitrogen, molecular weight = 28

r = \(\frac{R}{28}=\frac{8.314 \times 10^7}{28}\)

= \(0.297 \times 10^7 \mathrm{erg} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}\)

4. For carbon dioxide, molecular weight = 44

r = \(\frac{R}{44}=\frac{8.314 \times 10^7}{44}\)

= \(0.189 \times 10^7 \mathrm{erg} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}\)

Universal gas Constant Numerical Examples

Example 1. The mass of 1 litre of hydrogen at STP is 0.0896 g. Calculate the value of R from this data.
Solution:

Volume of 0.0896 g of hydrogen at STP = 1000 cm³.

Hence, a volume of 2 g or 1 mol of hydrogen at STP = \(\frac{1000 \times 2}{0.0896}=22321.4 \mathrm{~cm}^3.\)

Standard pressure = 76x 13.6×981 dyn · cm^-2; standard temperature = 0°C = 273 K

∴ R = \(\frac{p V}{T}=\frac{76 \times 13.6 \times 981 \times 22321.4}{273} \mathrm{erg} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\)

= \(8.29 \times 10^7 \mathrm{erg} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\)

Example 2. The mass of 3.76 litre of oxygen at 2 standard atmo¬sphere pressure and 20°C is 10 g. Find the value of R
Solution:

Given, p = 2 standard atmosphere = 2 x 76 x 13.6 x 981 dyn · cm^-2,

V = 3.76 x 10³ cm³, T = 273 + 20 = 293 K and n = 10/32 mol, [where 32 is the molecular weight of oxygen]

∴ pV=nRT

R = \(\frac{p V}{n T}=\frac{2 \times 76 \times 13.6 \times 981 \times 3.76 \times 10^3 \times 32}{10 \times 293}\)

= \(8.33 \times 10^7 \mathrm{erg} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\)

Example 3. The density of air at STP = 1.293 g · L^-1 and that of mercury = 13.6 g ·  cm^-3. Find the value of the gas constant for 1 g of air.
Solution:

If k is the constant for 1 g of air, then k = pV/T

According to the problem, 1.293 g of air occupies a volume of 1000 cm³

∴ 1g of air occupies a volume of \(\frac{1000}{1.293} \mathrm{~cm}^3\)

Here, p = \(76 \times 13.6 \times 981 \mathrm{dyn} \cdot \mathrm{cm}^{-1}, T=273 \mathrm{~K}\)

∴ k = \(76 \times 13.6 \times 981 \times \frac{1000}{1.293} \times \frac{1}{273}\)

= \(0.287 \times 10^7 \mathrm{erg} \cdot \mathrm{g}^{-1} \cdot \mathrm{K}^{-1}\)

Example 4. The masses, volumes, and pressures of two samples of oxygen and hydrogen gases are equal. Find the ratio of their absolute temperatures.
Solution:

Let the volume of each gas = V, the pressure of each gas = p, and the absolute temperatures of the gases be T₁ and T₂ respectively.

If the mass of each sample is m g, then the number of moles of the gases are respectively, \(n_1=\frac{m}{32} \quad \text { and } n_2=\frac{m}{2} \text {. }\)

As per the equation pV = nRT, for oxygen gas, \(p V=\frac{m}{32} R T_1\) and for hydrogen gas, \(p V=\frac{m}{3} R T_2\)

∴ \(\frac{m}{32} R T_1=\frac{m}{2} R T_2 \quad \text { or, } \quad \frac{T_1}{T_2}=\frac{32}{2}=16: 1\)

 Expansion Of Gases Conclusion

Boyle’s law: At constant temperature, the volume (V) of a fixed mass of gas is inversely proportional to the pressure (p) of the gas.

i.e \(V \propto \frac{1}{p}\) or, pV = constant.

Charles’ law: At constant pressure, the volume of a fixed mass of gas increases or decreases by 1/273 of its volume at 0°C per degree Celsius rise or fall in temperature.

Pressure law: At constant volume, the pressure of a fixed mass of gas increases or decreases by 1/273 of its pressure at 0°C per degree Celsius rise or fall in temperature.

Volume coefficient: The volume coefficient of a fixed mass of a gas at a constant pressure is the increment of its volume per unit volume when its temperature is raised by 1°C from 0°C.

Pressure coefficient: The pressure coefficient of a fixed mass of a gas at a constant volume is the increment of its pressure per unit pressure when its temperature is raised by 1°C from 0°C.

• The volume coefficient of all gases is equal.
• The pressure coefficients of all gases are equal.
• In the case of any ideal gas, the volume coefficient and the pressure coefficient are equal, i.e., \(\gamma_p=\frac{1}{273}{ }^{\circ} \mathrm{C}^{-1}=\gamma_v.\)
• While determining the volume and pressure coefficients of a gas, we always refer to the initial volume or pressure at 0°C.
• The gases which obey Boyle’s and Charles’ laws at all temperatures are known as ideal gases. But in actual practice no real gas is ideal.

Absolute zero temperature: The temperature at which the volume and the pressure of an ideal gas theoretically become zero is called the absolute zero temperature. This is the lowest possible temperature in reality.

The scale of temperature in which the temperature -273°C is taken as zero and each degree interval is equal to a degree interval in the Celsius scale is called the absolute scale of temperature or Kelvin scale.

Absolute zero temperature = 0K = -273°C = 459.4°F.

Universal or molar gas constant.

R =8.314 x 10⁷ erg · mol^-1  K^-1

= 8.314 J ⋅ mol^-1 K^-1

At constant pressure, the density of a gas is inversely proportional to its absolute temperature.

At constant temperature, the density of a gas is directly proportional to its pressure.

Expansion Of Gases Useful Relations For Solving Numerical Problems

If the volume of a definite mass of a gas is V and its pressure is p, then according to Boyle’s law pV = constant

Let at constant pressure, the volume of some definite mass of a gas at 0°C be V₀. According to Charles’ law the final volume of the gas due to riC rise or fall in temperature,

⇒ \(V_t=V_0\left(1 \pm \frac{t}{273}\right)\)

Let at constant volume, the pressure of some definite mass of a gas at 0°C be p₀. According to pressure law. the final pressure of the gas due to t°C rise or fall in temperature,

⇒ \(p_t=p_0\left(1 \pm \frac{t}{273}\right)\)

Volume coefficient of a gas at constant pressure, \(\gamma_p=\frac{V_t-V_0}{V_0 \cdot t}\)

Pressure coefficient of a gas at constant volume, \(\gamma_v=\frac{p_t-p_0}{p_0 \cdot t}\)

⇒ \(\gamma_p=\gamma_v=\frac{1}{273}{ }^{\circ} \mathrm{C}^{-1}\)

T = t + 273 lf any temperature is represented by t and T in Celsius and Kelvin scales respectively]

For n mol of an ideal gas, pV = nRT = \(\frac{m}{M} R T\) [where m and M are the mass and molecular weight of the gas respectively]

If ρ is the density of an ideal gas, then \(\frac{p}{\rho T}=\frac{R}{M}\) [symbols have usual meanings]

Expansion Of Gases Very Short Answer Type Questions

Question 1. At what Celsius temperature, does the volume of a gas become zero according to Charles’ law?
Answer: -273°C

Question 2. How does the volume of a definite mass of gas change with pressure at constant temperature?
Answer: Inversely proportional

Question 3. How does the volume of a definite mass of gas change with its absolute temperature at constant pressure?
Answer: Directly proportional

Question 4. At constant volume, the pressure of a definite mass of gas is directly proportional to its absolute temperature. Is the statement true or false?
Answer: True

Question 5. What is the value of the volume coefficient of a gas?
Answer: 1/273 °C^-1

Question 6. What is the value of the pressure coefficient of a gas?
Answer: 1/273 °C^-1

Expansion Of Gases Assertion Reason Type Question And Answers

Direction: These questions have statement 1 and statement 2 Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: Equal masses of helium and oxygen gases are given equal quantities of heat. There will be a greater rise in the temperature of helium compared to that of oxygen.

Statement 2: The molecular weight of oxygen is more than the molecular weight of helium.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 2.

Statement 1: In the upper part of the atmosphere, the temperature of air is of the order of 1000 K, even then it is quite cold there.

Statement 2: Molecular density at high altitudes is low.

Answer:  1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 3.

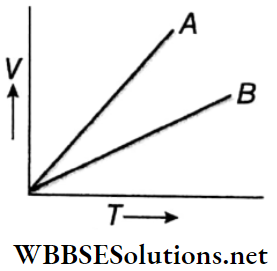
Statement 1: Shows the V – T graphs of a certain mass of an ideal gas at two pressures p₁ and p₂. It follows from the graph that p₁ is greater than p₂.

Statement 2: The slope of V- T graph for an ideal gas is directly proportional to pressure.

Answer: 3. Statement 1 is true, statement 2 is false.

Question 4.

Statement 1: V-T graph in a process is a rectangular hyperbola. Then p-T graph in the same process will be a parabola.

Statement 2: If the V-T graph is a rectangular hyperbola, with an increase in T, the volume will decrease and hence, pressure will increase.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 5.

Statement 1: The size of a hydrogen balloon increases as it rises in the air.

Statement 2: The material of the balloon can be easily stretched.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Expansion Of Gases Match Column 1 With Column 2

Question 1. The V-T graph of two gases A and B is shown.

Answer: 1. D, 2. D, 3. D, 4. D

Expansion Of Gases Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. An air bubble starts rising from the bottom of a lake. Its diameter is 3.6 mm at the bottom and 4 mm at the surface. The depth of the lake is 250 cm and the temperature at the surface is 40°C. The atmospheric pressure is 76 cm of Hg and g = 980 cm · s^-2.

1. What is the pressure at the bottom of the lake?

1. 1279325 dyn • cm^-2
2. 1359943 dyn • cm^-2
3. 1257928 dyn • cm^-2
4. 1378174 dyn • cm^-2

Answer:  1. 1279325 dyn • cm^-2

2. What is the temperature at the bottom of the lake?

1. 9.77°C
2. 10.37°C
3. 11.31°C
4. 11.67°C

Answer: 2. 10.37°C

Question 2. A fixed thermally conducting cylinder has a radius of R and a height of L₀. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L, from the top surface as shown. The atmospheric pressure is p₀.

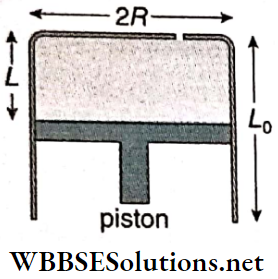
1. The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then be

1. \(\frac{p_0}{2}+\frac{M g}{\pi R^2}\)
2. \(\frac{p_0}{2}\)
3. \(p_0\)
4. \(\frac{p_0}{2}-\frac{M g}{\pi R^2}\)

Answer: 1. \(\frac{p_0}{2}+\frac{M g}{\pi R^2}\)

2. When the piston is at a distance 2L from the top the hole at the top is sealed. The piston is then released, at a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is

1. \(\left(\frac{2 p_0 \pi R^2}{\pi R^2 p_0+M g}\right)(2 L)\)
2. \(\left(\frac{p_0 \pi R^2-M g}{\pi R^2 p_0}\right)(2 L)\)
3. \(\left(\frac{p_0 \pi R^2+M g}{\pi R^2 p_0}\right)(2 L)\)
4. \(\left(\frac{p_0 \pi R^2}{\pi R^2 p_0-M g}\right)(2 L)\)

Answer: 4. \(\left(\frac{p_0 \pi R^2}{\pi R^2 p_0-M g}\right)(2 L)\)

3. The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown.

The density of the water is ρ. In equilibrium, the height H of the water column in the cylinder satisfies

1. \(\rho g\left(L_0-H\right)^2+p_0\left(L_0-H\right)+L_0 p_0=0\)
2. \(\rho g\left(L_0-H\right)^2-p_0\left(L_0-H\right)-L_0 p_0=0\)
3. \(\rho g\left(L_0-H\right)^2+p_0\left(L_0-H\right)-L_0 p_0=0\)
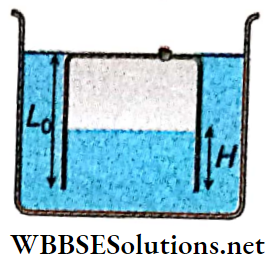
4. \(\rho g\left(L_0-H\right)^2-p_0\left(L_0-H\right)+L_0 p_0=0\)

Answer: 3. \(\rho g\left(L_0-H\right)^2+p_0\left(L_0-H\right)-L_0 p_0=0\)

Expansion Of Gases Integer Type Questions And Answers

In this type, the answer to each of the questions Is a single-digit integer ranging from 0 to 9.

Question 1. An ideal gas is heated from 27 °C to 627°C at constant pressure. If the initial volume was 3 m³, then what would be the final volume (in m³) of gas?
Answer: 9

Question 2. An air bubble of diameter 1 cm is formed at a depth of 238 ft in a lake. What will be the diameter (in cm) of the bubble when it reaches the free surface? Given that the temperature from top to bottom in the lake is the same and the height of a water barometer is 34 ft.
Answer: 2

Question 3. The volume of some air saturated with water vapor is 80 cm³ at a pressure of 74 cm Hg. Keeping the temperature fixed if pressure is made 146 cmHg then the volume becomes halved. What will be the pressure (in cm Hg) of water vapor then?
Answer: 2

Question 4. Find the percentage increase in the pressure when air enclosed at 30 °C is raised to 57 °C at a constant volume.
Answer: 9

Expansion Of Gases Short Answer Type Questions And Answers

Question 1. The temperature of an open room of volume 30 m³ increases from 17°C to 27°C due to the sunshine. The atmospheric pressure in the room remains 1 x 10⁵ Pa. If n_i and n_f are the number of molecules in the room before and after heating, then n_f – n_i will be

1. 1.61 x 10²³
2. 1.38 x 10²³
3. 2.5 x 10²⁵
4. -2.5 x 10²⁵

Answer:

If n₁ and n₂ are the number of moles at the initial and final temperature inside the room respectively, then

⇒ \(n_1 =\frac{p_1 V_1}{R T_1}=\frac{10^5 \times 30}{8.31 \times(273+17)}\)

= \(1.245 \times 10^3\)

⇒ \(n_2 =\frac{p_2 V_2}{R T_2}=\frac{p_1 V_1}{R T_2}=\frac{10^5 \times 30}{8.31 \times(273+27)}\)

= \(1.203 \times 10^3\)

Therefore \(n_f-n_1=\left(n_2-n_1\right) \times 6.023 \times 10^{23}\)

= \(-2.5 \times 10^{25}\)

The option 4 is correct.

Question 2. Explain why air pressure in a car increases during driving.
Answer:

The temperature of air inside the increases due to motion. We know from Charles’ law, p ∝ T, therefore air pressure inside the the increases during driving.