Rotation Of Rigid Bodies Angular Momentum
The rotational analogues of the mass (m) of a body and its linear velocity (v) are moment of inertia (I) and angular velocity (ω), respectively. Hence, the rotational analogue of the linear momentum (mv) of the body is Iω. This physical quantity is called the angular momentum (L) of the body.
Angular Momentum Definition: The dynamical property generated in a body under rotational motion, due to the moment of inertia about an axis and angular velocity, is called the angular momentum of the body about that axis.
Angular momentum is measured by the product of moment of inertia and angular velocity, i.e., L = Iω.
Since I is a scalar and ω is an axial vector, angular momentum L is also an axial vector whose direction is along the axis of rotation, and in the direction of ω.
Unit And Dimension Of Angular Momentum:
CGS System: g · cm² · s-1
SI: kg · m² · s-1
Dimension of L = dimension of I x dimension of ω = ML² x T-1 = ML²T-1
Relation Between Linear Momentum And Angular Momentum: Suppose a body is revolving with an angular velocity ω about an axis. If m1, m2, m3,…. are the constituent particles of that body and they are at distances r1, r2, r3,…. respectively from the axis of rotation, then the moment of inertia of the body,
I = \(m_1 r_1^2+m_2 r_2^2+m_3 r_3^2+\cdots=\sum_i m_i r_i^2\)
In the case of pure rotation, the angular velocity of each particle becomes equal to the angular velocity of the body.
So, the angular momentum of the body,
L = \(I \omega=\sum_i m_i r_i^2 \cdot \omega=\sum_i m_i r_i v_i\) (because \(v_i=\omega r\))
= \(\sum_i r_i \times m_i v_i=\sum_i r_i \times p_i\)
[pi = mivi = linear momentum of i-th particle]
For the particles, the quantities r1 x m1v1, r2 x m2v2,…… etc., can be called the moments of linear momentum, or in brief, moments of momentum (in analogy with the moment of force).
So, the angular momentum of a body about an axis is the algebraic sum of the moments of linear momentum about the same axis, of all particles constituting the body.
Thus, for a particle rotating about a circle of radius r and having a linear momentum p, the angular momentum will be L = rp.
Vector Representation: The vector representation for the relation between linear and angular momentum is \(\vec{L} = \vec{r} \times \vec{p}\). This is often referred to as the defining equation of \(\vec{L}\).
We know the vector representation for the relation between linear velocity and angular velocity is \(\vec{v}=\vec{\omega} \times \vec{r}\).
If \(\vec{v}\) and \(\vec{\omega}\) are replaced by \(\vec{p}\) and \(\vec{L}\), respectively, the geometric form for the relation of \(\vec{L}\), \(\vec{p}\) and \(\vec{r}\) is obtained.
Relation Between Angular Momentum And Torque: In case of rotational motion, when a torque is applied to a body, an angular acceleration is produced in it. If the initial angular velocity of the body is ω1 and its angular velocity after time t is ω2, then the angular acceleration of the body,
α = \(\frac{\omega_2-\omega_1}{t}\)
Again, torque = moment of inertia x angular acceleration
or, \(\tau=I \alpha=I \times \frac{\omega_2-\omega_1}{t}=\frac{I \omega_2-I \omega_1}{t}\)
or, \(\tau t=I \omega_2-I \omega_1\)
Hence, torque x time = change in angular momentum of the body during that interval
This is the relation between torque and angular acceleration. From this relation, it is evident that a change in angular momentum takes place about the axis along which the torque acts on the body.
We know that in the case of translational motion, Ft = mv – mu and the rotational analogue of this equation is τt = Iω2 – Iω1. The quantity Ft is known as the impulse of force. Similarly, the quantity τt is known as the angular impulse or the impulse of torque.
Law Of Conservation Of Angular Momentum: Suppose the moment of inertia of a body changes from I1 to I2 in time t. In this case, the equation τt = Iω2 – Iω1 changes to τt = I2ω2 – I1ω1 Now, if no external torque acts on the body, i.e., if τ = 0, then from the equation, τt = I2ω2 – I1ω1 we get, I2ω2 – I1ω1 = 0, or, τt = I2ω2 = I1ω1
It means that the final angular momentum of the body is equal to its initial angular momentum, i.e., the angular momentum is conserved.
Law: if the net external torque on a body is zero, the angular momentum of the body rotating about an axis always remains conserved.
So, this law is nothing but the rotational analogue of the law of conservation of linear momentum.
Again we know, \(\frac{dL}{dT}\) = τext
From this, it is clear that, if total external torque acts on a body is zero; its angular velocity decreases with the increase of its moment of inertia and vice versa i.e., angular momentum remains constant.
Related Experiments And Practical Examples:
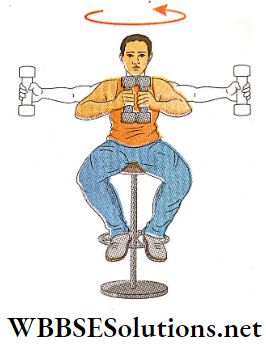
1. A man is sitting on a turntable holding a pair of dumbbells of equal mass, one in each hand with his arms out-stretched while the turntable rotates with a definite angular velocity, If the man suddenly draws the dumbbells towards his chest, the speed of rotation of the turntable is found to increase.
- This is due to the fact that when the man draws the dumbbells towards his chest, the moment of inertia of the man about the axis of rotation decreases and his angular velocity increases due to conservation of angular momentum.
- If the man again stretches his arms, his angular velocity decreases due to an increase in moment of inertia, and the turntable consequently rotates slowly.
2. In a diving event, when a competitor dives from a high platform or springboard into water, he keeps his legs and arms outstretched and starts descending with less angular velocity, After that he curls his body by rolling the legs and arms inwards, his moment of inertia decreases.
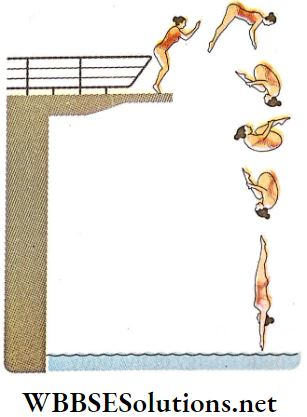
- As angular momentum is conserved, his angular velocity goes on increasing rapidly. As a result, his body begins to spin rapidly and before reaching the surface of the water, he can perform a good number of somersaults.
- In the case of skating on the surface of ice or during the performance of acrobatics, the principle of conservation of angular momentum can be applied in a similar way.
Rotation Of Rigid Bodies Angular Momentum Numerical Examples
Example 1. If the radius of the earth decreases by \(\frac{1}{2}\)%, then what will be the change in the length of a day? Assume that the earth is a uniform sphere and its moment of inertia, I = \(\frac{2}{5}\)MR², where M and R are the mass and the radius of the earth.
Solution:
If the mass of a solid sphere remains unaltered, then its moment of inertia ∝ (radius)².
Here, the changed radius \(=\frac{100-\frac{1}{2}}{100} R=\frac{199}{200} R\).
So, if the moment of inertia of the earth for its present radius R is I and the moment of inertia for its changed radius is I’, then
⇒ \(\frac{I}{I^{\prime}}=\frac{R^2}{\left(\frac{199 R}{200}\right)^2}=\left(\frac{200}{199}\right)^2\)
If the present angular velocity of the earth is ω and its changed angular velocity is ω’, then according to the principle of conservation of angular momentum,
⇒ \(I \omega=I^{\prime} \omega^{\prime}\)
or, \(\omega^{\prime}=\frac{I \omega}{I^{\prime}}\)
or, \(\frac{2 \pi}{T^{\prime}}=\frac{I}{I^{\prime}} \times \frac{2 \pi}{T}\)
or, \(T^{\prime}=\frac{I^{\prime}}{I} \cdot T=\left(\frac{199}{200}\right)^2 \times 24=23.76 \mathrm{~h}\)
∴ The length of the day will decrease by (24-23.76) = 0.24 h = 14 min 24 s
Example 2. A solid sphere of mass 1 kg and of radius 10 cm is rotating about one of its diameters with an angular; velocity of π rad · s-1. Calculate the kinetic energy of the sphere by using the relevant formula.
Solution:
Let the moment of inertia of the sphere about its diameter I = \(\frac{2}{5}\)MR², M = mass of the sphere and R = radius of the sphere.
The kinetic energy of the body = rotational kinetic energy of the body
= \(\frac{1}{2} I \omega^2=\frac{1}{2} \times \frac{2}{5} M R^2 \cdot \omega^2\)
= \(\frac{1}{5} \times 1000 \times(10)^2 \times \pi^2\)
= \(197392.09 \mathrm{erg} .\)
Example 3. A thin rod of length l and mass m per unit length is rotating about an axis passing through the midpoint of its length and perpendicular to it. Prove that its kinetic energy \(\frac{1}{24}\) mω2l3 = ω = angular velocity of the rod.
Solution:
Kinetic energy of the rod = \(\frac{1}{2}\) mω2
According to the problem,
I = \(\frac{1}{12}\)Ml² [M = mass of the rod = ml]
= \(\frac{1}{12}\) x ml x l² = \(\frac{m l^3}{12}\)
∴ Kinetic energy of the rod = \(\frac{1}{2} \times \frac{m l^3}{12} \times \omega^2=\frac{1}{24} m \omega^2 l^3 .\)
Example 4. Calculate the moment of inertia of a solid cylinder of I length 10 cm and of radius 20 cm about its own axis. The density of the material of the cylinder = 9 g · cm-3.
Solution:
L= length of the cylinder, R = radius of the cylinder and M = mass of the cylinder
= volume of the cylinder x density
= πR²L X density
= π x (20)² x 10 x 9 g
Moment of inertia of a solid cylinder about its own axis,
I = \(\frac{1}{2} M R^2\)
I = \(\frac{1}{2} \times \pi \times(20)^2 \times 10 \times 9 \times(20)^2\)
= \(22.6 \times 10^6 \mathrm{~g} \cdot \mathrm{cm}^2\)
Example 5. A solid sphere of diameter 2 cm and of mass 20 g is rolling with a velocity of 3 cm · s-1. What is the total kinetic energy of the sphere?
Solution:
Let M = mass of the sphere, R = radius of the sphere, V = linear velocity of the sphere, I = \(\frac{2}{5}\)MR² (moment of inertia of the sphere about its diameter), ω = \(\frac{V}{R}\)
Total kinetic energy of the sphere = translational kinetic energy + rotational kinetic
= \(\frac{1}{2} M V^2+\frac{1}{2} I \omega^2=\frac{1}{2} M V^2+\frac{1}{2} \times \frac{2}{5} M R^2\left(\frac{V}{R}\right)^2\)
= \(\frac{1}{2} M V^2+\frac{1}{5} M V^2=\frac{7}{10} M V^2=\frac{7}{10} \times 20 \times(3)^2\)
= \(126 \mathrm{erg}\)
Example 6. A stone of mass m tied with a thread Is rotating along a horizontal circular path (force of gravity is neglected). The length of the thread decreases gradually in such a manner that the angular momentum of the stone remains constant with respect to the centre of the circle. If the tension in the thread Is T = Arn, where A = constant, r = instantaneous radius of the circle, then find the value of n.
Solution:
If the instantaneous angular velocity of the stone is w, then angular momentum,
L = Iω = mr²ω = constant (according to the problem)
or, ω = \(\frac{L}{m r^2}\)
Here the tension in the thread provides the necessary centripetal force for rotation.
So, T = \(A r^n=m \omega^2 r=m \cdot \frac{L^2}{m^2 r^4} r=\frac{L^2}{m} r^{-3}\)
= \(A r^{-3} \quad\left(A=\frac{L^2}{m}=\text { constant }\right)\)
∴ n=-3 .
Example 7. Two ends of a uniform rod weighing W, are placed on supports so that the rod remains horizontal. If a support at one end is suddenly removed, what will be the force exerted on the horizontal rod by the support at the other end?
Solution:
Let the length of the rod = l cm, its weight = W = Mg, where M is the mass of the rod. When the support at one end is removed suddenly, the centre of gravity of the rod falls downwards with an acceleration a. Let R = reaction force at the end with the support. Hence, if the C.G. now falls with an acceleration a, the rod will turn about the point P.
The torque on the rod = Mg · \(\frac{l}{2}\)
Also, Mg – R = Ma or, \(a=\frac{M g-R}{M}\)
Here moment of inertia, I = \(\frac{1}{3}\)Ml² = moment of inertia of the rod about the perpendicular axis passing through the end of the rod and the angular acceleration, α = \(\frac{a}{V / 2}=\frac{2 a}{l}\)
∴ \(\frac{1}{3} M l^2 \alpha=M g \frac{l}{2}\) (because \(\tau=I \alpha\))
or, \(\frac{1}{3} M R^2 \cdot \frac{2 a}{l}=M g \frac{l}{2} \text { or, } \frac{2}{3} a=\frac{g}{2} \text { or, } \frac{2}{3}\left(\frac{M g-R}{M}\right)=\frac{g}{2}\)
R = \(\frac{M g}{4}=\frac{W}{4}\)
Therefore, when one support is removed, the support at the other end will exert a reaction force of \(\frac{W}{4}\)
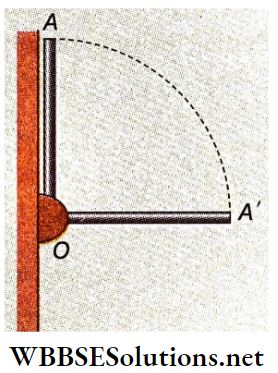
Example 8. A rod of length L and M is attached with a hinge on a wall at point O. After releasing the rod from its vertical position OA, when it comes to position OA’, what is the reaction on point O of the rod by the hinge?
Solution:
Let, the angular velocity of the rod at the horizontal position OA’ is ω.
∴ At that instant its kinetic energy = \(\frac{1}{2} I \omega^2=\frac{1}{2} \cdot \frac{M L^2}{3} \cdot \omega^2=\frac{M L^2 \omega^2}{6}\)
The centre of mass of the rod shifts down by \(\frac{L}{2}\) from OA to OA’.
So, decrease in potential energy of the rod = Mg\(\frac{L}{2}\)
According to the kinetic energy conservation law, \(M g \frac{L}{2}=\frac{M L^2 \omega^2}{6} \quad \text { or, } \omega=\sqrt{\frac{3 g}{L}}\)…(1)
Two forces act on the rod at position OA’
- Gravitational force (Mg) vertically downward direction and
- Reaction force (n) of the hinge
Let, the horizontal and the vertical n components of n are nx and ny respectively; the horizontal and the vertical components of the acceleration of the centre of mass of the rod area ax and ay respectively.
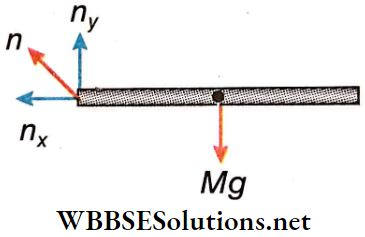
∴ According to \(M g-n_y=M a_y\)….(2)
and \(n_x=M a_x=M \omega^2 \cdot \frac{L}{2}\)
(because \(a_x=\) centripetal acceleration)
= \(M \cdot \frac{3 g}{L} \cdot \frac{L}{2}=\frac{3}{2} M g\)
[putting the value of ω from equation (1)]
The rod starts to rotate due to the action of torque created by ny and Mg.
If the angular acceleration of the rod is α, \(M g \cdot \frac{L}{2}=I \alpha=\frac{M L^2}{3} \alpha\)
∴ \(\alpha=\frac{3 g}{2 L}\)
The acceleration along the vertical direction, \(a_y=\frac{L}{2} \alpha=\frac{3 g}{4}\)
Putting the value of ay in equation (2) we get, \(M g-n_y=\frac{3 M g}{4} \text { or, } n_y=\frac{M g}{4}\)
∴ n = \(\sqrt{n_x^2+n_y^2}=\sqrt{\left(\frac{3}{2} M g\right)^2+\left(\frac{M g}{4}\right)^2}=\frac{\sqrt{37}}{4} M g\)
