WBCHSE Class 11 Physics For Simple Harmonic Motion: Definition, Examples

Oscillation And Waves

Simple Harmonic Motion Mathematical Analysis Of SHM

Differential Equation: Let x be the displacement from the equilibrium position of a particle executing SHM.

Then the velocity of the particle is, v = \(\frac{d x}{d t}\)

The acceleration of the particle (i.e., the rate of change of velocity), a = \(\frac{d v}{d t}=\frac{d}{d t}\left(\frac{d x}{d t}\right)=\frac{d^2 x}{d t^2}\)

So, the equation of SHM can be written as \(\frac{d^2 x}{d t^2}=-\omega^2 x \text { or, } \frac{d^2 x}{d t^2}+\omega^2 x=0\)…(1)

Equation (1) is called the differential equation of SHM.

Solution Of The Differential Equation: Let x = e^pt be a solution for equation (1).

∴ \(\frac{d x}{d t}=p e^{p t} \text { and } \frac{d^2 x}{d t^2}=p^2 e^{p t}\)

Putting the values obtained above in equation (1) we have,

⇒ \(p^2 e^{p t}+\omega^2 e^{p t}=0\)

or, \(\left(p^2+\omega^2\right) e^{p t}=0\)

or, \(p^2+\omega^2=0\) (because \(e^{p t} \neq 0\))

or, \(p^2=-\omega^2 \text { or, } p= \pm i \omega \quad[\text { Here, } i=\sqrt{-1}]\)

So, the general solution of equation (1) is x = \(A^{\prime} \sin \omega t+B^{\prime} \cos \omega t\)…..(2)

Where A’ and B’ are Integration constants.

Inserting e^mx in the equation \(\frac{d^2 y}{d x^2}+c_1 \frac{d y}{d x}+c_2 y=0\), if we get m = a’±ib’, then the general solution of the equation is y = \(e^{a^{\prime} x}\left(A^{\prime \prime} \sin b^{\prime} x+B^{\prime \prime} \cos b^{\prime} x\right) .\)

Let us put A’ = Acosα and B’ = Asinα in equation (2).

Then, A = \(\sqrt{A^{\prime 2}+B^{\prime 2}} \text { and } \alpha=\tan ^{-1} \frac{B^{\prime}}{A^{\prime}}\)

Thus, x = A(sinωtcosα + cosωtsinα) or, x = Asin(ωt+α)…..(3)

This represents the general equation of simple harmonic motion expressing the displacement of the particle.

Differential Equation Special Cases:

1. If A’ = A and B’ = 0, i.e., α= 0, we have from equation (2) or (3), x = Asinωt ……(4)

From this equation, it is seen that, at t = 0, x = 0,

i.e., initially the particle is at its position of equilibrium.

2. If A’ = 0 and B’ = A, i.e., a = \(\frac{\pi}{2}\), we have from equation (2) or (3), x = Asost……..(5)

From this equation, it is seen that when t = 0, x = A, which is the maximum value of displacement of the particle.

So, if a particle executing SHM starts its motion from its equilibrium position, its displacement is expressed as a sine function. If it starts its motion from one end of its path, its displacement is expressed as a cosine function.

If the particle executing SHM starts its motion from another point of its path, then equation (3) is directly used.

Relation Between SHM And Uniform Circular Motion: SHM is the simplest form of linear periodic motion. Again, uniform circular motion is the simplest form of rotational periodic motion.

• The relation between SHM and uniform circular motion can be shown by a mechanical example.
• A wheel is rotating with uniform speed about its center. A rod is connected between the circumference of the wheel and the handle of a frictionless piston fitted within a cylinder.
• With the uniform rotation of the wheel, the piston moves to and fro along the shown path uniformly. As the motion of the wheel is uniform, the motion of the piston will be simple harmonic.

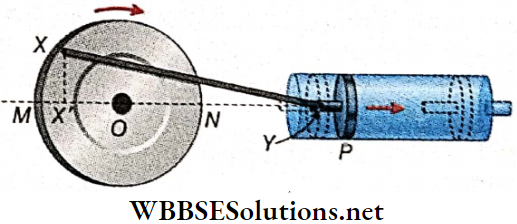
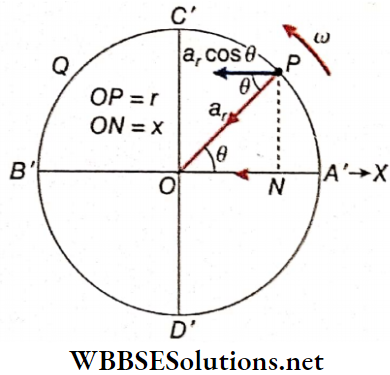
Geometrical Proof: Suppose a panicle is moving with a uniform angular velocity in an anticlockwise direction. This is shown by an arrow, along the circumference A’C’B’D’ of a circle hating its center at O. The foot of the perpendicular, drawn from different positions of the particle on the diameter B’OA’ (or C’OD’), will execute the simple harmonic motion. This is proved below.

• When the particle is at P, the foot of the perpendicular drawn from P on the diameter B’OA’ is at N. Now, as the particle moves around the circle, the foot of the perpendicular moves along the diameter A’OB’. Let the particle starting from A’, move around the circle in an anticlockwise direction and come back to A’.
• Its projection on A’OB’ (N) also moves along A’OB’, reverses its direction, and then comes back along the same path to its starting point simultaneously. This to-and-fro motion of N along A’B’ is a linear periodic motion.

Similarly, if we draw a perpendicular from P on the diameter C’OD’, the foot to the perpendicular will execute a linear periodic motion along the diameter C’OD’. This linear periodic motion will be simple harmonic if it can be shown that the acceleration of N is proportional to its displacement from O and is directed towards the position of equilibrium O.

Let ω be the uniform angular velocity of the particle and r be the radius of the circular path.

∴ The uniform linear speed of the particle is, ν = ωr

The centripetal acceleration of the particle at P along PO is, \(a_r=\frac{v^2}{r}=\omega^2 r\)

Let at any instant, OP make an angle θ with the diameter B’OA’ (taken as x-axis) and the displacement of the foot of the perpendicular (N) be x from the position of equilibrium.

∴ x = ON = OPcosθ = rcosθ

Again, the component of nr along the diameter A’OB’, i.e., die acceleration of N at that instant is a = a_rcosθ = ω²r cosθ = ω²x

Hence, the acceleration of N is proportional to its displacement from its position of equilibrium.

The component of ar along A’OB’ is related to the motion of N. Obviously, if the particle is at P, this component of acceleration is directed towards O, the position of equilibrium. So the motion of N is simple harmonic.

Therefore, when a particle is in a uniform circular motion, the motion of its projection on any diameter of the circular path is simple harmonic. The circle in the example above is called the circle of reference and the particle is called the reference particle.

Related To SHM Displacement: We know that the general equation for the displacement of a particle executing SHM is, x = Asin(ωt+α)….(1)

Related To SHM Displacement Special Cases:

1. If the particle starts its motion from one of the extremities B or C of its path, then the equation becomes x = Acosωt …..(2)
2. If the particle starts its motion from O, the position of equilibrium, then the equation becomes x = Asinωt……(3)

Related To SHM Velocity: From equation (1) we get,

sin (ωt+a) = \(\frac{x}{A}\)

∴ cos(ωt+ a) = \(\pm \sqrt{1-\frac{x^2}{A^2}}\)

So, the velocity of the particle executing SHM is

∴ v = \(\frac{d x}{d t}=A \omega \cos (\omega t+\alpha)= \pm A \omega \sqrt{1-\frac{x^2}{A^2}}\)

or, v = \(\pm \omega \sqrt{A^2-x^2}\)….(4)

It shows that the velocity of the particle depends on its displacement.

Related To SHM Velocity Special Cases:

1. When x = 0, i.e., when the particle is at O, the position of equilibrium, v = ± ωA, which is the maximum velocity. ie.., ν_max = ± ωA
2. When x = ±A, i.e., when the particle is at B or C, the two extremities of its path, \(\nu= \pm \omega \sqrt{A^2-A^2}=0\), which is the minimum velocity. i.e., v_min = 0.

So, a particle executing SHM has different velocities at different points on its path. It passes the position of equilibrium with maximum velocity. The magnitude of its velocity gradually decreases as the particle moves towards its extremities from the equilibrium position and it momentarily comes to rest at the extreme points of its path.

Related To SHM Acceleration: From equation (1), we get

velocity, v = \(\frac{d x}{d t}=\omega A \cos (\omega t+\alpha)\)

∴ Acceleration, a = \(\frac{d v}{d t}=-\omega^2 A \sin (\omega t+\alpha)\)

or, a = -ω²x…..(5)

From this equation, we see that the acceleration of the particle depends on its displacement from its mean position. The negative sign indicates that acceleration and displacement are mutually opposite in direction.

Related To SHM Acceleration Special Cases:

1. When x = 0, i.e., when the particle is at O, the position of equilibrium, a = 0, which is the minimum acceleration.
2. When x = ±A, i.e., when the particle is at B or C, the extremities of its path, a =\(\mp\)ω²A, which is the maximum acceleration.

A particle undergoing SHM possesses different accelerations at different points on its path. It has zero acceleration at equilibrium and attains the maximum acceleration at the extreme positions of its path.

Instead of equation (1) if we use equation (2) or (3), we get the same equations (4) and (5) for velocity and acceleration.

Related To SHM Time Period And Frequency: Let the equation of a simple harmonic motion: x = Acosωt. In this case, at the beginning of the motion, i.e., at time t = 0, ωt = 0, and x = Acos0 = A. This implies that the particle begins its motion from one extreme end of its path.

Now, as time advances, when t = \(\frac{2 \pi}{\omega}\), again we get, x = Acos2π = A, i.e., the particle returns to the initial point from which it began its motion. Thus, an oscillation is completed.

So, for one complete oscillation, change in ωt = 2π-0 = 2π, i.e., for one complete oscillation, time taken is \(\frac{2 \pi}{\omega}\)(ωt = 2π).

As the total time elapsed for one complete oscillation is called the time period (T) of a SHM, we have, T = \(\frac{2 \pi}{\omega}\)….(6)

Related To SHM Time Period And Frequency Definition: Frequency is defined as the number of complete oscillations per second of a particle executing SHM.

In time T the number of oscillations is 1. Hence in unit time, the number of oscillations is \(\frac{1}{T}\).

∴ Frequency, n = \(\frac{1}{T}=\frac{\omega}{2 \pi}\) …..(7)

or, ω = 2πn

ω is called the angular frequency.

Considering only the magnitude of the acceleration of a particle executing SHM, we get from equation (5), \(\omega^2=\frac{a}{x} \text { or, } \omega=\sqrt{\frac{a}{x}}\)

∴ Time period, T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{x}{a}}\)

= \(2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}}\)…(8)

∴ Frequency, n = \(\frac{1}{T}=\frac{1}{2 \pi} \sqrt{\frac{a}{x}}\)

= \(\frac{1}{2 \pi} \sqrt{\frac{\text { acceleration }}{\text { displacement }}}\)….(9)

Related To SHM Amplitude: The amplitude of simple harmonic motion = OB = OC. Since, -1 ≤ sinθ≤+ 1 and -1≤ cosθ ≤ + 1, we get from equation (1), the maximum value of displacement x = amplitude = |±A| = A

∴ \(\overrightarrow{O B}=\vec{A} \quad \text { and } \overrightarrow{O C}=-\vec{A}\)

From equations (8) and (9) it is evident that the time period and frequency of an SHM do not depend on the amplitude A. So, if the amplitude of oscillation of a simple pendulum diminishes gradually due to air resistance, its time period remains unchanged (law of isochronism). For this, simple harmonic motion is called an isochronous motion.

Related To SHM Phase: The phase of a particle executing SHM at any instant, is defined as its state of motion at that instant. The term ‘state of motion’ indicates displacement, velocity, acceleration, etc., of the particle at any instant.

Suppose in equation (1),  θ= ωt + α……(10)

velocity, v = \(\pm \omega \sqrt{A^2-x^2}= \pm \omega A \cos \theta \text {; }\)

acceleration, a = -ω²x = -ω²Asinθ

Now, ω and A are both constants. So displacement, velocity, and acceleration of the particle at any instant depend entirely on the angle θ. The angle θ, expressed by equation (10), is called the phase angle of the simple harmonic motion. It is seen from equation (10), that, θ depends on time t. Thus, the phase of a particle executing SHM changes continuously with respect to time.

Related To SHM Phase Special Cases:

1. If θ = 0, then x = Asinθ = 0, i.e., the particle is at O. If the value of θ becomes 90°, then x = Asin90° = A, i.e., the particle is at the end B of its path, i.e., the change of phase = 90° = \(\frac{\pi}{2}\).
2. If θ = 270°, then x = Asin270° = -A, i.e., the particle is at C. So, when the particle moves from B to C, the change of phase angle = 270° -90° = 180° = π. The positions B and C are then said to be in opposite phases.

If θ = 450° = 360° + 90° , then x = Asin450° = Asin90° = A;

i.e., the particle is at B. So, when the particle starts its motion from B, goes to C, and then returns to B, the change of phase angle = 450° – 90° = 360° = 2π. In this case, the initial and the final positions are in the same phase.

Related To SHM Epoch: It is defined as the initial phase of motion (i.e., at t = 0) of the particle executing SHM.

If the equation of SHM is x = Asin(ωt+ α), then phase angle, θ = ωt+ α.

Putting t = 0 in this equation, we get epoch, θ = α

As a special case, if the particle starts its motion from one extremity of its path we have,

x = \(A \cos \omega t=A \sin \left(\omega t+\frac{\pi}{2}\right)\).

Here phase angle, θ = cot+\(\frac{\pi}{2}\) . If t = 0 , epoch = \(\frac{\pi}{2}\).

Again, if the particle starts its motion from the position of equilibrium, we have, x = Asinωt

Here, phase angle θ= ωt. Putting t = 0, epoch = 0 .

Related To SHM Epoch Phase Difference: In the case of two particles executing SHM, if the phase angle of the first particle is θ₁ and that of the second particle is θ₂ at an instant, then the phase difference of the SHMs is θ = θ₂ – θ₁ (or θ₁ – θ₂). Two simple harmonic motions having the same time period, frequency, and amplitude may have different phases. For example, if at an instant when the first particle reaches C, the second particle is at B, then their phase difference = 180°= π.

If the phase difference between two SHMs remains constant, i.e., it does not change with time, they are said to be coherent; the particles executing these SHMs are said to be in coherent motion.

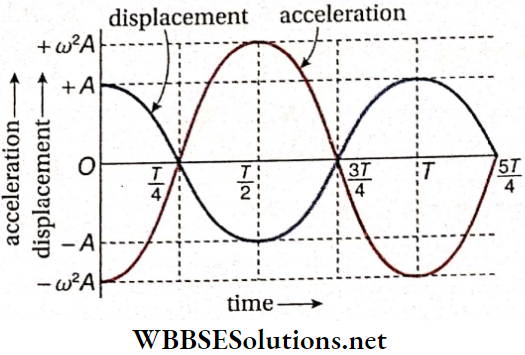
Relations Among Displacement Velocity And Acceleration: Suppose a particle executing SHM starts its motion from the extremity B of its path. If T is the time period, then the particle crosses the position of equilibrium O in time \(\frac{T}{4}\); reaches C, the other extremity of the path in time \(\frac{T}{2}\) again on its way back crosses O, the position of equilibrium in time \(\frac{3T}{4}\) and returns to B in time T.

Using v = \(\pm \omega \sqrt{A^2-x^2} \text { and } a=-\omega^2 x\), we can calculate displacement, velocity, and acceleration of the particle at different times, as shown in the table below.

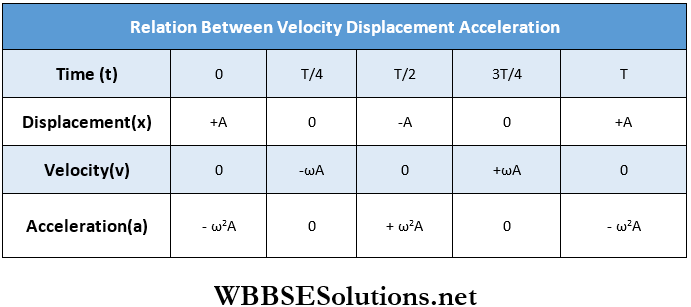
The graph of displacement and velocity against time is shown, and the graph of displacement and acceleration against time.

Phase Difference Of Velocity And Acceleration With Displacement: Displacement of a particle executing a SHM is, x = Acosωt,

velocity, v = \(-A \omega \sin \omega t=A \omega \cos \left(\omega t+\frac{\pi}{2}\right)\)

and acceleration, a = -Aω² cosωt = Aω²cos(ωt+π)

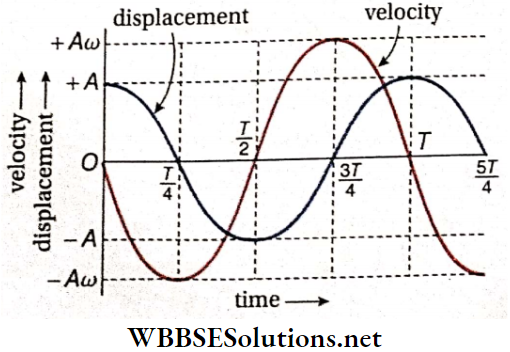
So, the phase difference between velocity and displacement is \(\frac{\pi}{2}\) or 90°, and the difference between acceleration and displacement is π or 180°.

Characteristics Of SHM

1. Simple harmonic motion is a kind of linear periodic motion, i.e., in this motion, the particle moves to and fro following the same path repeatedly at regular time intervals.
2. The acceleration of the particle executing SHM is always directed towards the position of equilibrium.
3. The acceleration of the particle is proportional to its displacement from the position of equilibrium at any instant.
4. When the particle passes the position of equilibrium, its velocity becomes maximum. The velocity of the particle gradually reduces and momentarily comes to zero at the extremities of its path.
5. The time period of SHM does not depend on the amplitude. Though the amplitude decreases gradually due to various external resistances, the time period remains unchanged.

It is to be noted that SHM is a special form of periodic motion. If the periodic motion is

1. Linear and
2. The acceleration of the particle is proportional to its displacement from the position of equilibrium and is directed towards it, only then the motion of the particle is called simple harmonic.

The motion of the hands of a clock or the motions of the planets and satellites are periodic, but as these motions do not satisfy the above two conditions, they are not considered as simple harmonic. So, it can be said that all simple harmonic motions are periodic, but all periodic motions are not simple harmonic.

 Oscillation And Waves

Simple Harmonic Motion Mathematical Analysis Of SHM Numerical Examples

Example 1. A particle of mass 0.5 g is executing SHM with a time period of 2 s and an amplitude of 5 cm. Calculate its

1. Maximum velocity,
2. Maximum acceleration and
3. Velocity, acceleration, and force acting on the particle when it is at a distance of 4 cm from its position of equilibrium.

Solution:

Amplitude, A = 5 cm; time period, T = 2 s

∴ ω = \(\frac{2 \pi}{T}=\frac{2 \pi}{2}=\pi \mathrm{rad} \cdot \mathrm{s}^{-1}\)

1. Maximum velocity, \(v_{\max }=\omega A=\pi \cdot 5=5 \pi =5 \times 3.14=15.7 \mathrm{~cm} \cdot \mathrm{s}^{-1}=0.157 \mathrm{~m} \cdot \mathrm{s}^{-1}\)
2. Maximum acceleration, \(a_{\max }=\omega^2 A=\pi^2 \cdot 5 =5 \times(3.14)^2=49.298 \mathrm{~cm} \cdot \mathrm{s}^{-2} \approx 0.493 \mathrm{~m} \cdot \mathrm{s}^{-2}\)
3. When x = 4cm,

velocity, v = \(\omega \sqrt{A^2-x^2}=\pi \sqrt{5^2-4^2}\)

= \(3.14 \times 3=9.42 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

= \(0.094 \mathrm{~m} \cdot \mathrm{s}^{-1}\)
\end{aligned}

acceleration, = \(39.438 \mathrm{~cm} \cdot \mathrm{s}^{-2}\)

= \(0.394 \mathrm{~m} \cdot \mathrm{s}^{-2}\)

And force,F = \(m a=0.5 \times 39.438\)

= 19.72 dyn \(\approx 0.197 \times 10^{-3} \mathrm{~N} .\)

Example 2. A particle executing SHM possesses velocities 20cm · s^-1 and 15cm · s^-1 at distances 6 cm and 8 cm respectively from its mean position. Calculate the amplitude and the time period of the particle.
Solution:

Given:

A particle executing SHM possesses velocities 20cm · s^-1 and 15cm · s^-1 at distances 6 cm and 8 cm respectively from its mean position.

Velocity of the particle executing SHM, \(\nu=\omega \sqrt{A^2-x^2}\)

In the first case, 20 = \(\omega \sqrt{A^2-6^2}\)….(1)

In the second case, 15 = \(\omega \sqrt{A^2-8^2}\)…(2)

Dividing (1) by (2) we get, \(\frac{20}{15}=\frac{\omega \sqrt{A^2-6^2}}{\omega \sqrt{A^2-8^2}} \text { or, } \frac{4}{3}=\frac{\sqrt{A^2-36}}{\sqrt{A^2-64}} \text { or, } \frac{A^2-36}{A^2-64}=\frac{16}{9}\)

or, \(16 A^2-1024=9 A^2-324\)

or, \(7 A^2=700 \text { or, } A^2=100 \text { or, } A=10 \mathrm{~cm}=0.1 \mathrm{~m}\)

From equation (1) we get,

20 = \(\omega \sqrt{10^2-6^2}=8 \omega \text { or, } \omega=\frac{20}{8}=\frac{5}{2} \mathrm{rad} \cdot \mathrm{s}^{-1}\)

∴ T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{5} \times 2=\frac{4}{5} \times 3.14=2.51 \mathrm{~s} .\)

Example 3. The time period and amplitude of a particle executing SHM are 10 s and 0.12 m respectively. Find its velocity at a distance of 0.04 m from its position of equilibrium.
Solution:

Given:

The time period and amplitude of a particle executing SHM are 10 s and 0.12 m respectively.

Here T = 10 s; A = 0.12 m

∴ \(\omega=\frac{2 \pi}{T}=\frac{2 \pi}{10}=\frac{\pi}{5} \mathrm{rad} \cdot \mathrm{s}^{-1}\)

So, v = \(\omega \sqrt{A^2-x^2}=\frac{\pi}{5} \sqrt{0.12^2-0.04^2}=\frac{\pi}{5} \sqrt{0.0128}\)

= \(0.071 \mathrm{~m} \cdot \mathrm{s}^{-1}\).

Example 4. The frequency of a vibrating wire is 200 Hz. The velocity of a particle on the wire is 4.35m · s^-1 when it is at a distance of half its amplitude. Calculate the acceleration of the particle at that instant
Solution:

Given:

The frequency of a vibrating wire is 200 Hz. The velocity of a particle on the wire is 4.35m · s^-1 when it is at a distance of half its amplitude.

Here, ω = 2πn = 2π ·200 = 400π rad · s^-1 [n = 200 Hz]

Let A be the amplitude of the particle.

If x = \(\frac{A}{2}\), then v = 4.35 m · s^-1

∴ v = \(\omega \sqrt{A^2-x^2}\)

or, \(4.35=400 \pi \sqrt{A^2-\frac{A^2}{4}}=400 \pi \cdot \frac{A \sqrt{3}}{2}\)

or, \(A=\frac{4.35 \times 2}{400 \pi \times \sqrt{3}} \mathrm{~m}\).

∴ Required acceleration, a = \(\omega^2 x=\omega^2 \cdot \frac{A}{2}=(400 \pi)^2 \times \frac{1}{2} \times \frac{4.35 \times 2}{400 \pi \sqrt{3}}\)

= \(\frac{400 \pi \times 4.35}{\sqrt{3}}=3154 \mathrm{~m} \cdot \mathrm{s}^{-2} \text { (approx.) }\)

The acceleration of a rapidly vibrating object may reach an exceptionally high value.

Example 5. Two particles executing SUM possess the same frequency. When the first particle just pusses the mean position of its path, the second particle moving lit the same direction is at a distance of 3 cm from its mean position. If the amplitude of vibration of the second particle is 6 cm, what is the phase difference of the two particles?
Solution:

Given:

Two particles executing SUM possess the same frequency. When the first particle just pusses the mean position of its path, the second particle moving lit the same direction is at a distance of 3 cm from its mean position. If the amplitude of vibration of the second particle is 6 cm

If A is the amplitude and θ is the phase angle, then displacement, x = Acosθ

For the first particle, \(x_1=A_1 \cos \theta_1 \text { or, } 0=A_1 \cos \theta_1\)

or, \(\cos \theta_1=0 or, \theta_1= \pm 90^{\circ}\)

For the second particle, \(x_2 =A_2 \cos \theta_2 \text { or, } \cos \theta_2=\frac{x_2}{A_2}=\frac{3}{6}=\frac{1}{2}\)

or, \(\theta_2= \pm 60^{\circ}\)

At the given instant, the two particles are in motion in the same direction.

So,

1. If θ₁ = 90° , then θ₂ = 60°; phase difference θ₂-θ₁ = -30°
2. If θ₁ =-90°, then θ₂ = -60°; phase difference θ₂-θ₁ = +30°

∴ The required phase difference is ± 30°.

Example 6. A particle executing SHM possesses velocities v₁ and v₂ when it is at distances x₁ and x₂ respectively from its mean position. Show that, the time period of oscillation is given by T = \(2 \pi\left(\frac{x_2^2-x_1^2}{v_1^2-v_2^2}\right)^{1 / 2}\)
Solution:

Given:

A particle executing SHM possesses velocities v₁ and v₂ when it is at distances x₁ and x₂ respectively from its mean position.

We know, \(v=\omega \sqrt{A^2-x^2}\)

According to the question, \(v_1=\omega \sqrt{A^2-x_1^2} \text { or, } v_1^2=\omega^2\left(A^2-x_1^2\right)\)…..(1)

Also, \(v_2=\omega \sqrt{A^2-x_2^2} or, v_2^2=\omega^2\left(A^2-x_2^2\right)\)

Subtracting (2) from (1) we get, \(v_1^2-v_2^2=\omega^2\left(x_2^2-x_1^2\right) or, \quad \omega^2=\frac{v_1^2-v_2^2}{x_2^2-x_1^2}\)

or, \(\omega=\left(\frac{v_1^2-v_2^2}{x_2^2-x_1^2}\right)^{\frac{1}{2}}\)

We know that, T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{\left(\frac{u_1^2-u_2^2}{x_2^2-x_1^2}\right)^{\frac{1}{2}}}=2 \pi\left(\frac{x_2^2-x_1^2}{u_1^2-u_2^2}\right)^{\frac{1}{2}}\),

Example 7. The equation of a simple harmonic motion is  x = \(10 \sin \left(\frac{\pi}{3} t-\frac{\pi}{12}\right) \mathrm{cm}\). Calculate its

1. Amplitude,
2. Time period,
3. Maximum speed,
4. Maximum acceleration,
5. Epoch and
6. Speed after 1s of initiation of motion

Solution:

x = \(10 \sin \left(\frac{\pi}{3} t-\frac{\pi}{12}\right) \mathrm{cm}\)

Comparing this equation with the equation of SHM, x = A sin(ωt + α) we get,

1. Amplitude, A = 1.0 cm.
2. \(\omega=\frac{\pi}{3}\) so time period, T = \(\frac{2 \pi}{\omega}=\frac{2 \pi \times 3}{\pi}=6 \mathrm{~s} \text {. }\)
3. Maximum speed, \(\omega A=\frac{\pi}{3} \times 10=\frac{10 \pi}{3} \mathrm{~cm} \cdot \mathrm{s}^{-1} \text {. }\)
4. Maximum Acceleration, \(\omega^2 A=\left(\frac{\pi}{3}\right)^2 \times 10=\frac{10 \pi^2}{9} \mathrm{~cm} \cdot \mathrm{s}^{-2}\)
5. Epoch = \(-\frac{\pi}{12}=-15^{\circ}\)
6. Displacement after 1s of initiation of motion, \(x_1=10 \sin \left(\frac{\pi}{3} \cdot 1-\frac{\pi}{12}\right)=10 \sin \left(60^{\circ}-15^{\circ}\right)\)

= \(10 \sin 45^{\circ}=\frac{10}{\sqrt{2}}=5 \sqrt{2} \mathrm{~cm}\)

And speed after 1 s of initiation of motion, \(v_1=\omega \sqrt{A^2-x_1^2}=\frac{\pi}{3} \sqrt{(10)^2-(5 \sqrt{2})^2}\)

= \(\frac{\pi}{3} \sqrt{50}=\frac{5 \sqrt{2}}{3} \pi \mathrm{cm} \cdot \mathrm{s}^{-1}\)

Example 8. Write down the equation of a simple harmonic motion whose amplitude Is 5 cm, epoch Is 0° and the number of vibrations per minute is 150.
Solution:

Given:

Amplitude Is 5 cm, epoch Is 0° and the number of vibrations per minute is 150.

According to the problem, amplitude, A = 0.05 m; epoch, α = 0°; frequency, n = \(\frac{150}{60}=\frac{5}{2} \mathrm{~Hz}\)

∴ \(\omega=2 \pi n=2 \pi \cdot \frac{5}{2}=5 \pi \mathrm{rad} \cdot \mathrm{s}^{-1}\)

So, the equation of the simple harmonic motion is

x = \(A \sin (\omega t+\alpha) \quad \text { or, } x=0.05 \sin 5 \pi t \mathrm{~m}\).

Example 9. The displacement of a vibrating particle at time t is given by x = \(A^{\prime} \sin \left(\frac{\pi}{6} t\right)+B^{\prime} \cos \left(\frac{\pi}{6} t\right)\), where A’ = 0. 03 m, B’ = 0.04m. Calculate the

1. Amplitude,
2. Epoch,
3. Displacement, velocity, and acceleration of the particle after 2 seconds.

Solution:

Given:

The displacement of a vibrating particle at time t is given by x = \(A^{\prime} \sin \left(\frac{\pi}{6} t\right)+B^{\prime} \cos \left(\frac{\pi}{6} t\right)\), where A’ = 0. 03 m, B’ = 0.04m.

x = \(A^{\prime} \sin \left(\frac{\pi}{6} t\right)+B^{\prime} \cos \left(\frac{\pi}{6} t\right)\)….(1)

Let \(A^{\prime}=A \cos \alpha and B^{\prime}=A \sin \alpha\)

∴ \(A^2\left(\cos ^2 \alpha+\sin ^2 \alpha\right)=A^{\prime 2}+B^{\prime 2}\)

or, \(A=\sqrt{A^{\prime 2}+B^{\prime 2}} and \tan \alpha=\frac{B^{\prime}}{A^{\prime}}\)

So, x = \(A \sin \left(\frac{\pi}{6} t\right) \cos \alpha+A \cos \left(\frac{\pi}{6} t\right) \sin \alpha\)

or, x = \(A \sin \left(\frac{\pi}{6} t+\alpha\right)\)….(2)

From this equation we get,

1. Amplitude, A = \(\sqrt{A^{\prime 2}+B^{\prime 2}}\) = \(\sqrt{(0.03)^2+(0.04)^2}=0.05 \mathrm{~m}\)
2. Epoch, \(\alpha=\tan ^{-1} \frac{B^{\prime}}{A^{\prime}}=\tan ^{-1} \frac{4}{3}\)
3. When t = 2 s, we get from equation (1) displacement, x = \(A^{\prime} \sin \left(\frac{\pi}{6} t\right)+B^{\prime} \cos \left(\frac{\pi}{6} t\right)\)

= \(0.03 \sin \frac{\pi}{3}+0.04 \cos \frac{\pi}{3}\)

= \(0.03 \times \frac{\sqrt{3}}{2}+0.04 \times \frac{1}{2}\)

= \(0.04598 \mathrm{~m} \approx 0.046 \mathrm{~m}\)

From equation (2) we get, \(\omega=\frac{\pi}{6} \mathrm{rad} \cdot \mathrm{s}^{-1}\)

So, velocity after \(2 \mathrm{~s}\),

ν = \(\omega \sqrt{A^2-x^2}\)

= \(\frac{\pi}{6} \sqrt{(0.05)^2-(0.046)^2}=1.03 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Again, acceleration after 2s,

a = \(\omega^2 x=\left(\frac{\pi}{6}\right)^2 \times 0.046=1.26 \mathrm{~m} \cdot \mathrm{s}^{-2}\).

Example 10. The equation of motion of a particle executing SHM is expressed by x = \(10 \sin \left(10 t-\frac{\pi}{6}\right)\). Establish an equation to express its velocity and also calculate the magnitude of its maximum acceleration.
Solution:

Given, x = \(10 \sin \left(10 t-\frac{\pi}{6}\right)\)

∴ Velocity, \(\nu=\frac{d x}{d t}=10 \times 10 \cos \left(10 t-\frac{\pi}{6}\right)\)

= \(100 \cos \left(10 t-\frac{\pi}{6}\right) \text { unit. }\)

Again, acceleration, a = \(\frac{d v}{d t}=-10 \times 100 \sin \left(10 t-\frac{\pi}{6}\right)\)

= \(-1000 \sin \left(10 t-\frac{\pi}{6}\right) \text { unit. }\)

Acceleration will be maximum when, \(\sin \left(10 t-\frac{\pi}{6}\right)=1\)

∴ Magnitude of maximum acceleration, \(a_{\max }=1000\) units.

Example 11. Equation of a simple harmonic motion is y = \(2 \sin \left(4 t+\frac{\pi}{6}\right)\).  Find out its time period and initial phase.
Solution:

Given:

Equation of a simple harmonic motion is y = \(2 \sin \left(4 t+\frac{\pi}{6}\right)\).

Comparing the given equation with the general equation of SHM, y = Asin(ωt+θ), we get, ω = 4, i.e., time period, T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{4}=\frac{3.14}{2}=1.57 \mathrm{~s}\)

Phase = \(4 t+\frac{\pi}{6}\); and initial phase, i.e., phase at t = 0

∴ \(\theta=\frac{\pi}{6}=30^{\circ}\)

Example 12. The equations of the two SHMs are x₁ = Asin(ωt + δ₁) and x₂ = Asin(ωt+δ₂) respectively. They superimpose on each other. Find the amplitude of the resultant.
Solution:

Given:

The equations of the two SHMs are x₁ = Asin(ωt + δ₁) and x₂ = Asin(ωt+δ₂) respectively. They superimpose on each other.

Resultant, x = \(x_1+x_2\)

= \(A\left[\sin \left(\omega t+\delta_1\right)+\sin \left(\omega t+\delta_2\right)\right]\)

= \(2 A \sin \frac{\left(\omega t+\delta_1\right)+\left(\omega t+\delta_2\right)}{2} \cos \frac{\left(\omega t+\delta_1\right)-\left(\omega t+\delta_2\right)}{2}\)

= \(2 A \cos \frac{\delta_1-\delta_2}{2} \sin \left(\omega t+\frac{\delta_1+\delta_2}{2}\right)\)

∴ The amplitude of the resultant SHM is \(2 A \cos \frac{\delta_1-\delta_2}{2}\).

Example 13. The displacements of a particle executing SHM at three consecutive seconds are 6 cm, 10 cm, and 6 cm respectively. Find out the frequency of oscillation of the particle.
Solution:

Given:

The displacements of a particle executing SHM at three consecutive seconds are 6 cm, 10 cm, and 6 cm respectively.

Displacement, x = A cos(ωt+θ)

Let initially at t = 0, displacement = 6 cm.

So, at t = 1 s, displacement = 10 cm

and at t = 2s, displacement is = 6 cm

∴ 6 = A cosθ….(1)

10 = A cos(ω + θ)…(2)

6 = A cos(2ω + θ)…(3)

From (1) and (3) we get,

cos(2ω + θ) = cosθ = cos(-θ)

or, 2ω + θ = -θ or, ω = -θ

∴ From (2), we get,

10 = A cos0 or, A = 10 cm .

From (1), we get,

6 = 10cos(-ω) or, cosω = \(\frac{3}{5}\)

or, ω = 0.927 rad · s^-1

∴ Frequency = \(\frac{\omega}{2 \pi}=\frac{0.927}{2 \times 3.14}=0.148 \mathrm{~s}^{-1} \text {. }\)

Example 14. The equation of a SHM is y = 3sin60πt. Calculate its amplitude, time period, and acceleration at its position of maximum displacement.
Solution:

Given:

The equation of a SHM is y = 3sin60πt.

Comparing the given equation with y = Asinωt, we get amplitude, A = 3 units; ω = 60π.

∴ Time period, T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{60 \pi}=\frac{1}{30} \mathrm{~s}\)

∴ Acceleration at its position of maximum displacement = ω²A = (60π)² x 3 = 1.065 x 10⁵ unit · s^-2.

Example 15. Displacement of a particle is given by x = 4(cosπt + sinπt) m. Find its amplitude.
Solution:

Given:

Displacement of a particle is given by x = 4(cosπt + sinπt) m.

x = \(4(\cos \pi t+\sin \pi t)\)

= \(4 \sqrt{2}\left(\cos \pi t \cdot \frac{1}{\sqrt{2}}+\sin \pi t \cdot \frac{1}{\sqrt{2}}\right)\)

= \(4 \sqrt{2}\left(\cos \pi t \cdot \cos \frac{\pi}{4}+\sin \pi t \cdot \sin \frac{\pi}{4}\right)\)

= \(4 \sqrt{2} \cos \left(\pi t-\frac{\pi}{4}\right) \mathrm{m}\)

∴ Amplitude = 4√2 m.

Example 16. Equation of motion of a particle executing SHM is x = \(5 \sin \left(4 t-\frac{\pi}{6}\right) \mathrm{m}\), where x is the displacement. If the displacement is 3 m, find the velocity of the particle.
Solution:

Given:

Equation of motion of a particle executing SHM is x = \(5 \sin \left(4 t-\frac{\pi}{6}\right) \mathrm{m}\), where x is the displacement. If the displacement is 3 m.

Velocity, v = \(\frac{d x}{d t}=5 \times 4 \cos \left(4 t-\frac{\pi}{6}\right)\)

= \(20 \sqrt{1-\sin ^2\left(4 t-\frac{\pi}{6}\right)}=20 \sqrt{1-\left(\frac{x}{5}\right)^2}\)

If x = 3m, then v = \(20 \sqrt{1-\left(\frac{3}{5}\right)^2}=20 \times \frac{4}{5}=16 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)

Example 17. A point mass oscillates along the axis according to the law, x = \(x_0 \cos \left(\omega t-\frac{\pi}{4}\right)\). If the acceleration of the particle is written as a = Acos(ωt+δ), find A and δ.
Solution:

Given:

A point mass oscillates along the axis according to the law, x = \(x_0 \cos \left(\omega t-\frac{\pi}{4}\right)\). If the acceleration of the particle is written as a = Acos(ωt+δ),

x = \(x_0 \cos \left(\omega t-\frac{\pi}{4}\right)\)

∴ Velocity, \(v=\frac{d x}{d t}=-\omega x_0 \sin \left(\omega t-\frac{\pi}{4}\right)\)

and acceleration, \(\alpha=\frac{d v}{d t}=-\omega^2 x_0 \cos \left(\omega t-\frac{\pi}{4}\right)\)

= \(+\omega^2 x_0 \cos \left(\omega t-\frac{\pi}{4}+\pi\right)\)

= \(\omega^2 x_0 \cos \left(\omega t+\frac{3 \pi}{4}\right)\)

Given \(\alpha=A \cos (\omega t+\delta)\)

So comparing the two equations we have, \(A=\omega^2 x_0\) and \(\delta=\frac{3 \pi}{4}\)

Example 18. Two simple harmonic motions are represented by the equations \(y_1=0.1 \sin \left(100 \pi t+\frac{\pi}{3}\right)\) and y₂ = 0.1 cos πt. What is the initial phase difference of the velocity of the first particle with respect to the second?
Solution:

Given:

Two simple harmonic motions are represented by the equations \(y_1=0.1 \sin \left(100 \pi t+\frac{\pi}{3}\right)\) and y₂ = 0.1 cos πt.

∴ \(y_1=0.1 \sin \left(100 \pi t+\frac{\pi}{3}\right)\);

Velocity, \(v_1=\frac{d y_1}{d t}=100 \pi \times 0.1 \cos \left(100 \pi t+\frac{\pi}{3}\right)\)

= \(10 \pi \cos \left(100 \pi t+\frac{\pi}{3}\right)\)

Phase, ø₁ = \(\frac{\pi}{3}\) at time t = 0

y₂ = 0.1 cos πt

Velocity, \(\nu_2=\frac{d y_2}{d t}=-0.1 \pi \sin \pi t=0.1 \pi \cos \left(\pi t+\frac{\pi}{2}\right)\)

Phase, \(\phi_2=\frac{\pi}{2}\) at time t = 0

∴ Phase difference = \(\theta_1-\theta_2=\frac{\pi}{3}-\frac{\pi}{2}=-\frac{\pi}{6}\)

Example 19. The displacement of an object attached to a spring and executing SHM is given by x = 2 x 10^-2 cosπtm. In what time the object attain maximum speed first?
Solution:

Given:

The displacement of an object attached to a spring and executing SHM is given by x = 2 x 10^-2 cosπtm.

x = 2 x 10^-2 cosπt

∴ v = \(\frac{d x}{d t}=-\left(2 \times 10^{-2} \pi\right) \sin \pi t\)

v is maximum when sinπt = ±1.

or, \(\pi t=\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2} \ldots\)

The speed becomes maximum first when n t = \(\frac{\pi}{2}\)

or, t = \(\frac{1}{2}\) = 0.5

Example 20. If x, v, and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, show that the expressions \(\frac{aT}{x}\) and a²T² + 4π²v² do not change with time.
Solution:

Given:

If x, v, and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T

If A is the amplitude, ω is the angular frequency and x is the displacement of a particle executing SHM then,

velocity v = \(\pm \omega \sqrt{A^2-x^2}\)

acceleration a = \(-\omega^2 x\)

time period T = \(\frac{2 \pi}{\omega}\)

∴ \(\frac{a T}{x}=\frac{-\omega^2 x \cdot \frac{2 \pi}{\omega}}{x}\)

∴ \(a^2 T^2+4 \pi^2 v^2=\left(-\omega^2 x\right)^2\left(\frac{2 \pi}{\omega}\right)^2+4 \pi^2 \omega^2\left(A^2-x^2\right)\)

= \(\omega^4 x^2 \frac{4 \pi^2}{\omega^2}+4 \pi^2 \omega^2 A^2-4 \pi^2 \omega^2 x^2 \)

= \(4 \pi^2 \omega^2 A^2=\text { constant }\)

Example 21. Two simple harmonic motions of angular frequencies 100 and 1000 rad · s^-1 have the same displacement amplitude. What is the ratio of their maximum acceleration?
Solution:

Given:

Two simple harmonic motions of angular frequencies 100 and 1000 rad · s^-1 have the same displacement amplitude.

Acceleration, f= -ω²x

If the amplitude is a, maximum acceleration =ω²a

∴ Ratio of maximum accelerations = \(\frac{\omega_1^2 a}{\omega_2^2 a}=\left(\frac{\omega_1}{\omega_2}\right)^2=\left(\frac{100}{1000}\right)^2=\frac{1}{100}\)

Example 22. A particle initially at rest at a distance of 5 cm from its mean position performs a SHM completing 60 oscillations in 2 seconds. Find the equation representing the displacement of the particle at any subsequent instant. What will be its equation if initially the particle were at the mean position?
Solution:

Given:

A particle initially at rest at a distance of 5 cm from its mean position performs a SHM completing 60 oscillations in 2 seconds. Find the equation representing the displacement of the particle at any subsequent instant.

Time taken by the particle in SHM to complete 60 oscillations = 2 s.

∴ Time period of the particle, T = \(\frac{2}{60}\) =\(\frac{1}{30}\) s .

Angular velocity of the particle, \(\omega=\frac{2 \pi}{T}=\frac{2 \pi}{\frac{1}{30}}=60 \pi\)

The particle was at rest and about 5 cm away from its equilibrium position.

∴ The amplitude of the particle, a = 5 cm.

Let, at any time t, the particle is x cm away from its equilibrium position.

∴ Displacement of the particle, x = 5cos(60πt+ θ) cm

At t = 0, x = 5 cm

∴ 5 = 5cosθ or, cosθ =1 or, θ = 0

∴ x = 5cos60πt

If the particle starts its oscillation from the equilibrium position, then, x = 5 sin60πt.

Example 23. The equation of two SHMs are \(y_1=10 \sin \left(4 \pi t+\frac{\pi}{4}\right)\), \(y_2=5(\sin 3 \pi t+\sqrt{3} \cos 3 \pi t)\), What is thne ratio of therir amplitudes?
Solution:

Given:

The equation of two SHMs are \(y_1=10 \sin \left(4 \pi t+\frac{\pi}{4}\right)\), \(y_2=5(\sin 3 \pi t+\sqrt{3} \cos 3 \pi t)\),

The amplitude of the first SHM, A₁= 10

Now, \(y_2=5(\sin 3 \pi t+\sqrt{3} \cos 3 \pi t)\)

= \(5 \times 2\left(\frac{1}{2} \sin 3 \pi t+\frac{\sqrt{3}}{2} \cos 3 \pi t\right) \)

= \(10\left(\cos \frac{\pi}{3} \sin 3 \pi t+\sin \frac{\pi}{3} \cos 3 \pi t\right) \)

= \(10 \sin \left(3 \pi t+\frac{\pi}{3}\right)\)

∴ The amplitude of the second SHM, \(A_2=10\)

Hence, \(\frac{A_1}{A_2}=\frac{10}{10}=1 or, A_1: A_2=1: 1\).

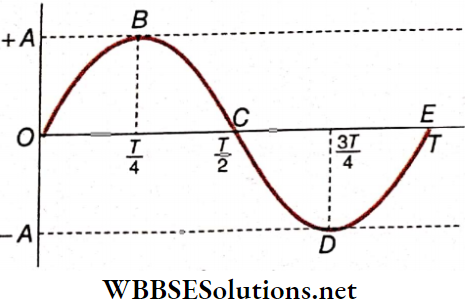
Graphical Representation Of SHM: If a particle executing simple harmonic motion begins its motion from the position of equilibrium, then the equation of motion of the particle is x = \(A \sin \omega t=A \sin \frac{2 \pi}{T} t\)

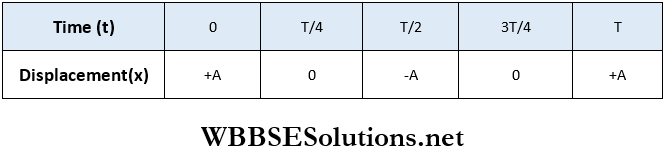
During a complete period, i.e., from t = 0 to t = T, the variation of displacement with time is shown in the following table:

Now on graph paper, time is placed along the horizontal axis and displacement along the vertical axis. The points O, B, C, D, and E are plotted according to their corresponding coordinates in the above table. The points are connected with a curved line. The graph OBCDE is obtained. This is a sine curve. This curve represents a simple harmonic motion.

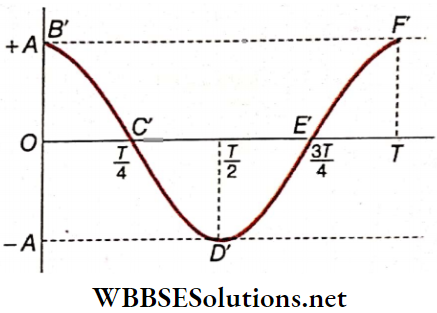
If a particle executing simple harmonic motion starts its motion from one end of Its path, then the equation of motion of the particle is x = \(A \cos \omega t=A \cos \frac{2 \pi}{T} t\)

Proceeding similarly, we get the following table and the graph. The graph B’C’D’E’F’ is a cosine curve.

The sine and the cosine curves are identical except for their initial phase difference. For their special symmetry, sine and cosine functions are called sinusoidal functions. As a simple harmonic motion is represented by any one of these sinusoidal functions, they are also known as harmonic functions.

Composition Of Two Colinear SHMs Of The Same Frequency By Graphical And Analytical Methods: Two simple harmonic motions, having the same frequency n (i.e., time period, T = \(\frac{1}{n}\) and angular frequency, ω = 2πn, are being executed along the x-axis, i.e., they are collinear. To obtain the resultant motion due to the superposition of the two SHMs, we have to know their phase difference.

1. Two SHMs Are In Phase: The two SHMs of the same time period are in phase.

Let the equation of the first motion be \(x_1=A \sin \omega t=A \sin \frac{2 \pi}{T} t.\)

and the equation of the second motion be \(x_2=B \sin \omega t=B \sin \frac{2 \pi}{T} t.\)

The resultant displacement at any instant is the vector sum of the displacements of the two individual motions at that instant.

So, the resultant displacement, \(x=x_1+x_2=A \sin \frac{2 \pi}{T} t+B \sin \frac{2 \pi}{T} t=(A+B) \sin \frac{2 \pi}{T} t\)

Therefore, the resultant motion is an SHM of the same frequency with an amplitude equal to (A + B).

The displacements of the two individual motions and their resultant displacement at different times (from t = 0 to t = T) are shown in the table below.

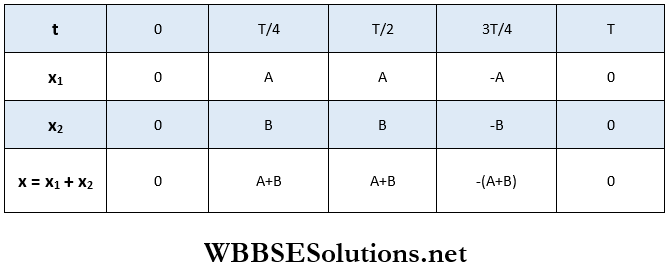
Plotting the referred values in the table, we get the graph of the resultant displacement x. From the graph, we come to know

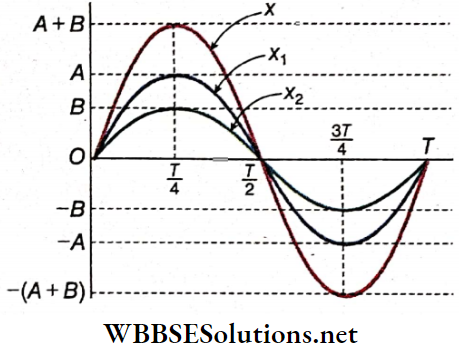
1. The resultant motion is also simple harmonic.
2. The frequency and the time period of the resultant motion are equal to those of the individual motions.
3. The amplitude of the resultant motion is equal to the sum of the amplitudes of the individual motions.
4. The resultant motion is also in phase with the individual motions.

2. Two SHMs In Opposite Phase: Two simple harmonic motions have the same frequency and the same time period, but they are in opposite phases.

So, the equation of the first SHM: \(x_1=A \sin \omega t=A \sin \frac{2 \pi}{T} t\).

The equation of the second SHM: \(x_2=B \sin (\omega t+\pi)=-B \sin \omega t=-B \sin \frac{2 \pi}{T} t \text {. }\)

[As the two motions are in opposite phases, the phase difference between them = 180° = π]

∴ Resultant displacement, x = \(x_1+x_2=A \sin \frac{2 \pi}{T} t-B \sin \frac{2 \pi}{T} t=(A-B) \sin \frac{2 \pi}{T} t\)

From t = 0 to t = T, the values of x₁, x₂, and x are given in the tables below.

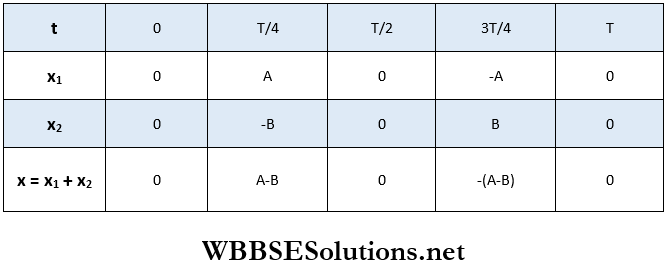
Plotting the referred values in the table, we get the graph of the resultant displacement x. From the graph, we come to know

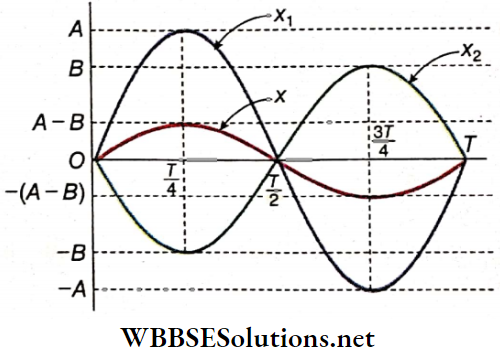
1. The resultant motion is also simple harmonic.
2. The frequency and the time period of the resultant motion are equal to those of the individual motions.
3. The amplitude of the resultant motion is equal to the difference of the amplitudes of the individual motions.
4. The resultant motion is in phase with the motion having a larger amplitude but in the opposite phase with the motion having a smaller amplitude.

Due to the superposition of two SHMs of the same amplitude but of opposite phases, the resultant displacement is x = x₁ + x₂ = 0 for all values of t. It implies that the particle, on which these two SHMs superpose, remains at rest.