Solid Geometry Chapter 2 Theorems On Transversal And Mid Points
Chapter 2 Theorems On Transversal And Mid Points Theorems On Mid Points
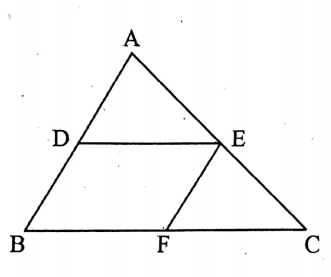
Let ABC be any triangle. D and E are the mid-points of its AB and AC sides respectively.
Then, DE || BC and DE = \(\frac{1}{2}\) BC.
Similarly, if F is the mid-point of BC, then DF || AC
and DF = \(\frac{1}{2}\) AC, EF || AB and EF = \(\frac{1}{2}\) AB
Therefore, the straight line obtained by joining the mid-points of any two sides of a triangle is parallel to its third side and is half of its length.
Read and Learn More WBBSE Solutions For Class 9 Maths
We shall now prove this theorem geometrically.
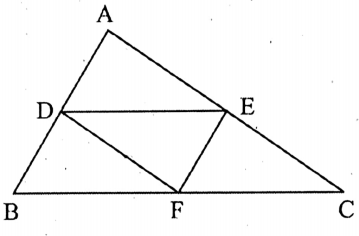
Theorem 1. The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it in length.
Given: Let D and E be the mid-points of the sides AB and AC respectively of the triangle ABC.
Let us join D and E.
To prove DE || BC and DE = \(\frac{1}{2}\) BC.
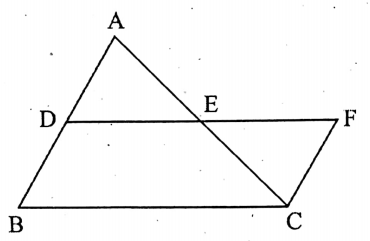
Construction: Let DE be extended to F such that DE EF and let us join F, C.
Proof: In triangles, ΔADE and ΔCEF, AE = CE
[∵ E is the mid-point of AC. ]
<AED = <CEF [∵ opposite angles ] and DE = EF [by construction]
∴ ΔADE ≅ ΔCEF [ by the condition of S-A-S congruent ]
∴ AD = FC
or, BD = CF [since D is the mid-point of AB, AD = BD]
Again, DAEFCE, but these are alternative angles,
∴ DA || CF
or, BA || CF
or, BD || CF.
Thus, in the quadrilateral BDFC, BD || CF and BD = CF,
∴ BDFC is a parallelogram.
DF || BC and DF = BC
or, DE || BC and DE+ EF = BC
or, DE + DE = BC [∵ DE = EF]
or, 2DE = BC
or, DE = \(\frac{1}{2}\) BC
∴ DE = BC and DE = \(\frac{1}{2}\) BC. (Proved)
We shall now prove the converse of Theorem-1.
Theorem 2. The line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Given: Let us draw DE parallel to BC through the mid-point D of AB of the ΔABC, which intersects AC at E.
To prove : AE = CE and DE = \(\frac{1}{2}\) BC.
Construction: ED is extended to F such that ED = DF.
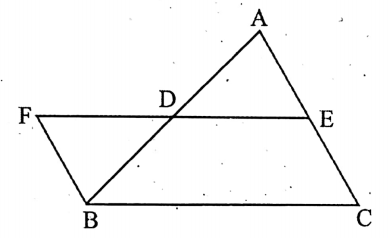
Let us join B, F.
Proof: In triangles A ADE and A BDF, AD = BD [∵ D is the mid-point of AB ],
∠EDA = ∠FDB [… opposite angles] and ED=DF [by construction]
∴ AADE ≅ ABDF [ by the condition of S-A-S congruence]
∴ AE = BF [ similar sides of congruent triangles ]
∠AED= ∠BFD. But these are alternate angles.
∴ AE || FB or, EC || FB…… (1)
Also, given that DE || BC or, FE || BC…… (2)
From (1) and (2) we get, BCEF is a parallelogram.
FB = CE or, AE = CE [ FB = AE] and FE = BC
[∵ opposite sides of any parallelogram are equal ]
or, FD + DE = BC or, DE + DE = BC [∵ FD = DE ]
or, 2DE = BC or, DE= \(\frac{1}{2}\) BC
∴ AE = CE and DE = \(\frac{1}{2}\) BC. (Proved)
We shall now prove theorem-1 with the help of the application of theorem-2.
Alternate proof of THEOREM-2
Given: Let D and E be the mid-points of the sides AB and AC respectively of the AABC and let us join D and B.
To prove: DE || BC and DE= \(\frac{1}{2}\) BC.
Construction: Let us draw EF through E, the mid-point of AC, parallel to AB, which intersects BC at F.
Proof: E is the mid-point of AC and EF || AB [by construction]
F is the mid-point of BC, i.e., BF = \(\frac{1}{2}\) BC and EF = \(\frac{1}{2}\) AB.
Again, EF = \(\frac{1}{2}\) AB = DB [∵ D is the mid-point of AB.]
Thus, in the quadrilateral DBFE, EF = DB and EF || DB.
∴ DBFE is a parallelogram.
∴ DE || BF or, DE || BC and DE = BF
or, DE =\(\frac{1}{2}\) BC.
∴ DE || BC and DE = \(\frac{1}{2}\) BC. (Proved)
Now, PR 10 cm,
∴ SR- cm 5 cm.
∴ the required length of QS = 5 cm.
Alternative Method:
We know that the median of any triangle drawn from the vertex forming the right-angle of any right-angled triangle to its hypotenuse is half of the hypotenuse.
QS = \(\frac{1}{2}\) PR = \(\frac{1}{2}\)x10 cm = 5 cm.
∴ the required length of QS = 5 cm
Chapter 2 Theorems On Transversal And Mid Points Theorems On Transversal
You have already studied in your previous classes the properties of the angles obtained by the intersection of a straight line (which is generally called the transversal) with two or more two straight lines (parallel or unparallel). In this chapter, we shall prove geometrically one theorem on this transversal.
Theorem 1. If a transversal intersects equal parts from three or more than three parallel straight lines, then they also intersect equal parts from another transversal.
Given: The parallel straight lines AB, CD and EF have intersected two equal parts GH and HI from the transversal PQ, i.e., GH = HI. The same parallel straight lines have also intersected A two parts LM and MN from another transversal RS.
To prove LM = MN.
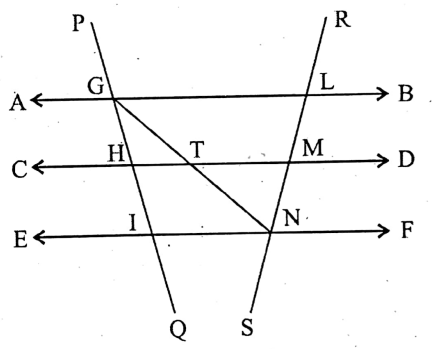
Construction: Let us join G and N.
Also, let GN intersects CD at point T.
Proof: In triangle GIN, H is the mid-point of GI
[∵ GH = HI] and HT || IN [Given]
∴ T is the mid-point of GN [by theorem-2]
Again, in AGLN, T is the mid-point of GN and TM || GL (Given)
∴ M, is the mid-point of LN [by theorem-2]
∴ LM = MN. (Proved)
Chapter 2 Theorems On Transversal And Mid Points Select The Correct Answer (MCQ)
Question 1. In ΔPQR, ∠PQR = 90° and PR = 10 cm. If S is the mid-point of PR, the length of QS is-
- 4 cm
- 5 cm
- 6 cm
- 3 cm
Solution:
Given
ΔPQR, ∠PQR = 90° And PR = 10 cm
S is the mid-point of PR.
Let us draw, SR’⊥ QR.
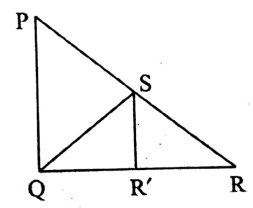
PQR = 90° and SR’R = 90°,
∴ PQ || SR.
Again, S is the mid-point of PR and SR’ || PQ.
∴ R’ is the mid-point of QR,
i.e., QR’ = RR’
Now, in A QSR’ and A RSR’, QR’ = RR’, SR’ is common to both the triangles and ∠SRQ = ∠SRR
[∵ each is 90° ]
ΔQSR’ = ΔRSR’
∴ QS = SR [∵ similar sides]
Now, PR 10 cm,
∴ SR = \(\frac{PR}{2}\) cm 5 cm.
∴ the required length of QS = 5 cm.
Alternative Method:
We know that the median of any triangle drawn from the vertex forming the right-angle of any right-angled triangle to its hypotenuse is half of the hypotenuse.
QS = \(\frac{1}{2}\) PR = \(\frac{1}{2}\)x10 cm = 5 cm.
∴ the required length of QS = 5 cm
Question 2. The mid-point of the median AD of AABC is E. Extended BE intersects AC at F. If AC = 10-5 cm, then AF =
- 3 cm
- 3.5 cm
- 2.5 cm
- 5 cm
Solution:
Given
The mid-point of the median AD of AABC is E.
Extended BE intersects AC at F. If AC = 10-5 cm.
Let us draw EF || DP.
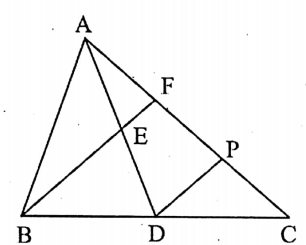
Also, let DP intersects AC at P.
E is the mid-point of AD and DP || BF.
∴ P is the mid-point of CF, i.e., CP – \(\frac{1}{2}\) CF = PF
Now, AF + FP+ PC = AC
or, AF+AF+ PF AC [ FP= AF and PC = PF]
or, AF+AF+AF= AC.
or, 3 AF = AC
or, AF = \(\frac{1}{3}\)AC = \(\frac{1}{3}\) x 10.5 cm = 3.5 cm
∴ the required length, AF = 3.5 cm.
Question 3. In the trapezium ABCD, AB || DC and AB =7 cm and DC=5 cm. If E and F be the mid-points of AD and BC respectively, then EF =
- 5 cm
- 6 cm
- 7 cm
- 12 cm
Solution:
Given
In the trapezium ABCD, AB || DC and AB =7 cm and DC=5 cm.
E and F be the mid-points of AD and BC respectively.
Let us join B and D. Let BD intersects EF at P.
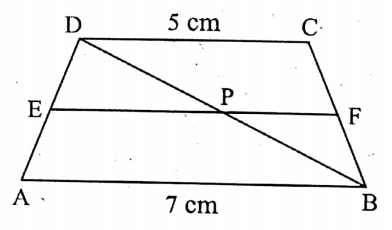
∴ DC || EF || AB and E and F are the mid-points of AD and BC respectively.
∴ EP = \(\frac{1}{3}\) AB and FP = \(\frac{1}{2}\) DC
∴ EF = EP + PF = \(\frac{1}{2}\) AB+ \(\frac{1}{2}\) DC = \(\frac{1}{2}\) (AB+DC)
= \(\frac{1}{2}\) (7+5) cm = \(\frac{1}{2}\) x 12 cm
= 6cm
∴ the required length of EF = 6 cm.
Question 4. D, E, and F are the mid-points of BC, CA, and AB respectively of the AABC. If BE and DF intersect at X and CF and DE intersect at Y, then XY
- \(\frac{1}{2}\) BC
- \(\frac{1}{4}\) BC
- \(\frac{1}{3}\) Bc
- \(\frac{1}{8}\) BC
Solution:
Given
D, E, and F are the mid-points of BC, CA, and AB respectively of the AABC.
BE and DF intersect at X and CF and DE intersect at Y.
D and E are the mid-points of BC and AC ofΔABC respectively.
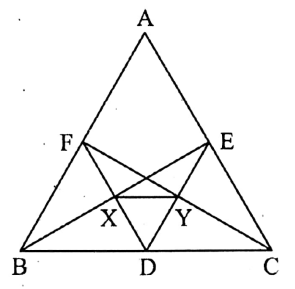
∴ DE || BA and DE = \(\frac{1}{2}\) BA = BF………..(1)
Similarly, DF || CA and DF = CA = \(\frac{1}{2}\) CA = CE……………(2)
Now, in ΔBXF and ΔDXE,
∠XBF = ∠XED [ ∵ alternate angles]
<XFB = ∠XDE [∵ alternate angles ] and BF = DE [by (1)]
∴ ΔBXF ≅ΔDXE.
∴ BX=XE [ ∵ similar sides of congruent Δ’s]
∴ X is the mid-point of BE.
Similarly, it can be proved that Y is the mid-point of DE.
∴ in ABDE, X and Y are the mid-points of BE and DE respectively.
∴ XY = \(\frac{1}{2}\) BD = \(\frac{1}{2}\) x \(\frac{1}{2}\) BC
[∵ BD = \(\frac{1}{2}\) BC] = \(\frac{1}{4}\)BC.
∴ the required length of XY = \(\frac{1}{4}\)BC
Question 5. D is the mid-point of the side BC of AABC. The line segment through D and parallel to CA and BA intersects BA and CA at E and F respectively. Then EF =
- \(\frac{1}{4}\)BC
- \(\frac{1}{2}\) BC
- BC
- 2 BC
Solution:
Given
D is the mid-point of the side BC of AABC.
The line segment through D and parallel to CA and BA intersects BA and CA at E and F respectively.
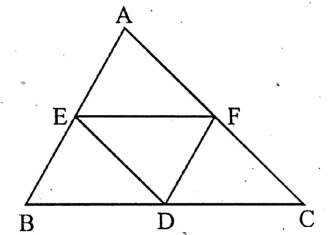
DF || BA, F is the mid-point of AC and DF = \(\frac{1}{2}\)AB ……………..(1)
Again, DE | CA, E is the mid-point of AB, and DE = \(\frac{1}{2}\) AC.
∴ E is the mid-point AB,
∴ \(\frac{1}{2}\) AB= BE
or, DF = BE [by (1)]
∴ in the quadrilateral BDFE, BE || DF and BE = DF,
∴ BDFE is a parallelogram.
∴ EF = BD = \(\frac{1}{2}\) BC [ D is the mid-point of BC]
∴ the required length of EF = = BC.
Question 6. E is the mid-point of the side BC of the parallelogram ABCD. DE and the extended AB meet at point F. Then AF =
- \(\frac{3}{2}\)AB
- 2 AB
- 3 AB
- \(\frac{5}{4}\) AB
Solution:
Given
E is the mid-point of the side BC of the parallelogram ABCD. DE and the extended AB meet at point F.
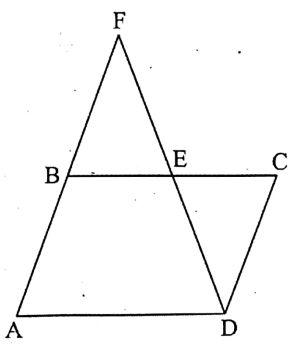
AF || DC and BC are their transversals,
∠FBC = ∠DCB [alternate angles ]
or, <FBE = ∠DCE………..(1)
Again, AF | DC and DF are their transversal,
∴ ∠AFD = ∠CDF [alternate angles ]
or, <BFE = ∠CDE………….(2)
Now, in ABEF and ACDE,
<FBE = ∠DCE [ by (1)],
∠BFE = ∠CDE [ by (2)]
and BE = CE [E is the mid-point of BC]
ΔBEF ≅ ΔCDE. [by the condition of A-A-S congruence]
∴ BF = DC [∵similar sides of congruent triangles ]
∴ BF = AB………….(3) [ opposite sides of the parallelogram ABCD are equal, ∴ DC = AB. ]
Now, AF = AB + BF = AB + AB [by (3)] = 2AB
∴ AF = 2AB.
Chapter 2 Theorems On Transversal And Mid Points Short Answer Type Questions
Question 1. AD and BE are the medians of AABC and DF, parallel to BE, intersect AC at a point F. If the length of AC is 8 cm, find the length of CF.
Solution:
Given
AD and BE are the medians of AABC and DF, parallel to BE, intersect AC at a point F.
The length of AC is 8 cm.
∴ D is the mid-point of BC and DF BE.
∴ F is the mid-point of CE.
Now, CF = \(\frac{1}{2}\) CE = \(\frac{1}{2}\) x \(\frac{1}{2}\) AC
[∵ BE is the median, E is the mid-point of AC]
= \(\frac{1}{4}\) AC = \(\frac{1}{4}\) x 8 cm
= 2 cm.
The length of CF = 2 cm.
Question 2. P, Q, and R are the mid-points of the sides BC, CA, and AB of the AABC. If AC = 21 cm, BC = 29 cm, and AB = 30 cm, then find the perimeter of the quadrilateral ARPQ.
Solution:
Given
P, Q, and R are the mid-points of the sides BC, CA, and AB of the AABC.
AC = 21 cm, BC = 29 cm, and AB = 30 cm.
AR = \(\frac{1}{2}\) AB = \(\frac{1}{2}\) x 30 cm = 15 cm
RP = AQ [∵ ARPQ is a parallelogram, RP || AQ and PQ ||RA]
= \(\frac{1}{2}\) AC
= \(\frac{1}{2}\) x 21 cm
= 10.5 cm
∴ the perimeter of the quadrilateral
ARPQ=AR+RP + PQ+QA.
=AR+RP + AR+RP [ ∵ PQ-AR, QA=RP]
=2 (AR+ RP)=2(15+10-5) cm
=2 x 25.5 cm
= 51 cm
∴ the required perimeter = 51 cm.
Question3. The medians BE and CF of the AABC intersect each other at G. P and Q are the mid-points of BG and CG respectively. If PQ = 3 cm, find the length of BC.
Solution:
Given
The medians BE and CF of the AABC intersect each other at G. P and Q are the mid-points of BG and CG respectively.
PQ = 3 cm
In A BGC, P and Q are the mid-points of BG and CG respectively,
∴ PQ || BC and PQ = \(\frac{1}{2}\) BC.
Given that PQ-3 cm.
∴ 3 = \(\frac{1}{2}\) BC
or, BC= 3 x 2 cm
= 6 cm
The length of BC = 6 cm
Question 4. D is any point on the side AC of the AABC. P, Q, X, Y are the mid-points of AB, BC, AD and DC respectively. If PX = 5 cm, then find the length of QY.
Solution:
Given
D is any point on the side AC of the AABC. P, Q, X, Y are the mid-points of AB, BC, AD and DC respectively.
PX = 5 cm.
Let us join P and Q.
PQ || AC, [ ∵ P and Q are the mid-points of the sides AB and BC respectively]
or, PQ || XY and PQ = \(\frac{1}{2}\) AC ……..……..…(1)
Now, XY = DX+DY= \(\frac{1}{2}\) AD + \(\frac{1}{2}\) DC
= \(\frac{1}{2}\) (AD + DC)
= \(\frac{1}{2}\) AC…………………(2)
From (1) and (2) we get, PQ = XY
in the quadrilateral PXYQ, PQ = XY and PQ II XY
∴ PXYQ is a parallelogram.
PX=QY or, 5 cm=QY [∵ PX = 5 cm]
∴ QY = 5 cm.
The length of QY = 5 cm
Question 5. D and E lie on the AABC such that AD = \(\frac{1}{4}\) AB and AE = \(\frac{1}{4}\) AC. Prove that DE || BC and DE = \(\frac{1}{4}\) BC.
Solution:
Given
D and E lie on the AABC
AD = \(\frac{1}{4}\) AB and AE = \(\frac{1}{4}\) AC.
Let P and Q be the mid-points of AB and AC respectively and let us join P and Q.
Then, PQ || BC and PQ = \(\frac{1}{2}\) BC ………………(1)
Again AD = \(\frac{1}{4}\) AB = \(\frac{1}{2}\) x \(\frac{1}{2}\) AB = \(\frac{1}{2}\) AP [∵ \(\frac{1}{2}\) AB = AP]
AE = \(\frac{1}{4}\) AC = \(\frac{1}{2}\) x \(\frac{1}{2}\) AC = \(\frac{1}{2}\) AQ [∵ \(\frac{1}{2}\) AC = AQ]
Then, in A APQ, D, and E are the mid-points of AP and AQ respectively,
DE || PQ and DE = \(\frac{1}{2}\) PQ
or, DE || BC and DE = \(\frac{1}{2}\) x \(\frac{1}{2}\) BC [by (1)] = \(\frac{1}{4}\)BC
∴ DE || BC and DE = \(\frac{1}{4}\) BC. (Proved)
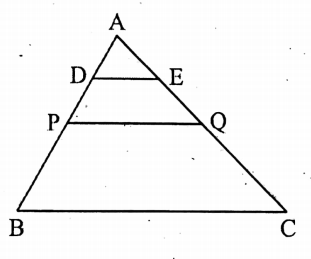
Question 6. D, E, and F are the mid-points of the sides BC, CA, and AB respectively of the AABC. FE intersects AD at O. If AD = 6 cm, find the length of AO.
Solution:
Given
D, E, and F are the mid-points of the sides BC, CA, and AB respectively of the AABC.
FE intersects AD at O.
AD = 6 cm.
D and E are the mid-points of BC and CA respectively.
∴ DE | BA or, DE || FA……………(1)
Again, D and F are the mid-points of BC and BA respectively,
∴ DF || CA
or, DF || EA……..(2)
From (1) and (2) we get, AEDF is a parallelogram, and AD and FE are two diagonals.
We know that diagonals of a parallelogram bisect each other.
∴ AO = DO
Now, AO + OD = AD
or, AO + AO = AD [∵ OD=AO]
or, 2AO = 6 cm
or, AO = \(\frac{6}{2}\)cm = 3 cm.
∴ the required length of AO = 3 cm.
The length of AO = 3 cm.
Chapter 2 Theorems On Transversal And Mid Points Long Answer Type Questions
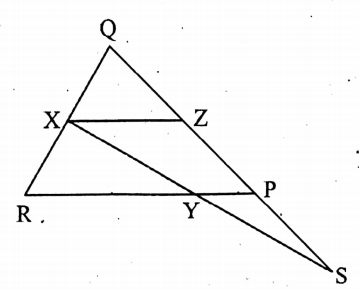
Question 1. X and Z are the mid-points of the sides QR and QP respectively of the APQR. The side QP is extended to S such that PS = ZP. SX intersects PR at Y. Prove that PY= \(\frac{1}{4}\) PR.
Given: X and Z are the mid-points of the sides QR and QP respectively of the APQR.
The side QP is extended to S such that PS = ZP. SX intersects PR at Y.
To prove : PY = \(\frac{1}{4}\) PR
Proof: ∵ X and Z are the mid-points of QR and QP respectively of the ΔPQR,
∴ XZ || RP and XZ = \(\frac{1}{2}\) PR …………..(1)
Again, ∵ ZP = PS,
∴ P is the mid-point of ZS.
PY is part of PR,
∴ ZX || PR ⇒ PY || ZX
in ΔSZX, PY || ZX and P is the mid-point of ZS.
PY =\(\frac{1}{2}\) ZX = \(\frac{1}{2}\) x \(\frac{1}{2}\) PR [by (1)]
∴ PY = \(\frac{1}{4}\) PR. (Proved)
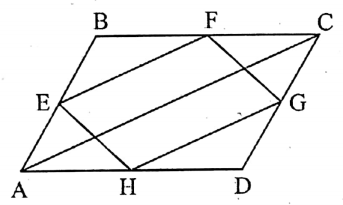
Question 2. Prove that the quadrilateral formed by joining the mid-points of a parallelogram is also a parallelogram.
Given: E, F, G, and H are the mid-points of the sides AB, BC, CD, and DA respectively of the parallelogram ABCD.
A quadrilateral EFGH is constructed by joining the pair of points (E, F), (F, G), (G, H), and (H. E).
To prove: EFGH is a parallelogram.
Construction: Let us draw the diagonal AC of the parallelogram ABCD.
Proof: In Δ ABC, E, and F are the mid-points of BA and BC respectively,
∴ EF || AC and EF = \(\frac{1}{2}\) AC…………….(1)
Again, in Δ ACD, H, and G are the mid-points of DA and DC respectively,
∴ HG || AC and HG = \(\frac{1}{2}\) AC……………(2)
Now, from (1) and (2) we get, EF = HG and EF || HG, i.e., two opposite sides of the quadrilateral EFGH are equal and parallel.
Hence, EFGH is a parallelogram. (Proved)
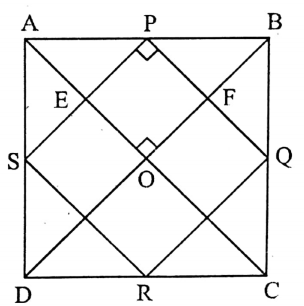
Question 3. Prove that the quadrilateral formed by joining the mid-points of the sides of a square is also a square.
Given: Let P, Q, R, and S be the mid-points of the sides AB, BC, CD, and DA respectively of the square ABCD.
A quadrilateral PQRS is constructed by joining these points.
To prove: PQRS is a square.
Construction: Let us draw the diagonals AC and BD of the square ABCD and let AC and BD intersect each other at O and also let AC intersect PS at E, and BD intersect PQ at F.
Proof: In ΔABD, S and P are the mid-points of AD and AB respectively,
∴ SP || DB and SP = \(\frac{1}{2}\) DB ……………(1)
Again, ΔBCD, Q, and R are the mid-points of CB and CD respectively,
∴ RQ | DB and RQ = \(\frac{1}{2}\) DB…………….(2)
Now, from (1) and (2) we get, SP = RQ and SP || RQ.
∴ PQRS is a parallelogram.
Again, in A ABC, P, and Q are the mid-points of AB and BC, PQ || AC and PQ=AC….(3)
SP = \(\frac{1}{2}\) DB and PQ = \(\frac{1}{2}\) AC.
But, DB = AC,
∴ SP = PQ, i.e.,
in quadrilateral EPFO, EP || OF and PF || EO.
∴ EPFO is a parallelogram.
∴ ∠EPF = ∠EOF [ ∵ opposite angles of a parallelogram]
= 90° [∵ the diagonals of a square bisect each other orthogonally. ]
∴ PQRS is such a rhombus, one angle of which is a right angle,
∴ PQRS is a square. (Proved)
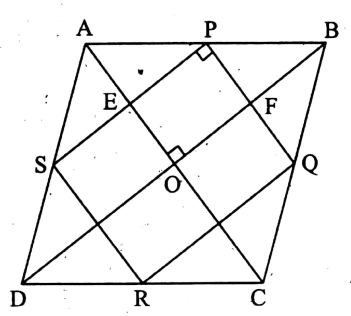
Question 4. Prove that the quadrilateral formed by joining the mid-points of a rhombus is a rectangle.
Given: P. Q, R, and S are the mid-points of AB, BC, CD, and DA respectively of the rhombus ABCD.
A quadrilateral PQRS is constructed by joining these points.
To prove: PQRS is a rectangle.
Construction: Let us draw the diagonals AC and BD of the rhombus ABCD. Also, let AC and BD intersect each other at O and AC intersect SP at E, and BD intersects PQ at F.
Proof: In A ABD, S, and P are the mid-points of AD and AB respectively, SP || DB and SP = \(\frac{1}{2}\) DB……….(1)
Again, in ΔBCD, R and Q. are the mid-points of CD and CB respectively, RQ || DB and RQ=DB …………..(2)
From (1) and (2) we get, SP || PQ and SP = RQ.
∴ PQRS is a parallelogram.
Now, in ΔABC, P, and Q are the mid-points of AB and BC respectively,
PQ || AC and PQ = \(\frac{1}{2}\) AC……………..(3)
From (1) and (3) we get, SP = \(\frac{1}{2}\) DB and PQ = \(\frac{1}{2}\)AC
But DB ≠ AC
∴ SP PQ, i.e., two adjacent sides of the parallelogram PQRS are not equal.
∴ PQRS is neither a rhombus nor a square.
Again, in the quadrilateral PEOF, PE || FO and EO || PF.
∴ PEOF is a parallelogram.
:. ∠EPF = ∠EOF [ ∵ opposite angles of a parallelogram]
= 90° [ ∵ the diagonals of a rhombus bisect each other orthogonally. ]
∴ PQRS is a parallelogram, one of the angles of which is a right angle, but the sides of which are not equal.
∴ PQRS is a rectangle. (Proved)
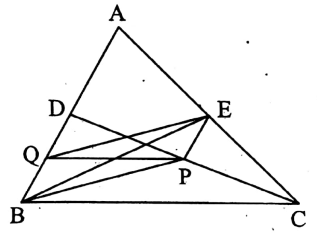
Question 5. D and E are the mid-points of AB and AC respectively of the ΔABC. P and Q are the mid-points of CD and BD respectively. Prove that BE and PQ bisect each other.
Given: D and E are the mid-points of AB and AC respectively of the Δ ABC.
P and Q are the mid-points of CD and BD respectively. Let us join B, E, and P, Q.
To prove: BE and PQ bisects each other.
Construction: Let us join P, E; Q, E, and B, P.
Proof: In ΔACD, P, and E are the mid-points of CD and CA respectively,
PE || DA and PE = \(\frac{1}{2}\) DA……….(1)
Again, DA, BA, and BQ are the line segments of the same straight line
∴ PE || BQ.
Now, D is the mid-point of AB.
∴ DA = DB or, DA = DQ + QB
or, DA=BQ+ BQ [∵ Q is the mid-point of BD]
or, DA = 2 BQ
∴from (1) we get, PE = \(\frac{1}{2}\) DA =\(\frac{1}{2}\) × 2BQ = BQ.
in the quadrilateral PEQB, PE || BQ and PE = BQ, i.e., two of the opposite sides of PEQB are equal and parallel.
PEQB is a parallelogram, and BE and PQ is two of its diagonals.
∴ BE and PQ bisects each other. (Proved)
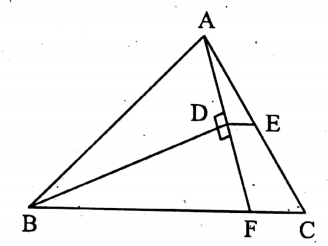
Question 6. AD is a perpendicular drawn from A to the bisector of the ∠ABC. The line segment DE is drawn through D, parallel to the line segment BC, which intersects AC at E. Prove that AE = EC.
Given: AD is the perpendicular, drawn from A to the bisector of ∠ABC.
The line segment DE is drawn through D, parallel to the line segment BC, which intersects AC at E.
To prove AE = EC.
Construction: Let us extend AD to a point F which intersects BC at F.
Proof: In Δ ABD and ΔFBD. ∠ABD = ∠FBD [∵ BD is the bisector of ∠ABC]
∠ADB = ∠FDB [ each is right-angle] and BD is common to both the triangles.
∴ ΔABD ≅ ΔFBD [ by the condition of A-A-S congruence]
AD = DF [∵ similar sides of congruence triangles ]
∴ D is the mid-point of AF.
Again, DE || BC (Given)
or, DE || FC. [∵ BC and FC are the segments of the same straight line]
Then, in ΔAFC, D is the mid-point of AF and DE || FC.
∴ E is the mid-point of AC.
∴ AE = EC. (Proved)
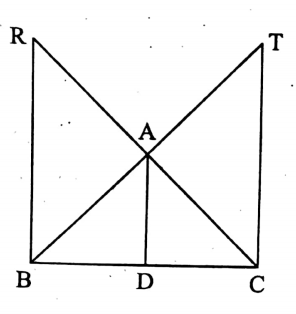
Question 7. AD is a median of AABC. Line segments BR and CT through B and C respectively are drawn parallel to AD, which intersects extended BA at T and extended CA at R. Prove \(\frac{1}{\mathrm{AD}}=\frac{1}{\mathrm{RB}}+\frac{1}{\mathrm{TC}}\) that
Given: AD is a median of AABC. The line segments BR and CT through B and C respectively are drawn parallel to AD which intersects extended BA at T and extended CA at R.
To prove : \(\frac{1}{\mathrm{AD}}=\frac{1}{\mathrm{RB}}+\frac{1}{\mathrm{TC}}\)
AD RB TC
Proof: In ABCR, D is the mid-point of CB and DA || BR (by construction)
∴ A is the mid-point of CR and DA = \(\frac{1}{2}\) BR or, RB = 2 AD………(1)
Again, in ΔBCT, D is the mid-point of BC and DA||CT (by construction)
A is the mid-point of BT and DA = \(\frac{1}{2}\) CT
or, TC = 2 AD……….(2)
\(\frac{1}{\mathrm{RB}}+\frac{1}{\mathrm{TC}}=\frac{1}{2 \mathrm{AD}}+\frac{1}{2 \mathrm{AD}}\) [from (1) and (2)]
= \(\frac{1+1}{2 \mathrm{AD}}=\frac{2}{2 \mathrm{AD}}=\frac{1}{\mathrm{AD}}\)
∴ \(\frac{1}{\mathrm{AD}}=\frac{1}{\mathrm{RB}}+\frac{1}{\mathrm{TC}}\) (Proved)
Alternative Method:
\(\frac{1}{\mathrm{AD}}=\frac{2}{2 \mathrm{AD}}=\frac{1+1}{2 \mathrm{AD}}=\frac{1}{2 \mathrm{AD}}+\frac{1}{2 \mathrm{AD}}=\frac{1}{\mathrm{RB}}+\frac{1}{\mathrm{TC}}\) [by (1) and (2) ]
∴ \(\frac{1}{\mathrm{AD}}=\frac{1}{\mathrm{RB}}+\frac{1}{\mathrm{TC}}\) (proved)
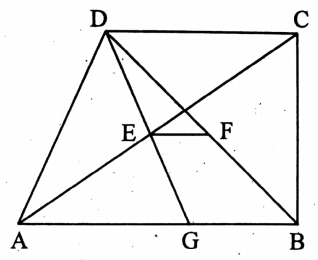
Question 8. In the trapezium ABCD, AB || DC and AB > DC; E and F are the mid-points of the diagonals AC and BD respectively. Prove that EF = \(\frac{1}{2}\) (AB-DC).
Given: In the trapezium ABCD, AB || DC and AB > DC; E and F are the mid-points of the diagonals AC and BD respectively.
To prove: EF = \(\frac{1}{2}\) (AB-DC).
Construction: The line segment DE is extended to G, which intersects AB at G.
Proof: In ΔAEG and ΔCED, ∠GAE = alternate ∠DCE [∵ AB || DC and AC are their transversal ]
∠AGE = alternate ∠CDE [ ∵ AB || DC and DG is their transversal ].
and AE = CE [∵ E is the mid-point of the diagonal AC]
:. ΔAEG = ΔCED
∴ AG=CD…………(1) [∵ similar sides of congruent triangles] and DE GE, i.e., E is the mid-point of DG.
Now, in ΔBDG, F and E are the mid-points of BD and GD respectively.
∴ FE BG and FE = \(\frac{1}{2}\) BG.
∴ EF = BG = \(\frac{1}{2}\) (AB-AG) = \(\frac{1}{2}\) (AB-CD) [by (1) AG = CD]
∴ EF = \(\frac{1}{2}\) (AB-DC). (Proved)
Question 9. C is the mid-point of the line segment AB and PQ is any straight line. The least distances of PQ from A, B and C are AR, BS and CT respectively. Prove that AR + BS = 2 CT.
Given: C is the mid-point of the line segment AB and PQ is any straight line.
The least distances of PQ from A, B, and C are AR, BS, and CT respectively.
To prove AR + BS = 2 CT.
Construction: Let us join A and ‘S and let AS intersects CT at D.
Proof: Since the least distances of PQ from A, B, and C are AR, BS, and CT respectively, AR, BS, and CT are all perpendiculars to PQ.
∴ AR || BS || CT.
Now, in ΔABS, CD || BS,
∴ CD = \(\frac{1}{2}\) BS [∵ C is the mid-point of AB and D is the mid-point of AS]
or, BS = 2CD…………(1)
Again, in ΔARS, DT || AR,
∴ DT = \(\frac{1}{2}\) AR [ ∵ D is the mid-point of AS ]
or, AR = 2 DT ………..(2)
Now, AR + BS2 DT+2 CD [∵ from (1) and (2)]
= 2 (DT + CD)
= 2 CT
∴ AR + BS = 2CT. (Proved)
Question 10. ABCD is a square. The diagonals AC and BD of it intersects each other at O. The bisector of <BAC intersects BO at P and BC at Q. Prove that OP = \(\frac{1}{2}\) CQ.
Given: The diagonals AC and BD of the square ABCD intersect each other at O.
The bisector of <BAC intersects BO at P and BC at Q.
prove : OP = \(\frac{1}{2}\) CQ.
Construction: Let us draw DB || CR. CR intersects the extended AQ at R.
Proof: O is the mid-point of AC [∵ diagonals of a rhombus intersect each other orthogonally.]
and OP || CR [by construction]
∴ OP = CR………….(1)
Now, ∠BAQ = <CAR (Given),
∠ABQ = ∠AOP [ each are 90° ]
= similar ACR [ ∵ OP || CR and AC is their transversal ]
∴ in ΔABQ and ΔACR, ∠BAQ= ∠CAR and ∠ABQ = ∠ACR.
∴ ∠AQB = ∠ARC [ third angles ], But ∠AQB = ∠CQR [opposite angles]
∴ ∠ARC=∠CQR
or, ∠QRC = ∠CQR.
∴ CR = CQ. [∵ opposite sides of equal angles. ]
∴ From (1) we get, OP = \(\frac{1}{2}\) CQ [∵ CR=CQ] (Proved)