Coordinate Geometry Chapter 3 Area Of Triangles
WBBSE Class 9 Area of Triangles Overview
Chapter 3 Area Of Triangles Determination of the area of the triangle formed by the given three points:
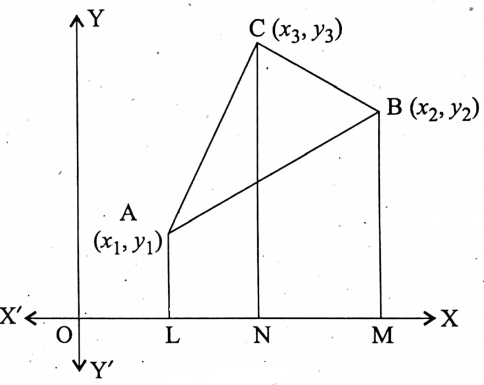
Let the coordinates of the points A, B, and C concerning the rectangular coordinate axes \(\overleftrightarrow{X’OX}\) and \(\overleftrightarrow{Y’OY}\) are \(\left(x_1, y_1\right),\left(x_2, y_2\right) \text { and }\left(x_3, y_3\right)\) respectively.
We have to find the area of the triangle ΔABC obtained by joining these points A, B, and C.
Let us draw perpendiculars AL, BM, and CN from A, B, and C respectively to the x-axis.
Then,
Read and Learn More WBBSE Solutions For Class 9 Maths
\(\overline{\mathrm{OL}}=x_1, \overline{\mathrm{OM}}=x_2, \overline{\mathrm{ON}}=x_3\)
and \(\overline{\mathrm{AL}}=y_1, \overline{\mathrm{BM}}=y_2, \overline{\mathrm{CN}}=y_3\)
∴ \(\overline{\mathrm{LN}}=x_3-x_1, \overline{\mathrm{LM}}=x_2-x_1 ; \overline{\mathrm{NM}}=\dot{x}_2-x_3\)
Now, area of the ΔABC = [(area of the trapezium ALNC) + (area of the trapezium CNMB) – (area of the trapezium ALMB)]
= \(\frac{1}{2}(\overline{\mathrm{AL}}+\overline{\mathrm{NC}}) \cdot \overline{\mathrm{LN}}+\frac{1}{2}(\overline{\mathrm{CN}}+\overline{\mathrm{MB}}) \cdot \overline{\mathrm{NM}}-\frac{1}{2}(\overline{\mathrm{AL}}+\overline{\mathrm{BM}}) \cdot \overline{\mathrm{LM}}\)
= \(\frac{1}{2}\left(y_1+y_3\right)\left(x_3-x_1\right)+\frac{1}{2}\left(y_3+y_2\right)\left(x_2-x_3\right)-\frac{1}{2}\left(y_1+y_2\right)\left(x_2-x_1\right) \text { Sq-units }\)
= \(\frac{1}{2}\left[x_1 y_2-y_1 x_2+x_2 y_3-y_2 x_3+x_3 y_1-y_3 x_1\right] \text { Sq-units }\)
= \(=\frac{1}{2}\left[x_1 y_2-y_1 x_2+x_2 y_3-y_2 x_3+x_3 y_1-y_3 x_1\right] \text { Sq-units }\)
∴ \(\Delta \mathrm{ABC}=\frac{1}{2}\left[y_1\left(x_2-x_3\right)+y_2\left(x_3-x_1\right)+y_3\left(x_1-x_2\right)\right] \text { Sq-units }\)
Chapter 3 Area Of Triangles To Determine The Condition Of Three Given Points To Be Collinear
Let \(\mathrm{A}\left(x_1, y_1\right), \mathrm{B}\left(x_2, y_2\right) \text { and } \mathrm{C}\left(x_3, y_3\right)\) be three collinear points.
∴ the area of the triangle produced by these three points must be 0.
∴ the required condition is
\(\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]=0\) \(\Rightarrow x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)=0\)
Chapter 3 Area Of Triangles Select The Correct Answer (MCQ)
Formulas for Area of Different Types of Triangles
Question 1. In the right-angled triangle ABC, ∠ABC = 90°. If the coordinates of A and C be (0, 4) and (3, 0) respectively then the area of the ΔABC is
- 12 Sq-units
- 6 Sq-units
- 24 Sq-units
- 8 Sq-units
Solution:
The coordinates of A and C are (0, 4) and (3, 0) respectively, and ∠ABC = 90°.
∴ the coordinates of B are (0, 0).
area of the ΔABC = \(\frac{1}{2} \mathrm{AB} \times \mathrm{BC}\)
= \(\frac{1}{2} \times 4 \times 3 \text { Sq-units }\)
= 6 Sq-units
∴ area of the ΔABC = 6 Sq-units.
Question 2. If the points (0, 0), (4, -3), and (x, y) are collinear, then
- x = 8, y = -6
- x = 8, y = 6
- x = 4, y = -6
- x = -8, y=-6
Solution: The given points (0, 0), (4, -3), and (x, y) are collinear, then
∴ \(\frac{1}{2}[0(-3-y)+4(y-0)+x(0+3)]=0 \Rightarrow \frac{1}{2}[4 y+3 x]=0 \Rightarrow 4 y+3 x=0\)
Now, x 8, y=-6 [∵ 4y+ 3.8 = 0⇒ 4y = -24⇒ y = -6]
∴ x = 8, y = -6.
Question 3. If the area of the triangle, the vertices of which are (2, 7), (5, 1), and (x, 3), is 18 sq-units, then the value of x is
- 10
- 2
- – 2
- – 10
Solution: The area of the triangle with vertices (2, 7), (5, 1), and (x, 3) is 18 Sq-units.
∴ \(\frac{1}{2}[2(1-3)+5(3-7)+x(7-1)]=18\)
\(\frac{1}{2}[-4-20+6 x]=18\)
⇒-24+6x=36
6x=60
⇒x=10
Question 4. If the points (1, 3), (2, h), and (5, 1) are collinear, then the value of h is
- 1
- 0
- 2
- None of these
Solution: The given points are colinear, the area of the triangle formed by them is equal to zero.
Now, area of the triangle = \(\frac{1}{2}[-1(h+1)+2(-1-3)+5(3-h)] \text { Sq-units }\)
= \(\frac{1}{2}[-h-1-8+15-5 h] \text { Sq-units }\)
= \(\frac{1}{2}[-6 h+6] \text { Sq-units }\)
= (3-3h) Sq-units.
3-3h = 0 ⇒ (1-h) = 0 ⇒ h = 1.
Heron’s Formula for Area of a Triangle
Chapter 3 Area Of Triangles Short Answer Type Questions
Question 1. Examine whether points (2, 3), (4, 5) and (6, 5) are collinear or not.
Solution:
Given Points (2, 3), (4, 5) and (6, 5)
Let the points be A (2, 3), B (4, 5), and C (6, 5).
∴ area of ΔABC = \(\frac{1}{2}[2(5-5)+4(5-3)+6(3-5)] \text { Sq-units }\)
= \(\frac{1}{2}[0+8-12] \text { Sq-units }\)
= -2 Sq-units
Since the area of the triangle formed by the given points is not 0.
∴ the given points are not collinear.
Question 2. The centroid of a triangle is (6, 9) and two of its vertices are (15, 0) and (0, 10). Find the coordinates of the third vertex.
Solution:
Given
The centroid of a triangle is (6, 9) and two of its vertices are (15, 0) and (0, 10)
Let the coordinates of the third vertex be (h, k).
Two given vertices are (15, 0) and (0, 10).
∴ centroid = \(\left(\frac{15+0+h}{3}, \frac{0+10+k}{3}\right)=\left(\frac{15+h}{3}, \frac{10+k}{3}\right)\)
As per question, \(\frac{15+h}{3}=6\) ⇒ 15+h=18 ⇒h=3
Again, \(\frac{10+k}{3}=9\) ⇒ 10+k=27 ⇒ k=17
∴ the third vertex is (3, 17).
Calculating Area of Right-Angled Triangles
Question 3. If the points (a, 0), (0, b), and (1, 1) are collinear, then show that \(\frac{1}{a}+\frac{1}{b}=1\)
Solution:
Given Points (a, 0), (0, b), and (1, 1) are collinear
Since the points (a, 0), (0, b), and (1, 1) are collinear,
∴ the area of the triangle formed by them is zero.
Now, area of the triangle = \(\left.\frac{1}{2}[a(b-1)+0(1-0)+1(0-b)] \text { Sq-units }=\frac{1}{2}[a b-a-b)\right] \text { Sq-units }\)
As per question, \(\frac{1}{2}[a b-a-b]=0\) ⇒ ab – a – b = 0 ⇒ ab = a+b ⇒ a+b = ab
⇒ \(\frac{a}{a b}+\frac{b}{a b}=1\)
⇒ \(\frac{1}{b}+\frac{1}{a}=1\)
∴ \(\frac{1}{a}+\frac{1}{b}=1\) (Proved)
Question 4. Find the centroid of the triangle formed by the points (xy, yz), (x, y), and (y, z).
Solution:
Given Points (xy, yz), (x, y), and (y, z)
The required centroid = \(\left(\frac{x-y-x+y}{3}, \frac{y-z-y+z}{3}\right)=\left(\frac{0}{3}, \frac{0}{3}\right)\) =(0,0)
∴ the centroid is (0, 0).
Chapter 3 Area Of Triangles Long Answer Type Questions
Question 1. For what value of k the points (1, 1), (2, 1), and (k, 1) are collinear?
Solution:
Given Points (1, 1), (2, 1), and (k, 1)
Let the given points be A (1, 1), B (2, 1), and C (k, – 1).
The given points are collinear if ΔABC = 0
Now, ΔABC = \(\frac{1}{2}\) [1 (− 1 + 1) + 2 ( − 1 + 1) + k ( − 1 + 1)] Sq-units = \(\frac{1}{2}\) [0+0+0] Sq-units = 0
Hence, for any real value of k, the given points are collinear.
Applications of Triangle Area Formulas in Real Life
Question 2. Prove that the line segment obtained by joining the points (1, 2) and (-2,-4) passes through the origin.
Solution:
Given Points (1, 2) and (-2,-4)
The area of the triangle formed by the points (1, 2) and (-2,-4) and the origin (0, 0)
= \(\frac{1}{2}\) [1(−4 −0) − 2 (0 −2)+0(2+4)] Sq-units = \(\frac{1}{2}\) [-4+4+0] Sq-units
= \(\frac{1}{2}\) x.0 Sq-units = 0
Since the area of the triangle formed by the given points is 0, the given points are collinear. Hence the line segment joining (1, 2) and (-2, -4) passes through the origin. (Proved)
Question 3. Prove that the mid-point of the line segment obtained by joining the points (2, 1) and (6, 5) lie on the line segment obtained by joining the points (-4, -5) and (9, 8).
Solution:
The midpoint of the line segment was obtained by joining the points (2, 1) and (6, 5)
= \(\left(\frac{2+6}{2}, \frac{1+5}{2}\right)\) = (4, 3).
Now, the area of the triangle formed by the points
= \(\frac{1}{2}\) [-4(8-3)+9(3+5)+4(-5-8)] Sq-units
= \(\frac{1}{2}\) [-20+72-52] Sq-units
= \(\frac{1}{2}\) x 0 Sq-units = 0
∴ (4, 5), (9, 8), and (4, 3) are collinear.
∴ the mid-point of the line segment joining (2, 1) and (6, 5) lies on the line segment joining the points (4; 5) and (9, 8). (Proved)
Common Mistakes in Area Calculations of Triangles
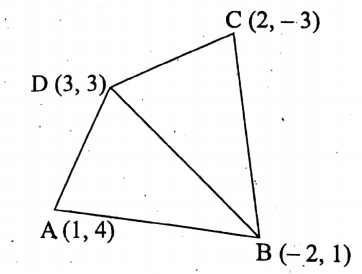
Question 4. Find the area of the quadrilateral formed by the points (1, 4), (2, 1), (2, 3), and (3, 3).
Solution:
Given Points (1, 4), (2, 1), (2, 3), and (3, 3)
Let the given points be A (1, 4), B(-2, 1), C (2, 3), and D (3, 3).
Let us draw the diagonal BD
Now, ΔABD = \(\frac{1}{2}\) [1(1 −3) −2(3-4)+3(4 − 1)] Sq-units
= \(\frac{1}{2}\) (-2+2+9] Sq-units
= \(\frac{9}{2}\) Sq-units.
Also, ABCD = \(\frac{1}{2}\) [-2(-3-3)+2(3-1)+3(1+3)] Sq-units
= \(\frac{1}{2}\) [12+4+12] Sq-units
= 14 Sq-units
∴ quadrilateral ABCD = ΔABD + ΔBCD
= \(\left(\frac{9}{2}+14\right)\)
= \(18 \frac{1}{2} S q \text {-units }\)
∴ the required area = \(18 \frac{1}{2} S q \text {-units }\) Sq-units.
Question 5. The coordinates of A, B, and C are (3, 4), (4, 3), and (8,6) respectively; Find the area of the ΔABC and also find the perpendicular distance of BC from the vertex A.
Solution:
Given
The coordinates of A, B, and C are (3, 4), (4, 3), and (8,6) respectively
The coordinates of A, B, and C are (3, 4), (- 4, 3), and (8, -6).
∴ area of ΔABC = \(\frac{1}{2}\) [3(3+6) 6)-4(-6-4)+8(4-3)] Sq-units
= \(\frac{1}{2}\) [27+40+8] Sq-units
= \(\frac{1}{2}\) x 75 Sq-units
= 37 \(\frac{1}{2}\) Sq-units.
Now, length of BC = \(\sqrt{(-4-8)^2+(3+6)^2} \text { units }\)
= √144+81 units
=√225 units
= 15 units Let the perpendicular distance of BC from A be x-units.
∴ \(\frac{1}{2} \times x \times 15=\frac{75}{2} \Rightarrow \frac{15 x}{2}=\frac{75}{2}\)
⇒ x = 5
∴ the required length of the perpendicular is 5 units.
Understanding Base and Height in Triangle Area Calculation
Question 6. The coordinates of A of the ΔABC are (2, 5) and the coordinates of its centroid are (-2, 1). Find the coordinates of the mid-point of BC.
Solution:
Given
The coordinates of A of the ΔABC are (2, 5) and the coordinates of its centroid are (-2, 1)
Let the mid-point of BC be D (h, k).
∴ the line segment AD is divided internally at (2, 1) into the ratio 2: 1.
∴ \(\frac{2 \times h+1 \times 2}{2+1}=-2\)
or, \(\frac{2 h+2}{3}=-2\)
or, 2h + 2 = -6
or, 2h = -8
or, h = -4
Again, \(\frac{2 \times k+1 \times 5}{2+1}=1\)
or, \(\frac{2 k+5}{3}=1\)
or, 2k + 5 = 3
or, 2k = -2
or, k = -1
∴ the mid-point of BC is (4, 1).
Question 7. A (1, 5), B (3, 1), and C (5, 7) are the vertices of the ΔABC. D, E, and F are the mid-points of BC, CA, and AB respectively. Find the area of ADEF and show that ΔABC = 4 ADEF.
Solution:
Given
A (1, 5), B (3, 1), and C (5, 7) are the vertices of the ΔABC. D, E, and F are the mid-points of BC, CA, and AB respectively
The vertices of the ΔABC are given A (- 1, 5), B (3, 1), and C (5, 7).
area of ΔABC = \(\frac{1}{2}\) [-1(1-7)+3(7-5)+5(5-1)] Sq-units
= \(\frac{1}{2}\)[6+6+20] Sq-units
= \(\frac{1}{2}\) x 32 Sq-units
= 16 Sq-units
The mid-points of BC, CA, and AB are D, E, and F respectively.
∴ Coordinates of D = \(\left(\frac{3+5}{2}, \frac{1+7}{2}\right)\) = (4,4)
∴ Coordinates of E = \(\left(\frac{-1+5}{2}, \frac{5+7}{2}\right)\) = (2,6)
∴ Coordinates of F = \(\left(\frac{-1+3}{2}, \frac{5+1}{2}\right)\) =(1,3)
area of ΔDEF = \(\frac{1}{2}[4(6-3)+2(3-4)+1(4-6)] \text { Sq-units }\)
= \(\frac{1}{2}[12-2-2] \text { Sq-units }=\frac{1}{2} \times 8 \text { Sq-units }\)
= 4 Sq-units
∴ ΔABC= 16 Sq-units = 4 x 4 Sq-units = 4 ΔDEF. (Proved)
Word Problems Involving Area of Triangles
Question 8. The coordinates of A, B, C, and D are (0, 1), (1, 2), (15, 2), and (4, 5) respectively. In what ratio does AC divide BD?
Solution:
Given
The coordinates of A, B, C, and D are (0, 1), (1, 2), (15, 2), and (4, 5) respectively
Let AC divide BD at P into the ratio m: n.
BD is divided at P into the ratio m: n.
∴ the coordinates of P = \(\left(\frac{4 m-n}{m+n}, \frac{-5 m+2 n}{m+n}\right)\)
Clearly, A, C, and P are collinear.
∴ the area of the triangle formed by them is zero.
∴ \(\frac{1}{2}\left[0\left(2-\frac{-5 m+2 n}{m+n}\right)+15\left(\frac{-5 m+2 n}{m+n}+1\right)+\frac{4 m-n}{m+n} \cdot(-1-2)\right]=0\)
\(15 \times \frac{-5 m+2 n+m+n}{m+n}-\frac{3(4 m-n)}{m+n}=0 \Rightarrow \frac{15(-4 m+3 n)-3(4 m-n)}{m+n}=0\)
\(5(-4 m+3 n)=4 m-n \quad \Rightarrow-20 m+15 n=4 m-n \quad \Rightarrow-24 m=-16 n\)
\(\frac{m}{n}=\frac{16}{24}=\frac{2}{3} \quad \Rightarrow m: n=2: 3\)
∴ \(\overline{\mathrm{AC}} \text { divides } \overline{\mathrm{BD}}\) internally into the ratio 2: 3.
AC divides BD = 2: 3.
Visual Representation of Triangle Areas
Question 9. The vertices of the triangle ABC are A (3, 0), B (0, 6), and C (6, 9). The sides AB and AC of ΔABC are intersected by DE at D and E respectively into a ratio of 1: 2. Prove by coordinate geometry that ΔABC = 9 ΔADE.
Solution:
Given
The vertices of the triangle ABC are A (3, 0), B (0, 6), and C (6, 9).
The sides AB and AC of ΔABC are intersected by DE at D and E respectively into a ratio of 1: 2
As per the question, AB is divided at D internally into the ratio 1 2.
∴ The coordinates of D = \(\left(\frac{1 \cdot 0+2 \cdot 3}{2+1}, \frac{1 \cdot 6+2 \cdot 0}{2+1}\right)\) = (2, 2)
Similarly, the coordinates of E = \(\left(\frac{1 \cdot 6+2 \cdot 3}{2+1}, \frac{1 \cdot 9+2 \cdot 0}{2+1}\right)\) = (4, 3)
Now, the area of ΔABC = \(\frac{1}{2}\) [3(6-9)+0(9-0)+6(0-6)] Sq-units
= \(\frac{1}[2]\) (-9-36) Sq-units
∴ the area of ΔABC = \(\frac{45}{2}\) Sq-units [∵ area can never be negative ]
Similarly, area of ΔADE = \(\frac{1}{2}\) [3(2−3)+2(3 +2(3-0)+4(0-2)] Sq-units
= \(\frac{1}{2}\) [−3+6–8] Sq-units
= – \(\frac{5}{2}\) Sq-units
area of ΔADE= \(\frac{5}{2}\) Sq-units [∵ area can never be negative ]
∴ \(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{ADE}}=\frac{\frac{45}{2}}{\frac{5}{2}}=9\)
or, ΔABC = 9 ΔADE (Proved)
ΔABC = 9 ΔADE
