WBBSE Solutions For Class 9 Maths Coordinate Geometry Chapter 2 Section Formulas

Coordinate Geometry Chapter 2 Section Formulas

Chapter 2 Section Formulas Determination of the coordinates of the point dividing a given line segment into a certain ratio:

Formula-1 When the line segment is divided internally

Let the coordinates of P and Q of the line segment \(\overleftrightarrow{\mathrm{PQ}}\) with respect to the axes \(\overleftrightarrow{\mathrm{OX}}\) and \(\overleftrightarrow{\mathrm{OY}}\) are \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) respectively.

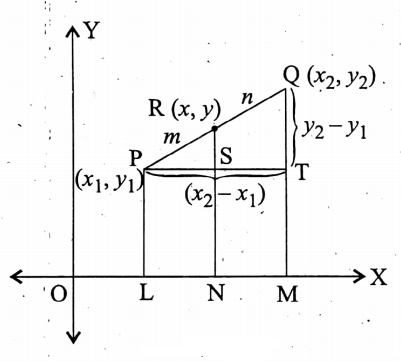
Also, let the point R divides \overleftrightarrow{\mathrm{OX}} internally at a ratio m: n, i.e., PR: RQ = m: n; We have to determine the coordinates of R.

Read and Learn More WBBSE Solutions For Class 9 Maths

Let the coordinates of R be (x, y)

Now, let us draw perpendiculars PL, QM, and RN from P, Q, and R respectively to \(\overleftrightarrow{\mathrm{OX}}\) 

Also, let us draw \(\overline{\mathrm{PT}}\) perpendicular to \(\overline{\mathrm{QM}}\) from P.

Let this perpendicular intersects \(\overline{\mathrm{RN}}\) at S and \(\overline{\mathrm{QM}}\) at T.

Clearly, \(\overleftrightarrow{\mathrm{RS}}\) || \(\overleftrightarrow{\mathrm{QT}}\)

∴ \(\frac{\overline{\mathrm{PS}}}{\overline{\mathrm{PT}}}=\frac{\overline{\mathrm{RS}}}{\overline{\mathrm{QT}}}=\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{PQ}}}\)

Now,

\(\overline{\mathrm{PS}}=\overline{\mathrm{LN}}=\overline{\mathrm{ON}}-\overline{\mathrm{OL}}=x-x_1\)

\(\overline{\mathrm{PT}}=\overline{\mathrm{LM}}=\overline{\mathrm{OM}}-\overline{\mathrm{OL}}=x_2-x_1\)

\(\overline{\mathrm{RS}}=\overline{\mathrm{RN}}-\overline{\mathrm{SN}}=\overline{\mathrm{RN}}-\overline{\mathrm{PL}}=y-y_1\)

and \(\overline{\mathrm{QT}}=\overline{\mathrm{QM}}-\overline{\mathrm{TM}}=\overline{\mathrm{QM}}-\overline{\mathrm{PL}}=y_2-y_1\)

Again, \(\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{RQ}}}=\frac{m}{n}\)

or, \(\frac{\overline{\mathrm{RQ}}}{\overline{\mathrm{PR}}}\) = \(\frac{n}{m}\)

=\(\frac{n}{m} \Rightarrow \frac{\overline{\mathrm{RQ}}}{\overline{\mathrm{PR}}}+1\)

=\(\frac{n}{m}+1 \Rightarrow \frac{\overline{\mathrm{RQ}}+\overline{\mathrm{PR}}}{\overline{\mathrm{PR}}}\)

=\(\frac{n+m}{m} \Rightarrow \frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}}\)

=\(\frac{m+n}{m}\)

∴ From (1) we get, \(\frac{\overline{\mathrm{PS}}}{\overline{\mathrm{PT}}}=\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{PQ}}}\)

or, \(\frac{x-x_1}{x_2-x_1}=\frac{m}{m+n} \quad \text { or, } x(m+n)-x_1(m+n)=m x_2-m x_1\)

or, \(x(m+n)=m x_2-m x_1+m x_1+n x_1\)

or, \(x(m+n)=m x_2-m x_1+m x_1+n x_1\)

∴ \(x=\frac{m x_2+i x_1}{m+n}\)

Again, \(\frac{\overline{\mathrm{RS}}}{\overline{\mathrm{QT}}}=\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{PQ}}} \quad[\text { by }(1)]\)

or, \(\frac{y-y_1}{y_2-y_1}=\frac{m}{m+n}\)

or, \(y=\frac{m y_2+n y_1}{m+n}\) [ by simplification ]

∴ Coordinates of R is \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)

 

 

Formula-2 When the line segment is divided externally

Let the coordinates of P and Q of the line segment \(\overleftrightarrow{\mathrm{PQ}}\) with respect to the coordinate axes \(\overleftrightarrow{\mathrm{OX}}\) and \(\overleftrightarrow{\mathrm{OY}}\) be \(\left(x_1, y_1\right) \text { and }\left(x_2, y_2\right)\) respectively and let the point R divides \(\overleftrightarrow{\mathrm{PQ}}\) externally with a ratio m: n,

i.e., \(\overline{\mathrm{PR}}\): \(\overline{\mathrm{QR}}\) = m: n.

We have to determine the coordinates of R.

Let the coordinates of R be (x, y)

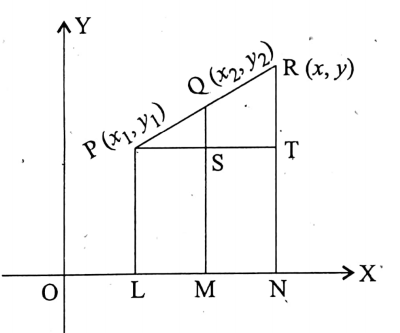
Let us draw perpendiculars \(\overline{\mathrm{PL}}\), \(\overline{\mathrm{QM}}\), and \(\overline{\mathrm{RN}}\) from P, Q, and R respectively to \(\overleftrightarrow{\mathrm{OX}}\).

Let us also draw perpendicular \(\overline{\mathrm{PT}}\) from P to \(\overline{\mathrm{RN}}\), which intersects \(\overline{\mathrm{QM}}\) at S and \(\overline{\mathrm{RN}}\) at T. 

Clearly, \(\overleftrightarrow{\mathrm{QS}} \| \overleftrightarrow{\mathrm{RT}}\)

∴ \(\frac{\overline{\mathrm{PS}}}{\overline{\mathrm{PT}}}=\frac{\overline{\mathrm{QS}}}{\overline{\mathrm{RT}}}=\frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}}\) …………….(1)

Now, 

\(\overline{\mathrm{PS}}=\overline{\mathrm{LM}}=\overline{\mathrm{OM}}-\overline{\mathrm{OL}}=x_2-x_1\)

\(\overline{\mathrm{PT}}=\overline{\mathrm{LN}}=\overline{\mathrm{ON}}-\overline{\mathrm{OL}}=x-x_1\)

\(\overline{\mathrm{QS}}=\overline{\mathrm{QM}}-\overline{\mathrm{SM}}=\overline{\mathrm{QM}}-\overline{\mathrm{PL}}=y_2-y_1\)

and \(\overline{\mathrm{RT}}=\overline{\mathrm{RN}}-\overline{\mathrm{TN}}=\overline{\mathrm{RN}}-\overline{\mathrm{PL}}=y-y_1\)

Again, \(\frac{\overline{\mathrm{PR}}}{\overline{\mathrm{QR}}}=\frac{m}{n}, \quad \text { or, } \frac{\overline{\mathrm{QR}}}{\overline{\mathrm{PR}}}=\frac{n}{m} \quad \text { or, } 1-\frac{\overline{\mathrm{QR}}}{\overline{\mathrm{PR}}}=1-\frac{n}{m}\)

or, \(\frac{\overline{\mathrm{PR}}-\overline{\mathrm{QR}}}{\overline{\mathrm{PR}}}=\frac{m-n}{m} \quad \text { or, } \frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}}=\frac{m-n}{m}\)

∴ From (1) we get, \(\frac{\overline{\mathrm{PS}}}{\overline{\mathrm{PT}}}=\frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}} \text { or, } \frac{x_2-x_1}{x-x_1}=\frac{m-n}{m}\)

or, \(x(m-n)-x_1(m-n)=m x_2-m x_1\)

Or, \(x(m-n)=m x_2-m x_1+m x_1-n x_1 \text { or, } x(m-n)=m x_2-n x_1\)

∴ \(x=\frac{m x_2-n x_1}{m-n}\)

Again, \(\frac{\overline{\mathrm{QS}}}{\overline{\mathrm{RT}}}=\frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{PR}}} \quad \text { or, } \frac{y_2-y_1}{y-y_1}=\frac{m-n}{m}\)

or, \(y=\frac{m y_2-n y_1}{m-n}\)      [ by simplification ]

∴ the coordinates of R is \(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right)\)

 

 

Formula-3: Determination of coordinates of mid-point

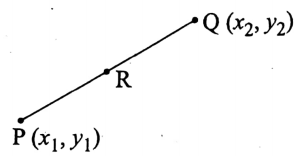
Let the coordinates of P and Q of the line segment  \(\overline{\mathrm{PQ}}\) be \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) respectively and let R is the mid-point of \(\overline{\mathrm{PQ}}\).

Clearly, R divides PQ internally in the ratio 1: 1.

∴ the required coordinates of R are \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

 

 

Formula-4: Determination of the centroid of a triangle:

In the solid geometry section, you have studied that the medians of any triangle are concurrent and the point of intersection of the medians of the triangle is called its centroid.

We shall now prove with the help of coordinate geometry the medians of any triangle are concurrent and the centroid divides the medians internally into a radio of 2: 1.

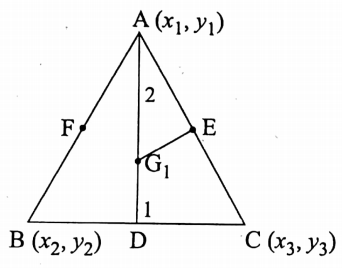
Let D, E, and F be the mid-points of the sides BC, AC, and AB respectively of the ΔABC. 

Also, let the coordinates of its vertices A, B, and C be \(\left(x_1; y_1\right),\left(x_2, y_2\right) \text { and }\left(x_3, y_3\right)\) respectively.

Then the coordinates of D, E, and F are

\(\left(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}\right),\left(\frac{x_3+x_1}{2}, \frac{y_3+y_1}{2}\right) \text { and }\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\) respectively.

Let G be any point on AD such that \(\overline{\mathrm{AG}_1}: \overline{\mathrm{G}_1 \mathrm{D}}=2: 1\) =2: 1.

Clearly, the coordinates of G₁ will be

\(\left(\frac{2 \cdot \frac{x_2+x_3}{2}+1 \cdot x_1}{2+1}, \frac{2 \cdot \frac{y_2+y_3}{2}+1 \cdot y_1}{2+1}\right)=\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

Similarly, if G₂ and G₃ be any two points on the medians BE and CF respectively such that \(\overline{\mathrm{BG}_2}: \overline{\mathrm{G}_2 \mathrm{E}}=2: 1 \text { and } \overline{\mathrm{CG}_3}: \overline{\mathrm{G}_3 \mathrm{~F}}=2: 1\), then in a similar process discussed above we can show that the coordinates of both \(\mathrm{G}_2 \text { and } \mathrm{G}_3\) will be \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

Thus \(\mathrm{G}_1, \mathrm{G}_2, \mathrm{G}_3\) expresses the same point.

Hence, the medians \(\overline{\mathrm{AD}}\), \(\overline{\mathrm{BE}}\), and \(\overline{\mathrm{CF}}\) are concurrent and the point of intersection of them divides them internally into a ratio of 2 1.

Also, the coordinates of the centroid are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

 

Chapter 2 Section Formulas Select The Correct Answer (MCQ)

 

Question 1. The coordinates of the mid-point of the line segment joining the points (l, 2m) and (-l+2m, 2l-2m) are

1. (1, m) 
2. (1, – m)
3. (m, -1)
4. (m, 1)

Solution: 

Given line segment joining the points (l, 2m) and (-l+2m, 2l-2m)

The coordinates of the required mid-point are \(\left(\frac{l-l+2 m}{2}, \frac{2 m+2 l-2 m}{2}\right)\)

 

Question 2. If the two endpoints of the diameter of a circle be (7, 9) and (1,3); then the centre of the circle is

1. (3, 3)
2. (4, 6)
3. (3, 3)
4. (4, 6)

Solution:

Given The two endpoints of the diameter of a circle be (7, 9) and (1,3)

The mid-point of the diameter of a circle is its centre.

∴ the required centre is \(\left(\frac{7-1}{2}, \frac{9-3}{2}\right)\)

 

Question 3. If any point divides the line segment joining the points (2,5) and (- 3,-2) into the ratio 4 3 externally. Then the ordinate of the point is

1. 18
2. – 7
3. 18
4. 7

Solution:

Given 

Any point divides the line segment joining the points (2,5) and (- 3,-2) into the ratio 4 3 externally

The required ordinate = \(\frac{4 \times(-2)-3 \times(-5)}{4-3}=\frac{-8+15}{1}=7\)

 

Question 4. If P (1, 2), Q (4, 6), R (5, 7) and S (x, y) are the successive four vertices of the parallelogram PQRS, then

1. x = 2, y = 4
2. x =3, y = 4
3. x = 2, y = 3
4. x = 2, y = 5

Solution:

Given 

P (1, 2), Q (4, 6), R (5, 7) and S (x, y) are the successive four vertices of the parallelogram PQRS

The mid-point of the diagonal \(\overline{\mathrm{PR}}\) is \(\left(\frac{1+5}{2}, \frac{2+7}{2}\right)=\left(3, \frac{9}{2}\right)\)

The mid-point of the diagonal \(\overline{\mathrm{QS}}\) is \(\left(\frac{4+x}{2}, \frac{6+y}{2}\right)\)

Since the mid-points of the diagonals of a parallelogram are the same,

∴ \(\frac{4+x}{2}=3 and \frac{6+y}{2}=\frac{9}{2}\)

⇒ x+4=6

⇒x=2

⇒ y+6=9

⇒y=3

∴ x=2, y = 3

 

Chapter 2 Section Formulas Short Answer Type Questions

 

Question 1. C is the centre of a circle and AB is its diameter. The coordinates of A and C are (6, 7) and (5, 2) respectively. Find the coordinates of B.

Solution:

Given 

C is the centre of a circle and AB is its diameter. The coordinates of A and C are (6, 7) and (5, 2) respectively

Let the coordinates of point A be (6, –7) and of point B is (h, k).

∴ the coordinates of C, mid-point of AB are \(\left(\frac{6+h}{2}, \frac{-7+k}{2}\right)\)

\(\frac{6+h}{2}=5\)

⇒ h + 6 = 10

⇒ h = 4

Also, \(\frac{-7+k}{2^{\prime}}=-2\)

⇒ k-7 = -4

⇒ k=3

∴ the coordinates of B are (4, 3).

 

Question 2. The points P and Q are on the first and third quadrants respectively and their distances of them from the x-axis and y-axis are 6 units and 4 units respectively. Find the coordinates of mid-point \(\overline{\mathrm{PQ}}\).

Solution:

Given

The points P and Q are on the first and third quadrants respectively and their distances of them from the x-axis and y-axis are 6 units and 4 units respectively

Since P is on the first quadrant,

∴ both the coordinates of P will be positive.

∴ The coordinates of P are (4, 6).

Also, since Q lies on the third quadrant, both the coordinates will be negative.

∴ the coordinates of Q are (-4, -6).

∴ the coordinates of the mid-point of \(\overline{\mathrm{PQ}}\) are

\(\left(\frac{4-4}{2}, \frac{6-6}{2}\right)\) = (0,0).

∴ the required coordinates of \(\overline{\mathrm{PQ}}\) are (0, 0).

 

 

 

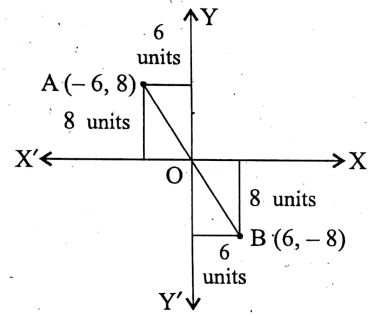
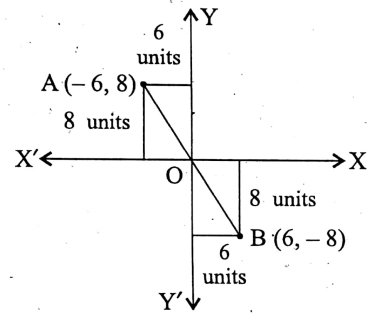
Question 3. The points A and B lie on the second and fourth quadrants respectively and the distances of them from the x-axis and y-axis are 8 units and 6 units respectively. Find the coordinates of the mid-point of AB.

Solution

Given

The points A and B lie on the second and fourth quadrants respectively and the distances of them from the x-axis and y-axis are 8 units and 6 units respectively

Since A lies on the second quadrant,

∴ its abscissa is negative and the ordinate is positive.

∴ coordinates of A are (- 6, 8).

Similarly, since B lies on the fourth quadrant, its abscissa is positive and the ordinate is negative.

∴ coordinates of B are (6,8).

∴ coordinates of the mid-point of \(\overline{\mathrm{AB}}\) are \(\left(\frac{-6+6}{2}, \frac{8-8}{2}\right)\) = (0,0)

∴ the required coordinates of the midpoint of \(\overline{\mathrm{AB}}\) are (0, 0).

 

 

Question 4. P is a point on the line segment \(\overline{\mathrm{AB}}\) such that AP PB. If the coordinates of A and B are (3, 4) and (5, 2) respectively find the coordinates of P.

Solution:

∵ AP = PB.

∴ P is the mid-point of \(\overline{\mathrm{AB}}\).

∴ the coordinates of P are \(\left(\frac{3-5}{2}, \frac{-4+2}{2}\right)=\left(\frac{-2}{2}, \frac{-2}{2}\right)=(-1,-1)\)

∴ the coordinates of P are (-1,-1).

 

The coordinates of P are (-1,-1)

 

Chapter 2 Section Formulas Long Answer Type Questions

 

Question 1. Determine the ratio in which the x-axis divides the line segment joining the points (5, 4) and (2, 3).

Solution:

Given 

The x-axis divides the line segment joining the points (5, 4) and (2, 3)

Let the given points be A (5; 4) and B (2, 3) and the x-axis divides \(\overline{\mathrm{AB}}\) into the ratio m: n 

∴ Coordinates of P are \(\left(\frac{2 m+5 n}{m+n}, \frac{3 m-4 n}{m+n}\right)\)

Since P lies on the x-axis, the ordinate of P is 0.

∴ \(\frac{3 m-4 n}{m+n}=0^i \Rightarrow 3 m-4 n=0 \Rightarrow 3 m=4 n \Rightarrow \frac{m}{n}=\frac{4}{3}=4: 3\)

\(\overline{\mathrm{AB}}\) is divided by the x-axis into the ratio 4: 3 internally.

 

Question 2. Determine the ratio into which the line segment joining the points (- 1, 2) and (4, 5) are intersected at the point (-11, 16).

Solution:

Given

The line segment joining the points (- 1, 2) and (4, 5) are intersected at the point (-11, 16)

Let the given points be A (1, 2) and B (4, 5) and AB is divided into the ratio m: n at (-11, 16).

∴ \(-11=\frac{m .4+n(-1)}{m+n}\)

-11m-11n = 4m-n

⇒ -15m =10n

⇒ \(\frac{m}{n}=-\frac{2}{3}\)

⇒ m: n=2: 3

Hence, \(\overline{\mathrm{AB}}\) is divided externally into the ratio 2 : 3 at (-11, 16).

 

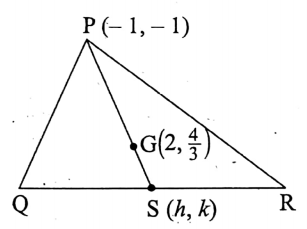
Question 3. The coordinates of P of the APQR are (-1, -1); If the centroid of the triangle is \(\left(2, \frac{4}{3}\right)\), then find the mid-point of QR.

Solution:

Given

The coordinates of P of the APQR are (-1, -1)

Let the centroid of the APQR be G\(\left(2, \frac{4}{3}\right)\)and the mid-point of QR be S (h, k); Since

G \(\left(2, \frac{4}{3}\right)\) divides the median \(\overline{\mathrm{PS}}\) internally into the ratio 2: 1, we get,

\(\frac{2 \cdot h+1(-1)}{2+1}=2\)

⇒ 2h – 1 = 6

⇒ 2h = 7

⇒ h = \(\frac{7}{2}\)

And, \(\frac{2 \cdot k+1 \cdot(-1)}{2+1}=\frac{4}{3}\)

⇒ 2k – 1 = \(\frac{4}{3}\) x 3

⇒ 2k = 4 + 1

⇒ k = \(\frac{5}{2}\)

∴ the mid-point of \(\overline{\mathrm{QR}}\) is \(\left(\frac{7}{2}, \frac{5}{2}\right)\)

 

 

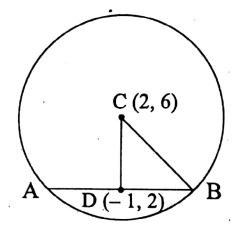
Question 4. (2, 6) is the centre of a circle and one of its chords of length 24 units is bisected at (-1, 2). Find the radius of the circle.

Solution:

Given 

(2, 6) is the centre of a circle and one of its chords of length 24 units is bisected at (-1, 2)

Let the chord AB of the circle with centre C is bisected at D.

As per the question, the coordinates of C and D are (2, 6) and (-1, 2).

∴ \(\mathrm{CD}^2=(2+1)^2+(6-2)^2=3^2+4^2=9+16=25 \text { and } \overline{\mathrm{AB}}=24\)

∴ \(\overline{\mathrm{BD}}\) = \(\frac{1}{2}\) \(\overline{\mathrm{AB}}\) = \(\frac{1}{2}\) x 24 = 12

Now, C and B are joined.

Since D is the mid-point of AB.

∴ \(\overline{\mathrm{CD}}\)  is perpendicular to \(\overline{\mathrm{AB}}\).

∴ from the right-angled triangle BCD, we get,

\(\mathrm{BC}^2=\mathrm{CD}^2+\mathrm{DB}^2=25+12^2 \Rightarrow \mathrm{BC}^2=169, \overline{\mathrm{BC}}=13\)

the required radius of the circle is 13 units.

 

 

Question 5. Determine the ratio in which the line segment joining the points (7, 3) and (-9, 6) is divided by the y-axis.

Solution: 

Given

The line segment joining the points (7, 3) and (-9, 6) is divided by the y-axis

Let the line segment joining the points (7, 3) and (-9, 6) be divided by the y-axis into the ratio mn at P.

∴ the coordinates of P are \(\left(\frac{m \cdot(-9)+n .7}{m+n}, \frac{m .6+n .3}{m+n}\right)=\left(\frac{-9 m+7 n}{m+n}, \frac{6 m+3 n}{m+n}\right)\)

Since P lies on the y-axis, 

∴ the abscissa of P is 0.

∴ \(\frac{-9 m+7 n}{m+n}=0\)

⇒ -9m + 7n = 0

⇒ +9m = +7n

⇒ \(\frac{m}{n}=\frac{7}{9}\)

∴ the required ratio is 7: 9.

 

Question 6. Prove that points A (7, 3), B (9, 6), C (10, 12) and D (8, 9) when joined consecutively produce a parallelogram.

Solution:

Given 

Points A (7, 3), B (9, 6), C (10, 12) and D (8, 9)

The mid-point of the diagonal AC of ABCD = mid-point of the line segment joining (7, 3) and (10, 12).

∴ mid-point of \(\overline{\mathrm{AC}}\) is \(\left(\frac{7+10}{2}, \frac{3+12}{2}\right)=\left(\frac{17}{2}, \frac{15}{2}\right)\)

Again, the mid-point of the diagonal BD of ABCD = mid-point of the line segment joining (9, 6) and (8, 9).

mid-point of \(\overline{\mathrm{BD}}\) is \(\left(\frac{9+8}{2}, \frac{6+9}{2}\right)=\left(\frac{17}{2}, \frac{15}{2}\right)\)

∴ Since the mid-points of both the diagonals \(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\) are \(\left(\frac{17}{2}, \frac{15}{2}\right)\)

i.e., the same,

\(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\) bisect each other.

∴ ABCD is a parallelogram. (Proved)

 

Question 7. Find (x,y) if the points (3, 2), (6, 3), (x, y) and (6, 5) produce a parallelogram when joined successively.

Solution:

Given 

The points (3, 2), (6, 3), (x, y) and (6, 5) produce a parallelogram when joined successively

Let the vertices of the parallelogram ABCD be A (3, 2), B (6, 3), C (x, y) and D (6, 5) and the diagonals AC and BD intersect each other at P.

∴ the diagonals of a parallelogram bisect each other,

P is the mid-point of both the diagonals \(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\).

∴ the coordinates of P, the mid-point of AC are \(\left(\frac{3+x}{2}, \frac{2+y}{2}\right)\)

and the coordinates of P, the mid-point of BD are \(\left(\frac{6+6}{2}, \frac{3+5}{2}\right)\) = (6,4);

∴ \(\left(\frac{3+x}{2}, \frac{2+y}{2}\right)=(6,4) \Rightarrow \frac{3+x}{2}=6 \Rightarrow x+3=12 \Rightarrow x=9\) 

and \(\frac{2+y}{2}=4 \Rightarrow y+2=8 \Rightarrow y=6\)

∴ (x, y) = (9, 6)

 

Question 8. If the points \(\left(x_1, y_1\right),\left(x_2, y_2\right),\left(x_3, y_3\right) \text { and }\left(x_4, y_4\right)\) when joined successively produce a parallelogram, prove that \(x_1+x_3=x_2+x_4 \text { and } y_1+y_3=y_2+y_4\)

Solution:

The mid-point of the diagonal joining the points \(\left(x_1, y_1\right) \text { and }\left(x_3, y_3\right)\) are

= \(\left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\right)\)

Again, the mid-point of the diagonal joining the points \(\left(x_2, y_2\right) \text { and }\left(x_4, y_4\right)=\left(\frac{x_2+x_4}{2}, \frac{y_2+y_4}{2}\right)\)

Since the diagonals of a parallelogram bisect each other, the mid-points of its diagonals will be the same.

∴ \(\left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\right)=\left(\frac{x_2+x_4}{2}, \frac{y_2+y_4}{2}\right)\)

∴ \(\frac{x_1+x_3}{2}=\frac{x_2+x_4}{2} \Rightarrow x_1+x_3=x_2+x_4\)   (proved)

Again, \(\frac{y_1+y_3}{2}=\frac{y_2+y_4}{2} \Rightarrow y_1+y_3=y_2+y_4\)     (Proved)

 

Question 9. (2, 4), (6, 2) and (- 4, 2) are the vertices of a triangle. Find the length of its medians.

Solution:

Given 

(2, 4), (6, 2) and (- 4, 2) are the vertices of a triangle

Let the given vertices be A (2, -4), B (6, -2) and C (-4, 2).

If D, E and F be the mid-points of BC, CA and AB respectively, then the coordinates of D are

\(\left(\frac{6-4}{2}, \frac{-2+2}{2}\right)\)= (1,0).

The coordinates of E are \(\left(\frac{2-4}{2}, \frac{-4+2}{2}\right)\) = (-1,-1).

The coordinates of F are \(\left(\frac{2+6}{2}, \frac{-4-2}{2}\right)\) = (4, -3)

∴ \(\overline{\mathrm{AD}}=\sqrt{(2-1)^2+(-4-0)^2}\) units = √1+16 units 

= √17 units

∴ \(\overline{\mathrm{BE}}=\sqrt{(6+1)^2+(-2+1)^2}\) units = √49+1 units 

= √50 units 

= 5√2 units

∴ \(\overline{\mathrm{CF}}=\sqrt{(-4-4)^2+(2+3)^2}\) units = √64+25 units

 = √89 units

∴ the required lengths of the medians are √17 units, 5√2 units and √89 units.

 

Question 10. Find the coordinates of the midpoint of the line segment intersected by the axes of the straight line 4x + 3y+ 12 = 0.

Solution:

Given 

straight line 4x + 3y+ 12 = 0

Putting x = 0 in 4x + 3y+ 120 we get, 3y= – 12 or, y = -4

∴ the straight line intersects the y-axis at (0, -4).

Also, putting y = 0 in 4x + 3y+ 12 = 0, we get 4x + 12 = 0 or, 4x = -12 or x = -3

∴ the straight line intersects the x-axis at (-3, 0).

So, the mid-point of (-3, 0) and (0, 4) is \(\left(\frac{-3+0}{2}, \frac{0-4}{2}\right)=\left(\frac{-3}{2},-2\right)\)

∴ the required coordinates are \(\left(\frac{-3}{2},-2\right)\)

 

Question 11. Determine the ratio in which the straight line 3x + 4y = 21 divides the line segment obtained by joining the points (-9, 5) and (7, 9).

Solution: 

Given 

The straight line 3x + 4y = 21 divides the line segment obtained by joining the points (-9, 5) and (7, 9)

Let the straight line 3x + 4y = 21 divide the line segment joining (-9, 5) and (7, 9) into the ratio m: n.

Now, the coordinates of the point of intersection are \(\left(\frac{7 m-9 n}{m+n}, \frac{9 m+5 n}{m+n}\right)\)

Clearly, this point lies on the straight line 3x + 4y = 21.

∴ \(\text { 3. } \frac{7 m-9 n}{m+n}+4 \cdot \frac{9 m+5 n}{m+n}=21\)

⇒ 21m-27n+36m+20n = 21m + 21n 

⇒ 36m = 28n

⇒ \(\frac{m}{n}=\frac{28}{36}=\frac{7}{9}\)

∴ m: n = 7:9

∴ the required ratio is 7: 9.

 

Question 12. If the points (5, 2), (x, 7), (1, 4) and (1, y) after joining successively produce a parallelogram, find the values of x and y.

Solution:

Given 

The points (5, 2), (x, 7), (1, 4) and (1, y) after joining successively produce a parallelogram

Let the given points denote the vertices A (5, 2), B (x, 7), C (- 1, 4) and D (1, y) of the parallelogram ABCD.

Then, mid-point of the diagonal AC = \(\left(\frac{5-1}{2}, \frac{2+4}{2}\right)\) = (2, 3)

Again, mid-point of the diagonal BD = \(\left(\frac{x+1}{2}, \frac{7+y}{2}\right)\)

Since mid-points of the diagonals of a parallelogram are equal.

\(\frac{x+1}{2}=2 \Rightarrow x+1=4 \Rightarrow x=3\) and

\(\frac{7+y}{2}=3 \Rightarrow y+7=6 \Rightarrow y=-1\)

∴ the values of x and y are 3 and -1 respectively.