WBBSE Solutions For Class 7 Maths Geometry Chapter 2 Miscellaneous Constructions Exercise 2 Solved Example Problems

Geometry Chapter 2 Miscellaneous Constructions Exercise 2 Solved Example Problems

Introduction

In class 6 you have studied the uses of different instruments found in the geometrical box. A very important topic in geometry is to construct different geometric figures accurately with the help of those instruments.

In this chapter, our aim is to construct various geometric figures mainly with the help of a scale, protractor, pair of dividers and pair of pencil compasses. While constructing those geometrical figures you should keep in mind two important aspects.

Firstly the end of your pencil must be very sharp and the use of an eraser should be minimised. If you can draw accurate geometrical figures at this early stage then it will help you a lot in the higher classes where more complicated figures will be required to construct.

To draw a 60° angle without the help of a protractor

Without the help of a protractor, an angle is to be drawn whose measure is 60°.

Read and Learn More WBBSE Solutions For Class 7 Maths

 

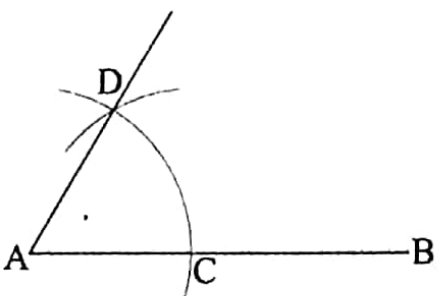
Construction: Take any straight line AB.

With A as centre and any radius draw an arc which intersects AB at C.

Again with C as centre and same radius draw another arc which intersects the former arc at D. AD is joined.

Then ∠DAB is the required angle whose measure is 60°.

To draw a 90° and a 120° angle without the help of protractor.

 

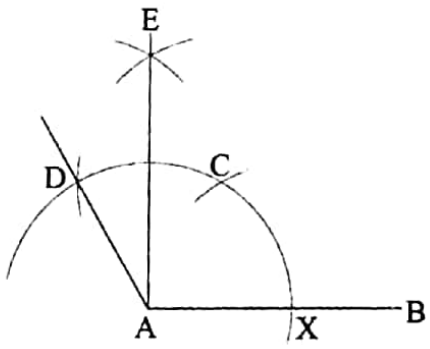
Without the help of protractor two angles are to be drawn whose measures are 90° and 120°.

Construction: Take any straight line AB. With A as centre and any radius draw an arc which intersects AB at X.

With X as centre and any radius draw an arc which intersects AB at X. With X as center and same radius draw another arc which intersects the former arc at C.

Again with C as centre and same radius draw another arc which intersects the former arc at D.

Now, with C and D as centres and same radius draw two arcs which intersect each other at the point E. Join AD and AE.

Then  ∠EAB = 90° and ∠DAB = 120° are the two required angles.

To construct an angle equal to a given angle

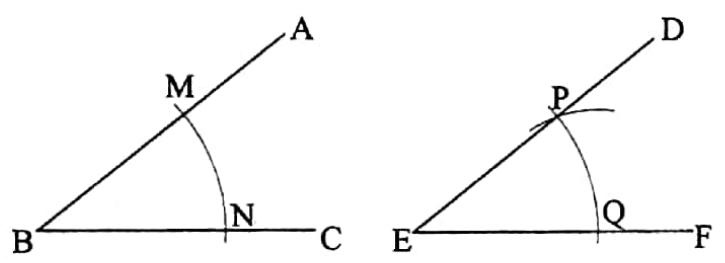
Let ∠ABC be a given angle.

It is required to construct an angle equal to ∠ABC.

Construction: Take any straight-line EF in the plane of the ∠ABC. With the vertex B of ∠ABC as centre and any radius draw an arc which intersects AB and BC at M and N respectively.

WBBSE Class 7 Geography Notes	WBBSE Solutions For Class 7 History
WBBSE Solutions For Class 7 Geography	WBBSE Class 7 History Multiple Choice Questions
WBBSE Class 7 Geography Multiple Choice Questions	WBBSE Solutions For Class 7 Maths

 

Now with E as centre and with the same radius as before draw an arc which intersects EF at Q. Now with Q as centre and radius equal to NM draw an arc which intersects the former arc at P. Join EP and produce it upto D.

Thus, ∠DEF is equal to ∠ABC.

Verification: If you measure the angles ABC and DEF with protractor you will find that they are of equal measure.

Construction of triangles

You have learnt earlier that a triangle has six parts, namely three sides and three angles.

A definite triangle can be constructed if three mutually independent parts are known. In fact, we can construct a triangle in the following cases:

1. When the three sides of a triangle are known.
2. When the two sides and the included angle of the triangle are known.
3. When the two sides and the angle opposite to one of them are known.
4. When one side and the angles adjacent to it are known.
5. When the hypotenuse and one side of a right-angled triangle are known.

To construct a triangle when the lengths of its three sides are given

Let a, b, and c be the lengths of the three sides of a triangle.

It is required to construct the triangle.

Construction: Draw any straight-line BD. Now from BD cut off BC equal to the length of the given side a.

WBBSE Class 7 Geometry Construction Examples

Now with B as the centre and radius equal to the length of the side c draws arc of a circle.

Again with C as the centre and radius equal to the length of the side b draw another arc of a circle on the same side of BD to cut the previous arc at A. Join BA and CA.

Thus, ΔABC is the required triangle.

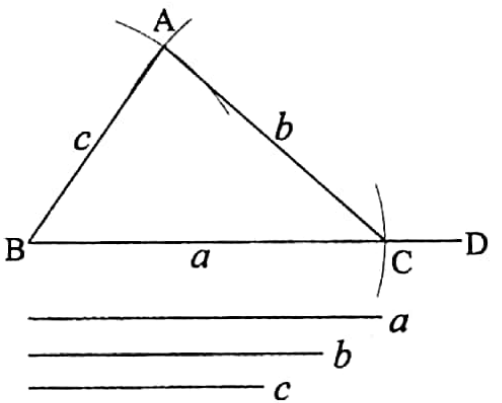
Verification: You may measure the lengths of the sides BC, CA and AB of the triangle ABC by a scale.

You will find that BC = a, CA = b and AB = c.

Thus, AABC is the required triangle whose three sides are equal to a, b and c respectively.

To construct a triangle when the lengths of its two sides and their included angle are given

Let a and c be the lengths of the two sides of a triangle and their included angle be ∠B. It is required to construct the triangle.

Construction: Draw any straight line BD.

Now from BD cut off BC equal to the length of the given side a.

Now at the point B on BC draw an angle ∠CBE equal to the given angle B.

From BE cut off BA equal to the length of the given side c.

Join AC. Thus, ΔABC is the required triangle.

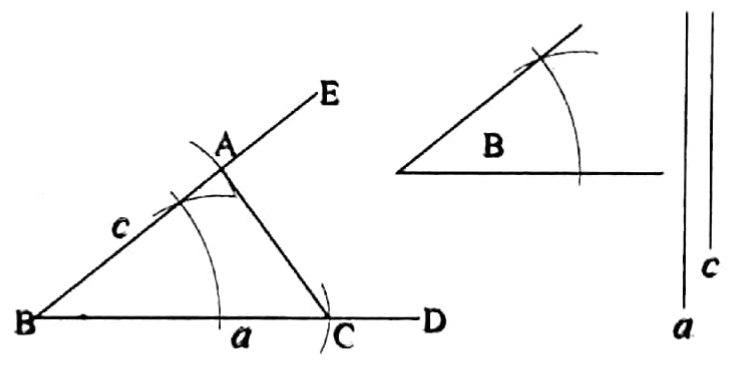
Verification: Measuring the sides BC and BA with a scale and the angle ∠ABC with a protractor you will find that BC = a, BA = c and ∠ABC is equal to ∠B.

Thus, ΔABC is the required triangle whose two sides are a and c and their included angle is ∠B.

Step-by-Step Solutions for Class 7 Geometry Problems

To construct a triangle when the lengths of its two sides and the angle opposite to one of them are given

Let b and c be the lengths of the two sides of a triangle and the angle opposite to the side b be ∠B.

It is required to construct the triangle.

Construction: Draw any straight-line BD. Now at the point B of the straight line BD construct an angle ∠DBE equal to the given angle B.

Now from BE, cut off BA equal to the length of the given side c.

With A as centre and radius equal to the length of the given side b construct an arc of a circle.

Let this arc intersect BD at C₁ and C₂. Join AC₁ and AC₂

Then both ΔABC₁ and ΔABC₂ are the required triangles.

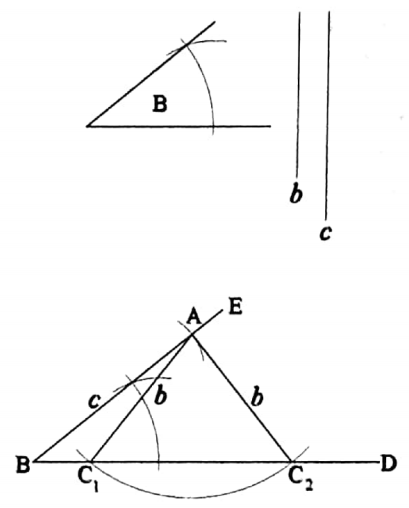
Verification: In the triangle ABC₁ if you measure the sides AB and AC₁ with a scale and the angle ∠ABC₁ with a protractor you will find that AB = c, AC₁ = b and ∠ABC₁ is equal to ∠B.

Similarly, in the triangle ABC₂, AB = c, AC₂ = b and ∠ABC₂ is equal to ∠B.

To construct a triangle when the length of its one side and the angles adjacent to it are given

Let a be the length of one side of a triangle and ∠B and ∠C be the angles adjacent to side a.

It is required to construct the triangle.

Solved Problems for Class 7 Miscellaneous Constructions

Construction: Draw any straight line BD. Now from BD cut off BC equal to the length of the side a.

Now at the point B on BC draw an angle ∠CBE equal to the given angle B.

Also at the point C on BC draw an angle ∠BCF equal to the given angle C.

Let BE and CF intersect each other at A. Thus, ΔABC is the required triangle.

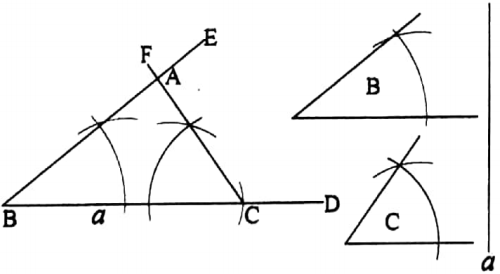
Verification: Measuring the side BC with a scale and the angles ∠ABC and ∠ACB with protractor you will find that BC = a, ∠ABC and ∠ACB are equal to the angles B and C respectively.

To construct a right-angled triangle when the lengths of its hypotenuse and one side are given

Let the length of the hypotenuse of a right-angled triangle be b and a be the length of its another side.

It is required to construct the triangle.

Construction: Draw any straight-line BD. Now from BD cut off BC equal to the length of the side a.

Draw a perpendicular BE on BC at B. With C as the centre and radius equal to the length of the hypotenuse b draw an arc of a circle to intersect BE at A. Join AC.

Thus, ΔABC is the required triangle.

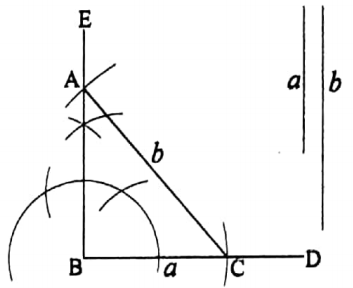
Verification: Measuring the sides BC and AC with a scale and the angle ∠ABC with a protractor you will find that, BC = a, AC = b and ∠ABC = 90°.

To construct a right-angled triangle when the length of its hypotenuse and an acute angle is given

Let the length of the hypotenuse of a right-angled triangle be b and an acute angle be a.

It is required to construct the triangle.

Class 7 Maths Exercise 2 Solutions on Constructions

Construction: Draw any straight line BD. Now from BD cut off BC equal to the length of the side b. At the point B draw ∠CBY equal to the angle a. Now from the point C draw the perpendicular CN on BY.

Thus, ΔBCN is the required triangle.

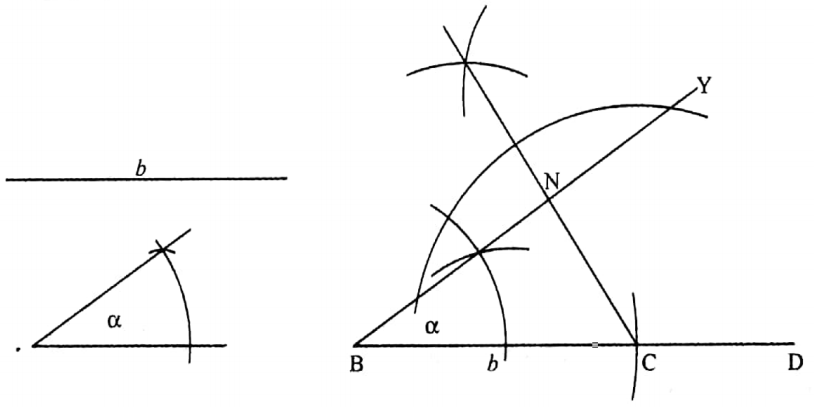
Verification: Measuring the length of the side BC it is found that BC = b and measuring ∠NBC and ∠BNC with protractor it is found that ∠NBC = α and ∠BNC = 90°

Construction of quadrilaterals

You have learnt earlier that a quadrilateral has four sides. A definite quadrilateral can be constructed if five mutually independent parts are known.

In fact, we can construct a quadrilateral in the following cases:

1. When the four sides and one angle of the quadrilateral are known.
2. When the three sides and two included angle between them are known.
3. When the four sides and one diagonal of a quadrilateral are known.

Besides the above possibilities we can also construct some quadrilaterals under given conditions, such as:

1. When the two adjacent sides and their included angle of a parallelogram are given.
2. When the length of the side of a square is known.
3. When the length of the side of a rhombus and the measure of its one angle are given.

To construct a quadrilateral when the lengths of its four sides and the measure of an angle are given

Let a, b, c, d be the lengths of the four sides of a quadrilateral, and ∠X be the included angle between the sides of lengths a and b.

It is required to construct the quadrilateral.

Construction: Draw any straight line AP. From AP cut off AB equal to the length of the diagonal l.

With centers A and C and radii equal to the lengths of the sideas a and b respectively draw two arcs of circles on the same side of AC.

Let these arcs intersects at B.

Again with centred A and C and radii  equal to the given angle X.

From AQ cut off AD equal to the length of the side b. Now with centres D and B construct two arcs of the circles of radii c and d respectively.

Let these two arcs intersect each other at C. Join DC and BC.

West Bengal Board Class 7 Geometry Assistance

Thus, ABCD is the required quadrilateral.

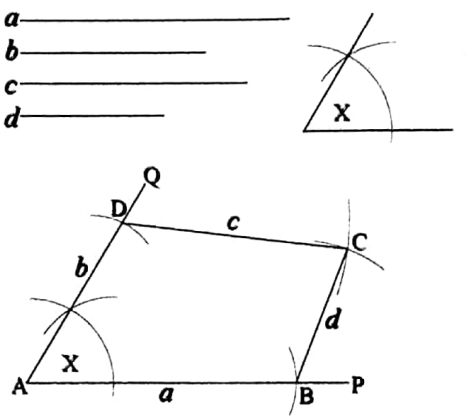
Verification: You may easily verify with scale and protractor that in the quadrilateral ABCD, AB = a, AD = b, DC = c, BC = d and ∠DAB = ∠X.

To construct a quadrilateral when the lengths of its three sides and the measures of two included angles between them are given

Let a, b, c be the lengths of the three sides of a quadrilateral and ∠X be the included angle between a and b, and ∠Y be the included angle between a and c.

It is required to construct the quadrilateral.

Construction: Draw any straight line AP. From AP, cut off AB equal to the length of the side a.

Now at the points A and B of the straight line AB draw angles ∠BAQ and ∠ABR equal to the angles X and Y respectively.

Now from AQ cut off AD equal to the length of the side b and from BR cut off BC equal to the length of the side c. Join DC.

Thus, ABCD is the required quadrilateral.

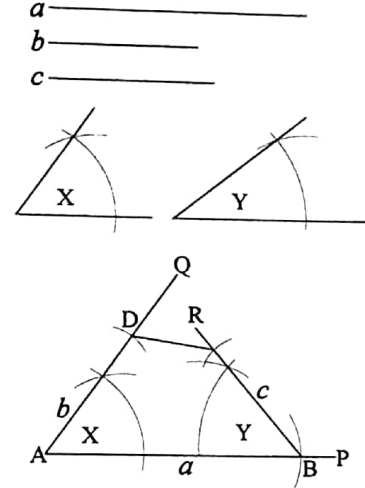
Verification: You may easily verify with scale and protractor that in the quadrilateral ABCD, AB = a, AD = b, BC = c, ∠DAB = ∠X and ∠CBA = ∠Y.

To construct a quadrilateral when the lengths of its four sides and one diagonal are given

Let, a, b, c, d be the lengths of the four sides of a quadrilateral and l be the length of its diagonal.

It is required to construct the quadrilateral.

Understanding Miscellaneous Constructions for Class 7

Construction: Draw any straight line AP.

From AP cut off AC equal to the length of the diagonal l. With centres A and C and radii equal to the lengths of the sides a and b respectively draw two arcs of circles on the same side of AC.

Let these arcs intersect at B. Again with centres A and C and radii equal to the lengths of the sides c and d respectively draw two arcs of circles on the other side of AC.

Let these arcs intersect at D. Join AB, BC, AD and CD. Thus, ABCD is the required quadrilateral.

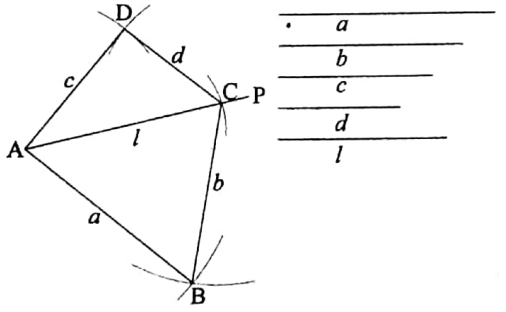
Verification: You may easily verify with a scale that in the quadrilateral ABCD, AB = a, BC = b, AD = c, CD = d and AC = l.

To construct a parallelogram when the lengths of its two adjacent sides and their included angle are given

Let a and b be the two adjacent sides and ZX be their included angle in a parallelogram. It is required to construct the parallelogram.

Construction: Draw any straight line AP. From AP cut off AB equal to the length of the side a. At the point A on AB draw an angle ∠BAQ equal to the given angle X.

From AQ, cut off AD equal to the length of the given side b.

Now with D and B as centres and radius equal to a and b respectively draw two arcs of circles intersecting each other at C. Joint BC and CD.

Thus, ABCD is the required parallelogram.

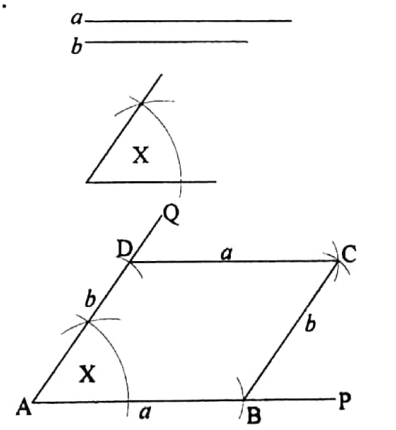
Verification: You can easily verify with scale and protractor that in the parallelogram ABCD, AB = a, AD = b, ∠BAD = X.

To construct a rectangle whose two adjacent sides are given

Let the length of the two adjacent sides of a rectangle be a and b.

It is required to construct the rectangle.

Construction: Draw any straight line AP. From AP cut off AB equal to the given side a. Now at the point A of the straight line AB construct a perpendicular AQ.

From AQ cut off AD equal to the side b.

Now draw two arcs with centres D and B and radius equal to a and b respectively which intersect each other at point C. Join BC and DC.

Thus, ABCD is the required rectangle

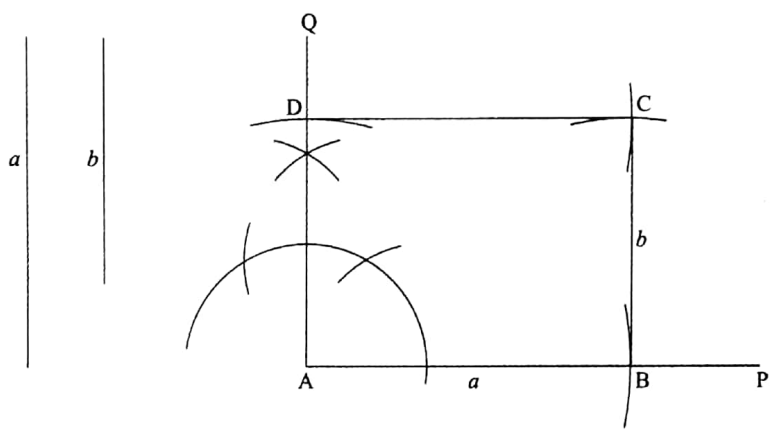
Verification: It can be verified easily by a scale that, for the rectangle, ABCD, AB = DC = a and AD = BC = b.

To construct a square the length of whose side is given

Let the length of the side of a square be a. It is required to construct the square.

Construction: Draw any straight line AP. From AP cut off AB equal to the given side a.

Now at the point A of the straight line AB constructs a perpendicular AQ. It is required to construct the rectangle.

WBBSE Class 7 Chapter 2 Construction Guide

Construction: Draw any straight line AP. From AP cut off AB equal to the given side a.

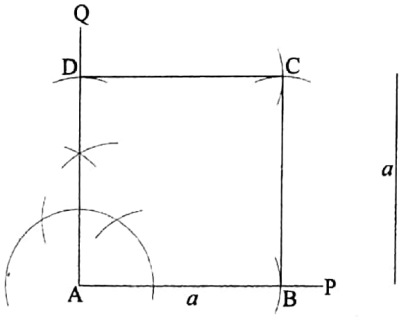
Now at the point A of the straight line AB construct a perpendicular AQ.

From AQ cut off AD equal to the side b.

Now draw two arcs with centres D and B and radius equal to a and b respectively which intersect each other at the point C. Join BC and DC.

Thus, ABCD is the required rectangle.

AQ cut off AD equal to the given side a.

Now with D and B as centres and radius equal to a construct two arcs of circles intersecting at C. Join BC and DC.

Thus, ABCD is the required square.

Verification: It can be verified easily by a scale that the length of each side of the square ABCD is a.

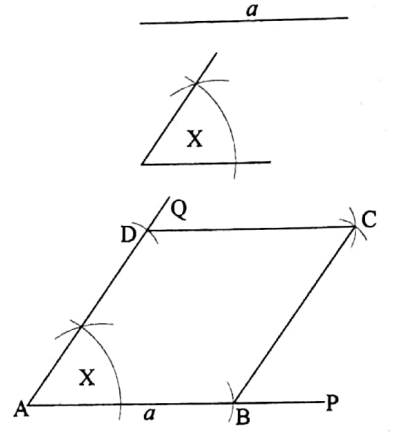
To construct a rhombus when the length of its side and the measure of one angle are given

Let the length of each side of a rhombus be a and the measure of its one angle be X.

It is required to construct the rhombus.

Construction: Draw any straight line AP. From AP cut off AB equal to the given side a.

Now at the point Aof the straight line AB construct an angle ∠BAQ equal to the given angle X.

From AQ cut off AD equal to the given side a. Now with D and B as centres and radius equal to a construct two arcs of circles intersecting at C. Join BC and DC.

Thus, ABCD is the required rhombus.

Class 7 Maths Exercise 2 Solved Examples

Verification: It can be verified easily with a scale and a protractor that the length of each side of the rhombus ABCD is a and the measure of the angle ∠BAD is equal to X.