Modulus of Elasticity – Elasticity Types, Elastic Stress and Strain

Properties Of Matter – Elasticity Different Kinds Of Strain And Moduli Of Elasticity

• Longitudinal Strain
• Longitudinal Stress
• Young’s Modulus

If force is applied along the length of a body usually whose length is much greater than all of its other dimensions (like breadth, height, etc., as in the case of a long thin wire or other rod-like bodies), then the body undergoes longitudinal strain.

Read and Learn More: Class 11 Physics Notes

• In other words, if, under the influence of an external force, a body undergoes an increase or decrease primarily in length, then this body is associated with a longitudinal strain. The ratio of the change in length (increase or decrease) to the original length of the body is the measure of its longitudinal strain.
• Longitudinal strain is possible only in the case of a solid substance. The stress developed inside the body, i.e., the reaction force developed per unit cross-sectional area while it undergoes longitudinal strain is called longitudinal stress.

Young’s modulus: Within the elastic limit, longitudinal stress divided by longitudinal strain is called Young’s modulus.

Yound’s modulus (Y) =\(\frac{\text { longitudinal stress }}{\text { longitudinal strain }}\)

• If longitudinal stress tends to infinity and longitudinal strain tends to zero, Young’s modulus tends to infinity. This is the case for a perfectly rigid body, for which Young’s modulus Y is infinite. On the other hand, if any external force is applied on a plastic body, its longitudinal stress is zero and Young’s modulus (Y) becomes zero.
• Liquids and gases cannot produce longitudinal stress at all, i.e., on the application of even a very small longitudinal force, they begin to flow. Therefore, Young’s modulus (Y) is a characteristic only of solids and not of liquids and gases.
• Let us consider a wire of length L and cross-sectional area A suspended from a rigid support. Now a force of magnitude F is applied perpendicularly to the cross-sectional area A on the wire i.e., the force will act downwards along the length of the wire. As a result, the wire will show a slight increase in length.

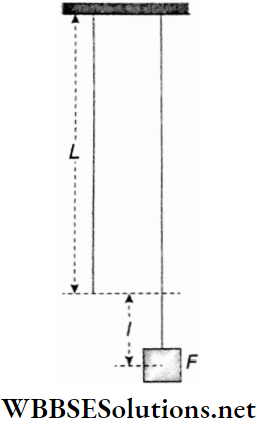
Let the increase in the length of the wire = l.

Longitudinal strain = \(\frac{\text { increase in length }}{\text { original length }}=\frac{l}{L}\)

Longitudinal stress = \(\frac{\text { applied force }}{\text { area of cross-section }}=\frac{F}{A}\)

∴ Young’s modulus, Y= \(\frac{\text { longitudinal stress }}{\text { longitudinal strain }}\)

= \(\frac{F}{\frac{F}{L}}=\frac{F L}{A l}\)….(1)

If the wire is of circular cross-section of radius r and a mass m is hung from its lower end, then, A = πr², F = mg

So, Y =\(\frac{m g L}{\pi r^2 l}\) …….(2)

Units of Young’s modulus:

• dyn · cm^-2 CGs
• N · m^-2 or p

Young’s modulus for copper is 1.26 x 10¹² dyn · cm^-2 — which means that a force of 1.26 x 10¹² dyn must be applied per cm² area of cross-section of a copper wire to produce unit longitudinal strain in it.

Sagging of an elastic body due to its own weight: In our daily life, we observe many bodies sag due to their own weights when they are suspended from a rigid support.

Examples: a wet towel suspended across a horizontal rope, a cloth bag containing a few kilograms of rice suspended from a hook, etc. However, these are not perfectly elastic bodies, and no theoretical expression for their sagging can be obtained.

Now, we turn our attention to elastic bodies. Suppose a cylindrical rod made of an elastic metal (say, steel) is hung vertically from a rigid support. It definitely sags due to its own weight, although the sagging is relatively small. But using elastic properties of the material, a clear expression for the sagging can be found out.

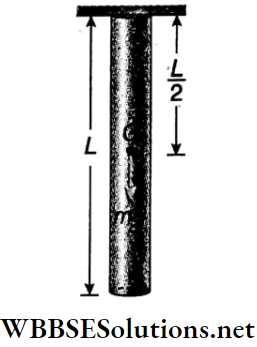
Let m be the mass of body B made of an elastic material. One of its ends is hung from a rigid support.

Then mg = weight of B, L = its length, and A = area of its cross-section.

If B is a body of uniform density and its cross section is also uniform throughout its height, the centre of gravity G is situated at the midpoint at a depth 1/2 from the rigid support.

A force due to the weight mg acts downwards at the centre of mass (G). It may be assumed that this force stretches the body above the point G. So the effective initial length that is strained is L/2. If the body B sags downwards through a length l, then,

longitudinal strain = \(\frac{\text { elongation }}{\text { initial length }}=\frac{l}{\frac{L}{2}}=\frac{2 l}{L}\)

Also, longitudinal stress = \(\frac{\text { applied force }}{\text { area of cross-section }}=\frac{m g}{A}\)

Again the mass of the body B is,

m = volume x density = LAρ [ρ = density of the material]

So Young’s modulus,

Y = \(\frac{\text { stress }}{\text { strain }}=\frac{\frac{m g}{A}}{\frac{2 l}{L}}=\frac{m g L}{2 A l}=\frac{L A \rho g L}{2 A l}=\frac{\rho g L^2}{2 l}\)

Hence the sagging of the body is,

l = \(\frac{\rho g L^2}{2 Y}\) ……….(3)

It is important to note that this expression is independent of A.

So the sagging of a thin wire is the same as that of a thick rod if their initial lengths are equal and they are made of the same elastic material.

• Bulk or Volume Strain
• Bulk or Volume Stress
• Bulk Modulus

When a body is subjected to uniform pressure acting normally at every point on its surface, then it undergoes a change in volume, without any change in its shape.

• For example, when a cube or a sphere is subjected to a uniform normal pressure, their shape remains unchanged, but they undergoes a volume strain.
• Under the influence of external forces, when a body undergoes an increase or decrease in volume without any change in its shape, then the strain of the body is called bulk or volume strain.
• The ratio of the change in volume (increase or decrease) of the body to its initial volume gives the measure of the volume strain of the body.
• The stress, developed in the body, i.e., the reaction force developed per unit surface area due to its volume strain is called bulk or volume stress.

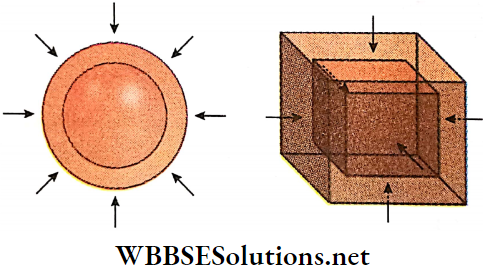
Bulk modulus: Within the elastic limit, volume stress divided by volume strain is called the bulk modulus of elasticity.

Bulk modulus (K) = \(\frac{\text { volume stress }}{\text { volume strain }}\)

Every substance—solid, liquid, or gas—has some volume, and hence the bulk modulus is meaningful for all substances.

The bulk moduli of a perfectly rigid body and a perfectly plastic body are infinite and zero respectively.

Since liquid and gaseous substances undergo only volume strain, the bulk modulus is the only elastic modulus for them. Among the different bulk moduli of a gas, very useful are its isothermal and adiabatic bulk moduli [for details see the chapter First and Second Law of Thermodynamics].

The isothermal bulk modulus of air = 1.01 x 10⁵ Pa and the adiabatic bulk modulus of air = 1.42 x 10⁵ Pa.

Let V = initial volume of a body,

p = applied force per unit surface area of the body = applied pressure,

ν = corresponding decrease in volume,

so, -ν = change in volume.

∴ Volume strain = \(\frac{\text { change in volume }}{\text { initial volume }}=-\frac{\nu}{V}\),

and volume stress = \(\frac{\text { reaction force developed }}{\text { surface area }}\)

= \(\frac{\text { applied force }}{\text { surface area }}\)

= applied pressure = p.

Therefore, the bulk modulus of elasticity of the material of the body is,

K = \(\frac{\text { volume stress }}{\text { volume strain }}=\frac{p}{-\frac{v}{V}}=-\frac{p V}{v}\) …..(4)

On application of pressure, the change in volume of all gases, and of a few materials like rubber, cotton, etc., is fairly large. This means that ν is large even for a relatively small applied pressure p.

So, the bulk moduli of all gases, and of the said materials, are fairly low. On the other hand, almost all solids and liquids show very small changes in volume on application of external forces. As a result, their bulk moduli are much higher.

For more mathematical rigor, the applied pressure is denoted by Δp (instead of p) and the corresponding decrease in volume by Δν (instead of ν). Then, equation (4) becomes,

If Δν is very low, which is usually observed in practice, we can put the limit Δν → 0. Then, from the definition of a derivative, we can replace \(\frac{\Delta p}{\Delta \nu}\) by the differential coefficient \(\frac{d p}{d v} .\).

Then we get, K = \(-V \frac{d p}{d v}\) ….(5)

This equation (5) is treated as the defining equation of the bulk modulus of elasticity.

For magnitudes only, the negative sign on the right-hand side of equations (4) and (5) is ignored.

Units of bulk modulus:

• dym · cm^-2
• N · m^-2

Compressibility: It is defined as the change in volume due to a unit change in pressure if a unit volume of a substance is taken initially. Like bulk modulus, compressibility is also a characteristic property of all substances—solids, liquids, and gases.

Again, let V = initial volume, Δp = applied pressure, and -ΔV = corresponding change in volume.

Then, from definition,

compressibility = \(\text { compressibility }=\frac{\text { change in volume }}{\text { initial volume } \times \text { change in pressure }}\)

= \(\frac{-\Delta V}{V \Delta p}=-\frac{1}{V} \frac{\Delta V}{\Delta p} .\)

In the limit Δp → 0, we have

compressibility = \(-\frac{1}{V} \frac{d V}{d p}\) …….(6)

Comparing equations (5) and (6), we observe that

compressibility = \(\frac{1}{\text { bulk modulus }} \text {. }\)

So, bulk modulus and compressibility are not independent properties. If one is known, the other can be calculated.

The compressibility of a solid or a liquid is very small, compared to that of a gas due to lack of space between molecules and larger intermolecular forces.

The compressibility of a perfectly rigid body is zero. The compressibility of water is 44 x 10^-6 atm^-1, meaning that the volume strain of water becomes 44 x 10^-6 on the application of 1 standard atmosphere pressure.

Units of compressibility:

• cm².dyn^-1
• m².N^-1

Another useful unit of compressibility is atmosphere^-1.

• Shearing Strain
• Shearing Stress
• Modulus of Rigidity or Shear Modulus

If the matchbox is held firmly on a table and a tangential force is applied on the upper surface of the box with the help of a finger, the shape of the box changes. This is known as shearing strain. In this condition, however, the change in the volume of the box is negligible as well as irrelevant.

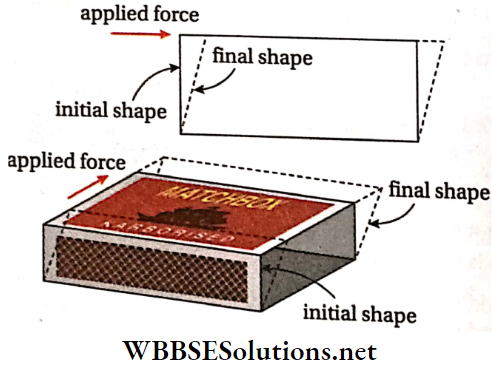
Under the influence of an external force, if a body undergoes a change in its shape, then the strain of the body is called shearing strain or shear. The corresponding stress developed inside the body is called shearing stress.

Modulus of rigidity: Within the elastic limit, shearing stress divided by shearing strain is called the modulus of rigidity or shear modulus.

Modulus of rigidity (n) = \(\frac{\text { shearing stress }}{\text { shearing strain }}\)

The modulus of rigidity is a characteristic property of solids because only solids have definite shapes.

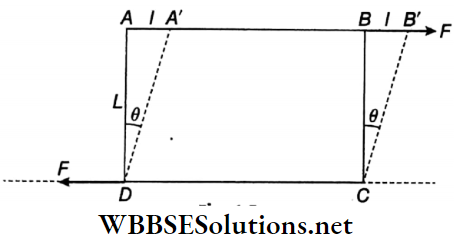
• Let us consider a rectangular parallelepiped ABCD. ABCD is only the front surface of the parallelepiped for convenience, the depth has not been shown in the figure.
• AD and BC denote the vertical side faces, whereas AB and CD are the top and the bottom faces respectively. The lower face CD is kept fixed to the horizontal surface.
• A tangential force F is applied on its upper face AB. An equal but opposite reaction force F will act tangentially on the lower surface DC of the block.

These two forces constitute a couple and due to its action, each layer parallel to the surface DC will be displaced in the direction of the applied force. The layers that are farther from the surface DC will have larger relative displacements during deformation.

• As a result, the block will undergo a change in its shape. It will be seen that each vertical surface parallel to F takes the form of a parallelogram from the original rectangular shape, i.e., the surface ABCD will become a parallelogram A’B’CD.
• This kind of strain is called a shearing strain. It should be noted that, if the displacement AA’ is large, the surface A’B’ will come down a bit, and its position will be lower relative to the original position AB.
• As a result, the area of the parallelogram and the volume of the parallelepiped will decrease. However, in most cases, particularly for metals, AA’ is so small that the change in volume may safely be ignored.

The angle formed between the initial and the final positions of any vertical line drawn perpendicular to the direction of the applied force is called shearing strain or the angle of shear. Usually, this angle is small, as the displacement AA’ is small.

Let ∠ADA’ = ∠BCB’ = θ; AD = L; AA’ = l;

Since θ is very small, tanθ ≈ θ. [where θ is expressed in radian]

∴ Shearing strain = θ = tanθ = l/L

= \(\frac{\begin{array}{c}
\text { relative displacement between two } \\
\text { parallel layers of the body }
\end{array}}{\text { distance between the layers }}\)

Now, if L = 1, then θ=1, which means that the relative displacement between two layers situated at a unit distance apart is the measure of shearing strain.

Shearing stress is measured by the applied tangential force per unit area. If the area of the surface AB is a, then shearing stress = \(=\frac{F}{a}\).

∴ Modulus of rigidity,

n = \(\frac{\text { shearing stress }}{\text { shearing strain }}=\frac{\frac{F}{a}}{\theta}=\frac{F}{a \theta}=\frac{F}{a} \cdot \frac{L}{l}\)

Units of the modulus of rigidity:

• dyn.cm^-2
• N.m^-2 or pa

Poisson’s Ratio: Under the influence of an external force, when a body elongates in any direction, it also undergoes contraction in a perpendicular direction.

• Conversely, when a body contracts in any direction under the influence of an external force, it also elongates at the same time in perpendicular directions.
• So, longitudinal strain and lateral strain occur simultaneously in a body. If the lateral strain is low, then it is proportional to its longitudinal strain. The ratio of lateral strain to longitudinal strain is called the Poisson’s ratio.

Poissons ratio \((\sigma)=\frac{\text { lateral strain }}{\text { longitudinal strain }}\)

Let us consider a wire of initial length L and initial diameter D. If the increase in the length of the wire under the influence of the external force is l and the decrease in its diameter is d, then lateral strain = \(\frac{d}{D}\), longitudinal strain = \(\frac{l}{L}\)

∴ Poisson’s ratio, \(\sigma=\frac{\frac{d}{D}}{\frac{l}{L}}=\frac{d}{D} \cdot \frac{L}{l}\)

Poisson’s ratio depends only on the nature of the material of a body. It is a pure number and has no unit since it is a ratio between two strains. It is applicable only to solids. In the case of liquids and gases, Poisson’s ratio is meaningless.

Poisson’s ratio is not an elastic modulus because it is not the ratio of stress to strain. It is an elastic constant.

Limiting values of Poisson’s ratio: Theoretically, it can be shown that the maximum value of Poisson’s ratio is +1/2 and its minimum value is -1.

But Poisson’s ratio becomes negative only when a body undergoes lateral expansion along with its longitudinal expansion. It cannot be realized in practice. For this reason, the practical values of Poisson’s ratio lie between 0 and +1/2.

Poisson’s ratio—when the volume does not change due to elongation: Let l and r be the length and the radius of circular cross-section of a wire. Then, the volume of the wire, V = πr²l.

Differentiating both sides, we get, dV = πr²dl + πl · 2rdr.

Here, dV = change in volume

dl = change in length, dr = change in radius.

Since, the volume remains unchanged, dV = 0.

∴ 0 = πr² dl+ π l2r dr

or, 0 = πrdl+ π2ldr

or, rdl = -2 ldr or, \(-\frac{d r}{r}=\frac{d l}{2 l}\)

or, \(-\frac{d r / r}{d l / l}=\frac{1}{2}\) = 1/2 [negative sign indicates that if l increases, then r decreases].

∴ Poisson’s ratio: \(\sigma=\frac{\text { lateral strain }}{\text { longitudinal strain }}=\frac{-d r / r}{d l / l}=\frac{1}{2}=0.5\)

Properties Of Matter – Elasticity Poisson’s Ration Numerical Examples

Example 1. An 8 kg mass is suspended from one end of an iron wire of length 2 m and diameter 1 mm. If Young’s modulus of iron is 2 x 10¹² dyn · cm^-2, then what is the increase in length of the wire? [g = 980 cm · s^-2]
Solution:

An 8 kg mass is suspended from one end of an iron wire of length 2 m and diameter 1 mm. If Young’s modulus of iron is 2 x 10¹² dyn · cm^-2

Young’s modulus, Y = \(\frac{m g L}{\pi r^2 l} \quad \text { or, } l=\frac{m g L}{Y \pi r^2}\)

Here, m = 8 kg = 8000 g , g = 980 cm • s^-2 .

L = 2 m = 200 cm , r = 1/2 mm = 0.05 cm,

Y = 2 x 10¹² dyn.cm^-2

∴ l =\(\frac{8000 \times 980 \times 200}{2 \times 10^{12} \times 3.14 \times(0.05)^2}\) = 0.1 cm = 1 mm

Example 2. The volume of 1 litre of glycerine decreases by, 0.42 cm³ on application of a pressure of 20 kg.cm^-2.  Calculate the bulk modulus of glycerine.
Solution:

The volume of 1 litre of glycerine decreases by, 0.42 cm³ on application of a pressure of 20 kg.cm^-2.

Bulk modulus, K= \(\frac{p V}{v}\)

Here, p = 20 kg • cm^-2 = 20 x 1000 x 980 dyn • cm^-2

V = 1 litre = 1000 cm³ , v = 0.42 cm³

∴ Bulk modulus, K =\(K=\frac{20 \times 1000 \times 980 \times 1000}{0.42}\)

= 4.67 x 10¹⁰ dyn · cm^-2

= 4.67 x 10⁹ N · m^-2

Example 3. The upper surface of an aluminium cube of side 10 cm is displaced by 0.03 cm with respect to its firmly held lower surface by a tangential force of 7.5 x 10¹⁰ dyn. Calculate the modulus of rigidity of aluminium.
Solution:

The upper surface of an aluminium cube of side 10 cm is displaced by 0.03 cm with respect to its firmly held lower surface by a tangential force of 7.5 x 10¹⁰ dyn.

Modulus of rigidity, n = \(\frac{F}{A \theta}\)

Here, F= 7.5 x 10¹⁰ dyn , A = 10 x 10 = 100 cm²

θ = \(\frac{0.03}{10}=0.003\)

∴ Modulus of rigidity,

n = \(\frac{7.5 \times 10^{10}}{100 \times 0.003}\)

= 2.5 x 10¹¹ dyn · cm^-2

= 2.5 x 10¹⁰ N · m^-2

Example 4. A metallic wire of length 3 m Is stretched to producean elongation of 2 nun. If the diameter of the wire is l mm, then find the decrease In its diameter due to this elongation. Poisson’s ratio for the material of the wire is 0.24.
Solution:

A metallic wire of length 3 m Is stretched to producean elongation of 2 nun. If the diameter of the wire is l mm

Poisson’s ratio, \(\sigma=\frac{d}{D} \cdot \frac{L}{l} \quad \text { or, } d=\frac{\sigma D l}{L}\)

Here. σ = 0.24 , D = 1 mm = 10^-3 m . L = 3 m .

l = 2 mm = 2 x 10^-3 m

∴ d = \(\frac{0.24 \times 10^{-3} \times 2 \times 10^{-3}}{3}=1.6 \times 10^{-7} \mathrm{~m}\)

Example 5. When a body of mass 5 kg is hung from a wire of length 1 m and radius 2 mm, the length increases by 0.1 mm. If the Poisson’s ratio is 0.4, what will be the change in the radius of the wire? If the load is reduced to 2 kg, how will the radius change?
∴ Solution:

When a body of mass 5 kg is hung from a wire of length 1 m and radius 2 mm, the length increases by 0.1 mm. If the Poisson’s ratio is 0.4, what will be the change in the radius of the wire? If the load is reduced to 2 kg

Poisson’s ratio, \(\sigma=\frac{d}{D} \cdot \frac{L}{l}\)

[where D, L are the initial diameter and the length of the wire and d, l are the changes in tire diameter and in the length of the wire respectively]

∴ d = \(\frac{\sigma D l}{L}=\frac{0.4 \times 0.004 \times 0.0001}{1} \mathrm{~m}\)

[σ = 0.4 , D = 2 x 2 = 4 mm = 0.004 m , 7 = 0.1 mm = 0.0001 m, I = 1 m]

or, d = 16 x 10^-8 m

∴ Change in radius = \(=\frac{16 \times 10^{-8}}{2}=8 \times 10^{-8} \mathrm{~m}\)

Now, Y = \(\frac{m g L}{\pi r^2 l} \quad \text { or, } l=\frac{m g L}{Y \pi r^2}\)

So, for the same wire, l ∝ m. Then we get,

⇒ \(\frac{m_1}{m_2}=\frac{l_1}{l_2} \text { or, } \frac{5}{2}=\frac{0.0001}{l_2} \text { or, } l_2=4 \times 10^{-5} \mathrm{~m}\)

∴ Change in diameter, \(d_2=\frac{\sigma D l_2}{L}=\frac{0.4 \times 0.004 \times 4 \times 10^{-5}}{1}=64 \times 10^{-9} \mathrm{~m}\)

∴ Change in radius = \(\frac{64 \times 10^{-9}}{2}=3.2 \times 10^{-8} \mathrm{~m}\)

Example 6. The change in length of a wire of a circular cross section is found to be 0.01% due to longitudinal stress. If the Poisson’s ratio for the material is 0.2, what is the percentage change in volume?
Solution:

The change in length of a wire of a circular cross section is found to be 0.01% due to longitudinal stress. If the Poisson’s ratio for the material is 0.2

Let the length of the wire be 7, its radius be r and
volume be V.

So, V = \(\pi r^2 l\)

∴ dV = \(\pi r^2 d l+2 \pi l r d r\) [because \(\sigma=\frac{-d r / r}{d L / l}\), dr = -rσ \(\frac{d l}{l}\)]

= \(\pi r^2 d l-2 \pi r^2 \sigma d l\)

= \(\pi r^2 d l(1-2 \sigma)\)

∴ Volume strain

= \(\frac{d V}{V}=\frac{\pi r^2 d l(1-2 \sigma)}{\pi r^2 l}\)

= \(\frac{d l}{l}(1-2 \sigma)\left[\text { Here, } \frac{d l}{l}=0.01 \%=0.0001\right.\)]

= \(0.0001(1-2 \times 0.2)=6 \times 10^{-5}\)

∴ Percentage change in volume

= \(\frac{d V}{V} \times 100=6 \times 10^{-5} \times 100=0.006 \%\)

Example 7. A metallic wire of length and diameter 3 m and 0.001 m respectively is stretched by a load of 10 kg. Young’s modulus and Poisson’s ratio of the material of the wire are respectively 20 x 10¹⁰ N • m^-2 and 0.26. Calculate the decrease In the diameter of the wire, (g = 9.8 m • s^-2)
Solution:

A metallic wire of length and diameter 3 m and 0.001 m respectively is stretched by a load of 10 kg. Young’s modulus and Poisson’s ratio of the material of the wire are respectively 20 x 10¹⁰ N • m^-2 and 0.26.

Young’s modulus Y = \(\frac{F \cdot L}{A \cdot l}\)

or, \(\quad \frac{l}{L}=\frac{F}{Y A}=\frac{10^6 \times 9.8 \times 4}{20 \times 10^{10} \times 3.14 \times(0.001)^2}\)

Again, \(\sigma=\frac{d}{D} \cdot \frac{L}{l}\)

[F = \(10 \times 9.8 \mathrm{~N}\)]

or, \(d=\frac{\sigma D l}{L}=0.26 \times 0.001 \times \frac{10 \times 9.8 \times 4}{20 \times 10^{10} \times 3.14 \times(0.001)^2}\) = 16.23 x 10^-8 m

Decrease in the diameter of the wire = 16.23 x 10^-8 m

Example 8. A wire of length 2 m and diameter 2 cm is suspended vertically with its top end fixed. Its Poisson’s ratio and Young’s modulus are 0.2 and 1.8 x 10¹¹ N • m^-2 respectively. What will be its lateral strain if a load of 1000 kg is suspended at its lower end?
Solution:

A wire of length 2 m and diameter 2 cm is suspended vertically with its top end fixed. Its Poisson’s ratio and Young’s modulus are 0.2 and 1.8 x 10¹¹ N • m^-2 respectively.

Young’s modulus, Y = \(\frac{m g}{\pi r^2} \cdot \frac{L}{l}\)

∴ Longitudinal strain, \(\frac{l}{L}=\frac{m g}{\pi r^2 \cdot Y}=\frac{1000 \times 9.8 \times 7}{22 \times(0.01)^2 \times 1.8 \times 10^{11}}\)

[Here, r = D/2= 2/2 cm = 1 cm = 0.01 nr]

Again, Poisson’s ratio, \(\sigma=\frac{d / D}{l / L}\)

∴ Lateral strain, \(\frac{d}{D}=c \cdot \frac{l}{L}=\frac{0.2 \times 1000 \times 9.8 \times 7}{22 \times(0.01)^2 \times 1.8 \times 10^{11}}\) = 3.46 x 10^-5

Example 9. A rubber cord of length 10 m is suspended vertically. How much does It stretch under its own weight? Density of rubber = 1.5 x 10³ kg · m^-3 Young’s modulus of rubber =6 x 10⁶ gf • cm^-2; g = 9.8 m • s^-2
Solution:

A rubber cord of length 10 m is suspended vertically.

Given, L = 10m; ρ = 1.5 x 10³ kg • m^-3

Y = 6x 10⁶ gf • cm^-2 = 6 x 10⁶ x 980 dyn • cm^-2

= 5.88 x 10⁸ N • m^-2

Let a be the area of cross-section of the rubber cord. Then

F = weight of the rubber cord

= L x a x ρ x g

The weight of the rubber cord acts at its centre of gravity and hence the weight of the rubber cord will produce an extension in the length L/2 of the cord.

Now, Y = \(\frac{F\left(\frac{L}{2}\right)}{a l} \quad \text { or, } l=\frac{F \times L}{2 a \times Y}\)

l = \(\frac{L a \rho g \times L}{2 a \times Y}=\frac{L^2 \rho g}{2 Y}=\frac{10^2 \times 1.5 \times 10^3 \times 9.8}{2 \times 5.88 \times 10^8}\)

= \(1.25 \times 10^{-3} \mathrm{~m}=1.25 \mathrm{~mm}\)

Example 10. A force of 10⁸ N • m^-2 is required for breaking a material. If the density of the material is 3 x 10³ kg • m^-3, then what should be the length of the wire made of this material, so that it breaks due its own weight? [g = 9.8 m • s^-2]
Solution:

A force of 10⁸ N • m^-2 is required for breaking a material. If the density of the material is 3 x 10³ kg • m^-3

Let L be the length of the wire which will break under its own weight.

If a is the cross section and ρ is the density of the material of the wire, then, breaking weight = a x L x ρ x g

= a x L x 3 x 10³ x 9.8 ………(1)

(Here ρ = 3 x 10³ kg • m^-3 ; g = 9.8m•s^-2]

Also, breaking stress = 10⁶ N • m^-2

Therefore, breaking weight = 10⁶ x a ……(2)

From equations (1) and (2) we have,

a x L x 3 x 10³ x 9.8 = 10⁶ x a

or, L = \(\frac{10^6}{3 \times 10^3 \times 9.8} \approx 34 \mathrm{~m}\)

Example 11. A cupper wire of negligible mass of length 1 m and cross sectional area 10^-6 m² is kept on a smooth horizontal table with one end fixed. A ball of mass 1 kg is attached to the other end. The wire and the ball are revolving with an angular velocity of 20 rad • s^-1. If the elongation in the length of the wire is 10^-3 m, obtain the Young’s modulus. If on increasing the angular velocity to 100 rad • s^-1 the wire breaks down, obtain the breaking stress.
Solution:

A cupper wire of negligible mass of length 1 m and cross sectional area 10^-6 m² is kept on a smooth horizontal table with one end fixed. A ball of mass 1 kg is attached to the other end. The wire and the ball are revolving with an angular velocity of 20 rad • s^-1. If the elongation in the length of the wire is 10^-3 m

The stretching force developed in the wire due to the revolution of the ball is,

F = \(\frac{m v^2}{r}=m r \omega^2=1 \times 1 \times(20)^2=400 \mathrm{~N}\)

Stress in the wire = \(\frac{F}{A}=\frac{400}{10^{-6}}=4 \times 10^8 \mathrm{~N} \cdot \mathrm{m}^{-2}\)

Strain in the wire = \(\frac{10^{-3}}{1}=10^{-3}\)

∴ Young’s modulus = \(\frac{\text { stress }}{\text { strain }}=\frac{4 \times 10^8}{10^{-3}}=4 \times 10^{11} \mathrm{~N} \cdot \mathrm{m}^{-2}\)

If the breaking angular velocity be \(\omega_0\) then breaking stress

= \(\frac{m r \omega_0^2}{A}=\frac{1 \times 1 \times(100)^2}{10^{-6}}=1 \times 10^{10} \mathrm{~N} \cdot \mathrm{m}^{-2}\)

Example 12. A steel cable with a radius of 1.5 cm supports a chair-lift at a ski area. If the maximum stress does not exceed 10⁸ N • m^-2, what is the maximum load that the cable can support?
Solution:

A steel cable with a radius of 1.5 cm supports a chair-lift at a ski area. If the maximum stress does not exceed 10⁸ N • m^-2

The breaking stress is 10⁸ N • m^-2.

Therefore, the breaking load = breaking stress x cross-sectional area

= 10⁸ x [3.14 x (1.5 x 10^-2)²] = 7.065 x 10⁴ N

Relations among the Elastic Constants: Relations among Young’s modulus (Y), bulk modulus (K) , modulus of rigidity (n), and Poisson’s ratio (σ) are shown below.

These relations show that any two of the four quantities are independent. If the values of any two quantities are known, then the other two can be found out.