Hydrostatic Pressure: Definition, Equation and Calculations

Hydrostatics Pressure

Pressure Definition: The force acting normally on unit area of a surface is called pressure.

Let the force or thrust acting normally on an area A be F. Therefore, pressure,

p = \(\frac{\text { normal force }}{\text { area }}=\frac{F}{A}\)

Examples:

1. The area of the cross-section of the pointed edge of a nail is very small. When its head is hammered, due to a large force exerted on the small area of its point, the pressure is high and the nail enters the surface easily.
2. The area of the cross-section of the sharpened edge of a knife is small. So when a force is applied on the blade, it cuts through easily because of the large pressure developed.
3. When a person stands on his feet, the contact area with the ground becomes less than that when he lies down. That is why when a person stands on soft clay or sand, his feet sink into the surface.

Read and Learn More: Class 11 Physics Notes

Pressure and Thrust of a Liquid: When a liquid is kept in a container, it exerts a force on the bottom and on the walls of the container.

• This force acts normally at every point of contact in the container. From our experience, we know that if there is a hole in the wall of a container of water, the water comes out of the hole at a high speed.
• If we try to block the flow of water with a finger, we feel the pressure. So, we can infer that water exerts pressure on the walls of the container.

Pressure of a liquid: The pressure at a point inside a liquid is defined as the normal force exerted by the liquid on a unit area surrounding the point.

Sometimes, liquid pressure is also called hydrostatic pressure, if the liquid is at rest and no pressure is developed due to its motion.

Let F be the normal force exerted by a liquid on a surface area A surrounding a point inside a liquid. The pressure p at that point is

p = F/A or, F = pA

Thrust of a liquid: The normal force exerted by a liquid on any surface in contact with it is called the thrust of the liquid.

Thrust (F) = pressure (p) x area (A)

Thrust is a force and hence it is a vector quantity. But pressure is a scalar quantity. The direction of thrust \(\vec{F}\) is defined as the direction of the area vector \(\vec{A}\), where A is a plane surface i.e., \(\vec{F}\) = p\(\vec{A}\).

Dimension of pressure: \([p]=\frac{[F]}{[A]}=\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^2}=\mathrm{ML}^{-1} \mathrm{~T}^{-2} .\)

Dimension of thrust: As thrust and force are the same physical quantity, the dimension of thrust is MLT^-2 .

Units of pressure and thurst

Absolute unit

Pressure:

• dyn • cm^-2 CGS System
• N · m^-2 or pascal(pa) SI

Thurst:

• dyn
• N

Relation: 1N = 10⁵ dyn

⇒ \(1 \mathrm{~N} \cdot \mathrm{m}^{-2}\)

or, \(1 \mathrm{~Pa}=\frac{1 \mathrm{~N}}{1 \mathrm{~m}^2}\)

= \(\frac{10^5 \mathrm{dyn}}{10^4 \mathrm{~cm}^2}\)

= \(10 \mathrm{dyn} \cdot \mathrm{cm}^{-2}\)

The magnitude of pressure at a point within a Liquid: Let us consider a liquid of density ρ kept in a vessel. We have to determine the pressure exerted by the liquid at a point C at a depth h below the surface of the liquid. Let us imagine a vertical cylinder of small horizontal area A surrounding the point C inside the liquid. The weight of the liquid column inside the cylinder is the thrust or normal force applied on the area A.

Now, weight of the liquid column

= mass of the liquid column x g

= volume of the liquid column x density of the liquid column x g = Ah x ρ x g

∴ Thrust exerted on the area A, F = Ahρg

∴ Pressure exerted by the liquid at the point C,

p = \(\frac{F}{A}=\frac{A h \rho g}{A}=h \rho g\) …….(1)

∴ The pressure exerted by the liquid = depth x density x acceleration due to gravity

So, at a particular place (where g is a constant), the pressure at a point in a liquid is

1. directly proportional to the depth of the point when the density of the liquid is a constant (p ∝ h) and
2. directly proportional to the density of the liquid when the depth is kept constant (p ∝ ρ).

If the surface of the liquid is exposed to air, then the atmospheric pressure also acts on the surface of the liquid If the atmospheric pressure is R, then the net pressure at a point inside the liquid is given by

p = B+ hρg ………(2)

Sometimes, pressure is expressed in terms of the height of a liquid column. The pressure exerted by a liquid of height h is hρg.

So, ‘atmospheric pressure is 76 cm of mercury’ means that in the CGS system, it is equal to a pressure of 76 x 13.6 x 980 = 1.013 x 10⁶ dyn · cm^-2.

Pressure at a Point in a Liquid at Rest

Experiment: A glass funnel (F) is taken whose mouth has been closed with a stretched rubber sheet. It is connected by means of a rubber tube (R) to a glass tube of Fine bore (T). The glass tube is kept horizontal with a scale (S) attached to it.

• A drop of a coloured liquid (l) is j introduced in the tube and it serves as an index. VY’ hence the rubber sheet is pressed, the air inside the tube gets compressed and pushes the index towards right. From the movement of the drop, we can study the variation of pressure on the rubber sheet.
• If the funnel is introduced in a liquid kept in a vessel and is gradually immersed, it will be seen that the index (l) gradually moves towards right. As the funnel is submerged deeper into the liquid, the index moves more towards right. This proves that with the increase in depth within the liquid, the pressure of the liquid increases.

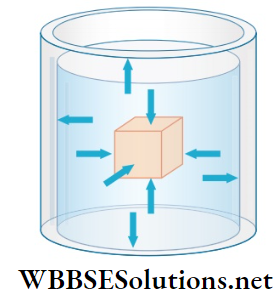
Now, keeping the funnel fixed at a particular depth below the liquid surface, if its mouth is turned in diluent directions, the index remains stationary. It indicates that at a point inside a liquid, the pressure exerted by the liquid is equal in all directions.

If the funnel is now moved to different points at the same horizontal level, the position of

the index will still remain stationary. From this, it may be concluded that the pressure exerted by a liquid at different points at the same depth is equal.

From this experiment, we can infer that the characteristics of pressure exerted by a liquid at rest are:

1. A liquid exerts pressure at a point inside it equally in all directions.
2. The pressure exerted at different points on the same horizontal plane inside it is the same.
3. The pressure exerted by a liquid at a point inside it increases with the increase in its depth.

Action of a small hole on the wall of a container: Let a small hole be made on the wall at a depth h of a vessel containing a liquid. We know that for a liquid of density ρ, pressure at a depth h of the liquid is hρg.

So, the lateral pressure exerted by the liquid on the mouth of the hole = hρg.

Due to this lateral pressure, the liquid comes out through the hole. Naturally, with the ejection of liquid through the hole, the level of water goes down in the container and hence the lateral pressure exerted by the liquid gradually decreases. For this reason, the rate of flow of the liquid through the hole also decreases gradually.

Nature Of The Free Surface Of A Liquid At Rest:

1. The free surface of a liquid at rest always remains horizontal.

Take a container with some liquid at rest. Let us assume that the free surface of the liquid is not horizontal but way. Two points A and B are taken on the same horizontal plane inside the liquid, which are at depths h₁ and h₂ respectively from the free surface of the liquid.

If the density of the liquid is p then, pressure of the liquid at the point A = h₁ρg and pressure of the liquid at the point B = h₂ρg.

We know that, at all points on the same horizontal plane inside a liquid at rest, the pressure exerted by the liquid is the same.

So, liquid pressure at the point A = liquid pressure at the point B

or, h₁ρg = h₂ρg or, h₁ = h₂, i.e., h₁ and h₂ cannot be unequal. Since A and B lie on the same horizontal plane and h₁ is equal to h₂, the free surface of a liquid at rest always remains horizontal.

2. The free surfaces of a liquid at rest in connected vessels always remain on the same horizontal plane: A system of connected vessels of different shapes is taken and a liquid is poured into it. Though the shapes and volumes of the vessels are different, it is seen that the liquid rises up to the same horizontal level in all the vessels.

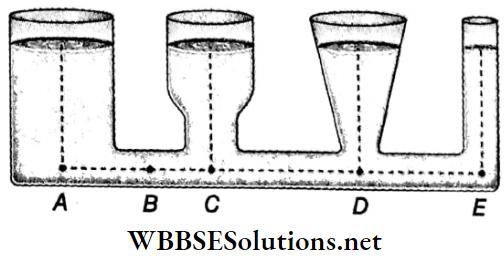
Let us consider a horizontal plane passing through the common interconnecting tube of the system. We know that at different points (for example, A, B, C, D, E) on that horizontal plane, the pressure exerted by the liquid is the same.

Since the liquid pressure at a point depends on the depth of that point from the free surface of the liquid, we can say that the free surfaces of the liquid in the vessels must remain on the same horizontal plane. Hence, a liquid seeks its own level— which is regarded as a general property of a liquid.

If the diameters of the different vessels become very small (2 mm or less that), then due to the surface tension of the liquid, it rises to different heights in different vessels. In that case, the free surfaces of the liquid in different vessels will not remain on the same horizontal plane.

Equilibrium Of Two Different Liquids In A U-Tube: When two immiscible liquids are poured into the two limbs of a U-tube, it is found that the free surfaces of the liquids in the two limbs remain horizontal, but they attain different heights.

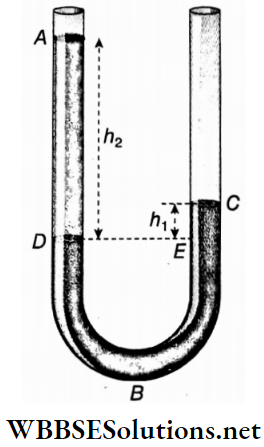
Let ADBEC be a U-tube made of glass. Into one of the limbs (say, the right one), mercury is poured and it is seen that mercury enters the other limb and rises up to the same horizontal level in the two limbs.

Now, another liquid lighter than mercury is poured into the left limb of the U-tube and it is observed that the mercury level falls in this limb and rises in the other limb through the same height.

In equilibrium, the interface of the liquids in the left arm is at D, the free surface of the liquid is at A and that of mercury is at C. In equilibrium, at the same horizontal level DE, liquid pressure at the point D = mercury pressure at the point E.

Now, the pressure at the point D = h₂ρ₂g

[AD = h₂ , density of the liquid = ρ₂, acceleration due to gravity = g]

and pressure at the point E = h₁ρ₁g[CE = h₁, density of mercury = ρ₁]

∴ \(h_2 \rho_2 g=h_1 \rho_1 g \text { or, } \frac{h_1}{h_2}=\frac{\rho_2}{\rho_1}\) ……(1)

Therefore, in equilibrium, the height of the liquid column from the level of the interface is inversely proportional to the respective density.

If the density of one liquid is known, then with the help of equation (1), the density of the other liquid can also be found out.

Lateral Thrust On A Surface Immersed Vertically In A Liquid: Consider a horizontal surface in a liquid at rest. At every point on that surface, the pressure exerted by the liquid will be the same and the pressure multiplied by the area of the immersed surface gives the total thrust.

• But if the surface is placed in a vertical or an inclined position inside the liquid, then different points of the surface will lie at different depths and hence the pressure will vary from point to point.
• In this case, the average pressure exerted on the surface is calculated. The total thrust acting on the surface can be obtained by multiplying the average pressure with the area of the surface.

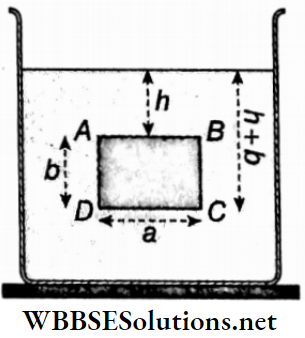
Let the length and breadth of a rectangular surface ABCD, immersed vertically inside a liquid of density p, be a and b respectively.

Let us assume that the depth of the side AB from the free surface of the liquid is h.

∴ Depth of the side CD = (h+ b).

∴ Pressure at any point on the side AB = hρg and that at any point on the side CD = (h+ b)ρg.

∴ Average pressure on the surface ABCD

= \(\frac{h \rho g+(h+b) \rho g}{2}=\frac{2 h \rho g+b \rho g}{2}\)

= \(h \rho g+\frac{1}{2} b \rho g=\left(h+\frac{b}{2}\right) \rho\)

So, the lateral thrust on the surface ABCD

= average pressure x area = \(\left(h+\frac{b}{2}\right) \rho g \times a b\)

Unit 7 Properties Of Bulk Matter Chapter 2 Hydrostatics Pressure Numerical Examples

Example 1. Calculate the pressure at the bottom of a freshwater lake of depth 10 m. The atmospheric pressure = 76 cm of mercury and the density of mercury = 13.6 g · cm^-3.
Solution:

Pressure at the bottom of the lake = atmospheric pressure + pressure exerted by a 10 m water column

= 76 x 13.6 x 980 + 10 x 100 x 1 x 980

= 980(76 x 13.6 + 1000)

= 980 x 2033.6 = 1.993 x 10  dyn ·cm^-2.

Example 2. The length of a right circular cylinder filled with water is 4 m and its diameter is 1 m. At first, it is held upright on its base, and then is positioned laterally. Find the ratio of the thrusts exerted on its circular base in the above two cases.
Solution:

The length of a right circular cylinder filled with water is 4 m and its diameter is 1 m. At first, it is held upright on its base, and then is positioned laterally.

When the cylinder is held upright, the thrust exerted on its circular base,

⇒ \(F_1=\text { pressure } \times \text { area }=4 \times 1000 \times 9.8 \times \pi\left(\frac{1}{2}\right)^2 \mathrm{~N}\)

When the cylinder is kept laterally, the thrust exerted on its circular base,

F₂ = average pressure x area

= \(\frac{1}{2} \times 1000 \times 9.8 \times \pi\left(\frac{1}{2}\right)^2 \mathrm{~N}\)

∴ \(\frac{F_1}{F_2}=\frac{4 \times 1000 \times 9.8 \times \pi\left(\frac{1}{2}\right)^2}{\frac{1}{2} \times 1000 \times 9.8 \times \pi\left(\frac{1}{2}\right)^2}\)

∴ \(F_1: F_2=8: 1\)

Example 3. A hollow right circular cone of height h and of semi-vertical angle θ is placed with its base on a horizontal table. If the cone is filled with a liquid of density ρ and the weight of the empty cone is equal to the weight of the liquid that it contains, find the thrust of the liquid on the base of the cone and the pressure exerted on the table.
Solution:

A hollow right circular cone of height h and of semi-vertical angle θ is placed with its base on a horizontal table. If the cone is filled with a liquid of density ρ and the weight of the empty cone is equal to the weight of the liquid that it contains

According to Fig, r = h tan θ = radius of the circular base of the cone.

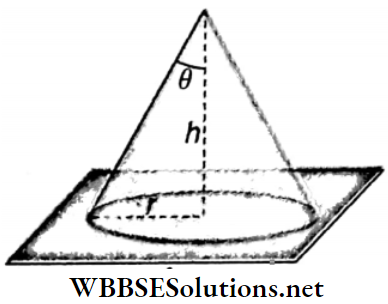
Volume of the cone, V = \(\frac{1}{3} \pi r^2 h\)

Mass of the liquid inside the cone, M = \(\frac{1}{3} \pi \rho r^2 h\)

Liquid pressure on the base of the cone = \(h \rho g\)

∴ Thrust exerted by the liquid on the base of the cone

= pressure x area = \(h \rho g \times \pi r^2=\pi \rho g h^3 \tan ^2 \theta\)

Again, mass of the empty cone = M = \(\frac{1}{3} \pi \rho r^2 h\)

∴ Total force exerted on the table = weight of the cone + weight of the liquid

= \(\frac{1}{3} \pi \rho r^2 h \cdot g+\frac{1}{3} \pi \rho r^2 h \cdot g=\frac{2}{3} \pi \rho g r^2 h\)

∴ Pressure on the table = \(\frac{\text { force }}{\text { area }}=\frac{\frac{2}{3} \pi \rho g r^2 h}{\pi r^2}=\frac{2}{3} h \rho g\).

Example 4. The lock gate of a canal is 4.8 m broad. The depth of water on one side of the lockgate is 4.5 m and on the other side is 3 m. Calculate the total thrust on the lock gate. The density of water = 1000 kg · m³.
Solution:

The lock gate of a canal is 4.8 m broad. The depth of water on one side of the lockgate is 4.5 m and on the other side is 3 m.

Thrust exerted by the water column of depth 4.5 m on one side of the lock gate

= 1/2 x 4.5 x 1000 x (4.5 x 4.8) xg = 48600 kg x g

Thrust exerted by the water column of depth 3 m on the other side of the lock gate

= 1/2 x 3 x 1000 x (3 x 4.8) xg = 21600 kg x g

Since, these two thrusts are mutually opposite in direction, the net thrust on the lockgate

= (48600-21600) xg = 2.65 x 10⁵ N.

Example 5. An air bubble of diameter 1 mm is formed at the bottom of a lake and when it rises to the surface of the water, its diameter becomes 2 mm. If the atmospheric pressure is 76 cm of mercury, then find the depth of the lake. (Density of mercury = 13.6 g · cm^-3)
Solution:

An air bubble of diameter 1 mm is formed at the bottom of a lake and when it rises to the surface of the water, its diameter becomes 2 mm. If the atmospheric pressure is 76 cm of mercury

Pressure at the bottom of the lake = (76 x 13.6 x 980 + h x 1 x 980) dyn · cm^-2

[h = depth of the lake; p = atmospheric pressure =76 x 13.6 x 980 dyn · cm^-2]

Volume of the bubble at the bottom of the lake = 4/3π(0.05)³ cm³ and volume of the bubble at the surface of the lake = 4/3π(0.1)³ cm³.

If the temperature of the lake water is uniform, then pV = constant.

∴ \((76 \times 13.6+h) \times 980 \times \frac{4}{3} \pi(0.05)^3\)

= \(76 \times 13.6 \times 980 \times \frac{4}{3} \pi(0.1)^3\)

∴ h = 7235 cm = 72.35 m.

Example 6. A large container with a cylindrical mouth is filled with water and closed with a piston. A vertical tube is now inserted through the piston. The radius of the 1 tube is 5 cm, the radius of the piston is 10 cm and the mass of the piston is 20 kg. To what height will the water rise inside the tube?
Solution:

A large container with a cylindrical mouth is filled with water and closed with a piston. A vertical tube is now inserted through the piston. The radius of the 1 tube is 5 cm, the radius of the piston is 10 cm and the mass of the piston is 20 kg.

Area of the piston

= \(\pi\left(r_2^2-r_1^2\right)=\pi\left(10^2-5^2\right)=75 \pi \mathrm{cm}^2\).

Weight of the piston = 20 x 1000 x g dyn

Let the height of the water column in the tube be hem.

Now, pressure of the piston = pressure of the water column in the tube

or, \(\frac{20 \times 1000 \times g}{75 \pi}=h \times 1 \times g\)

∴h = \(\frac{20000}{75 \pi}=84.88 \mathrm{~cm}\)

Example 7. At what depth below the surface of a lake will the total pressure be twice the atmospheric pressure? (Atmospheric pressure = 76 cm Hg and the density of mercury = 13.6 g · cm^-3)
Solution:

If the required depth is h and the atmospheric pressure is p, then 2p = p + hρg

or, p = hρg or, 76 x 13.6 x g = h x 1 x g

∴ h = 76 x 13.6 = 1033.6 cm.

Example 8. A U-tube is partially filled with mercury. Kerosene oil is poured into one of its limbs and glycerine into the other. It is observed that, when the height of the kerosene oil becomes 20 cm and that of glycerine becomes 12.68 cm, the levels of the mercury column in the two limbs are at the same horizontal level If the density of kerosene oil is 0.8 g · cm^-3, then find that of glycerine.
Solution:

A U-tube is partially filled with mercury. Kerosene oil is poured into one of its limbs and glycerine into the other. It is observed that, when the height of the kerosene oil becomes 20 cm and that of glycerine becomes 12.68 cm, the levels of the mercury column in the two limbs are at the same horizontal level If the density of kerosene oil is 0.8 g · cm^-3

In the U-tube, mercury levels in the two limbs are at the same horizontal level.

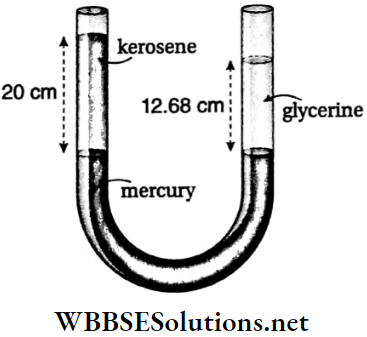
So, pressure exerted by 20 cm of kerosene oil = pressure exerted by 12.68 cm of glycerine. Let the density of glycerine be ρ.

∴ 20 x 0.8 x g = 12.68 x ρ x g

or, \(\rho=\frac{20 \times 0.8}{12.68}=1.26 \mathrm{~g} \cdot \mathrm{cm}^{-3}\)

Example 9. A vertical U-tube of uniform cross-section contains mercury. Through one of its limbs, some water is poured such that the mercury level in that limb goes down by 2 cm. What will be the height of the water column?
Solution:

A vertical U-tube of uniform cross-section contains mercury. Through one of its limbs, some water is poured such that the mercury level in that limb goes down by 2 cm.

Let the height of the water column be h. If the mercury level falls down by 2 cm in one limb, then it will rise by 2 cm in the other limb.

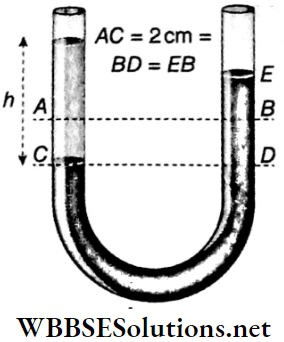
From fig, AC = 2cm, BE = 2cm

∴ DE = 2 + 2 = 4 cm

Now, pressure at the point C = pressure at the point D

∴ h x l x g = 4 x 13.6 x g or, h = 54.4 cm

Example 10. The cross-sections of the two limbs of a U-tube are 3 cm² and 1 cm² respectively. Keeping the tube vertical, some mercury is poured into it. Now 60 cm³ of water is poured into the wider limb. To what height will the mercury rise in the narrow limb? The density of mercury = 13.6 g · cm^-3.
Solution:

The cross-sections of the two limbs of a U-tube are 3 cm² and 1 cm² respectively. Keeping the tube vertical, some mercury is poured into it. Now 60 cm³ of water is poured into the wider limb.

In Fig, we can see the final state after water is poured. The mercury column in the wider limb will fall and that in the narrow limb will rise.

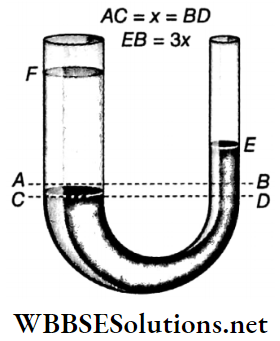
The height of the water column in the wider limb

= \(\frac{\text { volume of water }}{\text { area of cross-section of the wider limb }}=\frac{60}{3}=20 \mathrm{~cm}\)

∴ FC = 20 cm

After water is poured into the wider limb, suppose the mercury column Tails by x. So, mercury will rise through 3x in the narrower limb (v the area of the cross-section of the wider limb is 3 times that of tire narrower limb).

∴ AC = x and BE = 3x

∴ DE = x+3x = 4x

Now, pressure at the point C = pressure at tire point D

or, 20 x 1 x g = 4x x 13.6 x g

or, x = \(\frac{20}{4 \times 13.6}=0.368 \mathrm{~cm}\)

∴ The mercury column will rise through 0.368 x 3 = 1.1 cm in the narrower limb.

Example 11. One of the two limbs of a U-tube of uniform bore is closed by means of a cork. Some water and paraffin oil are in the tube. Water level in the open tube is 2 cm higher than that in the closed tube and a 10 cm column of paraffin is above it. If the cork is removed, then by what height will the level of water in the closed limb rise or fall? (Density of paraffin = 0.8 g · cm^-3)
Solution:

One of the two limbs of a U-tube of uniform bore is closed by means of a cork. Some water and paraffin oil are in the tube. Water level in the open tube is 2 cm higher than that in the closed tube and a 10 cm column of paraffin is above it.

Let us assume that, when the cork is removed, the water level below the oil column will fall by h with respect to the level of water in the other limb.

Now,pressure at D = pressure at A’

or, h x 1 x g = 10 x 0.8 x g or, h = 8 cm .

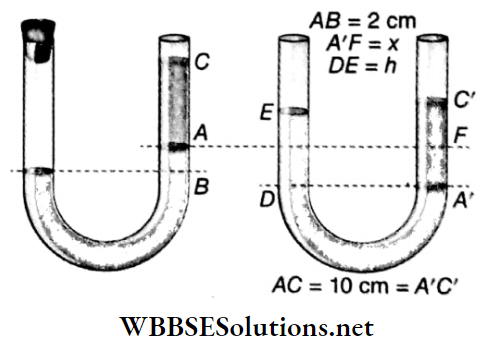
Here, the cross-section of the U-tube is uniform. So, if the height of the water column falls through x cm in one limb, the difference in the level of water in the two limbs will increase by 2x cm.

So, the initial difference in the levels of water = -2 cm, and the final difference = + 8 cm.

∴ 2x = 8-(-2) = 10

∴ x = 5 cm

So, when the cork is removed, the height of the water column
will rise by 5 cm in that limb.

Example 12. A vertical U-tube of uniform cross-section contains mercury in both Its arms. A glycerine (density 1.3 g · cm^-3) column of height 10 cm is introduced into one of the arms. Oil of density 0.8 g · cm^-3 is poured into the other arm until the upper surfaces of oil and glycerine are at the same level. Find the height of the oil column. The density of mercury is 13.6 g · cm^-3.
Solution:

A vertical U-tube of uniform cross-section contains mercury in both Its arms. A glycerine (density 1.3 g · cm^-3) column of height 10 cm is introduced into one of the arms. Oil of density 0.8 g · cm^-3 is poured into the other arm until the upper surfaces of oil and glycerine are at the same level.

Let the height of the oil column be h

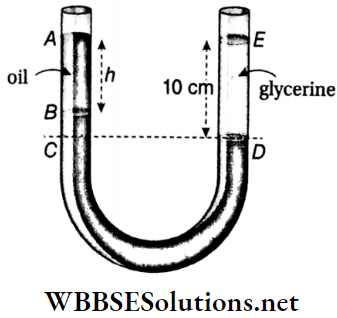
According to the figure, AC = ED

or, h + BC = 10

or, BC = (10 – h) cm

Now,pressure at the point C = pressure at the point D

or, h x 0.8 x g + (10 – h) x 13.6 x g =10 x 1.3 x g

or, h x 0.8 + 136 – 13.6h = 13 or, 12.8 h = 123

or, h =\(\frac{123}{12.8}=9.61 \mathrm{~cm}\)

Example 13. The cross-sections of the two sides of a U-tube are 1 cm² and 0.1 cm² respectively. Some water is poured inside the tube when it rises to the same height in both the limbs. What volume of a liquid of density 0.85 g · cm^-3 should be poured into the wider limb so that the water level rises by 15 cm in the narrow limb?
Solution:

The cross-sections of the two sides of a U-tube are 1 cm² and 0.1 cm² respectively. Some water is poured inside the tube when it rises to the same height in both the limbs.

At first, water rises up to the same level in both the arms. When the liquid is poured into the wider limb, sup¬pose the level of waterfalls by x cm and rises by 15 cm in the narrow limb.

AC = BF = x

volume of the part AC = volume of the part BD

or, x x 1 = 15×0.1 or, x = 1.5 cm

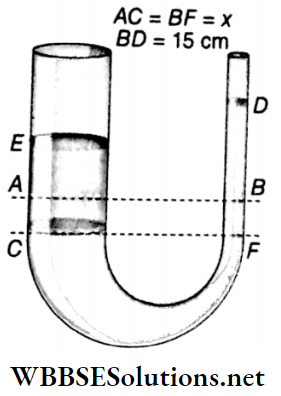
Let EC = h.

Pressure at the point C = pressure at the point F

or, h x 0.85 x g = (15 + 1.5) x 1 x g

or, h = \(\frac{16.5}{0.85}\) = 19.41 cm

So, the volume of liquid poured into the wider limb = 19.41 x 1 = 19.41 cm³.

Example 14. The cross-sectional area of the left limb of a U-tube is one-third of that of its right limb. It contains some mercury. The empty space in the left limb measures to 40 cm. If water is poured to fill it up, then find the rise of the mercury column in the right limb. (Specific gravity of mercury = 13.6)
Solution:

The cross-sectional area of the left limb of a U-tube is one-third of that of its right limb. It contains some mercury. The empty space in the left limb measures to 40 cm.

At first, the mercury is at the same level in both the limbs. When water is poured, suppose the fall in the mercury level in the narrow limb is x and the corresponding rise in the mercury level in the wider limb is y.

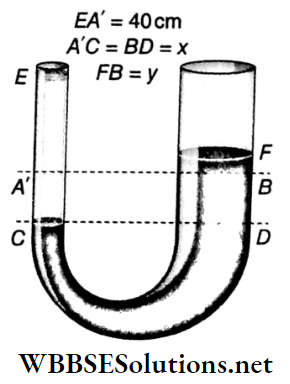
If the cross-sectional area of the narrow limb is A, then, according to the problem, the cross-sectional area of the wider limb will be 3A.

From Fig. 2.14, we see,

volume of the part A’ C – volume of the part FB

or, x x A = y x 3A or, x = 3y

Now, pressure at point C = pressure at point D

or, EC x 1 x g = FD x 13.6 x g or, (40 + x) = (x + y) x 13.6

or, 40 + 3y= (3y+y)x 13.6

or, (13.6 x 4 – 3)y = 40

or, y = \(\frac{40}{54.4-3}=0.78 \mathrm{~cm} .\)

Example 15. A U-tube of uniform cross-section contains some mercury. If water is poured into one of the limbs up to a height of 13.4 cm, then find the rise in the mercury level in the other limb. The density of mercury = 13.4 g · cm^-3.
Solution:

A U-tube of uniform cross-section contains some mercury. If water is poured into one of the limbs up to a height of 13.4 cm

At first, the mercury will attain the same height in both the limbs. Now a column of water 13.4 cm high is poured into the left limb and, due to this, the mercury level falls through a depth of x cm from its initial position.

Since the cross-sectional areas of both the limbs are the same, the mercury level will rise through a height of x cm from its original position in the other limb.

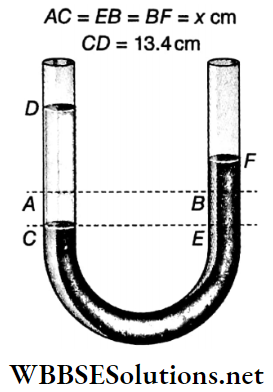
Now, pressure at point C = pressure at point E

or, 13.4 x 1 x g = 2JC X 13.4 xg or, x = 1/2 = 0.5 cm

The mercury level in the other limb will rise by 0.5 cm from its original position.

Example 16. Two cylindrical vessels of the same type contain a liquid of density ρ. The bases of both the vessels lie on the same horizontal plane. The depth of the liquid in the left vessel is h₁ and that in the right vessel is h₂. The area of the cross-section of the base of each vessel is A. If the vessels are connected by a tube, then how much is the work done by gravity to equalize the levels of the liquid in the vessels (suppose h₁ >h₂)?
Solution:

Two cylindrical vessels of the same type contain a liquid of density ρ. The bases of both the vessels lie on the same horizontal plane. The depth of the liquid in the left vessel is h₁ and that in the right vessel is h₂. The area of the cross-section of the base of each vessel is A.

When the vessels are connected, the level of the liquid in the left-hand vessel will fall, and that in the right-hand one will go up.

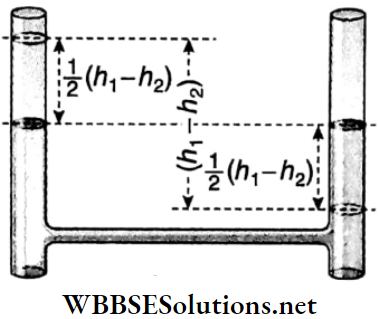
The initial difference in the liquid levels in the vessels = h₁-h₂. When the levels in both vessels become the same, the level of liquid in the left-hand vessel will fall by 1/2(h₁-h₂), and that in the right-hand vessel will rise by 1/2(h₁-h₂).

Mass of this liquid = 1/2(h₁-h₂)Aρ.

The centre of gravity of this liquid moves up against gravity by 1/2(h₁-h₂).

∴ Increase in potential energy of this liquid = work done against gravity

= \(\frac{1}{2}\left(h_1-h_2\right) A \rho \times g \times \frac{1}{2}\left(h_1-h_2\right)=\frac{1}{4} A \rho g\left(h_1-h_2\right)^2\).

Example 17. A tank closed tightly with a lid, is completely filled with water and is rigidly fixed on a car. The car moves with a constant acceleration of 20 cm · s^-2. Determine the pressure at a point 10 cm below the lid and at a distance of 10 cm from the front wall of the tank.
Solution:

A tank closed tightly with a lid, is completely filled with water and is rigidly fixed on a car. The car moves with a constant acceleration of 20 cm · s^-2.

Let us consider a vertical disc of unit area kept at a depth h from the upper surface of the tank. The disc is at a distance x from the front wall of the car and its width is dx. Let the pressures at distances x and (x + dx) be p and (p+dp) respectively.

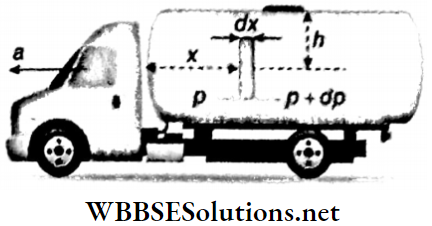
∴ p + dp – p = p – dx- a

[ρ = density of the liquid, ρdx = mass of the liquid displaced by the disc, and a = acceleration of the car]

or, dp = aρdx

∴ ∫dp = ap ∫dx

or, p = aρx+ c [c = integration constant]

Now, if x = 0, then p = hρg.

∴ hρg = c

∴ p = aρx+ hρg = ρ(ax+ hg)

∴ The pressure at a point 10 cm below the lid and at a distance of 10 cm from the front wall of the tank,

p = 1(20 x 10 + 10×980) =200 + 9800

= 10000 dyn · cm^-2.