Gravitation Multiple Choice Question And Answers

Gravitation

Question 1. The acceleration due to gravity at a height of 1 km above the earth’s surface is the same as that at a depth d below the surface of the earth. The,

1. d =1 km
2. d = 1.5 km
3. d = 0.5 km
4. d = 2 km

Answer: 4. d = 2km

The value of g at a height h (= 1 km) is

⇒ \(\frac{g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}=g\left(1+\frac{h}{R_{\mathrm{E}}}\right)^{-2} \approx g\left(1-\frac{2 h}{R_{\mathrm{E}}}\right)\) […h << RE]

At a depth d, \(g^{\prime}=g\left(1-\frac{d}{R_{\mathrm{E}}}\right)\)

Given that \(g\left(1-\frac{2 \times 1 \mathrm{~km}}{R_{\mathrm{E}}}\right)=g\left(1-\frac{d}{R_{\mathrm{E}}}\right)\)

∴ d = 2 km

Question 2. Starting from the centre of the earth (having the radius RE) the variation of g (acceleration due to gravity) is represented by

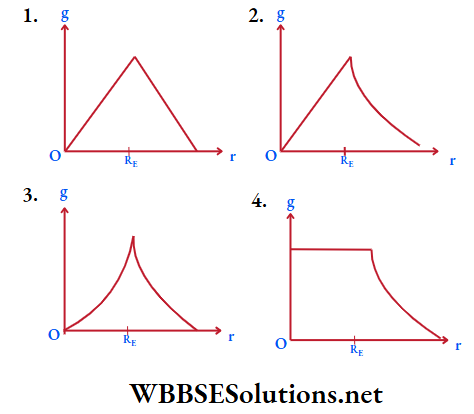
Answer: 2.

At the centre of the earth, g = 0. The value of g increases linearly as we move radially towards the surface, and then moving away from the earth, g decreases nonlinearly. The figure given in the option (b) shows the correct variation.

Question 3. The height h at which the weight of a body becomes (1/16)th of its weight on the surface of the earth (radius = RE) is

1. h = R_E
2. h = 2R_E
3. h = 3R_E
4. h = 4R_E

Answer: 3. h = 3R_E

The weight w’ at a height h is \(\frac{m g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}\)

Given that w’ = \(\frac{w}{16}\)

∴ \(\frac{m g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}=\frac{m g}{16} \Rightarrow h=3 R_{\mathrm{E}}\)

Question 4. The force between a hollow sphere and a point mass at P inside it, as shown in the adjoining figure, is

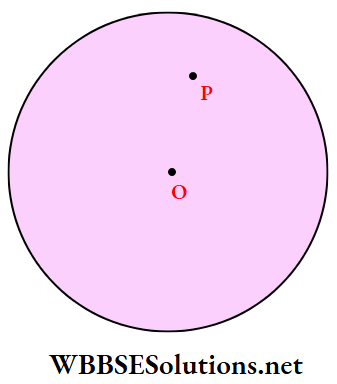
1. Attractive and constant
2. Attractive but depends on the separation of the PO
3. Zero
4. Repulsive and constant

Answer: 3. Zero

The gravitational field in the cavity of a spherical shell is zero, so the force on the mass m inside is zero.

Question 5. If the mass of the earth is 80 times that of the moon and the radius of the earth is 4 times that of the moon, the ratio gM-gE will be

1. 1:1
2. 1:2
3. 1:3
4. 1:5

Answer: 4. 1:5

The value of g at the surface of a planet is \(\frac{G M}{R^2}\)

∴ \(\frac{g_{\mathrm{M}}}{g_{\mathrm{E}}}=\frac{\mathrm{M}_{\mathrm{M}}}{M_{\mathrm{E}}} \times \frac{R_{\mathrm{E}}^2}{R_{\mathrm{M}}^2}\)

=\(\frac{\mathrm{M}_{\mathrm{M}}}{80 \mathrm{M}_{\mathrm{M}}} \times \frac{16 R_{\mathrm{M}}^2}{R_{\mathrm{M}}^2}\)

= \(\frac{1}{5}\)

= 1: 5

Question 6. The value of g at a given point on the earth is 9.8 m s^-2. Let the earth suddenly shrink uniformly to half its present size without any loss of mass. The value of g at the same point (assuming that the distance of the given point from the centre of the earth remains unchanged) will now be

1. 4.9 ms^-2
2. 9.8 ms^-2
3. 3.3 m s^-2
4. 19.6 ms^-2

Answer: 2. 9.8 ms^-2

The gravitational field and the potential point external to the aspherical body remain the same as if its total mass is at the centre. Hence, the shrinkage will not change g and its value remains unchanged at 9.8 m s^-2

Question 7. If the radius of the earth were to shrink by 1%, its mass remaining the same, the acceleration due to gravity on the earth’s surface would

1. Increase by 1%
2. Increase by 2%
3. Decrease by 2%
4. Decrease by 1%

Answer: 2. Increase by 2%

∴ \(g=\frac{G M_{\mathrm{E}}}{R_{\mathrm{F}}^2}=G M_{\mathrm{E}} R_{\mathrm{E}}^{-2}\)

∴ \(\frac{d g}{g}=-2\left(\frac{d R_{\mathrm{E}}}{R_{\mathrm{E}}}\right)=-2(-1 \%)\)

= 2%

Thus, g increases by 2%.

Question 8. If the value of g at a height h above the earth’s surface is the same as that at a depth x below it then (assuming h << R_E and X << R_E)

1. x = h
2. x = 2h
3. x = \(\frac{h}{2}\)
4. x = 4h

Answer: 2. x = 2h

Given that,

⇒ \(\frac{g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}=g\left(1-\frac{x}{R_{\mathrm{E}}}\right)\)

∴ \(g\left(1+\frac{h}{R_{\mathrm{E}}}\right)^{-2}=g\left(1-\frac{x}{R_{\mathrm{E}}}\right)\)

⇒ \(\left(1-\frac{2 h}{R_{\mathrm{E}}}\right)=\left(1-\frac{x}{R_{\mathrm{E}}}\right)\)

x = 2h.

Question 9. If the angular speed co of the earth is doubled, the value of the acceleration due to gravity at the north pole

1. Is doubled
2. Is halved
3. Remains the same
4. Becomes zero

Answer: 3. Remains the same

The value of g’ at a place where the latitude is y, is given by

⇒ \(g^{\prime}=g-\omega^2 R_E \cos ^2 \lambda\)

At the poles, y = 90°.

So, g’ =g.

Hence, g’ remains unaffected.

Question 10. The escape velocity of an object from the Earth is about 11 km s^-1. Assuming the mass of the earth to be about 81 times the mass of the moon and the radius of the earth to be 4 times the radius of the moon, the escape velocity from the surface of the moon will be

1. 0.54 km s^-1
2. 2.44 km s^-1
3. 11 km s^-1
4. 49.5 km s^-1

Answer: 2. 2.44 km s^-1

Escape velocity,

⇒ \(v_{\mathrm{e}}=\sqrt{2 g R_{\mathrm{E}}}=\sqrt{\frac{2 \mathrm{GM}}{R_{\mathrm{E}}}}\)

∴ \(\frac{v_e}{v_m}=\sqrt{\frac{M_e}{M_m} \times \frac{R_m}{R_e}}\)

=\(\sqrt{81 \times \frac{1}{4}}\)

=\(\frac{9}{2}\)

∴ the escape velocity from the moon is

⇒ \(v_{\mathrm{m}}=\frac{2}{9} v_{\mathrm{e}}\)

=\(\frac{2}{9} \times 11 \mathrm{~km} \mathrm{~s}^{-1}\)

=\(2.44 \mathrm{~km} \mathrm{~s}^{-1}\)

Question 11. The given figure shows the motion of a planet around the sun in an elliptical orbit with the sun(S) at the focus. The shaded areas A and B shown in the figure can be assumed to be equal. If t₁ and t₂ represent the time intervals taken by the planet to move from a to b and c to d respectively then

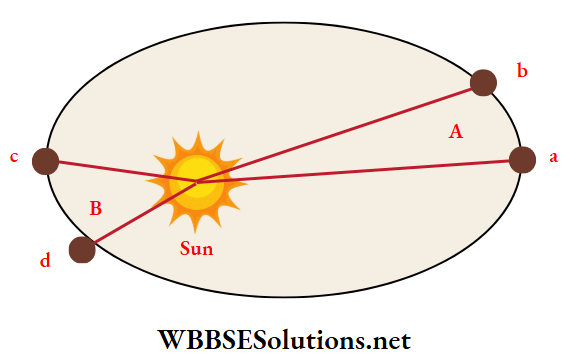
1. t₁ > t₂
2. t₁ < t₂
3. t₁ = t₂
4. t₁ = 2t₂

Answer: 3. t₁ = t₂

According to Kepler’s second law, the areal velocity \(\left(\frac{\Delta A}{\Delta t}\right)\)of a planet around the sun remains constant.

So,

⇒ \(\frac{A}{t_1}=\frac{B}{t_2} \Rightarrow \frac{\Delta \mathrm{Sab}}{t_1}=\frac{\Delta \mathrm{Scd}}{t_2}\)

t₁ = t₂ Since the shaded areas are equal

Question 12. Which of the following graphs is a consequence of the orbital motion of a planet moving around the sun, where T = time of revolution and r = radius of the orbit?

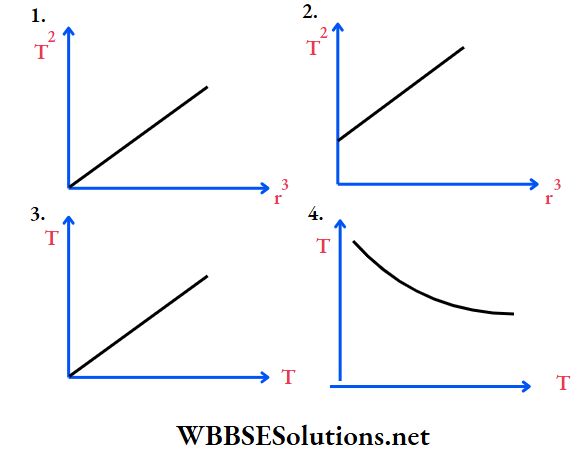
Answer: 1.

According to Kepler’s third law, T₂ α r₃ the T₂-r₃ graph must be a straight line passing through the origin.

Question 13. If an orbiting satellite suddenly comes to rest in its orbit then the satellite will

1. Fly off tangentially
2. Move radially towards the centre of the earth
3. Escape to outer space
4. Continue to move in the same orbit

Answer: 2. Move radially towards the centre of the earth

When the satellite suddenly comes to rest in its orbit, the earth’s attraction continues to exist. So, it will move radially towards the earth’s centre.

Question 14. The mean distance of Jupiter from the sun is nearly 5.2 times the corresponding earth-sun distance. Jupiter’s year in its orbit will be n times the earth’s year, where n is

1. 5
2. 7.5
3. 12
4. 25

Answer: 3. 12

According to Kepler’s third law, T²

So,

⇒ \(\frac{T_{\mathrm{J}}^2}{T_{\mathrm{E}}^2}=\left(\frac{5.2 r}{r}\right)^3 \Rightarrow \frac{T_{\mathrm{J}}}{T_{\mathrm{E}}}=(5.2)^{3 / 2}\)

T_J = 5.2√5.2(1 y)

= 11.8 y ≈ 12 y.

Question 15. The orbital speed of a body orbiting close to the surface of the Earth is approximately

1. 8 km s^-1
2. 11.2 km s^-1
3. 3 x 10⁶ m s^-1
4. 2.2 km s^-1

Answer: 1. 8 km s^-1

Close to the surface of the earth, die centripetal force \(\left(\frac{m v^2}{R_{\mathrm{E}}}\right)\) is provided by the weight (mg).

So,

⇒ \(\frac{m v^2}{R_{\mathrm{E}}}=m g\)

⇒ \(v=\sqrt{g R_{\mathrm{E}}}\)

=\(\sqrt{\left(9.8 \mathrm{~m} \mathrm{~s}^{-2}\right)(6400 \mathrm{~km})}\)

⇒ \(\sqrt{9.8 \times 10^{-3} \times 6400 \mathrm{~km}^2 \mathrm{~s}^{-2}}\)

= 7.9 km s^-1 ≈ 8kms^-1.

Question 16. The orbital speed of an artificial satellite in a circular orbit just above the earth’s surface is v₂. For a satellite orbiting at an altitude of half the Earth’s radius, the orbital speed is

1. \(\frac{3}{2} v_0\)
2. \(\sqrt{\frac{3}{2}} v_0\)
3. \(\sqrt{\frac{2}{3}} v_0\)
4. \(\frac{2}{3} v_0\)

Answer: 3. \(\sqrt{\frac{2}{3}} v_0\)

The orbital speed dose to the earth’s surface is \(v_{\mathrm{o}}=\sqrt{g R_{\mathrm{E}}}\)

Ata height \(h=\frac{R_{\mathrm{E}}}{2}\), orbital speed = v.

∴ \(\frac{m v^2}{r}=\frac{G m M}{r^2}\)

⇒ \(v=\sqrt{\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+h}}=\sqrt{\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+\frac{R_{\mathrm{E}}}{2}}}\)

=\(\sqrt{\frac{2}{3} g R_{\mathrm{E}}}\)

=\(\sqrt{\frac{2}{3}} v_{\mathrm{o}}\)

Question 17. Two artificial satellites of masses m₁ and m₂ (where m₁ > m₂) are revolving around the earth in circular orbits of radii r₁ and r₂ (where r₁ > r₂) respectively. Which of the following statements is true regarding their speeds v₁ and v₂?

1. v₁ = v₂
2. v₁ > v₂
3. v₁< v₂
4. \(\frac{v_1}{r_1}=\frac{v_2}{r_2}\)

Answer: 3. v1< v2 Orbital speed = \(v=\sqrt{\frac{g R_{\mathrm{E}}^2}{r}}\) .. \(\frac{v_1}{v_2}=\sqrt{\frac{r_2}{r_1}}\)

Since r₁ > r₂, we have v₁ < v₂

Question 18. An artificial satellite in a circular orbit around the earth has a total (kinetic + potential) energy E₀. Its potential energy is

1. -E₀
2. \(\frac{3 E_0}{2}\)
3. 2E₀
4. E₀

Answer: 3. 2E₀

The potential energy and the kinetic energy in orbital motion are respectively given by

⇒ \(\mathrm{PE}=-\frac{\mathrm{GM} m}{r} \text { and } \mathrm{KE}=\frac{1}{2} m v^2=\frac{\mathrm{GMm}}{2 r}\)

∴ total energy = \(E_0=\mathrm{PE}+\mathrm{KE}=-\frac{G M m}{2 r}\)

∴ \(\mathrm{PE}=2\left(-\frac{G M m}{2 r}\right)=2 E_0\)

Question 19. If the speed of a satellite revolving around a planet is increased by 41.4%, it will

1. Orbit the planet with a greater radius
2. Orbit the planet with a lesser radius
3. Escape the gravitational pull of the planet
4. Fall into the planet

Answer: 3. Escape the gravitational pull of the planet

Let the initial speed be v₀ = √gR.

increased speed = v = \(v_0+\frac{41.4}{100} v_0\)

= 1.414v₀

= √2v₀

= √2gR

The increased speed is the escape speed, so the satellite will escape the planet’s gravitational pull.

Question 20. Two artificial satellites with their mass ratio \(\frac{m_1}{m_2}=\frac{2}{1}\) are orbiting around the earth in the same circular orbit. If T₁ and T₂ be their time periods of revolution then

1. \(\frac{T_1}{T_2}=2\)
2. \(\frac{T_1}{T_2}=\frac{1}{2}\)
3. \(\frac{T_1}{T_2}=1\)
4. \(\frac{T_1}{T_2}=\frac{1}{4}\)

Answer: 3. \(\frac{T_1}{T_2}=1\)

The orbital speed of a satellite around the planet is

v₀ = \(\sqrt{\frac{G M}{r}}\) which is independent of the satellite’s mass.

So, on the same orbit, T₁ = T₂.

Question 21. A geostationary satellite is established in a higher orbit. Its distance from the centre of the earth in the new orbit is twice that of the previous orbit. The time period of revolution in the second orbit is

1. 24 hours
2. 48√2 hours
3. 48 hours
4. 24√2 hours

Answer: 2. 48√2 hours

From Kepler’s third law, T₂ α r₃.

∴ \(\frac{T_0^2}{T^2}=\frac{r_0^3}{r^3} \Rightarrow \frac{T_0}{T}=\left(\frac{r_0}{2 r_0}\right)^{3 / 2}\)

⇒ \(\frac{24 \mathrm{~h}}{T}=\left(\frac{1}{2}\right)^{3 / 2}=\frac{1}{2 \sqrt{2}}\)

⇒ \(T=48 \sqrt{2} \mathrm{~h}\)

Question 22. A satellite revolving around the earth in a circular orbit whose radius is R. The work done by the earth’s gravitational force during half of its revolution is

1. 2mgR
2. πmgR
3. \(\frac{1}{2}\) mgR
4. Zero

Answer: 2. πmgR

The orbital motion of a satellite is a uniform circular motion in which the force is radial and the work, done is

⇒ \(W=\vec{F} \cdot \overrightarrow{d S}\)

=\(F d S \cos 90^{\circ}=0\)

Question 23. A simple pendulum has its time period T₁ when on the earth’s surface and T₂ when taken to a height equal to RE above the earth’s surface, where RE is the radius of the earth. The value of \(\frac{T_2}{T_1}\) is

1. 2
2. 4
3. √2
4. 1

Answer: 1. 2

⇒ \(T_1=2 \pi \sqrt{\frac{l}{g}} \text { and } T_2\)

=\(2 \pi \sqrt{\frac{l}{g^{\prime}}}\)

=\(2 \pi \sqrt{\frac{l}{\frac{g R_{\mathrm{E}}^2}{4 R_{\mathrm{E}}^2}}}\)

=\(4 \pi \sqrt{\frac{l}{g}}\)

⇒ \(\frac{T_2}{T_1}=\frac{2}{1}\)

= 2.

Question 24. An object when projected vertically upwards from the earth’s surface with a velocity v₀, attains a height RE (the radius of the earth). Ifg is the acceleration due to gravity on the earth’s surface then

1. v₀² = gR_E
2. v₀² = 2gRE
3. v₀²> 2gRE
4. v₀²< gRE

Answer: 4. v₀²< gRE

At the surface, \(\mathrm{KE}=\frac{1}{2} m v_0^2 \text { and } \mathrm{PE}=-\frac{\mathrm{GMm}}{R_{\mathrm{E}}} \text {. }\)

The velocity at a height h = RE is zero, so total energy on the surface = total energy at the height RE

⇒ \(\frac{1}{2} m v_0^2-\frac{G M m}{R_{\mathrm{E}}}=0+\left(-\frac{G M m}{2 R_{\mathrm{E}}}\right)\)

⇒ \(v_0^2=\frac{G M}{R_{\mathrm{E}}}\)

=\(\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}}\)

=\(g R_{\mathrm{E}}\)

⇒ \(v_0^2=g R_{\mathrm{E}}\)

Question 25. An object is projected vertically upwards from the earth’s surface with a velocity equal to half the escape velocity from the earth. If RE be the radius of the earth, the maximum height attained by the object is

1. \(\frac{R_{\mathrm{E}}}{2}\)
2. \(\frac{R_{\mathrm{E}}}{3}\)
3. \(\frac{R_{\mathrm{E}}}{5}\)
4. \(\frac{R_{\mathrm{E}}}{4}\)

Answer: 2. \(\frac{R_{\mathrm{E}}}{3}\)

Let x be the maximum height attained. Conserving the mechanical energy, we have

⇒ \(\frac{1}{2} m\left(\frac{v_e}{2}\right)^2-\frac{G M m}{R_{\mathrm{E}}}=-\frac{G M m}{R_{\mathrm{E}}+x}\)

or, \(\frac{1}{2} \cdot \frac{m}{4}\left(2 g R_{\mathrm{E}}\right)=m g R_{\mathrm{E}}-\frac{m g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+x}\)

or, \(\frac{R_{\mathrm{E}}}{4}=R_{\mathrm{E}}-\frac{R_{\mathrm{E}}^2}{R_{\mathrm{E}}+x} \text { or } \frac{R_{\mathrm{E}}}{R_{\mathrm{E}}+x}=\frac{3}{4}\)

∴ \(x=\frac{R_E}{3}\)

Question 26. Two artificial satellites of different masses are revolving in the same orbit. They have the same

1. Mechanical energy
2. Angular momentum
3. Time period
4. Linear momentum

Answer: 3. Time period

In the same orbit, only the time period of revolution is the same and is independent of the mass of the satellite.

Question 27. A body of mass m is moved from the earth’s surface to a height equal to the radius of the earth (RE). The increase in its gravitational potential energy is

1. mgRE
2. 2mgRE
3. \(\frac{1}{2} m g R_{\mathrm{E}}\)
4. \(\frac{1}{4} m g R_{\mathrm{E}}\)

Answer: 3. \(\frac{1}{2} m g R_{\mathrm{E}}\)

Increase in gravitational PE = U_f-U_i

⇒ \(-\frac{G M m}{2 R_{\mathrm{E}}}-\left(-\frac{G M m}{R_{\mathrm{E}}}\right)=\frac{G M m}{2 R_{\mathrm{E}}}\)

⇒ \(\frac{g R_E^2 m}{2 R_{\mathrm{E}}}=\frac{1}{2} m g R_{\mathrm{E}}\)

Question 28. The escape velocity of an object when projected vertically upwards from the surface of the earth is ve. If the object is projected in a direction making an angle θ with the vertical, the escape velocity will be

1. v_ecos θ
2. v_esin θ
3. v_e
4. v tan θ

Answer: 3. v_e

The escape velocity does not depend on the direction of projection (θ). So, it remains v_e.

Question 29. If the gravitational force of attraction between two material bodies were to vary as 1/r³ instead of 1/r², the period of revolution of a planet around the sun would vary as

1. √r
2. r
3. r^3/2
4. r²

Answer: 4. r²

Assuming F = \(F=\frac{G M m}{r^3}\), we have

or, \(\frac{m v^2}{r}=\frac{G M m}{r^3}\)

or, \(\left(\frac{2 \pi r}{T}\right)^2=\frac{g R^2}{r^2}\)

or, \(T^2=\frac{4 \pi^2 \cdot r^4}{g R^2} \quad\)

or, \(\quad T=\left(\frac{2 \pi}{\sqrt{g} R}\right) r^2\)

∴ T α r².

Question 30. Let r be the orbital radius of a geostationary satellite of the earth. What will be the time period of revolution of a satellite orbiting the earth at a height equal to 2.5R_E, where the radius of the earth is RE (Take r = 7R_E.)

1. 6√2 hours
2. 6√3 hours
3. 12 hours
4. 6√7 hours

Answer: 1. 6√2 hours

According to Kepler’s third law, T₂ α r₃.

∴ \(\frac{T_1}{T_2}=\left(\frac{r_1}{r_2}\right)^{3 / 2}\)

For the geostationary satellite,

T₁ = one day = 24 h

and r₁ = R_E + 6R_E = 7R_E.

For the other satellite, r₂ = 2.5R_E + R_E = 3.5R_E.

∴ \(T_2=\left(\frac{r_2}{r_1}\right)^{3 / 2} T_1\)

=\(\left(\frac{3.5 R_{\mathrm{E}}}{7 R_{\mathrm{E}}}\right)^{3 / 2}(24 \mathrm{~h})\)

=\(\frac{24 \mathrm{~h}}{2 \sqrt{2}}=6 \sqrt{2} \mathrm{~h}\)

Question 31. If the angular momentum of a planet of mass m, moving around the sun in a circular orbit, is L about the centre of the sun, its areal velocity is

1. \(\frac{4 L}{m}\)
2. \(\frac{L}{m}\)
3. \(\frac{L}{2 m}\)
4. \(\frac{2 L}{m}\)

Answer: 3. \(\frac{L}{2 m}\)

Angular momentum = \(L=I \omega=m r^2 \frac{d \theta}{d t}\)

∴ \(r^2 \frac{d \theta}{d t}=\frac{L}{m}\)

∴ areal velocity = \(\frac{d A}{d t}=\frac{1}{2}\left(r^2 \frac{d \theta}{d t}\right)\)

=\(\frac{1}{2}\left(\frac{L}{m}\right)\)

=\(\frac{L}{2 m}\)

Question 32. A uniform sphere of mass M and radius R exerts a force F on a point mass m situated at a distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is formed inside _ the sphere by extracting a portion, as shown in the figure. The force of attraction between the remaining mass of the sphere and the point mass is

1. \(\frac{F}{3}\)
2. \(\frac{2F}{3}\)
3. \(\frac{4F}{9}\)
4. \(\frac{7F}{9}\)

Answer: 4. \(\frac{4F}{9}\)

The mass of the cutout portion of the sphere is

⇒ \(M^{\prime}=\frac{4}{3} \pi\left(\frac{R}{2}\right)^3 \rho=\frac{1}{8}\left(\frac{4}{3} \pi R^3 \rho\right)=\frac{M}{8}\)

The force of attraction due to the solid sphere is

⇒ \(F=\frac{G M m}{(2 R)^2}=\frac{G M m}{4 R^2}\)

The force due to the cavity (assumed as a negative mass) is

⇒ \(f=\frac{G\left(\frac{M}{8}\right) \cdot m}{\left(2 R-\frac{R}{2}\right)^2}=\frac{G M m}{8\left(\frac{9 R^2}{4}\right)}=\frac{G M m}{18 R^2}\)

∴ net force = \(F-f=\frac{G M m}{4 R^2}-\frac{G M m}{18 R^2}\)

⇒ \(\frac{7}{36}\left(\frac{G M m}{R^2}\right)\)

=\(\frac{7}{9}\left(\frac{G M m}{4 R^2}\right)\)

=\(\frac{7 F}{9}\)

Question 33. The radius of the earth is JRE and g is the acceleration due to gravity on its surface. What should be the angular speed of the earth about its axis, so that bodies lying on the equator become weightless?

1. \(\sqrt{\frac{g}{R_{\mathrm{E}}}}\)
2. \(\sqrt{\frac{2 g}{R_{\mathrm{E}}}}\)
3. \(\sqrt{\frac{8}{2 R_E}}\)
4. \(2 \sqrt{\frac{g}{R_E}}\)

Answer: 1. \(\sqrt{\frac{g}{R_{\mathrm{E}}}}\)

For circular motion,

⇒ \(m g-\propto V=\frac{m v^2}{R_{\mathrm{E}}}=m \omega^2 R_{\mathrm{E}}\)

For weightlessness,

⇒ \(\alpha=0 \Rightarrow m \omega^2 R_E=m g\)

Hence, angular velocity = \(\omega=\sqrt{\frac{g}{R_{\mathrm{E}}}}\)

Question 34. A hollow spherical shell is compressed uniformly to half its initial radius. The gravitational potential at the centre

1. Increases
2. Decreases
3. Remains unchanged
4. Varies during the process of compression

Answer: 2. Decreases

Initially, thegravitational potentialatthecentre oftheshellis \(V_{\mathrm{i}}=-\frac{G M}{R}\)

Finally, when R’ = \(R^{\prime}=\frac{R}{2}, V_{\mathrm{f}}=-\frac{G M}{\frac{R}{2}}=-\frac{2 G M}{R}\)

So, the potential is reduced (being more negative).

Question 35. A planet revolves around the sun in an elliptical orbit. The areal velocity (dA/dt) of the planet is 4.0 x 10¹⁶ m² s^-1, and the least distance between the planet and the sun is 2 x 10¹² m. The maximum linear speed of the planet is

1. 10 km s^-1
2. 2010ns^-1
3. 40 km s^-1
4. 80 km s^-1

Answer: 3. 40 km s^-1

Areal velocity = \(\frac{d A}{d t}=\frac{1}{2} r(r \omega)=\frac{1}{2} r v\)

∴ \(\frac{1}{2} r v=\frac{d A}{d t}\)

Hence, linear speed = \(=v=\frac{2}{r} \frac{d A}{d t}\)

⇒ \(\frac{2}{2 \times 10^{12} \mathrm{~m}}\left(4.0 \times 10^{16} \mathrm{~m}^2 \mathrm{~s}^{-1}\right)\)

= 4 x 104 m s^-1

= 40 km s^-1

Question 36. A particle of mass m on the earth’s surface has imparted a velocity twice the escape velocity ve on the earth. Its total mechanical energy will be

1. \(\frac{1}{2} m v_{\mathrm{e}}^2\)
2. \(\frac{2}{3} m v_{\mathrm{e}}^2\)
3. \(\frac{3}{2} m v_{\mathrm{e}}^2\)
4. 3mv_e²

Answer: 3. \(\frac{3}{2} m v_{\mathrm{e}}^2\)

⇒ \(\mathrm{PE}=-\frac{G M m}{R_{\mathrm{E}}}\)

and \(\mathrm{KE}=\frac{1}{2} m\left(2 v_{\mathrm{e}}\right)^2\)

=\(\frac{1}{2} m \cdot 4\left(\frac{2 G M}{R_{\mathrm{E}}}\right)\)

=\(\frac{4 G M m}{R_{\mathrm{E}}}\)

∴ the total mechanical energy is

⇒ \(E_{\mathrm{tot}}=\mathrm{KE}+\mathrm{PE}\)

=\(\frac{3 G M m}{R_{\mathrm{E}}}\)

=\(\frac{3}{2} m\left(\frac{2 G M}{R_{\mathrm{E}}}\right)\)

=\(\frac{3}{2} m v_{\mathrm{e}}^2\)

Question 37. Two artificial satellites are revolving in the same circular orbit around the centre of the earth. They must have the same

1. Mass
2. Kinetic energy
3. Angular momentum
4. Linear speed

Answer: 4. Linear speed

The linear speed of the earth’s satellite is \(v=\sqrt{\frac{G M}{r}}\), which is constant (independent of mass) for all satellites.

Question 38. The work done in slowly lifting a body from the earth’s surface to a height equal to RE (radius of the earth) is equal to twice the work done in lifting the same body from the earth’s surface to a height h, where h is equal to

1. \(\frac{R_{\mathrm{E}}}{4}\)
2. \(\frac{R_{\mathrm{E}}}{3}\)
3. \(\frac{R_{\mathrm{E}}}{6}\)
4. \(\frac{R_{\mathrm{E}}}{2}\)

Answer: 2. \(\frac{R_{\mathrm{E}}}{3}\)

Work done = change in PE = ΔPE.

Initial \(\mathrm{PE}=-\frac{G M m}{R_{\mathrm{E}}} \text { and final } \mathrm{PE}=-\frac{G M m}{R_{\mathrm{E}}+h}\)

When raised to a height RE,

⇒ \(\Delta \mathrm{PE}_1=U_{\mathrm{f}}-U_{\mathrm{i}}\)

=\(-\frac{G M m}{R_{\mathrm{E}}+R_{\mathrm{E}}}-\left(-\frac{G M m}{R_{\mathrm{E}}}\right)\)

=\(\frac{G M m}{2 R_{\mathrm{E}}}\)

When raised to a height of h,

⇒ \(\Delta \mathrm{PE}_2=-\frac{G M m}{R_{\mathrm{E}}+h}+\frac{G M m}{R_{\mathrm{E}}}\)

Given that ΔPE₁ = 2ΔPE₂.

∴ \(\frac{G M m}{2 R_{\mathrm{E}}}=-\frac{2 G M m}{R_{\mathrm{E}}+h}+\frac{2 G M m}{R_{\mathrm{E}}}\)

⇒ \(h=\frac{R_{\mathrm{E}}}{3}\)

Question 39. For a system of three uniform spherical shells, each of mass M and radius R, are kept so as to touch each other as shown in the figure. The magnitude of the gravitational force on any of the shells due to the other two is

1. \(\frac{\sqrt{3}}{2}\left(\frac{G M^2}{R^2}\right)\)
2. \(\frac{\sqrt{3}}{4}\left(\frac{G M^2}{R^2}\right)\)
3. \(\frac{3}{2}\left(\frac{G M^2}{R^2}\right)\)
4. \(\sqrt{\frac{G M^2}{R^2}}\)

Answer: 2. \(\frac{\sqrt{3}}{4}\left(\frac{G M^2}{R^2}\right)\)

The spherical shells may be considered as point masses at the centre. These are at the vertices of an equilateral triangle of side 2R.

The gravitational force between two shells is \(f=\frac{G M^2}{4 R^2}\)

Hence, the net force on any shell is

⇒ \(F=\sqrt{f^2+f^2+2 f \cdot f \cos 60^{\circ}}=\sqrt{3} f=\frac{\sqrt{3}}{4}\left(\frac{G M^2}{R^2}\right)\)

Question 40. The mass and diameter of a planet are thrice the respective values of the Earth. The period of oscillations of a simple pendulum on the earth is 2 s. The period of oscillations of the same pendulum on the planet would be

1. \(\frac{2}{\sqrt{3}} \mathrm{~s}\)
2. 2√3 s
3. \(\frac{\sqrt{3}}{2} \mathrm{~s}\)
4. \(\frac{3}{2} \mathrm{~s}\)

Answer: 2. 2√3 s

⇒ \(\frac{g_{\mathrm{E}}}{g_{\mathrm{P}}}=\frac{G M_{\mathrm{E}} / R_{\mathrm{E}}^2}{G M_{\mathrm{p}} / R_{\mathrm{P}}^2}\)

=\(\frac{M_{\mathrm{E}}}{M_{\mathrm{P}}} \times\left(\frac{R_{\mathrm{P}}}{R_{\mathrm{E}}}\right)^2\)

=\(\frac{M_{\mathrm{E}}}{3 M_{\mathrm{E}}} \times\left(\frac{3 R_{\mathrm{E}}}{R_{\mathrm{E}}}\right)^2\)

= 3.

Time period = \(T=2 \pi \sqrt{\frac{l}{g}}\)

∴ \(\frac{T_{\mathrm{p}}}{T_{\mathrm{E}}}=\sqrt{\frac{g_{\mathrm{E}}}{g_{\mathrm{p}}}}\)

⇒ \(=\sqrt{3}\)

⇒ \(T_{\mathrm{p}}=2 \sqrt{3} \mathrm{~s}\)

Question 41. A black hole is an object whose gravitational field is so strong that even light cannot escape it. To what approximate radius would the earth (mass = 5.98 x 10²⁴ kg) have to be compressed to make it a black hole?

1. 10^-9 m
2. 10^-6m
3. 10^-2m
4. 100 m

Answer: 3. 10^-2m

For the Earth to be a black hole, the escape velocity from the Earth must be equal to the speed of light.

Hence,

⇒ \(v_{\mathrm{e}}=\sqrt{\frac{2 G M}{r}}=c\)

⇒ \(r=\frac{2 G M}{c^2}=\frac{2\left(6.67 \times 10^{-11}\right)\left(5.98 \times 10^{24}\right)}{\left(3 \times 10^8\right)^2} \mathrm{~m}\)

= 8.86 x 10^-3 m ≈ 10^-2 m.

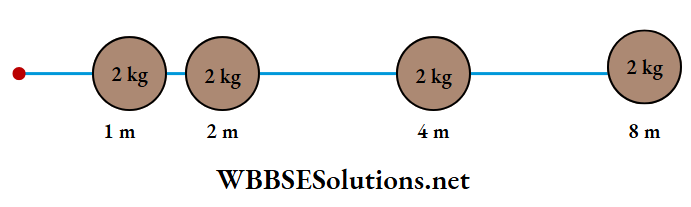
Question 42. An infinite number of spherical bodies, each of mass m = 2 kg, are placed on the x-axis at the distances 1 m, 2 m, 4 m, 8 m, etc., respectively from the origin. The resulting gravitational potential due to this system at the origin in SI units will be

1. \(-\frac{4}{3} G\)
2. -4 G
3. -G
4. \(-\frac{8}{3} G\)

Answer: 2. -4 G

Gravitational potential due to the masses at 0 the origin O is

⇒ \(V_{\mathrm{O}}=-\frac{G(2 \mathrm{~kg})}{1 \mathrm{~m}}-\frac{G(2 \mathrm{~kg})}{2 \mathrm{~m}}-\frac{G(2 \mathrm{~kg})}{4 \mathrm{~m}}-\frac{G(2 \mathrm{~kg})}{8 \mathrm{~m}}-\ldots\)

⇒ \(-G(2 \mathrm{~kg})\left(\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots\right)\)

⇒ \(-G(2 \mathrm{~kg})\left(\frac{1}{1-\frac{1}{2}}\right)\)

= -2G(2 kg)

= -4G units.

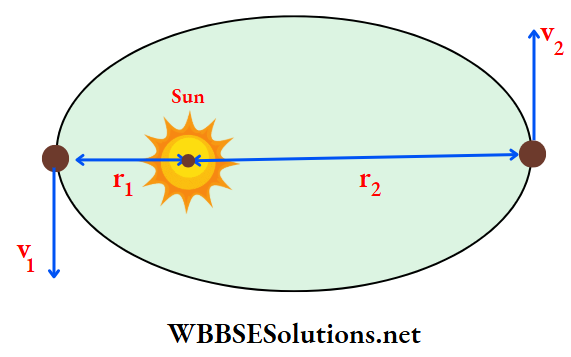
Question 43. A planet moving along an elliptical orbit is closest to the sun at a distance r₁ and farthest at a distance r₂ as shown in the figure. If v₁ and v₂ are their linear velocities at these points respectively, the ratio v₁/v₂ is equal to

1. \(\left(\frac{r_1}{r_2}\right)^2\)
2. \(\frac{r_2}{r_1}\)
3. \(\left(\frac{r_2}{r_1}\right)^2\)
4. \(\frac{r_1}{r_2}\)

Answer: 2. \(\frac{r_2}{r_1}\)

Since the angular momentum is conserved,

L₁ = L₂

mv₁r₁ = mv₂r₂

⇒ \(\frac{v_1}{v_2}=\frac{r_2}{r_1}\)

Question 44. The earth (mass = 6 x 10²⁴ kg) revolves around the sun with an angular velocity of 2 x 10⁷ rad s^-1 in a circular orbit of radius 1.5 x 10⁸ km. The force exerted by the sun on the earth is

1. 36 x 10²¹ N
2. 27 x 10³⁹ N
3. 18 x 10²⁵ N
4. Zero

Answer: 1. 36 x 10²¹ N

Gravitational pull by the sun on the earth provides the necessary centripetal force. Hence, the force exerted by the sun is

F = m

= 36 x 10²¹ N.

Question 45. The mean radius of the earth is R& its angular speed on its own axis is to, and the acceleration due to gravity on the earth’s surface is g. What will be the radius of the orbit of a geostationary satellite?

1. \(\left(\frac{R_{\mathrm{E}}^2 g}{\omega^2}\right)^{1 / 3}\)
2. \(\left(\frac{R_{\mathrm{E}} g}{\omega^2}\right)^{1 / 3}\)
3. \(\left(\frac{R_{\mathrm{E}}^2 \omega^2}{g}\right)^{1 / 3}\)
4. \(\left(\frac{R_{\mathrm{E}}^2 g}{\omega}\right)^{1 / 3}\)

Answer: 1. \(\left(\frac{R_{\mathrm{E}}^2 g}{\omega^2}\right)^{1 / 3}\)

For a geostationary satellite, the angular velocity must be equal to that of the earth (ω). For circular motion, the centripetal force (mω²r) is provided by the gravitational attraction \(\left(\frac{G M m}{r^2}\right)\) by the earth on the satellite.

Thus,

⇒ \(m \omega^2 r=\frac{G M m}{r^2}\)

=\(\frac{g R_{\mathrm{E}}^2 m}{r^2}\)

= \(\left(\frac{R_{\mathrm{E}}^2 g}{\omega^2}\right)^{1 / 3}\)

Question 46. A satellite is orbiting the earth at a constant speed v in a circular orbit of radius r. An object of mass m is ejected from the satellite such that it just escapes from die gravitational pull of the earth. At the time of ejection, the kinetic energy of the object is

1. \(\frac{3}{2} m v^2\)
2. mv²
3. 2mv²
4. \(\frac{1}{2} m v^2\)

Answer: 2. mv²

The orbital speed of the satellite is \(v=\sqrt{\frac{G M}{r}}\) To escape the earth’s gravity, its total mechanical energy (PE + KE) must be zero. So,

(KE of the mass m) + \(\left(-\frac{G M m}{r}\right)=0\)

(KE of the mass m) = \(\frac{G M m}{r}\)

= \(m\left(\sqrt{\frac{G M}{r}}\right)^2\)

=\(m v^2\)

Question 47. A body weighs 200 N on the surface of the earth. How much will it weigh halfway down to the centre of the earth?

1. 150 N
2. 200 N
3. 250 N
4. 100 N

Answer: 4. 100 N

The acceleration due to gravity at a depth x below the earth’s surface is

⇒ \(g^{\prime}=g\left(1-\frac{\dot{x}}{R_{\mathrm{E}}}\right)=g\left(1-\frac{\frac{R_{\mathrm{E}}}{2}}{R_{\mathrm{E}}}\right)=\frac{g}{2}\)

∴ \(\frac{w^{\prime}}{w}=\frac{\frac{m g}{2}}{m g}=\frac{1}{2} \Rightarrow w^{\prime}=\frac{w}{2}=\frac{200 \mathrm{~N}}{2}\)

= 100N.

Question 48. The work done to raise a body of mass m from the surface of the earth to a height h, which is equal to the radius of the earth, is

1. mgR_E
2. 2mgR_E
3. \(\frac{1}{2} m g R_{\mathrm{E}}\)
4. \(\frac{3}{2} m g R_{\mathrm{E}}\)

Answer: 3. \(\frac{1}{2} m g R_{\mathrm{E}}\)

The gravitational field is conservative, for which KE + PE = constant and the change in potential energy equals the work done.

Initial PE at the surface = \(U_{\mathrm{i}}=-\frac{G M m}{R_{\mathrm{E}}}\)

At a height \(h=R_{\mathrm{E}} \text {, final } \mathrm{PE}=U_{\mathrm{f}}=-\frac{G M m}{R_{\mathrm{E}}+h}=-\frac{G M m}{2 R_{\mathrm{F}}}\)

Hence, increase in \(\mathrm{PE}=U_{\mathrm{f}}-U_{\mathrm{i}}=-\frac{G M m}{2 R_{\mathrm{E}}}-\left(-\frac{G M m}{R_{\mathrm{E}}}\right)\)

⇒ \(\frac{G M m}{2 R_{\mathrm{E}}}=\frac{\left(g R^2\right) m}{2 R_{\mathrm{E}}}=\frac{1}{2} m g R_{\mathrm{E}}\)

This is equal to the work done by the agent.

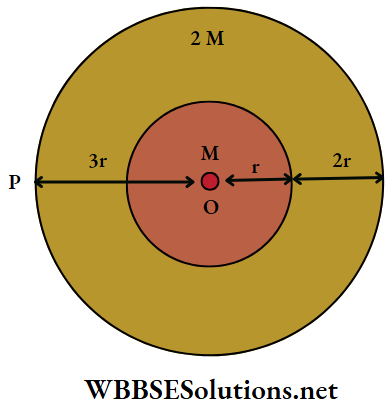
Question 49. A solid sphere of mass M and radius r is surrounded by a uniform concentric spherical shell of thickness 2r and mass 2M. The gravitational field at a distance 3r from the common centre will be GM

1. \(\frac{2 G M}{3 r^2}\)
2. \(\frac{2 G M}{9 r^2}\)
3. \(\frac{G M}{3 r^2}\)
4. \(\frac{G M}{9 r^2}\)

Answer: 3. \(\frac{G M}{3 r^2}\)

The point P at a distance 3r from the centre lies on the surface of the outer thick shell. Now, for a spherical mass distribution, the field at an external point will be the same as if its total mass is considered as a point mass at the centre. Hence, the required field has the magnitude

⇒ \(E=\frac{G(M+2 M)}{(3 r)^2}=\frac{G M}{3 r^2}\)

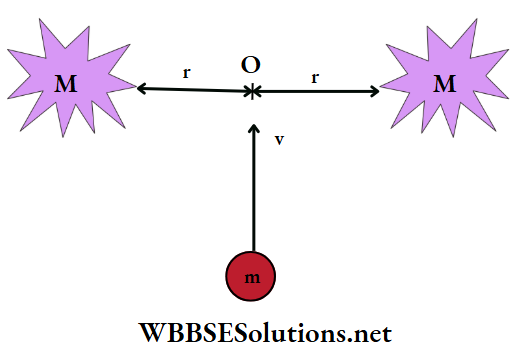
Question 50. Two stars of masses 3 x 10³¹ kg each and at a separation of 2 x 10¹¹ m rotate in a plane about their common centre of mass O. A meteorite passes through O moving perpendicular to the star’s plane of rotation. In order to escape the gravitational pull of this double-star system, the minimum speed that the meteorite should have at O is

1. 2.8 x 10⁵ m s^-1
2. 3.8 x 10⁴ m s^-1
3. 1.4 x 10⁵ m s^-1
4. 2.4 x 10⁴ ms^-1

Answer: 1. 2.8 x 10⁵ m s^-1

Let KE of the meteorite of mass m while crossing the centre O be \(\frac{1}{2} m v^2\) and its PE be

⇒ \(\left(-\frac{G M m}{r}\right)+\left(-\frac{G M m}{r}\right)=-\frac{2 G M m}{r}\)

∴ the total energy of the meteorite is

⇒ \(E_0=\frac{1}{2} m v^2-\frac{2 G M m}{r}\)

When it moves to the infinity, the total mechanical energy must be zero, so,

E_t = 0.

Conserving the energy,

⇒ \(\frac{1}{2} m v^2-\frac{2 G M m}{r}=0\)

⇒ \(v=2 \sqrt{\frac{G M}{r}}\)

Substituting the values,

⇒ \(v=2 \sqrt{\frac{\left(6.67 \times 10^{-11}\right)\left(3 \times 10^{31}\right)}{1 \times 10^{11}}} \mathrm{~m} \mathrm{~s}^{-1}\)

=\(2.8 \times 10^5 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 51. A satellite is revolving in a circular orbit at a height h above the earth’s surface such that h« RE, where RE is the radius of the earth. Assuming the effect of the earth’s atmosphere to be negligible, the minimum increase in the speed required so that the satellite could escape the gravitational pull of the earth is

1. \(\sqrt{\frac{g R_{\mathrm{E}}}{2}}\)
2. √gR_E
3. √2gR_E
4. \((\sqrt{2}-1) \sqrt{g R_{\mathrm{E}}}\)

Answer: 4. \((\sqrt{2}-1) \sqrt{g R_{\mathrm{E}}}\)

The orbital speed (v₁) of the satellite at a height h above the earth’s surface is given by

⇒ \(\frac{m v_1^2}{r}=\frac{G M m}{r^2}\)

or \(v_1=\sqrt{\frac{G M}{r}}=\sqrt{\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+h}}\)

For this satellite to escape the gravitational pull of the earth, the escape speed v₂ is given by

⇒ \(\frac{1}{2} m v_2^2-\frac{G M m}{r}=0 \quad \text { or } \quad v_2=\sqrt{\frac{2 G M}{R_{\mathrm{E}}+h}}=\sqrt{\frac{2 g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+h}}\)

increase in velocity = v₂-v₁

⇒ \((\sqrt{2}-1) \sqrt{\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+h}} \approx(\sqrt{2}-1) \sqrt{g R_{\mathrm{E}}}\) [… h<<Rg]

Question 52. If the acceleration due to gravity at a height x above the earth’s surface is the same as that below the earth’s surface at the same depth then x in terms of the earth’s radius RE is

1. \((\sqrt{5}-1) \frac{R_{\mathrm{E}}}{2}\)
2. √2RE
3. \(\frac{R_{\mathrm{E}}}{\sqrt{2}}\)
4. \((\sqrt{5}+1) \frac{R_{\mathrm{E}}}{2}\)

Answer: 1. \((\sqrt{5}-1) \frac{R_{\mathrm{E}}}{2}\)

At a height x above the earth’s surface,

⇒ \(\delta_1=\frac{g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+x\right)^2}\)

At a depth x below the earth’s surface,

⇒ \(g_2=g\left(1-\frac{x}{R_E}\right)\)

Given that g₁ = g₂. Hence,

⇒ \(\frac{R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+x\right)^2}=\left(1-\frac{x}{R_{\mathrm{E}}}\right)\)

(R_E+X)(R_E²-X²)=R_E³.

x² + R_Ex-R_E² =0

⇒ \(x=(\sqrt{5}-1) \frac{R_{\mathrm{E}}}{2}\)

Question 53. The orbital velocity v₀ of a satellite revolving close to the earth is increased to \(\sqrt{\frac{3}{2}} v_0\). The radius of the satellite’s orbit around the earth will now be (given that the earth’s radius is RE)

1. \(\sqrt{\frac{3}{2}} R_{\mathrm{E}}\)
2. 2R_E
3. 3R_E
4. 4R_E

Answer: 3. \(\sqrt{\frac{3}{2}} R_{\mathrm{E}}\)

Let the satellite get established in an orbit of radius r with the orbital velocity v₀.

Conserving the mechanical energy,

⇒ \(\frac{1}{2} m\left(\sqrt{\frac{3}{2}} v_0\right)^2-\frac{G M m}{R_{\mathrm{E}}}=\frac{1}{2} m v^2-\frac{G M m}{r}\)…..(1)

Conserving the angular momentum,

⇒ \(m \cdot \sqrt{\frac{3}{2}} \cdot v_{\mathrm{o}} R_{\mathrm{E}}=m v r \text { or } v=\sqrt{\frac{3}{2}} \cdot \frac{v_{\mathrm{o}} R_{\mathrm{E}}}{r}\)….(2)

Substituting v from (2) and putting \(v_{\mathrm{o}}=\sqrt{g R_{\mathrm{E}}} \text { and } G M=g R_{\mathrm{E}}^2\) in (1),

⇒ \(\frac{1}{2} m \frac{3}{2} g R_{\mathrm{E}}-m g R_{\mathrm{E}}=\frac{3}{4} m\left(\frac{g R_{\mathrm{E}}^3}{r^2}\right)-\frac{m g R_{\mathrm{E}}^2}{r}\)

or, \(-\frac{1}{4}=\frac{3}{4}\left(\frac{R_{\mathrm{E}}^2}{r^2}\right)-\frac{R_{\mathrm{E}}}{r} \text { or } r^2-4 R_{\mathrm{E}} r+3 R_{\mathrm{E}}^2=0\)

Solving we get, r = 3RE

Question 54. Two bodies A and B have equal weights when A is placed at the equator of the earth and B is situated at a height h above the pole of the earth. Express h in terms of the earth’s radius RE, the earth’s angular speed CD and the acceleration due to gravity g close to the earth.

1. \(\frac{R_E \omega^2}{2 g}\)
2. \(\frac{R_{\mathrm{B}}^2 \omega^2}{2 g}\)
3. \(\frac{R_{\mathrm{E}} g}{\omega^2}\)
4. \(\frac{g}{\omega^2}\)

Answer: 2. \(\frac{R_{\mathrm{B}}^2 \omega^2}{2 g}\)

For the same weight, g_A = g_B.

But \(g_{\mathrm{A}}=g-\omega^2 R_{\mathrm{E}}\)

and \(g_{\mathrm{B}}=\frac{g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}\)

=\(g\left(1+\frac{h}{R_{\mathrm{E}}}\right)^{-2}\)

= \(g\left(1-\frac{2 h}{R_{\mathrm{E}}}\right)\)

∴ \(\omega^2 R_{\mathrm{E}}=\frac{2 g h}{R_{\mathrm{E}}}\)

⇒ \(h=\frac{\omega^2 R_{\mathrm{E}}^2}{2 g}\)

Question 55. A satellite is in an elliptical orbit around a planet. It is observed that the speed of the satellite when it is farthest from the planet is 6 times less than that when it is closest to the planet. The ratio of the distances between the satellite and the planet at the closest and farthest points is

1. 3:4
2. 1:1
3. 1:2
4. 1:6

Answer: 4. 1:6

Conserving the angular momentum,

⇒ \(m r_1^2 \omega_1=m r_2^2 \omega_2\)

⇒ \(w r_1^2\left(\frac{v_0}{r_1}\right)=r_2^2\left(\frac{v_2}{r_2}\right)\)

⇒ \(r_1(6 v)=r_2(v)\)

⇒ \(\frac{r_1}{r_2}=\frac{1}{6}\)

r₁: r₂= 1: 6

Question 56. Two planets have masses M and 16M, and radii R and 2R. The separation between their centres is 10R. An object of mass m is fired from the surface of the larger planet towards the smaller planet along the line joining their centres. For the object to strike the surface of the smaller planet, the minimum speed of projection is

1. \(\sqrt{\frac{G M^2}{m R}}\)
2. \(\sqrt{\frac{G M}{R}}\)
3. \(\frac{3}{2} \sqrt{\frac{5 G M}{R}}\)
4. \(\sqrt{\frac{G M}{R}}\)

Answer: 3. \(\frac{3}{2} \sqrt{\frac{5 G M}{R}}\)

For the object to reach the smaller planet, the speed of projection v must be such so as to just cross the point P, where the net gravitational field due to the planets is zero.

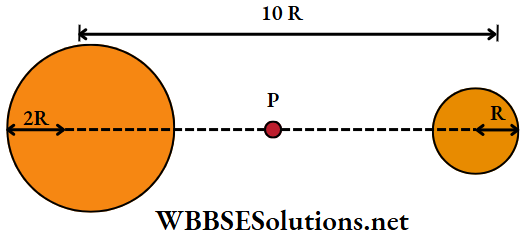
∴ \(\frac{G(16 M)}{r^2}=\frac{G M}{(10 R-r)^2}\)

r = 8R

Conserving the mechanical energy,

⇒ \(-\frac{G \cdot 16 M m}{2 R}-\frac{G M m}{10 R-2 R}+\frac{1}{2} m v^2\)

=\(-\frac{G \cdot 16 M m}{8 R}-\frac{G M m}{2 R}\)

or, \(v=\frac{3}{2} \sqrt{\frac{5 G M}{R}}\)