Coulomb’s Law of Electrostatics Notes

Coulomb’s Law Of Electrostatics Notes

Electrostatics Synopsis

• An electric charge (q or Q) is always associated with electrons and protons which are constituents of atoms.
• The SI unit of charge is the coulomb (symbol: C). The elementary charge is e = 1.6 x 10^-19 C.
• 1 C of charge is contained in 6.25 x 10¹⁸ electrons (or protons).
• A charge is quantized as Q = ne, where n = 1, 2, 3,…
• A charging process involves a gain or loss of electrons. An object becomes positively charged due to the loss of electrons and negatively charged due to the gain of electrons.

“electrostatics physics “

• Coulomb’s law: \(F=\frac{1}{4 \pi \varepsilon_0}\left(\frac{q_1 q_2}{r^2}\right)=K\left(\frac{q_1 q_2}{r^2}\right)\)
  where ε₀ = permittivity of free space
  = 8.85 x 10^-12 F m^-1 (or C² N^-1 m^-2)
  and \(K=\frac{1}{4 \pi \varepsilon_0}\)
• = \(9 \times 10^9 \mathrm{~N} \mathrm{~m}^2 \mathrm{C}^{-2}\)
• Principle of superposition: The net force on any charge q due to other charges in space equals the vector sum of all the forces on it on account of the constituent charges in space. Thus,
  ⇒ \(\vec{F}=\vec{F}_1+\vec{F}_2+\ldots=\frac{1}{4 \pi \varepsilon_0}\left[q\left(\frac{q_1}{r_1^2} \cdot \hat{r}_1+\frac{q_2}{r_2{ }^2} \cdot \hat{r}_2+\ldots\right)\right]\)
• The electric field (or field strength or field intensity) \(\vec{E}\) is defined as the force per unit test charge \(\left(\vec{E}=\frac{\vec{E}}{q_0}\right)\). Its SI unit is NC^-1(≡V m^-1).
  The electric field due to a single charge Q (monopole) is
  ⇒ \(\vec{E}=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{r^2} \cdot \hat{r}\right)\)
• Electric dipole: Two equal and opposite point charges separated at a short distance constitute an electric dipole.
• The electric dipole moment \((\vec{p})\) is the product of one charge |± q| and the separation (δl) between the charges. Thus,
  ⇒ \(|\vec{p}|=|q| \delta l \Rightarrow \vec{p}=|q| \vec{\delta} l\)
  Here \(\vec{p}\) is a vector directed from the negative charge to the positive charge, and its SI unit is the coulomb meter (C m).

Coulomb’s Law of Electrostatics Notes 

“coulomb’s law for electrostatic force “

• Dipole field:
  • At a point on the axis,
    ⇒ \(\vec{E}_{\text {axial }}=\frac{1}{4 \pi \varepsilon_0}\left[\frac{2 \vec{p} r}{\left(r^2-l^2\right)^2}\right] \approx \frac{1}{4 \pi \varepsilon_0}\left(\frac{2 \vec{p}}{r^3}\right)\)
  • At an equatorial point,
    ⇒ \(\vec{E}_{\text {equatorial }}=\frac{1}{4 \pi \varepsilon_0}\left[\frac{-\vec{p}}{\left(r^2+l^2\right)^{3 / 2}}\right] \approx \frac{1}{4 \pi \varepsilon_0}\left(\frac{-\vec{p}}{r^3}\right)\)
  • At any point P(r, θ),
    ⇒ \(E=\frac{1}{4 \pi \varepsilon_0}\left(\frac{p}{r^3} \sqrt{1+3 \cos ^2 \theta}\right)\)
• Torque on a dipole in a uniform field \(\vec{E}\):
  ⇒ \(\vec{\tau}=\vec{p} \times \vec{E} \Rightarrow \tau=p E \sin \theta\)
• Flux of an electric field:
  ⇒ \(\phi=\int \vec{E} \cdot \overrightarrow{d A}=\int E d A \cos \theta\)
  Φ is a scalar quantity, and its SI unit is V m (≡ N m² C^-1).
• Gauss’s law: \(\Phi=\frac{1}{\varepsilon_0}\) (net charge enclosed).
• Expressions for an electric field:
  • For a line charge, \(\vec{E}=\frac{\lambda}{2 \pi \varepsilon_0 r} \cdot \hat{r}\)
  • For a plane charge sheet, \(\vec{E}=\frac{\sigma}{2 \varepsilon_0} \cdot \hat{n}\)
  • For a uniformly charged spherical shell of radius R,
    ⇒ \(\vec{E}=\left\{\begin{array}{cc}
    \frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{r^2} \cdot \hat{r}\right) & \text { for } r>R \\
    \frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{R^2} \cdot \hat{R}\right) & \text { for } r=R \\
    0 & \text { for } r<R
    \end{array}\right.\)
  • For a solid sphere of radius R having a total charge of Q distributed uniformly,
    ⇒ \(\vec{E}=\left\{\begin{array}{l}
    \frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{r^2} \cdot \hat{r}\right) \text { for } r>R \\
    \frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{R^2} \cdot \hat{R}\right) \text { for } r=R \\
    \frac{1}{4 \pi \varepsilon_0}\left(\frac{Q r}{R^3} \cdot \hat{r}\right) \text { for } r<R
    \end{array}\right.\)

Class 11 Physics	Class 12 Maths	Class 11 Chemistry
NEET Foundation	Class 12 Physics	NEET Physics

 

“electrostatic charges examples “

• Potential energy between two charges:
  ⇒ \(U=\frac{1}{4 \pi \varepsilon_0}\left(\frac{q_1 q_2}{r}\right)\)
• The potential energy of a system of three charges:
  ⇒ \(U_{\text {sys }}=U_{12}+U_{13}+U_{23}=\frac{1}{4 \pi \varepsilon_0}\left(\frac{q_1 q_2}{r_{12}}+\frac{q_1 q_3}{r_{13}}+\frac{q_2 q_3}{r_{23}}\right)\)
• Potential at a point in an electric field:
  V = \(\frac{U}{q}\) = potential energy per unit test charge.
  • The potential due to a monopole (single charge) Q is
    ⇒ \(V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{r}\right)\)
  • The potential due to a system of charges is
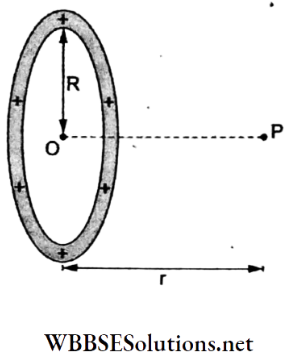
    ⇒ \(V=V_1+V_2+\ldots=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q_1}{r_1}+\frac{Q_2}{r_2}+\ldots\right)\)
  • The potential due to a uniformly charged ring of radius R is
    ⇒ \(V=\left\{\begin{array}{l}
    \frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{\sqrt{R^2+r^2}}\right) \text { atP } \\
    \frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{R}\right) \text { atO }
    \end{array}\right.\)

“physics coulomb’s law “

“coulomb’s law of electrostatics “

Electrostatics Lecture Notes 

• Potential due to an electric dipole:
  • At an axial point, V = \(V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{p}{r^2}\right)\)
  • At an equatorial point, V = 0.
  • At any point \(\mathrm{P}(r, \theta), V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{p \cos \theta}{r^2}\right)\)
• Potential due to a uniformly charged spherical shell of radius R:
  • At an external point, \(V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{r}\right)\)
  • On the surface of the shell, \(V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{R}\right)\)
  • Inside theshell, \(V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{R}\right)\) (the same as thaton thesurface).
• Potential due to a spherical charge distribution:
  • At an external point, \(V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{r}\right) \text { for } r>R\)
  • On the surface of the sphere, \(V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{R}\right)\)
  • Inside the sphere at a distance r (where r < R) from the center,
    ⇒ \(V=\frac{1}{4 \pi \varepsilon_0}\left[\frac{Q\left(3 R^2-r^2\right)}{2 R^3}\right]\)
• The potential energy of an electric dipole in a uniform electric field \(\vec{E}\):
  ⇒ \(U=-\vec{p} \cdot \vec{E}=-p E \cos \theta\)
• The potential difference in an electric field:
  ⇒ \(V_2-V_1=-\int_1^2 \vec{E} \cdot \vec{d} r\)
• Relation between the field \(\vec{E}\) and the potential (V):
  ⇒ \(|\vec{E}|=-\frac{d V}{d r}, \text { where } E_x=-\frac{\partial V}{\partial x}, E_y=-\frac{\partial V}{\partial y} \text { and } E_z=-\frac{\partial V}{\partial z}\)
• The electric field in the material of a conductor is \(\vec{E}\) = 0, and that in a dielectric medium of dielectric constant K is \(\vec{E}=\frac{\vec{E}_0}{K} \text {, where } \vec{E}_0\) is the external field strength.
• Dielectric strength: A sufficient increase in the external electric field reduces the ability of atoms and molecules to hold the outer electrons, which get detached to cause a dielectric breakdown. The maximum electric field that- the dielectric can sustain without breaking down is called its dielectric strength. For dry air, the dielectric strength is around 3 x 10⁶ V m^-1.
• Electrical capacitance, C = \(\frac{Q}{V}\). Its SI unit is the farad (symbol F).
  Thus,
  1F = \(\frac{1C}{1V}\)

Coulomb’s Law Physics Notes 

• The capacitance of a sphere of radius R is C = 4nε₀R
• Electrostatic energy, \(U=\frac{1}{2} C V^2=\frac{Q^2}{2 C}\)
• The capacitance of a parallel-plate capacitor:
  • With air, \(C_0=\frac{\varepsilon_0 A}{d}\)
  • With a dielectric, \(C=K C_0=\frac{K \varepsilon_0 A}{d}\)
  • With a thin dielectric plate, \(C=\frac{\varepsilon_0 A}{d-t+\frac{t}{K}} \text { for } t<d\)
  • With a thin metal plate, \(C=\frac{\varepsilon_0 A}{d-t} \text { for } t<\underline{d} \text { and } K_{\text {metal }}=\infty\)
• Equivalent capacitance:
  • In series, \(\frac{1}{C_s}=\frac{1}{C_1}+\frac{1}{C_2}+\ldots\)
  • In parallel, C_p = C₁ + C₂ + ….
    C_s is less than the least in the combination, C_p is greater than the greatest in the combination.

“state coulomb’s law “