Oscillation And Waves – Simple Harmonic Motion
Motion Of A Body In A Tunnel Through The Center Of The Earth
Let the earth be considered as a sphere of uniform density (same density at every part of the earth). Let AB be the diameter of the earth. A frictionless tunnel is imagined along AB. (Such a tunnel has no physical existence.)
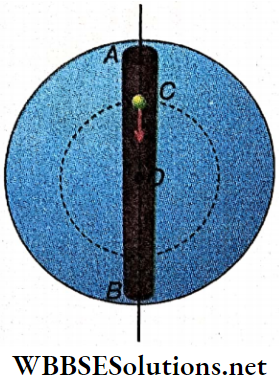
To show the characteristic features of the acceleration due to gravity below the surface of the earth, such a tunnel is imagined. It can be shown that on releasing a body through the tunnel, the body will execute a simple harmonic motion.
Let a body of mass m be dropped in the tunnel AB. After some time, it reaches point C, at a distance x from the center of the earth. Taking O as the center and OC = x as the radius, a sphere is drawn. Here only the gravitational force due to the sphere of radius x is effective and the spherical shell of thickness AC(=R-x) applies no force on the body.
Hence, the force of attraction on the body at C,
F = \(\frac{G \times \text { mass of sphere of radius } x \times m}{x^2}\)
= \(G \cdot \frac{\frac{4}{3} \pi x^3 \rho m}{x^2}(\rho=\text { average density of the earth })\)
= \(\frac{4}{3} \pi G \rho m x\)
∴ Acceleration produced a = \(\frac{F}{m}=\frac{4}{3} \pi G \rho x\)…(1)
Hence, aαx [as \(\frac{\pi}{3}\)Gρ = constant]
Therefore,
- The acceleration of the body is directly proportional to its distance from the centre of the earth and
- It is always directed towards the center of the earth
Since, the gravitational force of attraction is always directed towards the center of the earth, but the distance is always measured away from the center of the earth, we may write, a ∝ -x.
Whenever the acceleration of a body with respect to a fixed point fulfills conditions (1) and (2) simultaneously, the body executes simple harmonic motion.
Time period of this motion, \(T=2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}}=2 \pi \sqrt{\frac{x}{a}}\)
From equation(1), \(\frac{x}{a}=\frac{3}{4 \pi G \rho}\)
∴ \(T=2 \pi \sqrt{\frac{3}{4 \pi G \rho}}\)=\(2 \pi \sqrt{\frac{3 \times 4 \pi R G}{4 \pi G \times 3 g}}\) as \(\rho=\frac{3 g}{4 \pi R G}\)
∴ T = \(2 \pi \sqrt{\frac{R}{g}}\)
Hence, the time period does not depend on the mass of the body.
Taking the radius of the earth R = 6400 km and the acceleration due to gravity on the surface of the earth g = 9.8 m · s-2,
T = \(2 \pi \sqrt{\frac{6400 \times 10^3}{9.8}}=1 \mathrm{~h} 24 \mathrm{~min} 38 \mathrm{~s}\)
The body will move from A to B in exactly half of the above-calculated time. Thus, anybody, from a certain point on the earth’s surface, will reach exactly the opposite endpoint in about 42 min.
If the tunnel were not through the center, but along a straight line joining any two points on the earth’s surface, the body would still have executed simple harmonic motion of the same period and would have taken 42 min to reach one end from the other.
Oscillation And Waves – Simple Harmonic Motion
Motion Of A Body In A Tunnel Through The Center Of The Earth Numerical Examples
Example 1. The normal length of a steel spring is 8 cm. Keeping one end of the spring fixed at a point, if a weight is attached to the other end, its length becomes 14 cm. The weight is pulled down slightly and then released. Find the time period of oscillation of the spring.
Solution:
The increase in length of the spring for the mass m is, l = 14- 8 = 6 cm.
So, force constant, k (force required for a unit increase in length) = \(\frac{m g}{6} \mathrm{dyn} \cdot \mathrm{cm}^{-1}\)
Time period, T = \(2 \pi \sqrt{\frac{m}{k}}=2 \pi \sqrt{\frac{m}{\frac{m}{6}}}\)
= \(2 \pi \sqrt{\frac{6}{g}}=2 \times 3.14 \times \sqrt{\frac{6}{980}}=0.49 \mathrm{~s}\)
Example 2. Two bodies of mass m1 and m2 are suspended from a weightless spring. The force constant of the spring is k. When die bodies are in an equilibrium position, the body of mass m1 is taken away from the system such that the equilibrium condition of the system is not disturbed at that very moment. Determine the angular frequency and the amplitude of motion for the body of mass m2.
Solution:
If the increase in length of the spring due to the two masses m1 and m2, is l. then
k = \(\frac{\left(m_1+m_2\right) g}{l} \text { or, } l=\frac{\left(m_1+m_2\right) g}{k}\)
Similarly for the mass m2 increase in length, \(l_2=\frac{m_2 g}{k}\).
This l2 is the increase in length for the final equilibrium position. So with the mass m1, displacement from the equilibrium position = amplitude of motion
= \(l-l_2=\frac{\left(m_1+m_2\right) g}{k}-\frac{m_2 g}{k}=\frac{m_1 g}{k}\)
Since only the mass m2 vibrates, the angular frequency & is given by, \(\omega^2=\frac{k}{m_2} \text { or, } \omega=\sqrt{\frac{k}{m_2}} \text {. }\)
Example 3. A spring is elongated by 2 cm due to a 80 g mass attached to it Another body of mass 600 g is attached to the end of the spring and it is displaced by 8 cm from its equilibrium position. Calculate the energy of the system in this position. Considering the principle of conservation of energy, determine the velocity of the body when it is at a distance of 4 cm.
Solution:
The force constant of the spring, k = \(\frac{80 \times 980}{2}=40 \times 980 \mathrm{dyn} \cdot \mathrm{cm^-1}\)
Mass, m = 600 g; amplitude, A = 8 cm.
Total energy, E = maximum potential energy = potential energy at the ends of the path of the motion = \(\frac{1}{2} k t^2=\frac{1}{2} \times 40 \times 980 \times(8)^2=1254400 \mathrm{erg}=0.12544 \mathrm{~J}\)
Even x = 4 cm, the total energy remains unchanged, If v is the velocity at this position, then \(\frac{1}{2} m v^2+\frac{1}{2} k x^2=\frac{1}{2} \times 40 \times 980 \times 64\)
or, \(\frac{1}{2} m v^2 =\frac{1}{2} \times 40 \times 980 \times 64-\frac{1}{2} \times 40 \times 980 \times 4^2\)
= \(\frac{1}{2} \times 40 \times 980 \times(64-16)\)
= \(\frac{1}{2} \times 40 \times 980 \times 48\)
or, \(t^2=\frac{40 \times 980 \times 48}{m}=\frac{40 \times 980 \times 48}{600}=4 \times 49 \times 16\)
or, v = \(\sqrt{4 \times 49 \times 16}=2 \times 7 \times 4=56 \mathrm{~cm} \cdot \mathrm{s}^{-1} .\)
Example 4. A particle is executing SHM. If time is measured from when it is at one end of its path of motion, calculate the ratio of its kinetic energy to the potential energy at t = \(\frac{T}{12}\). Here T is the time padod of the motion. Suppose the initial phase is zero.
Solution:
If time is measured from when the particle is at one end of the path of motion, then the equation of SHM is x = Acosωt.
If t = \(\frac{T}{12}\), then \(x=A \cos \frac{2 \pi}{T} \cdot \frac{T}{12}=A \cos \frac{\pi}{6}=\frac{A \sqrt{3}}{2}=\frac{\sqrt{3}}{2} A\)
Kinetic energy of the particle at that time, K = \(\frac{1}{2} m l^2=\frac{1}{2} m \omega^2\left(A^2-x^2\right)\)
= \(\frac{1}{2} m \omega^2\left(A^2-\frac{3 A^2}{4}\right)=\frac{1}{8} m \omega^2 A^2\)
The potential energy of the particle at that time,
U = \(\frac{1}{2} m \omega^2 x^2=\frac{1}{2} m\left(\omega^2 \cdot \frac{3 A^2}{4}\right)=\frac{3}{8} m \omega^2 A^2\)
∴ \(\frac{K}{U}=\frac{\frac{1}{8} m \omega^2 A^2}{\frac{3}{3} m \omega^2 A^2}=\frac{1}{3} \quad therefore \quad K: U=1: 3 \)
Example 5. When a man of mass 6okg sist inside a car, the center of gravity of the car descends by 0.3 cm, If the mass of the car is 1000kg, calculate the frequency of oscillation of the empty car.
Solution:
Frequency of oscillation of the car, n = \(\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\)
The force constant of the spring of the car, k = \(\frac{F}{x}=\frac{60 \times 9.8}{0.3 \times 10^{-2}}\)=\(196 \times 10^3 \mathrm{~N} \cdot \mathrm{m}^{-1}\)
∴ Frequency, n = \(\frac{1}{2 \times \frac{22}{7}} \sqrt{\frac{196 \times 10^3}{1000}}\)
= \(\frac{14 \times 7}{44}=2.23 \mathrm{~s}^{-1} .\)
Example 6. A wooden block of cross-sectional area 10 cm² is floating vertically on water. The volume of the immersed portion of the block is 200 cm³. The block is depressed slightly inside the water and then released. Calculate the time period of vibration of the block.
Solution:
Volume of displaced water = 200 cm³
∴ Mass of displaced water = 200 g, and mass of the wooden block = 200 g
Let the block be depressed inside water through x cm and then released.
∴ Upward restoring force on the block, F = 10x x 1 x g = 10xg
∴ Acceleration of the block, a = \(\frac{F}{m}=\frac{10 x g}{200}=\frac{x g}{20}\)
∴ Time period of vibration of the block, T = \(2 \pi \sqrt{\frac{x}{a}}=2 \pi \sqrt{\frac{20}{g}}=2 \pi \sqrt{\frac{20}{980}}=0.897 \mathrm{~s} .\)
Example 7. A small coin is kept on a horizontal platform. The platform oscillates vertically with a time period of 0.5 s. What should be the maximum amplitude of vibration so that the coin always remains in contact with the platform?
Solution:
The coin will always remain in contact with the platform if the downward acceleration of the platform does not exceed the acceleration of the coin due to gravity.
If A is the maximum amplitude of vibration, then ω²A = g
or, A = \(\frac{g}{\omega^2}=\frac{g}{\left(\frac{2 \pi}{T}\right)^2}=\frac{g T^2}{4 \pi^2}\)
= \(\frac{9.8 \times(0.5)^2}{4 \times(3.14)^2}=0.06205 \mathrm{~m} \approx 0.06 \mathrm{~m}\)
Example 8. Two identical bodies, each of mass m, are connected by a spring having constant k and they are placed on a frictionless floor. The spring is compressed a little and then released. What will be the frequency of oscillation of the system?
Solution:
If the maximum compression of the spring from its position of equilibrium is A, then restoring force = -kA.
In this condition, the whole energy of the spring is its potential energy = \(\frac{1}{2}\)kA².
Again, during oscillation, when the two bodies just cross the position of equilibrium, the potential energy becomes zero and the total energy is then equal to the kinetic energy of the two bodies. At this stage, the velocity of each body = maximum velocity = ω\(\frac{A}{2}\), where = ω angular frequency and \(\frac{A}{2}\) = amplitude of vibration of each body.
∴ Kinetic energy of the two bodies = \(\frac{1}{2} m \omega^2\left(\frac{A}{2}\right)^2+\frac{1}{2} m \omega^2\left(\frac{A}{2}\right)^2=\frac{1}{4} m \omega^2 A^2 .\)
According to the principle of conservation of energy, \(\frac{1}{2} k A^2=\frac{1}{4} m \omega^2 A^2 \quad \text { or, } \omega=\sqrt{\frac{2 k}{m}} \text {. }\)
∴ Frequency of oscillation of the system = \(\frac{\omega}{2 \pi}=\frac{1}{2 \pi} \sqrt{\frac{2 k}{m}} .\)
Example 9. The time period of a body of mass M executing SHM, connected to a spring, is 2 s. If the mass of the body is increased by 2 kg, its time period increases by 1 s. Considering that Hooke’s law is obeyed, calculate the initial mass M.
Solution:
The time period of SHM executed by the body connected to the spring, \(T=2 \pi \sqrt{\frac{M}{k}}[/latex; k = force constant of the spring
So, in the first case, 2 = [latex]2 \pi \sqrt{\frac{M}{k}}\)…(1)
and in the second case, 2 + 1 = 3 = \(2 \pi \sqrt{\frac{M+2}{k}}\)…(2)
Dividing (2) by (1) we get, \(\frac{3}{2}=\sqrt{\frac{M+2}{M}} \text { or, } \frac{9}{4}=\frac{M+2}{M}\)
or, 9M = 4M + 8 or, M = 1.6 kg
Example 10. The time period of a spring of negligible mass, with a mass M hanging from it, is T. The time period changes to \(\frac{5T}{3}\) on attaching an additional mass m to it. Find out the value of \(\frac{m}{M}\)
Solution:
From the formula, T = \(2 \pi \sqrt{\frac{m}{k}}\), we get, \(\frac{T}{T^{\prime}}=\sqrt{\frac{m}{m^{\prime}}}\)
For the given cases, \(\frac{T}{\frac{5 T}{3}}=\sqrt{\frac{M}{M+m}} \text { or, } \frac{3}{5}=\sqrt{\frac{M}{M+m}}\)
or, \(\frac{M+m}{M}=\frac{25}{9} \text { or, } 1+\frac{m}{M}=\frac{25}{9}\)
∴ \(\frac{m}{M}=\frac{25}{9}-1=\frac{16}{9} .\)
Example 11. A smooth-walled tunnel is made along the straight line connecting any two points on the earth’s surface. A body is released at one end of the tunnel. Considering the earth to be a sphere of uniform density, calculate the time period of oscillation of the partide for its simple harmonic motion.
Solution:
Let a body of mass m be dropped into the tunnel AB and after some time, suppose the body reaches C. Force of attraction on the body at C,
F= \(\frac{G \cdot \frac{4}{3} \pi r^3 \rho m}{r^2}[\rho=\text { average density of the earth }]\)
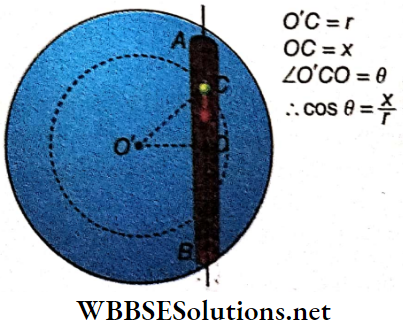
= \(\frac{4}{3} \pi G \rho \cdot m r=\frac{g}{R} m r\)
because \(\rho=\frac{3 g}{4 \pi R G}\)(R= radius of the earth)
F acts along \(C O^{\prime}\). So component of F along CO,
F \(\cos \theta=\frac{m g r}{R} \times \frac{x}{r}=\frac{m g}{R} x\)
∴ Acceleration of the body a = \(\frac{F \cos \theta}{m}=\frac{g}{R} x\)…(1)
Hence, a ∝ x (g/R is a consant)
Therefore,
- The acceleration of the body is directly proportional to its distance from O
- This acceleration is always directed toward the center O of the tunnel. Hence, it executes a simple harmonic motion, and its time period
T = \(2 \pi \sqrt{\frac{x}{a}}\)
From, (1) and (2), T = \(2 \pi \sqrt{\frac{R}{g}}\)
Example 12. A particle at the end of a spring executes SHM with a period t1, while the corresponding period for another spring is t2. If the period of oscillation when the two springs are connected in series is T, then prove that, \(t_1^2+t_2^2=T^2\)
Solution:
Let the mass of the particle be m and the spring constants of the springs be k1 and k2.
In first case, \(t_1=2 \pi \sqrt{\frac{m}{k_1}} \text { or, } t_1^2=4 \pi^2\left(\frac{m}{k_1}\right)\)…(1)
In second case, \(t_2=2 \pi \sqrt{\frac{m}{k_2}} \text { or, } t_2^2=4 \pi^2\left(\frac{m}{k_2}\right)\)…(2)
In series the equivalent spring constant is k,
Then, \(\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2} \quad \text { or, } k=\frac{k_1 k_2}{k_1+k_2}\)
∴ Time period of the combination,
T = \(2 \pi \sqrt{\frac{m}{k}}\)=\(2 \pi \sqrt{\frac{m\left(k_1+k_2\right)}{k_1 k_2}}\)
or, \(T^2=\frac{4 \pi^2 m\left(k_1+k_2\right)}{k_1 k_2}\)
adding (1) and (2) we get, \(t_1^2+t_2^2=4 \pi^2\left(\frac{m}{k_1}+\frac{m}{k_2}\right)=4 \pi^2 m\left(\frac{1}{k_1}+\frac{1}{k_2}\right)\)
= \(4 \pi^2 m\left(\frac{k_1+k_2}{k_1 k_2}\right)\)
∴ \(t_1^2+t_2^2=T^2 \text { (Proved). }\)

