Centre of Mass and Rotation
Question 1. Consider a system of two particles of masses m1 and m2. If is pushed towards the centre of mass of the system through a distance d, by what distance should the second particle be moved so as to keep the position of the centre of mass unchanged?
- \(\left(\frac{m_1}{m_1+m_2}\right) d\)
- \(\left(\frac{m_2}{m_1}\right) d\)
- \(\left(\frac{m_1}{m_2}\right) d\)
- \(\left(\frac{m_2}{m_1+m_2}\right) d\)
Answer: 3. \(\left(\frac{m_1}{m_2}\right) d\)
The position of the centre of mass is given by
⇒ \(x_{\mathrm{CM}}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
For \(\Delta x_{\mathrm{CM}}=0\), we have
⇒ \(\frac{m_1 \Delta x_1+m_2 \Delta x_2}{m_1+m_2}=0\)
or, m1d+ m2ΔX2 = 0
or, \(\Delta x_2=-\left(\frac{m_1}{m_2}\right) d\)
∴ \(\left|\Delta x_2\right|=\left(\frac{m_1}{m_2}\right) d\)
Question 2. A cubical block of ice of mass m and edge L is placed in a big plate of mass M. If the whole ice melts, and the centre of mass of the ice-tray system will come down by
- \(\frac{M L}{m+M}\)
- \(\frac{m L}{2(m+M)}\)
- \(\frac{M L}{2(M+m)}\)
- \(\frac{m L}{m+M}\)
Answer: 2. \(\frac{m L}{2(m+M)}\)
If the block of ice melts fully, water will spread over the plate. So, the CM will go down by \(\frac{L}{2}\), while the position of the CM of the plate will remain unchanged.
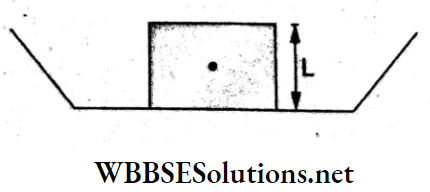
Since \(x_{\mathrm{CM}}=\frac{m x_1+M x_2}{m+M}\) the shiftin the CM of the system will be
⇒ \(\Delta x_{\mathrm{CM}}=\frac{1}{m+M}\left(m \Delta x_1+M \Delta x_2\right)\)
⇒ \(\frac{1}{m+M}\left(m \cdot \frac{L}{2}+M \cdot 0\right)\)
= \(\frac{m L}{2(m+M)}\)
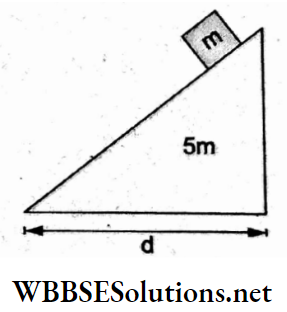
Question 3. A block of mass m is placed on the top of a bigger wedge of mass 5m, as shown in the figure. All the surfaces are frictionless. The system is released from rest. At the instant when the smaller block reaches the ground, the bigger block will move through
- \(\frac{d}{6}\) towards left
- \(\frac{d}{6}\) towards right
- \(\frac{d}{5}\) towards left
- \(\frac{d}{5}\) towards right
Answer: 2. \(\frac{d}{5}\) towards left
Since there is no external force along the horizontal, the net displacement of the CM of the system will be zero.
Thus,
⇒ \(x_{\mathrm{CM}}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}=0\)
∴ \(\Delta x_{\mathrm{CM}}=0=\frac{1}{m_1+m_2}\left(m_1 \Delta x_1+m_2 \Delta x_2\right)\)
Here, m1 = m, m2 = 5m, Δx1=d-x and Δx2 = x, where x = displacement of the wedge to the right so as to keep the position of the CM unchanged.
Thus,
m(d-x) = 5mx
x =\(\frac{d}{6}\) (towards right).
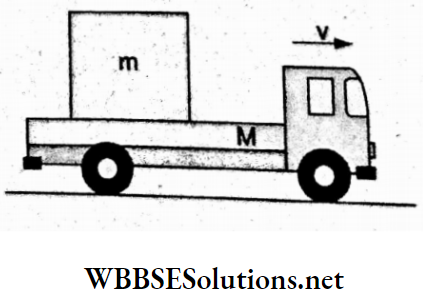
Question 4. On a truck of mass M, moving with uniform velocity on a horizontal road, a rock of mass m drops from above and strikes the floor of the truck vertically. The final velocity of the truck will be
- \(\frac{M v}{m}\)
- \(\frac{(M+m) v}{m}\)
- \(\frac{M v}{M+m}\)
- \(\frac{m v}{M+m}\)
Answer: 3. \(\frac{M v}{M+m}\)
Conserving the linear momentum along the horizontal,
we have Mv =(M+ m)v’
⇒ \(v^{\prime}=\frac{M v}{M+m}\)
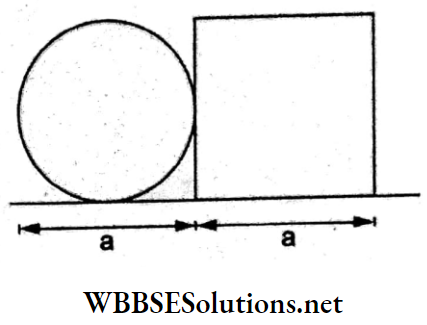
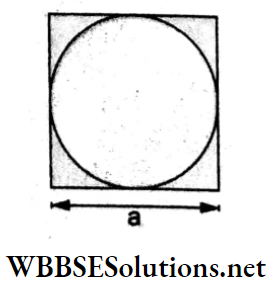
Question 5. A circular plate of diameter a is kept in contact with a square plate of edge in the same plane, as shown in the figure. The surface density of the material and the thickness are the same everywhere. The centre of mass of the combined system will be
- Inside the circular plate
- Inside the square plate
- At the point of contact
- At the midpoint of the radius of the circular plate
Answer: 2. Inside the square plate
Let p be the surface mass density. So, the mass of the circular plate,
m1 = \(\pi\left(\frac{a^2}{4}\right) \rho\) and mass of the square plate = m2 = a²p.
Taking the centre of the circular plate as the origin,
⇒ \(x_{\mathrm{CM}}=\frac{m_1 \cdot 0+m_2 x_2}{m_1+m_2}\)
=\(\frac{a^2 \rho a}{\pi\left(\frac{a^2}{4}\right) \rho+a^2 \rho}\)
=\(\frac{a}{1+\frac{\pi}{4}}=\frac{a}{1.785}\)
=\(0.56 a>\frac{a}{2}\)
Thus, the CM lies inside the square plate
Question 6. Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised vertically through 7 cm. By what distance should the second block be moved so as to raise the centre of mass of the system by 1 cm?
- 1 cm downwards
- 1 cm upwards
- 2 cm downwards
- 2 cm upwards
Answer: 1. 1 cm downwards
⇒ \(x_{\mathrm{CM}}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
⇒ \(\Delta x_{\mathrm{CM}}=\frac{m_1 \Delta x_1+m_2 \Delta x_2}{m_1+m_2}\)
Hence, mx- 10 kg, m2 = 30 kg, AxCM =1 cm (upward) and Ax1-7 cm.
∴ \(1 \mathrm{~cm}=\frac{(10 \mathrm{~kg})(7 \mathrm{~cm})+(30 \mathrm{~kg}) \Delta x_2}{40 \mathrm{~kg}}\)
30 ΔX2 = 40 cm- 70 cm
= -30 cm
Δx2 =-1 cm.
Hence, the second block must be moved by 1 cm downwards.
Question 7. The balloon (of mass M), the light string (of length L) and the monkey (of mass m) shown in the figure are at rest in the air. If the monkey reaches the top of the rope, the balloon will descend vertically through the distance
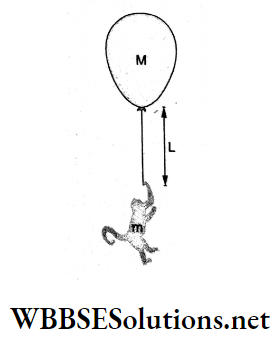
- \(\frac{m L}{M}\)
- \(\frac{M L}{m}\)
- \(\frac{M L}{M+m}\)
- \(\frac{m L}{M+m}\)
Answer: 4. \(\frac{m L}{M+m}\)
Since the system is initially at rest, the position of the CM of the system must be unchanged. Let the balloon move down by x. Then,
Mx = m(L- x)
=> (M + m)x= mL
⇒ \(x=\frac{m L}{M+m}\)
Question 8. A boy of mass m is standing on one end of a long boat of mass M and length L. Neglecting friction, how far does the boat move if the boy slowly moves to the other end?
- \(\frac{m L}{M}\)
- \(\frac{M L}{m}\)
- \(\frac{m L}{M+m}\)
- \(\frac{M L}{m+M}\)
Answer: 3. \(\frac{m L}{M+m}\)
As the boy moves towards the right, let the boat move towards the left by x so as to keep the position of the CM of the system unchanged.
Thus,
m(L-x)=Mx
=> mL = (M+ m)x
⇒ \(x=\frac{m L}{M+m}\)
Question 9. The linear mass density of a rod of length 3m is directly proportional to the distance x from one end. The distance of the centre of mass of the rod from that end will be
- 1.5m
- 2 m
- 2.5 m
- 3.0m
Answer: 2. 2 m
⇒ \(x_{\mathrm{CM}}=\frac{1}{M} \int_0^L x d m\), where the total mass is
⇒ \(M=\int d m=\int_0^L \lambda x d x=\frac{\lambda L^2}{2}\)
Now, \(\int_0^L x d m=\int_0^L x(\lambda x d x)=\lambda \int_0^L x^2 d x=\frac{\lambda L^3}{3}\)
⇒ \(x_{\mathrm{CM}}=\frac{\frac{\lambda L^3}{3}}{\frac{\lambda L^2}{2}}=\frac{2}{3} L=\frac{2}{3} \cdot(3 \mathrm{~m})\)
= 2m.
Question 10. Three particles of the same mass lie in the xy-plane. The x and y-coordinates of their positions are given by (1, 1), (2, 2) and (3, 3) respectively. The x and y-coordinates of the centre of mass of the system are given by
- (1,2)
- (2,2)
- (2, 3)
- (4,5)
Answer: 2. (2,2)
The x- and y-coordinates of the CM are respectively,
⇒ \(x_{\mathrm{CM}}=\frac{1}{3 m}(m \cdot 0+m \cdot a+m \cdot 0)=\frac{a}{3}\)
and \(y_{\mathrm{CM}}=\frac{1}{3 m}(m \cdot 0+m \cdot 0+m \cdot b)=\frac{b}{3}\)
= \(\frac{1}{3}\) (1+2+3)
= 2.
Thus, the x- and y-coordinates of the CM are given by (2, 2)
Question 11. Three particles, each of mass m, are placed at the vertices of a right-angled triangle OAB, as shown in the figure. If OA = a and OB = b then the position vector of the centre of mass of the given system is
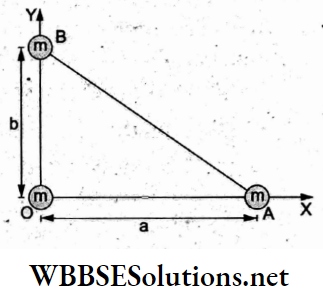
- \(\frac{1}{3}(a \hat{i}+b \hat{j})\)
- \(\frac{1}{3}(a \hat{i}-b \hat{j})\)
- \(\frac{2}{3}(a \hat{i}+b \hat{j})\)
- \(\frac{2}{3}(a \hat{i}-b \hat{j})\)
Answer: 1. \(\frac{1}{3}(a \hat{i}+b \hat{j})\)
With reference to the origin O,
⇒ \(x_{\mathrm{CM}}=\frac{1}{3 m}(m \cdot 0+m \cdot a+m \cdot 0)=\frac{a}{3}\)
and \(y_{\mathrm{CM}}=\frac{1}{3 m}(m \cdot 0+m \cdot 0+m \cdot b)=\frac{b}{3}\)
∴ the position vector of the centre of mass is
⇒ \(\vec{r}_{C M}=\left(\frac{a}{3}\right) \hat{i}+\left(\frac{b}{3}\right) \hat{j}=\frac{1}{3}(a \hat{i}+b \hat{j})\)
Question 12. Three particles, each of mass m, are placed at the vertices of an equilateral triangle of side a, as shown in the figure. The position vector of the centre of mass of the system is
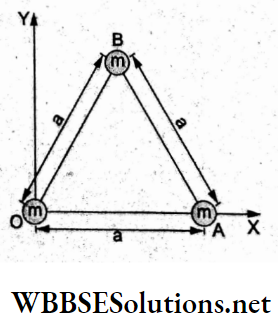
- \(\frac{a}{2}\left(\hat{i}+\frac{1}{\sqrt{3}} \hat{j}\right)\)
- \(\frac{a}{2}(3 \hat{i}+\sqrt{3} \hat{j})\)
- \(\frac{a}{2}\left(3 \hat{i}+\frac{1}{\sqrt{3}} \hat{j}\right)\)
- \(\frac{a}{2}(\hat{i}+\hat{j})\)
Answer: 1. \(\frac{a}{2}\left(\hat{i}+\frac{1}{\sqrt{3}} \hat{j}\right)\)
With reference to the origin O,
⇒ \(x_{\mathrm{CM}}=\frac{1}{3 m}\left(m \cdot 0+m \cdot a+m \cdot \frac{a}{2}\right)\)
= \(\frac{a}{2}\)
and \(y_{\mathrm{CM}}=\frac{1}{3 m}\left(m \cdot 0+m \cdot 0+m \cdot \frac{\sqrt{3}}{2} a\right)\)
= \(\frac{\sqrt{3} a}{2}\)
∴ \(\vec{r}_{\mathrm{CM}}=\left(\frac{a}{2}\right) \hat{i}+\left(\frac{\sqrt{3} a}{2}\right) \hat{j}\)
= \(\frac{a}{2}\left(\hat{i}+\frac{\sqrt{3}}{3} \hat{j}\right)\)
= \(\frac{a}{2}\left(\hat{i}+\frac{1}{\sqrt{3}} \hat{j}\right)\)
Question 13. A one-metre-long uniform-disbent at a right angle at its midpoint. The distance of the centre of mass from the centre of the rod is
- 17.7 cm
- 25.2 cm
- 34.1cm
- Zero
Answer: 1. 17.7 cm
⇒ \(x_{\mathrm{CM}}=\frac{\frac{m}{2}\left(\frac{L}{4}\right)}{m}=\frac{L}{8} \text { and } y_{\mathrm{CM}}=\frac{L}{8}\)
∴ \(\vec{r}_{\mathrm{CM}}=\frac{L}{8}(\hat{i}+\hat{j})\)
∴ the distance of the CM from O is
⇒ \(\left|\vec{r}_{\mathrm{CM}}\right|=\frac{\sqrt{2}(1 \mathrm{~m})}{8}\)
= 0.177m
= 17.7 cm.
Question 14. Two particles of mass m1 and m2, initially at rest, move towards each other under a mutual force of attraction. At any instant when their respective speeds are v1 and v2 the speed of the centre of mass of the system is
- \(\frac{m_1 v_1}{m_1+m_2}\)
- \(\frac{m_2 v_2}{m_1+m_2}\)
- \(\frac{v_1+v_2}{2}\)
- Zero
Answer: 4. Zero
Since there is no external force, the linear momentum of the system will be conserved.
The initial momentum = 0,
so, \(m_1 \vec{v}_1+m_2 \vec{v}_2=0\)
Now, the velocity of the CM is
⇒ \(\vec{v}_{\mathrm{CM}}=\frac{m_1 \vec{v}_1+m_2 \vec{v}_2}{m_1+m_2}=0\)
Question 15. Two blocks of masses 10kg and 4kg are connected by a light spring and placed on a frictionless horizontal surface. An impulse to the heavier block imparts a velocity of 14 m s-1 in the direction of the lighter block. The velocity of the centre of mass of the system is
- 5 ms-1
- 10 m s-1
- 15m s-1
- 20 m s-1
Answer: 2. 10 m s-1
Given that m1 = 10 kg and m2 = 4 kg.
The initial velocity imparted to m1 is w1 = 14m-1 and u2 = 0.
∴ the velocity of the CM of the system is
⇒ \(\vec{v}_{\mathrm{CM}}=\frac{1}{m_1+m_2}\left(m_1 \vec{u}_1+m_2 \vec{u}_2\right)\)
⇒ \(\frac{1}{14 \mathrm{~kg}}\left[(10 \mathrm{~kg})\left(14 \mathrm{~m} \mathrm{~s}^{-1}\right)+0\right]\)
= 10 ms-1.
Question 16. A wheel rotates with a constant acceleration of 2.0 rad s-2 starting from rest. The number of revolutions made in the first 10 seconds is
- 5
- 10
- 16
- 20
Answer: 3. 16
Given that angular acceleration = a = 2.0 rad s-2, time = t = 10 s and angular frequency = ω0 = 0.
For angular motion,
⇒ \(\theta=2 \pi N=\omega_0 t+\frac{1}{2} \alpha t^2=\frac{1}{2}\left(2 \mathrm{rad} \mathrm{s}^{-2}\right)\left(100 \mathrm{~s}^2\right)\)
⇒ \(N=\frac{100}{2 \pi}=15.9 \approx 16\)
Question 17. A motor wheel, accelerated uniformly from rest, rotates through 2.5 rad during the first second. The angle rotated through the next second is
- 5 rad
- 10 rad
- 7.5 rad
- 12.5 rad
Answer: 3. 7.5 rad
ω0 = θ and θ1 = 2.5 rad in the first second.
For the first second,
⇒ \(\theta_1=\omega_0 t+\frac{1}{2} \alpha t^2\)
or, \(2.5 \mathrm{rad}=\frac{1}{2} \alpha(1 \mathrm{~s})^2\)
∴ angular acceleration= α = 5.0 rad s-2.
For the first two seconds,
⇒ \(\theta_2=\frac{1}{2} \alpha(2 \mathrm{~s})^2=\frac{1}{2}(5.0)(4) \mathrm{rad}\)
= 10 rad
and \(\theta_1=\frac{1}{2} \alpha(1 s)^2=\frac{1}{2}(5)(1)\)
= 2.5 rad.
θ2 – θ1 = (10- 2.5)rad
= 7.5 rad.
Question 18. A wheel revolves about its axis with uniform angular acceleration. Starting from rest, it attains an angular velocity of 100 rev s-2 in 4 seconds. The angular acceleration of the wheel is
- 10 revs-2
- 15 revs-2
- 20 revs-2
- 25 rev s-2
Answer: 4. 25 rev s-2
⇒ \(\omega=\omega_0+\alpha t\)
⇒ \(100 \mathrm{rps}=0+\alpha(4 \mathrm{~s})\)
∴ angular acceleration= a = 25 rev s-2
Question 19. In the preceding question, the angle rotated by the wheel during the first four seconds is 6
- 200ft rad
- 400ft rad
- 100ft rad
- 300ft rad
Answer: 2. 400ft rad
⇒ \(\theta=\omega_0 t+\frac{1}{2} \alpha t^2\)
= \(0+\frac{1}{2}\left(25 \times 2 \pi \mathrm{rad} \mathrm{s}^{-2}\right)(4 \mathrm{~s})^2\)
= 400n rad.
Question 20. A disc of radius 10 cm is rotating uniformly about its axis at an angular speed of 20rad s-1. The linear speed of a point on the rim of the disc is
- 0.5 ms-1
- 1.0ms-1
- 1.5 ms-1
- 2.0 ms-1
Answer: 4. 2.0 ms-1
Angular speed = to = 20 rad s-1 and radius = r
= 10 cm
= 0.1 m.
∴ linear speed, v = ωr
= (20rad s-1)(0.1 m)
= 2m s-1
Question 21. In the preceding question, what is the ratio of the linear speed at the rim to that at the midpoint of the radius of the disc?
- 1:1
- 1:2
- 2:1
- None of these
Answer: 3. 2:1
⇒ \(\frac{v_r}{v_{r / 2}}=\frac{\omega r}{\omega(r / 2)}=2: 1\)
Question 22. Three-point masses m1 m2 and m3 are located at the vertices of an equilateral triangle of side a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
- \(\left(m_1+m_2\right) \frac{a^2}{4}\)
- \(\left(m_2+m_3\right) \frac{a^2}{4}\)
- \(\left(m_1+m_3\right) \frac{a^2}{4}\)
- \(\left(m_1+m_2+m_3\right) \frac{a^2}{4}\)
Answer: 2. \(\left(m_2+m_3\right) \frac{a^2}{4}\)
The mass lies on the axis of rotation, so it does not contribute to the moment of inertia.
∴ \(I=m_2 r_2^2+m_3 r_3^2\)
⇒ \(\left(m_2+m_3\right)\left(\frac{a}{2}\right)^2\)
⇒ \(\left(m_2+m_3\right) \frac{a^2}{4}\)
Question 23. Four particles of masses m, 2m, 3m and 4m are connected by a rod of negligible mass, as shown in the figure. The radius of gyration of the system about the axis AB is
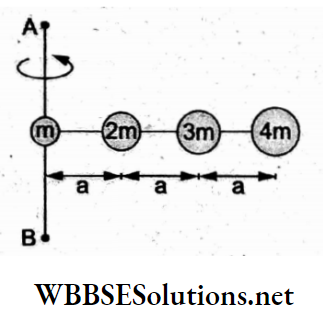
- 2a
- √5a
- √3a
- √2a
Answer: 2. √5a
The moment of inertia of the given system about the axis AB is
I = m(0) + 2m(a2) + 3m(2a)2 + 4m(3a)2
= 50ma2
= (m + 2m + 3m + 4m)k2
= 10mk2.
∴ the radius of gyration = k
⇒ \(\sqrt{\frac{50}{10} a^2}=\sqrt{5} a\)
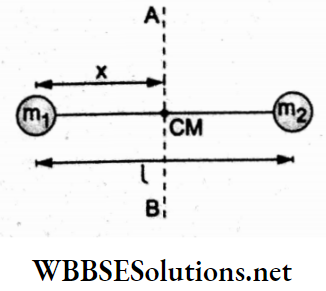
Question 24. A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the length of the rod and passing through the centre of mass is
- \(\left(m_1+m_2\right) l^2\)
- \(\sqrt{m_1 m_2} l^2\)
- \(\left(\frac{m_1 m_2}{m_1+m_2}\right) l^2\)
- \(\left(\frac{m_1+m_2}{m_1 m_2}\right) l^2\)
Answer: 3. \(\left(\frac{m_1 m_2}{m_1+m_2}\right) l^2\)
Let x be the distance of the CM from the A; m1 end. So,
⇒ \(x=\frac{m_1 \cdot 0+m_2 l}{m_1+m_2}=\left(\frac{m_2}{m_1+m_2}\right) l\)
∴ the distance between the CM and m2,
⇒ \(l-x=\left(\frac{m_1}{m_1+m_2}\right) l\)
Hence, the moment of inertia of the given system about AB will be
⇒ \(I=m_1 x^2+m_2(l-x)^2\)
⇒ \(m_1 \cdot \frac{m_2{ }^2 l^2}{\left(m_1+m_2\right)^2}+m_2 \cdot \frac{m_1{ }^2 l^2}{\left(m_1+m_2\right)^2}=\left(\frac{m_1 m_2}{m_1+m_2}\right) l^2\)
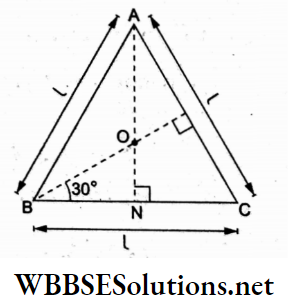
Question 25. Three thin metal rods, each of mass M and length l are welded to form an equilateral triangle. The moment of inertia of the composite system about an axis passing through the centre of mass of the structure and perpendicular to its plane is
- \(\frac{M l^2}{2}\)
- \(\frac{M l^2}{4}\)
- \(\frac{M l^2}{8}\)
- \(\frac{M l^2}{12}\)
Answer: 1. \(\frac{M l^2}{2}\)
From the given figure,
⇒ \(\frac{O N}{B N}=\tan 30^{\circ}\)
⇒ \(O N=B N \tan 30^{\circ}=\frac{l}{2 \sqrt{3}}\)
The moment of inertia of BC about an axis through N and perpendicular to the plane of the rods is
⇒ \(I_{\mathrm{N}}=\frac{1}{12} M l^2\)
From the parallel-axes theorem,
⇒ \(I_{\mathrm{O}}=I_{\mathrm{N}}+M(O N)^2=\frac{M l^2}{12}+M\left(\frac{l}{2 \sqrt{3}}\right)^2=\frac{M l^3}{6}\)
For the total system comprising the triangle,
⇒ \(I=3 I_{\mathrm{O}}=3\left(\frac{M l^2}{6}\right)=\frac{M l^2}{2}\)
Question 26. Four metal rods, each of mass M and length L, are welded to form a square-shaped structure ABCD, as shown in the figure. The moment of inertia of the composite structure about the file axis bisecting the rods AB and CD and coplanar with the structure is
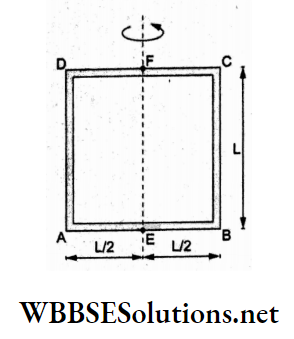
- \(\frac{M L^2}{6}\)
- \(\frac{M L^2}{3}\)
- \(\frac{M L^2}{12}\)
- \(\frac{2}{3} M L^2\)
Answer: 4. \(\frac{2}{3} M L^2\)
About the given axis, the moment of inertia of AB is
⇒ \(I_{\mathrm{AB}}=\frac{M L^2}{12}\),
that for \(\mathrm{BC} \text { is } I_{\mathrm{BC}}=M\left(\frac{L}{2}\right)^2=\frac{M L^2}{4}\)
that for \(\mathrm{CD} \text { is } I_{\mathrm{CD}}=\frac{M L^2}{12}\),
and that for \(\mathrm{AD} \text { is } I_{\mathrm{AD}}=\frac{M L^2}{4}\)
∴ the moment of inertia of the system is
⇒ \(I=2\left(\frac{M L^2}{4}\right)+2\left(\frac{M L^2}{12}\right)=\frac{2}{3} M L^2\)
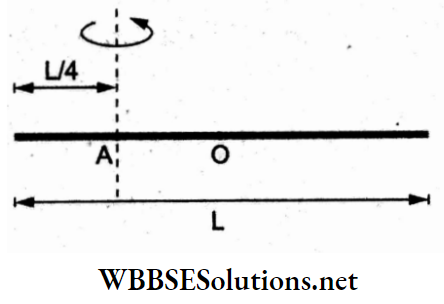
Question 27. The moment of inertia of a thin rod of mass M and length L about an axis passing perpendicularly at a distance \(\frac{L}{4}\) from one end of the rod is
- \(\frac{7}{48} M L^2\)
- \(\frac{1}{3} M L^2\)
- \(\frac{1}{12} M L^2\)
- \(\frac{1}{8} M L^2\)
Answer: 1. \(\frac{7}{48} M L^2\)
The moment of inertia of the rod about the axis through the centre of mass (O) is
⇒ \(I_{\mathrm{CM}}=\frac{M L^2}{12}\)
∴ the moment of inertia about the parallel axis through Ais.
⇒ \(I_{\mathrm{A}}=I_{\mathrm{CM}}+M d^2=\frac{M L^2}{12}+M\left(\frac{L}{4}\right)^2\)
=\(\frac{7}{48} M L^2\)
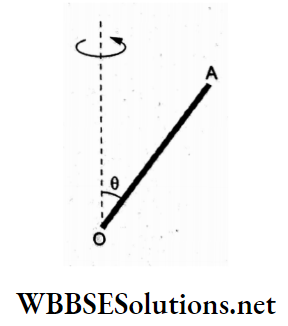
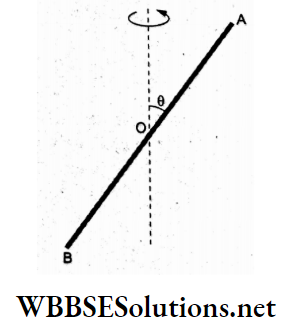
Question 28. A uniform rod OA of mass M and length L is inclined at an angle θ to the vertical. What is its moment of inertia about the vertical axis passing through its end O, as shown in the figure?
- \(\frac{1}{3} M L^2\)
- \(\frac{1}{3} M L^2 \sin ^2 \theta\)
- \(\frac{1}{3} M L^2 \cos ^2 \theta\)
- \(\frac{1}{12} M L^2\)
Answer: 2. \(\frac{1}{3} M L^2 \cos ^2 \theta\)
The mass of an element dx at a distance x from one end O is dm = \(\frac{M}{L}\)dz, and its perpendicular distance from the axis of
AN= OA sin θ = xsin θ.
∴ the moment of inertia is
⇒ \(I=\int d^2 d m=\int_0^L(x \sin \theta)^2\left(\frac{M}{L} d x\right)\)
⇒ \(\frac{M}{L}\left(\sin ^2 \theta\right) \frac{L^3}{3}=\frac{1}{3} M L^2 \sin ^2 \theta\)
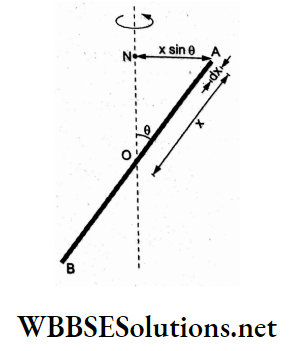
Question 29. A uniform rod AB of mass M and length L is inclined at an angle θ to the vertical. What is its moment of inertia about the vertical axis passing through its midpoint O, as shown in the figure?
- \(\frac{1}{3} M L^2\)
- \(\frac{1}{12} M L^2\)
- \(\frac{1}{12} M L^2 \sin ^2 \theta\)
- \(\frac{1}{12} M L^2 \cos ^2 \theta\)
Answer: 3. \(\frac{1}{12} M L^2 \sin ^2 \theta\)
As solved in the preceding question,
⇒ \(d I=\left(\frac{M}{L} d x\right)(x \sin \theta)^2\)
For the total,
⇒ \(I=\left(\frac{M}{L} \sin ^2 \theta\right)_{-l / 2}^{l / 2} x^2 d x\)
⇒ \(2\left(\frac{M}{L} \sin ^2 \theta\right)\left[\frac{x^3}{3}\right]_0^{l / 2}\)
⇒ \(\frac{1}{12} M L^2 \sin ^2 \theta\)
Question 30. Two identical uniform rods, each of mass M and length L, are welded together at their centre and placed in a horizontal plane. The rods are inclined at an angle of θ, as shown in the figure. The moment of inertia of the combination about a vertical axis (perpendicular to the plane of the rods) passing through their midpoint O is
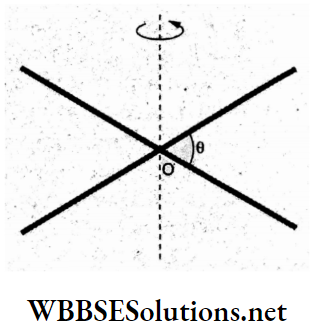
- \(\frac{1}{3} M L^2\)
- \(\frac{1}{6} M L^2\)
- \(\frac{1}{12} M L^2 \sin ^2 \theta\)
- \(\frac{1}{6} M L^2 \cos ^2 \theta\)
Answer: 2. \(\frac{1}{6} M L^2\)
The moment of inertia of each rod about the given axis is
⇒ \(\frac{M L^2}{12}\)
The moment of inertia is a scalar quantity and does not depend on their inclination θ. So,
⇒ \(I_{\text {net }}=2 I=2\left(\frac{M L^2}{12}\right)\)
=\(\frac{M L^2}{6}\)
Question 31. A thin rod AB of mass M and length L is hinged at one end A to a horizontal floor. It is gently allowed to fall from its initial vertical position. The angular velocity of the rod when its free end strikes the floor is
- \(2 \sqrt{\frac{g}{L}}\)
- \(\sqrt{\frac{2 g}{L}}\)
- \(\sqrt{\frac{g}{L}}\)
- \(\sqrt{\frac{3 g}{L}}\)
Answer: 4. \(\sqrt{\frac{3 g}{L}}\)
As the rod falls, its PE is converted to rotational KE. Thus,
⇒ \(M g \cdot \frac{L}{2}=\frac{1}{2} I \omega^2\)
⇒ \(\frac{1}{2}\left(\frac{1}{3} M L^2\right) \omega^2\)
⇒ \(\omega=\sqrt{\frac{3 g}{L}}\)
Question 32. A uniform thin wire of length L and linear mass density X is bent into a circular loop. The moment of inertia of the loop about its tangent is
- \(\frac{\lambda L^3}{8 \pi^2}\)
- \(\frac{3 \lambda L^3}{8 \pi^2}\)
- \(\frac{\lambda L^3}{16 \pi^2}\)
- \(\frac{\lambda L^3}{2 \pi^2}\)
Answer: 2. \(\frac{3 \lambda L^3}{8 \pi^2}\)
The moment of inertia of a circular loop about its diameter is given by
⇒ \(I_{\mathrm{dia}}=\frac{1}{2} M R^2\),
where \(M=\lambda L \text { and } R=\frac{L}{2 \pi}\) =radius.
∴ the moment of inertia about the tangents given by
⇒ \(I_{\mathrm{tan}}=I_{\mathrm{dia}}+M R^2\)
=\(\frac{3}{2} M R^2=\frac{3}{2}(\lambda L)\left(\frac{L}{2 \pi}\right)^2\)
=\(\frac{3 \lambda L^3}{8 \pi^2}\)
Question 33. A tube of uniform cross-section and length L is completely filled with an incompressible liquid of mass M and closed at both ends. The tube is then revolved in a horizontal plane about an axis passing perpendicularly through its one end with uniform angular velocity ω. The force exerted by the liquid at the other end is
- \(\frac{1}{4} M \omega^2 L\)
- \(\frac{1}{2} M \omega^2 L\)
- \(\omega^2 L\)
- \(\frac{M \omega^2 L^2}{2}\)
Answer: 2. \(\frac{1}{2} M \omega^2 L\)
In circular motion, the centripetal force exerted by an element of length dx at a distance x is \(d F=\left(\frac{M}{L} d x\right) \omega^2 x\)
∴ total force \(F=\int d F=\frac{M \omega^2}{L} \int_0^L x d x\)
=\(\frac{1}{2} M \omega^2 L\)
Question 34. A uniform circular disc of mass M and radius R is rotating about its axis of symmetry at a uniform rate. A lump of wax of mass m is gently stuck on the disc at a distance r = R/2 from its centre. The new angular velocity of the system is
- \(\frac{2 \omega M}{2 M+m}\)
- \(\frac{2 \omega M}{M+2 m}\)
- \(\frac{\omega m}{M}\)
- \(\frac{\omega M}{m}\)
Answer: 1. \(\frac{2 \omega M}{2 M+m}\)
Conserving the angular momentum, we have
⇒ \(I \omega=I^{\prime} \omega^{\prime} \quad\)
⇒ \(\quad \frac{1}{2} M R^2 \omega=\left[\frac{1}{2}\left(M R^2\right)+\frac{m R^2}{4}\right] \omega^{\prime}\)
Simplifying, we get
⇒ \(\omega^{\prime}=\frac{2 M \omega}{2 M+m}\)
Question 35. From a disc of radius R and mass M, a circular hole of diameter is cutItsrimpassesthrough the centre of the disc. What is the moment of inertia of the remaining part of the disc about a perpendicular axis passing through the centre?
- \(\frac{15}{32} M R^2\)
- \(\frac{11}{32} M R^2\)
- \(\frac{13}{32} M R^2\)
- \(\frac{9}{32} M R^2\)
Answer: 3. \(\frac{13}{32} M R^2\)
The total mass of the disc is M. Then, the mass of the cutout portion is
⇒ \(m=\left(\frac{M}{\pi R^2}\right) \pi\left(\frac{R}{2}\right)^2=\frac{M}{4}\)
The moment of inertia of the total disc about the given axis through O is
⇒ \(I=\frac{1}{2} M R^2\)
The moment of inertia of the cutout portion about the perpendicular axis through its centre
⇒ \(I_{\mathrm{O}^{\prime}}=\frac{1}{2}\left(\frac{M}{4}\right)\left(\frac{R}{2}\right)^2=\frac{M R^2}{32}\)
From the theorem of parallel axes, its moment of inertia about the perpendicular axis through O is
⇒ \(I_{\mathrm{O}}=I_{\mathrm{O}^{\prime}}+\frac{M}{4}\left(O O^{\prime}\right)^2=\frac{M R^2}{32}+\frac{M R^2}{16}=\frac{3}{32} M R^2\)
Now, the net moment of inertia is
⇒ \(I_{\text {net }}=I-I_0=\frac{M R^2}{2}-\frac{3}{32} M R^2=\frac{13}{32} M R^2\)
Question 36. Three identical spherical shells, each of mass m and radius r, are placed touching each other, as shown in the figure. Consider an axis XX’, which is touching the two shells and passing through the file diameter of the fluid shell. The moment of inertia of the system consisting of these three shells about XX’is
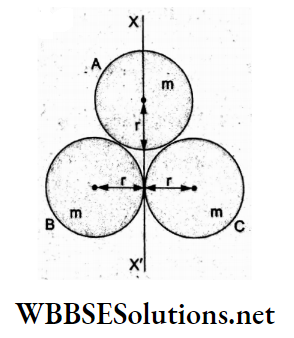
- \(\frac{16}{5} m r^2\)
- \(\frac{11}{5} m R^2\)
- 4mr²
- 3mr²
Answer: 3. 4mr²
The moment of inertia of the shell A about XX’ is
⇒ \(I_{\mathrm{A}}=\frac{2}{3} m r^2\)
Similarly, \(I_{\mathrm{B}}=\frac{2}{3} m r^2+m r^2=\frac{5}{3} m r^2\)
∴ the net moment of inertia of the system is
⇒ \(I=I_{\mathrm{A}}+I_{\mathrm{B}}+I_{\mathrm{C}}=4 m r^2\)
Question 37. The ratio of the radii of gyration of a circular ring and a circular disc of the same mass and radius about an axis passing through their centres and perpendicular to their planes is
- 1:√2
- √2:1
- 2:1
- 3:2
Answer: 2. √2:1
Moment of inertia of the ring = \(I_{\text {ring }}=M R^2=M k_{\text {ring }}^2\)
Moment of inertia of the disc = \(I_{\text {disc }}=\frac{1}{2} M R^2=M k_{\text {disc }}^2\)
∴ \(\frac{I_{\text {ring }}}{I_{\text {disc }}}=\frac{M R^2}{\frac{1}{2} M R^2}=\frac{M k_{\text {ring }}^2}{M k_{\text {disc }}^2}=\frac{k_{\text {ring }}^2}{k_{\text {disc }}^2}\)
⇒ \(k_{\text {ring }}: k_{\text {disc }}\)
= \(\sqrt{2}: 1\)
Question 38. The moment of inertia of the uniform circular disc shown in the figure is maximum about an axis perpendicular to the disc and passing through
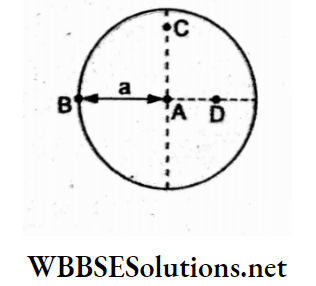
- A
- D
- B
- C
Answer: 3. B
According to the theorem of parallel axes, \(I=I_{\mathrm{CM}}+M a^2\)
The distance from the centre is maximum for the point B, so I is a maximum of about B.
Question 39. The instantaneous angular position of a point on a rotating wheel is given by the equation θ(t) = 2t- 6t². The torque on the wheel becomes zero at
- t = 1s
- t = 0.5s
- t = 2s
- t = 1.5s
Answer: 1. t = 1s
Given that θ = 2t³- 6t². Hence, angular velocity = \(\omega=\frac{d \theta}{d t}=6 t^2-12 t\) and
angular acceleration \(\alpha=\frac{d \omega}{d t}=12 t-12\)
For torque \(\tau=I \alpha\) to be zero,
α = 12t – 12 = 0
=> t =1 s.
Question 40. From a circular disc of radius R and mass 9M, a small disc of mass M and radius R/3 is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
- 8MR²
- 4MR²
- \(\frac{40}{9} M R^2\)
- \(\frac{4}{9} M R^2\)
Answer: 3. \(\frac{40}{9} M R^2\)
The moment of inertia of the remaining disc is
⇒ \(I=\frac{1}{2}(9 M) R^2-\frac{1}{2}(M)\left(\frac{R}{3}\right)^2\)
= \(\frac{1}{2} M R^2\left(9-\frac{1}{9}\right)\)
= \(\frac{40}{9} M R^2\)
Question 41. The moment of inertia of a uniform disc of mass M and radius R about an axis touching the disc at its edge and normal to the plane of the disc is
- \(\frac{1}{2} M R^2\)
- MR²
- \(\frac{3}{2} M R^2\)
- 2MR²
Answer: 3. \(\frac{3}{2} M R^2\)
From the theorem of parallel axes,
⇒ \(I=I_{\mathrm{CM}}+M R^2=\frac{1}{2} M R^2+M R^2\)
= \(\frac{3}{2} M R^2\)
Question 42. Two bodies A and B have their moments of inertia I and 21 about their axes of rotation. If their kinetic energies of rotation are equal, their angular velocities will be in the ratio
- 2: 1
- 1: 2
- √2: 1
- 1: √2
Answer: 3. √2: 1
The kinetic energies of the bodies A and B are respectively
⇒ \(E_{\mathrm{A}}=\frac{1}{2} I \omega_{\mathrm{A}}^2 \text { and } E_{\mathrm{B}}=\frac{1}{2}(2 I) \omega_{\mathrm{B}}^2 \text {. }\)
Given that EA = EB. So,
⇒ \(\omega_A{ }^2=2 \omega_B{ }^2\)
∴ \(\frac{\omega_A}{\omega_B}=\frac{\sqrt{2}}{1}\)
⇒ \(\omega_A: \omega_B=\sqrt{2}: 1\)
Question 43. A circular disc of the moment of inertia I2 about its axis perpendicular to its plane and passing through its centre is gently placed over another disc of the moment of inertia I1 rotating with an angular velocity GO about the same axis. The final angular velocity of the combination of discs is
- \(\frac{I_2 \omega}{I_1+I_2}\)
- \(\frac{I_1 \omega}{I_1+I_2}\)
- \(\frac{\left(I_1+I_2\right) \omega}{I_1}\)
- \(\frac{I_1 \omega}{I_2}\)
Answer: 2. \(\frac{I_1 \omega}{I_1+I_2}\)
Initial angular momentum = I1ω
and final angularmomentum=(I1 + I2)ω.
Conserving the angularmomentum \(\omega^{\prime}=\frac{I_1 \omega}{I_1+I_2}\)
Question 44. The ratio of the radius of gyration of a disc about a coplanar tangential axis to that of a ring of the same radius about a coplanar tangential axis is
- 2:3
- 2:1
- √5: √6
- √1: √3
Answer: 3. \(\frac{I_1 \omega}{I_1+I_2}\)
The moment of inertia of a uniform disc about its tangent is given by
⇒ \(I_{\text {disc }}=\frac{1}{4} M R^2+M R^2=\frac{5}{4} M R^2\)
where \(\frac{1}{4} M R^2\) is the moment ofinertia of the disc aboutits diameter.
Similarly, for the ring,
⇒ \(I_{\text {ring }}=\frac{M R^2}{2}+M R^2=\frac{3}{2} M R^2\)
∴ \(\frac{I_{\text {disc }}}{I_{\text {ring }}}=\frac{\frac{5}{4} M R^2}{\frac{3}{2} M R^2}=\frac{5}{6}=\frac{M k_{\text {disc }}^2}{M k_{\text {ring }}^2}\)
⇒ \(\frac{k_{\text {disc }}}{k_{\text {ring }}}=\sqrt{\frac{5}{6}} \Rightarrow k_{\text {disc }}: k_{\text {ring }}=\sqrt{5}: \sqrt{6}\)
Question 45. A heavy disc is rotating with an angular speed co. If a child gently sits on it, what is conserved?
- Linear momentum
- Angular momentum
- Kinetic energy
- Potential energy
Answer: 2. Angular momentum
Since there is no external torque, the angular momentum will be conserved.
Question 46. ABC is a triangular plate of uniform thickness. The sides are in the ratio 3: 4: 5, as shown in the figure. IAB, IBC and ICA are the moments of inertia of the plate about AB, BC and CA respectively. Which of the following is correct?
- \(I_{\mathrm{AB}}+I_{\mathrm{BC}}=I_{\mathrm{CA}}\)
- ICA is maximum
- \(I_{\mathrm{AB}}>I_{\mathrm{BC}}\)
- \(I_{\mathrm{BC}}>I_{\mathrm{AB}}\)
Answer: 4. \(I_{\mathrm{BC}}>I_{\mathrm{AB}}\)
Adding the shaded part APC, we get a rectangular plate for which the moment of inertia is
⇒ \(I_{\mathrm{AB}}=\frac{1}{3}(2 M)(3)^2=6 M \text { units, }\)
⇒ \(I_{\mathrm{BC}}=\frac{1}{3}(2 M)(4)^2=\frac{32}{3} M=10.67 M \text { units, }\)
and ICA=minimum.
Thus, IBC > IAB.
Question 47. In a rectangular plate ABCD A (where BC = 2AB), the moment of inertia is minimum along the axis passing through the points E
- B and C
- B and D
- H and F
- E and G
Answer: 2. B and D
The moment of inertia depends on the mass distribution of the rotational axis.
For the axis BD or AC, the maximum distance of the points A and C is less than the smaller side AB.
Hence, IBD is minimal.
Question 48. The moment of inertia of a body about a given axis is 1.2 kg m². Initially, the body is at rest. In order to produce a rotational kinetic energy of 1500 J, an angular acceleration of 25 rad s-2 must be applied about that axis for a duration of
- 4 s
- 2 s
- 8 s
- 10 s
Answer: 2. 2 s
⇒ \(\mathrm{KE}=\frac{1}{2} I \omega^2=\frac{1}{2} I\left(\omega_0+\alpha t\right)^2=\frac{1}{2} I \alpha^2 t^2\)
⇒ \(\text { time }=t=\sqrt{\frac{2(\mathrm{KE})}{I \alpha^2}}=\frac{1}{\alpha} \sqrt{\frac{2(\mathrm{KE})}{I}}\)
Substituting the given values,
⇒ \(t=\frac{1}{25} \sqrt{\frac{2(1500)}{1.2}} \mathrm{~s}=\frac{1}{25} \times 50 \mathrm{~s}\)
= 2s.
Question 49. The moment of inertia of a uniform circular disc about its diameter is I. Its moment of inertia about an axis perpendicular to its plane and touching a point on its rim will be
- 5I
- 3I
- 4I
- 6I
Answer: 4. 6I
The moment of inertia of the disc about its diameter is \(I=\frac{M R^2}{4}\) and
that about the axis of symmetry is
⇒ \(I_{\mathrm{O}}=\frac{M R^2}{2}=2 I\)
From the theorem of parallel axes,
I = Io+MR²
= 2I+ 4I
= 6I
Question 50. A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with an angular velocity co. Its kinetic energy is
- mr²ω²
- \(\frac{1}{2} m r^2 \omega^2\)
- mrω²
- \(\frac{1}{2} m r \omega^2\)
Answer: 2. \(\frac{1}{2} m r^2 \omega^2\)
The kinetic energy of the ring about the given axis is
⇒ \(\frac{1}{2} I \omega^2=\frac{1}{2} m r^2 \omega^2\)
Question 51. Two discs of moments of inertia I1 and I2 rotating about their respective axes, with angular frequencies co1 and co2 respectively, are gently brought into contact face to face, with their axes of rotation coincident. The angular frequency of the composite disc will be
- \(\frac{I_1 \omega_1-I_2 \omega_2}{I_1-I_2}\)
- \(\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)
- \(\frac{I_1 \omega_2+I_2 \omega_1}{I_1+I_2}\)
- \(\frac{I_1 \omega_2-I_2 \omega_1}{I_1-I_2}\)
Answer: 2. \(\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)
Conserving the angular momentum, we have
⇒ \(I_1 \omega_1+I_2 \omega_2=\left(I_1+I_2\right) \omega^{\prime}\)
⇒ \(\omega^{\prime}=\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)
Question 52. If the earth were to suddenly contract to half its present size without any change in its mass, the duration of the day would have been
- 12 hours
- 6 hours
- 18 hours
- 30 hours
Answer: 2. 6 hours
The earth revolves in its orbit due to the gravitational attraction of the sun, and the torque is zero. So, the angular momentum is conserved.
∴ \(I \omega=I^{\prime} \omega^{\prime} \Rightarrow \frac{2}{5} M R^2 \cdot \frac{2 \pi}{24 \mathrm{~h}}=\frac{2}{5} M\left(\frac{R}{2}\right)^2 \cdot \frac{2 \pi}{T}\)
∴ 24h= 4T
T= 6h
Question 53. A solid cylinder of mass M and radius R rotates about its axis with a constant angular speed a. Its kinetic energy is
- 2MR²ω²
- \(\frac{1}{2} M R^2 \omega^2\)
- \(\frac{1}{4} M R^2 \omega^2\)
- MR²ω²
Answer: 3. \(\frac{1}{4} M R^2 \omega^2\)
The KE of the solid cylinder is
⇒ \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{1}{2} M R^2\right) \omega^2=\frac{1}{4} M R^2 \omega^2\)
Question 54. A circular disc of mass m and radius rerolling on a rough horizontal surface with a constant speed v. Its kinetic energy is
- \(\frac{1}{4} m v^2\)
- \(\frac{1}{2} m v^2\)
- \(\frac{3}{4} m v^2\)
- mv²
Answer: 3. \(\frac{3}{4} m v^2\)
KE of a rolling disc \(\mathrm{KE}_{\text {trans }}+\mathrm{KE}_{\text {rot }}=\frac{1}{2} m v^2+\frac{1}{2} I \omega^2\)
The condition for rolling is v = ωr. Hence
⇒ \(E_{\mathrm{tot}}=\frac{1}{2} m v^2+\frac{1}{2}\left(\frac{1}{2} m R^2\right) \frac{v^2}{R^2}=\frac{3}{4} m v^2\)
Question 55. A solid sphere is rotating about its diameter at a constant angular velocity ω. If its size is slowly reduced to 1/n of its original value without any change in its mass, its angular velocity becomes
- \(\frac{\omega}{n}\)
- nω
- \(\frac{\omega}{n^2}\)
- n²ω
Answer: 4. n²ω
Conserving the angular momentum,
⇒ \(I \omega=I^{\prime} \omega^{\prime} \Rightarrow\left(\frac{2}{5} M R^2\right) \omega=\frac{2}{5} M\left(\frac{R}{n}\right)^2 \omega^{\prime}\)
ω = n²ω
Question 56. A circular disc of radius R is free to oscillate about an axis passing through a point on its rim and perpendicular to its plane. The disc is turned through an angle of 60° and released. Its angular velocity when it reaches the equilibrium position will be
- \(\sqrt{\frac{g}{3 R}}\)
- \(\sqrt{\frac{2g}{3 R}}\)
- \(\sqrt{\frac{2g}{R}}\)
- \(\sqrt{\frac{3g}{2 R}}\)
Answer: 2. \(\sqrt{\frac{2g}{3 R}}\)
Loss in PE = mgR(1- cos 60°) = \(\frac{m g R}{2}\)
Gain in KE = \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{1}{2} m R^2+m R^2\right) \omega^2\)
Conserving the energy,
⇒ \(\frac{1}{2}\left(\frac{3}{2} m R^2\right) \omega^2=\frac{m g R}{2}\)
⇒ \(\omega=\sqrt{\frac{2 g}{3 R}}\)
Question 57. The moment of inertia of a thick shell of mass and internal and external radii R and 2R respectively, about its diameter is
- \(\frac{13}{35} M R^2\)
- \(\frac{3}{2} M R^2\)
- \(\frac{62}{35} M R^2\)
- \(\frac{31}{35} M R^2\)
Answer: 3. \(\frac{62}{35} M R^2\)
We consider the given hollow sphere as if a solid sphere of radius R and mass M2 be removed from a solid sphere of radius 2R and mass M1.
Thus,
⇒ \(M=M_1-M_2=\frac{4}{3} \pi(2 R)^3 \rho-\frac{4}{3} \pi R^3 \rho=\frac{28}{3} \pi R^3 \rho\)
∴ the moment of inertia of the given hollow sphere is
⇒\(\frac{2}{5} M_1(2 R)^2-\frac{2}{5} M_2 R^2\)
⇒ \(\frac{2}{5} \times \frac{32}{3} \pi R^3 \cdot \rho \cdot 4 R^2-\frac{2}{5} \cdot \frac{4}{3} \pi R^3 \rho \cdot R^2\)
⇒ \(\frac{2}{5}(32-1) \frac{4}{3} \pi R^5 \rho=\frac{62}{5}\left(\pi R^3\right)\left(\frac{4}{3} R^2 \rho\right)\)
⇒ \(\frac{62}{5}\left(\frac{3 M}{28 \rho}\right)\left(\frac{4}{3} R^2 \rho\right)=\frac{62}{35} M R^2\)
Question 58. A disc of mass M and radius 2R has a concentric hole of radius R. Its moment of inertia about an axis through its centre is
- \(\frac{3}{2} M R^2\)
- \(\frac{5}{3} M R^2\)
- \(\frac{5}{2} M R^2\)
- \(\frac{2}{5} M R^2\)
Answer: 3. \(\frac{5}{2} M R^2\)
The disc with a concentric hole may be considered as a solid disc of radius 2R and mass M1 with a concentric cutout disc of radius R and mass M2.
The mass of the given discs
⇒ \(M=M_1-M_2=\pi(2 R)^2 \sigma-\pi R^2 \sigma=3 \pi R^2 \sigma,\)
where is the surface mass density?
The moment of inertia of the given disc is
⇒ \(I=\frac{1}{2} M_1(2 R)^2-\frac{1}{2} M_2 R^2\)
⇒ \(\frac{1}{2}\left(4 \pi R^2 \sigma\right)\left(4 R^2\right)-\frac{1}{2}\left(\pi R^2 \sigma\right) R^2\)
⇒ \(\frac{1}{2} \pi R^4 \sigma(16-1)=\frac{15}{2}\left(\pi R^4\right) \frac{M}{3 \pi R^2}\)
⇒ \(\frac{5}{2} M R^2\)
Question 59. A mass m is moving at a constant velocity along a straight line parallel to the x-axis away from the origin. It’s angular with respect to the origin
- Goes on increasing
- Goes on decreasing
- Remains constant
- Is zero
Answer: 3. Remains constant
The angular momentum of the mass m about the origin is
⇒ \(\vec{L}=\vec{r} \times \vec{p}=\vec{r} \times(m \vec{v})=m(\vec{r} \times \vec{v})\)
Position vector = \(\overrightarrow{O P}=(x \hat{i}+y \hat{j})\), where (x, y) gives the coordinates of P, and
velocity = \(\vec{v}=v \hat{i}\)
∴ \(\vec{L}=m(x \hat{i}+y \hat{j}) \times v \hat{i}=m y v(-\hat{k})\)
Here m and v are constant, and y is also constant as the particle moves parallel to the x-axis.
Thus, \(|\vec{L}|\) = myv
= constant.
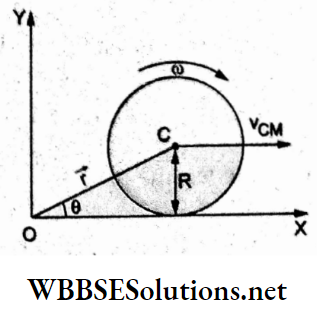
Question 60. A disc of mass and radius R is rolling with an angular speed ω on a horizontal plane, as shown in the figure. The magnitude of the angular momentum of the disc about the origin O is
- \(\frac{1}{2} M R^2 \omega\)
- MR²ω
- \(\frac{3}{2} M R^2 \omega\)
- 2MR²ω
Answer: 3. \(\frac{3}{2} M R^2 \omega\)
Let \(\overrightarrow{O C}=\vec{r} \text { and } \vec{v}_{\mathrm{CM}}\) = velocity of the centre of mass of the disc.
Hence, the linear momentum of the disc is
⇒ \(\vec{p}_{\mathrm{C}}=m \vec{v}_{\mathrm{CM}}\)
If Lc = angular momentum about C, the angular momentum about the origin is
⇒ \(\vec{L}_{\mathrm{O}}=\vec{L}_{\mathrm{C}}+\vec{r} \times \vec{p}_{\mathrm{C}}\)
⇒ \(I_{C^\omega} \omega+r \times M v_{C M} \sin \theta\)
⇒ \(\frac{1}{2} M R^2 \omega+M R v_{\mathrm{CM}}\) [∵ r sinθ = R]
⇒ \(\frac{1}{2} M R^2 \omega+M R^2 \omega\) [∵ vCM = Rω]
⇒ \(\frac{3}{2} M R^2 \omega\)
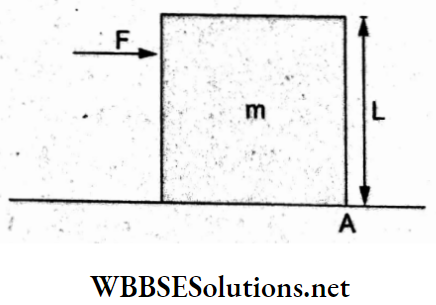
Question 61. A cubical block of mass m and side L rests on a rough horizontal surface having the coefficient of friction μ, A horizontal force F is applied on the block, as shown in the figure. The coefficient of friction is sufficiently large so that the block does not slide before toppling. The minimum force required to topple the block is
- mg
- \(\frac{m g}{2}\)
- \(\frac{m g}{4}\)
- mg (1-μ)
Answer: 2. \(\frac{m g}{2}\)
By the applied force, the cubical block will turn about the edge at A.
Hence, the torque of the force F about A is
⇒ \(\tau_1=F L\) (clockwise).
The torque due to the weight mg about A is
⇒ \(\tau_2=m g\left(\frac{L}{2}\right)=\frac{m g L}{2}\) (anticlockwise).
For turning, must slightly exceed \(\tau_2\).
So, in the limit
⇒ \(\tau_1=\tau_2 \Rightarrow F L=m g\left(\frac{L}{2}\right) \Rightarrow F=\frac{m g}{2}\)
Question 62. A solid metallic sphere of radius R has a moment of inertia I about its diameter. The sphere is melted and recast into a solid disc of radius r and uniform thickness. The moment of inertia of the disc about an axis passing through its edge and perpendicular to its plane is also equal to I. The ratio r/R is
- \(\frac{2}{\sqrt{10}}\)
- \(\frac{2}{\sqrt{5}}\)
- \(\frac{2}{\sqrt{15}}\)
- \(\frac{1}{\sqrt{2}}\)
Answer: 3. \(\frac{2}{\sqrt{15}}\)
Themomentofinertia of the solid sphere is \(I_1=\frac{2}{5} M R^2\) , and the moment of inertia of the disc is
Given that I1 = I2, we have
⇒ \(\frac{2}{5} M R^2=\frac{3}{2} M r^2 \Rightarrow \frac{r}{R}=\frac{2}{\sqrt{15}}\)
Question 63. A circular disc rolls down an inclined plane without slipping. What fraction of its total energy is translational?
- \(\frac{1}{\sqrt{2}}\)
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- \(\frac{2}{3}\)
Answer: 4. \(\frac{2}{3}\)
At any instant during rolling,
v = ωr,
KE of translation = \(\frac{1}{2}\)mv²
and KE of rotation = \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{1}{2} m r^2\right)\left(\frac{v^2}{r^2}\right)=\frac{1}{4} m v^2\)
∴ total energy = \(\frac{1}{2} m v^2+\frac{1}{4} m v^2=\frac{3}{4} m v^2\)
Hence, the ratio is
⇒ \(\frac{\mathrm{KE} \text { of translation }}{\text { total KE }}=\frac{\frac{1}{2} m v^2}{\frac{3}{4} m v^2}=\frac{2}{3}\)
Question 64. A solid sphere rolls down an inclined plane without slipping. What fraction of its total energy is rotational?
- \(\frac{2}{7}\)
- \(\frac{3}{7}\)
- \(\frac{2}{3}\)
- \(\frac{3}{5}\)
Answer: 1. \(\frac{2}{7}\)
KE of translation = \(\frac{1}{2}\) mv²
and KE of rotation = \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{2}{5} m R^2\right)\left(\frac{v}{R}\right)^2\)
⇒ \(\frac{1}{5}\) [∵ v = Rω for rolling].
∴ total energy = \(\frac{1}{2} m v^2+\frac{1}{5} m v^2=\frac{7}{10} m v^2\)
Hence, \(\frac{\text { rotational KE }}{\text { total } \mathrm{KE}}=\frac{\frac{1}{5} m v^2}{\frac{7}{10} m v^2}=\frac{2}{7}\)
Question 65. A solid cylinder of mass M and radius R rolls down without slipping on a rough inclined plane from a height of h. The rotational kinetic energy of the cylinder, when it reaches the bottom of the plane, will be
- Mgh
- \(\frac{M g h}{2}\)
- \(\frac{M g h}{3}\)
- \(\frac{2M g h}{3}\)
Answer: 3. \(\frac{M g h}{3}\)
The initial PE (= mgh) will change into the total KE.
Now,KE of rotation = \(=\frac{1}{2} I \omega^2\)
=\(\frac{1}{2}\left(\frac{1}{2} m R^2\right) \omega^2\)
=\(\frac{1}{4} m R^2\left(\frac{v^2}{R^2}\right)\)
⇒ \(\frac{1}{4} m v^2\)
and KE of translation = \(\frac{1}{2}\)mv².
∴ total KE = \(\mathrm{KE}=\frac{1}{2} m v^2+\frac{1}{4} m v^2\)
=\(\frac{3}{4} m v^2\)
Now, \(\frac{3}{4} m v^2=m g h \Rightarrow v^2\)
=\(\frac{4}{3} g h\)
∴ the KE of rotation at the bottom is
⇒ \(\frac{1}{4} m v^2=\frac{1}{4} m\left(\frac{4}{3} g h\right)\)
=\(\frac{1}{3} m g h\)
Question 66. A solid sphere rolls down from the top of a rough inclined plane. Its velocity on reaching the bottom of the incline is v. When the same sphere slides down from the top of a smooth but similar inclined plane, its velocity is v’. The ratio v’/v is equal to
- \(\sqrt{\frac{3}{5}}\)
- \(\sqrt{\frac{7}{5}}\)
- 1
- \(\frac{3}{\sqrt{5}}\)
Answer: 2. \(\sqrt{\frac{7}{5}}\)
While rolling down the inclined plane,
total KE= mgh
⇒ \(\frac{1}{2} m v^2+\frac{1}{2} I \omega^2=m g h\)
⇒ \(\frac{1}{2} m v^2+\frac{1}{2}\left(\frac{2}{5} m R^2\right) \frac{v^2}{R^2}=m g h\)
⇒ \(\frac{7}{10} m v^2=m g h\)
While slipping,
⇒ \(\frac{1}{2} m v^{\prime 2}=m g h\)
⇒ \(\frac{1}{2} m v^{\prime 2}=\frac{7}{10} m v^2\)
⇒ \(\frac{v^{\prime}}{v}=\sqrt{\frac{7}{5}}\)
Question 67. A solid sphere rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout the motion). The directions of the static frictional force acting on the cylinder are
- Up the incline while ascending and down the incline while descending
- Up the incline while ascending as well as descending
- Down the incline while ascending and up the incline while descending
- Down the incline while ascending as well as descending
Answer: 2. Up the incline while ascending as well as descending
When the sphere rolls up the inclined plane, friction opposes rolling and acts up along the plane so as to produce an anticlockwise torque.
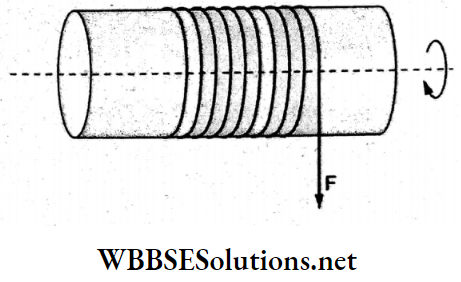
When the sphere rolls down the inclined plane, friction supports rolling and acts up along the plane, thus producing an anticlockwise torque, which increases the angular speed.
Question 68. A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a constant force of 30 N?
- 0.25 rad s-2
- 25 rad s-2
- 5 ms-2
- 25 ms-2
Answer: 2. 25 ms-2
Torque = FR =Ia = MR²a.
∴ angular acceleration
⇒ \(\alpha=\frac{F R}{M R^2}\)
= \(\frac{F}{M R}=\frac{30 \mathrm{~N}}{(3 \mathrm{~kg})\left(\frac{40}{100} \mathrm{~m}\right)}\)
= \(25 \mathrm{rad} \mathrm{s}^{-2}\)
Question 69. Two discs of the same moment of inertia rotate about their regular axes passing through the centre and perpendicular to their planes with angular velocities ω1 and ω2. They are brought into contact face to face coinciding their axes of rotation. The expression for the loss of energy during this process is
- \(\frac{1}{4} I\left(\omega_1-\omega_2\right)^2\)
- \(I\left(\omega_1-\omega_2\right)^2\)
- \(\frac{1}{8} I\left(\omega_1-\omega_2\right)^2\)
- \(\frac{1}{2} I\left(\omega_1-\omega_2\right)^2\)
Answer: 1. \(\frac{1}{4} I\left(\omega_1-\omega_2\right)^2\)
Conserving the angular momentum,
⇒ \(I \omega_1+I \omega_2=2 I \omega \Rightarrow \omega=\frac{\omega_1+\omega_2}{2}\)
Initial KE = \(\frac{1}{2} I \omega_1{ }^2+\frac{1}{2} I \omega_2{ }^2\)
and final KE = \(\frac{1}{2}(2 I) \omega^2=I\left(\frac{\omega_1+\omega_2}{2}\right)^2\)
∴ loss of energy = KEi-KEf
= \(\frac{I}{2}\left[\left(\omega_1^2+\omega_2^2\right)-\frac{\left(\omega_1+\omega_2\right)^2}{2}\right]\)
=\(\frac{1}{4} I\left(\omega_1-\omega_2\right)^2\)
Question 70. Two rotating bodies A and B of respective masses m and 2m with moments of inertia IA and IB (where IA > IA) have the same kinetic energy of rotation. If LA and LB are their angular momenta respectively then
- \(L_{\mathrm{A}}=\frac{L_{\mathrm{B}}}{2}\)
- LA = 2LB
- LB>LA
- LA>LB
Answer: 3. LB>LA
KEin terms of angular momentum (L) is \(\frac{L^2}{2 I}\)
∴ \(\frac{L_{\mathrm{A}}^2}{2 I_{\mathrm{A}}}=\frac{L_{\mathrm{B}}^2}{2 I_{\mathrm{B}}}\)
⇒ \(\frac{L_{\mathrm{A}}^2}{L_{\mathrm{B}}^2}=\frac{I_{\mathrm{A}}}{I_{\mathrm{B}}}\)
Since IB > IA, we have LB > LA
Question 71. A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and the same radius is also rotating about a geometrical axis with an angular speed of twice that of the sphere. The ratio of their kinetic energies of rotation EAsph:EAcyl will be
- 2:3
- 1:5
- 1:4
- 3:1
Answer: 2. 1:5
The kinetic energy of the solid sphere is \(E_1=\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{2}{5} M R^2\right) \omega^2\)
The kinetic energy of the solid cylinder is \(E_2=\frac{1}{2} I(2 \omega)^2=\frac{1}{2}\left(\frac{M R^2}{2}\right) 4 \omega^2\)
∴ \(\frac{E_1}{E_2}=\frac{\frac{1}{5} M R^2 \omega^2}{M R^2 \omega^2}\)
= 1: 5.
Question 72. A disc and a sphere of the same radius roll down on two inclined planes from the same altitude and length. Which of the two objects gets to the bottom of the plane first?
- Both read at the same time.
- The disc
- It depends on their masses.
- The sphere
Answer: 4. The sphere
The acceleration of a body rolling down an inclined plane is given
⇒ \(a=\frac{g \sin \theta}{1+\frac{k^2}{R^2}}\)
For the disc, \(\frac{k^2}{R^2}=\frac{1}{2} \Rightarrow a_{\mathrm{disc}}=\frac{2}{3} g \sin \theta\)
For the sphere, \(\frac{k^2}{R^2}=\frac{2}{5} \Rightarrow a_{\mathrm{sph}}=\frac{5}{7} g \sin \theta\)
Since \(a_{\mathrm{sph}}>a_{\text {disc }}\), the sphere will reach the bottom before the disc.
Question 73. A uniform circular di9c of radius 50 cm at rest is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2.0 rad s-2. Its net acceleration at the end of 2.0 s is approximately
- 6.0 ms-2
- 3.0 m s-2
- 7.0 ms-2
- 8.0 ms-2
Answer: 4. 8.0 ms-2
Given that radius = R = 50 cm = 0.5 m and angular acceleration
α = 2.0 rad s-2.
The angular velocity (ω) at the end of 2.0 s will be
ω = ω0 + at = 0 + (2.0rad s-2)(2.0 s)= 4rad s-1.
Tangential acceleration atan = Rα = (0.5m)(2.0rad s-2) = 1.0m s-2
and radial acceleration= arad = ω2R = (4rad s-1)2(0.5m) = 8.0m s-2.
∴ net acceleration = \(\sqrt{a_{\mathrm{tan}}^2+a_{\mathrm{rad}}^2}=\sqrt{\left(1.0 \mathrm{~m} \mathrm{~s}^{-2}\right)^2+\left(8.0 \mathrm{~m} \mathrm{~s}^{-2}\right)^2}\)
⇒ \(\sqrt{65 \mathrm{~m}^2 \mathrm{~s}^{-4}} \approx 8.0 \mathrm{~m} \mathrm{~s}^{-2}\)
Question 74. A force \(F=\alpha \hat{i}+3 \hat{j}+6 \hat{k}\) is acting at a point \(\vec{r}=2 \hat{i}-6 \hat{j}-12 \hat{k}\). The value of α for which the angular momentum about the origin is conserved is
- 1
- -1
- 2
- Zero
Answer: 2. -1
The angular momentum is conserved when the torque \((\vec{\tau}=\vec{r} \times \vec{p})\) is zero.
Given that \(\vec{r}=2 \hat{i}-6 \hat{j}-12 \hat{k} \text { and } \vec{F}=\alpha \hat{i}+3 \hat{j}+6 \hat{k}\)
∴ \(\vec{\tau}=\vec{r} \times \vec{p}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & -6 & -12 \\
\alpha & 3 & 6
\end{array}\right|\)
⇒ \((-36+36) \hat{i}+(-12 \alpha-12) \hat{j}+(6+6 \alpha) \hat{k}\)
⇒ \(-\hat{j}(12+12 \alpha)+\hat{k}(6+6 \alpha)\)
Since x = 0, we have,
12 + 12α = 0
or, α =-1 and 6 + 6α = 0
or, α= -1.
Question 75. A solid cylinder of mass 50kg and radius 0.5m is free to rotate about the horizontal axis. A light string is wound around the cylinder with one end attached to it and the other hanging freely. The tension in the string required to produce an angular acceleration of 2 rev s-2 is
- 25N
- 50N
- 78.5N
- 157N
Answer: 4. 157N
Given that M = 50 kg, R = 0.5 m
and angular acceleration = α = 2 rev s-2
= 4π rad s-2.
Let T be the required tension.
∴ torque = \(\tau=T R=I \alpha\)
tension = \(T=\frac{I \alpha}{R}=\frac{\left(\frac{1}{2} M R^2\right) \alpha}{R}=\frac{1}{2} M R \alpha\)
⇒ \(\frac{1}{2}(50 \mathrm{~kg})\left(\frac{1}{2} \mathrm{~m}\right)\left(4 \pi \mathrm{rad} \mathrm{s}^{-2}\right)\)
= 50πN
= 157N.
Question 76. A rod PQ of mass m and length L is hinged at the end P. The rod is kept horizontal by a massless string tied to the point Q, as shown in the figure. When the string is cut, the initial angular acceleration of the rod is
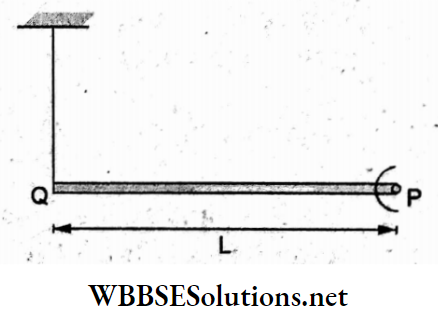
- \(\frac{3 g}{2 L}\)
- \(\frac{2 g}{3 L}\)
- \(\frac{g}{L}\)
- \(\frac{2 g}{L}\)
Answer: 1. \(\frac{3 g}{2 L}\)
When the string is cut, the weight mg acting at the centre of the rod will produce a torque of \(\tau=m g\left(\frac {L}{2}\right)\)
But \(\tau=I \alpha=\frac{1}{3} m L^2 \alpha\)
∴ \(\frac{1}{3} m L^2 \alpha=m g\left(\frac{L}{2}\right)\)
Question 77. A small object of uniform density rolls up a curved surface with an initial velocity of v. It reaches up to a maximum height of \(\frac{3 v^2}{4 g}\) with respect to the initial position. The object is a
- Ring
- Shell
- Disc
- Solid sphere
Answer: 3. Disc
The kinetic energy at the base gets converted into the PE at the maximum height.
Thus, at the base,
⇒ \(\frac{1}{2} m v^2\left(1+\frac{k^2}{R^2}\right)=m g h=m g\left(\frac{3 v^2}{4 g}\right)\)
or, \(1+\frac{k^2}{R^2}=\frac{3}{2} \quad\)
or, \(\quad \frac{k^2}{R^2}=\frac{1}{2}\), which is true for a disc
Question 78. A solid cylinder and a hollow cylinder, both of the same mass and the same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping. Which will reach the bottom first?
- The hollow cylinder
- The solid cylinder
- Both together
- Both together only when the angle of inclination of the plane is 45°
Answer: 2. The solid cylinder
The acceleration of a body rolling down an inclined plane is
⇒ \(a=\frac{g \sin \theta}{1+\frac{k^2}{R^2}}\)
For a solid cylinder, \(\frac{k^2}{R^2}=\frac{1}{2}\)
For a hollow cylinder, \(\frac{k^2}{R^2}=1\)
⇒ \(a_{\text {solid }}=\frac{g \sin \theta}{1+\frac{1}{2}}=\frac{2}{3} g \sin \theta=0.66 g \sin \theta\)
and \(a_{\text {hollow }}=\frac{g \sin \theta}{2}=0.5 g \sin \theta\)
Since \(a_{\text {solid }}>a_{\text {hollow }}\), the solid cylinder will reach the bottom before the hollow one.
Question 79. A cylindrical shell of mass M and radius R rolls down without slipping along an inclined plane of inclination θ. The frictional force
- Dissipates energy as heat
- Decreases the rotational motion only
- Decreases both the rotational and translational motion
- Converts translational energy to rotational energy
Answer: 4. Converts translational energy to rotational energy
In the case of pure rolling, there is no slipping or relative motion between the rolling body and the surface at the point of contact. Only static friction exists. It supports rolling downwards but does not dissipate energy. It simply converts translational energy to rotational energy due to the torque produced by static friction.
Question 80. Consider a point P in contact with the wheel on the ground. The wheel rolls on the ground without slipping. The magnitude of displacement of the point P when the wheel completes half the revolution is (where the radius of the wheel is 1 m)
- 2 m
- πm
- \(\sqrt{\pi^2+4} \mathrm{~m}\)
- \(\sqrt{\pi^2+2} \mathrm{~m}\)
Answer: 3. \(\sqrt{\pi^2+4} \mathrm{~m}\)
During the rotation, the contact point moves horizontally and through d= 2r vertically as shown.
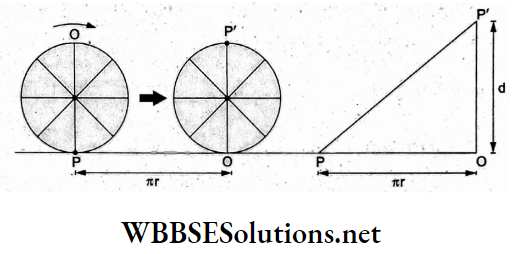
Hence, the magnitude of the displacement is
⇒ \(P P^{\prime}=\sqrt{(P O)^2+\left(O P^{\prime}\right)^2}=\sqrt{(\pi r)^2+(2 r)^2}\)
⇒ \(\sqrt{\pi^2(1 m)^2+(2 m)^2}=\sqrt{\pi^2+4} m\)
Question 81. The speed of a homogeneous solid sphere after rolling down an inclined plane of vertical height h from rest without slipping is
- \(\sqrt{\frac{4}{3} g h}\)
- √gh
- \(\sqrt{\frac{6}{5} g h}\)
- \(\sqrt{\frac{10}{7} g h}\)
Answer: 4. \(\sqrt{\frac{10}{7} g h}\)
⇒ \(\frac{1}{2} m v^2\left(1+\frac{k^2}{R^2}\right)=m g h\)
⇒ \(\frac{1}{2} m v^2\left(1+\frac{2}{5}\right)=m g h\)
⇒ \(v=\sqrt{\frac{10}{7} g h}\)
Question 82. A solid sphere rolls up along a rough inclined plane of inclination θ = 30° with an initial velocity of 2.8 m s-1. The maximum distance covered by the sphere is approximately
- 5.45 m
- 2.74 m
- 1.10m
- 3.25 m
Answer: 3. 1.10m
From the work-energy theorem, work done by gravity = change in kinetic energy
⇒ \(-m g s \sin 30^{\circ}=-\frac{1}{2} m v^2\left(1+\frac{k^2}{R^2}\right)\)
⇒ \(g s\left(\frac{1}{2}\right)=\frac{1}{2} v^2\left(1+\frac{2}{5}\right)=\frac{7}{10} v^2\)
⇒ \(s=\frac{7}{10}\left(2.8 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\left(\frac{2}{10 \mathrm{~m} \mathrm{~s}^{-2}}\right)=1.097 \mathrm{~m} \approx 1.10 \mathrm{~m}\)
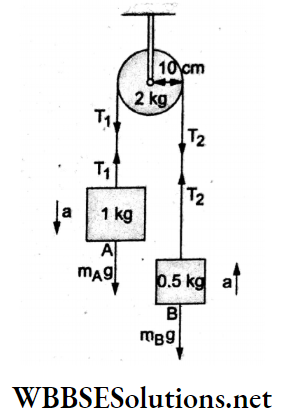
Question 83. Consider a system of two blocks A and B connected by a light, inextensible string passing over a pulley of mass M = 2 kg and radius R = 10 cm. Find the acceleration of the block A if mA =1 kg and mB = 0.5 kg.
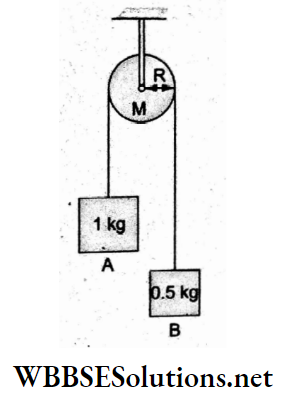
- 3.5m s-2
- 2ms-2
- 1.5 ms-2
- 2.5 ms-2
Answer: 2. 2ms-2
The magnitudes of the accelerations of both the blocks are equal (a), but the tensions will be different (T1 > T2).
For thepulley, \(\left(T_1-T_2\right) R=I \alpha=\left(\frac{M R^2}{2}\right)\left(\frac{a}{R}\right)\)
⇒ \(T_1-T_2=\left(\frac{M}{2}\right) a\)…..(1)
For theblock A, mAg – T1 = mAa…..(2)
For theblock B, T1-mBg = mBa…..(3)
Adding (1), (2) and (3),
⇒ \(\left(m_{\mathrm{A}}-m_{\mathrm{B}}\right) g=\left(m_{\mathrm{A}}+m_{\mathrm{B}}+\frac{M}{2}\right) a\)
Substituting the given values,
(1.0kg- 0.5 kg)(10m s-2) = (1.0kg + 0.5kg +1 kg)a
⇒ \(\left(\frac{1}{2} \mathrm{~kg}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)\)
= (2.5 kg)a
a = 2ms-2
Question 84. A disc of mass 0.5 kg and radius 20 cm rolls down an inclined plane. Find the force of friction required for pure rolling.
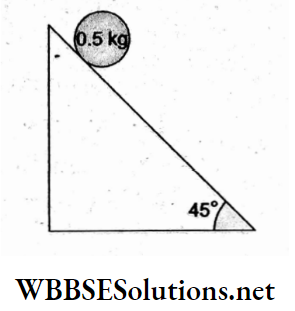
- \(\frac{5}{3 \sqrt{2}} \mathrm{~N}\)
- \(\frac{5 \sqrt{2}}{3} \mathrm{~N}\)
- \(\frac{5}{2 \sqrt{3}} \mathrm{~N}\)
- \(\frac{5}{\sqrt{2}} \mathrm{~N}\)
Answer: 1. \(\frac{5}{3 \sqrt{2}} \mathrm{~N}\)
The force of friction for pure rolling down a rough inclined plane is given by
⇒ \(f=\frac{m g \sin \theta}{1+\frac{R^2}{k^2}}\)
⇒ \(\frac{(0.5 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right) \sin 45^{\circ}}{1+\frac{2}{1}}\)
= \(\frac{5}{3} \times \frac{1}{\sqrt{2}} \mathrm{~N}\)
= \(\frac{5}{3 \sqrt{2}} \mathrm{~N}\)
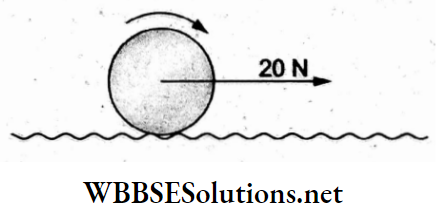
Question 85. A disc of mass 2 kg and radius 10 cm undergoes pure rolling on a rough horizontal surface, as shown. Find the ratio of the linear and angular accelerations (a/α).
- \(\frac{1}{15} m\)
- \(\frac{1}{10} m\)
- \(\frac{1}{20} m\)
- \(\frac{1}{5} m\)
Answer: 2. \(\frac{1}{10} m\)
Due to the force F at the centre of mass, the point of contact A has a tendency to slip towards the right. Hence, static friction/acts towards the left. This friction produces a torque for pure rolling.
For translational motion,
F-f= ma and forrotation,
⇒ \(\tau=f R=I \alpha\)
or, \(f R=\frac{1}{2} m R^2\left(\frac{a}{R}\right) \quad \text { or } \quad f=\frac{1}{2} m a\)
or, \(f=\frac{1}{2} m a\)
∴ \(F=\frac{3}{2} m a\)
⇒ \(f=\left(\frac{1}{2} m\right)\left(\frac{2 F}{3 m}\right)=\frac{F}{3}\)
Now, \(\frac{F-f}{f R}=\frac{m a}{I \alpha}\)
⇒ \(\frac{F-\frac{F}{3}}{\left(\frac{F}{3}\right) R}=\left(\frac{a}{\alpha}\right)\left(\frac{m}{\frac{1}{2} m R^2}\right)\)
⇒ \(\left(\frac{a}{\alpha}\right)\left(\frac{2}{R^2}\right)\)
⇒ \(\frac{2}{R}=\left(\frac{a}{\alpha}\right)\left(\frac{2}{R^2}\right)\)
⇒ \(\frac{a}{\alpha}=R=10 \mathrm{~cm}\)
= \(\frac{1}{10} \mathrm{~m}\)
Question 86. A disc of radius 2 m and mass 100 kg rolls on a horizontal floor. Its centre of mass has a speed of 20 cm s-1. How much work is needed to stop it?
- 1J
- 2J
- 3J
- 20 J
Answer: 3. 3J
The kinetic energy of a rolling body is \(\frac{1}{2} M v_{\mathrm{CM}}^2\left(1+\frac{k^2}{R^2}\right)\)
Given that M = 100kg and \(v_{\mathrm{CM}}=20 \mathrm{~cm} \mathrm{~s}^{-1}=0.2 \mathrm{~m} \mathrm{~s}^{-1}\)
and \(\frac{k^2}{R^2}=\frac{1}{2}\)
Hence, \(\mathrm{KE}=\frac{1}{2}(100 \mathrm{~kg})\left(0.2 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\left(\frac{3}{2}\right)\)
= 3J.
According to the work-energy theorem,
| work done | = | KEf-KEi |
= 3J.
Question 87. A solid cylinder of mass 2kg and radius 4 cm rotating about its axis at a rate of 3 rpm. The torque required to stop after 2π rev is
- 2 x 10-6Nm
- 2 x 10-3N m
- 12 x 10-4Nm
- 2 x 104N m
Answer: 1. 2 x 10-6Nm
The moment of inertia of the solid cylinder is
⇒ \(I=\frac{1}{2} M R^2=\frac{1}{2}(2 \mathrm{~kg})\left(4 \times 10^{-2} \mathrm{~m}\right)^2=16 \times 10^{-4} \mathrm{~kg} \mathrm{~m}^2\)
Initial angular speed = \(=\omega_0=\frac{3 \times 2 \pi}{60} \mathrm{rad} \mathrm{s}^{-1}\)
=\(\frac{\pi}{10} \mathrm{rad} \mathrm{s}^{-1}\)
Angular displacement θ = 2θ rev = 2π(2π) rad = 4π² rad
Now, \(\omega^2=\omega_0^2-2 \alpha \theta\)
∴ angular acceleration \(\alpha=\frac{\omega_0^2}{2 \theta}\)
=\(\frac{\left(\frac{\pi}{10}\right)^2}{2 \times 4 \pi^2} \mathrm{rad} \mathrm{s}^{-2}\)
=\(\frac{1}{800} \mathrm{rad} \mathrm{s}^{-2}\)
Hence, the required torque is
⇒ \(\tau=I \alpha=\left(16 \times 10^{-4} \mathrm{~kg} \mathrm{~m}^2\right)\left(\frac{1}{800} \mathrm{rad} \mathrm{s}^{-2}\right)\)
=\(2 \times 10^{-6} \mathrm{~N} \mathrm{~m}\)
Question 88. A disc of mass 5 g and radius 1 cm is fixed to a thin stick AB of negligible mass, as shown in the figure. The system is initially at rest. A constant torque required to rotate the disc about AB at 25 rps in 5 s is close to
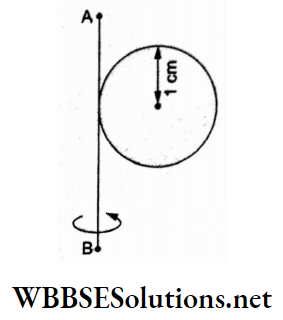
- 4.0 x 10-66N m
- 1.6 x 10-5N m
- 2.0 x 10-5N m
- 6.5 x 10-4N m
Answer: 3. 2.0 x 10-5N m
The moment of inertia of the disc about the axis AB (a tangent) is
⇒ \(I=\frac{M R^2}{4}+M R^2=\frac{5}{4} M R^2\)
Angular acceleration
⇒ \(\alpha=\frac{d \omega}{d t}=\frac{25 \mathrm{rps}}{5 \mathrm{~s}}=10 \pi \mathrm{rad} \mathrm{s}^{-2}\)
Hence, the required torque is
⇒ \(\tau=I \alpha=\left(\frac{5}{4} M R^2\right)(10 \pi)\)
∴ \(\tau=\frac{5}{4}\left(5 \times 10^{-3} \mathrm{~kg}\right)\left(10^{-2} \mathrm{~m}\right)^2\left(10 \pi \mathrm{rad} \mathrm{s}^{-2}\right)\)
= 19.6 x 10-6 Nm ≈ 2 x 10-5N m.
Question 89. The magnitude of the torque on a particle of mass 1 kg is 2.5 N m about the origin. If the force acting on it is 1 N and the distance of the particle from the origin is 5 m. Then, the angle between the force and the position vector is
- \(\frac{\pi}{3}\)
- \(\frac{\pi}{4}\)
- \(\frac{\pi}{8}\)
- \(\frac{\pi}{6}\)
Answer: 4. \(\frac{\pi}{6}\)
Torque = \(|\vec{\tau}|=|\vec{r} \times \vec{F}|\) = rF sin0
=> (2.5Nm) = (5m)(lN) sinθ
⇒ \(\sin \theta=\frac{1}{2} \Rightarrow \theta=\frac{\pi}{6}\)
Question 90. A rod of length 0.5 m is pivoted at one end. It is raised such that it makes an angle of 30° from the horizontal, as shown, and then released from rest. Its angular speed when it passes through the horizontal will be
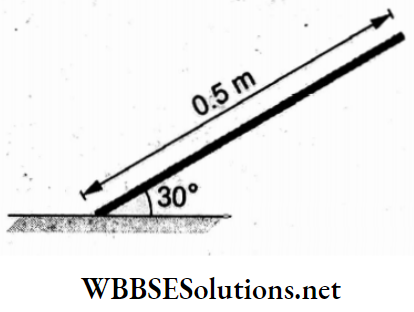
- \(\frac{\sqrt{30}}{2} \mathrm{rad} \mathrm{s}^{-1}\)
- 30 rad s-1
- \(\frac{\sqrt{20}}{2} \mathrm{rad} \mathrm{s}^{-1}\)
- √15 rad s-1
Answer: 2. √30 rad s-1
Work done by gravity = \(W_{\text {grav }}=M g\left(\frac{L}{2}\right) \sin 30^{\circ}=\frac{M g L}{4}\)
Change in KE = \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{M L^2}{3}\right) \omega^2\)
From the work-energy theorem,
⇒ \(\frac{1}{2}\left(\frac{M L^2}{3}\right) \omega^2=\frac{M g L}{4} \Rightarrow \omega=\sqrt{\frac{3 g}{2 L}}\)
Substituting the values,
⇒ \(\omega=\sqrt{\frac{3\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}{2(0.5 \mathrm{~m})}}=\sqrt{30} \mathrm{rad} \mathrm{s}^{-1}\)
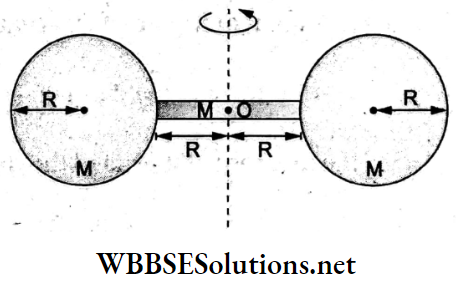
Question 91. Two identical solid spheres of mass Mandradius R each are stuck on the two ends of a uniform rod of length 2R and mass M, as shown in the figure. The moment of inertia of the system about the axis passing perpendicularly through the centre of the rod is
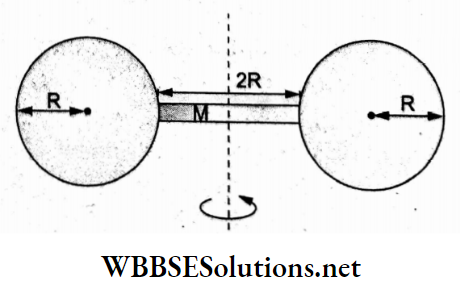
- \(\frac{137}{15} M R^2\)
- \(\frac{209}{15} M R^2\)
- \(\frac{17}{15} M R^2\)
- \(\frac{152}{15} M R^2\)
Answer: 1. \(\frac{137}{15} M R^2\)
The moment of inertia of a solid cp sphere about its own diameter is given by
ICM = \(\frac{2}{5}\)MR².
From the theorem of parallel axes, the moment of inertia of each sphere about the parallel axis through O is given
⇒ \(I=I_{\mathrm{CM}}+M d^2\)
= \(\frac{2}{5} M R^2+M(2 R)^2\)
= \(\frac{22}{5} M R^2\)
So, the moment of inertia of the whole system about the axis through O is
⇒ \(2\left(\frac{22}{5} M R^2\right)+\frac{M(2 R)^2}{12}=\frac{137}{15} M R^2\)
Question 92. A solid sphere and a solid cylinder of equal radii approach an incline with the same linear velocity. Both roll without slipping throughout their motion. The two respectively reach the maximum heights of hsph and hcyl on the incline. The ratio \(\frac{h_{\mathrm{sph}}}{h_{\mathrm{cyl}}}\) is equal to
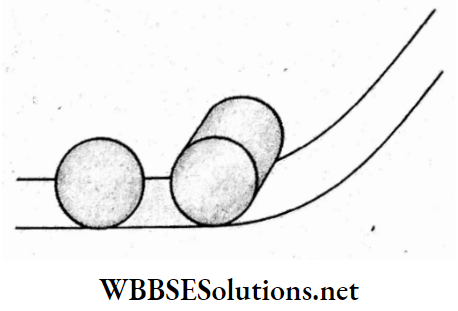
- \(\frac{4}{5}\)
- \(\frac{14}{15}\)
- \(\frac{2}{\sqrt{5}}\)
- 1
Answer: 2. \(\frac{14}{15}\)
For a solid sphere, the KE of rolling motion is
⇒ \(E_{\mathrm{sph}}=\frac{1}{2} M v^2\left(1+\frac{k^2}{R^2}\right)\)
=\(\frac{1}{2} M v^2\left(1+\frac{2}{5}\right)\)
If the height reached on the incline is hsph then
⇒ \(M g h_{\mathrm{sph}}=\frac{1}{2} M v^2\left(\frac{7}{5}\right)\)……..(1)
Similarly, for a solid cylinder, we have
⇒ \(M g h_{\mathrm{cyl}}=\frac{1}{2} M v^2\left(1+\frac{k^2}{R^2}\right)=\frac{1}{2} M v^2\left(1+\frac{1}{2}\right)\)
⇒ \(M g h_{\mathrm{cyl}}=\frac{1}{2} M v^2\left(\frac{3}{2}\right)\)……(2)
Now, by dividing (1) by (2), we get the ratio
⇒ \(\frac{h_{\text {sph }}}{h_{\text {cyl }}}=\frac{\frac{7}{5}}{\frac{3}{2}}=\frac{14}{15}\)
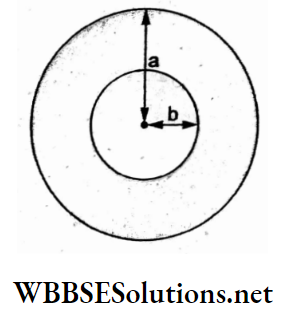
Question 93. A circular disc of radius a has a hole of radius b around its centre. If surface density (mass per unit area) varies as \(\sigma=\frac{\sigma_0}{r}\) (where r is the radius of a concentric ring), the radius of gyration (k) of the disc about the axis passing through its centre and perpendicular to its plane is equal to
- \(\frac{a+b}{2}\)
- \(\frac{a+b}{3}\)
- \(\sqrt{\frac{a^2+b^2+a b}{2}}\)
- \(\sqrt{\frac{a^2+b^2+a b}{3}}\)
Answer: 4. \(\sqrt{\frac{a^2+b^2+a b}{3}}\)
Let us consider a concentric ring of radius r and width dr. Its mass is i
⇒ \(d M=2 \pi r d r\left(\frac{\sigma_0}{r}\right)\)
Then, the total mass of the disc is
⇒ \(M=2 \pi \sigma_0 \int_b^a d r=2 \pi \sigma_0(a-b)\)……(1)
The moment of inertia ofthisringis
⇒ \(d I=(\text { mass }) r^2=(2 \pi r d r)\left(\frac{\sigma_0}{r}\right) r^2=2 \pi \sigma_0 r^2 d r\)
∴ the moment of inertia of the disc is
⇒ \(I=\int d I=2 \pi \sigma_0 \int_b^a r^2 d r=\frac{2}{3} \pi \sigma_0\left(a^3-b^3\right)\)…..(2)
But I = Mk². Hence, the radius of gyration is
⇒ \(k=\sqrt{\frac{I}{M}}=\sqrt{\frac{\frac{2}{3} \pi \sigma_0\left(a^3-b^3\right)}{2 \pi \sigma_0(a-b)}}=\sqrt{\frac{a^2+b^2+a b}{3}}\)
Question 94. Two coaxial discs of moments of inertia I and I/2 are rotating with angular velocities ω and ω/2 about their common axis. They are brought in contact with each other and then they rotate with a common angular velocity. If Ef and be the final and initial total energies respectively, Ef– Ei is equal to
- \(-\frac{I \omega^2}{12}\)
- \(\frac{I \omega^2}{6}\)
- \(-\frac{I \omega^2}{24}\)
- \(\frac{3}{8} I \omega^2\)
Answer: 3. \(-\frac{I \omega^2}{24}\)
Conserving the angular momentum,
⇒ \(I \omega+\left(\frac{I}{2}\right)\left(\frac{\omega}{2}\right)=\left(I+\frac{I}{2}\right) \omega_0 \Rightarrow \omega_0=\frac{5}{6} \omega\)……(1)
Initial KE = \(E_{\mathrm{i}}=\frac{1}{2} I \omega^2+\frac{1}{2}\left(\frac{I}{2}\right)\left(\frac{\omega}{2}\right)^2=\frac{9}{16} I \omega^2\)
Final KE = Ef = \(E_{\mathrm{f}}=\frac{1}{2}\left(I+\frac{I}{2}\right) \omega_0^2=\frac{1}{2}\left(\frac{3}{2} I\right)\left(\frac{5 \omega}{6}\right)^2\) [from (1)]
= \(\frac{25}{48} I \omega^2\)
∴ \(E_{\mathrm{f}}-E_{\mathrm{i}}=\left(\frac{25}{48}-\frac{9}{16}\right) I \omega^2=-\frac{I \omega^2}{24}\)
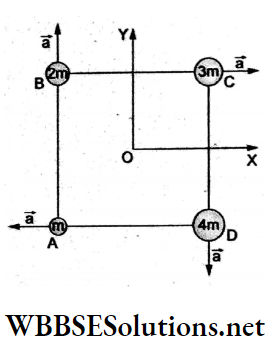
Question 95. Four particles A, B, C and D of masses m, 2m, 3m and 4m respectively are at the comers of a square. They have accelerations of the same magnitude \(|\vec{a}|\) and the directions as shown in the figure. The acceleration of the centre of mass of the system of particles is
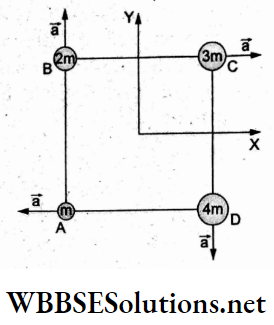
- \(\frac{a}{5}(\hat{i}-\hat{j})\)
- \(\frac{a}{5}(\hat{i}+\hat{j})\)
- Zero
- \(a(\hat{i}+\hat{j})\)
Answer: 1. \(\frac{a}{5}(\hat{i}-\hat{j})\)
The acceleration of the centre of mass of the system is
⇒ \(\vec{a}_{\mathrm{CM}}=\frac{1}{M}\left(m_1 \vec{a}_1+m_2 \vec{a}_2+m_3 \vec{a}_3+m_4 \vec{a}_4\right)\)
⇒ \(\frac{[m a(-\hat{i})+2 m a(\hat{j})+3 m a(\hat{i})+4 m a(-\hat{j})]}{m+2 m+3 m+4 m}\)
⇒ \(\frac{a}{10}(2 \hat{i}-2 \hat{j})\)
=\(\frac{a}{5}(\hat{i}-\hat{j})\)
Question 96. A thin smooth rod of length L and mass M is rotating freely with an angular speed ω0 about an axis perpendicular to the length of the rod and passing through its centre of mass. Two beads of mass m each and of negligible sizes are at the centre of the rod initially. The beads are free to slide along the rod. The angular speed of the system, when the beads reach the opposite ends of the rod, will be
- \(\frac{M \omega_0}{M+2 m}\)
- \(\frac{M \omega_0}{M+3 m}\)
- \(\frac{M \omega_0}{M+6 m}\)
- \(\frac{M \omega_0}{M+m}\)
Answer: 3. \(\frac{M \omega_0}{M+6 m}\)
Conserving the angular momentum,
⇒ \(I \omega_0=I^{\prime} \omega \Rightarrow \frac{M L^2}{12} \omega_0=\left[\frac{M L^2}{12}+2 m\left(\frac{L}{2}\right)^2\right] \omega\)
⇒ \(\frac{M \omega_0}{12}=\left(\frac{M}{12}+\frac{m}{2}\right) \omega=\left(\frac{M+6 m}{12}\right) \omega\)
⇒ \(\omega=\left(\frac{M}{M+6 m}\right) \omega_C\)
Question 97. A man of mass 80 kg is standing at the edge of a circular disc of mass 200 kg. The disc rotates about the vertical axis through its centre at 5 revolutions per second. If the moves to the centre of the disc, the angular speed of the disc becomes
- 9rps
- 3rps
- 6rps
- 12rps
Answer: 1. 9rps
The initial moment of inertia of the man-disc system is
⇒ \(I_1=\frac{1}{2} M R^2+m R^2=\left(\frac{M}{2}+m\right) R^2\)
where M and m are the masses of the disc and them respectively.
Finally, when the man is at the centre,
⇒ \(I_2=\frac{1}{2} M R^2\)
Conserving the angular momentum,
⇒ \(\left(\frac{M}{2}+m\right) R^2 \omega_1=\frac{1}{2} M R^2 \omega^{\prime}\)
final angular speed
⇒ \(\omega^{\prime}=\frac{(180 \mathrm{~kg})(5 \mathrm{rps})}{100 \mathrm{~kg}}\)
= 9rps
Question 98. A one-metre-long uniform rod AB of mass 2mpivoted atAishithorizontally at the free end B by a ball of mass m moving at 6 m s-1. If the ball sticks to the rod after a collision, find the maximum angular displacement (θ) of the rod. (Given that cos 63° = 0.46.)
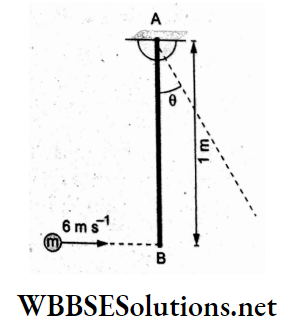
- 53°
- 63°
- 59°
- 69°
Answer: 2. 63°
Conserving the angular momentum,
⇒ \(\frac{1}{2} I \omega^2=2 m g\left(\frac{l}{2}\right)(1-\cos \theta)+m g l(1-\cos \theta)\)
the initial angular speed of the rod is
Conserving the mechanical energy,
⇒ \(\frac{1}{2}\left(\frac{5}{3} m l^2\right)\left(\frac{3 v}{5 l}\right)^2=2 m g l(1-\cos \theta)\)
⇒ \(\frac{1}{2}\left(\frac{5}{3} m l^2\right)\left(\frac{3 v}{5 l}\right)^2=2 m g l(1-\cos \theta)\)
Substituting l=1 m and v = 6ms-1, we have
⇒ \(\cos \theta=\frac{23}{50}=0.46=\cos 63^{\circ}\)
⇒ \(\theta \approx 63\)
Question 99. A block of mass 3m is suspended by a metre scale of mass m, as shown. If the tension in the string A is kmg A in equilibrium, then the value of k will be
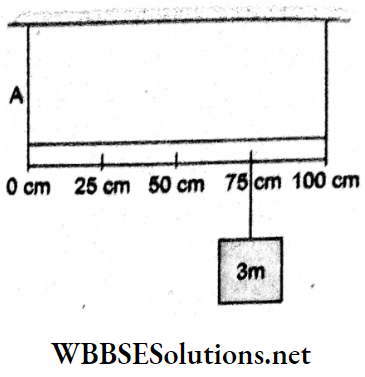
- \(\frac{5}{4}\)
- \(\frac{4}{5}\)
- \(\frac{1}{5}\)
- \(\frac{3}{5}\)
Answer: 1. \(\frac{5}{4}\)
The forces acting on the system are:
- Weight of the scale through its centre of
- Tension TA and T acting vertically upward.
- Weight of the suspended block = 3mg.
Since the system is in equilibrium, the torque of all forces about any point must be zero.
Taking the torque about O, kmg (100cm)
= mg(50cm) + 3mg(25cm)
⇒ \(k(100)=125\)
⇒ \(k=\frac{5}{4}\)

Question 100. Two discs having the moments of inertia I1 = 0.10 kg m² and I2 = 0.20 kg m² and rotating with the angular velocities ω1 = 10 rad s-1 and ω2 = 5 rad s-1 respectively are brought into contact coaxially and thereafter they rotate together. What is the kinetic energy of the system when they have a common angular velocity?
- Zero
- 10J
- 5 J
- \(\frac{20}{3}\)J
Answer: 4. \(\frac{20}{3}\)J
Conserving the angular momentum,
⇒ \(L=I_1 \omega_1+I_2 \omega_2=\left(I_1+I_2\right) \omega\)
The kinetic energy of the system when they rotate together will be
⇒ \(E=\frac{L^2}{2 I}\)
=\(\frac{\left(I_1 \omega_1+I_2 \omega_2\right)^2}{2\left(I_1+I_2\right)}\)
=\(\frac{(0.1 \times 10+0.2 \times 5)^2}{2(0.1+0.2)} \mathrm{J}=\frac{20}{3} \mathrm{~J}\)
Question 101. A square of side a/2 is drilled in a uniform disc of radius a, as shown in the adjoining figure. The position of the centre of mass of the remaining part is at
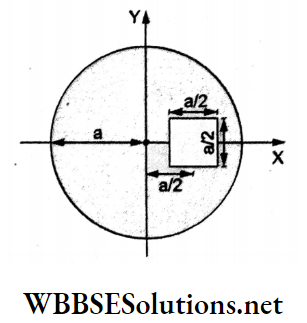
- \(x=-\frac{2 a}{\pi}\)
- \(x=-\frac{4 a}{3 \pi}\)
- \(x=-\frac{a}{8 \pi-2}\)
- \(x=\frac{3 a}{4 \pi}\)
Answer: 3. \(x=-\frac{a}{8 \pi-2}\)
Mass per unit area of the disc = \(\frac{M}{\pi R^2}\)
Mass of the square area \(\left(\frac{M}{\pi R^2}\right)\left(\frac{a^2}{4}\right)=\frac{M}{4 \pi}\) [∵ a = R]
The distance of the centre of mass of the remaining part of the disc from the centre O is
⇒ \(x=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}=\frac{M \cdot 0+\left(-\frac{M}{4 \pi}\right)\left(\frac{a}{2}\right)}{M+\left(-\frac{M}{4 \pi}\right)}=\frac{-a}{8 \pi-2}\)
Question 102. Two discs A and B of the same mass have the radii R and R/2. A rotates with an angular speed of co; while B is at rest. When A is placed gently on B, both rotate with the same angular velocity. In the process, the percentage loss of kinetic energy is
- 20
- 40
- 10
- 30
Answer: 1. 20
For disc A, \(I_1=\frac{1}{2} m R^2 \text { and } \omega_1=\omega\)
For disc B, \(I_2=\frac{1}{2} m\left(\frac{R^2}{4}\right)=\frac{m R^2}{8}=\frac{I_1}{4}\)
and \(\omega_2=0\)
The angular momentum remains constant.
Initial KE = \(E_1=\frac{L^2}{2 I_1}\)
and final,
⇒ \(\mathrm{KE}=E_2=\frac{L^2}{2\left(I_1+I_2\right)}=\frac{L^2}{2\left(\frac{5 I_1}{4}\right)}\)
∴ fractional change in KE, \(\frac{\Delta E}{E_1}=1-\frac{E_2}{E_1}=1-\frac{4}{5}=\frac{1}{5}\)
Hence, the percentage decrease
⇒ \(\frac{\Delta E}{E_1} \times 100 \%=\frac{1}{5} \times 100 \%=20 \%\)
Question 103. Two discs of radii R and aR are of the same thickness and made of the same material. If their moments of inertia about their own axis are in the ratio 1: 16, the value of α is
- \(\frac{1}{2}\)
- 2
- \(\frac{1}{4}\)
- 1
Answer: 2. 2
Let a denote the mass per unit area.
Hence,\(m_1=\pi R^2 \sigma \text { and } m_2=\pi \alpha^2 R^2 \sigma\)
∴ \(\frac{I_1}{I_2}=\frac{\frac{1}{2} m_1 R^2}{\frac{1}{2} m_2 \alpha^2 R^2}\)
=\(\frac{\sigma \pi R^4}{\sigma \pi \alpha^4 R^4}\)
=\(\frac{1}{\alpha^4}\)
=\(\frac{1}{16} \text { (given) }\)
∴ a = 2
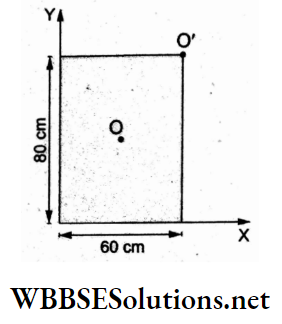
Question 104. The ratio of the moments of inertia of the rectangular plate of uniform thickness about the axes through O and O’ perpendicular to the plane of the plate is
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- \(\frac{1}{4}\)
- \(\frac{1}{5}\)
Answer: 3. \(\frac{1}{4}\)
About the axis through O,
⇒ \(I_0=M\left(\frac{a^2+b^2}{12}\right)\)
About the axis through O’
⇒ \(I^{\prime}=I_0+M r^2=M\left(\frac{a^2+b^2}{12}\right)+M\left(\frac{a^2+b^2}{4}\right)\)
⇒ \(M\left(\frac{a^2+b^2}{3}\right)\)
∴ \(\frac{I_0}{I^{\prime}}=\frac{1}{4}\)
Question 105. Find the torque about the origin when a force \(\vec{F}=(3 \mathrm{~N}) \hat{j}\); acts on a particle whose position vector is \((2 \mathrm{~m}) \hat{k}\).
- \(6 \hat{j} \mathrm{Nm}\)
- \(-6 \hat{i} \mathrm{Nm}\)
- \(6 \hat{k} \mathrm{Nm}\)
- \(6 \hat{i} \mathrm{Nm}\)
Answer: 2. \(-6 \hat{i} \mathrm{Nm}\)
Given that \(\vec{F}=(3 \mathrm{~N}) \hat{j} \text { and } \vec{r}=(2 \mathrm{~m}) \hat{k}\)
∴torque = \(\vec{\tau}=\vec{r} \times \vec{F}=(3 \times 2 \mathrm{~N} \mathrm{~m})(\hat{k} \times \hat{j})\)
⇒ \((6 \mathrm{Nm})(-\hat{i})\)
⇒\(-6 \hat{i} \mathrm{Nm}\)