Algebra Chapter 4 Linear Equations
Chapter 4 Linear Equations Introduction:
You have studied a lot of what are equations in one and two variables, what are simultaneous linear equations in one and two variables, how graphs of these linear equations are drawn in the graph papers, and also how they are solved with the help of a graph, etc, in the previous chapter.
In the present chapter, we shall discuss the different methods of solving these simultaneous linear equations, especially in two variables without any drawing of graphs.
But first, we want to know the conditions for which two given simultaneous linear equations in two variables are solvable or not.
Read and Learn More WBBSE Solutions For Class 9 Maths
Chapter 4 Linear Equations Conditions For Which Two Simultaneous Linear Equations In Two Variables Are Solvable Or Not
- You have already known that the general or standard form of two simultaneous linear equations in two variables is:
- a1 + b1y + r, =0. where a1, b1, c1 are constants and both a1 and b1, are hot zero simultaneously.
- a2x + b2y + c2 = 0, where a2, b2, c2 are constants and both a2 and b2 are not zero simultaneously.
We can determine whether these two equations are solvable or not by two methods :
- By drawing graphs
- By finding the relations among the ratios of the co-efficient of the same variable and of the constant terms of the two equations.
By drawing graphs :
- You have already learned the methods of drawing graphs of linear equations in one or two variables.
- So, it is now easy to you to draw the graphs of the above equations given in the standard form.
- You have also learned previously that the graphs of any linear equations, either in one or two variables are always some straight lines.
- Therefore, the two graphs of the given two simultaneous linear equations, in two variables must also be two straight lines.
Now, if these two straight lines—
- Intersect to each other, then the given two simultaneous equations are solvable and there is one and only one solution set of these two equations.
- Coincide then the given two simultaneous linear equations are solvable and there are infinitely many solution sets of these two equations.
- Are parallel to each other and the given two simultaneous linear equations are not solvable.
Accordingly, there is no solution set for these two equations.
By finding the relations among the ratios between the coefficients of the same variable and of the constant terms of the two equations:
The coefficient of the variable x in the two simultaneous linear equations a1 x + b1 y + c1 = 0 and a2x + b2y + c2 = 0 are and a2 respectively.
The ratio of them is \(\frac{a_1}{a_2}\) The coefficient of the variable y are b1 and b2, the ratio of which is \(\frac{b_1}{b_2}\) The constant terms of the two equations are c1 and c2 the ratio of which is \(\frac{c_1}{c_2}\)
Now, if—
1. \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\), then the given two simultaneous linear equations are solvable and there is one and only one set of solutions in this case.
2. \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) then the given two simultaneous linear equations are solvable and there are infinitely many sets of solutions in this case.
3. \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\), then the two given simultaneous linear equations are not solvable and there is no set of solutions in this case.
From the above discussion, we can say that,
1. If \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\), then the graph of the given two simultaneous linear equations intersect each other. The converse is also true.
2. \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\), then the graph of the given two simultaneous linear equations coincide. The converse is also true.
3. If \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\), then the graph of the given two simultaneous linear equations are parallel to each other. It is also true conversely.
Your conceptions about the solvability of two simultaneous linear equations will be clear in the following given examples.
Chapter 4 Linear Equations Select The Correct Answer (MCQ)
Question 1.
1. If the simultaneous linear equations 3x + 4y 18 and kx 4y = 180 have no solution then the value of k is-
1. 0
2. 1
3. – 2
4. – 3
Solution:
3x + 4y = 18 and kx – 4y= 180 have no solution
⇔ \(\frac{3}{k}\) = \(\frac{4}{-4}\) ≠ \(\frac{18}{180}\)
⇒ 4k = –12
⇒ k = -3
The correct answer is 4. – 3
2. If the simultaneous linear equations ax + by + c = 0 and ax + b2y + c2 = 0 have only one solution, then the required condition is-
1. \(a_1 b_2=a_2 b_1\)
2. \(a_1 a_2=b_1 b_2\)
3. \(a_1 a_2=b_1 b_2 \neq c_1 c_2\)
4. \(a_1 b_2 \neq a_2 b_1\)
Solution:
If the simultaneous linear equations \(a_1 x+b_1 y+c_1=0 \text { and } a_2 x+b_2 y+c_2=0\) have only one solution.
∴ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(a_1 b_2 \neq a_2 b_1\)
∴ The correct answer is 4. \(a_1 b_2 \neq a_2 b_1\)
3. Two simultaneous linear equations in two variables will be inconsistent if their graphs be-
1. Intersecting
2. Parallel
3. Coincident
4. None of these
Solution:
Two simultaneous linear equations in two variables
will be inconsistent if their graphs be parallel.
∴ The correct answer is 2. Parallel
Chapter 4 Linear Equations Short Answer Type Questions
Question 1. Write the equation of such a straight line which
1. are parallel,
Solution:
The Equation Of A Stright Line
The equation of the straight line parallel to the graph of the equation x + 2y = 6
is x+2y= 10 (the alternate answer may be), since \(\frac{1}{1}=\frac{2}{2} \neq \frac{6}{10}\)
[by the formula: \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)]
2. intersect with each other
Solution:
The equation of a straight line intersecting with the graph of the equation x + 2y = 6 is 2x + y
= 6 (the alternate answer may be), since \(\frac{1}{2} \neq \frac{2}{1}\)
[by the formula: \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)]
3. coincide with the graph of a linear equation x + 2y = 6.
Solution:
Given x + 2y = 6
The equation of a straight line coinciding with the graph of the equation x + 2y = 6 is 4x + 8y= 24 (the alternate answer may be), since \(\frac{1}{4}=\frac{2}{8}=\frac{6}{24}\)
[by the formula: \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)]
Question 2. Find the value of p for which the equations 3x-4y = 1 and 9x+py = 2 will have only one set of solutions.
Solution:
Given 3x-4y = 1 And 9x+py = 2
The equations 3. x 4y = 1 and 9x+ py= 2 will have only one set of solutions if \(\frac{3}{9} \neq \frac{-4}{p}\)
[by the formula: \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
or, \(\frac{1}{3} \neq \frac{-4}{p} \text { or, } p \neq-12\)
The given two equations will have only one set of solutions for all real values of p except (-12).
Question 3. Find the values of r for which the equations rx + 2y = 5 and (r+ 1)x + 3y = 2 have no solution.
Solution:
Given rx + 2y = 5 And (r+ 1)x + 3y = 2
Consider the Given Equations that rx + 2y = 5…….. (1) and (r + 1) x + 3y = 2………….(2)
Now, since equations (1) and (2) have no solution,
\(\frac{r}{r+1}=\frac{2}{3}\) [by the formula: \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
or, 3r = 2r + 2
or, 3r – 2r = 2
or, r = 2.
. The required value of r is 2.
Question 4. Find the value of p for which the equations px + 6yp = 0 and (p-1) x + 4y + (p-5)=0 have infinitely many sets of solutions.
Solution:
Given rx + 2y = 5 And (r+ 1)x + 3y = 2
The equations px + 6y-p=0….. (1) and (p-1) x + 4y + (p – 5) = 0…. (2)
will have infinitely many sets of solutions if \(\frac{p}{p-1}=\frac{6}{4}=\frac{-p}{p-5}\)
[by the formula: \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
or, 3p – 3 = 2p
or, 3p – 2p = 3
or, p = 3.
Again, \(\frac{6}{4}=\frac{-p}{p-5} \quad \text { or, } \quad \frac{3}{2}=\frac{-p}{p-5}\)
or, 3p – 15 = – 2p
or, 3p + 2p = 15
or, 5p = 15
or, p = 3.
.. The required value of p is 3.
Question 5. If x = 3t and y = \(\frac{2 t}{3}-1\)
Solution:
Given that x= 3y,
3t = 3 \(\frac{2 t}{3}-1\) [ x = 3t and y = \(\frac{2t}{3}\) – 1]
or, 3t = 2t – 3
or, 3t – 2t = -3
or, t = – 3.
Question 6. Find the value of k for which the equations 2x+5y= 8 and 2x-ky = 3 will have no solution.
Solution:
Given 2x+5y= 8 And 2x-ky = 3
The equations 2x+5y=8…….. (1) and 2x – ky = 3………. (2) will have no solution if \(\frac{2}{2}=\frac{5}{-k}\)
[by the formula: \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)]
or, 1 = \(\frac{5}{-k}\)
or, k = 5 or, k = 5.
∴ The required value of k is (-5).
Question 7. If x and y are real numbers and (x – 5)² + (x – y)²= 0, then find the value of x and y.
Solution:
Given (x – 5)² + (x – y)²= 0
In the equation (x – 5)² + (x – y)² = 0, the sum of two squares (x-5)² and (x – y)² is zero.
So, the value of these two squares will be zero each separately.
(x-5)² = 0x – 5 = 0
⇒ x = 5 and (x – y)² = 0
x – y = 0
⇒x = y
y = 5 [ ∵ x = 5]
∴ The required values of x = 5 and y = 5.
Question 8. Find the values of x and y if x² + y² – 2x + 4y=5.
Solution:
Given x² + y² – 2x + 4y=5
x²+ y² – 2x + 4y = –5
or, (x² – 2x + 1) + (y²+ 4y + 4) = 0
or, (x – 1)² + (y + 2)² = 0.
Since the sum of two squares equals zero implies that the value of each of the squares is zero separately,
we get, (x 1)² = 0
x – 1 = 0
⇒ x = 1 and (y+ 2)² = 0
y+2 = 0
y = -2.
The values of x = 1 and y = -2.
Question 9. Find the values of r for which the equations rx – 3y – 1 = 0 and (4-r) x – y + 1= 0 will have no solution.
Solution:
Given rx – 3y – 1 = 0 And (4-r) x – y + 1= 0
The equations rx – 3y – 1 = 0………………..(1) and (4-r) x – y + 1 = 0………..(2)
will have no solution if \(\frac{r}{4-r}=\frac{-3}{-1}\)
[by the formula: \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)]
or, 12 -3r = r
or, 4r = 12
or, r = 3.
The required value of r = 3.
Question 10. Write the equation \(a_1 x+b_1 y+c_1=0, b_1 \neq 0\) b ≠ 0, in the form of y = mx + c, where m and c are constants.
Solutions:
We have, \(a_1 x+b_1 y+c_1=0 \text { or, } b_1 y=-a_1 x-c_1\)
or, y = \(-\frac{a_1}{b_1} x-\frac{c_1}{b_1}\)
or, y= \(\left(-\frac{a_1}{b_1}\right) x+\left(-\frac{c_1}{b_1}\right)\)
or, y = mx + c, where m = \(-\frac{a_1}{b_1} \text { and } c=-\frac{c_1}{b_1}\)
Question 11. Find the value of k for which the equations kx 21y+ 150 and 8r – 7y = 0 will have only one set of solutions.
Solution:
Given kx 21y+ 150 And 8r – 7y = 0
The equations kx 21y+ 15 = 0 ……(1) and 8x7y = 0 (2)
will have only one set of solutions if \(\frac{k}{8} \neq \frac{-21}{-7}\)
[by the formula:\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)]
\(\frac{k}{8}\) ≠ 3
or, k ≠ 24.
∴ The equations (1) and (2) will have only one set of solutions for all real values of k, except 24.
Question 12. Find the values of a and b for which the equations 5x + 8y = 7 and (a + b) x + (a – b) y = (2a + b + 1) will have infinitely many sets of solutions.
Solutions:
Given 5x + 8y = 7 And (a + b) x + (a – b) y = (2a + b + 1)
The solutions 5x + 8y = 7……(1) and (a + b) x + (a – b) y = (2a + b + 1)……………(2)
will have infinitely many sets of solutions if \(\frac{5}{a+b}=\frac{8}{a-b}=\frac{7}{2 a+b+1}\)
[by the formula: \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)]
Now, \(\frac{5}{a+b}=\frac{8}{a-b}\)
or, 8a + 8b = 5a – 5b
or, 3a = –13 b
or, a = – \(\frac{13}{3}\) b…………..(3)
Again, \(\frac{8}{a-b}=\frac{7}{2 a+b+1}\)
or, 16a + 8b + 8 = 7a – 7b
or, 9a + 15b + 8 = 0
or, 9 x (– \(\frac{13}{3}\) b) + 15b +8 = 0 [by (3)]
or, –39b + 15b + 8 = 0
or, – 24b = 8
or, b = \(\frac{-8}{-24}\)
= \(\frac{1}{3}\)
∴ a = \(-\frac{13}{3} \times \frac{1}{3}\) =\(-\frac{13}{9}\)
Chapter 4 Linear Equations Long Answer Type Questions
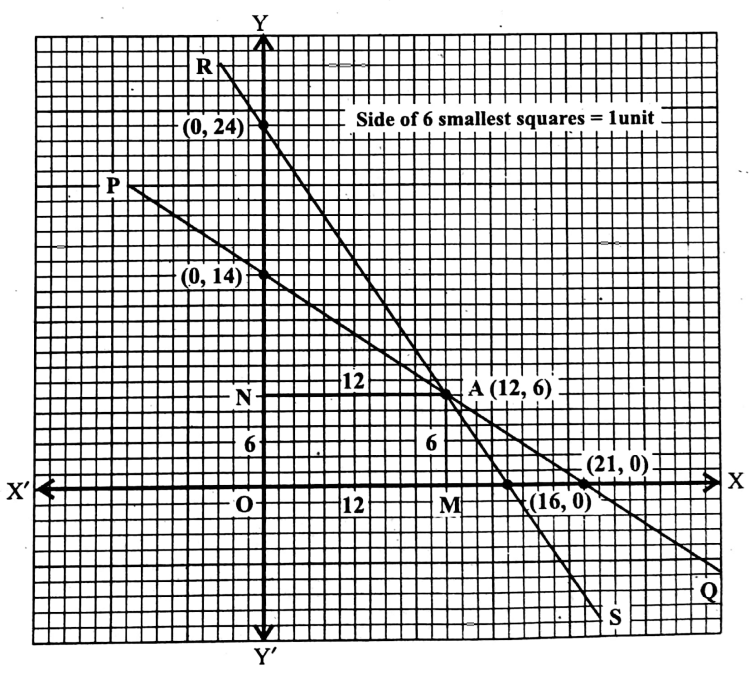
Question 1. Draw the graphs of the following equations to determine whether they are solvable or not. If solvable, find the set of solutions for a single solution and three sets of solutions for an infinite number of solutions :
1. 2x + 3y – 7 = 0; 3x + 2y 8 = 0
Solution:
Given 2x + 3y – 7 = 0; 3x + 2y 8 = 0
We have, 2x + 3y-7=0
From (1) we get. \(\frac{2 x}{7}+\frac{3 y}{7}=1 \text { or, } \frac{x}{\frac{7}{2}}+\frac{y}{\frac{7}{3}}=1\)
∴ the graph of equation (1) intersects the x-axis at \(\left(\frac{7}{2}, 0\right)\) and the y-axis at \(\left(0, \frac{7}{3}\right)\)
From (2) we, get \(\frac{3 x}{8}+\frac{2 y}{8}=1 \text { or, } \frac{x}{\frac{8}{3}}+\frac{y}{4}=1\)
∴ the graph of the equation intersects the x-axis at \(\left(\frac{8}{3}, 0\right)\) and the y-axis at (0, 4).
Now, by taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin and side of each smallest square = \(\frac{1}{6}\) unit, let us plot the point
\(\left(\frac{7}{2}, 0\right) \equiv\left(\frac{7}{2} \times 6,0 \times 6\right)=(21,0):\left(0, \frac{7}{3}\right) \equiv\left(0 \times 6, \frac{7}{3} \times 6,\right)=(0,14)\)
\(\left(\frac{8}{3}, 0\right) \equiv\left(\frac{8}{3} \times 6,0 \times 6\right)\) (16, 0) and (0, 4) = (0 x 6, 4 × 6) = (0,24) in the graph paper.
Then by joining the points (21, 0) and (0, 14) we get a straight line which is the required graph of equation (1).
Let this straight line be PQ.
By joining the points (16, 0) and (0, 24) we get another straight line which is the graph of equation (2).
Let this straight line be RS.
It is clear from the graph that PQ and RS intersect each other at point A, the coordinates of which are (12, 6).
But, since the side of 6 smallest squares = 1 unit, the real value of (12, 6) = (\(\frac{12}{6}\), \(\frac{6}{6}\)) = (2, 1).
∴ the given equations are solvable and there is only one set of solutions, the values of which are
r = 2 and y = 1.
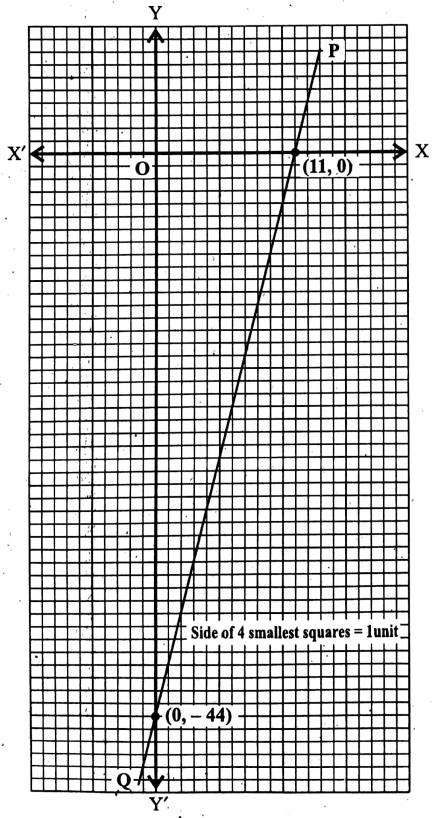
2. 4xy = 11; – 8x + 2y = 22
Solution:
Given 4xy = 11; – 8x + 2y = 22
Given that 4x – y = 11……..(1) and –8x + 2y = 22…….(2)
From (1) we get, \(\frac{4 x}{11}+\frac{y}{-11}=1 \quad \text { or } \frac{x}{\frac{11}{4}}+\frac{y}{-11}=1\)
∴ the graph of equation (1) intersects the x-axis at \(\left(\frac{11}{4}, 0\right)\) and the y-axis at (0, -11).
From (2) we get, \(\frac{-8 x}{-22}+\frac{2 y}{-22}=1 \text { or, } \frac{x}{\frac{11}{4}}+\frac{y}{-11}=1\)
∴ the graph of equation (2) intersects the x-axis at \(\left(\frac{11}{4}, 0\right)\) and the y-axis at (0, -11).
Now, by taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin and side of the 4 smallest squares = 1 unit,
let us plot the points \(\left(\frac{11}{4}, 0\right)\) = \(\left(\frac{11}{4} \times 4,0 \times 4\right)\)
= (11, 0) (0, -11) = (0 × 4, -11 x 4) = (0, 44) in the graph paper.
By joining these two points we get a straight X-line PQ (let).
Since the next two points (11, 0) and (0, 44) are also the same by joining them we shall get the same straight-line PQ.
Therefore, the graphs of equations (1) and (2) coincide.
∴ there are infinitely many sets of solutions to the given two equations.
Now let x = 0 for the equation (1).
∴ by (1) we get, 4 x 0 – y = 11
or, y = -11
∴ x = 0 and y = -11 is one set of solutions of the given equation (1).
Similarly, from (1) we get, if y = 0, x = and if y = 1, x 3.
∴ the required three sets of solutions the equations (1) and (2) are:
x = 0 and y = -11
x = \(\frac{11}{4}\) and y = 0
x = 3 and y = 1.
3. 7x+3y= 42; 21x+9y= 42.
Solution:
Given 7x+3y= 42 ; 21x+9y= 42
Given that 7x+3y= 42……………(1)
and 21x+9y= 42…………….(2)
From (1) we get, \(\frac{7 x}{42}+\frac{3 y}{42}=1 \text { or, } \frac{x}{6}+\frac{y}{14}=1\)
∴ the graph of equation (1) intersects the
x-axis at (6, 0) and the y-axis at (0, 14).
Again, from (2) we get, \(\frac{21 x}{42}+\frac{9 y}{42}=1 \text { or, } \frac{x}{2}+\frac{y}{\frac{14}{3}}=1 .\)
the graph of equation (2) intersects
the x-axis at (2, 0) and the y-axis at \(\left(0, \frac{14}{3}\right)\)
Now, by taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin and side of 3 smallest squares = 1 unit, let us plot the points (6, 0) = (6 x 3, 0 x 3) = (18, 0), (0, 14) = (0 x 3, 14 x 3) = (0, 42), (2, 0) = (2 x 3, 0 × 3) = (6, 0)
and \(\left(0, \frac{14}{3}\right) \equiv\left(0 \times 3, \frac{14}{3} \times 3\right)\) = ( (0, 14) in the graph paper.
Then by joining the points (18, 0) and (0, 42), we get a straight line, say PQ.
Again, by joining the points (6, 0) and (0, 14) we get another straight line, says RS.
From the graph, we see that PQ || RS, i.e., the graphs of the given equations (1) and (2) are parallel to each other.
The given equations (1) and (2) are not solvable.
Question 2. Determine whether each pair of the following equations are solvable or not by finding the relations among the ratios of the coefficients of the same variable and the constant terms of each pair. Also, write whether the graphs of the equations of each pair are parallel or intersecting or coinciding, or not.
1. 5x + 3y= 11; 2x – 7y = 12
Solution:
Given x + 3y= 11; 2x – 7y = 12
We have, 5x + 3y = 11……………….(1) and 2x – 7y = 12…………..(2)
Here, the ratio of the coefficients of x = \(\frac{5}{2}\) and the ratio of the coefficients of y = \(\frac{3}{-7}\)
Since, \(\frac{5}{2}\) ≠ \(\frac{3}{-7}\), the given equations (1) and (2) will have only one solution and they intersect to each
2. 6x-8y = 2; 3x-4y = 1
Given 6x-8y = 2; 3x-4y = 1
We have, 6x – 8y = 2…..…. (1) and 3x – 4y = 1………..(2)
Here, the ratio of the co-efficients of x = \(\frac{6}{3}\) = 2 and the co-efficients of y = =2.
Also, the ratio of the constant terms of (1) and (2) is \(\frac{2}{1}\) = 2.
Since the ratios are all equal, the given two equations are solvable and their graphs of them coincide.
3. 8x – 7y = 0; 8x – 7y = 56
Solution:
Given 8x – 7y = 0; 8x – 7y = 56
We have 8x – 7y = 0………(1) and 8x – 7y= 56…….(2)
Here, the ratio of the coefficients of x = \(\frac{8}{8}\) = 1, the coefficients of y = \(\frac{-7}{-7}\) =1
and the ratio of the constant terms = \(\frac{0}{56}\) =0.
Since, 1 = 1 ≠ 0,
∴ the given equations are not solvable and their graph of them are parallel to each other.
Different methods of solving two simultaneous linear equations in two variables:
- You have studied the easy method of solving linear equations in one variable in your earlier classes.
- In the present, we shall discuss the different methods of solving two simultaneous linear equations in two variables.
The methods are:
- Method of elimination
- Method of comparison
- Method of substitution
- Method of cross-multiplication.
1. Method of Elimination:
- In this method, the solution of one of the two given variables (generally x and y) is determined by eliminating the other variable with the help of simple algebraic operations.
- Since one variable of the two is eliminated to determine the other one, the method is known as the method of elimination.
- You have learned that the value of an equation does not change when it is multiplied or divided by a non-zero real number.
- Applying this principle, the coefficients of any one of the two variables (generally of that variable the signs of which are opposite to each other in the two equations) in the given two simultaneous linear equations, are made equal in this method and then that very variable is eliminated by the simple algebraic operations-addition or subtraction.
The working rule of this method is:
STEP-1: Equalize one of the two coefficients of any one of the two variables of the given simultaneous linear equations by multiplying or dividing them by any non-zero real numbers.
STEP-2: Eliminate that very variable by simple algebraic operations of addition or subtraction.
STEP-3: Determine the value of the rest variable by solving the equation thus obtained in STEP-2.
STEP-4: On putting the value of the variable thus determined in any one (as per convenience) of the given two equations, find the solved value of the eliminated variable.
Therefore, the values of the variables thus obtained are the solutions of the two given simultaneous linear equations.
You can check whether the solutions thus determined are correct or not immediately by the following process:
1. Calculate the values of the LHS of both the given equations by putting the values of the variables thus obtained.
2. If these values are equal to the RHS in both equations, then your solved solutions are correct. If not, obviously they are incorrect.
Observe the following example minutely:
Solve: 8x + 5y = 11; 3x – 4y = 10
Solution:
Given 8x + 5y = 11; 3x – 4y = 10
Consider THe Given Equation that 8x + 5y = 11………….(1) and 3x – 4y = 10……………(2).
Here the coefficients of x in both the equations are positive but the coefficients of y are in opposite signs, the first is ‘+’ and the second is ‘ – ‘;
So, it is convenient to equalize the coefficients of y.
Now, the co-efficient of y in the first equation is 5 and in the second, it is 4.
The LCM of 5 and 4 is 20, i.e., we have to multiply the first equation by 4 to make 5 a number 20 and the second equation by 5 to make 4 a number 20.
Thus, by multiplying (1) by 4 and (2) by 5, we get,
32x + 20y = 44…..(3)
15x – 20y = 50………(4)
Adding (3) and (4), 47x = 94 or, x = \(\frac{94}{47}\)
∴ x = 2.
Now, putting x = 2 in (1), we get, 8 x 2+5y= 11
or, 16+5y = 11
or, 5y = 11 16
or, 5y = -5
or, y = -1.
∴ the required solution is x = 2, y = -1.
Proof of correctness:
LHS of (1) = 8x + 5y = 8 x 2 + 5 x (-1)
= 16 – 5
= 11
= RHS.
LHS of (2) = 3x- 4y = 3 x 2 – 4 x ( -1)
= 6 + 4
= 10
= RHS.
Hence the required solutions are correct.
2. Method of Comparison:
In this method, one of the two variables of the given two simultaneous linear equations is expressed in terms of the other variable and then the expressed parts of both equations are compared to get a new linear equation of one variable.
Hence the value of that variable is determined by solving this equation.
Since comparison is made to solve the given two simultaneous linear equations, the method is known as the method of comparison.
The working rule of this method is :
STEP-1: Express anyone (as per convenience) of the two variables in the first equation in terms of the other variable (i.e., there will be only one variable in the LHS of the first equation.)
STEP-2: Express the same variable in the second equation in terms of the other variable similarly.
STEP-3: Compare the RHSS of both the equation, thus expressed to get a new linear equation of one variable, i.e. write RHS of the first equation equal to the RHS of the second equation.
STEP-4: Determine the value of the variable by solving the equation obtained in STEP-3.
Find the value of the other variable by putting the value of the variable obtained in STEP-4 in any one of the expressed equations in STEP-1 or STEP-2 and solving thereafter.
Therefore, the values of the variables thus obtained are the required solutions of the given two simultaneous linear equations.
Observe the following example :
Solve: 4x-3y = 18, 4y 5x=-7.
Solution:
Given 4x-3y = 18, 4y 5x=-7
We have, 4x – 3y = 18
or, 4x = 18+ 3y
or, x = \(\frac{18 + 3y}{4}\)…………(i)
4y – 5x = -7
or, 5x = 7 – 4y
or, x = \(\frac{4y + 7}{5}\) ……………(ii)
Now, comparing the RHSS of (1) and (2) we get,
\(\frac{3y + 18}{4}\) = \(\frac{4y + 7}{5}\) [ …LHSS are equal]
or, 16y+ 28 = 15y + 90
or, 16y – 15y = 90 – 28
or, y = 62,
∴ y = 62.
Now putting y = 62 in (1) we get, x = \(\frac{3 \times 62+18}{4}=\frac{186+18}{4}=\frac{204}{4}\) =51.
∴ the required solution is x = 51, y = 62.
3. Method of Substitution :
In this method, one variable of any one of the given two simultaneous linear equations is expressed in terms of the other variable.
Then this expressed the value of the variable is substituted against that variable in the other equation to get a linear equation of one variable.
Solving this equation we get the value of that variable.
Since the expressed value of one variable of any one of the given two simultaneous linear equations is substituted against the same variable in the other equation to get the solutions of the given equations, the method is known as the method of substitution.
The working rule of this method is:
STEP-1: Express one of the two variables of any one of the given two simultaneous linear equations in terms of the other variable.
STEP-2: In the other equation substitute that variable with this expressed value of the variable to get a linear equation of one variable.
STEP-3: Find the value of that variable by solving this linear equation.
STEP-4: Find the value of the other variable by putting the value of the variable obtained in STEP-3 in the expressed equation in STEP-1.
Therefore, the values of the variables thus obtained are the solutions of the given two simultaneous linear equations.
Observe the following equations:
Solve: 3xy = 7; 2x + 4y = 0
Solution:
Given 3xy = 7; 2x + 4y = 0
We have, 3x – y = 7
or, 3x = y + 7
or, x = \(\frac{y+7}{3}\) …………(1)
Substituting \(\frac{y+7}{3}\) in respect to x in 2x + 4y = 0 we get,
\(2 \times \frac{y+7}{3}+4 y\) = or, \(\frac{2 y+14}{3}+4 y=0\)
or, 2y + 14+ 12y = 0
or, 14y = -14
or, y = \(\frac{-14}{14}\)
or, y = -1.
Now, putting y = -1 in (1) we get, x = \(\frac{-1+7}{3}=\frac{6}{3}\) = 2.
∴ the required solution is x = 2, y = -1.
4. Method of Cross-multiplication:
In this method, two simultaneous linear equations given in the standard form (If not they should be expressed in the standard form) are solved by a formula.
The formula is:
If \(a_1 x+b_1 y+c_1=0 \text { and } a_2 x+b_2 y+c_2=0\) be two given simultaneous linear equations, then
\(\frac{x}{b_1 c_2-b_2 c_1}=\frac{-y}{a_1 c_2-a_2 c_1}=\frac{1}{a_1 b_2-a_2 b_1} \quad\left(a_1 b_2-a_2 b_1 \neq 0\right)\)
i.e., x = \(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}\)
and y = \(\frac{a_2 c_1-a_1 c_2}{a_1 b_2-a_2 b_1}\)
This formula can be obtained by the cross-multiplication of the coefficients of the variables of the given two simultaneous linear equations. For this reason, this method is known as the method of cross-multiplication.
We can solve the simultaneous linear equations \(a_1 x+b_1 y+c_1=0\)…… (1) and
\(a_2 x+b_2 y+c_2=0\)………..(2) by the method of elimination.
Such as- multiplying (1) by a2 and (2) by a1 we get,
\(a_1 a_2 x+a_2 b_1 y+a_2 c_1=0\)…… (3)
and \(a_1 a_2 x+a_1 b_2 y+a_1 c_2=0\)……. (4)
Now, subtracting (3) from (4) we get, \(a_1 b_2 y-a_2 b_1 y+a_1 c_2-a_2 c_1=0\)
or, \(y\left(a_1 b_2-a_2 b_1\right)=a_2 c_1-a_1 c_2\)
or, \(\frac{a_2 c_1-a_1 c_2}{a_1 b_2-a_2 b_1}\)………………..(5)
Again, multiplying (1) by b2 and (2) by b1, we get
\(a_1 b_2 x+b_1 b_2 y+b_2 c_1=0\)………………….(vi)
and \(\frac{a_2 c_1-a_1 c_2}{a_1 b_2-a_2 b_1}\)…..(vii)
Now, subtracting (vi) from (vii) we get, \(a_2 b_1 x+a_1 b_2 x+b_1 c_2-b_2 c_1=0\).
or, \(\left(a_2 b_1-a_1 b_2\right) \ddot{x}=\left(b_2 c_1-b_1 c_2\right)\)
or,\(\frac{b_2 c_1-b_1 c_2}{a_2 b_1-a_1 b_2}=\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}\)……………(8)
From (v) and (viii) we get,
\(\frac{x}{b_1 c_2-b_2 c_1}=\frac{y}{a_2 c_1-a_1 c_2}=\frac{1}{a_1 b_2-a_2 b_1}\)
or, \(\frac{x}{b_1 c_2-b_2 c_1}=\frac{-y}{a_1 c_2-a_2 c_1}=\frac{1}{a_1 b_2-a_2 b_1}, \quad\left(a_1 b_2-a_2 b_1 \neq 0\right)\)
Therefore, the method of cross-multiplication is nothing but the summarisation of the method of elimination.
Therefore, the required solution is
x = \(=\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1} \text { and } y=\frac{a_2 c_1-a_1 c_2}{a_1 b_2-a_2 b_1}\)
The working rule of this method is :
STEP-1: Express the given two simultaneous linear equations in the standard form (ax+by+ c = 0) (if it is not given in the standard form).
STEP-2: Write
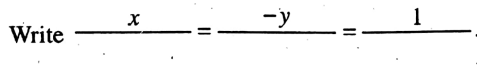
STEP-3: Write below the variable x the result of the following cross-multiplication:
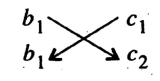
,i.e. write \(\left(b_1 c_2-b_2 c_1\right)\) below x.
STEP-4: Write below the variable (-y), the result of the following cross-multiplication:
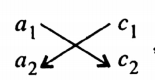
i.e. write \(\left(a_1 c_2-a_2 c_1\right)\) below (- y).
STEP-5: Write below (1), the result of the following cross-multiplication :
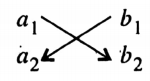
i.e. write \(\left(a_1 b_2-a_2 b_1\right)\) below (1).
STEP-6: After STEP-V, you shall get the equations
\(\frac{x}{b_1 c_2-b_2 c_1}=\frac{-y}{a_1 c_2-a_2 c_1}=\frac{1}{a_1 b_2-a_2 b_1}\)From this equations write x = \(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1} \text { and } y=\frac{a_2 c_1-a_1 c_2}{a_1 b_2-a_2 b_1}\)
Therefore, the values of x and y thus, obtained are the solutions of the given two simultaneous linear equations.
Observe the following example:
Solve: 7x – 3y – 31= 0; 9x – 5y – 41 = 0.
Solution:
Given 7x – 3y – 31= 0; 9x – 5y – 41 = 0
We have, 7x-3y 31 = 0…………….(1) and 9x – 5y – 41 = 0…………(2)
We get from (1) and (2) by the method of cross multiplication,
\(\begin{aligned}& \frac{x}{\left|\begin{array}{ll}
b_1 & c_1 \\
b_2 & c_2
\end{array}\right|}=\frac{-y}{\left|\begin{array}{ll}
a_1 & c_1 \\
a_2 & c_2
\end{array}\right|}=\frac{1}{\left|\begin{array}{ll}
a_1 & b_1 \\
a_2 & b_2
\end{array}\right|} \text {, where } \\
& \left|\begin{array}{ll}
b_1 & c_1 \\
b_2 & c_2
\end{array}\right|=b_1 c_2-b_2 c_1 ;\left|\begin{array}{ll}
a_1 & c_1 \\
a_2 & c_2
\end{array}\right|=\left(a_1 c_2-a_2 c_1\right) ;\left|\begin{array}{ll}
a_1 & b_1 \\
a_2 & b_2
\end{array}\right|=\left(a_1 b_2-a_2 b_1\right) .
\end{aligned}\)
∴ the required solution is x = 4 and y = –1.
How to solve any two given simultaneous linear equations in two variables by all of the four methods described above is thoroughly discussed in the following examples:
Chapter 4 Linear Equations Select The Correct Answer (MCQ)
Question 1.
1. If y of equation \(\frac{2}{x}\) + \(\frac{7}{y}\) = 1 is expressed in term of x we get
1. y = \(\frac{7 x}{x-2}\)
2. y = \(y=\frac{7(x-2)}{x}\)
3. x = \(x=\frac{2 y}{y-7}\)
4. x = \(x=\frac{2(x-7)}{y}\)
Solution:
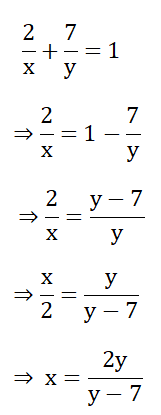
∴ The correct answer is 3. x = \(x=\frac{2 y}{y-7}\)
2. The value of x when y = \(\frac{7-4 x}{-5}\) is substituted in the equation 2x + 3y = 9 is
1. 1
2. 2
3. 3
4. 4
Solution:
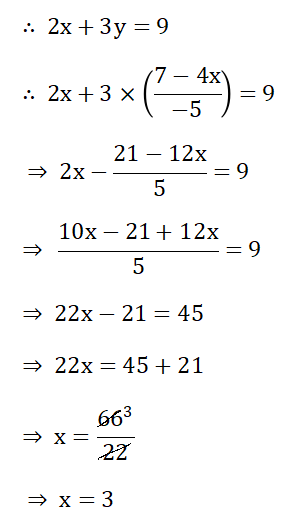
∴ The correct answer is 3. 3
3. If r (x + y) = 2rs………(1) and s (x – y) = 2rs……..(2) be two equations, then the value of x obtained from (1) that should be substituted in equation (2) so as to determine the value of y is-
1. s – r
2. y – 2s
3. 2r – y
4. 2r+ y
Solution:
Given r (x + y) = 2rs And s (x – y) = 2rs
r (x + y) = 2rs…………..(1)
x + y = 2s
⇒ x = 2s – y
s (x – y) = 2rs…………..(2)
⇒ x – y = 2r
=> 2s-y- y = 2r
⇒ -2y= 2r – 2s
⇒ 2y = 2s – 2r
y = s – r
:. The correct answer is 1. s – r
Chapter 4 Linear Equations Short Answer Type Questions
Question 1. Solve the following simultaneous linear equations in two variables by the method of elimination.
1. \(x+y=48 ; \quad x+4=\frac{5}{2}(y+4)\)
Solution:
x + y = 48……..(1) \(x+4=\frac{5}{2}(y+4)\)…………….(2)
Subtracting (2) from (1) we get, \(y-4=48-\frac{5}{2}(y+4) \text { or; } y-4=48-\frac{5 y}{2}-10\)
or, \(y+\frac{5 y}{2}=38+4 \text { or, } \frac{7 y}{2}=42 \text { or, } y=42 \times \frac{2}{7}=12\)
Now, putting y = 12 in (1) we get, x + 12 = 48
or, x= 48 – 12
or, x = 36
The required solution is x = 36, and y = 12.
2. \(3 x-\frac{2}{y}=5 ; \quad x+\frac{4}{y}=4\)
Solution:
3x – \(\frac{2}{y}\) = 5……………………(1)
x + \(\frac{4}{y}\) = 2……………………(2)
Multiplying (1) by 2 we get,
6x – \(\frac{4}{y}\) = 10……………………(1)
x + \(\frac{4}{y}\) = 2……………………(2)
Adding, 6x + x = 10 + 4,
or, 7x = 14
or, x= \(\frac{14}{7}\) = 2
Putting x 2 in (1) we get, 3 x 2 – \(\frac{2}{y}\) = 5
or, 6 – \(\frac{2}{y}\) = 5
or, – \(\frac{2}{y}\) = -1
or, y = 2
∴ The required solution is x = 2, y = 2.
3. \(\frac{x}{2}+\frac{y}{3}=1 ; \frac{x}{3}+\frac{y}{2}=1\)
Solution:
\(\frac{x}{2}+\frac{y}{3}=1\)……………..(1)
\(\frac{x}{3}+\frac{y}{2}=1\)………………..(2)
Multiplying (1) by 3 and (2) by 2 we get,
\(\frac{3 x}{2}+y=3\)…………………(3)
\(\frac{2 x}{3}+y=2\)…………………(4)
\(\frac{3x}{2}\) – \(\frac{2x}{3}\) = 3 -2 (Subtracting)
or, \(\frac{9 x-4 x}{6}\) = 1
or, \(\frac{5x}{6}\) = 1
or, x = \(x=\frac{6}{5}=1 \frac{1}{5}\)
Putting x = \(\frac{6}{5}\) in (4) we get,
\(\frac{2}{3} \times \frac{6}{5}+y=2 \text { or, } \frac{4}{5}+y=2 \text { or, } y=2-\frac{4}{5}=\frac{6}{5}=1 \frac{1}{5}\)
∴ The required solution is x = 1 \(\frac{1}{5}\) , y = 1 \(\frac{1}{5}\).
4. \(\frac{x+y}{2}+\frac{3 x-5 y}{4}=2 ; \quad \frac{x}{14}+\frac{y}{18}=1\)
Solution:
\(\frac{x+y}{2}+\frac{3 x-5 y}{4}=2 \text { or, } \frac{x}{2}+\frac{y}{2}+\frac{3 x}{4}-\frac{5 y}{4}=2\)or, \(\frac{5 x}{4}-\frac{3 y}{4}=2\)……………………(1)
\(\frac{x}{14}+\frac{y}{18}=1\)…………………….(2)
Multiplying (1) by \(\frac{2}{27}\) we get,
\(\frac{5 x}{54}-\frac{y}{18}=\frac{4}{27}\)……………..(3)
\(\frac{x}{14}+\frac{y}{18}=1\)…………………..(4)
\(\frac{5 x}{54}+\frac{x}{14}=\frac{4}{27}+1\) (Adding)
or, \(\frac{35 x+27 x}{378}=\frac{4+27}{27}\)
or, \(\frac{62 x}{378}=\frac{31}{27}\)
or, x = \(\frac{31}{27} \times \frac{378}{62}=7\)
∴ x = 7.
Putting x = 7 in (2) we get, \(\frac{7}{14}+\frac{y}{18}\) =1
or, \(\frac{1}{2}+\frac{y}{18}\) = 1
or, \(\frac{y}{18} = 1-\frac{1}{2}\)
\(\frac{y}{18}=\frac{1}{2}\)y =\(\frac{18}{2}\) = 9
∴ The required solution is x = 7, y = 9.
5. \(\frac{x y}{x+y}=\frac{1}{5} ; \quad \frac{x y}{x-y}=\frac{1}{9}\)
Solution:
\(\frac{x y}{x+y}=\frac{1}{5}\)………………….(1)
and \(\frac{x y}{x-y}=\frac{1}{9}\)………………….(2)
from (1) we get, \(\frac{x+y}{x y}=5 \text { or, } \frac{x}{x y}+\frac{y}{x y}=5 \text { or, } \frac{1}{y}+\frac{1}{x}=5\)……………….(3)
From (2) we get, \(\frac{x-y}{x y}=9 \text { or, } \frac{x}{x y}-\frac{y}{x y}=9 \text { or, } \frac{1}{y}-\frac{1}{x}=9\)…………………(4)
Adding (3) and (4) we get, \(\frac{1}{y}+\frac{1}{y}=5+9 \text { or, } \frac{2}{y}=14 \text { or, } y=\frac{2}{14}=\frac{1}{7}\)
Putting y = \(\frac{1}{7}\)
or, \(\frac{1}{y}\) = 7 in (3) we get, \(7+\frac{1}{x}=5 \text { or, } \frac{1}{x}=-2 \text { or, } x=-\frac{1}{2}\)
∴ The required solution is x = – \(\frac{1}{2}\), y = \(\frac{1}{7}\)
6. \(\frac{1}{x-1}+\frac{1}{y-2}=3 ; \frac{2}{x-1}+\frac{3}{y-2}=5\)
Solution:
\(\frac{1}{x-1}+\frac{1}{y-2}=3\)…………………(1)
\(\frac{2}{x-1}+\frac{3}{y-2}=5\)……………………(2)
Multiplying (1) by 3 we get, \(\frac{3}{x-1}+\frac{3}{y-2}=9\)……………….(3)
Subtracting (2) from (3) we get, \(\frac{3}{x-1}-\frac{2}{x-1}\) = 9 – 5
or, \(\frac{3-2}{x-1}=4\)
or, \(\frac{1}{x-1}=4\)
or, 4x – 4 = 1
or, 4x = 5
or, x = \(x=\frac{5}{4}=1 \frac{1}{4}\)
Now, putting \(\frac{1}{x-1}=4\) in (1) we get, \(4+\frac{1}{y-2}=3\)
or, \(\frac{1}{y-2}=-1\)
or, -y + 2 = 1
or, y = 1
∴ The required solution is x = 1 \(\frac{1}{4}\), y = 1.
Alternative Method:
Let, \(\frac{1}{x-1}=u\) and \(\frac{1}{y-2}=v\)
∴ From (1) we get, u + v = or 2u + 2v…………….(3)
From (2) we get,, 2u + 3v = 5………………………(4)
Subtracting, -v = 1 or v = -1.
from u + v = 3 we get, u – 1 = 3
or, u = 4
∴ u = 4 and v = -1.
or, \(\frac{1}{x-1}=4\)
or, \(\frac{1}{y-2}=-1\) [∵ \(u=\frac{1}{x-1} \text { or, } v=\frac{1}{y-2}\)]
or 4x – 4 = 1
or, -y + 2 = 1
or, 4x = 5
or, -y = – 1
or, y = 1
or, x = \(\frac{5}{4}\)
= 1 \(\frac{1}{4}\)
∴ The required solution is x = 1 \(\frac{1}{4}\), y= 1.
7. \((7 x-y-6)^2+(14 x+2 y-16)^2=0\)
Solution:
\((7 x-y-6)^2+(14 x+2 y-16)^2=0\)∴ (7x – y – 6)² = 0
or, 7x – y – 6 = 0…………….(1)
[Since if the sum of two squares is zero, then the value of each of the squares must be zero separately.]
and (14x + 2y – 16)² = 0
or, 14x + 2y – 16 = 0
or, 7x + y – 8 = 0………………(2)
Now, subtracting (1) from (2) we get, y + y – 8 + 6 = 0
or, 2y – 2 = 0
or, 2y = 2
or, y = \(\frac{2}{2}\) =1
Putting y = 1 in (1) we get, 7x – 1 – 6 = 0
or, 7x – 7 = 0
or, 7x = 7
or, x= \(\frac{7}{7}\) = 1
The required solution is x = 1, y = 1.
8. \(a x+b y=1 ; b x+a y=\frac{(a+b)^2}{a^2+b^2}-1,(a \neq b)\)
Solution:
ax + by 1…………………..(1)
bx+ay = \(\frac{(a+b)^2}{a^2+b^2}-1\) = -1
or, bx+ay = \(\frac{a^2+2 a b+b^2-a^2-b^2}{a^2+b^2}\)
or, bx+ay = \(\frac{2 a b}{a^2+b^2}\)………………….(2)
Now, multiplying (1) by a and (2) by b we get,
\(a^2 x+a b y=a\)…………………..(3)
\(b^2 x+a b y=\frac{2 a b^2}{a^2+b^2}\)……………..(4)
\(a^2 x-b^2 x=a-\frac{2 a b^2}{a^2+b^2}\) (Subtracting)
or, \(x\left(a^2-b^2\right)=\frac{a^3+a b^2-2 a b^2}{a^2+b^2}\)
or, \(x\left(a^2-b^2\right)=\frac{a^3-a b^2}{a^2+b^2}\)
or, x=\(\frac{a\left(a^2-b^2\right)}{\left(a^2+b^2\right)\left(a^2-b^2\right)}\)
or, \(\frac{a}{a^2+b^2}\)
Putting x = \(\frac{a}{a^2+b^2}\) in (1) we get, \(a \times \frac{a}{a^2+b^2}+b y=1\) = 1
or, \(\frac{a^2}{a^2+b^2}+b y=1\)
or, \(b y=1-\frac{a^2}{a^2+b^2}\)
or, \(b y=\frac{a^2+b^2-a^2}{a^2+b^2}\)
or, \(b y=\frac{b^2}{a^2+b^2}\)
or, \(y=\frac{b^2}{b\left(a^2+b^2\right)}\)
or, \(y=\frac{b}{a^2+b^2}\) [∵b ≠ 0]
∴ The required solution is \(\frac{a}{a^2+b^2}, \quad y=\frac{b}{a^2+b^2}\)
Question 2. Solve the following simultaneous linear equations in two variables by the method of comparison.
1. \(2 x+\frac{3}{y}=5 ; 5 x-\frac{2}{y}=3\)
Solution:
\(2 x+\frac{3}{y}=5 \text { or, } 2 x=5-\frac{3}{y} \text { or, } x=\frac{1}{2}\left(5-\frac{3}{y}\right)\)…………………..(1)
\(5 x-\frac{2}{y}=3 \text { or, } 5 x=3+\frac{2}{y} \quad \text { or, } x=\frac{1}{5}\left(3+\frac{2}{y}\right)\)………………(2)
the LHSs of (1) and (2) are equal, by comparing the RHSs we get,
\(\frac{1}{2}\left(5-\frac{3}{y}\right)=\frac{1}{5}\left(3+\frac{2}{y}\right)\)or, \(\frac{5}{2}-\frac{3}{2 y}=\frac{3}{5}+\frac{2}{5 y}\)
or, \(-\frac{3}{2 y}-\frac{2}{5 y}=\frac{3}{5}-\frac{5}{2}\)
or, \(\frac{-15-4}{10 y}\) =\(\frac{6-25}{10}\)
or, \(\frac{-19}{y}=\frac{-19}{1}\)
or, y =1.
Putting y 1 in (1) we get, x = \(\frac{1}{2}\left(5-\frac{3}{1}\right)=\frac{1}{2}(5-3)\)
or, x = \(\frac{1}{2} \times 2=1\)
∴ The required solution is x = 1, y = 1
2. \(2 x-3 y=8 ; \frac{x+y}{x-y}=\frac{7}{3}\)
Solution:
2x – 3y = 8 or, 2x = 8 + 3y or, x = \(\frac{8+3 y}{2}\)……………(1)
\(\frac{x+y}{x-y}=\frac{7}{3}\)
or, 7x – 7y = 3x + 3y
or, 7x – 3x = 3y + 7y
or, 4 x = 10 y
or, x = \(\frac{10y}{4}\)
or, x = \(\frac{5y}{2}\)……………………..(2)
the LHSs of (1) and (2) are equal, comparing the RHSs we get, \(\frac{8+3 y}{2}=\frac{5 y}{2}\)
or, 8+ 3y = 5y
or, 3y – 5y = -8
or, – 2y – 8
or, -2y = -8
or, y = \(\frac{-8}{-2}\)
= 4.
Putting y = 4 in (2) we get, x = \(\frac{5 \times 4}{2}=10\)
∴ The required solution is x = 10, y = 4.
3. \(\frac{1}{3}(x-y)=\frac{1}{4}(y-1) ; \frac{1}{7}(4 x-5 y)=x-7\)
Solution:
\(\frac{1}{3}\) (x – y) = \(\frac{1}{4}\) (y – 1)
or, 4x – 4y = 3y – 3
or, 4x = 3y – 3 + 4y
or, 4x = 7y – 3
or, x = \(\frac{7 y-3}{4}\)……………. (1)
Again, \(\frac{1}{7}\) (4x-5y) = x – 7
or, 4x – 5y = 7x – 49
or, 4x – 7x = – 49 + 5y
or, – 3x = − (49 – 5y)
or, x = \(\frac{-(49-5 y)}{-3} \text { or, } x=\frac{49-5 y}{3}\)……………..·(2)
The LHSs of (1) and (2) are equal, comparing the RHSs we get, \(\frac{7 y-3}{4}=\frac{49-5 y}{3}\)
or, 21y – 9 = 196 – 20y
or, 21y + 20y = 196 + 9
or, 41y = 205
or, y = \(\frac{205}{41}\)
Now, putting y = 5 in (1) we get, x = \(\frac{7 \times 5-3}{4}\)
or, x =\(\frac{35-3}{4}\)
or, x =\(\frac{32}{4}\)
or, x = 8
∴ The required solution is x = 8, y = 5.
4. \(\frac{x+1}{y+1}=\frac{4}{5} ; \quad \frac{x-5}{y-5}=\frac{1}{2}\)
Solution:
\(\frac{x+1}{y+1}=\frac{4}{5}\)or, 5x + 5 = 4y + 4
or, 5x = 4y + 4 -5+or, x = \(\frac{4 y-1}{5}\)………………..(1)
Again, \(\frac{x-5}{y-5}=\frac{1}{2}\)
or, 2x – 10 = y -5
or, 2x = y – 5 + 10
or, x = \(\frac{y+5}{2}\)……………..(2)
The LHSs of (1) and (2) are equal, comparing the RHSs we get,
or, 8y – 2 = 5y + 25
or, 8y- 5y = 25 + 2
or, 3y = 27
or, y = \(\frac{27}{3}\)
= 9
The required solution is x = 7, y = 9.
5. \(\frac{1}{x}+\frac{1}{y}=\frac{5}{6} ; \frac{1}{x}-\frac{1}{y}=\frac{1}{6}\)
Solution:
\(\frac{1}{x}+\frac{1}{y}=\frac{5}{6}\)or, \(\frac{1}{x}=\frac{5}{6}-\frac{1}{y}\)………………….(1)
and \(\frac{1}{x}-\frac{1}{y}=\frac{1}{6} \text { or, } \frac{1}{x}=\frac{1}{6}+\frac{1}{y}\)…………………..(2)
The LHSS of (1) and (2) are equal, comparing the RHSS we get,
\(\frac{1+1}{y}=\frac{5-1}{6} \text { or, } \frac{2}{y}=\frac{4}{6}\)4y = 12
or, y = 3.
Now putting y = 3 in (1) we get, \(\frac{1}{x}=\frac{5}{6}-\frac{1}{3}\)
\(\frac{1}{x}=\frac{5-2}{6}\) \(\frac{1}{x}=\frac{3}{6}\)or, x = 2
∴ The required solution is x = 2, y = 3.
Alternative method:
Let \(\frac{1}{x}\) = u and \(\frac{1}{y}\) = v.
∴ \(\frac{1}{x}+\frac{1}{y}=\frac{5}{6} \Rightarrow u+v=\frac{5}{6} \text { or, } u=\frac{5}{6}-v\)…………………(1)
\(\frac{1}{x}-\frac{1}{y}=\frac{1}{6} \Rightarrow u-v=\frac{1}{6} \text { or, } u=\frac{1}{6}+v\)………………….(2)
The LHSs of (1) and (2) are equal, comparing the RHSs we get,
\(\frac{5}{6}-v=\frac{1}{6}+v \text { or, } v+v=\frac{5}{6}-\frac{1}{6} \text { or, } 2 v=\frac{4}{6} \text { or, } v=\frac{4}{2 \times 6}=\frac{1}{3}\)From (1) we get, \(u=\frac{5}{6}-\frac{1}{3} \text { or, } u=\frac{5-2}{6}=\frac{3}{6}=\frac{1}{2}\)
∴ \(u=\frac{1}{2} \quad \text { or, } \frac{1}{x}=\frac{1}{2} \quad \text { or, } x=2\)
and \(v=\frac{1}{3} \quad \text { or, } \frac{1}{y}=\frac{1}{3} \quad \text { or, } y=3\)
∴ The required solution is x = 2, y = \(\frac{2}{3}\)
6. \(\frac{x+y}{x y}=2 ; \quad \frac{x-y}{x y}=1,(x \neq 0, y \neq 0)\)
Solution:
\(\frac{x+y}{x y}=2 \text { or, } \frac{x}{x y}+\frac{y}{x y}=2 \text { or, } \frac{1}{y}+\frac{1}{x}=2 \text { or, } \frac{1}{y}=2-\frac{1}{x}\)………………(1)
\(\frac{x-y}{x y}=1 \text { or, } \frac{x}{x y}-\frac{y}{x y}=1 \text { or, } \frac{1}{y}-\frac{1}{x}=1 \text { or, } \frac{1}{y}=1+\frac{1}{x}\)………………..(2)
The LHSS of (1) and (2) are equal, comparing the RHSS we get,
\(2-\frac{1}{x}=1+\frac{1}{x} \text { or, } \frac{1}{x}+\frac{1}{x}=2-1 \text { or, } \frac{2}{x}=1\)x = 2
Now putting x = 2
or, \(\frac{1}{x}\) = \(\frac{1}{2}\) in (1) we get,
\(\frac{1}{y}=2-\frac{1}{2} \text { or, } \frac{1}{y}=\frac{3}{2} \text { or, } y=\frac{2}{3}\)∴ The required solution is x = 2, y = \(\frac{2}{3}\)
Alternative Method:
\(\frac{x+y}{x y}=2\)or, x + y = 2xy
or, 2xy – x = y
or, x (2y – 1) = y
or, \(x=\frac{y}{2 y-1}\)………………….(1)
\(\frac{x-y}{x y}=1\)or, x – y = xy
or, x – xy = y
or, x (1 – y) = y
or, \(x=\frac{y}{1-y}\)……………….(2)
The LHSS of (1) and (2) are equal, comparing the RHSS we get, \(\frac{y}{2 y-1}=\frac{y}{1-y}\)
or, 2y – 1 = 1 – y [ y ≠ 0]
or, 3y = 2
or, y = 2/3
putting y = 2/3 we get,
\(x=\frac{\frac{2}{3}}{1-\frac{2}{3}}=\frac{\frac{2}{3}}{\frac{1}{3}}=2\)
∴ The required solution is x = 2 y = 2/3
7. \(\frac{x+y}{5}+\frac{x-y}{4}=5 ; \frac{x+y}{4}+\frac{x-y}{5}=5 \frac{4}{5}\)
Solution:
\(\frac{x+y}{5}+\frac{x-y}{4}=5\)or, \(\frac{4 x+4 y+5 x-5 y}{20}=5\)
or, 9x – y = 100
or, y = 9x – 100……………………(1)
\(\frac{x+y}{4}+\frac{x-y}{5}=5 \frac{4}{5}\)or, \(\frac{5 x+5 y+4 x-4 y}{20}=\frac{29}{5}\)
or, 9x + y = 116 – 9x
or, y = 116 – 9x………………..(2)
The LHSs of (1) and (2) are equal, comparing the RHSs we get, 9x – 100 = 116 – 9x
or, 9x + 9x = 116+ 100
or, 18x = 216
or, x= \(\frac{216}{18}\)
Putting x = 12 in (1) we get, y = 9 x 12 100
or, y = 108 – 100
or, y = 8.
∴ The required solution is x = 12, y = 8.
Alternative Method:
\(\frac{x+y}{5}+\frac{x-y}{4}=5\)………….(1)
\(\frac{x+y}{4}+\frac{x-y}{5}=5 \frac{4}{5}\)…………….(2)
Let x + y = u and x – y = v
∴ from (1) we get, \(\frac{u}{5}+\frac{v}{4}=5\)
or, 4u + 5v = 100 [multiplying by 20]
or, 4u = 100 – 5v
or, u = \(u=\frac{100-5 v}{4}\)………………(3)
From (2) we get, \(\frac{u}{4}+\frac{v}{5}=\frac{29}{5}\)
or, 5u + 4v = 116 [multiplying by 20]
or, 5u = 116 – 4v
or, u = \(u=\frac{116-4 v}{5}\)………………..(4)
The LHSS of (3) and (4) are equal, comparing the RHSS we get,
\(\frac{100-5 v}{4}=\frac{116-4 v}{5}\)
or, 500 – 25v = 464 – 16v
or, -16 + 25v = 500 – 464
or, 9v = 36
or, \(\frac{36}{9}\)
= 4
putting v = 4 in (3) we get, u = \(\frac{100-5 \times 4}{4} \text { or, } u=\frac{100-20}{4} \text { or, } u=\frac{80}{4}\)
or, u = 20.
∴ u = 20
or, x + y = 20
or, x = 20-y……………………(5)
and v = 4
or, x – y = 4
or, x = 4 +y……………………(6)
Comparing equations (5) and (6) we get
20 – y = 4 + y
or, y + y = 20 – 4
or, 2y = 16
or, y = \(\frac{16}{2}\)
or, y = 8.
∴ putting y = 8 in (5) we get, x = 20 – 8
or, x = 12.
∴ the required solution is x = 12, y = 8.
8. 2 – 2 (3x – y) = 10(4 – y) – 5x = 4(y – x)
Solution:
Given 2 – 2 (3x – y) = 10(4 – y) – 5x = 4(y – x)
2 – 2 (3x – y) = 10(4 – y) – 5x = 4(y – x)
∴ 2 – 2(3x – y) = 4 (y – x)
or, 2 – 6x +2y = 4y – 4x
or, 2 – 6x +4x = 4y -2y
or, 2 – 2x = 2y
or, x = 1 – y……………..(1)
and 10(4 – y) – 5x = 4(y – x)
or, 40 – 10y – 5x = 4y – 4x
or, 40 – 5x + 4x = 4y + 10y
or, 40 – x = 14y
or, x = 40 – 14y…………………..(2)
The LHSs of (1) and (2) are equal, comparing the RHSs. we get, 1 – y = 40 – 14y
or, 13y = 39
Or, y = \(\frac{39}{13}\) = 3.
Question 3. Solve the following simultaneous linear equations in two variables by the method of substitution:
1. \(2 x+\frac{3}{y}=1 ; 5 x-\frac{2}{y}=\frac{11}{12}\)
Solution:
\(2 x+\frac{3}{y}=1\)………………(1)
\(5 x-\frac{2}{y}=\frac{11}{12}\)…………………(2)
From (1) we get, \(\frac{3}{y}\) = 1 – 2x
or, y = \(\frac{3}{y}=1-2 x \text { or, } y=\frac{3}{1-2 x}\)……………..(3)
Substituting y = \(y=\frac{3}{1-2 x}\) in (2) we get, \(5 x-\frac{2}{\frac{3}{1-2 x}}=\frac{11}{12}\)
or, \(5 x-\frac{2(1-2 x)}{3}=\frac{11}{12}\)
or, \(\frac{15 x-2+4 x}{3}=\frac{11}{12}\)
or, \(\frac{19 x-2}{3}=\frac{11}{12}\)
or, 76x – 8 = 11
or, 76x = 19
or, x = \(\frac{19}{76}\)
or, x = \(\frac{1}{4}\)
putting x = \(\frac{1}{4}\) in (3) we get,
\(y=\frac{3}{1-2 \times \frac{1}{4}}\)or, \(y=\frac{3}{1-\frac{1}{2}}\)
or, \(y=\frac{3}{\frac{1}{2}}\)
or, y = 6
∴ The required solution is x = \(\frac{1}{4}\), y = 6.
2. \(\frac{2}{x}+\frac{5}{y}=1 ; \frac{3}{x}+\frac{2}{y}=\frac{19}{20}\)
Solution:
\(\frac{2}{x}+\frac{5}{y}=1\)………………….(1)
and \(\frac{3}{x}+\frac{2}{y}=\frac{19}{20}\)……………………..(2)
From (1) we get, \(\frac{2}{x}\) = 1 – \(\frac{5}{y}\)
or, \(x=\frac{2}{1-\frac{5}{y}}\)
or, \(x=\frac{2}{\frac{y-5}{y}}\)
or, \(x=\frac{2 y}{y-5}\)………………..(3)
Substituting x = \(x=\frac{2 y}{y-5}\) in (2) we get,
\(\frac{3}{\frac{2 y}{y-5}}+\frac{2}{y}=\frac{19}{20}\)or, \(\frac{3 y-15}{2 y}+\frac{2}{y}=\frac{19}{20}\)
or, \(\frac{3 y-15+4}{2 y}=\frac{19}{20}\)
or, \(\frac{3 y-11}{y}=\frac{19}{10}\)
or, 30y – 110 = 19y
or, 30y – 19y = 110
or, 11y = 110
or y = \(\frac{110}{11}\)
or, y = 10.
putting y = 10 in (3) we get, \(x=\frac{2 \times 10}{10-5}=\frac{20}{5}=4\)
Alternative Method:
Let \(\frac{1}{x}\) = u and \(\frac{1}{y}\) = v.
∴ from (1) we get, 2u + 5v = 1or 2u = 1 – 5v
or, u = \(\frac{1-5 v}{2}\)……………………(3)
From (2) we get, 3u + 2v = \(\frac{19}{20}\)
or, \(3\left(\frac{1-5 v}{2}\right)+2 v=\frac{19}{20}\) (putting u = \(\frac{1-5 v}{2}\))
or, \(\frac{3-15 v+4 v}{2}=\frac{19}{20}\)
or, \(\frac{3-11 v}{1}=\frac{19}{10}\)
or, 30 – 110 v = 19
or, 110v = 11
or, v = \(\frac{11}{110}=\frac{1}{10}\)
(putting v = \(\frac{1}{10}\) in 93) we get, u = \(\frac{1-5 \times \frac{1}{10}}{2}\)
or, u = \(\frac{1-\frac{1}{2}}{2}=\frac{\frac{1}{2}}{2}=\frac{1}{4}\)
∴ u = \(\frac{1}{4}\)
or, \(\frac{1}{x}=\frac{1}{4}\)
or, x = 4 and v = \(\frac{1}{10}\)
or, \(\frac{1}{y}=\frac{1}{10}\)
o, y = 10
∴ The required solution is x = 4, y = 10.
3. \(\frac{x+y}{x y}=3 ; \quad \frac{x-y}{x y}=1\)
Solution:
\(\frac{x+y}{x y}=3\)……(1)
\(\frac{x-y}{x y}=1\)…………..(2)
from (1) we get, x + y = 3xy
or, 3xy – x = y
or, x (3y – 1) = y
or, \(x=\frac{y}{3 y-1}\)………..(3)
Substituting x = \(\frac{y}{3 y-1}\) in (2) we get, \(\frac{\frac{y}{3 y-1}-y}{\frac{y}{3 y-1} \times y}=1\)
or, \(\frac{\frac{y-3 y^2+y}{3 y-1}}{\frac{y^2}{3 y-1}}=1\)
or, \(\frac{\frac{2 y-3 y^2}{3 y-1}}{\frac{y^2}{3 y-1}}=1\)
or, \(\frac{2 y-3 y^2}{y^2}=1\)
or, 2y – 3y² = y²
or, 2y = 4y²
or, y = \(\frac{1}{2}\)
putting y = \(\frac{1}{2}\) in (3) we get, x = \(\frac{\frac{1}{2}}{3 \times \frac{1}{2}-1}=\frac{\frac{1}{2}}{\frac{1}{2}}=1\)
∴ The required solution is x = 1, y = \(\frac{1}{2}\)
Alternative Method:
\(\frac{x+y}{x y}=3\)………….(1)
\(\frac{x-y}{x y}=1\)………………(2)
From (1) we get, \(\frac{x}{x y}+\frac{y}{x y}=3\)
or, \(\frac{1}{y}+\frac{1}{x}=3\)
or, \(\frac{1}{y}=3-\frac{1}{x}\)………………………(3)
From (2) we get, \(\frac{x}{x y}-\frac{y}{x y}=1\)
or, \(\frac{1}{y}-\frac{1}{x}=1\)
or, \(3-\frac{1}{x}-\frac{1}{x}=1\) (putting \(\frac{1}{y} = 3 – \frac{1}{x}\))
or, 3 – \(\frac{2}{x}\) = 1
or, \(\frac{2}{x}\)
or, x = 1.
putting x = 1 in (3) we get, \(\frac{1}{y}=3-\frac{1}{1} \text { or, } \frac{1}{y}=3-1 \text { or, } \frac{1}{y}=2 \text { or, } y=\frac{1}{2}\)
∴ The required solution is x = 1 y = \(\frac{1}{2}\)
4. \(\frac{x+y}{x-y}=\frac{7}{3} ; x+y=\frac{7}{10}\)
Solution:
\(\frac{x+y}{x-y}=\frac{7}{3}\)…………(1)
\(x+y=\frac{7}{10}\)……………(2)
From (1) we get, \(\frac{x+y}{x-y}=\frac{7}{3}\)
or, 7x – 3x = 3y + 7y
or, 4x = 10y
or, x = \(\frac{10y}{4}\)
or, x = \(\frac{5y}{2}\)………………(3)
Substituting x = \(\frac{5y}{2}\) in (2) we get,
\(\frac{5 y}{2}+y=\frac{7}{10} \text { or, } \frac{5 y+2 y}{2}=\frac{7}{10} \text { or, } \frac{7 y}{1}=\frac{7}{5} \text { or, } y=\frac{7}{5} \times \frac{1}{7} \text { or, } y=\frac{1}{5}\)
Putting y in (3) we get, x = \(\frac{5 \times \frac{1}{5}}{2} \text { or, } x=\frac{1}{2}\)
∴ the required solution is x = \(x=\frac{1}{2}, \quad y=\frac{1}{5}\)
5. \(\frac{x}{2}+\frac{y}{3}=1 ; \frac{x}{3}+\frac{y}{2}=1\)
Solution:
\(\frac{x}{2}+\frac{y}{3}=1\)………………(1)
\(\)……………….(2)
From (1) we get, \(\frac{y}{3}=1-\frac{x}{2} \text { or, } \frac{y}{3} \times \frac{3}{2}=\left(1-\frac{x}{2}\right) \times \frac{3}{2} \text { or, } \frac{y}{2}=\frac{3}{2}-\frac{3 x}{4}\)………….(3)
From (2) we get, \(\frac{x}{3}+\frac{3}{2}-\frac{3 x}{4}=1 \cdot\left[\text { Putting } \frac{y}{2}=\frac{3}{2}-\frac{3 x}{4}\right]\)
or, \(\frac{4 x-9 x}{12}=1-\frac{3}{2} \cdot \text { or, } \frac{-5 x}{12}=-\frac{1}{2} \text { or, } x=\frac{6}{5}=1 \frac{1}{5}\)
putting x = \(\frac{6}{5}\) in (1)we get,
\(\frac{\frac{6}{5}}{2}+\frac{y}{3}=1 \quad \text { or, } \frac{y}{3}=1-\frac{3}{5} \text { or, } \frac{y}{3}=\frac{2}{5} \quad \text { or, } y=\frac{6}{5} \quad \text { or, } y=1 \frac{1}{5}\)∴ the required solution is \(=1 \frac{1}{5}, \quad y=1 \frac{1}{5}]\)
6. \(\frac{1}{3}(x-y)=\frac{1}{4}(y-1) ; \frac{1}{7}(4 x-5 y)=x-7\)
Solution:
\(\frac{1}{3}(x-y)=\frac{1}{4}(y-1)\)…………….(1)
\(\frac{1}{7}(4 x-5 y)=x-7\)…………….(2)
From (1) we get, 4x – 4y = 3y – 3
or, 4x = 7y -3
or,\(x=\frac{7 y-3}{4}\)………………(3)
Substituting \(x=\frac{7 y-3}{4}\) in (2) we get,
\(\frac{1}{7}\left(4 \times \frac{7 y-3}{4}-5 y\right)=\frac{7 y-3}{4}-7\)or, \(\)
or, \(\frac{1}{7}(2 y-3)=\frac{7 y-31}{4}\)
or, 49y – 217 = 8y – 12
or, 49y – 8y = -12 + 217
or, 41y = 205
or, y = \(\frac{205}{41}\)
or, y = 5.
Now putting y = 5 in (3) we get,
\(x=\frac{7 \times 5-3}{4} \text { or, } x=\frac{35-3}{4} \text { or, } x=\frac{32}{4}=8\)∴the required solution is x = 8, y = 5.
7. \(\frac{x}{14}+\frac{y}{18}=1 ; \frac{x+y}{2}+\frac{3 x-5 y}{4}=2\)
Solution:
\(\frac{x}{14}+\frac{y}{18}=1\)…………………(1)
\(\frac{x+y}{2}+\frac{3 x-5 y}{4}=2\)…………..(2)
From (2) we get, \(\frac{2 x+2 y+3 x-5 y}{4}=2\)or, 5x – 3y = 8
or, 5x = 3y + 8
or,\(x=\frac{3 y+8}{5}\)………….(3)
Now , substituting \(x=\frac{3 y+8}{5}\) in (1) we get, \(\frac{\frac{3 y+8}{5}}{14}+\frac{y}{18}=1\)
or, \(\frac{3 y+8}{70}+\frac{y}{18}=1 \text { or, } \frac{27 y+72+35 y}{630}=1\)
or, 62y + 72 = 360
or, 62y = 558
or, \(\frac{558}{62}\)
= 9
Now, putting y =9 in (3), we get, \(x=\frac{3 \times 9+8}{5}\)
or, \(\frac{35}{5}
or, x = 7.
∴ The required solution is x = 7, y = 9.
8. [latex]p(x+y)=q(x-y)=2 p q \quad(p, q \neq 0)\)
Solution:
p (x + y) = q (x − y) = 2 pq
∴ p (x + y) = 2 pq
or, x + y = 2q
or, x = 2q-y……(1)
and q (x-y) = 2 pq
or, x – y = 2p……(2)
Substituting x = 2q-y in (2) we get, 2q-y- y = 2p
or, 2q-2y= 2p
or, q-y=p
or, y = q- p.
Putting y = q-p in (1) we get, x = 2q-q+p
or, x = p + q
∴ The required solution is x = p + q, y=q-p.
Question 4. Solve the following simultaneous linear equations in two variables by the method of cross-multiplication
1. \(x+5 y=36 ; \frac{x+y}{x-y}=\frac{5}{3}\)
Solution:
x + 5y = 36 ……..(1)
and \(\frac{x+y}{x-y}=\frac{5}{3}\)…………..(2)
From (1) we get, \(\frac{x+y}{x-y}=\frac{5}{3}\)
or, 5x – 5y = 3x + 3y
or, 5x-3x= 3y+5y
or, 2x= 8y
or, x = 4y
or, x–4y+0=0…………….(4)
Now, by the method of cross-multiplication, we get from (3) and (4),
\(\frac{x}{0-144}=\frac{-y}{0+36}=\frac{1}{-4-5}\)
[ ∵ \(\frac{x}{\left|\begin{array}{cc}
5 & -36 \\
-4 & 0
\end{array}\right|}=\frac{-y}{\left|\begin{array}{cc}
1 & -36 \\
1 & 0
\end{array}\right|}=\frac{1}{\left|\begin{array}{rr}
1 & 5 \\
1 & -4
\end{array}\right|} \quad \text { or, } \frac{x}{-144}=\frac{-y}{36}=\frac{1}{-9}\)
or, \(\frac{x}{-144}=\frac{1}{-9} \quad \text { or, } x=\frac{-144}{-9}\)
or, x = 16
and \(\frac{-y}{36}=\frac{1}{-9} \text { or, }-y=\frac{36}{-9}\)
or, y = 4
∴ The required solution is x = 16, and y = 4.
2. \(\frac{x}{5}+\frac{y}{3}=\frac{x}{4}-\frac{y}{3}-\frac{3}{20}=0\)
Solution:
\(\frac{x}{5}+\frac{y}{3}=\frac{x}{4}-\frac{y}{3}-\frac{3}{20}=0\)\(\frac{x}{5}+\frac{y}{3}+0=0\)………………(1)
and \(\frac{x}{4}-\frac{y}{3}-\frac{3}{20}=0\)………….(2)
From (1) and (2) by the method of cross-multiplication, we get,
\(\frac{x}{\frac{1}{3} \times\left(-\frac{3}{20}\right)-0 \times\left(-\frac{1}{3}\right)}=\frac{-y}{\frac{1}{5} \times\left(-\frac{3}{20}\right)-0 \times \frac{1}{4}}=\frac{1}{\frac{1}{5} \times\left(-\frac{1}{3}\right)-\frac{1}{3} \times \frac{1}{4}}\)
[ ∵ \(\frac{x}{\left|\begin{array}{rr}
\frac{1}{3} & 0 \\
-\frac{1}{3} & -\frac{3}{20}
\end{array}\right|}=\frac{-y}{\left|\begin{array}{cc}
\frac{1}{5} & 0 \\
\frac{1}{4} & -\frac{3}{20}
\end{array}\right|}=\frac{1}{\left|\begin{array}{rr}
\frac{1}{5} & \frac{1}{3} \\
\frac{1}{4} & -\frac{1}{3}
\end{array}\right|}\) ]
or, \(\frac{x}{-\frac{1}{20}}=\frac{-y}{-\frac{3}{100}}=\frac{1}{-\frac{1}{15}-\frac{1}{12}}\)
or, \(\frac{x}{\frac{1}{20}}=\frac{-y}{\frac{3}{100}}=\frac{1}{\frac{9}{60}}\)
∴ \(\frac{x}{\frac{1}{20}}=\frac{1}{\frac{9}{60}} \quad \text { or, } \quad x=\frac{\frac{1}{20}}{\frac{9}{60}}\)
or, \(x=\frac{1}{20} \times \frac{60}{9} \text { or, } x=\frac{1}{3}\)
and \(\frac{-y}{\frac{3}{100}}=\frac{1}{\frac{9}{60}} . \quad \text { or, }-y=\frac{\frac{3}{100}}{\frac{9}{60}}\)
or, \(-y=\frac{3}{100} \times \frac{60}{9} \text { or, } y=-\frac{1}{5}\)
∴ The required solution is x = \(\frac{1}{3}\), y =- \(\frac{1}{5}\)
3. \(\frac{x+2}{7}+\frac{y-x}{4}=2 x-8 ; \frac{2 y-3 x}{3}+2 y=3 x+4\)
Solution:
\(\frac{x+2}{7}+\frac{y-x}{4}=2 x-8\)……………(1)
\(\frac{2 y-3 x}{3}+2 y=3 x+4\)……………..(2)
From (1) we get, 4x + 8 + 7y – 7x = 56x – 224 [multiplying by 28]
or, 59x – 7y – 232 = 0………………….(3)
From (2) we get, 2y – 3x+6y=9x+12 [multiplying by 3]
or, 12x – 8y+12= 0
or, 3x – 2y+3=0……………………(4)
From (3) and (4) by the method of cross-multiplication, we get,
\(\frac{x}{(-7) \times 3-(-232) \times(-2)}=\frac{-y}{59 \times 3-(-232) \times 3}=\frac{1}{59 \times(-2)-(-7) \times 3}\)
[ ∵ \(\frac{x}{\left|\begin{array}{cc}
-7 & -232 \\
-2 & 3
\end{array}\right|}=\frac{-y}{\left|\begin{array}{cc}
59 & -232 \\
3 & 3
\end{array}\right|}=\frac{1}{\left|\begin{array}{cc}
59 & -7 \\
3 & -2
\end{array}\right|}\) ]
or, \(\frac{x}{-21-464}=\frac{-y}{177+696}=\frac{1}{-118+21}\)
or, \(\frac{x}{-485}=\frac{-y}{873}=\frac{1}{-97}\)
∴ \(\frac{x}{-485}=\frac{1}{-97} \text { or, } x=\frac{-485}{-97}\)
or, x = 5 and \(\frac{-y}{873}=\frac{1}{-97}\)
or, \(-y=\frac{873}{-97}\)
or, y = 9
∴ The required solution is x = 5, y = 9.
4. \(x+y=2 b ; x-y=2 a\)
Solution:
x+y=2b…..(1) and x-y=2a…..(2)
From (1) we get, x + y – 2b= 0…….(3)
From (2) we get, x- y-2a = 0…………….(4)
From (3) and (4) by the method of cross-multiplication, we get,
\(\frac{x}{1 \times(-2 a)-(-1) \times(-2 b)}=\frac{-y}{1 \times(-2 a)-1 \times(-2 b)}=\frac{1}{1 \times(-1)-1 \times 1}\)
[ ∵ \(\frac{x}{\left|\begin{array}{rr}
1 & -2 b \\
-1 & -2 a
\end{array}\right|}=\frac{-y}{\left|\begin{array}{ll}
1 & -2 b \\
1 & -2 a
\end{array}\right|}=\frac{1}{\left|\begin{array}{rr}
1 & 1 \\
1 & -1
\end{array}\right|}\) ]
or, \(\frac{x}{-2 a-2 b}=\frac{-y}{-2 a+2 b}=\frac{1}{-1-1}\)
or, \(\frac{x}{-2(a+b)}=\frac{-y}{-2(a-b)}=\frac{1}{-2}\)
∴ \(\frac{x}{-2((1+b))}=\frac{1}{-2}\)
or, \(\frac{-2(a+b)}{-2} \text { and } \frac{-y}{-2(a-b)}=\frac{1}{-2}\)
or, \(-y=\frac{-2(a-b)}{-2}\)
or, -y = a – b
or, y = b – a
x = a + b
∴ The required Solution is x = a + b, y = b – a
5. \(\frac{x}{a}+\frac{y}{b}=2 ; a x-b y=a^2-b^2\)
Solution:
\(\)………….(1)
and ax – by = a² – b²……….(2)
From (1) we get, \(\)…………….(3)
From (3) and (4) by the method of cross-multiplication, we get,

or, x = a
or, -y = -b
or, y = b
∴ The required solution is x = a, y = b.
6. \(a x+b y=1 ; b x+a y=\frac{2 a b}{a^2+b^2}\)
Solution:
ax + by = 1………….(1)
and \(b x+a y=\frac{2 a b}{a^2+b^2}\)…………….(2)
From (1) we get, ax + by – 1 = 0…………….(3)
From (2) we get, \(b x+a y-\frac{2 a b}{a^2+b^2}=0\)………………(4)
From (3) and (4) we get by the method of cross-multiplication,
\(\frac{x}{b \times\left(-\frac{2 a b}{a^2+b^2}\right)-(-1) \times a}=\frac{-y}{a \times\left(-\frac{2 a b}{a^2+b^2}\right)-(-1) \times b}=\frac{1}{a \times a-b \times b}\)
[ ∵ \(\frac{x}{\left|\begin{array}{cc}
b & -1 \\
a & -\frac{2 a b}{a^2+b^2}
\end{array}\right|}=\frac{-y}{\left|\begin{array}{cc}
a & -1 \\
b & -\frac{2 a b}{a^2+b^2}
\end{array}\right|}=\frac{1}{\left|\begin{array}{ll}
a & b \\
b & a
\end{array}\right|}\) ]
or, \(\frac{x}{-\frac{2 a b^2}{a^2+b^2}+a}=-\frac{-y}{-\frac{2 a^2 b}{a^2+b^2}+b}=\frac{1}{a^2-b^2}\)
or, \(\frac{x}{\frac{-2 a b^2+a^3+a b^2}{a^2+b^2}}=\frac{-y}{\frac{-2 a^2 b+a^2 b+b^3}{a^2+b^2}}=\frac{1}{a^2-b^2}\)
or, \(\frac{x}{\frac{a^3-a b^2}{a^2+b^2}}=\frac{-y}{\frac{-a^2 b+b^3}{a^2+b^2}}=\frac{1}{a^2-b^2}\)
or, \(\frac{x}{\frac{a\left(a^2-b^2\right)}{a^2+b^2}}=\frac{-y}{\frac{-b\left(a^2-b^2\right)}{a^2+b^2}}=\frac{1}{a^2-b^2}\)
∴ \(\frac{x}{\frac{a\left(a^2-b^2\right)}{a^2+b^2}}=\frac{1}{a^2-b^2}\)
and \(\frac{-y}{\frac{-b\left(a^2-b^2\right)}{a^2+b^2}}=\frac{1}{a^2-b^2}\)
or, \(x=\frac{1}{a^2-b^2} \times \frac{a\left(a^2-b^2\right)}{a^2+b^2}\)
or, \(-y=\frac{1}{a^2-b^2} \times \frac{-b\left(a^2-b^2\right)}{a^2+b^2}\)
or, \(x=\frac{a}{a^2+b^2}\)
or, \(y=\frac{b}{a^2+b^2}\)
∴ the required solution is \(x=\frac{a}{a^2+b^2}, y=\frac{b}{a^2+b^2}\)

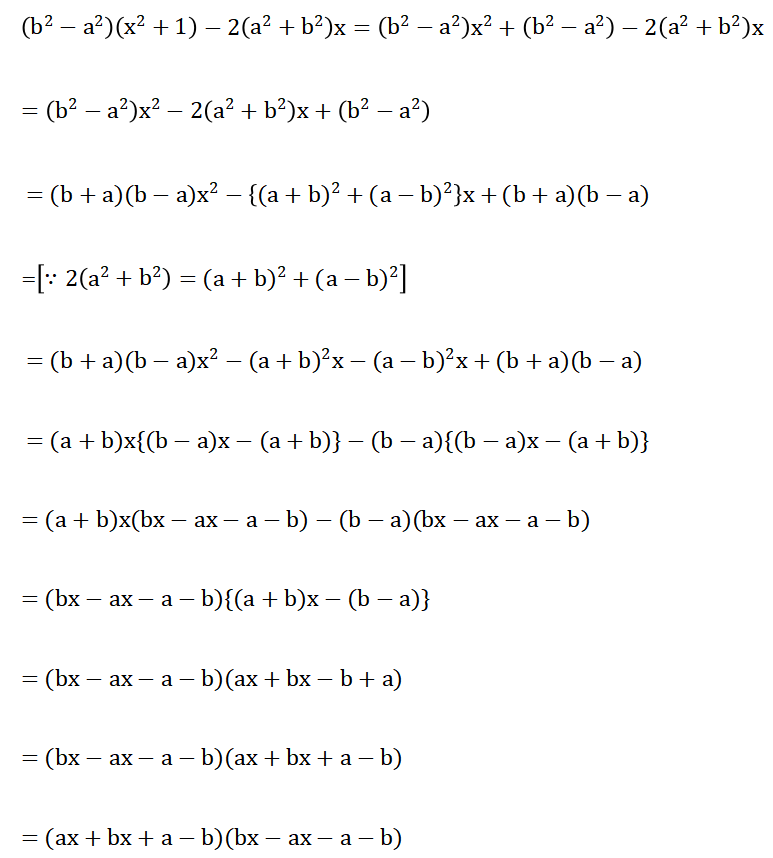
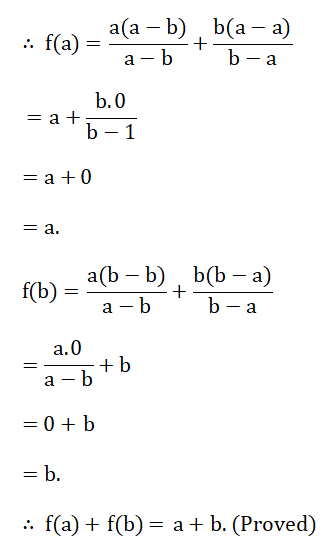
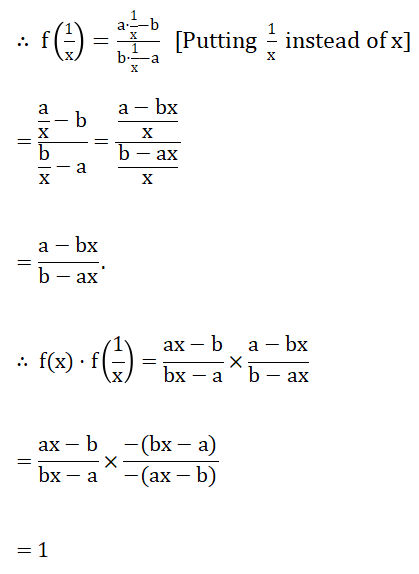

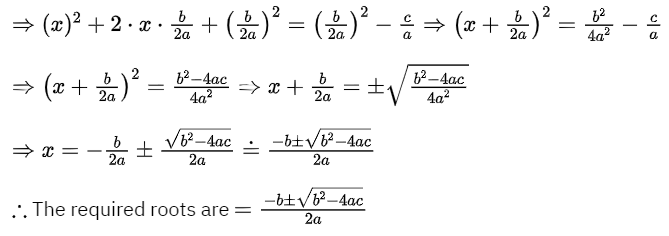

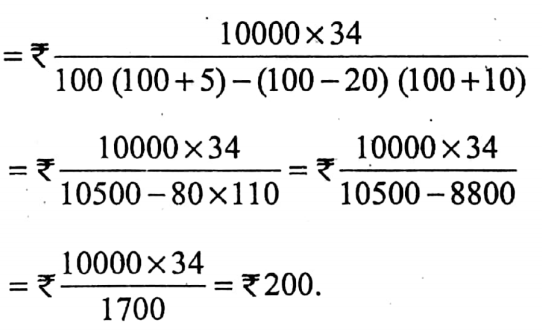

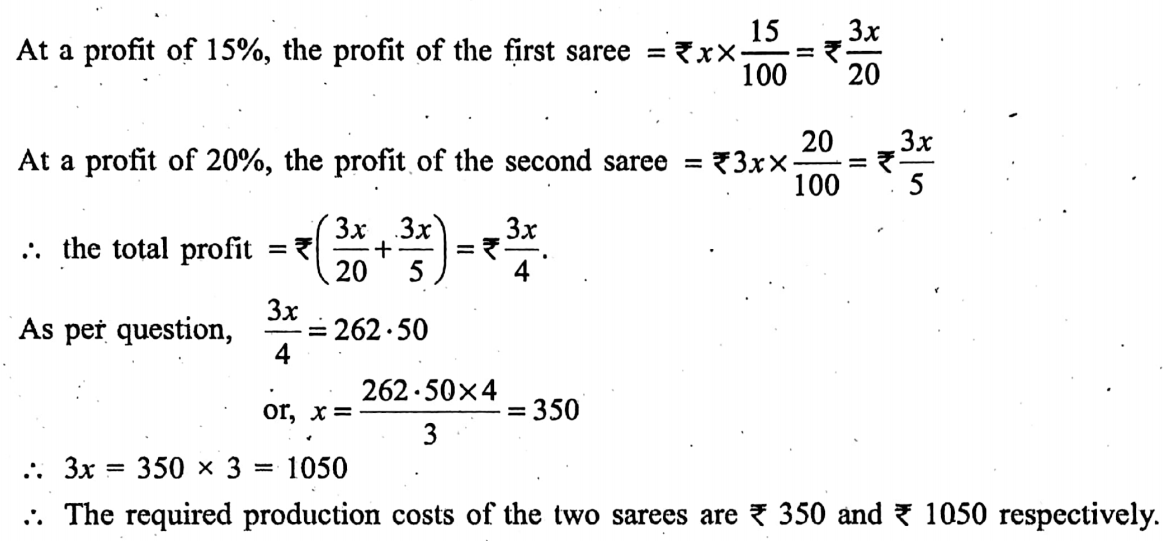
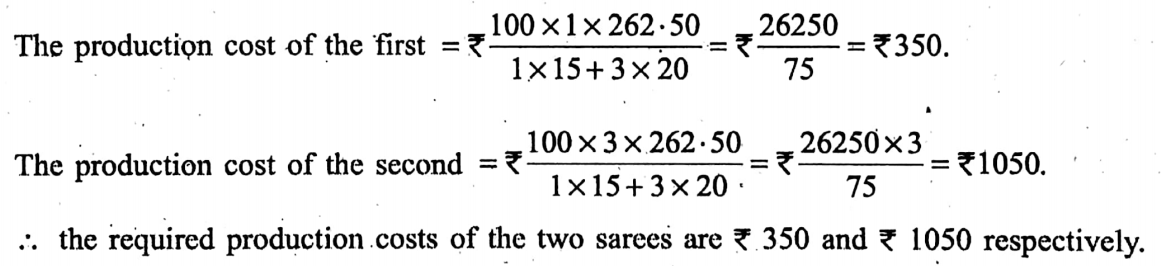

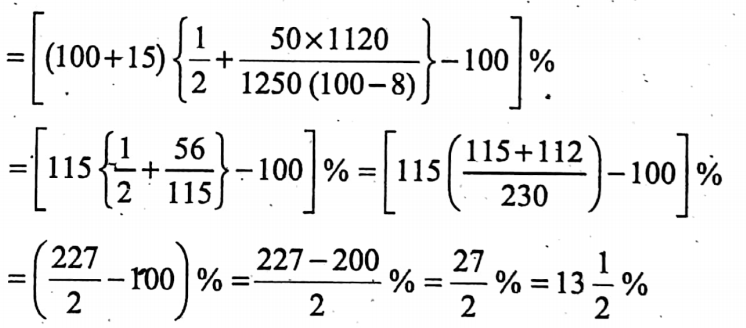

















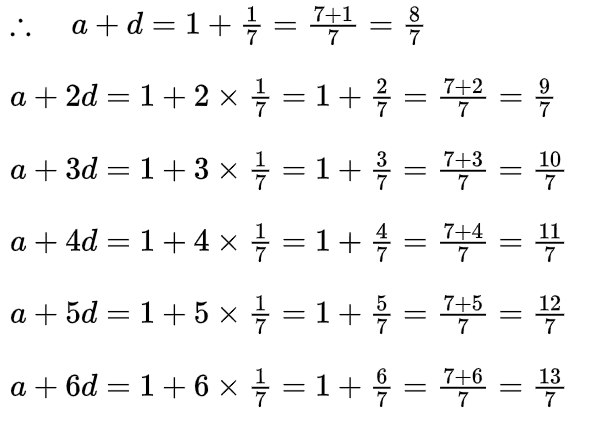










 .
.