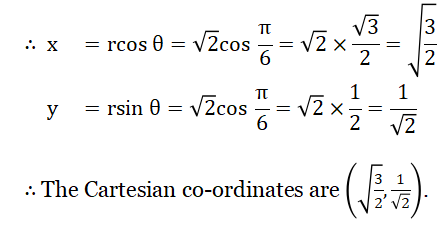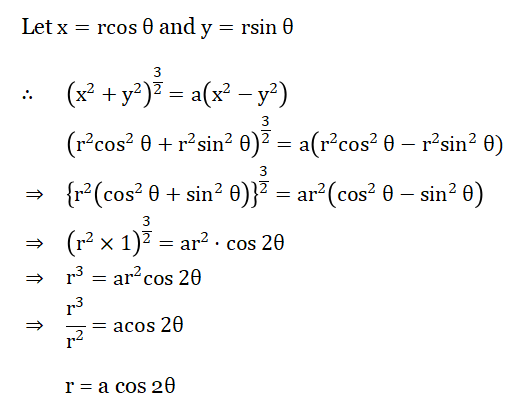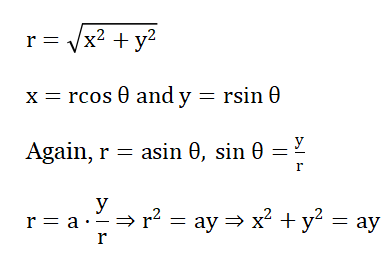Algebra Chapter 3 Graphs
Chapter 3 Graphs Introduction:
- It is said that Necessity is the mother of invention.
- To fulfill the different types of necessities, human beings have devoted themselves to new inventions continuously.
- Such a necessity leads mathematicians to build a vast branch of coordinate geometry in Mathematics and the necessity was to find the exact position of any object or point in this universe.
- We know that a point or an object can be
1. in a two-dimensional plane, like a plane, a table, a floor, etc., or
2. in a three-dimensional place, like a reading room, a classroom, etc.
- The branch of mathematics in which the positions of a point or an object situated in a plane along with its different measurements are discussed is called two-dimensional coordinates geometry.
- While the branch of mathematics in which the positions of a point or an object situated in a three-dimensional place or space along with its different measurements are discussed is called three-dimensional coordinate geometry.
- In this chapter, we shall confine our discussion only to two-dimensional coordinate geometry.
Read and Learn More WBBSE Solutions For Class 9 Maths
Chapter 3 Graphs What Is Coordinate Geometry
- The branch of geometry in which different measurements and properties of the positions of an object (or objects), with respect to certain reference frames, are calculated by using the concepts obtained in arithmetic and algebra is called coordinate geometry.
- The calculations or the measurements with respect to a certain reference frame are called coordinates.
- If the reference frame is two in number, then it is called two-dimensional geometry.
- However, if the reference frame is three in number, then we call it three-dimensional geometry.
- Co-ordinate geometry is also known as Cartesian geometry or analytical geometry.
- The great French philosopher and mathematician Rene Descartes (1596-1650) rooted this branch of mathematics.
- According to his Latin name, this branch of mathematics is named cartesian geometry.
- Co-ordinate geometry is in general of two kinds-
1. Two-dimensional coordinate geometry and
2. Three-dimensional coordinate geometry.
Chapter 3 Graphs Two-Dimensional Coordinate Geometry
The branch of coordinate geometry in which the different measurements of the position of a point or of an object are calculated with respect to two certain reference frames is called two-dimensional coordinate geometry.
There are two types of two-dimensional coordinate geometry. Such as-
1. Rectangular Cartesian co-ordinates system
2. Polar co-ordinates system
Chapter 3 Graphs What Are The Rectangular Cartesian Coordinates
- You have studied a lot in class VIII about rectangular Cartesian coordinates. Here it is again discussed in brief.
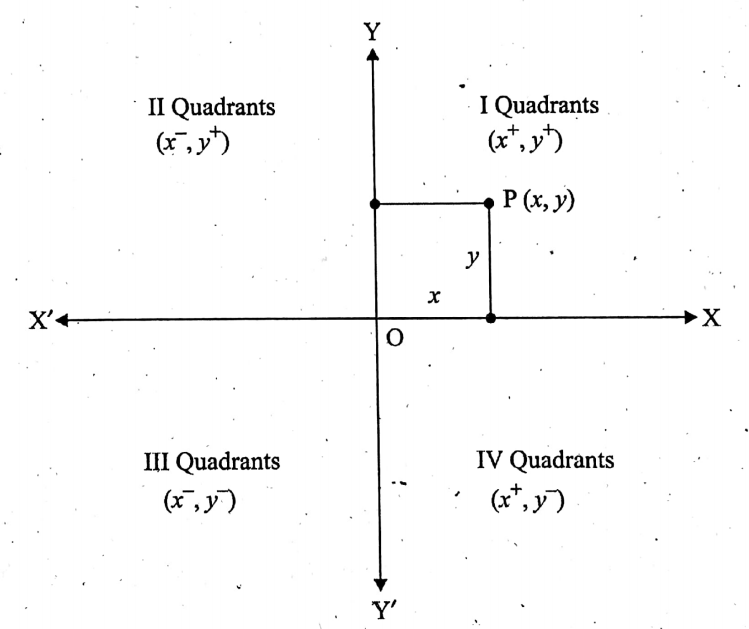
- Let X’OX and Y’OY be two straight lines in a plane intersecting perpendicularly to each other at O.
- The st. line X’OX is horizontal and the st. line Y’OY is vertical. Then the plane should be divided into 4 equal regions by these two st. lines.
- Let P be any point in this plane.
- Knowing the exact position of point P in this plane is our ultimate goal.
1. Cartesian plane or Co-ordinate plane or xy-Plane:
The plane mentioned above, i.e., the plane in which two st. line intersect perpendicularly to each other at a point is known as the Cartesian plane or Co-ordinate plane or xy-plane.
2. x-axis :
- The st. line X’OX is called the x-axis.
- The part OX of X’OX on the right-hand side of O is called the positive x-axis and the part OX of X’OX on the left-hand side of O is called the negative x-axis.
3. y-axis:
- The st. line Y’OY is called the y-axis.
- The part OY of Y’OY above point O is called the positive y-axis and the part OY’ of Y’OY below point O is called the negative y-axis.
4. Origin:
- The point at which the axes, i.e., the st. lines X’OX and Y’OY intersect is called the origin.
- Here point O is the origin.
- The distance of the origin, i.e., of the point O from both axes is O.
5. x-ordinate or Abscissa:
- In the xy-plane, the perpendicular distance of any point, say P from the y-axis is called the x-coordinate or abscissa of that point P.
- If the point is on the right side of the y-axis, then the x-coordinate or abscissa of that point is always positive.
- If it is on the left side of the y-axis, then the x-coordinate or abscissa of that point is always negative.
- However, if the point is on the y-axis, then the x-coordinate or abscissa of that point is always 0.
6. y-co-ordinate or Ordinate:
- In the xy-plane, the perpendicular distance of any point, say P, from the x-axis, is called the y-coordinate or ordinate of that point P.
- If the point is on the upper region of the x-axis, then its y-coordinate or ordinate is always positive While if it is on the lower region of the x-axis, then its y-coordinate or ordinate is always negative.
- However, if the point is on the x-axis, then its y-coordinate or ordinate, is always Q.
7. Co-ordinates of the point P:
- If the x-co-ordinate or abscissa of P is x and the y-coordinate or ordinate of P is y, then the coordinates of P are represented by the ordered pair (x, y).
- Accordingly, if the abscissa of any point is 2 and the ordinate is (-1), then the coordinates of that point are (2, 1).
- On the other hand, if the coordinates of any point be (1, 3), then its abscissa and ordinate are 1 and 3 respectively.
- Obviously, the perpendicular distance of the point from the y-axis=1-1=-(-1)= 1, since the distance is always positive and the perpendicular distance of the point from the x-axis = 3.
- The general form of the coordinates of any point on the x-axis is (a, 0), and that on the y-axis is (0, b).
- ∴ The point (2, 0) is on the x-axis since its ordinate is 0 and the point (0, -3) is on the y-axis since its abscissa is 0.
- Thus, to find the abscissa of any point, we determine the perpendicular distance of that point from the y-axis and to find the ordinate of the point, we determine the same from the x-axis.
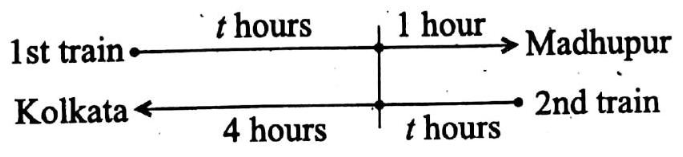
8. Quadrants:
- The x-axis and the y-axis divide the xy-plane into four equal regions, such as XOY, YOX’, X’OY’, and Y’OX.
- The interior region of XOY is known as I (first) quadrant;
- The interior region of YOX’ is known as the II (second) quadrant;
- The interior region of X’OY’ is known as III (third) quadrant;
- The interior region of Y’OX is known as the IV (fourth) quadrant;
- In the first quadrant, both the x- and y-coordinates of any point are positive.
- In the second quadrant, the x- and y-coordinates of any point are negative and positive respectively.
- In the third quadrant, the x- and the y-coordinates of any point are negative and positive respectively.
- In the fourth quadrant, the x- and y-coordinates of any point are positive and negative respectively.
Chapter 3 Graphs What Are The Polar Coordinates
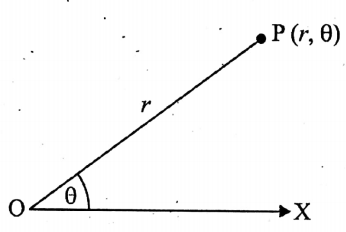
- To determine the position of a point P on any plane, let O is a fixed point on that plane and \(\overrightarrow{\mathrm{OX}}\) be
- a directed line segment. Then O is called the origin or the pole and \(\overrightarrow{\mathrm{OX}}\) is called the initial line. If the distance | OP of P from O is denoted by x and ∠XOP is denoted by 0, then the ordered pair (x, 0) is called the polar coordinates of the point P.
- The distance r is called the radius vector and the angle 0 is called the vectorial angle.
- If \(\overrightarrow{\mathrm{OX}}\) revolves anti-clockwise, then the vectorial angle e is positive and if it revolves clockwise, then the vectorial angle is negative.
- The coordinates of the pole or the origin are (0,0).
Relation between Cartesian coordinates and Polar coordinates:
Let the Cartesian coordinates of a point P in any plane be (x, y) and the polar coordinates of the same point P in the same plane be (r, 0).
Then by the adjoined,
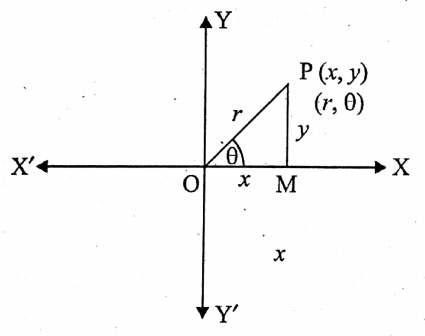
x = r cos θ………………(1)
y = r sin θ…………………….(2)
∴ x2 + y2 = (r cosθ)2 + (r sinθ)2
= r2 cos2θ+ rsin2θ
= r2 (cos2θ+ sin2θ)
= r2
∴ \(\)………………………..(1)
and tan θ = \(\frac{PM}{OM}\) = \(\frac{y}{x}\)
∴ \(\theta=\tan ^{-1} \frac{y}{x}\)…………….(2)
For example, if the Cartesian coordinates of any point P be (√3, 1), then we get, x = √3 and y = 1.
∴ \(r=\left|\sqrt{x^2+y^2}\right|=\left|\sqrt{(\sqrt{3})^2+1^2}\right|=|\sqrt{3+1}|=2\) and
\(\theta=\tan ^{-1} \frac{\sqrt{3}}{1}=\tan ^{-1} \sqrt{3}=\tan ^{-1} \tan 60^{\circ}=60^{\circ}\)
∴ The polar coordinates of the point are (2, 60°).
On the other hand, if the polar co-ordinates of a point P are (√2, 225°) then we get, r = √2 and
0 = 225°.
:. x=rcose = √2 cos225° = \(\sqrt{2} \times-\frac{1}{\sqrt{2}}\) = -1
y = r sinθ = √2 sin 225°= \(\sqrt{2} \times-\frac{1}{\sqrt{2}}\) = -1
∴ The Cartesian co-ordinates of P are (-1,-1).
Chapter 3 Graphs What Is Graph Paper
Graph Paper:-
- Graph papers are a special type of ruled paper. In such papers, equal squares are constructed by drawing equidistant parallel lines, horizontal and vertical.
- Generally, each side of the smallest square on the graph paper is equal to \(\frac{1}{10}\)th inch or \(\frac{1}{5}\)th cm.
- If the given measurements are in integers, then the length of each side of the smallest squares is taken as the unit length.
- However, in some special cases, the length of each side of the smallest squares is taken as more than one unit of length.
- If the given measurements are in fraction or decimal fraction, then the length of each side of the smallest squares is taken conveniently, such as, if the given length be cm, then it is convenient to take the length of each side of the smallest squares as 2 cm, if it is 1cm, then 3 cm, if it is 4cm, then 4 cm and so on.
Plotting of points in the graph paper:
Working Rule:
STEP-1: Draw the x- and y-axis with the help of a scale and a pencil and mark the origin as O.
STEP 2: Select the scale of the graph paper, i.e., take the length of each side of the smallest squares as units conveniently.
STEP 3: If the x-coordinate or abscissa of the given point be-
1. positive, then count the squares starting from O on the right side of O, along with the x-axis equal to the given abscissa, and mark the point thus obtained.
2. negative, then count the squares, starting from O on the left side of O, along with the x-axis, and mark the point thus obtained.
STEP 4: If the y-coordinate or ordinate of the given point be-
1. positive, then count the squares starting from the point obtained in STEP-3, upwards parallel to the y-axis, equal to the given ordinate, and mark the point.
2. negative, then count the squares, starting from the point obtained in STEP-3, downwards parallel to the y-axis, equal to the given ordinate, and mark the point.
Now, the point at which you have reached finally after STEP-4 is the required position of the given point.
Chapter 3 Graphs Determination Of The Coordinates Of A Point Plotted In The Graph Paper
Working Rule:
STEP 1: Draw a perpendicular on the y-axis from the plotted point and note the length of the perpendicular.
Let this length = a unit.
STEP 2: Draw a perpendicular on the x-axis from the plotted point and note the length of the perpendicular.
Let this length = b unit.
Then the required coordinates of the plotted point are given by (a, b).
Chapter 3 Graphs Linear Equations Of One Variable
Linear Equation Of One Variable:-
If there is only one variable in an equation and if the highest power of the variable is 1, then the equation is called a linear equation of one variable.
The standard form of a linear equation is ax + b = 0, where a 0 and a and b are any real numbers.
Some special cases:
- If x = 0, then it is the equation of the y-axis.
- If x = a, then it is a st. line parallel to the y-axis. When a is positive such as x = 2, x = a is a st. line parallel to the y-axis and which lies on the right side of the y-axis.
- When a is negative, such as x2, x = a is a st. line parallel to the y-axis.
If y = 0, then it is the equation of the x-axis.
- If y = b, then it is the equation of a st. line parallel to the x-axis.
When b is positive (such as y = 4), it is a st. line parallel to the x-axis and above the x-axis.
When b is negative (such as y=3), it is a st. line parallel to the x-axis and below the x-axis.
Chapter 3 Graphs Drawing Of The Graphs Of The Linear Equations
Working Rule:
STEP 1: Write the given equation in the standard form y = ax + b, a 0.
STEP 2: Determine three corresponding values of y for any three values of x. Let the values of y be b1, b2, and b3 for the values of a1, a2, and a3 of x respectively.
STEP 3: Construct the following table

STEP 4: Select the x-axis and y-axis.
STEP 5: Select the scale of the graph.
STEP 6: Plot the points (a1, b1), (a2, b2), and (a3, b3) in the graph paper.
STEP 7: Join the three points by a scale.
If the three points thus plotted in the graph paper lie on a st. line, then we say that the drawing is correct and the st. line thus obtained is the graph of the given linear equation.
Some special cases:
1. To draw the graph of the equation x = 0, let x.= 0.y + 0.
Then for any three values of y, find the corresponding values of x.
Obviously, for any value of y, the value of x will be zero, such as-
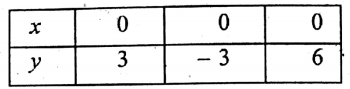
Now, plot the points on the graph paper and join them to get a st.line which is the required graph of the given linear equation.
2. To draw the graph of the linear equation y = 0, let y = 0x+0. Then find at least three values of y corresponding to any three values of x.
Obviously, for any value of x, the respective values of y are always zero. Such as-
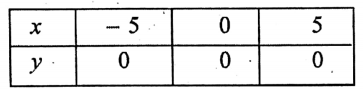
Now, plot the points (-5, 0), (0, 0), and (5, 0) in the graph papers and join them to get a st. line, which is the required graph of the given linear equation y = 0.
3. To draw the graphs of the linear equations of type x = a (such as x = 2, x=-3,…. etc.), let x=0. y + a. Then follow the procedures described above.
4. To draw the graphs of the linear equations of type y = b (such as y = 1 or, y=-5,…. etc.), let y = 0.x + b. Then follow the procedures described in (2) above.
Chapter 3 Graphs Linear Equations Of Two Variables
Linear Equations Of Two Variables:-
The equations having two variables and the highest power of the variables is 1, are called linear equations of two variables.
The standard form of linear equations of two variables is ax+by+c= 0, where both a and b are not together zero and a, b, c are any real numbers.
Some special cases:
1. If a = 0, then 0.x + by + c = 0 or, by + c = 0 or, by = c or, y = – \(\frac{c}{b}\) or, y = k where k = – \(\frac{c}{b}\) and k is a constant.
∴ if a = 0, then the graph of the linear equation of two variables ax + by + c = 0 is a st. line parallel to the x-axis.
2. If b = 0, then a.x +0.y + c = 0 or, ax + c = 0 or, ax = -c or, x= – \(\frac{c}{a}\) or, x = p where p = – \(\frac{c}{a}\)and p is a constant.
∴ if b = 0, the graph of the equation ax+by+c=0 is a st. line parallel to the y-axis.
3. If c = 0, then ax+by+0=0 or, ax + by=0, or by =-ax or, y = – \(\frac{a}{b}\) x or, y = mx, where m = – \(\frac{a}{b}\) and m is a constant……………… (1)
Now putting x = 0 in (1) we get, ym.0 = 0,
∴ (0, 0), i.e., the origin is on the st. line is given by (1).
∴ if c = 0, the graph of ax + by + c = 0 is an st. a line passing through the origin.
4. We know that the equation of the x-axis is y = 0.
∴ putting y 0 in ax + by + c = 0 we get, ax + b.0 + c = 0
or, ax + c = 0
or, ax = c
or, x= – \(\frac{c}{a}\)
∴ The graph of ax+by+c=0 intersects the x-axis at the point \(\left(-\frac{c}{\dot{a}}, 0\right)\)
5. We know that the equation of the y-axis is x = 0.
∴ Putting x 0 in ax + by + c = 0 we get a.0 +by+ c = 0.
or, by + c = 0
or, by = -c
or, y= – \(\frac{c}{b}\)
∴ The graph of ax + by + c = 0 intersects the y-axis at the point \(\left(0,-\frac{c}{b}\right)\)
6. The distance between the two points \(\left(-\frac{c}{\dot{a}}, 0\right)\) and \(\left(0,-\frac{c}{b}\right)\)
= \(\sqrt{\left(-\frac{c}{a}-0\right)^2+\left(0+\frac{c}{b}\right)^2}=\sqrt{\frac{c^2}{a^2}+\frac{c^2}{b^2}}=c \sqrt{\frac{1}{a^2}+\frac{1}{b^2}}\)
∴ the length of the interception of the graph of the equation ax+by+c=0 by the co-ordinate axes
= c \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}\)
For example, the length of the interception of the graph of equation 2x + 3y+ 50 by the co-ordinate axes \(5 \sqrt{\frac{1}{2^2}+\frac{1}{3^2}}=5 \sqrt{\frac{1}{4}+\frac{1}{9}}=\frac{5}{6} \sqrt{13}\)
7. Length of the interception of the x-axis = \(\left|-\frac{c}{a}\right|=-\left(-\frac{c}{a}\right)=\frac{c}{a}\)
Length of the interception of the y-axis = \(\left|-\frac{c}{b}\right|=-\left(-\frac{c}{b}\right)=\frac{c}{b}\)
∴ if these two interceptions are equal, then \(\frac{c}{a}\) = \(\frac{c}{b}\) =>a= b.
if ab, then the graph of ax+by+c=0 intercepts equal lengths from the coordinate axes. For example, the length of the interception of the x-axis by the graph of the equation 2x+2y-1=0 is equal to = \(\left|-\frac{1}{2}\right|=\frac{1}{2}\) which are both equal.
Chapter 3 Graphs To Draw The Graphs Of Linear Equations Having Two Variables
Working Rule:
STEP 1 : Write the equation ax + by + c = 0 in the form of y = px + q, where p = – \(\frac{a}{b}\) and q = – \(\frac{c}{b}\)
STEP 2: Take three arbitrary values of x and determine the corresponding three values of y.
Let the arbitrary values of x be a1, a2, and a3 and the corresponding values of y are b1, b2, and b3 respectively.
∴ The points thus obtained are (a1, b1), (a2, b2) and (a3, b3).
STEP 3: Select the coordinate axes.
STEP 4: Select the scale of the graph paper.
STEP 5: Plot the points (a1,b1), (a2, b2), and (a3, b3) in the graph paper and join them by a scale to get a st. line.
∴ The st. line thus obtained is the graph of the given linear equation of two variables.
Simultaneous equations:
Two or more two equations are said to be simultaneous equations, if for certain values of each variable of them, each of the equations are satisfied.
For example, 2x + 3y-10 is a linear equation of two variables. Then its simultaneous equation will be another linear equation, i.e., 3x+y+2=0 will be a simultaneous equation of the above-mentioned equation. It is true conversely.
In general, the number of simultaneous equations of any linear equation having two variables is 2, having three variables is 3 having 4 variables is 4, and so on.
Simultaneous linear equations have two variables :
If the number of variables of two linear equations is two and if for certain values of the two variables both the equations are satisfied, then the equations are called simultaneous linear equations having two variables.
The standard or general form of linear equations having two variables is :
a1x+b1y+c1 = 0 and a2x+b2y+ c2 = 0, where a1, b1, c1, a2, b2, c2 are all real numbers and a and b, a and b, are not zero altogether.
For example, x + 2y – 30 and 2x-3y+4= 0 are two simultaneous linear equations having two variables x and y.
Solution of two simultaneous linear equations by drawing graphs:
Let, ax+by+c1 = 0….. (1) and ax + b²y + c² = 0…….. (2) be two given linear equations of two variables.
We want to solve these equations.
Then the following working rule should be followed:
Working Rule:
STEP – 1: Draw the graph of equation no. (1). (It has already been practiced earlier).
STEP 2: Draw the graph of the equation no. (2) similarly.
STEP 3: The graphs drawn in STEP-1 and STEP-2 are two st. lines that intersect each other at a point.
Mark this intersecting point.
STEP 4: Let the coordinates of the intersecting point be (a, b).
Then the solutions are x = a and y = b.
Chapter 3 Graphs Select The Correct Answer (MCQ)
Question 1.
1. The Cartesian coordinates of the point (√2,\(\frac{π}{6}\)) is
1. \(\left(\sqrt{\frac{2}{3}}, \frac{1}{\sqrt{2}}\right)\)
2. \(\left(\sqrt{\frac{2}{3}}, \frac{1}{2}\right)\)
3. \(\left(\sqrt{3}, \frac{1}{\sqrt{2}}\right)\)
4. \(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\)
Solution:
Here, r = √2, θ = \(\frac{π}{6}\)
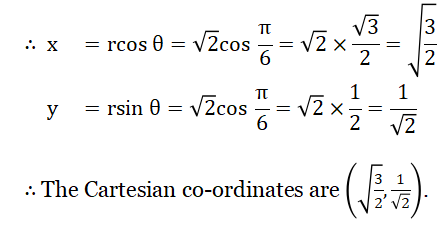
∴ The correct answer is 1. \(\left(\sqrt{\frac{3}{2}}, \frac{1}{\sqrt{2}}\right)\)
2. The polar form of the equation (x2 + y2)3/2 = a(x2 – y2 ) in the Cartesian form is
1. r = a cos θ
2. r = a sin θ
3. r = a cos 2θ
4. r = a sin 2θ
Solution:
Given Polar Form Of The Equation (x2 + y2)3/2 = a(x2 – y2 )
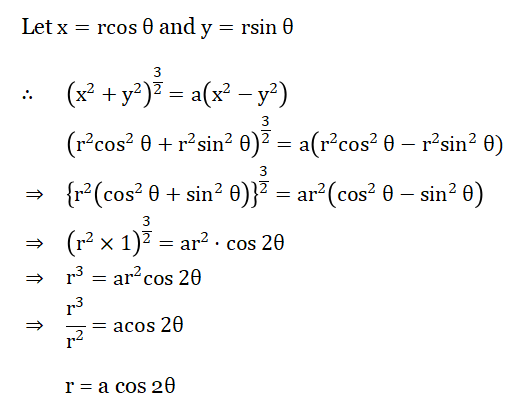
∴ The correct answer is 3. r = a cos 2θ
3. The Cartesian form of the equation r = a.sin θ in the polar form is
1. x2 + y2 = ax
2. x2 + y2 = ay
3. x2 – y2 = ax
4. x2-y2= ay
Solution:
Given
Cartesian Form Of The Equation r = a.sin θ
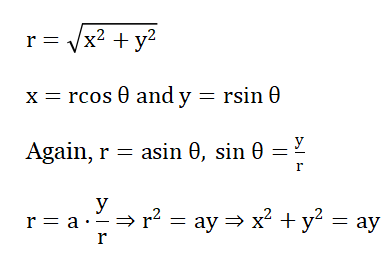
∴ The correct answer is 2. x2 + y2 = ay
Chapter 3 Graphs Short Answer Type Questions
Question 1.
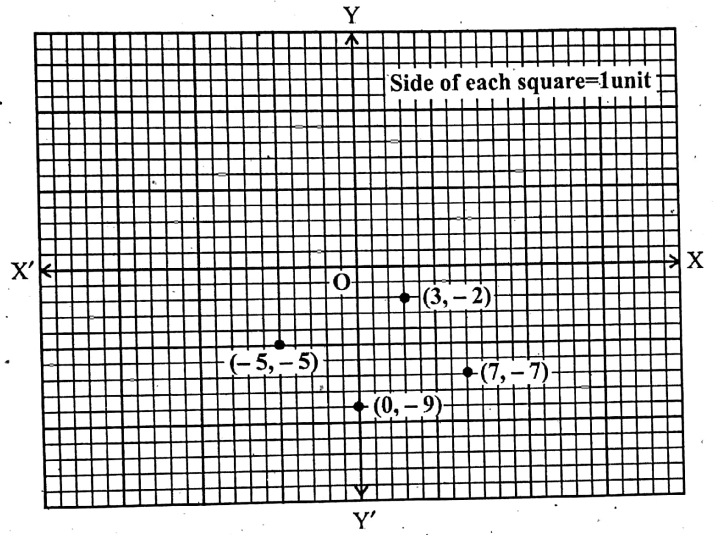
1. Plot the following points on the graph paper and write whether they are above or below the x-axis :
1. (3,2)
2. (-5,-5)
3. (7, -7)
4. (0, -9)
Solution:
Taking X’OX as the x-axis and YOY’ as y- the axis, O as the origin, and the length of each side of the smallest squares equal to 1 unit, locate the given points in the graph paper (as shown in the above).
According to the figures in the graph paper:
1. The point (3,-2) lie below the x-axis.
2. The point (- 5, -5) lies below the x-axis.
3. The point (7, -7) lie below the x-axis.
4. The point (0, -9) lies below the x-axis.
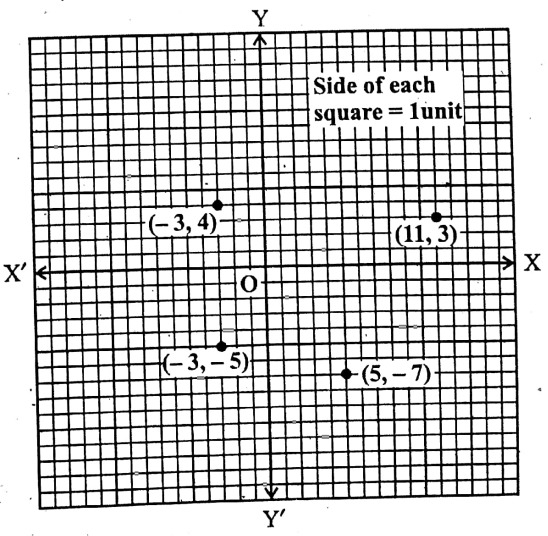
2. Plot the following points on graph paper and write whether they are on the right side or on the left side of the y-axis.
1. (5,7)
2. (-3,-5)
3. (-3, 4)
4. (11, 3)
Solution:
1. The point (5,-7) lie on the right side of the y-axis.
2. The point (-3,-5) lies on the left side of the y-axis.
3. The point (-3, 4) lies on the left side of the y-axis.
4. The point (11, 3) lies on the right side of X’ the y-axis.
Question 2.
1. Write four points on the x-axis.
Solution:
The ordinate or y-co-ordinate of any point on the x-axis is always 0.
Therefore, the coordinates of any four points on the x-axis are:
(-3, 0), (2, 0), (4, 0), (10, 0).
2. Write four points on the y-axis.
The abscissa or the x-co-ordinate of any point on the y-axis is always 0.
Therefore, the coordinates of any four points on the y-axis are (0,7), (0,3), (0, 4), and (0, 11).
Question 3.
1. Write the coordinates of a point in each of the quadrants.
Solution:
Coordinates Of A Point In Each Of The Quadrants:-
The sign of both abscissa and ordinate of a point in the first quadrant is positive.
∴ The coordinates of any point in the first quadrant are (2, 4).
In the second quadrant, the abscissa of any point is negative and the ordinate is positive.
Therefore, the coordinates of any in the second quadrant are (-3, 10).
In the third quadrant, both the abscissa and the ordinate of a point are negative.
Therefore, the coordinates, of any point in the second quadrant are (-1,-5).
In the fourth quadrant, the abscissa of any point is positive and the ordinate of any point is negative.
Therefore, the coordinates of a point in the fourth quadrant are (4,7).
2. The distance of a point from the x-axis in the positive direction is 5 and from the y-axis in the positive direction is 7. Find the coordinates of the point.
Solution:
Given
The Distance Of A Point From The X-Axis In The Positive Direction Is 5 And From The Y-Axis In The Positive Direction Is 7
The abscissa of the point = 7 (∴ the distance of the point from the y-axis in the positive direction is 7.)
The ordinate of the point = 5 (∵ the distance of the point from the x-axis in the positive direction is 5.)
∴ The coordinates of the point are (7, 5).
Chapter 3 Graphs Long Answer Type Questions
Question 1. Express the following statements in the form of simultaneous linear equations:
1. The total value of 3 copies (khata) and 2 pens is Rs. 44 and that of 4 copies (khata) and 3 pens is Rs. 61.
Solution:
Let the value of I copy (khata) be Rs. x and that of 1 pen be Rs. y.
by reversing the two digits of the number, is 27 less than the original number.
by the first condition given. 3x+2y= 44………….(1)
and by the second condition given, 4x + 3y = 61……….(2)
∴ (1) and (2) are the required simultaneous linear equations.
2. The sum of two different numbers is 80 and 3 times the difference between the two numbers is 20 more than the greater one.
Solution:
Let the greater number be x and the smaller number be y.
∴ by the first condition given, x + y = 80………(1)
and by the second condition given, 3 (x – y) = x + 20……..(2)
∴ (1) and (2) are the required simultaneous linear equations.
3. If 2 is added to both the numerator and denominator of a fraction, its value becomes \(\frac{7}{9}\) and if 3 is subtracted from both the numerator and denominator of it, the fraction becomes \(\frac{1}{2}\)
Solution:
Let the numerator = x and the denominator = y of the fraction.
∴ by the given first condition, \(\) or, 9x+18 = 7y+ 14
or, 9x – 7y + 4 = 0…… (1)
By the given second condition, \(\) or, 2x-6=y – 3
or, 2x – y = 3…………(2)
.. (1) and (2) are the required simultaneous linear equations.
4. The tens’ digit of a number of two digits is double its unit’s digit. The number, obtained?
Solution:
Let the units’ digit = y and the tens’ digit = x.
∴ The number 10x + y.
by the given first condition, x = 2y……. (1)
If the digits of the number be reversed, the units digit is x and the tens’ digit is y.
Then, the number thus obtained is 10y + x.
By the given second condition, 10y + x = 10x + y – 27
or, 9x – 9y = 27
or, x – y=3…….(2)
∴ (1) and (2) are the required simultaneous linear equations.
Question 2.
1. Find the distance of the point (6, -8) from both axes.
Solution:
The ordinate of the point (6, 8) = -8.
∴ The distance of the point (6, -8) from the x-axis is 8 units in the negative direction.
The abscissa of the point (6, – 8) = 6.
∴ The distance of the point (6,8) from the x-axis is 6 units in the positive direction.
2. Determine the coordinates of the point of intersection of equation 2x + 3y = 12 on the x-axis.
We know that the equation of the x-axis is y = 0.
∴ putting y = 0 in the equation 2x + 3y = 12 we get, 2x + 3.0 = 12
or, 2x = 12
or, x = 6.
2x + 3.0 = 12
or, 2x = 12
or, x = 6.
∴ The co-ordinates of the required point of intersection are (x, y) = (6, 0) [x= 6 and y = 0]
3. Find the coordinates of the point of intersection of the equation 2x-3y = 12 on the y-axis.
Solution:
We know that the equation of the y-axis is x = 0.
∴ Putting x = 0 in the equation 2x-3y= 12, we get, 2.0-3y= 12
or, 3y= 12
or, y = 4.
∴ The coordinates of the required point of intersection are (x, y) = (0,4) [x=0 and y=4]
Question 3.
1. Find the area of the triangle formed by the graph of equation 3x + 4y = 12 and the coordinate axes.
Solution:
Method-1:
Given that 3x + 4y = 12 ….. (1)
Putting y = 0 in (1) we get, 3x + 4.0 = 12 or, x = 4.
Putting x = 0 in (1) we get, 3.0+ 4y = 12 or, y = 3.
∴ The graph of the given equation intersects 4 units from
The x-axis and 3 units from the y-axis.
the required area of the triangle
= \(\frac{1}{2}\) x 4 x 3 sq.units ×3 sq. units [∵ area of Δ = \(\frac{1}{2}\)× Base x Height] = 6sq, units.
The required area of the triangle = 6 sq. units.
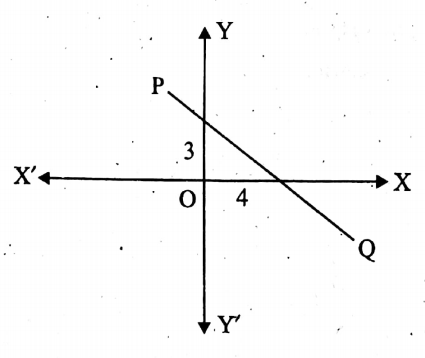
Method 2 (With the help of a graph):
Let us draw the graph of the given equation 3x + 4y = 12.
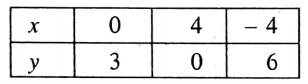
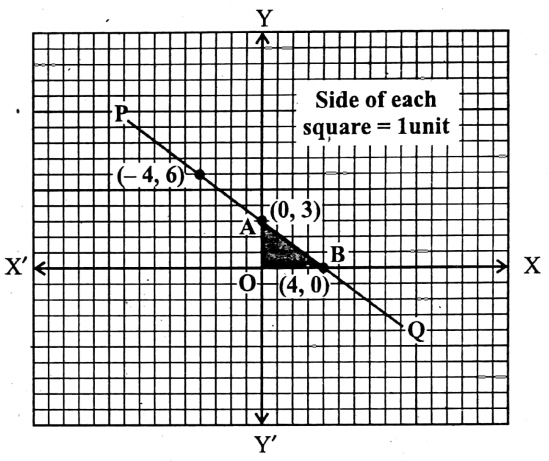
Let us now place the points (0, 3), (4, 0), and (4, 6) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each of the smallest square = 1 unit.
By joining these points we get a straight-line PQ.
From the graph, it is clear that the base OB of the right-angled triangle OAB is 4 units and the height OA of it is 3 units.
∴ The area of the ΔAOB
= \(\frac{1}{2}\) OB X OA [∵ Δ = \(\frac{1}{2}\) x Base x Height]
= \(\frac{1}{2}\) x 4 x 3 sq. units
= 6 sq. units.
The required area = 6 sq. units.
Method-3 (By higher mathematics) :
We have 3x+4y = 12 or,
or, \(\frac{3x}{12}\) + \(\frac{4y}{12}\) = 1 (Dividing by 12) or, \(\frac{x}{4}\) + \(\frac{y}{3}\) = 1.
∴ The intercept of x-axis = 4 units and that of y-axis = 3 units
∴ The required area of the triangle
= \(\frac{1}{2}\) x 4 x 3sq. units
= 6 sq. units.
2. Determine the angle which the graph of equation x = y makes with the positive x-axis.
Method-1 :
Let us draw the graph of the equation x = y.
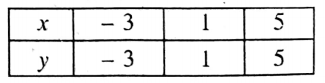
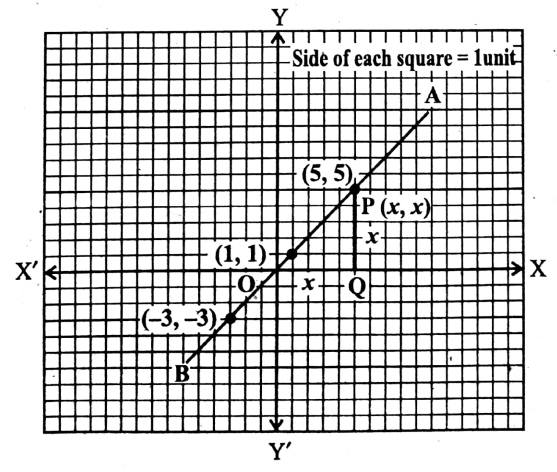
Let us now plot the points (3,3), (1, 1), and (5, 5) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each of the smallest square= I unit.
By joining these points we get a St. line AB.
From the graph it is clear that the graph of the given equation is a st. line which passes through the origin. Let P (x, y) be any point on the st.line.
∴ y = x,
. the co-ordinates of P will be (x, x), i.e., OQ = PQ.
∴ ∠POQ = ∠OPQ
Now, in the right-angled triangle POQ = ∠OPQ.
∴ OPQ is a right-angled bilateral triangle.
We know that the angles of any right-angled bilateral triangle are 90°, 45° and 45°, POQ = 45°.
The graph of equation x = y makes an angle of 45° with the positive x-axis.
Method 2 (By higher mathematics) :
Given that x = y ‘or, y=x or, y = 1. x
∴ If the graph of the given equation makes an angle with the positive x-axis, then tanθ = 1 = tan 45° [tan 45° = 1]
∴ θ = 45°.
The required angle = 45°.
Question 4. Draw the graphs of the following equations
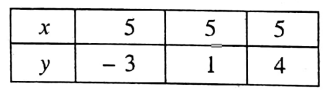
1. x = 5
Solution:
x= 5
or, x = 0y + 5……………………(1)
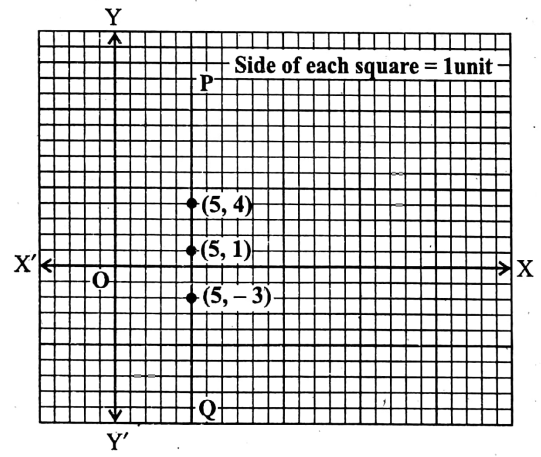
Putting y=3, 1, 4 in (1) we get, x = 5, 5, 5 respectively. We get the following list:
Let us now plot the points (5, 3), (5, 1) x, and (5, 4) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each of the smallest square = 1 unit.
By joining these points we get a st. line PQ.
∴ PQ is the required graph.
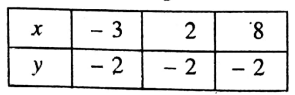
2. y + 2 = 0
Solution:
Given that y+2=0
y=-2
y = 0.x-2….… (1)
Putting x = -3, 2, 8 in (1) we get
x = -2, -2, -2 respectively.
∴ we get the following table
Let us now plot the points (-3,-2), (2,-2), and (8.2) in the graph paper
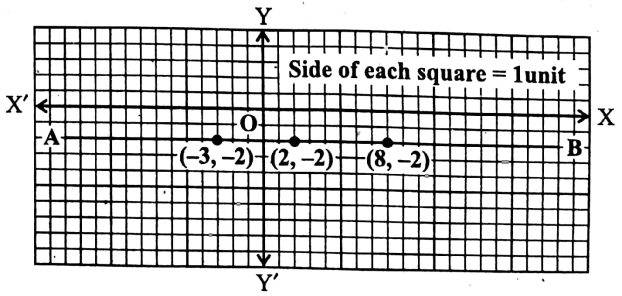
by taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin and side of each of the smallest squares = 1 unit.
We get a st. line AB parallel to the x-axis by joining these points.
∴ AB is the required graph.
3. 3x – 7y = 21
Solution:
Given that 3x-7y= 21
or, 7y = 3x-21
or, y = \(\frac{3}{7}\) x – 3………………(1)
Putting x = 0 in (1) we get,
y= \(\frac{3}{7}\) x 0 – 3 = -3.
Putting x = -7 in (1) we get,
Y = \(\frac{3}{7}\) x (-7) -3 = -6
Putting x 7 in (1) we get,
y=\(\frac{3}{7}\) x 7 – 3 = 0
We get the following table:
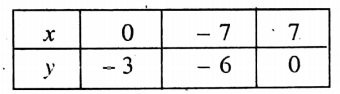
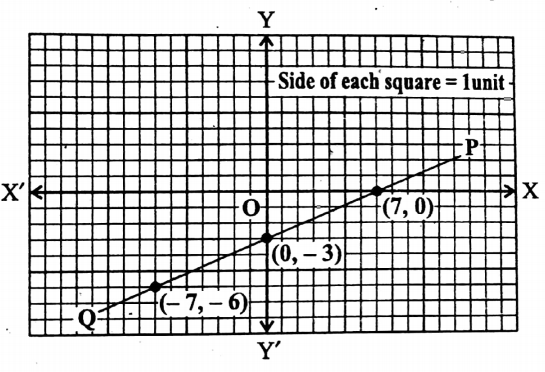
Let us now plot the points (0,3), (-7, -6), and (7, 0) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each of the smallest squares = 1 unit. We get a straight-line PQ by joining the points.
∴ PQ is the required graph of the given equation.
Alternative Method 1 :
Given that 3x – 7y = 21
or, \(\frac{3x}{21}\) – \(\frac{7y}{21}\) = 1 [Dividing by 21]
or,\(\frac{x}{7}\) – \(\frac{y}{3}\) = 1.
∴ The graph of the given equation intersects the x-axis at (7, 0) and the y-axis at (0,3).
Let us now plot the points (7, 0) and (0, -3) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin and side of each of the smallest squares = 1 unit.
by joining, these two points and expanding in both sides we get a straight-line PQ.
PQ is the required graph of the given equation.
Alternative Method 2:
3x-7y= 21…….. (1)
Putting y = 0 in (1) we get 3.x 7.0 = 21
or, x = 7
∴ The graph of the given equation intersects the x-axis at the point (7, 0).
Again, putting = 0 in (1) we get, 3.0 – 7y= 21
or, y = -7
The graph intersects the y-axis at the point (0, -3)
Now, by taking the previous axes, origin, and scale, we plot the points (7, 0) and (0,3).
Therefore, by joining the points and expanding thereafter on both sides we get a straight-line PQ.
∴ PQ is the required graph of the given equation.
4. \(\frac{x}{3} + \frac{y}{4}\) = 0.
Solution:
Given that \(\frac{x}{3}\) + \(\frac{y}{4}\) = 0
or, \(\frac{y}{4}\) = – \(\frac{x}{3}\)
or, y = – \(\frac{4x}{3}\)…………….(1)
Now, putting x = 0 in (1) we get, y = \(\frac{4}{3}\) x 0 = 0.
Putting x 6 in (1) we get, y = – \(\frac{4 \times-6}{3}\) =8
Putting x 6 in (1) we get,
y = – \(\frac{4 \times-6}{3}\) =8
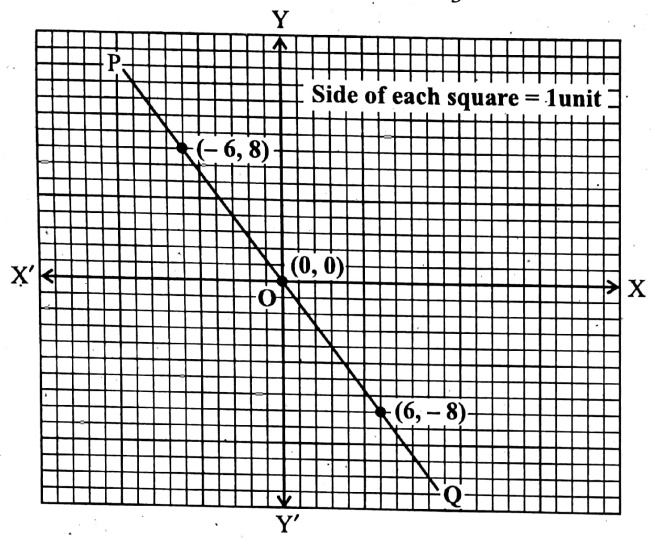
∴ We get the following table
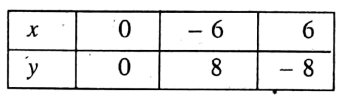
Let us now plot the points (0, 0), X (-6, 8), and (6, -8) by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each of the smallest squares = 1 unit.
By joining these points we get a St. line PQ.
∴ PQ is the required graph of the given equation.
Question 5. Express the following statements in the form of linear equations of two variables and draw the graphs of them :
1. The sum of two numbers is 15
Solution:
1. Let the numbers be x and y.
As per question, x + y = 15…….. (1)
∴ The required linear equation of two variables x + y = 15.
Drawing of graph:
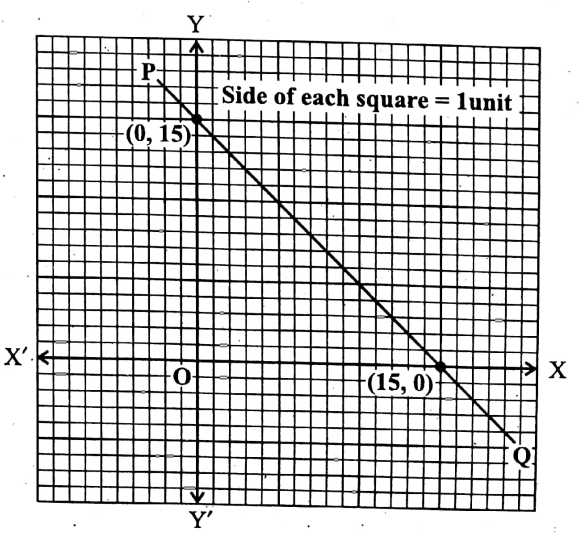
Putting y = 0 in (1) we get, x = 15.
∴ the graph of equation (1) intersects the x-axis at the point (15, 0).
Again, putting x = 0 in (1) we get y = 15.
∴ the graph of equation (1) intersects the y-axis at the point (0, 15)..
Let us now plot the points (15, 0) and (0, 15) in the graph paper by taking X’OX as the x-axis, YOY’
as the y-axis, O as the origin and side of each of the smallest squares = 1 unit.
By joining these two points and expanding in both directions, we get a st. line PQ.
∴ PQ is the required graph.
2. If 2 is added to both the numerator and denominator of a fraction, the value of the fraction becomes \(\frac{7}{9}\)
Let the numerator of the fraction be x and the denominator be y.
As per question, \(\frac{x+2}{y+2}=\frac{7}{9}\)
or, 9x + 18 = 7y + 14
or, 9x – 7y + 4 = 0………….(1)
the required linear equation of two variables is 9x7y+4= 0.
Drawing of graph:
Putting y 0 in (1) we get, 9x – 7.0 + 4 = 0
or, x = – \(\frac{4}{9}\)
∴ the graph intersects the x-axis
at the point \(\left(-\frac{4}{9}, 0\right)\)
Also putting x = 0 in (1) we get
9.0 – 7y+ 4 = 0 or, y = \(\frac{4}{7}\)
∴ the graph intersects the y-axis
at the point \(\left(0, \frac{4}{7}\right)\)
Now, let us take the sum of the sides of the 63 smallest squares = 1 unit.
∵ the L.C.M. of 7 and 9 = 63.
∴ Side of – \(\frac{4}{9}\) smallest squares
= – \(\frac{4}{9}\) x 63 units = -28 units.
And side of \(\frac{4}{7}\) smallest squares\(\frac{4}{7}\) x 63 units = 36 units.
∴ With this calculation (- \(\frac{4}{9}\) = (-28, 0) and (0, \(\frac{4}{7}\)) = (0, 36).
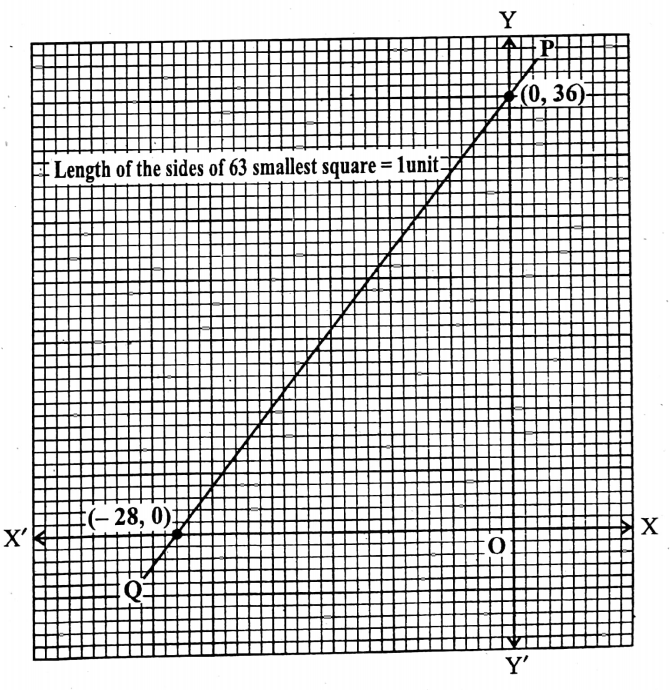
Therefore, by taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin and side of the 63 smallest squares = 1 unit, let us plot the points (-28, 0) and (0, 36) in the graph paper.
We get a St. line PQ by joining these two points and expanding in both directions.
∴ PQ is the required graph.
Question 6. Draw the graphs of the following simultaneous linear equations:
1. y = 5 and 2x + 3y = 11
Solution:
Given Linear Equations y = 5 And 2x + 3y = 11
Graph of equation 2x + 3y = 11:
Putting y = 0 in the equation 2x + 3y = 11, we get 2x + 3.0 11 or, x=-
the graph of this equation intersects the x-axis at
Again, putting = 0 in the given equation we get, 2.0 + 3y = 11 or,
∴ The graph of the equation intersects the y-axis at (0.4).
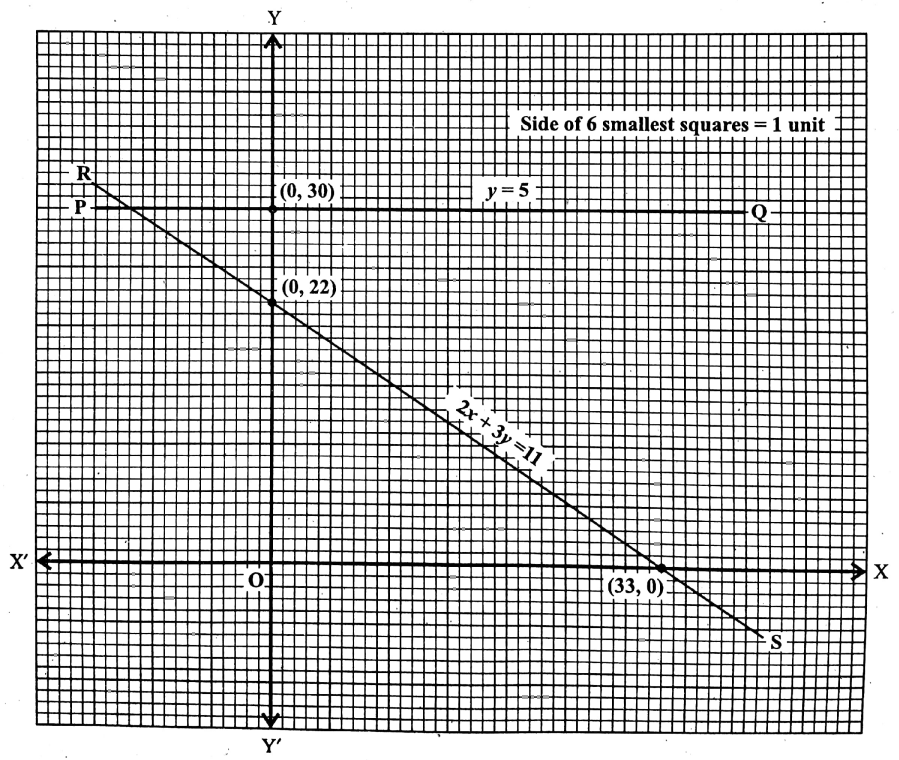
Now, by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of 6 smallest squares
= 1 unit
∵ [L.C.M. of 2 and 3 is 6], we get, \(\frac{11}{2}\) units = side of 6 x \(\frac{11}{2}\) smallest square
= side of 33 smallest squares.
\(\frac{11}{3}\) units = side of 6 x \(\frac{11}{3}\) smallest square
= side of 22 smallest squares.
∴ (\(\frac{11}{2}\) , 0) = (33.0) and (0, \(\frac{11}{3}\)) = (0, 22).
Let us plot the points (33, 0) and (0, 22) in the graph paper and join them.
Also, let the St. the line thus obtained is RS.
∴ RS is the graph of equation 2x + 3y = 11.
Graph of the equation y = 5:
We know that the graph of the equation y = 5 is a st. line parallel to the x-axis and at a distance of 5 units above the x-axis.
Let us draw an st. line PQ by taking the same axes, origin, and scale in the graph paper.
∴ PQ is the graph of the equation y = 5.
2. 3x-5y= 16 and 2x-9y=5.
Given 3x-5y= 16 And 2x-9y=5
Graph of the equation 3x-5y = 16:
We have, 3x – 5y = 16 or, 5y = 3x – 16
or, y = \(\frac{3x – 16}{5}\)……....(1)
Putting x 7 in (1) we get. y = \(\frac{3.7 – 16}{5}\) = \(\frac{5}{5}\) = 1
Putting x 2 in (1) we get, y= \(\frac{3.2 – 16}{5}\) = \(\frac{-10}{5}\) = -2
Putting x = 12 in (1) we get, y= \(\frac{3.12 – 16}{5}\) = \(\frac{20}{5}\) = 4
∴ We get the following table
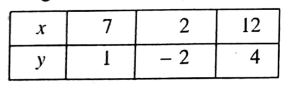
Now, let us plot the points (7, 1), (2, 2), and (12, 4) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each smallest square = 1 unit. By joining these points we get a st. line PQ.
∴ PQ is the graph of the equation 3x-5y = 16.
Graph of the equation 2x – 9y= 5:
We have, 2x 9y= 5
or, 9y = 2x-5
or, y = \(\frac{2x – 5}{9}\)…………....(2)
Putting x = 7 in (2) we get, y = \(\frac{2.7 – 5}{9}\) = \(\frac{9}{9}\) = 1.
Putting x = 16 in (2) we get, \(\frac{2.16 – 15}{9}\) = \(\frac{27}{9}\) = 3.
Putting x = –2 in (2) we get,
y = \(\frac{2 \times(-2)-5}{9}\) = – \(\frac{9}{9}\) = -1.
∴ We get the table
Let us now plot the point (7, 1), (16, 3), and (-2, 1) on the same graph paper by taking the same axes, origin, and scale.
By joining these points we get a st. line RS.
Then RS is the graph of equation 2x – 9y= 5.
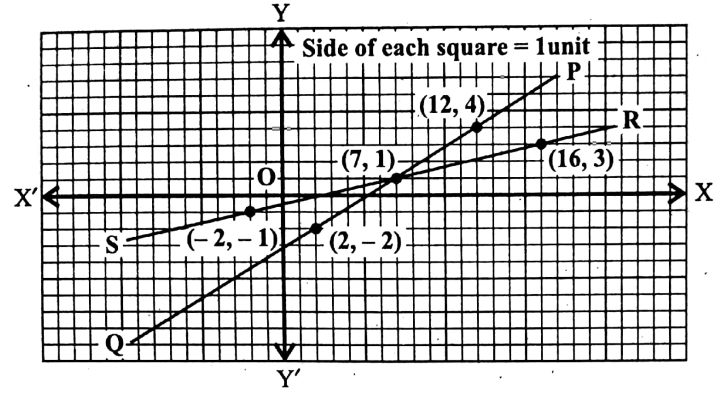
Question 7. Draw the graphs of the following simultaneous linear equations and determine the coordinates of the point of intersection of each of them. Also, find their solutions.
1. 3xy = 5, 4x + 3y = 11
Solution:
Given 3xy = 5, 4x + 3y = 11
3x – y = 5 or, y = 3x-5…………………(1)
Putting x = -2 in (1) we get,
y = 3x (-2) – 5 = -11
Putting x = 2 in (1) we get, y = 3 x 2 – 5 = 1
Putting x = 6 in (1) we get, y = 3 x 6 – 5 = 13
∴ We get the following table
Let us now plot the points (-2, –11), (2, 1), and (6, 13) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each smallest square = 1 unit.
By joining these points we get a st. line PQ.
∴ PQ is the graph of equation 3x – y = 5.
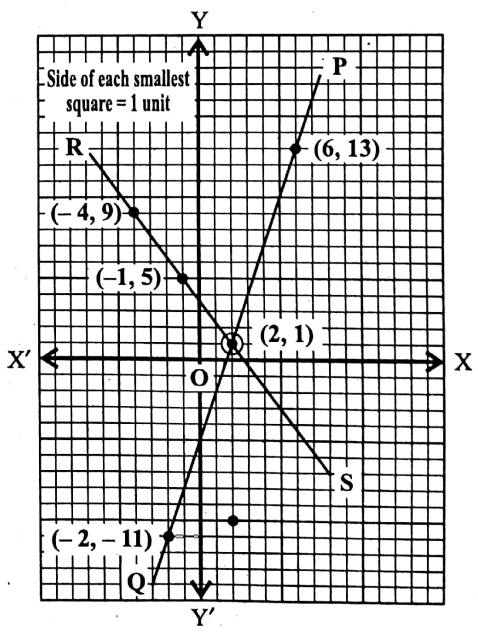
Graph of the equation 4x + 3y = 11:
We have, 4x + 3y = 11
or, 3y = 11 – 4x
or, y = \(\frac{11 – 4x}{3}\)………...(2)
Putting x = -1 in (2) we get, y = \(\frac{11-4 \times(-1)}{3}=\frac{15}{3}=5\)
Putting x 2 in (2) we get, y = \(\frac{11-4 \times 2}{3}=\frac{3}{3}=1\)
Putting x 4 in (2) we get, y = \(\frac{11-4 \times(-4)}{3}=\frac{27}{3}=9\)
∴ We get the table
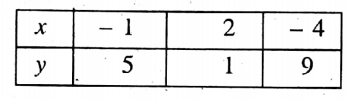
Let us now plot the points (1, 5), (2, 1), and ( 4, 9) on the same graph paper by taking the same axes, origin, and scale.
By joining these points we get an st. line RS.
Then RS is the graph of equation 4x + 3y = 11.
It is clear from the graphs that the point of intersection of the two graphs is (2, 1).
The required solutions are x = 2, and y = 1.
2. 2x + 3y = 12, 2x = 3y.
Solution:
Graph of equation 2x + 3y = 12
We have, 2x + 3y= 12 or, 3y = 12 – 2x
or, y = \(\frac{12 – 2x}{3}\)………….(1)
Putting 0 in (1) we get,
y = \(\frac{12-2 \times 0}{3}=\frac{12}{3}=4\)
Putting x = 3 in (1) we get,
y = \(\frac{12-2 \times 3}{3}=\frac{6}{3}=2\)
Putting x 6 in (1) we get,
y = \(\frac{12-2 \times 6}{3}=\frac{0}{3}=0\)
∴ We get the table
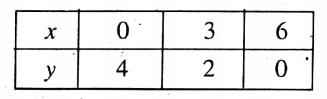
Now taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin and side of each smallest square = 1 unit, we plot the points (0, 4), (3, 2) and (6, 0) in the graph paper. By joining these points we get a st. line AB.
Hence, AB is the graph of equation 2x + 3y = 12.
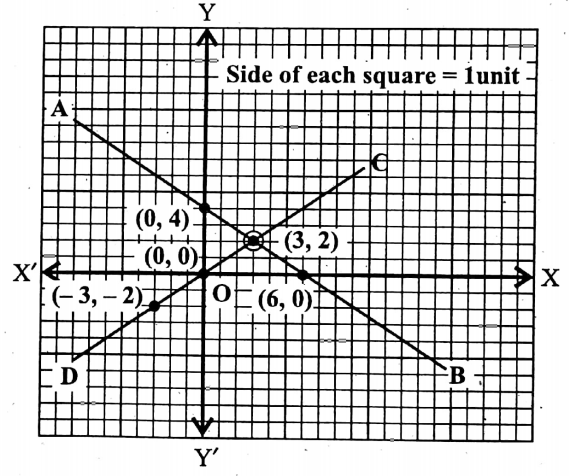
Graph of the equation 2x = 3y:
We have, 2x = 3y or, y = \(\frac{2x}{3}\)………………….(2)
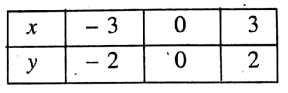
Putting 3 in (2) we get, y = \(\frac{2 \times-3}{3}=-2\)
Putting x = 0 in (2) we get, y= \(\frac{2 \times 0}{3}=0\)
Putting x 3 in (2) we get, y= \(\frac{2 \times 3}{3}=2\)
∴ We get the table
Let us now plot the points (3,2), (0, 0), and (3, 2) on the same graph paper by taking the same axes, origin, and scale.
By joining these points we get a St. Line CD
∵ The CD is the graph of equation 2. x = 3y.
It is clear from the graphs that the point of intersection of the two St. lines AB and CD are (3,2).
Hence, the required solutions are x = 3 and y = 2.
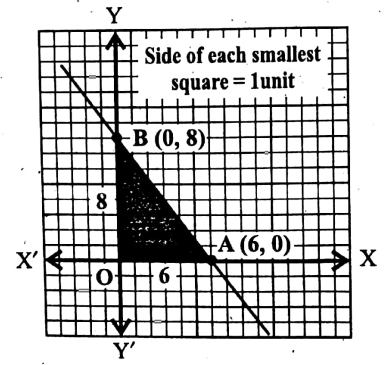
Question 8. Draw the graph of the equation \(\frac{x}{3}\) + \(\frac{y}{4}\) = 2. Also, find the area of the triangle which is produced by this graph with the coordinate axes.
Solution:
We have \(\frac{x}{3}\) + \(\frac{y}{4}\) = 2
or, \(\frac{x}{6}\) + \(\frac{y}{8}\) =1 [Dividing by 2]
∴ the graph of the given equation intersects the x-axis at A (6; 0) and the y-axis at B (0, 8).
[Standard form: \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1]
Now, by taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin and side of each smallest 1 unit, let us plot the points A (6, 0) and B (0, 8) in the graph paper and join them.
∵ ∠AOB = 90°, the hypotenuse of ΔOAB = AB.
∴ We can take OA (= 6 units) as the base and OB (= 8 units) as the height of the triangle OAB.
∴ the area of the
ΔAOB = \(\frac{1}{2}\) X OA X OB [∵ A = \(\frac{1}{2}\) x Base x Height]
= \(\frac{1}{2}\) x 6 x 8 sq. units = 24 units.
∴ the required area = 24 sq. units.
Question 9. Draw the graphs of equations x = 4, y = 3, and 3x+4y= 12. Also, find the area of the triangle formed by these three graphs.
Solution:
The graph of the equation x = 4 is a straight line parallel to the y-axis and at a distance of 4 units from the y-axis on the right-hand side. (∵ 4 > 0)
The graph of the equation y = 3 is a straight line parallel to the x-axis and at a distance of 3 units above the x-axis [∵ 3 > 0].
Again, Putting y = 0 in 3x + 4y = 12 we get, 3x + 4.0 = 12
or, 3x = 12
or, x = \(\frac{12}{3}\) = 4.
∴ the graph of equation 3x + 4y = 12 intersects the x-axis at P (4, 0).
Putting x = 0 in 3x + 4y = 12 ,we get, 3.0 + 4y = 12
or, 4y = 12
or, y = 3.
∴ The graph of equation 3x + 4y = 12 intersects the y-axis at Q (0, 3).
Let us now draw the graphs of the equations x = 4 and y = 3 and plot the points P (6, 0) and Q (0,3) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each smallest square = 1 unit.
From the graph, we see that the triangle formed by the three graphs is PQR of which ∠PRQ = 90°, QR = 4 units, and PR = 3 units.
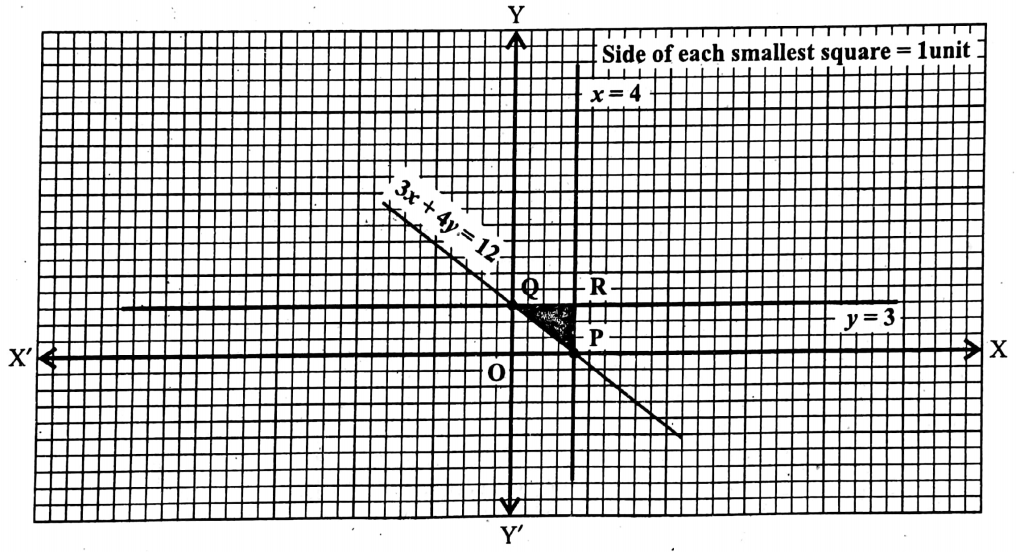
PQR is a right-angled triangle and PR ⊥ QR.
PQ is the hypotenuse of the ΔPQR.
∴ if QR is to be taken as the base of the ΔPQR, PR will be its height of it.
∴ the area of the ΔPQR = \(\frac{1}{2}\) × QR x PR = \(\frac{1}{2}\) x 4 x 3 sq. units
= 6 sq. units.
∴ The required area = 6 sq. units.
Question 10. Draw the graph of y = \(\frac{x+2}{3}\). Find the value of y when x = – 2 from the graph. Also, find from the graph the value of x for which the value of y is 3.
Solution:
We have, y = \(\frac{x+2}{3}\) ……………(1)
Putting x 1 in (1) we get,
y = \(\frac{1+2}{3}=\frac{3}{3}=1\)
Putting x 4 in (1) we get,
y = \(\frac{4+2}{3}=\frac{6}{3}=2\)
Putting x 10 in (1) we get,
y = \(\frac{10+2}{3}=\frac{12}{3}=4\)
∴ We get the table
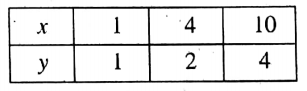
Let us now plot the points (1, 1), (4, 2), and (10, 4) in the graph paper by taking X’OX as the x-axis. YOY’as the y-axis, O as the origin and side of each smallest square = 1 unit.
By joining these points we get a straight-line PQ.
∴ PQ is the graph of the equation y = \(\frac{x+2}{3}\)
From the graph, we see that y = 0 when x = -2.
∴ the required value of y is 0 when x = – 2
Again, let us take OC = 3 units and draw a straight line parallel to the x-axis through point C, which intersects PQ at A. Let us draw a perpendicular AB from A to the x-axis, which intersects the x-axis at point B.
∴ AB = CO = 3 units.
By observation, we see that OB = 7 units.
The required value of x is 7 for which the value of y is 3.
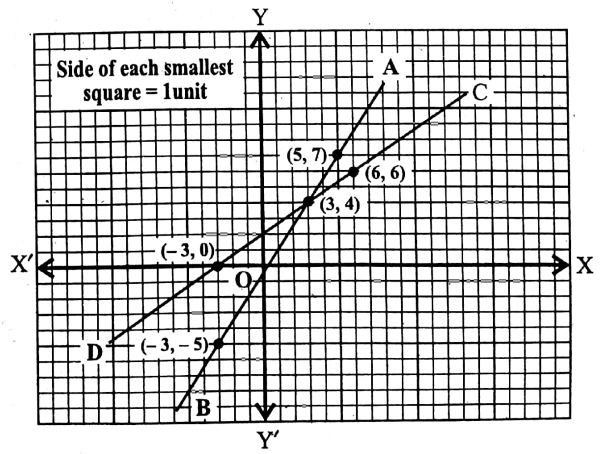
Question 11. Solve : \(\frac{3 x-1}{2}=\frac{2 x+6}{3}\)by drawing its graph.
Solution:
Let y = \(\frac{3 x-1}{2}\)……………...(1)
Putting x = -3 in (1) we get, y = \(\frac{3 \times(-3)-1}{2}=\frac{-10}{2}=-5\)
Putting x = 3 in (1) we get, y = \(\frac{3 \times3-1}{2}=\frac{8}{2}=4\)
Putting x = 5 in (1) we get, y = \(\frac{3 \times(5)-1}{2}=\frac{14}{2}=7\)
∴ We get the table:
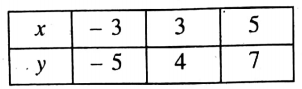
Now. by taking X’OX as the x-axis. YOY’ as the y-axis, O as the origin and side of each smallest square = I unit, let us plot the points (3, 5), (3, 4) and (5, 7) in the graph paper.
By joining these plotted points we get a straight line. Let the straight line be AB.
∴ AB is the graph of the equation y = \(\frac{3x-1}{2}\)
As per question, y = \(\frac{2x+1}{3}\)……………..(2)
Putting x 3 in (2) we get, y = \(\frac{2 \times(-3)+6}{3}=\frac{0}{3}=0\)
Putting x 3 in (2) we get, y = \(\frac{2 \times3+6}{3}=\frac{12}{3}=4\)
Putting x 6 in (2) we get, y = \(\frac{2 \times6+6}{3}=\frac{18}{3}=6\)
Thus, we get a table
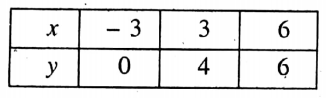
Now, we plot the points (-3, 0), (3, 4), and (6, 6) in the same graph paper by taking the same axes, origin and scale.
Lastly, we join the points to get a straight line.
Let the straight line be CD.
∴ CD is the graph of the equation y = \(\frac{2x+6}{3}\)
We see that the graphs of the given equations intersect to each other at a point (3, 4).
∴ The required solution is x = 3.
Question 12. At present your uncle is elder than you by 16 years. After 8 years, the age of your uncle will be 2 times of your age. Find the present ages of you and your uncle with the help of graphs.
Solution:
Let your present age be x years and your uncle’s present age be y years.
By the first condition given, y = x + 16……. (1), and by the second condition given,
y + 8 = 2(x+8)
or, y = 2x + 16 – 8
or, y = 2x + 8……………..(2)
Now, putting y = 0 in (1) we get, 0 = x+ 16
or, x = – 16
∴ the graph of the equation y = x + 16 intersects the x-axis at the point (-16, 0).
Also on putting x = 0 in (1) we get, y = 0+ 16
or, y = 16.
∴ the graph of the equation y = x + 16 intersects the y-axis at a point (0, 16).
By taking X’OX as the x-axis, YOY’ as the y-axis, O as the origin and side of each smallest squares
= 1 unit, we plot the points (-16, 0) and (0, 16). By joining these two points we get a straight line. Let the straight line be PQ.
Again, putting y = 0 in (2) we get, 0= 2x + 8
or, x = -4
∴ The graph of the equation y = 2x + 8 intersects the x-axis at (-4, 0).
Putting x = 0 in (2) we get, y = 2 x 0 + 8
or, y = 8.
the graph of the equation y = 2x + 8 intersects the y-axis at (0, 8).
Now, by taking the same axes, origin, and scale, let us plot the points (-4, 0) and (0, 8) on the same graph paper so that we get another straight line RS.
∴ RS is the graph of the equation y = 2x + 8.
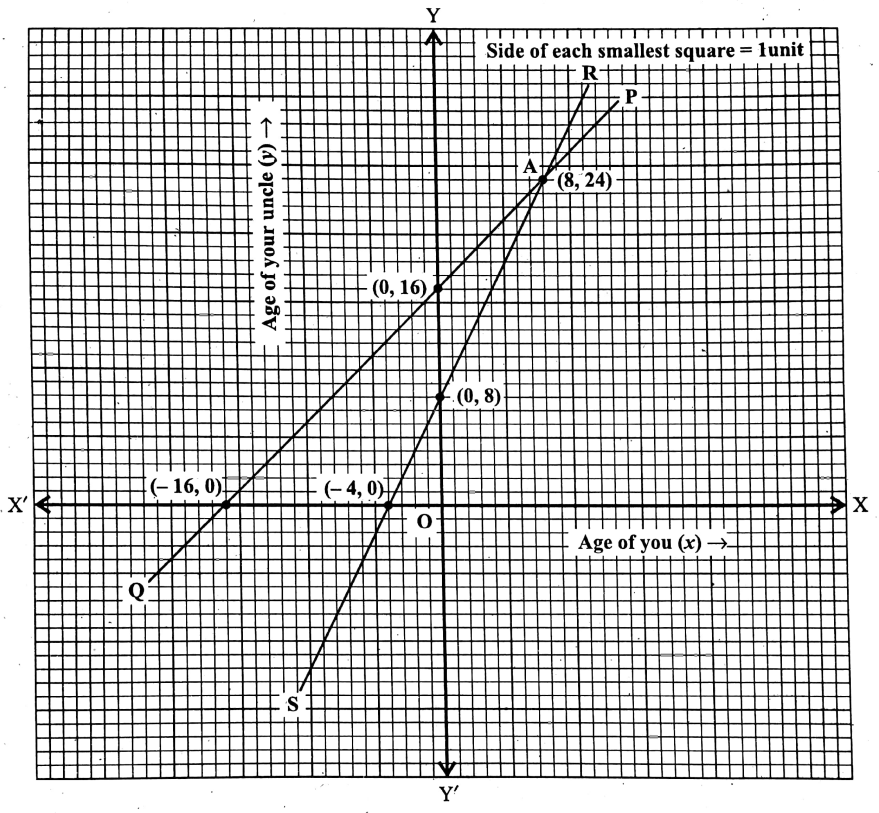
From the graph, we see that the two straight lines PQ and RS intersect each other at point A, the coordinates of which are (8, 24), i.e., abscissa = 8 and ordinate = 24.
∴ At present your age of you is 8 years and the age of your uncle is 24 years.
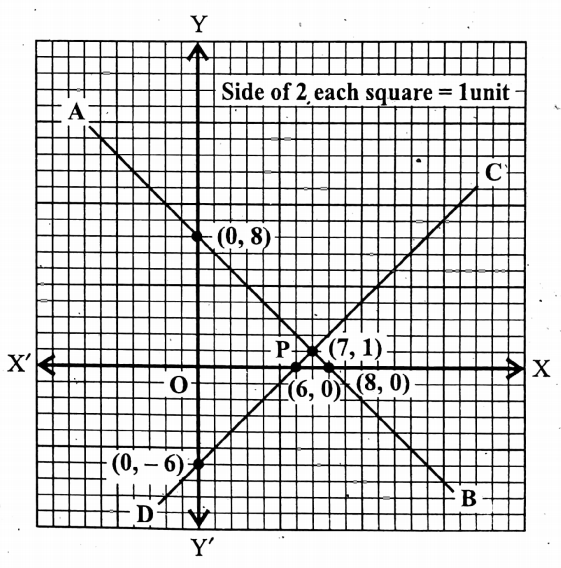
Question 13. A boat travels 64 km in 16 hours in favor of the current and 24 km in 8 hours against the current of the river. Find the velocity of the boat in steady water and the velocity of the current with the help of a graph.
Solution:
Let the velocity of the boat in steady water be x km/hour and the velocity of the current be y km/hour (x > y).
∴ The velocity of the boat in favor of the current = (x + y) km/hour and the velocity of the boat against the current = (x − y) km/hour.
∴ by the first condition, 16 (x + y) = 64
or, x + y = 4
or, y = 4-x………….(1)
By the second condition, 8 (x – y) = 24
or, x – y = 3
or, y = x – 3…………(2)
Now, putting y = 0 in (1) we get, 0 = 4 – x
or, x = 4.
∴ the graph of the equation y = 4
Again, putting x = 0 in (1) we get,
the graph of the equation y = 4
x intersects the x-axis at a point (4, 0).
y = 4 – 0
or, y = 4.
x intersects the y-axis at a point (0, 4).
Let us now plot the points (4, 0) and (0, 4) in the graph paper by taking X’OX as the x-axis, YOY’ as the y-axis, and O as the origin, and side of each 2 smallest squares = 1 unit.
∴ 4 units side of 2 x 4 smallest squares = side of 8 smallest squares.
∴ (4, 0) ≡ (8, 0). Similarly, (0, 4) ≡ (0, 8)
We then join the points (8, 0) and (0, 8) to get a straight line AB.
∴ AB is the graph of the equation y = 4-x.
Again, putting y = 0 in (2) we get, 0=x -3
or, x = 3.
∴ the graph of the equation y=x -3 intersects the x-axis at a point (3, 0).
According to the previous scale (3, 0) = (3 x 2, 0) = (6, 0).
Again putting = 0 in (2) we get, y = 0-3
or, y = -3.
the graph of the equation y = x – 3 intersects the y-axis at a point (0, -3).
According to the previous scale (0,–3) ≡ (0,-3 x 2) = (0,6).
Now, by plotting the points (6, 0) and (0, -6) in the same graph paper taking the same axes, origin, and scale, we get a straight-line CD.
∴ The CD is the graph of the equation y = x-3.
It is clear from the graph that the straight lines AB and CD intersect at a point P, the coordinates of which are (7, 1).
∴ x = 7 and y = 1.
But we have assumed the side of each 2 smallest squares = 1 unit.
∴ the real value of x = \(\frac{7}{2}\) = 3.5 and that of y = \(\frac{1}{2}\) = 0.5
∴ The required solutions are
∴ the velocity of the boat in steady water = 3.5 km/hour and the velocity of the current = 0.5 km/ hour.
Question 14.
1. Find the value of t if the point (4, t² – 4t + 4) lie on the x-axis.
Solution:
Given (4, t² – 4t + 4) Lies On x-axis
We know that the ordinate or the y-coordinate of any point on the x-axis is 0.
∴ t² – 4t + 4 = 0
or, (t – 2)² = 0
or, t – 2 = 0
or, t = 2.
∴ The required value of t is 2.
2. For what value of t does the point (t²-(2+√3)t +2√3, 8) lie on the y-axis?
Solution:
Given (t²-(2+√3)t +2√3, 8)
The abscissa of any point on the y-axis is 0.
t² – (2+√3)t + 2√3 = 0
or t² – 2t – √3t + 2√3=0
or, t(t-2) – √3(t – 2)=0
or, (t-2)(t-√3)=0.
∴ either t – 2 = 0
t = 2
or, t – √3 = 0
t = √3.
∴ The required value of t is 2 or √3.
Question 15.
1. Find the equation of the straight line parallel to the x-axis and passing through the point (3,5).
Solution:
Given (3,5)
We know that the equation of any straight line parallel to the x-axis is given by y = b.
b constant ………(1)
∴ the straight line (1) passes through (- 3,-5), the equation (1) will be satisfied by (-3, – 5).
∴ – 5 = b [by co-ordinate = 5] or, b = -5.
we get from (1), y = -5
or, y + 5 = 0.
The required equation is y + 5 = 0.
2. Find the equation of the straight line parallel to the y-axis and passing through the point (-1, -7).
Solution:
Given Point (-1, -7)
We know that the equation of any straight line parallel to the y-axis is given by x = a,
a constant……………(2)
∴ the straight line (2) passes through (-1, -7),
∴ the equation (2) will be satisfied by (-1, -7).
∴ -1 = a [x co-ordinate = –1]
or, a = –1.
∴ from (2) we get, x = -1
or, x+1 = 0.
The required equation is x + 1 = 0.
Question 16.
1. Determine the value of a if the straight line ax + 7y = 3 (a – 2) passes through the origin.
Solution:
The straight line ax + 7y = 3 (a – 2) passes through the origin, i.e., through the point (0, 0).
∴ the equation of this straight line will be satisfied by x = 0 and y = 0.
So, we get, a.0 + 7.0 = 3 (a – 2) or, 0+0= 3 (a – 2) or, 3 (a-2) = 0 or, a2 = 0 or, a = 2.
∴ The required value of a is 2.
2. Determine the value of a if the straight line 2x + ay = 10 (a-3) passes through the point (1, 2).
Solution:
The straight line 2x + ay = 10 (a – 3) passes through (1, 2).
∴ the equation of this straight line will be satisfied by x= 1 and y = 2.
∴ 2.1 + a.2 = 10 (a – 3)
or, 2 + 2a = 10 (a – 3)
or, 2 + 2a = 10a – 30
or, 8a = 32
or, a = 4.
∴ The required value of a is 4.
Question 17.
1. Determine the coordinates of the point on the straight line 2x-3y = 12 whose abscissa is double its ordinate.
Solution:
Given Straight Line 2x-3y = 12
Let the ordinate of the point be a.
∴ abscissa = 2a (as per question)
∴ the coordinates of the point are (2a, a).
The point lies on the straight line 2x-3y = 12.
∴ 2.2a – 3.a = 12
a = 12.
∴ 2a = 2 x 12 = 24.
∴ The required coordinates of the point are (24, 12).
2. Determine the coordinates of the point on the straight line 11x – 7y + 10 = 0 whose ordinate is 3 times of its abscissa.
Solution:
Let the abscissa of the point be a.
∴ Ordinate = 3a (as per question)
∴ the coordinates of the point are (a, 3a).
The point (a, 3a) lies on the straight line 11x – 7y+ 10 = 0.
∴ 11.a – 7 x 3a + 100 (x = a and y = 3a)
or, 11a – 21a + 10 = 0
∴ 11.a – 7 x 3a + 10 = 0 (∵ x = a and y = 3a)
or, 11a – 21a + 10 = 0
or, -10a = -10
or, a = \(\frac{-10}{-10}\)
∴ 3a = 3 x 1 = 3.
∴ The required coordinates are (1, 3).
Question 18.
1. Find the polar coordinates of a point whose Cartesian coordinates are (-1, 1).
Solution:
The abscissa of the given point is (-1) and the ordinate of it is 1, i.e., here x= 1 and y = 1.
By formula, r = \(\sqrt{x^2+y^2}=\sqrt{(-1)^2+(1)^2}=\sqrt{1+1}\) =√2.
Also, tan θ = \(\frac{y}{x}\) (by formula)
or, tan θ = \(\frac{-1}{-1}\) = -1.
or, tan θ = – tan 45° [tan 45° = 1]
or, tan (180°- 45°) [by formula]
or, tan 135°
θ = 135°.
The required polar co-ordinates are = (r, θ) = (√2, 135°)
2. Find the Cartesian coordinates of a point whose polar coordinates are (√2, \(\frac{5π}{4}\)).
The radius vector of the point r = √2
and the vectorial angle of the point θ = \(\frac{5π}{4}\) = \(\frac{5 \times 180^{\circ}}{4}=225^{\circ}\)
We know by the formula that x = r cos θ
⇒ x = √2 cos 225°.
⇒ x = √2 cos (180° +45°)
⇒ x= √2 (−cos45°)
⇒ x = √2 × – \(\frac{1}{√2}\)
⇒ x = -1.
and y = r sin θ
⇒ y=√2 sin 225°
⇒ y = √2 sin (180° +45°).
⇒ y = √2(-sin 45°) [ by formula ]
⇒ y = √2x – √2
∴ The required Cartesian coordinates are (-1, -1).
Question 19.
1. Transfer the equation x² + y² = 2ax Cartesian co-ordinates into an equation of polar co-ordinates.
Solution:
Given x² + y² = 2ax
We know by a formula that x = r cos θ and y = r sin θ.
∴ Putting x = r cos θ and y = r sin θ in the equation x² + y² = 2ax,
we get, (r cos θ)² + (r sin θ)² = 2 a. r cos θ.
or, r²cos²θ + r²sin²θ = 2ar cosθ
or, r²(cos²θ+ sin²θ) = 2 ar cos θ
or, r².1 = 2ar cos θ [ cos²θ+ sin²θ = 1]
or, r = 2 a cos θ.
∴ The required equation of polar coordinates is r = 2a cos θ.
2. Transfer the equation r = a cos e of polar coordinates into an equation of Cartesian coordinates.
Solution:
Given r = a cos e
Given that r = cos or, = ar cos 0 [Multiplying both the sides by r]
or, x2 + y2 = ax [:: r = √x2 + y2 or 72 = x2 + y2 and r cos 0 = x] ̧
or, x2+ y2 = ax.
The required equation of Cartesian coordinates is x2 + y2 = ax.
Question 20. If the variables C and R denote the temperature in Centigrade and Romer scales respectively, then the relation between them is given by \(\frac{C}{5}\) = \(\frac{R}{4}\)
1. Express this relation by a graph, i.e. draw a graph of this relation.
Solution:
Given that \(\frac{C}{5}\) = \(\frac{R}{4}\)…………………..(1)
or, C = \(\frac{5R}{4}\)
Putting R = 0 in (1) we get,
C = \(\frac{5 \times0}{4}\) = 0
Putting R = -4 in (1) we get,
C = \(\frac{5 \times(-4)}{4}=-5\)
Putting R = 4 in (1) we get,
C = \(\frac{5 \times(4)}{4}=5\)
∴ We get the following table
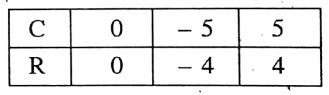
Let us now plot the points (0, 0), (5, 4), and (5, 4) in the graph paper by taking X’OX as the C-axis, YOY’ as the R-axis, O as the origin and side of each smallest square 1 unit. We then join these three points by a scale to get a straight line, say, PQ.
∴ PQ is the required graph of the relation given by \(\frac{C}{5}\) = \(\frac{R}{4}\)
2. What will be the temperature of a place on the Romer scale if the temperature of the place on the centigrade scale is 10°C?
Solution:
Given The Temperature Of The Place On The Centigrade Scale Is 10°C
Let us now take point B on the C axis at a distance of 10 units from the origin O moving towards the right-hand side of O along the C-axis and let us draw a perpendicular AB to the C-axis from point B.
Let the perpendicular AB intersects the st. line PQ on point A.
By observation, it is found that AB = 8 units.
the coordinates of A are (10, 8). i.e., if C is 10, then R = 8.
if the temperature of any place in the centigrade scale is 10°C, then the temperature of the place on the Romer scale will be 8° R.
Question 21. Determine the area of the plane region formed by the graphs of the equations x=6, y – 30, x+4=0, and y + 5 = 0.
Solution:
Given x=6, y – 30, x+4=0, And y + 5 = 0
The given equation x = 6 is of the form x = a.
∴ The graph of this equation is a straight line parallel to the y-axis and at a distance of 6 units from the y-axis on the right-hand side of it ( 6> 0).
Let the straight line be PQ.
We have, y – 3 = 0 or, y = 3 which is an equation of the form y = b.
∴ the graph of this equation is a straight line parallel to the x-axis and at a distance of 3 units above the x-axis (3>0). Let the straight line be RS.
We also have x + 4 = 0 or, x= -4, which is an equation of the form x = a.
∴ the graph of this equation is a straight line parallel to the y-axis and at a distance of 4 units on the left-hand side of it [4 < 0].
Let the straight line be EF.
Lastly, y + 5 = 0
y = 5, which is an equation of a straight line in the form y = b.
∴ the graph of this equation is a straight line parallel to the x-axis and at a distance of 5 units below the x-axis [5 < 0].
Let the straight line be GH.
By taking X’OX as the x-axis, YOY as the y-axis, and O as the origin and side of each smallest square = 1 unit, let us draw the straight lines PQ, RS, EF, and GH on the same graph paper.
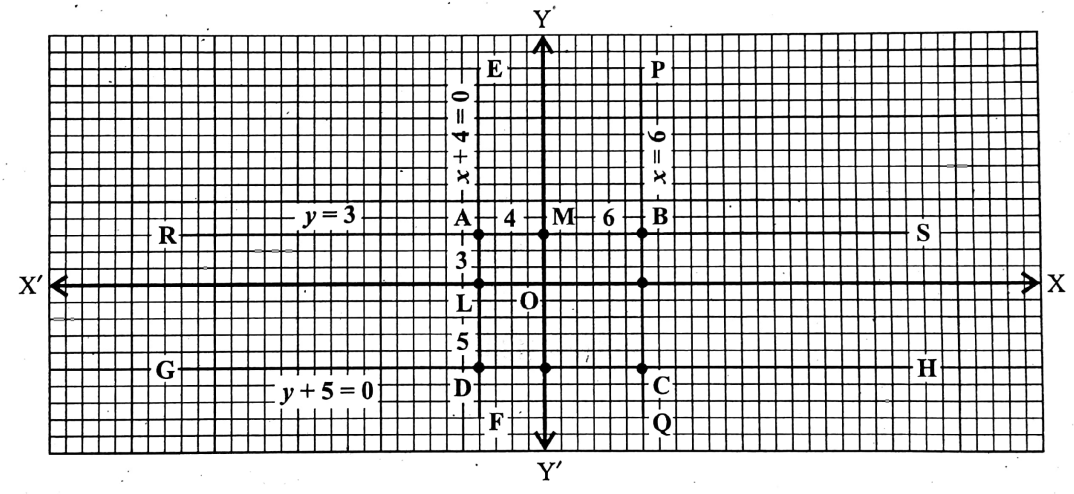
Let RS and EF intersect with each other at point A, PQ, and RS at point B, PQ, and GH at point C, and EF and GH at point D.
Thus, the plane region ABCD is formed, which is nothing but a rectangle (the opposite sides are parallel and the angles are 90°).
Now, the length of the rectangle ABCD is AB and AB = AM + BM = (4+6) units = 10 units (by the graph).
Also, the breadth of the rectangle ABCD is AD, and AD = AL + DL = (3+ 5) units = 8 units (by the graph).
∴ Area of the rectangle ABCD = AB x AD [ ∵ area = length x breadth]
= 10 x 8 sq. units = 80 sq. units.
Hence the required area = is 80 sq. units.
![]() PQRS have the same base PQ and they lie within the same parallels PQ
PQRS have the same base PQ and they lie within the same parallels PQ![]() PQRS ……………….(3)
PQRS ……………….(3)![]() PQRS
PQRS ![]() PQRS…… (4)
PQRS…… (4)![]() PQRS.
PQRS.