Class 7 Maths

Algebra Chapter 3 Laws Exercise 3 Solved Example Problems

Algebra Introduction

In this chapter, we shall discuss some phenomena known to you in a different manner.

Actually, out of the four basic operations namely addition, subtraction, multiplication, and division only addition and multiplication (and in some special cases division also) abide by some laws.

Math Solution Of Class 7 Wbbse

Read and Learn More WBBSE Solutions For Class 7 Maths

These laws are:

1. Commutative law
2. Associative law and
3. Distributive law.

These laws play an important role in higher mathematics, especially in classical and modern algebra and also in the theory of sets. Let us have a look at these laws, starting with very simple examples.

Wbbse Class 7 Maths Solutions

Commutative law 

You know that, 7 + 8 = 15

Again, 8 + 7 = 15

Therefore, 7 + 8 = 8 + 7.

So, it may be said that, if a and 6 be any two integers then, a+b = b+a.

In the above equation, we see that on the left-hand side a is in the first position and b is after a while on the right-hand side b is in the first position and a is after b.

This law, where a and b interchange their positions is known as commutative law.

Also, you know that, 7 x 4 = 28 and also, 4 x 7 = 28

Therefore, 7 x 4 = 4 x 7.

Math Solution Of Class 7 Wbbse

So, it may be said that, if a and b are two integers then, axb= bxa.

Thus, the commutative law is also applicable in the case of multiplication.

Illustration: 1. Suppose, you have 6 mangoes and your brother has 4 mangoes. Thus the total number of mangoes can be obtained by adding your mangoes with your brother’s share i.e., 4 + 6 = 10.

Again we can find the total number of mangoes by adding your brother’s mangoes with your mangoes i.e., 6 + 4 = 10. Therefore, 4 + 6 = 6 + 4.

Hence, we can say that the addition of 6 with 4 and the addition of 4 with 6 give the same result. Thus if 4 and 6 change their places, their sum remains unaltered.

2. Suppose, in a garden, there are 4 rows of trees and in each row, there are 3 trees.

Then the total number of trees in the garden = 3 x 4 = 12.

Also in another garden, there are 3 rows of trees and in each row, there are 4 trees.

Then the total number of trees in the garden is 4 x 3 = 12. Thus we see that, 3×4 = 4×3.

Associative law

The sum 4 + 5 + 7 may be written in different ways.

If, at first 5 is added with 4 and then 7 is added with this result of addition then it may be written as (4 + 5) + 7 = 9 + 7=16; again, if at first 7 is added with 5 and then the result of this addition is added with 4 then it may be written as 4 + (5 + 7) = 4 + 12 = 16.

So, it is clear that (4 + 5) + 7 = 4 + (5 + 7).

Therefore, in general, if a, 6 and c be three integers then, (a + 6) + c = a + (6 + c).

This is known as the associative law of addition.

The associative law is also applicable in the case of multiplication.

For example, we see that (2 x 3) x 4 = 6 x 4 = 24 and 2 x (3 x 4) = 2×12 = 24.

Therefore, in general, if a, b and c be three integers then it may be written in general that, (a x b) x c = a x (b x c).

Math Solution Of Class 7 Wbbse

Illustration: 1. Suppose, you have 4 pens. Your brother has 3 pens and your sister has 2 pens.

At first, adding your and your brother’s pens the total number of pens becomes 4 + 3 = 7.

Now adding this number the number of your sister’s pens the total number of pens becomes (4 + 3) + 2 = 7 + 2 = 9.

Again, adding your brother’s and sister’s pens, the total number of pens = 3+2 = 5.

Now adding with your pens, the sum of your brother’s and sister’s pens the total number of pens becomes 4+(3+2) = 4+5 – 9.

Thus counting the total number of pens in both ways we get, (4 + 3) + 2 = 4 + (3 + 2).

2. Suppose, a boy can do 5 sums per day and we are to find the number of sums that can be done by the boy in 4 weeks.

Since in 1 day the boy can do 5 sums therefore in 1 week (i.e., 7 days) the boy can do 5 x 7 = 35 sums.

Thus in 4 weeks the boy can do (5 x 7) x 4 = 35 x 4 = 140 sums.

Also we may think the issue from another point of view. The total number of days in 4 weeks = 7 x 4 = 28.

Since in 1 day the boy can do 5 sums therefore in 7 x 4 days the boy can do 5 x (7 x 4) = 5 x 28 = 140 sums.

Thus the total number of sums done by the boy is same in both cases.

Math Solution Of Class 7 Wbbse

Distributive law

You know that, 15 x 6 = 90

Again, since 6 = 4 + 2

∴ 15 x 6 = 15 x (4 + 2) = 15 x 4 + 15 x 2 = 60 + 30 = 90.

So, it may be said in general that, if a, b, and c are three integers then,

a x (b+c) = a x b + a x c and a x (b-c) = a x b -a x c.

So, in the case of multiplication, the distributive law is always applicable.

The distributive law of multiplication may also have the following forms:

(a+b) x c=a x c+b x c and (a-b) x c=a x c- b x c.

Let us now see that, how the distributive law may be applied in the case of division.

You know that, 35 ÷ 5 = 7 and 35 = 25 + 10

Now, (25+10) ÷ 5 = 25÷5 + 10 ÷ 5 = 5 + 2 = 7.

So, it may be said in general that, if a, b, and c are three integers then,

(a+b) ÷ c= a ÷ c + b ÷ c and (a-b) ÷ c= a ÷ c- b ÷c.

This distributive law of division is only applicable for the right-hand side.

If a, b, and c be three integers then it may be shown that,

c ÷ (a + b) ≠ c ÷ a + c ÷ b and c ÷ (a-b) ≠ c ÷a – c ÷ b.

Therefore, the distributive law of division is not applicable in this case.

Illustration: Suppose you can do 12 sums daily and your brother can do 8 sums daily.

In 10 days what will be the total number of sums done by you? We may solve this problem in two ways.

In one day the total sum done by you and your brother is (12 + 8) = 20.

Hence, the number of sums done in 10 days = {(12 + 8) x 10} = 20 x 10 = 200.

Again in 10 days, you can do 12 x 10 – 120 sums and in 10 days your brother can do 8 x 10 = 80 sums.

Hence, the total number of sums done by you and your brother in 10 days = 12 x 10 + 8 x 10 = 120 + 80 = 200.

Thus, we can say that, (12 + 8) x 10 = 12 x 10 + 8 x 10.

Use of brackets: In algebra brackets are used in the same manner as in arithmetic. In general, four types of brackets are used.

They are:

1. Line bracket —
2. First bracket ( )
3. Second bracket { }
4. Third bracket [ ]

If in a question all the brackets are present then first of all, the operation under the line bracket is performed. After that, the operation under first bracket, second bracket and third bracket are done in series after finding values inside the corresponding brackets.

 

Algebra Chapter 3 Laws Exercise 3 Some Problems With Commutative, Associative, And Distributive Laws And The Use Of Brackets

Example 1. Prove on the number axis that 4 + 3 = 3 + 4.

Solution:

Moving 4 units to the right of 0

we get to point 4. After this, moving 3 more units in the same direction we get point 7.

Thus, 4 + 3 = 7.

Again, at first moving 3 units to the right of 0 we get point 3. After this, moving 4 more units in the same direction we get to point 7. Thus, 3 + 4 = 7.

Hence, 4 + 3 = 3 + 4 (proved).

Example 2. Prove that : 4 x 5 = 5 x 4.

Solution:

4 x 5 = 5 + 5 + 5 + 5 = 20

5 x 4=4+4+4+4+4=20

Hence, 4 x 5 = 5 x 4 (proved).

Wbbse Class 7 Maths Solutions

Example 3. Rewrite 2 + 3 + 5 in two different ways such that a single bracket is used in each case.

Solution: 2 + 3 + 5 = (2 + 3) + 5 and 2 + 3 + 5 = 2 + (3 + 5).

Example 4. Rewrite 5 x 6 x 7 in two different ways such that a single bracket is used in each case.

Solution:  5 x 6 x 7 = (5 x 6) x7 and 5 x 6 x 7 = 5 x (6 x 7).

Example 5.  In each of the following cases, determine which law of which operation has been used.

1. a + b = b + a.
2. a x b – b x a,
3. (a + y) + z – x + (y + z).
4. m x (n x p) = (m x n) x p.
5. a x (6 + c) = a x b + a x c.
6. (a + b) ÷ c = a ÷ c + b ÷ c.

Solution:

1. Commutative law of addition.
2. Commutative law of multiplication.
3. Associative law of addition.
4. Associative law of multiplication.
5. Distributive law of multiplication,
6. Distributive law of division.

Example 6. Add the sum of 3 and 7 with 5 and find the result.

Solution:

Given:

5 + (3 + 7) = 5 + 10 = 15

∴ 15.

The  Result is 15.

Example 7. From 50, subtract the sum of 25 and 15 and find the result.

Solution:

Given:

From 50, subtract the sum of 25 and 15

50 – (25 + 15) = 50 – 40 = 10

∴ 10.

The  Result is 10.

Wbbse Class 7 Maths Solutions

Example 8. Using the result (a + b). c = a.c + b.c prove that,

1. (a – b).c=a.c -b.c.
2. a. (b-c) = a.b- a.c.

Solution:

Given:

Using the result (a + b). c = a.c + b.c

1. (a – b).c + b.c = x.c + b.c [Assuming x = a – b]= (x + b).c [Using the given relation]

= {(a – b) + b}.c [Putting the value of x] = [a + {(-b + b)}].c [By associative property]

= [a + o].c [According to the definition of zero]

= a.c + o.c [Using the given relation]

= a.c + o = a.c [According to the definition of zero]

Now, a.c – b.c = {(a – b).c + b.c} – b.c [Putting the value of a.c]

= (a – b).c + {b.c – b.c} [By associative property]

= (a – b).c + o = (a – b).c

Hence, it is proved that, (a – b).c = a.c – b.c.

2. a.(b – c)= (b – c).a [By commutative property]

= b.a – c.a [From the proof of 1st part]= a.b – a.c [By commutative property]

Hence, it is proved that a.(b – c) = a.b – a.c.

Example 9. Prove that,

1. (a + b + c).x = a.x+ x + c.x.
2. (a + b + c) = x.a+ x.b + x.c.

Solution:

Wbbse Class 7 Maths Solutions

Example 10. Prove that, (a + b) ÷ x = (a ÷ x) + (b ÷ x).

Solution: [(a ÷ x) + (b ÷ x)].x

Hence, (a + b) ÷ x = (a ÷ x) + (b ÷ x) [Proved].

Example 11. Simplify xyz (x + y + z).

Solution:

The given expression = xyz (x + y + z)

= xyz X x + xyz X y + xyz X z

∴ x²yz + xy²z + xyz²

xyz (x + y + z) = x²yz + xy²z + xyz²

Example 12. Simplify : a(a² + 5a – 6).

Solution:

The given expression

= a(a² + 5a – 6)

= a x a² + a x 5a – a x 6 = a³ + 5a² – 6a

∴ a³ + 5a² – 6a.

a(a² + 5a – 6) = a³ + 5a² – 6a.

Wbbse Class 7 Maths Solutions

Example 13.  Simplify: \(\frac{x}{x-y}\)+\(\frac{y}{y-x}\)

Solution:

The given expression

Example 14. Simplify 

Solution:

The given expression

∴ 9

Example 15. Simplify

Wbbse Class 7 Maths Solutions

Solution :

The given expression

∴ – 3

Class Vii Math Solution Wbbse

Example 16. Simplify: 

Solution:

The given expression

∴ y-x

 

Arithmetic Chapter  Square Measure Exercise 6 Solved Example Problems

 

Plane

If we keep the face of a solid on a flat white paper with which it coincides and indicate its boundary with a pencil, we obtain a plane.

Keeping a rectangular parallelopiped on a white paper, and moving a pencil through its edge we obtain a rectangle. If a cube is taken and the same process is applied we obtain a square.

In other words, the portion of a plane enclosed by three or more straight lines or by one or more curves is called a plane.

Area

The measure of the portion of a plane enclosed by a plane figure is called its area. The plane area enclosed by the straight lines is called a polygon.

The measure of the portion enclosed by the sides of a polygon is called its area.

Perimeter

The sum of the lengths of the sides of a polygon is called its perimeter.

Rectangle

A quadrilateral whose opposite sides are equal and the angles are right angles is called a rectangle.

 

 

Square

The quadrilateral whose four sides are equal and the angles are right angles is called a square.

 

 

Some useful measurements

1. Area of rectangle Length x Breadth.
2. Perimeter of rectangle = 2 x (Length + Breadth).
3. Area of square = (Side)².
4. Perimeter of square = 4 x Side.

Areas in connection with a room: A rectangular or square-shaped room has the following parts

1. One floor and one roof
2. Two walls along the length of the room (equal in size & shape and placed opposite to each other)
3. Two walls along the breadth of the room (equal in size & shape and placed opposite to each other)
4. There may be one or more doors and windows in the four walls.

The following images gives a clear idea about the above parts

 

 

Useful measurements in connection with a room:

1. Area of the roof or floor of the room = Length x breadth
2. Area of two walls along the length of the room = 2 x length x height
3. Area of two walls along the breadth of the room = 2 x breadth x height
4. Area of the four walls of the room =2 (length + breadth)x height = Perimeter of room (or floor) x height
5. Number of floor tiles = \(\frac{Area of floor}{Area of one tile}\)
6. One has to consider the total area of the four walls and that of the roof to either paint or whitewash or plaster the room.
7. If the room contains windows and/or door(s), then their total area has to be subtracted from the total area of roof and four walls to get the effective total area.

Height and Area of a triangle

The perpendicular drawn from any vertex on its opposite side is called the height of the triangle. In the image a perpendicular AD is drawn from the vertex A on its opposite side BC in the triangle ABC.

 

 

Hence AD is the height of the triangle. Here BC is the base of the triangle. If AC is taken as the base of the triangle, then the perpendicular drawn on AC from the opposite vertex B shall be taken as the height of the triangle.

Similarly, if AB is taken as the base of the triangle, then the perpendicular drawn on AB from the opposite vertex C shall have to be taken as the height of the triangle ABC.

The following images show the heights of an equilateral triangle, an isosceles triangle and a right-angled triangle.

 

 

It is not mandatory that the height of a triangle should lie within its area enclosed by the three sides.

 

 

The adjacent figure shows that if one of the adjacent sides of the obtuse angle of an obtuse-angled triangle is taken as the base of the triangle, then the height of the triangle shall lie outside the area of the triangle bounded by its three sides.

The images shows that AD lies outside the bounded area of the triangle ABC when BC is taken as the base.

Some useful measurements in connection with a triangle:

1. Perimeter of a triangle = Sum of lengths of three sides = AB + BC + CA
2. Half or semiperimeter of a triangle = \(\frac{AB + BC + CA}{2}\)
3. Area of triangle = \(\frac{1}{2}\) X base x height = \(\frac{1}{2}\) X BC X AD
4. Area of a right-angled triangle = \(\frac{1}{2}\) X BC X AB

Unit of area

While writing the unit of area we have to write the word, ‘square’.

For example square metre, square centimetre etc.

Some points to note

1. To indicate the area of rectangle having length 10 cm and breadth 6 cm we write 10 cm x 6 cm, and read it as 10 cm by 6 cm.

2. Metre x Metre = Square metre.

10 square metres + 5 metres = 2 metres.
10 sq metres + 8 sq metres = 18 sq metres.
10 sq metres-8 sq metres = 2 sq metres.
25 sq metres + 5 sq metres = 5.

3. 12 inches = 1 foot, 144 sq inches = 1 sq foot.

3 feet = 1 yard, 9 sq feet = 1 sq yard.

4840 sq yards = 1 acre.

640 acres = 1 sq mile.

4. 10 mm = 1 cm, 100 sq mm = 1 sq cm

10 cm = 1 dm, 100 sq cm = 1 sq dm.

10 dm = 1 m, 100 sq dm 1 sq m.

10 m = 1 Dm, 100 sq m = 1 sq Dm.

10 Dm 1 Hm,  100 sq Dm = 1 sq Hm.

10 Hm = 1 Km, 100 sq Hm = 1 sq km.

1 are = 1 sq Dm = 100 sq m.

100 centiares = 1 are.

100 are 1 hectare.

100 hectares = 1 sq Kilometres.

5. To calculate area, both length and breadth must be reduced to same unit. The area is expressed in terms of sq unit.

Some problems on square measure

Example 1.  The length of a rectangle is 15 m 25 cm and its breadth is 10 m 2 cm. Find its area.

Solution:

Given:

The length of a rectangle is 15 m 25 cm and its breadth is 10 m 2 cm.

Here, length = 15 m 25 cm = 1525 cm breadth = 10 m 2 cm = 1002 cm

∴ Area of the rectangle = length x breadth = 1525 x 1002 sq cm

= 1528050 sq cm

= 152 sq m 80 sq dm 50 sq cm

∴ 152 sq m 80 sq dm 50 sq cm.

Area = 152 sq m 80 sq dm 50 sq cm.

Example 2.  The page of an exercise book is 15 cm long and 12 cm broad. A margin of width 2 cm is drawn on all sides and something was written on the remaining portion. What is the area of the written portion? What is the area of the portion where nothing was written?

Solution:

Given:

The page of an exercise book is 15 cm long and 12 cm broad. A margin of width 2 cm is drawn on all sides and something was written on the remaining portion.

Area of the page = 15 cm x 12 cm = 180 sq cm.

The portion on which something was written, was of length (15-2x 2) cm 11 cm and breadth (12-2 × 2) cm = 8 cm

∴ Area = 11 cm x 8 cm = 88 sq cm.

 

 

The portion on which nothing was written was of area (180 -88) sq cm = 92 sq cm.

∴ 88 sq cm, 92 sq cm.

= (4 × 100 + 50) sq cm = 450 sq cm. its breadth = 10 cm

The area of the portion where nothing was written = (4 × 100 + 50) sq cm = 450 sq cm. its breadth = 10 cm

Example 3. The area of a rectangle is 4 sq dm 50 sq cm Find the area of the path. and its breadth 10 cm. Find its length.

Solution:

Given:

The area of a rectangle is 4 sq dm 50 sq cm

Area of the rectangle = 4 sq dm 50 sq cm

= (40 x 100 + 50) sq cm

= 450 sq cm.

its breadth = 10 cm

∴ Its length = \(\frac{Area}{breadth}\) = \(\frac{450 sq cm}{10 cm}\)

∴ 45 cm.

Length =  45 cm.

Example 4. The length and breadth of a rectangular plot are 36 m and 24 m. There is a path 2 m wide all around outside of the plot.

1. Find the length and breadth of the plot of land including the path.
2. Find the area of the plot of land excluding the path.
3. What is the area of the path?

Solution:

1. Length of the rectangular plot including the path (36+2×2) m = 40 m

Breadth of the rectangular plot including path = (24+2×2)m = 28 m

∴ 40 m, 28 cm.

2. Excluding the path, area of the rectangular plot = 36 x 24 sq m = 864 sq m

∴ 864 sq m.

3. Area of the path = (40 x 28-36 x 24) sq m = (1120-864) sq m = 256 sq m.

Example 5. How many tiles, each 5 dm by 2 dm will be required to cover the floor of a room 15 m by 12 m?

Solution:

The area of the floor = 15 x 12 sq m = 180 sq m = 18000 sq dm.

The area of each tile = 5 dm x 2 dm

∴ The number of tiles required = \(\frac{18000}{10}\) = 1800

∴ 1800

The number of tiles required = 1800.

Example 6. There is a square plot of land of side 20 m. A path 1 m wide runs all around outside of it.

Solution:

Given:

There is a square plot of land of side 20 m.

Including the path, length of the square plot of land (20+2 x 1) m = 22 m.

Including the path, area of the square plot of land = 22 x 22 sq m = 484 sq m.

Excluding the path, area of the square plot of land = 20 x 20 sq m = 400 sq m.

∴ Area of the path = (484-400) sq m = 84 sqm.

∴ 84 sq m.

Area of the path 84 sq m.

Example 7. Find the perimeter of a rectangle whose length is 15 m 5 dm and breadth is 8 m 7 dm.

Solution:

The perimeter of the rectangle = 2 x (length + breadth)

= 2x (155+ 87) dm

= 2x (242) m = 484 dm = 48 m 4 dm

∴ 48 m 4 dm.

The perimeter of a rectangle 48 m 4 dm.

Example 8. The area of a square plot of land is 6400 sq m. Find the cost of fencing all around the land at 3.50 per metre.

Solution:

Given:

The area of a square plot of land is 6400 sq m.

Area of the square plot of land = 6400 sq m

length of side of the square plot of land = √6400 m = 80 m

The perimeter of the square plot of land = 4 x 80m = 320 m

Cost of fencing 1 m = ₹ 3.50

Cost of fencing 320 m = ₹ 3.50 x 320 = ₹ 1120

Example 9. One plot is 4 sq metres and another plot is 4 metres square. Which one is of the greater area? 

Solution:

Given:

One plot is 4 sq metres and another plot is 4 metres square.

By 4 sq metres is meant a plot whose area rectangle. is 4 sq metres.

[It may be a square, the length of whose side is 2 m and hence its area = 2 m x 2 m = 4 sq m

or, it may be a rectangle whose length is 4 m and breadth is 1 m and hence its area = 4

or, it may be triangular or circular or it may have the shape of any plane whose area is equal to 4 sq m.

On the other hand, by the sentence ‘a plot is 4 metres square’ we mean only a square the length of whose side is 4 metres i.e., its area (4)2 sq m = 16 sq m.

∴ The plot ‘4 metres square’ is of the greater area.

Example 10. The length of a rectangular plot of land is twice its breadth and its area is 578 sq m. Find the length, breadth and perimeter of the land.

Solution:

Given:

The length of a rectangular plot of land is twice its breadth and its area is 578 sq m.

Let, the breadth of the rectangular plot of land = x m then its length = 2x m.

∴ 2x x x = 578

or, 2x² = 578 or, x² = 289

or, x= √28917

∴ Breadth 17 m, Length = 2 x 17 m = 34 m Perimeter = 2 × (34 +17) m = 102 m

∴ Length is 34 m, breadth is 17 m and perimeter is 102 m.

Example 11. How much fencing will be required to fence a square field of area 625 sq metres?

Solution:

The area of the square field = 625 sq metres

∴ The length of its side = √625 m = 25 m .

∴ Its perimeter = 4 x 25 m = 100 metres.

Since the total length of fencing is equal to the 4 x 80 m = 320 m perimeter, therefore the required length of fencing 100 metres.

Cost of fencing 1 m = 3.50 Cost of fencing 320 m = 3.50 x 320=1120

Example 12. The length of a rectangle is 1 \(\frac{1}{2}\) times its breadth. If the area of a square be 100 sq m and its perimeter be equal to the perimeter of the rectangle then find the length of the rectangle.

Solution:

Area of the square = 100 sq m

Length of side of the square = √100 m = 10m

∴ Perimeter of the square= 4 x 10 m = 40 m

Let, the breadth of the rectangle = xm, 3х then length of the rectangle = \(\frac{3x}{2}\) m

∴ 2 X (x + \(\frac{3x}{2}\)) = 40

or, \(\frac{5x}{2}\)=20

or, x =\(\frac{2 X 20}{5}\) = 8

∴ Length of the rectangle = \(\frac{3 X 8}{2}\)

∴ 12 m.

Length of the rectangle =12 m.

Example 13. The length of a room is 8 m, its breadth is 6 m and its height is 5 m. What will be the cost of polishing the floor of the room at 70 per sq m?

Solution:

Given:

The length of a room is 8 m, its breadth is 6 m and its height is 5 m.

Area of the floor of the room = 8 x 6 sq m = 48 sq m

Cost in 1 sq m = ₹ 70

Cost in 48 sq m = ₹ 70 x 48 = ₹ 3360

∴ ₹ 3360

Cost in 48 sq m = ₹ 3360

Example 14. A rectangular plot of length 200 m and breadth 120 m has been divided in 4 equal parts by two paths 10 m wide parallel to length and breadth. What is the area of that path?

Solution:

Given:

A rectangular plot of length 200 m and breadth 120 m has been divided in 4 equal parts by two paths 10 m wide parallel to length and breadth.

Area of the path parallel to length = 200 x 10 sq m = 2000 sq m

Area of the path parallel to breadth = 120 x 10 sq m = 1200 sq m

Area of the portion where the two paths intersect 10 x 10 sq m = 100 sq m

∴ The required area of the path =(2000+ 1200-100) sq m = 3100 sq m

∴ 3100 sq m

The required area of the path = 3100 sq m

Example 15. If both length and breadth of a rectangle are doubled then how many times will be its area?

Solution:

Let, length of the rectangle = x m and its breadth = y m

∴ Area of the rectangle = x y sq m

Changed length = 2x m and breadth = 2ym

∴ Changed area = 2x × 2y sq m = 4 xy sq m

∴ Area of the rectangle will be 4 times

∴ 4 times.

Example 16. The length of a rectangular stage of a theatre is twice its breadth. It costs ₹ 6048 to cover the whole stage with tarpaulin. If one sq m of tarpaulin costs ₹21, find the length and breadth of the stage.

Solution:

Given:

The length of a rectangular stage of a theatre is twice its breadth. It costs ₹ 6048 to cover the whole stage with tarpaulin. If one sq m of tarpaulin costs ₹21

Since the total expenditure is ₹ 6048 to cover the stage at the rate ₹21 per square metre, therefore, the area of the stage = (6048 ÷ 21) sq m = 288 sqm

Let, the breadth of the stage =  x m then its length  = 2x m.

∴ 2x X x = 288  or, 2x² = 288

or, x² = \(\frac{288}{2}\) = 144

or, x=√144 = 12

∴ Breadth = 120m and length = 2 x 12 m = 24 m

∴ Length is 24 m and breadth is 12 m

Example 17. A garden is 30 m long and 20 m broad. All round outside of it, there is a path 3 m broad. What is the area of the path?

Solution:

Given:

A garden is 30 m long and 20 m broad. All round outside of it, there is a path 3 m broad

Length of the garden including the path = (30+3×2) m = (30 + 6) m = 36 m

Breadth of the garden including the path = (20 + 3 x 2) m = (20 + 6) m = 26 m

 

 

Area of the garden including the path = 36 m x 26 m = 936 sq m

Area of the garden excluding the path = 30 m x 20 m = 600 sq m.

Area of the path = (936- 600) sq m = 336 sq m

∴ 336 sq m

Area of the path = 336 sq m

Example 18. The length and breadth of a rectangular garden are 60 m and 40 m respectively. Two 5 m wide path is divided Find the cost of paving the path at ₹80 per rectangular garden into four equal parts. sq. metre. Find also the area of each part of the land.

Solution:

Given:

The length and breadth of a rectangular garden are 60 m and 40 m respectively. Two 5 m wide path is divided Find the cost of paving the path at ₹80 per rectangular garden into four equal parts. sq. metre.

Area of the path parallel to the length = 60 x 5 sq m = 300 sq m.

Area of the path parallel to the breadth = 40 x 5 sq m = 200 sq m.

Area of the portion where two paths intersect each other = 5 x 5 sq m = 25 sq m.

Area of the path = (300 + 200- 25) sq m = 475 sq m

cost of paving 1 sq m path = ₹ 80

cost of paving 475 sq m path = ₹ 80 x 475 = ₹ 38000

 

 

length of one part of the garden =\(\frac{60 -5}{2}\) m = \(\frac{55}{2}\)

breadth of one part of the garden = \(\frac{40 -5}{2}\) m = \(\frac{35}{2}\)

area of one part of the garden = \(\frac{55}{2}\) x \(\frac{35}{2}\) sq m

= \(\frac{1925}{4}\) sq m = 481.25 sq m

∴ ₹ 38000, 481 .25 sq m.

Example 19. A garden is 25 metres square. All around inside of it, there is a path 2\(\frac{1}{2}\) m broad. What is the area of the path?

Solution:

Given:

A garden is 25 metres square. All around inside of it, there is a path 2\(\frac{1}{2}\) m broad.

Area of the garden = 25 x 25 sq m = 625 sq m

Length of the side of the garden excluding the path

= (25 – \(\frac{5}{2}\) x 2) m = 25 -5 m = 20 m

∴ Area of the garden excluding the path = 20 m x 20 m = 400 sq m.

∴ Area of the path = (625-400) sq m = 225 sq m.

∴ 225 sq m.

Area of the path = 225 sq m.

Example 20. The path that leads to a man’s house is 2 m wide. The path divides the garden in front of the house in two equal squares. The path is constructed for 8000 at the rate of 500 per sq m. Calculate the area of each square portion of the garden. The house is built in rectangular land. If the length of the rectangular land is 4 m, calculate the area occupied by the house.

Solution:

Given:

The path that leads to a man’s house is 2 m wide. The path divides the garden in front of the house in two equal squares. The path is constructed for 8000 at the rate of 500 per sq m. Calculate the area of each square portion of the garden.

Since the total expenditure of constructing the path is ₹ 8000 at the rate of ₹ 500 per sq m therefore, area of the path

\(\frac{8000}{500}\) sq m = 16 sq m

Since the breadth of the path = 2 m

therefore its length = \(\frac{16}{2}\) m = 8 m

∴ Area of each square portion of the garden = 8 x 8 sq m = 64 sq m

Length of the portion occupied by the house = (8 + 2 + 8)m = 18m and its breadth = 4 m.

Therefore, its area = 18 x 4 sq m = 72 sq m

∴ 64 sq m, 72 sq m

Area= 64 sq m, 72 sq m

Example 21. The length, breadth and height of a room are 4 m, 3 m and 5 m respectively. What will be the cost of cementing the floor of that room at? ₹15 per square metre? What will be the cost of white washing the four walls at ? ₹5 per square metre?

Solution:

Given:

The length, breadth and height of a room are 4 m, 3 m and 5 m respectively.

Area of the floor of the room = 4 x 3 sq m = 12 sq m.

cost of cementing 1 sq m =  ₹ 15

cost of cementing 12 sq m =  ₹ 15 x 12 = ₹ 180

Again, the area of the four walls of the room = 2 x (4+3) x 5 sq m

= 2x7x5 sq m = 70 sq m

cost of whitewashing 1 sq m = ₹ 5

cost of whitewashing 70 sq m = ₹ 5 x 70 = ₹ 350

∴ Cost of cementing the floor =₹ 180.

Cost of whitewashing the four walls = ₹ 350.

Example 22.  The cost of cultivating a 30 m long piece of land is ₹ 150. Had the breadth of the land been 5 m less, the cost would have been ₹ 120. Calculate the breadth of the land.

Solution:

Given:

The cost of cultivating a 30 m long piece of land is ₹ 150. Had the breadth of the land been 5 m less, the cost would have been ₹ 120.

Let the breadth of the land = xm

The area of the land = 30x sq m

Had the breadth of the land been 5 m less the breadth would have been (x-5) m.

The area would have been 30 (x-5) sq m

According to the question,

\(\frac{30x}{30(x -5)}\) = \(\frac{x}{x – 5}\) = \(\frac{5}{4}\)

or, 5x-25= 4x or, 5x-4x= 25 or, x = 25

∴ The breadth of the land is 25 m.

Example 23. The area of four walls of a room is 154 sq m If its length and breadth be 6 m and 5 m respectively then what will be its height?

Solution:

Given:

The area of four walls of a room is 154 sq m If its length and breadth be 6 m and 5 m respectively

2 × (length + breadth) x height = area of four walls.

or, 2 x (6+ 5) m x height = 154 sq m or, 22 m x height = 154 sq m

or, height = \(\frac{154}{22}\) m = 7 m

∴ 7 m.

Height = 7 m.

Example 24. The length and breadth of a rectangular hall are 30 m and 18 m respectively. Find how many square tiles of side 3 dcm will be required for flooring the hall.

Solution:

Given:

The length and breadth of a rectangular hall are 30 m and 18 m respectively.

Area of the floor of the hall = 30 x 18 sq m = 540 sq m.

Area of one tile = 3 dcm x 3 dcm = .3 mx .3 m = .09 sq m

∴ Number of tiles = \(\frac{540}{.09}\) = 6000

∴ 6000 tiles will be required.

Example 25. Find the greatest measure of each stone of the same square shape to cover a rectangular courtyard 36 m long and 28 m broad. Find the number of such stones.

Solution:

The H.C.F. of 36 m and 28 m is 4 m.

∴ Each stone of the greatest area will be 4 metres square.

∴ Area of each stone = (4)² sq m = (4×4) sq m

∴ The required number of stones = \(\frac{36 X 28}{4 X 4}\) =63

∴ Each stone is 4 metres square and a number of stones is 63.

Example 26. Mahim’s family has an 18 m x 14 m rectangular plot of land. There is a square portion of the garden of side 3.4 m within the rectangular plot of land. Calculate the area of the plot of land without the garden. Find how many square tiles of side 2 dcm will be required to cover the empty portion of land.

Solution:

Given:

Mahim’s family has an 18 m x 14 m rectangular plot of land. There is a square portion of the garden of side 3.4 m within the rectangular plot of land.

Area of a rectangular plot of land = (18 x 14) sq m = 252 sq m.

Area of the square portion of the garden of side 3.4 m = (3.4 x 3.4) sq m = 11.56 sq m.

Area of the empty portion of land excluding the garden (252-11.56) sq m = 240.44 sq m.

Area of one tile = 2 dcm x 2 dcm = .2 m x .2 m = .04 sq m

∴ Number of tiles = \(\frac{240.44}{.0.4}\) = 6011

∴ Area of empty plot of land = 240.44 sq m, 6011 tiles will be required.

Example 27. Find the perimeter of a square field having twice the area of a rectangular field of length 25 m and breadth 8 m.

Solution: Area of the rectangular field = 25 x 8 sq m = 200 sq m

∴ Area of the square field = 2 x 200 sq m = 400 sq m

∴ Each side of the square field = √400 m = 20 m

∴ Perimeter of the square field = 4 × 20 m = 80 m

∴ 80 metres.

Perimeter of the square field = 80 metres.

Example 28. The length, breadth and height of a room of a school are 8 m, 6 m and 5 m respectively.

1. Find the cost of cementing the floor at ₹ 75 per square metre.
2. Find the cost of whitewashing the ceiling at ₹ 52 per square metre.
3. The room has 2 doors each 1.5 m wide and 1.8 m high and has 2 windows each 1.2 m wide and 1.4 m high. Calculate the cost of painting doors and windows at ₹ 260 per square metre.
4. Calculate the total cost of plastering the four walls without doors and windows at ₹ 95 per square metre and painting the walls at ₹ 40 per square metre.

Solution:

1. Area of the floor = (8 x 6) sq m = 48 sq m.

The cost of cementing 48 sq m at the rate ₹ 75 per square metre ₹ 75 x 48= ₹3600

∴ ₹ 3600.

2. Area of the ceiling area of the floor = 48 sq m.

Cost of whitewashing 48 sq m at the rate ₹ 52 per square metre = ₹ 52 x 48= ₹ 2496

∴ ₹ 2496.

3. Total area of two doors each 1.5 m wide and 1.8 m high = 2x (1.5 x 1.8) sq m = 5.4 sq m.

Total area of two windows each 1.2 m wide and 1.4 m high = 2 × (1.2 x 1.4) sq m = 3.36 sq m.

Total area of the doors and windows = (5.4+ 3.36) sq m = 8.76 sq m.

Cost of painting doors and windows at the rate ₹ 260 per square metre ₹ (260 x 8.76)= ₹ 2277.60

∴ ₹ 2277.60.

4.  Total area of the four walls = 2 × (length +breadth) x height = 2 x (6+8) x sq m = 140 sq m

area of the four walls without doors and windows (140-8.76) sq m = 131.24 sq m.

cost of plastering and painting per square metre (95+40) = ₹ 135

Total cost in 131.24 sq m at the rate of  ₹135 per square metre ₹ (135 x 131.24)= ₹ 17717.40

∴ ₹ 17717.40.

Example 29. What will be the cost of paper 3 m wide, at 25 paise per metre for covering the four walls of a room 15 m long, 12 m broad and 10 m high?

Solution:

The area of the paper =the area of the four walls

= 2 x (length + breadth) x height

= 2 x (15 m + 12 m) x 10 m

= 2 x 27 x 10 sq m

The length of the paper used = \(\frac{2 X 27 X 10}{3}\) m = 180 m

The required cost = 180 x 25 paise = 4500 paise = ₹ 45

∴ ₹45.

The required cost ₹45.

Example 30. A club room is square in the shape of side 15 m long and 5 m high. There are 4 doors in the club room each 1.5 m wide and 2 m high. Calculate the cost of oil painting its four walls without doors at 350 per square metre.

Solution:

Given:

A club room is square in the shape of side 15 m long and 5 m high. There are 4 doors in the club room each 1.5 m wide and 2 m high

Area of the 4 walls of the club room =2x (15+15) x 5 sq m = 300 sq m.

Area of 4 doors each 1.5 m wide and 2 m high = 4 x (1.5 × 2) sq m = 12 sq m.

Area of 4 walls without doors (300-12) sqm=288 sqm

Cost of oil painting 4 walls without doors at the rate ₹350 per sq m = ₹350 x 288 = ₹100800.

∴ ₹ 100800.

Cost of oil painting 4 walls without doors at the rate ₹350 per sq m = ₹ 100800.

Example 31. The length, breadth and height of a room are equal. If the area of four walls be 100 sq m then find its length, breadth and height.

Solution:

Given:

The length, breadth and height of a room are equal. If the area of four walls be 100 sq m

Let, the length of the room = its breadth = its height = a metres.

∴ 2x (a + a) x a = 100

or, 2 x 2a x a = 100

or, 4a² = 100

or, a² = 100 = 25

or, a = √25 = 5

∴ Each of length, breadth and height is equal to 5 m.

Example 32. What will be the cost of preparing a road of length 12 km and breadth 4 m at ₹ 3.50 per square metre?

Solution:

Area of the road= 12000×4 sq m. = 48000 sq m.

∴ Cost of preparing the road

= ₹ 48000 x 3.50 = ₹ 168000

∴ ₹ 168000

Cost of preparing the road is ₹ 168000

Example 33. ₹57800 is required to fence a square park with iron railing at 50 per metre. Find the length of one side of the park.

Solution:

Since, to fence the square park with iron railing at ₹ 50 per metre, ₹ 57800 is needed therefore, the perimeter of the square park

= \(\frac{57800}{50}\) metres = 1156 metres

Hence, the length of its one side = \(\frac{1156}{4}\) metres = 289 metres.

∴ 289 metres.

The length of its one side 289 metres.

Example 34. The length of a rectangular field is three times its breadth and its area is 192 sq metres. How much greater will be the area of the square field than that of the rectangular field if the perimeter of the square field is equal to that of the rectangular field?

Solution:

Given:

The length of a rectangular field is three times its breadth and its area is 192 sq metres.

Area of the rectangle = 192 sq m

∴ length x breadth = 192 sq m.

or, 3 x breadth x breadth = 192 sq m

or, (breadth)² = \(\frac{192}{3}\) sq m = 64 sq m

or, breadth = 8 m

∴ Length = 3 x 8 m = 24 m

Hence, the perimeter of the rectangular field = 2 (24 + 8) m = 64 m

Therefore, the perimeter of the square field is also 64m

∴ Length of each side of the square field = \(\frac{64}{3}\) = 16 m

∴ Area of the square field = (16)² sq m = 256 sq m

∴ Area of the square field is greater than that of the rectangular field by (256- 192) sq m = 64 sq m

∴ Greater by 64 sq m

Example 35. The length, breadth and height of a room are 6 m, 5 m and 3.5 m respectively. There are two doors each measuring 1.75 m by 1.2 m and two windows each measuring 1.4 m by 1 .2 m. What will be the cost of cementing the floor at? ₹65 per sq m? What will be the cost of whitewashing the four walls? ₹15 per sqm leaving the doors and the windows?

Solution:

Given:

The length, breadth and height of a room are 6 m, 5 m and 3.5 m respectively. There are two doors each measuring 1.75 m by 1.2 m and two windows each measuring 1.4 m by 1 .2 m.

Area of the floor of the room = 6 x 5 sq m = 30 sq m.

Total cost of cementing the floor at the rate of  ₹ 65 per sq m = ₹ 65 x 30 = ₹ 1950.

The area of the four walls of the room = 2 x (6 + 5) x 3.5 sq m = 77 sq m

Total area of two doors and two windows = (2 x 1.2 x 1.75 + 2 x 1.4 x 1.2) sqm

= (4.2 + 3.36) sq m = 7.56 sq m

∴ Area of the four walls excepting the doors and the windows = (77-7.56) sq m = 69.44 sq m.

Total cost of whitewashing at the rate of  ₹ 15 per square metre = ₹ 69.44 × 15 = ₹ 1041.60.

∴ ₹ 1950, 1041.60.

Example 36. There is a path 1 metre broad all round outside of a square garden of side 20 m. Find the cost of paving the path at ₹ 35.50 per sq m.

Solution:

Given:

There is a path 1 metre broad all round outside of a square garden of side 20 m.

Length of the square garden including the path = (20 + 2) m = 22 m.

∴ Area of the square garden including the path = (22)² sq m = 484 sq m.

area of the square garden excluding the path = (20)² sq m = 400 sq m.

∴ Area of the path =(484-400) sq m = 84 sq m.

The total cost of paving the path at ₹ 35.50 per square metre = ₹ (35.50 x 84) = ₹ 2982.

∴ The required cost is  ₹ 2982.

Example 37. Boundary walls are made along the bank of a pond to surround it. The length of the pond is 6 m more than its breadth. Now widening the edge of this pond by 8 m, a railing of length 192 m was made towards the waterside. What is the outside length and breadth of the boundary walls along the bank? What is the perimeter of the pond along the outside boundary?

Solution:

Given:

Boundary walls are made along the bank of a pond to surround it. The length of the pond is 6 m more than its breadth. Now widening the edge of this pond by 8 m, a railing of length 192 m was made towards the waterside.

Considering the water side 2 x (length + breadth) = 192 m

or, length + breadth = 96 m

or, breadth + 6 m + breadth = 96 m

 

 

or, 2 x breadth = 90 m or, breadth =\(\frac{90}{2}\) 45 m

Hence, length (45+6) m = 51 m.

Now, the outside length of the boundary wall along the bank = (51 +16) m = 67 m and the outside breadth = (45+16) m = 61 m.

Perimeter of the pond along the outside boundary=2x (67 +61) m = 256 m.

Example 38. Find the height of a triangle if its area and length of the base be x sq. units and y units respectively.

Solution:

Area of triangle =\(\frac{1}{2}\) x base x height

or, x = \(\frac{1}{2}\)  x y x height

or, height = \(\frac{2x}{y}\)

∴ \(\frac{2x}{y}\) unit.

Example 39. The perimeter of a triangle is (3a + b)cm. If the length of its two sides are (2a-b)cm and b cm, then find the length of the third side.

Solution:

Given:

The perimeter of a triangle is (3a + b)cm. If the length of its two sides are (2a-b)cm and b cm

Sum of lengths of two sides = (2a – b) + b = 2a cm.

∴ Length of third side = (3a + b) – 2a = (a + b) cm.

∴ (a + b) cm.

Length of third side = (a + b) cm.

Example 40. If the adjacent sides of the right angle in a right-angled triangle measure 4 cm and 10 cm in length, then find the area of the triangle.

Solution:

If one side adjacent to the right angle be considered as the base, then the other side becomes the height or altitude of the right angles triangle.

∴ Area of the triangle

= \(\frac{1}{2}\) x 4 x 10 sq.cm = 20 cm

Area of the triangle = 20 cm.

Example 41. The length of the base of a triangular-shaped land is thrice its height. A sum of ₹4,50,000 has been expended to cultivate the land at a rate of ₹30 per sq.m. Calculate the length of height of the land.

Solution:

Given:

The length of the base of a triangular-shaped land is thrice its height. A sum of ₹4,50,000 has been expended to cultivate the land at a rate of ₹30 per sq.m.

Area of land = sq.m 15000 sq.m.

Let the height of the triangular-shaped land be x m.

∴ Length of its base = 3x m.

∴ Area of triangle = \(\frac{1}{2}\) × 3x X x = 3x²/2 sq.m

Therefore, 3x²/2= 15000

or, x² = 3 x 15000 = 10,000

or, x=√10,000 = 100

∴ Height of land, x = 100m and length of the base, 3x=300m.

∴ 300m and 100m.

Height of land = 300m and 100m.

Example 42. The ratio of the lengths of the two sides = (2a – b) + b = 2a cm. adjacent to the right angle in a right-angled triangle is 3 4. If the area of the triangle is 1014 sq. cm, then find out the length of these sides.

Solution:

Given: 

The ratio of the lengths of the two sides = (2a – b) + b = 2a cm. adjacent to the right angle in a right-angled triangle is 3 4. If the area of the triangle is 1014 sq. cm

Let the lengths of the two sides be 3x and 4x.

∴ Area of triangle =\(\frac{1}{2}\) x 3x x 4x=\(\frac{12}{2}\) x² = 6x²

Therefore, 6x² =1014

or, x² = \(\frac{1014}{6}\) = 169

or, x =√169 = 13

∴ Length of two sides, 3×13 = 39 cm and 4×13 = 52 cm.

∴ 39 cm and 52 cm.

Length of two sides = 39 cm and 52 cm.

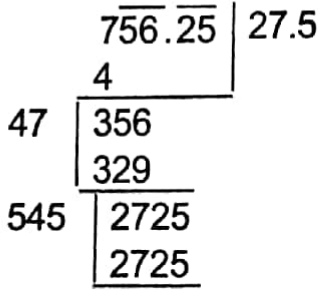
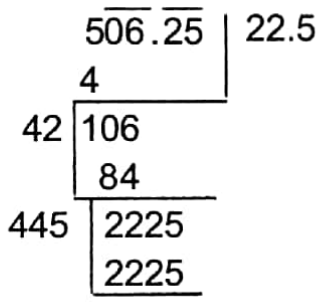
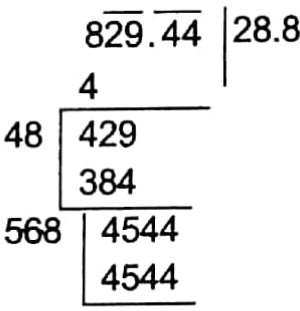
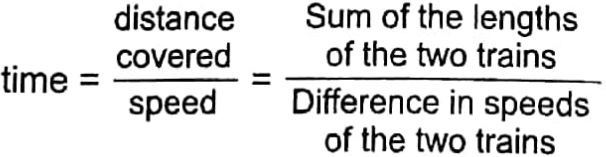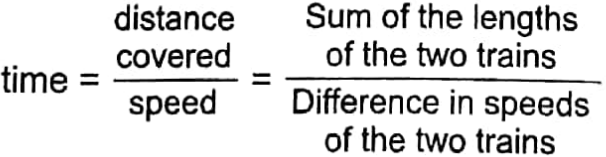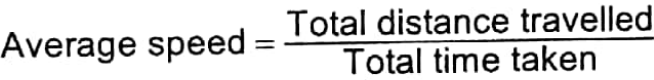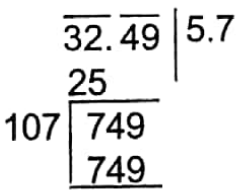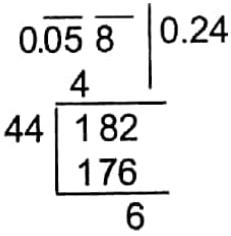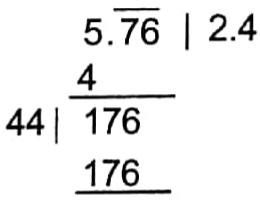Arithmetic Chapter 5 Time And Distance Exercise 5 Solved Example Problems

 

Introduction:

The problem of time and distance arises from travelling. In our daily life, we have to travel from one place to the other. Travelling may be of different types. Some people walk on foot and some travel by cycle.

Other than these there are several vehicles by which we may go from one place to the other. There are buses, trams, trains, boats, ships, aeroplanes, etc., for our travelling.

In every case of travelling, to cover some distance, some time elapse. Thus to work out problems on time and distance we shall have to concentrate on two main things-

1. The distance travelled
2. The time required to travel that distance.

Uniform and non-uniform speed

When a body covers a particular distance in a particular time, we say that the body is travelling with uniform speed; otherwise, the speed of the body is said to be non-uniform.

In the case of uniform speed, if a car travels 40 km in one hour, it will travel 80 km in two hours and 120 km in three hours. This indicates that the car is travelling at a uniform speed of 40 km per hour.

But if a car travels 40 km is the first hour, 45 km in the second hour, and 35 km in the third hour then say that the speed of the car is non-uniform.

In this chapter, we shall assume that the objects are moving with uniform speed. We shall use ratio and proportion and unitary methods to solve the problems on uniform speed.

Relation between time, distance and speed

The distance traversed by any vehicle or person in unit time is called speed. By the term ‘unit time’ we mean ‘per hour’ or ‘per minute’ or ‘per second’.

If a train travels 50 kilometres per hour then its speed is written as, “50 km per hour” or, “50 km/hour”.

We get the following relations among time, distance and speed.

1. Distance travelled = Speed x Time. Distance Travelled

2. Speed= \(\frac{Distance travelled}{Time}\)

3. Time= \(\frac{Distance travelled}{Speed}\)

Two important rules

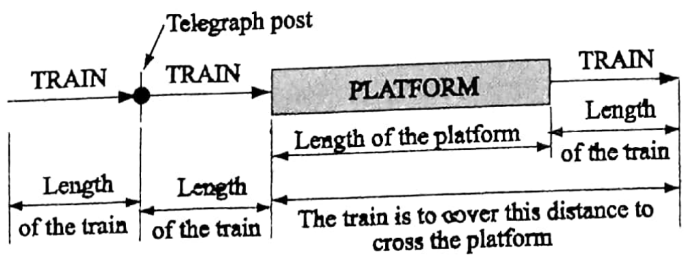
1. Since a tree or a telegraph post does not possess any length, they can be represented either by a dot or a point. Hence, when a train crosses a tree (or a telegraph post), it travels a distance equal to its own length.

2. When a train crosses a platform (or a bridge), it travels a distance equal to the sum of the lengths of the train and the platform (or the bridge).

 

 

Relative speed

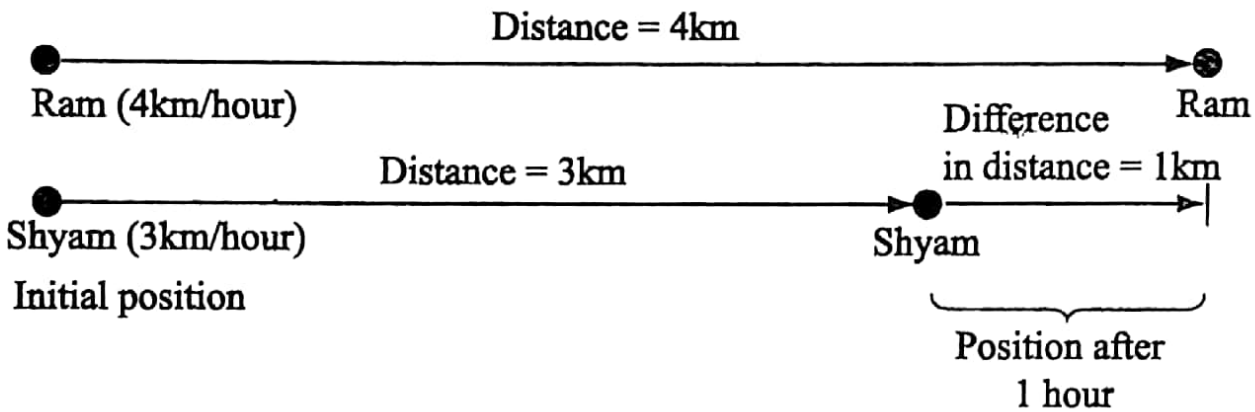
Let, Ram and Shyam, start walking from the same place in the same direction. Let the speed of Ram be 4 km/hour and that of Shyam be 3 km/hour. Then in 1 hour, Ram travels (4-3) km or, 1 km more than Shyam. So it is clear that

When two men walk in the same direction the difference of their speeds is their relative speed.

 

 

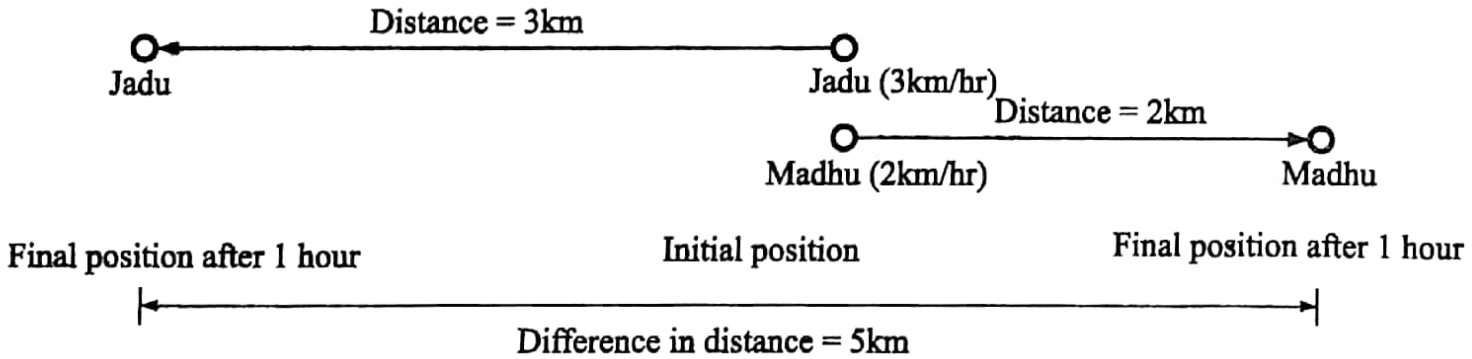
Again, let Jadu and Madhu start walking from the same place in the opposite direction.

Let the speed of Jadu be 3 km/hour and that of Madhu be 2 km/hour. Then in 1 hour the distance between Jadu and Madhu increases by (3+2) km or, 5 km. So it is clear that

When two men walk in the opposite direction the sum of their speeds is their relative speed.

 

 

Thus from the idea of relative speed, we which the high-speed train crosses the slow can say that:

1. Between two trains moving towards the same direction in parallel tracks, the time in which the high-speed train crosses the slow-speed train is, speed train is,

 

 

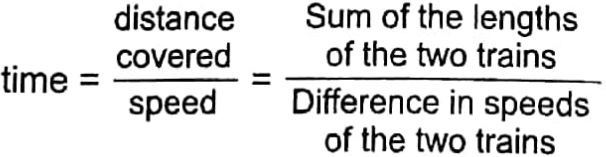
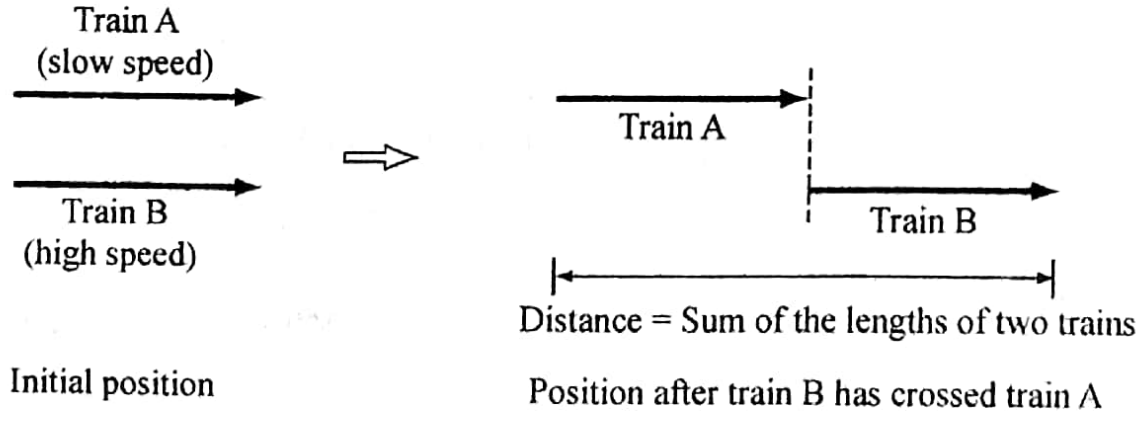
2. When two trains are moving towards opposite directions in parallel tracks, the time in which the trains would cross each other is,

 

 

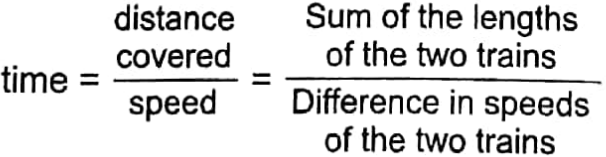
Average speed

When the speed of a body is not uniform throughout the journey, the average speed of the same is considered.

Boat and Stream

When a boat moves in a river then we have to consider two things:
1. Speed of the boat.
2. Speed of the river current.

The actual speed of a boat: By actual speed of a boat we mean the distance covered by a boat in unit time in still water (i.e., when there is no current) under the influence of oars.

 

 

Speed of a boat under the current of a river: When a boat moves under the current of a river, there may arise two cases.

If the boat moves along the current (downstream) the effective speed is greater than the actual speed of the boat and if the boat moves against the current (upstream) the effective speed is less than the actual speed of the boat.

 

 

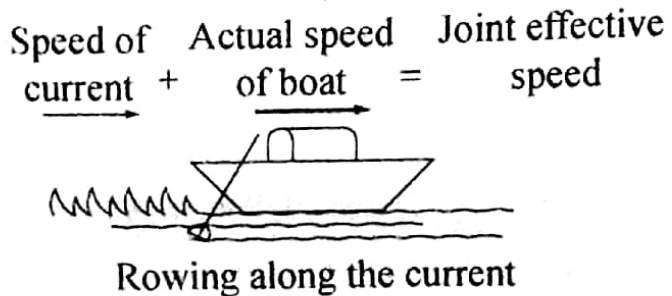
When the boat rows along the current, then the joint effective speed = actual speed of the boat + speed of the river current.

When the boat rows against the current, then the joint effective speed = actual speed of the boat-speed of the river current.

 

 

Arithmetic Chapter 5 Time And Distance Exercise 5 Some Problems On Time And Distance

Example 1. A train travels 24 km in 4 hours. What distance will it travel in 10 minutes?

Solution:

Given:

A train travels 24 km in 4 hours.

Time
4 x 60 minutes
10 minutes

Distance
24 km
x km (say)

Since, distance is directly proportional to time,

∴\(\frac{40 X 60}{10}\) = \(\frac{24}{x}\)

or, x = \(\frac{24 X 10}{4 X 60}\) = 1

∴ The required distance = 1 km.

Alternative method:

In 4 x 60 minutes, the train travels 24 km

In 1 minute the train travels \(\frac{24}{4 X 60}\) km

In 10 minutes the train travels \(\frac{24 X 10}{4 X 60}\) = 1 km

Example 2. On Monday, Ram was cycling at a speed of 13 km/hour. He covered a certain distance in 2 hours. On Tuesday, cycling for the same time at a speed of 11 km/hour he covered a certain distance. On which day, Ram travelled how much more distance in 2 hours?

Solution:

Given:

On Monday, Ram was cycling at a speed of 13 km/hour. He covered a certain distance in 2 hours. On Tuesday, cycling for the same time at a speed of 11 km/hour he covered a certain distance.

On Monday In 1 hour he travelled 13 km In 2 hours he travelled 13 x 2 = 26 km

On Tuesday – In 1 hour he travelled 11 km In 2 hours he travelled 11 x 2 km = 22 km

On Monday he travelled (26-22) km or 4 km more distance.

∴ On Monday, he travelled 4 km more distance.

Example 3. A man can travel 5 metres in 6 seconds by a cycle. Find his speed in km/hour.

Solution:

Given:

A man can travel 5 metres in 6 seconds by a cycle.

Time
6 seconds
60 x 60 seconds

Distance
5 metres
x metres (say)

Since, distance is directly proportional to time,

∴ \(\frac{6}{60 X 60}\)

or, 6x= 5 x 60 x 60

or, x= \(\frac{5 X 60 X 60}{6}\) = 3000

∴ In 1 hour the main travel of 3000 metres = 3km

∴ The speed of the man is 3km/hour.

Alternative method:

In 6 seconds the man travels 5 m

In 1 second the man travels \(\frac{5}{6}\) m

In 60 x 60 seconds, the man travels \(\frac{5}{6}\) x 60 x 60

= 3000 metres = 3km

Speed in km/hour = 3km

Example 4. On Saturday, Jadu went to the market cycling at a speed of 12 km/hour. But on Sunday he went to market cycling at a speed of 15 km/hour. If the distance between the house and the market is 2 km, on which day, Jadu took how much less time to reach the market?

Solution:

Given:

On Saturday, Jadu went to the market cycling at a speed of 12 km/hour. But on Sunday he went to market cycling at a speed of 15 km/hour. If the distance between the house and the market is 2 km,

On Saturday, he travelled 12 km in 60 minutes

On Saturday, he travelled 1 km in \(\frac{60}{12}\) x 2 = 10 minutes

On Sunday, he travelled 15 km in 60 minutes

On Sunday, he travelled 1 km in \(\frac{60}{15}\) minutes

On Sunday, he travelled 2 km in \(\frac{60}{15}\) x 2 minutes = 8 minutes

On Sunday he took (108) min or 2 min less to reach the market.

∴ On Sunday, he took 2 min less time.

Example 5. Find the time taken to travel 600 km by train whose speed is 25 km/hour.

Solution

Distance
25 km
600 km

Time
1 hour
x hours (say)

Since, distance is proportional to time,

∴ \(\frac{25}{600}\) = \(\frac{1}{x}\)

or, 25x= 600 or, x = \(\frac{600}{25}\) = 24

∴ The required time is 24 hours.

Alternative method:

The train travels 25 km in 1 hour

The train travels 1 km in \(\frac{1}{25}\) hour

The train travels 600 km in \(\frac{600}{25}\) hour = 24 hours.

Example 6. A man covered a distance of 12 km in 40 minutes by bus. Find the speed of the bus.

Solution:

Given:

A man covered a distance of 12 km in 40 minutes by bus.

That man, in 40 minutes travelled 12 km

That man, in 1 minute travelled \(\frac{12}{40}\) km

That man, in 60 minutes travelled \(\frac{12}{40}\) x 60 = 18 km

∴ Speed of the bus is 18 km/hour.

Example 7.  A train went from Kolkata to Burdwan at a speed of 45 km/hour and then returned from Burdwan to Kolkata at a speed of 36 km/hour. Find the average speed of the train.

Solution:

Given:

A train went from Kolkata to Burdwan at a speed of 45 km/hour and then returned from Burdwan to Kolkata at a speed of 36 km/hour.

While going from Kolkata to Burdwan

The train travelled 45 km in 1 hour

The train travelled 1 km in \(\frac{1}{45}\) hour

While returning from Burdwan to Kolkata

The train travelled 36 km in 1 hour

∴ The train travelled 1 km in \(\frac{1}{36}\) hour

∴ To travel 2 km the train takes

(\(\frac{1}{45}\) + \(\frac{1}{36}\)) hr = \(\frac{4 + 5}{180}\) hr = \(\frac{1}{20}\) hour.

In \(\frac{1}{20}\) hour the train travels 2 km

In 1 hour the train travels 2 x 20 km = 40 km

∴ The average speed of the train is 40 km/hour.

Alternative method:

Let the distance between Kolkata and Burdwan be 180 km. (L.C.M. of 45 and 36 is 180).

∴ To travel from Kolkata to Burdwan the train \(\frac{180}{45}\) hours = 4 hours.

To return from Burdwan to Kolkata the train takes \(\frac{180}{36}\) hours = 5 hours.

∴ In (4+5) hours or 9 hours, the train travels (180+180) km = 360 km.

∴ Average speed of the train is \(\frac{1}{36}\)km/hour = 40 km/hour.

Example 8. A train of length 100 metres passed a tree moving at a speed of 60 km/hour. How much time did it take?

Solution:

Given:

A train of length 100 metres passed a tree moving at a speed of 60 km/hour.

When a train crosses a tree it travels its own length

100 metres = \(\frac{100}{1000}\) km = \(\frac{1}{10}\) km.

The train travels 60 km in 60 x 60 sec

The train travels 1 km in \(\frac{60 X 60}{60}\) sec

The train travels \(\frac{1}{10}\) km in \(\frac{1}{10}\) x 60 sec = 6 sec

Example 9. A train of length 210 metres crosses a telegraph post in 7 seconds. Express the speed of the train in the “km/hour” unit.

Solution:

Given:

A train of length 210 metres crosses a telegraph post in 7 seconds.

When a train crosses a telegraph post it travels a distance equal to its own length.

Time
7 seconds
60 x 60 seconds

Distance
210 metres
x metres (say)

Since, distance is directly proportional to time,

∴ \(\frac{7}{60 X 60}\) = \(\frac{210}{x}\)

or, 7x= 210 × 60 × 60

∴ in 1 hour the train travels 108000 metres = 108 km.

∴ The speed of the train is 108 km/hour.

Alternative method:

In 7 seconds the train crosses 210 m

In 1 second the train crosses \(\frac{210}{7}\) m

In 60 x 60 second the train crosses \(\frac{210}{7}\) x 60 x 60 m

= 108000 metres = 108 km.

Example 10. Moving with a uniform speed a taxi takes 6 hours 12 min to cover a distance of 217 km. How much time will it take to cover a distance of 273 km?

Solution:

Given:

Moving with a uniform speed a taxi takes 6 hours 12 min to cover a distance of 217 km.

6 hour 12 min (6 x 60+12) min = 372 min

To travel 217 km time required = 372 min

To travel 1 km time required = \(\frac{372}{217}\) min

To travel 273 km time required = \(\frac{372}{217}\) x 273

= 468 mon = 7 hours 48 min

∴ 7 hour 48 min.

7 hour 48 min time will it take to cover a distance of 273 km

Example 11. A train crosses a platform in 30 seconds travelling at a speed of 60 km/hour. If the length of the train be 200 metres, then find the length of the platform.

Solution:

Given:

A train crosses a platform in 30 seconds travelling at a speed of 60 km/hour. If the length of the train be 200 metres

When a train crosses a platform, it travels a distance equal to the sum of the lengths of the train and the platform.

Time
60 x 60 seconds
30 seconds

Distance
60 km
x km (say)

Since the distance is directly proportional to time,

∴  \(\frac{60 X 60}{30}\) = \(\frac{60}{x}\)

or, x X 60 x 60 = 30 × 60

or, x = \(\frac{30 X 60}{60 X 60}\) = \(\frac{1}{2}\)

∴ Distance travelled by train in 30 seconds

= \(\frac{1}{2}\) km = \(\frac{1}{2}\) x 1000 metres = 500 metres.

Now, the length of the train + length of the platform = 500 metres

∴ length of the platform = (500 – 200) metres = 300 metres.

Alternative method:

The speed of the train is 60 km/hour

∴ In 60 x 60 seconds the travel 60 x 1000 m

In 1 second the travel \(\frac{60 X 1000}{60 X 60}\) m

In 30 seconds the travel \(\frac{60 X 1000 X 30}{60 X 60}\) m= 500 metres

∴ length of the platform = (500-200) metres = 300 metres

Example 12. Ram covered a distance of 100 km in 2 hours and 5 min on his motorbike. Shyam covered the same distance on his cycle in 6 hours and 40 min. Find the ratio of the speeds of the motorbike and cycle.

Solution:

Given:

Ram covered a distance of 100 km in 2 hours and 5 min on his motorbike. Shyam covered the same distance on his cycle in 6 hours and 40 min.

2 hour 5 min = (2 x 60+ 5) min = 125 min.

In 125 min Ram travels 100 km

In 1 min Ram travels \(\frac{100}{125}\) = \(\frac{4}{5}\) km

6 hour 40 min = (6 x 60+40) min = 400 min

In 400 min Shyam travels 100 km

In 1 min Shyam travels \(\frac{100}{400}\) km = \(\frac{1}{4}\) km

Ratio of the speeds of the motorbike and cycle

= \(\frac{4}{5}\) ÷ \(\frac{1}{14}\)

= \(\frac{4}{5}\) X \(\frac{1}{14}\)

= \(\frac{16}{5}\) = 16: 5

The ratio of the speeds of the motorbike and cycle = 16: 5

Example 13. A train of length 160 metres crosses a platform of length 320 metres in 36 seconds. Find the speed of the train.

Solution:

Given:

A train of length 160 metres crosses a platform of length 320 metres in 36 seconds.

In order to cross the platform, the train has to travel (160+320) metres = 480 metres.

Time
36 seconds
60 X 60 seconds

Distance
480 metres
x metres(say)

Since, the distance is directly proportional to time,

∴ \(\frac{36}{60 X 60}\) = \(\frac{480}{x}\)

or, 36x = 480 X 60X 60

or, x = \(\frac{480 X 60 X 60}{36}\) = 48000

∴ Speed of the train is 48000 metres/hour = 48 km/hour

Alternative method:

∴ In 36 seconds the train travels 480 m

In 1 seconds the train travels \(\frac{480}{36}\) m

In 60 X 60 seconds the train travels \(\frac{480 X 60 X 60}{36}\)

= 48000 metres = 48 km.

Example 14. Moving with a uniform speed a goods train covers a distance of 49.5 km in 2 hours 45 min. How long will it take to reach a station situated at a distance of 58.5 km?

Solution:

Given:

Moving with a uniform speed a goods train covers a distance of 49.5 km in 2 hours 45 min.

2 hr 45 min = 2 \(\frac{45}{60}\) hr = 2 \(\frac{3}{4}\) hour = \(\frac{11}{4}\) hr.

To travel 49.5 km time taken = \(\frac{11}{4}\) hour

To travel 1 km time taken = \(\frac{11}{4 X 49.5}\) hour

To travel 58.5 km time taken = \(\frac{11 X 58.5}{4 X 49.5}\) hour

= \(\frac{11 X 585}{4 X 495}\) hour = \(\frac{13}{4}\) hour

= 3 \(\frac{1}{4}\)

∴ 3 hour 15 min

3 hour 15 min will it take to reach a station situated at a distance of 58.5 km

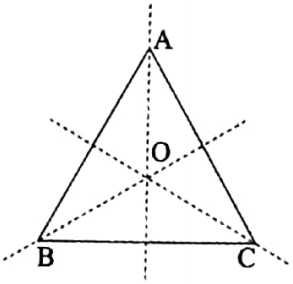
Example 15. Two trains are travelling towards each other on parallel lines. Their speeds are 40 km/hour and 30 km/hour respectively. They reached their destinations after 4 and 5 hours respectively from the time they met each other. Find the distance between the destinations of the two trains. (The lengths of the trains may be neglected in comparison with the distance travelled by them.)

Solution:

Given:

Two trains are travelling towards each other on parallel lines. Their speeds are 40 km/hour and 30 km/hour respectively. They reached their destinations after 4 and 5 hours respectively from the time they met each other.

Let the destination of the first train be point B and that of the second train be A.

Let O be the point at which they meet.

In 4 hours the first train travels the distance OB, with a speed of 40 km/hour.

∴ OB = 40 x 4 km = 160 km.

In 5 hours the second train travels the distance OA, with a speed of 30 km/hour.

∴ OA 30 x 5 km = 150 km.

Hence, AB = OB + OA = (160 + 150) km

∴ 310 km

The distance between the destinations of the two trains 310 km.

Example 16. Your father went to Bandel on his motorcycle, worked there for an hour and returned home in 3 hours and 30 minutes. If the uniform speed of the motorcycle is 40 km/hour finds the distance of Bandel from your home.

Solution:

Given:

Your father went to Bandel on his motorcycle, worked there for an hour and returned home in 3 hours and 30 minutes. If the uniform speed of the motorcycle is 40 km/hour

Since your father has worked for 1 hour, therefore the time is taken to Bandel and return 2 hours 30 min.

Therefore, time taken only to go to Bandel = 2 hours 30 min ÷ 2 = 1 hour 15 min = 75 min.

In 60 min he travels 40 km

In 1 min he travels \(\frac{40}{60}\) km

In 75 min he travels \(\frac{40}{60}\) X 75 km = 50 km

∴ The required distance = 50 km

Example 17. Two trains start at the same time towards each other from two stations 120 km apart. The speeds of the trains are 50 km/hour and 40 km/hour respectively. Find the distance between them after 1 hour 15 minutes. Find also the distance between them after 2 hours. (Here assume that the two trains are travelling on parallel lines.)

Solution:

Given:

Two trains start at the same time towards each other from two stations 120 km apart. The speeds of the trains are 50 km/hour and 40 km/hour respectively. Find the distance between them after 1 hour 15 minutes.

In 1 hour the distance between the two trains decreases by (50+40) km = 90 km.

Now, 1 hr 15 m = 1 \(\frac{15}{60}\) hrs = 1 \(\frac{1}{4}\)hrs = \(\frac{5}{4}\)hrs.

In 1 hour distance between the two trains decreases by 90 km

∴ In \(\frac{5}{4}\) hours distance between the two trains decreases by 90 x \(\frac{5}{4}\) km = 112.5 km.

∴ The distance between them after 1 hour 15 minutes will be (120-112.5) km = 7.5 km.

Again, in 2 hours the two trains advance towards each other by 90 x 2 km = 180 km.

∴ The distance between them after 2 hours will be (180120) km = 60 km.

∴ 7.5 km, 60 km.

The distance between them after 2 hours 7.5 km, 60 km.

Example 18. A 70-metre-long train runs at a speed of 75 km/hour. How long will it take to cross a platform of length 105 metres?

Solution:

Given: 

A 70-metre-long train runs at a speed of 75 km/hour.

To cross a platform of length 105 metres a train of length 70 metres will travel (70+105) metre = 175 metres.

The train travels 75 x 1000 m in 60 x 60 sec

The train travels 1 m in \(\frac{60 X 60}{75 X 1000}\) sec

The train travels 175 m in \(\frac{60 X 60 X 175}{75 X 1000}\) sec

= \(\frac{42}{5}\) sec = 8 \(\frac{8}{5}\) sec.

∴ 8 \(\frac{8}{5}\) sec.

8 \(\frac{8}{5}\) sec. it will take to cross a platform of length 105 metres.

Example 19. A passenger train and a goods train start from the same station on parallel lines at the same time and in the same direction. The speed of the passenger train is 50 km/hour. After 30 minutes it is found that the passenger train is 5 km ahead of the goods trains. Find the speed of the goods trains.

Solution:

Given:

A passenger train and a goods train start from the same station on parallel lines at the same time and in the same direction. The speed of the passenger train is 50 km/hour. After 30 minutes it is found that the passenger train is 5 km ahead of the goods trains

In 60 minutes the passenger train goes 50 km

In 1 minute the passenger train goes \(\frac{50}{60}\) km

In 30 minutes the passenger train goes \(\frac{50}{60}\) x 30 km = 25 km

By this time, the goods train goes (25-5) km = 20 km

In 30 minutes the goods train goes 20 km.

In 1 minute the passenger train goes \(\frac{20}{30}\) km

In 60 minutes the passenger train goes \(\frac{20}{30}\) x 60 km = 40 km

∴ Speed of the goods train is 40 km/hour.

Example 20. A 90-metre-long train takes 25 sec to cross a pillar. Calculate the speed of the train in km/ hour.

Solution:

Given:

A 90-metre-long train takes 25 sec to cross a pillar.

When a train crosses a pillar it crosses a distance equal to it own length.

In 25 sec the train crosses \(\frac{90}{1000}\) km

In 1 sec the train crosses \(\frac{90}{25 X 1000}\) km

In 60 X 60 sec the train crosses \(\frac{90 X 60 X 60}{25 X 1000}\) km

= \(\frac{324}{25}\) km = 12.96 km

∴ 12.96 km/hour.

The speed of the train in km/ hour 12.96 km/hour..

Example 21. Two trains of lengths 200 metres and 240 metres approach each other in two parallel lines running side by side with speeds of 42.5 km/hour and 36.7 km/hour respectively. What time will they take to cross each other after they meet?

Solution:

Given:

Two trains of lengths 200 metres and 240 metres approach each other in two parallel lines running side by side with speeds of 42.5 km/hour and 36.7 km/hour respectively.

In 1 hour the distance between the two trains decreases by (42.5+ 36.7) km = 79.2 km.

The two trains will have to travel a total distance of (200+ 240) metres = 440 metres in order to cross each other.

79.2 X 1000 metres distance decreases in 60 x 60 seconds

1-metre distance decreases in \(\frac{60 X 60}{792 X 1000}\) sec

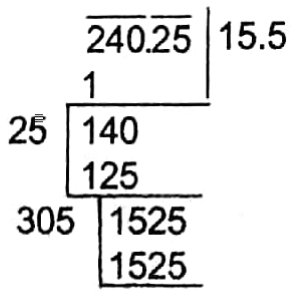
440-metre distance decreases in \(\frac{60 X 60 X 400}{79.2 X 1000}\) seconds 20 seconds.

∴ 20 seconds.

20 seconds time will they take to cross each other after they meet.

Example 22. To cross a bridge of length 250 metres a train of length 150 metres takes 30 sec. How long will this train take to cross a platform 130 metres long?

Solution:

Given:

To cross a bridge of length 250 metres a train of length 150 metres takes 30 sec.

When a train of length 150 metres crosses a bridge of length 250 metres then it travels (150+250) metre = 400 metres.

When a train of length 150 metres crosses a platform of length 130 metres then it travels (150+130) metres 280 metres.

The train travels 400 metres in 30 sec

The train travels 1 metre in \(\frac{30}{400}\) sec

The train travels 280 metre in \(\frac{30 X 280}{400}\) sec = 210 sec

Example 23. A bus starts from Kolkata at 7-30 A.M. and reaches Digha at 12 noon. If the speed of the bus be 45 km/hour, what is the distance between Kolkata and Digha?

Solution:

Given:

A bus starts from Kolkata at 7-30 A.M. and reaches Digha at 12 noon. If the speed of the bus be 45 km/hour

Total time from 7-30 A.M. to 12 noon

= 4 hours 30 minutes = 4 hours = hours.

Now, in 1 hour the bus goes 45 km

Now, in \(\frac{9}{2}\) hours the bus goes 45 Χ \(\frac{9}{2}\) km = 202.5 km

Example 24. A train takes 4 sec to cross a telegraph post and 20 sec to cross a 264-metre-long bridge. Find the length of the train and its speed.

Solution:

Given:

A train takes 4 sec to cross a telegraph post and 20 sec to cross a 264-metre-long bridge.

Let the length of the train be x metre. Then the train travels x metre in 4 sec and (x+264) metre in 20 sec.

∴ \(\frac{4}{20}\) = \(\frac{x}{x + 264}\)

or, 5x=x+264 or, 5x-x= 264

or, 4x = 264 or, x = 264 = 66

∴ The length of the train is 66 metres.

In 4 sec the train travels \(\frac{66}{1000}\) km

In 1 sec the train travels \(\frac{66}{4 X 1000}\) km

In 60 X 60 sec the train travels \(\frac{66 X 60 X 60}{4 X 1000}\) km = 59.4 km

∴ The length of the train is 66 metres and its speed is 59.4 km/hour.

Example 25. An up train and a down train started their journey at the same time after meeting at a station. After 24 minutes, the two trains reached two opposite stations, the distance between them being 30 km. If the speed of the up train be 40 km/hour, find the speed of the down train.

Solution:

Given:

An up train and a down train started their journey at the same time after meeting at a station. After 24 minutes, the two trains reached two opposite stations, the distance between them being 30 km. If the speed of the up train be 40 km/hour

In 60 minutes the up train travels 40 km

In 1 minute the up train travels \(\frac{40}{60}\) km

In 24 minutes the up train travels \(\frac{40}{60}\) X 24 km = 16 km.

Therefore, the down train travels (30-16) km = 14 km.

In 24 minutes the down train travels 14 km

In 1 minute the down train travels \(\frac{14}{24}\) km

In 60 minutes the down train travels \(\frac{14}{24}\) X 60 km = 35 km

∴ The speed of the down train is 35 km/ hour.

Example 26. A 100-metre-long train, at a speed of 48 km/ hour crosses a tunnel in 21 sec. Calculate the length of the tunnel.

Solution:

Given:

A 100-metre-long train, at a speed of 48 km/ hour crosses a tunnel in 21 sec

In 60 x 60 sec the train travels 48000 metre

In 1 sec the train travels \(\frac{48000}{60 X 60}\) metre

In 21 sec the train travels \(\frac{48000 X 21}{60 X 30}\) = 280 metres.

Since the length of the train is 100 metres, therefore, the length of the tunnel = (280-100) metres = 180 metres.

Example 27. A 250-metre-long goods train is travelling with a speed of 33 km/hour. A 200 metre-long mail train approaches it from the back side in a parallel line with a speed of 60 km/hour. How long will it take to cross the goods train after catching it?

Solution:

Given:

A 250-metre-long goods train is travelling with a speed of 33 km/hour. A 200 metre-long mail train approaches it from the back side in a parallel line with a speed of 60 km/hour.

In 1 hour the distance between the two trains (60-33) km = 27 km.

In order to overtake the goods train, the mail train will have to travel (250 + 200) metres = 450 metres.

Now, the distance is 27 x 1000 m in 60 min.

the distance is 1 m in \(\frac{60}{27 X 1000}\) min.

the distance is 450 m in \(\frac{60 X 450}{27 X 1000}\) = 1 minute.

Example 28. A train takes 10 sec to cross a man standing on a platform 150 metres long and crosses the platform in 22 sec. Calculate the length and the speed of the train.

Solution:

Given:

A train takes 10 sec to cross a man standing on a platform 150 metres long and crosses the platform in 22 sec.

Let, the length of the train be x metre. In 10 sec the train crosses x metre and in 22 sec the train crosses (x + 150) metre.

∴ \(\frac{10}{22}\) = \(\frac{x}{x + 150}\)

or, 11x=5x+750

or, 11x-5x=750

or, 6x = 750

or, x = \(\frac{750}{6}\) = 125

Length of the train is 125 metres

In 10 sec the train crosses 125 metre

In 1 sec the train crosses \(\frac{125}{1000 X 10}\) km

In 60 x 60 sec the train crosses \(\frac{125 X 60 X 60}{1000 X 10}\) km = 45 km

∴ The length of the train is 125 metres and its speed is 45 km/hour.

Example 29. A train crosses two bridges of lengths 210 metres and 122 metres in 25 seconds and 17 seconds respectively. Find the length and the speed of the train.

Solution:

Given:

A train crosses two bridges of lengths 210 metres and 122 metres in 25 seconds and 17 seconds respectively.

Let, the length of the train be x

Then in 25 seconds, the train travels (x+210) metres and in 17 seconds it travels (x + 122) metres.

Hence, \(\frac{25}{17}\) = \(\frac{x + 210}{x + 122}\)

or, 25x+3050 = 17x+3570
or, 25x-17x=3570-3050

or, 8x = 520

or, x = \(\frac{520}{8}\) = 65

∴ Length of the train = 65 metres.

Now, in 25 seconds the train travels (65+ 210) metres 275 metres.

In 25 seconds it travels 275 metres

In 1 second it travels \(\frac{275}{25}\) metres

In 60 X 60 seconds it travels \(\frac{275 X 60 X 60}{25}\) metres

= 39600 metres = 39.6 km

∴ The speed of the train is 39.6 km/hour

∴ The length of the train = 65 metres and its speed is 39.6 km/hour

Example 30. The distance between A and B along a river is 96 km. The speed of the river current is 4 km/ hour from A towards B. A boat takes 8 hours to travel from A to B. What time will it take to return from B to A?

Solution:

Given:

The distance between A and B along a river is 96 km. The speed of the river current is 4 km/ hour from A towards B. A boat takes 8 hours to travel from A to B.

For the journey from A to B,

In 8 hours the boat travels 96 km.

In 1 hours the boat travels \(\frac{96}{8}\) km = 12 km

∴ The actual speed of the boat = (12-4) km/ hour = 8 km/hour.

Therefore, the speed of the boat against the current = (8-4) km/hour = 4 km/hour.

So, for the journey from B to A,

To travel 4 km the boat takes 1 hour

To travel 1 km the boat takes \(\frac{1}{4}\) hour

To travel 96 km the boat takes \(\frac{96}{4}\) hours = 24 hours

Example 31. A boat can travel 8 km/hour in still water. But upstream it takes 4 times of that time to cover the same distance. What time will the boat take to cover 56 km downstream?

Solution:

Given:

A boat can travel 8 km/hour in still water. But upstream it takes 4 times of that time to cover the same distance.

Against the Current-

In 4 hours the boat goes 8 km.

In 1 hour the boat goes \(\frac{8}{4}\) = 2 km

Also, in still water, the boat travels 8 km/hour.

Hence, the speed of the river current is (8-2) km/hour 6 km/hour.

Therefore, downstream, in 1 hour the boat travels (8+6) km = 14 km.

So, along the current the boat covers-

14 km in 1 hour

1 km in \(\frac{1}{14}\) hour

56 km in \(\frac{56}{14}\) hours = 4 hours.

Example 32. P and Q are two places on the bank of a river. The speed of the river current is from P towards Q. At the same time, a boat starts from P towards Q with an actual speed of 8 km/ hour and another boat starts from Q towards P with an actual speed of 7 km/hour. If the distance between P and Q be 150 km, when will the two boats meet?

Solution:

Given:

P and Q are two places on the bank of a river. The speed of the river current is from P towards Q. At the same time, a boat starts from P towards Q with an actual speed of 8 km/ hour and another boat starts from Q towards P with an actual speed of 7 km/hour. If the distance between P and Q be 150 km

Let the speed of the river current be x km/hour.

In 1 hour the first boat covers (8 + x) km and in 1 hour the second boat covers (7-x) km

In 1 hour the distance between the two boats decreases by (8+x+7-x) km = 15 km

The distance decreases by- 15 km in 1 hour

1 km in \(\frac{1}{15}\) hour

150 km  in \(\frac{150}{15}\) hours = 10 hours

∴ The two boats will meet after 10 hours.

Example 33. Speeds of a boat along and against the current are 12 km/hour and 8 km/hour respectively. Find the actual speed of the boat and the speed of the current.

Solution:

Given:

Speeds of a boat along and against the current are 12 km/hour and 8 km/hour respectively.

Actual speed of the boat = \(\frac{20}{2}\) km/hr = 10 km/hr

∴ Speed of the current = (120- 10) km/hr = 2 km/hr.

∴ Actual speed of the boat = 10 km/hr.

Speed of the current = 2 km/hr

Example 34. The speed of a boat in still water is 10 km/ hour. The boat can cover 90 km in 6 hours downstream. What time will the boat take to cover the same distance upstream?

Solution:

Given:

The speed of a boat in still water is 10 km/ hour. The boat can cover 90 km in 6 hours downstream.

Downstream, in 6 hours the boat covers 90 km

Downstream, in 1 hour the boat covers \(\frac{90}{6}\) km = 15 km

Therefore, the speed of the current = (15- 10) km/hour = 5 km/hour.

Hence, against the current in 1 hour, the boat covers (10-5) km = 5 km.

Therefore, upstream the boat covers—

5 km in 1 hour

1 km in \(\frac{1}{5}\) hour

90 km in \(\frac{90}{5}\) hours = 18 hours.

∴ 18 hours.

18 hours Time will the boat take to cover the same distance upstream

Arithmetic Chapter 4 Square Root Of Fraction Exercise 4 Solved Example Problems

 

 Introduction

You have learnt the method of finding the square root of the perfect square integers in the previous class. Here, you will be able to learn the method of finding the square root of fractions and decimals.

As in our practical life we have to deal not only with integers but also with fractions and decimals so it is necessary to know the method of finding the square root of fractions and decimals as well.

The square roots of fractions and decimals are calculated in a similar way as that of integers but here the method is slightly complicated.

Square root of decimal fraction

If a decimal fraction is multiplied by itself then the product is called the square of the decimal fraction and the original decimal fraction is called the square root of the product.

Example:

Square of 0.2 0.2 0.2 = 0.04; the therefore square root of 0.04 = √0.04= 0.2.

Square of 0.7 0.7 x 0.7 = 0.49; therefore square root of 0.49 = √0.49 = 0.7.

Similarly, (0.12)²= 0.12 x 0.12 = 0.0144, hence √0.0144 = 0.12

(0.24)² = 0.24 x 0.24 = 0.0576, hence √0.0576 = 0.24

Rule:

1. Mark pair of digits, for an integral part, starting from the digit in the units’ place (i.e., from the digit immediately before the decimal point), towards the left in a similar way as you have done in the case of integers.

Then, similarly, mark the digits immediately after the decimal point in pairs towards the right.

2. If the decimal fraction do not contain any integral part then perform marking the pairs after the decimal point.

3. If the given decimal fraction has an odd number of decimal places, put a zero at the end to make the number of digits after decimal point even.

4. The decimal point should be put in the square root immediately when the pair of digits from the decimal part is brought down at the end of an integral part.

Example: Find the square root of: 150.0625

∴ The required square root is 12.25.

Example: (0.1)² = 0.01; Here, 0.01 < 0.1

And (1.5)² = 2.25; here 2.25 > 1.5

The square root of a vulgar fraction

If a vulgar fraction is multiplied by itself then the product is called the square of that vulgar fraction and the original vulgar fraction is called the square root of the product.

Example: Square of \(\frac{1}{2}\) = \(\frac{1}{2}\) x \(\frac{1}{2}\) = \(\frac{1}{4}\)

therefore square root of \(\frac{1}{2}\) = = \(\frac{1}{2}\)

 

Arithmetic Chapter 4 Square Root Of Fraction Exercise 4 Some Problems On Square Root Of Decimal Fractions

Example 1. The area of a square is 32.49 sq cm. What is the length of one side of the square?

Solution:

Given:

The area of a square is 32.49 sq cm.

The length of the side of the square = √32.49 cm = 5.7 cm.

∴ 5.7 cm

The length of one side of the square 5.7 cm.

 Example 2. What least number must be subtracted from 0.0582 so that the result of subtraction be a perfect square decimal number?

Solution:

Given:

0.0582

Hence, it is found that the number 0.0582 exceeds the square of 0.24 by 0.0006.

Hence, at least 0.0006 should be subtracted from 0.0582 so that the result of subtraction will be a perfect square decimal number.

∴ At least 0.0006 should be subtracted.

Example 3. Find the length of one side of a square whose area is equal to the sum of the areas of two rectangles whose areas are 2.1214 sq m and 2.9411 sq m.

Solution:

Given:

2.1214 sq m And 2.9411 sq m

Total area of the two rectangles = (2.1214+2.9411) sq m = 5.0625 sq m

∴ Area of the square = 5.0625 sq m

∴ Length of the side of the square = √5.0625 m = 2.25 m

∴ 2.25 m

Length of the side of the square 2.25 m

Example 5. What must be added with 0.28 so that the square root of 1?

Solution:

Given:

0.28

Since, square root of the sum is 1 therefore, sum is also 1.

Number to be added = (1-0.28) = 0.72 = 0.72

∴ 0.72

Example 6. Find the square root of the product of 0.032 and 0.2.

Solution:

Given:

0.032 And 0.2

The required square root

= √0.032×0.2= √0.0064=0.08

= 0.08

The square root of the product 0.08

Example 7. Find the value of √240.25 + √2.4025 + √0.024025

Solution:

Given:

√240.25 + √2.4025 + √0.024025

∴ √240.25 = 15.5

Similarly, √240.25 = 1.55 and,

√0.024025 = 0.155

∴ The required sum = 15.5 + 1.55 + 0.155 = 17.205

∴ 17.205

The value of √240.25 + √2.4025 + √0.024025 = 17.205

Example 8. Which number should be subtracted from 48.03 so that the square root of the difference is 5.7?

Solution:

Since, the square root of the difference is 5.7 therefore, the difference = (5.7)² = 32.49.

Hence, the number to the subtracted = 48.03 – 32.49 = 15.54

Example 9. Find the decimal number which when multiplied by itself gives 1.1025 as the product.

Solution: The required number will be the square root of 1.1025 = √1.1025 = 1.05

∴ 1.05

Example 10. Find the square root of 2 upto 3 places of decimals.

Solution:

Given:

Here, although 2 is an integer it is not a perfect square number.

Hence, the square root of 2 must be a decimal fraction.

Also, we may consider 2 as 2.000000…

∴ The required square root = 1.414.

Example 11. Which decimal number is to be added with 0.75 so that square root of the sum will be 2?

Solution:

Since, the square root of the sum will be 2 therefore the sum will be 4.

∴ Number to be added = 4-0.75 = 3.25

∴ 3.25.

Example 12. Find the square root of 5.842 up to 3 places of decimals.

Solution:

∴ The required square root is 2.417.

Example 13. Find the approximate value of √15 upto 2 decimal places. Find how greater or less than 15 is the square of this approximate value.

Solution:

Therefore, the approximate value of upto 2 decimals places is 3.87.

Now, square of 3.87 = (3.87)² = 14.9769.

Therefore, the square is less than 15 by (15-14.9769)=0.0231.

∴  3.87, 0.0231 less.

Example 14. Find the square root of 52.983841 correct upto two places of decimals

Solution:

Hence, the square root of 52.983841 correct up to two places of decimals is 7.28

Example 15. Find the value of √0.5 correct up to three decimal places.

Solution:

∴ The value of √0.5 correct up to three decimal places is 0.707.

Example 16. Which decimal fraction multiplied by itself will give a product 7.5625?

Solution: The required decimal fraction will be the square root of 7.5625

∴ 2.75

Example 17. Find the least number which when added to 31.69 will make it a perfect square having 4 places after the decimal.

Solution:

Example 18. Find the difference of the lengths of the sides The area of the new square of the squares whose areas are 1.4641 sq m and 1.0609 sq m.

Solution:

The length of side of the first square. Each side of the new square = √14641 m = 1.21 m.

The length of side of the second square = √1.0609 m = 1.03 m

Example 19. Find the length of the side of the square whose area is equal to the sum of the areas of two rectangles having areas 3.24 sq m and 2.52 sq m.

Solution:

The sum of the areas of two rectangles (3.24 + 2.52) sq m = 5.76 sq m.

∴ Length of the side of the square = √5.76 m = 2.4 m

∴ The length of the side of the square is 2.4 m.

Example 20. The sides of two squares are 16.5 and 22 metres respectively. Find the side of a square whose area is equal to the sum of the areas of the two squares.

Solution:
Area of the first square = (16.5)² sq m = 272.25 sq m

Area of the second square = (22)² sq m = 484 sq m

The area of the new sqaure = (272.25 + 484)  sq m = 756.25 sq m

∴ Each side of the new square = √756.25 m = 27.5 m

∴ 27.5 meters.

Example 21. A man spent ₹ 506.25 and each day he spent as many rupees as the number of days in which the money was spent. How much did he spend each day?

Solution:

Since the number of days and the number of rupees spent each day are equal, therefore the product of two equal numbers = 506.25

∴ Each number = √506.25 = 22.5

Example 22. A ladder 36 metres long, stands against a wall so that its bottom is 21.6 metres away from the wall. How high is its top on the wall?

Solution:

Let Bc = 36 metres be the ladder and AB = 21.6 metres.

Let AC = h metres.

Now h²+ (21.6)² = (36)²

or, h = (36)² – (21.6)²

= 1296 – 466.56 = 829.44

or, h =√829.44 = 28.8

 

Arithmetic Chapter 4 Square Root Of Fraction Exercise 4 Some Problems On Square Root Of Vulgar Fractions

Example 1. Find the square root of \(\frac{324}{625}\)

Solution:

Square root of

∴ \(\frac{18}{25}\)

Example 2. The area of a square is \(\frac{1089}{825}\) sq. cm.What is 825 the length of one side of the square?

Solution:

Length of the side of the square

∴ Length of one side of the square is \(\frac{33}{25}\) cm.

Example 3. A vulgar fraction multiplied by itself gives the product \(\frac{841}{2025}\) Find the fraction.

Solution:

Here the required vulgar fraction is the Square root of \(\frac{841}{2025}\)

∴ \(\frac{29}{45}\)

Example 4. Find the square root of 6 \(\frac{433}{676}\)

Solution:

 

∴ The required square root = 2 \(\frac{15}{26}\)

Example 5. Extract the square root of \(\frac{2}{5}\) to two places of decimals.

Solution:

∴ 0.63

Example 6. By what should the square root of \(\frac{121}{169}\) be multiplied so that the product will be 1?

Solution: Square root of

Now, \(\frac{11}{13}\) should be multiplied by \(\frac{13}{11}\) so that the product will be 1.

∴ To be multiplied by \(\frac{13}{11}\)

Example 7. The product of two numbers is \(\frac{75}{121}\) and one of them is threice the other. Find the  numbers

Solution:

Greater number x smaller number = \(\frac{75}{121}\)

or, 3 x smaller x smaller number = \(\frac{75}{121}\)

or,(smaller number)² = \(\frac{75}{3 x 121}\) = \(\frac{25}{121}\)

or, smaller number =

∴ greater number = 2 x \(\frac{7}{8}\) = \(\frac{7}{4}\)

∴ The two numbers are \(\frac{7}{4}\) and \(\frac{7}{8}\)

Example 9. Find the smallest whole number by which \(\frac{64}{125}\) should be multiplied so that the product will be a fraction which is a perfect square.

Solution:

\(\frac{64}{125}\) = \(\frac{8 x 8}{5 x 5 x 5}\)

Clearly, it should be multiplied at least by 5 so that the product will be a fraction which is a perfect square.

∴ 5

Example 10. Find a fraction, which when multiplied by itself gives 6 \(\frac{145}{256}\)

Solution:

6 \(\frac{145}{256}\) = \(\frac{1681}{256}\)

The required fraction will be the sqaure root of \(\frac{1681}{256}\)

 

∴ The required fraction = \(\frac{41}{61}\)

Example 11. Find the square root of

Solution:

= \(\frac{9}{25}\) + \(\frac{16}{25}\) = \(\frac{9 + 16}{25}\) = \(\frac{25}{25}\) = 1

the square root of 1 is 1

Question 12. By which fraction should \(\frac{49}{91}\) be multiplied so that the square root of the product is 1?

Solution:

Square root of the product will be 1. Therefore, product will also be 1.

\(\frac{49}{91}\) should be multiplied by \(\frac{91}{49}\) sp, that the product is 1.

∴To be multiplied by \(\frac{91}{49}\)

Example 13.  =what?

Solution:

∴ 2

Example 14. By which fraction should \(\frac{35}{42}\) be multiplied so that the square root of the product is 2?

Solution:

\(\frac{35}{42}\) = \(\frac{5}{6}\)

If the square root of the product is 2 then the product is 4.

∴ The required number = 4 ÷ \(\frac{5}{6}\)

= 4 x \(\frac{5}{6}\) = \(\frac{24}{5}\) = 4 \(\frac{4}{5}\)

∴ To multiplied by 4 \(\frac{4}{5}\)

Example 15. By what number should the square root of \(\frac{625}{144}\) be multiplied nso that the product will be 1?

Solution:

Square root of

Now, the number by which \(\frac{25}{12}\) should be multiplied so that the product will be 1 is \(\frac{12}{25}\)

∴ \(\frac{12}{25}\)

Example 16. Find the least positive integer by which \(\frac{9}{50}\) should be multiplied so that the product will be a perfect square.

Answer:

\(\frac{9}{50}\) = \(\frac{3 X 3}{5 X 5 X 2}\)

Therefore, it should be multiplied at least by 2, so that the product will be a perfect sqaure.

∴ To be multiplied by 2.

Example 17. One number is thrice the other, If the product of the two numbers be 15\(\frac{3}{16}\) then what are the numbers?

Solution:

The greater number x smaller number = 15 \(\frac{3}{16}\)

or, 3x smaller number x smaller number= \(\frac{243}{16}\)

or, (smaller number)² = \(\frac{243}{16 X 3}\) = \(\frac{81}{16}\)

or, smaller number =

∴ greater number = 3 x \(\frac{9}{4}\) = \(\frac{27}{4}\) = 6 \(\frac{3}{4}\)

∴ The numbers are 2 \(\frac{1}{4}\) and 6 \(\frac{3}{}\)

Example 18. The product of two positive numbers is \(\frac{14}{15}\) and their quotient is \(\frac{35}{24}\). Find the numbers.

Solution:

Let the two numbers be x and y.

∴ The two numbers are \(\frac{7}{6}\) and \(\frac{4}{5}\)

Example 19. Out of the three numbers, the product of the first and the second number is 3, that of the second and the third number is 8 \(\frac{2}{5}\) and that of the third and the first number is 4 \(\frac{3}{8}\). Find the three numbers.

Solution:

First number x second number=3…………..(1)

Second number x third number = \(\frac{42}{5}\) …..(2)

Third number x first number = \(\frac{35}{8}\) ……(3)

By (1) x (2) x (3) we get,

(First number x second numnber x third number)²

= 3 x \(\frac{42}{5}\) x \(\frac{35}{8}\) = \(\frac{21 X 21}{4}\)

∴ First number x second number x third number =   = \(\frac{21}{2}\)

By (4) ÷ (1) we get, the third number

= \(\frac{21}{2}\) x \(\frac{1}{3}\) = \(\frac{7}{2}\) = 3 \(\frac{1}{2}\)

By (4) ÷ (2) we get, first number

= \(\frac{21}{2}\) x \(\frac{5}{42}\) = \(\frac{5}{4}\) = 1 \(\frac{1}{4}\)

By (4) ÷ (3) we get, second number

= \(\frac{21}{2}\) x \(\frac{8}{35}\) = \(\frac{12}{5}\) = 2 \(\frac{2}{5}\)

∴ The numbers are 1 \(\frac{1}{4}\), 2 \(\frac{2}{5}\), 3 \(\frac{1}{2}\)

Example 20. Find by what magnitude is (√25+ √81) more than (√16 + √36).

Solution:

√16+ √36=4+6=10

√25+√815+9=14

Now, 14-10=4

∴  Is more by 4.

Example 21. The area of a square is 4225 sq metres. If it is divided into 9 equal parts then each part becomes a square. What is the length of each side of such a square?

Solution:

If a square of area 4225 sq metres is divided into 9 equal parts then area of each part becomes \(\frac{4225}{9}\) sq metres.

If these parts are squares, then length of each side of such a square= meters =

= \(\frac{65}{3}\) metres = 21 \(\frac{2}{3}\)

∴ 21 \(\frac{2}{3}\)

Example 22. Find the value of

Solution:

= \(\frac{1}{2}\) + \(\frac{1}{3}\) – \(\frac{1}{4}\) – \(\frac{1}{5}\)

⇒ 2 x 3 x 10 = 60

= (\(\frac{1}{2}\) + \(\frac{1}{3}\)) – (\(\frac{1}{4}\) + \(\frac{1}{5}\))

= \(\frac{5}{6}\) – \(\frac{9}{20}\) = \(\frac{50- 27}{60}\) = \(\frac{23}{60}\)

∴ \(\frac{23}{60}\)

Example 23. Area of the square ‘A’ is \(\frac{225}{289}\)th of the area of the square ‘B’. What fraction of the side of ‘B’ is the side of ‘A’?

Solution:

Area of the square ‘A’ = Area of the square ‘B’ x \(\frac{225}{289}\)

∴ Length of the side of ‘A’ = Length of the side of ‘B’ x

∴ Length of the side of ‘A’ = Length of the side of ‘B’ x \(\frac{15}{17}\)

Hence, length of the side of the square ‘A’ is \(\frac{15}{17}\) th part of the length of the side of the square ‘B’.

∴ \(\frac{15}{17}\)
Example 24. Arrange the following in the descending order of their magnitude:

Solution:

∴ In descending order of magnitude the numbers are:

Example 25. The areas of two rectangles are \(\frac{24}{25}\) sq metres and \(\frac{12}{25}\) sq metres respectively, Find the length of each side of a square whose area is equal to the sum of the areas of these two rectangles.

Solution:

Given:

The areas of two rectangles are \(\frac{24}{25}\) sq metres and \(\frac{12}{25}\) sq metres respectively

The sum of the areas of the two rectangles = (\(\frac{24}{25}\) + \(\frac{12}{25}\)) sq metres = \(\frac{36}{25}\) sq meters.

Hence, the area of the square = \(\frac{35}{25}\) sq metres.

Hence, the length of each side of the square

= metres

= \(\frac{6}{5}\) metres = 1 \(\frac{1}{5}\) metres.

∴ 1 \(\frac{1}{5}\) metres.

Example 26. 308 square stones are required to pave a square of area 1925  square metres. Find the length of each side of such a stone.

Solution:

Given:

308 square stones are required to pave a square of area 1925  square metres.

By 308 stones 1925 sq metres is paved

By 1 stones \(\frac{1925}{308}\) sq metres is paved

= \(\frac{25}{4}\)  sq metres is paved

Therefore, area ofeach stone = \(\frac{25}{4}\) sq metres.

∴ Length of each side of a stone = metres =\(\frac{5}{2}\) metres = 2 \(\frac{1}{2}\) metres.

∴ 2 \(\frac{1}{2}\) metres.

Example 27. The sides of two squares are \(\frac{12}{5}\) metres. metres and \(\frac{9}{5}\) metres.respectively. Find the side of a a square whose area is equal to the sum of the areas of the two squares.

Solution:

Given:

The sides of two squares are \(\frac{12}{5}\) metres. metres and \(\frac{9}{5}\) metres.respectively.

The area of the first square = (\(\frac{1}{2}\))² sq metres

= \(\frac{144}{25}\) = sq metres

∴ The area of the second square = (\(\frac{9}{5}\))²

= \(\frac{81}{25}\) sq metres.

∴ Area of the new square

=(\(\frac{144}{25}\) + \(\frac{81}{25}\))

= \(\frac{225}{25}\) sq metres = 9 sq metres.

∴ Each side of the new square=√9 metres = 3 metres

∴ 3 metres.

The side of a a square whose area is equal to the sum of the areas of the two squares is 3 metres.

Arithmetic Chapter 3 Approximate Value Exercise 3 Solved Example Problems

 

Approximate Value
In our daily life, in many cases, it is not possible to calculate the actual value of a quantity or the actual price or weight of a body accurately.

Therefore, in such cases for practical purpose, a value is taken nearest to the actual value, actual price, or actual weight.

It is called the approximate value of that quantity or the approximate price or weight of that body.

Suppose, ₹262.50 is to be divided among 50 boys. Then each boy will get ₹262.50 +50 =₹5.25.

Now observe that, if each boy is given ₹5 then each boy gets 25 paise less than what he would have obtained.

Again, if each boy is given ₹6 then each boy gets 75 paise more than his due.

Therefore, neither ₹5 nor ₹6 is due for that boy. Hence, this less or more is to be termed an error.

Since there is an error in both cases, therefore, the less is the amount of error more is the degree of purity.

In the above case, if ₹5 is given then an error is 25 paise and if ₹6 is given the error is 75 paise. Hence, if each is given 5 then he will be given the nearest money due for him.

Again, let ₹287.50 is to be divided among 50 boys equally. Then each boy will get ₹287.50÷ 50= ₹5.75.

Therefore, in this case, if each boy is given 6 then he will be given the nearest money due for him.

Rule: In order to calculate the approximate value instead of the actual value of any quantity, if the digit after the decimal be less than 5 (₹ 5 and paise 25 = ₹ 5.25) then it is to be ignored and if it be 5 or greater than 5 (₹ 5 and paise 75 =₹ 5.75) then 1 is to be added with the digit in the units’ place.

Approximate value of the integer

If the value of the number 5832 is written as 5000 then 832 less than the actual value is written. Again if 6000 is written instead of 5832 then, (60005832) or 168 more than the actual value is written.

Now observe that between 6000 and 5000 the former is nearer to the actual value of 5832.

Therefore, the value of 5832 in the approximate thousands of places is 6000. Similarly, the value of 5832 in the approximate hundreds’ place is 5800, and in the approximate tens’ place is 5830.

Approximate value of decimal fraction

In order to find the approximate value of any decimal fraction up to a definite decimal place, write the digits up to that decimal place and reject the next remaining digits.

But if the first digit from the left-hand side of the rejected digits be 5 or more than 5 then 1 is to be added with the last digit of that particular place.

For example, the approximate value of 3.65038 up to integer = 4. (Since, the number 6 at the left end of the rejected portion after 3 is greater than 5 therefore, 4 is the result after adding 1 with 3).

Its approximate value up to 1 decimal place =3.7 (Here, since the first digit of the rejected portion is 5 therefore, 1 is added with the previous digit.

Its approximate value up to 2 decimal places = 3.65.
(Here, since the first digit of the rejected portion is 0 therefore, nothing has been added to the previous digit.)

Its approximate value up to 3 decimal places = 3.650.

Its approximate value up to 4 decimal places = 3.6504.

Examples:

1. Find the correct value of 0.655172 up to 4 decimal places.

Solution: 0.6552 (first digit of the rejected portion is 7)

2. Express 3628753 in approximate hundred.

Solution: 3628800

3. Find the correct values of 1.218713 upto 3 and 4 decimal places and express the approximate value of their difference corrected to 2 decimal places.

Solution:

The subtracted value, when corrected upto 2 decimal places, is 0.00

Significant digit

The numbers are formed by the digits 1 to 9. They are called significant digits. If between two significant digits, there is/are one or more than one zeroes (0) then those zeroes are also taken as significant digits.

If in any decimal fraction, there is a decimal point in the beginning and there are some zeroes after the decimal point then digits other than zeroes are called significant digits. The last zero or zeroes of an integer or decimal fraction are sometimes significant digits and sometimes they are not so.

Example:

1. The approximate value of 30.23046 up to 4 significant digits 30.23. But its approximate value corrects up to 4 decimal places = 30.2305.

2. In the case of the number 0.12065 the value is correct up to 4 decimal places and also the approximate value up to 4 significant digits are both equal to 0.1207.

3. In the case of the number 0.00147, the value corrects up to one significant digit = 0.001 and the value corrects up to two significant digits= 0.0015.

4. The approximate value of 0.000240079 up to five decimal places= is 0.00024. But its approximate value up to 5 significant digits= 0.00024008.

5. In the case of the number 0.44598 the correct value up to 4 decimal places and the approximate value up to 4 significant digits are both equal to 0.4460 (Here 0 is the significant digit; here since the rejected digit is 8, therefore, adding 1 with the last digit 9 of 0.4459 we obtained 0.4460.)

6. The approximate value of 163289 up to 4 significant digits is 163300. (Here, the two zeroes are not significant digits).

7. In case of 705769, the approximate value up to a thousand and the approximate value up to a hundred are 706000 and 705800 respectively. (In both cases the last zeroes are not significant digits).

Error

If a value other than the actual value is taken then there occurs an error. In practical case this error should be as small as possible. Let us roughly take the weight of 100 kg of coal.

If the weight is taken more accurately then it may be found that the weight of coal is 99 \(\frac{1}{2}\) kg. In this \(\frac{1}{2}\) kg of coal, the loss is not significant.

But if it is gold in and that would not be negligible. Therefore, in lieu of coal then there would be a great loss if a goldsmith is compelled to measure gold more accurately.

 

Arithmetic Chapter 3 Approximate Value Exercise 3 Absolute Error, Relative Error, And Percentage Error

The difference between the actual value and the approximate value is called the absolute error of the approximate value.

That means, absolute error = Actual value ∼ approximate value.

The ratio of absolute error and the actual value is called the relative error.

That means, relative error = \(\frac{Absolute error}{Actual value}\).

The percentage error of the approximate value is that percentage of the actual value which the absolute error is.

That means, percentage error = \(\frac{Absolute error}{Actual value} \)

Example 1. Express 4325 kg in approximate hundred kg and find an absolute error, relative error, and percentage error.

Solution:

Given:

4325 kg

4325 kg = 4300 kg (in approximately 100 kg)

∴ absolute error = 4325 kg-4300 kg = 25 kg 25 kg

relative error = \(\frac{25 \mathrm{~kg}}{4325 \mathrm{~kg}}=\frac{1}{173}\)

and percentage error = relative error x 100 = \(\frac{1}{173}\) x100= 0.58 (correct up to 2 decimal places).

Example 2. Find the approximate value up to first two significant digits and the absolute error of 3.068.

Solution:

Given:

3.068

The approximate value of 3.068. The required sum = 13.67489.
up to first two significant digits = 3.1. absolute error = 3.068-3.1 = 0.032.

Example 3. A man measured a path of length 12 \(\frac{7}{200}\) km and told its length as 12.01 km. At this find his absolute error, relative error, and percentage error.

Solution:

Given:

A man measured a path of length 12 \(\frac{7}{200}\) km and told its length as 12.01 km.

12 \(\frac{7}{200}\) = 12.035

Absolute error = 12.035 km -12.01 km = 0.025 km

Relative error = \(\frac{0.025 \mathrm{~km}}{12035 \mathrm{~km}}=\frac{5}{2407}\)

and percentage error = \(\frac{5}{2407}\) x 100 = 0.21%

(correct up to 2 decimal places).

 

Arithmetic Chapter 3 Approximate Value Exercise 3 To Find The Addition And Subtraction In Approximate Value Of Decimal

Rule: When the result of addition and subtraction are to be known approximately up to a definite decimal place, it is necessary to know the next digit.

Therefore, we have to find the result of addition and subtraction up to two more digits than the digits up to which approximation is required to be done. Then the answer is to be given in approximate value as per requirement.

Example 1. What is the sum of 4.3074, 0.0028391, and 9.364 approximate up to five decimal places?

Solution:

Given:

4.3074, 0.0028391,And 9.364

Here, to get the approximate 5 decimal place the 6th decimal place must be known correctly.

So, writing up to one more decimal place i.e., 7th decimal place the sum is to be determined.

∴ The required sum = 13.67489

Example 2. Find the difference of 30.406 and 23.139 approximately up to 4 decimal places.

Solution:

Given:

30.406 And 23.139

∴ The required difference of 7.2670

Example 3. Find the sum of 7.302, 0.0865, 32.87, and 3.02 approximately up to 3 significant digits.

Solution:

Given:

7.302, 0.0865, 32.87, And 3.02

∴The required sum = 43.3.

 

Algebra Chapter 2 Addition Subtraction Multiplication And Division Of Integers Exercise 2

Solved Example Problems

Integers are all natural numbers including Zero (0) i.e., all whole numbers with a positive or negative sign.

For example 0, 3, (-3), 5, (-8), etc., are all integers.

Addition and Subtraction of the integers

You have already learned the number line and the representation of the numbers in the number line to attain the value of an expression in class 6.

Let us find the value of the expression 0+(+2)+( + 5)+(- 10)+(-6).

Wbbse Class 7 Maths Solutions

Read and Learn More WBBSE Solutions For Class 7 Maths

 

 

The value of the expression 0 + 2 + 5-10-6 = (-9).

Step 1 >	(+ 0) + (+ 2) = + 2.
Step 2 >	(+ 2 ) + (+ 5) = + 7	(adding both integers with the same signs gives the result with that sign).
Step 3 >	(+ 7) + (- 10) = 7- 10 =-3	(By adding the integers with different signs the result will be the difference between the numbers with the sign of the greater number.)
Step 4 >	(-3) + (-6) =  (-9)	(adding both integers with the same signs gives the result with that sign).

 

Let us find the value of {( + 3) – (- 3)} – ( – 8) from the number line.

{(+ 3) – (- 3)} – (- 8) = {(+ 3) + ( 3)} + ( + 8)= ▭

 

 

So, we get {( + 3) – (- 3)} – (- 8) = + 14.

Commutative Property

Wbbse Class 7 Maths Solutions
We know 3 + 5 = 5 + 3 = 8. This infers that whole numbers can be added in any order.

So, the addition of whole numbers is commutative.

But let us see what happens in the case of integers

We know 4 + (- 6)= – 2 and (-6) + 4 = -2.

So, 4 + (-6) = (-6) + 4.

So, it is known that addition is commutative for integers, a + b = b + a

But subtraction is not commutative for whole numbers as well as integers.

Let us consider the integers 6 and ( – 3 ).

Example 1. 6-(- 3) = 6 + 3 = 9.

Example 2. – 3 – 6 = – 9.

So, we can conclude that subtraction is not commutative for integers.

Example 1. By selling each kg of mango, a fruit seller gains ₹ 5 per kg but loses ₹4 per kg of lichi. If he sells 10 kg mango and 14 kg of lichi, find his overall profit or loss.

Solution:

Given:

By selling each kg of mango, a fruit seller gains ₹ 5 per kg but loses ₹4 per kg of lichi. If he sells 10 kg mango and 14 kg of lichi,

On selling 1 kg mango, he earns ₹ 5

So, profit in 10 kg of mango = ₹ 5 x 10 = ₹50

Again, on selling 1 kg of lichi, the fruit seller losses ₹ 4, in other words, he earns – ₹ 4.

So his earning on selling 14 kg lichi = – ₹ 4 x 14 = – ₹ 56

So, his overall profit = ₹ 50 + ₹ (- 56) = – ₹ 6, that means he losses ₹ 6 after the sale.

Example 2. In an examination, 6 marks are given for correct answers, and – 3 marks are given for incorrect answers. If Rabin makes 7 correct answers and 5 incorrect answers, then what is his score?

Solution :

Given:

In an examination, 6 marks are given for correct answers, and – 3 marks are given for incorrect answers. If Rabin makes 7 correct answers and 5 incorrect answers

For 7 correct answers Rabin gets = 7 x 6 = 42 marks

For 5 incorrect answers, Rabin gets = 5 x (- 3) = – 15 marks.

So, his total marks = 42 + (-15) = 27 marks.

His total Score  = 27 marks.

Wbbse Class 7 Maths Solutions

Example 3. In a quiz competition, Manika’s scores in five successive rounds were 25, – 2, – 10,15 and 10 with negative markings for wrong answers. Find her total score at the end of 5th round.

Solution:

Given:

In a quiz competition, Manika’s scores in five successive rounds were 25, – 2, – 10,15 and 10 with negative markings for wrong answers.

Her total score = 25 + (- 2) + ( – 10) + 15 + 10

= 25-2-10+15+10

= 50 – 12 = 38.

Her total score at the end of 5th round = 38

 

Algebra Chapter 2 Addition Subtraction Multiplication And Division Of Integers Exercise 2 Examples For Associative Properties

⇔ Consider the integers + 3,-5, and – 7.

Example 1. Let us find out the value of the expression by number line {(+ 3) + (- 5)} + (- 7).

Solution:

 

Example 2. If the expression be (+ 3)+{(-5)+(-7)} then find the value.

Solution:

 

We get, {( + 3) + (- 5)} + ( – 7) = ( + 3) + {(- 5) + (- 7).

We find that addition is associative for integers.

In general, for any integers a, b, and c, we can say, (a + b) + c = a + (b + c)

 

Algebra Chapter 2 Addition Subtraction Multiplication And Division Of Integers Exercise 2 Examples For Multiplication Of Integers

We know that the multiplication of whole numbers is repeated addition.

Example: 4 x 2 = 2 + 24-2 + 2 = 8.

Example 1. Let us find the value of 3 x 2 (both the integers are +ve).

Solution:

 

We get from number line 3×2 = ( + 2) + ( + 2) + ( + 2) = + 6.

Example 2. Now, find the value of 2 x 3.

Solution:

 

We get from number line =2×3=(+3)+(+3)=+6

∴ We find that in both cases the value is same.

So, 3 x 2 = 2 x 3 or a x b = b x a

Example 3. Now, let us find out the product value of 3 x (- 4) (One integer is +ve and the other is -ve).

Solution:

 

We get from number line 3x(-4)-(-4)+(- 4)+(-4)-12-(3×4)

Again, in case of 2x(- 4) = (-41) + (- 4) = (- 8) = (- 2 ) x 4

= (- 2) + (- 2)+ (-2 ) + (-2)

So, a x (-6) = (-a) x b = – (ab)

We thus find that while multiplying a positive integer and a negative integer, we multiply them as whole numbers and put a minus (-) sign before the product. We thus get a negative integer.

So, we learn that when signs of integers are same, the answer is a +ve number.

( + )x( + )or(-)x(-) are always +ve.

When the signs of the integers are different, the answer is always – ve (+) x (-) or (-) x ( + ) are always – ve.

Multiplication of negative integers:

Now let us see the product of two negative integers

(-3) x (-2) = + 6

(-4) x (-5)= + 20

(- 4) x (- 3) = + 12.

So, after observing these products we understand that there is a rule prevailing over states that the product of two negative integers is always a positive integer.

So, (-a) x (-b) = a x b

Now, let us see the product of three or more negative integers:

1. (-5) x (-3) x (-2) = [-5 x -3] x (-2) = 15 x (-2) =-30.

2.( -3)x( -5)x( -2)x(-4) = [ -3 x -5] x [-2 x -4] = (+15) x ( + 8) = +120.

From the above results we observe that:

1. Product of two negative integers is a positive integer.
2. Product of three negative integers is a negative integer.
3. Product of four negative integers is a positive integer.

So, we can conclude that if the number of negative integers in a product is even then the product is always a positive integer. If the number of negative integers in a product is odd, then the product is always a negative integer.

 

Algebra Chapter 2 Addition Subtraction Multiplication And Division Of Integers Exercise 2 Examples For Commutative Property Of Multiplication

Now we observe the following results

Pattern -1	Pattern – 2	Conclusion
3x(-4) =-12, (-15) x 10 =-150, (-4)x(-5) = 20	(-4)x3= -12, 10 x (-15)=-150, (-5)x(-4)=20	3x(-4) = (-4 )x3, (-15)x10 = 10 x (-15), (-4)x(-5) = (-5)x(-4)

 

All the cases shown above confirm that multiplication is commutative in the case of integers.

So, a x b = b x a (where a & b are integers)

Distributive property of multiplication: We know that, 15 x (8 + 2) =(15 x 8) + (15 x 2) = 150

Now, let us see the cases for negative integers also: (- 3) x (2 + 5) = – 3 x 7 = – 21.

Also, [(-3)x 2] + [(-3) x5] =-6+-15=-21.

So, we can conclude that

a x (b + c) = a x b + a x c

We know, 5(9 – 3) = 5 x 6 = 30

Again, ( 5 x 9) – (5 x 3) = 45 – 15 = 30.

So, we can conclude that if a, b, c are there integers then we can write, a x ( b – c ) = a x b – a x c

Similarly,

(-5) x 3 = (- 15) > 1. (-15) + (- 5) = 3,2. (-15) + 3 = (-5)

(-3) x (-5) = 15 > 1. 15 ÷ (- 3) = (- 5), 2. 15 + (- 5) = (- 3)

Rule for division:

1. When we divide a +ve integer by a -ve integer or a -ve integer by a + ve integer, division is done considering whole numbers but putting a minus sign ( – ) before the quotient. Hence, the result is negative.

\(\frac{-15}{3}\) = – \(\frac{15}{3}\) = -5

So, a ÷ (-b) = (-a) ÷ b = – \(\frac{a}{b}\)

2. When we divide a negative integer by a negative integer, we divide the integers considering whole numbers but putting a ( + ) positive sign before the quotient.

\(\frac{-15}{5}\) = + \(\frac{15}{5}\) = +3

So, (- a) + (- b) = a ÷ b = \(\frac{a}{b}\)

3. Now let us take two integers like 24, ( – 3). If we divide one by other, then let us see the result.

24 ÷ ( – 3) = \(\frac{24}{-3}\) = – \(\frac{24}{3}\) = -8 ….(1)

Again, (-3) + 24= \(\frac{-3}{24}\) = – \(\frac{1}{8}\) …..(2)

We find (1) & (2) are not same.

So, we can write, a ÷ b ≠ b ÷ a

4. Let us take three integers like – 30, – 5, and + 2. We now set the number in two ways.

 

Set 1	Set 2
(-30) ÷ {(-5) + 2} = (-30) ÷ (-3) = 10	(-30) ÷ (-5)+ (-30) ÷ 2 = 6 +(-15) = 6 – 15 = – 9

 

∴ (-30) {(-5) + 2} ≠ (-30) ÷ (-5) + (-30) ÷ 2

So, we can write, a ÷ ( b + c) ≠ a ÷ b + a ÷ c

5. We now take three integers – 30, + 2, and 7. Let us set the numbers in two ways.

Set 1	Set 2
{(- 30) + 2 } ÷ 7 = – 28 ÷ 7 = – 4	{(-30) + 2}÷ 7 = \(\frac{-30}{7}\) + \(\frac{2}{7}\) = \(\frac{-30+2}{7}\) = \(\frac{-28}{7}\) = -4

 

So, we can write, (b + c) ÷ a = b ÷ a + c ÷ 4

 

Algebra Chapter 2 Addition Subtraction Multiplication And Division Of Integers Exercise 2 Examples For Multiplication And Division

Example 1. Find the value of the following products:

1. (- 18) x (- 9) x 9
2. (- 20) x (- 2) x { – 5) x 6
3. (- 1) x (- 5) x ( – 4) x (- 6)

Solution:

1. (- 18) x (- 9) x 9 = [(- 18) x (-9)] x 9 = 162 x 9 = 1458.
2. (- 20) x(-2)x(-5)x6 = (- 20 x – 2) x (- 5) x 6 = 40 x (- 5) x 6 = – 200 x 6 . = -1200.
3. (- 1) x (_ 5) x (- 4) x (- 6) = [(- 1) x (- 5)] x [(- 4) x (- 6)] = 5×24 = 120.

Example 2.  In a test containing 12 questions, 4 marks are given for every correct answer, and ( – 2) marks are given for every incorrect answer. Raju attempted all questions but only 8 of his answers were correct. Find his total score.

Solution:

Given:

In a test containing 12 questions, 4 marks are given for every correct answer, and ( – 2) marks are given for every incorrect answer. Raju attempted all questions but only 8 of his answers were correct.

Marks are given for each correct answer = 4

So, marks for 8 correct answers = 8 x 4 = 32

Marks given for one incorrect answer = – 2

So, marks for (12 – 8) = 4 incorrect answers = (-2) x 4 = -8.

Therefore, Raju’s total score = 32 + (- 8) = 32-8 =24.

Example 3. A shopkeeper earns a profit of ₹2 by sealing one pen and incurs a loss of ₹ 1 per pencil. In a particular month, he incurs a loss of ₹ 15, During this period, he sold 45 pens. How many pencils did he sell in this period?

Solution:

Given:

A shopkeeper earns a profit of ₹2 by sealing one pen and incurs a loss of ₹ 1 per pencil. In a particular month, he incurs a loss of ₹ 15, During this period, he sold 45 pens.

Profit earned by selling one pen = ₹ 2.

Profit earned by selling 45 pens = ₹2 x 45 = ₹ 90.

Loss incurred =₹ 15, which is denoted by – ₹ 15.

We know profit earned + loss incurred = Total loss

Therefore, Loss incurred =  Total loss – Profit earned = -₹ 15 – ₹90 = – ₹ 105.

Loss incurred by selling one pencil = ₹ 1.

So, number of pencils sold = – ₹ 105 ÷ – ₹1 = 105.

Number of pencils sold in this period = 105.

 

Algebra Chapter 1 Some Problems On Symbols

Symbols Introduction:

In the previous class, you have known the contribution of famous mathematicians in the study of algebra.

Here we shall not repeat it. In this chapter, our aim is to discuss briefly the algebraic system of numbers, directed numbers, the use of algebraic symbols and four basic operations which you have learnt in the previous class.

Wbbse Class 7 Maths Solutions

Algebraic system of numbers and directed numbers

Read and Learn More WBBSE Solutions For Class 7 Maths

In arithmetic, we form all the numbers with the help of the ten digits 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. But we cannot write “any number” by these digits. Also, the numbers considered in arithmetic are positive numbers.

In arithmetic + sign denotes addition and – sign denotes subtraction. In algebra, these two signs are used in much wider sense.

In arithmetic when we subtract 5 from 10 then we say 10 – 5 = 5.

But when we are asked to subtract 15 from 10 then we say that 10 – 15 cannot be calculated as a greater number cannot be subtracted from a smaller number.

Thus, 10-15 becomes meaningless. But in algebra 10 – 15 = – 5. The consideration of negative numbers in algebra helps us to overcome many difficulties.

Also to express some quantities of same kind but of opposite nature, we use positive and negative numbers.

Thus to express profit and loss, increase and decrease rise and fall, and income and expenditure we take one as + quantity and the other as -quantity.

In arithmetic, there is no place of negative numbers. The numbers +1, +2, +3…. and -1, -2, -3…. considered in algebra are called directed numbers since the idea of direction is associated with these numbers.

Here, the signs + and – are called the signs of affection.

Use of algebraic symbols

To express ‘any number’ we use the letters of the alphabet as symbols. Thus we use the letters x, y, z etc., as symbols to represent numbers.

When such alphabetic symbols are used instead of numbers then those symbols express numbers— although their values are not fixed.

For example, x + 5 represents a number but its value is not fixed as the value of x is not fixed.

We may express all the 90 numbers of two digits with the help of a single symbol 10b + a in which a represents the digit in the units’ place and b represents the digit in the tens’ place.

In arithmetic, we find the relation, Dividend = Divisor x Quotient + Remainder. This relation cannot be expressed, in general, by the ten digits of arithmetic.

But if we assume that, if the number a is divided by b then the quotient is c and the remainder is d, then we may write, a = b c + d in this relation a, b, c, d may represent any number.

Wbbse Class 7 Maths Solutions

Four basic operations

Addition, Subtraction, Multiplication and Division are the four basic operations.

We use these operations in algebra in the same way as we use them in arithmetic.

For example:

1. Sum of a and b is represented by a + b.
2. Result of subtracting b from a is represented by a – b.
3. Product of a and b is represented by a x b.
4. Result of dividing a by b is represented by \(\frac{a}{b}\).

Opposite numbers: If x is a natural number then + x and – x are opposite to each other.

Example: -7 is the opposite number of +7.

Absolute value: The value of a positive or negative number without its sign is called its absolute value. For example, the absolute value of both -10 and +10 is 10.

Addition:

1. To add two positive numbers, the absolute values of the numbers are added and the sign of the sum is +.

For Example:(+6) + (+4) = + 10
(+15) +(+6) = + 21.

2. To add two negative numbers, the absolute values of the numbers are added and the sign of the sum is -.

For Example: (-7) + (- 5) = -12
(-12) + (- 8) = -20.

3. To add one positive and one negative number the smaller absolute value is subtracted from the greater absolute value and the sign of the result is that of the greater number.

For Example: (+8) + (-3) = +5
(-12) + (+4) – -8.

Subtraction:

Wbbse Class 7 Maths Solutions
Subtracting the integral number y from the integral number x means adding the opposite of the integral number y to the integral number x. For example, to subtract -5 from +7 we have to add +5 with +7.

So, (+7) – (-5) = (+7) + (+5) = (+12).

Similarly, (+8) – (+3) = (+8) + (-3) = (+5).

Multiplication:

In order to find the product of two numbers we have to multiply their absolute values and the sign of the product will be “+’ if the given two numbers are of the same sign and the sign of the product will be —’ if the given two numbers are of the opposite sign.

Example: (+5)x(+4) = + 20
(- 4) x (+ 7) = – 28
(+ 3) x (- 8) = – 24
(-7) x (- 2) = + 14

Division:

In order to find the quotient of two numbers we have to divide their absolute values and the sign of the quotient will be + if the dividend and the divisor are of the same sign and the sign of the quotient will be – if they are of opposite sign.

Example: (+30) ÷ (+ 5) = (+ 6)
(+ 28) ÷ (- 4) = (- 7)
(- 42) ÷ (+ 6) = (- 7)
(- 40) ÷ (- 5) = (+ 8)

Algebra Chapter 1 Revision Of Previous Lessons Exercise 1 Some Problems On Symbols

Example 1. Write in words:

1. x + y
2. \(\frac{x}{3}\)
3. 2x + 3
4. x ≥ 14
5.  x ≤ 8.

Solution:

1. The sum of x and y.
2. One-third of x.
3. 3 more than twice x.
4. The value of x is greater than or equal to 14.
5. The value of x is less than or equal to 8.

Example 2. Write with the help of a sign 

1. 7 less than p
2. 20 times q
3. 3 less than one-fourth of x
4. The value of x is not greater than 25
5. The value of y is not less than 30.

Solution:

1.  p – 7
2. 20 q
3. \(\frac{x}{4}\) – 3
4. x 25
5. y 30.

Example 3.  If a = 2, b = 5 and c = 8 then write 582 by the alphabetic symbol.

Wbbse Class 7 Maths Solutions

Solution : 582 = 5 x 100 + 8 x 10 + 2 = b x 100 + c x 10 + a = 100b + 10c + a

∴ 1006 + 10c + a.

Example 4. Ram had ₹ x, and Ram’s father gave him ₹y more. How many rupees has Ram at present?

Solution: ∴(x + y).

Example 5. The product of two numbers is 30. If one of them be x then find the other.

Solution: \(\frac{30}{x}\)

Example 6. 20 years ago, a man’s age was (x- 10) years. What will be his age after 20 years?

Solution: 20 years ago, the man’s age was (x -10) years.

So at present his age = (x – 10 + 20) years = (x + 10) years.

∴ After 20 years his age will be (x + 10 + 20) years = (x + 30) years

∴ (x + 30) years.

Wbbse Class 7 Maths Solutions

Example 7. Ram is x years older than Shyam, and y years younger than Jadu. If Jadu is 2 years old then find the ages of Ram and Shyam.

Class Vii Math Solution Wbbse
Solution: Jadu is z years old.

Ram is y years younger than Jadu.

So Ram’s age = (z – y) years.

Again, Shyam is x years younger than Ram.

So, Shyam’s age = (z-y-x) years

∴ Ram’s age is (z-y) years and Shyam’s age is (z – y – x) years.

Example 8. Hari’s age will be b years, after a year. What was his age c years ago?

Solution:

Given:

Hari’s age will be b years, after a year.

At present, Hari’s age is (b – a) years, c years ago his age was (b – a-c) years

∴ (b- a-c) years.

Example 9. The number of members of a club is x. If each member contributes? ₹y, what will be the total contribution? If z number of footballs are bought by that money, find the price of each football.

Solution:

Given:

The number of members of a club is x. If each member contributes? ₹y,

1 member contributes ₹y

x members contribute ₹ xy

The price of z footballs is ₹ xy

The price of 1 football is ₹ \(\frac{xy}{z}\)

∴ ₹ \(\frac{xy}{z}\), ₹ xy

Class Vii Math Solution Wbbse

Example 10. The product of two numbers is p; if their H. C. F. be m then what will be their L. C. M.?

Solution:

Given:

The product of two numbers is p; if their H. C. F. be m

L. C. M. X H. C. F. = Product of the numbers

or, L. C. M. X m =p

or, L, C. M. = \(\frac{p}{m}\)

∴ \(\frac{p}{m}\)

Concept of Index

In case of the number xⁿ, we say that x is the main number and n is power or index.

Three basic rules of the index are:

1. x^m X xⁿ= x^m+n,

2. x^m ÷ xⁿ= x^m-n,

3. (x^m)ⁿ = x^mn.

Class Vii Math Solution Wbbse

Example: x^mn x x⁴ = x⁸⁺⁴ = x¹²,

x⁸ ÷ x⁴ = x^8-4 =  x⁴ and (x⁸)⁴ = X^{8 x 4} = x³².

Also, x° = 1, because x° = x^n-n = xⁿ ÷ xⁿ= 1.

Any integer can also be expanded is terms of the index as follows:

915 = 9 x 100 + 10 x 1 + 5 = 9 x 10² + 10¹+ 5

Also, 81 = 3 x 3 x 3 x 3 = 3⁴

Here, 3 is the main number and 4 is the index.

Some problems on directed numbers:

Example 1. Arrange the following numbers in the ascending order of their values: 5,-3,-7, 0, 4,-13.

Solution: In the ascending order of their values the numbers are: -13, -7, -3, 0, 4, 5.

Example 2. Arrange the following numbers in the descending order of their values: -7,- 15,-8, 5, 0,-20, 25, 15.

Solution: In the descending order of their values, the numbers are: 25, 15, 5, 0, – 7, – 8, – 15, – 20.

Example 3. Write the opposite of the following expressions.

1. Expenditure of ₹ 30.
2. – 3 km towards north.
3. A capital of ₹ 50.
4. Rise of temperature by 42°C.
5. Descending – 20 metres.
6. Fall of temperature by – 20°C.

Solution:

1.  An income of ₹ 30.
2. 3 km towards the north.
3. A loan of ₹ 50.
4. Fall of temperature by 42°C.
5. Descending 20 metres.
6. Fall of temperature by 20°C.

Example 4. What do the following expressions mean?

1. A loan of  ₹ -10.
2. An income of ₹ -40.
3. Ascending -70 metres.
4. A profit of  ₹-100.
5. Fall of temperature by -5°C.
6. -15 km towards north.

Solution:

1. A capital of  ₹ 10.
2. An expenditure of ₹ 40.
3. Descending 70 metres.
4. A loss of  ₹ 100.
5. Rise of temperature by 5°C.
6. 15 km towards south.

Example 5. If +x represents an income of  ₹ 20. then which will represent an expenditure of  ₹ 100?

Solution:

Given:

+x represents an income of  ₹ 20.

An income of ₹ 20 is represented by + x

An income of ₹ 1 is represented by \(\frac{+x}{20}\)

An income of ₹ 100 is represented by \(\frac{+x}{20}\) X 100 = + 5x

∴ An expenditure of  ₹ 100 will be represented by – 5x.

Class Vii Math Solution Wbbse

Example 6. If x = a profit of ₹ 7 and y = a loss of ₹ 15 then find what amount of profit or loss will be represented by 12x + 3y?

Solution:

Given:

x = a profit of ₹ 7 and y = a loss of ₹ 15

12x = 12 X a profit of ₹ 7 = a profit of ₹ 84

3y = 3 X a loss of ₹ 15 = a loss of ₹ 45 .

∴ 12x+3y = a profit of ₹ (84 – 45) = a profit of ₹ 39

Solution: A profit of ₹ 39.

Example 7.  If an expenditure of ₹ 50 is denoted by -5 \(\frac{1}{2}\) then what will be denoted by + 33?

Solution: – \(\frac{11}{2}\) denotes an expenditure of ₹ 50

-1 denotes an expenditure of ₹ 50 X \(\frac{2}{11}\)

∴ -33 denotes an expenditure of ₹ 50 X \(\frac{2}{11}\) X 33

+ 33 denotes an income of  ₹ 300

∴ An income of ₹ 300.

Wbbse Class 7 Maths Solutions

Example 8. If a man earns ₹ 10 daily and his total expenses in 7 days be ₹ 60, what will be his total savings after 7 days?

Solution:

Given:

A man earns ₹ 10 daily and his total expenses in 7 days be ₹ 60,

In 1 day the man earns ₹ 10

In 7 days the man earns ₹ 70

Also in 7 days his total expenses is ₹ 60

∴ his savings after 7 days = ₹ (70 – 60) = ₹ 10

∴ ₹ 10.

Total savings after 7 days ₹ 10.

Example 9. Find the product :

1. x⁷ X x³
2. (- x⁵) X x³
3. x⁴  X (- x⁵)
4. (-x⁴) X (- x⁷)
5. x^m X xⁿ

Solution:

1. x⁷ X x³ = x^{7 + 3} = x¹⁰.
2. x⁴  X (- x⁵) = -x^{5 + 3} = -x⁸.
3. x⁴  X (- x⁵) = -x^{4 + 5} = -x⁹.
4. (-x⁴) X (- x⁷) = x⁴⁺⁷=x¹¹
5. x^m X xⁿ = x^m+n.

Example 10. Find the quotient :

1. x⁸ ÷ x³
2. (- x¹¹) ÷ x³
3. x¹² ÷ (- x⁴)
4.  (-x⁵)÷ (-x²)
5. x^m ÷ xⁿ.

Solution:

1. x⁸ ÷ x³ = x^{8 – 3} = x⁵.
2. (- x¹¹) + x³=-x^11-3 = -x⁸.
3. x¹² + (- x⁴) = -x^{12- 4} = – x⁸.
4. (-x⁵)+ (-x²) = x^5-2 – x³.
5. x^m + xⁿ= x^m-n.

Example 11. If a =-2,b = 4 and c = – 5 then find the value of a³ + b³ + c³.

Solution:

Given:

a =-2,b = 4 and c = – 5

a³ + b³ + c³ = (- 2)³ + (4)³ + (- 5)³

= (- 2) x (- 2) x (- 2) + 4 x 4 x 4 + (- 5) x (- 5) x (- 5)

= – 8 + 64 – 125 = 64 – (8 + 125)

= 64- 133

= -69

∴ -69.

a³ + b³ + c³ = -69

Example 12. If a = 2, b = – 3, c = 4 find the value of a²b³c⁴.

Solution :

Given:

a = 2, b = – 3, c = 4

a²b³c⁴ = (2)² x (- 3)³ x (4)⁴

= 2x2x(-3)x(-3)x(-3)x 4 x 4 x 4 x 4 = 4 x (- 27) x 256

= – 27648

∴ -27648.

a²b³c⁴= -27648.

Arithmetic Chapter 7 Bar Graph Exercise 7 Solved Example Problems

 

When different data are represented by some bars then it is called a bar graph. You have seen the runs scored in different overs in a cricket match by means of bar graph in television. We shall discuss the application of bar graphs in different fields of society.

Example 1.

Let, the number of boys in your school from Class 6 to 9 be as follows :

Class 6 — 45 boys

Class 7 — 48 boys

Class 8 — 50 boys

Class 9 — 40 boys

Solution: This data may be represented as follows :

 

 

This way the pictorial representation of the numerical data by a number of bars (rectangles) of uniform width is called a bar graph. In the above example, the bar graph has been drawn following the undermentioned methods:

1. The classes of 6, 7, 8 and 9 are marked along the horizontal axis (X-axis) at uniform gaps.

2. Keeping in mind the maximum and minimum number of boys among the given classes, a suitable scale is chosen to determine the heights of the rectangles or bars that have been erected vertically along the vertical axis (Y-axis).

The given example shows that 1 scale division represents 10 boys between the origin (0-mark) and the 50 mark.

3. At last the number of boys in each class is drawn as bars (of equal width) corresponding to each class. The bars of different heights have equal spacing between them. Thus the bar graph is drawn completely.

Now the obvious question is what is the utility of bar graph or what do we come to know from a bar graph.

The information obtained from a bar graph may be stated as:

1. Pictorial representation of data in the form of bars helps easy the understanding of data. This makes comparative analysis easier and which in turn facilitates the process of decision-making about future corrective actions, if any.
2. The maximum and minimum values of obtained data and the range or the difference between these two values become clear in front of our eyes.
3. This sort of data handling makes the computation of the average value of gathered data easier and more meaningful.

The above points related to the utilities of the bar graph will be more clear from the next example.

Example 2. The bar graph of the boys of your school from class 5 to 8 in the year 2013 is given below

Solution:

 

From the bar graph the following information are known:

1. In the year 2013, the number of boys of class 5 was nearly 30.
2. In the year 2013, the number of boys of class 6 was 40.
3. In the year 2013, the number of boys of class 7 was between 40 and 50.
4. In the year 2013, the number of boys of class 8 was between 30 and 40.

Double bar graph:

The simultaneous pictorial representation of two series of data using two bars drawn side by side following the same scale is known as a double bar graph.

Both the bars are shaded separately and the shading is usually shown in the top right corner of the graph paper.

Example 3. You obtained the following marks in different subjects In two consecutive tests.

Subject	Bengali	English	Maths	History	Geography
1st test	72	85	86	85	90
2nd test	80	77	90	80	85

 

Solution:

 

The most important utility of a double bar graph is that it gives us the opportunity to carry out fruitful comparative analysis of two series of data without elaborate mathematical computations.

The matter will be clear to you once you go through the following examples.

Example 4. In a Girls’ school participation of the girls in dance, singing and recitation is as follows: 

Activity	Dance	Singing	Recitation
Class 7	15	12	16
Class 8	10	8	20

 

Represent the above data by a double bar graph and answer the following questions from the bar graph:

1. In which activity is the participation of girls of both classes 7 & 8 maximum?
2. In which activities have the students of class 7 participated in more number than those of class 8?

Solution:

 

It is seen from the above double bar graph that:

1. Maximum participation of girls of both class 7 & 8 has occurred in recitation.
2. Students of class 7 have participated in both dance and music in more numbers than those of class 8.

Example 5. The production of motorcycles and cycles (in number) of four companies in the last 6 months is summarised hereunder: 

Company	1st	2nd	3rd	4th
Motor cycle(in No)	8000	15,000	20,000	10,000
Cycle(in No.)	3000	5000	6000	4000

 

Represent the production figures with help of a double bar graph and give answers to the following questions :

1. Which company has produced the maximum number of motorcycles compared to that of cycles?
2. Which company has produced a minimum number of motorcycles compared to that of cycles?
3. Which company has produced the maximum number of motorcycles.
4. Which company has produced a minimum number of cycles.

Solution:

 

1. Company #3 has produced the maximum number of motorcycles compared to that of cycles.
2. Company #4 has produced a minimum number of motorcycles compared to that of cycles.
3. Company #3 has produced a maximum number of motorcycles.
4. Company #1 has produced a minimum number of cycles.

Example 6. The five-year production (in Ton) data of a state in connection with paddy and oil seeds is provided as below:

Year	2010	2011	2012	2013	2014
Paddy(Ton.)	210	200	195	210	180
Oil seeds(Ton)	85	110	115	120	125

 

Draw a double bar graph of the above data. Answer the following questions from the bar graph:

1. Which year has seen the minimum production of paddy?
2. In which two years the paddy productions are same?
3. In which year the production of oil seeds has been the maximum?
4. Which year has recorded the maximum production of paddy in comparison to that of oil seeds?

Solution:

 

From the double bar graph we come to know that:

1. Production of paddy has been minimum in 2014.
2. Paddy productions are found to be the same in both 2010 and 2013
3. Maximum production of oil seeds has occurred in 2014.
4. The Year 2010 has recorded the maximum production of paddy in comparison to that of oil seeds.

 

Geometry Chapter 4 Congruence Exercise 4 Solved Example Problems

Congruence

We say that the two objects are congruent when they are of the same size and shape.

In our daily life we come across many objects which are of the same size and shape.

For example, fifty paise coins, sheets of paper of a particular exercise book, keys of the same lock, shaving blades of the same brand etc.

These objects are called congruent objects. The relation of two objects being congruent is called congruence.

We shall, however, confine our attention to the congruence relation among plane figures only. In other words, we shall study those Figures which lie in the same plane and which have the same size and shape.

Read and Learn More WBBSE Solutions For Class 7 Maths

Congruence of triangles

Two triangles are said to be congruent or equal in all respects if all the six parts namely three sides and three angles of one triangle are respectively equal to the corresponding six parts of other triangles.

If two triangles are congruent and we place one of them on the other then they will coincide.

In the two triangles ABC and DEF,

\(\overline{A B} \cong \overline{D E}, \quad \overline{B C} \cong \overline{E F}, \quad \overline{C A} \cong \overline{F D}\)

Wbbse Class 7 Maths Solutions

∠BAC ≅ ∠EDF, ∠ABC ≅ ∠DEF, ∠BCA ≅ ∠EFD

Hence, the two triangles ABC and DEF are congruent and we write ΔABC ≅ ΔDEF.

Now place triangle ABC on triangle DEF so that \(\overline{B C}\) falls on \(\overline{E F}\) and the points B and C coincide respectively with the points E and F.

Then you will find that point A will coincide with point D and the two triangles will coincide entirely.

Corresponding sides and corresponding angles of two congruent triangles

If two triangles are congruent, then the sides opposite to the equal angles are called corresponding sides and the angles opposite to the equal sides are called corresponding angles.

Thus, in the two congruent triangles, ABC and DEF discussed in the previous article the corresponding sides are: AB and DE, BC and EF, and CA and FD.

Also, the corresponding angles are ∠BAC and ∠EDF, ∠ABC and ∠DEF, ∠BCA and ∠EFD.

Conditions of congruence of two triangles

The conditions under which the two triangles become congruent are :

1. Of the two triangles, if the two sides and their included angle of one, are respectively equal to the two sides and their included angle of the other, then the triangles are congruent. (It is called Side-Angle- Side congruence or SAS congruence.)
2. Of the two triangles, if the two angles and one side of one, are respectively equal to the two angles and one side of the other, then the triangles are congruent. (It is called Angle-Angle-Side congruence or AAS congruence.)
3. Of the two triangles, if the three sides of one are respectively equal to the three sides of the other, then the triangles are congruent. (It is called Side-Side-Side congruence or SSS congruence.)
4. Of two right triangles, if the hypotenuse and one side of the one are respectively equal to the hypotenuse and one side of the other, then the two right triangles are congruent. (It is called Right Angle-Hypotenuse — Side congruence or RHS congruence).

Verification of SAS congruence

Let us suppose that between two triangles ABC and DEF, AB = DE, AC = DF and the included ∠BAC = ∠EDF.

It is required to verify that ΔABC = ΔDEF.

Wbbse Class 7 Maths Solutions

Cut off the triangle DEF along its border and place it on the triangle ABC such that A D EF coincides with BC.

You will find that D will coincide with A and the triangles DEF and ABC will also coincide.

Hence, it is verified that the two triangles are congruent.

Alternative method

Let ABC be a given triangle. Take a line segment DF congruent to AC. Now construct at the point D an angle ∠FDP congruent to ∠CAB. From DP cut off DE congruent to AB. Join EF.

Now measuring the angles of ΔDEF by a protractor it is found that ∠DEF = ∠ABC and ∠DFE =∠ACB.

Also measuring with a scale it is found that BC = EF.

Now if we set a correspondence between the two triangles ABC and DEF, such that A → D, B → E and C → F then all the six parts of ΔABC are congruent to the corresponding parts of ΔDEF. Hence, the two triangles are congruent.

But according to the construction two sides and their included angle of the triangle DEF were made congruent to the corresponding parts of the triangle ABC.

By actual measurement, the triangles are found to be congruent. Hence, the axiom is verified.

Verification of the AAS congruence

Let us suppose that between two triangles ABC and DEF, ∠ABC = ∠DEF, ∠BCA = ∠EFD and BC = EF.

It is required to verify that ΔABC ≅ ΔDEF.

Cut off the triangle DEF along its border and place it on the triangle ABC such that EF coincides with BC.

You will find that D will coincide with A and the triangles DEF and ABC will also coincide. Hence, it is verified that the two triangles are congruent.

Wbbse Class 7 Maths Solutions

Alternative method

Let ABC be a given triangle. Take a line segment EF congruent to BC.

At the point E draw ∠DEF = ∠ABC and at point F draw ∠DFE = ∠ACB.

Now measuring with a protractor it will be found that ∠EDF = ∠BAC.

Also measuring with a scale it will be found that DE = AB and DF = AC.

Now, if we set a correspondence between the two triangles ABC and DEF, such that A → D, B → E and C → F then all the six parts of ΔABC are congruent to the corresponding parts of ΔDEF. Hence the two triangles are congruent.

But according to the construction two angles and one side of ΔDEF were made congruent to the corresponding parts of the ΔABC.

By actual measurement, the triangles are found to be congruent. Hence the axiom is verified.

Verification of SSS congruence

Let us suppose that between two triangles ABC and DEF, AB = DE, BC = EF and AC = DF.

It is required to verify that ΔABC = ΔDEF.

In this case, also we may verify the axiom by the two methods namely

1. Paper cutting and
2. Constructing on the basis of given parts as has already been discussed in two other cases.

Congruence of circles

If one of the two circles can be made to coincide with the other by translation, rotation, reflection or a combination of them, then the two circles are called congruent circles. It is obvious that the radii of two congruent circles are equal.

Axioms on congruent circles

1. Incongruent circles (or in the same circle) equal chords cut off equal arcs and they subtend equal angles at the centre.
2. Incongruent circles (or in the same circle) are those chords which cut off equal arcs or subtend equal angles at the centre at equal.

Verification of the above axioms 

Let us consider two circles having centres O₁ and O₂. Let the circles be of the same radius r. Hence, the circles are congruent.

Consider the equal chords AB, CD and EF of the circles.

Let AGB, CHD and EIF be the minor arcs cut off by the chords AB, CD and EF respectively.

By measuring the lengths of these minor arcs with threads it is found that these minor arcs are equal in length.

Also, the circumferences of the two circles will be found to be equal by measuring with threads.

Also since the length of a major arc = length of the circumference – length of the corresponding minor arc

It is found that all the major arcs are also of equal length.

Wbbse Class 7 Maths Solutions

Now join AO₁,BO₂,CO_1,DO₁,EO₂ and FO₂.

By measuring the angles ∠AO₁B, ∠CO₁D, ∠EO₂F it is found that they are equal.

Repeating this process for different pair of circles and obtaining the same result you may conclude that :

Incongruent circles (or in the same circle) equal chords cut off equal arcs and they subtend equal angles at the centre.

To verify the second axiom i.e., the converse of the first take two congruent circles with centres O₁ and O₂ and construct at the centres the angles ∠AO₁B, ∠CO₁D and ∠EO₂F of equal measure.

You may verify by a thread that the arcs AGB, CHD and EIF are equal in length and also measured by a scale you will find that the chords AB, CD and EF are equal in length.

Some examples

Example 1. Explain with reasons whether the following triangles are congruent or not.

Solution: Of the two triangles ΔABC and ΔDEF, we have AB = DF = 5 cm, BC = DE = 6 cm and AC = EF = 7 cm.

∴ ΔABC is congruent to ΔDEF as per SSS congruence condition.

Example 2. It is given that ΔABC: AB = 17 cm, BC = 15 cm, AC = 18 cm ΔPQR: PQ = 18 cm, QR = 17 cm, PR= 15 cm Verify if the two triangles are congruent. If they are congruent, write which angles are same among the two triangles.

Solution:

Given:

It is given that ΔABC: AB = 17 cm, BC = 15 cm, AC = 18 cm ΔPQR: PQ = 18 cm, QR = 17 cm, PR= 15 cm Verify if the two triangles are congruent.

Among the two triangles,

BC = PR = 15 cm, AB=QR= 17 cm and AC=PQ=18 cm.

The triangles are congruent as per SSS congruence condition.

According to the condition of congruency, the opposite angles of equal sides shall be equal to each other among the two triangles.

Hence, ∠A = ∠Q, ∠C = ∠P and ∠B = ∠R.

∠A = ∠Q, ∠C = ∠P and ∠B = ∠R angles are same among the two triangles

Example 3. Justify with reasons whether the two triangles are congruent or not.

Solution: Between the two triangles, ∠B = ∠F = 60°

∠C = ∠D = 45°

But BC ≠ FD

∴ The two triangles are not congruent.

Example 4. In given AB∥DC and AB=DC. Explain with reasons whether the triangles ΔACD and ΔCAB are congruent or not. Name the angle which is equal to ∠CAD.

Solution:

Given:

In given image AB∥DC and AB=DC.

Since ABIICD and AB=DC, hence quadrilateral ABCD is a parallelogram.

Among the two triangles ΔACD and ΔCAB, AB=DC (Given)

AC is the common side.

∠BAC = ∠ACD (ABIICDC, AC is the transversal, alternate internal angles are equal).

∴ The triangles are congruent as per SAS congruence condition.

According to the condition of congruency, the respective opposite angles of CD and AB shall be equal to each other.

∠CAD = ∠ACB.

Class Vii Math Solution Wbbse

Example 5. Justify whether the given triangles are congruent or not.

Solution: The given triangles are right triangles each of which has PR, the opposite side of the right angle, as the hypotenuse.

Between the two triangles ΔPQR and ΔPSR, QR = SR = 4 cm

PR is the common hypotenuse

∠Q = ∠S = 90°.

ΔPQR and ΔPSR are congruent as per RHS congruence condition.

 

 

Geometry Chapter 3 Symmetry Exercise 3 Solved Example Problems

Introduction

In the natural world around us we come across various shapes and objects in our daily life. Some of them are symmetrical and some of them are not so.

Imagine a straight line on a two-dimensional shape or object and if the portions of the shape or object on both sides of that straight line become identical then the shape or object is called symmetrical.

For example, if you imagine a vertical straight line just through the middle of the blackboard of your classroom, you will find that the parts of the blackboard on the left-hand and the right-hand side of that straight line are identical.

Hence, the blackboard is a symmetrical object.

Read and Learn More WBBSE Solutions For Class 7 Maths

Again, take a piece of coal of irregular shape in your hand. No straight line or plane can be imagined through it so that the portions on both sides of this straight line or plane are identical.

Hence, a piece of coal of irregular shape is not a symmetrical object.

Different types of symmetry

Symmetry are mainly of two types.

1. Linear symmetry and
2. Rotational symmetry.

Linear symmetry

If an image is cut into two identical parts by a straight line then it is said that the image is symmetrical with respect to that straight line and the straight line is called the line of symmetry or axis of symmetry.

If these are folded along the dotted lines (line of symmetry) then the portions on the left-hand side of the dotted lines would coincide or match exactly on the portions on the right-hand side of it.

Hence, they are parted or divided into two identical portions with respect to the dotted lines.

To examine whether a figure has linear symmetry or not we have to fold it along the line of symmetry and we have to observe whether the two parts of the figure coincide or not.

A geometric may or may not have a line of symmetry. Also, a geometrical image may have more than one line of symmetry.

Wbbse Class 7 Maths Solutions

Linear symmetry geometrical images

1. A scalene triangle has no line of symmetry (or axis of symmetry).

ΔABC is a scalene triangle. This triangle has no line of symmetry.

2. An isosceles triangle has one line of symmetry. This line of symmetry is the perpendicular bisector of the base.

ΔABC is an isosceles triangle of which AD is the perpendicular bisector of the base BC.

AD has divided the triangle ABC into two congruent triangles ΔABD and ΔACD. Hence, the line of symmetry of the triangle ABC is the straight line AD.

3. An equilateral triangle has three lines of symmetry. The perpendicular bisectors of each side are its three lines of symmetry.

ΔABC is an equilateral triangle. Each of the three perpendicular bisectors of BC, CA and AB namely AD, BE and CF is a line of symmetry.

4. A non-isosceles trapezium has no line of symmetry.

ABCD is a non-isosceles trapezium. That means its sides AD and BC are unequal. This trapezium has no line of symmetry

Wbbse Class 7 Maths Solutions

5. An isosceles trapezium has one line of symmetry. This line of symmetry is the line, joining the mid-points of the two parallel sides.

ABCD is an isosceles trapezium of which the lengths of the sides AD and BC are equal.

Now, E and F are the mid-points of the parallel sides AB and DC. The straight line EF is the line of symmetry of the trapezium ABCD.

6. A parallelogram has no line of symmetry.

ABCD is a parallelogram. The parallelogram has no line of symmetry.

7. A rectangle has two lines of symmetry

ABCD is a rectangle. It has two lines of symmetry. One is the line joining the mid-points of AB and DC.

Wbbse Class 7 Maths Solutions

8. A square has four line of symmetry

ABCD is a square. It has four lines of symmetry.

1. The line joining the midpoints of AB and DC
2. The line joins the midpoints of AD and BC.
3. The straight line along the diagonal AC.
4. The straight line along the diagonal BD.

9. A rhombus has two lines of symmetry 

ABCD is a rhombus. Its two lines of symmetry are the two straight lines along the diagonals AC and BD.

10. A kite has one line of symmetry 

ABCD is a kite. Its one line of symmetry is the straight line along the diagonal AC.

11. An arrowhead has one line of symmetry

ABCD is an arrowhead. Its one line of symmetry is the straight line along AC.

12. A line segment has two lines of symmetry.

AB is a line segment. It has two lines of symmetry. One is the perpendicular bisector of AB and the other is the straight line along AB.

13. An angle with equal arms has one line of symmetry.

∠ABC is an angle with equal arms such that AB = AC. Its one line of symmetry is the internal bisector of ∠ABC.

Linear symmetry of some regular polygons

Class Vii Math Solution Wbbse

We have seen earlier that, an equilateral triangle has three lines of symmetry and a square has four lines of symmetry.

Now, we shall show that a regular pentagon has 5 lines of symmetry, a regular hexagon has 6 lines of symmetry and a regular heptagon has 7 lines of symmetry.

Linear symmetry of a circle

A circle has an infinite number of lines of symmetry.

Any straight line along any diameter of a circle is its line of symmetry.

Since a circle has an infinite number of diameters therefore it has an infinite number of lines of symmetry.

Linear symmetry of the letters of the English alphabet

Some letters from A to Z of the English alphabet have no axis of symmetry, some have one axis of symmetry and some have two axes of symmetry.

The axes of symmetry are marked with dotted lines.

Reflection in the plane mirror and symmetry

Class Vii Math Solution Wbbse

When reflection takes place in a plane mirror then the image formed in the plane mirror has some characteristics. For example :

1. Size of object = size of the image.
2. Distance of object from the mirror = Distance of image from the mirror.

We can understand these two things easily. Because, when we stand in front of a mirror we Find our image identical with ourselves. If we proceed towards the mirror then the image also proceeds towards the mirror.

Hence, it is found that the concept of symmetry is associated with the reflection by the plane mirror.

But if you watch carefully you will find in the mirror shows your right hand as the left hand and the left hand as the right hand. This phenomenon is called lateral inversion.

That means the phenomenon of inversion of the image of an object by the plane mirror is called lateral inversion.

In this case, it should be noticed that symmetric objects do not undergo any lateral inversion. Then the formed by a mirror of some letters is shown below.

Also, from the phenomenon of reflection by a plane mirror, it can be said that, the axis of symmetry of the symmetrical image is such a line of reflection that, when the image is reflected with respect to that line it remains unaltered in the same position. The original image and its image coincide.

The image of the right-hand side of the letter ‘A’ coincides with the left-hand side of the letter ‘A’.

Hence, the reflecting line l is the axis of symmetry of the letter A.

Class Vii Math Solution Wbbse

The symmetry of rotation (or rotational symmetry)

Suppose, a body changes its position while moving in a circular path, about a fixed point and along a plane.

Now, if the angle between the two straight lines, obtained by joining the initial and terminal positions of any point on the body, with the centre remains unchanged throughout, then the motion of the body is called rotation.

It can be said in easy language that —

If each point of a moving body rotates through equal angle then its motion is called rotation.

The fixed point about which an object rotates is called the centre of rotation. As a result of rotation, an object does not change its shape.

When due to the rotation of a geometrical figure about a fixed point within it, the image, coincides with itself time and again then we say that, the image, has the symmetry of rotation.

The point about which there is rotational symmetry is called the centre of symmetry of rotation.

The measure of a minimum number of degrees through which angle, when a geometrical image, is rotated to make it coincide with itself, is called the angle of symmetry of rotation of that figure.

The number, through which a geometrical image, coincides with its initial position when it makes a complete rotation, which means it rotates through an angle 360°, is called the order of rotation.

Class Vii Math Solution Wbbse

Therefore, if an image which is symmetrical with respect to the rotation has a symmetry of rotation of order n then the measure of the angle symmetry of rotation of that image is 360°/n

If the side is rotated through 90° about the centre of symmetry of rotation the image comes back to its initial position.

The order of the symmetry of rotation of this image is 4.

Also, the measure of its angle of symmetry of rotation is 360°/4 ⁼ 90°. 4

The symmetry of rotation of some geometrical images

1. A scalene triangle and an isosceles triangle have no symmetry of rotation.

2. An equilateral triangle has the symmetry of rotation. An equilateral triangle has three axes of symmetry. Their point of intersection is the centre of symmetry of rotation.

The centre O of the symmetry of rotation of the equilateral triangle ABC is the point of intersection of the three axes of

Its order of symmetry of rotation is 3 and the angle of symmetry of rotation is 120°.

3. A trapezium has no symmetry of rotation.

4. A parallelogram has the symmetry of rotation.

ABCD is a parallelogram. If the parallelogram is rotated through 180° about the point of intersection O of the diagonals the parallelogram it will coincide with itself.

Therefore, in the case of a parallelogram, the centre of symmetry of rotation is the point of intersection of its diagonals. The angle of symmetry of rotation is 180°. The order of symmetry of rotation is 2.

5. A rectangle has the symmetry of rotation.

In the image, below ABCD is a rectangle. If the rectangle is rotated through 180° with respect to the point of intersection O of the diagonals then the rectangle will coincide with itself.

Therefore, in the case of a rectangle, the centre of symmetry of rotation is the point of intersection of its diagonals.

The angle of symmetry of rotation is 180°. The order of symmetry of rotation is 2.

6. A square has the symmetry of rotation.

The next page ABCD is a square. If the square is rotated through 90° about the point of intersection of the diagonals then the square will coincide with itself.

Therefore, in case of a square, the centre of symmetry of rotation is the point O of the intersection of the diagonals.

The angle of symmetry of rotation is 90°. The order of symmetry of rotation is 4.

7. A rhombus has the symmetry of rotation.

Below ABCD is a rhombus. If the rhombus is rotated through 180° about the point of intersection of the diagonals then the rhombus will coincide with itself.

Class Vii Math Solution Wbbse

Hence, in case of a rhombus the centre of symmetry of rotation is the point of intersection of the two diagonals. The angle of symmetry of rotation is 180°.

The order of symmetry of rotation is 2.

8. A kite has no symmetry of rotation.

9. An arrow head has no symmetry of rotation.

10. A given line segment has the symmetry of rotation with respect to its mid-point. The angle of symmetry of rotation is 180°.

The order of symmetry of rotation is 2.

The symmetry of rotation of some regular polygons

1. The centre of symmetry of rotation of a regular pentagon is the point of intersection of the five axes of symmetry. Its angle of symmetry of rotation is 72° and the order of symmetry of rotation is 5.
2. The centre of symmetry of rotation of a regular hexagon is the point of intersection of the six axes of symmetry. Its angle of symmetry of rotation is 60° and the order of symmetry of rotation is 6.
3. Similarly, the centres of symmetry of rotation of different regular polygons are the point of intersection of their axes of symmetry. The angle of symmetry of rotation = (360° + number of sides). The order of symmetry of rotation = a number of sides.

Point symmetry

It is said to have symmetry with respect to a point if the image, remains unaltered when it is rotated in that plane through 180° about the point.

That point is called the point of symmetry or centre of symmetry.

Since in this case there is a rotation of 180° therefore such type of symmetry is also called half-turn symmetry.

The following letters have point symmetry about the point marked by a dot.