Oscillation And Waves
Simple Harmonic Motion Preliminary Topics
Periodic Motion Definition: Any motion, that repeats itself at regular intervals of time, is known as periodic motion.
The motion of planets around the sun, the hands of a clock, and the blades of a revolving electric fan are some examples of periodic motion. A characteristic of this motion is that each moves along a definite circular or elliptical path repeatedly in a regular time interval.
- The motion along an elliptical path is called elliptical or orbital periodic motion, while the other motions are called rotational periodic motion.
- On the other hand, if the bob of a simple pendulum is pulled aside slightly and then released, it swings to the other side passing through its equilibrium position.
- On its way back, the bob again passes through its equilibrium position and returns to its point of release.
- Then it goes on repeating this to and fro motion. Thus the bob covers a definite path repeatedly. If the angular displacement of oscillation of the pendulum is less than 4°, the amplitude or range of oscillation is small compared to the radius of curvature of the oscillatory path and so the path of the bob may be taken as a straight line.
Hence, this motion is called linear periodic motion. The motion of an elastic spring and that of a piston in the cylinder of an automobile engine are examples of linear periodic motion.
Oscillation Or Vibration: If a body undergoing periodic motion has an equilibrium position somewhere inside its path, it experiences no net external force at that point. Hence, if it is left there at rest, it remains there forever.
Now, if the body is given a small displacement from the equilibrium position, a restoring force comes into play which tries to bring the body back to its equilibrium point, giving rise to oscillations or vibrations.
Oscillation Or Vibration Definition: If a particle that executes periodic motion moves to and fro along the same path, the motion is called oscillation or vibration.
Simple Pendulum: A pendulum is suspended from a rigid support. Let P be the point of suspension and O be the mean or equilibrium position of the body. If the bob is pulled to position B and then released, it oscillates along the path BOC.
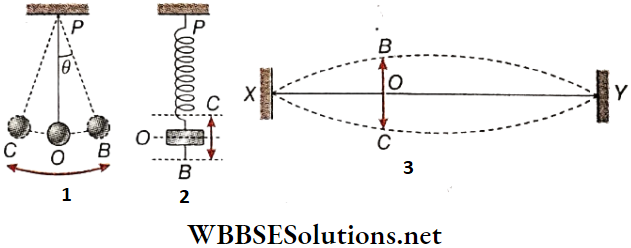
If the angular displacement, i.e., ∠OPB or∠OPC is less than 4°, then the path BOC or COB may be taken as a straight line. The pendulum is then called a simple pendulum and its oscillation is a linear periodic motion.
Elastic Spring: The upper end of an elastic spring is attached with a rigid support, Let P be the point of suspension. If a heavy body is suspended from its lower end, the spring stretches and the body hangs at rest, at some position of equilibrium O.
If the body is slightly pulled to B and then released, the spring executes an up-and-down oscillatory motion along the straight path BOC and COB. The oscillation of the elastic spring is therefore a linear periodic motion.
Stretched String: A string XY is attached to two rigid supports at points X and Y, It remains at a position of equilibrium along the straight line XY, If the string is pulled slightly upwards or downwards and then released, it vibrates about its position of equilibrium.
- If we consider a point O on the string, it is seen that the point vibrates along the straight path BOC, This vibration is also a linear periodic motion. Although any kind of oscillation or vibration is a periodic motion, the converse is not true. All periodic motions are not oscillations or vibrations.
- For example, the earth completes one revolution around the sun in 1 year, but it is not a to-and-fro motion about any mean position. Hence the motion is periodic but not oscillatory.
Some Quantities Related To Oscillation: It is evident from the different examples of oscillation above that the motion of the particle is restricted to a line segment, say BC.
Complete Oscillation: If a vibrating particle starts its motion from any point on its path towards a certain direction, returns to the same point, and then follows the same path in the same direction then it is said to have executed one complete oscillation or one complete vibration.
- If the particle starts its motion from B and after tracing the paths BOC and COB returns to B, then the particle executes one complete oscillation. It is seen that for a complete oscillation, the particle moves along the entire straight path twice.
- So, if the particle starts its motion from D and after tracing the paths DOC, COB, and BD, finally returns to D, then also it can be said that the particle has executed one complete oscillation. A complete oscillation is also known as a period.
Time Period: Time period of oscillation of a vibrating particle is defined as the time taken by it to execute one complete oscillation. Its dimension is T and its unit in all systems is second (s).
Frequency: The frequency of oscillation of a vibrating particle is defined as the number of complete oscillations executed by it in 1 second.
In time T the particle executes one complete oscillation, Thus the number of complete oscillations executed by the particle In ls is \(\frac{1}{T}\). Hence, the frequency n of the particle is n = \(\frac{1}{T}\).
The dimension of frequency is T-1 and its unit in all systems is second-1 or per second. This unit of frequency Is called hertz (Hz). So, 1 Hz = ls-1.
Amplitude: The amplitude of oscillation of a vibrating particle is defined as Its maximum displacement from Its equilibrium position.
- Amplitude, A = OB or OC. The dimension of amplitude is 1, and Its units In the CGS system and SI are centimeters (cm) and meters (m) respectively. It is to be noted that in the above discussions, sometimes we have used the term ‘oscillation1 and sometimes ‘vibration’. In fact, oscillation and vibration are synonymous.
- Usually, when the time period of the particle is large, i.e., frequency is low, the motion of the particle is called oscillation.
Amplitude Example: Oscillation of a simple pendulum or an elastic spring. On the other hand, when the time period of the particle is small, i.e., frequency is high, the motion of the particle is called vibration. Examples of vibration are the vibration of a stretched string or that of a tuning fork.
Periodic Functions: A function f(t) is periodic if the function repeats itself after a regular interval of the independent variable t.
The simplest examples of a periodic motion can be represented by any of the following functions.
f(t) = \(A \cos \frac{2 \pi}{T} t\)….(1)
and \(g(t)=A \sin \frac{2 \pi}{T} t\)….(2)
Here T is the time period of the periodic motion.
To check the periodicity of these functions t is to be replaced by (t+ T), In the above equations simultaneously.
Hence equation (1) gives us,
f(t+T) = \(A \cos \left[\frac{2 \pi}{T}(t+T)\right]=A \cos \left[\frac{2 \pi}{T} t+2 \pi\right]\)
= \(A \cos \frac{2 \pi}{T} t[because \cos (\theta+2 \pi)=\cos \theta]\)
= f(t)
And equation (2) gives us,
g(t+T) = \(A \sin \left[\frac{2 \pi}{T}(t+T)\right]=A \sin \left(\frac{2 \pi}{T} t+2 \pi\right)\)
= \(A \sin \frac{2 \pi}{T} t[because \sin (\theta+2 \pi)=\sin \theta]\)
= g(t)
So, for a periodic function with period T, f(t+T) = f(t) or, g(t+T) = g(t)
The result will be the same if we consider a linear combination of sine and cosine functions of period T,
i.e., f(t) = \(A \sin \frac{2 \pi}{T} t+B \cos \frac{2 \pi}{T} t\)
Another example of a periodic function is, f(t)= sinωt + cos2ωt + cos4ωt But, f(t) = e-ωt is not a periodic function, because it decreases monotonically with the increase in time and tends to zero as t → ∞
Displacement As A Function Of Time: Displacement can be represented by a mathematical function of time. In the case of periodic motion, this function is periodic in nature. One of the simple periodic functions is, f(t) = Acoscot
When the argument cot, is increased by an integral multiple of 2π radians, the value of the function remains the same.
Properties Of Simple Harmonic Motion Or SHM: Simple harmonic motion is the simplest form of oscillation. From the properties of simple harmonic motion, we can analyze any complex oscillation or vibration.
Any type of oscillatory motion can be considered to be the result of two or more simple harmonic motions acting on a particle. Thus, it is of great importance to discuss SHM in detail.
Restoring Force: When a vibrating particle is at its position of equilibrium, the resultant force acting on it is zero. For example, when a simple pendulum is at its equilibrium position the downward force due to the weight of the bob is balanced by the upward tension of the string.
- So, the resultant force acting on the bob is zero. If the bob is displaced slightly from its equilibrium position and released, then a resultant force acts on the bob which tries to bring it to its equilibrium position.
- This force is called the restoring force. Since force is a vector quantity, this restoring force has a magnitude and a direction.
- If the magnitude and the direction of the restoring force satisfy the following two conditions, the motion of the particle is termed simple harmonic motion (SHM),
- The restoring force Is always directed towards the position of equilibrium of the particle.
- The magnitude of the restoring force is proportional to the displacement of the particle from its position of equilibrium.
Equation Of Simple Harmonic Motion: Suppose, a particle is executing linear periodic motion along x-axis, and the point O, which is the origin (x = 0), is the position of equilibrium of the particle. Let D be any point on the path of the particle with position coordinate x.
According to condition (2), if F is the restoring force acting on the particle at D, then F ∝ x
Again from condition (1), as the restoring force F is directed towards the equilibrium position, it is taken as negative since the displacement OD = x is taken as positive.
So, F = -kx …..(1)
k is called the force constant and it is positive. Therefore, the magnitude of the restoring force acting on the particle when it is at a position of unit displacement is called the force constant. The units of k are dyn · cm-1 (CGS) and N · m-1 (SI).
If m is the mass of the particle and a is its acceleration then F = ma. So, from equation (1) we get, ma = -kx
or, a = \(-\frac{k}{m} x=-\omega^2 x\)…(2)
Here, \(\omega=+\sqrt{\frac{k}{m}}=\text { constant }\)…… (3)
Any one of the equations (1) or (2) is called the equation of simple harmonic motion. As the forms of these equations are identical, it can be said that the properties of acceleration of the particle and those of the restoring force are identical. Simple harmonic motion can be defined with reference to the properties of acceleration.
Simple Harmonic Motion Definition: The motion of a particle is said to be simple harmonic if its acceleration
- Is proportional to its displacement from the position of equilibrium and
- Is always directed towards that position.
It is to be noted that the acceleration of a particle executing simple harmonic motion is expressed as a = -ω²x. Conversely, if the acceleration of a particle obeys the equation a = -ω²x, then we can say that the motion of the particle is simple harmonic.
Oscillation And Waves
Simple Harmonic Motion Energy Of Simple Harmonic Motion
Let m be the mass of a particle executing simple harmonic motion, A be the amplitude and T be the time period of the motion. The particle possesses kinetic energy due to its velocity all along its path of motion except at the extremities.
Again restoring force acts on the particle all along its path of motion except at the position of equilibrium. So, the work that is to be done to move the particle against the restoring force remains stored in the particle as potential energy.
Kinetic Energy: At a displacement x from the position of equilibrium, the velocity of the particle, v = \(\omega \sqrt{A^2-x^2}\)
So, the kinetic energy of the particle of mass m at that instant, K = \(\frac{1}{2} m v^2=\frac{1}{2} m \omega^2\left(A^2-x^2\right)\)….(1)
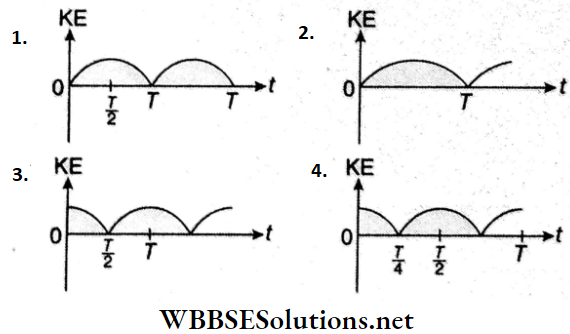
- When the particle is just at the position of equilibrium, the kinetic energy at that instant, K = \(\frac{1}{2}\)mω²A² this is the maximum value of the kinetic energy.
- As the particle reaches any end of its path, X = ± A, the kinetic energy at that instant, K = 0 this is the minimum value of the kinetic energy.
So, the kinetic energy of a particle executing SHM is maximum at the position of equilibrium and zero at the two ends, i.e., at the two extremities of its path of motion.
Potential Energy: When the particle is at a distance x from its position of equilibrium, the restoring force acting on it is, F = mω²x.
Again, when the particle is just at the position of equilibrium, x = 0, the restoring force F = 0, i.e., no force acts on the particle.
So, within the displacement from 0 to x, the average force acting on the particle = \(\frac{0+m \omega^2 x}{2}=\frac{1}{2} m \omega^2 x\)
Now potential energy of the particle, U = work done to move the particle through the distance x against this average force = average force x displacement acting on the particle = \(\frac{1}{2} m \omega^2 x \cdot x=\frac{1}{2} m \omega^2 x^2\)…(2)
- When the particle is just at the position of equilibrium, x = 0, the potential energy at that instant, U = 0 this is the minimum value of the potential energy.
- As the particle reaches any end of its path, x = ± A, the potential energy at that instant, U = \(\frac{1}{2}\) mω²A² this is the maximum value of the potential energy.
Calculation Of Potential Energy With The Help Of Calculus: When the displacement of the particle is x from the position of equilibrium, the restoring force acting on it is, mω²x. Let dx be a further infinitesimal displacement of the particle such that the above force acting on the particle remains constant throughout this displacement.
So, work done in moving the dx = mω²x · dx
Hence, the total work done in moving it from 0 to x, i.e., the potential energy of the particle is,
U = \(\int_0^x m \omega^2 x d x=\frac{1}{2} m \omega^2 x^2\)
Total Mechanical Energy: Total energy of a particle executing simple harmonic motion,
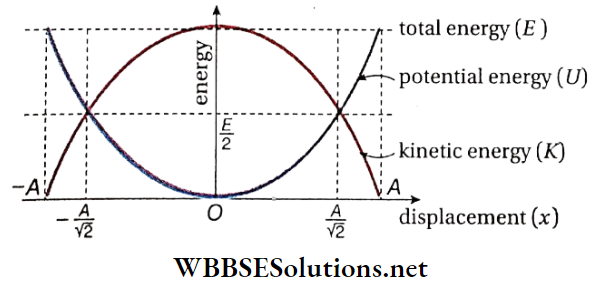
E = K+ U = \(\frac{1}{2} m \omega^2\left(A^2-x^2\right)+\frac{1}{2} m \omega^2 x^2=\frac{1}{2} m \omega^2 A^2 .\)
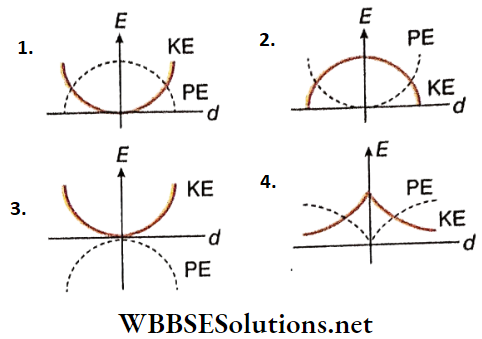
- Since m and co are constants, if the amplitude A remains unchanged, then E = constant, i.e., the total energy of the particle does not depend on its displacement. As the particle moves away from the position of equilibrium, kinetic energy gradually gets transformed into potential energy.
- While returning from the extreme position towards the position of equilibrium, its potential energy gradually gets converted into kinetic energy. This conversion is in accordance with the law of conservation of energy.
- Due to any external cause (for example, air resistance), if the amplitude of the motion decreases, the total energy will also decrease. In that case, the energy of the particle is transferred to the surroundings (for example, different air particles).
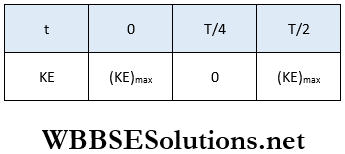
- The conversion of kinetic energy to potential energy and vice versa with the change in displacement of the particle executing SHM are shown in the following table. Using this table, the energy-displacement curve is plotted.
From the table, we see that when the displacement of the particle is ± \(\frac{A}{\sqrt{2}}\)
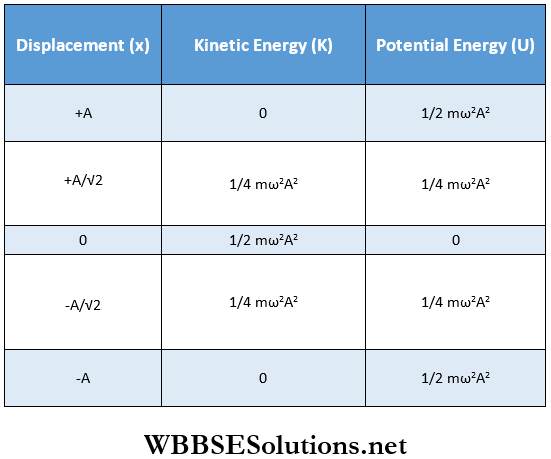
then kinetic energy = potential energy = \(\frac{1}{4} m \omega^2 A^2=\frac{E}{2}\)
Oscillation And Waves
Simple Harmonic Motion Energy Of Simple Harmonic Motion Numerical Examples
Example 1. When a particle executing SHM is at a distance of 0.02 m from its mean position, then its kinetic energy is thrice its potential energy. Calculate the amplitude of motion of the particle.
Solution:
According to the question, K = 3U
i.e., \(\frac{1}{2} m \omega^2\left(A^2-x^2\right)=3 \times \frac{1}{2} m \omega^2 x^2\) or, \(A^2-x^2=3 x^2 or, A^2=4 x^2\) or, \(A=| \pm 2 x|=0.04\)
[since x = 0.02m]
∴Amplitude = 0.04 m.
Example 2. When a particle executing SHM is at a distance of 0.02 m from its position of equilibrium, then its kinetic energy is twice its potential energy. Calculate the distance from the position of equilibrium where its potential energy is twice its kinetic energy.
Solution:
In the first case, when x = 0.02 m, K = 2 U
i.e., \(\frac{1}{2} m \omega^2\left(A^2-x^2\right)=2 \times \frac{1}{2} m \omega^2 x^2\)
or, \(A^2-x^2=2 x^2 or, A^2=3 x^2\)
or, \(A^2=3 \times(0.02)^2=0.0012\)
In the second case, 2 K=U
i.e., \(2 \times \frac{1}{2} m \omega^2\left(A^2-x^2\right)=\frac{1}{2} m \omega^2 x^2\)
or, \(2\left(A^2-x^2\right)=x^2 or, 3 x^2=2 A^2\)
or, \(x^2=\frac{2}{3} A^2=\frac{2}{3} \times 0.0012=.0008\)
or, x = \(\sqrt{0.0008}=0.0282 \mathrm{~m} \approx 0.03 \mathrm{~m}\)
Example 3. A particle of mass 0.2 kg is executing SHM along the x-axis with a frequency of \(\frac{25}{\pi}\)Hz. If its kinetic energy is 0.5 J at x = 0.04 m, then find its amplitude of vibration.
Solution:
Here, n = \(\frac{25}{\pi} \mathrm{Hz}\); so, \(\omega=2 \pi \cdot \frac{25}{\pi}=50 \mathrm{rad} \cdot \mathrm{s}^{-1}\)
We know, K = \(\frac{1}{2} m \omega^2\left(A^2-x^2\right) or, \frac{2 K}{m \omega^2}=A^2-x^2\)
or, \(A^2=\frac{2 K}{m \omega^2}+x^2=\frac{2 \times 0.5}{0.2 \times(50)^2}+(0.04)^2=0.0036 or, A=0.06 \mathrm{~m}\).
Example 4. The total energy of a particle executing SHM is 3 J. A maximum force of 1.5 N acts on it the Time period and epoch of the SHM are 2 s and 30° respectively. Establish the equation of this SHM and also find the mass of the particle.
Solution:
Total energy = \(\frac{1}{2} m \omega^2 A^2=3\)…(1)
Maximum force = mass x maximum acceleration
= m x ω²A = 1.5
Dividing (1) by (2) we get, \(\frac{1}{2}\) A = 2 or, A = 4 m
Time period, T = 2s
∴ \(\omega=\frac{2 \pi}{T}=\frac{2 \pi}{2}=\pi \mathrm{rad} \cdot \mathrm{s}^{-1}\)
Epoch, \(\alpha=30^{\circ}=\frac{\pi}{6}\)
So, the equation of SHM is x = Asin(ωt+α)
or, x = \(4 \sin \left(\pi t+\frac{\pi}{6}\right) \mathrm{m}\)
Again from equation (2), m = \(\frac{1.5}{\omega^2 A}=\frac{1.5}{\pi^2 \cdot 4}=0.038 \mathrm{~kg}\)
Example 5. The equation of motion of a particle executing SHM is x = Asin(ωt+ θ). Calculate the velocity and acceleration of the particle. If m is the mass of the particle, then what is the maximum value of its kinetic energy?
Solution:
Given equation ofSHM, x = Asin(ωt+ θ)….(1)
So, velocity v = \(\frac{d x}{d t}=\omega A \cos (\omega t+\theta)\)
From equation (1) we get, \(\sin (\omega t+\theta)=\frac{x}{A}\)
∴ \(\cos (\omega t+\theta)=\sqrt{1-\sin ^2(\omega t+\theta)}=\sqrt{1-\frac{x^2}{A^2}}=\sqrt{\frac{A^2-x^2}{A^2}}\)
∴ v = \(\omega A \sqrt{\frac{A^2-x^2}{A^2}}=\omega \sqrt{A^2-x^2}\)
Again, the acceleration of the particle,
a = \(\frac{d \nu}{d t} =\frac{d}{d t}\{\omega A \cos (\omega t+\theta)\}=-\omega^2 A \sin (\omega t+\theta)\)
= \(-\omega^2 x\) (x = \(A \sin (\omega t+\theta)\))
As the maximum value of \(\cos (\omega t+\theta)\) is 1 ,
the maximum value of velocity, \(v_{\max }=\omega \mathrm{A}\)
∴ Maximum kinetic energy of the particle
= \(\frac{1}{2} m v_{\max }^2=\frac{1}{2} m \omega^2 A^2 .\)
Example 6. The amplitude of a particle of mass 0.1 kg executing SHM is 0.1m. At the mean position, its kinetic energy is 8×10-3 J. Find the time period of its vibration.
Solution:
At the mean position, the potential energy of the particle =0
Hence, kinetic energy of the particle at the mean position = total energy = \(\frac{1}{2}\)A
∴ \(\frac{1}{2} m \omega^2 A^2=E \text { or, } \omega^2=\frac{2 E}{m A^2} \text { or, } \omega=\sqrt{\frac{2 E}{m A^2}}\)
i.e., time period,
T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m A^2}{2 E}}\)
= \(2 \times 3.14 \times \sqrt{\frac{0.1 \times(0.1)^2}{2 \times 8 \times 10^{-3}}}\)
= \(2 \times 3.14 \times \sqrt{\frac{1}{16}}=\frac{2 \times 3.14}{4}=1.57 \mathrm{~s} .\)
Example 7. An object of mass 10 kg executes SHM. Its time period and amplitude are 2 s and 10 m respectively. Find Its kinetic energy when it is at a distance of
- 2 m and
- 5 m respectively from its position of equilibrium.
Justify the two different results for (1) and (2).
Solution:
T = \(2 \mathrm{~s}\), i.e., \(\omega=\frac{2 \pi}{T}=\frac{2 \pi}{2}=\pi \mathrm{rad} \cdot \mathrm{s}^{-1}\)
Kinetic energy, K = \(\frac{1}{2} m \omega^2\left(A^2-x^2\right)\)
- When x = 2m, K = \(\frac{1}{2} \times 10 \times(\pi)^2 \times\left\{(10)^2-(2)^2\right\}\) = \(5 \times(3.14)^2 \times 96=4732.6 \mathrm{~J} .\)
- When x = 5m, K = \(\frac{1}{2} \times 10 \times(\pi)^2 \times\left\{(10)^2-(5)^2\right\}\) = \(5 \times(3.14)^2 \times 75=3697.35 \mathrm{~J}\)
The velocity of a particle executing SHM becomes maximum at its mean position. As the displacement increases, i.e., as it moves away from the equilibrium position, its velocity decreases and so the kinetic energy also decreases.
Example 8. A particle of mass m executes SHM with amplitude and frequency n. What is the average kinetic energy of the particle during its motion from the position of equilibrium to the end?
Solution:
KE in the mean position = \(\frac{1}{2} m a^2 w^2\)
= \(\frac{1}{2} m a^2(2 \pi n)^2\)
= \(2 \pi^2 m a^2 n^2\)
KE at the end = 0
∴ Average kinetic energy = \(\frac{0+2 \pi^2 m a^2 n^2}{2}=\pi^2 m a^2 n^2\)
Oscillation And Waves
Simple Harmonic Motion Simple Pendulum
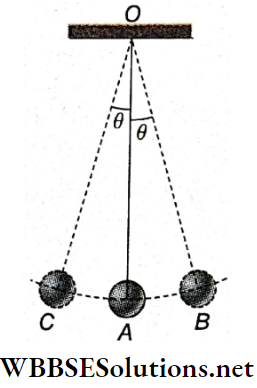
A simple pendulum is nothing but a small, heavy body suspended from a rigid support with the help of a long string. The heavy body remains in its lowest position A when the string is vertical.
- This position OA is called the position of equilibrium of the pendulum. The heavy body is called the pendulum bob. The support (O) from which the bob is suspended is called the point of suspension.
- The center of gravity of the suspended bob Is the point of oscillation, When the bob Is displaced from the equilibrium position by a little distance and then released, the pendulum oscillates about its equilibrium position on either side.
For convenience in the mathematical treatment of the properties of a pendulum, an Ideal simple pendulum Is considered. A simple pendulum will be ideal If
- The string is weightless,
- The string is inextensible,
- No frictional resistance acts on the bob during its oscillation and
- The bob is a point mass. Conforming to all the conditions stated above is not practically possible; we never get an ideal simple pendulum. Hence, for laboratory use, a small, heavy metal ball is tied to one end of a long, light string and the system is suspended from a rigid support.
Simple Pendulum Definition: If a small, heavy body, suspended from a rigid support by a long, weightless, and inextensible string, can be set into oscillation, then the arrangement is called a simple pendulum.
- When the pendulum bob is slightly displaced from position A to B and then released, it starts oscillating along arc BAC and CAB. This means that the position of the pendulum periodically changes from OB to OC.
- This to-and-fro oscillatory motion is periodic. But practical experience shows that due to air resistance and friction at the suspension point, this oscillation slowly subsides and ultimately the pendulum comes to rest along OA, its equilibrium position.
A Few Definitions Related To Simple Pendulum
Plane Of Oscillation: In the given diagram, the straight lines OA, OB, and OC lie on the same vertical plane. The pendulum does not leave that plane during oscillation. This plane is called the plane of oscillation.
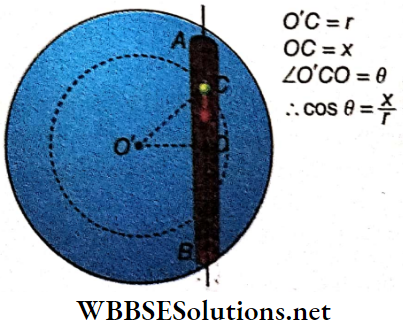
Effective Length: The distance of the center of gravity of the bob from the point of suspension is called the effective length of the pendulum. In the case of a spherical bob of radius r, the center of gravity lies at the center of the sphere, and if the length of the string is l, then the effective length L = l+r.
Amplitude And Angular Amplitude: The maximum displacement of The pendulum hob on either side of its equilibrium position is called amplitude. In the given diagram, AB or AC is the amplitude of the pendulum.
The angle subtended at the point of suspension by the equilibrium position and the maximum displaced position of the pendulum bob is the angular amplitude of the pendulum. The angular amplitude ∠AOB = ∠AOC = θ.
It is to be noted that, the angular amplitude should be less than 4° so that the arc CAB is almost a straight line.
Complete Oscillation And Period Of Oscillation Or Time Period: Starting from an endpoint, when the pendulum bob again and returns to the same point, the pendulum completes one complete oscillation.
- The bob starting from point B reaches C and returns to B. This completes one complete oscillation. During one complete oscillation, the pendulum bob covers twice the total path of its movement. Hence, let us assume that the bob starts from point A towards point B.
- After reaching point B, the bob starts moving in the opposite direction, crosses A, and reaches point C, then from C the bob reaches A. A complete oscillation is executed in this manner also. After executing one complete oscillation the pendulum returns to its initial phase.
- The time taken by a pendulum to complete one oscillation is called the period of oscillation or the time period. In other words, the time period is the minimum time taken by the pendulum to return to its starting phase.
The movement from B to C is a half oscillation of the pendulum, and the time required for it is called the half-time period or half the period of oscillation.
Simple Pendulum Frequency: The number of complete oscillations executed in one second by a pendulum is its frequency. If the time period of a pendulum is T, then as per definition, the number of complete oscillations in time T = 1. Hence, in unit time, the number of complete oscillations = \(\frac{1}{t}\).
Now, from definition, the frequency n = \(\frac{1}{t}\).
The unit of frequency is s-1 or hertz or Hz; the dimension is T-1.
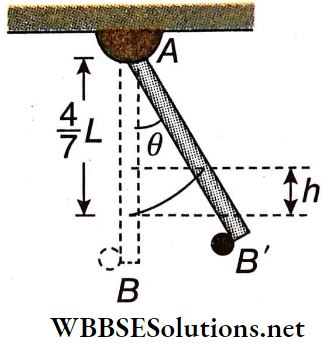
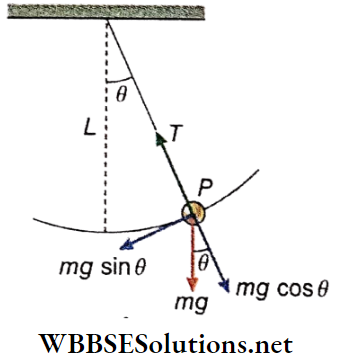
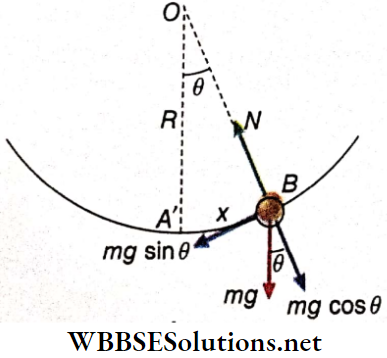
Motion Of A Simple Pendulum: A simple pendulum of effective length*1 L is oscillating with m angular amplitude not exceeding 4°. The bob of the pendulum oscillates from B to C on either side of its position of equilibrium, O.
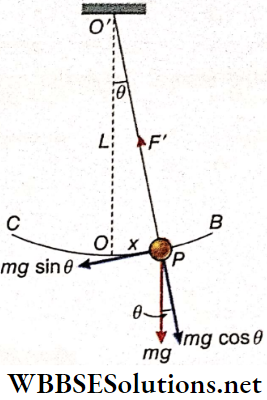
Let at any instant of motion, the bob of mass m be at P and its displacement from the position of equilibrium OP = x. If the angular displacement is θ, then θ = \(\frac{x}{L}\) rad, provided θ is small and sinθ ≈ θ ≈ tanθ.
At P, the weight mg of the bob acts vertically downwards. The component mg sinθ tries to bring the bob to the position of equilibrium. As this force acts in a direction opposite to that of displacement, it is the restoring force, expressed as
F = -mg sinθ
= -mgθ[since # is less than 4°]
= -mg\(\frac{X}{L}\)
Now, the acceleration of the bob,
a = \(\frac{F}{m}=\frac{-g}{L} x=-\omega^2 x \quad\left[\text { where, } \omega=\sqrt{\frac{g}{L}}\right]\)
As the motion of the bob obeys the equation, a = -ω²x, it can be said that the motion of a simple pendulum with an angular amplitude less than 4° is simple harmonic.
Time Period: Time period of the pendulum,
T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\frac{g}{L}}}\)
= \(2 \pi \sqrt{\frac{L}{g}}\)…(1)
Mechanical Energy Of The Pendulum: The kinetic energy of the pendulum,
K = \(\frac{1}{2} m \omega^2\left(A^2-x^2\right)=\frac{1}{2} m \frac{g}{L}\left(A^2-x^2\right)\)
The potential energy of the pendulum,
U = \(\frac{1}{2} m \omega^2 x^2=\frac{1}{2} m \frac{g}{L} x^2\)
∴ The total mechanical energy of a simple pendulum,
E = K+ U = \(\frac{1}{2} m \omega^2 A^2=\frac{1}{2} m \frac{g A^2}{L}=\frac{m g A^2}{2 L}\)
Thus, if the angular amplitude is less than 4°, the total mechanical energy of a simple pendulum is
- Directly proportional to the mass of the bob,
- Inversely proportional to the effective length of the pendulum and
- Directly proportional to the square of the amplitude of the SHM executed by the pendulum.
Tension On The String: When the pendulum oscillates about its point of suspension, a centripetal force is required for the circular motion of the bob. At the instant when the bob passes through the position of equilibrium O, its velocity becomes maximum. So, the upward centripetal force, Fc, becomes maximum at O. The resultant of downward weight mg and tension F’ on the string becomes equal to this force F.
Therefore, Fc = F’ – mg or, F’ = Fc + mg
The kinetic energy of the pendulum at P,
K = \(\frac{1}{2} m v^2=\frac{1}{2} m \omega^2\left(A^2-x^2\right)=\frac{1}{2} m \frac{g}{L}\left(A^2-x^2\right)\)
So, \(m v^2=\frac{m g\left(A^2-x^2\right)}{L}\)
Therefore, the centripetal force at P,
∴ \(F_c=\frac{m v^2}{L}=\frac{m g\left(A^2-x^2\right)}{L^2}\)
∴ \(F^{\prime}=m g+F_c=m g+m g \frac{\left(A^2-x^2\right)}{L^2}\)
= \(m g\left(1+\frac{A^2-x^2}{L^2}\right)\)
When the bob passes through O (where x = 0 ), the tension F1 on the string becomes the maximum
∴ \(F_{\max }^{\prime}=m g\left(1+\frac{A^2}{L^2}\right)\)
Seconds Pendulum Pendulum Clock Definition: A simple pendulum of a time period of 2 seconds, or a half-time period of 1 second, is called a seconds pendulum.
A seconds pendulum has a time period, T = 2s
It is known, T = \(2 \pi \sqrt{\frac{L}{g}} or, 2=2 \pi \sqrt{\frac{L}{g}}\)
or, \(1=\pi \sqrt{\frac{L}{g}} or, L=\frac{g}{\pi^2}=\frac{981}{\pi^2}=99.40 \mathrm{~cm}=0.9940 \mathrm{~m}\).
Pendulum Dock Running Fast Or Slow: A pendulum clock marks time by means of its time period. From the equation T = \(2 \pi \sqrt{\frac{L}{g}},\), it can be shown that if
- The effective length l of a pendulum changes, or
- The value of the acceleration due to gravity changes, the time period of a second pendulum does not remain 2 s, but increases or decreases accordingly.
An increase in the time period means that the pendulum oscillates slowly, i.e., the clock goes slow. On the other hand, a decrease in the time period makes the clock run fast.
- For example, when a pendulum clock is taken from the poles to the equator, or from the sea level to the top of a mountain, or from the earth’s surface to deep inside a mine, the acceleration due to gravity g decreases; hence, the time period increases. Thus, in each case, the clock goes slow.
- A pendulum clock may run slow or fast depending on the temperature. At a higher temperature, due to the expansion of the metallic suspender and the bob, the effective length increases, and the time period also increases.
On the other hand, at low temperatures, the time period decreases. Therefore, a pendulum clock runs slow in summer and fast in winter. To get the correct time from the same pendulum at different temperatures, compensated pendulums are used.
Some Uses Of A Simple Pendulum
Finding The Value Of g: From equation (1) we get, g = \(4 \pi^2 \frac{L}{T^2}\)…(1)
Using this equation, the value of acceleration due to gravity (g) of a place can be determined. For different lengths of strings, the time period (T) and the effective length (L) of a pendulum can be evaluated by experiment.
Then \(\frac{L}{T^2}\) value in each case is determined and the average value of \(\frac{L}{T^2}\) is calculated. Substituting this average value in equation (1), the value of g can be obtained.
Determining The Height Of A Place: Let R = radius of the earth, h = height of a place (say, top of a hill), g = value of acceleration due to gravity on earth’s surface, g’ = value of acceleration due to gravity at height h, T =time period of a simple pendulum al a fixed place on the earth surface and T’ = time period of the same pendulum at height h.
From equation (1) Newtonian Gravitation and Planetary Motion,
⇒ \(\sqrt{\frac{g}{g^{\prime}}}=\frac{R+h}{R}=1+\frac{h}{R}\)…(2)
Also \(T=2 \pi \sqrt{\frac{L}{g}} and T^{\prime}=2 \pi \sqrt{\frac{L}{g^{\prime}}}\)
∴ \(\frac{T}{T^{\prime}}=\sqrt{\frac{g}{g}}\)
or, \(\sqrt{\frac{g}{g^{\prime}}}=\frac{T^{\prime}}{T}\)
From (2) and (3),
1 + \(\frac{h}{R}=\frac{T^{\prime}}{T} \text { or, } \frac{h}{R}=\frac{T^{\prime}}{T}-1\)
or, h = \(\frac{R}{T}\left(T^{\prime}-T\right)\)
Knowing the value of R and determining the values of T and T’ using a stopwatch, the value of h can be determined from equation (4).
Finding The Depth Of A Mine: Let h = depth of the mine, g = value of acceleration due to gravity on earth’s surface, g’ = value of acceleration due to gravity at the depth h below earth’s surface, T = time period of a simple pendulum on the earth surface, T’ = time period of the same pendulum at depth h.
In this case, \(T=2 \pi \sqrt{\frac{L}{g}}\) and \(T^{\prime}=2 \pi \sqrt{\frac{L}{g^{\prime}}}\)
or, \(\frac{T}{T^{\prime}}=\sqrt{\frac{g^{\prime}}{g}} or, g^{\prime}=g \frac{T^2}{T^{\prime 2}}\)…(5)
From equation (4) Newtonian Gravitation and Planetary Motion, we get
⇒ \(g^{\prime}=g\left(1-\frac{h}{R}\right)\)…(6)
From equations (5) and (6), \(\frac{T^2}{T^{\prime 2}}=1-\frac{h}{R}\)
or, \(h=R\left(1-\frac{T^2}{T^{\prime 2}}\right)\)
Knowing the value of R and determining the values of T and T’ using a stopwatch, the value of h can be determined from equation (7).
Oscillation And Waves
Simple Harmonic Motion Simple Pendulum Numerical Examples
Example 1. A simple pendulum executes 40 complete oscillations in a minute. What is the effective length of the pendulum? g = 980 cm · s-2.
Solution:
Time period (T) = \(\frac{60}{40}=\frac{3}{2} \mathrm{~s}\)
Now, T = \(2 \pi \sqrt{\frac{L}{g}} or, T^2=4 \pi^2 \frac{L}{g}\)
or, \(L=\frac{g T^2}{4 \pi^2}=\frac{980 \times\left(\frac{3}{2}\right)^2}{4 \times \pi^2}=55.9 \mathrm{~cm}\).
Example 2. What will be the percentage increase in the time period of a simple pendulum when its length is increased by 21%?
Solution:
Given, the increase in length of the pendulum = 0.21 L, where L is the initial length
Hence, increased length L’ = L + 0.21L = 1.211
Let, the time period change to T’ from T due to the change in length.
As T ∝ √L,
⇒ \(\frac{T}{\sqrt{L}}=\text { constant }\)
Thus, \(\frac{T}{\sqrt{L}}=\frac{T^{\prime}}{\sqrt{L}}\)
or, \(T^{\prime}=\sqrt{\frac{L^{\prime}}{L}} T=\sqrt{\frac{1.21 L}{L}} T=1.1 T\)
∴ Increase in time period = \(T^{\prime}-T=1.1 T-T\)
= 0.1 T = 10% of T
Hence, the time period increases by 10%.
Example 3. Two simple pendulums of lengths 100 cm and 101 cm are set Into oscillation at the same time. After what time does one pendulum gain one complete oscillation over the other?
Solution:
The length of the First pendulum is comparatively less, and hence, its time period is also less; thus the first pendulum oscillates faster.
By the time the second pendulum executes n oscillations, suppose the first one completes (n + 1) oscillations.
Hence, if T1 and T2 are time periods of the first and the second pendulums, \((n+1) T_1=n T_2 \text { or, } \frac{T_2}{T_1}=\frac{n+1}{n}=1+\frac{1}{n}\)…(1)
Again \(\frac{T_2}{T_1}=\sqrt{\frac{L_2}{L_1}}=\sqrt{\frac{101}{100}}=\left(1+\frac{1}{100}\right)^{1 / 2}\)
= \(1+\frac{1}{2} \times \frac{1}{100}\)=\(1+\frac{1}{200}\)…(2)
From equations (1) and (2) \(\frac{1}{n}=\frac{1}{200} \text { or, } n=200 \text {, i.e., } n+1=201\)
Thus, the required time = time of 201 complete oscillations of the first pendulum = \(201 \times T_1\)
= \(201 \times 2 \pi \sqrt{\frac{L_1}{g}}\)
= \(201 \times 2 \times \pi \sqrt{\frac{100}{980}} \approx 403 \mathrm{~s}=6 \mathrm{~min} 43 \mathrm{~s} .\)
Example 4. Find the length of a simple pendulum on the surface of the moon that has a time period same as that of a simple pendulum on the earth’s surface. The mass of Earth is 80 times that of the moon and the radius of Earth is 4 times that of moon.
Solution:
If masses of the earth and the moon are and respectively, \(\frac{M_1}{M_2}=80\)
Again, their radii are R1 and R2 (say).
So, \(\frac{R_1}{R_2}=4\)
Acceleration due to gravity on earth, \(g_1=\frac{G M_1}{R_1^2}\); acceleration due to gravity on moon, \(g_2=\frac{G M_2}{R_2^2}\)
∴ \(\frac{g_1}{g_2}=\frac{M_1}{M_2} \times \frac{R_2^2}{R_1^2}=\frac{M_1}{M_2} \times\left(\frac{R_2}{R_1}\right)^2=80 \times\left(\frac{1}{4}\right)^2=5\)
Also, in the case of a simple pendulum, time period on earth’s surface T = \(2 \pi \sqrt{\frac{L_1}{g_1}}\)
and time period on the moon’s surface T = \(2 \pi \sqrt{\frac{L_2}{g_2}}\)
∴ \(\sqrt{\frac{L_1}{g_1}}=\sqrt{\frac{L_2}{g_2}} \text { or, } \frac{L_1}{L_2}=\frac{g_1}{g_2}=5\)
∴ \(L_2=\frac{L_1}{5}\)
Hence, the length of the pendulum on the moon’s surface should be 1/5 th of its length on the earth’s surface.
Example 5. Two pendulums of time periods 1.8 s and 2 s are set Into oscillation at the same time. After how many seconds will the faster-moving pendulum execute one complete oscillation more than the other? How many oscillations will the faster-moving pendulum execute during this time?
Solution:
Suppose the faster pendulum executes one more oscillation than the other after t s.
Number of complete oscillations of the first pendulum in t s = \(\frac{t}{1.8}\)
Number of oscillations of the second pendulum in t s = \(\frac{t}{2}\)
According to the given condition, \(\frac{t}{1.8}\) – \(\frac{t}{2}\) = 1
or, 0.2t= 2×1.8 or, t = 18 s
Number of complete oscillations executed by the faster pen¬dulum (time period 1.8 s) = \(\frac{1.8}{1.8}\) = 10.
Example 6. A pendulum clock runs 20s slow per day. What should be the change in length of the clock so that it records the correct time? Take the pendulum as a simple pendulum.
Solution:
Half time period of a simple pendulum t = \(\frac{T}{2}=\pi \sqrt{\frac{L}{g}}\)
For a perfect seconds pendulum t = 1s
∴ 1 = \(\pi \sqrt{\frac{L}{g}} \text { or, } L=\frac{g}{\pi^2}\)….(1)
Also, 1d = 24 x 60 x 60 = 86400 s.
Number of half oscillations executed in a day by a pendulum that runs 20 s slow per day = 86400 – 20 = 86380.
Hence, the time period of that pendulum \(t_1=\frac{86400}{86380} \mathrm{~s}\)
If the length of this simple pendulum is L1, then \(t_1=\pi \sqrt{\frac{L_1}{g}} \text { or, } L_1=\frac{g t_1^2}{\pi^2}\)…(2)
Subtracting equation (1) from equation (2), \(L_1-L=\frac{g}{\pi^2}\left(t_1^2-1\right)\) = \(\frac{980}{\pi^2}\left[\left(\frac{86400}{86380}\right)^2-1\right]\)
Hence, to get the correct time, the length of the pendulum is to be decreased by 0.46 mm.
Alternative Method: Half-time period of a perfect seconds pendulum = 1 s.
Number of Half oscillations of a clock that runs slow by t0 s in a day = 86400 – t0.
Hence, half time period = \(\frac{86400}{86400-t_0} \mathrm{~s} \)
∴ Increase in the value of half time period, dt = \(\frac{86400}{86400-t_0}-1=\frac{t_0}{86400-t_0} \mathrm{~s}\)
If the value of t0 is negligibly smaller than 86400, dt \(=\frac{t_0}{86400} \mathrm{~s}\)
Now, t = \(pi \sqrt{\frac{L}{g}} or, \log t=\log \pi+\frac{1}{2} \log L-\frac{1}{2} \log g\)
Differentiating, \(\frac{d t}{t}=\frac{1}{2} \frac{d L}{L}-\frac{1}{2} \frac{d g}{g}\)…(1)
Here, dL = increase in length and dg = increase in acceleration due to gravity.
Putting values of t and dt in (1), \(\frac{t_0}{86400}=\frac{1}{2}\left(\frac{d L}{L}-\frac{d g}{g}\right)\)
or, \(t_0=43200\left(\frac{d L}{L}-\frac{d g}{g}\right)\)…(2)
This equation can be used as a rule for a seconds pendulum. For a second pendulum L = \(\frac{g}{\pi^2}\) and on the surface of the earth g = 980 cm · s-2. If the clock runs fast, the value of t0 is negative.
In the given problem, t0 = 20 s;
If there is no change in the value of g, dg = 0
∴ \(t_0=43200 \times \frac{a L}{L}\)
or, \(d L=\frac{20 \times L}{43200}=\frac{20}{43200} \times \frac{980}{\pi^2}=0.046 \mathrm{~cm}=0.46 \mathrm{~mm}\)
Hence, the length of the defective clock has increased by 0.46 mm. Thus to get the correct time, its length needs to be decreased by 0.46 mm.
Example 7. A pendulum of length 60 cm is suspended inside an airplane. The aeroplane is flying up with an acceleration of 4 m · s-2 making an angle of 30° with the horizontal. Find the time period of oscillation of the pendulum.
Solution:
Horizontal component of acceleration a of the plane = acos30° and vertical component = asin30°
Hence, the downward acceleration experienced by the pendulum bob = g- (-a sin30°) = g+ a sin30°
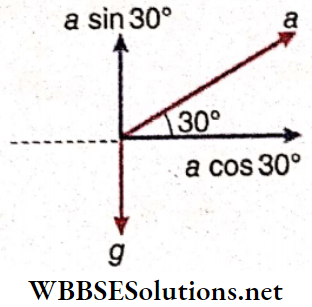
So, the acceleration of the pendulum bob
g’ = \(\sqrt{\left(g+a \sin 30^{\circ}\right)^2+\left(a \cos 30^{\circ}\right)^2} \)
= \(\sqrt{\left(9.8+4 \times \frac{1}{2}\right)^2+\left(4 \times \frac{\sqrt{3}}{2}\right)^2}=\sqrt{(11.8)^2+12}\)
= \(\sqrt{151.24}=12.3 \mathrm{~m} \cdot \mathrm{s}^{-2}\)
∴ The time period of the pendulum
T = \(2 \pi \sqrt{\frac{L}{g^{\prime}}}=2 \times \pi \sqrt{\frac{0.60}{12.3}}=1.38 \mathrm{~s} .\)
Example 8. The effective length of a simple pendulum is 1 m and the mass of its bob is 5 g. If the amplitude of motion of the pendulum is 4 cm, what is the maximum tension on the string to which the bob is attached?
Solution:
The velocity of the bob is maximum at its position of equilibrium.
The maximum velocity \(v_{\max }=\omega A=\frac{2 \pi A}{T} .\)
At this position, centripetal force is also maximum, whose value is \(F_c=\frac{m \nu_{\max }^2}{L}=\frac{m \omega^2 A^2}{L}\)
[L = effective length of the pendulum]
The resultant of the weight mg of the bob and tension F on the string becomes equal to this force Fc .
∴ F = \(m g+F_c=m g+\frac{m \omega^2 A^2}{L}=m\left(g+\frac{\omega^2 A^2}{L}\right)\)
Again, \(T=2 \pi \sqrt{\frac{L}{g}} ; so, \omega=\frac{2 \pi}{T}=\sqrt{\frac{g}{L}} or, \omega^2=\frac{g}{L}\)
∴ F = \(m\left(g+\frac{g A^2}{L^2}\right)=m g\left(1+\frac{A^2}{L^2}\right)\)
= \(5 \times 980\left(1+\frac{4^2}{100^2}\right)[because L=1 \mathrm{~m}=100 \mathrm{~cm}]\)
= \(4908 \mathrm{dyn}=0.04908 \mathrm{~N} \approx 0.05 \mathrm{~N}\)
Example 9. Prove that the change in the time period t of a simple pendulum due to a change AT of temperature is, \(\Delta t=\frac{1}{2} \alpha t \Delta T\), where α = coefficient of linear expansion.
Solution:
If L is the effective length of a simple pendulum, then its time period is, t = \(2 \pi \sqrt{\frac{L}{g}}\)
For a change ΔT of temperature, the length becomes, L’ = L(1 +αΔT)
Therefore the time period,
t’ = \(2 \pi \sqrt{\frac{L}{g}}=2 \pi \sqrt{\frac{L}{g}(1+\alpha \Delta T)}\)
= \(2 \pi \sqrt{\frac{L}{g}}(1+\alpha \Delta T)^{1 / 2}=t\left(1+\frac{1}{2} \alpha \Delta T\right)=t+\frac{1}{2} \alpha t \Delta T\)
[neglecting the terms containing a², a³, etc. since a is very small]
The change in time period, Δt = t’ -t = \(\frac{1}{2}\)αtΔT (Proved).
Alternative Method: t = \(2 \pi \sqrt{\frac{L}{g}}\)
log t = \(\log 2 \pi+\frac{1}{2} \log L-\frac{1}{2} \log g\)
Differentiating with respect to L, \(\frac{1}{t} d t=\frac{1}{2 L} d L\)
∴ \(\frac{d t}{t}=\frac{1}{2} \frac{d L}{L}\)…(1)
Now \(L_t=L(1+\alpha \Delta T)\)
or, \(L_t-L=L \alpha \Delta T or, d L=L \alpha \Delta T\)
or, \(\frac{d L}{L}=\alpha \Delta T\)…(2)
From equations (1) and (2) we get, \(\frac{d t}{t}=\frac{1}{2} \alpha \Delta T \text { or, } d t=\frac{1}{2} \alpha \Delta T \cdot t \text { (Proved). }\)
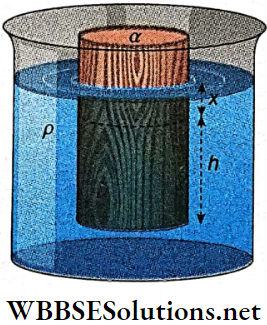
Example 10. The bob of a simple pendulum is made of brass and its time period is T. It is completely immersed in a liquid and is allowed to oscillate. If the density of the liquid is 1/8 th of the density of brass, what will be the time period of oscillation of the pendulum now?
Solution:
Initial time period of the simple pendulum, T = \(2 \pi \sqrt{\frac{L}{g}}\)
[L = effective length of the pendulum]
If m is the mass, V is the volume of the bob and d is the density of brass, then the apparent weight of the hob inside the liquid,
W1 = W- buoyancy (weight of the displaced liquid)
= \(V d g-V \frac{d}{8} g=\frac{7}{8} V d g\)
If g1 is the effective acceleration due to gravity in the immersed condition, then
⇒ \(W_1=m g_1=\frac{7}{8} V d g \text { or, } g_1=\frac{7}{8} \frac{m g}{m}=\frac{7}{8} g\)
∴ Final time period, \(T_1=2 \pi \sqrt{\frac{L}{g_1}}=2 \pi \sqrt{\frac{8 L}{7 g}}=\sqrt{\frac{8}{7}} T\).
Example 11. A brass sphere is hung from one end of a massless and inextensible thread. When the sphere is set into oscillation, it oscillates with a time period of T. If now the sphere is dipped completely into a non-viscous liquid, then what will be the time period of its oscillation? (The density of the liquid is 1/10th of that of brass)
Solution:
Let the volume of the sphere be V, the density of brass be ρ, the density of the liquid be ρ’.
∴ Apparent weight of the sphere when immersed in the liquid = real weight – weight of displaced liquid = Vρg-Vρ’g =Vg(ρ-ρ’)
∴ Apparent acceleration due to gravity of the sphere immersed in the liquid,
g’ = \(\frac{\text { apparent weight }}{\text { mass }}=\frac{V g\left(\rho-\rho^{\prime}\right)}{V \rho}=g\left(1-\frac{\rho^{\prime}}{\rho}\right)\)
According to the problem, \(\frac{\rho^{\prime}}{\rho}=\frac{1}{10}\);
hence \(g^{\prime}=g\left(1-\frac{1}{10}\right)=\frac{9}{10} g \text {. }\)
In the case of a simple pendulum, \(T\propto \frac{1}{\sqrt{g}}\); so, if the rime period of oscillation of the sphere, when unmersed in die liquid, is T’, then \(\frac{T^{\prime}}{T}=\sqrt{\frac{g}{g^{\prime}}}=\sqrt{\frac{10}{9}} \text { or, } T^{\prime}=\frac{\sqrt{10}}{3} T \text {. }\)
Oscillation And Waves
Simple Harmonic Motion A Few Examples Of SHM
Oscillation Of A Mass Attached To A Vertical Elastic Spring: Let a body of mass m be attached to the bottom of a vertical elastic spring of negligible mass suspended from a rigid support, As a result of this, let the increase in length of the spring be l.
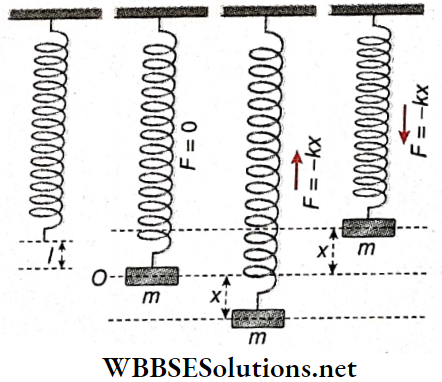
So the force constant of the spring.
k = force required for a unit increase in length = \(\frac{mg}{l}\)
Now the mass is pulled downwards through a distance x from its position of equilibrium O. If the extension of the spring does not exceed its elastic limit, then a reaction force, – kx, equal and opposite to the applied force is developed in the spring.
This force acts as the restoring force. If a is the acceleration of the suspended body, then restoring force -kx = ma
or, a = \(\frac{-k}{m} x=-\omega^2 x \quad\left[\text { where } \omega=\sqrt{\frac{k}{m}}\right]\)
As the motion of the body of mass m obeys the equation a = -ω²x, it can be said that the motion of the body attached to the spring is simple harmonic.
In this case, the time period of oscillation,
T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m}{k}} .\)
Now, k = \(\frac{m g}{l}\); therefore T = \(2 \pi \sqrt{\frac{m}{\frac{m g}{l}}}=2 \pi \sqrt{\frac{l}{g}}\)
Here, the initial increase in length of the spring due to suspension of the body of mass m is l. So by measuring this increase in length with a meter scale and the time period T with a stopwatch, acceleration due to gravity g can be calculated from the above relation.
Oscillation Of A Mass Attached To A Horizontal Elastic Spring: Let one end of an elastic spring of negligible mass be attached to a vertical support and its other end to a body of mass m. The body lies on a smooth horizontal plane. At this moment, no force acts on the body due to the spring as it is not stretched. So the body is at rest.
If the body is now moved towards the right, the spring will be elongated and a restoring force F will act on the body towards the left, trying to bring the mass to its equilibrium position.
If the force constant of the spring is k and the body is moved through a distance x towards the right, then F = – kx.
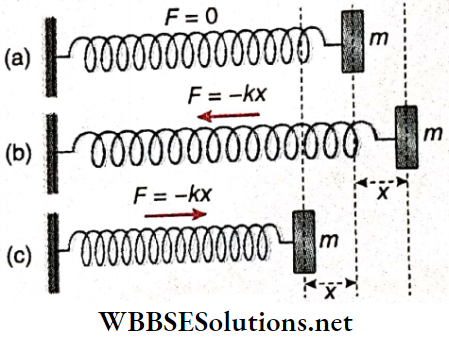
∴ Acceleration of the body, a = \(\frac{F}{m}=\frac{-k x}{m}=-\omega^2 x\left[\text { where } \omega=\sqrt{\frac{k}{m}}\right]\)
As the motion of the body obeys the equation, a = -ω²x, it can be said that the motion of the body attached to the spring is simple harmonic.
Time period of oscillation, T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m}{k}}\)
It is to be noted that the time periods of vertical oscillation and horizontal oscillation of a spring are equal.
Oscillation Of A Liquid In A U-Tube: Consider that a U-tube of uniform cross-section a contains a liquid of density ρ. Let the length of the liquid column in each limb at equilibrium be L. Therefore the total length of the liquid column is 2L, if the horizontal separation between the two limbs is negligibly small.
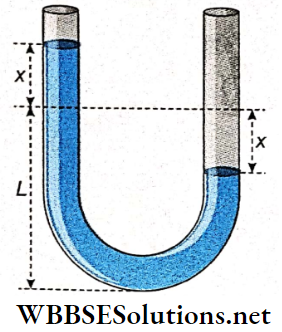
Then the mass of the liquid column, m = 2Lαρ
If the liquid in one limb is depressed by x then the liquid level in the other limb will be raised by x. Hence the difference in the height of the liquid levels in the two limbs will be 2x.
Weight of this liquid head = 2xαρg.
This weight provides a restoring force trying to bring the liquid to its initial equilibrium. This force acts opposite to the direction of displacement x in the two limbs.
Thus, restoring force = -2xαρg.
Due to this force, if a is the acceleration of the liquid level, then ma = -2xαρg
or, 2Lαρa = -2xαρg
or, a = \(\frac{-g \cdot x}{L}=-\omega^2 x\left[\text { where } \omega=\sqrt{\frac{g}{L}}\right]\)
As the motion of the liquid level obeys the equation a = -ω²x, it follows a simple harmonic motion. So, if the liquid in one limb of a U-tube is depressed and then released, the up and down motion of the liquid column would be simple harmonic.
Time period of this motion, T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{L}{g}}\)
Oscillation Of A Piston In A Gas Cylinder: Suppose, some amount of gas is enclosed in a cylinder fitted with a frictionless piston. Let the piston be initially at C, the position of equilibrium, the pressure of the gas enclosed be P and the length of the gas column be L.
The piston is now pushed down slightly to B very slowly and then released. The compressed gas will then expand and cause the piston to oscillate up and down.
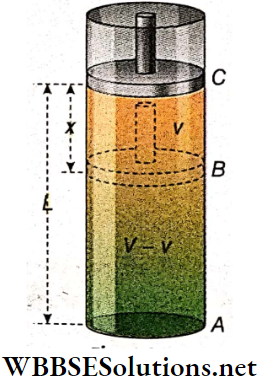
When the piston is moved through a distance x from C to B, suppose the pressure of the enclosed gas increases from P to P + p and the volume decreases to (V- v) from V. If this change takes place isothermally, then according to Boyle’s law, PV = (P + p) (V- v)
or, PV = PV-Pv+ pV-pv
or, Pv = pV [neglecting pν as it is very small]
or, p = \(\frac{P v}{V}=\frac{P \alpha x}{\alpha L}=\frac{P x}{L}\)
[α = cross-sectional area of the piston]
An additional force acts on the piston for this excess pressure p and tries to bring the piston to its initial position of equilibrium.
So, the restoring force = \(-p \alpha=\frac{-P \alpha x}{L}\)
∴ Acceleration of the piston,
a = \(\frac{\text { restoring force }}{\text { mass of the piston }}=-\frac{P \alpha x}{L M}\)
[M = mass of the piston]
or, a = \(-\omega^2 x, \text { where } \omega=\sqrt{\frac{P \alpha}{L M}}\)
The motion of the piston obeys the equation a = -ω2x.
So this motion is simple harmonic. –
Time period of this motion, T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{L M}{P \alpha}}=2 \pi \sqrt{\frac{L \alpha M}{P \alpha^2}}=2 \pi \sqrt{\frac{V M}{P \alpha^2}} .\)
Simple Harmonic Motion Synopsis
Periodic Motion: Any motion, which repeats itself at regular intervals of time is called periodic motion.
Oscillation Or Vibration: If a particle executing periodic motion moves to and fro along the same path, the motion is called oscillation or vibration.
Complete Oscillation: If an oscillating particle starting from any point on its path towards a certain direction returns to the same point and then moves in the same direction, it is said to have executed a complete oscillation.
Time Period: The time period of oscillation of a vibrating particle (T) is defined as the time taken by it to execute one complete oscillation.
Frequency: The frequency of oscillation of a vibrating particle (n) is defined as the number of complete oscillations executed by it in 1 second.
Amplitude: The magnitude of the maximum displacement of a vibrating particle on either side of its position of equilibrium is called the amplitude (A) of vibration.
Phase: The state of the motion at any instant of a particle executing simple harmonic motion is called its phase.
Initial Phase Or Epoch: Epoch or phase constant is the phase of the particle executing simple harmonic motion at the initial instant, i.e., at t = 0.
Simple Harmonic Motion: If the acceleration of a vibrating particle is
- Directly proportional to the displacement of the particle from the position of equilibrium and
- Is always directed towards the equilibrium position, then the motion is called a simple harmonic motion.
- All simple harmonic motions are periodic motions but all periodic motions are not simple harmonic.
- If it is possible to oscillate a small but heavy body suspended from a rigid support by means of a long, weightless, and inextensible string, then that system is called a simple pendulum.
- The motion of a simple pendulum is simple harmonic in nature if the angular amplitude of oscillation of the pendulum is less than 4°.
- A simple pendulum that has a time period of 2s or a half time period of Is is called a seconds pendulum.
Simple Harmonic Motion Useful Relations For Solving Numerical Problems
For a SHM, F ∝-x or, F = -kx; [where, F = restoring force, k = force constant, x = displacement of the particle from its equilibrium position,]
a = -ω²x and ω = 2πn [where, a = acceleration of the particle, n = frequency, ω = angular frequency]
Differential Equation Of Simple Harmonic Motion: \(\frac{d^2 x}{d t^2}=-\omega^2\)
The General Equation For Displacement In A Simple Harmonic Motion: x = A sin(ωt+ α)
(where, A = amplitude, α = initial phase]
The velocity of a particle executing simple harmonic motion, v = \(\pm \omega \sqrt{A^2-x^2}\) maximum velocity vmax = ± Aω [where x = A]; minimum velocity vmin = 0 (where x = ±A)
Acceleration, a = -ω²x, maximum acceleration, amax = ω²A [where x = ±A]; minimum acceleration, amin = 0 (where x = 0)
Kinetic energy, K = \(\frac{1}{2} m v^2=\frac{1}{2} m \omega^2\left(A^2-x^2\right)\)
Potential energy, U = \(\frac{1}{2} m \omega^2 x^2\)
Total energy, E = \(K+U=\frac{1}{2} m \omega^2 A^2=\text { constant }\)
Time period, T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{x}{a}}=2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}}\)
Frequency, n = \(\frac{1}{T}\)
Time period of a simple pendulum oscillating at an angular amplitude less than 4° is T = \(2 \pi \sqrt{\frac{L}{g}}\)
[where, L = effective length of the pendulum = length from the point of suspension of the pendulum to the center of gravity of the bob.]
In case of oscillation of a mass attached to a vertical elastic spring, time period, T = \(2 \pi \sqrt{\frac{m}{k}}=2 \pi \sqrt{\frac{l}{g}}\)
[where, k = spring constant, l = initial elongation of the spring due to the attachment of the mass m]
In case of oscillation of a mass attached to a horizontal elastic spring, time period, T = \(2 \pi \sqrt{\frac{m}{k}}\)
In case of oscillation of a liquid in a U-tube, time period, T = \(2 \pi \sqrt{\frac{L}{g}}\)
[Where L = length of the liquid column in each limb at equilibrium].
Simple Harmonic Motion Very Short Answer Type Questions
Question 1. If the time period of an SHM is 2 s, then what will be its frequency?
Answer: \(\frac{1}{2}\)Hz
Question 2. If the frequency of an SHM is 200 Hz, then what will be its time period?
Answer: \(\frac{1}{200}s\)
Question 3. What is the unit of force constant of SHM in SI?
Answer: N • m-1
Question 4. The motion of the earth around the sun is a ______ motion.
Answer: Periodic
Question 5. What is the maximum displacement of a vibrating particle from the equilibrium position called?
Answer: Amplitude
Question 6. What is the phase difference between the displacement and the velocity of a particle executing SHM?
Answer: 90°
Question 7. What is the phase difference between the displacement and the acceleration of a particle executing SHM?
Answer: 180°
Question 8. If the time period is T then what will be the time taken by a particle executing SHM to traverse from the position of equilibrium to an extremity?
Answer: \(\frac{T}{4}\)
Question 9. What will be the change in the time period of a simple pendulum if the metallic bob of the pendulum is replaced by a wooden bob of the same radius? provided both bobs are of uniform density
Answer: Time Period Remains The same
Question 10. In which direction is the acceleration of a particle executing SHM directed?
Answer: Equilibrium
Question 11. At which points of its path, the velocity of a particle executing SHM becomes zero?
Answer: Extreme
Question 12. At which position, the velocity of a particle executing SHM becomes maximum?
Answer: Equilibrium
Question 13. At which position, the acceleration of a particle executing SHM become zero?
Answer: Equilibrium
Question 14. At which points of its path, the acceleration of a particle executing SHM becomes maximum?
Answer: Extreme
Question 15. A simple pendulum is oscillating in a vertical plane with a small amplitude. State whether the total energy at any point in its motion will be equal to that at an extreme point.
Answer: Yes
Question 16. At which position, the kinetic energy of a particle executing SHM becomes maximum?
Answer: Equilibrium
Question 17. At which points of its path, the potential energy of a particle executing SHM becomes maximum?
Answer: Extreme
Question 18. Total mechanical energy of a simple pendulum is directly proportional to the mass of the pendulum. Is the statement true or false?
Answer: True
Question 19. How is the total mechanical energy of a simple pendulum related to the length of the pendulum?
Answer: Inversely proportional
Question 20. Total mechanical energy of a simple pendulum is directly proportional to the amplitude of the pendulum. Is the statement true or false?
Answer: False
Question 21. The bob of a simple pendulum is made of iron. A powerful magnetic pole is placed below the bob in its equilibrium position. How will the time period of the pendulum change?
Answer: Decrease
Question 22. A body attached to a spring is executing SHM. If the force constant of the spring is increased then what will be the change in the frequency of oscillation?
Answer: Frequency will increase
Question 23. If a straight tunnel is bored from the north pole to the south pole of the earth and if a body is dropped into that tunnel then what time will the body take to move from one end to the other end of the tunnel?
Answer: 42 min
Question 24. What is the type of motion of a body along the tunnel passing through the centre of the earth?
Answer: Simple harmonic
Simple Harmonic Motion Assertion Reason Type Question And Answers
Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.
- Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
- Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
- Statement 1 is true, statement 2 is false.
- Statement 1 is false, and statement 2 is true.
Question 1.
Statement 1: The total energy of a particle performing simple harmonic motion could be negative.
Statement 2: The potential energy of a system could be negative.
Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
Question 2.
Statement 1: The spring constant of a spring is k. When it is divided into n equal parts, then the spring constant of each piece is k/n.
Statement 2: The spring constant is independent of the material used for the spring.
Answer: 4. Statement 1 is false, statement 2 is true.
Question 3.
Statement 1: A particle performs a simple harmonic motion with amplitude A and angular frequency ω. To change the angular frequency of the simple harmonic motion to 3ω and amplitude to A/2, we have to supply an extra energy of (5/4) mω²A², where m is the mass of the particle executing simple harmonic motion.
Statement 2: The angular frequency of simple harmonic motion is independent of the amplitude of oscillation.
Answer: 4. Statement 1 is false, statement 2 is true.
Simple Harmonic Motion Match Column 1 With Column 2
Question 1. A particle of mass 2 kg is moving on a straight line under the action of force F = (8 – 2x)N. The particle is released from rest at x = 6m. For the subsequent motion match the following (all the values in Column 2 are in their SI units.)

Answer: 1. C, 2. D, 3. D, 4. B
Question 2. Two particles ‘ P ’ and ‘ Q ’ start SHM at t = 0. Their positions as a function of time are given by \(x_p=A \sin \omega t; \quad x_Q=A \sin \left(\omega t+\frac{\pi}{3}\right)\)
Answer: 1. B, 2. A, 3. D, 4. C
Simple Harmonic Motion Comprehension Type Question And Answers
Read the following passages carefully and answer the questions at the end of them.
Question 1. A block of mass m is connected to a spring of spring constant k as shown. The block is found at its equilibrium position at t = 14 and it has a velocity of 0.25 m · s-1 at t = 2s. The time period of oscillation is 6s.
1. The amplitude of oscillation is
- \(\frac{3}{2 \pi} \mathrm{m}\)
- \(3 \mathrm{~m}\)
- \(\frac{1}{\pi} \mathrm{m}\)
- \(1.5 \mathrm{~m}\)
Answer: 1. \(\frac{3}{2 \pi} \mathrm{m}\)
2. Determine the velocity of a particle at t = 5s.
- -0.4 m · s-1
- 0.5 m · s-1
- -0.25 m · s-1
- None of these.
Answer: 3. -0.25 m · s-1
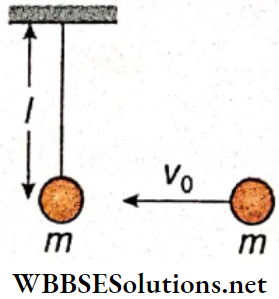
Question 2. Two identical blocks A and B, each of mass m = 3 kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown. Another identical block C moving with velocity v0 = 0.6 m · s-1 collides with A and sticks to it. As a result, the motion of the system takes place in some way.
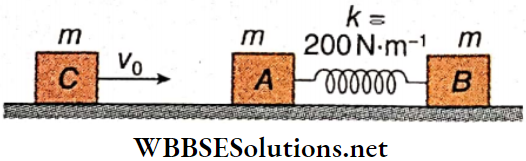
1. After the collision of C and A, the combined body and block B would
- Oscillate about the center of mass of the system and the center of mass is at rest
- Oscillate about the center of mass of the system and the center of mass is moving
- Oscillate but about different locations other than the center of mass
- Not oscillate
Answer: 2. Oscillate about the center of mass of the system and the center of mass is moving
2. Oscillation energy of the system, i.e., part of the energy which is oscillating (changing) between potential and kinetic forms, is
- 0.27 J
- 0.09 J
- 0.18 J
- 0.45 J
Answer: 2. 0.09 J
3. The maximum compression of the spring is
- 3√30 mm
- 3√20 mm
- 3√10 mm
- 3√50 mm
Answer: 3. 3√10 mm
Question 3. A particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation, the spring becomes unstretched. Take g = π² m • s-2
1. The maximum speed of the particle is
- 5π cm · s-1
- 4π cm · s-1
- 3π cm · s-1
- 2π cm · s-1
Answer: 1. 5π cm · s-1
2. The speed of the particle when the spring is stretched by 0.2 cm is
- 15.4 cm · s-1
- 12.8 cm · s-1
- 10.8 cm · s-1
- 11.4 cm · s-1
Answer: 1. 15.4 cm · s-1
Question 4. Two identical balls A and B each of mass 0.1 kg are attached to two identical massless springs. The spring-mass system is constrained to move inside a rigid smooth pipe bent in the form of a circle as shown. The pipe is in the horizontal plane. The centers of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and a spring constant of 0.1 N · m-1. Initially, both the balls are displaced by an angle θ = \(\frac{\pi}{6}\) radian with respect to the diameter PQ of the circle.
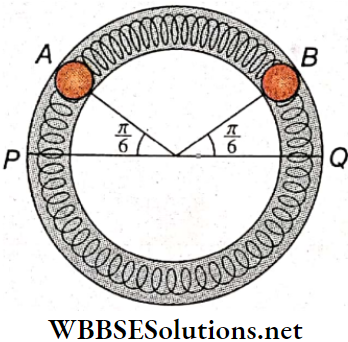
1. The frequency of oscillation of ball B is
- π HZ
- π-1 HZ
- π² HZ
- π-2 Hz
Answer: 1. π HZ
2. Speed of ball A when A and B are at the two ends of the diameter PQ
- 0.05 m · s-1
- 0.071 m · s-1
- 0.0628 m · s-1
- 0.083 m · s-1
Answer: 3. 0.0628 m · s-1
3. The total energy of the system is
- 4 x 10-4 J
- 5 x 10-3 J
- 4 x 10-3J
- 5 x 10-4 J
Answer: 1. 4 x 10-4 J
Question 5. A man has an antique pendulum clock of 1832 which bears the signature of the purchaser. He does not want to replace it in the fond memory of his great-grandparents. It ticks off one second in each side-to-side swing. It keeps the correct time at 20 °C. The pendulum shaft is made of steel and its mass can be ignored as compared to the mass of the bob. The linear expansion coefficient of steel is 1.2x 10-5 °C-1
1. What is the fractional change in length if the shaft is cooled to 10 °C?
- 0.01 %
- 1.2 x 10-1 %
- 1.2 x 10-3 %
- 1.2 x 10-4 %
Answer: 1. 1.2 x 10-2 %
2. How many seconds will the clock gain or lose in a day at 10 ºC?
- Gains 5.2 s
- Loses 5.2 s
- Gains 10.4 s
- Loses 10.4 s
Answer: 1. Gains 5.2 s
3. How closely must the temperature be controlled so that it does not gain or lose more than a second in a day?
- ± 0.2 °C
- ± 0.1 °C
- ± 1 °C
- ± 2 °C
Answer: 4. ± 2 °C
4. The pendulum mentioned in the paragraph is called _____ and its time period is_______
- Seconds pendulum, 1s
- Seconds pendulum, 2s
- 2 Second pendulum, 2s
- None
Answer: 2. Seconds pendulum, 2s
Simple Harmonic Motion Integer Type Question And Answers
In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.
Question 1. If the displacement (x) and velocity (v) of a particle executing SHM are related through the expression 4v² = 25-x², what should be the value of (T/π)? [T is the time period (in second) of the SHM.]
Answer: 4
Question 2. Starting from the origin, a body oscillates simply harmonically with a period of 2s. After a certain time (t) its kinetic energy will be 75% of the total energy. What should be the value of 1/t (in s-1)?
Answer: 6
Question 3. A particle executing SHM can be expressed by the equation x = 3cosωt+ 4sinωt. Find the amplitude of the resultant SHM.
Answer: 5
Question 4. Two pendulums of lengths 100 cm and 225 cm start oscillating in phase simultaneously. After how many oscillations will they again be in phase together?
Answer: 2
Question 5. At a certain temperature, the pendulum of a clock keeps the correct time. The coefficient of linear expansion for the pendulum material = 1.85 x 10-5 K-1. How much will the clock gain or lose in 24 h if the ambient temperature is 10 °C higher?
Answer: 8