Hydrostatics Buoyancy And Buoyant Force
A body appears lighter when it is immersed totally or partly in a liquid or a gas. For example, a pitcher full of water appears lighter when immersed in water.
On drawing a bucket full of water from a well, it appears lighter as long as it is inside water. But once it rises above water, it appears heavier. In no case does the actual weight of a body decrease, but the body experiences an apparent loss of weight.
Buoyancy And Buoyant Force Definition: The ability of a liquid or a gas at rest to exert an upward force on a body immersed in that fluid is called buoyancy.
- When a body is immersed in a liquid or a gas, the liquid or the gas exerts pressure that is different on different parts of the body. The pressure at any point on the body depends on the depth of that point from the free surface or the upper surface of that liquid or gas.
- Since the immersed body experiences different forces at different points, we can say that the body experiences a resultant force or thrust which acts in the upward direction. This resultant upward thrust balances a part of the downward force due to the weight of the body and hence the body suffers an apparent loss of weight.
Read and Learn More: Class 11 Physics Notes
Definition: The upward thrust exerted by a liquid or a gas at rest on a body partly or totally immersed in it is called buoyant force.
The terms buoyancy and buoyant force usually have the same meaning.
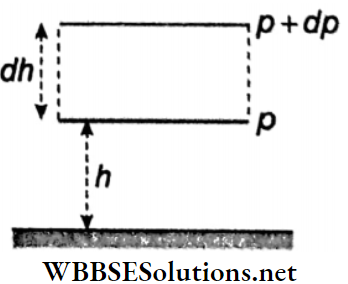
The Magnitude Of Buoyancy On A Body Immersed In A Liquid: Let a cube ABCDEFGH be immersed in a liquid of density ρ. The depths of the surfaces ABCD and EFGH of the cube from the upper surface of the liquid are h1 and h2 respectively. Each side of the cube is length of l.
The surfaces ABCD and EFGH of the cube are horizontal but the other surfaces are vertical. The liquid exerts a normal thrust on each surface of the cube.
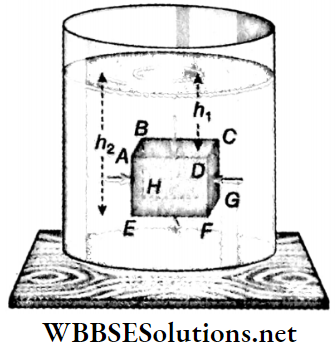
The lateral thrusts acting horizontally on the mutually opposite vertical faces ABHE and CDFG, being equal and opposite, balance each other. Similarly, the lateral thrusts acting on the side faces AEFD and BCGH balance each other.
So, no lateral resultant thrust acts on the cube in the horizontal direction. But, due to the difference in the depths of the surfaces ABCD and EFGH from the upper surface of the liquid, unequal thrusts act on these two surfaces.
The downward pressure of the liquid at any point on the surface ABCD = h1ρg
The downward thrust on the surface ABCD = pressure x area = h1ρg · l²
The upward pressure of the liquid at any point on the surface EFGH = h2ρg
The upward thrust on the surface EFGH = h2ρg· l²
Since h2> h1, the upward thrust acting on the cube becomes greater than the downward thrust.
∴The net upward thrust on the cube
= \(h_2 \rho g l^2-h_1 \rho g l^2=l^2 \rho g\left(h_2-h_1\right)=l^3 \rho g\)
[because \(h_2-h_1=l\)]
But, l³ = V = volume of the cube
∴ l³ρg = Vρg = weight of the liquid of a volume equal to that of the cube.
- So, the buoyancy on the cube due to the liquid = weight of the liquid displaced by the cube.
- This inference is applicable to any object of any shape whatsoever.
- Hence, we can say that when a body is immersed partly or totally in a liquid, then the body feels an upward thrust and this upthrust or buoyant force is equal to the weight of the liquid displaced by the body.
- From the presence of the factor g in the expression of the buoyant force, it is evident that buoyancy is a direct consequence of the effect of gravity on fluid pressure.
Characteristics Of Buoyant Force:
1. The buoyant force depends on
- The volume of the immersed portion of the body,
- The density of the displaced liquid and
- The acceleration due to gravity. Gd the buoyant force acts in the direction opposite to the weight of the body.
2. For a totally immersed body, the buoyant force does not depend on the depth up to which the body is immersed inside the liquid.
3. If the volume of a body is kept unaltered, then
- The buoyant force on a totally immersed body does not depend on the size, physical state (i.e., Solid, liquid, or gas), and mass of the body but
- For a partly immersed body, the buoyant force on it does not depend upon its size or physical state but depends on its mass.
- It is clear that there will be no buoyant force acting on a body if both the body and the liquid are in a weightless condition. This situation arises in an artificial satellite or for a freely falling system.
Units And Dimension Of Buoyant Force:
- dyne CGS System
- newton SI
The dimension of the buoyant force is MLT-2.
Centre Of Buoyancy : The point where the centre of gravity of the liquid or gas is located before it is displaced by the immersed body is the centre of buoyancy or the centre of floatation of the immersed body.
The buoyant force on an immersed body acts through the centre of buoyancy. The centre of gravity and the centre of buoyancy coincide for a totally immersed body in a fluid. But for a partly immersed body, these two points are different.
Reaction Of Buoyant Force : when a body is immersed in a liquid, the displaced liquid exerts an upthrust or buoyant force on the body, and according to Newton’s third law of motion, the body also exerts an equal but opposite reaction on the liquid. The existence of this reaction can be realised from the following experiment.
Reaction Of Buoyant Force Experiment: A beaker containing water is placed on one pan of a common balance and by placing the required counterpoising weights on the other pan, the balance beam is made horizontal.
- Now, a piece of iron is tied by a thread and is immersed in water by holding the free end of the thread so that the piece of iron does not touch the wall of the beaker.
- It is seen that the pan with the beaker immediately goes down. As the liquid exerts an upthrust on the piece of iron, the iron piece at the same time applies a downward reaction on the liquid. This reaction ultimately acts on the pan and hence it goes down.
Apparent Weight Of A Body Immersed In A Liquid : Let the real weight of a body be W1 this weight acts vertically downwards through the centre of gravity of the body. When the body is immersed in a liquid, then the buoyancy W2 acts in the upward direction through the centre of buoyancy.
So, apparent weight of the body immersed in a liquid = real weight of the body – buoyant force acting on the body (i.e., weight of liquid displaced by the body)
= W1-W2
Hence, the apparent weight of the body < its real weight. So, a body suffers an apparent loss of weight due to the upthrust of the liquid when it is immersed in that liquid.
Hydrostatics Floatation And Immersion Of A Body In A Liquid At Rest
When a body is immersed in a liquid at rest, then the following two forces act on the body simultaneously.
- The weight W1 of the body which acts vertically downwards through the centre of gravity of the body.
- The buoyancy of the liquid W2 (weight of the liquid displaced by the body) which acts vertically upwards through the centre of buoyancy.
The value of W1 may be greater than, equal to, or less than W2, and hence any one of the three cases may arise.
Case 1: If W1>W2, i.e., the weight of the body is greater than the weight of the liquid displaced by the body, then the body will sink in the liquid.
In this case, the net downward force = W1-W2.
If the body is homogeneous and if its density and volume are ρ1 and V1 respectively, then W1= V1ρ1g. If the density of the liquid is ρ2, then the weight of the liquid displaced by the body, W2 = V2ρ2g.
∴ If W1 > W2 , then, ρ1 > ρ2
So, if the density of the material of the body is greater than the density of the liquid, then the body sinks in the liquid. For example, a piece of stone or iron sinks in water.
Case 2: If W1 = W2, i.e., the weight of the body is equal to the weight of the liquid displaced by the body, then the body will float at rest in any position in the liquid and be totally immersed in that liquid.
In this case, the weight of the body and the buoyancy i balance each other and hence the net force acting on the body becomes zero. So, the body becomes appar- . ently weightless.
Since, \(W_1=W_2, V_1 \rho_1 g=V_1 \rho_2 g \text { or, } \rho_1=\rho_2\)
Hence, if the density of the material of the body is equal to the density of the liquid, then the body can float remaining totally immersed within the liquid.
Case 3: If W1<W2, i.e., the weight of the body is less than that of the liquid displaced by it, then the body floats remaining partially immersed in the liquid.
If the body is released after immersing it completely inside the liquid, then under the influence of the force (W2-W1), it will move up through the liquid and, after some time, a part of the body will gradually come out of the liquid.
As a result, the amount of liquid displaced by the body is less. When the weight of the body is equal to that of the liquid displaced by it, the body floats remaining partially immersed in the liquid.
Since, \(W_1<W_2, \rho_1<\rho_2\)
So, when the density of the material of the body is less than the density of the liquid, the body floats on the liquid. For example, the density of wood is 0.7 – 0.9 g · cm-3 and that of pure water is 1 g · cm-3.
So, a piece of wood floats on water. Again, as the density of iron (7-7.9 g · cm-3) is less than that of mercury (13.68 g · cm-3), a piece of iron floats on mercury.
A floating body has no apparent weight: when a body floats in a liquid, the weight of the body becomes equal to the weight* of the liquid displaced by the body. According to Archimedes’ principle, the apparent loss of weight of the body inside the liquid is equal to the weight of the liquid displaced by that body, and hence the apparent weight of the body in the liquid = weight of the body – weight of liquid displaced by the body = 0.
So, a floating body in a liquid has no apparent weight. The weight of the floating body is balanced by the buoyant force exerted by the liquid.
Hydrostatics Properties Of A Floating Body
Conditions of Equilibrium of a Floating Body: Two equal but opposite forces act on a floating body—one is the weight of the body which acts downwards and another is the buoyancy of the liquid which acts in the upward direction.
To keep the floating body in equilibrium, these two forces must act along the same straight line. Otherwise, these two forces will constitute a couple and will produce a rotational motion in the body. Hence, for the equilibrium of a floating body, the following two conditions must be satisfied.
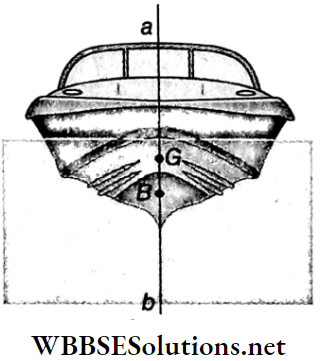
1. Condition of floatation: The weight of the floating body must be equal to the weight of the liquid displaced by the body.
2. Condition of equilibrium: The centre of gravity of the body and the centre of buoyancy must lie on the same vertical line.
In Fig, a body is floating in equilibrium. The centre of gravity of the body is G, centre of buoyancy is B, and weight of the body (W1) = weight of the displaced liquid (W2). In equilibrium, the vertical line ab passes through the centre of gravity G and the center of buoyancy B. The line ab is called the centre line.
Stability of a Floating Body: The equilibrium of a floating body may be of three types
- Neutral equilibrium,
- Stable equilibrium and
- unstable equilibrium.
If the floating body is tilted slightly, then the state of its equilibrium can be studied.
- If a slight tilt of the floating body from its equilibrium position does not produce any shift of the centre of buoyancy, i.e., if the new centre of buoyancy coincides with its previous position, then the body is said to be floating in neutral equilibrium.
- In this case, the centre of gravity of the body and the centre of buoyancy lie on the same vertical line. A sphere floating on a liquid is always in neutral equilibrium,
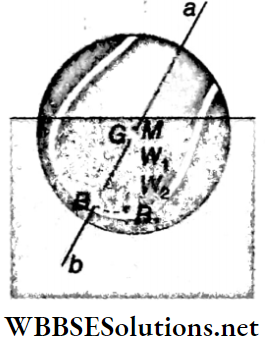
State equilibrium and unstable equilibrium: Usually, when a floating body is tilted, the centre of buoyancy shifts towards the leaning side as more liquid is displaced on that side of the body.
- Let be the new position of the centre of buoyancy. In this situation, the weight of the body (W1) and the buoyant force (W2) do not act along the same vertical line. These two equal but parallel forces constitute a couple.
- If this couple can return the body to its original position, then the equilibrium is said to be stable. But if the couple does not return the body to its original position, but rather it tends to tilt the body further, then the equilibrium is said to be unstable.
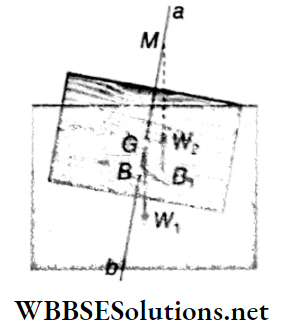
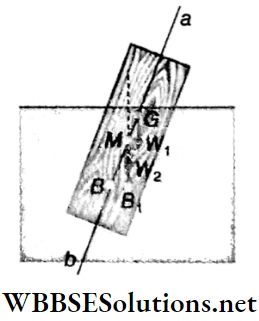
Metacentre: In the tilted position of a floating body, the point at which the vertical line drawn through the centre of buoyancy (B1) cuts the centre line ab is called the metacentre (M) of the body.
- From Fig, it is understood that if the metacenter (M) lies above the centre of gravity (G) of the body, then the equilibrium of the body is stable. But if the metacenter (M) lies below the centre of gravity (G) of the body, then the equilibrium is unstable.
- Hence, for stable equilibrium of a floating body, the metacentre of the body should be situated above its centre of gravity. In the case of neutral equilibrium, the points G and M coincide with each other.
- The distance GM is called metacentric height. The more the distance of the centre of gravity of the body below the metacentre, the stronger the moment of the restoring couple acting on the body and the equilibrium will be more stable.
Stability of ships and boats: Boats, ships, etc., are so constructed that they can float in water at stable equilibrium. For this, two conditions should be followed.
- The external shapes of these vehicles are so designed that the metacentre lies at a suitable height. For this, the width of the vehicles are made greater at the top them at the bottom.
- The centre of gravity of these vehicles is kept as low as possible by filling the bottom with heavy cargo. For this, some additional weights, called ballast, are kept loaded in the hold of an empty ship.
Two Important Relations in Connection with a Floating Body
1. Let a body of volume V and density D be allowed to float on a liquid of density d. If the volume of the immersed part of the body in that liquid is ν, then the volume of liquid displaced by the body will also be ν. So, according to the condition of floatation,
weight of the body = weight of the displaced liquid
or vDg or, \(\frac{v}{V}=\frac{D}{d}\)
∴ \(\frac{\text { volume of the immersded of part of a body }}{\text { total volume of the body }}\)
= \(\frac{\text { density of the body }}{\text { density of the liquid }}\)
2. if n is the fraction of volume of the body that remains immersed in the liquid, then
⇒ \(\frac{\nu}{V}=n=\frac{D}{d} \text { or, } D=n \times d\)
Application and Illustration of the Principle of Floatation
The upward motion of a balloon: The upward motion of a balloon depends on the upthrust of air. The net weight of an inflated balloon containing hydrogen gas is much less than the weight of air displaced by it (due to lower density of hydrogen).
- As a result, the buoyant force exerted by air on the balloon becomes greater than the weight of the balloon. Due to this reason, the balloon experiences a net upward force and it moves up. We know that with the increase in altitude from the surface of the earth, the density of air decreases and hence the upthrust exerted on the balloon decreases.
- After attaining a certain height, the weight of the balloon becomes equal to the buoyant force acting on it and then the balloon cannot rise any further; it remains floating at a particular altitude.
- Again, another situation may arise. Due to the lower atmospheric pressure at a higher altitude, the volume of the balloon gradually increases.
- As a result, the weight of air displaced by the balloon, i.e., the upthrust also increases and, in consequence, the balloon rises more and more and finally may burst due to excessive expansion in its volume.
- Besides hydrogen, helium is also used as a filling agent in a balloon. Hydrogen is lighter than helium, but is inflammable whereas helium is not. For this reason, helium is used in balloons.
Why does ice float on water: The mass of 1 cm³ of ice is 0.917 g. The mass of 1 cm³ of water is 1 g. So, the same volume of ice is lighter than water. Since the density of ice is less than that of water, it floats partially immersed in water. If nth part of a lump of ice remains submerged, then n = density of ice = 0.917 = 11/12 (approx.)
So, in its floating condition, 11/12 th part of a lump of ice remains immersed in water and 1/12 th part remains above the water surface. The density of sea water is 1.03 g· cm-3. So, 1/9 th part (approx.) of an iceberg remains exposed to air while floating on sea water.
To float on water, we have to learn swimming, but to animals swimming comes naturally-explain why: The average density of the human body 1.01 g · cm-3 (approx.).
- The weight of the body of a man is less than the weight of an equal volume of water. But the head is heavier than the weight of an equal volume of water.
- Hence, a man can float on water, but his head sinks in it. So, we have to learn swimming to float on water. A man strives to keep his head afloat by moving his limbs in water. This is the act of swimming.
- For animals, both their heads and bodies are lighter than an equal volume of water and hence they can float on water effortlessly.
- It is easier to float in sea water than in fresh river water because the density of sea water is more than that of river water. Hence, the upthrust of sea water is more than that of river water.
A piece of iron sinks into water but a ship made of iron floats on it—explain how: This is due to the special shape of a ship. The bottom of a ship is made wider and hollow. It is given a concave shape so that the weight of displaced water by the ship becomes equal to the weight of the ship.
According to the condition of floatation, if the weight of a body becomes equal to the upthrust exerted on it by the displaced liquid then the body floats on that liquid. That is why a ship floats on water. The weight of a piece of iron is more than the weight of water displaced by it and so it sinks in water.
How does a submarine submerge and float on water: A submarine can float on water, but can also be submerged. A submarine contains a large number of tanks which can be filled up with air or water.
- These tanks are called ballast tanks. When the ballast tanks are filled with air, the submarine floats on water as the weight of the submarine becomes less than the weight of water displaced by it.
- When water is admitted into the ballast tanks using a pump, tire submarine becomes slightly heavier than the water displaced by it and hence it submerges. To raise the submarine again to the surface of water, water is driven out of the ballast tanks by compressed air.
Why are life-belts used: Steamers and ships are provided with life-belts. If a steamer or a ship sinks, then the passengers can float by wearing these life-belts. A life-belt is nothing but an air-filled bag. The weight of this bag along with the weight of the person is less than the weight of the displaced water so the person is able to keep afloat.
1 kilogram of cotton is heavier than 1 kilogram of iron: For a body in air,
apparent weight = actual weight (i.e., weight in vacuum) – buoyancy of air
So, actual weight = apparent weight + buoyancy of air
= apparent weight + weight of air displaced by the body
When we weigh 1 kg of cotton and 1kg of iron in air, those are their apparent weights. So the actual weight depends on the weight of air displaced by them.
Clearly, 1kg of cotton has a much larger volume, and it displaces a much larger amount of air. so the actual weight of 1kg of cotton is higher than that of 1kg of iron. Therefore, it is said that, 1kg of cotton is heavier than 1kg of iron.
Hydrostatics Pressure Difference And Buoyant Force In A Liquid Of A Uniformly Accelerated Container Filled With The Liquid
The mathematical expression used so far for the buoyant force acting on a body immersed in a liquid holds true for any liquid at rest. However, those equations are to be modified for a uniformly accelerated container filled with the liquid.
In the Case of a Moving Lift
Case 1: When a lift with a liquid-filled container moves upwards with an acceleration a (or moves downwards with a retardation a):
Difference: In pressure Let us imagine a liquid column of height h and cross-sectional area A inside the lift. If the density of the liquid is ρ, then the mass of the liquid column, m = hAρ.
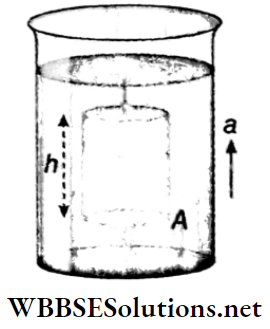
Different forces exerted on the liquid column:
- If p1 is the pressure on the upper surface of the liquid column, then the thrust on that surface F1 = p1A; this force acts vertically downwards.
- If p1 is the pressure on the lower surface of the liquid column, then the thrust on that surface F2 = ρ2A; this force acts vertically upwards.
- The weight of the liquid column mg = hAρg; this force acts vertically downwards.
Therefore, the equation of motion of the liquid column is
⇒ \(F_2-F_1-m g=m a\)
or, \(p_2 A-p_1 A=m a+m g\)
or, \(\left(p_2-p_1\right) A=m(a+g)\)…..(1)
= \(h A \rho(a+g)\)
or, \(p_2-p_1=h \rho(g+a)\)…….(2)
So the difference in pressure increases by hρa.
Buoyant force: The buoyant force or upthrust on the liquid column, W’ = (p2– p1)A
From equation (1) we get, W’ = m(g+ a)…. (3)
So, the buoyant force increases by ma.
Case 2: When the lift with a liquid-filled container moves downwards with an acceleration a (or moves upwards with a retardation a):
Following the previous calculation, it can be seen that \(p_2-p_1=h \rho(g-a)\)
i.e., the difference in pressure, in this case, decreases by ρa.
Similarly, the buoyant force, W’ = m(g- a)
i.e., the buoyant force, in this case, decreases by ma.
Case 3: When the lift with a liquid-filled container moves downwards freely (i.e., a = g):
In this case, the difference in pressure, p2– p1 = 0 and the buoyant force, W’ = 0
i.e., both the pressure at any point inside a liquid and the upthrust on any immersed object become nil.
Case 4: When the lift with a liquid-filled container is at rest or moves up or down with uniform speed:
Here, a = 0.
∴ Difference in pressure, p2-p1 = hρg and buoyant force, W’ = mg.
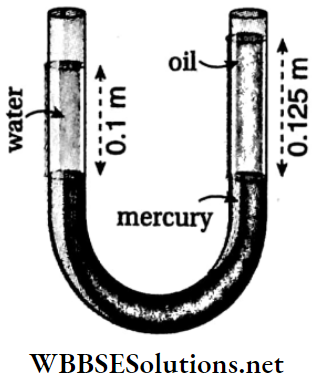
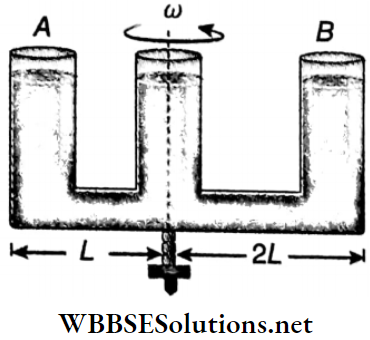
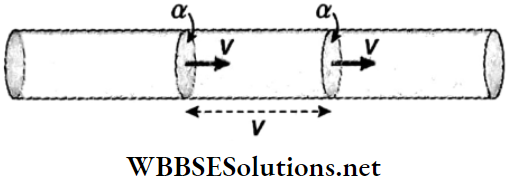
Free Surface in a Liquid-filled Container Moving horizontally with Uniform Acceleration a: A horizontal cylinder of length l and cross-sectional area a is imagined inside a liquid.
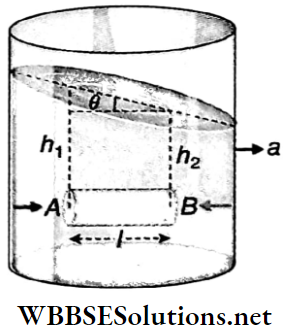
If the density of the liquid is ρ, then the mass of the said liquid cylinder, m = lap.
Let the liquid exert pressures pA and pB respectively at the two ends A and B of the cylinder.
∴ The equation of motion of the liquid cylinder is \(p_A \alpha-p_B \alpha=m a\)
or, \(\alpha\left(p_A-p_B\right)=l \alpha \rho a \text { or, } p_A-p_B=l \rho a\)…..(1)
Pressures at two points on the same horizontal line inside a liquid-filled container moving horizontally with uniform acceleration are not the same.
Due to the absence of any vertical acceleration of the container, the pressure at any point inside the liquid is similar to that in the case of a liquid at rest. But in this case, the free surface of the liquid does not remain horizontal. Suppose the free surface makes angle 6 with the horizontal.
Now, \(p_A=h_1 \rho g\) and \(p_B=h_2 \rho g\)
∴ According to equation (1),
⇒ \(h_1 \rho g-h_2 \rho g=l \rho a\)
or, \(\frac{h_1-h_2}{l}=\frac{a}{g}\)
or, \(\tan \theta=\frac{a}{g}\)
or, \(\theta=\tan ^{-1}\left(\frac{a}{g}\right)\)
Hydrostatics Pressure Difference And Buoyant Force In A Liquid Of A Uniformly Accelerated Container Filled With The Liquid Numerical Examples
Example 1. A body weighs 100gxg and 40gxg In air and water respectively. Calculate the weight of the body when Immersed in a liquid of specific gravity 0.8.
Solution:
A body weighs 100gxg and 40gxg In air and water respectively.
Weight of the body in air = 100 g x g, weight of the body in water = 40 g x g.
∴ Weight of displaced water = (100 – 40) x g = 60 g x g.
∴ Volume of displaced water = 60 cm3
So, the volume of the body = 60 cm3
The specific gravity of the liquid =0.8
∴ Density of the liquid =0.8 g · cm-3.
∴ Weight of the displaced liquid = (60 x 0.8) x g = 48 g x g.
Weight of the body in the liquid = weight of the bodyin air – weight of the displaced liquid
= (100 – 48) x g = 52 g x g = 50960 dyn .
Example 2. The mass of a steamer is 10 tonnes. When it enters a fresh water lake from the sea, it displaces 50 L more water than before. Calculate the density of seawater. (Mass of 1 L of fresh water = 1 kg)
Solution:
The mass of a steamer is 10 tonnes. When it enters a fresh water lake from the sea, it displaces 50 L more water than before.
Mass of displaced seawater = mass of the streamer = 10 x 103 kg = 107 g.
∴ The volume of displaced seawater = \(\frac{10^7}{\rho} \mathrm{cm}^3\) [p = density of sea water)
Mass of displaced take water = 107 g
As the density of fresh water is 1 g · cm-3, the volume of dis¬placed lake water = 107 cm3.
According to the problem,
⇒ \(10^7-\frac{10^7}{\rho}=50 \times 10^3 \text { or, } 10^7\left(1-\frac{1}{\rho}\right)-5 \times 10^4\)
or, \(1-\frac{1}{\rho}=\frac{5}{10^3} \text { or, } \frac{1}{\rho}=1-\frac{5}{1000}=\frac{995}{1000}\)
∴ \(\rho=\frac{1000}{995}=1.005 \mathrm{~g} \cdot \mathrm{cm}^{-3}\)
Example 3. The internal and external diameters of a sphere are 8cm and 10cm respectively. The sphere neither floats nor sinks in a liquid of specific gravity 1.5 g ⋅ cm-3. Calculate the density of the material of the sphere.
Solution:
The internal and external diameters of a sphere are 8cm and 10cm respectively. The sphere neither floats nor sinks in a liquid of specific gravity 1.5 g ⋅ cm-3.
Let the density of the material of the given sphere be ρ.
According to the condition of floatation, volume of the sphere x density of the material of the sphere = volume of displaced liquid x density of that liquid.
or, \(\left\{\frac{4}{3} \pi(5)^3-\frac{4}{3} \pi(4)^3\right\} \times \rho=\frac{4}{3} \pi(5)^3 \times 1.5\)
or, \(\left\{(5)^3-(4)^3\right\} \times \rho=(5)^3 \times 1.5\)
or, \((125-64) \rho=125 \times 1.5\)
or, \(\rho=\frac{125 \times 1.5}{61}=3.07 \mathrm{~g} \cdot \mathrm{cm}^{-3}\)
Example 4. A body of density ρ is placed slowly on the surface of a liquid of density δ. If the depth of the liquid is d, then prove that the time taken by the body to reach the bottom of the liquid is \(\left[\frac{2 d \rho}{g(\rho-\delta)}\right]^{1 / 2}\) second.
Solution:
A body of density ρ is placed slowly on the surface of a liquid of density δ.
Let the mass of the body be m.
∴ Its volume = \(\frac{m}{\rho}\).
Volume of liquid displaced = \(\frac{m}{\rho}\)
∴ Mass of liquid displaced = \(\frac{m}{\rho}\) x 8
If the downward acceleration of the body in the liquid is a, then by the problem
mg – \(\frac{m}{\rho}\).δg= ma
or, \(a=\left(1-\frac{\delta}{\rho}\right) g=\left(\frac{\rho-\delta}{\rho}\right) g\)
If the time taken by the body to reach the bottom of the liquid is t, then
d = \(u t+\frac{1}{2} a t^2=\frac{1}{2} a t^2 \quad(because u=0)\)
= \(\frac{1}{2} \frac{(\rho-\delta)}{\rho} g t^2 \text { or, } t^2=\frac{2 d \rho}{(\rho-\delta) g}\)
∴ t = \(\left[\frac{2 d \rho}{(\rho-\delta) g}\right]^{\frac{1}{2}}\)
Example 5. The weight of a body in air is 0.4 g x g. Its weight along with an sinker in water = 3.37 gx g.The weight of the sinker in air = 4 g x g. Find the specific gravity of the body. [Specific gravity of the sinker = 8]
Solution:
The weight of a body in air is 0.4 g x g. Its weight along with an sinker in water = 3.37 gx g.The weight of the sinker in air = 4 g x g.
Let the density of the body be d g • cm-3.
Volume of the body = \(\frac{0.4}{d} \mathrm{~cm}^3\); volume of the sinker = 4/8 = 0.5 cm3
Volume of water displaced by the body along with the sinker = \(\left(0.5+\frac{0.4}{d}\right)\) cm
.-. Weight of displaced water = (\(\left(0.5+\frac{0.4}{d}\right)\)) g x g
Again, weight of displaced water = weight of the body along with sinker in air – weight of the body along with sinker in water
= (0.4 + 4) x g- 3.37 x g =(4.4-3.37) x g = 1.03g x g
.-. \(0.5+\frac{0.4}{d}=1.03 \text { or, } \frac{0.4}{d}=0.53\)
or, d = \(\frac{0.4}{0.53}\)= 0.75
∴ The specific gravity of the body = 0.75.
Example 6. A piece of wood of volume 20.5 cm3 is tied to a piece of lead of volume 1 cm3. State whether the combination will sink or float in water. [Specific gravity of wood and lead are respectively 0.5 and 11.4]
Solution:
A piece of wood of volume 20.5 cm3 is tied to a piece of lead of volume 1 cm3.
Weight of the piece of wood = 20.5 x 0.5 x g = 10.25 g x g
Weight of lead = 1 x 11.4 x g = 11.4 g x g
∴ Total weight of the combination = (10.25 +11.4) x g = 21.65 g xg
Total volume of wood and lead = (20.5+1) = 21.5 cm3
∴ Weight of displaced water by wood and lead = 21.5 g x g
∴ Weight of combination > weight of displaced water
So, when the piece of wood and lead are tied together, the combination will sink in water.
Example 7. A piece of an alloy of gold and silver weighs 25 g xg in air and 23 g x g in water. Find out the amount of gold and silver in the piece of alloy. [The specific gravity of silver is 10.8 and that of gold is 19.3]
Solution:
A piece of an alloy of gold and silver weighs 25 g xg in air and 23 g x g in water.
Let the amount of gold in the alloy be x g.
∴ Amount of silver =(25-x)g
Volume of gold = \(\frac{x}{19.3} \mathrm{~cm}^3 \text {; }\)
volume of silver = \(\frac{25-x}{10.8} \mathrm{~cm}^3\)
volume of alloy = \(\left(\frac{x}{19.3}+\frac{25-x}{10.8}\right) \mathrm{cm}^3\)
Again, weight of water displaced by the alloy = (25 – 23) x g = 2 g x g
i.e., mass of this displaced water = 2 g
∴ Volume of displaced water = 2 cm3
∴ \(\frac{x}{19.3}+\frac{25-x}{10.8}=2\)
or, 10.8x + 19.3 x 25 – 19.3x = 2 x 19.3 x 10.8
or, x = 7.72
∴ Amount of gold =7.72 g and amount of silver = 25-7.72 = 17.28 g.
Example 8. There is a cavity inside a piece of metal of mass 237.3 g. The apparent weight of the piece of metal immersed completely in water is 192.1 g x g. If the density of the metal is 7.91 g · cm-3, then find the volume of the cavity.
Solution:
There is a cavity inside a piece of metal of mass 237.3 g. The apparent weight of the piece of metal immersed completely in water is 192.1 g x g. If the density of the metal is 7.91 g · cm-3,
Volume of the material of the metal piece = \(\frac{237.3}{7.91}=30 \mathrm{~cm}^3 \text {; }\)
mass of water displaced by the metal piece = (237.3-192.1) x g = 45.2g x g
∴ Volume of displaced water = 45.2 cm3
∴ Volume of the metal piece including the cavity = 45.2 cm3
∴ Volume of the cavity =45.2-30 = 15.2 cm3
Example 9. A piece of wood weighs 40 g x g In air. A piece of brass of mass 12 g is tied to the wooden piece and the combination floats just totally immersed in water. If the specific gravity of brass is 8.5, calculate the specific gravity of wood. [Density of water = 1g · cm-3]
Solution:
A piece of wood weighs 40 g x g In air. A piece of brass of mass 12 g is tied to the wooden piece and the combination floats just totally immersed in water. If the specific gravity of brass is 8.5,
Let the density of the piece of wood be ρ g • cm-3.
Total volume of the pieces of wood and brass = \(\left(\frac{40}{\rho}+\frac{12}{8.5}\right) \mathrm{cm}^3\)
Volume of displaced water = \(\left(\frac{40}{\rho}+\frac{12}{8.5}\right) \mathrm{cm}^3\)
By the condition, the weight of the piece of wood + weight of the piece of brass = weight of water displaced by both of them
or, 40 + 12 = \(\left(\frac{40}{\rho}+\frac{12}{8.5}\right) \times 1 \text { or, } 52=\frac{40}{\rho}+\frac{12}{8.5}\)
or, \(\frac{40}{\rho}=52-1.41 \text { or, } \rho=\frac{40}{50.59}=0.79\)
∴ Specific gravity of wood is 0.79.
Example 10. The apparent weights of two bodies suspended from the two ends of a balance beam and immersed in water are the same. The mass and density of one body are 32 g and 8 g · cm-3 respectively. If the density of the other body is 5 g · cm-3, then find its mass.
Solution:
The apparent weights of two bodies suspended from the two ends of a balance beam and immersed in water are the same. The mass and density of one body are 32 g and 8 g · cm-3 respectively.
Let the mass of the second body be mg.
Volume of the first body = 32/8 = 4 cm3
∴ Volume of water displaced by the first body = 4 cm3
Volume of the second body = m/5 cm3
∴ Volume of water displaced by the second body = m/5 cm3
By the problem, apparent weight of the first body = apparent weight of the second body
∴ Real weight of the first body – weight of water displaced by the first body
= real weight of the second body – weight of water displaced by the second body
or, 32 – 4 = m – m/5 or, 28 = 4m/5 or, m = 35
∴ Mass of the second body is 35 g.
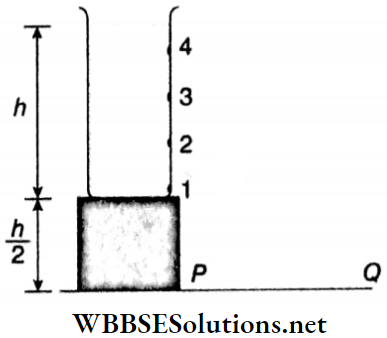
Example 11. body of mass 25 g is underwater at a depth of 50 cm. If the specific gravity of the material of the body is 5 and g = 980 cm • s-2, find the amount of work required to lift it very slowly to the surface.
Solution:
Body of mass 25 g is underwater at a depth of 50 cm. If the specific gravity of the material of the body is 5 and g = 980 cm • s-2,
The volume of water displaced by the body = volume of the body = 25/5 = 5 cm3
∴ Weight of displaced water = 5 g x g
∴ Downward resultant force = (25 x 980 – 5 x 980)
= 20 x 980 = 19600 dyn
∴ Required work done = 19600 x 50 = 9.8 x 105 erg.
Example 12. A solid spherical ball having density d and volume v floats on the interface of two immiscible liquids. The density of the liquid in the upper portion is d1 and that of the liquid in the lower portion is d2. What parts of the ball will remain in the liquids in the upper and lower portions respectively, if d1 < d < d2?
Solution:
A solid spherical ball having density d and volume v floats on the interface of two immiscible liquids. The density of the liquid in the upper portion is d1 and that of the liquid in the lower portion is d2.
Suppose a volume x of the ball remains in the liquid in the upper portion. So, a volume (ν- x) remains in the liquid in the lower portion.
According to the principle of floatation, weight of the body = weight of displaced liquid
or, \(v d=x d_1+(\nu-x) d_2 \text { or, } x\left(d_1-d_2\right)=v\left(d-d_2\right)\)
or, \(\frac{x}{v}=\frac{d-d_2}{d_1-d_2}=\frac{d_2-d}{d_2-d_1}\)
∴ The part of the ball that remains in the liquid in the upper portion = \(\frac{d_2-d}{d_2-d_1}\)
and the part of the ball that remains in the liquid in the lower = \(\left(1-\frac{d_2-d}{d_2-d_1}\right)=\frac{d-d_1}{d_2-d_1} .\)
Example 13. An object of density 12 g · cm-3 is weighed with some counterpoising weights made of brass with the help of a common balance. Density of brass = 8 g · cm-3. If the buoyancy of air is neglected in this measurement, then calculate the percentage error in the measurement of mass. Density of air = 1.2 x 10-3 g · cm-3.
Solution:
An object of density 12 g · cm-3 is weighed with some counterpoising weights made of brass with the help of a common balance. Density of brass = 8 g · cm-3. If the buoyancy of air is neglected in this measurement
Let the real weight of the body be mgxg; real weight of the brass weights = m’ g x g.
Here, apparent weight of the body = apparent weight of the brass weights
or, real weight of the body – weight of air displaced by the body
= real weight of the brass weights – weight of air displaced by the brass weights
or, \(m-\frac{m}{12} \times 1.2 \times 10^{-3}=m^{\prime}-\frac{m^{\prime}}{8} \times 1.2 \times 10^{-3}\)
or, \(m-m \times 10^{-4}=m^{\prime}-m^{\prime} \times 1.5 \times 10^{-4}\)
or, \(\frac{m^{\prime}}{m}=\frac{1-10^{-4}}{1-1.5 \times 10^{-4}}\)
or, \(\frac{m^{\prime}-m}{m}=\frac{(1.5-1) \times 10^{-4}}{1-1.5 \times 10^{-4}}=0.5 \times 10^{-4}\)
∴ Error = \(\frac{m^{\prime}-m}{m} \times 100=0.5 \times 10^{-4} \times 100=0.005 \%\).
Example 14. A robber ball of mass 10 g and radius 2 cm is submerged in water up to a depth of 5 cm and released. Find the height up to which the ball pops up above the surface of water, neglecting the resistance of water and air. The density of water = 1 g · cm-3.
Solution:
A robber ball of mass 10 g and radius 2 cm is submerged in water up to a depth of 5 cm and released.
Volume of the rubber ball,
V = \(\frac{4}{3} \times \frac{22}{7} \times(2)^3 \mathrm{~cm}^3=\frac{704}{21} \mathrm{~cm}^3\)
Resultant upward force = buoyant force – weight of the rubber
or, 10a = V x 1 x g – 10 x g [a = upward accleration]
or, \(10 a=\frac{704 \mathrm{~g}}{21}-10 \mathrm{~g} \text { or, } a=\frac{494}{210} \mathrm{~g} \mathrm{~cm} \cdot \mathrm{s}^{-2}\)
Let the velocity of the ball when it reaches the surface of water be v, then
⇒ \(\nu =\sqrt{2 a s}=\sqrt{\frac{2 \times 494}{210} \times 980 \times 5}\)
= \(\sqrt{\frac{2 \times 494 \times 14 \times 5}{3}}=151.83 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)
If the ball pops up to a height x above the surface of water, then
⇒ \(\nu^2=2 g x \text { of, } x=\frac{v^2}{2 g}=\frac{(151.83)^2}{2 \times 980}=11.76 \mathrm{~cm} .\)
Example 15. The density of the material of a hollow sphere of radius 11 Is ρ. Prove that the sphere can float on water If the thickness (t) of Its wall satisfies the relation: \(t<\frac{R}{3 \rho}\).
Solution:
The density of the material of a hollow sphere of radius 11 Is ρ.
According to the condition of floatation, weight of the sphere ≤ weight of the same volume of water
or, \(\left[\frac{4}{3} \pi R^3-\frac{4}{3} \pi(R-t)^3\right] \rho\) ≤ \(\frac{4}{3} \pi R^3 \times 1\)
or, \(\left[\frac{4}{3} \pi R^3-\frac{4}{3} \pi R^3\left(1-\frac{t}{R}\right)^3\right] \rho\) ≤ \(\frac{4}{3} \pi R^3\)
or, \(\frac{4}{3} \pi R^3\left[1-\left(1-\frac{t}{R}\right)^3\right] \rho\) ≤ \(\frac{4}{3} \pi R^3\)
or, \(\left[1-\left(1-\frac{3 t}{R}\right)\right] \rho\) ≤1
[t ≤ R terms containing \(\frac{t^3}{R^3}, \frac{t^2}{R^2}\) are neglected]
or, \(\frac{3 t}{R} \rho\) ≤ 1 or, \(t ≤ \frac{R}{3 \rho}\).
Example 16. When a body is Immersed separately into three liquids of specific gravities S1, S2, and S3, its apparent weights become W1, W2, and W3 respectively. Show that \(S_1\left(W_2-W_3\right)+S_2\left(W_3-W_1\right)+S_3\left(W_1-W_2\right)=0\).
Solution:
When a body is Immersed separately into three liquids of specific gravities S1, S2, and S3, its apparent weights become W1, W2, and W3 respectively.
Let the real weight of the body be W and the volume of the body be V.
∴ \(W_1=W-V \cdot S_1\)……..(1)
∴\(W_2=W-V \cdot S_2\)…..(2)
∴\(W_3 =W-V \cdot S_3\)…..(3)
Subtracting (2) from (1), we get
∴ \(W_1-W_2=V\left(S_2-S_1\right)\)
Subtracting (3) from (2), we get \(W_2-W_3=V\left(S_3-S_2\right)\)
Subtracting (1) from (3), we get \(W_3-W_1=V\left(S_1-S_3\right)\)
∴ \(S_1\left(W_2-W_3\right)+S_2\left(W_3-W_1\right)+S_3\left(W_1-W_2\right)\)
= \(S_1 V\left(S_3-S_2\right)+S_2 V\left(S_1-S_3\right)+S_3 \cdot V\left(S_2-S_1\right)\)
= \(V\left[S_1\left(S_3-S_2\right)+S_2\left(S_1-S_3\right)+S_3\left(S_2-S_1\right)\right]\)
= 0
Example 17. A body Is floating on mercury keeping its – th part inside mercury. Now, water is poured into the container such that the body remains just immersed totally in water. Now what part of the body will remain immersed in mercury? (Density of mercury = 13.6 g · cm-3]
Solution:
A body Is floating on mercury keeping its – th part inside mercury. Now, water is poured into the container such that the body remains just immersed totally in water.
Let the volume of the body be V; density of its material be d.
In the case of floatation in mercury, \(V \times d=\frac{V}{4} \times 13.6 \text { or, } d=\frac{13.6}{4}=3.4 \mathrm{~g} \cdot \mathrm{cm}^{-3}\)
When water is added, suppose x part of the volume of the body remains immersed in mercury and (1 – x) part of its volume in water.
∴ x 3.4 = V x x x 13.6 + V(1 – x) x 1
or, 3.4 = 13.6 + 1 -x
or, 12.6x = 2.4
or, \(x=\frac{2.4}{12.6}=\frac{4}{21}\)
So, 4/21 th part of the given body will remain immersed in
Example 18. A sugar crystal of mass 40 g is coated with wax of mass 5.76 g. The specific gravity of wax is 0.96. If the wax-coated sugar crystal weighs 14.76 g xg inside i water, calculate the specific gravity of sugar.
Solution:
A sugar crystal of mass 40 g is coated with wax of mass 5.76 g. The specific gravity of wax is 0.96. If the wax-coated sugar crystal weighs 14.76 g xg
Let the density of sugar be \(d \mathrm{~g} \cdot \mathrm{cm}^{-3}\).
∴ Volume of sugar = \(\frac{40}{d} \mathrm{~cm}^3\);
volume of wax = \(\frac{5.76}{0.96} \mathrm{~cm}^3 \text {. }\)
Mass of water displaced by the coated sugar
=(40+5.76) x g -14.76 x g
= 31 g x g.
∴ Volume of displaced water = 31 \(\mathrm{~cm}^3\)
∴ \(\frac{40}{d}+\frac{5.76}{0.96}=31\)
or, \(\frac{40}{d}+6=31\)
or, \(\frac{40}{d}=25\)
or, \(d=\frac{40}{25}=1.6\)
∴ Specific gravity of sugar =1.6
Example 19. When a loaded cargo ship enters a river from the sea, it sinks by a length x. When the ship is totally unloaded, it rises by a length y. When the unloaded ship again enters the sea, it rises by z cm more. If the density of water of the river is ρw and the body of the ship is vertical, show that the density of sea water is \(\frac{y \rho_w}{(z-x+y)}\).
Solution:
When a loaded cargo ship enters a river from the sea, it sinks by a length x. When the ship is totally unloaded, it rises by a length y. When the unloaded ship again enters the sea, it rises by z cm more. If the density of water of the river is ρw and the body of the ship is vertical,
Let the weight of the loaded ship be w; the weight of cargo be w’ the base-area of the ship be A and the density of seawater be p.
Let us also assume that the loaded ship sinks a length h in sea water.
∴ In the case of floatation in seawater, w = Ahρ ……(1)
In the case of floatation in river water, w = A(h + x)ρw …(2)
When the ship is unloaded, w- w’ = A(h + x-y)ρw ….(3)
When the unloaded ship enters the sea, w-w’ = A(h + x-y-z)ρ….(4)
From (1) and (2), we get
⇒ \(A h \rho=A(h+x) \rho_w \text { or, } h+x=\frac{h \rho}{\rho_w}\)
From (3) and (4), we get
or, \(h+x-y=(h+x-y-z) \frac{\rho}{\rho_w}\)
or, \(\frac{h \rho}{\rho_w}-y=\frac{h \rho}{\rho_w}+(x-y-z) \frac{\rho}{\rho_w}\)
or, \(y=(y+z-x) \frac{\rho}{\rho_w}\)
or, \(\rho=\frac{y \rho_w}{(z-x+y)}\).
Example 20. A cubical steel block floats on mercury erectly. If each side of the cube is 10 cm,
- How much of the body is above the mercury surface?
- If water is poured over mercury and it just covers the upper surface of the cube, then what will be the depth of the water column? Densities of steel and mercury are 7.8 g · cm-3 and 13.6g · cm-3 respectively.
Solution:
A cubical steel block floats on mercury erectly. If each side of the cube is 10 cm,
1. Suppose x cm of the cube remajps immersed in mercury.
So, according to the condition of floatation, volume of the cube x density of the material of the cube = volume of mercury displaced x density of mercury
∴ 103³x 7.8 = 10² x xx 13.6 or, x = 7.8/13.6 = 5.74
∴ (10-5.74) = 4.26 cm height of the cube remains above mercury.
2. Let the length of the cube that remains in water be h cm and that in mercury be (10 – h) cm.
∴ According to the condition of floatation, volume of the cube x density of the material of the cube = volume of displaced water x density of water + volume of displaced mercury x density of mercury
∴ 10³ x 7.8 = 10² x h x 1 + 10² x (10-h) x 13.6
or, 78 = h + (10- h) x 13.6 or, h =
∴ Depth of the water column = 4.6 cm.
Example 21. A and B are two cylinders identical in size but made of different materials. A floats with half of itself immersed in a liquid. When B is placed on A, both j the cylinders remain floating in the liquid, but completely immersed in it. Compare the density of the liquid and the densities of the materials of A and B.
Solution:
A and B are two cylinders identical in size but made of different materials. A floats with half of itself immersed in a liquid. When B is placed on A, both j the cylinders remain floating in the liquid, but completely immersed in it.
Let the volume of each of the cylinders A and B be V. Also, let the densities of the materials of A and B and that of the liquid be d1, d2, and d3 respectively.
When cylinder A alone floats on the liquid, then volume of the cylinder x density of its material = volume of displaced liquid x density of the liquid
or, \(V \times d_1=\frac{V}{2} \times d_3 \text { or, } d_1=\frac{d_3}{2}\)
When cylinders A and B together float in the liquid, then volume of the cylinder A x its density + volume of the cylinder B x its density = volume of displaced liquid x its density
or, \(V d_1+V d_2=2 V \times d_3\)
or, \(d_1+d_2=2 d_3\)
or, \(\frac{d_3}{2}+d_2=2 d_3\)
or, \(d_2=2 d_3-\frac{d_3}{2}=\frac{3 d_3}{2}\)
∴ \(d_1: d_2: d_3=\frac{d_3}{2}: \frac{3 d_3}{2}: d_3=1: 3: 2\)
Example 22. The apparent weight of a body In a liquid of density d1 is m1 and, in another liquid of density d2, its apparent weight is m2. What will be its apparent weight in a liquid of density d3?
Solution:
The apparent weight of a body In a liquid of density d1 is m1 and, in another liquid of density d2, its apparent weight is m2.
Let the real weight of the body be M and its volume be V.
∴ M- Vd1 = m1 ………(1)
and M- Vd2 = m2 ……..(2)
From equations (1) and (2), we get
V = \(\frac{m_1-m_2}{d_2-d_1}\)
Let the apparent weight of the body in the liquid of density d3 be m3.
∴ \(m_3=M-V d_3=m_1+V d_1-V d_3\) [with the help of equation (1)]
= \(m_1+V\left(d_1-d_3\right)\)
= \(m_1+\frac{\left(m_1-m_2\right)\left(d_1-d_3\right)}{\left(d_2-d_1\right)}\)
= \(\frac{m_1\left(d_2-d_1\right)+\left(m_1-m_2\right)\left(d_1-d_3\right)}{\left(d_2-d_1\right)}\)
= \(\frac{m_1\left(d_2-d_3\right)-m_2\left(d_1-d_3\right)}{\left(d_2-d_1\right)}\)
Example 23. A glass ball of density 2.6 g · cm-3 is coated with a thick layer of wax of density 0.8 g · cm-3. If the combination floats in water remaining completely submerged, find the ratio of the volume of wax to that of the glass ball.
Solution:
A glass ball of density 2.6 g · cm-3 is coated with a thick layer of wax of density 0.8 g · cm-3.
Let volume of glass be V1 cm3 and volume of wax be V2 cm3.
According to the problem, weight of glass ball + weight of wax = weight of displaced water
or, \(V_1 \times 2.6 \times g+V_2 \times 0.8 \times g=\left(V_1+V_2\right) \times 1 \times g\)
or, \(V_1(2.6-1)=V_2(1-0.8)\)
or, \(\frac{V_2}{V_1}=\frac{1.6}{0.2}=\frac{8}{1}\)
∴ Volume of wax: volume of glass =8:1.
Example 24. A body can float on a liquid keeping J th of It vol-ume outside the liquids The body is completely immersed inside the liquid and then released. What will be its upward acceleration at that time?
Solution:
A body can float on a liquid keeping J th of It vol-ume outside the liquids The body is completely immersed inside the liquid and then released.
Let volume of the body be V and density be ρ; density of the liquid be ρ’.
According to the condition of floatation,
⇒ \(V \times \rho \times g=\frac{3}{4} V \times \rho^{\prime} \times g \text { or, } \rho^{\prime}=\frac{4 \rho}{3}\)
When the body is completely immersed in the liquid, the net upward force = buoyant force – weight
or, \(V \rho a=V \rho^{\prime} g-V \rho g\)
[a= upward acceleration]
or, \(V \rho a=V \cdot \frac{4}{3} \rho \cdot g-V \rho g=\frac{1}{3} V \rho g\)
or, \(a=\frac{1}{3} g\).
Example 25. A drop of oil rises within water with an upward acceleration of ag. If or is a constant and g is the acceleration due to gravity, find the specific gravity of the oil Neglect the friction of water.
Solution:
A drop of oil rises within water with an upward acceleration of ag. If or is a constant and g is the acceleration due to gravity
Let the densities of oil and water be D and d respectively and the mass of the oil drop be m.
∴ Volume of the oil drop = \(\frac{m}{D}\) = volume of water displaced by the oil drop
∴ Mass of displaced water = density of water x volume of displaced water = \(\frac{d m}{D}\)
∴ Buoyancy = weight of displaced water = \(\frac{d m g}{D}\)
∴ Net upward thrust on the oil drop = buoyant force – weight of the oil drop
= \(\frac{d m g}{D}-m g=\left(\frac{d}{D}-1\right) m g\)
∴ Acceleration of the oil drop inside water,
⇒ αg= \(\frac{\left(\frac{d}{D}-1\right) m g}{m}\) or, α =\(\left(\frac{d}{D}-1\right)\)
or, \(\frac{d}{D}=1+\alpha\)
Example 26. A stone of density 2.5 g · cm-3 Is completely Immersed In sen water and Is allowed to sink from rest. Calculate the depth uttalned by the stone In 2 s. Neglect the effect of friction. The specific gravity of seawater Is 1.025, acceleration due to gravity = 980 cm · s-2.
Solution:
A stone of density 2.5 g · cm-3 Is completely Immersed In sen water and Is allowed to sink from rest
Let the mass of the stone be m g, So, the volume of the stone = 3/2.5 cm3.
When the stone is allowed to sink in seawater, the resultant downward force weight of the stone upthrust
or, \(m a=m g-\frac{m}{2.5} \times 1.025 \times g\)
[a = downward acceleration of the stone]
or, \(a=980-\frac{1.025}{2.5} \times 980=578.2 \mathrm{~cm} \cdot \mathrm{s}^{-2} .\)
If the stone attains a depth h in 2 8, then
h = \(\frac{1}{2} a t^2=\frac{1}{2} \times 578.2 \times(2)^2=1156.4 \mathrm{~cm}=11.564 \mathrm{~m} \text {. }\)
Example 27. A uniform cube of side 10 cm weighs 880 g x g. It is floating in saline water (specific gravity of saline water = 1.1). What will be the thrust on each face of the cube?
Solution:
A uniform cube of side 10 cm weighs 880 g x g. It is floating in saline water (specific gravity of saline water = 1.1).
Density of the material of the cube
= \(\frac{880}{10^3}=0.88 \mathrm{~g} \cdot \mathrm{cm}^{-3} \text {. }\)
Since the density is less than the density of saline water, some part of the cube remains above water. Let the lower surface of the cube be at a depth of x cm from the upper surface of saline water.
So, according to the condition of floatation, weight of the cube = weight of the saline water displaced by the cube

or, 880 x g = x x 10 x 10 x l .l x g or, x = 8 cm
So, the area of the part of a side of the cube that remains immersed in the saline water, A = 8×10 = 80 cm²
and the average depth that of the surface = \(\frac{0+x}{2}=\frac{x}{2}\)
Hence, the thrust on each lateral surface of the cube
= \(\frac{x}{2} \times 1.1 \times g \times A=\frac{8}{2} \times 1.1 \times 981 \times 80\)
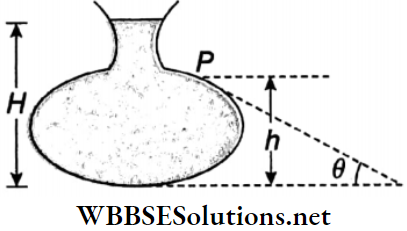
Example 28. A glass test tube with a plane base has a diameter of 4 cm and mass 30 g. Centre of gravity of the empty test tube is at a height of 10 cm from the base. Find the amount of water to be taken in the test tube so that when it floats vertically, its centre of gravity shifts to the midpoint of the immersed portion of the tube.
Solution:
A glass test tube with a plane base has a diameter of 4 cm and mass 30 g. Centre of gravity of the empty test tube is at a height of 10 cm from the base
The centre of gravity P of the empty tube is 10 cm above the point O. Let the height of water level taken in the tube be h cm. Midpoint of the water column is Q.
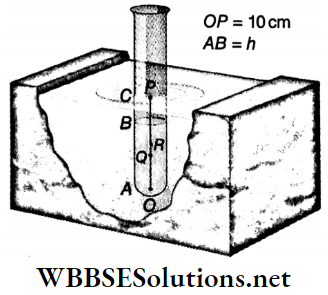
Let the centre of gravity of the test tube-water system be at R. Hence, part of the tube immersed in water, AC = 2x OR.
Volume of water in the tube = \(\pi(2)^2 h=4 \pi h \mathrm{~cm}^3\)
Mass of the tube + water in it = \((30+4 \pi h) \mathrm{g}\)
From the condition of floatation,
⇒ \(\pi\left(2^2\right) \times A C=30+4 \pi h\)
∴ AC = \(2 \times O R=\frac{30}{4 \pi}+h=d \text { (say). }\)
Taking a moment about the point R, \(4 \pi h \times R Q \stackrel{\circ}{=} 30 \times P R\)
or, \(4 \pi h[O R-O Q]=30 \times[O P-O R]\)
or, h = 8.806 cm
Hence the required mass of water -n x 8.806 = 110.66 g
or, \(4 \pi h\left[\frac{d}{2}-\frac{h}{2}\right]=30\left[10-\frac{d}{2}\right]\)
or, \(4 \pi h\left[\frac{1}{2}\left(\frac{30}{4 \pi}+h\right)-\frac{h}{2}\right]=30\left[10-\frac{1}{2}\left(\frac{30}{4 \pi}+h\right)\right]\)
or, h=8.806 cm
Hence the required mass of water = \(4 \pi \times 8.806=110.66 \mathrm{~g}\).
Example 29. A body of uniform cross-section remains floating in a liquid. The density of the liquid is 3 times that of the body. What part of that body remains outside the liquid?
Solution:
A body of uniform cross-section remains floating in a liquid. The density of the liquid is 3 times that of the body.
Let the volume of the body be V, density be ρ and density of the liquid be 3ρ.
Let us assume that x part of the body remains immersed in the liquid.
So, according to the condition of floatation, weight of the body = weight of displaced liquid
or, \(V \rho g=V x \cdot 3 \rho \cdot g \text { or, } x=\frac{1}{3}\)
∴ \(\left(1-\frac{1}{3}\right) \text { or } \frac{2}{3}\) part of the body remains outside the liquid.
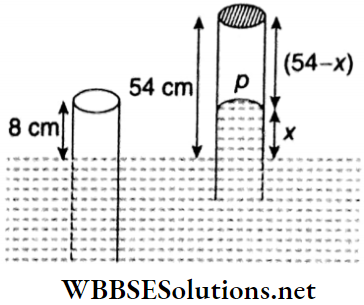
Example 30. When a 300 g mass is placed over a wooden cube, the cube just floats in water. When the mass is removed, the cube comes out by 4 cm from the water. Determine the length of each side of the cube.
Solution:
When a 300 g mass is placed over a wooden cube, the cube just floats in water. When the mass is removed, the cube comes out by 4 cm from the water.
Let the mass of the cube be mg; the length of each side of the cube be l cm.
∴ According to the problem for the first case, (m + 300)g = l³ x 1 x g ….(1)
For the second case, mg = l²(l-4) x 1 x g….(2)
∴ From (1) and (2), we get
300 = l³ – l³ + 4l²
or, l² = 75
or, l = 5√3
∴ Each side of the cube is 5√3 cm in length.
Example 31. From the two arms of a beam balance, a metal body weighing 20 g and a piece of glass are suspended. The apparent weights of these two bodies when measured in water are found to be the same. If immersed in alcohol instead of water, the mass of the metal needs to be increased by 0.84 g for balancing the beam. Calculate die mass of the glass piece. [Given, density of water =1 g·cm-3; density of alcohol = 0.96 g·cm-3]
Solution:
From the two arms of a beam balance, a metal body weighing 20 g and a piece of glass are suspended. The apparent weights of these two bodies when measured in water are found to be the same. If immersed in alcohol instead of water, the mass of the metal needs to be increased by 0.84 g for balancing the beam.
Let us assume that the weight of the glass piece is mg
Let the density of the metal body = d1 g · cm-3, and the density of glass = d1 g · cm-3
According to the question, when the bodies are immersed in water, apparent weight of the metal body = apparent weight of the glass piece
or, real weight of the metal body – weight of the water displaced by the metal body
= real weight of the glass piece – weight of the water displaced by the glass piece
or, \(\left(20-\frac{20 \times 1}{d_1}\right) \times g=\left(m-\frac{m \times 1}{d_2}\right) \times g\)
or, \(\frac{m}{d_2}-\frac{20}{d_1}=m-20\)
When immersed in alcohol,
⇒ \(\left(20-\frac{20}{d_1} \times 0.96\right) \times g+0.84 \times g=\left(m-\frac{m}{d_2} \times 0.96\right) \times g\)
or, \(m\left(1-\frac{0.96}{d_2}\right)-20\left(1-\frac{0.96}{d_1}\right)=0.84\)
or, \(m-\frac{m \times 0.96}{d_2}-20+\frac{20 \times 0.96}{d_1}=0.84\)
or, \(m-0.96\left(\frac{m}{d_2}-\frac{20}{d_1}\right)=20.84\)
or, \(m-0.96(m-20)=20.84\) [From equation (1)]
or, \(0.04 m=20.84-19.2\)
or, \(m=\frac{1.64}{0.04}=41\)
∴ The mass of the glass piece is 41g.
Example 32. A piece of silver weighing 105 gf and another piece of glass weighing 130 gf are placed on the right and left pan of a balance respectively. Which pan will move down when the die balance is immersed in water? [Given, the density of silver, ρ1 = 10.5 g • cm-3 and density of glass, ρ2 = 2.6 g · cm-3]
Solution:
A piece of silver weighing 105 gf and another piece of glass weighing 130 gf are placed on the right and left pan of a balance respectively.
Here weight of the piece of silver, W1 = 105 gf, and weight of the piece of glass, W2 = 130 gf.
Now, volume of the piece of silver,
⇒ \(V_1=\frac{105}{\rho_1}=\frac{105}{10.5}=10 \mathrm{~cm}^3\)
and volume of the piece of glass,
⇒ \(V_2=\frac{130}{\rho_2}=\frac{130}{2.6}=50 \mathrm{~cm}^3\)
Since density of water is 1 g · cm-3, weight of the water displaced by the pieces of silver and glass will be 10 gf and 50 gf respectively.
Therefore on immersing the balance in water, the apparent weight of the piece of silver,
W’1 = W1 – 10 = 105-10 = 95 gf
and the apparent weight of the piece of glass,
W’2 = W2 -50 = 130-50 = 80 gf
Since W’1 < W’2, the right pan i.e. the pan having piece of silver on it, will move down.
Example 33. A body Is fully immersed in water. Calculate the change in potential energy of the body, raised to a height h inside the water.
Solution:
A body Is fully immersed in water.
Let ρ and ρ0 be the density of the material of the body and the water respectively. If V is the volume of the body, then apparent weight of the body
= Vρg- Vρ0g = V(ρ-ρ0)g
Therefore, increase in potential energy of the body,
ΔU = work done in raising the body to a height h = V(ρ-ρ0)g x h
Example 34. A solid uniform ball of volume V and density ρ floats on the interface of two immiscible liquids as shown In the figure. The density of the upper liquid is ρ1 and that of the lower liquid is ρ2 (ρ2>ρ>ρ1).What fraction of the volume of the ball will be in the upper liquid and what fraction will be in the lower one?
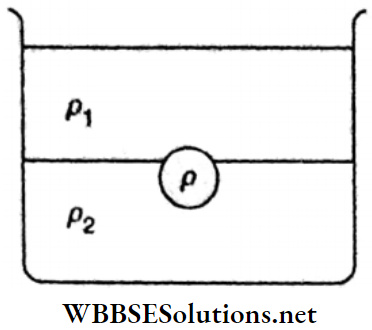
Solution:
Let V be the volume of the ball and a fraction x of its volume is in the upper liquid.
Then, volume of the ball inside the upper liquid =xV, and volume of the ball inside the lower liquid = V- xV = (1-x)V
Due to buoyancy, the net force on the ball in upward direction = [xρ1+(1-x)ρ2]Vg
At equilibrium, \(\left[x \rho_1+(1-x) \rho_2\right] V g\)=\(V \rho g\)
or, \(x \rho_1+(1-x) \rho_2=\rho\)
or, \(x\left(\rho_2-\rho_1\right)=\rho_2-\rho\)
Hence, the fraction of the volume of the ball inside the upper liquid,
x = \(\frac{\rho_2-\rho}{\rho_2-\rho_1}\)
Example 35. To what height should a cylindrical vessel be filled with a homogeneous liquid such that the force exerted by the liquid on the wall of the vessel be equal to the force exerted by the liquid on the bottom of the vessel?
Solution:
Let h be the height of the liquid of density p in the cylinder of radius r. The pressure of the liquid column at the bottom of the cylinder is hρg.
Therefore, the force exerted by the liquid column on the bottom of the cylinder is
F1 = pressure x area of the bottom = hρg x πr²
The pressure of the liquid column on the wall of the vessel varies from zero at the top of the column to hρg at the bottom.
Thus, the average pressure on the wall is \(\frac{0+h \rho g}{2}=\frac{1}{2} h \rho g\)
Therefore, the force exerted by the liquid column on the wall of the cylinder is
F2 = pressure x area of wall = 1/2 hρgx 2πrh
For F2 = F1 we should have 1/2 hρg x 2πrh = hρg x πr²
or, h = r
i.e., the height of the liquid column in the cylinder should be equal to the radius of the cylinder.









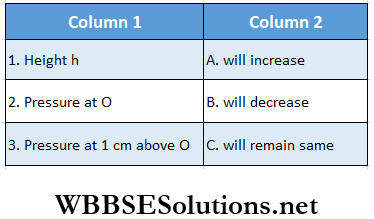
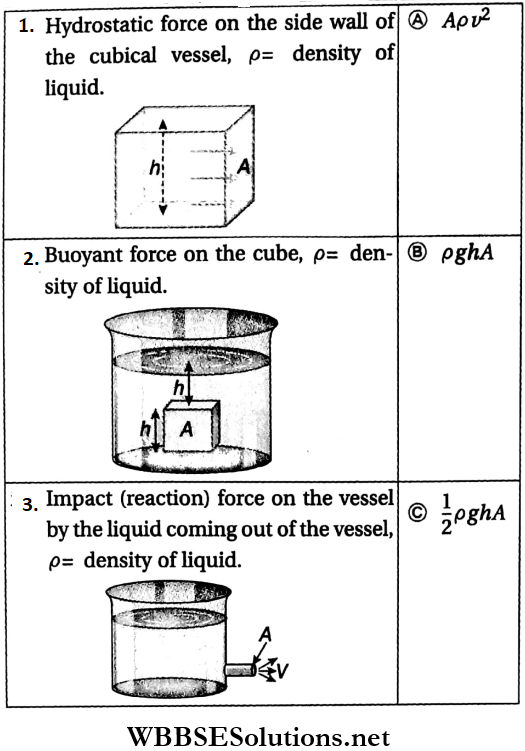
 Answer: 1
Answer: 1