Haritha

Thermodynamics

First And Second Law Of Thermodynamics Introduction

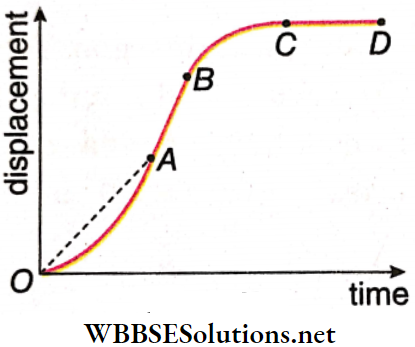
Position, displacement, velocity, acceleration, etc., are external properties of a body. From them, we get no information about the nature of the body. They are discussed in the subject of mechanics.

• On the other hand, properties like mass (M), volume (V), pressure (p), temperature (T), density (ρ), etc., are internal properties of a body. These are bulk (macroscopic) properties and can be measured by simple experiments.
• Any change in these properties generally involves the transfer of energy in the form of heat or work. All of these are studied in a branch of Physics, known as thermodynamics. The above-mentioned properties and similar others are called thermodynamic properties.
• The subject is based only on experi¬mental data and every thermodynamic formula comes from the analysis of this data. For example, suppose a fixed mass of an ideal gas is studied at constant temperature.
• Any change of pressure produces a change in volume and different sets of p and V are obtained. An analysis of these measured values shows that the product pV = constant. This is the well-known Boyle’s law. As it is experiment-based, it is a thermodynamic law.

Thermodynamic Systems: A body or, a part of a body, or a combination of a number of bodies that is being studied is usually called a thermodynamic system. In general, such a system interacts with its surroundings or, environment and exchanges energy and mass.

The environment or surroundings include all external objects that have some influence on the system. For example, if a room in a house is considered as a system and its thermal properties are to be studied, the sun at a distance of 1.5 x 10⁸ km is an important component of the environment, but another house only 100 m away need not be included as a component. Thermodynamic systems are of three types.

Isolated system: This system does not exchange any energy or mass with the surroundings.

Closed system: Energy is exchanged with the surroundings, but the mass remains fixed.

Open system: Both energy and mass are exchanged. We shall not discuss open systems in this chapter.

Properties like a number of molecules, molecular velocity, etc., are internal microscopic properties of a body. They are not directly measurable and experimental data is absent. Hence, the study of this subject is based on theoretical assumptions and is known as kinetic theory.

Thermodynamics – First And Second Law Of Thermodynamics Nature Of Heat

Heat is a form of energy which can be identified only when it is in transit. It can be converted into other forms of energy and vice versa. To measure the amount of heat energy, different units are used:

CGS System: calorie: (cal)

SI: Joule (J)

• In SI, the unit of energy is directly used to measure some quantity of heat. So, Joule (J) is the unit of heat in SI, as it is the SI unit of energy. Similarly, other energy units like erg may also be used.
• Immediately it becomes clear that the energy units must have definite relations with the conventional units of heat. This topic is discussed in the next section.
• In thermodynamics, the definition of temperature comes earlier from the zeroth law of thermodynamics. The definition of heat is based on the concept of temperature.

Nature of heat Definition: Heat is a form of energy which is transmitted from one place to another due to their temperature differences only.

It is interesting to note the difference between this and the calorimetric definition of heat.

Thermodynamics – First And Second Law Of Thermodynamics Mechanical Equivalent Of Heat Joules Law

The widely used unit of heat is calorie (or cal, in CGS system). We know that heat is a form of energy; so energy units like erg (CGS system) and joule (J in SI) should somehow be related to the units of heat.

• James Prescott Joule was the first experimentalist who accurately measured the mechanical energy equivalent to some amount of heat energy i.e., the mechanical equivalent of heat.
• This measurement determines the amount of mechanical energy expressed in joule (or erg) which is equivalent to heat energy of 1 cal.
• Mechanical energy may be used to do work and work produces heat. On the other hand, heat may be converted to work or mechanical energy. This indicates that there is a natural relationship between work and heat. This relation is known as Joule’s law.

Joule’s law: If some amount of work is entirely converted to heat, then the work done and the heat produced are proportional to each other.

If W=workdoneand H=heat produced,then from Joule’slaw,

W ∝ H or, W = JH…..(1)

Here, J is a constant. This constant is called the mechanical equivalent of heat or Joule’s equivalent.

Definition of J and Hs magnitudes in different systems: In equation (1), if H = 1, then W = J. So mechanical equivalent of heat is defined as the amount of work done to produce a unit amount of heat.

Clearly, the unit and the magnitude of J depends on the unit of heat and work in different systems of units.

CGS system: The unit of H is calorie and the unit of W is erg.

As J = \({W}{H}\) the unit of J is erg · cal^-1 and the measured value of J = 4.2 x 10⁷ erg · cal^-1.

As 1 J = 10⁷ erg, the value of J = 4.2 J · cal-1.

The units like erg · cal^-1 and J · cal^-1 indicate that the mechanical equivalent of heat J actually denotes the conversion factor between two units. For example, J = 4.2 J · cal^-1.

This means that 1 cal = 4.2 J, i.e., each calorie should be multiplied by 4.2 to express the energy in joule.

In SI: Here W and H are expressed in the same unit, which is joule (J). So, no conversion factor is necessary. The mechanical equivalent of heat is J = 1. This means that the concept of J is unnecessary in SI.

Relation of calories with erg and joule: 1 cal = 4.2 x 10⁷ erg = 4.2 J.

Thermodynamics – First And Second Law Of Thermodynamics Mechanical Equivalent Of Heat Numerical Examples

Example 1. 800 g lead balls are kept in a 1 m long, vertical tube which is a bad conductor and the tube is then closed at both ends. The tube is suddenly inverted so that the balls fall from one end to the other. The I temperature of the lead balls increases by 3.89°C after 50 such inversions. Find out the mechanical equivalent of heat assuming that the lead balls have retained the entire amount of heat produced.
Solution:

Work done, W= loss of potential energy of the balls = n x mgh

= 50 x 800 x 980 x 100 erg (1 m = 100 cm)

Heat produced, H = mst = 800 x 0.03 x 3.89 cal

∴ J = \(\frac{W}{H}=\frac{50 \times 800 \times 980 \times 100}{800 \times 0.03 \times 3.89}=4.2 \times 10^7 \mathrm{erg} \cdot \mathrm{cal}^{-1}\).

Example 2. Water drops from a height of 50 m in a waterfall. Find out the rise in temperature of water, if 75% of its energy is converted into heat and absorbed by water. (\(J=4.2 \times 10^7 \mathrm{erg} \cdot \mathrm{cal}^{-1} ; \mathrm{g}=9.8 \mathrm{~m} \cdot \mathrm{s}^{-2}\))
Solution:

Here, W = mgh x 75/100 and H = mst

Now, W = JH

or, \(m g h \times \frac{75}{100}=J m s t\)

or, \(t=\frac{m g h \times \frac{75}{100}}{J m s}\)

[s = \(J \mathrm{cal} \cdot \mathrm{g}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\) for water, g = \(9.8 \mathrm{~m} \cdot \mathrm{s}^{-2}\)=980 \(\mathrm{~cm} \cdot \mathrm{s}^{-2}, h=50 \mathrm{~m}=50 \times 100 \mathrm{~cm}\))

= \(\frac{g h}{J s} \times \frac{75}{100}=\frac{980 \times 50 \times 100}{4.2 \times 10^7 \times 1} \times \frac{75}{100}=0.0875^{\circ} \mathrm{C}\)

Example 3. The velocity of a 42 kg celestial body reduces from 20 km · min^-1 to 5 km · min^-1 due to its passage through the earth’s atmosphere. Find out the heat produced in calories. (J = 4.2 x 10⁷ erg · cal^-1)
Solution:

The initial velocity of the celestial body,

u = \(20 \mathrm{~km} \cdot \mathrm{min}^{-1}=\frac{20 \times 1000}{60} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Final velocity of the celestial body,

v = \(5 \mathrm{~km} \cdot \min ^{-1}=\frac{5 \times 1000}{60} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Work done, W = change in kinetic energy

= \(\frac{1}{2} m u^2-\frac{1}{2} m v^2=\frac{1}{2} m\left(u^2-v^2\right)\)

= \(\frac{1}{2} \times 42 \times\left(\frac{1000}{60}\right)^2\left(20^2-5^2\right)\)

= \(\frac{42 \times 10^4 \times 375}{2 \times 36} \text { joule }\)

∴ Heat produced,

H = \(\frac{W}{J}=\frac{42 \times 10^4 \times 375}{2 \times 36 \times 4.2} \)

(J = \(4.2 \times 10^7 \mathrm{erg} \cdot \mathrm{cal}^{-1}=4.2 \mathrm{~J} \cdot \mathrm{cal}^{-1}\))

= \(5.2 \times 10^5 \mathrm{cal}\).

Example 4. Find out the amount of work done to convert 100 g ice at 0°C to water at 100°C. (Latent heat of fusion of ice = 80 cal · g^-1; the mechanical equivalent of heat = 4.2 J · cal^-1).
Solution:

Total heat supplied,

H = 100 x 80 + 100 x 1 x (100-0)

= 8000 + 10000 = 18000 cal

∴ Work done, W = JH = 4.2 x 18000 = 75600 J.

Example 5. What will be the temperature difference between the top and the bottom of a 400 m high waterfall, assuming that 80% of the heat produced is retained by the water?
Solution:

Work done, W = loss in potential energy

= mg(h- 0) = mgh

∴ Heat produced, H = \(\frac{W}{J}=\frac{m g h}{J}\)

∴ Amount of heat retained by water = \(\frac{m g h}{J} \times \frac{80}{100}\)

If the increase in temperature of water is t, required heat = mst

According to the question,

mst = \(\frac{m g h}{J} \times \frac{80}{100}\)

or, t = \(\frac{g h}{J s} \times \frac{80}{100}=\frac{9.8 \times 400}{4.2 \times 1000} \times \frac{80}{100}\)

(specific heat of water in SI s = \(1000 \mathrm{cal} \cdot \mathrm{kg}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\))

or, t = 0.747 °C

Example 6. Find out the minimum height from which a piece of ice at 0°C should be dropped so that it melts completely due to its impact with the ground. Assume that half of the energy loss due to the fall is responsible for the fusion of ice. (Latent heat of fusion of ice = 80 cal · g^-1, g = 980 cm · s^-2, J = 4.2 J · cal^-1)
Solution:

Let the piece of ice of mass m be allowed to fall from height h.

Now, energy loss due to the fall = loss in potential energy = mgh = work done, W.

Half of it, i.e., W/2 amount of energy is converted into heat and it is responsible for the fusion of ice.

∴ Heat produced, \(H=\frac{W / 2}{J}=\frac{m g h}{2 J}\)

As mg of ice melts into water, required latent heat = 80 m cal

So, \(\frac{m g h}{2 J}=80 \mathrm{~m}\)

or, \(h=\frac{80 \times 2 J}{g}=\frac{80 \times 2 \times 4.2 \times 10^7}{980}\)

(J = \(4.2 \mathrm{~J} \cdot \mathrm{cal}^{-1}=4.2 \times 10^7 \mathrm{erg} \cdot \mathrm{cal}^{-1}\))

= \(6.857 \times 10^6 \mathrm{~cm}=68.57 \mathrm{~km}\)

Example 7. A piece of ice at 0°C is dropped to the ground from some height. The piece of ice melts completely due to its impact on the ground. Find the height from which the piece was dropped considering that 60% of its energy is converted into heat. (J = 4.2 J · cal^-1)
Solution:

The potential energy of the piece of ice of mass m at height h = mgh, kinetic energy = 0

So, total mechanical energy = mgh

This energy is conserved till it touches the ground. Due to the impact with the ground, 60% of this energy,

i.e., mgh x 60/100 or 0.6 mgh is converted into heat energy.

∴ Heat produced = \(\frac{0.6 \mathrm{mgh}}{J}\)

Again, heat required to melt m g of ice = mL

[L = latent heat of fusion of ice]

∴ \(\frac{0.6 m g h}{J}=m L\)

or, h = \(\frac{J L}{0.6 g}\left[L=80 \mathrm{cal} \cdot \mathrm{g}^{-1}=80 \times 1000 \mathrm{cal} \cdot \mathrm{kg}^{-1}\right]\)

= \(\frac{4.2 \times(80 \times 1000)}{0.6 \times 9.8}=5.71 \times 10^4 \mathrm{~m}=57.1 \mathrm{~km}\)

Example 8. A stirrer rotates in 1 l of water against a damping force of 0.1 N at 360 rpm in a circle of radius 5 cm. Calculate the rise in water temperature in 1 h, neglecting heat loss due to radiation. (J = 4.2 J · cal^-1)
Solution:

Mass of 1 l of water, m = 1 kg.

If t is the rise in temperature of water in 1 h, then heat produced, H = mst.

Now, circumference of the circle =2πr; number of rotations in 1 h = 360 x 60

∴ Displacement of the stirrer, d = 360 x 60 x 2πr

Work done, W = force x displacement = Fd

∴ W = JH or, Fd = Jmst

or, t = \(\frac{F d}{J m s}=\frac{0.1 \times(360 \times 60 \times 2 \times \pi \times 0.05)}{4.2 \times 1 \times 1000}\)

(F = \(0.1 \mathrm{~N} ; r=5 \mathrm{~cm}=0.05 \mathrm{~m}\))

s = \(1000 \mathrm{cal} \cdot \mathrm{kg}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

= 0.162°C.

Example 9. 10 l of water is dropped from a height of 250 m. How much heat (in calories) will be generated when the water reaches the bottom? Assuming that the entire heat will be retained by the mass of water, what will be the rise in temperature of the water? (Given J = 4.18 J · cal^-1)
Solution:

Mass of 10 l of water, m = 10 kg.

Kinetic energy on impact with the ground

= initial potential energy = mgh = work done (W)

So, heat generated,

H = \(\frac{W}{J}=\frac{m g h}{J} \mathrm{cal}\)

The specific heat of water,

s = \(1000 \mathrm{cal} \cdot \mathrm{kg}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

If t is the rise in temperature, then

mst = H = \(\frac{m g h}{J}\)

or, t = \(\frac{g h}{J s}=\frac{9.8 \times 250}{4.18 \times 1000}=0.586^{\circ} \mathrm{C}\)

Example 10. What will be the time required to heat a 151 bucket full of water from 20°C to 40°C using a 1500W immersion heater?
Solution:

Mass of 15 1 of water, m = 15 kg specific heat of water, s = 1000 cal · kg^-1 · °C^-1

Now, W = JH or, Pt = Jmsθ

where P = power of the heater = 1500W; t = time required; θ = rise in temperature = 40 – 20 = 20°C.

So, t = \(\frac{J m s \theta}{P}=\frac{4.2 \times 15 \times 1000 \times 20}{1500}=840 \mathrm{~s}=14 \mathrm{~min} \text {. }\)

Example 11. The temperature of a piece of lead is 27°C. Find out the minimum velocity of its impact with a wall so that it melts completely. Suppose 58% of the heat generated is dissipated. Given, J = 4.2 J · cal^-1; melting point, specific heat, and latent heat of fusion of lead are 327°C, 0.03 cal · g^-1 · °C^-1 and 5 cal · g^-1, respectively.
Solution:

⇒ \(H \times \frac{100-58}{100}=m s t+m l\)

or, \(H=(m s t+m l) \times \frac{100}{42}\)

Again, W = \(\frac{1}{2} m v^2\)

Now, W=J H

or, \(\frac{1}{2} m v^2=J(m s t+m l) \times \frac{100}{42}\)

or, \(v^2=2 J(s t+l) \times \frac{100}{42}\)

= \(2 \times\left(4.2 \times 10^7\right) \times[0.03 \times(327-27)+5] \times \frac{100}{42}\)

= \(28 \times 10^8\)

So, \(v=5.29 \times 10^4 \mathrm{~cm} \cdot \mathrm{s}^{-1}=529 \mathrm{~m} \cdot \mathrm{s}^{-1}\).

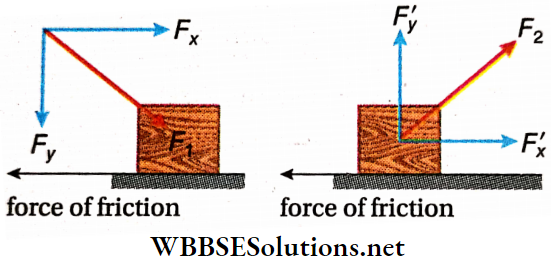
Example 12. A body of mass 2 kg is pulled with a velocity of 2 m · s^-1 on a horizontal surface. What will be the heat produced in 5s, if the coefficient of friction between the body and the surface is 0.2? Given, J = 4.21 • cal^-1; g = 9.8 m• s^-2.
Solution:

Force of friction on the body, F = μmg

So the work done, W = Fs = μ mg · vt

∴ Heat produced, H = \(\frac{W}{J}=\frac{\mu \mathrm{mg \nu t}}{J}\)

= \(\frac{0.2 \times 2 \times 9.8 \times 2 \times 5}{4.2}\)

= 9.33 cal

Example 13. Two pieces of ice, of equal mass moving towards each other with the same velocity, collide head-on and are vaporized due to this collision. Find out the minimum initial velocity of the pieces of ice. Given, that the initial temperature, specific heat, and latent heat of fusion of ice are -12°C, 0.5 cal · g^-1 · °C^-1, and 80 cal · g^-1 respectively latent heat of steam is 540 cal · g^-1.
Solution:

Let m = mass of each piece of ice; v = minimum initial velocity.

Here, work done due to collision, W

= loss in kinetic energy = 2 x 1/2 mv² = mv²

Heat produced, H = 2[m x 0.5 x 12 + m x 80 + m x 1 x 100 + m x 540]

= 1452 m cal

∴ W = JH or, mv² = J x 1452m

or, v² = (4.2 x 10⁷)x 1452 = 6.1 x 10¹⁰

So, v = 2.47 x 10⁵ cm · s^-1 = 2.47 km · s^-1.

Example 14. The top of a waterfall is at a temperature 0.49°C below that of the bottom. The work done by water due to its fall is converted entirely into heat. Find the height of the waterfall. Given, g = 980 cm · s^-2, J = 4.2 J · cal^-1.
Solution:

Let m = mass of water falling from height h.

Work done, W = kinetic energy of impact

= initial potential energy = mgh.

Now, W = JH or, mgh = Jmst

or, h = \(\frac{J s t}{g}\)

= \(\frac{\left(4.2 \times 10^7\right) \times 1 \times 0.49}{980}\)

= 21000 cm =210 m.

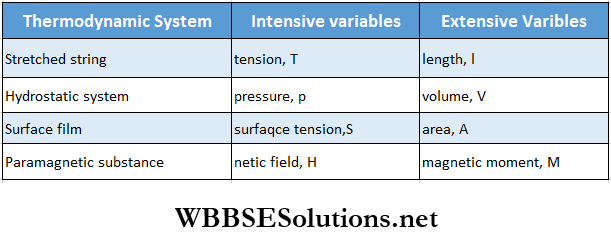
Thermodynamics – First And Second Law Of Thermodynamics Intensive And Extensive Variables

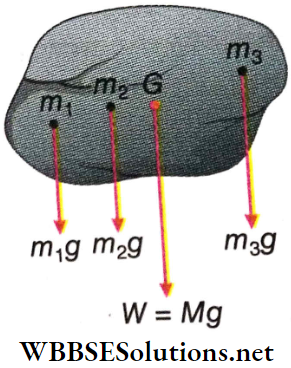
Let us consider a wooden table and a wooden chair. The mass (m) and volume (V) of them are different because such properties depend on the whole body. These are the extrinsic thermodynamic properties.

On the other hand, the density (ρ) is the same for both the bodies. This property does not depend on the whole body, but only on the material (in this case, wood) of the body. This is an intrinsic thermodynamic property.

Generally, thermodynamic variables are of two types

1. Intensive variable and
2. Extensive variable.

The variables that do not depend on the amount of matter or mass in a thermodynamic system are called intensive variables. Pressure, temperature, density, surface tension, etc., are intensive variables.

• The variables that are proportional to the amount of matter or mass in a thermodynamic system are called extensive variables. Volume, magnetic moment, internal energy, entropy, etc., are extensive variables.
• As an illustration we may consider some amount of gas of mass m, volume V, pressure p, temperature T, and density ρ, enclosed in a container.

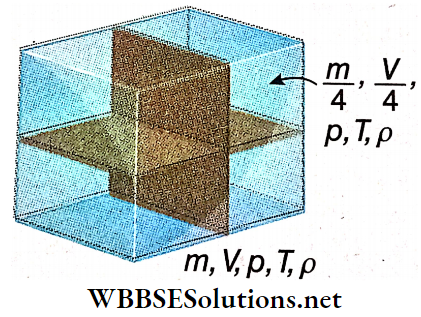
Now we divide the gas into 4 equal parts. Clearly, mass, volume, pressure, temperature, and density of each part arc \(\frac{m}{4}, \frac{V}{4}, p, T \text { and } \rho\), respectively.

• It means that m and V depend on the whole amount of the gas; they are extensive variables. But ρ, p, T do not depend on the amount; they are intensive variables.
• We consider a relation like mass = density x volume or, m = ρV. On the left-hand side, mass m changes proportionally with the amount of matter in a system. On the right-hand side, volume V changes similarly.
• Thus, the two sides remain equal only if ρ remain the same. So, whereas m and V are extensive, ρ is intensive. In general, in a product of two or more thermodynamic properties, only one is an extensive variable and the others are intensive variables.

So we can have a product like ρV which is extensive (V is extensive, but ρ is intensive). But a product like mV is not allowed, as both m and V are extensive.

Intensive and extensive variable in thermodynamics systems

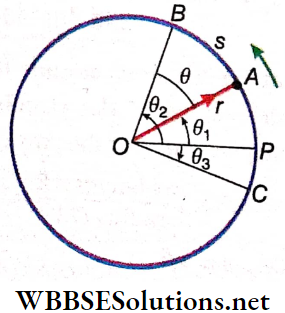
State Function and Path Function: If a system is in equilibrium, the variables like its volume (V), pressure (p), temperature (T), etc. have definite values. So these values refer to the state of the system and do not depend on the path followed to reach that state. So variables like volume, pressure, temperature, etc. are called state functions or properties of the system.

• On the other hand, the two functions—work (W) and heat (Q) are not related to any state of the system, rather they are relevant to any process of the system. A statement—W_A is the amount of work done in the state A—has no meaning.
• Rather the statement ‘WAB is the amount of work done in die process A → B’ is meaningful. There can be various paths from the state A to the state B. The values of W_AB or Q_AB in each path are different, i.e., these values depend on the paths between the states A and B. So W and Q are called path functions.
• They are not state functions. It is to be noted that if V_A and V_B are the volumes of the system in the states A and B respectively, then the change in volume in the process A → B = V_B– V_A.
• Whatever may be the path taken from A to B the change in volume, V_B-V_A, remains the same. It does not depend on the path. So any change of a state function is independent of the path.

 Thermodynamics – First And Second Law Of Thermodynamics Thermodynamic Equilibrium And Process

Thermodynamic equilibrium: The macroscopic properties that are used to describe a system may change spontaneously or due to an external influence. During such a change, the system and its surroundings interact with each other.

1. The absence of unbalanced force or torque in the interior of a system or between a system and its surroundings implies mechanical equilibrium has been established.
2. For a system in mechanical equilibrium, when there is no spontaneous change of internal structure (by means of a chemical reaction) or transfer of matter from one part of the system to another (by means of diffusion) chemical equilibrium is said to be established.
3. For a system in mechanical and chemical equilibrium, thermal equilibrium is set to be attained if no exchange of heat occurs between the system and its surroundings. Hence it is obvious that in thermal equilibrium, the temperature remains the same throughout the system and is identical with that of the surroundings.

When all the three types of equilibrium stated above an attained by a system, it is said to be in a thermodynami equilibrium in an equilibrium state, or simply, in state.

• A closed thermodynamic system, i.e., a system having a fixed mass, can be described completely by three of its properties—volume (V), pressure (p), and temperature (T). All other properties of the system depend on these properties and therefore are functions of, V, p, and T.
• In thermodynamic equilibrium none of the tires properties of a system— volume, pressure, or temperature—changes with time. In our study, we shall deal with equilibrium states, and V, p, and T will not be treated as functions of time. So, the quantity time will never appear in our formulation of thermodynamic relations.

Moreover, volume, pressure, and temperature are related among themselves by an equation of state. Thus, if two of them are known, the third can be calculated using that equation of state. Hence, there are only two independent properties for a closed thermodynamic system. For example, let a fixed mass of 1 mol of a gas be taken at STP. Then,

p = 1 atm = 76 cm of mercury

= 76 x 13.6 x 980 dyn · cm^-2

T = 0 °C = 273K

If die gas is assumed to be ideal, then from the equation of state pV = RT, we have

V = \(\frac{R T}{p}=\frac{8.31 \times 10^7 \mathrm{erg} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1} \times 273 \mathrm{~K}}{76 \times 13.6 \times 980 \mathrm{dyn} \cdot \mathrm{cm}^{-2}}\)

= \(22400 \mathrm{~cm}^3 \cdot \mathrm{mol}^{-1}=22.4 \mathrm{l} \cdot \mathrm{mol}^{-1}\)

Here, p and T played the role of independent properties and V could be calculated from them.

Thermodynamic process: Let a system be initially at an equilibrium state A. Now, if the system exchanges energy, in the form of work or heat, with its surroundings, then the values of V, p, and T would change, in general. So, the system would deviate from the state A.

• But eventually, when the energy exchange stops, the system would attain a new equilibrium state, say B. The transition of a system from an initial state A to a final state B is known as a thermodynamic process and is usually denoted as A → B.
• It should be noted that the transition between two states may occur along different paths 1, 2, …. Each of these paths corresponds to a separate process.

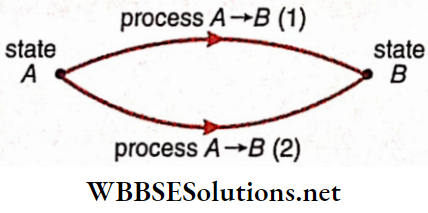
A process, in general, involves simultaneous changes of all the three properties—volume (V), pressure (p), and temperature (T). However, for simplicity of analysis, some special processes are often considered:

1. Isochoric process: The volume of a system remains constant in this process. But, both pressure and temperature undergo some changes.
2. Isobaric process: Here, p remains constant and Vand T change their values.
3. Isothermal process: T is a constant, whereas there are changes in V and p.
4. Adiabatic process: The heat exchange between the system and its surroundings remains zero there are changes in all of V, p, and T.

Thermodynamics – First And Second Law Of Thermodynamics External Work

Hydrostatic system: A system that obeys Pascal’s law is called a hydrostatic system. Important characteristics of such a system are:

1. The pressure is uniform throughout the system and acts normally outwards at every point on the walls.
2. Any additional pressure applied at any point gets transmitted throughout the system in such a way that the pressure everywhere continues to remain uniform.

These conditions are obeyed by

1. Small amounts of liquids for which the effect of gravity may be neglected and
2. Gaseous systems.

However, all liquids are nearly incompressible, i.e., any change in pressure does not produce an appreciable change in volume. Due to this reason, for the thermodynamic analysis of a hydrostatic system, it is convenient to take a closed gaseous system.

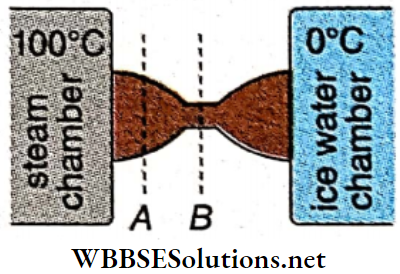
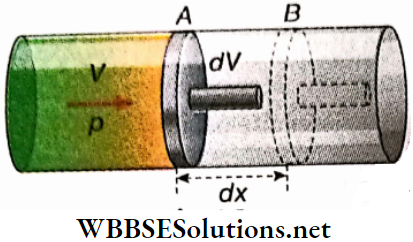
Hydrostatic work: An amount of gas is enclosed by an airtight cylinder-piston arrangement. where the piston can move without friction along the inner walls of the cylinder.

These conditions are obeyed by

1. Small amounts of liquids for which the effect of gravity may be neglected and
2. Gaseous systems.

However, all liquids are nearly incompressible, i.e., any change in pressure does not produce an appreciable change in volume. Due to this reason, for the thermodynamic analysis of a hydrostatic system, it is convenient to take a closed gaseous system.

Hydrostatic work: An amount of gas is enclosed by an airtight cylinder-piston arrangement. where the piston can move without friction along the inner walls of the cylinder.

Let p = pressure of the enclosed gas,

a = area of cross-section of the piston.

So, the force acting on the piston = pa.

• Now, suppose the piston goes through a very small displacement outwards from position A to position B; displacement AB = dx.
• This displacement occurs when a slight difference develops between the pressures of this system and its surroundings. A small outwards pull on the piston, a gain of a small amount of heat from the surroundings, etc., may initiate such a displacement.
• During this displacement, however small, the pressure p of the system may change. But at even instant, the pressure must be uniform throughout the system. A sufficiently slow motion of the piston is required to satisfy this hydrostatic condition.

Due to the small displacement dx, the gas expands from volume V to V+dV. Clearly, dV = adx. So, the small work done in this infinitesimal process is,

dW = force x displacement

= (pα)(dx) = p(αdx) = pdV

or concisely, dW = pdV …(1)

Work done in a finite process, for which the volume changes from V₁ to V₂, is

W = \(\int d W=\int_{V_1}^{V_2} p d V\)…(2)

The relation (1) can be interpreted as:

1. When there is no change in volume, V = constant and dV = 0. So, dW = 0 no work is done in such a process.

2. When the volume increases, i.e., for an expansion, dV is positive, i.e., dV> 0. So, dW>0; positive amount of work is done in this process. The system releases some energy to its surroundings it is termed as work done by the system.

3. When the volume decreases, i.e., for a contraction occurring due to an inward motion of the piston, dV is negative, i.e., dV<0.

So, dW< 0; a negative work is done in this process. The system receives some energy from its surroundings it is termed as work done on the system.

The integral in relation (2) can be evaluated for special processes:

1. Isochoric process: V = constant and dV = 0.

So, W = 0 …(3)

2. Isobaric process:

p = constant.

So, W = \(\int_{V_1}^{V_2} p d V=p \int_{V_1}^{V_2} d V=p\left(V_2-V_1\right)\)….(4)

But, when the pressure p of a system changes in a process, the integral cannot be evaluated unless p can be expressed as a function of volume V.

It is only possible if the equation of state of the system is known. Later in this chapter, the expressions for isothermal work and adiabatic work for an ideal gas will be evaluated, using the ideal gas equation of state, pV = R.

There are systems in thermodynamics that are not hydrostatic. For them, the work equations (1) and (2) would be different. However, in this chapter, we shall restrict ourselves mainly to hydrostatic systems.

 

Unit 8 Thermodynamics Chapter 1 First And Second Law Of Thermodynamics Reverse And Irreversible Process

Let a thermodynamic system be in an initial state A. Owing to heat exchange and external work, the system attains its final state B. That is, the process is A → B. Now, we shall state the conditions under which the process may be called ‘reversible’. A Process A → B is reversible, if

1. The process B → A occurs in nature and
2. After the processes A →B →A, there is no net change in the surroundings.

The conditions 1 and 2 are called the conditions of reversibility. Process A → B is an irreversible process, if these conditions are not satisfied.

• The concepts of reversibility and irreversibility are direct consequences of the second law of thermodynamics. The words ‘self-acting machine’ in Clausius or Kelvin-Planck statements are closely related to the words ‘no net change in the surroundings’ in the reversibility conditions.
• For example, we consider the process of heat flow from higher to lower temperatures. The reverse process does occur in nature — a domestic refrigerator actually transfers heat from its cool container to comparatively hotter surroundings.
• But it is not self-acting, because some work in the form of electrical energy must be supplied from the surroundings. As a result, the environment suffers a net change.

So we may say that heat transfer from higher to lower temperature is an irreversible process. This is because heat, on its own, cannot flow from lower to higher temperatures (Clausius statement).

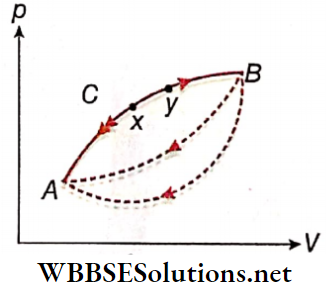
• We now consider a process A →B on a p V diagram. Let the process occur along a particular path ACB.
• The opposite process B → A can take different paths from B to A. However, for reversibility, only the path BCA is important.
• Then for each elementary step (say, xy) the heat exchange and the work done in the forward process (x → y) are exactly equal and opposite to those in the reverse process (y → x) – This is essentially the condition for reversibility, equivalent to the conditions discussed earlier.

A process A→ B is reversible, if

1. The process B → A occurs in nature and
2. The heat exchange and the work done for each step in the forward process are exactly equal and opposite to those for the reverse process.

Conditions of reversibility:

1. A process is reversible if there is no dissipation of energy during this process. The origin of dissipative energy are friction, surface tension, resistance, etc. So, a process that occurs against friction, surface tension, etc., cannot be reversible.

2. A process is reversible if it occurs infinitesimally slowly. Every real process in nature is irreversible. A reversible process is only an ideal process, never occurring in nature. Still, the concept is very useful to formulate important thermodynamic relations.

Conditions of reversibility Example:

1. Let a gas be enclosed inside a cylinder-piston arrangement. Now the gas is allowed to get compressed very slowly through an isothermal process by applying force from its surroundings. So work is done on the gas by the piston.

• Now after this process, if the gas by itself expands very slowly pushing the piston up, it returns to the initial state. So work is done on the piston by the gas.
• This work done is nearly equal to the previous one. So apparently, the process is reversible. But actually, in each piston movement, some heat is generated due to friction.
• This heat is absorbed by the surroundings which cannot be restored. So strictly speaking, the process is irreversible, but becomes nearly reversible only when the piston movements are very slow and heat generated due to friction becomes almost negligible.

2. Let us take a container having 10 g of ice floating on 100 g of water at 0°C. If 80 cal of heat is supplied from the surroundings, 1 g of ice melts into 1 g of water.

• Now, if 80 cal of heat is taken away, we again get 10 g of ice on 100 g of water. Here, the surroundings also come to its initial state. So the process of fusion of ice is apparently reversible.
• However, some heat exchange with the surroundings can never be avoided. That heat cannot be recovered in any manner.
• So the surroundings suffer a permanent change. For this reason, processes like fusion and vaporisation are only approximately reversible.

3. Free fall of a body due to gravity from a height h to the ground is an irreversible process because the body on its own cannot move up to the height of h.

4. When containers with two different gases are connected, the gases mix with each other. The gases cannot separate themselves on their own and so the process is irreversible.

 

Unit 8 Thermodynamics Chapter 1 First And Second Law Of Thermodynamics Very Short Answer Type Questions

Question 1. Which branch of physics deals with the study of the relationship between heat and various forms of energy?
Answer: Thermodynamics

Question 2. How is the work done related to the heat produced when work is completely converted into heat?
Answer: Mutually proportional

Question 3. If some amount of work is completely converted into heat, what is the name of the ratio of work done and amount of heat?
Answer: Mechanical equivalent of heat

Question 4. What is the value of the mechanical equivalent of heat in a CGS system?
Answer: 4.2 x 10⁷ erg · cal^-1

Question 5. What is the value of the mechanical equivalent of heat in SI?
Answer: 1

Question 6. What would be the amount of heat generated if 4.2 x 10⁷ erg of work is completely converted into heat?
Answer: 1 cal

Question 7. Give an example of intensive variable.
Answer: Temperature

Question 8. Give an example of an extensive variable.
Answer: Volume

Question 9. Which one of the four quantities does not indicate the thermodynamic state of a substance—volume, temperature, pressure, and work?
Answer: Work

Question 10. What is the change in temperature of water when it falls from the top to the bottom in a waterfall?
Answer: Increases

Question 11. Is pressure intensive or extensive variable?
Answer: Intensive

Question 12. Is magnetic moment intensive or extensive variable?
Answer: Extensive

Question 13. What would be the amount of heat required to increase the temperature of 1 g of water by 1°C?
Answer: 4.2

Question 14. What is the change in internal energy of a substance when it is heated?
Answer: Increases

Question 15. On which factor does the internal energy of a certain amount of an ideal gas depend?
Answer: On its temperature

Question 16. Will there be any change in the internal energy of a certain amount of gas, if its pressure or volume changes at constant temperature?
Answer: No

Question 17. In case of expansion of a gas, would the work done by the gas be positive or negative?
Answer: Positive

Question 18. What is the SI unit of molar-specific heat?
Answer: J · mol^-1 · K^-1

Question 19. The first law of thermodynamics is the mathematical form of a universal law. Name it.
Answer: Law of conservation of energy

Question 20. How many types of specific heat of a gas are used in practice?
Answer: Two

Question 21. How many types of molar-specific heat of a gas are used in practice?
Answer: Two

Question 22. Which is greater — specific heat at constant volume, c_v, or specific heat at constant pressure, c_p?
Answer: c_p

Question 23. How is the heat supplied to a substance in an isothermal process used?
Answer: External work

Question 24. In which process does the heat accepted or rejected become zero?
Answer: Adiabatic

Question 25. Is the reversible process slow or fast?
Answer: Slow

Question 26. Which process does not suffer dissipative forces reversible or irreversible?
Answer: Reversible process

Question 27. Is the isothermal process slow of fast?
Answer: Very slow process

Question 28. Is the adiabatic process slow or fast?
Answer: Very fast process

Question 29. Is rusting of iron a reversible process?
Answer: No

Question 30. Hot milk is poured into a cup of tea a. d is mixed with a spoon. Is this an example of a reversible process?
Answer: No

Question 31. The sum of kinetic and potential energies of the molecules of a substance is equal to its ______
Answer: Internal energy

Question 32. In a process, if dU, dW, and dQ are changes in internal energy, work done, and heat accepted respectively for a system, what is the relation between dU, dQ, and dW?
Answer: dQ = dU+dW

Question 33. p and V are the pressure and volume respectively of a gas of a particular mass. If volume changes to V+ dV, what is the work done in the process?
Answer: pdV

Question 34. The molecular weight of a gas is M. If the specific heat and molar specific heat at constant volume of the gas is c_v and C_v respectively. Write down the relation between c_v > C_v and M.
Answer: C_v = Mc_v

Question 35. A bicycle pump becomes hot when air is pumped into the tube. Why?
Answer: Due to adiabatic compression

Question 36. Air coming out from a burst bicycle or motorcar tube appears to be cold. Why?
Answer: Due to adiabatic expansion

Question 37. If γ of a gas is equal to 1.66 then what is the number of atoms in a molecule of the gas?
Answer: 1

Question 38. Adiabatic curves are comparatively _______ than isothermal curves.
Answer: Steeper

Question 39. If the pressure and the temperature of a gas changes at constant volume, what is the work done by the gas?
Answer: Zero

Question 40. What is the change in internal energy in an isothermal process?
Answer: Zero

Question 41. In which expansion the internal energy of a gas be decrease?
Answer: Adiabatic

Question 42. If M is the molecular weight of a gas, what is the difference between the two specific heats of 1 g of an ideal gas?
Answer: \(\frac{R}{M}\)

Question 43. In case of 1 mol of an ideal gas, write down the value of C_v -C_p
Answer: -R

Question 44. An ideal gas rejects 10 cal of heat at constant volume. Find the work done
Answer: Zero

Question 45. What is the relation between p and V in an adiabatic process?
Answer: pV^γ = constant

Question 46. A process against frictional force cannot be ______
Answer: Reversible

Question 47. Two balls of the same mass, one of iron and the other of copper, are dropped from the same height. Which one would become hotter?
Answer: Copper

Question 48. In an isothermal process, the gas containers should be made of highly _____ materials.
Answer: Conducting

Question 49. In an adiabatic process, the gas containers should be made of highly _______ materials.
Answer: Non-conducting

Question 50. Is Joule’s heating process reversible or irreversible?
Answer: Irreversible

Question 51. Write down the coefficient of performance of an ideal refrigerator.
Answer: Infinite

Question 52. What is the value of the efficiency of an ideal heat engine?
Answer: 1

Question 53. Heat engine is a mechanical device that converts heat into _____
Answer: Work

Question 54. When heat is gained or lost by heat reservoir, its temperature ______
Answer: Remains constant

Unit 8 Thermodynamics Chapter 1 First And Second Law Of Thermodynamics Assertion Reason Type Question And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: In an isothermal process the whole heat energy supplied to the body is converted into internal energy.

Statement 2: According to the first law of thermodynamics ΔQ = ΔU+pΔV.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 2.

Statement 1: The specific heat of a gas in an adiabatic process is zero but it is infinite in an isothermal process.

Statement 2: Molar specific heat of a gas is directly proportional to heat exchanged with the system and inversely proportional to change in temperature.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: In an adiabatic process, the change in internal energy of a gas is equal to work done on or by the gas in the process.

Statement 2: The temperature of the gas remains constant in an adiabatic process.

Answer: 3. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 4.

Statement 1: The internal energy of an ideal gas does not depend on the volume of the gas.

Statement 2: This is because internal energy of an ideal gas depends on the temperature of the gas.

Answer: Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.

Unit 8 Thermodynamics Chapter 1 First And Second Law Of Thermodynamics Match Column 1 With Column 2

Question 1. For 1 mol of a monatomic gas match the following:

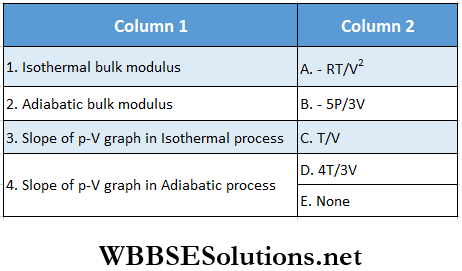
Answer: 1. D, 2. A, D, 3. D, 4. B, C

Question 2. Heat given to it pi recess is taken to be positive. Then mutch two options in column l with the corresponding options in column 2 for the given cycle.

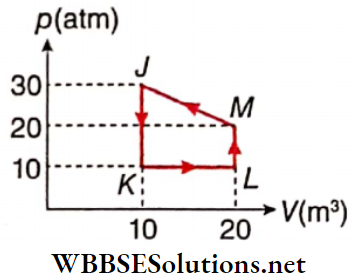
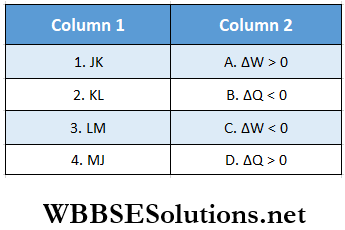
Answer: 1. E, 2. E, 3. A, 4. B

Question 3. Column 1 contains a list of processes Involving the expansion of an ideal gas. Match this with column 2 describing the thermodynamic change during this process.

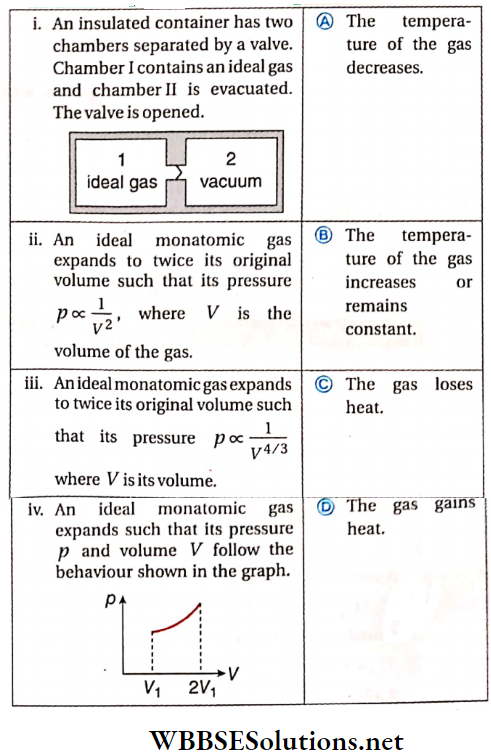
Answer: 1. B, 2. A, C, 3. A, D, 4. B, D

Question 4. Volume versus pressure curves are given for four processes as shown. Match the entries of column 1 with the entries of column 2.

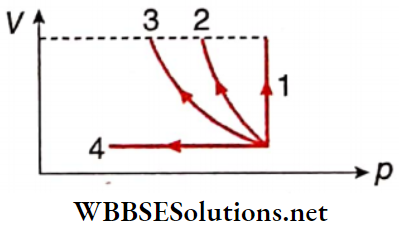
Answer: 1. A, C, D, 2. C, D 3. C, 4. B

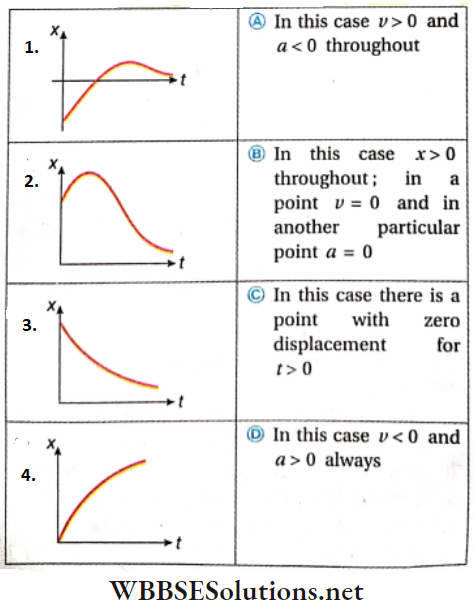
Question 5. A sample of gas goes from state A to state B in four different manners, as shown by the graphs. Let W be the work done by the gas and ΔU be the change in internal energy along the path AB. Match the graphs with the statements provided correctly.

Answer: 1. D, 2. B, 3. C, 4. B

Question 6. One mole of a monatomic ideal gas is taken along two cyclic processes E → F → G → E and E → F → H → E.

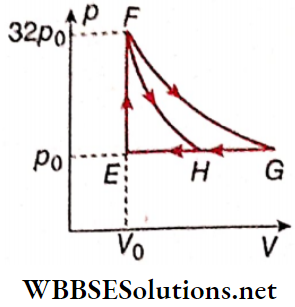
The processes involved are purely isochoric, isobaric, isothermal, or adiabatic. Match tire column 1 with the magnitudes of the work done in column 2.

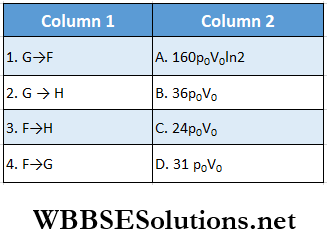
Answer: 1. D, 2. C, 3. B, 4. A

Question 7. One mole of a monoatomic ideal gas is taken through a cycle ABCDA as shown in the p-V diagram. Column 2 gives the characteristics involved in the cycle. Match them with each of the processes given in column 1.

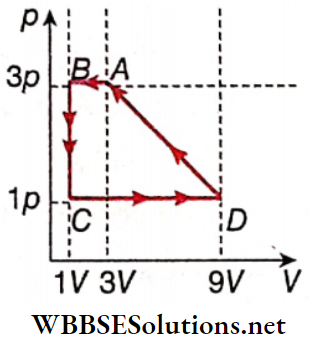
Answer: 1. A, C, E 2. A, C, 3. B, D 4. C, E

Unit 8 Thermodynamics Chapter 1 First And Second Law Of Thermodynamics Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A Fixed mass of gas is taken through a process A → B → C→ A. Here A→B is isobaric, B→ C is adiabatic and C→A is isothermal. (Take γ = 1.5)

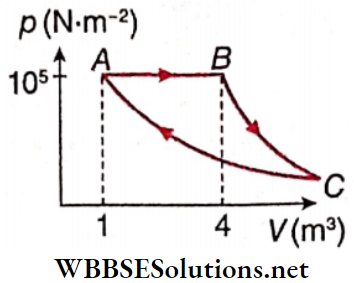
1. Find pressure at C.

1. \(\frac{10^5}{64} \mathrm{~N} \cdot \mathrm{m}^{-2}\)
2. \(\frac{10^5}{32} \mathrm{~N} \cdot \mathrm{m}^{-2}\)
3. \(\frac{10^5}{12} \mathrm{~N} \cdot \mathrm{m}^{-2}\)
4. \(\frac{10^5}{6} \mathrm{~N} \cdot \mathrm{m}^{-2}\)

Answer: 1. \(\frac{10^5}{64} \mathrm{~N} \cdot \mathrm{m}^{-2}\)

2. Find volume at C.

1. 32 m³
2. 100m³
3. 64m³
4. 25m³

Answer: 3. 64m³

3. Find work done in the process.

1. 4.9 x 10⁵ J
2. 3.2 x 10⁵ J
3. 1.2 x 10⁵ J
4. 7.2 x 10⁵ J

Answer: 1. 4.9 x 10⁵ J

Question 2. One mole of an ideal gas has an internal energy given by U = U₀ + 2pV, where p is the pressure and V is the volume of the gas. U₀ is a constant. This gas undergoes the quasistatic cyclic process ABCD as shown in the U-V diagram.

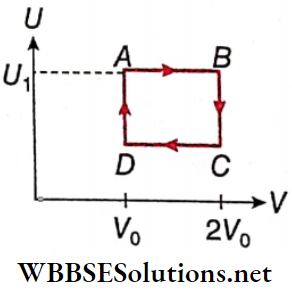
1. The molar heat capacity of the gas at constant pressure is

1. 2R
2. 3R
3. 5/2R
4. 4R

Answer: 2. 3R

2. The work done by the ideal gas in the process AB is

1. Zero
2. \(\frac{U_1-U_0}{2}\)
3. \(\frac{U_0-U_1}{2}\)
4. \(\frac{U_1-U_0}{2} \log _e 2\)

Answer: 4. \(\frac{U_1-U_0}{2} \log _e 2\)

3. Assuming that the gas consists of a mixture of two gases, the gas is

1. Monatomic
2. Diatomic
3. A mixture of monatomic and diatomic gases
4. A mixture of diatomic and triatomic gases

Answer: 3. A mixture of diatomic and triatomic gases

Question 3. A cylinder containing an ideal gas and closed by a movable piston is submerged in an ice-water mixture. The piston is quickly pushed down from position X to position Y (process AB). The piston is held at position Y until the gas is again at 0°C (process BC). Then the piston is slowly raised back to position X (process CA).

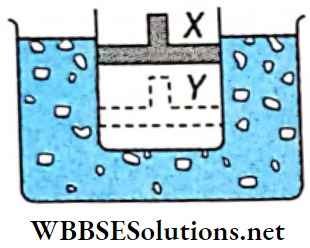
1. Which of the following p-V diagrams will correctly represent the processes AB, BC, and CA and the cycle ABCA?

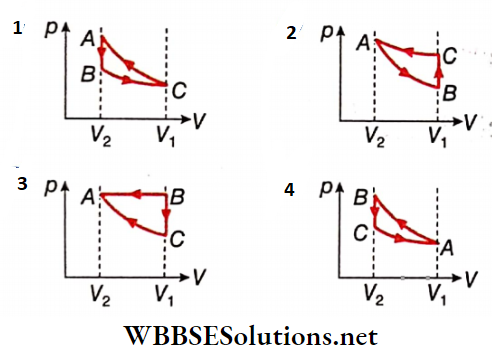
Answer: 4.

2. If 100 g of ice is melted during the cycle ABCA, how much work is done on the gas?

1. 8kcal
2. 5kcal
3. 2.1 kJ
4. 4.2 kJ

Answer: 1. 8kcal

3. If p is the atmospheric pressure acting on the piston and change in the volume is (V₁ – V₂). the work done (in N · m^-2) during the cycle is

1. \(\frac{p V}{2} \mathrm{~J}\)
2. \(\frac{2 p V}{3} J\)
3. \(p V J\)
4. None of these

Answer: 4. None of these

Question 4. 1 mol of an ideal monatomic gas undergoes thermodynamic cycle 1-2-3-1 as shown. The initial temperature of the gas is T₀= 300 K.

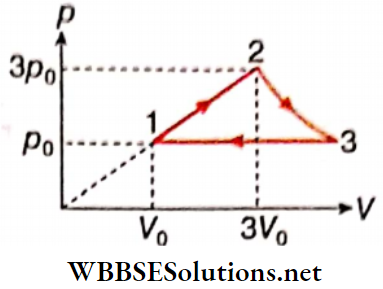
• Process 1 → 2 : p = aV
• Process 2 → 3 : pV = constant
• Process 3 → 1 : p = constant (Take In|3| = 1.09)

1. Find the net work done in the cycle.

1. 3.27 RT₀
2. 6.83 RT₀
3. 4.53 RT₀
4. 5.81 RT₀

Answer: 4. 5.81 RT₀

2. Determine the heat capacity of each process.

1. 20.75 J · mol^-1 -K^-1
2. 10.23 J · mol^-1 · K^-1
3. 22.37 J · mol^-1 · K^-1
4. 15.96 J · mol^-1 · K^-1

Answer: 1. 20.75 J · mol^-1 K^-1

Question 5. A container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. The heat capacities per mole of an ideal monatomic gas are \(C_V=\frac{3}{2} R, C_p=\frac{5}{2} R\), and those for an ideal diatomic gas are \(C_V=\frac{5}{2} R, C_p=\frac{7}{2} R\)

1. Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gases will be

1. 550 K
2. 525 K
3. 513 K
4. 490 K

Answer: 4. 490 K

2. Now consider the partition to be free to move without friction so that the pressure of gases in both compartments is the same. Then total work done by the gases till the time they achieve equilibrium will be

1. 250R
2. 200R
3. 100R
4. -100R

Answer: 4. -100R

Unit 8 Thermodynamics Chapter 1 First And Second Law Of Thermodynamics Integer Type Questions And Answers

In this type, the answer to each of the questions Is a single-digit integer ranging from 0 to 9.

Question 1. A diatomic ideal gas is compressed adiabatically to 1/32 of its initial volume. If the initial temperature of the gas is T₁ (in kelvin) and the final temperature is aT₁ find the value of a.

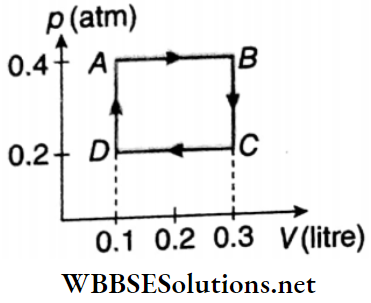
Answer: 4

Question 2. 1 mol of an ideal gas p(atm) undergoes a cyclic change A ABCDA as shown. What is the net work done (in J) in the process? (Take. 1 atm = 10⁵Pa)
Answer: 4

Question 3. During adiabatic expansion of 10 mol of a gas, internal energy decreases by 700 J.Work clone during (the process is x x 10² J. What Is the value of x?
Answer: 7

Question 4. Two Carnot engines A and U operate respectively between 500 K and 400 K and 400 K and 300 K. What is the difference in their efficiencies (in percentage)?
Answer: 5

Question 5. Calculate the pressure required to compress a gas adiabatically at atmospheric pressure to one-third of its volume. Given γ = 1.47.
Answer: 5

Question 6. A thermodynamic system is taken from an initial state I with internal energy U_i = 100 J to the final state f along two different paths iaf and ibf, as shown.

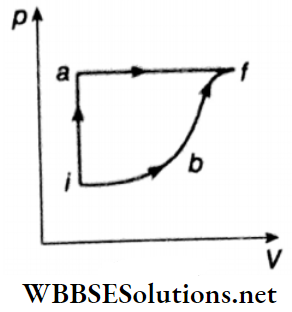
The work done by the system along the paths af, ib, and bf is \(W_{af}=200 \mathrm{~J}, \quad W_{i b}=50 \mathrm{~J} \quad \text { and } \quad W_{b f}=100 \mathrm{~J}\) respectively. The heat supplied to the system along the path iaf, ib, and bf is Q_iaf, Q_ib, and Q_bf respectively. If the internal energy of the system in the state b is U_b = 200 J and Q_iaf = 500 J then find out the ratio of Q_bf/Q_ib.

Answer: 2

 

 

 

Statics – Rigid Bodies

Rigid Bodies: Statics is a branch of mechanics where the equilibrium of bodies under the action of a number of forces and the conditions for equilibrium are studied.

The concept of rigid bodies has to be introduced in the discussions of rotation, in particular. The particle description of material bodies is not sufficient in that context.

Rigid Bodies Definition: A body that does not change its shape or size under the action of forces is called a rigid body.

No substance is perfectly rigid. However, most material bodies may be assumed to be rigid when the forces acting on them do not exceed a certain limit.

Read and Learn More: Class 11 Physics Notes

Statics – Resultant Of Parallel Forces

Forces acting in the same direction are called parallel forces. \(\vec{F}_1, \vec{F}_2 \text { and } \vec{F}_3\) are examples of like parallel forces. When two forces act in opposite directions, they constitute a pair of, unlike parallel forces. \(\vec{F}_4\) and \(\vec{F}_5\) are two unlike parallel forces.

The straight line along which a force acts is called the line of action of that force. For example, AB is the line of action of forces \(\vec{F}_1\) and \(\vec{F}_2\), CD is the line of action of force \(\vec{F}_3\).

Resultant Of Two Like Parallel Forces: Let \(\vec{F}_1\) and \(\vec{F}_2\) be a pair of like parallel forces acting at points A and B. Their resultant has to be calculated. O is a point on the plane of the forces.

Line OX is drawn perpendicular to the lines of action of \(\vec{F}_1\) and \(\vec{F}_2\). OX is taken as the x-axis. OY is the y-axis on the same plane.

Since \(\vec{F}_1\) and \(\vec{F}_2\) do not have any components along the x-axis, the resultant \(\vec{R}\)(say) will also have no component along the x-axis and its line of action will be perpendicular to the line OX, i.e., parallel to the lines of action of \(\vec{F}_1\) and \(\vec{F}_2\). Hence, component of \(\vec{R}\) along y-axis is, R = F₁ + F₂….(1)

Hence, the magnitude of the resultant is the sum of the magnitudes of the forces and its direction will be the same as the direction of the parallel forces.

To find the line of action of R, let us assume that \(\vec{R}\) acts at point C. \(\vec{R}\) is the resultant of \(\vec{F}_1\) and \(\vec{F}_2\). It implies that the effect of forces \(\vec{F}_1\) and \(\vec{F}_2\) together, should be the same as that of R acting alone.

Hence, the algebraic sum of moments due to \(\vec{F}_1\) and \(\vec{F}_2\) about the point O should be equal to the moment of \(\vec{R}\) about O,

or, F₁ x OA + F₂ x OB = R x OC

or, F₁(OC-AC) + F₂(OC+CB) = (F₁ + F₂) x OC

or, F₁ x AC = F₂ x BC

or, \(\frac{F_1}{F_2}=\frac{B C}{A C}\)….(2)

Hence, the line of action of the resultant divides the distance AB into two parts in the inverse ratio of the magnitudes of the forces.

Suppose the line A’B’ is obtained by joining any two points on the lines of action of F₁ and F₂. Obviously, the line of action of the resultant divides it into two parts in the inverse ratio of the magnitude of the forces \(\vec{F}_1\) and \(\vec{F}_2\).

Position of the point C can also be determined in terms of points A and B. If OA = x₁, OB = x₂ and OC = x, then, taking moments about the point O of the forces \(\vec{F}_1\), \(\vec{F}_2\) and resultant \(\vec{R}\) we get,

∴ \(F_1 x_1+F_2 x_2=R \times x=\left(F_1+F_2\right) x\)

∴ x = \(\frac{F_1 x_1+F_2 x_2}{F_1+F_2}\)…(1)

Resultant of Two Unlike Parallel Forces: Let \(\vec{F}_1\) and \(\vec{F}_2\) be two unlike parallel forces acting at points A and B as shown. Let \(F_1\) > \(F_2\). Suppose \(\vec{R}\) is the resultant of these two forces. Then, R = \(F_1\) – \(F_2\)

The resultant acts along the direction of the greater force.

Taking moments about point O and from the definition of resultant we get, F₁ x OA – F₂ x OB = R x OC

or, F₁(OC+ CA) – F₂(OC+ CB) = (F₁ – F₂) x OC

or, \(\frac{F_1}{F_2}=\frac{B C}{A C}\)

and x = \(\frac{F_1 x_1-F_2 x_2}{F_1-F_2}\)…(2)

Hence, the line of action of the resultant divides externally the distance of separation of the two forces in the inverse ratio of their magnitudes.

Resultant Of Three Or More Parallel Forces: When a body is acted upon by the parallel forces \(\vec{F}_1\), \(\vec{F}_2\), \(\vec{F}_3\),…… simultaneously, the resultant force \(\vec{R}\) can be obtained by framing an equation similar to equation (1).

R = \(F_1+F_2+F_3+\cdots=\sum_i F_i\)….(5)

Any one of the forces may be taken as positive. Correspondingly, forces in the same direction as this force are positive and those in the opposite direction are negative. If the forces are coplanar. the distance of the line of action of the resultant from any point O on that plane is,

x = \(\frac{F_1 x_1+F_2 x_2+F_3 x_3 \cdots}{R} \text { or, } x=\frac{\sum_i F_i x_i}{\sum_i F_i}\)…(6)

where x₁, x₂, x₃,…are the perpendicular distances of the point O from the lines of action of the forces, \(\vec{F}_1\), \(\vec{F}_2\), \(\vec{F}_3\)… etc.

The moment of the resultant about the point O can be positive or negative. The direction of rotation caused by the resultant about the point O is determined by this positive or negative sign.

 

 Statics- Centre Of Gravity

It is known that an extended object is an aggregation of a large number of particles. If the masses of these constituents are m₁, m₂, m₃, …., the earth pulls these particles with respective forces m₁g, m₂g, m₃g,…. towards its centre.

• The resultant of these parallel forces acting on the particles is the weight W of the object. This weight W, acts vertically downward through a definite point.
• This point is called the centre of gravity (G) of the body. Like the centre of mass, the centre of gravity may be located inside or outside the body.
• The respective distances between the particles remain fixed. Hence, the resultant of the weights also remains the same both in magnitude and in direction and acts through the same point.
• Thus, it can be stated that the position of the centre of gravity of a body does not depend on the orientation of the body.

Centre Of Gravity Definition: The force of gravity that is exerted on an extended object always acts through a unique point. This point; is the centre of gravity of the object.

To Find The Position Of The Centre Of Gravity: The position of the centre of gravity (G) can be determined using the rules for finding the resultant of parallel forces. The magnitude of the resultant is equal to the weight of the body:

W = m₁g + m₂g + m₃g + …. = Mg

[Here, M=m₁ + m₂ + m₃ + = total mass of the object]

Let the coordinates of \(m_1, \quad m_2, \ldots\) be \(\left(x_1, y_1, z_1\right)\), \(\left(x_2, y_2, z_2\right)\), …respectively and the point of action of the resultant W, i.e., the coordinates of the centre of gravity be (x, y,z).

∴ \(\left.\begin{array}{l}
\begin{array}{rl}
therefore \quad x & =\frac{m_1 g x_1+m_2 g x_2+\cdots}{m_1 g+m_2 g+\cdots} \\
& =\frac{m_1 x_1+m_2 x_2+\cdots}{m_1+m_2+\cdots} \\
& =\frac{\sum_i m_i x_i}{\sum_i m_i}
\end{array} \\
\text { Similarly, } y=\frac{\sum_i m_i y_i}{\sum_i m_i} \text { and } z=\frac{\sum_i m_i z_i}{\sum_i m_i}
\end{array}\right\}\)

Some Important Information About The Centre Of Gravity: To establish equation (1), the magnitude of g is assumed to be the same for all particles constituting the body. This assumption is acceptable for small objects only, where the variation of g is negligible. But if the body is very large, the magnitude of g varies from point to point and equation (1) is not applicable.

Equation (1) of this section and equation (2) are identical. Hence, if the magnitudes of acceleration due to gravity at all points within a body are the same, the centre of mass and the centre of gravity become identical.

Uniqueness Of Centre Of Gravity: A body cannot have more than one centre of gravity. This is called the uniqueness of the centre of gravity. Let us assume a body has two centres of gravity G and G’. From the definition of centre of gravity, irrespective of the orientation of the body, its weight should act through G and G’.

But the weight of a body always acts vertically downwards. Therefore, GG’ must always be a vertical line. But for aflPoftlntations of the body, GG’ cannot be vertical. Hence a body having two centres of gravity is not a possibility.

Statics – Difference Between Centre Of Mass And Centre Of Gravity

The Centre of mass of a body is such a point that a force applied at this point produces linear motion only and does not produce any rotational motion.

1. The Centre of gravity is the point through which the weight of a body acts vertically downwards.
2. As the mass of a body remains constant anywhere in the universe, a body always has a definite centre of mass. But at places where the weight of the body becomes zero, there is no centre of gravity, for example, a body inside an artificial satellite rotating around the earth or a free-falling body is weightless. So in these cases, the body has no centre of gravity.
3. If the magnitude of acceleration due to gravity remains the same at all points of a body, the centre of mass and the centre of gravity will be identical.
   • But if the magnitude of gravitational acceleration is different at different points of a body, then the centre of mass will not coincide with the centre of gravity, For example, for very large mountains like the Himalayas acceleration due to gravity is greater at the bottom of the mountain, that’s why even for an object of uniform density earth’s attraction is greater at the bottom.
   • Again position of the centre of mass depends only on the density and not on the weight of the body. That is why for massive and tall objects like these centre of gravity remains below the centre of mass.

Statics – Centre Of Mass And Centre Of Gravity Numerical Examples

Example 1. A rod of weight W is kept horizontally on two knife edges with a distance d between them. The Centre of gravity of the rod is at a distance x from A. Find the normal reactions at points A and B.

Solution:

Let the centre of gravity of the rod be C. Normal reactions at A and B are R₁ and R₂. Weight W through C acting downwards, and R₁ and R₂ are the three coplanar forces that keep the rod in equilibrium.

Hence, W- R₁ – R₂ = 0 or, W = R₁ + R₂

Taking the moment of the forces about C, \(-R_1 \cdot x+R_2(d-x)=0 \text { or, } R_1 x=R_2(d-x)\)

or, \(x\left(R_1+R_2\right)=R_2 d \text { or, } W x=R_2 d\)

∴ \(R_2=\frac{x}{d} W\)

and \(R_1=W-R_2=W-\frac{W x}{d}=W\left(1-\frac{x}{d}\right)\)

Example 2. Show that the centre of gravity of three equal weights suspended from three vertices of a triangle coincides with the centre of mass of the triangle.
Solution:

Let the median of the triangle ABC be AD. Identical weights W are hung from each of the vertices A, B and C. Resultant of the weights suspended from B and C = 2W and it acts from the point D.

The resultant of the forces 2 W at D and W at A is 3 W. Suppose this resultant acts at G.

Hence, W x AG = 2 W x DG

or, AG = 2 DG

Thus, G is the point of intersection of the medians of the triangle, which is the centre of mass.

Example 3. A person of mass 80 kg is standing on the top of an 18 kg ladder of length 6 m. The upper end of the ladder rests on a smooth vertical wall and the lower end is on the ground 3 m away from the vertical wall. What should be the minimum coefficient of friction between the floor and the ladder so that the system remains in equilibrium?
Solution:

Given that, for the ladder weight W acts through the centre of gravity, C (mid-point of AB) of the ladder.

Weight W’ of the man acts at B downwards.

Normal reaction R’ by the wall acts at B.

Normal reaction R by the ground acts at A.

Limiting friction that acts along the floor at A, f = μR where, n is the coefficient of friction, required for equilibrium.

At equilibrium, the sum of all horizontal forces and the sum of all vertical forces will be zero separately.

⇒ \(\mu R-R^{\prime}=0 \text { or, } \mu R=R^{\prime}\)…(1)

⇒ \(R-W-W^{\prime}=0 \text { or, } R=W+W^{\prime}\)…(2)

Again the sum of the moments of all forces taken about A will be zero.

∴ \(R^{\prime} \times B D-W \times A E-W^{\prime} \times A D=0\)

or, \(\mu\left(W+W^{\prime}\right) \times B D=W \times A E+W^{\prime} \times A D\)

∴ \(\mu=\frac{W \times A E+W^{\prime} \times A D}{\left(W+W^{\prime}\right) \times B D}\)

Here, AB = \(6 \mathrm{~m}, A D=3 \mathrm{~m}\).

∴ AE = \(\frac{A D}{2}=\frac{3}{2} \mathrm{~m} ; B D=\sqrt{A B^2-A D^2}=5.2 \mathrm{~m}\)

W = \(18 \mathrm{~kg} \times g ; W^{\prime}=80 \mathrm{~kg} \times \mathrm{g}\)

∴ \(\mu=\frac{18 \times \frac{3}{2}+80 \times 3}{(18+80) \times 5.2}=0.52\).

Example 4. A uniform cylinder of diameter 8 cm is kept on a rough inclined plane, whose angle of inclination with the ground is 30°. What should be the maximum height of the cylinder so that it does not topple?
Solution:

The cylinder ABCD is kept on the plane of inclination 30°. Suppose the cylinder is on the verge of toppling over when its height is 2h. At this stage, the line of action of gravity must pass vertically through the endpoint A at the base of the cylinder.

From \(tan 30^{\circ}=\frac{A E}{E G}\)

or, \(\frac{1}{\sqrt{3}}=\frac{r}{h} or, h=\sqrt{3} r=4 \sqrt{3} \mathrm{~cm}\)

Hence, maximum permissible height = 2h = x 4√3 = 8√3 cm.

Example 5. A hollow cylinder of height 100 cm and diameter 8 cm has its top end open. It contains water up to a height of 50 cm. The mass per square centimetre of the hollow cylinder is 9 g. Find the height of the centre of gravity of the water cylinder system from the base of the cylinder.
Solution:

The Centre of gravity of the curved surface of the empty cylinder is 50 cm above its base at P.

The weight of the base of the empty cylinder

= π(4)² x 9 x g dyn [g = acceleration due to gravity]

Weight of curved surface of the cylinder = 2π x 4 x 100 x 9 x g dyn. Its centre of gravity is at G₁, where PG₁ = 50 cm.

Weight of water in the cylinder =π(4)² x 50 x 1 x g dyn and the centre of gravity of this water is at G₂ which is 25 cm above the base of the cylinder.

Suppose the centre of mass of the cylinder filled with water is at G, which is h cm above its base. The centre of gravity coincides with this centre of mass.

Taking moments of all the weights about P, \(2 \pi \times 4 \times 100 \times 9 \times G_1 P+\pi \times 16 \times 50 \times 1 \times G_2 P\)

= \((\pi \times 16 \times 9+2 \pi \times 4 \times 100 \times 9+\pi \times 16 \times 50 \times 1) \times G P\)

or, \(2 \pi \times 4 \times 100 \times 9 \times 50+\pi \times 16 \times 50 \times 1 \times 25\)

= \((\pi \times 16 \times 9+2 \pi \times 4 \times 100 \times 9 +\pi \times 16 \times 50 \times 1) \times h\)

or, h = 46.7 cm.

Example 6. A uniform narrow rod of mass M and length 2 L is kept vertically, along the y-axis, on a smooth horizontal plane. The lower end of the rod coincides with the origin (0,0). Due to a slight disturbance at time t = 0, the rod slides along the positive x-axis and begins to fall. Determine

1. The shift in the centre of gravity during the fall,
2. The equation of the locus of a point at a distance r from the lower end of the rod also mentions the shape of the locus.

Solution:

Initially (0, L) was the coordinates of the centre of gravity of the rod. Let B be the point at a distance r, from point O (0, 0), on the rod. So, (0, r) denotes the point B.

At t = 0, the rod is disturbed and it falls. During this fall there is no other force acting on it except the downward gravitational force.

1. We know that the centre of gravity is influenced only by an external force which is gravity in this case. So the centre of gravity will be shifted vertically downwards from (0, L) to (0, 0).
2. Let (x, y) be the position of B’ at any moment dining the fall of the rod, where B’ is the point at a distance r, from the lower end O’ of the rod.

From, \(\frac{O G^{\prime}}{O^{\prime} G^{\prime}}=\frac{C B^{\prime}}{O^{\prime} B^{\prime}}\)

or, \(\frac{a}{L}=\frac{y}{r}\)

Again, \(\frac{O^{\prime} O}{O C}=\frac{O^{\prime} G^{\prime}}{G^{\prime} B^{\prime}}\)

or, \(\frac{O C}{G^{\prime} B^{\prime}}=\frac{O^{\prime} O}{O^{\prime} G^{\prime}} or, \frac{x}{r-L}=\frac{b}{L}\)

∴ \(\frac{x^2}{(r-L)^2}=\frac{b^2}{L^2}=\frac{L^2-a^2}{L^2}=1-\frac{a^2}{L^2}=1-\frac{y^2}{r^2}\)

or, \(\frac{x^2}{(r-L)^2}+\frac{y^2}{r^2}=1\)

This is the equation of the locus of a point (x, y) and it is elliptical with its centre at the origin.

Example 7. A circular metal plate of uniform thickness has a radius of 10 cm. A hole of radius 4 cm is punched on the plate a little away from its centre. The centres of the plate and of the hole are 5 cm apart. Find the centre of gravity of the plate with the hole.
Solution:

The Centre of gravity of the plate before the hole was punched was at its centre G. The centre of gravity of the circular part before the punching was at its centre G₁. Suppose the centre of gravity of the plate with the hole is at G₂, on the line GG₁.

Let W₁ = weight of the plate with a hole, W₂ = weight of the disc that is cut off

∴ \(W_1 \times G G_2=W_2 \times G G_1 \text { or, } G G_2=\frac{W_2}{W_1} \times G G_1\)

But \(G G_1=5 \mathrm{~cm}, W_1=\pi\left(10^2-4^2\right) \times \rho\)(ρ= weight per unit area) and \(W_2=\pi \times 4^2 \times \rho\)

∴ \(G G_2=\frac{4^2}{10^2-4^2} \times 5=\frac{20}{21} \mathrm{~cm}\)

Hence, the centre of gravity of the system will be \(\frac{20}{21}\) cm to the left of the centre of the plate.

Example 8. A mass of 10 kg is suspended using two strings. One string makes an angle of 60° with the vertical. What should be the angle made by the other string so that the tension in the string will be minimum? Find the tension in each wire.
Solution:

As the mass is in equilibrium, from the force diagram we get \(T_1 \cos \theta_1+T_2 \cos \theta_2=m g\)

or, \(T_1 \cos \theta_1=m g-T_2 \cos \theta_2\)….(1)

Also \(T_1 \sin \theta_1=T_2 \sin \theta_2\)…(2)

From (2) and (1) we get, \(\frac{\sin \theta_1}{\cos \theta_1}=\frac{T_2 \sin \theta_2}{m g-T_2 \cos \theta_2}\)

or, \( m g \sin \theta_1=T_2\left(\sin \theta_1 \cos \theta_2+\cos \theta_1 \sin \theta_2\right)\)

∴ \(T_2=\frac{m g \sin \theta_1}{\sin \left(\theta_1+\theta_2\right)}\)….(3)

As m, g and θ are constants, the minimum value of T₂ corresponds to the maximum value of sin(θ₁ + θ₂) i.e., sin(θ₁ + θ₂) = 1 = sin90°

∴ θ₁+ θ₂ = 90° or, θ₂ = 90° – θ₁ = 90° -60° = 30°

From equation (3) we get, \(T_2=\frac{10 \times g \sin 60^{\circ}}{1}=84.87 \mathrm{~N}\)

From equation (2) we get, \(T_1=\frac{T_2 \sin \theta_2}{\sin \theta_1}=\frac{5 \sqrt{3} \times 9.8 \times \sin 30^{\circ}}{\sin 60^{\circ}}=49 \mathrm{~N} \text {. }\)

Example 9. A chain of mass m and length l is kept on a horizontal frictionless table, such that \(\frac{1}{4}\) th of the length of chain is the hanging part of the chain onto the table.
Solution:

Mass per unit length of the chain = \(\frac{m}{l}\)

∴ Mass of hanging part of the chain = \(\frac{m}{l}\) x  \(\frac{l}{4}\) =  \(\frac{m}{4}\)

∴ The Centre of gravity of this portion is at \(\frac{l}{4 \times 2}=\frac{l}{8}\) below the top of the table.

∴ Work to be done to lift the hanging part of the chain = \(\frac{m}{4} \times g \times \frac{l}{8}=\frac{m g l}{32}\)

Statics – Equilibrium Of A Body Under Gravity

Suppose a chair is at rest with its legs resting on the floor. This stationary state of the chair is its equilibrium position. If the chair is tilted a little, it has to be held in that position to prevent it from falling.

• This shows that this position is not the equilibrium position of the chair. On tilting it further the chair falls to the ground on its side and comes to rest again.
• This is another equilibrium position of the chair. In general, under the influence of gravity, a body may have one or more equilibrium states.

Under The Influence Of Gravity, A Body May Stay In Three Types Of Equilibrium States:

1. Stable Equilibrium: If a substance is disturbed from its equilibrium state, and if on release it gets back to the same equilibrium state, then the body is initially in a stable equilibrium.
   • If a book, placed on a table with its largest surface resting on the table, is lifted a little by any one of the edges and then released, it falls back and returns to its initial state of equilibrium.
2. Unstable Equilibrium: If a body, when displaced a little from its equilibrium position, tends to move away further, then the body was in an unstable equilibrium.
   • Unstable Equilibrium Examples:
     • A pencil made to balance on its pointed end
     • An egg is made to stand on its narrow end (it is almost impossible to keep a pencil or an egg in this position by hand). If a slight push is given these fall over.
3. Neutral Equilibrium: Let a body be displaced a little from its state of equilibrium and then released. If it still remains in equilibrium in its new position, then it is said to be in a neutral equilibrium. Let a sphere be placed on a smooth horizontal plane.
   • On being pushed, it rolls a bit and comes to rest in a new position. Hence the sphere is said to be in a neutral equilibrium state. Different equilibrium states of a body can be ascertained by either of the following two methods.

Extension Of The Base: A chair on a floor rests with all four legs in contact with the floor. The quadrilateral obtained by joining the contact points of its legs with the floor is called the base of the chair. A body that has a larger base area compared to the area of its upper regions is always in stable equilibrium if the vertical line through its centre of gravity passes through its base.

From everyday experience, we know that, for an object of a given height, stability increases with the extent of the base area. For a stable object, the line of action of its weight always lies within its base.

Extension Of The Base Stable Equilibrium: Consider two possible ways of placing a brick on a horizontal surface. In the brick is placed on its largest face AB. This is a position of stable equilibrium and the lines of action of the weight W and the normal reaction R coincide. If we tilt the brick to stand it on the edge through point A, as shown, the lines of action of W and R do not lie on the same straight line.

• Consequently, when we release the brick, the couple created by W and R brings it back on the original base AB. Note that the line of action of the weight W still passes through the base AB when the brick is tilted. So the initial state of the brick is a state of stable equilibrium.
• To topple the brick, it needs to be tilted further about the edge through A so that the line of action of W goes outside the base AB. The brick is on the verge of toppling.
• The same brick is shown to be standing on one of its smaller faces like BC. In this case, it will be easier to topple the brick because the line of action of W goes outside the base BC on turning the brick through a smellier angle. But this initial state is also a stable equilibrium state. Thus, we can say that stability increases with the extent of the base area.

Unstable Equilibrium: A cone is shown balanced on its tip. Since the lines of action of W and R coincide, we can say that the cone is in equilibrium.

• However, a minute displacement from this position is enough to make it lose its balance and topple over. Thus, the cone standing on its tip is an example of unstable equilibrium.
• In this state, if the object is disturbed and then released, it does not return to its initial position but seeks a position of stable equilibrium.
• Note that when the cone is displaced slightly, the lines of action of W and R do not lie on the same straight line and the line of action of W does not pass through the base A. The bricks are at state of unstable equilibrium.

Neutral Equilibrium: Consider a ball resting on a horizontal surface as shown. In this situation, the lines of action of W and R coincide. We conclude that the ball is in equilibrium. If we roll the ball to a new position, we find that it is in a similar kind of equilibrium as before.

• As a matter of fact, the lines of action of W and R coincide in any orientation. Such an equilibrium is called a neutral equilibrium. When a body is displaced from a position of neutral equilibrium does not tend to return to its initial position; rather it settles into a new position of neutral equilibrium.
• Thus, if the line of action of its weight does not pass through the base of the body, it cannot remain in equilibrium. Once displaced from its equilibrium position, a body comes to a new equilibrium either by returning to the old base or on a new base.
• A chair is not stable when it stands on two legs, as the line of action of its weight does not pass through the baseline defined by the two legs. Quadrupeds are more stable than animals who walk on two legs.
• Hence, in the latter case, the technique of standing on two legs has to be learned. When a bucket full of water is carried in the right hand, the body is leaned towards the left in order to keep the line of action of the weight of the body and the bucket together within our feet.

Position Of Centre Of Gravity: Objects tend to move towards the centre of the earth due to the gravitational pull of the earth. Since the point of action of this attractive force (i.e., weight) is the centre of gravity of the body, the natural tendency of the centre of gravity is to attain the least height. Therefore, the lower the position of the centre of gravity of a body, the more stable its equilibrium.

If on displacing a body, it’s centre of gravity

1. Goes up, then the body was at a stable equilibrium initially,
2. Goes down, the body attains a more stable equilibrium than before,
3. Remains at the same height, and then the body is said to be in neutral equilibrium.

Position Of Centre Of Gravity Example:

1. A person standing with his feet apart is more stable than when his feet are together. By placing his feet apart, the person increases the base area so he can stand more comfortably.
   • When a person lies down, along with the increase in the base area, there is a considerable lowering of the centre of gravity. Hence, the lying-down position is the most stable equilibrium for a person.
2. Boxes and books, when placed on the floor, are usually kept with their largest surfaces in contact with the ground. This lowers the centre of gravity and the equilibrium becomes most stable.
3. Passengers are not allowed to stand on the upper deck of a double-decker bus in order to keep the centre of gravity low.
4. Hydrometers, lactometers, special types of toys, etc. are loaded with lead in their lower part (base) so that the centre of gravity of the system remains very low. Hence, the vertical position is the most stable equilibrium position in these cases.
   • The toys can be tilted about their bases through large angles, but they will come back to their vertical positions as soon as they are released. Hence, each of these toys has only one state of equilibrium.

Relationship Of The Centre Of Gravity And Gravitational Potential With Different Types Of Equilibrium: Gravitational potential energy is related to the position of the centre of gravity of a body. Potential energy depends on the height of the centre of gravity from the ground.

• Lower the position of the centre of gravity, lower the potential energy and higher the stability of the body.
• Thus, when the centre of gravity of a body or a system attains the lowest possible height and hence has the lowest possible gravitational potential energy, the body achieves stable equilibrium. When the centre of gravity is at its maximum height, potential energy is also the maximum and therefore, the equilibrium becomes unstable.
• The body tends to deviate from that position to a state of lower potential energy.
• For a body in neutral equilibrium, the height of the centre of gravity does not change when it is displaced and the potential energy remains the same. Hence, the body remains in equilibrium even in the displaced state.

Statics Conclusion

Centre Of Mass is a unique point for an extended object or a system of particles such that, any force applied through that point produces only translational motion of the body, but no rotational motion.

1. No object can have more than one centre of mass,
2. The centre of mass of an object can be outside the material of the object.
3. The position of the centre of mass changes as the shape of an object changes.

The vector quantity which tends to rotate a body by the combination of the force acting on the body and the perpendicular distance of the line of action of that force from the axis of rotation is called the moment of the applied force with respect to that axis of rotation.

The magnitude of the moment of force is expressed by the product of the magnitude of the force and the perpendicular distance of the force from the axis of rotation.

The vector form of the relation between the moment of force and the applied force is \(\vec{G}=\vec{r} \times \vec{F}\).

• A number of forces acting in the same direction are called parallel forces. Two forces acting in mutually opposite directions are called unlike parallel forces.
• The straight line along which a force acts is called the line of action of that force.
• The line of action of the resultant of two like parallel forces acting at two different points on a body divides the distance between the like parallel forces in inverse ratio of the magnitudes of the two forces.
• The line of action of the resultant of two unlike parallel forces acting at two different points on a body divides externally the distance between the unlike parallel forces in inverse ratio of the magnitudes of the forces.
• A body is said to be in equilibrium when it is at rest moving with uniform linear velocity moving with a uniform angular speed or moving with both uniform linear and angular velocities.

Conditions of equilibrium of a body under the action of a number of coplanar forces:

1. 1st Condition: The resultant of all coplanar forces acting on the body should be zero. If this condition is fulfilled, the linear acceleration of the body will be zero.
2. 2nd Condition: The algebraic sum of the moments of coplanar forces acting on the body, taken about any point on the plane, should be zero. If this condition is fulfilled, the angular acceleration of the body will be zero.

Both conditions, satisfied simultaneously, keep a body in equilibrium.

• Conditions of equilibrium under the action of two forces: Two forces acting on a body should be equal, collinear and opposite to each other.
• Conditions of equilibrium under the action of three non-parallel forces:
• Three forces must be on the same plane and the resultant of any two should be equal and opposite to the third force and the lines of action of all three forces must pass through the same point.
• The single force that cancels the action of all other forces acting on a body is called an equilibrant.

Centre of gravity is a fixed point of an object through which the weight of the body acts. Its position is independent of the orientation of an object of fixed shape and volume.

1. No object can have more than one centre of gravity.
2. When acceleration due to gravity at all points of an object becomes the same, the centre of mass coincides with the centre of gravity.

At zero gravity, the centre of mass exists but the centre of gravity has no significance.

Under the action of gravity, objects may have three types of equilibrium:

1. Stable,
2. Unstable and
3. Neutral.

A body with a wider base compared to its upper regions, becomes stable. Also if the line drawn vertically through the centre of gravity of the object passes through its base, the object remains in a stable equilibrium.

Statics Useful Relations For Solving Numerical Problems

Let \(\vec{F}_1\) and \(\vec{F}_2\) be two like parallel forces. They act on two different points on x-axis with coordinates x₁ and x₂ respectively. The resultant (\(\vec{R}\)) of the above forces act through a point with coordinate x. Here,

R = \(F_1+F_2 \text { and } x=\frac{F_1 x_1+F_2 x_2}{F_1+F_2}\)

If \(\vec{F}_1\) and \(\vec{F}_2\) are unlike parallel forces then,

R = \(\left|F_1-F_2\right| \text { and } x=\frac{F_1 x_1-F_2 x_2}{F_1-F_2}\)

For n number of parallel forces

R = \(\sum_{i=1}^n F_i \text { and } x=\frac{\sum_{i=1}^n F_i x_i}{\sum_{i=1}^n F_i}\)

For n number of parallel forces \(R=\sum_{i=1}^n F_i \text { and } x=\frac{\sum_{i=1}^n F_i x_i}{\sum_{i=1}^n F_i}\)

For equilibrium og n number of coplanar forces, according to the 1st condition, \(R_x=\sum_{i=1}^n F_{i x}=0 \text { and } R_y=\sum_{i=1}^n F_{i y}=0\)

and according to the 2nd condition, \(\tau=\sum_{i=1}^n F_i x_i=0\)

Mathematical expressions for Lami’s theorem, \(\frac{P}{\sin (Q, R)}=\frac{Q}{\sin (R, P)}=\frac{R}{\sin (P, Q)}\)

Suppose particles of masses m₁, m₂,…..m_n constitute an extended object or a system of particles. The positional coordinates of the particles are (x₁, y₁, z₁, (x₂, y₂, z₂),…..(x_n, y_n, z_n) and that of the centre of mass are (x_cm, y_cm, z_cm), Then

∴ \(x_{\mathrm{cm}}=\frac{\sum_{i=1}^n m_i x_i}{\sum_{i=1}^n m_i}, y_{\mathrm{cm}}=\frac{\sum_{i=1}^n m_i y_i}{\sum_{i=1}^n m_i}, z_{\mathrm{cm}}=\frac{\sum_{i=1}^n m_i z_i}{\sum_{i=1}^n m_i}\)

Statics Assertion Reason Type Questions And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 1 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: The centre of mass of the system will not alter in any direction if the external force is not exerted on it.

Statement 2: If net external force is zero then the linear momentum of the system remains constant.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 2.

Statement 1: The position of the centre of mass of a body is independent of the shape and size of the body.

Statement 2: The centre of mass of a body may be in a position where there is no mass.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 3.

Statement 1: Centre of mass of a rigid body always lies inside the body.

Statement 2: Centre of mass and centre of gravity coincide if gravity is uniform.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 4.

Statement 1: The centre of mass of an electron-proton system, when released, moves faster towards the proton.

Statement 2: Proton is heavier than an electron.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 5.

Statement 1: When a body dropped from a height explodes in mid-air, its centre of mass keeps moving in a vertically downward direction.

Statement 2: Explosion occurs under internal forces only External force is zero.

Answer: 3. Statement 1 is true, statement 2 is false.

Statics Match The Columns

Question 1.

Answer: 1. A, 2. C, 3. D, 4. B

Question 2. The two-block systems shown, match the following.

Answer: 1. C, D, 2. C, D, 3. B, 4. B

Question 3.  If the net force on a system of particles is zero, then match the following columns

Answer: 1. B, 2. C, 3. C, 4. D

Question 4. The arrangement is shown to match the following.

Answer: 1. B, 2. B, 3. B, 4. A

Statics Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A solid cylinder rolls up an inclined plane with an angle of inclination of 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m · s^-1.

1. The distance up to which the cylinder goes up the plane is

1. 4m
2. 3.8m
3. 3.6m
4. 3m

Answer: 2. 3.8m

2. The time taken for the cylinder to return to the bottom is

1. 3.5 s
2. 3.7 s
3. 3.0 s
4. 3.8 s

Answer: 3. 3.0 s

Question 2. Four particles of masses 1 kg, 2 kg, 3 kg and 4 kg are placed at the four vertices A, B, C and D of a square of side 1 m.

1. Taking D as origin, x -coordinates of centre of mass is

1. 0.7 m
2. 0.8 m
3. 0.5 m
4. 0.6 m

Answer: 3. 0.5 m

2. Taking D as origin, y -coordinates of the centre of mass is

1. 0.5 m
2. 0.6 m
3. 0.3 m
4. 0.4 m

Answer: 3. 0.3 m

3. Taking C as the origin, the position of the centre of mass of the particles is

1. (0.7 m, 0.6 m)
2. (-0.5 m, 0.3 m)
3. (0.6 m, 0.4 m)
4. (-0.5 m, 0.6 m)

Answer: 2. (-0.5 m, 0.3 m)

Question 3. Two balls having masses m₁ = 4 kg and m₂ = 5 kg have initial velocities of 5m • s^-1 in the directions shown. They collide at the origin. (Take all integer values)

1. Velocity of the centre of mass 3 s before the collision is

1. \((-2 \hat{i}+1 \hat{j}) \mathrm{m} \cdot \mathrm{s}^{-1}\)
2. \((-2 \hat{i}-1 \hat{j}) \mathrm{m} \cdot \mathrm{s}^{-1}\)
3. \((2 \hat{i}+1 \hat{j}) \mathrm{m} \cdot \mathrm{s}^{-1}\)
4. \((2 \hat{i}+1 \hat{j}) \mathrm{m} \cdot \mathrm{s}^{-1}\)

Answer: 1. \((-2 \hat{i}+1 \hat{j}) \mathrm{m} \cdot \mathrm{s}^{-1}\)

2. The position of the centre of mass 2 s after the collision is

1. \(-4 \hat{i}-2 \hat{j}\)
2. \(4 \hat{i}-2 \hat{j}\)
3. \(-4 \hat{i}+2 \hat{j}\)
4. \(4 \hat{i}+2 \hat{j}\)

Answer: 3. \(-4 \hat{i}+2 \hat{j}\)

Question 4. A particle of mass 1 kg has velocity \(\overrightarrow{v_1}=(2 t) \hat{i}\) and another particle of mass 2 kg has velocity \(\overrightarrow{v_2}=\left(t^2\right) \hat{j}\)

1. Net force on the centre of mass at 2 s

1. \(\frac{20}{9}\) unit
2. \(\sqrt{68}\) unit
3. \(\frac{\sqrt{80}}{3}\) unit
4. None of these

Answer: 2. \(\sqrt{68}\) unit

2. Velocity of the centre of mass at 2 s

1. \(\frac{20}{9}\) unit
2. \(\sqrt{68}\) unit
3. \(\frac{\sqrt{80}}{3}\) unit
4. None of these

Answer: 3. \(\frac{\sqrt{80}}{3}\) unit

3. Displacement of the centre of mass in 2 s

1. \(\frac{20}{9}\) unit
2. \(\sqrt{68}\) unit
3. \(\frac{\sqrt{80}}{3}\) unit
4. None of these

Answer: 1. \(\frac{20}{9}\) unit

Statics Integer Answer Type Questions And Answers

In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.

Question 1. Two ice skaters A and B approach each other at right angles. Skater A has a mass of 30 kg and a velocity 1 m · s^-1, and skater B has a mass 20 kg and a velocity 2m · s^-1. They meet and cling together. Find the final velocity (in m · s^-1) of the couple.
Answer: 1

Question 2. Both the blocks as shown in the given arrangement are given a horizontal velocity towards the right together. If a_cm is the subsequent acceleration of the centre of mass of the system of blocks then find the value of a_cm (in m · s^-2).
Answer: 2

Question 3. Blocks A and B shown have equal masses m. The system is released from rest with the spring unstretched. The string between A and the ground is cut when there is a maximum extension in the spring. Find the acceleration of the centre of mass (in terms of how many times of g) of the two blocks.
Answer: 2

 

 Newtonian Gravitation And Planetary Motion

Newtonian Gravitation And Planetary Motion Introduction: Since ancient times, scientists have been extremely curious to learn more about the stars and planets.

• Since the time of Copernicus, it is known that planets move around the sun. But to investigate the cause and nature of this motion, it was necessary to know the exact positions of the planets in the sky at different times.
• Astrophysicist Tycho Brahe, for many years, observed the positions of planets without a telescope (Galileo discovered the telescope after the death of Brahe) and published a lot of information about this.
• Kepler analysed the observational findings of Tycho Brahe and arrived at three laws about planetary motion. These laws are known as Kepler’s laws of planetary motion.

Read and Learn More: Class 11 Physics Notes

 Newtonian Gravitation And Planetary Motion – Kepler’s Laws

Kepler’s Laws First Law: Every planet moves in an elliptical orbit with the sun at one of its foci.

Kepler’s Laws Second Law: The line joining the sun and a planet sweep out equal areas in equal intervals of time, i.e., the areal velocity of a planet is constant.

Kepler’s Laws Third Law: The square of the time period of revolution of a planet is directly proportional to the cube of the length of the semi-major axis of its elliptical orbit.

The orbits of planets are known as Keplerian orbits while their motions are known as Keplerian motions.

Proof Of Kepler’s Second Law: Let us consider a planet of mass m moving in an elliptical orbit with the sun at focus S. Also, let \(\vec{r}\) be the position vector of the planet with respect to the sun and \(\vec{F}\) be the required centripetal force for the planet.

The torque exerted on this planet by this force about the sun, \(\)

(\(\vec{r}\) and \(\vec{F}\) are oppositely directed)

But \(\) (\(\vec{L}\) = angular momentum of the planet)

∴ \(\frac{d \vec{L}}{d t}=0 \quad \text { or, } \vec{L}=\text { constant }\)

Now, if the planet moves from position P to P’ in very small time A t, then the area swept out by the radius vector \(\vec{r}\) is,

⇒ \(\Delta \vec{A}=\text { area of triangular region } S P P^{\prime}\)

= \(\frac{1}{2} \vec{r} \times \overrightarrow{P P^{\prime}}\)

Now, \(\quad \overrightarrow{P P^{\prime}} =\Delta \vec{r}=\vec{v} \Delta t=\frac{\vec{p}}{m} \Delta t\)

∴ \(\quad \Delta \vec{A}=\frac{1}{2} \vec{r} \times \frac{\vec{p}}{m} \Delta t\)

or, \(\quad \frac{\Delta \vec{A}}{\Delta t}=\frac{1}{2 m}(\vec{r} \times \vec{p})=\frac{\vec{L}}{2 m}\) (because \(\vec{L}=\vec{r} \times \vec{p}\))

Hence, \(\quad \frac{\Delta \vec{A}}{\Delta t}=\text { constant }\) (because \(\vec{L} \text { and } m\)) are constant

Thus, the areal velocity of the planet remains constant, i.e., the radius vector joining the sun and a planet sweeps out equal areas in equal intervals of time.

Gravitational Attraction Of Extended Bodies

Any extended body comprises a large number of particles. Thus, to find the mutual force of attraction between two extended bodies, the force of attraction between each particle of the first body and that of the second body is to be determined individually.

• The resultant of these forces, given by the vector addition method, gives the magnitude and direction of the force of attraction between the two extended bodies. Clearly, this method is complicated and unwieldy. This method can only be used in the case of regular-shaped bodies.
• But in the case of two extended bodies, however large they may be, if the distance separating them is much greater than their sizes, it can be assumed that the entire mass of each body is concentrated at its centre of mass. As a result, two extended bodies can be considered as two particles at their respective centres of mass.
• In this way, the complication involved in applying Newton’s law of gravitation may be removed. This approach can be applied to celestial bodies, like the earth and the moon, even if they are large in size and cannot be considered as particles.
• The distance between them is so large in comparison to their sizes that they may be considered as particles situated at their respective centres of mass for the purpose of measuring the gravitational force between them.

Now taking M = mass of the earth, m = mass of the moon and r = the distance between their centres of mass, the force of gravitation between them = \(\frac{G M m}{r^2}\).

When the distance between the two bodies is small compared to their sizes, this method of calculation fails.

When the gravitational attraction between a homogeneous spherical body and a particle situated outside the body is considered, it is assumed that the entire mass of the spherical body is concentrated at its centre of mass.

Hence, the earth, the sun, the moon and other planets are taken as spherical and the law is applied. A substance is called homogeneous when the physical properties (like density) of its different parts are identical.

Newtonian Gravitation And Planetary Motion – Sun Earth Moon Numerical Examples

Example 1. Assuming that the moon moves around the earth in a circular orbit of radius 3.8 x 10⁵ km in 27 days and the earth moves around the sun in a circular orbit of radius 1.5 x 10⁸ km in 365 days, find the ratio of the masses of the sun and the earth.
Solution:

From Kepler’s law, \(\frac{T^2}{r^3}\) = constant

where T = time period, r = radius of the orbit.

If the mass of the sun is M₀ and the radius of the earth’s orbit around the sun is r₀, the orbital speed,

⇒ \(v_0=\sqrt{\frac{G M_0}{r_0}}\)

∴ Time period T₀ of the earth = \(\frac{2 \pi r_0}{v_0}=2 \pi r_0 \sqrt{\frac{r_0}{G M_0}}=2 \pi \sqrt{\frac{r_0^3}{G M_0}}\)

Similarly, if the mass of the earth is M, the radius of the moon’s orbit is r, time period,

T = \(2 \pi \sqrt{\frac{r^3}{G M}}\)

∴ \(\frac{T}{T_0}=\sqrt{\left(\frac{r}{r_0}\right)^3 \frac{M_0}{M}} \text { or, }\left(\frac{T}{T_0}\right)^2=\left(\frac{r}{r_0}\right)^3 \cdot \frac{M_0}{M}\)

or, \(\frac{M_0}{M}=\left(\frac{T}{T_0}\right)^2 \cdot\left(\frac{r_0}{r}\right)^3=\left(\frac{27}{365}\right)^2 \cdot\left(\frac{1.5 \times 10^8}{3.8 \times 10^5}\right)^3\)

= 3.37 x 10⁵ = 337000

Hence, the sun is 337000 times more massive than the Earth.

Example 2. Find the mass of the sun considering the orbit of the earth to be circular. Given, a distance of the earth from the sun = 1.49 x 10¹³ cm and G = 6.66 x 10^-8 CGS unit.
Solution:

Let the mass of the sun be M₀, the distance of the earth from the sun r, and the time period of the earth around the sun T.

∴ Mass of the Sun, \(M_0=\frac{4 \pi^2 r^3}{G T^2}\)

= \(\frac{4 \times \pi^2 \times\left(1.49 \times 10^{13}\right)^3}{6.67 \times 10^{-8} \times(365 \times 24 \times 60 \times 60)^2}\)

= \(2 \times 10^{33} \mathrm{~g}=2 \times 10^{30} \mathrm{~kg}\)

Newtonian Gravitation And Planetary Motion – Mass And Average Density Of The Earth Numerical Examples

Example 1. The average density of the earth is 5500 kg · m^-3, the gravitational constant is 6.7 x 10^-11 N · m² · kg^-2 and the radius of the earth is 6400 km. Using the given values, find the magnitude of the acceleration due to gravity on the surface of the earth.
Solution:

It is known \(\rho=\frac{3 g}{4 \pi R G}\)

or, \(g=\frac{4 \pi \rho R G}{3}\)

g =\(\frac{4 \times 22 \times 5500 \times 6400 \times 10^3 \times 6.7 \times 10^{-11}}{7 \times 3}\)

= \(9.88 \mathrm{~m} \cdot \mathrm{s}^{-2} .\)

Example 2. If the earth is considered as a solid sphere of iron of; radius 6.37 x 10⁶ m and of density 7.86 g · cm^-3, what will be the magnitude of the acceleration due to gravity on the earth’s surface? Gravitational constant = 6.58 x 10^-8 CGS unit.
Solution:

It is known \(\rho=\frac{3 g}{4 \pi R G}\)

∴ g = \(\frac{4 \pi \rho R G}{3}=\frac{4 \times 22 \times 7.86 \times 6.37 \times 10^8 \times 6.58 \times 10^{-8}}{7 \times 3}\)

= \(1380.55 \mathrm{~cm} \cdot \mathrm{s}^{-2}\)

Newtonian Gravitation And Planetary Motion Conclusion

The force with which any two material particles in the universe attract each other is called gravitation.

Newton’s Law Of Gravitation: Any two material particles in the universe attract each other along their line of joining. This force of attraction is directly proportional to the product of the masses of the two particles and inversely proportional to the square of the distance separating them.

• The amount of force with which any two material particles of unit mass kept at a unit distance apart attract each other is called the gravitational constant.
• If a body of unit mass is kept at a point in any gravita¬tional field, the gravitational force acting on that body is called gravitational intensity at that point.
• The amount of work done to bring a body of unit mass from infinity to any point in a gravitational field is called the gravitational potential at that point.
• The force with which anybody on or near the earth’s surface is attracted by the earth is called gravity.
• The acceleration produced in a body falling under the influence of the force of gravity is called the acceleration due to gravity.

Kepler’s laws related to the motion of planets and satellites:

1. First Law: Keeping the sun at one of the foci, each planet revolves in an elliptical path around the sun.
2. Second Law: The line joining the sun and a planet covers equal areas in equal intervals of time.
3. Third Law: The square of the time period of revolution of a planet around the sun is directly proportional to the cube of the semimajor axis of its orbit.

The minimum velocity that should be given to a body so that it can escape from the earth or other planets or sat¬ellites is called its escape velocity.

Some uses of an artificial satellite:

1. Weather information,
2. Communication,
3. Military and defence surveillance,
4. Remote sensing.

If the relative angular velocity of an artificial satellite revolving in the equatorial plane is zero with respect to the diurnal motion of the earth, then, from the earth’s surface, the satellite appears to be at rest at the same place. This kind of satellite is called a geostationary satellite.

Newtonian Gravitation And Planetary Motion Useful Relations For Solving Numerical Problems

If the distance between two particles of masses m₁ and m₂ is r and if the mutual force of attraction between the two particles is F, then according to Newton’s law of gravitation,

F = \(\) where G is the gravitational constant whose value in SI is 6.67 x 10^-11 N · m² · kg^-2.

Gravitational intensity at a point situated at a distance r from the centre of a body of mass M is E = \(\frac{G M}{r^2}\)

Work done in bringing a body of unit mass from infinity to the position r, i.e., the gravitational potential at a distance r from the centre of a body of mass M is V = –\(\frac{G M}{r}\)

The relation between the gravitational field intensity and potential is E = \(\frac{d V}{d r}\)

Acceleration due to gravity at any point on the earth’s surface, g = \(\frac{G M}{R^2}\), where M is the mass and R is the radius of the earth, and G is the gravitational constant.

The relation between the gravitational constant G and the mean density (ρ) of the earth is \(\frac{3 g}{4 \pi R G}\).

1. The relation between the acceleration due to gravity at an altitude h above the surface of the earth (g’) and the acceleration due to gravity on the earth’s surface (g) is g’ = g(1-\(\frac{2h}{R}\)) (this equation is valid for h<<R)
2. The relation between the acceleration due to gravity at a depth h below the earth’s surface (g’) with the acceleration due to gravity on the earth’s surface (g) is g’ = g = (1-\(\frac{h}{R}\)
3. The value of the acceleration due to gravity at θ – latitude (g’) of the earth is \(g^{\prime}=g\left(1-\frac{\omega^2 R}{g} \cos ^2 \theta\right)\)
   1. At the poles, θ = 90° ; so, g’ = g.
   2. At the equator, θ = 0°; so, \(g^{\prime}=g\left(1-\frac{\omega^2 R}{g}\right)\)

If a planet of mass m revolves around the sun of mass M₀ along a circular path of radius r, then the orbital speed of that planet, v = \(v=\sqrt{\frac{G M_0}{r}}.\).

Orbital angular velocity, \(\omega=\sqrt{\frac{G M_0}{r^3}}\)

Time period of revolution, T = \(T=2 \pi \sqrt{\frac{r^3}{G M_0}}\)

The value of the escape velocity of a body from the surface of the earth, \(v_e=\sqrt{2 g R}.\).

If the mass of the earth = M, radius of the earth = R, mass of an artificial satellite = m, the orbital speed of the satellite = v and the height of the orbit above the surface of the earth = h, then the orbital speed of the artificial satellite, v \(=\sqrt{\frac{G M}{R+h}}\) and the time period of revolution of the satellite, T = \(2 \pi \sqrt{\frac{r^3}{8}}\), where r = R+h.

In the case of a satellite revolving very close to the surface of the earth, its orbital speed, \(v=\sqrt{g R}\)

and the time period of revolution, T = \(2 \pi \sqrt{\frac{R}{g}}\)

If the mass of the earth = M, the radius of the earth = R, the mass of a geostationary satellite = m, the distance of the satellite from the centre of the earth = r and its time period of revolution = T, then the orbital speed of the geostationary satellite,

v = \(\sqrt{\frac{g R^2}{r}}\)

and the height of the orbit of the geostationary satellite, r \(=\left(\frac{g R^2 T^2}{4 \pi^2}\right)^{1 / 3}\)

If an artificial satellite of mass m revolves along a circular path of radius r, the kinetic energy of the satellite,

K = \(\frac{G M M}{2 r}\) [where M = mass of the earth]

The potential energy is U = –\(\frac{G M m}{r}\)

Total energy of the satellite, E = –\(\frac{G M m}{2r}\)

Newtonian Gravitation And Planetary Motion Assertion Reason Type Questions And Answers

Direction: These questions have statement 1 and statement 2 of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, statement 1 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is true; statement 2 is false.

Question 1.

Statement 1: The force of gravitation between a sphere of mass M₁ and a rod of mass M₂ is = \(\frac{G M_1 M_2}{r} \text {. }\)

Statement 2: Newton’s law of gravitation holds correct for point masses.

Answer: 4. Statement 1 is true; statement 2 is false.

Question 2.

Statement 1: An astronaut in an orbiting space station above the earth experiences weightlessness

Statement 2: An object moving around the earth under the influence of the earth’s gravitational force is in a state of free fall.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: If time period of a satellite revolving in a circular orbit in the equatorial plane is 24 h, then it must be a geostationary satellite.

Statement 2: Time period of a geostationary satellite is 24 hours.

Answer: 4. Statement 1 is true; statement 2 is false.

Question 4.

Statement 1: Gravitational force between two masses in the air is F. If they are immersed in the water force will remain F.

Statement 2: Gravitational force does not depend on the medium between the masses.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 5.

Statement 1: The binding energy of a satellite does not depend upon the mass of the satellite.

Statement 2: Binding energy is the negative value of the total energy of the satellite.

Answer: 4. Statement 1 is true; statement 2 is false.

Question 6.

Statement 1: Kepler’s laws for planetary motion are a consequence of Newton’s laws.

Statement 2: Kepler’s laws can be derived by using Newton’s laws.

Answer: 4. Statement 1 is true; statement 2 is false.

Newtonian Gravitation And Planetary Motion Match Column A With Column B.

Question 1.

Answer: 1. A, C, 2. A, B, C, D, 3. A, B, C, D, 4. A, C, D

Question 2. In Column A, four artificial satellites of Earth are shown. In Column B, some statements are given related to motion or other facts about the satellites.

Answer: 1. A, D, 2. B, D, 3. B, D, 4. C

Question 3.

Answer: 1. C, 2. B, 3. A

Question 4. In the elliptical orbit of a planet, as the planet moves from the apogee position to the perigee position, match the following columns.

Answer: 1. C, 2. B, 3. B, 4. A

Newtonian Gravitation And Planetary Motion Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. The PE of the earth-satellite system is shown by a solid line as a function of distance r (the separation between the earth’s centre and satellite). The total energy of two objects which may or may not be bound to earth are shown in the graph by dotted lines,

1. Mark the correct statement(s).

1. The object having total energy E₁ is the bounded one
2. The object having total energy E₂ is the bounded one
3. Both objects are bounded

Answer: 1. The object having total energy E₁ is the bounded one

2. If the object having total energy E₁ is having the same PE curve as shown, then

1. r₀ is the maximum distance of the object from the earth’s centre
2. This object and earth system is a bounded one
3. The KE of the object is zero when r = r₀
4. All of the above

Answer: 4. All of the above

3. If both the objects gave the same PE curve as shown, then

1. For the object having total energy E₂, all values of r are possible
2. For the object having total energy E₂ only values of r < r₀ are possible
3. For the object having total energy E₁ all values of r are possible
4. None of the above

Answer: 1. For the object having total energy E₂, all values of r are possible

Question 2. A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a. The centre of the shell falls on the surface of the inner sphere.

1. Find the gravitational field intensity at point P₁.

1. \(\frac{G M}{16 a^2}\)
2. \(\frac{G M}{8 a^2}\)
3. \(\frac{G M}{2 a^2}\)
4. \(\frac{G M}{4 a^2}\)

Answer: 1. \(\frac{G M}{16 a^2}\)

2. Find the gravitational field intensity at point P₂.

1. \(\frac{21 G M}{900 a^2}\)
2. \(\frac{61 G M}{450 a^2}\)
3. \(\frac{61 G M}{900 a^2}\)
4. \(\frac{61 G M}{1800 a^2}\)

Answer: 3. \(\frac{61 G M}{900 a^2}\)

Question 3. The gravitational field in a region is given by \(\vec{E}=\left(5 \mathrm{~N} \cdot \mathrm{kg}^{-1}\right) \hat{i}+\left(12 \mathrm{~N} \cdot \mathrm{kg}^{-1}\right) \hat{j}\)

1. Find the magnitude of the gravitational force acting on a particle of mass 2 kg placed at the origin.

1. 26 N
2. 30 N
3. 20 N
4. 35 N

Answer: 1. 26 N

2. Find the potential at the points (12 m, 0) and (0,5 m) if the potential at the origin is taken to be zero.

1. -30J · kg^-1_, -30 J · kg^-1
2. -40J · kg^-1_, -30 J · kg^-1
3. -60J · kg^-1_, -60 J · kg^-1
4. -40J · kg^-1_, -50 J · kg^-1

Answer: 3. -60J · kg^-1_, -60 J · kg^-1

3. Find the change in gravitational potential energy if a particle of mass 2 kg is taken from the origin to the point (12 m, 5 m).

1. -225 J
2. -240 J
3. -245 J
4. -250 J

Answer: 2. -240 J

4. Find the change in potential energy if the particle is taken from (12 m, 0) to (0,5 m).

1. -10 J
2. -50 J
3. Zero
4. -60 J

Answer: 3. Zero

Newtonian Gravitation And Planetary Motion Integer Answer Type Questions

In this type, the answer to each of the questions Is a single-digit integer ranging from 0 to 9.

Question 1. Gravitational acceleration on the surface of a planet is (√6/11)g, where g is the gravitational acceleration on the surface of the earth. The average mass density of the planet is \(\frac{2}{3}\)times that of the earth. If the escape speed on the surface of the earth is taken to be 11 km · s^-1, the escape speed on the surface of the planet in km · s^-1 will be
Answer: 3

Question 2. A binary star consists of two stars A (mass 2.2 M_s) and B (mass 11 M_s), where M_s is the mass of the sun. They are separated by distance d and are rotating about their centre of mass, which is stationary. The ratio of the total angular momentum of the binary star to the angular momentum of star B about the centre of mass is
Answer: 6

Question 3. A particle is projected vertically upwards from the surface of the earth of radius R, with a kinetic energy equal to half of the minimum value needed for it to escape. The maximum height to which it rises above the surface of the earth is nR. What should be the value of n?
Answer: 1

Question 4. The time period of a satellite A, whose orbital radius is r₀, is T₀ and the time period of a satellite B having radius 4r₀ is T_B. Find the ratio of T_B and T₀.
Answer: 8

Question 5. Two particles of masses m₁ and m₂ are kept at a separation of r. When a third particle is kept at a distance of \(\frac{d}{3}\) from m, then it does not experience any net force. Determine the ratio \(\frac{m_2}{m_1}\).
Answer: 4

 

Transmission of Heat

Different Mechanisms Of Heat Transfer: When two bodies having different temperatures are brought in contact with each other, heat flows from the hot¬ter body to the colder one.

Again, when there is a temperature difference between different points of a body, heat flows in die body from the point of higher temperature to the point of lower temperature.

The flow of heat from one place to another is called transmission of heat: Heat is transmitted in three different processes:

1. Conduction,
2. Convection and
3. Radiation.

 

1. Conduction: It is the process in which heat energy is transmitted from a hotter region to a colder region of a material without any displacement of molecules. Conduction usually takes place in solids. When one end of an iron rod is placed in fire, the other end becomes so hot that it becomes difficult to hold that end with our hand. In this case heat gets transmitted through the rod from the end held in fire to the other end. This is known as heat conduction.
2. Convection: It is the process in which heat is transmitted from a hotter region to a colder region of a material by the actual movement of heated molecules. This happens only in fluids i.e., in liquids and gases because here molecules can move freely. If we take some liquid in a container and heat it from below, the top part of the liquid gets heated mainly through convection.
3. Radiation: This is the process in which heat is transferred from one place to another in the form of electro-magnetic radiation in the absence of any material medium or without heating a material medium if it is present between the two places. Heat from the sun reaches the earth by radiation.

Comparison among the three modes of transmission of heat

 

Transmission Of Heat Numerical Examples

Example 1. Four metal pieces of the same surface area and of thickness 1 cm, 2 cm, 3cm, and 4cm respectively are connected serially with each other; Coefficients of thermal conductivity of the respective pieces are 0.2 CGS, 0.3 CGS, 0.1 CGS, and 0.4 CGS units. Find the equivalent conductivity of the system.
Solution:

It is known that, \(\frac{x_1+x_2+x_3+x_4}{k}=\frac{x_1}{k_1}+\frac{x_2}{k_2}+\frac{x_3}{k_3}+\frac{x_4}{k_4}\)

or, \(\frac{1+2+3+4}{k}=\frac{1}{0.2}+\frac{2}{0.3}+\frac{3}{0.1}+\frac{4}{0.4} \)

or, \(\frac{10}{k}=51.67 \text { or, } k=0.1935 \text { CGS. }\)

Example 2. A thick composite plate is formed by two plates of equal thickness kept one over the other. If the conductivities of the material of the constituent plates are k₁ and k₂, show that the equivalent conductivity of the thick plate, k = \(\frac{2 k_1 k_2}{k_1+k_2}\)
Solution:

Is is known, \(\frac{x_1+x_2}{k}=\frac{x_1}{k_1}+\frac{x_2}{k_2}\)

Here, \(x_1=x_2=x\) (say)

∴ \(\frac{x+x}{k}=\frac{x}{k_1}+\frac{x}{k_2} or, \frac{2}{k}=\frac{1}{k_1}+\frac{1}{k_2} or, k=\frac{2 k_1 k_2}{k_1+k_2}\).

Example 3. A 75 cm long copper rod and a 125 cm long steel rod are joined face to face. Each rod is of a circular cross-section of diameter 2 cm. Temperatures at the two ends of the composite rod are 100 °C and 0°C and the outer surface of the rod is insulated. Find the temperature at the junction of the two rods What is the rate of conduction of heat through the junction?

1. k for copper = 9.2 x 10^-2 kcal · m^-1 · °C^-1 · s^-1 and
2. k for steel = 1.1 x 10^-2  kcal · m^-1 · °C^-1 · s^-1

Solution: Let the temperature of the junction = θ Conductivity of copper,

⇒ \(k_1=\frac{9.2 \times 10^{-2} \times 10^3}{10^2}=0.92 \text { CGS unit }\)

and that of steel, \(k_2=\frac{1.1 \times 10^{-2} \times 10^3}{10^2}=0.11 \text { CGS unit }\)

Area of cross-section of each rod, \(A=\pi(1)^2=\pi \mathrm{cm}^2\)

∴ Rate of flow of heat through the junction, \(\frac{Q}{t}=\frac{k_1 A\left(\theta_2-\theta\right)}{l_1}=\frac{k_2 A\left(\theta-\theta_1\right)}{l_2}\)

or, \(k_1 l_2(100-\theta)=k_2 l_1 \theta\)

or, \(0.92 \times 125 \times(100-\theta)=0.11 \times 75 \times \theta \text { or, } \theta=93.3^{\circ} \mathrm{C}\)

∴ Rate of conduction, \(\frac{Q}{t}=\frac{k_2 A\left(\theta-\theta_1\right)}{l_2}=\frac{0.11 \times \pi \times 93.3}{125}=0.258 \mathrm{cal} \cdot \mathrm{s}^{-1}\)

Example 4. The thickness of each metal in a composite bar is 0. 01 m and the temperature of the two external surfaces are 100 °C and 30 °C. If the conductivities of the metals be 0.2 CGS unit and 0.3 CGS unit respectively, find the temperature on the interface.
Solution:

Let the temperature on the interface = θ.

At steady state, rate of flow of heat will be the same through both the plates.

∴ \(\frac{Q}{t}=\frac{k_1 A(100-\theta)}{x_1}=\frac{k_2 A(\theta-30)}{x_2}\)

or, \(\frac{0.2(100-\theta)}{1}=\frac{0.3(\theta-30)}{1} \text { or, } 200-2 \theta=3 \theta-90\)

or, \(5 \theta=290 \text { or, } \theta=58^{\circ} \mathrm{C} .\)

Example 5. Three metal rods of the same length and area of cross-section are attached in series. Conductivity of the three metals are k, 2k, and 3k. Free end of the first rod is kept at 200°C while the other end of the combination is kept of 100 °C. Find the temperatures of the two junctions at steady state. Assume that no heat loss occurs due to radiation.
Solution:

Let the required temperatures be θ₁  and θ₂.

At steady state, \(\frac{Q}{t}=\frac{k A\left(200-\theta_1\right)}{l}=\frac{2 k A\left(\theta_1-\theta_2\right)}{l}=\frac{3 k A\left(\theta_2-100\right)}{l}\)

∴ \(200-\theta_1=2\left(\theta_1-\theta_2\right)=3\left(\theta_2-100\right)\)

As \(200-\theta_1=2\left(\theta_1-\theta_2\right)\)

∴ \(3 \theta_1-2 \theta_2=200\)…..(1)

Also, \(200-\theta_1=3\left(\theta_2-100\right)\)

or, \(\theta_1+3 \theta_2=500\)…..(2)

Solving (1) and (2), \(\theta_1=145.45^{\circ} \mathrm{C} \text { and } \theta_2=118.18^{\circ} \mathrm{C} \text {. }\)

Example 6. A composite block is constructed with three plates of equal thickness and of equal cross-sectional area. The coefficients of conductivity of the three plates are k₁, k₂, and k₃ respectively. If the coefficient of conductivity of the composite block is k, then prove that k = \(=\frac{3}{\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}}\)
Solution:

Let the thickness of each plate be d and cross-sectional area be A.

Q amount of heat flows through each plate in time t, The temperatures of the two ends of the composite slab are T₁ and T₂ respectively.

Also, the temperatures of the consecutive junctions

So, \(Q=\frac{k_1 A\left(T_1-T_1{ }^{\prime}\right) t}{d}\)

= \(\frac{k_2 A\left(T_1{ }^{\prime}-T_2{ }^{\prime}\right) t}{d}=\frac{k_3 A\left(T_2{ }^{\prime}-T_2\right) t}{d}\) or, \(\frac{Q d}{A t}=\frac{T_1-T_1{ }^{\prime}}{\frac{1}{k_1}}=\frac{T_1{ }^{\prime}-T_2{ }^{\prime}}{\frac{1}{k_2}}=\frac{T_2{ }^{\prime}-T_2}{\frac{1}{k_3}}\)

or, \(\frac{Q d}{A t}=\frac{T_1-T_2}{\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}}\)…(1)

[by componendo and dividendo process]

Again, since thickness of the composite slab is 3d,

Q = \(\frac{k A\left(T_1-T_2\right) t}{3 d} \text { or, } \frac{Q d}{A t}=\frac{T_1-T_2}{\frac{3}{k}}\)….(2)

From (1) and (2) we get, \(\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}=\frac{3}{k} \text { or, } k=\frac{3}{\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}}\)

Example 7. The temperature of a room is kept fixed at 20 °C with the help of an electric heater of resistance 20Ω. The heater is connected to a 200 V main. Temperature is same everywhere in the room. The area of the window through which heat is conducted outside from the room is 1 m² and the thickness of the glass is 0.2 cm. Then calculate the temperature outside. [Given, coefficient of thermal conductivity of glass = 0.002 cal • m^-1 • ° C^-1 • s^-1 and / = 4.2 J/s
Solution:

Heat generated by the heater in 1s,

⇒ \(H_1=\frac{V^2}{R J}=\frac{(200)^2}{20 \times 4.2}=\frac{200 \times 2000}{20 \times 42}=476.19 \mathrm{cal}\)

Heat conducted through the window in 1s,

⇒ \(H_2=\frac{k A\left(\theta_2-\theta_1\right)}{d}=\frac{0.002 \times 10^4 \times\left(\theta_2-\theta_1\right)}{0.2} \mathrm{cal}\)

Here, \(H_2=H_1 \quad \text { or, } \frac{0.002 \times 10^4 \times\left(\theta_2-\theta_1\right)}{0.2}=476.19\)

or, \(\left(\theta_2-\theta_1\right)=4.7619\)

∴ \(\theta_1=\theta_2-4.76=20-4.76=15.24^{\circ} \mathrm{C}\)

Example 8. The temperature of a room is kept fixed at 20°C. With the help of an electric heater when the temperature outside is -10°C. The total area of the walls in the room is 137 m2. The walls have three layers—the innermost layer is made of wood and 2.5 cm thick, the middle layer is made of cement and 1 cm thick, the outermost layer is made of bricks and 25 cm thick. Then calculate the power of the heater. [Given, coefficients of thermal conductivity of wood, cement, and brick are 0.125 W · m^-1 • °C^-1, 1.5 W · m^-1 • °C^-1 and 1.0 W • m^-1 • °C^-1 respectively]
Solution:

If k is the equivalent thermal conductivity of the wall made of three layers of different materials then,

k = \(\frac{x_1+x_2+x_3}{\frac{x_1}{k_1}+\frac{x_2}{k_2}+\frac{x_3}{k_3}}\)

Here, \(x_1=2.5 \mathrm{~cm}, x_2=1.0 \mathrm{~cm}, x_3=25 \mathrm{~cm}\)

⇒ \(k_1=0.125 \mathrm{~W} \cdot \mathrm{m}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}, k_2=1.5 \mathrm{~W} \cdot \mathrm{m}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1},\)

⇒ \(k_3=1 \mathrm{~W} \cdot \mathrm{m}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

k = \(\frac{2.5+1+25}{\frac{2.5}{0.125}+\frac{1}{1.5}+\frac{25}{1}}=0.624 \mathrm{~W} \cdot \mathrm{m}^{-1} \cdot{ }^{\circ} \mathrm{C}^{-1}\)

Heat conducted outside through the walls per second

= \(\frac{k A\left(\theta_2-\theta_1\right)}{d}=\frac{0.624 \times 137 \times\{20-(-10)\}}{28.5 \times 10^{-2}}\)

= 8998,7 W ≈ 8999 J s^-1

To keep the temperature of the room fixed the healer must generate 8999 J or 8.999 kJ heat per second.

Hence, power of the heater = 9 kW.

Example 9. The temperature gradient at the earth’s surface is 32 C/km and the average thermal conductivity of earth is 0.005 CGS unit. Find the loss of heat per day from the earth surface taking its radius to be  6000 km.
Solution:

We know, Q = \(k \cdot \Lambda \frac{d \theta}{d x} t \quad\left[\frac{d \theta}{d x}=\frac{\theta_2-\theta_1}{d}\right]\)

Here, k = 0.008 CGS unit, A = 4 x (6000 x 105)² cm²

∴ \(\frac{d \theta}{d x} = 32^{\circ} \mathrm{C} / \mathrm{km}=\frac{32}{10^5}{ }^{\circ} \mathrm{C} / \mathrm{cm},\)

t = \(1 \text { day }=24 \times 60 \times 60 \mathrm{~s}\)

∴ Q = \(\frac{0.008 \times 4 \pi \times 36 \times 10^{16} \times 32 \times 24 \times 60 \times 60}{10^5}\)

= \(1.0006 \times 10^{18} \mathrm{cal}\)

Example 10. Three rods made of material X and three rods of material Y are connected as shown. Each rod has equal length and equal cross-section. If the temperatures of end A and junction E are 60°C and 10°C respectively, find the temperatures of junctions B, C, and D. Coefficients of thermal conductivity of the materials X and Y are 0.92 CGS units and 0.46 CGS units respectively.
Solution:

Let the temperatures of the junctions B, C, and D be θ₁, θ_2, and θ₃ respectively.

Now, heat conducted from A to B

= heat conducted from B to C + heat conducted from B to D

or, 0.46(60 – θ₁) = 0.92(θ₁ -θ₂) + 0.46(θ₁ – θ₃)

or, 60 -θ₁ =2(θ₁ – θ₂) + (θ₁ – θ₃)

or, 4θ₁ -2θ₁-θ₃ = 60 …(1)

Again, heat conducted from B to D

= heat conducted from D to C + heat conducted from D to E

or, \(0.46\left(\theta_1-\theta_3\right)=0.92\left(\theta_3-\theta_2\right)+0.46\left(\theta_3-10\right)\)

or, \(\theta_1-\theta_3=2\left(\theta_3-\theta_1\right)+\left(\theta_3-10\right)\)

or, \(-\theta_1-2 \theta_2+4 \theta_3=10\)….(2)

Similarly, heat conducted from B to C+ heat conducted from D to C= heat conducted from C to E

or, \(0.92\left(\theta_1-\theta_2\right)+0.92\left(\theta_3-\theta_2\right)=0.92\left(\theta_2-10\right)\)

or, \(\theta_1-\theta_2+\theta_3-\theta_2=\theta_2-10\)

or, \(\theta_1-3 \theta_2+\theta_3=-10\)…(3)

Solving (1), (2), and (3), we get, \(\theta_1=30^{\circ} \mathrm{C} ; \theta_2=\theta_3=20^{\circ} \mathrm{C}\)

Example 11. Determine the equivalent thermal conductivity of the system shown. when

1. Heat flows from left to right and
2. Heat flows downwards.

Given, k₁ = 2k₂ and the length and cross section are same for all the slabs.

Solution:

1. Let, the equivalent thermal conductivity is k

Area of cross-section of each plate = A

Temperature difference between the two ends of each Plate =θ

Then heat conducted, \(Q_1=2 \frac{k_1 A \theta t}{l}+2 \frac{k_2 A \theta t}{l}\)

= \(4 \frac{k A \theta t}{l}\)

or, \(\frac{2 A \theta t}{l}\left(k_1+k_2\right)=\frac{4 k A \theta t}{l}\)

or, \(k_1+k_2=2 k\)

or, \(k=\frac{k_1+k_2}{2}=\frac{2 k_1+k_2}{2}=\frac{3 k_2}{2}=1.5 k_2\)

2. In this case if \(k^{\prime}\) be the equivalent thermal conductivity then,

⇒ \(\frac{l}{k^{\prime}} =\frac{\frac{l}{4}}{k_1}+\frac{\frac{l}{4}}{k_2}+\frac{\frac{l}{4}}{k_1}+\frac{\frac{l}{4}}{k_2}\)

or, \(\frac{1}{k^{\prime}}=\frac{1}{2 k_1}+\frac{1}{2 k_2} \frac{1}{4 k_2}+\frac{1}{2 k_2}=\frac{3}{4 k_2}\)

or, \(k^{\prime}=\frac{4 k_2}{3}=1.33 k_2\)

Conduction of Heat through a Slab of Varying Thickness: The thickness of a slab can vary during thermal conduction.

• In cold countries when temperature falls below 0°C, the water on the surface of the lakes and ponds slowly freeze to ice.
• Heat from rest of the mass of water is conducted to the atmosphere through the top frozen layer and the thickness of the ice layer on the surface gradually increases.
• So this is a fine example of conduction of heat through a slab of varying thickness. When the temperature of the atmosphere falls below 0°C, the uppermost surface of water loses its latent heat to the atmosphere and forms a thin sheet of ice.
• In this way, as the thickness of the layer of ice increases, heat will have to be conducted through a thicker layer too.

Let the coefficient of conductivity of ice = k, the density of ice at 0°C = ρ, the temperature of air above the ice surface = -θ °C and the uppermost surface area of the water body = A

After a time t s from the beginning of the formation of ice, let the thickness of ice formed on the water body be x.

If in a small interval of time dt, the increase in thickness of ice is dx, then the volume of ice formed in dt is Adx.

∴ The mass of that ice =Aρdx.

Therefore, the heat lost by water or the heat conducted to air in time dt through ice of thickness x is,

dQ = Aρdx- L [where L = latent heat of ice]

∴ Rate of flow of heat, \(\frac{d Q}{d t}=A \rho L \frac{d x}{d t}=\frac{k A[0-(-\theta)]}{x}=\frac{k A \theta}{x}\)

or, \(xdx  =\frac{k}{\rho L} \theta d t\)…(1)

2. Let us assume that at t = 0, x = x₁ and at t = t₁, x = x₂. This means that in t₁ s time if the thickness of ice slab has increased from x₁ to x₂, integrating the equation (1) we get,

⇒ \(\int_{x_1}^{x_2} x d x=\int_0^{t_1} \frac{k \theta}{\rho L} d t\)

or, \(\frac{1}{2}\left(x_2^2-x_1^2\right)=\frac{k \theta}{\rho L} t_1\)

∴ \(t_1=\frac{\rho L}{2 k \theta}\left(x_2^2-x_1^2\right)\)

1. If x₁ = 0 when t = 0 and x2-x when t = t₁

∴ \(t_1=\frac{\rho L}{2 k \theta} x^2\)….(3)

This equation gives the time (t₁) required for the deposi¬tion of a layer of ice of thickness x.

Note that in both equations (1) and (2), t₁ is independent of the surface area A of the lake. So in the same weather conditions, water bodies of all sizes from ice in this same rate.

Transmission Of Heat Conductivity Of Ice Numerical Examples

Example 1. A 3 cm thick layer of ice is formed over a water reservoir. Temperature over the reservoir is -20°C. In what time, the thickness of the ice layer increase by 1 mm? The conductivity of ice = 0.005 CGS unit; latent heat of fusion of ice = 80 cal · g^-1; density of ice at 0°C = 0.91 g · cm^-3.
Solution:

We shall use the equation, \(t=\frac{\rho L}{2 k \theta}\left(x_2^2-x_1^2\right)\)

where ρ = 0.91 g · cm^-3, L = 80 cal · g^-1,

k = 0.005 CGS unit, θ = 0 – (-20) = 20°C , x₁ = 3cm, x₂ = 3.1 cm

∴ t = \(\frac{0.91 \times 80}{2 \times 0.005 \times 20}\left[(3.1)^2-(3)^2\right]\)

= \(\frac{0.91 \times 80}{2 \times 0.005 \times 20} \times 0.61\)

= 222.04 s = 3 min 42 s

Example 2. The surface of a lake is covered with a layer of ice of a thickness 10 cm. For increase in thickness of the ice layer by 1 mm, time taken is found to be 49 min9s. Conductivity of ice = 0.005 CGS unit, latent heat of fusion of ice = 80 cal · g^-1, and density of ice = 0. 917 g • cm^-3. Find the outside temperature.
Solution:

Let the temperature of air outside = -θ

It is known that, t = \(\frac{\rho L}{2 k \theta}\left(x_2^2-x_1^2\right) \quad \text { or, } \theta=\frac{\rho L}{2 k t}\left(x_2^2-x_1^2\right)\)

In this case, t = 49 min 9 s = 2949 s, x₁ = 10.1 cm, x₂ = 10 cm, ρ = 0.917 g · cm^-3, L = 80 cal · g^-1, k = 0.005 CGS unit

∴ \(\theta =\frac{0.917 \times 80}{2 \times 0.005 \times 2949}\left[(10.1)^2-(10)^2\right]\)

= \(\frac{0.917 \times 80 \times 2.01}{2 \times 0.005 \times 2949}=5\)

∴ The outside temperature is -5°C

Example 3. Water in a tank at 0°G is in contact with a surrounding temperature of -20°C. Prove that the rate of increase of thickness x (in cm) ofice on the surface, is related to time t (in s) as x² = 0.00273t. The density of ice =0.917 g · cm^-3, latent heat of fusion of ice =80 cal • g^-1, and conductivity of ice =0.005 CGS unit.
Solution:

Let, A be the surface area of the tank, x be the initial thickness of ice floating on the tank surface and dx be the increase in thickness in time dt.

Hence, mass of ice formed in the time dt = Adx x ρ [ρ = density of ice]

Heat released by water = Adx x ρ xL [L = latent heat of fusion of ice]

This is the amount of heat that is conducted from water in the tank through the ice of thickness x to the surroundings.

∴ Rate of release of heat, \(\frac{d Q}{d t}=A \rho L \frac{d x}{d t}=\frac{k A[0-(-\theta)]}{x}\)

[-θ°C being the temperature of the surroundings]

or, \(x d x=\frac{k \theta}{\rho L} d t\)

Integrating, \(\int_0^x x d x=\frac{k \theta}{\rho L} \int_0^t d t\)

or, \(x^2=\frac{2 k \theta}{\rho L} t=\frac{2 \times 0.005 \times 20 \times t}{0.917 \times 80}\)

or, \(]y=0.00273 t\) (Proved).

Example 4. A 14.9 cm thick layer of ice floats on a deep lake. The temperature of the upper surface of the ice layers is the same as that of the surrounding air. If this temperature remains constant at -1°C then determine the time required for the layer to increase by 2mm in thickness. Given, latent heat of melting of ice =80 cal · g^-1, density of ice = 0.9 g cm^-3 and coefficient of thermal conductivity of ice = 0.006 CGS unit.
Solution:

We know, \(t=\frac{\rho L}{2 k \theta}\left(x_2^2-x_1^2\right)\)

Here, \(\rho=0.9 \mathrm{~g} \cdot \mathrm{cm}^{-3}, L=80 \mathrm{cal} \cdot \mathrm{g}^{-1}\)

k = \(0.006 \mathrm{CGS} \text { unit }, \theta=1^{\circ} \mathrm{C}\)

∴ \(x_1 =14.9 \mathrm{~cm}, x_2=14.9+0.2=15.1 \mathrm{~cm}\)

t = \(\frac{0.9 \times 80}{2 \times 0.006 \times 1}\left[(15.1)^2-(14.9)^2\right]\)

= \(\frac{0.9 \times 80}{0.012} \times 30 \times 0.2=36000 \mathrm{~s}=10 \mathrm{~h}\)

 

Energy Distribution In Black Body Radiation Wien’s Displacement Law

Radiation from a hot body consists of electromagnetic waves of different wavelengths (λ). However the energy is not evenly distributed in all wavelengths of radiation.

The intensity of wavelengths in black body radiation, obtained by experimental observations, reveals a pattern as shown by the graph.

The abscissa of the graph denotes the wavelengths A of radiated heat and the ordinate denotes radiation per unit area per unit time (Eλ) for different wavelengths.

Interpretation of the graph:

1. At a temperature T₁, the source

1. Energy distribution is unequal for different wavelengths and
2. The intensity is maximum at a certain wavelength \(\lambda_{m_1}\) as represented by point P on graph A.

2. Radiations from the body at different temperatures T₁, T₂, T_3, and the corresponding intensity distribution can be compared from graphs A, B, C. Clearly

1. As temperature increases the total intensity, represented by the area under the curve, also increases,
2. The wavelength of maximum intensity shifts towards the lower wavelength side, with the increase in temperature of the source.

The observations referred to above led to the formulation of Wien’s displacement law which can be stated as: With the increase in the temperature of a body, the wavelength corresponding to the maximum intensity shifts towards the lower wavelength side.

The mathematical representation of Wien’s displacement law is, λ_mT = b (constant), where λ_m is the wavelength having maximum intensity at a temperature T of the source.

The value of Wien’s constant b, is about 0.0029 m K in SI unit. Thus, if λ_m is known, the temperature of the source T can be calculated. This method is widely used in estimating the temperature of stars. For example, if the temperature of a black body (star) is 1000 K,

∴ \(\lambda_m=\frac{0.0029}{1000}=2.9 \times 10^{-6} \mathrm{~m}\)

= \(29000 \times 10^{-10} \mathrm{~m}=29000\)Å

This wave lies in the infrared region of the electromagnetic spectrum.

Transmission Of Heat Energy Distribution In Black Body Radiation Numerical Examples

Example 1. The wavelength of the radiation of maximum Intensity from the solar surface Is 4.9 x 10^-7 m. From Wien’s displacement law, find the surface temperature of the sun. [ b = 0.0029 m • K]
Solution:

As per Wien’s displacement law, \(\lambda_m T=b=0.0029 \mathrm{~m} \cdot \mathrm{K}\)

Hence, \(T=\frac{0.0029}{4.9 \times 10^{-7}}=5918 \mathrm{~K}\).

Example 2. Assume that a star, which has a surface temperature of 5 x 10⁴ K, is a black body. Calculate the length of maximum intensity In Its radiation [b = 0.0029 m · K]
Solution:

From Wien’s displacement law, \(\lambda_m T=b\); given, \(T=5 \times 10^4 \mathrm{~K}\) and \(b=0.0029 \mathrm{~m} \cdot \mathrm{K}\).

∴ \(\lambda_m=\frac{b}{T}=\frac{0.0029}{5 \times 10^4}=\frac{29}{5} \times 10^{-8}=5.8 \times 10^{-8} \mathrm{~m}\).

 

Transmission Of Heat Long Answer Type Questions

The capability of a material to conduct heat is called its thermal conductivity.

• The quantity of heat conducted per second perpendicularly across the opposite faces of a unit cube, when the difference of temperature between its opposite faces is unity, is called the coefficient of thermal conductivity or simply thermal conductivity (k) of that material.
• In case of an ideal conductor k → ∞ and in case of an ideal insulator k = 0. So in reality, 0 < k < ∞.

Dimension of k: \(\mathrm{MLT}^{-3} \Theta^{-1}\)

• In the pre-steady state, the rate of increase in temperature of any layer of a conducting rod depends on the coefficient of thermal conductivity, the density and the specific heat of the material of the rod.
• In steady state, no layer of the rod has any increase in temperature and hence, the transmission of heat along the rod depends only on the coefficient of thermal conductivity.
• The ratio of the thermal conductivity of a substance to the thermal capacity per unit volume of that substance is called the thermal diffusivity of the substance.

In the radiation process, heat energy spreads all around in the form of electromagnetic waves. This thermal wave is called thermal radiation or radiant heat.

Prevost’s theory of heat exchange: The rise and fall of temperature of a body depends on the heat exchange of the body with its surroundings.

• The body which is a good absorber is also a good radiator of heat. Conversely, a bad absorber is also a bad radiator of heat.
• The body which absorbs all the incident radiations without reflecting or transmitting any part of it is called a perfectly black body. Since a perfectly black body is an ideal absorber of heat, it is also an ideal radiator of heat.

Kirchhoff’s law: At a particular temperature, the ratio of the emissive power and the absorptive power of a substance is always a constant and is equal to the emissive power of a perfectly black body at that temperature.

Stefan’s law: The total radiation of all wavelengths emitted per unit time per unit area of a perfect blackbody is directly proportional to the fourth power of its absolute temperature.

Newton’s law of cooling: For a small difference in temperature, heat lost per unit time by a body is directly proportional to the difference in temperature of the body with its surroundings.

Men’s law: With the increase in temperature of a body, the wavelength of the radiation corresponding to the maximum intensity shifts towards the lower wavelengths.

Transmission Of Heat Useful Relations For Solving Numerical Problems

If the temperature of the two faces of a rectangular plate of cross-sectional area A and of thickness d be θ₂ and θ₁ (θ₂ > θ₁) then the amount of heat conducted in time t from the hot to the cold face of the plate will be

Q = \(\frac{k A\left(\theta_2-\theta_1\right) t}{d}\)

Thermal resistance of conductor = \(\frac{1}{k} \cdot \frac{d}{A} .\)

Thermal resistivity of a substance = \(\frac{1}{k}\)

Thermal diffusivity of a substance, \(h=\frac{k}{\rho s}\)

[k = coefficient of thermal conductivity, ρ = density, s = specific heat]

If the equivalent thermal conductivity of a combined slab is k, then, \(\frac{x_1+x_2+\cdots+x_n}{k}=\frac{x_1}{k_1}+\frac{x_2}{k_2}+\cdots+\frac{x_n}{k_n}\)

where, x_n = thickness of n-th slab, k_n= thermal conductivity of the n-th slab. The temperature of the interface,

⇒ \(\theta=\frac{k_1 \theta_2 x_2+k_2 \theta_1 x_1}{k_2 x_1+k_1 x_2}\)

Emissive power (e) of a surface = amount of radiation emitted at a particular temperature from unit area of the surface in unit time.

Relative emittance of a surface (e) = \(\begin{gathered}
=\frac{\text { the amount of heat radiated by that surface }}{\text { the amount of heat radiated by the same surface area }} \\
\text { of a black body at the same temperature } \\
\text { in an equal interval time }
\end{gathered}\)

Absorptive power (a) of a surface = \(\frac{\text { the amount of heat absorbed }}{\text { the amount of heat incident on the surface }}\)

If the emissive power and absorptive power of a surface at a particular temperature be e and a respectively and the emissive power of a perfectly black body is E, then according to Kirchhoff’s law, \(\frac{e}{a}\) = E.

According to the Stefan’s law, E = σT⁴ (where σ = Stefan’s constant]

If the absolute temperature of an ideal black body and its surroundings be T and T₀, then by Prevosfs theory of heat exchange, the net rate of radiation of heat from the black body, \(E=\sigma\left(T^4-T_0^4\right)\)

Let mass of a body be m, its specific heat s, and the temperature of the surroundings θ₀. If at time t the temperature of the body drops from θ₁ to θ₂, then

t = \(\frac{1}{C} \ln \left(\frac{\theta_1-\theta_0}{\theta_2-\theta_0}\right)\)

According to the Wien’s law, λ_mT= constant.

[where, λ_m = wavelength of the radiation corresponding to the maximum intensity emitted from a black body kept at an absolute temperature T.]

Solar temperature T = \(\left[\left(\frac{R}{r}\right)^2 \times \frac{s}{\sigma}\right]^{1 / 4}\)

(where r = radius of the sun, R = mean distance of the earth from the sun, s = solar constant and σ = Stefan’s constant)

 

Transmission Of Heat Assertion Reason Type Questions And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 Is true, statement 2 Is true; statement 2 Is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 Is false, and statement 2 Is true.

Question 1.

Statement 1: The equivalent thermal conductivity of two plates of same thickness in contact is less than the smaller value of thermal conductivity.

Statement 2: For two plates of equal thickness contact, the equivalent thermal conductivity is given by \(\frac{2}{k}=\frac{1}{k_1}+\frac{1}{k_2} \text {. }\)

Answer: 4. Statement 1 Is false, statement 2 Is true.

Question 2.

Statement 1: If the thermal conductivity of a rod is 5 units, then its thermal resistivity is 0.2 units.

Statement 2: Thermal conductivity = \(\frac{1}{\text { thermal resistivity }}\)

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: When the temperature difference across the two sides of a wall is increased, its thermal conductivity increases.

Statement 2: Thermal conductivity depends on the nature of material of the wall.

Answer: 4. Statement 1 Is false, statement 2 Is true.

Question 4.

Statement 1: If the temperature of a star is doubled then the rate of loss of heat from it becomes 16 times.

Statement 2: The specific heat varies with temperature.

Answer: 3. Statement 1 is true, statement 2 is false.

Question 5.

Statement 1: Radiant heat is an electromagnetic wave.

Statement 2: Heat from the sun reaches the earth by convection.

Answer: 3. Statement 1 is true, statement 2 is false.

Transmission Of Heat Match Column 1 With Column 2

Question 1. On average, the temperature of the earth’s crust increases 1°C for every 30 m of depth. The average thermal conductivity of the earth’s crust is 0.75 J • m^-1 • K^-1 • s^-1. Solar constant is 1.35 kW • m^-2.

Answer: 1. A, 2. 3. 4. E

Question 2. Three rods of equal length of the same material are joined form an equilateral triangle ABC as shown. Area of a cross-section of rod AB is S, of rod BC is 2S and that of AC is S.

Answer: 1. C, 2. D, 3. 1, 4. B

Question 3. A copper rod (initially at room temperature 20°C) of the non-uniform cross section is placed between a steam chamber at 100°C and an ice water chamber at 0°C. A and B are cross sections as shown. Then match the statements in Column 1 with results in Column 2 using comparing only cross sections A and B.

Answer: 1. A, C, 2. D, 3. B

Transmission Of Heat Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A body cools in a surrounding of constant temperature 30°C. Its heat capacity is 2 J • °C^-1. The initial temperature of die body is 40°0. Assume Newton’s law of cooling is valid. The body cools to 38°C in 10 minutes.

1. In further 10 min it will cool from 38 °C to

1. 36°C
2. 36.4 °C
3. 37°C
4. 37.5°C

Answer: 2. 36.4 °C

2. The temperature of the body in T. denoted by θ. The variation of θ versus time t is best denoted as

Answer: 1

3. When the body temperature has reached 38°C, it is heated again so that it reaches 40°C in 10 min. The heat required from a heater by the body is

1. 3.6J
2. 0.364J
3. 8J
4. 4J

Answer: 3. 4

Question 2. Two insulated metal bars each of length 5 cm and rectangular cross-sections with sides 2 cut and 3 cm are wedged between two walls one held at 100°C and the other at 0°C. The bars are lead (Pb) and silver (Ag) k_Pb = 350 W m^-1 K^-1, k_Ag = 425 W m^-1 K^-1

1. Thermal current through lead bar is

1. 210W
2. 420W
3. 510W
4. 930W

Answer: 2. 420W

2. Total thermal current through the two-bar system is

1. 210 W
2. 420W
3. 510 W
4. 930W

Answer: 4. 930W

3. Equivalent thermal resistance of the two-bar system is

1. 0.1 W
2. 0.23 W
3. 0.19 W
4. 0.42W

Answer: 1. 0.1 W

Question 3. Assume that the thermal conductivity of copper is twice that of aluminum and four times that of brass. Three metal rods made of copper, aluminum, and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminum between the other two. The free ends of the copper and brass rods are maintained at 100°C and 0°C, respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere,

1. Under steady-state condition, the equilibrium temperature of the copper-aluminum junction will be

1. 86°C
2. 18.8°C
3. 57°C
4. 73°C

Answer: 1. 86°C

2. When steady state condition is reached everywhere,

1. No heat is transmitted across the copper-aluminium or aluminium-brass junction
2. More heat is transmitted across the copper-aluminium junction than across the aluminium-brass junction
3. More heat is transmitted across the aluminium-brass junction than the copper-aluminium junction
4. Equal amount of heat is transmitted at the copper-aluminum and aluminium-brass junction

Answer: 4. Equal amount of heat is transmitted at the copper-aluminium and aluminium-brass junction

3. Under steady-state conditions, the equilibrium temperature of the aluminum-brass junction will be

1. 57°C
2. 35°C
3. 18.8°C
4. 28.5°C

Answer: 1. 57°C

Transmission Of Heat Integer Type Questions And Answers

In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.

Question 1. A metal rod AB of length 10x has its one end A in. ice at 0°C and the other end B in water at 100°C if a point P on the rod is maintained at 400°C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540 cal · g^-1 and the latent heat of melting of ice is 80 cal · g^-1. If the point P is at a distance of λx from the ice end A, find the value of λ. (Neglect any heat loss to the surroundings.)
Answer: 9

Question 2. Two spherical bodies A (radius 6 cm] and B (radius IS cm) are at temperature T₁ and T₂, respectively. The maximum intensity in the emission spectrum of A is at 500 runs and of B is at 1500 nm. Considering them to be blackbodies, what will be the ratio of the rare of total energy radiated by A to that of B?
Answer: 9

Question 3. A liquid takes 5 minutes to cool from 80°C to 50°C- How much time (in min) will it take to cool from 60°C to 30 °C? The temperature of the surroundings is 20°C
Answer: 9

Question 4. The ends of the two rods of different materials with their thermal conductivities, radii of cross-section, and lengths in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat through the larger rod is 4 cal · s^-1, what is the rate of flow of heat (in cal • s^-1) through the shorter rod?
Answer: 1

 

Expansion Of Solid And Liquids Introduction Expansion Of Solids

Usually, all solid substances expand on heating and contract on cooling. For a certain rise in temperature, this change is so small for solids, compared to that of liquids and gases, that the change is not always noticeable.

But with the help of proper experiments, it can be shown that solids expand on heating. This phenomenon of expansion with a change in temperature is called thermal expansion. Expansions in solids by the application of external forces have been discussed in the chapter Elasticity.

Thermal expansion in solids is of three types

1. Linear expansion (a change in length),
2. Surface or superficial expansion (the change in surface area) and
3. Volume or cubical expansion (change in volume).

The thermal expansion of different solids, for the same rise in temperature, is different. For example, copper undergoes a greater thermal expansion than iron, for the same rise in temperature with respect to their initial length, surface or volume.

Generally, with the rise in temperature, a solid expands equally in all directions. But there are exceptions as well. A few crystals expand differently in different directions when heated. Again an alloy of iron and nickel, called invar, practically does not show any expansion with the rise in temperature.

Reason for thermal expansion of solids: From the simple considerations of the structure of a crystalline solid, it can be said that the atoms of the crystal are arranged in a regular array under the elastic force.

Between two adjacent atoms this elastic force behaves like an almost inextensible spring. At a fixed temperature, two atoms thus maintain an average distance between them and vibrate. This average distance increases with rise in temperature. Hence, solids expand with the rise in temperature.

 

Expansion Of Solid And Liquids – Coefficient Of Surface Or Superficial Expansion

Superficial Expansion Definition: The increase in surface area for a unit rise in temperature for a unit surface area of a solid is called the coefficient of surface expansion of the material of that solid.

Let S₁ and S₂ be the surface areas of a solid at temperatures t₁ and t₂ respectively, where t₂ > t₁

Proceeding in a way similar, we get, the coefficient of surface expansion,

⇒ \(\beta=\frac{S_2-S_1}{S_1\left(t_2-t_1\right)}\)

= \(\frac{\text { increase in area }}{\text { initial area } \times \text { rise in temperature }}\) …….(1)

or, \(S_2-S_1=S_1 \beta\left(t_2-t_1\right)\)

or, \(S_2=S_1\left\{1+\beta\left(t_2-t_1\right)\right\}\) ….(2)

If the initial temperature = 0 and the final temperature = t, we may write, S_t = S₀ {1 + βt}……..(3)

where S₀ = surface area at zero temperature.

1. The coefficient of surface expansion β is not a constant For precise measurements of β, the surface area at 0°C is to be taken as the initial surface area.
2. Value of β does not depend on the unit of surface area,
3. Value of β depends on the unit of temperature.

Unit of β is °C or °F^-1. The change in temperature by 1°F = 5/9°C change in temperature.

∴ \(\beta_F=\frac{5}{9} \beta_C \text {, where } \beta_F\) = value of 0 in Fahrenheit scale, and 0C = value of 0 in Celsius scale.

 

Expansion Of Solid And Liquids – Relation Among The Three Coefficients of Expansion Numerical Examples

Example 1. At 30°C the diameter of a brass disc is 8 cm. What will be the increase in surface area if it is heated to 80°C? a of brass = 18 x 10^-6 °C^-1.
Solution:

Increase in surface area = \(S_2-S_1=\beta S_1\left(t_2-t_1\right)\)

Here, \(\beta=2 \alpha=2 \times 18 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1} \text { and } S_1=\pi \times\left(\frac{8}{2}\right)^2 \mathrm{~cm}^2\)

Increase in temperature = t₂– t₁ = 80-30 = 50 °C

∴ Increase in surface area, \(S_2-S_1\)=\(2 \times 18 \times 10^{-6} \times \pi \times\left(\frac{8}{2}\right)^2 \times 50\)

= \(36 \times 10^{-6} \times 16 \pi \times 50=0.0905 \mathrm{~cm}^2 .\)

Example 2. A rectangular copper block measures 20 cm x 12 cm x 3 cm. What will be the change in volume of the block when it is heated from 0°C to 800°C? The coefficient of linear expansion of copper is 0. 16 x 10^-4 °C^-1.
Solution:

Initial volume of the block, V₀ =20 X 12 X 3 = 720 cm³, increase in temperature = t₂ – t₁ = 800 – 0 = 800°C.

γ = 3α = 3 x 0.16 x 10^-4 °C^-1

Cubical expansion, \(V_{800}-V_0=V_0 \times \gamma \times(800-0)\)

= 720 x 3 x 0.16 x 10^-4 x 800 = 27.65 cm³.

Example 3. A lead bullet has a volume of 2.5 cm³ at 0°C. Its volume increases by 0.021 cm³ when heated to 98°C. Find the coefficient of linear expansion of lead.
Solution:

By definition, the coefficient of volume expansion of lead, \(\gamma=\frac{V_t-V_0}{V_0 t}\)

Given, \(V_t-V_0=0.021 \mathrm{~cm}^3, V_0=2.5 \mathrm{~cm}^3 \text { and } t=98^{\circ} \mathrm{C}\)

∴ \(\gamma=\frac{0.021}{2.5 \times 98}=85.7 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)

∴ Coefficient of linear expansion of lead \(\alpha=\frac{\gamma}{3}=\frac{8.57 \times 10^{-6}}{3}=2.86 \times 10^{-6 \circ} \mathrm{C}^{-1}\)

Example 4. An aluminium sphere of diameter 20 cm Is heated from 0°C to 100°C. What will be its change in volume? Coefficient of linear expansion of aluminium = 23x 10^-6 °C^-1.
Solution:

The initial volume of the aluminium sphere,

= \(\frac{4}{3} \pi\left(\frac{20}{2}\right)^3=\frac{4}{3} \pi(10)^3 \mathrm{~cm}^3\)

Value of γ for aluminium =3 x α =3x23x 10^-6 °C^-1.

Hence, increase in volume, \(V_t-V_0=V_0 \gamma t=\frac{4}{3} \pi \times 10^3 \times 3 \times 23 \times 10^{-6} \times 100\)

= 28.9 cm³.

Example 5. A piece of metal weighs 46 g xg in air. When immersed in a liquid of relative density 1.24, kept at 27°C, its weight is 30 g x g. When the temperature of the liquid is raised to 42°C, the metal piece in it weighs 30.5 g x g. At 42°C, the relative density of the liquid is 1.20. Find the coefficient of linear expansion of the metal.
Solution:

The apparent loss in weight of the metal at 27°C = weight of an equal volume of the liquid = (46 – 30) g x g;

Thus the volume of the displaced liquid at 27 °C = \(\frac{46-30}{1.24}=\frac{16}{1.24} \mathrm{~cm}^3\) = volume of the metal piece at 27°C(= V₁).

Similarly, the volume of the metal piece at 42 °C (= V₂)

= \(\frac{46-30.5}{1.20}=\frac{15.5}{1.20} \mathrm{~cm}^3\)

∴ Coefficient of volume expansion of the metal,

⇒ \(\gamma=\frac{V_2-V_1}{V_1\left(t_2-t_1\right)}=\frac{1}{\left(t_2-t_1\right)}\left(\frac{V_2}{V_1}-1\right)\)

= \(\frac{1}{42-27}\left(\frac{15.5}{1.2} \times \frac{1.24}{16}-1\right)=\frac{1}{15}\left(\frac{961}{960}-1\right)\)

= \(\approx 6.94 \times 10^{-5 \circ} \mathrm{C}^{-1}\)

∴ The coefficient of linear expansion of the metal piece \(\alpha=\frac{\gamma}{3}=\frac{6.94 \times 10^{-5}}{3}{ }^{\circ} \mathrm{C}^{-1}=23.15 \times 10^{-6{ }^{\circ}} \mathrm{C}^{-1}\)

Change Of Density Of A Solid Due To Change Of Temperature

It is known that the density of a substance = \(\frac{\text { mass }}{\text { volume }}\).

With the change in temperature, while the mass of a solid remains the same, its volume changes. Hence, with the change in temperature, the density of a solid changes.

With the rise in temperature, volume increases, thus density decreases and with the decrease in temperature, volume decreases, thus density increases.

Let for a solid of mass m at temperature t₁, the volume be V₁ and density be D₁; while at temperature t₂, its volume becomes V₂ and density becomes D₂.

∴ \(D_1=\frac{m}{V_1} \text { and } D_2=\frac{m}{V_2}\)

∴ \(\frac{D_1}{D_2}=\frac{V_2}{V_1}\)

If the coefficient of volume expansion of the solid is γ, then

⇒ \(V_2=V_1\left[1+\gamma\left(t_2-t_1\right)\right] \quad \text { or, } \frac{D_1}{D_2}=\frac{V_1\left[1+\gamma\left(t_2-t_1\right)\right]}{V_1}\)

or, \(D_1=D_2\left[1+\gamma\left(t_2-t_1\right)\right]\)

or, \(D_2=\frac{D_1}{\left[1+\gamma\left(t_2-t_1\right)\right]}=D_1\left[1+\gamma\left(t_2-t_1\right)\right]^{-1}\)

or, \(D_2=D_1\left[1-\gamma\left(t_2-t_1\right)\right]\)

[neglecting higher powers of γ(t₂ – t₂), as γ is very small]

If t₂ > t₁, D₂ < D₁

If D₀ and D_t are the densities of the solid at 0 and t degree temperatures respectively, equation (2) reduces to D_t = D₀(1-γt).

Expansion Of Solid And Liquids – Change Of Density Of A Solid Due To Change Of Temperature Numerical Examples

Example 1. Density of glass at 10°C is 2.6 g · cm^-3 and that at 60°C is 2.596 g • cm^-3. What is the average value of the coefficient of linear expansion of glass between these two temperatures?
Solution:

Using the equation D₁ = D₂ [1 +γ(t₂ -t₁)], and substituting the given values,

D₁ = 2.6 g · cm^-3, D₁ = 2.596 g · cm^-3, t₁ = 10°C and t₂ = 60°C,

we get, 2.6 = 2.596 [1 + γ(60 – 10)]

or, \(1+50 \gamma=\frac{2.6}{2.596} \quad \text { or, } 50 \gamma=\frac{2.6-2.596}{2.596}\)

or, 50γ = 1.00154 – 1

or, \(\gamma=\frac{0.00154}{50}=30.8 \times 10^{-6 \circ} \mathrm{C}^{-1}\)

∴ \(\alpha=\frac{\gamma}{3}=10.27 \times 10^{-6 \circ} \mathrm{C}^{-1}\)

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Thermal Stress

A change in temperature causes a change in the length of a metal rod. But if the two ends of the rod are rigidly fixed at fixed supports, expansion or contraction of the rod gets obstructed. Hence, a large force is generated along the rod. This force, measured per unit area of the rod is called ther¬mal stress.

Experimental demonstration of thermal stress: A metal rod B is set within the gap of a heavy iron frame Y. One end of the rod B is threaded and two holes P₁ and P₂ are at the other end.

• A screw N is fitted at the threaded end of B. A cast iron pin is introduced through the hole P₁ and the rod B is heated.
• When the rod expands, the pin at P₁ is tightly fitted with the frame by adjusting the screw N.
• If the rod is cooled now, the pin obstructs the contraction of the rod developing a huge force which breaks the pin inserted through P₁.
• Expansion of the rod, when obstructed, also generates a huge force. To demonstrate this, a pin is inserted through P₂ and the rod is fixed rigidly by adjusting the screw N. If now the rod is heated, the pin P₂ gets broken due to the force developed in the rod on expansion.

Magnitude of thermal stress: Let a rod of length l, cross-sectional area A, coefficient of linear expansion α be heated so that the rise in temperature is t. The rod, therefore expands by l∝t.

• Now if the two ends of the rod are rigidly fixed and it is cooled to its original temperature, it tends to contract back to its original length and this contraction is opposed by a force F (say).
• Therefore, the reaction to the force F, which is equal and opposite to F, is the thermal force developed in the rod due to expansion lα t.

From Hooke’s law, the Young’s modulus of the rod,

Y = \(\frac{\text { stress }}{\text { strain }}=\frac{\text { applied force } / \text { area }}{\text { change in length } / \text { initial length }}=\frac{F / A}{l a t / l}\)

∴ F = AYαt

Therefore, the thermal stress = F/A = Yαt

Clearly, thermal stress is independent of length or area of the cross-section of the rod (or a wire).

Expansion Of Solid And Liquids Thermal Stress Numerical Examples

Example 1. Two ends of a steel rod are rigidly fixed with two supports. At 30° C its area of cross-section is 4 cm². How much force will be exerted on the supports by the ends of the rod if the temperature of the rod is raised by 60°C? [Young’s modulus of steel = 2.1 x 10¹² dyn · cm^-2 and its coefficient of linear expansion is 12 x 10^-6 °C^-1
Solution:

In this case, A = 4 cm², Y = 2.1 x 10¹² dyn · cm^-2, α = 12 x 10^-6 °C^-1 and t = 60 – 30 = 30°C

∴ The force exerted

=AYαt =4×2.1 x 10¹² x 12 x 10^-6 x 30 = 3.024x 10⁹ dyn.

Example 2. Two ends of a wire are rigidly clamped. If its temperature is decreased by 10°C, find the change in the tension of the wire. Area of cross-section of the wire =0.01 cm²; α= 16 x 10 ^-6 °C^-1, Y = 20 x 10¹¹ dyn · cm^-2
Solution:

Here A = 0.01 cm², Y = 20 x 10¹¹ dyn · cm^-2,α = 16 x 10^-6 °C^-1, t = 10°C

∴ Change in tension

AYαt = 0.01 x 20 x 10¹¹ x 16 x 10^-6 x 10 = 32 x 10⁵ dyn.

 

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Apparent And Real Expansion Of Liquids

To heat a liquid, it has to be kept in a container. When heat is applied, the container also expands along with the liquid. As the liquid expands more than the container for the same change in temperature, expansion of the container is sometimes neglected and only the expansion of the liquid is recorded.

• Hence, the recorded expansion of the liquid, ignoring the expansion of the container, is less than the actual expansion of the liquid.
• The expansion of a liquid, ignoring the expansion of the container, is called the apparent expansion of the liquid.
• The sum of the apparent expansion of the liquid and the expansion of the container is called the real expansion of the liquid.

Experiment: Let, surface of the liquid in a flask rest at mark O. If the flask is heated from outside, at first the flask expands and the surface of the liquid comes down at mark A.

Thus the length OA represents expansion of the flask. Then the supplied heat reaches the liquid and surface of the liquid rises up to mark B. Therefore, volume of AB is the real expansion of the liquid.

On the other hand, if the first change of volume is unnoticed, it seems like the surface rises from initial position O to final position B. So, volume of OB is the apparent expansion of the liquid.

∴ For a liquid, real expansion = apparent expansion of the liquid + expansion of container

Coefficients of Apparent and Real Expansion of Liquids

Since liquid expansions are of two types, two separate coefficients of expansion are to be considered:

1. Coefficient of apparent expansion and
2. Coefficient of real expansion.

Coefficient of apparent expansion of a liquid Definition: The apparent expansion of unit volume of a liquid for a temperature rise of 1° is called the coefficient of apparent expansion (γ’) of the liquid.

Expression for γ’: Let the volume of a certain amount of liquid be V₁ at temperature t₁, and its apparent volume be V’₂ at temperature t₂.

∴ For a rise in temperature of (t₂ – t₁), apparent expansion of the liquid of volume \(V1 = (V2′ – Vx).V_1=\frac{V_2^{\prime}-V_1}{\left(t_2-t_1\right)}\)

∴ For a unit rise in temperature, the apparent expansion per unit volume = \(\frac{V_2^{\prime}-V_1}{V_1\left(t_2-t_1\right)}\)

By definition, \(\gamma^{\prime} =\frac{V_2^{\prime}-V_1}{V_1\left(t_2-t_1\right)}\)

= \(\frac{\text { apparent expansion }}{\text { initial volume } \times \text { rise in temperature }}\) ….(1)

From (1), we get, \(V_2^{\prime}=V_1\left\{1+\gamma^{\prime}\left(t_2-t_1\right)\right\}\)…(2)

It is important to note that, the coefficient of apparent expansion of a liquid is not an intrinsic property of the liquid. It depends on the material of the container. Hence, a liquid may have different values of γ’ when heated in containers of different materials.

Coefficient of real expansion of a liquid Definition: The actual or real increase of unit volume of a liquid for a temperature rise of 1° is called the coefficient of real expansion (γ) of the liquid.

Expression for γ: Let the volume of a fixed amount of a liquid at a temperature t₁ be V₁, and at a temperature t₂ be V₂.

Hence, volume increases by (V₂-V₁) for a rise (t₂ – t₁) in temperature.

∴ By definition, \(\gamma=\frac{V_2-V_1}{V_1\left(t_2-t_1\right)}\)

= \(\frac{\text { real expansion }}{\text { initial volume } \times \text { rise in temperature }}\)…(3)

∴ \(V_2 =V_1\left\{1+\gamma\left(t_2-t_1\right)\right\}\) …(4)

The coefficient of real expansion is an intrinsic property of the liquid and does not depend on the material of the container.

1. It is clear from equations (1) and (3) that the values of γ and γ’ are independent of the unit of volume but depend on scale of temperature used.

• For example, the coefficient of real expansion of mercury in the Celsius and the Fahrenheit scales are 18.18 x 10^{-5 °}C^-1 and 10.1 x 10^{-5 °}F^-1 respectively.
• The coefficient of volume expansion of a liquid is the same in the Celsius and the Kelvin scales but in the Fahrenheit scale it is 5/9 times that in Celsius and Kelvin scales.

2. It is assumed during the derivations of (2) and (4) that the value of the coefficient of expansion of a liquid is the same for all ranges of temperature. Precise observations show that the value changes, though the changes are very small.

Hence, the values deduced above are the average values of γ and γ’ for the temperature range between t₁ and t₂. However, in practice, the values of γ and γ’ of a liquid are taken as constants for all temperature ranges.

3. While defining γ or γ’, initial volume at any temperature is taken. But for finer measurements, volume at 0°C should be taken as the initial volume In practice, the difference is ignored.

Values of the coefficient of real expansion of a few liquids are shown in the following table.

Relation between the Coefficients of Apparent and Real Expansions of Liquids

Let the volume of certain mass of a liquid in a container at a temperature t₁ = V₁. At a temperature t₂, the apparent volume of that liquid = V’₂ and its real volume = V₂.

The part of the container, that contained the liquid at t₁, has a volume V at t₂.

∴ Apparent expansion of the liquid = V₂‘ – V₁ and real expansion = V₂ – V₁.

Expansion of the part of the container containing the liquid at t₁ = V- V₁

Since for a liquid, real expansion = apparent expansion + expansion of container, \(V_2-V_1=\left(V_2^{\prime}-V_1\right)+\left(V-V_1\right)\)

Dividing both sides by V₁ t (where t = t₂ – t₁)

⇒ \(\frac{V_2-V_1}{V_1 t}=\frac{V_2^{\prime}-V_1}{V_1 t}+\frac{V-V_1}{V_1 t}\)

or, γ = γ’ + γ_g[γ_g = coefficient of volume expansion of the material of the container]

Hence, the coefficient of real expansion of a liquid = the coefficient of apparent expansion of the liquid + the coefficient of volume expansion of the material of the container.

Relation between Density and Coefficient of Real Expansion of Liquids: The volume of a liquid increases with the increase in temperature. Thus the density decreases. Water between 0°C and 4°C is an exception, and that will be discussed later. Let the mass of some liquid be m, the volume of that liquid be V₁ and the density be ρ₁, at temperature t₁.

At temperature t₁, its volume becomes V₁ and density ρ₂. Consider t₂> t₁.

Hence, \(m_1=V_1 \rho_1=V_2 \rho_2 \quad \text { or, } \frac{\rho_1}{\rho_2}=\frac{V_2}{V_1}\)…(1)

If the coefficient of real expansion of the liquid is γ, then

⇒ \(V_2 =V_1\left\{1+\gamma\left(t_2-t_1\right)\right\}\)

or, \(\frac{V_2}{V_1}=1+\gamma\left(t_2-t_1\right)\)…..(2)

From equations (1) and (2) we get,

⇒ \(\frac{\rho_1}{\rho_2}=\left\{1+\gamma^{\prime}\left(t_2-t_1\right)\right\}\)

or, \(\rho_1=\rho_2\left[1+\left(t_2-t_1\right)\right]\)….(3)

\(\rho_2 =\frac{\rho_1}{1+\gamma\left(t_2-t_1\right)}=\rho_1\left\{1+\gamma\left(t_2-t_1\right)\right\}^{-1}\)

= \(\rho_1\left[1-\gamma\left(t_2-t_1\right)\right]\)

neglecting higher powers of γ, as it is very small.

Hence, the density of a liquid decreases with the increase in temperature.

Equations (3) and (4) both give the relation between the coefficient of real expansion and the density of the liquid.

Equation (4) can be written as \(\gamma=\frac{\rho_1-\rho_2}{\rho_1\left(t_2-t_1\right)}\)

Thus if the densities of a liquid at two different temperatures are known, its coefficient of real expansion can be found out.

 

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Apparent Loss In Weight Of A Solid Immersed In A Liquid At Different Temperatures

There is an apparent loss in the weight of a solid when it is immersed in a liquid. This loss in weight is due to the upthrust it receives in a liquid. This upthrust depends directly on the density of the liquid as well as the volume of the immersed portion of the body.

With the change in temperature, density of the liquid and volume of the solid, both change. Hence, the apparent weight of a solid will be different at different temperatures.

Let the weight of a solid in air = W.

Weight of the solid completely immersed in a liquid at temperature t₁ = W₁ and that at temperature t₂ = W₂.

Hence, the apparent loss in weight at temperature t₁ = W- W₁ = M₁g, and that at t₂ = W- W₂ = M₂g,

where M₁ and M₂ are the masses of the liquid displaced by the body.

If V₁ and ρ₁ are the volume and density at t₁, and V₂ and ρ₂ are those at t₂ respectively, then, \(M_1=V_1 \rho_1 \text { and } M_2=V_2 \rho_2\)

If the coefficient of real expansion of the liquid is γ and the coefficient of volume expansion of the material of the solid is γ_s, then,

⇒ \(\rho_1=\rho_2\left[1+\gamma\left(t_2-t_1\right)\right]\)

= \(\rho_2[1+\gamma t]\left[\text { Let } t_2-t_1=t\right]\)

and \(V_2=V_1\left(1+\gamma_s t\right)\)

∴ \(M_2 =V_2 \rho_2=\frac{\rho_1 V_1\left(1+\gamma_s t\right)}{1+\gamma t}\)

= \(\rho_1 V_1\left(1+\gamma_s t\right)(1+\gamma t)^{-1}\)

= \(\rho_1 V_1\left(1+\gamma_s t\right)(1-\gamma t)\)

[neglecting the higher powers of γ]

= \(M_1\left[1-\left(\gamma-\gamma_s\right) t\right]\) neglecting the term \(\gamma \gamma_s t^2\)

Usually \(\gamma \gg \gamma_s and t=t_2-t_1>0\),

∴ \(M_1>M_2 \text { or, } M_1 g>M_2 g \text { i.e., } W_1<W_2 \text {. }\)

Hence, the apparent weight of a body immersed in a liquid increases with the increase in temperature of the liquid.

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Apparent Loss In Weight Of A Solid Immersed In A Liquid At Different Temperatures Numerical Examples

Example 1. A piece of metal weighs 50 g x g in air. It weighs45 g x g when immersed in a liquid at 25°C, and 45.1 g x g at 100°C. If the coefficient of linear expansion of the metal is 12 x 10^-6 °C^-1, find the coefficient of real expansion of the liquid.
Solution:

Apparent loss in weight at 25°C = M₁g = (50 – 45) gxg = 5gxg Apparent loss in weight at 100°C

= \(M_1 g=(50-45) g \times g=5 g \times g\)

Apparent loss in weight at \(100^{\circ} \mathrm{C}\)

= \(M_2 g=(50-45.1) g \times g=4.9 \mathrm{~g} \times \mathrm{g}\)

As \(M_2=M_1\left[1-\left(\gamma-\gamma_s\right)\left(t_2-t_1\right)\right]\)

∴ 4.9 = \(5\left[1-\left(\gamma-12 \times 10^{-6} \times 3\right)(100-25)\right]\)

or, 4.9 = \(5\left[1-\left(\gamma-12 \times 10^{-6} \times 3\right) \times 75\right]\left[\right. as \left.\gamma_s=3 \times \alpha_s\right]\)

or, \(\left(\gamma-36 \times 10^{-6}\right) \times 75 \times 5=5-4.9\)

or, \(\gamma-36 \times 10^{-6}=\frac{0.1}{75 \times 5}\)

or, \(\gamma=36 \times 10^{-6}+2.67 \times 10^{-4}=3.03 \times 10^{-4}{ }^{\circ} \mathrm{C}^{-1}\).

Example 2. A glass rod weighs 90g x g In air. It weighs 49.6 g x g when immersed In n liquid at 12°C, and 51.9 g x g at 97°C. Wnd the real expansion coefficient of the liquid. Volume expansion coefficient of glass = 2.4 x 10^-5 °C^-1
Solution:

let the volume of the glass rod be V₁, at 12°C, and density of the liquid be ρ₁.

The mass of the displaced liquid at that temperature = 90-49.6 =40.4 g

∴ Volume of the glass rod at that temperature, \(V_1=\frac{40.4}{\rho_1}\)……(1)

Again at 97°C, mass of the displaced liquid = 90-51.9 = 38.1 g

Let at 97°C the volume of the glass rod be V₂, and density of the liquid be ρ₂.

∴ \(V_2=\frac{38.1}{\rho_2}\) ….(2)

From (1) and (2), \(\frac{V_2}{V_1}=\frac{\rho_1}{\rho_2} \times \frac{38.1}{40.4}\)….(3)

Now for the glass rod, V₂ = V₁ [1 + 2.4 x 10^-5 x 85]

∴ \(\frac{V_2}{V_1}=1+2.4 \times 10^{-5} \times 85=1.00204\)

In case of liquid, \(\rho_1=\rho_2[1+\gamma \times 85]\)

∴ \(\frac{\rho_1}{\rho_2}=1+\gamma \times 85\)

From equation (3), \(1.00204=(1+\gamma \times 85) \times \frac{38.1}{40.4}\)

or, \(1+85 \gamma=\frac{1.00204 \times 40.4}{38.1}\)

or, \(85 \gamma=\frac{1.00204 \times 40.4}{38.1}-1=\frac{2.382}{38.1}\)

or, \(\gamma=7.35 \times 10^{-4 \circ} \mathrm{C}^{-1} .\)

Example 3. Apparent weights of a solid in a liquid are 50 g x g and 52 g x g at 25°C and 75°C respectively. If the coefficient of linear expansion of the solid Is ag α_s = 6.6 x 10^-6 °C^-1, and γ for the liquid Is 7.3 x 10^-4 °C^-1, what Is the real weight of the solid In air?
Solution:

Let the real weight of the solid in air = M g x g.

Apparent loss in weight at \(225^{\circ} \mathrm{C}:-M_1 g=(M-50) g \times g\)

and apparent loss in weight at \(75^{\circ} \mathrm{C}=M_2 g \circ(M-52) \mathrm{g} \times g\)

∴ \(M_2=M_1\left|1-\left(\gamma-\gamma_s\right) \times t\right|\)

⇒ \((M-52)=(M-50) \mid 1-\left(7.3 \times 10^{-4}\right.\) \(-19.8 \times\left(0^{-6}\right) \times 501\)

= \((M-50)\left\{1-7.102 \times 10^{-4} \times 50\right\}\)

= \((M-50) \times 0.96449\)

M = 0.96449 M-48.2245+52

or, 0.03551 M=3.7755

M = \(\frac{3.7755}{0.03551}=106.32 \mathrm{~g}\)

∴ Real weigth of the solid is 106.32 g x g

Example 4. A sphere of mass 266.5 g and of diameter 7 cm floats on a liquid. When the liquid Is heated to 35°C the sphere sturts sinking In the liquid. If the density of the liquid at 0°C Is 1.527 g • cm^-3, find the coefficient of volume expansion. Neglect the expansion of the sphere.
Solution:

Volume of the sphere = \(\frac{4}{3} \pi\left(\frac{7}{2}\right)^3 \mathrm{~cm}^3\)

∴ Volume of displaced liquid at 35°C = \(\frac{4}{3} \pi\left(\frac{7}{2}\right)^3 \mathrm{~cm}^3\)

If the density of the liquid at 35°C is ρ₃₅, then the mass of the displaced liquid at 35°C = \(\frac{4}{3} \pi\left(\frac{7}{2}\right)^3 \times \rho_{35} g .\)

From the condition of floatation, \(\frac{4}{3} \pi\left(\frac{7}{2}\right)^3 \times \rho_{35}=266.5\)…(1)

Now, \(\rho_{35}=\frac{\rho_0}{1+\gamma \times 35}\)

= \(\frac{1.527}{1+\gamma \times 35}\)

From equations (1) and (2), we get, \(\frac{1.527}{1+\gamma \times 35}=\frac{266.5}{\frac{4}{3} \pi\left(\frac{7}{2}\right)^3}\)

or, \(1+35 \gamma=\frac{4 \times 22 \times(7)^3 \times 1.527}{3 \times 7 \times(2)^3 \times 266.5}\)

or, \(35 \gamma=1.029-1\)

or, \(\gamma=\frac{0.029}{35}=8.28 \times 10^{-4}{ }^{\circ} \mathrm{C}^{-1}\).

Example 5. A piece of metal weighs 46 g x g in air. It weighs 30 g x g in a liquid of specific gravity 1.24 at 27°C. At 42°C, when the specific gravity of the liquid is 1.20, the weight of the piece immersed in it is 30.5 g x g. Find the coefficient of linear expansion (α) of the metal.
Solution:

Mass of the displaced liquid at 27°C = 46-30 = 16 g

Volume of the displaced liquid at 27°C, \(V_{27}=\frac{16}{1.24} \mathrm{~cm}^3\)

Similarly volume of the displaced liquid at 42 °C, \(V_{42}=\frac{46-30.5}{1.20}=\frac{15.5}{1.20} \mathrm{~cm}^3\)

So the volume of the piece at 27 °C and 42° C are \(\frac{16}{1.24} \mathrm{~cm}^3\) and \(\frac{15.5}{1.20} \mathrm{~cm}^3\) respectively.

Now, \(V_{42}=V_{27}\{1+\gamma(42-27)\}\)

[where γ = coefficient of volume expansion of the metal]

or, \(\frac{15.5}{1.20}=\frac{16}{1.24}\{1+\gamma \times 15\} or, 1+15 \gamma=\frac{15.5 \times 1.24}{1.20 \times 16}\)

or, \(15 \gamma=1.001-1\)

or, \(\gamma=\frac{0.001}{15}=3 \alpha\)

∴ Coefficient of linear expansion of the metal \(\alpha=\frac{\gamma}{3}=\frac{0.001}{45}=2.2 \times 10^{-5 \circ} \mathrm{C}^{-1}\)

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Anomalous Expansion Of Water

When a liquid is heated, its volume increases and density decreases with rise in temperature. Exceptions are observed in case of water for a certain range of temperatures.

• When heated from 0°C to 4°C, the volume of water decreases and the density increases. Above 4°C, the volume of water increases again with the increase in temperature.
• Hence, water has a maximum density and a minimum volume at 4°C. Also, on cooling from 4°C to 0°C, the volume of water increases instead of decreasing. This exceptional behaviour of water in respect of expansion within the range of 0°C to 4°C, is called anomalous expansion of water.
• The two graphs below represent the change In volume and density of 1 g of water, with the Increase in temperature.

Conclusions from the two graphs are:

1. Volume of water decreases as its temperature rises from 0°C to 4°C. Hence, expansion of water is anomalous and does not follow the general rule. Consequently, the coefficient of volume expansion of water is negative for this temperature range.
2. Water has the least volume and the maximum density at 4°C.
3. After 4°C, expansion of water takes place following the general rule. This means that, with the increase in tem-perature, the volume also starts increasing. The expan¬sion is no longer anomalous.
4. The slope of the curves for volume or for density, at temperature close to 4°C is almost zero. So, there is practically no change in volume or density for a small variation of temperature at and around 4°C. Hence, the density of water at 4°C is taken as unity.

Effect of Anomalous Expansion of Water on Marine Life: Due to anomalous expansion of water, fishes and various living creatures can survive under frozen lakes, rivers or seas.

• In cold countries, with the fall in atmospheric temperature, upper surface of lakes, seas and various ponds gradully, cool. Water of the upper surface, then being denser and heavier, moves down.
• Water below it, being comparatively warmer and lighter, moves up. This convection process in water continues until the density of the water in the lower part becomes maximum i.e., the temperature of the lower water reaches 4°C.
• As the temperature of the upper surface decreases further below 4°C, density begins to decrease. So water cannot move down further. It then begins to cool further and at last turns into ice. As ice is lighter than water, a thick layer of ice, thus formed, floats over the surface of water.

Both ice and water are bad conductors of heat. So, a negligible amount of heat can be conducted from the lower levels of water to the atmosphere outside. So, the entire vol¬ume of water (top to bottom) in a pond cannot freeze.

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Anomalous Expansion Of Water Numerical Examples

Example 1. The area of the cross-section of the capillary tube of a mercury thermometer is A₀ and the volume of the bulb filled with mercury is V₀ at 0°C. Find the length of the mercury column in the capillary tube as the bulb is heated to t°C. The coefficient of linear expansion of glass is α and coefficient of volume expansion of mercury is β.
Solution:

Let V_g and V_m be the volumes of the bulb and mercury at t°C.

∴ \(V_g=V_0\left(1+\gamma_g t\right)=V_0(1+3 \alpha t)\)

and \(V_m=V_0(1+\beta t)\)

Hence, volume of mercury entering the tube is \(V_m-V_g=V_0(1+\beta t)-V_0(1+3 \alpha t)=V_0 t(\beta-3 \alpha)\)

If the area of the cross-section of the capillary tube at t°C is A_t then A_t = A₀(1+2αt).

If the length of the mercury column in the tube is l, then \(A_t \times l=V_0 t(\beta-3 \alpha)\)

∴ l = \(\frac{V_0 t(\beta-3 \alpha)}{A_0(1+2 \alpha t)}\)….(1)

= \(\frac{V_0 t(\beta-3 \alpha)(1+2 \alpha t)^{-1}}{A_0}=\frac{V_0}{A_0} t(\beta-3 \alpha)(1-2 \alpha t)\)

= \(\frac{V_0}{A_0}(\beta-3 \alpha) t\)…..(2)

[neglecting αβ and α² as they are very small]

Both the equations (1) and (2), indicate the length of mercury column in the capillary tube at t °C.

Example 2. A 1L flask contains some mercury. It is observed that the volume of air in the flask remains unchanged at all temperatures. What is the volume of mercury in the flask? The coefficient of linear expression of the material of the flask = 9 x 10^-6 °C^-1 and coefficient of real expansion of mercury = 1.8 x 10^-4 °C^-1
Solution:

Due to expansion of the scale, the actual barometric reading will be greater than the apparent reading. Let the real reading be h and the apparent reading be H.

∴ h = \(H(1+\alpha t)=75.34\left(1+18 \times 10^{-6} \times 5\right)\)

= \(75.34\left(1+9 \times 10^{-5}\right)\)

h = \(75.34 \times 1.00009 \mathrm{~cm}\)

Again, mercury expands with increase in temperature. Hence, the barometric reading at 0°C will be less than that at 20°C. Let at 0°C, the barometric reading be H₀.

∴ \(H_0=h(1-\gamma t)=75.34 \times 1.00009\left[1-18 \times 10^{-5} \times 25\right]\)

= 75.34 x 1.00009[1 -0.0045]

= 75.34 x 1.00009 x 0.9955 = 75.01 cm.

Example 4. Coefficients of volume expansion of benzene and wood are 1.2×10^-3 °C^-1 and 1.5 x 10^-4 °C^-1 respectively. Their respective densities at 0°C are 900 kg · m^-3 and 880 kg · m^-3. Find the temperature at which wood will just immerse in benzene.
Solution:

The wood will just immerse in benzene at a temperature for which the densities are equal. Let the required temperature be t°C, when the density of both is ρ.

∴ 900 = \(\rho\left[1+1.2 \times 10^{-3} \times t\right]\)

and \(880=\rho\left[1+1.5 \times 10^{-4} \times t\right]\)

Dividing (1) by (2) we get, \(\frac{900}{880}=\frac{1+1.2 \times 10^{-3} t}{1+1.5 \times 10^{-4} t}\)

or, \(t\left(900 \times 1.5 \times 10^{-4}-880 \times 1.2 \times 10^{-3}\right)=880-900 or, \quad t=21.7^{\circ} \mathrm{C}\).

Example 5. A metal piece of density 8g · m^-3 is suspended from a wooden hook by a weightless string. The tension in the string is 56 g x g. What will be the tension in the string, if the system is Immersed in a liquid at 40°C? The surrounding temperature during the experiment is 20°C. At 20°C the specific gravity of the liquid is 1.24. The coefficients of volume expansion of the liquid and the metal are 4 x 10^-5 °C^-1 and 8 x 10^-4 °C^-1 respectively.
Solution:

Volume of the metal piece at 20°C, \(V_{20}=\frac{56}{8}=7 \mathrm{~cm}^3\)

∴ Volume at 40°C, \(V_{40}=V_{20}\left[1+8 \times 10^{-4} \times 20\right]\)

= \(7\left(1+8 \times 10^{-4} \times 20\right) \mathrm{cm}^3\)

Volume of the displaced liquid = V₄₀

∴ Mass of displaced liquid = V₄₀ x ρ₄₀

[ρ₄₀ = density of the liquid at 40°C]

i.e, weight of the displaced liquid = V₄₀ x ρ₄₀ x g

∴ Upthrust = \(V_{40} \times \rho_{40} \times g\)

= \(7\left[1+8 \times 10^{-4} \times 20\right] \times \frac{1.24}{1+20 \times 4 \times 10^{-5}} \times 980\)

= \(7 \times 1.24[1+0.016]\left[1+8 \times 10^{-4}\right]^{-1} \times 980 \)

= \(7 \times 1.24 \times 1.016[1-0.0008] \times 980\)

= \(7 \times 1.24 \times 1.016 \times 0.9992 \times 980=8.81 \times 980 \mathrm{dyn}\)

∴ Tension in the string = \((56-8.81) \times 980=4.625 \times 10^4 \mathrm{dyn} .\)

Example 6. A body, at 4°C, floats with 0.98 part of its volume immersed in water. At what temperature the body will just be immersed in water? Coefficient of real expansion of water = 3.3 x 10^-4 ° C^-1. Neglect expansion of the solid body.
Solution:

Let the required temperature be t°C, and the volume of the body = V.

Let the densities of water at 4°C and t°C be d₁ and d₂ respectively.

∴ From the condition of floatation, Vx 0.98 x d₁ = Vxd₂

∴ \(\frac{d_1}{d_2}=\frac{1}{0.98}=\frac{50}{49}\)

As \(d_1=d_2\left\{1+3.3 \times 10^{-4}(t-4)\right\},\)

∴ \(\frac{d_2}{d_2}\left\{1+3.3 \times 10^{-4}(t-4)\right\}=\frac{50}{49}\)

∴ \(3.3 \times 10^{-4} \times(t-4)=\frac{50}{49}-1=\frac{1}{49}\)

∴ t = \(\frac{1}{49 \times 3.3 \times 10^{-4}}+4=61.84+4=65.84^{\circ} \mathrm{C} .\)

Example 7. A solid at 0°C floats with 98% of its volume immersed in a liquid. The solid floats completely immersed when the temperature is raised to 25°C. If the coefficient of volume expansion of the solid is 2.6 x 10^-6 °C^-1, find the coefficient of real expansion of the liquid.
Solution:

Let at 0°C, volume of the solid = V₀, density of the liquid = ρ₀; at 25°C, volume of the solid = V’ and density of the liquid = ρ’

Now, \(V^{\prime}=V_0\left[1+2.6 \times 10^{-6} \times 25\right]\)

and \(\rho_0=\rho^{\prime}[1+\gamma \times 25]\)

where γ = coefficient of real expansion of’tlre liquid.

From the condition of floatation, \(V_0 \times 0.98 \times \rho_0=V^{\prime} \rho^{\prime}\)

or, \(V_0 \times 0.98 \times \rho^{\prime}[1+\gamma \times 25]\)

= \(V_0\left[1+2.6 \times 10^{-6} \times 25\right] \times \rho^{\prime}\)

or, \(1+25 \gamma=\frac{1+0.000065}{0.98} \quad \text { or, } 25 \gamma=1.02047-1\)

∴ \(\gamma=8.19 \times 10^{-4 \circ \mathrm{C}^{-1} .}\)

Example 8. A mercury thermometer contains 0.4 cm³ of mercury at 0°C. The diameter of the capillary tube of the thermometer is 0.2 mm. What should be the length of the scale to measure temperatures between 0°C to 100°C? The coefficient of apparent expansion of mercury = 1.7 x 10^{-4 °}C^-1.
Solution:

The apparent expansion of mercury due to increase in temperature from 0°C to 100°C = 0.4 x 1.7 x 10^-4 x 100 = 0.0068 cm³

The cross-section of the capillary tube = π(0.01)² cm²

∴ The length of the temperature measuring scale = \(\frac{0.0068}{\pi(0.01)^2}=21.6 \mathrm{~cm}\)

Example 9. A and B are two thermometers made of glass and both contain the same liquid. Both thermometers have spherical bulbs. The internal diameter of the bulb of A is 7.5 mm and radius of the capillary tube is 1.25 mm. The corresponding values for B are 6.2 mm and 0.9 mm. Find the ratio of the lengths between two consecutive graduations in thermometers A and B.
Solution:

Let the separations between two consecutive graduations for 1° in thermometers A and B be x cm and y cm respectively.

Hence, for the thermometer A, volume expansion of liquid in the bulb due to an increase of 1°C in temperature = vol¬ume of x cm length in the tube,

⇒ \(\frac{4}{3} \pi\left(\frac{0.75}{2}\right)^3 \times \gamma^{\prime} \times 1=x \times \pi(0.125)^2\)…..(1)

where γ’ is the coefficient of apparent expansion of the liquid.

Similarly for the thermometer B, \(\frac{4}{3} \pi\left(\frac{0.62}{2}\right)^3 \times \gamma^{\prime} \times 1=y \times \pi \times(0.09)^2\)….(2)

Dividing equation (1) by (2) we get,

⇒ \(\frac{x \times \pi \times(0.125)^2}{y \times \pi \times(0.09)^2}=\frac{\frac{4}{3} \pi\left(\frac{0.75}{2}\right)^3 \times \gamma^{\prime} \times 1}{\frac{4}{3} \pi\left(\frac{0.62}{2}\right)^3 \times \gamma^{\prime} \times 1}\)

or, \(\frac{x}{y}=\frac{(0.75)^3 \times(0.09)^2}{(0.62)^3 \times(0.125)^2}=0.92 \text { (approx.). }\)

Example 10. A container is filled up to the brim with 500 g of water and 1000 g of mercury. When 21200 cal of heat is supplied to the system, 3.52 g of water flows out of the container. Neglecting the expansion of the container, find the coefficient of real expansion of mercury. Given, the volume expansion coefficient of water =1.5x 10^{-4 °}C^-1, density of mercury ss 13.6 g · cm^-3, density of water 1 g · cm^-3 and speciflc heat capacity of mercury = 0.03 cal · g^-1 · °C^-1. 
Solution:

Due to the application of heat, 3.52 g i.e., 3.52 cm³ of water flows out of the container.

∴ The total expansion of mercury and water = 3.52 cm³.

Let the rise in temperature = t°C.

Heat absorbed by mercury + heat absorbed by water = 21200

∴ 500 x 1 x t + 1000 x 0.03 x t= 21200 or, t = 40°C

Expansion of water = 500 x 1.5 x 10^-4 x 40 =3 cm³

∴ Expansion of mercury = (3.52-3) = 0.52 cm3 1000

∴ \(\frac{1000}{13.6} \times \gamma \times 40=0.52\)

[γ = volume expansion coefficient of mercury] 7

∴ γ= 1.768 x 10^-4 C^-1.

Example 11. A glass bulb is filled in at 0°C by 350 g of mercury. When a few steel balls are put in the bulb, it can then hold only 265 g of mercury. When the bulb is heated to 100°C, with the steel balls in mercury, 5 g of mercury flows out. Find the coefficient of linear expansion of steel. Given, the coefficient of real expansion of mercury = 18 x 10^{-5 °}C^-1. Neglect expansion of glass.
Solution:

Let ρ₀ and ρ₁₀₀ be the densities of mercury at 0°C and 100°C respectively.

∴ Volume of mercury in the glass bulb at 0°C = \(\frac{350}{\rho_0}\)

Volume of mercury in the glass bulb after the steel balls are put = \(\frac{265}{\rho_0}\)

∴ Volume occupied by the steel balls at 0°C = \(\frac{350}{\rho_0}-\frac{265}{\rho_0}=\frac{85}{\rho_0}\)

Expansion of mercury at 100°C = \(\frac{265}{\rho_0} \times 18 \times 10^{-5} \times 100=\frac{4.77}{\rho_0}\)

Expansion of the steel balls at 100°C = \(\frac{85}{\rho_0} \times \gamma_s \times 100=\frac{8500 \gamma_s}{\rho_0}\)

[γ_s = coefficient of volume expansion of steel]

Now, expansion of mercury + expansion of the steel balls = volume of mercury expelled

i.e., \(\frac{4.77}{\rho_0}+\frac{8500 \gamma_s}{\rho_0}=\frac{.5}{\rho_{100}}\)

or, \(4.77+8500 \gamma_s=\frac{5 \rho_0}{\rho_{100}}=\frac{5 \rho_{100}\left(1+18 \times 10^{-5} \times 100\right)}{\rho_{100}}\)

= \(5 \times 1.018\)

⇒ \(\left[because \rho_0=\rho_{100}\left(1+18 \times 10^{-5} \times 100\right)\right]\)

or, \(8500 \gamma_s=0.32\) or, \(\gamma_s=\frac{0.32}{8500}=37.65 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\).

∴ Coefficient of linear expansion, \(\alpha_s=\frac{\gamma_s}{3}=\frac{37.65}{3} \times 10^{-6}=12.55 \times 10^{-6{ }^{\circ}} \mathrm{C}^{-1}\)

Example 12. Between two similar thermometers, one is filled with mercury and another with alcohol of the same volume at 0°C. The gap for each degree in the mercury thermometer is l and that in the alcohol thermometer is l’. Show that \(\frac{l}{l^{\prime}}=\frac{\gamma-3 \alpha}{\gamma_1-3 \alpha}\)
coefficient of real expansion of mercury, γ₁ = coefficient of real expansion of alcohol and a = coefficient of linear expansion of glass.
Solution:

In both thermometers, let the area of the cross-section of the tube be A and the volume of the bulb be V.

For 1° rise in temperature in mercury thermometer, apparent expansion of mercury = volume of length l of the tube

i.e., \(V(\gamma-3 \alpha) \times 1=l \times A \quad\left[because \gamma^{\prime}=\gamma-\gamma_g\right]\)….(1)

Similarly, for 1° rise in temperature in alcohol thermometer,

∴ \(V\left(\gamma_1-3 \alpha\right) \times 1=l^{\prime} \times A\)….(2)

Dividing (1) by (2) we get,

⇒ \(\frac{l \times A}{l^{\prime} \times A}=\frac{V(\gamma-3 \alpha)}{V\left(\gamma_1-3 \alpha\right)} \text { or, } \frac{l}{l^{\prime}}=\frac{\gamma-3 \alpha}{\gamma_1-3 \alpha}\)

Example 13. A cylindrical container contains some liquid. The coefficient of linear expansion of the material of the container is a. When the container is heated it is observed that the liquid level inside the container remains unchanged. What is the volume expansion coefficient of the liquid?
Solution:

Let height of the liquid level inside the container be x and area of the cross-section be A.

Now, the level of liquid surface inside the container will remain unchanged when volume expansion of the container due to an increase in temperature t = volume expansion of the liquid due to increase in temperature t.

∴ xA x 3α x t = xA x γ x t [y = volume expansion coefficient of the liquid]

∴ γ = 3α

Example 14. A body weighs W₀ in air. Its apparent weights in a liquid at t₁ °C and t₂ °C are W₁ and W₂ respectively. If the coefficient of volume expansion of the material of the body is γ, find the coefficient of real expansion of the liquid.
Solution:

Weight of displaced liquid at t₁ °C = W₀-W₁

Let V₁ and V₂ be the volumes of the body and d₁ and d₂ be the densities of the liquid at t₁°C and t₂°C respectively.

We have, \(W_0-W_1=V_1 d_1 g\)….(1)

and \(W_0-W_2=V_2 d_2 g\)

Dividing equation (1) by equation (2) we get,

⇒ \(\frac{W_0-W_1}{W_0-W_2}=\frac{V_1 d_1}{V_2 d_2} .\)

Now \(V_2=V_1\left[1+\gamma\left(t_2-t_1\right)\right] and d_1=d_2\left[1+\gamma_l\left(t_2-t_1\right)\right]\),

where \(\gamma_l\) is the coefficient of real expansion of the liquid.

∴ \(\frac{W_0-W_1}{W_0-W_2}=\frac{1+\gamma_l \times t}{1+\gamma \times t} [where \left.t=\left(t_2-t_1\right)\right]\)

or, \(1+\gamma_l t=\frac{W_0-W_1}{W_0-W_2} \times(1+\gamma t)=\frac{W_0-W_1}{W_0-W_2}+\frac{\gamma t\left(W_0-W_1\right)}{W_0-W_2}\)

or, \(\gamma_l t=\frac{W_2-W_1}{W_0-W_2}+\frac{\gamma t\left(W_0-W_1\right)}{W_0-W_2}\)

or, \(\left(W_0-W_1\right)(1+\gamma t)=\left(W_0-W_2\right)\left(1+\gamma_l \times t\right)\)

or, \(\gamma_l=\frac{W_2-W_1}{\left(W_0-W_2\right) t}+\frac{\gamma\left(W_0-W_1\right)}{W_0-W_2}\)

Example 15. Using two different containers A and B, the coefficients of apparent expansion of a liquid are found to be γ₁  and γ₂ respectively. If the coefficient of linear expansion of the material A is α, find that of the material B.
Solution:

We have, γ = γ’ + γ_g or, γ = γ’ + 3α

[γ’ = Coefficient of apparent expansion of the liquid, γ = coefficient of real expansion of the liquid, γ_g = coefficient of volume expansion of the material of the container.]

For container A, \(\gamma=\gamma+\gamma_g=\gamma_1+3 \alpha\)

and for container B, \(\gamma=\gamma_2+3 \alpha^{\prime}\)

[α’ = coefficient of linear expansion of the material of the container B ]

∴ \(\gamma_2+3 \alpha^{\prime}=\gamma_1+3 \alpha\)

or, \(3 \alpha^{\prime}=\gamma_1+3 \alpha-\gamma_2 \quad or, \alpha^{\prime}=\frac{1}{3}\left(\gamma_1-\gamma_2\right)+\alpha\).

Example 16. A hollow iron ball floats completely immersed in water at 10°C temperature. What will happen if the temperature of both of them is raised to 50°C?
Solution:

The iron ball will sink in water if the temperature of the ball and of water is raised to 50°C from 10°C.

Let dy be the density of water and be the volume of the iron ball at 10°C.

So, the apparent loss in weight of the ball at 10°C = V₁d₁g.

Again, if d₂ is the density of water and V₂, is the volume of the iron ball at 50°C, the apparent loss in weight of the bull at 50°C = V₂d₂g

Now, \(V_2=V_1\left[1+\gamma_i(50-10)\right]\)

[\(\gamma_i=\) coefficient of volume expansion of iron]

and \(d_2=d_1\left[1-\gamma_w(50-10)\right]\)

⇒ \(\gamma_w\). coefficient of volume expansion of water]

∴ \(V_2 d_2=V_1 d_1\left[1+40 \gamma_i\right]\left[1-40 \gamma_w\right]\)

= \(V_1 d_1\left[1-40\left(\gamma_w-\gamma_i\right)\right] \text { (approx.) }\)

Since \(\gamma_w>\gamma_i, V_2 d_2 g<V_1 d_1 g\).

Therefore, the loss in weight of the ball at 50°C temperature is less. Hence its apparent weight increases. So the ball will sink in water.

 

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Useful Relations For Solving Numerical Problems

1. If the length of a rod at temperature is t₁ is l and that at temperature t₂ is l₂ then,

coefficient of linear expansion, \(\alpha=\frac{l_2-l_1}{l_1\left(t_2-t_1\right)}\)

2. If the initial length of the rod at temperature 0 is l₀ and the, final length of the rod at temperature t is l_t, then, \(l_t=l_0(1+\alpha t)\)

3. If the values of α in Celsius and Fahrenheit scales are α_C and α_F then, \(\alpha_F=\frac{5}{9} a_C\)

If the surface area of a solid at temperature t₁, is S₁ and that at temperature t₂, is S₂, then,

coefficient of surface expansion, \(\beta=\frac{S_2-S_1}{S_1\left(t_2-t_1\right)}\)

⇒ \(\beta_F=\frac{5}{9} \beta_C\)

If the volume of a solid body at temperature t₁ is V₁ and that at temperature t₂ is V₂ then,

coefficient of volume expansion, \(\gamma=\frac{V_2-V_1}{V_1\left(t_2-t_1\right)}\)

⇒ \(\gamma_F=\frac{5}{9} \gamma_C\)

⇒ \(\alpha=\frac{\beta}{2}=\frac{\gamma}{3}\)

If the density of a solid at temperature t₁ is D₁ and that at temperature t₂ is D₂ then, \(D_2=D_1\left\{1+\gamma\left(t_2-t_1\right)\right\}^{-1} \approx D_1\left\{1-\gamma\left(t_2-t_1\right)\right\}\)

If area of the cross-section of a rod is A, rise in temperature is t, Young’s modulus for the material is Y, coefficient of linear expansion is a and the force developed inside the rod, when its length is kept unchanged, is F then,
thermal stress = \(\frac{F}{A}=Y \alpha t\)

Real expansion of a liquid = apparent expansion of the liquid + expansion of the container.

Coefficient of real expansion of a liquid = coefficient of apparent expansion of the liquid + coefficient of volume expansion of the material of the container, i.e., \(\gamma=\gamma^{\prime}+\gamma_g \)

⇒ \(\gamma=\frac{\rho_1-\rho_2}{\rho_1\left(t_2-t_1\right)}\) [where ρ₁ = density of the liquid at the temperature t₁, ρ₂ = density of the liquid at the temperature t₂]

Apparent loss in weight of a solid body immersed completely in a liquid is M₂ = M₁{1-(γ-γ_s)t}

where M₁g= apparent loss in weight of the body at the temperature t₁, M₂g = apparent loss in weight of the body at the temperature t₂,t = t₂-t₁, γ = coefficient of real expansion of the liquid and γ_s = coefficient of volume expansion of the immersed solid.

 

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Very Short Answer Type Questions

Question What is the unit of the coefficient of linear expansion of a substance?
Answer: °C^-1

Question 2. What is the relation between the coefficient of linear expansion (α) and the coefficient of volume expansion (γ) of a solid?
Answer: γ = 3α

Question 3. A bimetallic strip made up of brass and iron remains linear at 20 °C. When the temperature is decreased to 0°C, the strip bends. Which material remains on the convex side of the bent strip?
Answer: Iron

Question 4. Coefficient of linear expansion of platinum is 9 x 10^-6 °C^-1. What will be the value of this coefficient when the temperature is expressed in Fahrenheit unit?
Answer: 5 x10^-6 °F^-1

Question 5. If the coefficient of linear expansion of iron is 0. 0000067 °F^-1, then what is its value in the Celsius scale?
Answer: 0.000012°C^-1

Question 6.Due to rise in temperature, if each side of a copper cube increases by 0.1%, then find out the increase in volume of that cube.
Answer: 0.3%

Question 7.Write down the variation of density of a solid with increase in temperature.
Answer: Decreases

Question 8. Thermal expansion of invar is _______ than that of all other metals or alloys.
Answer: Less

Question 9.Between the coefficient of apparent expansion (γ’) and the coefficient of real expansion (γ) of a liquid which one is a characteristic property of the liquid?
Answer: y

Question 10. A glass vessel is filled with water up to its brim. Now what will happen if temperature is increased?
Answer: Water will overflow

Question 11. At what temperature density of water will be the maximum?
Answer: 4°C

Question 12. How does the density of a liquid change with temperature?
Answer: Density decreases

Question 13. At what temperature under standard atmospheric pressure, the density of pure water will be the maximum?
Answer: 4°C

Question 14. Real expansion of a liquid = apparent expansion of the liquid + volume expansion of the _______.
Answer: vessel

Question 15. Coefficient of real expansion of water from 0°C to 4°C is ___________.
Answer: Negative

Question 16. ‘Usually, the thermal expansion of a liquid is greater than the thermal expansion of an equal volume of a solid.’ State whether the statement is true or false.
Answer: True

Question 17. ‘Usually, the thermal expansion of a liquid is greater than
the thermal expansion of an equal volume of a gas.’ State whether the statement is true or false.
Answer: False

Question 18. What is the density of pure water at 4°C in SI?
Answer: 1000 kg • m^-3

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Assertion Reason Type Question And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, statement 2 is true.

Question 1.

Statement 1: A brass disc just fits in a hole in a steel plate. The system must be cooled to loosen the disc from the hole.

Statement 2: The coefficient of linear expansion for brass is greater than the coefficient of linear expansion for steel.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 2.

Statement 1: A beaker is completely filled with water at 4 °C. It will overflow, both when heated or cooled.

Statement 2: There is expansion of water below and above 4°C.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: The coefficient of real expansion of the liquid is independent of the nature of container.

Statement 2: ϒ_r = γ_a + γ_v where γ_v = coefficient of real expansion, γ_a = coefficient of expansion and γ_v = coefficient of apparent expansion of vessel.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 4.

Statement 1: The coefficient of apparent expansion can be negative.

Statement 2: Coefficient of real expansion of a liquid can be less than the coefficient of expansion of vessel.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 5.

Statement 1: A solid and a hollow sphere of same material when heated through the same temperature, wall expand by the same amount.

Statement 2: The change in volume is independent of the original mass but depends on original volume.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Match Column 1 With Column 2.

Question 1. A piece of metal of density ρ₁ floats on mercury of density ρ₂. The coefficients of expansion of the metal and mercury are. γ₁ and γ₂ respectively. The temperatures of both mercury and metal are increased by ΔT.

Answer: 1. C, 2. A, 3. D, 4. B

Question 2.

Answer: 1. B, 2. C, 3. A

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Comprehension Type Question And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A copper collar is to fit tightly about a steel shaft that has a diameter of 6 cm at 20 °C. The inside diameter of the copper collar at that temperature is 5.98 cm.

1. To what temperature must the copper collar be raised so that it will just slip on the steel shaft, assuming the steel shaft remains at 20 °C? (α_copper= 17 x 10^-6 K^-1)

1. 324 °C
2. 21.7 °C
3. 217 °C
4. 32.4 °C

Answer: 3. 217 °C

2. The tensile stress in the copper collar when its temperature returns to 20 °C is (Y = 11 x 10¹⁰ N • m^-2)

1. 1.34 x 10⁵ N • m^-2
2. 3.68 x 10^-12 N • m^-2
3. 3.68 x 10⁸ N • m^-2
4. 1.34 x 10^-12 N • m^-2

Answer: 3. 3.68 x 108^-12 N • m^-2

3. If the breaking stress of copper is 230 N • m^-2, at what temperature will the copper collar break as it cools?

1. 20 °C
2. 47 °C
3. 94 °C
4. 217 °C

Answer: 3. 94 °C

Unit 7 Properties Of Bulk Matter Chapter 5 Expansion Of Solid And Liquids Integer Type Question And Answers

In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.

Question 1. A composite rod is made by joining a copper rod, end to end, with a second rod of a different material but of same cross-section. At 25 °C, the composite rod is lm in length of which the length of the copper rod is 30 cm. At 125 °C the length of the composite rod increases by 1.91 mm. The coefficient of linear expansion of copper is α = 1.7 x 10^-5 °C^-1 and that of the second rod is β = n x 10^-5 °C^-1. Find the value of n
Answer: 2

Question 2. The volume of a metal sphere increases by 0.24% when its temperature is raised by 40 °C. The coefficient of linear expansion of the metal is n x 10^-5 °C^-1.Find the value of n.
Answer: 2

Question 3. The coefficient of real expansion of mercury is 18 x 10^-6 °C^-1. A thermometer has a bulb of volume 10^-6 m³ and the cross-section of the stem is 0.002 cm². Assuming the bulb to be filled with mercury at 0 °C, find the length (in cm) of the mercury column at 100 °C.
Answer: 9

Question 4. A thin copper wire of length l increases in length by 1 % when heated from 0 °C to 100 °C. If a thin copper plate of area 2lx l is heated from 0 °C to 100 °C, find the percentage increase in its area.
Answer: 2

 

 

One-Dimensional Motion

One-Dimensional Motion Introduction: Mechanics is the branch of science which deals with the motion of bodies and the effect of force on stationary or moving bodies.

The Branches Of MechanicsAre As Follows:

1. Dynamics: A branch of mechanics in which the motion of a body and the effect of force on the motion of the body are discussed.
2. Kinematics: It is restricted to the study of motion and not the causes of motion.
3. Kinetics: It incorporates the study and analysis of the motion of a body together with the causes of motion. Also, the mass of a body and the effect of force on the mass are studied here.
4. Statics: A branch of mechanics which deals with the equilibrium of a body under the action of a number of forces and studies the conditions of equilibrium.

One-Dimensional, Two-Dimensional And Three-Dimensional Motions: We will be discussing only one-dimensional motion in this chapter. The motion which is confined to a straight line is called one-dimensional motion or rectilinear motion.

• This type of motion can be explained by one-dimensional, two-dimensional or three-dimensional coordinates. The motion of a car moving in a straight line or the motion of a body under gravity are examples of one-dimensional motion.
• The motion which is confined to a plane is called two-dimensional motion or planar motion is called two- dimensional motion can only be described by two-dimensional or three-dimensional coordinates. The motion of a planet around the sun, a body revolving in a circle, a billiard ball moving over the billiard table etc. are examples of two-dimensional motion.
• The motion which is not confined to a plane is called three-dimensional motion. This type of motion can only be explained by three-dimensional coordinates, flic examples of three-dimensional motion are the spiral motion of a particle or the motion of an aeroplane

Read and Learn More: Class 11 Physics Notes

Speed And Velocity Numerical Examples

Example 1. A particle moves in a circular path of radius 7 cm. It covers

1. Half of the circle in 4 s and
2. One complete round in 10 s. In each case find the average speed and average velocity.

Solution:

The circumference of the circle = 2πr = 2 x \(\frac{22}{7}\) x 7 = 44cm

1. The distance travelled by the particle = half of the circumference = \(\frac{44}{2}\) = 22 cm and time taken = 4 s.

∴ Average speed, v = \(\frac{22}{4}\) = 5.5 cm · s^-1.

Displacement = diameter of the circle = 2 x 7 = 14 cm and time taken = 4s.

Hence average velocity, \(\vec{v}\) = \(\frac{14}{4}\) = 3.5 cm · s^-1 along AB.

2. The distance travelled by the particle = circumference of the circle = 44 cm and time taken = 10 s.

∴ Average speed = = 4.4 cm · s^-1.

Displacement in this case is 0 (as initial and final positions are the same.)

Hence, average velocity = \(\frac{\text { displacement }}{\text { time }}\)

Example 2. An aeroplane travels 2000 km to the west It then turns north and moves 2000 km more. Finally, it follows the shortest path to return to its starting point If the speed of the plane is 200 km · h^-1, find its average velocity for the total journey.
Solution:

Since initial and final positions are the same, displacement is zero.

∴ Average velocity = \(\frac{\text { displacement }}{\text { total time }}=\frac{0}{\text { total time }}=0 \text {. }\)

Example 3. Find the speed of the tip of a 3 cm long second’s hand in a clock.
Solution:

The tip of the second’s hand describes an angle of 360° in 60 seconds when it completes the total circular path once.

Hence, distance travelled = circumference of the circle = 2π x 3 = 6π cm; time = 60 s.

∴ Speed = \(=\frac{6 \pi}{60}=\frac{\pi}{10}=0.314 \mathrm{~cm} \cdot \mathrm{s}^{-1} .\)

Example 4. A train travels from station A to station B at a constant speed of 40 km · h^-1 and returns from B to A at 60 km · h^-1. Find the average speed and average velocity of the train.
Solution:

Let the distance between stations A and B be x km.

Time taken by the train to move from A to B = \(\frac{x}{40}\)h and time taken to move from B to A = \(\frac{x}{60}\)h.

Total distance travelled = 2x km.

∴ Average speed = \(\frac{2 x}{\left(\frac{x}{40}+\frac{x}{60}\right)}=\frac{2 \times 40 \times 60}{100}=48 \mathrm{~km} \cdot \mathrm{h}^{-1}\)

Initial and final positions are the same so the total displacement becomes zero and hence average velocity is zero.

Example 5. The motion of a particle, along the x-axis, follows the relation x = 8t – 3t². Here x and t are expressed in metre and second respectively. Find

1. The average velocity of the particle in time interval 0 to 1 s and
2. Its instantaneous velocity at t = 1s.

Solution:

1. Let at t = 0, x = x₁ and at t = 1, x = x₂.

∴ x₁ = 8 x 0 -3 x 0² = 0 and x₂ = 8 x 1 -3 x 1² = 5m

∴ Displacement = x₂ – x₁ =5 m and time taken is 1 s

∴ Average velocity = \(\frac{5 m}{1 s}\) = 5 m · s^-1.

2. Here instantaneous velocity,

v = \(\frac{d x}{d t}=\frac{d}{d t}\left(8 t-3 t^2\right)=8-2 \times 3 t=8-6 t\)

At t = \(1 \mathrm{~s}, \frac{d x}{d t}=8-6 \times 1=2 \mathrm{~m} \cdot \mathrm{s}^{-1}\).

Acceleration: When the velocity of a particle increases with time, the particle is said to be accelerating. So, in case of acceleration, the final velocity is greater than the initial velocity.

Acceleration Definition: The rate of change of velocity with time is called acceleration.

Thus, acceleration (a) = \(\frac{\text { change in velocity }}{\text { time }}\)

= \(\frac{\text { final velocity }- \text { initial velocity }}{\text { time }}\)

Acceleration Example: A train at rest starts from a station and speeds up. In this case, we can say that the train is moving with acceleration.

Sometimes, acceleration is represented by the symbol ‘f’.

Nature Of Acceleration: Acceleration is related to the change in velocity of a body. So, like velocity, acceleration is also a vector quantity. It has to be specified by its magnitude and direction. However, to specify the acceleration vector, we have to use vector algebra to determine the change in the velocity.

This shows that velocity and change in velocity may have different directions, in general. Thus, the direction of the acceleration may or may not be the same as that of velocity.

Units And Dimension: Unit of acceleration = \(\frac{\text { unit of velocity }}{\text { unit of time }} \text {. }\)

CGS System: cm · s^-2

SI: m · s^-2

Dimension of acceleration = \(\frac{\text { dimension of velocity }}{\text { dimension of time }}=\frac{\mathrm{LT}^{-1}}{\mathrm{~T}}=\mathrm{LT}^{-2}\)

Motion With Uniform And Non-Uniform Acceleration: Uniform acceleration corresponds to a motion in which the velocity of a body changes equally in equal intervals of time.

If a particle moves with uniform acceleration, then its acceleration remains the same, both in magnitude and direction, at each point on its path. When a body falls freely from a height under gravity, its velocity increases. But its acceleration is uniform on or near the surface of the earth and is known as the acceleration due to gravity.

Non-uniform Acceleration corresponds to a motion in which the velocity of a body does not change equally in equal intervals of time.

The motion of an oscillating pendulum is an example of motion with non-uniform acceleration. The acceleration of the bob becomes maximum at its maximum displaced position and becomes zero at its mean position.

Average Acceleration: The acceleration of a particle may not always be uniform. Generally, we can find out the average acceleration using the following relation:

(a) = \(\frac{\text { final velocity }- \text { initial velocity }}{\text { time taken }}\)

= \(\frac{\text { change in velocity }}{\text { time }}\)

Instantaneous Acceleration: The acceleration of a particle at any moment is called its instantaneous acceleration.

Instantaneous Acceleration Definition: The instantaneous acceleration of a particle at a given point is the limiting value of the rate of change in velocity with respect to time when the time interval tends to zero.

According to differential calculus, instantaneous acceleration, a = \(\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}=\frac{d v}{d t}=\frac{d}{d t}\left(\frac{d s}{d t}\right)=\frac{d^2 s}{d t^2}\)

Deceleration Or Retardation: when the velocity of a particle decreases with time, the particle is in a state of deceleration or retardation. Here, the final velocity is less than the initial velocity.

Deceleration Or Retardation Definition: The rate of decrease of velocity with time is called deceleration or retardation.

Deceleration Or Retardation Example: When a train approaches a station, it slows down and finally stops. During this period the train decelerates to come to a halt.

Deceleration is a special case of acceleration where the final velocity is less than the initial velocity. Thus, deceleration is essentially a negative acceleration. It is not a different physical quantity.

Let us consider a particle moving with a velocity of 10 cm · s^-1. It then slows down to 4 cm · s^-1 in 3 s. Its acceleration is given by,

a = \(\frac{\text { final velocity }- \text { initial velocity }}{\text { time interval }}\)

= \(\frac{4-10}{3}=-2 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

This example clearly shows that deceleration is described mathematically as negative acceleration.

Distinction Between Acceleration And Retardation

Acceleration Due To Gravity: The earth attracts other bodies towards itself because of its gravity. A body released near the earth’s surface falls freely under the action of the force due to gravity. Whenever a body is allowed to fall freely, it undergoes an acceleration directed towards the earth. This is referred to as the acceleration due to gravity and is denoted by g. Its characteristics are:

1. It is always directed towards the centre of the earth, i.e., vertically downwards.
2. Its value is the greatest on the earth’s surface. It decreases slightly as we go away from the surface in such a way that at an altitude of 3.2 km, its value decreases only by 0.1%. Thus, for practical purposes, we may consider its value to be constant and equal to its value on the earth’s surface.
3. It is independent of the characteristics of an object, such as mass, density or shape.

Bodies that move vertically downwards undergo constant acceleration, while bodies moving vertically upwards undergo constant retardation. In this discussion, we have neglected the small variations in g at different locations and the air resistance faced by freely falling bodies.

The value of g is usually taken as, g = 980 cm · s^-2 = 9.8 m · s^-2

Motion In A Straight Line

When a body moves without changing its direction, the motion is naturally along a straight line. It is also known as rectilinear motion.

Vertical fall of a body under gravity, the motion of a car on a straight road, etc. are examples of such motion. The discussions henceforth in this chapter will be restricted to rectilinear motions only.

Representation Of The Physical Quantities Of Motion: For the rectilinear motion of a particle, the straight line of motion itself may be chosen as an axis (say, the x-axis) and a point O on it as the origin. Obviously, the motion is one-dimensional.

• There is a basic difference in the representations of the scalar and the vector quantities related to rectilinear motion. The scalar quantities like distance travelled and speed have magnitudes only, and are always expressed by positive numbers. However, two directions, exactly opposite to each other, exist for the motion in a straight line.
• So a vector quantity is expressed by a positive number for one direction and by a negative number for the exactly opposite direction. The direction towards the right may be taken as positive; then the direction towards the left naturally becomes negative. As an example, we may consider the vertical motion of a particle under gravity.
• For a downward motion, we may take each of displacement, velocity and acceleration to be positive. Then, for an upward motion, displacement and velocity would be negative; but acceleration would still remain positive since the acceleration due to gravity (g) is always directed downwards.
• It is important to note that simple algebraic operations are sufficient for calculations involving any quantity, a scalar or a vector, in a rectilinear motion. It means that vector algebra is not at all necessary even for the calculations involving vector quantities of a rectilinear motion.

For motion along a straight line,

1. Distance travelled by a particle = magnitude of its displacement,
2. Speed of the particle at any point = magnitude of its velocity at that point
3. Displacement, velocity and acceleration vectors are along the same straight line.

Rectilinear Motion with Uniform Velocity: If a particle moves with a uniform velocity, its acceleration is zero. Let v be the uniform velocity of a particle and s be its displacement in time t. Therefore, according to the definition of uniform velocity, the particle moves a distance v x 1 in Is, v x 2 in2s, etc.

∴ In t s its displacement is v x t.

∴ s = vt…..(1)

i.e., displacement = uniform velocity x time .

Motion In A Straight Line Numerical Example

Example 1. A person travels half of a distance at an average velocity of 24 km · h^-1. At what average velocity should he move to cover the second half of the path so that his average velocity for the total path becomes 32 km · h^-1?
Solution:

Let the total length of the path = 2s km.

∴ Time required to cover the first half of the path = \(\frac{s}{24}\) h.

If the man travels the total path with an average velocity of 32 km · h^-1, then the total time taken by him = \(\frac{2 s}{32}\) = \(\frac{s}{16}\) h.

∴ Time required to cover the second half of the path = \(\frac{s}{16}\) – \(\frac{s}{24}\) = \(\frac{s}{48}\) h

∴ Average velocity of second half = \(\frac{\text { distance }}{\text { time }}=\frac{s}{\frac{s}{48}}=48 \mathrm{~km} \cdot \mathrm{h}^{-1}\)

Rectilinear Motion With Uniform Acceleration

Rectilinear Motion With Uniform Acceleration: For a particle in motion, let

u = initial velocity

v = final velocity after a time t and

corresponding uniform acceleration = a.

Let the displacement = s in that time.

Then the above variables obey the following equations:

1. v = u+at,
2. s= ut+1/2 at²
3. v² = u² + 2as
4. s_t = M + \(\frac{1}{2}\) a(2t – 1) [where s_t = the displacement in the t th second]

Rectilinear Motion With Uniform Acceleration Derivations:

1. v= u+at

Let the initial velocity of a particle be u and its final velocity after time t be v.

∴ In time t, change in velocity = v – u

∴ Rate of change of velocity with time = \(\frac{v – u}{t}\) = a, by definition.

Hence, at = v – u or, v = u + at….(1)

For a particle starting from rest, u = 0 and thus, v = at ….(2)

In case of retardation, the relationship becomes v = u – at …(3)

2. s = ut + \(\frac{1}{2}\) at²

If a particle with initial velocity u and uniform acceleration a, attains final velocity v after time t, the average velocity, considering the two endpoints, is \(\frac{u + v}{2}\).

The acceleration a implies that the velocity increases by an after every second. Hence, the velocity 1 s after the start of motion = u + a and 1 s before the end of motion = v – a

∴ Average velocity = \(\frac{u+a+v-a}{2}=\frac{u+v}{2}\)

Hence, the particle can be considered to have travelled a distance s with the average velocity \(\frac{(u+v)}{2}\) in time t.

Hence, displacement, s = \(\frac{u+v}{2} \times t=\frac{u+(u+a t)}{2} \times t\) (because v=u+a t)

or, \(s=\frac{2 u t}{2}+\frac{1}{2} a t^2\) or, \(s=u t+\frac{1}{2} a t^2\)…..(4)

For a particle starting from rest, u=0

So, \(s=\frac{1}{2} a t^2\)…..(5)

For a retarding particle, s = \(u t-\frac{1}{2} a t^2\)…..(6)

3. \(v^2=u^2+2 a s\)

From equation (1) we have, v=u+a t

or, \(v^2=(u+a t)^2=u^2+2 u a t+a^2 t^2\)

= \(u^2+2 a\left(u t+\frac{1}{2} a t^2\right)\)

or, \(v^2=u^2+2\) as [using equation (4)]…….(7)

Hence, for a particle starting from rest \(\nu^2=2 a s\)……(8)

and in case of retardation \(v^2=u^2-2 a s\)……(9)

4. \(s_t=u+\frac{1}{2} a(2 t-1)\)

Displacement in t seconds, s = \(u t+\frac{1}{2} a t^2\), from equation (4).

Displacement in (t-1) seconds, \(s^{\prime}=u(t-1)+\frac{1}{2} a(t-1)^2\)

Hence, the displacement in the t th second, \(s_t=s-s^{\prime}\)

or, \(s_t=u t+\frac{1}{2} a t^2-\left\{u(t-1)+\frac{1}{2}(t-1)^2 a\right\}\)

= \(u t+\frac{1}{2} a t^2-u t+u-\frac{1}{2} a t^2+\frac{1}{2} \cdot 2 t a-\frac{a}{2}\)

= \(u+a t-\frac{a}{2}=u+\frac{1}{2} a(2 t-1)\)…….(10)

For a particle starting from rest \(s_t=\frac{1}{2} a(2 t-1)\)……(11)

and in case of retardation \(s_t=u-\frac{1}{2} a(2 t-1)\)…..(12)

Rectilinear Motion With Uniform Acceleration Numerical Examples

Example 1. A velocity of 60 km · h^-1 of a train is reduced by the application of brakes. A retardation of 40 cm · s^-2 is produced. After how much time will the train stop? What will be the velocity of the train after 20 seconds?
Solution:

Given, \(u=60 \mathrm{~km} \cdot \mathrm{h}^{-1}=\frac{60 \times 1000}{60 \times 60}=\frac{50}{3} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

a = 40 cm · s^-2 = 0.4 m · s^-2 and v = 0

Hence, from the relation v = u- at, we get \(0=\frac{50}{3}-0.4 \times t \quad \text { or, } t=\frac{50}{3 \times 0.4}=41.7 \mathrm{~s}\)

∴ The train will stop after 41.7.

The velocity after 20 s, v = \(\frac{50}{3}-0.4 \times 20\)

= \(\frac{26}{3} \mathrm{~m} \cdot \mathrm{s}^{-1}=8.7 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

= \(\frac{8.7 \times 60 \times 60}{1000} \mathrm{~km} \cdot \mathrm{h}^{-1}\)

= \(31.3 \mathrm{~km} \cdot \mathrm{h}^{-1}\)

Example 2. A body covers 200 cm in the first 2 s of motion and 220 cm in the next 4 s. Calculate the velocity 7 s after the start.
Solution:

We know, s = ut + \(\frac{1}{2}\) at²

∴ Putting t = 2 s

200 = u x 2 + \(\frac{1}{2}\) a x 4 = 2u + 2a

or, u + a = 100….(1)

The displacement in (4 + 2) or 6 s = 200 + 220 = 420 cm

∴ 420 = u x 6 + \(\frac{1}{2}\) a x 36 = 6u + 18a

or, u + 3a = 70…..(2)

From equations (1) and (2) we get, a = -15 cm · s^-2 and u = 115 cm · s^-1

Velocity after 7 s of motion, v = u + at = 115 – 15 x 7 = 115 – 105 = 10cm · s^-1

Example 3. A man is 9 m behind a train at rest. The train starts with an acceleration of 2 m · s^-2 and simultaneously the man starts running. He is able to board the train somehow after 3 seconds. Find the acceleration of the man.
Solution:

While boarding the train, the positions of the man and of the train must be the same.

Let the acceleration of the man be a and the distance traversed by the train in 3 s be x.

We know, s = ut + \(\frac{1}{2}\)at².

Here u = 0 as the train as well as the man starts from rest.

So, for the train, x = \(\frac{1}{2}\) x 2 x (3)² or, x = 9 m

Thus, the distance traversed by the man in this time = 9 + 9 = 18 m

Then, s = 18 m , u = 0 and t = 3 s

∴ a = \(\frac{2 s}{t^2}\) = \(\frac{2}{3 ^2}\) x 18 = 4 m s

Example 4. A particle moves with a uniform acceleration along a straight line. It covers 41 cm and 49 cm in the 6th and the 10th seconds respectively. What will be the distance covered by the particle in 15 seconds?
Solution:

We know, distance covered in the nth second, s = u + \(\frac{1}{2}\)a(2n- 1)

According to the question, s₀ = u + \(\frac{1}{2}\)a(2 x 6-1) or, 41 = u + \(\frac{11}{2}\) a….(1)

ans s₁₀ = u + \(\frac{1}{2}\)a(2 x 10- 1) or, 49 = u + \(\frac{19}{2}\)a…..(2)

By solving equations (1) and (2) we get, u = 30 and a = 2

Now, putting t = 15 in s = ut + \(\frac{1}{2}\) at² we get,

s = 30 x 15 = \(\frac{1}{2}\) x 2 x (15)² = 450 + 225 = 675 cm

∴ The particle traverses 675 cm in 15 s.

Example 5. A train begins its journey from station A and stops at station B after 45 min. C is a certain point between A and B where the train attains its maximum velocity of 50 km · h^-1. If the train travels from A to C with a uniform acceleration and from C to B with a uniform retardation, calculate the distance between A and B.
Solution:

Let the train start from A with a uniform acceleration a₁ and reach C in time t₁. From here it travels to B in time t₂ with a uniform retardation a₂.

The maximum velocity of A the train is v at point C.

Let AC = s₁ and CB = s₂

So for the motion from A to C, v = \(a_1 t_1 \text { and } s_1=\frac{1}{2} a_1 t_1^2\)

and for the motion from C to B, \(0=v-a_2 t_2 \quad \text { or, } v=a_2 t_2\)

and \(s_2=v t_2-\frac{1}{2} a_2 t_2^2=a_2 t_2^2-\frac{1}{2} a_2 t_2^2=\frac{1}{2} a_2 t_2^2\)

So the distance between A and B,

s = \(A B=A C+C B=s_1+s_2\)

= \(\frac{1}{2} a_1 t_1^2+\frac{1}{2} a_2 t_2^2\)

= \(\frac{1}{2} v t_1+\frac{1}{2} v t_2\) (because \(v=a_1 t_1=a_2 t_2\))

= \(\frac{1}{2} v\left(t_1+t_2\right)=\frac{1}{2} \times 50 \times \frac{3}{4}\)

(\(v=50 \mathrm{~km} \cdot \mathrm{h}^{-1}, t_1+t_2=45 \mathrm{~min}=\frac{3}{4} \mathrm{~h}\))

=18.75 km

Example 6. A train moving with constant acceleration crosses an observer standing on the platform. The first and the second compartments, each 15 m long, cross the observer in 2 s and 2.5 s, respectively. Find the velocity of the train when its first compartment just crosses the observer and also find its acceleration.
Solution:

Let the velocity and the acceleration of the train as its 1st compartment just reaches the observer be u and a, respectively.

Hence, displacement in 2 s = length of the 1st compartment = 15 m

and displacement in (2 + 2.5) or, 4.5 s = total length of the two compartments = 2 x 15 = 30 m

Now from the equation s = ut + \(\frac{1}{2}\) at² we get,

∴ 15 = 2u + \(\frac{1}{2}\)a(2)²

or, u + a = \(\frac{15}{2}\)….(1)

and 30 = 4.5 u + \(\frac{1}{2}\) a(4.5)²

or, 36u + 81a = 240….(2)

Solving equations (1) and (2), we get, u = \(\frac{49}{6}\) and a = –\(\frac{2}{3}\)

The 1st compartment crosses the observer in 2 s; the velocity at that moment,

v = u + at = \(\frac{49}{6}\) x 2 = \(\frac{41}{6}\)

Therefore, the velocity and acceleration of the train as its 1st compartment just crosses the observer are \(\frac{41}{6}\) m · s^-1 and –\(\frac{2}{3}\)m · s^-2 respectively.

Example 7. A bullet with an initial velocity u penetrates a target. After penetrating a distance x, its velocity decreases by \(\frac{u}{n}\). How much farther will the bullet move through the target before it comes to rest?
Solution:

Let us assume that the retardation of the bullet inside the target is a and it is uniform.

After penetrating a distance x, the velocity, v = u – \(\frac{u}{n}\) = \(\frac{u(n-1)}{n}\)

∴ From \(v^2=u^2-2 a s\), we get, \(\frac{u^2(n-1)^2}{n^2}=u^2-2 a x\)

or, \(2 a x=u^2-\frac{u^2(n-1)^2}{n^2}\)

= \(u^2\left(1-\frac{n^2-2 n+1}{n^2}\right)=u^2 \cdot \frac{2 n-1}{n^2}\)

or,  a = \(\frac{u^2(2 n-1)}{2 x n^2}\)

Let the bullet travel an additional distance y before it comes to rest.

∴ \((0)^2=u^2-2 a(x+y) \quad \text { or, } x+y=\frac{u^2}{2 a}\)

or, \(y=\frac{u^2}{2 a}-x=\frac{u^2 \cdot 2 x n^2}{2 u^2(2 n-1)}-x=\frac{x n^2}{2 n-1}-x\)

= \(x\left(\frac{n^2-2 n+1}{2 n-1}\right)=\frac{x(n-1)^2}{2 n-1}\)

Example 8. Starting from rest, a train travels a certain distance with a uniform acceleration α. Then it travels with a uniform retardation β and finally comes to rest again. If the total time of motion is t, find

1. The maximum velocity attained and
2. The total distance travelled by the train.

Solution:

1. Let t₁ be the time taken to travel a distance s₁ with acceleration α, and t₂ be the time taken to travel a farther distance s₂ with retardation β. Let the maximum velocity attained by the train be v.

Here t = t₁ + t₂

∴ For the motion of the train with acceleration α,

v = \(\alpha t_1 \quad \text { or, } t_1=\frac{\nu}{\alpha}\)…..(1)

and \(\nu^2=2 \alpha s_1 or, s_1=\frac{\nu^2}{2 \alpha}\)…..(2)

Similarly, for the motion of the train with retardation β,

0 = \(\nu-\beta t_2\)

or, \(t_2=\frac{v}{\beta}\) and \(0^2=v^2-2 \beta s_2\) or, \(s_2=\frac{\nu^2}{2 \beta}\)

From (1) and (3) we get, \(t=t_1+t_2=v\left(\frac{1}{\alpha}+\frac{1}{\beta}\right) \quad \text { or, } \quad v=\frac{\alpha \beta t}{\alpha+\beta}\)

2. From (2) and (4), the total distance travelled,

s = \(s_1+s_2=\frac{\nu^2}{2}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right) \)

= \(\left(\frac{\alpha \beta t}{\alpha+\beta}\right)^2 \times \frac{1}{2}\left(\frac{\alpha+\beta}{\alpha \beta}\right)=\frac{\alpha \beta t^2}{2(\alpha+\beta)} .\)

Example 9. A particle travelling with uniform acceleration along a straight line has average velocities v₁, v₂ and v₃ in successive time intervals t₁, t₂ and t₃, respectively. Prove that, \(\frac{v_2-v_1}{v_3-v_2}=\frac{t_1+t_2}{t_2+t_3}\)
Solution:

Let the initial velocity of the particle be w and its acceleration be a. Also, x, y and z are the velocities after the respective time intervals t₁, t₂ and t₃.

∴ \(x=u+a t_1, y=u+a\left(t_1+t_2\right), z=u+a\left(t_1+t_2+t_3\right) \)

Again, \(v_1=\frac{u+x}{2}, v_2=\frac{x+y}{2}, v_3=\frac{y+z}{2}\)

∴ \(\frac{v_2-v_1}{v_3-v_2}=\frac{\frac{1}{2}(x+y)-\frac{1}{2}(u+x)}{\frac{1}{2}(y+z)-\frac{1}{2}(x+y)}\)

= \(\frac{y-u}{z-x}=\frac{u+a\left(t_1+t_2\right)-u}{u+a\left(t_1+t_2+t_3\right)-\left(u+a t_1\right)}\)

= \(\frac{t_1+t_2}{t_2+t_3}\)

Example 10. A bullet, moving with a velocity of 200 m • s-1 can just go through a 4 cm thick plank. What should be the velocity of a bullet for just going through a 10 cm thick identical plank?
Solution:

The retardation (a) should be the same inside both the planks. The final velocity of the bullet in both cases is zero.

Let the initial velocities of the bullet in the two cases be u₁ and u₂, respectively.

Then 0 = \(u_1^2-2 a s_1 or, u_1^2=2 a s_1\)

Similarly, \(u_2^2=2 a s_2\)

∴ \(\frac{u_1^2}{u_2^2}=\frac{s_1}{s_2}\)

or, \(u_2=u_1 \sqrt{\frac{s_2}{s_1}}=200 \times \sqrt{\frac{10}{4}}\)

= \(100 \sqrt{10}=316.2 \mathrm{~m} \cdot \mathrm{s}^{-1}\).

Example 11. The speed of a train drops from 48 km h^-1 to 24 km h^-1 after moving through a distance of 108 m with uniform retardation. How much farther would it move with the same retardation before coming to rest?
Solution:

⇒ \(v^2=u^2+2\) as; \(s=108 \mathrm{~m}=0.108 \mathrm{~km}\)

∴ \(a=\frac{v^2-u^2}{2 s}\)

= \(\frac{(24)^2-(48)^2}{2 \times 0.108}=-8000 \mathrm{~km} \cdot \mathrm{h}^{-2}\)

For the second part of the motion, u = \(24 \mathrm{~km} \cdot \mathrm{h}^{-1} \text { and } v=0\)

∴ \(s=\frac{v^2-u^2}{2 a}\)

= \(\frac{0-(24)^2}{2 \times(-8000)}=0.036 \mathrm{~km}=36 \mathrm{~m}\)

Example 12. A particle starts with a velocity u with a uniform acceleration f. In the p-th, q-th and r-th seconds, it moves through distances a, b and c respectively. Prove that, a(q- r) + b(r- p) + c(p- q) = 0.
Solution:

Distance travelled in the n-th second, \(s_n=u+\frac{1}{2} f(2 n-1)\)

∴ a = \(u+\frac{1}{2} f(2 p-1)\)

= \(u+f p-\frac{f}{2}=\left(u-\frac{f}{2}\right)+f p\)…..(1)

Similarly, b = \(\left(u-\frac{f}{2}\right)+f q\)…..(2)

and c = \(\left(u-\frac{f}{2}\right)+f r\)……(3)

Multiplying (1), (2) and (3) by (q-r),(r-p) and (p-q) respectively, and then adding, we get a(q-r)+b(r-p)+c(p-q)

= \(\left(u-\frac{f}{2}\right)[(q-r)+(r-p)+(p-q)]\) + \(f[p(q-r)+q(r-p)+r(p-q)]\)

= \(\left(u-\frac{f}{2}\right) \cdot 0+f \cdot 0=0\)

Example 13. From two stations A and B, two trains started simultaneously towards each other with velocities v₁ and v₂ respectively. After they crossed each other, the first train reached B in time t₁ and the second train reached A in time t₂. Show that v₁: v₂ = √t₂:√t₁

Solution:

Let the two trains cross each other at point O after time t.

So, AO = v₁t and BO = v₂t, i.e., \(\frac{A O}{B O}=\frac{v_1}{v_2}\)

Again, for the first train, OB = v₁t₁

and for the second train, OA = v₂t₂

∴ \(\frac{O A}{O B}=\frac{A O}{B O}=\frac{v_2 t_2}{v_1 t_1}\)

Then, \(\frac{v_1}{v_2}=\frac{v_2 t_2}{v_1 t_1} \quad or, \frac{v_1^2}{v_2^2}=\frac{t_2}{t_1} \quad or, \frac{v_1}{v_2}=\frac{\sqrt{t_2}}{\sqrt{t_1}}\)

Example 14. A train attains a velocity v after starting from rest with a uniform acceleration α. Then the train travels for some time with uniform velocity, and at last, comes to rest with a uniform retardation β. If the overall displacement is s in time t, show that \(t=\frac{s}{v}+\frac{v}{2}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)\).
Solution:

For the accelerated motion, \(\nu=0+\alpha t_1 \quad \text { or, } t_1=\frac{\nu}{\alpha}\)

and \(v^2=0+2 \alpha s_1 \quad or, s_1=\frac{v^2}{2 \alpha}\)

For the uniform motion, \(s_2=v t_2 or, t_2=\frac{s_2}{v}\)

For the retarded motion, \(0=v-\beta t_3 \quad or, t_3=\frac{\nu}{\beta}\)

and 0 = \(v^2-2 \beta s_3 \quad or, s_3=\frac{v^2}{2 \beta}\)

∴ \(s=s_1+s_2+s_3=\frac{\nu^2}{2 \alpha}+s_2+\frac{\nu^2}{2 \beta}\)

or, \(s_2=s-\frac{v^2}{2}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)\)

Then, t = \(t_1+t_2+t_3=\frac{\nu}{\alpha}+\frac{s_2}{\nu}+\frac{\nu}{\beta}=\frac{v}{\alpha}+\frac{1}{\nu}\left[s-\frac{v^2}{2}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)\right]+\frac{\nu}{\beta}\)

= \(v\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+\frac{s}{v}-\frac{\nu}{2}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)=\frac{s}{v}+\frac{\nu}{2}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)\)

Graphical Proof Of The Equations Of Motion: AB represents the velocity-time graph of a particle starting with an initial velocity u, attaining a final velocity v in time t, moving with a uniform acceleration a.

Along the time and the velocity axes, OC = t, OA = u and CB = v.

∴ a = slope of AB

= tan θ= \(\tan \theta=\frac{D B}{A D}=\frac{C B-C D}{A D}=\frac{C B-O A}{O C}=\frac{\nu-u}{t} .\)

Proof Of v = u + at: We know the equation of a straight line of slope m with an intercept c on the y-axis is y = mx + c …..(1)

Comparing the corresponding values for AB, we get, y = v, m = a, x = t and c = u.

∴ The graph AB follows the equation v = u + at….(2)

Proof Of s = ut + \(\frac{1}{2}\)at²: The area under the graph AB and the time-axis, gives the displacement of the particle in time t.

The area under AB is the area of the trapezium OABC, which is the sum of the areas of the rectangle OADC and the triangle ABD.

Hence, the displacement of the particle in time t,

s = \(O A \times O C+\frac{1}{2} A D \times D B=O A \times O C+\frac{1}{2} \times \frac{D B}{A D} \times A D^2\)

∴ \(s=u t+\frac{1}{2} a t^2\) (because A D=O C=t) ……(3)

Proof Of v² = u² + 2as: Slope of AB = a = tanθ = \(\frac{D B}{A D}\)=\(\frac{DB}{O C}\)

∴ as = slope of AB X area of the trapezium OABC

= \(\frac{B D}{O C} \times \frac{1}{2}(O A+C B) \times O C\)

= \(\frac{1}{2} B D(O A+C B)=\frac{1}{2}(C B-C D)(O A+C B)\)

∴ as = \(\frac{1}{2}(v-u)(v+u)=\frac{1}{2}\left(v^2-u^2\right)\)

∴ 2as =\(v^2-u^2\)

or, \(v^2=u^2+2 a s\)

Proof Of s_t = u + \(\frac{1}{2}\)a(2t-1): Let AP represent the velocity-time graph of a particle starting with an initial velocity u and moving with a uniform acceleration a.

Let points D and E represent the times (t – 1) and t respectively in the motion. Hence, the area of the trapezium BCED denotes the displacement s_t in the t th second.

∴ s_t = \(\frac{1}{2}\) (DB + EC) x DE

DE = OE- OD = t- (t- 1) = 1 s

DB = the velocity attained in time (t- 1) = u+ a(t- 1)

EC = velocity attained in time t = u+ at.

∴ s_t = \(\frac{1}{2}\)[{u+ a(t—1)} + (u+ at)] x 1

= u + \(\frac{1}{2}\) a(2t- 1)….(5)

Derivation Of The Equations Of Motion Using Calculus

Derivation of v = u + at: From definition, acceleration is the rate of change of velocity,

i.e., a = \(\frac{dv}{dt}\) or, dv = a dt

For motion with a uniform acceleration, a = constant.

∴ ∫dv = a∫dt

or, v = at + A [A = integration constant]……(1)

At t = 0, v = u. Then from equation (1), we get,

u = a·0 + A or, A = u

Hence, equation (1) becomes, v = u + at

Derivation of s = ut + \(\frac{1}{2}\) at²: We know the velocity of a particle is the rate of change of its displacement with time.

∴ v = \(\frac{ds}{dt}\) or, \(\frac{ds}{dt}\) = u + at

or, ds = u dt+ at dt, a and u are constants

∫ds = u∫dt+ a∫t dt

or, s = ut + \(\frac{1}{2}\) at² + A [A = integration constant]……(2)

From initial condition, at t = 0 , s = 0

∴ A = 0

∴ Equation (2) becomes, s = ut + \(\frac{1}{2}\) at²

Derivation Of v² = u² + 2as: Velocity of the particle,

v = \(\frac{ds}{dt}\) and acceleration, a = \(\frac{dv}{dt}\) \(\frac{ds}{dt}\) = v\(\frac{dv}{ds}\)

or, a ds = v dv, where a is a constant, a∫ds = ∫v dv

or, as = \(\frac{v^2}{2}\) + B [B = integration constant]…..(3)

At the start of motion, v = u and s = 0

∴ 0 = \(\frac{u^2}{dt}\) + B or, B = –\(\frac{u^2}{2}\)

Substituting this in equation (3), we get,

as = \(\frac{v^2}{2}\) – \(\frac{u^2}{2}\)

or, v² = u² + 2as…..(4)

Derivation Of The Equations Of Motion Using Calculus Numerical Examples

Example 1. s-t graph for a particle, moving with a constant acceleration, subtends 45° angle with the time axis at time t. That angle becomes 60° 1 s later. Find the acceleration of the particle.
Solution:

Let the velocity of the particle at P₁ and P₂ be u and v respectively.

∴ u = tanθ₁ and v = tanθ₂

∴ Acceleration of the particle

a = \(\frac{\nu-u}{t_2-t_1}\)

= \(\frac{\tan \theta_2-\tan \theta_1}{t_2-t_1}\)

= \(\frac{\tan 60^{\circ}-\tan 45^{\circ}}{1}\)

= \(\sqrt{3}-1=0.732 \text { unit. } \mathrm{s}^{-2} .\)

Example 2. Displacement x and time t, in a rectilinear motion of a particle, are related as t= √x+3. Here x is measured in metres and t in seconds. Find the displacement of the particle when its velocity is zero.
Solution:

Given, t = √x + 3 or, √x = t-3 or, x = (t-3)².

Velocity, v = \(\frac{dx}{dt}\) = 2(t – 3)

If velocity =0, 2(t – 3) = 0 or, t = 3 s

∴ At t = 3 s , the displacement, x = (3 -3)² = 0

Hence at zero velocity, the displacement is also zero

Example 3. A body starts from rest and moves with an acceleration proportional to time,

1. Find its velocity n s after starting,
2. What distance will it travel in ns?

Solution:

According to the problem, a ∝ t

or, a = kt, where k is the constant of proportionality.

Now, a = \(\frac{dv}{dt}\)

dv = kt dt or, ∫dv = k∫t dt

∴ v = \(\frac{k t^2}{2}\) = A(where A = integration constant) ……(1)

Also, as v = 0 at t = 0 , we get A = 0

∴ From equation (1 ) we get, v = \(\frac{k t^2}{2}\)….(2)

Again, if the displacement of the object is s, then v = \(\frac{ds}{dt}\)

∴ From equation (2), \(\)

On integration we get,

s = \(\frac{k t^3}{6}\) + B [where B = integration constant]

Also, at t = 0 , s = 0

∴ B = 0

∴ s = \(\frac{k t^3}{6}\)….(3)

At t = ns, from equations(2) and (3) we get,

1. v = \(\frac{k n^2}{2}\)
2. s = \(\frac{k n^2}{6}\)

Example 4. The velocity of a moving particle v decreases with its displacement. Given, v = v₁ – ax where v₀ = initial velocity, x = displacement and a is a constant. How long will the particle take to reach point B on the x-axis at a distance x_m from the origin?
Solution:

Given, v = v₀ – ax.

At the starting point, v = v₀.

∴ v₀ = v₀– ax or, x= 0 [a = constant]

Hence, the particle was initially at the origin.

Now, \(v=\frac{d x}{d t}=v_0-\alpha x\)

or, \(\frac{d x}{v_0-\alpha x}=d t or, \frac{-\alpha d x}{v_0-\alpha x}=-\alpha d t\)

Then, \(\int \frac{-\alpha d x}{v_0-\alpha x}=-\alpha \int d t or, \log _e\left(\nu_0-\alpha x\right)=-\alpha t+c\); [c is the integration constant]

At t=0 (initially), x=0

∴ \(c=\log _e v_0\)

Therefore, \(\log _e\left(v_0-\alpha x\right)=-\alpha t+\log _e v_0\)

or, \(t=\frac{1}{\alpha} \log _e \frac{v_0}{v_0-\alpha x}\)

At the point \(B, x=x_m\).

Let the corresponding time be \(t_m\).

∴ \(t_m=\frac{1}{\alpha} \log _e \frac{v_0}{v_0-\alpha x_m} \text {. }\)

Example 5. The relation between the time taken and the displacement of a moving body is s = 2t²- 3t² + 4t³, where the unit of s is in metres and that of t is in seconds. Find out the displacement, velocity and acceleration of the body 2 s after initiation of the journey.
Solution:

Here, s = 2t – 3t³ + 4t³……(1)

∴ In 2 s the displacement of the body is,

s = (2 x 2)- [3 x (2)²] + [4 x (2)³]

= (4-12 + 32) = 24 m

Now, the velocity is, v = \(\frac{ds}{dt}\) = 2 – 6t + 12t²

∴ After 2s, v = 2- (6 x 2) +[12 x (2)²] = 38 m · s^-1

Again, the acceleration is, a = \(\frac{dv}{dt}\) -6 + 24t

∴ Acceleration after 2 s, a = – 6 +.24 X 2 = -6 + 48 = 42 m · s^-2.

Example 6. For a particle travelling along a straight line, the equation of motion is s = 16t + 5t². Show that it will always travel with uniform acceleration.
Solution:

Here, s = 16t + 5t²

∴ Velocity, v = \(\frac{ds}{dt}\) = 16 + 10t

Again acceleration, a = \(\frac{dv}{dt}\) = 10 = constant

∴ The particle will always travel with uniform acceleration.

Example 7. If a, b and c are constants of motion and s = at² + bt + c, then prove that 4a(s – c) = v² – b².
Solution:

Here, s = at² + bt+ c

∴ v = \(\frac{ds}{dt}\) = 2at+ b

∴ v² – b² =  (2at+ b)²- b² = 4a²t² + 4abt

= 4a(at² + bt) = 4a(at² + bt + c – c)

or, v² – b² = 4a(s-c) (Proved)

Example 8. The retardation of a particle in rectilinear motion is proportional to the square root of its velocity v. Assume that the constant A of proportionality Is positive. The initial velocity of the particle is v₀. How far would the particle move before coming to rest? What would be the time required to travel that distance?
Solution:

⇒ \(a \propto-\sqrt{v}\)

∴ \(a=-A \sqrt{v}=-A \nu^{1 / 2}\)

or, \(\frac{d \nu}{d t}=-A v^{1 / 2}\)

or, \(v^{-1 / 2} d v=-A d t\)

∴ \(\int v^{-1 / 2} d v=-A \int d t+c\) [c=integration constant]

or, \(2 v^{1 / 2}=-A t+c\)…..(1)

Given, at t=0, v=\(v_0\). Putting in (1), \(c=2 v_0^{1 / 2}\)

∴ \(2 v^{1 / 2}=-A t+2 v_0^{1 / 2}\)

or, \(2\left(\sqrt{v_0}-\sqrt{v}\right)\)= At…..(2)

When the particle comes to rest after a time T, we have v=0 at t=T.

From (2), \(2 \sqrt{v_0}=A T \quad \text { or, } T=\frac{2}{A} \sqrt{v_0}
\)

Now, \(a=\frac{d v}{d t}=\frac{d v}{d x} \frac{d x}{d t}=\frac{d v}{d x} v\)

or, \(d x=\frac{1}{a} v d v=-\frac{1}{A \sqrt{v}} v d v=-\frac{1}{A} v^{1 / 2} d v\)

∴ \(\int d x=-\frac{1}{A} \int v^{1 / 2} d v+k\) [k = integration constant]

or, \(x=-\frac{1}{A} \cdot \frac{2}{3} \nu^{3 / 2}+k=-\frac{2}{3 A} v^{3 / 2}+k\)….(3)

At start, x=0 and \(v=v_0\), Putting in (3),

0 = \(-\frac{2}{3 A} v_0^{3 / 2}+k \quad \text { or, } k=\frac{2}{3 A} v_0^{3 / 2}\)

So, equation (3) becomes, \(x=\frac{2}{3 A}\left(v_0^{\frac{3}{2}}-v^{\frac{3}{2}}\right)\)……..(4)

When the particle comes to rest, v=0. Then the total distance travelled is, \(x_0=\frac{2}{3 A} v_0^{3 / 2}\)

Example 9. The acceleration-time graph of a particle starting from rest is given. Draw the corresponding velocity-time graph and hence find out the displacement in 6s.

Solution:

In the intervals (0 →1), (2 → 3) and (4 → 5) seconds, acceleration is zero, i.e., velocity = constant.

Again, in the intervals (1 → 2), (3 → 4) and (5 → 6) seconds, the velocity increases uniformly and rises to 1 m/s, 2 m/s and 3 m/s respectively, because the uniform acceleration in each interval is 1 m/s²

∴ The velocity-time graph of the motion is ABCDEF

Displacement in 6 s = area under ABCDEF

= area of 6 unit squares + area of 3 triangles

= 6 x (1 x 1) + 3 x (\(\frac{1}{2}\) x 1 x 1) = 7.5 m

Vertical Motion Under Gravity

Acceleration Due To Gravity: when an object is released from a certain height above the earth’s surface, it moves with vertically downward acceleration. Again, when an object is thrown vertically upwards from the ground, it moves up with a deceleration. An upward deceleration is equivalent to a downward acceleration.

Actually, the acceleration is always downward, and its magnitude is the same for both downward and upward motions.

So, the equations of vertical motion are,

v = u + at ….(1)

h = ut + \(\frac{1}{2}\)at² ……(2)

and v² = u² + 2ah ……(3)

Here, initial velocity is u, velocity after time r is v, vertical displacement in time t is h, and acceleration is a.

This acceleration a is called the acceleration due to gravity or free fall acceleration and is represented by the letter g.

The direction of g is always vertically downwards.

If the downward direction is taken as positive, i.e., a = g, then we get the following equations of motion:

v = u + gt …..(4)

h = ut + \(\frac{1}{2}\)gt² …..(5)

and v² = u² + 2 gh …(6))

If the upward direction is taken as positive, i.e., a = we get the following equations: -g, then

v = u – gt …….(7)

h = ut – \(\frac{1}{2}\)gt² …..(8)

and v² = u² – 2gh …..(9)

Maximum Height Attained: When a body is thrown vertically upwards with a velocity u, it momentarily comes to rest on attaining the maximum height and then again starts falling vertically downwards.

Hence, at maximum height H, the velocity of the body, v = 0.

∴ 0 = u² – 2gH [from equation (9)]

or, H = \(\frac{u^2}{2g}\)…….(10)

Time To Reach The Maximum Height: Let the time required to reach the maximum height be T.

∴ 0 = u² – gT [from equation (7)]

or, T= \(\frac{u}{g}\)……(11)

Time Taken To Fall From The Maximum Height: if T₁ is the time taken by the body to fall from the maximum height to the initial position then, using equation (5),

H = \(\frac{1}{2} g T_1^2\)[as at maximum height, u = 0]

or, \(T_1^2=\frac{2 H}{g}=\frac{2}{g} \cdot \frac{u^2}{2 g}=\frac{u^2}{g^2}\)

∴ \(T_1=\frac{u}{g}\)….(12)

Hence, the time to reach the maximum height is equal to the time to return to the starting point.

Time Of Flight: it is the total time required for upward and downward motions

T’ = T + T₁ = \(\frac{u}{g}\) + \(\frac{u}{g}\) = \(\frac{2u}{g}\)

Time Of Flight Alternative Method: After completion of the upward and downward motions, the displacement becomes zero. Thus, using equation (8),

0 = uT’ – \(\frac{1}{2}\)gT’² or, u = \(\frac{1}{2}\)gT’ or, T’ = \(\frac{2u}{g}\).

Time Taken To Reach A Certain Height: Let the object reach a height h at time f. The initial upward velocity = u.

∴ h = \(u t-\frac{1}{2} g t^2\)

or, \(\frac{1}{2} g t^2-u t+h=0\)

or, \(t=\frac{u}{g} \pm \frac{\sqrt{u^2-2 g h}}{g}\)

From this equation, two different values of t are obtained. This is because the object crosses the point at a height h twice, first during the upward motion and then during the downward motion.

Velocity At Any Height: From the equation \(v^2=u^2-2 g h, \text { we get, } v= \pm \sqrt{u^2-2 g h} \text {. }\).

The positive (+) sign is applicable for upward motion and the negative (-) sign is applicable for downward motion. So, an object crosses any point with the same magnitude of velocity in its upward and downward motions.

Velocity Of Projection And Velocity Of Return: Let u = velocity of projection, v = velocity of return and total time of flight = T’.

∴ From equation (7), we can write,

v = u – gT’ = u – g · \(\frac{2u}{g}\) = -u (T’ = \(\frac{2u}{g}\))

Hence, the upward velocity of projection is equal in magnitude to the downward velocity with which an object hits the ground.

Vertical Motion Under Gravity Numerical Examples

Example 1. A stone is dropped from a height of 19.6 m. What is the time taken by the stone to travel the last metre of the path?
Solution:

In this case u = 0

∴ \(h=\frac{1}{2} g t^2 \quad \text { or, } t=\sqrt{\frac{2 h}{g}}\)

Let t₁ and t₂ be the time taken by the stone to travel (19.6-1) = 18.6 m and 19.6 m, respectively.

∴ \(t_1=\sqrt{\frac{2 \times 18.6}{9.8}} \text { and } t_2=\sqrt{\frac{2 \times 19.6}{9.8}}\)

or, \(t_1=1.948 \mathrm{~s} \) and \(t_2=2 \mathrm{~s}\)

Hence, the time taken to travel the last metre, \(t_2-t_1=2-1.948=0.052 \mathrm{~s}\)

Example 2. An object is thrown vertically upwards with an initial velocity of 40 m · s^-1.

1. How long will the object move upwards?
2. What will be the maximum height attained?
3. How much time will it take to reach the ground?
4. When will the object be at a height of 25 m from the ground?
5. What will be its velocity after 2 s ? [g = 9.8 m · s^-2]

Solution:

1. Let the time taken for upward motion be t s. At maximum height, its velocity is zero. From equation v = u – gt, we get, 0 = 40 – 9.8 x t or, t = 4.1s.

2. Let the maximum height attained be h.

From equation v² = u² – 2gh, we get,

0 = (40)² – 2 x 9.8h or, h = 81.6 m .

3. Let the time taken to reach the ground be t₁ starting from the time of projection. Considering both upward and downward motions of the body and using the equation h = ut – \(\frac{1}{2}\)gt², we get,

0 = \(40 t_1-\frac{1}{2} \times 9.8 \times t_1^2\) [total displacement is zero in this case]

∴ t₁ = 8.2 s

4. Let the time after which the body is at a height of 25 m be x.

Hence, from h = ut – \(\frac{1}{2}\)gt² we get,

25 = 40 x – \(\frac{1}{2}\) · 9.8x² or, 49x² – 400x + 250 = 0

or, \(x=\frac{400 \pm \sqrt{(400)^2-4 \cdot 49 \cdot 250}}{2 \cdot 49}=\frac{400 \pm 10 \sqrt{1110}}{2 \cdot 49}\)

or, x = 0.682 s and x = 7.481 s

Two values of x signify that the object will be at a height of 25 m twice during its flight, once (x = 0.682 s) while moving upwards and the next (x = 7.481 s) during its downward motion.

5. Let the velocity acquired 2 s after the projection be v.

∴ v = 40 – 9.8 x 2 = 20.4 m · s^-1.

Example 3. A ball falls freely on a perfectly elastic plate from a height of 3 m. At the instant t = 0, the velocity of the ball is zero. Draw a velocity-time graph for the motion of the ball, [g = 9.8 m · s^-2]
Solution:

In this case, h = \(\frac{1}{2}\) gt²

The time taken by the ball to fall through 3 m is given by t = \(\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 3}{9.8}}=0.783 \mathrm{~s}\)

According to the equation, v² = 2gh, the velocity of the ball just before striking the plate is given by

v = \(\sqrt{2 g h}=\sqrt{2 \times 9.8 \times 3.0}=7.67 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Since the plate is perfectly elastic, the ball after striking it will rebound with the same velocity (7.67 m · s^-1) and its velocity will become zero after the same time (0.78 s). This motion will be repeated again and again as shown in the above graph.

Example 4. A body is thrown vertically upwards. After attaining half of its maximum height its velocity becomes 14 m · s^-1.

1. How high will the body rise?
2. What will be the velocity of the body 1 s and 3 s after its projection?
3. What is the average velocity of the body in the first half second?

Solution:

1. Let the velocity of projection be u.

Hence, maximum height attained by the body, h = \(\frac{u^2}{2g}\) [using v² = u² – 2 gh]

or, u² = 2 gh

For half the maximum height, i.e., \(\frac{h}{2}\), we get

(14)² = u² – 2g\(\frac{h}{2}\) = 2gh –\(\frac{h}{2}\)(2gh) = gh

∴ h = 20 m [where g = 9.8 m · s^-2]

∴ The body will rise up to a height of 20 m. nil Here, the velocity of projection,

2. Here, the velocity of projection, \(u=\sqrt{2 g h}=\sqrt{2 \times 9.8 \times 20}=19.8 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

∴ The velocity of the body 1 s after projection is, v₁ = u – g ·1 = 19.8 – 9.8 = 10 m · s^-1.

Velocity 3 s after projection, v₂ = u – g x 3 = 19.8 – 9.8 x 3 = -9.6 m · s^-1

(Negative sign indicates downward motion of the body.)

3. Velocity after  \(\frac{1}{2}\)s

v’ = u – g x \(\frac{1}{2}\) = 19.8 – 9.8 x \(\frac{1}{2}\) = 149 m · s^-1

Hence, average velocity during the given period = \(\frac{u+v^{\prime}}{2}=\frac{(19.8+14.9)}{2}=17.35 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)

Example 5. A piece of stone was dropped from a stationary balloon. The stone covered 13.9 m during the last 1/7 s of its descent. Find the height of the balloon and the velocity of the stone when it strikes the ground, [g = 9.8 m · s^-2]
Solution:

Let h = height of the balloon, t = total time of fall of the stone, h’ = downward displacement in time (t – \(\frac{1}{7}\))s.

Hence, \(h-h^{\prime}=\frac{1}{2} g t^2-\frac{1}{2} g\left(t-\frac{1}{7}\right)^2\)

or, \(13.9=\frac{1}{2} \times 9.8 \times t^2-\frac{1}{2} \times 9.8\left(t-\frac{1}{7}\right)^2\)

or, \(13.9=4.9 t^2-4.9 t^2+1.4 t-0.1\)

or, \(1.4 t=14\) or, t=10

∴ Height of the balloon, \(h=\frac{1}{2} g t^2=\frac{1}{2} \times 9.8 \times(10)^2=490 \mathrm{~m}\)

The velocity of the stone when it strikes the ground is, \(v=u+g t=0+9.8 \times 10=98 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)

Example 6. A stone is dropped from the top of a tower 400 m high. At the same time, another stone is thrown upwards from the ground with a velocity of 100 m · s^-1. When and where will they meet each other? (g = 9.78 m · s^-2).
Solution:

Let the two stones meet after a time t at a distance h from the top of the tower.

h = \(\frac{1}{2}\) gt² = \(\frac{1}{2}\) x 9.8 t² ……(1)

Considering the downward motion of the 1st stone 400 – h = 100t – \(\frac{1}{2}\) x 9.8 t² …..(2)

From equations (1) and (2) we get, 400 – \(\frac{1}{2}\)x 9.8t² = 100t – \(\frac{1}{2}\) x 9.8t²

or, 100t = 400 or, t = 4 s

Hence, from equation (1) we get, h = \(\frac{1}{2}\) x 9.8 x (4)² = \(\frac{1}{2}\) x 9.8 x 16 = 78.4 m

Hence, the two stones meet at 78.4 m below the top of the tower after 4 s.

Example 7. A stone is dropped from the top of a vertical pillar. When the stone has fallen through a height x, another stone is dropped from height y below the top of the pillar. Both the stones touch the ground at the same time. Prove that the height of the pillar should be \(\frac{(x+y)^2}{4 x}\).
Solution:

Let the height of the pillar be h and the velocity of the stone at x below the top of the pillar be v.

∴ \(v^2=2 g x \text { or, } v=\sqrt{2 g x}\)…..(1)

Let the first stone take \(t \mathrm{~s}\) to cover the distance (h-x).

∴ \(h-x=v t+\frac{1}{2} g t^2\)….(2)

According to the problem, the second stone is dropped from a height of (h-y) and this stone takes time t to cross that distance.

∴ \(h-y=\frac{1}{2} g t^2\)…..(3)

From equations (2) and (3) we get, \(h-x=\nu t+h-y \text { or, } y-x=v t \text { or, } y-x=t \sqrt{2 g x}\)

∴ t = \(\frac{y-x}{\sqrt{2 g x}}\)

From equation (3) we get, \(h-y=\frac{1}{2} g \frac{(y-x)^2}{2 g x}=\frac{(y-x)^2}{4 x}\)

or, \((h-y) \cdot 4 x=(y-x)^2 or, 4 x h-4 x y=y^2-2 y x+x^2\)

or, \(h=\frac{(x+y)^2}{4 x}\) (Proved).

Example 8. A, B, C and D are four points on a vertical line such that AB = BC = CD. A body is allowed to fall freely from A. Prove that the respective times required by the body to cross the distances AB, BC, and CD should be in the ratio 1: (√2- 1): (√3-√2).
Solution:

Let AB – BC = CD = x and the time taken by the body to cover these distances be t₁, t₂ and t₃ respectively.

Now, \(x=\frac{1}{2} g t_1^2 \text { or, } t_1=\sqrt{\frac{2 x}{g}}\)…..(1)

2x = \(\frac{1}{2} g\left(t_1+t_2\right)^2 \text { or, } t_1+t_2=\sqrt{\frac{4 x}{g}}\)…..(2)

3 x = \(\frac{1}{2} g\left(t_1+t_2+t_3\right)^2 \text { or, } t_1+t_2+t_3=\sqrt{\frac{6 x}{g}}\)…..(3)

From (1) and (2) we get, \(t_2=\sqrt{\frac{4 x}{g}}-\sqrt{\frac{2 x}{g}}=\sqrt{\frac{2 x}{g}}(\sqrt{2}-1)\)

From (2) and (3) we get, \(t_3=\sqrt{\frac{6 x}{g}}-\sqrt{\frac{4 x}{g}}=\sqrt{\frac{2 x}{g}}(\sqrt{3}-\sqrt{2})\)

∴ \(t_1: t_2: t_3=1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2})\) (Proved).

Example 9. A rubber ball is thrown vertically downwards from the top of a tower with an Initial velocity of 14 m · s^-1. A second ball is dropped 1 s later from the same place. In 2 s the first ball reaches the ground and rebounds upwards with the same velocity. When will they collide with each other?
Solution:

Height of the tower, h = distance covered by the first ball in 2s = 14 x 2 + \(\frac{1}{2}\)  x 9.8 x (2)² = 47.6 m

(h = ut + \(\frac{1}{2}\)gt²)

The velocity of the first ball just before touching the ground is v = 14 + 9.8 x 2 = 33.6 m · s^-1

Hence, its velocity just after bouncing = 33.6 m · s^-1

Downward displacement of the second ball in 1 s, x = \(\frac{1}{2}\) x 9.8 x (1)² = 4.9 m

Velocity of second ball after 1 s = 9.8 x 1 = 9.8 m · s^-1

Hence, the distance between the two balls, 2 s after the projection of the first ball = 47.6- 4.9 = 42.7 m.

Let the two balls collide with each other ts after the first ball bounces off the ground.

Upward displacement of the first ball in ts, x₁ = 33.6t – \(\frac{1}{2}\) X 9.8 x t² = 33.6t- 4.9t²

Downward displacement of the second ball in t s, x₂ = 9.8t+ \(\frac{1}{2}\) x 9.8 x t² = 9.8t + 4.9t²

Now, x₁ + x₂ = 42.7

or, 33.6t – 4.9t + 9.8t+ 4.9 t³ = 42.7 or, 43.4t = 42.7

∴ t = \(\frac{42.7}{43.78}\) = 0.98 s

Example 10. A lift starts to move up with a constant acceleration of 2 m · s^-2 from the earth’s surface. A piece of stone is dropped outside from the lift 4 s after the start of the lift When will the stone reach the earth’s surface?
Solution:

Initial velocity of the lift, u = 0; acceleration, a = 2 m · s^-2

Let the rise of the lift in 4 s be s and its velocity at that point be v.

Hence, from equation v = u+ at we get,

v = 0 + 2 x 4 = 8 m · s^-1

Also from equation s = ut + \(\frac{1}{2}\) at² we get

s = 0 x 4 + \(\frac{1}{2}\) x 2 (4)² = 16 m

∴ The stone piece was dropped with an initial upward velocity of 8 m · s^-1 and was at a height of 16 m from the ground. If t is the time taken by the stone to reach the ground, then from equation h = ut + \(\frac{1}{2}\)gt²,

16 = \(-8 t+\frac{1}{2} \times 9.8 t^2\)

(because for the stone, \(u=-8 \mathrm{~m} \cdot \mathrm{s}^{-1}, g=9.8 \mathrm{~m} \cdot \mathrm{s}^{-2}\), h=16 m)

or, \(4.9 t^2-8 t-16=0\)

or, \( t=\frac{8 \pm \sqrt{(8)^2-4 \times 4.9 \times(-16)}}{2 \times 4.9}=\frac{8 \pm 19.4}{9.8}\)

Since time cannot be negative, \(t=\frac{8+19.4}{9.8}=2.8 \mathrm{~s}\).

Example 11. Two bodies released from different heights fall freely and reach the ground at the same time. The first body takes a time, t₁ = 2 s and the second body takes a time, t₂ = 1 s. What was the height of the first body at the time of the release of the second body?
Solution:

Let the height from which the first body is released be h₁ above the ground. When it is at a height h₂, the second body is released.

So, the first body falls through a height (h₁ – h₂) in time (t₁– t₂) before the release of the second body.

According to the problem, \(h_1=\frac{1}{2} g t_1^2 \text { and } h_1-h_2=\frac{1}{2} g\left(t_1-t_2\right)^2\)

or, \(\frac{1}{2} g t_1^2-h_2=\frac{1}{2} g\left(t_1-t_2\right)^2\)

or, \(h_2=\frac{1}{2} g\left(2 t_1-t_2\right) t_2\)

= \(\frac{1}{2} \times 9.8(2 \times 2-1) \times 1=14.7 \mathrm{~m} .\)

Example 12. A balloon moves vertically upwards with a uniform velocity v₀. A weight is tied to the balloon with a rope. When the balloon attains a height of h₀, the rope snaps. How much time will the weight take to reach the ground?
Solution:

Let the time taken by the weight, after the rope snaps, to reach the ground be t. From the question, the weight ascends with the same velocity as that of the balloon, i.e., v₀.

So, when the rope snaps the initial velocity of the weight =- v₀ [the negative sign comes as the velocity of the weight is directed upwards just when the rope snaps].

∴ For the free fall of the weight, \(h_0=-v_0 t+\frac{1}{2} g t^2 \text { or, } \frac{1}{2} g t^2-v_0 t-h_0=0\)

∴ \(t=\frac{v_0 \pm \sqrt{v_0^2-4 \times \frac{1}{2} g\left(-h_0\right)}}{2 \cdot \frac{1}{2} g}=\frac{v_0 \pm \sqrt{v_0^2+2 g h_0}}{g}\)

So, the time taken by the weight to reach the ground is \(\frac{v_0+\sqrt{v_0^2+2 g h_0}}{g}\) (becasue t>0).

Example 13. According to the, three cars P, Q and R are at three points along the x-axis at a given moment. Now car P starts its motion towards P₁ parallel to the y-axis with a uniform velocity v. Again, R is in motion parallel to the y-axis along RRX with uniform acceleration a. If car Q too moves parallel to the y-axis then under what condition will all of them remain collinear? Given PQ = QR

Solution:

Let the time be t after which P and R are at and respectively.

PP₁ = vt and RR₁ = \(\frac{1}{2}\)at²

According to the question, after time t, Q will be at Q₁.

From the figure we have, \(\frac{P P_1}{P M}=\frac{Q Q_1}{Q M}=\frac{R R_1}{R M}=k\) (say)

∴ \(P P_1=k \cdot P M=k(P Q+Q M)\)

⇒ \(Q Q_1=k \cdot Q M\)

and \(R R_1=k \cdot R M=k(Q R-Q M)\)

∴ \(P P_1-R R_1=k \cdot(Q M+Q M)\) (because P Q=Q R)

= \(2 k \cdot Q M\)

∴ \(k \cdot Q M=\frac{P P_1-R R_1}{2}\)

∴ \(Q Q_1=k \cdot Q M\)

= \(\frac{P P_1-R R_1}{2}=\frac{P P_1}{2}-\frac{R R_1}{2}=\frac{\nu t}{2}-\frac{1}{4} a t^2\)

∴ \(Q Q_1=\left(\frac{\nu}{2}\right) t-\frac{1}{2}\left(\frac{a}{2}\right) \cdot t^2\)……..(1)

Comparing equation (1) with s = ut- \(\frac{1}{2}\)at², we can say that to remain in the same straight line joining the other two cars, the initial velocity of the car Q must be \(\frac{v}{2}\) along the positive y-axis and it should move with retardation \(\frac{a}{2}\).

 

 One-Dimensional Motion Conclusion

Dynamical quantities related to an object are determined with reference to some other object in the surroundings. This external object forms a frame of reference. A frame of reference is represented in forms like cartesian, polar, spherical etc.

• The change of position of a moving object in a fixed direction is called displacement. Displacement is a vector quantity.
• The rate of Hie distance covered by a body with respect to time is called speed. Speed is a scalar quantity.
• The rate of the distance travelled from a point by a particle with respect to an infinitesimal interval of time is called the instantaneous speed of the particle at that point.
• The rate of displacement of a body with respect to time is called velocity. Velocity is a vector quantity.

The rate of the displacement of a particle from a certain point with respect to an infinitesimally small time interval is called the instantaneous velocity of the particle at that point.

• An object moving in a straight line with uniform speed is said to be moving with uniform velocity.
• An object with uniform velocity must have uniform speed but an object with uniform speed may not have uniform velocity.
• For a moving object, zero average velocity does not necessarily mean a zero average speed, but zero speed always implies zero velocity.
• For an object moving with a uniform velocity, its average velocity is the same as its instantaneous velocity.

The rate of change of velocity of an object with respect to time is called acceleration. Acceleration is a vector quantity.

• The rate of change in velocity of a body at a point with respect to an infinitesimally small time interval is the instantaneous acceleration of the body at that position.
• On a displacement-time graph of a particle, the inclination of the tangent at a point on the graph gives the instantaneous velocity of the particle at that point.
• In a velocity-time graph for a particle, the inclination of the tangent at any point gives the instantaneous acceleration of the particle at that point.

The area enclosed between the velocity-time graph of a particle and the time axis gives the magnitude of the displacement of the particle.

 One-Dimensional Motion Useful Relations For Solving Problems

Speed, v = \(\frac{l}{t}\), where l = distance covered in time t.

Average speed = \(\frac{\text { total distance }}{\text { total time }}\)

or, \(v=\frac{l_1+l_2+l_3+\cdots+l_n}{t_1+t_2+t_3+\cdots+t_n}\)

Instantaneous speed, \(v_i=\lim _{\Delta t \rightarrow 0} \frac{\Delta l}{\Delta t}=\frac{d l}{d t}\)

Velocity, v = \(\frac{s}{t}\), where s= displacement in time t.

Average velocity = \(\frac{\text { total displacement }}{\text { total time }}\)

or, (v)= \(\frac{s_1+s_2+s_3+\cdots+s_n}{t_1+t_2+t_3+\cdots+t_n}\)

Instantaneous velocity, \(v_i=\lim _{\Delta t \rightarrow 0} \frac{\Delta s}{\Delta t}=\frac{d s}{d t}\)

For A Particle In Motion

• Initial velocity = u
• Acceleration = a
• Distance covered in the n-th second =sn
• Acceleration due to gravity = g
• The final velocity after time t = v
• Displacement in time t = s_n
• Height in time t = h

Acceleration or average acceleration = \(\frac{\text { final velocity }- \text { initial velocity }}{\text { time }}=\frac{\text { change in velocity }}{\text { time }}\)

or, (a) =\(\frac{v-u}{t}\)

Instantaneous acceleration, \(a_i=\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}=\frac{d v}{d t}=\frac{d^2 s}{d t^2}\)

For a particle in motion with uniform acceleration,

1. v = u + at,
2. s = ut +\(\frac{1}{2}\)at²,
3. v² = u² + 2as,

The displacement in the t th second s_t = u + \(\frac{l}{2}\)a(2t-1) In case of retardation,

1. v – u -at,
2. s_t = ut – \(\frac{1}{2}\)at²,
3. v² = u² – 2as,
4. s_t = u – \(\frac{1}{2}\)a(2t-1)

Equations of vertical motion under gravity (downward direction positive):

1. v = u + gt,
2. h = ut + \(\frac{1}{2}\)gt²,
3. v² = u² + 2gh

(upward direction positive):

1. v = u – gt,
2. h = ut- \(\frac{l}{2}\)gt²,
3. v² = u² – 2gh

 

One-Dimensional Motion Very Short Answer Type Questions

Question 1. A particle is in uniform motion with respect to a reference frame. Is it possible for the particle to be at rest with respect to another frame?
Answer: Yes

Question 2. Retardation is essentially a _______ acceleration
Answer: Negative

Question 3. For a particle, displacement (x) and time (t) are related by the following equation: x = (3t² + 2t+5)m. If time is expressed in seconds, find the initial velocity of the particle.
Answer: 2 m · s^-1

Question 4. The displacement of a moving particle is directly proportional to the square of the time duration. State whether the particle is moving at a constant velocity or at a constant acceleration.
Answer: Constant acceleration

Question 5. When is the average velocity of a particle equal to its instantaneous velocity?
Answer: In motion with uniform velocity

Question 6. Does a particle with a uniform speed in a curved path possess any acceleration?
Answer: Yes

Question 7. How many dimensions are there in the motion of a ship in a turbulent sea?
Answer: Three

Question 8. If the position of a particle at instant t is given by x = t⁴, find the acceleration of the particle.
Answer: 12t²

Question 9.For a moving body, displacement y (in metre) and time t (in second) are related as y = – \(\frac{2}{3}\) t²+16t+2. When will the body stop?
Answer: After 12s

Question 10. The displacement equation for a particle moving in a straight line is x = αt³ + βt² + γt+ δ. The ratio of the initial acceleration to the initial velocity depends only on _______
Answer: β and γ

Question 11. The motion of an artificial satellite around the earth is a _________ dimensional motion.
Answer: Two

Question 12. An athlete runs with a velocity of 18 km · h^-1. How much distance will he cover in 10 min?
Answer: 3 km

Question 13. What is the nature of the time-displacement graph for a particle moving with a constant velocity?
Answer: A straight line

Question 14. What does the slope of a position-time graph represent?
Answer: Velocity of a body

Question 15. The area under v-t graph =?
Answer: Displacement of the particle

Question 16. In the same displacement-time graph, two motions are represented by two straight lines having slopes of 45° and 60° respectively. Which line represents a higher velocity and what is the ratio between the first and the second velocities?
Answer: Second: 1: √3

Question 17. Velocity (in m · s^-1 unit)-time (in s unit) graph, of a particle moving in a straight line, is a straight line and it is inclined at an angle 45 with the time axis. What is the acceleration of the particle?
Answer: 1 m s^-2

One-Dimensional Motion Assertion Reason Type Questions And Answers

These questions have statements 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: The average velocity of a particle may be equal to its instantaneous velocity.

Statement 2: For a given time interval of a given motion, average velocity is single-valued while average speed can have many values.

Answer: 3. Statement 1 is false, statement 2 is true.

Question 2.

Statement 1: A scooter moves towards the north and then moves towards the south with the same speed. There will be no change in the velocity of the scooter.

Statement 2: Velocity is a vector quantity.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 3.

Statement 1: An object can possess acceleration even when it has a uniform speed.

Statement 2: When the direction of motion of an object keeps changing, its velocity also changes with time.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 4.

Statement 1: Acceleration of a moving particle can change its direction without any change in the direction of velocity.

Statement 2: If the direction of the change in the velocity vector changes, the direction of the acceleration vector also changes.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 5.

Statement 1: The distance between two particles moving with constant velocities always remains constant.

Statement 2: The relative motion between two particles moving with a constant is velocities.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 6.

Statement 1: A particle with zero velocity may have a non-zero acceleration.

Statement 2: A particle comes to rest at the instant of reversing its direction of motion.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 7.

Statement 1: A particle moving with uniform accelera¬tion has its displacement proportional to the square of time.

Statement 2: If the motion of a particle is represented by a straight line on the velocity-time graph, its acceleration is uniform.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 8.

Statement 1: A freely falling body travels through distances in this ratio 1: 3: 5: 7:…… in successive equal intervals of time (Galileo’s law of odd integers).

Statement 2: In one-dimensional motion, a particle with zero speed may have a non-zero velocity.

Answer: 3. Statement 1 is true, statement 2 is false.

Question 9.

Statement 1: If the average velocity of a body is equal in two successive time intervals, its velocity is a constant.

Statement 2: When a body travels with constant velocity, its displacement is proportional to time.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 10.

Statement 1: If two bodies of different masses one dropped simultaneously from the same height, then they touch the ground simultaneously.

Statement 2: The time of flight of a freely falling body is independent of its mass.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 11.

Statement 1: The distance between two bodies does not change if they move in the same direction with the same constant acceleration.

Statement 2: Two bodies moving with the same velocity are at rest relative to each other.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 12.

Statement 1: A body is dropped from a height h and another body is thrown simultaneously from the ground with a velocity u in the vertically upward direction. They meet after a time of \(\frac{h}{u}\).

Statement 2: For a body projected in the vertically upward direction, the ascent in the last second is always 4.9 m, whatever the velocity of projection.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

One-Dimensional Motion Match Column A And Column B

Question 1. In column 1 velocity-time graphs of a particle moving along a straight line are given and in column 2 the corresponding acceleration-time graphs are given.

Answer: 1. A, 2. E, 3. D, 4. C

Question 2. In column 1 some statements related to various physical quantities are given while in column 2 information about the motion of a particle moving along a straight line are given.

Answer: 1. C, 2. B, 3. D, 4. A

Question 3. The displacement-time curve of a moving particle is given.

Answer: 1. A, 2. C, 3. B, 4. D

Question 4.

Answer: 1. A, B, 2. A, B, 3. C, 4. A, B

Question 5.

Answer: 1. A, 2. B, E, 3. C, 4. D

Question 6.

Answer: 1. A, B, 2. C 3. A, B, D, 4. C

Question 7.

Answer: 1. C, 2. B, 3. D, 4. A

Question 8. For a moving particle, displacement and velocity at time t are s and v, respectively.

Answer: 1. A, 2. A, 3. D, 4. B

Question 9. Two cars start from the origin and move along the x-axis. Their displacements (in m) are related to time (in s) as, x_A = 4t+ t² and x_B = 2t² + 2t³. Then

Answer: 1. D, 2. B, 3. C, 4. A

One-Dimensional Motion Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. The vertical rise or fall of a particle under gravity is governed by the equations:

1. v = u + gt,
2. h = ut + \(\frac{1}{2}\)gt², and
3. v² = u2² + 2gh, the symbols having their usual meanings. Then for a particle dropped from the top of a tower and falling freely, choose the correct options:

1. The distance covered by it after n seconds is directly proportional to

1. n¹
2. n
3. 2n-1
4. 2n²-1

Answer: 1. n²

2. The distance covered in the nth second is proportional to

1. n²
2. n
3. 2n-1
4. 2n²-1

Answer: 3. 2n-1

3. The velocity of the body after n seconds is proportional to

1. n²
2. n
3. 2n-1
4. 2n²-1

Answer: 2. n

Question 2. Shows the speed-time graph of two cars A and B which are travelling in the same direction over a period of 40 s. Car A travelling at a constant speed of 40 m · s^-1, overtakes car B at t = 0. In order to catch up with car A, car B immediately accelerates uniformly for 20 s.

1. Distance travelled by car B in 20 s is

1. 800 m
2. 750 m
3. 1000 m
4. 500 m

Answer: 2. 750m

2. What is the acceleration of car B for the first 20 s?

1. 1.25 m · s^-2
2. 3.75 m · s^-2
3. 2.5 m · s^-2
4. 5 m · s^-2

Answer: 1. 1.25 m · s^-2

3. At what time car B overtake car A?

1. 12 s
2. 50 s
3. 18 s
4. 25 s

Answer: 4. 25 s

4. What is the distance travelled by car A before car B overtakes it?

1. 480 m
2. 1000 m
3. 800 m
4. 1200 m

Answer: 2. 1000 m

5. What is the maximum separation between the two cars during the 40 s interval?

1. 150 m
2. 480 m
3. 390 m
4. None of these

Answer: 1. 150 m

Question 3. A ball is thrown up with velocity u = 50 m · s^-1 as shown. The origin and positive and negative directions are also indicated in the figure. Neglect air resistance and take g = 10 m · s^-2.

1. How much time does the ball take to reach half the maximum height?

1. 1.46 s
2. 2.5 s
3. 3s
4. 1.82s

Answer: 1. 1.46 s

2. After how much time will it again cross the same position?

1. 7.07 s
2. 7.5 s
3. 8.18 s
4. Would not cross again

Answer: 1. 7.07 s

3. Determine the distance travelled by the ball in the 3rd second of its motion.

1. Zero
2. 45 m
3. 25 m
4. 80 m

Answer: 3. 25

One-Dimensional Motion Integer Answer Type Questions

In this type, the answer to each of the questions is a single-digit integer between 0 and 9.

Question 1. The displacement x of a particle moving in one dimension, under the action of a constant force, is related to time t by the equation t = √x + 3, where x is in meters and t is in seconds. Find the displacement (in metres) of the particle when its velocity is zero.
Answer: 0

Question 2. The motion of a body is defined by \(\frac{dv(t)}{dt}\) = 6-3v(t) where v(t) is the velocity (in m/s) of the body at time t (in seconds). If the body was at rest at t = 0, find its velocity (in m/s) when the acceleration is half the initial value.
Answer: 1

Question 3. A balloon is at a height of 40 m and is ascending with a velocity of 10 m · s^-1. A bag of 5 kg weight is dropped from it. When will the bag reach the surface of the earth? Given g = 10 m · s^-2.
Answer: 4

Question 4. A bike, initially at rest, travels the first 20 m in 4s along a straight line with constant acceleration. Determine the acceleration of the bike in m · s^-2. Consider the bike as a particle.
Answer: 5

Question 5. Starting from rest, a particle moving along a straight line attains a speed of 2 m · s^-1 in 1.5 s. What is the particle’s speed after an additional 3 s has elapsed assuming that the particle is moving with constant acceleration?
Answer: 6

 

Circular Motion

A Material Particle May Possess Two Kinds Of Motion:

1. Translational motion and
2. Circular or rotational motion.

Sometimes the particle may possess both kinds of motion simultaneously. This is known as a mixed motion. We have already discussed translational motion elaborately in the chapter on One-dimensional Motion.

Circular Motion Definition: If a particle is moving along a circular path about a point as the centre then the motion of that particle is called circular or rotational motion.

• The surface in which the circular path lies is called the plane of rotation. A straight line drawn through the centre of the circular path and perpendicular to the plane of rotation is called the axis of rotation.
• Let us consider a particle is revolving along a circular path of radius r and centre O. The perpendicular drawn through the point O on the plane of rotation is the axis of rotation.

Read and Learn More: Class 11 Physics Notes

• The radius r of the circle is called the radius vector whose direction is towards the particle away from the centre. During the revolution of the particle, the radius vector also keeps on rotating.

Angular Coordinate: Let OP be the radius of the circle, and be taken as the reference for rotation i.e., at time t = 0, the position of the particle is at point P. Let us assume that the position of the particle is at point A on the circumference of the circle after time t and the arc AP makes an angle θ₁ with OP at the centre O.

• This angle θ₁ is called the angular coordinate for the position A of the particle with respect to the radius OP. Similarly, the angular coordinates of the points B and C are θ₂ and -θ₃, respectively.
• So, the position of the particle on a particular circular path can be determined from its angular coordinate only. It should be noted that the angular coordinate for position C in the given figure is negative.
• Usually, for anticlockwise rotational motion, θ is taken as positive and for clockwise motion, negative.

Angular Acceleration

Angular Acceleration Definition: The rate of change of angular velocity of a particle with time is called the angular acceleration of that particle.

Let us consider a particle under rotational motion whose initial angular velocity is ω₁ and final angular velocity after time t is ω₂. So, according to the definition

angular acceleration (α) = \(\frac{\text { change in angular velocity }}{\text { time }}\)

= \(\frac{\omega_2-\omega_1}{t}\)

Compared with the definition of average acceleration in the chapter One-dimensional Motion, this can be referred to as the average angular acceleration.

Instantaneous angular acceleration: The instantaneous angular acceleration of a particle at a given point is the limiting value of the rate of the change in velocity with respect to a time interval when the time interval tends to zero.

If the change in angular velocity of a particle in a small time interval Δt is Δω, then instantaneous angular acceleration,

α = \(\alpha=\lim _{\Delta t \rightarrow 0} \frac{\Delta \omega}{\Delta t}=\frac{d \omega}{d t} .\)

Since, \(\omega=\frac{d \theta}{d t}, \alpha=\frac{d}{d t}\left(\frac{d \theta}{d t}\right)=\frac{d^2 \theta}{d t^2}\)

If the angular velocity of a particle increases gradually, the particle is said to be moving with an angular acceleration.

For example, when an electric fan is switched on, it undergoes angular acceleration before attaining its velocity.

On the other hand, if the angular velocity of a body decreases gradually, it is said to be moving with an angular deceleration or angular retardation. For example, when an electric fan is switched off, it undergoes angular deceleration until it stops.

In the case of angular retardation, the initial angular velocity ω₁ is greater than the final angular velocity ω₂.

Hence, \(\alpha=\frac{\omega_2-\omega_1}{t}\) = a negative quantity.

So, angular retardation is nothing but a negative angular acceleration.

Angular Acceleration Is An Axial Vector: As \(\vec{\omega}_1\) and \(\vec{\omega}_2\) are axial vectors, \(\vec{\omega}_2\) – \(\vec{\omega}_1\) and, hence, \(\vec{\alpha}\) is also an axial vector. When \(\vec{\alpha}\) is positive, its direction is the same as that of \(\vec{\omega}\) and when \(\vec{\alpha}\) is negative, its direction is opposite to that of \(\vec{\omega}\).

Unit And Dimension Of Angular Acceleration: Unit of angular acceleration

= \(\frac{\text { unit of angular velocity }}{\text { unit of time }}\)

= \(\mathrm{radian} / \mathrm{second}{ }^2=\left(\mathrm{rad} \cdot \mathrm{s}^{-2}\right)\)

Dimension of angular acceleration = \(\frac{\text { dimension of angular velocity }}{\text { dimension of time }}=\frac{T^{-1}}{T}=T^{-2} \text {. }\)

Relation Between Linear Acceleration And Angular Acceleration: Let us consider a particle moving along a circular path of radius r, whose linear velocity changes from \(\vec{v}_1 \text { to } \vec{v}_2\) in time t. During this time interval, its angular velocity changes from \(\vec{\omega}_1\) to \(\vec{\omega}_2\).

∴ \(\vec{v}_1=\vec{\omega}_1 \times \vec{r}\) and \(\vec{v}_2=\vec{\omega}_2 \times \vec{r}\)

∴ The value of linear acceleration, \(\vec{a}=\frac{\vec{v}_2-\vec{v}_1}{t}=\frac{\left(\vec{\omega}_2 \times \vec{r}\right)-\left(\vec{\omega}_1 \times \vec{r}\right)}{t}=\frac{\left(\vec{\omega}_2-\vec{\omega}_1\right)}{t} \times \vec{r}\)

Again, angular acceleration is, \(\vec{\alpha}=\frac{\vec{\omega}_2-\vec{\omega}_1}{t}\)

∴ \(\vec{a}=\vec{\alpha} \times \vec{r}\)

Thus, the magnitude of instantaneous linear acceleration = the magnitude of instantaneous angular acceleration x radius of the circular path.

It should be remembered that in the case of pure rotation, linear acceleration changes its direction continuously, but the direction of angular acceleration remains unaltered. Whenever the axis of rotation remains fixed, the direction of angular acceleration does not change.

Geometrical Representation: Putting \(\vec{a} \text { and } \vec{\alpha}\) instead of \(\vec{v} \text { and } \vec{\omega}\), respectively, we will obtain the geometrical representation for the relation among \(\vec{a}\), \(\vec{\alpha}\) and \(\vec{r}\).

Kinematical Equations Of Rotational Motion

From the analogy of the three equations s = θ, v = rω and a = rα, it can be inferred that in case of rotational motion, angular displacement θ, angular velocity co and angular acceleration α, respectively, play the same role as that of displacement s, velocity v and acceleration a in the case of translational motion.

For this reason θ, ω and α are called the rotational analogues of s, v and a respectively. (If a quantity has similarities with another quantity, then that quantity is called the analogue of the other.)

Kinematical Equations For Uniformly Accelerated Motion Are:

1. v = u + at
2. s = ut + 1/2at²
3. v² = u² + 2as

For a uniformly accelerated rotational motion, the analogues of these equations are:

1. \(\omega_2=\omega_1+\alpha t\)
2. \(\theta=\omega_1 t+\frac{1}{2} \alpha t^2\)
3. \(\omega_2^2=\omega_1^2+2 \alpha \theta\)

Here, initial angular velocity = ω₁, final angular velocity after time t = ω₂, angular acceleration = α and angular displacement after time t = θ.

In the case of translational motion with uniform velocity, s = vt. In the case of uniform rotational motion, the analogue of this equation is θ= ωt.

Comparison Of Linear And Angular Motion With Constant Acceleration:

1. Straight Line Motion With Constant Linear Acceleration: For an object that starts moving along a straight line with initial velocity u and constant linear acceleration a, we have
   1. a =constant,
   2. v= u+at,
   3. s =ut+ 1/2at²,
   4. v² = u² + 2as
2. Fixed Axis Rotation With Constant Angular Acceleration: For an object that starts revolving with initial angular velocity ω₀ and uniform angular acceleration α, we have
   1. \(\alpha\) = constant,
   2. \(\omega_1=\omega_0+\alpha t\),
   3. \(\theta=\omega_0 t+\frac{1}{2} \alpha t^2\),
   4. \(\omega^2=\omega_0^2+2 \alpha \theta\)

Kinematical Equations Of Rotational Motion Numerical Examples

Example 1. An electric fan is revolving with a velocity of 210 rpm. When its morion Is Increased with the help of a regulator, it attains a velocity of 630 rpm in 11 s. What is the angular acceleration of the fan? Also, calculate the number of revolutions completed by the fan in that 11s.
Solution:

Initial angular velocity, \(\omega_1=\frac{2 \pi \times 210}{60}=7 \pi \mathrm{rad} \cdot \mathrm{s}^{-1}\)

Final angular velocity, \(\omega_2=\frac{2 \pi \times 630}{60}=21 \pi \mathrm{rad} \cdot \mathrm{s}^{-1}\)

Now, from the equation ω₂ = ω₁+ αt we get, angular acceleration,

α = \(\frac{\omega_2-\omega_1}{t}=\frac{21 \pi-7 \pi}{11}=\frac{14 \pi}{11}=\frac{14}{11} \times \frac{22}{7}\)

= \(4 \mathrm{rad} \cdot \mathrm{s}^{-2}\)

Again, angular displacement, \(\theta=\omega_1 t+\frac{1}{2} \alpha t^2=7 \pi \times 11+\frac{1}{2} \times 4 \times(11)^2\)

θ = \(11(7 \pi+22)=484 \mathrm{rad}\)

Since in a single revolution, the angular displacement is 2π, the number of revolutions

= \(\frac{\theta}{2 \pi}=\frac{484}{2 \pi}=77\)

Example 2. A wheel rolls on a horizontal path with uniform velocity. Prove that the velocity of any point on the circumference of the wheel with respect to its centre is equal to the velocity of the wheel What will be the instantaneous velocity of the point on the wheel which touches the ground?
Solution:

If the radius of the wheel is r then its circumference = 2πr, and velocity of the wheel = \(\frac{2 \pi r}{T}=\frac{2 \pi r}{\frac{2 \pi}{\omega}}=\omega r\)

here, ω = angular velocity of the wheel

Again, the linear velocity of any point on the circumference of the wheel with respect to its centre is, v = ωr. So, this velocity is the same as the velocity of the wheel.

At any moment, when a point on the wheel touches the ground, its linear velocity with respect to the centre of the wheel is v and its direction is just opposite to the direction of the linear velocity v of the wheel Hence, the instantaneous resultant velocity of the point on the wheel which touches the ground = v-v = 0.

Example 3. Starting from rest, a wheel, with uniform acceleration, attains an angular velocity of 60 rad · s^-1 at the end of 30 complete revolutions. What Is the angular acceleration of the wheel?
Solution:

Initial angular velocity, ω₁ =0.

Angular displacement at the end of 30 revolutions, θ = 30 x 2π = 60π rad

Final angular velocity, ω₁ = 60 rad · s^-1

Now, from the equation \(\omega_2^2=\omega_1^2+2 a \theta\)

(α = angular acceleration of the wheel) we get, (60)2 = 0 + 2a x 60/r

or, \(\alpha=\frac{30}{\pi}=9.55 \mathrm{rad} \cdot \mathrm{s}^{-2} .\)

 

 Circular Motion Conclusion

If any particle moves along a circular path about a point as the centre, then the motion of that particle is called circular motion or rotational motion.

• The angle subtended by the initial and final positions of a rotating particle at the centre of its path is called the angular displacement of the particle.
• Angular displacement is a dimensionless physical quantity.
• The rate of angular displacement of a particle with time is called the angular velocity of the particle.
• The rate of change of angular velocity of a particle with time is called the angular acceleration of the particle.
• If the angular velocity of a particle rotating along a circular path is constant, its motion is known as uniform circular motion.

When an object moves in a circular path with a varying speed, then the motion of the object is called non-uni-form circular motion.

There are two unit vectors of circular motion. One is the radial unit vector and the other is the tangential unit vector. The radial unit vector is directed along the radius of the circular path away from the centre.

• The tangential unit vector is directed along the tangent of the circular path. There are two components of the acceleration in non-uniform circular motion. One is radial acceleration and the other is tangential.
• In the case of a particle revolving along a circular path with uniform speed i.e., in the case of uniform circular motion, the acceleration which always acts towards the centre of the circle, known as the radial or centripetal or normal acceleration.
• The force that acts normally to the direction of its velocity to rotate a body along a circular path and is directed towards the centre of that circular path from the body along the radius of the circle is called the centripetal force.

If an observer rotates with a body with the same angular velocity as that of the body rotating along a circular path, the observer will feel that a force is acting on this body which is equal but opposite in direction to the centripetal force. This force is called the centrifugal force.

Circular Motion Useful Relations For Solving Numerical Examples

1° = π/100 rad or, 1 rad = 57.296°

Distance travelled by a rotating particle (s) = radius of the path (r) x angular displacement(θ)

While revolving along a circular path, if the angular displacement of a particle is θ in time f, then the average angular velocity of the particle, \(\omega=\frac{\theta}{t}\)

If in a time interval Δt, the angular displacement of a particle is Δθ0, then the instantaneous angular velocity, \(\omega=\lim _{\Delta t \rightarrow 0} \frac{\Delta \theta}{\Delta t}=\frac{d \theta}{d t}\)

1 rpm = \(\frac{\text { one complete revolution }}{1 \text { minute }}=\frac{2 \pi}{60} \mathrm{rad} \cdot \mathrm{s}^{-1}\)

= \(\frac{\pi}{30} \mathrm{rad} \cdot \mathrm{s}^{-1}\)

The value of linear velocity at any moment (v) = value of angular velocity (ω) at that moment x radius of the circular path (r)

If the initial angular velocity of a rotating particle be ω₁ and that after time t is ω₂, then angular acceleration (a) = \(\frac{\omega_2-\omega_1}{t}\)

Value of instantaneous linear acceleration (a) = radius of the circular path (r) x value of instantaneous angular acceleration (α)

Equations for pure circular motion of a particle with uniform angular acceleration are

1. \(\omega_2=\omega_1+\alpha t\)
2. \(\theta=\omega_1 t+\frac{1}{2} \alpha t^2\)
3. \(\omega_2^2=\omega_1^2+2 \alpha \theta\)

Here, initial angular velocity = ω₁, final angular velocity after time t = ω₂, angular acceleration = α and angular displacement in time t = d.

If a particle of mass m revolves along a circular path of radius r with uniform speed v, the normal or centripetal acceleration of the particle = \(\omega^2 r=\frac{v^2}{r}\)(ω = angular velocity of the particle, ω = \(\frac{v}{r}\))

If the mass of the body is m, the radius of its circular path is r, its linear velocity is v and its angular velocity is ω, then centrifugal force = \(m \omega^2 r=\frac{m v^2}{r}\)

If a body of mass m revolves along a circular path of radius r with velocity v (angular velocity ω), then centrifugal force = \(\frac{m v^2}{r}=m \omega^2 r\)

Circular Motion Assertion Reason Type Question And Answers

These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 Is true, statement 2 Is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 Is true, and statement 2 Is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false,
4. Statement 1 Is false, and statement 2 is true.

Question 1.

Statement 1: A pendulum is oscillating between points A, B and C. Acceleration of bob at points A or C is zero.

Statement 2: Velocity at A and C is zero.

Answer: 4. Statement 1 Is false, and statement 2 is true.

Question 2.

Statement 1: A particle of mass m undergoes uniform horizontal circular motion inside a smooth funnel as shown, The Normal reaction in this case is not mgcosθ.

Statement 2: Acceleration of particle is not along the surface of the funnel.

Answer: 1. Statement 1 Is true, statement 2 Is true; statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: If a car is taking a turn on a banked road, then the normal contact force between the car and the road is greater than the weight of the car (neglecting friction).

Statement 2: On a banked road, the horizontal component of normal contact force between the car and the road provides the necessary centripetal force. Assume friction is absent.

Answer: 2. Statement 1 is true, statement 2 is false,

Question 4.

Statement 1: A car takes a turn of radius 20 m with a constant velocity of 10 m · s^-1.

Statement 2: In circular motion, velocity can never be constant.

Answer: 4. Statement 1 Is false, and statement 2 is true.

Question 5.

Statement 1: A particle can perform circular motion without having any tangential component of acceleration.

Statement 2: For circular motion to take place, radial acceleration should exist.

Answer: 2. Statement 1 Is true, and statement 2 Is true; statement 2 is not a correct explanation for statement 1.

Question 6.

Statement 1: Uniform circular motion is uniformly accelerated motion.

Statement 2: Acceleration in uniform circular motion is always towards the centre.

Answer: 4. Statement 1 Is false, and statement 2 is true.

Question 7.

Statement 1: In circular motion average speed and average velocity are never equal.

Statement 2: In any curvilinear path these two are never equal.

Answer: 1. Statement 1 Is true, statement 2 Is true; statement 2 is a correct explanation for statement 1.

Circular Motion Match Column A With Column B

Question 1. In Column A some physical quantities related to translational motion are given, while in Column B physical quantities associated with rotational motion are mentioned.

Answer: 1. C, 2. B, 3. D, 4. A

Question 2. A particle is rotating in a circle of radius R = \(\frac{2}{\pi}\)m, with constant speed 1 m • s^-1. Match the following two columns for the time interval when it completes 1/4 th of the circle.

Answer: 1. D, 2. B, 3. C, 4. B

Circular Motion Comprehension Type Question And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A particle is moving along a circular path of radius 0.7 m with constant tangential acceleration of 5 m · s^-2. The particle is initially at rest. Based on the above information, answer the following questions

1. The speed of the particle after 7 s is

1. 5 m • s^-1
2. 7 m • s^-1
3. 35 m • s^-1
4. 48 m • s^-1

Answer: 3. 35 m • s^-1

2. The radial acceleration of the particle at t = 7 s is

1. 1200 m · s^-2
2. 1750 m · s^-2
3. 70 m · s^-2
4. 250 m · s^-2

Answer: 2. 1750 m · s^-2

3. Distance travelled by the particle in 7 s is

1. 123 m
2. 725 m
3. 728 m
4. 426 m

Answer: 1. 123 m

4. The number of revolutions made by the particle in 7 s is

1. 27.8
2. 164.8
3. 165.52
4. 96.85

Answer: 1. 27.8

Question 2. A small particle of mass m attached with a light inextensible thread of length L is moving in a vertical circle. In the given case the particle is moving in a complete vertical circle and ratio of its maximum to minimum velocity is 2: 1.

1. Minimum velocity of the particle is

1. \(\sqrt[4]{\frac{g L}{3}}\)
2. \(2 \sqrt{\frac{g L}{3}}\)
3. \(\sqrt{\frac{g L}{3}}\)
4. \(3 \sqrt{\frac{g L}{3}}\)

Answer: 2. \(2 \sqrt{\frac{g L}{3}}\)

2. The kinetic energy of the particle at the lowest position is

1. \(\frac{4 m g L}{3}\)
2. \(2 m g L\)
3. \(\frac{8 m g L}{3}\)
4. \(\frac{2 m g L}{3}\)

Answer: 3. \(\frac{8 m g L}{3}\)

3. The velocity of the particle when it is moving vertically downward is

1. \(\sqrt{\frac{10 g L}{3}}\)
2. \(2 \sqrt{\frac{g L}{3}}\)
3. \(\sqrt{\frac{8 g L}{3}}\)
4. \(\sqrt{\frac{13 g L}{3}}\)

Answer: 1. \(\sqrt{\frac{10 g L}{3}}\)

Question 3. The earth rotates once per day about an axis passing through the north and south poles, that is perpendicular to the plane containing the equator. Assume the earth as a sphere of radius 6400 km. The two particles A and B are considered on the surface of the earth as shown. The particle A is situated at the equator and B is situated at a latitude of 30° north of the equator.

1. The speed of particle A is

1. 465.4 m · s^-1
2. 850 m · s^-1
3. 243.6 m · s^-1
4. 1.675 x 106 m · s^-1

Answer: 1. 465.4 m · s^-1

2. The acceleration of particle A is

1. 3.38 x 10^-7 m · s^-2
2. 3.38 x 10^-5 m · s^-2
3. 3.38 x 10^-2 m · s^-2
4. 3.38 x 10^-1 m · s^-2

Answer: 3. 3.38 x 10^-2 m · s^-2

3. The speed of particle B is

1. 405 m · s^-1
2. 403 m · s^-1
3. 706.5 m · s^-1
4. 210 m · s^-1

Answer: 2. 403 m · s^-1

Circular Motion Integer Answer Type Questions

In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.

Question 1. A particle is moving along a circular path of radius 2 m with a constant angular velocity of 3 rad • s^-2. Determine the angular displacement (in rad) of the particle in 3 s.
Answer: 9

Question 2. A particle moves in a circle of radius 1.0 cm at a speed given by v = 2.0t, where v is in cm · s^-1 and t in seconds. Find the radial acceleration of the particle at t = 1s.
Answer: 4

Question 3. If the earth was to suddenly contract to half its present size, without any change in its mass, then what would be the duration of the new days (in hours)?
Answer: 6

 

Law of Motion Class 11 Notes Physics

Laws Of Motion – Friction

Friction Introduction: It is a common experience that, when a book lying on a table is pushed, it moves some distance and then stops. However according to Newton’s first law of motion, after being pushed, the book should have continued moving with a uniform velocity in the absence of any external force.

• The fact that the book stops clearly shows the existence of some external force that affects the motion of the body. This force is the force of friction, or simply friction, or dry friction. Also, if the book is pushed slightly, it often does not move at all.
• If the force on the book is gradually increased, it begins to move after a while. So, initially, the frictional force can balance the applied force. But, later, it is not enough to resist the motion.
• A large number of phenomena in our daily lives, prove the existence of frictional force. Discussions in this chapter will be restricted to friction between two dry surfaces only.

Read and Learn More: Class 11 Physics Notes

Friction Definition: When two surfaces are in contact with each other and there exists a relative motion between them or an attempt is made to impart a relative motion, then a force comes into play that resists this motion or this attempt. This force is called the force of friction, or simply, friction.

The respective areas of the two bodies which remain in contact with each other are called the surfaces of contact. Friction acts parallel to the surfaces of contact in a direction opposite to the direction of relative motion that is attempted or actually occurs.

Origin Of Friction: From our experience, we find that friction between two smooth surfaces is less than that between two rough surfaces. An apparently smooth surface when examined under a powerful microscope, also shows considerable roughness on the atomic scale.

• At the points of contact A₁, A₂, and A₃,……. atoms of the two surfaces come very close to each other, and interatomic forces act between them. Hence, adhesion takes place between the planes. Such adhesion is the source of friction.
• Also, due to the relative motion between the surfaces, the shape and size of the grooves change continuously. This creates waves and atomic motion which also give rise to friction.

Law of Motion Class 11 Notes Physics

Class 11 Physics Notes For Angle Of Repose

Consider a body of weight W, placed on a surface inclined at an angle θ with the horizontal. The normal force of the inclined plane on the body is R = W cosθ. In this case, the component W sinθ along the plane tries to set up a downward motion of the body.

• Consequently, a frictional force develops upwards along the surface. If the inclination θ is such that the surface just prevents the downward motion of the body, then the frictional force f is the limiting friction, expressed as f = W sinθ.
• Hence, the coefficient of friction, \(\mu=\frac{f}{R}=\frac{W \sin \theta}{W \cos \theta}=\tan \theta\)
• Therefore, when the tangent of the angle of inclination equals the coefficient of friction, the body remains in limiting equilibrium on the inclined plane. If the angle of inclination θ is increased further, W sinθ also increases.
• Then the limiting friction f cannot balance the body and it starts to slide down the inclined plane. The angle of inclination θ in this case, is called the angle of repose of the inclined plane.

Angle Of Repose Definition: The maximum value of the angle of inclination of a surface, for which an object placed on it is just on the verge of downward motion due to its own weight, is called the angle of repose.

Law of Motion Class 11 Notes Physics – Angle Of Repose Discussion

1. For a very smooth surface, i.e., for μ ≈ 0, the angle of repose becomes approximately equal to 0°. This means that the surface cannot prevent the downward motion of this body, even when it is very slightly inclined.
2. When the angle of inclination exceeds the angle of repose, then the frictional force can no longer keep the body in equilibrium on the inclined plane.
3. The angle of repose of different objects, placed on the same inclined surface, may be different.
4. We know μ = tanλ, where λ is the angle of friction, and also μ = tanθ, where θ is the angle of repose, for a pair of surfaces in contact.

∴ tanλ= tanθ or, λ = 6.

Thus, the angle of repose and the angle of friction are numerically equal. However, they are two different physical quantities. The angle of friction is a quantity related to friction between any two surfaces; on the other hand, the angle of repose is a property of inclined surfaces only.

Law of Motion Class 11 Notes Physics – Acceleration Of A Body On An Inclined Plane

Consider a body of mass m sliding down an inclined plane with an acceleration a. Let the angle of inclination be θ. Since the body slides down, θ must be greater than the angle of repose.

Here kinetic friction acts upwards along the incline. Let the normal force of the inclined plane be R, and the coefficient of sliding friction be μ’. Hence, sliding frictional force, f = μ’ R.

Also, R = mgcosθ. The component of the weight of the body along the plane is mg sinθ, which is in the opposite direction of f. The equation of the downward motion, of the body along this inclined plane is, mg sinθ-f= ma

or, ma = mg sinθ – μ’R = mg(sinθ-μ’cosθ)

or, a = g(sinθ-μ’cosθ)

If the inclined plane is perfectly smooth, then μ’ = 0 and a = g sinθ. Hence, the frictional force reduces the downward acceleration of the body along the plane by an amount gμ’ cosθ.

Equilibrium Of A Body On An Inclined Plane

A body of weight W is kept on a plane inclined at an angle θ with the horizontal. If θ is greater than the angle of repose, the frictional force alone is not sufficient to keep the body at rest; an external force F is required for equilibrium. Let it be assumed that the force F makes an angle α with the inclined plane.

There can be either of the two limiting equilibrium conditions—

1. The body is about to move down along the inclined plane, or,
2. The body is about to move up along the inclined plane.

Case 1: Equilibrium Against Downward Motion: The force of limiting friction acts on the body in an upward direction. For equilibrium, the resultants of the components of the forces acting

1. Along The Incline, And
2. Perpendicular To The Incline, Both Should Be Zero.

Here, f + F cosα = W sinθ …(1) and

R + F sinα = W cosθ …(2)

If the coefficient of friction is μ, then f = μR and from equation (1), μR+ F cosα = W sinθ …..(3)

Multiplying equation (2) by θ and then subtracting from (3) we get,

∴ \(F(\cos \alpha-\mu \sin \alpha)=W(\sin \theta-\mu \cos \theta)\)

or, \(F=W \cdot \frac{\sin \theta-\mu \cos \theta}{\cos \alpha-\mu \sin \alpha}\)

Again, if \(\lambda\) is the angle of friction then, \(\mu=\tan \lambda\)

∴ F = \(W \cdot \frac{\sin \theta-\tan \lambda \cos \theta}{\cos \alpha-\tan \lambda \sin \alpha}\)

= \(W \cdot \frac{\sin \theta \cos \lambda-\cos \theta \sin \lambda}{\cos \alpha \cos \lambda-\sin \lambda \sin \alpha}\)

= \(W \cdot \frac{\sin (\theta-\lambda)}{\cos (\alpha+\lambda)}\)…(4)

For given values of θ and λ, F wdll be minimum when cos(α +λ) is maximum,

i.e., when cos(α +λ) = 1 = cos 0

∴ a + λ = 0 or, λ = -λ ….(5)

∴ Minimum applied force, F_min – W sin(θ – λ)

Class 11 Physics Friction Notes

Case 2: Equilibrium Against Upward Motion: If the body is about to move up along the incline, the limiting friction, f= μR acts downwards along the incline. The forces acting when the body is just about to move are shown. Conditions for limiting equilibrium are,

F cosα = μR + W sinθ or, F cosα-μR = W sinθ…..(6)

and F sinα + R = Wcosθ or, μF sinα + μR = W μcosθ…..(7)

On adding (6) and (7), we get F(cosα + μsinα) = W(sinθ + μcosθ)

or, F = \(W \cdot \frac{\sin \theta+\mu \cos \theta}{\cos \alpha+\mu \sin \alpha}\)

Expressing μ in terms of the angle of friction λ, i.e., μ = tanλ,

F = \(W \cdot \frac{\sin \theta+\tan \lambda \cos \theta}{\cos \alpha+\tan \lambda \sin \alpha}\)

= \(W \cdot \frac{\sin \theta \cos \lambda+\sin \lambda \cos \theta}{\cos \alpha \cos \lambda+\sin \lambda \sin \alpha}\)

= \(W \cdot \frac{\sin (\theta+\lambda)}{\cos (\alpha-\lambda)}\)

For given values of θ and λ for F to be minimum, cos(α-λ) = 1 = cos 0 or,α = λ

Class 11 Physics Friction Notes

and F_min = W sin(θ + λ).

Special Cases: When F is applied along the plane, i.e., if α = 0, then the force required to prevent the body from moving downwards is F = \(W \cdot \frac{\sin (\theta-\lambda)}{\cos \lambda}\)…(9)

Again, the force required to bring the body on the verge of moving upwards along the inclined plane is F = \(\frac{W \sin (\theta+\lambda)}{\cos \lambda}\)…(10)

Equilibrium Of A Body On An Inclined Plane Numerical Examples

Example 1. A body is kept on a horizontal rough plane. The plane is then gradually raised to an inclination of 30° with the horizontal and the body starts to slide down. The body descends 12 m along the inclined plane in the next 4 s. Find the coefficients of static and magnetic friction between the surfaces in contact.
Solution:

In this case, the angle of repose = 30°.

∴ Coefficient of static friction, μ = tan30° = 1/√3 = 0.577

As the body begins to slide down, kinetic friction starts acting against the motion.

Downward acceleration, a = g(sinθ-μ’cosθ) [μ’ = coefficient of kinetic friction]

= \(9.8\left(\frac{1}{2}-\mu^{\prime} \frac{\sqrt{3}}{2}\right)=9.8\left(0.5-0.866 \mu^{\prime}\right) \mathrm{m} \cdot \mathrm{s}^{-2}\)

As the body travels 12 m in 4 s from rest, from the equation, s = \(\frac{1}{20}\) at², we get,

12 = \(\frac{1}{2} a \cdot(4)^2 \quad \text { or, } a=\frac{3}{2}=1.5 \mathrm{~m} \cdot \mathrm{s}^{-2}\)

∴ \(9.8\left(0.5-0.866 \mu^{\prime}\right)=1.5\)

or, \(4.9-8.5 \mu^{\prime}=1.5 \quad \text { or, } \mu^{\prime}=\frac{3.4}{8.5}=0.4\)

Class 11 Physics Friction Notes

Example 2. To initiate an upward motion of a body along an inclined plane, the minimum force required is twice the force required to keep the body at rest on the same incline. If the coefficient of friction is μ, prove that the inclination of the plane is θ = tan^-1 (3μ).
Solution:

Let the mass of the body be m, and the minimum force required to keep the body at rest on the inclined plane be F₁.

In this case, the force of limiting friction f acts in the direction of the applied force.

∴ F₁+f=mgsinθ

or, F₁ + μmg cosθ = mg sinθ or, F₁ = mg(sinθ – μcosθ). If F₂ is the minimum force needed to set the body in an upward motion, then limiting friction acts downwards.

∴ F₂ = mg sinθ + f = mg sinθ + μmg cosθ

= mg(sinθ +μcosθ)….(1)

As F₂ = 2F₁ (given),

mg(sinθ + μcosθ) = 2mg(sinθ- μ cosθ) or, sinθ = 3 μ cosθ

or, tanθ = 3μ or, θ = tan^-1(3μ) (Proved).

Example 3. A body of mass 5 x 10^-3 kg is projected upwards along a plane inclined at an angle of 30° with the horizontal. If the time required by the body to move up the incline is half the time required for it to slide down, find the coefficient of friction between the surface and the body.
Solution:

Let the mass of the body be m, and its upward acceleration be a₁. Let the force of friction be f.

∴ ma₁ = mg sinθ + f = mg sinθ + μmg cosθ

or, a₁ = g(sinθ + μcosθ)

If a₂ is the acceleration during the downward motion, then, ma₂ = mgsindθ – f = mgsinθ – μmgcosθ

or, a₂ = g(sinθ-μcosθ)

Class 11 Physics Friction Notes

∴ \(\frac{a_1}{a_2}=\frac{\sin \theta+\mu \cos \theta}{\sin \theta-\mu \cos \theta}=\frac{\tan \theta+\mu}{\tan \theta-\mu}\)

If the displacement along the inclined plane is s, and the time taken to move up and to come down are t₁ and t₂ respectively, then,

s = \(\frac{1}{2} a_1 t_1^2=\frac{1}{2} a_2 t_2^2\)

∴ \(a_1=\frac{2 s}{t_1^2} \text { and } a_2=\frac{2 s}{t_2^2}\)

⇒ \(\frac{a_1}{a_2}=\frac{t_2^2}{t_1^2}=\left(\frac{t_2}{t_1}\right)^2=2^2=4 \quad\left[because t_1=\frac{t_2}{2}\right]\)

∴ \(\frac{\tan \theta+\mu}{\tan \theta-\mu}=4 \text { or, } \mu=\frac{3}{5} \tan \theta=0.6 \tan 30^{\circ}=0.346\)

Example 4. The upper half of an inclined surface is perfectly smooth but the lower half is rough. A body starts sliding down the plane and stops immediately upon reaching the bottom. The inclination of the plane is 30° with the horizontal. Show that the frictional resistance of the rough part of the surface is equal to the weight of the body.
Solution:

Class 11 Physics Friction Notes

Let the length of the inclined plane be 2l, and the vertical height from the ground be h.

Then we get, \(\sin 30^{\circ}=\frac{h}{2 l} \quad \text { or, } \frac{1}{2}=\frac{h}{2 l} \quad \text { or, } h=l \text {. }\)

The potential energy of the body of mass m at maximum height on the plane = mgh = mgl.

The body comes to rest at the bottom. Hence, all its potential energy at the top is spent in doing work against the force of friction, which acts along the length of the lower half of the surface. If f is the frictional force, then f x l = mgl

or, f = mg = weight of the body (Proved).

Rolling Friction

So far we have discussed only the examples of motions where a body slides over a surface. Common examples are, pulling a chair on a floor, skiing on ice, pushing a book over a table, and so on.

• A characteristic feature of this sliding motion is that the contact plane of the moving body remains unaltered. In other words, the force of friction acts on a particular surface of the sliding body all the time.
• When a body rolls over a surface, the area of contact of the rolling body changes continuously with time. So, the frictional force does not act on any specific surface of the body.

Types Of Friction

Consider the motion of a wheel over a horizontal plane. In this case the area of contact of the two surfaces at any time during the motion is very small.

• When a rigid (or hard) wheel is placed on a horizontal plane, the plane of contact practically becomes a straight line, Now, let a horizontal force P be applied at the center C of the wheel.
• It will initiate a translatory motion of the wheel, along the horizontal surface. Then, a frictional force F will act in the backward direction at the line of contact OA. As a result, the moment of F about C will generate a rotation of the wheel.
• Line OA will be displaced, and new lines like O’B will come in contact with the horizontal surface. The overall effect is that two types of motion (translational and rotational) are set up in the wheel. Such composite motion of the wheel is called rolling.

Rolling Friction Definition: When a body translates, as well as rotates over a surface without slipping, its motion is known as rolling; the frictional force developed opposite to the direction of motion is called rolling friction.

• We already know that sliding or kinetic friction is less than the limiting value of static friction (limiting friction). Rolling friction is much lower than even sliding friction. So it is considerably easier to overcome the rolling friction, and thus to set a body in motion.
• This is how all-wheeled vehicles move. Wheels and tracks are always designed so that the applied force is greater than the rolling friction but less than the sliding friction. Car and bicycle tires have grooved surfaces that increase sliding friction.

If, for some reason, the sliding friction suddenly drops below the applied force, the wheel of the bicycle slides, or ‘skids’. Vehicles with wheels are not used at all where the sliding friction is very low—for example, flat-bottomed carts are used on ice surfaces.

Source Of Rolling Friction: When a wheel rolls on a surface, its motion gets obstructed due to deformation of the wheel, the surface, or both, at the plane of contact.

Types Of Friction

• In real life, usually, the and the ground are not perfectly rigid and both get deformed to some extent.
• Such deformation is easily noticeable when a heavy wheel rolls over soft ground. At the point of contact of the wheel and the ground, an indentation is created on the surface due to the weight of the wheel. The ground just in front of the wheel swells up slightly.
• At the point of contact, the wheel also gets deformed and a slight flattening is easily observed. These deformations at the point of contact are the source of rolling friction. When the air pressure is low in a cycle tube, the is flattened, and frictional force increases.
• If both the surfaces in contact are rigid enough, then the deformation is negligible, and so the rolling friction is quite low. For this reason, the friction is considerably low in the case of a train running over a railway track.

Note that, the deformations of the surfaces in contact, in case of a rolling motion, are temporary. As soon as the point of contact shifts, the wheel and the surface regain their original shapes and the deformation shifts to a new point of contact.

Difference Between Sliding Friction And Rolling Friction:

1. The surface of contact remains unchanged in case of sliding friction while in case of rolling friction, the surface of contact keeps changing.
2. In case of sliding friction, two surfaces in contact are in motion with respect to each other. In the case of rolling friction, there is no relative motion between the two surfaces in contact.
3. The frictional force opposing the sliding motion (sliding friction) is much more than the force opposing the rolling motion (rolling friction).

Class 11 Physics Notes For Friction

Friction Conclusion

When two surfaces are in contact with each other, and there exists a relative motion between them, or an attempt is made to impart a relative motion, a force comes into play that resists the movement. This force is called the force of friction, or simply friction.

• Force of friction is a self-adjusting force that balances the applied force as long as there is no relative motion in which case it is known as static friction.
• The maximum possible magnitude of static friction is called limiting friction.
• The force of limiting friction and kinetic friction, between two surfaces in contact, are directly proportional to the normal force.
• When the normal force remains constant, friction between the two surfaces in contact is independent of the area of contact and the relative velocity between the surfaces.
• The ratio between the force of limiting friction and the normal force is called the coefficient of static friction for two surfaces in contact. Again, the ratio between the kinetic friction and the normal force is the coefficient of kinetic friction.

The coefficient of friction (μ) does not have any unit; it is just a number. Usually, it is less than 1, but can be equal to or greater than 1 in special cases.

• For a pair of surfaces in contact the resultant of the force of limiting friction and the normal force makes an angle with the normal force itself. That is called the angle of friction.
• The maximum value of the angle of inclination of an inclined plane, for which an object is just on the verge of downward motion along the incline only due to its weight is called the angle of repose.
• For the same system, the angle of friction is equal to the angle of repose.
• When a body rolls over a surface without slipping, the frictional force developed at the point of contact, that opposes the rotation of the rolling body, is called rolling friction.

 Friction Useful Relations For Solving Numerical Examples

When R = normal force, f = limiting friction or sliding friction, and μ = coefficient of friction, f = μR,

Acceleration produced on a body of mass m, kept on a rough surface, by a force F applied along the surface, is a = \(\frac{F-\mu R}{m}\)

If a body of mass m remains in equilibrium on a plane, inclined at the angle of repose θ, then R = mg cosθ and f = μR= mg sinθ; hence, μ = tanθ.

If the angle of repose is θ and the angle of friction is λ then, μ = tanθ = tanλ

∴ θ = λ.

Resultant of the limiting friction and the normal force R between two surfaces in contact,

Q = \(R \sqrt{1+\mu^2}\)

Acceleration of a body moving over an incline, under the action of gravity is a = g(sinθ – μcosθ)

Friction Very Short Answer Type Questions

Question 1. Can the value of the coefficient of friction be greater than 1?
Answer: Yes

Question 2. Does the force of friction depend on the area of contact?
Answer: No

Question 3. On what factors does the coefficient of static friction depend?
Answer:

1. Nature of the surfaces in contact
2. Nature of the material in contact

Question 4. What is wet friction?
Answer: The force of friction between a solid and the layer of liquid

Question 5. Value of the angle of friction ______ on increasing the smoothness of the plane.
Answer: Decreases

Question 6. Rolling friction is _______ than both static friction and kinetic friction.
Answer: Less

Friction Assertion Reason Type Question And Answers

These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: If a body tries to slip over a surface then friction acting on the body is necessarily equal to the limiting friction.

Statement 2: Static friction can be less than the limiting friction.

Answer: 4. Statement 1 is false, statement 2 is true

Question 2.

Statement 1: Frictional heat generated by the moving ski is the chief factor that promotes sliding in skiing and waxing the ski makes skiing easier.

Statement 2: Due to friction, energy dissipates in the form of heat. As a result, it melts the snow below it. Wax is water-repellent.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 3.

Statement 1: The coefficient of friction can be greater than unity.

Statement 2: Frictional force depends on normal reaction and the ratio of force of friction and normal reaction cannot exceed unity.

Answer: 3. Statement 1 is true, statement 2 is false.

Question 4.

Statement 1: Static frictional force is always greater than the kinetic frictional force.

Statement 2: Coefficient of static friction, μ_s > coefficient of kinetic friction, μ_k.

Answer: 4. Statement 1 is false, statement 2 is true

Question 5.

Statement 1: The driver of a moving car sees a wall in front of him. To avoid a collision, he should apply brakes rather than take a turn away from the wall.

Statement 2: Force of friction is needed to stop the car or take a turn on a horizontal road.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 6.

Statement 1: Friction opposes the motion of a body.

Statement 2: Static friction is self-adjusting while kinetic friction is constant.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 7.

Statement 1: A particle is thrown vertically upwards. If air resistance is taken into consideration then retardation in the upward journey is more than the acceleration in the downward journey.

Statement 2: Some mechanical energy is lost in the form of heat due to air friction.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Friction Match Column A With Column B

Question 1.

Answer: 1. B, 2. A, C, 3. B, 2. A, C

Question 2. For the situation shown, in Column A, the statements regarding frictional forces are mentioned, while in Column B some information related to frictional forces is given.

Answer: 1. B, D, 2. C, 3. A, D, 4. C

Question 3. A body of mass 200 g is moving with a velocity of 5 m • s^-1 along the positive x -x-direction. At time t = 0, when the body is at x = 0, a constant force of 0.4 N directed along the negative x-direction is applied to the body for 10 s.

Answer: 1. C, 2. A, 3. B, 4. D

Question 4. The coefficient of friction between the block and the surface is 0.4.

Answer: 1. A, C, 2. B, D 3. A, B 4. C, D

Question 5. Both the pulleys are massless and frictionless. A force F (of any possible magnitude) is applied in the horizontal direction. There is no friction between M and the ground. μ₁ and μ₂ are the coefficients of friction as shown between the blocks. Column A gives the different relations between μ₁ and μ₂ and Column B is regarding the motion of M.

Answer: 1. C, 2. C, 3. B, D, 4. A, D

Question 6. For the diagram shown, match the following columns.

Answer: 1. D, 2. A, 3. D

Question 7. A block of mass m is thrown upwards with some initial velocity as shown. On the block:

Answer: 1. C, 2. D, 3. B 4. A

 Friction Comprehension Type Question And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A man wants to slide down a block of mass m which is kept on a fixed inclined plane of inclination 30° as shown. Initially, the block is not sliding. To just start sliding the man pushes the block down the incline with a force F. Now, the block starts accelerating. To move it downwards with constant speed the man starts pulling the block with the same force. Surfaces are such that ratio of maximum static friction to kinetic friction is 2.

1. What is the value of F?

1. \(\frac{m g}{4}\)
2. \(\frac{m g}{6}\)
3. \(\frac{m g \sqrt{3}}{4}\)
4. \(\frac{m g}{2 \sqrt{3}}\)

Answer: 2. \(\frac{m g}{6}\)

2. What is the value of μ_s, friction?

1. \(\frac{4}{3 \sqrt{3}}\)
2. \(\frac{2}{3 \sqrt{3}}\)
3. \(\frac{3}{3 \sqrt{3}}\)
4. \(\frac{1}{2 \sqrt{3}}\)

Answer: 1. \(\frac{4}{3 \sqrt{3}}\)

3. If the man continues pushing the block by force F, its acceleration would be

1. \(\frac{g}{6}\)
2. \(\frac{g}{4}\)
3. \(\frac{g}{2}\)
4. \(\frac{g}{3}\)

Asnwer: 4. \(\frac{g}{3}\)

Question 2. A lift with a mass 1200 kg is raised from rest by a cable with a tension of 1350g N. After some time the tension drops to 1000g N and the lift comes to rest at a height of 25 m above its initial point. (1gN = 9.8 N).

1. What is the height at which the tension changes?

1. 10.8 m
2. 12.5 m
3. 14.3 m
4. 16 m

Answer: 3. 14.3 m

2. What is the greatest speed of the lift?

1. 9.8 m s^-1
2. 7.5 m s^-1
3. 5.92 m s^-1
4. None Of These

Answer: 3. 5.92 m s^-1

Question 3. A 6 kg block is kept on an inclined rough surface as shown. Based on this information answer the following questions (Take g = 10 m · s^-2).

1. The amount of force (F) required to keep the block stationary is

1. 34N
2. 40 N
3. 35 N
4. 36 N

Answer: 1. 34N

2. The amount of force (F) required to move the block downwards with constant velocity is

1. 35 N
2. 37 N
3. 40 N
4. 44 N

Answer: 3. 40 N

3. The amount of force (F) required to move the block upwards with an acceleration of 4 m • s^-2 is

1. 90 N
2. 92 N
3. 88 N
4. 80 N

Answer: 3. 88 N

Friction Integer Answer Type Questions

In this type, the answer to each of the questions li a tingle digit Integer ranging from 0 to 9.

Question 1. A horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. What is the weight of the block (in N)?
Answer: 2

Question 2. The coefficient of friction between two blocks is μ = 0.6. The blocks are given velocities in the directions shown in the figure. Find the common velocity (in m • s^-1) of the two blocks.
Answer: 4

 

 

 

Kinematics Vector

Definition Of Scalar And Vector Quantities

Physical quantities, used in science and technology are broadly classified into two groups, scalar quantities and vector quantities.

Scalar Quantities Definition: A scalar quantity is a physical quantity having only magnitude but no direction.

Physical quantities like length, mass, time, relative density, energy, temperature, etc. are fully described by their magnitudes. These quantities do not have any direction. These are examples of scalar quantities.

Scalar Definition: Any number, that has a real magnitude only but no direction, is called a scalar.

Essentially, any real number—like 8, -2, √3, etc. is a scalar. Naturally, if an appropriate unit is added to a scalar, it becomes a scalar quantity.

Scalar Example:

1. The distance of a railway station is 10 km from my residence.
2. It takes me 30 minutes (time) to reach school from my home.

In all the above examples we can see that a scalar quantity is completely expressed by a real number and a unit and thus have complete information about the quantities.

Mathematical operations of scalars follow simple algebraic rules.

Read and Learn More: Class 11 Physics Notes

Vector Quantities Definition A vector quantity is defined as a physical quantity, having both magnitude and direction.

• For physical quantities like displacement, velocity, acceleration, force, etc. the magnitude does not define the quantity fully. If we express the position of our school by saying that it is 4 km away from my residence then this statement is incomplete.
• The school cannot be located until we say that it is 4 km west of my residence. Thus position is a vector quantity. A statement such as ‘the bus stop is 200 m from where one is standing’ may not be useful until a direction is specified, like 200 m east.

Vector Definition: Any number, that has a real magnitude as well as a direction, is called a vector.

A vector quantity is expressed by a real number, a unit, and a specific direction.

Vector Example: Velocity of a particle = 10 m · s^-1 towards the east. If the unit is omitted, we get a vector. In this example, the vector is ‘10 towards east’.

5 towards the south, -8 downwards, \(\frac{1}{2}\) along the north-west, 2√2 from the south-west, etc. are examples of vectors. Obviously, the vector ‘-8 downwards’ is identical to the vector ‘8 upwards’. If an appropriate unit is added to a vector, it becomes a vector quantity.

Differences Between Scalar And Vector Quantities:

It is to be noted that, scalars and vectors are mathematical elements only. After all mathematical operations, a proper unit must be added to the final result to obtain a meaningful physical quantity.

Geometrical Representation Of A Vector

A vector is represented by a line segment with an arrowhead. The length of the line segment (in a predetermined scale), is the magnitude of the vector and the arrowhead denotes the direction. The front end (carrying the arrow) is called the head and the rear end is called the tail.

The velocity of a particle 6 cm • s^-1 towards the east is represented by the line segment AB. If the scale is chosen such that CD =0.5 in. represents 2cm · s^-1, then the length of the segment AB should be 1.5 in.

So, the 1.5 in. long line segment AB with the arrowhead pointing towards the east represents both the magnitude and direction (towards the east) of the velocity of the particle. The velocity vector is represented as \(\overrightarrow{A B}\), where A is the initial point and B is the terminal point.

Generally, a vector is expressed as an algebraic quantity by using a letter with an arrowhead like \(\vec{a}, \vec{b}, \vec{c},\), etc. The magnitude or absolute value of a vector is a scalar and is always positive. It is called the modulus of the vector. It is expressed as a, b, c (without an arrow) or \(|\vec{a}|,|\vec{b}|,|\vec{c}|\).

Modulus of the velocity vector \(\overrightarrow{A B}\), as shown.

Therefore, \(|\stackrel{\rightharpoonup}{\nu}|=|\overrightarrow{A B}|=A B \text { (length) }=6 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

Some Facts About Vectors

Equal Vectors: Two vectors, equal in magnitude as well as in direction, are called equal vectors. \(\overrightarrow{A B}\) and \(\overrightarrow{C D}\) are equal vectors as both have the same magnitude (length) and direction.

If \(\overrightarrow{A B}\) represents 20 towards the north, then \(\overrightarrow{C D}\) will also represent 20 towards the north. If \(\overrightarrow{A B}\) = \(\vec{a}\), then \(\overrightarrow{C D}\) is also = \(\vec{a}\), i.e., \(\overrightarrow{A B}\) = \(\overrightarrow{C D}\).

Two vectors may be equal even when their initial and final points are not the same. This means that we can translate a vector keeping its magnitude and direction unchanged.

Opposite Vectors: Two vectors having the same absolute value but opposite directions are called opposite vectors. \(\overrightarrow{F E}\) and \(\overrightarrow{A B}\) or \(\overrightarrow{C D}\) are opposite vectors.

∴ \(\overrightarrow{F E}\) represents a vector with a magnitude same as that of \(\overrightarrow{A B}\) or \(\overrightarrow{C D}\) = a (say), but the direction of \(\overrightarrow{F E}\) is opposite to that of \(\overrightarrow{A B}\) or \(\overrightarrow{C D}\).

Hence, if \(\overrightarrow{A B}\) = \(\overrightarrow{C D}\) = \(\vec{a}\), then \(\overrightarrow{F E}\) = –\(\vec{a}\). It may also be written as \(\overrightarrow{A B}\) = \(\overrightarrow{C D}\) = –\(\overrightarrow{F E}\).

As magnitudes or moduli of two opposite vectors are the same, we have, \(|\vec{a}|=a,|-\vec{a}|=a\).

Collinear Vectors: Vectors that are of the same or different magnitudes, but jure parallel or anti-parallel to one another, are known as collinear vectors. \(\vec{d}, \vec{e}, \vec{f}\) are collinear vectors. Also \(\vec{x}, \vec{y}, \vec{z}\) acting along the same line, represent a set of collinear vectors.

Coplanar Vectors: Vectors lying on the same plane are coplanar vectors. \(\vec{a}\) and –\(\vec{a}\) and all vectors lie on the plane of the paper and hence are coplanar.

Unit Vector: A vector in the direction of a given vector with unit magnitude is called a unit vector. A unit vector is often denoted by a lowercase letter with circumflex or ‘hat’ (^).

The absolute value of any vector is a scalar. This scalar, multiplied by the unit vector in that direction, gives the corresponding vector.

Unit Vector Example: \(|\vec{A}|\) = A and \(A \hat{n}=\vec{A}\) where \(\hat{n}\) is the unit vector in the direction of \(\vec{A}\). This means \(\frac{\vec{A}}{A}=\hat{n}\).

Therefore a vector divided by its magnitude gives the unit vector in the direction of that vector. In the cartesian coordinate system, unit vectors along x, y, and z axes are conventionally represented as \(\hat{i}, \hat{j} \text { and } \hat{k}\) respectively.

Composition Of Scalars And Vectors

Scalars have only magnitudes. So addition or subtraction of scalars means the addition or subtraction of their magnitudes only. Accordingly, scalar addition follows simple algebraic rules.

Vectors have both magnitude and direction. Therefore, during addition or subtraction of vectors, their directions should be taken into account as well. Thus, they cannot be added or subtracted by using simple algebraic rules. Hence, the geometrical method or analytical method of vector algebra is used for vector addition.

Addition Or Two Vectors

Suppose a particle starting from its initial position O undergoes \(\vec{a}\) displacement a and reaches point A. Hence, \(\vec{a}\) = \(\overrightarrow{O A}\). After a further displacement of \(\vec{b}\) in a  different direction, the particle reaches point B.

Hence, \(\vec{a}\) = \(\overrightarrow{A B}\). Starting from point O, the net displacement of the particle is thus \(\overrightarrow{O B}\) = \(\vec{c}\) (say).

Vector \(\vec{c}\) is called the sum or the resultant of \(\vec{a}\) and \(\vec{b}\), expressed as \(\vec{c}\) = \(\vec{a}\) + \(\vec{b}\).

This sum will obviously be a vector sum, because by adding only the magnitudes of \(\vec{a}\) and \(\vec{b}\), \(\vec{c}\) cannot be found. The magnitudes of \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) can be determined from the lengths of the sides OA, AB and OB respectively.

This method of finding the resultant of two displacements also holds good for finding the sum of any two vectors. Illustrates one such case where forces \(\vec{P}\) and \(\vec{Q}\) pull a boat simultaneously. As a result, the boat moves along the resultant \(\vec{R}\), and \(\vec{P}\) + \(\vec{Q}\) = \(\vec{R}\).

Addition Of Two Vectors Resultant: A single vector, which represents the result of the summation of a number of vectors both in magnitude and in direction, is called the resultant of those vectors.

∴ \(\overrightarrow{O B}\) is the resultant.

To find the sum of \(\vec{P}\) and \(\vec{Q}\), draw the vectors \(\vec{P}\) as shown and name it as AB i.e., \(\overrightarrow{A B}\) = \(\vec{P}\).

Now move the vector \(\vec{Q}\) parallel to itself such that its tail coincides with the tip B of the vector \(\vec{P}\).

Mark the tip of the vector \(\vec{Q}\) as C i.e., \(\overrightarrow{B C}\) = \(\vec{Q}\). Join the tail of the vector \(\vec{P}\) to the tip of the vector \(\vec{Q}\) i.e., \(\overrightarrow{A C}\) = \(\vec{R}\) where \(\vec{Q}\) represents the sum of the vectors \(\vec{P}\) and \(\vec{Q}\). Thus, \(\vec{R}\) = \(\vec{P}\) + \(\vec{Q}\).

Vector addition follows either of the following equivalent laws:

1. Law of triangle of vectors,
2. Law of parallelogram of vectors and
3. Polygon law of vectors.

Magnitude In vector Addition: Let us consider two vectors a and b whose resultant is found to be \(\vec{c}\) i.e., \(\vec{a}\) + \(\vec{b}\) = \(\vec{c}\). Now to think, that the magnitude of \(\vec{c}\) is actually the sum of the magnitude of \(\vec{a}\) and magnitude of \(\vec{b}\) is incorrect. This is because we can see that \(|\vec{c}|<|\vec{a}|+|\vec{b}|\).

It means that the magnitude of resultant vector \(\vec{c}\) not only depends on the magnitude of \(\vec{c}\) and \(\vec{c}\) but also depends on the angle between the two vectors \(\vec{a}\) and \(\vec{b}\).

To find out the relationship between \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) and the angle between the vectors, let us study the following law of vector addition.

Law Of Triangle Of Vectors

Law Of Triangle Of Vectors Geometrical Method: \(\vec{a}\) + \(\vec{b}\) = \(\vec{c}\) or \(\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}\). Vectors \(\overrightarrow{O A}, \overrightarrow{A B} \) and their resultant \(\overrightarrow{O B}\), therefore represent the three sides of the A OAB. The following triangle law of vector addition can be obtained by considering the magnitudes and directions of the vectors.

Law Of Triangle Of Vectors Geometrical Method Statement: When the magnitudes and directions of two vectors, are represented by two adjacent sides of a triangle taken in order, the third side taken in the opposite order, represents the magnitude and direction of the resultant of the two vectors.

Two adjacent sides taken in order and the third side taken in the opposite order—means that if the former is in a clockwise direction in the triangle, the third side, representing the resultant, should be in an anticlockwise direction.

Law Of Triangle Of Vectors Geometrical Method Corollary: With reference to the A OAB, \(\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}\) or, \(\overrightarrow{O A}+\overrightarrow{A B}-\overrightarrow{O B}=0\)

or, \(\overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{B O}=0\)

Hence, if three vectors are completely represented by the three sides of a triangle taken in order (all clockwise or all anticlockwise), then the resultant of the vectors will be zero.

Law Of Triangle Of Vectors Analytical Method: Let the two vectors \(\vec{a}\) and \(\vec{b}\) be represented both in magnitude and direction by the sides \(\overrightarrow{O A}\) and \(\overrightarrow{A B}\) of ΔOAB is taken in the same order. Then according to the triangle law of vector addition, the resultant \(\vec{c}\) is given by the side OB taken in the reverse order, as shown.

Law Of Triangle Of Vectors Analytical Method Magnitude Of The Resultant \(\vec{c}\): BE is the perpendicular drawn from B on the extension of OA. The angle between the vectors \(\vec{a}\) and \(\vec{b}\), ∠BAE = α. It is to be noted that to measure the angle between two vectors, their initial points are superimposed on each other without changing the directions of the vectors.

Now from right-angled ΔAEB we have \(BE \frac{B E}{A B}=\sin \alpha\)

or, \(B E=A B \sin \alpha\)

or, \(B E=b \sin \alpha\) and \(\frac{A E}{A B}=\cos \alpha\) or, \(A E=A B \cos \alpha\)

or, \(A E=b \cos \alpha\)

Applying Pythagoras theorem in right-angled ΔOEB we get, \((O B)^2=(O E)^2+(E B)^2=(O A+A E)^2+(E B)^2\)

or, \(c^2=(a+b \cos \alpha)^2+(b \sin \alpha)^2\)

= \(a^2+2 a b \cos \alpha+b^2 \cos ^2 \alpha+b^2 \sin ^2 \alpha\)

or, \(c^2=a^2+2 a b \cos \alpha+b^2\left(\cos ^2 \alpha+\sin ^2 \alpha\right)\)

or, \(c^2=a^2+b^2+2 a b \cos \alpha\) (because \(\cos ^2 \alpha+\sin ^2 \alpha=1\))

or \(c=\sqrt{a^2+b^2+2 a b \cos \alpha}\)….(1)

Law Of Triangle Of Vectors Analytical Method Direction Of The Resultant \(\vec{c}\): Let the resultant vector (\(\vec{c}\)) make an angle α with the first vector \(\vec{a}\). Then from right-angled ΔOEB, we get, \(\tan \theta=\frac{B E}{O E}=\frac{B E}{O A+A E}\)

or, \(\tan \theta=\frac{b \sin \alpha}{a+b \cos \alpha}\)….(2)

Therefore, if the magnitudes a and b, and the value of the angle α are known, then from equations (1) and (2), the magnitude of the resultant vector and its direction can be determined.

Law Of Parallelogram Of Vectors

Law Of Parallelogram Of Vectors Geometrical Method: The law of parallelogram of vector addition is just an alternative form of the law of triangle of vector addition. let \(\overrightarrow{O A}=\vec{a}\) and \(\overrightarrow{A B}=\vec{b}\).

Therefore, from the triangle law of vector addition, the vector \(\overrightarrow{O B}\) represents the magnitude and direction of the resultant \(\vec{c}\). Hence, \(\vec{a}+\vec{b}=\vec{c}\) or, \(\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}.\)

Now the parallelogram OABD is completed. AB and OD being the opposite sides of the parallelogram, are equal and parallel.

Hence, \(\overrightarrow{A B}=\overrightarrow{O D}=\vec{b}\).

So, \(\overrightarrow{O A}+\overrightarrow{O D}=\overrightarrow{O B}\)

Law Of Parallelogram Of Vectors Geometrical Method Statement: If the magnitudes and directions of two vectors are represented by two adjacent sides of a parallelogram, the diagonal drawn from the point of origin of the two vectors represents the magnitude and direction of the resultant.

Law Of Parallelogram Of Vectors Analytical Method:

Law Of Parallelogram Of Vectors Analytical Method Magnitude Of Resultant \(\vec{c}\): Let the point of origin of the vectors \(\vec{a}\) and \(\vec{b}\) be O. The two vectors are represented by the line segments OA and OD.

The parallelogram OABD is completed by drawing DB parallel to OA and AB parallel to OD. Then the diagonal OB from point 0 represents the magnitude and direction is the resultant of the vectors \(\vec{a}\) and \(\vec{b}\).

Here, \(\vec{a}=\overrightarrow{O A}, \vec{b}=\overrightarrow{O D}=\overrightarrow{A B} \text { and } \vec{c}=\overrightarrow{O B}\)

Perpendicular BE is drawn from B on the extension of OA. Then ∠BAE = ∠DOA = α

Here, the length of the side OA = \(|\vec{a}|\) = a

length of the side OD = length of the side AB = \(|\vec{b}|\) = b and length of the side OB = \(|\vec{c}|\) = c

From right angled ΔBAE we have, \(\frac{B E}{A B}=\sin \alpha\) or, BE = \(A B \sin \alpha\)

∴ BE = \(b \sin \alpha\)

Again, \(\frac{A E}{A B}=\cos \alpha\) or, \(A E=A B \cos \alpha\)

∴ AE = \(b \cos \alpha\)

Using Pythagoras theorem in right-angled ΔOEB, we get, \((O B)^2=(O E)^2+(B E)^2=(O A+A E)^2+(B E)^2\)

or, \(c^2=(a+b \cos \alpha)^2+(b \sin \alpha)^2\)

or, \(c^2=a^2+b^2 \cos ^2 \alpha+2 a b \cos \alpha+b^2 \sin ^2 \alpha\)

= \(a^2+b^2\left(\cos ^2 \alpha+\sin ^2 \alpha\right)+2 a b \cos \alpha\)

∴ \(c^2=a^2+b^2+2 a b \cos \alpha\) (because \(\cos ^2 \alpha+\sin ^2 \alpha=1\))

or, c = \(\sqrt{a^2+b^2+2 a b \cos \alpha}\)…….(1)

Law Of Parallelogram Of Vectors Analytical Method Direction Of Resultant \(\vec{c}\): Let the resultant \(\vec{c}\) make an angle θ with the direction of \(\vec{a}\). Then from right-angled ΔOEB, we get,

tanθ= \(\frac{B E}{O E}=\frac{B E}{O A+A E} \text { or, } \tan \theta=\frac{b \sin \alpha}{a+b \cos \alpha}\)…..(2)

Equations (1) and (2) are identical to those in the previous section.

It may be noted that two vectors and their resultant are always confined on a plane. This is not the case for three or more vectors and their resultant. The vectors and their resultant are, in general, distributed in 3-dimensional space.

Some Special Cases Of Addition Of Two Vectors

1. Two Parallel Vectors (α = 0): In this case, sinα = 0 and cosα = 1. Thus from equation (1), we can write,

c = \(\sqrt{a^2+b^2+2 a b}=\sqrt{(a+b)^2}=(a+b)\)

From equation (2), we can conclude that tanθ = 0, or, θ = 0°.

Hence, the magnitude of the resultant is the sum of the magnitudes of the vectors and it is directed along the vectors. It is simply a scalar addition.

2. Two anti-parallel vectors (α = 180°): In this case, sinα = 0 and cosα = -1.

Therefore, from equation (1), we get, c = \(\sqrt{a^2+b^2-2 a b}=\sqrt{(a-b)^2}\) or, \(c=|a-b|\) and from equation (2), tanθ = 0 or, θ = 0° when a > b or θ= 180° when b> a.

Hence, the magnitude of the resultant is the difference in the magnitudes of the vectors and its direction is along the larger vector. It is also a simple scalar operation.

3. Two Equal And Anti-Parallel Vectors (a = b and α = 180°): In this case sinα = 0 and cosα = -1.

Hence, using equation (1), c = \(\sqrt{a^2+a^2+2 a^2 \cos 180^{\circ}}=\sqrt{2 a^2-2 a^2}=0\)

Therefore, the magnitude of the resultant is zero. It is essentially a null vector.

4. Two Orthogonal (Perpendicular To Each Other) Vectors (α = 90°): In this case, sinα = 1 and cosα= 0

∴ From equation (1) and (2), c = \(\sqrt{a^2+b^2+2 a b \cos 90^{\circ}}=\sqrt{a^2+b^2}\) and \(\tan \theta=\frac{b}{a}\)

Therefore, we can conclude that,

1. The maximum possible value of the resultant = sum of magnitudes of the vectors i.e., c(max) = a + b
2. The minimum possible value of the resultant = difference of magnitudes of the vectors i.e., c (min) = |a- b|
3. If the vectors are equal in magnitude and anti-parallel, then the resultant will be 0.

Properties Of Vector Addition (Commutative And Associative Rules)

Properties Of Vector Addition Commutative Rule: Vector addition is commutative. If \(\vec{a}\) and \(\vec{b}\) are two vectors, then by this rule, \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\). This means that vectors can be added in any order.

Properties Of Vector Addition Commutative Rule Proof: OA and OC representing two vectors are two adjacent arms of the parallelogram OABC.

Here, \(\vec{a}=\overrightarrow{O A}=\overrightarrow{C B}\) and \(\vec{b}=\overrightarrow{O C}=\overrightarrow{A B}\)

So, \(\vec{a}+\vec{b}=\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}=\vec{c}\), (as per the triangle law of addition of vectors).

Again, \(\vec{b}+\vec{a}=\overrightarrow{O C}+\overrightarrow{C B}=\overrightarrow{O B}=\vec{c}\)

Hence, \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\) or in other words, vector sum is commutative.

Properties Of Vector Addition Associative Rule: Vector addition is associative. To add any three vectors, the addition may be initiated with any two of the vectors. Mathematically, \((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\), where \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are the given vectors. This rule holds good for the addition of more than three vectors as well.

Properties Of Vector Addition Associative Rule Associative Rule Proof: Let \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) be represented by the three arms OA, AB and BC of the quadrilateral OABC.

As shown, \(\vec{a}+\vec{b}=\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}\) and \(\overrightarrow{O B}+\overrightarrow{B C}=(\vec{a}+\vec{b})+\vec{c}=\overrightarrow{O C}\)

Again, as per figure, \(\vec{b}+\vec{c}=\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\)

∴ \(\vec{a}+(\vec{b}+\vec{c})=\overrightarrow{O A}+\overrightarrow{A C}=\overrightarrow{O C}\)

Hence, \(\vec{a}+(\vec{b}+\vec{c})=(\vec{a}+\vec{b})+\vec{c}\)

Itis noted that scalar addition also follows these two rules.

Law Of Polygon Of Vectors: Addition Of Three Or More Vectors: The sum (resultant) of two vectors can be determined by the law of triangle for vector addition. If the number of vectors is three or more, then by applying the law of triangle successively the law of polygon of vectors is derived. By the application of the law of polygon of vectors, the addition of any number of vectors is possible.

Suppose the resultant of four vectors \(\vec{a}, \vec{b}, \vec{c} \text { and } \vec{d}\) is to be determined. For this, vector \(\overrightarrow{O A}\) equal to \(\vec{a}\) is drawn from any point O.

Now taking A as the initial point, \(\overrightarrow{A B}\) equal to \(\vec{b}\) is drawn. Similarly, \(\overrightarrow{B C}\) equal to \(\vec{c}\) and \(\overrightarrow{C D}\) equal to \(\vec{d}\) are drawn one after another.

Then, the vector \(\overrightarrow{O D}\) drawn by joining the initial point O of the first vector and the terminal point D of the last vector represents the resultant of the vectors \(\vec{a}, \vec{b}, \vec{c} \text { and } \vec{d}\).

∴ \(\overrightarrow{O D}=\vec{R}=\vec{a}+\vec{b}+\vec{c}+\vec{d}=\overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}\)

This is called the law of polygon of vectors and with this law, the resultant of any number of vectors can be determined.

Laws Of Polygon Of Vectors Statement: If the magnitudes and directions of a number of vectors are represented by the sides of a closed polygon, taken in order, then the last side of the polygon, taken in the opposite order, represents the magnitude and direction of the resultant of the vectors.

The coplanarity of the vectors is not necessary for the validity of polygon law. Vectors can be added by using the polygon law irrespective of their number and sequence.

Proof Of The Law Of Polygon Of Vectors: Let the magnitudes and directions of the vectors \(\vec{a}, \vec{b}, \vec{c}, \vec{d}\) be represented, by the arms of the polygon OABCD, taken in order: \(\overrightarrow{O A}, \overrightarrow{A B}, \overrightarrow{B C}, \overrightarrow{C D}\).

From Triangle Law,

In triangle OAB, \(\overrightarrow{O B}=\overrightarrow{O A}+\overrightarrow{A B}\),

In triangle OBC, \(\overrightarrow{O C}=\overrightarrow{O B}+\overrightarrow{B C}=\overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{B C}\) and

In triangle OCD, \(\overrightarrow{O D}=\overrightarrow{O C}+\overrightarrow{C D}=\overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}\)

∴ \(\overrightarrow{O D}\)=\(\vec{R}=\overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}\)=\(\vec{a}+\vec{b}+\vec{c}+\vec{d}\)

Hence, \(\overrightarrow{O D}\) is the resultant of the vectors \(\vec{a}, \vec{b}, \vec{c}\) and \(\vec{d}\). The arm \(\overrightarrow{O D}\) is the remaining arm of the polygon taken in the opposite order. This proves the law and also shows that it is nothing but an extension of the law of triangle of vector addition.

Polygon Of Vector Corollary: In the pentagon OABCD, \(\overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}=\overrightarrow{O D}\)

or, \(\overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}-\overrightarrow{O D}=0\)

or, \(\overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D O}=0\)

In other words, if three or more vectors can be represented by the sides of a closed polygon, taken in order, the resultant of the vectors must be zero.

The physical quantities that have both magnitude and direction and obey all the laws of vector addition such as

1. Triangle law of vectors,
2. Parallelogram law of vectors and
3. The Polygon law of vectors are called vector quantities.

Unit 2 Chapter 2 Vector

Polygon Of Vectors Numerical Examples

Example 1. If \(\vec{a}+\vec{b}=\vec{c}\) and a + b = c, find the angle between \(\vec{a}\) and \(\vec{b}\).
Solution:

Let the angle between \(\vec{a}\) and \(\vec{b}\) be

Here, \(\vec{a}+\vec{b}=\vec{c}\) = \(\vec{c}\)

∴ c² = a² + b² + 2 ab cosα……..(1)

Again, a+b=c or, a² + b²+ 2ab = c²……(2)

Hence from (1) and (2), a² + b² + 2ab = a² + b² + 2ab cosα

or, 2ab = 2ab cosα or, cosα = 1 = cos0°

∴ α = 0°

Example 2. Can the magnitude of the resultant of two equal vectors be equal to the magnitude of each of the vectors? Explain.
Solution:

Let the magnitude of each vector and of the resultant be a and the angle between the vectors be α.

Hence, a² = a² + a² + 2a · a cosα

or, a² = 2a²(1+ cosα) or, 2(1 + cosα) = 1

or, cosα = \(\frac{1}{2}\) – 1 = –\(\frac{1}{2}\) = cos 120°

∴ α = 120°

Hence, the magnitude of the resultant of two equal vectors is equal to that of each of the given vectors when they are inclined at an angle of 120° with each other.

Example 3. 2P and P are two vectors inclined to each other at such an angle that if the 1st vector is doubled, the value of the resultant becomes three times. What is the angle between the two vectors?
Solution:

Let the initial resultant be R and the angle between the two vectors 2 P and P be α.

∴ \(R^2=(2 P)^2+P^2+2 \cdot 2 P \cdot P \cos \alpha\)

or, \(R^2=5 P^2+4 P^2 \cos \alpha\)…..(1)

In the second case, 1st vector =2 P x 2 = 4P and resultant = 3R

or, \((3 R)^2=(4 P)^2+P^2+2.4 P \cdot P \cos \alpha\)

or, \(9 R^2=17 P^2+8 P^2 \cos \alpha\)

or, \(R^2=\frac{17}{9} P^2+\frac{8}{9} P^2 \cos \alpha\)…..(2)

From (1) and (2), \(5 P^2+4 P^2 \cos \alpha=\frac{17}{9} P^2+\frac{8}{9} P^2 \cos \alpha\)

or, \(\left(4-\frac{8}{9}\right) \cos \alpha=\frac{17}{9}-5\)

or, \(\frac{28}{9} \cos \alpha=-\frac{28}{9}\)

or, \(\cos \alpha=-1=\cos 180^{\circ}\)

∴ \(\alpha=180^{\circ}\)

Example 4. Using vectors, prove that the line joining the midpoints of two sides of a triangle is parallel to the base and half its length.
Solution:

From the triangle law of vector addition in ΔABC, \(\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\)

or, \(\frac{1}{2} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{B C}=\frac{1}{2} \overrightarrow{A C}\)…..(1)

As D and E are the mid-points of sides AB and AC, \(\overrightarrow{A D}\)=\(\frac{1}{2} \overrightarrow{A B}\) and \(\overrightarrow{A E}=\frac{1}{2} \overrightarrow{A C}\)

From the triangle law of vector addition in ΔADE \(\overrightarrow{A D}+\overrightarrow{D E}\)=\(\overrightarrow{A E}\)

or, \(\frac{1}{2} \overrightarrow{A B}+\overrightarrow{D E}=\frac{1}{2} \overrightarrow{A C}\)……(2)

From (1) and (2), \(\overrightarrow{D E}=\frac{1}{2} \overrightarrow{B C}\)

Hence, \(\overrightarrow{D E}\) and \(\overrightarrow{B C}\) are parallel and DE = \(\frac{1}{2}\)BC.

Example 5. When will the magnitude of the resultant of two equal vectors be

1. √2 times and
2. √3 times the magnitude of each of them?

Solution:

Let the value of each vector be a and the angle between the two vectors be α.

1. In this case, the magnitude of the resultant =√2a

∴ (√2a)² = a² + a² + 2a · acosα

or, 2a² cosα = 0 or, cosα = 0 = cos 90°

∴ α = 90°

Hence, the angle between the two vectors will be 90°.

2. In this case, the magnitude of the resultant = √3a

∴ (√3a)² = a² + a²+ 2a · acosα

or, 2a² cosα = a² or, cosα = 1/2 = cos 60°

∴ α = 60°

The angle between the two vectors will be 60°.

Example 6. The maximum and the minimum values of the resul¬tant of two forces are 15 N and 7 N respectively. If the magnitude of each force is increased by 1 N and these new forces act at an angle of 90° to each other, find the magnitude and direction of their resultant.
Solution:

Let the magnitudes of the two forces be P and Q.

As per given condition, P + Q = 15 N…..(1)

and P-Q = 7N……(2)

By solving (1) and (2), we get, P = 11 N and Q = 4 N.

When each of the two forces is increased by 1 N in magnitude, the new magnitudes are P= (11 + 1) = 12 N and Q = (4 + 1) = 5 N and since the angle between these new forces is 90°, new resultant = \(\sqrt{12^2+5^2}=13 \mathrm{~N}\)

Let the angle of inclination of the resultant with the force 12 N be d.

Then, tanθ = \(\frac{5}{12}\) or, d = tan-1 \(\frac{5}{12}\)

∴ The magnitude of the resultant is 13 N and it is inclined with the force 12 N at an angle tan \(\frac{5}{12}\).

Example 7. The resultant \(\vec{R}\) of two vectors has a magnitude equal to one of the vectors and is at a right angle to it. Find the value of the other vector.
Solution:

Let Q be the value of the other vector.

R² + R² = Q² or, Q² = 2 R²

∴ Q = √2R

Example 8. The maximum magnitude of the resultant of two vectors, \(\vec{P}\) and \(\vec{Q}\)(where P> Q) is x times the minimum magnitude of the resultant When the angle between \(\vec{P}\) and \(\vec{Q}\) is θ, the magnitude of the resultant Is equal to half the sum of the magnitudes of the two vectors. Prove that, \(\cos \theta=\frac{x^2+2}{2\left(1-x^2\right)}\).
Solution:

P+Q=x(P-Q) (given) or, Q = \(\frac{x-1}{x+1} \cdot P\)

If R is the resultant of the two vectors when the angle between them is θ, then \(R^2=P^2+Q^2+2 P Q \cos \theta\)…..(1)

Given, \(R=\frac{P+Q}{2}=\frac{P+\frac{x-1}{x+1} \cdot P}{2}=\frac{x P}{x+1}\)

Putting in (1),

∴ \(\frac{x^2 P^2}{(x+1)^2}=P^2+\frac{(x-1)^2}{(x+1)^2} P^2+2 P^2\left(\frac{x-1}{x+1}\right) \cos \theta\)

or, \(\frac{x^2}{(x+1)^2}=1+\frac{(x-1)^2}{(x+1)^2}+\frac{2(x-1)}{x+1} \cos \theta\)

or, \(\frac{-\left(x^2+2\right)}{(x+1)^2}=\frac{2(x-1)}{(x+1)} \cos \theta\)

or, \(\cos \theta=\frac{-\left(x^2+2\right)}{2\left(x^2-1\right)}=\frac{x^2+2}{2\left(1-x^2\right)}\)

Example 9. Out of two vectors, the larger one is √2 times the smaller one. Show that the resultant cannot make an angle greater than π/4 with the larger one.
Solution:

Let the two vectors be √2Q and Q and the resultant be R. Angle between R and √2 Q is θ and ∠ADB = α.

From ΔABD, \(\frac{A B}{\sin \angle A D B}=\frac{B D}{\sin \angle D A B} \text { or, } \frac{\sqrt{2} Q}{\sin \alpha}=\frac{Q}{\sin \theta}\)

or, \(\sin \theta=\frac{1}{\sqrt{2}} \sin \alpha\)

∴ sinα ≯ 1, sinθ ≯  \(\frac{1}{\sqrt{2}}\)

Hence, θ ≯ \(\frac{\pi}{4}\)

Example 10. Show that If three forces are represented by the three medians of a triangle, they will be In equilibrium.
Solution:

Let the medians of the A ABC be \(\overrightarrow{A D}, \overrightarrow{B E} \text { and } \overrightarrow{C F}\). Vectors AD, BE and CF represent the three forces.

We have to show: \(\overrightarrow{A D}+\overrightarrow{B E}+\overrightarrow{C F}=\overrightarrow{0} \text {. }\)

As per triangle law of vector addition, \(\overrightarrow{A D}=\overrightarrow{A C}+\overrightarrow{C D}=\overrightarrow{A C}+\frac{1}{2} \overrightarrow{C B}\)

⇒ \(\overrightarrow{B E}=\overrightarrow{B A}+\overrightarrow{A E}=\overrightarrow{B A}+\frac{1}{2} \overrightarrow{A C}\)

⇒ \(\overrightarrow{C F}=\overrightarrow{C B}+\overrightarrow{B F}=\overrightarrow{C B}+\frac{1}{2} \overrightarrow{B A}\)

Hence, \(\overrightarrow{A D}+\overrightarrow{B E}+\overrightarrow{C F}=\frac{3}{2}(\overrightarrow{A C}+\overrightarrow{C B}+\overrightarrow{B A})=\overrightarrow{0}\)

[as the sum of 3 vectors, represented by the 3 sides of a triangle taken in order, is zero].

Example 11. The magnitude of the resultant of two forces P and Q acting at a point is (2m+1) \(\sqrt{P^2+Q^2}\) when the angle between them is a, and is (2m- 1)\(\sqrt{P^2+Q^2}\) when the angle is \(\left(\frac{\pi}{2}-\alpha\right)\) Prove that, \(\tan \alpha=\frac{m-1}{m+1}\).
Solution:

When the angle is, the magnitude of the resultant is, R = \(\sqrt{P^2+Q^2+2 P Q \cos \alpha}\)

Given, \(R=(2 m+1) \sqrt{P^2+Q^2}\)

On comparison, \(P^2+Q^2+2 P Q \cos \alpha=(2 m+1)^2\left(P^2+Q^2\right)\)

or, \(2 P Q \cos \alpha=\left(P^2+Q^2\right)\left\{(2 m+1)^2-1\right\}\)

= \(\left(P^2+Q^2\right)\left(4 m^2+4 m+1-1\right)\)

or, \(P Q \cos \alpha=2\left(P^2+Q^2\right) m(m+1)\)

= \(2 m(m+1)\left(P^2+Q^2\right)\)….(1)

Again, when the angle is \(\left(\frac{\pi}{2}-\alpha\right)\), the magnitude of the resultant is,

R’ = \(=\sqrt{P^2+Q^2+2 P Q \cos \left(\frac{\pi}{2}-\alpha\right)}=\sqrt{P^2+Q^2+2 P Q \sin \alpha}\)

Given, \(R^{\prime}=(2 m-1) \sqrt{P^2+Q^2}\).

On comparison, \(P^2+Q^2+2 P Q \sin \alpha=(2 m-1)^2\left(P^2+Q^2\right)\)

or, \(2PQ \sin \alpha=\left(P^2+Q^2\right)\left\{(2 m-1)^2-1\right\}\)

= \(\left(P^2+Q^2\right)\left(4 m^2-4 m+1-1\right)\)

or, \(P Q \sin \alpha=2\left(P^2+Q^2\right) m(m-1)\)

= \(2 m(m-1)\left(P^2+Q^2\right)\)….(2)

Dividing (2) by (1), we have, \(\tan \alpha=\frac{m-1}{m+1}\).

Example 12. Two forces P and Q have a resultant R. This resultant is doubled, either when Q Is doubled, or when Q is reversed. Show that, P:Q:P = √2:√3:√2.
Solution:

Let the angle between P and Q be \(\alpha\).

So, \(R^2=P^2+Q^2+2 P Q\) cosα

or, \(2 P Q \cos \alpha=R^2-P^2-Q^2\)…..(1)

When Q is doubled, \((2 R)^2=P^2+(2 Q)^2+2 P \cdot 2 Q \cos \alpha\)

or, \(2 P Q \cos \alpha=2 R^2-\frac{1}{2} P^2-2 Q^2\)…..(2)

Again, when Q is reversed, \((2 R)^2=P^2+Q^2+2 P Q \cos \left(180^{\circ}-\alpha\right)\)

or, \(2 P Q \cos \alpha=-4 R^2+P^2+Q^2\)…..(3)

From (1) and (3), \(R^2-P^2-Q^2=-4 R^2+P^2+Q^2\)

or, \(2 P^2+2 Q^2-5 R^2=0\)…..(4)

From (1) and (2), \(R^2-P^2-Q^2=2 R^2-\frac{1}{2} P^2-2 Q^2\)

or, \(P^2-2 Q^2+2 R^2=0\)…….(5)

Adding (4) and (5), \(3 P^2-3 R^2=0\) or, \(P=R\)

Putting this in (5), \(P^2-2 Q^2+2 P^2=0\) or, \(3 P^2=2 Q^2\) or, \(Q=\frac{\sqrt{3}}{\sqrt{2}} P\)

∴ \(P: Q: R=P: \frac{\sqrt{3}}{\sqrt{2}} P: P=1: \frac{\sqrt{3}}{\sqrt{2}}: 1=\sqrt{2}: \sqrt{3}: \sqrt{2}\)

Example 13. The resultant of two forces P and Q, inclined at a fixed angle, is it which makes an angle θ with P. If P is replaced by (P+ Q) keeping the direction unchanged, show that the resultant of (P+ R) and Q would be inclined at \(\frac{\theta}{2}\) with P+ R.
Solution:

Let a = angle between P and Q.

Then, R² = P² + Q² + 2PQcosα….(1)

and \(\tan \theta=\frac{Q \sin \alpha}{P+Q \cos \alpha}\)…..(2)

In the second case, if the resultant makes an angle θ₁ with P+R, then \(\tan \theta_1=\frac{Q \sin \alpha}{(P+R)+Q \cos \alpha}\)….(3)

Now, \(\tan \left(\theta-\theta_1\right)=\frac{\tan \theta-\tan \theta_1}{1+\tan \theta \tan \theta_1}\)

= \(\frac{\frac{Q \sin \alpha}{P+Q \cos \alpha}-\frac{Q \sin \alpha}{(P+R)+Q \cos \alpha}}{1+\frac{Q^2 \sin ^2 \alpha}{[P+Q \cos \alpha][(P+R)+Q \cos \alpha]}}\)

= \(\frac{R Q \sin \alpha}{[P+Q \cos \alpha][(P+R)+Q \cos \alpha]+Q^2 \sin ^2 \alpha}\)

= \(\frac{R Q \sin \alpha}{P^2+Q^2+2 P Q \cos \alpha+P R+R Q \cos \alpha}\)

= \(\frac{R Q \sin \alpha}{R^2+R(P+Q \cos \alpha)}=\frac{Q \sin \alpha}{(P+R)+Q \cos \alpha}\)

= \(\tan \theta_1 \text { [using equation (1) and (3)] }\)

∴ \(\theta-\theta_1=\theta_1 \quad \text { or, } \theta_1=\frac{\theta}{2}\)

Example 14. Four forces 2 P, P, P, and 2P acton a point towards NE, NW, SW, and SE directions respectively. Find the resultant of the forces.
Solution:

The forces 2P along NE, P along NW, P along SW, and 2P along SE are represented by \(\overrightarrow{O A}, \overrightarrow{A B}, \overrightarrow{B C} \text { and } \overrightarrow{C D}\) respectively.

The initial point O and the terminal point D are joined. Hence, the resultant of the four given vectors is \(\overrightarrow{O D}\).

Let ∠EOD = θ.

The quadrilateral EABC is a square. So, from ΔODE, DE = OE =P and ∠OED = 90°

∴ OD = \(\sqrt{P^2+P^2}=\sqrt{2 P^2}=\sqrt{2 P}\)

and \(\tan \theta=\frac{D E}{O E}=\frac{P}{P}=1 \quad \text { or, } \theta=45^{\circ}\)

Since, \(\overrightarrow{O A}\) is along NE, \(\overrightarrow{O D}\) is along east.

Alternative solution: The forces 2 P and P along NE and SW directions respectively are opposite to each other. Hence, their resultant = (2P-P) is equal to a force P directed towards NE.

Similarly, the resultant of P directed towards NW and 2P towards SE is equal to a force P along SE.

Now there two forces, P along NE and P along SE, are perpendicular to each other. So, the resultant is, F = \(\sqrt{P^2+P^2}=\sqrt{2} P\)

If the resultant F makes an angle 6 with P along NE, then tan9 = \(\frac{P}{P}\) = 1 or, 6 = 45°

Thus, F is in the eastward direction.

Hence, the resultant of the four forces is 72 P along the x-axis, i.e., along the east.

 

Resolutions Of Vectors

A vector can be resolved into many components just as many vectors can be added to give a single resultant vector.

Resolutions Of vectors Definition: When a vector is split into two or more vectors in such a manner that, the original vector becomes the resultant of the resolved parts or components of the vector, this splitting is called the resolution of vectors.

• Apparently, it may seem that the resolution of vectors is just the opposite of the addition of vectors. But it may be noted that, when two vectors are added, it gives only one resultant vector. On the other hand, in the resolution of vectors, different sets of components can be formed.
• The resolution of vectors into two or three components is an elegant technique to solve most of the problems related to vectors. Splitting into more than three components is very rare in practice.

Resolution In Two Dimensions

Resolution Of Vectors Into Two Components: Let the magnitude and direction of a given vector \(\vec{R}\) be represented by \(\overrightarrow{O A}\). OM and ON are inclined to OA by angles α and β respectively, in such a way that OA, OM, and ON lie on the same plane. The vector \(\vec{R}\) is to be resolved into components along OM and ON.

AC parallel to OM and AB parallel to ON are drawn to complete the parallelogram. Now, from the law of parallelogram of vectors, \(\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O A}\)

Thus, the two components of \(\overrightarrow{O A}\) are \(\overrightarrow{O B}\) and \(\overrightarrow{O C}\)  and their magnitudes are a and b respectively.

∴ OB = a and OC = BA = b

Applying trigonometric rules to ΔOAB, we get, \(\frac{O B}{\sin \angle O A B}=\frac{B A}{\sin \angle A O B}=\frac{O A}{\sin \angle A B O}\)

or, \(\frac{a}{\sin \beta}=\frac{b}{\sin \alpha}=\frac{R}{\sin [\pi-\{\alpha+\beta\}]}\)

or, \(\frac{a}{\sin \beta}=\frac{b}{\sin \alpha}=\frac{R}{\sin (\alpha+\beta)}\)

Hence, \(a=\frac{R \sin \beta}{\sin (\alpha+\beta)}\) and \(b=\frac{R \sin \alpha}{\sin (\alpha+\beta)}\)…..(1)

Since α and β can have many sets of values, a and b can also have many values. Hence, a vector can be resolved into different pairs of components.

The two most useful components of a vector are the two mutually perpendicular components when α + β = 90°. Then from equation (1), we get

a = \(\frac{R \sin \left(90^{\circ}-\alpha\right)}{\sin 90^{\circ}}=R \cos \alpha\)

and b = \(\frac{R \sin \alpha}{\sin 90^{\circ}}=R \sin \alpha\)…..(2)

Again, depending on α, different pairs of orthogonal components are possible.

Resolution Of Vectors Into Rectangular Or Orthogonal Components: \(\vec{R}\) has been resolved into two components along two mutually perpendicular axes OX and OY.

Let \(\overrightarrow{O B}=\vec{a}, \overrightarrow{O C}=\vec{b} \text { and } \angle A O B=\alpha\); i.e., the component \(\vec{a}\) is inclined to the vector R at an angle α.

According to \(\cos \alpha=\frac{O B}{O A}=\frac{a}{R}\)

or, a = Rcosα…..(1)

and \(\sin \alpha=\frac{A B}{O A}=\frac{b}{R} \text { or, } b=R \sin \alpha\)….(2)

Hence, the component of \(\vec{R}\) along a direction that makes an angle α with \(\vec{R}\) is Rcosα, and the other component is Rsinα.

Resolution Of Vectors Into Rectangular Or Orthogonal Components Special Cases: To determine the component of a vector \(\vec{R}\) along its own direction, we put α = 0° in equation (1) and get a = Rcos0° = R.

Again, by putting α = 0° in equation (2) [or, α = 90° in equation (1)], we get the other component, i.e., the component in the direction perpendicular to \(\vec{R}\), as, b = Rsin 0° = 0.

Hence, we may conclude that,

1. The component (or resolved part) of a vector along its own direction is the vector itself.
2. There is no component in a direction perpendicular to the vector.

Practical Example—Pull Or Push: A body can be set into motion along a horizontal plane by pushing it from the back or by pulling it towards the front. When the body is pushed, the applied force F₁ usually acts downwards at an angle with the horizontal.

• Horizontal motion of the body is due to the horizontal component F_x of the applied force F₁. The vertical component F_y, acting downwards, adds to the weight of the body, and hence, pushing becomes difficult.
• On the other hand, while pulling, the applied force F₂ acts upwards at an angle with the horizontal. In this case, also, the horizontal component F’_x of F₂ produces the horizontal motion of the body. The vertical component F’_y acting upwards, effectively reduces the weight of the body. Hence pulling becomes easier.

Thus, it is easier to pull a body than to push it.

Resolutions In Two Dimensional Numerical Examples

Example 1. A force of 30 dyn Is inclined to the y-axis at an angle of 60°. Find the components of the force along the x and y axes respectively.
Solution:

Given, F = 30 dyn and θ = 60°

Hence, a component of F along the y-axis, F_y = F cosθ = F cos60° = 30 x 1/2 = 15 dyn

and a component of F along x-axis \(F_x=F \sin 60^{\circ}=30 \times \frac{\sqrt{3}}{2}=15 \sqrt{3} \text { dyn }.\)

Example 2. The value of the resultant of two mutually perpendicular forces is 80 Dyn. The resultant makes an angle 60° with one of the forces. Find the magnitudes of the forces.
Solution:

Let the forces be \(\vec{P}\), \(\vec{R}\) and the resultant that makes an angle 60° with \(\vec{P}\) be  \(\vec{R}.\)

Here, R = 80 dyn

∴ P = R cosθ – 80 cos60° = 80 x 1/2 = 40 dyn

and Q = R sin60° =80 sin60° = \(80 \times \frac{\sqrt{3}}{2}\) = 40√3 dyn .

 

Motion Of A Projectile

Motion Of A Projectile Definition: A body thrown upwards in any direction from the earth’s surface or a point close to it, is called a projectile. Common examples of projectiles are

1. A javelin thrown by an athlete,
2. A bullet fired from a rifle,
3. An object dropped from an airplane,
4. A jet of water coming out from the side hole of a vessel,
5. A stone thrown from the top of a hill or a tower,
6. A rocket after its fuel is exhausted.

The path traced out by a projectile is called its trajectory. The motion of a projectile is two-dimensional as it is always confined to a vertical plane.

• To study the projectile motion the horizontal direction is taken along the x-axis and the vertical direction is taken along the y-axis. The only force acting on the projectile is the gravitational force.
• So the projectile has acceleration in the y direction which is equal to the acceleration due to gravity. The force acting on the projectile is zero along the x-axis. So the horizontal acceleration is zero. This means, that projectile motion is a combination of horizontal motion with constant velocity and vertical motion with uniform acceleration.
• Let a body be projected from a point O with velocity u making an angle α with the horizontal. The body reaches B following the path OAB through the highest point A. Points B and O lie on the same horizontal plane.

O is the point of projection, u is the velocity of projection, the angle of projection, and OB is the horizontal range; the time taken for traveling the path OAB is called the time of flight. Velocity of projection u has a horizontal component = \(u_{x_0}=u \cos \alpha\) and a vertical component = \(u_{y_0}=u \sin \alpha\).

• As acceleration due to gravity (g) acts vertically downward, the velocity component usina gradually changes. Hence, the vertical motion of the body is a motion under gravity. But since g has no component along the horizontal direction, the acceleration or deceleration of the horizontal component of motion is zero.
• Hence, the motion of the body along the horizontal direction is uniform, i.e., horizontal velocity \(u_{x_0}=u \cos \alpha\) = constant. It is convenient to use the vertical motion and the horizontal motion separately in discussions related to projectile motion.

Principle Of Physical Independence Of Motions: In the absence of air resistance the motion of a projectile is considered as the combination of the following two independent motions.

1. Motion along the horizontal direction with uniform velocity.
2. Motion along vertical direction under gravity i.e., uniform acceleration equal to g.

The two motions of a projectile along horizontal and vertical directions are independent of each other. This is called the principle of physical independence of motion.

Principle Of Physical Independence Of Motions Key Points:

1. A projectile returns to the ground at the same angle and with the same velocity with which it is projected.
2. When a projectile is at the highest point of its trajectory
   1. It possesses velocity only along horizontal,
   2. The velocity and acceleration of the projectile are perpendicular to each other.

Equations For Projectile Motion: Let the time taken by the projectile to reach the point P be t.

For the horizontal motion of the projectile we have, \(v_x=u_{x_0}+a_x t\)

or, \(v_x=u \cos \alpha\) (because \(a_x=0\))….(1)

where v_x is the horizontal component of the velocity of the projectile after time t.

Again, \(x=u_{x_0} t+\frac{1}{2} a_x t^2\)

or, \(x=u_{x_0} t=u \cos \alpha t\)….(2)

From this equation, we get the horizontal position of the projectile after time t.

For the vertical motion of the projectile, a_y=-g

∴ \(v_y=u_{y_0}+a_y t\)

[v_y is the vertical component of velocity of the projectile after time t]

or, \(v_y=u_{y_0}-g t\) (because \(a_y=-g\))……(3)

Again, \(v_y^2=u_{y_0}^2-2 g y\)

and \(y=u_{y_0} t+\frac{1}{2} a_y t^2=u_{y_0} t-\frac{1}{2} g t^2\)

From equation (4), we get the vertical position of the projectile after time t.

Equations For Projectile Motion Maximum Height: The maximum height of a projectile is the maximum vertical distance attained by the projectile above the horizontal plane of projection. It is denoted by H. To calculate the height of the projectile, consider only its vertical motion. The vertical component of the velocity of projection = u sinα and velocity at the highest point = 0.

If H = maximum height, \(0=(u \sin \alpha)^2-2 g H \text { or, } H=\frac{u^2 \sin ^2 \alpha}{2 g}\)….(5)

It should be noted that the body attains maximum height by reaching a point that is not exactly above point O. Because of the horizontal component of motion, the body has a horizontal displacement as well. the highest point on the trajectory of the projectile is point A and maximum height (H) = AC.

Time Of Flight: It is the time taken by the projectile from the instant it is projected till it reaches a point in the horizontal plane of its projection. As shown the total time taken to reach point B from point O is the time of flight.

Let the time taken to reach the maximum height be T₁

Hence, \(0=u \sin \alpha-g T_1 \text { or, } T_1=\frac{u \sin \alpha}{g}\)….(6)

On reaching the highest point, the body starts descending again. At the same time, the body covers a horizontal path due to its horizontal component of motion. Finally, the body reaches B. Thus, the body follows the trajectory OAB.

The height of B with respect to the point of projection, O is zero, i.e., the vertical displacement of the object is zero. Hence, if T is the time required to cover the path OAB,

0 = \(u \sin \alpha \cdot T-\frac{1}{2} g T^2\) [from equation (4)]

∴ \(2 u \sin \alpha=g T or, T=\frac{2 u \sin \alpha}{g}\)…..(7)

Comparing equations (6) and (7), \(2 T_1=\frac{2 u \sin \alpha}{g}=T \text { or, } T_1=\frac{T}{2}\)

So, the time required to reach the maximum height is equal to half the time of flight.

Horizontal Range: Let the horizontal range be OB = R. The horizontal distance traversed by the body in time T is R. Since the body crosses the distance R horizontally with a uniform velocity ucosα,

R = \(u \cos \alpha \cdot T=u \cos \alpha \cdot \frac{2 u \sin \alpha}{g}\)

= \(\frac{2 u^2 \sin \alpha \cos \alpha}{g}=\frac{u^2}{g} \sin 2 \alpha\)…..(8)

The value of R is maximum when sin 2α is maximum. Therefore, the condition for covering the maximum horizontal distance for a particular initial velocity u, is sin 2α = 1 = sin90° or, α = 45°.

∴ \(R_{\max }=\text { Maximum range }=\frac{u^2}{g}\)…..(9)

To send a projectile to the maximum possible distance, it has to be thrown at an angle of 45° with the horizontal. This is why sportsmen try to throw the javelin or discus at 45°.

It should be noted that if the angle of projection is (\(\frac{\pi}{2}-\alpha\)) instead of a, the horizontal range remains the same for a particular velocity of projection, since, \(R^{\prime}=\frac{u^2}{g} \sin \left\{2\left(\frac{\pi}{2}-\alpha\right)\right\}\) = \(\frac{u^2}{g} \sin (\pi-2 \alpha)=\frac{u^2}{g} \sin 2 \alpha=R\)

Locus Of A Projectile: Let us take a reference frame such that, its positive y-axis extends vertically upwards, and the positive x-axis extends horizontally in the direction of the horizontal component of the velocity of the projectile. The origin is taken as the point of projection

Let the point reached by the body from O in time f be P and the coordinates of P be (x, y).

y = \(u \sin \alpha \cdot t-\frac{1}{2} g t^2\)…………(10)

Again, as the horizontal velocity =ucosa = constant, x = ucosα · t

or, \(t=\frac{x}{u \cos \alpha}\)

From (10) and (11), \(y=u \sin \alpha \frac{x}{u \cos \alpha}-\frac{1}{2} g \frac{x^2}{u^2 \cos ^2 \alpha}\)

or, y = \(x \tan \alpha-\frac{g}{2 u^2 \cos ^2 \alpha} x^2\)

This equation is the locus of the projectile.

The equation is of the type y=ax+bx² which is the equation of a parabola. Hence, the trajectory of a projectile is parabolic.

Motion Of A Projectile Numerical Examples

Example 1. A body is projected with a velocity of 20 m s^-1, making an angle of 45° with the horizontal. Calculate—

1. The time taken to reach the ground [g = 10 m s^-2],
2. The maximum height it can attain and
3. Horizontal range.

Solution:

The vertical and horizontal components of the velocity of 20 m s^-1 are \(u_H=20 \cos 45^{\circ}=20 \times \frac{1}{\sqrt{2}}=10 \sqrt{2} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

and \(u_V=20 \sin 45^{\circ}=20 \times \frac{1}{\sqrt{2}}=10 \sqrt{2} \mathrm{~m} \cdot \mathrm{s}^{-1}\).

1. Let the total time of flight of the body be t. Considering the vertical motion of the body, we get from the equation h = ut-\(\frac{1}{2}\)gt²,

0 = \(10 \sqrt{2} t-\frac{1}{2} \cdot 10 \cdot t^2 \quad[\text { as } h=0]\)

or, \(5 t^2=10 \sqrt{2} t\)

∴ Total time of flight, \(t=\frac{10 \sqrt{2}}{5}=2 \sqrt{2}=2 \times 1.414=2.828 \mathrm{~s}\)

2. Let the maximum height attained be h. Vertical velocity at the maximum height = 0.

Considering the vertical motion of the body, we get from the equation v² = u²- 2gh,

0 = (10√2)² -2 ·10 · h

∴ h = 10m

3. Let the distance from the point of projection to the point at the ground where the body touches be x. By considering the horizontal motion of the body, we get,

x = u_H x t = 10√2 x 2√2 = 40 m.

∴ The horizontal range = 40 m.

Example 2.  A plane is flying horizontally at a height of 196 m at 600 km · h^-1 with respect to the ground. On reaching a point directly above A, the plane drops an object that reaches the ground at B. Find the distance AB.
Solution:

Let the point directly above A from where the object is dropped be O

Therefore, OA = 1960 m. Let the time taken by the object to hit the ground at B be t.

Since the plane is flying horizontally, the initial vertical velocity of the object = 0 and vertical (downward) A displacement = 1960 m.

Considering the vertical motion of the object, we get from the equation h = ut + \(\frac{1}{2}\) gt²,

1960 = \(0 \times t+\frac{1}{2} \times 9.8 \times t^2\)

or, \(t^2=\frac{2 \times 1960}{9.8}=400\) or, \(t=20 \mathrm{~s}\)

The initial horizontal velocity of the body = \(600 \mathrm{~km} \cdot \mathrm{h}^{-1}=\frac{600 \times 1000}{60 \times 60} \mathrm{~m} \cdot \mathrm{s}^{-1}=\frac{500}{3} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

So, the object moves at a uniform velocity of \(\frac{500}{3} \mathrm{~m} \cdot \mathrm{s}^{-1}\) in the horizontal direction. Hence,

AB = \(\frac{500}{3} \times 20 \mathrm{~m}=\frac{500 \times 20}{3 \times 1000} \mathrm{~km}=\frac{10}{3}=3.33 \mathrm{~km}\)

Example 3.  A particle falls from rest from the highest point of a vertical circle of radius r, along a chord without any friction. Show that the time taken by the particle to come down is independent of the chord’s length. Find the time in terms of r and g.
Solution:

Let the chord along which the particle falls be CD. The CD makes an angle θ with the vertical diameter as shown. CD = 2 r cosθ. The component of acceleration due to gravity along CD = g cosθ.

Let the time taken by this particle to fall from rest along CD be t.

Hence, from the equation s = ut + \(\frac{1}{2}\) at²,

2r \(\cos \theta\) = \(0+\frac{1}{2} g \cos \theta \cdot t^2\)

or, \(t^2=\frac{4 r}{g} \text { or, } t=2 \sqrt{\frac{r}{g}}\)

The time is independent of θ, and hence on the length of the chord CD.

Example 4. At what angle with respect to the horizontal, should a projectile be thrown with a velocity of 19.6 m · s^-1, to just clear a wall 14.7 m high, at a distance of 19.6 m?
Solution:

Let the angle of projection be θ. Hence horizontal component of velocity = 19.6 cosθ m · s^-1 and its vertical component = 19.6 sinθ m · s^-1.

Let the time after which the projectile crosses the wall be t.

Considering horizontal motion, 19.6 = 19.6 cosθ x t or, t = secθ

For the vertical motion, 14.7 =19.6 sinθ x t \(\frac{1}{2}\) x 9.8 x t²

or, 14.7 = 19.6 sinθ x secθ-4.9 sec²θ

or, 3 = 4 tanθ – (1 + tan²θ) or, tan²θ-4tanθ + 4 = 0

or, (tanθ – 2)³ = 0 or, tanθ = 2

∴ θ = tan^-1 2 = 63.4°

Example 5. A block of ice is sliding down the sloping roof of a house and the angle of inclination of the roof with the horizontal is 30°. The maximum and minimum heights of the roof from the ground are 8.1 m and 5.6 m. How far from the starting point, measured horizontally, does the block land? [ignore friction].
Solution:

Let the highest point of the roof be A and the lowest point be P as shown.

∴ AC= 8.1 m; PD = 5.6 m

∴ AB =AC-BC =AC-PD= 8.1 -5.6 = 2.5 m

AP = \(\frac{A B}{\sin 30^{\circ}}=\frac{2.5}{\frac{1}{2}}=5 \mathrm{~m}\)

Let the velocity of the block at P be v.

Considering the motion of the block from A to P,

v² = 2g sin30° xAP = 2 x 9.8 x \(\frac{1}{2}\) x 5 = 49 or, v = 7 m · s^-1.

The horizontal and vertical components of the velocity at P are \(v \cos 30^{\circ}=\frac{7 \sqrt{3}}{2} \mathrm{~m} \cdot \mathrm{s}^{-1} \quad \text { and } \quad v \sin 30^{\circ}=\frac{7}{2} \mathrm{~m} \cdot \mathrm{s}^{-1}\) respectively.

Let the total time taken by the block to come from P to E be t. Considering the vertical motion of the block,

5.6 = \(\frac{7}{2} t+\frac{1}{2} \times 9.8 \times t^2 \quad \text { or, } 7 t^2+5 t-8=0\)

∴ t = \(\frac{-5 \pm \sqrt{25+224}}{14}=0.77 \mathrm{~s}\) [taking the positive value of t]

Now, DE =  \(\nu \cos 30^{\circ} \times t=\frac{7 \sqrt{3}}{2} \times 0.77=2.7 \sqrt{3} \mathrm{~m}\)

∴ CE = \(C D+D E=2.5 \sqrt{3}+2.7 \sqrt{3}\)

(\(\tan 30^{\circ}=\frac{A B}{P B} \text { or, } P B=2.5 \sqrt{3} \mathrm{~m}\) and, DC = \(P B=2.5 \sqrt{3} \mathrm{~m}]\))

= \(5.2 \sqrt{3}=9 \mathrm{~m}\)

Example 6. The equation of the trajectory of a projectile on s vertical plane is y = ax- bx², where a and b are constants, and x and y respectively are the horizontal distances of the projectile from the point of projection. Find out the maximum height attained by the projectile, and also the angle of projection with respect to the horizontal.
Solution:

Let, u = velocity of projection; α = angle of projection

The velocity ucosα in the horizontal direction is uniform.

So, in time t, x = \(u \cos \alpha \cdot t \quad \text { or, } t=\frac{x}{u \cos \alpha}\)

The velocity u sin α in the vertically upward direction is under a uniform retardation -g, where g is the acceleration due to gravity.

Then, in time t, y = \(u \sin \alpha \cdot t-\frac{1}{2} g t^2=u \sin \alpha \cdot \frac{x}{u \cos \alpha}-\frac{1}{2} g \frac{x^2}{u^2 \cos ^2 \alpha}\)

or, \(y=x \tan \alpha-\frac{g}{2 u^2 \cos ^2 \alpha} x^2\)

Comparing with the given equation y=a x-bx², we get

1. a =θ, or angle of projection, \(\theta=\tan ^{-1} a\).
2. b = \(\frac{g}{2 u^2 \cos ^2 \alpha} \quad or, u^2=\frac{g}{2 b \cos ^2 \alpha}\)

At maximum height H, the velocity of the projectile is zero.

Considering vertical motion, we have

0 = \((u \sin \alpha)^2-2 g H\)

or, H = \(\frac{u^2 \sin ^2 \alpha}{2 g}=\frac{g}{2 b \cos ^2 \alpha} \cdot \frac{\sin ^2 \alpha}{2 g}\)

= \(\frac{\tan ^2 \alpha}{4 b}=\frac{a^2}{4 b}\)

Example 7. A gun fires at an angle 30° with the horizontal and hits a target at a distance of 3 km. Can another target at a distance of 5 km be hit by changing the angle of projection but keeping the velocity of projection unchanged?
Solution:

Horizontal range, \(R=\frac{u^2 \sin 2 \alpha}{g}\)

In the first case, 3 = \(\frac{u^2 \sin \left(2 \times 30^{\circ}\right)}{g}=\frac{u^2}{g} \frac{\sqrt{3}}{2}\)

or, \(\frac{u^2}{g}=2 \sqrt{3}\)

If the velocity of projection is unchanged, the maximum horizontal range for \(\alpha=45^{\circ}\), is \(R_{\max }=\frac{u^2 \sin \left(2 \times 45^{\circ}\right)}{g}=\frac{u^2}{g}=2 \sqrt{3}\)

= \(2 \times 1.732=3.464 \mathrm{~km}\)

So, a target at a distance of 5 km cannot be hit.

Example 8. A gun is kept on a horizontal road and is used to hit a running car. The uniform speed of the car is 72 km/h. At the instant of firing at an angle of 45° with the horizontal, the car is at a distance of 500 m from the gun. Find out the distance between the gun and the car at the instant of hitting. Given, 10 m/s².
Solution:

Velocity of the car, v = 72 km/h = 20 m/s;

if it is hit after a time s, then its displacement = 201 m

∴ Distance between the gun and the car at that instant,

D =  500 + 20tm.

If u be the initial velocity of the bullet, then its horizontal range,

R = \(\frac{u^2 \sin \left(2 \times 45^{\circ}\right)}{g}=\frac{u^2}{g}\)

∴ \(\frac{u^2}{g}=500+20 t\)…..(1)

Considering the vertical motion of the bullet in time t, we have

0 = \(u \sin 45^{\circ} \cdot t-\frac{1}{2} g t^2 \quad \text { or, } \frac{u t}{\sqrt{2}}=\frac{1}{2} g t^2\)

or, u = \(\frac{1}{\sqrt{2}} g t\)

∴ \(u^2=\frac{1}{2} g^2 t^2 \quad \text { or, } \frac{u^2}{g}=\frac{1}{2} g t^2=\frac{1}{2} \times 10 \times t^2=5 t^2\)

Putting in (1), we get \(5 t^2=500+20 t \text { or, } t^2-4 t-100=0\)

∴ t = \(\frac{4 \pm \sqrt{16-4 \times 1 \times(-100)}}{2 \times 1}=2 \pm \sqrt{104}\)

Keeping only the positive value of t, we have \(t=2 \pm \sqrt{104}=12.2 \mathrm{~s}\)

So, we get, \(D=500+20 t=500+20 \times 12.2=744 \mathrm{~m} \text {. }\)

Example 9. The initial velocity of a projectile is (\(\hat{i}+2 \hat{j}\)) m/s, where i and j are unit vectors along the horizontal and vertical directions respectively. Find out the locus of the projectile, taking g = 10 m/s².
Solution:

Horizontal and vertical components of initial velocity are, respectively,

u_x = 1 m/s and u_y = 2 m/s

Let, at t = 0, the initial coordinates of the projectile are (0, 0); at time t, these are (x, y).

So, \(x=u_x t=t \mathrm{~m}\)

y = \(u_y t-\frac{1}{2} g t^2=\left(2 t-5 t^2\right)=2 x-5 x^2\)

∴ \(y=2 x-5 x^2\) is the locus of the projectile.

Example 10. Two objects are thrown simultaneously from the same point with the same initial velocity at angles of projection α and β respectively. If they reach the top and the bottom of a tower simultaneously, then prove that tanα – tanβ = tanθ where θ = angle of elevation of the tower from the point of projection.
Solution:

Horizontal range of the 2nd projectile

OB = \(x=\frac{u^2 \sin 2 \beta}{g}=\frac{2 u^2}{g} \sin \beta \cos \beta\)…..(1)

Time of flight of the 2nd projectile, t = \(\frac{2 u \sin \beta}{g}\)

= time taken by the 1st projectile from O to A

For the horizontal motion of the 1st projectile,

OB = \(x=u \cos \alpha \cdot t=u \cos \alpha \cdot \frac{2 u \sin \beta}{g}\)

= \(\frac{2 u^2}{g} \sin \beta \cos \alpha\)……….(2)

Comparing (1) and (2), we have \(\cos \alpha=\cos \beta\)…….(3)

For the vertical motion of the 1st projectile, AB = \(y=u \sin \alpha \cdot t-\frac{1}{2} g t^2\)

= \(u \sin \alpha \frac{2 u \sin \beta}{g}-\frac{1}{2} g\left(\frac{2 u \sin \beta}{g}\right)^2\)

= \(\frac{2 u^2}{g}\left(\sin \alpha \sin \beta-\sin ^2 \beta\right)\)…….(4)

Diving (4) by (1), we have \(\tan \theta=\frac{A B}{O B}=\frac{y}{x}=\frac{\sin \alpha \sin \beta-\sin ^2 \beta}{\sin \beta \cos \beta}\)

= \(\frac{\sin \alpha}{\cos \beta}-\frac{\sin \beta}{\cos \beta}=\frac{\sin \alpha}{\cos \alpha}-\tan \beta\)

= \(tan \alpha-\tan \beta\) (using (3))

Example 11. A truck starts from rest and accelerates uniformly. at 2 m · s^-2 At t = 10 s, a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What are the

1. Velocity and
2. Acceleration of the stone at t = 11 s? (Neglect air resistance).

Solution:

The velocity of the truck after 10s = at = 2 x 10 = 20 m · s^-1

So, at the time of release, the stone has a horizontal velocity of 20 m • s^-1, but no vertical velocity. Its horizontal acceleration = 0 and vertical acceleration, g = 9.8 m • s^-2.

1. At 11 s, i.e., 1 s after release, the horizontal velocity of the stone = 20 m • s^-1;

vertical velocity = gt = 9.8 x 1 = 9.8 m • s^-1

So, the resultant velocity = \(\sqrt{(20)^2+(9.8)^2}=22.27 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

2. The acceleration of the stone = downward acceleration due to gravity = 9.8 m • s^-2

 

Vector Synopsis

Geometrical Representation Of A Vector:

1. A vector is represented by a line segment with an arrowhead,
2. The magnitude of the vector is the length of the line segment and
3. The direction of the vector is shown by the arrowhead.

Triangle Law Of Vector Addition: If two sides of a triangle taken in order, represent the magnitudes and directions of two vectors, the third side, taken in the opposite order, represents the magnitude and direction of the resultant of the two vectors.

If three vectors can be represented by the three sides of a triangle, taken in order, the resultant of the vectors is a zero vector.

Parallelogram Law Of Vector Addition: If two adjacent sides of a parallelogram represent the magnitudes and directions of two vectors, then the diagonal, drawn through the intersection of the two sides of the parallelogram, represents the magnitude and direction of the resultant of the two vectors. In this case the point of intersection is the initial point of the two vectors and their resultant.

Polygon Law Of Vector Addition: If the magnitudes and directions of a number of vectors are represented by the sides of a polygon, taken in order, then the last side, taken in the opposite order, represents the magnitude and direction of the resultant of the vectors.

• If any vector is split into two or more vectors such that the original vector becomes the resultant of the split parts or components of the vector, then this splitting is called the resolution of vectors.
• Component of a vector in the same direction as the vector has the same magnitude as the vector itself.
• No vector has a component at right angles to itself.
• When the position of a point with respect to the origin is represented by a vector, then that vector is called the position vector.
• The apparent velocity of a body, with respect to another body at rest or in motion, is called its relative velocity.
• The apparent acceleration of a body, with respect to another body moving with or without, is called its relative acceleration.
• The scalar product or dot product of two vectors is a scalar, whereas the vector product or cross product of two vectors is another vector.
• A body thrown obliquely from the earth’s surface or from a point close to it is called a projectile.
• The path of a projectile is parabolic except for those projected along the vertical direction. In that case, it is a straight line.

Resultant of \(\vec{a}\) and \(\vec{b}\), when the angle between them is \(\alpha\), is \(\vec{c}\) such that \(c=\sqrt{a^2+b^2+2 a b \cos \alpha}\). [equation giving the magnitude of the resultant]

If the angle between \(\vec{a}\) and \(\vec{c}\) is \(\theta\), then \(\tan \theta=\frac{b \sin \alpha}{a+b \cos \alpha}\) [equation giving the direction of the resultant]

1. When \(\alpha=0\), \(c=a+b=c_{\max }\) (maximum possible value of the resultant) and \(\theta=0\).
2. For \(\alpha=\pi\), \(c=|a-b|=c_{\text {min }}\) (minimum possible value of c) and \(\theta=0\), (when a>b) or \(\theta=\pi\) (when a<b)
   • Note: α or θ is usually measured from \(\vec{a}\).
3. When \(\alpha=\frac{\pi}{2}\) then \(c=\sqrt{a^2+b^2}\) and \(\theta=\tan ^{-1} \frac{b}{a}\).

Characteristics Of Vector Addition:

1. \(\vec{A}+\vec{B}=\vec{B}+\vec{A}\) [Commutative rule]
2. \(\vec{A}+(\vec{B}+\vec{C})=(\vec{A}+\vec{B})+\vec{C}\)[Associative rule]
3. \(\vec{A}-\vec{B}=\vec{A}+(-\vec{B})\)
4. \((-n) \vec{A}=n(-\vec{A})=-n \vec{A}\)

If two components of \(\vec{R}\) are \(\vec{a}\) and \(\vec{b}\), angle between \(\vec{R}\) and \(\vec{a}\) is \(\alpha\), and angle between \(\vec{R}\) and \(\vec{b}\) is \(\beta\), then

a = \(\frac{R \sin \beta}{\sin (\alpha+\beta)} \text { and } b=\frac{R \sin \alpha}{\sin (\alpha+\beta)}\)

When \(\alpha+\beta=\frac{\pi}{2}\) then \(a=R \cos \alpha, b=R \sin \alpha\)

If coplanar vectors \(\vec{P}, \vec{Q}\) and \(\vec{R}\) are at angles \(\alpha, \beta\) and \(\gamma\) respectively with respect to the positive x-axis, then the component of their resultant \(\vec{F}\) along the positive x-axis, \(F_x=P \cos \alpha+Q \cos \beta+R \cos \gamma\)

and component of \(\vec{F}\)

along the positive y-axis \(F_y=P \sin \alpha+Q \sin \beta+R \sin \gamma\)

and hence, \(F=\sqrt{F_x^2+F_y^2}\)

When \(\vec{F}\) makes an angle \(\theta\) with the positive x-axis \(\theta=\tan ^{-1} \frac{F_y}{F_x}\)

Taking O as the origin of the three-dimensional cartesian coordinate system, we get the position vector of A(x, y, z) as, \(\vec{r}=\overrightarrow{O A}=x \hat{i}+y \hat{j}+z \hat{k}\)

∴ r = \(\sqrt{x^2+y^2+z^2}\)

If \(\vec{r}\) makes angles \(\alpha, \beta, \gamma\), with x, y, z axes respectively, then the direction cosines of \(\vec{r}\) are \(\cos \alpha=\frac{x}{r}, \cos \beta=\frac{y}{r}\) and \(\cos \gamma=\frac{z}{r}\) where, \(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1\)

The resultant of \(\vec{r}_1=x_1 \hat{i}+y_1 \hat{j}+z_1 \hat{k}\) and \(\vec{r}_2=x_2 \hat{i}+y_2 \hat{j}+z_2 \hat{k}\) is \(\vec{r}_1+\vec{r}_2=\left(x_1+x_2\right) \hat{i}+\left(y_1+y_2\right) \hat{j}+\left(z_1+z_2\right) \hat{k}\)

If \(\theta\) is the angle between \(\vec{A}\) and \(\vec{B}\), vector and scalar products of the vectors \(\vec{A}\) and \(\vec{B}\) are respectively \(\vec{A} \times \vec{B}=A B \sin \theta \hat{n} \text { and } \vec{A} \cdot \vec{B}=A B \cos \theta\)

(where \(\hat{n}\) is the unit vector perpendicular to both \(\vec{A}\) and \(\vec{B}\))

If the velocities of two particles are \(\vec{v}_1\) and \(\vec{v}_2\), then the relative velocity of the second particle with respect to the first is, \(\vec{v}=\vec{v}_2-\vec{v}_1\)

If velocity and angle of projection of a projectile are u and \(\alpha\) respectively, then

1. Maximum height, \(H=\frac{u^2 \sin ^2 \alpha}{2 g}\)
2. Time of flight, \(T=\frac{2 u \sin \alpha}{g}\)
3. Range of the projectile, \(R=\frac{u^2 \sin 2 \alpha}{g}\)
4. Equation of the locus of the projectile, y = \(x \tan \alpha-\frac{g}{2 u^2 \cos ^2 \alpha} x^2 \text { (a parabola). }\)

 

Vector Match The Columns

Question 1. \(\vec{A}=(3 \hat{i}+4 \hat{j}-5 \hat{k})\)

Answer: 1-B, 2-C, 3-D, 4-D

Question 2. \(|\vec{A}|=2 \text { and }|\vec{B}|=4\). \(\theta\) is the angle between \(\vec{A} \text { and } \vec{B} \text {. }\)

Answer: 1-B, 2-A, 3-D, 4-C

Question 3. \(|\vec{A}|=2 \text { and }|\vec{B}|=4\). \(\theta\) is the angle between A and B

Answer: 1-D, 2-C, 3-A, 4-B

Question 4. If θ is the angle between two vectors A and B, then match the following columns.

Answer: 1-D, 2-B, C, 3-A, 4-A

Question 5. Vector A is pointing eastwards and vector B is northwards. Then match the following two columns.

Answer: 1-A, 2-D, 3-B, 4-D

Question 6. Given below in Column A is the relations between vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) and in Column B are the orientations of \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) in the XY plane.

Answer: 1-D, 2-C, 3-A, 4-B

Question 7. For a projectile thrown from the ground at an angle with the horizontal

Answer: 1-C, 2-B, 3-D, 4-E

Vector Comprehension Type Questions And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A farmer goes 500 m due north, 400 m due east and 200 m due south to reach his field. He takes 20 min to reach the field.

1. How much distance does he to walk to reach the field?

1. 900 m
2. 1100 m
3. 1300 m
4. 700 m

Answer: 2. 1100 m

2. What is the displacement from his house to the field?

1. 550 m
2. 700 m
3. 500 m
4. 714 m

Answer: 3. 500 m

3. What is the average speed of the farmer during the walk?

1. 35 m • min^-1
2. 63 m • min^-1
3. 55m · min^-1
4. 65 m · min^-1

Answer: 3. 55m · min^-1

4. What is the average velocity of the farmer during the walk?

1. 27 m · min^-1
2. 30 m · min^-1
3. 35 m · min^-1
4. 25 m · min^-1

Answer: 4. 25 m · min^-1

Question 2. A man crosses a river in a boat. If he crosses the river in minimum time he takes 10 min with a drift 120 m. If he crosses the river taking the shortest path, he takes 12.5 min.

1. What is the width of the river?

1. 250 m
2. 200 m
3. 300 m
4. 230 m

Answer: 2. 200 m

2. What is the velocity of the boat in still water?

1. 21 m · min^-1
2. 24 m · min^-1
3. 20 m · min^-1
4. 18 m · min^-1

Answer: 3. 20 m · min^-1

3. What is the speed of the current?

1. 13 m · min^-1
2. 12 m · min^-1
3. 14 m · min^-1
4. 15 m · min^-1

Answer: 2. 12 m · min^-1

Question 3. A particle is projected from the surface of the earth with a speed of 20 m · s^-1 at an angle 30° with the horizontal.

1. The time of flight of that particle is

1. 3 s
2. 4s
3. 2s
4. 1s

Answer: 3. 2s

2. The range of that particle is

1. 10 m
2. 12√2 m
3. 20√3 m
4. 30 m

Answer: 3. 20√3 m

3. The maximum height the particle can reach is

1. 3 m
2. 7 m
3. 5m
4. 12 m

Answer: 3. 5m

Vector Integer Answer Type Questions

In this type, the answer to each of the questions is a single-digit Integer between 0 and 9.

Question 1. A projectile is launched from the ground and it returns to the ground level. The horizontal range of the projectile is R = 175 m. If the horizontal component of the projectile’s velocity at any instant is 25 m · s^-1, then determine the time of flight of the projectile.
Answer: 7

Question 2. A food packet is to be dropped by a helicopter on a flood relief mission. The helicopter is moving horizontally with a constant speed of y = 50 m · s^-1. At the time of dropping the food packet, it is at a height of 2 km from the ground level. For the person shown to receive the packet, what should be the value of x in km? [Given, g = 10 m · s^-2]

Answer: 1

Question 3. Two men are running on a straight north-south track. Person A moves north with a speed of 5 m · s^-1 while B moves south with a speed of 2 m · s^-1. Determine the velocity (magnitude only) of

1. A with respect to B.
2. The ground with respect to A.
3. B with respect to A.

Answer: 7, 5, 7

 

Newton Law Of Motion

Statements Of The Laws Of Motion

In 1687, Sir Isaac Newton, in his book Principia, published three laws of motion related to all the moving objects in the universe. These are known as Newton’s laws of motion. These laws cannot be proved using any old concept of physics. Yet, their validity has been confirmed through successful explanations and predictions on numerous events in nature. Hence, the laws founded a new branch of physics called kinetics.

The Laws Are:

1. 1st Law: Everybody continues to be in its state of rest or of uniform motion in a straight line unless the body is compelled to change its state by a net external force.
2. 2nd Law: The rate of change of momentum of a body is proportional to the impressed force and takes place in the direction in which the force acts.
3. 3rd Law: To every action, there is an equal and opposite reaction.

These laws involve the new concepts of

1. Inertia,
2. Force and
3. Momentum.

Read and Learn More: Class 11 Physics Notes

The study of these laws is the subject of this chapter and is called Newtonian mechanics. It should be mentioned, however, that Newtonian mechanics does not apply to all situations.

1. If the interacting bodies are moving with the speed of light (or an appreciable fraction of the speed of light), Newtonian mechanics should be replaced by Einstein’s special theory of relativity.
2. If the interacting bodies are of atomic dimensions (for example, electrons in an atom), Newtonian mechanics should be replaced by quantum mechanics.

In short, Newtonian mechanics may be treated as a special case of these two more comprehensive theories.

Weight Of A Body Gravitational Unit Of Force

Gravitational Unit Of Force Definition: The weight of a body is the force with which the earth attracts the body.

• The earth’s attraction is the force of gravity, the acceleration produced by it is called the acceleration due to gravity, g, and it is always directed towards the center of the earth.
• Hence, using the relation \(\vec{F}=m \vec{a}\), the weight of a body of mass m is formulated as \(\vec{W}=m \vec{g}\)
• So, weight = mass x acceleration due to gravity at the place. The value of g varies at different places and hence the weight also changes. For example, a bowling ball of mass 7.2 kg weighs 71N on Earth, but only 12N on the Moon.
• The mass of the ball is the same on both earth and the moon but the free fall acceleration on the moon is only 1.6 m/s².

Gravitational unit Of force: The force with which the earth pulls a body of unit mass, is the unit of gravitational force.

Gravitational units are no longer accepted for use with the SI units by BIPM.

From the above definitions, we see that gravitational units depend on acceleration due to gravity which varies at different places. So we cannot use these units as standard.

But accepting a value of g as a standard, a standard gravitational unit of force can be defined. Kilogram-force or kgf is the most commonly used standard unit.

1 kgf is the weight of a mass of 1 kg at a place where the acceleration due to gravity, g = 9.80665 m · s^-2, and

therefore 1 kgf = 1 kg x 9.80665 m · s^-2 = 9.80665 N .

However, this unit has become almost obsolete at present.

Inertial Mass: Suppose, two small pieces, one of wood and the other of iron, are at rest on the floor. From experience, we know that, on applying the same amount of force, the piece of wood will have an acceleration greater than that of the iron piece.

• Conversely, to produce the same acceleration on both pieces, the force applied on the iron piece will have to be greater. So, the inertia of rest for the iron piece is more than that for the piece of wood. Thus, the mass of a body is a measure of inertia of rest.
• This is also true for the inertia of motion. For instance, to stop a bicycle and a truck, moving with the same velocity within the same distance, i.e., to produce the same retardation, the force applied on the truck has to be greater. So, in this case, too, the masses of the vehicles give a measure of their inertia of motion.

Therefore, to produce the same acceleration in any two different objects, at rest or in motion, force required will be different if their masses are unequal. Thus, the mass of an object is the measure of its inertia. So mass is also called Inertial mass. The mass m in the equation \(\vec{F}=m \vec{a}\), is the inertial mass.

Newton Law Of Motion Weigt Of Body Numerical Examples

Example 1. A paratrooper of mass 75 kg falls with a constant velocity. Find the air resistance acting on him.
Solution:

As the acceleration is zero, there is no resultant force acting on the paratrooper. The weight acting downwards = 75 x 9.8 = 735 N.

Therefore, the air resistance, acting upwards, is R = 735 N.

 Newton Law Of Motion – Analysis Of Different Motions

Walking On A Horizontal Plane: AB is a horizontal plane. A man wants to walk on the plane towards B. He applies an oblique force F on the plane. The plane too, exerts a reaction force R on the man.

• The vertical component of R acts opposite to the weight of the man and the horizontal component H provides the force for the forward movement. So, the motion of the man is not directly due to the force F that he exerts, but due to the opposite reaction.
• In fact, this force decides the type of the motion. As the frictional force is low on a smooth surface, it is not possible to exert a large force. If the horizontal component of F becomes much larger than the frictional force, the man may slip.
• Hence one cannot walk fast on a very smooth surface as there is a high chance of slipping.

Flight Of Birds: If a bird intends to fly along OC, it flaps its wings along OA and OB, thus exerting some force on the air. At the same time, the reaction forces on the bird are OE and OD.

• If both the wings of the bird exert equal force on air, the resultant reaction force will be along OC. The bird moves forward due to this reaction force.
• By adjusting the force applied by the wings, the resultant may be shifted to the left or right of the direction of OC, and the bird can thus change its course.
• In the absence of air, i.e., in a vacuum, the reaction forces OD and OE cannot be generated, and so birds cannot fly.

Motion Of A Hand-Pulled Rickshaw: A man is trying to pull a rickshaw on a horizontal plane, towards point B. He exerts an oblique force P on the plane. The reaction R of the plane has a vertical component N and a horizontal component F. Force N is balanced by the weight of the man. Horizontal component F sets up the motion of the man.

• Let the force exerted by the man on the handles of the rickshaw be T. The rickshaw also pulls the man backward with the same force T.
• Due to the motion of the wheel on the plane, frictional force F’ acts at the point of contact of the wheel and the plane in a direction opposing the motion.
• Hence, the resultant of forces acting on the man = F- T in the forward direction and that on the rickshaw in the same direction = T-F’
• Let the masses of the man and the rickshaw be m₁ and m₂ respectively and common acceleration in the forward direction be a.

For the man, F- T = m₁a or, T = F-m₁a

For the rickshaw, \(T-F^{\prime}=m_2 a \text { or, } T=F^{\prime}+m_2 a\)

∴ \(F-m_1 a=F^{\prime}+m_2 a \text { or, }\left(m_1+m_2\right) a=F-F^{\prime}\)

or, \(a=\frac{F-F^{\prime}}{\left(m_1+m_2\right)}\)

The expression for the acceleration shows that,

1. Individual masses m₁ or m₂ are not significant but the sum of the masses (m₁ + m₂) matters,
2. The rickshaw will start moving, i.e., Accelerating when F> T>F’,
3. During the early stages of motion, F > T > F’. It attains a uniform speed when F =T= F’ and then of course a = 0, and
4. If F< F’, the rickshaw cannot be set into motion at all.

There are many similar examples in nature, where a force (action) is applied backward, and the reaction force generated is actually responsible for the intended forward motion.

Newton Law Of Motion – Equation Of Motion And Its Solution

The body, whose motion is to be analyzed, should be identified at first.

1. This ‘‘body” may consist of a single body a combination of bodies (often called a system of bodies’) or even a part of a single body.
2. Then we have to consider the surroundings (or environment). Every other body having a direct influence on our chosen body is a part of the surroundings. In general, action-reaction-type forces act between the body and its surroundings.
3. Now we search for every force acting on our body. Each of the forces is either a force of action on the body or a force of reaction on it due to some other body in the surroundings.
4. Once the forces are identified, we regard them on the same footing, i.e., we no longer differentiate between actions and reactions. In this sense, the body under consideration acts as a free body, subject to a system of forces acting on it.
5. If the active forces are \(\vec{F}_1, \vec{F}_2, \vec{F}_3, \cdots\), then the resultant or net force is \(\vec{F}=\vec{F}_1+\vec{F}_2+\vec{F}_3+\cdots\)

For a body of constant mass m, we get from Newton’s 2nd law, m \(\vec{a}=\vec{F}=\vec{F}_1+\vec{F}_2+\vec{F}_3+\cdots\)…(1)

This equation (1) is to be solved to find out the acceleration \(\vec{a}\) of the body.

As \(\vec{a}\) is related to the velocity \(\vec{v}\) as \(\vec{a}\) = \(\frac{d \vec{v}}{d t}\), equation (1) may be written as \(m \frac{d \vec{v}}{d t}=\vec{F}\)…(2)

Clearly, this is the differential equation to be solved if the velocity of the body is to be found. Similarly, as \(\vec{v}=\frac{d \vec{r}}{d t}\)(\(\vec{r}\) = position vector of the body), we may write m \(\frac{d^2 \vec{r}}{d t^2}=\vec{F}\)…(3)

This 2nd-order differential equation is to be solved to obtain \(\vec{r}\) at any instant.

Any of the equations (1) to (3) is then called the equation of motion of a body.

It is to be noted that the equation of motion is a vector equation. Each vector has three independent components. So the solution of an equation of motion involves, in general, a solution of three independent equations corresponding to three mutually orthogonal coordinate axes.

However, this is not always the case we come across plenty of examples of one or two-dimensional motions where one or two equations, respectively, are relevant.

Newton Law Of Motion Problems On Tension

Horizontal Motion With The Help Of A Smooth Pulley: A body A of mass m is resting on a frictionless horizontal plane. To set body A into motion along the plane, it is tied, using a massless, inextensible string passing over a massless, frictionless pulley, with another m body B of mass M as shown.

Both the bodies, A and B, get the same constant acceleration and the tension in the string remains constant (as the pulley is frictionless).

Let the tension in the string = T; acceleration produced = a

∴ For the motion of A, T = ma …(1)

For the downward motion of B, Mg- T = Ma ….(2)

From (1) and (2), (M+ m)a = Mg

or, a = \(\frac{M}{M+m^g} g\)…(3)

As, \(\frac{M}{M+m}<1, a<g\), though the surface and the pulley are frictionless.

Also, inserting the value of an in equation (1) we get, T = \(\frac{M m}{M+m^2} g=\frac{M}{1+\frac{M}{m}^g}\)

Here, \(\frac{M}{1+\frac{M}{m}}<M\), and hence T < mg, i.e., the tension in the string is less than the weight of the body B.

Vertical Motion With The Help Of A Smooth Pulley; To raise a body A of mass m vertically, a heavy body B of mass M is connected to A using a massless inextensible string passing over a massless smooth frictionless pulley as shown.

Let the tension developed in the string be T and the common acceleration of A and B be a. Mass of B is more than that of A. Hence B will move downwards, A will move upwards.

Considering the motion of B, Mg – T = Ma …(1)

and the motion of A, T – mg = ma …(2)

Adding equations (1) and (2), (M- m)g = (M+ m)a

or, a = \(\frac{M-m}{M+m} g\)…(3)

From (3), a < g though the pulley is smooth.

Again, inserting the value of an in (1),

T = \(M g-\frac{M(M-m)}{M+m} g=M g\left(1-\frac{M-m}{M+m}\right)\)

= \(\frac{2 M m}{M+m^2} g\)…(4)

The value of a in equation (3) is positive (i.e., acceleration of A is upwards), if M> m, i.e., if the mass of B is more than that of A. As M > m, we get from equation (4), T> mg and T< Mg, i.e., the tension in the string is more than the weight of A (mg), but less than the weight of B. The net force on the pulley,

2T = \(\frac{4 M m}{M+m} g\)…(5)

 Newton Law Of Motion Problems On Tension Numerical Examples

Example 1. A block of mass m₂ = 100 g is suspended from one end of an inextensible string. The other end of the string is tied to another block of mass m₁ = 200 g, kept on a frictionless table surface. The string passes over a pulley. Find the tension in the string and the acceleration of the blocks.

Solution:

Let the tension in the string = T, and the acceleration of each block be a.

So, the equations of motion of the two blocks are, T = m₁a and m₂g – T = m₂a

On adding the two equations, we get, m₂g = m₁a + m₂a

or, \(a=\frac{m_2}{m_1+m_2} \cdot g=\frac{100}{200+100} \times 980=326.7 \mathrm{~cm} \cdot \mathrm{s}^{-2}\)

and T = m₁a  = 200 x 326.7 = 65340 dyn.

Example 2. Two blocks of masses 2.9 kg and 1.9 kg are suspended from a rigid support, using two inextensible wires, each of length 1 m, as shown. The mass of the upper string is negligible and that of the lower string is 0.2 kg • m^-1. If the whole system is moving up with an acceleration of 0.2 ms^-2, find

1. The tension at the midpoint of the lower string and
2. The tension at the midpoint of the upper string.Acceleration due to gravity = 9.8 m · s^-2.

Solution:

1. Mass of the lower string =0.2 x 1 = 0.2 kg. Its midpoint is B, and so the total mass hanging from B, \( m_B=\left (1.9+\frac{0.2}{2}\right)=2 \mathrm{~kg} \text {. }\)

Hence, downward force at B = m_Bg

Upward force at B = T_B

So applying Newton’s 2nd law of motion for the mass below B, m_Ba = T_B– m_Bg

or, T_B = m_Ba + m_Bg = m_B(a + g)

= 2(0.2 + 9.8) = 20 N

2. Midpoint of the upper string is A; total mass hanging below A, m_A = 2.9 + 0.2 + 1.9 =5.0 kg.

Hence, downward force at A = m_Ag

Upward force at A = T_A

Hence applying Newton’s 2nd law of motion for the whole system, m_Aa = T_A– m_Ag

or, T_A = m_A(g+ a) = 5(9.8 + 0.2) = 50 N

Example 3. Two bodies of mass 7 kg and 5 kg 200 N are joined with a rope of mass 4 kg. An upward force of 200 N is applied on the upper body. Find

1. The acceleration of the system,
2. Tension at the top end of the rope and
3. Tension at the midpoint of the rope.

Solution:

Let the acceleration be a.

1. From Newton’s 2nd law, 16a = 200- 16g or, 16a = 200- 16 x 9.8

∴ a = 2.7 m · s^-2.

2. The upper end of the rope carries the masses of the second body and the rope. If the tension is T, then T- (4 + 5)g = (4 + 5)a

or, T =9(g+ a) =9(9.8 + 2.7) =112.5 N.

3. The mass carried by the midpoint of the rope is half the mass of the rope and the whole mass of the lower body. Hence, if the tension is T’ at the midpoint, the equation of motion is T’-(2 + 5)g= (2 + 5)a

or, T’ = 7(g+ a) = 7(9.8 + 2.7) = 87.5 N.

Example 4. A double inclined— plane A is placed on a horizontal table and two blocks of masses m₁ and m₂ are placed on the two frictionless inclined planes of A. Two ends of a rope wound over a pulley are tied to the two blocks. Find out the horizontal acceleration to be imparted to the system so that the blocks are at rest relative to A. In this condition, what will be the tension in the rope?

Solution:

Let the tension in the rope be T and the horizontal acceleration be a .

The forces acting on the two blocks have been shown. They are at rest relative to A, if

∴ \(T-m_2 g \sin \beta-m_2 a \cos \beta=0\)…(1)

∴ \(T-m_1 g \sin \alpha+m_1 a \cos \alpha=0\)…(2)

Subtracting (2) from (1), we get, \(g\left(m_1 \sin \alpha-m_2 \sin \beta\right)=a\left(m_1 \cos \alpha+m_2 \cos \beta\right)\)

or, \(a=\frac{m_1 \sin \alpha-m_2 \sin \beta}{m_1 \cos \alpha+m_2 \cos \beta} \times g\)

∴ T = \(m_2 a \cos \beta+m_2 g \sin \beta\)

= \(m_2 g\left[\frac{m_1 \sin \alpha-m_2 \sin \beta}{m_1 \cos \alpha+m_2 \cos \beta} \cdot \cos \beta+\sin \beta\right]\)

= \(\frac{m_1 m_2 \sin (\alpha+\beta)}{m_1 \cos \alpha+m_2 \cos \beta} g .\)

Newton Law Of Motion Reaction In A Moving Lift Apparent Weight

When a person of mass m stands on a floor, a downward force mg acts on the floor due to his weight. At the same time, the floor exerts an upward reaction force or normal force R on the man.

• As R acts on the person, the person feels his weight. From the third law of motion, R = mg.
• So, in this case, the actual weight mg, and the normal reaction, R, is the same. If the normal force R is absent, the person feels weightless.
• For example, while jumping from a height, one feels weightless before touching the earth’s surface, because the normal force R is absent.
• The normal force R varies inside a lift due to its vertical motion. The floor of the lift, in this case, provides the reaction. A person feels lighter or heavier than his actual weight depending on the reaction force R. This is called apparent weight.

Let the mass of a man in a lift be m.

The downward attractive force acting on him = real weight = mg

The upward normal force of the floor – apparent weight = R

∴ The net upward force F = R- mg.

We can determine the apparent weight R using F = ma for different types of motion of the lift.

1. The Lift Is Moving Up With An Acceleration a(Or, Moving Down With A Retardation a): Here the upward acceleration is a.

∴ R- mg = ma

or, R = mg+ ma = m(g+ a)….(1)

∴  As R> mg, the man feels heavier.

2. The Lift Is Moving Down With An Acceleration a(Or, Moving Up With A Retardation a): Here the downward acceleration = a or upward acceleration =-a (here a < g).

∴ R- mg = -ma

or, R = m(g- a)…(2)

He feels lighter as m(g- a) < mg.

3. The Cable Of The Lift Snaps And The Lift With The Man, Falls Freely Due To Gravitational Pull: Here, the acceleration, a = g. Hence from (2),

R = m(g- g) = 0…(3)

As no normal force acts on the man, he feels weightless.

This apparent weightlessness is true for all freely falling bodies.

4. The Lift Is At Rest Or In Uniform Motion: The value of a is zero and so the reaction force, R = mg. Hence, the apparent weight is the same as the real or true weight.

5. The Lift Falls With A Downward Acceleration Greater Than g: Here, a > g. From equation (2), R = m(g-a) or, R = -m(a- g).

The negative sign indicates that the apparent weight is negative, i.e., it is directed upwards. The man thus loses contact with the floor and hits the ceiling of the lift. Any item on the floor of the lift will hit the roof when exposed to similar conditions. This is termed as super-weightlessness.

Newton Law Of Motion – Reaction In A Moving Lift Apparent Weight Numerical Examples

Example 1. A body of mass 1 kg is suspended from a spring balance calibrated for acceleration due to gravity of 10 m · s^-2. What is the reading on the spring balance when the system

1. Is ascending with an acceleration of 5 m · s^-2 and
2. Is descending with the same acceleration? [g = 10 m · s^-2]

Solution:

1. Reaction force on the balance when it ascends, R = m(g+ a) = 1(10 + 5) = 15 N.

∴ In this case, the reading of the spring balance = 15/100 = 1.5 kg

Reaction force when the system descends, R = m(g – a) =1(10-5) = 5N.

∴ In this case, the reading of the spring balance = 5/10 = 0.5 kg

Example 2. A man of 50 kg is standing on a weighing machine in a lift. As the lift moves with a constant acceleration, the weighing machine registers the man’s weight as 45 kg. State whether the lift is ascending or descending. Give reasons for your answer. What is the acceleration of the lift? [g = 9.8 m · s^-2]
Solution:

The weighing machine shows a reading lower than the real weight of the man. So, the lift is descending with an acceleration, because in such cases, apparent weight R = m(g- a) < mg.

The downward acceleration, a = \(g-\frac{R}{m}=9.8-\frac{45 \times 9.8}{50}=0.98 \mathrm{~m} \cdot \mathrm{s}^{-2}\)

Example 3. A man of mass 70 kg is sitting in a motor car. The car is moving with an acceleration of 5 m · s^-2. What is the gravitational force on the man? [g = 9.8 m s^-2]

Solution:

Let the horizontal acceleration of the car be \(\vec{a}\).

The apparent acceleration due to gravity with respect to the car, \(\vec{g}^{\prime}=\vec{g}-\vec{a}=[\vec{g}+(-\vec{a})]\)

which is the resultant of the vectors \(\vec{g}\) and –\(\vec{a}\).

From, \(g^{\prime}=\sqrt{g^2+a^2}=\sqrt{(9.8)^2+5^2}\)

= \(11 \mathrm{~m} \cdot \mathrm{s}^{-2}\)

Force of gravitation on the man =70 x 11 = 770 N,

which acts in the direction of g’.

[The apparent weight of the man is, W’ = \(\frac{770}{9.8}\) = 78.6 kg]

The force of gravity, acting on the man, remains constant but, because of acceleration, the man feels a greater pull of gravity.

Example 4. A man of mass 60 kg is standing in a lift at rest. What will be the reaction force on the man when the lift is

1. Stationary,
2. Moving up with an acceleration of 4.9 m · s^-2,
3. Moving up at a constant speed, and
4. Moving up with a retardation of 4.9 m · s^-2? [G = 9.8 m · s^-2]

Solution:

1. The reaction of the lift floor when the lift is stationary R = mg = 60 x 9.8 N = 588 N.

2. The lift is moving up with an acceleration, of a = 4.9 m · s^-2.

Reaction, R=m(g+a) =60(9.8 + 4.9) N =882N,

3. When the lift is moving up at a constant speed, a = 0.

∴ R = mg =60 x 9.8 N = 588 N.

4. When the  lift moves up with a retardation of 4.9 m · s^-2,

R = m[g+ (-a)] = m(g- a) = 60(9.8- 4.9) N = 294 N

Example 5. A man of mass 98 kg, is standing on a weighing machine in a lift. What will be the readings of the weighing machine in the following cases:

1. The lift ascends at 100 cm per second,
2. The lift descends with an acceleration of 30 cm · s^-2. [g= 980 cm · s^-2]

Solution:

1. When the lift ascends with uniform velocity (acceleration a = 0 ) then, R = mg = 98 x 9.8 N.

Reading of the weighing machine = \(\frac{98 \times 9.8}{9.8} \mathrm{~kg}=98 \mathrm{~kg} .\)

2. When the lift descends, R = m(g- a)

= 98(9.8-0.3) [30 cm · s^-2 = 0.3 m · s^-2]

= 98 x 9.5 N

∴ Reading of the weighing machine = \(\frac{98 \times 9.5}{9.8} \mathrm{~kg}=95 \mathrm{~kg} .\)

Example 6. A man weighing 60 kg is in a lift that descends with an acceleration of 4 cm · s^-2. What force will the man exert on the floor of the lift? If the lift begins to ascend with the same acceleration, what reaction force will act on the man? For what acceleration of the lift, while descending, will the man experience weightlessness? [g = 980 cm · s^-2]
Solution:

If the lift descends with an acceleration a, and if the reaction force exerted by the lift on the man in the upward direction is R, then mg- R = ma …(1)

The force exerted by the man on the lift’s floor, R = mg – ma [4cm · s^-2 = 0.04m · s^-2] = 60(9.8-0.04) = 585.6 N

If the lift ascends with the same acceleration, then the reaction force on the man is, R’ = mg+ ma [4 cm · s^-2 = 0.04 m · s^-2]

= 60(9.8 + 0.04) = 590.4 N

When the acceleration of the lift, while descending, is a = g, then from equation (1), we get, R = mg- mg = 0 . For this zero reaction force, the man feels weightless.

So, for a lift falling freely with an acceleration g, the man inside it will feel no weight.

Example 7. A lift of mass 200 kg is moving up with an acceleration of 4 m · s^-2. What is the tension in the lift cable? If the lift moves down with the same acceleration, what will be the tension in that case? [g = 9.8 m · s^-2]
Solution:

Let the tension in the cable be T when the lift is moving with an acceleration a.

The equation of motion for the lift is, T- mg = ma

or, T = m(g+a)…(1)

Substituting the values for m, g, and a in equation (1), for upward motion,

T =200(9.8 + 4) = 200×13.8 = 2760 N

For the lift moving downwards, a = -4m · s^-2,

T= 200(9.8-4) = 200×5.8 = 1160 N

Example 8. A lift of mass 2000 kg is supported by thick steel ropes. If the maximum upward acceleration of the lift be 1.2 m/s², and the breaking stress for the ropes be 2.8 x 10⁸ N/m², what should be the minimum diameter of the rope?
Solution:

Here, m = 2000 kg, a = 1.2 m/s²

Breaking stress =2.8 x 10⁸ N/m²

Let the diameter of the rope be D.

When the lift moves upwards, the tension in the rope is T= m(g+ a) = 2000(9.8 + 1.2) = 22000 N.

Now, breaking stress = \(\frac{\text { force }}{\text { area }}=\frac{T}{\pi D^2 / 4}=\frac{4 T}{\pi D^2}\)

or, 2.8 x \(10^8=\frac{4 \times 22000 \times 7}{22 \times D^2}\)

or, \(D^2=\frac{4 \times 22000 \times 7}{22 \times 2.8 \times 10^8}=10^{-4} \quad \text { or, } D=1 \mathrm{~cm}\)

Newton Law Of Motion – Law Of Conservation Of Linear Momentum

Newton’s second law of motion states that the rate of change of momentum of a body is directly proportional to the applied force. Hence, in the absence of an external force, there is no change in the momentum of a body.

This law is also applicable for a system consisting of a number of bodies. The members in a many-body system may have interactions among themselves due to collisions, attractions, repulsions, etc. These forces are to be treated as internal forces, not external forces.

Law Of Conservation Of Linear Momentum Statement: In the absence of any external force acting on a system of bodies, even if interactions exist among the bodies, the total linear momentum of the system remains constant.

• This statement is the law of conservation of linear momentum. For a system of bodies, we can calculate the components of linear momentum, of all the bodies present, in any chosen direction. The stun of these individual components in this direction will be a constant.
• We shall illustrate the law for a one-dimensional collision. Suppose two particles of mass m₁ and m₂, moving with velocities u₁ and u₂ respectively in a straight line, collide with each other. After the collision, the particles move with velocities v₁ and v₂ respectively in the same direction.

Hence, total momentum before collision =m₁u₁ + m₂u₂, and total momentum after collision =m₁v₁ + m₂v₂.

If there is no external force, as per the conservation law of linear momentum, m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂…….(1)

Law Of Conservation Of Linear Momentum From Newton’s Third Law Of Motion: In the absence of any external force, two bodies, during a collision, exert an impulsive force on each other. From Newton’s third law of motion, impulsive force on the first body is equal and opposite to that exerted on the second body.

Forces F₁₂ and F₂₁ are shown: F₂₁ = -F₁₂

If the collision lasts for a time t, the impulse of F₂₁ on the first body = F₂₁ • t = change of momentum of the first body = m₁u₁– m₂u₂

Similarly, impulse of F₁₂ on the second body = F₁₂ x t = change of momentum of the second body = \(m_2 v_2-m_2 u_2\)

As \(F_{21}=-F_{12}, \quad m_1 v_1-m_1 u_1=-\left(m_2 v_2-m_2 u_2\right)\)

or, \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)

As total momentum before collision = total momentum after collision, the total linear momentum remains conserved.

Alternative Method: Suppose two bodies of masses m₁ and m₂, moving along the same straight line with velocities v₁ and v₂ respectively, collide with each other.

Since there is no external force present, let the force on the first body exerted by the second body be F₂₁, and that on the second body exerted by the first body be F₁₂.

∴ \(a_1=\frac{d v_1}{d t} \text { and } a_2=\frac{d v_2}{d t}\) = are the respective accelerations of the bodies.

From Newton’s third law of motion, \(F_{21}=-F_{12}\)

or, \(m_1 \frac{d v_1}{d t}=-m_2 \frac{d v_2}{d t}\)

or, \(\frac{d}{d t}\left(m_1 v_1+m_2 v_2\right)=0 or, \quad m_1 v_1+m_2 v_2\)= constant

Hence, the total linear momentum remains conserved.

Newton’s Third Law Of Motion From The Law Of Conservation Of Linear Momentum: Let the initial momentum of two bodies be p₁ and p₂. They come in contact for a time t and their momenta change to p₁‘ and p₂‘ respectively.

In the absence of any external force, as per law of conservation of linear momentum, \(p_1+p_2=p_1^{\prime}+p_2^{\prime}\)

or, \(p_1^{\prime}-p_1=-p_2^{\prime}+p_2 \quad \text { or, } \frac{p_1^{\prime}-p_1}{t}=-\frac{p_2^{\prime}-p_2}{t}\)

The left-hand side of the equation is the rate of change of the momentum of the first body = force on the first body = F₂₁; similarly, the right-hand side is -F₁₂.

Hence F₂₁ = -F₂₁ or, action = – reaction.

So action and reaction between two bodies are equal and opposite. This is nothing but Newton’s third law of motion.

Practical Applications Of The Principle Of Conservation Of Linear Momentum:

1. Recoil Of A Gun: When a bullet is fired from a gun, the gun recoils or gives a kick in the backward direction. It can be explained as follows:

• let m₁ be the mass of the bullet and m₂ be the mass of the gun. Initially, both the gun and the bullet are at rest. On firing the gun, let the bullet move with a velocity \(\vec{v}_1\), and the gun move with a velocity \(\vec{v}_2\).
• According to the principle of conservation of linear momentum, the total momentum of gun and bullet before firing = total momentum of gun and bullet after firing.

i.e., 0 = \(m_1 \vec{\nu}_1+m_2 \vec{\nu}_2 \quad \text { or, } \vec{\nu}_2=-\frac{m_1}{m_2} \vec{v}_1\)

• The negative sign shows that \(\vec{v}_2\) and \(\vec{v}_2\) are in opposite directions, i.e., as the bullet moves forward, the gun will move in backward direction. This backward motion of the gun is called the recoil of the gun.
• Hence, while firing a bullet, the gun must be held tight to the shoulder otherwise, because of the recoil velocity of the gun, the shoulder of the man who fires the gun, may get hurt.
• If the gun is held tight to the shoulder then the gun and the body of the man recoil as a single system. As the mass is quite large, the recoil velocity will be very small and the shoulder of the man will not get hurt.

2. Explosion Of A Bomb: Let a bomb of mass M be initially at rest. So, the initial momentum = 0.

After the explosion, suppose that the bomb is split into a few fragments of masses m₁, m₂, m₃ ……; the fragments fly away from the center of the explosion with velocities \(\vec{v}_1\), \(\vec{v}_2\), \(\vec{v}_3\)…

Thus, the final momentum is,\(\vec{p}=\vec{p}_1+\vec{p}_2+\vec{p}_3+\cdots=m_1 \vec{v}_1+m_2 \vec{v}_2+m_3 \vec{v}_3+\cdots\)

As no external force acts on the bomb, the momentum must be conserved, i.e., final momentum = initial momentum, or, \(\vec{p}=\vec{p}_1+\vec{p}_2+\vec{p}_3\)+….. = 0

As a special case, if the bomb explodes into two fragments only, then \(\vec{p}_1+\vec{p}_2=0 \text {, or } m_1 \vec{v}_1+m_2 \vec{v}_2=0 \text {, or } m_1 \vec{v}_1=-m_2 \vec{v}_2\)

Again, if the two fragments are of equal mass, \(m_1=m_2 \text { then } \vec{v}_1=-\vec{v}_2\)

Hence, the two fragments would acquire equal and opposite velocities due to the explosion.

Newton Law Of Motion – Law Of Conservation Of Linear Momentum Numerical Examples

Example 1. A bullet of mass 6 g is fired with a velocity of 500 m s-1 from a gun of mass 4 kg. Find the recoil velocity of the gun.
Solution:

A bullet of mass 6 g is fired with a velocity of 500 m s-1 from a gun of mass 4 kg.

As the bullet and the gun were at rest before the firing, the initial momentum of the system was zero. Let the speed of the bullet after the firing be v, and that of the gun be V.

From the law of conservation of linear momentum, 0 = MV+ mv

[mass of the bullet = m , mass of the gun = M]

or, \(V=-\frac{m}{M} \nu=-\frac{6 \times 10^{-3}}{4} \times 500=-0.75 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Hence, the recoil velocity of the gun = 0.75 m · s^-1.

Example 2. While firing a bullet of mass 8 g, the recoil velocity of the gun of mass 5 kg becomes 64 cm · s^-1. The bullet penetrates 50 cm through a target and then stops. Express the average resistance on the bullet in Newton.
Solution:

While firing a bullet of mass 8 g, the recoil velocity of the gun of mass 5 kg becomes 64 cm · s^-1. The bullet penetrates 50 cm through a target and then stops.

The initial momenta of the gun and the bullet were zero, as both were at rest. Let the masses of the gun and the bullet be M and m respectively and the respective velocities after firing be V and v.

From the law of conservation of Linear momentum, 0 = MV+ mu

∴ \(\nu=-\frac{M}{m} V=-\frac{5}{8 \times 10^{-3}} \times 0.64=-400 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

The bullet comes to rest after penetrating a distance of 50 cm or 0.5 m. If the retardation is due to the resistance of the material of the target, 0 = (400)² – 2a · 0.5 or, a = 16 x 10⁴ m · s^-2

Hence, average resistance, F = ma = 0.008 x 16 x 10⁴ = 1280 N.

Example 3. A body of mass m moving with velocity V along the X-axis collides with another mass M moving with velocity v along the Y-axis. The masses coalesce after the collision. Find the velocity and the direction of motion of the combined mass.
Solution:

A body of mass m moving with velocity V along the X-axis collides with another mass M moving with velocity v along the Y-axis. The masses coalesce after the collision.

Let the velocity of the combined mass be u which makes an angle θ with the X- axis.

Applying the law of conservation of linear momentum along the X-axis, mV+ 0 = (m + M)u cosθ…(1)

Similarly, along Y-axis, 0 + Mv = (m + M)u sinθ…(2)

Squaring and adding (1) and (2), \(m^2 V^2+M^2 v^2=(m+M)^2 u^2\)

or, \(u^2=\frac{m^2 V^2+M^2 v^2}{(m+M)^2}\)

Hence, u = \(\frac{\sqrt{m^2 V^2+M^2 v^2}}{M+m}\)

Also, (2) ÷ (1) gives, \(\tan \theta=\frac{M v}{m V} \text { or, } \theta=\tan ^{-1} \frac{M v}{m V} .\)

Example 4. A body of mass 50 kg is projected vertically upwards with a velocity of 100 m s^-1. After 5 s it splits up into two parts due to an explosion. One part of mass 20 kg moves vertically upwards with a velocity of 150 m s^-1. Find the velocity of the second body. Find the sum of the momenta of the two parts 3 s after the explosion and show that if there was no explosion, the momentum of the body would have been constant.
Solution:

Let the velocity of the projectile 5 s after the projection and just before the explosion be v.

∴ v = 100- 9.8 x 5 = 51 m · s^-1

Let the velocity of the second part after the explosion be v₁.

Applying the law of conservation of linear momentum along the direction of projection, 50 x 51 = 20 x 150 + 30 x v₁.

or, \(v_1=\frac{50 \times 51-3000}{30}=-15 \mathrm{~m} \cdot \mathrm{s}^{-1} \text { (downwards) }\)

Let the velocity of the 20 kg mass, produced due to the explosion, 3 seconds after the explosion be v’.

∴ v’ = 150- 9.8 x 3

= 150-29.4 = 120.6 m · s^-1 (upwards)

If v” is the velocity of the 30 kg mass 3 seconds after the explosion, then v” =15 + 9.8×3

= 15 + 29.4 = 44.4 m · s^-1 (downwards)

Thus the total momentum 3 seconds after the explosion = 20 x 120.6- 30 x 44.4 = 1080 kg · m · s^-1

In the case of no explosion, the velocity after 8 seconds of projection would have been v₂ = 100-9.8×8 = 100-78.4 = 21.6 m · s^-1

Hence, its momentum after 8 s would have been 50 x 21.6 = 1080 kg · m ·  s^-1

Example 5. A body P of mass 20 g and another body Q of mass 40 g are projected at the same time from points A A and B on the earth’s surface. The velocity of projection for each was 49 m · s^-1 and it was directed at an angle of 45° with the horizontal. Distance AB = 245 m. P and Q collide on the same vertical plane. After the collision, P retraces its path to the ground. Find the position where Q touches the ground. How long will Q take to reach the ground after the collision? [g = 9.8 m · s^-2]

Solution:

A body P of mass 20 g and another body Q of mass 40 g are projected at the same time from points A A and B on the earth’s surface. The velocity of projection for each was 49 m · s^-1 and it was directed at an angle of 45° with the horizontal. Distance AB = 245 m. P and Q collide on the same vertical plane. After the collision, P retraces its path to the ground.

As the two bodies P and Q are projected at the same time with the same velocity u = 49 m · s^-1 and angle = 45°, the horizontal range for both P and Q is the same an equal to, \(\frac{u^2 \sin 2 \alpha}{g}=\frac{(49)^2 \times \sin 90^{\circ}}{9.8}=245 \mathrm{~m} .\)

Hence the two bodies P and Q will meet at a point on the perpendicular bisector of AB.

Let the time when P and Q meet after projection be t. Hence horizontal distance moved by each x = \(49 \cos 45^{\circ} \times t=\frac{245}{2}, \quad \text { or, } t=\frac{5}{\sqrt{2}} \mathrm{~s}\)

During the collision, the vertical velocity of P and Q \(u_y=u \sin 45^{\circ}-g t=\frac{49}{\sqrt{2}}-\frac{9.8 \times 5}{\sqrt{2}}=0\)

Horizontal velocity of P and Q \(u_x=u \cos 45^{\circ}=\frac{49}{\sqrt{2}} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Hence horizontal component of the total momentum before collision p_x = (0.02 u_x – 0.04 u_x) kg · m · s^-1

P retraces its path after the collision. Hence horizontal velocity of P after collision =-u_x and for Q it is = v (say).

Hence horizontal component of the total momentum of the system after the collision = (- 0.02 u_x + 0.04 v) kg · m · s^-1

From the law of conservation of momentum, 0.02 u_x– 0.04 u_x = (- 0.02 u_x + 0.04 V)

or, v = 0

Thus Q does not have any horizontal component of velocity and hence it falls down vertically at the midpoint of AB, at a distance 245/2 = 122.5 m from both A and B

Let t = time required by Q to reach the ground after the collision.

t = \(\frac{u \sin 45^{\circ}}{g}=\frac{49 \times 1}{\sqrt{2} \times 9.8}=3.53 \mathrm{~s} .\)

Example 6. A car of mass 2000 kg collides with a truck of mass 10⁴ kg moving at 48 km · h^-1. After the collision, the car rides up the truck, and the truck-car combination moves at 15 km · h^-1. What was the velocity of the car before the collision?
Solution:

A car of mass 2000 kg collides with a truck of mass 10⁴ kg moving at 48 km · h^-1. After the collision, the car rides up the truck, and the truck-car combination moves at 15 km · h^-1.

Suppose a body of mass m moving with velocity u collides along a straight line with a body of mass M and velocity v. After collision the two masses combine and move with velocity V. Applying the law of conservation of equal to, momentum, mu + mv = (m + M)V

or, mu = (m + M)V- Mv

or, \(u=\frac{m+M}{m} V-\frac{M}{m} v=\left(1+\frac{M}{m}\right) V-\frac{M}{m} v\).

Here \(m=2000 \mathrm{~kg}, v=48 \mathrm{~km} \cdot \mathrm{h}^{-1}, M=10000 \mathrm{~kg}\),

V = \(15 \mathrm{~km} \cdot \mathrm{h}^{-1}\)

∴ \(\frac{M}{m}=\frac{10000}{2000}=5\)

u = \((1+5) \times 15-5 \times 48=90-240=-150 \mathrm{~km} \cdot \mathrm{h}^{-1}\)

The negative sign indicates that before collision the car was moving in the direction opposite to that of the truck.

Example 7. A ball weighing 100 g was thrown vertically upwards with a velocity 49 m · s^-1. At the same moment, another identical ball was dropped from a height of 98 m vertically above the first ball. After some time the two balls collided and got stuck together. This combined mass reached the ground finally. Determine how long the balls were in motion.
Solution:

A ball weighing 100 g was thrown vertically upwards with a velocity 49 m · s^-1. At the same moment, another identical ball was dropped from a height of 98 m vertically above the first ball. After some time the two balls collided and got stuck together. This combined mass reached the ground finally.

Let the height attained by the balls above the ground in time t₁ be h when they collide with each other.

Analyzing the upward motion of the first ball, we get \(h=49 t_1-9.8 t_1^2 / 2\)…(1)

Analyzing the downward motion of the second ball, we get \(98-h=9.8 t_1^2 / 2\)…(2)

From equations (1) and (2), 98 = 49 t₁ or, t₁ = 2 s

At the time of collision, the velocity of the ball thrown in the upward direction is v₁ and that of the ball thrown in the downward direction is v₂.

∴ v₁ = 49 -9.8 x 2 = 29.4 m · s^-1(upward)

and v₂ = 9.8 x 2 = 19.6 m · s^-1 (downward)

After collision, the velocity of the combined mass is V. Then according to the law of conservation of momentum, 0.1 x 29.4- 0.1 x 19.6 = 2 x 0.1 x V

or, V = 4.9m · s^-1 (upward)

From equation (1), we get h = 49 x 2- 9.8 x (2)²/2 = 78.4 m

Let the time taken by the combined mass to reach the ground be t₂.

Then \(78.4=-4.9 t_2+9.8 \times t_2^2 / 2 \quad \text { or, } t_2^2-t_2-16=0\)

or, \(t_2=(1 \pm \sqrt{1+64}) / 2=4.53 \mathrm{~s}\) (because t 0)

∴ Total time = \(t_1+t_2=2+4.53=6.53 \mathrm{~s} .\)

Example 8. A body of mass m is at rest on a smooth horizontal plane. A force F = kt is applied on the body making an angle α with the horizontal. In the equation of force, t is time and k is a constant. At the instant the object loses contact with the plane, how far will it move along the plane and what will be its velocity?
Solution:

A body of mass m is at rest on a smooth horizontal plane. A force F = kt is applied on the body making an angle α with the horizontal. In the equation of force, t is time and k is a constant. At the instant the object loses contact with the plane

As F= kt, the force increases with time. The vertical component of the force = Fsinα.

The body loses contact with the plane when the vertical force equals the weight of the body, i.e., Fsinα = mg. Let the time after which the body loses contact be t₀.

∴ Fsinα = kt₀sinα = mg

∴ \(t_0=\frac{m g}{k \sin \alpha}\)

The horizontal component of the force F = Fcosα = ktcosα

Hence horizontal acceleration = \(\frac{k t \cos \alpha}{m}=\frac{d v_x}{d t}\)

∴ \(d v_x=\frac{k t \cos \alpha}{m} \cdot d t\)

Integrating, \(v_x=\frac{k \cos \alpha}{m} \frac{t^2}{2}+A\)…(1)

[where A = integration constant]

As the body starts from rest, at t = 0, v = 0.

Inserting this in equation (1), A = 0

∴ \(v_x=\frac{k \cos \alpha}{2 m} t^2\)…(2)

If the displacement along the plane is s, then \(v_x=\frac{d s}{d t}=\frac{k \cos \alpha}{2 m} t^2 \quad \text { or, } d s=\frac{k \cos \alpha}{2 m} t^2 d t\)

Integrating again, \(s=\frac{k \cos \alpha}{6 m} t^3+B\)…(3)

[where B = integration constant]

As at the initial moment, the displacement is zero, i.e., at t = 0, s = 0.

From equation (3), we get B = 0

Inserting the value of B in equation (3), \(s=\frac{k \cos \alpha}{6 m} r^3\)

Hence, displacement along the plane in time t0, \(s_0=\frac{k \cos \alpha}{6 m} t_0^3=\frac{k \cos \alpha}{6 m}\left(\frac{m g}{k \sin \alpha}\right)^3\)

or, \(s_0=\frac{m^2 g^3 \cos \alpha}{6 k^2 \sin ^3 \alpha}\) and corresponding velocity, \(v_0=\frac{k \cos \alpha}{2 m}\left(\frac{m g}{k \sin \alpha}\right)^2\)

∴ \(v_0=\frac{m g^2 \cos \alpha}{2 k \sin ^2 \alpha} .\)

Example 9. A cannonball of mass 50 kg is fired with a velocity of 40 m s^-1 from a cannon of mass 1000 kg. What will be the recoil velocity of the cannon? If the force of friction between the surface and the wheels of the cannon is 1/10th of the weight of the cannon, how far will the cannon move before coming to rest? [Given, g = 10 m s^-2].
Solution:

A cannonball of mass 50 kg is fired with a velocity of 40 m s^-1 from a cannon of mass 1000 kg. What will be the recoil velocity of the cannon? If the force of friction between the surface and the wheels of the cannon is 1/10th of the weight of the cannon

Let the velocity of the recoil of the cannon be V.

Hence, from the law of conservation of momentum \(0=m v+M V \quad \text { or, } V=-\frac{m v}{M}\)

Here, m = mass of the cannonball = 50 kg, v = its velocity = 40 m · s^-1, and M = mass of the cannon = 1000 kg.

From given data, V \(=-\frac{50 \times 40}{1000}=-2 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Hence, the recoil velocity of the cannon = 2 m · s^-1 (backward).

Frictional force between the wheels and the land surface = 1/10 x 1000 x 10 = 1000N

∴ Retardation of the cannon = \(\frac{1000 \mathrm{~N}}{1000 \mathrm{~kg}}=1 \mathrm{~m} \cdot \mathrm{s}^{-2}\)

∴ Distance traveled by the cannon before coming to rest is, \(s=\frac{V^2}{2 a}=\frac{2^2}{2 \times 1}=2 \mathrm{~m}\)

Example 10. Four identical blocks, each of mass m, are connected as shown and are kept on a horizontal table. A force F Is applied on the first block. Find the tension in each string, neglecting friction.
Solution:

Four identical blocks, each of mass m, are connected as shown and are kept on a horizontal table. A force F Is applied on the first block.

Let the acceleration of the system, on applying force F on the first block, be a. Let tension in the string connecting the 1st and the 2nd block be T₁, 2nd, and that for the 3rd be T₂ and for the 3rd and the 4th be T₃.

Equations of motion for the

1st block, F- T₁ = ma…(1)

2nd block, T₁-T₂ = ma……(2)

3rd block, T₂-T₃ = ma….(3)

and 4th block, T₃ = ma …(4)

Since T₃ = ma, T₂ = ma+ T₃ = 2ma and T₁ = 3ma.

Hence, applied force, F = ma+ T₁ = 4 ma

Expressing the tensions in terms of the applied force F, we get \(T_1=\frac{3}{4} F, T_2=\frac{F}{2} \text { and } T_3=\frac{F}{4} \text {. }\)

Newton Law Of Motion – Motion Of An Object Or A System Of Objects With Variable Mass

The mass of an object or a system of objects may change with time. Newton’s second law of motion can be applied in this case only after taking into account the time-variation of mass.

• Suppose you are cycling along a road with a uniform velocity, carrying your friend in the backseat. You ask your friend to get down by jumping from the running cycle.
• Then you can realize that suddenly your velocity has increased a bit. The change of velocity would depend on the momentum with which your friend got down from the cycle.

Many examples of this type can be cited which are part of our day-to-day experience.

Equation Of Motion Of An Object Or A System Of Objects With Variable Mass: Let us suppose, at any moment t, the mass and velocity of an object (moving in a straight line) be m and v respectively and the external fixed net force acting on the object be F.

At that moment, another object of an infinitesimal mass dm moving in the same straight line with velocity u is added with the first one. As a result, after an infinitesimal interval of time, i.e., at the moment (f + dt), the mass of the system of objects becomes (m + dm), and let us assume that the velocity becomes (v + dv).

Now the initial and final momentum of the system of the objects would be respectively, p = mv+ udm….(1)

and p+dp = (m+ dm)(v+ dv)

= mv+ mdv+ vdm…….(2)

As the quantity dmdv is very very small, it is ignored.

So, change in momentum of the system of objects in time dt (p+ dp) – p = mv+ mdv+ vdm – mv- udm

or, dp = mdv-(u-v)dm

Therefore, according to Newton’s second law of motion, F = \(\frac{d p}{d t}=m \frac{d v}{d t}-(u-v) \frac{d m}{d t}\)

It is to be noted that, (u-v) is the relative velocity of dm with respect to m. Putting u_rel in place of (u – v) in equation (3) we get,

F = \(m \frac{d v}{d t}-u_{\text {rel }} \frac{d m}{d t} \quad \text { or, } F+u_{\text {rel }} \frac{d m}{d t}=m \frac{d v}{d t}\)…(4)

The resulting acceleration of the system is \(\frac{dv}{dt}\) = a.

So from equation (4), \(m a=F+u_{\mathrm{rel}} \frac{d m}{d t}\)….(5)

In the case of time-varying mass, equation (4) or (5) is the effective form of Newton’s second law of motion. Note that, due to time-variation of mass the last term in equation (5) is added to the familiar equation ma = F.

 Newton Law Of Motion – Rocket And Jet Plane

Rocket And Jet Plane Working Principle: A rocket or a jet plane works on the principle of conservation of momentum. In a rocket or a jet engine, there is a combustion chamber with a small aperture (exhaust) H at its rear end.

Solid or liquid fuel is ignited in the chamber. As a result of combustion, a large amount of spent fuel, in gaseous form, escapes at a high velocity through the exhaust. This provides a forward thrust to the rocket.

Force On The Rocket And Acceleration: Suppose, at time t, m= mass of a rocket, and v= its velocity in an inertial frame of reference. So, initial momentum of the system, p = mv.

When fuel is burnt in the combustion chamber, a gas is formed. High pressure within the chamber forces the gas out of a nozzle at the back of the rocket. Let the gas eject at a constant speed u relative to the rocket (u is assumed to be constant); the actual speed with respect to the same inertial frame = (u + v).

Let, dm = mass of the gas ejected in time dt

m – dm = residual mass of the rocket

and, v+ dv = velocity of the rocket after time dt

Then, total momentum after time dt, p+ dp = (u+ v)dm + (m- dm)(v+ dv) = mv+ udm + mdv [ignoring the product dmdv]

So, the change of momentum in time dt, dp = (p+ dp) – p = udm + mdv

And, external force = rate of change of momentum =\(\frac{d p}{d t}=u \frac{d m}{d t}+m \frac{d v}{d t}=u \frac{d m}{d t}+m a\)

where, a = \(\frac{dv}{dt}\) = acceleration of the rocket.

As no external force is acting on the rocket, we have 0 = \(u \frac{d m}{d t}+m a, \quad \text { or, } a=-\frac{u}{m} \frac{d m}{d t}\)…(1)

The negative sign shows that the rocket is accelerated in a direction opposite to that of u. Therefore, the rocket increases its speed in the forward direction as a result of the backward exhaust of the burnt fuel.

A jet plane cannot fly where there is no air, because oxygen from air is used for combustion. Otherwise, its motion follows the same working principle as that of a rocket.

Newton Law Of Motion – Rocket And Jet Plane Numerical Examples

Example 1. A wagon is moving along a straight railway track with a velocity of 3.2 m · s^-1. The wagon is being loaded with coal in moving condition at a rate of 540 kg · min^-1. How much force is to be applied to move the wagon at a constant velocity? Mention the direction of force. Assume, the initial velocity of the coal in the horizontal direction is zero.
Solution:

A wagon is moving along a straight railway track with a velocity of 3.2 m · s^-1. The wagon is being loaded with coal in moving condition at a rate of 540 kg · min^-1.

The velocity of the wagon, v = 3.2 m · s^-1,

and the rate of change of mass of the wagon, \(\frac{d m}{d t}=540 \mathrm{~kg} \cdot \mathrm{min}^{-1}=\frac{540}{60} \mathrm{~kg} \cdot \mathrm{s}^{-1}=9 \mathrm{~kg} \cdot \mathrm{s}^{-1}\)

Hence, force to be applied on the wagon to maintain its constant velocity (acceleration, a = \(\frac{dv}{dt}\) = 0),

F = \(v \frac{d m}{d t}+m \frac{d v}{d t}=3.2 \times 9+0=28.8 \mathrm{~N}\)

In this case, the direction of applied force and the direction of velocity of the wagon is identical.

Example 2. A rocket loses 1/40th of its mass in one second, during its upward motion. The speed of ejection of gas is 4000 m · s^-1. Find the acceleration gained.
Solution:

A rocket loses 1/40th of its mass in one second, during its upward motion. The speed of ejection of gas is 4000 m · s^-1.

In this case, \(\frac{dm}{m}\) = \(\frac{1}{40}\), dt = 1s,

u = – 4000 m ·  s^-1 (since u is in a downward direction)

Hence, acceleration, a = \(-\frac{u}{m} \frac{d m}{d t}=-\frac{u}{d t} \frac{d m}{m} \)

= \(4000 \times \frac{1}{40}=100 \mathrm{~m} \cdot \mathrm{s}^{-2} .\)

The positive value shows that the acceleration is upwards.

Example 3. A rocket is using 200 kg of fuel per second for its flight. Gas produced during combustion is ejected at a velocity of 6000 m • s^-1. What is the force acting on the rocket?
Solution:

A rocket is using 200 kg of fuel per second for its flight. Gas produced during combustion is ejected at a velocity of 6000 m • s^-1.

Force acting on the rocket, F = \(\frac{dm}{dt}\)u.

Given, rate of combustion of fuel, \(\frac{dm}{dt}\) = 200 kg · s^-1, the velocity of ejection of gas, u = 6000 m · s^-1.

∴ F = -200 x 6000 kg · m- s^-2 = -1.2 x 10⁶ N

The negative sign indicates that the force acts in the direction opposite to that of the ejected gas.

Example 4. A machine gun fires bullets at the rate of 180 shots per minute. Each bullet is of mass 20 g and moves with a velocity of 1 km · s^-1. After colliding perpendicularly with a steel plate, the bullets rebound at half the incident speed. What will be the force required to keep the steel plate in position?
Solution:

A machine gun fires bullets at the rate of 180 shots per minute. Each bullet is of mass 20 g and moves with a velocity of 1 km · s^-1. After colliding perpendicularly with a steel plate, the bullets rebound at half the incident speed.

Velocity of each bullet before impact = 1 km · s^-1 = 1000 m · s^-1

Velocity of each bullet after impact

= -1/2 km · s^-1 = -1/2 x 1000 m · s^-1 = -500 m · s^-1

The negative sign indicates this velocity is oppositely directed.

∴ Change in velocity of each bullet after impact = 1000 – (-500) = 1500 m · s^-1

Number of bullets incident per second on the steel plate = \(\frac{180}{60}\) = 3

∴ Rate of change of momentum of the three bullets = 3 x \(\frac{2}{1000}\) x 1500 = 90 N = force exerted on the steel plate.

Hence, the force required to hold the steel plate in position = 90 N.

Example 5. Just before take-off, the mass of a rocket is 4000 kg and the velocity of ejection of the burnt fuel is 400 m · s^-1. What should be the rate of combustion of the fuel so that the rocket can take off vertically?
Solution:

Just before take-off, the mass of a rocket is 4000 kg and the velocity of ejection of the burnt fuel is 400 m · s^-1.

Let the mass of gas ejected per second be m.

∴ Change of momentum of the ejected gas per second = mv = 400m N.

∴ Force on the ejected gas =400mN = upward vertical reaction on the rocket.

Weight of the rocket = 4000 x 9.8 N.

For taking off, the vertical reaction force on the rocket must be slightly greater than the weight of the rocket.

As the limiting case, the vertical reaction force = weight of the rocket.

∴ 400m = 4000 x 9.8 or, m = 98 kg · s^-1.

Newton Law Of Motion Synopsis

Newton’s First Law: Everybody continues to be in its state of rest or of uniform motion in a straight line unless the body is compelled to change its state by a net external force.

Newton’s Second Law: The rate of change of momen¬tum of a body is proportional to the impressed force and takes place in the direction in which the force acts.

Newton’s Third Law: To every action, there is an equal and opposite reaction.

• Property by the virtue of which a body tries to retain its state of rest or of uniform motion is called inertia of the body. There are two types of inertia—inertia of rest and inertia of motion.
• The tendency of a stationary body to remain at rest forever is called its inertia of rest.
• The tendency of a moving body to maintain its motion in a straight line at a constant velocity is called its inertia of motion.

The external influence that changes or tends to change the state of rest or state of uniform motion of a body is called force. Force is a vector quantity.

• The dynamic property arising from the combined effect of mass and velocity of a moving body is called its momentum.
• A frame of reference, at rest or in uniform motion, is called an inertial frame of reference.
• All three of Newton’s laws of motion are applicable in an inertial frame of reference.

An accelerating frame of reference is called a non-inertial frame of reference. None of Newton’s laws of motion holds good in a non-inertial frame of reference.

• Mass of a body determines its inertia. Hence this mass is called inertial mass.
• For a force acting on a body for an interval of time, the product of this force and the time is called the impulse of that force.
• If a large force acts on a body for a very short interval of time, it is called an impulsive force.
• Law of conservation of linear momentum: In the absence of any external force acting on a system of bodies—even if action-reaction forces exist among them, the total linear momentum of the system remains conserved.
• A rocket’s or a jet plane’s motion is based on the law of conservation of linear momentum.

The oxidant (oxygen) required for the combustion of rocket fuel is carried in the rocket itself so the rocket can travel in outer space where there is no air. A jet plane requires atmospheric oxygen to bum its fuel. Therefore, a jet plane cannot fly in space.

Newton Law Of Motion Useful Relations For Solving Numerical Problems

Momentum, p = mv

Applied force, F = \(m a=m\left(\frac{v-u}{t}\right)=\frac{m v-m u}{t}\)

Impulse of a force, Ft = mv- mu.

If the reaction force or normal force of a moving lift is R, its value when the lift

Ascends with an acceleration a is, R = m(g+ a)

Descends with an acceleration a is, R = m(g- a)

Ascends with a retardation a is, R = m(g- a)

Descends with a retardation a is, R = m(g+ a)

When the lift is at rest or ascending or descending with uniform velocity, R – mg

During free fall R = 0.

Law of conservation of linear momentum between two bodies: m₁u₁ + m₂u₂ = m₁v₁+ m₂v₂

The form of Newton’s second law of motion for time-varying mass, \(F+u_{\mathrm{rel}} \frac{d m}{d t}=m a\)

 

Newton Law Of Motion Very Short Answer Type Questions

Question 1. As per Newton’s laws of motion, only an external force can change the inertia of a body. When a car is brought to rest by the application of brakes, which external force stops the car?
Answer: Frictional force applied by road

Question 2. A man, in a train in uniform motion, throws a ball vertically upwards. Will the ball return to his hand?
Answer: Yes

Question 3. From the roof of a train, a metal ball is suspended by a string. When the train moves with uniform velocity, will the string remain vertical?
Answer: Yes

Question 4. A body in motion is acted upon by a force. Will the body stop at the moment of withdrawal of the force?
Answer: No

Question 5. A force of 200 dyn acts on a mass of 10 g for 5 s. Initially the body was at rest. What will be the final velocity of the mass?
Answer: 100cm · s^-1

Question 6. A man is coming down a hanging rope. The rope can bear up to 2/3 of his weight. The minimum acceleration with which the man can come down is _________
Answer: g/ 3

Question 7. Write the name of the physical quantity whose unit is the same as that of the impulse of a force.
Answer: Momentum

Question 8. A body of weight W₁ is suspended from the ceiling of a room by a rope of weight W₂. What is the force exerted by the ceiling on the rope?
Answer: W₁ + W₂

Question 9. Arrangements of two identical pulleys are shown in Fig. 1.49. The strings have negligible masses. In (1) mass m is pulled up by attaching a mass 2 m at the other end of the string and (2) mass m is pulled up by applying a downward force of 2 mg at the other end of the string. What are the accelerations in the two cases?

Answer: g/3,g

Question 10. A spring balance is set in a stationary lift. A person of mass 50 kg is standing on that balance. What will be the change in the reading of the balance if the lift moves upwards with constant velocity?
Answer: No change

Question 11. A spring balance is set in a stationary lift. A person of mass 50 kg is standing on the balance. What will be the change in the balance reading when the lift moves upwards with a constant acceleration?
Answer: An increase

Question 12. A man of mass 50 kg is descending at a constant velocity using a parachute. What is the air resistance on the man?
Answer: 490 N

Question 13. Two bodies of equal masses are kept on the scale pans of a beam balance in a lift. If the lift starts moving up with an acceleration, will the beam balance be in equilibrium?
Answer: Yes

Question 14. Can a rocket operate in free space?
Answer: Yes

Question 15. What is the principle of Rocket propulsion?
Answer: Conservation of linear momentum

Question 16. A bomb explodes in mid-air into two equal fragments. What is the direction of motion of the two fragments?
Answer: Opposite to each other

Newton Law Of Motion Assertion Reason Type Question And Answers

Direction: These questions have statement 1 and statement 2. Of the four choices given below, choose the one that best describes the two statements.

1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
2. Statement 1 is true, and statement 2 is true; statement 2 is not a correct explanation for statement 1.
3. Statement 1 is true, statement 2 is false.
4. Statement 1 is false, and statement 2 is true.

Question 1.

Statement 1: A cloth covers a table. Some dishes are kept on it. The cloth can be pulled out without dislodg¬ing the dishes from the table.

Statement 2: For every action, there is an equal and opposite reaction.

Answer: 2. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.

Question 2.

Statement 1: A reference frame attached to the earth is an inertial frame of reference.

Statement 2: The reference frame which has zero acceleration is called an inertial frame of reference.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 3.

Statement 1: A concept of pseudo forces is valid both for inertial as well as non-inertial frames of reference.

Statement 2: A frame accelerated with respect to an inertial frame is a non-inertial frame.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 4.

Statement 1: Block A is moving on a horizontal surface towards right under the action of force F. All surfaces are smooth. At the instant shown, the force exerted by block A on block B is equal to the net force on block B.

Statement 2: From Newton’s third law of motion, the force exerted by block A on B is equal in magnitude to the force exerted by block B on A.

Answer: 4. Statement 1 is false, statement 2 is true.

Question 5.

Statement 1: During free fall of a person one feels weightlessness because his weight becomes zero.

Statement 2: He falls with an acceleration of g.

Answer: 1. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.

Question 6.

Statement 1: When a person walks on a rough surface, the net force exerted by the surface on the person in the direction of his motion.

Statement 2: It is the force exerted by the road on the person that causes the motion.

Answer: 4. Statement 1 is false, statement 2 is true.

Newton Law Of Motion Match Column 1 With Column 2

Question 1. A block of mass m is released from rest when the spring was in its natural length. The pulley also has mass m but it is frictionless. Suppose the value of m is such that finally it is able to just lift the block M.

Answer: 1. C, 2. C,3. C, 4. B, D

Question 2. In the diagram shown, match the following column, (g = 10 m/s²)

Answer: 1. B, 2. D, 3. A, 4. D

Newton Law Of Motion Comprehension Type Question And Answers

Read the following passages carefully and answer the questions at the end of them.

Question 1. A ball of mass 200 g is thrown with a speed 20 m · s^-1. The ball strikes a bat and rebounds along the same line at a speed of 40 m · s^-1. Variation in the interaction force, as long as the ball remains in contact with the bat, is shown.

1. Maximum force F₀ exerted by the bat on the ball is

1. 4000 N
2. 5000 N
3. 3000 N
4. 2500 N

Answer: 1. 4000 N

2. Average force exerted by the bat on the ball is

1. 5000 N
2. 2000 N
3. 2500 N
4. 6000 N

Answer: 2. 2000 N

3. What is the speed of the ball at the instant the force acting on it is maximum?

1. 40 m · s^-1
2. 30 m · s^-1
3. 20 m · s^-1
4. 10 m · s^-1

Answer: 3. 20 m · s^-1

Question 2. Three blocks m₁ = 10 kg, m₂ = 20 kg, and m₃ = 30 kg are on a smooth horizontal table, connected to the adjacent blocks by light horizontal strings. A horizontal force F = 60 N is applied to m₃, towards the right.

1. The tension (T₁) acting between m₁ and m₂ is

1. 10N
2. 15N
3. 20N
4. 25N

Answer: 1. 10N

2. Tension (T₂) acting between m₂ and m₃ is

1. 25N
2. 30N
3. 24N
4. 15N

Answer: 2. 30N

3. The tension (T₂), if all of a sudden the string between m₁ and m₂ snaps, is

1. 30N
2. 24N
3. 25N
4. 15N

Answer: 2. 24N

Question 3. A stone of mass 0.05 kg is thrown in vertically by upward direction (take g = 10 m · s^-2). Neglect air friction,

1. The net force acting on the stone during its upward motion is

1. 0.5 N, upward
2. 0.5 N, downward
3. 5 N, upward
4. Zero

Answer: 2. 0.5 N, downward

2. The net force acting on the stone during its downward motion is

1. 0.5 N, upward
2. 0.5 N, downward
3. 5 N, upward
4. Zero

Answer: 2. 0.5 N, downward

Newton Law Of Motion Integer Answer Type Questions

In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.

Question 1. On planet X, a man throws a 500 g mass with a speed of 20 m · s^-1 and catches it as it comes down 20 seconds later. Find the weight of the mass (in N units).
Answer: 1

Question 2. The elevator shows it is descending with an acceleration of 2 m · s^-1. The mass of the block A = 0.5 kg. What should be the force (in N) exerted by the block A on the block B? Given g = 10 m • s^-2.

Answer: 4

Question 3. A monkey of mass 30 kg climbs a rope that can withstand a maximum tension of 360 N. Find the maximum acceleration (in m · s^-2) of the climbing monkey which this rope can tolerate, (g = 10m · s^-2)
Answer: 2

Question 4. In the arrangement shown the mass M is very heavy compared to m (M»m). The tension in the string is nmg. Find the value of n.

Answer: 4

Question 5. Find the acceleration of three blocks (in m • s^-2) as shown. Each surface of the system is smooth.

Answer: 3