Ameerun

Electrostatics

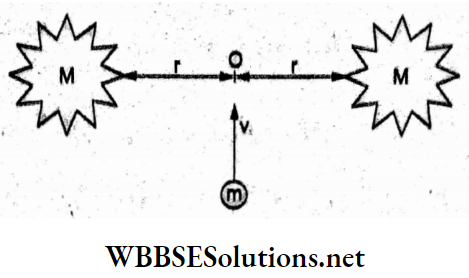
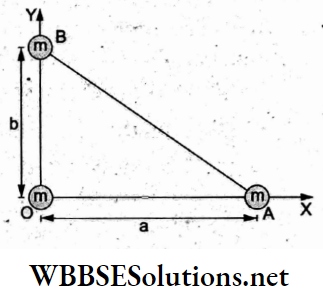
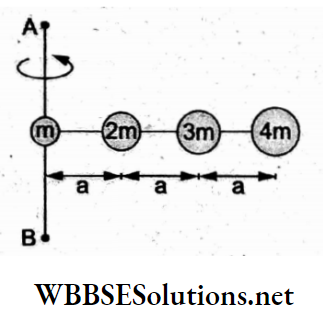
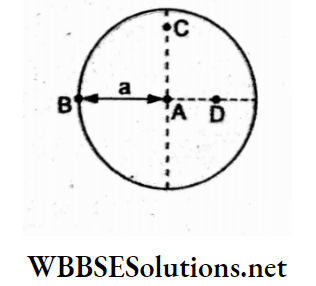
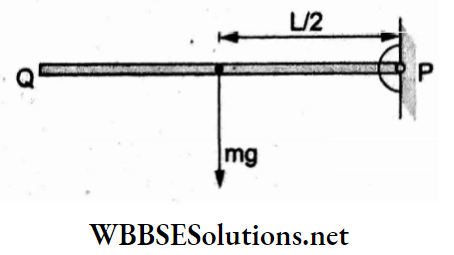
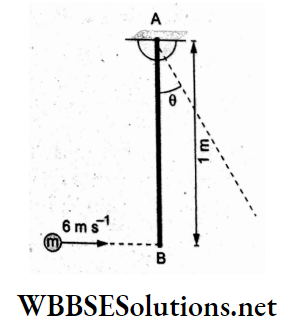
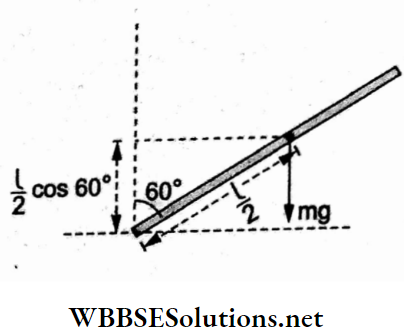
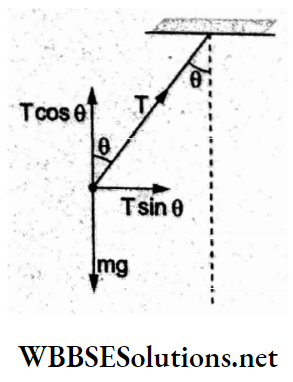
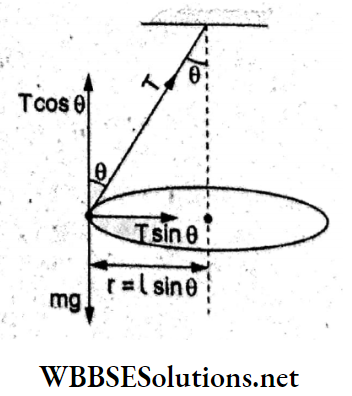
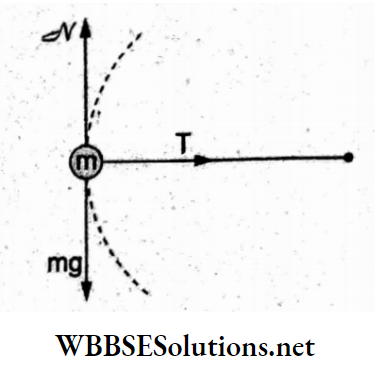
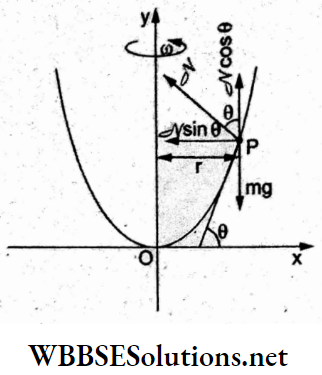
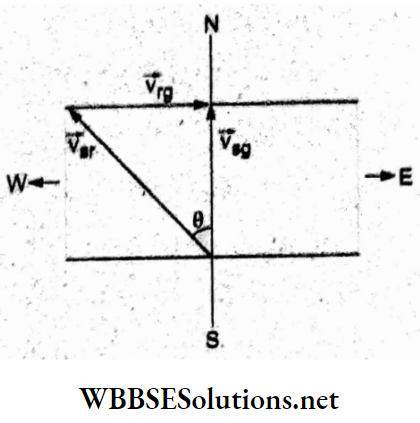
Question 1. Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d (d << l) apart because of their mutual repulsion. The charges begin to leak from both spheres at a constant rate. As a result, the spheres approach each other with a velocity v. Then v varies with separation x between the spheres as

1. v ∝ x^-1/2
2. v ∝ x^-1
3. v ∝ x^1/2
4. v ∝ x

Answer: 1. v α x^-1/2

Resolving the tension T along the horizontal and vertical directions and equating the component forces,

⇒ \(T \sin \theta=F=\frac{K q^2}{x^2}\)…..(1)

and Tcosθ = mg…..(2)

Dividing (1) by (2),

⇒ \(\tan \theta=\frac{K q^2}{m g x^2}\)

For θ → 0, tan 0 → sin θ = \(\frac{x / 2}{l}\)

⇒ \(\frac{x}{2 l}=\frac{K q^2}{m g x^2}\)

⇒ \(x^3=\frac{K \cdot 2 l}{m g} q^2\)

⇒ \(q^2=\frac{m g}{2 k l} x^3=\text { constant } x^3\)

=> q = constant x^3/2.

Differentiating w.r.t time t,

⇒ \(\frac{d q}{d t}=\text { constant } \frac{3}{2} x^{1 / 2} \cdot \frac{d x}{d t}\)

∵ \(\frac{d q}{d t}\) is constant, x^-1/2 . v = constant

=> v ∝ x^-1/2

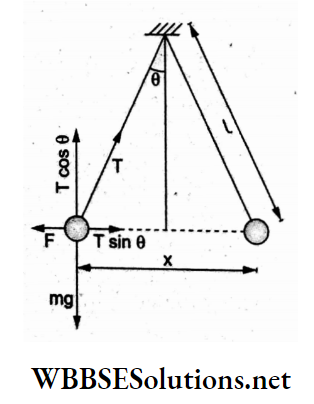
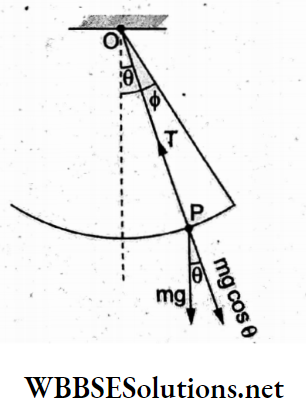
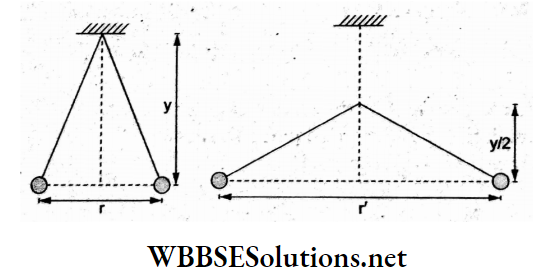
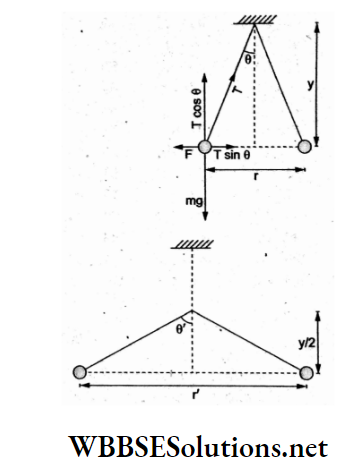
Question 2. Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them being r. Now, if the strings are rigidly clamped at half the height, the equilibrium separation r’ between the balls becomes

1. \(\frac{2 r}{\sqrt{3}}\)
2. \(\frac{2 r}{3}\)
3. \(\frac{r}{\sqrt{2}}\)
4. \(\frac{r}{\sqrt[3]{2}}\)

Answer: 4. \(\frac{r}{\sqrt[3]{2}}\)

In the first case, let θ be the deflection of the string and r be the separation between the balls, so

⇒ \(T \sin \theta=F=K \frac{q^2}{r^2}\)

and Tcosθ = mg.

∴ \(\frac{r / 2}{y}=\frac{K q^2}{m g r^2}\)……..(1)

Similarly, in the 2nd case,

⇒ \(\tan \theta^{\prime}=\frac{r^{\prime} / 2}{y / 2}=\frac{K q^2}{m g r^{\prime 2}}\)

Dividing (2) by (1), \(\frac{2 r^{\prime}}{r}=\frac{r^2}{r^{\prime 2}}\)

⇒ \(r^3=\frac{1}{2} r^3\)

⇒ \(r^{\prime}=\frac{r}{\sqrt[3]{2}}\)

Question 3. Two positive ions, each having a charge q, are separated by a distance d. If F is the force of repulsion between the ions, the number of electrons missing from each ion will be (e = charge on the electron)

1. \(\frac{4 \pi \varepsilon_0 F d^2}{e^2}\)
2. \(\sqrt{\frac{4 \pi \varepsilon_0 e^2}{d^2}}\)
3. \(\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}}\)
4. \(\frac{4 \pi \varepsilon_0 e^2}{F d^2}\)

Answer: 3. \(\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}}\)

Let q = Ne, where N is the number of missing electrons.

From Coulomb’s law,

⇒ \(F=\frac{1}{4 \pi \varepsilon_0} \frac{q^2}{d^2}\)

⇒ \(q=N e=\sqrt{4 \pi \varepsilon_0 F d^2}\)

⇒ \(N=\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}} .\)

Question 4. The electric field at a distance \(\frac{3R}{2}\) from the center of a charged conducting spherical shell of radius JR is E. The electric field at a distance \(\frac{R}{2}\) from the centre of the sphere is

1. E
2. \(\frac{E}{2}\)
3. \(\frac{E}{3}\)
4. Zero

Answer: 4. Zero

The electric field due to a spherical conducting shell of radius R is given by

⇒ \(E=\frac{1}{4 \pi \varepsilon_0} \frac{Q}{r^2} \text { for } r>R \text { and } E=0 \text { for } r<R\)

In this case, since r = \(\frac{R}{2}\) , the value of the field \(\vec{E}\) is zero.

Question 5. A thin conducting ring of radius R is given a charge +Q. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on the part ACDB of the ring is

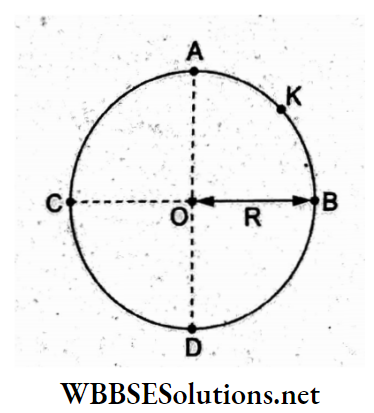
1. E along KO
2. 3E along OK
3. 3E along OK
4. E along OK

Answer: 4. E along OK

The field at the center O of the ring is zero. This is because the field at each quadrant will cancel out the field of the opposite quadrant. The field due to each quadrant is given as E.

Due to the part ACDB (consisting of three quadrants), the field due to parts AC and BD will cancel out and the net field will be due to part CD, which is E and directed along the bisector OK.

Question 6. The electric field at the centre O of semicircle of radius R having linear charge density yyy is given by

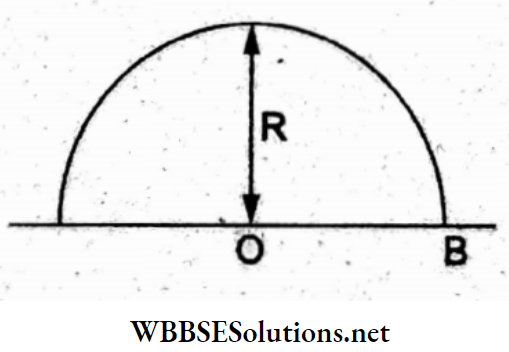
1. \(\frac{2 \lambda}{\varepsilon_0 R}\)
2. \(\frac{\pi \lambda}{\varepsilon_0 R}\)
3. \(\frac{\lambda}{2 \pi \varepsilon_0 R}\)
4. \(\frac{\lambda}{\pi \varepsilon_0 R}\)

Answer: 3. \(\frac{\lambda}{2 \pi \varepsilon_0 R}\)

Charge on the element AB of the ring is dq = XR dQ.

The field at the centre O due to this element,

⇒ \(d E=K \frac{d q}{R^2}=\frac{k \lambda R d \theta}{R^2}\)

This is directed radially along AO.

From considerations of symmetry, the x-components cancel out, and the net field is along the y-axis.

Thus, \(d E_y=d E \sin \theta=\frac{K \lambda R}{R^2} \sin \theta d \theta\)

Integrating,

⇒ \(E_y=\int d E_y=\frac{1}{4 \pi \varepsilon_0} \frac{\lambda}{R} \int_0^\pi \sin \theta d \theta=\frac{1}{4 \pi \varepsilon_0} \frac{\lambda}{R}[\cos \theta]_\pi^0=\frac{\lambda}{2 \pi \varepsilon_0 R}\)

Question 7. A hollow insulated conducting sphere is given a positive charge of 10 μC. The electric field at the centre of the sphere, if its radius is 2 meters, will be

1. 20 μCm^-2
2. 5 μCm^-2
3. Zero
4. 8 μCm^-2

Answer: 3. Zero

The electric field in the cavity of a hollow, charged conducting spherical shell is zero.

Question 8. A particle of mass m with charge q is placed at rest in a uniform electric field £ and then released. The kinetic energy gained by the particle after moving a distance y is

1. qEy
2. qE²y
3. qEy²
4. q2Ey

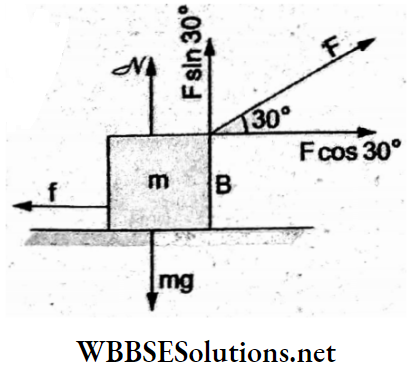
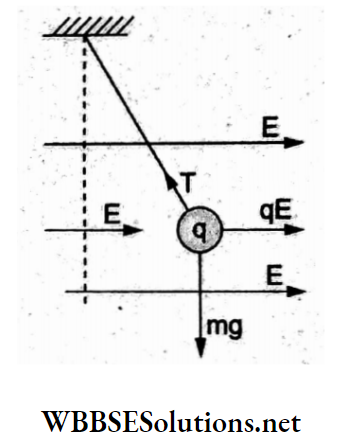
Answer: 1. qEy

Force on the charged particle = F = qE.

Work done by the electric field = Fy = qEy.

According to the work-energy theorem,

work done = change in \(\mathrm{KE}=\mathrm{KE}_{\text {final }}-\mathrm{KE}_{\text {initial }}\)

⇒ \(q E y=\frac{1}{2} m v^2\)

∴ KE gained = qEy

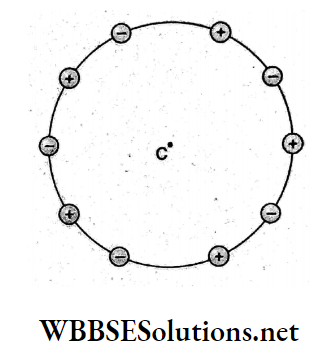
Question 9. The given figure represents electric field lines due to two charges q₁ and q₂. What are the signs of the two charges?

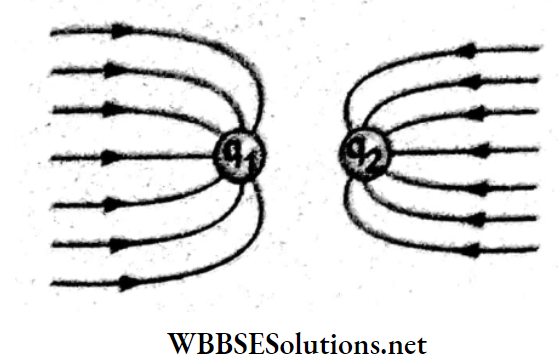
1. q₁ is positive but q₂ is negative.
2. q₁ is negative but q₂ is positive.
3. Both are negative.
4. Both are positive.

Answer: 3. Both are negative.

According to the convention, electric field lines emerge from positive charges and end at negative charges. In the given figure, the field lines end at both q₁ and q₂. Hence both q₁ and q₂ are negative charges.

Question 10. An electron is moving around the nucleus of a hydrogen atom in a circular orbit of radius r. The Coulomb force F between the two is

1. \(K \frac{e^2}{r^3} \vec{r}\)
2. \(-K \frac{e^2}{r^3} \vec{r}\)
3. \(K \frac{e^2}{r^2} \hat{r}\)
4. \(-K \frac{e^2}{r^3} \hat{r}\)

Answer: 2. \(-K \frac{e^2}{r^3} \vec{r}\)

The force of attraction between the proton and electron has magnitude \(F=\frac{K e^2}{r^2}\) and is directed along PO.

Taking O as the origin,

⇒ \(\vec{F}=-\frac{K e^2}{r^2} \hat{r}=-\frac{K e^2}{r^3} \vec{r}\)

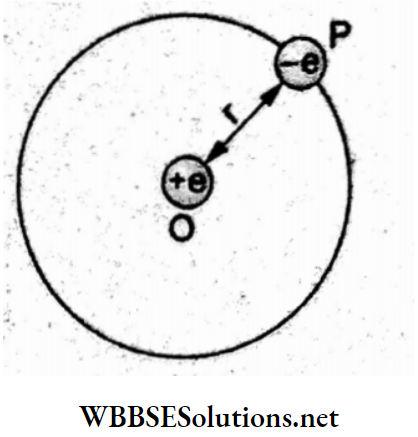
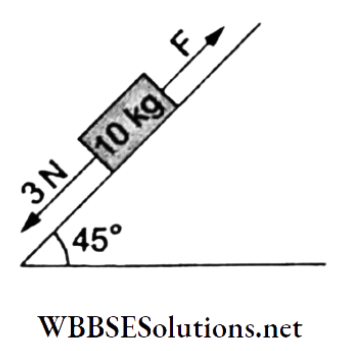
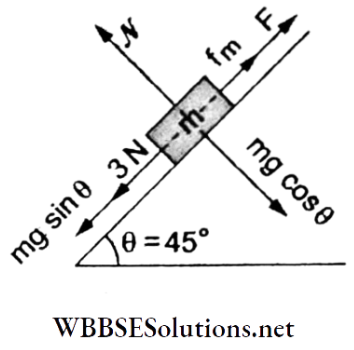
Question 11. A pendulum bob of mass 30.7 x 10^-6 kg carrying a charge of 2 x 10^-8 C is at rest in a horizontal uniform electric field of intensity 2 x 10⁴ V m¹. The tension in the thread of the pendulum is (g = 9.8 m s^-2)

1. 3 x 10^-4 N
2. 3 x 10^-4 N
3. 5 x 10^-4 N
4. 6 x 10^-4 N

Answer: 3. 5 x 10^-4 N

Forces acting on the bob are (1) weight mg, (2) force due to electric field (\(\vec{E}\)) qE, and (3) tension T. For the system to be in equilibrium

⇒ \(T=\sqrt{(m g)^2+(q E)^2}\)

⇒ \(\sqrt{\left(30.7 \times 10^{-6} \times 10\right)^2+\left(2 \times 10^{-8} \times 2 \times 10^4\right)^2}\)

⇒ \(\sqrt{\left(3 \times 10^{-4}\right)^2+\left(4 \times 10^{-4}\right)^2}=5 \times 10^{-4} \mathrm{~N}\)

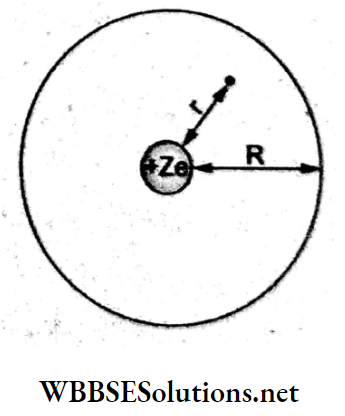
Question 12. According to an early model, an atom was considered to have a positively charged point nucleus of charge Ze, surrounded by a uniform density of negative charge up to a radius R. The atom as a whole was considered neutral even then. The electric field at a distance r(r<R) from the nucleus would then be

1. \(\frac{Z e}{4 \pi \varepsilon_0}\left(\frac{1}{r^2}-\frac{r}{R^3}\right)\)
2. \(\frac{1}{4 \pi \varepsilon_0}\left(\frac{1}{r^3}-\frac{r}{R^2}\right)\)
3. \(\frac{\mathrm{Ze}}{4 \pi \varepsilon_0}\left(\frac{r}{R^3}-\frac{1}{r^2}\right)\)
4. \(\frac{1}{4 \pi \varepsilon_0}\left(\frac{r}{R^3}+\frac{1}{r^2}\right)\)

Answer: 1. \(\frac{Z e}{4 \pi \varepsilon_0}\left(\frac{1}{r^2}-\frac{r}{R^3}\right)\)

Since the atom as a whole is neutral, the negative charge (-Ze) is uniformly distributed within the radius R of a sphere concentric with a tire nucleus.

Thus, the charge density is

⇒ \(\rho=\frac{(-Z e)}{\frac{4}{3} \pi R^3}=-\frac{3}{4 \pi} \frac{Z e}{R^3}\)

The negative charge enclosed within a sphere of radius r is

⇒ \(Q^{\prime}=-\frac{3}{4 \pi} \frac{Z e}{R^3} \cdot \frac{4}{3} \pi r^3=-\frac{Z e r^3}{R^3}\)

The net charge enclosed in this sphere is

⇒ \(Q_i=Q^{\prime}+Z e=Z e\left(1-\frac{r^3}{R^3}\right)\)

Applying Gauss’s theorem, electric flux = \(E A=\frac{1}{\varepsilon_0} Q_i\)

⇒ \(E \cdot 4 \pi r^2=\frac{1}{\varepsilon_0} Z e\left(1-\frac{r^3}{R^3}\right)\)

⇒ \(E=\frac{Z e}{4 \pi \varepsilon_0}\left(\frac{1}{r^2}-\frac{r}{R^3}\right)\)

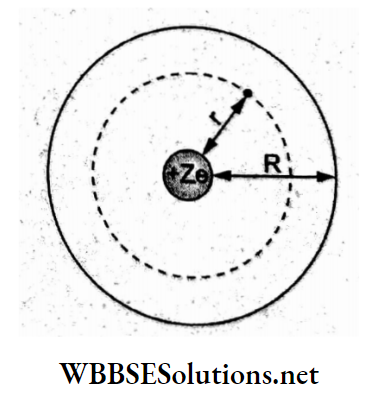
Question 13. The electric field strength (or dielectric strength) of dry air at stp is 3 x 10⁶ V m^-1. The maximum charge that can be given to a spherical conductor of radius 3 m is

1. 3 x 10^-4 C
2. 3 x 10^-4 C
3. 3 x 10^-2 C
4. 0.3 C

Answer: 2. 3 x 10^-3 C

Dielectric strength is the maximum electric field that the dielectric can sustain without breaking down.

Given, \(E_{\max }=3 \times 10^6 \mathrm{Vm}^{-1}=\frac{1}{4 \pi \varepsilon_0} \frac{Q}{R^2}\)

∴ Q = 4πE₀R² (3 x 10⁶ V m^-1)

⇒ \(\frac{1}{9 \times 10^9}(3 \mathrm{~m})^2\left(3 \times 10^6 \mathrm{Vm}^{-1}\right)\)

= 3 x 10^-3 C.

Question 14. A charge Q is enclosed by a Gaussian spherical surface of radius R. If the radius is doubled, the outward electric flux will

1. Be reduced to half
2. Remain the same
3. Be doubled
4. Increase four times

Answer: 2. Remain the same

The electric flux through a closed spherical surface is \(\phi=\frac{Q}{\varepsilon_0}\), where Q is the charge enclosed. The flux is independent of the radius of the spherical surface.

Hence, a change in the radius will not affect the value of the flux

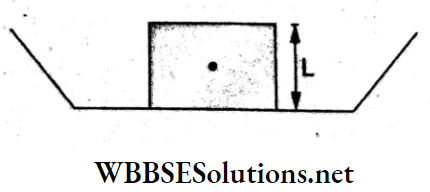
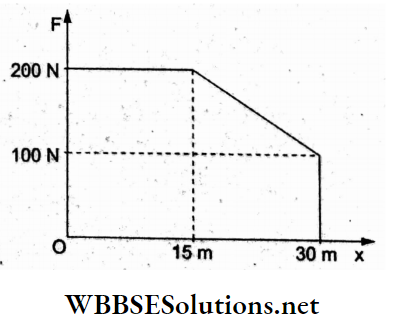
Question 15. In a square, the plane surface of the paper side is L placed(in m) in a uniform electric field E (in V m^-1) acting along the same plane L at an angle θ with the horizontal side of the square as shown. The electric flux linked to the surface in the unit of V m is

1. EL²
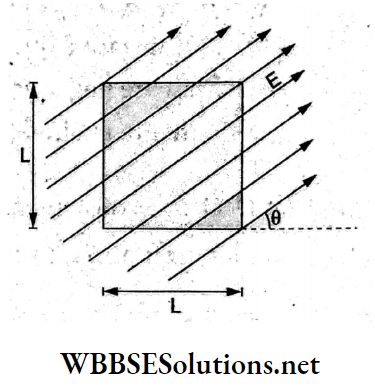
2. EL² cosθ
3. EL² sinθ
4. Zero

Answer: 4. Zero

In a uniform electric field, the flux of the electric field linked with a surface is \(\phi=\vec{E} \cdot \vec{A}\). The area vector is normal to the surface area, so the

angle between \(\vec{E}\) and \(\vec{A}\) is 90°.

Hence Φ = EA cos 90°

= 0.

Question 16. A hollow cylinder has a charge q coulomb within it. If is the electric flux in units of voltmetres associatedwiththecurvedsurface B, the flux linked with the plane surface A in volt metres will be

1. \(\frac{1}{2}\left(\frac{q}{\varepsilon_0}-\phi\right)\)
2. \(\frac{q}{2 \varepsilon_0}\)
3. \(\frac{\phi}{\varepsilon_0}\)
4. \(\frac{q}{\varepsilon_0}-\phi\)

Answer: 1. \(\frac{1}{2}\left(\frac{q}{\varepsilon_0}-\phi\right)\)

The total electric flux through the cylinder is linked partly through the curved surface (=Φ ) and partly through two plane faces (2Φ_p)

According to Gauss’s theorem,

total flux = \(\phi+2 \phi_{\mathrm{p}}=\frac{q}{\varepsilon_0}\)

⇒ \(\phi_{\mathrm{p}}=\frac{1}{2}\left(\frac{q}{\varepsilon_0}-\phi\right)\)

Question 17. A square surface of a side L meter is in the plane of the paper. A uniform electric field E (in V m^-1) also in the plane of the paper is limited only to the lower half of the square surface (see figure). The electric flux in SI units linked With the surface is

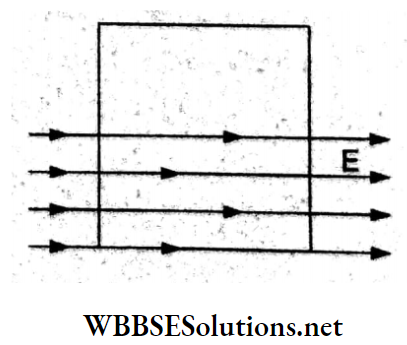
1. \(\frac{E L^2}{2 \varepsilon_0}\)
2. \(\frac{E L^2}{2}\)
3. Zero
4. EL²

Answer: 3. Zero

The area vector is directed perpendicular to the plane of the square

surface, so the angle between \(\vec{E}\) and \(\vec{A}\) is 90°.

Hence, \(\phi=\left(\frac{A}{2}\right)(E) \cos 90^{\circ}=0\)

Question 18. A charge q is situated at the center of a cube. The electric flux through any face of the cube is

1. \(\frac{\pi q}{4 \pi \varepsilon_0}\)
2. \(\frac{q}{6\left(4 \pi \varepsilon_0\right)}\)
3. \(\frac{2 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)
4. \(\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)

Answer: 4. \(\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)

When the charge is at the center of a cube, its position is symmetrical.

The flux linked with each of the six faces will be equal. Hence, the electric flux through any face is

⇒ \(\phi_0=\frac{1}{6}(\text { total flux })=\frac{1}{6}\left(\frac{q}{\varepsilon_0}\right)=\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)

Question 19. Suppose the charge of a proton differs slightly from that of an electron. One of them is -e, and the other is (e + Δe). If the net of electrostatic force and gravitational force between two hydrogen atoms placed a distance d (much greater than atomic size) apart is zero then Ae is of the order of (given that mH = 1.67 x 10^-27 kg)

1. 10^-23 C
2. 10^-37 C
3. 10^-47 C
4. 10^-20 C

Answer: 2. 10^-37 C

The net charge on one H atom is cj = (-e) + (e + Δe) = Δe.

The repulsive force between two H atoms is F_e = \(F_{\mathrm{e}}=\frac{K q^2}{d^2}=\frac{K(\Delta e)^2}{d^2}\) .

The gravitational attractive force between two H atoms is

⇒ \(F_{\mathrm{g}}=\frac{G m_{\mathrm{H}}^2}{d^2}\)

Given that F_net = 0, we have

⇒ \(F_{\mathrm{g}}=F_{\mathrm{e}}\)

⇒ \(\frac{K(\Delta e)^2}{d^2}=\frac{G m_{\mathrm{H}}^2}{d^2}\)

⇒ \(\Delta e=\sqrt{\frac{G m_{\mathrm{H}}^2}{K}}\)

= \(m_{\mathrm{H}} \sqrt{\frac{G}{K}}\)

= \(\left(1.6 \times 10^{-27}\right) \sqrt{\frac{\left(6.67 \times 10^{-11}\right)}{9 \times 10^9}}\)

=1.38 x 10^-37C ≈ 10^-37C

Question 20. The accompanying figure shows a S distribution of charges. The flux of the electric field due to these charges through the closed surface S is

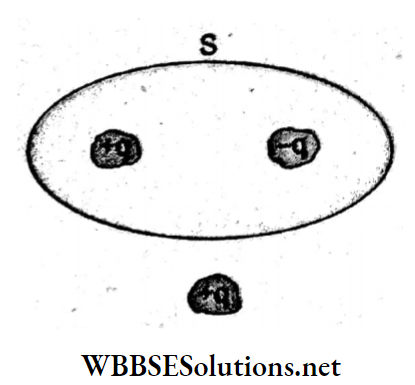
1. \(\frac{3 q}{\varepsilon_0}\)
2. \(\frac{2 q}{\varepsilon_0}\)
3. \(\frac{q}{\varepsilon_0}\)
4. Zero

Answer: 4. Zero

The total flux through a dosed surface is \(\phi=\frac{1}{\varepsilon_0}\) (total net charge enclosed).

In the given case, the outer charge +q does not contribute to the electric flux while the net charge enclosed is zero. Hence, the net flux is zero.

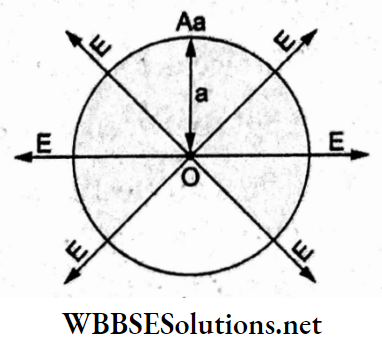
Question 21. The electric field in a certain region is acting radially outward and is given by E = At. A charge contained in a sphere of radius centered at the origin of the field will be given by

1. 4πε₀Aa³
2. ε₀Aa³
3. 4πε₀Aa²
4. Aε₀a²

Answer: 1. 4πε₀Aa³

The electric field at the surface of the sphere of radius a is Aa, radially directed from the center O.

The total electric flux through the sphere = Φ = 4πa².E = 4πa² (Aa).

If q is the charge enclosed then according to Gauss’s law,

⇒ \(\phi=\frac{q}{\varepsilon_0}\)

\(q=\phi \varepsilon_0\)

= \(4 \pi \varepsilon_0\left(A a^3\right)\)

Question 22. A charge q is placed at the center of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to

1. –\(\frac{Q}{4}\)
2. \(\frac{Q}{4}\)
3. –\(\frac{Q}{2}\)
4. \(\frac{Q}{2}\)

Answer: 1. –\(\frac{Q}{4}\)

The charge q is symmetrically placed between two equal charges +Q placed at A and B. Hence, for any value of q, the force on q will be zero. The system is in equilibrium, meaning each Q must experience zero net force.

So, \(F_{\text {net }}=K \frac{Q q}{(r / 2)^2}+K \frac{Q^2}{r^2}=0 \Rightarrow q=-\frac{Q}{4}\)

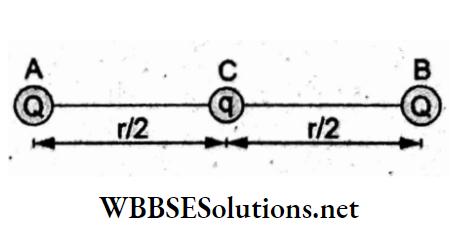
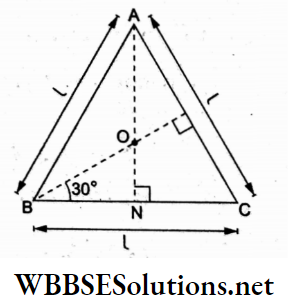
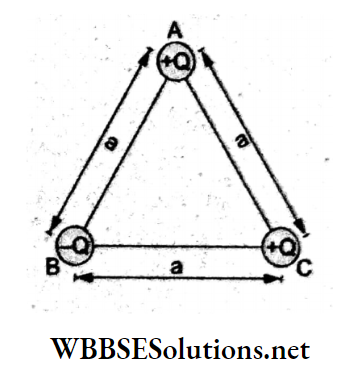
Question 23. Three charges are placed at the vertices of an equilateral triangle of side a as shown in the figure. The force experienced by the charge placed at the vertex A in a direction normal to BC is

1. \(\frac{Q^2}{4 \pi \varepsilon_0 a^2}\)
2. -Q²(4πε₀a²)
3. Zero
4. \(\frac{Q^2}{4 \pi \varepsilon_0 a^2}\)

Answer: 3. Zero

The force on +Q at A due to +Q at C is

⇒ \(f_1=\frac{K Q^2}{a^2}\) along CA,

and that due to -Q at B is

⇒ \(f_2=\frac{K Q^2}{a^2}\) along AB

These are equal in magnitudes (f₁ = f₂) and inclined at an angle of 120°.

Their net force F makes an angle of 60° with f₁ as well as f₂.

Since the direction of \(\vec{F}\) is parallel to BC, its component normal to BC will be zero.

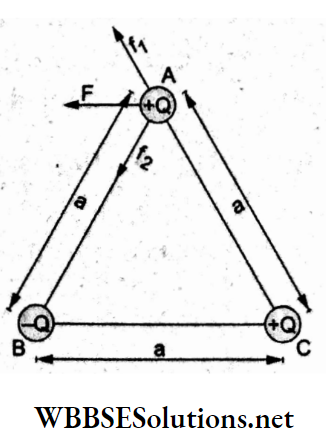
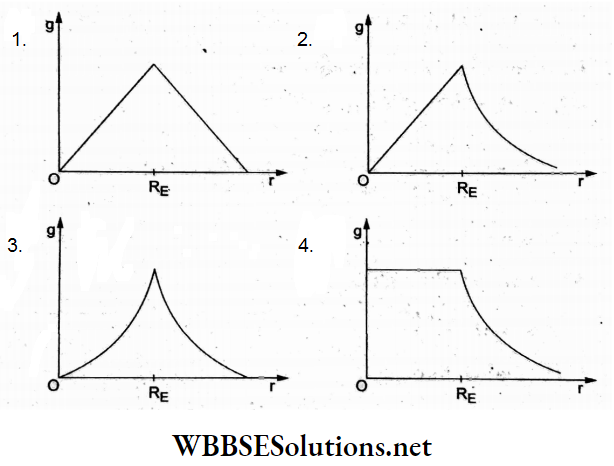
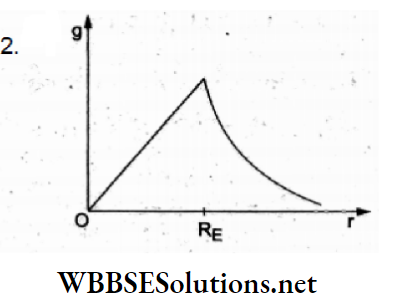
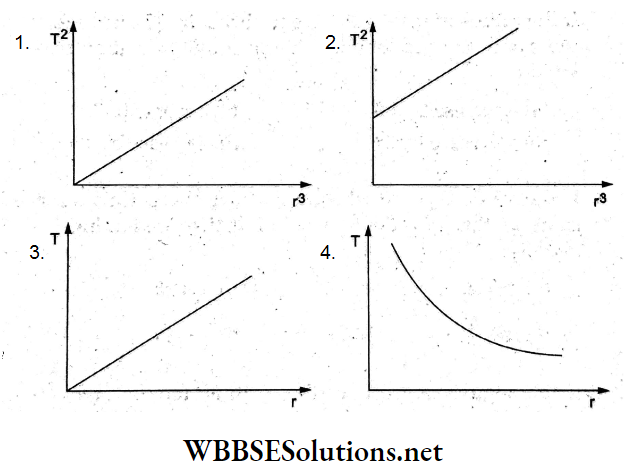
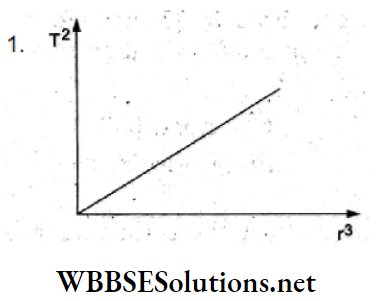
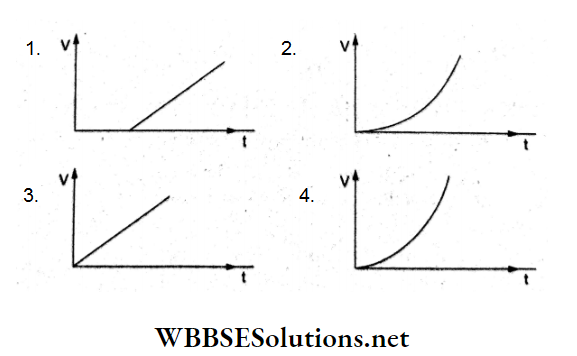
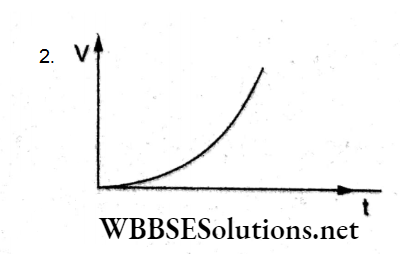
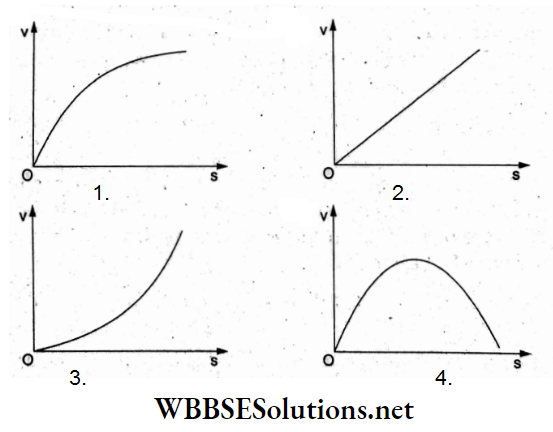
Question 24. The variation of electric field due to a uniformly charged conducting solid sphere of radius Rasa function of distance r from its centre is graphically represented by

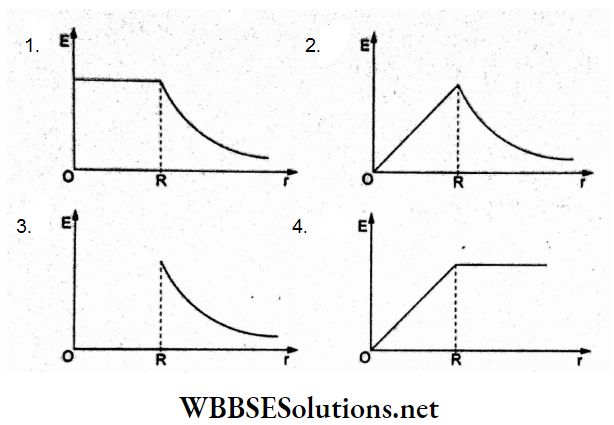
Answer: 2.

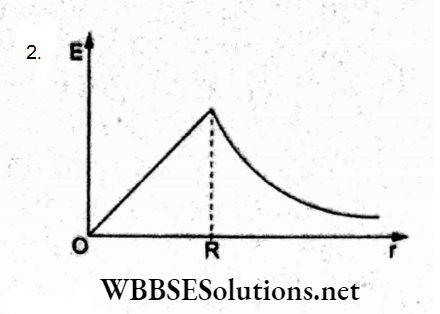
When charge Q is uniformly distributed throughout the volume of a solid sphere of radius R, the electric field inside the sphere at a distance r(r<R) from its center is \(E(r)=\frac{1}{4 \pi \varepsilon_0} \frac{Q}{R^3} r\), so E ∝ r, which represents a straight line through the origin.

For a point outside, \(E=\frac{1}{4 \pi \varepsilon_0} \frac{Q}{r^2}\) which means E decreases nonlinearly with r.

This represents the graph (b).

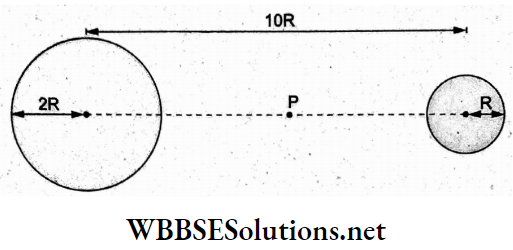
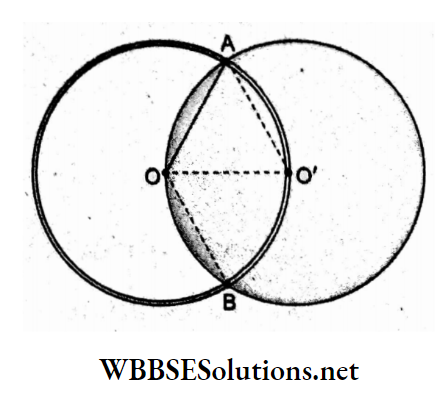
Question 25. A charge q is uniformly distributed on a ring of radius R. A sphere of an equal radius is constructed with its centre lying on the periphery of the ring. The flux of the electric field through the surface of the sphere will be

1. \(\frac{q}{\varepsilon_0}\)
2. \(\frac{q}{2 \varepsilon_0}\)
3. \(\frac{q}{3 \varepsilon_0}\)
4. \(\frac{q}{4 \varepsilon_0}\)

Answer: 3. \(\frac{q}{3 \varepsilon_0}\)

From the figure,

OA = radius of the ring,

O’A = radius of the sphere, and

OO’ = distance between their centers.

Since OA = O’A = OO’ = JR, ΔAOO’ is equilateral.

∴ \(\angle A O B=120^{\circ}=\frac{2 \pi}{3}\)

Arc AO’B of the ring enclosed within the sphere is \(R\left(\frac{2 \pi}{3}\right)\) contains the charge \(\frac{q}{2 \pi R} \cdot R \cdot \frac{2 \pi}{3}=\frac{q}{3}\) the flux of the electric field through the sphere is

⇒ \(\phi=\frac{1}{\varepsilon_0}\left(\frac{q}{3}\right)=\left(\frac{q}{3 \varepsilon_0}\right)\)

Question 26. Four charges are arranged at the corners of a square as shown in the figure. The direction of the electric field at the centre of the square will be along

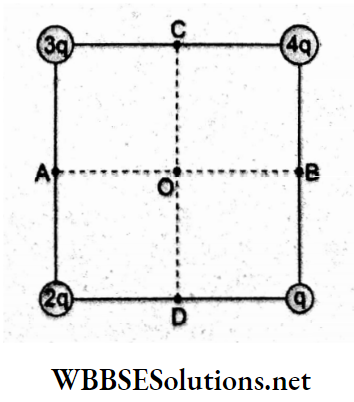
1. CD
2. BC
3. AD
4. AB

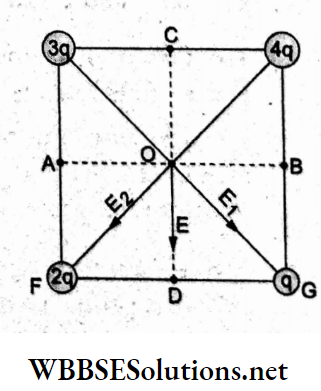
Answer: 1. CD

The field at a point is the force per unit test charge (+ve).

The field at the centre O due to charges 3q and q at the opposite comers is

⇒ \(E_1=K \frac{2 q}{r^2}\),directed along OG.

Similarly, the field at O due to the pair of charges 4q and 2q is

⇒ \(E_2=K \frac{2 q}{r^2}\), directed along OF.

The fields E₁ and E₂ are equal in magnitude so that the net field will be along CD.

Question 27. The electric field due to a charged straight conductor outside will be proportional to the distance r as

1. \(\frac{1}{r}\)
2. \(\frac{1}{r^2}\)
3. \(\frac{1}{r^{3 / 5}}\)
4. \(\frac{1}{r^{3 / 2}}\)

Answer: 1. \(\frac{1}{r}\)

In order to find the electric field due to a straight-charged conductor, we consider a coaxial cylindrical surface and apply Gauss’s theorem.

∴ \(E 2 \pi r l=\frac{\lambda l}{\varepsilon_0} \Rightarrow E=\frac{\lambda}{2 \pi \varepsilon_0 r}\)

Hence, H oc \(\frac{1}{r}\)

Question 28. An electron is projected with velocity \(\vec{v}=v_0 \hat{i}\) in the electric’ field \(\vec{E}=E_0 \hat{j}\). The path followed by the electron is a

1. Parabola
2. Circle
3. Straight line in the positive y-direction
4. Straight line in the negative y-direction

Answer: 1. Parabola

The motion of the title electron is along the and the force is along the negative y-direction as die field is along the y-direction. At t = 0, let the electron be at the origin. At time t,

⇒ \(x=v_0 t \text { and } y=\frac{1}{2} a t^2=\frac{1}{2}\left(\frac{e E}{m}\right)\left(\frac{x}{v_0}\right)^2\)

∴ \(y=\frac{1}{2}\left(\frac{e E}{m v_0^2}\right) x^2=k x^2\)

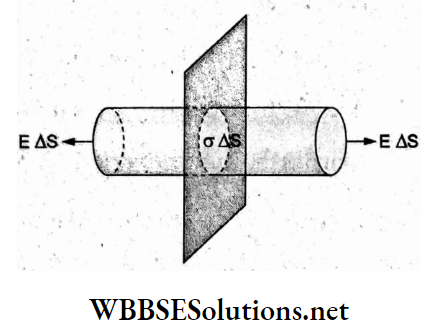
Question 29. The electric field at a distance r from an infinitely long uniformly charged conducting sheet is

1. Proportional to r^-1
2. Proportional to r^-2
3. Proportional to r^-3/2
4. Independent of r

Answer: 4. Independent of r

According to Gauss’s theorem, the total outward flux is

⇒ \(E=\Delta S+E \Delta S=\frac{1}{\varepsilon_0}(\sigma \Delta S)\)

where σ = surface charge density.

∴ \(E=\frac{\sigma}{2 \varepsilon_0}\)

which is independent of distance r.

Question 30. A solid conducting sphere is placed in a uniform electric field. Which path correctly 2 indicates the electric field lines in the given diagram?

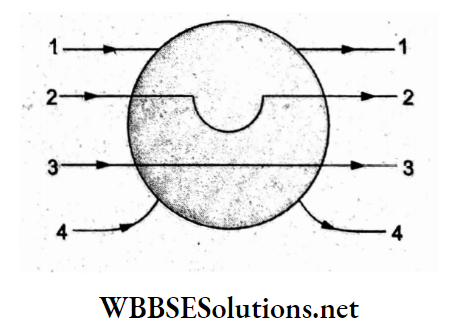
1. 1
2. 2
3. 3
4. 4

Answer: 4. 4

The surface of a conductor is equipotential, where the direction of the electric field lines is always perpendicular to the surface.

For a sphere, the normal direction is radial (directed towards the center) and hence the field lines terminate radially on the left side and restart radially from the right side, as shown by line 4.

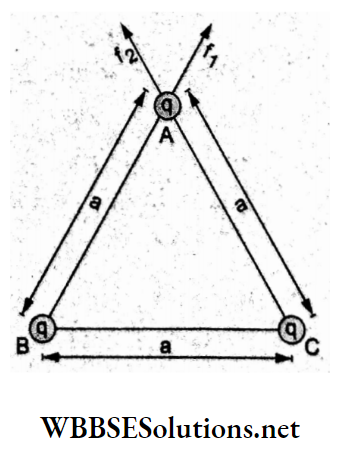
Question 31. Three identical charges, each equal to q, are placed at the vertices of an equilateral triangle of side a. The magnitude of the force experienced by each charge is

1. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q^2}{a^2}\)
2. \(\frac{1}{4 \pi \varepsilon_0} \frac{q^2}{2 a^2}\)
3. \(\frac{1}{4 \pi \varepsilon_0} \frac{\sqrt{3} q^2}{a^2}\)
4. \(\frac{1}{4 \pi \varepsilon_0} \frac{q^2}{\sqrt{2} a^2}\)

Answer: 3. \(\frac{1}{4 \pi \varepsilon_0} \frac{\sqrt{3} q^2}{a^2}\)

Forces acting on charge cj at A due to the remaining equal charges are

⇒ \(f=f_1=f_2=\frac{1}{4 \pi \varepsilon_0} \frac{q}{a^2}\)

∴ the magnitude of the net force is

⇒ \(F_{\text {net }}=\sqrt{f_1^2+f_2^2+2 f_1 f_2 \cos 60^{\circ}}\)

⇒ \(\sqrt{2 f^2+2 f^2 \times \frac{1}{2}}\)

= \(\sqrt{3} f\)

= \(\frac{1}{4 \pi \varepsilon_0} \frac{\sqrt{3} q^2}{a^2}\)

Question 32. An electric dipole is placed at an angle of 30° with an electric field of intensity 2 x 10⁵ N C^-1. It experiences a torque equal to 4 N m. The charge on the dipole, if the dipole length is 2 cm, is

1. 8 mC
2. 2 mC
3. 5 mC
4. 7 μC

Answer: 2. 2mC

Given that electric field = = 2 x 10⁵ NC^-1, 0 = 30°,E torque = \(\tau\) = 4 N m, dipole length = 2l = 2 x 10^-2 m.

⇒ \(\tau=p E \sin \theta\)

∴ \(p=q 2 l=\frac{\tau}{E \sin \theta}\)

or, \(q=\frac{\tau}{E(2 l) \sin \theta}\)

Substituting the values,

⇒ \(q=\frac{4 \mathrm{~N} \mathrm{~m}}{\left(2 \times 10^5 \mathrm{~N} \mathrm{C}^{-1}\right)\left(2 \times 10^{-2} \mathrm{~m}\right)(0.5)}\)

= 2 x 10^-3C

= 2mC.

Question 33. The potential (in volts) in a region is expressed as V(x, y, z) = 6xy- y + 2yz. The electric field (in N C^-1) at point (1,1, 0) is

1. \(-(2 \hat{i}+3 \hat{j}+\hat{k})\)
2. \(-(6 \hat{i}+9 \hat{j}+\hat{k})\)
3. \(-(3 \hat{i}+5 \hat{j}+3 \hat{k})\)
4. \(-(6 \hat{i}+5 \hat{j}+2 \hat{k})\)

Answer: 4. \(-(6 \hat{i}+5 \hat{j}+2 \hat{k})\)

Given that the potential is a function of x, y, z, i.e.,

V(x,y,z) = 6xy – y + 2yz.

The electric field along the x-direction is

⇒ \(E_x=-\frac{\delta V}{\delta x}=-6 y\)

Similarly, \({E_y}=-\frac{\delta V}{\delta y}=-6 x+1-2 z\)

⇒ \(E_z=-\frac{\delta V}{\delta z}=-2 y\)

At point (1,1,0) \(\vec{E}_x=-6 \hat{i}, \vec{E}_y=-5 \hat{j} \text { and } \vec{E}_z=-2 \hat{k}\)

Thus, \(\vec{E}=-(6 \hat{i}+5 \hat{j}+2 \hat{k})\)

Question 34. In a region, the potential is represented as V(x, y, z) = 6x – 8xy – 8y + 6yz, where Vis in volts and x, y, z are in meters. The electric force experienced by a charge of 2 coulombs situated at point (1,1, 1) is

1. 6√5 N
2. 30 N
3. 24 N
4. \(4 \sqrt{35} \mathrm{~N}\)

Answer: 4. \(4 \sqrt{35} \mathrm{~N}\)

Potential = V = 6x – 8xy – 8y + 6yz.

∴ \(E_x=-\frac{\partial V}{\partial x}=-6+8 y\)

⇒ \(E_y=-\frac{\partial V}{\partial y}=8 x+8-6 z, \text { and }\)

⇒ \(E_z=-\frac{\partial V}{\partial z}=-6 y\)

At point (1, 1,1), \(\vec{E}=2 \hat{i}+10 \hat{j}-6 \hat{k}\)

The magnitude of the electric field is,

⇒ \(|\vec{E}|=\sqrt{2^2+10^2+(-6)^2} \mathrm{Vm}^{-1}\)

= \(2 \sqrt{35} \mathrm{Vm}^{-1}\)

∴ the force on the charge Q = 2C is

F = QE

= \((2 \mathrm{C})\left(2 \sqrt{35} \mathrm{Vm}^{-1}\right)\)

= \(4 \sqrt{35} \mathrm{~N}\)

Question 35. An electric dipole of dipole moment \(\vec{p}\) is aligned parallel to a uniform electric field \(\vec{E}\). The energy required to rotate the dipole by 90° is

1. p²E
2. pE
3. pE²
4. Infinite

Answer: 2. pE

The energy required to rotate the dipole from θ = 0 to θ is

W = pE(1-cosθ).

Here θ = 90°, so die energy required is W = pE

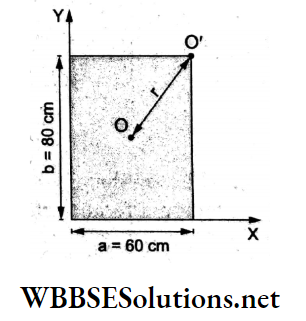
Question 36. A cube of side 10 cm has charge Q at each of its eight comers. If the potential at the center of the cube is 144 x 10⁴ V, the charge Q in coulombs is

1. √2 μC
2. √3 μC
3. 2 μC
4. 3μC

Answer: 2. √3 μC

The distance of each comer of the cube from the centre is \(r=\frac{\sqrt{3}}{2} a\)

Hence, the total potential at the centre is

⇒ \(V=\frac{1}{4 \pi \varepsilon_0} \frac{8 Q}{r}=\left(9 \times 10^9\right) \frac{8 Q}{\left(\frac{\sqrt{3}}{2} a\right)}\)

⇒ \(Q=\left(\frac{\sqrt{3}}{2} a\right) \frac{V}{8\left(9 \times 10^9\right)} \mathrm{C}\)

⇒ \(\frac{\sqrt{3}}{2} \frac{\left(10 \times 10^{-2}\right)\left(144 \times 10^4\right)}{72 \times 10^9} \mathrm{C}\)

√3 x 10^-6C

= √3μC.

Question 37. A straight wire of length L has charge Q distributed uniformly along its length. If the wire is bent into a semicircular shape, the potential at the centre of curvature of the semicircle is

1. \(\frac{Q}{L}\)
2. \(\frac{Q}{\varepsilon_0 L}\)
3. \(\frac{Q}{4 \pi \varepsilon_0 L}\)
4. \(\frac{Q}{4 \varepsilon_0 L}\)

Answer: 4. \(\frac{Q}{4 \varepsilon_0 L}\)

Given that length = L = πR, where R is the radius of the semi circle.

∴ the potential at the centre is

⇒ \(V=\frac{1}{4 \pi \varepsilon_0} \frac{Q}{R}=\frac{1}{4 \pi \varepsilon_0} \frac{Q}{L / \pi}=\frac{Q}{4 \varepsilon_0 L}\)

Question 38. The electric potential at a point P(x, y, z) in space is expressed as V = A(xy + yz + zx), where A is a constant. The electric field at P will be

1. \(-A(x \hat{i}+y \hat{j}+z \hat{k})\)
2. \(-A[(x+y) \hat{i}+(y+z) \hat{j}+(z+x) \hat{k}]\)
3. \(-A[(y+z) \hat{i}+(z+x) \hat{j}+(x+y) \hat{k}]\)
4. \(\frac{A}{\sqrt{x^2+y^2+z^2}}(x \hat{i}+y \hat{j}+z \hat{k})\)

Answer: 3. \(-A[(y+z) \hat{i}+(z+x) \hat{j}+(x+y) \hat{k}]\)

Given that potential = V = A(xy + yz + zx).

⇒ \(E_x=-\frac{\partial V}{\partial x}=-A(y+z)\)

⇒ \(E_y=-\frac{\partial V}{\partial y}=-A(x+z)\)

⇒ \(E_z=-\frac{\partial V}{\partial z}=-A(x+y)\)

∴ \(\vec{E}=E_x \hat{i}+E_y \hat{j}+E_z \hat{k}\)

= \(-A[(y+z) \hat{i}+(x+z) \hat{j}+(x+y) \hat{k}]\)

Question 39. An electric dipole of moment p is placed in an electric field of intensity £. The dipole acquires a position such that its axis makes an angle 0 with the direction of the field. Assuming that the potential energy of the dipole to be zero when 0 = 90°, the torque and the potential energy of the dipole will respectively be

1. pE sin θ and -pE cos θ
2. pE sin θ and-2pE cos θ
3. pE sin θ and 2pE cos θ
4. pE cos θ and -pE sin θ

Answer: 1.

Torque on the dipole \(\vec{\tau}=\vec{p} \times \vec{E} . \text { So }|\vec{\tau}|=p E \sin \theta\)

Potential energy \(U=-\vec{p} \cdot \vec{E}=-p E \cos \theta\)

Question 40. Four point charges -Q,-q, 2q and 2Q are placed, one at each comer of a square. The relation between Q and q for which the potential at the centre of the square is zero will be

1. Q = -q
2. Q = –\(\frac{1}{q}\)
3. Q = q
4. Q = \(\frac{1}{q}\)

Answer: 1. Q = -q

Let the distance of each comer from the centre of the square = r.

∴ the net potential at the centre is,

⇒ \(V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{-Q}{r}+\frac{-q}{r}+\frac{2 q}{r}+\frac{2 Q}{r}\right)\)

⇒ \(\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q+q}{r}\right)\)

∵ V = 0,Q + q = 0

=> Q = -q.

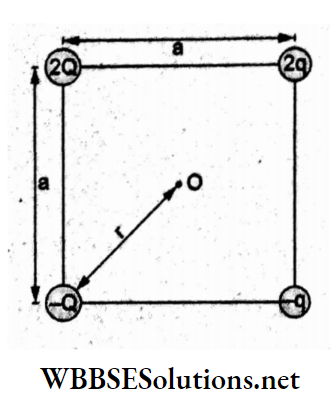
Question 41. Four electric charges +q, +q, -q, -q are placed at the comers of a square of side 2L. The electric potential at A, midway between the two charges +q and +q, is

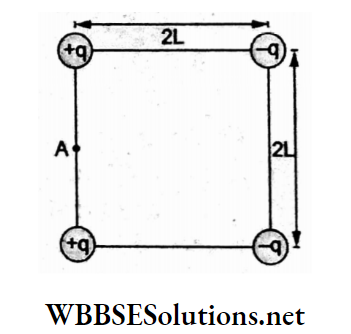
1. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}(1+\sqrt{5})\)
2. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1+\frac{1}{\sqrt{5}}\right)\)
3. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)
4. Zero

Answer: 3. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)

Potential at A due to the pair of charges \((+q,+q) \text { is } V_1=\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\)

Distance of A from each-q charge = \(\sqrt{4 L^2+L^2}=\sqrt{5} L\)

∴ the potential at A due to the pair ofcharges \((-q,-q), V_2=\frac{1}{4 \pi \varepsilon_0} \frac{-2 q}{(\sqrt{5 L})}\)

∴ the total potential at A is \(V=V_1+V_2=\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)

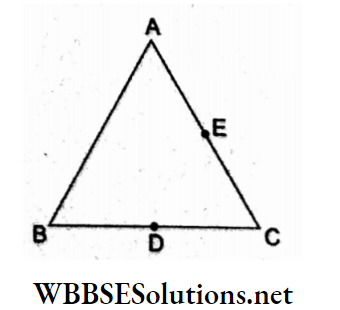
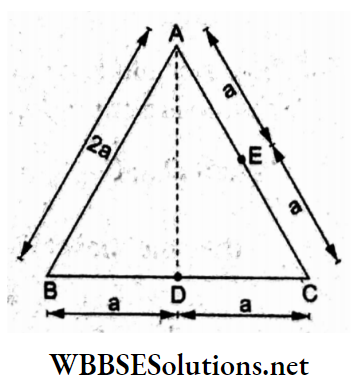
Question 42. Three charges, each +q, are placed at the comers of an equilateral triangle ABC of side 2a. D and E are the midpoints of BC and CA. The work done in taking a charge Q from D to

1. \(\frac{3 Q q}{4 \pi \varepsilon_0 a}\)
2. \(\frac{3 Q_q}{8 \pi \varepsilon_0 a}\)
3. \(\frac{Q q}{4 \pi \varepsilon_0 a}\)
4. Zero

Answer: 4. Zero

The potential at E due to the three charges is

⇒ \(V_{\mathrm{B}}=\frac{1}{4 \pi \varepsilon_0}\left(\frac{q}{a}+\frac{q}{a}+\frac{q}{\sqrt{3} a}\right)\)

⇒ \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{a}\left(2+\frac{1}{\sqrt{3}}\right)\)

Similarly at D, \(V_{\mathrm{D}}=\frac{1}{4 \pi \varepsilon_0} q\left(2+\frac{1}{\sqrt{3}}\right)\)

∴ V_D = V_B, the work done is W = Q (V_D – V_E) = 0

Question 43. The electric potential V at any point (x, y, z), all in meters, in space, is given by V = 4x² volts. The electric field of the point (1, 0, 2) in V m^-1 is

1. 8 along the negative x-axis
2. 8 along the positive x-axis
3. 16 along the negative x-axis
4. 16 along the positive x-axis

Answer: 1. 8 along the negative x-axis

Given that V = 4x².

Electric field = \(E=-\frac{\partial V}{\partial x}=-8 x\)

For \(x=1, \vec{E}_x=-8 \mathrm{~V} \mathrm{~m}^{-1} \hat{i}\)

Hence, the field is 8 V m^-1 along the negative x-axis.

Question 44. The electric potential at a point (x, y, z) is given by V = -x²y- xz³ + 4. The electric field at that point is

1. \(\vec{E}=2 x y \hat{i}+\left(x^2+y^2\right) \hat{j}+\left(3 x z+y^2\right) \hat{k}\)
2. \(\vec{E}=z^3 \hat{i}+x y z \hat{j}+z^2 \hat{k}\)
3. \(\vec{E}=\left(2 x y-z^3\right) \hat{i}+x y^2 \hat{j}+3 x z^2 \hat{k}\)
4. \(\vec{E}=\left(2 x y+z^3\right) \hat{i}+x^2 \hat{j}+3 x z^2 \hat{k}\)

Answer: 4. \(\vec{E}=\left(2 x y+z^3\right) \hat{i}+x^2 \hat{j}+3 x z^2 \hat{k}\)

Given that V = -x²y- xz³ + 4.

The electric field \(\vec{E}\) has the following components:

⇒ \(E_x=-\frac{\partial V}{\partial x}=+2 x y+z\)

⇒ \(E_y=-\frac{\partial V}{\partial y}=x^2\)

and \(E_z=-\frac{\partial V}{\partial z}=3 x z^2\)

∴ \(\vec{E}=E_x \hat{i}+E_y \hat{j}+E_z \hat{k}\)

= \(\left(2 x y+z^3\right) \hat{i}+x^2 \hat{j}+3 x z^2 \hat{k}\)

Question 45. The electric potential at a point in free space due to charge Q coulombs is Q x 10¹¹ volts. The electric field at that point is

1. 4πε₀Q x 10²⁰ V m^-1
2. 12πε₀Q x 10²² V m^-1
3. 4πε₀Q x 10²² V m^-1
4. 12πε₀Q x 10²⁰ V m^-1

Answer: 3. 4πε₀Q x 10²² V m^-1

The electric potential due to a charge Q at a distance r is

⇒ \(V=K \frac{Q}{r}=Q \times 10^{11}\)….(1)

At the same point, the electric field

⇒ \(E=K \frac{Q}{r^2} \mathrm{~V} \cdot \mathrm{m}^{-1}\)….(2)

From (1),

⇒ \(\frac{K}{r}=10^{11}\)

⇒ \(r=\frac{K}{10^{11}}\)

From (2),

⇒\(E=\frac{K Q V m^{-1}}{\left(K / 10^{11}\right)^2}\)

= \(\frac{10^{22} Q}{K}\)

= \(4 \pi \varepsilon_0 Q \times 10^{22} \mathrm{Vm}^{-1}\)

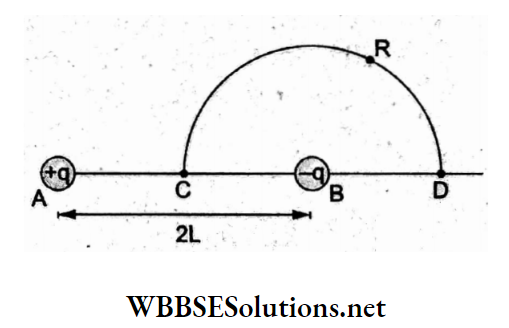
Question 46. Charges +q and -q are placed at points A and B respectively, which are a distance 2L apart. C is the midpoint between A and B. The work done in moving a charge Q along the semicircle CRD is

1. \(\frac{Q q}{2 \pi \varepsilon_0 L}\)
2. \(\frac{Q q}{6 \pi \varepsilon_0 L}\)
3. –\(\frac{Q q}{6 \pi \varepsilon_0 L}\)
4. \(\frac{Q q}{4 \pi \varepsilon_0 L}\)

Answer: 3. –\(\frac{Q q}{6 \pi \varepsilon_0 L}\)

The electric field is conservative, so the work done for the displacement of charge is path-independent.

Potential at \(\mathrm{C}=V_{\mathrm{C}}=\frac{K(+q)}{L}+\frac{K(-q)}{L}=0\)

∴ the potential at D,

⇒ \(V_{\mathrm{D}}=\frac{K(+q)}{3 L}+\frac{K(-q)}{L}=-\frac{2}{3} \frac{K q}{L}\)

∴ potential difference

⇒ \(\Delta V=V_D-V_C=\frac{-2}{3} \frac{K q}{L}\)

∴ work done \(W=Q \Delta V=\frac{-2}{3}\left(\frac{1}{4 \pi \varepsilon_0}\right) \frac{Q q}{L}=-\frac{Q q}{6 \pi \varepsilon_0 L}\)

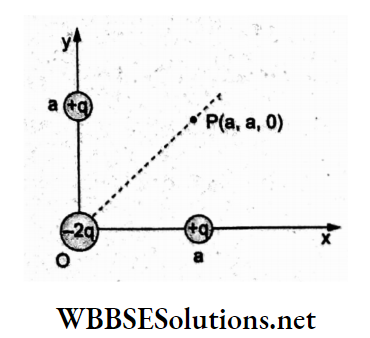
Question 47. Three point charges +q, -2q and +q are placed at points (x – 0, y =0a, z = 0), (x = 0, y = 0, z = 0) and (x = a, y = 0, z = 0) respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are

1. √2qa along the line joining the points (x = 0, y = 0, z = 0) and
   (x = a,y = a,z = 0)
2. qa along the line joining the points (x = 0, y = 0, z = 0) and
   (x = a,y = q,z = 0)
3. √2qa along the positive r-direction
4. √2qa along the positive y-direction

Answer: 1. √2qa along the line joining the points (x = 0, y = 0, z = 0) and
(x = a,y = a,z = 0)

The given system of charges constitutes yi two electric dipoles of the same magnitude (qa) directed along the x- and y-axes.

Thus, \(\vec{p}=(q a) \hat{i}+(q a) \hat{j}\)

The magnitude of the dipole moment is,

⇒ \(p=\sqrt{p_x^2+p_y^2}\)

= \(\sqrt{(q a)^2+(q a)^2}\)

= \(\sqrt{2} q a\)

Here \(\vec{p}\) makes an angle of 45° with the x-axis, and hence is along the line OP, where the coordinates of P are (a, a, 0)

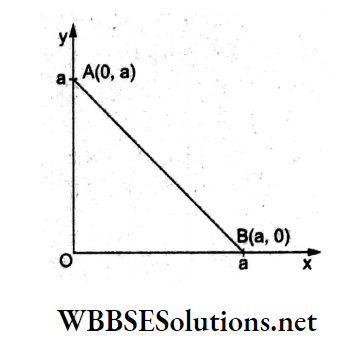
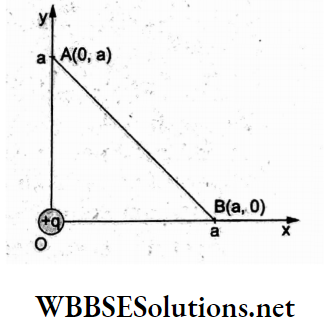
Question 48. As shown in the figure, a point charge +q is placed at the origin O. Work done in taking another charge -Q’from the point A(0, a) to another point B(a, 0) along the straight path AB is

1. Zero
2. \(\left(\frac{Q q}{4 \pi \varepsilon_0 a^2}\right) \sqrt{2} a\)
3. \(\left(\frac{-Q q}{4 \pi \varepsilon_0 a^2}\right) \sqrt{2} a\)
4. \(\left(\frac{Q q}{4 \pi \varepsilon_0 a^2}\right) \frac{a}{\sqrt{2}}\)

Answer: 1. Zero

Points A and B are equidistant from the charge q at O, so the potential is

⇒ \(V_{\mathrm{A}}=V_{\mathrm{B}}=K \frac{Q}{a}\)

Work done = W = (-Q)(V_B– V_A)

= -Q x 0

= 0

Question 49. A bullet of mass 2 g has a charge of 2 pC. Through what potential difference must it be accelerated, starting from rest, so as to acquire a speed of 10 m s^-1?

1. 5kV
2. 50 kV
3. 5 V
4. 50 V

Answer: 2. 50 kV

Work done = change in KE

=> QV = KE_final-KE_initial = \(\frac{1}{2}\) mv².

Given: Q = 2μC = 2 x 10^-6C,

m = 2 g

= 2 x 10^-3 kg,

v = 10 m s^-1.

Potential difference = \(V=\frac{1}{2} \frac{m v^2}{Q}\)

⇒ \(\frac{1}{2} \frac{\left(2 \times 10^{-3} \mathrm{~kg}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)^2}{\left(2 \times 10^{-6} \mathrm{C}\right)}\)

= 50 x 10³ V

= 50 kV.

Question 50. If E_a be the electric field due to an electric dipole on its axial line and Eq be the field on its equatorial line at the same distance r then the relation between Ea and Eq is

1. Ea = Eq
2. Ea = 2Eq
3. Eq = 2E.
4. Ea = 3Eq

Answer: 2. Ea = 2Eq

The magnitude of the electric field at the axial point is \(E_{\mathrm{ax}}=K\left(\frac{2 p}{r^3}\right)\)
and that at the equatorial point is \(E_{\text {eq }}=K\left(\frac{p}{r^3}\right)\)

Hence, the ratio is \(\frac{E_{\mathrm{ax}}}{E_{\mathrm{eq}}}=2 \Rightarrow E_{\mathrm{ax}}=2 E_{\mathrm{eq}}\)

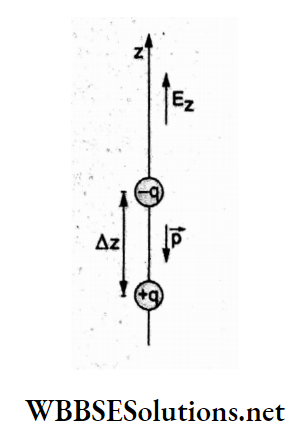
Question 51. In a certain region of space, an electric field is along the positive z-direction throughout. The magnitude of the electric field, however, is not constant but increases uniformly along the positive z-direction at a constant rate of 10⁵ N C^-1 m^-1. The force experienced by the system having a total dipole moment equal to 10⁷ C m in the negative z-direction will be

1. -10^-2 N
2. 10^-2 N
3. 10^-4 N
4. -10^-4 N

Answer: 1. -10^-2 N

In the given figure, the direction of the dipole moment p is along the negative z-direction and the field is increasing along the positive z-direction.

Force on the the charge +q is E+ = qE and that on charge (-q) is E_ = (-q)(E + AE)

⇒ \((-q)\left(E+\frac{d E}{d z} \cdot \Delta z\right)\)

∴ the net force on the dipole is,

⇒ \(F=q E-q E-q\left(\frac{d E}{d z} \cdot \Delta z\right)\)

⇒ \(-(q \Delta z) \frac{d E}{d z}\)

= \(-p\left(\frac{d E}{d z}\right)\)

= -(10^-7 C m) (10⁵ N C^-1 m^-1)

=-10^-2 N.

Question 52. The magnitude of the charge of an electric dipole is q and its dipole moment is p. The dipole is placed in a uniform electric field \(\vec{E}\). Its dipole moment vector \(\vec{p}\) is along the direction of the field \(\vec{E}\). The net force on it and its potential energy are respectively

1. 2qE and minimum
2. qE and pE
3. qE and maximum
4. Zero and minimum

Answer: 3. qE and maximum

An electric dipole consists of two, equal and opposite charges ±q and experiences equal and opposite forces. Hence, the net force on the dipole in a uniform electric field is zero. The potential energy of the dipole is,

⇒ \(U(\theta)=-\vec{p} \cdot \vec{E}=-p E \cos \theta\)

For θ = 0, U = -pE, which is minimum.

Question 53. Some charge is given to a conductor. Then it’s potential

1. Is maximum at the surface
2. Is maximum at the centre
3. Remains the same throughout the conductor
4. Is maximum somewhere between the surface and center

Answer: 3. Remains the same throughout the conductor

The surface of a charged conductor of any shape is equipotential and its potential remains the same throughout the conductor as \(\vec{E}\) = 0 inside.

Question 54. If a dipole of dipole moment \(\vec{p}\) is placed in a uniform electric field \(\vec{E}\) then die torque acting on it is given by

1. \(\vec{\tau}=\vec{p} \cdot \vec{E}\)
2. \(\vec{\tau}=\vec{p} \times \vec{E}\)
3. \(\vec{\tau}=\vec{p}+\vec{E}\)
4. \(\vec{\tau}=\vec{p}-\vec{E}\)

Answer: 2. \(\vec{\tau}=\vec{p} \times \vec{E}\)

Torque = \(\tau\) = pE smQ and in vector notation it is expressed as \(\vec{\tau}=\vec{p} \times \vec{E}\)

Question 55. While bringing an electron towards another electron, the electrostatic potential energy of the system

1. Becomes zero
2. Increases
3. Decreases
4. Remains the same

Answer: 2. Increases

The electrostatic potential energy of a system of two charges is,

⇒ \(U=\frac{1}{4 \pi \varepsilon_0} \frac{Q_1 Q_2}{r}\)

Here, \(Q_1=Q_2=(-e)\)

So, \(U=\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r}\)

With decreased inseparation r, the potential energy increases.

Question 56. A point charge Q is placed on the perpendicular bisector of an electric dipole of dipole moment p. If the distance of Q from the dipole is r (much larger than the size of the dipole) then the electric field at Q is proportional to

1. p² and r^-3
2. p and r^-2
3. p-1 and r^-2
4. p and r^-3

Answer: 4. p and r^-3

The electric field at the perpendicular bisector of an electric dipole is

given by \(E=\frac{1}{4 \pi \varepsilon_0} \frac{p}{r^3}\), which is proportional to (1) and (2) r^-3.

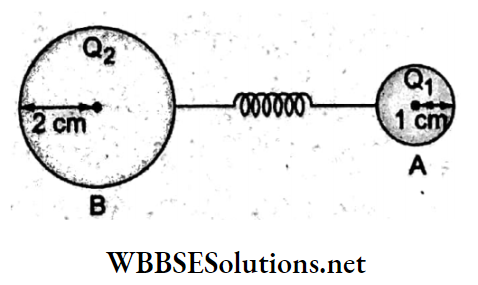
Question 57. Two metallic spheres of radii 1 cm and 2 cm are given charges10^-2C and 5 x 10^-2 C respectively. If they are connected by a conducting wire, die final charge on the smaller sphere is

1. 3 x 10^-2C
2. 4 x 10^-2 C
3. 1 x 10^-2C
4. 2 x 10^-2 C

Answer: 4. 2 x 10^-2 C

For the smaller sphere A, r₁ = 1cm and charge q₁ = 10^-2C.

For the sphere B, r₂ = 2 cm and charge q₂ = 5 x 10^-2C.

When connected by a conducting wire, the system has a common potential V with charge redistribution.

Let q’₁ and q’₂ be the charges on A and B respectively.

⇒ \(V=K \frac{q_1^{\prime}}{r_1}\)

= \(K \frac{q_2^{\prime}}{r_2}\)

= \(K \frac{\left(q_1^{\prime}+q_2^{\prime}\right)}{r_1+r_2}\)

= \(\frac{K Q}{r_1+r_2}\), where Q = total charge.

∴ charge on \(\mathrm{A}=q_1^{\prime}=\frac{Q}{r_1+r_2} \cdot r_1=\frac{10^{-2} \mathrm{C}+5 \times 10^{-2} \mathrm{C}}{(1 \mathrm{~cm}+2 \mathrm{~cm})}(1 \mathrm{~cm})\)

⇒ \(\frac{6 \times 10^{-2}}{3} \mathrm{C}=2 \times 10^{-2} \mathrm{C}\)

Question 58. There is an electric field \(\vec{E}\) along the x-direction. If the work done on moving a charge of 0.2 C through a distance of 2 m along a line making an angle 60° with the x-axis is 4 J then the value of E is

1. 5 NC^-1
2. 20 NC^-1
3. √3 NC^-1
4. 4 NC^-1

Answer: 2. 20 NC^-1

Work done = \(W=\vec{F} \cdot \vec{S}=q \vec{E} \cdot \vec{S}=q E S \cos \theta\)

Here, q = 0.2 C, S = 2 m, 0 = 60° and W = 4J.

Substituting the values, 4 J = (0.2 C) E(2 m) cos 60° = E(0.2 C m).

∴ \(E=\frac{4 \mathrm{~J}}{0.2 \mathrm{Cm}}\)

= 20 V m^-1 or 20 NC^-1

Question 59. An electric dipole of dipole moment p is placed in the position of stable equilibrium in a uniform electric field E. It is rotated through an angle 0 from the initial position. The potential energy of the electric dipole in the final position is

1. -pE cos θ
2. pE (1- cos θ)
3. pE cos θ
4. pE sin θ

Answer: 1. -pE cos θ

The PE of an electric dipole of the moment \(\vec{p}\) in a uniform electric field \(\vec{E}\) is given by \(U=-\vec{p} \cdot \vec{E}=-p E \cos \theta\)

The dipole is the most stable when the PE is minimal and this occurs
at θ = 0°.

When rotated through an angle θ, work done = U_f– U_i

=> pE(1- cos θ) = U_f– (-pE)

=> U_f = -pE cosθ.

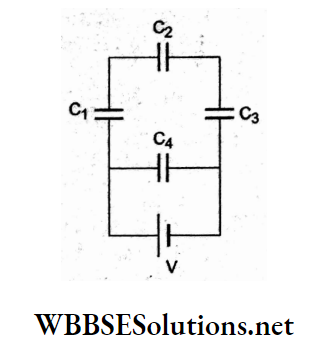
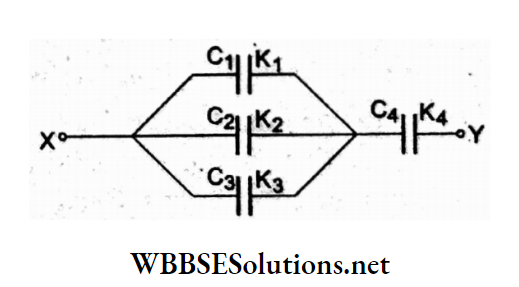
Question 60. A network of four capacitors of capacitances C₁ = C, C₂ = 2C, C₃ = 3C, and C₄ = 4C is connected to a battery as shown in the adjoining figure. The ratio of the charges on C₂ and C₄ is

1. \(\frac{4}{7}\)
2. \(\frac{3}{22}\)
3. \(\frac{7}{4}\)
4. \(\frac{22}{3}\)

Answer: 2. \(\frac{3}{22}\)

The given network can be redrawn as shown.

The equivalent capacitance of the series combination is \(\frac{6}{11}\)C.

Charge Q is the same on each capacitor in series, where Q = Q₁ = Q₂ = Q₃ = C_eq.V = \(\frac{6}{11}\)CV.

The charge on C₄ is Q₄ = (4C) V

⇒ \(\frac{Q_2}{Q_4}=\frac{\frac{6}{11} C V}{4 C V}\)

= \(\frac{3}{22}\)

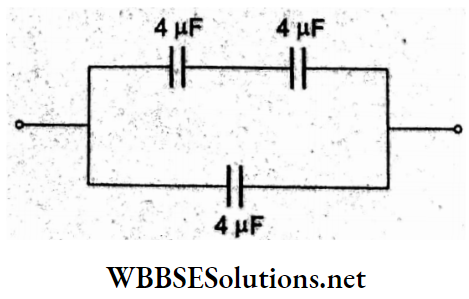
Question 61. Three capacitors, each of capacitance 4μF, are to be connected in such a way that the effective capacitance is 6 μF. This can be done by

1. Connecting All Of them in a series
2. Connecting Them in parallel
3. Connecting Two In series and one in parallel
4. Connecting Two In parallel and one in series

Answer: 3. Connecting two in series and one in parallel

Two capacitors in series give a capacitance of 2 μF. When this combination is connected in parallel to the 3rd capacitor, we get

C_eq = 2 μF + 4 μF

= 6 μF.

Question 62. A capacitor of capacitance C₁ is charged up to V volts and then connected to an uncharged capacitor of capacitance C₂. The final potential difference across each will be

1. \(\frac{C_2 V}{C_1+C_2}\)
2. \(\frac{C_1 V}{C_1+C_2}\)
3. \(\left(1+\frac{C_2}{C_1}\right) V\)
4. \(\left(1-\frac{C_2}{C_1}\right) V\)

Answer: 2. \(\left(1+\frac{C_2}{C_1}\right) V\)

When the capacitor C₁ is charged to a potential of V volts, its charge is Q = C₁V. When connected in parallel to the uncharged C₂, the common potential is

⇒ \(V=\frac{Q_1}{C_1}=\frac{Q_2}{C_2}\)

= \(\frac{Q_1+Q_2}{C_1+C_2}\)

= \(\frac{\text { total charge }}{C_1+C_2}\)

= \(\frac{Q}{C_1+C_2}\)

= \(\frac{C_1 V}{C_1+C_2}\)

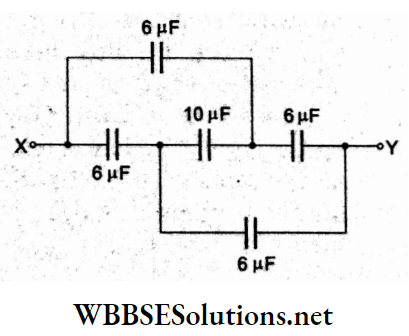
Question 63. What is the effective capacitance across the terminals x and y?

1. 12 μF
2. 18 μF
3. 24μF
4. 6 μF

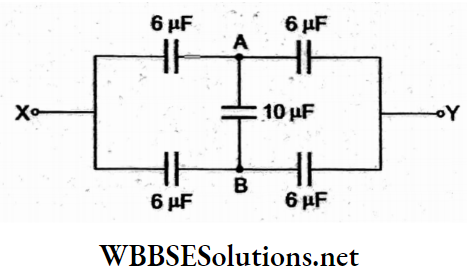
Answer: 4. 6 μF

The given network of capacitors can be redrawn as shown in the figure. The applied voltage across X and Y is equally divided across the two capacitors of equal capacitance in the upper and lower branches, so points A and B will be at the same potential. The 10-μF capacitor will be ineffective.

Hence, the equivalent I capacitance across X and Y will be

⇒ \(C_{e q}=3 \mu \mathrm{F}+3 \mu \mathrm{F}=6 \mu \mathrm{F}\)

Question 64. Two parallel metal plates having charges +Q and -Q face each other at a certain distance. If the plates are now dipped in kerosene oil and kept in a tank, the electric field between the plates will

1. Become zero
2. Increase
3. Decrease
4. Remain the same

Answer: 3. Decrease

The electric field between the plates of a charged capacitor with air between the plates is

⇒ \(E=\frac{\sigma}{\varepsilon_0}\), where a = surface charge density.

When immersed in a liquid (here kerosene oil), the field is charged to \(E^{\prime}=\frac{\sigma}{K \varepsilon_0}\) where K = relative permittivity (or dielectric constant) of kerosene oil.
Since K >1, E’ < E.

Question 65. Three capacitors, each of capacitance C and of breakdown voltage V, are joined in series. The capacitance and breakdown voltage for the given combination will be

1. 3C, \(\frac{V}{3}\)
2. \(\frac{C}{3}\),3V
3. 3C,3V
4. \(\frac{C}{3}\), \(\frac{V}{3}\)

Answer: 2. \(\frac{C}{3}\),3V

The equivalent capacitance in series grouping is

⇒ \(\frac{1}{C_{\mathrm{eq}}}=\frac{1}{C}+\frac{1}{C}+\frac{1}{C}\)

= \(\frac{3}{C}\)

⇒ \(C_{\text {eq }}=\frac{C}{3}\)

Since the voltage across each equal capacitor in series is the same (equal to breakdown voltage V), the breakdown voltage across the combination is 3V.

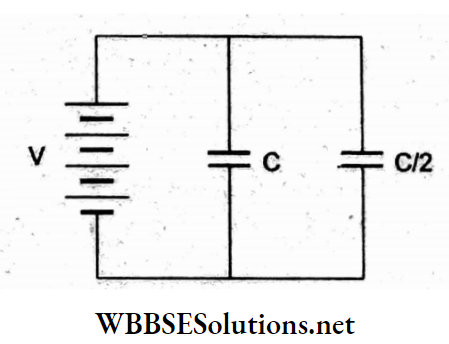
Question 66. Two capacitors, one of capacitance C and the other of capacitance C/2, are connected to a V-volt battery as shown in the figure. The work in fully charging both the capacitors is

1. \(\frac{1}{4}\)CV²
2. \(\frac{3}{4}\)CV²
3. \(\frac{1}{2}\)CV²
4. 2CV²

Answer: 2. \(\frac{3}{4}\)CV²

Work done in charging toe capacitor = electrostatic energy stored in the capacitor, hence

⇒ \(W=\frac{1}{2} C V^2\).

The equivalent capacitance (in the parallel combination) is \(C+\frac{C}{2}=\frac{3}{2} C\) C and the voltage across it is V.

Hence, the total work done is

⇒ \(W=\frac{1}{2}\left(\frac{3}{2} C\right) V^2=\frac{3}{4} C V^2\)

Question 67. A parallel-plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery, the separation between the plates of the capacitor is increased using an insulating handle. As a result, the potential difference between the plates

1. Increases
2. Decreases
3. Does not change
4. Becomes zero

Answer: 1. Increases

After the charging battery is disconnected, the charge on the plates of the capacitor will remain unchanged. When the separation between the plates (4) is increased, the capacitance \(\left(C=\frac{\varepsilon_0 A}{d}\right)\) will decrease.

Consequently, the potential difference between the plates \(\left(V=\frac{Q}{C}\right)\) will increase.

Question 68. Two thin dielectric slabs of dielectric constants K₁ and K₂ (K₁ < K₂) are inserted between the plates of a parallel-plate capacitor, as shown in the figure. The variation of the electric field between the plates with a distance d as measured from the plate P is correctly shown in

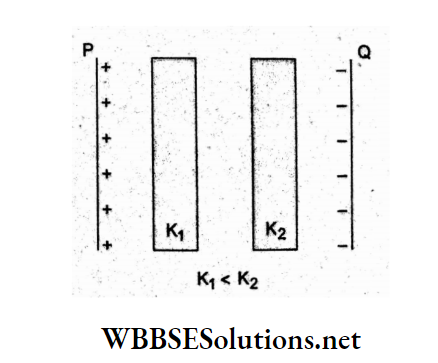
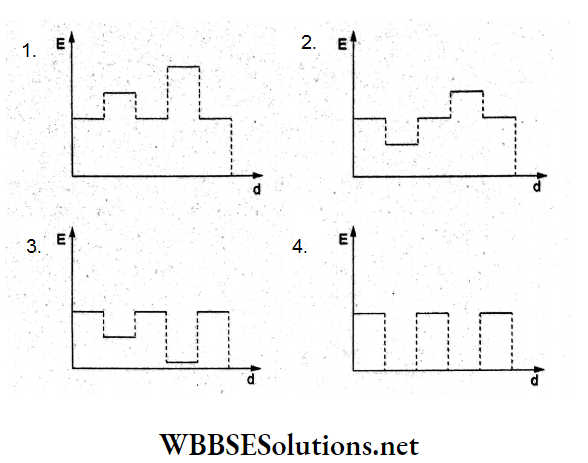
Answer: 3.

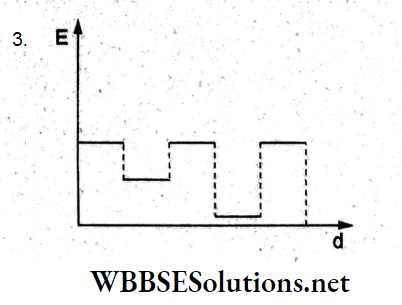
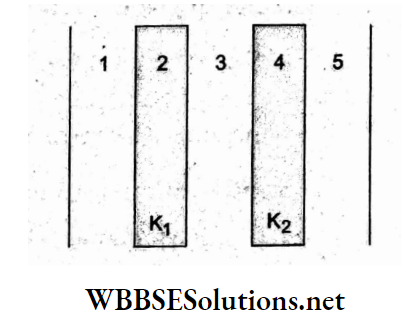
Let us divide the space between the plates of the charged capacitor into five regions.

In regions 1, 3, and 5 the medium is air, so the field

⇒ \(E_1=E_3=E_5=\frac{\sigma}{2 \varepsilon_0}\)

In the region 2, field \(E_2=\frac{\sigma}{2 K_1 \varepsilon_0}\) and in die region 4, field \(E_4=\frac{\sigma}{2 K_2 \varepsilon_0}\)

Since K₁ < K₂, E₂ > E₄.

Thus, E₁ = E₃ = E₅ > E₂ > E₄ as shown in option (3).

Question 69. A series combination of n₁ capacitors, each of value C₁ is charged by a source of potential difference 4V. When another parallel combination of n₂ capacitors, each of value C₂, is charged by a voltage source of V, it has the same (total) energy stored in it as the series combination has. The value of C₂, in terms of C₁, is then

1. \(\frac{2 C_1}{n_1 n_2}\)
2. \(\frac{16 n_2 C_1}{n_1}\)
3. \(\frac{2 n_2 C_1}{n_1}\)
4. \(\frac{16 C_1}{n_1 n_2}\)

Answer: 4. \(\frac{16 C_1}{n_1 n_2}\)

Equivalent capacitance in series grouping = \(\frac{C_1}{n_1}\) . When connected across a voltage source of 4V, the energy stored is

⇒ \(u_1=\frac{1}{2}\left(\frac{C_1}{n_1}\right)(4 V)^2\)

Equivalent capacitance in parallel grouping = n2C2. When connected across the source of voltage V, the energy stored is \(U_2=\frac{1}{2}\left(n_2 C_2\right) V^2\)

Given,

⇒ \(U_1=U_2\)

⇒ \(\frac{1}{2}\left(\frac{C_1}{n_1}\right) 16 V^2\)

⇒ \(\frac{1}{2} n_2 C_2 V^2\)

⇒ \(C_2=\frac{16 C_1}{n_1 n_2}\)

Question 70. A parallel-plate air capacitor has capacitance C and the separation between the plates is d. A potential difference V is applied between the plates. The force of attraction between the plates will be

1. \(\frac{C V^2}{d}\)
2. \(\frac{C^2 V^2}{2 d^2}\)
3. \(\frac{C^2 V^2}{2 d}\)
4. \(\frac{C V^2}{2 d}\)

Answer: 4. \(\frac{C V^2}{2 d}\)

The electric field between the plates of a charged capacitor is

⇒ \(E=\frac{\sigma}{\varepsilon_0}=\frac{V}{d} \Rightarrow \sigma=\frac{\varepsilon_0 V}{d}\)….(1)

The field due to a single plate is \(\frac{\sigma}{2 \varepsilon_0}\)

The negative plate will experience an attractive force in this field \(\left(\frac{\sigma}{2 \varepsilon_0}\right)\).

This force is given by

⇒ \(F=Q\left(\frac{\sigma}{2 \varepsilon_0}\right)=(\sigma A)\left(\frac{\sigma}{2 \varepsilon_0}\right)=\sigma^2 \frac{A}{2 \varepsilon_0}\)

Substituting σ from the equation (1),

⇒ \(F=\left(\frac{\varepsilon_0 V}{d}\right)^2 \cdot \frac{A}{2 \varepsilon_0}\)

= \(\left(\frac{\varepsilon_0 A}{d}\right) \frac{V^2}{2 d}\)

= \(\frac{C V^2}{2 d}\)

Question 71. A parallel-plate air capacitor of capacitance C is connected to a cell of emf Vand and then disconnected from it. A dielectric slab of dielectric constant K, which can just fill the air gap between the plates is now inserted in it. Which of the following statements is incorrect?

1. The change in potential energy stored is \(\frac{1}{2} C V^2\left(\frac{1}{K}-1\right)\)
2. The charge on the capacitor is not conserved.
3. The potential difference between the plates decreases K times.
4. The energy stored in the capacitor decreases K times.

Answer: 2. The charge on the capacitor is not conserved.

When the plates of the capacitor are not touched, the charge always remains conserved. So, the option (2) is incorrect.

Change in potential energy = \(u_f-u_i=\frac{Q^2}{2 C^{\prime}}-\frac{Q^2}{2 C}\)

⇒ \(\frac{Q^2}{2 K C}-\frac{Q^2}{2 C}=\frac{1}{2} C V^2\left(\frac{1}{K}-1\right)\)

So, the option (1) is correct.

Potential difference are \(V=\frac{Q}{C} \text { and } V^{\prime}=\frac{Q}{C^{\prime}}=\frac{Q}{K C}\)

So, V’ < V. Therefore, option (3) is correct.

From option (4), (U_f– U_i) is negative, so the energy stored in the capacitor decreases, which is correct. Hence, all the options are correct except (2).

Question 72. A parallel-plate capacitor has a uniform electric field E in the space between the plates. If the separation between the plates is d and the area of each plate is A, the energy stored in the capacitor is

1. \(\frac{1}{2} \varepsilon_0 E^2\)
2. \(\frac{E^2 A d}{\varepsilon_0}\)
3. \(\frac{1}{2} \varepsilon_0 E^2 A d\)
4. E0EAd

Answer: 3. \(\frac{1}{2} \varepsilon_0 E^2 A d\)

The energy stored in the capacitor is \(U=\frac{1}{2} C V^2, \text { where } C=\frac{\varepsilon_0 A}{d}\), and the

electric field is \(E=\frac{V}{d} \Rightarrow V=E d\)

Substituting these values, energy stored, U is

⇒ \(\frac{1}{2}\left(\frac{\dot{\varepsilon}_0 A}{d}\right)(E d)^2=\frac{1}{2} \varepsilon_0 E^2 A d\)

Question 73. A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system

1. Decreases by a factor of 2
2. Remains unchanged
3. Increases by a factor of 2
4. Increases by a factor of 4

Answer: 1. Decreases by a factor of 2

The energy of a charged capacitor is \(U_i=\frac{Q^2}{2 C}\). When another identical capacitor is connected in parallel with the battery removed, the charge Q remains unchanged but C increases to 2C. Hence, the final energy

\(U_f=\frac{1}{2} \cdot \frac{Q^2}{2 C}\)

∴ the decrease in energy is \(U_i-U_f=\frac{Q^2}{2 C}-\frac{Q^2}{4 C}=\frac{1}{2}\left(\frac{Q^2}{2 C}\right)\).

The energy decreases by a factor of 2.

Question 74. A capacitor of 2μF is charged as shown in the diagram. When the switch S is turned to the position 2, the percentage of stored energy dissipated is

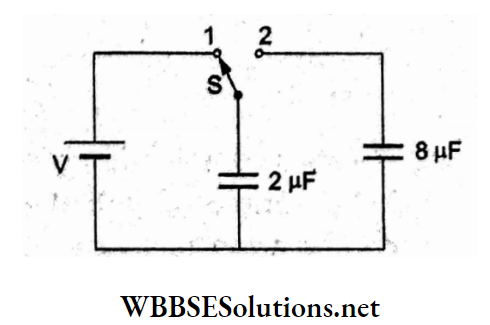
1. 75
2. 80
3. 10
4. 20

Answer: 2. 80

The energy stored in the 2-μF capacitor is \(U_1=\frac{Q^2}{2 C_1}\) When the switch is turned to position 2, the battery is disconnected and the capacitors are joined in parallel with charge Q remaining the same and the capacitors are joined in parallel with charge Q remaining the same.

Thus, final energy = \(U_2=\frac{Q^2}{2\left(C_1+C_2\right)}\)

Hence, fractional loss of energy = \(\frac{u_1-u_2}{u_1}=\left(1-\frac{u_2}{u_1}\right)\)

⇒ \(=\left(1-\frac{C_1}{C_1+C_2}\right)\)

= \(\left(1-\frac{2}{10}\right)\)

= \(\frac{8}{10}\)

∴ per cent loss = \(\frac{8}{10}\) x 100%

= 80%.

Question 75. A parallel-plate capacitor of area A, plate separation d, and capacitance C is filled with four dielectric materials having dielectric constants K₁, K₂, K₃, and K₄4 as shown in the figure. If a single dielectric material is to be used to have the same capacitance C in the capacitor then its dielectric constant K will be given by

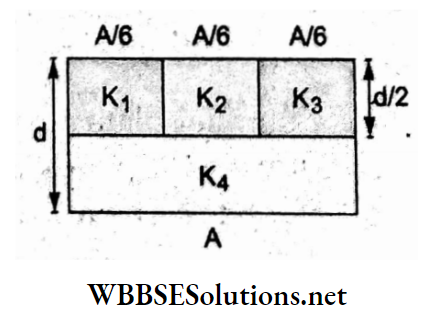
1. k = k₁ + k₂ + k₃ + 3k₄
2. \(\mathrm{k}=\frac{2}{3}\left(k_1+k_2+k_3\right)+2 k_4\)
3. \(\frac{2}{k}=\frac{3}{k_1+k_2+k_3}+\frac{1}{k_4}\)
4. \(\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}+\frac{3}{2 k_4}\)

Answer: 3. \(\frac{2}{k}=\frac{3}{k_1+k_2+k_3}+\frac{1}{k_4}\)

The given system can be considered as a combination of four capacitors, as shown in the adjoining figure

The capacitances are:

⇒ \(C_1=\frac{K_1 \varepsilon_0 A / 3}{d / 2}=\frac{2}{3} \frac{K_1 \varepsilon_0 A}{d}\)

⇒ \(C_2=\frac{2}{3} \frac{K_2 \varepsilon_0 A}{d}, C_3=\frac{2}{3} \frac{K_3 \varepsilon_0 A}{d}\)

⇒ \(C_4=\frac{2 K_4 \varepsilon_0 A}{d}\)

If C is the equivalent capacitance then

⇒ \(\frac{1}{C}=\frac{1}{C_1+C_2+C_3}+\frac{1}{C_4}\)

⇒ \(\frac{d}{K \varepsilon_0 A}=\frac{3 d}{2 \varepsilon_0 A\left(K_1+K_2+K_3\right)}+\frac{d}{2 K_4 \varepsilon_0 A}\)

⇒ \(\frac{2}{K}=\frac{3}{K_1+K_2+K_3}+\frac{1}{K_4}\)

Question 76. The voltage of some clouds is 4 x 10⁶, volts with respect to the ground. In a lightning strike lasting for 100 milliseconds, a charge of 4 coulombs is delivered to the ground. The power of the lightning strike is

1. 160 MW
2. 80 MW
3. 20 MW
4. 500 MW

Answer: 2. 80 MW

Given that potential difference V = 4 x 10⁶ V, time = 100 ms = 100 x 10^-3 s, charge = Q = 4C.

Work done = W = \(\frac{1}{2}\) QV.

Hence power of the lightning strike is

⇒ \(P=\frac{W}{t}=\frac{1}{2} \frac{Q V}{t}=\frac{1}{2} \frac{\left(4 \times 4 \times 10^6\right) J}{0.18}\)

= 8 x 10⁷ W

= 80 MW.

Question 77. Five capacitors, each of capacitance C, are connected as shown in the figure. The ratio of the capacitance between P and R and that between P and R is

1. 3:1
2. 5:2
3. 2:3
4. 1:1

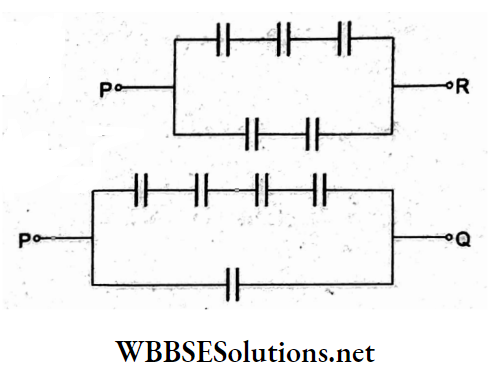
Answer: 3. 2:3

The two adjoining figures show the connection between P and R and that across P and Q.

In the first case, \(C_{\mathrm{PR}}=\frac{C}{3}+\frac{C}{2}=\frac{5}{6} C\)

In the second case, \(C_{\mathrm{PQ}}=\frac{C}{4}+C=\frac{5}{4} C\)

∴ required ratio = \(\frac{C_{P R}}{C_{P Q}}=\frac{5 C / 6}{5 C / 4}\)

= \(\frac{2}{3}\)

Question 78. What is the energy stored in the capacitor between terminals a and b of the network shown in the figure? (Given the capacitance of each capacitor, C = 1μF.)

1. 12.5 μJ
2. Zero
3. 25 μJ
4. 50μJ

Answer: 1. 12.5 μJ

The circuit consisting of five identical capacitors, each of capacitance 1 pF, is redrawn as shown in the figure.

The potential difference across each capacitor is equally divided and the combination constitutes a balanced Wheatstone bridge.

The energy stored in the capacitor across ab is

⇒ \(U=\frac{1}{2} C V^2=\frac{1}{2}\left(10^{-6} \mathrm{~F}\right)(5 \mathrm{~V})^2=12.5 \mu \mathrm{J}\)

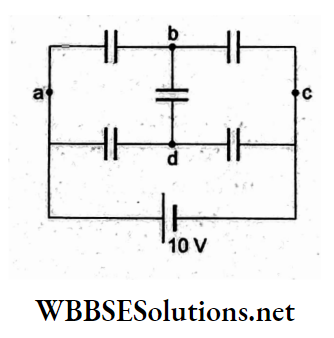
Question 79. What would be the voltage across C₃?

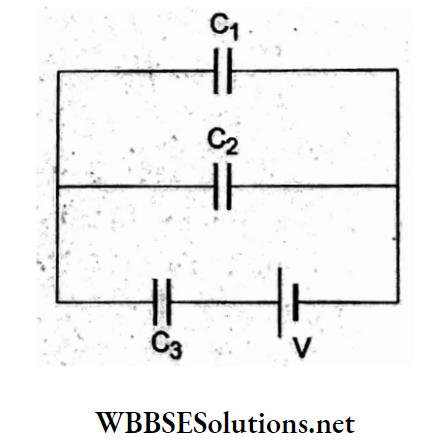
1. \(\frac{\left(C_1+C_2\right) V}{C_1+C_2+C_3}\)
2. \(\frac{C_1 V}{C_1+C_2+C_3}\)
3. \(\frac{C_2 V}{C_1+C_2+C_3}\)
4. \(\frac{C_3 V}{C_1+C_2+C_3}\)

Answer: 1. \(\frac{\left(C_1+C_2\right) V}{C_1+C_2+C_3}\)

The given combination of capacitors consists of C₁ and C₂ in parallel, which is connected in series with C₃ as shown in the adjoining figure. The equivalent combination of C₁ and C2 is (C₁ + C₂). This, in series with C₃, gives,

⇒ \(\frac{1}{C_{\mathrm{eq}}}=\frac{1}{C_1+C_2}+\frac{1}{C_3}\)

= \(\frac{C_1+C_2+C_3}{\left(C_1+C_2\right) C_3}\)

⇒ \(C_{\text {eq }}=\frac{\left(C_1+C_2\right) C_3}{C_1+C_2+C_3}\)

Charge delivered to the combination = Q = C_eq.V

⇒ \(\frac{\left(C_1+C_2\right) C_3 V}{C_1+C_2+C_3}\)

∴ the voltage across C₃, is

⇒ \(\frac{Q}{C_3}=\frac{\left(C_1+C_2\right) V}{C_1+C_2+C_3}\)

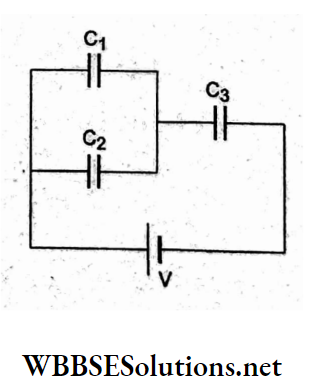
Question 80. The diameter of the plate of a parallel-plate capacitor is 6 cm. If its capacitance is equal to that of a sphere with a diameter of 200 cm, the Separation between the plates of the capacitor is

1. 4.5 x 10^-4 m
2. 2.25 x 10^-4 m
3. 6.75 x 10^-4 m
4. 9 x 10^-4 m

Answer: 2. 2.25 x 10^-4 m

The capacitance of a parallel-plate capacitor is

⇒ \(C_1=\frac{\varepsilon_0 A}{d}\)

= \(\frac{\varepsilon_0\left(\pi D^2 / 4\right)}{d}\)

This is equal to the capacitance of a sphere of radius R = \(\frac{200}{2}\) cm =1.0 m, which is C₂ = 4πε₀R.

∵ \(C_1=C_2 \text { (given), } \frac{\varepsilon_0 \pi D^2}{4 d}\)

= \(4 \pi \varepsilon_0 R\)

∴ the separation between the plates is,

⇒ \(d=\frac{D^2}{16 R}\)

= \(\frac{\left(6 \times 10^{-2} \mathrm{~m}\right)^2}{16(1.0 \mathrm{~m})}\)

= \(\frac{36}{16} \times 10^{-4} \mathrm{~m}\)

= 2.25 x 10^-4 m.

Question 81. A parallel-plate capacitor with air as a dielectric has capacitance C. A slab of dielectric constant K having the same thickness as the separation between the plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be

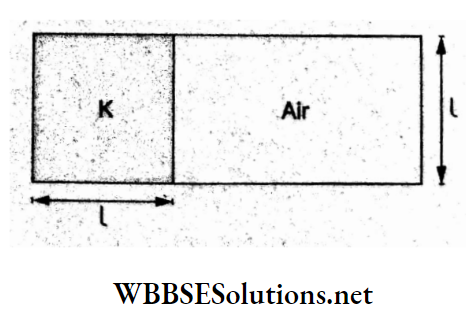
1. (K + 3) [lartex]\frac{C}{4}[/latex]
2. (K + 2) [lartex]\frac{C}{4}[/latex]
3. (K + 1) [lartex]\frac{C}{4}[/latex]
4. [lartex]\frac{KC}{4}[/latex]

Answer: 1. (K + 3) [lartex]\frac{C}{4}[/latex]

For the air capacitor, the capacitance is C = where A is the total area of each plate.

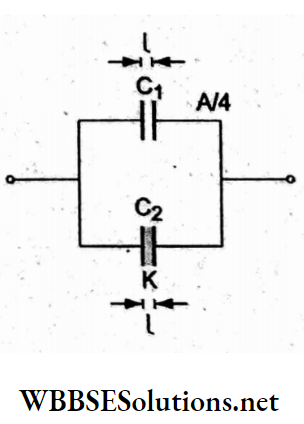
After the dielectric is introduced between the plates, we have a situation equivalent to a parallel combination of two capacitors, as shown in the figure.

In this, \(C_1=\frac{\varepsilon_0 3 A / 4}{l}\)

and, \(C_2=\frac{K \varepsilon_0 A / 4}{l}\)

∴ equivalent capacitance \(C_{\mathrm{eq}}=C_1+C_2=\frac{3}{4} \frac{\varepsilon_0 A}{l}+\frac{K}{4} \frac{\varepsilon_0 A}{l}\)

⇒ \((3+K) \frac{\varepsilon_0 A}{4 l}\)

= \((k+3) \frac{C}{4}\)

Question 82. A hollow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the center

1. Increases as r increases for r < R and for r > Rasa
2. Is zero as r increases for r < R, decreases as r increases for r > R
3. Is zero as r increases for r < R, increases as r increases for r > R
4. Decreases as r increases for r < R and for r > R

Answer: 2. Is zero as r increases for r < R, decreases as r increases for r > R

A charged conducting spherical shell has zero electric fields in the cavity, so E = 0 for 0 < r < R. At an external point, the field E is the same as if the total charge were centered at the center of the sphere, obeying the inverse square law \(\left(E \propto \frac{1}{r^2}\right)\) Thus, E decreases as r increased for r>R.

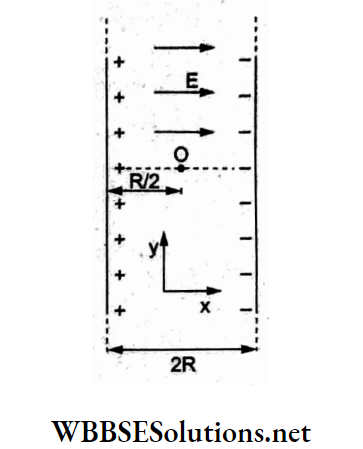
Question 83. Two parallel, infinite line charges with uniform line charge densities +λ. C m^-1 and -λ C m^-1 are placed at a distance of 2R from each other in free space. What is the electric field midway between the two line charges?

1. \(\frac{2 \lambda}{\pi \varepsilon_0 R} \mathrm{NC}^{-1}\)
2. \(\frac{\lambda}{2 \pi \varepsilon_0} \mathrm{NC}^{-1}\)
3. \(\frac{\lambda}{\pi \varepsilon_0 R} \mathrm{NC}^{-1}\)
4. Zero

Answer: 3. \(\frac{\lambda}{\pi \varepsilon_0 R} \mathrm{NC}^{-1}\)

According to Gauss’s theorem, the electric

field due to a line charge is

⇒ \(\vec{E}=\frac{\lambda}{2 \pi \varepsilon_0 r} \hat{i}\)

where r is the distance from the line charge. Here, at the midpoint 0,r = R, and the fields due to the two line charges are along the same direction (along the x-axis). These fields add up to give the net field

⇒ \(\vec{E}=\frac{\lambda}{2 \pi \varepsilon_0 R} \hat{i}+\frac{\lambda}{2 \pi \varepsilon_0 R} \hat{i}=\frac{\lambda}{\pi \varepsilon_0 R} \hat{i} \mathrm{~N} \mathrm{C}^{-1}\)

Question 84. Two points A and B having charges +Q and -Q respectively are placed a certain distance apart. The force between them is F. If 25% charge of A is transferred to B then the force between the charges becomes

1. F
2. \(\frac{9F}{16}\)
3. \(\frac{16F}{9}\)
4. \(\frac{4F}{3}\)

Answer: 2. \(\frac{9F}{16}\)

Initially, the charges are + Q and -Q, so F = \(F=K \frac{Q^2}{r^2}\) (attraction).

Finally, when \(\frac{Q}{4}\) is transferred from A to B, the charge on A is \(Q_1=Q-\frac{Q}{4}=\frac{3}{4} Q\) and the charge on B is \(Q_2=(-Q)+\left(\frac{Q}{4}\right)=-\frac{3}{4} Q\)

∴ the force F’ = \(\frac{K Q_1 Q_2}{r^2}=\frac{K\left(\frac{3}{4} Q\right)\left(\frac{3}{4} Q\right)}{r^2}\) (attraction)

⇒ \(\frac{9}{16}\left(K \frac{Q^2}{r^2}\right)\)

= \(\frac{9}{16} F\)

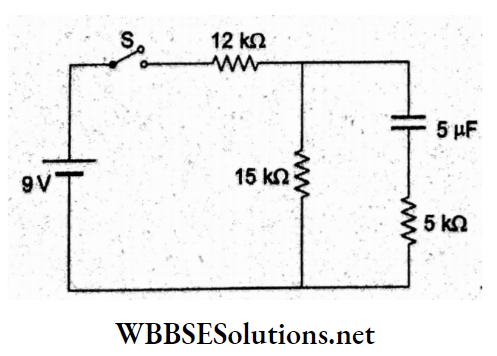
Question 85. Find the charge on the capacitor 1 s after the switch is opened at t = ∞.

1. 20 e^-10 μC
2. 30 e^-10 μC
3. 35 e^-10 μC
4. 25 e^-10 μC

Answer: 4. 25 e^-10 μC

In the state, the current through the 15-kΩ resistance,

⇒ \(I=\frac{9 \mathrm{~V}}{27 \mathrm{k} \Omega}=\frac{1}{3} \times 10^{-3} \mathrm{~A} .\)

The PD across the capacitor is

V = \((15 \mathrm{k} \Omega)\left(\frac{10^{-3}}{3} \mathrm{~A}\right)\)

= 5 V.

Charge Q₀ = CV

=(5x 10⁶ F) (5 V)

= 25 pC.

= time constant CR = (5 μF) (20 kΩ) = 0.1 s

= \(Q=Q_0 e^{-t / C R}\)

= \((25 \mu \mathrm{C}) e^{-1 \mathrm{~s} / 0.1 \mathrm{~s}}\)

= \(\frac{25 \mu \mathrm{C}}{e^{10}}\)

= \(25 \times e^{-10} \mu \mathrm{C}\)

Question 86. A capacitor of capacitance 15 nF having a dielectric slab of 2.5 and dielectric strength of 30 MV m^-1 has a potential difference of 30 V across its plates. The minimum area of its plates is

1. 8.4 x 10^-4 m²
2. 6.7 x 10^-4 m²
3. 9.8 x 10^-4 m²
4. 42 x 10^-4 m²

Answer: 2. 6.7 x 10^-4 m²

The electric field between the plates of the capacitor,

⇒ \(E=\frac{\sigma}{K \varepsilon_0}=\frac{Q}{K \varepsilon_0 A}\)

Plate area = \(A=\frac{Q}{K \varepsilon_0 A}\)

But \(Q=C V \Rightarrow A=\frac{C V}{K \varepsilon_0 E}\)

Substituting the given values,

⇒ \(A=\frac{\left(15 \times 10^{-9} \mathrm{~F}\right)(30 \mathrm{~V})}{(2.5)\left(8.85 \times 10^{-12} \mathrm{Fm}^{-1}\right)\left(30 \times 10^6 \mathrm{Vm}^{-1}\right)}\)

= 6.7 x 10^-4 m².

Question 87. In the steady state, the charge on the capacitor is

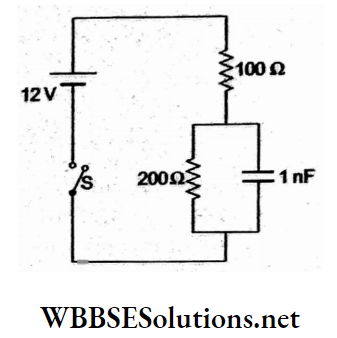
1. 8 nC
2. 10 nC
3. 12 nC
4. 5 nC

Answer: 1. 8nC

In the steady state, current through the 200-Ω resistor \(I=\frac{12 \mathrm{~V}}{300 \Omega}=\frac{4}{100} \mathrm{~A}\) Charge \(Q=C V\)

= \(\left(1 \times 10^{-9} \mathrm{~F}\right)\left(\frac{4}{100} \times 200 \mathrm{~V}\right)\)

= 8nC.

Question 88. Four equal point charges Q are placed in the xy-plane at (0, 2), (4, 2), (4, -2) and (0, -2). The work required to put a fifth charge Q at the origin of the coordinate system will be

1. \(\frac{Q^2}{4 \pi \varepsilon_0}\)
2. \(\frac{Q^2}{4 \pi \varepsilon_0}\left(1-\frac{1}{\sqrt{3}}\right)\)
3. \(\frac{Q^2}{2 \sqrt{2} \pi \varepsilon_0}\)
4. \(\frac{Q^2}{4 \pi \varepsilon_0}\left(1+\frac{1}{\sqrt{5}}\right)\)

Answer: 4. \(\frac{Q^2}{4 \pi \varepsilon_0}\left(1+\frac{1}{\sqrt{5}}\right)\)

The positions of four equal charges are given in the figure.

The net potential at the origin O is

⇒ \(V=K Q\left(\frac{1}{2}+\frac{1}{2}+\frac{2}{\sqrt{20}}\right)\)

= \(\frac{2 K Q}{2}\left(1+\frac{1}{\sqrt{5}}\right)\)

Work done W=QV

= \(K Q^2\left(1+\frac{1}{\sqrt{5}}\right)\)

⇒ \(\frac{Q^2}{4 \pi \varepsilon_0}\left(1+\frac{1}{\sqrt{5}}\right)\)

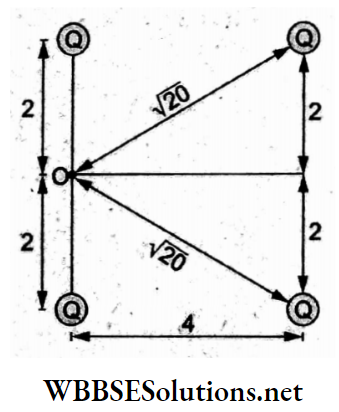
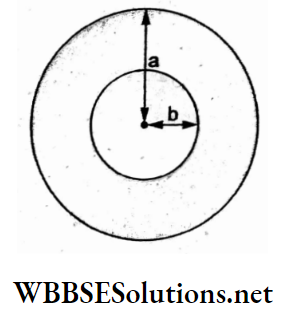
Question 89. A charge Q is distributed over three concentric spherical shells of radii a, b, and c (a < b < c) such that their surface densities of charge are equal. The total potential at a point at a distance r (r < a) from their common center would be

1. \(\frac{Q\left(a^2+b^2+c^2\right)}{4 \pi \varepsilon_0\left(a^3+b^3+c^3\right)}\)
2. \(\frac{Q(a+b+c)}{4 \pi \varepsilon_0\left(a^2+b^2+c^2\right)}\)
3. \(\frac{Q}{4 \pi \varepsilon_0(a+b+c)}\)
4. \(\frac{Q}{12 \pi \varepsilon_0} \frac{a b+b c+c a}{a b c}\)

Answer: 2. \(\frac{Q(a+b+c)}{4 \pi \varepsilon_0\left(a^2+b^2+c^2\right)}\)

Let the charges on the three spherical shells be q1,q2 and q3. For equal surface densities,

⇒ \(\sigma=\frac{q_1}{4 \pi a^2}=\frac{q_2}{4 \pi b^2}=\frac{q_3}{4 \pi c^2}\)

⇒ \(\frac{q_1}{a^2}=\frac{q_2}{b^2}=\frac{q_3}{c^2}=\alpha\)

= \(\frac{q_1+q_2+q_3}{a^2+b^2+c^2}\)

⇒ \(\frac{Q}{a^2+b^2+c^2}\)

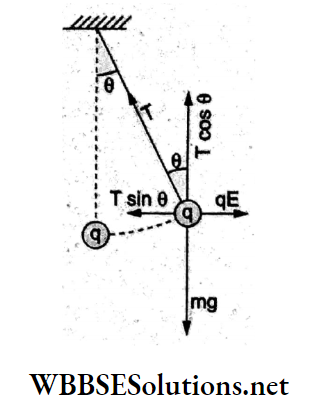
Question 90. The bob of a simple pendulum has a mass of 2 g and a charge of 5.0 μC. It rests in a uniform horizontal electric field of intensity 2000 V m^-1. At equilibrium, the angle that the pendulum makes with the vertical is

1. tan^-1 (5.0)
2. tan^-1 (2.0)
3. tan^-1 (0.5)
4. tan^-1 (0.2)

Answer: 3. tan^-1 (0.5)

Resolving the tension T along the horizontal and vertical directions,

Tsin θ = qE and Tcos θ = mg.

Dividing, we get,

⇒ \(\tan \theta=\frac{q E}{m g}=\frac{\left(5 \times 10^{-6} \mathrm{C}\right)\left(2 \times 10^3 \mathrm{~V} \mathrm{~m}^{-1}\right)}{\left(2 \times 10^{-3} \mathrm{~kg}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}\) = 0.5

=> 0 = tan^-1(0.5).

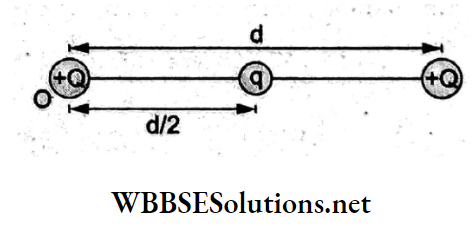
Question 91. Three charges + Q,q, and + Q are placed at distances 0, \(\frac{d}{2}\) and d from the origin on the x-axis. If the net force experienced by +Q placed at x = 0 is zero, the value of q is

1. +\(\frac{Q}{2}\)
2. +\(\frac{Q}{4}\)
3. –\(\frac{Q}{2}\)
4. –\(\frac{Q}{4}\)

Answer: 4. –\(\frac{Q}{4}\)

The net force on charge +Q at the origin O will be zero if the force due to q at x = \(\frac{d}{2}\)is equal and opposite to that due to +Q at x = d.

Hence, q must have a negative value.

∴ \(F_{\text {net }}=-\frac{K Q q}{\left(\frac{d}{2}\right)^2}\)

= \(-\frac{K Q^2}{d^2}\)

Hence, q = –\(\frac{Q}{4}\)

Question 92. A solid conducting sphere having a charge Q is surrounded by a hollow spherical shell that is uncharged and conducting. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a charge of -4Q, the new potential difference between the same two surfaces is

1. V
2. 2 V
3. -2 V
4. 4 V

Answer: 1. V

The potential at any point in a spherical shell’s cavity is constant and the same as that on its surface. Hence, adding a charge (= -4Q) to this shell will cause an equal change of potential in the outer and inner spheres, keeping the initial potential difference V unchanged.

Question 93. For a uniformly charged ring of radius R, the electric field on its axis has the maximum value at a distance x from its center. The value of x is

1. \(\frac{R}{\sqrt{2}}\)
2. R√2
3. R
4. \(\frac{R}{\sqrt{5}}\)

Answer: 1. \(\frac{R}{\sqrt{2}}\)

The electric field at a point P on the axis of a uniformly charged ring is given by +

⇒ \(E=\frac{1}{4 \pi \varepsilon_0} \frac{Q x}{\left(R^2+x^2\right)^{3 / 2}}\)

The variation of E with x is shown in the adjoining graph.

The field E is maximum at A where the slope

⇒ \(\frac{d E}{d x}=0\)

Thus,

⇒ \(\frac{1}{\left(R^{2+}+x^2\right)^{3 / 2}}-\frac{3}{2} \frac{x \cdot 2 x}{\left(R^2+x^2\right)^{5 / 2}}=0\)

3x² = R²+x².

⇒ \(x= \pm \frac{R}{\sqrt{2}}\)

Question 94. In free space, a particle A of charge1 pC is held fixed at a point P. Another particle B of the same charge and mass 4 pg is kept at a distance of 1 m from P. If B is released then its velocity at a distance of 9 m from P is

1. 2.0 x 10³ m s^-1
2. 3.0 x 10⁴ m s^-1
3. 1.0 m s^-1
4. 1.5 x 10² m s^-1

Answer: 1. 2.0 x 10³ m s^-1

From the work-energy theorem, the work done by the electric field is equal to the gain in KE of the mass.

Thus, the initial PE is \(\frac{K Q_q}{r_1}\) and the final PE is ⇒ \(\frac{K Q_q}{r_2}\) .

Now, loss in \(\mathrm{PE}=\left(\frac{k Q q}{r_1}-\frac{k Q q}{r_2}\right)=\frac{1}{2} m v^2\)

⇒ \(K Q q\left(\frac{1}{r_1}-\frac{1}{r_2}\right)=\frac{1}{2} m\left(v^2\right)\)

Substituting proper values,

⇒ \(\left(9 \times 10^9\right)\left(1 \times 10^{-6} \mathrm{C}\right)\left(1 \times 10^{-6} \mathrm{C}\right)\left(\frac{1}{1}-\frac{1}{9}\right)=\frac{1}{2}\left(4 \times 10^{-9}\right) v^2\)

⇒ \(\left(9 \times \frac{8}{9}\right)\left(10^{-3}\right)=\left(2 \times 10^{-9}\right) v^2\)

⇒ \(v=\sqrt{4 \times 10^6} \mathrm{~m} \mathrm{~s}^{-1}\)

= 2 x 10³ m s^-1.

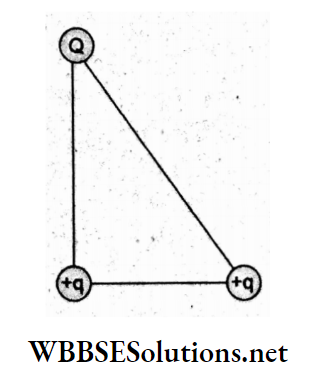
Question 95. Three charges Q, +q, and +q are placed at the vertices of a right-angled isosceles triangle, as shown in the figure. The net electrostatic energy of the system is zero if the value of Q is

1. +q
2. -q
3. \(\frac{-q}{1+\sqrt{2}}\)
4. \(\frac{-\sqrt{2} q}{1+\sqrt{2}}\)

Answer: 4. \(\frac{-\sqrt{2} q}{1+\sqrt{2}}\)

The electrostatic potential energy of the given system of charges is

⇒ \(U=\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q q}{a}+\frac{q^2}{a}+\frac{Q q}{\sqrt{2} a}\right)\)

For U to be zero, \(Q q+q^2+\frac{Q q}{\sqrt{2}}=0\)

⇒ \(Q\left(1+\frac{1}{\sqrt{2}}\right)=-q\)

⇒ \(Q=-\frac{\sqrt{2} Q}{\sqrt{2}+1}\)

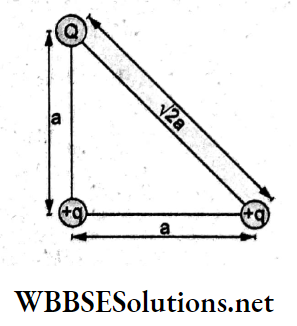
Question 96. A uniformly charged ring of radius 3a and total charge Q is placed in the xy-plane centered at the origin. A point charge q moves towards the ring along the z-axis and has speed v at z = 4a. The minimum value of v such that it crosses the origin is

1. \(\sqrt{\frac{2}{m}}\left(\frac{2}{15}, \frac{q^2}{4 \pi \varepsilon_0 a}\right)^{1 / 2}\)
2. \(\sqrt{\frac{2}{m}}\left(\frac{1}{15} \cdot \frac{q^2}{15 \times 4 \pi \varepsilon_0 a}\right)^{1 / 2}\)
3. \(\sqrt{\frac{2}{m}}\left(\frac{1}{5} \cdot \frac{q^2}{4 \pi \varepsilon_0 a}\right)^{1 / 2}\)
4. \(\sqrt{\frac{2}{m}}\left(\frac{4}{15} \cdot \frac{q^2}{4 \pi \varepsilon_0 a}\right)^{1 / 2}\)

Answer: 1. \(\sqrt{\frac{2}{m}}\left(\frac{2}{15}, \frac{q^2}{4 \pi \varepsilon_0 a}\right)^{1 / 2}\)

The minimum speed of the point charge at P should be such that it just reaches the center O of the ring. Conserving energy,

(KE)p + (PE)P = (KE)0f (PE)0.

Thus,

⇒ \(\frac{1}{2} m v^2+K \frac{q^2}{5 a}=0+\frac{K q^2}{3 a}\)

⇒ \(\frac{1}{2} m v^2=\frac{K q^2}{a}\left(\frac{1}{3}-\frac{1}{5}\right)\)

= \(\frac{1}{4 \pi \varepsilon_0} \frac{q^2}{a} \cdot \frac{2}{15}\)

⇒ \(v=\sqrt{\frac{1}{4 \pi \varepsilon_0} \frac{4 q^2}{15 m a}}=\sqrt{\frac{2}{m}}\left(\frac{2}{15} \frac{q^2}{4 \pi \varepsilon_0 a}\right)^{1 / 2}\)

Question 97. Determine the electric dipole moment of the system of three charges placed at the vertices of an equilateral triangle, as shown in the figure.

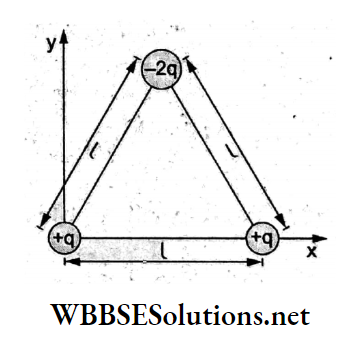
1. \(\sqrt{\frac{3}{2}} q l(\hat{j}-\hat{i})\)
2. \(2 q l \hat{j}\)
3. \(-\sqrt{3} q l \hat{j}\)
4. \(\frac{q l}{\sqrt{2}}(\hat{i}+\hat{j})\)

Answer: 3. \(-\sqrt{3} q l \hat{j}\)

The system of charges constitutes two dipoles having magnetic moments of equal magnitude (qa) inclined at 30° with the negative y-axis as shown. The cancel out and the net dipole moment becomes

⇒ \((2 p \cos \theta)(-\hat{j})=2 q l \cos 30^{\circ}(-\hat{j})=-\sqrt{3} q l \hat{j} .\)

Question 98. An electric field of 1000 V m^-1 is applied to an electric dipole at an angle of 45° to the dipole axis. The electric dipole moment is 10^-29 C m. The potential energy of the electric dipole is

1. -20 x 10^-18 J
2. -7 x 10^-27 J
3. -10 x 10^-29 J
4. -9 x 10^-20 J

Answer: 2. -7 x 10^-27 J

The potential energy of an electric dipole in a uniform electric field (E) is given by

⇒ \(U=-\vec{p} \cdot \vec{E}=-p E \cos \theta\)

⇒ \(-\left(10^{-29} \mathrm{Cm}\right)\left(10^3 \mathrm{~V} \mathrm{~m}^{-1}\right)\left(\cos 45^{\circ}\right)\)

⇒ \(-\frac{1}{\sqrt{2}} 10^{-26} \mathrm{~J}\)

= \(-7 \times 10^{-27} \mathrm{~J}\)

Question 99. The system of charges +q and -q shows an electric dipole with the midpoint at O and length AB = la. OP is perpendicular to AB. A charge Q is placed at P, where OP -y and y >> 2a. The charge Q experiences an electrostatic force F. If Q is moved along the equatorial line to P’ such that OP’ = \(\frac{y}{3}\)the force on Q will be close to (assuming \(\frac{y}{3}\) >> 2a)

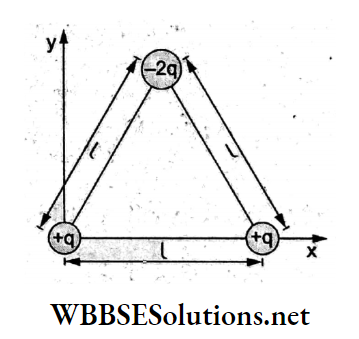
1. \(\frac{F}{3}\)
2. 3F
3. 9F
4. 27F

Answer: 4. 27F

The electric field at the equatorial point P is given by \(E=\frac{1}{4 \pi \varepsilon_0} \frac{p}{y^3}\) where OP = y.

AtP’, where OP’ = \(\frac{y}{3}\), the field

⇒ \(E^{\prime}=\frac{1}{4 \pi \varepsilon_0} \frac{p}{\left(\frac{y}{3}\right)^3}\)

⇒ \(\frac{E^{\prime}}{E}=27\)

Hence, \(\frac{F^{\prime}}{F}=\frac{Q E^{\prime}}{Q E}=27\)

=> F = 27F.

Question 100. The voltage rating of a parallel-plate capacitor is 500 V. Its dielectric can withstand a maximum electric field of 106 V m^-1. The plate area is 10^-4 m². What is the dielectric constant if the capacitance is 15 pF?

1. 3.8
2. 4.5
3. 6.2
4. 8.5

Answer: 4. 8.5

Since E = \(\frac{V}{d}\), the separation between the plates is

⇒ \(d=\frac{V}{E}\)

= [\(\frac{500 \mathrm{~V}}{10^6 \mathrm{Vm}^{-1}}\)

= \(\frac{1}{2000} \mathrm{~m}\)

Capacitance = \(C=\frac{K \varepsilon_0 A}{d}\)

Hence the dielectric constant is

⇒ \(k=-\frac{c \cdot d}{\varepsilon_0 A}\)

= \(\frac{\left(15 \times 10^{-12} \mathrm{~F}\right)\left(\frac{1}{2000} \mathrm{~m}\right)}{\left(8.86 \times 10^{-12} \mathrm{Fm}^{-1}\right)\left(10^{-4} \mathrm{~m}^2\right)}\)

= 8.5.

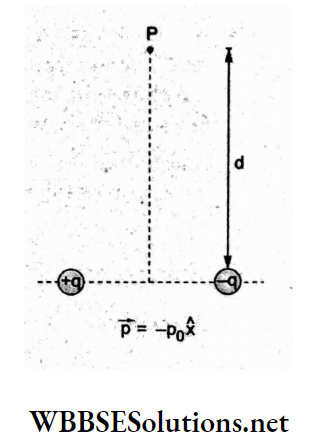
Question 101. A point dipole \(\vec{p}=-p_0 \hat{x}\) is kept at the origin. The potential and electric field due to this dipole on the y-axis at a distance d are respectively,

1. \(\frac{|\vec{p}|}{4 \pi \varepsilon_0 d^2} \text { and } \frac{-\vec{p}}{4 \pi \varepsilon_0 d^2}\)
2. \(\frac{|\vec{p}|}{4 \pi \varepsilon_0 d^2} \text { and } \frac{\vec{p}}{4 \pi \varepsilon_0 d^3}\)
3. \(0 \text { and } \frac{-\vec{p}}{4 \pi \varepsilon_0 d^3}\)
4. \(0 \text { and } \frac{\vec{p}}{4 \pi \varepsilon_0 d^3}\)

Answer: 3. \(0 \text { and } \frac{-\vec{p}}{4 \pi \varepsilon_0 d^3}\)

The potential at any point P on the equatorial line of the electric dipole is zero (0). At the same point, the electric field \(\vec{E}\) has a magnitude \(\frac{1}{4 \pi \varepsilon_0} \frac{p}{d^3}\) and direction antiparallel to \(\vec{p}\),

⇒ \(\vec{E}=\frac{1}{4 \pi \varepsilon_0}\left(\frac{-\vec{p}}{d^3}\right)\)

= \(\frac{1}{4 \pi \varepsilon_0}\left[-\left(\frac{-p_0 \hat{x}}{d^3}\right)\right]\)

⇒ \(\frac{p_0 \hat{x}}{4 \pi \varepsilon_0 d^3}=\frac{-\vec{p}}{4 \pi \varepsilon_0 d}\)

Question 102. Two electric dipoles A and B with respective dipole moment vectors \(\vec{p}_{\mathrm{A}}=4 q a \hat{i} \text { and } \vec{p}_{\mathrm{B}}=-2 q a \hat{i}\) are placed on the x-axis with a separation R as shown in the figure. The distance from Aat which both of them produce the same potential is

1. \(\frac{\sqrt{2} R}{\sqrt{2}+1}\)
2. \(\frac{\sqrt{2} R}{\sqrt{2}-1}\)
3. \(\frac{R}{\sqrt{2}+1}\)
4. \(\frac{R}{\sqrt{2}-1}\)

Answer: 2. \(\frac{\sqrt{2} R}{\sqrt{2}-1}\)

Let AP = x, where both the dipoles produce the same potential.

Thus, for V₁ = V₂, we have

⇒ \(\frac{K p_1}{x^2}=\frac{K p_2}{(R-x)^2}\)

⇒ \(\frac{2 p}{x^2}=\frac{p}{(R-x)^2}\)

⇒ \(x=\sqrt{2}(R-x)\)

⇒ \(x=\frac{\sqrt{2} R}{1+\sqrt{2}}\)

Question 103. A parallel-plate capacitor having a capacitance of 12 μF is charged by a battery to a potential difference of 10 V between its plates. The charging battery is now disconnected and a dielectric slab of dielectric constant 6.5 is inserted between the plates. The work done by the capacitor on the slab is

1. 560 pJ
2. 508 pJ
3. 692 pJ
4. 600 pJ

Answer: 2. 508 pJ

The initial electrostatic energy of the capacitor is

⇒ \(U_i=\frac{1}{2} C V^2=\frac{1}{2}\left(12 \times 10^{-12} \mathrm{~F}\right)(10 \mathrm{~V})^2\)

= 600 x 10^-12J.

Disconnecting the battery will maintain the charge on the capacitor unchanged but introducing a dielectric slab will increase the capacitance.

Thus, the final energy is \(U_{\mathrm{f}}=\frac{Q^2}{2 k C}=\frac{C^2 V^2}{2 k C}=\frac{C V^2}{2 k}=\frac{600 \times 10^{-12} \mathrm{~J}}{(6.5)}\)

decrease in energy \(\Delta U=U_i-U_f=\left(600 \times 10^{-12} \mathrm{~J}\right)\left(1-\frac{1}{6.5}\right)\)

= 507.7 x 10^-12J

= 508 pJ

This gives the amount of work done by the capacitor.

Question 104. A parallel-plate capacitor has a capacitance of 1 μF. One of its two plates is given a charge of +2 μC and the other plate is given a charge of +4 μC. The potential difference developed across the capacitor is

1. 5 V
2. 3 V
3. 1 V
4. 2 V

Answer: 3. 1 V

If the plates of a capacitor are H Jo, given unequal charges Q₁ and Q₂, the charges appearing on its four faces are as shown in the figure. The charge on the capacitor is the charge on its inner faces.

Thus, charge = \(Q=\frac{Q_1-Q_2}{2}\)

= \(\frac{4 \mu C-2 \mu C}{2}\)

= \(1 \mu C\)

∴ the potential difference across the plates of the capacitor is

⇒ \(V=\frac{Q}{C}=\frac{1 \mu \mathrm{C}}{1 \mu \mathrm{F}}\)

= 1V.

Question 105. See the given circuit diagram. After the switch S is turned from position A to B, the energy dissipated in the circuit in terms of capacitance C and total charge Q is

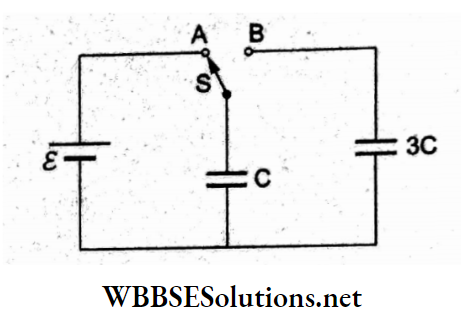
1. \(\frac{5}{8} \frac{Q^2}{C}\)
2. \(\frac{9}{5} \frac{Q^2}{C}\)
3. \(\frac{9}{4} \frac{Q^2}{C}\)
4. \(\frac{1}{8} \frac{Q^2}{C}\)

Answer: 2. \(\frac{9}{5} \frac{Q^2}{C}\)

The initial energy associated with C is \(U_i=\frac{1}{2} C \mathcal{E}^2=\frac{Q^2}{2 C}\)

When the switch is turned to B, there is a charge redistribution with the total charge Q remaining the same. Thus, the final energy is

⇒ \(U_{\mathrm{f}}=\frac{1}{2} \frac{Q^2}{C_{\mathrm{eq}}}=\frac{Q^2}{2(C+3 C)}=\frac{Q^2}{8 C}\)

∴ dissipated energy = \(\Delta U=U_{\mathrm{i}}-U_{\mathrm{f}}=\frac{3}{8} \frac{Q^2}{\mathrm{C}}\)

Question 106. A parallel-plate capacitor has an area of 6 cm² and a separation of 3 mm. The space between the plates is filled with three dielectric materials of equal thickness (see figure) with dielectric constants K₁ = 10, K₂ = 12, and K₃ = 14. The dielectric constant of the material which gives the same capacitance when fully inserted in the above capacitor would be

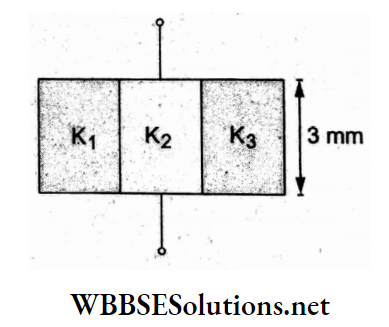
1. 4
2. 36
3. 12
4. 14

Answer: 3. 12

The combination forms three capacitors in parallel. Hence, the equivalent capacitance is

⇒ \(C=C_1+C_2+C_3=\frac{\varepsilon_0 A}{d}\left(K_1+K_2+K_3\right)\)

⇒ \(\frac{\varepsilon_0 A}{d}(10+12+14)\)

= \(36 \frac{\varepsilon_0 A}{d}\)

With a single dielectric of dielectric constant K, we get the same capacitance.

Hence, \(\frac{K \varepsilon_0(3 A)}{d}=36 \frac{\varepsilon_0 A}{d}\)

K = 12.

Question 107. In the file given the combination of capacitors, find the value of C if the effective capacitance of the whole Circuit across AB is to be 0.5 pF. All values in the circuit are in pF.

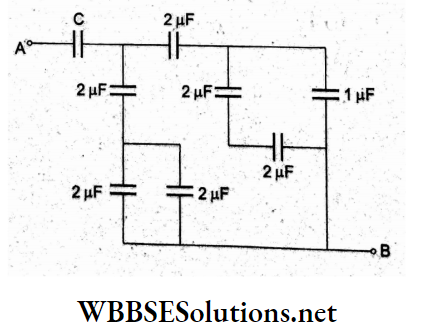
1. \(\frac{6}{5} \mu \mathrm{F}\)
2. \(\frac{7}{10} \mu \mathrm{F}\)
3. \(\frac{7}{11} \mu \mathrm{F}\)
4. \(\frac{3}{2} \mu \mathrm{F}\)

Answer: 3. \(\frac{7}{11} \mu \mathrm{F}\)

The given combination of capacitors can be redrawn as shown.

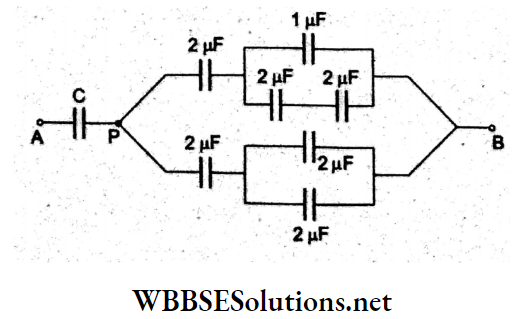
The equivalent capacitance in the upper branch across PB is

⇒ \(\frac{2 \times 2}{2+2}=1 \mu \mathrm{F}\),

and in the lower branch, it is

⇒ \(\frac{2 \times 4}{2+4}=\frac{8}{6}=\frac{4}{3} \mu \mathrm{F}\).

Hence, \(C_{\mathrm{PB}}=\left(1+\frac{4}{3}\right) \mu \mathrm{F}\)

= \(\frac{7}{3} \mu \mathrm{F}\)

Net capacitance across \(A B=\frac{C \times \frac{7}{3} \mu \mathrm{F}}{C+\frac{7}{3} \mu \mathrm{F}}=0.5 \mu \mathrm{F}=\frac{1}{2} \mu \mathrm{F}\)

⇒ \(\frac{14}{3} C=C+\frac{7}{3} \mu \mathrm{F}\)

⇒ \(\frac{11}{3} C=\frac{7}{3} \mu \mathrm{F}\)

⇒ \(C=\frac{7}{11} \mu F\)

Question 108. In the given figure the charge on the left plate of the 10-μF capacitor is -30 μC. The charge on the right plate of the 6-μF capacitor is

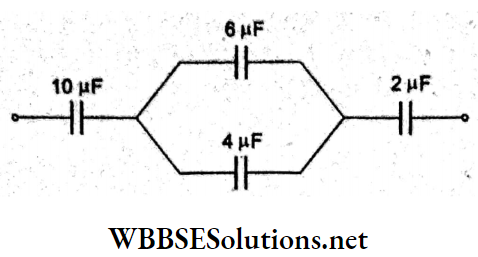
1. +12 μC
2. -18 μC
3. -12 μC
4. +18 μC

Answer: 4. +18 μC

Since the potential difference (V_A – V_B) is the same across both the capacitors in parallel, therefore charges are

q₁ = (V_A – V_B) (6 μF),

and q₂ = (V_A-V_B)(4μF).

∴ \(\frac{q_1}{q_2}=\frac{6}{4}=\frac{3}{2}\)

⇒ \(q_2=\frac{2}{3} q_1\)

Now, q₁ + q₂ = 30μC

⇒ \(\frac{5}{3}\)q₁ = 30μC

∴ the charge on the right plate of the upper capacitor q₁ = +18 μC.

Question 109. The parallel combination of two air-filled parallel-plate capacitors of capacitance C and nC is connected to a battery of voltage V. When the capacitors are fully charged, the battery is removed and after that, a dielectric plate of dielectric constant K is inserted between the two plates of the first capacitor. The new potential difference of the combined system is

1. \(\frac{V}{n+k}\)
2. \(\left(\frac{n+1}{n+k}\right) V\)
3. \(\left(\frac{n \cdot}{n+k}\right) V\)
4. V

Answer: 2. \(\left(\frac{n+1}{n+k}\right) V\)

In the first case, let Q₁ and Q₂ be the charges on the capacitors.

Hence, Q₁ = CV and Q₂ = nCV.

∴ the total charge is Q = Q₁ + Q₂ = CV(n + 1)…. (1)

In the 2nd case, when the battery is removed and a dielectric plate is inserted in the first capacitor, there will be a redistribution of charge at a new PD V such that Q₁ = KCV’ and Q₂ = nCV’.

∴ the total charge is Q = Q₁+ Q₂ = C(K + n)V’…(2)

Equating (1) and (2),

C(n + K)V’ = (n + 1) CV

⇒ \(V^{\prime}=\left(\frac{n+1}{n+K}\right) V\)

Question 110. The given figure shows the charge (q) versus voltage (V) graphs for series and parallel combinations of two given capacitors. The capacitances are

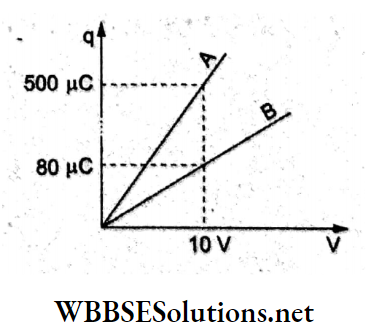
1. 50 μF, 30 μF
2. 60 μF, 40 μF
3. 40 μF, 10 μF
4. 20 μF, 30 μF

Answer: 3. 40μF, 10μF

The slope of the two lines is \(\frac{q}{v}\), which is the equivalent capacitance.

Hence,

⇒ \(C_{\text {parallel }}=\frac{500 \mu \mathrm{C}}{10 \mathrm{~V}}\)

= \(50 \mu \mathrm{F}\)

and \(C_{\text {series }}=\frac{80 \mu \mathrm{C}}{10 \mathrm{~V}}\)

= \(8 \mu \mathrm{F}\)

∴ \(C_1+C_2=50 \mu \mathrm{F} ; \frac{C_1 C_2}{C_1+C_2}\)

= 8μF.

Solving, we get C₁ = 40 μF and C₂ = 10 μF.

Question 111. A 5-pF capacitor is charged by a 220-V source. The source is disconnected and a 2.5-μF uncharged capacitor is connected to the charged capacitor. The heat dissipated during the process is

1. \(\frac{121}{3}\) mJ
2. 200 mJ
3. \(\frac{1210}{5}\) mJ
4. \(\frac{121}{3}\) mJ

Answer: 4. \(\frac{121}{3}\) mJ

Given: C₁ = 5 μF, C₂ = 2.5μF; V₁ = 220 V, V₂ = 0 (uncharged)

Common Fpotential = \(V=\frac{C_1 V_1+C_2 V_2}{C_1+C_2}\)

= \(\frac{5 \times 220}{7.5} \mathrm{~V}\)

= \(\frac{440}{3} \mathrm{~V}\)

Initial energy = \(U_1=\frac{1}{2} C_1 V_1^2\)

= \(\frac{1}{2}(5 \mu \mathrm{F})(220 \mathrm{~V})^2\)

Final energy = \(U_2=\frac{1}{2}\left(C_1+C_2\right) V^2\)

= \(\frac{1}{2}(7.5 \mu \mathrm{F})\left(\frac{5 \times 220}{7.5} \mathrm{~V}\right)^2\)

Heat dissipation = \(U_1-U_2=\frac{1}{2}(220 \mathrm{~V})^2\left(5-\frac{2.5}{7.5}\right) \mu \mathrm{F}\)

⇒ \(\frac{1}{2}(22,0)^2\left(5-\frac{10}{3}\right) \mu \mathrm{J}\)

= \(\frac{121}{3} \mathrm{~mJ}\)

Alternative method:

Loss of energy \(\Delta U=\frac{1}{2} \frac{C_1 C_2}{C_1+C_2}\left(V_1-V_2\right)^2\)

⇒ \(\frac{1}{2} \frac{(5 \mu \mathrm{F})(2.5 \mu \mathrm{F})}{(7.5 \mu \mathrm{F})}(220 \mathrm{~V})^2\)

⇒ \(\frac{121}{3}\)

Question 112. What is the potential across capacitors of capacitance C in the steady state? All resistors have an equal resistance of 2Ω.

1. 0 V
2. 2 V
3. 8 V
4. 4 V

Answer: 3. 8 V

Current through the cell = l = \(\frac{10 \mathrm{~V}}{\frac{10}{3} \Omega}\) = 3A

∴ X = \(\frac{4}{6}\) x 3A = 2A, Y = l A.

The potential difference across the capacitor

V = (V_A-V_B) + (V_B-V_C)

= (2Ω)(1A) + (2Ω)(3A)

= 8 V.

Question 113. A 20-μF capacitor is charged up to 50 V and disconnected from the source. When connected to an uncharged capacitor of unknown capacitance C, the common potential becomes 20 V. The value of C is

1. 10 μF
2. 20 μF
3. 30 μF
4. 40 μF

Answer: 3. 30μF

Given: C₁ = 20 μF, C₂ = C;

V₁ = 50V, V₂ = 0.

Common potential \(V=\frac{C_1 V_1+C_2 V_2}{C_1+C_2}\)

⇒ \(20 \mathrm{~V}=\frac{(20 \mu \mathrm{F})(50 \mathrm{~V})+C \times 0}{20 \mu \mathrm{F}+C}\)

=> 20μF + C = 50μF

=> C = 30 pF

Question 114. In the given circuit, C₁ = 15μF, C₃ = 8 μF, the potential difference across C₃ is 20 V, and the total charge delivered by the cell is Q = 750 μC. The charge on C₂ is

1. 450μC
2. 630 μC
3. 160 μC
4. 590 μC

Answer: 4. 590μC

Total charge = Q = Q₂ + Q₃

= (C₂ + C₃) (20 V)

=> 750 μC = (C2 + 8 μF) (20 V)

C₂ = (37.5-8) μF

= 29.5 μF.

∴ the charge on C₂ is Q₂ = C₂ (20 V)

= (29.5 μF) (20 V)

= 590μC.

Question 115. Two parallel-plate capacitors of capacitances C and 2C are respectively charged to potential differences of V and 2V between their plates. These capacitors are connected in such a way that the positive plate of one is connected to the negative plate of the other. The change in the potential energy of the system is

1. 3CV²
2. CV²
3. \(\frac{1}{2}\)CV²
4. 2CV²

Answer: 1. 3CV²

The initial energy of the capacitors is

⇒ \(U_i=\frac{1}{2} C V^2+\frac{1}{2}(2 C)(2 V)^2=\frac{9}{2} C V^2\)

When connected with polarity reversed, the common potential of the system is

⇒ \(V_{\mathrm{c}}=\frac{C V+(2 C)(-2 V)}{C+2 C}=-V\)

⇒ \(\left|V_{\mathrm{c}}\right|=V\)

The final energy of the system is

⇒ \(U_{\mathrm{f}}=\frac{1}{2} C \cdot V_{\mathrm{c}}^2+\frac{1}{2}(2 C) V_{\mathrm{c}}^2=\frac{3}{2} C V^2\)

∴ change in energy \(\Delta U=\frac{9}{2} C V^2-\frac{3}{2} C V^2\)

= \(3 C V^2\)

Question 116. A particle having a charge q is released from rest in an electric field E = E₀ (1 – αx²) from the origin. Find its position when it again comes to momentary rest for the first time.

1. \(\sqrt{\frac{1}{\alpha}}\)
2. \(\sqrt{\frac{2}{\alpha}}\)
3. \(\sqrt{\frac{3}{\alpha}}\)
4. \(\sqrt{\frac{1}{2 \alpha}}\)

Answer: 3. \(\sqrt{\frac{3}{\alpha}}\)

Force = F = qE = qE₀ (1- αx²).

∴ acceleration \(a=\frac{F}{m}=\frac{q E_0}{m}\left(1-\alpha x^2\right)\)

But \(a=\frac{d v}{d t}=\frac{d v}{d x} \cdot \frac{d x}{d t}=v \frac{d v}{d x}\)

⇒ \(v d v=\frac{q E_0}{m}\left(1-\alpha x^2\right) d x\)

Integrating, \(\int_0^x v d v=\frac{q E_0}{m} \int_0^x\left(1-\alpha x^2\right) d x\)

⇒ \(\frac{q E}{m}\left(x-\frac{\alpha x^3}{3}\right)=0\)

or, \(x=\sqrt{\frac{3}{\alpha}}\)

Question 117. Charge Q is distributed on two concentric spheres of radii r and R (r<R). If the charge density on both spheres is the same, the electric potential at the common center is

1. \(K Q\left(\frac{1}{r}+\frac{1}{R}\right)\)
2. \(\frac{k Q(r+R)}{r^2+R^2}\)
3. \(\frac{k Q r R}{r+R}\)
4. \(\frac{k Q\left(R^2+r^2\right)}{R+r}\)

Answer: 2. \(\frac{k Q(r+R)}{r^2+R^2}\)

Total charge = Q = q₁ + q₂ = 4πr²σ + 4πR²σ.

∴ surface charge density \(\sigma=\frac{Q}{4 \pi\left(r^2+R^2\right)}\)

∴ the potential at the common center is

⇒ \(V=V_1+V_2=K\left(\frac{q_1}{r}+\frac{q_2}{R}\right)\)

= K(4πrσ + 4πσR) = K4πσ (r + R)

⇒ \(\frac{K Q(r+R)}{r^2+R^2}\)

Question 118. Two concentric spherical shells of radii r and 4r are given charges Q₁ and Q₂ respectively. The potential difference between the shells is

1. \(\frac{3}{4 \pi \varepsilon_0} \frac{Q_1}{r}\)
2. \(\frac{3}{16 \pi \varepsilon_0} \frac{Q_1}{r}\)
3. \(\frac{k Q r R}{r+R}\)
4. \(\frac{k Q\left(R^2+r^2\right)}{R+r}\)

Answer: 2. \(\frac{3}{16 \pi \varepsilon_0} \frac{Q_1}{r}\)

Potential of the inner shell due to its own charge Q₁ is \(\frac{1}{4 \pi \varepsilon_0} \frac{Q_1}{r}\) and that due to charge Qz on the outer shell is \(\frac{1}{4 \pi \varepsilon_0} \frac{Q_2}{4 r}\)

∴ the total potential of the inner shell is

⇒ \(V_1=\frac{1}{4 \pi \varepsilon_0}\left[\frac{Q_1}{\dot{r}}+\frac{Q_2}{4 r}\right]\)

Potential of the outer shell due to its own charge Q₂ is \(\frac{1}{4 \pi \varepsilon_0} \frac{Q_2}{4 r}\) and that due to the inner shell (with charge Q₁) is \(\frac{1}{4 \pi \varepsilon_0} \frac{Q_1}{4 r}\)

∴ the total potential of the outer shell is

⇒ \(V_{\mathrm{o}}=\frac{1}{4 \pi \varepsilon_0}\left[\frac{Q_2}{4 r}+\frac{Q_1}{4 r}\right]\)

Hence, potential difference \(V_1-V_0=\frac{1}{4 \pi \varepsilon_0}\left[\frac{Q_1}{r}-\frac{Q_1}{4 r}\right]=\frac{3}{16 \pi \varepsilon_0} \frac{Q_1}{r}\)

Question 119. Charges Q₁ and Q₂ are at points A and B of a right-angled triangle OAB. If the resultant electric field at point O is perpendicular to the hypotenuse then \(\frac{Q_1}{Q_2}\) is proportional to

1. \(\frac{x_1^2}{x_2^2}\)
2. \(\frac{x_2^2}{x_1^2}\)
3. \(\frac{x_2}{x_1}\)
4. \(\frac{x_1}{x_2}\)

Answer: 4. \(\frac{x_1}{x_2}\)

From the given figure,

⇒ \(E_1=K \frac{Q_1}{x_1^2}, E_2=K \frac{Q_2}{x_2^2}\)

⇒ \(\frac{E_1}{E_2}=\frac{Q_1}{Q_2} \frac{x_2^2}{x_1^2}\)

But \(\frac{E_1}{E_2}=\tan \theta+\frac{x_2}{x_1}\)

From (1) and (2),

⇒ \(\frac{Q_1}{Q_2}=\frac{x_1}{x_2}\)

Question 120. Ten charges are placed on the circumference of a circle of radius R with constant angular separation between successive charges. Alternate charges numbered 1, 3, 5, 7, and 9 have charge +q each, while 2, 4, 6, 8, and 10 have charge -q each. The potential V and the electric field E at the center of the circle are respectively (take V = 0 at infinity)

1. \(V=\frac{10 q}{4 \pi \varepsilon_0 R} \text { and } E=0\)
2. V = 0; E = 0
3. \(V=0 \text { and } E=-\frac{10 q}{4 \pi \varepsilon_0 R^2}\)
4. \(V=\frac{10}{4 \pi \varepsilon_0 R} \text { and } E=\frac{10 q}{4 \pi \varepsilon_0 R}\)

Answer: 2. V = 0; E = 0

The potential at the center is

⇒ \(V=\frac{K q}{r}+\frac{K}{r}(-q)+\frac{K}{r}(+q) \ldots=0\)

Due to a symmetrical charge distribution, the net field at the center of symmetry is always zero.

Hence,

⇒ \(\vec{E}\) = \(\vec{0}\).

Gravitation

Question 1. The acceleration due to gravity at a height of 1 km above the earth’s surface is the same as that at a depth d below the surface of the earth. The,

1. d =1 km
2. d = 1.5 km
3. d = 0.5 km
4. d = 2 km

Answer: 4. d = 2km

The value of g at a height h (= 1 km) is

⇒ \(\frac{g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}=g\left(1+\frac{h}{R_{\mathrm{E}}}\right)^{-2} \approx g\left(1-\frac{2 h}{R_{\mathrm{E}}}\right)\) […h << RE]

At a depth d, \(g^{\prime}=g\left(1-\frac{d}{R_{\mathrm{E}}}\right)\)

Given that \(g\left(1-\frac{2 \times 1 \mathrm{~km}}{R_{\mathrm{E}}}\right)=g\left(1-\frac{d}{R_{\mathrm{E}}}\right)\)

∴ d = 2 km

Question 2. Starting from the centre of the earth (having the radius RE) the variation of g (acceleration due to gravity) is represented by

Answer: 2.

At the centre of the earth, g = 0. The value of g increases linearly as we move radially towards the surface, and then moving away from the earth, g decreases nonlinearly. The figure given in the option (b) shows the correct variation.

Question 3. The height h at which the weight of a body becomes (1/16)th of its weight on the surface of the earth (radius = RE) is

1. h = R_E
2. h = 2R_E
3. h = 3R_E
4. h = 4R_E

Answer: 3. h = 3R_E

The weight w’ at a height h is \(\frac{m g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}\)

Given that w’ = \(\frac{w}{16}\)

∴ \(\frac{m g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}=\frac{m g}{16} \Rightarrow h=3 R_{\mathrm{E}}\)

Question 4. The force between a hollow sphere and a point mass at P inside it, as shown in the adjoining figure, is

1. Attractive and constant
2. Attractive but depends on the separation of the PO
3. Zero
4. Repulsive and constant

Answer: 3. Zero

The gravitational field in the cavity of a spherical shell is zero, so the force on the mass m inside is zero.

Question 5. If the mass of the earth is 80 times that of the moon and the radius of the earth is 4 times that of the moon, the ratio gM-gE will be

1. 1:1
2. 1:2
3. 1:3
4. 1:5

Answer: 4. 1:5

The value of g at the surface of a planet is \(\frac{G M}{R^2}\)

∴ \(\frac{g_{\mathrm{M}}}{g_{\mathrm{E}}}=\frac{\mathrm{M}_{\mathrm{M}}}{M_{\mathrm{E}}} \times \frac{R_{\mathrm{E}}^2}{R_{\mathrm{M}}^2}\)

=\(\frac{\mathrm{M}_{\mathrm{M}}}{80 \mathrm{M}_{\mathrm{M}}} \times \frac{16 R_{\mathrm{M}}^2}{R_{\mathrm{M}}^2}\)

= \(\frac{1}{5}\)

= 1: 5

Question 6. The value of g at a given point on the earth is 9.8 m s^-2. Let the earth suddenly shrink uniformly to half its present size without any loss of mass. The value of g at the same point (assuming that the distance of the given point from the centre of the earth remains unchanged) will now be

1. 4.9 ms^-2
2. 9.8 ms^-2
3. 3.3 m s^-2
4. 19.6 ms^-2

Answer: 2. 9.8 ms^-2

The gravitational field and the potential point external to the aspherical body remain the same as if its total mass is at the centre. Hence, the shrinkage will not change g and its value remains unchanged at 9.8 m s^-2

Question 7. If the radius of the earth were to shrink by 1%, its mass remaining the same, the acceleration due to gravity on the earth’s surface would

1. Increase by 1%
2. Increase by 2%
3. Decrease by 2%
4. Decrease by 1%

Answer: 2. Increase by 2%

∴ \(g=\frac{G M_{\mathrm{E}}}{R_{\mathrm{F}}^2}=G M_{\mathrm{E}} R_{\mathrm{E}}^{-2}\)

∴ \(\frac{d g}{g}=-2\left(\frac{d R_{\mathrm{E}}}{R_{\mathrm{E}}}\right)=-2(-1 \%)\)

= 2%

Thus, g increases by 2%.

Question 8. If the value of g at a height h above the earth’s surface is the same as that at a depth x below it then (assuming h << R_E and X << R_E)

1. x = h
2. x = 2h
3. x = \(\frac{h}{2}\)
4. x = 4h

Answer: 2. x = 2h

Given that,

⇒ \(\frac{g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}=g\left(1-\frac{x}{R_{\mathrm{E}}}\right)\)

∴ \(g\left(1+\frac{h}{R_{\mathrm{E}}}\right)^{-2}=g\left(1-\frac{x}{R_{\mathrm{E}}}\right)\)

⇒ \(\left(1-\frac{2 h}{R_{\mathrm{E}}}\right)=\left(1-\frac{x}{R_{\mathrm{E}}}\right)\)

x = 2h.

Question 9. If the angular speed co of the earth is doubled, the value of the acceleration due to gravity at the north pole

1. Is doubled
2. Is halved
3. Remains the same
4. Becomes zero

Answer: 3. Remains the same

The value of g’ at a place where the latitude is y, is given by

⇒ \(g^{\prime}=g-\omega^2 R_E \cos ^2 \lambda\)

At the poles, y = 90°.

So, g’ =g.

Hence, g’ remains unaffected.

Question 10. The escape velocity of an object from the Earth is about 11 km s^-1. Assuming the mass of the earth to be about 81 times the mass of the moon and the radius of the earth to be 4 times the radius of the moon, the escape velocity from the surface of the moon will be

1. 0.54 km s^-1
2. 2.44 km s^-1
3. 11 km s^-1
4. 49.5 km s^-1

Answer: 2. 2.44 km s^-1

Escape velocity,

⇒ \(v_{\mathrm{e}}=\sqrt{2 g R_{\mathrm{E}}}=\sqrt{\frac{2 \mathrm{GM}}{R_{\mathrm{E}}}}\)

∴ \(\frac{v_e}{v_m}=\sqrt{\frac{M_e}{M_m} \times \frac{R_m}{R_e}}\)

=\(\sqrt{81 \times \frac{1}{4}}\)

=\(\frac{9}{2}\)

∴ the escape velocity from the moon is

⇒ \(v_{\mathrm{m}}=\frac{2}{9} v_{\mathrm{e}}\)

=\(\frac{2}{9} \times 11 \mathrm{~km} \mathrm{~s}^{-1}\)

=\(2.44 \mathrm{~km} \mathrm{~s}^{-1}\)

Question 11. The given figure shows the motion of a planet around the sun in an elliptical orbit with the sun(S) at the focus. The shaded areas A and B shown in the figure can be assumed to be equal. If t₁ and t₂ represent the time intervals taken by the planet to move from a to b and c to d respectively then

1. t₁ > t₂
2. t₁ < t₂
3. t₁ = t₂
4. t₁ = 2t₂

Answer: 3. t₁ = t₂

According to Kepler’s second law, the areal velocity \(\left(\frac{\Delta A}{\Delta t}\right)\)of a planet around the sun remains constant.

So,

⇒ \(\frac{A}{t_1}=\frac{B}{t_2} \Rightarrow \frac{\Delta \mathrm{Sab}}{t_1}=\frac{\Delta \mathrm{Scd}}{t_2}\)

t₁ = t₂ Since the shaded areas are equal

Question 12. Which of the following graphs is a consequence of the orbital motion of a planet moving around the sun, where T = time of revolution and r = radius of the orbit?

Answer: 1.

According to Kepler’s third law, T₂ α r₃ the T₂-r₃ graph must be a straight line passing through the origin.

Question 13. If an orbiting satellite suddenly comes to rest in its orbit then the satellite will

1. Fly off tangentially
2. Move radially towards the centre of the earth
3. Escape to outer space
4. Continue to move in the same orbit

Answer: 2. Move radially towards the centre of the earth

When the satellite suddenly comes to rest in its orbit, the earth’s attraction continues to exist. So, it will move radially towards the earth’s centre.

Question 14. The mean distance of Jupiter from the sun is nearly 5.2 times the corresponding earth-sun distance. Jupiter’s year in its orbit will be n times the earth’s year, where n is

1. 5
2. 7.5
3. 12
4. 25

Answer: 3. 12

According to Kepler’s third law, T²

So,

⇒ \(\frac{T_{\mathrm{J}}^2}{T_{\mathrm{E}}^2}=\left(\frac{5.2 r}{r}\right)^3 \Rightarrow \frac{T_{\mathrm{J}}}{T_{\mathrm{E}}}=(5.2)^{3 / 2}\)

T_J = 5.2√5.2(1 y)

= 11.8 y ≈ 12 y.

Question 15. The orbital speed of a body orbiting close to the surface of the Earth is approximately

1. 8 km s^-1
2. 11.2 km s^-1
3. 3 x 10⁶ m s^-1
4. 2.2 km s^-1

Answer: 1. 8 km s^-1

Close to the surface of the earth, die centripetal force \(\left(\frac{m v^2}{R_{\mathrm{E}}}\right)\) is provided by the weight (mg).

So,

⇒ \(\frac{m v^2}{R_{\mathrm{E}}}=m g\)

⇒ \(v=\sqrt{g R_{\mathrm{E}}}\)

=\(\sqrt{\left(9.8 \mathrm{~m} \mathrm{~s}^{-2}\right)(6400 \mathrm{~km})}\)

⇒ \(\sqrt{9.8 \times 10^{-3} \times 6400 \mathrm{~km}^2 \mathrm{~s}^{-2}}\)

= 7.9 km s^-1 ≈ 8kms^-1.

Question 16. The orbital speed of an artificial satellite in a circular orbit just above the earth’s surface is v₂. For a satellite orbiting at an altitude of half the Earth’s radius, the orbital speed is

1. \(\frac{3}{2} v_0\)
2. \(\sqrt{\frac{3}{2}} v_0\)
3. \(\sqrt{\frac{2}{3}} v_0\)
4. \(\frac{2}{3} v_0\)

Answer: 3. \(\sqrt{\frac{2}{3}} v_0\)

The orbital speed dose to the earth’s surface is \(v_{\mathrm{o}}=\sqrt{g R_{\mathrm{E}}}\)

Ata height \(h=\frac{R_{\mathrm{E}}}{2}\), orbital speed = v.

∴ \(\frac{m v^2}{r}=\frac{G m M}{r^2}\)

⇒ \(v=\sqrt{\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+h}}=\sqrt{\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+\frac{R_{\mathrm{E}}}{2}}}\)

=\(\sqrt{\frac{2}{3} g R_{\mathrm{E}}}\)

=\(\sqrt{\frac{2}{3}} v_{\mathrm{o}}\)

Question 17. Two artificial satellites of masses m₁ and m₂ (where m₁ > m₂) are revolving around the earth in circular orbits of radii r₁ and r₂ (where r₁ > r₂) respectively. Which of the following statements is true regarding their speeds v₁ and v₂?

1. v₁ = v₂
2. v₁ > v₂
3. v₁< v₂
4. \(\frac{v_1}{r_1}=\frac{v_2}{r_2}\)

Answer: 3. v1< v2 Orbital speed = \(v=\sqrt{\frac{g R_{\mathrm{E}}^2}{r}}\) .. \(\frac{v_1}{v_2}=\sqrt{\frac{r_2}{r_1}}\)

Since r₁ > r₂, we have v₁ < v₂

Question 18. An artificial satellite in a circular orbit around the earth has a total (kinetic + potential) energy E₀. Its potential energy is

1. -E₀
2. \(\frac{3 E_0}{2}\)
3. 2E₀
4. E₀

Answer: 3. 2E₀

The potential energy and the kinetic energy in orbital motion are respectively given by

⇒ \(\mathrm{PE}=-\frac{\mathrm{GM} m}{r} \text { and } \mathrm{KE}=\frac{1}{2} m v^2=\frac{\mathrm{GMm}}{2 r}\)

∴ total energy = \(E_0=\mathrm{PE}+\mathrm{KE}=-\frac{G M m}{2 r}\)

∴ \(\mathrm{PE}=2\left(-\frac{G M m}{2 r}\right)=2 E_0\)

Question 19. If the speed of a satellite revolving around a planet is increased by 41.4%, it will

1. Orbit the planet with a greater radius
2. Orbit the planet with a lesser radius
3. Escape the gravitational pull of the planet
4. Fall into the planet

Answer: 3. Escape the gravitational pull of the planet

Let the initial speed be v₀ = √gR.

increased speed = v = \(v_0+\frac{41.4}{100} v_0\)

= 1.414v₀

= √2v₀

= √2gR

The increased speed is the escape speed, so the satellite will escape the planet’s gravitational pull.

Question 20. Two artificial satellites with their mass ratio \(\frac{m_1}{m_2}=\frac{2}{1}\) are orbiting around the earth in the same circular orbit. If T₁ and T₂ be their time periods of revolution then

1. \(\frac{T_1}{T_2}=2\)
2. \(\frac{T_1}{T_2}=\frac{1}{2}\)
3. \(\frac{T_1}{T_2}=1\)
4. \(\frac{T_1}{T_2}=\frac{1}{4}\)

Answer: 3. \(\frac{T_1}{T_2}=1\)

The orbital speed of a satellite around the planet is

v₀ = \(\sqrt{\frac{G M}{r}}\) which is independent of the satellite’s mass.

So, on the same orbit, T₁ = T₂.

Question 21. A geostationary satellite is established in a higher orbit. Its distance from the centre of the earth in the new orbit is twice that of the previous orbit. The time period of revolution in the second orbit is

1. 24 hours
2. 48√2 hours
3. 48 hours
4. 24√2 hours

Answer: 2. 48√2 hours

From Kepler’s third law, T₂ α r₃.

∴ \(\frac{T_0^2}{T^2}=\frac{r_0^3}{r^3} \Rightarrow \frac{T_0}{T}=\left(\frac{r_0}{2 r_0}\right)^{3 / 2}\)

⇒ \(\frac{24 \mathrm{~h}}{T}=\left(\frac{1}{2}\right)^{3 / 2}=\frac{1}{2 \sqrt{2}}\)

⇒ \(T=48 \sqrt{2} \mathrm{~h}\)

Question 22. A satellite revolving around the earth in a circular orbit whose radius is R. The work done by the earth’s gravitational force during half of its revolution is

1. 2mgR
2. πmgR
3. \(\frac{1}{2}\) mgR
4. Zero

Answer: 2. πmgR

The orbital motion of a satellite is a uniform circular motion in which the force is radial and the work, done is

⇒ \(W=\vec{F} \cdot \overrightarrow{d S}\)

=\(F d S \cos 90^{\circ}=0\)

Question 23. A simple pendulum has its time period T₁ when on the earth’s surface and T₂ when taken to a height equal to RE above the earth’s surface, where RE is the radius of the earth. The value of \(\frac{T_2}{T_1}\) is

1. 2
2. 4
3. √2
4. 1

Answer: 1. 2

⇒ \(T_1=2 \pi \sqrt{\frac{l}{g}} \text { and } T_2\)

=\(2 \pi \sqrt{\frac{l}{g^{\prime}}}\)

=\(2 \pi \sqrt{\frac{l}{\frac{g R_{\mathrm{E}}^2}{4 R_{\mathrm{E}}^2}}}\)

=\(4 \pi \sqrt{\frac{l}{g}}\)

⇒ \(\frac{T_2}{T_1}=\frac{2}{1}\)

= 2.

Question 24. An object when projected vertically upwards from the earth’s surface with a velocity v₀, attains a height RE (the radius of the earth). Ifg is the acceleration due to gravity on the earth’s surface then

1. v₀² = gR_E
2. v₀² = 2gRE
3. v₀²> 2gRE
4. v₀²< gRE

Answer: 4. v₀²< gRE

At the surface, \(\mathrm{KE}=\frac{1}{2} m v_0^2 \text { and } \mathrm{PE}=-\frac{\mathrm{GMm}}{R_{\mathrm{E}}} \text {. }\)

The velocity at a height h = RE is zero, so total energy on the surface = total energy at the height RE

⇒ \(\frac{1}{2} m v_0^2-\frac{G M m}{R_{\mathrm{E}}}=0+\left(-\frac{G M m}{2 R_{\mathrm{E}}}\right)\)

⇒ \(v_0^2=\frac{G M}{R_{\mathrm{E}}}\)

=\(\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}}\)

=\(g R_{\mathrm{E}}\)

⇒ \(v_0^2=g R_{\mathrm{E}}\)

Question 25. An object is projected vertically upwards from the earth’s surface with a velocity equal to half the escape velocity from the earth. If RE be the radius of the earth, the maximum height attained by the object is

1. \(\frac{R_{\mathrm{E}}}{2}\)
2. \(\frac{R_{\mathrm{E}}}{3}\)
3. \(\frac{R_{\mathrm{E}}}{5}\)
4. \(\frac{R_{\mathrm{E}}}{4}\)

Answer: 2. \(\frac{R_{\mathrm{E}}}{3}\)

Let x be the maximum height attained. Conserving the mechanical energy, we have

⇒ \(\frac{1}{2} m\left(\frac{v_e}{2}\right)^2-\frac{G M m}{R_{\mathrm{E}}}=-\frac{G M m}{R_{\mathrm{E}}+x}\)

or, \(\frac{1}{2} \cdot \frac{m}{4}\left(2 g R_{\mathrm{E}}\right)=m g R_{\mathrm{E}}-\frac{m g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+x}\)

or, \(\frac{R_{\mathrm{E}}}{4}=R_{\mathrm{E}}-\frac{R_{\mathrm{E}}^2}{R_{\mathrm{E}}+x} \text { or } \frac{R_{\mathrm{E}}}{R_{\mathrm{E}}+x}=\frac{3}{4}\)

∴ \(x=\frac{R_E}{3}\)

Question 26. Two artificial satellites of different masses are revolving in the same orbit. They have the same

1. Mechanical energy
2. Angular momentum
3. Time period
4. Linear momentum

Answer: 3. Time period

In the same orbit, only the time period of revolution is the same and is independent of the mass of the satellite.

Question 27. A body of mass m is moved from the earth’s surface to a height equal to the radius of the earth (RE). The increase in its gravitational potential energy is

1. mgRE
2. 2mgRE
3. \(\frac{1}{2} m g R_{\mathrm{E}}\)
4. \(\frac{1}{4} m g R_{\mathrm{E}}\)

Answer: 3. \(\frac{1}{2} m g R_{\mathrm{E}}\)

Increase in gravitational PE = U_f-U_i

⇒ \(-\frac{G M m}{2 R_{\mathrm{E}}}-\left(-\frac{G M m}{R_{\mathrm{E}}}\right)=\frac{G M m}{2 R_{\mathrm{E}}}\)

⇒ \(\frac{g R_E^2 m}{2 R_{\mathrm{E}}}=\frac{1}{2} m g R_{\mathrm{E}}\)

Question 28. The escape velocity of an object when projected vertically upwards from the surface of the earth is ve. If the object is projected in a direction making an angle θ with the vertical, the escape velocity will be

1. v_ecos θ
2. v_esin θ
3. v_e
4. v tan θ

Answer: 3. v_e

The escape velocity does not depend on the direction of projection (θ). So, it remains v_e.

Question 29. If the gravitational force of attraction between two material bodies were to vary as 1/r³ instead of 1/r², the period of revolution of a planet around the sun would vary as

1. √r
2. r
3. r^3/2
4. r²

Answer: 4. r²

Assuming F = \(F=\frac{G M m}{r^3}\), we have

or, \(\frac{m v^2}{r}=\frac{G M m}{r^3}\)

or, \(\left(\frac{2 \pi r}{T}\right)^2=\frac{g R^2}{r^2}\)

or, \(T^2=\frac{4 \pi^2 \cdot r^4}{g R^2} \quad\)

or, \(\quad T=\left(\frac{2 \pi}{\sqrt{g} R}\right) r^2\)

∴ T α r².

Question 30. Let r be the orbital radius of a geostationary satellite of the earth. What will be the time period of revolution of a satellite orbiting the earth at a height equal to 2.5R_E, where the radius of the earth is RE (Take r = 7R_E.)

1. 6√2 hours
2. 6√3 hours
3. 12 hours
4. 6√7 hours

Answer: 1. 6√2 hours

According to Kepler’s third law, T₂ α r₃.

∴ \(\frac{T_1}{T_2}=\left(\frac{r_1}{r_2}\right)^{3 / 2}\)

For the geostationary satellite,

T₁ = one day = 24 h

and r₁ = R_E + 6R_E = 7R_E.

For the other satellite, r₂ = 2.5R_E + R_E = 3.5R_E.

∴ \(T_2=\left(\frac{r_2}{r_1}\right)^{3 / 2} T_1\)

=\(\left(\frac{3.5 R_{\mathrm{E}}}{7 R_{\mathrm{E}}}\right)^{3 / 2}(24 \mathrm{~h})\)

=\(\frac{24 \mathrm{~h}}{2 \sqrt{2}}=6 \sqrt{2} \mathrm{~h}\)

Question 31. If the angular momentum of a planet of mass m, moving around the sun in a circular orbit, is L about the centre of the sun, its areal velocity is

1. \(\frac{4 L}{m}\)
2. \(\frac{L}{m}\)
3. \(\frac{L}{2 m}\)
4. \(\frac{2 L}{m}\)

Answer: 3. \(\frac{L}{2 m}\)

Angular momentum = \(L=I \omega=m r^2 \frac{d \theta}{d t}\)

∴ \(r^2 \frac{d \theta}{d t}=\frac{L}{m}\)

∴ areal velocity = \(\frac{d A}{d t}=\frac{1}{2}\left(r^2 \frac{d \theta}{d t}\right)\)

=\(\frac{1}{2}\left(\frac{L}{m}\right)\)

=\(\frac{L}{2 m}\)

Question 32. A uniform sphere of mass M and radius R exerts a force F on a point mass m situated at a distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is formed inside _ the sphere by extracting a portion, as shown in the figure. The force of attraction between the remaining mass of the sphere and the point mass is

1. \(\frac{F}{3}\)
2. \(\frac{2F}{3}\)
3. \(\frac{4F}{9}\)
4. \(\frac{7F}{9}\)

Answer: 4. \(\frac{4F}{9}\)

The mass of the cutout portion of the sphere is

⇒ \(M^{\prime}=\frac{4}{3} \pi\left(\frac{R}{2}\right)^3 \rho=\frac{1}{8}\left(\frac{4}{3} \pi R^3 \rho\right)=\frac{M}{8}\)

The force of attraction due to the solid sphere is

⇒ \(F=\frac{G M m}{(2 R)^2}=\frac{G M m}{4 R^2}\)

The force due to the cavity (assumed as a negative mass) is

⇒ \(f=\frac{G\left(\frac{M}{8}\right) \cdot m}{\left(2 R-\frac{R}{2}\right)^2}=\frac{G M m}{8\left(\frac{9 R^2}{4}\right)}=\frac{G M m}{18 R^2}\)

∴ net force = \(F-f=\frac{G M m}{4 R^2}-\frac{G M m}{18 R^2}\)

⇒ \(\frac{7}{36}\left(\frac{G M m}{R^2}\right)\)

=\(\frac{7}{9}\left(\frac{G M m}{4 R^2}\right)\)

=\(\frac{7 F}{9}\)

Question 33. The radius of the earth is JRE and g is the acceleration due to gravity on its surface. What should be the angular speed of the earth about its axis, so that bodies lying on the equator become weightless?

1. \(\sqrt{\frac{g}{R_{\mathrm{E}}}}\)
2. \(\sqrt{\frac{2 g}{R_{\mathrm{E}}}}\)
3. \(\sqrt{\frac{8}{2 R_E}}\)
4. \(2 \sqrt{\frac{g}{R_E}}\)

Answer: 1. \(\sqrt{\frac{g}{R_{\mathrm{E}}}}\)

For circular motion,

⇒ \(m g-\propto V=\frac{m v^2}{R_{\mathrm{E}}}=m \omega^2 R_{\mathrm{E}}\)

For weightlessness,

⇒ \(\alpha=0 \Rightarrow m \omega^2 R_E=m g\)

Hence, angular velocity = \(\omega=\sqrt{\frac{g}{R_{\mathrm{E}}}}\)

Question 34. A hollow spherical shell is compressed uniformly to half its initial radius. The gravitational potential at the centre

1. Increases
2. Decreases
3. Remains unchanged
4. Varies during the process of compression

Answer: 2. Decreases

Initially, thegravitational potentialatthecentre oftheshellis \(V_{\mathrm{i}}=-\frac{G M}{R}\)

Finally, when R’ = \(R^{\prime}=\frac{R}{2}, V_{\mathrm{f}}=-\frac{G M}{\frac{R}{2}}=-\frac{2 G M}{R}\)

So, the potential is reduced (being more negative).

Question 35. A planet revolves around the sun in an elliptical orbit. The areal velocity (dA/dt) of the planet is 4.0 x 10¹⁶ m² s^-1, and the least distance between the planet and the sun is 2 x 10¹² m. The maximum linear speed of the planet is

1. 10 km s^-1
2. 2010ns^-1
3. 40 km s^-1
4. 80 km s^-1

Answer: 3. 40 km s^-1

Areal velocity = \(\frac{d A}{d t}=\frac{1}{2} r(r \omega)=\frac{1}{2} r v\)

∴ \(\frac{1}{2} r v=\frac{d A}{d t}\)

Hence, linear speed = \(=v=\frac{2}{r} \frac{d A}{d t}\)

⇒ \(\frac{2}{2 \times 10^{12} \mathrm{~m}}\left(4.0 \times 10^{16} \mathrm{~m}^2 \mathrm{~s}^{-1}\right)\)

= 4 x 104 m s^-1

= 40 km s^-1

Question 36. A particle of mass m on the earth’s surface has imparted a velocity twice the escape velocity ve on the earth. Its total mechanical energy will be

1. \(\frac{1}{2} m v_{\mathrm{e}}^2\)
2. \(\frac{2}{3} m v_{\mathrm{e}}^2\)
3. \(\frac{3}{2} m v_{\mathrm{e}}^2\)
4. 3mv_e²

Answer: 3. \(\frac{3}{2} m v_{\mathrm{e}}^2\)

⇒ \(\mathrm{PE}=-\frac{G M m}{R_{\mathrm{E}}}\)

and \(\mathrm{KE}=\frac{1}{2} m\left(2 v_{\mathrm{e}}\right)^2\)

=\(\frac{1}{2} m \cdot 4\left(\frac{2 G M}{R_{\mathrm{E}}}\right)\)

=\(\frac{4 G M m}{R_{\mathrm{E}}}\)

∴ the total mechanical energy is

⇒ \(E_{\mathrm{tot}}=\mathrm{KE}+\mathrm{PE}\)

=\(\frac{3 G M m}{R_{\mathrm{E}}}\)

=\(\frac{3}{2} m\left(\frac{2 G M}{R_{\mathrm{E}}}\right)\)

=\(\frac{3}{2} m v_{\mathrm{e}}^2\)

Question 37. Two artificial satellites are revolving in the same circular orbit around the centre of the earth. They must have the same

1. Mass
2. Kinetic energy
3. Angular momentum
4. Linear speed

Answer: 4. Linear speed

The linear speed of the earth’s satellite is \(v=\sqrt{\frac{G M}{r}}\), which is constant (independent of mass) for all satellites.

Question 38. The work done in slowly lifting a body from the earth’s surface to a height equal to RE (radius of the earth) is equal to twice the work done in lifting the same body from the earth’s surface to a height h, where h is equal to

1. \(\frac{R_{\mathrm{E}}}{4}\)
2. \(\frac{R_{\mathrm{E}}}{3}\)
3. \(\frac{R_{\mathrm{E}}}{6}\)
4. \(\frac{R_{\mathrm{E}}}{2}\)

Answer: 2. \(\frac{R_{\mathrm{E}}}{3}\)

Work done = change in PE = ΔPE.

Initial \(\mathrm{PE}=-\frac{G M m}{R_{\mathrm{E}}} \text { and final } \mathrm{PE}=-\frac{G M m}{R_{\mathrm{E}}+h}\)

When raised to a height RE,

⇒ \(\Delta \mathrm{PE}_1=U_{\mathrm{f}}-U_{\mathrm{i}}\)

=\(-\frac{G M m}{R_{\mathrm{E}}+R_{\mathrm{E}}}-\left(-\frac{G M m}{R_{\mathrm{E}}}\right)\)

=\(\frac{G M m}{2 R_{\mathrm{E}}}\)

When raised to a height of h,

⇒ \(\Delta \mathrm{PE}_2=-\frac{G M m}{R_{\mathrm{E}}+h}+\frac{G M m}{R_{\mathrm{E}}}\)

Given that ΔPE₁ = 2ΔPE₂.

∴ \(\frac{G M m}{2 R_{\mathrm{E}}}=-\frac{2 G M m}{R_{\mathrm{E}}+h}+\frac{2 G M m}{R_{\mathrm{E}}}\)

⇒ \(h=\frac{R_{\mathrm{E}}}{3}\)

Question 39. For a system of three uniform spherical shells, each of mass M and radius R, are kept so as to touch each other as shown in the figure. The magnitude of the gravitational force on any of the shells due to the other two is

1. \(\frac{\sqrt{3}}{2}\left(\frac{G M^2}{R^2}\right)\)
2. \(\frac{\sqrt{3}}{4}\left(\frac{G M^2}{R^2}\right)\)
3. \(\frac{3}{2}\left(\frac{G M^2}{R^2}\right)\)
4. \(\sqrt{\frac{G M^2}{R^2}}\)

Answer: 2. \(\frac{\sqrt{3}}{4}\left(\frac{G M^2}{R^2}\right)\)

The spherical shells may be considered as point masses at the centre. These are at the vertices of an equilateral triangle of side 2R.

The gravitational force between two shells is \(f=\frac{G M^2}{4 R^2}\)

Hence, the net force on any shell is

⇒ \(F=\sqrt{f^2+f^2+2 f \cdot f \cos 60^{\circ}}=\sqrt{3} f=\frac{\sqrt{3}}{4}\left(\frac{G M^2}{R^2}\right)\)

Question 40. The mass and diameter of a planet are thrice the respective values of the Earth. The period of oscillations of a simple pendulum on the earth is 2 s. The period of oscillations of the same pendulum on the planet would be

1. \(\frac{2}{\sqrt{3}} \mathrm{~s}\)
2. 2√3 s
3. \(\frac{\sqrt{3}}{2} \mathrm{~s}\)
4. \(\frac{3}{2} \mathrm{~s}\)

Answer: 2. 2√3 s

⇒ \(\frac{g_{\mathrm{E}}}{g_{\mathrm{P}}}=\frac{G M_{\mathrm{E}} / R_{\mathrm{E}}^2}{G M_{\mathrm{p}} / R_{\mathrm{P}}^2}\)

=\(\frac{M_{\mathrm{E}}}{M_{\mathrm{P}}} \times\left(\frac{R_{\mathrm{P}}}{R_{\mathrm{E}}}\right)^2\)

=\(\frac{M_{\mathrm{E}}}{3 M_{\mathrm{E}}} \times\left(\frac{3 R_{\mathrm{E}}}{R_{\mathrm{E}}}\right)^2\)

= 3.

Time period = \(T=2 \pi \sqrt{\frac{l}{g}}\)

∴ \(\frac{T_{\mathrm{p}}}{T_{\mathrm{E}}}=\sqrt{\frac{g_{\mathrm{E}}}{g_{\mathrm{p}}}}\)

⇒ \(=\sqrt{3}\)

⇒ \(T_{\mathrm{p}}=2 \sqrt{3} \mathrm{~s}\)

Question 41. A black hole is an object whose gravitational field is so strong that even light cannot escape it. To what approximate radius would the earth (mass = 5.98 x 10²⁴ kg) have to be compressed to make it a black hole?

1. 10^-9 m
2. 10^-6m
3. 10^-2m
4. 100 m

Answer: 3. 10^-2m

For the Earth to be a black hole, the escape velocity from the Earth must be equal to the speed of light.

Hence,

⇒ \(v_{\mathrm{e}}=\sqrt{\frac{2 G M}{r}}=c\)

⇒ \(r=\frac{2 G M}{c^2}=\frac{2\left(6.67 \times 10^{-11}\right)\left(5.98 \times 10^{24}\right)}{\left(3 \times 10^8\right)^2} \mathrm{~m}\)

= 8.86 x 10^-3 m ≈ 10^-2 m.

Question 42. An infinite number of spherical bodies, each of mass m = 2 kg, are placed on the x-axis at the distances 1 m, 2 m, 4 m, 8 m, etc., respectively from the origin. The resulting gravitational potential due to this system at the origin in SI units will be

1. \(-\frac{4}{3} G\)
2. -4 G
3. -G
4. \(-\frac{8}{3} G\)

Answer: 2. -4 G

Gravitational potential due to the masses at 0 the origin O is

⇒ \(V_{\mathrm{O}}=-\frac{G(2 \mathrm{~kg})}{1 \mathrm{~m}}-\frac{G(2 \mathrm{~kg})}{2 \mathrm{~m}}-\frac{G(2 \mathrm{~kg})}{4 \mathrm{~m}}-\frac{G(2 \mathrm{~kg})}{8 \mathrm{~m}}-\ldots\)

⇒ \(-G(2 \mathrm{~kg})\left(\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots\right)\)

⇒ \(-G(2 \mathrm{~kg})\left(\frac{1}{1-\frac{1}{2}}\right)\)

= -2G(2 kg)

= -4G units.

Question 43. A planet moving along an elliptical orbit is closest to the sun at a distance r₁ and farthest at a distance r₂ as shown in the figure. If v₁ and v₂ are their linear velocities at these points respectively, the ratio v₁/v₂ is equal to

1. \(\left(\frac{r_1}{r_2}\right)^2\)
2. \(\frac{r_2}{r_1}\)
3. \(\left(\frac{r_2}{r_1}\right)^2\)
4. \(\frac{r_1}{r_2}\)

Answer: 2. \(\frac{r_2}{r_1}\)

Since the angular momentum is conserved,

L₁ = L₂

mv₁r₁ = mv₂r₂

⇒ \(\frac{v_1}{v_2}=\frac{r_2}{r_1}\)

Question 44. The earth (mass = 6 x 10²⁴ kg) revolves around the sun with an angular velocity of 2 x 10⁷ rad s^-1 in a circular orbit of radius 1.5 x 10⁸ km. The force exerted by the sun on the earth is

1. 36 x 10²¹ N
2. 27 x 10³⁹ N
3. 18 x 10²⁵ N
4. Zero

Answer: 1. 36 x 10²¹ N

Gravitational pull by the sun on the earth provides the necessary centripetal force. Hence, the force exerted by the sun is

F = m

= 36 x 10²¹ N.

Question 45. The mean radius of the earth is R& its angular speed on its own axis is to, and the acceleration due to gravity on the earth’s surface is g. What will be the radius of the orbit of a geostationary satellite?

1. \(\left(\frac{R_{\mathrm{E}}^2 g}{\omega^2}\right)^{1 / 3}\)
2. \(\left(\frac{R_{\mathrm{E}} g}{\omega^2}\right)^{1 / 3}\)
3. \(\left(\frac{R_{\mathrm{E}}^2 \omega^2}{g}\right)^{1 / 3}\)
4. \(\left(\frac{R_{\mathrm{E}}^2 g}{\omega}\right)^{1 / 3}\)

Answer: 1. \(\left(\frac{R_{\mathrm{E}}^2 g}{\omega^2}\right)^{1 / 3}\)

For a geostationary satellite, the angular velocity must be equal to that of the earth (ω). For circular motion, the centripetal force (mω²r) is provided by the gravitational attraction \(\left(\frac{G M m}{r^2}\right)\) by the earth on the satellite.

Thus,

⇒ \(m \omega^2 r=\frac{G M m}{r^2}\)

=\(\frac{g R_{\mathrm{E}}^2 m}{r^2}\)

= \(\left(\frac{R_{\mathrm{E}}^2 g}{\omega^2}\right)^{1 / 3}\)

Question 46. A satellite is orbiting the earth at a constant speed v in a circular orbit of radius r. An object of mass m is ejected from the satellite such that it just escapes from die gravitational pull of the earth. At the time of ejection, the kinetic energy of the object is

1. \(\frac{3}{2} m v^2\)
2. mv²
3. 2mv²
4. \(\frac{1}{2} m v^2\)

Answer: 2. mv²

The orbital speed of the satellite is \(v=\sqrt{\frac{G M}{r}}\) To escape the earth’s gravity, its total mechanical energy (PE + KE) must be zero. So,

(KE of the mass m) + \(\left(-\frac{G M m}{r}\right)=0\)

(KE of the mass m) = \(\frac{G M m}{r}\)

= \(m\left(\sqrt{\frac{G M}{r}}\right)^2\)

=\(m v^2\)

Question 47. A body weighs 200 N on the surface of the earth. How much will it weigh halfway down to the centre of the earth?

1. 150 N
2. 200 N
3. 250 N
4. 100 N

Answer: 4. 100 N

The acceleration due to gravity at a depth x below the earth’s surface is

⇒ \(g^{\prime}=g\left(1-\frac{\dot{x}}{R_{\mathrm{E}}}\right)=g\left(1-\frac{\frac{R_{\mathrm{E}}}{2}}{R_{\mathrm{E}}}\right)=\frac{g}{2}\)

∴ \(\frac{w^{\prime}}{w}=\frac{\frac{m g}{2}}{m g}=\frac{1}{2} \Rightarrow w^{\prime}=\frac{w}{2}=\frac{200 \mathrm{~N}}{2}\)

= 100N.

Question 48. The work done to raise a body of mass m from the surface of the earth to a height h, which is equal to the radius of the earth, is

1. mgR_E
2. 2mgR_E
3. \(\frac{1}{2} m g R_{\mathrm{E}}\)
4. \(\frac{3}{2} m g R_{\mathrm{E}}\)

Answer: 3. \(\frac{1}{2} m g R_{\mathrm{E}}\)

The gravitational field is conservative, for which KE + PE = constant and the change in potential energy equals the work done.

Initial PE at the surface = \(U_{\mathrm{i}}=-\frac{G M m}{R_{\mathrm{E}}}\)

At a height \(h=R_{\mathrm{E}} \text {, final } \mathrm{PE}=U_{\mathrm{f}}=-\frac{G M m}{R_{\mathrm{E}}+h}=-\frac{G M m}{2 R_{\mathrm{F}}}\)

Hence, increase in \(\mathrm{PE}=U_{\mathrm{f}}-U_{\mathrm{i}}=-\frac{G M m}{2 R_{\mathrm{E}}}-\left(-\frac{G M m}{R_{\mathrm{E}}}\right)\)

⇒ \(\frac{G M m}{2 R_{\mathrm{E}}}=\frac{\left(g R^2\right) m}{2 R_{\mathrm{E}}}=\frac{1}{2} m g R_{\mathrm{E}}\)

This is equal to the work done by the agent.

Question 49. A solid sphere of mass M and radius r is surrounded by a uniform concentric spherical shell of thickness 2r and mass 2M. The gravitational field at a distance 3r from the common centre will be GM

1. \(\frac{2 G M}{3 r^2}\)
2. \(\frac{2 G M}{9 r^2}\)
3. \(\frac{G M}{3 r^2}\)
4. \(\frac{G M}{9 r^2}\)

Answer: 3. \(\frac{G M}{3 r^2}\)

The point P at a distance 3r from the centre lies on the surface of the outer thick shell. Now, for a spherical mass distribution, the field at an external point will be the same as if its total mass is considered as a point mass at the centre. Hence, the required field has the magnitude

⇒ \(E=\frac{G(M+2 M)}{(3 r)^2}=\frac{G M}{3 r^2}\)

Question 50. Two stars of masses 3 x 10³¹ kg each and at a separation of 2 x 10¹¹ m rotate in a plane about their common centre of mass O. A meteorite passes through O moving perpendicular to the star’s plane of rotation. In order to escape the gravitational pull of this double-star system, the minimum speed that the meteorite should have at O is

1. 2.8 x 10⁵ m s^-1
2. 3.8 x 10⁴ m s^-1
3. 1.4 x 10⁵ m s^-1
4. 2.4 x 10⁴ ms^-1

Answer: 1. 2.8 x 10⁵ m s^-1

Let KE of the meteorite of mass m while crossing the centre O be \(\frac{1}{2} m v^2\) and its PE be

⇒ \(\left(-\frac{G M m}{r}\right)+\left(-\frac{G M m}{r}\right)=-\frac{2 G M m}{r}\)

∴ the total energy of the meteorite is

⇒ \(E_0=\frac{1}{2} m v^2-\frac{2 G M m}{r}\)

When it moves to the infinity, the total mechanical energy must be zero, so,

E_t = 0.

Conserving the energy,

⇒ \(\frac{1}{2} m v^2-\frac{2 G M m}{r}=0\)

⇒ \(v=2 \sqrt{\frac{G M}{r}}\)

Substituting the values,

⇒ \(v=2 \sqrt{\frac{\left(6.67 \times 10^{-11}\right)\left(3 \times 10^{31}\right)}{1 \times 10^{11}}} \mathrm{~m} \mathrm{~s}^{-1}\)

=\(2.8 \times 10^5 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 51. A satellite is revolving in a circular orbit at a height h above the earth’s surface such that h« RE, where RE is the radius of the earth. Assuming the effect of the earth’s atmosphere to be negligible, the minimum increase in the speed required so that the satellite could escape the gravitational pull of the earth is

1. \(\sqrt{\frac{g R_{\mathrm{E}}}{2}}\)
2. √gR_E
3. √2gR_E
4. \((\sqrt{2}-1) \sqrt{g R_{\mathrm{E}}}\)

Answer: 4. \((\sqrt{2}-1) \sqrt{g R_{\mathrm{E}}}\)

The orbital speed (v₁) of the satellite at a height h above the earth’s surface is given by

⇒ \(\frac{m v_1^2}{r}=\frac{G M m}{r^2}\)

or \(v_1=\sqrt{\frac{G M}{r}}=\sqrt{\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+h}}\)

For this satellite to escape the gravitational pull of the earth, the escape speed v₂ is given by

⇒ \(\frac{1}{2} m v_2^2-\frac{G M m}{r}=0 \quad \text { or } \quad v_2=\sqrt{\frac{2 G M}{R_{\mathrm{E}}+h}}=\sqrt{\frac{2 g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+h}}\)

increase in velocity = v₂-v₁

⇒ \((\sqrt{2}-1) \sqrt{\frac{g R_{\mathrm{E}}^2}{R_{\mathrm{E}}+h}} \approx(\sqrt{2}-1) \sqrt{g R_{\mathrm{E}}}\) [… h<<Rg]

Question 52. If the acceleration due to gravity at a height x above the earth’s surface is the same as that below the earth’s surface at the same depth then x in terms of the earth’s radius RE is

1. \((\sqrt{5}-1) \frac{R_{\mathrm{E}}}{2}\)
2. √2RE
3. \(\frac{R_{\mathrm{E}}}{\sqrt{2}}\)
4. \((\sqrt{5}+1) \frac{R_{\mathrm{E}}}{2}\)

Answer: 1. \((\sqrt{5}-1) \frac{R_{\mathrm{E}}}{2}\)

At a height x above the earth’s surface,

⇒ \(\delta_1=\frac{g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+x\right)^2}\)

At a depth x below the earth’s surface,

⇒ \(g_2=g\left(1-\frac{x}{R_E}\right)\)

Given that g₁ = g₂. Hence,

⇒ \(\frac{R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+x\right)^2}=\left(1-\frac{x}{R_{\mathrm{E}}}\right)\)

(R_E+X)(R_E²-X²)=R_E³.

x² + R_Ex-R_E² =0

⇒ \(x=(\sqrt{5}-1) \frac{R_{\mathrm{E}}}{2}\)

Question 53. The orbital velocity v₀ of a satellite revolving close to the earth is increased to \(\sqrt{\frac{3}{2}} v_0\). The radius of the satellite’s orbit around the earth will now be (given that the earth’s radius is RE)

1. \(\sqrt{\frac{3}{2}} R_{\mathrm{E}}\)
2. 2R_E
3. 3R_E
4. 4R_E

Answer: 3. \(\sqrt{\frac{3}{2}} R_{\mathrm{E}}\)

Let the satellite get established in an orbit of radius r with the orbital velocity v₀.

Conserving the mechanical energy,

⇒ \(\frac{1}{2} m\left(\sqrt{\frac{3}{2}} v_0\right)^2-\frac{G M m}{R_{\mathrm{E}}}=\frac{1}{2} m v^2-\frac{G M m}{r}\)…..(1)

Conserving the angular momentum,

⇒ \(m \cdot \sqrt{\frac{3}{2}} \cdot v_{\mathrm{o}} R_{\mathrm{E}}=m v r \text { or } v=\sqrt{\frac{3}{2}} \cdot \frac{v_{\mathrm{o}} R_{\mathrm{E}}}{r}\)….(2)

Substituting v from (2) and putting \(v_{\mathrm{o}}=\sqrt{g R_{\mathrm{E}}} \text { and } G M=g R_{\mathrm{E}}^2\) in (1),

⇒ \(\frac{1}{2} m \frac{3}{2} g R_{\mathrm{E}}-m g R_{\mathrm{E}}=\frac{3}{4} m\left(\frac{g R_{\mathrm{E}}^3}{r^2}\right)-\frac{m g R_{\mathrm{E}}^2}{r}\)

or, \(-\frac{1}{4}=\frac{3}{4}\left(\frac{R_{\mathrm{E}}^2}{r^2}\right)-\frac{R_{\mathrm{E}}}{r} \text { or } r^2-4 R_{\mathrm{E}} r+3 R_{\mathrm{E}}^2=0\)

Solving we get, r = 3RE

Question 54. Two bodies A and B have equal weights when A is placed at the equator of the earth and B is situated at a height h above the pole of the earth. Express h in terms of the earth’s radius RE, the earth’s angular speed CD and the acceleration due to gravity g close to the earth.

1. \(\frac{R_E \omega^2}{2 g}\)
2. \(\frac{R_{\mathrm{B}}^2 \omega^2}{2 g}\)
3. \(\frac{R_{\mathrm{E}} g}{\omega^2}\)
4. \(\frac{g}{\omega^2}\)

Answer: 2. \(\frac{R_{\mathrm{B}}^2 \omega^2}{2 g}\)

For the same weight, g_A = g_B.

But \(g_{\mathrm{A}}=g-\omega^2 R_{\mathrm{E}}\)

and \(g_{\mathrm{B}}=\frac{g R_{\mathrm{E}}^2}{\left(R_{\mathrm{E}}+h\right)^2}\)

=\(g\left(1+\frac{h}{R_{\mathrm{E}}}\right)^{-2}\)

= \(g\left(1-\frac{2 h}{R_{\mathrm{E}}}\right)\)

∴ \(\omega^2 R_{\mathrm{E}}=\frac{2 g h}{R_{\mathrm{E}}}\)

⇒ \(h=\frac{\omega^2 R_{\mathrm{E}}^2}{2 g}\)

Question 55. A satellite is in an elliptical orbit around a planet. It is observed that the speed of the satellite when it is farthest from the planet is 6 times less than that when it is closest to the planet. The ratio of the distances between the satellite and the planet at the closest and farthest points is

1. 3:4
2. 1:1
3. 1:2
4. 1:6

Answer: 4. 1:6

Conserving the angular momentum,

⇒ \(m r_1^2 \omega_1=m r_2^2 \omega_2\)

⇒ \(w r_1^2\left(\frac{v_0}{r_1}\right)=r_2^2\left(\frac{v_2}{r_2}\right)\)

⇒ \(r_1(6 v)=r_2(v)\)

⇒ \(\frac{r_1}{r_2}=\frac{1}{6}\)

r₁: r₂= 1: 6

Question 56. Two planets have masses M and 16M, and radii R and 2R. The separation between their centres is 10R. An object of mass m is fired from the surface of the larger planet towards the smaller planet along the line joining their centres. For the object to strike the surface of the smaller planet, the minimum speed of projection is

1. \(\sqrt{\frac{G M^2}{m R}}\)
2. \(\sqrt{\frac{G M}{R}}\)
3. \(\frac{3}{2} \sqrt{\frac{5 G M}{R}}\)
4. \(\sqrt{\frac{G M}{R}}\)

Answer: 3. \(\frac{3}{2} \sqrt{\frac{5 G M}{R}}\)

For the object to reach the smaller planet, the speed of projection v must be such so as to just cross the point P, where the net gravitational field due to the planets is zero.

∴ \(\frac{G(16 M)}{r^2}=\frac{G M}{(10 R-r)^2}\)

r = 8R

Conserving the mechanical energy,

⇒ \(-\frac{G \cdot 16 M m}{2 R}-\frac{G M m}{10 R-2 R}+\frac{1}{2} m v^2\)

=\(-\frac{G \cdot 16 M m}{8 R}-\frac{G M m}{2 R}\)

or, \(v=\frac{3}{2} \sqrt{\frac{5 G M}{R}}\)

Centre of Mass and Rotation

Question 1. Consider a system of two particles of masses m₁ and m₂. If is pushed towards the centre of mass of the system through a distance d, by what distance should the second particle be moved so as to keep the position of the centre of mass unchanged?

1. \(\left(\frac{m_1}{m_1+m_2}\right) d\)
2. \(\left(\frac{m_2}{m_1}\right) d\)
3. \(\left(\frac{m_1}{m_2}\right) d\)
4. \(\left(\frac{m_2}{m_1+m_2}\right) d\)

Answer: 3. \(\left(\frac{m_1}{m_2}\right) d\)

The position of the centre of mass is given by

⇒ \(x_{\mathrm{CM}}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)

For \(\Delta x_{\mathrm{CM}}=0\), we have

⇒ \(\frac{m_1 \Delta x_1+m_2 \Delta x_2}{m_1+m_2}=0\)

or, m₁d+ m₂ΔX₂ = 0

or, \(\Delta x_2=-\left(\frac{m_1}{m_2}\right) d\)

∴ \(\left|\Delta x_2\right|=\left(\frac{m_1}{m_2}\right) d\)

Question 2. A cubical block of ice of mass m and edge L is placed in a big plate of mass M. If the whole ice melts, and the centre of mass of the ice-tray system will come down by

1. \(\frac{M L}{m+M}\)
2. \(\frac{m L}{2(m+M)}\)
3. \(\frac{M L}{2(M+m)}\)
4. \(\frac{m L}{m+M}\)

Answer: 2. \(\frac{m L}{2(m+M)}\)

If the block of ice melts fully, water will spread over the plate. So, the CM will go down by \(\frac{L}{2}\), while the position of the CM of the plate will remain unchanged.

Since \(x_{\mathrm{CM}}=\frac{m x_1+M x_2}{m+M}\) the shiftin the CM of the system will be

⇒ \(\Delta x_{\mathrm{CM}}=\frac{1}{m+M}\left(m \Delta x_1+M \Delta x_2\right)\)

⇒ \(\frac{1}{m+M}\left(m \cdot \frac{L}{2}+M \cdot 0\right)\)

= \(\frac{m L}{2(m+M)}\)

Question 3. A block of mass m is placed on the top of a bigger wedge of mass 5m, as shown in the figure. All the surfaces are frictionless. The system is released from rest. At the instant when the smaller block reaches the ground, the bigger block will move through

1. \(\frac{d}{6}\) towards left
2. \(\frac{d}{6}\) towards right
3. \(\frac{d}{5}\) towards left
4. \(\frac{d}{5}\) towards right

Answer: 2. \(\frac{d}{5}\) towards left

Since there is no external force along the horizontal, the net displacement of the CM of the system will be zero.

Thus,

⇒ \(x_{\mathrm{CM}}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}=0\)

∴ \(\Delta x_{\mathrm{CM}}=0=\frac{1}{m_1+m_2}\left(m_1 \Delta x_1+m_2 \Delta x_2\right)\)

Here, m₁ = m, m₂ = 5m, Δx₁=d-x and Δx₂ = x, where x = displacement of the wedge to the right so as to keep the position of the CM unchanged.

Thus,

m(d-x) = 5mx

x =\(\frac{d}{6}\) (towards right).

Question 4. On a truck of mass M, moving with uniform velocity on a horizontal road, a rock of mass m drops from above and strikes the floor of the truck vertically. The final velocity of the truck will be

1. \(\frac{M v}{m}\)
2. \(\frac{(M+m) v}{m}\)
3. \(\frac{M v}{M+m}\)
4. \(\frac{m v}{M+m}\)

Answer: 3. \(\frac{M v}{M+m}\)

Conserving the linear momentum along the horizontal,

we have Mv =(M+ m)v’

⇒ \(v^{\prime}=\frac{M v}{M+m}\)

Question 5. A circular plate of diameter a is kept in contact with a square plate of edge in the same plane, as shown in the figure. The surface density of the material and the thickness are the same everywhere. The centre of mass of the combined system will be

1. Inside the circular plate
2. Inside the square plate
3. At the point of contact
4. At the midpoint of the radius of the circular plate

Answer: 2. Inside the square plate

Let p be the surface mass density. So, the mass of the circular plate,

m₁ = \(\pi\left(\frac{a^2}{4}\right) \rho\) and mass of the square plate = m₂ = a²p.

Taking the centre of the circular plate as the origin,

⇒ \(x_{\mathrm{CM}}=\frac{m_1 \cdot 0+m_2 x_2}{m_1+m_2}\)

=\(\frac{a^2 \rho a}{\pi\left(\frac{a^2}{4}\right) \rho+a^2 \rho}\)

=\(\frac{a}{1+\frac{\pi}{4}}=\frac{a}{1.785}\)

=\(0.56 a>\frac{a}{2}\)

Thus, the CM lies inside the square plate

Question 6. Two blocks of masses 10 kg and 30 kg are placed along a vertical line. The first block is raised vertically through 7 cm. By what distance should the second block be moved so as to raise the centre of mass of the system by 1 cm?

1. 1 cm downwards
2. 1 cm upwards
3. 2 cm downwards
4. 2 cm upwards

Answer: 1. 1 cm downwards

⇒ \(x_{\mathrm{CM}}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)

⇒ \(\Delta x_{\mathrm{CM}}=\frac{m_1 \Delta x_1+m_2 \Delta x_2}{m_1+m_2}\)

Hence, mx- 10 kg, m2 = 30 kg, AxCM =1 cm (upward) and Ax1-7 cm.

∴ \(1 \mathrm{~cm}=\frac{(10 \mathrm{~kg})(7 \mathrm{~cm})+(30 \mathrm{~kg}) \Delta x_2}{40 \mathrm{~kg}}\)

30 ΔX₂ = 40 cm- 70 cm

= -30 cm

Δx₂ =-1 cm.

Hence, the second block must be moved by 1 cm downwards.

Question 7. The balloon (of mass M), the light string (of length L) and the monkey (of mass m) shown in the figure are at rest in the air. If the monkey reaches the top of the rope, the balloon will descend vertically through the distance

1. \(\frac{m L}{M}\)
2. \(\frac{M L}{m}\)
3. \(\frac{M L}{M+m}\)
4. \(\frac{m L}{M+m}\)

Answer: 4. \(\frac{m L}{M+m}\)

Since the system is initially at rest, the position of the CM of the system must be unchanged. Let the balloon move down by x. Then,

Mx = m(L- x)

=> (M + m)x= mL

⇒ \(x=\frac{m L}{M+m}\)

Question 8. A boy of mass m is standing on one end of a long boat of mass M and length L. Neglecting friction, how far does the boat move if the boy slowly moves to the other end?

1. \(\frac{m L}{M}\)
2. \(\frac{M L}{m}\)
3. \(\frac{m L}{M+m}\)
4. \(\frac{M L}{m+M}\)

Answer: 3. \(\frac{m L}{M+m}\)

As the boy moves towards the right, let the boat move towards the left by x so as to keep the position of the CM of the system unchanged.

Thus,

m(L-x)=Mx

=> mL = (M+ m)x

⇒ \(x=\frac{m L}{M+m}\)

Question 9. The linear mass density of a rod of length 3m is directly proportional to the distance x from one end. The distance of the centre of mass of the rod from that end will be

1. 1.5m
2. 2 m
3. 2.5 m
4. 3.0m

Answer: 2. 2 m

⇒ \(x_{\mathrm{CM}}=\frac{1}{M} \int_0^L x d m\), where the total mass is

⇒ \(M=\int d m=\int_0^L \lambda x d x=\frac{\lambda L^2}{2}\)

Now, \(\int_0^L x d m=\int_0^L x(\lambda x d x)=\lambda \int_0^L x^2 d x=\frac{\lambda L^3}{3}\)

⇒ \(x_{\mathrm{CM}}=\frac{\frac{\lambda L^3}{3}}{\frac{\lambda L^2}{2}}=\frac{2}{3} L=\frac{2}{3} \cdot(3 \mathrm{~m})\)

= 2m.

Question 10. Three particles of the same mass lie in the xy-plane. The x and y-coordinates of their positions are given by (1, 1), (2, 2) and (3, 3) respectively. The x and y-coordinates of the centre of mass of the system are given by

1. (1,2)
2. (2,2)
3. (2, 3)
4. (4,5)

Answer: 2. (2,2)

The x- and y-coordinates of the CM are respectively,

⇒ \(x_{\mathrm{CM}}=\frac{1}{3 m}(m \cdot 0+m \cdot a+m \cdot 0)=\frac{a}{3}\)

and \(y_{\mathrm{CM}}=\frac{1}{3 m}(m \cdot 0+m \cdot 0+m \cdot b)=\frac{b}{3}\)

= \(\frac{1}{3}\) (1+2+3)

= 2.

Thus, the x- and y-coordinates of the CM are given by (2, 2)

Question 11. Three particles, each of mass m, are placed at the vertices of a right-angled triangle OAB, as shown in the figure. If OA = a and OB = b then the position vector of the centre of mass of the given system is

1. \(\frac{1}{3}(a \hat{i}+b \hat{j})\)
2. \(\frac{1}{3}(a \hat{i}-b \hat{j})\)
3. \(\frac{2}{3}(a \hat{i}+b \hat{j})\)
4. \(\frac{2}{3}(a \hat{i}-b \hat{j})\)

Answer: 1. \(\frac{1}{3}(a \hat{i}+b \hat{j})\)

With reference to the origin O,

⇒ \(x_{\mathrm{CM}}=\frac{1}{3 m}(m \cdot 0+m \cdot a+m \cdot 0)=\frac{a}{3}\)

and \(y_{\mathrm{CM}}=\frac{1}{3 m}(m \cdot 0+m \cdot 0+m \cdot b)=\frac{b}{3}\)

∴ the position vector of the centre of mass is

⇒ \(\vec{r}_{C M}=\left(\frac{a}{3}\right) \hat{i}+\left(\frac{b}{3}\right) \hat{j}=\frac{1}{3}(a \hat{i}+b \hat{j})\)

Question 12. Three particles, each of mass m, are placed at the vertices of an equilateral triangle of side a, as shown in the figure. The position vector of the centre of mass of the system is

1. \(\frac{a}{2}\left(\hat{i}+\frac{1}{\sqrt{3}} \hat{j}\right)\)
2. \(\frac{a}{2}(3 \hat{i}+\sqrt{3} \hat{j})\)
3. \(\frac{a}{2}\left(3 \hat{i}+\frac{1}{\sqrt{3}} \hat{j}\right)\)
4. \(\frac{a}{2}(\hat{i}+\hat{j})\)

Answer: 1. \(\frac{a}{2}\left(\hat{i}+\frac{1}{\sqrt{3}} \hat{j}\right)\)

With reference to the origin O,

⇒ \(x_{\mathrm{CM}}=\frac{1}{3 m}\left(m \cdot 0+m \cdot a+m \cdot \frac{a}{2}\right)\)

= \(\frac{a}{2}\)

and \(y_{\mathrm{CM}}=\frac{1}{3 m}\left(m \cdot 0+m \cdot 0+m \cdot \frac{\sqrt{3}}{2} a\right)\)

= \(\frac{\sqrt{3} a}{2}\)

∴ \(\vec{r}_{\mathrm{CM}}=\left(\frac{a}{2}\right) \hat{i}+\left(\frac{\sqrt{3} a}{2}\right) \hat{j}\)

= \(\frac{a}{2}\left(\hat{i}+\frac{\sqrt{3}}{3} \hat{j}\right)\)

= \(\frac{a}{2}\left(\hat{i}+\frac{1}{\sqrt{3}} \hat{j}\right)\)

Question 13. A one-metre-long uniform-disbent at a right angle at its midpoint. The distance of the centre of mass from the centre of the rod is

1. 17.7 cm
2. 25.2 cm
3. 34.1cm
4. Zero

Answer: 1. 17.7 cm

⇒ \(x_{\mathrm{CM}}=\frac{\frac{m}{2}\left(\frac{L}{4}\right)}{m}=\frac{L}{8} \text { and } y_{\mathrm{CM}}=\frac{L}{8}\)

∴ \(\vec{r}_{\mathrm{CM}}=\frac{L}{8}(\hat{i}+\hat{j})\)

∴ the distance of the CM from O is

⇒ \(\left|\vec{r}_{\mathrm{CM}}\right|=\frac{\sqrt{2}(1 \mathrm{~m})}{8}\)

= 0.177m

= 17.7 cm.

Question 14. Two particles of mass m₁ and m₂, initially at rest, move towards each other under a mutual force of attraction. At any instant when their respective speeds are v₁ and v₂ the speed of the centre of mass of the system is

1. \(\frac{m_1 v_1}{m_1+m_2}\)
2. \(\frac{m_2 v_2}{m_1+m_2}\)
3. \(\frac{v_1+v_2}{2}\)
4. Zero

Answer: 4. Zero

Since there is no external force, the linear momentum of the system will be conserved.

The initial momentum = 0,

so, \(m_1 \vec{v}_1+m_2 \vec{v}_2=0\)

Now, the velocity of the CM is

⇒ \(\vec{v}_{\mathrm{CM}}=\frac{m_1 \vec{v}_1+m_2 \vec{v}_2}{m_1+m_2}=0\)

Question 15. Two blocks of masses 10kg and 4kg are connected by a light spring and placed on a frictionless horizontal surface. An impulse to the heavier block imparts a velocity of 14 m s^-1 in the direction of the lighter block. The velocity of the centre of mass of the system is

1. 5 ms^-1
2. 10 m s^-1
3. 15m s^-1
4. 20 m s^-1

Answer: 2. 10 m s^-1

Given that m₁ = 10 kg and m₂ = 4 kg.

The initial velocity imparted to m1 is w₁ = 14m^-1 and u₂ = 0.

∴ the velocity of the CM of the system is

⇒ \(\vec{v}_{\mathrm{CM}}=\frac{1}{m_1+m_2}\left(m_1 \vec{u}_1+m_2 \vec{u}_2\right)\)

⇒ \(\frac{1}{14 \mathrm{~kg}}\left[(10 \mathrm{~kg})\left(14 \mathrm{~m} \mathrm{~s}^{-1}\right)+0\right]\)

= 10 ms^-1.

Question 16. A wheel rotates with a constant acceleration of 2.0 rad s^-2 starting from rest. The number of revolutions made in the first 10 seconds is

1. 5
2. 10
3. 16
4. 20

Answer: 3. 16

Given that angular acceleration = a = 2.0 rad s^-2, time = t = 10 s and angular frequency = ω₀ = 0.

For angular motion,

⇒ \(\theta=2 \pi N=\omega_0 t+\frac{1}{2} \alpha t^2=\frac{1}{2}\left(2 \mathrm{rad} \mathrm{s}^{-2}\right)\left(100 \mathrm{~s}^2\right)\)

⇒ \(N=\frac{100}{2 \pi}=15.9 \approx 16\)

Question 17. A motor wheel, accelerated uniformly from rest, rotates through 2.5 rad during the first second. The angle rotated through the next second is

1. 5 rad
2. 10 rad
3. 7.5 rad
4. 12.5 rad

Answer: 3. 7.5 rad

ω₀ = θ and θ₁ = 2.5 rad in the first second.

For the first second,

⇒ \(\theta_1=\omega_0 t+\frac{1}{2} \alpha t^2\)

or, \(2.5 \mathrm{rad}=\frac{1}{2} \alpha(1 \mathrm{~s})^2\)

∴ angular acceleration= α = 5.0 rad s^-2.

For the first two seconds,

⇒ \(\theta_2=\frac{1}{2} \alpha(2 \mathrm{~s})^2=\frac{1}{2}(5.0)(4) \mathrm{rad}\)

= 10 rad

and \(\theta_1=\frac{1}{2} \alpha(1 s)^2=\frac{1}{2}(5)(1)\)

= 2.5 rad.

θ₂ – θ₁ = (10- 2.5)rad

= 7.5 rad.

Question 18. A wheel revolves about its axis with uniform angular acceleration. Starting from rest, it attains an angular velocity of 100 rev s^-2 in 4 seconds. The angular acceleration of the wheel is

1. 10 revs^-2
2. 15 revs^-2
3. 20 revs^-2
4. 25 rev s^-2

Answer: 4. 25 rev s^-2

⇒ \(\omega=\omega_0+\alpha t\)

⇒ \(100 \mathrm{rps}=0+\alpha(4 \mathrm{~s})\)

∴ angular acceleration= a = 25 rev s^-2

Question 19. In the preceding question, the angle rotated by the wheel during the first four seconds is 6

1. 200ft rad
2. 400ft rad
3. 100ft rad
4. 300ft rad

Answer: 2. 400ft rad

⇒ \(\theta=\omega_0 t+\frac{1}{2} \alpha t^2\)

= \(0+\frac{1}{2}\left(25 \times 2 \pi \mathrm{rad} \mathrm{s}^{-2}\right)(4 \mathrm{~s})^2\)

= 400n rad.

Question 20. A disc of radius 10 cm is rotating uniformly about its axis at an angular speed of 20rad s^-1. The linear speed of a point on the rim of the disc is

1. 0.5 ms^-1
2. 1.0ms^-1
3. 1.5 ms^-1
4. 2.0 ms^-1

Answer: 4. 2.0 ms^-1

Angular speed = to = 20 rad s^-1 and radius = r

= 10 cm

= 0.1 m.

∴ linear speed, v = ωr

= (20rad s^-1)(0.1 m)

= 2m s^-1

Question 21. In the preceding question, what is the ratio of the linear speed at the rim to that at the midpoint of the radius of the disc?

1. 1:1
2. 1:2
3. 2:1
4. None of these

Answer: 3. 2:1

⇒ \(\frac{v_r}{v_{r / 2}}=\frac{\omega r}{\omega(r / 2)}=2: 1\)

Question 22. Three-point masses m₁ m₂ and m₃ are located at the vertices of an equilateral triangle of side a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m₁?

1. \(\left(m_1+m_2\right) \frac{a^2}{4}\)
2. \(\left(m_2+m_3\right) \frac{a^2}{4}\)
3. \(\left(m_1+m_3\right) \frac{a^2}{4}\)
4. \(\left(m_1+m_2+m_3\right) \frac{a^2}{4}\)

Answer: 2. \(\left(m_2+m_3\right) \frac{a^2}{4}\)

The mass lies on the axis of rotation, so it does not contribute to the moment of inertia.

∴ \(I=m_2 r_2^2+m_3 r_3^2\)

⇒ \(\left(m_2+m_3\right)\left(\frac{a}{2}\right)^2\)

⇒ \(\left(m_2+m_3\right) \frac{a^2}{4}\)

Question 23. Four particles of masses m, 2m, 3m and 4m are connected by a rod of negligible mass, as shown in the figure. The radius of gyration of the system about the axis AB is

1. 2a
2. √5a
3. √3a
4. √2a

Answer: 2. √5a

The moment of inertia of the given system about the axis AB is

I = m(0) + 2m(a²) + 3m(2a)² + 4m(3a)²

= 50ma²

= (m + 2m + 3m + 4m)k²

= 10mk².

∴ the radius of gyration = k

⇒ \(\sqrt{\frac{50}{10} a^2}=\sqrt{5} a\)

Question 24. A light rod of length l has two masses m₁ and m₂ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the length of the rod and passing through the centre of mass is

1. \(\left(m_1+m_2\right) l^2\)
2. \(\sqrt{m_1 m_2} l^2\)
3. \(\left(\frac{m_1 m_2}{m_1+m_2}\right) l^2\)
4. \(\left(\frac{m_1+m_2}{m_1 m_2}\right) l^2\)

Answer: 3. \(\left(\frac{m_1 m_2}{m_1+m_2}\right) l^2\)

Let x be the distance of the CM from the A; m1 end. So,

⇒ \(x=\frac{m_1 \cdot 0+m_2 l}{m_1+m_2}=\left(\frac{m_2}{m_1+m_2}\right) l\)

∴ the distance between the CM and m₂,

⇒ \(l-x=\left(\frac{m_1}{m_1+m_2}\right) l\)

Hence, the moment of inertia of the given system about AB will be

⇒ \(I=m_1 x^2+m_2(l-x)^2\)

⇒ \(m_1 \cdot \frac{m_2{ }^2 l^2}{\left(m_1+m_2\right)^2}+m_2 \cdot \frac{m_1{ }^2 l^2}{\left(m_1+m_2\right)^2}=\left(\frac{m_1 m_2}{m_1+m_2}\right) l^2\)

Question 25. Three thin metal rods, each of mass M and length l are welded to form an equilateral triangle. The moment of inertia of the composite system about an axis passing through the centre of mass of the structure and perpendicular to its plane is

1. \(\frac{M l^2}{2}\)
2. \(\frac{M l^2}{4}\)
3. \(\frac{M l^2}{8}\)
4. \(\frac{M l^2}{12}\)

Answer: 1. \(\frac{M l^2}{2}\)

From the given figure,

⇒ \(\frac{O N}{B N}=\tan 30^{\circ}\)

⇒ \(O N=B N \tan 30^{\circ}=\frac{l}{2 \sqrt{3}}\)

The moment of inertia of BC about an axis through N and perpendicular to the plane of the rods is

⇒ \(I_{\mathrm{N}}=\frac{1}{12} M l^2\)

From the parallel-axes theorem,

⇒ \(I_{\mathrm{O}}=I_{\mathrm{N}}+M(O N)^2=\frac{M l^2}{12}+M\left(\frac{l}{2 \sqrt{3}}\right)^2=\frac{M l^3}{6}\)

For the total system comprising the triangle,

⇒ \(I=3 I_{\mathrm{O}}=3\left(\frac{M l^2}{6}\right)=\frac{M l^2}{2}\)

Question 26. Four metal rods, each of mass M and length L, are welded to form a square-shaped structure ABCD, as shown in the figure. The moment of inertia of the composite structure about the file axis bisecting the rods AB and CD and coplanar with the structure is

1. \(\frac{M L^2}{6}\)
2. \(\frac{M L^2}{3}\)
3. \(\frac{M L^2}{12}\)
4. \(\frac{2}{3} M L^2\)

Answer: 4. \(\frac{2}{3} M L^2\)

About the given axis, the moment of inertia of AB is

⇒ \(I_{\mathrm{AB}}=\frac{M L^2}{12}\),

that for \(\mathrm{BC} \text { is } I_{\mathrm{BC}}=M\left(\frac{L}{2}\right)^2=\frac{M L^2}{4}\)

that for \(\mathrm{CD} \text { is } I_{\mathrm{CD}}=\frac{M L^2}{12}\),

and that for \(\mathrm{AD} \text { is } I_{\mathrm{AD}}=\frac{M L^2}{4}\)

∴ the moment of inertia of the system is

⇒ \(I=2\left(\frac{M L^2}{4}\right)+2\left(\frac{M L^2}{12}\right)=\frac{2}{3} M L^2\)

Question 27. The moment of inertia of a thin rod of mass M and length L about an axis passing perpendicularly at a distance \(\frac{L}{4}\) from one end of the rod is

1. \(\frac{7}{48} M L^2\)
2. \(\frac{1}{3} M L^2\)
3. \(\frac{1}{12} M L^2\)
4. \(\frac{1}{8} M L^2\)

Answer: 1. \(\frac{7}{48} M L^2\)

The moment of inertia of the rod about the axis through the centre of mass (O) is

⇒ \(I_{\mathrm{CM}}=\frac{M L^2}{12}\)

∴ the moment of inertia about the parallel axis through Ais.

⇒ \(I_{\mathrm{A}}=I_{\mathrm{CM}}+M d^2=\frac{M L^2}{12}+M\left(\frac{L}{4}\right)^2\)

=\(\frac{7}{48} M L^2\)

Question 28. A uniform rod OA of mass M and length L is inclined at an angle θ to the vertical. What is its moment of inertia about the vertical axis passing through its end O, as shown in the figure?

1. \(\frac{1}{3} M L^2\)
2. \(\frac{1}{3} M L^2 \sin ^2 \theta\)
3. \(\frac{1}{3} M L^2 \cos ^2 \theta\)
4. \(\frac{1}{12} M L^2\)

Answer: 2. \(\frac{1}{3} M L^2 \cos ^2 \theta\)

The mass of an element dx at a distance x from one end O is dm = \(\frac{M}{L}\)dz, and its perpendicular distance from the axis of

AN= OA sin θ = xsin θ.

∴ the moment of inertia is

⇒ \(I=\int d^2 d m=\int_0^L(x \sin \theta)^2\left(\frac{M}{L} d x\right)\)

⇒ \(\frac{M}{L}\left(\sin ^2 \theta\right) \frac{L^3}{3}=\frac{1}{3} M L^2 \sin ^2 \theta\)

Question 29. A uniform rod AB of mass M and length L is inclined at an angle θ to the vertical. What is its moment of inertia about the vertical axis passing through its midpoint O, as shown in the figure?

1. \(\frac{1}{3} M L^2\)
2. \(\frac{1}{12} M L^2\)
3. \(\frac{1}{12} M L^2 \sin ^2 \theta\)
4. \(\frac{1}{12} M L^2 \cos ^2 \theta\)

Answer: 3. \(\frac{1}{12} M L^2 \sin ^2 \theta\)

As solved in the preceding question,

⇒ \(d I=\left(\frac{M}{L} d x\right)(x \sin \theta)^2\)

For the total,

⇒ \(I=\left(\frac{M}{L} \sin ^2 \theta\right)_{-l / 2}^{l / 2} x^2 d x\)

⇒ \(2\left(\frac{M}{L} \sin ^2 \theta\right)\left[\frac{x^3}{3}\right]_0^{l / 2}\)

⇒ \(\frac{1}{12} M L^2 \sin ^2 \theta\)

Question 30. Two identical uniform rods, each of mass M and length L, are welded together at their centre and placed in a horizontal plane. The rods are inclined at an angle of θ, as shown in the figure. The moment of inertia of the combination about a vertical axis (perpendicular to the plane of the rods) passing through their midpoint O is

1. \(\frac{1}{3} M L^2\)
2. \(\frac{1}{6} M L^2\)
3. \(\frac{1}{12} M L^2 \sin ^2 \theta\)
4. \(\frac{1}{6} M L^2 \cos ^2 \theta\)

Answer: 2. \(\frac{1}{6} M L^2\)

The moment of inertia of each rod about the given axis is

⇒ \(\frac{M L^2}{12}\)

The moment of inertia is a scalar quantity and does not depend on their inclination θ. So,

⇒ \(I_{\text {net }}=2 I=2\left(\frac{M L^2}{12}\right)\)

=\(\frac{M L^2}{6}\)

Question 31. A thin rod AB of mass M and length L is hinged at one end A to a horizontal floor. It is gently allowed to fall from its initial vertical position. The angular velocity of the rod when its free end strikes the floor is

1. \(2 \sqrt{\frac{g}{L}}\)
2. \(\sqrt{\frac{2 g}{L}}\)
3. \(\sqrt{\frac{g}{L}}\)
4. \(\sqrt{\frac{3 g}{L}}\)

Answer: 4. \(\sqrt{\frac{3 g}{L}}\)

As the rod falls, its PE is converted to rotational KE. Thus,

⇒ \(M g \cdot \frac{L}{2}=\frac{1}{2} I \omega^2\)

⇒ \(\frac{1}{2}\left(\frac{1}{3} M L^2\right) \omega^2\)

⇒ \(\omega=\sqrt{\frac{3 g}{L}}\)

Question 32. A uniform thin wire of length L and linear mass density X is bent into a circular loop. The moment of inertia of the loop about its tangent is

1. \(\frac{\lambda L^3}{8 \pi^2}\)
2. \(\frac{3 \lambda L^3}{8 \pi^2}\)
3. \(\frac{\lambda L^3}{16 \pi^2}\)
4. \(\frac{\lambda L^3}{2 \pi^2}\)

Answer: 2. \(\frac{3 \lambda L^3}{8 \pi^2}\)

The moment of inertia of a circular loop about its diameter is given by

⇒ \(I_{\mathrm{dia}}=\frac{1}{2} M R^2\),

where \(M=\lambda L \text { and } R=\frac{L}{2 \pi}\) =radius.

∴ the moment of inertia about the tangents given by

⇒ \(I_{\mathrm{tan}}=I_{\mathrm{dia}}+M R^2\)

=\(\frac{3}{2} M R^2=\frac{3}{2}(\lambda L)\left(\frac{L}{2 \pi}\right)^2\)

=\(\frac{3 \lambda L^3}{8 \pi^2}\)

Question 33. A tube of uniform cross-section and length L is completely filled with an incompressible liquid of mass M and closed at both ends. The tube is then revolved in a horizontal plane about an axis passing perpendicularly through its one end with uniform angular velocity ω. The force exerted by the liquid at the other end is

1. \(\frac{1}{4} M \omega^2 L\)
2. \(\frac{1}{2} M \omega^2 L\)
3. \(\omega^2 L\)
4. \(\frac{M \omega^2 L^2}{2}\)

Answer: 2. \(\frac{1}{2} M \omega^2 L\)

In circular motion, the centripetal force exerted by an element of length dx at a distance x is \(d F=\left(\frac{M}{L} d x\right) \omega^2 x\)

∴ total force \(F=\int d F=\frac{M \omega^2}{L} \int_0^L x d x\)

=\(\frac{1}{2} M \omega^2 L\)

Question 34. A uniform circular disc of mass M and radius R is rotating about its axis of symmetry at a uniform rate. A lump of wax of mass m is gently stuck on the disc at a distance r = R/2 from its centre. The new angular velocity of the system is

1. \(\frac{2 \omega M}{2 M+m}\)
2. \(\frac{2 \omega M}{M+2 m}\)
3. \(\frac{\omega m}{M}\)
4. \(\frac{\omega M}{m}\)

Answer: 1. \(\frac{2 \omega M}{2 M+m}\)

Conserving the angular momentum, we have

⇒ \(I \omega=I^{\prime} \omega^{\prime} \quad\)

⇒ \(\quad \frac{1}{2} M R^2 \omega=\left[\frac{1}{2}\left(M R^2\right)+\frac{m R^2}{4}\right] \omega^{\prime}\)

Simplifying, we get

⇒ \(\omega^{\prime}=\frac{2 M \omega}{2 M+m}\)

Question 35. From a disc of radius R and mass M, a circular hole of diameter is cutItsrimpassesthrough the centre of the disc. What is the moment of inertia of the remaining part of the disc about a perpendicular axis passing through the centre?

1. \(\frac{15}{32} M R^2\)
2. \(\frac{11}{32} M R^2\)
3. \(\frac{13}{32} M R^2\)
4. \(\frac{9}{32} M R^2\)

Answer: 3. \(\frac{13}{32} M R^2\)

The total mass of the disc is M. Then, the mass of the cutout portion is

⇒ \(m=\left(\frac{M}{\pi R^2}\right) \pi\left(\frac{R}{2}\right)^2=\frac{M}{4}\)

The moment of inertia of the total disc about the given axis through O is

⇒ \(I=\frac{1}{2} M R^2\)

The moment of inertia of the cutout portion about the perpendicular axis through its centre

⇒ \(I_{\mathrm{O}^{\prime}}=\frac{1}{2}\left(\frac{M}{4}\right)\left(\frac{R}{2}\right)^2=\frac{M R^2}{32}\)

From the theorem of parallel axes, its moment of inertia about the perpendicular axis through O is

⇒ \(I_{\mathrm{O}}=I_{\mathrm{O}^{\prime}}+\frac{M}{4}\left(O O^{\prime}\right)^2=\frac{M R^2}{32}+\frac{M R^2}{16}=\frac{3}{32} M R^2\)

Now, the net moment of inertia is

⇒ \(I_{\text {net }}=I-I_0=\frac{M R^2}{2}-\frac{3}{32} M R^2=\frac{13}{32} M R^2\)

Question 36. Three identical spherical shells, each of mass m and radius r, are placed touching each other, as shown in the figure. Consider an axis XX’, which is touching the two shells and passing through the file diameter of the fluid shell. The moment of inertia of the system consisting of these three shells about XX’is

1. \(\frac{16}{5} m r^2\)
2. \(\frac{11}{5} m R^2\)
3. 4mr²
4. 3mr²

Answer: 3. 4mr²

The moment of inertia of the shell A about XX’ is

⇒ \(I_{\mathrm{A}}=\frac{2}{3} m r^2\)

Similarly, \(I_{\mathrm{B}}=\frac{2}{3} m r^2+m r^2=\frac{5}{3} m r^2\)

∴ the net moment of inertia of the system is

⇒ \(I=I_{\mathrm{A}}+I_{\mathrm{B}}+I_{\mathrm{C}}=4 m r^2\)

Question 37. The ratio of the radii of gyration of a circular ring and a circular disc of the same mass and radius about an axis passing through their centres and perpendicular to their planes is

1. 1:√2
2. √2:1
3. 2:1
4. 3:2

Answer: 2. √2:1

Moment of inertia of the ring = \(I_{\text {ring }}=M R^2=M k_{\text {ring }}^2\)

Moment of inertia of the disc = \(I_{\text {disc }}=\frac{1}{2} M R^2=M k_{\text {disc }}^2\)

∴ \(\frac{I_{\text {ring }}}{I_{\text {disc }}}=\frac{M R^2}{\frac{1}{2} M R^2}=\frac{M k_{\text {ring }}^2}{M k_{\text {disc }}^2}=\frac{k_{\text {ring }}^2}{k_{\text {disc }}^2}\)

⇒ \(k_{\text {ring }}: k_{\text {disc }}\)

= \(\sqrt{2}: 1\)

Question 38. The moment of inertia of the uniform circular disc shown in the figure is maximum about an axis perpendicular to the disc and passing through

1. A
2. D
3. B
4. C

Answer: 3. B

According to the theorem of parallel axes, \(I=I_{\mathrm{CM}}+M a^2\)

The distance from the centre is maximum for the point B, so I is a maximum of about B.

Question 39. The instantaneous angular position of a point on a rotating wheel is given by the equation θ(t) = 2t- 6t². The torque on the wheel becomes zero at

1. t = 1s
2. t = 0.5s
3. t = 2s
4. t = 1.5s

Answer: 1. t = 1s

Given that θ = 2t³- 6t². Hence, angular velocity = \(\omega=\frac{d \theta}{d t}=6 t^2-12 t\) and

angular acceleration \(\alpha=\frac{d \omega}{d t}=12 t-12\)

For torque \(\tau=I \alpha\) to be zero,

α = 12t – 12 = 0

=> t =1 s.

Question 40. From a circular disc of radius R and mass 9M, a small disc of mass M and radius R/3 is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is

1. 8MR²
2. 4MR²
3. \(\frac{40}{9} M R^2\)
4. \(\frac{4}{9} M R^2\)

Answer: 3. \(\frac{40}{9} M R^2\)

The moment of inertia of the remaining disc is

⇒ \(I=\frac{1}{2}(9 M) R^2-\frac{1}{2}(M)\left(\frac{R}{3}\right)^2\)

= \(\frac{1}{2} M R^2\left(9-\frac{1}{9}\right)\)

= \(\frac{40}{9} M R^2\)

Question 41. The moment of inertia of a uniform disc of mass M and radius R about an axis touching the disc at its edge and normal to the plane of the disc is

1. \(\frac{1}{2} M R^2\)
2. MR²
3. \(\frac{3}{2} M R^2\)
4. 2MR²

Answer: 3. \(\frac{3}{2} M R^2\)

From the theorem of parallel axes,

⇒ \(I=I_{\mathrm{CM}}+M R^2=\frac{1}{2} M R^2+M R^2\)

= \(\frac{3}{2} M R^2\)

Question 42. Two bodies A and B have their moments of inertia I and 21 about their axes of rotation. If their kinetic energies of rotation are equal, their angular velocities will be in the ratio

1. 2: 1
2. 1: 2
3. √2: 1
4. 1: √2

Answer: 3. √2: 1

The kinetic energies of the bodies A and B are respectively

⇒ \(E_{\mathrm{A}}=\frac{1}{2} I \omega_{\mathrm{A}}^2 \text { and } E_{\mathrm{B}}=\frac{1}{2}(2 I) \omega_{\mathrm{B}}^2 \text {. }\)

Given that EA = EB. So,

⇒ \(\omega_A{ }^2=2 \omega_B{ }^2\)

∴ \(\frac{\omega_A}{\omega_B}=\frac{\sqrt{2}}{1}\)

⇒ \(\omega_A: \omega_B=\sqrt{2}: 1\)

Question 43. A circular disc of the moment of inertia I₂ about its axis perpendicular to its plane and passing through its centre is gently placed over another disc of the moment of inertia I₁ rotating with an angular velocity GO about the same axis. The final angular velocity of the combination of discs is

1. \(\frac{I_2 \omega}{I_1+I_2}\)
2. \(\frac{I_1 \omega}{I_1+I_2}\)
3. \(\frac{\left(I_1+I_2\right) \omega}{I_1}\)
4. \(\frac{I_1 \omega}{I_2}\)

Answer: 2. \(\frac{I_1 \omega}{I_1+I_2}\)

Initial angular momentum = I₁ω

and final angularmomentum=(I₁ + I₂)ω.

Conserving the angularmomentum \(\omega^{\prime}=\frac{I_1 \omega}{I_1+I_2}\)

Question 44. The ratio of the radius of gyration of a disc about a coplanar tangential axis to that of a ring of the same radius about a coplanar tangential axis is

1. 2:3
2. 2:1
3. √5: √6
4. √1: √3

Answer: 3. \(\frac{I_1 \omega}{I_1+I_2}\)

The moment of inertia of a uniform disc about its tangent is given by

⇒ \(I_{\text {disc }}=\frac{1}{4} M R^2+M R^2=\frac{5}{4} M R^2\)

where \(\frac{1}{4} M R^2\) is the moment ofinertia of the disc aboutits diameter.

Similarly, for the ring,

⇒ \(I_{\text {ring }}=\frac{M R^2}{2}+M R^2=\frac{3}{2} M R^2\)

∴ \(\frac{I_{\text {disc }}}{I_{\text {ring }}}=\frac{\frac{5}{4} M R^2}{\frac{3}{2} M R^2}=\frac{5}{6}=\frac{M k_{\text {disc }}^2}{M k_{\text {ring }}^2}\)

⇒ \(\frac{k_{\text {disc }}}{k_{\text {ring }}}=\sqrt{\frac{5}{6}} \Rightarrow k_{\text {disc }}: k_{\text {ring }}=\sqrt{5}: \sqrt{6}\)

Question 45. A heavy disc is rotating with an angular speed co. If a child gently sits on it, what is conserved?

1. Linear momentum
2. Angular momentum
3. Kinetic energy
4. Potential energy

Answer: 2. Angular momentum

Since there is no external torque, the angular momentum will be conserved.

Question 46. ABC is a triangular plate of uniform thickness. The sides are in the ratio 3: 4: 5, as shown in the figure. I_AB, I_BC and I_CA are the moments of inertia of the plate about AB, BC and CA respectively. Which of the following is correct?

1. \(I_{\mathrm{AB}}+I_{\mathrm{BC}}=I_{\mathrm{CA}}\)
2. ICA is maximum
3. \(I_{\mathrm{AB}}>I_{\mathrm{BC}}\)
4. \(I_{\mathrm{BC}}>I_{\mathrm{AB}}\)

Answer: 4. \(I_{\mathrm{BC}}>I_{\mathrm{AB}}\)

Adding the shaded part APC, we get a rectangular plate for which the moment of inertia is

⇒ \(I_{\mathrm{AB}}=\frac{1}{3}(2 M)(3)^2=6 M \text { units, }\)

⇒ \(I_{\mathrm{BC}}=\frac{1}{3}(2 M)(4)^2=\frac{32}{3} M=10.67 M \text { units, }\)

and I_CA=minimum.

Thus, I_BC > I_AB.

Question 47. In a rectangular plate ABCD A (where BC = 2AB), the moment of inertia is minimum along the axis passing through the points E

1. B and C
2. B and D
3. H and F
4. E and G

Answer: 2. B and D

The moment of inertia depends on the mass distribution of the rotational axis.

For the axis BD or AC, the maximum distance of the points A and C is less than the smaller side AB.

Hence, I_BD is minimal.

Question 48. The moment of inertia of a body about a given axis is 1.2 kg m². Initially, the body is at rest. In order to produce a rotational kinetic energy of 1500 J, an angular acceleration of 25 rad s^-2 must be applied about that axis for a duration of

1. 4 s
2. 2 s
3. 8 s
4. 10 s

Answer: 2. 2 s

⇒ \(\mathrm{KE}=\frac{1}{2} I \omega^2=\frac{1}{2} I\left(\omega_0+\alpha t\right)^2=\frac{1}{2} I \alpha^2 t^2\)

⇒ \(\text { time }=t=\sqrt{\frac{2(\mathrm{KE})}{I \alpha^2}}=\frac{1}{\alpha} \sqrt{\frac{2(\mathrm{KE})}{I}}\)

Substituting the given values,

⇒ \(t=\frac{1}{25} \sqrt{\frac{2(1500)}{1.2}} \mathrm{~s}=\frac{1}{25} \times 50 \mathrm{~s}\)

= 2s.

Question 49. The moment of inertia of a uniform circular disc about its diameter is I. Its moment of inertia about an axis perpendicular to its plane and touching a point on its rim will be

1. 5I
2. 3I
3. 4I
4. 6I

Answer: 4. 6I

The moment of inertia of the disc about its diameter is \(I=\frac{M R^2}{4}\) and

that about the axis of symmetry is

⇒ \(I_{\mathrm{O}}=\frac{M R^2}{2}=2 I\)

From the theorem of parallel axes,

I = I_o+MR²

= 2I+ 4I

= 6I

Question 50. A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with an angular velocity co. Its kinetic energy is

1. mr²ω²
2. \(\frac{1}{2} m r^2 \omega^2\)
3. mrω²
4. \(\frac{1}{2} m r \omega^2\)

Answer: 2. \(\frac{1}{2} m r^2 \omega^2\)

The kinetic energy of the ring about the given axis is

⇒ \(\frac{1}{2} I \omega^2=\frac{1}{2} m r^2 \omega^2\)

Question 51. Two discs of moments of inertia I₁ and I₂ rotating about their respective axes, with angular frequencies co₁ and co₂ respectively, are gently brought into contact face to face, with their axes of rotation coincident. The angular frequency of the composite disc will be

1. \(\frac{I_1 \omega_1-I_2 \omega_2}{I_1-I_2}\)
2. \(\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)
3. \(\frac{I_1 \omega_2+I_2 \omega_1}{I_1+I_2}\)
4. \(\frac{I_1 \omega_2-I_2 \omega_1}{I_1-I_2}\)

Answer: 2. \(\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)

Conserving the angular momentum, we have

⇒ \(I_1 \omega_1+I_2 \omega_2=\left(I_1+I_2\right) \omega^{\prime}\)

⇒ \(\omega^{\prime}=\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)

Question 52. If the earth were to suddenly contract to half its present size without any change in its mass, the duration of the day would have been

1. 12 hours
2. 6 hours
3. 18 hours
4. 30 hours

Answer: 2. 6 hours

The earth revolves in its orbit due to the gravitational attraction of the sun, and the torque is zero. So, the angular momentum is conserved.

∴ \(I \omega=I^{\prime} \omega^{\prime} \Rightarrow \frac{2}{5} M R^2 \cdot \frac{2 \pi}{24 \mathrm{~h}}=\frac{2}{5} M\left(\frac{R}{2}\right)^2 \cdot \frac{2 \pi}{T}\)

∴ 24h= 4T

T= 6h

Question 53. A solid cylinder of mass M and radius R rotates about its axis with a constant angular speed a. Its kinetic energy is

1. 2MR²ω²
2. \(\frac{1}{2} M R^2 \omega^2\)
3. \(\frac{1}{4} M R^2 \omega^2\)
4. MR²ω²

Answer: 3. \(\frac{1}{4} M R^2 \omega^2\)

The KE of the solid cylinder is

⇒ \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{1}{2} M R^2\right) \omega^2=\frac{1}{4} M R^2 \omega^2\)

Question 54. A circular disc of mass m and radius rerolling on a rough horizontal surface with a constant speed v. Its kinetic energy is

1. \(\frac{1}{4} m v^2\)
2. \(\frac{1}{2} m v^2\)
3. \(\frac{3}{4} m v^2\)
4. mv²

Answer: 3. \(\frac{3}{4} m v^2\)

KE of a rolling disc \(\mathrm{KE}_{\text {trans }}+\mathrm{KE}_{\text {rot }}=\frac{1}{2} m v^2+\frac{1}{2} I \omega^2\)

The condition for rolling is v = ωr. Hence

⇒ \(E_{\mathrm{tot}}=\frac{1}{2} m v^2+\frac{1}{2}\left(\frac{1}{2} m R^2\right) \frac{v^2}{R^2}=\frac{3}{4} m v^2\)

Question 55. A solid sphere is rotating about its diameter at a constant angular velocity ω. If its size is slowly reduced to 1/n of its original value without any change in its mass, its angular velocity becomes

1. \(\frac{\omega}{n}\)
2. nω
3. \(\frac{\omega}{n^2}\)
4. n²ω

Answer: 4. n²ω

Conserving the angular momentum,

⇒ \(I \omega=I^{\prime} \omega^{\prime} \Rightarrow\left(\frac{2}{5} M R^2\right) \omega=\frac{2}{5} M\left(\frac{R}{n}\right)^2 \omega^{\prime}\)

ω = n²ω

Question 56. A circular disc of radius R is free to oscillate about an axis passing through a point on its rim and perpendicular to its plane. The disc is turned through an angle of 60° and released. Its angular velocity when it reaches the equilibrium position will be

1. \(\sqrt{\frac{g}{3 R}}\)
2. \(\sqrt{\frac{2g}{3 R}}\)
3. \(\sqrt{\frac{2g}{R}}\)
4. \(\sqrt{\frac{3g}{2 R}}\)

Answer: 2. \(\sqrt{\frac{2g}{3 R}}\)

Loss in PE = mgR(1- cos 60°) = \(\frac{m g R}{2}\)

Gain in KE = \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{1}{2} m R^2+m R^2\right) \omega^2\)

Conserving the energy,

⇒ \(\frac{1}{2}\left(\frac{3}{2} m R^2\right) \omega^2=\frac{m g R}{2}\)

⇒ \(\omega=\sqrt{\frac{2 g}{3 R}}\)

Question 57. The moment of inertia of a thick shell of mass and internal and external radii R and 2R respectively, about its diameter is

1. \(\frac{13}{35} M R^2\)
2. \(\frac{3}{2} M R^2\)
3. \(\frac{62}{35} M R^2\)
4. \(\frac{31}{35} M R^2\)

Answer: 3. \(\frac{62}{35} M R^2\)

We consider the given hollow sphere as if a solid sphere of radius R and mass M₂ be removed from a solid sphere of radius 2R and mass M₁.

Thus,

⇒ \(M=M_1-M_2=\frac{4}{3} \pi(2 R)^3 \rho-\frac{4}{3} \pi R^3 \rho=\frac{28}{3} \pi R^3 \rho\)

∴ the moment of inertia of the given hollow sphere is

⇒\(\frac{2}{5} M_1(2 R)^2-\frac{2}{5} M_2 R^2\)

⇒ \(\frac{2}{5} \times \frac{32}{3} \pi R^3 \cdot \rho \cdot 4 R^2-\frac{2}{5} \cdot \frac{4}{3} \pi R^3 \rho \cdot R^2\)

⇒ \(\frac{2}{5}(32-1) \frac{4}{3} \pi R^5 \rho=\frac{62}{5}\left(\pi R^3\right)\left(\frac{4}{3} R^2 \rho\right)\)

⇒ \(\frac{62}{5}\left(\frac{3 M}{28 \rho}\right)\left(\frac{4}{3} R^2 \rho\right)=\frac{62}{35} M R^2\)

Question 58. A disc of mass M and radius 2R has a concentric hole of radius R. Its moment of inertia about an axis through its centre is

1. \(\frac{3}{2} M R^2\)
2. \(\frac{5}{3} M R^2\)
3. \(\frac{5}{2} M R^2\)
4. \(\frac{2}{5} M R^2\)

Answer: 3. \(\frac{5}{2} M R^2\)

The disc with a concentric hole may be considered as a solid disc of radius 2R and mass M₁ with a concentric cutout disc of radius R and mass M₂.

The mass of the given discs

⇒ \(M=M_1-M_2=\pi(2 R)^2 \sigma-\pi R^2 \sigma=3 \pi R^2 \sigma,\)

where is the surface mass density?

The moment of inertia of the given disc is

⇒ \(I=\frac{1}{2} M_1(2 R)^2-\frac{1}{2} M_2 R^2\)

⇒ \(\frac{1}{2}\left(4 \pi R^2 \sigma\right)\left(4 R^2\right)-\frac{1}{2}\left(\pi R^2 \sigma\right) R^2\)

⇒ \(\frac{1}{2} \pi R^4 \sigma(16-1)=\frac{15}{2}\left(\pi R^4\right) \frac{M}{3 \pi R^2}\)

⇒ \(\frac{5}{2} M R^2\)

Question 59. A mass m is moving at a constant velocity along a straight line parallel to the x-axis away from the origin. It’s angular with respect to the origin

1. Goes on increasing
2. Goes on decreasing
3. Remains constant
4. Is zero

Answer: 3. Remains constant

The angular momentum of the mass m about the origin is

⇒ \(\vec{L}=\vec{r} \times \vec{p}=\vec{r} \times(m \vec{v})=m(\vec{r} \times \vec{v})\)

Position vector = \(\overrightarrow{O P}=(x \hat{i}+y \hat{j})\), where (x, y) gives the coordinates of P, and

velocity = \(\vec{v}=v \hat{i}\)

∴ \(\vec{L}=m(x \hat{i}+y \hat{j}) \times v \hat{i}=m y v(-\hat{k})\)

Here m and v are constant, and y is also constant as the particle moves parallel to the x-axis.

Thus, \(|\vec{L}|\) = myv

= constant.

Question 60. A disc of mass and radius R is rolling with an angular speed ω on a horizontal plane, as shown in the figure. The magnitude of the angular momentum of the disc about the origin O is

1. \(\frac{1}{2} M R^2 \omega\)
2. MR²ω
3. \(\frac{3}{2} M R^2 \omega\)
4. 2MR²ω

Answer: 3. \(\frac{3}{2} M R^2 \omega\)

Let \(\overrightarrow{O C}=\vec{r} \text { and } \vec{v}_{\mathrm{CM}}\) = velocity of the centre of mass of the disc.

Hence, the linear momentum of the disc is

⇒ \(\vec{p}_{\mathrm{C}}=m \vec{v}_{\mathrm{CM}}\)

If Lc = angular momentum about C, the angular momentum about the origin is

⇒ \(\vec{L}_{\mathrm{O}}=\vec{L}_{\mathrm{C}}+\vec{r} \times \vec{p}_{\mathrm{C}}\)

⇒ \(I_{C^\omega} \omega+r \times M v_{C M} \sin \theta\)

⇒ \(\frac{1}{2} M R^2 \omega+M R v_{\mathrm{CM}}\) [∵ r sinθ = R]

⇒ \(\frac{1}{2} M R^2 \omega+M R^2 \omega\) [∵ v_CM = Rω]

⇒ \(\frac{3}{2} M R^2 \omega\)

Question 61. A cubical block of mass m and side L rests on a rough horizontal surface having the coefficient of friction μ, A horizontal force F is applied on the block, as shown in the figure. The coefficient of friction is sufficiently large so that the block does not slide before toppling. The minimum force required to topple the block is

1. mg
2. \(\frac{m g}{2}\)
3. \(\frac{m g}{4}\)
4. mg (1-μ)

Answer: 2. \(\frac{m g}{2}\)

By the applied force, the cubical block will turn about the edge at A.

Hence, the torque of the force F about A is

⇒ \(\tau_1=F L\) (clockwise).

The torque due to the weight mg about A is

⇒ \(\tau_2=m g\left(\frac{L}{2}\right)=\frac{m g L}{2}\) (anticlockwise).

For turning, must slightly exceed \(\tau_2\).

So, in the limit

⇒ \(\tau_1=\tau_2 \Rightarrow F L=m g\left(\frac{L}{2}\right) \Rightarrow F=\frac{m g}{2}\)

Question 62. A solid metallic sphere of radius R has a moment of inertia I about its diameter. The sphere is melted and recast into a solid disc of radius r and uniform thickness. The moment of inertia of the disc about an axis passing through its edge and perpendicular to its plane is also equal to I. The ratio r/R is

1. \(\frac{2}{\sqrt{10}}\)
2. \(\frac{2}{\sqrt{5}}\)
3. \(\frac{2}{\sqrt{15}}\)
4. \(\frac{1}{\sqrt{2}}\)

Answer: 3. \(\frac{2}{\sqrt{15}}\)

Themomentofinertia of the solid sphere is \(I_1=\frac{2}{5} M R^2\) , and the moment of inertia of the disc is

Given that I₁ = I₂, we have

⇒ \(\frac{2}{5} M R^2=\frac{3}{2} M r^2 \Rightarrow \frac{r}{R}=\frac{2}{\sqrt{15}}\)

Question 63. A circular disc rolls down an inclined plane without slipping. What fraction of its total energy is translational?

1. \(\frac{1}{\sqrt{2}}\)
2. \(\frac{1}{2}\)
3. \(\frac{1}{3}\)
4. \(\frac{2}{3}\)

Answer: 4. \(\frac{2}{3}\)

At any instant during rolling,

v = ωr,

KE of translation = \(\frac{1}{2}\)mv²

and KE of rotation = \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{1}{2} m r^2\right)\left(\frac{v^2}{r^2}\right)=\frac{1}{4} m v^2\)

∴ total energy = \(\frac{1}{2} m v^2+\frac{1}{4} m v^2=\frac{3}{4} m v^2\)

Hence, the ratio is

⇒ \(\frac{\mathrm{KE} \text { of translation }}{\text { total KE }}=\frac{\frac{1}{2} m v^2}{\frac{3}{4} m v^2}=\frac{2}{3}\)

Question 64. A solid sphere rolls down an inclined plane without slipping. What fraction of its total energy is rotational?

1. \(\frac{2}{7}\)
2. \(\frac{3}{7}\)
3. \(\frac{2}{3}\)
4. \(\frac{3}{5}\)

Answer: 1. \(\frac{2}{7}\)

KE of translation = \(\frac{1}{2}\) mv²

and KE of rotation = \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{2}{5} m R^2\right)\left(\frac{v}{R}\right)^2\)

⇒ \(\frac{1}{5}\) [∵ v = Rω for rolling].

∴ total energy = \(\frac{1}{2} m v^2+\frac{1}{5} m v^2=\frac{7}{10} m v^2\)

Hence, \(\frac{\text { rotational KE }}{\text { total } \mathrm{KE}}=\frac{\frac{1}{5} m v^2}{\frac{7}{10} m v^2}=\frac{2}{7}\)

Question 65. A solid cylinder of mass M and radius R rolls down without slipping on a rough inclined plane from a height of h. The rotational kinetic energy of the cylinder, when it reaches the bottom of the plane, will be

1. Mgh
2. \(\frac{M g h}{2}\)
3. \(\frac{M g h}{3}\)
4. \(\frac{2M g h}{3}\)

Answer: 3. \(\frac{M g h}{3}\)

The initial PE (= mgh) will change into the total KE.

Now,KE of rotation = \(=\frac{1}{2} I \omega^2\)

=\(\frac{1}{2}\left(\frac{1}{2} m R^2\right) \omega^2\)

=\(\frac{1}{4} m R^2\left(\frac{v^2}{R^2}\right)\)

⇒ \(\frac{1}{4} m v^2\)

and KE of translation = \(\frac{1}{2}\)mv².

∴ total KE = \(\mathrm{KE}=\frac{1}{2} m v^2+\frac{1}{4} m v^2\)

=\(\frac{3}{4} m v^2\)

Now, \(\frac{3}{4} m v^2=m g h \Rightarrow v^2\)

=\(\frac{4}{3} g h\)

∴ the KE of rotation at the bottom is

⇒ \(\frac{1}{4} m v^2=\frac{1}{4} m\left(\frac{4}{3} g h\right)\)

=\(\frac{1}{3} m g h\)

Question 66. A solid sphere rolls down from the top of a rough inclined plane. Its velocity on reaching the bottom of the incline is v. When the same sphere slides down from the top of a smooth but similar inclined plane, its velocity is v’. The ratio v’/v is equal to

1. \(\sqrt{\frac{3}{5}}\)
2. \(\sqrt{\frac{7}{5}}\)
3. 1
4. \(\frac{3}{\sqrt{5}}\)

Answer: 2. \(\sqrt{\frac{7}{5}}\)

While rolling down the inclined plane,

total KE= mgh

⇒ \(\frac{1}{2} m v^2+\frac{1}{2} I \omega^2=m g h\)

⇒ \(\frac{1}{2} m v^2+\frac{1}{2}\left(\frac{2}{5} m R^2\right) \frac{v^2}{R^2}=m g h\)

⇒ \(\frac{7}{10} m v^2=m g h\)

While slipping,

⇒ \(\frac{1}{2} m v^{\prime 2}=m g h\)

⇒ \(\frac{1}{2} m v^{\prime 2}=\frac{7}{10} m v^2\)

⇒ \(\frac{v^{\prime}}{v}=\sqrt{\frac{7}{5}}\)

Question 67. A solid sphere rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout the motion). The directions of the static frictional force acting on the cylinder are

1. Up the incline while ascending and down the incline while descending
2. Up the incline while ascending as well as descending
3. Down the incline while ascending and up the incline while descending
4. Down the incline while ascending as well as descending

Answer: 2. Up the incline while ascending as well as descending

When the sphere rolls up the inclined plane, friction opposes rolling and acts up along the plane so as to produce an anticlockwise torque.

When the sphere rolls down the inclined plane, friction supports rolling and acts up along the plane, thus producing an anticlockwise torque, which increases the angular speed.

Question 68. A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a constant force of 30 N?

1. 0.25 rad s^-2
2. 25 rad s^-2
3. 5 ms^-2
4. 25 ms^-2

Answer: 2. 25 ms^-2

Torque = FR =Ia = MR²a.

∴ angular acceleration

⇒ \(\alpha=\frac{F R}{M R^2}\)

= \(\frac{F}{M R}=\frac{30 \mathrm{~N}}{(3 \mathrm{~kg})\left(\frac{40}{100} \mathrm{~m}\right)}\)

= \(25 \mathrm{rad} \mathrm{s}^{-2}\)

Question 69. Two discs of the same moment of inertia rotate about their regular axes passing through the centre and perpendicular to their planes with angular velocities ω₁ and ω₂. They are brought into contact face to face coinciding their axes of rotation. The expression for the loss of energy during this process is

1. \(\frac{1}{4} I\left(\omega_1-\omega_2\right)^2\)
2. \(I\left(\omega_1-\omega_2\right)^2\)
3. \(\frac{1}{8} I\left(\omega_1-\omega_2\right)^2\)
4. \(\frac{1}{2} I\left(\omega_1-\omega_2\right)^2\)

Answer: 1. \(\frac{1}{4} I\left(\omega_1-\omega_2\right)^2\)

Conserving the angular momentum,

⇒ \(I \omega_1+I \omega_2=2 I \omega \Rightarrow \omega=\frac{\omega_1+\omega_2}{2}\)

Initial KE = \(\frac{1}{2} I \omega_1{ }^2+\frac{1}{2} I \omega_2{ }^2\)

and final KE = \(\frac{1}{2}(2 I) \omega^2=I\left(\frac{\omega_1+\omega_2}{2}\right)^2\)

∴ loss of energy = KE_i-KE_f

= \(\frac{I}{2}\left[\left(\omega_1^2+\omega_2^2\right)-\frac{\left(\omega_1+\omega_2\right)^2}{2}\right]\)

=\(\frac{1}{4} I\left(\omega_1-\omega_2\right)^2\)

Question 70. Two rotating bodies A and B of respective masses m and 2m with moments of inertia I_A and I_B (where I_A > I_A) have the same kinetic energy of rotation. If L_A and L_B are their angular momenta respectively then

1. \(L_{\mathrm{A}}=\frac{L_{\mathrm{B}}}{2}\)
2. L_A = 2L_B
3. L_B>L_A
4. L_A>L_B

Answer: 3. L_B>L_A

KEin terms of angular momentum (L) is \(\frac{L^2}{2 I}\)

∴ \(\frac{L_{\mathrm{A}}^2}{2 I_{\mathrm{A}}}=\frac{L_{\mathrm{B}}^2}{2 I_{\mathrm{B}}}\)

⇒ \(\frac{L_{\mathrm{A}}^2}{L_{\mathrm{B}}^2}=\frac{I_{\mathrm{A}}}{I_{\mathrm{B}}}\)

Since I_B > I_A, we have L_B > L_A

Question 71. A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and the same radius is also rotating about a geometrical axis with an angular speed of twice that of the sphere. The ratio of their kinetic energies of rotation E_Asph:E_Acyl will be

1. 2:3
2. 1:5
3. 1:4
4. 3:1

Answer: 2. 1:5

The kinetic energy of the solid sphere is \(E_1=\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{2}{5} M R^2\right) \omega^2\)

The kinetic energy of the solid cylinder is \(E_2=\frac{1}{2} I(2 \omega)^2=\frac{1}{2}\left(\frac{M R^2}{2}\right) 4 \omega^2\)

∴ \(\frac{E_1}{E_2}=\frac{\frac{1}{5} M R^2 \omega^2}{M R^2 \omega^2}\)

= 1: 5.

Question 72. A disc and a sphere of the same radius roll down on two inclined planes from the same altitude and length. Which of the two objects gets to the bottom of the plane first?

1. Both read at the same time.
2. The disc
3. It depends on their masses.
4. The sphere

Answer: 4. The sphere

The acceleration of a body rolling down an inclined plane is given

⇒ \(a=\frac{g \sin \theta}{1+\frac{k^2}{R^2}}\)

For the disc, \(\frac{k^2}{R^2}=\frac{1}{2} \Rightarrow a_{\mathrm{disc}}=\frac{2}{3} g \sin \theta\)

For the sphere, \(\frac{k^2}{R^2}=\frac{2}{5} \Rightarrow a_{\mathrm{sph}}=\frac{5}{7} g \sin \theta\)

Since \(a_{\mathrm{sph}}>a_{\text {disc }}\), the sphere will reach the bottom before the disc.

Question 73. A uniform circular di9c of radius 50 cm at rest is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2.0 rad s^-2. Its net acceleration at the end of 2.0 s is approximately

1. 6.0 ms^-2
2. 3.0 m s^-2
3. 7.0 ms^-2
4. 8.0 ms^-2

Answer: 4. 8.0 ms^-2

Given that radius = R = 50 cm = 0.5 m and angular acceleration

α = 2.0 rad s^-2.

The angular velocity (ω) at the end of 2.0 s will be

ω = ω₀ + at = 0 + (2.0rad s^-2)(2.0 s)= 4rad s^-1.

Tangential acceleration a_tan = Rα = (0.5m)(2.0rad s^-2) = 1.0m s^-2

and radial acceleration= a_rad = ω2R = (4rad s^-1)2(0.5m) = 8.0m s^-2.

∴ net acceleration = \(\sqrt{a_{\mathrm{tan}}^2+a_{\mathrm{rad}}^2}=\sqrt{\left(1.0 \mathrm{~m} \mathrm{~s}^{-2}\right)^2+\left(8.0 \mathrm{~m} \mathrm{~s}^{-2}\right)^2}\)

⇒ \(\sqrt{65 \mathrm{~m}^2 \mathrm{~s}^{-4}} \approx 8.0 \mathrm{~m} \mathrm{~s}^{-2}\)

Question 74. A force \(F=\alpha \hat{i}+3 \hat{j}+6 \hat{k}\) is acting at a point \(\vec{r}=2 \hat{i}-6 \hat{j}-12 \hat{k}\). The value of α for which the angular momentum about the origin is conserved is

1. 1
2. -1
3. 2
4. Zero

Answer: 2. -1

The angular momentum is conserved when the torque \((\vec{\tau}=\vec{r} \times \vec{p})\) is zero.

Given that \(\vec{r}=2 \hat{i}-6 \hat{j}-12 \hat{k} \text { and } \vec{F}=\alpha \hat{i}+3 \hat{j}+6 \hat{k}\)

∴ \(\vec{\tau}=\vec{r} \times \vec{p}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & -6 & -12 \\
\alpha & 3 & 6
\end{array}\right|\)

⇒ \((-36+36) \hat{i}+(-12 \alpha-12) \hat{j}+(6+6 \alpha) \hat{k}\)

⇒ \(-\hat{j}(12+12 \alpha)+\hat{k}(6+6 \alpha)\)

Since x = 0, we have,

12 + 12α = 0

or, α =-1 and 6 + 6α = 0

or, α= -1.

Question 75. A solid cylinder of mass 50kg and radius 0.5m is free to rotate about the horizontal axis. A light string is wound around the cylinder with one end attached to it and the other hanging freely. The tension in the string required to produce an angular acceleration of 2 rev s^-2 is

1. 25N
2. 50N
3. 78.5N
4. 157N

Answer: 4. 157N

Given that M = 50 kg, R = 0.5 m

and angular acceleration = α = 2 rev s^-2

= 4π rad s^-2.

Let T be the required tension.

∴ torque = \(\tau=T R=I \alpha\)

tension = \(T=\frac{I \alpha}{R}=\frac{\left(\frac{1}{2} M R^2\right) \alpha}{R}=\frac{1}{2} M R \alpha\)

⇒ \(\frac{1}{2}(50 \mathrm{~kg})\left(\frac{1}{2} \mathrm{~m}\right)\left(4 \pi \mathrm{rad} \mathrm{s}^{-2}\right)\)

= 50πN

= 157N.

Question 76. A rod PQ of mass m and length L is hinged at the end P. The rod is kept horizontal by a massless string tied to the point Q, as shown in the figure. When the string is cut, the initial angular acceleration of the rod is

1. \(\frac{3 g}{2 L}\)
2. \(\frac{2 g}{3 L}\)
3. \(\frac{g}{L}\)
4. \(\frac{2 g}{L}\)

Answer: 1. \(\frac{3 g}{2 L}\)

When the string is cut, the weight mg acting at the centre of the rod will produce a torque of \(\tau=m g\left(\frac {L}{2}\right)\)

But \(\tau=I \alpha=\frac{1}{3} m L^2 \alpha\)

∴ \(\frac{1}{3} m L^2 \alpha=m g\left(\frac{L}{2}\right)\)

Question 77. A small object of uniform density rolls up a curved surface with an initial velocity of v. It reaches up to a maximum height of \(\frac{3 v^2}{4 g}\) with respect to the initial position. The object is a

1. Ring
2. Shell
3. Disc
4. Solid sphere

Answer: 3. Disc

The kinetic energy at the base gets converted into the PE at the maximum height.

Thus, at the base,

⇒ \(\frac{1}{2} m v^2\left(1+\frac{k^2}{R^2}\right)=m g h=m g\left(\frac{3 v^2}{4 g}\right)\)

or, \(1+\frac{k^2}{R^2}=\frac{3}{2} \quad\)

or, \(\quad \frac{k^2}{R^2}=\frac{1}{2}\), which is true for a disc

Question 78. A solid cylinder and a hollow cylinder, both of the same mass and the same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping. Which will reach the bottom first?

1. The hollow cylinder
2. The solid cylinder
3. Both together
4. Both together only when the angle of inclination of the plane is 45°

Answer: 2. The solid cylinder

The acceleration of a body rolling down an inclined plane is

⇒ \(a=\frac{g \sin \theta}{1+\frac{k^2}{R^2}}\)

For a solid cylinder, \(\frac{k^2}{R^2}=\frac{1}{2}\)

For a hollow cylinder, \(\frac{k^2}{R^2}=1\)

⇒ \(a_{\text {solid }}=\frac{g \sin \theta}{1+\frac{1}{2}}=\frac{2}{3} g \sin \theta=0.66 g \sin \theta\)

and \(a_{\text {hollow }}=\frac{g \sin \theta}{2}=0.5 g \sin \theta\)

Since \(a_{\text {solid }}>a_{\text {hollow }}\), the solid cylinder will reach the bottom before the hollow one.

Question 79. A cylindrical shell of mass M and radius R rolls down without slipping along an inclined plane of inclination θ. The frictional force

1. Dissipates energy as heat
2. Decreases the rotational motion only
3. Decreases both the rotational and translational motion
4. Converts translational energy to rotational energy

Answer: 4. Converts translational energy to rotational energy

In the case of pure rolling, there is no slipping or relative motion between the rolling body and the surface at the point of contact. Only static friction exists. It supports rolling downwards but does not dissipate energy. It simply converts translational energy to rotational energy due to the torque produced by static friction.

Question 80. Consider a point P in contact with the wheel on the ground. The wheel rolls on the ground without slipping. The magnitude of displacement of the point P when the wheel completes half the revolution is (where the radius of the wheel is 1 m)

1. 2 m
2. πm
3. \(\sqrt{\pi^2+4} \mathrm{~m}\)
4. \(\sqrt{\pi^2+2} \mathrm{~m}\)

Answer: 3. \(\sqrt{\pi^2+4} \mathrm{~m}\)

During the rotation, the contact point moves horizontally and through d= 2r vertically as shown.

Hence, the magnitude of the displacement is

⇒ \(P P^{\prime}=\sqrt{(P O)^2+\left(O P^{\prime}\right)^2}=\sqrt{(\pi r)^2+(2 r)^2}\)

⇒ \(\sqrt{\pi^2(1 m)^2+(2 m)^2}=\sqrt{\pi^2+4} m\)

Question 81. The speed of a homogeneous solid sphere after rolling down an inclined plane of vertical height h from rest without slipping is

1. \(\sqrt{\frac{4}{3} g h}\)
2. √gh
3. \(\sqrt{\frac{6}{5} g h}\)
4. \(\sqrt{\frac{10}{7} g h}\)

Answer: 4. \(\sqrt{\frac{10}{7} g h}\)

⇒ \(\frac{1}{2} m v^2\left(1+\frac{k^2}{R^2}\right)=m g h\)

⇒ \(\frac{1}{2} m v^2\left(1+\frac{2}{5}\right)=m g h\)

⇒ \(v=\sqrt{\frac{10}{7} g h}\)

Question 82. A solid sphere rolls up along a rough inclined plane of inclination θ = 30° with an initial velocity of 2.8 m s^-1. The maximum distance covered by the sphere is approximately

1. 5.45 m
2. 2.74 m
3. 1.10m
4. 3.25 m

Answer: 3. 1.10m

From the work-energy theorem, work done by gravity = change in kinetic energy

⇒ \(-m g s \sin 30^{\circ}=-\frac{1}{2} m v^2\left(1+\frac{k^2}{R^2}\right)\)

⇒ \(g s\left(\frac{1}{2}\right)=\frac{1}{2} v^2\left(1+\frac{2}{5}\right)=\frac{7}{10} v^2\)

⇒ \(s=\frac{7}{10}\left(2.8 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\left(\frac{2}{10 \mathrm{~m} \mathrm{~s}^{-2}}\right)=1.097 \mathrm{~m} \approx 1.10 \mathrm{~m}\)

Question 83. Consider a system of two blocks A and B connected by a light, inextensible string passing over a pulley of mass M = 2 kg and radius R = 10 cm. Find the acceleration of the block A if m_A =1 kg and mB = 0.5 kg.

1. 3.5m s^-2
2. 2ms^-2
3. 1.5 ms^-2
4. 2.5 ms^-2

Answer: 2. 2ms^-2

The magnitudes of the accelerations of both the blocks are equal (a), but the tensions will be different (T₁ > T₂).

For thepulley, \(\left(T_1-T_2\right) R=I \alpha=\left(\frac{M R^2}{2}\right)\left(\frac{a}{R}\right)\)

⇒ \(T_1-T_2=\left(\frac{M}{2}\right) a\)…..(1)

For theblock A, m_Ag – T₁ = m_Aa…..(2)

For theblock B, T₁-m_Bg = m_Ba…..(3)

Adding (1), (2) and (3),

⇒ \(\left(m_{\mathrm{A}}-m_{\mathrm{B}}\right) g=\left(m_{\mathrm{A}}+m_{\mathrm{B}}+\frac{M}{2}\right) a\)

Substituting the given values,

(1.0kg- 0.5 kg)(10m s^-2) = (1.0kg + 0.5kg +1 kg)a

⇒ \(\left(\frac{1}{2} \mathrm{~kg}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)\)

= (2.5 kg)a

a = 2ms^-2

Question 84. A disc of mass 0.5 kg and radius 20 cm rolls down an inclined plane. Find the force of friction required for pure rolling.

1. \(\frac{5}{3 \sqrt{2}} \mathrm{~N}\)
2. \(\frac{5 \sqrt{2}}{3} \mathrm{~N}\)
3. \(\frac{5}{2 \sqrt{3}} \mathrm{~N}\)
4. \(\frac{5}{\sqrt{2}} \mathrm{~N}\)

Answer: 1. \(\frac{5}{3 \sqrt{2}} \mathrm{~N}\)

The force of friction for pure rolling down a rough inclined plane is given by

⇒ \(f=\frac{m g \sin \theta}{1+\frac{R^2}{k^2}}\)

⇒ \(\frac{(0.5 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right) \sin 45^{\circ}}{1+\frac{2}{1}}\)

= \(\frac{5}{3} \times \frac{1}{\sqrt{2}} \mathrm{~N}\)

= \(\frac{5}{3 \sqrt{2}} \mathrm{~N}\)

Question 85. A disc of mass 2 kg and radius 10 cm undergoes pure rolling on a rough horizontal surface, as shown. Find the ratio of the linear and angular accelerations (a/α).

1. \(\frac{1}{15} m\)
2. \(\frac{1}{10} m\)
3. \(\frac{1}{20} m\)
4. \(\frac{1}{5} m\)

Answer: 2. \(\frac{1}{10} m\)

Due to the force F at the centre of mass, the point of contact A has a tendency to slip towards the right. Hence, static friction/acts towards the left. This friction produces a torque for pure rolling.

For translational motion,

F-f= ma and forrotation,

⇒ \(\tau=f R=I \alpha\)

or, \(f R=\frac{1}{2} m R^2\left(\frac{a}{R}\right) \quad \text { or } \quad f=\frac{1}{2} m a\)

or, \(f=\frac{1}{2} m a\)

∴ \(F=\frac{3}{2} m a\)

⇒ \(f=\left(\frac{1}{2} m\right)\left(\frac{2 F}{3 m}\right)=\frac{F}{3}\)

Now, \(\frac{F-f}{f R}=\frac{m a}{I \alpha}\)

⇒ \(\frac{F-\frac{F}{3}}{\left(\frac{F}{3}\right) R}=\left(\frac{a}{\alpha}\right)\left(\frac{m}{\frac{1}{2} m R^2}\right)\)

⇒ \(\left(\frac{a}{\alpha}\right)\left(\frac{2}{R^2}\right)\)

⇒ \(\frac{2}{R}=\left(\frac{a}{\alpha}\right)\left(\frac{2}{R^2}\right)\)

⇒ \(\frac{a}{\alpha}=R=10 \mathrm{~cm}\)

= \(\frac{1}{10} \mathrm{~m}\)

Question 86. A disc of radius 2 m and mass 100 kg rolls on a horizontal floor. Its centre of mass has a speed of 20 cm s^-1. How much work is needed to stop it?

1. 1J
2. 2J
3. 3J
4. 20 J

Answer: 3. 3J

The kinetic energy of a rolling body is \(\frac{1}{2} M v_{\mathrm{CM}}^2\left(1+\frac{k^2}{R^2}\right)\)

Given that M = 100kg and \(v_{\mathrm{CM}}=20 \mathrm{~cm} \mathrm{~s}^{-1}=0.2 \mathrm{~m} \mathrm{~s}^{-1}\)

and \(\frac{k^2}{R^2}=\frac{1}{2}\)

Hence, \(\mathrm{KE}=\frac{1}{2}(100 \mathrm{~kg})\left(0.2 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\left(\frac{3}{2}\right)\)

= 3J.

According to the work-energy theorem,

| work done | = | KE_f-KE_i |

= 3J.

Question 87. A solid cylinder of mass 2kg and radius 4 cm rotating about its axis at a rate of 3 rpm. The torque required to stop after 2π rev is

1. 2 x 10^-6Nm
2. 2 x 10^-3N m
3. 12 x 10^-4Nm
4. 2 x 10⁴N m

Answer: 1. 2 x 10^-6Nm

The moment of inertia of the solid cylinder is

⇒ \(I=\frac{1}{2} M R^2=\frac{1}{2}(2 \mathrm{~kg})\left(4 \times 10^{-2} \mathrm{~m}\right)^2=16 \times 10^{-4} \mathrm{~kg} \mathrm{~m}^2\)

Initial angular speed = \(=\omega_0=\frac{3 \times 2 \pi}{60} \mathrm{rad} \mathrm{s}^{-1}\)

=\(\frac{\pi}{10} \mathrm{rad} \mathrm{s}^{-1}\)

Angular displacement θ = 2θ rev = 2π(2π) rad = 4π² rad

Now, \(\omega^2=\omega_0^2-2 \alpha \theta\)

∴ angular acceleration \(\alpha=\frac{\omega_0^2}{2 \theta}\)

=\(\frac{\left(\frac{\pi}{10}\right)^2}{2 \times 4 \pi^2} \mathrm{rad} \mathrm{s}^{-2}\)

=\(\frac{1}{800} \mathrm{rad} \mathrm{s}^{-2}\)

Hence, the required torque is

⇒ \(\tau=I \alpha=\left(16 \times 10^{-4} \mathrm{~kg} \mathrm{~m}^2\right)\left(\frac{1}{800} \mathrm{rad} \mathrm{s}^{-2}\right)\)

=\(2 \times 10^{-6} \mathrm{~N} \mathrm{~m}\)

Question 88. A disc of mass 5 g and radius 1 cm is fixed to a thin stick AB of negligible mass, as shown in the figure. The system is initially at rest. A constant torque required to rotate the disc about AB at 25 rps in 5 s is close to

1. 4.0 x 10^-66N m
2. 1.6 x 10^-5N m
3. 2.0 x 10^-5N m
4. 6.5 x 10^-4N m

Answer: 3. 2.0 x 10^-5N m

The moment of inertia of the disc about the axis AB (a tangent) is

⇒ \(I=\frac{M R^2}{4}+M R^2=\frac{5}{4} M R^2\)

Angular acceleration

⇒ \(\alpha=\frac{d \omega}{d t}=\frac{25 \mathrm{rps}}{5 \mathrm{~s}}=10 \pi \mathrm{rad} \mathrm{s}^{-2}\)

Hence, the required torque is

⇒ \(\tau=I \alpha=\left(\frac{5}{4} M R^2\right)(10 \pi)\)

∴ \(\tau=\frac{5}{4}\left(5 \times 10^{-3} \mathrm{~kg}\right)\left(10^{-2} \mathrm{~m}\right)^2\left(10 \pi \mathrm{rad} \mathrm{s}^{-2}\right)\)

= 19.6 x 10^-6 Nm ≈ 2 x 10^-5N m.

Question 89. The magnitude of the torque on a particle of mass 1 kg is 2.5 N m about the origin. If the force acting on it is 1 N and the distance of the particle from the origin is 5 m. Then, the angle between the force and the position vector is

1. \(\frac{\pi}{3}\)
2. \(\frac{\pi}{4}\)
3. \(\frac{\pi}{8}\)
4. \(\frac{\pi}{6}\)

Answer: 4. \(\frac{\pi}{6}\)

Torque = \(|\vec{\tau}|=|\vec{r} \times \vec{F}|\) = rF sin0

=> (2.5Nm) = (5m)(lN) sinθ

⇒ \(\sin \theta=\frac{1}{2} \Rightarrow \theta=\frac{\pi}{6}\)

Question 90. A rod of length 0.5 m is pivoted at one end. It is raised such that it makes an angle of 30° from the horizontal, as shown, and then released from rest. Its angular speed when it passes through the horizontal will be

1. \(\frac{\sqrt{30}}{2} \mathrm{rad} \mathrm{s}^{-1}\)
2. 30 rad s^-1
3. \(\frac{\sqrt{20}}{2} \mathrm{rad} \mathrm{s}^{-1}\)
4. √15 rad s^-1

Answer: 2. √30 rad s^-1

Work done by gravity = \(W_{\text {grav }}=M g\left(\frac{L}{2}\right) \sin 30^{\circ}=\frac{M g L}{4}\)

Change in KE = \(\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{M L^2}{3}\right) \omega^2\)

From the work-energy theorem,

⇒ \(\frac{1}{2}\left(\frac{M L^2}{3}\right) \omega^2=\frac{M g L}{4} \Rightarrow \omega=\sqrt{\frac{3 g}{2 L}}\)

Substituting the values,

⇒ \(\omega=\sqrt{\frac{3\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}{2(0.5 \mathrm{~m})}}=\sqrt{30} \mathrm{rad} \mathrm{s}^{-1}\)

Question 91. Two identical solid spheres of mass Mandradius R each are stuck on the two ends of a uniform rod of length 2R and mass M, as shown in the figure. The moment of inertia of the system about the axis passing perpendicularly through the centre of the rod is

1. \(\frac{137}{15} M R^2\)
2. \(\frac{209}{15} M R^2\)
3. \(\frac{17}{15} M R^2\)
4. \(\frac{152}{15} M R^2\)

Answer: 1. \(\frac{137}{15} M R^2\)

The moment of inertia of a solid cp sphere about its own diameter is given by

I_CM = \(\frac{2}{5}\)MR².

From the theorem of parallel axes, the moment of inertia of each sphere about the parallel axis through O is given

⇒ \(I=I_{\mathrm{CM}}+M d^2\)

= \(\frac{2}{5} M R^2+M(2 R)^2\)

= \(\frac{22}{5} M R^2\)

So, the moment of inertia of the whole system about the axis through O is

⇒ \(2\left(\frac{22}{5} M R^2\right)+\frac{M(2 R)^2}{12}=\frac{137}{15} M R^2\)

Question 92. A solid sphere and a solid cylinder of equal radii approach an incline with the same linear velocity. Both roll without slipping throughout their motion. The two respectively reach the maximum heights of h_sph and h_cyl on the incline. The ratio \(\frac{h_{\mathrm{sph}}}{h_{\mathrm{cyl}}}\) is equal to

1. \(\frac{4}{5}\)
2. \(\frac{14}{15}\)
3. \(\frac{2}{\sqrt{5}}\)
4. 1

Answer: 2. \(\frac{14}{15}\)

For a solid sphere, the KE of rolling motion is

⇒ \(E_{\mathrm{sph}}=\frac{1}{2} M v^2\left(1+\frac{k^2}{R^2}\right)\)

=\(\frac{1}{2} M v^2\left(1+\frac{2}{5}\right)\)

If the height reached on the incline is h_sph then

⇒ \(M g h_{\mathrm{sph}}=\frac{1}{2} M v^2\left(\frac{7}{5}\right)\)……..(1)

Similarly, for a solid cylinder, we have

⇒ \(M g h_{\mathrm{cyl}}=\frac{1}{2} M v^2\left(1+\frac{k^2}{R^2}\right)=\frac{1}{2} M v^2\left(1+\frac{1}{2}\right)\)

⇒ \(M g h_{\mathrm{cyl}}=\frac{1}{2} M v^2\left(\frac{3}{2}\right)\)……(2)

Now, by dividing (1) by (2), we get the ratio

⇒ \(\frac{h_{\text {sph }}}{h_{\text {cyl }}}=\frac{\frac{7}{5}}{\frac{3}{2}}=\frac{14}{15}\)

Question 93. A circular disc of radius a has a hole of radius b around its centre. If surface density (mass per unit area) varies as \(\sigma=\frac{\sigma_0}{r}\) (where r is the radius of a concentric ring), the radius of gyration (k) of the disc about the axis passing through its centre and perpendicular to its plane is equal to

1. \(\frac{a+b}{2}\)
2. \(\frac{a+b}{3}\)
3. \(\sqrt{\frac{a^2+b^2+a b}{2}}\)
4. \(\sqrt{\frac{a^2+b^2+a b}{3}}\)

Answer: 4. \(\sqrt{\frac{a^2+b^2+a b}{3}}\)

Let us consider a concentric ring of radius r and width dr. Its mass is i

⇒ \(d M=2 \pi r d r\left(\frac{\sigma_0}{r}\right)\)

Then, the total mass of the disc is

⇒ \(M=2 \pi \sigma_0 \int_b^a d r=2 \pi \sigma_0(a-b)\)……(1)

The moment of inertia ofthisringis

⇒ \(d I=(\text { mass }) r^2=(2 \pi r d r)\left(\frac{\sigma_0}{r}\right) r^2=2 \pi \sigma_0 r^2 d r\)

∴ the moment of inertia of the disc is

⇒ \(I=\int d I=2 \pi \sigma_0 \int_b^a r^2 d r=\frac{2}{3} \pi \sigma_0\left(a^3-b^3\right)\)…..(2)

But I = Mk². Hence, the radius of gyration is

⇒ \(k=\sqrt{\frac{I}{M}}=\sqrt{\frac{\frac{2}{3} \pi \sigma_0\left(a^3-b^3\right)}{2 \pi \sigma_0(a-b)}}=\sqrt{\frac{a^2+b^2+a b}{3}}\)

Question 94. Two coaxial discs of moments of inertia I and I/2 are rotating with angular velocities ω and ω/2 about their common axis. They are brought in contact with each other and then they rotate with a common angular velocity. If Ef and be the final and initial total energies respectively, E_f– E_i is equal to

1. \(-\frac{I \omega^2}{12}\)
2. \(\frac{I \omega^2}{6}\)
3. \(-\frac{I \omega^2}{24}\)
4. \(\frac{3}{8} I \omega^2\)

Answer: 3. \(-\frac{I \omega^2}{24}\)

Conserving the angular momentum,

⇒ \(I \omega+\left(\frac{I}{2}\right)\left(\frac{\omega}{2}\right)=\left(I+\frac{I}{2}\right) \omega_0 \Rightarrow \omega_0=\frac{5}{6} \omega\)……(1)

Initial KE = \(E_{\mathrm{i}}=\frac{1}{2} I \omega^2+\frac{1}{2}\left(\frac{I}{2}\right)\left(\frac{\omega}{2}\right)^2=\frac{9}{16} I \omega^2\)

Final KE = E_f = \(E_{\mathrm{f}}=\frac{1}{2}\left(I+\frac{I}{2}\right) \omega_0^2=\frac{1}{2}\left(\frac{3}{2} I\right)\left(\frac{5 \omega}{6}\right)^2\) [from (1)]

= \(\frac{25}{48} I \omega^2\)

∴ \(E_{\mathrm{f}}-E_{\mathrm{i}}=\left(\frac{25}{48}-\frac{9}{16}\right) I \omega^2=-\frac{I \omega^2}{24}\)

Question 95. Four particles A, B, C and D of masses m, 2m, 3m and 4m respectively are at the comers of a square. They have accelerations of the same magnitude \(|\vec{a}|\) and the directions as shown in the figure. The acceleration of the centre of mass of the system of particles is

1. \(\frac{a}{5}(\hat{i}-\hat{j})\)
2. \(\frac{a}{5}(\hat{i}+\hat{j})\)
3. Zero
4. \(a(\hat{i}+\hat{j})\)

Answer: 1. \(\frac{a}{5}(\hat{i}-\hat{j})\)

The acceleration of the centre of mass of the system is

⇒ \(\vec{a}_{\mathrm{CM}}=\frac{1}{M}\left(m_1 \vec{a}_1+m_2 \vec{a}_2+m_3 \vec{a}_3+m_4 \vec{a}_4\right)\)

⇒ \(\frac{[m a(-\hat{i})+2 m a(\hat{j})+3 m a(\hat{i})+4 m a(-\hat{j})]}{m+2 m+3 m+4 m}\)

⇒ \(\frac{a}{10}(2 \hat{i}-2 \hat{j})\)

=\(\frac{a}{5}(\hat{i}-\hat{j})\)

Question 96. A thin smooth rod of length L and mass M is rotating freely with an angular speed ω₀ about an axis perpendicular to the length of the rod and passing through its centre of mass. Two beads of mass m each and of negligible sizes are at the centre of the rod initially. The beads are free to slide along the rod. The angular speed of the system, when the beads reach the opposite ends of the rod, will be

1. \(\frac{M \omega_0}{M+2 m}\)
2. \(\frac{M \omega_0}{M+3 m}\)
3. \(\frac{M \omega_0}{M+6 m}\)
4. \(\frac{M \omega_0}{M+m}\)

Answer: 3. \(\frac{M \omega_0}{M+6 m}\)

Conserving the angular momentum,

⇒ \(I \omega_0=I^{\prime} \omega \Rightarrow \frac{M L^2}{12} \omega_0=\left[\frac{M L^2}{12}+2 m\left(\frac{L}{2}\right)^2\right] \omega\)

⇒ \(\frac{M \omega_0}{12}=\left(\frac{M}{12}+\frac{m}{2}\right) \omega=\left(\frac{M+6 m}{12}\right) \omega\)

⇒ \(\omega=\left(\frac{M}{M+6 m}\right) \omega_C\)

Question 97. A man of mass 80 kg is standing at the edge of a circular disc of mass 200 kg. The disc rotates about the vertical axis through its centre at 5 revolutions per second. If the moves to the centre of the disc, the angular speed of the disc becomes

1. 9rps
2. 3rps
3. 6rps
4. 12rps

Answer: 1. 9rps

The initial moment of inertia of the man-disc system is

⇒ \(I_1=\frac{1}{2} M R^2+m R^2=\left(\frac{M}{2}+m\right) R^2\)

where M and m are the masses of the disc and them respectively.

Finally, when the man is at the centre,

⇒ \(I_2=\frac{1}{2} M R^2\)

Conserving the angular momentum,

⇒ \(\left(\frac{M}{2}+m\right) R^2 \omega_1=\frac{1}{2} M R^2 \omega^{\prime}\)

final angular speed

⇒ \(\omega^{\prime}=\frac{(180 \mathrm{~kg})(5 \mathrm{rps})}{100 \mathrm{~kg}}\)

= 9rps

Question 98. A one-metre-long uniform rod AB of mass 2mpivoted atAishithorizontally at the free end B by a ball of mass m moving at 6 m s^-1. If the ball sticks to the rod after a collision, find the maximum angular displacement (θ) of the rod. (Given that cos 63° = 0.46.)

1. 53°
2. 63°
3. 59°
4. 69°

Answer: 2. 63°

Conserving the angular momentum,

⇒ \(\frac{1}{2} I \omega^2=2 m g\left(\frac{l}{2}\right)(1-\cos \theta)+m g l(1-\cos \theta)\)

the initial angular speed of the rod is

Conserving the mechanical energy,

⇒ \(\frac{1}{2}\left(\frac{5}{3} m l^2\right)\left(\frac{3 v}{5 l}\right)^2=2 m g l(1-\cos \theta)\)

⇒ \(\frac{1}{2}\left(\frac{5}{3} m l^2\right)\left(\frac{3 v}{5 l}\right)^2=2 m g l(1-\cos \theta)\)

Substituting l=1 m and v = 6ms^-1, we have

⇒ \(\cos \theta=\frac{23}{50}=0.46=\cos 63^{\circ}\)

⇒ \(\theta \approx 63\)

Question 99. A block of mass 3m is suspended by a metre scale of mass m, as shown. If the tension in the string A is kmg A in equilibrium, then the value of k will be

1. \(\frac{5}{4}\)
2. \(\frac{4}{5}\)
3. \(\frac{1}{5}\)
4. \(\frac{3}{5}\)

Answer: 1. \(\frac{5}{4}\)

The forces acting on the system are:

1. Weight of the scale through its centre of
2. Tension TA and T acting vertically upward.
3. Weight of the suspended block = 3mg.

Since the system is in equilibrium, the torque of all forces about any point must be zero.

Taking the torque about O, kmg (100cm)

= mg(50cm) + 3mg(25cm)

⇒ \(k(100)=125\)

⇒ \(k=\frac{5}{4}\)

Question 100. Two discs having the moments of inertia I₁ = 0.10 kg m² and I₂ = 0.20 kg m² and rotating with the angular velocities ω₁ = 10 rad s^-1 and ω₂ = 5 rad s^-1 respectively are brought into contact coaxially and thereafter they rotate together. What is the kinetic energy of the system when they have a common angular velocity?

1. Zero
2. 10J
3. 5 J
4. \(\frac{20}{3}\)J

Answer: 4. \(\frac{20}{3}\)J

Conserving the angular momentum,

⇒ \(L=I_1 \omega_1+I_2 \omega_2=\left(I_1+I_2\right) \omega\)

The kinetic energy of the system when they rotate together will be

⇒ \(E=\frac{L^2}{2 I}\)

=\(\frac{\left(I_1 \omega_1+I_2 \omega_2\right)^2}{2\left(I_1+I_2\right)}\)

=\(\frac{(0.1 \times 10+0.2 \times 5)^2}{2(0.1+0.2)} \mathrm{J}=\frac{20}{3} \mathrm{~J}\)

Question 101. A square of side a/2 is drilled in a uniform disc of radius a, as shown in the adjoining figure. The position of the centre of mass of the remaining part is at

1. \(x=-\frac{2 a}{\pi}\)
2. \(x=-\frac{4 a}{3 \pi}\)
3. \(x=-\frac{a}{8 \pi-2}\)
4. \(x=\frac{3 a}{4 \pi}\)

Answer: 3. \(x=-\frac{a}{8 \pi-2}\)

Mass per unit area of the disc = \(\frac{M}{\pi R^2}\)

Mass of the square area \(\left(\frac{M}{\pi R^2}\right)\left(\frac{a^2}{4}\right)=\frac{M}{4 \pi}\) [∵ a = R]

The distance of the centre of mass of the remaining part of the disc from the centre O is

⇒ \(x=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}=\frac{M \cdot 0+\left(-\frac{M}{4 \pi}\right)\left(\frac{a}{2}\right)}{M+\left(-\frac{M}{4 \pi}\right)}=\frac{-a}{8 \pi-2}\)

Question 102. Two discs A and B of the same mass have the radii R and R/2. A rotates with an angular speed of co; while B is at rest. When A is placed gently on B, both rotate with the same angular velocity. In the process, the percentage loss of kinetic energy is

1. 20
2. 40
3. 10
4. 30

Answer: 1. 20

For disc A, \(I_1=\frac{1}{2} m R^2 \text { and } \omega_1=\omega\)

For disc B, \(I_2=\frac{1}{2} m\left(\frac{R^2}{4}\right)=\frac{m R^2}{8}=\frac{I_1}{4}\)

and \(\omega_2=0\)

The angular momentum remains constant.

Initial KE = \(E_1=\frac{L^2}{2 I_1}\)

and final,

⇒ \(\mathrm{KE}=E_2=\frac{L^2}{2\left(I_1+I_2\right)}=\frac{L^2}{2\left(\frac{5 I_1}{4}\right)}\)

∴ fractional change in KE, \(\frac{\Delta E}{E_1}=1-\frac{E_2}{E_1}=1-\frac{4}{5}=\frac{1}{5}\)

Hence, the percentage decrease

⇒ \(\frac{\Delta E}{E_1} \times 100 \%=\frac{1}{5} \times 100 \%=20 \%\)

Question 103. Two discs of radii R and aR are of the same thickness and made of the same material. If their moments of inertia about their own axis are in the ratio 1: 16, the value of α is

1. \(\frac{1}{2}\)
2. 2
3. \(\frac{1}{4}\)
4. 1

Answer: 2. 2

Let a denote the mass per unit area.

Hence,\(m_1=\pi R^2 \sigma \text { and } m_2=\pi \alpha^2 R^2 \sigma\)

∴ \(\frac{I_1}{I_2}=\frac{\frac{1}{2} m_1 R^2}{\frac{1}{2} m_2 \alpha^2 R^2}\)

=\(\frac{\sigma \pi R^4}{\sigma \pi \alpha^4 R^4}\)

=\(\frac{1}{\alpha^4}\)

=\(\frac{1}{16} \text { (given) }\)

∴ a = 2

Question 104. The ratio of the moments of inertia of the rectangular plate of uniform thickness about the axes through O and O’ perpendicular to the plane of the plate is

1. \(\frac{1}{2}\)
2. \(\frac{1}{3}\)
3. \(\frac{1}{4}\)
4. \(\frac{1}{5}\)

Answer: 3. \(\frac{1}{4}\)

About the axis through O,

⇒ \(I_0=M\left(\frac{a^2+b^2}{12}\right)\)

About the axis through O’

⇒ \(I^{\prime}=I_0+M r^2=M\left(\frac{a^2+b^2}{12}\right)+M\left(\frac{a^2+b^2}{4}\right)\)

⇒ \(M\left(\frac{a^2+b^2}{3}\right)\)

∴ \(\frac{I_0}{I^{\prime}}=\frac{1}{4}\)

Question 105. Find the torque about the origin when a force \(\vec{F}=(3 \mathrm{~N}) \hat{j}\); acts on a particle whose position vector is \((2 \mathrm{~m}) \hat{k}\).

1. \(6 \hat{j} \mathrm{Nm}\)
2. \(-6 \hat{i} \mathrm{Nm}\)
3. \(6 \hat{k} \mathrm{Nm}\)
4. \(6 \hat{i} \mathrm{Nm}\)

Answer: 2. \(-6 \hat{i} \mathrm{Nm}\)

Given that \(\vec{F}=(3 \mathrm{~N}) \hat{j} \text { and } \vec{r}=(2 \mathrm{~m}) \hat{k}\)

∴torque = \(\vec{\tau}=\vec{r} \times \vec{F}=(3 \times 2 \mathrm{~N} \mathrm{~m})(\hat{k} \times \hat{j})\)

⇒ \((6 \mathrm{Nm})(-\hat{i})\)

⇒\(-6 \hat{i} \mathrm{Nm}\)

Work Energy Power And Collisions

Question 1. A particle moves from a point \((-2 \hat{i}+5 \hat{j}) \text { to }(4 \hat{j}+3 \hat{k})\) when a force of \((4 \hat{i}+3 \hat{j})\)N is applied. How much work has been done by this force?

1. 8J
2. 11J
3. 5J
4. 2J

Answer: 3. 5J

The position vector of the initial position of the particle is,

⇒ \(\vec{r}_1=-2 \hat{i}+5 \hat{j}\)

and that of the final position is,

⇒ \(\overrightarrow{r_2}=4 \hat{j}+3 \hat{k}\).

∴ the displacement vector is \(\vec{s}=\vec{r}_2-\vec{r}_1=(2 \hat{i}-\hat{j}+3 \hat{k}) \mathrm{m}\).

Force \(\vec{F}=(4 \hat{i}+3 \hat{j}) \mathrm{N}\)

∴ work done is \(W=\vec{F} \cdot \vec{s}=(4 \hat{i}+3 \hat{j}) \mathrm{N} \cdot(2 \hat{i}-\hat{j}+3 \hat{k}) \mathrm{m}\)

= (8 – 3) J

= 5 J

Question 2. A body of mass 1 kg is thrown upwards with a velocity of 20ms^-1. It momentarily comes to rest after attaining a height of 18m. How much energy is lost due to air friction? (Take g = 10ms^-2).

1. 30J
2. 40J
3. 10J
4. 20J

Answer: 4. 20J

Work done by gravity = mgh = (1 kg)(-10 m s^-2)(18 m)

= -180 J.

Initial \(\mathrm{KE}=\frac{1}{2} m v^2=\frac{1}{2}(1 \mathrm{~kg})\left(20 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\)

= 200 J.

By the work-energy theorem,

⇒ \(W_{\text {grav }}+W_{\text {air }}=\mathrm{KE}_{\mathrm{f}}-\mathrm{KE}_{\mathrm{i}}\)

=> -180 J + W_air = 0J -200J.

∴ work done by air friction = 180 J- 200 J

= 20 J.

Hence, the energy lost due to air friction is 20 J.

Question 3. A child is swaying on a swing. Its minimum and maximum heights from the ground are 0.75 are 2.0m respectively. Its maximum speed will be

1. 10 m s^-1
2. 5 m s ^-1
3. 8 m s^-1
4. 15 m s^-1

Answer: 2. 5 m s ^-1

At the maximum height (h₂= 2.0m), the KE is zero, and at the minimum height (h₁ = 0.75 m), the KE is the maximum

⇒ \(\left(=\frac{1}{2} m v_{\max }^2\right)\)

Hence, by the principle of conservation of energy

⇒ \(\frac{1}{2} m v_{\max }^2=m g\left(h_2-h_1\right)\)

⇒ \(v_{\max }=\sqrt{2 g\left(h_2-h_1\right)}=\sqrt{2\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(1.25 \mathrm{~m})}\)

= 5ms^-1

Question 4. A particle having a kinetic energy K is projected making an angle of 60 with the horizontal. The kinetic energy at the highest point will be

1. K
2. \(\frac{K}{2}\)
3. \(\frac{K}{4}\)
4. \(\frac{K}{8}\)

Answer: 3. \(\frac{K}{4}\)

The horizontal component of the velocity of projection remains unchanged.

At the highest point, the velocity is along the horizontal and equals u cos 60°= \(\frac{u}{2}\)

Initial kinetic energy

⇒ \(K=\frac{1}{2} m u^2\)

At the highest point,

⇒ \(K^{\prime}=\frac{1}{2} m\left(\frac{u}{2}\right)^2=\frac{1}{2} m u^2 \times \frac{1}{4}=\frac{K}{4}\)

Question 5. A body moves through a distance of 10 m long in a straight line under the action of a 5-N force. If the work done is 25J, the angle between the force direction of the body is

1. 30°
2. 45°
3. 60°
4. 75°

Answer: 3. 60°

Work done = W = Fs cos θ.

∴ 25 J= (5N)(10 m)cos θ

⇒ \(\cos \theta=\frac{25 \mathrm{~J}}{50 \mathrm{~J}}=\frac{1}{2}\)

θ = 60°.

Question 6. A force on a 3-g particle in such a way that the position of the particle as a function of time is given by \(x = 3t- At² + t³\), where x is in meters and t is in seconds. The work done during the first four seconds is

1. 490 3J
2. 450 mJ
3. 528 mJ
4. 530 mJ

Answer: 3. 528 mJ

Given that position x = 3t- At² + t³.

So, velocity \(0=\frac{d x}{d t}=3-8 t+3 t^2\)

Initial velocity \(u=\left.\frac{d x}{d t}\right|_{t=0}=3 \mathrm{~m} \mathrm{~s}^{-1}\)

Final velocity

⇒ \(v=\left.\frac{d x}{d t}\right|_{t=4 \mathrm{~s}}=(3-32+48) \mathrm{m} \mathrm{s}^{-1}=19 \mathrm{~m} \mathrm{~s}^{-1}\)

∴ the change in kinetic energy is

⇒ \(\Delta \mathrm{KE}=\frac{1}{2} m\left(v^2-u^2\right)=\frac{1}{2}(3 \mathrm{~g})\left[\left(19 \mathrm{~m} \mathrm{~s}^{-1}\right)^2-\left(3 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\right]\)

= 528mJ

Question 7. Two bodies with their kinetic energies in the ratio 4:1 are moving with equal linear momenta. The ratio of their masses is

1. 4: 1
2. 1: 2
3. 2: 1
4. 1: 4

Answer: 4. 1: 4

Let m₁ and m₂ be the masses of the bodies and p be their equal momentum.

Now, \(\mathrm{KE}=\frac{1}{2} m v^2=\frac{m^2 v^2}{2 m}=\frac{p^2}{2 m}\)

Given that,

⇒ \(\frac{\mathrm{KE}_1}{\mathrm{KE}_2}=\frac{4}{1}=\frac{\frac{p^2}{2 m_1}}{\frac{p^2}{2 m_2}}=\frac{m_2}{m_1}\)

⇒\(\frac{m_1}{m_2}=\frac{1}{4} \Rightarrow m_1: m_2\)

= 1: 4

Question 8. Two bodies of masses m and 4m are moving with equal kinetic energies. The ratio of their linear momenta is

1. 1: 2
2. 1: 4
3. 4: 1
4. 1: 1

Answer: 1. 1: 2

Given that m₁ = m, m₂ = 4m and K₁ = K₂

⇒ \(\frac{p_1^2}{2 m_1}=\frac{p_2^2}{2 m_2} \Rightarrow \frac{p_1}{p_2}=\sqrt{\frac{m_1}{m_2}}=\sqrt{\frac{m}{4 m}}=\frac{1}{2}\)

= 1: 2

Question 9. A body constrained to move along the y-axis is subjected to a force given by \(\vec{F}=(-2 \hat{i}+15 \hat{j}+6 \hat{k})\)N. The work done by this force in moving the body through a distance of \(10 \hat{j}\) m along the y-axis is

1. 160J
2. 20J
3. 150J
4. 190J

Answer: 3. 150J

Work done \(W=\vec{F} \cdot \vec{s}=(-2 \hat{i}+15 \hat{j}+6 \hat{k}) \mathrm{N} \cdot(10 \hat{j}) \mathrm{m}\)

= 150J

Question 10. A position-dependent force F=(7- 2x + 3X²)N acts on a small body of mass 2kg and displaces it from x= 0 to x= 5m. The work done is

1. 35 J
2. 70 J
3. 135 J
4. 270 J

Answer: 3. 135 J

The work done by the given variable force is

⇒ \(W=\int d W=\int F d x=\int_0^{5 \mathrm{~m}}\left[\left(7-2 x+3 x^2\right) \mathrm{N}\right] d x\)

⇒ \(\left[\left(7 x-x^2+x^3\right) \mathrm{N}\right]_0^{5 \mathrm{~m}}=(35-25+125) \mathrm{J}\)

= 135J

Question 11. A bullet of mass 10 g leaves a rifle with an initial velocity of 1000m s^-1 and strikes the ground at the same horizontal level with a velocity of 500m s^-1. The work done in overcoming the air resistance will be

1. 375 J
2. 500 J
3. -3750 J
4. 5000 J

Answer: 3. -3750 J

By the work-energy theorem, the work done by the bullet in overcoming the air resistance is

W = change in \(\mathrm{KE}=\frac{1}{2} m v^2-\frac{1}{2} m u^2\)

⇒ \(\frac{1}{2}(10 \mathrm{~g})\left[\left(500 \mathrm{~m} \mathrm{~s}^{-1}\right)^2-\left(10^3 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\right]\)

Question 12. The kinetic energy acquired by a mass m in traveling through a distance d, starting from rest, under the action of a constant force is directly proportional to

1. m
2. m°
3. √m
4. \(\frac{1}{\sqrt{m}}\)

Answer: 2. m°

v² = u² + 2as

= 2as = 2ad [here, u = θ and s = d].

∴ \(\mathrm{KE}=\frac{1}{2} m v^2=\frac{1}{2} m(2 a s)\)

= mas

= F.s

Hence, the KE acquired is independent of m and is thus proportional to m°

Question 13. Water falls from a height of 60 m at the rate of 15 kg s^-1 to operate a turbine. The losses due to frictional forces are 10% of the energy. How much power is generated by the turbine? (Takeg = 10m s^-2.)

1. 12.3 kW
2. 7.0 kW
3. 8.1 kW
4. 10.2 kW

Answer: 3. 8.1 kW

The mass of water falling per second is 15 kg, the height is 60 m, and g = 10 ms^-2.

Now, the loss of energy is 10%.

∴ available energy = 90%.

∴ power generated = \(\left(15 \mathrm{~kg} \mathrm{~s}^{-1}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(60 \mathrm{~m})\left(\frac{90}{100}\right)\)

= 8100W

= 8.1 W.

Question 14. An engine pumps water continuously through a hose. Water leaves the hose with a velocity of v, and m is the mass per unit length of the water jet. What is the rate at which the kinetic energy is imparted to the water?

1. mv³
2. \(\frac{1}{2} m^2 v^2\)
3. \(\frac{1}{2} m v^2\)
4. \(\frac{1}{2} m v^3\)

Answer: 4. \(\frac{1}{2} m v^3\)

Given that velocity of water = v and mass flowing per unit length = m. In one second, the length of the water jet is v, so the mass contained is mv.

∴ the KE imparted to water in one second is

⇒ \(\frac{1}{2}(m v) v^2=\frac{1}{2} m v^3\)

Question 15. A block of mass M is attached to the lower end of a vertical spring, which is hung from the ceiling and has a force constant of k. The block is released from rest with the initial stretch. The maximum extension produced in the length of the spring will be

1. \(\frac{M g}{2 k}\)
2. \(\frac{2 M g}{k}\)
3. \(\frac{4 M g}{k}\)
4. \(\frac{M g}{k}\)

Answer: 2. \(\frac{2 M g}{k}\)

Let x be the extension in the spring.

So, PE lost by the block = PE gained by the spring

⇒ \(M g x=\frac{1}{2} k x^2 \Rightarrow x=\frac{2 M g}{k}\)

Question 16. A block2kof mass m, starting from rest, undergoes a uniform acceleration. If the speed acquired in a time t be v, the power delivered to the block is

1. \(\frac{m v^2}{t}\)
2. \(\frac{m v^2}{2 t^2}\)
3. \(\frac{m v^2}{t^2}\)
4. \(\frac{m v^2}{2 t}\)

Answer: 4. \(\frac{m v^2}{2 t}\)

Power delivered = \(\frac{\text { work done }}{\text { time }}=\frac{\text { change in the } \mathrm{KE}}{t}\)

⇒ \(\frac{\frac{1}{2} m v^2}{t}=\frac{m v^2}{2 t}\)

Question 17. A block of mass 10 kg, moving along the x-axis with a constant speed of 10 m s^-1, is subjected to a retarding force F = -0.1x J m^-1 during its travel from x = 20 m to x = 30 m. Its final kinetic energy will be

1. 275 J
2. 450 J
3. 475J
4. 250 J

Answer: 3. 475J

By the work-energy theorem, work done by the retarding force = change in the KE.

∴ \(W=\int F d x=-(0.1) \int x d x=\frac{1}{2} m u^2-\frac{1}{2} m v^2\)

∴ final \(\mathrm{KE}=\frac{1}{2} m v^2=\frac{1}{2}(10 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)^2-0.1\left[\frac{x^2}{2}\right]_{20 \mathrm{~m}}^{30 \mathrm{~m}}\)

⇒ \(=500 \mathrm{~J}-\frac{0.1}{2}[900-400] \mathrm{J}\)

= 50Q J- 25 J

= 475 J.

Question 18. The force F acting on an object varies with the distance x as shown in the adjoining figure. The forceFisinnewtons and x are in metres. The work done by the force in moving the object from x = θ to x = 6m is

1. 9.0 J
2. 4.5 J
3. 13.5 J
4. 18.0 J

Answer: 3. 13.5 J

The work done by a variable force is given by

W = \(\int d W=\int F d x\) = area under the F-x graph.

From the given figure, the total work done is

W= area of the rectangle + area of the triangle

⇒ \((3 m)(3 N)+\frac{1}{2}(3 m)(3 N)\)

= 13.5J.

Question 19. The force F on a particle moving along a straight line varies with the distance d as shown in the following figure. The work done on the particle during its displacement of 12m is

1. 13 J
2. 18 J
3. 21 J
4. 30 J

Answer: 1. 13 J

From the given figure, the force from d = 0 to d = 3m is zero.

So, the work done is

⇒ \(W=(7-3) m \times(2 N)+\frac{1}{2}(12 m-7 m)(2 N)\)

= 8J + 5J

= 13J.

Question 20. A car of mass m starts from rest and accelerates so that the instantaneous power delivered to the car has a constant magnitude P₀. The instantaneous velocity of this car is proportional to

1. \(t^2 P_0\)
2. t^1/2
3. t ^-1/2
4. \(\frac{t}{\sqrt{m}}\)

Answer: 2. t^1/2

Instantaneous power is given by

⇒ \(P_0=F v=\left(m \frac{d v}{d t}\right) v\)

∴ P₀dt = mv dv.

Integrating, \(P_0 t=\frac{m v^2}{2}\)

∴ velocity = \(v=\sqrt{\frac{2 P_0 t}{m}}\)

∴ \(v \propto t^{1 / 2}\).

Question 21. A particle of mass m is driven by a machine that delivers a constant power P. If the particle starts from rest, the force on the particle at a time t is

1. \(\sqrt{\frac{2 m P}{t}}\)
2. \(\frac{1}{2} \sqrt{\frac{m P}{t}}\)
3. \(\sqrt{\frac{m P}{2 t}}\)
4. \(\sqrt{\frac{m P}{t}}\)

Answer: 3. \(\sqrt{\frac{m P}{2 t}}\)

Constant power = P = \(\frac{d W}{d t}\)

So, W = \(\int d W=\int P d t=P t\)

Now, work done = change in the KE = \(\frac{1}{2} m v^2-0=\frac{1}{2} m v^2\)

∴ \(P t=\frac{1}{2} m v^2 \text { or } v=\sqrt{\frac{2 P t}{m}}\)

Now, acceleration = a = \(\frac{d v}{d t}=\sqrt{\frac{2 P}{m}}\left(\frac{1}{2 \sqrt{t}}\right)\)

The force on the particle is

⇒ \(F=m a=m \cdot \sqrt{\frac{2 P}{m}}\left(\frac{1}{2 \sqrt{t}}\right)=\sqrt{\frac{m P}{2 t}}\)

Question 22. A particle of mass 10 g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal to 8 x 10^-4J at the end of the second revolution after the beginning of the motion?

1. 0.2 ms^-2
2. 0.15 m s^-2
3. 0.1 m s^-2
4. 0.18 m s^-2

Answer: 3. 0.1 m s^-2

Given: mass = m = 10 g = 10 x 10^-3 kg,

radius = R = 6.4 cm = 6.4 x 10^-2 m,

final KE = 8x 10^-4J

and initial KE = 0.

By the work-energy theorem,

work done = change in the KE

=> maT. 2(2πR) = KE_f.

Hence, tangential acceleration = aT = \(\frac{\mathrm{KE}_{\mathrm{f}}}{4 \pi R m}\)

⇒ \(\frac{8 \times 10^{-4} \mathrm{~J}}{4 \times 3.14 \times 6.4 \times 10^{-2} \times 10^{-2} \mathrm{~kg} \mathrm{~m}}\)

= 0.099m s^-2

= 0.1m s^-2

Question 23. Consider a drop of rainwater of mass 1 g falling from a height of 1 km. It hits the ground with a speed of 50 m s^-1 Take g equal to 10 m s^-2 The work done by the gravitational force and that by the resistive force of air are respectively

1. 1.25 J and -8.25 J
2. 100 J and 8.75 J
3. 10 J and -8.75 J
4. -10 J and -8.25 J

Answer: 3. 10 J and -8.75 J

The work done by the gravitational force is

⇒ \(W_{\text {grav }}=m g h=\left(1 \times 10^{-3} \mathrm{~kg}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(1000 \mathrm{~m})\)

= 10 J.

If W_fric = work done by the resistive force then

⇒ \(W_{\text {grav }}+W_{\text {fric }}=\text { change in the } \mathrm{KE}=\frac{1}{2} m v^2-0\)

⇒ \(10 \mathrm{~J}+W_{\text {fric }}=\frac{1}{2}\left(10^{-3} \mathrm{~kg}\right)\left(50 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\)

= 1.25 J.

Hence, \(W_{\text {fric }}=(1.25-10) \mathrm{J}\)

= -8.75 J.

Question 24. A body of mass 1 kg begins to move under the action of a time-dependent force \(\vec{F}=\left(2 t \hat{i}+3 t^2 \hat{j}\right) \mathrm{N}, \text { where } \hat{i} \text { and } \hat{j}\) are the unit vectors along the x- and y-axes. The power developed by the force at a time t will be

1. (2t³ + 3t⁴)W
2. (2t³ + 3t⁵)W
3. (2t² + 3t³)W
4. (2t² + 4t⁴)W

Answer: 2. (2t³ + 3t⁵)W

Given: force = \(F=\left(2 t \hat{i}+3 t^2 \hat{j}\right)\) N and mass = m =1 kg.

∴ acceleration = \(\vec{a}=\frac{\vec{F}}{m}=\frac{\left(2 t \hat{i}+3 t^2 \hat{j}\right) \mathrm{N}}{1 \mathrm{~kg}}\)

Hence, the velocity at the time t is

⇒ \(\vec{v}=\int_0^t \vec{a} d t=\int_0^t\left(2 t \hat{i}+3 t^2 \hat{j}\right) d t=\left(t^2 \hat{i}+t^3 \hat{j}\right) \mathrm{m} \mathrm{s}^{-1}\)

∴ the instantaneous power delivered at the time t will be

⇒ \(P=\vec{F} \cdot \vec{v}=\left(2 t \hat{i}+3 t^2 \hat{j}\right) \mathrm{N} \cdot\left(t^2 \hat{i}+t^3 \hat{j}\right) \mathrm{m} \mathrm{s}^{-1}=\left(2 t^3+3 t^5\right) \mathrm{W}\)

Question 25. What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?

1. √gR
2. √2gR
3. √5gR
4. √3gR

Answer: 3. √5gR

⇒ At the highest point, the centripetal force (mv2/R) is provided by the weight (mg).

So,

⇒ \(\frac{m v^2}{R}=m g \text { and } \mathrm{KE}=\frac{1}{2} m v^2=\frac{1}{2} m g R\)

By the work-energy principle,

⇒ \(W_{\text {grav }}=\mathrm{KE}_{\mathrm{f}}-\mathrm{KE}_{\mathrm{i}}\)

or \(m g \cdot 2 R=\frac{1}{2} m v_{\mathrm{f}}^2-\frac{1}{2} m g R\)

∴ the required speed is \(v_{\mathrm{f}}=\sqrt{5 g R}\)

Question 26. The heart of a man pumps 5 liters of blood through the arteries per minute at a pressure of 150 mmHg. If the density of mercury be 13.6 x 10³ kg m^-3 and g = 10 m s^-2 then the power is

1. 1.50 W
2. 2.35 W
3. 3.0 W
4. 1.70 W

Answer: 3. 3.0 W

The flow rate of blood is \(5 \mathrm{~L} \mathrm{~m}^{-1}=\frac{5 \times 10^{-3} \mathrm{~m}^3}{60 \mathrm{~s}}\)

Blood pressure =p = 150mmHg = hpg

= (150 x 10^-3m)(13.6 x 10³kgm^-3)(10m s^-2)

= 20.4 x 10³Pa.

∴ the power of the heart is

⇒ \(P=\frac{W}{t}=\frac{p V}{t}=\frac{\left(20.4 \times 10^3 \mathrm{~Pa}\right)\left(5 \times 10^{-3} \mathrm{~m}^3\right)}{60 \mathrm{~s}}\)

= 1.70 W.

Question 27. A bullet is fired from a rifle which recoils after firing. The ratio of the kinetic energy of the rifle to that of the bullet is

1. One
2. Zero
3. Less Than One
4. More Than One

Answer: 3. Less Than One

Let M = mass of the gun, m = mass of die bullet, V = recoil speed of the gun, and v = speed of the bullet.

By the principle of conservation of linear momentum, MV = mv = p.

⇒ \(\mathrm{KE}_{\text {gun }}=\frac{p^2}{2 M} \text { and } \mathrm{KE}_{\text {bullet }}=\frac{p^2}{2 m}\)

Now,

∴ \(\frac{\mathrm{KE}_{\text {gun }}}{\mathrm{KE}_{\text {bullet }}}=\frac{m}{M}<1\)

Question 28. A body of mass 0.5 kg, moving at a speed of 1.5 m s^-1 on a smooth horizontal surface, collides with a light spring of force constant k = 5ON m^-1. The maximum compression of the spring will be

1. 1.5 m
2. 0.15 m
3. 0.5 m
4. 0.12 m

Answer: 2. 0.15 m

By the principle of conservation of energy,

KE of the body = PE in the spring

⇒ \(\frac{1}{2} m v^2=\frac{1}{2} k x^2\)

Here, the maximum compression of the spring is

⇒ \(x=\sqrt{\frac{m v^2}{k}}=\sqrt{\frac{(0.5)(1.5)^2}{50}} \mathrm{~m}\)

= 0.15m.

Question 29. A block of mass m moves up an inclined plane of inclination 0. If p is the coefficient of friction between the block and the inclined plane, the work done in moving the block through a distance s up along the plane is

1. mgs (sin θ + μ cos θ)
2. mgs sin θ
3. mgs(sm θ- μ cos θ)
4. μmgs cos θ

Answer: 1. mgs(sin 0 + μ cos 0)

Since the block is pulled up the incline, the applied force will overcome the components of the weight (mg sin 9) and the kinetic friction (mmg cos 0).

Hence, the work done by the pulling force is

W = Fs = (mg sin θ + μmg cos θ)s

= mgs(sin θ + μ cos θ).

Question 30. Amovingbullethits a solid target resting on a frictionless horizontal surface and gets embedded in the target. What is conserved in this process?

1. The momentum and the kinetic energy
2. The momentum alone
3. The kinetic energy alone
4. Neither the momentum nor the kinetic energy

Answer: 2. The momentum alone

In all types of collisions, it is only the momentum that is conserved.

Question 31. The potential energy of a particle in a force field is \(U=\frac{A}{r^2}-\frac{B}{r}\), where A and B are positive constants and r is the distance of the particle from the center of the field. For stable equilibrium, the distance of the particle is

1. \(\frac{B}{2 A}\)
2. \(\frac{B}{A}\)
3. \(\frac{2 A}{B}\)
4. \(\frac{A}{B}\)

Answer: 3. \(\frac{2 A}{B}\)

Given that PE = \(U(r)=\frac{A}{r^2}-\frac{B}{r}\)

For equilibrium,

⇒ \(\frac{d U}{d r}=0=-\frac{2 A}{r^3}+\frac{B}{r^2} \Rightarrow r=\frac{2 A}{B}\)

For stable equilibrium,

⇒ \(\frac{d^2 U}{d r^2}>0 \Rightarrow \frac{d^2 U}{d r^2}=\frac{6 A}{r^4}-\frac{2 B}{r^3}\)

Substituting r = \(\frac{2A}{B}\), we have

⇒ \(\frac{d^2 U}{d r^2}=6 A\left(\frac{B}{2 A}\right)^4-2 B\left(\frac{B}{2 A}\right)^3=\frac{B^4}{8 A^3}>0\)

Thus, for stable equilibrium,

⇒ \(r=\frac{2 A}{B}\)

Question 32. A body projected vertically from the earth reaches a height equal to the earth’s radius before returning to the earth’s surface. When is the power delivered by the gravitational force of the earth the greatest?

1. At the highest position of the body
2. At the instant before the body hits the ground
3. Constant all through
4. At the instant after the body is projected

Answer: 2. At the instant before the body hits the ground

The instantaneous power delivered is P= Fv.

Just before hitting the ground, the velocity v is maximum, so the power delivered is also maximum.

Question 33. A body of mass 5 kg rests on a rough horizontal surface having a coefficient of friction of 0.2. The body is pulled through a distance of 10 m by a horizontal force of 25 N. The kinetic energy acquired by it is (assuming g = 10 m s^-2)

1. 200 J
2. 150 J
3. 100 J
4. 50 J

Answer: 2. 150 J

The work done by the applied force is

⇒ \(W_1=\vec{F} \cdot \vec{s}=F s \cos \theta\)

= (25 N)(10 m) cos θ°

= 250 J,

and the work done by friction is

⇒ \(W_2=-(\mu m g) s\)

= -(0.2)(5)(10)(10) J

= -100 j.

Net work done = change in the KE.

∴ KE acquired = W₁ + W₂

= 250 J- 100 J

= 150 J.

Question 34. A body is moving up an inclined plane of angle 0 with an initial kinetic energy E. The coefficient of friction between the plane and the body is p. The work done against the friction before the body comes to rest is

1. \(\frac{\mu \cos \theta}{E \sin \theta+\cos \theta}\)
2. \(\mu E \cos \theta\)
3. \(\frac{\mu E \cos \theta}{\mu \cos \theta+\sin \theta}\)
4. \(\frac{\mu E \cos \theta}{\mu \cos \theta-\sin \theta}\)

Answer: 3. \(\frac{\mu E \cos \theta}{\mu \cos \theta+\sin \theta}\)

By the work-energy theorem,

gain in KE = E = total work done

⇒ \(W_{\text {grav }}+W_{\text {fric }}=m g s \sin \theta+W_{\text {fric }}\)

∴ \(W_{\text {fric }}=E-m g s \sin \theta\)……(1)

Now, the upward acceleration along the rough plane is

a = g(sin0 + mcos 0).

Hence, u² = 2as= 3g (sinθ+ m cos θ)s

or, \(s=\frac{u^2}{2 g(\sin \theta+\mu \cos \theta)}\)

Substituting s in(1),

⇒ \(W_{\text {fric }}=E-\frac{m g \sin \theta \cdot u^2}{2 g(\sin \theta+\mu \cos \theta)}\)

⇒ \(E-\frac{E \sin \theta}{\sin \theta+\mu \cos \theta}=\frac{\mu E \cos \theta}{\mu \cos \theta+\sin \theta}\)

Question 35. A bullet is fired normally on an immovable wooden plank. It loses 25% of its momentum penetrating a thickness of 3.5 cm. The total thickness penetrated by the bullet is

1. 7 cm
2. 8 cm
3. 10 cm
4. 12 cm

Answer: 2. 8 cm

KE = \(\frac{p^2}{2 m}\)

Loss in momentum = \((25 \% \text { of } p)=\frac{p}{4}\)

∴ remaining momentum = \(\frac{3 p}{4}\)

∴ final \(\mathrm{KE}=\frac{\left(\frac{3 p}{4}\right)^2}{2 m}=\frac{9 p^2}{32 m}\)

According to the work-energy theorem,

⇒ \(F(3.5 \mathrm{~cm})=\Delta \mathrm{KE}=\frac{p^2}{2 m}-\frac{9 p^2}{32 m}=\frac{7 p^2}{32 m}\)

At the moment when the bullet finally comes to rest,

⇒ \(F(s)=\Delta K E=\frac{p^2}{2 m}-0=\frac{p^2}{2 m}\)

⇒ \(\frac{F(s)}{F(3.5 \mathrm{~cm})}=\frac{\frac{p^2}{2 m}}{\frac{7 p^2}{32 m}}=\frac{16}{7}\)

⇒ \(s=(3.5 \mathrm{~cm}) \frac{16}{7}\)

= 8 cm

Question 36. A uniform rod of mass m and length is held inclined at an angle of 60° with the vertical. What will be its potential energy in this position?

1. \(\frac{m g l}{4}\)
2. \(\frac{m g l}{3}\)
3. \(\frac{m g l}{2}\)
4. mgl

Answer: 1. \(\frac{m g l}{4}\)

PE of the uniform rod

= weight x height of the CM from the ground

⇒ \(m g\left(\frac{l}{2} \cos 60^{\circ}\right)\)

⇒ \(\frac{1}{4} m g l\)

Question 37. An engine pulls a car of mass 1500 kg on a level road at a constant speed of 18 km h^-1. If the frictional force is 1500N, what power does the engine generate?

1. 5.0kW
2. 7.5 kW
3. 10 kW
4. 12.5 kW

Answer: 2. 7.5 kW

Since the car moves at a constant velocity (c = 5ms ^-2), acceleration = 0.

Hence, F_net = 0.

The force F exerted by the engine must be equal and opposite to the frictional force (F = 1500 N).

∴ the power delivered by the engine is

P = Fv = (1500N)(5m s^-1)

= 7500 W

= 7.5kW

Question 38. In the preceding question, what extra power must the engine develop to maintain the same speed up along an inclined plane having a gradient of 1 in 10? (Take g = 10 m s^-2.)

1. 2.5 kW
2. 5.0 kW
3. 7.5 kW
4. 10 kW

Answer: 3. 7.5 kW

Extra power required = (mg sin θ)v

⇒ \((1500 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)\left(\frac{1}{10}\right)\left(5 \mathrm{~m} \mathrm{~s}^{-1}\right)\)

= 7500 W

= 7.5kW.

Question 39. Each of two identical cylindrical vessels, with their bases at the same level, contains a liquid of density p. The height of the liquid in one vessel is hx and that in the other is h₂. The area of either base is A. What is the work done by gravity in equalizing the levels when the vessels are interconnected?

1. \(A \rho g\left(h_1-h_2\right)^2\)
2. \(A \rho g\left(h_1+h_2\right)^2\)
3. \(A \rho g\left(\frac{h_1-h_2}{2}\right)^2\)
4. \(A \rho g\left(\frac{h_1+h_2}{2}\right)^2\)

Answer: 3. \(A \rho g\left(\frac{h_1-h_2}{2}\right)^2\)

The work done by gravity is equal to the change in the PE of the system.

The total initial PE of the system is

⇒ \(U_i=m_1 g\left(\frac{h_1}{2}\right)+m_2 g\left(\frac{h_2}{2}\right)\)

⇒ \(A h_1 \rho g\left(\frac{h_1}{2}\right)+A h_2 \rho g\left(\frac{h_2}{2}\right)=\frac{A \rho g}{2}\left(h_1^2+h_2^2\right)\)

When the vessels are interconnected, the height of the liquid in each

⇒ \(\frac{h_1+h_2}{2}\).

Hence, the final PE of the system is

⇒ \(U_{\mathrm{f}}=2\left[A\left(\frac{h_1+h_2}{2}\right) \rho g\left\{\frac{\left(h_1+h_2\right) / 2}{2}\right\}\right]=\frac{A \rho g}{4}\left(h_1+h_2\right)^2\)

∴ the change in the PE is

⇒ \(\Delta U=U_{\mathrm{f}}-U_{\mathrm{i}}=\frac{A \rho g}{4}\left(h_1+h_2\right)^2-\frac{A \rho g}{2}\left(h_1^2+h_2{ }^2\right)\)

⇒ \(\frac{A \rho g}{4}\left[\left(h_1+h_2\right)^2-2\left(h_1^2+h_2^2\right)\right]=-\frac{A \rho g}{4}\left(h_1-h_2\right)^2\)

∴ the work done by gravity is

⇒ \(W=-\Delta U=A \rho g\left(\frac{h_1-h_2}{2}\right)^2\)

Question 40. An electric pump on the ground floor of a building takes 10 minutes to fill a tank of volume 30 m3 with water. If the tank is 60 m above the ground and the efficiency of the engine is 30%, how much electric power is consumed by the pump in filling the tank? (Takeg = 10 m s^-2.)

1. 100 kW
2. 150 kW
3. 200 kW
4. 250 kW

Answer: 1. 100 kW

Output power = \(\frac{\text { work }}{\text { time }}=\frac{m g h}{t}=\frac{V \rho g h}{t}\)

⇒ \(\frac{\left(30 \mathrm{~m}^3\right)\left(10^3 \mathrm{~kg} \mathrm{~m}^{-3}\right)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(60 \mathrm{~m})}{10 \times 60 \mathrm{~s}}\)

= 30 x 10³ W.

⇒ \(\text { Efficiency }=\frac{\text { output power }}{\text { input power }}\)

⇒ \(30 \%=\frac{30}{100}=\frac{30 \times 10^3 \mathrm{~W}}{\text { input power }}\)

⇒ input power = power consumed by the engine

⇒ \(\left(30 \times 10^3 \mathrm{~W}\right) \times \frac{100}{30}\)

= 100kW.

Question 41. A ball of mass m is thrown vertically upwards with a velocity of v. The height at which the kinetic energy of the ball will reduce to half its initial value is given by

1. \(\frac{v^2}{g}\)
2. \(\frac{v^2}{2 g}\)
3. \(\frac{v^2}{3 g}\)
4. \(\frac{v^2}{4 g}\)

Answer: 4. \(\frac{v^2}{4 g}\)

Initial KE = E = \(\frac{1}{2} m v^2\)

At the height h,KE = \(\frac{E}{2}=\frac{1}{4} m v^2\)

By the work-energy theorem,

⇒ \(W_{\text {grav }}=\Delta \mathrm{KEE}=\frac{E}{2}-E=-\frac{E}{2}\)

⇒ \(-m g h=-\frac{1}{4} m v^2 \Rightarrow h=\frac{v^2}{4 g}\)

Question 42. In a hydroelectric power station, the height of the dam is 10 m. How many kilograms of water must fall per second on the blades of a turbine so as to generate 1 MW of electrical power? (Take g = 10 m s^-2.)

1. 10³
2. 10⁴
3. 10⁵
4. 10⁶

Answer: 2. 10⁴

Power generated =1 MW = 10⁶ W = \(\frac{m g h}{t}\)

Given that h = 10m,g = 10m s^-2 and t = 1 s.

∴ \(m=\frac{\left(10^6 \mathrm{~W}\right)(1 \mathrm{~s})}{\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(10 \mathrm{~m})}=10^4 \mathrm{~kg} \mathrm{~s}^{-1}\)

Question 43. A metal ball of mass 2 kg, moving at a speed of 36 km h, undergoes a perfectly inelastic head-on collision with a stationary ball of mass 3 kg. The loss in its kinetic energy during the collision is

1. 40 J
2. 100 J
3. 140 J
4. 60 J

Answer: 4. 60 J

By the conservation of linear momentum,

⇒ \(m_1 u=\left(m_1+m_2\right) v \Rightarrow v=\frac{m_1 u}{m_1+m_2}\)

Initial KE = \(\frac{1}{2}(2 \mathrm{~kg})\left(36 \times \frac{5}{18} \mathrm{~m} \mathrm{~s}^{-1}\right)^2=100 \mathrm{~J}\)

and final KE = \(\frac{1}{2}\left(m_1+m_2\right) \frac{m_1^2 u^2}{\left(m_1+m_2\right)^2}=\frac{1}{2}\left(\frac{m_1^2 u^2}{m_1+m_2}\right)\)

⇒ \(\frac{\frac{1}{2}(2 \mathrm{~kg})^2\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)^2}{5 \mathrm{~kg}}=40 \mathrm{~J}\)

∴ loss in KE = 100j – 40J

= 60J.

Question 44. A ball is thrown vertically downwards from a height of 20 m with an initial velocity v₀. It collides with the ground, loses 50% of its energy during the collision, and rebounds to the same height. The initial velocity v₀ is equal to

1. 10 ms^-1
2. 14 ms^-1
3. 28 ms^-1
4. 20 ms^-1

Answer: 4. 20 ms^-1

Let the velocity of the ball just before it strikes the ground be v.

⇒ \(v^2=v_0^2+2 g h\)

⇒ \(\frac{1}{2} m v^2=\frac{1}{2} m v_0^2+m g h\)

⇒ \(E=E_0+m g h\)

The remaining energy E’ after the 50% loss will be

⇒ \(E^{\prime}=\frac{E}{2}=\frac{1}{2}\left(E_0+m g h\right)\)

∴ \(\frac{1}{2}\left(\frac{1}{2} m v_0^2+m g h\right)=m g h\) [ … at h, velocity = 0]

⇒ \(v_0=\sqrt{2 g h}=\sqrt{2\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(20 \mathrm{~m})}\)

= 20m s^-1.

Question 45. A bullet of mass 10 g, moving horizontally at a velocity of 400m s^-1, strikes a wooden block of mass 2 kg, which is suspended by a light, inextensible string of length 5 m. As a result, the center of gravity of the block is found to rise vertically through 10 cm. The speed of the bullet after it emerges horizontally from the block will be

1. 80 ms^-1
2. 100 ms^-1
3. 120 ms^-1
4. 160 ms^-1

Answer: 3. 120 ms^-1

Given that m = 10 g, u = 400m s^-1, and M = 2 kg.

If V₁ = velocity of the block just after the collision,

⇒ \(\frac{1}{2} M v_1^2=M g h\)

⇒ \(\dot{v}_1=\sqrt{2 g h}=\sqrt{2(10)\left(10 \times 10^{-2}\right)} \mathrm{ms}^{-1}\)

⇒ \(\sqrt{2} \mathrm{~ms}^{-1}\)

By the conservation of linear momentum,

mu =Mv₁ + mv

⇒ \(\left(10 \times 10^{-3} \mathrm{~kg}\right)\left(400 \mathrm{~m} \mathrm{~s}^{-1}\right)=(2 \mathrm{~kg})\left(\sqrt{2} \mathrm{~m} \mathrm{~s}^{-1}\right)+\left(10 \times 10^{-3} \mathrm{~kg}\right) v\)

⇒ \(v=\frac{4-2 \sqrt{2}}{0.01} \mathrm{~m} \mathrm{~s}^{-1}=117.15 \mathrm{~m} \mathrm{~s}^{-1} \approx 120 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 46. A block of mass m, moving at a speed v on a frictionless horizontal surface, collides elastically with another block of the same mass m, initially at rest. After the collision, the first block moves at an angle 0 to the initial direction and has a speed of  The speed of the second block after the collision is 3

1. \(\frac{\sqrt{3}}{2} v\)
2. \(\frac{3}{4} v\)
3. \(\frac{3}{\sqrt{2}} v\)
4. \(\frac{2 \sqrt{2}}{3} v\)

Answer: 4. \(\frac{2 \sqrt{2}}{3} v\)

Let vx be the speed of the second block. In an elastic collision, the kinetic energy is conserved.

So,

⇒ \(\frac{1}{2} m v^2+0=\frac{1}{2} m\left(\frac{v}{3}\right)^2+\frac{1}{2} m v_1^2\)

⇒ \(v_1^2=v^2-\frac{v^2}{9}=\frac{8}{9} v\)

⇒ \(v_1=\frac{2 \sqrt{2}}{3} v\)

Question 47. A body of mass 4m is lying in the xy-plane at rest. It suddenly explodes into three pieces. Two pieces, each of mass m, fly off perpendicular to each other with equal speeds of v. The total kinetic energy generated due to the explosion is

1. mv²
2. \(\frac{3}{2} m v^2\)
3. 2mv²
4. 4 muv²

Answer: 2. \(\frac{3}{2} m v^2\)

The resultant of the momentum vectors of A and B is √2mv.

Before the explosion, the momentum is zero.

So, for the final momentum to be zero, we have from the adjoining figure,

⇒ \(2 m v^{\prime}=\sqrt{2} m v \Rightarrow v^{\prime}=\frac{v}{\sqrt{2}}\)

∴ the KE generated due to the explosion is

⇒ \(\frac{1}{2} m v^2+\frac{1}{2} m v^2+\frac{1}{2}(2 m)\left(\frac{v}{\sqrt{2}}\right)^2\)

⇒ \(\frac{3}{2} m v^2\)

Question 48. A mass m, moving horizontally (along the *-axis) at a velocity v, collides with sand sticks to a mass of 3m, moving vertically upwards (along die y-axis) at a velocity 2v. The final velocity of the combination is

1. \(\frac{1}{3} v \hat{i}+\frac{2}{3} v \hat{j}\)
2. \(\frac{2}{3} v \hat{i}+\frac{1}{3} v \hat{j}\)
3. \(\frac{3}{2} v \hat{i}+\frac{1}{4} v \hat{j}\)
4. \(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)

Answer: 4. \(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)

The initial momentum of the mass m is \(\vec{p}_1=m v \hat{i}\), and that of the mass

⇒ \(3 m \text { is } \vec{p}_2=3 m(2 v) \hat{j}\)

∴ the total initial momentum is

⇒ \(\vec{p}_1=\vec{p}_1+\vec{p}_2=m v \hat{i}+6 m v \hat{j}\)

Finally, when the masses stick and move together, let the final momentum be \(\vec{p}_{\mathrm{f}}=4 m \vec{v}_0\)

Conserving the momentum, we have

⇒ \(4 m \vec{v}_0=m v \hat{i}+6 m v \hat{j} \Rightarrow \vec{v}_0=\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)

Question 49. A body of mass 2 kg has an initial velocity \(\vec{v}_i=(\hat{i}+\hat{j}) \mathrm{m} \mathrm{s}^{-1}\). After a collision with another body, its velocity becomes \(\vec{v}_{\mathrm{f}}=(5 \hat{i}+6 \hat{j}+\hat{k}) \mathrm{m} \mathrm{s}^{-1}\). If the time of impact is 0.02 s, the average force of impact on the body is

1. \(100(4 \hat{i}+5 \hat{j}-\hat{k}) \mathrm{N}\)
2. \(100(4 \hat{i}+5 \hat{j}+\hat{k}) \mathrm{N}\)
3. \(50(4 \hat{i}-5 \hat{j}-\hat{k}) \mathrm{N}\)
4. \(50(4 \hat{i}+5 \hat{j}+\hat{k}) \mathrm{N}\)

Answer: 2. \(100(4 \hat{i}+5 \hat{j}+\hat{k}) \mathrm{N}\)

Initial momentum = \(\vec{p}_{\mathrm{i}}=(2 \mathrm{~kg})(\hat{i}+\hat{j}) \mathrm{m} \mathrm{s}^{-1}\)

and final momentum = \(\vec{p}_{\mathrm{f}}=(2 \mathrm{~kg})(5 \hat{i}+6 \hat{j}+\hat{k}) \mathrm{m} \mathrm{s}^{-1}\)

∴ changeinmomentum = \(\Delta \vec{p}=\vec{p}_{\mathrm{f}}-\vec{p}_{\mathrm{i}}\)

⇒ \((2 \mathrm{~kg})(4 \hat{i}+5 \hat{j}+\hat{k}) \mathrm{m} \mathrm{s}^{-1}\)

∴ average force = \(\vec{F}_{\mathrm{av}}=\frac{\Delta \vec{p}}{\Delta t}=\frac{(2 \mathrm{~kg})(4 \hat{i}+5 \hat{j}+\hat{k}) \mathrm{m} \mathrm{s}^{-1}}{0.02 \mathrm{~s}}\)

⇒ \(100(4 \hat{i}+5 \hat{j}+\hat{k}) \mathrm{N}\)

Question 50. A ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass at rest. After the collision, if the two balls move at equal speeds, the angle between their directions of motion will be

1. 60°
2. 30°
3. 90°
4. 120°

Answer: 3. 90°

Let \(\vec{p}_1 \text { and } \vec{p}_2\) be the momenta of the two balls after the elastic collision.

Hence, conserving the momentum, we have

⇒ \(\vec{p}=\overrightarrow{p_1}+\overrightarrow{p_2} \text {, where } \vec{p}\) = initial momentum.

Taking the self-dot-product,

⇒ \(\vec{p} \cdot \vec{p}=\left(\overrightarrow{p_1}+\overrightarrow{p_2}\right) \cdot\left(\overrightarrow{p_1}+\overrightarrow{p_2}\right)\)

or \(p^2=p_1^2+p_2^2+2 \vec{p}_1 \cdot \vec{p}_2\)

or \(\frac{p^2}{2 m}=\frac{p_1^2}{2 m}+\frac{p_2^2}{2 m}+\frac{2 \vec{p}_1 \cdot \overrightarrow{p_2}}{2 m}\) ……(1)

⇒ In an elastic collision, the KE (=p²/2m) is conserved.

∴ \(E=E_1+E_2 \text { or } \frac{p^2}{2 m}=\frac{p_1^2}{2 m}+\frac{p_2^2}{2 m}\) …(2)

From (1) and(2),

⇒ \(\overrightarrow{p_1} \cdot \overrightarrow{p_2}=0 \text {, i.e., } \overrightarrow{p_1} \text { is perpendicular to } \overrightarrow{p_2}\)

So, the angle between the velocities of the two balls is 90°.

Question 51. A body of mass 2 kg moving at a velocity \((\hat{i}+2 \hat{j}-3 \hat{k}) \mathrm{m} \mathrm{s}^{-1}\) collides with another body of mass 3 kg moving at a velocity \((2 \hat{i}+\hat{j}+\hat{k}) \mathrm{m} \mathrm{s}^{-1}\). If they stick together, the velocity of the composite body will be

1. \(\frac{1}{5}(8 \hat{i}+7 \hat{j}-3 \hat{k}) \mathrm{m} \mathrm{s}^{-1}\)
2. \(\frac{1}{5}(-4 \hat{i}+\hat{j}-3 \hat{k}) \mathrm{m} \mathrm{s}^{-1}\)
3. \(\frac{1}{5}(8 \hat{i}+\hat{j}-\hat{k}) \mathrm{m} \mathrm{s}^{-1}\)
4. \(\frac{1}{5}(-4 \hat{i}+7 \hat{j}-3 \hat{k}) \mathrm{m} \mathrm{s}^{-1}\)

Answer: 1. \(\frac{1}{5}(8 \hat{i}+7 \hat{j}-3 \hat{k}) \mathrm{m} \mathrm{s}^{-1}\)

Conserving the momentum,

⇒ \((2 \mathrm{~kg})(\hat{i}+2 \hat{j}-3 \hat{k}) \mathrm{m} \mathrm{s}^{-1}+(3 \mathrm{~kg})(2 \hat{i}+\hat{j}+\hat{k}) \mathrm{m} \mathrm{s}^{-1}\)

⇒ \((2 \mathrm{~kg}+3 \mathrm{~kg}) \vec{v}\)

or, \((5 \mathrm{~kg}) \vec{v}=(8 \hat{i}+7 \hat{j}-3 \hat{k}) \mathrm{kg} \mathrm{m} \mathrm{s}^{-1}\)

Hence, the velocity of the composite body is

⇒ \(\vec{v}=\frac{1}{5}(8 \hat{i}+7 \hat{j}-3 \hat{k}) \mathrm{m} \mathrm{s}^{-1}\)

Question 52. A steel ball falls from a height on a floor for which the coefficient of restitution is e. The height attained by the ball after two rebounds is

1. eH
2. e²H
3. e³H
4. e⁴H

Answer: 4. e⁴H

We know that the coefficient of restitution (e) is expressed by the relation velocity of separation

= e(velodty of approach).

The initial speed (u) when the ball hits the ground is given by

⇒ \(u^2=2 g H \quad \Rightarrow \quad u=\sqrt{2 g H}\)

The first recoil speed is u₁ = eu and the second recoil speed is

⇒ \(u_2=e u_1=e(e u)=e^2 u=e^2 \sqrt{2} g H .\)

If H² is the maximum height,

⇒ \(u_2^2=2 g H_2 \Rightarrow 2 g H_2=e^4(2 g H)\)

=> H² = e⁴H.

Question 53. A body of mass m, moving at a constant speed, undergoes an elastic collision with a body of mass m₂, initially at rest. The ratio of the kinetic energy of the first body after the collision to that before the collision is

1. \(\left(\frac{m_1-m_2}{m_1+m_2}\right)^2\)
2. \(\left(\frac{m_1+m_2}{m_1-m_2}\right)^2\)
3. \(\left(\frac{2 m_1}{m_1+m_2}\right)^2\)
4. \(\left(\frac{2 m_1}{m_1-m_2}\right)^2\)

Answer: 1. \(\left(\frac{m_1-m_2}{m_1+m_2}\right)^2\)

Conserving the momentum,

⇒ \(m_1 u=m_1 v_1+m_2 v_2\)….(1)

where u is the initial speed of the ball before the collision, and v₁ and v₂ are the speeds of the balls after the collision.

For an elastic collision, the coefficient of restitution = e = 1.

∴ \(\left(v_2-v_1\right)=1 \times u \Rightarrow v_2=u+v_1\)

Substituting for v₂ in (1), we get

⇒ \(m_1 u=m_1 v_1+m_2\left(u+v_1\right)\)

=> (m₁– m₂)u = (m₁ + m₂)v₁

⇒ \(v_1=\left(\frac{m_1-m_2}{m_1+m_2}\right) u\)

⇒ \(\frac{\mathrm{KE}_{\text {after }}}{\mathrm{KE}_{\text {before }}}=\frac{\frac{1}{2} m_1 v_1^2}{\frac{1}{2} m_1 u^2}=\left(\frac{v_1}{u}\right)^2=\left(\frac{m_1-m_2}{m_1+m_2}\right)^2\)

Question 54. A radioactive nucleus of mass number A, initially at rest, emits an a-particle with a speed v. What will be the recoil speed of the daughter nucleus?

1. \(\frac{2 v}{A-4}\)
2. \(\frac{2 v}{A+4}\)
3. ⇒ \(\frac{4 v}{A-4}\)
4. \(\frac{4 v}{A+4}\)

Answer: 3. \(\frac{4 v}{A-4}\)

The scheme of decay is shown in the adjoining figure. After the decay,

themomentaofthe fragments are \(4 m v \hat{i} \text { and }(A-4) m v^{\prime}(-\hat{i})\) respectively.

Conserving the momentum,

⇒ \(4 m v \hat{i}-(A-4) m v^{\prime} \hat{i}=0 \Rightarrow 4 v=(A-4) v^{\prime}\)

⇒ \(v^{\prime}=\frac{4 v}{A-4}\)

Question 55. Consider a system comprising a light string, a light spring, and a block of mass M suspended from a rigid support, as shown in the adjacent figure. The spring constant is k and the block is released when the spring

1. \(\frac{M g}{2}\)
2. Mg
3. 3Mg
4. 2Mg

Answer: 4. 2Mg

The initial of the block is zero, and finally, at the maximum extension (x) of the file spring, it comes to momentary rest.

Thus, by the work-energy theorem,

⇒ \(W_{\mathrm{grav}}+W_{\mathrm{sp}}=\Delta \mathrm{KE}=0\)

⇒ \(M g x+\left(-\frac{1}{2} k x^2\right)=0 \Rightarrow x=\frac{2 M g}{k}\)

∴ the maximum tension in the spring is

⇒ \(F_{\max }=k x_{\max }=k\left(\frac{2 M g}{k}\right)\)

= 2Mg.

Question 56. In the given figure, the spring has its natural length, the blocks are at rest, and there is no friction anywhere. If the spring constant is k= 20Nm^-1, the maximum extension in the spring will be

1. \(\frac{10}{3} \mathrm{~cm}\)
2. \(\frac{20}{3} \mathrm{~cm}\)
3. \(\frac{40}{3} \mathrm{~cm}\)
4. \(\frac{19}{3} \mathrm{~cm}\)

Answer: 1. \(\frac{10}{3} \mathrm{~cm}\)

When the extension in the spring is maximum (= x0), the blocks have the same velocity and the same acceleration (= a).

The system can be considered as connected bodies, and we apply Newton’s second law from the given free-body diagram.

For A, F-kx₀ = m₁a…(1)

For B, kx₀ = m₂a….(2)

Adding (1) and (2),

⇒ \(a=\frac{F}{m_1+m_2}\)….(3)

Substituting a from (3) in (2), the maximum extension becomes

⇒ \(x_0=\frac{m_2 a}{k}=\frac{m_2 F}{k\left(m_1+m_2\right)}\)

Substituting the given values

⇒ \(x_0=\frac{(1 \mathrm{~kg})(1 \mathrm{~N})}{\left(20 \mathrm{~N} \mathrm{~m}^{-1}\right)\left(\frac{3}{2} \mathrm{~kg}\right)}=\frac{10}{3} \mathrm{~cm}\)

Question 57. Find the maximum force if the potential energy is \(U=\frac{a}{r^2}-\frac{b}{r}\) (Given that a = 2 and b = 4.)

1. \(-\frac{16}{27} \mathrm{~N}\)
2. \(-\frac{32}{27} \mathrm{~N}\)
3. \(+\frac{32}{27} \mathrm{~N}\)
4. \(+\frac{16}{27} \mathrm{~N}\)

Answer: 1. \(-\frac{16}{27} \mathrm{~N}\)

By definition, \(F=-\frac{d U}{d r} \Rightarrow F=\frac{2 a}{r^3}-\frac{b}{r^2}\)

For F to be maximum,

⇒ \(\frac{d F}{d r}=0 \Rightarrow-\frac{6 a}{r^4}+\frac{2 b}{r^3}=0\)

⇒ \(r=\frac{3 a}{b}=3\left(\frac{2}{4}\right)=\frac{3}{2}\)

∴ \(F_{\max }=\frac{2 a}{r^3}-\frac{b}{r^2}\)

⇒ \(\frac{2(2)}{\left(\frac{3}{2}\right)^3} \mathrm{~N}-\frac{4}{\left(\frac{3}{2}\right)^2} \mathrm{~N}\)

⇒ \(\frac{32}{27} \mathrm{~N}-\frac{16}{9} \mathrm{~N}\)

⇒ \(-\frac{16}{27} \mathrm{~N}\)

Question 58. Initially when the spring is relaxed, having its natural length, block A of mass 0.25 kg is released. Find the maximum force exerted by the system on the floor.

1. 20N
2. 15N
3. 30N
4. 25N

Answer: 4. 25N

By the work-energy theorem,

⇒ \(W_{\text {grav }}+W_{\text {sp }}=\Delta \mathrm{KE}=0\)

⇒ \(m_{\mathrm{A}} g x_0-\frac{1}{2} k x_0^2=0\), where x0= maximum compression

⇒ \(x_0=\frac{2 m_A g}{k}\)

∴ the maximum force on the floor is

⇒ \(F_{\max }=m_{\mathrm{B}} g+k x_0=m_{\mathrm{B}} g+2 m_{\mathrm{A}} g\)

⇒ \(\left(m_{\mathrm{B}}+2 m_{\mathrm{A}}\right) \mathrm{g}=(2 \mathrm{~kg}+0.5 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)\)

= 25N.

Question 59. A force F = 20x + 10y acts on a particle in the y-direction, where F is in newtons and y is in meters. The work done by this force to move the particle from y = 0 to y = 1 m is

1. 30 J
2. 5 J
3. 25 J
4. 20 J

Answer: 3. 25 J

The total work done is

⇒ \(W=\int d W=\int \vec{F} \cdot d \vec{y}=\int_0^1m(20+10 y) d y\)

⇒ \(\left[20 y+5 y^2\right]_0^{1 m}\)

= 25J

Question 60. A constant force acts on a 2-kg object so that its position is given as a function of time by x = 3t²-5. What is the work done by this force in the first five seconds?

1. 850 J
2. 875 J
3. 900 J
4. 950 J

Answer: 3. 900 J

Since x = 3t2 – 5, the instantaneous velocity is

⇒ \(v=\frac{d x}{d t}=6 t\)

and the acceleration is

⇒ \(a=\frac{d v}{d t}=6 \mathrm{~m} \mathrm{~s}^{-2}=\text { constant }\)

∴ force = F = ma = (2kg)(6m s^-2)

= 12N.

The distance covered in 5 s is

⇒ \(x=u t+\frac{1}{2} a t^2=0 \cdot t+\frac{1}{2}\left(6 \mathrm{~m} \mathrm{~s}^{-2}\right)\left(25 \mathrm{~s}^2\right)\)

= 75m.

∴ work done =Fx = (12N)(75m) = 900 J

Question 61. A particle undergoes a displacement under the action of a \(\vec{r}=4 \hat{i}\) constant force \(\vec{F}=3 \hat{i}-12 \hat{j}\);. If the initial kinetic energy of the particle is 3 J, the kinetic energy at the end of the displacement will be

1. 9 J
2. 15 J
3. 12 J
4. 10 J

Answer: 2. 15 J

Work done = \(\vec{F} \cdot \vec{r}=(3 \hat{i}-12 \hat{j}) \mathrm{N} \cdot 4 \hat{i} \mathrm{~m}\)

=12 J.

∴ change in the KE = KE_f – KE_i = work done.

∴ \(\mathrm{KE}_{\mathrm{f}}=3 \mathrm{~J}+12 \mathrm{~J}=15 \mathrm{~J}\)

Question 62. Ablockofmassm, lying on a smooth horizontal surface, is attached to a light spring of spring constant k. The other end of the spring is fixed, as shown in the adjoining figure. The block is initially at rest in its equilibrium position. If the block is now pulled with a constant force F, the maximum speed of the block will be

1. \(\frac{\pi F}{\sqrt{m k}}\)
2. \(\frac{F}{\sqrt{m k}}\)
3. \(\frac{2 F}{\sqrt{m k}}\)
4. \(\frac{F}{\pi \sqrt{m k}}\)

Answer: 2. \(\frac{F}{\sqrt{m k}}\)

As the force produces elongation (x) in the spring, a retarding force (-kx) develops and we have

F_net= F-kx = ma.

When the velocity is maximum, the acceleration \(\left(\frac{d v}{d t}\right)\) is zero.

Thus,

⇒ \(F-k x=0 \Rightarrow x=\frac{F}{k}\)

According to the work-energy theorem,

⇒ \(W_{\text {fric }}+W_{\text {sp }}=\mathrm{KE}_{\max }=\frac{1}{2} m v_{\max }^2\)

⇒ \(F x-\frac{1}{2} k x^2=\frac{1}{2} m v_{\max }^2\)……(1)

Substituting x = \(\frac{F}{k}\) in (1) the condition for the maximum velocity,

⇒ \(F\left(\frac{F}{k}\right)-\frac{1}{2} k\left(\frac{F}{k}\right)^2=\frac{1}{2} m v_{\max }^2\)

⇒ \(\frac{F^2}{2 k}=\frac{1}{2} m v_{\max }^2 \Rightarrow v_{\max }=\frac{F}{\sqrt{m k}}\)

Question 63. A block of mass m is kept on a platform that starts from rest with a constant acceleration \(\frac{g}{2}\) upwards, as shown in the adjoining figure. The work done by the normal reaction on the block in a time t will be

1. \(\frac{m g^2 t^2}{8}\)
2. \(\frac{3 m g^2 t^2}{8}\)
3. \(-\frac{m g^2 t^2}{8}\)
4. Zero

Answer: 2. \(\frac{3 m g^2 t^2}{8}\)

The height reached by the block in the time t is

⇒ \(h=\frac{1}{2}\left(\frac{g}{2}\right) t^2=\frac{g t^2}{4}\)

and the velocity at that time is

⇒ \(v=\left(\frac{g}{2}\right) t=\frac{g t}{2}\)

The work done by gravity is

⇒ \(W_{\mathrm{grav}}=-(m g) h=-m g\left(\frac{g t^2}{4}\right)\)

Change in the

⇒ \(\mathrm{KE}=\frac{1}{2} m\left(\frac{g t}{2}\right)^2=\frac{1}{2}\left(\frac{m g^2 t^2}{4}\right)\)

From the work-energy theorem,

⇒ \(\mathrm{W}_{\mathrm{grav}}+W_{O V}=\frac{1}{2} m v^2\)

⇒ \(-\frac{m g^2 t^2}{4}+W_{\delta V}=\frac{1}{2} m\left(\frac{g^2 t^2}{4}\right)\)

∴ the work done by the normal reaction is

⇒ \(W N =\frac{m g^2 t^2}{4}+\frac{m g^2 t^2}{8}=\frac{3}{8} m g^2 t^2\)

Question 64. Throe blocks A, B, and C are placed on a smooth horizontal surface, as shown in the given figure. A and B have equal masses of m, while C has a mass of M. Block A is given an initial speed of v towards B, due to which it collides with B perfectly inelastically. The combined mass collides with C, also perfectly inelastically. If in the whole process, \(\frac{5}{6}\) of its initial kinetic energy is lost, the value of the ratio \(\frac{M}{m}\) is

1. 4
2. 2
3. 3
4. 5

Answer: 1. 4

Since momentum is conserved during each impact, p = mu = (M + 2m) v₀, where v₀ is the final velocity of the combined system.

Initial kinetic energy of A is \(\frac{p^2}{2 m}\) and final kinetic energy of the combined system is

⇒ \(\frac{1}{6}\left(\frac{p^2}{2 m}\right), \text { since } \frac{5}{6} \text { part in loss }\)

⇒ \(\frac{1}{6}\left(\frac{p^2}{2 m}\right)=\frac{p^2}{2(M+2 m)}\)

or, 6m = (M+2m)

Hence \(\frac{M}{m}=4 .\)

Question 65. A gun exerts a time-dependent force on a bullet given by

F = [100- (0.5 x 10⁵)t] N.

If the bullet emerges with a speed of 400 m s^-1, find the impulse delivered to the bullet till the force F is reduced to zero.

1. 0.1 Ns
2. 0.3Ns
3. 0.5Ns
4. 0.4Ns

Answer: 1. 0.1 Ns

When F is reduced to zero at a time t, we have

⇒ \(t=\frac{100}{(0.5) 10^5} \mathrm{~s}=\frac{2}{1000} \mathrm{~s}\)

The impulse delivered to the bullet is

⇒ \(I=\int_0^t F d t=\left[100 t-\left(0.5 \times 10^5\right) \frac{t^2}{2}\right]_0^{(2 / 1000)}\)

⇒ \(100\left(\frac{2}{1000}\right)-\frac{1}{2} \times \frac{10^5}{2}\left(\frac{2}{10^3}\right)^2\)

=(0.2- 0.1)N s

= 0.1N s.

Question 66. A block A of mass 4m, moving towards block B of mass 2m at rest, undergoes an elastic head-on collision. The fraction of energy lost by the colliding body A is

1. \(\frac{4}{9}\)
2. \(\frac{5}{9}\)
3. \(\frac{8}{9}\)
4. \(\frac{2}{9}\)

Answer: 3. \(\frac{8}{9}\)

Let v₁ and v₂ be the velocities of the blocks A and B after the collision.

Conserving the momentum,

4mu₁ + 2m(0) = 4mv₁ +2mv₂

=> 2u₁= 2v₁+v₂…..(1)

For an elastic collision, e = 1.

Thus,

v₂-v₁ = e(u₁-u₂)

=> v₂-v₁ = u₁…..(2)

Subtracting(2) from(1),

⇒ \(3 v_1=u_1 \Rightarrow v_1=\frac{u_1}{3}\)

The fractional loss of energy the block A is

⇒ \(\frac{\Delta \mathrm{KE}_{\mathrm{A}}}{\mathrm{KE}_{\mathrm{A}}}=\frac{\frac{1}{2} m_{\mathrm{A}} u_1^2-\frac{1}{2} m_{\mathrm{A}} v_1^2}{\frac{1}{2} m_{\mathrm{A}} u_1^2}\)

⇒ \(1-\left(\frac{v_1}{u_1}\right)^2=1-\left(\frac{1}{3}\right)^2\)

⇒ \(\frac{8}{9}\)

Question 67. A block rests on a rough horizontal surface. A horizontal force that increases linearly with time (t) starts acting on the block at t = 0. Which of the following velocity-time graphs will be correct?

Answer: 2.

Given that \(F=m \frac{d v}{d t}=\alpha t \Rightarrow d v=\frac{\alpha}{m}, t d t\)

Integrating, \(v=\frac{\alpha}{2 m} \cdot t^2\)

Due to its roughness, the block starts moving after some time when

F≥f_k.

Question 68. A particle of mass m is moving at a speed 2v and collides with a particle of mass 2m, moving at a speed v in the same direction. After the collision, the first particle is stopped, while the second particle splits up into two smaller particles, each of mass m, which move at 45° with respect to the original direction. The speed of each moving particle will be

1. \(\frac{v}{2 \sqrt{2}}\)
2. 2 √2v
3. \(\frac{v}{\sqrt{2}}\)
4. √2v

Answer: 2. 2 √2v

The situations before and after the collision are shown in the figure below.

Conserving the momentum along the direction of motion,

m.2v + 2m.v = mv’cos45°+ mv’cos45°

⇒ \(4 m v=2 m v^{\prime}\left(\frac{1}{\sqrt{2}}\right)\)

⇒ \(v^{\prime}=\frac{4}{\sqrt{2}} v=2 \sqrt{2} v\)

Question 69. A body of mass m, moving at a velocity \(\hat{u i}\), collides elastically with a stationary body of mass 3m. If the velocity of the lighter body after the collision is \(\hat{v j}\) then this velocity has the magnitude After the collision

1. \(v=\frac{u}{2}\)
2. \(v=\frac{u}{\sqrt{3}}\)
3. \(v=\frac{u}{\sqrt{2}}\)
4. \(v=\frac{4}{3}\)

Answer: 3. \(v=\frac{u}{\sqrt{2}}\)

Conserving the KE, we have

⇒ \(\frac{1}{2} m u^2=\frac{1}{2} m v^2+\frac{1}{2}(3 m) v^{\prime 2}\)

or, \(u^2-v^2=3 v^2\)

Conserving the momentum, we have along the

x-axis: mu = 3mv’cosθ

and along the y-axis: 0 = mv-3mv’sin θ.

∴ \(u^2+v^2=9 v^{\prime 2}\)

From (1) and (2)

⇒ \(u^2+v^2=3\left(u^2-v^2\right) \Rightarrow v=\frac{u}{\sqrt{2}}\)

Question 70. Five blocks are placed on a smooth, horizontal, plane surface along the same line, as shown. The first block (of mass m) is given a velocity v so that the blocks successively undergo a perfectly inelastic collision. The percentage loss in the kinetic energy after the last collision is

1. 88.5%
2. 93.75%
3. 90.2%
4. 85.5%

Answer: 3. 90.2%

The momentum (p) is conserved during the collision.

However, due to the perfectly inelastic collision, the mass has changed from m to 16m.

Initial KE = \(\frac{p^2}{2 m} \text { and final } \mathrm{KE}=\frac{p^2}{2(16 m)}\)

∴ AKE = changee in the KE = \(\)

∴ % loss in KE = \(\frac{p^2}{2 m}-\frac{p^2}{2(16 m)}\)

Question 71. The force-displacement graph of a particle moving along the x-axis is shown in the given figure. The work done by the force from x = 0 to x = 30m is

1. 4550 J
2. 5250 J
3. 4250 J
4. 7500 J

Answer: 2. 5250 J

The area under the force-displacement graph gives the work done.

Hence,

W = area of the rectangle + area of the trapezium

= (200N)(15 m) + \(\frac{1}{2}\) (200N + 100 N)(15m)

= 3000 J + 2250 J

= 5250 J

Question 72. A block of mass m starts slipping down an inclined plane from the topmost point B and finally comes to rest at the lowermost point A. If BC = 2AC and the friction coefficient of the rough part ACis A m = k tan 6 then the value of k is

1. 0.5
2. 0.35
3. 0.75
4. 3.0

Answer: 4. 3.0

Let AC = x and BC = 2x.

∴ AB = 3x.

Work done by gravity = \(W_{\mathrm{grav}}=m g h=m g(3 x \sin \theta)\)

Work done by friction = \(W_{\text {fric }}=-f x=-(\mu m g \cos \theta) x\)

From the work-energy theorem,

⇒ \(W_{\text {grav }}+W_{\text {fric }}=\Delta K E=K_f-K_1=0\)

=> (mg)(3x) sin θ = (μmg cosθ)x

=> 3 tan θ = m = k tan 0 [ given ]

=> k=3.

Question 73. A 100-g bullet moving horizontally at 20m s^-1 strikes a stationary block of mass 1.9 kg and comes to rest inside. The kinetic energy of the block just before hitting the ground is

1. 11 J
2. 21 J
3. 24 J
4. 32 J

Answer: 2. 21 J

Conserving the linear momentum,

(100 g)(20m s^-1) = (100 g + 1.9 kg)v

=> v = 1m s^-1.

From the work-energy principle,

Wgrav = changein the KE

⇒ \((2 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(1 \mathrm{~m})=\mathrm{KE}_{\mathrm{f}}-\mathrm{KE}_{\mathrm{i}}\)

=\(\mathrm{KE}_{\mathrm{f}}-\frac{1}{2}(2 \mathrm{~kg})\left(1 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\)

Hence, KE_f = 20J +1J

= 21J.

Question 74. A block is pushed up along a rough inclined plane with a speed V₀, as shown in the given figure. After some time, it is again back to the starting point with a reduced Find the coefficient of speed \(\frac{v_0}{2}\) fiction (μ).

1. 0.15
2. 0.45
3. 0.35
4. 0.75

Answer: 3. 0.35

Applying the work-energy theorem,

⇒ \(W_{\text {grav }}+W_{\text {fric }}=\Delta K E=K_f-K_i\)

The work done by gravity is zero, and the work done by friction is

⇒ \(W_{\text {fric }}=-\mu \delta N(2 s)=-\left(\mu m g \cos 30^{\circ}\right)(2 s)\)

The change in KE is

⇒ \(\frac{1}{2} m\left(\frac{v_0}{2}\right)^2-\frac{1}{2} m v_0^2=-\frac{1}{2}\left(\frac{3}{4} m v_0^2\right)\)

∴ \(\frac{1}{2} \cdot \frac{3}{4} m v_0^2=(\mu m g \sqrt{3}) s\)

⇒ \(v_0^2=\frac{8}{\sqrt{3}} \mu g s\)…..(1)

For demotion down the plane,

⇒ \(\left(\frac{v_0}{2}\right)^2=0+2 g(\sin \theta-\mu \cos \theta) s\)

⇒ \(v_0^2=8 g\left(\frac{1}{2}-\frac{\sqrt{3}}{2} \mu\right) s\) …..(2)

Equating (1) and(2),

⇒ \(4 g s(1-\sqrt{3} \mu)=\frac{8}{\sqrt{3}} \mu g s\)

⇒ \(\mu\left(\sqrt{3}+\frac{2}{\sqrt{3}}\right)=1\)

⇒ \(\mu=\frac{\sqrt{3}}{5}\)

= 0.35

Question 75. A block of mass 2 kg at rest is driven by a constant power of 1.0 W. The distance covered by the block in 6 s is

1. 2√6 m
2. 4√6 m
3. 3√3 m
4. 4√3 m

Answer: 2. 4√6 m

Instantaneous power P = Fv = \(\left(m \frac{d v}{d t}\right) v\)

∴ \(\frac{P}{m} d t=v d v\)

Integrating, \(\left(\frac{P}{m}\right) t=\frac{y^2}{2}\)

Hence, velocity = \(v=\frac{d s}{d t}=\sqrt{\frac{2 P}{m}} t^{1 / 2}\)

Integrating again,

⇒ \(s=\sqrt{\frac{2 P}{m}}\left(\int t^{1 / 2} d t\right)=\sqrt{\frac{2 P}{m}}\left(\frac{2}{3} t^{3 / 2}\right)=\frac{2}{3} \sqrt{\frac{2 \times 1}{2}}\left(6^{3 / 2}\right)=4 \sqrt{6} \mathrm{~m}\)

Friction and Circular Motion

Question 1. A block released on a rough inclined plane of inclination 0 = 30° Or slides down the plane with a constant acceleration of \(\frac{g}{4}\), where g is the acceleration due to gravity. What is the coefficient of friction between the block and the inclined plane?

1. \(\frac{1}{\sqrt{3}}\)
2. \(\frac{1}{2}\)
3. \(\frac{1}{2 \sqrt{2}}\)
4. \(\frac{1}{2 \sqrt{3}}\)

Answer: 4. \(\frac{1}{2 \sqrt{3}}\)

The acceleration of a block sliding down an inclined plane is given by a =g(sin θ- cos θ).

Given that a = \(\frac{g}{4}\) and θ = 30°.

∴ \(\frac{g}{4}=g\left(\sin 30^{\circ}-\mu \cos 30^{\circ}\right)=\frac{g}{2}(1-\sqrt{3} \mu) .\)

∴ Coefficient offriction = \(\mu=\frac{1}{2 \sqrt{3}}\)

Question 2. A block takes twice as much time to slide down a rough 45°-inclined plane as it takes to slide down an identical but smooth 45°-inclined plane. The coefficient of kinetic friction between the block and the rough inclined plane is

1. 0.25
2. 0.50
3. 0.75
4. 0.90

Answer: 3. 0.75

The acceleration down a rough incline is

⇒ \(a_{\text {rough }}=g(\sin \theta-\mu \cos \theta)=\frac{g}{\sqrt{2}}(1-\mu)\) [∵ θ = 45°]

and that down a smooth incline is

⇒ \(a_{\text {smooth }}=g \sin \theta=\frac{8}{\sqrt{2}} \text {. }\)

Time to slide, \(t=\sqrt{\frac{2 s}{a}}\)

∴ \(t \propto \frac{1}{\sqrt{a}} .\)

Now, \(\frac{t_{\text {rough }}}{t_{\text {smooth }}}=\sqrt{\frac{a_{\text {smooth }}}{a_{\text {rough }}}}=\sqrt{\frac{\frac{g}{\sqrt{2}}}{\frac{g}{\sqrt{2}}(1-\mu)}}=\sqrt{\frac{1}{1-\mu}}\)

⇒ \(2=\frac{1}{\sqrt{1-\mu}}\)

⇒ \(\mu=\frac{3}{4}=0.75\)

Question 3. The upper half of an inclined plane of inclination θ is perfectly smooth, while the lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom of the coefficient of friction between the block and the lower half of the plane is given by

1. p = 2 tan θ
2. p = tan θ
3. \(\mu=\frac{2}{\tan \theta}\)
4. p = cot θ

Answer: 1. p = 2 tan θ

For the motion along the upper (smooth) half,

⇒ \(v_0^2=2 g \sin \theta \cdot \frac{s}{2}=g \sin \theta\)

For the motion on the lower (rough) half,

⇒ \(v^2=v_0^2-2 a\left(\frac{s}{2}\right)=g s \sin \theta-2(\sin \theta-\mu \cos \theta) g \cdot \frac{s}{2}\)

⇒ \(2(\sin \theta-\mu \cos \theta)\left(\frac{g s}{2}\right)=g^s \sin \theta\) [∵ v = 0]

Simplifying, we gel \(\mu\) = 2tanθ.

Question 4. A 20-kg block is pulled by a force of 100 N acting at an angle of 30° above the horizontal with a uniform speed on a horizontal surface. The coefficient of friction between the surface and the block is

1. 0.75
2. 0.85.
3. 0.43
4. 0.58

Answer: 4. 0.58

For vertical equilibrium, N + F sin 30° = mg.

Hence, the normal reaction is

N = mg-Fsin 30°

= 200 N-50 N

= 150 N.

Since the block moves with a uniform velocity,

⇒ \(F_{\text {net }}=0 \Rightarrow F \cos 30^{\circ}=f=\mu \nu\)

∴ \(\mu=\frac{100\left(\frac{\sqrt{3}}{2}\right)}{150}=\frac{\sqrt{3}}{3}=0.58\)

Question 5. A uniform chain of length L lies on the horizontal surface of a table. The coefficient of static friction between the chain and the table is p. The maximum length of the chain that can hang over the edge of the table so that the entire chain can remain at rest will be

1. \(\frac{\mu L}{1+\mu}\)
2. \(\frac{\mu L}{1-\mu}\)
3. \(\frac{L}{1-\mu}\)
4. \(\frac{L}{1+\mu}\)

Answer: 1. \(\frac{\mu L}{1+\mu}\)

Let X be the mass per unit length of the chain and xL be its maximum length that can hang.

∴ The pulling force on the chain is \(\lambda\)xLg, while the weight of the chain lying on the table is \(\lambda(1-x) L g\), which is equal to the normal reaction N.

For the limiting static equilibrium,

⇒ \(\lambda x L g=\mu \delta V=\mu \lambda(1-x) L g\)

Simplifying, we get \(x=\frac{\mu}{1+\mu}\)

∴ The maximum length of the Overhanging part is

⇒ \(x L=\frac{\mu L}{1+\mu}\)

Question 6. A boy weighing 40 kg is climbing a vertical pole at a constant speed. If the coefficient of friction between his palms and the pole is 0.8 and g = 10 m s^-2, the force exerted by him on the pole is

1. 500 N
2. 300 N
3. 400 N
4. 600 N

Answer: 1. 500 N

Given that the weight of the boy is mg = 40 kg x g = 400 N.

The force exerted by the boy on the pole is F = N.

Hence, the force of friction = \(f=\mu \nu =\mu F.\)

For uniform motion,

⇒ \(F_{\text {net }}=m g-\mu \nu=0 \Rightarrow \mu F=m g\) [∵ F = N]

⇒ \(F=\frac{m g}{\mu}=\frac{400 \mathrm{~N}}{0.8}=500 \mathrm{~N}\)

Question 7. A boy of mass m is sliding down a vertical pole by pressing it with a horizontal force f. If \(\mu\) is the coefficient of friction between his palms and the pole, the acceleration with which he slides down will be

1. g
2. \(\frac{\mu f}{m}\)
3. \(g-\frac{\mu f}{m}\)
4. \(g+\frac{\mu f}{m}\)

Answer: 3. \(g-\frac{\mu f}{m}\)

Normal reaction = force exerted horizontally.

The upward force of friction = μf.

∴ \(F_{\text {net }}=m g-\mu f=m a\)

∴ downward acceleration

⇒ \(a=\frac{F_{\text {net }}}{m}=g-\frac{\mu f}{m} .\)

Question 8. A block B is pushed momentarily along a horizontal surface with an initial velocity of v. If (A is the coefficient of sliding friction between B and the surface, B will come to rest after a time

1. \(\frac{\mu g}{v}\)
2. \(\frac{g}{v}\)
3. \(\frac{v}{g}\)
4. \(\frac{v}{\mu g}\)

Answer: 4. \(\frac{v}{\mu g}\)

Initial velocity = v.

Frictional force = \(f=\mu \nu =\mu m g\)

∴ acceleration = \(a=\frac{L}{m}=\mu g\)

Now, applying v = u-at, we have

⇒ \(0=v-\mu g t \Rightarrow t=\frac{v}{\mu g}\)

Question 9. The coefficient of static friction between μ_s the block A (of mass 2 kg) and the table is shown in the. figure is 0.2. What should be the maximum mass of the block B so that the two blocks do not move? (The string and the pulley are assumed to be smooth and light, and g = 10 m s^-2.)

1. 2.0 kg
2. 4.0 kg
3. 0.2 kg
4. 0.4 kg

Answer: 4. 0.4 kg

The limiting static friction for block A is

⇒ \(\mu m_A g=0.2(2 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)=4 \mathrm{~N}\)

The tension in the string is also T = 4 N.

For the block B,

⇒ \(m_{\mathrm{B}} g=T=4 \mathrm{~N} \Rightarrow m_{\mathrm{B}}=\frac{4 \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-2}}{10 \mathrm{~m} \mathrm{~s}^{-2}}=0.4 \mathrm{~kg}\)

Question 10. The system consists of three masses m_1, m₂, and m₃, connected by a string passing over a pulley P. The mass m₁ hangs freely, and m₂ and m₃ are on a rough horizontal table (the coefficient of friction being p). The pulley is frictionless and of negligible mass. The downward acceleration of mass m₁ is (assuming m₁= m₂ = m₃ = m)

1. \(\left(\frac{1-\mu}{9}\right) g\)
2. \(\frac{2}{3} \mu g\)
3. \(\left(\frac{1-2 \mu}{3}\right) 8\)
4. \(\left(\frac{1-2 \mu}{2}\right) g\)

Answer: 3. \(\left(\frac{1-2 \mu}{3}\right) 8\)

Let the common acceleration of the system be a, the tension connecting the hanging mass ml be T₁, and that connecting m₂ and m₃ be T₂. From Newton’s law, we obtain the following.

For the mass m₁, m₁g-T₁ = m₁a.

For the mass \(m_2, T_1-T_2-\mu m_2 g=m_2 a\)

For the mass \(m_3, T_2-\mu m_3 g=m_3 a\)

Adding the three equations and putting m₁ = m₂ = m₃ = m, we get

⇒ \(m g(1-2 \mu)=3 m a\) = 3ma.

Hence, acceleration = \(a=\left(\frac{1-2 \mu}{3}\right) g\)

Question 11. A block released from rest from the top of a smooth inclined plane of inclination 0 has a speed of v when it reaches the bottom. The same block, released from the top of a rough inclined plane of the same inclination 9, acquires a speed \(\frac{v}{n}\) on reaching the bottom, where n > 1. The coefficient of friction is given by

1. \(\mu=\sqrt{1-\frac{1}{n^2}} \cdot \tan \theta\)
2. \(\mu=\sqrt{1-\frac{1}{n^2}} \cdot \cot \theta\)
3. \(\mu=\sqrt{1-\frac{1}{n^2}} \cdot \sin \theta\)
4. \(\mu=\left(1-\frac{1}{n^2}\right) \tan \theta\)

Answer: 4. \(\mu=\left(1-\frac{1}{n^2}\right) \tan \theta\)

For the motion down the smooth inclined plane,

v² = 2(gsinθ)s……(1)

For the rough inclined plane, the acceleration down the plane is

⇒ \(a=g(\sin \theta-\mu \cos \theta)\).

Hence,

⇒ \(\left(\frac{v}{n}\right)^2=2 g(\sin \theta-\mu \cos \theta) s\)…….(2)

Dividing (1) by (2),

⇒ \(n^2=\frac{\sin \theta}{\sin \theta-\mu \cos \theta}\)

⇒ \(\mu=\left(1-\frac{1}{n^2}\right) \tan \theta\)

Question 12. Two blocks of masses m₁-m and m₂-m are connected by a light inextensible string that passes over a smooth pulley fixed on the top of an inclined plane, as shown in the figure. When θ = 30°, the block of mass ml just begins to move up along the inclined plane. The coefficient of kinetic friction between the block of mass m₁ and the inclined plane is

1. \(\frac{1}{\sqrt{3}}\)
2. \(\frac{1}{\sqrt{2}}\)
3. \(\frac{1}{2 \sqrt{2}}\)
4. \(\frac{1}{3 \sqrt{2}}\)

Answer: 1. \(\frac{1}{\sqrt{3}}\)

Since the block of mass m₁ just begins to move, it is friction, and the net force on each block is zero.

For m₂, m₂g – T = 0.

For \(m_1, T-m_1 g \sin \theta-\mu m_1 g \cos \theta=0\)

Taking m₁ = m₂ = m and adding the two equations,

⇒ \(m g-m g \sin \theta-\mu m g \cos \theta=0\)

⇒ \(\mu=\frac{1-\sin \theta}{\cos \theta}=\frac{1-\sin 30^{\circ}}{\cos 30^{\circ}}=\frac{1}{\sqrt{3}}\)

Question 13. A block rests on an inclined plane. If the angle of inclination is gradually increased, the block just begins to slide down the plane when the angle of inclination is 30°. The coefficient of friction between the block and the inclined plane is

1. \(\frac{1}{3}\)
2. \(\frac{1}{2 \sqrt{3}}\)
3. \(\frac{1}{2 \sqrt{3}}\)
4. \(\frac{1}{2 \sqrt{2}}\)

Answer: 2. \(\frac{1}{2 \sqrt{3}}\)

According to the given question, θ is the angle of repose, for which

⇒ \(\mu=\tan \theta=\tan 30^{\circ}=\frac{1}{\sqrt{3}}\)

Alternative method:

⇒ \(m g \sin \theta=f=\mu \sigma V=\mu m g \cos \theta\)

⇒ \(\mu=\tan \theta=\tan 30^{\circ}=\frac{1}{\sqrt{3}}\)

Question 14. A plank with a block on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches 30°, the block just starts to slip down the plank and slides 4.0 m in 4.0 s. The coefficients of static and kinetic frictions between the block and the plank will respectively be

1. 0.5 and 0.6
2. 0.4 and 0.3
3. 0.6 and 0.6
4. 0.6 and 0.5

Answer: 4. 0.6 and 0.5

When the die block just tends to slip down, it is a case of static limiting friction, for which

⇒ \(\mu_{\mathrm{s}}=\tan \theta=\tan 30^{\circ}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}=0.58 \approx 0.6\)

When the block slides down the plane, the acceleration is

⇒ \(a=g\left(\sin 30^{\circ}-\mu \cos 30^{\circ}\right)=\frac{g}{2}(1-\sqrt{3} \mu) .\)

∵ \(s=u t+\frac{1}{2} a t^2\)

⇒ \(4.0 \mathrm{~m}=0+\frac{1}{2} \cdot 5\left(1-\sqrt{3} \mu_{\mathrm{k}}\right)(4 \mathrm{~s})^2\)

⇒ \(\sqrt{3} \mu_{\mathrm{k}}=1-\frac{1}{10}=\frac{9}{10}\)

Hence, \(\mu_k=\frac{0.9}{\sqrt{3}}=0.5\)

Question 15. A car is negotiating a curved road of radius R. The road is banked at an angle θ. The coefficient of friction between the tire of the car and the road is μ_s. The maximum safe velocity on this road is

1. \(\sqrt{\frac{g}{R} \cdot \frac{\mu_{\mathrm{s}}+\tan \theta}{1-\mu_{\mathrm{s}} \tan \theta}}\)
2. \(\sqrt{\frac{g}{R^2} \cdot \frac{\mu_s+\tan \theta}{1-\mu_s \tan \theta}}\)
3. \(\sqrt{g R^2 \cdot \frac{\mu_s+\tan \theta}{1-\mu_s \tan \theta}}\)
4. \(\sqrt{g R \cdot \frac{\mu_{\mathrm{s}}+\tan \theta}{1-\mu_{\mathrm{s}} \tan \theta}}\)

Answer: 4. \(\sqrt{g R \cdot \frac{\mu_{\mathrm{s}}+\tan \theta}{1-\mu_{\mathrm{s}} \tan \theta}}\)

The forces acting on the car moving on a banked road are the weight (mg), the normal reaction (N), and the friction (f).

Resolving f and N along the vertical and horizontal directions (as shown in the adjoining figure), we obtain the following.

For vertical equilibrium,

⇒ \(\mathcal{N} \cos \theta=m g+f \sin \theta\)

or, \(m g=\alpha N \cos \theta-f \sin \theta\) ….. (1)

The centripetal force is provided by

⇒ \(f \cos \theta+\propto N \sin \theta=\frac{m v^2}{R}\)….(2)

Dividing (2) by (1),

⇒ \(\frac{f \cos \theta+\delta N \sin \theta}{\delta N \cos \theta-f \sin \theta}=\frac{v^2}{R g}\)

In the limiting case, when \(f=f_{\max }=\mu_{\mathrm{s}} \nu\)

⇒ \(\frac{v_{\max }^2}{R g}=\frac{\mu_{\mathrm{s}} N \cos \theta+N \sin \theta}{\alpha N \cos \theta-\mu_{\mathrm{s}} \nu \sin \theta}\)

⇒ \(v_{\max }=\sqrt{R g\left(\frac{\mu_s+\tan \theta}{1-\mu_s \tan \theta}\right)}\)

Question 16. A block of mass 10 kg is placed on a rough horizontal surface having a coefficient of friction μ = 0.5. If a horizontal force of 100 N acts on it, the acceleration of the block will be

1. 10ms^-2
2. 5ms^-2
3. 15 ms^-2
4. 0.5ms^-2

Answer: 2. 5ms^-2

Maximum kinetic friction = \(f_{\max }=\mu \subset N=(0.5)(10 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)\)

= 50 N.

Applied force = F = 100 N.

∴ \(F_{\text {net }}=F-f_{\max }=m a\)

100 N – 50 N = (10kg)4.

∴ acceleration = a = 5ms^-2.

Question 17. A car is negotiating a curved level road of radius r. If the coefficient of friction between the tyre and the road is μ_s, the car will skid if its speed exceeds

1. \(\sqrt{2 \mu_s r g}\)
2. \(\sqrt{3 \mu_s r g}\)
3. \(\sqrt{\mu_s r g}\)
4. \(2 \sqrt{\mu_s r g}\)

Answer: 3. \(\sqrt{\mu_s r g}\)

Since \(\mu_{\mathrm{s}}\) is the coefficient of static friction between the tyre and the road, its maximum value is \(f_{\max }=\mu_s m g\); and for a safe turn (without skidding),

⇒ \(\frac{m v^2}{r} \leq \mu_s m g \Rightarrow v \leq \sqrt{\mu_s r g}\)

∴ \(v_{\max }=\sqrt{\mu_s r g}\)

Question 18. A 20-kg box is placed gently on a horizontal conveyor belt moving at a speed of 4 m s^-1. If the coefficient of friction between the box and the belt is 0.8, through what distance will the block slide on the belt?

1. 0.6 m
2. 0.8 m
3. 1.0 m
4. 1.2 m

Answer: 3. 1.0 m

Theforce offrictionon theboxis \(f=\mu m g\), so the accelerationisa \(a=\frac{f}{m}=\mu g\)

The box will slide on the belt until it attains the speed of the belt (v).

The distance moved by the box is (applying v² = u²- 2as)

⇒ \(s=\frac{v^2}{2 a}\) [∵ u=0]

⇒ \(\frac{\left(4 \mathrm{~m} \mathrm{~s}^{-1}\right)^2}{2(0.8)\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}=1 \mathrm{~m}\)

Question 19. A car is negotiating a circular horizontal track of radius 10 m with a constant speed of 10 m s^-1. A bob is suspended from the roof of the car by a light thread of length 1.0 m. The angle made by the thread with the vertical is

1. \(\frac{\pi}{3} \mathrm{rad}\)
2. \(\frac{\pi}{6} \mathrm{rad}\)
3. \(\frac{\pi}{4} \mathrm{rad}\)
4. 0°

Answer: 3. \(\frac{\pi}{4} \mathrm{rad}\)

Let the thread make an angle 0 with the vertical when T is the tension.

Resolving T, we have

⇒ \(T \sin \theta=\frac{m v^2}{R} \text { and } T \cos \theta=m g\)

Dividing, we get

⇒ \(\tan \theta=\frac{v^2}{R g}=\frac{\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)^2}{(10 \mathrm{~m})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)}=1\)

⇒ \(\theta=45^{\circ}=\frac{\pi}{4} \mathrm{rad}\)

Question 20. A Block A of mass m₁ rests on a horizontal table. A light string connected to it passes over a frictionless pulley fixed at the edge of the table, and a block B of mass m₂ is suspended from its other end. The coefficient of kinetic friction between block A and the table is μ_k. When the block A is sliding on the table, the tension in the string is

1. \(\frac{m_1 m_2\left(1+\mu_{\mathrm{k}}\right) g}{m_1+m_2}\)
2. \(\frac{m_1 m_2\left(1-\mu_k\right) g}{m_1+m_2}\)
3. \(\frac{m_2+\mu_{\mathrm{k}} m_1 g}{m_1+m_2}\)
4. \(\frac{m_2-\mu_{\mathrm{k}} m_1 g}{m_1+m_2}\)

Answer: 1. \(\frac{m_1 m_2\left(1+\mu_{\mathrm{k}}\right) g}{m_1+m_2}\)

The given figure shows the situation. Let a be the acceleration of the system and T be the tension in the connecting string.

For the block of mass m₁, T – μ_km₁g= m₁a,

and for the block of mass m₂, m₂g – T = m₂a.

Dividing the first equation by the second,

⇒ \(\frac{T-\mu_{\mathrm{k}} m_1 g}{m_2 g-T}=\frac{m_1}{m_2}\)

Simplifying, we get

⇒ \(T=\frac{m_1 m_2\left(1+\mu_{\mathrm{k}}\right) g}{m_1+m_2}\)

Question 21. A block of mass m is in contact with a cart C, as shown in the figure. The coefficient of static friction between the block and the cart is μ. The acceleration α of the cart that will prevent the block from falling down satisfies the relation

1. \(\alpha>\frac{m g}{\mu}\)
2. \(\alpha>\frac{g}{\mu m}\)
3. \(\alpha \geq \frac{g}{\mu}\)
4. \(\alpha<\frac{g}{\mu}\)

Answer: 3. \(\alpha \geq \frac{g}{\mu}\)

The pseudo-force acting on the block is

Fps = -(mass of the block)(acceleration of the frame)

= -mα towards right

= mα towards the left,

This pressing force produces the normal reaction N, and in the limiting case, c \(f_{\max }=\mu \propto N=\mu m \alpha,\), which will act against the weight mg. The block will not fall as long as \(f \geq m g \text { or } \mu m \alpha \geq m g \text { or } \alpha \geq g / \mu\)

Question 22. On a horizontal surface (p = 0.6) of a truck, a block of mass1 kg is placed, and the truck is moving with an acceleration of 5 m s^-2. The frictional force exerted on the block is

1. 5 N
2. 6 N
3. 5.88 N
4. 8 N

Answer: 1. 5 N

Here the truck is the accelerated frame of reference with a = 5 m s^-2.

The pseudo-force acting on the block is

F_ps = ma = ( 1 kg)(5ms^-2)

= 5 N (towards left).

The friction/acts to the right and has the maximum value

⇒ \(f_{\max }=\mu N=(0.6)(1 \mathrm{~kg})\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)=6 \mathrm{~N}\)

Since friction is a self-adjusting force, the frictional force

f = 5 N

Question 23. A bridge over a river is in the form of an arc of radius of curvature R. If m is the total mass of the bike and the rider, and the rider is crossing the bridge at a speed v, the thrust on the bridge at the highest point will be

1. \(\frac{m v^2}{R}\)
2. mg
3. \(\frac{m v^2}{R}-m g\)
4. \(m g-\frac{m v^2}{R}\)

Answer: 4. \(m g-\frac{m v^2}{R}\)

The thrust on the topmost point of the river bridge will be the normal reaction N by the bike.

The centripetal force \(\left(\frac{m v^2}{R}\right)\) is provided by mg – N

Thus, \(\frac{m v^2}{R}=m g-N\)

⇒ \(\mathcal{N}=m g-\frac{m v^2}{R}\) = thrust on the bridge.

Question 24. A block is placed on a smooth hemispherical surface of radius R. The block is given a small horizontal push so that it slides down along the curved spherical surface. The block loses its contact with the hemisphere at a point whose height from file ground is

1. \(\frac{3}{4} R\)
2. \(\frac{2}{3} R\)
3. \(\frac{R}{2}\)
4. \(\frac{2}{\sqrt{3}} R\)

Answer: 2. \(\frac{2}{3} R\)

Let the block start from point A and leave its contact at point P, where ΔAOP = 9.

Now, gain in KE = \(\text { loss in } \mathrm{PE} \Rightarrow \frac{1}{2} m v^2=m g \cdot A B=m g R(1-\cos \theta)\)

⇒ \(v^2=2 g R(1-\cos \theta)\)……(1)

At P, centripetal force = \(\frac{m v^2}{R}=m g \cos \theta-N\)

Here, N = θ (for no contact). So,

v² = gR cosθ…….(3)

Equating (1) and (2),

⇒ \(2 g R(1-\cos \theta)=g R \cos \theta \Rightarrow 3 \cos \theta=2\)

⇒ \(\cos \theta=\frac{2}{3} .\)

∴ height = \(O B=R \cos \theta=\frac{2}{3} R\)

Question 25. A block is placed on a smooth hemispherical surface of radius R. What minimum horizontal velocity must be imparted to the block so that it leaves the hemisphere without sliding over it?

1. \(\frac{\sqrt{8 R}}{2}\)
2. \(2 \sqrt{8 R}\)
3. \(\sqrt{\frac{g R}{2}}\)
4. \(\sqrt{g R}\)

Answer: 3. \(\sqrt{\frac{g R}{2}}\)

Let u be the velocity imparted to the block so that it strikes the ground without touching the sphere. The motion of the block will be like that of a projectile, for which

⇒ \(R=\frac{1}{2} g t^2 \Rightarrow t=\sqrt{\frac{2 R}{g}}\)

Further, \(R=u t=u \sqrt{\frac{2 R}{g}}\)

⇒ \(u=R \sqrt{\frac{g}{2 R}}=\sqrt{\frac{g R}{2}} .\)

Question 26. A 1-m-long string is fixed to a rigid support and carries a mass of 100 g at its free end. The string makes √5/π revolutions per second about a vertical axis passing through the fixed end of the string. What is the angle of inclination of the string with the vertical? (Take g = 10 m s^-2.)

1. 30°
2. 45°
3. 60°
4. 75°

Answer: 3. 60°

Given that m = 100 g = 0.1 kg,

⇒ \(\omega=2 \pi n=\frac{2 \pi \sqrt{5}}{\pi}=2 \sqrt{5} \mathrm{rad} \mathrm{s}^{-1}\) and l =1 m.

The horizontal component of the tension T is

⇒ \(T \sin \theta=m \omega^2 r\)…..(1)

and the vertical component is

⇒ \(T \cos \theta=m g\)…..(2)

Dividing (1) by (2)

⇒ \(\tan \theta=\frac{\omega^2 r}{g}=\frac{(2 \sqrt{5})^2(l \sin \theta)}{10}\)

⇒ \(\frac{\sin \theta}{\cos \theta}=\frac{(4 \times 5)(1 \times \sin \theta)}{10}\)

⇒ \(\cos \theta=\frac{1}{2} \Rightarrow \theta=60^{\circ} \text {. }\)

Question 27. One end of a string of length l is connected to a particle of mass m, and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in a circle at a uniform speed v, the net force on the particle (directed towards the center) will be (T being the tension in the string) 

1. T
2. \(T-\frac{m v^2}{l}\)
3. T + mg
4. \(T+\frac{m v^2}{l}\)

Answer: 1. T

The forces acting on the particle of mass m are the weight (mg), the normal reaction (N), and the tension (T) in the string. Here mg and N balance. So, the net force on the particle will be T, which will provide the required centripetal force.

Question 28. A string can break due to a tension just exceeding 25N. The great. the speed with which a body of mass1 kg can be whirled in a horizontal circle using such a string of length m (without breaking it) is

1. 10 m s^-1
2. 2.5 m s^-1
3. 5 ms^-1
4. 7.5 ms^-1

Answer: 3. 5 ms^-1

Gravity acts vertically downwards. Its component along the horizontal is zero, so only the tension T along the string provides the required centripetal force

⇒ \(\left(\frac{m v^2}{R}\right)\)

∴ \(25 \mathrm{~N}=\frac{(1 \mathrm{~kg}) v^2}{1 \mathrm{~m}} \Rightarrow v=5 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 29. A simple pendulum with a bob of mass m swings with an angular amplitude \(\phi\). When the angular displacement is θ (where θ < \(\phi\)), the tension in the string is

1. mg cos θ
2. mg sin θ
3. Greater than mg cos θ
4. Greater than mg sin θ

Answer: 3. Greater than mg cos θ

When the bob is at P with the angular displacement θ (where θ < Φ), the forces acting are the weight (mg) and the tension (T). The component of mg along the string is mg cosθ.

Then, the net force along the string directed toward the center is

T- mg cos θ, which provides the required

centripetal force \(\left(\frac{m v^2}{r}\right)\)

Thus,

T- mgcosθ = \(\frac{m v^2}{r}\)

⇒ \(T=m g \cos \theta+\frac{m v^2}{r}\)

∴ \(T>m g \cos \theta\)

Question 30. A bridge over a river is in the form of an arc of radius of curvature 10 m. The highest speed with which a motorcyclist can cross the bridge without his bike losing contact with the ground is

1. 10 ms^-1
2. 10 2 ms^-1
3. 10 √3 m s^-1
4. 20 ms^-1

Answer: 1. 10 ms^-1

At the highest point of the river bridge, the forces acting are the weight mg (downward) and the normal reaction N (upward).

The net force (mg- N) towards the center provides the required centripetal force \(\left(\frac{m v^2}{R}\right)\)

Thus, \(m g – N=\frac{m v^2}{R}\)

⇒ \(\mathcal{N}=m g-\frac{m v^2}{R}\)

An increase in the speed (v) of the bike will reduce N and for N = 0 (when the contact will just go),

⇒ \(\frac{m v_{\max }^2}{R}=m g \Rightarrow v_{\max }=\sqrt{g R}=\sqrt{\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(10 \mathrm{~m})}=10 \mathrm{~m} \mathrm{~s}^{-1} .\)

Question 31. A mass m attached to a thin wire is whirled in a vertical circle. The wire is most likely to break when the

1. Mass is at the highest point
2. Wire is horizontal
3. Mass is at the lowest point
4. The wire is inclined at an angle of 60° to the vertical

Answer: 3. Mass is at the lowest point

At the lowest point of the vertical circle, the centripetal \(\left(\frac{m v^2}{l}\right)\) force is provided by T- mg.

Thus, \(T-m g=\frac{m v^2}{l}\)

⇒ \(T=m g+\frac{m v^2}{l}\)

Hence, the tension is maximum at the lowest point, so the chance of breaking is maximum at this point.

Question 32. A particle moving at a velocity v is acted upon by three forces P, Q, and R, shown by the vector triangle in the p figure. The velocity of the particle will

1. Increase
2. Decrease
3. Remain constant
4. Change with time periodically

Answer: 3. Remain constant

According to the triangle rule for vector addition, \(\vec{P}+\vec{Q}+\vec{R}=\overrightarrow{0}\). So, for net force = θ, acceleration = θ; hence the velocity will remain constant.

Question 33. Two particles A and B are undergoing uniform circular motion in concentric circles of radii r_A and r_B with speeds v_A and v_B respectively. Their time periods of revolution are equal. The ratio of the angular speed of A to that of B will be

1. r_A:r_B
2. v_A: v_B
3. r_B:r_A
4. 1:1

Answer: 4. 1:1

The particles A and B are synchronous since they have the same period of revolution (T_A = T_B). Hence, the ratio of their angular speeds is

⇒ \(\frac{\omega_{\mathrm{A}}}{\omega_{\mathrm{B}}}=\frac{\frac{2 \pi}{T_{\mathrm{A}}}}{\frac{2 \pi}{T_{\mathrm{B}}}}=\frac{T_{\mathrm{B}}}{T_{\mathrm{A}}}=1=1: 1 .\)

Question 34. A block of mass 10 kg is in contact with the inner surface of a hollow cylindrical drum of radius 1 m. The coefficient of friction between the block and the surface is 0.1. The minimum angular speed ω required for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis will be

1. √10 rad s^-1
2. \(\frac{10}{2 \pi} \mathrm{rad} \mathrm{s}^{-1}\)
3. 10 rad s^-1
4. 10π rad s^-1

Answer: 3. 10 rad s^-1

The forces acting on the block are its weight mg (vertically downward), the normal reaction \(\mathcal{N}=m \omega^2 r\) (towards the center), and the force of friction

⇒ \(f_{\max }=\mu \propto N\) vertically upward.

For the block to remain stationary,

⇒ \(f_{\max } \geq m g \Rightarrow \mu\left(m \omega^2 r\right) \geq m g\)

⇒ \(\omega_{\min }=\sqrt{\frac{g}{\mu r}}\)

⇒ \(\sqrt{\frac{10 \mathrm{~m} \mathrm{~s}^{-2}}{(0.1)(1 \mathrm{~m})}}\)

= 10 rad s^-1

Question 35, A smooth parabolic wire rotates about the vertical y-axis (expressed as y= 4cx²), as shown below. If a bead of mass m does not slip at (a,b), the value of to is

1. \(2 \sqrt{\frac{2 g c}{b}}\)
2. \(2 \sqrt{2 g c}\)
3. \(2 \sqrt{\frac{2 g c}{a b}}\)
4. \(\sqrt{\frac{g c}{2 a b}}\)

Answer: 4. \(\sqrt{\frac{g c}{2 a b}}\)

Let the bead stay in equilibrium at P. The forces acting on the bead are the weight (mg) and the normal reaction (N). The vertical component N cos θ balances the weight (mg), while the horizontal component N sin 0 provides the centripetal force \(\left(\frac{m v^2}{r}\right)\) for the circular motion.

Hence,

⇒ \(\propto N \sin \theta=\frac{m v^2}{r} \text { and } \alpha \cos \theta=m g\)

∴ \(\tan \theta=\frac{v^2}{r g}\)

From the figure, the slope at P is

⇒ \(\tan \theta=\frac{d y}{d x}=\frac{d}{d x}\left(4 c x^2\right)=8 c x=8 c r\)

Hence,

⇒ \(8 c r=\frac{\omega^2 r}{g} \Rightarrow \omega=\sqrt{8 c g}=2 \sqrt{2 c g}\)

Question 36. An insect is at the bottom of a hemispherical ditch of radius 1 m. It crawls up the ditch but starts slipping after it reaches a height h above the bottom. If the coefficient of friction between the ground and the insect is 0.75 then h is (assuming g = 10 m s^-2)

1. 0.60 m
2. 0.20 m
3. 0.80 m
4. 0.45 m

Answer: 4. 0.45 m

The insect starts slipping when

⇒ \(m g \sin \theta \geq f\)

or, \(m g \sin \theta \geq \mu m g \cos \theta\)

or, \(\tan \theta=\mu=\frac{3}{4}\)

or, \(\frac{P A}{O A}=\mu\)

or, \(\mu=\frac{R \sin \theta}{R-h} .\)

Substituting the values,

⇒ \(\frac{3}{4}=\frac{\frac{3}{5}}{1-h}\)

or, \(1-h=\frac{3}{5} \times \frac{4}{3}=\frac{4}{5}\)

or, \(h=\left(1-\frac{4}{5}\right)=\frac{1}{5} \mathrm{~m}\)

= 20cm

= 0.20m

Motion in a Straight Line

Question 1. If the velocity of a particle is v = At+Bt², where A and B are constants, the distance traveled by it between 1 s and 2 s is

1. \(\frac{3}{2} A+4 B\)
2. \(\frac{A}{2}+\frac{B}{3}\)
3. 3A + 7B
4. \(\frac{3}{2} A+\frac{7}{3} B\)

Answer: 4. \(\frac{3}{2} A+\frac{7}{3} B\)

Given that the velocity at the time t is

⇒ \(v=A t+B t^2 \text { or } \quad \frac{d x}{d t}=A t+B t^2\)

Integrating,

⇒ \(\int d x=\int\left(A t+B t^2\right) d t\)

or, \(x=\frac{A t^2}{2}+\frac{B t^3}{3}+c\)

At t=1s, \(x_1=\frac{A}{2}+\frac{B}{3}+c\)

and at t = 2s, x₂ =2A + \(\frac{8}{3}\)B + c.

∴ The distance covered in the given time interval is

⇒ \(x_2-x_1=\left(2 A+\frac{8}{3} B+c\right)-\left(\frac{A}{2}+\frac{B}{3}+c\right)=\frac{3}{2} A+\frac{7}{3} B\)

Question 2. The motion of a particle along a straight line is described by the equation x =8 +12t-t², where x is in meters and t is in seconds. The retardation of the particle when its velocity becomes zero is

1. 6ms^-2
2. zero
3. 12 m s^-2
4. 24 m s^-2

Answer: 3. 12 m s^-2

The equation representing the position (x) as a function of time (t) is

x = 8 +12t-t³.

Hence, the instantaneous velocity is

⇒ \(v=\frac{d x}{d t}=12-3 t^2\)

and the instantaneous acceleration

⇒ \(a=\frac{d v}{d t}=-6 t\)

When = 0, 12- 3t² = 0 and t = 2 s.

Hence, the magnitude of the acceleration at t = 2 s is

⇒ \(|a|_{t=2 s}=6(2) \mathrm{ms}^{-2}=12 \mathrm{~m} \mathrm{~s}^{-2} \text {. }\)

∴ retardation =12 ms^-2

Question 3. Preeti reached a metro station and found that the escalator was not working. She walked up the stationary escalator in a time tv On other days, if she remains stationary on the moving escalator, the escalator takes her up in a time t₂. The time taken by her to walk up the moving escalator is

1. t₁ – t₂
2. \(\frac{t_1 t_2}{t_1+t_2}\)
3. \(\frac{t_1 t_2}{t_2-t_1}\)
4. \(\frac{t_1+t_2}{2}\)

Answer: 2. \(\frac{t_1 t_2}{t_1+t_2}\)

Let the velocity of Preeti on the stationary escalator be u₀ and the length of the escalator be s. Hence,

⇒ \(u_0=\frac{s}{t_1}\) ….(1)

When the escalator is moving with a velocity u_e,

⇒ \(u_{\mathrm{e}}=\frac{s}{t_2}\) …(2)

Finally, Preeti’s resultant velocity relative to the ground when both are moving will be u₀ + u_e. So,

⇒ \(u_0+u_{\mathrm{e}}=\frac{s}{T}\) …(3)

Adding (1) and (2),

⇒ \(u_0+u_{\mathrm{e}}=s\left(\frac{1}{t_1}+\frac{1}{t_2}\right)\)

Equating (3) and (4),

⇒ \(\frac{s}{T}=s\left(\frac{t_1+t_2}{t_1 t_2}\right)\)

Hence, the time T needed for Preeti to walk up the moving escalator is

⇒ \(T=\frac{t_1 t_2}{t_1+t_2}\)

Question 4. The displacement x (in meters) of a particle of mass m (in kilograms) moving in one dimension under the action of a force is related to the time t (in seconds) by t = √x + 3. The displacement of the particle when its velocity is zero will be

1. 2 m
2. Zero
3. 4 m
4. 6 m

Answer: 2. Zero

Time (t) as a function of position (x) is t = √x +3 or √x =t- 3.

Squaring, x = t²- 6t + 9 = (t- 3)².

∴ instantaneous velocity, \(v=\frac{d x}{d t}=2 t-6\)

For 0 = 0, 2t = 6 or t = 3.

Hence, the position at t = 3 will be x =(t- 3)² = 0.

Question 5. Two cars P and Q start from a point at the same time in a straight line, and their positions are represented by \(x_{\mathrm{P}}(t)=a t+b t^2\) and \(x_{\mathrm{Q}}(t)=f t-t^2\) respectively. At what time do the cars have the velocity?

1. \(\frac{a+f}{2(1+b)}\)
2. \(\frac{a+f}{2(b-1)}\)
3. \(\frac{a-f}{1+b}\)
4. \(\frac{f-a}{2(1+b)}\)

Answer: 4. \(\frac{f-a}{2(1+b)}\)

For the car P, x_p(t) = at + bt², and for the car Q, x_Q(t) =ft- f².

∴ The velocity of P is

⇒ \(v_{\mathrm{P}}=\left(\frac{d x}{d t}\right)_{\mathrm{P}}=a+2 b t\)

and the velocity of Q is

⇒ \(v_{\mathrm{Q}}=\left(\frac{d x}{d t}\right)_{\mathrm{Q}}=f-2 t\)

At the time t, let P and Q have the same velocity. So,

V_p = V_Q

or, a + 2bt = t – 2t or 2t(b + 1) = f-a.

∴ \(t=\frac{f-a}{2(1+b)}\)

Question 6. A particle covers half its journey with a speed vl and the other half with a speed v₂. Its average speed during the complete journey is

1. \(\frac{v_1 v_2}{v_1+v_2}\)
2. \(\frac{2 v_1 v_2}{v_1+v_2}\)
3. \(\frac{v_1+v_2}{2}\)
4. \(\frac{v_1^2 v_2^2}{v_1^2+v_2^2}\)

Answer: 3. \(\frac{v_1+v_2}{2}\)

Let s be the total distance covered.

For the first half,

⇒ \(\frac{s}{2}=v_1 t_1 \Rightarrow t_1=\frac{s}{2 v_1}\)

Similarly, in the second half,

⇒ \(\frac{s}{2}=v_2 t_2 \Rightarrow t_2=\frac{s}{2 v_2}\)

Hence, the average velocity is

⇒ \(v_{\mathrm{av}}=\frac{\text { total displacement }}{\text { total time taken }}=\frac{s}{t_1+t_2}=\frac{s}{\frac{s}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)}=\frac{2 v_1 v_2}{v_1+v_2} \text {. }\)

Question 7. A particle starts moving from rest with a uniform acceleration of (4/3) m s^-2. The distance traveled by the particle during the third second of its motion is

1. 4 m
2. 6 m
3. \(\frac{10}{3} \mathrm{~m}\)
4. \(\frac{19}{3} m\)

Answer: 3. \(\frac{10}{3} \mathrm{~m}\)

The distance covered in the nth second is

⇒ \(s_n=u+\left(\frac{2 n-1}{2}\right) a\)

Given that u =0,n = 3, a = \(\frac{10}{3}\) ms^-2.

∴ The distance covered in the third second is

⇒ \(s_3=0+\left(\frac{2 \times 3-1}{2}\right) \frac{4}{3} \mathrm{~m}=\frac{10}{3} \mathrm{~m}\)

Question 8. A car moves from X to Y with a uniform speed v₁ and returns to X with a uniform speed v₂. The average speed during this round trip is

1. \(\sqrt{v_1 v_2}\)
2. \(\frac{v_1 v_2}{v_1+v_2}\)
3. \(\frac{v_1+v_2}{2}\)
4. \(\frac{2 v_1 v_2}{v_1+v_2}\)

Answer: 4. \(\frac{2 v_1 v_2}{v_1+v_2}\)

Average speed = \(\frac{\text { total distance covered }}{\text { total time taken }}\)

⇒ \(\frac{s+s}{\frac{s}{v_1}+\frac{s}{v_2}}=\frac{2 s}{s\left(\frac{1}{v_1}+\frac{1}{v_2}\right)}=\frac{2 v_1 v_2}{v_1+v_2}\)

Question 9. A particle moves along a straight line OX. At a time t (in seconds), the distance x (in meters) of the particle from O is given by \(x=40+12 t-t^3\). How long would the particle travel before coming to rest?

1. 16 m
2. 24 m
3. 40 m
4. 50 m

Answer: 1. 16 m

Given that x = 40+12t-t3.

∴ instantaneous velocity, v = \(\frac{d x}{d t}\) =12-3t².

For v = 0,

12-3t2 = 0 => t = 2s.

The distance covered by the particle before coining to rest will be

⇒ \(s=\int d s=\int_{t=0}^{t=2 s} v d t=\int_0^{2 s}\left(12-3 t^2\right) d t\)

⇒ \(\left[12 t-t^3\right]_0^2=\left(12 \times 2-2^3\right) \mathrm{m}\)

= 16 m.

Question 10. The position s (in meters) of a particle as a function of time t (in seconds) is expressed as \(s=3 t^3+7 t^2+14 t+8\) The value of the acceleration of the particle at time t =1 s is

1. 16 ms^-2
2. 32 ms^-2
3. 10 ms^-2
4. 30 ms^-2

Answer: 2. 32 ms^-2

Given that s = 3³ +7t² +14t +8.

Hence, velocity = \(v=\frac{d s}{d t}=9 t^2+14 t+14\)

and acceleration = \(a=\frac{d v}{d t}=18 t+14\)

The value of the acceleration t =1 s is

⇒ \(|a|_{t=1 \mathrm{~s}}=|18 \mathrm{t}+14|_{t=1 \mathrm{~s}}\)

=32 ms^-2.

Question 11. The position x of a particle varies with time t as \(x=a t^2-b t^3\). The time at which acceleration will be zero is equal to

1. \(\frac{a}{3 b}\)
2. \(\frac{3 a}{2 b}\)
3. \(\frac{a}{b}\)
4. Zero

Answer: 1. \(\frac{a}{3 b}\)

The position (x) of the given particle as a function of time (t) is

⇒ \(x=a t^2-b t^3\)

∴ instantaneous velocity = \(v=\frac{d x}{d t}=2 a t-3 b t^2\)

and instantaneous acceleration = \(a=\frac{d v}{d t}=2 a-6 b t\)

When A = 0, the required time is t = \(\frac{2 a}{6 b}=\frac{a}{3 b}\)

Question 12. The displacement * of a particle varies with the time t as \(x=a e^{-\alpha t}+b e^{\beta t}\), where a, b, a and p are positive constants. The velocity of the particle will

1. Drop to zero when a = p
2. Go on decreasing with time
3. Be independent of p
4. Go on increasing with time

Answer: 4. Go on increasing with time

Given that \(x=a e^{-\alpha t}+b e^{\beta t}\)

Hence, velocity = \(v=\frac{d x}{d t}=-a \alpha e^{-\alpha t}+b \beta e^{\beta t}\)

The velocity of the particle will increase with time, being an exponential function

Question 13. A car is moving along a straight road with a uniform acceleration. It passes two points P and Q separated by some distance with a velocity of 30 km h^-1 and 40 km h^-1 respectively. The velocity of the car while crossing the midpoint between P and Q will be

1. 33.5 km h^-1
2. \(20 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\)
3. \(25 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\)
4. 38 km h^-1

Answer: 3. \(25 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\)

Given that \(v_{\mathrm{P}}=30 \mathrm{~km} \mathrm{~h}^{-1} \text { and } v_{\mathrm{Q}}=40 \mathrm{~km} \mathrm{~h}^{-1}\)

Let the velocity at the midpoint O be v0 and the uniform acceleration
be a.

For the motion from P to Q,

⇒ \(v_{\mathrm{Q}}^2-v_{\mathrm{P}}^2=2 a L\)

or, \(40^2-30^2=2 a L\) ….(1)

For the motion from to Q,

⇒ \(v_{\mathrm{Q}}{ }^2-v_{\mathrm{O}}{ }^2=2 a\left(\frac{L}{2}\right)\)

or, \(40^2-v_{\mathrm{O}}^2=a L .\) ….(2)

Dividing (1) by (2),

⇒ \(\frac{40^2-30^2}{40^2-v_O^2}=2\)

Solving, we get \(v_0=25 \sqrt{2} \mathrm{kmh}^{-1}\).

Question 14. The acceleration of a particle is increasing linearly with time as bt. The particle starts from the origin with an initial velocity v₀. The distance traveled by the particle in time t will be

1. \(v_0 t+\frac{1}{3} b t^2\)
2. \(v_0 t+\frac{1}{6} b t^3\)
3. \(v_0 t+\frac{1}{2} b t^2\)
4. \(v_0 t+\frac{1}{3} b t^3\)

Answer: 2. \(v_0 t+\frac{1}{6} b t^3\)

Acceleration = a = bt = \(\frac{dv}{dt}\).

So,dv = bt dt.

Integrating,

⇒ \(\int^v d v=b \int^t t d t \Rightarrow v-v_0=\frac{b}{2} \cdot t^2 \Rightarrow v=\frac{d x}{d t}=v_0+\frac{b t^2}{2}\)

Integrating again,

⇒ \(x=\int v d t=\int_0^t\left(v_0+\frac{b t^2}{2}\right) d t=\left[v_0 t+\frac{b t^3}{6}\right]_0^t\)

∴ the distance traveled in the time this

⇒ \(x=v_0 t+\frac{b t^3}{6}\)

Question 15. A particle starts sliding down a smooth inclined plane. If sn is the distance traversed by it from a time t = (n-1) s to a time t = n s then the ratio \(s_n / s_{n+1}\) is

1. \(\frac{2 n-1}{2 n+1}\)
2. \(\frac{2 n+1}{2 n}\)
3. \(\frac{2 n}{2 n+1}\)
4. \(\frac{2 n+1}{2 n-1}\)

Answer: 1. \(\frac{2 n-1}{2 n+1}\)

Given that u = 0. So, the distance covered during the nth second is

⇒ \(s_n=u+(2 n-1) \frac{a}{2}=(2 n-1) \frac{a}{2}\)

and that during the (n + l)th second is

⇒ \(s_{n+1}=[2(n+1)-1] \frac{a}{2}\)

∴ \(\frac{S_n}{S_{n+1}}=\frac{2 n-1}{2 n+1}\)

Question 16. A particle is moving with a velocity \(\vec{v}=k(y \hat{i}+x \hat{j})\), where k is constant. The general equation for its path is

1. y² – x² + constant
2. y = x² + constant
3. y² = x + constant
4. xy = constant

Answer: 1. y² – x² + constant

Given that \(\vec{v}=k(y \hat{i}+x \hat{j})=v_x \hat{i}+v_y \hat{j}\)

∴ \(v_x=\frac{d x}{d t}=k y \text { and } v_y=\frac{d y}{d t}=k x\)

∴ \(\frac{v_y}{v_x}=\frac{x}{y}=\frac{d y / d t}{d x / d t}=\frac{d y}{d x}\)

∴ ydy = xdx.

Integrating,

⇒ \(\frac{y^2}{2}=\frac{x^2}{2}\) + constant

y² = x² + constant.

Question 17. A particle, located at x = 0 at a time t = 0, starts moving along the positive x-direction with a velocity v, which varies as v = a√x. The displacement of the particle varies with time as

1. t³
2. t²
3. t
4. t½

Answer: 2. t²

Instantaneous velocity = \(v=\frac{d x}{d t}=\alpha \sqrt{x}\)

∴ \(\frac{d x}{\sqrt{x}}=\alpha d t\)

Integrating,

⇒ \(2 \sqrt{x}=\alpha t \Rightarrow 4 x=\alpha^2 t^2 \Rightarrow x \propto t^2\).

Question 18. The velocity of a particle is \(v=v_0+g t+f t^2\). If its position at t= 0 gt is x = 0 then its displacement after a unit time (f = 1 s) is

1. \(v_0+2 g+3 f\)
2. \(v_0+\frac{g}{2}+\frac{f}{3}\)
3. \(v_0+g+f\)
4. \(v_0+\frac{g}{2}+f\)

Answer: 2. \(v_0+\frac{g}{2}+\frac{f}{3}\)

Given that \(v=\frac{d x}{d t}=v_0+g t+f^2\).

So, the displacement at a time t will be

⇒ \(x=\int d x=\int v d \dot{t}=\int\left(v_0+g t+f t^2\right) d t\)

⇒ ⇒ \(\left[v_0 t+g \frac{t^2}{2}+f \frac{t^3}{3}\right]_{t=0}^{t=1 \mathrm{~s}}\)

⇒ \(v_0+\frac{g}{2}+\frac{f}{3}\)

Question 19. The relation between the time t and the displacement x is t = ax² + bx, where a and b are constants. The acceleration is

1. -2abv²
2. 2bv³
3. -2av³
4. 2av²

Answer: 3. -2av³

Given that t = ax² + bx.

Differentiating with respect to time t,

⇒ \((2 a x+b) \frac{d x}{d t}=1\)

or v(2ax + b) =1

or \(v=\frac{1}{2 a x+b}\)

Differentiating again with respect to time t,

acceleration = \(\frac{d v}{d t}=\frac{-2 a v}{(2 a x+b)^2}=-(2 a v) v^2=-2 a v^3\)

Question 20, The speeds of two identical cars are u and 4u at a given instant. The ratio of their respective distances at which the two cars are stopped after that instant is

1. 1:1
2. 1:4
3. 1:8
4. 1:16

Answer: 4. 1:16

If d = stopping distance then

⇒ \(v^2=0=u^2-2 a d \text { or } d=\frac{u^2}{2 a}\)

∴ \(\frac{s_1}{s_2}=\frac{u_1^2}{u_2^2}\) [∵ a is the same for the two identical cars]

\(\frac{u^2}{(4 u)^2}\)

= 1:16.

Question 21. An object moving with a speed of 6.25 m s^-1 is decelerated at a rate given \(\frac{d v}{d t}=-2.5 \sqrt{v}\), where v is the instantaneous speed. The time taken by the object to come to rest would be

1. 2 s
2. 4 s
3. 8 s
4. 1 s

Answer: 1. 2 s

Given that \(\frac{d v}{d t}=-2.5 \sqrt{v}\)

∴ \(\frac{d v}{\sqrt{v}}=-2.5 d t\)

Integrating, 2√v = -2.5f + c.

At t = 0, v = 6.25ms^-1, soc = 5.

For the object to come to rest,

2V0 = -2.5t + 5

=> t = 2s

Question 22. A particle is moving eastwards with a velocity of 5 m s^-1. In 10 s the velocity changes to 5 m s^-1 northwards. The average acceleration during tins time is

1. \(\frac{1}{\sqrt{2}} \mathrm{~m} \mathrm{~s}^{-2} \text { towards } \mathrm{NE}\)
2. \(\frac{1}{2} \mathrm{~m} \mathrm{~s}^{-2} \text { towards north }\)
3. Zero
4. \(\frac{1}{\sqrt{2}} \mathrm{~m} \mathrm{~s}^{-2} \text { towards NW }\)

Answer: 4. \(\frac{1}{\sqrt{2}} \mathrm{~m} \mathrm{~s}^{-2} \text { towards NW }\)

The average acceleration is

⇒ \(\vec{a}_{\mathrm{av}}=\frac{\text { change in velocity }}{\text { time }}=\frac{\vec{v}_{\mathrm{f}}-\vec{v}_{\mathrm{i}}}{t}\)

⇒ \(\frac{\left(5 \mathrm{~ms}^{-1}\right) \hat{j}-\left(5 \mathrm{~ms}^{-1}\right) \hat{i}}{10 \mathrm{~s}}=\frac{1}{2}(\hat{j}-\hat{i}) \mathrm{ms}^{-2}\)

∴ \(\left|\vec{a}_{\mathrm{av}}\right|=\frac{\sqrt{2}}{2} \mathrm{~ms}^{-2}=\frac{1}{\sqrt{2}} \mathrm{~ms}^{-2} \text { (towards NW)}\)

Question 23. The adjoining figure shows the variation of the acceleration of a particle with time. The particle is moving along a straight line and has a velocity v = 2 m s^-1 at f = 0. The velocity after 2 s will be

1. 2 ms^-1
2. 4 ms^-1
3. 6 ms^-1
4. 8 m s^-1

Answer: 3. 6 ms^-1

The area enclosed under the given-t graph is

⇒ \(A=\frac{1}{2}(2 \mathrm{~s})\left(4 \mathrm{~ms}^{-2}\right)=4 \mathrm{~ms}^{-1}\)

But this area = \(\int a d t=\int \frac{d v}{d t} d t=[v]_{v_{\mathrm{i}}}^{v_{\mathrm{i}}}\)

∴ 4 m s^-1 = v_f – v_i = v_f-2 m s^-1

∴ The velocity after 2 s is v_f = 6 m s^-1.

Question 24. The given figure shows the velocity-time graph of two particles A and B moving along the same straight line in the same direction. Which of the following statements is true?

1. The relative velocity is zero.
2. The relative velocity is nonzero but constant.
3. The relative velocity increases continuously.
4. The relative velocity decreases continuously.

Answer: 3. The relative velocity increases continuously.

The relative velocity (ur) and relative acceleration (ar) of two particles

are related by vr = ur + art.

Here, ur = 0 and at = (aA – aB) = constant.

∴ relative velocity = vT = (aA- aB)t.

∴ \(v_{\mathrm{r}} \propto t .\)

Hence, the relative velocity increases continuously with time.

Question 25. The position of a particle moving along a straight line is expressed as a function of time (t) as x = 6 + 12t- 2t², where x is in meters and t is in seconds. The distance covered by the particle in the first 5 s is

1. 32 m
2. 24 m
3. 20 m
4. 26 m

Answer: 4. 26 m

Given that x = 6 + 12t- 2t².

Hence, velocity = u = \(v=\frac{d x}{d t}=12-4 t\)

and acceleration = \(a=\frac{d v}{d t}=-4 \mathrm{~m} \mathrm{~s}^{-2}\)

Initial velocity = \(u=[12-4 t]_{t=0}=12 \mathrm{~m} \mathrm{~s}^{-1}\)

Due to the retardation of -4 ms^-2, the particle comes to rest when
u = 0 =12-4t or t =3s.

The distance covered in3s is

⇒ \(s_1=u t+\frac{1}{2} a t^2=(12 \times 3) \mathrm{m}+\frac{1}{2}(-4)(9) \mathrm{m}=18 \mathrm{~m}\)

The distance covered backward in 2s is

⇒ \(s_2=\frac{1}{2}(4)(2)^2 \mathrm{~m}=8 \mathrm{~m}\)

Hence, total distance = s = s1 + s2

= 18 m + 8 m

= 26 m.

Question 26. A particle starts moving along a straightlinesuchthattheacceleration varies with the displacement (s) as shown in the given figure. Which of the following represents the velocity-displacement graph?

Answer: 2.

The graph showing the variation of acceleration (a) with displacement (s) is linear. Hence, a = ks, where k- constant,

∴ \(a=\frac{d v}{d t}=\frac{d v}{d s} \frac{d s}{d t}=k s\)

or, \(v \frac{d v}{d s}=k s\) [∵ \(\frac{d s}{d t}=v\)]

or, vdv = ks ds.

Integrating,

⇒ \(\frac{v^2}{2}=\frac{k s^2}{2} \text { or } v \propto s\).

⇒ Question 27. Two particles moving along the same straight line and leaving the same point O at the same time have their initial velocities u and 2u and uniform accelerations 2a and a respectively. The distance of the two particles from O when one particle overtakes the other is

1. \(\frac{u^2}{a}\)
2. \(\frac{4 u^2}{a}\)
3. \(\frac{6 u^2}{a}\)
4. \(\frac{8 u^2}{a}\)

Answer: 3. \(\frac{6 u^2}{a}\)

When one particle overtakes the other at a time t, both travel the same distance s.

Hence, for the first particle,

⇒ \(s=u t+\frac{1}{2}(2 a) t^2\)

and for the second particle,

⇒ \(s=2 u t+\frac{1}{2} a t^2\)

Equating,

⇒ \(u t+a t^2=2 u t+\frac{a}{2} t^2 \Rightarrow \frac{a}{2} t=u \Rightarrow t=\frac{2 u}{a} .\)

Hence,

⇒ \(s=u t+\frac{1}{2}(2 a) t^2=u\left(\frac{2 u}{a}\right)+\frac{1}{2}(2 a)\left(\frac{2 u}{a}\right)^2=\frac{2 u^2}{a}+\frac{4 u^2}{a}=\frac{6 u^2}{a}\)

Question 28. A particle moves a distance x in a time t according to the equation x = {t + 5)^-1. The acceleration of the particle is proportional to

1. (velocity)^2/3
2. (distance)²
3. (distance)^-2
4. (velocity)^3/2

Answer: 1. (distance)²

The displacement (x) of the given particle at a time t is x = (t + 5)^-1.

∴ velocity = \(v=\frac{d x}{d t}=-(t+5)^{-2}\)

and acceleration = \(a=\frac{d v}{d t}=2(t+5)^{-3}\)

∴ \(a=2\left[(t+5)^{-1}\right]^3=2 x^3 \Rightarrow a \propto x^3\)

But

⇒ \(v^{3 / 2}=-(t+5)^{-3} \text {. Hence, } a \propto v^{3 / 2} \text {. }\)

Question 29. A particle starts moving from rest under the action of a constant force. If it covers a distance of sx in the first s and a distance s² in the first 20 s then

1. s₂ = s₁
2. s₂ = 4s₁
3. s₂ = 3s₁
4. s₂ = 2s₁

Answer: 2. s₂ = 4s₁

Initial velocity = u = 0.

The distance covered in the first s is

⇒ \(s_1=\frac{1}{2} a\left(10^2\right)=50 a,\)

and the distance covered in the first 20 s is

⇒ \(s_2=\frac{1}{2} a\left(20^2\right)=200 a=4(50 a)=4 s_1\)

∴ \(s_2=4 s_1\)

Question 30. A particle moves in a straight line with a constant acceleration. It changes its velocity from 10ms^-1 to 20ms^-1 while passing through a distance of 135 m in a time t. The value of t is

1. 10 s
2. 9 s
3. 12 s
4. 1.8 s

Answer: 2. 9 s

Given that, u = 10 m s^-1, v = 20m s^-1, and s = 135 m.

∴ acceleration = \(a=\frac{v^2-u^2}{2 s}=\frac{400-100}{2 \times 135} \mathrm{~ms}^{-2}=\frac{10}{9} \mathrm{~ms}^{-2} .\)

Now, v = u + at, so the required time is

⇒ \(t=\frac{v-u}{a}=\frac{20 \mathrm{~ms}^{-1}-10 \mathrm{~ms}^{-1}}{\frac{10}{9} \mathrm{~ms}^{-2}}=9 \mathrm{~s}\)

Question 31. The position x of a particle with respect to the time t along the x-axis is given by \(x=9 t^2-t^3\), where x is in meters and t is in seconds. What will be the position of the particle when it achieves the maximum speed in the positive

1. 54 m
2. 32m
3. 24 m
4. 81m

Answer: 1. 54 m

The position as a function of time (t) is x = 9t²-t³ and thus the velocity

is \(v=\frac{d x}{d t}=18 t-3 t^2\)

For v to be the maximum,

\(\frac{d v}{d t}\) = 0 or 18 — 6f = 0 or t = 3s.

The position at f = 3 s willbe

⇒ \(|x|_{t=3 \mathrm{~s}}=\left|9 t^2-t^3\right|_{t=3 \mathrm{~s}}\)

= 81m-27m

= 54m.

Question 32. A bus is moving at a speed of 10 ms^-1 on a straight road. A scooterist wishes to overtake the bus in 100s. If the bus is at a distance of 1 km from the scooterist, with what speed should the scooterist chase the bus?

1. 20 ms^-1
2. 10 ms^-1
3. 40 ms^-1
4. 25 ms^-1

Answer: 1. 20 ms^-1

Let the velocity of the scooter be v sc.

Given that the velocity of the bus = 10 m s^-1 and its initial (relative) separation between the two vehicles =1 km = 1000 m.

The acceleration values of both are zero. So, for the relative separation to reduce to zero,

⇒ \(s_{\mathrm{r}}=u_{\mathrm{r}} t \Rightarrow t=\frac{s_{\mathrm{r}}}{u_{\mathrm{r}}}=\frac{1000 \mathrm{~m}}{v_{\mathrm{sc}}-10 \mathrm{~m} \mathrm{~s}^{-1}}=100 \mathrm{~s}\)

⇒ \(v_{\mathrm{sc}}-10 \mathrm{~m} \mathrm{~s}^{-1}=10 \mathrm{~m} \mathrm{~s}^{-1} \Rightarrow v_{\mathrm{sc}}=20 \mathrm{~m} \mathrm{~s}^{-1}\)

Hence, the velocity of the scooter is v sc = 20 m s^-1.

Question 33. If a car at rest accelerates uniformly to a speed of 144 km h^-1 in 20 s, it covers a distance of

1. 2980 m
2. 1440 m
3. 400 m
4. 20 m

Answer: 3. 400 m

Given that u = 0, v = 144 km h^-1  = 144 x \(\frac{5}{18}\) m s^-1  = 40 m s^-1  and the time taken = 20 s.

∵ v = u + at,

∴ \(a=\frac{v}{t}=\frac{40 \mathrm{~m} \mathrm{~s}^{-1}}{20 \mathrm{~s}}=2 \mathrm{~m} \mathrm{~s}^{-2}\)

∴ The distance covered is

⇒ \(s=u t+\frac{1}{2} a t^2=0+\frac{1}{2}\left(2 \mathrm{~m} \mathrm{~s}^{-2}\right)(20 \mathrm{~s})^2\)

= 400m.

Question 34. A car accelerates from rest at a constant rate for some time, after which it decelerates at a constant rate of P and comes to rest. If the total time elapsed is t, the maximum velocity acquired by the car will be

1. \(\left(\frac{\alpha^2+\beta^2}{\alpha \beta}\right) t\)
2. \(\left(\frac{\alpha \beta}{\alpha+\beta}\right) t\)
3. \(\left(\frac{\alpha^2-\beta^2}{\alpha \beta}\right) t\)
4. \(\left(\frac{\alpha+\beta}{\alpha \beta}\right) t\)

Answer: 2. \(\left(\frac{\alpha \beta}{\alpha+\beta}\right) t\)

Let v max be the maximum velocity. While accelerating, sa

⇒ \(v_{\max }=\alpha t_1 \Rightarrow t_1=\frac{v_{\max }}{\alpha} .\)

Similarly, while decelerating to stop finally,

⇒ \(\frac{0-v_{\max }}{t_2}=-\beta \text { or } t_2=\frac{v_{\max }}{\beta}\)

Total time = \(t=t_1+t_2=v_{\max }\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)\)

∴ \(v_{\max }=\left(\frac{\alpha \beta}{\alpha+\beta}\right)\)

Question 35. 11M? displacement 9 (in meters) of a particle moving along a straight line is expressed as a function of time t (in seconds) by the equation \(s=\left(t^3-6 t^2+3 t+4\right)\). When the acceleration is zero, the velocity will be

1. 42 m s^-1
2. -9 m s^-1
3. 5ms^-1
4. -12 m s^-1

Answer: 2. -9 m s^-1

Given that s = t³-6t² + 3t + 4.

Hence, velocity = \(y=\frac{d s}{d t}=3 t^2-12 t+3\)

and acceleration = a = \(\frac{d v}{d t}\)

= 6t-12 = 0.

So, t = 2 s.

The required velocity is

⇒ \(v=\left|3 t^2-12 t+3\right|_{t=2 \mathrm{~s}}\)

= (12-24+3) ms^-1

= -9 ms^-1.

Question 36. A bus travels the first one-third distance at a speed of 10 km h^-1 the next one-third distance at 20 km h^-1 and the last one-third distance at 60 km h^-1. The average speed of the bus is

1. 10 km h^-1
2. 16 km h^-1
3. 18 km h^-1
4. 40 km hr^-1

Answer: 3. 18 km h^-1

Let the total distance covered by s.

∴ \(T=t_1+t_2+t_3=\frac{s}{3 u_1}+\frac{s}{3 u_2}+\frac{s}{3 u_3}=\frac{s}{3}\left(\frac{1}{u_1}+\frac{1}{u_2}+\frac{1}{u_3}\right)\)

Hence, the total time of travel is

⇒ \(\frac{s}{3}\left(\frac{1}{10}+\frac{1}{20}+\frac{1}{60}\right)=\frac{s \times 10}{3 \times 60}\)

∴ average speed \(=v_{\mathrm{av}}=\frac{\mathrm{s}}{T}=18 \mathrm{~km} \mathrm{~h}^{-1}\)

Question 37. A car covers a distance of 200 m. It covers the first half of the distance at a speed of 40 km h^-1 and the second half at a speed v. If the average speed of the car is 48 km h^-1, the value of vis

1. 48 km h^-1
2. 45 km h^-1
3. 60 km h^-1
4. 50 km h^-1

Answer: 3. 60 km h^-1

Since the motion of the car is uniform, its acceleration is zero. During the first half,

⇒ \(\frac{s}{2}=u_1 t_1 \quad \text { or } \quad t_1=\frac{s}{2 u_1}\)

and during the second half,

⇒ \(t_2=\frac{s}{2 u_2}\)

the total time of travel is

⇒ \(T=t_1+t_2=\frac{s}{2}\left(\frac{1}{u_1}+\frac{1}{u_2}\right)\)

the average speed is

⇒ \(v_{\mathrm{av}}=\frac{s}{T}=\frac{2}{\frac{1}{u_1}+\frac{1}{u_2}}\)

Substituting the values,

⇒ \(48=\frac{2}{\frac{1}{40}+\frac{1}{v}}\)

or, \(\frac{1}{40}+\frac{1}{v}=\frac{1}{24}\)

or, v = 60 km^-1

Question 38. A car starting from rest and moving with a constant acceleration covers a distance of s₁ in the fourth second and a distance of s₂ in the sixth second The ratio s₁/s₂ is

1. \(\frac{4}{9}\)
2. \(\frac{6}{11}\)
3. \(\frac{7}{11}\)
4. \(\frac{2}{3}\)

Answer: 3. \(\frac{7}{11}\)

Given that u = 0. So, in the fourth second,

⇒ \(s_4=u+\left(\frac{2 n-1}{2}\right) a=\frac{7}{2} a\)

and in the sixth second

⇒ \(s_6=\frac{11}{2} a .\)

∴ \(\frac{s_4}{s_6}=\frac{\frac{7}{2} a}{\frac{11}{2} a}=\frac{7}{11}\)

Question 39. The acceleration a of a body starting from rest varies with the time t according to the relation a = 3t + 4. The velocity of the body at the time t = 2s will be

1. 10 ms^-1
2. 12 ms^-1
3. 14 m s^-1
4. 16 m s^-1

Answer: 3. 14 m s^-1

Given that

⇒ \(a=\frac{d v}{d t}=3 t+4\)

∴ \(v=\int_0^t(3 t+4) d t=\frac{3}{2} t^2+4 t\)

Aat t=2s, \(v=\left[\frac{3}{2}\left(2^2\right)+4(2)\right] \mathrm{ms}^{-1}\)

= 143s ^-1.

Question 40. The displacement y meters) of a body varies with the time t Cm seconds) as \(y=-\frac{2}{3} t^2+16 t+2\) How long does the body take to come to rest? 

1. 8 s
2. 10 s
3. 12s
4. 16 s

Answer: 3. 12s

The position is given by

⇒ \(y=-\frac{2}{3} t^2+16 t+2\)

Comparing the equation with the standard equation of a uniformly accelerated motion,

⇒ \(s=u t+\frac{1}{2} a t^2\) we have

u = 16ms^-1

and \(\frac{a}{2}=-\frac{2}{3} \text { or } a=-\frac{4}{3} \mathrm{~ms}^{-2}\)

For the body to come to rest, v = 0.

∴ \(v=u+a t \Rightarrow 0=16 \mathrm{~m} \mathrm{~s}^{-1}+\left(-\frac{4}{3} \mathrm{~m} \mathrm{~s}^{-2}\right) t\)

t = 12s.

Question 41. The given figure represents the speed-time graph of a body moving along a straight line. How much distance does it cover during the last 10 seconds of its motion?

1. 40m
2. 100 m
3. 60 m
4. 120 m

Answer: 3. 60 m

The area under the v-t graph gives the displacement. So, the distance covered in the last 10 s will be the area of ΔABC, i.e.,

⇒ \(\frac{1}{2}(B C)(A B)\)

⇒ \(\frac{1}{2}(20 \mathrm{~s}-10 \mathrm{~s})\left(20 \mathrm{~m} \mathrm{~s}^{-1}\right)\)

= 100m.

Question 42. The velocity-time graph of a stone thrown vertically upwards with an initial velocity of 30 m s^-1 is shown in the given figure. The velocity in the upward direction is taken as positive. What is the maximum height to which the stone rises?

1. 30m
2. 45m
3. 80m
4. 90m

Answer: 2. 45m

Given that u = 30m s^-1.

Acceleration = slope of the line AB, so a = \(\frac{0-30 \mathrm{~ms}^{-1}}{3 \mathrm{~s}}=-10 \mathrm{~m} \mathrm{~s}^{-2}\)

At the maximum height, v = 0.

Hence, by \(v^2=u^2-2 g h\)

⇒ \(h=\frac{u^2}{2 g}=\frac{900}{20} \mathrm{~m}\)

= 45m

Question 43. The driver of train A moving at a speed of 30 m s^-1 sights another train B moving on the same track at a speed of 10 m s^-1 in the same direction. He immediately applies the brakes and achieves a uniform retardation of 2 m s^-2. To avoid a collision, what must be the minimum distance between the two trains?

1. 100 m
2. 120 m
3. 60m
4. 160 m

Answer: 1. 100 m

The relative speed of the train A with respect to the train B,

vAB = vA -vB

= (30- 10) m s^-1

= 20 m s^-1.

To avoid a collision, let the minimum separation between them be s.

This means that the relative speed must reduce to zero when the distance covered is s.

Thus,

⇒ \(v_{\mathrm{r}}^2-u_{\mathrm{r}}^2=2 a_{\mathrm{r}} s\)

⇒ \(0-\left(20 \mathrm{~m} \mathrm{~s}^{-1}\right)^2=2\left(-2 \mathrm{~m} \mathrm{~s}^{-2}\right) \mathrm{s}\)

s = 100m.

Question 44. Three particles P, Q, and R are projected from the top of a tower with the same speed u. P is thrown straight up, Q is thrown straight down and R is thrown horizontally. They hit the ground with speeds of v_p, v_Q, and v_R respectively. Then,

1. \(v_{\mathrm{P}}>v_{\mathrm{Q}}=v_{\mathrm{R}}\)
2. \(v_{\mathrm{P}}=v_{\mathrm{Q}}>v_{\mathrm{R}}\)
3. \(v_{\mathrm{P}}=v_{\mathrm{Q}}=v_{\mathrm{R}}\)
4. \(v_{\mathrm{P}}>v_{\mathrm{Q}}>v_{\mathrm{R}}\)

Answer: 3. \(v_{\mathrm{P}}=v_{\mathrm{Q}}>v_{\mathrm{R}}\)

The net vertical displacement for each of the three particles is the same (= h).

For P, work done by gravity is mph.

Hence, change in KE = \(\frac{1}{2} m_{\mathrm{P}}\left(v_{\mathrm{P}}^2-u^2\right) \Rightarrow \frac{1}{2} m_{\mathrm{P}}\left(v_{\mathrm{P}}^2-u^2\right)=m_{\mathrm{P}} g h\)

vp² =2gh+u².

Similarly, \(v_{\mathrm{O}}^2=2 g h+u^2 \text { and } v_{\mathrm{R}}^2=2 g h+u^2\)

∴ \(v_{\mathrm{P}}=v_{\mathrm{Q}}=v_{\mathrm{R}}\)

Question 45. A body dropped from a tower of height h covers a distance h/2inthe last second of its motion. The height of the tower is approximately (taking g = 10 ms^-1)

1. 50 m
2. 55 m
3. 58 m
4. 60 m

Answer: 3. 58 m

Let the total time of fall be t. So,

⇒ \(h=\frac{1}{2} g t^2\) ……(1)

The distance covered in the final second is h/2. So, for the upper half (h/2), time = t^-1.

∴ \(\frac{h}{2}=\frac{1}{2} g(t-1)^2\) …..(2)

Now, dividing (1) by (2),

⇒ \(2=\left(\frac{t}{t-1}\right)^2\)

Solving, we get

⇒ \(t=(2+\sqrt{2}) \mathrm{s}\)

the height of the tower is

⇒ \(h=\frac{1}{2}(10)(2+\sqrt{2})^2 m=58.3 m \approx 58 m\)

Question 46. A body is projected vertically upwards with a velocity u. It crosses three points A, B, and C in succession in its upward journey with velocities u/2, u/3, and u/4. The ratio AB/BC is

1. \(\frac{10}{7}\)
2. \(\frac{20}{7}\)
3. \(\frac{3}{2}\)
4. \(\frac{2}{1}\)

Answer: 2. \(\frac{20}{7}\)

For the motion along AB,

⇒ \(\left(\frac{u}{3}\right)^2-\left(\frac{u}{2}\right)^2=-2 g(A B) \Rightarrow A B=\frac{5 u^2}{72 g}\)

Similarly, for the motion along BC,

⇒ \(\left(\frac{u}{4}\right)^2-\left(\frac{u}{3}\right)^2=-2 g(B C)^{\prime} \Rightarrow B C=\frac{7 u^2}{288 g}\)

Hence,

⇒ \(\frac{A B}{B C}=\frac{5}{72} \times \frac{288}{7}=\frac{20}{7}\)

Question 47. From the top of a 40-m-high tower, a stone is projected vertically upwards with an initial velocity of 10 m s^-1. After how much time will the stone hit the ground? (Take g = 10 m s^-2.)

1. 4 s
2. 1 s
3. 2 s
4. 3 s

Answer: 1. 4 s

Let us take the point of rejection as the origin. Applying the coordinate sign convention, velocity of projection = u = +10 ms^-1 net displacement

= h = -40 m and g =-10 m s^-2.

Thus, \(-h=+u t-\frac{1}{2} g t^2\)

or, -40 = 10t -5t²

or t²-2t-8=0 or (t-4)(t + 2)=0.

The acceptable solution is = 4s.

Question 48. In the preceding question, what will be the speed of the stone when it hits the ground?

1. 20 ms^-1
2. 30 m s^-1
3. 35m sr^-1
4. 40 m s^-1

Answer: 3. 35m srl

Applying the standard equation v = u+gt, we have

-v =10 m s^-1-10 m s^-2 x 4s

= -30 m s^-1

v = 30ms^-1.

Question 49. A stone dropped from the top of a tower hits the ground after 4 s. How much time does it take to travel the first half of the distance from the top of the tower?

1. 1 s
2. 2√2 s
3. 2 s
4. √3 s

Answer: 2. 2√2 s

For the total flight of the stone,

⇒ \(h=\frac{1}{2} g t^2\) [∵ u=0]

⇒ \(h=\frac{1}{2} \times 10 \times 4^2=80\)

⇒ \(\frac{h}{2}=40=\frac{1}{2} \cdot(10) t^2=5 t^2\)

So, the required time

⇒ \(t=2 \sqrt{2} \mathrm{~s}\)

Question 50. A stone is projected vertically downwards with a velocity u from the top of a tower. It strikes the ground with a velocity of 3M. The time taken by the stone to reach the ground is

1. \(\frac{u}{g}\)
2. \(\frac{3 u}{g}\)
3. \(\frac{2 u}{g}\)
4. \(\frac{4 u}{g}\)

Answer: 3. \(\frac{2 u}{g}\)

For the downward motion,

v = u+gt

⇒ 3u = u +gt

⇒ \(t=\frac{2 u}{g}\)

Question 51. In the preceding question, what is the height of the tower?

1. \(\frac{u^2}{g}\)
2. \(\frac{2 u^2}{g}\)
3. \(\frac{3 u^2}{8}\)
4. \(\frac{4 u^2}{g}\)

Answer: 4. \(\frac{4 u^2}{g}\)

Let h be the height of the tower.

Hence,

⇒ \(h=u t+\frac{1}{2} g t^2=u\left(\frac{2 u}{g}\right)=\frac{1}{2} g\left(\frac{2 u}{g}\right)^2=\frac{4 u^2}{g}\)

Question 52. A stone falls freely under gravity. It covers the distances hv h₂ and h₃ in the first 5 s, the second 5 s, and the third 5 s respectively. The relation between h₁, h₂ and h₃ is given by

1. \(h_2=3 h_1 \text { and } h_3=2 h_2\)
2. \(h_1=h_2=h_3\)
3. \(h_1=2 h_2=3 h_3\)
4. \(h_1=\frac{h_2}{3}=\frac{h_3}{5}\)

Answer: 4. \(h_1=\frac{h_2}{3}=\frac{h_3}{5}\)

The stone is dropped from O.

So, \(O A=h_1=\frac{1}{2} g\left(5^2\right)=\frac{25 g}{2}\)

⇒ \(O B=h_1+h_2=\frac{1}{2} g\left(10^2\right)=\frac{100 g}{2}\)

and \(O C=h_1+h_2+h_3=\frac{1}{2} g\left(15^2\right)=\frac{225 g}{2}\)

∴ \(h_2 \doteq O B-O A=\frac{75 g}{2} \text { and }\)

⇒ \(h_3=O C-O B=\frac{125 g}{2}\)

Hence,

⇒ \(h_1: h_2: h_3=25: 75: 125=1: 3: 5\)

∴ \(h_1=\frac{h_2}{3}=\frac{h_3}{5}\)

Question 53. A ball is dropped from a high-rise platform at t = 0. After 6 s, another ball is thrown downwards from the same platform with a speed v. The two balls meet at t – 18 s. What is the value of 7 (Take g = 10 m s^-2.)

1. 40 ms^-1
2. 75ms^-1
3. 60 ms^-1
4. 55 ms^-1

Answer: 2. 75ms^-1

The two balls meet at time t=18s. Hence, for the first ball,

⇒ \(h=\frac{1}{2} g t^2=\frac{1}{2}\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(18 \mathrm{~s})^2\)

= 5 (18)² m.

For the second ball, time = (t-6) s when the two balls meet.

Hence,

h = v(t-6)+ \(\frac{1}{2}\)g(t- 6)²

= v(t8- 6) + 5(18- 6)²

=12v + 5 x 12².

Equating the two expressions for h, we have

12v + 5 x 144 = 5 x 18 x 18

⇒ \(v=\frac{5 \times 18^2}{12} \mathrm{~ms}^{-1}-\frac{5 \times 144}{12} \mathrm{~ms}^{-1}=75 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 54. Two bodies A (of mass 1 kg) and B (of mass 3 kg) are dropped from the heights of 16 m and 25 m respectively. The ratio of the time taken by them to reach the ground is

1. \(\frac{12}{5}\)
2. \(\frac{5}{4}\)
3. \(\frac{5}{12}\)
4. \(\frac{4}{5}\)

Answer: 3. \(\frac{5}{12}\)

Theoretically, the time of fall is independent of mass.

So, applying \(h=\frac{1}{2} g t^2\)

or, \(t=\sqrt{\frac{2 h}{g}}\), we obtain

⇒ \(\frac{t_{\mathrm{A}}}{t_{\mathrm{B}}}=\sqrt{\frac{h_{\mathrm{A}}}{h_{\mathrm{B}}}}=\sqrt{\frac{16 \mathrm{~m}}{25 \mathrm{~m}}}=\frac{4}{5}\)

Question 55. A ball is projected vertically upwards. It attains a speed of 10 m s^-1 when it reaches half its maximum height. How high does the ball rise? (Take g = 10 m s^-2.)

1. 5 m
2. 20 m
3. 10 m
4. 15 m

Answer: 3. 10 m

v² = u² – 2gh, where o = 0 at the maximum height (h) and u = 10 m s^-1.

∴ \(0=10^2-2 g\left(\frac{h}{2}\right)=100-10 h\)

Hence, h = 10 m.

Question 56. If a ball is thrown vertically upwards with speed u, the distance covered during the last t seconds of its ascent is

1. \(\frac{1}{2} g t^2\)
2. ut
3. \(u t-\frac{1}{2} g t^2\)
4. (u+gt)t

Answer: 1. \(\frac{1}{2} g t^2\)

Let A be the point at the maximum height, where the speed is reduced to zero. Let AB be the distance during the last f seconds. Hence, time of ascent = time of descent, where BA = AB = h

∴ \(h=u_{\mathrm{A}} t+\frac{1}{2} g t^2=0+\frac{1}{2} g t^2=\frac{1}{2} g t^2\)

Note This value of h is independent of u.

Question 57. A particle is thrown vertically upwards. Its velocity at half the maximum height is 10 m s^-1. The maximum height attained is (taking g = 10 m s^-2)

1. 8 m
2. 10 m
3. 16 m
4. 20 m

Answer: 2. 10 m

During the descent of the particle from the maximum height, the speed will be the same (= 10 m s^-1) at half the height. Hence,

⇒ \(v^2=u^2+2 g\left(\frac{h}{2}\right)(\text { from the top) }\)

⇒ \(\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)^2=0^2+2\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right) \frac{h}{2}\)

⇒ \(h=\frac{100}{10} \mathrm{~m}=10 \mathrm{~m}\)

Question 58. A man throws balls with the same speed vertically upwards, one after another, at an interval of 2 s. What should be the speed of projection so that more than two balls are in the sky at any time? (Given that g = 9.8m s^-2.)

1. More than 19.6 m s^-1
2. At least 9.8 m s^-1
3. Any speed less than 19.6 m s^-1
4. 19.6 m s^-1 only

Answer: 1. More than 19.6 m s^-1

The time interval between the two balls thrown is 2 s. If more than two balls (or at least three balls) remain in the air, the time of flight of the first ball must be greater than 2 x 2 s = 4 s.

∴ \(T>4 \mathrm{~s} \Rightarrow \frac{2 u}{g}>4 \mathrm{~s} \Rightarrow u>2 g=19.6 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 59. A rubber ball is dropped from a height of 5 m on the ground. On bouncing, it rises to 1.8 m. The fractional loss in the velocity bouncing is (taking g – 10 m s^-2)

1. \(\frac{9}{25}\)
2. \(\frac{16}{25}\)
3. \(\frac{2}{5}\)
4. \(\frac{3}{5}\)

Answer: 3. \(\frac{2}{5}\)

The velocity of the ball when it hits the ground for the first time is

⇒ \(v=\sqrt{2 g h}=\sqrt{2 \times 10 \times 5} \mathrm{~m} \mathrm{~s}^{-1}=10 \mathrm{~m} \mathrm{~s}^{-1}\)

The velocity of rebmmd is \(v^{\prime}=\sqrt{2 g \times 1.8} \mathrm{~m} \mathrm{~s}^{-1}=6 \mathrm{~m} \mathrm{~s}^{-1}\)

∴ the fractional loss in velocity is

⇒ \(\frac{\Delta v}{v}=\frac{v-v^{\prime}}{v}=\frac{10-6}{10}=\frac{2}{5}\)

Question 60. A body dropped from a height h strikes the ground with a velocity of 3 m s^-1. Another body of the same mass is projected from the same height h with an initial velocity of 4 m s^-1. The final velocity of the second body with which it strikes the ground is (assuming g = 10 m s^-2)

1. 3 ms^-1
2. 5ms^-1
3. 4 ms^-1
4. 12 m s^-1

Answer: 2. 5ms^-1

For the first body,

⇒ \(v^2=u^2+2 g h\)

or (3 ms^-1)² = 0² + 2gh = 2gh.

For the second body,

⇒ \(v^2=\left(4 \mathrm{~m} \mathrm{~s}^{-1}\right)^2+2 g h\)

or, \(2 g h=v^2-\left(4 \mathrm{~m} \mathrm{~s}^{-1}\right)^2\)

Equating (1) and (2),

v²-(4ms^-1)² = (3ms^-1)²

v = 5m s^-1.

Question 61. Water drops fall at regular intervals from a tap 5 m above the ground. The third drop leaves the tap at the instant the first drop touches the ground. How far above the ground is the second drop at that instant? (Take g = 10 m s^-2.)

1. 1.25 m
2. 4.00 m
3. 3.75 m
4. 2.50 m

Answer: 3. 3.75 m

Given that h = 5 m. For the time of flight t of the first water drop,

⇒ \(5 \mathrm{~m}=\frac{1}{2} g t^2 \Rightarrow t^2=1 \mathrm{~s}^2\) t = 1 s. Hence, the third drop leaves one second after the first drop.

So, the time gap between two successive drops is (1/2) s.

Now, the distance covered by the second drop after (1/2) s will be

⇒ \(\frac{1}{2} g t^2=5\left(\frac{1}{2}\right)^2 \mathrm{~s}=\frac{5}{4} \mathrm{~s}\)

Thus, the distance of the second drop above the ground will be

⇒ \(5 \mathrm{~m}-\frac{5}{4} \mathrm{~m}=\frac{15}{4} \mathrm{~m}\)

= 3.75 m.

Question 62. A body dropped from the top of a tower fell through 40 m during the last two seconds of its fall. The height of the tower is (assuming g = 10 m s^-2)

1. 45 m
2. 50 m
3. 80 m
4. 60 m

Answer: 1. 45 m

Let h = height of the tower and t = time of flight.

Now, \(h=\frac{1}{2} g t^2 \text { and } h-40=\frac{1}{2} g(t-4)^2\)

Subtracting,

⇒ \(40=\frac{g}{2}\left[t^2-(t-4)^2\right]\)

= 5(2t-4)(4)

=> 2t = 6s

=> t = 3s.

∴ \(h=\frac{1}{2} g t^2=5\left(3^2\right) \mathrm{m}\)

= 45 m

Question 63. What will be the ratio of the distances covered by a freely falling body from rest in the fourth and fifth seconds of its fall?

1. 1:1
2. 7:9
3. 16:25
4. 4:5

Answer: 2. 7:9

The distance covered in the nth second is given by

⇒ \(s_n=u+\left(\frac{2 n-1}{2}\right) a\)

Hence, for the fourth second,

⇒ \(s_4=\frac{7 g}{2}\)

and for the fifth second,

⇒ \(s_5=\frac{9 g}{2}\) [∵ u = 0]

∴ \(\frac{s_4}{s_5}=\frac{7}{9} \quad \text { or } \quad s_4: s_5=7: 9\)

Question 64. A balloon is rising vertically upwards with a velocity of 10 m s^-1, When it is at a height of 45 m above the ground, a parachutist bails out from it. After 3 s, he opens the parachute and decelerates at a constant rate of Sms^-2. What was the height of the parachute above the ground when he opened the parachute? (Take g = 10 m s^-2.)

1. 30 m
2. 15 m
3. 60 m
4. 45 m

Answer: 1. 30 m

When the parachutist bails out, he has the velocity of the balloon, which is 10 m s^-1 upwards.

∴ the net displacement in 3 s is

⇒ \(s=u t+\frac{1}{2}\left(-g t^2\right)=10 \times 3-\frac{10}{2}(3)^2\)

= -15 m.

Here the negative sign indicates a downward displacement.

Hence, the height above the ground when he opens the parachute is

= 45m-15m

= 30m.

Question 65. In the previous problem, how far was the parachutist from the balloon at t^-3 s?

1. 15 m
2. 30 m
3. 45 m
4. 60 m

Answer: 3. 45 m

The balloon rises up in 3 s by a height of (10 m s^-1)(3 s) = 30 m. Hence, the parachutist is now at a distance of 30 m + 15 m = 45 m from the balloon.

Question 66. In the preceding problem, how much time does the parachutist take to hit the ground after his exit from the balloon?

1. 4 s
2. 5 s
3. 6 s
4. 7 s

Answer: 2. 5 s

The total time the parachutist takes after his exit from the balloon to hit the ground is 3 s + 2 s = 5 s.

Question 67. From the top of a tower, a stone is thrown up and it reaches the ground in a time tx. A second stone is thrown down with the same speed and it reaches the ground in a time t². A third stone is released from rest and it reaches the ground in a time t³. The relationship of t, t², and t³ is given by

1. \(\frac{1}{t_3}=\frac{1}{t_1}+\frac{1}{t_2}\)
2. \(t_3=\sqrt{t_1 t_2}\)
3. \(t_3=\frac{1}{2}\left(t_1+t_2\right)\)
4. \(t_3{ }^2=t_1{ }^2-t_2{ }^2\)

Answer: 2. \(t_3=\sqrt{t_1 t_2}\)

Taking the coordinate sign convention into consideration, we have

for the firststone, \(-h=u t_1-\frac{1}{2} g t_1^2\) …(1)

for the second stone, \(h=u t_2+\frac{1}{2} g t_2^2\) ….(2)

and for the third stone, \(h=\frac{1}{2} g t_3{ }^2\)…(3)

In order to eliminate u, multiplying (1) by t2 and (2) by itself and then subtracting, we obtain

⇒ \(-h\left(t_2+t_1\right)=-\frac{1}{2} g\left(t_1+t_2\right) t_1 t_2 \Rightarrow h=\frac{g}{2}\left(t_1 t_2\right)\)

But from (3) \(h=\frac{1}{2} g t_3{ }^2\)

∴ \(t_3{ }^2=t_1 t_2 \Rightarrow t_3=\sqrt{t_1 t_2}\)

Question 68. Water drops fall at regular intervals from a tap in the roof. At an instant when a drop is about to leave the tap, the separation between three successive drops is in the ratio

1. 1:2:3
2. 1:4:9
3. 1:3:5
4. 1:5:13

Answer: 3. 1:3:5

Let the time interval between two successive drops be f.

For the first drop (being detached), h₁=0.

For the second drop, \(h_2=\frac{1}{2} g t^2\)

For the third drop, \(h_3=\frac{1}{2} g(2 t)^2=\frac{g}{2}\left(4 t^2\right)\)

For the fourth drop, \(h_4=\frac{1}{2} g(3 t)^2=\frac{g}{2}\left(9 t^2\right)\)

Hence, the separations between two successive drops are

⇒ \(h_2-h_1=\frac{1}{2} g t^2, h_3-h_2=\frac{1}{2} g\left(3 t^2\right) \text { and } h_4-h_3=\frac{1}{2} g\left(5 t^2\right)\)

∴ The required ratio is \(\frac{1}{2} g t^2: \frac{1}{2} g\left(3 t^2\right): \frac{1}{2} g\left(5 t^2\right)\)

= 1:3:5.

Question 69. A balloon starts rising up from the ground with an acceleration of 1.25 m s^-2. After 8 s, a stone is released from the balloon. The stone will

1. Cover a distance of 40 m
2. Have a displacement of 50 m
3. Reach the ground in 4 s
4. Begin to move down after being released

Answer: 3. Reach the ground in 4 s

The balloon starts moving upwards with an acceleration of 1.25 m s^-2.
Hence, its height at t = 8s will be

⇒ \(h=\frac{1}{2} a t^2=\frac{1}{2}\left(1.25 \mathrm{~m} \mathrm{~s}^{-2}\right)(8 \mathrm{~s})^2=40 \mathrm{~m}\)

and its velocity at that instant will be

⇒ \(n=a t=\left(1.25 \mathrm{~m} \mathrm{~s}^{-2}\right)(8 \mathrm{~s})=10 \mathrm{~m} \mathrm{~s}^{-1}\)

At this instant, the stone shares the motion of the balloon and falls

freely under gravity for which

⇒ \(u=10 \mathrm{~m} \mathrm{~s}^{-1}, h=-40 \mathrm{~m} \text { and } g=-10 \mathrm{~m} \mathrm{~s}^{-2}\)

∵ \(h=u t+\frac{1}{2} g t^2 \Rightarrow-40=10 t-\frac{1}{2}(10) t^2\)

⇒ \(5 t^2-10 t-40=0 \Rightarrow t^2-2 t-8=0\)

(t- 4)(t + 2) = 0

=> t = 4 s.

Thus, the stone strikes the ground in 4 s.

Question 70. A body is thrown vertically upwards- Which of the following graphs correctly represents the variation of its velocity against time?

Answer: 4.

The slope of the v-t graph is the acceleration (g). At t = 0, the velocity is maximum and positive.

It goes on decreasing (remaining positive), and at the highest point (A), v 0.

Further, it becomes negative and increases with the same acceleration.

Hence, the correct graph is given in (d).

Question 71. A parachutist after bailing out falls 50 m without any friction. When the parachute opens, it decelerates at 2 m s^-2. He reaches the ground at a speed of 3 m s^-1. At what height has he bailed out?

1. 91m
2. 182 m
3. 293 m
4. 111 m

Answer: 3. 293 m

When the parachutist falls freely through a height of 50 m, let his
speed be u.

So, u² = 2gh

= 2(9.8 m s^-2)(50 m)

= 980 (m s^-1)².

When he opens the parachute, he falls through a height of h, where

32- 980 + 2(-2)h.

∴ \(h=\frac{980-9}{4} \mathrm{~m}=242.75 \mathrm{~m} \approx 243 \mathrm{~m}\)

Hence, the height at bailing out is H = 50 m + 243 m

= 293 m.

Question 72. Two identical balls are thrown upwards with the same initial velocity of 40 m s^-1 in the same vertical direction at an interval of 2 s. The balls collide at a height of (taking g = 10 m s^-2)

1. 210 m
2. 125 m
3. 75 m
4. 40 m

Answer: 3. 75 m

Given that u = 40 m s^-1.

Let the height at which the balls collide be h.

For the first ball, \(h=u t-\frac{1}{2} g t^2\)

and for the second ball, \(h=u(t-2)-\frac{1}{2} g(t-2)^2\)

Equating the expressions for h, we obtain

⇒ \(u(t-2)-\frac{1}{2} g(t-2)^2=u t-\frac{1}{2} g t^2\)

Simplifying, we get

2u = 2g(t^-1).

Substituting the values,

2(40 m s^-1) = (20 ms^-1)(t – Is).

∴ The time of collision is t- 5 s.

Hence, the balls collide at a height of

⇒\(h=u t-\frac{1}{2} g t^2=(40 \times 5-5 \times 25) \mathrm{m}\)

= 75m.

Question 73. A ball is projected vertically upwards from the ground. It experiences a constant air resistance of 2 m s^-2 directed opposite to the direction of its motion. The ratio of the time of ascent to the time of descent equals (assuming g = 10 m s^-2)

1. 1
2. \(\frac{2}{3}\)
3. \(\sqrt{\frac{4}{3}}\)
4. \(\sqrt{\frac{2}{3}}\)

Answer: 4. \(\sqrt{\frac{2}{3}}\)

During the ascent,

⇒ \(v=0=u-(g+a) t_1 \Rightarrow t_1=\frac{u}{g+a}\)… (1)

During the descent,

⇒ \(h=0\left(t_2\right)+\frac{1}{2}(g-a) t_2{ }^2=\frac{1}{2}(g-a) t_2{ }^2 .\)

For the upward motion,

⇒ \(h=u t_1-\frac{1}{2}(g+a) t_1^2\)

Substituting for t₁ from (1),

⇒ \(h=\frac{u^2}{g+a}-\frac{1}{2}(g+a) \cdot \frac{u^2}{(g+a)^2}=\frac{u^2}{2(g+a)}\)

Equating the expressions for h,

⇒ \(\frac{1}{2}(g-a) t_2^2=\frac{u^2}{2(g+a)} \Rightarrow t_2=\frac{u}{\sqrt{g^2-a^2}}\)

Hence,

⇒ \(\frac{t_1}{t_2}=\frac{u}{g+a} \cdot \frac{\sqrt{g^2-a^2}}{u}=\sqrt{\frac{g-a}{g+a}}=\sqrt{\frac{10-2}{10+2}}=\sqrt{\frac{2}{3}}\)

Question 74. A ball is projected vertically upwards from the foot of a tower. It crosses the top of the tower twice after a time interval of 8s and strikes the ground after 16 seconds. The height of the tower is (taking g = 10 m s^-2)

1. 140 m
2. 240 m
3. 100 m
4. 200 m

Answer: 2. 240 m

The velocity of the ball while crossing the top of the tower during its
descent is

⇒ \(v=0+g t=10 \mathrm{~m} \mathrm{~s}^{-2} \times \frac{8}{2} \mathrm{~s}=40 \mathrm{~m} \mathrm{~s}^{-1}\)

The time taken to cover the height of the tower is \(\frac{1}{2}(16 s-8 s)\) = 4s.

∴ height of the tower is

⇒ \(h=u t+\frac{1}{2} g t^2=\left(40 \mathrm{~m} \mathrm{~s}^{-1}\right)(4 \mathrm{~s})+\frac{1}{2}\left(10 \mathrm{~m} \mathrm{~s}^{-2}\right)(4 \mathrm{~s})^2\)

= 160 m + 80 m

= 240 m.

Question 75. When an object is shot from the bottom of a long and smooth inclined plane kept at an angle of 60° with the horizontal, it can travel a distance xx along the plane. But when the inclination is decreased to 30° and the same object is shot with the same velocity, it can travel a distance of x₂. The ratio of x₁ to x₂ will be

1. 1:√2
2. √2:1
3. 1:√3
4. 1:2√3

Answer: 3. 1:√3

In Case I, work done by gravity

⇒ \(-m g h_1=-m g x_1 \sin 60^{\circ}\)

and change in KE = \(-\frac{1}{2} m v^2\)

Hence, \(m g x_1\left(\frac{\sqrt{3}}{2}\right)=\frac{1}{2} m v^2\)

Similarly, in Case 2

⇒ \(m g x_2 \sin 30^{\circ}=\frac{1}{2} m v^2 .\)

∴ \(m g x_1\left(\frac{\sqrt{3}}{2}\right)=m g x_2\left(\frac{1}{2}\right)\)

⇒ \(\frac{x_1}{x_2}=\frac{1}{\sqrt{3}} \Rightarrow x_1: x_2=1: \sqrt{3}\)

Question 76. The speed of a swimmer in still water is 20 m s^-1. The speed of the water of a river, flowing due east, is 10 m s^-1. If the swimmer is standing on the south bank and wishes to cross the river along the shortest path, the angle at which he should make his strokes relative to the north is given by

1. 30° west
2. 0°
3. 60° west
4. 45° west

Answer: 1. 30° west

Given that the velocity of the swimmer relative to the river is v st = 20 m s^-1 and the velocity of the river relative to the ground is urg = 10 m s^-1. These are shown vectorially in the adjoining diagram.

According to the vector diagram,

⇒ \(\vec{v}_{\mathrm{sg}}=\vec{v}_{\mathrm{sr}}+\vec{v}_{\mathrm{rg}}\)

and \(\sin \theta=\frac{v_{\mathrm{rg}}}{v_{\mathrm{sr}}}=\frac{10 \mathrm{~ms}^{-1}}{20 \mathrm{~ms}^{-1}}=\frac{1}{2} \Rightarrow \theta=30^{\circ}\)

Hence, the direction of the strokes is 30° due west.

Question 77. A particle is moving along a circular path with a constant speed of 10 m s^-2. What is the magnitude of the change in velocity of the particle when it moves through an angle of 60° around the center of the circular path?

1. 10√2 m s^-2
2. 1.m s^-1
3. 10√3 m s^-1
4. Zero

Answer: 2. 1.m s^-1

The initial velocity at A is

⇒ \(\vec{u}=\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right) \hat{i}\)

and the final velocity at B is

⇒ \(\vec{v}=\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)\left(\cos 60^{\circ}\right) \hat{i}+\left(10 \mathrm{~m} \mathrm{~s}^{-1}\right)\left(\sin 60^{\circ}\right) \hat{j}\)

⇒ \(\left(5 \mathrm{~m} \mathrm{~s}^{-1}\right) \hat{i}+\left(5 \sqrt{3} \mathrm{~m} \mathrm{~s}^{-1}\right) \hat{j}\)

∴ the change in velocity is

⇒ \(\Delta \vec{v}=\vec{v}-\vec{u}=(5-10) \mathrm{m} \mathrm{s}^{-1} \cdot \hat{i}+5 \sqrt{3} \mathrm{~m} \mathrm{~s}^{-1} \cdot \hat{j}\)

Hence, the magnitude of change in velocity is

⇒ \(|\Delta \vec{v}|=|-5 \hat{i}+5 \sqrt{3} \hat{j}| \mathrm{m} \mathrm{s}^{-1}\)

⇒ \(\sqrt{25+75} \mathrm{~m} \mathrm{~s}^{-1}=10 \mathrm{~m} \mathrm{~s}^{-1}\)

Question 78. The position (x) of a particle as a function of time (t) is given by x(t) = at + bt² -ct³, where a, b, and c are constants. When the particle attains zero acceleration, its velocity will be

1. \(a+\frac{b^2}{2 c}\)
2. \(a+\frac{b^2}{c}\)
3. \(a+\frac{b^2}{3 c}\)
4. \(a+\frac{b^2}{4 c}\)

Answer: 3. \(a+\frac{b^2}{3 c}\)

Given that x = at + bt²- ct³.

∴ velocity = \(v=\frac{d x}{d t}=a+2 b t-3 c t^2\) …..(1)

and acceleration = \(a=\frac{d v}{d t}=2 b-6 c t\) …..(2)

For a = 0, 2b-6cf = 0

⇒ \(t=\frac{2 b}{6 c}=\frac{b}{3 c}\)

From (1), the velocity at this time t is

⇒ \(v=a+2 b\left(\frac{b}{3 c}\right)-3 c\left(\frac{b}{3 c}\right)^2=a+\frac{2 b^2}{3 c}-\frac{b^2}{3 c}=a+\frac{b^2}{3 c}\)

Question 79. A helicopter is rising vertically upwards from the ground with an acceleration g starting from rest. When it reaches a height of h, a packet is dropped at t = 0. Find the time t when the packet strikes the ground.

1. \(\sqrt[4]{\frac{2 g}{h}}\)
2. \(\sqrt{\frac{2 h}{8}}\)
3. \(2 \sqrt{\frac{2 h}{g}}\)
4. \((1+\sqrt{2}) \sqrt{\frac{2 h}{g}}\)

Answer: 4. \((1+\sqrt{2}) \sqrt{\frac{2 h}{g}}\)

Let the velocity of the helicopter at tire height h be v.

∴ \(v^2=2 g h \Rightarrow v=\sqrt{2 g h} \text { (upward). }\)

For free fall of the packet from the height h,

⇒ \(-h=u t-\frac{1}{2} g t^2=\sqrt{2 g h} t-\frac{1}{2} g t^2\)

⇒ \(\left(\frac{g}{2}\right) t^2-\sqrt{2 g h} t-h=0\)

Solving for t, we get

⇒ \(t=\frac{1}{g}[\sqrt{2 g h}+\sqrt{2 g h+2 g h}]=\frac{(2+\sqrt{2}) \sqrt{g h}}{g}\)

⇒ \((1+\sqrt{2}) \sqrt{\frac{2 h}{g}}\)